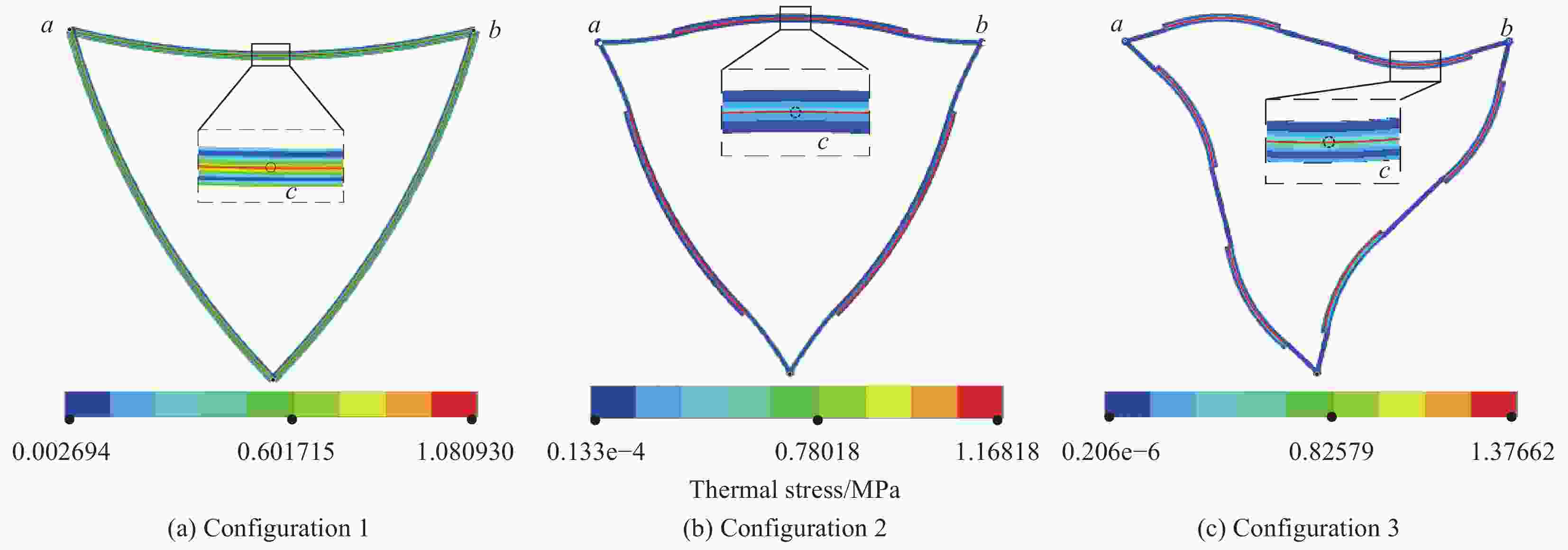
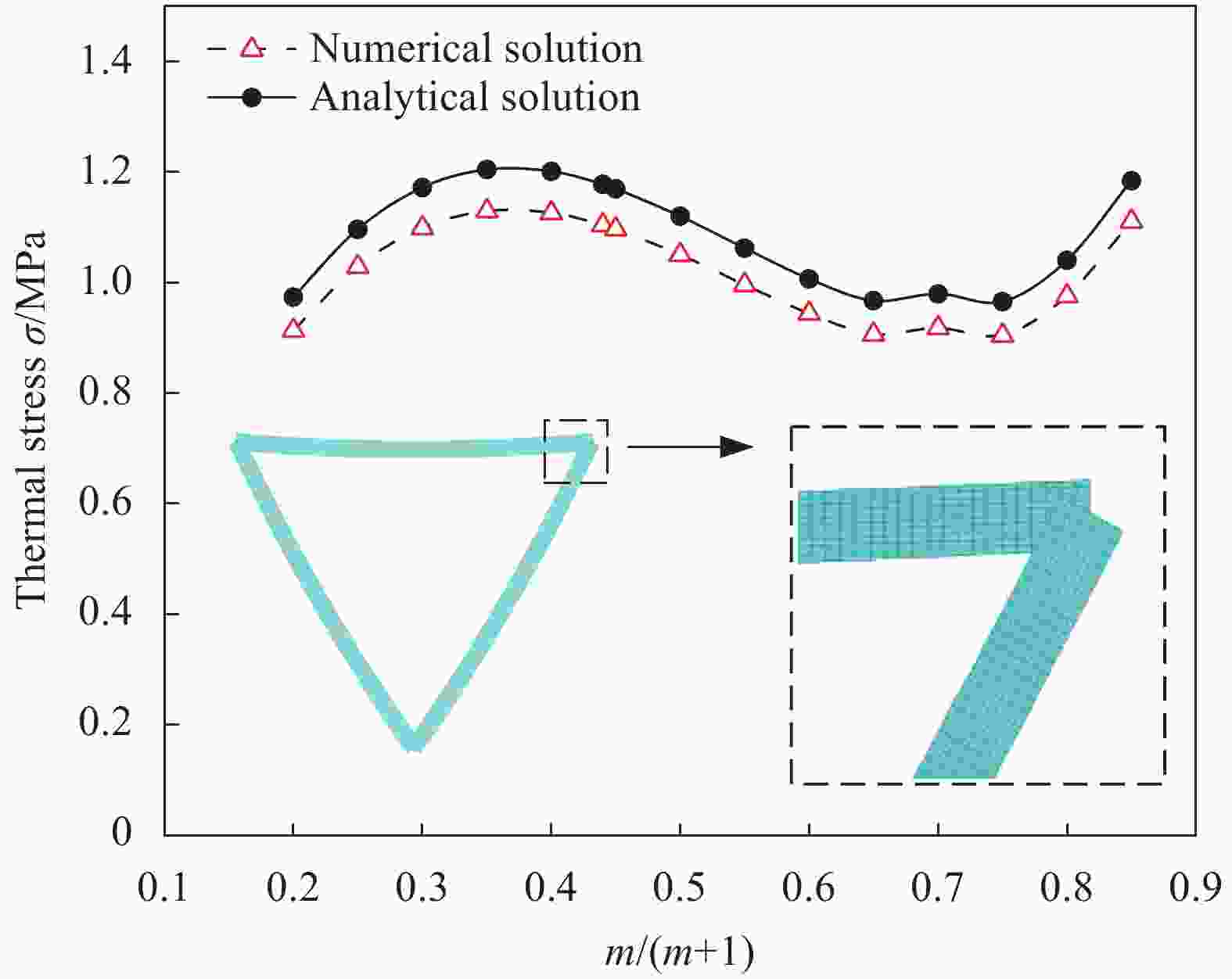
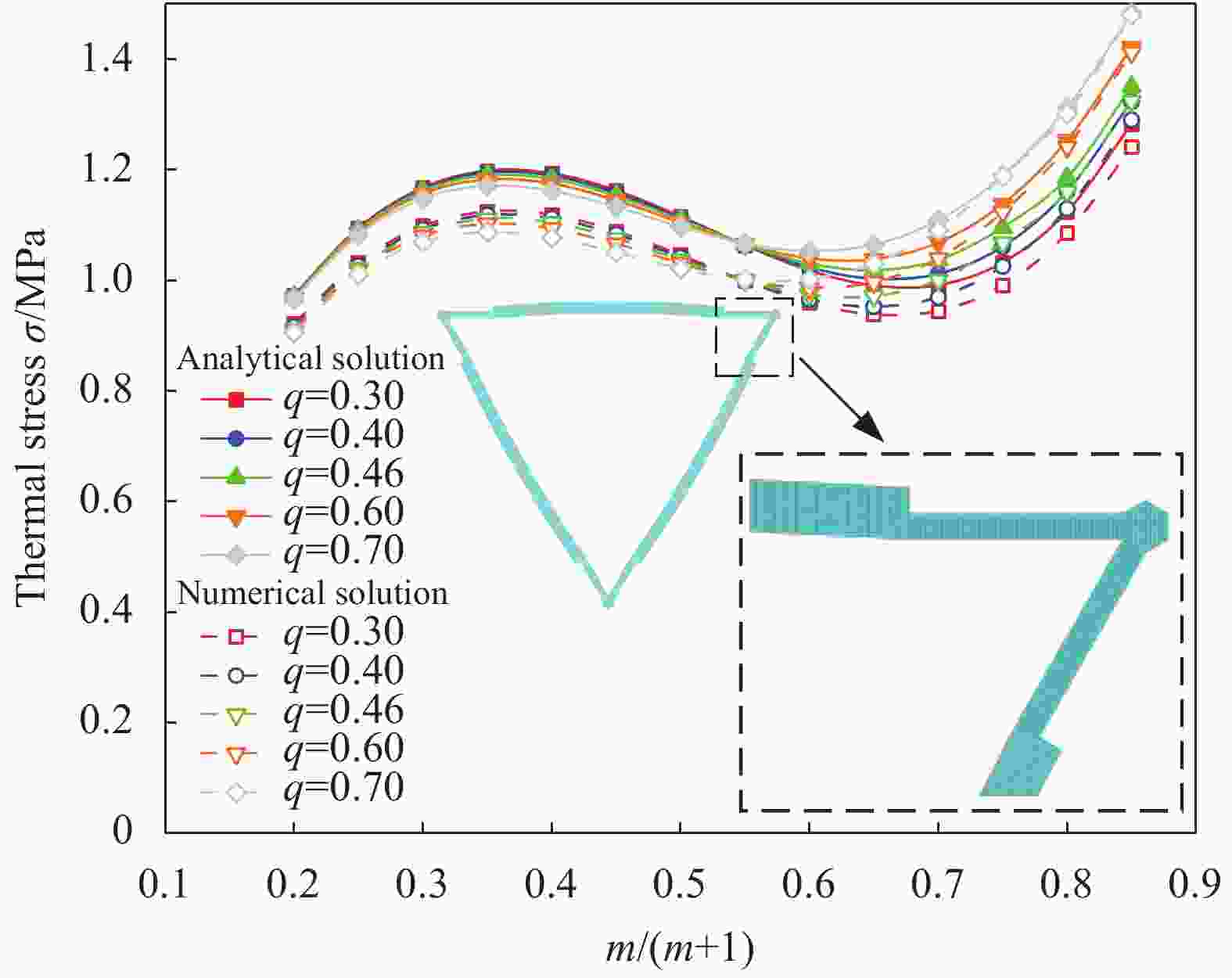
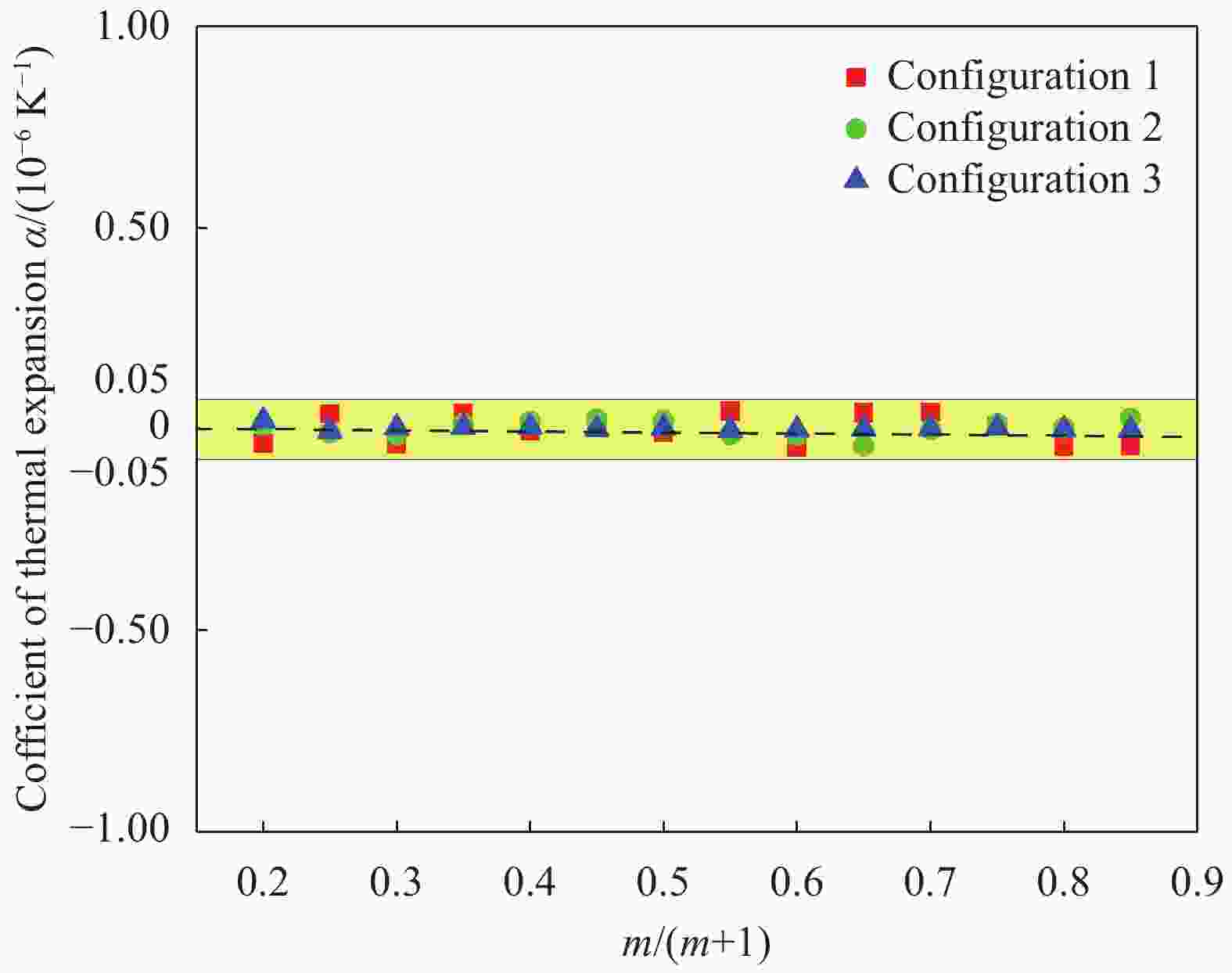
Design of higher allowable temperature range for zero thermal expansion composites considering stiffness characteristic
-
摘要: 材料的宏观零热膨胀可以通过两种不同的正热膨胀材料在单胞尺度上的复合实现。该类材料虽然能在较大温度波动环境下保持较高的几何稳定性，但两种材料之间过大的热应力很容易导致材料失效，从而限制其许用温度变化范围(简称许用温变)。为此，提出以单位温升的最大热应力作为零热膨胀材料许用温变的衡量指标，通过解析和有限元数值仿真两种方法，对三种典型弯曲变形机制的零热膨胀材料进行许用温变和刚度特性分析，揭示了单胞可设计参数对其性能的影响规律。结果表明：在满足零热膨胀条件下，通过合理的单胞结构设计和选材设计，可以实现刚度与许用温变双目标共赢。Abstract: The macroscopic zero thermal expansion of material could be obtained through combining two kinds of materials with different positive thermal expansion coefficients within a unit cell. These composites usually possess higher thermally geometric stability in the large temperature fluctuation. However, it readily produces excessive thermal stress on the interface between the two constituent materials and therefore limits the allowable temperature range of the material. A new evaluation index of the maximum thermal stress of unit temperature rise was resorted to perform allowable temperature and stiffness analyses for the three types of typical bending-dominated zero expansion materials. Both the analytic and numerical simulation methods were adopted and the influences of cell design parameters on these aspects were also discussed. The results show that when the designed zero expansion attribute is achieved, the high stiffness and high allowable temperature range can be obtained at the same time if the reasonable constituent materials and structural parameters are selected.
-
Key words:
- composite /
- zero thermal expansion /
- allowable temperature range /
- optimal design /
- collaborative design
-
图 1 弯曲主导型零热膨胀点阵复合材料
Figure 1. Bending-dominated zero thermal expansion lattice composites
图 2 零热膨胀复合材料有限元热应力数值仿真
Figure 2. Finite element thermal stress numerical simulation of zero thermal expansion composites
图 3 构型1中测点c单位温升的热应力随
$m/(m + 1)$ 变化Figure 3. Thermal stress of unit temperature rise at measuring point c of configuration 1 varied with
$m/(m + 1)$ 
图 4 构型2中测点c单位温升的热应力随
$m/(m + 1)$ 变化Figure 4. Thermal stress of unit temperature rise at measuring point c of configuration 2 varied with
$m/(m + 1)$ 
图 5 构型3中测点c单位温升的热应力随
$m/(m + 1)$ 变化Figure 5. Thermal stress of unit temperature rise at measuring point c of configuration 3 varied with
$m/(m + 1)$ 
图 6 不同厚度条件下各构型的零热膨胀材料设计
Figure 6. Zero thermal expansion designs for all configurations with different thickness ratios
图 7 构型1的等效刚度和单位温升的热应力随厚度变化
Figure 7. Equivalent stiffness and thermal stress of unit temperature rise vary with different thickness ratios for configuration 1
图 8 构型2的等效刚度和单位温升的热应力随厚度变化
Figure 8. Equivalent stiffness and thermal stress of unit temperature rise vary with different thickness ratios for configuration 2
图 9 构型3的等效刚度和单位温升的热应力随厚度变化
Figure 9. Equivalent stiffness and thermal stress of unit temperature rise vary with different thickness ratios for configuration 3
图 10 双材料热膨胀系数差值(
${\alpha _2} - {\alpha _1}$ )对单位温升的热应力影响Figure 10. Effect of thermal expansion coefficient difference (
${\alpha _2} - {\alpha _1}$ ) on thermal stress of unit temperature rise
图 11 双材料热膨胀系数比值(
${\alpha _2}/{\alpha _1}$ )对等效刚度的影响Figure 11. Effect of thermal expansion coefficient ratio (
${\alpha _2}/{\alpha _1}$ ) of two materials on equivalent stiffness表 1 零热膨胀复合材料单胞几何参数和材料属性定义
Table 1. Definition of cell geometric parameters and material properties of zero thermal expansion composites
L Total dual-constituent cell length L0 Bi-layer curve panel length θ Included angle of bi-layer curve panel t Total thickness of dual-constituent cell t1 Thickness of layer 1 t2 Thickness of layer 2 m Two layer thickness ratio t1/t2 q Length ratio of curved part to total cell L0/L E1, E2 Young’s modulus of two constituent materials ν1, ν2 Poisson’s ratios of two constituent materials α1, α2 CTEs of two constituent materials n Young’s modulus ratio E1/E2 
下载: 导出CSV
表 2 零热膨胀复合材料热膨胀系数、等效刚度及界面热应力公式
Table 2. Formulas of cell thermal expansion coefficient, equivalent stiffness and interfacial thermal stress of zero thermal expansion composites
Configuration 1 $\alpha _{ {\rm{sum} } }^1=\left( { {\alpha _1} + {\alpha _2} } \right)/2 + ({\alpha _2} - {\alpha _1}) \left\{ {\dfrac{ {4{m^2} + 3m + 1/mn} }{ { {m^3}n + 4{m^2} + 6m + 1/mn + 4} } - \left( {\dfrac{\theta }{ { {\rm{12} } } }\dfrac{ { {L_{} } } }{t} } \right)\dfrac{ {6{ {(1 + m)}^2} } }{ {[3{ {(1 + m)}^2} + (1 + mn)({m^2} + 1/mn)]} } - \dfrac{1}{2} } \right\}$ $E_{\rm{H} }^1=\dfrac{2}{ {\sqrt 3 } } \dfrac{ { {E_1}m + {E_{\rm{2} } } } }{ {(m + 1)} } \left( {\dfrac{t}{L} } \right) 2{\theta ^3}\Biggr/\left[ {24{ {\left( {\dfrac{L}{t} } \right)}^2}\left( {\dfrac{\theta }{2}\cos \theta + \theta - \dfrac{3}{2}\sin \theta } \right) + 3{\theta ^2}\sin \theta - {\theta ^3} } \right]$ ${\sigma ^1}=\left\{ \begin{array}{l} \dfrac{ {\Delta \alpha \Delta t} }{ {\lambda {t_{\rm{1} } } }} \left[ {1 + \dfrac{ {3\left( { {t_1} + {t_2} } \right){D_1} } }{ { {t_1} D} } } \right] \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } L/2} \right)} \right] \\ - \dfrac{ {\Delta \alpha \Delta t} }{ {\lambda {t_2} } } \left[ {1 + \dfrac{ {3\left( { {t_1} + {t_2} } \right){D_2} } }{ { {t_2} D} } } \right] \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } L/2} \right)} \right] \\ \end{array} \right.$ Thermal stress on side of material 1 Thermal stress on side of material 2 Configuration 2 $\begin{array}{l}\alpha _{{\rm{sum}}}^2 = {a_1} + q({\alpha _2} - {\alpha _1})\left\{ {\left[ {\dfrac{{4{m^2} + 3m + 1/mn}}{{{m^3}n + 4{m^2} + 6m + 1/mn + 4}}} \right] - \dfrac{{{\rm{6}}{{(1 + m)}^2}}}{{[3{{(1 + m)}^2} + (1 + mn)({m^2} + 1/mn)]}}} \right.\left. {\dfrac{{(1 - q)(1 + n){{(1 + m)}^3}}}{{2qn{m^3} + (1 - q)(1 + n){{(1 + m)}^3}}}\left( {\dfrac{\theta }{{12}}\dfrac{{qL}}{t} + \dfrac{m}{{2(m + 1)}}} \right)} \right\}\end{array}$ $E_{\rm{H} }^2=\dfrac{2}{ {\sqrt 3 } } \dfrac{ { {E_1}m + {E_2} } }{ {(m + 1)} } \left( {\dfrac{t}{L} } \right) 2{\theta ^3} \Bigr/ \left\{ \left[ {12{ {\left( {qL/t} \right)}^2}\left( {\theta \cos \theta + 2\theta - 3\sin \theta } \right) + 3{\theta ^2}\sin \theta - {\theta ^3} } \right]q + 2(1 - q)\left( {nm + 1} \right){\theta ^3}/mn \right\}$ ${\sigma ^2}=\left\{ \begin{array}{l} \dfrac{ {\Delta \alpha \Delta t} }{ {\lambda {t_1} } } \left[ {1 + \dfrac{ {3\left( { {t_1} + {t_2} } \right){D_1} } }{ { {t_1} D} } } \right] \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } qL/2} \right)} \right] + \\ \dfrac{ {\Delta \alpha \Delta t} }{\lambda } \dfrac{ { {E_{\rm{I} } }{I_{\rm{I} } }{E_{ {\rm{II} } } }{I_{ {\rm{II} } } }q} }{ {q{E_{\rm{I} } }{I_{\rm{I} } } + {E_{ {\rm{II} } } }{I_{ {\rm{II} } } }(1 - q)} } \dfrac{ { {t_1} + {t_2} } }{ {2D} } \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } {L_0}/2} \right)} \right] \dfrac{ {({y_{\rm{c} } } - {t_{\rm{1} } })} }{ { {I_{ {\rm{II} } } } } } \\ - \dfrac{ {\Delta \alpha \Delta t} }{ {\lambda {t_2} } } \left[ {1 + \dfrac{ {3\left( { {t_1} + {t_2} } \right){D_2} } }{ { {t_{\rm{2} } } D} } } \right] \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } qL/2} \right)} \right] +\\ \dfrac{ {\Delta \alpha \Delta t} }{\lambda } \dfrac{ { {E_{\rm{I} } }{I_{\rm{I} } }{E_{ {\rm{II} } } }{I_{ {\rm{II} } } }q} }{ {q{E_{\rm{I} } }{I_{\rm{I} } } + {E_{ {\rm{II} } } }{I_{ {\rm{II} } } }(1 - q)} } \dfrac{ { {t_1} + {t_2} } }{ {2D} } \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } {L_0}/2} \right)} \right] \dfrac{ {({y_{\rm{c} } } - {t_1})} }{ { {I_{ {\rm{II} } } } } } \\ \end{array} \right.$ Thermal stress on side of material 1 Thermal stress on side of material 2 Configuration 3 $\alpha _{ {\rm{sum} } }^3={\alpha _1} + q({\alpha _2} - {\alpha _1}) \left\{ {\left[ {\dfrac{ {4{m^2} + 3m + \dfrac{1}{ {mn} } } }{ { {m^3}n + 4{m^2} + 6m + \dfrac{1}{ {mn} } + 4} } } \right] - \dfrac{ { {\rm{6} }{ {(1 + m)}^2} } }{ {\left[3{ {(1 + m)}^2} + (1 + mn)\left({m^2} + \dfrac{1}{ {mn} }\right)\right]} } \left( {\dfrac{\theta }{ {12} }\dfrac{ {qL} }{ {2t} } + \dfrac{m}{ {2(1 + m)} } } \right)} \right\}$ $E_{\rm{H} }^3=\dfrac{2}{ {\sqrt 3 } } \dfrac{ { {E_1}m + {E_2} } }{ {(m + 1)} } \left( {\dfrac{t}{L} } \right) 2{\theta ^3}\Bigr/\left\{ \left[ {12{ {\left( {qL/2t} \right)}^2}\left( {\theta \cos \theta + 2\theta - 3\sin \theta } \right) + 3{\theta ^2}\sin \theta - {\theta ^3} } \right]q + 2(1 - q)\left( {nm + 1} \right){\theta ^3}/mn\right\}$ ${\sigma ^3}=\left\{ \begin{array}{l} \dfrac{ {\Delta \alpha \Delta t} }{ {\lambda {t_1} } } \left[ {1 + \dfrac{ {3\left( { {t_1} + {t_2} } \right){D_1} } }{ { {t_1} D} } } \right] \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } qL/4} \right)} \right] \\ - \dfrac{ {\Delta \alpha \Delta t} }{ {\lambda {t_2} } } \left[ {1 + \dfrac{ {3\left( { {t_1} + {t_2} } \right){D_2} } }{ { {t_2}D} } } \right] \left[ {1 - \cosh \left( { {K_ * } x} \right)/\cosh \left( { {K_ * } qL/4} \right)} \right] \\ \end{array} \right.$ Thermal stress on side of material 1 Thermal stress on side of material 2 ${E_{\rm{I} } }={E_1}, {E_{ {\rm{II} } } }{\rm{=(} }{E_1} + {E_2})/2, {I_{\rm{I} } }{\rm{=} }t_{\rm{1} }^3/12 , {I_{ {\rm{II} } } }{\rm{=} }t_{}^3/12,{D_{\rm{1} } }={E_1}t_1^3\Bigr/\left[ {12\left( {1 - \nu_1^2} \right)} \right], {D_2}={E_2}t_2^3\Bigr/\left[ {12\left( {1 - \nu_2^2} \right)} \right]$ ${k_1}=2\left( {1 + {\nu_1} } \right){t_1}/\left( {3{E_1} } \right), {k_2}=2\left( {1 + {\nu_2} } \right){t_2}/\left( {3{E_2} } \right), k={k_1} + {k_2},{y_{\rm{c} } }={t_2}\left( { {t_2}/2 + {t_1} } \right) + nt_1^2{\rm{/} }\left[ { {\rm{2(} }{t_2} + {t_1}n{\rm{)} } } \right]$ $\lambda =\left[ {t_1^2/{D_1} + t_2^2/{D_2} + 3{ {\left( { {t_1} + {t_2} } \right)}^2}/D} \right]/12, K_ * ^2=\lambda /k$
下载: 导出CSV
表 3 零热膨胀复合材料有限元分析参数
Table 3. Material parameters of zero thermal expansion composites in finite element analysis
$E$/GPa $\alpha $/(10−6 K−1) $\nu$ Material 1 (Invar) 140 1 0.25 Material 2 (Steel) 200 12 0.25
下载: 导出CSV
表 4 零热膨胀复合材料有限元模型几何尺寸
Table 4. Geometric parameters of zero thermal expansion composites in finite element model
$L$/mm $q$ ${L_0}$/mm $t$/mm 50 0.3–0.9 L0=qL 1
下载: 导出CSV
-
[1] LIU S, HU R, LI Q, et al. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope[J]. Applied Optics,2014,53(35):8318-8325. doi: 10.1364/AO.53.008318 [2] HU R, CHEN W, LI Q, et al. Design optimization method for additive manufacturing of the primary mirror of a large-aperture space telescope[J]. Journal of Aerospace Engineering,2016,30(3):04016093. [3] TOROPOVA M M, STEEVES C A. Adaptive bimaterial lattices to mitigate thermal expansion mismatch stresses in satellite structures[J]. Acta Astronautica,2015,113:132-141. doi: 10.1016/j.actaastro.2015.03.022 [4] ZHENGCHUN D, MENGRUI Z, ZHIGUO W, et al. Design and application of composite platform with extreme low thermal deformation for satellite[J]. Composite Structures,2016,152:693-703. doi: 10.1016/j.compstruct.2016.05.073 [5] CUI E J. Research statutes, development trends and key technical problems of near space flying vehicles[J]. Advances in Mechanics,2009,39(6):658-672. [6] ENTEL P, HOFFMANN E, MOHN P, et al. First-principles calculations of the instability leading to the Invar effect[J]. Physical Review B,1993,47(14):8706-8720. doi: 10.1103/PhysRevB.47.8706 [7] 韦凯, 裴永茂. 轻质复合材料及结构热膨胀调控设计研究进展[J]. 科学通报, 2017, 62(1):47-60. doi: 10.1360/N972016-00630WEI Kai, PEI Yongmao. Development of designing lightweight composites and structures for tailorable thermal expansion[J]. Chinese Science Bulletin,2017,62(1):47-60(in Chinese). doi: 10.1360/N972016-00630 [8] STEEVES C A, E LUCATO S L S, HE M, et al. Concepts for structurally robust materials that combine low thermal expansion with high stiffness[J]. Journal of the Mechanics and Physics of Solids,2007,55(9):1803-1822. doi: 10.1016/j.jmps.2007.02.009 [9] WEI K, CHEN H, PEI Y, et al. Planar lattices with tailorable coefficient of thermal expansion and high stiffness based on dual-material triangle unit[J]. Journal of the Mechanics and Physics of Solids,2016,86:173-191. doi: 10.1016/j.jmps.2015.10.004 [10] LAKES R. Cellular solid structures with unbounded thermal expansion[J]. Journal of Materials Science Letters,1996,15(6):475-477. doi: 10.1007/BF00275406 [11] LEHMAN J, LAKES R S. Stiff lattices with zero thermal expansion[J]. Journal of Intelligent Material Systems and Structures,2012,23(11):1263-1268. doi: 10.1177/1045389X12445647 [12] LEHMAN J, LAKES R S. Stiff, strong zero thermal expansion lattices via the Poisson effect[J]. Journal of Materials Research,2013,28(17):2499-2508. doi: 10.1557/jmr.2013.154 [13] LEHMAN J, LAKES R S. Stiff, strong, zero thermal expansion lattices via material hierarchy[J]. Composite Structures,2014,107:654-663. doi: 10.1016/j.compstruct.2013.08.028 [14] SIGMUND O, TORQUATO S. Design of materials with extreme thermal expansion using a three-phase topology optimization method[J]. Journal of the Mechanics and Physics of Solids,1997,45(6):1037-1067. doi: 10.1016/S0022-5096(96)00114-7 [15] SIGMUND O, TORQUATO S. Composites with extremal thermal expansion coefficients[J]. Applied Physics Letters,1996,69(21):3203-3205. doi: 10.1063/1.117961 [16] LEHMAN J, LAKES R S. Stiff lattices with zero thermal expansion and enhanced stiffness via rib cross section optimization[J]. International Journal of Mechanics and Materials in Design, 2013, 9(3): 213-225. [17] ZHANG Y C, LIANG Y J, LIU S T, et al. A new design of dual-constituent triangular lattice metamaterial with unbounded thermal expansion[J]. Acta Mechanica Sinica,2019,35(3):507-517. [18] ZHANG Y, LIANG Y, LIU S, et al. A new design for enhanced stiffness of dual-constituent triangular lattice metamaterial with unbounded thermal expansion[J]. Materials Research Express,2018,6(1):015705. doi: 10.1088/2053-1591/aae5be [19] TIMOSHENKO S. Analysis of bi-metal thermostats[J]. Josa,1925,11(3):233-255. doi: 10.1364/JOSA.11.000233 [20] SUHIR E. Interfacial stresses in bimetal thermostats[J]. Journal of Applied Mechanics,1989,56(3):595-600. doi: 10.1115/1.3176133 -
下载:
点击查看大图
计量
- 文章访问数: 950
- HTML全文浏览量: 328
- PDF下载量: 71
- 被引次数: 0
