Mechanical behavior of bamboo scrimber filled steel tube under different loading modes
-
摘要: 本文将重组竹与钢管复合形成新型钢管约束重组竹。对24个新型钢管约束重组竹圆柱试件进行了轴压试验，研究了钢管厚度和加载方式(全截面与核心加载)对其轴压性能的影响。试验结果表明：外加钢管能够有效地提高结构承载力和变形能力；钢管约束重组竹圆柱主要破坏形态为剪切破坏；结构的峰值应力、峰值应变均与钢管厚度呈正相关，随着钢管厚度增加，试件的峰值应力最大增长22.4%，峰值应变最大增长6.1%；核心受压钢管重组竹较全截面受压试件展现了更好的承载潜力和变形能力。根据全截面受压和核心受压的曲线不同，考虑了钢管套箍系数，分别提出了两种加载方式下新型钢管约束重组竹的极限应力、极限应变和峰值应力、峰值应变的预测模型，应力计算模型误差均在10%以内。最后建议了应力-应变全曲线模型，预测了不同加载方式下新型钢管约束重组竹的应力-应变变化规律。Abstract: By means of structural innovation, a new type of bamboo scrimber filled steel tube was formed by composite materials of bamboo scrimber and steel tube. Axial compression tests were carried out on 24 cylindrical specimens of the new type of bamboo scrimber filled steel tube to study the effect of steel tube thickness and loading mode (full section and core loading) on its axial compression performance. The test results show that the external steel tube can effectively improve the structural bearing capacity and deformation capacity, and the main failure mode of the bamboo scrimber filled steel tube is shear failure. The peak stress and peak strain of the structure are positively correlated with the steel tube thickness. As the steel tube thickness increases, the maximum increase in peak stress of the specimens reaches 22.4%, while the maximum increase in peak strain is 6.1%. The core loading specimens exhibit better load bearing potential and deformation capacity than the full section loading specimens. Based on the different curves of full section loading and core loading, and considering the steel tube confinement factor, the prediction models of ultimate stress, ultimate strain, peak stress and peak strain of the new type of bamboo scrimber filled steel tube under different loading modes are proposed, and the error of the stress calculation model is less than 10%. Finally, the stress-strain full curve model is proposed, and the stress-strain variation of the new bamboo scrimber filled steel tube under different loading modes is predicted.
-
竹材因其资源丰富、节能环保、经济效益好等诸多优点而具有广阔的工程应用前景，可作为钢和混凝土材料的补充材料[1]。然而，天然竹子存在尺寸不均、容易开裂和耐久性差等缺陷，为了满足更复杂的工程需求，现有加工技术已经开发出各种新型竹复合材料。其中重组竹是以竹材为主要原料，经过碾压、干燥、施胶、干燥、组坯成型等加工工艺热压而成的板状或其他形式的新型竹基复合材料[2]，是中国自主研发的一种高附加值竹材产品。重组竹不仅具有较好的韧性，而且其抗压、抗拉强度均优于普通木材，可以满足不同场合下工程材料的性能需求[3-6]。
目前，学者们围绕重组竹轴压力学性能进行了一系列研究。Liu等[7]以福建毛竹为原料制备重组竹，并进行了单轴纵向拉伸和压缩试验压缩过程，根据竹纤维和周围基体的变形阶段分为4个阶段：弹性、弹塑性、塑性和破坏阶段，并根据试验结果提出了两种应力-应变本构模型。朱彦等[8]进行了高温环境下重组竹顺纹和横纹的单轴抗压试验，研究了高温对重组竹轴向抗压强度、初始弹性模量和质量的影响，比较了不同温度下重组竹的微观结构变化，并结合了重组竹在高温环境下的受压破坏机制进行分析。Wei等[9]研究了重组竹短柱在循环压缩荷载下的压缩行为。结果表明，重组竹柱的破坏模式包括屈曲、剪切和劈裂，在高应变范围内，重组竹的残余塑性应变比远低于混凝土，进而建立了一个循环应力-应变模型。
随着可持续绿色建材的推广，钢-竹复合结构逐渐受到广泛关注，该复合结构能进一步提高竹材的承载能力，充分发挥钢材和竹材的强度，提高竹材利用率，同时能有效克服钢材过早屈曲的问题，提高钢结构的稳定性[10-13]。重组竹抗压能力强于普通竹材，但容易产生劈裂破坏，如果利用钢管施加约束，有望更好发挥其承载性能。但目前对于钢管重组竹复合结构研究较少，钢-竹复合结构主要集中于梁柱、组合墙板及构件连接方式等方面的研究[14-17]，Zhang等[18]将冷弯薄壁钢与竹材组合形成钢-竹复合结构，探讨了钢-竹界面的破坏模式和机制，研究了剪切应力的分布。Zhao等[19]研制了一种新型薄壁钢管/竹胶合板带约束钢筋空心组合柱。结果表明，竹胶合板的压缩破坏模式主要为压碎破坏、粘接界面部分脱粘破坏和屈曲失稳破坏。试件的极限承载力与净截面面积、长细比及约束钢筋有关。Gan等[20]提出了一种新型钢管-竹-混凝土结构，将混凝土填充在外部钢管和内部原竹之间的空间中，研究了钢管-竹-混凝土轴压短柱的组合效应，结果表明，随着钢管径厚比的减小，组合柱的轴压承载力明显提高，变形能力明显改善。
1. 新型钢管重组竹结构概念及特点
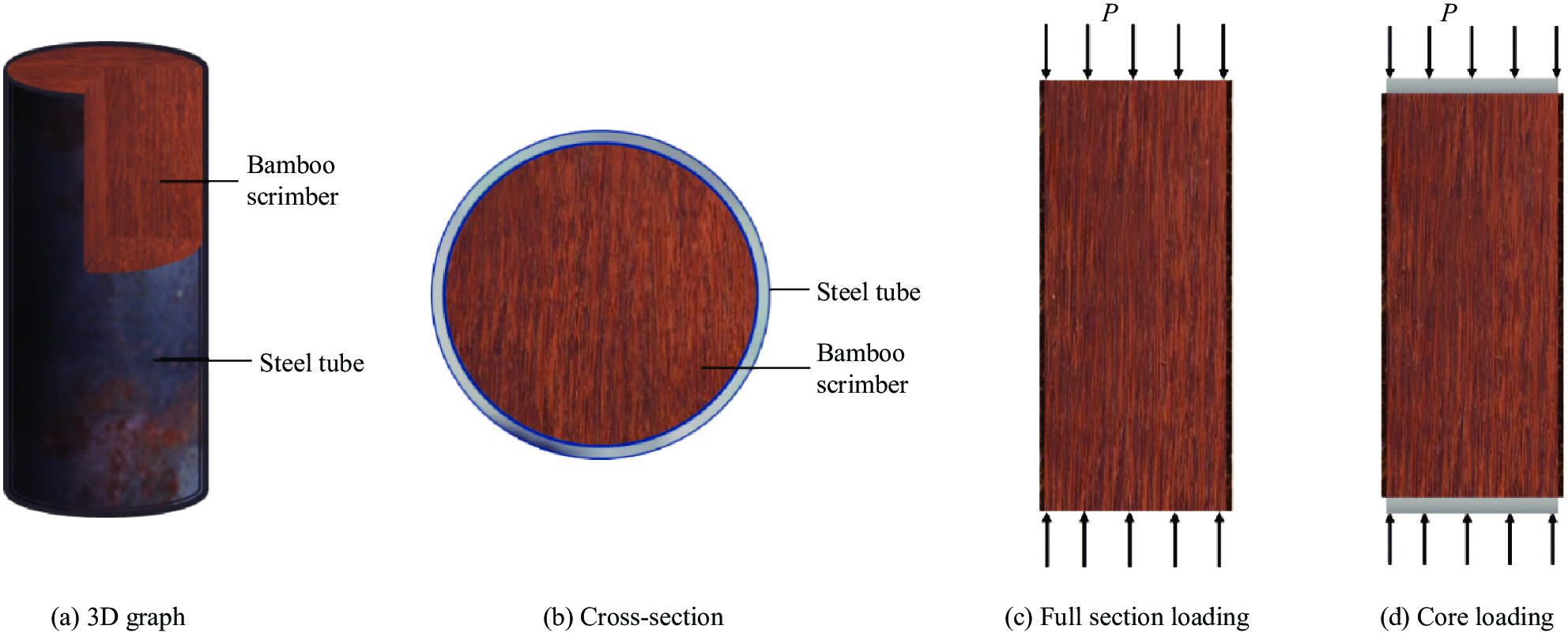
本文采用重组竹与钢管复合制成新型钢管约束重组竹，如图1所示。该新型结构特点在于利用钢管有效抑制重组竹的劈裂破坏，同时重组竹作为钢管内部填充材料，避免钢管过早屈曲，有望提高结构的承载能力，同时保证结构的延性，替代传统钢管混凝土应用于桥墩、立柱、桁架腹杆等竖向承载构件。
![]()
图 1 圆形钢管重组竹柱结构概念图P—Vertical loadFigure 1. Structural concept diagram of bamboo scrimber-filled steel tube2. 试验概况
2.1 试件设计及制备
本试验共制备了24个钢管约束重组竹组合试件。全截面加载和核心加载各4组(每组3个)，钢管重组竹试件高度H分别为345 mm、400 mm，对应的钢管外径D分别为114 mm、133 mm，高径比为3。主要参数为加载方式(全截面加载、核心加载)及钢管厚度(4.5 mm、6.0 mm)，具体参数见表1。为准确区分每一个试件，根据试件参数不同对试件进行编号，相同参数试件分别制备了3个，以“-1”、“-2”和“-3”区别。分别以“D1S4.5-1F”、“D2S6.0-2C”为例介绍试件命名规则，“D”表示直径、“S”表示钢管厚度，“F”、“C”表示加载方式。比如D1S4.5-1F表示4.5 mm厚度钢管，钢管外径为114 mm，采用全截面加载的钢管约束重组竹柱1号试件；D2S6.0-2C则表示4.5 mm厚度钢管，钢管外径为133 mm，采用核心加载的钢管约束重组竹柱2号试件。
表 1 钢管约束重组竹柱轴压试验结果Table 1. Axial compression test result of bamboo scrimber filled steel tubeSpecimen H/mm Db/mm Ds/mm Pcu/kN fce/MPa εce fcy/MPa εcy fcc/MPa εcc Ebs/GPa D1S4.5-F 345 103 114 1628.8 92.56 0.0019 — — 159.58 0.064 44.5 D1S6.0-F 345 100 114 1994.2 113.32 0.0021 — — 195.37 0.063 52.3 D2S4.5-F 400 122 133 1882.3 78.58 0.0019 — — 135.49 0.063 42.1 D2S6.0-F 400 119 133 2292.6 95.71 0.0018 — — 165.02 0.065 43.8 D1S4.5-C 345 103 114 1412.0 — — 142.78 0.033 169.46 0.086 15.8 D1S6.0-C 345 100 114 1413.2 — — 162.90 0.047 179.94 0.087 16.2 D2S4.5-C 400 122 133 1630.3 — — 122.86 0.033 139.46 0.075 16.7 D2S6.0-C 400 119 133 1674.3 — — 131.55 0.031 150.54 0.075 15.2 Notes: Specimens were numbered according to the different parameters of the specimens; D—Diameter of specimen; S—Thickness of the steel tube; F—Full section loading; C—Core loading; H—Height of all specimens; Db—Diameter of bamboo scrimber; Ds—Outer diameter of steel tube; Pcu—Peak load; fce—Proportional limit stress; εce—Proportional limit strain; fcy—Yield stress; εcy—Yield strain; fcc—Peak stress; εcc—Peak strain; Ebs—Nominal initial compressive elastic modulus. 新型钢管-重组竹复合管圆柱试件的制备过程包括圆形重组竹的工厂加工、同一批次的钢管加工及除锈、钢管重组竹复合构件的制作。试件的具体制备过程如下：(1) 将原竹剖分成竹片，疏解成竹丝束，经干燥浸胶，高温高压热固化制成板状重组竹，再用卡盘将制作好的重组竹固定，对准中心，利用切削刀将矩形构件逐渐削圆，形成圆柱形重组竹，最后裁剪成设计长度；(2) 用直磨机对钢管内壁进行抛光，确保截面清洁，与重组竹配合紧密；(3) 将钢管底部用热熔胶固定在平板上；(4) 钢管外侧用塑料膜包裹，防止胶水污染钢管表面；(5) 将配制好的环氧树脂倒入钢管中，均匀涂刷钢管内部和重组竹表面；(6) 将重组竹柱放入钢管中，用环氧树脂胶填充缝隙，为使环氧树脂胶更好地填满空隙，将重组竹慢慢放入钢管，防止底部因冲击过大漏胶。图2为试件准备的关键步骤。
2.2 材料性能试验
钢管材料性能依据《金属材料拉伸试验：第一部分：室温试验方法》(GB/T 228.1—2010)[21]测得，钢管的详细材料性能见表2。本次试验使用的重组竹为中国安徽宏宇竹业有限公司提供的热压重组竹，测得的密度为1100 kg /m3。根据重组竹出厂检验报告，重组竹的耐腐蚀性为I级，抗霉性为95.8%，吸水厚度膨胀率在5%以内。根据厂家提供，环氧树脂胶的拉伸强度为67.7 MPa，弹性模量为2.9 GPa，拉伸极限应变为0.029。
表 2 钢管力学性能指标Table 2. Mechanical properties of steel tubeDs/mm ts/mm fy/MPa fu/MPa Es/GPa 114 4.5 327.4 465.9 205.2 133 4.5 336.8 502.2 206.1 114 6.0 376.0 510.2 206.4 133 6.0 381.2 499.2 205.1 Notes: ts—Thickness of steel tube; fy—Yield strength of steel tube; fu—Ultimate tensile strength of steel tube; Es—Elastic modulus of steel tube. 根据美国材料试验标准(ASTM D143—09)[22]的抗压试验要求，按标准尺寸制作10个拉伸试样，按50 mm×50 mm×200 mm的尺寸制作10个抗压重组竹试样，测定了竹材的抗压强度fc0为112.01 MPa、抗压极限应变εc0为0.050、抗拉强度108.37 MPa和弹性模量15.65 GPa。同时根据钢管重组竹试件尺寸设计并试验了相应尺寸的重组竹试件，具体数据见表3。
表 3 重组竹试件力学性能指标Table 3. Properties of bamboo scrimberSpecimen H/mm Db/mm Pbu/kN fby/MPa εby fbu/MPa εbu Eb/GPa D103 345 103 823.8 95.41 0.029 98.87 0.050 18.6 D100 345 100 767.0 94.24 0.029 97.66 0.050 15.6 D122 400 122 1121.9 92.61 0.028 95.97 0.052 15.0 D119 400 119 1053.4 91.40 0.026 94.71 0.048 14.8 Notes: Pbu—Ultimate load; fby—Yield stress of the bamboo scrimber; εby—Yield strain of the bamboo scrimber; fbu—Ultimate stress of the bamboo scrimber; εbu—Ultimate strain of the bamboo scrimber; Eb—Initial compressive elastic modulus. 2.3 试验加载及采集制度
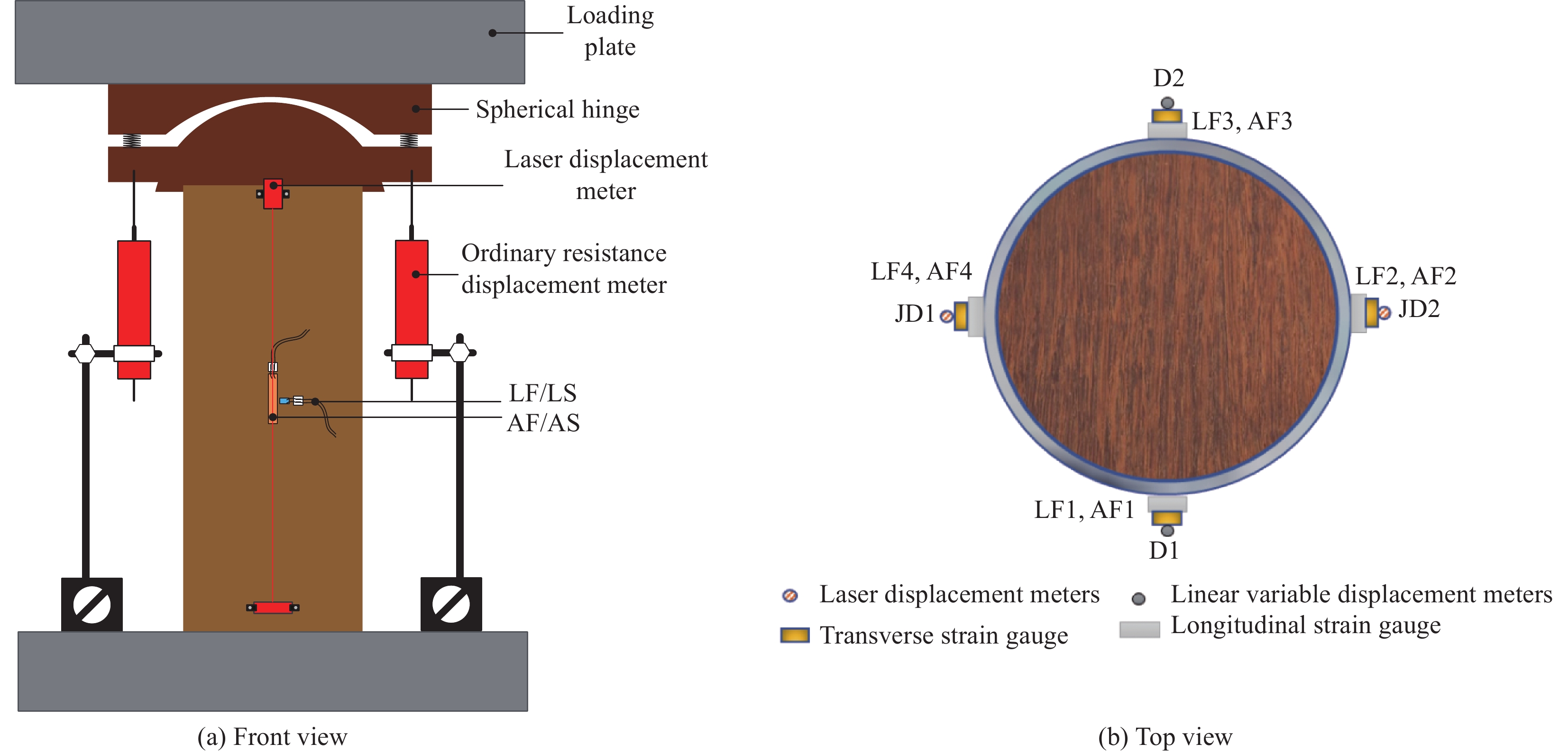
本文采用的加载装置为杭州邦威3000 kN高刚度岩石混凝土试验机，同时采用Tokyo Sokki Kenkyulo生产的TDS-530数据采集仪进行同频率收集试验应变、位移等数据，试验加载及测量装置如图3所示。试件两侧对称垂直布置两普通电测位移计(D1/D2)，用于测量试件全高度范围内的变形，在另外两侧对称布置两激光位移计(JD1/JD2)，均距端部30 mm，用于测量试件沿部分高度方向的位移，同时，在每个试件的中部四周分别对称粘贴4个纵向应变片(AF/AS)和4个横向应变片(LF/LS)。试验加载采用位移控制，0.5 mm/min的速率，最后以试件变形达到30 mm或超出位移计量程停止试验[23]。对于核心加载试件，加载前在试件两个端面放置直径低于内部重组竹1 mm的钢垫板，以保证仅核心重组竹承受轴向荷载。
3. 试验结果与分析
3.1 试验现象及破坏形态
图4给出了全截面受压钢管约束重组竹的试件破坏状态。在初始加载阶段，试件表面无明显变形，钢管和重组竹共同受载，此时试件处于弹性工作阶段，有部分锈迹脱落，钢管的环向约束作用未被激活。随着加载的继续，试件首先在中部膨胀变形明显，出现屈曲，随后屈曲现象延伸到两端，最后中部及两端钢管变形显著，出现严重凸起，以剪切形式破坏。
![]()
图 4 全截面受压钢管重组竹破坏形态Figure 4. Typical failure modes of bamboo scrimber filled steel tube under full section loading图5给出了核心受压钢管约束重组竹的破坏形态。在加载初始阶段，试样表面没有明显变化，继续加载，有细微内部纤维断裂的声音，重组竹内部发生了轻微压缩损伤。随着荷载的增加，钢管约束了重组竹的横向变形，有效提高了纵向抗压强度。当荷载达到极限荷载的95%左右时，钢管中部出现腰鼓现象，横向变形增大，钢管表面锈迹脱落，当重组竹剪切力超过其承受能力时，组合试件内部出现剪切破坏，钢管表面形成剪切滑移线。停止试验时，试件承载力仍呈缓慢上升趋势，重组竹仍具有一定的抗压能力。考虑到钢管与重组竹形成了较强的粘结作用，在有限变形范围内，剪切破坏较小，钢管未表现出明显的屈曲现象，而试件表面出现明显的剪切滑移线[24]，故整体呈现剪切破坏形态。
![]()
图 5 核心受压钢管重组竹破坏形态Figure 5. Typical failure modes of bamboo scrimber filled steel tube under core loading3.2 钢管约束重组竹柱应力-应变关系
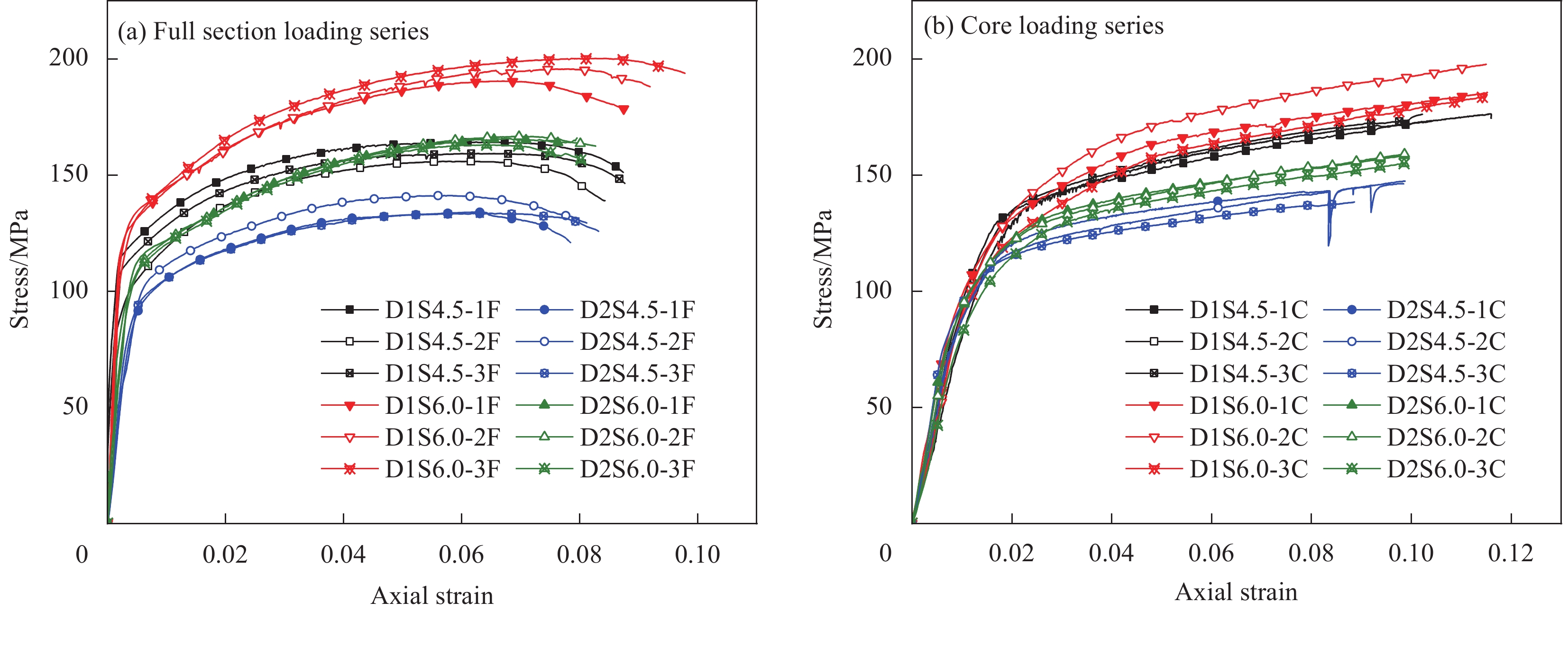
图6给出了钢管约束重组竹柱应力-应变关系曲线。图6(a)为全截面加载组，图6(b)为核心加载组，其中纵坐标名义应力为试验轴向荷载与试件横截面面积的比值，全截面加载组中，曲线弹性阶段横坐标的纵向应变采用应变片所测得数据，弹性阶段过后的曲线采用普通电测位移计测得数据。核心加载组采用试件全高范围普通电测位移计测得数据计算。
![]()
图 6 钢管重组竹应力-应变关系曲线Figure 6. Stress-strain curves of bamboo scrimber filled steel tube全截面受压钢管约束重组竹柱的应力-应变关系曲线如图6(a)所示，主要分为弹性阶段、弹塑性阶段、下降段。在弹性阶段，钢管和重组竹一般分别承担荷载，应力-应变曲线呈线性增加，初始刚度由重组竹和钢管共同提供。钢管重组竹柱的塑性性能逐渐突出，弹塑性曲线的斜率逐渐减小，相应的应变增长快于应力。同时，两种材料之间产生箍向力，使钢管处于纵向压力、环张力和径向压力的受力状态，钢管环向拉应力逐渐增大，根据Von Mises屈服准则，钢管纵向压应力减小；重组竹处于纵向压力、环压力和径向压力三向受压状态，抗压强度显著提高。钢管的约束使重组竹的应力分布更加均匀，减小了竹材中心出现局部损伤的可能性。当复合结构达到峰值应力，试件的应力开始缓慢下降，应变不断增大，直至最终破坏。
核心受压钢管约束重组竹柱的应力-应变关系曲线可分为弹性阶段和弹塑性阶段，如图6(b)所示。线弹性阶段，外层钢管对重组竹的约束作用较小，重组竹的应力近似线性增大，初始刚度由重组竹提供。在弹塑性阶段，应力-应变曲线斜率减小，钢管提供的约束主导了试件的力学行为，钢管施加的侧向压力限制了重组竹横向膨胀变形，抑制了重组竹劈裂破坏，重组竹的抗压强度得到有效提高。试件在弹性阶段的初始刚度基本相同，随着轴向荷载的逐渐增大，曲线继续上升，曲线斜率随尺寸增大而减小，钢管的约束作用减小，导致刚度减小，所有曲线均未出现下降段。由于测试仪器的限制，后续应力-应变曲线的变化尚不清楚。从曲线的变化趋势可以看出，该结构仍具有较大的承压能力，未来需采用更大的测量范围。
3.3 参数化分析
图7、图8为钢管厚度及加载方式参数变化对钢管约束重组竹柱峰值应力、峰值应变影响的对比分析图，定性定量地对比分析了各参数变化对圆形钢管重组竹柱受压性能的影响规律。
![]()
图 7 不同钢管厚度钢管重组竹应力-应变曲线对比Figure 7. Comparisons of stress-strain curves of bamboo scrimber filled steel tube with different steel tube thicknessfc—Peak stress of bamboo scrimber filled steel tube specimen; fc0—Ultimate stress of the bamboo scrimber; εc0—Ultimate strain of the bamboo scrimber; εc—Peak strain of bamboo scrimber filled steel tube specimen![]()
图 8 不同加载模式钢管重组竹峰值应力-应变对比Figure 8. Comparison of peak stress and peak strain of bamboo scrimber filled steel tube under different loading modes3.3.1 钢管厚度的影响
全截面受压试件中，钢管厚度为6.0 mm的试件峰值应力较钢管厚度为4.5 mm的试件上升显著，D1、D2组试件峰值应力fcc分别增强22.4%、21.8%，峰值应变εcc分别增强5.9%和0.8%。钢管厚度越大，弹性阶段较长，且弹塑性阶段斜率较大，试件的整体承载力明显增强，变形能力明显改善，下降段斜率也较平坦。
核心受压试件中，当钢管厚度从4.5 mm增加到6.0 mm时，D1、D2组试件峰值应力fcc分别增强6.1%、7.9%，而峰值应变εcc分别增强6.1%和0%。钢管厚度不同的钢管重组竹试件初始刚度基本相同，进入弹塑性阶段时的应力-应变一致。而钢管厚度为6.0 mm的试件的弹塑性阶段斜率较大，上升更快，同样地，弹塑性阶段上升斜率随着尺寸增大而减小。D2S4.5-C与D2S6.0-C弹塑性阶段斜率几乎相同，此时两种不同厚度的钢管对于重组竹横向膨胀的约束效果近似。
3.3.2 加载方式的影响
如图8所示，同种钢管厚度情况下，不同加载方式下试件的峰值应力和峰值应变有所不同。主要表现为核心受压与全截面受压的钢管重组竹试件的峰值应力相差不大，峰值应变稍高于全截面受压的钢管重组竹试件。受仪器量程限制，同时保证统一性，核心受压试件试验数据在取峰值应力应变时，由于不存在下降段，取位移30 mm，试验结束时的点作为峰值点，故会产生核心受压试件峰值应力试验值低于全截面受压试件的情形，但应力-应变曲线的后续变化是未知的。从曲线的趋势可以看出，核心受压试件仍然具有较大的承压潜力，未来将进行更大范围的测量。本文中建立的核心受压试件的承载力模型属于保守型，核心受压试件的峰值应变均大于全截面受压试件，主要是由于核心受压中仅重组竹承受荷载，由于外加钢管约束，钢管提供更多侧向约束作用，限制重组竹的侧向膨胀，从而提高试件的抗压强度和变形能力。全截面受压试件中，钢管快速屈服，约束力不足，两者组合结构的变形较小。
3.4 模型提出
典型全截面受压钢管约束重组竹柱应力-应变曲线特征点如图9所示。钢管约束重组竹柱的应力-应变曲线主要由3个阶段构成。在第一阶段，应力随着应变的增加呈现线性增加，该阶段的斜率与钢管厚度成正相关，为E'bs。进入第二阶段后，钢管出现屈服现象，应力增长速度减小；在第三阶段中，钢管约束重组竹柱达峰值承载力后开始出现下降段，下降段斜率与钢管厚度呈负相关。将第二阶段最大应力点定义为峰值点，为(fcc, εcc)，其中fcc、εcc分别为试件的峰值应力、峰值应变。第一阶段与第二阶段的交叉点定义为弹性极限点，为(fce, εce)，其中 fce、εce分别为试件的弹性应力、弹性应变。弹性极限与峰值点之间的中点定义为阶段屈服点，为(fcy, εcy)，其中 fcy、εcy分别为试件的屈服应力、屈服应变。第三阶段终点定义为 (fcu, εcu)，其中fcu、εcu分别为试件的极限应力、极限应变，fcu=85%fcc。
![]()
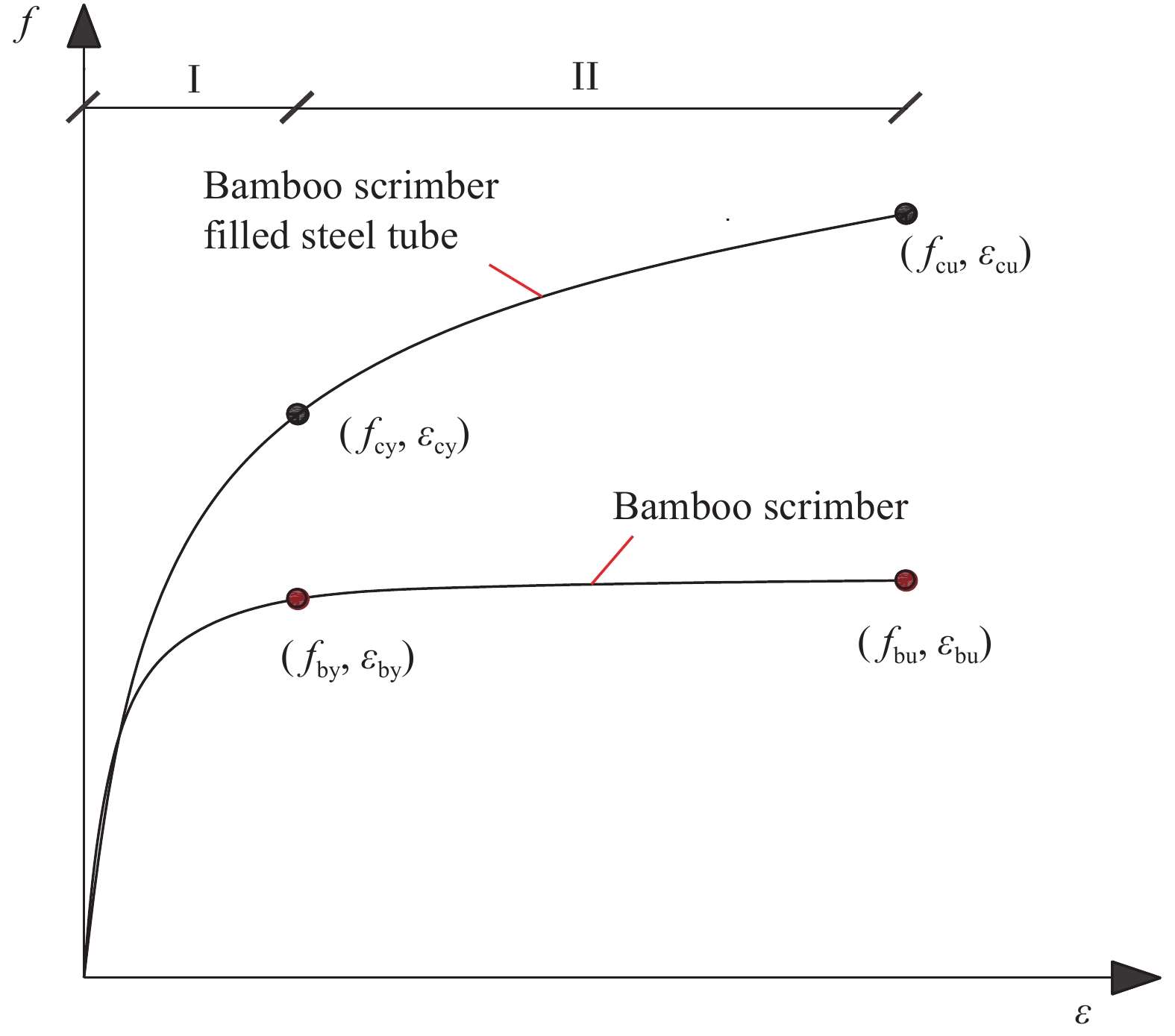
图 9 全截面受压钢管约束重组竹柱应力-应变曲线Ey—Elastic-plastic stage stiffness; E'bs—Proportional stage stiffness; fcu—Ultimate stress; εcu—Ultimate strain; f—Stress; ε—StrainFigure 9. Stress-strain curve of bamboo scrimber filled steel tube under full-section loading核心受压重组竹应力-应变曲线有所不同，如图10所示，根据重组竹的应力-应变曲线特征和重组竹通用函数模型[25]与钢管混凝土复合柱的应力-应变曲线模型，确定了钢管约束重组竹复合试件的特征点，包括屈服点和极限点。应力-应变曲线的终点定义为极限点(fcu, εcu)，其中 fcu、εcu分别为试件的极限应力、极限应变。曲线中从弹性阶段到弹塑性阶段的转折点定义为屈服点(fcy, εcy)，其中 fcy、εcy分别为试件的屈服应力、屈服应变由于屈服点的取值界限不够清晰，因此无法一次精确确定。过程中根据实际情况进行反复验证应力-应变全曲线模型并反复取值来找到误差最小的屈服点，以最大程度地减小误差。
![]()
图 10 核心受压钢管约束重组竹柱应力-应变曲线Figure 10. Stress-strain curves of bamboo scrimber filled steel tube under core loading在钢管混凝土理论中，套箍系数ξs是影响极限承载力的主要指标，它反映了钢管对混凝土的约束程度[26]。本文研究对象为钢管约束重组竹柱，将套箍系数ξs引入到试件的模型计算中，同时考虑到钢管重组竹构件实际制作中，套箍的作用会受到许多因素的影响，如钢管与重组竹之间的粘结、间隙、钢管的尺寸等影响因素，最后给出了峰值应力的一般规律，并给出了计算方法，提出了应力-应变模型特征点的计算公式。本文在试验结果的基础上，建议具体计算公式如下，其中Ab为重组竹表面积，As为钢管表面积，Ag为钢管约束重组竹组合面积。
全截面受压：
ξs=AsfyAbfbu (1) E′bs=AbEb+AsEsAg (2) fce=E′bsεce (3) fcy=12(fcc−fce)+fce (4) εcy=0.18εcc (5) Ey=fcy−fceεcy−εce (6) fccfbu=1+0.83ξs (7) εccεbu=1+0.51ξs (8) 核心受压：
fcyfby=1+0.6ξs0.69 (9) εcyεby=1+0.5ξs1.4 (10) fcufbu=1+0.85ξs (11) εcuεbu=1+1.1ξs (12) 核心受压钢管重组竹试件在本文的模型中预测偏保守，这与试验方案和试验方法等因素有关。因此，在进一步的研究中，可以调整采用更加细致和精确的试验方法，进一步研究核心受压试件的极限承载力和变形能力，同时对所建议公式进行修正。
根据不同的应力-应变全曲线形式，全截面受压和核心受压分别提出了更相符的模型，其中全截面受压是基于改进的Chang-Mander钢筋本构模型[27]，全截面受压的钢管重组竹全曲线弹塑性阶段应力-应变关系采用非线性包络曲线计算，下降段采用线性计算公式，其中Ecu为下降段斜率。
fc={E′bsεcεc⩽ (13) 基于魏洋等模型[28]，提出了适用于核心受压钢管重组竹柱的应力-应变全曲线公式，Esec为峰值点处割线模量，具体如下：
f(x) = \frac{{{f_{{\rm{c}}}}}}{{{f_{{{\rm{cc}}}}}}} = \frac{{x a}}{{a - 1 + {x^{a{{(x + \delta )}^b} + c}}}} (14) a = \frac{{{E_{{\rm{c}}}}}}{{{E_{{\rm{c}}}} - {E_{{{\rm{sec}}}}}}} (15) {E_{\sec }} = \frac{{{f_{{{\rm{cc}}}}}}}{{{\varepsilon _{{{\rm{cc}}}}}}} (16) 为全面评估各模型精准性，通过理论计算值与试验值的平均值(Average，AV)、标准差(Standard deviation，SD)和平均绝对误差(Average absolute error，AAE)这三大指标进行评价数据的离散性。
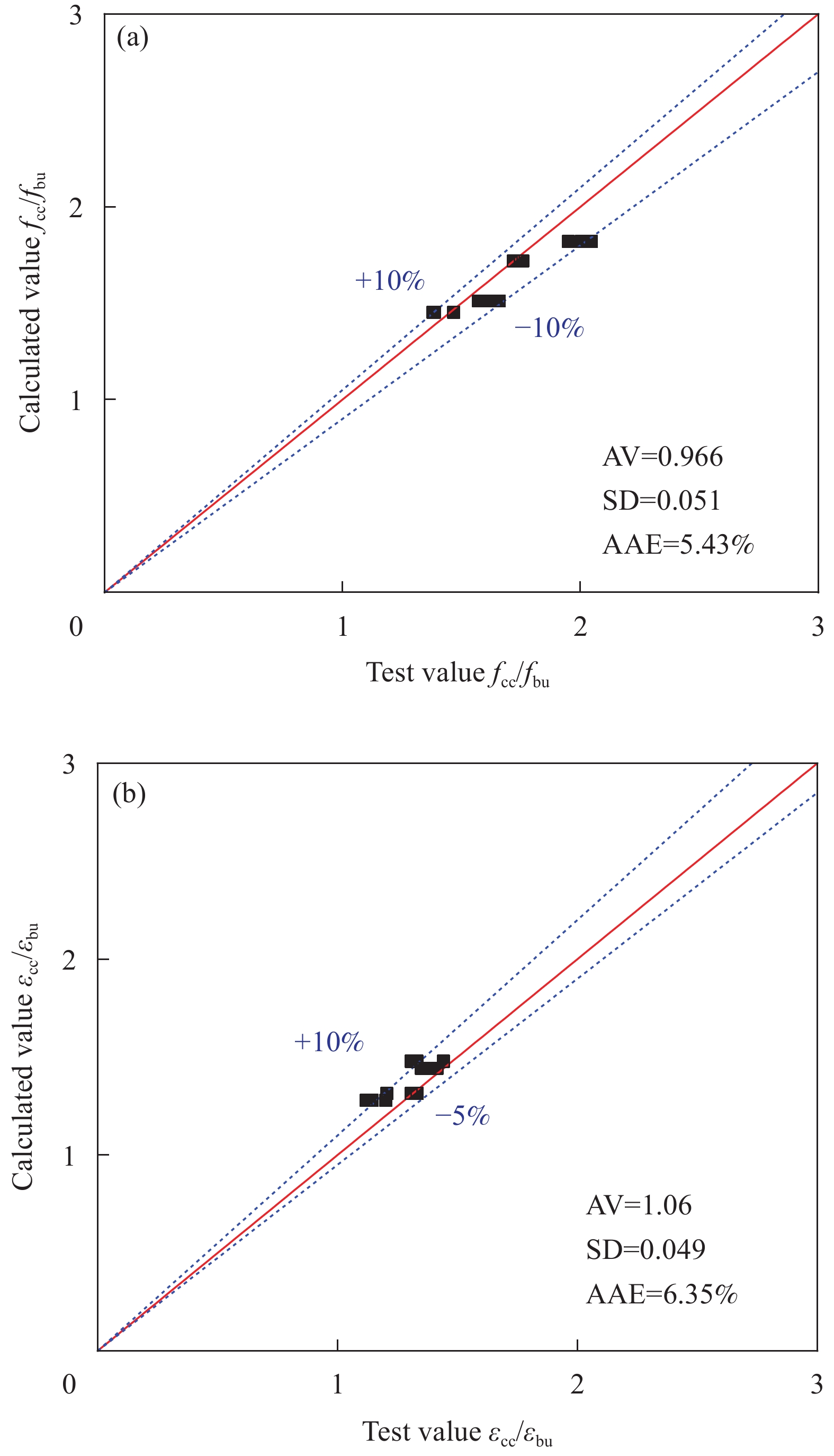
{\text{AV}} = {{\sum {\left( {\frac{{{\text{Theo}}.}}{{{\text{Expe}}.}}} \right)} } \mathord{\left/ {\vphantom {{\sum {\left( {\frac{{{\text{Theo}}.}}{{{\text{Expe}}.}}} \right)} } n}} \right. } n} (17) {\text{SD}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {\frac{{{\text{Theo}}.}}{{{\text{Expe}}.}} - {\text{AV}}} \right)}^2}} } (18) {\text{AAE}} = {{\sum {\frac{{\left| {{\text{Expe}}. - \left. {{\text{Theo}}.} \right|} \right.}}{{\left| {{\text{Expe}}.} \right|}}} } \mathord{\left/ {\vphantom {{\sum {\frac{{\left| {{\text{Expe}}. - \left. {{\text{Theo}}.} \right|} \right.}}{{\left| {{\text{Expe}}.} \right|}}} } n}} \right. } n} (19) 对比结果表明，模型预测值与试验值较吻合，如图11所示。峰值应力模型的AV、SD和AAE值分别为0.966、0.051和5.43%，峰值应变模型的AV、SD和AAE值分别为1.06、0.049和6.35%，试验值与计算值误差较小，模型预测较准确。
![]()
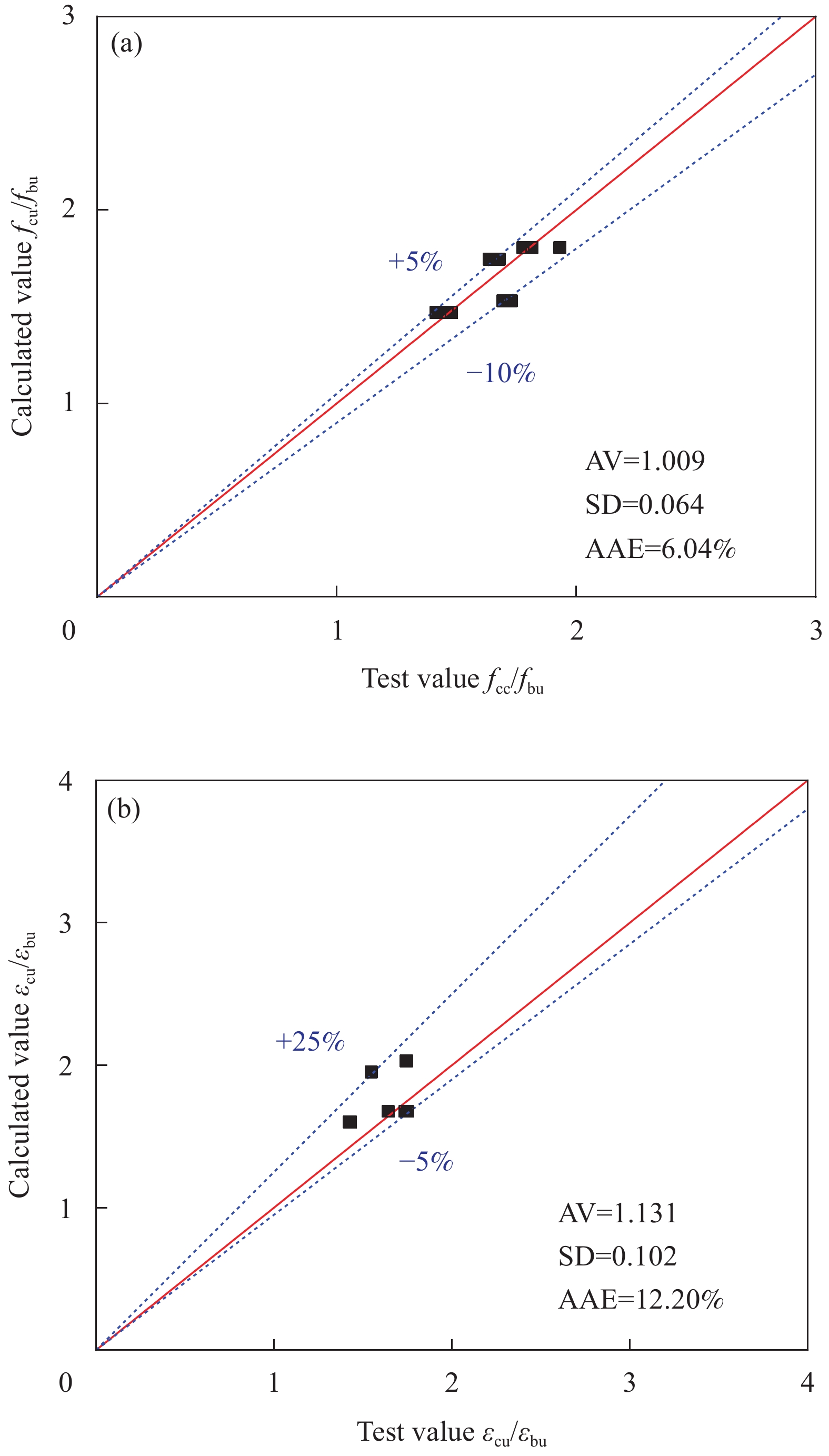
图 11 全截面受压钢管约束重组竹柱极限应力-应变模型评估AV—Average; SD—Standard deviation; AAE—Average sbsolute errorFigure 11. Verification of peak stress and peak strain model under full-section loading极限应力-应变模型与计算值对比如图12所示。结果表明，该模型具有理想的性能，极限应力模型的AV、SD和AAE值分别为1.009、0.064和6.04%，极限应变模型的AV、SD和AAE值分别为1.131、0.102和12.20%。试验值与计算值的误差较小，证明了公式的合理性，表明公式预测钢管重组竹复合柱在轴向荷载作用下的行为是可行的。
![]()
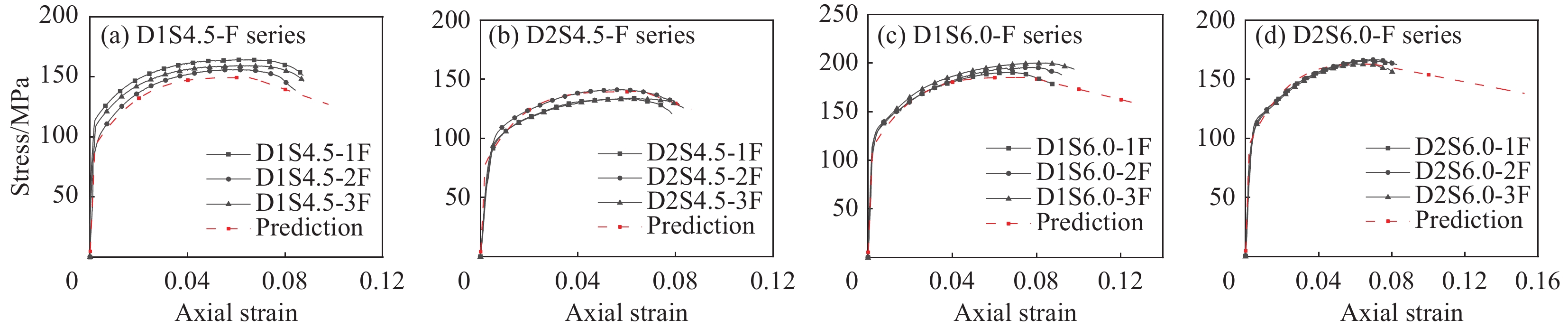
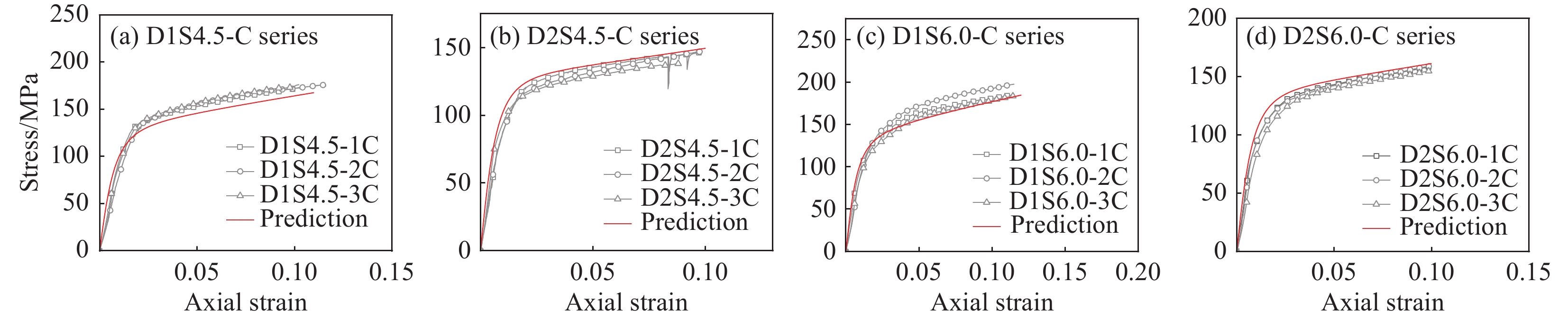
图 12 核心受压钢管约束重组竹柱极限应力-应变模型评估Figure 12. Verification of peak stress and peak strain model under core loading图13、图14给出了预测模型与试件实际试验值的对比。对于钢管重组竹柱在轴压作用下的弹性阶段和弹塑性阶段，模型与实际试验值吻合较好，能够描述钢管重组竹的本构行为，为重组竹的设计和应用提供了理论支持，也能准确预测试验后期承载力的增长趋势。总体而言，该模型描述了钢管重组竹的完整轴压性能，具有较好的精度、简单性和通用性。
![]()
图 13 全截面受压钢管约束重组竹全曲线模型验证Figure 13. Full curve model verification of bamboo scrimber filled steel tube under full section loading![]()
图 14 核心受压钢管约束重组竹全曲线模型验证Figure 14. Full curve model verification of bamboo scrimber filled steel tube under core loading4. 结 论
(1) 钢管重组竹柱轴压主要破坏模式为剪切破坏。对于全截面受压试件，破坏形态较明显，钢管明显屈曲。对于核心受压试件，试件表面钢管鼓起而无明显屈曲，剪切破坏通过试件表面明显的剪切滑移线判定。
(2) 全截面受压钢管重组竹柱的应力-应变曲线分为3个阶段：弹性阶段、弹塑性阶段和下降段。钢管厚度越大，弹性阶段较长，且弹塑性阶段斜率较大，试件的整体承载力和变形能力均有明显的增强。随着钢管厚度增加，试件的峰值应力最大增长22.4%，峰值应变最大增长6.1%，且下降段斜率也较平坦。核心受压钢管重组竹柱应力-应变曲线分为两个阶段：弹性阶段、弹塑性阶段。弹性阶段的初始刚度由重组竹提供，钢管厚度大的试件的弹塑性阶段斜率较大，上升更快，试件的强度和变形能力同样有明显的增强。
(3) 核心受压与全截面受压的钢管重组竹试件的峰值应力相差不大，峰值应变稍高于全截面受压的钢管重组竹试件。主要是由于核心受压中仅重组竹承受荷载，钢管能够提供更多侧向约束作用，限制重组竹的侧向膨胀，从而提高试件的抗压强度和变形能力。全截面受压试件中，钢管承受纵向压力而快速屈服，约束力不足，两者组合结构的变形较小。
(4) 考虑了钢管套箍系数，提出了适用于圆形新型钢管约束重组竹的极限应力、应变和峰值应力、应变的预测模型，应力计算模型误差均在10%以内。建议的应力-应变全曲线模型预测结果与试验结果吻合较好，能够很好地模拟出圆形钢管约束重组竹的应力-应变全曲线各阶段的应力-应变变化规律，为实际工程应用奠定了基础。
-
![]()
图 1 圆形钢管重组竹柱结构概念图
P—Vertical load
Figure 1. Structural concept diagram of bamboo scrimber-filled steel tube
![]()
图 4 全截面受压钢管重组竹破坏形态
Figure 4. Typical failure modes of bamboo scrimber filled steel tube under full section loading
![]()
图 5 核心受压钢管重组竹破坏形态
Figure 5. Typical failure modes of bamboo scrimber filled steel tube under core loading
![]()
图 6 钢管重组竹应力-应变关系曲线
Figure 6. Stress-strain curves of bamboo scrimber filled steel tube
![]()
图 7 不同钢管厚度钢管重组竹应力-应变曲线对比
Figure 7. Comparisons of stress-strain curves of bamboo scrimber filled steel tube with different steel tube thickness
fc—Peak stress of bamboo scrimber filled steel tube specimen; fc0—Ultimate stress of the bamboo scrimber; εc0—Ultimate strain of the bamboo scrimber; εc—Peak strain of bamboo scrimber filled steel tube specimen
![]()
图 8 不同加载模式钢管重组竹峰值应力-应变对比
Figure 8. Comparison of peak stress and peak strain of bamboo scrimber filled steel tube under different loading modes
![]()
图 9 全截面受压钢管约束重组竹柱应力-应变曲线
Ey—Elastic-plastic stage stiffness; E'bs—Proportional stage stiffness; fcu—Ultimate stress; εcu—Ultimate strain; f—Stress; ε—Strain
Figure 9. Stress-strain curve of bamboo scrimber filled steel tube under full-section loading
![]()
图 10 核心受压钢管约束重组竹柱应力-应变曲线
Figure 10. Stress-strain curves of bamboo scrimber filled steel tube under core loading
![]()
图 11 全截面受压钢管约束重组竹柱极限应力-应变模型评估
AV—Average; SD—Standard deviation; AAE—Average sbsolute error
Figure 11. Verification of peak stress and peak strain model under full-section loading
![]()
图 12 核心受压钢管约束重组竹柱极限应力-应变模型评估
Figure 12. Verification of peak stress and peak strain model under core loading
![]()
图 13 全截面受压钢管约束重组竹全曲线模型验证
Figure 13. Full curve model verification of bamboo scrimber filled steel tube under full section loading
![]()
图 14 核心受压钢管约束重组竹全曲线模型验证
Figure 14. Full curve model verification of bamboo scrimber filled steel tube under core loading
表 1 钢管约束重组竹柱轴压试验结果
Table 1 Axial compression test result of bamboo scrimber filled steel tube
Specimen H/mm Db/mm Ds/mm Pcu/kN fce/MPa εce fcy/MPa εcy fcc/MPa εcc Ebs/GPa D1S4.5-F 345 103 114 1628.8 92.56 0.0019 — — 159.58 0.064 44.5 D1S6.0-F 345 100 114 1994.2 113.32 0.0021 — — 195.37 0.063 52.3 D2S4.5-F 400 122 133 1882.3 78.58 0.0019 — — 135.49 0.063 42.1 D2S6.0-F 400 119 133 2292.6 95.71 0.0018 — — 165.02 0.065 43.8 D1S4.5-C 345 103 114 1412.0 — — 142.78 0.033 169.46 0.086 15.8 D1S6.0-C 345 100 114 1413.2 — — 162.90 0.047 179.94 0.087 16.2 D2S4.5-C 400 122 133 1630.3 — — 122.86 0.033 139.46 0.075 16.7 D2S6.0-C 400 119 133 1674.3 — — 131.55 0.031 150.54 0.075 15.2 Notes: Specimens were numbered according to the different parameters of the specimens; D—Diameter of specimen; S—Thickness of the steel tube; F—Full section loading; C—Core loading; H—Height of all specimens; Db—Diameter of bamboo scrimber; Ds—Outer diameter of steel tube; Pcu—Peak load; fce—Proportional limit stress; εce—Proportional limit strain; fcy—Yield stress; εcy—Yield strain; fcc—Peak stress; εcc—Peak strain; Ebs—Nominal initial compressive elastic modulus. 
下载: 导出CSV
表 2 钢管力学性能指标
Table 2 Mechanical properties of steel tube
Ds/mm ts/mm fy/MPa fu/MPa Es/GPa 114 4.5 327.4 465.9 205.2 133 4.5 336.8 502.2 206.1 114 6.0 376.0 510.2 206.4 133 6.0 381.2 499.2 205.1 Notes: ts—Thickness of steel tube; fy—Yield strength of steel tube; fu—Ultimate tensile strength of steel tube; Es—Elastic modulus of steel tube.
下载: 导出CSV
表 3 重组竹试件力学性能指标
Table 3 Properties of bamboo scrimber
Specimen H/mm Db/mm Pbu/kN fby/MPa εby fbu/MPa εbu Eb/GPa D103 345 103 823.8 95.41 0.029 98.87 0.050 18.6 D100 345 100 767.0 94.24 0.029 97.66 0.050 15.6 D122 400 122 1121.9 92.61 0.028 95.97 0.052 15.0 D119 400 119 1053.4 91.40 0.026 94.71 0.048 14.8 Notes: Pbu—Ultimate load; fby—Yield stress of the bamboo scrimber; εby—Yield strain of the bamboo scrimber; fbu—Ultimate stress of the bamboo scrimber; εbu—Ultimate strain of the bamboo scrimber; Eb—Initial compressive elastic modulus.
下载: 导出CSV
-
[1] HARELIMANA V, ZHU J, YUAN J, et al. Investigating the bamboo as alternative partial replacement of steel bars in concrete reinforcement members[J]. The Structural Design of Tall and Special Buildings,2022,6:31.
[2] 陈思, 魏洋, 赵鲲鹏, 等. 重组竹顺纹受压蠕变性能及预测模型[J]. 复合材料学报, 2021, 38(3):944-952. DOI: 10.13801/j.cnki.fhclxb.20200615.002 CHEN Si, WEI Yang, ZHAO Kunpeng, et al. Creep performance and prediction model of bamboo scrimber under compression[J]. Acta Materiae Compositae Sinica,2021,38(3):944-952(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20200615.002
[3] CHEN S, WEI Y, ZHU J, et al. Experimental investigation of the shear performance of bamboo scrimber beams reinforced with bamboo pins[J]. Construction and Building Materials,2023,365:130044. DOI: 10.1016/j.conbuildmat.2022.130044
[4] YU Y, LIU R, HUANG Y, et al. Preparation, physical, mechanical, and interfacial morphological properties of engineered bamboo scrimber[J]. Construction and Building Materials,2017,157:1032-1039. DOI: 10.1016/j.conbuildmat.2017.09.185
[5] 盛叶, 黄庚浪, 叶小凡, 等. 重组竹抗拉力学性能分析[J]. 林业工程学报, 2023, 8(1):46-52. SHENG Ye, HUANG Genglang, YE Xiaofan, et al. Analysis on mechanical properties of bamboo scrimber under tension stress[J]. Journal of Forestry Engineering,2023,8(1):46-52(in Chinese).
[6] 杨娜, 张亚慧. 重组竹材料技术创新与面临的关键问题[J]. 世界竹藤通讯, 2021, 19(5):64-68. YANG Na, ZHANG Yahui. Technological innovation for bamboo scrimber and its key technical problems faced[J]. World Bamboo and Rattan,2021,19(5):64-68(in Chinese).
[7] LIU W, LIU M, HUANG J, et al. Constitutive relation models of bamboo scrimber under uniaxial loading along the fibre direction[J]. European Journal of Wood and Wood Products,2021,79:811-820. DOI: 10.1007/s00107-021-01680-8
[8] 朱彦, 卞玉玲, 周爱萍, 等. 重组竹高温下单轴受压性能试验研究[J]. 建筑结构学报, 2021, 42(9):127-134. DOI: 10.14006/j.jzjgxb.2019.0866 ZHU Yan, BIAN Yuling, ZHOU Aiping, et al. Experimental study on uniaxial compressive properties of parallel strand bamboo at high temperatures[J]. Journal of Building Structures,2021,42(9):127-134(in Chinese). DOI: 10.14006/j.jzjgxb.2019.0866
[9] WEI Y, JI X, DUAN M, et al. Flexural performance of bamboo scrimber beams strengthened with fiber-reinforced polymer[J]. Construction and Building Materials,2017,142:66-82. DOI: 10.1016/j.conbuildmat.2017.03.054
[10] ZHANG J, TONG K, WU P, et al. Research status on steel-bamboo composite structure[J]. MATEC Web of Conferences,2019,275:1018. DOI: 10.1051/matecconf/201927501018
[11] LI Y S, YAO J, LI R, et al. Thermal and energy performance of a steel-bamboo composite wall structure[J]. Energy and Buildings,2017,156:225-237. DOI: 10.1016/j.enbuild.2017.09.083
[12] ZHANG X, XU J, ZHANG X, et al. Life cycle carbon emission reduction potential of a new steel-bamboo composite frame structure for residential houses[J]. Journal of Building Engineering,2021,39(4):102295.
[13] SHI D, DEMARTINO C, LI Z, et al. Axial load-deformation behavior and fracture characteristics of bolted steel to laminated timber and glubam connections[J]. Composite Structures,2023,305:116486. DOI: 10.1016/j.compstruct.2022.116486
[14] HASSANIEH A, VALIPOUR H, BRADFORD M. Load-slip behaviour of steel-cross laminated timber (CLT) composite connections[J]. Journal of Constructional Steel Research,2016,122:110-121. DOI: 10.1016/j.jcsr.2016.03.008
[15] CRISTIANO L, FRANGI A. Experimental investigation on in-plane stiffness and strength of innovative steel-timber hybrid floor diaphragms[J]. Engineering Structures,2017,138:229-244. DOI: 10.1016/j.engstruct.2017.02.032
[16] SHAN Q, ZHANG J, TONG K, et al. Study on flexural behaviour of box section bamboo-steel composite beams[J]. Advances in Civil Engineering,2020,2020:8878776.
[17] 刘战江, 王占良, 吴时旭, 等. 装配式钢-竹组合结构建筑施工工艺及工程应用[J]. 建筑技术, 2023, 54(1):45-48. LIU Zhanjiang, WANG Zhanliang, WU Shixu, et al. Research on building construction technology and engineering application of prefabricated steel-bamboo composite structure[J]. Architecture Technology,2023,54(1):45-48(in Chinese).
[18] ZHANG J, ZHANG Z, TONG K, et al. Bond performance of adhesively bonding interface of steel-bamboo composite structure[J]. Journal of Renewable Materials,2020,8(6):687-702. DOI: 10.32604/jrm.2020.09513
[19] ZHAO W, LUO Z, LI Y. Axial compression testing of bamboo-laminated encased steel tube composite columns[J]. Iranian Journal of Science and Technology Transactions of Civil Engineering,2020,44(2):645-655. DOI: 10.1007/s40996-020-00381-1
[20] GAN D, ZHANG T, ZHOU X, et al. Experimental investigation on the bamboo-concrete filled circular steel tubular stub columns[C]//Proceedings of the 12th International Conference on Advances in Steel-Concrete Composite Structures. Spain: Universitat Politècnica de València, 2018: 385-391.
[21] 中国国家标准化管理委员会. 金属材料拉伸试验: 第一部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2010. Standardization Administration of the People's Republic of China. Tensile test of metallic materials: Part 1: Test method at room temperature: GB/T 228.1—2010[S]. Beijing: Standards Press of China, 2010(in Chinese).
[22] ASTM. Standard test methods for small clear specimens of timber: ASTM D143—09[S]. West Conshohocken: ASTM International, 2009.
[23] 柏佳文, 魏洋, 张依睿, 等. 新型碳纤维增强复合材料-钢复合管海水海砂混凝土圆柱轴压试验[J]. 复合材料学报, 2021, 38(9):3084-3093. BAI Jiawen, WEI Yang, ZHANG Yirui, et al. Axial compression behavior of new seawater and sea sand concrete filled circular carbon fiber reinforced polymer-steel composite tube columns[J]. Acta Materiae Compositae Sinica,2021,38(9):3084-3093(in Chinese).
[24] 郭莹, 许天祥, 刘界鹏. 圆CFRP-钢复合管约束高强混凝土短柱轴压试验研究[J]. 建筑结构学报, 2019, 40(5):124-131. GUO Ying, XU Tianxiang, LIU Jiepeng. Experimental study on axial behavior of circular CFRP-steel composite tubed high-strength concrete stub columnss[J]. Journal of Building Structures,2019,40(5):124-131(in Chinese).
[25] 魏洋, 纪雪微, 端茂军, 等. 重组竹轴向应力-应变关系模型[J]. 复合材料学报, 2018, 35(3): 572-579. WEI Yang, JI Xuewei, DUAN Maojun, et a. Model for axial stress strain relationship of bamboo scrimber[J]. Acta Materiac Compositae Sinica, 2018, 35(3): 572-579(in Chinese).
[26] WEI Y, BAI J, ZHANG Y, et al. Compressive performance of high-strength seawater and sea-sand concrete-filled circular FRP-steel composite tube columns[J]. Engineering Structures,2021,240:112357. DOI: 10.1016/j.engstruct.2021.112357
[27] CHANG G, MANDER J. Seismic energy based fatigue damage analysis of bridge columns: Part I—Evaluation of seismic capacity[M]. Buffalo: National Center for Earthquake Engineering Research, 1994: 2.
[28] 张依睿, 魏洋, 柏佳文, 等. 纤维增强聚合物复合材料-钢复合圆管约束混凝土轴压性能预测模型[J]. 复合材料学报, 2019, 36(10):2478-2485. ZHANG Yirui, WEI Yang, BAI Jiawen, et al. Models for predicting axial compression behavior of fiber reinforced polymer-steel composite circular tube confined concrete[J]. Acta Materiae Compositae Sinica,2019,36(10):2478-2485(in Chinese).
-
期刊类型引用(1)
1. 韦宝幸，魏洋，王高飞，邢泽，林煜. 钢管约束竹-混凝土组合柱轴压力学性能. 复合材料学报. 2024(06): 3115-3128 . 
本站查看
其他类型引用(0)
-
目的
随着乡村振兴及碳中和、碳达峰国家战略的不断深入推进，竹结构逐渐成为实现绿色发展的重要组成部分。重组竹不仅具有较好的韧性，而且其抗压、抗拉强度均大于普通木材，有望在工程结构中广泛应用，然而研究表明其受压时胶合处脆弱，易产生劈裂破坏。如果能够很好的解决重组竹的劈裂破坏问题，则能更好的发挥重组竹承载性能。本文将重组竹与钢材组合形成钢-竹组合结构，且使得重组竹位于钢管的核心，形成新型钢管约束重组竹。可望克服重组竹承载时过早的劈裂破坏，同时提升钢结构在稳定性和屈曲性能方面的不足，发挥多种材料共同工作的优点。重组竹替代传统混凝土，一定程度上实现了未来社会对现代工程结构提出的绿色、可持续发展要求。为了更好地在工程实际中推广钢管重组竹组合柱，本文提出了这种新型结构在轴向荷载作用下的应力-应变曲线模型。
方法本文分析了钢管重组竹组合柱在不同加载模式下的轴压作用下的典型应力-应变关系曲线，研究了加载方式和钢管厚度等因素对钢管约束重组竹轴压性能的影响规律，分析了其破坏特征和受力性能，考虑了钢管套箍系数，提出了适用于圆形新型钢管约束重组竹的极限应力、极限应变和峰值应力、峰值应变的预测模型以及应力-应变全曲线模型，并利用24个试验数据对提出的模型进行了验证，结果表明提出的模型具有较好的精确性和适用性。
结果从对不同加载模式下钢管重组竹组合柱轴压性能、应力-应变模型验证结果的分析发现：①全截面受压钢管约束重组竹柱的应力应变关系曲线主要分为弹性阶段、弹塑性阶段、下降段；核心受压钢管约束重组竹柱的应力-应变关系曲线可分为弹性阶段和弹塑性阶段。②核心受压与全截面受压的钢管重组竹试件的峰值应力相差不大，峰值应变稍高于全截面受压的钢管重组竹试件，主要是因为核心受压中仅重组竹承受荷载，钢管能够提供更多侧向约束作用，限制重组竹的侧向膨胀，从而提高试件的抗压强度和变形能力。全截面受压试件中，钢管承受纵向压力而快速屈服，约束力不足，两者组合结构的变形较小。③对于不同试验参数的钢管重组竹组合柱，钢管厚度的增加对于试件应力-应变曲线的影响主要体现在弹塑性阶段，钢管厚度越大，弹性阶段较长，且弹塑性阶段斜率较大，试件的整体承载力明显增强，变形能力明显改善。④提出的极限应变、峰值应力和峰值应变计算模型模拟出的数据与试验数据也较为吻合；利用提出的应力-应变曲线模型计算得到的预测曲线与试验曲线较为吻合。
结论新型钢管重组竹组合柱为重组竹在工程实际中的直接利用提供了可能性，两者的组合不仅解决了重组竹劈裂破坏的问题，又有效提高了结构的承载能力和变形能力。本文提出的钢管重组竹组合柱的应力-应变曲线模型计算结果与试验结果较吻合，表明此模型适用于本文的结构。
-
重组竹不仅具有较好的韧性，而且其抗压、抗拉强度均大于普通木材，有望在工程结构中广泛应用，然而研究表明其受压时胶合处脆弱，易产生劈裂破坏。如果能够很好的解决重组竹的劈裂破坏问题，则能更好的发挥重组竹承载性能。将重组竹与钢材组合形成钢-竹组合结构，且使重组竹位于钢管的核心，可望克服重组竹承载时过早的劈裂破坏，同时提升钢结构在稳定性和屈曲性能方面的不足，发挥多种材料共同工作的优点。重组竹替代传统混凝土，一定程度上实现了未来社会对现代工程结构提出的绿色、可持续发展要求。
本文将重组竹与钢管复合形成新型钢管约束重组竹。对24个新型钢管约束重组竹圆柱试件进行了轴压试验，研究了钢管厚度和加载方式(全截面与核心加载)对其轴压性能的影响。试验结果表明，外加钢管能够有效地提高结构承载力和变形能力；钢管约束重组竹圆柱主要破坏形态为剪切破坏；结构的峰值应力、峰值应变均与钢管厚度呈正相关，随着钢管厚度增加，试件的峰值应力最大增长22.4%，峰值应变最大增长6.1%；核心受压钢管重组竹较全截面受压试件展现了更好的承载潜力和变形能力。根据全截面受压和核心受压的曲线不同，考虑了钢管套箍系数，分别提出了两种加载方式下钢管约束重组竹的极限应力、极限应变和峰值应力、峰值应变的预测模型，应力计算模型误差均在10%以内。最后建议了应力-应变全曲线模型，预测了不同加载方式下新型钢管约束重组竹的应力-应变变化规律。
钢管约束重组竹组合柱 (a)结构截面图；(b) 全截面加载全曲线模型；(c) 核心加载全曲线模型
计量
- 文章访问数: 632
- HTML全文浏览量: 430
- PDF下载量: 30
- 被引次数: 1
