Meso-structure analysis and permeability prediction of satin fabric based on Micro-CT
-
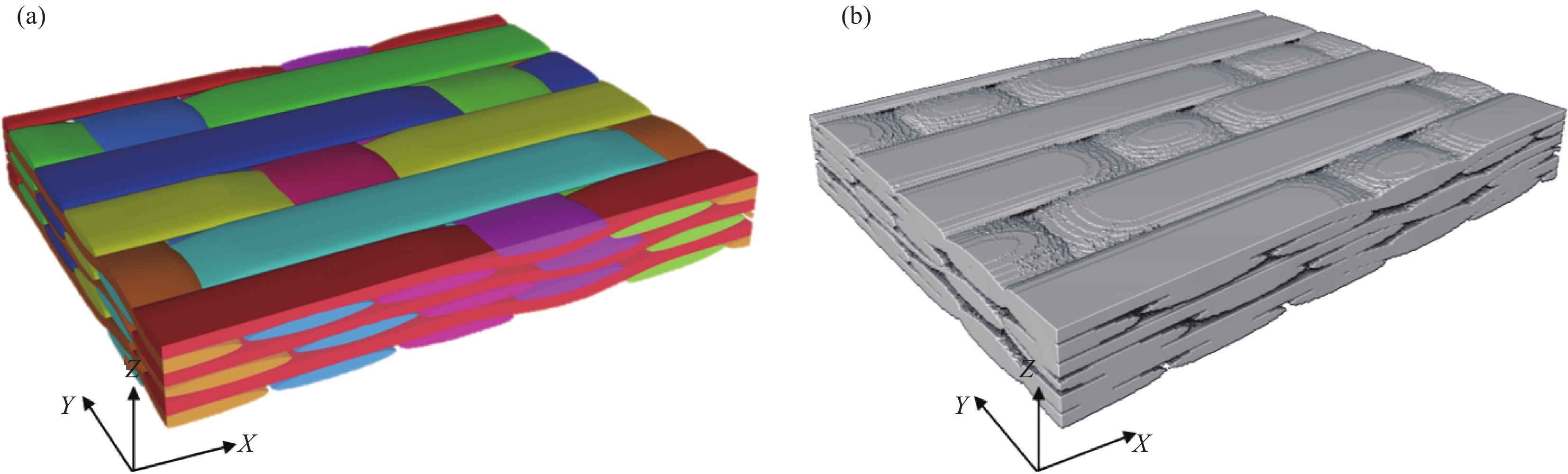
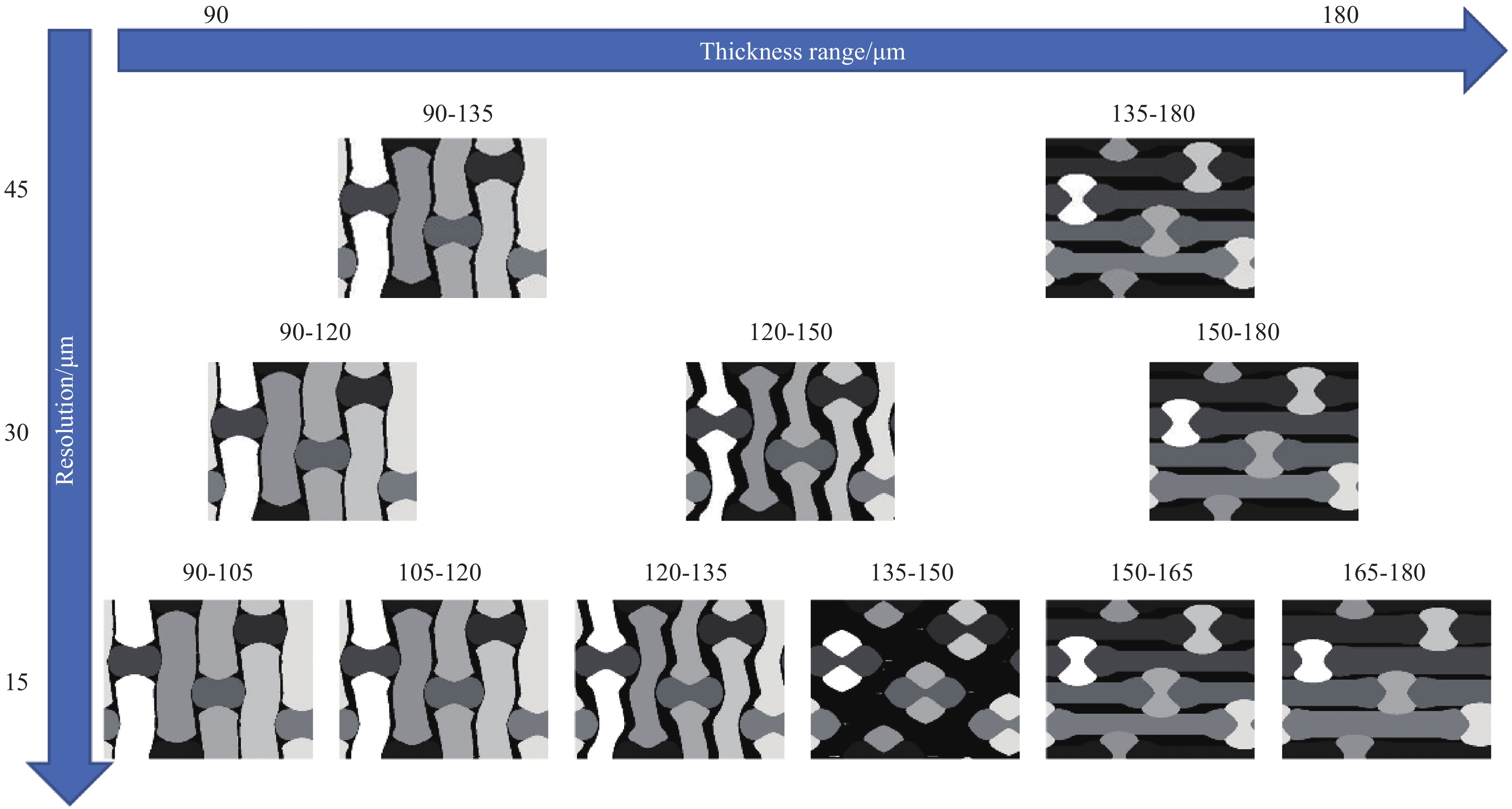
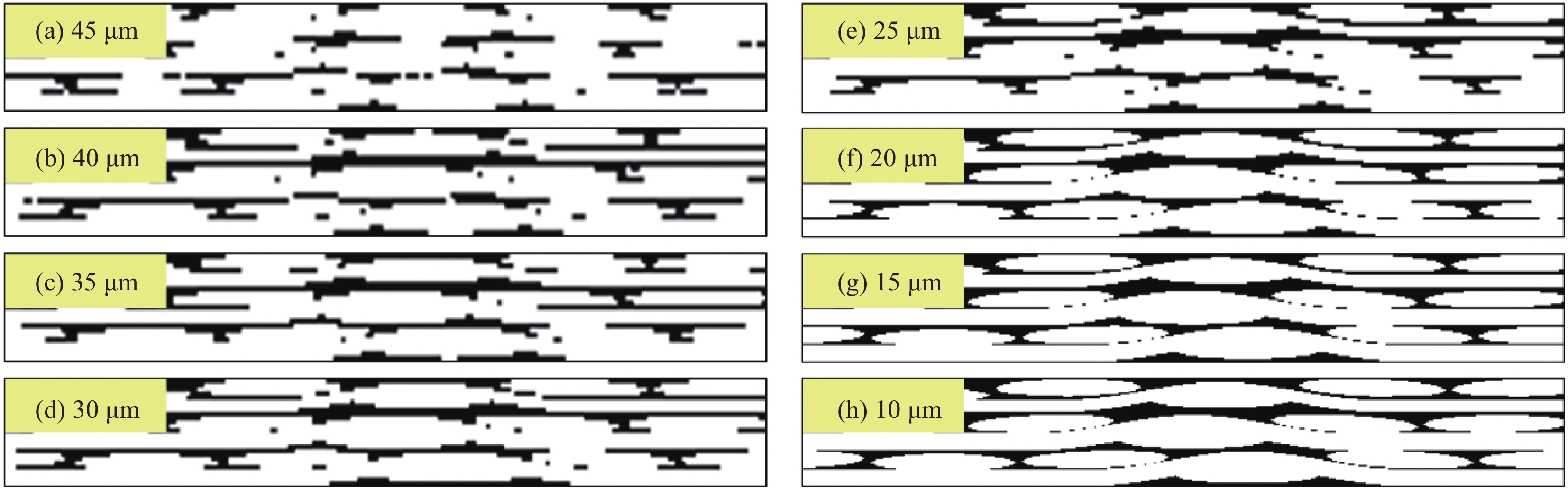
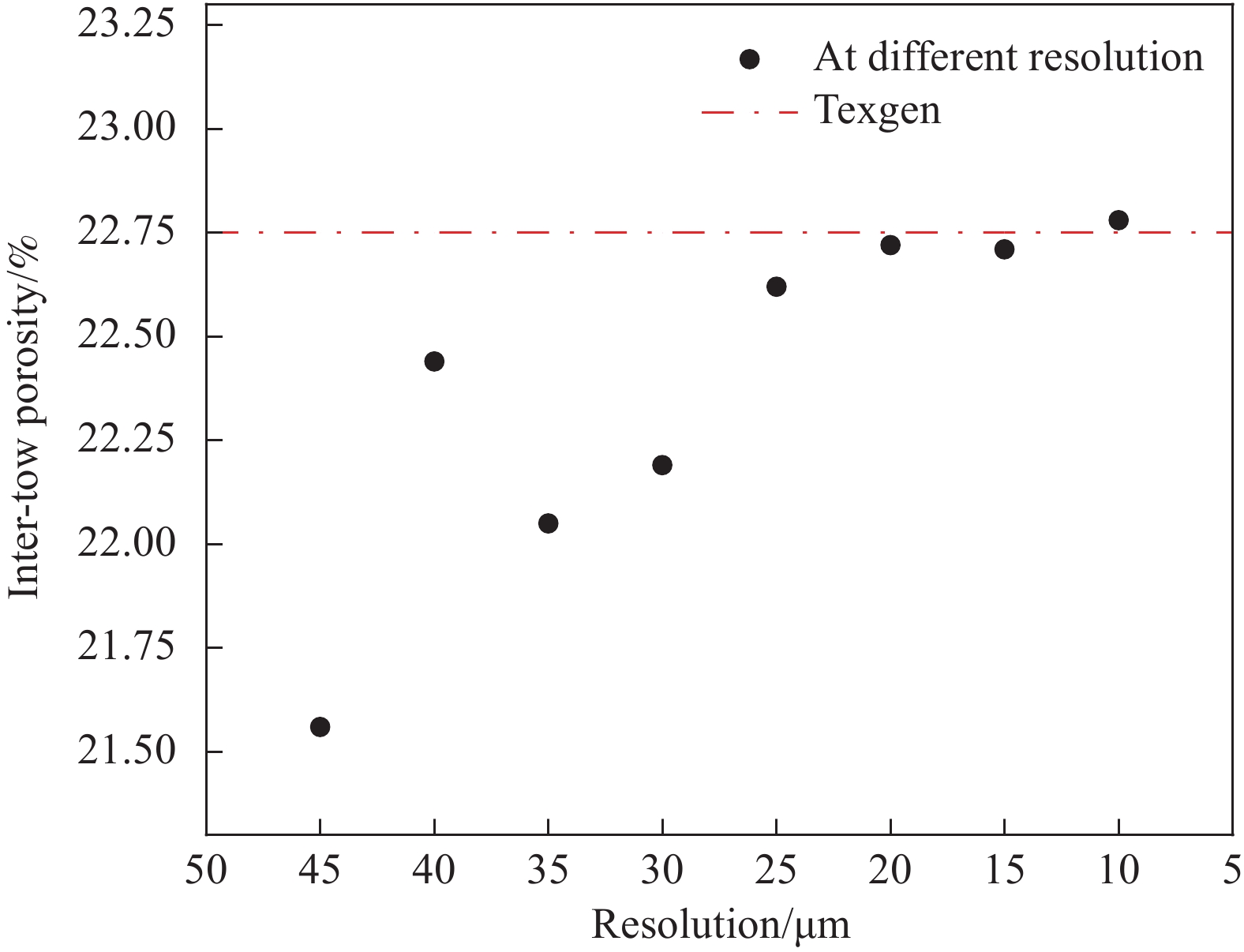
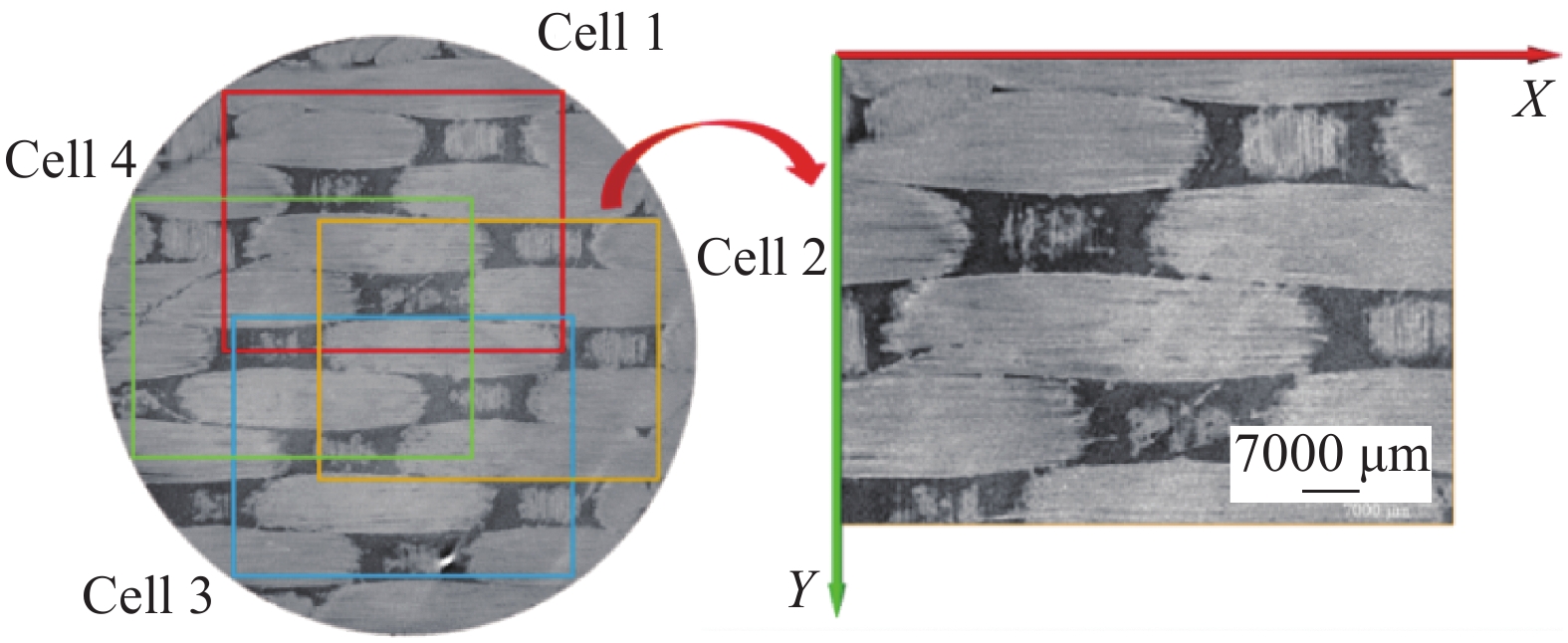
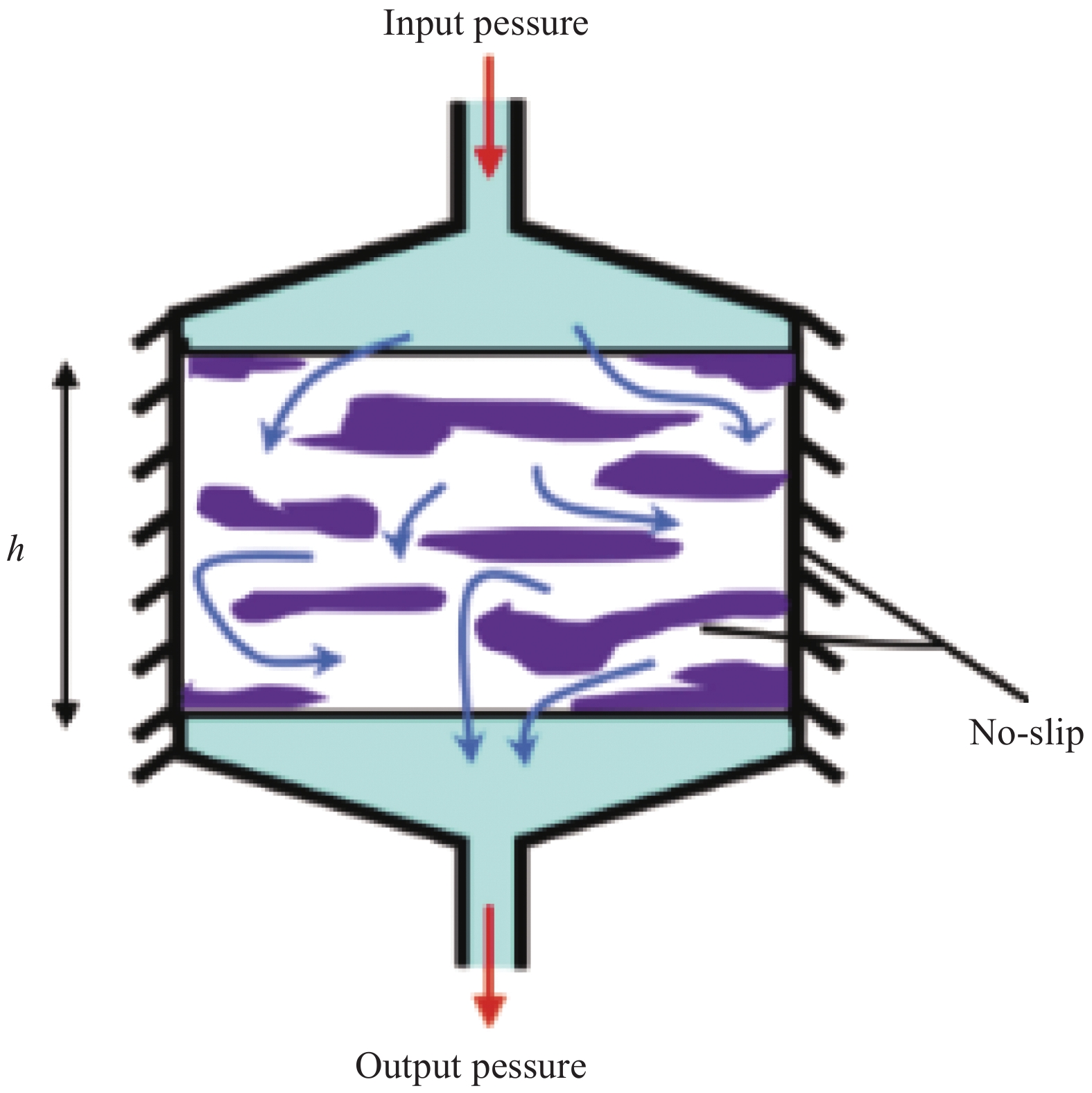
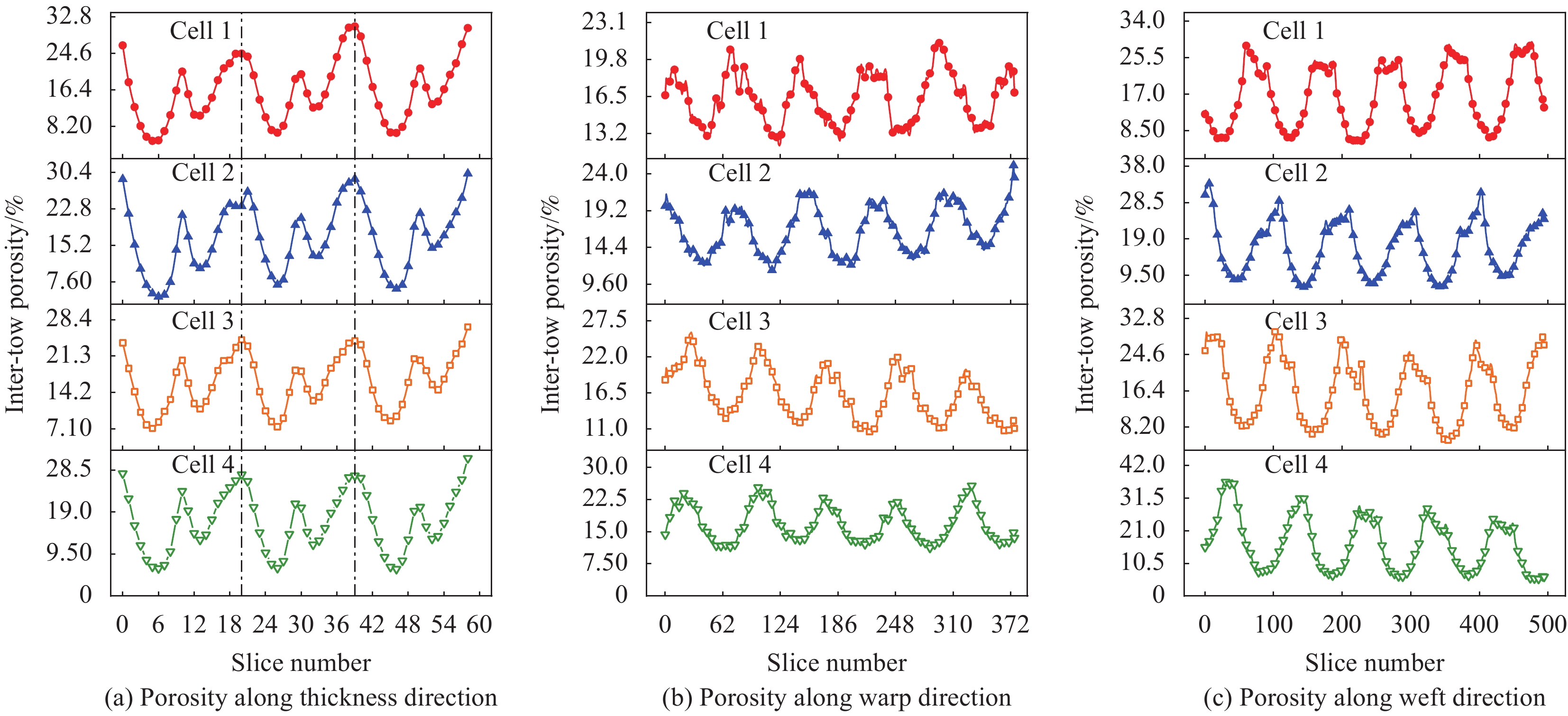
摘要: 建立了确定显微计算机断层扫描技术(Micro-CT)扫描最合适分辨率的方法,并基于CT图像分析了3K五枚缎纹织物的结构,预测了渗透率。首先,将织物理想单胞模型转换为不同分辨率二维切片,考察分辨率对单胞结构、渗透率表征的影响,提出了确定Micro-CT扫描最合适分辨率的方法;其次,采用确定的分辨率对织物进行Micro-CT扫描,获取织物细观结构;最后,使用CT三维细观结构进行厚度方向渗透率数值预测,研究了织物结构的空间离散性对厚度方向渗透率的影响。结果表明:对于本文所用五枚缎纹织物,采用15 μm分辨率进行Micro-CT扫描最合适;通过Micro-CT可准确获取织物纤维束的路径及截面变化;多层织物的孔隙沿3个主方向均呈现周期性排布,且束间孔隙率均值为16.6%;使用真实CT模型的厚度方向渗透率预测结果与实验值具有良好的吻合性。Abstract: The optimal resolution determination method of micro-computed tomography (Micro-CT) scanning was presented here based on two-dimensional slices at different resolutions for ideal unit cell model, and the meso-structure and permeability of 3K 5-harness satin woven fabric were characterized based on the CT image at the optimal resolution. Firstly, the ideal unit cell model of the fabric was converted into 2D slices at different resolutions and the effects of resolution on the characterization of cell structure and permeability were investigated. Thereafter, the optimal resolution was determined for fabric CT scanning. Then, the CT image of the fabric with the optimal resolution was used for the meso-structure and through-thickness permeability characterizations of the fabric. The results show that the optimal resolution for the CT scanning of 5-harness satin woven fabric is 15 μm. The path and cross-sectional variation of the yarns in the fabric can be obtained by Micro-CT accurately. The inter-tow voids of the multilayer fabric are arranged periodically along the three main directions with an average inter-tow porosity of 16.6%. The through-thickness permeabilities obtained based on Micro-CT are in good agreement with experimental results.
-
Keywords:
- satin fabric /
- resolution /
- CT image /
- inter-tow voids /
- numerical simulation /
- permeability
-
由微纳米尺寸纤维随机排布组成的纤维网络材料是一类广泛存在且具有重要应用前景的材料,例如生物细胞中维持细胞形状的蛋白质骨架[1-2]及纳米纸[3]、生活用纸[4]、无纺布[5]等都属于纤维网络材料;此外,以纤维网络为基础的复合薄膜材料在防雷击涂层[6]、电磁屏蔽[7-8]、应变传感器[9]等诸多领域也有重要应用。纤维网络材料由于纤维分布的随机性及网络疏密和纤维连接强弱的不均匀性而具有显著的非均质特点,其非均质性使该类材料的失效分析变得极为复杂。近些年,为了设计制备出更高强度、更高韧性的纤维网络材料,学者们从不同角度出发对纤维网络的失效问题展开了研究。起初,仿真[10]和试验[11]结果均表明网络的强度与网络密度呈线性关系,网络密度越高,强度越大。随后,Deogekar等[12]发现并不是所有网络材料的强度都与网络密度呈线性关系,对于只存在连接损伤而无纤维损伤的网络,其强度与网络中纤维密度无关,而是与连接密度和连接强度呈线性关系。为了进一步探究实际纤维网络非均质特点对其失效的影响,学者们研究了纤维间连接分布及纤维几何尺寸分布等因素的影响。例如,Borodulina等[13]在小厚度三维网络纤维间相互作用的模拟研究中发现,如果连接强度分布接近对称分布,则其分散性在一定范围内对纤维网络强度的影响不大,而增大纤维长度的分散性却会显著降低网络强度。Deogekar等[14]进一步研究了连接强度的分散性对损伤的影响,发现连接强度相同的高密度网络损伤通常集中在局部,而连接强度分散性较大的网络中损伤则分散于整个网络,表现出更好的韧性。此外,Kulachenko等[15]和Deogekar等[12]分析了纤维形貌的影响,结果表明纤维的弯曲程度不会对网络结构强度产生显著影响。
上述研究大多针对的是单一纤维组成的网络,然而实际应用中大部分纤维网络是由不同性质的两类或多类纤维构成的混杂网络,多种类型纤维的引入使混杂纤维网络具有了更好的可设计性。例如,日常用纸便是由多类纤维混杂而成的,通过选择不同力学性能和长细比的纤维可以设计出不同强度和韧性的纸[16];在大部分生物胶原网络中,纤维会形成不同尺寸的纤维束[17],纤维束进一步组成网络结构,因此这些网络结构也可以看作是混杂纤维网络,正是由于不同类型、不同尺寸纤维(束)的存在,生物材料才能表现出异常丰富的性能[18-19]。混杂纤维网络的性能与纤维组分占比密切相关,现有研究表明,混杂纤维网络的刚度随纤维组分占比的变化呈现出非线性关系[20]。Lin等[21]发现在纤维状肌动蛋白网络中加入少量高刚度纤维会引起其力学性能的巨大变化,使剪切大变形下原本的软化现象转变为硬化现象。Bai等[22]通过数值方法系统地研究了高刚度纤维的加入对网络刚度的影响,他们发现对于低密度纤维网络,少量高刚度纤维的加入能够显著增大网络的剪切模量;而对于高密度纤维网络,网络剪切模量会随着夹杂纤维数量增加呈现线性增加,即少量高刚度纤维的加入并不会引起网络剪切模量的显著增加。在此基础之上,Shahsavari等[16]深入探究了刚度增加的机制,他们发现高刚度纤维的加入会在原有刚度较低的网络中,形成一个椭圆形的仿射变形区域,当仿射变形区域联通后,混杂网络会出现明显的刚度增加现象。
目前混杂纤维网络的研究主要集中在网络的刚度,对于其强度和韧性的研究较少。尽管已有研究者针对柔软水凝胶网络的强度展开了研究[23-26],然而水凝胶网络中柔软基体的存在使得其失效机制与强度特点不同于常见的半柔软混杂纤维网络。因此,半柔软混杂纤维网络的失效问题仍有待深入研究。相关实验研究表明,混杂纤维网络强度随着纤维组分占比变化先升后降,存在强度峰值现象。例如,在芳纶纸中,保持纤维总体积含量不变,逐渐增加芳纶浆粕的占比,芳纶纸的强度先增大后减小[27-28]。然而,其中的力学机制尚不清楚,这种规律是否普遍存在于混杂纤维网络也有待研究。
为了揭示混杂纤维网络的失效机制,深入理解其强度存在峰值现象的原因,本文综合考虑纤维和纤维间连接的失效,系统地研究了混杂纤维网络的拉伸失效过程。通过典型拉伸失效过程分析发现了混杂纤维网络中连接失效和纤维失效的“竞争”机制,并系统讨论了纤维混杂比、纤维间连接强度和纤维总体积分数等材料微观结构参数对失效强度的影响,揭示了其强度存在峰值现象的原因,可用于指导纤维网络材料力学性能的进一步提升。
1. 模型
1.1 网络结构和参数
结合实际应用中混杂纤维网络的特点,本文建立了如图1(a)所示的二维混杂纤维网络代表性面积单元(Representative area element,RAE)。模型中包含两种不同类型的圆形截面纤维,一类是高强度高模量纤维,记作H纤维;另一类是低强度低模量纤维,记作L纤维。两类纤维的分布均采用均匀随机分布,每根纤维由中点坐标x0、y0和偏角θ确定,对于边长为Lx×Ly的长方形区域,分别在(0, Lx]、(0, Ly]和(0, π]范围按照均匀分布生成x0、y0和θ,若所生成的纤维落在长方形区域之外,则按照如图1(b)所示的方法进行平移,进而得到如图1(a)所示的周期性RAE。
![]() 图 1 混杂纤维网络模型:(a) 网络代表性面积单元(RAE)示意图;(b) 周期性代表单元建模过程示意图Figure 1. Hybrid fiber networks: (a) Representative area element (RAE) of fiber networks; (b) Schematic diagram of the modeling process of a periodic RAELx×Ly—Size of the representative area element; θ—Angle between the fiber and x-axis; A', B'—Corresponding point of A, B for the period boundray; A2, B2 and C2—Corresponding point of A1, B1 and C1
图 1 混杂纤维网络模型:(a) 网络代表性面积单元(RAE)示意图;(b) 周期性代表单元建模过程示意图Figure 1. Hybrid fiber networks: (a) Representative area element (RAE) of fiber networks; (b) Schematic diagram of the modeling process of a periodic RAELx×Ly—Size of the representative area element; θ—Angle between the fiber and x-axis; A', B'—Corresponding point of A, B for the period boundray; A2, B2 and C2—Corresponding point of A1, B1 and C1H纤维和L纤维的模量分别为EfH和EfL,长度分别为lfH和lfL,直径分别为dfH和dfL(dfH>dfL),长细比分别为λfH=lfH/dfH和λfL=lfL/dfL。在边长为Lx×Ly的纤维网络代表单元中,纤维总数为Ntotal,两类纤维的数量分别为NH和NL,需要注意的是,NH和NL是在对纤维进行平移前的两类纤维的数量。纤维相交处产生连接点,两类纤维产生三种类型的连接,分别记作HH连接、HL连接和LL连接,连接数分别为nHH、nHL和nLL,连接总数n=nHH + nHL + nLL。
为了方便后续分析,此处做如下约定:假定纤维网络RAE边长Lx=Ly=LE,对于由H和L两类纤维构成的混杂纤维网络,空间中纤维总体积分数Vf为
Vf = π (NHlfHd2fH+NLlfLd2fL)4L2EdfH (1) H纤维占比VfH定义为H纤维在所有纤维中占据的体积分数,即
VfH = VHVf = NHlfHd2fHNHlfHd2fH+NLlfLd2fL (2) 式中,VH为空间中H纤维的体积分数。同样地,L纤维占比VfL定义为L纤维在所有纤维中占据的体积分数,即
VfL = 1−VfH = NLlfLd2fLNHlfHd2fH+NLlfLd2fL (3) 低刚度低强度L纤维的长度和直径均小于H纤维,在纤维总体积分数保持不变时,增加L纤维体积占比,网络中纤维总数量会增加,连接总数量也会因此增大。
纤维网络材料作为结构材料使用时,纤维网络的密度通常较高,因此本文仅针对高密度混杂网络进行研究,即网络相对密度在弯-拉转变阈值以上,网络中的纤维处于拉压主导的变形状态。由文献[29-31]可知,网络处于弯-拉转变状态时,纤维总体积分数为26.6vol%。因此,在本文的研究中保持网络中Vf大于26.6vol%。
1.2 纤维及连接性能
(1) 纤维
为了避免复杂的材料本构关系给网络的损伤机制分析带来干扰,本文纤维材料使用弹脆性本构。在材料发生损伤之前,材料保持线弹性,弹性模量为Ef。纤维失效采用最大应力准则进行判断,纤维失效的临界条件为
|σ1|=σbf (4) 式中:σ1为纤维中的轴向应力;
σbf 为纤维材料的轴向失效应力,这里假设纤维材料的轴向拉压失效应力相同。达到失效应力后,纤维发生脆断,但在有限元模拟中为了保证模拟的稳定性,将纤维刚度折减为原刚度的0.5%,而后在应变较大时进一步将纤维刚度缓慢折减为0.01%。本研究中的混杂纤维网络由H纤维和L纤维两类纤维构成,表1为其相关模量、轴向拉压强度、长度和直径。
表 1 纤维的力学及几何参数Table 1. Mechanical and geometric parameters for fibersFiber type Modulus Ef/GPa Strengthσbf/MPa Length lf/mm Diameter df/μm H 134 3000 1.0 10.0 L 35 150 0.5 7.1 (2) 纤维间连接
基于纤维网络中连接的变形和失效机制[32],可以通过粘结区域模型模拟连接的整体力学行为[10, 13-14, 33],为了避免复杂的材料本构关系给网络的损伤机制分析带来干扰,纤维间连接也采用弹脆性本构,在连接发生失效之前,连接单元保持线弹性状态,刚度为kc,连接单元中的载荷Fc可写作
Fc=kcΔuc (5) 式中:
Δuc 为连接单元两节点的相对位移。连接的失效使用载荷失效准则[14],连接的等效载荷Fc达到连接单元的临界载荷Fbc 时,连接发生失效,即Fc=Fbc (6) 失效发生后,连接单元不能再承受载荷,在有限元分析中为了保证模拟的稳定性,将连接单元的刚度kc折减为原刚度的0.5%,为了避免大变形后损伤连接上产生较大的力,在载荷较大时进一步将连接刚度缓慢折减为0.01%。
通过试验方法精确测量连接强度非常困难,在已有文献[34-35]中,纤维连接强度的测试数据差异非常大,在1~60 mN间变化。本文的目标是研究混杂纤维网络的力学响应规律,不失一般性,首先基于可用的试验结果选择特定的一组纤维连接数据进行研究,而后在参数研究中讨论连接力学性能变化的影响。三种连接的刚度均取为8.7 N/m[36],HH连接的强度较小,设为1 mN;为简化分析,假设HL连接和LL连接的强度相等,均为4.8 mN(表2)。为了方便后续参数研究,此处定义无量纲连接强度
ˆFc 为纤维连接失效载荷Fbc 和L纤维单向拉伸失效载荷FbfL 的比值,即ˆFc = FbcFbfL=4Fbcπd2fLσbfL (7) 式中,
σbfL 为L纤维的失效应力。表 2 纤维间连接的本构和参数Table 2. Constitutive relations and the relative parameters for connections
Type Stiffness kc/(N·mm−1) Failure load Fbc/mN HH 8.7 1.0 HL 8.7 4.8 LL 8.7 4.8 Notes: Δuc—Relative displacement of two nodes of a connected element; Fb c-LL, Fb c-HL, Fbc-HH—Critical failure load of LL connection, HL connection and HH connection. 1.3 有限元模拟
有限元模型中,可以根据网络的疏密采用欧拉(Euler)梁或者铁摩辛柯(Timoshenko)梁对网络中的纤维进行模拟[37-40],本文研究高密度网络,使用两节点铁摩辛柯梁单元模拟[12]。纤维间连接的相互作用采用带有两个节点的连接单元(ABAQUS中的CONN2 D2)进行模拟[14, 41],忽略纤维间的扭转相互作用,假设纤维间的连接只能传递力,不能传递扭矩。
为研究网络在x方向单向拉伸时的力学响应,在胞元的边界上施加周期性边界条件(图1(a)),垂直于拉伸方向的两条平行边上的节点对A-A'控制方程为
ux=LE−ux=0=LEˉεxvx=LE−vx=0=0wx=LE−wx=0=0} (8) 平行于拉伸方向的两个边界上的节点对B-B'的位移控制方程为
uy=LE−uy=0=0vy=LE−vy=0=0wy=LE−wy=0=0} (9) 式中:u和v分别表示纤维网络中梁单元节点沿x方向和y方向的位移;w表示纤维网络中梁单元节点转角;LE为RAE的边长;
ˉεx 表示RAE在x方向施加的宏观应变。有限元模拟中,在参考点上施加的位移为LEˉεx 。模型尺寸收敛性验证表明,RAE的边长LE = 3lH时可以满足计算精度要求,与文献[33, 42]中的研究结果一致。本文中的模拟使用商业有限元软件ABAQUS开展分析,分析中考虑纤维和连接的损伤以及大转角,采用非线性方法进行分析。由于网络中纤维分布具有随机性,每组参数计算约30个模型,以消除随机性的影响。
为了使研究结果更具有一般性,采用无量纲量进行分析,纤维网络的无量纲平均应力
ˆσnet 定义为网络平均应力ˉσnet 和低刚度L纤维拉伸强度σbfL 的比值,即ˆσnet = ˉσnetσbfL = FxLEtnetσbfL (10) 网络的无量纲模量
ˆEnet 可以写为ˆEnet = ˆσnetˉεx = FxˉεxLEtnetσbfL (11) 式中:
ˉσnet 表示给定宏观应变ˉεx 下纤维网络的平均应力;Fx表示在纤维网络产生的宏观应变为ˉεx 时的外力;tnet=dH表示纤维网络的厚度;纤维网络的无量纲强度ˆSnet 定义为ˆSnet = Fxmax (12) 式中:
F_x^{\max } 表示纤维网络在加载过程中的最大载荷。网络的无量纲韧性{\hat T_{{\text{net}}}} 定义为{\hat T_{{\text{net}}}}{\text{ = }}\int {{{\hat \sigma }_{{\text{net}}}}} {\text{d}}{\bar \varepsilon _x} (13) 即无量纲应力在应变上的积分,在具体分析中当应力降至一定程度便认为彻底失效,其积分上限即为失效应变。
2. 失效过程分析
本节将结合典型算例研究纤维组分占比不同时混杂纤维网络的失效过程,以揭示混杂纤维网络的失效机制。本节选取的典型算例的参数如表1和表2所示,连接的无量纲强度由式(7)给出,HH连接无量纲强度
{\hat F_{{\text{c-HH}}}} = 0.17 ,LL连接及HL连接的无量纲强度{\hat F_{{\text{c-LL}}}} = {\hat F_{{\text{c-HL}}}} = 0.8 ;高刚度H纤维和低刚度L纤维为均匀随机分布,纤维总体积分数Vf=40vol%。图2(a)展示了Vf=40vol%的混杂纤维网络中不同低刚度L纤维占比对应的典型应力-应变曲线。对于低刚度L纤维体积占比VfL<15vol%的纤维网络,峰值应力后,网络应力迅速下降,表现出明显的脆性。对于低刚度L纤维体积占比VfL在15vol%和60vol%之间的混杂纤维网络,应力达到最大值后,应力-应变曲线缓慢下降,表现出明显的韧性失效特征。对于低刚度L纤维体积占比VfL超过60vol%的纤维网络,峰值应力后,网络应力迅速下降,表现出明显的脆性。低刚度L纤维体积占比VfL较低和较高的混杂纤维网络,与VfL=0vol%和VfL=100vol%的单一纤维网络一样,具有一定的脆性;而VfL在15vol%和60vol%之间的混杂纤维网络则具有明显的韧性;图2(b)也表明VfL在15vol%和60vol%之间的混杂纤维网络具有更高的韧性。下面将结合有限元结果详细分析不同纤维网络的损伤演化过程,揭示混杂纤维网络的失效机制。
![]() 图 2 纤维总体积分数Vf=40vol%时不同低刚度L纤维体积占比VfL对应的应力-应变曲线 (a) 和网络韧性随低刚度L纤维体积占比VfL的变化规律 (b)Figure 2. Stress-strain curves of networks with different volume fractions of the L fiber VfL (a) and toughness with variable volume fractions of the L fiber VfL for the networks (b) with the total fiber volume fraction Vf=40vol%
图 2 纤维总体积分数Vf=40vol%时不同低刚度L纤维体积占比VfL对应的应力-应变曲线 (a) 和网络韧性随低刚度L纤维体积占比VfL的变化规律 (b)Figure 2. Stress-strain curves of networks with different volume fractions of the L fiber VfL (a) and toughness with variable volume fractions of the L fiber VfL for the networks (b) with the total fiber volume fraction Vf=40vol%对于单一H纤维网络(VfL=0vol%),由于H纤维间HH连接强度较低,加载后连接很快发生失效,导致网络强度非常低。由于H纤维的强度较高,加载过程中仅会发生纤维间HH连接损伤和失效(图3(a)),网络应力达到最大值时,连接失效比例为0.95%,和文献[14]中的结果(0.5%)一样都是很小的值。对于只有连接失效的高密度网络,当很少的连接发生失效时,网络的应力便达到最大值,此后开始降低。这是由于网络密度较高时,在发生局部损伤之前连接的载荷分布相对均匀,一旦局部连接发生失效,周围的连接需要分担失效连接的载荷,很快便会达到连接强度,发生失效。因此,连接失效极易在失效区域附近扩展形成一条主裂纹(图3(c))。主裂纹的形成,会导致网络承载能力突然下降,整体网络表现为脆性失效。这与文献[14]中对于单一纤维网络的研究结果是一致的。
![]() 图 3 低刚度L纤维体积占比VfL=0vol%时纤维网络应力-应变曲线和损伤-应变曲线 (a)、网络应力
图 3 低刚度L纤维体积占比VfL=0vol%时纤维网络应力-应变曲线和损伤-应变曲线 (a)、网络应力{\sigma _{{\text{net}}}} = \sigma _{{\text{net}}}^{\max } (A点)时的损伤分布 (b) 和网络应力{\sigma _{{\text{net}}}}{\text{ = }}0.7\sigma _{{\text{net}}}^{{\text{max}}} (B点)时的损伤分布 (c)Figure 3. Stress-strain curve and damage fraction-strain curves (a), damage distributions when the stress of the network{\sigma _{{\text{net}}}} = \sigma _{{\text{net}}}^{\max } (point A) (b) and damage distributions when{\sigma _{{\text{net}}}}{\text{ = }}0.7\sigma _{{\text{net}}}^{{\text{max}}} (point B) (c) for the networks with the volume fraction of the L fiber VfL=0vol%图4(a)为低刚度L纤维体积占比VfL在15vol%和60vol%之间的混杂纤维网络加载过程中纤维和连接损伤变化。由于高刚度H纤维间HH连接强度较低,加载后HH连接首先发生失效。继续加载,HH连接失效数量快速增加,同时低刚度L纤维开始出现损伤和失效,随着HH连接和L纤维失效数量的增加,应力-应变曲线进入非线性阶段。尽管在局部HH连接发生失效后周边连接的载荷同样会快速增加,但是由于HL连接和LL连接的强度较高,不会迅速发生失效形成主裂纹,而是网络中的HH连接继续失效形成分散的损伤模式(图4(c))。分散的损伤会引起宏观应变的显著增加,从而减缓网络应力-应变曲线的下降。因此,网络整体表现出韧性失效特征。
![]() 图 4 低刚度L纤维体积占比VfL=40vol%时纤维网络应力-应变曲线和损伤-应变曲线 (a)、网络应力
图 4 低刚度L纤维体积占比VfL=40vol%时纤维网络应力-应变曲线和损伤-应变曲线 (a)、网络应力{\sigma _{{\text{net}}}} = \sigma _{{\text{net}}}^{\max } (A点)时损伤分布 (b) 及网络应力{\sigma _{{\text{net}}}}{\text{ = }}0.7\sigma _{{\text{net}}}^{{\text{max}}} (B点)时损伤分布 (c)Figure 4. Stress-strain curve and damage fraction-strain curves (a), damage distributions when the stress of the network{\sigma _{{\text{net}}}} = \sigma _{{\text{net}}}^{\max } (point A) (b) and damage distributions when{\sigma _{{\text{net}}}}{\text{ = }}0.7\sigma _{{\text{net}}}^{{\text{max}}} (point B) (c) for the networks with the volume fraction of the L fiber VfL=40vol%图5(a)为低刚度L纤维体积占比VfL=80vol%的混杂纤维网络中连接失效和纤维失效变化。最大应力对应的连接损伤比例约为0.16%,远小于单一H纤维网络(VfL=0vol%)对应的0.95%,由此可以推断VfL=80vol%的混杂纤维网络应力-应变曲线的失效并非由连接失效主导。此外,随着加载的继续,纤维失效比例的增速远大于总连接失效比例的增速,由此可以认为VfL=80vol%的混杂纤维网络的失效由纤维失效主导。低刚度L纤维体积占比VfL=100vol%的网络,在整个加载过程中,没有发生连接失效,纤维网络的失效完全由纤维失效主导。因此,可以认为当L纤维体积占比VfL≥80vol%时,网络的失效由纤维失效主导。对于纤维失效主导的高密度网络,和只有连接失效的网络相近,网络中纤维在失效前承载相对均匀,发生失效后,周边未失效纤维中的应力会快速增加,很快达到纤维的失效载荷而发生失效。因此,纤维失效极易在失效区域附近扩展形成主裂纹(图5(c))。主裂纹的形成会导致网络承载能力突然下降,发生脆性失效。
![]() 图 5 低刚度L纤维体积占比VfL=80vol%时纤维网络应力-应变曲线和损伤-应变曲线 (a)、网络应力
图 5 低刚度L纤维体积占比VfL=80vol%时纤维网络应力-应变曲线和损伤-应变曲线 (a)、网络应力{\sigma _{{\text{net}}}} = \sigma _{{\text{net}}}^{\max } (A点)时损伤分布 (b) 和网络应力{\sigma _{{\text{net}}}}{\text{ = }}0.7\sigma _{{\text{net}}}^{{\text{max}}} (B点)时损伤分布 (c)Figure 5. Stress-strain curve and damage fraction-strain curves (a), damage distributions when the stress of the network{\sigma _{{\text{net}}}} = \sigma _{{\text{net}}}^{\max } (point A) (b) and damage distributions when{\sigma _{{\text{net}}}}{\text{ = }}0.7\sigma _{{\text{net}}}^{{\text{max}}} (point B) (c) for the networks with the volume fraction of the L fiber VfL=80vol%综上所述,Vf=40vol%的纤维网络中,对于连接失效主导的网络(0vol%≤VfL<15vol%)或纤维失效主导的网络(60vol%<VfL≤100vol%),在单向拉伸载荷作用下,只要很少的连接或纤维发生失效,网络的应力即达到最大值,随着加载位移增加,网络中纤维或连接的失效沿着先前的失效区域扩展,形成主裂纹,导致网络应力快速下降,纤维网络表现出脆性失效。对于连接失效和纤维失效共同作用的混杂纤维网络(15vol%≤VfL≤60vol%),应力达到最大值后,继续增加位移,由于纤维及纤维间HL连接和LL连接强度较高,网络在强度较低的连接(HH连接)失效后周边的纤维和连接可以承担相应的载荷而不发生失效,峰值应力后,混杂网络中的失效呈现分散的分布形式,没有主裂纹的形成,使网络中应力缓慢下降,网络表现出韧性失效。
3. 影响参数讨论
本节将首先保持Vf不变,讨论混杂纤维比例和纤维间连接强度对网络整体力学性能的影响,而后研究Vf的影响。
3.1 混杂比例的影响
本节主要研究混杂纤维网络的刚度和强度随纤维组分的变化规律,纤维网络中连接强度参数与第2节相同。
图6(a)为混杂纤维网络的弹性模量随低刚度L纤维体积占比的变化。随着低刚度L纤维体积占比的增加,弹性模量不断下降,且与L纤维的体积含量呈现线性关系,这和Bai等[22]的研究是一致的。对于混杂纤维网络,弹性模量可以用混合率公式进行预测。
{E_{{\rm{net}}}}{\rm{ = }}{V_{{\rm{fH}}}}{E_{{\rm{net - H}}}} + {V_{{\rm{fL}}}}{E_{{\rm{net - L}}}} (14) 式中:
{E_{{\rm{net - H}}}} 和{E_{{\rm{net - L}}}} 分别表示纤维总体积分数为Vf时高刚度H纤维和低刚度L纤维构成的单一纤维网络的弹性模量。图6(b)为混杂纤维网络强度随低刚度L纤维体积占比的变化。随着低刚度L纤维体积占比VfL的增大,强度先增加后下降,无法使用混合率公式进行估算。在低刚度L纤维体积占比VfL为40vol%左右时,混杂纤维网络的强度最高。由此可见,不同纤维构成的混杂纤维网络,可以通过纤维体积占比的设计使其强度高于相应的单一纤维网络强度,这一现象与柔软的双网络水凝胶表现出的现象类似[24, 43]。
混杂纤维网络强度的先升后降与其失效机制密切相关。根据第2节的分析,不同L纤维占比的混杂纤维网络对应的失效机制和失效模式也不同。对于L纤维占比适中的混杂纤维网络(15vol%≤VfL≤60vol%),网络失效由HH连接失效和L纤维失效共同主导。在保持纤维总体积不变的情况下,增加L纤维体积占比,HL连接和LL连接的数量会增多,这两种连接的强度高于HH连接,因此在VfL≤60vol%时,增加L纤维意味着增加强连接,网络整体强度随L纤维占比的增加呈现明显的上升趋势。对于VfL>60vol%的混杂纤维网络,失效是由L纤维失效主导的,此时高强度的H纤维可以看作是L纤维网络的增强相,因此随着L纤维体积占比的增加,增强相体积含量降低,承载能力下降,网络强度呈现降低趋势。
综上所述,混杂纤维网络强度随L纤维体积占比增加出现先升后降现象的原因在于失效机制的转变,在L纤维体积占比较低时,混杂纤维网络的失效由连接失效和L纤维失效共同主导,此时连接是影响网络强度“短板”,增加L纤维体积占比意味着增加强连接;当L纤维体积占比较高时,网络失效由L纤维失效主导,此时高强度H纤维充当增强相,增加L纤维体积占比意味着减少增强相。增加强连接和减少增强相两种机制的竞争,使混杂纤维网络强度随L纤维体积占比增加呈现出了先升后降的现象。因此,可以通过设计混杂网络中不同纤维的占比来达到网络强度的最优。
3.2 连接强度的影响
在上述分析中,HL连接强度
F_{{\rm{c-HL}}}^{\rm{b}} 和LL连接强度F_{{\text{c-LL}}}^{\rm{b}} 高于HH连接强度F_{{\text{c-HH}}}^{\rm{b}} ,这一设定是否会影响强度的变化趋势?换言之,前文分析得到的强度先升后降现象是否普遍存在于所有纤维网络?本节将对这一问题予以讨论分析。为了便于分析,本节保持HH连接强度F_{{\text{c-HH}}}^{\rm{b}} 不变,改变HL连接和LL连接的强度(F_{{\text{c-LL}}}^{\rm{b}}{\rm{ = }}F_{{\text{c-HL}}}^{\rm{b}} )分析网络强度的变化规律。图7给出了不同LL连接无量纲强度
{\hat F_{{\text{c-LL}}}} 对应的混杂纤维网络强度随L纤维体积占比VfL的变化规律。可以看出,{\hat F_{{\text{c-LL}}}} 增大时,混杂纤维网络的强度会出现明显增加;{\hat F_{{\text{c-LL}}}} 不同时,随着L纤维体积占比VfL增加,混杂纤维网络的强度变化规律会发生变化。![]() 图 7 混杂纤维网络中LL连接强度变化时网络强度随低刚度L纤维体积占比VfL的变化规律(纤维总体积分数Vf=40vol%)Figure 7. Strength of networks with variable strength of the LL connection and variable volume fractions of the L fiber (Total fiber volume fraction Vf=40vol%){\hat F_{{\text{c-HL}}}} —Dimensionless strength of HH connection; {\hat F_{{\text{c-HH}}}} —Dimensionless strength of LL connection
图 7 混杂纤维网络中LL连接强度变化时网络强度随低刚度L纤维体积占比VfL的变化规律(纤维总体积分数Vf=40vol%)Figure 7. Strength of networks with variable strength of the LL connection and variable volume fractions of the L fiber (Total fiber volume fraction Vf=40vol%){\hat F_{{\text{c-HL}}}} —Dimensionless strength of HH connection; {\hat F_{{\text{c-HH}}}} —Dimensionless strength of LL connection当强连接的强度很弱时,即
{\hat F_{{\text{c-HL}}}} ={\hat F_{{\rm{c-LL}}}} ≈{\hat F_{{\text{c-HH}}}} =0.17,随着L纤维体积占比VfL的增大,网络的强度不断增加。这是由于所有连接的强度都比较低,对于任意的L纤维体积占比VfL,网络的失效均由纤维间的连接失效主导(图8(a)和图8(b))。由于模型中单根L纤维的体积较小,在保持纤维总体积分数不变的前提下增加L纤维体积占比实质上增加了总纤维数量,也相应地增加了网络中的总连接数量。因此,随着L纤维体积占比VfL的增大,网络的强度不断增加。![]() 图 8 纤维总体积分数Vf=40vol%时不同无量纲强度
图 8 纤维总体积分数Vf=40vol%时不同无量纲强度{\hat F_{{\rm{c - LL}}}} 及L纤维体积占比VfL下纤维网络应力-应变曲线和损伤-应变曲线:(a){\hat F_{{\rm{c - LL}}}} = 0.17 ,VfL=20vol%;(b){\hat F_{{\rm{c - LL}}}} = 0.17 ,VfL =100vol%;(c){\hat F_{{\rm{c - LL}}}} = 0.3 ,VfL =20vol%;(d){\hat F_{{\rm{c - LL}}}} = 0.3 ,VfL =40vol%Figure 8. Stress-strain curves and damage fraction-strain curves of fiber networks with variable dimensionless connection strength{\hat F_{{\rm{c - LL}}}} and volume fractions of the L fiber VfL for the total fiber volume fraction Vf=40vol%: (a){\hat F_{{\rm{c - LL}}}} = 0.17 , VfL=20vol%; (b){\hat F_{{\rm{c - LL}}}} = 0.17 , VfL=100vol%; (c){\hat F_{{\rm{c - LL}}}} = 0.3 , VfL=20vol%; (d){\hat F_{{\rm{c - LL}}}} = 0.3 , VfL=40vol%当强连接的强度比弱连接略高时,例如,
{\hat F_{{\text{c-LL}}}} = 0.3 ,随着L纤维体积占比VfL的增大,网络的强度最初几乎线性增加,之后逐步变得平缓(图7)。这是由于网络尽管与3.1节讨论的情况类似,连接失效和纤维失效两种模式处于“竞争”的态势,随着VfL的增加,网络中纤维失效的影响越来越大,削弱了连接数量增加对于强度的提升作用,导致网络强度的增势逐渐趋缓。但由于强连接不够强,连接失效的作用始终较纤维失效更显著(图8(c)和图8(d)),导致纤维失效对强度的削弱不足以引起整体网络强度的下降。3.3 纤维总体积分数Vf 的影响
为研究Vf不同时,混杂网络刚度和强度随L纤维体积占比VfL的变化规律,本节取Vf分别为30vol%、40vol%和50vol%,网络中连接和纤维参数与3.1节相同。
图9展示了不同Vf时的纤维网络模量和强度随L纤维体积占比的变化。可以看出,Vf增大时,由于网络中可以承载的纤维和连接数量均会明显增加,网络的模量和强度均会明显增大。若Vf一定,随着低刚度L纤维体积占比VfL的增加,混杂网络的模量线性下降,满足式(14)所示的混合率;对于不同Vf的网络,都存在网络强度随着低刚度L纤维体积占比VfL的增加而先增加后下降的现象。
图10为Vf从30vol%至50vol%变化时单一纤维网络和混杂纤维网络的模量-强度可设计空间和强度-韧性可设计空间。可以看出,对于单一纤维网络,网络的模量和强度的可设计空间在两个实线线段上,而对于含有两类纤维的混杂纤维网络,网络模量和强度的可设计空间可达到红色区域(图10(a));同样,在强度-韧度空间中,混杂纤维网络能够达到的空间也远大于单一纤维网络(图10(b))。可见,不同纤维混合而成的混杂纤维网络,展现出了单一纤维网络并不具备的力学性能,大大拓展了纤维网络的可设计空间。在实际应用中,可以通过改变网络中不同纤维的含量,满足不同的使用要求。
![]() 图 10 纤维总体积分数Vf从30vol%至50vol%变化时单一纤维网络和混杂纤维网络的模量-强度可设计空间 (a) 和强度-韧性可设计空间 (b) (区域边界由线性插值获得)Figure 10. Modulus-strength phase diagram (a) and strength-toughness phase diagram of networks (b) for the fiber networks with the total fiber volume fraction Vf changing from 30vol% to 50vol% (Region boundary is obtained by linear interpolation)
图 10 纤维总体积分数Vf从30vol%至50vol%变化时单一纤维网络和混杂纤维网络的模量-强度可设计空间 (a) 和强度-韧性可设计空间 (b) (区域边界由线性插值获得)Figure 10. Modulus-strength phase diagram (a) and strength-toughness phase diagram of networks (b) for the fiber networks with the total fiber volume fraction Vf changing from 30vol% to 50vol% (Region boundary is obtained by linear interpolation)4. 结 论
建立了同时考虑纤维失效和多种连接失效的混杂纤维网络模型,分析了混杂纤维网络的损伤失效过程,揭示了试验中发现的混杂纤维网络强度随纤维组分变化出现先升后降现象的原因,同时研究了连接强度变化和纤维总体积分数对混杂纤维网络的力学性能的影响。可以得出如下结论:
(1) 混杂纤维网络具有单一纤维网络不具备的良好韧性。对于只有连接失效的网络或纤维失效主导的网络,网络中纤维或连接的失效沿着初始失效区域扩展,形成一条主裂纹,导致网络应力快速下降,纤维网络表现出一定的脆性特征。对于连接失效和纤维失效共同作用的混杂纤维网络,由于纤维及强度较高的纤维间连接能够有效承担失效区域释放的载荷而不会快速失效形成主裂纹,此时网络中低强度连接逐渐失效,呈现出分散分布的形式,使网络中应力缓慢下降,表现出韧性特征;
(2) 混杂纤维网络强度随低强度低模量纤维(L纤维)体积占比增加出现先升后降现象的原因在于失效机制的转变。在L纤维体积占比较低时,失效由连接失效和L纤维失效共同主导,此时连接属于“短板”,增加L纤维体积占比意味着增加强连接;当L纤维体积占比较高时,失效由L纤维失效主导,此时可将高强度高模量纤维(H纤维)看作增强相,增加L纤维体积占比意味着减少增强相。增加强连接和减少增强相两种机制的竞争,使混杂纤维网络强度随L纤维体积占比增加而出现先升后降现象;
(3) 相比于单一纤维构成的网络,混杂纤维网络的强度和韧性更高,性能区间更广。在实际应用中,通过改变网络中不同纤维的含量和引入不同强度的连接,可以大大拓展纤维网络的可设计空间,满足不同的使用要求。
-
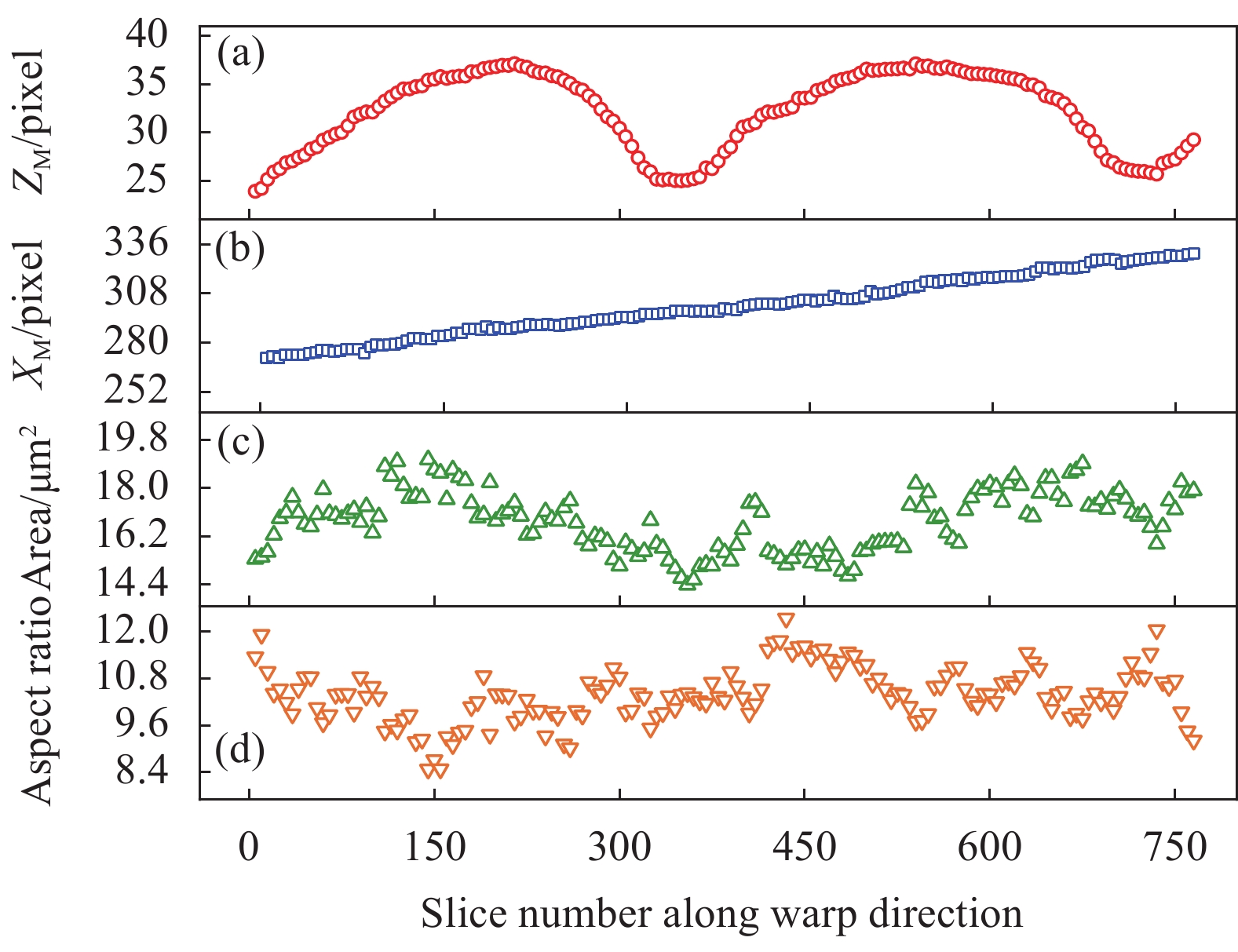
图 14 五枚缎纹织物经向纤维束结构特征:(a) 面内波动参数变化;(b) 面外波动参数变化;(c) 面积变化;(d) 长宽比变化
Figure 14. Structural characteristics of warp yarns of 5-harness satin woven fabric: (a) Variation of in-plane fluctuation parameter; (b) Variation of out-of-plane fluctuation parameter; (c) Changes in area; (d) Changes in aspect ratio
表 1 五枚缎纹织物细观几何参数
Table 1 Geometry parameters of the 5-harness satin woven fabric
Parameter Average/μm Coefficient of variation/% Weft Width 1157±41 2.8 Height 164±13 5.5 Warp Width 1520±31 1.0 Height 144±9 3.7 Fiber diameter 7.0±1.4 7.3 表 2 不同分辨率下五枚缎纹织物厚度方向渗透率计算结果
Table 2 Through-thickness permeability of 5-harness satin woven fabric calculated at different resolutions
Resolution/μm 45 40 35 30 25 20 15 10 Number of voxels 436020 633650 935220 1464870 2539008 5069200 11010285 39603600 KZ/10−12 m2 2.16 1.48 2.36 1.64 1.71 1.74 1.71 1.73 CPU time/min <10 <10 <10 12 14 26 47 75 Notes: KZ—Permeability of 5-harness satin woven fabric in thickness direction; CPU—Central processing unit. 表 3 实验测得的五枚缎纹织物KZ值
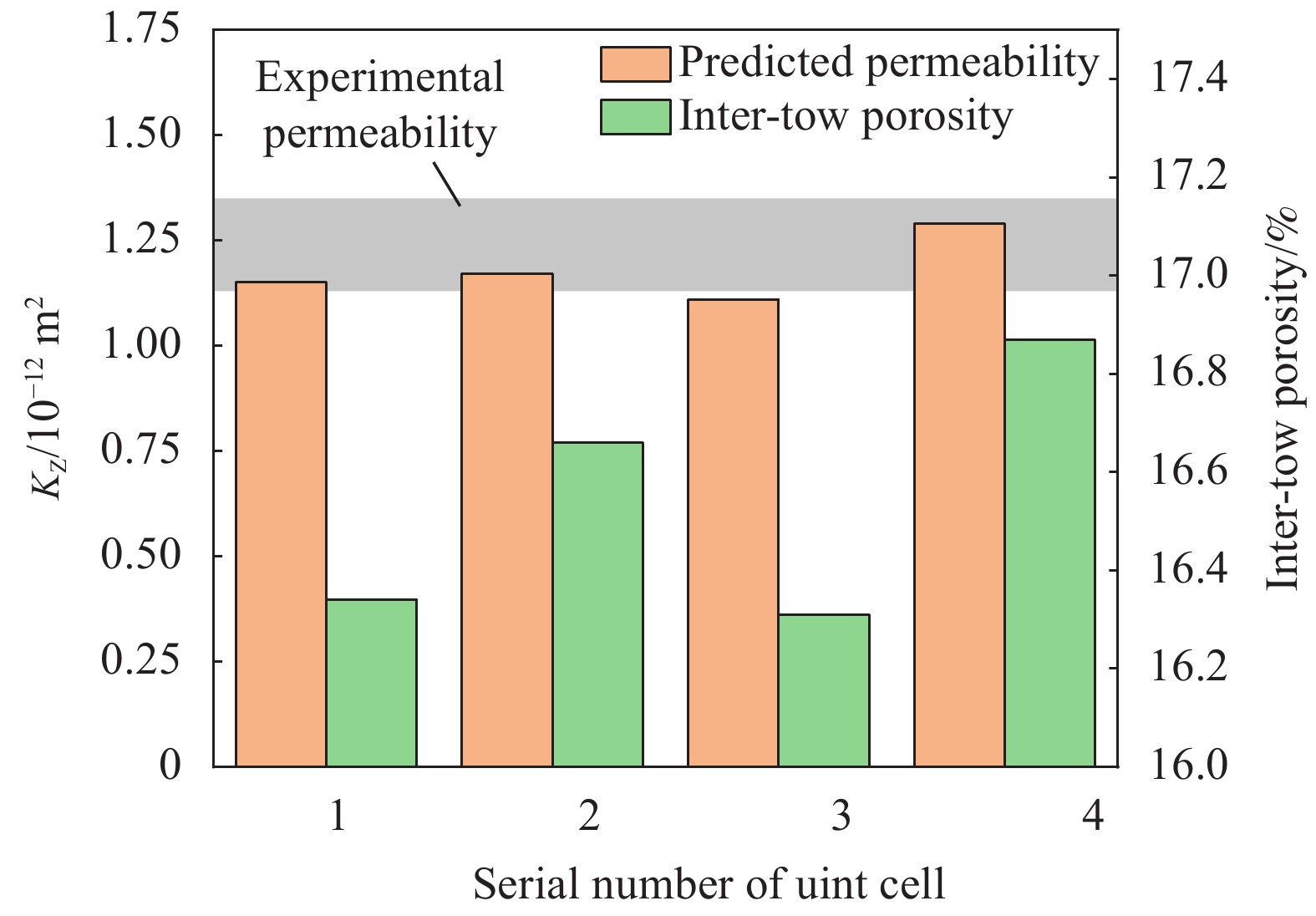
Table 3 KZ values measured by experiment of 5-harness satin woven fabric
Number Permeability/10−12 m2 1 1.35 2 1.32 3 1.28 4 1.17 5 1.13 Average/10−12 m2 1.25 Coefficient of variation/% 7.65 -
[1] KONSTANTOPOULOS S, HUEBER C, ANTONIADIS I, et al. Liquid composite molding reproducibility in real-world production of fiber reinforced polymeric composites: A review of challenges and solutions[J]. Advanced Manufacturing: Polymer & Composites Science,2019,5(3):85-99.
[2] 杨旭静, 王跃飞, 韦凯, 等. 基于孔隙控制的车身结构树脂传递模塑成型工艺设计[J]. 复合材料学报, 2017, 34(5):970-977. YANG Xujing, WANG Yuefei, WEI Kai, et al. Design of resin transfer molding process for vehicle body structure based on porosity control[J]. Acta Materiae Compositae Sinica,2017,34(5):970-977(in Chinese).
[3] 马彦旭, 王继辉, 倪爱清, 等. 大厚度复合材料曲面典型构件的工艺优化[J]. 复合材料学报, 2021, 38(10):3302-3313. MA Yanxu, WANG Jihui, NI Aiqing, et al. Process optimization of typical composite cambered components with large thickness[J]. Acta Materiae Compositae Sinica,2021,38(10):3302-3313(in Chinese).
[4] 李嘉禄, 吴晓青, 冯驰. RTM中纤维渗透率预测的研究进展[J]. 复合材料学报, 2006, 23(6):1-8. DOI: 10.3321/j.issn:1000-3851.2006.06.001 LI Jialu, WU Xiaoqing, FENG Chi. Research progress on the permeability prediction of f iber in RTM[J]. Acta Materiae Compositae Sinica,2006,23(6):1-8(in Chinese). DOI: 10.3321/j.issn:1000-3851.2006.06.001
[5] 詹明樊, 王继辉, 倪爱清, 等. 基于数字图像技术的纤维织物面内渗透率表征[J]. 复合材料学报, 2021, 38(12):4180-4189. ZHAN Mingfan, WANG Jihui, NI Aiqing, et al. In-plane permeability characterization of fiber fabric based on digital image technology[J]. Acta Materiae Compositae Sinica,2021,38(12):4180-4189(in Chinese).
[6] 李香林, 王继辉, 倪爱清, 等. 液体模塑成型工艺用纤维织物厚度方向饱和渗透率的预测模型[J]. 复合材料学报, 2019, 36(6):1428-1437. LI Xianglin, WANG Jihui, NI Aiqing, et al. Prediction model of through-thickness saturated permeability of fabric for liquid composite molding[J]. Acta Materiae Compositae Sinica,2019,36(6):1428-1437(in Chinese).
[7] HUANG W, CAUSSE P, HU H, et al. Numerical and experimental investigation of saturated transverse permeability of 2D woven glass fabrics based on material twins[J]. Polymer Composites,2020,41(4):1341-1355. DOI: 10.1002/pc.25458
[8] 张浩, 李书欣, 王继辉, 等. 基于新型测试装置的网孔板层开孔率对纤维厚度方向渗透率的影响[J]. 复合材料学报, 2020, 37(5):1175-1183. ZHANG Hao, LI Shuxin, WANG Jihui, et al. Influence of ratio of hole area for mesh plate layer on through-thickness permeability based on a new designed test bench[J]. Acta Materiae Compositae Sinica,2020,37(5):1175-1183(in Chinese).
[9] VERNET N, RUIZ E, ADVANI S, et al. Experimental determination of the permeability of engineering textiles: Benchmark II[J]. Composites Part A: Applied Science and Manufacturing,2014,61:172-184. DOI: 10.1016/j.compositesa.2014.02.010
[10] YONG A, AKTAS A, MAY D, et al. Out-of-plane permeability measurement for reinforcement textiles: A benchmark exercise[J]. Composites Part A: Applied Science and Manufacturing,2021,148(1):106480.
[11] YANG B, HUANG W, CAUSSE P, et al. On the design of test molds based on unidirectional saturated flows to measure transverse permeability in liquid composite molding[J]. Polymer Composites,2022,43(4):2234-2251. DOI: 10.1002/pc.26536
[12] 李永静, 晏石林, 李德权, 等. 液体模塑成型工艺中纤维束横向渗透率的细观数值模拟[J]. 纺织学报, 2015, 36(8):22-27. LI Yongjing, YAN Shilin, LI Dequan, et al. Microscopic numerical simulation of transverse permeability of fiber bundles in liquid composite molding[J]. Journal of Textile Research,2015,36(8):22-27(in Chinese).
[13] 倪爱清, 王继辉, 朱以文. 复合材料液体模塑成型工艺中预成型体渗透率张量的数值预测[J]. 复合材料学报, 2007, 24(6):50-56. DOI: 10.3321/j.issn:1000-3851.2007.06.009 NI Aiqing, WANG Jihui, ZHU Yiwen. Numerical prediction of saturated permeability tensor of a woven fabric for use in the fluid simulation of liquid composite molding[J]. Acta Materiae Compositae Sinica,2007,24(6):50-56(in Chinese). DOI: 10.3321/j.issn:1000-3851.2007.06.009
[14] CHEN Z R, YE L, LU M. Permeability predictions for woven fabric preforms[J]. Journal of Composite Materials,2010,44(13):1569-1586. DOI: 10.1177/0021998309355888
[15] ZENG X, ENDRUWEIT A, BROWN L P, et al. Numerical prediction of in-plane permeability for multilayer woven fabrics with manufacture-induced deformation[J]. Composites Part A: Applied Science and Manufacturing,2015,77:266-274. DOI: 10.1016/j.compositesa.2015.03.027
[16] 金天国, 魏雅君, 杨波, 等. 预成型体渗透率预测及其受压缩变形的影响[J]. 复合材料学报, 2015, 32(3):840-847. JIN Tianguo, WEI Yajun, YANG Bo, et al. Permeability prediction of preform and influence of compression deformation[J]. Acta Materiae Compositae Sinica,2015,32(3):840-847(in Chinese).
[17] 张璇, 白国娟, 王星星, 等. 三维织物厚度方向渗透率研究[J]. 中国胶粘剂, 2017, 26(5):21-24. ZHANG Xuan, BAI Guojuan, WANG Xingxing, et al. Study on the thickness-permeability of three-dimensional fabric[J]. China Adhesives,2017,26(5):21-24(in Chinese).
[18] YOUSAF Z, POTLURI P, WITHERS P J, et al. Digital element simulation of aligned tows during compaction validated by computed tomography (CT)[J]. International Journal of Solids and Structures,2018,154:78-87. DOI: 10.1016/j.ijsolstr.2017.05.044
[19] ALI M A, UMER R, KHAN K A, et al. In-plane virtual permeability characterization of 3 D woven fabrics using a hybrid experimental and numerical approach[J]. Composites Science and Technology,2019,173:99-109. DOI: 10.1016/j.compscitech.2019.01.030
[20] STRAUMIT I, HAHN C, WINTERSTEIN E, et al. Computation of permeability of a non-crimp carbon textile reinforcement based on X-ray computed tomography images[J]. Composites Part A: Applied Science and Manufacturing,2016,81:289-295. DOI: 10.1016/j.compositesa.2015.11.025
[21] 王法琪 严亚波, 温鑫鑫, 等. Micro-CT分辨率对松质骨微观结构及生物力学测量的影响[J]. 现代生物医学进展, 2015, 15(10):1877-1880,1835. WANG Faqi, YAN Yabo, WEN Xinxin, et al. The effect of micro-CT resolution on measuring microstructure and mechanical parameters of human lumbar vertebral trabecular bone[J]. Progress in Modern Biomedicine,2015,15(10):1877-1880,1835(in Chinese).
[22] 耿冲, 杨永飞, 高莹. 不同分辨率岩石CT图像的优化处理方法[J]. 科学技术与工程, 2014, 14(2):1-4. DOI: 10.3969/j.issn.1671-1815.2014.02.001 GENG Chong, YANG Yongfei, GAO Ying. Optimization of image processing method based on rock CT images of different resolutions[J]. Science Technology and Engineering,2014,14(2):1-4(in Chinese). DOI: 10.3969/j.issn.1671-1815.2014.02.001
[23] ALI M A, UMER R, KHAN K A. A virtual permeability measurement framework for fiber reinforcements using micro CT generated digital twins[J]. International Journal of Lightweight Materials and Manufacture,2020,3(3):204-216. DOI: 10.1016/j.ijlmm.2019.12.002
[24] 王晨晨, 姚军, 杨永飞, 等. 基于CT扫描法构建数字岩心的分辨率选取研究[J]. 科学技术与工程, 2013, 13(4):1050-1052. WANG Chenchen, YAO Jun, YANG Yongfei, et al. Study of resolution selection for construction of digtal rock with CT scanning method[J]. Science Technology and Engineering,2013,13(4):1050-1052(in Chinese).
[25] RATHORE J S, VIENNE C, QUINSAT Y, et al. Influence of resolution on the X-ray CT-based measurements of metallic AM lattice structures[J]. Welding in the World,2020,64(8):1367-1376. DOI: 10.1007/s40194-020-00920-4
[26] BIGGEMANN J, KLLNER D, SCHATZ J, et al. Influence of CT scanning resolution and volume on FEM-simulation of periodic 3D-printed porous ceramics[J]. Materials Letters,2021,303:130529.
[27] 杨斌. 复合材料用纤维织物压缩与渗流性能表征方法研究[D]. 武汉: 武汉理工大学, 2018. YANG Bin. Research on compressibility and seepage property characterization methods of preform for FRP[D]. Wuhan: Wuhan University of Technology, 2018(in Chinese).
[28] ZENG X, BROWN L P, ENDRUWEIT A, et al. Geometrical modelling of 3D woven reinforcements for polymer composites: Prediction of fabric permeability and composite mechanical properties[J]. Composites Part A: Applied Science and Manufacturing,2014,56(1):150-160.
[29] 王浩. 平纹织物复合材料微观结构特征对材料弹性常数的影响研究[D]. 长沙: 国防科学技术大学, 2016. WANG Hao. Effects of microstructure characteristics on elastic properties of plain-weave composites[D]. Changsha: National University of Defense Technology, 2016(in Chinese).
[30] RAJAB M A, GEORGE L E. Stamps extraction using local adaptive k-means and ISODATA algorithms[J]. Indonesian Journal of Electrical Engineering and Computer Science,2021,21(1):137-145. DOI: 10.11591/ijeecs.v21.i1.pp137-145
[31] TAHIR M W, HALLSTR M S, KERMO M. Effect of dual scale porosity on the overall permeability of fibrous structures[J]. Composites Science & Technology,2014,103:56-62.
-
期刊类型引用(15)
1. 吕晋书,马玉钦,庞利沙,王浩,张育洋,许怡,虢海银. 基于ANSYS的多尺度GO-CF/EP复合材料弯曲性能仿真及试验验证. 复旦学报(自然科学版). 2024(04): 481-491 .  百度学术
百度学术
2. 李臻,贾紫茹,程嘉瑞. 功能化环氧树脂涂层的研究进展. 石油化工腐蚀与防护. 2022(01): 24-27 .  百度学术
百度学术
3. 陈官,马传国,付泽浩,王静,王亚珍. 磁场作用下氧化石墨烯包覆羟基氧化铁增强碳纤维/环氧树脂复合材料的层间断裂韧性. 航空材料学报. 2022(03): 89-96 .  百度学术
百度学术
4. 刘文军,严建龙,周川,李伟东,周玉敬,邱虹,白华,胡晓兰. 氧化石墨烯改性碳纤维/环氧树脂复合材料的湿热性能及微观形貌. 复合材料学报. 2021(05): 1416-1425 .  本站查看
本站查看
5. 刘义,李树锋,张策,闫民杰,孙颖颖. 碳纳米管对碳纤维复合材料防辐射性能的影响. 天津纺织科技. 2021(04): 40-43 .  百度学术
百度学术
6. 刘刚,欧宝立,赵欣欣,彭彩茹,汪雨微. 共价功能化石墨烯超疏水防腐复合涂层材料的制备. 复合材料学报. 2021(10): 3236-3246 .  本站查看
本站查看
7. 罗佳妮,李丽君,张晓思,邹汉涛,刘雪婷. 氧化石墨烯掺杂TiO_2改性活性炭纤维. 纺织学报. 2020(01): 8-14 .  百度学术
百度学术
8. 刘桂艳. 氧化石墨烯/环氧树脂复合材料特性研究. 塑料科技. 2020(04): 10-13 .  百度学术
百度学术
9. 段雯雯,王建军,辛振祥,王洪振. 环氧化天然橡胶改性石墨烯-炭黑/天然橡胶复合材料的制备及性能. 复合材料学报. 2020(07): 1667-1674 .  本站查看
本站查看
10. 刘新,陈铎,何辉永,孙涛,武湛君. 热塑性颗粒-无机粒子协同增韧碳纤维增强环氧树脂复合材料. 复合材料学报. 2020(08): 1904-1910 .  本站查看
本站查看
11. 段瑛涛,武肖鹏,王智文,敬敏,栗娜,刘强,宁慧铭,胡宁. 碳纤维增强树脂复合材料-热成型钢超混杂层合板层间力学性能. 复合材料学报. 2020(10): 2418-2427 .  本站查看
本站查看
12. 任志东,郝思嘉,邢悦,杨程,戴圣龙. 氧化石墨烯改性环氧树脂及其复合材料的性能. 航空材料学报. 2019(02): 25-32 .  百度学术
百度学术
13. 李欣儒,郑力军,石华强,吴彦飞. P(AA-AM)复合石墨烯凝胶暂堵剂的研制及性能评价. 应用化工. 2019(08): 1805-1808 .  百度学术
百度学术
14. 姜浩田,鞠艾洵,肖润平,王博,王欣,于显利. 氧化石墨烯/碳纤维复合材料的制备及表征. 安全与电磁兼容. 2019(04): 58-61 .  百度学术
百度学术
15. 张策,徐志伟,郭兴峰. 基于微波等离子体方法生长的纳米碳对碳纤维/环氧树脂复合材料界面性能的影响. 复合材料学报. 2018(11): 2994-3000 .  本站查看
本站查看
其他类型引用(12)
-





 下载:
下载: