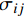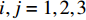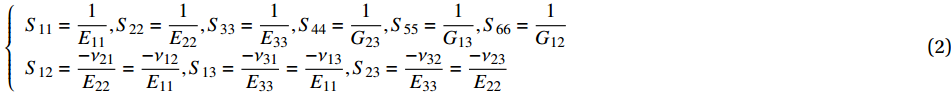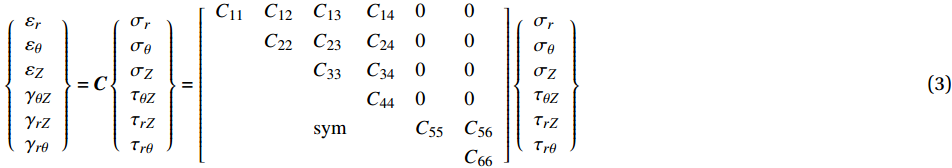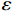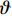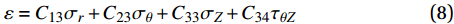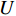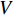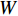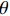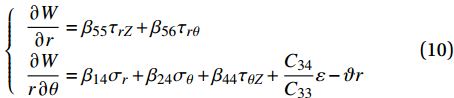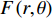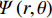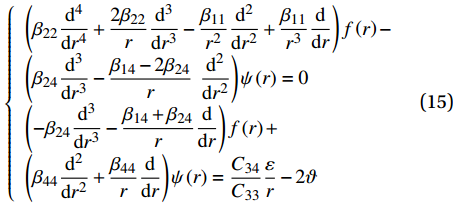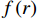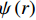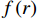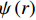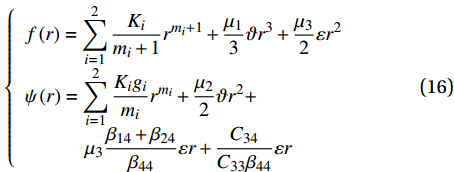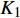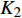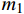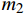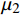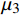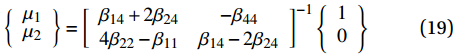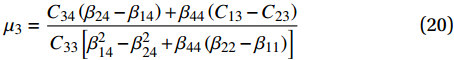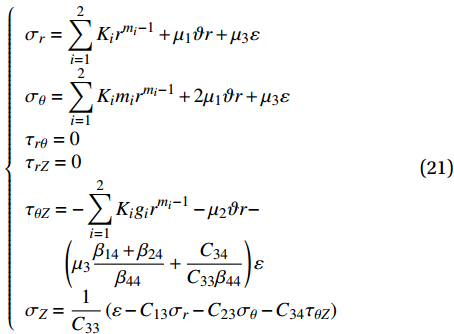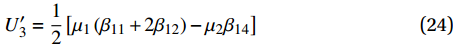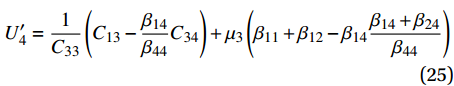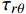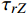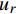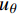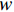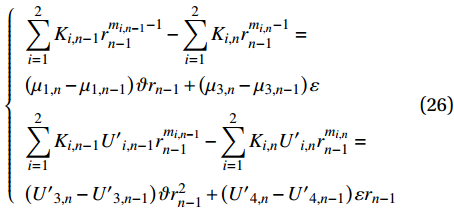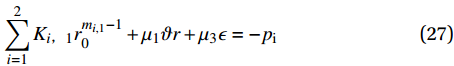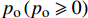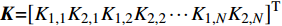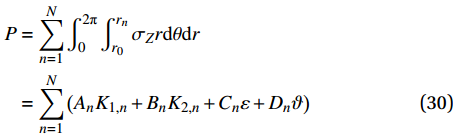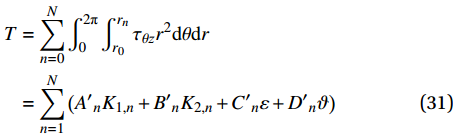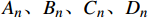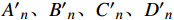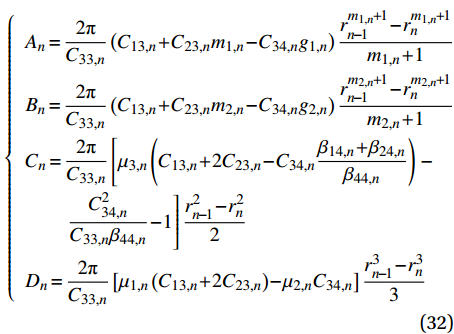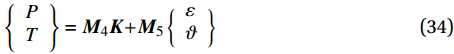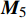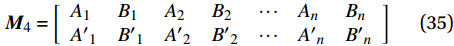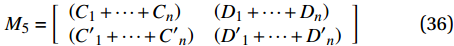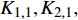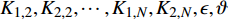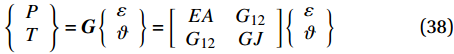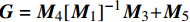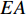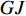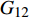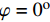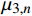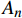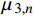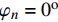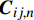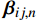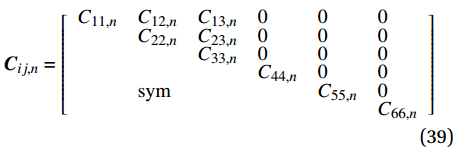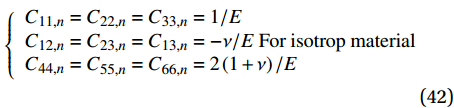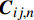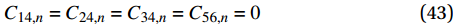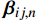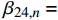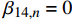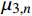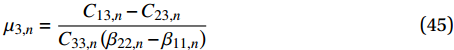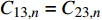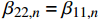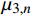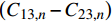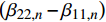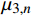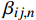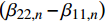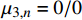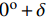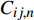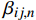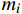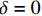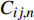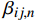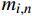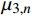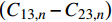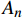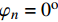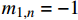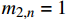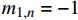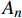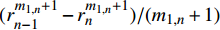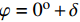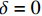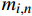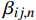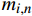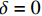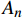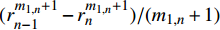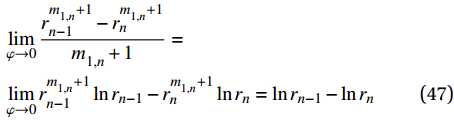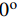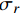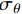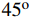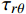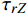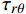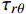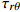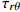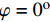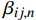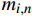A method to analyze the axially symmetric problem of composite thick tubes with arbitrary angles
-
摘要: 提出了一种任意角度复合材料厚壁管的轴对称问题的分析方法。传统的Lekhnitskii理论能够获得普通缠绕层复合材料厚壁管的精确弹性解,但是,当厚壁管内存在0°缠绕层或者各项同性材料层时,该两种特殊层都会出现奇异参数,从而导致特殊层与普通层界面的连续性条件不能被满足。因此,讨论了特殊层存在奇异参数的原因,并对这类参数进行连续性分析和极限计算,从而解决了参数奇异的问题,使Lekhnitskii理论的应用范围扩展到任意缠绕角的复合材料厚壁管。最后,通过有限元计算软件ABAQUS分析了不同复合材料组合管的力学响应,有限元计算结果与改进理论结果基本一致。Abstract: A method was proposed to analysis the axisymmetric problem of composite tubes made up of winding layers with arbitrary angles. The traditional Lekhnitskii theory can obtain the exact elastic solution of the thick composite tubes with common winding layers. However, when there are 0° winding layers or isotropic layers in the thick walled tubes, singular parameters will appear in the both special layers. And the discontinuity condition between the special layer and the common layer could not be satisfied. Therefore, the reasons for the existence of singular parameters in special layers were discussed. Then, the continuity analysis and limit calculation of these parameters were carried out, so that the problem of parameter singularity was solved and the application of Lekhnitskii theory was extended to composite thick tubes with arbitrary angles. Finally, the mechanical responses of different compo-site tubes were analyzed by ABAQUS, and the results of finite element calculation were basically consistent with the developed theoretical results.
-
Keywords:
- composite material /
- axisymmetric problem /
- winding angles /
- thick tubes /
- theoretical analysis
-
复合材料厚壁管作为一种主承力构件,目前在航空航天、民用和交通等领域有着广泛的应用前景,如火箭筒身、燃料储箱[1-4],氢燃料电池汽车中用于存储H2的Ⅲ型和Ⅳ型气瓶[5-7]及复合材料传动轴[8-9]等。上述这些应用领域使几何轴对称的复合材料管承受如内压、外压、扭矩和轴向力等轴对称载荷的作用。在小变形假设的基础上,由于管内的应力和应变关于管中心轴对称并与管的环向坐标无关,工程上通常将这类问题称为轴对称问题。
为了满足工程应用的需要,在设计过程中对复合材料厚壁管的精确计算显得非常重要。通常,有限元数值分析方法具有较高的计算精度,但复合材料厚壁管通常是由不同材料按不同厚度和不同角度缠绕而成,这进一步地增加有限元分析软件的建模周期和计算成本。因此,理论分析方法对这类结构的初期设计显得更方便和高效。传统的经典层合板理论[10]及JIANG等[11-12]提出的均质等效理论能够满足薄壁筒结构的计算精度,而对于厚壁管,传统理论难以满足计算精度的要求。并且,理论及实验研究表明[13-15],由于圆柱壳不能严格地实现对称铺层,面内通常存在剪切应力,并由此产生扭转变形,传统的理论并没有考虑这一现象,因此,发展精确的复合材料厚壁管的三维弹性理论成为结构可靠性设计的关键。
目前,复合材料厚壁管的三维弹性理论方法主要包括以Lekhnitskii[16]为代表的柔度法和以Stroh[17]、Xia等[13]和Zu等[18]为代表的刚度法。相比刚度法,柔度法通过引入应力函数来获得系统的偏微分方程组,并已被工程界广泛采用[19]。Lekhnitskii[16]最早提出双应力函数柔度法求解复合材料圆柱筒结构,但只采用单个应力函数求解了90°单层缠绕管的弯曲问题。Jolicoeur和Cardou[20]在Lekhnitskii双应力函数法[16]的基础上,通过引入两个函数之间的联系参数,获得了多层纤维缠绕管的纯弯曲问题和轴对称问题的解。之后,张灿辉等[21]、柯淼宏[22]、刘沛[23]、Zhang等[24-25]发现Jolicoeur和Cardou[20]所提出的复合材料厚壁管纯弯曲问题的方法中,当厚壁管中存在0°和90°特殊缠绕层时,部分联系参数出现0/0不定型的现象,并且其极限为无穷大,不能直接进行求解;为了解决这一问题,分别提出了统一联系参数法和独立的双应力函数法,这两种方法避免了计算过程中联系参数出现0/0不定型的情况,从而发展了与复合材料厚壁管纯弯曲问题相关的Lekhnitskii理论。
进一步研究发现,针对复合材料厚壁管的轴对称问题,Jolicoeur和Cardou[20]的理论方法同样不能直接求解包含0°铺层或各向异性层的复合材料厚壁管。事实上,采用拉挤工艺或缠绕工艺制备得到的复合材料压力容器及管道既具有0°铺层还具有用于密封的各向同性金属内胆。在计算中,通常将各向同性内胆视为特殊的0°铺层。因此,0°铺层对于复合材料厚壁管是普遍存在的,进一步地扩展复合材料厚壁管轴对称问题弹性理论的应用范围,具有十分重要的意义。
本文在Jolicoeur和Cardou[20]所提出的多层复合材料厚壁管轴对称问题的理论基础上,讨论了当缠绕层中0°或各向同性层出现奇异参数的原因,并对奇异参数进行连续性分析,同时采用极限分析法解决了参数的奇异性问题。最后通过有限元计算软件ABAQUS分析了不同复合材料组合管的力学响应,并与改进的理论结果进行对比。
1. 复合材料厚壁管轴对称问题的传统方法
复合材料厚壁管是由多层纤维以不同角度缠绕而成的各向异性的复杂结构。在轴向力P、扭矩T、内压
pi 和外压po 四种轴对称载荷作用下的复合材料厚壁管如图1所示,厚壁管的端面圆心处建立了X-Y-Z直角坐标系,在此直角坐标系的基础上继续建立了如图1所示的标准柱坐标系,其径向、环向和轴向分别用r 、θ 和Z 三个符号表示。该缠绕管共有N个缠绕层,图1中,r0 、rN 分别为厚壁管的内径和外径,rn 和φn(n=1,2,⋯,N) 则为第n层的外径和缠绕角;σZ 为管的轴向应力分量;σr 、σθ 和τrθ 为平行于横截面的应力分量;τθZ 和τrZ 为垂直于横截面的应力分量。轴对称载荷作用下,复合材料厚壁管的弹性理论主要基于以下两个基本假设:(1) 复合材料厚壁管变形前后保持轴对称,任意位置的应力分量都与坐标θ 无关(∂σij/∂θ=0 );(2) 由于厚壁管变形的对称性,假设两个面外剪切应力分量τrZ 和τrθ 都为0。![]() 图 1 轴对称载荷作用下的复合材料厚壁管Figure 1. Composite tube subjected to axisymmetric loadsP, T, pi and po—Axial load, torque, internal pressure and outer pressure, respectively; r0 and rN—Internal radius and outer radius of the composite thick tube; rn and φn—Outer radius and winding angle of the nth layer; σZ—Axial stress component; σr, σθ and τrθ—Stress components parallel to the cross section; τθZ and τrZ—Stress components perpendicular to the cross section
图 1 轴对称载荷作用下的复合材料厚壁管Figure 1. Composite tube subjected to axisymmetric loadsP, T, pi and po—Axial load, torque, internal pressure and outer pressure, respectively; r0 and rN—Internal radius and outer radius of the composite thick tube; rn and φn—Outer radius and winding angle of the nth layer; σZ—Axial stress component; σr, σθ and τrθ—Stress components parallel to the cross section; τθZ and τrZ—Stress components perpendicular to the cross section对于单层复合材料缠绕层,其在材料主轴坐标系下的应变与应力关系如下式所示:
\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _{11}}}\\ {{\varepsilon _{22}}}\\ {{\varepsilon _{33}}}\\ {{\gamma _{23}}}\\ {{\gamma _{13}}}\\ {{\gamma _{12}}} \end{array}} \right\} = {\boldsymbol{S}}\left\{ {\begin{array}{*{20}{l}} {{\sigma _{11}}}\\ {{\sigma _{22}}}\\ {{\sigma _{33}}}\\ {{\tau _{23}}}\\ {{\tau _{13}}}\\ {{\tau _{12}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{l}} {{S_{11}}}&{{S_{12}}}&{{S_{13}}}&0&0&0\\ {}&{{S_{22}}}&{{S_{23}}}&0&0&0\\ {}&{}&{{S_{33}}}&0&0&0\\ {}&{}&{}&{{S_{44}}}&0&0\\ {}&{}&{{\rm{sym}}}&{}&{{S_{55}}}&0\\ {}&{}&{}&{}&{}&{{S_{66}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\sigma _{11}}}\\ {{\sigma _{22}}}\\ {{\sigma _{33}}}\\ {{\tau _{23}}}\\ {{\tau _{13}}}\\ {{\tau _{12}}} \end{array}} \right\} (1) 式中,下标1、2和3分别表示纤维方向和面内垂直于纤维的方向及面外平行于厚度的方向;
{\varepsilon _{ij}} 和{\sigma _{ij}} (i,j = 1,2 , 3 )为对应方向的应变和应力分量;柔度矩阵{\boldsymbol{S}} 为对称矩阵,其元素分别为\left\{\begin{array}{l} {S}_{11}=\dfrac{1}{{E}_{11}},{S}_{22}=\dfrac{1}{{E}_{22}},{S}_{33}=\dfrac{1}{{E}_{33}},{S}_{44}=\dfrac{1}{{G}_{23}},{S}_{55}=\dfrac{1}{{G}_{13}},{S}_{66}=\dfrac{1}{{G}_{12}}\\ {S}_{12}=\dfrac{-{\nu }_{21}}{{E}_{22}}=\dfrac{-{\nu }_{12}}{{E}_{11}},{S}_{13}=\dfrac{-{\nu }_{31}}{{E}_{33}}=\dfrac{-{\nu }_{13}}{{E}_{11}},{S}_{23}=\dfrac{-{\nu }_{32}}{{E}_{33}}=\dfrac{-{\nu }_{23}}{{E}_{22}}\end{array}\right. (2) 式中:E1、E2和E3弹性模量;v12、v13和v23为泊松比;G12、G13和G23为剪切模量,下标1、2和3分别表示纤维方向和铺层面内垂直于纤维方向及缠绕层厚度方向。
柱坐标系下复合材料管内各缠绕层均具有以下形式的本构关系:
\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _r}}\\ {{\varepsilon _\theta }}\\ {{\varepsilon _{\textit{Z}}}}\\ {{\gamma _{\theta {\textit{Z}}}}}\\ {{\gamma _{r{\textit{Z}}}}}\\ {{\gamma _{r\theta }}} \end{array}} \right\} = {\boldsymbol{C}}\left\{ {\begin{array}{*{20}{l}} {{\sigma _r}}\\ {{\sigma _\theta }}\\ {{\sigma _{\textit{Z}}}}\\ {{\tau _{\theta {\textit{Z}}}}}\\ {{\tau _{r{\textit{Z}}}}}\\ {{\tau _{r\theta }}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{l}} {{C_{11}}}&{{C_{12}}}&{{C_{13}}}&{{C_{14}}}&0&0\\ {}&{{C_{22}}}&{{C_{23}}}&{{C_{24}}}&0&0\\ {}&{}&{{C_{33}}}&{{C_{34}}}&0&0\\ {}&{}&{}&{{C_{44}}}&0&0\\ {}&{}&{{\rm{sym}}}&{}&{{C_{55}}}&{{C_{56}}}\\ {}&{}&{}&{}&{}&{{C_{66}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\sigma _r}}\\ {{\sigma _\theta }}\\ {{\sigma _{\textit{Z}}}}\\ {{\tau _{\theta {\textit{Z}}}}}\\ {{\tau _{r{\textit{Z}}}}}\\ {{\tau _{r\theta }}} \end{array}} \right\} (3) 其中
{\boldsymbol{C}} = {\boldsymbol{T}}^{\rm{T}}{\boldsymbol{S}} {\boldsymbol{T}}^{} (4) 并且
{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 0&{{{\sin }^2}\varphi }&{{{\cos }^2}\varphi }&{ - 2 \sin \varphi \cos \varphi }&0&0 \\ 0&{{{\cos }^2}\varphi }&{{{\sin }^2}\varphi }&{2 \sin \varphi \cos \varphi }&0&0 \\ 1&0&0&0&0&0 \\ 0&0&0&0&{ - \sin \varphi }&{ - \cos \varphi } \\ 0&0&0&0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi \cos \varphi }&{ - \sin \varphi \cos \varphi }&{{{\sin }^2}\varphi - {{\cos }^2}\varphi }&0&0 \end{array}} \right] (5) 为了方便地表示应力及应变的表达式,Lekhnitskii[16]引入了缩减弹性系数
{\beta _{ij}} :{\beta _{ij}} = {C_{ij}} - \frac{{{C_{i3}}{C_{3j}}}}{{{C_{33}}}} (6) 通过对应变张量进行积分运算[20] (见Lekhnitskii[16]第3章),可得到位移表达式:
\left\{ \begin{array}{l} {u_r} = U \\ {u_\theta } = \vartheta _{r{\textit{Z}} }+ V \\ w = {\textit{Z}}\varepsilon + W \end{array} \right. (7) 式中:
{u_r} 、{u_\theta } 和w 分别为厚壁管的径向、环向和轴向位移;\varepsilon 和\vartheta 表示厚壁管的轴向应变和扭曲率(angle/unit length),并且轴向应变\varepsilon 可由下式表示:\varepsilon = {C_{13}}{\sigma _r} + {C_{23}}{\sigma _\theta } + {C_{33}}{\sigma _{\textit{Z}}} + {C_{34}}{\tau _{\theta {\textit{Z}}}} (8) U 、V 和W 分别是与r 和\theta 有关的位移函数:\left\{ \begin{array}{l} \varepsilon _r^0 \equiv \dfrac{{\partial U}}{{\partial r}} = {\beta _{11}}{\sigma _r} + {\beta _{12}}{\sigma _\theta } + {\beta _{14}}{\tau _{\theta {\textit{Z}}}} + \dfrac{{{C_{13}}}}{{{C_{33}}}}\varepsilon \\ \varepsilon _\theta ^0 \equiv \dfrac{1}{r}\dfrac{{\partial V}}{{\partial \theta }} + \dfrac{U}{r} = {\beta _{12}}{\sigma _r} + {\beta _{22}}{\sigma _\theta } + \\ \qquad {\beta _{24}}{\tau _{\theta {\textit{Z}}}} + \dfrac{{{C_{23}}}}{{{C_{33}}}}\varepsilon \\ \gamma _{r\theta }^0 \equiv \dfrac{1}{r}\dfrac{{\partial U}}{{\partial \theta }} + \dfrac{{\partial V}}{{\partial r}} - \dfrac{V}{r} = {\beta _{56}}{\tau _{r{\textit{Z}}}} + {\beta _{66}}{\tau _{r\theta }} \end{array} \right. (9) \left\{ \begin{array}{l} \dfrac{{\partial W}}{{\partial r}} = {\beta _{55}}{\tau _{r{\textit{Z}}}} + {\beta _{56}}{\tau _{r\theta }} \\ \dfrac{{\partial W}}{{r\partial \theta }} = {\beta _{14}}{\sigma _r} + {\beta _{24}}{\sigma _\theta } + {\beta _{44}}{\tau _{\theta {\textit{Z}}}} + \dfrac{{{C_{34}}}}{{{C_{33}}}}\varepsilon - \vartheta r \end{array} \right. (10) 极坐标系中厚壁管的应变协调方程[16]为
\left( {\frac{{{\partial ^2}}}{{\partial {\theta ^2}}} - r\frac{\partial }{{\partial r}}} \right)\varepsilon _r^0 + r\frac{{{\partial ^2}}}{{\partial {r^2}}}\left( {r\varepsilon _\theta ^0} \right) - \frac{{{\partial ^2}}}{{\partial r \partial \theta }}\left( {r\gamma _{r\theta }^0} \right) = 0 (11) 对于复合材料厚壁管的轴对称问题,Jolicoeur和Cardou[20]采用了Lekhnitskii[16]所提出的双应力函数
{{F}}\left( {r,\theta } \right) 和\varPsi \left( {r,\theta } \right) ,来表示如下应力分量:\left\{ \begin{array}{l} {\sigma _r} = \dfrac{1}{r}\dfrac{{\partial {{F}} }}{{\partial r}} + \dfrac{1}{{{r^2}}}\dfrac{{{\partial ^2}{{F}} }}{{\partial {\theta ^2}}} \\ {\sigma _\theta } = \dfrac{{{\partial ^2}{{F}} }}{{\partial {r^2}}} \\ {\tau _{r\theta }} = - \dfrac{{{\partial ^2}}}{{\partial r\partial \theta }}\left( {\dfrac{{{F}} }{r}} \right) \\ \end{array} \right. (12) \left\{ \begin{array}{l} {\tau _{r{\textit{Z}}}} = \dfrac{1}{r}\dfrac{{\partial \varPsi }}{{\partial \theta }} \\ {\tau _{\theta {\textit{Z}}}} = - \dfrac{{\partial \varPsi }}{{\partial r}} \end{array} \right. (13) 考虑到轴对称问题应力函数与坐标
\theta 无关,双应力函数仅为与坐标r 相关的函数,应力函数可表示为\left\{ \begin{array}{l} {{F}} = f\left( r \right) \\ \varPsi = \psi \left( r \right) \\ \end{array} \right. (14) 分别将式(9)代入应变协调方程式(11),并将式(10)中两个式子分别微分并整合,分别消去
U 、V 和W 三个变量函数,并将所有应力分量用式(12)和式(13)中的应力函数表示,从而获得如下式所示的常微分方程组:\left\{ \begin{array}{l} \left( {{\beta _{22}}\dfrac{{{{\rm{d}}^4}}}{{{\rm{d}}{r^4}}} + \dfrac{{2{\beta _{22}}}}{r}\dfrac{{{{\rm{d}}^3}}}{{{\rm{d}}{r^3}}} - \dfrac{{{\beta _{11}}}}{{{r^2}}}\dfrac{{{{\rm{d}}^2}}}{{{\rm{d}}{r^2}}} + \dfrac{{{\beta _{11}}}}{{{r^3}}}\dfrac{{\rm{d}}}{{{\rm{d}}r}}} \right)f\left( r \right)- \\ \left( {{\beta _{24}}\dfrac{{{{\rm{d}}^3}}}{{{\rm{d}}{r^3}}} - \dfrac{{{\beta _{14}} - 2{\beta _{24}}}}{r}} \right.\left. {\dfrac{{{{\rm{d}}^2}}}{{{\rm{d}}{r^2}}}} \right)\psi \left( r \right) = 0 \\ \left( { - {\beta _{24}}\dfrac{{{{\rm{d}}^3}}}{{{\rm{d}}{r^3}}} - \dfrac{{{\beta _{14}} + {\beta _{24}}}}{r}\dfrac{{\rm{d}}}{{{\rm{d}}r}}} \right)f\left( r \right) + \\ \left( {{\beta _{44}}\dfrac{{{{\rm{d}}^2}}}{{{\rm{d}}{r^2}}} + \dfrac{{{\beta _{44}}}}{r}\dfrac{{\rm{d}}}{{{\rm{d}}r}}} \right)\psi \left( r \right) = \dfrac{{{C_{34}}}}{{{C_{33}}}}\dfrac{\varepsilon }{r} - 2\vartheta \\ \end{array} \right. (15) 为了求解式(15)所示常微分方程组的通解,Jolicoeur和Cardou[20]通过引进联系参数建立起双应力函数之间的桥梁,得到了应力函数
f\left( r \right) 和\psi \left( r \right) 的通解。应力函数表达式
f\left( r \right) 和\psi \left( r \right) 中最初具有6个任意常数,由于该应力函数需要满足式(12)和式(13)所示的应力分量,可以证明应力函数其中3个常数必须等于0;并且,该应力函数还需要满足式(9)和式(10)所示的位移函数关于管中心轴对称的特性,从而得到1个与该层材料参数相关的已知常数[20],最终,该应力函数仅剩下2个未知常数,如下式:\left\{ \begin{array}{l} f\left( r \right) = \displaystyle\sum\limits_{i = 1}^2 {\dfrac{{{K_i}}}{{{m_i} + 1}}{r^{{m_i} + 1}}} + \dfrac{{{\mu _1}}}{3}\vartheta {r^3} + \dfrac{{{\mu _3}}}{2}\varepsilon {r^2} \\ \psi \left( r \right) = \displaystyle\sum\limits_{i = 1}^2 {\dfrac{{{K_i}{g_i}}}{{{m_i}}}{r^{{m_i}}}} + \dfrac{{{\mu _2}}}{2}\vartheta {r^2} + \\ \qquad\quad {\mu _3}\dfrac{{{\beta _{14}} + {\beta _{24}}}}{{{\beta _{44}}}}\varepsilon r + \dfrac{{{C_{34}}}}{{{C_{33}}{\beta _{44}}}}\varepsilon r \\ \end{array} \right. (16) 其中:组合系数
{K_1} 和{K_2} 为未知常数;特征参数{m_1} 和{m_2} 为特征方程的根,如下式所示:\left\{ \begin{array}{l} {m_1} \\ {m_2} \\ \end{array} \right. = \pm \sqrt {\frac{{{\beta _{11}}{\beta _{44}} - \beta _{14}^2}}{{{\beta _{22}}{\beta _{44}} - \beta _{24}^2}}} (17) 联系参数
{g_1} 和{g_2} 如下式所示:{g}_{i}=\frac{\beta {}_{14}+\beta {}_{24}m{}_{i}}{\beta {}_{44}}\qquad\qquad(i=1,2) (18) 参数
{\mu _1} 、{\mu _2} 和{\mu _3} 则分别由以下两个式子计算得到:\left\{ \begin{array}{l} {\mu _1} \\ {\mu _2} \\ \end{array} \right\} = {\left[ {\begin{array}{*{20}{c}} {{\beta _{14}} + 2{\beta _{24}}}&{ - {\beta _{44}}} \\ {4{\beta _{22}} - {\beta _{11}}}&{{\beta _{14}} - 2{\beta _{24}}} \end{array}} \right]^{ - 1}} \left\{ \begin{array}{l} 1 \\ 0 \\ \end{array} \right\} (19) {\mu _3} = \frac{{{C_{34}}\left( {{\beta _{24}} - {\beta _{14}}} \right) + {\beta _{44}}\left( {{C_{13}} - {C_{23}}} \right)}}{{{C_{33}}\left[ {\beta _{14}^2 - \beta _{24}^2 + {\beta _{44}}\left( {{\beta _{22}} - {\beta _{11}}} \right)} \right]}} (20) 得到应力函数之后,将式(16)代入式(12)~(13),得到如下式所示应力分量表达式:
\left\{ \begin{array}{l} {\sigma _r} = \displaystyle\sum\limits_{i = 1}^2 {{K_i}{r^{{m_i} - 1}}} + {\mu _1}\vartheta r + {\mu _3}\varepsilon \\ {\sigma _\theta } = \displaystyle\sum\limits_{i = 1}^2 {{K_i}{m_i}{r^{{m_i} - 1}}} + 2{\mu _1}\vartheta r + {\mu _3}\varepsilon \\ {\tau _{r\theta }} = 0 \\ {\tau _{r{\textit{Z}}}} = 0 \\ {\tau _{\theta {\textit{Z}}}} = - \displaystyle\sum\limits_{i = 1}^2 {{K_i}{g_i}{r^{{m_i} - 1}}} - {\mu _2}\vartheta r - \\ \qquad\left( {{\mu _3}\dfrac{{{\beta _{14}} + {\beta _{24}}}}{{{\beta _{44}}}} + \dfrac{{{C_{34}}}}{{{C_{33}}{\beta _{44}}}}} \right)\varepsilon \\ {\sigma _{\textit{Z}}} = \dfrac{1}{{{C_{33}}}}\left( {\varepsilon - {C_{13}}{\sigma _{{r}}} - {C_{23}}{\sigma _\theta } - {C_{34}}{\tau _{\theta {\textit{Z}}}}} \right) \end{array} \right. (21) 位移函数
U 、V 和W 分别为\left\{ \begin{array}{l} U = \displaystyle\sum\limits_{i = 1}^2 {{K_i}{{U'}_i}{r^{{m_i}}} + {{U'}_3}\vartheta {r^2} + {{U'}_4}\varepsilon r} \\ V = 0 \\ \\ W = 0 \\ \end{array} \right. (22) 其中,
{U'_i} = \frac{1}{{{m_i}}}\left( {{\beta _{11}} + {\beta _{12}}{m_i} + {\beta _{14}}{g_i}} \right)\;\;\;\;\;\; i = 1,2 (23) {U'_3} = \frac{1}{2}\left[ {{\mu _1}\left( {{\beta _{11}} + 2{\beta _{12}}} \right) - {\mu _2}{\beta _{14}}} \right] (24) {U'_4} = \frac{1}{{{C_{33}}}}\left( {{C_{13}} - \frac{{{\beta _{14}}}}{{{\beta _{44}}}}{C_{34}}} \right) + {\mu _3}\left( {{\beta _{11}} + {\beta _{12}} - {\beta _{14}}\frac{{{\beta _{14}} + {\beta _{24}}}}{{{\beta _{44}}}}} \right) (25) 2. 理论的改进方法
2.1 边界条件及奇异参数现象
第一节获得了单层缠绕管的应力函数的通解,对于多层复合材料圆柱管,其轴对称问题的复杂性主要体现在:各相邻层之间的应力和位移需要保持连续性。基于层与层之间不会出现滑移的假设,厚壁管的相邻层之间需要保持应力
{\sigma _r} 、{\tau _{r\theta }} 和{\tau _{rZ}} 及位移{u_r} 、{u_\theta } 和w 之间的连续性,根据位移表达式(7)和应力表达式(21),可以获得2N个方程,其中共有N−1个接触面和内、外2个自由面。以第n−1层与第n层的界面连续条件为例:\left\{ \begin{array}{l} \displaystyle\sum\limits_{i = 1}^2 {{K_{i,n - 1}}r_{ n - 1}^{ {m_{i,n - 1}} - 1}} - \displaystyle\sum\limits_{i = 1}^2 {{K_{i,n}}r_{ n - 1}^{ {m_{i,n}} - 1}} = \\ \left( {{\mu _{1,n}} - {\mu _{1,n - 1}}} \right)\vartheta {r_{n - 1}} + \left( {{\mu _{3,n}} - {\mu _{3,n - 1}}} \right)\varepsilon \\ \displaystyle\sum\limits_{i = 1}^2 {{K_{i,n - 1}}{{U'}_{i,n - 1}}r_{ n - 1}^{ {m_{i,n - 1}}}} - \displaystyle\sum\limits_{i = 1}^2 {{K_{i,n}}{{U'}_{i,n}}r_{ n - 1}^{ {m_{i,n}}}}= \\ \left( {{{U'}_{3,n}} - {{U'}_{3,n - 1}}} \right)\vartheta r_{ n - 1}^{ 2} + \left( {{{U'}_{4,n}} - {{U'}_{4,n - 1}}} \right)\varepsilon {r_{n - 1}} \end{array} \right. (26) 当管内存在内压
{p_{\rm{i}}}\left( {{p_{\rm{i}}} \geqslant 0} \right) 时,{\sigma _r} = - {p_{\rm{i}}} {\rm{at}} r = {r_0} ,可具体表示为{\displaystyle \sum _{i=1}^{2}{K}_{i,1}{r}_{0}^{{m}_{i,1}-1}}+{\mu }_{1}\vartheta r+{\mu }_{3}\epsilon =-{p}_{\rm{i}} (27) 当管外壁存在外压
{p_{\rm{o}}}\left( {{p_{\rm{o}}} \geqslant 0} \right) 时,{\sigma _r} = - {p_{\rm{o}}} {\rm{at}} r = {r_N} ,可具体表示为\sum\limits_{i = 1}^2 {{K_{i,n}}r_{ n}^{ {m_{i,n}} - 1}} + {\mu _{1,n}}\vartheta {r_n} + {\mu _{3,n}}\varepsilon = - {p_{\rm{o}}} (28) 因此,以上2N个方程,可用如下矩阵形式表示:
{{\boldsymbol{M}}_{\rm{1}}}*{\boldsymbol{K}}{\rm{ = }}{{\boldsymbol{M}}_2} + {{\boldsymbol{M}}_3}\left[ {\begin{array}{*{20}{c}} \varepsilon \\ \vartheta \end{array}} \right] (29) 其中:
{\boldsymbol{K}}{\rm{ = }}{\left[ {{K_{1,1}} {K_{2,1}} {K_{1,2}} {K_{2,2}} \cdots {K_{1,N}} {K_{2,N}}} \right]^{\rm{T}}} ;{{\boldsymbol{M}}_{\rm{1}}} 和{{\boldsymbol{M}}_3} 分别为式(26)~(28)所示2N个方程的系数矩阵,并且{{\boldsymbol{M}}_2}{\rm{ = }}{\left[ { - {p_{\rm{i}}},0 , \cdots ,0 , - {p_{\rm{o}}}} \right]^{\rm{T}}} 。此外,当厚壁管在端部受轴向载荷P和扭矩T的作用时,需满足以下端部边界条件:
\begin{split} P &= \sum\limits_{n = 1}^N {\int_0^{2{\rm{{\text{π}} }}} {\int_{{r_0}}^{{r_n}} {{\sigma _{\textit{Z}}}} } r {\rm{d}}\theta {\rm{d}}r} \\ & = \sum\limits_{n = 1}^N {\left( {{A_n}{K_{1,n}} + {B_n}{K_{2,n}} + {C_n}\varepsilon + {D_n}\vartheta } \right)} \end{split} (30) \begin{split} T &= \sum\limits_{n = 0}^N {\int_0^{2{\rm{{\text{π}} }}} {\int_{{r_0}}^{{r_n}} {{\tau _{\theta {\textit{z}}}}} } r{ ^2} {\rm{d}}\theta {\rm{d}}r} \\ & = \sum\limits_{n = 1}^N {\left( {{{A'}_n}{K_{1,n}} + {{B'}_n}{K_{2,n}} + {{C'}_n}\varepsilon + {{D'}_n}\vartheta } \right)} \end{split} (31) 其中,端部边界条件表达式中的参数
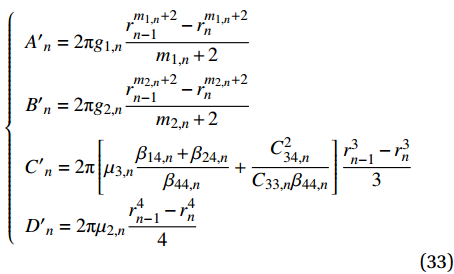
{A}_{n}、{B}_{n}、{C}_{n}、{D}_{n} 和{{A}^{\prime }}_{n}、{{B}^{\prime }}_{n}、{{C}^{\prime }}_{n}、{{D}^{\prime }}_{n} 分别为\left\{ \begin{array}{l} {A_n} = \dfrac{{2{\rm{{\text{π}} }}}}{{{C_{33,n}}}}\left( {{C_{13,n}} + {C_{23,n}}{m_{1,n}} - {C_{34,n}}{g_{1,n}}} \right)\dfrac{{r_{ n - 1}^{{m_{1,n}} + 1} - r_{ n}^{{m_{1,n}} + 1}}}{{{m_{1,n}} + 1}} \\ {B_n} = \dfrac{{2{\rm{{\text{π}} }}}}{{{C_{33,n}}}}\left( {{C_{13,n}} + {C_{23,n}}{m_{2,n}} - {C_{34,n}}{g_{2,n}}} \right)\dfrac{{r_{ n - 1}^{{m_{2,n}} + 1} - r_{ n}^{{m_{2,n}} + 1}}}{{{m_{2,n}} + 1}} \\ {C_n} = \dfrac{{2{\rm{{\text{π}} }}}}{{{C_{33,n}}}}\left[ {{\mu _{3,n}}\left( {{C_{13,n}} + 2{C_{23,n}} - {C_{34,n}}\dfrac{{{\beta _{14,n}} + {\beta _{24,n}}}}{{{\beta _{44,n}}}}} \right)} \right.- \\ \qquad \left. {\dfrac{{C_{34,n}^2}}{{{C_{33,n}}{\beta _{44,n}}}} - 1} \right]\dfrac{{r_{ n - 1}^{ 2} - r_{ n}^2}}{2} \\ {D_n} = \dfrac{{2{\rm{{\text{π}} }}}}{{{C_{33,n}}}}\left[ {{\mu _{1,n}}\left( {{C_{13,n}} + 2{C_{23,n}}} \right) - {\mu _{2,n}}{C_{34,n}}} \right]\dfrac{{r_{ n - 1}^{ 3} - r_{ n}^3}}{3} \end{array} \right. (32) \left\{ \begin{array}{l} {{A'}_n} = 2{\rm{{\text{π}} }}{g_{1,n}}\dfrac{{r_{ n - 1}^{{m_{1,n}} + 2} - r_{ n}^{{m_{1,n}} + 2}}}{{{m_{1,n}} + 2}} \\ {{B'}_n} = 2{\rm{{\text{π}} }}{g_{2,n}}\dfrac{{r_{ n - 1}^{{m_{2,n}} + 2} - r_{ n}^{{m_{2,n}} + 2}}}{{{m_{2,n}} + 2}} \\ {{C'}_n} = 2{\rm{{\text{π}} }}\left[ {{\mu _{3,n}}\dfrac{{{\beta _{14,n}} + {\beta _{24,n}}}}{{{\beta _{44,n}}}} + \dfrac{{C_{34,n}^2}}{{{C_{33,n}}{\beta _{44,n}}}}} \right]\dfrac{{r_{ n - 1}^{ 3} - r_{ n}^3}}{3} \\ {{D'}_n} = 2{\rm{{\text{π}} }}{\mu _{2,n}}\dfrac{{r_{ n - 1}^{ 4} - r_{ n}^4}}{4} \end{array} \right. (33) 为了方便计算,将式(30)和式(31)用矩阵的形式表示:
\left\{ \begin{array}{l} P \\ T \\ \end{array} \right\} = {{\boldsymbol{M}}_{\rm{4}}}{\boldsymbol{K}}{\rm{ + }}{{\boldsymbol{M}}_5}\left\{ \begin{array}{l} \varepsilon \\ \vartheta \\ \end{array} \right\} (34) 其中,矩阵
{{\boldsymbol{M}}_{\rm{4}}} 和{{\boldsymbol{M}}_5} 分别为{{\boldsymbol{M}}_{\rm{4}}} = \left[ {\begin{array}{*{20}{l}} {{A_1}}&{{B_1}}&{{A_2}}&{{B_2}}& \cdots &{{A_n}}&{{B_n}}\\ {{{A'}_1}}&{{{B'}_1}}&{{{A'}_2}}&{{{B'}_2}}& \cdots &{{{A'}_n}}&{{{B'}_n}} \end{array}} \right] (35) {M_5} = \left[ {\begin{array}{*{20}{l}} {\left( {{C_1} + \cdots + {C_n}} \right)}&{\left( {{D_1} + \cdots + {D_n}} \right)}\\ {\left( {{{C'}_1} + \cdots + {{C'}_n}} \right)}&{\left( {{{D'}_1} + \cdots + {{D'}_n}} \right)} \end{array}} \right] (36) 联立式(29)和式(34)两个方程组,共组成了2N+2个方程,此时可将2N+2个未知数(
{K}_{1,1},{K}_{2,1}, {K}_{1,2},{K}_{2,2}, \cdots ,{K}_{1,N},{K}_{2,N},\epsilon ,\vartheta )求解出来。进一步地将式(29)代入式(34),可以得到:
\left\{ \begin{array}{l} P \\ T \\ \end{array} \right\} = {{\boldsymbol{M}}_{\rm{4}}}{\left[ {{{\boldsymbol{M}}_1}} \right]^{ - 1}}{{\boldsymbol{M}}_2}{\rm{ + }}\left[ {{{\boldsymbol{M}}_{\rm{4}}}{{\left[ {{{\boldsymbol{M}}_1}} \right]}^{ - 1}}{{\boldsymbol{M}}_3}{\rm{ + }}{{\boldsymbol{M}}_5}} \right]\left\{ \begin{array}{l} \varepsilon \\ \vartheta \\ \end{array} \right\} (37) 当仅存在轴向力或扭矩时,式(37)可简化为
\left\{ \begin{array}{l} P \\ T \\ \end{array} \right\} = {\boldsymbol{G}}\left\{ \begin{array}{l} \varepsilon \\ \vartheta \\ \end{array} \right\} = \left[ {\begin{array}{*{20}{c}} {EA}&{{G_{12}}} \\ {{G_{12}}}&{GJ} \end{array}} \right]\left\{ \begin{array}{l} \varepsilon \\ \vartheta \\ \end{array} \right\} (38) 其中:刚度矩阵
{\boldsymbol{G}} = {{\boldsymbol{M}}_{\rm{4}}}{\left[ {{{\boldsymbol{M}}_1}} \right]^{ - 1}}{{\boldsymbol{M}}_3}{\rm{ + }}{{\boldsymbol{M}}_5} 为对称矩阵;EA 为复合材料厚壁管的轴向刚度;GJ 则为扭转刚度;{G_{12}} 为耦合系数。通过求解以上2N+2个未知数,即可计算多层纤维缠绕管轴对称问题的弹性响应。而在计算过程中,当复合材料厚壁管中第n层为特殊缠绕角
\varphi = {0^{\rm{o}}} 或含有各向同性层时,将会导致参数{\mu _{ 3,n}} 和参数{A_n} 中的分式表达式出现0/0的奇异现象,使特殊层与普通层界面的连续性条件不能满足,程序无法继续计算。下面对这两种奇异参数问题分别讨论,并提出解决方法。2.2 参数
{\mu _{{\kern 1pt} 3,n}} 的奇异性及解决方法当厚壁管中第n层缠绕角为
{\varphi _n} = {0^{\rm{o}}} 或第n层为各向同性层时,由式(4)和式(6)可求出弹性系数矩阵{{\boldsymbol{C}}_{ij,n}} 和缩减弹性系数矩阵{{\boldsymbol{\beta }}_{ij,n}} 为{{\boldsymbol{C}}_{ij,n}} = \left[ {\begin{array}{*{20}{l}} {{C_{11,n}}}&{{C_{12,n}}}&{{C_{13,n}}}&0&0&0\\ {}&{{C_{22,n}}}&{{C_{23,n}}}&0&0&0\\ {}&{}&{{C_{33,n}}}&0&0&0\\ {}&{}&{}&{{C_{44,n}}}&0&0\\ {}&{{\rm{sym}}}&{}&{}&{{C_{55,n}}}&0\\ {}&{}&{}&{}&{}&{{C_{66,n}}} \end{array}} \right] (39) {{\boldsymbol{\beta }}_{ij,n}} = \left[ {\begin{array}{*{20}{l}} {{\beta _{11,n}}}&{{\beta _{12,n}}}&0&0&0&0\\ {}&{{\beta _{22,n}}}&0&0&0&0\\ {}&{}&0&0&0&0\\ {}&{}&{}&{{\beta _{44,n}}}&0&0\\ {}&{{\rm{sym}}}&{}&{}&{{\beta _{55,n}}}&0\\ {}&{}&{}&{}&{}&{{\beta _{66,n}}} \end{array}} \right] (40) 其中:
\left\{ \begin{array}{l} {C_{11,n}} = {S_{33,n}}, {C_{22,n}} = {S_{22,n}}, {C_{33,n}} = {S_{11,n}} \\ {C_{12,n}} = {S_{23,n}}, {C_{23,n}} = {S_{12,n}}, {C_{13,n}} = {S_{13,n}} \;{\rm{For}} \; \varphi = {0^{\rm{o}}} \\ {C_{44,n}} = {S_{66,n}}, {C_{55,n}} = {S_{55,n}}, {C_{66,n}} = {S_{44,n}} \\ \end{array} \right. (41) \left\{ \begin{array}{l} {C_{11,n}} = {C_{22,n}} = {C_{33,n}} = 1/E \\ {C_{12,n}} = {C_{23,n}} = {C_{13,n}} = - \nu/E \; {\rm{For}}\; {\rm{isotrop}} \; {\rm{material}} \\ {C_{44,n}} = {C_{55,n}} = {C_{66,n}} = 2\left( {1 + \nu } \right)/E \\ \end{array} \right. (42) 相比一般缠绕角的情况,特殊层的弹性系数矩阵
{{\boldsymbol{C}}_{ij,n}} 中增加了以下4个零系数:{C_{14,n}} = {C_{24,n}} = {C_{34,n}} = {C_{56,n}} = 0 (43) 同时,缩减弹性系数矩阵
{{\boldsymbol{\beta }}_{ij,n}} 增加了以下3个零缩减系数:{\beta _{14,n}} = {\beta _{24,n}} = {\beta _{56,n}} = 0 (44) 因此,当第n层为特殊层时,由于
{\beta _{24,n}} = {\beta _{14,n}} = 0 ,式(20)所示的参数{\mu _{ 3,n}} 可简化为{\mu _{ 3,n}} = \frac{{{C_{13,n}} - {C_{23,n}}}}{{{C_{33,n}}\left( {{\beta _{22,n}} - {\beta _{11,n}}} \right)}} (45) 由于复合材料具有横观各向同性的性质,这将导致系数
{C_{13,n}} = {C_{23,n}} ,{\beta _{22,n}} = {\beta _{11,n}} ,此时参数{\mu _{ 3,n}} 分式表达式中,分子中的因式\left( {{C_{13,n}} - {C_{23,n}}} \right) 和分母中的因式\left( {{\beta _{22,n}} - {\beta _{11,n}}} \right) 同时为0;使参数{\mu _{ 3,n}} 成为0/0型。事实上,为了简化表达式,Lekhnitskii[16]引入了如式(6)所示的缩减弹性系数
{\beta _{ij,n}} ,而当计算特殊层时,因式\left( {{\beta _{22,n}} - {\beta _{11,n}}} \right) 包含了零因式\left( {{C_{13,n}} - {C_{23,n}}} \right) ,从而出现了{\mu _{3,n}} = 0/0 的情况。Zhang等[25]在处理复合材料管的纯弯曲问题时,针对缠绕角为\varphi = {0^{\rm{o}}} + \delta 或\varphi = {90^{\rm{o}}} + \delta 时,推导了对应缠绕角的弹性系数{C_{ij,n}} 和缩减弹性系数{\beta _{ij,n}} 的导数,并将特征参数{m_i} 进行泰勒展开,证明了当\delta = 0 时,弹性系数{C_{ij,n}} 、缩减弹性系数{\beta _{ij,n}} 和特征参数{m_{i,n}} 的连续性。因此,当第n层为 缠绕层或为各向同性层时,奇异参数{\mu _{3,n}} 分式中的零因式\left( {{C_{13,n}} - {C_{23,n}}} \right) 可通过求极限的方式约掉,如下式所示:\begin{split} {\mu _{3,n}} &= \mathop {\lim }\limits_{ \varphi \to {0^{\rm{o}}}} \dfrac{{{C_{13,n}} - {C_{23,n}}}}{{{C_{33,n}}\left( {{\beta _{22,n}} - {\beta _{11,n}}} \right)}} \\ & = \mathop {\lim }\limits_{ \varphi \to {0^{\rm{o}}}} \dfrac{{{C_{13,n}} - {C_{23,n}}}}{{{C_{33,n}}\left( {{C_{22,n}} - {C_{11,n}} - \dfrac{{{C_{23,n}}{C_{32,n}} - {C_{13,n}}{C_{31,n}}}}{{{C_{33,n}}}}} \right)}} \\ & = \dfrac{1}{{{C_{13,n}} + {C_{23,n}}}} \\[-12pt] \end{split} (46) 2.3 参数
{A_n} 的奇异性及解决方法当第n层缠绕角为
{\varphi _n} = {0^{\rm{o}}} 或为各向同性层时,式(17)计算的特征参数分别为{m_{1,n}} = - 1 ,{m_{2,n}} = 1 ;当{m_{1,n}} = - 1 时,式(32)所示参数{A_n} 中的因式( {{r_{ n - 1}^{{m_{1,n}} + 1} - r_{ n}^{{m_{1,n}} + 1}}})/({{{m_{1,n}} + 1}} ) 将会出现0/0的奇异情况。对于复合材料厚壁管的轴对称问题,前面已经讨论了当缠绕角为\varphi = {0^{\rm{o}}} + \delta 时,弹性系数{C_{ij,n}} 和缩减弹性系数{\beta _{ij,n}} 在变量\delta = 0 的邻域内是连续的,并且,式(17)所示的特征参数{m_{i,n}} 为{\beta _{ij,n}} 的连续函数,可以证明特征参数{m_{i,n}} 在\delta = 0 处是连续的。因此,参数{A_n} 中因式( {{r_{ n - 1}^{{m_{1,n}} + 1} - r_{ n}^{{m_{1,n}} + 1}}})/({{{m_{1,n}} + 1}} ) 的大小可以通过求极限的方法计算得到:\begin{split} & \mathop {\lim }\limits_{\varphi \to 0} \frac{{r_{n - 1}^{m_{ 1,n}^{} + 1} - r_n^{m_{ 1,n}^{} + 1}}}{{m_{1,n}^{} + 1}}= \\ & \mathop {\lim }\limits_{\varphi \to 0} r_{n - 1}^{m_{ 1,n}^{} + 1}\ln{r_{n - 1}} - r_n^{m_{ 1,n}^{} + 1}\ln {r_n}= \ln{r_{n - 1}} - \ln {r_n} \end{split} (47) 此时,
{A_n} 的表达式需更改为{A_n} = \frac{{2{\rm{{\text{π}} }}}}{{{C_{33,n}}}}\left( {{C_{13,n}} + {C_{23,n}}{m_{1,n}} - {C_{34,n}}{g_{1,n}}} \right)\left( { \ln{r_{n - 1}} - \ln {r_n}} \right) (48) 因此,当第n层为
{0^{\rm{o}}} 缠绕层或为各向同性层时,将式(46)代入式(20)并将式(48)代入式(32)中的第一个式子,即可解决传统方法遇到的参数奇异性问题,从而实现任意角度复合材料厚壁管轴对称问题的计算。3. 数值算例
为了验证文中改进理论的可靠性和准确性,将正交各向异性材料的弹性本构关系编写进UMAT用户子程序,用于ABAQUS 13.0有限元软件的隐式求解器,并分别对如图2所示的两个的复合材料组合管进行三维弹性计算。其中,管1分别由碳纤维和玻璃纤维组成,且仅受扭矩的作用;管2由钢内衬、碳纤维层和玻璃纤维层组成,内表面受内压的作用,同时承受轴向拉伸载荷的作用,这与复合材料压力容器筒身的受力情况一致。表1为各层材料的力学性能参数。
表 1 各层材料的力学性能参数Table 1. Material property for each layerCarbon fiber/epoxy-resin E1=155 GPa, E2=E3=12.1 GPa; v12=v13=0.248; v23=0.458; G12=G13=4.4 GPa; G23=3.2 GPa Glass fiber/epoxy-resin E1=60 GPa, E2=E3=11 GPa;
v12 = v13=0.26; v23=0.4; G12=G13=7.6 GPa; G23=3.7 GPaSteel E=210 GPa;v=0.3 Notes: E1, E2, E3—Modulus in fiber direction, in-plane transverse modulus and out-of-plane transverse modulus respectively; ν12, G12—Poisson's ratio and shear modulus of fiber direction and in-plane transverse direction; ν13 and G13—Poisson's ratio and shear modulus of fiber direction and out-of-plane transverse direction; ν23 and G23—Poisson's ratio, shear modulus of in-plane transverse direction and out-of-plane transverse direction; E and v—Modulus and poisson’s ratio of the steel. 有限元计算模型采用C3D8R实体单元,每个缠绕层厚度方向的网格数量为10份,环向网格数量为60份,管1和管2的长度都为600 mm,并且长度方向网格数量为100份;管1边界条件为一端端面施加轴向约束和环向约束,另一端端面与端面圆心上的参考点进行coupling约束,并在此参考点上施加8×106 N·mm大小的扭矩;管2的边界条件为一端施加轴向约束,另一端端面与端面圆心上的参考点进行coupling约束,并在参考点上施加19625 N的拉力,同时在内表面施加10 MPa的内压。需要注意的是管1的载荷条件和约束条件在柱坐标系环境中施加,而管2的载荷条件和约束条件则在全局坐标系环境中施加。
将本文所提出的改进理论应用于管1和管2,并与有限元应力结果进行对比。在柱坐标系下,两种复合材料组合管的应力分量随半径的变化曲线分别如图3和图4所示。其中,
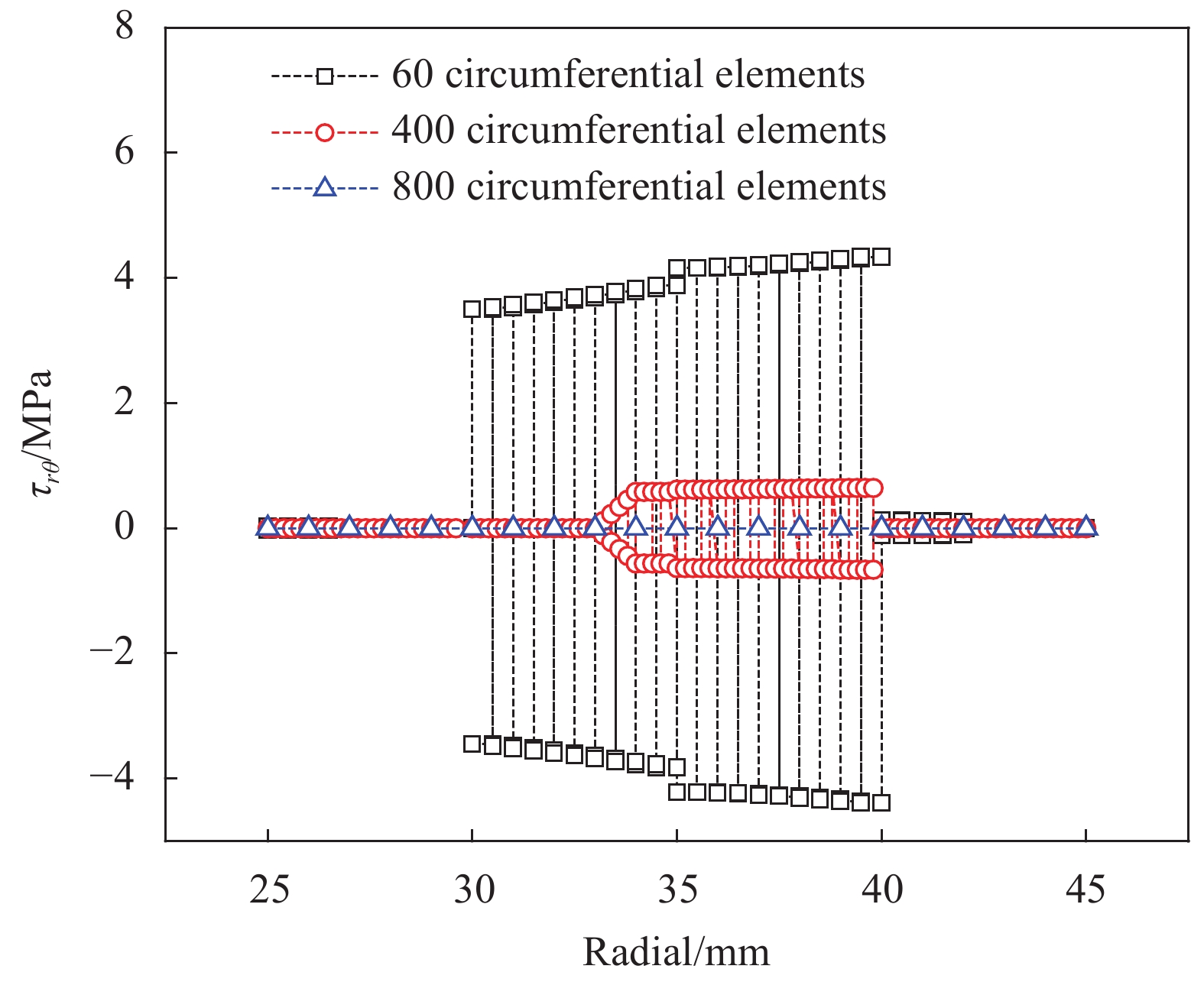
{\sigma _{\textit{Z}}} 、{\sigma _r} 、{\sigma _\theta } 和{\tau _{\theta {\textit{Z}}}} 四个应力分量的理论结果与有限元数值模拟结果吻合较好,而管1内{45^{\rm{o}}} 和- {45^{\rm{o}}} 两层的面外剪切应力分量{\tau _{r\theta }} 和{\tau _{r{\textit{Z}}}} 两种有限元计算结果在0值水平线上下震荡,管2内胆层的面外剪切应力分量{\tau _{r\theta }} 有限元计算结果也出现了相同的情况。剪切应力出现震荡的主要原因是环向网格数量较少,并且模型中的网格单元类型为C3D8R,此单元中心仅有1个积分点,虽然,这类单元可以提高计算效率,但也降低了计算精度。以管1面外剪切应力
{\tau _{r\theta }} 为例,如图5所示,随着环向网格数量的增加,管1面外剪切应力{\tau _{r\theta }} 在{45^{\rm{o}}} 和- {45^{\rm{o}}} 两个缠绕层内的震荡逐渐趋于0值水平线,这一模拟结果与面外剪切应力为0的基本理论假设一致。显然,增加环向网格数量可以获得较精确的结果,但网格数量的增加需耗费更多的计算机资源和计算周期,这也从侧面证明了本文改进理论的重要价值。4. 结 论
首先介绍了多层复合材料圆柱筒轴对称问题的传统计算方法,而后讨论了复合材料厚壁管中存在特殊缠绕角
\varphi = {0^{\rm{o}}} 或含有各向同性层时,参数\mu { _{3,n}} 和参数{A_n} 出现奇异性现象的原因,通过讨论缩减弹性系数{\beta _{ij,n}} 和特征参数{m_{i,n}} 在0°缠绕角邻域内的连续性,将参数的奇异性问题转化为对参数的极限分析。从而进一步地扩展了Lekhnitskii理论的应用范围,使得该理论适用于任意缠绕角。最后,通过有限元计算软件ABAQUS分析了不同复合材料组合管的力学响应,结果显示,基于精细化模型的有限元计算结果与改进理论结果基本一致。 -
图 1 轴对称载荷作用下的复合材料厚壁管
Figure 1. Composite tube subjected to axisymmetric loads
P, T, pi and po—Axial load, torque, internal pressure and outer pressure, respectively; r0 and rN—Internal radius and outer radius of the composite thick tube; rn and φn—Outer radius and winding angle of the nth layer; σZ—Axial stress component; σr, σθ and τrθ—Stress components parallel to the cross section; τθZ and τrZ—Stress components perpendicular to the cross section
表 1 各层材料的力学性能参数
Table 1 Material property for each layer
Carbon fiber/epoxy-resin E1=155 GPa, E2=E3=12.1 GPa; v12=v13=0.248; v23=0.458; G12=G13=4.4 GPa; G23=3.2 GPa Glass fiber/epoxy-resin E1=60 GPa, E2=E3=11 GPa;
v12 = v13=0.26; v23=0.4; G12=G13=7.6 GPa; G23=3.7 GPaSteel E=210 GPa;v=0.3 Notes: E1, E2, E3—Modulus in fiber direction, in-plane transverse modulus and out-of-plane transverse modulus respectively; ν12, G12—Poisson's ratio and shear modulus of fiber direction and in-plane transverse direction; ν13 and G13—Poisson's ratio and shear modulus of fiber direction and out-of-plane transverse direction; ν23 and G23—Poisson's ratio, shear modulus of in-plane transverse direction and out-of-plane transverse direction; E and v—Modulus and poisson’s ratio of the steel. -
[1] VASILIEV V, BARYNIN V A, RASIN A F. Anisogrid lattice structures-survey of development and application[J]. Composite Structures,2001,54(2):361-370.
[2] VASILIEV V, BARYNIN V A, RASIN A F. Anisogrid composite lattice structures development and aerospace applications[J]. Composite Structures,2012,94(3):1117-1127. DOI: 10.1016/j.compstruct.2011.10.023
[3] FAN Hualin, FANG Daining, CHEN Liming, et al. Manufacturing and testing of a CFRC sandwich cylinder with Kagome cores[J]. Composites Science and Technology,2009,69(15-16):2695-2700. DOI: 10.1016/j.compscitech.2009.08.012
[4] FAN H L, JING F N, FANG D N, et al. Mechanical properties of hierarchical cellular materials, Part I: Analysis[J]. Composites Science & Technology,2008,68:3380-3387. DOI: 10.1016/j.compscitech.2008.09.022
[5] 郑津洋, 李静媛, 黄强华. 车用高压燃料气瓶技术发展趋势和我国面临的挑战[J]. 压力容器, 2014(2):43-51. DOI: 10.3969/j.issn.1001-4837.2014.02.007 ZHENG Jinyang, LI Jingyuan, HUANG Qianghua. Technology trends of high pressure vehicle fuel tanks and challenges for China[J]. Pressure Vessel Technology,2014(2):43-51(in Chinese). DOI: 10.3969/j.issn.1001-4837.2014.02.007
[6] 中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会. 车用压缩氢气铝内胆碳纤维全缠绕气瓶: GB/T 35544—2017[S]. 北京: 中国标准出版社, 2017. Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Management Committee. FuIly-wrapped carbon fiber reinforced cylinders with an aluminum liner for the on-board storage of compressed hydrogen as a fuel for land vehicles: GB/T 35544—2017[S]. Beijing: China Standards Press, 2017(in Chinese).
[7] 顾付伟, 顾周越, 朱晓磊, 等. 一种无焊缝连接金属内衬复合材料压力容器的制备工艺及其液压实验[J]. 复合材料学报, 2021, 38(1):198-208. GU Fuwei, GU Zhouyue, ZHU Xiaolei, et al. The design and hydraulic tests of a metal liner composite overwrapped pressure vessels with seamless connection technology[J]. Acta Materiae Compositae Sinica,2021,38(1):198-208(in Chinese).
[8] 蔡光胜, 张锦光, 毛戈. 碳纤维复合材料直升机传动轴设计研究[J]. 玻璃钢/复合材料, 2019(10):71-75. CAI Guangsheng, ZHANG Jinguang, MAO Ge. Design and research of carbon fiber composite helicopter drive shaft[J]. Fiber Reinforced Plastics/Composites,2019(10):71-75(in Chinese).
[9] 胡晶, 李晓星, 张天敏, 等. 碳纤维复合材料传动轴承扭性能优化设计[J]. 复合材料学报, 2009, 26(6):177-181. DOI: 10.3321/j.issn:1000-3851.2009.06.030 HU Jing, LI Xiaoxing, ZHANG Tianmin, et al. Design optimization on torsion property of carbon-fiber composite drive shaft[J]. Acta Materiae Compositae Sinica,2009,26(6):177-181(in Chinese). DOI: 10.3321/j.issn:1000-3851.2009.06.030
[10] 沈观林. 复合材料力学[M]. 北京: 清华大学出版社, 2013. SHEN Guanlin. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2013(in Chinese).
[11] JIANG S Y, SUN F, FAN H L. Multi-failure theory of composite orthogrid sandwich cylinder[J]. Aerospace Science and Technology,2017,70(11):520-525.
[12] JIANG S Y, SUN F, FAN H L, et al. Fabrication and testing of composite orthogrid sandwich cylinder[J]. Composites Science & Technology,2017,142(4):171-179.
[13] XIA M, TAKAYANAGI H, KEMMOCHI K. Analysis of multi-layered filament-wound composite pipes under internal pressure[J]. Composite Structures,2001,53(4):483-491. DOI: 10.1016/S0263-8223(01)00061-7
[14] ROY A K, TSAI S W. Design of thick composite cylinders[J]. Journal of Pressure Vessel Technology,1988,110:255-262. DOI: 10.1115/1.3265597
[15] HYER M W. Hydrostatic response of thick laminated composite cylinders[J]. Journal of Reinforced Plastics and Composites,1988,7(4):321-340. DOI: 10.1177/073168448800700402
[16] LEKHNITSKII S G. Theory of elasticity of an anisotropic elastic body[M]. Moscow: Mir Publishers, 1981: 215-262.
[17] STROH A N. Dislocations and cracks in anisotropic elasticity[J]. Philosophical Magazine,1958,3:625-646. DOI: 10.1080/14786435808565804
[18] ZU L, WANG J, LI S. Analysis of multi-layered thick-walled filament-wound hydrogen storage vessels[J]. International Journal of Hydrogen Energy,2014,39(36):21083-21096. DOI: 10.1016/j.ijhydene.2014.10.075
[19] TING T C T. Anisotropic elasticity theory and applications[M]. Oxford: Oxford University Press, 1996: 118-163.
[20] JOLICOEUR C, CARDOU A. Analytical solution for bending of coaxial orthotropic cylinders[J]. Journal of Engineering Mechanics,1994,120(12):2556-2574. DOI: 10.1061/(ASCE)0733-9399(1994)120:12(2556)
[21] 张灿辉, 张建霖, 柯淼宏, 等. 采用独立双应力函数分析纯弯曲复合材料厚壁管[J]. 厦门大学学报(自然科学版), 2017, 56(6):900-906. ZHANG Canhui, ZHANG Jianlin, KE Miaohong, et al. Analysis of composite material thick walled tubes subjected to pure bending loading using two stress functions independent to each other[J]. Journal of Xiamen University (Natural Science),2017,56(6):900-906(in Chinese).
[22] 柯淼宏. 纯弯曲复合材料组合管统一联系参数法的进一步研究[D]. 厦门: 厦门大学, 2017. KE Miaohong. More investigation of unified-connected-parameter method for composite material combined tubes under pure bending loading[D]. Xiamen: Xiamen University, 2017(in Chinese).
[23] 刘沛. 复合材料厚壁管弯曲性能分析的统一参数法及杂交应力有限元最佳假设应力场构造的定量方法[D]. 厦门: 厦门大学, 2014. LIU Pei. The unified-parameter method for bending perfor-mance analysis of composite thick tube as well as the quanti-tave method to determine the optimal assumed stress fields for hybrid stress finite elements[D]. Xiamen: Xiamen University, 2014(in Chinese).
[24] ZHANG C H, HOA S V. Limit based approach to the stress analysis of cylindrically orthotropic composite cylinders (0/90) subjected to pure bending[J]. Composite Structure,2012,94:2610-2619. DOI: 10.1016/j.compstruct.2012.02.030
[25] ZHANG C H, HOA S V, LIU P. A method to analyze the pure bending of tubes of cylindrically anisotropic layers with arbitrary angles including 0 and 90[J]. Composite Structure,2014,109:57-67. DOI: 10.1016/j.compstruct.2013.10.038
-
期刊类型引用(1)
1. 黄德流. 厚壁管焊接接头中间射线检验技术探究. 现代工业经济和信息化. 2022(11): 283-285+294 .  百度学术
百度学术
其他类型引用(1)
-





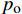

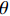

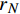
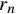
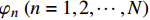
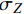
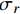
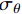
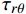

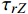

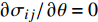



 下载:
下载: