复合材料帽型加筋板等效弯曲刚度

吴菁; 胡明勇; 章向明; 杨少红; 王安稳

doi:10.13801/j.cnki.fhclxb.20211208.001

复合材料帽型加筋板等效弯曲刚度

海军工程大学　基础部，武汉 430033

基金项目: 国家自然科学基金(51479206)；海军工程大学2022年自主研发项目(425317T00G)

详细信息

通讯作者:
胡明勇，博士，教授，硕士生导师，研究方向为船舶结构力学和复合材料力学　E-mail: shuai_humingyong@163.com

中图分类号: TB330.1
计量
- 文章访问数: 1508
- HTML全文浏览量: 798
- PDF下载量: 141
出版历程
- 收稿日期: 2021-10-13
- 修回日期: 2021-11-21
- 录用日期: 2021-11-25
- 网络出版日期: 2021-12-10
- 刊出日期: 2022-11-30

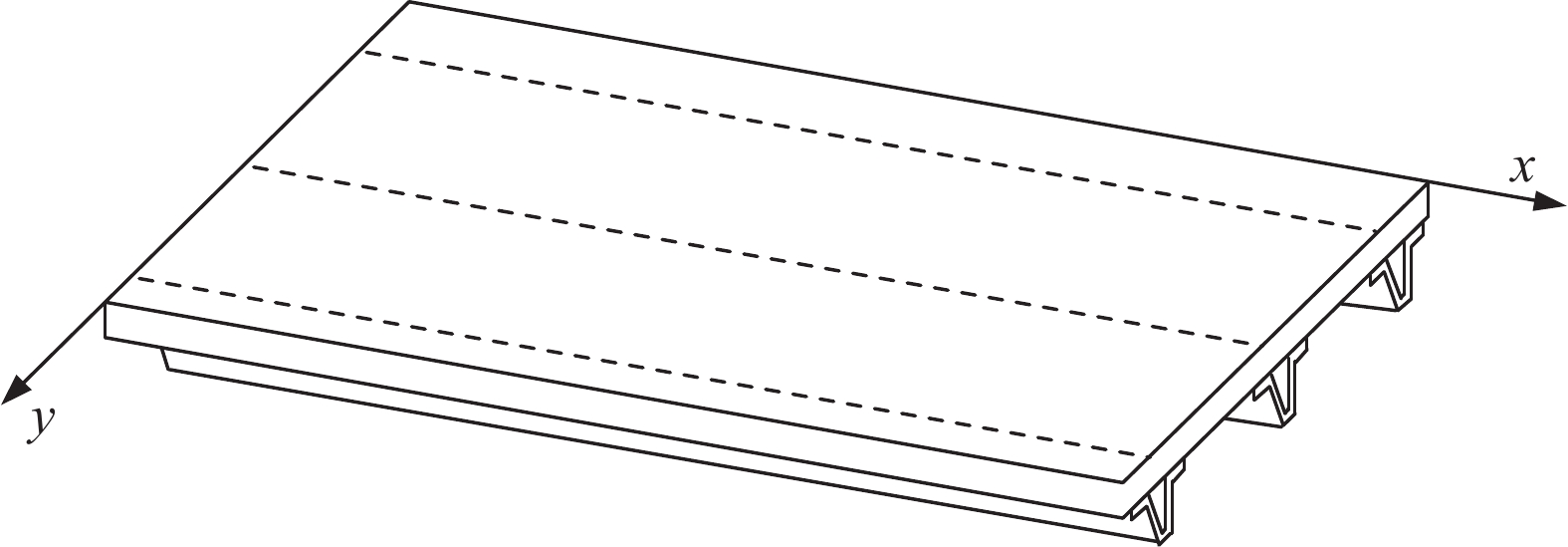
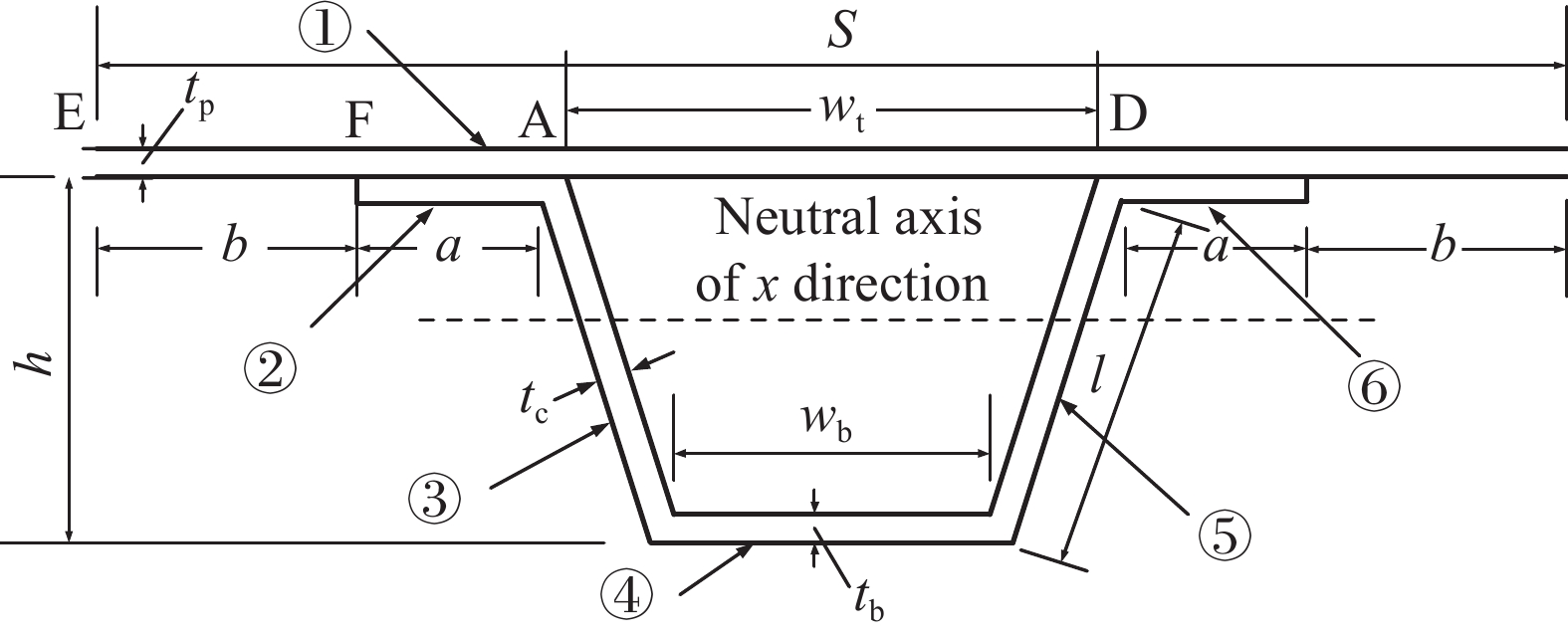
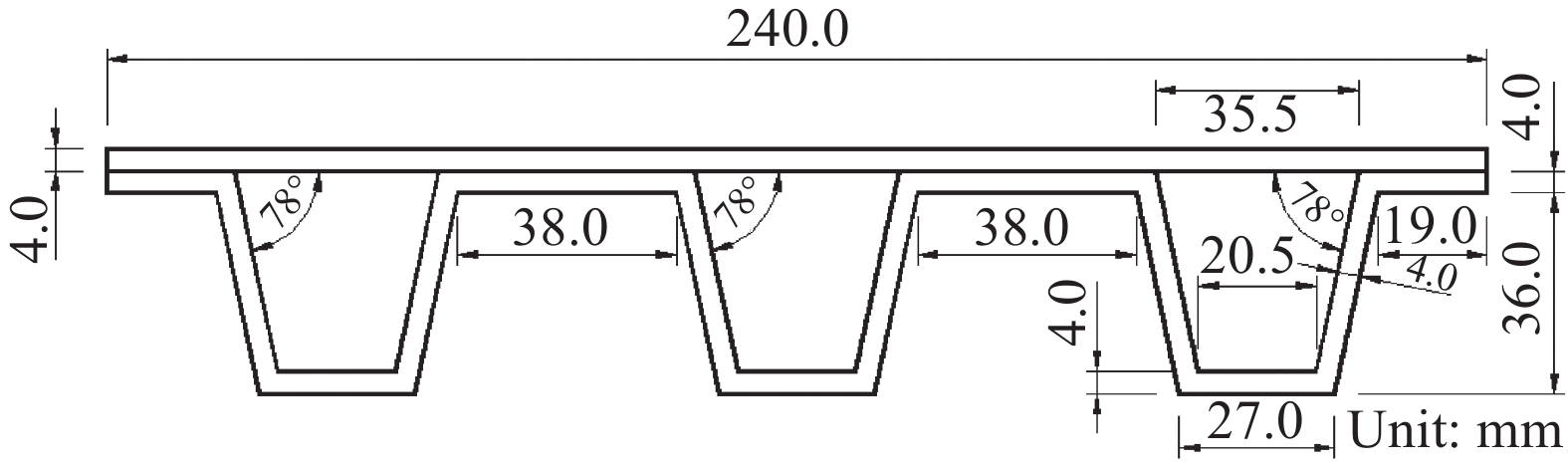
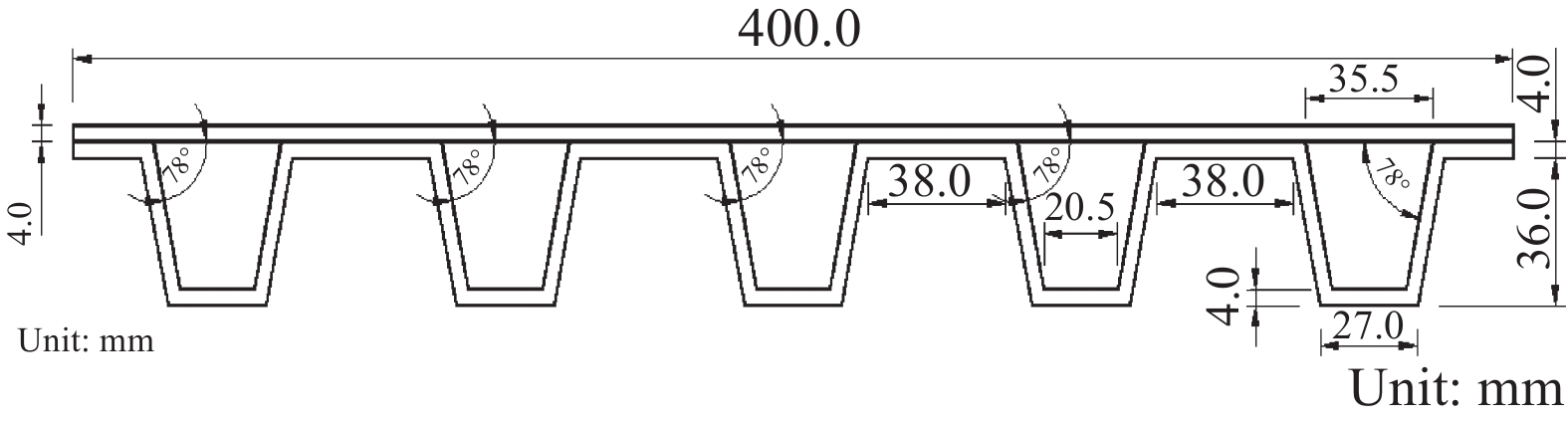
Equivalent bending stiffness of composite hat-stiffened panel

Department of Basic Courses, Naval University of Engineering, Wuhan 430033, China

摘要

摘要: 复合材料船体结构主要由纵向或横向加筋板架构成，复合材料加筋板设计可以近似处理成正交异性板，需要定量计算复合材料加筋板的等效刚度。利用卡氏定理推导了复合材料帽型加筋层合板的纵向和横向弯曲刚度，给出了等效层合板弯曲刚度的解析表达式。通过复合材料帽型加筋层合板纵向和横向三点弯曲试验实测梁的跨中挠度并与等效弯曲刚度对应的解析解比较；用ABAQUS有限元软件计算三点弯曲纵向和横向复合材料帽型加筋梁和四边简支复合材料帽型加筋板中心点的挠度并与等效弯曲刚度对应的解析解比较。结果表明：解析解与数值计算及试验结果对比，吻合较好，验证了等效弯曲刚度解析表达式的正确性，且具有较好的计算精度，可作为复合材料帽型加筋板设计的计算依据。
- 复合材料船体 /
- 帽型加筋板 /
- 等效弯曲刚度 /
- 解析解 /
- 弯曲试验
Abstract: The composite hull is mainly composed of longitudinally or transversely stiffened laminates. The design of composite stiffened laminates can be approximated as an orthogonal anisotropic plate and the equivalent stiffness of stiffened composite plates needs to be calculated quantitatively. The longitudinal and transverse bending stiffness of hat-stiffened panel were derived using the Castigliano's theorem. The analytical expressions for the equivalent bending stiffness were provided. The longitudinal and transverse three-point bending tests of the hat-stiffened laminates were designed to measure the mid-span deflection of the beam and the obtained test data were compared with the analytical solution corresponding to the equivalent bending stiffness. The deflection at the center point of longitudinally and transversely hat-stiffened composite beam in three-point bending and the four-sided simply-supported hat-stiffened composite laminates was calculated by ABAQUS and compared with the analytical solution corresponding to the equivalent bending stiffness. The results show that the analytical solutions are in good agreement with the numerical calculations and the experimental results, which verifies the correctness of the analytical expression of the equivalent bending stiffness. It can be used confidently in the design of the hat-stiffened panel.
- composite hull /
- hat-stiffened panel /
- equivalent bending stiffness /
- analytic solution /
- bending test

HTML全文

具有轻质、高强、免锈蚀及抗疲劳性能良好等诸多优点的碳纤维增强聚合物复合材料(Carbon fiber reinforced polymer，CFRP)筋有望成为传统钢制筋材的替代品，特别是对于在恶劣环境下工作的预应力结构^[1-3]。相较于易导致CFRP筋出现“切口效应”而过早发生横向破坏的夹持型锚固系统，粘结型锚固系统通过CFRP筋-粘结介质界面的化学胶着力、摩擦力及机械咬合力可实现对CFRP筋更可靠、有效的锚固^[4-5]。活性粉末混凝土(Reactive powder concrete，RPC)以其优异的力学性能和耐久性能可成为有效锚固CFRP筋的粘结介质^[6]。RPC灌注的CFRP筋粘结型锚固系统已在实际工程中得以成功应用，并表现出优异的锚固性能^[7-8]。然而，CFRP筋及其粘结型锚固系统在建造和运营过程中可能遭受火灾作用^[9-12]。火灾下CFRP筋及CFRP筋-粘结介质界面因树脂基体较弱的耐高温性能而易成为受力薄弱环节，则高温下CFRP筋及其粘结型锚固系统的力学性能值得关注。因此，对CFRP筋及其粘结型锚固系统的高温力学性能进行研究是十分必要的。

国内外部分学者对高温下CFRP筋的力学性能开展了研究。Wang等^[13]试验研究了20~600℃作用下CFRP筋力学性能退化规律，结果表明：高温下CFRP筋应力-应变始终呈线性关系；CFRP筋抗拉强度随处理温度升高而近似线性衰减，并在500℃时完全丧失；处理温度高于350℃时，CFRP筋弹性模量急剧下降。杨桢楠^[14]试验研究了100~500℃作用下CFRP筋的力学性能，结果表明：处理温度大于200℃时，CFRP筋的抗拉强度与弹性模量均大幅下降。周飞^[15]对20~500℃作用下CFRP筋力学性能进行了试验研究，提出了适于表征高温下CFRP筋轴拉性能退化规律的指数函数模型。上述研究所采用CFRP筋的树脂玻璃化转变温度T_g均小于200℃。

另有部分学者对高温下纤维增强塑料(Fiber reinforce plastic，FRP)筋-混凝土界面的粘结性能进行了试验研究。吕西林等^[16]研究了处理温度、混凝土强度与粗骨料粒径等参数对20~250℃作用下玻璃纤维增强聚合物复合材料(Glass fiber reinforced polymer，GFRP)筋-混凝土界面粘结性能的影响规律，结果表明处理温度高于110℃时，界面粘结强度相较于常温下降低了85%~90%。Katz等^[17-18]对20~250℃作用下GFRP筋-混凝土界面粘结性能进行了研究，给出了适于表征界面粘结强度衰减规律的半经验模型，结果表明处理温度为250℃时，界面粘结强度仅为常温时的10%~20%；筋材表面处理方式是影响界面粘结强度的重要因素。王晓璐等^[19]研究了20~350℃作用下FRP (GFRP、玄武岩纤维增强聚合物复合材料(Basalt fiber reinforced polymer，BFRP))筋-混凝土界面的粘结性能，提出了高温下界面粘结强度衰减模型与粘结-滑移本构模型，结果表明处理温度由60℃增至120℃时，界面粘结强度的衰减幅度最大；200℃时界面粘结强度仅为常温时的15%。鞠竹等^[20]对20~190℃作用下GFRP筋-混凝土界面的粘结性能进行了研究，并提出了适用于表征高温下界面粘结-滑移行为的双折线模型。

综上所述，现有研究侧重于高温下具有较低T_g(T_g<200℃) FRP筋材轴拉性能及FRP筋-混凝土界面粘结性能，鲜见关于高温下CFRP筋(T_g>200℃)及其粘结型锚固系统力学性能研究的报道。为此，本文将在方志等^[21]的研究(侧重于研究高温后CFRP筋及其粘结型锚固系统的残余力学性能，是开展火灾后相应评估工作的依据)的基础上，对高温下一种抗火性能优良的CFRP筋(T_g>200℃)及其粘结型锚固系统的静力性能进行试验研究，以揭示处理温度对高温下CFRP筋轴拉性能及其锚固性能的影响规律，提出适于表征高温下CFRP筋轴拉性能及其锚固性能的实用计算公式，为评估CFRP筋及其锚固系统的抗火性能提供依据。本文与前期研究的成果将共同为高性能CFRP筋材的工程应用提供理论基础。

1. 试验概况

1.1 试件设计

参照《纤维增强复合材料筋基本力学性能试验方法》(GB/T 30022—2013)^[22]设计CFRP筋轴拉试件，以筋材处理温度T(分别为25℃、100℃、210℃和300℃)为试验参数，设计4组试件，每组3个试件，共计12个试件。

CFRP筋轴拉试件由长为680 mm的自由段及其两端长为360 mm的粘结型锚固系统组成，总长共计1400 mm，如图1所示。其中，锚固CFRP筋的粘结型锚固系统通过在外径为42 mm、内径为36 mm的钢套筒内灌注RPC形成，筋材周围RPC保护层厚度为12 mm。

选取试验锚的处理温度T (分别为25℃、100℃、210℃、300℃)为锚固性能试验的参数，设计4组试件，每组2个试件，共计8个试件。锚固性能试件的粘结长度l均设置为5d，其中d为CFRP筋的公称直径，d=12 mm。

CFRP筋-RPC锚固性能试件由CFRP筋材自由段及其位于左右两侧的工具锚与试验锚组成，如图2所示。以CFRP筋轴拉试件的粘结型锚固系统作为锚固性能试件的工具锚。为便于测定CFRP筋-RPC界面粘结-滑移性能，锚固性能试件右侧的试验锚通过在外径为76 mm、内径为72 mm的钢套筒内灌注RPC形成。试验锚长度设置为420 mm，以与高温炉炉腔长度380 mm相匹配。为获取试验预设的粘结长度l=5d，试验锚加载端与自由端的CFRP筋外侧均预埋长度为180 mm的耐高温陶瓷套管。利用耐高温胶密封陶瓷套管与CFRP筋间的孔隙，以防止灌注粘结介质时RPC进入陶瓷套管内。此外，利用耐高温胶带将K型热电偶的较少部分金属探头固定于CFRP筋-RPC界面，以实时监测试验过程中粘结界面的温度。

图 1 碳纤维增强聚合物复合材料(CFRP)筋轴拉试件

Figure 1. Axial tensile specimen of carbon fiber reinforced polymer (CFRP) bar

下载: 全尺寸图片幻灯片

图 2 CFRP筋-活性粉末混凝土(RPC)锚固性能试件

Figure 2. Anchorage performance specimen of CFRP bar-reactive powder concrete (RPC)

下载: 全尺寸图片幻灯片

利用设置在锚筒两端的聚乙烯封盖中心处圆孔精确定位轴拉试件或锚固系统性能试件的CFRP筋。浇筑钢锚筒的粘结介质RPC形成粘结型锚固系统，将其静置24 h后再采用90℃蒸汽养护48 h。

1.2 试验材料

轴拉与锚固性能试验所用的CFRP筋材均由江苏连云港中复碳芯电缆科技有限公司提供，其外观尺寸及T_g如图3和表1所示。CFRP筋由体积含量为66.3vol%的T700SC连续碳纤维丝束与TP224环氧树脂拉挤而成。

CFRP筋粘结型锚固系统的粘结介质-RPC由不含钢纤维的商品预混料加水拌制而成，其设计强度等级为RPC150。边长100 mm的立方体实测抗压强度为158 MPa，RPC配合比(单方质量比)如表2所示。

图 3 CFRP筋及其外观尺寸

Figure 3. CFRP bar and its external dimensions

下载: 全尺寸图片幻灯片

表 1 CFRP筋外观尺寸及玻璃化转变温度T_g

Table 1. Dimensions and glass transition temperatureT_g of CFRP bar

Nominal diameter/mm	Rib width/mm	Rib height/mm	Embossing space/mm	T_g/℃
12	9.26	0.27	14.8	210

下载: 导出CSV

| 显示表格

表 2 RPC配合比及抗压强度

Table 2. Mix proportion and compressive strength of RPC

Strength grade	Cement	Silica fume	Quartz flour	Quartz sand	Water reducer	Water binder ratio
RPC150	1	0.25	0.25	1.1	0.02	0.16

下载: 导出CSV

| 显示表格

1.3 温升加载方式与测点布置

轴拉与锚固性能试验的温升加载及测量装置分别如图4、图5所示。试验中采用的温升加载方式参考金属材料高温拉伸试验方法(GB/T 4338—2006)^[23]，如图6所示。将轴拉试件的筋材自由段或锚固性能试件的试验锚放置于高温试验炉(尺寸为380 mm (长)×410 mm (宽)×650 mm (高)) 中，以3℃/min的温升速率温升至目标温度，恒温一定时间(对于轴拉试件，通常恒温20 min；对于锚固性能试件，恒温至CFRP筋-RPC界面温度达到目标温度)后再进行单调加载。高温炉由长沙科辉炉业科技有限公司提供，其升温区间和最大升温速率分别为100~1200℃和100℃/min。利用设置在CFRP筋表面与CFRP筋-RPC界面的K型热电偶分别监测轴拉与锚固性能试件的实时温度。

图 4 轴拉试验的温升及加载装置

MTS—Mechanical testing and simulation

Figure 4. Setups of elevated temperature and loading of axial tensile test

下载: 全尺寸图片幻灯片

图 5 锚固性能试验的温升及加载装置

Figure 5. Setups of elevated temperature and loading of anchorage performance test

下载: 全尺寸图片幻灯片

图 6 温升及加载过程

Figure 6. Processes of elevated temperature and loading

T₀—Room temperature; T_a—Target temperature; P_u—Ultimate load; T—Temperature; P—Load; t—Time; t₀—Test start time; t₁—Time to target temperature; t₂—Start load time; t₃—Time to failure

下载: 全尺寸图片幻灯片

当试件温度达到目标温度且稳定时，利用600 kN液压伺服试验机(南京诺尔泰设备制造有限公司)以1 mm/min的位移加载速率对试件施加轴向拉力或拉拔力。其中，锚固性能试件的拉拔力需借助固定于液压伺服试验机夹具上的工具锚，对放置在反力架上的试验锚进行施加，如图5所示。为使锚固性能试件始终处于铅直受力状态，在反力架与试验锚之间设置了可转动的开孔球铰。利用液压伺服试验机的力传感器采集试件拉拔力。采用与CFRP筋表面紧密接触的高温引伸计测量轴拉试件筋材自由段中部的应变。锚固性能试件加载端CFRP筋-RPC界面滑移通过固定于CFRP筋上的位移传感器获取。

2. CFRP筋轴拉试验结果及分析

2.1 CFRP筋轴拉试件的破坏形态

高温下各CFRP筋轴拉试件的典型破坏形态均为拉断破坏，破断位置均分布于筋材自由段区域内；随着处理温度逐渐升高，拉断破坏形态由筋材断口破坏与少量丝束分离的片状形态转变为纤维丝“蓬松”的形态，如图7所示。

常温下，试件的轴拉应力超过80%极限抗拉强度后，少量纤维丝破断而发出细小声响；当轴拉应力达到极限抗拉强度时，试件会突然破坏而形成位于自由段中部的断口，并伴随有轻微的炸裂现象。但文中常温试件炸裂程度较轻，且筋材自由段左侧区域因炸裂形成的碳纤维细条未能及时收集而丢失，导致图7中所示常温试件的破坏形态与典型的纤维束爆裂形态(纤维束炸开的扫帚状)存在一定的差别。

图 7 CFRP筋轴拉试件的破坏形态

Figure 7. Typical failure modes of CFRP bar axial tensile specimens

下载: 全尺寸图片幻灯片

对于处理温度为100~210℃的轴拉试件，其轴拉应力接近极限抗拉强度时因少量纤维丝破断而发出细小声响。由于树脂性能退化较轻微，少量破断的纤维丝呈丝束分离的片状形态。筋材轴拉应力达到极限抗拉强度后突然发生伴有清脆响声的破断，其断口位置靠近筋材自由段中间区域。

对于处理温度不低于T_g=210℃的轴拉试件，其自由段中部树脂因高温作用而逐渐软化、甚至部分分解(厂家提供的树脂基体5wt%质量损失相应温度为318℃)，导致树脂-纤维界面粘结性能快速衰减、部分纤维丝间无树脂而裸露。筋材轴拉应力达到极限抗拉强度后，其自由段中部裸露的纤维丝发生破断而呈现“蓬松”的状态。

2.2 CFRP筋轴拉试验结果

各轴拉试件的主要试验结果、应力-应变曲线如表3与图8所示。可见，高温下轴拉试件破断前的应力-应变基本呈线性关系。利用应力-应变曲线中0.2~0.5倍极限抗拉强度范围内的割线模量确定筋材轴向试件的弹性模量^[24]。高温下CFRP筋轴拉性能的衰减规律如图9所示。

表 3 CFRP筋轴向拉伸试验结果

Table 3. Results of axial tensile test for CFRP bar

Specimen	P_u/kN	f_u/MPa	${\overline f _{\text{u}}}/{\text{MPa}}$	E/GPa	$\overline E /{\text{GPa}}$	${ \varepsilon _{\text{u}}}/{10^{ - 6}}$	${\overline \varepsilon _{\text{u}}}/{10^{ - 6}}$
AT-T25-1	280.8	2631	2650	162.2	159.9	15627	15513
AT-T25-2	283.1	2653		161.8		15464
AT-T25-3	284.5	2666		155.6		15448
AT-T100-1	274.2	2569	2588	133.0	141.6	18506	18387
AT-T100-2	278.0	2605		143.5		18343
AT-T100-3	276.3	2589		148.3		18312
AT-T210-1	198.9	1864	1861	98.7	102.9	18298	18201
AT-T210-2	192.7	1806		105.5		18254
AT-T210-3	204.3	1914		104.4		18051
AT-T300-1	176.0	1649	1566	82.6	87.9	17963	17816
AT-T300-2	157.0	1471		92.4		17762
AT-T300-3	168.3	1577		88.8		17723
Notes: In the specimen code, AT is axial tensile, T indicates the treatment temperature, the last number indicates the same specimen number; P_u—Ultimate bearing capacity; f_u—Tensile strength; ${\overline f _{\text{u}}}$ —Average value; E—Elastic modulus; $\overline E$ —Average value; ${ \varepsilon _{\text{u}}}$ —Ultimate tensile strain; ${\overline \varepsilon _{\text{u}}}$ —Average value.

下载: 导出CSV

| 显示表格

图 8 CFRP筋轴拉试件的应力-应变曲线

Figure 8. Stress-strain curves of CFRP bar axial tensile specimen

下载: 全尺寸图片幻灯片

相较于常温试件，100℃下轴拉试件的抗拉强度、弹性模量分别减小了2.3%、11.4%，而极限拉应变增大了18.5%；210℃和300℃下轴拉试件的抗拉强度、弹性模量分别减小了(29.8%、40.9%)和(35.6%、45%)，而极限拉应变分别增大了17.3%和14.8%。可见，高温下筋材弹性模量较抗拉强度受处理温度的影响更为显著，两者的衰减幅度在处理温度由100℃增至210℃时达到最大。高温下筋材的极限拉应变较常温下有所增大，并随处理温度升高而呈先增大后减小的变化趋势。究其原因，处理温度为T_g时，筋材自由段区域的树脂逐渐软化，导致筋材整体性退化明显，各纤维间的受力更趋不均，使筋材抗拉强度与弹性模量退化显著。此外，高温下筋材的弹性模量(或轴拉刚度)较抗拉强度更依赖于树脂基体的力学性能。高温下树脂基体的力学性能因其较差的耐高温性能而快速衰减，其退化幅度远大于碳纤维，进而导致高温下筋材弹性模量的衰减幅度较抗拉强度更大、极限拉应变较常温下有所增加。

图 9 高温下CFRP筋轴拉性能衰减规律

$f_u(T)/f_u$ —Reduction coefficient of tensile strength under high-temperature;

$E_u(T)/E_u$ —Reduction coefficient of elastic modulus under high-temperature;

$\varepsilon _u(T)/\varepsilon_u$ —Reduction coefficient of ultimate tensile strain under high-temperature

Figure 9. Decay law of axial tensile performance of CFRP bar exposed to elevated temperature

下载: 全尺寸图片幻灯片

3. CFRP筋-RPC锚固性能试验结果及分析

3.1 CFRP筋-RPC锚固性能试件的破坏形态

图10为CFRP 筋-RPC 锚固性能试件破坏形态。将锚固性能试件破坏后的试验锚加载端含陶瓷套管区域切除，以便观察CFRP筋-RPC界面的破坏形态，如图10(a)所示。高温下锚固性能试件的破坏形态均为滑移破坏，具体表现为筋材表面压纹肋发生剪切破坏，其核心部分从锚固区被拔出，筋材肋间RPC未被拔出。随着处理温度升高，筋材压纹肋及肋间表面树脂逐渐软化、甚至部分分解，而高温下RPC的剩余剪切性能远高于树脂；导致压纹肋更易发生剪切破坏、从锚固区拔出的筋材核心部分表面压纹肋残留的痕迹越发模糊，无树脂包裹而裸露的部分纤维丝因与肋间RPC发生摩擦而破坏，如图10(b)所示。因此，高温下CFRP筋-RPC界面粘结性能主要取决于树脂的剩余剪切性能。

图 10 CFRP筋-RPC锚固性能试件破坏形态

Figure 10. Typical failure modes of CFRP bar-RPC anchorage performance specimens

下载: 全尺寸图片幻灯片

3.2 CFRP筋-RPC锚固性能试件的粘结-滑移曲线

各锚固性能试件的试验结果、高温下的粘结-滑移曲线分别如表4和图11所示。可见，各锚固性能试件的粘结-滑移曲线均可分为以下四个阶段：(1) 线性段。粘结-滑移基本呈线性关系，加载端的粘结界面滑移较小，均在0~1 mm之间。粘结界面的切应力主要由筋材与RPC间化学胶着力抵抗。粘结界面的化学胶着力随处理温度升高而逐渐减小，导致加载端的初期滑移逐渐增大；(2) 非线性上升段。粘结-滑移呈明显的非线性关系，筋材与粘结介质间化学胶着力丧失，粘结界面的切应力主要由筋材与RPC间摩擦力、筋材表面凸起的压纹肋及肋间RPC形成的机械咬合力共同抵抗。筋材表面的压纹肋树脂抗剪性能逐渐衰减，导致粘结强度逐渐降低；(3) 下降段。筋材表面的部分压纹肋发生剪切破坏，其与肋间RPC的机械咬合力丧失。抵抗粘结界面切应力的机械咬合力逐渐减小，导致CFRP筋-RPC界面滑移继续增大；(4) 残余段。界面的切应力主要由未拔出的筋材核心部分与RPC界面间摩擦力抵抗。随着滑移增大，试验锚陶瓷管内的带肋筋材进入锚固区，其表面压纹肋与RPC间机械咬合力参与抵抗粘结界面切应力，进而导致残余段可承担的粘结界面切应力逐渐增加。

图 11 高温下CFRP筋-RPC锚固性能试件的粘结-滑移曲线

Figure 11. Bond-slip curves of CFRP bar-RPC anchorage performance specimens exposed to elevated temperature

下载: 全尺寸图片幻灯片

采用下式计算试件锚固区CFRP筋-RPC界面的平均粘结强度τ_u，并将计算结果示于表4：

${\tau _{\text{u}}} = \frac{{{P_{\text{u}}}}}{{{\text{π}}dl}}$

(1)

式中：P_u为极限荷载值；d为筋材公称直径；l为粘结长度。

表 4 CFRP筋-RPC锚固性能试验结果

Table 4. Results of CFRP bar-RPC anchorage performance test

Specimen	T/℃	P_u/kN	${\overline P _{\text{u}}}/{\text{kN}}$	τ_u/MPa	s/mm	$\overline s_{\rm{u}} /{\text{mm}}$
A-T25-L5d-1	25	66.74	66.38	29.36	6.74	6.67
A-T25-L5d-2	25	66.02	66.38	29.36	6.60	6.67
A-T100-L5d-1	100	50.58	52.84	23.37	6.44	6.53
A-T100-L5d-2	100	55.10	52.84	23.37	6.62	6.53
A-T210-L5d-1	210	34.30	31.47	13.92	5.88	6.01
A-T210-L5d-2	210	28.64	31.47	13.92	6.14	6.01
A-T300-L5d-1	300	11.85	9.85	4.36	5.69	5.63
A-T300-L5d-2	300	7.85	9.85	4.36	5.57	5.63
Notes: In the specimen code, A is anchorage, T indicates the treatment temperature, the last number indicates the same specimen number; T—Treatment temperature; L—Bond length; τ_u—Average bond strength; s—Slip of loading end corresponding to P_u; d—Diameter of CFRP bar; $\bar P_{\rm{u}}$ —Average value of ultimate bearing capacity for anchorage system; $\bar s_{\rm{u}}$ —Average value of the slip of loading end corresponding to P_u。

下载: 导出CSV

| 显示表格

3.3 温度对CFRP筋-RPC锚固性能试件粘结强度的影响

锚固性能试件粘结强度随温度的变化规律如表4与图12所示。可见，试件粘结强度随处理温度升高而线性退化。相较于常温下的锚固性能试件，100℃、210℃和300℃下试件粘结强度分别减小了20.4%、52.6%和85.1%。究其原因为随着处理温度逐渐升至210℃和300℃，筋材表面的压纹肋树脂逐渐软化、甚至部分分解，导致用于抵抗粘结界面切应力的主要抗力—筋材压纹肋与肋间RPC的机械咬合力大幅退化。

4. 公式建立

4.1 高温下CFRP筋轴拉性能

对本文高温下轴拉试验结果进行回归分析，构建适于表征高温下(25℃ $\leqslant$ T $\leqslant$ 300℃) CFRP筋轴拉性能退化规律的计算模型，如以下两式及图9(a)、图9(b)所示：

$\frac{{{f_{\rm{u}}} \left( T \right)}}{{{f_{\rm{u}}}}} = 0.387 \exp \left[ { - 3 {{\left( {\frac{{T - {T_0}}}{{{T_{\rm{g}}}}}} \right)}^4}} \right] + 0.613$

(2)

$\frac{{{E_{\rm{u}}} \left( T \right)}}{{{E_{\rm{u}}}}} = 0.47 \exp \left[ { - 3 {{\left( {\frac{{T - {T_0}}}{{{T_{\rm{g}}}}}} \right)}^2}} \right] + 0.53$

(3)

将式(2)除以式(3)，可得高温下CFRP筋极限拉应变退化规律的计算公式为

$\frac{{{\varepsilon _{\rm{u}}} \left( T \right)}}{{{\varepsilon _{\rm{u}}}}} = \frac{{0.387 \exp \left[ { - 3 {{\left( {\dfrac{{T - {T_0}}}{{{T_{\rm{g}}}}}} \right)}^4}} \right] + 0.613}}{{0.47 \exp \left[ { - 3 {{\left( {\dfrac{{T - {T_0}}}{{{T_{\rm{g}}}}}} \right)}^2}} \right] + 0.53}}$

(4)

式中：f_u(T)、E_u(T)、ε_u(T)分别为高温下CFRP筋的抗拉强度、弹性模量及极限拉应变；f_u、E_u、ε_u为常温下CFRP筋的抗拉强度、弹性模量及极限拉应变；T₀为常温25℃；25℃ $\leqslant$ T $\leqslant$ 300℃。

图 12 处理温度对CFRP筋-RPC界面黏结强度的影响

Figure 12. Effect of elevated temperature on bond strength of CFRP bar-RPC interface

下载: 全尺寸图片幻灯片

利用式(4)计算本文各轴拉试件的极限拉应变，并将其与试验值进行对比分析，结果如表5与图9(c)所示。试验值/计算值的平均值及变异系数分别为1.010与0.01，表明式(4)可较准确地表征高温下(25℃ $\leqslant$ T $\leqslant$ 300℃) CFRP筋极限拉应变的退化规律，亦表明式(2)、式(3)均具有较高计算精度。

为明确T_g对高温下CFRP筋轴拉性能的影响规律，将本文CFRP筋(T_g=210℃)轴拉性能退化规律与文献[15]中CFRP筋(T_g=126℃)相应结果进行对比分析，如图9(a)、图9(b)及图13所示。可见本文CFRP筋极限抗拉强度和弹性模量随温度的衰减规律与文献[15]试验结果基本相似；相较于文献[15]选用的CFRP筋(T_g=126℃)，本文筋材(T_g=210℃)的高温轴拉性能更优，300℃下本文筋材的轴拉性能较常温试件仅退化46%~50%，如图9(a)与图9(b)所示；但本文筋材轴拉性能受(T−T₀)/T_g的影响更显著，如图13所示。

表 5 CFRP筋轴拉试件极限拉应变试验值与计算值对比

Table 5. Comparison of measured and predicted ultimate tensile strain of CFRP bar axial tensile specimens

Specimen	ε_u,t/10⁻⁶	ε_u,c/10⁻⁶	ε_u,t/ε_u,c
AT-T25	15513	15513	1.000
AT-T100	18387	17902	1.030
AT-T210	18201	18227	0.999
AT-T300	17816	17852	0.998
Average			1.010
Variation coefficient			0.01
Note: ε_u,t, ε_u,c—Experimental and calculated values of ultimate tensile strain of axial tensile specimen respectively.

下载: 导出CSV

| 显示表格

图 13 (T−T₀)/T_g对高温下CFRP筋轴拉性能的影响

Figure 13. Effect of (T−T₀)/T_g on axial tensile performance of CFRP bar exposed to elevated temperature

下载: 全尺寸图片幻灯片

4.2 高温下CFRP筋-RPC锚固性能试件界面粘结强度

基于ACI 440.1R-15^[24]中FRP筋-普通混凝土界面粘结强度的理论模型，对表4中的实测数据进行回归分析，构建适于表征高温下CFRP筋-RPC界面粘结强度退化规律的计算公式，如下式所示：

$\frac{{{\tau _{\rm{u}}}(T)}}{{\sqrt {{f_{{\rm{cu}}}}} }} = \left[ {1 - \frac{{0.64(T - {T_0})}}{{{T_{\rm{g}}}}}} \right]\left( {2 + 1.89\frac{d}{l}} \right)$

(5)

式中：f_cu为RPC的立方体抗压强度；T₀为室温，25℃；25℃ $\leqslant$ T $\leqslant$ 300℃。

利用式(5)预测各试件的平均粘结强度，结果如表6所示，实测值/预测值的平均值及变异系数分别为0.99与0.06，表明式(5)可较准确地表征高温下(25℃ $\leqslant$ T $\leqslant$ 300℃) CFRP筋-RPC界面粘结强度的退化规律。

表 6 CFRP筋-RPC界面粘结强度试验值与计算值对比

Table 6. Comparison between measured and predicted bond strength of CFRP bar-RPC interface

Specimen	f_cu/MPa	τ_u,t/MPa	τ_u,c/MPa	τ_u,t/τ_u,c
A-T25-L5d	158	29.36	29.89	0.98
A-T100-L5d	158	23.37	23.06	1.01
A-T210-L5d	158	13.92	13.04	1.07
A-T300-L5d	158	4.36	4.84	0.90
Average				0.99
Variation coefficient				0.06
Notes: f_cu—Cube compressive strength of RPC; τ_u,t, τ_u,c—Experimental and calculated values of interfacial bond strength between CFRP bars and RPC, respectively.

下载: 导出CSV

| 显示表格

4.3 高温下CFRP筋-RPC锚固性能试件临界锚固长度

将温升处理下CFRP筋的拉断破坏与高温下锚固区滑移破坏同时发生时所对应的筋材锚固长度定义为高温下筋材的临界锚固长度l_cr(T)，则由临界破坏时的平衡条件可知：

${\tau _{\text{u}}}(T){\text{π}}d{l_{{\text{cr}}}}(T) = {f_{\text{u}}}(T)({\text{π}}{d^2} /4)$

(6)

将式(5)代入式(6)，可得高温下CFRP筋的临界锚固长度(25℃ $\leqslant$ T $\leqslant$ 300℃)为

${l_{{\rm{cr}}}}(T) = \frac{{{f_{\rm{u}}}(T)d}}{{8\sqrt {{f_{{\rm{cu}}}}} \left( {1 - \dfrac{{0.64(T - {T_0})}}{{{T_{\rm{g}}}}}} \right)}} - 0.945d$

(7)

利用式(7)计算本文中各试件的临界锚固长度，并将其与试件实际锚固长度进行比较，以预测试件发生的破坏形态，结果如表7所示。可见，基于式(7)预测的破坏形态与实际情况吻合。

表 7 CFRP筋-RPC锚固性能试件临界锚固长度计算值及预测的破坏形态

Table 7. Critical anchorage length determined by formula and predicted failure mode of CFRP bar-RPC anchorage performance test

Specimen	T/℃	Anchorage length/mm	Actual failure mode	Critical anchorage length/mm	Predicted failure mode
A-T25-L5d	25	60	Slip	304.9	Slip
A-T100-L5d	100			389.0
A-T210-L5d	210			497.8
A-T300-L5d	300			1142.9

下载: 导出CSV

| 显示表格

5. 结论

(1) 相较于常温试件，100℃、210℃和300℃下轴拉试件的抗拉强度、弹性模量分别下降了(2.3%、11.4%)、(29.8%、40.9%)和(35.6%、45%)；而极限拉应变分别增大了18.5%、17.3%和14.8%。高温下筋材的弹性模量较抗拉强度受处理温度的影响更为显著；筋材的极限拉应变随处理温度升高而先增大后减小。

(2) 锚固性能试件碳纤维增强聚合物复合材料(CFRP)筋-活性粉末混凝土(RPC)界面的粘结强度随处理温度升高而线性退化。100℃、210℃和300℃下CFRP筋-RPC界面的粘结强度较常温试件分别下降20.4%、52.6%与85.1%。

(3) 构建了适于表征高温下CFRP筋及其粘结型锚固系统力学性能退化规律的实用计算公式，均具有较高计算精度。

(4) 高温下文中所用筋材轴拉性能较玻璃化转变温度T_g<200℃的CFRP筋更优良，但本文筋材轴拉性能受(T−T₀)/T_g(T为处理温度，T₀为室温)的影响更显著。

(5) 文中针对CFRP筋及其锚固系统高温力学性能的研究均未考虑筋材初应力的影响，与预应力结构中CFRP筋的实际受力情形存在一定偏差。但本文研究可视为后续含初应力的CFRP预应力筋及其锚固系统高温力学性能研究的基础，有必要先行开展。

图 1 帽型加筋层合板

Figure 1. Hat-stiffened panel

下载: 全尺寸图片幻灯片

图 2 帽型加筋层合板典型单元横截面

Figure 2. Representative sectional element of hat-stiffened panel

①-⑥—Elementary component; S—Width of representative unit; a—Foot width; b—Extending width; w_t—Bottom width; w_b—Top width; t_p—Panel thickness; t_c—Side thickness; t_b—Top thickness; l—Side length; h—Hat height

下载: 全尺寸图片幻灯片

图 3 受横向弯矩作用的加筋帽单元

Figure 3. Hat-stiffened element under transverse bending

ξ—Natural coordinate; θ—Angle of sides; M_P—Plate bending moment; M_c—Hat bending moment; P—Load; M_y—Total bending moment

下载: 全尺寸图片幻灯片

图 4 纵向弯曲帽型加筋板试件截面尺寸

Figure 4. Dimensions of transverse section of longitudinally-bending-test hat-stiffened panel

下载: 全尺寸图片幻灯片

图 5 横向弯曲帽型加筋板试件截面尺寸

Figure 5. Dimensions of longitudinal section of transversely-bending-test hat-stiffened panel

下载: 全尺寸图片幻灯片

图 6 试验装置

Figure 6. Test device

下载: 全尺寸图片幻灯片

图 7 帽型加筋板挠度随载荷变化

Figure 7. Relation between the load and mid-span deflection of hat-stiffened panel

下载: 全尺寸图片幻灯片

图 8 帽型加筋板的弯曲变形：(a) 沿纵向(F=2 kN)；(b) 沿横向(F=0.2 kN)

Figure 8. Displacement of hat-stiffened composite laminates: (a) Under longitudinally bending (F=2 kN); (b) Under transversely bending (F=0.2 kN)

U—Displacement; U2—Displacement in y dirction

下载: 全尺寸图片幻灯片

图 9 帽型加筋板结构示意图

Figure 9. Geometry of hat-stiffened plate

下载: 全尺寸图片幻灯片

图 10 四边简支帽型加筋板最大挠度

Figure 10. Maximum deflection of four-sided simply-supported hat-stiffened composite laminates

下载: 全尺寸图片幻灯片

图 11 四边简支帽型加筋板的弯曲变形

Figure 11. Displacement of four-sided simply-supported hat-stiffened composite laminates

下载: 全尺寸图片幻灯片

参考文献(23)

[1]	唐红艳, 王继辉, 徐鹏遥. 复合材料在舰艇上的国外应用现状及进展[J]. 船舶, 2006(2):6-11. DOI: 10.3969/j.issn.1001-9855.2006.02.002 TANG Hongyan, WANG Jihui, XU Pengyao. Worldwide application and development of compound material in naval ships[J]. Ship and Boat,2006(2):6-11(in Chinese). DOI: 10.3969/j.issn.1001-9855.2006.02.002
[2]	司卫华. 船舶复合材料国外最新进展[J]. 塑料工业, 2011, 39(6):1-7. SI Weihua. The foreign latest progress of composite materials for ships[J]. China Plastics Industry,2011,39(6):1-7(in Chinese).
[3]	任茶仙, 张铎. 复合材料层合结构铺层顺序优化设计的免疫遗传算法[J]. 强度与环境, 2007, 34(2):43-50. REN Chaxian, ZHANG Duo. Immuntity genetic algorithm for stacking sequence optimization in composite laminated structures[J]. Structure & Environment Engineering,2007,34(2):43-50(in Chinese).
[4]	蔡忠云, 唐文勇, 陈念众, 等. 复合材料船体层合板的极限强度分析[J]. 船舶力学, 2009, 13(1):72-81. DOI: 10.3969/j.issn.1007-7294.2009.01.010 CAI Zhongyun, TANG Wenyong, CHEN Nianzhong, et al. Ultimate strength analysis of composite laminated ship panels[J]. Journal of Ship Mechanics,2009,13(1):72-81(in Chinese). DOI: 10.3969/j.issn.1007-7294.2009.01.010
[5]	章向明, 王安稳, 姚国文, 等. 复合材料偏心加筋壳特性分析[J]. 海军工程大学学报, 2005, 17(3):19-26. DOI: 10.3969/j.issn.1009-3486.2005.03.005 ZHANG Xiangming, WANG Anwen, YAO Guowen, et al. Analysis of behaviors of composite laminated eccentrically stiffened shell[J]. Journal of Naval University of Engineering,2005,17(3):19-26(in Chinese). DOI: 10.3969/j.issn.1009-3486.2005.03.005
[6]	葛东云, 莫与明, 何柏灵, 等. 复合材料帽型加筋板轴压试验及承载能力预测[J]. 复合材料学报, 2016, 33(7):1531-1539. GE Dongyun, MO Yuming, HE Boling, et al. Test and ultimate load capacity prediction of hat-stiffened composite panel under axial compression[J]. Acta Materiae Compo-sitae Sinica,2016,33(7):1531-1539(in Chinese).
[7]	YETMAN J E. Skin stiffener debonding of top-hat stiffened composite structures[D]. Southampton: University of Southampton, 2016.
[8]	RICCIO A, RAIMONDO A, FRAGALE S, et al. Delamination buckling and growth phenomena in stiffened composite panels under compression. Part I: An experimental study[J]. Journal of Composite Materials,2014,48(23):2843-2855. DOI: 10.1177/0021998313502741
[9]	张永强, 刘龙权, 余音. 复合材料帽型加筋板冲击损伤后的弯曲性能[J]. 实验室研究与探索, 2020, 39(6):32-36. DOI: 10.3969/j.issn.1006-7167.2020.06.008 ZHANG Yongqiang, LIU Longquan, YU Yin. Bending performance of composite top-hat stiffened panel after impact damage[J]. Research and Exploration in Laboratory,2020,39(6):32-36(in Chinese). DOI: 10.3969/j.issn.1006-7167.2020.06.008
[10]	张国凡, 孙侠生, 吴存利. 复合材料帽型加筋壁板的失效机制分析与改进设计[J]. 复合材料学报, 2017, 34(11):2479-2486. ZHANG Guofan, SUN Xiasheng, WU Cunli. Failur mechanism analysis and design of omega stiffened composite panel[J]. Acta Materiae Compositae Sinica,2017,34(11):2479-2486(in Chinese).
[11]	徐丽, 李宏源, 王大政, 等. 复合材料帽型骨材强度及刚度影响因素研究[J]. 武汉理工大学学报, 2014, 3(5):974-978. XU Li, LI Hongyuan, WANG Dazheng, et al. Research of influencing factors on strength and stiffness of composite cap-shape cirder[J]. Journal of Wuhan University of Technology,2014,3(5):974-978(in Chinese).
[12]	梅蕾, 李宏源, 徐丽, 等. 复合材料船舶帽型加筋结构静力分析[J]. 舰船科学技术, 2015, 37(4):41-46. DOI: 10.3404/j.issn.1672-7649.2015.04.008 MEI Lei, LI Hongyuan, XU Li, et al. Static analysis of hat stiffeners on the composite ship[J]. Ship Science and Technology,2015,37(4):41-46(in Chinese). DOI: 10.3404/j.issn.1672-7649.2015.04.008
[13]	胡珍伍. 标准化玻璃钢示范渔船船体结构优化设计研究[D]. 大连: 大连理工大学, 2013. HU Zhenwu. Research on hull structure optimal design for standardized FRP fishing vessel[D]. Dalian: Dalian University of Technology, 2013.
[14]	NISHIHARA S. Analysis of ultimate strength of stiffened rectangular plate(4th report)-On the ultimate bending moment of ship hull girder[J]. Journal of the Society of Naval Architects of Japan, 1983, 154: 367-375.
[15]	PAIK P K, MANSOUR A E. A simple formula-ion for predicting the ultimate strength of ships[J]. Journal of Marine Science and Technology,1995,1(1):52-62. DOI: 10.1007/BF01240013
[16]	KUTT L M, PIASZCZYK C M, CHEN Y K. Evaluation of longitudinal ultimate strength of various ship hull configurations[J]. SNAME Trans,1985,93:33-55.
[17]	JONES B J. Design equations and criteria of or-thotropic composite pannels[R]. West Bethesda: Department of Defense, 2004.
[18]	史明, 陈普会. 基于多学科耦合的复合材料帽型加筋板制造仿真[J]. 复合材料学报, 2021, 38(12):4162-4172. SHI Ming, CHEN Puhui. Simulation of manu facture of the hat-stiffened composite plate based on multidisciplinary coupling[J]. Acta Materiae Compositae Sinica,2021,38(12):4162-4172(in Chinese).
[19]	吴德财, 徐元铭, 贺天鹏. 新的复合材料格栅加筋板的平铺等效刚度法[J]. 力学学报, 2007, 39(4):495-502. DOI: 10.3321/j.issn:0459-1879.2007.04.010 WU Decai, XU Yuanming, HE Tianpeng. A new smeared stiffener theory for grid-stiffened composite panels[J]. Chinese Journal of Theoretical and Applied Mechanics,2007,39(4):495-502(in Chinese). DOI: 10.3321/j.issn:0459-1879.2007.04.010
[20]	KIDANEA S, LI G Q, HELMS J, et al. Buckling loadanalysis of grid stiffened composite cylinders[J]. Composites,2003,34B:1-9.
[21]	NAVIN J, NORMAN F K J. Optimal design of grid-stiffened composite panels using global and localbuckling analyses[J]. Journal of Aircraft,1998,35(3):478-486. DOI: 10.2514/2.2321
[22]	赵群, 丁运亮, 金海波. 基于压弯刚度匹配论则的复合材料加筋板结构优化设计[J]. 南京航空航天大学学报, 2010, 42(3):357-362. DOI: 10.3969/j.issn.1005-2615.2010.03.020 ZHAO Qun, DING Yunliang, JIN Haibo. Structural optimization design of composite stiffened panels based on matching regulations of compression and bending stiffnesses[J]. Journal of Nanjing University of Aeronautics & Astronautics,2010,42(3):357-362(in Chinese). DOI: 10.3969/j.issn.1005-2615.2010.03.020
[23]	胡明勇, 王安稳, 章向明, 等. 复合材料帽形加筋梁强度及刚度实用计算与试验[J]. 海军工程大学学报, 2014, 26(5):53-56. HU Mingyong, WANG Anwen, ZHANG Xiangming, et al. Experimenal research and calculation of strength and stiffness of hat-stiffened composite beam[J]. Journal of Naval University of Engineering,2014,26(5):53-56(in Chinese).

施引文献(7)

期刊类型引用(6)

1.	辛雨柯，邓庆田，宋学力，李新波. 加筋曲板结构抗弯承载能力分析. 塑性工程学报. 2024(02): 189-198 . 百度学术
2.	梁永廷，于文学，熊芯，乔珂. 碳纤维复合材料超大开度门结构设计与仿真. 北京交通大学学报. 2024(06): 144-153 . 百度学术
3.	吴菁，章向明，胡明勇，朱子旭，王安稳. 复合材料船体帽型加筋板弯曲应力. 船舶力学. 2023(07): 1084-1095 . 百度学术
4.	吴菁，章向明，朱子旭，胡明勇，王安稳. 复合材料船体帽型加筋板面内刚度. 海军工程大学学报. 2023(04): 1-6+28 . 百度学术
5.	刘宸宇，骆烜赫，刘康翔，孟增，肖山. 基于平铺刚度法的弧形加筋板的轻量化设计. 应用数学和力学. 2023(08): 953-964 . 百度学术
6.	邱家波. 复合材料加筋壁板的弯曲计算和刚度优化. 中国造船. 2023(05): 119-129 . 百度学术