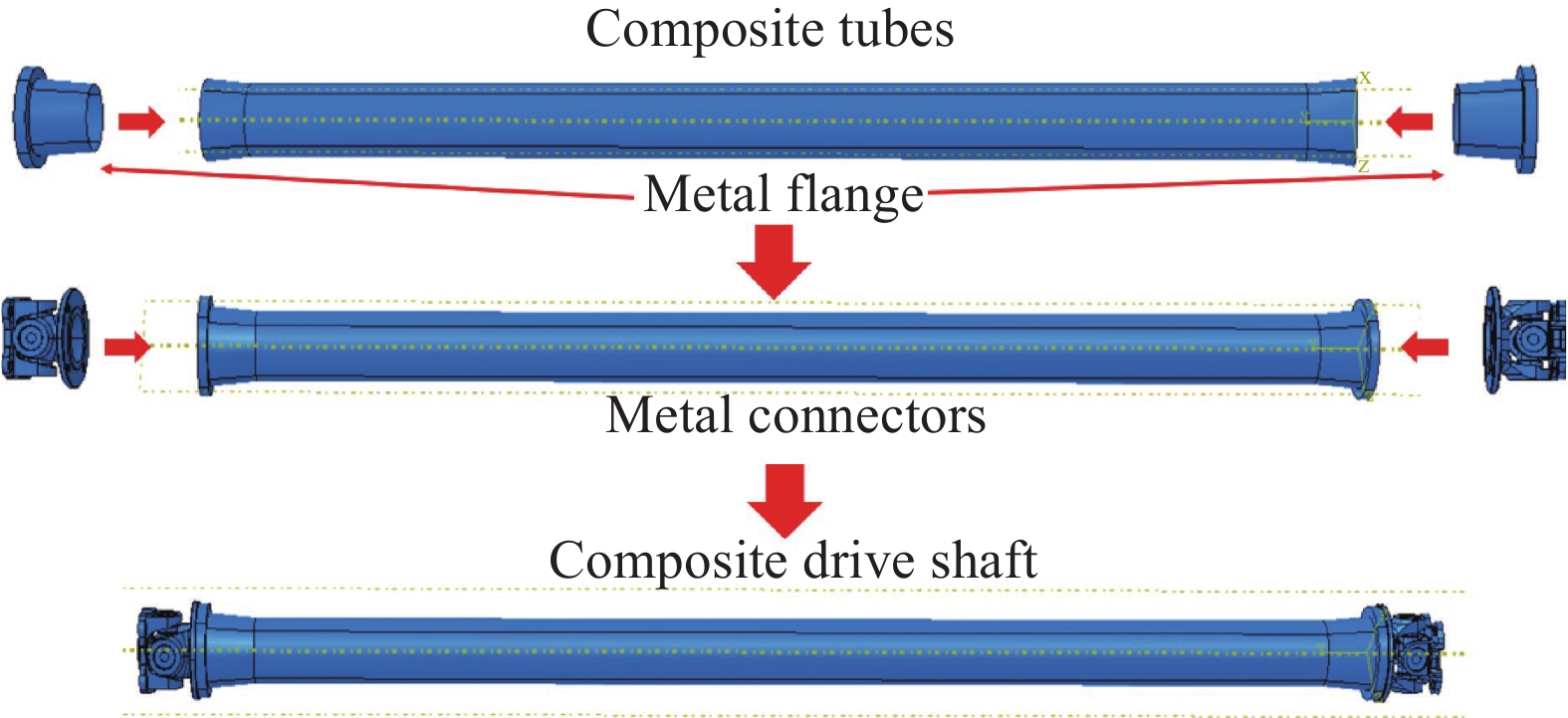
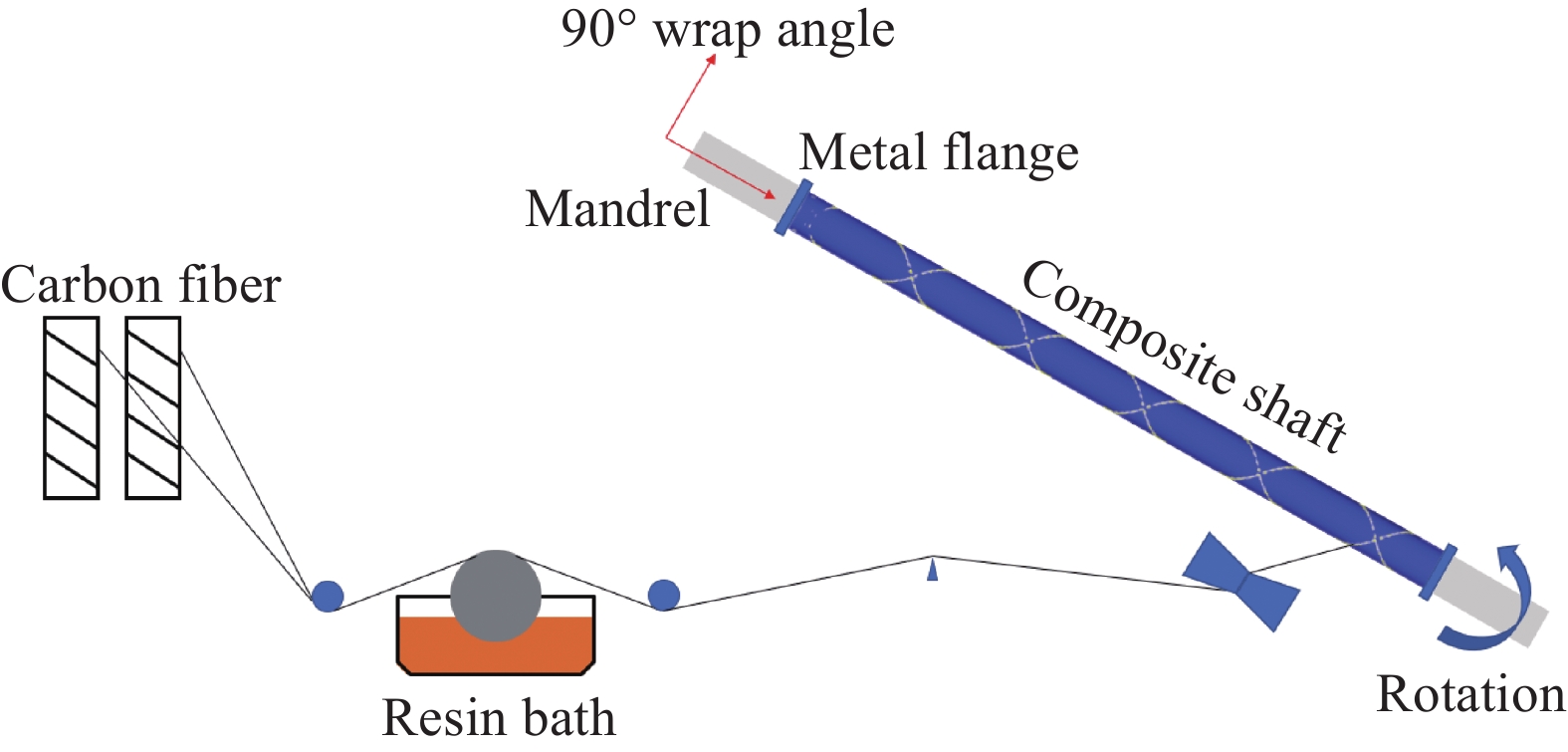
Torsional characteristics and failure mechanism of composite drive shafts formed by variable-angle winding
-
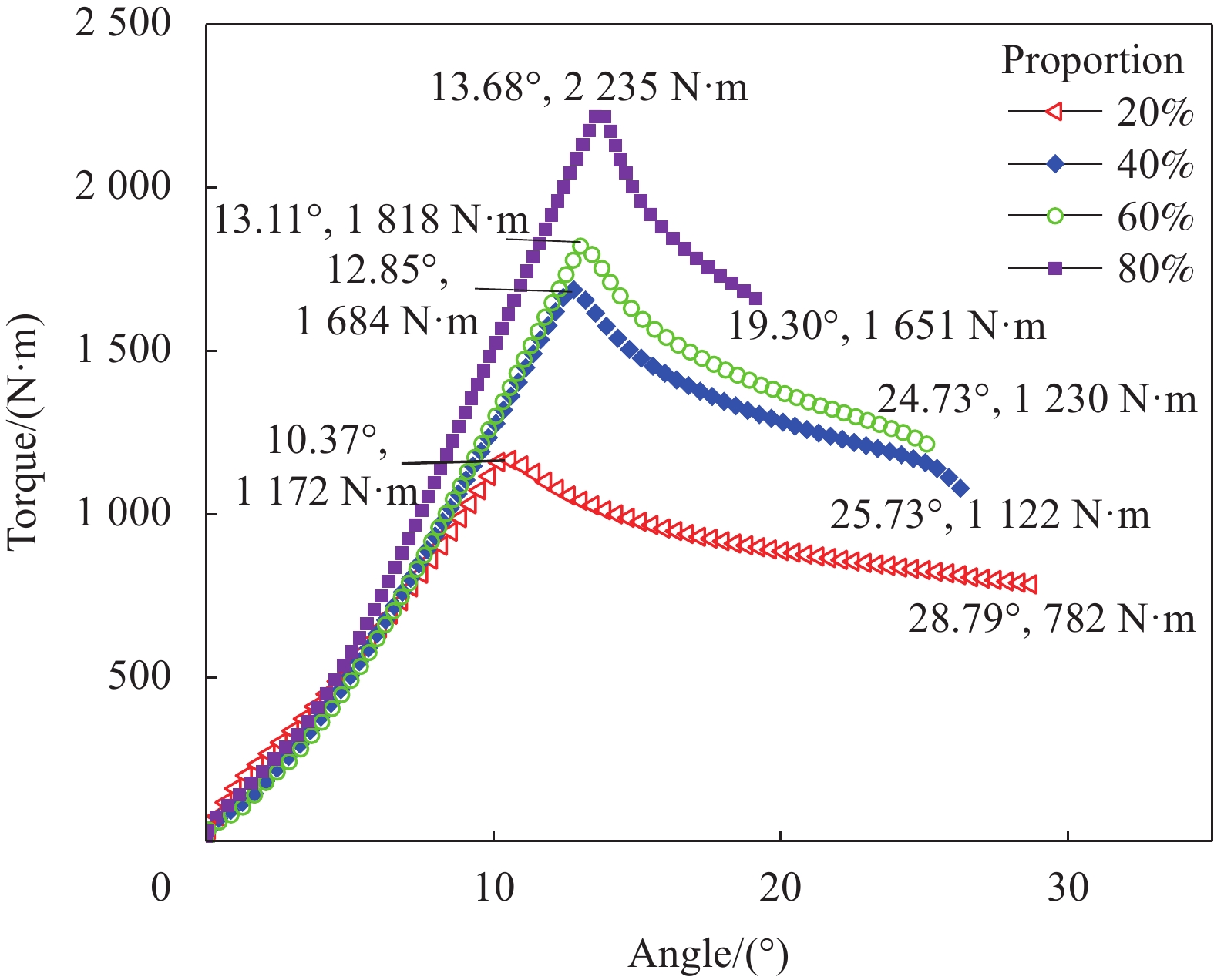
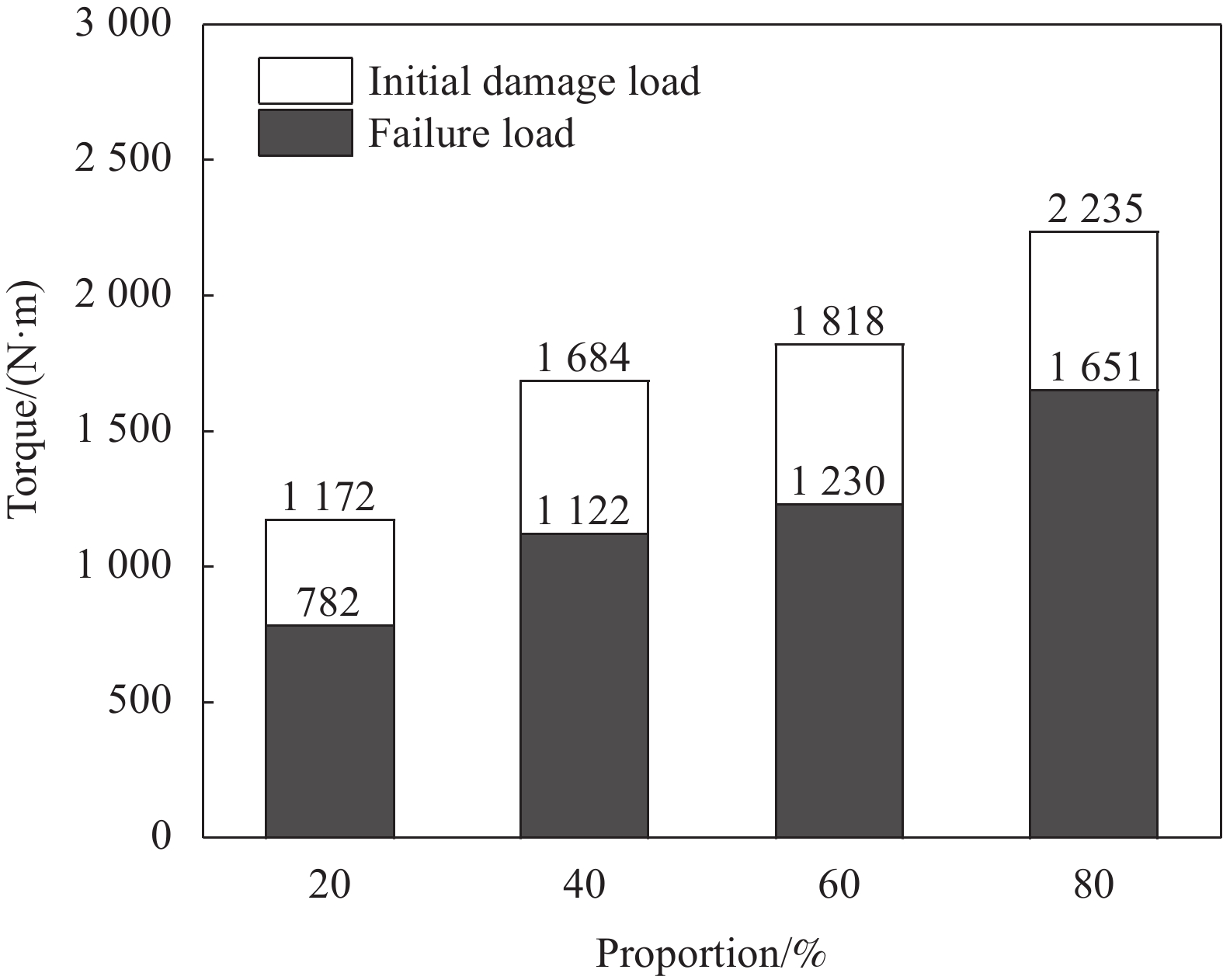
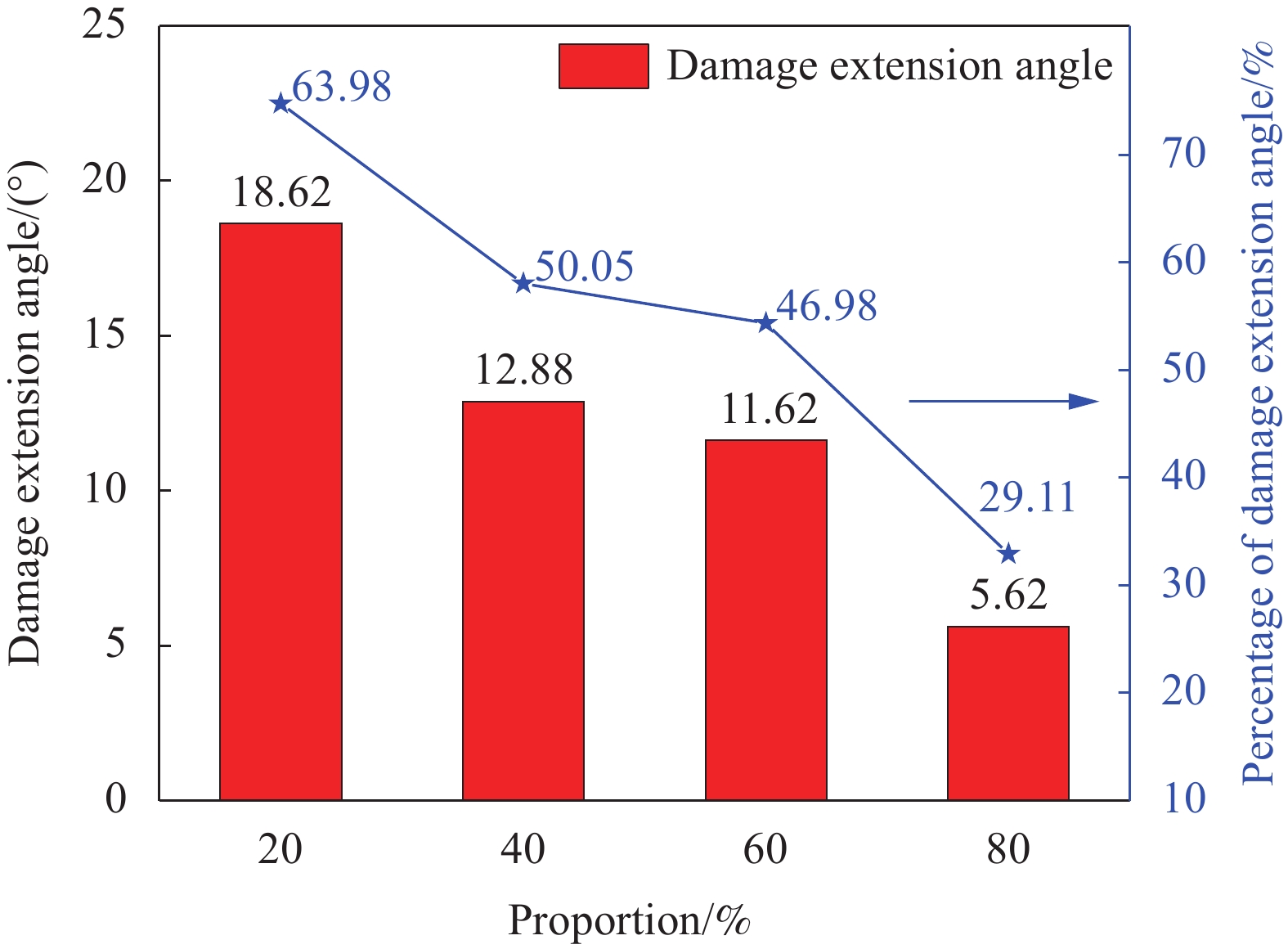
摘要: 基于非测地线缠绕和纤维滑移理论，提出采用非测地线缠绕成型一体化复合材料传动轴。设计了多组不同比例纤维变角度过渡区复合材料传动轴，并利用有限元分析和扭转实验深入研究了传动轴的扭转性能及其失效机制。结果表明，含有的变角度过渡区比例越大，传动轴扭转性能越好，过渡区从20%提高到80%，传动轴的失效载荷提高111%，峰值载荷提高90.7%。随着过渡区占比的提高，屈曲形变导致的损伤失效得到有效缓解，损伤扩展角度降低了54.5%。结合有限元仿真和扭转实验分析可知，过渡区纤维角度的增加抑制了屈曲形变，减少了分层损伤带来的界面上力学传导失效，提高了轴管承载能力。Abstract: Based on the theory of non-geodesic winding and fiber slippage, it was proposed to use non-geodesic winding to form integrated composite drive shafts. Multiple groups of variable-angle composite drive shafts with different proportions of transition zone were designed, and the torsion performance and failure mechanism of the drive shafts were deeply studied by finite element analysis and torsional experiment. The results show that the greater the proportion of the transition zone with variable angles, the better the torsional performance of the drive shafts. The transition zone increases from 20% to 80%, the failure load of the drive shafts increases by 111%, and the peak load increases by 90.7%. With the increase in the proportion of the transition zone, the damage failure caused by buckling deformation is effectively alleviated, and the damage angle is reduced by 54.5%. According to the finite element simulation and torsional experiment analysis, it can be concluded that the increase of the fiber angle in the transition zone suppresses the buckling deformation and reduces mechanical conduction failure on the interface caused by delamination damage. As a result, it improves the bearing capacity of the drive shafts.
-
纤维增强复合材料具有轻质高强，耐腐蚀性好[1]等特点，随着拉挤成型工艺的发展，拉挤型材在复合材料结构方面受到越来越多的关注，具有加工方便，成本低的特点。拉挤型材中纤维主要沿轴向分布，构件具有较好的抗压承载力[2]，可以直接作为轻质结构使用，也可以作为模板浇筑混凝土，构成纤维增强复合材料管约束混凝土结构，加工方便，强度高[3–7]。然而，受拉挤型材特殊加工工艺影响，拉挤型材在受压过程中表现为明显的脆性特征；与混凝土组合受力过程中极易发生局部屈曲，混凝土约束效率低。Guo等[8-9]研究了不同截面拉挤型材约束混凝土柱的受力性能，结果表明拉挤型材在受压过程中面外位移较大，并发生撕裂破坏现象，但与矩形截面相比，圆形截面受力性能明显较好，混凝土约束率较高。Alhawamdeh等[10]也得出过类似结论，与圆形截面相比，矩形截面更容易发生局部屈曲。其原因在于，拉挤型材的弯曲刚度比轴压刚度小，而矩形柱四边在加载过程中主要受弯曲作用，易发生局部屈曲[11]。虽然对矩形截面进行倒角处理有效改善结构受力性能，但在与混凝土组合时约束效率依然低于圆形截面[12]。
为改善矩形拉挤型材受力性能，提高混凝土约束效率，本文提出了一种多腔矩形纤维增强复合材料约束混凝土组合柱。受内部肋板支撑，多腔结构有效延缓面层局部屈曲，与单腔结构相比，承载力及延性大幅提高[13–16]。Huang等[14-15]提出一种矩形纤维增强复合材料管约束十字型钢混凝土柱，其中十字型钢与纤维增强复合材料矩形管构成多腔结构；轴压试验结果表明，多腔结构有效限制纤维增强复合材料管面外变形，受约束混凝土强度大幅提高。Togay等[16]对一种全纤维增强复合材料多腔组合结构进行了轴压试验研究，结果表明，纤维增强复合材料多腔结构有效增强混凝土约束效率，结构极限承载力大幅提高。但文献中成型工艺较复杂，无法满足工程快速成型需求；现有拉挤工艺只能制造单孔或双孔截面，无法制造复杂多腔截面。
纤维增强复合材料约束混凝土柱的受力性能除与截面形状相关外，还受纤维铺层角度显著影响。Vincent等[17]研究了不同纤维角度对纤维增强复合材料约束混凝土结构受力性能的影响，结果表明，过多的轴向纤维导致面层过早的局部屈曲，而增加环向纤维有效提高纤维增强复合材料管对混凝土的约束效率。Al-saadi等[18]研究表明，拉挤型材中，增加轴向纤维有效提高结构刚度；增加环向纤维改善局部屈曲，结构强度大幅增加。因此，为改善结构环向刚度，Guo等[19]和Zhang等[20]对不同截面的碳纤维增强拉挤型材约束混凝土柱进行了轴压试验研究。结果表明，对于圆形截面柱，碳纤维环向增强有效提高混凝土约束效率，结构破坏具有延性特征；而对于矩形截面柱，由于较小的转角半径，碳纤维面层与拉挤型材发生过早界面剥离现象，改善效果不明显。
为充分利用矩形拉挤型材受压强度，发挥纤维增强复合材料管约束混凝土结构优势，基于格构结构，采用纤维面层加强多腔组合构件。其中，格构结构由面层、格构腹板及芯材组成，采用真空导入工艺一体成型，加工方便，截面形式灵活；以拉挤型材及其约束混凝土构件作为芯材，外包纤维面层，基于真空导入，可快速制造多腔组合柱；纤维面层由多轴向纤维组成，以提高结构轴向及环向刚度；增设格构腹板以改善纤维布与拉挤型材界面粘结性能[21-23]。Liu等 [24]对一种格构增强复合材料矩形木柱进行了轴压试验研究，结果表明，格构增强结构显著增强芯材受力性能，面层与芯材的抗剥离能力和协同工作能力极大提高，构件破坏有明显伪延性特征。目前，格构结构主要采用木材、泡沫等轻质芯材，结构刚度较低。以拉挤型材约束混凝土为芯材，有效改善结构承载力，增加结构多样性，具有较好的应用前景。
为研究格构增强多腔纤维增强复合材料约束混凝土组合柱结构的破坏模式、峰值承载力及延性，并考虑增设格构腹板对其受力性能的影响，分别对格构增强多腔组合构件及无格构构件进行了轴压试验研究。此外，针对多腔矩形纤维增强复合材料约束混凝土组合柱的峰值承载力提出了一种简易计算公式，为工程应用提供参考。
1. 试验概况
1.1 构件设计及制作
多腔纤维增强复合材料约束混凝土组合柱如图1所示。试验共设计12个构件，包括2组多腔混凝土组合构件，2组多腔空心组合构件和2组控制构件，所有构件纤维体量相同。基于结构不同对各构件进行命名，其中“H”表示多腔空心组合构件；C表示多腔混凝土组合构件；L表示增设格构腹板构件；F表示无格构构件。控制构件为空心拉挤型材单管(HPT)及其约束混凝土柱(CPC)。每组包含两个构件，其中构件“1”和“2”结构相同，以验证试验可靠性。
![]()
图 1 多腔纤维增强复合材料约束混凝土组合柱Figure 1. Concrete-filled multi-cavity pultruded composite rectangular columns构件由四个相同的拉挤型材构成，高度均为400 mm，边长100 mm，壁厚6 mm，倒角半径3 mm。除控制构件外，所有构件名义高度均为400 mm，边长208 mm，倒角半径为3 mm；实测平均边长为207.46 mm，高度398.53 mm。具体见表1。
表 1 构件信息Table 1. Details of specimensLabels Size
(H×W×r)
/mmLayup of lattice-webs Layup of fibre skin Concrete HF-PT-1 400×208×3 — [(±45°)2/(0, 90°)2]2 — HF-PT-2 — HL-PT-1 (±45°)2 [(0, 90°)2/ (±45°)2] — HL-PT-2 — CF-PC-1 — [(±45°)2/(0, 90°)2]2 C60 CF-PC-2 C60 CL-PC-1 (±45°)2 [(0, 90°)2/ (±45°)2] C60 CL-PC-2 C60 HPT-1 400×100×3 — — HPT-2 CPC-1 C60 CPC-2 Notes: H—Height of specimens; W—Width of specimens; r is the corner radius of specimens. The thickness of GFRP wove fabrics of (±45°) and (0, 90°) was 0.5 mm. Labels of the specimens are as follows, “H”—hollow specimens; “C”—Concrete-filled specimens; “L”—Specimens reinforced with lattice-webs; “F”—Specimens without lattice-webs; “HPT” and “CPC”—Normal pultruded tubes and related concrete-filled specimens; the number “1” and “2” followed the labels represent two nominally identical specimens in each pair. 构件加工时，预制拉挤型材两端采用塑料片材进行封口，易于真空导入。单根管材按要求包裹纤维布(格构腹板)，搭接长度50 mm；摆放成型后整体包裹纤维布(纤维面层)，纤维铺设过程中持续喷涂干胶以固定位置，搭接长度100 mm。基于真空导入工艺，采用不饱和树脂浸满拉挤型材间纤维布，形成约束面层和肋板，其中约束面层由纤维面层、格构腹板及拉挤型材组成；肋板由格构腹板及拉挤型材组成。待固化24 h后脱模，并切除两端方形塑料片，两端打磨平整后灌注混凝土。端部手糊6层碳纤维布，避免集中应力破坏。制作流程如图2所示。
1.2 材料基本力学性能
依据ASTM D3410[25]和ASTM D3039[26]分别对多轴向纤维布及拉挤型材进行压缩及拉伸试验。纤维面层与格构腹板均由(0,90°)及(±45°)双轴向GFRP纤维布组成(如表1所示)，纤维体积分数约为65%，拉挤型材为单轴向GFRP拉挤型材，纤维体积分数约为50vol%。依据ASTM C39/C39 M [27]对混凝土进行轴压试验，其中混凝土为C60混凝土。试验结果如表2所示。
表 2 基本材料属性Table 2. Material propertiesProperty (±45°) (0, 90°) Pultruded tubes Concrete Mean Standard deviation Mean Standard deviation Mean Standard deviation Mean Standard deviation Axial compression fxc/MPa 137.53 3.54 181.26 8.26 140.23 6.89 59.53 1.13 Exc/GPa 22.92 1.86 26.16 4.63 18.03 2.14 36.53 2.01 Transverse compression fyc/MPa 137.53 3.54 181.26 8.26 1.56 — — — Eyc/GPa 22.92 1.86 26.16 4.63 6.78 — — — Axial tension strength fxt/MPa 185.23 18.65 330.52 11.63 — — — Transverse tension strength fyt/MPa 185.23 18.65 330.52 11.63 18.05 1.63 — — Poisson’s ratio ν12 0.30 0.031 0.30 0.031 0.28 0.028 0.2 — ν21 0.30 0.026 0.30 0.026 0.09 0.011 — Notes: f—Stress of each kind of material; E—Elastic modulus. 1.3 轴压试验方案
试验采用500 t伺服油压压剪试验机(MTS)，加载速度为0.5 mm/min。顶板采用球形接头与机器相连接，以确保荷载始终与构件相垂直。沿构件纵向对称布置两只杰尔德线性差动变压器(LVDT)-400位移计，以测量构件纵向位移。混凝土组合柱四边中点处各布置2组20 mm标距(SG-20)应变片，每组应变片由一个纵向应变片和一个环向应变片组成，用于测定构件的轴向及环向应变，如图3所示。结构预加载采用试验力控制，预加载荷载为100 kN，以消除构件与加载头之间缝隙。采用东华DH3816数据采集仪对构件的应变和LVDT读数进行连续采集。
2. 试验结果
2.1 试验现象
2.1.1 单管轴压试验
为研究多腔结构及格构增强结构对混凝土约束效率的影响，分别对空心拉挤单管(HPT)及其约束混凝土组合柱(CPC)进行了轴压试验，破坏模式如图4所示。构件加载前期均无明显试验现象，峰值荷载时，HPT构件局部屈曲并发生受压破坏；CPC构件中拉挤型材受压屈曲撕裂，混凝土受压破坏，混凝土与拉挤型材发生明显界面剥离。试验结果见表3，其中Npp为峰值荷载，εpp为峰值荷载点应变值，NppA为峰值荷载平均值，εppA为应变平均值。
CPC及HPT构件的荷载-应变曲线如图5所示，其中应变值采用位移计LVDT-400记录采集并取平均值。可知，单管结构曲线整体表现为线性，在达到峰值荷载后，荷载迅速下降，构件均表现为脆性破坏。构件CPC在破坏前，荷载有轻微波动，但曲线双线性特征不明显，混凝土约束效率极低。
2.1.2 多腔组合柱轴压试验
对于无格构多腔组合构件，典型破坏模式如图6(a)和图6(b)所示。与拉挤型材单管相比，多腔构件破坏时，脆性特征有所改善。构件HF-PT在开始加载时无明显试验现象；当荷载达到1280 kN时，构件表面出现大量鼓包，并伴随不断的滋滋声，约束面层发生明显界面剥离现象；当荷载达到峰值点时，约束面层与肋板受压破坏，构件中部出现压缩裂缝并迅速贯穿截面，构件丧失承载力。
![]()
图 3 轴压试验装置及仪器布置Figure 3. Axial compression test setup and instrumentationLVDT—Linear variable differential transformer; SG-20—Gauge with a standard distance of 20 mm表 3 单管轴压试验结果Table 3. Test results of single tubesSpecimen H×W/mm Npp /kN εpp/10−6 NppA/kN εppA/10−6 HPT-1 400×100 214.86 5308 211.65 5367 HPT-2 400×100 208.44 5426 CPC-1 400×100 625.00 3829 609.74 4088 CPC-2 400×100 618.62 4043 Notes: Npp—Peak load; εpp—Corresponding strain; NppA—Average peak load; εppA—Average strain at the peak point. ![]()
图 6 多腔组合柱轴压破坏模式Figure 6. Axial compressive failure modes of multi-cavity composite rectangular columns对于约束混凝土构件CF-PC，当荷载增加至2000 kN时，约束面层沿环向方向出现多条白痕，构件轴向纤维发生局部受压损伤；继续加载至3000 kN，构件表面白痕逐渐扩大并出现明显鼓包，约束面层发生界面剥离现象，由图6(b)可知，纤维面层局部屈曲并与拉挤型材脱粘；当达到峰值荷载时，约束面层发生撕裂破坏，环向约束力大幅下降，混凝土受压破坏。
图6(c)和图6(d)展示了格构增强多腔组合柱的典型破坏模式，构件在荷载作用下表现为渐进破坏模式，具有一定延性特征。对于构件HL-PT，当荷载达到1000 kN时，约束面层发生轻微界面剥离，构件表面泛白，无鼓包现象，结果表明增设格构腹板有效改善构件界面粘结能力；当加载至峰值荷载时，约束面层受压破坏，构件一侧出现压缩裂缝，此时构件尚未丧失承载力；继续加载，构件出现多条裂缝并迅速贯穿截面，荷载急剧下降，构件破坏。
约束混凝土构件CL-PC在峰值荷载前与CF-PC试验现象相似，荷载加至3300 kN后约束面层出现轻微界面剥离现象，由图6(d)可知，纤维面层局部屈曲后，格构腹板与拉挤型材未发生剥离，表现出更好的界面粘结能力；当达到峰值荷载后，约束面层受压开裂，但构件并未立刻破坏，受格构腹板限制，裂缝沿截面缓慢发展；继续加载，构件中部出现竖向白色线条，并随着荷载的增加而逐渐加深，约束面层发生拉伸损伤；加载至极限荷载时，格构腹板局部屈曲，约束面层面外位移快速增加，混凝土受压破坏，压缩裂缝沿面层快速发展，构件破坏。
2.2 主要试验结果
图7和图8为构件的荷载-应变曲线，应变值分别由LVDT-400及轴向应变片SG-20记录采集。在受压过程中，尤其是在峰值荷载之后，由于应变片发生脱落及破坏，无法准确反映构件的受力状态，因此基于LVDT测量值对曲线进行校正。
![]()
图 7 多腔组合柱荷载-应变曲线Figure 7. Load-axial strain curves of multi-cavity composite rectangular columns![]()
图 8 多腔混凝土组合柱荷载-环向应变曲线Figure 8. Load-hoop strain curves of concrete-filled multi-cavity composite rectangular columns由图7可知，多腔空心组合柱在加载初期处于弹性阶段，曲线均表现为线性。对于HF-PT，当约束面层发生损伤后，纤维面层与拉挤型材持续发生界面剥离，曲线开始进入非线性上升段，斜率小于第一段；当达到峰值荷载时，拉挤型材局部屈曲并发生受压破坏，荷载迅速下降。对于HL-PT，纤维面层局部屈曲并与格构腹板发生界面剥离，格构腹板与拉挤型材粘结良好，持续约束芯材受力，曲线具有较长的非线性段；当达到峰值荷载时，拉挤型材发生局部屈曲并受压破坏，荷载下降；由于格构腹板限制裂缝发展，结构仍具有一定承载力，荷载在峰值点后有明显波动，具有一定延性特征。
对于多腔混凝土组合柱，曲线主要分为线弹性阶段、非线性上升阶段和下降阶段。曲线在初始阶段表现为线性，此时混凝土环向变形较小，外部复合材料尚未激活。继续加载，混凝土变形增加，并受外部纤维增强复合材料约束，曲线斜率降低。由图7可知，CF-PC曲线斜率普遍高于CL-PC，具有更大的约束刚度。继续加载，CF-PC构件进入渐进损伤阶段，约束面层发生界面剥离，纤维面层局部屈曲，混凝土约束刚度降低，曲线斜率逐渐减小，荷载继续增加到峰值点。在达到峰值荷载后，拉挤型材局部屈曲，混凝土受压破坏，荷载下降。与拉挤型材约束混凝土单管相比，多腔混凝土组合构件具有明显的双线性特征，有效改善拉挤型材混凝土约束性能。对于CL-PC构件，纤维面层局部屈曲后，格构腹板继续约束内部芯材，曲线拥有更长的渐进损伤段和更大的峰值荷载，表现出更好的界面粘结性能[24]；荷载达到最大值后，格构腹板发生局部损伤，环向约束力大幅下降，混凝土受压破坏，荷载下降。CL-PC构件峰值承载力平均为3497 kN，是CF-PC构件(3083 kN)的1.13倍，结果表明，增设格构腹板进一步改善结构承载力。与多腔空心组合柱相比，由于混凝土的环向变形增加了多腔结构的不稳定性，混凝土组合柱轴向变形低于空心组合柱；其中，构件CL-PC与HL-PT应变值差距较小，结果表明，增设格构腹板有效增加结构变形能力。
图8中环向应变(HS)基于SG-20应变片采集记录并取平均值，以研究增设格构腹板对多腔结构混凝土约束效率的影响。由于HS-8应变片在面层搭接处，应变值无法准确反应结构状态[28]，因此未插入相关曲线。达到峰值荷载时，构件发生较明显的界面剥离现象，应变片多发生损坏与脱落，因此图中给出最大荷载值为构件的峰值荷载。由图8还可知，在加载初期，环向应变分布较均匀，此时混凝土变形较小，多腔纤维增强复合材料管受压产生环向应变。随着荷载的不断增加，混凝土发生不均匀膨胀，各应变差异明显；当面层发生局部屈曲后，损伤面应变快速增加，其中CF-PC构件局屈曲荷载为1500 kN，CL-PC构件局部屈曲荷载为3000 kN，增设格构腹板有效延缓约束面层局部屈曲。达到峰值荷载时，构件CL-PC平均环向应变为4247×10−6，约为构件CF-PC(ε=2632×10−6)的1.61倍。结果表明，增设格构腹板大幅增加复合材料环向应变值，改善混凝土约束效率。
2.3 多腔组合结构受力分析
基于荷载-轴向应变曲线，定义峰值荷载提高系数ψ，对空心复合材料组合柱和混凝土组合柱轴心受力性能进行分析，结果如表4所示。其中Np和εp为峰值荷载及其相对的峰值点应变，AP为复合材料组合柱截面面积；对于空心组合柱，NppA为单根空心拉挤型材平均承载力，Am为其截面面积；对于混凝土组合柱，NppA为单根拉挤型材约束混凝土均承载力，Am为其截面面积。系数ψ表达式如下：
表 4 拉挤型材组合柱试验结果Table 4. Test results of composite pultruded columnsSpecimen σc
/MPaNy
/kNεy
/10−6Np
/kNεp
/10−6Nu
/kNεu
/10−6ψ
/%η HF-PT-1 — 1293 5594 1323 5872 1125 6512 56.27 1.16 HF-PT-2 — 1283 5987 1319 6345 1121 7115 55.80 1.19 HL-PT-1 — 727 3344 1259 5606 1070 9054 48.71 2.71 HL-PT-2 — 1032 4648 1283 5998 1091 6825 51.55 1.47 CF-PC-1 74.28 2612 2951 3136 4036 2666 4750 7.44 1.61 CF-PC-2 72.35 1973 2072 3030 3872 2576 4472 7.23 2.16 CL-PC-1 79.29 2715 3047 3537 5011 3006 5475 21.17 1.80 CL-PC-2 80.03 2126 2251 3457 5518 2938 5978 18.43 2.66 Notes: σc—Compressive stress of confined concrete; Ny and εy—Yield load and corresponding strain of multi-cavity composite columns; Np and εp—Peak load and corresponding strain of multi-cavity composite columns; Nu and εu—Ultimate load and corresponding strain of multi-cavity composite columns; ψ and η—Load enhancement ratio and ductility coefficient of multi-cavity composite columns. ψ=NP/Ap−4×NppA/Am4×NppA/Am (1) 为量化不同参数对构件延性特征的影响，基于Tao等[29]的研究，定义延性系数η；极限承载力Nu(其中Nu=85%Np)及其对应的应变εu；屈服荷载Ny及相对的应变的εy[30]。延性系数η表达式如下：
η=εuεy (2) 由表4可知，多腔组合结构极限承载力大于各组分材料总和，拉挤型材及混凝土具有更好的组合效应。对于空心组构件，构件HF-PT中ψ值平均值为56.27%，高于构件HL-PT中的最大值51.55%，结果表明相同纤维体积分数下，增设格构腹板削弱了结构的整体性，结构承载力有所降低；构件HF-PT中η值最大1.16，低于构件HL-PT中最小值1.47，其中HL-PT构件中，η值最大可达2.71，结果表明，增设格构腹板有效延缓约束面层局部屈曲，大幅提高结构变形能力。
对于混凝土组合柱，构件CF-PC中ψ值平均为7.34%，构件CL-PC中ψ值平均为19.98%。结果表明，多腔结构有效提高结构峰值承载力；在相同纤维体积分数下，增设格构腹板对结构承载力改善效果最佳。构件CF-PC中延性系数η平均为1.88，构件CL-PC中延性系数η平均为2.23，结果表明，多腔结构有效改善拉挤型材脆性特征，结构具有一定延性特征。综上所述，多腔结构有效改善拉挤型材受力性能；增设格构腹板进一步提高结构承载力及变形能力。
2.4 混凝土受力分析
由于混凝土的应力-应变关系无法直接测量，因此将混凝土组合柱试件分为约束混凝土及多腔空心结构，并假定混凝土承担荷载为约束混凝土结构荷载减去空心结构荷载。基于上述假定及图7中的荷载-轴向应变曲线，可得混凝土的峰值荷载(如表4所示)及相应的应力-应变曲线，如图9所示。由于混凝土构件发生破坏时，轴向应变普遍低于相应空心结构，因此给出的应变仅为混凝土达到峰值荷载时的应变，并非试件最大应变。
由图9可知，与拉挤型材单管约束混凝土曲线相比，多腔混凝土组合构件曲线表现出较明显双线性，且当达到峰值应力时，混凝土具有更大的变形能力。结合表4可知，拉挤型材单管混凝土强度平均为60.11 MPa，无明显提高现象；多腔约束混凝土强度约为72.35~80.03 MPa，与无约束混凝土相比，强度平均提高约27.45%。结果表明，多腔结构有效改善拉挤型材约束效率，大幅提高约束混凝土强度。由于多腔截面中单孔混凝受压尺寸与单管相同，该结论不受尺寸效应影响。
![]()
图 9 多腔组合柱约束混凝土应力-应变曲线Figure 9. Axial stress-strain curves of confined concrete in multi-cavity composite rectangular columns对于多腔混凝土组合结构，相比于CF-PC，构件CL-PC具有更高的峰值应力及更大的轴向应变，结果表明，格构增强结构有效改善多腔结构变形能力，进一步提高被约束混凝土强度。值得注意的是，构件CF-PC曲线第二段斜率高于CL-PC，表明相同纤维含量下，无格构多腔结构约束刚度高于CF-PC。但由于界面粘结性能较差，纤维面层发生过早剥离，约束混凝土强度未有效增强。
为验证多腔结构中混凝土约束效率，分别对截面面积相同的圆形及矩形截面纤维增强复合材料管约束混凝土构件进行混凝土应力计算。具体构件尺寸如表5所示，其中S表示倒角半径r为3 mm的矩形构件，L表示内边长，t表示约束面层厚度；C表示为圆形构件，D为圆管内侧直径。其中构件CCL-PC及SCL-PC与构件CL-PC具有相同的等效约束面积和约束厚度，如图10所示；构件CCF-PC及SCF-PC也同理。
表 5 等效圆形及矩形截面约束混凝土计算值Table 5. Theoretical results of confined concrete in equivalent circle and rectangular sectionsSpecimen L(D)
/mmt
/mmσc0
/MPaεc0
/10−6εhrup
/10−6σcc
/MPaεcu
/10−6CCL-PC 214 9 59.53 2600 4508 75.23 7745 CCF-PC 212 10 5151 81.85 9372 SCL-PC 190 9 1667 61.98 4869 SCF-PC 188 10 1905 63.02 5030 Notes: L—Inner length; D—Inner diameter; C—Circular section specimens; "S"—Square section specimens; t—Thcikness of face sheets ; σc0—Unconfined concrete strength ; εhrup—Rupture hoop strain; σcc—Confined concrete strength ; εcu—Ultimate axial starin.of confined concrete. 受工艺限制，无法加工特定尺寸构件，因此采用Teng和Lam[31-32]模型分别对圆形及矩形截面构件进行约束混凝土强度计算，圆形截面表达式如下：
εcu/εc0=1.75+12(fl,afc0)(εhrupεc0)0.45 (3) fccfc0=1+3.3fl,afco (4) fl,a=2EfacetεhrupD (5) 其中：εcu为约束混凝土受压应变；εc0为无约束混凝土受压应变；fl,a为混凝土约束应力；εhrup为构件破坏时环向应变；fcc为约束混凝土受压强度；fc0为无约束混凝土受压强度；Eface为构件面层弹性模量；由于各构件面层均为正交各向异性层合板，因此采用经典层合板理论进行计算，公式如下所示：
Aij=t/2∫−t/2(Qij)kdz=N∑n=1(Qij)n(zn−zn - 1) (6) Ex=(A11A22−A212)tA22,Ey=(A11A22−A212)tA11,νxy=A12tA22 (7) 其中：Aij为层合结构拉伸(压缩)刚度；zn-1为第n层内表面距中面的距离；zn为第n层外表面距中面的距离；Ex为层合结构轴向弹性模量；Ey=Eface为层合结构横(环)向弹性模量；νxy为层合板纵向泊松比；Qij为单层板刚度分量，可基于材性参数直接计算获得。由于构件破坏时，面层未达到破坏应变，εhrup取值为材料破坏应变的0.63[32]，可表示为
εh,rup=0.63∑nfl,ntntEx (8) 其中，fl,n和tn分别为约束面层中第n层板的受拉强度和厚度。
对于矩形构件，计算公式如下：
εcuεc0=1.75+12ks(fl,afc0)(εh,rupεc0)0.45 (9) fccfc0=1+2ksfl,afc0 (10) fl,a=2Efacetεhrup√2L2 (11) ks=1−2(L−2r)23[L2−(4−π)r2] (12) 约束混凝土强度如表5所示，相同条件下，矩形截面约束混凝土强度平均为66.35 MPa，远低于多腔约束混凝土强度，结果表明多腔结构有效提高混凝土约束效率。对于无格构结构，约束混凝土强度低于同面积圆形截面构件，结果表明，构件受压过程中部分混凝土未有效约束；对于格构增强结构，约束混凝土强度高于同面积圆形截面构件，全截面混凝土被有效约束。基于上述分析，提出以下假设：(1) 格构增强多腔约束混凝土应力强度与同面积圆形约束混凝土应力强度相同；(2) 无格构多腔约束混凝土应力强度与同面积矩形约束混凝土应力强度相同。Huang等[15]基于该假定进行了多腔柱的轴压强度计算，结果较相符，具有一定安全储备。
由表5可知，约束混凝土极限受压应变的计算结果远高于试验值，结果表明，多腔结构具较好的约束刚度，但拉挤型材加剧了结构脆性特征，因此应变低于理论值。由2.2节结果可知，多腔结构有效缓解拉挤型材屈曲，增加结构变形能力，峰值荷载时多腔纤维增强复合材料管及其约束混凝土构件应变值差距较小，尤其是增加格构腹板后，CL-PC与HL-PT变形相近。因此，假定峰值荷载时，多腔组合管与受约束混凝土同时破坏，结构峰值荷载为多腔空心组合结构与受约束混凝土峰值荷载之和。
2.5 结构峰值荷载计算
Qiao等[33]研究了拉挤型材的受压性能，并假定拉挤型材由四块相互连接的层合板组成，拉挤型材承载力为层合板承载力总和，理论结果与试验较吻合。由于拉挤型材较厚，受压过程中未发生整体屈曲，因此基于上述研究成果，将多腔纤维增强复合材料管的承载力计算简化为层合板的受力性能计算。其中，层合板耦合刚度假设为0，轴压刚度基于式(6)计算，并采用首层失效准则计算层合板受力性能。层合板的荷载应变关系可表达为
(Nx00)=A(εxεyγxy)=(A11A120A21A22000A33)(εxεyγxy) (13) 其中：x表示沿荷载方向(轴向)；y表示垂直荷载方向(环向)；Nx为层合板所受轴压荷载；εx、εy和γxy分别为层合板中的轴向应变、环向应变和剪切应变。基于2.1节所述试验现象，首层破坏主要发生在纤维面层、格构腹板和拉挤管之间。因此，假定层合板由上述多轴单层板构成，多轴单层板刚度可以表示为
ˉQkij=Akijtk (14) 其中：Aijk(k=a、b、c···)为第k个多轴单层板的压缩刚度，可由式(6)计算获得；tk是第k个多轴单层板厚度。第k个多轴单层板的应力应变关系可以表示为
{σkxσkyσkz}=¯Qk{εkxεkyγkxy}=[¯Qk11¯Qk120¯Qk21¯Qk22000¯Qk66]{εkxεkyγkxy} (15) 其中，εkx、εky和γkxy是第k个多轴单层复合材料平面中的轴向应变、环向应变和剪切应变。将方程(13)代入方程(15)，每个多轴单层复合材料平面中的轴向应力可表示为
(σkxσkyτkxy=)¯Qk(εkxεkyγkxy)=(¯Qk11¯Qk120¯Qk21¯Qk22000¯Q33)(−A22A21εyεy0)=(−¯Qk11A22A21εy+¯Qk12εy−¯Qk21A22A21εy+¯Qk22εy0) (16) 根据最大应力准则，当面内应力达到多轴单层复合材料平面的极限强度时，发生损伤。首层破坏应变εx(1)等于k层多轴单层复合材料平面的最小应变，可表示为
εk(1)y=min(−S(−)L−¯Qk11A22A21+¯Qk12，S(+)T−¯Qk21A22A21+¯Qk22) (17) εk(1)x=−A22A21εk(1)y (18) ε(1)x=min (19) 其中，SL(−)和ST(+)是多轴单层复合材料板的纵向压应力和横向拉应力。层合板的首层破坏应力Nx(1)可表示为
{N^{(1)}_x} = \left( {{A_{11}} - \frac{{{A_{12}}{A_{21}}}}{{{A_{22}}}}} \right) {\varepsilon ^{(1)}_x} (20) 因此构件承载力可以表示为
{N}_{\text{p}}\text={\sigma }_{\text{c}}{A}_{\text{c}}+{N}^{(1)}{}_{{x}}l (21) 其中：Np是峰值荷载；σc和Ac分别是约束混凝土受压强度及面积；l是多腔纤维增强复合材料管轴横截面轮廓周长。计算结果如表6所示。
结果表明，所得计算荷载与试验值较相符，误差均在10%一下，该理论方法具有一定可行性。对于无格构增强多腔约束混凝土结构，由于面层过早发生局部屈曲，因此峰值轴向应变值远低于理论计算值；多腔拉挤型材轴向纤维含量较高，式(9)无法较准确地计算结构极限轴压应变；本文得到的试验数据有限，仅能解决部分问题，需要更多的试验数据完善相关模型。
表 6 多腔组合柱试验及理论结果对比Table 6. Comparison of theoretical and experimental results of multi-cavity composite rectangular columnsSpecimen Experimental Theoretical (Fp−Fp c)/Fp Peak load Fp/kN Axial strain at peak load/10−6 Peak load Fp c/kN Axial strain at peak load/10−6 HF-PT-1 1323 5872 1302 5334 1.587% HF-PT-2 1319 6345 1.288% HL-PT-1 1259 5606 1257 5355 0.1589% HL-PT-2 1283 5998 2.026% CF-PC-1 3136 4036 3254 5334 3.763% CF-PC-2 3030 3872 7.393% CL-PC-1 3537 5011 3587 5355 1.414% CL-PC-2 3457 5518 3.760% 3. 结 论
(1) 多腔结构有效改善拉挤型材脆性破坏特征，提高拉挤型材受力性能，构件承载力平均增加53.08%。多腔空心组合柱破坏模式表现为拉挤型材局部屈曲，面层受压破坏，在峰值荷载前有明显破坏特征。相同纤维体积分数下，增设格构腹板有效限制裂缝开展，曲线下降较为平缓，构件延性系数最大为2.71，远高于无格构构件的最大值(1.19)，拉挤截面变形能力极大提升。
(2) 多腔混凝土组合柱破坏模式表现为约束面层界面剥离，混凝土环向约束减小并受压破坏。其中构件受压曲线为明显双线性曲线，混凝土约束效率有效提高，受约束混凝土强度平均提高约27.45%；相同纤维体积分数下，增设格构腹板有效缓解约束面层屈曲，进一步提高混凝土约束效率，构件承载力最大增加21.17%， 远高于无格构构件的7.44%。
(3) 多腔结构有效改善拉挤型材变形能力，提高受约束混凝土强度。无格构增强多腔混凝土结构约束刚度大，但面层发生过早界面剥离，变形能力改善不明显，构件平均延性系数为1.88，约束混凝土平均强度为73.32 MPa；增设格构腹板有效提高纤维布与拉挤型材界面粘结性能，进一步提高结构变形能力，增加约束混凝土强度，其中构件延性系数为2.23，约束混凝土平均强度为79.66 MPa。
(4) 通过首层破坏原则，计算结构破坏时多腔拉挤型材峰值破坏荷载，并基于等效约束面积，确定不同结构下约束混凝土强度，计算得出了结构的峰值荷载，计算结果与试验较为一致。
-
![]()
图 3 缠绕过程中返回区中的丝束移动
Figure 3. Movement of the tow at return region during the winding process
![]()
图 4 复合材料传动轴过渡区示意图
Figure 4. Schematic diagram of composite drive shaft with transition zone
![]()
图 8 含过渡区的变角度缠绕复合材料轴管的角度-轴向距离关系曲线
Figure 8. Angle-axial distance relationship curve of variable-angle winding composite tube with transition zone
![]()
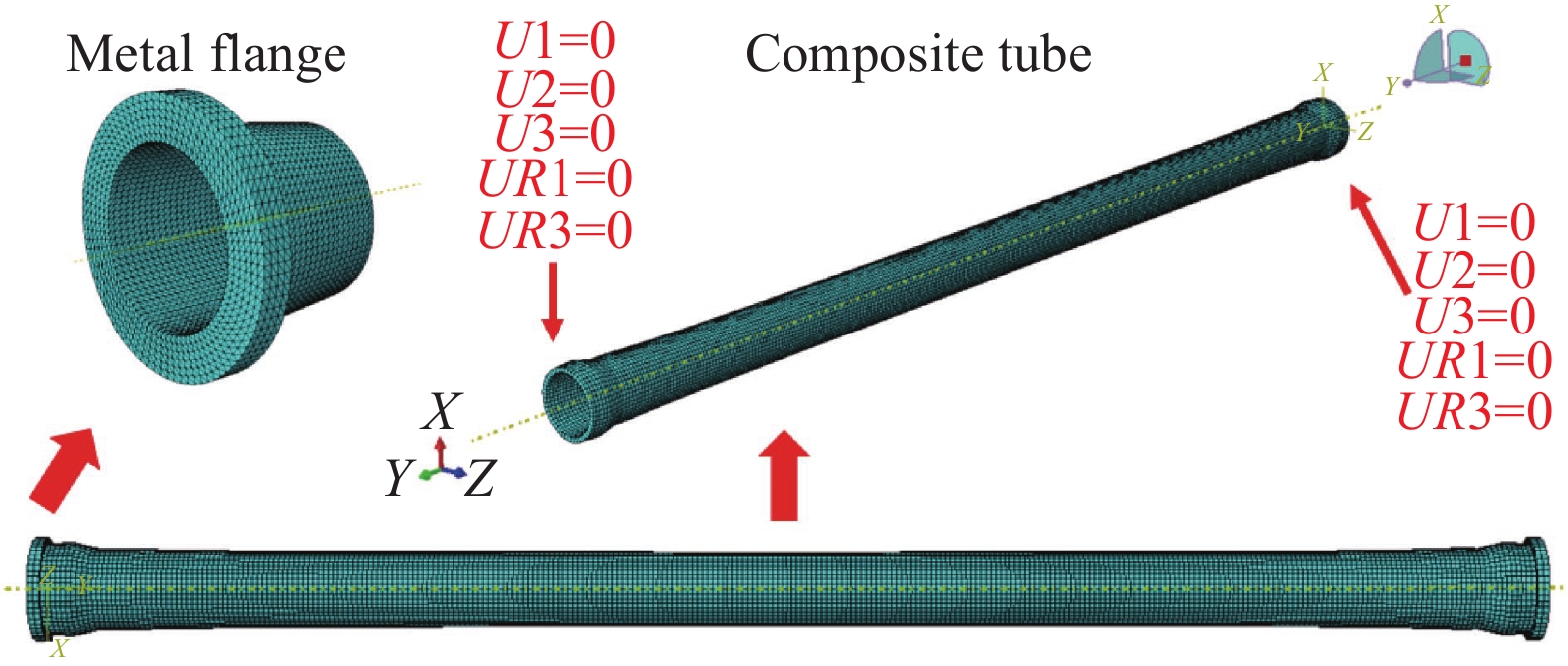
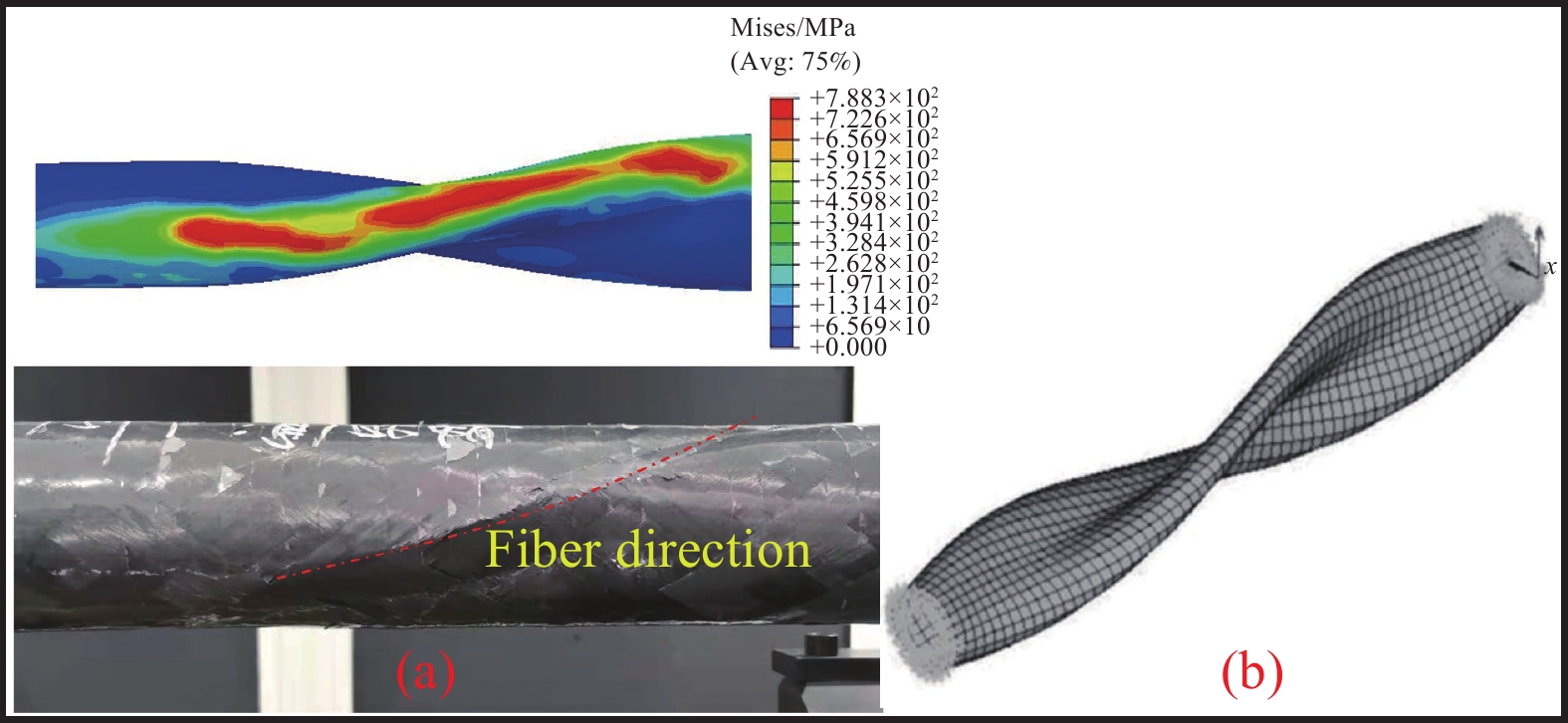
图 10 复合材料传动轴有限元(FEA)模型
Figure 10. Model of finite element analysis (FEA) of composite drive shaft
U1—Translational degrees of freedom in the X direction; U2—Translational degrees of freedom in the Y direction; U3—Translational degrees of freedom in the Z direction; UR1—Rotational degrees of freedom in the X direction; UR2—Rotation degrees of freedom in the Y direction; UR3—Rotational degrees of freedom in the Z direction
![]()
图 11 不同过渡区占比的复合材料传动轴扭矩-角度关系
Figure 11. Torque-twisting angle relations of composite drive shaft with different proportions of transition zone
![]()
图 12 不同过渡区占比的复合材料传动轴初始损伤载荷和失效载荷
Figure 12. Initial damage load and failure load of composite drive shaft with different proportions of transition zone
![]()
图 13 不同过渡区占比的复合材料传动轴扭转损伤扩展角度及其占比
Figure 13. Torsional damage propagation angle and percentage of composite drive shaft with different proportions of transition zone
![]()
![]()
图 15 复合材料传动轴样品横截面的扭转失效
Figure 15. Torsional damage of composite drive shaft sample at middle cross-section
![]()
图 16 含过渡区的变角度缠绕复合材料轴管扭矩-角度曲线
Figure 16. Torque-angle curve of variable-angle winding composite tube with transition zone
T—Torque; R—Torsional stress changes from non-uniform to uniform node; O—Initial point; Q—Damage initial node; P—Inflection point of rate of declinet; θ—Torsion angle
![]()
图 17 样品A的FEA结果：(a) Q点；(b) P点
Figure 17. FEA results of sample A: (a) Point Q; (b) Point P
![]()
图 18 不同过渡区占比复合材料传动轴管的扭转失效与FEA
Figure 18. Torsional failure and FEA of composite shaft with different transition zones
![]()
图 19 Q点的损伤初始角的FEA值和实验值
Figure 19. FEA value and experimental value of the damage initial angle at Q point
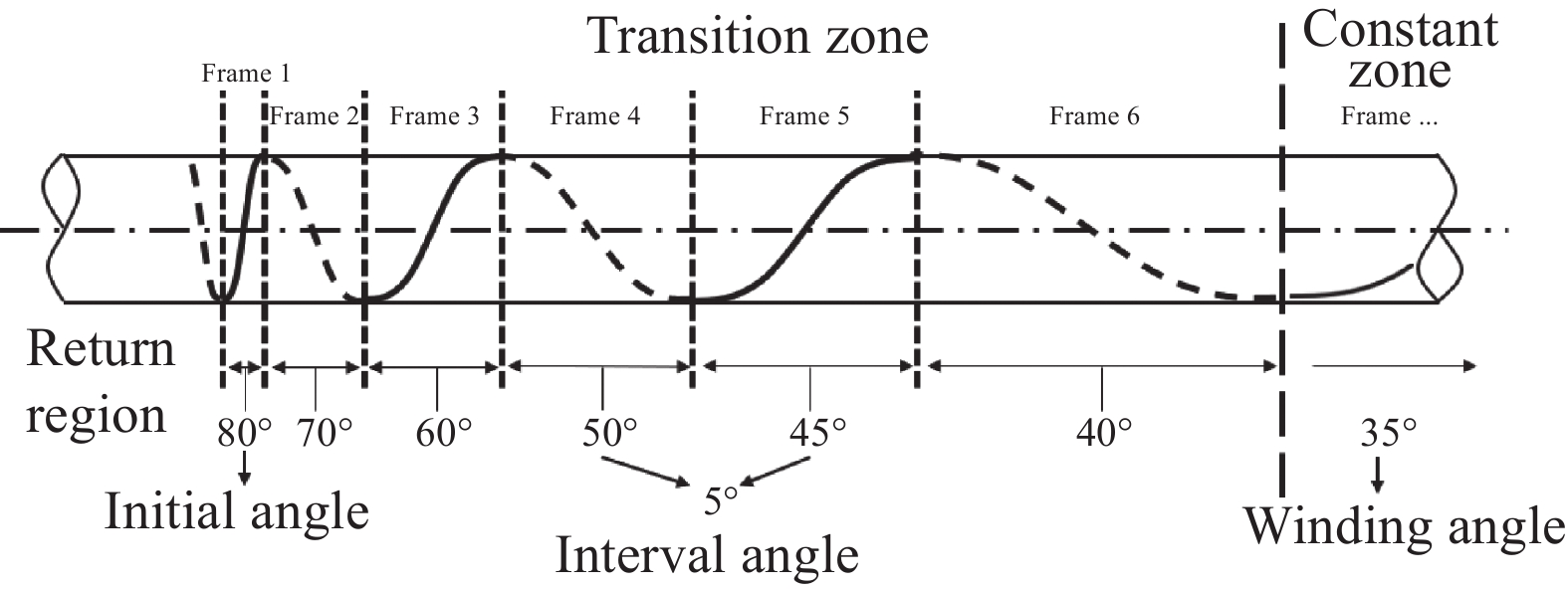
表 1 不同缠绕工艺参数的变角度缠绕稳定性
Table 1 Variable-angle winding stability of different parameters in filament winding process
Winding angle/(°) 55 45 35 25 15 5
Proportion/%20 □ □ □ □ × × 40 □ □ □ □ □ × 60 □ □ □ □ □ × 80 □ □ □ □ □ □ Interval angle/(°) 10 □ □ × × × × 7 □ □ □ × × × 5 □ □ □ □ × × 3 □ □ □ □ □ × 2 □ □ □ □ □ □ 1 □ □ □ □ □ □ Initial angle/(°) 65 □ □ □ □ × × 70 □ □ □ □ □ × 75 □ □ □ □ × × 80 □ □ □ × × × Notes: □—Without slip; ×—Slip. 
下载: 导出CSV
表 2 实验变量设置
Table 2 Setting of variable in the experiments
Sample Ply angles Proportion/% Thickness/mm A [±25°]4 20 2.20 B 40 2.25 C 60 2.29 D 80 2.25
下载: 导出CSV
表 3 T700SC 12K碳纤维/BAC-172环氧树脂复合材料的FEA参数
Table 3 FEA parameters of T700SC 12K carbon fiber/BAC-172 epoxy resin composites
Parameter Value Xt, Yt/MPa 1632, 34 E1t, E2t /GPa 123, 7.8 υ12, υ13 0.27 υ23 0.42 Xc, Yc/MPa 704, 68 G12/GPa 3.8 G13, G23/GPa 5.0 τ12/MPa 55 τ13, τ23/MPa 80 Notes: E1t, E2t—Tensile elastic modulus; υ12, υ13, υ23—Poisson’s ratio; G12, G13, G23—Shear modulus; Xt—Longitudinal tensile strength; Xc—Longitudinal compressive strength; Yt—Transverse tensile strength; Yc—Transverse compressive strength; τ12—Longitudinal shear strength; τ12, τ13—Transverse shear strength.
下载: 导出CSV
-
[1] QI L, LI C, YU X, et al. Effect of reinforced fibers on the vibration characteristics of fibers reinforced composite shaft tubes with metal flanges[J]. Composite Structures,2021,275:114460. DOI: 10.1016/j.compstruct.2021.114460
[2] SUN Z, XIAO J, YU X, et al. Vibration characteristics of carbon-fiber reinforced composite drive shafts fabricated using filament winding technology[J]. Composite Structures,2020,241:111725. DOI: 10.1016/j.compstruct.2019.111725
[3] ZU L, KOUSSIOS S, BEUKERS A. A novel design solution for improving the performance of composite toroidal hydrogen storage tanks[J]. International Journal of Hydrogen Energy,2012,37(19):14343-14350. DOI: 10.1016/j.ijhydene.2012.07.009
[4] 矫维成, 王荣国, 刘文博, 等. 缠绕纤维与芯模表面间滑线系数的测量表征[J]. 复合材料学报, 2012, 29(3):191-196. JIAO Weicheng, WANG Rongguo, LIU Wenbo, et al. Measurement of slippage coefficient between fiber and mandrel surface for non-geodesic filament winding[J]. Acta Materiae Compositae Sinica,2012,29(3):191-196(in Chinese).
[5] ZU L, XU H, WANG H, et al. Design and analysis of filament-wound composite pressure vessels based on non-geodesic winding[J]. Composite Structures,2019,207:41-52. DOI: 10.1016/j.compstruct.2018.09.007
[6] DALIBOR I H, LISBÔA T V, MARCZAK R J, et al. A geometric approach for filament winding pattern generation and study of the influence of the slippage coefficient[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering,2019,41(12):576. DOI: 10.1007/s40430-019-2083-2
[7] FU J, YUN J, JUNG Y, et al. Generation of filament-winding paths for complex axisymmetric shapes based on the principal stress field[J]. Composite Structures,2017,161:330-339. DOI: 10.1016/j.compstruct.2016.11.022
[8] ZHANG B, XU H, ZU L, et al. Design of filament-wound composite elbows based on non-geodesic trajectories[J]. Composite Structures,2018,189:635-640. DOI: 10.1016/j.compstruct.2018.02.008
[9] PARK H C, CHO C, CHOI Y. Torsional buckling analysis of composite cylinders[J]. AIAA Journal,2001,39(5):951-955. DOI: 10.2514/2.1400
[10] SHOKRIEH M M, HASANI A, LESSARD L B. Shear buckling of a composite drive shaft under torsion[J]. Composite Structures,2004,64(1):63-69. DOI: 10.1016/S0263-8223(03)00214-9
[11] SHEN H S, XIANG Y. Buckling and postbuckling of anisotropic laminated cylindrical shells under combined axial compression and torsion[J]. Composite Structures,2008,84(4):375-386. DOI: 10.1016/j.compstruct.2007.10.002
[12] 闫光, 韩小进, 阎楚良, 等. 复合材料圆柱壳轴压屈曲性能分析[J]. 复合材料学报, 2014, 31(3):781-787. YAN Guang, HAN Xiaojin, YAN Chuliang, et al. Buckling analysis of composite cylindrical shell under axial compression load[J]. Acta Materiae Compositae Sinica,2014,31(3):781-787(in Chinese).
[13] 胡晶, 李晓星, 张天敏, 等. 碳纤维复合材料传动轴承扭性能优化设计[J]. 复合材料学报, 2009, 26(6):177-181. DOI: 10.3321/j.issn:1000-3851.2009.06.030 HU Jing, LI Xiaoxing, ZHANG Tianmin, et al. Design optimization on torsion prosion property of carbon-fiber composite drive shaft[J]. Acta Materiae Compositae Sinica,2009,26(6):177-181(in Chinese). DOI: 10.3321/j.issn:1000-3851.2009.06.030
[14] MINAK G, ABRATE S, GHELLI D, et al. Residual torsional strength after impact of CFRP tubes[J]. Composites Part B: Engineering,2010,41(8):637-645. DOI: 10.1016/j.compositesb.2010.09.021
[15] BADIE M A, MAHDI E, HAMOUDA A M S. An investigation into hybrid carbon/glass fiber reinforced epoxy composite automotive drive shaft[J]. Materials & Design,2011,32(3):1485-1500.
[16] SEVKAT E, TUMER H, HALIDUN KELESTEMUR M, et al. Effect of torsional strain-rate and lay-up sequences on the performance of hybrid composite shafts[J]. Materials & Design,2014,60:310-319. DOI: 10.1016/j.matdes.2014.03.069
[17] TARIQ M, NISAR S, SHAH A, et al. Effect of carbon fiber winding layer on torsional characteristics of filament wound composite shafts[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering,2018,40(4):198-206. DOI: 10.1007/s40430-018-1099-3
[18] HAO W, HUANG Z, ZHANG L, et al. Study on the torsion behavior of 3-D braided composite shafts[J]. Composite Structures,2019,229:111384. DOI: 10.1016/j.compstruct.2019.111384
[19] ARMANFARD A, MELENKA G W. Experimental evaluation of carbon fibre, fibreglass and aramid tubular braided composites under combined tension-torsion loading[J]. Composite Structures,2021,269:114049. DOI: 10.1016/j.compstruct.2021.114049
[20] MAHDY W M, ZHAO L, LIU F, et al. Buckling and stress-competitive failure analyses of composite laminated cylindrical shell under axial compression and torsional loads[J]. Composite Structures,2021,255:112977. DOI: 10.1016/j.compstruct.2020.112977
[21] 高洪平, 孙泽玉, 陶雷, 等. 复合材料模量对汽车传动轴固有频率的影响[J]. 复合材料科学与工程, 2018(5):58-63. GAO Hongping, SUN Zeyu, TAO Lei, et al. Effect of fiber modulus on natural frequency of composite automobile drive shaft[J]. Composites Science and Engineering,2018(5):58-63(in Chinese).
[22] 孙泽玉, 余许多, 陶雷, 等. 不同内径碳纤维复合材料轴管的振动性能研究[J]. 复合材料科学与工程, 2020(5):63-68. DOI: 10.3969/j.issn.1003-0999.2020.05.009 SUN Zeyu, YU Xuduo, TAO Lei, et al. Study on vibration properties of carbon fiber reinforced composite tubes with different inner diameters[J]. Composite Science and Engineering,2020(5):63-68(in Chinese). DOI: 10.3969/j.issn.1003-0999.2020.05.009
[23] YE J, CHU C, CAI H, et al. A multi-scale model for studying failure mechanisms of composite wind turbine blades[J]. Composite Structures,2019,212:220-229. DOI: 10.1016/j.compstruct.2019.01.031
[24] CHRISTENSEN R M. Tensor transformations and failure criteria for the analysis of fiber composite materials[J]. Journal of Composite Materials, 1988, 22(9): 874-897.
[25] CHRISTENSEN R M. Failure criteria for fiber composite materials, the astonishing sixty year search, definitive usable results[J]. Composites Science and Technology, 2019, 182: 107718.
[26] GU J, CHEN P. Some modifications of Hashin’s failure criteria for unidirectional composite materials [J]. Composite Structures, 2017, 182: 143-152.
[27] MACEDO R, FERREIRA R, GUEDES J M, et al. Intraply failure criterion for unidirectional fiber reinforced compo-sites by means of asymptotic homogenization[J]. Compo-site Structures, 2017, 159: 335-349.
[28] MURTY A V K, NAIK G N, GOPALAKRISHNAN S. Towards a rational failure criterion for unidirectional composite laminae[J]. Mechanics of Advanced Materials and Structures, 2005, 12(2): 147-157.
[29] ZHAO H W, LIU X G, KENT A. Mechanical properties research of carbon fiber composite laminates [J]. Materials Science Forum, 2020, 980: 107-116.
[30] 宋涛, 余许多, 江晟达, 等. 变刚度碳纤维/环氧树脂复合材料薄壁圆管轴向压溃响应与破坏机制[J]. 复合材料学报, 2021, 38(11): 3586-3600. SONG Tao, YU Xuduo, JIANG Shengda, et al. Axial crushing response and failure mechanism of variable stiffness carbon fiber/epoxy resin composite thin-walled tube[J]. Acta Materiae Compositae Sinica, 2021, 38(11): 3586-3600(in Chinese).
[31] 孙伟, 关志东, 黎增山, 等 纤维增强复合材料薄壁圆管扭转失效分析[J]. 复合材料学报, 2016, 33(10): 2187-2196. SUN Wei, GUANG Zhidong, LI Zengshan, et al. Failure analysis of fiber reinforced composite thin walled tubes under torsion load [J]. Acta Materiae Compositae Sinica, 2016, 33(10): 2187-2196(in Chinese).
-
期刊类型引用(0)
其他类型引用(1)
-
计量
- 文章访问数: 1551
- HTML全文浏览量: 611
- PDF下载量: 106
- 被引次数: 1
