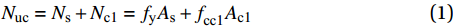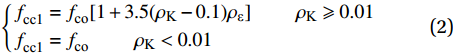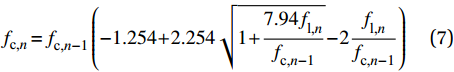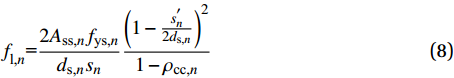Evaluation of axial compressive performance of FRP-confined steel-reinforced concrete column-to-reinforced concrete ring beam joint with seismic damage
-
摘要: 对2个具有不同环梁配筋率的纤维增强树脂复合材料(FRP)约束型钢混凝土(FCSRC)柱-钢筋混凝土(RC)梁节点震损试件进行轴压试验，结合有限元模拟和理论分析，对震损试件的轴压性能进行分析和评估。结果表明：震损试件在轴压荷载下的破坏均由玻璃纤维增强树脂复合材料(Glass fiber reinforced polymer，GFRP)管破裂引起，表明所设计的两个试件在震损后依然满足“强节点，弱构件”的设计原则；当环梁配筋率由1.4%增大到2.5%时，试件的屈服荷载和初始刚度变化不大，而峰值荷载和屈服后刚度分别增加了7.3%和60.2%，极限变形和延性系数分别减小了10.4%和8.5%；所建立的有限元模型可以较好地模拟震损试件的轴压行为；所提出的理论计算公式能够较准确地预测震损试件的轴压承载力，同时具有一定的安全储备。
-
关键词:
- 纤维增强树脂复合材料约束混凝土 /
- 节点 /
- 轴压性能 /
- 地震损伤 /
- 承载力
Abstract: Axial compressive tests were conducted on two fiber reinforced polymer (FRP)-confined steel-reinforced concrete (FCSRC) column-to-reinforced concrete (RC) beam joints with seismic damage which have different reinforcement ratios of the ring beam. The axial compressive performance of the specimen with seismic damage was analyzed and evaluated by finite element simulation and theoretical analysis. The results show that the failure of the specimens is caused by the rupture of the glass fiber reinforced polymer (GFRP) tubes, indicating that the designed specimens still meet the design principle of strong joint and weak members after seismic. When the ring beam reinforcement ratio is increased from 1.4% to 2.5%, the yield load and initial stiffness of the specimen do not change much, while the peak load and post-yield stiffness increase by 7.3% and 60.2%, respectively, and the ultimate deformation and ductility factor decrease by 10.4% and 8.5%, respectively. The established finite element model can better reflect the axial compressive behavior of the specimens with seismic damage. The proposed theoretical formulation could predict the axial compressive bearing capacity of the specimen with seismic damage accurately with certain safety reserves. -
纤维增强树脂复合材料(Fiber reinforced polymer，FRP)因其轻质高强、耐腐性等特点，一直被广泛用于既有结构的加固中[1-3]。近年来，将FRP与混凝土、钢材相结合，形成FRP-钢-混凝土组合结构，是将FRP应用于工程中的另一研究热点[4-8]。这种新型组合结构将FRP、钢和混凝土三种材料有机结合，在FRP的约束作用下，混凝土强度和延性得以提高，钢材的屈曲也得到了有效抑制，同时钢材的加入还进一步提升了构件的承载力和变形能力。
FRP约束型钢混凝土(FRP-confined steel-reinforced concrete，FCSRC)是具有代表性的FRP-钢-混凝土组合构件之一，近年来，国内外学者对该组合构件的力学性能展开了一系列研究[9-16]。Karimi等[9]、Yu等[10]和Zakaib等[11]分别对FCSRC柱的轴压性能、偏心受压性能和抗弯性能进行了试验研究。Ren等[12]在大量轴压试验的基础上，考虑了FRP管厚度、内置型钢截面形状和含钢率的影响，提出了FCSRC柱轴压应力-应变关系的分析模型。此外，部分学者还将高强混凝土[13]或再生混凝土[14-16]用于FCSRC柱，研究表明采用高强混凝土或再生混凝土的试件仍然具有良好的力学性能和抗震性能。
从已有研究成果中不难发现，对FCSRC的研究大都集中在构件层面(如梁、柱等)，而对于其在结构层面(如梁柱节点等)的研究较少，一个重要的原因是由于FRP作为一种无机非金属材料，难以像钢材一样通过焊接等方式与其他构件进行连接[17]。而新型结构构件梁柱节点的研究，对保证结构整体性能有着至关重要的作用，也是将其应用于工程实践的关键。
为此，本文作者所在课题组提出一种适用于FCSRC柱与钢筋混凝土(Reinforced concrete，RC)梁连接的RC环梁节点，并对其完成了抗震性能试验[18]，研究表明该种构造形式能够保证梁柱连接的可靠性和结构的整体性，同时具有良好的抗震性能。由于结构震后性能的评估对确保人员生命安全和财产安全具有重要的意义，同时也是灾后房屋加固和重建的重要依据[19-20]，为此本文在完成抗震性能试验后，对带损伤的FCSRC柱-RC环梁节点试件进行轴压试验，研究和分析节点损伤对试件轴压性能的影响，并结合有限元模拟和理论分析，对震损试件的轴压性能进行评估。
1. 试验概况
1.1 试件
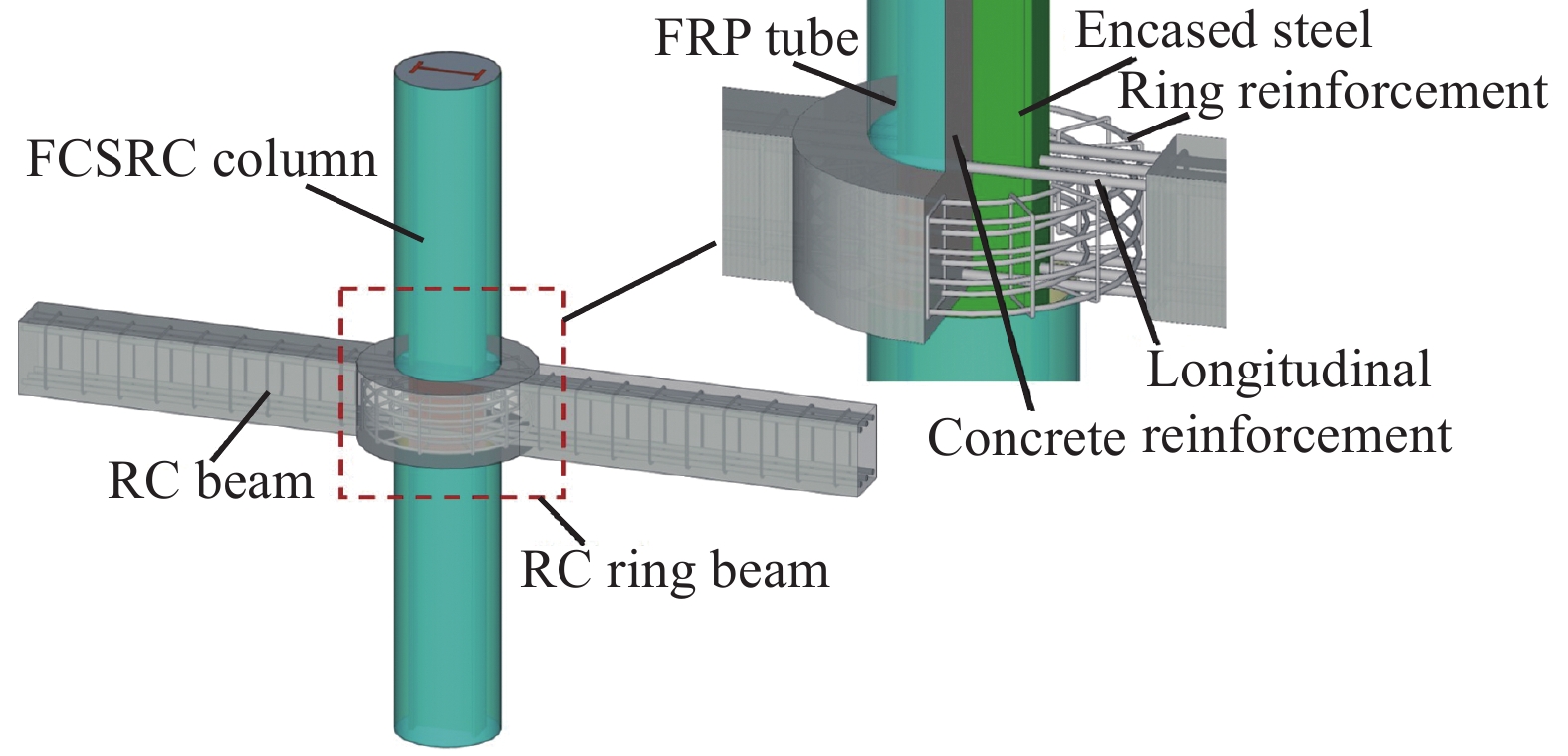
相关研究表明[21]，环梁配筋率和框架梁配筋率的比值是影响试件塑性铰发生位置的关键因素，为此设计了两个具有不同环梁配筋率的FCSRC柱-RC梁试件，如图1所示，FCSRC柱的内置型钢从节点贯通，FRP管在节点的上下表面截断，只对柱中的混凝土和型钢起到约束作用，节点内部的混凝土和型钢由RC环梁进行约束。梁内靠近边缘的纵向钢筋从柱的内置型钢两侧穿过，中部的纵向钢筋焊接在柱内置型钢的翼缘上。试件的详细尺寸和配筋如图2所示，环梁含有内外两圈环形钢筋和12个直径为8 mm(φ8)的箍筋。试件编号M-4、M-5分别表示RC环梁中有4层φ10和5层φ12的钢筋，环梁配筋率分别为1.4%和2.5%，分别低于和高于框架梁配筋率的1.7%。
![]()
图 1 纤维增强树脂复合材料(FRP)约束型钢混凝土(FCSRC)柱-钢筋混凝土(RC)梁节点Figure 1. Joint of fiber reinforced polymer (FRP)-confined steel-reinforced concrete (FCSRC) column-to-reinforced concrete (RC) beam![]()
图 2 试件截面尺寸及配筋GFRP—Glass fiber reinforced polymer; φ—Diameter; M-4, M-5—4, 5 layers of ring bars in the ring beamFigure 2. Details of specimens1.2 材料性能
在试件浇筑混凝土时，采用同批混凝土制作了6个高300 mm、直径150 mm的圆柱体试件并按ASTM C39/C39 M-18[22] 和ASTM C469/C469-14[23]要求在试验当天对其强度和弹性模量进行测试。试件制作所用混凝土的平均强度和弹性模量分别为41.2 MPa和30.8 GPa。
试验用GFRP管采用玻璃纤维通过缠绕成型工艺[24]制成，纤维共12层，缠绕角度与管轴向呈80°，GFRP管内径为400 mm，厚度为4.2 mm。采用文献[25]提供的轴压和水压试验方法对GFRP管进行材料性能测试。GFRP管的轴向和环向弹性模量分别为13.2 GPa和40.1 GPa，泊松比分别为0.13和0.39。
按照《金属材料拉伸试验 第1部分：室温试验方法》(GB/T 228.1—2010)[26]对试验所用钢材进行材性试验，测试结果见表1。
表 1 钢材力学性能Table 1. Mechanical properties of steelType of steel Thickness or diameter/mm fy/MPa fu/MPa Es/GPa Steel bar 8 306 456 211 10 459 627 200 12 448 609 201 14 422 612 208 22 418 591 205 Steel plate 16 286 411 191 Note: fy, fu, Es—Yield strength, ultimate strength and elastic modulus of steel, respectively. 1.3 抗震性能试验概况
按照《建筑抗震试验规程》(JGJ/T 101—2015)[27]的要求对试件进行抗震性能试验。试验加载装置如图3所示，试件上下两端通过锚杆固定在反力架上，在试验开始时首先通过顶部的液压千斤顶对柱施加2850 kN(试验轴压比为0.4)的轴向荷载，并在试验过程中保持荷载不变。接着通过左右两个竖向作动器在加载点处(图2)对试件施加反方向的循环往复荷载，直至试件承载力下降到峰值荷载的85%以下。
抗震性能试验的荷载-位移曲线如图4所示，可知荷载已经下降到峰值荷载的85%以下，表明节点已经达到了极限状态，抗震性能试验完成后节点的破坏情况如图5所示。受到环梁配筋率和框架梁配筋率比的影响[21]，试件M-4和M-5的塑性铰分别发生在RC环梁节点和框架梁端，尽管二者的RC环梁节点均出现一定程度的损伤，但由于后者的环梁配筋率较高，导致其破坏程度较轻。具体表现为M-4的裂缝深入环梁程度更高且裂缝宽度较大，同时伴有大块混凝土掉落，如图5(a)所示；而M-5的破坏主要是由于梁端混凝土破坏引起的，裂缝深入节点程度较低，节点损伤较小，两个试件的FCSRC柱在试验中并未发生明显现象。在试验过程中对试件各部分应变进行了测量，结果表明FCSRC柱内的型钢均未达到屈服应变。RC环梁节点内环形钢筋的应变结果如图6所示，可知靠近框架梁一侧的环形钢筋(R1)在进入极限状态时已经达到屈服应变，而试件中部的环形钢筋(R2)尚未屈服。
![]()
图 4 FCSRC柱-RC梁抗震性能试验荷载-位移曲线Figure 4. Load-displacement curves of FCSRC column-to-RC beam in seismic performance experiment![]()
图 5 FCSRC柱-RC梁抗震性能试验破坏模态Figure 5. Failure modes of FCSRC column-to-RC beam in seismic performance experiment![]()
图 6 FCSRC柱-RC梁抗震性能试验荷载-环梁应变曲线R1—Strain of ring bars at near the beam; R2—Strain of ring bars in the middle of the jointFigure 6. Load-strain curves for the ring beam of FCSRC column-to-RC beam in seismic performance experiment1.4 轴压试验
在抗震性能试验完成后，采用1500吨CSS-254压力试验机(长春试验机厂生产)对震后试件进行轴压试验。加载装置和量测装置如图7所示。使用位移计(Linear variable differential transformer，LVDT，扬州晶明科技有限公司生产)对试件全高变形进行测量，同时在GFRP管外侧沿柱高方向布置应变片，对其轴向和环形应变进行监测。采用位移控制进行加载，加载速率为0.5 mm/s。当试件承载力下降至峰值荷载的85%时停止加载。
![]()
图 7 轴压试验装置LVDT—Linear variable differential transformerFigure 7. Test set-up of axial compressive test2. 试验结果与讨论
2.1 试验现象与破坏模态
各试件试验现象与破坏模态如图8和图9所示。在试验初期试件并未发生明显现象，当轴向位移加载至12.5 mm时，两个试件的GFRP管开始出现白色带状条纹，如图8(a)和图9(a)所示。加载至36 mm时，试件M-4上柱和下柱的GFRP管均发生爆裂，如图8(b)所示，此后承载力急剧下降，同时还观察到试件节点部位发生明显的面外变形，如图8(c)所示。在RC环梁上观察到多条明显的竖向裂缝，裂缝最大宽度为8 mm，如图8(d)所示。对于试件M-5，当加载至32 mm时其上下柱的中部的GFRP管均发生爆裂，如图9(b)所示，此时承载力急剧下降，但并未观察到试件节点处发生明显的面外变形。与M-4相比，试件M-5的RC环梁也出现了多条竖向裂缝，如图9(c)所示，但后者裂缝宽度较小，最大宽度仅为2 mm，同时裂缝有向两侧延伸的趋势。这是由于试件M-5的环梁配筋率较高，环向钢筋对混凝土约束作用更强。
两个试件的破坏都是由于GFRP管破裂引起的，表明两个试件在震损后依然满足“强节点，弱构件”的设计要求。
2.2 FCSRC柱- RC环梁节点轴向荷载-位移曲线
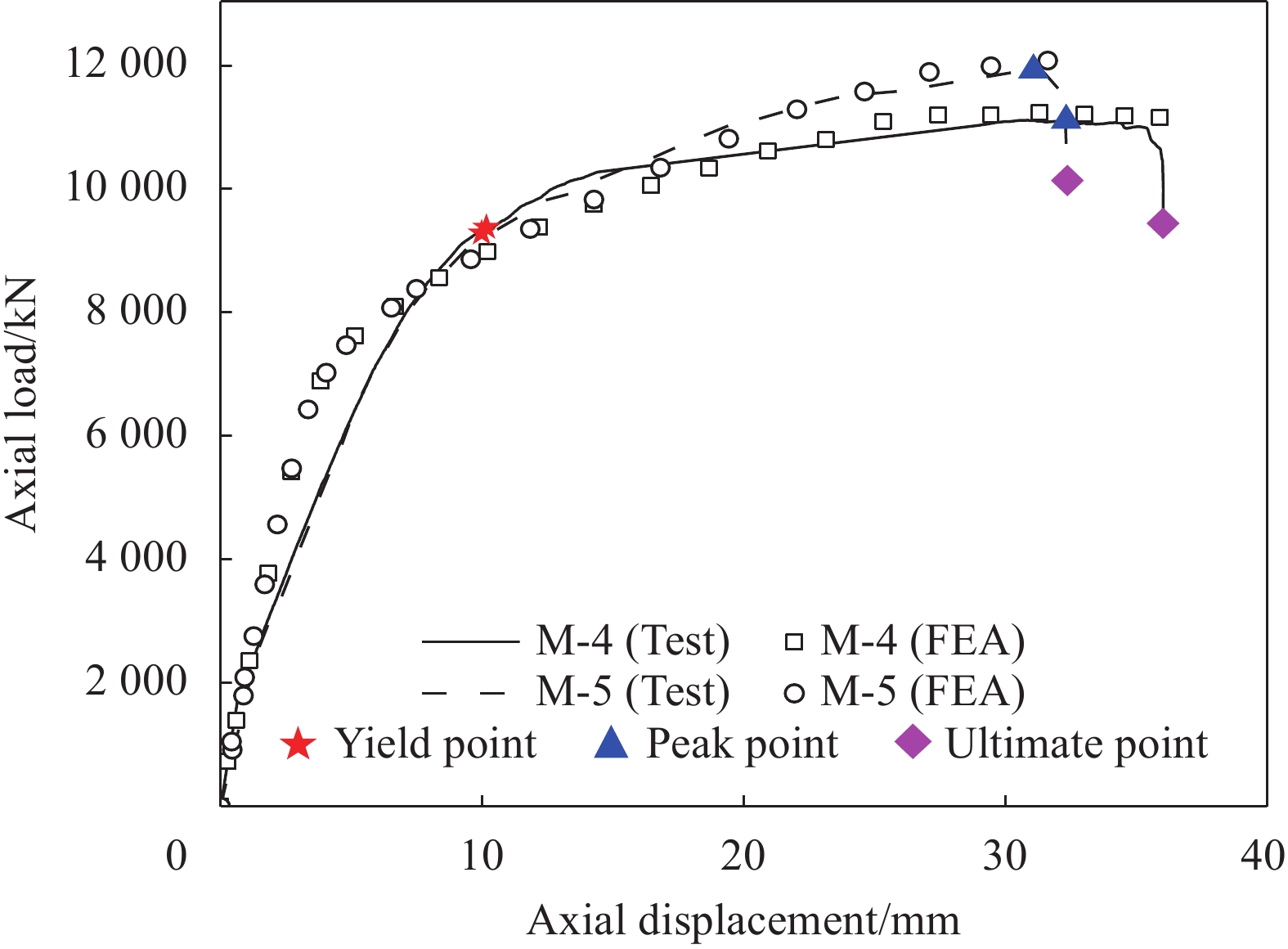
各试件的轴向荷载-位移曲线如图10所示。图中屈服点(Yield point)采用文献[28]提出的“最远点法”确定，峰值点(Peak point)为承载力最大时对应的点，极限点(Ultimate point)为承载力下降到峰值荷载85%时对应的点，各关键点对应的力和位移见表2。
![]()
图 10 FCSRC柱-RC环梁节点轴向荷载-位移曲线FEA—Finite element analysisFigure 10. Axial load-displacement curves of FCSRC column-to-RC ring beam joint表 2 FCSRC柱-RC环梁节点试验、有限元和理论分析结果Table 2. Results of experiment, finite element analysis and theoretical analysis for FCSRC column-to-RC ring beam jointFy/kN Δy/mm Fp/kN Δp/mm Fu/kN Δu/mm μ k0/(kN·mm−1) ks/(kN·mm−1) FFEA/kN Fthe/kN M-4 9351 10.15 11080 32.32 9408 36.02 3.55 1129 78 11256 10723 M-5 9258 9.98 11891 31.07 10107 32.27 3.23 1153 125 12042 10723 Notes: Fy, Fp, Fu—Yield load, peak load and ultimate load of the specimen, respectively; Δy, Δp, Δu—Displacement corresponding to Fy, Fp, Fu; μ—Ductility coefficient; k0—Initial stiffness of the specimen; ks—Post-yield stiffness of the specimen; FFEA, Fthe—Maximum load-bearing capacity calculated by FEA and theory. 由图10和表2可知，节点受损伤试件仍然具有一定的轴向承载能力和变形能力。随着环梁配筋率的增加(由1.4%增大到2.5%)，试件的屈服荷载变化不大(相差不超过1%)，而峰值荷载有小幅增加(7.3%)，可见在“强节点，弱构件”的设计原则下，环梁配筋率对试件的轴压承载力影响不大，这是由于两个试件的RC环梁承载力相对于FCSRC柱较高，试件的轴向承载力均主要由FCSRC柱来控制。
试件M-5的极限变形与M-4相比减小了10.4%，这是由于前者环梁节点配筋率较高，导致节点刚度较大，在相同加载位移下，FCSRC柱的轴向变形比后者大，因此M-5在更小的位移下到达了峰值荷载和极限荷载。延性系数μ为极限位移和屈服位移的比值，即Δu/Δy，是反映试件变形能力的重要指标之一，各试件的延性系数见表2。可知，M-5的延性系数与M-4相比减小了8.5%，这是由于二者屈服位移接近，但前者极限位移更大导致的。由此可见，在保证“强节点，弱构件”的前提下，环梁配筋率过大会降低试件的延性，因此不建议环梁配筋率过大。
将荷载-位移曲线在屈服荷载的1/6~1/2段割线刚度的斜率记为试件的初始刚度k0[12]，各试件的初始刚度见表2。结合图7可以看出，M-4和M-5的初始刚度相差2.1%，可见环梁配筋率对试件的初始刚度影响程度不大。将屈服点与峰值点连线的斜率定义为试件的屈服后刚度ks，屈服后刚度反映了试件屈服后荷载随位移增长的快慢程度，各试件的屈服后刚度见表2。可以看出M-5的屈服后刚度与M-4相比提高了60.2%，表明试件屈服后，环梁配筋量较高的试件达到峰值荷载时的位移更小。综上所述，在“强节点，弱构件”设计的前提下，环梁配筋率的增大对试件初始刚度影响不大，但会提高试件的屈服后刚度。
2.3 FCSRC柱-RC环梁节点应变分析
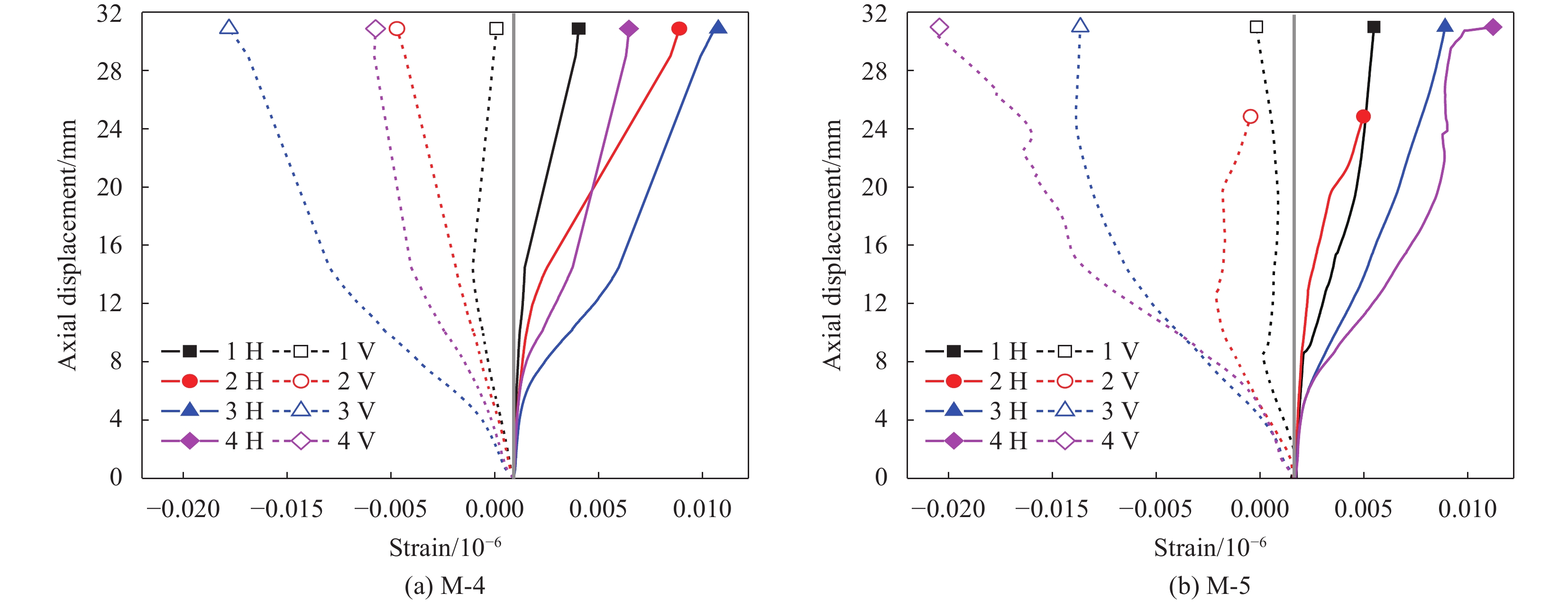
试件各截面应变监测点的应变值与轴向位移的关系曲线如图11所示，图中1~4分别表示图7(b)中截面1~4，H和V分别表示环向应变和轴向应变，应变受拉为正。可知，各试件轴向应变均为负值，环向应变基本均为正值，表明FCSRC柱在轴压荷载下，填充混凝土发生膨胀，引起GFRP管环向受拉，从而对混凝土起到约束作用。此外，相同加载位移下，环梁配筋率较高的试件M-5，其FCSRC柱的轴向应变较M-4更大，这一点与2.2节的讨论一致。此外，试件M-4和M-5的最大环向应变基本相同，均为0.011(M-4的3 H处和M-5的4 H处)，基本达到了GFRP管的环向断裂应变(一般为0.01~0.015)。
![]()
图 11 FCSRC柱-RC环梁节点轴向位移-应变曲线1-4—Section 1-4 in Fig.7(b); H—Hoop strain; V—Axial strainFigure 11. Axial displacement-strain curves of FCSRC column-to-RC ring beam joint3. 有限元分析
为了更深入地研究震损试件在轴压试验中的应力状态和受力机制，有必要对其进行有限元分析(Finite element analysis，FEA)。
3.1 FCSRC柱-RC梁有限元模型的建立
采用ABAQUS软件对试件进行有限元分析，如图12所示，混凝土和内置型钢采用C3 D8 R单元，GFRP管采用S4 R单元，钢筋采用Truss单元。通过收敛性研究，确定所有部件均采用50 mm网格进行划分。GFRP管与柱采用“绑定”连接，内置型钢和钢筋均“嵌入”混凝土中。柱的顶部和底部只对三个方向的平动自由度进行约束。
钢筋和内置型钢均采用双折线本构，硬化模量为弹性刚度的1%。GFRP管采用“Lamina”材料类型，其中环向弹模E1=40.1 GPa，环向泊松比ν12=0.39，其他参数均设置为较小值[29](本文中均设为1)。混凝土采用损伤塑形模型(Concrete damaged plasticity，CDP)，由于GFRP管、RC环梁节点的环形钢筋及RC框架梁的纵向钢筋对混凝土的约束效果不同，因此这三个部位的混凝土需要设置不同的材料参数。文献[21]和[29]分别给出了环形钢筋约束混凝土和FRP约束混凝土的本构参数及CDP模型参数计算方法，此处不再赘述。框架梁的混凝土本构参考《混凝土结构设计规范》(GB 50010—2010)[30]。
3.2 FCSRC柱-RC梁有限元模型的验证
采用3.1节的建模方法对试件M-4和M-5进行建模，首先按照抗震性能试验的加载方案对试件进行加载，然后对震后试件施加轴向荷载。两个试件左梁的抗震性能试验结果[18]和FEM模型计算结果对比如图13所示，可以看出，有限元分析与试验结果吻合程度较好，表明所采用的有限元建模方法和材料本构的选取能够较准确地反映试验情况。
![]()
图 13 FCSRC柱-RC环梁节点有限元模型验证RC—Type of beams; 4, 5—4, 5 layers of ring bars in the ring beam; 0.4—Axial load ratioFigure 13. Verification of FEA model of FCSRC column-to-RC ring beam joint3.3 FCSRC柱-RC环梁节点有限元结果分析
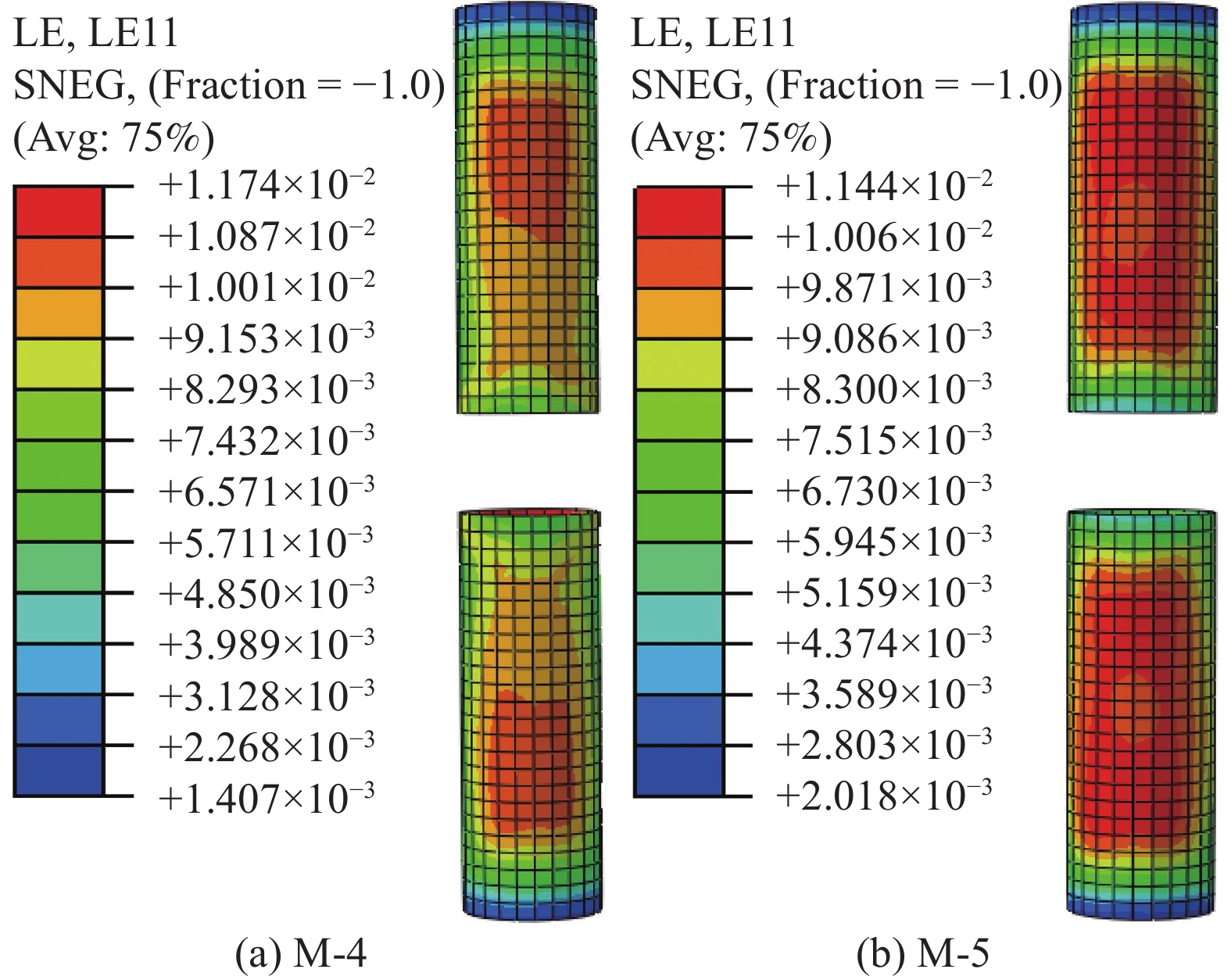
通过轴压分析得到震后试件在轴压下的荷载-位移曲线如图10所示，可以看出，试验结果和有限元结果基本吻合，特别是承载力吻合程度较高，由表2可知有限元分析的得到的峰值荷载与试验相比误差不超过2%。图14给出了试件在极限状态下GFRP管的环向应变分布，可以看出：(1) 两个试件在极限状态下的最大环向应变值(分别为0.0117和0.0114)与试验得到的最大环向应变(0.011)接近；(2) 从环向应变分布来看，柱中部的应变值较大，这与试验中GFRP管爆裂位置相近。综上所述，有限元模型能够对试件震后轴压承载力进行准确预测。
![]()
图 14 GFRP管环向应变LE—Strain; LE11—Hoop strain; SNEG—Face with negative normal direction of elementsFigure 14. Hoop strain distribution of GFRP tubes图15给出了轴向位移为25 mm时试件的轴向应变分布，ABAQUS中应力和应变值均是受拉为正，受压为负。相对柱而言，两个试件的RC环梁都出现不同程度的受拉变形，这是由于轴压下核心混凝土膨胀，引起环梁内混凝土受拉。此外可以明显看出，在相同加载位移下，试件M-4节点的轴向应变比M-5更大，前者FCSRC柱发生的轴向变形会较后者更小，其原因在于M-4较低的环梁配筋率使环梁节点刚度较小，这一点与2.2和2.3节的讨论相一致。
![]()
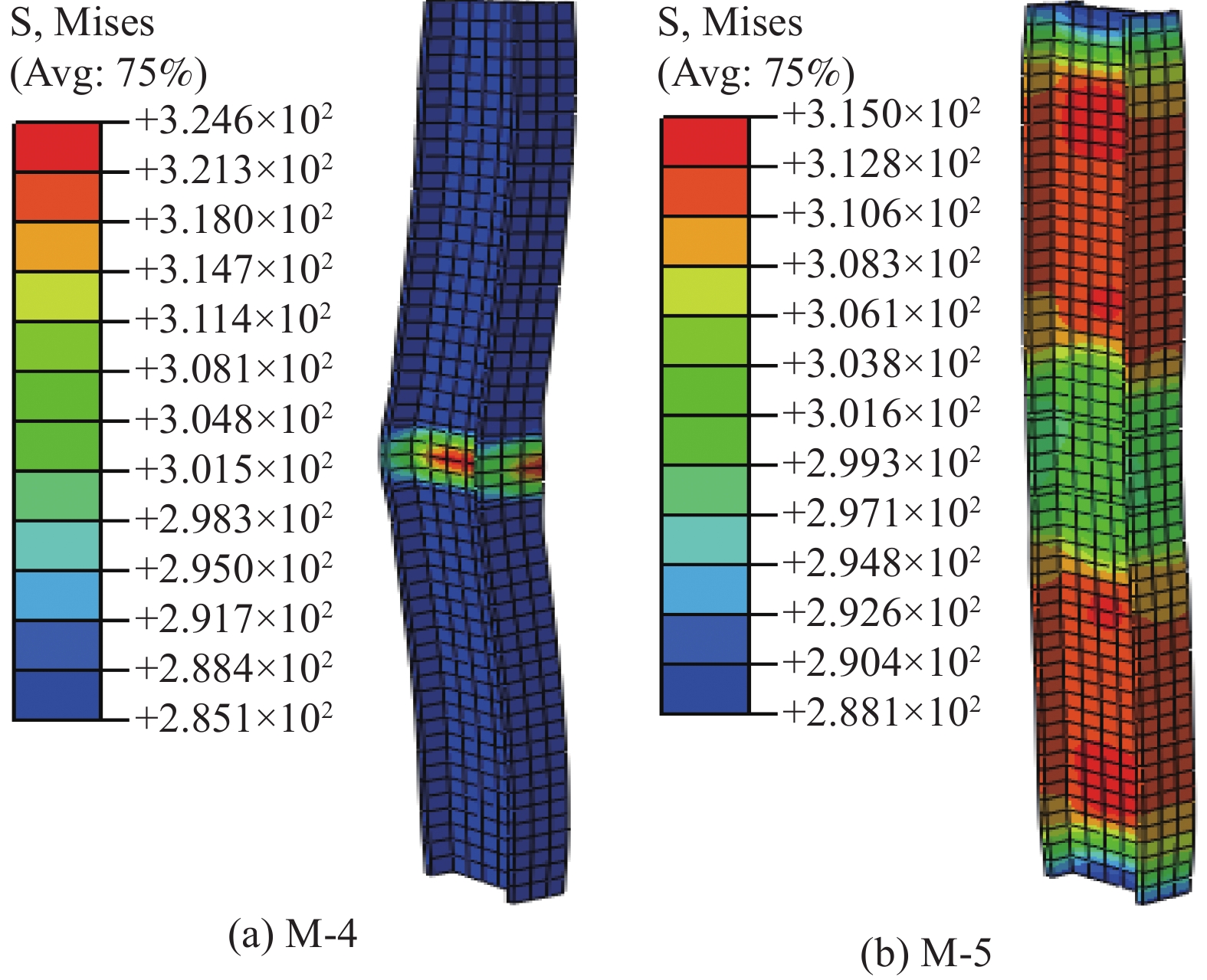
图 15 25 mm的FCSRC柱-RC环梁节点试件轴向应变分布Figure 15. Axial strain distribution of 25 mm FCSRC column-to-RC ring beam joint specimens图16分别为试件M-4和M-5在极限位移下环梁钢筋的轴向应力云图，可以看出在轴向荷载作用下，内圈和外圈环形钢筋应力均为正值，表明受到核心混凝土膨胀的作用，环梁中内圈和外圈的环形钢筋均受拉。但内圈环形钢筋的应力均小于外圈，可见内圈钢筋对核心混凝土起到的约束作用更强。M-4的环形钢筋最大应力高于M-5，这是由于前者环梁配筋率较低，在相同荷载下环形钢筋对核心混凝土的约束作用弱于后者，导致钢筋变形较大。两个试件FCSRC柱的内置型钢在极限位移下的应力云图如图17所示，可以发现两个试件的内置型钢均发生全截面屈服，但在GFRP管破裂处并未发生局部屈曲，表明GFRP管和填充混凝土能够有效抑制内置型钢翼缘的局部屈曲。此外，M-4的内置型钢中部出现了应力集中现象，为了便于观察，将面外变形放大10倍后可以明显看出，该试件中部(环梁节点处)发生了一定程度的面外变形，而试件M-5并未观察到这一现象，这一点也与试验结果相符(图8(c))，也进一步证明了有限元分析的准确性。
然而，有限元分析结果仍有不足之处，模拟得到的试件初始刚度偏高，特别是当荷载在3000~8000kN阶段。这是由于抗震性能试验后，节点的部分混凝土发生破碎掉落，如图5所示，导致试件初始刚度的降低，而混凝土的剥落在有限元分析中普遍很难模拟，这一点在今后的研究中有待进一步改进。
4. FCSRC柱-RC环梁节点轴压承载力理论分析
为了进一步对震损试件轴压承载力进行评估，本节从理论的角度，分别对未受损的FCSRC柱和RC环梁节点的承载力进行分析，并与震损试件的试验结果进行对比，以研究地震作用对试件轴压承载力的影响。
4.1 FCSRC柱轴压承载力
由于GFRP管主要是对FCSRC柱内的填充混凝土起到约束作用，其轴向刚度较小，因此不考虑GFRP管对试件轴压承载力的贡献。FCSRC柱的轴压承载力可以通过分别计算约束混凝土和内置型钢承担的轴向荷载后叠加得到：
Nuc=Ns+Nc1=fyAs+fcc1Ac1 (1) 式中：Nuc为FCSRC柱的轴压承载力；Ns、Nc1分别为内置型钢和填充混凝土的轴压承载力；fy和fcc1分别为钢材的屈服强度和FRP约束混凝土强度；As和Ac1分别表示内置型钢和填充混凝土的截面面积。Teng等[31]给出了fcc1的计算公式：
{fcc1=fco[1+3.5(ρK−0.1)ρε] ρK⩾ (2) {\rho _{\text{K}}}{\text{ = }}2{E_{{\text{FRP}}}}t/[(f_{{\text{co}}}^{}/{\varepsilon _{{\text{co}}}})D] (3) \; {\rho _{{\text{ε}}}}{\text{ = }}{\varepsilon _{{\text{h,rup}}}}/{\varepsilon _{{\text{co}}}} (4) 式中：fco为未约束混凝土强度；εco为其对应的应变；ρK和ρε分别为约束刚度比和应变比；EFRP、t、D和εh,rup分别为FRP管的环向弹性模量、壁厚、内径和环向断裂应变。
4.2 RC环梁节点轴压承载力
RC环梁节点的轴压承载力由两部分组成，即内置型钢和核心混凝土(环梁节点直接承压部分的混凝土，其截面面积与柱相同)，则节点轴压承载力为
{N_{\text{j}}} = {N_{\text{s}}} + {N_{{\text{c2}}}} (5) 式中，Nj和Nc2分别表示节点的轴压承载力和核心混凝土提供的轴压承载力。考虑核心混凝土受到多圈环形钢筋对其约束作用，Nc2的计算方法如下：
{N_{{\text{c2}}}} = f_{{\text{c,}n}}^{}{A_{{\text{c2}}}} (6) 式中：fc,n为从外向内第n圈环形钢筋内的约束混凝土强度；Ac2为节点直接承压的混凝土截面面积。结合Mander等[32]提出的约束混凝土理论，fc,n由叠加原理得到[33]：
f_{{\text{c,}n}}^{} = f_{{\text{c,}n-1}}^{}\left(-1.254 + 2.254\sqrt {1 + \frac{{7.94f_{{\text{l,}n}}^{}}}{{f_{{\text{c,}n-1}}^{}}}} - 2\frac{{f_{{\text{l,}n}}^{}}}{{f_{{\text{c,}n-1}}^{}}}\right) (7) 式中，fl,n表示从外向内第n圈环形钢筋对其内部混凝土产生的围压，其计算方法如下：
{f}_{\text{l,}n}^{}\text=\frac{2{A}_{\text{ss,}n}{f}_{\text{ys,}n}}{{d}_{\text{s,}n}{s}_{{n}}}\frac{{\left(1-\frac{{s}_{{n}}^{'}}{2{d}_{\text{s,}n}}\right)}^{2}}{1-{\rho }_{\text{cc,}n}} (8) 式中：Ass,n、fss,n和ds,n分别表示从外向内第n圈环形钢筋的截面面积、屈服强度和中线的直径；sn和sn′分别第n圈环形钢筋中心间距和净距；ρcc,n表示竖向钢筋面积与环形钢筋内混凝土截面面积的比值(竖向钢筋在本构造中为箍筋的单肢和内置型钢)。
研究表明[34]，采用式(6)计算的钢筋约束混凝土承载力偏于保守，Chen等[34]考虑了混凝土局部承压的影响，对钢筋约束混凝土的轴压承载力进行修正：
{N}_{\text{c2}}=0.85\beta {f}_{\text{c,}n}^{}{A}_{\text{c2}}\sqrt{{A}_{\text{c3}}/{A}_{\text{c2}}}\text{，}\text{ }\sqrt{{A}_{\text{c3}}/{A}_{\text{c2}}}\leqslant 2 (9) 式中：Ac3为混凝土局部受压计算底面积，为完全包含在支座内的最大圆台或棱台，其上表面为Ac2，下表面按照上表面的边缘按1/2坡度进行延伸；β为混凝土局部受压调整系数，由下式得到：
\;\beta {\text{ = 1/(}}1.1h/d + 0.28{\text{)}} (10) 式中，h和d分别表示环梁的高度和局部受压面的直径(即柱的直径)。
4.3 FCSRC柱-RC环梁节点轴压承载力计算
根据4.1节和4.2节给出的FCSRC和RC环梁节点的计算公式，分别计算M-4和M-5的轴压承载力。根据试验中监测到的最大GFRP管环向应变0.011，结合式(1)~(4)可得，试件M-4和M-5中FCSRC柱的轴压承载力均为10732 kN。根据式(5)~(10)可得试件M-4和M-5节点的轴压承载力分别为12004 kN和14684 kN。节点的轴压承载力均大于FCSRC柱，因此试件M-4和M-5的轴压承载力的理论值Fthe均为10732 kN，见表2。
通过与试验结果进行对比可以得出：(1) 从试验结果来看，两个试件失效均是由于FCSRC柱的GFRP管破坏引起的，因此FCSRC柱的轴压承载力决定了试件的最大轴压承载力，这与理论结果一致，也进一步证明两个试件的RC环梁节点在遭受地震作用后依然能够体现出“强节点，弱构件”的设计理念；(2) 震损试件轴压承载力的试验值与未震损试件轴压承载力理论值接近且偏大(M-4和M-5的误差分别为3.1%和9.7%)，表明本试验中节点损伤对试件的轴压承载力影响不大，同时理论值偏于保守，采用本文提出的理论公式得到的试件轴压承载力具有一定的安全储备。
5. 结 论
(1) 所设计的两个震损纤维增强树脂复合材料(FRP)约束型钢混凝土柱(FRP-confined steel-reinforced concrete，FCSRC)柱-钢筋混凝土(Reinforced concrete，RC)梁节点试件在轴向荷载作用下的失效均是由于玻璃纤维增强树脂复合材料(GFRP)管破裂引起的，表明震损后的试件依然满足“强节点，弱构件”的设计原则。
(2) 当环梁配筋率由1.4%增大到2.5%时，试件的屈服荷载和初始刚度变化不大，而峰值荷载和屈服后刚度分别增加了7.3%和60.2%，极限变形和延性系数分别减小了10.4%和8.5%。
(3) 所建立的有限元模型能够较准确地模拟震损试件在轴压荷载下的力学行为。
(4) 提出的理论公式计算结果与试验值接近，能够较准确地预测震损试件的轴压承载力，同时具有一定的安全储备。
-
![]()
图 1 纤维增强树脂复合材料(FRP)约束型钢混凝土(FCSRC)柱-钢筋混凝土(RC)梁节点
Figure 1. Joint of fiber reinforced polymer (FRP)-confined steel-reinforced concrete (FCSRC) column-to-reinforced concrete (RC) beam
![]()
图 2 试件截面尺寸及配筋
GFRP—Glass fiber reinforced polymer; φ—Diameter; M-4, M-5—4, 5 layers of ring bars in the ring beam
Figure 2. Details of specimens
![]()
图 4 FCSRC柱-RC梁抗震性能试验荷载-位移曲线
Figure 4. Load-displacement curves of FCSRC column-to-RC beam in seismic performance experiment
![]()
图 5 FCSRC柱-RC梁抗震性能试验破坏模态
Figure 5. Failure modes of FCSRC column-to-RC beam in seismic performance experiment
![]()
图 6 FCSRC柱-RC梁抗震性能试验荷载-环梁应变曲线
R1—Strain of ring bars at near the beam; R2—Strain of ring bars in the middle of the joint
Figure 6. Load-strain curves for the ring beam of FCSRC column-to-RC beam in seismic performance experiment
![]()
图 7 轴压试验装置
LVDT—Linear variable differential transformer
Figure 7. Test set-up of axial compressive test
![]()
图 10 FCSRC柱-RC环梁节点轴向荷载-位移曲线
FEA—Finite element analysis
Figure 10. Axial load-displacement curves of FCSRC column-to-RC ring beam joint
![]()
图 11 FCSRC柱-RC环梁节点轴向位移-应变曲线
1-4—Section 1-4 in Fig.7(b); H—Hoop strain; V—Axial strain
Figure 11. Axial displacement-strain curves of FCSRC column-to-RC ring beam joint
![]()
图 13 FCSRC柱-RC环梁节点有限元模型验证
RC—Type of beams; 4, 5—4, 5 layers of ring bars in the ring beam; 0.4—Axial load ratio
Figure 13. Verification of FEA model of FCSRC column-to-RC ring beam joint
![]()
图 14 GFRP管环向应变
LE—Strain; LE11—Hoop strain; SNEG—Face with negative normal direction of elements
Figure 14. Hoop strain distribution of GFRP tubes
![]()
图 15 25 mm的FCSRC柱-RC环梁节点试件轴向应变分布
Figure 15. Axial strain distribution of 25 mm FCSRC column-to-RC ring beam joint specimens
表 1 钢材力学性能
Table 1 Mechanical properties of steel
Type of steel Thickness or diameter/mm fy/MPa fu/MPa Es/GPa Steel bar 8 306 456 211 10 459 627 200 12 448 609 201 14 422 612 208 22 418 591 205 Steel plate 16 286 411 191 Note: fy, fu, Es—Yield strength, ultimate strength and elastic modulus of steel, respectively. 
下载: 导出CSV
表 2 FCSRC柱-RC环梁节点试验、有限元和理论分析结果
Table 2 Results of experiment, finite element analysis and theoretical analysis for FCSRC column-to-RC ring beam joint
Fy/kN Δy/mm Fp/kN Δp/mm Fu/kN Δu/mm μ k0/(kN·mm−1) ks/(kN·mm−1) FFEA/kN Fthe/kN M-4 9351 10.15 11080 32.32 9408 36.02 3.55 1129 78 11256 10723 M-5 9258 9.98 11891 31.07 10107 32.27 3.23 1153 125 12042 10723 Notes: Fy, Fp, Fu—Yield load, peak load and ultimate load of the specimen, respectively; Δy, Δp, Δu—Displacement corresponding to Fy, Fp, Fu; μ—Ductility coefficient; k0—Initial stiffness of the specimen; ks—Post-yield stiffness of the specimen; FFEA, Fthe—Maximum load-bearing capacity calculated by FEA and theory.
下载: 导出CSV
-
[1] 张剑, 周储伟, 艾军, 等. 高性能碳-玻璃纤维布加固混凝土梁的非线性响应[J]. 复合材料学报, 2017, 34(7):1617-1623. DOI: 10.13801/j.cnki.fhclxb.20160926.001 ZHANG Jian, ZHOU Chuwei, AI Jun, et al. Nonlinear response analysis of concrete beam reinforced with high performance CF-GF sheet[J]. Acta Materiae Compositae Sinica,2017,34(7):1617-1623(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20160926.001
[2] 李腾, 宁志华, 吴嘉瑜. CFRP加固钢板的粘结截面剥离破坏[J]. 复合材料学报, 2021, 38(12):4090-4105. LI Teng, NING Zhihua, WU Jiayu. Interfacial debonding failure of CFRP-strengthened steel structures[J]. Acta Materiae Compositae Sinica,2021,38(12):4090-4105(in Chinese).
[3] POHORYLES D A, MELO J, ROSSETTO T, et al. Seismic retrofit schemes with FRP for deficient RC beam-column joints: State-of-the-art review[J]. Journal of Composites for Construction,2019,23(4):03119001. DOI: 10.1061/(ASCE)CC.1943-5614.0000950
[4] TENG J G, YU T, WONG Y L, et al. Hybrid FRP-concrete-steel tubular columns: Concept and behavior[J]. Construction and Building Materials,2007,21(4):846-854. DOI: 10.1016/j.conbuildmat.2006.06.017
[5] HU Y M, YU T, TENG J G. FRP-confined circular concrete-filled thin steel tubes under axial compression[J]. Journal of Composites for Construction,2011,15(5):850-860. DOI: 10.1061/(ASCE)CC.1943-5614.0000217
[6] YU T, HU Y M, TENG J G. FRP-confined circular concrete-filled steel tubular columns under cyclic axial compression[J]. Journal of Constructional Steel Research,2014,94:33-48. DOI: 10.1016/j.jcsr.2013.11.003
[7] YE Y Y, ZHU D H, ZENG J J, et al. Rectangular double-tube concrete columns with an internal elliptical high-strength steel tube: Concrete and behavior[J]. Engineering Structures,2020,216:110742.
[8] XIE W, CHEN Y, HAN S, et al. Research on I steel reinforced concrete-filled GFRP tubular short columns[J]. Thin-Walled Structures,2017,120:282-296. DOI: 10.1016/j.tws.2017.08.031
[9] KARIMI K, TAIT M J, El-DAKHAKHNI W W. Testing and modeling of a novel FRP-encased steel-concrete compo-site column[J]. Composite Structures,2011,93(5):1463-1473. DOI: 10.1016/j.compstruct.2010.11.017
[10] YU T, LIN G, ZHANG S S. Compressive behavior of FRP-confined concrete-encased steel columns[J]. Composite Structures,2016,154:493-506. DOI: 10.1016/j.compstruct.2016.07.027
[11] ZAKAIB S, FAM A. Flexural performance and moment connection of concrete-filled GFRP tube-encased steel I-Sections[J]. Journal of Composites for Construction,2012,16(5):604-613. DOI: 10.1061/(ASCE)CC.1943-5614.0000288
[12] REN F M, LIANG Y W, HO J C M, et al. Behaviour of FRP tube-concrete-encased steel composite columns[J]. Composite Structures,2020,241:112139. DOI: 10.1016/j.compstruct.2020.112139
[13] CHEN G M, LAN Z H, XIONG M X, et al. Compressive behavior of FRP-confined steel-reinforced high strength concrete columns[J]. Engineering Structures,2020,220:110990. DOI: 10.1016/j.engstruct.2020.110990
[14] XIONG M X, XU Z, CHEN G M, et al. FRP-confined steel-reinforced recycled aggregate concrete columns: Concept and behaviour under axial compression[J]. Composite Structures,2020,246:112408. DOI: 10.1016/j.compstruct.2020.112408
[15] REN F M, WU D, CHEN G, et al. Slender FRP-confined steel-reinforced RAC columns under eccentric compression: Buckling behavior and design calculation models[J]. Engineering Structures,2021,246:113059. DOI: 10.1016/j.engstruct.2021.113059
[16] REN F M, TIAN S Y, MA W, et al. Seismic performance of FRP-confined steel-reinforced RAC columns[J]. Compo-site Structures,2021,51(6):115077. DOI: DOI:10.1016/j.compstruct.2021.115077
[17] 田时雨, 任凤鸣, 陈光明. 复材新结构梁柱节点: 研究现状及展望[J]. 工业建筑, 2021, 51(6):186-197. TIAN Shiyu, REN Fengming, CHEN Guangming. Beam-to-column joint of new structures incorporating FRP: Current status and prospects[J]. Industrial Construction,2021,51(6):186-197(in Chinese).
[18] REN F M, TIAN S Y, GONG L, et al. Seismic performance of a ring beam joint connecting FTCES column and RC/ESRC beam with NSC[J]. Journal of Building Engineering, 2022: 105366(in press). .
[19] 王艳云, 叶献国, 蒋庆, 等. 基于性能的钢筋混凝土框架结构震后损失评估[J]. 工程抗震与加固改造, 2016, 38(5):16-20, 43. DOI: 10.16226/j.issn.1002-8412.2016.05.003 WANG Yanyun, YE Xianguo, JIANG Qing. Performance-based seismic loss assessment in RC structure[J]. Earthquake Resistant Engineering and Retrofitting,2016,38(5):16-20, 43(in Chinese). DOI: 10.16226/j.issn.1002-8412.2016.05.003
[20] 许圆圆. 钢筋混凝土框架结构震后残余变形对其抗震性能影响的研究[D]. 西安: 西安建筑科技大学, 2017. XU Yuanyuan. Study on the residual deformation after earthquake of reinforced concrete frame structure for future seismic performance[D]. Xi’an: Xi’an University of Architecture and Technology, 2017(in Chinese).
[21] CHEN Q, CAI J, BRADFORD M A, et al. Seismic behaviour of a through-beam connection between concrete-filled steel tubular columns and reinforced concrete beams[J]. Engineering Structures,2014,80:24-39. DOI: 10.1016/j.engstruct.2014.08.036
[22] American Society of Testing Materials. Standard test method for compressive strength of cylindrical concrete specimens: C39/C39 M-18[S]. West Conshohocken: ASTM International, 2018.
[23] American Society of Testing Materials. Standard test method for static modulus of elasticity and poisson’s ratio of concrete in compression: C469/C469 M-14[S]. West Conshohocken: ASTM International, 2014.
[24] 吴智深, 汪昕, 吴刚. FRP增强工程结构体系[M]. 北京: 科学出版社, 2017. WU Zhishen, WANG Xin, WU Gang. FRP reinforced engi-neering structural systems[M]. Beijing: Science Press, 2017(in Chinese).
[25] XIE P. Behavior of large-scale hybrid FRP-concrete-steel double-skin tubular columns subjected to concentric and eccentric compression[D]. Hong Kong: The Hong Kong Polytechnic University, 2018.
[26] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of China. Metallic materials-Tensile testing-Part 1: Method of test at room temperature: GB/T 228.1—2010[S]. Beijing: Standards Press of China, 2011(in Chinese).
[27] 中华人民共和国住房和城乡建设部. 建筑抗震试验规程: JGJ/T 101—2015[S]. 北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Specification for seismic test of buildings: JGJ/T 101—2015[S]. Beijing: China Architecture and Building Press, 2015(in Chinese).
[28] 冯鹏, 强翰霖, 叶列平. 材料、构件、结构的“屈服点”定义与讨论[J]. 工程力学, 2017, 34(3):36-46. DOI: 10.6052/j.issn.1000-4750.2016.03.0192 FENG Peng, QIANG Hanlin, YE Lieping. Discussion and definition on yield points of materials, members and structures[J]. Engineering Mechanics,2017,34(3):36-46(in Chinese). DOI: 10.6052/j.issn.1000-4750.2016.03.0192
[29] FERROTTO M F, FISCHERB O, CAVALERI L. A strategy for the finite element modeling of FRP-confined concrete columns subjected to preload[J]. Engineering Structures,2018,173:1054-1067. DOI: 10.1016/j.engstruct.2018.07.047
[30] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture and Building Press, 2015(in Chinese).
[31] TENG J G, JIANG T, LAM L, et al. Refinement of a design-oriented stress-strain model for FRP-confined concrete[J]. Journal of Composites for Construction,2009,13:269-278. DOI: 10.1061/(ASCE)CC.1943-5614.0000012
[32] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering,1988,114(8):1804-1826. DOI: 10.1061/(ASCE)0733-9445(1988)114:8(1804)
[33] BAI Y, NIE J G, CAI C S. New connection system for confined concrete columns and beams. II: Theoretical modeling[J]. Journal of Structural Engineering,2008,134(12):1800-1809. DOI: 10.1061/(ASCE)0733-9445(2008)134:12(1800)
[34] CHEN Q J, CAI J, BRADFORD M A. Axial compressive behavior of through-beam connections between concrete-filled steel tubular columns and reinforced concrete beams[J]. Journal of Structural Engineering,2015,141(10):04015016. DOI: 10.1061/(ASCE)ST.1943-541X.0001249
-
期刊类型引用(3)
1. 植培斌，卢德辉，潘正玉，田时雨，韩靖. 分离式施工升降机基础施工工艺及力学性能研究. 广州建筑. 2024(09): 43-47 . 
百度学术
2. 周刚，田时雨，雷鸣，张溜. 环梁直径对CFST柱-RC梁节点力学性能的影响. 广州建筑. 2024(09): 10-13 . 百度学术
3. 张滨麟，金浏，陈凤娟，杜修力. 考虑剪跨比及配纤率影响的CFRP加固剪力墙抗剪承载力计算方法. 复合材料学报. 2023(10): 5902-5917 . 本站查看
其他类型引用(2)
-
计量
- 文章访问数: 1158
- HTML全文浏览量: 570
- PDF下载量: 61
- 被引次数: 5
