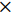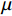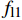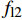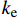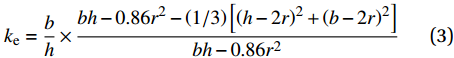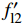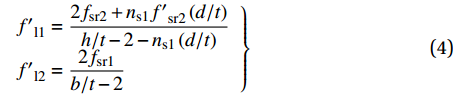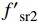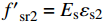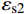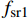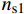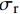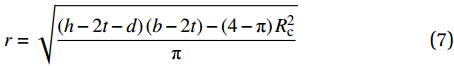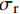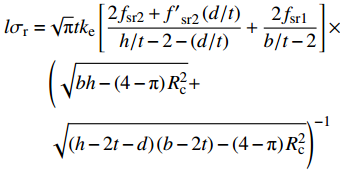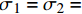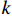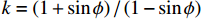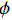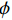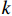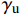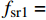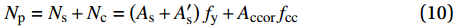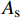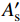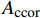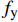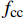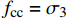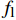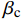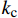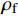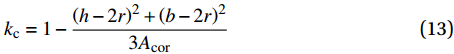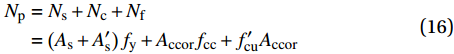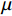玻璃纤维增强聚合物复合材料约束壁式钢管混凝土短柱轴压性能试验

程杰; 齐玉军; 谢志锦

doi:10.13801/j.cnki.fhclxb.20200827.001

玻璃纤维增强聚合物复合材料约束壁式钢管混凝土短柱轴压性能试验

南京工业大学　土木工程学院，南京 211816

基金项目: 国家自然科学基金面上项目(51778286)；江苏省基础研究计划(自然科学基金)面上项目(BK20171469)

详细信息

通讯作者:
齐玉军，博士，教授，研究方向为新材料及新型结构　Email：qiyujun@njtech.edu.cn

中图分类号: TU398.9
计量
- 文章访问数: 1290
- HTML全文浏览量: 500
- PDF下载量: 87
出版历程
- 收稿日期: 2020-06-14
- 录用日期: 2020-08-13
- 网络出版日期: 2020-08-27
- 刊出日期: 2021-06-22

Experiment on axial compression performance of glass fiber reinforced polymer-walled concrete-filled steel tube columns

College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China

摘要

摘要: 为研究玻璃纤维增强聚合物复合材料(GFRP)约束壁式钢管混凝土矩形短柱的轴压力学性能，对1组无GFRP约束试件和2组GFRP约束试件进行静力轴压试验；根据试验结果提出壁式柱的强弱约束模型，并基于双剪统一强度理论建立GFRP约束壁式钢管混凝土柱的轴压承载力计算公式；最后建立有限元模型，将计算结果与试验对比，并进行参数化分析，研究钢材屈服强度和混凝土强度对新型壁式钢管混凝土柱轴压性能的影响。结果表明：壁式钢管混凝土柱最终因柱中混凝土压碎、钢管屈曲、试件变形过大而失效；钢材在试件第二线性段起点处开始屈服，钢材强度得到充分发挥，GFRP能有效提高构件峰值承载力，但延性有所下降；理论公式计算结果与试验值吻合较好；混凝土强度及钢材屈服强度均能有效提高承载能力，且钢材屈服强度对承载力的影响明显大于混凝土强度的影响。
- 玻璃纤维增强聚合物复合材料 /
- 壁式钢管混凝土柱 /
- 矩形截面 /
- 承载力 /
- 参数分析
Abstract: In order to study the axial compression performance of glass fiber reinforced polymer (GFRP)-walled concrete-filled steel tube columns, the static axial compression tests were conducted on a group of non-GFRP constrained specimens and two groups of GFRP constrained specimens. According to the test results, a strong and weak constraint model of the wall column was proposed. Based on the twin-shear unified strength theory, the formula was established to calculate the axial compression bearing capacity of the GFRP-walled concrete-filled steel tube columns. Finally, the theoretical results, obtained through the establishment of the finite element model, were compared with the experimental results. And a parametric analysis was used to study the effect of the yield strength of steel and the strength of concrete on the axial compression performance of the new type wall-filled concrete-filled steel tube columns. The results show that the wall-filled concrete-filled steel tube columns eventually fail due to crushing of the concrete, buckling of the steel tube and excessive deformation of the specimens. At the beginning of the second linear section of the specimen, the steel begins to yield and its strength is fully exerted, which demonstrates that GFRP can effectively improve the peak load of the member, however, the ductility has decreased. The results of the theoretical formula are in agreement with the experimental results. The bearing capacity can be improved by increasing the strength of concrete and the yield strength of the steel. Compared with the strength of concrete, the yield strength of steel bars has a greater influence on the bearing capacity.
- glass fiber reinforced polymer /
- walled concrete-filled steel tube column /
- rectangular section /
- bearing capacity /
- parameter analysis

HTML全文

矩形钢管混凝土是一种在矩形钢管中填充混凝土，并由钢管和混凝土共同承担外荷载的组合构件。外部钢管对核心混凝土起到约束作用，从而可提高混凝土强度；内部混凝土可改善钢管屈曲，从而保证材料性能可得到充分发挥^[1]。该类结构以其施工方便、承载力高、经济效果好等特点而被广泛应用于结构工程中。

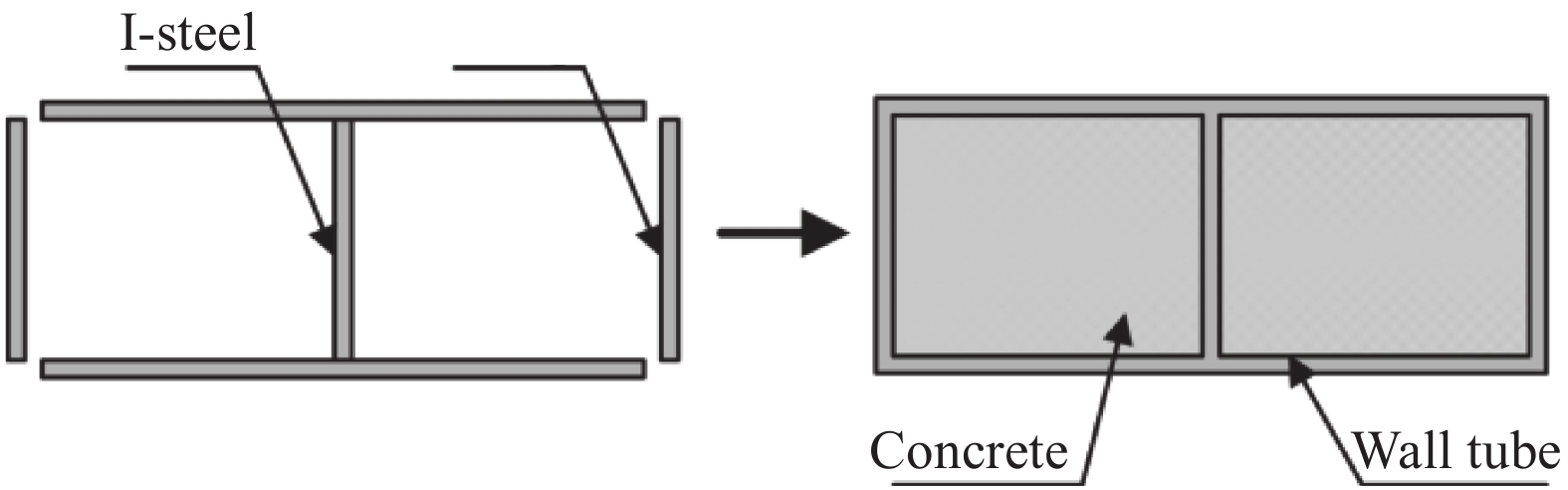
但在住宅结构中，钢管混凝土结构的框架柱常会凸出墙体，降低建筑功能^[2]。对此，孙晓岭等^[3]提出一种适用于钢结构住宅的壁式钢管混凝土柱(Walled concrete-filled steel tube column, WCFT column)，它沿围护墙方向适当增加截面高宽比，此种截面可减少甚至避免框架柱凸出墙体，显著提高钢结构住宅品质。典型的壁式柱构造形式如图1所示，此种截面虽然可以充分利用现有工字钢截面生产线，减少生产成本与工艺难度，但焊缝出现在角部，无法避免常见矩形钢管混凝土柱在轴压作用下纵向焊缝在角部撕裂的问题^[4-6]。国内外学者通过试验研究发现，对矩形截面做倒圆角处理能有效改善混凝土应力与纤维增强聚合物复合材料(FRP)应变分布不均匀，从而提高混凝土柱的约束效果。李晓霞^[7]进行了复合材料约束素混凝土方形短柱受压试验，发现倒圆角可有效提高约束方柱受压强度。

图 1 壁式柱典型构造

Figure 1. Typical structure of wall column

下载: 全尺寸图片幻灯片

在方形钢管内填充混凝土可有效限制空钢管向内局部屈曲的趋势，但向外屈曲的问题并没有得到改善。近年来，FRP由于其轻质高强的力学性能而被广泛应用于结构加固增强中。Xiao等^[8]最早提出FRP约束钢管混凝土组合柱(CCFT)的概念。采用FRP外包加固混凝土柱，通过约束混凝土的侧向膨胀，从而提高混凝土柱的抗压强度^[9-10]。

为解决现有壁式钢管混凝土柱角部焊缝开裂及改善钢管外部屈曲的问题，本文提出一种新型壁式钢管混凝土柱，该柱沿内隔板纵向焊接，内部填充混凝土，外部包裹玻璃纤维增强聚合物复合材料(GFRP)。通过对新型GFRP约束壁式钢管混凝土柱进行轴压试验，研究柱的荷载位移、破坏模式和延性等。并基于双剪统一强度理论，建立壁式柱轴压承载力的理论计算公式，以期给工程应用提供参考。

1. 试验概况

1.1 试件设计及制作

试验共设计6个试件，包括1组无GFRP约束壁式钢管混凝土柱，2组GFRP约束壁式钢管混凝土柱，每组试件2个，GFRP包裹层数为0层、2层、4层。试件截面尺寸均为100 mm $\times$ 200 mm，高度为600 mm，混凝土强度等级为C30，钢板及内隔板均采用同批次Q235B钢，壁式钢管倒角半径为15 mm，C形截面通过钢板折弯形成，角部无焊缝，两片C形截面与中间内隔板均在外部采用对焊形成，焊缝形式为单边V形焊缝，焊接采取满焊、焊透的方式，最后将焊接处用机器打磨光滑、平整；采用真空导入的方法外部粘贴GFRP布，GFRP布的搭接长度取为200 mm。试件上下端部采用同批次GFRP布进行端部约束，宽50 mm，缠绕两层，搭接区长度同样为200 mm。试件截面如图2所示，具体试件实测尺寸见表1。

图 2 试件几何尺寸及构造

Figure 2. Geometrical dimensions and structure of the specimens

下载: 全尺寸图片幻灯片

1.2 材料性能

所有构件采用同批次C30混凝土浇筑并预留试块，依据GB/T 50081—2019^[11]进行标准试验，测得混凝土的立方体抗压强度。构件中采用Q235B钢板，依据GB/T 228—2010^[12]规定的测试方法，实测钢材屈服强度及弹性模量，具体材料性能见表2。GFRP采用密度为800 g/m²的玻璃纤维布，依据ASTM D3039^[13]、ASTM D3410^[14]测试方法，测得本试验中GFRP的抗拉强度和模量，具体材料性能见表3。

表 1 玻璃纤维增强聚合物复合材料(GFRP)约束壁式钢管混凝土柱参数

Table 1. Parameters of glass fiber reinforce polymer (GFRP)-walled concrete-filled steel tube columns

Number	b×h×L/mm	t/mm	d/mm	R_c/mm	Fiber layer
C30-G0-1	100×200×600	5	5	15	0
C30-G0-2	100×200×600	5	5	15	0
C30-G2-1	100×200×600	5	5	15	2
C30-G2-2	100×200×600	5	5	15	2
C30-G4-1	100×200×600	5	5	15	4
C30-G4-2	100×200×600	5	5	15	4
Notes: C—Concrete, the number stands for the concrete grade; G—GFRP, the numbers are the number of package layers; 1 and 2—Two different test pieces; B—Length; h—Width; L—Height; t—Wall thickness; d—Thickness of the separator; R_c—Radius of the chamfer.

下载: 导出CSV

| 显示表格

表 2 钢材和混凝土的材料力学性能

Table 2. Material mechanical properties of steel and concrete

Material	${f_{\rm{y}}}/{\rm{MPa}}$	$E/{\rm{GPa}}$	${f_{{\rm{cu}}}}/{\rm{MPa}}$
Concrete	—	—	32.4
Steel plate	251	196	—
Notes: f_y—Yield strength; E—Tensile modulus; f_cu—Cube compressive strength.

下载: 导出CSV

| 显示表格

表 3 GFRP布的材料力学性能

Table 3. Mechanical properties of GFRP

Material	${\sigma _{\rm{b}}}/{\rm{MPa}}$	$E/{\rm{GPa}}$
GFRP	537.4	28.7
Note: ${\sigma _{\rm{b}}}$ —Tensile strength.

下载: 导出CSV

| 显示表格

1.3 加载及测量装置

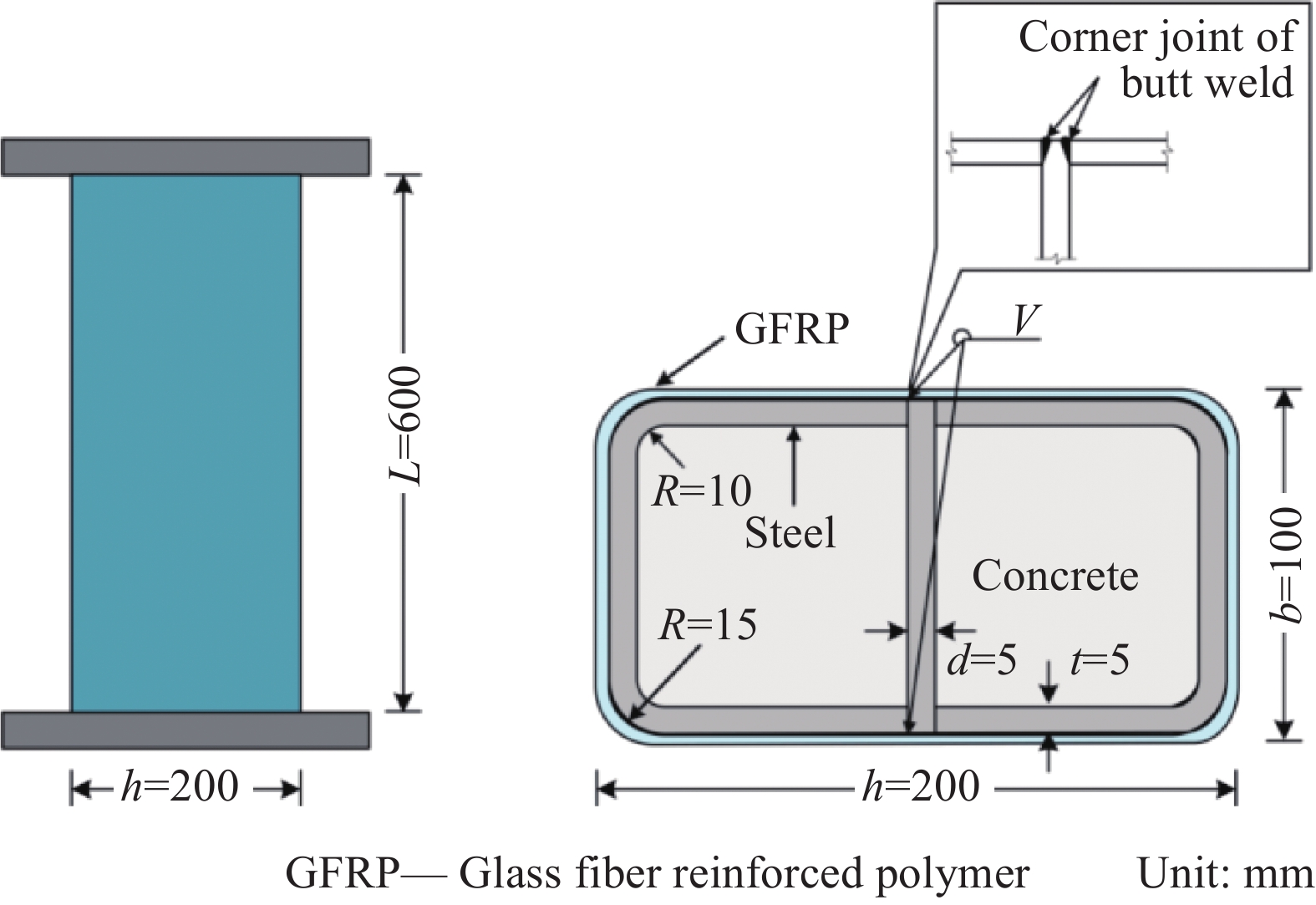
试验在复合材料试验室500 t压力试验机上进行，加载装置如图3所示。试验加载速度为2 mm/min，直至试件发生破坏，其中试件的破坏标志为发生严重变形或承载力下降到峰值70%以下。2个拉线式位移计(D₁、D₂)被固定在试件对角位置，用于对中并测量试件的轴向变形，为方便对试件破坏过程进行详细描述，将试件正对立面定义为1面，由顶往底看其余三面按照顺时针旋转，分别定义为2、3、4面，如图3所示。

图 3 GFRP约束壁式钢管混凝土柱轴压试验加载装置

Figure 3. Axial compressive test setup of GFRP-walled concrete-filled steel tube columns

下载: 全尺寸图片幻灯片

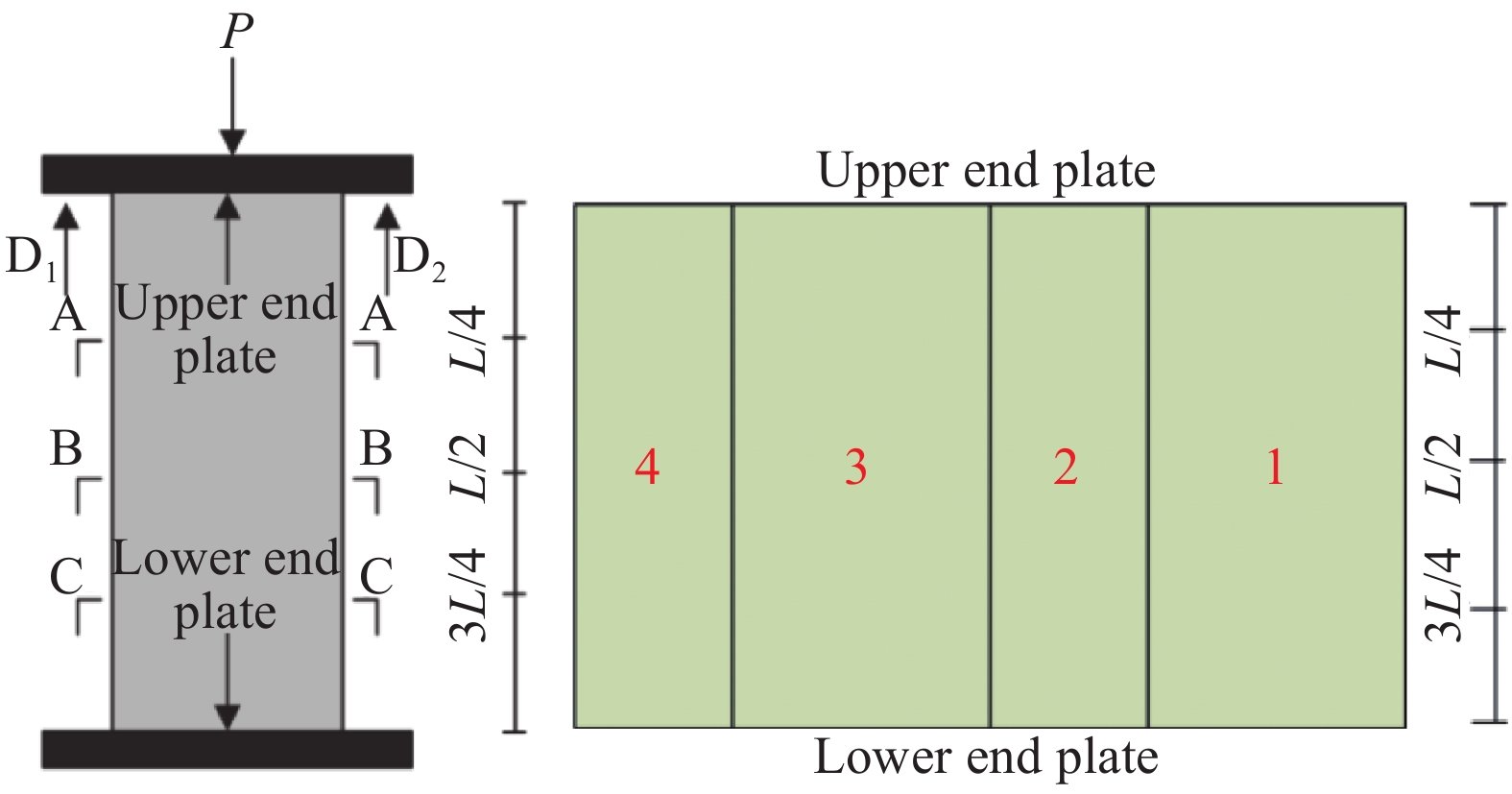
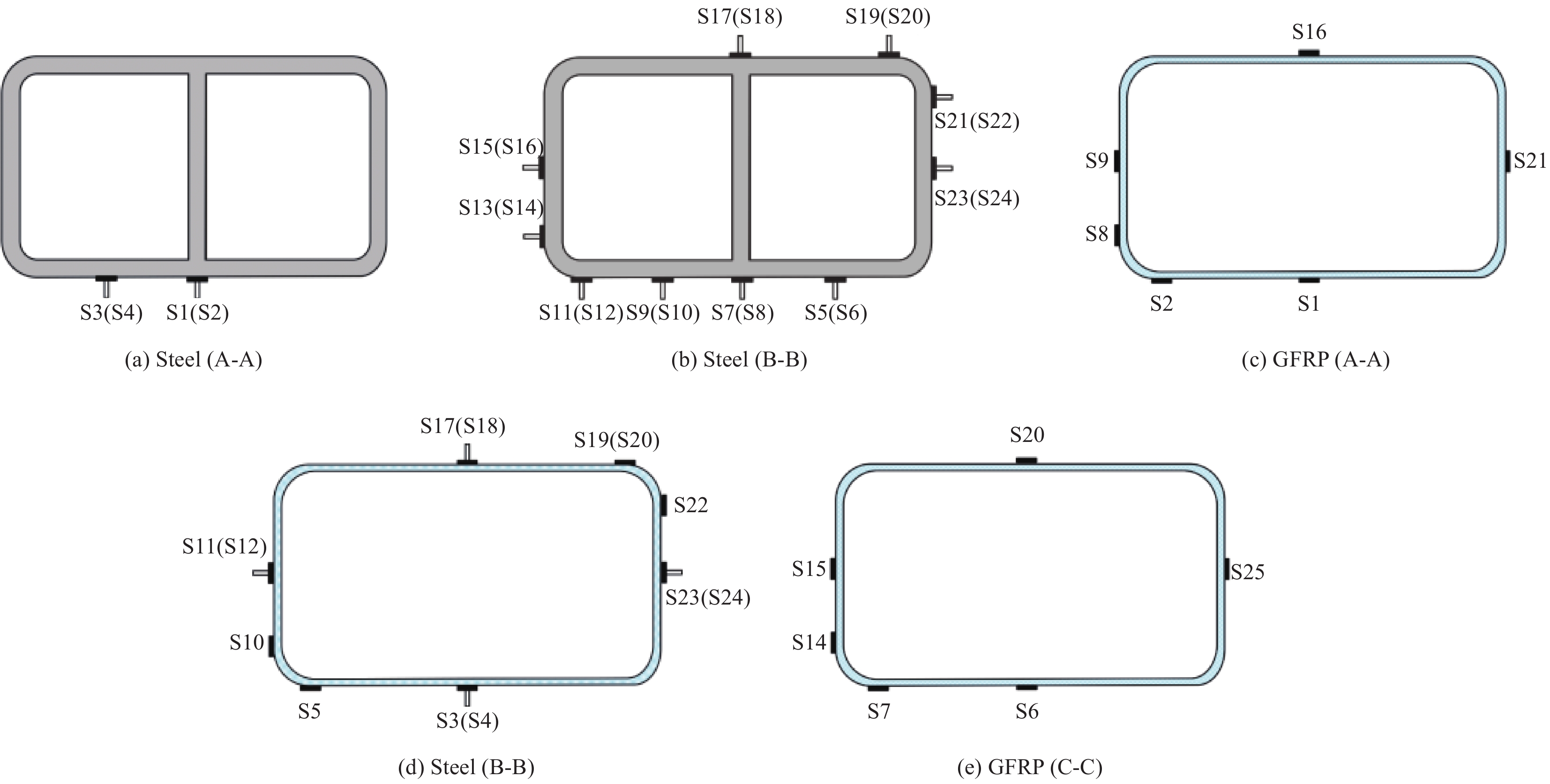
应变片主要布置在L/2和L/4截面处，用于测量加载过程中因变形所引起的壁式钢管和GFRP应变变化，应变片具体布置见图4。

图 4 试验柱测点布置

Figure 4. Arrangement of measuring points for tested columns

下载: 全尺寸图片幻灯片

2. 试验结果与分析

2.1 试验现象与破坏模式

对于无GFRP约束壁式钢管混凝土柱的破坏模式，以试件C30-G0-1为例，详细介绍试件的破坏过程，破坏过程见图5。加载初期试件处于弹性阶段，试件无明显变化；试件达到屈服荷载后，试件刚度下降，但此时试件承载力仍在增加；当荷载增加到峰值荷载的90%时，试件L/2截面处，1面长边与2面短边沿内隔板对称处出现褶皱形状的鼓曲，如图5(a)所示，同时试件4面L/4截面处开始出现鼓曲如图5(b)所示，且鼓曲随荷载的增加而不断明显；加载至峰值荷载后，荷载逐渐降低，此时试件沿L/2截面变形加剧，但由于短柱构件纵向压缩量有限，中部的混凝土不断压实，整个褶皱截面不断趋向于圆形如图5(c)所示，与陈梦成等^[15]研究的钢管约束混凝土试件破坏模式基本一致，试件最终因鼓曲处混凝土压碎，钢管屈服，试件变形过大而停止加载。

图 5 C30-G0-1的破坏过程

Figure 5. Failure process of C30-G0-1

下载: 全尺寸图片幻灯片

两组GFRP约束壁式钢管混凝土柱的破坏模式与试验现象基本一致，但与两层GFRP包裹试件相比，四层包裹试件纤维断裂前期无明显征兆，断裂发生突然且伴随巨响；纤维断裂延伸长度较长；纤维断裂后试件承载力出现骤降。

以试件C30-G2-1为例详细介绍破坏模式，破坏过程见图6。试验加载前期无明显现象，承载力快速线性增大；在试件达到屈服荷载时，GFRP开始与钢管发生剥离，试件刚度下降，承载力继续上升，如图6(a)所示。当荷载上升到峰值荷载的90%左右时，1面和3面出现白横纹，并不断向长边中部逐渐发展，短边基本无横向裂纹，如图6(b)和6(c)所示。在荷载继续增加并不断接近峰值荷载的过程中，短边2面与4面开始不断出现横向裂纹，如图6(d)所示。当试件达到峰值荷载时，试件中部3-4面L/2界面处角部出现纵向裂纹，单向布断裂，承载力开始快速下降，试件中部角部开始不断出现局部断裂，GFRP退出工作，如图6(e)所示。随着位移的继续增加，柱中鼓曲加剧，试件发生局部屈曲，如图6(f)所示，试件最终因鼓曲处混凝土压碎，钢管屈服，GFRP断裂，试件变形过大而停止加载。

图 6 C30-G2-1的破坏过程

Figure 6. Failure process of C30-G2-1

下载: 全尺寸图片幻灯片

与无GFRP约束试件相比，GFRP约束试件在钢管屈服时GFRP开始工作，约束钢管混凝土的侧向膨胀，极限承载力有所提高；随着荷载的继续增加GFRP断裂，试件承载力骤降，加固层数越多断裂现象越突然且承载力下降越快。壁式钢管混凝土柱角部无焊缝，有效地解决了传统矩形钢管混凝土柱在轴压作用下纵向焊缝在角部撕裂的问题。

2.2 GFRP约束壁式钢管混凝土柱荷载-位移曲线

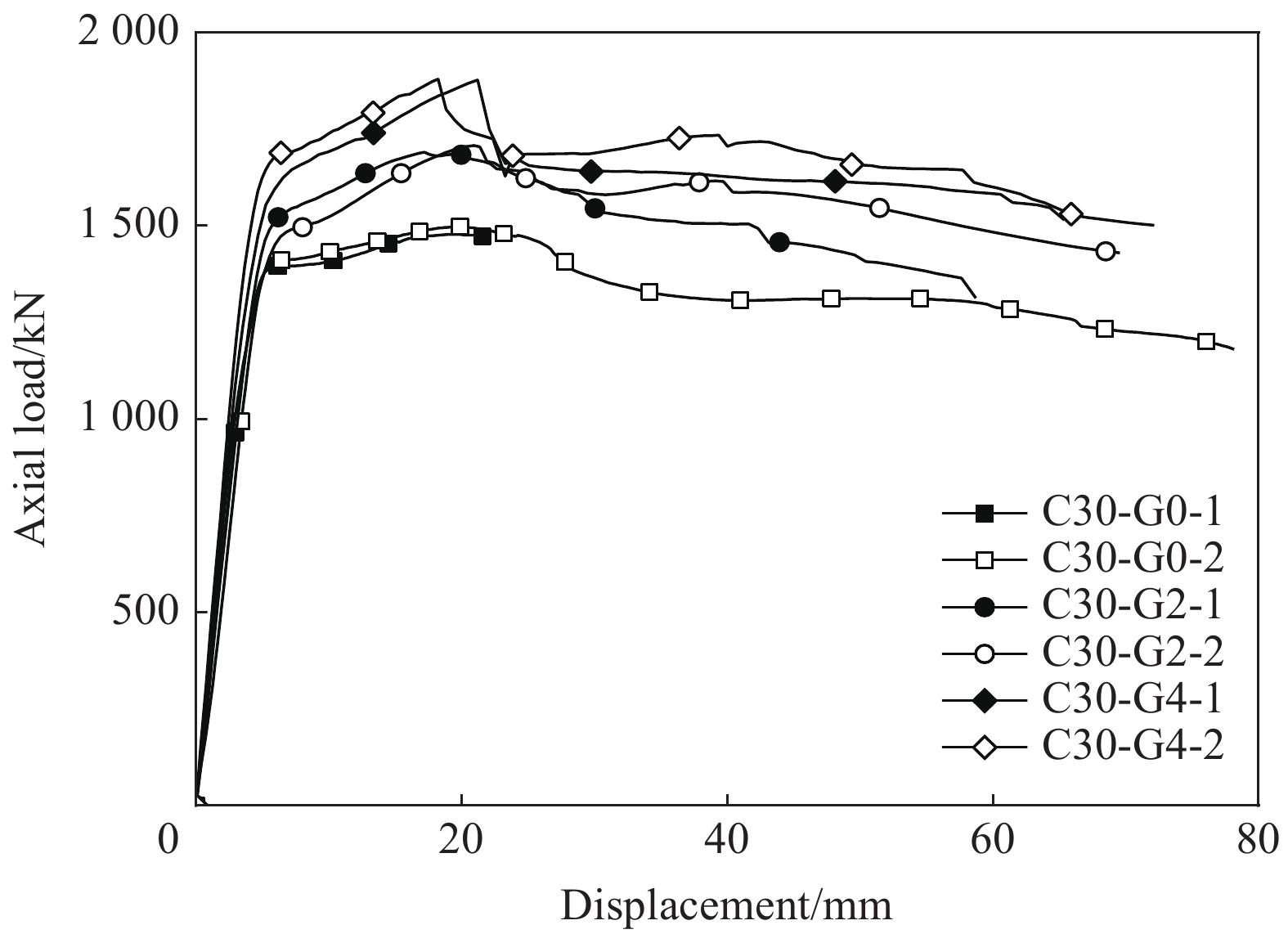
3组试件的荷载-位移曲线如图7所示。其中位移为两个对角位移计实测值的平均值，试件C30-G0-1因试验机采集故障，数据下降段未采集到。

图 7 GFRP约束壁式钢管混凝土柱轴向荷载-位移曲线

Figure 7. Axial load-deformation curves of GFRP-walled concrete-filled steel tube columns

下载: 全尺寸图片幻灯片

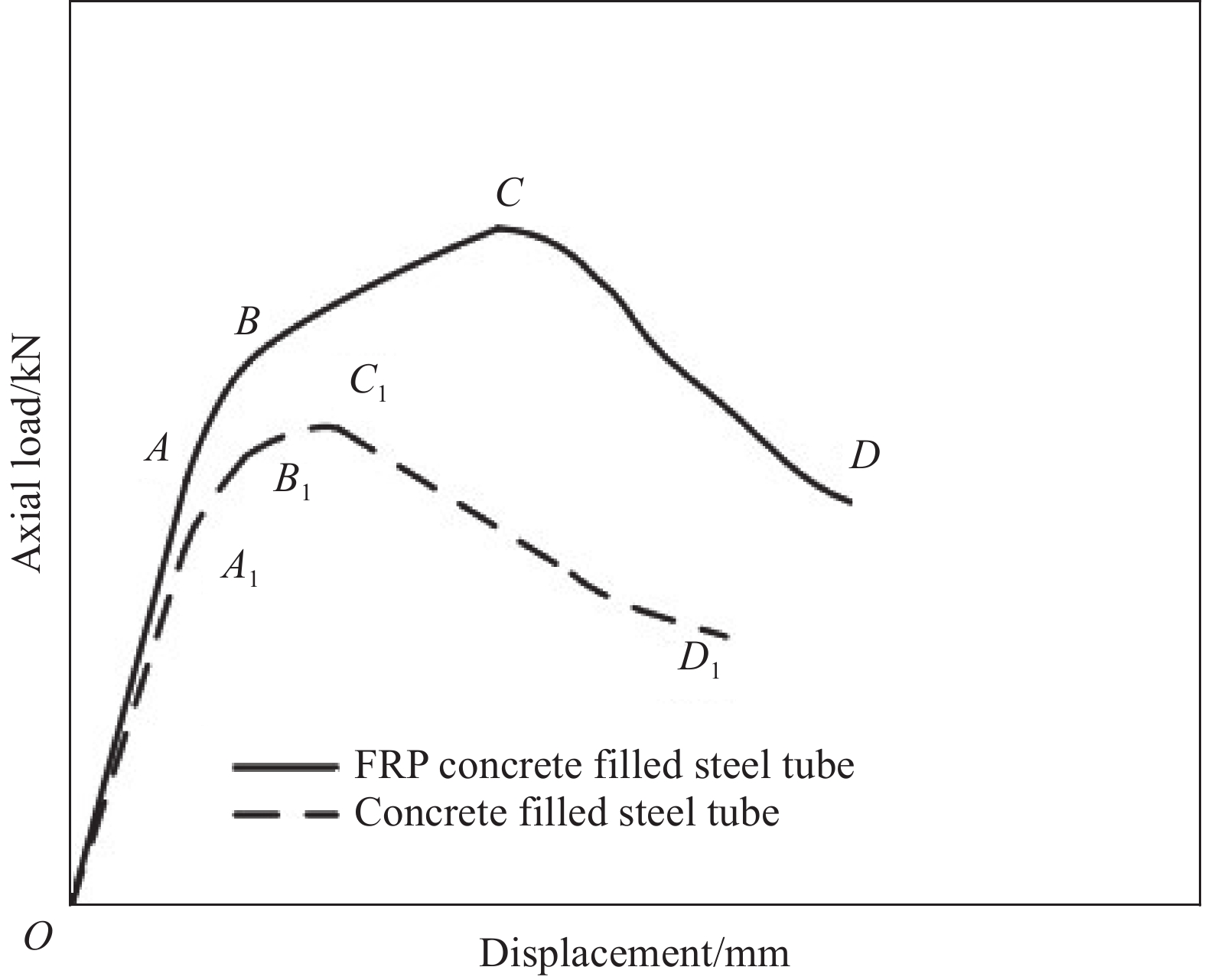
根据荷载-位移曲线的特点，可将构件的荷载位移曲线分为四个阶段：弹性阶段(OA)、弹塑性阶段(AB)、塑性强化阶段(BC)、软化阶段(CD)，本文典型曲线与张依睿等^[16]研究的FRP-钢复合约束混凝土轴压模型基本一致，如图8所示。

图 8 FRP-钢复合约束混凝土典型轴向荷载-位移曲线

Figure 8. Typical curves of axial load-displacement of FRP concrete filled steel tube

OA—Elastic stage; AB—Elastic-plastic stage; BC—Plastic strengthening stage; CD—Softening stage

下载: 全尺寸图片幻灯片

无GFRP包裹壁式钢管混凝土柱的受力过程如下：(1) OA₁，荷载随位移呈线性关系，此时试件无明显变化，钢管与混凝土二者仅存在界面黏结作用，直到A₁点钢管才对核心混凝土产生约束；(2) A₁B₁，随着轴向荷载的增加，核心混凝土的裂纹不断发展，而导致体积不断膨胀，其横向变形系数超过钢材泊松比，钢管混凝土进入弹塑性强化阶段，此后钢管混凝土柱开始发生横向膨胀。在B₁点钢管开始屈服；(3) B₁C₁，B₁开始钢管开始屈服，试件的承压刚度开始逐渐降低，钢管混凝土发生横向膨胀后，混凝土处于三向围压下的强度不断增长，荷载-位移曲线出现强化段。钢材环向应力不断增大，根据Vonmises准则，环向应力增加必然导致纵向应力减小，故此时钢材从纵向受压逐渐转变为承受环向拉应力。此时，轴向荷载增量主要由混凝土承担；(4) C₁D₁，当钢管失去对核心混凝土环向约束时，试件达到峰值承载力，平均峰值承载力为1 477 kN。

2层GFRP约束的壁式钢管混凝土柱在(1) OA，GFRP布在轴压方向上不承担竖向荷载，此阶段GFRP无明显效果；(2) AB，GFRP环向套箍作用开始发挥，可以观察到外包GFRP与钢管的逐渐剥离、泛白并伴有滋滋的声响；(3) BC，此阶段内GFRP断裂与钢管全面屈服同时进行，但GFRP的存在降低了钢材的屈服速率，表现为增加相同荷载情况下，BC比B₁C₁位移增加更少。由于GFRP是线弹性材料，当纤维丝达到其断裂应变时，GFRP断裂，C点对应组合试件的峰值荷载，平均峰值荷载为1 692 kN；(4) CD，试件承载力快速下降，位移急速增大。

4层GFRP包裹的壁式钢管混凝土，弹性阶段与0层和2层试件基本一致，试件有明显的弹塑性阶段；塑性强化阶段外包GFRP的剥离脱空表现的更加突然，声音也比2层的试件大；峰值荷载相对于0层和2层试件有一定程度的提升，平均峰值承载力为1 878 kN。

主要试验结果见表4，结果表明包裹层数的增加，可以进一步的延缓钢材屈服，提高组合构件的整体承载力，峰值承载力分别提高15%和27%。

表 4 GFRP约束壁式钢管混凝土柱主要试验结果

Table 4. Main test results of GFRP-walled concrete-filled steel tube columns

Number	${N_{\rm{p}}}$ /kN	${N_{{\rm{p1}}}}$ /kN	I/%
C30-G0-1	1 480	1 477	-
C30-G0-2	1 475	1 477	-
C30-G2-1	1 691	1 692	15
C30-G2-2	1 708	1 692	15
C30-G4-1	1 877	1 878	27
C30-G4-2	1 879	1 878	27
Notes: N_p—Peak load; N_p1—Average value of the peak load; I—Increment of N_p1.

下载: 导出CSV

| 显示表格

2.3 GFRP约束壁式钢管混凝土柱荷载-应变曲线

试件钢管表面L/2截面处长边、短边和倒角切线处的荷载-应变曲线如图9所示。在加载前期，曲线呈线性，纵向应变的增长速度明显大于横向应变；随着荷载的增加，曲线斜率减小，钢材开始逐渐屈服进入塑性阶段；荷载接近峰值荷载时，纵向应变全部达到屈服应变，曲线逐渐平缓。

图 9 钢管截面应力-应变曲线

Figure 9. Stress-strain curves of steel pipe section

下载: 全尺寸图片幻灯片

张忠杰等^[17]研究发现矩形薄壁钢管混凝土短柱长边约束弱于短边，但本文在长边中部增加内隔板有效提高长边约束能力，使长边与短边约束能力基本相同。以试件C30-G0-2为例，在L/2截面处，当长边S5测点和短边S15测点达到材性试验实测屈服应变1 300×10⁻⁶左右时(其中S5、S15均为横向应变测点)，长边与短边承载力基本一致，且长边与短边横向应变变化规律无明显差异。

GFRP可以有效延缓钢材的屈服。以试件C30-G0-2、C30-G2-2和C30-G4-1为例，钢管中部截面纵向平均应变达到钢材单轴屈服应变1 300×10⁻⁶时，试件的荷载对应分别为1 047 kN、1 394 kN和1 563 kN，这说明GFRP可以有效延缓钢材的屈服，使核心混凝土的承载力得到进一步的提高。

2.4 GFRP约束壁式钢管混凝土柱延性系数

采用延性系数 $\mu$ 描述构件塑性变形能力^[18]：

$\mu = \frac{{{e_{\rm{u}}}}}{{{e_{\rm{y}}}}}$

(1)

其中：e_u是峰值承载力所对应的纵向位移；e_y为试件屈服承载力所对应的纵向位移。试件屈服点的取值采用冯鹏等^[19]的研究中最远法进行定义。试件C30-G0-1由于试验设备出现故障，未采集到下降段荷载-位移曲线。三组无GFRP包裹的壁式钢管混凝土柱的平均延性系数见表5。可知，随着GFRP包裹层数的增加，试件的延性系数逐渐降低。与无GFRP包裹试件相比，试件在到达峰值荷载后，破坏更加突然，承载力骤降且随着包裹层数的增加骤降越明显，破坏模式的差异致使纤维约束试件的延性较差。

表 5 GFRP约束壁式钢管混凝土柱延性系数

Table 5. Ductility coefficients of GFRP-walled concrete-filled steel tube columns

Number	${e_{\rm{u}}}$ /mm	${e_{\rm{y}}}$ /mm	$\mu$	$\overline \mu$
C30-G0-1	—	5.12	—	11.53
C30-G0-2	60.11	5.08	11.53	11.53
C30-G2-1	58.76	5.71	10.29	10.97
C30-G2-2	65.64	5.64	11.64	10.97
C30-G4-1	56.09	6.15	9.12	10.53
C30-G4-2	60.27	5.21	11.57	10.53
Notes: e_u—Longitudinal displacement corresponding to the peak load; e_y—Longitudinal displacement corresponding to the yield bearing capacity; $\mu$ —Ductility coefficient； $\overline \mu$ —Average ductility coefficient of each group.

下载: 导出CSV

| 显示表格

3. GFRP约束壁式钢管混凝土柱承载力计算与试验值对比

对于矩形截面，箍筋约束混凝土与钢管约束混凝土柱在效果上本质相同，区别在于钢管可以实现对核心混凝土横向约束的纵向连续。参考Mander等^[20]针对箍筋约束混凝土提出的等效侧向约束力计算方法，确定矩形钢管长边、短边对核心混凝土的等效侧向约束应力 ${f_{{\rm{l1}}}}$ 和 ${f_{{\rm{l2}}}}$ ，可表示为

$\left. \begin{array}{l} {f_{{\rm{l1}}}} = {k_{\rm{e}}}{f'}_{{\rm{l1}}} \\ {f_{{\rm{l2}}}} = {k_{\rm{e}}}{f'}_{{\rm{l2}}} \\ \end{array} \right\}$

(1)

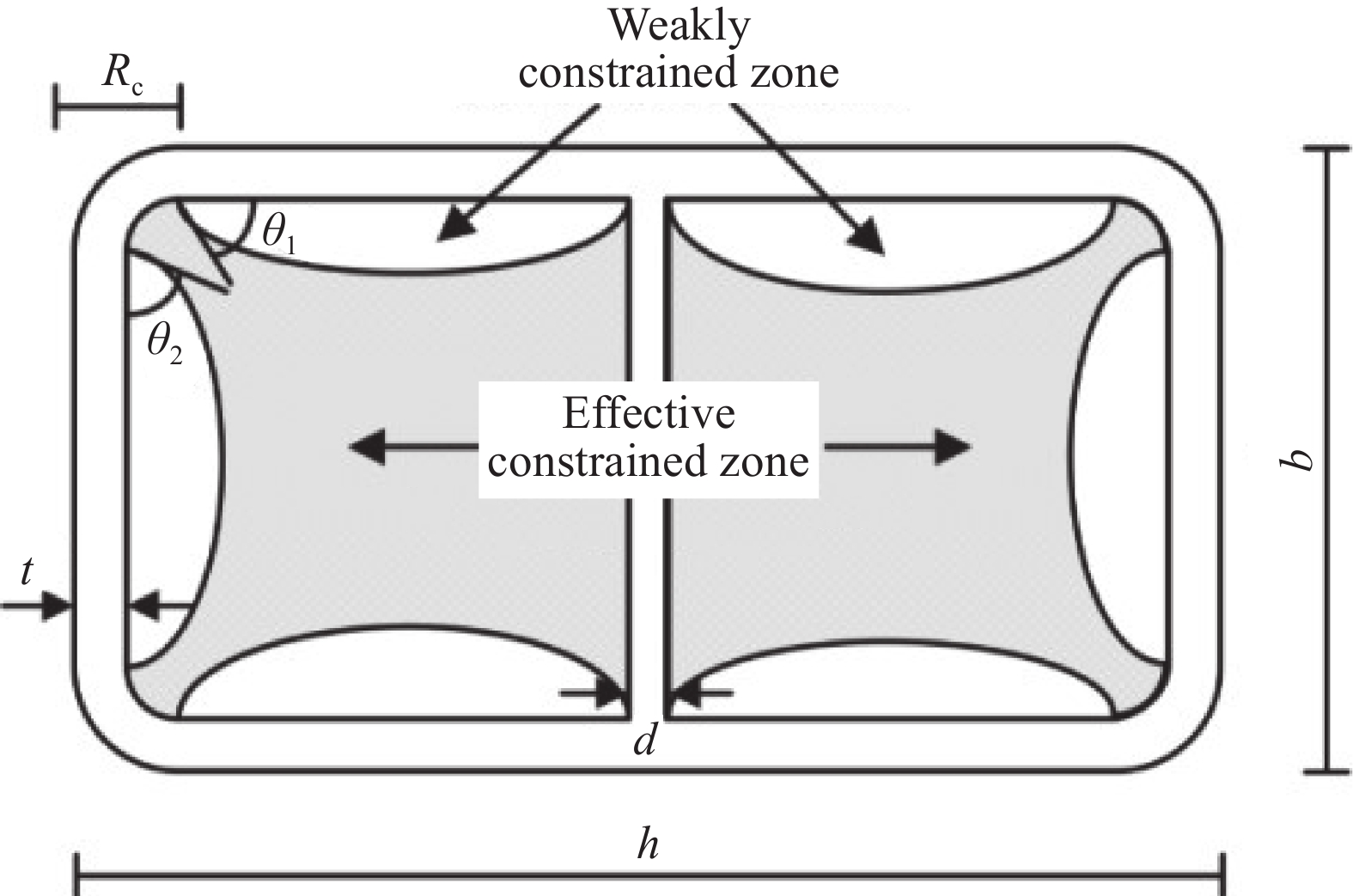
式中： ${f'}_{{\rm{l1}}}$ 和 ${f'}_{{\rm{l2}}}$ 分别为矩形钢管长边与短边平均侧向约束应力； ${k_{\rm{e}}}$ 为矩形钢管对核心混凝土提供的有效约束系数，可表示为^[21]

${k_{\rm{e}}} = \frac{b}{h} \times \frac{{bh - 0.86{r^2} - \left( {1/3} \right)\left[ {{{\left( {h - 2r} \right)}^2} + {{\left( {b - 2r} \right)}^2}} \right]}}{{bh - 0.86{r^2}}}$

(2)

式中：b为截面宽度；h为截面长度；r为倒角半径。GFRP 约束壁式钢管混凝土柱强弱约束分布如图10所示。

图 10 GFRP约束壁式钢管混凝土柱强弱约束分布

Figure 10. Distribution of strong and weak constraints of GFRP-walled concrete-filled steel tube columns

R_c—Chamfer radius; θ₁ and θ₂—Original angle; t—Pipe wall thickness; d—Thickness of the inner partition; h and b—Long and short side of steel pipes

下载: 全尺寸图片幻灯片

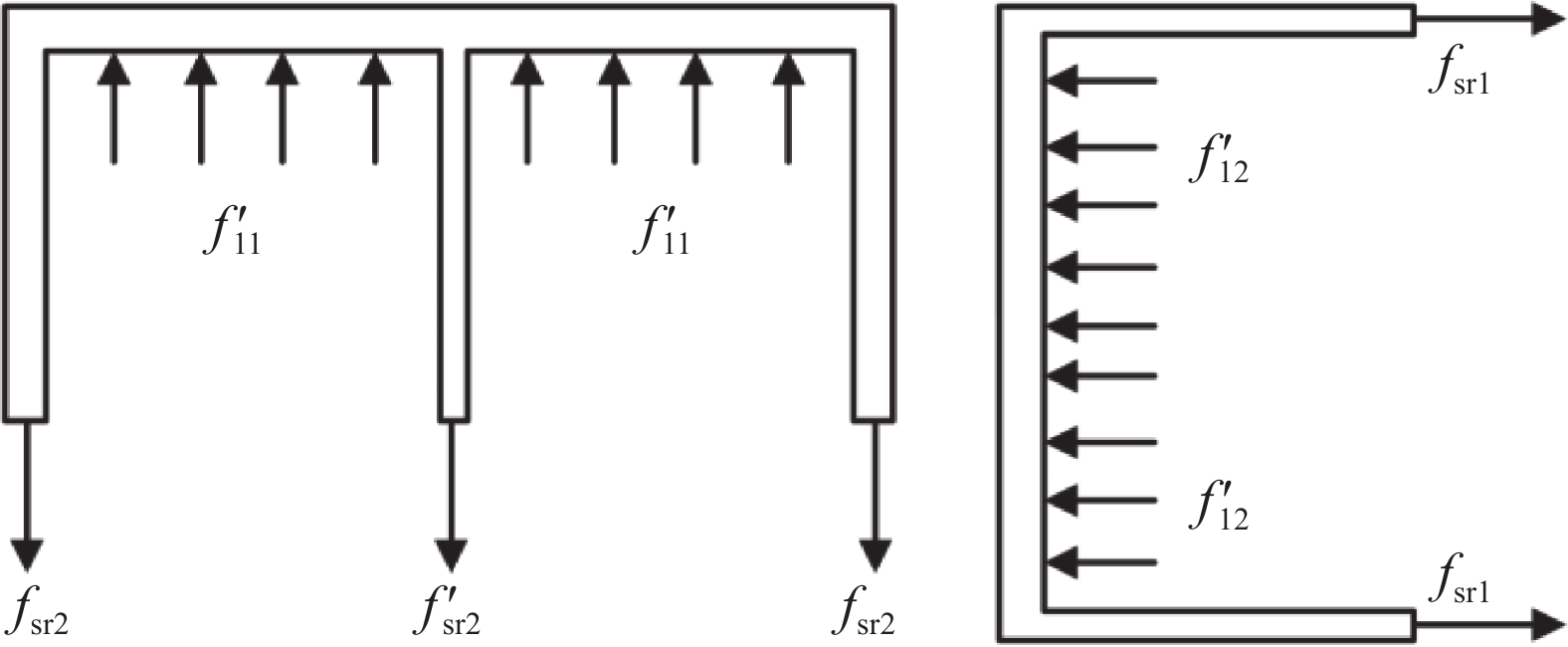
取壁式钢管截面作为受力体，则壁式钢管在水平向的受力如图11所示。

图 11 钢管截面受力示意图

Figure 11. Schematic diagram of cross-section force of steel pipe

${f_{{\rm{l1}}}}$ and

${f_{{\rm{l2}}}}$ —Equivalent lateral restraint stress of rectangular steel tube long side and short side to core concrete respectively;

${f'_{{\rm{l1}}}}$ and

${f'_{{\rm{l2}}}}$ —Average lateral constraint forces of long side and short side of rectangular steel tube, respectively;

${f'_{{\rm{sr2}}}}$ —Circumferential stress of inner diaphragm;

${f_{{\rm{sr1}}}}$ and

${f_{{\rm{sr2}}}}$ —Hoop stresses of long side and short side of wall steel tube, respectively

下载: 全尺寸图片幻灯片

${f'_{{\rm{l1}}}}$ 和 ${f'_{{\rm{l2}}}}$ 分别为矩形钢管长边与短边平均侧向约束应力，且假设其沿截面长边、短边均匀分布，则由平衡方程可得：

$\left. \begin{array}{l} {f'}_{{\rm{l1}}} = \dfrac{{2{f_{{\rm{sr2}}}} + {n_{{\rm{s1}}}}{f'}_{{\rm{sr2}}}\left( {d/t} \right)}}{{h/t - 2 - {n_{{\rm{s1}}}}\left( {d/t} \right)}} \\ {f'}_{{\rm{l2}}} = \dfrac{{2{f_{{\rm{sr1}}}}}}{{b/t - 2}} \\ \end{array} \right\}$

(3)

式中： ${f'}_{{\rm{sr2}}}$ 为内隔板环向应力， ${f'}_{{\rm{sr2}}} = {E_{\rm{s}}}{\varepsilon _{{\rm{s2}}}}$ ， ${\varepsilon _{{\rm{s2}}}}$ 为内隔板的平均受拉应变(拟取屈服应变)； ${f_{{\rm{sr1}}}}$ 和 ${f_{{\rm{sr2}}}}$ 分别为壁式钢管长边和短边的环向应力； ${n_{{\rm{s1}}}}$ 为隔板个数，本文为1；本文d=t。

参考文献[22-23]将矩形钢管等效为圆形钢管进行均匀侧压力 ${\sigma _{\rm{r}}}$ 的计算，等效原则为等效前后圆形与矩形截面含钢率相同且截面相等：

${\sigma _{\rm{r}}} = \frac{{t\left( {\left| {{f_{{\rm{l1}}}}} \right| + \left| {{f_{{\rm{l2}}}}} \right|} \right)}}{{R + r}}$

(4)

式中，R、r分别为等效圆钢管的外径与内径，则R与r可表示为

$R = \sqrt {\frac{{bh - \left( {4 - {\text{π}}} \right)R_{\rm{c}}^2}}{\text{π}}}$

(5)

$r = \sqrt {\frac{{\left( {h - 2t - d} \right)\left( {b - 2t} \right) - \left( {4 - {\text{π}}} \right)R_{\rm{c}}^2}}{\text{π}}}$

(6)

其中，R_c为倒角半径，联立上式，可得 ${\sigma _{\rm{r}}}$ ：

$\begin{aligned}{l} {\sigma _{\rm{r}}} =& \sqrt {\text{π}} t{k_{\rm{e}}}\left[ {\dfrac{{2{f_{{\rm{sr2}}}} + {f'}_{{\rm{sr2}}}\left( {d/t} \right)}}{{h/t - 2 - \left( {d/t} \right)}} + \dfrac{{2{f_{{\rm{sr1}}}}}}{{b/t - 2}}} \right] \times \\& \left( {\sqrt {bh - \left( {4 - {\text{π}}} \right)R_{\rm{c}}^2} + } \right. \\& {\left. {\sqrt {\left( {h - 2t - d} \right)\left( {b - 2t} \right) - \left( {4 - {\text{π}}} \right)R_{\rm{c}}^2} } \right)^{{\rm{ - 1}}}} \\ \end{aligned}$

等效圆钢管中，对于核心混凝土，取 ${\sigma _1} = {\sigma _2} =$ ${\sigma _{\rm{r}}}$ ，则由双剪统一强度理论^[24]可得：

$\left. \begin{aligned} & {\sigma _3} = {f_{\rm{c}}} + k{\gamma _{\rm{u}}}{\sigma _1} \\ & {\gamma _{\rm{u}}} = 1.67 \times {D^{ - 0.112}} \\ \end{aligned} \right\}$

(7)

式中： $k$ 为侧压系数， $k = \left( {1 + \sin \phi } \right)/\left( {1 - \sin \phi } \right)$ ，其中 $\phi$ 为混凝土的内摩擦角，本文参考文献[25]，取 $\phi$ =30°， $k$ =2； ${\gamma _{\rm{u}}}$ 为混凝土降低系数；D为等效圆钢管直径(取外径)。

对于矩形截面，长边对混凝土的约束作用较弱，试件破坏时，假设钢材长边已经屈服即 ${f_{{\rm{sr1}}}} =$ ${f_{\rm{y}}}$ 。对钢管角点进行取距，则可得：

${f_{{\rm{l1}}}} = \frac{{{b^2}}}{{{h^2}}}{f_{{\rm{l2}}}}$

(8)

则对于壁式钢管混凝土，其承载力计算公式可表示为

${N_{\rm{p}}} = {N_{\rm{s}}} + {N_{\rm{c}}} = \left( {{A_{\rm{s}}} + {A'_{\rm{s}}}} \right){f_{\rm{y}}} + {A_{{\rm{ccor}}}}{f_{{\rm{cc}}}}$

(9)

式中： ${A_{\rm{s}}}$ 、 $A'_{\rm{s}}$ 分别为钢管及内隔板的截面面积； ${A_{{\rm{ccor}}}}$ 为截面混凝土面积； ${f_{\rm{y}}}$ 、 ${f_{{\rm{cc}}}}$ 分别为钢材的屈服强度和核心混凝土的轴心抗压强度，其中 ${f_{{\rm{cc}}}} = {\sigma _3}$ 。

对于GFRP提供的侧向约束力参考GB 50367—2013^[26]对于强度的计算公式，计算公式表示如下：

${f_{{\rm{cu}}}} = {f_{{\rm{ck}}}} + 4{f_{\rm{l}}}$

(10)

${f_{\rm{l}}} = 0.5{\beta _{\rm{c}}}{k_{\rm{c}}}{\rho _{\rm{f}}}{E_{\rm{f}}}{\varepsilon _{{\rm{fe}}}}$

(11)

其中：f_cu为混凝土强度；f_ck为混凝土抗压强度； ${f_{\rm{l}}}$ 表示有效约束应力； ${\beta _{\rm{c}}}$ 表示混凝土强度影响系数，本文取1.0； ${k_{\rm{c}}}$ 表示有效约束系数； ${\rho _{\rm{f}}}$ 表示环向围束体积比；E_f表示GFRP弹性模量；ε_fe表示GFRP有效拉应变。其中：

${k_{\rm{c}}} = 1 - \frac{{{{\left( {h - 2r} \right)}^2} + {{\left( {b - 2r} \right)}^2}}}{{3{A_{{\rm{cor}}}}}}$

(12)

${\rho _{\rm{f}}} = \frac{{2{t_{\rm{f}}}\left( {b + h} \right)}}{{bh}}$

(13)

其中：A_cor表示混凝土截面的面积；t_f为GFRP的厚度。本文对于纤维单独对核心混凝土提高的附加承载力可表示为

$f'_{{\rm{cu}}} = {f_{^{{\rm{ck}}}}} + 4{f_{\rm{l}}} - {f_{^{{\rm{ck}}}}} = 4{f_{\rm{l}}}$

(14)

其中，f'_cu为纤维单独对核心混凝土提高的附加强度，则玻璃纤维包裹的壁式钢管混凝土短柱承载力计算公式可表示为

$\begin{aligned} {N_{\rm{p}}} &= {N_{\rm{s}}} + {N_{\rm{c}}} + {N_{\rm{f}}} \\& = \left( {{A_{\rm{s}}} + {A'_{\rm{s}}}} \right){f_{\rm{y}}} + {A_{{\rm{ccor}}}}{f_{{\rm{cc}}}} + f'_{{\rm{cu}}}{A_{{\rm{ccor}}}} \\ \end{aligned}$

(15)

其中：N_p为峰值负载；N_s为钢管混凝土柱轴心抗压承载力；N_c为钢管对核心混凝土提高的附加承载力；N_f为GFRP对核心混凝土提高的附加承载力；A_s为钢管的有效横截面积；A_s′为内隔板的截面面积；f_y为钢材屈服强度。主要计算结果见表6，试验值与承载力计算值比值的均值为1.09，承载力理论计算值普遍小于试验实测值，说明本文所提及的理论计算公式偏保守，但比值标准差为0.028，说明结果离散性较小，公式吻合较好，本文提出的公式可以较好地预测组合构件的承载力。

表 6 GFRP约束壁式钢管混凝土柱承载力计算值与试验值对比

Table 6. Comparison of calculation and test value of bearing capacity of GFRP-walled concrete-filled steel tube columns

Number	${\varepsilon _{\rm{v}}}$ /10⁻⁶	${t_{\rm{f}}}$ /mm	${A_{\rm{s}}}$ /mm²	${A_{\rm{c}}}$ /mm²	${N_{\rm{p}}}$ /kN	${N_{{\rm{pre}}}}$ /kN	${N_{\rm{p}}}/{N_{{\rm{pre}}}}$	${\overline X _1}$
C30-G0-1	—	0	2 957	16 336	1 480	—	—	1.06
C30-G0-2	—	0			1 475	1 393	1.06	1.06
C30-G2-1	4 968	1.2			1 691	1 568	1.07	1.09
C30-G2-2	6 080	1.2			1 708	1 550	1.10	1.09
C30-G4-1	10 672	2.4			1 877	1 672	1.12	1.12
C30-G4-2	10 700	2.4			1 879	1 684	1.12	1.12
$\overline X$	—	—	—	—	—	—	1.09
${\sigma _{\rm{S} } }$	—	—	—	—	—	—	0.028
Notes: ε_v—Measured value of the high-circumferential strain of the corresponding column when GFRP breaks; t_f—Thickness of GFRP; A_s—Effective cross-sectional area of the steel tube; A_c—Effective cross-sectional area of the concrete; N_p—Peak load; N_pre—Theoretically calculated value of peak load; N_p/N_pre—Ratio of the test value and the calculated value; ${\overline X _1}$ —Average ratio of each group; $\overline X$ —Mean of the ratio; ${\sigma _{\rm{S}}}$ —Standard deviation of the ratio.

下载: 导出CSV

| 显示表格

4. 有限元分析模型

4.1 材料模型

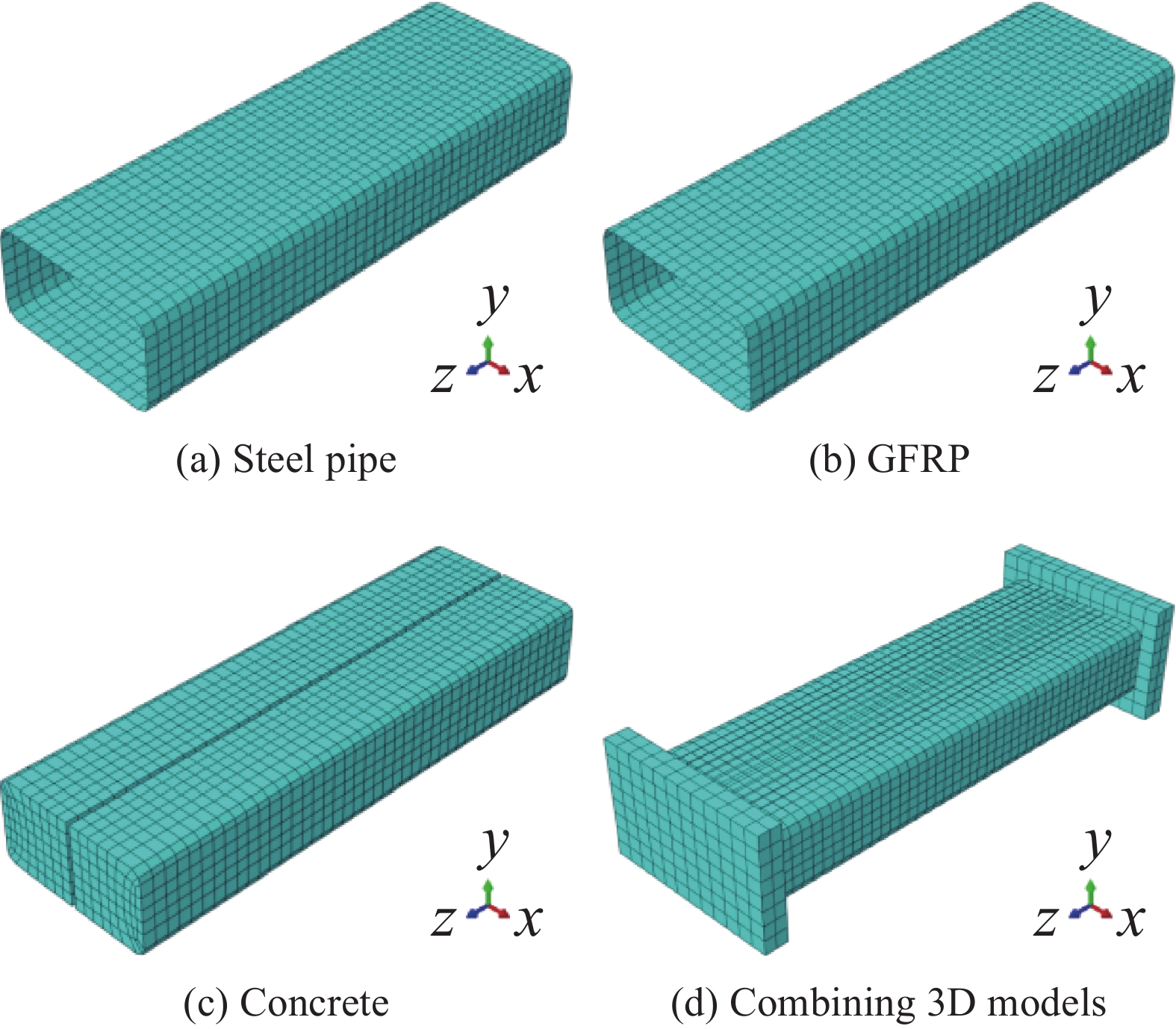
采用有限元软件ABAQUS对试验中的约束柱建立三维有限元模型进行模拟分析。混凝土、钢板均采用实体单元(C3D8R)，GFRP布采用壳单元。模型中采用“库伦摩擦”模拟钢管与混凝土之间的相互作用，其中摩擦系数 $\mu$ 取0.4。将GFRP与钢管采用“Tie”约束，即在纤维断裂之前，纤维与钢管变形一致，不发生滑移，保证协同变形实体，单元网格尺寸为10 mm×10 mm。柱三维模型如图12所示，模拟加载工程中，柱底设为固定端，在柱顶面设置耦合点进行轴向位移加载。

图 12 GFRP约束壁式钢管混凝土柱模型

Figure 12. GFRP-confined steel reinforced concrete column model

下载: 全尺寸图片幻灯片

材料模型主要由钢材模型、约束混凝土本构模型和GFRP材料模型组成。钢材的理想弹塑性模型对轴压作用下钢管应力途径的描述更加合理，因此模型中钢材采用理想弹塑性模型，不考虑钢材焊接处强度的微小差异，统一将屈服强度设置为251 MPa。对于核心混凝土，考虑到混凝土在壁式钢管中的受力关系，选取模型中混凝土材料破坏准则采用塑性损伤模型(Concrete damaged plasticity, CDP)，CDP的模拟参数取值见表7。混凝土的受压本构参考GB 50010—2010^[27]。GFRP布为单向理想线弹性材料。混凝土受压强度、钢材受拉强度和弹性模量及GFRP布弹性模量均同上文材性试验的结果。

表 7 塑性损伤参数取值

Table 7. Concrete damaged plasticity parameter values

$\psi$	$\varepsilon$	${\sigma _{{\rm{bo}}}}/{\sigma _{{\rm{co}}}}$	${K_{\rm{c}}}$	$\mu$
30	0.1	1.16	0.6667	0.005
Notes: $\psi$ —Expansion angle; $\varepsilon$ —Eccentricity; ${\sigma _{{\rm{bo}}}}/{\sigma _{{\rm{co}}}}$ —Ratio of the biaxial compressive strength to the uniaxial compressive ultimate strength value; ${K_{\rm{c}}}$ —Ratio of the invariable stress; $\mu$ —Viscous parameter.

下载: 导出CSV

| 显示表格

4.2 试验验证

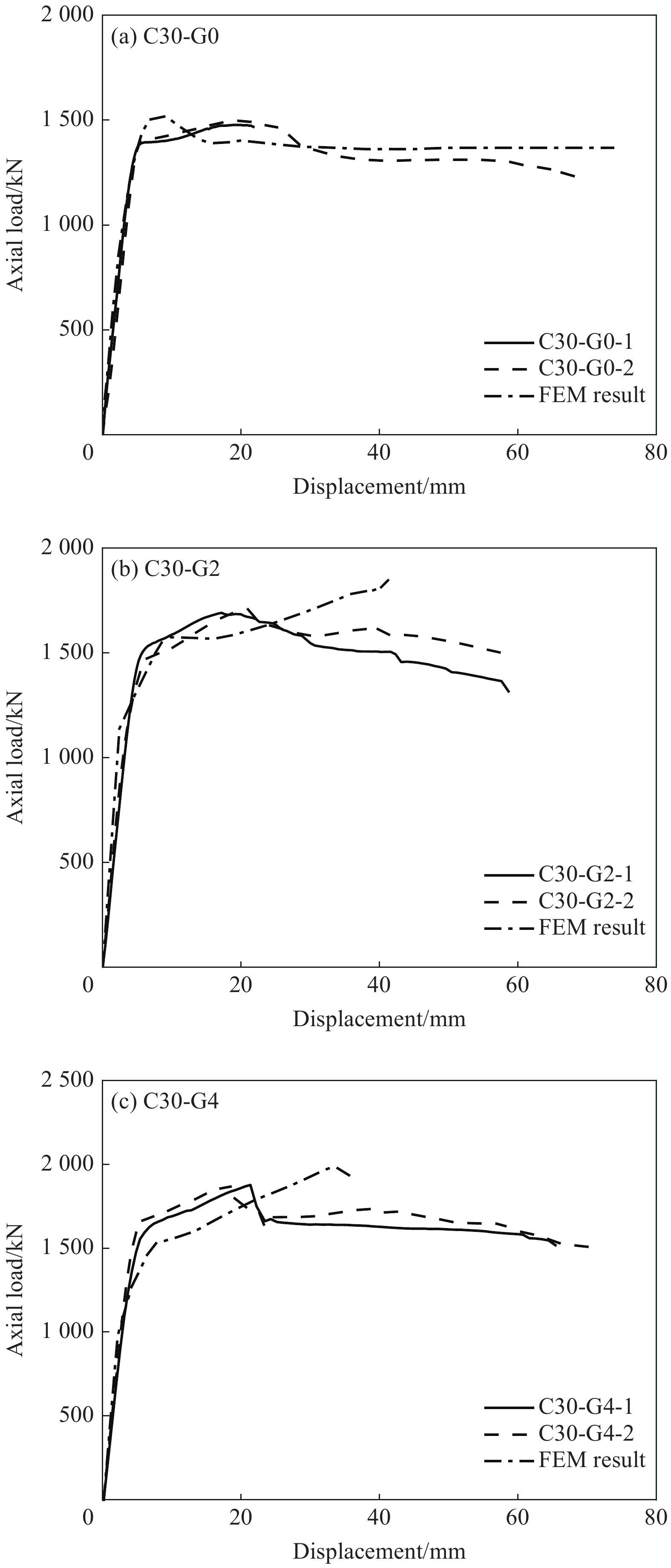
表8和图13对本文建立的有限元计算结果和试验结果进行了对比。计算结果表明有限元计算结果与试验结果总体吻合良好，但有限元模型弹性段刚度普遍比试验值大，这主要是由于试验过程中石膏抹面造成的一定影响；对于四层包裹的试件，模拟结果峰值承载力明显大于试验结果，表明实际试验加工工艺影响较大，试验未达到预期强度。本文建立的GFRP约束壁式钢管混凝土短柱数值分析模型可用于分析GFRP约束壁式钢管混凝土短柱的轴压性能。

表 8 GFRP约束壁式钢管混凝土短柱有限元结果与试验对比

Table 8. Comparison of finite element results and test results of GFRP-walled concrete-filled steel tube columns

Number	Fiber layer	${N_{{\rm{p1}}}}$ /kN	${N_{{\rm{Aba}}}}$ /kN	${N_{{\rm{p1}}}}$ / ${N_{{\rm{Aba}}}}$
C30-G0	0	1477	1516	0.97
C30-G2	2	1692	1747	0.97
C30-G4	4	1 878	1 981	0.95
Notes: N_p1—Average value of the peak load; N_Aba—Peak load of the finite element simulation; N_p1/N_Aba—Ratio of the measured peak load to the finite element simulated peak load.

下载: 导出CSV

| 显示表格

图 13 GFRP约束壁式钢管混凝土短柱荷载-位移曲线对比

Figure 13. Comparison of load-displacement curves of GFRP-walled concrete-filled steel tube columns

下载: 全尺寸图片幻灯片

4.3 参数分析

本节分别分析了钢材屈服强度f_y、混凝土强度f_cu对GFRP约束壁式钢管混凝土短柱轴压性能的影响，以试件C30-G2模型为基准，单次只改变一个参数。详细的数值模拟构件设计详见表9。

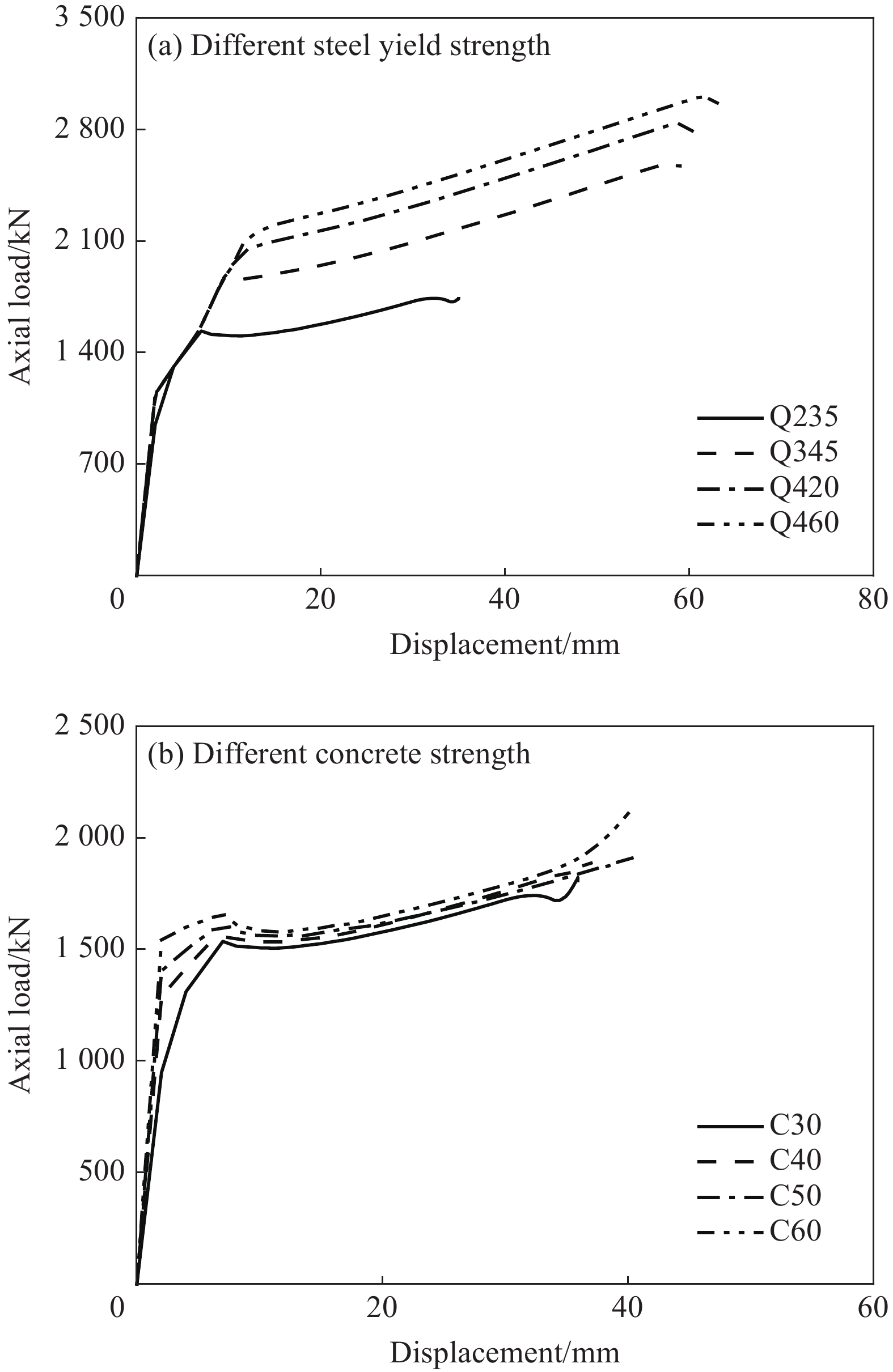
表 9 GFRP约束壁式钢管混凝土短柱模拟试件几何尺寸与材料强度

Table 9. Geometric dimensions and material strength of simulated specimens of GFRP-walled concrete-filled steel tube columns

Number	f_cu/MPa	f_y/MPa
TS-235-G2	30	235
TS-345-G2	30	345
TS-420-G2	30	420
TS-460-G2	30	460
TC-C30-G2	30	235
TC-C40-G2	40	235
TC-C50-G2	50	235
TC-C60-G2	60	235
Notes: T—Test; S—Steel; C—Concrete; G—GFRP; Numbers behind indicate the corresponding labels and types of materials; f_cu—Concrete strength; f_y—Steel yield strength.

下载: 导出CSV

| 显示表格

不同屈服强度钢材的GFRP约束壁式钢管混凝土短柱轴压的荷载-位移曲线见图14(a)和表10。分析结果表明：随着钢材屈服强度的增加，GFRP约束壁式钢管混凝土短柱的轴压承载力持续提高，与钢材屈服强度为235 MPa的构件相比，钢材屈服强度为345 MPa、420 MPa和550 MPa构件的承载力分别提高了45.55%、61.01%和70.29%。

图 14 不同钢材、混凝土强度的GFRP约束壁式钢管混凝土短柱荷载-位移曲线

Figure 14. Load-displacement curves of GFRP-walled concrete-filled steel tube columns with different steel and concrete strength

下载: 全尺寸图片幻灯片

表 10 不同钢材屈服强度的GFRP约束壁式钢管混凝土短柱有限元模拟结果

Table 10. Simulated results of GFRP-walled concrete-filled steel tube columns with different yield strength of steels

Number	f_y/MPa	N_y/kN	N_p/kN	I₁/%
TS-235-G2	235	1516	1767	—
TS-345-G2	345	1 817	2572	45.55
TS-420-G2	420	1 997	2845	61.01
TS-460-G2	460	2084	3009	70.29
Notes: N_y—Yield load; N_p—Peak load; I₁—Increment of N_p.

下载: 导出CSV

| 显示表格

图14(b)和表11为混凝土强度为30、40、50、60 MPa情况下GFRP约束壁式钢管混凝土短柱的荷载-位移曲线。随着混凝土强度的提高，GFRP约束壁式钢管混凝土短柱的轴压承载力逐渐增大。与混凝土强度为30 MPa的构件相比，当混凝土强度从30 MPa提高到40、50、60 MPa时，其轴压承载力分别提高了6.40%、11.45%和17.89%。

表 11 不同混凝土强度的GFRP约束壁式钢管混凝土短柱有限元模拟结果

Table 11. Simulated results of GFRP-walled concrete-filled steel tube columns with different strengths of concrete

Number	f_y/MPa	N_y/kN	N_p/kN	I₁/%
TC-C30-G2	30	1516	1767	—
TC-C40-G2	40	1563	1 880	6.40
TC-C50-G2	50	1598	1 970	11.45
TC-C60-G2	60	1614	2083	17.89

下载: 导出CSV

| 显示表格

提高钢材强度对GFRP约束壁式钢管混凝土短柱的轴压承载力的影响远大于混凝土强度的影响，可采用提高钢材强度来有效提高组合柱的轴压承载力。

5. 结论

(1) 壁式钢管混凝土柱最终因柱中混凝土压碎，钢管屈曲，试件变形过大而失效；柱角无焊缝，有效地解决了传统矩形钢管混凝土柱在轴压作用下纵向焊缝在角部撕裂的问题。

(2) 壁式钢管混凝土柱长边内置隔板能有效提高长边约束能力；玻璃纤维增强聚合物复合材料(GFRP)能有效延缓钢管屈服，提高试件峰值承载力但延性有所下降，承载力随包裹层数的增加而提高。

(3) 提出壁式柱的强弱约束模型，并基于双剪统一强度理论提出其轴压承载力计算公式，理论计算值与试验值吻合较好。

(4) 有限元数值模拟结果与实测值吻合较好，钢材强度、混凝土强度都能提高峰值承载力，其中钢材强度对承载力影响较大。

图 1 壁式柱典型构造

Figure 1. Typical structure of wall column

下载: 全尺寸图片幻灯片

图 2 试件几何尺寸及构造

Figure 2. Geometrical dimensions and structure of the specimens

下载: 全尺寸图片幻灯片

图 3 GFRP约束壁式钢管混凝土柱轴压试验加载装置

Figure 3. Axial compressive test setup of GFRP-walled concrete-filled steel tube columns

下载: 全尺寸图片幻灯片

图 4 试验柱测点布置

Figure 4. Arrangement of measuring points for tested columns

下载: 全尺寸图片幻灯片

图 5 C30-G0-1的破坏过程

Figure 5. Failure process of C30-G0-1

下载: 全尺寸图片幻灯片

图 6 C30-G2-1的破坏过程

Figure 6. Failure process of C30-G2-1

下载: 全尺寸图片幻灯片

图 7 GFRP约束壁式钢管混凝土柱轴向荷载-位移曲线

Figure 7. Axial load-deformation curves of GFRP-walled concrete-filled steel tube columns

下载: 全尺寸图片幻灯片

图 8 FRP-钢复合约束混凝土典型轴向荷载-位移曲线

Figure 8. Typical curves of axial load-displacement of FRP concrete filled steel tube

OA—Elastic stage; AB—Elastic-plastic stage; BC—Plastic strengthening stage; CD—Softening stage

下载: 全尺寸图片幻灯片

图 9 钢管截面应力-应变曲线

Figure 9. Stress-strain curves of steel pipe section

下载: 全尺寸图片幻灯片

图 10 GFRP约束壁式钢管混凝土柱强弱约束分布

Figure 10. Distribution of strong and weak constraints of GFRP-walled concrete-filled steel tube columns

R_c—Chamfer radius; θ₁ and θ₂—Original angle; t—Pipe wall thickness; d—Thickness of the inner partition; h and b—Long and short side of steel pipes

下载: 全尺寸图片幻灯片

图 11 钢管截面受力示意图

Figure 11. Schematic diagram of cross-section force of steel pipe

${f_{{\rm{l1}}}}$ and ${f_{{\rm{l2}}}}$ —Equivalent lateral restraint stress of rectangular steel tube long side and short side to core concrete respectively; ${f'_{{\rm{l1}}}}$ and ${f'_{{\rm{l2}}}}$ —Average lateral constraint forces of long side and short side of rectangular steel tube, respectively; ${f'_{{\rm{sr2}}}}$ —Circumferential stress of inner diaphragm; ${f_{{\rm{sr1}}}}$ and ${f_{{\rm{sr2}}}}$ —Hoop stresses of long side and short side of wall steel tube, respectively

下载: 全尺寸图片幻灯片

图 12 GFRP约束壁式钢管混凝土柱模型

Figure 12. GFRP-confined steel reinforced concrete column model

下载: 全尺寸图片幻灯片

图 13 GFRP约束壁式钢管混凝土短柱荷载-位移曲线对比

Figure 13. Comparison of load-displacement curves of GFRP-walled concrete-filled steel tube columns

下载: 全尺寸图片幻灯片

图 14 不同钢材、混凝土强度的GFRP约束壁式钢管混凝土短柱荷载-位移曲线

Figure 14. Load-displacement curves of GFRP-walled concrete-filled steel tube columns with different steel and concrete strength

下载: 全尺寸图片幻灯片

表 1 玻璃纤维增强聚合物复合材料(GFRP)约束壁式钢管混凝土柱参数

Table 1 Parameters of glass fiber reinforce polymer (GFRP)-walled concrete-filled steel tube columns

Number	b×h×L/mm	t/mm	d/mm	R_c/mm	Fiber layer
C30-G0-1	100×200×600	5	5	15	0
C30-G0-2	100×200×600	5	5	15	0
C30-G2-1	100×200×600	5	5	15	2
C30-G2-2	100×200×600	5	5	15	2
C30-G4-1	100×200×600	5	5	15	4
C30-G4-2	100×200×600	5	5	15	4
Notes: C—Concrete, the number stands for the concrete grade; G—GFRP, the numbers are the number of package layers; 1 and 2—Two different test pieces; B—Length; h—Width; L—Height; t—Wall thickness; d—Thickness of the separator; R_c—Radius of the chamfer.

下载: 导出CSV

表 2 钢材和混凝土的材料力学性能

Table 2 Material mechanical properties of steel and concrete

Material	${f_{\rm{y}}}/{\rm{MPa}}$	$E/{\rm{GPa}}$	${f_{{\rm{cu}}}}/{\rm{MPa}}$
Concrete	—	—	32.4
Steel plate	251	196	—
Notes: f_y—Yield strength; E—Tensile modulus; f_cu—Cube compressive strength.

下载: 导出CSV

表 3 GFRP布的材料力学性能

Table 3 Mechanical properties of GFRP

Material	${\sigma _{\rm{b}}}/{\rm{MPa}}$	$E/{\rm{GPa}}$
GFRP	537.4	28.7
Note: ${\sigma _{\rm{b}}}$ —Tensile strength.

下载: 导出CSV

表 4 GFRP约束壁式钢管混凝土柱主要试验结果

Table 4 Main test results of GFRP-walled concrete-filled steel tube columns

Number	${N_{\rm{p}}}$ /kN	${N_{{\rm{p1}}}}$ /kN	I/%
C30-G0-1	1 480	1 477	-
C30-G0-2	1 475	1 477	-
C30-G2-1	1 691	1 692	15
C30-G2-2	1 708	1 692	15
C30-G4-1	1 877	1 878	27
C30-G4-2	1 879	1 878	27
Notes: N_p—Peak load; N_p1—Average value of the peak load; I—Increment of N_p1.

下载: 导出CSV

表 5 GFRP约束壁式钢管混凝土柱延性系数

Table 5 Ductility coefficients of GFRP-walled concrete-filled steel tube columns

Number	${e_{\rm{u}}}$ /mm	${e_{\rm{y}}}$ /mm	$\mu$	$\overline \mu$
C30-G0-1	—	5.12	—	11.53
C30-G0-2	60.11	5.08	11.53	11.53
C30-G2-1	58.76	5.71	10.29	10.97
C30-G2-2	65.64	5.64	11.64	10.97
C30-G4-1	56.09	6.15	9.12	10.53
C30-G4-2	60.27	5.21	11.57	10.53
Notes: e_u—Longitudinal displacement corresponding to the peak load; e_y—Longitudinal displacement corresponding to the yield bearing capacity; $\mu$ —Ductility coefficient； $\overline \mu$ —Average ductility coefficient of each group.

下载: 导出CSV

表 6 GFRP约束壁式钢管混凝土柱承载力计算值与试验值对比

Table 6 Comparison of calculation and test value of bearing capacity of GFRP-walled concrete-filled steel tube columns

Number	${\varepsilon _{\rm{v}}}$ /10⁻⁶	${t_{\rm{f}}}$ /mm	${A_{\rm{s}}}$ /mm²	${A_{\rm{c}}}$ /mm²	${N_{\rm{p}}}$ /kN	${N_{{\rm{pre}}}}$ /kN	${N_{\rm{p}}}/{N_{{\rm{pre}}}}$	${\overline X _1}$
C30-G0-1	—	0	2 957	16 336	1 480	—	—	1.06
C30-G0-2	—	0			1 475	1 393	1.06	1.06
C30-G2-1	4 968	1.2			1 691	1 568	1.07	1.09
C30-G2-2	6 080	1.2			1 708	1 550	1.10	1.09
C30-G4-1	10 672	2.4			1 877	1 672	1.12	1.12
C30-G4-2	10 700	2.4			1 879	1 684	1.12	1.12
$\overline X$	—	—	—	—	—	—	1.09
${\sigma _{\rm{S} } }$	—	—	—	—	—	—	0.028
Notes: ε_v—Measured value of the high-circumferential strain of the corresponding column when GFRP breaks; t_f—Thickness of GFRP; A_s—Effective cross-sectional area of the steel tube; A_c—Effective cross-sectional area of the concrete; N_p—Peak load; N_pre—Theoretically calculated value of peak load; N_p/N_pre—Ratio of the test value and the calculated value; ${\overline X _1}$ —Average ratio of each group; $\overline X$ —Mean of the ratio; ${\sigma _{\rm{S}}}$ —Standard deviation of the ratio.

下载: 导出CSV

表 7 塑性损伤参数取值

Table 7 Concrete damaged plasticity parameter values

$\psi$	$\varepsilon$	${\sigma _{{\rm{bo}}}}/{\sigma _{{\rm{co}}}}$	${K_{\rm{c}}}$	$\mu$
30	0.1	1.16	0.6667	0.005
Notes: $\psi$ —Expansion angle; $\varepsilon$ —Eccentricity; ${\sigma _{{\rm{bo}}}}/{\sigma _{{\rm{co}}}}$ —Ratio of the biaxial compressive strength to the uniaxial compressive ultimate strength value; ${K_{\rm{c}}}$ —Ratio of the invariable stress; $\mu$ —Viscous parameter.

下载: 导出CSV

表 8 GFRP约束壁式钢管混凝土短柱有限元结果与试验对比

Table 8 Comparison of finite element results and test results of GFRP-walled concrete-filled steel tube columns

Number	Fiber layer	${N_{{\rm{p1}}}}$ /kN	${N_{{\rm{Aba}}}}$ /kN	${N_{{\rm{p1}}}}$ / ${N_{{\rm{Aba}}}}$
C30-G0	0	1477	1516	0.97
C30-G2	2	1692	1747	0.97
C30-G4	4	1 878	1 981	0.95
Notes: N_p1—Average value of the peak load; N_Aba—Peak load of the finite element simulation; N_p1/N_Aba—Ratio of the measured peak load to the finite element simulated peak load.

下载: 导出CSV

表 9 GFRP约束壁式钢管混凝土短柱模拟试件几何尺寸与材料强度

Table 9 Geometric dimensions and material strength of simulated specimens of GFRP-walled concrete-filled steel tube columns

Number	f_cu/MPa	f_y/MPa
TS-235-G2	30	235
TS-345-G2	30	345
TS-420-G2	30	420
TS-460-G2	30	460
TC-C30-G2	30	235
TC-C40-G2	40	235
TC-C50-G2	50	235
TC-C60-G2	60	235
Notes: T—Test; S—Steel; C—Concrete; G—GFRP; Numbers behind indicate the corresponding labels and types of materials; f_cu—Concrete strength; f_y—Steel yield strength.

下载: 导出CSV

表 10 不同钢材屈服强度的GFRP约束壁式钢管混凝土短柱有限元模拟结果

Table 10 Simulated results of GFRP-walled concrete-filled steel tube columns with different yield strength of steels

Number	f_y/MPa	N_y/kN	N_p/kN	I₁/%
TS-235-G2	235	1516	1767	—
TS-345-G2	345	1 817	2572	45.55
TS-420-G2	420	1 997	2845	61.01
TS-460-G2	460	2084	3009	70.29
Notes: N_y—Yield load; N_p—Peak load; I₁—Increment of N_p.

下载: 导出CSV

表 11 不同混凝土强度的GFRP约束壁式钢管混凝土短柱有限元模拟结果

Table 11 Simulated results of GFRP-walled concrete-filled steel tube columns with different strengths of concrete

Number	f_y/MPa	N_y/kN	N_p/kN	I₁/%
TC-C30-G2	30	1516	1767	—
TC-C40-G2	40	1563	1 880	6.40
TC-C50-G2	50	1598	1 970	11.45
TC-C60-G2	60	1614	2083	17.89

下载: 导出CSV

参考文献(27)

[1]	魏巍. 圆端形钢管混凝土构件偏压力学性能研究[D]. 武汉: 武汉理工大学, 2019. WEI Wei. Research on eccentric compressive behavior of round-ended concrete-filled steel tubular members[D]. Wuhan: Wuhan University of Technology, 2019(in Chinese).
[2]	郝际平, 孙晓岭, 薛强, 等. 绿色装配式钢结构建筑体系研究与应用[J]. 工程力学, 2017, 34(1):1-13. HAO Jiping, SUN Xiaoling, XUE Qiang, et al. Research and application of green prefabricated steel structure building system[J]. Engineering Mechanics,2017,34(1):1-13(in Chinese).
[3]	孙晓岭, 郝际平, 薛强, 等. 壁式钢管混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2018, 39(6):92-101. SUN Xiaoling, HAO Jiping, XUE Qiang, et al. Experimental study on seismic performance of walled concrete-filled steel tubular columns[J]. Journal of Building Structures,2018,39(6):92-101(in Chinese).
[4]	杜颜胜. 高强钢矩形钢管混凝土柱理论分析及试验研究[D]. 天津: 天津大学, 2017. DU Yansheng. Theoretical analysis and experimental study on rectangular concrete-filled steel tube columns using high-strength steel[D]. Tianjin: Tianjin University, 2017(in Chinese).
[5]	王灿灿, 夏之罡, 叶尹, 等. 焊缝质量对钢管混凝土柱影响研究[J]. 低温建筑技术, 2013, 35(7):69-71. WANG Cancan, XIA Zhigang, YE Yin, et al. Research on the influence of weld quality on concrete-filled steel tube columns[J]. Low Temperature Architecture Technology,2013,35(7):69-71(in Chinese).
[6]	颜燕祥, 徐礼华, 蔡恒, 等. 高强方钢管超高性能混凝土短柱轴压承载力计算方法研究[J]. 建筑结构学报, 2019, 40(12): 128-137. YAN Yanxiang, XU Lihua, CAI Heng, et al. Calculation methods of axial bearing capacity of short square UHPC filled high strength steel tubular columns[J]. Journal of Building Structures, 2019, 40(12): 128-137(in Chinese).
[7]	李晓霞. 倒角半径对FRP加固混凝土柱力学性能影响的试验研究[J]. 玻璃钢/复合材料, 2012, 4:19-22. LI Xiaoxia. Experimental study on mechanical behaviour of FRP-strengthend reinforced concrete columns based on the corner radius[J]. Fiber Reinforced Plastics/Composites,2012,4:19-22(in Chinese).
[8]	XIAO Y, HE W H, CHOI K K. Confined concrete-filled tubular columns[J]. Journal of Structural Engineering,2005,131(3):488-497. DOI: 10.1061/(ASCE)0733-9445(2005)131:3(488)
[9]	潘毅, 吴晓飞, 郭瑞, 等. 有初应力的FRP约束混凝土圆柱应力—应变分析型模型[J]. 中国铁道科学, 2017, 38(5):30-36. PAN Yi, WU Xiaofei, GUO Rui, et al. Stress-strain analysis model of FRP confined concrete cylinder with initial stress[J]. China Railway Science,2017,38(5):30-36(in Chinese).
[10]	朱春阳, 赵颖华, 李晓飞. FRP-钢管-混凝土构件抗震性能试验研究[J]. 复合材料学报, 2013, 30(1):180-186. ZHU Chunyang, ZHAO Yinghua, LI Xiaofei. Experimental study on seismic property of concrete filled FRP-steel tube[J]. Acta Materiae Compositae Sinica,2013,30(1):180-186(in Chinese).
[11]	中华人民共和国住房和城乡建设部. 混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for test methods of concrete physical and mechanical properties: GB/T 50081—2019[S]. Beijing: China Architecture & Building Press, 2019(in Chinese).
[12]	全国钢标准化技术委员会. 金属材料拉伸试验第1部分: 室温试验方法GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2011. Technical Committee on Steel of Standardization Committee of China. Metallic materials-Tensile testing-Part 1: Method of test at room temperature GB/T 228.1—2010[S]. Beijing: Standards Press of China, 2011(in Chinese).
[13]	American Society of Testing Materials. Standard test method for tensile properties of polymer matrix composite materials: ASTM D3039[S]. West Conshohocken: ASTM, 2002.
[14]	American Society of Testing Materials. Standard test method for compressive properties of polymer matrix composite materials with unsupported gage section by shear loading: ASTM D3410[S]. West Conshohocken: ASTM, 2002.
[15]	陈梦成, 刘京剑, 黄宏. 钢管再生矿渣混凝土轴压短柱试验研究[J]. 建筑结构学报, 2013, 34(S1):281-287. CHEN Mengcheng, LIU Jingjian, HUANG Hong. Experimental study on recycled slag aggregate concrete-filled steel tubular columns under axial compression[J]. Journal of Building Structures,2013,34(S1):281-287(in Chinese).
[16]	张依睿, 魏洋, 柏佳文, 等. 纤维增强聚合物复合材料-钢复合圆管约束混凝土轴压性能预测模型[J]. 复合材料学报, 2019, 36(10):2478-2485. ZHANG Yirui, WEI Yang, BAI Jiawen, et al. Models for predicting axial compression behavior of FRP-steel compo-site circular tube confined concrete[J]. Acta Materiae Compositae Sinica,2019,36(10):2478-2485(in Chinese).
[17]	张忠杰, 周新刚, 宋振宇, 等. 矩形薄壁钢管混凝土短柱轴心受压性能试验研究[J]. 烟台大学学报(自然科学与工程版), 2020, 33(2):218-224. ZHANG Zhongjie, ZHOU Xingang, SONG Zhenyu, et al. Experimental study on axially compressive behavior of rectangular concrete-filled thin-walled steel tube short column[J]. Journal of Yantai University (Natural Science and Engineering Edition),2020,33(2):218-224(in Chinese).
[18]	WANG X X, QI Y J, SUN Y L, et al. Compressive behavior of composite concrete columns with encased FRP confined concrete cores[J]. Sensors (Basel, Switzerland),2019,19(8):1792.
[19]	冯鹏, 强翰霖, 叶列平. 材料、构件、结构的“屈服点”定义与讨论[J]. 工程力学, 2017, 34(3):36-46. FENG Peng, QIANG Hanlin, YE Lieping. Discussion and definition on yield points of materials, members and structures[J]. Engineering Mechanics,2017,34(3):36-46(in Chinese).
[20]	MANDER J A B, PRIESTLEY M J N. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering,1988,114(8):1804-1826. DOI: 10.1061/(ASCE)0733-9445(1988)114:8(1804)
[21]	潘毅, 曹双寅, 敬登虎, 等. 负载下碳纤维布约束混凝土方柱轴压应力-应变关系的试验研究与分析[J]. 土木工程学报, 2009, 42(1):23-29. PAN Yi, CAO Shuangyin, JING Denghu, et al. Test and analysis of the axial stress-strain relationship of square section concrete columns confined by CFRP under preload[J]. China Civil Engineering Journal,2009,42(1):23-29(in Chinese).
[22]	郭红香, 赵均海, 魏雪英. 方钢管混凝土轴压短柱承载力分析[J]. 工业建筑, 2008(3):9, 14-16. GUO Hongxiang, ZHAO Junhai, WEI Xueying. Analysis of bearing capacity of concrete-filled square steel tube column under axial load[J]. Industrial Construction,2008(3):9, 14-16(in Chinese).
[23]	王娟, 赵均海, 吴赛, 等. 基于统一强度理论的矩形钢管混凝土短柱轴压承载力计算[J]. 建筑科学与工程学报, 2011, 28(3):88-92. WANG Juan, ZHAO Junhai, WU Sai, et al. Calculation of axial bearing capacity of rectangular concrete-filled steel tube short column based on twin shear unified strength theory[J]. Journal of Architecture and Civil Engineering,2011,28(3):88-92(in Chinese).
[24]	陶毅, 叶思君, 陈建飞. 内置约束芯柱的方钢管混凝土组合柱轴压承载力分析[J/OL]. 建筑结构学报: 1-12[2020-07-31]. 网址: doi.org/10.14006/j.jzjgxb.2020.0082. TAO Yi, YE Sijun, CHEN Jianfei. Analysis of axial compression bearing capacity of concrete-filled square steel tubular columns with built-in restraint cores[J/OL]. Journal of Building Structures: 1-12[2020-07-31]. Website: doi.org/10.14006/j.jzjgxb.2020.0082.(in Chinese).
[25]	魏锦, 赵均海, 刘彦东, 等. 钢管混凝土轴压短柱的极限承载力分析[J]. 建筑科学与工程学报, 2008(3):81-86. WEI Jin, ZHAO Junhai, LIU Yandong, et al. Analysis of the ultimate bearing capacity of concrete-filled steel tubular axial compression short columns[J]. Journal of Architecture and Civil Engineering,2008(3):81-86(in Chinese).
[26]	四川省住房和城乡建设厅. 混凝土结构加固设计规范: GB 50367—2013[S]. 北京: 中国建筑工业出版社, 2013. Sichuan housing and Urban Rural Development Department. Code for design of strengthening concrete structures: GB 50367—2013[S]. Beijing: China Architecture & Building Press, 2013(in Chinese).
[27]	中国建筑科学研究院. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015. China Academy of Building Research. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2015(in Chinese).

施引文献(15)

期刊类型引用(7)

1.	王百田，赵红娟，靳政闯，杨金凤. 改进关系阈值比的砖混结构建筑抗压强度检测. 计算机仿真. 2024(06): 549-553 . 百度学术
2.	管国东，张璐珂. 考虑尺寸效应的FRP约束混凝土分析模型. 湖南交通科技. 2023(04): 131-139 . 百度学术
3.	赵辉，曹玉贵，王攀峰，赵立峰. 不同应变速率下CFRP约束混凝土方柱的力学性能. 复合材料学报. 2022(10): 4847-4855 . 本站查看
4.	曹玉贵，赵国旭，尹亚运. 基于广义回归神经网络的纤维增强聚合物复合材料约束损伤混凝土强度预测. 复合材料学报. 2021(05): 1623-1628 . 本站查看
5.	任宏伟，严珊. CFRP约束高强混凝土圆柱抗压力学性能研究. 河南理工大学学报(自然科学版). 2021(06): 157-162 . 百度学术
6.	黄新良，陈文广，谭佩，徐金俊，钱四江. 纤维增强复材约束矩形混凝土轴压强度和极限压应变计算方法研究. 工业建筑. 2021(10): 170-176 . 百度学术
7.	张扬，卢志芳，曹玉贵. 基于Hoek-Brown破坏准则的FRP约束损伤混凝土圆柱与方柱统一强度模型（英文）. Journal of Central South University. 2020(12): 3807-3820 . 百度学术