Numerical simulation and theoretical analysis of flexural strengthening of RC beams with high-strength steel strand mesh/ECC
-
摘要:
采用有限元模拟与试验相结合的方法，研究了加固层材料用量、加固材料材性、加固钢筋混凝土(RC)梁特征参数等因素对高强钢绞线网/纤维增强水泥基复合材料(ECC)抗弯加固RC梁受弯性能的影响规律。首先，建立了高强钢绞线网/ECC加固既有无损RC梁有限元分析模型，并与试验结果比较，验证了其准确性和有效性，并采用该模型对关键参数对加固梁受弯性能的影响规律进行系统性分析。结果表明：该加固方法可显著提升RC梁的受弯承载力、刚度、延性，提升幅度分别为7.81%~61.84%、6.35%~40.90%、5.92%~50.16%；随着纵向钢绞线配筋率、加固层厚度和开裂应力的增大，承载力的提升幅度增大，而RC梁纵筋配筋率和截面高度增大会降低承载力的提升幅度；加固层厚度与纵向钢绞线配筋率的增大会增加刚度的提升幅度，而RC梁纵筋配筋率、混凝土强度和截面高度的增大会降低对刚度的提升幅度；延性的提升幅度随着混凝土强度的增大而增加。在此基础上结合相关力学理论，提出抗弯加固界限钢绞线用量计算公式及高强钢绞线网/ECC加固RC梁正截面承载力简化计算公式，与试验及数值模拟结果吻合良好。
Abstract:Using a combination of finite element simulation and experimentation, the impact of reinforcement layer material quantity, properties of reinforcement materials, and characteristic parameters of reinforced concrete (RC) beams on the flexural performance of RC beams strengthened with high-strength steel wire mesh/engineered cementitious composites (ECC) was investigated. Firstly, the finite element (FE) analysis model of existing nondestructive RC beams strengthened with high-strength steel wire mesh/ECC was established, and its effectiveness and accuracy were verified by comparing with the experimental results. The validated FE model was adopted to analyze the influencing factors of flexural performance of strengthened beams systematically. The results indicate that the strengthening method can significantly enhance the flexural bearing capacity, stiffness, and ductility of RC beams, with improvement ranges of 7.81% to 61.84%, 6.35% to 40.90%, and 5.92% to 50.16%, respectively. With the increase of longitudinal steel strand reinforcement ratio, thickness and cracking stress of ECC, the promotion range of bearing capacity increases, while the increase of longitudinal steel reinforcement ratio and section height of RC beams decrease the increment of bearing capacity. The increase of the thickness of ECC and the reinforcement ratio of longitudinal steel strand increase the promotion range of stiffness, but the promotion range decreases with the increment of longitudinal reinforcement ratio, concrete strength and section height of RC beams. The increment of ductility only increases with the increase of concrete strength. On this basis, combined with relevant mechanical theories, the calculation formula for the limit amount of steel strands for flexural strengthening and simplified calculation formulas for the normal-section bearing capacity of RC beams reinforced by high-strength steel wire strand mesh-reinforced ECC are proposed, calculation results are in good agreement with experimental and numerical simulation results.
-
目前，抗侵彻结构的发展趋势是轻量化和高防护性[1-2]。轻质材料的层状复合结构在合理的配置下能够充分发挥不同材料的物理特性，具有良好的抗侵彻性能，在防护领域受到广泛关注。目前层状复合抗侵彻结构中应用的材料主要包括陶瓷、金属合金和纤维复合材料[3-5]。陶瓷材料具有高硬度和高强度特点，用于复合结构的面板层，能够充分磨蚀弹体，消耗弹体大部分能量。但是陶瓷质地较脆并且抗拉强度低，因此需要和其它材料组合使用。纤维复合材料具有较高的比强度和比模量，与陶瓷组合使用能够进一步抵抗弹体的冲击，消耗其剩余能量。金属合金强度、硬度较高，用于复合结构中可以进一步提升防护性能。目前，应用较广泛的抗侵彻结构的形式包括陶瓷-纤维复合材料[6-7]、陶瓷-金属[8]。
泡沫铝等金属多孔材料由于具有轻质，高比强度和吸能性能好的特点，经常作为吸能构件应用于工程领域[9-11]。但是由于泡沫铝的强度较低，不能单独用来抵御弹体的侵彻或者是爆炸冲击波的毁伤。因此将泡沫铝与陶瓷、金属等高强度材料组成层状结构，在性能上形成互补，能够最大程度上发挥泡沫铝的优势。Mohan等[12]采用面板与泡沫铝组成夹芯结构，利用半球形冲头撞击夹芯结构，发现由于泡沫铝夹芯结构的存在明显提升了整体抗冲击性能。Vaidya等[13]研究了泡沫铝夹芯板在低速冲击下的响应，并计算了面板和芯层在最佳状态下的参数。肖先林等[14]通过子弹冲击试验总结出了碳纤维复合材料-泡沫铝夹芯板的失效形式，并通过有限元方法发现提高芯层的相对密度，刚度和强度能增强夹芯板抵抗冲击变形的能力，但是由于整体变形较小，不利于吸能。张元豪等[15]对泡沫铝夹芯结构开展了FSP侵彻试验，总结了夹芯结构的破坏机制，并分析了后面板的厚度对抗侵彻性能的影响。结果表明，泡沫铝芯层主要发生绝热剪切破坏，后面板的厚度越厚，抗弹性能越好。
金属丝缠绕材料(Entangled metallic wire material，EMWM)是一种特殊的多孔金属材料，综合性能好于泡沫铝。由于金属丝缠绕材料具有出色的阻尼性能，常用于航空航天、船舶等大型设备的减振和隔振装置。目前对金属丝缠绕材料的研究主要集中于宏观力学性能及其形成机制[16]、力学性能[17]及其影响因素[18]、制造工艺[19]等。受泡沫铝复合结构的启发，本文探索了金属丝缠绕材料复合结构在抗侵彻领域的应用。
对于3层及以上复合结构抗侵彻机制的研究目前还不深入，尤其是对金属丝缠绕材料夹芯复合结构的抗侵彻机制的研究还不成熟。本文基于设计的4种复合结构(碳化硅陶瓷/超高分子量聚乙烯/钛合金(SiC/UHMWPE/TC4)、SiC/TC4/UHMWPE、SiC/UHMWPE/EMWM/TC4和SiC/TC4/EMWM/UHMWPE)，通过分离式霍普金森压杆(SHPB)试验分析了复合结构的动态力学行为，并利用侵彻试验和数值模拟研究了复合结构的抗侵彻机制、防护性能和能量特性。最后，研究了金属丝缠绕材料约束对复合结构防护性能的影响。
1. 实验材料及方法
1.1 原材料
复合结构中应用的材料包括碳化硅陶瓷(SiC)、钛合金(TC4)、超高分子量聚乙烯层压板(UHMWPE)和金属丝缠绕材料(EMWM)。SiC、TC4、UHMWPE层压板和EMWM的厚度分别为5 mm、6 mm、5 mm和10 mm。UHMWPE层压板由涂有聚氨酯的单向纤维织物通过热压工艺制成，铺层角度[0°/90°/0°/90°]。UHMWPE纤维体积分数为83vol%，纤维直径为17 μm，抗拉强度为3.6 GPa，弹性模量为116 GPa。EMWM密度为2.38 g/cm3。金属丝是直径为0.3 mm的304奥氏体不锈钢丝(0Cr10Ni9)。
如表1所示，设计了4种复合结构。复合结构中UHMWPE和TC4置于不同位置以讨论材料排布顺序对抗侵彻性能的影响，进而得出复合结构的最优结构形式。如图1所示，侵彻试验所用复合结构的横截面尺寸为150 mm×150 mm。材料之间的界面均用环氧树脂粘合。
表 1 层状复合结构的排列形式Table 1. Arrangement forms of the layered composite structuresStructure Arrangement form SiC/UHMWPE/TC4 5 mm SiC/5 mm UHMWPE/6 mm TC4 SiC/TC4/UHMWPE 5 mm SiC/6 mm TC4/5 mm UHMWPE SiC/UHMWPE/EMWM/TC4 5 mm SiC/5 mm UHMWPE/10 mm
EMWM/6 mm TC4SiC/TC4/EMWM/UHMWPE 5 mm SiC/6 mm TC4/10 mm
EMWM/5 mm UHMWPENotes: UHMWPE—Ultra-high molecular weight polyethylene; TC4—Titanium alloy; EMWM—Entangled metallic wire material. 1.2 试验方法
1.2.1 侵彻试验
图2是侵彻试验装置。弹道枪用于发射弹体。弹体尺寸如图2所示，材料为T12A钢。待测复合结构被固定在约束装置上。速度测量装置用于测量弹体的初始速度。弹道枪与测速装置之间装有拦截装置。
侵彻试验中使用侵彻深度(DOP)方法评估复合结构的抗侵彻性能。如图3所示，在DOP方法中，603装甲钢置于复合结构后。通过测量603装甲钢的残余穿深Pres和参考穿深Pref，计算出复合结构的质量效率Fm和厚度效率FS。为减小试验误差，每种复合结构准备3个试样，分别进行3次射击，并取结果的有效值。Fm和FS的计算公式如下[8]：
![]()
图 3 侵彻深度(DOP)方法原理图Figure 3. Schematic of depth-of-penetration (DOP) methodPres—Residual penetration; δ—Thickness of the composite structureFm=(Pref−Pres)ρ603δρhs (1) Fs=Pref−Presδ (2) 式中：Pref是弹体侵彻603装甲钢的穿深，实验测试表明603装甲钢的Pref为32 mm；Pres是弹体穿透复合结构后在603装甲钢中的剩余穿深；ρ603是603装甲钢的密度，ρ603= 7.86 g/cm3；ρhs和δ分别是复合结构的平均密度和厚度。
1.2.2 数值模拟
使用LSDYNA有限元软件来模拟复合结构的侵彻过程。复合结构的边界被完全约束。由于系统的对称性和为了简化计算，建立了1/4模型。复合结构和弹体的有限元模型尺寸与试验一致，参考表1、图1和图2。建立了UHMWPE层压板的10层铺层结构，以反映侵彻过程中的变形特征。弹体的网格尺寸为1 mm。侵彻试验中，复合结构的变形和破坏主要集中在弹着点附近，其余区域变形不明显。在弹体半径2倍范围内对复合结构的网格进行了细化，细化网格尺寸0.1 mm。复合结构其余区域的网格沿着半径方向向外逐渐稀疏。模型和网格如图4所示。*CONTACT_ERODING_SURFACE_TO _SURF-ACE用于定义弹体与复合结构之间的接触。*CONTACT_TIED_SURFACE_TO_SURFACE用来定义环氧树脂粘合剂。环氧树脂的破坏拉伸应力和破坏剪切应力分别设定为120 MPa和80 MPa。材料模型的参数如表2~7[8,20-22]所示。
![]()
图 4 弹体和层状复合结构的有限元模型Figure 4. Finite element model of projectile and layered composite structure表 2 SiC的*MAT_JOHNSON_HOLMQUIST_CERAMICS[20]模型参数Table 2. *MAT_JOHNSON_HOLMQUIST_CERAMICS[20] constants for SiCConstant Value Density/(g·cm−3) 3.2 Shear modulus G/GPa 183 Intact strength coefficient A 0.96 Fracture strength coefficient B 0.35 Strain rate coefficient C 0.0045 Intact strength exponent N 0.65 Fracture strength exponent M 1.0 Maximum tensile pressure strength T/GPa 0.75 Pressure at HEL PHEL/GPa 14.567 Damage coefficient D1 0.48 Damage exponent D2 0.48 Bulk modulus K1/GPa 217.2 Pressure coefficient K2/GPa 0 Pressure coefficient K3/GPa 0 Constant Value Density/(g·cm−3) 0.97 Young’s modulus in a-direction Ea/GPa 29.8 Young’s modulus in b-direction Eb/GPa 29.8 Young’s modulus in c-direction Ec/GPa 1.91 Poisson’s ratio ba νba/GPa 0.008 Poisson’s ratio ca νca/GPa 0.044 Poisson’s ratio cb νcb/GPa 0.044 Shear modulus ab Gab/GPa 0.82 Shear modulus bc Gbc/GPa 0.75 Shear modulus ca Gca/GPa 0.75 Bulk modulus of failed material Kfail/GPa 2.2 AOPT 0 Material axes change flag for brick elements MACF 1 Shear strength Sc/GPa 0.36 Longitudinal tensile strength a-axis Xt /GPa 3.0 Transverse tensile strength b-axis Yt/GPa 3.0 Transverse compressive strength b-axis Yc/GPa 2.5 Shear stress parameter for the nonlinear term α 0.5 Normal tensile strength Sn/GPa 0.95 Transverse shear strength Syz/GPa 0.95 Transverse shear strength Sxz/GPa 0.95 Constant Value Density/(g·cm−3) 4.45 Shear modulus G/GPa 41.9 Static yield strength A/GPa 1.0 Strain hardening coefficient B/GPa 0.845 Strain hardening exponent n 0.58 Strain rate coefficient C 0.014 Reference Strain rate ˙ε0/s−1 1.0 Thermal softening exponent m 0.753 Reference temperature t0/K 298 Melting temperature tm/K 1 951 Damage constant D1 0.05 Damage constant D2 0.27 Damage constant D3 −0.48 Damage constant D4 0.014 Damage constant D5 3.8 Constant Value Density/(g·cm−3) 2.38 Young’s modulus E/MPa 36 Poisson’s ratio 1 Tensile stress cutoff/MPa 2.39 DAMP 0.1 Constant Value Density/(g·cm−3) 7.85 Shear modulus G/GPa 200 Static yield strength A/GPa 1.54 Strain hardening coefficient B/GPa 0.477 Strain hardening exponent n 0.26 Strain rate coefficient C 0 Reference Strain rate ˙ε0/s−1 1.0 Thermal softening exponent m 1.0 Reference temperature t0/K 298 Melting temperature tm/K 1763 Damage constant D1 2.0 Damage constant D2 0 Damage constant D3 0 Damage constant D4 0 Damage constant D5 0 Constant Value Density/(g·cm−3) 7.85 Shear modulus G/GPa 77 Static yield strength A/GPa 1.41 Strain hardening coefficient B/GPa 0.73 Strain hardening exponent n 0.26 Strain rate coefficient C 0.014 Reference strain rate ˙ε0/s−1 5000 Thermal softening exponent m 1.03 Reference temperature t0/K 298 Melting temperature tm/K 1793 Damage constant D1 0.05 Damage constant D2 3.44 Damage constant D3 −2.12 Damage constant D4 0.002 Damage constant D5 1.61 1.2.3 霍普金森压杆(SHPB)试验
SHPB测试系统如图5所示。SHPB入射杆和透射杆均由7075铝合金制成，直径为45 mm。其长度均为2 500 mm。使用高速摄像机(PCO.1200hs，PCO AG，Kelheim，Germany) 记录层状复合结构的冲击过程。每次实验撞击杆的速度为30 m/s。为了保证测试结果的准确性，每种复合结构分别进行3次测试，并取结果的平均值。
2. 结果与讨论
2.1 层状复合结构抗侵彻机制
如表8所示，侵彻试验结果与数值模拟结果较为吻合，可以通过建立的模型可以进一步研究复合结构的抗侵彻机制。
表 8 层状复合结构侵彻试验和数值模拟的残余穿深PresTable 8. Residual penetration Pres of penetration tests and numerical simulations of layered composite structuresStructure Incident velocity/(m·s−1) ρhs/(g·cm−3) δ/mm Pres/mm Experiment Numerical Error/% SiC/UHMWPE/TC4 812.0 2.791 17.1 2.51 2.74 9.16 SiC/TC4/UHMWPE 810.7 2.806 17.5 5.04 4.22 −16.27 SiC/UHMWPE/EMWM/TC4 814.3 2.498 27.6 5.63 4.75 −15.63 SiC/TC4/EMWM/UHMWPE 817.7 2.476 27.8 6.02 5.12 −15.00 Notes: ρhs—Density of composite structure. 复合结构SiC/UHMWPE/TC4的侵彻过程如图6所示。在弹体侵彻SiC的过程中，弹体发生塑性变形，SiC碎裂。随着进一步侵彻，弹体侵彻UHMWPE。UHMWPE的损伤形态如图7(a)所示。UHMWPE纤维首先经历拉伸变形，在纤维达到极限拉伸强度之前，在弹体的侵彻作用下会发生剪切破坏。TC4对UHMWPE的背表面的约束导致UHMWPE纤维在前表面上外翻。应力波在UHMWPE的基体和纤维之间反射形成拉伸应力波。当拉伸应力大于纤维层之间的粘合力时，UHMWPE发生分层破坏。TC4的损伤形态如图7(b)所示。TC4的失效模式是由塑性扩孔导致的崩落破坏。由于TC4的高强度和高硬度，弹体在TC4内部进一步损伤。
![]()
图 6 模拟复合结构SiC/UHMWPE/TC4的侵彻过程Figure 6. Simulation of penetration process of composite structure SiC/UHMWPE/TC4![]()
图 7 复合结构SiC/UHMWPE/TC4中各材料层的损伤形态Figure 7. Failure morphologies of each material layer in structure SiC/UHMWPE/TC4复合结构SiC/TC4/UHMWPE的侵彻过程如图8所示。TC4的损伤形态如图9(a)所示。TC4在复合结构SiC/TC4/UHMWPE中的失效模式是脆性破裂。TC4首先发生剪切破坏，并且随着弹体进一步推动TC4而发生脆性破裂。UHMWPE的损伤形态如图9(b)所示。复合结构SiC/TC4/UHMWPE中UHMWPE的失效模式为剪切破坏。在复合结构SiC/TC4/UHMWPE中，UHMWPE是TC4的背板。弹体穿透TC4后，弹体和TC4碎片形成组合弹体共同侵彻UHMWPE。UHMWPE的强度和刚度较低，在弹体和TC4碎片的组合侵彻下发生剪切破坏。TC4的限制导致UHMWPE变形小，不利于充分发挥UHMWPE的吸能性能。
![]()
图 8 模拟复合结构SiC/TC4/UHMWPE的侵彻过程Figure 8. Simulation of penetration process of composite structure SiC/TC4/UHMWPE![]()
图 9 复合结构SiC/TC4/UHMWPE中各层材料的的损伤形态Figure 9. Failure morphologies of each material layer in structure SiC/TC4/UHMWPE2.2 层状复合结构动态力学行为
EMWM具有出色的吸能和阻尼特性，在防护领域中具有应用价值。基于复合结构SiC/UHMWPE/TC4、SiC/TC4/UHMWPE的形式，设计了表1中的EMWM复合结构SiC/UHMWPE/EMWM/TC4、SiC/TC4/EMWM/UHMWPE。复合结构由多种不同物理性能的材料组成，其动态力学行为十分复杂。为了初步探索EMWM复合结构的动态力学行为，进行了SHPB试验，对研究EMWM复合结构的抗侵彻性能具有一定借鉴意义。根据SHPB试验设备的规格，用于SHPB试验的复合结构的横截面为直径40 mm的圆形。另外，为了避免复合结构中材料厚度变化对试验结果分析产生影响，SHPB试验中材料的厚度同侵彻试验中的厚度一致。SiC、TC4、UHMWPE和EMWM的厚度分别为5 mm、6 mm、5 mm和10 mm。
图10为SHPB冲击层状复合结构试验中得到的入射、反射和透射应变。对比复合结构SiC/UHMWPE/TC4、SiC/UHMWPE/EMWM /TC4或SiC/TC4/UHMWPE、SiC/TC4/EMWM/UHMWPE可以发现EMWM加入到复合结构中之后，反射波幅值与入射波幅值相近，透射波缓慢上升，并且透射波的幅值和波长显著减小。上述现象表明，EMWM可以延迟通过复合结构的弹性压缩波，并有效地阻碍了应力波的透射传播，减小透射波的能量。本文中透射率定义为透射应变的峰值与入射应变的峰值之比。通过计算，4种复合结构的透射率分别为0.8267、0.8800、0.2793和0.2953。复合结构SiC/UHMWPE/TC4、SiC/TC4/UHMWPE或结构SiC/UHMWPE/EMWM/TC4、SiC/TC4/EMWM/UHMWPE的透射率不同，证明材料的排布顺序会影响复合结构的应力波透射性能。
![]()
图 10 SHPB试验中层状复合结构的入射、反射和透射应变Figure 10. Incident, reflected and transmitted strain of layered composite structure in SHPB test、图11为4种复合结构冲击过程中的典型破坏形态。复合结构SiC/UHMWPE/TC4中陶瓷在应力波作用下碎裂成块状；结构SiC/TC4/UHMWPE中陶瓷碎片较结构SiC/UHMWPE/TC4中小，并且陶瓷碎片呈崩落状态；结构SiC/UHMWPE/EMWM/TC4中陶瓷与超高分子量聚乙烯保持粘接状态，虽然发生破坏，但是从陶瓷碎片大小及破坏形态可以看出，陶瓷完整度较高，破坏程度低；结构SiC/TC4/EMWM/UHMWPE陶瓷与钛合金背板保持粘接状态，碎裂程度较复合结构SiC/TC4/UHMWPE低。在复合结构SiC/UHMWPE/TC4、SiC/TC4/UHMWPE的基础上加入金属丝缠绕材料，能够减小陶瓷的损伤，说明金属丝缠绕材料具有良好的缓冲性能。4种复合结构破坏特征不同，说明材料的排布顺序对复合结构的动态力学性能有影响。
![]()
图 11 SHPB试验中层状复合结构的破坏形态Figure 11. Failure forms of layered composite structures in SHPB tests综上所述，金属丝缠绕材料在复合结构中能够有效地延迟，阻碍应力波的透射传播，并且具有缓冲作用，减小复合结构的损伤。另外，不同的材料排布也会影响复合结构的动态力学行为。基于金属丝缠绕材料复合结构出色的应力波延迟和阻碍效应，本文进一步探索了其在抗侵彻领域的应用。
2.3 EMWM复合结构破坏形态
复合结构SiC/UHMWPE/EMWM/TC4的侵彻过程如图12所示。复合结构SiC/UHMWPE/EMWM/TC4是在复合结构SiC/UHMWPE/TC4的基础上，在UHMWPE和TC4之间加入EMWM制成的。UHMWPE的损伤形态如图13(a)所示，UHMWPE在正面受到剪切破坏，在背面受到拉伸破坏。复合结构SiC/UHMWPE/TC4中UHMWPE在正面出现拉伸破坏现象。因此加入EMWM改变了UHMWPE的破坏机制。在弹体侵彻UHMWPE的过程中，由于EMWM的强度和硬度较低，EMWM和UHMWPE一起变形。因此，与复合结构SiC/UHMWPE/TC4中UHMWPE相比，复合结构SiC/UHMWPE/EMWM/TC4中UHMWPE的拉伸破坏程度相对较大。TC4的损伤形态如图13(b)所示，TC4产生由塑性扩孔导致的崩落破坏，加入EMWM没有改变TC4的失效模式。通过比较复合结构SiC/UHMWPE/TC4、SiC/UHMWPE/EMWM/TC4中TC4的破坏程度可以发现加入EMWM减小了TC4的破坏程度。EMWM的损伤形态如图13(c)，EMWM被弹体穿透，金属丝被剪断。
![]()
图 12 模拟层状复合结构SiC/UHMWPE/EMWM/TC4的侵彻过程Figure 12. Simulation of penetration process of layered composite structure SiC/UHMWPE/EMWM/TC4![]()
图 13 层状复合结构SiC/UHMWPE/EMWM/TC4中各层材料的损伤形态Figure 13. Failure morphologies of each material layer in layered composite structure SiC/UHMWPE/EMWM/TC4复合结构SiC/TC4/EMWM/UHMWPE的侵彻过程如图14所示。复合结构SiC/TC4/EMWM/UHMWPE是通过在复合结构SiC/TC4/UHMWPE中的TC4和UHMWPE之加入EMWM制成的。TC4的损伤形态如图15(a)所示，TC4发生脆性破裂，与复合结构SiC/TC4/UHMWPE中TC4的失效模式相同。UHMWPE的损伤形态如图15(b)所示，UHMWPE发生剪切破坏，与复合结构SiC/TC4/UHMWPE中UHMWPE的失效模式相同。通过比较可以发现加入EMWM减小了UHMWPE的损伤。EMWM的损伤形态如图15(c)所示，其失效模式与复合结构SiC/UHMWPE/EMWM/TC4中EMWM相同。
![]()
图 14 模拟层状复合结构SiC/TC4/EMWM/UHMWPE的侵彻过程Figure 14. Simulation of penetration process of layered composite structure SiC/TC4/EMWM/UHMWPE![]()
图 15 层状复合结构SiC/TC4/EMWM/ UHMWPE中各层材料的损伤形态Figure 15. Failure morphologies of each material layer in layered composite structure SiC/TC4/EMWM/ UHMWPE2.4 层状复合结构抗侵彻性能数值分析
如表9所示，为了比较复合结构的防护性能，通过数值方法计算了相同入射速度下复合结构的质量效率和厚度效率。除复合结构SiC/TC4/EMWM/UHMWPE的厚度效率为0.97外，其余质量效率和厚度效率均大于1，说明所设计的复合结构在减小质量和厚度方面具有优势。
表 9 层状复合结构的质量效率和厚度效率Table 9. Mass efficiency and thickness efficiency of layered composite structuresStructure Incident velocity/(m·s−1) ρhs/(g·cm−3) δ/mm Pres/mm Fm Fs SiC/UHMWPE/TC4 813.675 2.791 17.1 3.22 4.74 1.68 SiC/TC4/UHMWPE 813.675 2.806 17.5 4.48 4.40 1.57 SiC/UHMWPE/EMWM/TC4 813.675 2.498 27.6 3.75 3.22 1.02 SiC/TC4/EMWM/UHMWPE 813.675 2.476 27.8 4.98 3.09 0.97 Notes: Fm—Quality efficiency; Fs—Thickness efficiency. 如图16所示，通过有限元方法计算并提取出了不同材料的总能量。可以发现TC4的总能量的比重最大，说明TC4是复合结构抗侵彻性能的决定性因素。为了提高复合结构的抗侵彻性能，应充分利用TC4的耗能机制。TC4等金属材料主要依靠其高强度和高硬度来磨蚀弹体进而消耗弹体能量。TC4的脆性破裂属于低耗能失效模式，塑性扩孔导致的崩落破坏属于高耗能失效模式。因此，复合结构SiC/UHMWPE/TC4、SiC/UHMWPE/EMWM/TC4中TC4的总能量大于复合结构SiC/TC4/UHMWPE、SiC/TC4/EMWM/UHMWPE中TC4的总能量。TC4在复合结构SiC/UHMWPE/TC4中的总能量最高，说明TC4后置于UHMWPE时可以充分发挥其能量耗散性能，最大程度提高复合结构的抗侵彻性能。加入EMWM一定程度上减小了TC4的损伤，进而减小了TC4的耗能，导致抗侵彻性能下降。但是，EMWM复合结构仍有较高的防护系数，并且发挥了缓冲和减小损伤的作用，具有一定应用价值。
![]()
图 16 不同层状复合结构材料的总能量Figure 16. Total energy of different materials in layered composite structures2.5 层状复合结构改进
通过观察侵彻后的样品，EMWM在侵彻后出现明显的膨胀现象。基于这个特征，探索了EMWM约束结构。如图17所示，加工了EMWM的圆形约束结构和多圆约束结构来代替复合结构SiC/UHMWPE/EMWM/TC4中的EMWM。侵彻试验在相同的测试条件下进行。结果表明，圆形约束复合结构和多圆约束复合结构中603装甲钢的残余穿深分别为2.43 mm和1.95 mm。通过对EMWM施加约束显著地提高了复合结构的抗侵彻性能，并且多圆约束的效果更好。图18、图19是EMWM约束复合结构的损伤形态。圆形约束复合结构中，金属框架对EMWM产生约束作用，提高了弹体的侵彻阻力，提高了抗侵彻性能。多圆约束复合结构中，EMWM膨胀，金属框架限制EMWM并发生断裂，周向的EMWM进一步限制金属框架并产生变形，抗侵彻性能好于圆形约束复合结构。上述现象表明，通过约束EMWM，可以提高复合抗侵彻性能，并且通过对约束形式的设计可以进一步提高EMWM约束复合结构的抗侵彻性能。
![]()
图 18 圆形EMWM约束结构中各层材料的损伤形态Figure 18. Failure morphologies of each material layer in EMWM circular constraint composite strcuture![]()
图 19 多圆EMWM约束复合结构中各层材料的损伤形态Figure 19. Failure morphologies of each material layer in EMWM multi-circle constraint composite strcuture3. 结 论
(1) 超高分子量聚乙烯(Ultra-high molecular weight polyethylene，UHMWPE)前置于钛合金(Titanium alloy，TC4)或金属丝缠绕材料(Entangled metallic wire material，EMWM)时，UHMWPE会发生拉伸破坏；UHMWPE后置于TC4或EMWM时，UHMWPE发生剪切破坏。TC4前置于UHMWPE或EMWM时，TC4会发生脆性破裂；TC4后置于UHMWPE或EMWM时，TC4会发生由塑性扩孔引起的崩落破坏。EMWM由于侵彻作用产生剪断破坏。EMWM减小了材料的损伤。
(2) 加入EMWM延迟并阻碍了透射应力波的传播，减小了透射波的能量。EMWM具有良好的缓冲作用，有效地减小了复合结构的损伤。
(3) TC4在4种材料中的总能量的比重最大，在提高抗侵彻性能方面发挥重要作用。应当充分利用TC4的能量吸收性能，以提高复合结构的抗侵彻性能。TC4的崩落破坏属于高能耗破坏机制，脆性碎裂属于低能耗破坏机制。由于EMWM减小了TC4的损伤，导致TC4的总能量显著下降。
(4) 除了SiC/TC4/EMWM/ UHMWPE的厚度效率为0.97略小于1，其余复合结构的质量效率和厚度效率均大于1，说明设计的4种复合结构在减轻质量和厚度方面有优势，具有一定应用价值。此外，EMWM复合结构在减小损伤方面同样发挥重要作用，并且通过对EMWM施加合理的约束形式，可以进一步提高EMWM复合结构的抗侵彻性能。
-
![]()
图 1 加固梁有限元模型
RP—Reference point for adding constraints
Figure 1. Finite element model of strengthened beams
![]()
图 2 C-1试件破坏模式对比图
DAMAGET—Tensile damage variable of beam; U, U2—Vertical displacement of beam
Figure 2. C-1 specimen failure mode comparison diagram
![]()
图 4 各加固钢筋混凝土(RC)梁试件弯矩-跨中挠度曲线对比
Figure 4. Comparison of bending moment-midspan deflection curves of reinforced concrete (RC) beam specimens
![]()
图 5 各加固RC梁试件弯矩-跨中混凝土压应变曲线对比
Figure 5. Comparison of bending moment-midspan concrete compression-strain curves of strengthened RC beam specimens
![]()
图 6 各加固RC梁试件弯矩-受拉纵筋跨中应变曲线对比
Figure 6. Comparison of bending moment-strain curves of longitudinal reinforcement in tension of strengthened RC beam specimens
![]()
图 7 各加固RC梁试件弯矩-钢绞线跨中应变曲线对比
Figure 7. Comparison of bending moment-strain curves of steel strand in midspan of strengthened RC beam specimens
![]()
图 8 不同ECC加固层厚度试件荷载-挠度曲线
Figure 8. Load-deflection curves of specimens with different ECC strengthening layer thicknesses
![]()
图 9 不同纵向钢绞线配筋率试件荷载-挠度曲线
Figure 9. Load-deflection curves of specimens with different longitudinal steel strand reinforcement ratios
![]()
图 10 不同ECC开裂应力试件荷载-挠度曲线
Figure 10. Load-deflection curves of specimens with different ECC cracking stress
![]()
图 11 不同ECC极限抗拉强度试件荷载-挠度曲线
Figure 11. Load-deflection curves of specimens with different ECC ultimate tensile strength
![]()
图 12 不同纵筋配筋率试件弯矩-挠度曲线
Figure 12. Bending moment-deflection curves of specimens with different reinforcement ratios
![]()
图 13 不同混凝土强度试件荷载-挠度曲线
Figure 13. Load-deflection curves of specimens with different concrete strengths
![]()
图 14 不同RC梁高度试件荷载-挠度曲线
Figure 14. Load-deflection curves of specimens with different heights of RC beam
![]()
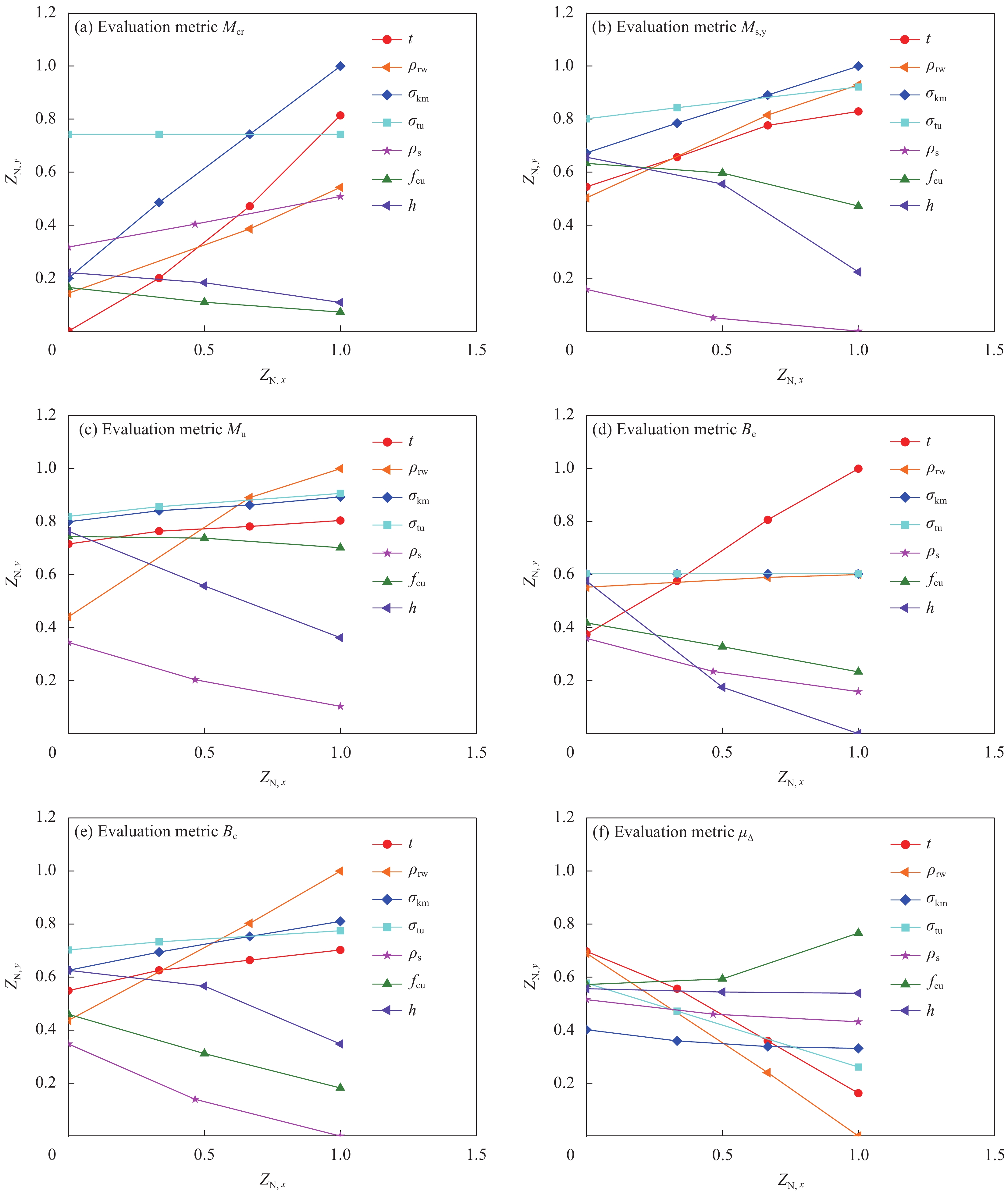
图 15 加固RC梁不同设计参数的评价指标均一化结果
t—Thickness of ECC; fcu—Compressive strength of concrete; h—Height of beam; ZN, y—Normalized value of evaluation index; ZN, x—Normalized values of design parameters
Figure 15. Normalized results of evaluation indicators for different design parameters of strengthened RC beams
![]()
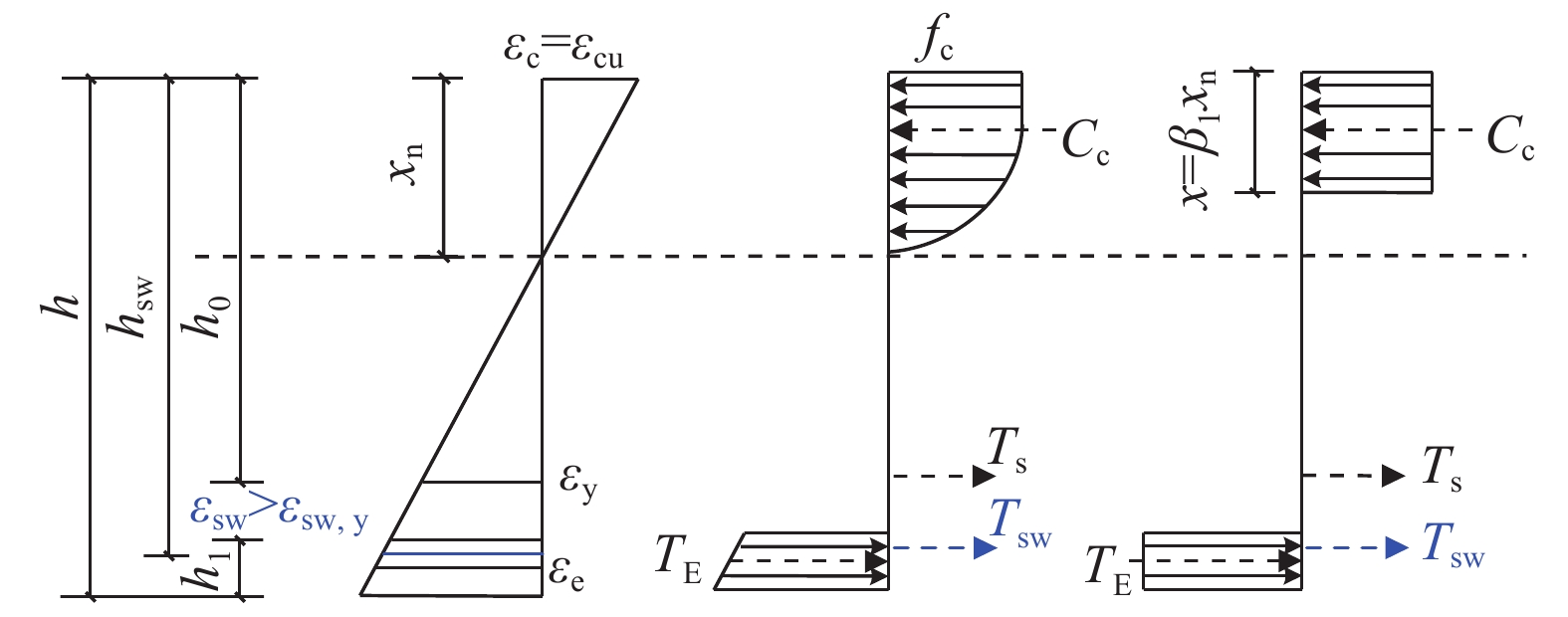
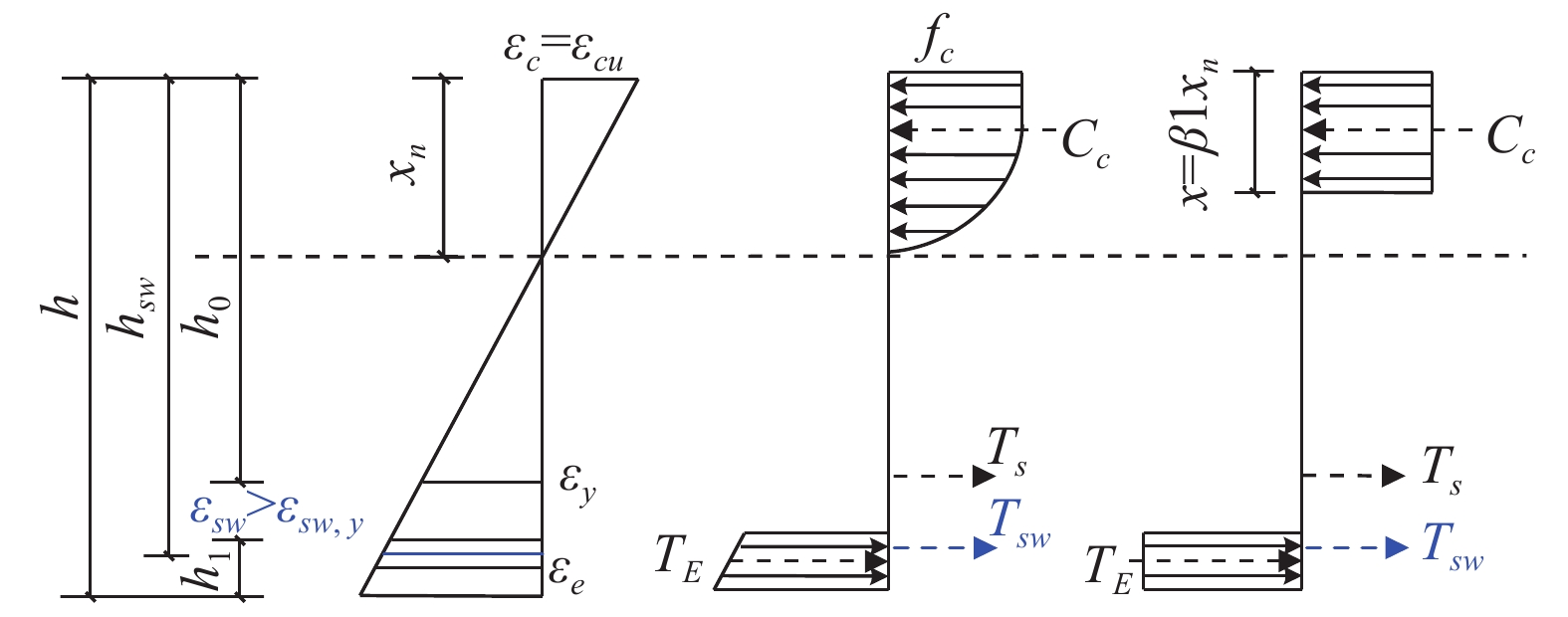
图 16 加固RC梁截面应变和应力分布
Figure 16. Distribution of cross-section strain and stress of strengthened RC beams
h—Height of the reinforced beam section; hsw—Distance from the steel strand to the top of the compression zone; h0—Effective height of the concrete section; h1—Thickness of the reinforcement layer; εc—Concrete compressive strain; εcu—Ultimate compressive strain value of concrete under non-uniform compression; xn—Height of the compression zone; εsw—Tensile strain in the steel strand; εsw,y—Strain corresponding to the nominal yield stress of the steel strand; εy—Ultimate tensile strain of the reinforcement; εe—Tensile strain of the reinforcement layer; Ts—Tensile force provided by the reinforcement; Tsw—Tensile force provided by the steel strand; TE—Tensile force provided by the reinforcement layer; Cc—Compressive force provided by the concrete; β1—Influence coefficient of concrete strength; fc—Design value of axial compressive strength of concrete
![]()
图 17 加固RC梁承载力公式计算值与试验值/模拟值间的离散程度
Figure 17. Dispersion degree between calculated value of bearing capacity formula and test value/simulation value of strengthened RC beams
表 1 试件设计
Table 1 Design of test specimens
Test specimen d/mm ρ/%(n) ECC formula[26] A-2 3.0 0.580 (5) Formula (1) A-3 3.0 0.812 (7) Formula (1) B-1 3.0 0.580 (5) Formula (2) B-2 3.0 0.580 (5) Formula (3) C-1 4.5 0.515 (2) Formula (1) D-1 3.6 0.686 (4) Formula (1) Notes: d—Diameter of steel strand; n—Number of longitudinal steel strands; ρ—Longitudinal steel strand reinforcement ratio; ECC—Engineered cementitious composites. 
下载: 导出CSV
表 2 增强水泥基复合材料(ECC)力学性能指标
Table 2 Mechanical properties of ECC
ECC
formula[26]fe/MPa Ee/GPa σkm/MPa εkm/% σtu/MPa εe,u/% (1) 37.3 14.1 1.37 0.025 2.18 1.88 (2) 46.5 14.6 1.91 0.035 2.81 0.75 (3) 36.6 14.3 1.86 0.032 2.30 2.47 Notes: fe—Compressive strength of ECC; Ee—Elastic modulus of ECC; σkm—Cracking stress of ECC; εkm—Cracking strain of ECC; σtu—Ultimate tensile strength of ECC; εe,u—Ultimate tensile strain of ECC.
下载: 导出CSV
表 3 高强钢绞线拉伸试验数据
Table 3 High-strength steel strand tensile test data
d/mm A/mm2 Erw/GPa σswu/MPa εu/% 3.0 4.35 139 1919.02 2.96 3.6 6.43 109 1521.21 3.47 4.5 9.65 130 1706.46 3.37 Notes: A—Cross-sectional area of the steel strand; Erw—Elastic modulus of steel strand; σswu—Ultimate tensile strength of the steel strand; εu—Ultimate tensile strain of the steel strand.
下载: 导出CSV
表 4 加固RC梁试件参数设计及有限元计算结果
Table 4 Parameter design of strengthened RC beam specimens and finite element calculation results
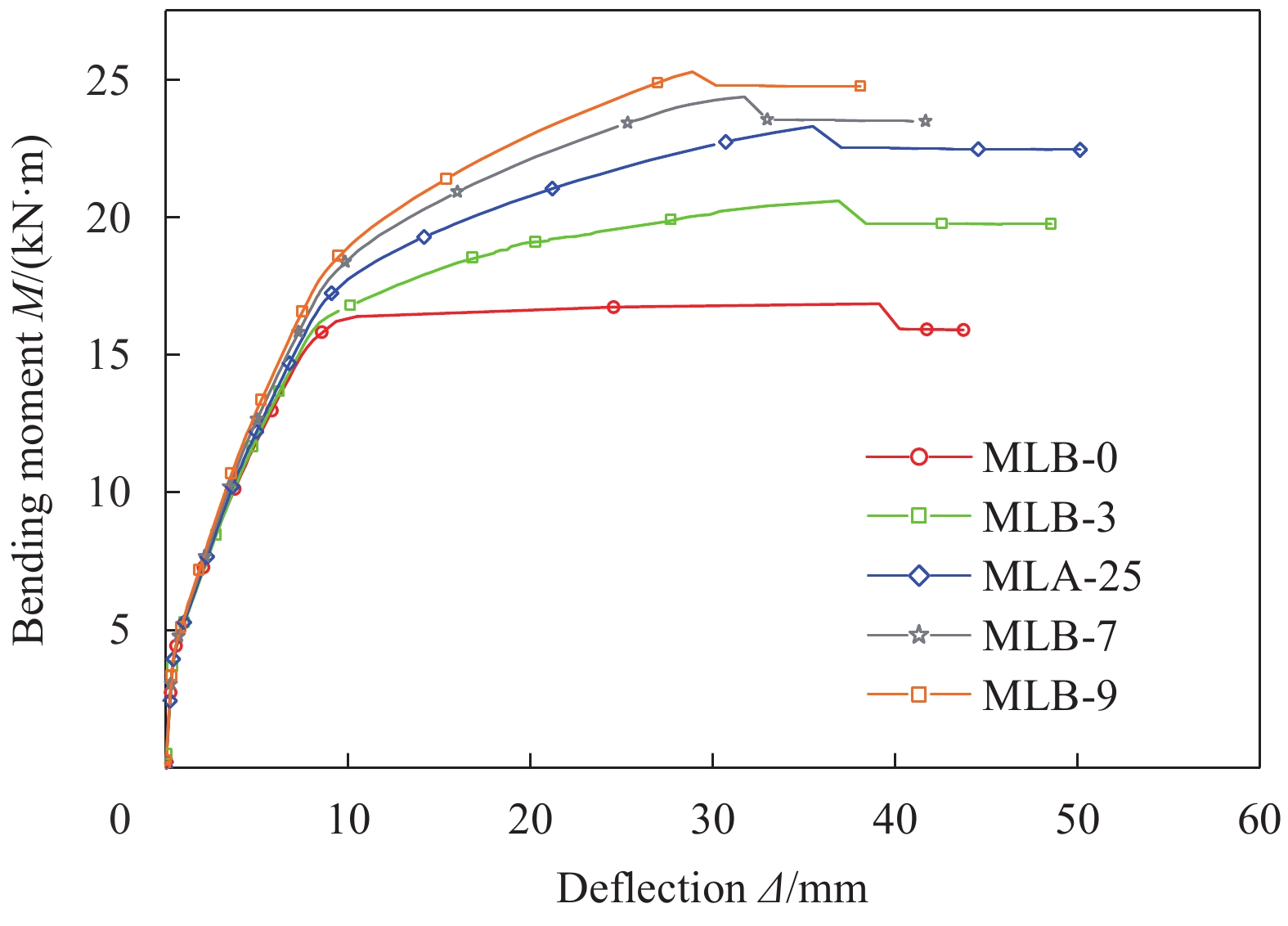
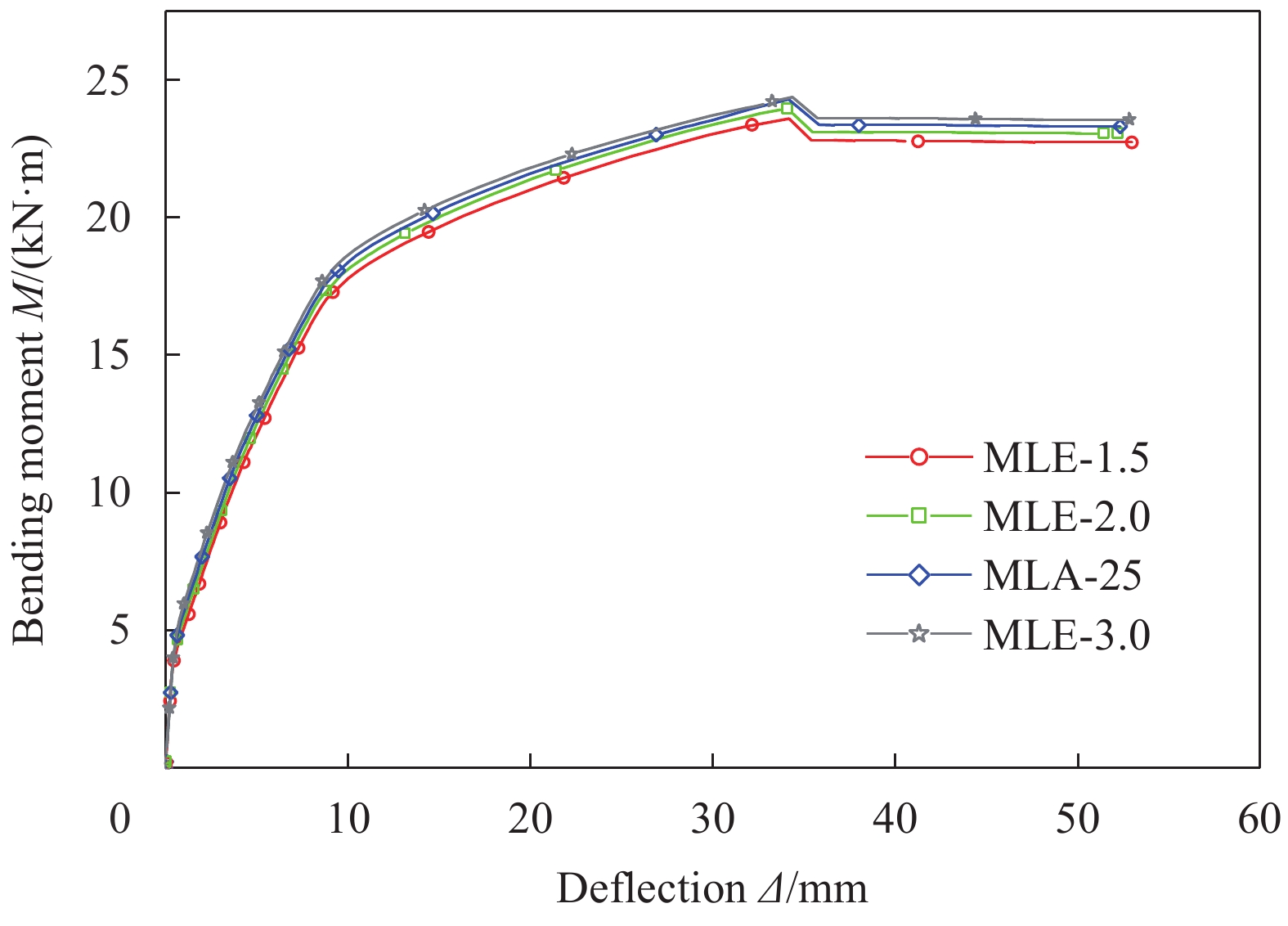
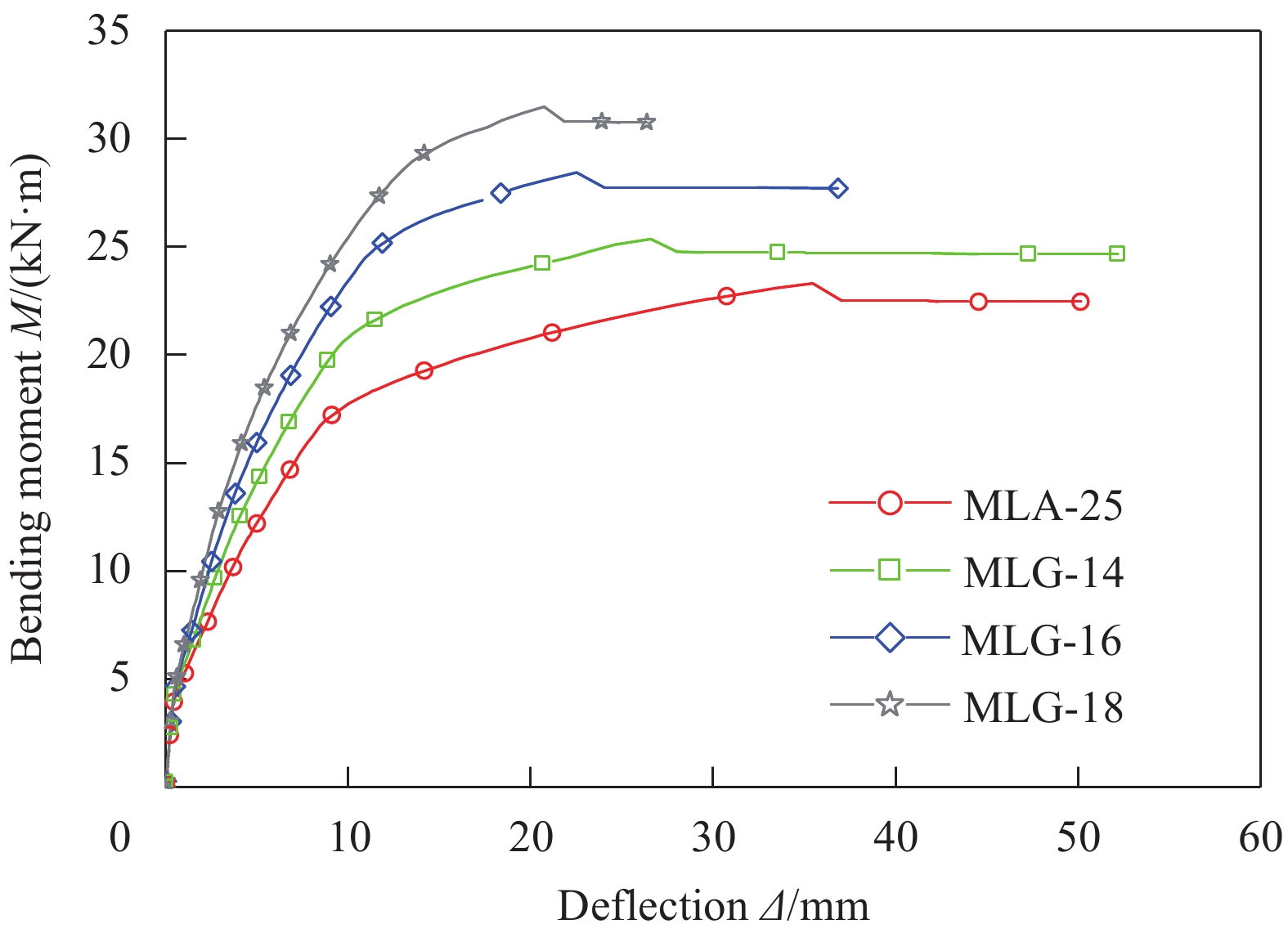
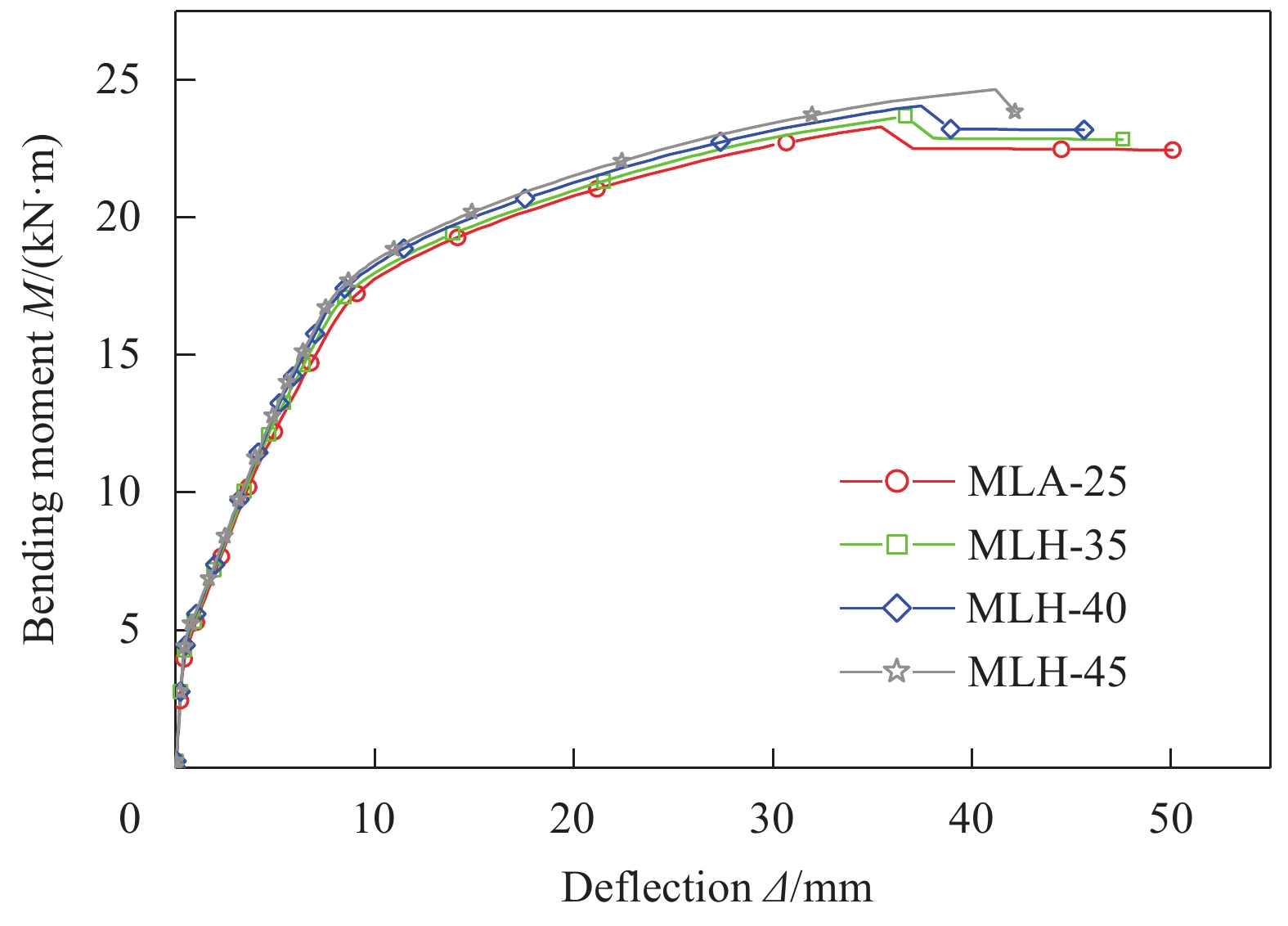
Specimen
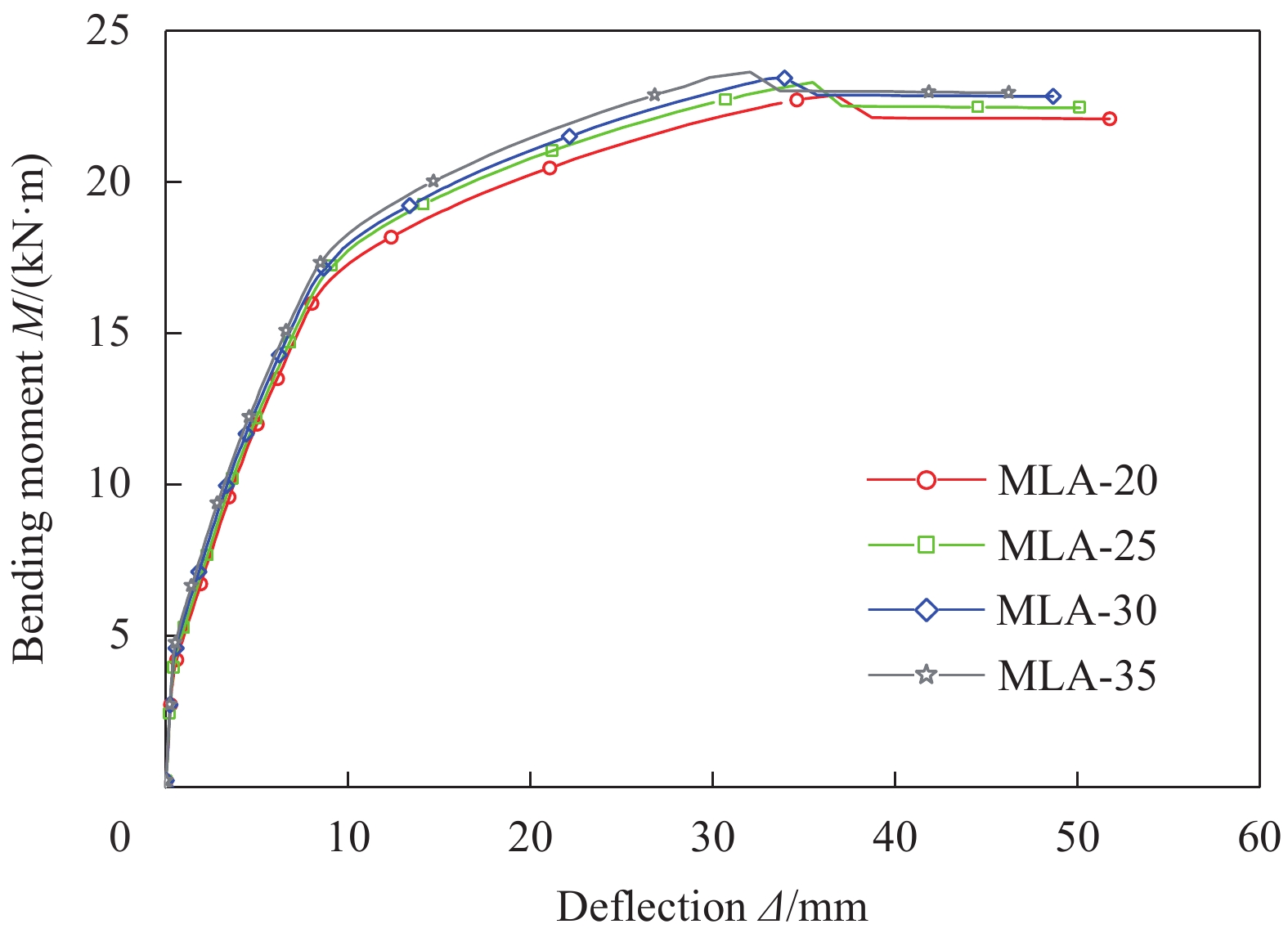
numberρs/% ρrw/% σkm/MPa σtu/MPa FM Mcr/(kN·m) Ms,y/(kN·m) Mu/(kN·m) Be Bc μ△ DB-0 0.936 – – – – 2.73 13.14 15.62 – – 3.21 DB-14 1.283 – – – – 2.77 17.87 20.07 – – 2.23 DB-16 1.686 – – – – 2.81 22.09 23.94 – – 1.56 DB-18 2.148 – – – – 2.86 25.89 27.21 – – 1.15 DB-35 0.936 – – – – 2.84 13.35 15.99 – – 3.33 DB-40 0.936 – – – – 2.97 13.64 16.28 – – 3.42 DB-45 0.936 – – – – 3.07 14.22 16.75 – – 3.59 DB-250 0.936 – – – – 3.97 21.89 25.89 – – 2.97 DB-300 0.936 – – – – 5.61 34.72 39.54 – – 2.52 MLA-20 0.936 0.58 1.5 2.5 CP 3.72 16.32 22.88 1.22 1.17 4.39 MLA-25 0.936 0.58 1.5 2.5 CP 3.86 16.72 23.29 1.28 1.18 4.19 MLA-30 0.936 0.58 1.5 2.5 CP 4.05 17.15 23.44 1.35 1.19 3.91 MLA-35 0.936 0.58 1.5 2.5 CP 4.29 17.34 23.63 1.41 1.2 3.63 MLB-0 0.936 0 1.5 2.5 CP 3.77 15.54 16.84 1.27 1.12 4.82 MLB-3 0.936 0.348 1.5 2.5 CP 3.82 16.17 20.56 1.27 1.15 4.38 MLB-7 0.936 0.812 1.5 2.5 CE 3.99 17.29 24.36 1.28 1.22 3.74 MLB-9 0.936 1.044 1.5 2.5 CE 4.1 17.7 25.28 1.29 1.25 3.4 MLE-1.5 0.936 0.58 1.5 4.5 CP 3.86 16.78 23.59 1.29 1.18 3.97 MLE-2.0 0.936 0.58 2 4.5 CP 4.06 17.18 23.94 1.29 1.2 3.91 MLE-2.5 0.936 0.58 2.5 4.5 CP 4.24 17.56 24.12 1.29 1.21 3.88 MLE-3.0 0.936 0.58 3 4.5 CP 4.42 17.95 24.38 1.29 1.22 3.87 MLF-2.5 0.936 0.58 2.5 2.5 CP 4.24 17.24 23.76 1.29 1.2 4.22 MLF-3.5 0.936 0.58 2.5 3.5 CP 4.24 17.39 24.07 1.29 1.2 4.07 MLF-5.5 0.936 0.58 2.5 5.5 CP 4.24 17.67 24.49 1.29 1.21 3.77 MLG-14 1.283 0.58 1.5 2.5 CP 4 20.31 25.37 1.21 1.13 2.87 MLG-16 1.686 0.58 1.5 2.5 CP 4.12 24.46 28.44 1.17 1.09 1.95 MLG-18 2.148 0.58 1.5 2.5 CE 4.27 28.31 31.49 1.15 1.06 1.42 MLH-35 1.283 0.58 1.5 2.5 CE 3.99 17.03 23.67 1.23 1.15 4.37 MLH-40 1.686 0.58 1.5 2.5 CP 4.13 17.26 24.04 1.2 1.12 4.52 MLH-45 2.148 0.58 1.5 2.5 CP 4.24 17.38 24.41 1.17 1.1 4.65 MLI-250 0.936 0.58 1.5 2.5 R 5.67 27.25 35.71 1.15 1.17 3.86 MLI-300 0.936 0.58 1.5 2.5 CP 7.8 40.08 50.36 1.1 1.13 3.27 Notes: Specimen number (DB—Non-reinforced; ML—Simulated RC beam, A-I—The group number; The number after the “-” indicates the value of the varying parameter in that group); ρs—RC beam longitudinal reinforcement ratio; ρrw—Longitudinal steel strand reinforcement ratio in the reinforcement layer; FM—Failure mode; CP—Due to concrete crushing to reach ultimate bearing capacity and concrete crushing occurs after the steel strand reaches nominal yield stress; CE—Due to concrete crushing to reach ultimate bearing capacity and concrete crushing occurs before the steel strand reaches nominal yield stress; R—Due to steel strand breaking to reach ultimate bearing capacity and steel strand breaking occurs before concrete crushing; Mcr—Cracking moment; Ms,y—Yield moment of reinforcement; Mu—Failure load; Be—Stiffness ratio in the elastic stage; Bc—Stiffness ratio during the cracked working stage; μ△—Displacement ductility factor.
下载: 导出CSV
表 5 高强钢绞线界限用量
Table 5 Limit dosage of high strength steel strand
Specimen
numberSectional area
of the steel
strand/mm2Relative values of stress and strain during concrete crushing σs/fy εs/εy σsw/fsw,y εsw/εsw,y MLB-0 0 – – – – MLB-1 4.35 (1) 1 11.98 Tensile rupture Tensile rupture MLB-2 6.70 (2) 1 10.53 1.16 2.05 MLB-3 13.05 (3) 1 9.98 1.14 1.77 MLB-4 17.40 (4) 1 9.46 1.13 1.42 MLB-5 21.75 (5) 1 9.04 1.09 1.33 MLB-6 26.10 (6) 1 8.65 1.04 1.14 MLB-7 30.45 (7) 1 7.23 0.99 0.99 MLB-8 34.80 (8) 1 6.32 0.98 0.95 MLB-9 39.15 (9) 1 3.99 0.96 0.87 Notes: σs—Stress of reinforcement; fy—Yield stress of rebar; εs—Strain of reinforcement; εy—Yield strain of rebar; σsw—Stress of high strength steel wire; fsw, y—Yield stress of high strength steel wire; εsw—Strain of high strength steel strand; εsw,y—Yield strain of high strength steel wire.
下载: 导出CSV
-
[1] 卢长福, 曹忠民. 高强钢绞线网-渗透性聚合物砂浆加固技术研究综述[J]. 江西科技, 2009, 27(26): 932-936. LU Changfu, CAO Zhongmin. Review of research on strengthening technique with strength steel wire mesh and polymer mortar[J]. Jiangxi Science, 2009, 27(26): 932-936(in Chinese).
[2] LI V C. High performance fiber reinforced cementitious composites as durable material for concrete structure repair international[J]. International Journal for Restoration, 2004, 10(2): 163-180.
[3] LI V C. Tailoring ECC for special attributes: A review[J]. International Journal of Concrete Structures and Materials, 2012, 6(3): 135-144. DOI: 10.1007/s40069-012-0018-8
[4] ZHENG Y Z, WANG W W, BRIGHAM J C. Flexural behavior of reinforced concrete beams strengthened with a composite reinforcement layer: BFRP grid and ECC[J]. Construction and Building Materials, 2016, 115: 424-437. DOI: 10.1016/j.conbuildmat.2016.04.038
[5] WU C, LI V C. CFRP-ECC hybrid for strengthening of the concrete structures[J]. Composite Structures, 2017, 178: 372-382. DOI: 10.1016/j.compstruct.2017.07.034
[6] 郑宇宙, 王文炜, 戴建国, 等. FRP-UHTCC复合层抗剪增强钢筋混凝土梁受力性能试验研究[J]. 建筑结构学报, 2019, 40(8): 118-126. ZHENG Yuzhou, WANG Wenwei, DAI Jianguo, et al. Experimental study on mechanical performance of reinforced concrete beams shear strengthened with FRP UHTCC composite[J]. Journal of Building Structures, 2019, 40(8): 118-126(in Chinese).
[7] 邓朗妮, 杨洲, 钟锰军, 等. FRP网格-ECC复合材料加固钢筋混凝土梁挠度[J]. 复合材料学报, 2023, 40(9): 4584-4596. DENG Langni, YANG Zhou, ZHONG Mengjun, et al. Deflection of reinforced concrete beams strengthened with FRP grid-engineered cementitious composite matrix composite[J]. Acta Materiae Compositae Sinica, 2023, 40(9): 4584-4596(in Chinese).
[8] 朱忠锋, 王文炜. FRP编织网/ECC复合加固钢筋混凝土圆柱力学性能的试验研究[J]. 东南大学学报(自然科学版), 2016, 46(5): 1082-1087. DOI: 10.3969/j.issn.1001-0505.2016.05.031 ZHU Zhongfeng, WANG Wenwei. Experimental study on mechanical behaviour of circular reinforced concrete columns strengthened with FRP textile and ECC[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(5): 1082-1087(in Chinese). DOI: 10.3969/j.issn.1001-0505.2016.05.031
[9] 郑宇宙, 王文炜. 复材网格-UHTCC复合增强钢筋混凝土梁抗弯性能试验研究[J]. 土木工程学报, 2017, 50(6): 23-32. ZHENG Yuzhou, WANG Wenwei. Experimental research on flexural behavior of RC beams strengthened with FRP grid-UHTCC composite[J]. China Civil Engineering Journal, 2017, 50(6): 23-32(in Chinese).
[10] 王冲. PVA-ECC钢丝网混凝土梁复合抗弯增强试验研究[D]. 南京: 东南大学, 2019. WANG Chong. Experimental study on the flexural behavior of concrete beams strengthened with PVA-ECC and steel wire meshes[D]. Nanjing: Southeast University, 2019(in Chinese).
[11] YANG X, GAO W Y, DAI J G, et al. Flexural strengthening of RC beams with CFRP grid-reinforced ECC matrix[J]. Composite Structures, 2018, 189: 9-26. DOI: 10.1016/j.compstruct.2018.01.048
[12] 朱忠锋, 王文炜, 郑宇宙, 等. 基于非接触式观测技术的FRP/ECC复合材料反复受拉本构关系模型[J]. 土木工程学报, 2019, 52(10): 36-45, 55. ZHU Zhongfeng, WANG Wenwei, ZHENG Yuzhou, et al. The constitutive model of FRP/ECC composite materials under uniaxial cyclic tensile loading based on the digital image correlation technique[J]. China Civil Engineering Journal, 2019, 52(10): 36-45, 55(in Chinese).
[13] HOU W, LI Z Q, GAO W Y, et al. Flexural behavior of RC beams strengthened with BFRP bars-reinforced ECC matrix[J]. Composite Structures, 2020, 241: 112092. DOI: 10.1016/j.compstruct.2020.112092
[14] 朱忠锋, 王文炜. 玄武岩格栅增强ECC复合材料反复荷载作用下本构关系模型[J]. 南京工业大学学报(自然科学版), 2017, 39(5): 44-50, 62. ZHU Zhongfeng, WANG Wenwei. Constitutive model of basalt fiber reinforced polymer grid reinforced engineered cement composite under cyclic loading[J]. Journal of Nanjing Tech University (Natural Science Edition), 2017, 39(5): 44-50, 62(in Chinese).
[15] 齐宝欣, 李宜人. PVA-ECC-钢筋复合梁抗冲击的影响因素及破坏特性研究[J]. 沈阳建筑大学学报(自然科学版), 2022, 38(2): 236-244. QI Baoxin, LI Yiren. Influence factors and failure characteristics of impact resistance of PVA-ECC-reinforced composite beams[J]. Journal of Shenyang Jianzhu University (Natural Science), 2022, 38(2): 236-244(in Chinese).
[16] ZHU J T, ZHANG K, WANG X L, et al. Bond-slip performance between high-strength steel wire rope meshes and engineered cementitious composites[J]. Journal of Materials in Civil Engineering, 2022, 34(5): 04022048. DOI: 10.1061/(ASCE)MT.1943-5533.0004184
[17] LI K, WEI Y X, LI Y P, et al. Flexural behavior of reinforced concrete beams strengthened with high-strength stainless steel wire rope meshes reinforced ECC[J]. Construction and Building Materials, 2023, 362: 129627. DOI: 10.1016/j.conbuildmat.2022.129627
[18] LI K, LIU W K, ZHANG K, et al. Bond behavior of stainless steel wire ropes embedded in engineered cementitious composites[J]. Construction and Building Materials, 2021, 281: 122622. DOI: 10.1016/j.conbuildmat.2021.122622
[19] WANG X L, YANG G H, QIAN W W, et al. Tensile behavior of high-strength stainless steel wire rope (HSSSWR)-reinforced ECC[J]. International Journal of Concrete Structures and Materials, 2021, 15(1): 43. DOI: 10.1186/s40069-021-00480-x
[20] 李可, 赵佳丽, 李志强, 等. 高强钢绞线网增强ECC抗弯加固无损RC梁试验[J]. 复合材料学报, 2022, 39(7): 3428-3440. LI Ke, ZHAO Jiali, LI Zhiqiang, et al. Experiment on non-damaged RC beams strengthened by high-strength steel wire strand meshes reinforced ECC in bending[J]. Acta Materiae Compositae Sinica, 2022, 39(7): 3428-3440(in Chinese).
[21] 李可, 王宇, 李志强, 等. 高强钢绞线网增强ECC加固无损RC梁受弯承载力研究[J]. 建筑结构学报, 2022, 43(12): 82-90. LI Ke, WANG Yu, LI Zhiqiang, et al. Research on flexural bearing capacity of non-damaged RC beams strengthened by high-strength steel wire strand mesh-reinforced ECC[J]. Journal of Building Structures, 2022, 43(12): 82-90(in Chinese).
[22] YUAN F, CHEN M C, PAN J L. Flexural strengthening of reinforced concrete beams with high-strength steel wire and engineered cementitious composites[J]. Construction and Building Materials, 2020, 254: 119284. DOI: 10.1016/j.conbuildmat.2020.119284
[23] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范(2015年版): GB/T 50010—2010[S]. 北京: 中国建筑工业出版社, 2016. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures (2015): GB/T 50010—2010[S]. Beijing: China Architecture & Building Press, 2016(in Chinese).
[24] 钱文文. 高强不锈钢绞线网增强ECC拉伸和弯曲性能试验及理论研究[D]. 郑州: 郑州大学, 2018. QIAN Wenwen. Experimental and theoretical research on tensile and flexural properties of high strength stainless steel strand mesh reinforced ECC[D]. Zhengzhou: Zhengzhou University, 2018(in Chinese).
[25] 刘伟康. ECC受压和受拉性能及本构模型研究[D]. 郑州: 郑州大学, 2018. LIU Weikang. Study on the compression and tensile properties and the constitutive model of ECC[D]. Zhengzhou: Zhengzhou University, 2018(in Chinese).
[26] 李志强. 高强钢绞线网/ECC加固无损伤RC梁受弯性能研究[D]. 郑州: 郑州大学, 2021. LI Zhiqiang. Study on the bending performance of non-damaged RC beams strengthened by high-strength steel wire mesh reinforced ECC[D]. Zhengzhou: Zhengzhou University, 2021(in Chinese).
[27] LIU X, JIANG Z J, YUAN Y, et al. Numerical investigation of the mechanical behavior of deformed segmental tunnel linings, strengthened by epoxy-bonded filament wound profiles[J]. Tunnelling and Underground Space Technology, 2018, 78: 231-244. DOI: 10.1016/j.tust.2018.04.033
-
期刊类型引用(1)
1. 刘晓军，战丽，邹爱玲，李志坤，赵俨梅，王绍宗. 纤维增强复合材料层间增韧技术研究进展. 复合材料科学与工程. 2022(01): 117-128 . 
百度学术
其他类型引用(1)
-
其他相关附件
-
目的
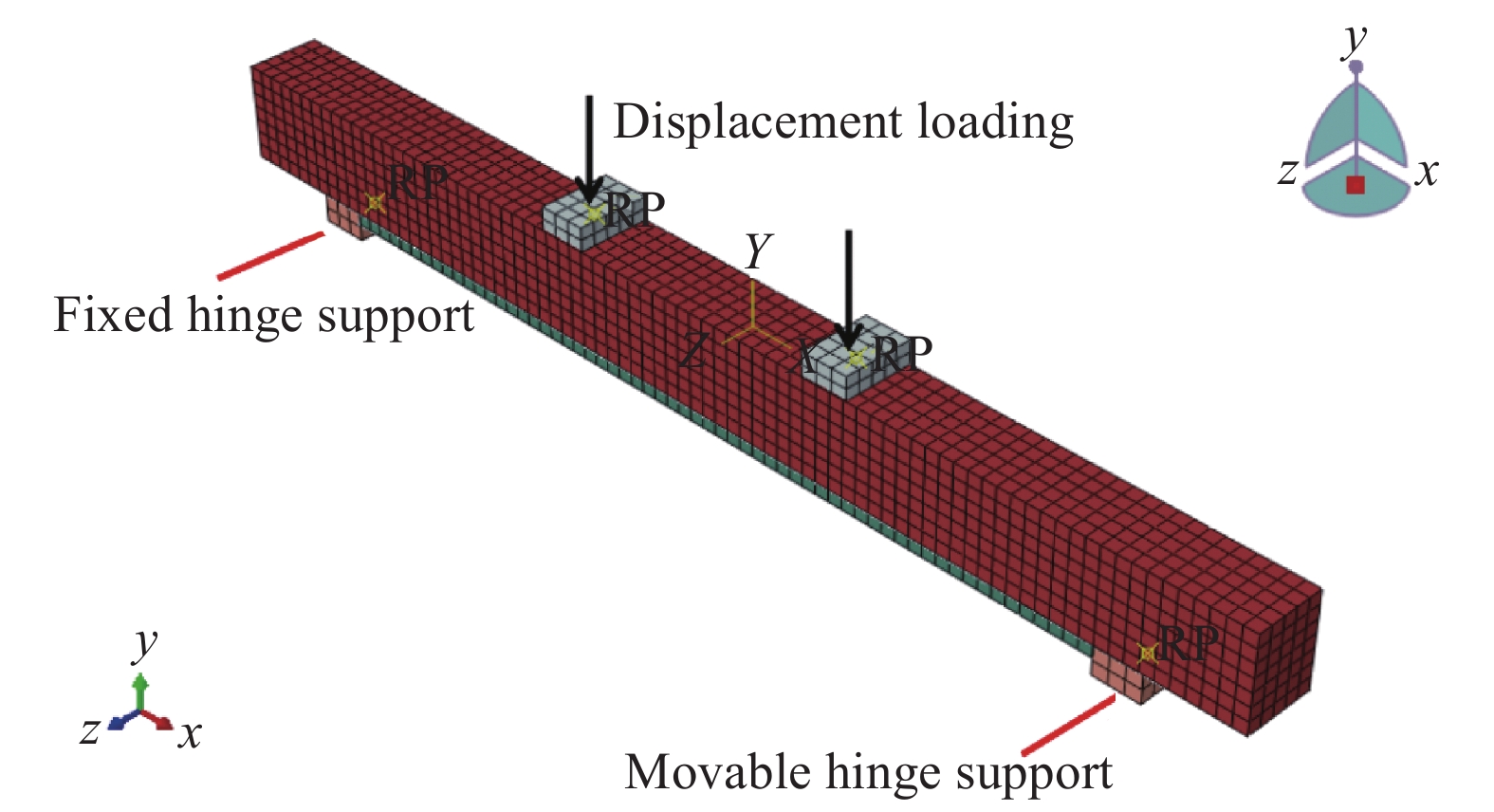
高强钢绞线网/ECC(Engineered Cementitious Composites) 这一新型高性能复合材料结合了高强钢绞线和ECC的优点，具有优异的延性、韧性及裂缝控制能力。考虑到目前对该新型高性能复合材料加固钢筋混凝土(Reinforced Concrete，RC)构件的研究尚不完善，且试验成本高、周期长、可能存在测试误差及难以充分考虑各种工况等问题，本文借助有限元软件ABAQUS，在对高强钢绞线网增强ECC加固无损RC梁受弯性能试验进行模拟验证分析的基础上，综合考虑多因素影响对加固梁受弯性能进行数值模拟分析。为完善现有研究成果，进一步将该新型复合材料应用于实际工程加固中，本文进行高强钢绞线网/ECC抗弯加固无损RC梁数值模拟及理论分析的研究。
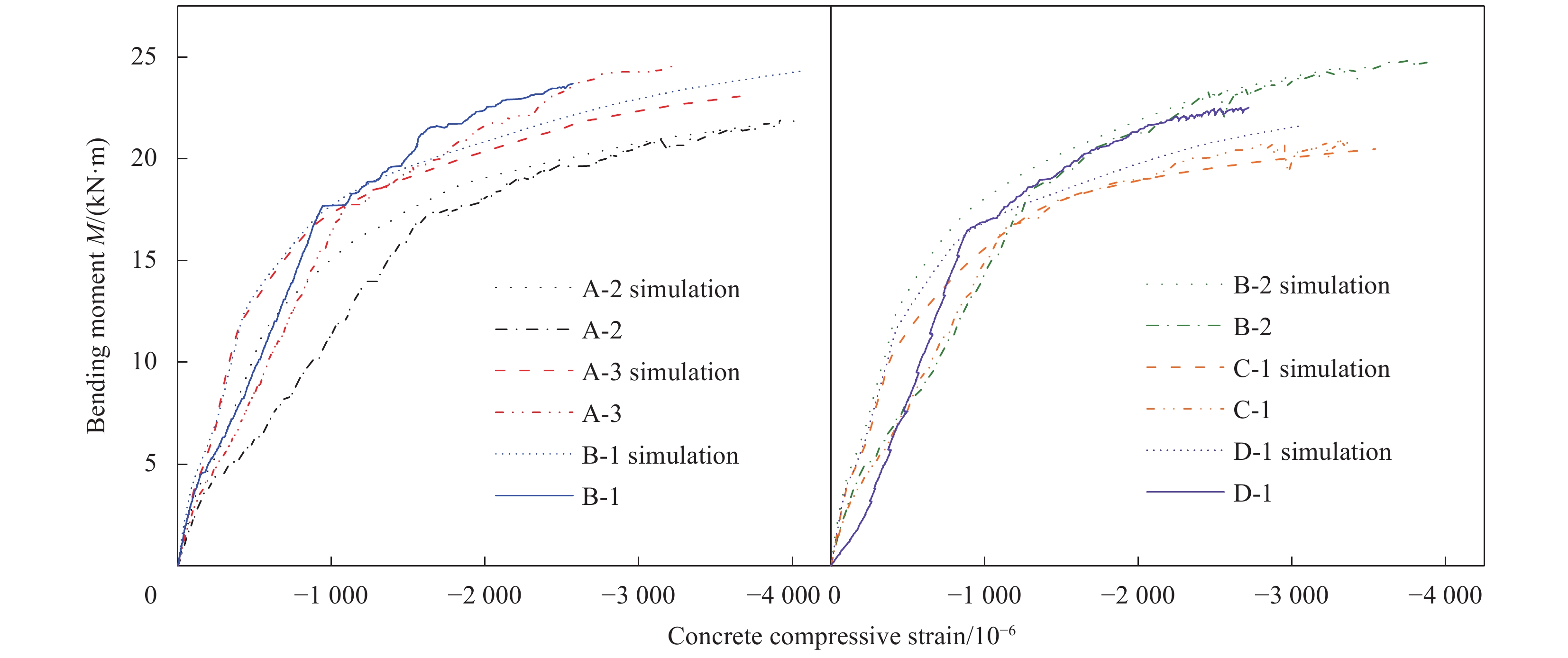
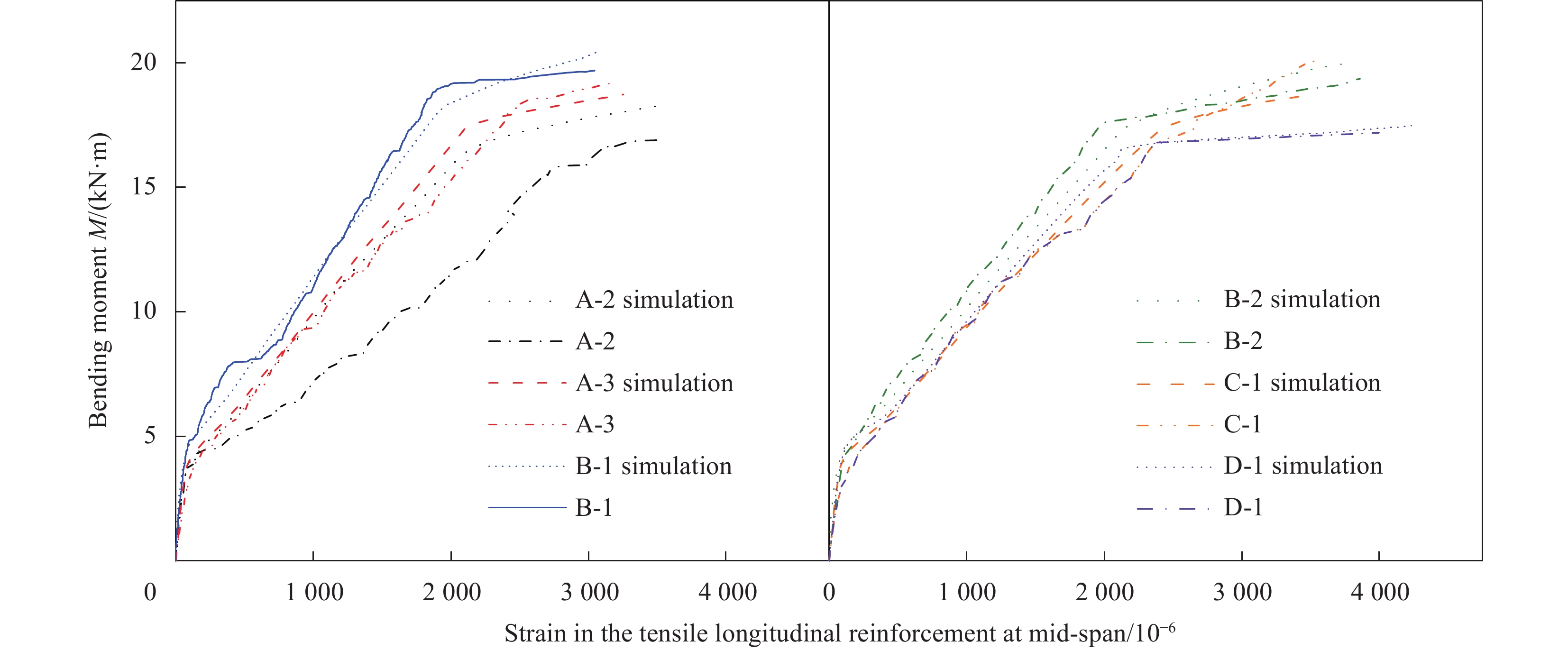
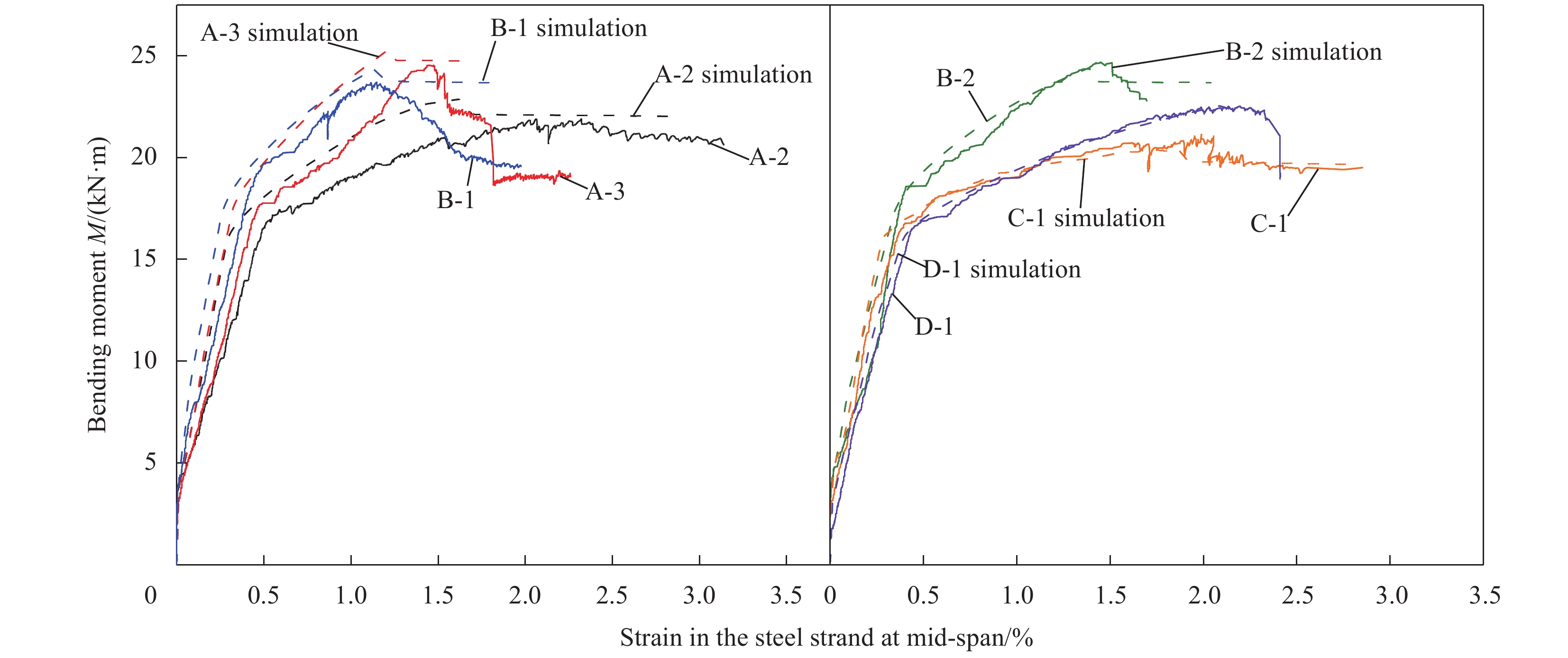
方法本文采用有限元模拟与试验相结合的方法，研究了加固层材料用量、加固材料材性、RC梁特征参数等因素对高强钢绞线网/ECC抗弯加固RC梁受弯性能的影响规律。首先建立了高强钢绞线网/ECC加固无损RC梁受弯分析模型，该模型计算结果与试验结果吻合良好，验证了其准确性和有效性，并采用该模型对关键参数对加固梁受弯性能的影响规律进行系统性分析。然后基于有限元分析结果绘制各试件曲线进行曲线分析，同时对试件的承载力、刚度和延性进行影响因素分析。
结果(1)该加固方法可显著提升RC梁的受弯承载力、刚度、延性，提升幅度分别7.81%~61.84%，6.35%~40.90%，5.92%~50.16%。(2)本文基于有限元分析结果与相关力学理论，提出抗弯加固界限钢绞线用量计算公式及高强钢绞线网/ECC加固RC梁正截面承载力简化计算公式，与试验及数值模拟结果吻合良好。
结论(1)本文建立的高强钢绞线网/ECC加固无损RC梁的有限元模型与试验结果吻合较好，证明了模型的有效性，并扩展影响因素分析表明：此加固方式能显著提升无损RC梁的开裂荷载、屈服荷载、极限承载力、刚度和延性，提升幅度分别为36.26%~61.90%，9.35%~36.61%，7.81%~61.84%，6.35%~40.90%，5.92%~50.16%。(2)各因素对加固梁开裂弯矩、屈服弯矩与极限弯矩影响规律：ECC加固层厚度和ECC开裂应力的增加会显著增大加固梁开裂弯矩的提升幅度，当ECC厚度由20mm增加至35mm时，开裂弯矩的提升幅度在36.26%至57.14%之间变化；纵向钢绞线配筋率的增大会明显提升屈服弯矩和极限弯矩的提升幅度，当纵向钢绞线配筋率由0增加至1.044%时，屈服弯矩由18.26%增加至34.70%，极限弯矩由7.81%增加至61.84%；RC梁纵向配筋率的增加会小幅度提升开裂弯矩的提升幅度、降低屈服弯矩和极限弯矩的提升幅度，而混凝土强度和梁高度的增大则会降低开裂弯矩、屈服弯矩与极限弯矩的提升幅度。(3)各因素对加固梁刚度与延性的影响规律：ECC加固层厚度和纵向钢绞线配筋率的增大会显著增加对加固后梁刚度的提升幅度，当ECC加固层厚度由20mm增加至35mm时，弹性阶段刚度的提升幅度由21.64%增加至40.90%，当纵向钢绞线配筋率由0增加至1.044%时，带裂缝阶段刚度的提升幅度由11.67%增加至25.37%， RC梁纵向配筋率、混凝土强度和梁截面高度的增大则会降低对刚度的提升幅度，ECC极限抗拉强度的增大会小幅度增加带裂缝工作阶段刚度的提升幅度；ECC加固层厚度、纵向钢绞线配筋率、RC梁纵向配筋率、ECC开裂应力、ECC极限抗拉强度和梁高度的增大会减少加固梁延性的提升幅度，当纵向钢绞线配筋率由0增加至1.044%时，延性系数提高幅度由50.16%降至5.92%，而混凝土强度的增大则会增加延性的提升幅度。(4)提出的高强钢绞线网/ECC抗弯加固RC梁界限钢绞线用量计算公式及正截面承载力简化计算公式，与试验及数值模拟结果吻合良好，验证了所提公式的准确性。
-
高强钢绞线网/ECC(Engineered Cementitious Composites)这一新型高性能复合材料结合了高强钢绞线和ECC的优点，具有强度高、超高延性、韧性及裂缝控制能力等优点。考虑到目前对该新型高性能复合材料加固钢筋混凝土(Reinforced Concrete，RC)构件的研究尚不完善，且试验成本高、周期长、可能存在测试误差及难以充分考虑各种工况等问题，本文借助有限元软件ABAQUS，在对高强钢绞线网增强ECC加固无损RC梁受弯性能试验进行模拟验证分析的基础上，综合考虑ECC厚度、纵向钢绞线配筋率、ECC开裂应力、ECC极限抗拉强度、RC梁纵筋配筋率、混凝土强度和RC梁截面高度7种影响因素对加固梁受弯性能进行数值模拟分析。
结果表明：提高纵向钢绞线的配筋率、加厚ECC加固层、增加ECC开裂应力与ECC极限抗拉强度，均能有效增强承载力；增加RC梁的纵筋配筋率、提高混凝土强度或增大截面高度，则会对承载力的增强效果产生负面影响；ECC加固层厚度、ECC开裂应力和纵向钢绞线配筋率的增加有助于提高结构刚度，而对于RC梁的纵筋配筋率、混凝土强度和截面高度的增加则会减少对刚度的提升效果；随着混凝土强度的提高，结构的延性也相应增加。
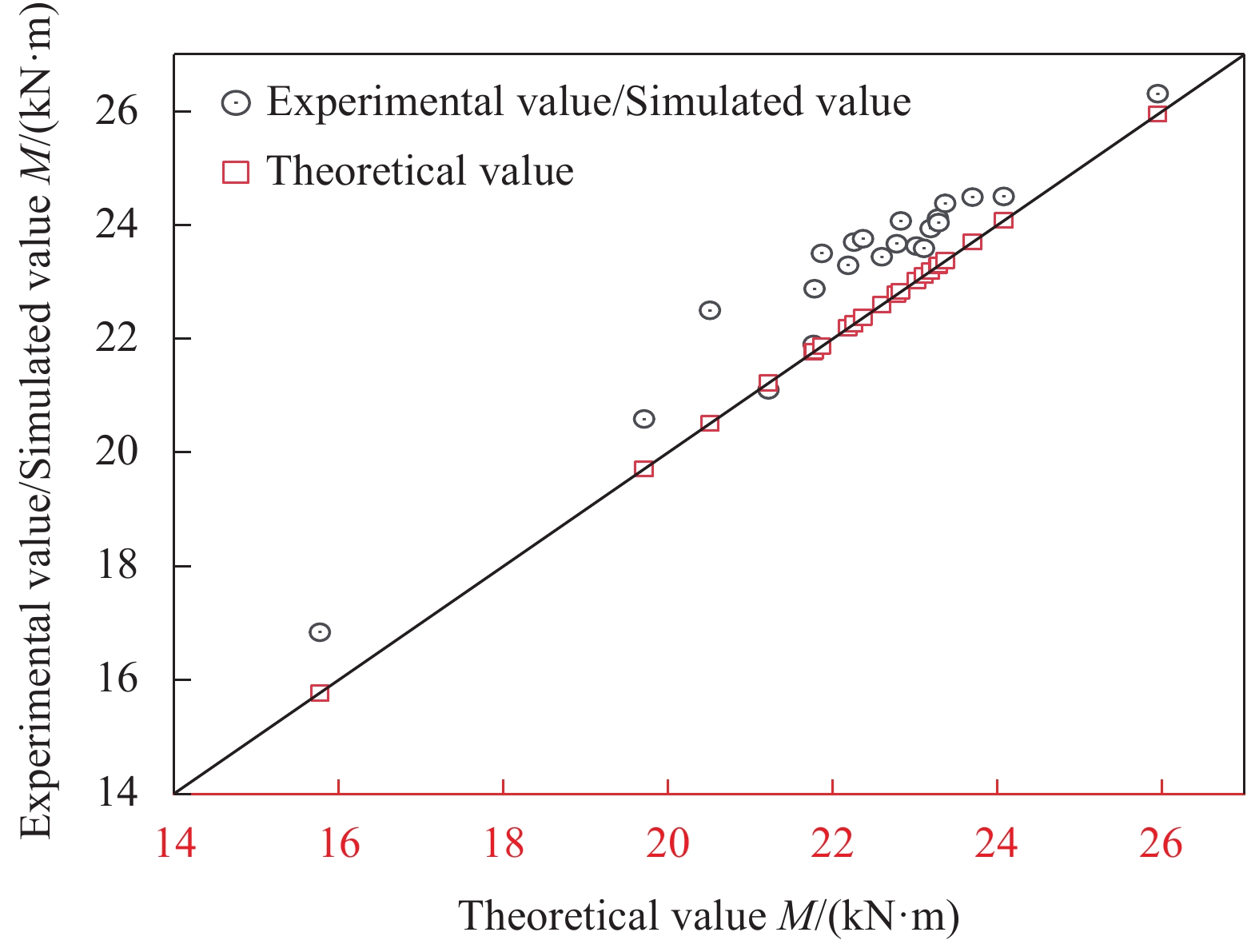
在此基础上，提出高强钢绞线网增强ECC抗弯加固无损RC梁界限钢绞线用量、正截面承载力简化计算公式，并将理论公式计算值与试验值及模拟值进行对比分析，结果吻合良好，验证了所提计算公式的准确性。
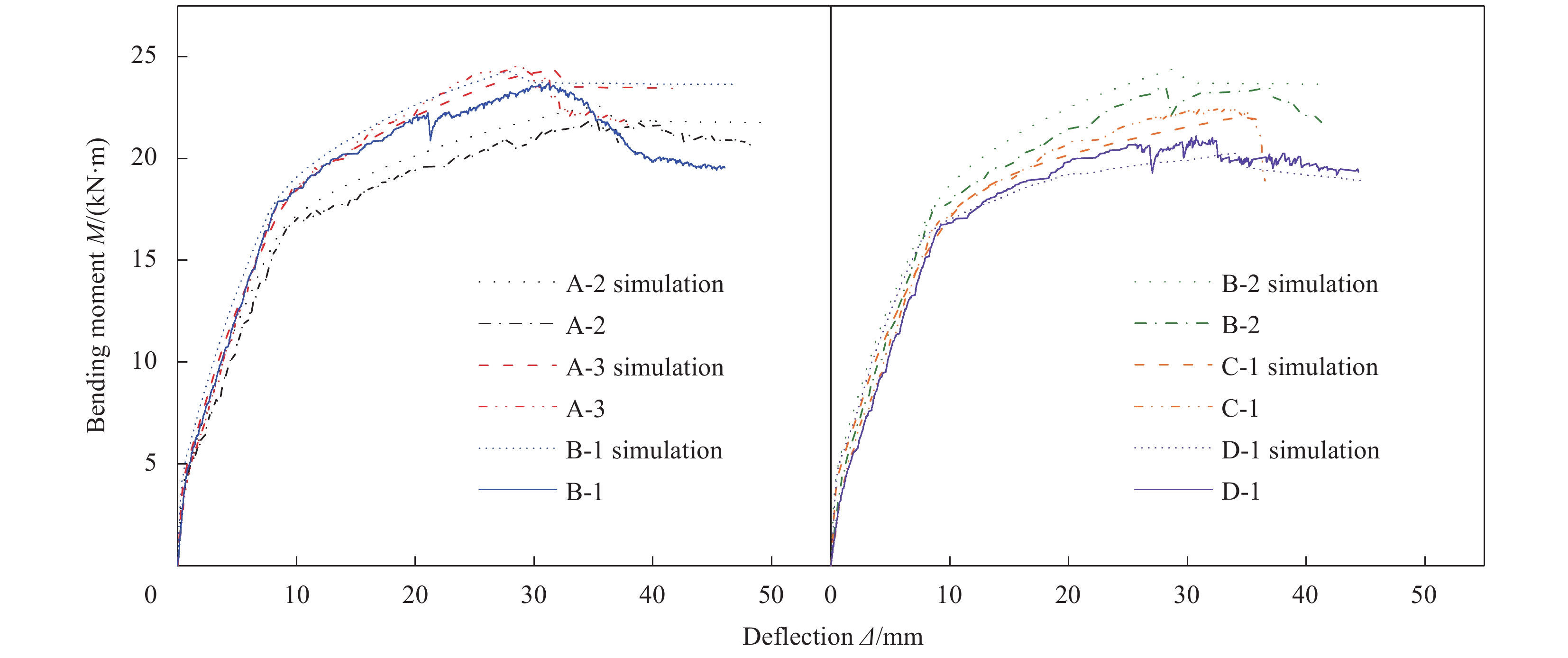
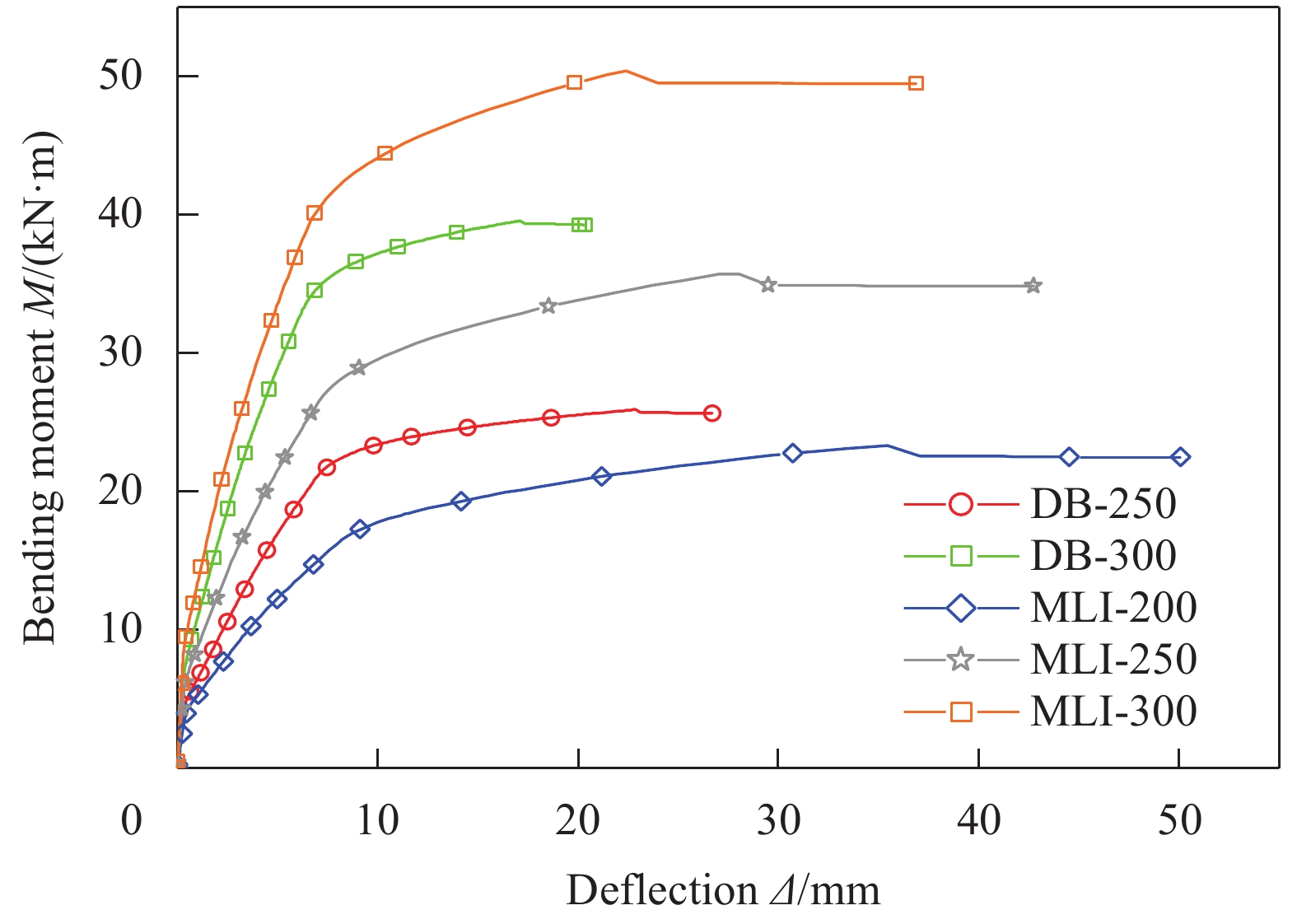
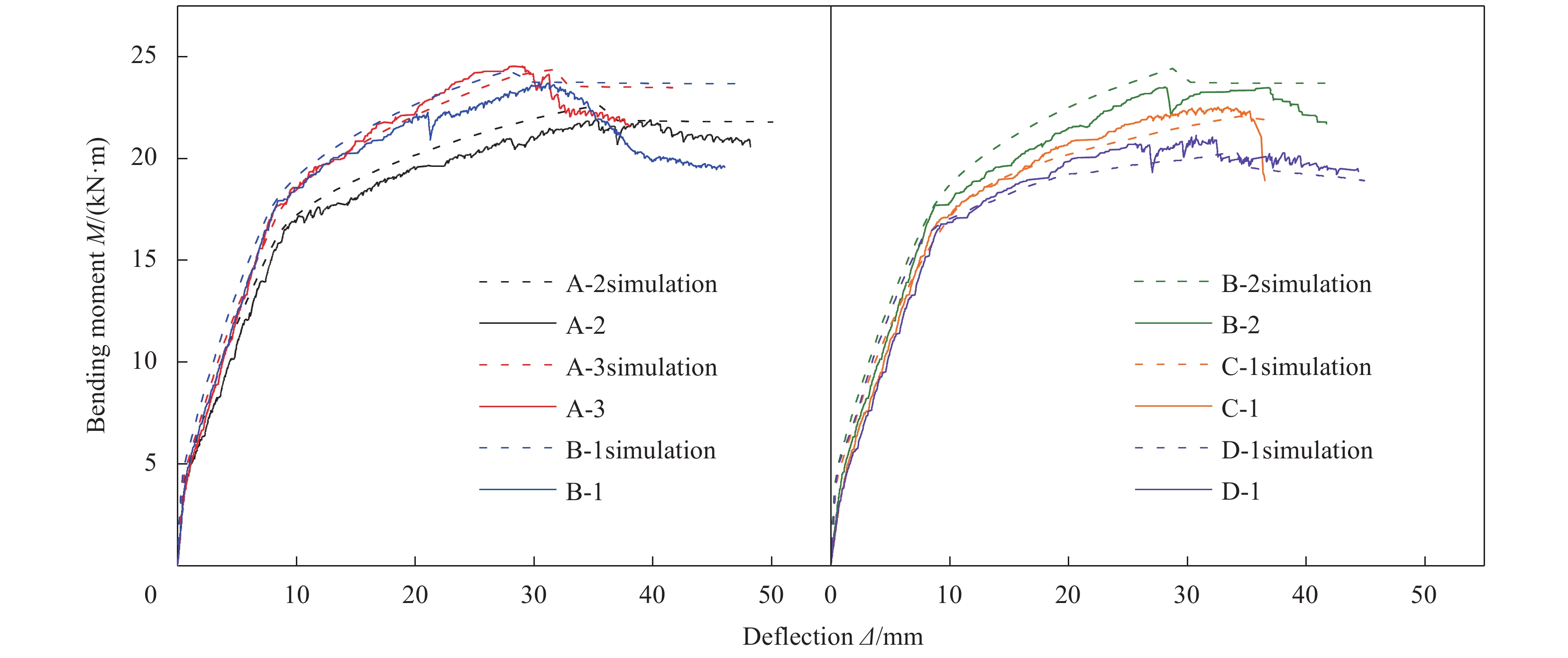
弯矩-跨中挠度曲线对比图
加固RC梁截面应变和应力分布
计量
- 文章访问数: 308
- HTML全文浏览量: 153
- PDF下载量: 14
- 被引次数: 2
