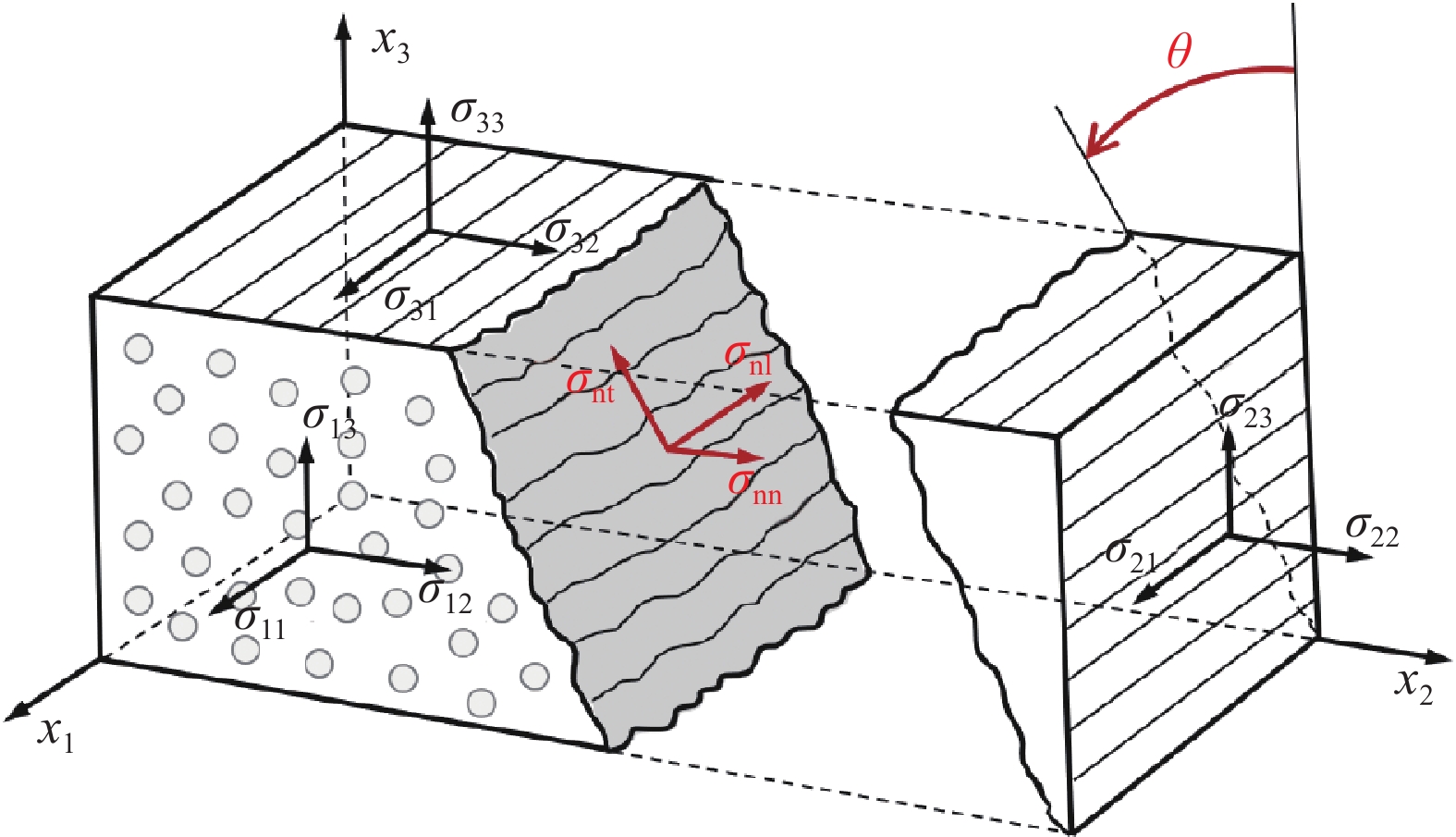
Assessment of damage prediction models for composite laminates under low-velocity impact
-
摘要:
针对碳纤维复合材料层合板低速冲击损伤的预测问题,采用数值模拟方法从结构外部力学响应、内部损伤状态两个方面,探讨三种损伤起始准则和三种演化方法对其影响。建立了分析层合板冲击问题的三维有限元模型,设计了包含起始判定、渐进演化及本构关系的损伤计算流程。研究了冲击过程损伤面积定量演变,为阐释损伤机制提供新视角。结合实验数据对冲击损伤数值模型进行了验证,并对不同起始准则、演化方法的预测能力进行了评价探讨。结果表明,数值预测与实验测试的动态力学响应曲线吻合度较高,证明该数值模型能够准确预测低速冲击损伤。同时发现起始准则与演化方法的结合对损伤模型预测性能十分关键,Hashin-Strain准则结合线性等效应变方法(Hashin-Strain-E1)和Puck准则结合指数型等效位移方法(Puck-E3)最优。然而,当Hashin-Strain准则结合线性或指数型等效位移方法时(Hashin-Strain-E2/E3),会由于刚度退化严重而引发穿透性损伤。研究成果为复合材料层合板低速冲击损伤预测与评估提供参考和借鉴。
Abstract:For the prediction of low-velocity impact damage in carbon fiber composite laminates, this study examined the influence of three damage initiation criteria and three evolution methods from structural overall mechanical response and internal damage state. To facilitate our investigation, a three-dimensional finite element model analyzing the impact behavior of laminate was established. Subsequently, a damage calculation process encompassing initiation determination, progressive evolution, and constitutive relationship was designed. Additionally, the quantitative evolution of damage area during impact was studied, which provided a new perspective for elucidating the damage mechanism. Based on experimental data, the accuracy of numerical simulation was verified. Then the prediction capabilities of different initiation criteria and evolution methods were evaluated and discussed. The results show that the numerical prediction agrees well with the experiment in dynamic mechanical response curve. This proves the numerical model can accurately predict the impact damage. Meanwhile, it has been found that the combination of initiation criteria and evolution methods significantly impacts the predictive efficacy of damage models. The pairing of the Hashin-Strain criterion with the linear equivalent strain method (Hashin-strain-E1) and the Puck criterion with the exponential equivalent displacement method (Puck-E3) yields optimal results. However, coupling the Hashin-Strain criterion with either the linear or exponential equivalent displacement method (Hashin-strain-E2/E3) can lead to penetrating damage due to severe degradation in stiffness. These research findings offer valuable insights into predicting low-velocity impact damage in composite laminates.
-
Keywords:
- Keywords: laminate /
- low-speed impact /
- initiation criterion /
- evolution method /
- damage prediction
-
泡沫混凝土是具有轻质、保温、耐火、减震等优点的轻质多孔材料[1-4],广泛用于建筑防火、路基填充和结构保温等领域[5]。泡沫混凝土的轻质、保温性能来源于其内部复杂的孔隙结构[6-8],但孔隙结构同时削弱了其力学性能,导致泡沫混凝土的应用和推广受限[9-11]。玄武岩纤维增强泡沫混凝土(BFRFC)是通过在泡沫混凝土制备过程中加入短切玄武岩纤维改进传统玄武岩纤维的新型材料。相较于泡沫混凝土,BFRFC借助纤维的桥接作用,整体力学性能得到显著改善[12-14]。
力学性能作为影响BFRFC的关键指标,诸多学者已展开了大量研究[15-19],研究发现:孔隙结构和玄武岩纤维掺量是影响其力学性能的关键因素。孔隙结构随BFRFC密度增加变得更为致密,BFRFC抵抗变形的能力也越强。BFRFC随着玄武岩纤维的掺量增加,材料强度也会明显得到改善。然而,现有研究成果多采用室内试验对BFRFC的力学性能进行宏观力学性能研究,对于BFRFC的微观受力机制尚不明确,缺乏数值仿真的验证。为更加全面了解BFRFC的微观力学性能,需建立基于实际孔隙参数的三维数值仿真模型对BFRFC的力学性能进行研究。
本文基于Matlab二次开发生成随机孔隙和纤维,根据Hashin失效准则和损伤变量考虑材料软化特性,建立BFRFC的渐进损伤模型,采用Comsol有限元软件对BFRFC的力学性能进行仿真分析。设计孔隙结构实验和单轴压缩实验,并借助Avizo软件对X射线计算机断层扫描(X-CT)数据进行滤波降噪、阈值分割等处理,对BFRFC微观结构进行三维重构,通过统计分析,获得BFRFC的微观结构特征。依据重构之后获得的孔隙参数,借助Matlab软件建立三维随机纤维孔隙模型,并采用Comsol有限元软件对BFRFC的力学性能进行数值仿真,分析BFRFC在单轴压缩载荷作用下的性能表现,同时探索玄武岩纤维在泡沫混凝土中的增强效应,研究不同纤维掺量的作用效果以及对BFRFC宏观性能的影响程度。此外,将BFRFC的数值仿真与试验结果进行对比,验证仿真结果的可靠性。研究结果有助于了解不同纤维掺量和密度下BFRFC的宏观及微观力学性能,从而更加全面地总结其工程特性,加快其在实际工程中的推广应用。
1. BFRFC的孔隙结构试验及单轴压缩实验
1.1 试验材料制备
本文所制BFRFC的原材料为水泥、发泡剂、9 mm短切玄武岩纤维和水。水泥选用P·O 42.5普通硅酸盐水泥;玄武岩纤维为海宁安捷复合材料公司生产的9 mm短切纤维,纤维体积掺量设计为0vol%、0.15vol%、0.30vol%、0.45vol%[20];发泡剂为河南华泰新材公司生产的HTW-1型复合发泡剂,稀释倍数为1∶30,如图1所示;水为自来水,水灰比为0.5。
按表1中的配比,参照《泡沫混凝土》(JG/T 266—2011)[21],首先将HTW-1发泡剂与水按照比例混合稀释并搅拌均匀,当密度、泡沫稳定性达到要求且发泡机(RH-30,荣信恒机械制造厂)能够稳定连续供泡时,称取预制泡沫备用。然后,将水泥加入砂浆搅拌机(BTJX-JBJ,鼎峰测绘仪器有限公司)中干拌90 s,加入1/3水搅拌1 min,随后加入玄武岩纤维和剩余2/3水,搅拌至少2 min,直至水泥浆体中没有胶凝材料团聚、结块。最后加入预制泡沫,并继续搅拌2 min,使泡沫与浆体均匀混合,形成具有泡孔结构的混凝土。将BFRFC浆体倒入模具中,静置24 h后脱模,混凝土标准养护箱(DF2C,郑州市博图机械有限公司)中养护28 d。本实验共制备8组设计干密度为800、
1000 kg/m3,尺寸为100 mm×100 mm×100 mm的BFRFC试样,同时每组浇筑多个尺寸为50 mm×50 mm×50 mm小型立方体试样用作X-CT扫描试验。表 1 玄武岩纤维增强泡沫混凝土(BFRFC)的配合比及密度(kg/m3)Table 1. Mix ratio and density of basalt fiber reinforced foam concrete (BFRFC) (kg/m3)Sample No. Cement Water Basalt fiber Foam Wet density Dry density A08-0 416.67 208.33 0 35.49 944.31 868.03 A08-0.15% 416.67 208.33 4.2 35.49 959.33 840.00 A08-0.30% 416.67 208.33 8.4 35.49 1002.33 891.33 A08-0.45% 416.67 208.33 12.6 35.49 965.33 846.00 A10-0 743.05 371.53 0 21.83 1187.60 1075.05 A10-0.15% 743.05 371.53 4.2 21.83 1240.33 1138.00 A10-0.30% 743.05 371.53 8.4 21.83 1226.00 1073.00 A10-0.45% 743.05 371.53 12.6 21.83 1235.67 1131.33 Note: Sample number A08-0.15% represents the design of dry density of 800 kg/m3 and the volume of basalt fiber mixed with 0.15vol%. 1.2 试验方法
BFRFC的孔隙结构试验采用德国Y.CT Precision微焦点X射线CT系统,扫描50 mm×50 mm×50 mm的立方体试件。该实验装置产生锥形X射线束,沿试件的水平断面自上而下逐层扫描,扫描完成后将样品台绕垂直轴旋转,采集多个旋转角度样品射线照片,获得
1600 张图像的空间分辨率为35.9 μm/Voxel的BFRFC试样的二维切片。通过Snake模型对X-CT二维切片进行预处理,提取纤维和孔隙的轮廓特征,并采用Avizo软件分离BFRFC的微观结构进行三维重构。具体过程如图2所示。首先,使用中值滤波法对CT图像进行降噪处理。其次,通过阈值方法对CT图像进行分割,水泥的分割阈值为21000 ~31500 ,孔隙的分割阈值为1110 ~21000 ,纤维的分割阈值为31500 ~65535 。然后,进行图像叠加,最后进行三维重构。BFRFC的单轴压缩试验参考《泡沫混凝土》(JG/T 266—2011) [21] 进行,试验装置采用MTS Landmark 370电液伺服万能试验机。试验采用位移控制的加载模式,设定加载速率为0.8 mm/min。当试样的轴向位移达到8 mm时停止加载并记录各试样的峰值荷载,每组设置3个平行试验。
2. BFRFC微观结构特征
2.1 BFRFC的孔隙率特征
孔隙结构特征是影响BFRFC宏观性能的重要指标。采用X-CT分析和饱和吸水率两种方法测算各试样的BFRFC孔隙率。X-CT分析通过Avizo中交互式阈值分割功能获取试样的孔隙率;而饱和吸水率法通过抽取试样真空使水充分进入孔隙,使试样处于充分饱和状态,计算试样烘干前后的质量差,间接获取孔隙体积,求得式样孔隙率。采用这两种方法计算两种密度等级(A08和A10)、不同纤维掺量共8组BFRFC试样的孔隙率,见表2。
表 2 各组BFRFC的孔隙率Table 2. Porosity of each group BFRFCDensity grade Fiber content/vol% Porosity/% X-CT analysis Saturated water absorption A08 0 15.43 15.87 0.15 14.91 15.29 0.30 14.44 14.84 0.45 14.02 13.75 A10 0 10.94 11.51 0.15 10.39 10.45 0.30 10.54 10.92 0.45 9.93 10.75 由表2可知,BFRFC的孔隙率随着密度的增大、纤维掺量的增加而逐渐减小,A08、A10等级的孔隙率分别在14%~15%、9%~10%范围内。使用饱和吸水率法得到的结果略大于X-CT分析,原因在于:对于BFRFC来说,靠近上下平面的孔隙率一般高于试样中段的孔隙率,而在处理X-CT数据时为了减小射束硬化的影响,会预先裁切掉试样上下面部分成像效果较差的数据;此外,受X-CT测试精度和分辨率的限制,部分微小孔隙不易被探测到[22],因此X-CT分析得到的孔隙率略小于实际孔隙率。
2.2 孔隙尺寸和形状特征
孔隙尺寸作为划分孔隙类型的重要指标之一,是影响BFRFC的宏观性能的重要因素。使用Avizo的“Label Analysis”工具对孔隙进行标记,生成每个孔隙的三维模型,对三维重构后分割出的孔隙部分进行统计,分析试样的孔隙直径、体积、表面积等特征,以此表征其微观结构的变化规律,不同密度和纤维掺量的孔隙尺寸特征如表3所示。采用SPSS软件拟合孔径分布情况,对BFRFC的孔隙分布曲线进行非线性拟合,发现其孔径近似服从非标准的对数正态分布,拟合曲线的相关系数均在0.95以上。因此,可用概率密度函数fd(d;μ,σ)来表征其分布规律,如下式所示:
fd(d;μ,σ)=1dσ√2π e−(lnd−μ)22σ2 (1) 式中:d为试样的直径,d>0 (μm);μ和σ分别为变量d对数的平均值和标准差。
表 3 BFRFC代表试样的孔隙尺寸特征Table 3. Pore size features of representative BFRFC specimensSample No. Fiber content/vol% Porosity/% Pore diameter/μm Distribution parameter Max Min Average μ σ A08 0 15.43 4480.61 44.54 425.15 5.99 0.34 0.15 14.91 4503.13 44.54 437.94 5.98 0.37 0.30 14.44 4534.57 44.54 447.85 6.11 0.34 0.45 14.02 4556.17 44.54 458.14 6.03 0.40 A10 0 10.94 3000.06 44.54 244.18 5.71 0.29 0.15 10.39 3035.25 44.54 245.92 5.66 0.30 0.30 10.54 3094.54 44.54 294.85 5.75 0.27 0.45 9.93 3136.87 44.54 307.14 5.77 0.32 Notes: The minimum pore diameter of the measured BFRFC specimens is 44.54 μm due to the limitation of testing accuracy and resolution of the X-CT equipment. In fact, the minimum pore diameter of each specimen should be less than 44.54 μm and different from each other; μ and σ are the mean and standard deviation of the logarithm of the pore diameter, respectively. 由表3可知:不同试样所测得的最小孔隙直径相同,均为44.54 μm,这是由于受X-CT设备测试精度的限制,实际上的最小孔径应小于该值,且彼此存在差异[23];考虑到该尺寸以下的孔隙占比较小(<1%),且影响BFRFC的宏观性能的孔隙直径大多在500 μm以上[24-25],因此,可忽略因设备精度带来的误差。通过统计各试样的孔隙直径的范围及频次,得到其孔径分布特征,见图3。
由图3可知,BFRFC的孔径分布特征与其密度等级关系密切,A08等级试样的孔径主要集中在400 μm左右,A10等级试样则为250~300 μm。
对数正态分布拟合曲线fd(d;μ,σ)的参数可表示BFRFC孔径分布特征。其中,孔隙对数平均值μ的数值越大,则对应试样的孔隙直径越大;对数标准差σ表示孔径分布的离散程度,其数值越大,试样孔径分布范围就越广。对比A08和A10两等级试样的分布参数,A08的平均值和标准差普遍大于A10试样,这表明BFRFC的孔径分布与其密度密切相关,密度等级越低,试样的孔径越大,分布范围越广。这是由于低密度的BFRFC使用较多的发泡剂,并且水泥含量较低,导致发泡剂形成的气孔更大、更不均匀,不仅增大了孔径而且增加孔径范围。
2.3 BFRFC的孔隙形状特征
除了孔隙率、孔隙直径外,孔隙形状同样对多孔水泥基材料有显著影响,BFRFC也不例外。本文借助Avizo的Label analysis命令,提取各孔隙的三维体积、表面积等数据,通过计算获得各BFRFC试样形状因子的分布情况,孔隙的形状因子定义如下:
δ=S336π V2 (2) 式中:S为孔隙表面积(μm2);V为孔隙体积(μm3)。标准球体的形状因子为1,形状因子偏离1的程度越大,表明该物体的形状越不规则。以A08-0、A10-0试样为例,通过计算两试样的孔隙形状因子、各类孔隙占比以其变化情况,得到两密度等级BFRFC的孔隙形状特征分布,见图4。
由图4可知,A08、A10两类密度等级BFRFC的孔隙形状因子数值主要位于1.0~2.0之间,孔隙类型以球状孔隙为主。A08试样的孔隙形状因子近似服从正态分布,其峰值位于1.4,分布范围较广,其球状孔隙的占比为58%;A10的形状因子集中在1.1附近,球状孔隙的占比高达71%,低密度等级的BFRFC由于配合比中胶凝材料的占比较低,包裹泡沫的水泥浆体较薄,在浇筑时更容易出现气泡合并的现象,使得孔隙的尺寸和形状分布更为离散[26],由此可知,BFRFC试样的孔隙形状与密度之间的关系较为密切。此外,通过计算得到A08和A10等级的BFRFC在的孔隙形状因子的数学期望值分别为1.56和1.21,由形状因子的定义可知,其数值越小意味着颗粒的形状越接近标准球形,力学性能越好[4]。因此,除了减小孔隙率和孔隙直径外,还可以通过改变孔隙形状来增强其力学性能。
2.4 BFRFC的纤维分布特征论
玄武岩纤维在 BFRFC内部起到了桥接增强的作用。本节通过分析BFRFC内部纤维的三维特征参数来定量描述其空间分布特征,并对比不同掺量下,纤维的分布差异,从微观结构角度探究其最优掺量,与后续BFRFC力学试验的结果相互验证。
对于玄武岩纤维来说,可用球坐标系描述其空间分布特征,主要参数为极角和方位角。极角为纤维长轴与Z轴间的夹角,表示纤维相对于Z轴的倾斜程度;方位角为纤维在XY平面的投影与X轴间的夹角,表示纤维在水平面的朝向。
在Avizo中通过自定义纤维模板命令,认为长径比大于100的部分为玄武岩纤维,通过该命令可以有效筛除其他非纤维的成分,从而精准统计BFRFC内部纤维的各参数特征。使用Avizo的“Skeletonization”工具,对每根纤维进行骨架化处理,获取纤维的中心线。然后,使用“Orien-tation Analysis”模块,计算纤维的角度取向。采用5组实验探究A08、A10两密度等级BFRFC不同纤维含量的纤维极角和方位角的分布情况,见图5。
由图5可知:A08、A10等级BFRFC内部纤维的极角分布情况存在明显一致性,即各等级试样的纤维极角θ主要集中在15°~90°的范围内。其中,BFRFC纤维极角接近90°的占比最高可达26.69%,而接近0°占比极低,均在3%以下。这是由于玄武岩纤维在浇筑的过程中受重力的影响,存在向XY平面倾倒的趋势。此外,BFRFC内部纤维的方位角分布较为均匀,整体较为均衡地分布在0°~360°范围内。尽管各试样间的方位角分布存在一定的差异,这主要是由于实际操作中搅拌不足所引起的。因此,为了改善纤维分布的均匀性并提升试样的整体力学性能,建议在实际浇筑过程中充分搅拌BFRFC浆体。
3. 基于实际微观结构参数的三维数值模型
3.1 基于Comsol LivelinkTM for MATLAB®的参数化建模方法
BFRFC内部微观结构的分布情况为参数化建模提供了思路。由前文研究结果可知:BFRFC的孔隙直径近似服从对数正态分布,纤维在X方向均匀分布在0°~360°之间,在Z方向均匀分布在15°~90°之间。由各试样孔径分布和纤维分布特征参数便可有效表征BFRFC的孔隙直径和纤维分布情况;此外,孔隙和纤维的中心位置可认为随机分布在试样内部。可利用Matlab软件中的对数正态分布Lognrnd函数和随机均匀分布rand函数实现参数化建模[5],同时借助Comsol LivelinkTM for MATLAB®接口将BFRFC数值模型导入Comsol软件中进行有限元分析。
前文中孔隙形状的分析结果表明:BFRFC内部孔隙主要以球状孔为主,占比高达71%,因此在仿真建模过程中可以将其内部孔隙简化为具有随机分布特征的球体。而其内部的异形孔隙可通过定义球体之间的重叠度δ来实现[27],试样的目标孔隙率作为孔隙生成的终止条件。玄武岩纤维可简化为具有固定长度和直径的圆柱体,可视为在BFRFC立方体内部随机分布且具有固定长度的空间向量,在定义纤维位置时只需定义向量起点的三维坐标,并通过生成随机旋转的角度来模拟其分布情况。为了避免纤维出现空间重叠问题,需要引入异面直线不重叠的判断方法。经过上述简化,便可建立基于实际微观结构的BFRFC三维概化模型,建模的基本步骤如下:
(1) 确定孔隙中心位置。基于孔隙结构的概化模型,假定BFRFC内部孔隙随机分布在试样中,可通过随机分布函数以及模型尺寸来确定各孔隙中心位置:
X=Lrand(1,1)cos(2πrand(1,1)) (3) Y=Lrand(1,1)sin(2πrand(1,1)) (4) Z=Lrand(1,1) (5) 式中:X、Y、Z分别为孔隙中心位置的三维坐标;L为BFRFC立方体试块的边长;rand(1,1)为Matlab中在0~1之间生成随机数的函数指令。
(2) 确定孔隙直径。借助前文分析得到的孔径分布特征参数μ和σ,使用Lognrnd函数生成服从对数正态分布的孔隙直径。同时为了防止出现尺寸过大或过小的孔隙,将随机生成的孔径控制在μ±2σ,保证具有95%的置信度[28],孔隙直径d可表示为
d=Lognrnd(μ,σ) (6) (3) 确定孔隙间关系。基于上文统计的各BFRFC试样孔隙形状因子的数学期望确定模型的孔隙重叠率δ,并通过限制相邻孔隙的中心距离确定孔隙间位置关系。
(4) 确定孔隙率。在生成孔隙过程中,通过计算每次生成新孔隙的当前孔隙率来控制BFRFC的整体材料孔隙率。终止孔隙生成的判断条件如下所示:
Vsum+Vpore⩾ (7) 式中:Vsum为截止至本次孔隙生成之前已有的全部孔隙体积;Vpore为当前随机生成的孔隙体积;Vsq为BFRFC立方体试样的体积;ε为目标孔隙率。
(5) 确定纤维起始端点坐标。由前文的假设可知:玄武岩纤维可视作服从随机分布的空间向量,其起点位置可借助随机分布函数rand(1,1)确定。为防止纤维另一端超出模型范围,需对纤维起点坐标设置限值Llim,使其分布在距离模型边缘距离为Llim的三维空间内,纤维起始端点坐标的定义如下:
X_0=\mathrm{rand}(1,1)(L-2L_{\text{lim}})+L_{\text{lim}} (8) Y_0=\mathrm{rand}(1,1)(L-2L_{\text{lim}})+L_{\text{lim}} (9) Z_0=\mathrm{rand}(1,1)(L-2L_{\text{lim}})+L_{\text{lim}} (10) 式中:X0、Y0、Z0分别为纤维起始端点的三维坐标, X_0,\ Y_0,\ Z_0\in\left[L_{\text{lim}},\ L-L_{\text{lim}}\right] ; {L_{{\text{lim}}}} 为起点坐标限值,在数值上等于纤维的长度。
(6) 确定纤维旋转角度。根据2.4节的各纤维的方向随机分布的特征,借助随机分布函数rand定义其旋转矩阵,如下式所示:
\alpha=\mathrm{rand}(1,1)\times2\text{π } (11) \beta=\mathrm{rand}(1,1)\times2\text{π } (12) \gamma=\frac{\text{π }}{12}+\mathrm{rand}(1,1)\left(\frac{\text{π }}{2}-\frac{\text{π }}{12}\right) (13) \begin{split} R=\;&\left(\begin{array}{ccc}1 & 0 & 0 \\ 0 & \mathrm{cos}\alpha & -\mathrm{sin}\alpha \\ 0 & \mathrm{sin}\alpha & \mathrm{cos}\alpha\end{array}\right) \cdot\left(\begin{array}{ccc}\mathrm{cos}\beta & 0 & \mathrm{sin}\beta \\ 0 & 1 & 0 \\ -\mathrm{sin}\beta & 0 & \mathrm{cos}\beta\end{array}\right)\cdot\\ &\left(\begin{array}{ccc}\mathrm{cos}\gamma & -\mathrm{sin}\gamma & 0 \\ \mathrm{sin}\gamma & \mathrm{cos}\gamma & 0 \\ 0 & 0 & 1\end{array}\right)\end{split} (14) 式中:α、β、γ为初始随机旋转角度;R为纤维的旋转矩阵。定义玄武岩纤维的起始端点坐标和旋转矩阵之后,可在三维空间中从起始端点沿随机生成的旋转角度构建出固定长度的纤维模型。
(7) 纤维干涉判断。由于玄武岩纤维属于实体结构,在三维空间中不能出现重叠现象,因此可以通过判断两纤维之间的最短距离大于纤维直径从而判断纤维是否相交。玄武岩纤维可视作服从随机分布的空间向量\overrightarrow {{a_1}{a_2}} 和\overrightarrow {{b_1}{b_2}} 。判断向量\overrightarrow {{a_1}{a_2}} 和\overrightarrow {{b_1}{b_2}} 是否相交,首先采用下式计算空间向量\overrightarrow {{a_1}{a_2}} 和\overrightarrow {{b_1}{b_2}} 单位向量的叉积 \vec c 。如果 \vec c 的模 \left\| c \right\| 为零,说明两条直线平行;反之,说明两条直线不平行 :
\vec c = \frac{{\overrightarrow {{a_1}{a_2}} }}{{\left\| {\overrightarrow {{a_1}{a_2}} } \right\|}} \times \frac{{\overrightarrow {{b_1}{b_2}} }}{{\left\| {\overrightarrow {{b_1}{b_2}} } \right\|}} (15) 当两条直线平行时,采用下式计算点到线的距离d:
d = \left\| {\left( {{b_1} - {a_1}} \right) - \left[ {\left( {{b_1} - {a_1}} \right) \cdot \left( {{a_2} - {a_1}} \right)} \right]\left( {{a_2} - {a_1}} \right)} \right\| (16) 否则采用下式计算两条直线之间的最近距离:
d = \frac{{\left| {\left( {{b_1} - {a_1}} \right) \cdot \vec c} \right|}}{{\left\| {\vec c} \right\|}} (17) 当最小距离小于纤维直径时,则认为纤维产生干涉。基于该特征设置判断条件,排除上述情景即可保证生成的玄武岩纤维模型在三维空间中不相交。
(8) 纤维掺量判断。纤维掺量的判断方法同孔隙率判断方法一致,以BFRFC每次加载条件下当前掺量与目标掺量的对比作为终止条件,当生成的纤维体积达到目标掺量时便停止生成,此处不再赘述。
基于上述建模步骤,可通过Matlab软件建立由参数控制的孔隙、纤维随机分布的BFRFC模型,建模流程及结果如图6(a)所示。基于上述流程可生成BFRFC的三维概化模型,如图6(b)所示。
3.2 参数设置与网格划分
将所生成的三维概化模型导入至Comsol Multiphysics®软件以进行结构力学分析。在执行参数化三维建模时,依据BFRFC微观结构分析的结果,包括孔隙率、孔径分布、孔隙形状和纤维分布等特性参数进行设置,以此构建基于实际微观结构参数的三维BFRFC数值模型,各试样的建模参数根据实验数据所取,如表3、图3和图4所示。根据建模参数和实际微观结构,通过定义水泥基质、玄武岩纤维和空气三类材料的基本属性,建立了BFRFC模型。其中,水泥基质的密度为
2300 kg/m3,弹性模量为30 GPa,泊松比为0.2;孔隙视为空气,密度为1.225 kg/m3,弹性模量为0.1 MPa,泊松比为0.3;玄武岩纤维的密度为2700 kg/m3,弹性模量为85 GPa,泊松比为0.25。采用物理场控制的方式划分网格,类型为自由四面体细化网格单元。纤维掺量为0.45vol%的A08的BFRFC数值模型,如图7所示。该试件仿真模型中网格单元总数为3426442 ,其中:孔隙单元网格数为130268 ,纤维单元网格数为543903 ,水泥基质网格数为2755047 ,模型大小为5.18 GB。3.3 基于Comsol模拟的BFRFC单轴压缩仿真
基于3.2节参数化建模的基本原理,建立BFRFC的三维数值模型,在Comsol软件中仿照单轴压缩的加载方式对模型设置荷载和边界条件,试样加载的示意图如图8所示。
采用Comsol内置结构力学模块,对BFRFC进行瞬态受压分析。模拟实际单轴压缩试验条件,通过在试样的上下表面各放置一块刚性平板来模拟单轴压缩装置。固定下板各方向的位移,并限制上面平板在X和Y方向的移动,同时在上板上施加一个随时间变化的Z方向位移,其增长速率定为−
0.013333 mm/s,以在10 min内实现8 mm的Z轴向下位移,确保与实际试验情况相吻合。设置上下压板与受压面之间的接触行为,两界面在法线和切向方向上分别采用粗糙接触和硬接触模型,其中,粗糙接触的摩擦系数设置为0.235[29]。在BFRFC仿真模拟过程中,所采用计算机的计算参数如表4所示。建立特征模型的耗时以及内存占用情况如下:网格剖分时间基本在15 min内完成;计算时间方面,采用正常的网格密度,整个计算过程均在5 h内完成。在计算过程中,需要注意的是模型所需的内存较大。例如,对于密度为A08纤维掺量为0.45vol%的BFRFC模型,其占用的内存达到54.56 GB。表 4 计算机性能表Table 4. Computer performance specificationsComponent Specification Processor (CPU) AMD Ryzen Threadripper 3990X; 32 cores/64 threads; Base frequency: 3.7 GHz;
Max boost frequency: 4.5 GHzGraphics processor (GPU) NVIDIA RTX 4090; VRAM: 24 GB GDDR6X Memory (RAM) 256 GB DDR4 ECC; Frequency: 3200 MHzPrimary storage 2 TB NVMe SSD (Samsung 980 PRO) Secondary storage 4 TB NVMe SSD (Samsung 970 EVO Plus) Mass storage 10 TB HDD (Seagate IronWolf Pro) Operating system Windows 11 Pro or Ubuntu 22.04 LTS Motherboard ASUS ROG Zenith II Extreme Alpha; Supports multiple GPU slots (PCIe 4.0); 8 DIMM slots;
USB 3.2; Wi-Fi 6; 10 G Ethernet对于BFRFC来说,其内部的主要受力结构为水泥基质和玄武岩纤维,两者在荷载作用下性能的变化规律决定了试样的力学行为。可使用Hashin失效准则来描述BFRFC单轴压缩过程中的损伤情况,Hashin是一种三维复合材料失效判定准则[30-33],现已广泛用于纤维增强复合材料的失效评估中。Hashin失效准则将纤维增强复合材料的失效模式分为4种:纤维方向拉伸、纤维方向压缩、水泥基质方向拉伸、水泥基质方向压缩,分别使用F_{\text{f}}^{\text{t}}、F_{\text{f}}^{\text{c}}、F_{\text{m}}^{\text{t}}和F_{\text{m}}^{\text{c}}表示上述4种失效指标,其计算公式如表5所示。只要任意一个失效指标不小于1,就可认定纤维复合材料发生破坏。
表 5 三维Hashin失效准则Table 5. Three-dimensional Hashin failure criteriaFailure mode Standard of judgment Fiber tension {\hat \sigma _{11}} \geqslant 0 F_{\text{f}}^{\text{t}} = {\left( {\dfrac{{{{\hat \sigma }_{11}}}}{{{X_{\text{T}}}}}} \right)^2} + \alpha {\left( {\dfrac{{{{\hat \tau }_{12}}}}{{{S_{\text{L}}}}}} \right)^2} \leqslant 1 Fiber compression {\hat \sigma _{11}} < 0 F_{\text{f}}^{\text{c}} = {\left( {\dfrac{{{{\hat \sigma }_{11}}}}{{{X_{\text{C}}}}}} \right)^2} \leqslant 1 Cement matrix tension {\hat \sigma _{22}} \geqslant 0 F_{\text{m}}^{\text{t}} = {\left( {\dfrac{{{{\hat \sigma }_{22}}}}{{{Y_{\text{T}}}}}} \right)^2} + {\left( {\dfrac{{{{\hat \tau }_{12}}}}{{{S_{\text{L}}}}}} \right)^2} \leqslant 1 Cement matrix compression {\hat \sigma _{22}} < 0 F_{\text{m}}^{\text{c}} = {\left( {\dfrac{{{{\hat \sigma }_{22}}}}{{2{S_{\text{T}}}}}} \right)^2} + \left[ {{{\left( {\dfrac{{{Y_{\text{C}}}}}{{2{S_{\text{T}}}}}} \right)}^2} - 1} \right] \dfrac{{{{\hat \sigma }_{22}}}}{{{Y_{\text{C}}}}} + {\left( {\dfrac{{{{\hat \tau }_{22}}}}{{{S_{\text{L}}}}}} \right)^2} \leqslant 1 Notes: X_{\text{T}}^{} and {X_{\text{C}}} represent the longitudinal tensile and compressive strengths, respectively; {Y_{\text{T}}} and {Y_{\text{C}}} denote the transverse tensile and compressive strengths of the specimen, respectively; {S_{\text{L}}}and {S_{\text{T}}} are the longitudinal and transverse shear strengths of the specimen, respectively; \alpha is the coefficient of contribution of shear stress to fiber tension (0 \leqslant \alpha \leqslant 1); \hat \sigma is the normal stress for material damage; \hat{\tau} is the shear stress for material damage; F_{\text{f}}^{\text{t}} , F_{\text{f}}^{\text{c}} , F_{\text{m}}^{\text{t}} and F_{\text{m}}^{\text{c}} represent four failure indices for the four directions: Fiber direction tension, fiber direction compression, cement matrix direction tension, and cement matrix direction compression, respectively. 材料损伤的评估系数\hat \sigma 可用下式计算:
\hat \sigma = M\sigma = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{1 - {d_{\text{f}}}}}}&0&0 \\ 0&{\dfrac{1}{{1 - {d_{\text{m}}}}}}&0 \\ 0&0&{\dfrac{1}{{1 - {d_{\text{s}}}}}} \end{array}} \right] \cdot \sigma (18) 式中:\sigma 为材料所受实际应力;M是损伤矩阵;{d_{\text{f}}}、{d_{\text{m}}}和{d_{\text{s}}}为纤维、基体和剪切损伤的内部变量,计算方式如下:
{d_{\text{f}}} = \left\{ {\begin{array}{*{20}{c}} {d_{\text{f}}^{\text{t}}}&{{\text{if}}\quad {{\hat \sigma }_{11}} \geqslant 0} \\ {d_{\text{f}}^{\text{c}}}&{{\text{if}}\quad {{\hat \sigma }_{11}} < 0} \end{array}} \right. (19) {d_{\text{m}}} = \left\{ {\begin{array}{*{20}{c}} {d_{\text{m}}^{\text{t}}}&{{\text{if}}\quad{{\hat \sigma }_{22}} \geqslant 0} \\ {d_{\text{m}}^{\text{c}}}&{{\text{if}}\quad{{\hat \sigma }_{22}} < 0} \end{array}} \right. (20) {d_{\text{s}}} = 1 - \left( {1 - d_{\text{f}}^{\text{t}}} \right){\text{ }}\left( {1 - d_{\text{f}}^{\text{c}}} \right){\text{ }}\left( {1 - d_{\text{m}}^{\text{t}}} \right){\text{ }}\left( {1 - d_{\text{m}}^{\text{c}}} \right) (21) BFRFC损伤演化参考Matzenmiller等[34]提出的纤维复合材料各向异性损伤本构模型,该模型将纤维复合材料的损伤过程视作应变能的释放过程,在这期间材料力学参数的退化引起试样整体强度的下降,材料软化的形式主要有线性和指数两种[35-36],本文假定BFRFC损伤过程中材料满足指数的应变-软化行为,如图9所示。
损伤变量{D_i}用来描述BFRFC在受压过程结构损伤的演化情况,可通过函数\phi \left( {{F_i}} \right)表示,各类损伤变量表达式如表6所示。
\phi \left( {{F_i}} \right)为损伤演化函数,其表达式如下:
{D_i} = \phi \left( {{F_i}} \right) = \left\{ {\begin{array}{*{20}{c}} {0{\text{ , }}F < {F_{{\text{min}}}}} \\ {{D_{{\text{max}}}} \left( {1 - {{\mathrm{e}}^{ - \frac{{{F^\beta } - F_{\min }^\beta }}{{e\beta }}}}} \right)} \end{array}} \right.{\text{ , }}F \geqslant {F_{{\text{min}}}} (22) 式中,\;\beta 为BFRFC材料的响应参数,其数值的变化能够影响失效指标F与损伤变量D之间的关系曲线,本文推荐参数\beta = 5,Fmin=1。
![]() 图 9 BFRFC材料本构关系Figure 9. BFRFC material ontological relationshipPoint A represents the onset of material damage, point B corresponds to the damage state at any given moment, and point C represents the moment when the material is completely degraded; Ei0 and Eid denote the initial elastic modulus and the hardening modulus of the material after yielding; \varepsilon _{{\rm{eq}}}^0 , εeq and \varepsilon _{{\rm{eq}}}^{\mathrm{f}} represent the yield strain, strain, and ultimate strain; εi and σi represent the strain and stress of concrete, respectively; Ri is the yield strength表 6 各类损伤变量DiTable 6. Impairment variables by category Di
图 9 BFRFC材料本构关系Figure 9. BFRFC material ontological relationshipPoint A represents the onset of material damage, point B corresponds to the damage state at any given moment, and point C represents the moment when the material is completely degraded; Ei0 and Eid denote the initial elastic modulus and the hardening modulus of the material after yielding; \varepsilon _{{\rm{eq}}}^0 , εeq and \varepsilon _{{\rm{eq}}}^{\mathrm{f}} represent the yield strain, strain, and ultimate strain; εi and σi represent the strain and stress of concrete, respectively; Ri is the yield strength表 6 各类损伤变量DiTable 6. Impairment variables by category DiDamage pattern Value of the damage variable Fiber material damage D{}_1 = \phi \left( {\max \left\{ {F_{\text{f}}^{\text{t}},F_{\text{f}}^{\text{c}}} \right\}{\text{ }}} \right) Cement matrix damage D{}_2 = \phi \left( {\max \left\{ {F_{\text{m}}^{\text{t}},F_{\text{m}}^{\text{c}}} \right\}{\text{ }}} \right) Composite shear damage {D_3} = 1 - (1 - {D_1})(1 - {D_2}) 4. 结果与讨论
根据Hashin失效准则和损伤变量可以得到考虑材料软化特性的渐进损伤模型,将其导入Comsol水泥基质与玄武岩纤维的材料属性中,得到改进后的BFRFC的数值模型,计算在单轴压缩仿真下改进后的应力-应变关系曲线如图10所示。
图10为各试样实测应力-应变关系曲线与仿真结果的对比图,实线部分为实际测试结果,虚线部分为仿真结果。由图可知:在材料属性中引入连续渐进损伤模型后,单轴压缩得到的应力-应变关系曲线各阶段的特征更为明显。屈服阶段之前,应力应变曲线呈现线弹性变化,内部材料结构破坏以弹性密实为主,应力应变曲线与实验结果基本吻合;屈服阶段之后,应力-应变关系先下降,内部孔隙逐渐进行脆性密实,然后进入平台阶段,此阶段中试样的承载力未大幅下降,与实际试验结果较为接近。总之,基于BFRFC损伤模型构建的仿真模型可以描述单轴压缩过程,且误差范围可以被接受。此外,通过提取各曲线的峰值强度,得到两类峰值强度的对比情况,见表7。
表 7 各BFRFC试样的峰值强度差异Table 7. Differences in peak strength of each BFRFC specimenDensity grade Fiber content/vol% Simulation result/MPa Actual result/MPa Absolute error/MPa Relative error/% A08 0.15 4.17 4.01 0.16 3.99 0.30 5.02 5.50 0.48 8.73 0.45 6.36 6.59 0.23 3.49 A10 0.15 7.44 7.04 0.40 5.68 0.30 8.12 8.33 0.21 2.52 0.45 10.59 11.18 0.59 5.25 由表7可知,A08、A10两等级不同纤维掺量试样的仿真结果与实际的绝对误差控制在0.59 MPa以下,相对误差保持在9%以内,整体较为接近。总体来说,基于连续介质损伤理论的BFRFC单轴压缩模型可以较为精准地模拟BFRFC在单轴压缩过程中的力学行为,因而可以借助该方法来模拟其他在试验室难以实现的加载情况,从而更全面地了解试样的力学性能。
BFRFC在单轴压缩过程中的缓冲性能可用总吸能E来表征,可通过对荷载-位移关系曲线积分进行计算:
E=\int_0^{l}P\mathrm{d}l (23) 式中:E为BFRFC在单轴压缩过程中总吸能量(J);P为压缩过程任意时刻的荷载值(N);l为试样在压缩过程中任意时刻的位移值(m)。
计算得到各BFRFC试样的吸能情况,如图11所示。可以看出,A10试样的整体吸能情况均大于A08试样,说明材料的吸能情况与试样的承载能力有关。A10试样的峰值应力和平台阶段应力较大,因此具有较强的吸能能力。此外,随着玄武岩纤维掺量的增大,BFRFC的总吸能也随之增加,A08、A10两试样纤维掺量从0.15vol%增至0.30vol%的过程中,总吸能分别提高了11.8%和20.5%,而从0.30vol%增至0.45vol%的过程中,总吸能分别提高2.1%和7.3%,可见当玄武岩纤维掺量过高时,由于纤维之间容易出现打结、团聚的现象,造成纤维增强效果的降低,进而引起总吸能的下降。
玄武岩纤维掺量的增加能够引起BFRFC峰值强度的提升,对比各冻融循环后的试样,玄武岩纤维对试样强度的提升效果随着密度的增大而不断降低。对于BFRFC来说,玄武岩纤维掺量过高时难以搅拌充分,降低了混凝土的工作性能,试样内部容易出现纤维重叠、交错等问题,使得纤维补强增韧的作用受限。冻融循环使得各试样的峰值强度均出现下降,而随着纤维掺量的提高,试样峰值强度的下降幅度有所收敛,纤维占比的提高抵消了因孔隙增大带来的强度损失问题,有助于试样抵抗冻融侵蚀等环境作用。
以A10-0.45%试样为例,分析Comsol软件模拟得到BFRFC的单轴压缩应力分布结果。由于试件应变为8 mm时,结构发生破碎,此时应力为0,难以分析完整试件的应力特征。因此,选取结构应力最大的状态进行分析,即压缩应变处于3 mm,计算结果如图12所示。
图12(a)为上表面在压板的作用下沿轴向位移至3 mm的BFRFC试样的变形图。可以看出压缩引起试样侧面向外发生变化,孔隙形状吸收能量,变为不规则的椭球状,而玄武岩纤维则未发生的明显变化。图12(b)展示了材料的应力分布情况。
观察试件的外表面,可以发现试件在接近底部的区域应力较高,而在中部区域应力较低。这种现象部分原因是由于底部受到加载装置的约束作用,导致其应力相对较低。对于试件内部,孔隙和纤维承受的力并不均匀,呈现出应力在中部集中的趋势,上下界面的应力较低。这一分布与孔隙在中部发生塌陷的规律相吻合。此外,孔隙越大,其集中的应力相对越高,孔隙吸能更高,孔隙更容易破碎,结构强度降低;相较之下,纤维虽受力更为均匀,但得益于其较长的形状及较高的强度,纤维有效地在材料内部重新分配了应力,显著提升了材料的整体强度。
在密度为A10纤维掺量为45vol%的BFRFC试样内部,布置5个域点探针来实时监测各位置处的应力大小,即空间坐标分别为A(10,10,10)、B(90,90,10)、C(50,50,50)、D(10,10,90)、E(90,90,90)。其中,A、B两点位于试样的下表面附近,D、E两点位于上表面附近,C点位于试样中心位置。提取各点数据可获得这5个点应力随时间的变化情况,如图13所示。
由图13可知:在t=0时刻,各点应力水平较为接近,加载刚开始进行,各点的应力水平均为0;随着压缩的进行,各探针位置的应力值均不断提升,其中位于试样的上下表面附近的A、B、D、E 4点的应力水平较为接近,而C点位于试样中心位置,在加载初期的应力值明显低于其他4点,且增幅略有所下降。因此,随着单轴压缩的持续进行,试样上下表面受外界荷载的影响程度最大,附近的玄武岩纤维在抵抗变形、传递荷载的过程中,内部的应力水平也随之提高;试样中部由于变形幅度较小,其内部应力主要由上下两侧的水泥基质和纤维传递而来,因此内部应力较小。
5. 结 论
(1)玄武岩纤维增强泡沫混凝土(BFRFC)的孔径分布近似服从对数正态分布。随着密度等级越高,内部水泥基占比增大,在浇筑的过程中不易出现气泡合并,从而降低了孔隙率和平均孔径,同时使孔径的分布范围变得更加集中。
(2) BFRFC的纤维在一定范围内大体分布均匀。由于玄武岩纤维在浇筑的过程中受重力的影响,BFRFC内部的纤维极角 \theta 主要集中在15°~90°之间,而方位角\varphi 则在0°~360°之间均匀分布。
(3)基于微观结构的随机分布采用Matlab的二次开发Comsol LivelinkTM for MATLAB®的建模技术可以准确地模拟BFRFC试样内部微观结构分布情况,这种方法不仅提升了数值仿真结果的准确度,而且为多孔混凝土结构的仿真研究提供了新的方向和思路。
(4) 基于Hashin失效准则和损伤变量的渐进损伤模型,考虑了材料软化特性,有效改进了BFRFC的数学仿真模型,从而使得仿真结果可以精准地模拟单轴压缩过程中的力学行为,为深入认识试样的细观力学性能提供了更为全面的视角。
(5) BFRFC单轴压缩过程中,材料的峰值强度和吸能能力随着纤维掺入量及材料密度的增加而显著提升,因此,玄武岩纤维可有效提升材料的力学性能特征。此外,试件的边缘应力相对于中心应力的增大,说明材料内部力学响应从外层向内层进行传递。
-
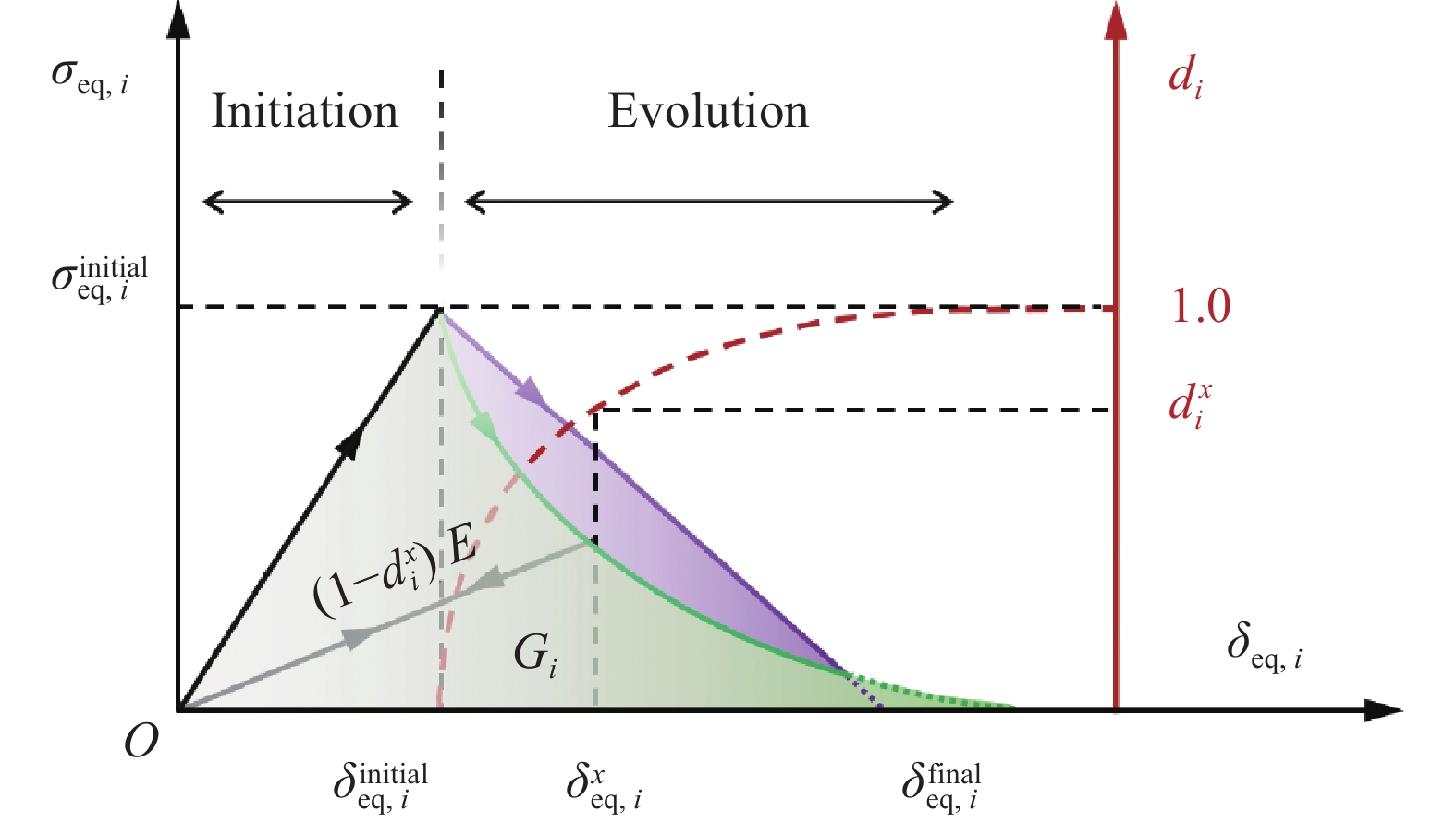
图 2 渐进演化方法中应力、损伤变量与位移的关系
Figure 2. Relationship between stress, damage variables and displacement in progressive evolution methods
{\delta }_{\mathrm{e}\mathrm{q},i} and {\sigma }_{\mathrm{e}\mathrm{q},i} are equivalent displacement and stress; {\delta }_{\mathrm{e}\mathrm{q},i}^{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}} and {\sigma }_{\mathrm{e}\mathrm{q},i}^{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}} are initiation equivalent displacement and stress. {\delta }_{\mathrm{e}\mathrm{q},i}^{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}} is failure equivalent displacement. {d}_{i} is damage state variable. {G}_{i} is fracture energy
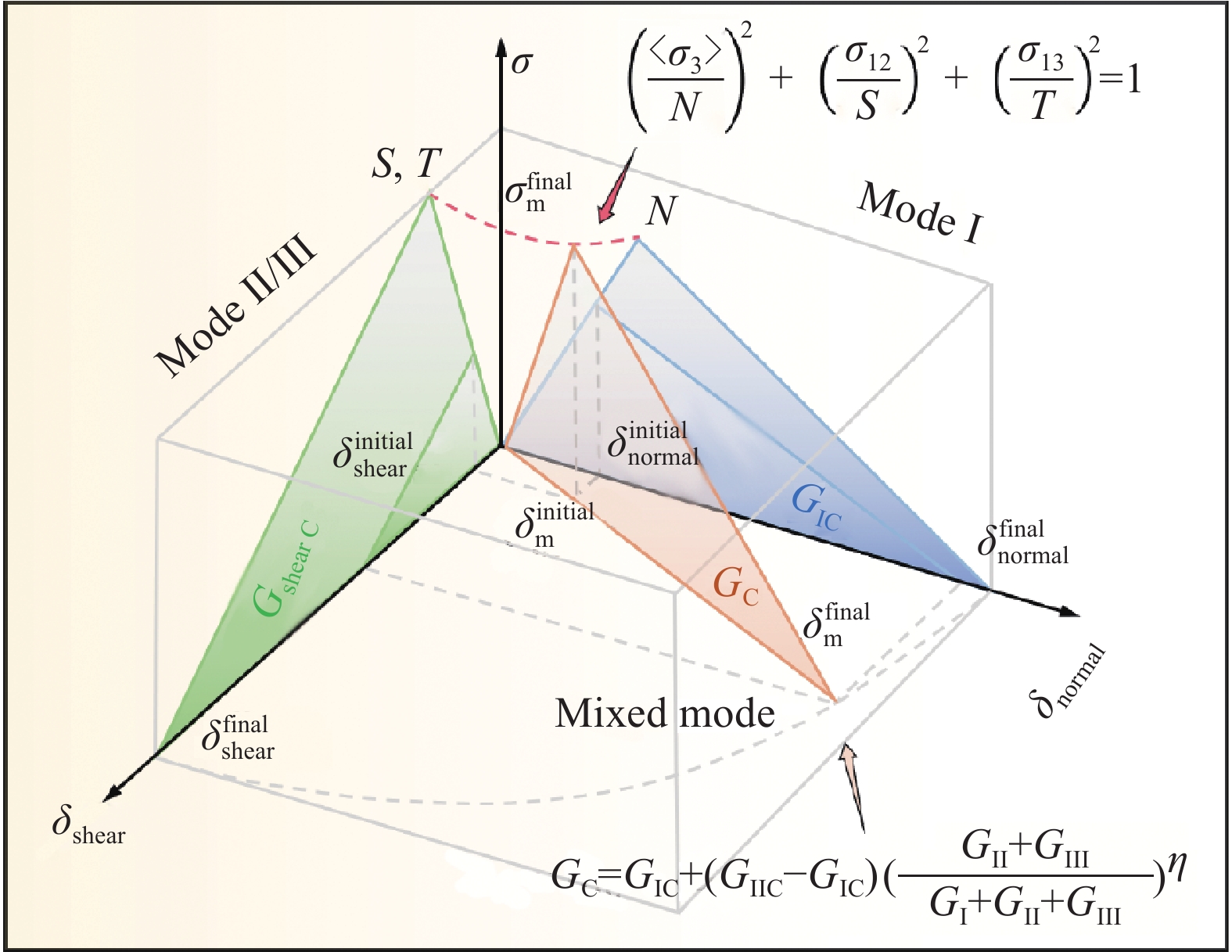
图 3 层间单元混合型双线性牵引-分离本构关系
Figure 3. Constitutive relation of the mixed-model bilinear traction-separation for cohesive element
{\delta }_{\mathrm{m}}^{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}} and {\delta }_{\mathrm{m}}^{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}} are initiation and failure equivalent displacement. Model Ⅰ, Ⅱ/Ⅲ are the failure model in out-of-plane direction and in-plane transverse direction. N, S and T are the strength in three directions
表 1 不同损伤模式下的等效位移和等效应力
Table 1 Equivalent displacement and equivalent stress for different damage modes
Modes Equivalent displacement Equivalent stress ft \delta _{{\mathrm{eq,ft}}}^{} = {l^{\mathrm{c}}} \cdot \sqrt {{{\left\langle {{\varepsilon _{11}}} \right\rangle }^2} + {{\left( {{\varepsilon _{12}}} \right)}^2} + {{\left( {{\varepsilon _{13}}} \right)}^2}} \sigma _{{\mathrm{eq,ft}}}^{} = {l^{\mathrm{c}}} \cdot \dfrac{{\left\langle {{\sigma _{11}}} \right\rangle \left\langle {{\varepsilon _{11}}} \right\rangle + {\sigma _{12}}{\varepsilon _{12}} + {\sigma _{13}}{\varepsilon _{13}}}}{{\delta _{{\mathrm{eq,ft}}}^{}}} fc \delta _{{\mathrm{eq,fc}}}^{} = {l^{\mathrm{c}}} \cdot \left\langle { - {\varepsilon _{11}}} \right\rangle \sigma _{{\mathrm{eq,fc}}}^{} = {l^{\mathrm{c}}} \cdot \dfrac{{\left\langle { - {\sigma _{11}}} \right\rangle \left\langle { - {\varepsilon _{11}}} \right\rangle }}{{\delta _{{\mathrm{eq,fc}}}^{}}} mt \delta _{{\mathrm{eq,mt}}}^{} = {l^{\mathrm{c}}} \cdot \sqrt {{{\left\langle {{\varepsilon _{22}}} \right\rangle }^2} + {{\left\langle {{\varepsilon _{33}}} \right\rangle }^2} + {{\left( {{\varepsilon _{12}}} \right)}^2} + {{\left( {{\varepsilon _{23}}} \right)}^2} + {{\left( {{\varepsilon _{13}}} \right)}^2}} \sigma _{{\mathrm{eq,mt}}}^{} = {l^{\mathrm{c}}} \cdot \dfrac{{\left\langle {{\sigma _{22}}} \right\rangle \left\langle {{\varepsilon _{22}}} \right\rangle + \left\langle {{\sigma _{33}}} \right\rangle \left\langle {{\varepsilon _{33}}} \right\rangle + {\sigma _{12}}{\varepsilon _{12}} + {\sigma _{13}}{\varepsilon _{13}} + {\sigma _{23}}{\varepsilon _{23}}}}{{\delta _{{\mathrm{eq,mt}}}^{}}} mc \delta _{{\mathrm{eq,mc}}}^{} = {l^{\mathrm{c}}} \cdot \sqrt {{{\left\langle { - {\varepsilon _{22}}} \right\rangle }^2} + {{\left\langle { - {\varepsilon _{33}}} \right\rangle }^2} + {{\left( {{\varepsilon _{12}}} \right)}^2} + {{\left( {{\varepsilon _{23}}} \right)}^2} + {{\left( {{\varepsilon _{13}}} \right)}^2}} \sigma _{{\mathrm{eq,mc}}}^{} = {l^{\mathrm{c}}} \cdot \dfrac{{\left\langle { - {\sigma _{22}}} \right\rangle \left\langle { - {\varepsilon _{22}}} \right\rangle + \left\langle { - {\sigma _{33}}} \right\rangle \left\langle { - {\varepsilon _{33}}} \right\rangle + {\sigma _{12}}{\varepsilon _{12}} + {\sigma _{13}}{\varepsilon _{13}} + {\sigma _{23}}{\varepsilon _{23}}}}{{\delta _{{\mathrm{eq,mc}}}^{}}} Notes: < > is Macaulay bracket. {\sigma }_{\mathrm{e}\mathrm{q},i} and {\delta }_{\mathrm{e}\mathrm{q},i} is equivalent stress and displacement, where i= ft, fc, mt and mc damage model. {l}^{\mathrm{c}} is the characteristic length of element. 表 2 T700 GC/M21单向板和界面材料参数
Table 2 Material parameters of unidirectional laminate and interlayer for T700 GC/M21 composite
Laminate properties Density/(kg·m−3) 1600 Young’s modulus/GPa E11 = 130; E22 = E33 = 7.7; G12 = G13 = 4.8; G23 = 3.8 Poisson’s ratio ν12 = ν13 = 0.33; ν23 = 0.35 Strength/MPa XT = 2080 ; XC =1250 ; YT = 60; YC =140; S12 = S13 = S23 = 110Fracture energy/(N·mm−1) Gft = 133; Gfc = 40; Gmt = 0.6 N; Gmc = 2.1 Interlayer properties Elastic modulus/GPa E = 5 Strength/MPa N = S = T = 30 Fracture energy/(N·mm−1) GIC = 0.6; GIIC = 2.1 Power exponent η 1.45 表 3 预测模型能力指标评价
Table 3 Index evaluation for the capability of prediction model
Peak force/kN Max. displacement/mm Impact time/ms Absorbed energy/J Experiment 8.65 5.11 3.60 13.00 Hashin-Stress E1 10.50(+21.4%) 4.72(−7.6%) 3.24(−10% 8.66(−33.4%) Hashin-Strain 8.84(+2.2%) 4.97(−2.7%) 3.70(+2.8%>) 10.03(−22.8%) Puck 11.44(+32.3%) 4.64(−9.2%) 3.11(−13.6%) 8.08(−37.8%) Hashin-Stress E2 8.74(+1.0%) 4.91(−3.9%) 3.70(2.8%) 11.00(−15.4%) Hashin-Strain — — — — Puck 8.62(−0.3%) 4.93(−3.5%) 3.50(−2.8%) 9.44(−27.4%) Hashin-Stress E3 9.40(+8.7%) 4.96(−2.9%) 3.70(+2.8%) 10.60(−18.5%) Hashin-Strain — — — — Puck 7.85(−9.2%) 5.09(−0.4%) 3.70(+2.8%) 9.44(−27.4%) -
[1] 罗忠兵, 张松, 钱恒奎, 等. CFRP复杂几何结构区相控阵超声检测建模与声传播规律[J]. 复合材料学报, 2021, 38(11): 3672-3681. Luo Z B, Zhang S, Qian H K, et al. Modelling and wave propagation behavior of phased array ultrasonic testing on carbon fiber reinforced plastics components with complex geometry[J]. Acta Materia Composite Sinica, 2021, 38(11): 3672-3681(in Chinese).
[2] Luo Z B, Zhang Song, Jin Shijie, et al. Heterogeneous ultrasonic time-of-flight distribution in multidirectional CFRP corner and its implementation into total focusing method imaging[J]. Composite Structures, 2022, 294: 115789. DOI: 10.1016/j.compstruct.2022.115789
[3] Luo Z B, Kang Jinli, Cao Huanqing, et al. Enhanced ultrasonic total focusing imaging of CFRP corner with ray theory-based homogenization technique[J]. Chinese Journal of Aeronautics, 2023, 36(1): 449-458.
[4] Hou YL, Huang J G, Liu Y T, et al. Low-velocity impact and compression after impact behaviors of rib-stiffened CFRP panels: Experimental and numerical study[J]. Aerospace Science & Technology, 2024, 146: 108948.
[5] 李英杰, 李继承, 李宁, 等. 纤维增强大块非晶的各向异性压缩力学行为原位实验研究[J]. 兵工学报, 2024, 28(7): 1-12. Li Y J, Li J C, Li N, et al. Research on anisotropic compressive mechanical behavior of fiber reinforced bulk metallic glass composite with in-situ test[J]. Acta Armamentarii, 2024, 28(7): 1-12(in Chinese).
[6] 钱奇伟, 张昕, 杨贞军, 等. 基于CT图像深度学习的三维编织C/C复合材料微观组分与缺陷智能识别[J]. 复合材料学报, 2024, 41(7): 3536-3543. Qian Q W, Zhang X, Yang Z J, et al. Intelligent identification of micro components and defects of 3D braided C/C composites based on deep learning of X-ray CT images[J]. Acta Materia Composite Sinica, 2024, 41(7): 3536-3543(in Chinese).
[7] 齐佳旗, 段玥晨, 铁瑛, 等. 结构参数对CFRP蒙皮-铝蜂窝夹层板低速冲击性能的影响[J]. 复合材料学报, 2020, 37(6): 1352-1363. Qi J Q, Duan Y C, Te Y, et al. Effect of structural parameters on the low-velocity impact performance of aluminum honeycomb sandwich plate with CFRP face sheets[J]. Acta Materia Composite Sinica, 2020, 37(6): 1352-1363(in Chinese).
[8] Chang F, Chang K. A progressive damage model for laminated composites containing stress concentrations[J]. Composites Material, 1987, 21: 832-855.
[9] Hou J, Petrinic N, Ruiz C. A delamination criterion for laminated composites under low-velocity impact[J]. Composites Science & Technology, 2001, 61: 2069-2074.
[10] Hashin Z. Failure criteria for unidirectional fiber composites, Journal of Applied Mechanics, 1980 47: 329–334.
[11] Puck A, Schurmann H. Failure analysis of frp laminates by means of physically based phenomenological models[J]. Composites Science & Technology, 2002, 62: 1633-1662.
[12] Liao B B, Liu P F. Finite element analysis of dynamic progressive failure of plastic composite laminates under low velocity impact[J]. Composite Structure, 2017, 159: 567-578. DOI: 10.1016/j.compstruct.2016.09.099
[13] Zhou J J, Liu B, Wang S N. Finite element analysis on impact response and damage mechanism of composite laminates under single and repeated low-velocity impact[J]. Aerospace Science & Technology, 2022, 129: 107810.
[14] Tuo H L, Lu Z X, Ma X P, J, et al. Zhang. Damage and failure mechanism of thin composite laminates under low-velocity impact and compression-after-impact loading conditions[J]. Composites Part B, 2019, 163: 642-654. DOI: 10.1016/j.compositesb.2019.01.006
[15] 拓宏亮, 马晓平, 卢智先. 基于连续介质损伤力学的复合材料层板低速冲击损伤模型[J]. 复合材料学报, 2018, 35(7): 1878-1888. Tuo H L, Ma X P, Lu Z X. A model for low velocity impact damage analysis of composite laminates based on continuum damage mechanics[J]. Acta Materia Composite Sinica, 2018, 35(7): 1878-1888(in Chinese).
[16] Long S, Yao X, Zhang X. Delamination prediction in composite laminates under low velocity impact[J]. Composite Structure, 2015, 132: 290-298. DOI: 10.1016/j.compstruct.2015.05.037
[17] Lyu Q, Wang B, Guo Z. Predicting post-impact compression strength of composite laminates under multiple low-velocity impacts[J]. Composites Part A, 2023, 164: 107322. DOI: 10.1016/j.compositesa.2022.107322
[18] Xu G, Cheng H, Zhang K, et al. Modeling of damage behavior of carbon fiber reinforced plastic composites interference bolting with sleeve[J]. Materials & Design, 2020, 194: 108904.
[19] 张辰, 饶云飞, 李倩倩, 等. 碳纤维-玻璃纤维混杂增强环氧树脂复合材料低速冲击性能及其模拟[J]. 复合材料学报, 2021, 38(1): 165-176. Zhang C, Rao Y F, Li Q Q, et al. Low-velocity impact behavior and numerical simulation of carbon fiber-glass fiber hybrid reinforced epoxy composites[J]. Acta Materia Composite Sinica, 2021, 38(1): 165-176(in Chinese).
[20] 杨姝, 陈鹏宇, 江峰, 等. 内凹弧形蜂窝夹芯板低速弹道冲击试验与数值仿真[J]. 振动与冲击, 2023, 42(6): 255-262. Yang S, Chen P Y, Jang F, et al. Low-speed ballistic impact test and numerical simulation on re-entrant circular honeycomb sandwich panels[J]. Journal of Vibration and Shock, 2023, 42(6): 255-262(in Chinese).
[21] Liu P F, Liao B B, Jia L Y, et al. Finite element analysis of dynamic progressive failure of carbon fiber composite laminates under low velocity impact[J]. Composite Structure, 2016, 149: 408-422. DOI: 10.1016/j.compstruct.2016.04.012
[22] Li X, Ma D, Liu H, et al. Assessment of failure criteria and damage evolution methods for composite laminates under low-velocity impact[J]. Composite Structure, 2019, 207: 727-739. DOI: 10.1016/j.compstruct.2018.09.093
[23] Maio L, Monaco E, Ricci F, et al. Simulation of low velocity impact on composite laminates with progressive failure analysis[J]. Composite Structure, 2013, 103: 75-85. DOI: 10.1016/j.compstruct.2013.02.027
[24] Zhou J J, Wen P H, Wang S N. Numerical investigation on the repeated low-velocity impact behavior of composite laminates[J]. Composites Part B, 2020, 185: 107771. DOI: 10.1016/j.compositesb.2020.107771
[25] Zhou J J, Wen P H, Wang S N. Finite element analysis of a modified progressive damage model for composite laminates under low-velocity impact[J]. Composite Structure, 2019, 225: 111113. DOI: 10.1016/j.compstruct.2019.111113
[26] Samareh-Mousavi S S, Mandegarian S, Taheri-Behrooz F. A nonlinear FE analysis to model progressive fatigue damage of cross-ply laminates under pin-loaded conditions[J]. International Journal of Fatigue, 2019, 119: 290-301. DOI: 10.1016/j.ijfatigue.2018.10.010
[27] ASTM International. Standard test method for measuring the damage resistance of a fiber-reinforced polymer matrix composite to a drop-weight impact event: ASTM D7136M-15[S]. West Conshohocken: ASTM International, 2015.
[28] Tan W, Falzon B G, Chiu L N S, et al. Predicting low velocity impact damage and compression-after-impact (CAI) behaviour of composite laminates[J]. Composites Part A, 2015, 71: 212-226. DOI: 10.1016/j.compositesa.2015.01.025
[29] Hongkarnjanakul N, Bouvet C, Rivallant S, et al. Validation of low velocity impact modelling on different stacking sequences of CFRP laminates and influence of fibre failure[J]. Composite Structure, 2013, 106: 549-559. DOI: 10.1016/j.compstruct.2013.07.008
[30] Johnson HE, Louca LA, Mouring S, et al. Modelling impact damage in marine composite panels[J]. International Journal of Impact Engineering, 2009, 36: 25-39. DOI: 10.1016/j.ijimpeng.2008.01.013
[31] Schwab M, Todt M, Wolfahrt M, et al. Failure mechanism-based modelling of impact on fabric reinforced composite laminates based on shell elements[J]. Composites Science & Technology, 2016, 128: 131-137.
[32] Lopes CS, Camanho P, Gürdal Z, et al. Low velocity impact damage on dispersed stacking sequence laminates. Part II: Numerical simulations[J]. Composites Science & Technology, 2009, 69: 926-936.
-
其他相关附件
-
本文图文摘要
点击下载
-
-
目的
CFRP层板结构在服役过程中不可避免会遇到外物的低速冲击而产生损伤。由于其内部复杂的应力作用,多种损伤机制之间会相互耦合,促使损伤萌生、扩展,严重降低结构强度甚至导致失效。考虑到试验测试存在结构内部损伤捕捉不足、实时监测成本高等问题,导致材料渐进损伤行为描述存在局限。本文从数值模拟的角度,采用宏观渐进分析方法,阐释了冲击损伤机制,并探索不同起始准则、演化方法对损伤预测的影响。
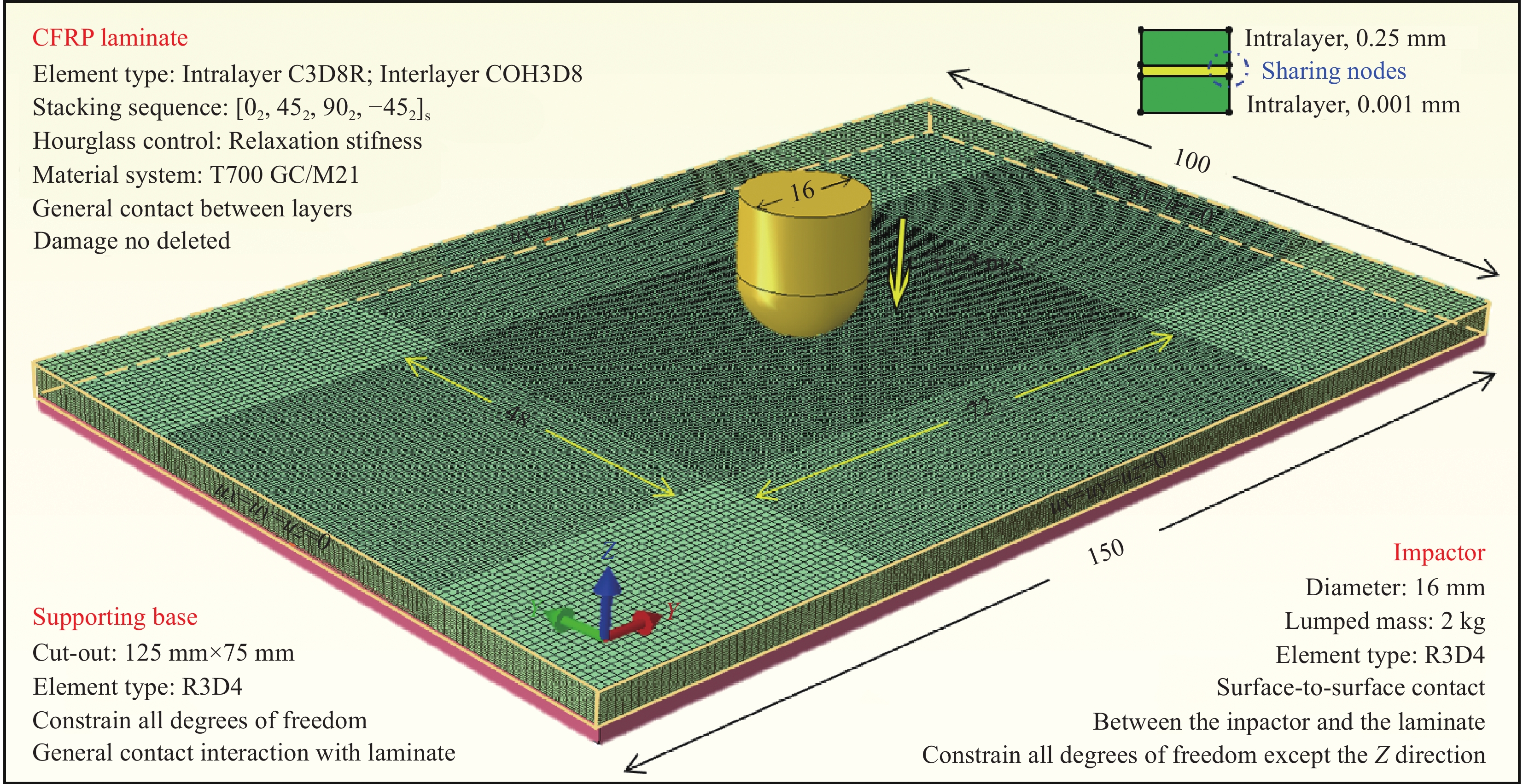
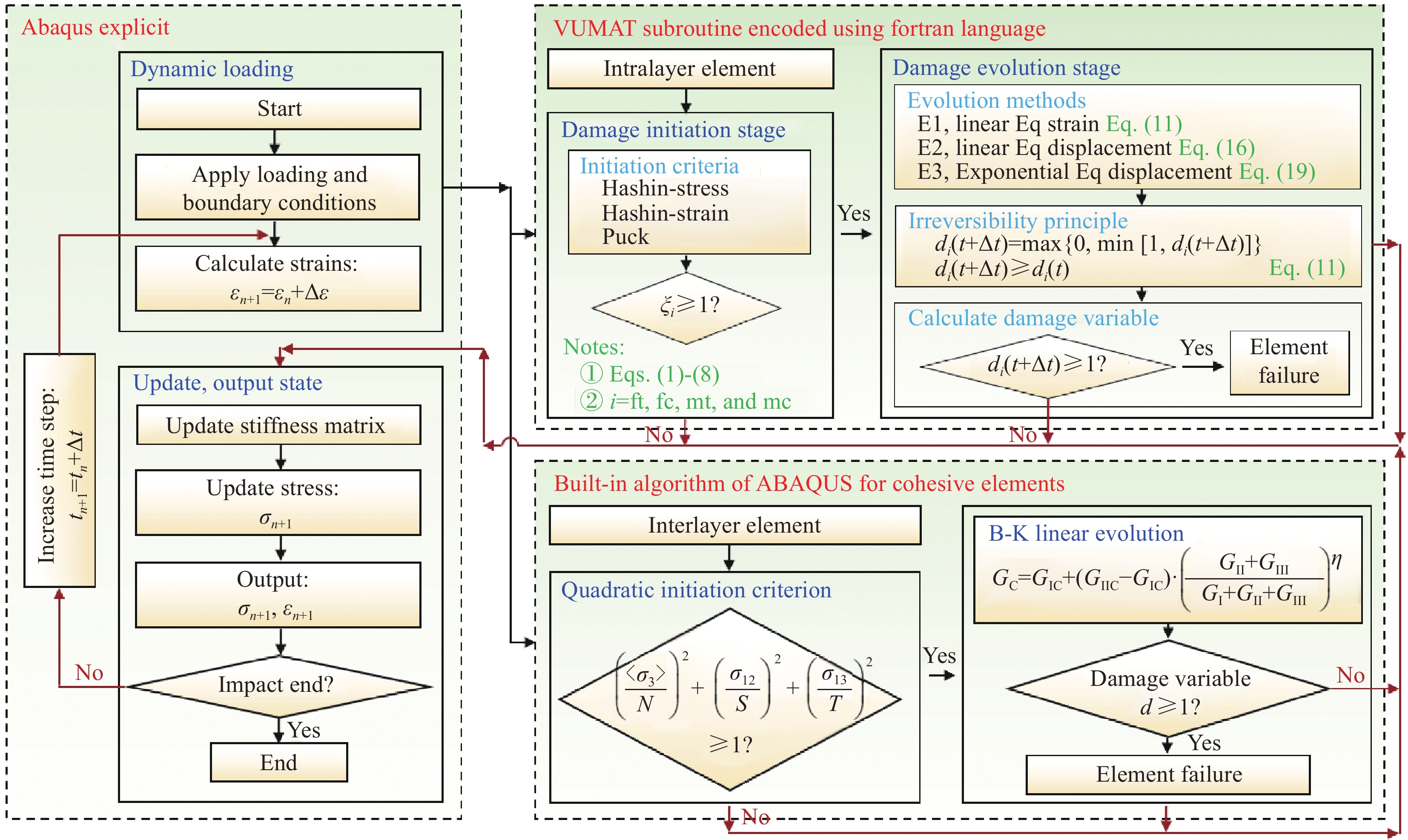
方法建立了分析层合板冲击问题的三维有限元模型,设计了包含起始判定、渐进演化及本构关系的损伤计算流程,并将其编码在ABAQUS/Explicit的VUMAT子程序中。通过提取损伤状态变量研究了损伤面积的定量、动态表征,进而对冲击损伤的渐进行为和形成机制进行描述和阐释。结合实验数据对冲击损伤数值模型进行了验证,并从结构外部力学响应、内部损伤状态两个方面,对三种损伤起始准则和三种演化方法的预测能力进行了评价探讨。
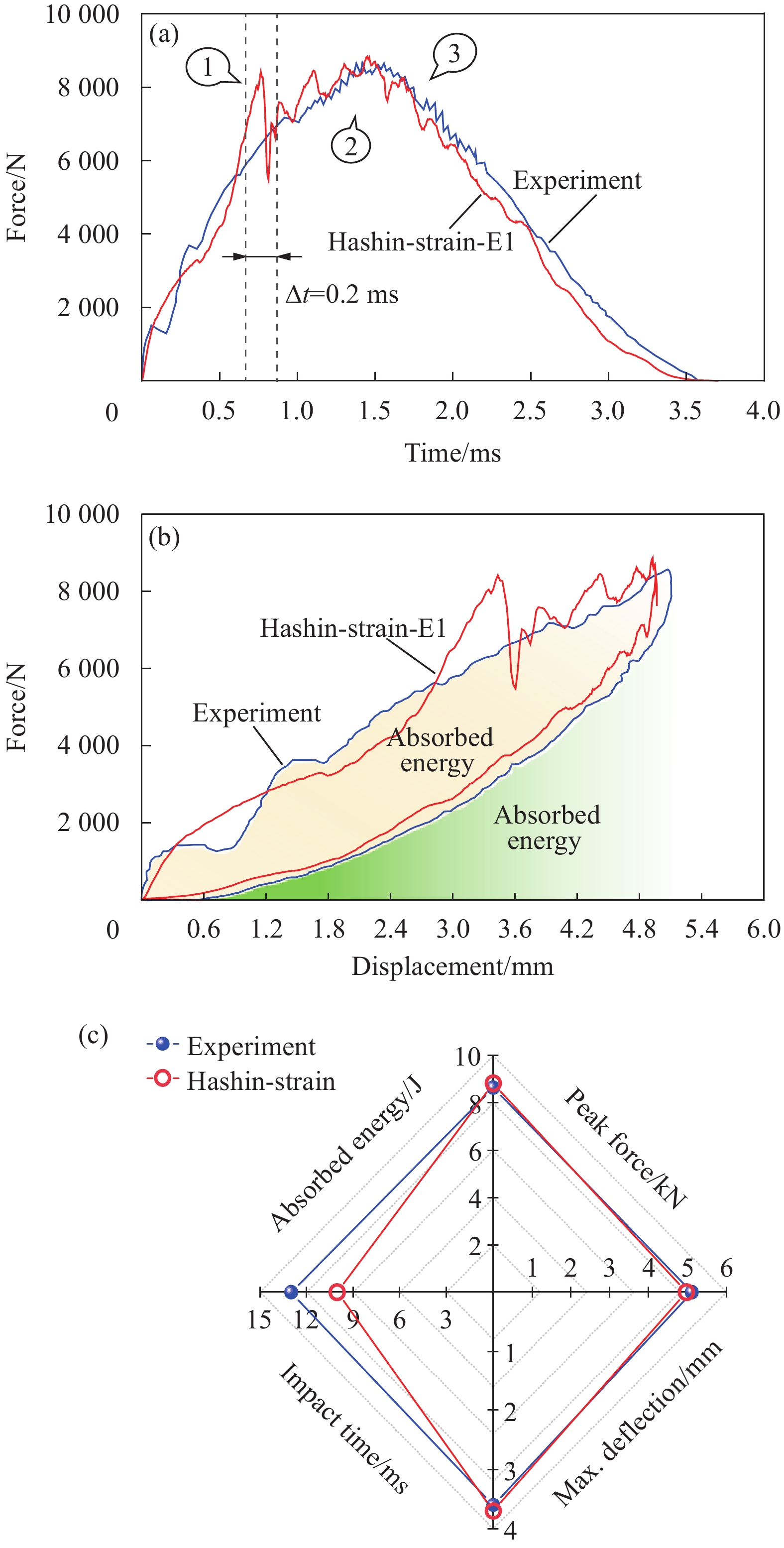
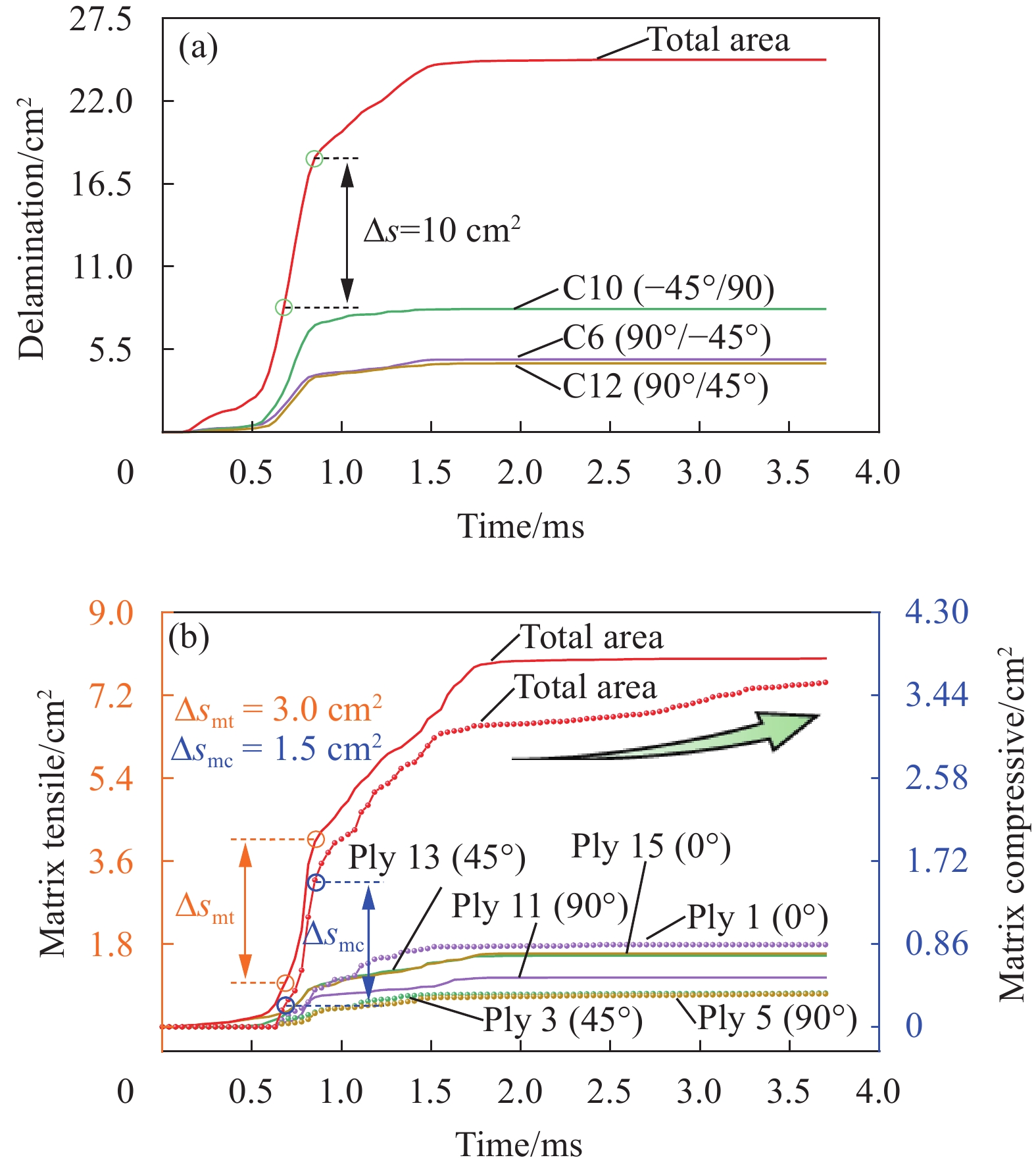
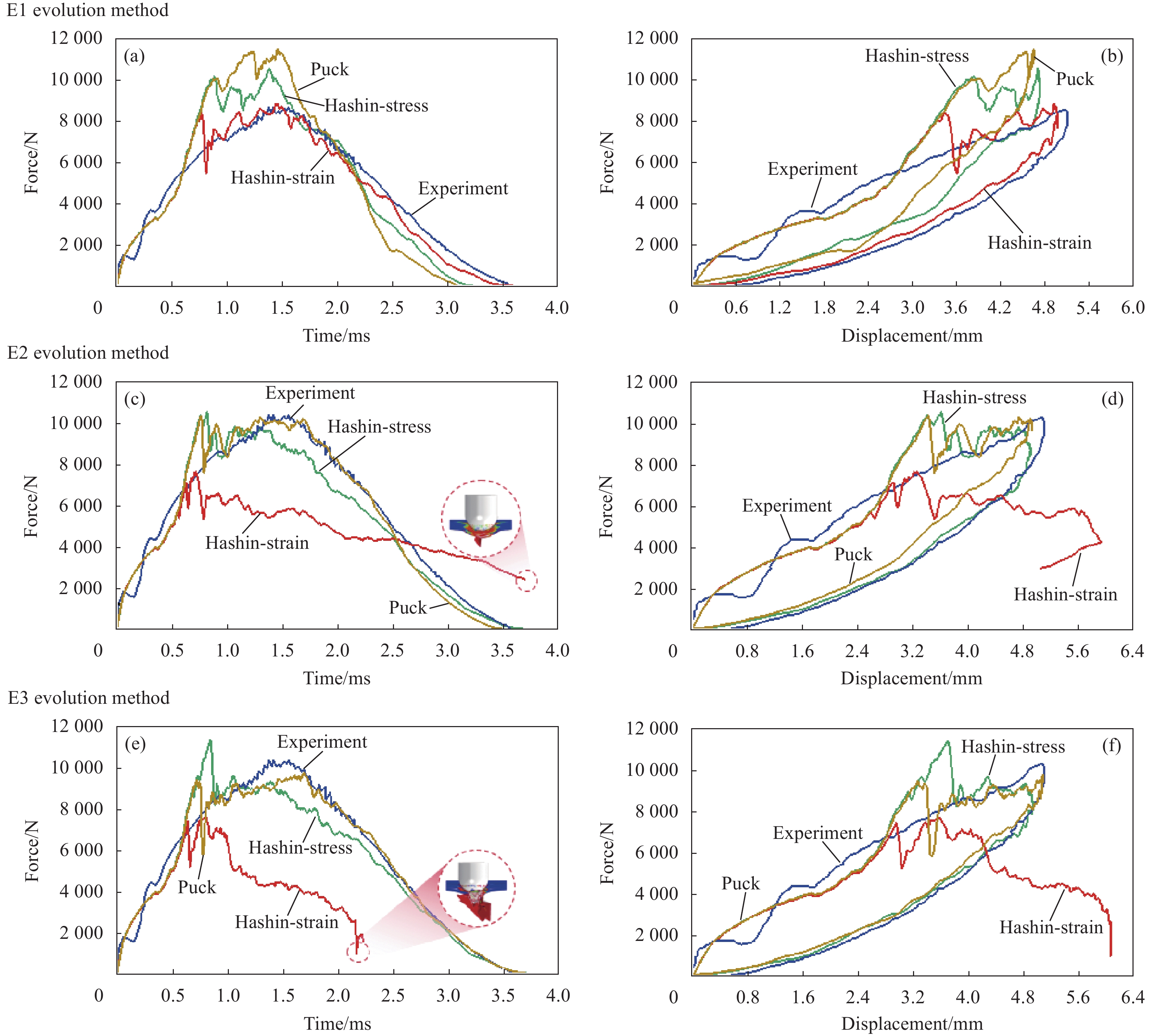
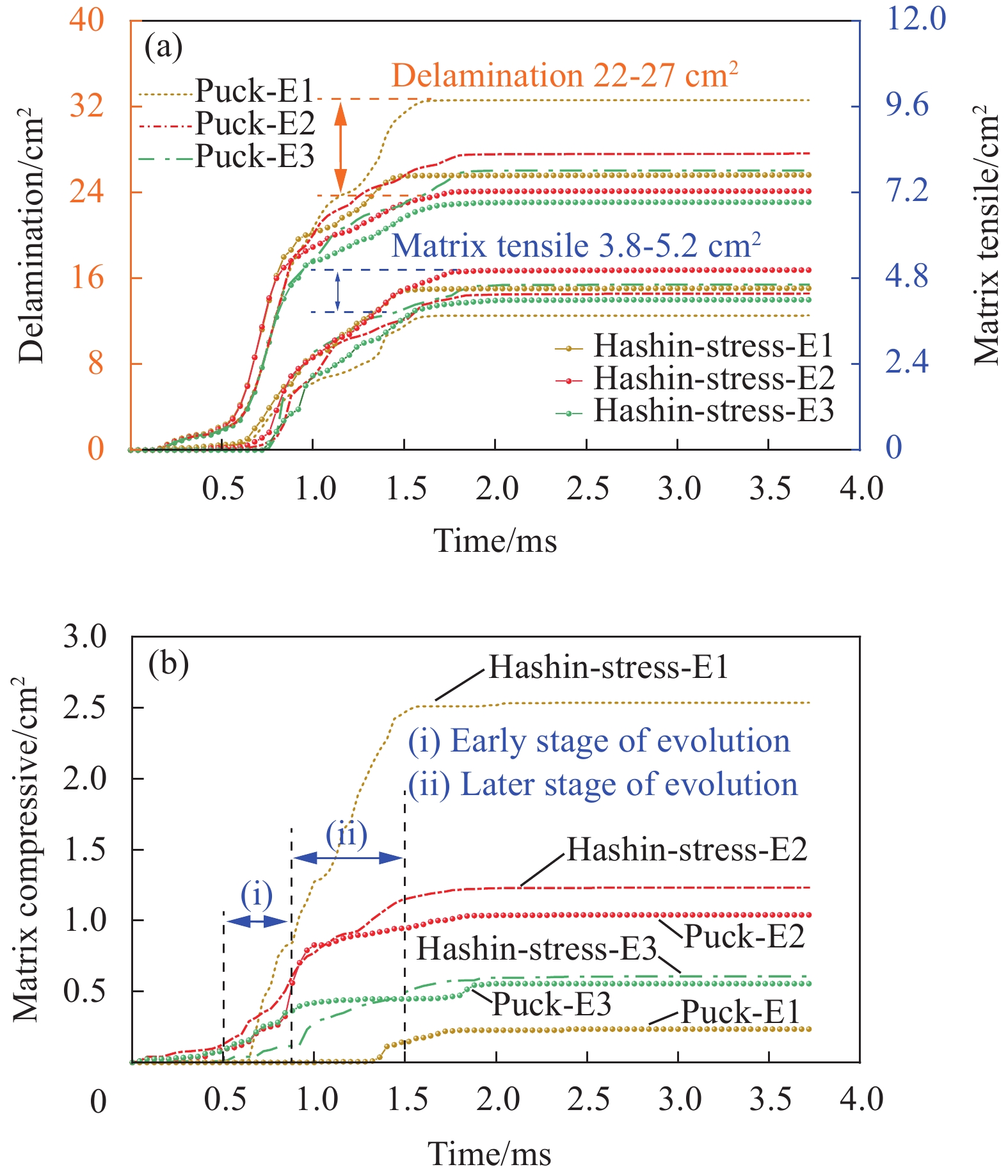
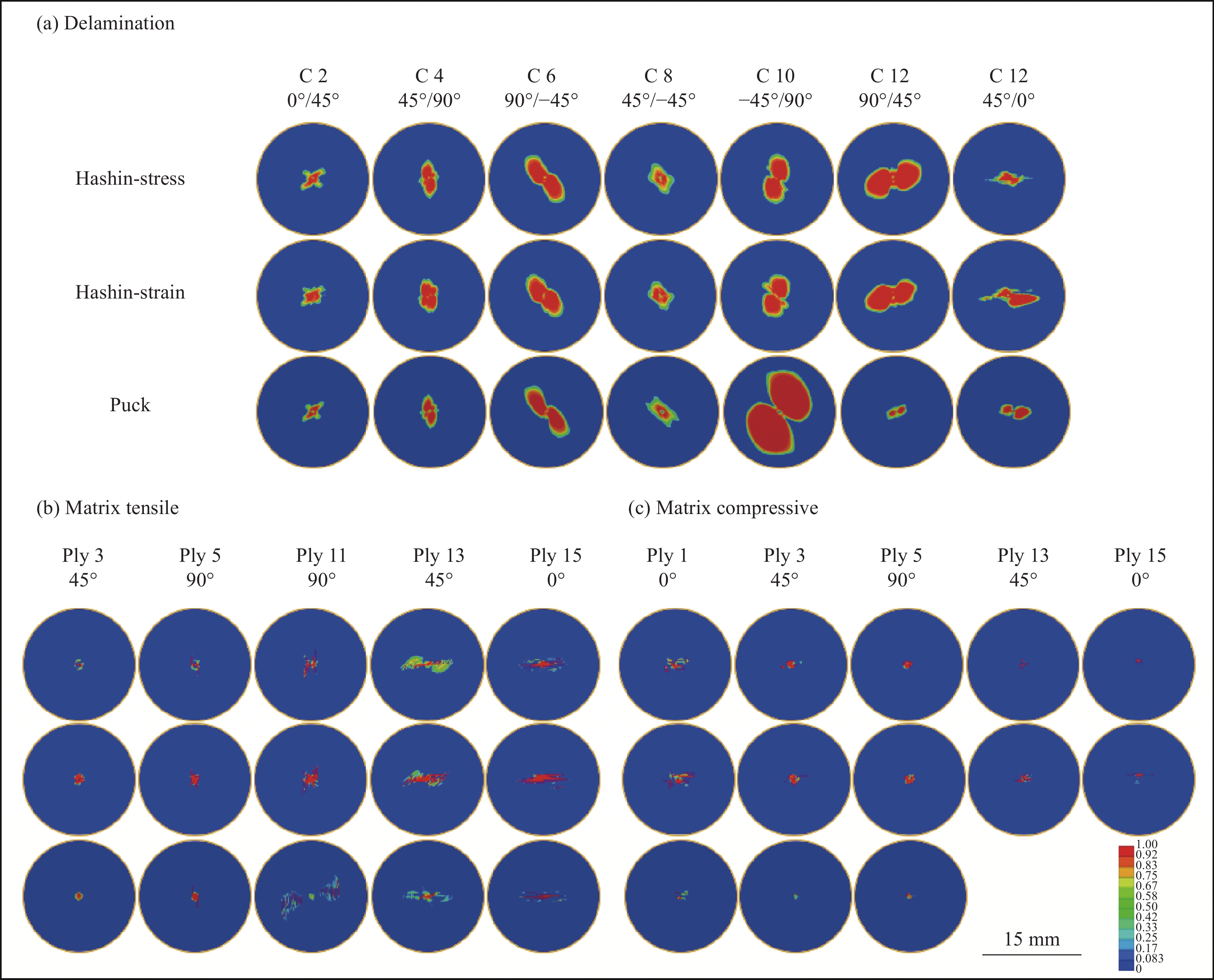
结果选用Hashin-Strain损伤起始准则结合E1演化方法(Hashin-Strain-E1)为代表的预测结果,与试验数据进行比较。动态力学响应曲线表现出二者吻合度较高,证明本文建立的数值模型能够准确预测冲击损伤。在此基础上通过损伤面积定量演化方法,解释了力学响应曲线上三次明显抖动的内在原因。对于第“1”次抖动,中性层及以下部分界面的分层是其对应一种损伤模式。此外,靠近冲击正面的第一层和中性层以下的层发生横向基体开裂是另一种损伤模式。故而,这次抖动是分层和基体损伤共同作用而导致的,但是分层占据主导地位。对于第“2”次抖动,分层和基体损伤的产生共同贡献了作用。然而相对基体损伤而言,分层损伤仍然起主要作用。第“3”次抖动是出现在层合板的回弹阶段,是由于局部区域的高压应力造成的。同时,对于不同损伤预测模型的能力评估和探索也有新发现。Hashin-Strain准则结合线性等效应变方法(Hashin-Strain-E1)和Puck准则结合指数型等效位移方法(Puck-E3)表现最优。然而,当Hashin-Strain准则结合线性或指数型等效位移方法时(Hashin-Strain-E2/E3),会由于结构刚度退化严重而引发穿透性损伤,进而呈现出最坏的的预测性能。此外,损伤起始准则对分层和基体拉伸损伤影响较小,但损伤之间的耦合作用会导致局部区域出现不同现象。起始准则对基体压缩损伤形貌影响较大,尤其是Puck准则。因为该准则不考虑贯穿层合板厚度方向的法向应力的作用,限制了损伤的向更深层方向扩展。损伤演化方法对基体压缩损伤影响显著,表现为预测的损伤面积分布更为分散,而对分层和基体拉伸损伤影响较小。
结论针对层合板低速冲击损伤的预测问题,本文建立数值模型探讨了三种损伤起始准则和三种演化方法对预测结果的影响。利用损伤状态变量研究了冲击过程中损伤面积的定量演变,为描述损伤渐进行为和阐释损伤机制提供新视角。损伤起始准则与演化方法的结合对损伤模型预测性能尤为关键,严重影响层合板结构内部损伤状态计算进而影响外部力学响应。本研究有助于减少与起始准则和演化方法间不同组合设计相关的试验工作量,为工程应用中更好预测冲击损伤性能提供参考。
-
CFRP层板结构在服役过程中不可避免会遇到外物的低速冲击而产生损伤。由于其内部复杂的应力作用,多种损伤机制之间会相互耦合,促使损伤萌生、扩展,严重降低结构强度甚至导致失效。考虑到试验测试无法呈现损伤内部状态、进而描述渐进损伤行为。因此,研究低速冲击过程的数值模拟就变得更为重要。
本文采用宏观渐进分析方法从结构外部力学响应、内部损伤状态两个方面,探讨不同的损伤起始准则和演化方法对层板损伤预测问题的影响。为此,建立了分析层板冲击问题的三维有限元模型,设计了包含起始判定、渐进演化及本构关系的损伤计算流程。同时,研究了冲击过程损伤面积定量演变,为阐释损伤机制提供新视角。发现Hashin-Strain准则结合线性等效应变方法和Puck准则结合指数型等效位移方法最优。然而,当Hashin-Strain准则结合线性或指数型等效位移方法时,会由于刚度退化严重而引发穿透性损伤。本研究有助于深入理解低速冲击下复合材料层合板的损伤演变机制,为工程中开展冲击损伤及性能评估提供参考和借鉴。
冲击过程中不同起始准则和演化方法下的动态力学响应






 下载:
下载: