碳纤维增强树脂基复合材料(Carbon Fiber-reinforced Polymer, CFRP)以其高比模量、高比强度、耐腐蚀、抗疲劳等显著特征，在航空航天、交通运输、能源等领域得到了广泛的应用^[1-3]。但由于在制造过程中纤维的预应力和固化温度的变化，致使复合材料结构在加热和固化过程中不可避免引入气泡^[4]、褶皱^[5]和分层^[6]等缺陷，严重削弱复合材料构件的强度、刚度和疲劳寿命^[1,7]。

褶皱缺陷是指纤维在复合材料内部或表面出现折痕或纤维层发生屈曲^[8]，而固化过程中基体和纤维热膨胀系数不同也会产生褶皱缺陷^[9]。为系统研究褶皱缺陷对复合材料力学性能影响，对褶皱缺陷的几何形貌特征进行理想化处理，通常使用高斯函数^[10,11]、正弦函数^[12,13]或余弦函数^[14]表征，主要参数包括波长λ、振幅A和纤维偏转角θ。

褶皱缺陷对强度性能影响方面，Mendonca等^[15]采用数值模拟与试验相结合对含褶皱缺陷玻纤复合材料板的疲劳损伤进行了研究，研究表明褶皱缺陷会导致复合材料疲劳寿命显著下降，并观察到缺陷区域产生裂纹起裂和分层扩展。Chen等^[16]对含褶皱缺陷复合材料板在受压和剪切载荷作用下材料失效行为进行了分析，结果表明：褶皱缺陷显著降低了层合板的抗压强度，并加剧了层合板的分层破坏，层合板的抗压强度和层间剪切强度分别下降了26.9%和2.8%。

在工业生产中，褶皱缺陷将导致复合材料结构的不均匀性以及加剧分层破坏^[17]，严重危害复合材料结构安全。因此，评估和量化褶皱缺陷对复合材料结构性能影响，对构件进行褶皱缺陷检测是十分必要的。

Miao等^[18]对从风力发电叶片梁帽部分切割下含褶皱缺陷的层合板进行疲劳加载，使用计算机断层扫描技术(CT)对层合板的疲劳裂纹进行检测，确定其疲劳载荷作用下的断裂模式和断裂路径。Chen^[19]使用CT对结构失效的风力发电机叶片进行检测，发现断裂面附近存在因富树脂区产生的褶皱缺陷。CT还可以测量单向铺层层合板内毫米级的纤维取向^[20]。Chakrapani等^[21]使用频率为120 Hz的空气耦合超声方法检测了风力发电机叶片中的纤维波纹度。虽然CT扫描和超声检测在一定程度上可以表征褶皱缺陷形貌特征，但对褶皱缺陷进行精确的定量化分析以及性能评价仍存在不足，无法获得含缺陷构件在给定工况下的位移响应。

激光剪切散斑干涉技术，因其高灵敏度和精度，在复合材料和金属结构的无损检测中显示出巨大的潜力^[22-24]。该技术通过记录位移导数的全场散斑干涉图像，实时捕捉到微小的位移梯度变化，从而实现对试样内部缺陷的高精度测量。Zhang等^[25]使用激光剪切散斑干涉技术记录了碳纤维复合材料损伤演化的实时成像过程，结果显示出比数字图像相关法更优越的缺陷成像能力。Guo等^[26]通过数值模型与实验结果的比较，讨论了剪切成像技术在不同载荷作用下检测最小缺陷尺寸和深度的能力。Gu等^[27]采用剪切成像技术与数字散斑干涉法相结合，实现了对金属薄板内部缺陷深度信息的表征，相对现有方法误差小于5%。

本文提出了一种基于激光剪切散斑干涉技术的碳纤维复合材料褶皱缺陷响应检测方法。研究内容如下：首先基于两步均匀化方法构建了梯度型褶皱的细观力学模型，推导了相应的等效刚度矩阵，分析了褶皱缺陷对层合板试样等效刚度系数影响，结合有限元分析，预测了不同褶皱缺陷参数(铺层顺序、波长λ、振幅A)以及不同拉伸载荷条件下褶皱缺陷的力学响应。基于激光剪切散斑干涉技术，开展了褶皱缺陷引起的位移响应测量实验，当施加微小的拉伸载荷时，褶皱缺陷区域因离面位移梯度变化而产生干涉条纹，且条纹随载荷增加变得更加密集。通过干涉条纹图的处理，得到褶皱缺陷引起的位移场。实验获取的离面位移值与有限元预测结果吻合良好，验证了梯度型褶皱细观力学模型在复合材料褶皱缺陷响应分析方面的可靠性。

1.   褶皱缺陷细观力学模型

1.1   梯度型褶皱几何形状

褶皱缺陷根据其几何特征可分为均匀型或梯度型褶皱。均匀型褶皱振幅与波长之比保持不变；梯度型褶皱沿厚度方向，振幅与波长之比呈现渐变趋势并逐渐减少^[28]。本研究中褶皱缺陷模型简化为梯度型褶皱，如图1所示。

图  1  梯度型褶皱

Figure  1.  Graded wrinkle

下载: 全尺寸图片 幻灯片

褶皱的形状由余弦函数^[14]描述，其具体表达式为

其中，x为平行于无褶皱缺陷的纤维方向，z为厚度方向。h为层合板中褶皱缺陷总高度，A为褶皱的振幅，λ为褶皱的波长。

A/λ为纤维波幅与波长的比值，定义为波纹比，用于表示褶皱缺陷的严重程度。由式(1)可知，当x=±λ/4时，褶皱缺陷区域内的纤维偏转角度$\phi$最大。

表1给出了最大纤维偏转角范围和波纹比A/λ比值之间的对应关系。

1.2   梯度型褶皱的细观力学模型

考虑一个代表性体积单元(Representative Volume Element, RVE)包含一个完整的梯度型褶皱缺陷时，可通过两步均匀化方法^[29]计算RVE的等效刚度矩阵，如图2所示。首先在RVE内部，含梯度型褶皱缺陷复合材料层合板沿水平方向分为许多窄带，在每个窄带内部先沿厚度方向进行均匀化，而后在RVE内部沿水平方向均匀化。[C_ij]表示单个窄带内部各层的刚度矩阵，可以通过材料坐标系下的刚度矩阵$\left[\bar{C}_{i j}\right]$变换得到：

表  1  复合材料褶皱缺陷中最大纤维偏转角范围和波纹比

Table  1.  Range of maximum misalignment angles and wrinkle ratio in wrinkle defects

A/λ	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50
${{\phi }_{\max }}$/(°)	32.14	43.30	51.49	57.52	62.05	65.55	68.30	70.52	72.34

下载: 导出CSV 

| 显示表格

图  2  梯度型褶皱的细观力学模型

Figure  2.  Meso-mechanical modeling of graded wrinkle

RVE−Representative Volume Element; C'_ij−Equivalent stiffness matrix of single prepreg layer; n−Number of layers in RVE; θⁿ−Fiber orientation angle of the n-th layer; m−Number of horizontal divisions in RVE; $\phi _{k}^{l}$−Misalignment angle of fiber in the k-th segment of the l-th layer; ^kC^*−Equivalent stiffness matrix of the k-th segment; [C^**]−Equivalent stiffness matrix of the homogenized

下载: 全尺寸图片 幻灯片

其中，θ是纤维铺层角度，$\phi$是指纤维在面外方向的偏转角度。T_θ和${{T}_{\phi }}$分别表示θ、$\phi$的刚度转换矩阵。

在第一步垂直均匀化中，假设σ_zz = $\sigma _{{\textit{z}}{\textit{z}}}^{*}$，σ_yz = $\sigma _{y{\textit{z}}}^{*}$，σ_zx = $\sigma _{{\textit{z}}x}^{*}$和ε_xx = $\varepsilon _{xx}^{*}$，ε_yy = $\varepsilon _{yy}^{*}$，ε_xy = $\varepsilon _{xy}^{*}$，其中上标*表示平均应力和应变。对于每条窄带内部的每一层材料的本构方程可表示为

其中：

依据$\left\{ {{\sigma }_{\text{A}}^*} \right\}$和$\left\{ {{\varepsilon }_{\text{B}}^*} \right\}$，式(5)亦可改写为

对于$\left\{ {{{\varepsilon }_{\text{A}}}} \right\}$和$\left\{ {{{\sigma }_{\text{B}}}} \right\}$的平均值即$\left\{ {{\varepsilon }_{\text{A}}^*} \right\}$和$\left\{ {{\sigma }_{\text{B}}^*} \right\}$，则可通过下式求得：

其中：

式(10)中的z_k 和 z_k−1表示每层的上下坐标，n为总层数。

通过求解式(9)，得到每条窄带垂直均匀化后的本构关系：

在第二步水平均匀化过程中，假设$\sigma _{xx}^{*}$ = $\sigma _{xx}^{**}$，$\sigma _{{\textit{z}}x}^{*}$ = $\sigma _{{\textit{z}}x}^{**}$，$\sigma _{xy}^{*}$ = $\sigma _{xy}^{**}$，$\varepsilon _{yy}^{*}$ = $\varepsilon _{yy}^{**}$，$\varepsilon _{{\textit{z}}{\textit{z}}}^{*}$ = $\varepsilon _{{\textit{z}}{\textit{z}}}^{**}$，$\varepsilon _{y{\textit{z}}}^{*}$ = $\varepsilon _{y{\textit{z}}}^{**}$。上标**表示两次均匀化后，z整个代表性体积单元内部等价或平均物理量。

其中：

根据$\left\{ {{\varepsilon }_{\text{E}}^{**}} \right\}$和$\left\{ {{\sigma }_{\text{F}}^{**}} \right\}$的表达式，式(13)改写为

对于$\left\{ {{\varepsilon }_{\text{E}}^*} \right\}$和$\left\{ {{\sigma }_{\text{F}}^*} \right\}$在RVE内部的平均值即$\left\{ {{\varepsilon }_{\text{E}}^{**}} \right\}$和$\left\{ {{\sigma }_{\text{F}}^{**}} \right\}$，则可通过下式求得：

其中：

通过求解式(16)，得到含有梯度型褶皱的RVE等效刚度：

1.3   褶皱缺陷等效刚度系数

采用上述的两步均匀化方法，推导了正交铺层[0/90]_2s、零度铺层[0]₃₀以及混合铺层[0/90/±45/0]_3s层合板试样的等效刚度系数，并探讨了褶皱缺陷存在与否对层合板试样等效刚度参数的影响，揭示褶皱缺陷对复合材料力学性能的影响。在下文的分析和实验中，组成层合板试样的单向板采用碳纤维(Carbon Fiber, CF)增强环氧树脂(Epoxy Resin, EP)复合材料，其性能参数如表2所示，含梯度型褶皱层合板试样参数见表3。

在有无褶皱缺陷条件下，表4分析了 [0/90]_2s、[0]₃₀和[0/90/±45/0]_3s三种不同铺层顺序层合板试样的等效刚度系数变化。结果表明，褶皱缺陷对材料在纤维方向上的纵向刚度系数C₁₁具有显著影响，其下降幅度分别为72.87%、72.59%和60.26%。在铺层顺序为[0/90]_2s和[0/90/±45/0]_3s的试样中，刚度系数C₁₃呈现增加趋势，而在铺层顺序为[0]₃₀的试样中，刚度系数C₁₃出现了减小趋势，表明褶皱缺陷在不同铺层顺序下对材料厚度方向的应变响应具有不同的敏感性。相比之下，面内横向刚度系数C₂₂变化幅度小于2.6%，表明褶皱缺陷对材料横向刚度的影响相对较小。

表  2  CF/EP复合材料弹性参数

Table  2.  Elastic parameters of CF/EP composites

E11/GPa	E22/GPa	E33/GPa	v12	v23	v31	G12/GPa	G23/GPa	G31/GPa
133.3	9.09	9.09	0.261	0.436	0.261	7.24	3.16	7.24

下载: 导出CSV 

| 显示表格

表  3  试样缺陷参数

Table  3.  Defect parameters of specimen

Specimen	Layup sequences	Wrinkle parameter
		Wavelength /mm	Amplitude /mm	Wrinkle ratio
Ⅰ	[0/90]2s	6.6	1.2	0.1818
Ⅱ	[0]30	8.3	1.0	0.1204
Ⅲ	[0/90/±45/0]3s	5.8	0.7	0.1206

下载: 导出CSV 

| 显示表格

表  4  铺层顺序和褶皱缺陷对等效刚度系数的影响

Table  4.  Effect of layup sequence and wrinkle defects on effective stiffness coefficients

Effective stiffness/GPa	Layup sequence
	[0/90]2 s			[0]30			[0/90/±45/0]3 s
	Wrinkle ratio=0.1818			Wrinkle ratio=0.1204			Wrinkle ratio=0.1206
	Without wrinkle	With wrinkle	Difference/%	Without wrinkle	With wrinkle	Difference/%	Without wrinkle	With wrinkle	Difference/%
C11	73.43	19.92	−72.87	135.53	37.14	−72.59	64.26	25.54	−60.26
C12	4.29	4.59	7.0	4.28	4.88	14.02	15.60	7.87	−49.55
C13	4.65	6.23	33.98	4.28	3.82	−10.75	4.64	5.94	28.2
C22	73.43	73.40	−0.04	11.36	11.35	−0.09	59.98	58.46	−2.53
C23	4.65	4.63	−0.43	5.02	5.01	−0.20	4.67	5.15	10.28
C33	11.36	13.85	21.92	11.36	13.24	16.55	11.36	12.40	9.15
C44	4.40	5.11	16.14	3.15	3.15	0	4.34	5.17	19.12
C55	4.40	7.35	67.05	7.24	9.06	25.14	4.46	6.08	36.32
C66	7.23	6.23	−13.83	3.16	3.16	0	18.54	15.58	−15.97

下载: 导出CSV 

| 显示表格

2.   试样制备

采用手工铺设和固化成型工艺来制备含有不同大小褶皱缺陷的碳纤维复合材料层合板试样。使用的预浸料为威海光威复合材料股份有限公司生产的USN 10000型号，其中单向纤维预浸料厚度为0.1 mm，纤维单位面积质量为100 g/m²，树脂体积含量为20%~40%。

通过采用文献[10]中描述的“钢棒法”，在预浸料层之间嵌入不同直径的钢棒，以控制褶皱缺陷的波幅和波长，进而制备含褶皱缺陷的复合材料层合板试样，梯度型褶皱缺陷的设计参数见表3，褶皱缺陷的形貌特征见图3。含褶皱缺陷试样的制备流程：将预浸料切割成300 mm×300 mm的方板，并按照预先设定的铺层顺序进行铺层。铺层顺序分别为[0/90]_2s，[0]₃₀和[0/90/±45/0]_3s。在预浸料底层放置一根钢棒，每铺设5层后抽真空处理，以排除预浸料间的空气。固化前移除钢棒，使环氧树脂在固化过程中聚集到钢棒留下的空隙中。固化过程中，将层合板置于表面光滑的模具上，覆盖透气毡并铺设真空袋，确保预浸料层间紧密贴合模具。固化成型过程中，升温速率为2℃/min，最高固化温度为120℃，保温时间为1.5 h，以确保预浸料中的环氧树脂充分硬化并与碳纤维形成牢固粘合。最后，为保证方板在切割过程中的稳定性以及后续拉伸实验的需求，需对方板夹持端进行加强处理，将其切割成尺寸为280 mm×25 mm的层合板试样。

图  3  梯度型褶皱缺陷试样：(a)试样几何参数示意图； (b)褶皱缺陷形貌特征

Figure  3.  Graded wrinkled specimen: (a) Geometric sketch of specimen; (b) Morphology of the wrinkle

下载: 全尺寸图片 幻灯片

3.   有限元数值分析

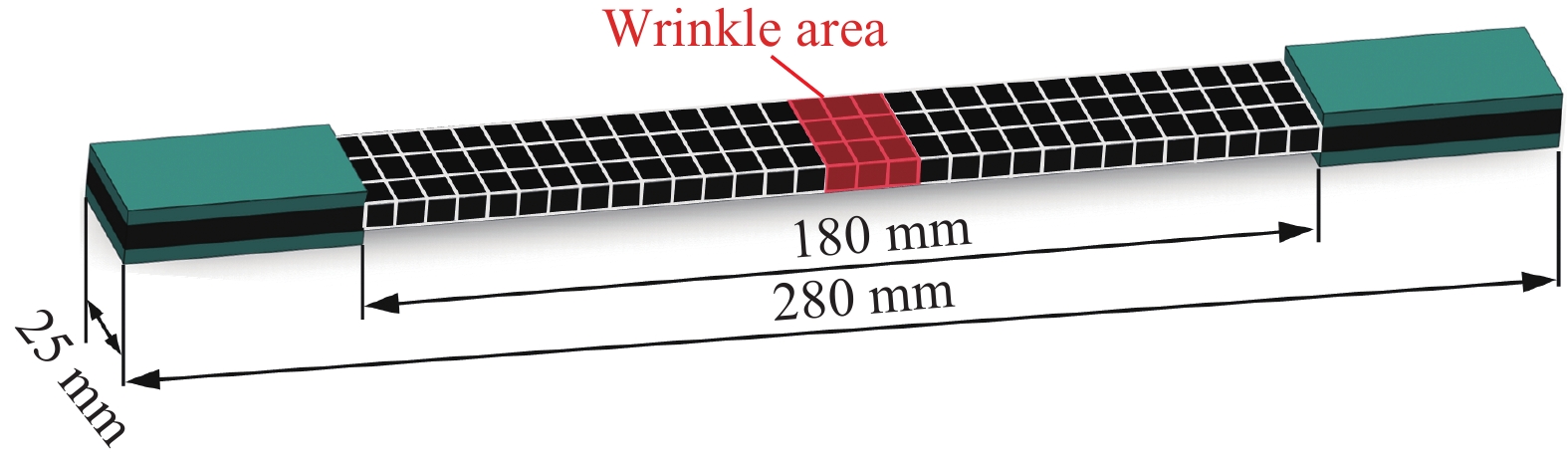
含褶皱缺陷层合板试样的有限元模型如图4所示，其中试样中部位置红色区域表示褶皱缺陷区域。有限元计算中，三种试样的单元类型均选用Solid185，其中试样Ⅰ的单元尺寸为1 mm×1 mm×0.8 mm，试样Ⅱ和试样Ⅲ的单元尺寸均为1 mm×1 mm×1 mm。材料模型采用1.3章节推导的等效刚度参数。层合板试样的计算模型约束条件：拉伸载荷条件下，模型左端面受到固支约束，右侧端面施加相应的载荷，有限元分析结果如图5所示。

图  4  含褶皱缺陷试样计算模型示意图

Figure  4.  Schematic of calculation model for wrinkled specimen

下载: 全尺寸图片 幻灯片

图  5  含褶皱缺陷试样与无缺陷试样的离面位移有限元结果对比

Figure  5.  Comparison of finite element results on out-of-plane displacement between wrinkled specimen and non-wrinkle specimen

下载: 全尺寸图片 幻灯片

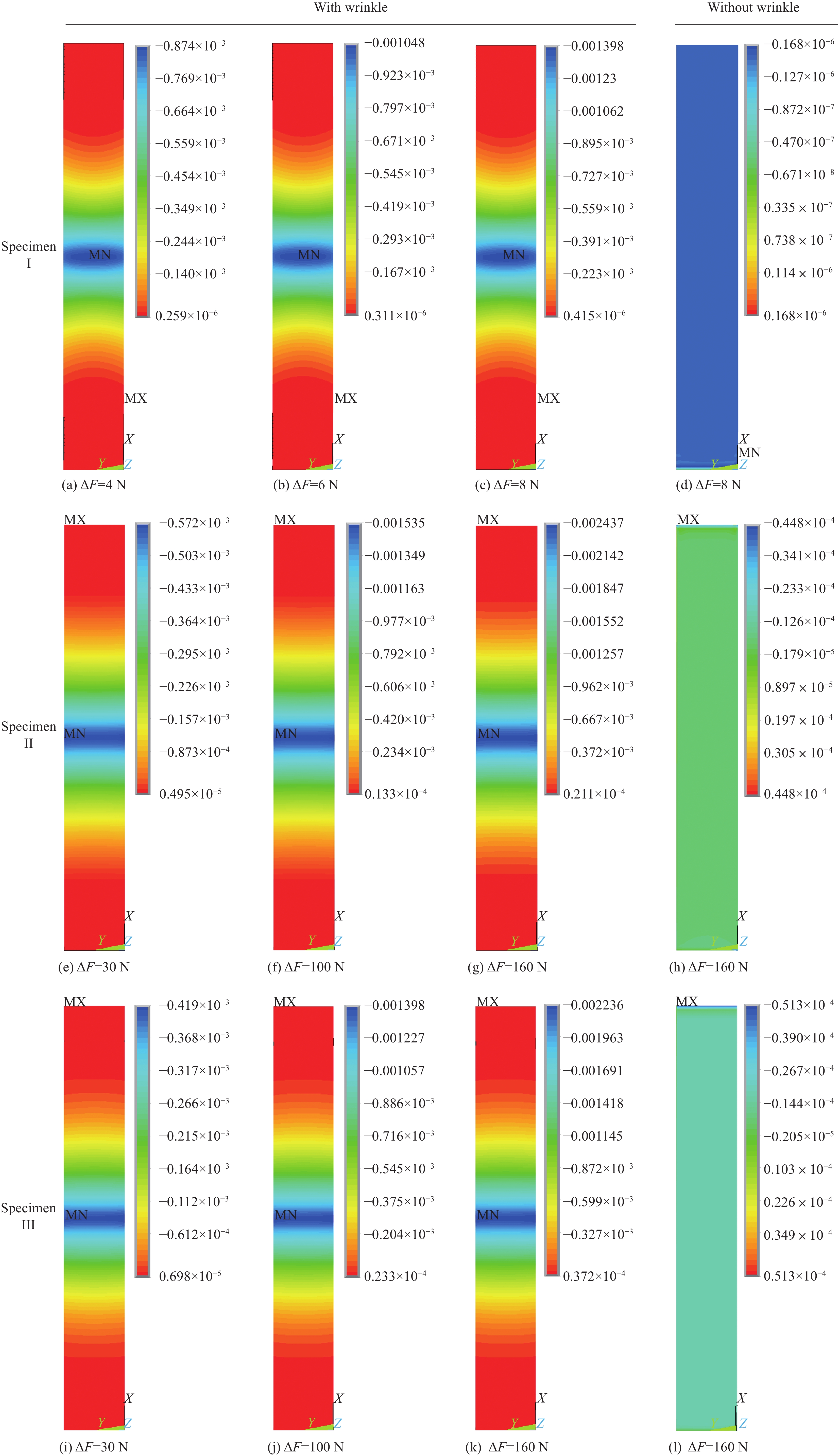
图5 展示了在单轴拉伸载荷作用下，三种试样的离面位移有限元结果。对于厚度约为1 mm含褶皱缺陷的试样Ⅰ，图5 (a)、5 (b)和5 (c)分别显示了在5 N、6 N和8 N的拉伸载荷下，其对应的最大离面位移分别达到874 nm、1048 nm和1398 nm，最大离面位移值产生的位置与缺陷所在的区域相吻合。图5 (c)、5 (d)分别对应含褶皱缺陷的试样和无缺陷的理想试样在8 N拉伸载荷下的离面位移有限元结果，从图中可以观察到，褶皱缺陷不仅改变了离面位移的分布，而且最大离面位移值相较理想试样约增加了8000倍。

图5 (e)~5 (n) 比较了两种不同铺层方式的碳纤维层合板试样(试样Ⅱ和试样Ⅲ)在相同铺层厚度、波纹比和拉伸载荷条件下的离面位移有限元结果。当试样中无褶皱缺陷时，单一方向铺层的试样Ⅱ的离面位移小于混合铺层试样III的离面位移。表明当试样II的纤维方向与施加拉伸载荷方向一致时，试样能有效承受拉伸载荷，展现出较低的变形。当两种试样中引入相同波纹比的褶皱缺陷时，在相同的拉伸载荷作用下，试样Ⅱ的最大离面位移值均大于试样Ⅲ的最大离面位移值。表明褶皱缺陷削弱了材料沿纤维方向的弹性模量，导致材料刚度降低。然而，混合铺层结构可通过其多方向的纤维取向，能够更好地分散载荷和应力，有效降低褶皱缺陷对材料力学性能的不利影响，使得在相同载荷条件下其离面位移值相对较小。

4.   激光剪切散斑干涉检测

4.1   实验装置

本文采用激光剪切散斑干涉技术测量拉伸加载下的褶皱缺陷试样的离面位移。

图6 (a)、6 (b) 是激光剪切散斑干涉系统(isi-sys GmbH，德国isi公司)实验测量示意图，其中拉伸载荷通过双立柱台式电子万能试验机(Instron 3369 型，美国英斯特朗公司)施加。激光剪切散斑干涉系统原理图如图6 (c) 所示，激光束照射到试样表面，经过漫反射后进入迈克尔逊干涉装置。其中一部分光束通过装置中的反光镜，而另一部分光束通过装置中的剪切镜。试样表面的两个相邻点反射的光束在CCD相机的成像平面上汇聚于同一点，发生干涉形成散斑干涉图像。当试样发生变形后，对变形前后的两幅散斑图像做相减处理，在计算机上实时显示出反映物体位移偏导数的干涉条纹图案。

图  6  激光剪切散斑干涉系统实验装置

Figure  6.  Experimental device with shearography system

下载: 全尺寸图片 幻灯片

4.2   条纹形成原理

被测物体加载前，散斑干涉图光强分布I可表示为^[30,31]

式中I₀是背景光强，μ是散斑图像的调制幅值，φ表示物体表面相邻两点相干光的相位差。

被测物体加载产生形变后，物体表面各点光程发生改变导致光波的相位发生改变，相位差变为 φ'= φ + Δ。变形后的散斑干涉图光强分布变为I'，表达式如下：

其中，Δ表示由于被测物体表面变形引起的相位变化。

对加载前后的散斑干涉图光强分布直接相减获得强度差I_d，表达式如下：

式中，sin(φ + Δ/2)属于高频正弦项，因包含随机变化φ，在干涉图中呈现随机散斑的形式。sin(Δ/2)属于低频项，其中相位变化Δ对应于被测物体的加载变形，在干涉图中呈现出条纹的形式。当I_d为最小值时，即Δ= 2nπ (n=1, 2, 3···为条纹级数)，干涉图上出现暗条纹；当I_d为最大值时，即Δ= (2n+1)π (n=1, 2, 3···)，干涉图上出现亮条纹。

如图7所示，对被测物进行加载后，物面上相邻两点P₁和P₂移动到${P}_{1}^{\prime}$和${P}_{2}^{\prime}$，其中(u, v, w)分别为沿x、y、z方向因加载产生的位移分量，δx为被测物表面发生干涉的相邻两点之间的距离，即沿x方向的剪切量。(δu, δv, δw)为变形后相邻两点的位移分量。Δ为相邻两点之间相对位移所产生的相位变化，其表达式如下：

图  7  剪切散斑变形量与相位的关系^[23]

Figure  7.  Relationship between shear and phase^[23]

P₁, P₂−Two adjacent points on the surface of specimen before surface deformation; P'₁, P'₂−New positions of P₁ and P₂ on the surface of specimen after surface deformation; S−Position of coherent light source; O−Position of image plane

下载: 全尺寸图片 幻灯片

其中，λ是激光器的波长，A、B和C为相对于光源位置S (x_s，y_s，z_s)和CCD相机位置O (x₀，y₀，z₀)的位移敏感因子，其表达式如下：

当剪切方向为x方向且剪切量很小时，令δx≠0、δy=0，式(22)中相对位移近似为u, v, w沿x剪切方向的位移梯度，相位差Δ可化为沿x剪切方向的相对相位差Δ_x,方程可写为

在实际应用的光学系统中，当光源方向与观察方向的夹角为α时：A=sinα; B=0; C=1+cosα。结合本文研究的层合板试样，通过有限元分析发现试样的面内位移远小于离面位移，故忽略面内位移，式(25)可变为

当调整光源方向与物面接近法向时，光照与观测方向之间的夹角α近似为零，因此相对相位差∆_x与离面位移导数${{\partial w}}/{{\partial x}}$的关系如下：

4.3   实验结果

图8展示了在拉伸载荷作用下，试样表面干涉条纹的变化情况。从图8 (a)可以观察到，对于总厚度为1 mm的试样Ⅰ，当拉伸载荷的增量达到2 N时，试样中部的褶皱缺陷区域开始显现出干涉条纹。随着拉伸载荷从2 N增加至10 N，缺陷区域的干涉条纹密度逐渐增加。

图  8  含褶皱缺陷试样随拉伸载荷变化得到的干涉条纹图：(a) 试样I；(b) 试样II；(c) 试样III

Figure  8.  Fringe patterns of specimen during tension test: (a) Specimen Ⅰ; (b) Specimen Ⅱ; (c) Specimen Ⅲ

下载: 全尺寸图片 幻灯片

图8 (b)与8 (c)分别展示了试样厚度为3 mm时的干涉条纹变化情况。与图8 (a)中厚度为1 mm的试样Ⅰ相比，引发干涉条纹形成的拉伸载荷分别为30 N、52 N。

图8展示了在拉伸载荷作用下，试样表面干涉条纹的变化情况。从图8 (a)可以观察到，对于总厚度为1 mm的试样Ⅰ，当拉伸载荷的增量达到2 N时，试样中部的褶皱缺陷区域开始显现出干涉条纹。随着拉伸载荷从2 N增加至10 N，缺陷区域的干涉条纹密度逐渐增加。

图8 (b)与8 (c)分别展示了试样厚度为3 mm时的干涉条纹变化情况。与图8 (a)中厚度为1 mm的试样Ⅰ相比，引发干涉条纹形成的拉伸载荷分别为30 N、52 N。

图9展示了试样在拉伸载荷作用下，通过解包裹和积分过程求解离面位移的步骤。在图9 (a)中，可以看到由激光剪切散斑干涉技术捕获的干涉条纹图像，干涉条纹随着拉伸载荷增大而变得更加密集。在图9 (b)中，通过解包裹处理，消除因包裹相位产生的不连续性，得到连续的位移偏导数分布图。在图9 (c)中，考虑到试样底部是固定约束，其位移近似为零，故选取试样底部的一个点作为基准参考点，进行定积分计算，得到实际的离面位移值。

图  9  解包裹和积分过程获得离面位移值

Figure  9.  Unwrapping and integral process to obtain out-of-plane

下载: 全尺寸图片 幻灯片

随着拉伸载荷增大，图9 (b)中的位移梯度相应提高，表明试样中部的褶皱缺陷区域发生严重变形。图9 (c)中的离面位移分布图展示了褶皱缺陷区域的具体位置和位移分布，试样Ⅰ由于褶皱缺陷引起的离面位移分别是542 nm、1050 nm和1316 nm，试样Ⅱ因缺陷引起的离面位移分别是565 nm、1620 nm和2178 nm，试样Ⅲ中因缺陷引起的离面位移是728 nm、1305 nm和2226 nm。观察到试样Ⅰ的褶皱缺陷影响区域面积较大，可能由于试样较薄，褶皱缺陷在拉伸过程中进而影响了层合板材料层间的粘结程度，从而使褶皱缺陷影响区域面积增大。

5.   分析与讨论

图10展示了在拉伸载荷作用下，试样沿评估线方向的离面位移实测数据和有限元模拟结果的对比，在图10 (a)中，对于厚度为1 mm的试样，在2 N、4 N的拉伸载荷下，实验测量的离面位移与有限元模拟的结果吻合较好，误差控制在4%以内。当拉伸载荷增至6 N、8 N和10 N时，实验数据与有限元模拟结果之间的误差开始增大达到7%。

图  10  沿评估线方向实验结果与有限元结果的离面位移对比

Figure  10.  Comparison of shearography measurement and FEA along evaluation line

下载: 全尺寸图片 幻灯片

在图10 (b)中，对于厚度为3 mm的单一铺层方向的试样Ⅱ，当拉伸载荷为30 N、56 N和102 N时，实验测量得到的离面位移与有限元模拟预测的结果表现出良好的一致性，误差维持在3%以内。随着拉伸载荷进一步增加162 N、180 N时，试验数据与模拟结果的误差开始增大，从7%上升到9%。

在图10 (c)中，对于厚度为3 mm的混合铺层试样Ⅲ，当拉伸载荷为52 N、165 N时，实验测量的离面位移与有限元模拟的预测值非常接近，误差仅为1.5%，并且非缺陷区域的变形趋势也保持一致。随着拉伸载荷增加到190 N时，实验数据与模拟结果之间的误差为6.0%。

另外产生误差的原因可能是有限元模拟是在理想化条件下进行的，而实际试样尤其是混合铺层试样在制作过程中形成的褶皱形貌特征可能不符合标准的余弦函数公式，导致实验结果与模拟预测之间的误差。

6.   结 论

(1)建立了表征梯度型褶皱缺陷的细观力学模型，推导了其等效刚度矩阵，分析褶皱缺陷对层合板试样等效刚度参数的影响，结合有限元分析预测了一定载荷作用下含褶皱缺陷试样的离面位移响应。

(2)开展了激光剪切散斑干涉测量缺陷位移响应的实验，在实验中仅需施加微小的拉伸载荷，褶皱缺陷区域即可出现反映离面位移梯度的干涉条纹，且条纹随载荷增加变得更加密集。通过分析干涉条纹图，能够准确测量出褶皱缺陷引起的位移变化值。实验得到的离面位移与数值模拟预测值具有较好的一致性，不仅证实了激光剪切散斑干涉技术在检测复合材料褶皱缺陷响应方面的有效性，也表明了文中所建立的细观力学模型在预测褶皱缺陷行为方面的准确性。

(3)对于风电叶片和碳纤维全缠绕储氢气瓶等可能存在褶皱缺陷的大型结构，本文所建立的细观力学模型可有效预测褶皱缺陷响应，对实际工程结构的缺陷评估具有重要的应用前景。