Stress-strain spectral response of Eu3+/Tb3+ doped YAG-ZrO2 fiber reinforced aluminum matrix composites
-
摘要:
复合材料的失效通常来自于外加载荷的周期循环过程中应力的积累与释放,因此,应力应变监测在纤维增强铝基复合材料的寿命评估和失效预警等方面具有非常重要的影响,但是复合材料变形区的应力应变很难直观地表征,利用稀土的荧光性能对应力-应变进行检测是一种可行的检测方法,其优点是稀土离子的荧光谱线丰富大多尖锐并且容易观测,而且大多对应力敏感性高。选取Eu3+和Tb3+作为发光中心,通过静电纺丝掺杂到YAG-ZrO2复合纤维中,以下简称(YAG:Eu3+-ZrO2)cf和(YAG:Tb3+-ZrO2)cf。通过热压烧结将(YAG:Eu3+/Tb3+-ZrO2)cf和2024铝粉复合,得到(YAG:Eu3+/Tb3+-ZrO2)cf增强铝基复合材料。利用动态拉伸荧光传感对(YAG:Eu3+/Tb3+-ZrO2)cf增强铝基复合材料在动态拉伸下的发光特性进行了表征,并通过发射光谱重心波长随应力的变化研究内应力的发光传感机制。结果表明,随着拉应力的增加,Eu3+的5D0→7F1跃迁表现出有规律的红移,Tb3+的5D4→7F5跃迁表现出有规律的蓝移,并且Eu3+表现出更高的传感精度。本文为基于Eu3+和Tb3+应力传感器材料的开发提供了思路。
Abstract:Composite materials typically fail due to the accumulation and release of stress during the cyclic loading process of external loads. Therefore, stress-strain monitoring plays a crucial role in the assessment of the lifespan and failure prediction of fiber-reinforced aluminum-based composite materials. However, it is challenging to visually characterize stress and strain in the deformation zone of composite materials. Using the fluorescence properties of rare earth ions for stress-strain detection is a feasible approach. The advantage of this method lies in the rich and sharp fluorescence spectra of rare earth ions, which are easy to observe and are highly sensitive to stress. In this study, Eu3+ and Tb3+ were selected as luminescent centers and incorporated into YAG-ZrO2 composite fibers, herein after referred to as (YAG:Eu3+/Tb3+-ZrO2)cf, these were combined with 2024 aluminum powder through hot pressing and sintering to create (YAG:Eu3+/Tb3+-ZrO2)cf-reinforced aluminum-based composite materials. Dynamic tensile fluorescence sensing was used to characterize the luminescent properties of (YAG:Eu3+/Tb3+-ZrO2)cf -reinforced aluminum-based composite materials under dynamic tensile conditions. Additionally, the change in emission spectrum centroid wavelength with stress was investigated to study the luminescence sensing mechanism of internal stress. The results indicate that with increasing tensile stress, Eu3+ displays a systematic red shift in the 5D0→7F1 transition, Tb3+ exhibits a consistent blue shift in the 5D4→7F5 transition, while with Eu3+ demonstrating higher sensing accuracy. This study provides insights into the development of stress sensor materials based on Eu3+ and Tb3+.
-
纺织复合材料相比传统金属材料拥有较高的比强度与比模量,且抗冲击性优异,有着较强的可设计性,被广泛应用于航空航天领域[1]。2.5D机织复合材料是纺织复合材料的一种[2],其经纱与纬纱之间形成联锁,在厚度方向上以一定角度进行交织,使其相比二维纺织复合材料具有更好的整体性和层间抗剪切性能。而相比三维正交复合材料,2.5D复合材料具有更低廉的制造成本和更短的生产周期,并且更易于制备回转构件,例如头锥、壳体等复杂构件,具有非常广泛的应用前景,得到了国内外学者的密切关注与研究。
针对2.5D机织复合材料的工程应用和结构设计,需对其真实力学性能和破坏机制有明确的认识。力学试验是获取材料力学性能最直接有效的方法之一。Jian等[3]通过试验研究了2.5D机织复合材料在不同温度下的力学响应、损伤演化和失效行为特征,发现随着温度的升高,材料的弹性模量和强度均呈下降趋势,但纤维束的强度对温度和加载方向均不敏感。Teng等[4]采用数字图像相关法开展了2.5D机织复合材料的面内拉伸试验研究,有效表征了应变的周期性分布特征,发现平均应变的偏差随计算面积的增加而减小,提出计算区域的大小应大于单位区域大小的两倍,且当面积大小是材料单胞大小的整数倍时,可以获得更准确的结果。Yuan等[5]制备了浅交弯联、浅交直联、深交联三种2.5D机织复合材料试样,并分别进行了低速冲击试验,试验结果对比显示三者中浅交弯联结构抗冲击性最佳。Younes等[6]基于三维Tsai-Wu强度准则,针对2.5D机织复合材料代表性体积单元的损伤容限和弹性模量进行了优化设计,并根据试验结果进行了验证。
解析模型是一种可以快速预测纺织复合材料力学性能的方法,其优点在于计算效率高及弹性性能预测基本准确,且相比于试验成本极低。杨振宇等[7]采用刚度平均法和有限元法分别预测了2.5D编织结构的等效力学性能,结果显示理论解与有限元解一致性较高。Hallal等[8]提出了一种2.5D机织复合材料的改进型解析模型—“三阶段均一化(3SHM)”,并通过与有限元结果的对比证明了模型的有效性与泛用性。Byun等[9]通过确定结构的结构参数与几何参数建立了一种2.5D复合材料理论模型,使用均一化方法和张量变换来预测弹性常数与纤维体积分数,并分析了各种参数对其有效弹性性能的影响。Chen等[10]则提出了一种根据2.5D机织复合材料的微观几何构型参数和结构特性来表达弹性常数的半解析方法,并分析了几何变量对2.5D机织复合材料力学性能的影响。
作为一种三维纺织结构,2.5D机织复合材料的损伤模式相比二维复合材料更加复杂多样;单纯通过力学试验及断面显微观测等方式难以观察到材料内部的损伤,而通过CT扫描等方式则无法对渐进损伤过程进行实时观测。另一方面,由于其几何构型的复杂性,2.5D复合材料的解析模型的建模极为复杂,且在强度预测和失效行为分析方面仍具有较大的局限性。因此,对2.5D机织复合材料的渐进损伤机制的研究,需借助计算机数值模拟方法进行辅助分析。
有限元模拟是一种可获取材料内部应力和损伤分布特征的较有效的数值模拟方法,近年来被广泛应用于各种复合材料的等效力学性能预测和渐进损伤行为分析。Dong等[11]建立了一种可以反映真实纤维束轮廓及走势的2.5D机织复合材料的有限元模型,并对模型进行了验证,发现模拟与试验结果相一致。Liu等[12]提出了一种可模拟渐进失效行为的多尺度非均匀有限元建模方法,分析了2.5D机织复合材料在单轴拉伸下的力学行为,成功地预测了该材料的弹性性能、断裂强度和渐进损伤过程。Zhang等[13]通过CT扫描获取2.5D机织复合材料的几何参数,进而建立了一种细观体素网格有限元模型,准确预测了材料的弹性模量、破坏强度及失效模式。Lu等[14]建立了考虑纤维损伤、基体开裂和界面损伤的2.5D角互锁编织复合材料的细观单胞模型,准确地预测了其拉伸应力-应变响应及损伤演化规律,并发现界面损伤对拉伸强度影响很大。
关于2.5D机织复合材料损伤失效行为的已有研究,大多以拉伸为主,相比之下对其压缩力学性能及失效模式的研究还较匮乏。卢子兴等[15]开展了2.5D机织复合材料的准静态压缩试验,并建立了单层有限元模型模拟了材料的压缩失效过程,但其并未分析简化模型与真实试样的尺寸及结构差异对模拟结果造成的影响。因此本文针对2.5D机织复合材料的压缩力学性能开展了试验测试,并建立了其细观尺度完整单胞的有限元模型,结合复合材料三维失效准则和损伤演化模型,采用ABAQUS/EXPLICIT求解器及VUMAT自定义子程序,模拟了2.5D机织复合材料在经向和纬向压缩载荷下的力学响应,并对材料的压缩损伤失效机制进行了系统的总结分析。
1. 试 验
2.5D机织复合材料使用增强纤维型号为Toray T800的碳纤维,基体材料为Cytec CYCOM® PR520,其力学性能参数分别来自Xing等[16]和Jia等[17]的报道。复合材料试样及结构示意图如图1所示,其最小体积代表性单胞(RVE)结构的尺寸为13.68 mm×9.74 mm×8.54 mm,并以此尺寸切割制备压缩试样。准静态压缩试验按照标准GB/T 1448—2005[18],分别对材料单胞试样的经向和纬向进行压缩试验;压缩试验采用DNS100电子万能试验机(长春试验机研究所),经向和纬向加载速度分别为0.82 mm/min和0.58 mm/min,以此来保证0.001/s的准静态加载应变率。两种工况各重复三次,试验得到的应力-应变曲线重复性较好。因此,本文选取了其中一条代表性曲线进行后续失效行为分析和模型验证。加载过程中,使用配备有远心镜头的V711高速摄像机(美国,Vision Research Inc)进行同步拍摄,并通过DIC技术计算得到试样的真实应变,试验装置系统见图2。
2. 2.5D机织复合材料细观有限元模型
细观有限元模型通过在几何上区分复合材料纤维束和纯基体区,可以很好地反映复合材料织物的真实纺织构型;通过分别对纤维束和基体赋予不同的材料属性与失效模型,细观有限元模型非常适用于分析纺织复合材料内部的应力分布和损伤演化规律。本文建立的2.5D机织复合材料细观有限元模型是基于复合材料单胞的真实几何构型之上建立的,且为全六面体网格,不易出现应力集中与单元畸变,计算效率高;使用区分损伤形式的三维失效准则即渐进损伤模型,可以较大程度模拟材料的真实局部变形、应力-应变分布及各种损伤的起始与扩展。
2.1 2.5D机织复合材料单胞几何模型的建立
2.5D角联锁结构是2.5D机织复合材料中最具代表性的结构之一,主要包含浅交直联、浅交弯联和深交联几种结构形式。本文研究的材料属于经向增强浅交直联形式,共有6层经纱层和7层纬纱层。在此结构中,接结经纱层间形成周期性联锁交织,纬纱近似呈现直线状,与经纱共同作用,提高结构厚度方向的力学性能;填充经纱则有效提高了材料整体的纤维体积分数,使纤维的性能得以充分利用。
本文通过四个步骤建立材料单胞的细观几何模型:(1) 纤维束几何尺寸测量;(2) 纤维束截面选型;(3) 理想单胞几何模型构建;(4) 单胞几何模型修正。
本文采用计算机图像测定法[19]计算复合材料纤维束的几何尺寸参数:通过体视显微镜分别拍摄试样垂直于经纱和纬纱的两个截面,作为含有经纱和纬纱横截面的一组切片。通过在图像处理软件Photoshop 2018中设置适当的灰度区间,将不同材料区域大致区分开,再通过人工调整完善灰度分区,如图3所示,最后利用下式计算单根纤维束横截面积S:
S=L1L2×M1n×M2 (1) 其中:L1和L2分别是切面的真实长度和宽度;M1为纤维束横截面区域像素点个数;M2为切片像素点总数;n为切片所包含具有完整横截面纤维束的数目。
模型中经纱和纬纱的纤维束截面形状采用椭圆截面,其中接结经纱与填充经纱尺寸及纤维体积分数相同。椭圆长短轴的真实长度a、b测量方法与纤维束截面测量方法类似,计算式如下:
a=xL1N1 (2) b=yL2N1 (3) 其中: x、y分别是其长短轴的像素长度;N1是切面长边的像素长度。对多个纤维束椭圆截面进行计算,最终取平均值作为模型的输入几何参数。
纤维束模型横截面的几何参数见表1,在此基础上,结合编织结构的纱线走势,利用三维织物建模软件(Texgen),可建立2.5D机织复合材料单胞模型,如图4(a)所示。可以观察到,此时的几何模型尺寸与真实试样有一定的偏差,且相邻纤维束之间存在一定程度的侵入。这是由于2.5D机织复合材料的制造工艺特点,成型后织物的实际结构与理论结构会有一定的差异,主要表现在纬纱和填充经纱不再为直线形状,接结经纱的波动角会有所改变。因此,需对理想几何模型进行一些修正调整。通过在Texgen中对经纱和纬纱中节点的面外方向坐标进行修改,使单胞模型的厚度及纤维波动角与真实试样一致,最终得到的几何模型如图4(b)所示。
表 1 纤维束模型截面几何参数Table 1. Section geometric parameters of fiber tow modelWidth/mm Height/mm Section power Warp yarn 1.21 0.47 1 Weft yarn 3.15 0.67 0.8 需要说明的是,由于真实试样中纤维束之间的相互挤压导致了部分纤维束截面的非对称变形和扭转,而本文建立的几何模型无法精确反映这些几何特征。本文的几何模型修正,仍是基于理想模型的近似几何修正,并结合纤维束体积分数的调整,实现纤维总体积分数与真实试样相一致的目的。
2.2 网格划分及加载条件
基于单胞的细观几何模型,通过Texgen软件内置功能可生成三维体素有限元网格,见图5。Zhang等[13]在其关于2.5D复合材料拉伸的论文中研究了大、中、小三种尺寸的体素网格对2.5D复合材料力学性能的影响,结果表明,模拟值随网格尺寸降低而逐渐收敛,且中、小网格模拟值与试验相当接近,并基于此结论在研究2.5D复合材料压缩性能时直接使用了中等网格,得到了较好的结果。本文模型的网格相对尺寸正是基于中网格尺寸所选取的,因此认为计算结果收敛。单胞模型单元总数量为80×64×98,所有单元类型均为八节点实体缩减积分单元(C3D8R)。由于压缩试验试样为单个单胞,因此有限元模型无需使用周期性边界条件,通过建立两个刚性平台模型,定义平台和试样的接触,设置相应的加载速度模拟试验平台的匀速压缩加载。
3. 材料本构模型
3.1 基体本构
基体材料PR520是一种高韧性的环氧树脂,其压缩力学响应可以用弹塑性本构来简化表征,并添加了基于位移的失效准则;基于Goldberg等[20]的试验数据,对其弹性和塑性响应进行了定义,对其在压缩、剪切、拉伸三种不同应力三轴度下的断裂应变分别设定为0.07、0.1、0.05。
3.2 纤维束本构
3.2.1 纤维束刚度与强度
2.5D机织复合材料的纤维束由碳纤维丝束和环氧树脂组成,在不考虑纤维束波动的前提下,可将其视为横观各向同性材料。纤维束轴向为1方向,垂直于纤维轴向为2和3方向,其刚度和强度参数可以用Huang[21]的桥联模型计算得到。其中,单向复合材料强度预测公式如下[22]:
轴向拉伸强度:
F1t=(VfEf11+VmEm)Ef11σft (4) 轴向压缩强度:
F1c=(VfEf11+VmEm)Ef11σfc (5) 横向拉伸强度:
F2t=(Vf+0.4Vm)Ef22+0.6VmEm(0.4Ef22+0.6Em)Kt22σmt (6) 横向压缩强度:
F2c=(Vf+0.4Vm)Ef22+0.6VmEm(0.4Ef22+0.6Em)Kc22σmc (7) 面内剪切强度:
Fls=(Vf+αVm)Gf12+(1−α)VmGmαGf12+(1−α)Gmσms (8) 式中:Vf与Vm为纤维和基体体积分数;
Ef11 、Ef22 、Gf12 为纤维丝的纵向、横向和剪切模量;Em 为基体的弹性模量;σft 、σfc 、σmt 、σmc 、σms 分别为纤维丝的拉伸、压缩强度、基体的拉伸、压缩、剪切强度;Kt22 和Kc22 分别为基体的横向拉伸应力集中系数和横向压缩应力集中系数,α为桥联参数,一般可在0.4到0.5之间取值,本文取0.45。表2为T800/PR520复合材料经纱和纬纱的刚度和强度性能参数。表 2 T800碳纤维/PR520环氧树脂纤维束的刚度与强度性能参数Table 2. Stiffness and strength properties of T800 carbon fiber/PR520 epoxy resin fiber towsWarp yarn Weft yarn Fiber volume fraction Vf /% 81 64 Elastic modulus E11/GPa 238.96 169.26 Elastic modulus E22(E33)/GPa 14.59 9.30 Shear modulus G12(G13)/GPa 7.63 3.62 Shear modulus G23/GPa 4.97 2.93 Tensile strength F1t/MPa 4 462 3160 Compression strength F1c/MPa 1 747 1 237 Tensile strength F2t/MPa 59 58 Compression strength F2c/MPa 119 130 Shear strength Fls/MPa 107 93 3.2.2 纤维束损伤模型
本文采用的纤维束失效准则基于Hashin[23]和Hou等[24]提出的失效判据改进得到:
纤维拉伸失效
(σ11>0) :eft=(σ11F1t)2+a(σ12+σ13Fls)2⩾ (9) 纤维压缩失效
\left( {{\sigma _{{\rm{11}}}} < 0} \right) :{e_{{\rm{fc}}}} = {\left( {\frac{{{\sigma _{{\rm{11}}}}}}{{{F_{{\rm{1c}}}}}}} \right)^2} \geqslant 1 (10) 基体拉伸失效
\left( {{\sigma _{{\rm{22}}}} > 0} \right) :{e_{{\rm{mt}}}} = {\left( {\frac{{{\sigma _{{\rm{22}}}}}}{{{F_{{\rm{2t}}}}}}} \right)^2} + {\left( {\frac{{{\sigma _{{\rm{12}}}}}}{{{F_{{\rm{ls}}}}}}} \right)^2} + {\left( {\frac{{{\sigma _{{\rm{23}}}}}}{{{F_{{\rm{ts}}}}}}} \right)^2} \geqslant 1 (11) 基体压缩失效
\left( {{\sigma _{{\rm{22}}}} < 0} \right) :{e_{{\rm{mc}}}} = \frac{1}{4}{\left( {\frac{{{\sigma _{{\rm{22}}}}}}{{{F_{{\rm{ls}}}}}}} \right)^2} + \frac{{F_{{\rm{2c}}}^{\rm{2}}{\rm{ }}{\sigma _{{\rm{22}}}}}}{{4{F_{{\rm{ls}}}}^2{F_{{\rm{2c}}}}}} - {\left( {\frac{{{\sigma _{{\rm{22}}}}}}{{{F_{{\rm{2c}}}}}}} \right)^2} + {\left( {\frac{{{\sigma _{{\rm{12}}}}}}{{{F_{{\rm{ts}}}}}}} \right)^2} \geqslant 1 (12) 式中,eft、efc、emt、emc为表征材料失效的变量,当其小于1时代表材料未失效,大于等于1时则表示材料失效。在材料发生失效前,材料表现为线弹性行为。式(9)中系数a为剪切应力对纤维拉伸失效的影响因子。
一旦某种损伤满足其失效判据,继续加载则会造成材料刚度下降,Zhao等[25]和刘鹏等[26]在文章里对其进行了详细的解释。在该模型的损伤演化表达式中,通过引入特征元素长度(实体单元体积的立方根),可计算单元的断裂能GI:
{G_{\rm{I}}} = \frac{1}{2} \sigma _{{\rm{eq}}}^{\rm{f}}\varepsilon _{{\rm{eq}}}^{\rm{f}}{l_{\rm{c}}} (13) 其中:
\sigma _{{\rm{eq}}}^{\rm{f}} 和\varepsilon _{{\rm{eq}}}^{\rm{f}} 分别为等效破坏强度和等效破坏应变;lc是单元特征长度。基于断裂能和失效时的等效应力可得到相应的等效失效位移,而单元的损伤变量的演化则可基于等效位移的线性关系得到:{d_i} = \frac{{\delta _{{{i}},{\rm{eq}}}^{\rm{f}}\left( {{\delta _{i,{\rm{eq}}}} - \delta _{i,{\rm{eq}}}^0} \right)}}{{{\delta _{i,{\rm{eq}}}}\left( {\delta _{i,{\rm{eq}}}^{\rm{f}} - \delta _{i,{\rm{eq}}}^0} \right)}} (14) 其中:i=ft、fc、mt、mc;
\delta _{i,{\rm{eq}}}^{\rm{f}} 表示相应失效模式下的等效失效位移;\delta _{i,{\rm{eq}}}^{\rm{0}} 表示相应失效模式的等效损伤起始位移;\delta _{i,{\rm{eq}}}^{} 则表示相应失效模式的实时等效位移。损伤起始后,复合材料性能的渐进退化可通过含损伤变量的二阶对称张量矩阵进行描述,其中di=0表示材料完好,di=1意味材料已完全失效,详细的参数退化方法参见文献[26]。
以上包含纤维束失效判据和损伤演化的三维渐进损伤模型可以通过ABAQUS用户子程序VUMAT实现,并结合ABAQUS/EXPLICIT进行求解。
4. 结果分析与讨论
采用所建立的2.5D机织复合材料细观有限元模型,开展了其准静态压缩仿真分析,结合试验结果,对材料内部的渐进损伤行为与失效机制进行了分析与讨论。
4.1 2.5D机织复合材料压缩试验结果
图6为2.5D机织复合材料单胞试样经向和纬向的压缩破坏形貌。由图6(a)可以看出,经向压缩的主要破坏模式包括经纱的横向开裂、纤维束和界面的分层破坏、纬纱边缘部分的压溃损伤及基体开裂,其中经纱的开裂一般随机发生在经纱波动角最大的位置附近,而分层破坏在经纱和纬纱的交织区域最明显。由图6(b)可以看出,纬向压缩的主要破坏模式为纬纱的压溃、纬纱纤维束的断裂及基体开裂;裂纹首先出现在个别纬纱中,随后扩展到纯基体区域,并继续发展至相邻的纬纱中,最终形成宏观剪切裂纹。值得关注的是,经纱损伤只出现在部分经纱中,而剩余经纱则保持了较高的完整性。
4.2 2.5D机织复合材料应力-应变曲线
图7(a)和图7(b)分别为有限元模拟的2.5D机织复合材料单胞试样经向和纬向压缩应力-应变曲线与试验结果的对比。其中应力是通过加载面的总支反力除以试样加载端面积得到,应变为加载方向的位移除以试样初始长度。通过计算在0.1%~0.2%应变范围内应力-应变曲线的斜率,可以得到材料的弹性模量。破坏应力与破坏应变分别为曲线峰值点对应的应力与应变值。在线弹性阶段,并未观察到明显损伤,仿真曲线与试验曲线吻合较好。表3为弹性模量、破坏应力和破坏应变的试验与模拟值对比。
表 3 T800/PR520 2.5D机织复合材料弹性模量、破坏应力、破坏应变的仿真预测和试验测试结果对比Table 3. Comparison of numerical predicted and experimental measured elastic modulus, failure stress and failure strain of T800/PR520 2.5D woven compositeWarp direction Weft direction Elastic modulus/GPa Strength/MPa Failure strain/% Elastic modulus/GPa Strength/MPa Failure strain/% Simulation 59.3 300.0 0.50 53.1 268.8 0.52 Experiment 56.5 308.6 0.51 48.6 211.5 0.49 Error/% 4.7 2.8 2.0 8.5 21.3 5.7 结合图7和表3可见,经向压缩模拟和仿真结果吻合度很好,对弹性模量、破坏应力、破坏应变的预测误差均在5%以内;纬向压缩仿真结果误差相对较大,其中弹性模量和破坏应变的误差较低,分别为8.5%和5.7%,但是破坏强度的误差较大,超过了20%。由图7(b)可见,试验曲线在高应变区间 (0.3%~0.5%)有明显的非线性行为,而仿真曲线未能有效地模拟该非线性响应。这种非线性行为主要是由于制造加工所产生的纤维束扭转,进而可能导致纤维束的提前屈曲失效。然而,由于本文细观模型存在一定局限性,未能重构纤维束的局部扭结行为,难以精确反映其所产生的非线性应力-应变响应,造成了模拟与试验曲线的差异。总体来说,本文建立的细观单胞有限元模型具有较高的准确性,可以用于2.5D机织复合材料的失效模式和渐进损伤行为分析。
4.3 2.5D机织复合材料渐进损伤分析
作为一种纤维增强复合材料,2.5D机织复合材料中纤维束的损伤状态直接影响着复合材料的实时力学响应和最终失效。基于验证后的细观有限元模型,可对不同加载状态下纤维束的损伤模式、损伤起始和失效过程进行系统的分析。
4.3.1 经向压缩
图8为2.5D机织复合材料在0.41%和0.5%经向压缩应变下,纤维束和基体的损伤云图。其中,数值0代表没有损伤,数值1代表完全损伤。图9为复合材料出现损伤前(压缩应变= 0.39%)的应力分布云图。由图8和图9可见,填充经纱承受了较高的轴向压缩载荷,并于0.41%应变时最先出现轴向压缩损伤。这主要有两方面的原因:从几何构型和力的传递来看,接结经纱穿插于不同的纬纱层之间,具有较大的纤维束波动角,在上升和下降波动处会产生方向相反的弯矩,使经纱波动角最小的位置外侧产生明显的轴向拉伸应力,内侧产生轴向压缩应力;同时,由于经纱轴向模量远大于横向模量,因而波动较小的填充经纱在经向的模量大于接结经纱,因此轴向填充经纱起主要承力作用。
此外,材料经向压缩会引起一定程度的纬向变形,该变形会导致经纱和基体及相邻经纱之间的挤压,从而产生横向压缩应力。随着该应力的增加,最终导致在接结经纱波动角最大位置附近出现横向压缩损伤,卢子兴等[15]在其研究中也对这一现象有所描述。在图6(a)中可以很明显地观察到,多根接结经纱断裂的位置几乎都位于波动角最大处,虽然由于试样的微观缺陷与工艺误差,断面分布具有随机性,在厚度方向并不是完全一致,但这仍然很好地证明了模拟结果的有效性。另一方面,接结经纱受到了与之相邻的纬纱的横向挤压,其反作用力在纬纱表面引起较高的横向压缩应力,从而使纬纱在受挤压位置发生局部横向压缩损伤。
随着压缩载荷的提高,当应变达到0.51%时,纤维束的损伤程度有显著上升。填充经纱中的局部轴向压缩损伤基本扩展至整个纤维束横截面,直接导致了填充经纱的断裂及应力-应变曲线的卸载;接结经纱上的横向压缩损伤也有所提高,但并没有达到完全失效的程度,因此个别接结经纱可能出现断裂,但大部分仍然可以继续承载,这也是经向压缩应力-应变曲线从峰值载荷下降后仍可以保持一定载荷的原因。在达到破坏应变时,纬纱中的横向压缩损伤由表面局部向纤维束内部扩展,具体表现为纬纱发生面外翘曲及横向压溃损伤。总体来说,2.5D机织复合材料在经向准静态压缩下的渐进损伤过程较复杂,其失效是由填充经纱的轴向压缩失效、接结经纱的横向压缩失效及纬纱的横向压溃共同作用而导致的。
4.3.2 纬向压缩
图10为2.5D机织复合材料在纬向压缩载荷下纤维束和基体的渐进损伤过程。图11为纤维束在纬向压缩应变0.35%时的应力分布云图。可见,在纬向压缩条件下,与压头接触的外侧经纱表现出较高的横向压缩应力,而接结经纱中的轴向应力集中在其最大波动角附近;纬纱承受了最大比例的压缩载荷,该载荷导致的轴向压缩应力主要分布于纬纱纤维最小波动角处的受压一侧。在全局应变达到0.38%时,导致沿纬纱分布的横向压缩损伤,此时纤维束和基体几乎没有其他损伤,材料整体压缩刚度基本保持不变。
随着压缩载荷的持续增加,在应变达到0.52%时,外侧经纱的损伤逐步扩展至整根经纱,内部经纱之间由于相互挤压而发生了明显的横向压缩损伤。另一方面,纬纱承受了大部分的压缩载荷,在其纤维束波动角最大的位置分解为轴向和横向的应力分量,并以轴向压缩损伤和横向压缩损伤的混合形式表现出来,导致了纬纱的断裂和压缩应力-应变曲线的卸载。此外,纬纱的损伤随着纤维束裂纹也扩展至基体中,并贯穿相邻的纬纱,形成明显的裂纹带,这一现象与试验的断裂模式图(图6(b))基本吻合。总体来说,2.5D机织复合材料在纬向准静态压缩下的失效是由纬纱的轴向压缩失效和横向压缩失效主导,并伴随着经纱的横向压缩损伤与基体失效。
5. 结 论
针对2.5D机织复合材料单胞试样分别开展了沿经向和纬向的准静态压缩试验,获得了相应的压缩应力-应变响应与材料破坏模式。另一方面,建立了带有三维失效准则和损伤演化模型的细观单胞有限元模型,并针对2.5D机织复合材料的压缩响应进行了数值模拟,基于模拟结果讨论了其损伤分布与失效机制。得到的主要结论如下。
(1) 所建立的细观有限元模型能够准确预测2.5D机织复合材料单胞在压缩载荷下的应力-应变曲线,证明了有限元模型的有效性。
(2) 经向压缩载荷下,2.5D机织复合材料的失效主要是由填充经纱的轴向压缩失效、接结经纱的横向开裂、纤维束间的界面分层破坏及纬纱的横向压溃共同作用而导致的。
(3) 纬向压缩载荷下,2.5D机织复合材料的失效主要是由纬纱的压溃和纬纱纤维束的断裂主导,并伴随有经纱的横向压缩失效与基体开裂的发生。
-
图 3 ((a), (b)) (YAG:Tb3+/Eu3+-ZrO2)cf的SEM图像;((c), (d))基体和(YAG:Tb3+/Eu3+-ZrO2)cf/Al复合材料断口形貌图;((e), (f)) (YAG:Tb3+/Eu3+-ZrO2)cf的EDS能谱图
Figure 3. ((a), (b)) SEM images of (YAG:Tb3+/Eu3+-ZrO2)cf; ((c), (d)) Fracture morphology of matrix and (YAG:Tb3+/Eu3+-ZrO2)cf aluminum matrix composite; ((e), (f)) EDS spectra of (YAG:Tb3+/Eu3+-ZrO2)cf
图 5 ((a), (b)) (YAG:Eu3+-ZrO2)cf/Al复合材料激发和发射光谱;((c), (d)) (YAG:Tb3+-ZrO2)cf/Al复合材料激发和发射光谱
Figure 5. ((a), (b)) Excitation and emission spectra of (YAG:Eu3+-ZrO2)cf/Al composite; ((c), (d)) Excitation and emission spectra of (YAG:Tb3+-ZrO2)cf/Al composite
λem—Emission wavelength; λex—Excitation wavelength
表 1 2024铝合金粉的化学成分
Table 1 Chemical composition of 2024 Al alloy powder
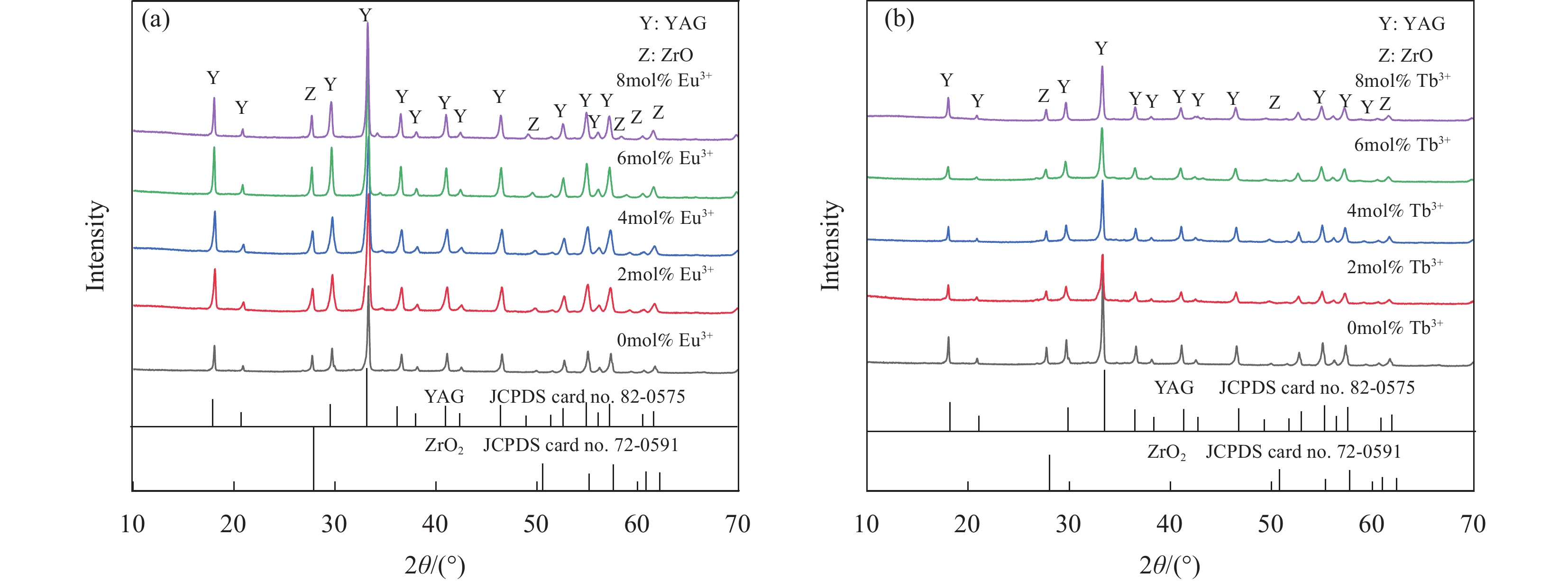
Element Cu Mg Fe Si Mn Zn Others Al Content/wt% 4.5 1.4 0.5 0.5 0.48 0.25 0.25 Balance 表 2 未掺杂Eu3+的YAG与8mol% Eu3+掺杂YAG的XRD数据
Table 2 XRD data of YAG undoped with Eu3+ and YAG doped with 8mol% Eu3+
Sample Crystal plane parameter (420) (521) (532) 2θ/(°) d/nm 2θ/(°) d/nm 2θ/(°) d/nm YAG 33.416 1.2021 41.249 1.2024 46.489 1.2024 YAG:Eu3+ (8mol%) 33.357 1.2048 41.159 1.2045 46.409 1.2037 Notes: 2θ—Incident angle of X-ray diffraction of the material; d—Crystal plane spacing. 表 3 Al基(111)晶面的弹性常数和泊松比
Table 3 Elastic constants and Poisson's ratios of Al-based (111) planes
Phase Crystal plane ν E Al (111) 0.19035 44.465 Notes: ν and E are the elastic constants and Poisson's ratios of the Al (111) plane. 表 4 (YAG:Eu3+-ZrO2)cf/Al复合材料内应力计算结果
Table 4 Calculation results of internal stress of (YAG:Eu3+-ZrO2)cf/Al composites
Tensile stress/MPa 2θ/(°) Β/(°) b/(°) β/rad εm/10−3 σ/MPa 50 41.2608 0.7577 0.096 0.0115 7.6689 340.9976 100 41.0534 0.7660 0.096 0.0117 7.8079 347.1783 150 40.9941 0.7739 0.096 0.0118 7.9125 351.8293 200 40.3919 0.7810 0.097 0.0119 8.1134 360.4623 250 40.3433 0.7993 0.097 0.0122 8.3414 370.9003 Notes: 2θ and B are the incident angles and half-width of (YAG:Eu3+ -ZrO2)cf/Al composite X-ray diffraction; b is the width of the instrument slit; β is the result of deducting the slit width; εm and σ are the microscopic strain and internal stress of the composite, respectively. -
[1] 黄文益, 江鸿杰, 王一博, 等. 6061铝颗粒层增强7075铝基复合材料的微观结构及阻尼性能[J]. 复合材料学报, 2021, 38(12): 4220-4227. HUANG Wenyi, JIANG Hongjie, WANG Yibo, et al. Microstructure and damping capacity of 7075 aluminum matrix composite enhanced by 6061 aluminum particles layer[J]. Acta Materiae Compositae Sinica, 2021, 38(12): 4220-4227(in Chinese).
[2] LI J C, CHEN X W, HUANG F L. FEM analysis on the deformation and failure of fiber reinforced metallic glass matrix composite[J]. Materials Science and Engineering: A, 2016, 652: 145-166.
[3] CHEN M, XING S L, LIU H B, et al. Determination of surface mechanical property and residual stress stability for shotpeened SAF2507 duplex stainless steel by in situ X-ray diffraction stress analysis[J]. Journal of Materials Research and Technology, 2020, 9(4): 7644-7654. DOI: 10.1016/j.jmrt.2020.05.028
[4] REZENDE A B, FONSECA S T, MINICUCCI D J, et al. Residual stress characterization by X-ray diffraction and correlation with hardness in a class D railroad wheel[J]. Journal of Materials Engineering and Performance, 2020, 29: 6223-6227. DOI: 10.1007/s11665-020-05097-x
[5] SANTOS D, MACHADO M A, MONTEIRO J, et al. Non-destructive inspection of high temperature piping combining ultrasound and eddy current testing[J]. Sensors, 2023, 23(6): 3348. DOI: 10.3390/s23063348
[6] CIECIELEG K, KECIK K, SKOCZYLAS A, et al. Non-destructive detection of real defects in polymer composites by ultrasonic testing and recurrence analysis[J]. Materials, 2022, 15(20): 7335. DOI: 10.3390/ma15207335
[7] XU Y, XU K, WANG H, et al. Research progress on magnetic memory nondestructive testing[J]. Journal of Magnetism and Magnetic Materials, 2023, 565: 170245. DOI: 10.1016/j.jmmm.2022.170245
[8] REBELO K J, HOFMANN M, GAN W M, et al. Non-destructive neutron surface residual stress analysis[J]. Journal of Nondestructive Evaluation, 2019, 38: 1-6. DOI: 10.1007/s10921-018-0529-6
[9] HUANG Y, SHANG J, REN L. Finite element simulation in laser ultrasound for non-destructive testing of aluminum defect materials[J]. Journal of Applied Optics, 2019, 40(1): 150-156.
[10] NAZAMI G R, PANDA B K, SAHOO S. Finite element simulation of residual stress in direct metal laser sintering of AlSi10Mg built part: Effect of laser spot overlapping[J]. Materials Today: Proceedings, 2021, 41: 445-450. DOI: 10.1016/j.matpr.2020.09.844
[11] JEON M H, CHO H J, SIM C H, et al. Experimental and numerical approach for predicting global buckling load of pressurized unstiffened cylindrical shells using vibration correlation technique[J]. Composite Structures, 2023, 305: 116460. DOI: 10.1016/j.compstruct.2022.116460
[12] REID A, MARSHALL M, MARTINZE I, et al. Measurement of strain evolution in overloaded roller bearings using time-of-flight neutron diffraction[J]. Materials & Design, 2020, 190: 108571.
[13] LIMA C R C, DOSTA S, GUILEMANY J M, et al. The application of photoluminescence piezospectroscopy for residual stresses measurement in thermally sprayed TBCs[J]. Surface and Coatings Technology, 2017, 318: 147-156. DOI: 10.1016/j.surfcoat.2016.07.084
[14] 岳俊昕, 张巍巍. 荧光方法测量应力[J]. 失效分析与预防, 2012, 7(1): 63-68. YUE Junxi, ZHANG Weiwei. Fluorescence method for measuring stress[J]. Failure Analysis and Prevention, 2012, 7(1): 63-68(in Chinese).
[15] QIAO J, MU X, QI L, et al. Construction of fluorescent polymeric nano-thermometers for intracellular temperature imaging: A review[J]. Biosensors and Bioelectronics, 2016, 85: 403-413. DOI: 10.1016/j.bios.2016.04.070
[16] WITTLIN A, PRZYBYLIŃSKA H, BERKOWSKI M, et al. Ambient and high pressure spectroscopy of Ce3+ doped yttrium gallium garnet[J]. Optical Materials Express, 2015, 5(8): 1868-1880. DOI: 10.1364/OME.5.001868
[17] WANG X, WU R T, ATKINSON A. Characterisation of residual stress and interface degradation in TBCs by photo-luminescence piezo-spectroscopy[J]. Surface and Coatings Technology, 2010, 204(15): 2472-2482. DOI: 10.1016/j.surfcoat.2010.01.035
[18] ZHANG J, CAI G, WANG W, et al. Tuning of emission by Eu3+ concentration in a pyrophosphate: The effect of local symmetry[J]. Inorganic Chemistry, 2019, 59(4): 2241-2247.
[19] BARZOWSKA J, SZCZODROWSKI K, KROŚNICKI M, et al. Influence of high pressure on Sr2SiO4:Eu2+ luminescence[J]. Optical Materials, 2012, 34(12): 2095-2100. DOI: 10.1016/j.optmat.2012.05.020
[20] DONG X, ZHANG H, YANG Y, et al. High pressure luminescence of InNbO4:Eu3+: A crystal-field analysis[J]. Journal of Molecular Structure, 2021, 1229: 129593. DOI: 10.1016/j.molstruc.2020.129593
[21] ZHAO S, YAN P, LI M, et al. Residual stress evolution of 8YSZ:Eu coating during thermal cycling studied by Eu3+ photoluminescence piezo-spectroscopy[J]. Journal of Alloys and Compounds, 2022, 913: 165292. DOI: 10.1016/j.jallcom.2022.165292
[22] WEI Y, WU Z, JIA Y, et al. Piezoelectrically-induced stress-luminescence phenomenon in CaAl2O4:Eu2+[J]. Journal of Alloys and Compounds, 2015, 646: 86-89. DOI: 10.1016/j.jallcom.2015.05.159
[23] ZHANG W, CHENG Y, LIN H, et al. Ratiometric mechanoluminescence in LiSrPO4:Eu2+/Eu3+ for stress sensing: Dopant concentration dependent sensitivity[J]. Materials Research Bulletin, 2023, 163: 112219. DOI: 10.1016/j.materresbull.2023.112219
[24] QIU L, MAO J, ZHAO Z, et al. Temperature sensing properties of self-crystalized Ba2LaF7:Tb3+ glass ceramics[J]. Ceramics International, 2021, 47(5): 6244-6250. DOI: 10.1016/j.ceramint.2020.10.202
[25] HE L, MA C, DONG Q Z, et al. Nondestructive stress detection of aluminum matrix composites based on luminescence characteristics of Eu3+ ions[J]. Journal of Materials Engineering and Performance, 2023, 32(5): 2445-2454. DOI: 10.1007/s11665-022-07269-3
[26] CHENG X, YUAN C, SU L, et al. Effects of pressure on the emission of CaWO4:Eu3+ phosphor[J]. Optical Materials, 2014, 37: 214-217. DOI: 10.1016/j.optmat.2014.05.030
[27] ZHANG W W, QIN C F, SHI J L, et al. Shear stress response and fluorescence piezo-spectroscopic properties of SrSiAlN3: Eu2+/epoxy composite[J]. Journal of Luminescence, 2019, 206: 240-243. DOI: 10.1016/j.jlumin.2018.10.049
[28] HE L, PAN L, LI W, et al. Spectral response characteristics of Eu3+ doped YAG-Al2O3 composite nanofibers reinforced aluminum matrix composites[J]. Optical Materials, 2020, 104: 109845. DOI: 10.1016/j.optmat.2020.109845
[29] QIN C F, ZHANG W, SHI J, et al. Fluorescence compressive stress sensing with SrSiAlN3:Eu2+/resin composites[J]. Chinese Journal of Sensors and Actuators, 2019, 32(1): 57-61.
[30] 黄继武. 多晶材料X射线衍射: 实验原理, 方法与应用[M]. 北京: 冶金工业出版社, 2012. HUANG Jiwu. X-ray diffraction of polycrystalline materials: Experimental principles, methods and applications[M]. Beijing: Metallurgical Industry Press, 2012(in Chinese).
[31] 中华人民共和国国家质量监督检验检疫总局. 纳米材料晶粒尺寸及微观应变的测定X射线衍射线宽化法: GB/T 23413—2009[S]. 北京: 中国标准出版社, 2009. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Determination of grain size and microstrain of nanomaterials X-ray diffraction line widening method: GB/T 23413—2009[S]. Beijing: Standards Press of China, 2009(in Chinese).
[32] LI L, MIYAMOTO G, ZHANG Y, et al. Quantitative analysis of microstructure evolution, stress partitioning and thermodynamics in the dynamic transformation of Fe-14Ni alloy[J]. Journal of Materials Science & Technology, 2024, 184: 221-234.
[33] GUPTA S S, VAN HUIS M A, DIJKSTRA M, et al. Depth dependence of vacancy formation energy at (100), (110), and (111) Al surfaces: A first-principles study[J]. Physical Review B, 2016, 93(8): 085432. DOI: 10.1103/PhysRevB.93.085432
-
期刊类型引用(7)
1. 唐宇哲,傅梅珍,刘恒. UHPC-NC组合梁抗弯承载能力影响因素分析. 公路工程. 2025(01): 41-49+120 .  百度学术
百度学术
2. 金清平,陈川,黄桥连,高永红,雷万雄,尹少龙. 超高性能混凝土中纤维作用效应研究综述. 水利与建筑工程学报. 2024(02): 55-65 .  百度学术
百度学术
3. 乔险涛,喻鹏,陈喜健,周佳乐,张连杰,李健朋. 非晶合金纤维和钢纤维单/混掺增强混凝土开裂及断裂性能研究. 硅酸盐通报. 2024(06): 2137-2148 .  百度学术
百度学术
4. 王冲,刘国磊,何国志,李公成,马秋峰,刘树龙,李庆国. 全尾砂固废基充填材料胶凝特性与纤维强化效应研究. 矿业研究与开发. 2024(06): 112-120 .  百度学术
百度学术
5. 刘志峰,卢涛,包杰,王祥雨,黄相又. 无粘结预应力UHPC梁剪切性能试验研究. 世界桥梁. 2024(05): 69-75 .  百度学术
百度学术
6. 梁林,王秋维,史庆轩. 粗骨料UHPC单轴拉伸性能及损伤本构模型. 建筑材料学报. 2024(09): 806-815 .  百度学术
百度学术
7. 郭旭,张品乐,胡静,查叶铭,陶忠. 钢-PVA混杂纤维水泥基力学性能与工程经济评价. 材料导报. 2024(S2): 179-184 .  百度学术
百度学术
其他类型引用(4)
-
其他相关附件
-
目的
铝基复合材料是一种用途广泛的基础工业材料,尤其应用于汽车零构件与航空航天器骨架中。由于外加载荷的周期循环过程中应力的积累与释放导致复合材料的失效,从而引起复合材料寿命的降低,因此开发一种有效检测材料内部应力的无损检测技术是很有必要的。本文选取(YAG-ZrO)作为基质材料,Eu、Tb作为发光中心,使纤维在增强材料力学性能的同时,赋予材料一种新的内应力检测的方法。
方法选取了Eu和Tb作为发光中心,使用静电纺丝技术制备了不同掺杂浓度的Eu和Tb复合YAG-ZrO复合纤维(简称(YAG:Eu-ZrO)和(YAG:Tb-ZrO)),使纤维具备了稀土的荧光性能。使用热压烧结技术将YAG-ZrO复合纤维用于增强2024铝合金(简称(YAG:Eu/Tb-ZrO)/Al复合材料),使复合材料在增强的同时具备了稀土荧光性能。利用SEM观察了复合荧光纤维的表面形貌、纤维直径大小,复合材料中纤维分布以及拉伸断裂后试样的断口形貌。通过分析材料的荧光性能与复合材料所受外应力得到了应力传感方程,并分析了荧光特征对应力传感的响应机制。通过原位拉伸XRD实验得到了(YAG:Eu-ZrO)/Al复合材料在拉伸过程中内应力与所受外应力之间的规律,与应力传感方程结合完成了对材料内应力的检测。
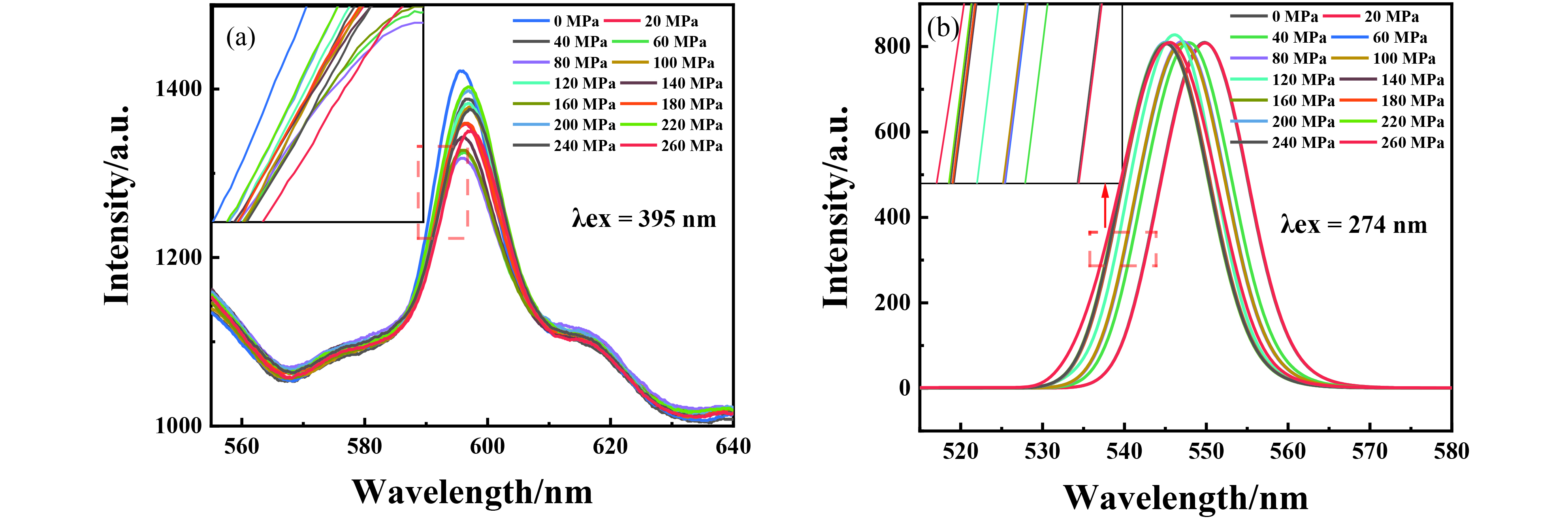
结果不同掺杂浓度的(YAG:Eu/Tb-ZrO)结晶性能良好,表面光滑,分散均匀。少量的纤维复合可以提高(YAG-ZrO)/Al复合材料的力学性能,当纤维掺杂量为3 wt%时,其致密度与硬度达到最大分别为98.3%和123.8 HV但当纤维掺杂量增加之后,纤维会发生团聚现象降低了复合材料的各项力学性能。Eu和Tb掺杂浓度不同的(YAG:Eu/Tb-ZrO)都具备良好的光学性能。其中Tb最佳掺杂量为6 mol%,Eu最佳掺杂量为4 mol%。并且(YAG:Tb-ZrO)/Al可以被波长为274nm的紫外光源激发发射出波长为544 nm(D-F跃迁)的绿光,(YAG:Eu-ZrO)/Al可以被波长为395 nm的紫外光源激发可以发射出波长为592nm(D-F跃迁)的橙红色光。(YAG:Eu-ZrO)/Al复合材料和(YAG:Tb-ZrO)/Al复合材料的发射光谱都对于拉应力具有敏感特性,通过分析重心波长与拉应力之间的关系,发现(YAG:Eu-ZrO)/Al复合材料的重心波长表现出了更高的拉伸应力传感精度,应力传感方程为λ=594.90616+0.01439σ,灵敏度为0.01439nm/MPa(等效于频移系数0.4058cm/MPa),与标准的荧光压谱材料红宝石的频移系数相比(0.0055 cm/MPa),灵敏度提高了约80倍。将得到的材料内应力随拉伸应力的变化规律,规律方程为σ=332.34674+0.14618σ,与(YAG:Eu-ZrO)/Al复合材料的重心波长传感方程λ=594.90616+0.01439σ相结合可得到内应力检测方程σ=10.1584λ-5710.9738。
结论通过静电纺丝制备的(YAG:Eu/Tb-ZrO)具有良好的结晶性。少量的纳米发光纤维添加到2024铝合金中可以提高其力学性能,并且具有良好的发光性能,这一功能为后续通过稀土荧光压谱效应来检测复合材料的内应力提供了可能性。随着拉应力的增加,Eu的D→F跃迁表现出有规律的红移,Tb的D-F跃迁表现出有规律的蓝移,并且Eu表现出更高的传感精度,通过将材料内应力随拉应力变化规律方程和复合材料重心波长传感方程结合,得到内部应力检测方程,即可通过材料的荧光性能检测拉伸过程中材料的内部应力。
-
铝基复合材料是一种用途广泛的基础工业材料,尤其应用于汽车零构件与航空航天器骨架中。由于外加载荷的周期循环过程中应力的积累与释放导致复合材料的失效,从而引起复合材料寿命的降低,因此有必要对其进行应力-应变监测。
本文选取了Eu3+和Tb3+作为发光中心,通过静电纺丝制备(YAG:Eu3+/Tb3+-ZrO2)cf,利用热压烧结技术制备了(YAG:Eu3+/Tb3+-ZrO2)cf/Al复合材料,使纤维具备了稀土的荧光性能,并将其用作(YAG:Eu3+/Tb3+-ZrO2)cf增强铝基复合材料内应力的传感探针。通过原位拉伸XRD实验得到了(YAG:Eu3+-ZrO2)cf/Al 复合材料在拉伸过程中内应力与所受外应力之间的规律,与应力传感方程结合完成了对材料内应力的检测。结果表明(1)少量的纤维复合可以提高(YAG:Eu3+/Tb3+-ZrO2)cf/Al复合材料的力学性能,当纤维掺杂量为3 wt%时,其致密度与硬度达到最大分别为98.3%和123.8 HV,(2)(YAG:Eu3+-ZrO2)cf/Al复合材料和(YAG:Tb3+-ZrO2)cf/Al复合材料的发射光谱都对于拉应力具有敏感特性,通过分析重心波长与拉应力之间的关系,发现(YAG:Eu3+-ZrO2)cf/Al复合材料的重心波长表现出了更高的拉伸应力传感精度,应力传感方程为λ=594.90616+0.01439σ,灵敏度为0.01439nm/MPa(等 效于频移系数0.4058 cm-1/MPa),与标准的荧光压谱材料红宝石的频移系数相比(0.0055 cm-1/MPa),灵敏度提高了约80倍。(3)通过分析原位拉伸过程中(YAG:Eu3+-ZrO2)cf/Al复合材料XRD图谱,得到材料内应力随拉伸应力的变化规律,规律方程为σIS=332.34674+0.14618σ,将此方程与(YAG:Eu3+-ZrO2)cf/Al复合材料的重心波长传感方程λ=594.90616+0.01439σ相结合可得到内应力检测方程σIS=10.1584λ-5710.9738。
归一化复合材料动态拉伸情况下的发射光谱变化(a) (YAG:Eu3+-ZrO2)cf/Al (b) (YAG:Tb3+-ZrO2)cf/Al





 下载:
下载: