Numerical study of the effect of compression-shear load ratio on the failure behavior of CFRP laminated plate
-
摘要: 碳纤维增强(Carbon fiber reinforced polymer, CFRP)复合材料层合板是飞行器中的常用结构。面内压缩和剪切载荷下，层合板结构失效同时受屈曲和材料损伤影响，失效形式复杂多变。本文建立了考虑就地效应、横向应力对剪切强度的影响以及剪切非线性的渐进损伤失效分析方法，开展压剪试验对分析方法进行了验证，并在此基础上研究了不同压缩和剪切载荷比下CFRP层合板的失效行为。研究表明，压剪载荷比低时，层合板先发生材料的初始损伤，然后达到最大载荷；压剪载荷比高时，直接发生屈曲，同时达到最大载荷，不发生材料损伤；载荷比处于两者之间时，先发生材料损伤，然后屈曲并且达到最大载荷。此外，压剪载荷比的变化还会对层合板的压缩承载能力、剪切承载能力、以及结构达到最大载荷时的损伤扩展程度产生影响。Abstract: Carbon fiber reinforced polymer (CFRP) composite laminated plates are commonly used structures in the aircraft. Under in-plane compression-shear loads, the failure of laminated plates is affected by both buckling and material damage, and the failure forms are complex and variable. In this paper, a progressive damage analysis method was established considering the in-situ effect, the influence of transverse stress on shear strength, and the shear nonlinearity of the material. The compression-shear test was carried out to validate the proposed method. Based on the validated method, the failure behavior of the CFRP plates with different compression-shear load ratios was investigated based on the finite element model. It is shown that when the compression-shear loads ratio is low, the initial material damage of the plate occurs first, and then the maximum load is reached. When the load ratio is high, buckling occurs directly, and at the same time, the maximum load is reached without material damage. When the load ratio is in between, material damage occurs first, then buckling occurs and maximum load is reached. In addition, the change of compression-shear load ratio will also have an effect on the compression and shear load bearing capacity of the plate, and the damage extension degree of the plate when the maximum load is reached.
-
作为典型的高性能轻质材料，碳纤维增强(Carbon fiber reinforced polymer, CFRP)复合材料被广泛地应用到了飞机、火箭和卫星等飞行器的各类结构中[1-4]。层合板是复合材料在飞行器结构中应用的主要形式之一[5,6]，通常承受面内的拉伸/压缩和剪切载荷[7]。拉伸载荷下结构不发生失稳，失效形式相对简单。但压缩和剪切载荷下结构失效同时受屈曲和材料损伤影响，失效形式更为复杂多变。且大多数飞行器结构在服役时需承受多轴组合应力。传统的设计和分析方法中通常将单轴试验数据代入简单的等效模型来解决多轴问题[8,9]。采用这种方法预测得到的失效载荷精度低，为了确保结构安全，需采用较大的安全系数，不可避免地导致设计结果过于保守。为了进一步提升结构效率，需要研究复合材料层合板结构在压缩和剪切组合载荷下的高精度失效预测方法和失效行为。
国内外学者分别基于试验和计算分析方法开展了研究工作。试验方面，受限于试验装置的复杂性和高昂成本[10-17]，研究较少。Peters[14]开展了板的压剪屈曲性能测试试验，采用测试结果验证了各向同性和正交各向异性板压剪屈曲理论曲线的适用性。Serra等[15]开展了含缺口CFRP多向层合板的拉剪失效试验，测试得到了层合板的拉剪失效包络线。此外，部分学者针对由复合材料层合板组成的夹层结构[16,17]和加筋结构[18,19]开展了平面内压剪失效性能测试试验，研究了结构在压剪载荷下的失效载荷和失效模式。
计算分析方面，刘鹏洋[20]基于解析方法对比了压剪载荷下复合材料方板和加筋板的线性屈曲载荷和屈曲模态，并基于二维有限元方法对比了两种结构的压剪失效载荷和失效模式。该项研究中仅考虑了一种比例的压缩和剪切组合载荷工况；且由于缺乏试验数据支持，其数值模拟方法的建立主要以工程经验为依据。陈庆远等[21,22]基于有限条法研究了载荷比对复合材料层合板屈曲后刚度的影响。李政和梁珂[23]基于二维有限元方法，研究了复合材料层合板屈曲载荷和屈曲前/后刚度随载荷比的变化。本文作者也在前期工作中基于解析方法开展了压剪载荷下复合材料层合板的线性屈曲和首层失效分析，研究了材料体系、结构尺寸和铺层角度对结构理论刚度和强度的影响[24,25]。但上述研究均未考虑材料损伤后的性能退化，以及结构刚度和材料损伤相互作用的复杂过程，不能反映层合板在压剪组合载荷作用下的承载特性。
为探究复合材料层合板结构在压缩和剪切组合载荷下的失效行为，本文建立了压剪载荷下CFRP层合板的渐进损伤失效分析方法，并通过试验对所建立方法进行了验证，之后基于数值模拟研究了不同压缩和剪切载荷比例下层合板的失效行为。
1. CFRP层合板压剪失效预测方法
本节在现有失效准则和材料刚度退化模型的基础上对材料强度和刚度参数进行了修正，提出了改进的渐进损伤分析方法，用于压剪载荷下的CFRP层合板失效预测。
1.1 失效准则
Lessard等提出的三维Hashin失效准则能够区分纤维拉伸/压缩、基体拉伸/压缩、纤基剪切以及层间拉伸/压缩7种失效模式，预测准确度高且计算量适中，常用于CFRP复合材料结构失效分析[26,27]。在该失效准则的基础上，本文通过考虑就地强度和横向应力对剪切强度的影响对准则中的强度参数进行了修正。
1.1.1 多向层合板的就地效应
复合材料的性能参数测试一般采用单向铺层试验件[28,29]。但现有研究表明，不同铺层方向的相邻层合板对基体开裂有一定的阻碍作用[30]，使得多向层合板与单向层合板中的子层合板表现出了不同的横向拉伸强度和剪切强度[31-33]。这种基体强度提升现象被称为就地效应。
考虑这一因素，本文在失效准则中采用就地强度代替基体相关强度。对于较薄单层(厚度小于0.8 mm[34])，其就地强度计算公式如下[35]：
YTis-e=√8GICπtΛo22 (1a) YTis-o=2√GICπtΛo22 (1b) SLis-e=√8GIICG12πt (1c) SLis-o=√4GIICG12πt (1d) STis-e=√8GIICG12πt (1e) STis-o=√8GIICG12πt (1f) 其中，YTis-e、YTis-o、SLis-e、SLis-o、STis-e和STis-o分别为中间层和表层的横向拉伸、纵向剪切(对应于材料坐标系的S12和S13)和横向剪切(对应于材料坐标系的S23)就地强度，GIC和GIIC分别为层板的I型和II型断裂韧度，Λo22为裂纹张量在y方向的非零分量：
Λo22=2(1E2−ν221E1) (2) 1.1.2 横向应力对剪切强度的影响
研究表明，横向应力会影响断裂面的张开程度：横向压缩应力对剪切失效的发生有一定的阻碍作用；横向拉伸应力会导致剪切失效加剧[34-37]。Lessard等的失效准则中仅对各应力与对应强度的比值进行叠加，无法准确预测这一现象。
因此，为表征横向应力对剪切强度的影响，在就地强度的基础上引入剪切强度修正式[35]：
SL=SLis−ηLσn (3a) ST=STis−ηTσn (3b) 其中，SL和ST分别为材料的实际纵向和横向剪切强度；σn为垂直于裂纹面的应力，在材料2方向和3方向相关项中分别近似取σ2和σ3[34]；ηL为材料的纵向摩擦系数，通常由试验测试获得；ηT为材料的横向摩擦系数:
ηT=−1tan2θf0 (4) θf0为纯横向压缩载荷下测得的断裂面角度。
1.1.3 考虑强度修正的三维Hashin失效准则
综合考虑就地效应和横向载荷对剪切失效的影响，本文对Lessard等提出的三维Hashin失效准则进行改进，提出考虑强度修正的三维Hashin失效准则：
纤维拉伸失效(FT)(σ11⩾：
\left(\frac{\sigma_{1}}{X_{\mathrm{T}}}\right)^{2}+\left(\frac{\tau_{12}}{S_{\mathrm{is}}^{\mathrm{L}}-\eta_{\mathrm{L}} \sigma_{2}}\right)^{2}+\left(\frac{\tau_{13}}{S_{\mathrm{is}}^{\mathrm{L}}-\eta_{\mathrm{L}} \sigma_{3}}\right)^{2} \geqslant 1 (5a) 纤维压缩失效(FC) ({\sigma _{11}} < 0) ：
-\frac{\sigma_{1}}{X_{{\rm{C}}}} \geqslant 1 (5b) 基体拉伸失效(MT) \left(\sigma_{22} \geqslant 0\right) ：
{\left( {\frac{{{\sigma _2}}}{{Y_{{\rm{is}}}^{\rm{T}}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{S_{{\rm{is}}}^{\rm{L}} - {\eta _{\rm{L}}}{\sigma _2}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{S_{{\rm{is}}}^{\rm{T}} - {\eta _{\rm{T}}}{\sigma _2}}}} \right)^2} \geqslant 1 (5c) 基体压缩失效(MC) \left(\sigma_{22}< 0\right) ：
{\left( {\frac{{{\sigma _2}}}{{{Y_{\rm{C}}}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{S_{{\rm{is}}}^{\rm{L}} - {\eta _{\rm{L}}}{\sigma _2}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{S_{{\rm{is}}}^{\rm{T}} - {\eta _{\rm{T}}}{\sigma _2}}}} \right)^2} \geqslant 1 (5d) 纤维基体剪切失效(FM) \left(\sigma_{11}< 0\right) ：
{\left( {\frac{{{\sigma _1}}}{{{X_{\rm{C}}}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{S_{{\rm{is}}}^{\rm{L}} - {\eta _{\rm{L}}}{\sigma _2}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{S_{{\rm{is}}}^{\rm{L}} - {\eta _{\rm{L}}}{\sigma _3}}}} \right)^2} \geqslant 1 (5e) 层间拉伸失效(IT) \left(\sigma_{3 \mathrm{3}} \geqslant 0\right) ：
{\left( {\frac{{{\sigma _3}}}{{Z_{{\rm{is}}}^{\rm{T}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{S_{{\rm{is}}}^{\rm{L}} - {\eta _{\rm{L}}}{\sigma _3}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{S_{{\rm{is}}}^{\rm{T}} - {\eta _{\rm{T}}}{\sigma _3}}}} \right)^2} \geqslant 1 (5f) 层间压缩失效(IC) \left(\sigma_{3 \mathrm{3}}>0\right) ：
{\left( {\frac{{{\sigma _3}}}{{{Z_{\rm{C}}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{S_{{\rm{is}}}^{\rm{L}} - {\eta _{\rm{L}}}{\sigma _3}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{S_{{\rm{is}}}^{\rm{T}} - {\eta _{\rm{T}}}{\sigma _3}}}} \right)^2} \geqslant 1 (5g) 其中，子层板分为中间层和表层， Y_{{\text{is}}}^{\text{T}} 、 S_{{\text{is}}}^{\text{L}} 和 S_{{\text{is}}}^{\text{T}} 按照其所在层的类型进行取值，根据横向各向同性假设和工程经验取 Z_{{\text{is}}}^{\text{T}} = Y_{{\text{is}}}^{\text{T}} 。
1.2 材料刚度退化模型
1.2.1 剪切非线性模型
对纤维增强复合材料的研究表明，受基体性能影响的材料刚度具有一定程度的非线性，其中纵向剪切应力-应变关系的非线性尤为显著[38.39]。因此，本文采用Hahn和Tsai提出的非线性模型[38]表征材料的纵向剪切非线性：
\gamma_{i j}=\frac{\tau_{1 j}}{G_{1 j}}+\beta\left(\tau_{1 j}\right)^{3} \quad(j=2,3) (6) 其中， \beta 为材料的剪切非线性系数。通过欧拉方法对公式(6)进行处理，可得到有限元计算中剪切刚度随载荷步 {n_{\text{L}}} 变化的表达式[40]:
\tau _{1j}^{\left( {{n_{\rm{L}}} + 1} \right)} = \left( {1 - {d_{1j}}} \right){G_{1j}}\gamma _{1j}^{\left( {{n_{\rm{L}}} + 1} \right)}\quad (j = 2,3) (7a) {d_{1j}} = \frac{{3\beta {G_{1j}}{{\left( {\tau _{1j}^{\left( {{n_{\rm{L}}}} \right)}} \right)}^2} - 2\beta {{\left( {\tau _{1j}^{\left( {{n_{\rm{L}}}} \right)}} \right)}^3}/\gamma _{1j}^{\left( {{n_{\rm{L}}}} \right)}}}{{1 + 3\beta {G_{1j}}{{\left( {\tau _{1j}^{\left( {{n_{\rm{L}}}} \right)}} \right)}^2}}}(j = 2,3) (7b) 1.2.2 损伤演化模型
考虑所建立失效准则中的七种失效模式，本文选用Zhang等[41,42]提出的材料损伤演化模型对材料损伤后的刚度性能进行表征。该准则以细观力学模型为基础，针对每种失效模式提供了不同的损伤演化方案：
纤维拉伸失效 ({\sigma _{11}} < 0) ：
E_{1}^{{\rm{d}}}=D E_{1} (8a) D=\left(1-c_{\mathrm{f}}\right) E_{\mathrm{m}}/ E_{1} (8b) 纤维压缩失效 ({\sigma _{11}} < 0) ：
E_{1}^{{\rm{d}}}=D E_{1} (8c) D \approx \frac{E_{2}}{E_{1}} (8d) 基体拉伸失效 \left(\sigma_{22} \geqslant 0\right) ：
\begin{split} &E_{2}^{\rm{d}}=D E_{2}, G_{12}^{\rm{d}}=D G_{12}, G_{23}^{\rm{d}}=D G_{23}, \\ &\qquad v_{12}^{\rm{d}}=D v_{12}, v_{23}^{\rm{d}}=D v_{23} \end{split} (8e) D=0 (8f) 基体压缩失效 \left(\sigma_{22}< 0\right) ：
\begin{split} &E_{2}^{\rm{d}}=\left\{\begin{array}{cc} D E_{2} & \left(\sigma_{1} \geqslant 0 \text { 且 } \sigma_{3} \geqslant 0\right) \\ E_{2} & \left(\sigma_{1}<0 \text { 的 } \sigma_{3}<0\right) \end{array}\right. \\ &G_{12}^{\mathrm{d}}=D G_{12} , \sigma_{23}^{\mathrm{d}}=D G_{23 } , v_{12}^{\mathrm{d}}=D_{12} , v_{23}^{\mathrm{d}}=D v_{23} \end{split} (8g) D=0 (8h) 纤维基体剪切失效 \left(\sigma_{11}< 0\right) ：
\begin{split} &G_{12}^{\rm{d}}=D G_{12}, G_{13}^{\rm{d}}=D G_{13}, G_{23}^{\rm{d}}=D G_{23}, \\ &\qquad v_{12}^{\rm{d}}=D v_{12}, v_{13}^{\rm{d}}=D v_{13}, v_{23}^{\rm{d}}=D v_{23} \end{split} (8i) D=\left[\frac{1-\sqrt{c_{\mathrm{f}}}}{1-\sqrt{c_{\mathrm{f}}}+c_{\mathrm{f}}}\right] \frac{G_{\mathrm{m}}}{G_{12}} (8j) 层间拉伸失效 \left(\sigma_{3 \mathrm{3}} \geqslant 0\right) ：
\begin{array}{c} E_{3}^{\rm{d}}=D E_{3}, G_{13}^{\rm{d}}=D G_{13}, G_{23}^{\rm{d}}=D G_{23}, \\ v_{13}^{\rm{d}}=D v_{13}, v_{23}^{\rm{d}}=D v_{23} \end{array} (8k) D=0 (8l) 层间压缩失效 \left(\sigma_{3 \mathrm{3}}>0\right) ：
\begin{split} &E_{3}^{\mathrm{d}}=\left\{\begin{array}{ll} D E_{3} & \left(\sigma_{1} \geqslant 0 \text { 且 } \sigma_{2} \geqslant 0\right) \\ E_{3} & \left(\sigma_{1}<0 \text { 或 } \sigma_{2}<0\right) \end{array}\right. \\ &G_{13}^{\mathrm{d}}=D G_{13}, G_{23}^{\mathrm{d}}=D G_{23}, v_{13}^{\mathrm{d}}=D v_{13}, v_{23}^{\mathrm{d}}=D v_{23} \end{split} (8m) D \approx \frac{E_{2}}{E_{1}} (8n) 式中， {c_{\text{f}}} 为材料中纤维体积分数， {E_{\text{m}}} 为基体材料拉伸模量， {G_{\text{m}}} 为基体材料剪切模量。
2. 方法验证
2.1 层合板压剪试验
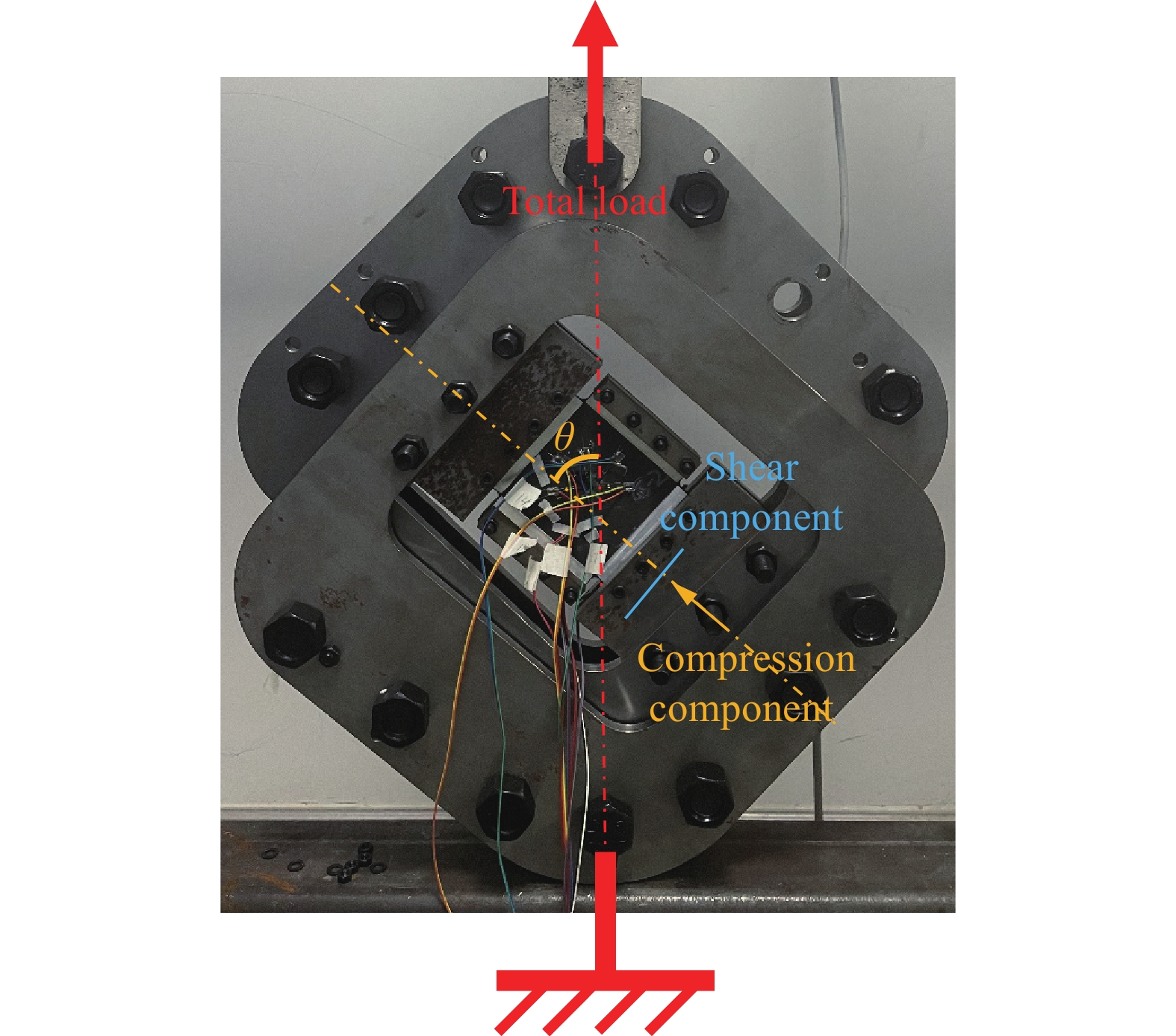
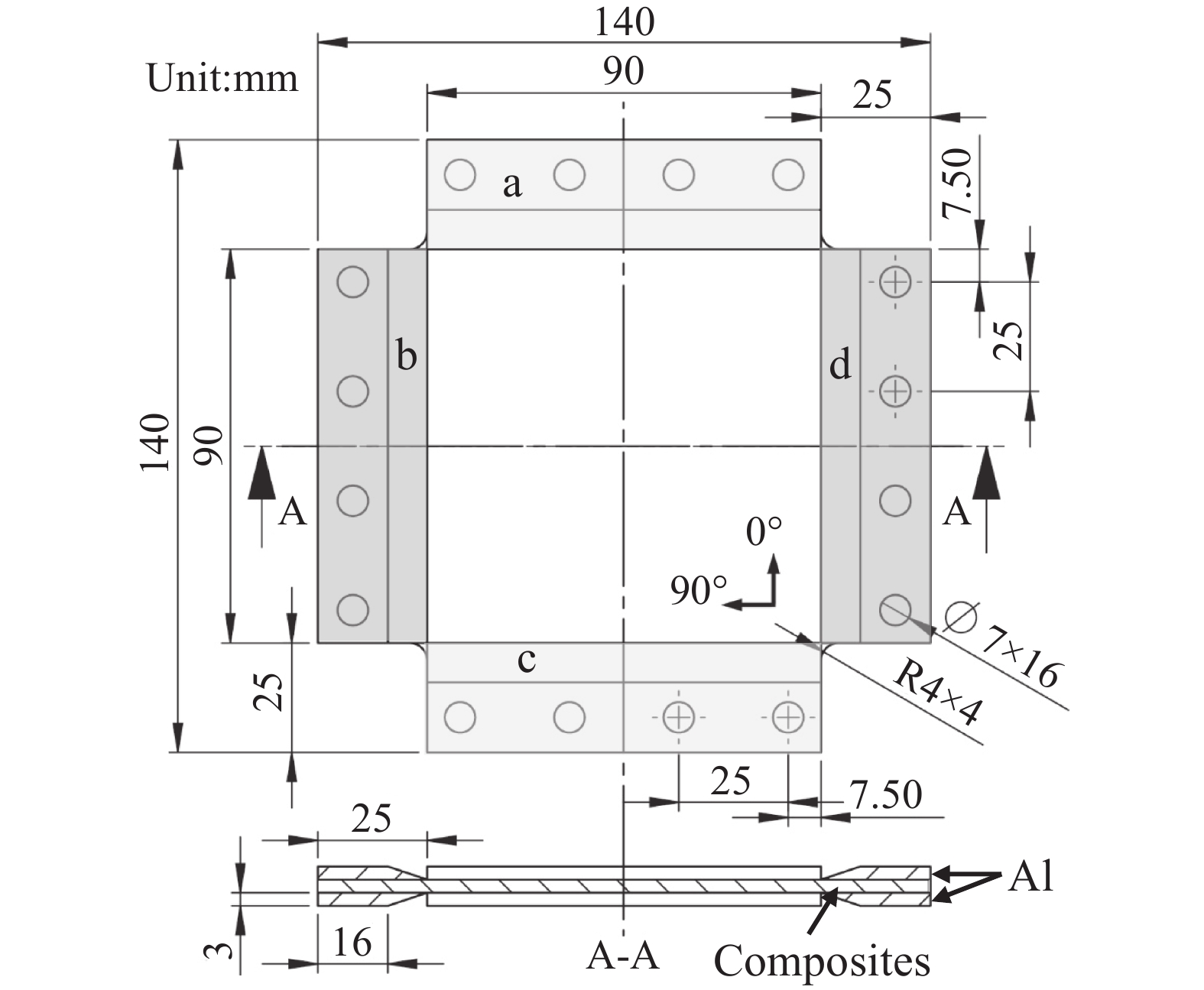
试验件尺寸如图1所示，铺层顺序为[±45]s，总厚度为0.52 mm。试验件四边伸长区域(灰色区域)均采用粘贴铝板的方式加强，其中区域a和区域c与夹具相连，区域b和区域d自由。压剪试验夹具如图2所示。定义加载方向与试验件铺层0°方向的夹角为加载方向角 \theta ，试验工况中 \theta =45°。本文研究中剪切载荷为正，因此加载方向与−45°纤维方向相同。所施加的总载荷分别通过4个螺栓(区域a、c各有4个螺栓孔)传递到试验件上，分解为对板的压缩载荷和剪切载荷。夹角 \theta =45°时，压缩载荷和剪切载荷的比值 \eta = {N_x}/{N_{xy}} =1。试验件材料为光威复合材料股份有限公司的T300级预浸料USN15000/EPW，材料性能如表1所示，其中z方向相关参数根据横观各向同性假设和工程经验与y方向取相同值。
表 1 USN15000/EPW材料参数Table 1. Properties of the USN15000/EPW materialE1/GPa E2/GPa v12 G12/GPa 129.96 9.62 0.35 4.99 XT/MPa XC/MPa YT/MPa YC/MPa S12/MPa 1564 997 44 180 77 GIC/(N/mm) GIIC/(N/mm) cf Em/GPa Gm/GPa 129.96 9.62 70% 3.52 1.2 Notes：E1, E2, v12, and G12 are the stiffness properties of the material; XT, XC, YT, YC, and S12 are the strength properties of the material; GIC and GIIC are the fracture toughness of the material; cf is the fiber volume fraction; Em and Gm are the stiffness properties of the matrix. 2.2 层合板渐进损伤模型
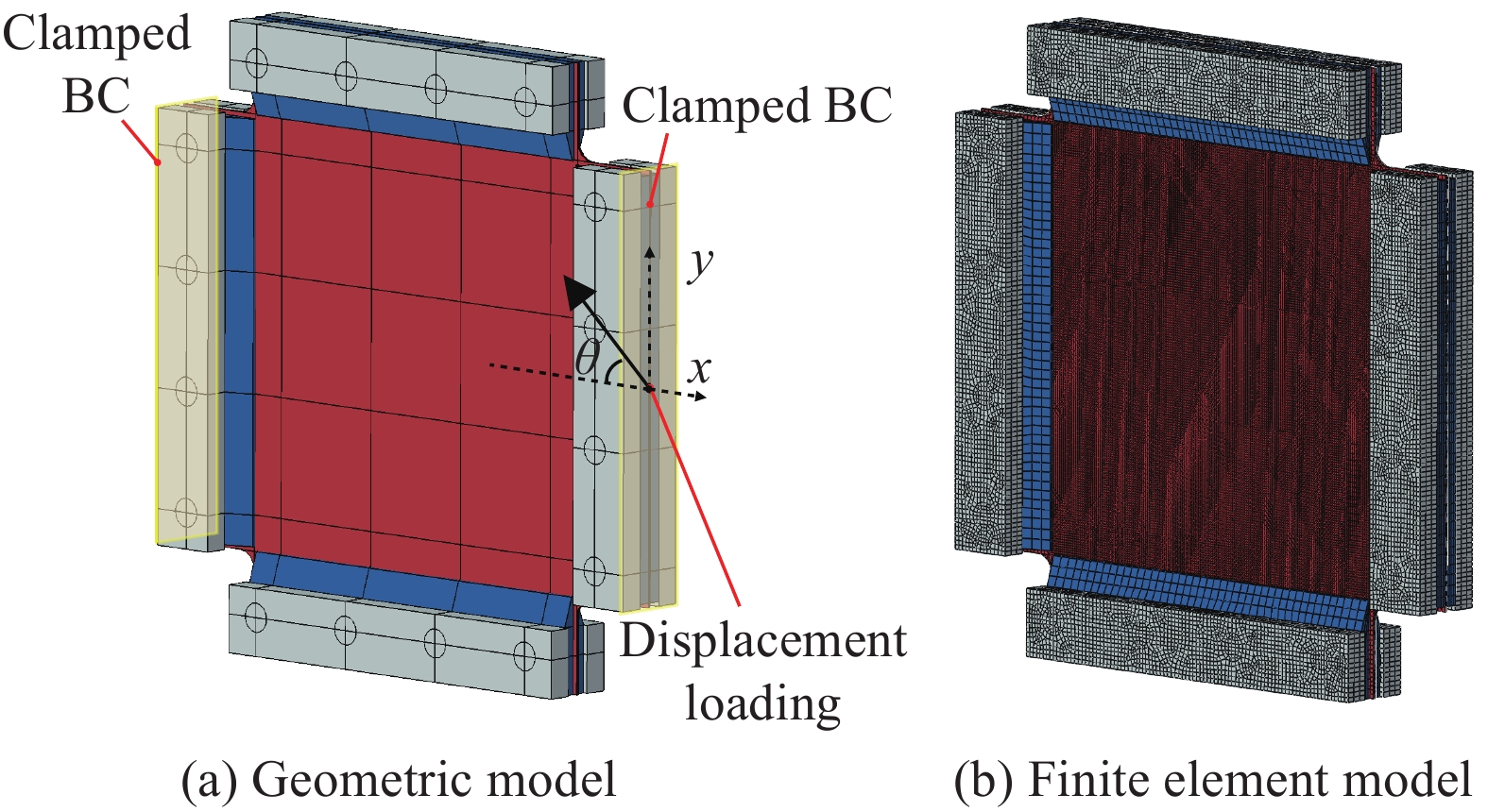
分别采用本文中所建立的渐进损伤方法和原有渐进损伤方法(不考虑就地效应和横向载荷对剪切失效的影响以及剪切刚度的非线性)，在ABAQUS®有限元软件中对试验过程进行了数值模拟。所建立的试验件几何模型和有限元模型如图3所示。模型中材料参数如表1所示，其中本文方法中的就地强度可根据公式(1)计算得到。
本文方法的失效准则中， {\eta _{\text{L}}} 参考文献中T300纤维增强树脂复合材料，取值0.082[43]； {\eta _{\text{T}}} 通过 {\theta _{{\text{f0}}}} 计算得到，碳纤维增强复合材料的 {\theta _{{\text{f0}}}} 一般为53°[34]。
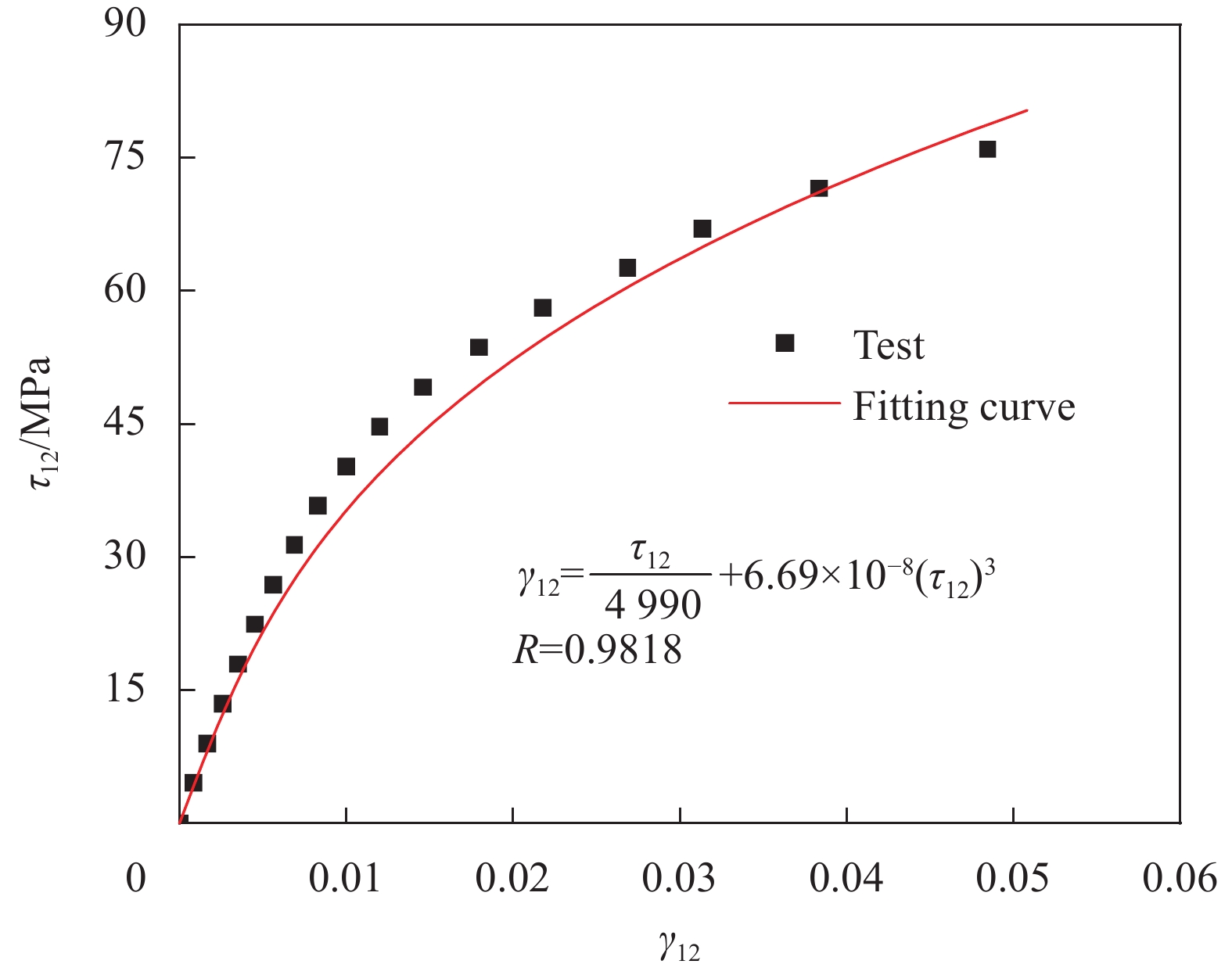
本文方法的材料刚度退化模型中，为确定 \beta 的取值，按照ASTM D3518/D3518 M试验标准[44]开展层合板的面内剪切性能测试试验，得到了层合板试验件的剪切应力-应变数据。采用公式(6)对试验数据进行拟合，拟合得到 \beta = 6.69 \times {10^{ - 8}} ，相关性系数为0.982。拟合曲线与试验结果的对比如图4所示。由图4可看出，试验测得的应力和应变之间存在明显的非线性关系，拟合曲线与试验数据吻合较好。
![]()
图 4 碳纤维增强(CFRP)层合板剪切非线性系数拟合Figure 4. Shear nonlinear coefficient fitting of the carbon fiber reinforced polymer (CFRP) plates将表1数据代入公式(8)中计算得到纤维拉伸损伤时 D = 0.008 ，纤维压缩失效时 D = 0.074 ，纤基剪切失效时 D = 0.046 ，其余情况下 D = 0 。
为了考虑制造公差缺陷等对非线性分析结果的影响，将层合板一阶屈曲模态作为初始缺陷加入模型，缺陷最大位移为层合板厚度的1%(推荐取0.5%-1%)[45]。求解时采用弧长法，施加力载荷，开展层合板试验件的渐进损伤失效分析。失效准则和材料刚度退化模型均通过UMAT子程序参与到计算中。
2.3 验证结果
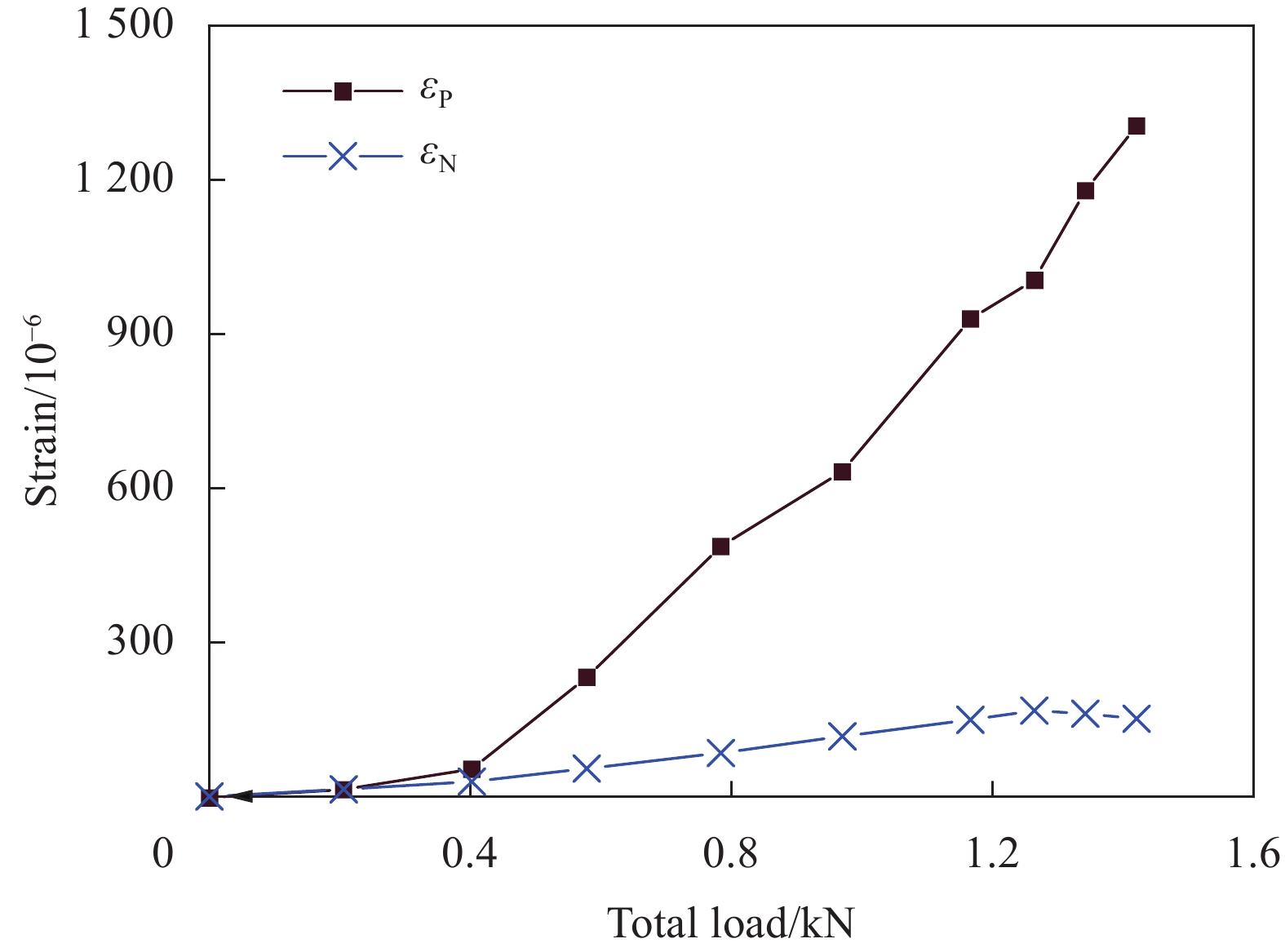
试验测试得到了层合板正反面中心点沿加载方向的应变-载荷曲线如图5所示。图5中，在206 N时正反面应变分别为13和14，差值为−1，相对误差为−7.14%；在402 N时正反面应变分别为53和29，差值为24，相对误差为82.76%，差值和相对误差均显著增大，说明402 N时出现了应变分叉现象，结构在达到该载荷时已经发生屈曲[46]。在
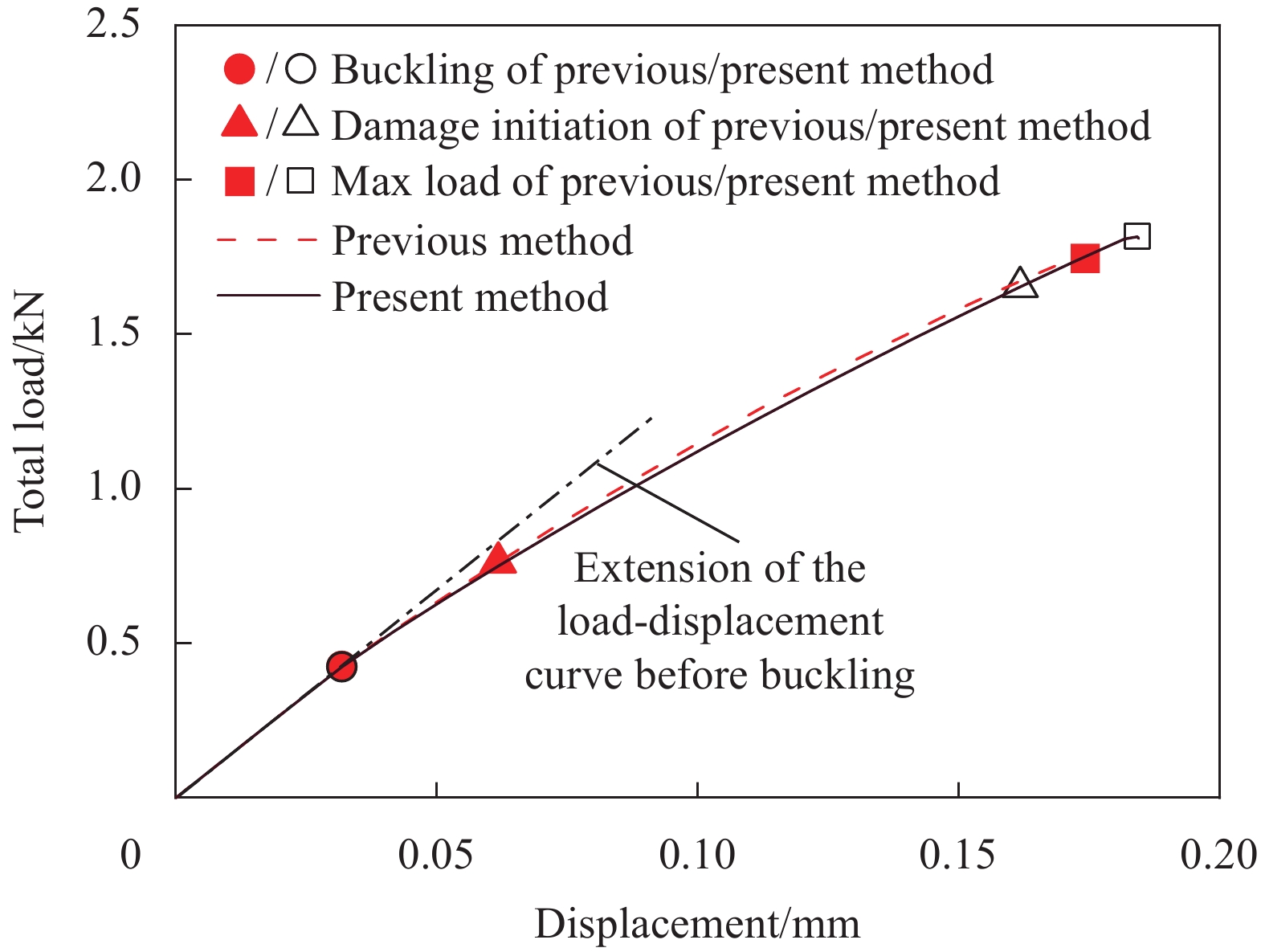
1509 N时首次听到材料损坏的声音，表明结构在该载荷附近发生初始损伤[47]。加载到1627 N时载荷突降，此时达到最大载荷。![]()
图 5 试验件正反面中心点应变-载荷曲线Figure 5. The strain-load curves at the center point of the front and back faces of the specimen分别对两种渐进损伤方法的计算结果进行数据处理和分析。当层板正反面中心点沿加载方向的应变分叉时，认为结构屈曲。读取试验件在每个载荷步下的7种损伤判断式计算结果及其中的最大值，当最大值增大至1时认为结构发生初始损伤。由此得到两种方法计算出的屈曲载荷、初始损伤载荷和最大载荷及各计算结果与试验结果的误差如表2所示。此外，对数值模拟结果中的总载荷和加载点沿加载方向的位移数据进行提取，得到两种方法的载荷位移曲线如图6所示。
表 2 数值模拟方法验证与对比Table 2. Validation and comparison of two numerical simulation methodsMethod Buckling Initial damage Max load Load/N Err/% Load/N Err/% Load/N Err/% Test 402 − 1509 − 1627 − Previous 425 5.72 761 −49.57 1792 10.14 Present 424 5.47 1653 9.54 1816 11.62 ![]()
图 6 数值模拟得到的试验件载荷位移曲线Figure 6. The load-displacement curve obtained by numerical simulation of the specimen由表2可见，本文方法与原有方法对屈曲载荷的预测值基本一致，误差分别为5.72%和5.47%。两种方法对最大载荷的预测结果相近，误差分别为10.14%和11.62%。但两种方法对初始损伤载荷的预测值差异较大，误差分别为-49.57%和9.54%，这是由于考虑就地效应和横向载荷对剪切失效的影响能够更准确地预测结构的初始损伤行为[37]。此外，由图6可见，两种方法预测得到的试验件刚度基本一致。综合各方面考虑，本文方法能够更准确地模拟层板试验件在压剪载荷下的承载行为。
由图6中载荷位移曲线的对比可以看出，屈曲前两种方法预测得到的载荷位移曲线基本重合。图中点划线为屈曲前载荷位移曲线的延长线。对比点划线与屈曲后的载荷位移曲线的斜率可知，屈曲发生后，结构刚度明显降低，载荷位移关系由线性转变为非线性。
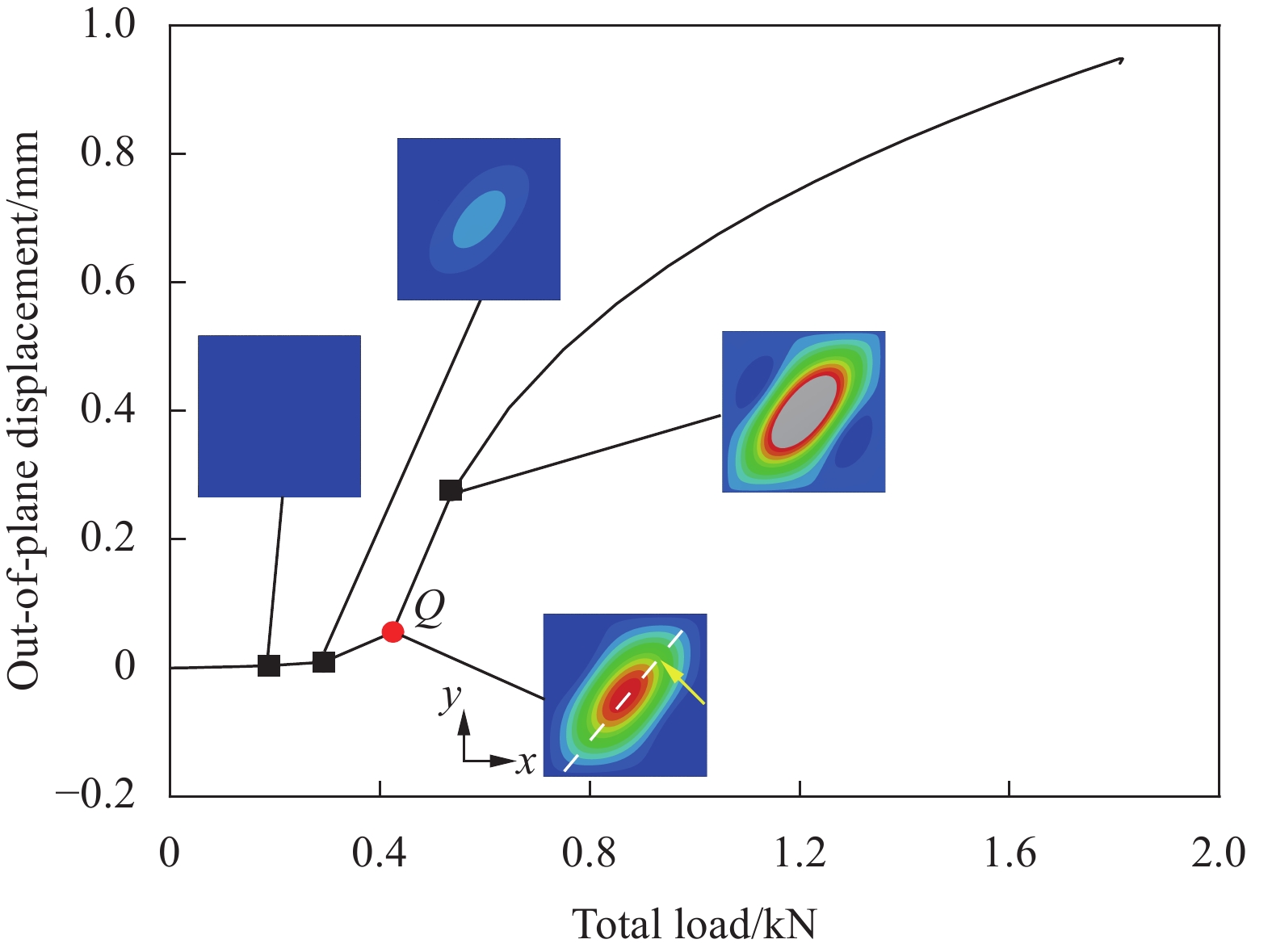
结构屈曲的一个明显特征是面外位移发生突变。图7给出了本文方法预测得到的试验件中心点面外位移-载荷曲线和试验件中心区域的面外位移云图。可见，载荷逐渐增加，在开始时面外位移很小；载荷增加到Q点时，面外位移突然增加，Q点也是计算结果中的应变分叉点；载荷超过Q点之后面外位移快速增加。对比4张位移云图可见，屈曲模态形状基本不变，仅是幅值增加。屈曲模态在x和y方向均只有1个半波，位移云图表现出椭圆形，椭圆长轴方向(白色虚线)与加载方向(黄色箭头)近似垂直。
![]()
图 7 试验件结构中心点的面外位移-载荷曲线Figure 7. The Out-of-plane displacement-load curve at the center of the structure the specimen本文方法预测得到试验件最大载荷时的失效云图与试验中观测到的最终失效形态的对比如图8所示。由图8可看出，计算结果的失效位置(黑色区域)与试验结果一致。最终失效时，计算得到的失效模式包括纤维压缩、基体拉伸、基体压缩、纤基剪切、层间拉伸和压缩。试验中最终失效部位层合板整体断裂，纤维和基体均发生破坏。上述对比结果表明，本文所建立的渐进损伤分析方法能够准确预测CFRP层合板在压剪载荷下的失效行为。
![]()
图 8 数值模拟结果与试验结果中的失效位置对比Figure 8. Comparison of the numerical and experimental failure locations3. 压剪载荷比例对层合板失效的影响
3.1 研究方案
基于本文提出的渐进损伤分析方法，对不同压剪载荷比下层合板的失效行为开展了数值模拟研究。考虑到蒙皮常见厚度范围，给定层合板总厚度为1 mm，铺层顺序为[±45]2 s，其他结构几何尺寸不变。载荷比取值分别为 \eta =0，0.1，0.5，1，2，10和∞共7种工况，对应的加载方向角 \theta =90°，84°，63°，45°，27°，6°和0°。
3.2 载荷比对层合板失效的影响规律
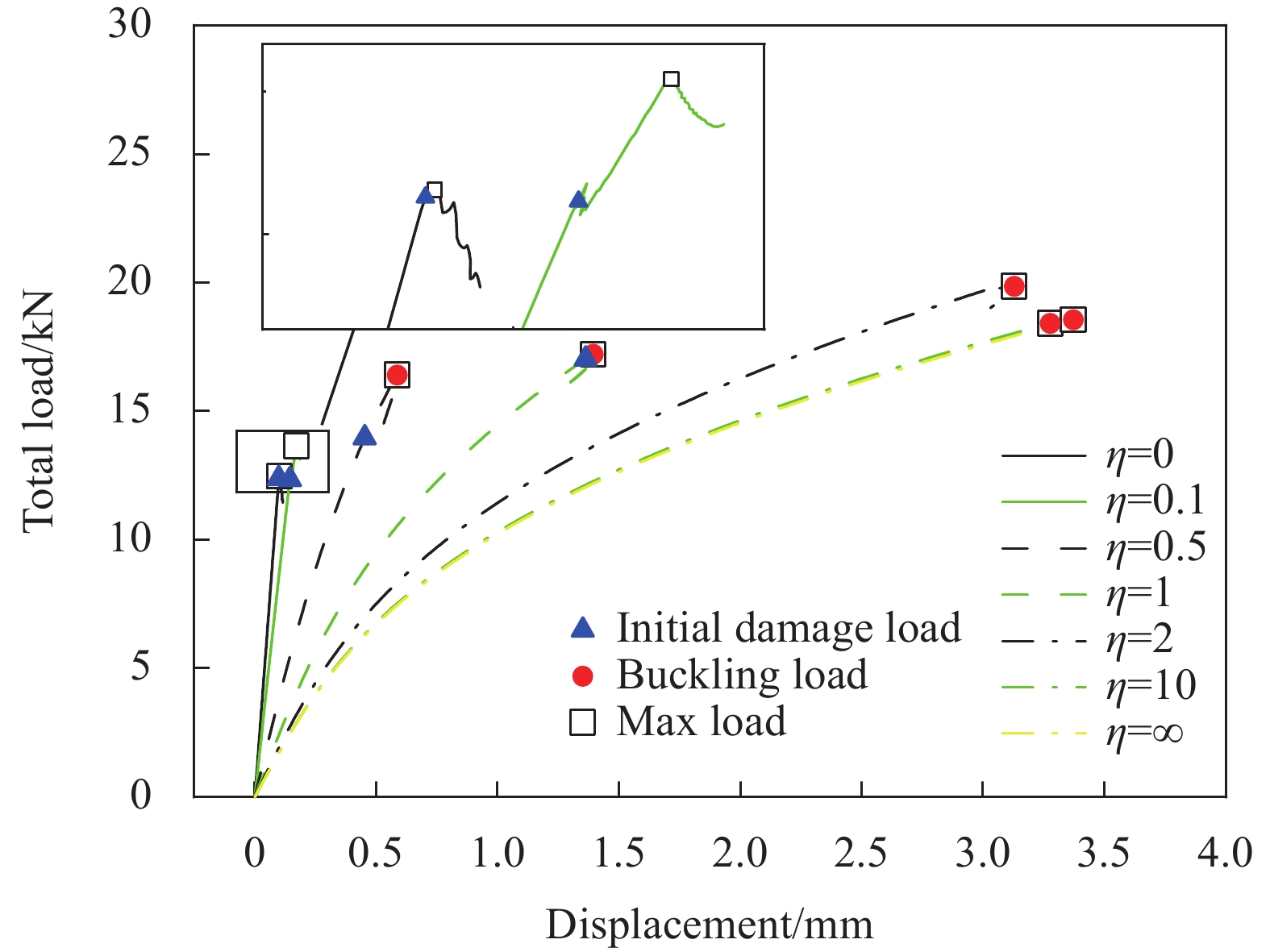
计算得到7种工况下本文结构的载荷位移曲线如图9所示。图中给出了各工况下本文结构的初始损伤载荷、屈曲载荷和最大载荷。
![]()
图 9 各载荷比下的CFRP层合板载荷位移曲线Figure 9. Load-displacement curves at various load ratios of CFRP platesη is the ratio of the compression load to the shear load由图9可知，不同载荷比下本文结构发生初始损伤、屈曲和最终失效的顺序不同。可以分成三类：1)材料失效导致破坏，2)材料失效和屈曲均发生后达到最大载荷，以及3)屈曲时达到最大载荷。当 \eta =0和0.1时，属于第1类，本文结构先发生初始损伤，损伤后仍能继续加载，直至达到最大载荷，承载过程中不发生屈曲；其中， \eta =0时初始损伤载荷与最大载荷非常接近， \eta =0.1时两者差别变大。当 \eta =0.5和1时，属于第2类，本文结构先发生初始损伤，继续加载后发生屈曲并同时达到最大载荷，结构进入后屈曲状态；其中， \eta =0.5时初始损伤载荷与最大载荷相差较大， \eta =1时两者接近。当 \eta =2，10和∞时，属于第3类，本文结构在发生屈曲同时达到最大载荷进入后屈曲状态，这种情况下不发生材料损伤。
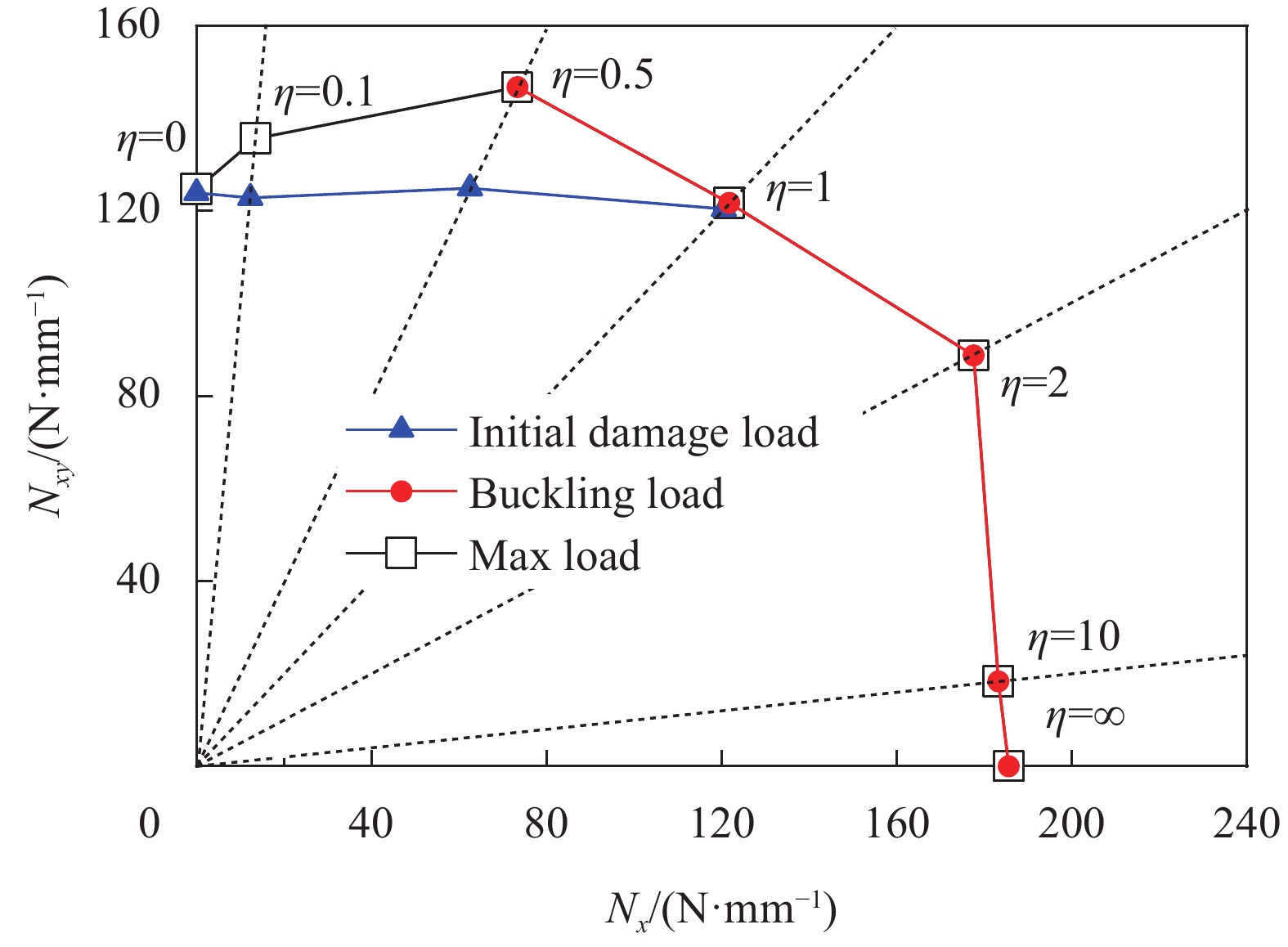
以压缩分量为横坐标，剪切分量为纵坐标，得到压缩剪切载荷平面内本文结构初始损伤载荷、屈曲载荷和最大载荷随载荷比的变化曲线如图10所示。
![]()
图 10 CFRP层合板各载荷随压剪载荷比的变化Figure 10. Variation of each load with the compression-shear load ratio of CFRP platesη is the ratio of the compression load to the shear load; Nx is the compression component of the loads; Nxy is the shear component of the loads由图10可知，当 \eta ≤1时，随着载荷比增大，初始损伤载荷的压缩分量单调递增，剪切分量基本不变；当 \eta ≥2时，初始损伤不发生。
由图10可知，当 \eta ≤0.1时，屈曲不发生；当 \eta ≥0.5时，随着载荷比增大，屈曲载荷的压缩分量单调递增，在 \eta ≥2后基本保持不变；剪切分量单调递减。
由图10可知，随着载荷比增大，最大载荷的压缩分量单调递增，在 \eta ≥2后基本保持不变；剪切分量在 \eta ≤0.5时增大，之后减小。
各工况在初始损伤和最大载荷时的损伤类型及载荷比如表3所示。
表 3 各工况下层合板失效扩展情况和载荷比Table 3. Damage initiation and extension each loading conditionsη Damage type Initial damage load/
Maximum loadInitial damage Ultimate failure 0 FC, FM FC, FM 0.994 0.1 FC, FM FC, MC, FM 0.903 0.5 FC, FM FC, MC, FM, IT 0.846 1 FC, FM FC, MC, FM 0.990 2 Undamaged Undamaged − 10 Undamaged Undamaged − ∞ Undamaged Undamaged − Notes: η is the ratio of the compression load to the shear load. 由表3可知， \eta ≤1时各工况初始损伤类型均为纤维压缩和纤基剪切，但最大载荷时的损伤类型不同。随着载荷比增大，初始损伤载荷与最大载荷的比值先减小后增大，最大载荷时所发生损伤种类的数量是先增多后减少。产生这一现象的主要原因是损伤后承载空间更大时，损伤扩展更充分，所诱发的损伤种类也更丰富。
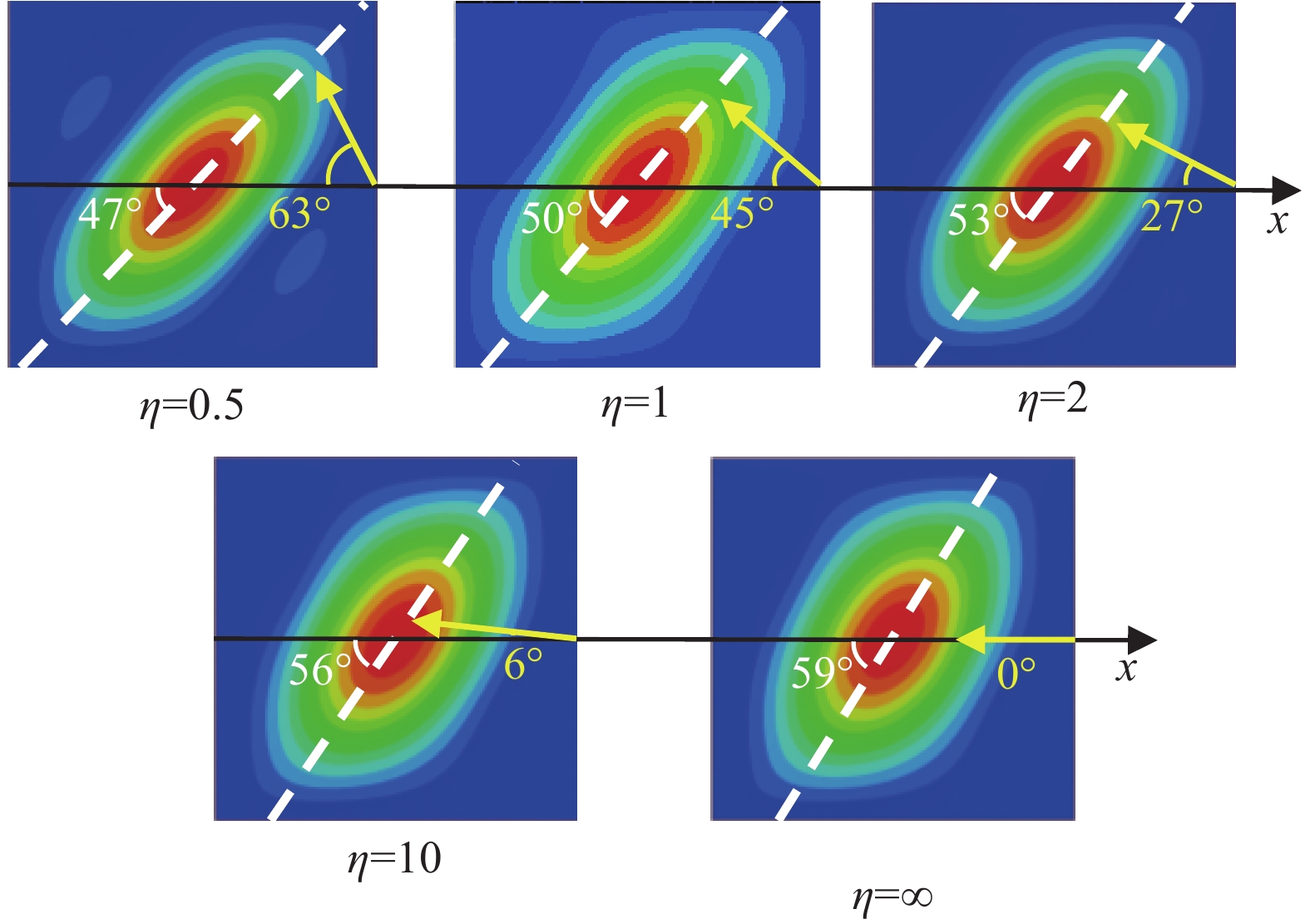
\eta ≥0.5时，本文结构在加载过程中会发生屈曲，各工况下结构中心区域的屈曲模态如图11所示。由图11可知，各工况下结构的屈曲模态在x和y方向的半波数均始终为1。随着加载方向(黄色箭头)逆时针旋转，压剪载荷比逐渐增大，椭圆长轴方向(白色虚线)同样沿逆时针方向小幅度旋转。定义椭圆长轴方向与x轴正方向的夹角为 \alpha 。当 \theta =63°时， \eta =0.5， \alpha =47°；随着 \theta 减小， \eta 和 \alpha 均增大；当 \theta =0°时 \eta =∞，为纯压缩载荷工况，此时本文结构的 \alpha =59°，与正交各向异性板屈曲变形关于x轴对称的情况明显不同。这是由于本文结构采用的[±45]2 s铺层虽然为均衡对称铺层，但因为±45°层与结构中面的距离不同，导致结构的刚度性能未关于x轴对称分布。
![]()
图 11 本文结构在不同载荷比下的屈曲模态Figure 11. Buckling modes of the structure under different compression-shear load ratios4. 结论
本文研究得到的主要结论如下：
(1)本文所建立的渐进损伤失效分析方法能够有效预测碳纤维增强(CFRP)层合板结构在面内压剪组合载荷下的失效行为。
(2)对于本文中层合板结构，随着压剪载荷比增大，结构失效形式可以分成三类：1)材料失效导致破坏，2)材料失效和屈曲共同导致破坏和3)屈曲时达到最大载荷。
(3)对于本文中层合板结构，随着压剪载荷比增大， \eta ≤1时，初始损伤载荷的压缩分量单调递增，剪切分量基本不变；当 \eta ≥0.5时，屈曲载荷的压缩分量单调递增，在 \eta ≥2时基本保持不变，剪切分量单调递减；在 \eta ≤1时最大载荷的压缩分量单调递增，在 \eta ≥2时基本保持不变，剪切分量在 \eta ≤0.5时增大，之后变为减小。
(4)对于本文中层合板结构， \eta ≤1时层合板在承载过程中会发生损伤，不同压剪载荷比下初始损伤类型相同，均为纤维压缩和纤基剪切；初始损伤载荷与最大载荷的比值先减小后增大，最大载荷时所发生损伤种类的数量先增多后减少。
(5) \eta ≥0.5时，本文结构在加载过程中会发生屈曲，屈曲模态在x和y方向的半波数均始终为1；随着压剪载荷比的增大，椭圆形屈曲模态的长轴方向会沿逆时针方向小幅度旋转，在 \eta =1时与加载方向近似垂直，在 \eta =∞时与x轴正方向的夹角约为59°。
-
![]()
图 4 碳纤维增强(CFRP)层合板剪切非线性系数拟合
Figure 4. Shear nonlinear coefficient fitting of the carbon fiber reinforced polymer (CFRP) plates
![]()
图 5 试验件正反面中心点应变-载荷曲线
Figure 5. The strain-load curves at the center point of the front and back faces of the specimen
![]()
图 6 数值模拟得到的试验件载荷位移曲线
Figure 6. The load-displacement curve obtained by numerical simulation of the specimen
![]()
图 7 试验件结构中心点的面外位移-载荷曲线
Figure 7. The Out-of-plane displacement-load curve at the center of the structure the specimen
![]()
图 8 数值模拟结果与试验结果中的失效位置对比
Figure 8. Comparison of the numerical and experimental failure locations
![]()
图 9 各载荷比下的CFRP层合板载荷位移曲线
Figure 9. Load-displacement curves at various load ratios of CFRP plates
η is the ratio of the compression load to the shear load
![]()
图 10 CFRP层合板各载荷随压剪载荷比的变化
Figure 10. Variation of each load with the compression-shear load ratio of CFRP plates
η is the ratio of the compression load to the shear load; Nx is the compression component of the loads; Nxy is the shear component of the loads
![]()
图 11 本文结构在不同载荷比下的屈曲模态
Figure 11. Buckling modes of the structure under different compression-shear load ratios
表 1 USN15000/EPW材料参数
Table 1 Properties of the USN15000/EPW material
E1/GPa E2/GPa v12 G12/GPa 129.96 9.62 0.35 4.99 XT/MPa XC/MPa YT/MPa YC/MPa S12/MPa 1564 997 44 180 77 GIC/(N/mm) GIIC/(N/mm) cf Em/GPa Gm/GPa 129.96 9.62 70% 3.52 1.2 Notes：E1, E2, v12, and G12 are the stiffness properties of the material; XT, XC, YT, YC, and S12 are the strength properties of the material; GIC and GIIC are the fracture toughness of the material; cf is the fiber volume fraction; Em and Gm are the stiffness properties of the matrix. 
下载: 导出CSV
表 2 数值模拟方法验证与对比
Table 2 Validation and comparison of two numerical simulation methods
Method Buckling Initial damage Max load Load/N Err/% Load/N Err/% Load/N Err/% Test 402 − 1509 − 1627 − Previous 425 5.72 761 −49.57 1792 10.14 Present 424 5.47 1653 9.54 1816 11.62
下载: 导出CSV
表 3 各工况下层合板失效扩展情况和载荷比
Table 3 Damage initiation and extension each loading conditions
η Damage type Initial damage load/
Maximum loadInitial damage Ultimate failure 0 FC, FM FC, FM 0.994 0.1 FC, FM FC, MC, FM 0.903 0.5 FC, FM FC, MC, FM, IT 0.846 1 FC, FM FC, MC, FM 0.990 2 Undamaged Undamaged − 10 Undamaged Undamaged − ∞ Undamaged Undamaged − Notes: η is the ratio of the compression load to the shear load.
下载: 导出CSV
-
[1] TRZEPIECIŃSKI T, NAJM S M, SBAYTI M, et al. New Advances and future possibilities in forming technology of hybrid metal–polymer composites used in aerospace applications[J]. Journal of Composites Science, 2021, 5(8): 217. DOI: 10.3390/jcs5080217
[2] 马志阳, 高丽敏, 徐吉峰. 复合材料在大飞机主承力结构上的应用与发展趋势[J]. 航空制造技术, 2021, 64(11): 24-30. MA Zhiyang, GAO Limin, XU Jifeng. Application and development for composite primary structure in large aircraft[J]. Aeronautical Manufacturing Technology, 2021, 64(11): 24-30(in Chinese).
[3] 陈佳. 运载火箭新型支承舱结构设计与分析 [D]. 南京: 南京航空航天大学, 2012. CHEN Jia. Structure design and analysis for advanced payload adapters [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese).
[4] 杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1): 1-12. DOI: 10.3321/j.issn:1000-3851.2007.01.001 DU Shanyi. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007, 24(1): 1-12(in Chinese). DOI: 10.3321/j.issn:1000-3851.2007.01.001
[5] 姜晓伟, 汪海, 朱建辉. 基于能量准则的复合材料层合板低速冲击近场动力学模拟[J]. 复合材料学报, 2024, 41(4): 2126-2136. JIANG Xiaowei, WANG Hai, ZHU Jianhui. Peridynamic modeling of composite laminate under low-velocity impact using energy-based criteria[J]. Acta Materiae Compositae Sinica, 2024, 41(4): 2126-2136(in Chinese).
[6] 俞鸣明, 朱雪莉, 刘雪强, 等. 低速多次冲击下碳纤维/环氧树脂基复合材料层合板失效机制及剩余强度评估[J]. 复合材料学报, 2023, 40 (09): 5359-5370. YU Mingming, ZHU Xueli, LIU Xueqiang, , et al. Failure mechanism and assessment of residual strength of carbon fiber/epoxy resin matrix composite laminates under multiple impacts at low velocities[J]. Acta Materiae Compositae Sinica, 2023, 40 (09): 5359-5370(in Chinese).
[7] 牛春匀, 程小全, 张纪奎. 实用飞机复合材料结构设计与制造 [M]. 北京: 航空工业出版社, 2010: 191-194. NIU Chunyun, CHENG Xiaoquan, ZHANG Jikui. Composite airframe structures [M]. Beijing: Aviation industry press, 2010: 191-194(in Chinese).
[8] MANSON S S, HALFORD G R. Multiaxial low-cycle fatigue of type 304 stainless steel[J]. Journal of Engineering Materials and Technology, 1977, 99(3): 283-285.
[9] MANSON S S, HALFORD G R. Treatment of multiaxial creep-fatigue by strainrange partitioning [C]// Proceedings of Symposium on Creep Fatigue Interaction. New York: American Society of Mechanical Engineers, 1976: 299-322.
[10] KLEIN H. General about buckling tests with thin-walled shells, 89-13 [R]. Cologne: DLR-Mitt, 1989.
[11] LIGHTFOOT M, AMBUR D. Open architecture data system for NASA Langley Combined Loads Test System [C]// Proceedings of 36th AIAA Aerospace Sciences Meeting and Exhibit. Reno: American Institute of Aeronautics and Astronautics, 1998: 0345.
[12] OESMANN W, SCHLERET J C, KOTZKE A, et al. Testing apparatus for compression and shear testing of a test component such as a curved aircraft component: US Patent, US7155982B2 [P]. 2007-01-02.
[13] LINDE P. Virtual Testing of stiffened composite panels at airbus[J]. International Journal of Structural Stability and Dynamics, 2010, 10(4): 589-600. DOI: 10.1142/S0219455410003634
[14] PETERS R W. Buckling tests of flat rectangular plates under combined shear and longitudinal compression, NACA-TN-1750 [R]. Washington: NACA, 1948: 1-2.
[15] SERRA J, PIERRé J E, PASSIEUX J C, et al. Validation and modeling of aeronautical composite structures subjected to combined loadings: The VERTEX project. Part 1: Experimental setup, FE-DIC instrumentation and procedures[J]. Composite Structures, 2017, 179: 224-244. DOI: 10.1016/j.compstruct.2017.07.080
[16] CASTANIE B, BARRAU J J, JAOUEN J P. Theoretical and experimental analysis of asymmetric sandwich structures[J]. Composite Structures, 2002, 55(3): 295-306. DOI: 10.1016/S0263-8223(01)00156-8
[17] CASTANIE B, BARRAU J J, JAOUEN J P, et al. Combined shear/compression structural testing of asymmetric sandwich structures[J]. Experimental Mechanics, 2004, 44(5): 461-472. DOI: 10.1007/BF02427957
[18] 马胜强. 复合材料壁板刚度匹配关系分析与试验研究 [D]. 哈尔滨: 哈尔滨工业大学, 2011. MA Shengqiang. Stiffness matching relations analysis and experimental study of composite panels [D]. Harbin: Harbin Institute of Technology, 2011(in Chinese).
[19] 姜海洋. 基于实测应变数据的复合材料加筋板工作行为分析 [D]. 哈尔滨: 哈尔滨工业大学, 2012. JIANG Haiyang. Work behavior analysis of stiffened composite panels based on measured strain data [D]. Harbin: Harbin Institute of Technology, 2012(in Chinese).
[20] 刘鹏洋. 复合材料加筋层合板屈曲分析理论及数值实现 [D]. 大连: 大连理工大学, 2020. LIU Pengyang. Analytical buckling analysis and numerical simulation of stiffened composite laminated plate [D]. Dalian: Dalian University of Technology, 2020(in Chinese).
[21] CHEN Q, QIAO P. Post-buckling analysis of composite plates under combined compression and shear loading using finite strip method[J]. Finite Elements in Analysis and Design, 2014, 83: 33-42. DOI: 10.1016/j.finel.2014.01.002
[22] 陈庆远. 复合材料薄壁结构的屈曲和后屈曲分析 [D]. 上海: 上海交通大学, 2015. CHEN qingyuan. Buckling and post-buckling analysis of thin-walled composite structures. Shanghai: Shanghai Jiao Tong University, 2015(in Chinese).
[23] 李政, 梁珂. 压剪联合载荷作用下复合材料壁板屈曲及后屈曲性能计算与优化方法研究[J]. 宇航总体技术, 2021, 5(6): 20-26. LI Zheng, LIANG Ke. A novel method for calculation and optimization of buckling and post-buckling performance of composite panels under combined compression and shear loads[J]. Astronautical Systems Engineering Technology, 2021, 5(6): 20-26(in Chinese).
[24] PIAN R, ZHANG L, YANG F, et al. The competition between buckling and overstress failure of composite laminated plates in compression and shear loads[J]. Composites Communications, 2023, 43: 101714. DOI: 10.1016/j.coco.2023.101714
[25] 骈瑢, 杨帆, 章凌, et al. 压剪载荷下复合材料层合板的失效模式研究[J/OL]. 北京航空航天大学学报. 网址: doi.org/10.13700/j.bh.1001-5965.2024.0084 PIAN Rong, YANG Fan, ZHANG Ling, et al. Failure mode study of composite laminated plates under compression-shear loading [J/OL]. Journal of Beijing University of Aeronautics and Astronautics. Website: doi.org/10.13700/j.bh.1001-5965.2024.0084(in Chinese).
[26] LESSARD L B. Compression failure in laminated composites containing an open hole [D]. Palo Alto: Stanford University, 1989.
[27] SHOKRIEH M M, LESSARD L B. Progressive fatigue damage modeling of composite materials, Part I: Modeling[J]. Journal of Composite Materials, 2000, 34(13): 1056-1080. DOI: 10.1177/002199830003401301
[28] 中国国家标准化管理委员会. 定向纤维增强聚合物基复合材料拉伸性能试验方法: GB/T 3354-2014 [S]. 北京: 中国标准出版社, 2014. Standardization Administration of the People’s Republic of China. Test method for tensile properties of orientation fiber reinforced polymer matrix composite materials: GB/T 3354-2014 [S]. Beijing: China Standards Press, 2014(in Chinese).
[29] American Society for Testing and Materials. Standard test method for compressive properties of polymer matrix composite materials using a combined loading compression (CLC) test fixture: ASTM D6641/D6641M-16e2 [S]. West Conshohocken: ASTM International, 2016.
[30] CAMANHO P P, DAVILA C G, PINHO S T, et al. Prediction of in situ strengths and matrix cracking in composites under transverse tension and in-plane shear[J]. Composites Part A: Applied Science and Manufacturing, 2006, 37(2): 165-176. DOI: 10.1016/j.compositesa.2005.04.023
[31] PARVIZI A, GARETT K W, BAILEY J E. Constrained cracking in glass fibre-reinforced epoxy cross-ply laminates[J]. Journal of Materials Science, 1978, 13(1): 195-201. DOI: 10.1007/BF00739291
[32] FLAGGS D L, KURAL M H. Experimental determination of the in situ transverse lamina strength in graphite/epoxy laminates[J]. 1982, 16 (2): 103-116.
[33] DVORAK G J, LAWS N. Analysis of progressive matrix cracking in composite laminates II. First Ply Failure[J]. 1987, 21 (4): 309-329.
[34] 张国凡. 复合材料加筋壁板结构屈曲承载特性研究 [D]. 西安: 西北工业大学, 2018. ZHANG Guofan. Study on buckling behavior of stiffened composite panels [D]. Xi’an: Northwestern Polytechnical University, 2018(in Chinese).
[35] PINHO S T, DARVIZEH R, ROBINSON P, et al. Material and structural response of polymer-matrix fibre-reinforced composites[J]. Journal of Composite Materials, 2012, 46(19-20): 2313-2341. DOI: 10.1177/0021998312454478
[36] PUCK A, SCHURMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models[J]. Composites Science and Technology, 2002, 62(12): 1633-1662.
[37] 李彪, 李亚智, 杨帆. 考虑复合材料层合板就地效应的强度理论[J]. 航空学报, 2014, 35(11): 3025-3036. DOI: 10.7527/S1000-6893.2014.0101 LI Biao, LI Yazhi, YANG Fan. Theoretical methodology for laminated composite strength including in-situ effect[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 3025-3036(in Chinese). DOI: 10.7527/S1000-6893.2014.0101
[38] HAHN H T, TSAI S W. Nonlinear elastic behavior of unidirectional composite laminae[J]. 1973, 7 (1): 102-118.
[39] PETIT P H, WADDOUPS M E. A method of predicting the nonlinear behavior of laminated composites[J]. 1969, 3 (1): 2-19.
[40] 路怀玉. 层—层角连锁机织复合材料的损伤行为研究 [D]. 哈尔滨: 哈尔滨工业大学, 2018. LU Huaiyu. Damage behaviors investigation of layer-to-layer angle interlock woven composites [D]. Harbin: Harbin Institute of Technology, 2018(in Chinese).
[41] ZHANG J, ZHOU L, CHEN Y, et al. A micromechanics-based degradation model for composite progressive damage analysis[J]. Journal of Composite Materials, 2016, 50(16): 2271-2287.
[42] SHAN M, ZHAO L, HONG H, et al. A progressive fatigue damage model for composite structures in hygrothermal environments[J]. International Journal of Fatigue, 2018, 111: 299-307. DOI: 10.1016/j.ijfatigue.2018.02.019
[43] SHIN E S, PAE K D. Effects of hydrostatic pressure on the torsional shear behavior of graphite/epoxy composites[J]. 1992, 26 (4): 462-485.
[44] American Society for Testing and Materials. Standard test method for in-plane shear response of polymer matrix composite materials by tensile test of a ±45° laminate: ASTM D3518/D3518M-18 [S]. West Conshohocken: ASTM International, 2018.
[45] 万春华, 段世慧, 吴存利, 等. 初始几何缺陷对加筋结构后屈曲分析的影响[J]. 航空计算技术, 2017, 47(1): 90-93. DOI: 10.3969/j.issn.1671-654X.2017.01.023 WAN Chunhua, DUAN Shihui, WU Cunli, et al. Influence of initial geometrical imperfection on post-buckling analysis for stiffened structure[J]. Aeronautical Computing Technique, 2017, 47(1): 90-93(in Chinese). DOI: 10.3969/j.issn.1671-654X.2017.01.023
[46] LI X, GAO W, LIU W. The Bearing behavior and failure characteristic of CFRP laminate with cutout under shearing load: Part I. Experiments[J]. Composite Structures, 2016, 141: 355-365. DOI: 10.1016/j.compstruct.2015.12.069
[47] HERMAN R J. Postbuckling behavior of graphite/epoxy cloth shear panels with 45-flanged lightening holes [D]. Naval Postgraduate School, 1982.
-
期刊类型引用(4)
1. 季文彬，王子豪，戴士杰，程鹏翔，吴润禾. 微波烧结复杂刃形TiB_2基陶瓷刀具的设计制备及力学性能. 复合材料学报. 2024(07): 3776-3788 . 
本站查看
2. 段俊彪，国秀花，皇涛，宋克兴，冯江，王旭. 基于SPS工艺制备的W-25 mass%Cu复合材料的组织与性能. 材料热处理学报. 2023(02): 37-45 . 百度学术
3. 庄蕾. (TiC-TiB_2)-Ni复合陶瓷的高温摩擦磨损性能. 材料保护. 2020(04): 58-61+83 . 百度学术
4. 张胜利，国秀花，宋克兴，梁淑华，周延军. 多粒径TiB_2颗粒增强铜基复合材料的制备与载流摩擦磨损性能. 复合材料学报. 2019(10): 2348-2356 . 本站查看
其他类型引用(3)
-
计量
- 文章访问数: 99
- HTML全文浏览量: 72
- PDF下载量: 14
- 被引次数: 7
