Direct shear performance and toughness evaluation of aligned steel fiber reactive powder concrete
-
摘要:
为研究准静态荷载下钢纤维长度、掺量及分布特征对活性粉末混凝土(Reactive powder concrete，RPC)试件剪切性能的影响，本文利用电磁场定向装置对RPC中的钢纤维进行定向处理，考虑3种纤维体积掺量(Vf=1.0vol%、1.5vol%、2vol%)、三种纤维长度(Lf=13 mm、16 mm、20 mm)制作了定向分布钢纤维活性粉末混凝土(Aligned steel fiber RPC，ASFRPC)试件和乱向分布钢纤维活性粉末混凝土(Steel fiber reinforced RPC，SFRPC)试件并开展双面直剪试验。分析了纤维方向、纤维掺量和纤维长度对钢纤维活性粉末混凝土试件抗剪强度、峰值剪切变形以及剪切韧性的影响。结果表明，ASFRPC试件的抗剪强度、剪切变形能力和剪切韧性相较SFRPC试件均得到了显著提高，钢纤维通过磁场定向分布后能够显著提升试件直剪力学性能。
Abstract:To investigate the effects of steel fiber length, volume fraction, and distribution characteristics on the shear performance of reactive powder concrete (RPC) specimens under quasi-static loads, an electromagnetic field orientation device was used to orient the steel fibers in RPC. Three fiber volume fractions (Vf=1.0vol%, 1.5vol%, 2vol%) and three fiber lengths (Lf=13 mm, 16 mm, 20 mm) were considered to produce aligned steel fiber reactive powder concrete (ASFRPC) specimens and randomly distributed steel fiber reinforced reactive powder concrete (SFRPC) specimens, and double-sided direct shear tests were conducted. The influence of fiber direction, fiber volume fraction, and fiber length on the shear strength, peak shear deformation, and shear toughness of all specimens were analyzed. The results show that the shear strength, shear deformation capacity, and shear toughness of ASFRPC specimens are significantly improved compared to SFRPC specimens. Steel fiber can significantly improve the direct shear mechanical properties of specimens after being oriented and distributed by a magnetic field.
-
混凝土中掺入纤维可以显著提升其抗弯、抗拉以及抗压强度[1]，改善混凝土脆性破坏特征。Romualdi等[2]基于线弹性断裂力学理论分析了纤维增强效果与纤维间距之间的关系，并通过试验验证了钢纤维混凝土的受拉、受剪性能与纤维间距的理论联系。Malvar[3]基于不同的围压值和固定的混凝土抗拉强度，对表面形状不同的玻璃纤维增强聚合物(Glass fiber reinforced polymer，GFRP)筋进行了研究，提出了FRP筋与混凝土粘结-滑移本构模型。高丹盈等[4]基于已有的粘结-滑移本构模型，比较了各个模型之间的差异性，提出了物理概念明确、形式简单实用的连续曲线模型，并通过大量试验数据验证了其实用性。
在各种纤维中，钢纤维因其高强度、高弹性模量以及与混凝土良好的粘接，在高弹模纤维混凝土中具有显著优势[5-6]。但是随机分布的钢纤维在单个受力方向上纤维方向效应系数(纤维在给定方向投影长度总和与实际长度总和之比)仅为0.4左右[7-11]，纤维在特定方向的增强效率偏低。为了解决此问题，提高混凝土中钢纤维的利用率，研究人员通过调整浇筑方式、浇筑顺序[12-15]等措施对钢纤维的分布进行调整或控制，将纤维方向效应系数提升至0.6，调整后试件的拉弯性能有显著提高。基于钢纤维在磁场中会磁化并转向与磁力线平行方向，慕儒等[16-19]利用均匀磁场将处于流体状态下拌合物中的钢纤维按照特定方向排列，制备出纤维方向系数达0.9的定向分布钢纤维混凝土(Aligned steel fiber concrete)试件，并对其断裂性能、弯曲抗拉性能进行了研究，结果表明调整方向后，同等纤维掺量时混凝土单向劈裂抗拉强度提高18%，弯曲抗拉强度提高程度达56%，剪切模量、抗剪强度分别提高30%和40%，断裂韧度和断裂能较乱向分布纤维试件更是近乎成倍增长。之后，又制备出在弯曲载荷作用下，钢纤维方向与主应力方向一致的全场对准钢纤维混凝土试件，其弯曲性能与定向和随机分布钢纤维试件相比显著提高[20]。为进一步提升纤维方向效应系数，作者选用镀铜微丝钢纤维，以纤维转动阻力更小的无粗骨料活性粉末混凝土(Reactive powder concrete，RPC)为基体，通过电磁场进行纤维定向获得了方向效应系数高于90%的定向钢纤维RPC (Aligned steel fiber RPC，ASFRPC)构件，其等效弯曲抗拉强度达到近30 MPa，残余强度以及韧度指数均较乱向分布RPC (Steel fiber reinforced RPC，SFRPC)试件显著提升[21-23]。
剪切性能对纤维混凝土同样重要，研究表明，钢纤维还可以有效地提高混凝土开裂后的直剪传递能力[24]，Boulekbache等[25]通过双面剪切试验系统地研究了基体强度、纤维方向、纤维掺量、纤维长径比对混凝土剪切性能的影响。Aveston[26]研究发现钢纤维混凝土发生剪切破坏时，具有一定的韧性并提出了多缝开裂理论。Soetens等[27]通过开展双面直接剪切试验，研究了钢纤维混凝土的剪切摩擦性能。结果表明，抗剪强度和纤维的掺量成正比关系，并通过对已有经验公式的检验提出了裂后钢纤维剪切-滑移模型。邓明科等[28]对高延性混凝土开展双面剪切试验，研究了聚乙烯醇纤维掺量和水胶比对高延性混凝土破坏形态、抗剪强度及峰值剪切变形的影响，并提出了采用初始能量密度与残余剪切韧度比作为延性混凝土剪切韧性评价方法。Mu等[29]通过双面直剪试验，发现纤维方向对混凝土的剪切性能有显著影响，定向钢纤维水泥基复合材料的抗剪强度、变形能力、剪切模量和韧性均优于乱向钢纤维水泥基复合材料。
为了进一步研究镀铜微丝钢纤维的定向分布对RPC直剪性能的影响，本文制作了不同掺量和纤维长度的ASFRPC和SFRPC构件，通过双面直剪试验，研究了钢纤维方向、钢纤维掺量和钢纤维长度对钢纤维活性粉末混凝土试件剪切破坏形态、剪切韧性的影响。
1. 试验概况
1.1 试验材料
为了减小纤维转向阻力，本次试验选用无粗骨料的RPC为基体，胶凝材料选用P·O 42.5R普通硅酸盐水泥和硅灰，骨料选用细度模数为2.32的天然河砂，添加剂选用密度为1.06 g/cm3的粉体聚羧酸高效减水剂，具体配比见表1。纤维选用镀铜微丝钢纤维，其外观和物理性能分别见图1和表2。
表 1 活性粉末混凝土(RPC)配合比Table 1. Mix proportion of reactive powder concrete (RPC)W/B/% Unit weight/(kg·m−3) Water Cement Sand Silica fume SP 26 244.4 710.0 1266.0 230.0 3.6 Notes: W/B—Water binder ratio; SP—Super plasticizer. ![]()
图 1 镀铜微丝钢纤维Figure 1. Copper coated microfilament steel fiberdf—Steel fiber diameter; Lf—Steel fiber length1.2 试件制作
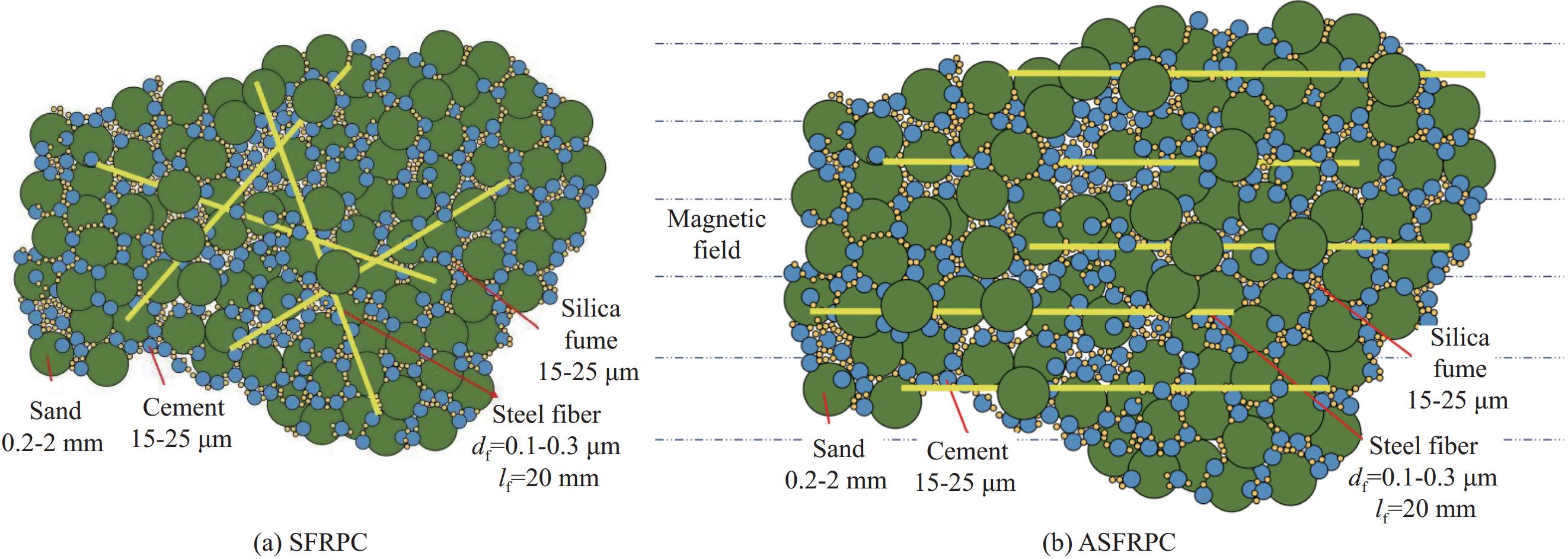
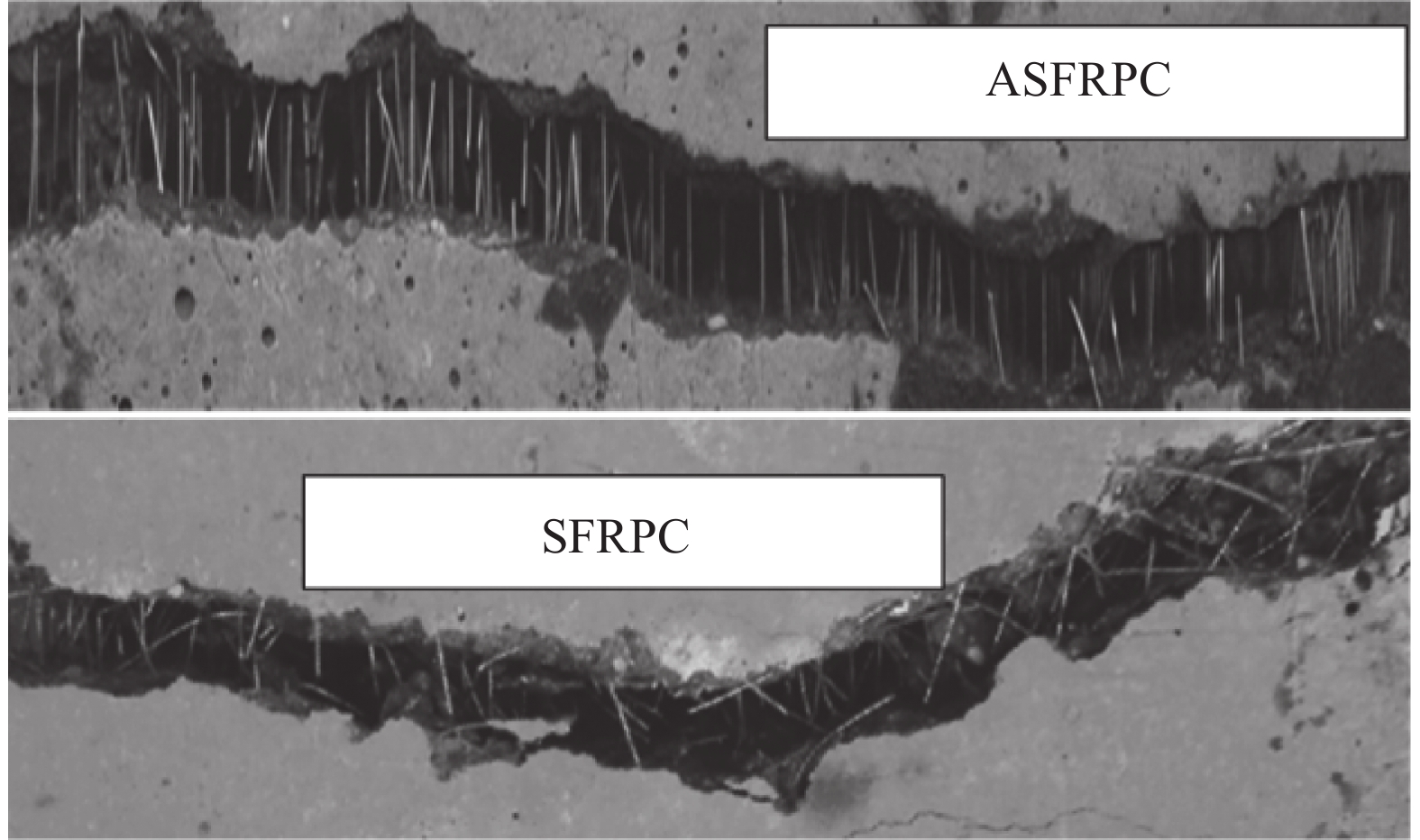
按表1的配合比制作ASFRPC和SFRPC试件。图2为试件制作实拍图，拌合物搅拌好后装入试模(图2(a))，SFRPC试件直接放在振动台上振动密实(图2(b))，ASFRPC试件需要放入强度250高斯的磁场中，再连同磁场线圈一起振捣定向(图2(c))，试件振捣完成后养护24~48 h，然后拆模并放入标准养护室(温度为(20±2)℃，相对湿度≥90℃)养护至28 d (图2(d))。纤维定向示意见图3，为确保定向效果，随机选择ASFRPC和SFRPC试件各一个进行弯折，破坏构件断口处纤维分布对比见图4。
本次试验考虑钢纤维分布、钢纤维掺量和钢纤维长度对钢纤维RPC剪切韧性的影响，制备了3种钢纤维体积掺量(Vf=1vol%、1.5vol%、2vol%)、3种钢纤维长度(Lf=13、16、20 mm)、尺寸为100 mm×100 mm×400 mm的ASFRPC和SFRPC试件，剪切试件每组4个，共18组。根据各组纤维分布、纤维掺量和纤维长度的不同对其进行编号，D、L分别表示定向、乱向分布钢纤维活性粉末混凝土试件，中间数字表示纤维长度，最后加上纤维的掺量。例如D13-2%表示纤维长度为13 mm，掺量为2vol%的定向分布钢纤维活性粉末混凝土试件。L0-0代表不掺钢纤维的试件，仅用于对照，具体编号说明见表3。
表 2 钢纤维的各项性能Table 2. Properties of steel fiberType Diameter df/mm Length Lf/mm Aspect ratio Lf/df Density/(g·cm−3) Tensile strength/MPa Elastic modulus/GPa S13 0.2 13 65 7.8 2900 200 S16 0.2 16 80 S20 0.2 20 100 ![]()
图 4 裂缝处定向分布钢纤维RPC (ASFRPC)与乱向分布钢纤维RPC (SFRPC)纤维分布对比Figure 4. Fiber distribution at the crack of aligned steel fiber RPC (ASFRPC) and randomly distributed steel fiber RPC (SFRPC) specimens表 3 试件编号Table 3. Specimen numberSpecimen number Fiber length/mm Fiber content/vol% Fiber distribution L13-1% 13 1 Randomly L13-1.5% 13 1.5 Randomly L13-2% 13 2 Randomly L16-1% 16 1 Randomly L16-1.5% 16 1.5 Randomly L16-2% 16 2 Randomly L20-1% 20 1 Randomly L20-1.5% 20 1.5 Randomly L20-2% 20 2 Randomly D13-1% 13 1 Aligned D13-1.5% 13 1.5 Aligned D13-2% 13 2 Aligned D16-1% 16 1 Aligned D16-1.5% 16 1.5 Aligned D16-2% 16 2 Aligned D20-1% 20 1 Aligned D20-1.5% 20 1.5 Aligned D20-2% 20 2 Aligned 1.3 试验及韧性评价方法
1.3.1 试验概况
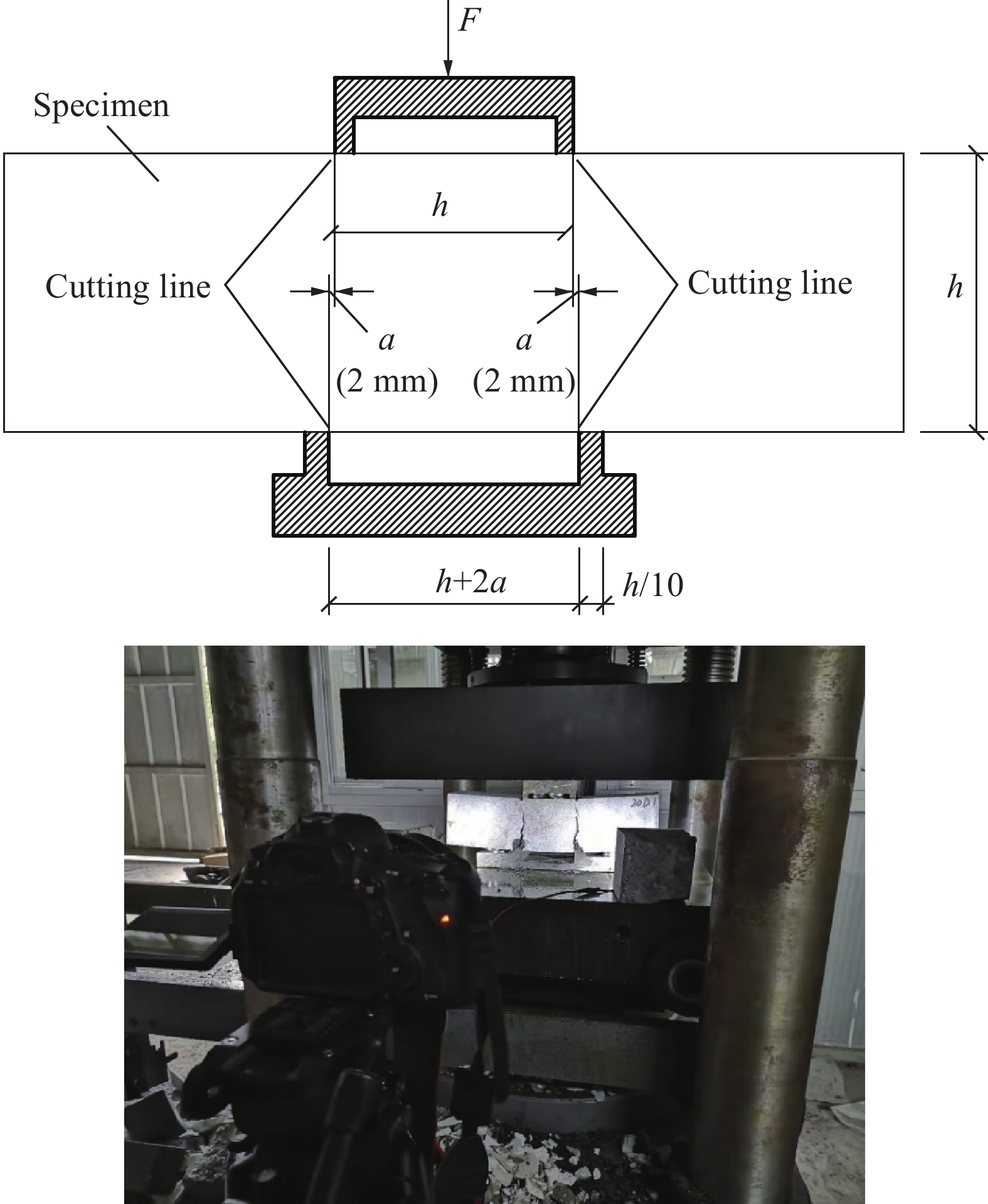
剪切试验参考《纤维混凝土试验方法标准》(CECS13: 2009)[30]中的规定进行。试件两个加载面用切割机环轴向分别切割2 mm深、2 mm宽的细缝，用来控制试件的直剪破坏的位置，避免局部压坏。双面剪切试验装置如图5所示。采用500吨的MTS电液伺服压力机，位移控制的方式进行加载，加载速度设置为0.1 mm/min。剪切强度采用下式计算：
![]()
图 5 双面剪切试验装置图Figure 5. Schematic of the double shear test setupa—Width of the cutting line; h—Height of the shear plane; F—Shear loadτ=Fmax2bh (1) 式中：τ为钢纤维RPC的抗剪强度(MPa)；Fmax为平均峰值剪切荷载(N)；b、h分别是剪切面的宽和高(mm)。
1.3.2 剪切韧性评价方法
在现有弯曲韧性评价方法的基础上，根据本次试验结果，以实测的试件剪切荷载-变形曲线为基础，参考邓明科等[28]提出的纤维混凝土剪切韧性评估方法，对材料的剪切韧性进行评价。
(1)峰值前韧性评价
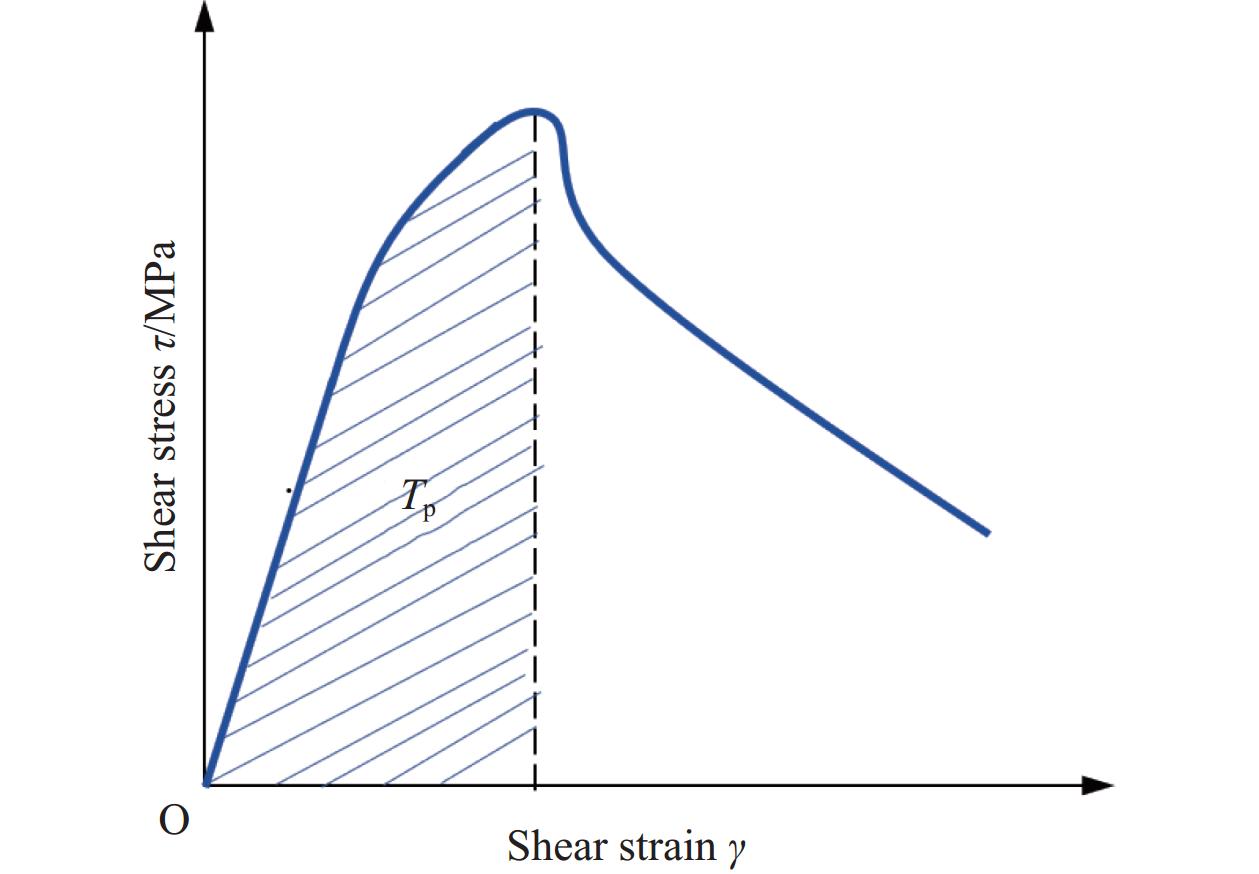
如图6所示以钢纤维RPC的等效初始剪切强度feq、峰值剪应变γp和初始能量密度Tp表征SFRPC剪切荷载达到峰值前的剪切强度、剪切变形和剪切韧性。feq、γp和Tp的计算公式如下：
feq=Ωp2bhδp (2) γp=δph (3) Tp=∫γp0τ(γ)dγ (4) 式中：δp为剪切变形曲线峰值荷载处的挠度；Ωp为峰值荷载前荷载-剪切变形曲线下的面积；τ(γ)是由荷载-剪切变形曲线计算得到的剪应力-剪应变相关函数。
从式(2)~(4)可以推导feq、γp与Tp的关系为
Tp=∫γp0τ(γ)dγ=∫(δph)0F(δ)2bhd(δh)=12bh2∫δp0F(δ)dδ=Ωp2bh2=Ωp2bhδpδph=feqγp (5) 从式(5)可以发现，初始剪切能量密度反映了峰值前强度与剪切变形能力的一个综合指标，可用来评价材料的初始剪切韧性。
(2) 峰值后韧性评价
如图7所示，以SFRPC的等效残余剪切强度fp,k和残余剪切韧度比Rp,k表征SFRPC剪切峰值后的残余持荷能力。fp,k和Rp,k的计算公式为
![]()
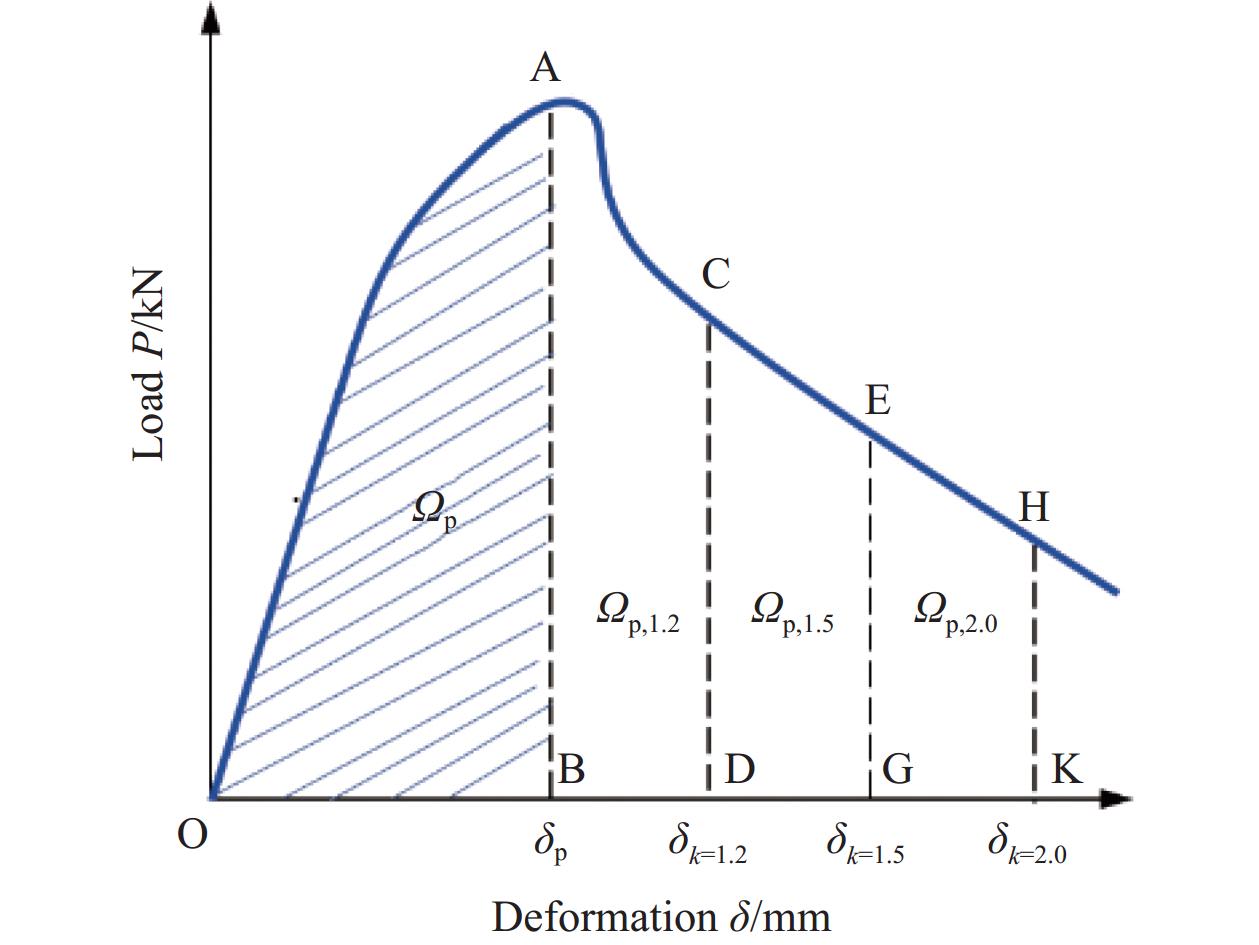
图 7 剪切韧性计算参数Figure 7. Definitions for shear toughness indexesδp is the deflection at the peak load of the shear deformation curve; Ωp is the area under the load shear deformation curve before the peak load; Ωp,k is the area under the load shear deformation curve from δp to δk; δp,k is the deformation difference of the corresponding δp to δk segment on the curve; k is the ratio of δk to the deflection δp at the peak loadfp,k=Ωp,k2bhδp,k (6) Rp,k=fp,kfp (7) 式中：Ωp,k为δp至δk段荷载变形曲线下的面积；为了更好地评价峰值后SFRPC材料的韧性，定义k为δk与峰值荷载处挠度δp的比值，k取值分为3个等级即1.2、1.5和2.0，与此相应曲线中BACD、BAEG、BAHK所包围的面积分别为Ωp,1.2、Ωp,1.5、Ωp,2.0；δp,k为曲线上对应的δp至δk段的变形差值；fp为抗剪强度。
2. 试验结果和分析
2.1 ASFRPC和SFRPC的破坏模式
图8表示以长度为20 mm，掺量1vol%的钢纤维RPC试件为例，显示了随着荷载增加，剪切面上的裂纹发展路径的详细过程。图9为不同钢纤维长度、掺量下ASFRPC和SFRPC的剪切破坏形态。
![]()
图 8 SFRPC试件直剪失效模式和裂纹形态(以L20-1%为例)Figure 8. Failure mode and crack morphology of SFRPC specimen (Take L20-1% as an example)![]()
图 9 ASFRPC和SFRPC试件直剪失效模式和裂纹形态Figure 9. Failure mode and crack morphology of the ASFRPC and SFRPC specimens由图8和图9可以看出，没有掺入钢纤维的RPC试件，剪切裂纹出现在两个剪切截面后，便迅速扩展，随即发生剪切破坏。破坏后，整个试件沿两个剪切破坏面被剪成3个独立的棱柱体，剪切破坏面光滑，断口整齐，没有钢纤维的增强作用，RPC试件呈现“一裂即坏”的完全脆性破坏模式。配置钢纤维的试件受载时，表现出明显的延性特征，第一条肉眼可见裂缝出现在受剪截面中间，如图8(a)所示；随着剪切荷载的不断增加，第一条微裂缝周围会相继出现其他的小竖向裂缝如图8(b)、图8(c)所示，裂缝的密集程度会随着钢纤维体积掺量、长径比的增加而增大；伴随着剪切裂缝的发展和贯通，沿着剪切面有部分钢纤维拔出，甚至有些钢纤维会沿着剪切面弯折，试件表面有部分基体材料剥落，如图8(d)所示；当试件达到极限剪切荷载时，裂纹局部化形成，大量剪切裂缝交叉贯通；经过峰值荷载后，剪切变形仍然不断增加，裂缝不断变宽，试件发生明显变形，直到试验结束，试件由于钢纤维在裂缝处的连接仍能保持一定的完整性，如图8(e)所示。
2.2 ASFRPC和SFRPC的荷载/应力-位移曲线
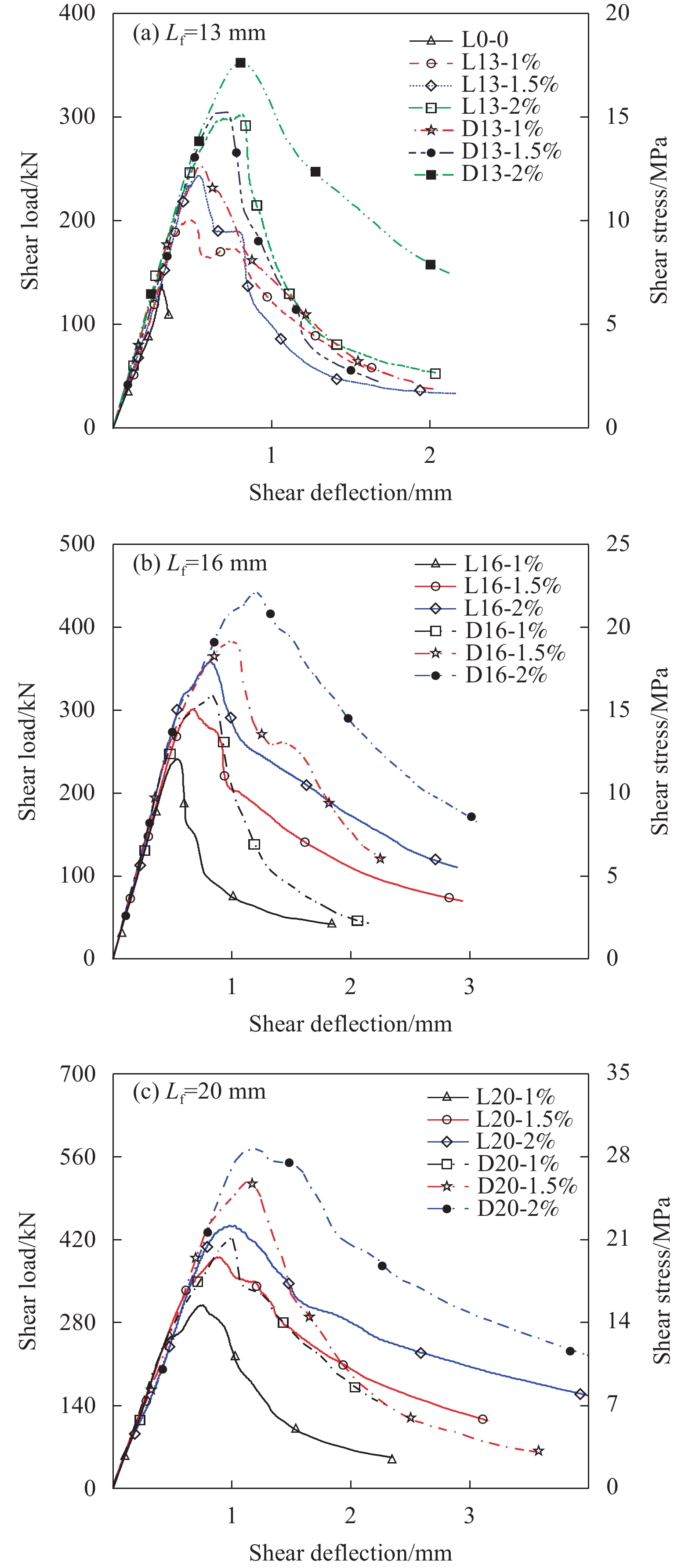
ASFRPC试件和SFRPC试件的剪切荷载/应力-变形关系曲线按照纤维长度分组如图10所示，可知，各试件开裂前的剪切荷载-变形曲线均为线性，荷载持续增大，不掺纤维的RPC试件的剪切-位移曲线随着第一条可见裂缝的出现立即下降，破坏极具突然性。而ASFRPC试件和SFRPC试件剪切荷载/应力-变形曲线均呈现出挠度硬化特点，且其剪切过程由线弹性阶段、挠度硬化阶段、挠度软化阶段3个部分组成，其原因主要是试件达到剪切开裂荷载后，基体退出工作，钢纤维承担主要荷载并抑制裂缝发展，钢纤维的桥接作用使得剪切荷载依然呈上升趋势。
![]()
图 10 SFRPC试件和ASFRPC试件剪切荷载/应力-位移关系曲线Figure 10. Shear load/stress-deformation curves of SFRPC specimens and ASFRPC specimens同等条件下，ASFRPC试件的承载能力和峰值剪切变形均高于SFRPC试件，并且相关性能随着纤维长径比和纤维掺量的增加而呈递增趋势。纤维掺量为1vol%，纤维长度分别为13 mm、16 mm、20 mm时，ASFRPC试件比SFRPC试件抗剪强度分别提升了27.05%、32.06%、36.43%，峰值剪切位移相应提高了8%、58%、30%。纤维掺量为1.5vol%，纤维长度分别为13 mm、16 mm、20 mm时，ASFRPC试件比SFRPC试件抗剪强度分别提升了25.7%、27.62%、33.13%，峰值剪切位移相应提高了33.96%、46.27%、35.96%；纤维掺量为2vol%，纤维长度为13 mm、16 mm、20 mm时，ASFRPC比SFRPC试件抗剪强度分别提升了16.79%、23.24%、29.67%。纤维长度为13 mm时，ASFRPC试件和SFRPC试件的峰值剪切位移相当，纤维长度为16 mm、20 mm时，峰值剪切位移相应提高了50%、24.49%。
纤维长度为13 mm，纤维掺量由1vol%增加至2vol%时，ASFRPC试件抗剪强度分别提高了20.11%、15.57%，相应的剪切变形分别提高了31.48%、17.14%；纤维长度为16 mm，纤维掺量由1vol%增加至2vol%时，ASFRPC试件抗剪强度分别提高了20.58%、15.04%，相应的剪切变形分别提高了16.67%、22.44%；当纤维长度为20 mm，纤维掺量由1vol%增加至2vol%时，ASFRPC试件抗剪强度分别提高了23.11%、5.61%，相应的剪切变形分别提高了23.49%、3.3%。
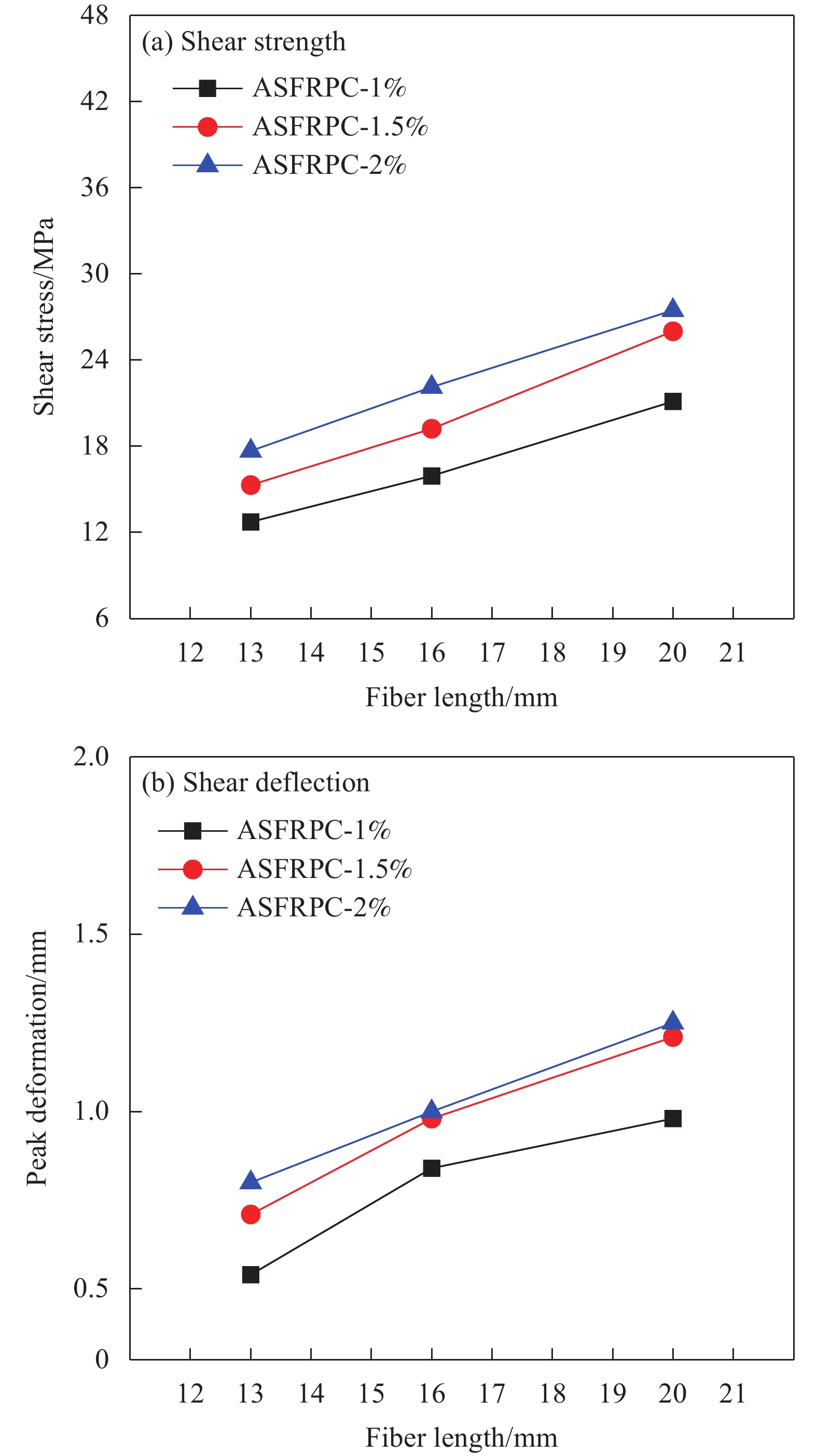
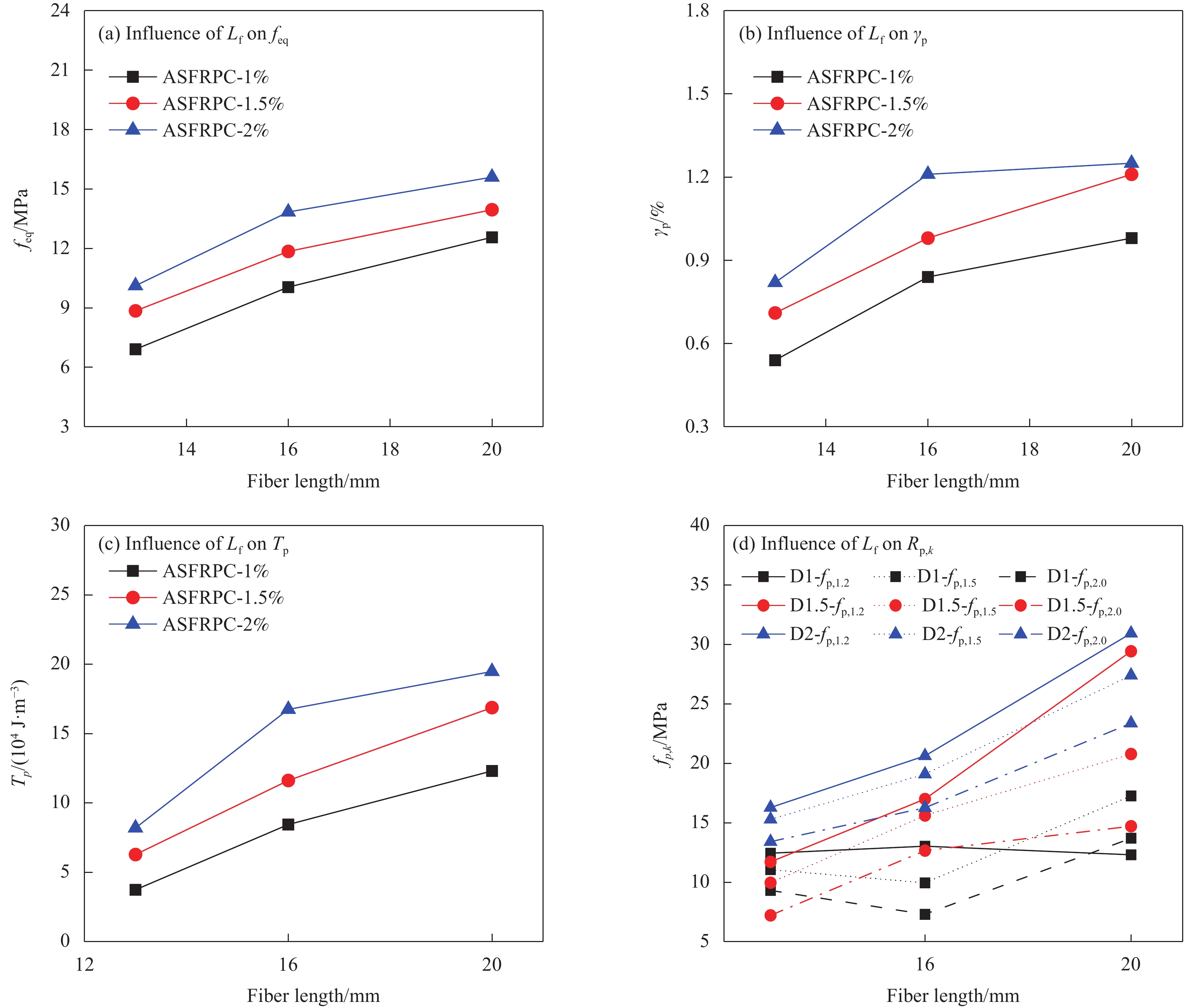
图11为纤维长度对ASFRPC试件抗剪强度与峰值变形的影响曲线。可知，当纤维掺量一定时，ASFRPC试件的抗剪强度和峰值变形均随着纤维长径比的增加而提高，纤维长径比越大，提高幅度越大。纤维掺量为1vol%时，纤维长度为16 mm、20 mm的ASFRPC试件较纤维长度为13 mm的试件抗剪强度分别提高了25.22%、65.90%，相应的剪切变形分别提高了55.56%、81.48%；纤维掺量为1.5vol%时，纤维长度为16 mm、20 mm的ASFRPC试件较纤维长度为13 mm的试件抗剪强度分别提高了25.70%、70.04%，相应的剪切变形分别提高了38.03%、70.42%；纤维掺量为2vol%时，纤维长度为16 mm、20 mm的ASFRPC试件较纤维长度为13 mm的试件抗剪强度分别提高了25.12%、63%，相应的剪切变形分别提高了25%、56.25%。当纤维掺量为1.5vol%时，ASFRPC试件的抗剪强度随纤维长径比的增加提高幅度最明显，其相应的峰值剪切变形增量也最大。
![]()
图 11 纤维长度对ASFRPC试件抗剪强度与峰值变形的影响Figure 11. Effect of fiber length on shear strength and peak deformation of ASFRPC specimens2.3 ASFRPC和SFRPC的试验数据汇总
表4给出了SFRPC、ASFRPC和RPC试件双面剪切试验最大剪切荷载Fmax、峰值变形Δp和相应立方体抗压强度fcu试验结果。
表 4 SFRPC、ASFRPC和RPC试件试验测量结果Table 4. Test measurements of SFRPC, ASFRPC and RPC specimensSpecimen type Group fcu/MPa Fmax/kN △p/mm SFRPC L13-1% 87.33 200.4 0.49 L13-1.5% 89.78 243.2 0.53 L13-2% 95.04 302.6 0.82 L16-1% 93.31 241.4 0.53 L16-1.5% 95.96 301.2 0.67 L16-2% 103.52 358.8 0.8 L20-1% 93.63 300.8 0.75 L20-1.5% 95.45 390.6 0.89 L20-2% 98.22 444.2 0.98 ASFRPC D13-1% 87.33 254.6 0.54 D13-1.5% 89.78 305.8 0.71 D13-2% 95.04 353.4 0.83 D16-1% 93.31 318.8 0.84 D16-1.5% 95.96 384.4 0.98 D16-2% 103.52 442.2 1.2 D20-1% 93.63 422.4 0.95 D20-1.5% 95.45 520 1.21 D20-2% 98.22 549.2 1.25 RPC L0-0 79.91 138.8 0.31 Notes: fcu—Cube compressive strength; Fmax—Peak shear load; △p—Peak deformation; L13-1% represents SFRPC specimens with a fiber length of 13 mm and a fiber content of 1vol%; D13-1% represents ASFRPC specimens with a fiber length of 13 mm and a fiber content of 1vol%, and the rest are the same. 2.4 ASFRPC和SFRPC的剪切韧性分析
根据表4结合本文提出的SFRPC韧性的评估方法计算得到的试件剪切荷载-变形曲线峰值前及峰值后的韧性指标列于表5中。计算结果表明，ASFRPC试件的等效初始强度、峰值剪切应变及初始能量密度相比RPC和SFRPC均有显著提高。
表 5 RPC试件剪切荷载-变形曲线峰值前及峰值后的韧性指标Table 5. Toughness index evaluation pre-peak and post-peak load of shear load-deformation curves of RPC specimenSpecimen type Group feq/MPa γp/% Tp/(104 J·m−3) fp,k/MPa Rp,k/% fp,1.2 fp,1.5 fp,2.0 Rp,1.2 Rp,1.5 Rp,2.0 RPC L0-0 3.13 0.31 0.97 — — — — — — SFRPC L13-1% 5.56 0.49 2.73 9.61 9.17 8.17 0.96 0.92 0.82 L13-1.5% 6.49 0.53 3.44 9.93 10.04 7.90 0.82 0.83 0.65 L13-2% 9.47 0.8 7.06 11.7 8.76 6.39 0.77 0.58 0.42 L16-1% 6.67 0.515 3.54 9.88 7.94 6.00 0.82 0.66 0.50 L16-1.5% 8.40 0.67 5.63 14.11 13.38 11.30 0.94 0.89 0.75 L16-2% 10.6 0.8 8.48 16.09 14.40 12.96 0.9 0.80 0.72 L20-1% 9.42 0.75 7.07 14.68 12.85 9.86 0.98 0.85 0.66 L20-1.5% 11.74 0.89 10.45 18.71 16.65 15.30 0.96 0.85 0.78 L20-2% 12.44 0.98 12.2 22.28 20.19 17.74 1.00 0.91 0.8 ASFRPC D13-1% 6.91 0.54 3.74 12.44 11.06 9.31 0.98 0.87 0.73 D13-1.5% 8.85 0.71 6.28 11.71 9.96 7.21 0.76 0.65 0.47 D13-2% 10.12 0.82 8.2 16.82 15.29 13.41 0.95 0.87 0.76 D16-1% 10.05 0.84 8.45 13.03 9.95 7.30 0.82 0.62 0.46 D16-1.5% 11.85 0.98 11.62 17.00 15.62 12.66 0.88 0.76 0.66 D16-2% 13.84 1.21 16.75 20.63 19.09 16.27 0.93 0.86 0.74 D20-1% 12.56 0.98 12.31 17.26 16.00 13.70 0.82 0.76 0.65 D20-1.5% 13.95 1.21 16.88 29.43 20.78 14.71 1.13 0.80 0.57 D20-2% 15.6 1.25 19.48 30.92 27.41 23.38 1.13 1.00 0.85 Notes: feq—Initial equivalent shear strength; γp—Peak shear strain; Tp—Initial energy density; fp,k—Equivalent residual shear strength; Rp,k—Residual shear toughness ratio. 2.4.1 钢纤维方向对剪切韧性的影响
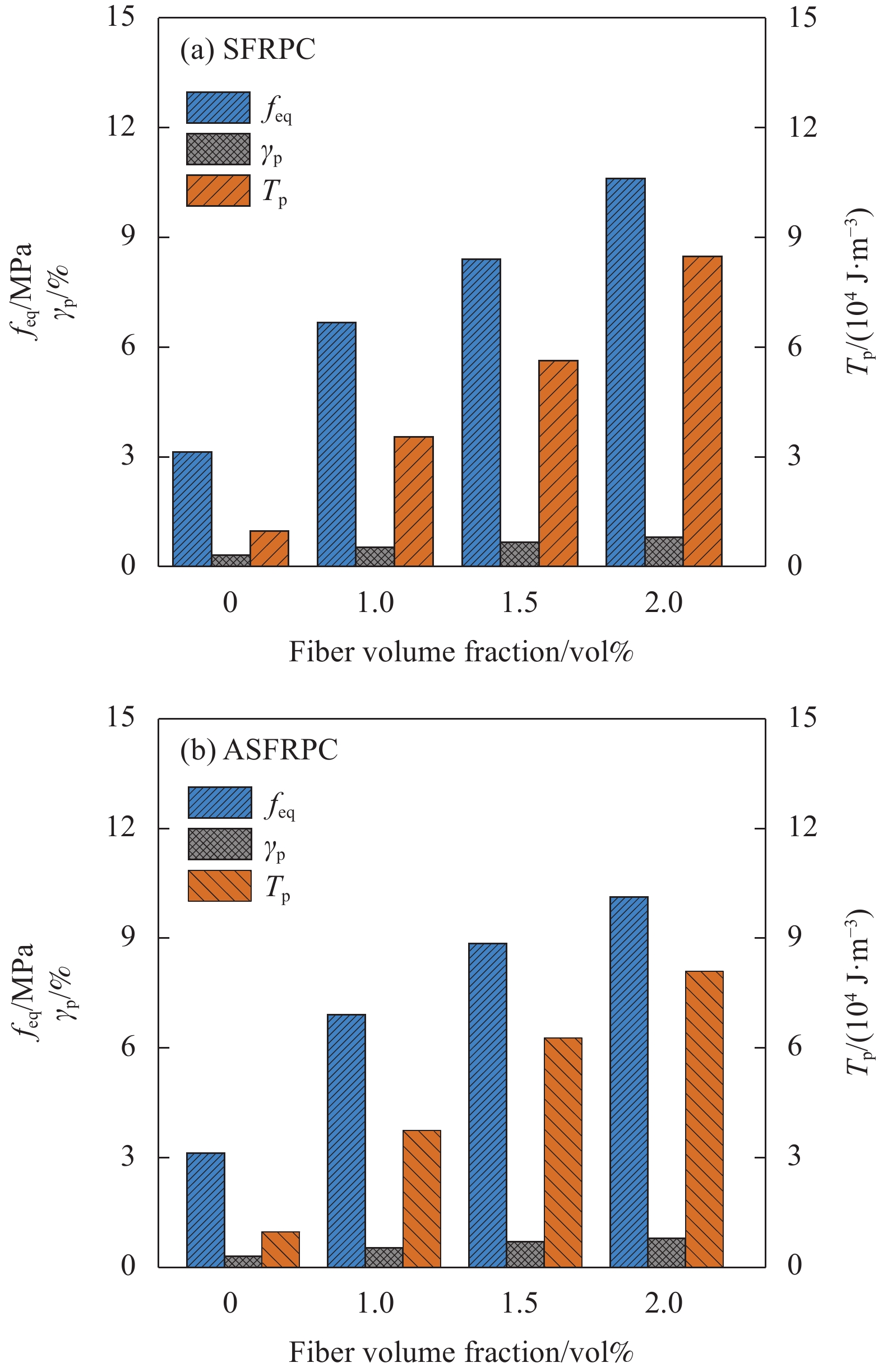
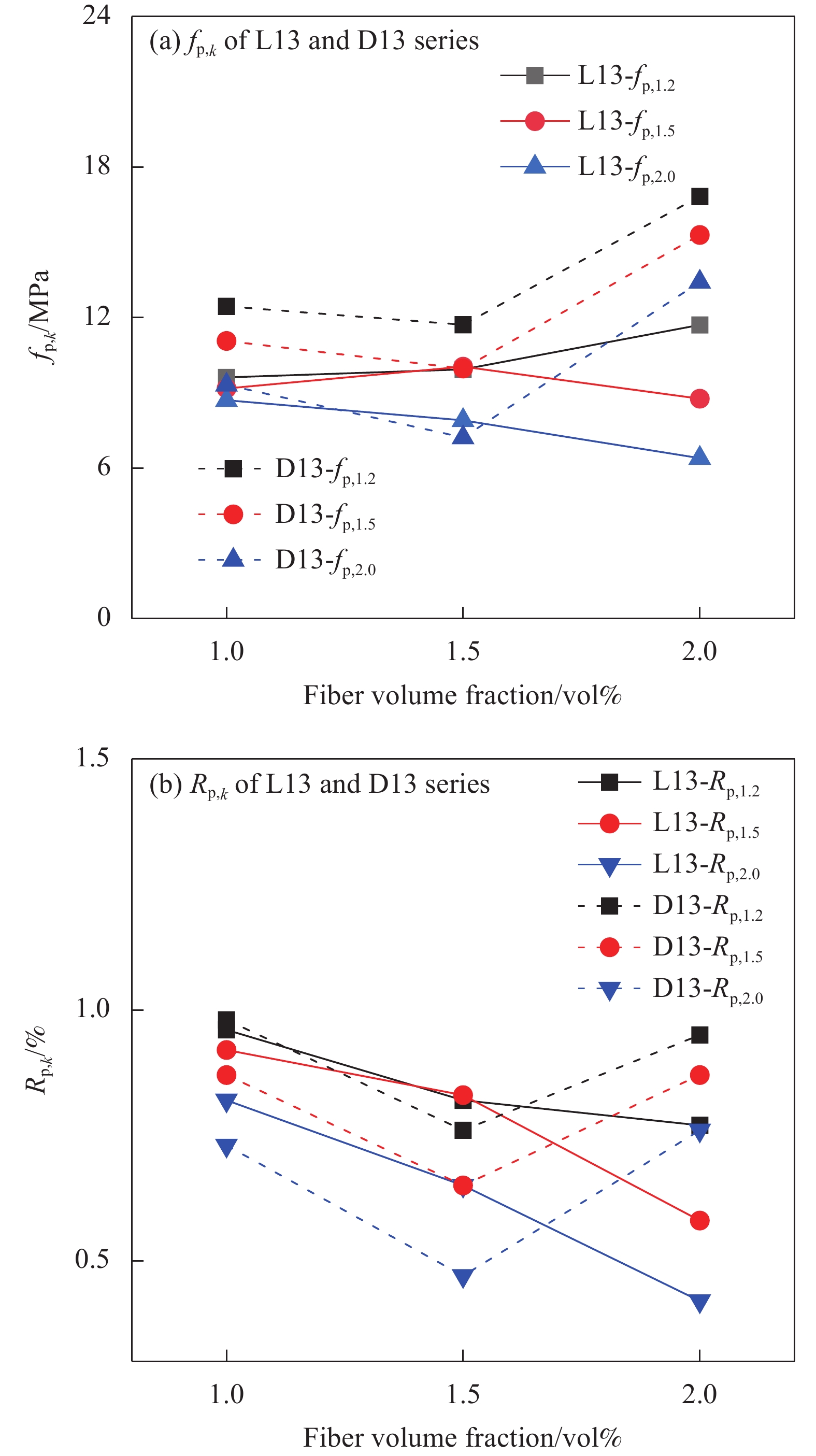
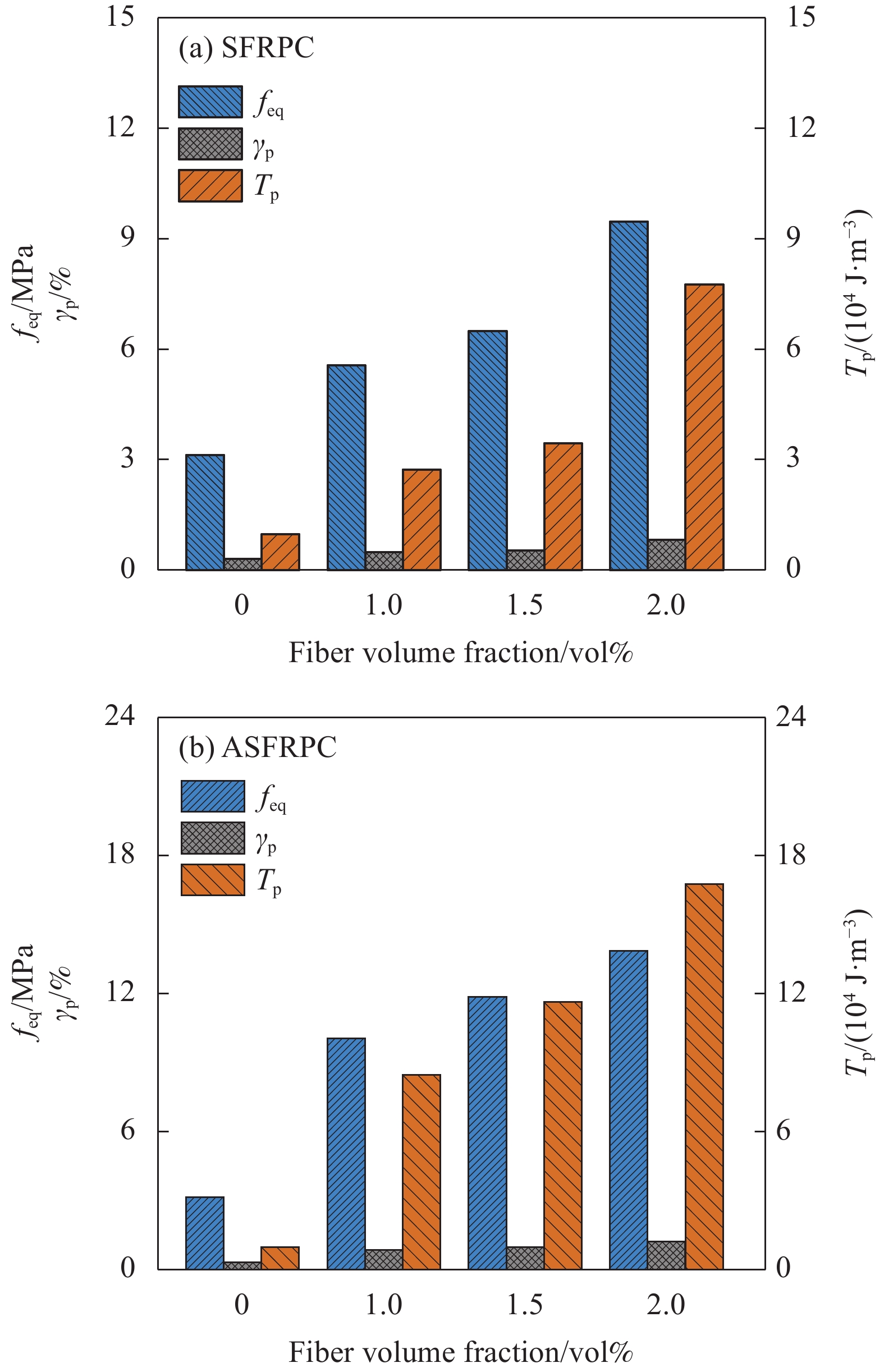
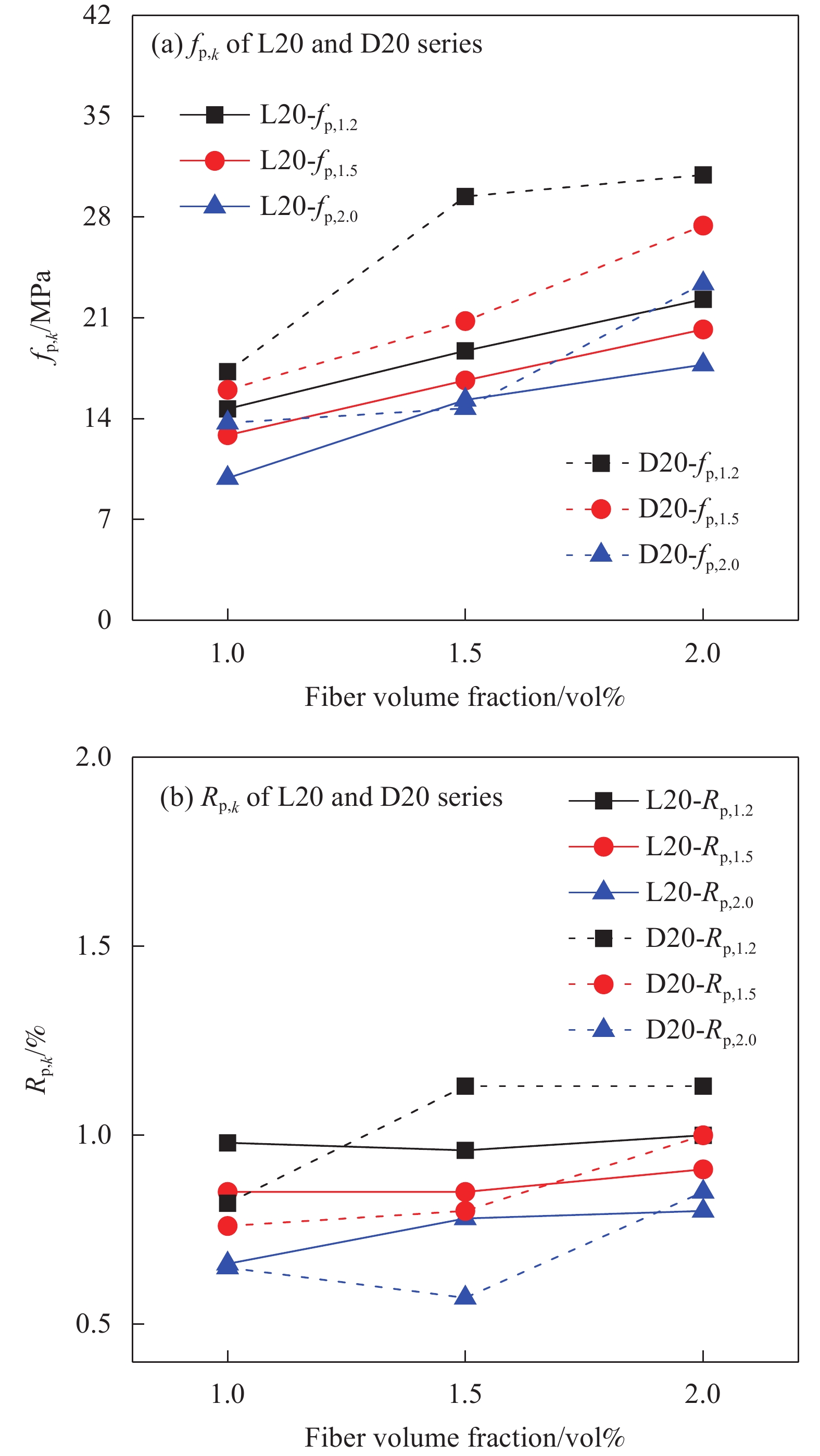
图12反映了纤维长度为13 mm时ASFRC试件和SFRPC试件的峰值前韧性指标。可知，ASFRPC和SFRPC试件的等效初始剪切强度、峰值剪应变及初始能量密度均随着纤维掺量的增加而增加。结合表5，当纤维掺量为1vol%、1.5vol%、2vol%时，ASFRPC试件的等效初始剪切强度feq比SFRPC试件高24.3%、36.36%和7%；峰值剪应变γp比SFRPC试件分别高10.2%、33.96%和2.5%；初始能量密度Tp比SFRPC试件分别高37%、82.56%和16.14%。图13(a)和图13(b)是峰值荷载后ASFRC和SFRPC试件的等效残余剪切强度fp,k和残余剪切韧度比Rp,k。当纤维掺量为2vol%时，ASFRPC的等效残余剪切强度fp,1.2、fp,1.5、fp,2.0较SFRPC提高幅度较为显著，分别约为43.76%、74.54%、109.86%，残余韧度在纤维掺量为1vol%和1.5vol%时两者相差不大。ASFRPC和SFPRC试件的残余剪切韧度比Rp,k未表现出明显规律，这主要是由于Rp,k是个相对值，当两类构件的峰值荷载和位移不同，但曲线形状类似时，二者不会有太大差别或者表现出与绝对值类似规律。
![]()
图 12 纤维方向对SFRPC-13试件峰值前剪切韧性的影响Figure 12. Effects of fiber orientation on toughness parameters pre-peak load of SFRPC-13 specimens![]()
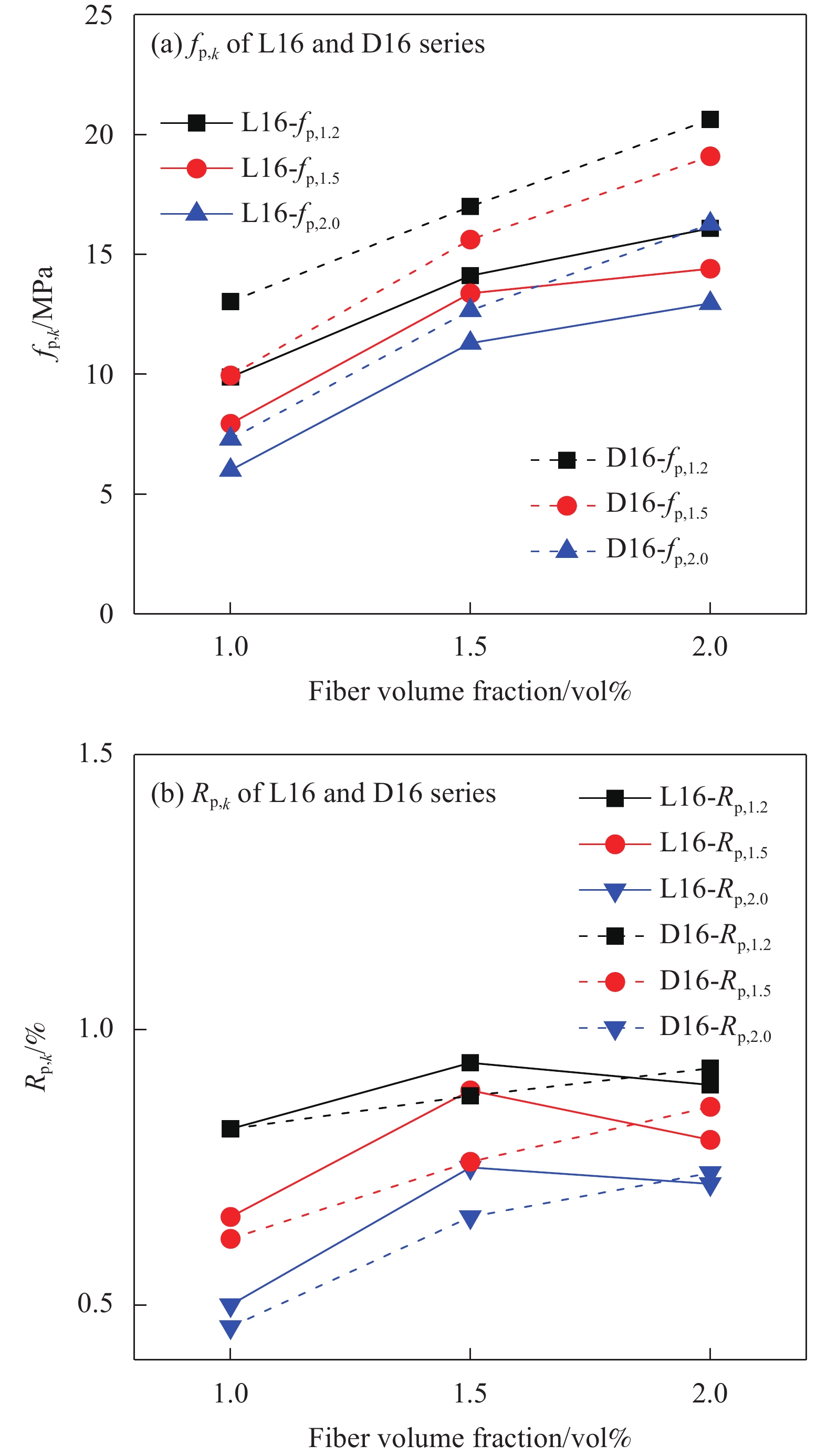
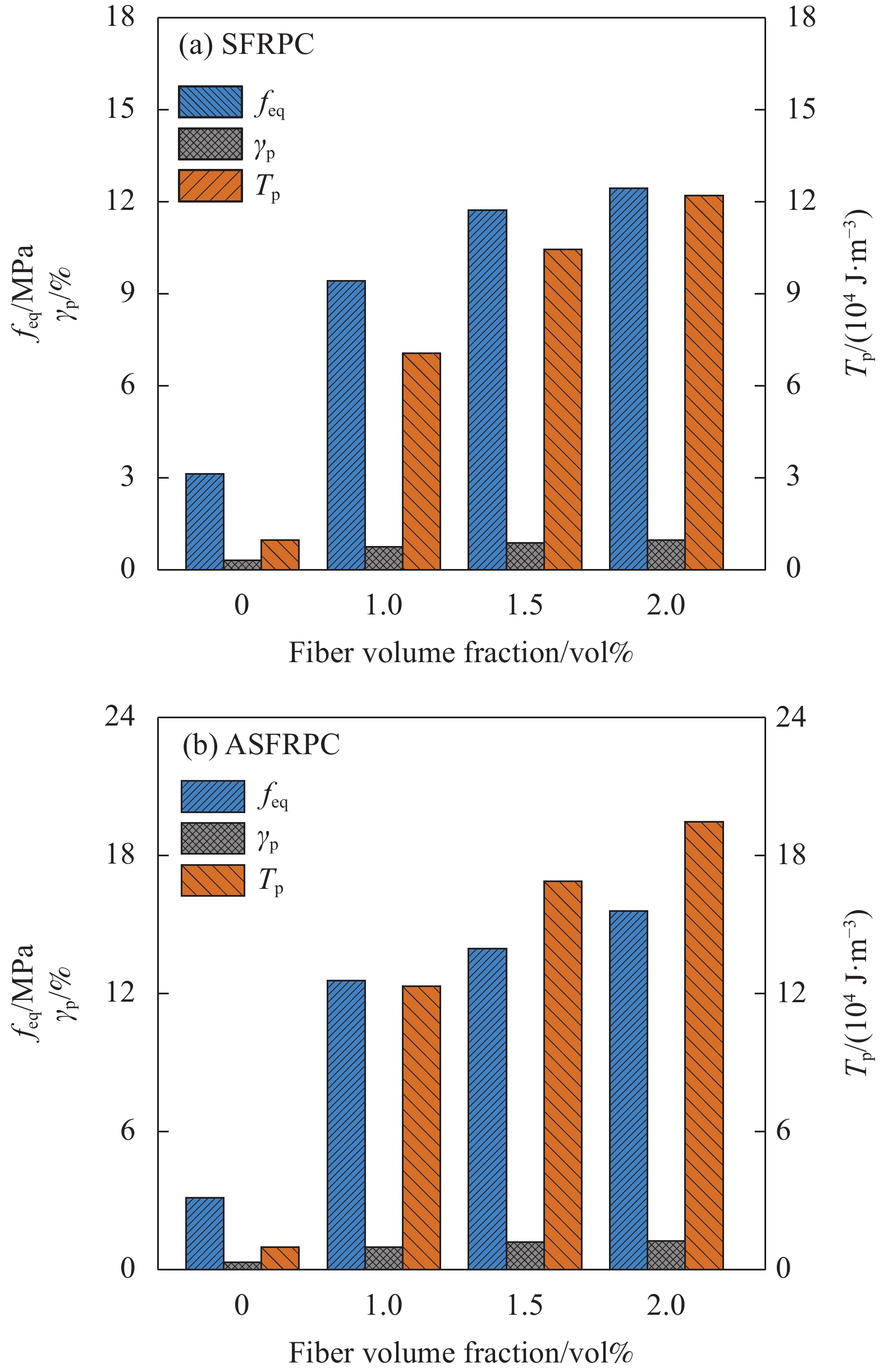
图 13 钢纤维方向对SFRPC-13试件峰值后剪切韧性的影响Figure 13. Effects of fiber orientation on toughness parameters post-peak load of SFRPC-13 specimens图14反映了纤维长度为16 mm时峰值荷载前ASFRC试件和SFRPC试件的韧性指标，与纤维长度为13 mm时类似，峰值前韧性指标同样随着纤维掺量增加而提高。当纤维掺量为1vol%、1.5vol%、2vol%时，ASFRPC试件的等效初始剪切强度feq比SFRPC试件分别高50.67%、41.07%和30.66%；其峰值剪应变γp分别比SFRPC试件高64.71%、46.27%和51.25%；初始能量密度Tp分别比SFRPC试件高138.7%、106.4%和97.52%。图15(a)和图15(b)分别是峰值荷载后ASFRC和SFRPC试件的等效残余剪切强度fp,k和残余剪切韧度比Rp,k。可知，ASFRPC试件的等效残余剪切强度fp,k均高于同参数的SFRPC试件。当纤维掺量为1vol%时，ASFRPC的等效残余剪切强度fp,1.2、fp,1.5、fp,2.0较SFRPC提高幅度大约为31.88%、39.36%、21.67%。另外，与纤维长度13 mm构件组的原因类似，由于ASFRPC试件抗剪强度值基数较大，导致计算出来的残余剪切韧度比Rp,k相比SFRPC试件无显著规律。
![]()
图 14 纤维方向对SFRPC-16试件峰值前剪切韧性指标的影响Figure 14. Effects of fiber orientation on toughness parameters pre-peak load of SFRPC-16 specimens![]()
图 15 钢纤维方向对SFRPC-16试件峰值后剪切韧性指标的影响Figure 15. Effects of fiber orientation on toughness parameters postpeak load of SFRPC-16 specimens图16反映了纤维长度为20 mm，ASFRC试件和SFRPC试件的峰值前韧性指标。可知峰值前韧性指标同样随着纤维掺量增加而提高。当纤维掺量为1vol%、1.5vol%和2vol%时，ASFRPC试件的等效初始剪切强度feq比SFRPC试件分别高33.33%、18.82%和25.4%；其峰值剪应变γp比SFRPC分别高30.67%、35.96%和30%；其初始能量密度Tp比SFRPC试件高200.41%、61.53%和59.67%。图17(a)和图17(b)分别是峰值后ASFRC和SFRPC试件的等效残余剪切强度fp,k和残余剪切韧度比Rp,k。图中除了L20-1.5%试件的fp,1.5以外，ASFRPC试件的等效残余剪切强度fp,k比SFRPC试件均有显著提高。当纤维掺量为2vol%时，ASFRPC的等效残余剪切强度fp,1.2、fp,1.5、fp,2.0较SFRPC提高幅度大约为38.78%、35.76%、31.8%。由于上述同样原因，两类构件的Rp,k未表现出显著规律。
![]()
图 16 纤维方向对SFRPC-20试件峰值前剪切韧性指标的影响Figure 16. Effects of fiber orientation on toughness parameters prepeak load of SFRPC-20 specimens![]()
图 17 纤维方向对SFRPC-20试件峰值后剪切韧性指标的影响Figure 17. Effects of fiber orientation on toughness parameters post-peak load of SFRPC-20 specimens2.4.2 钢纤维掺量对剪切韧性的影响
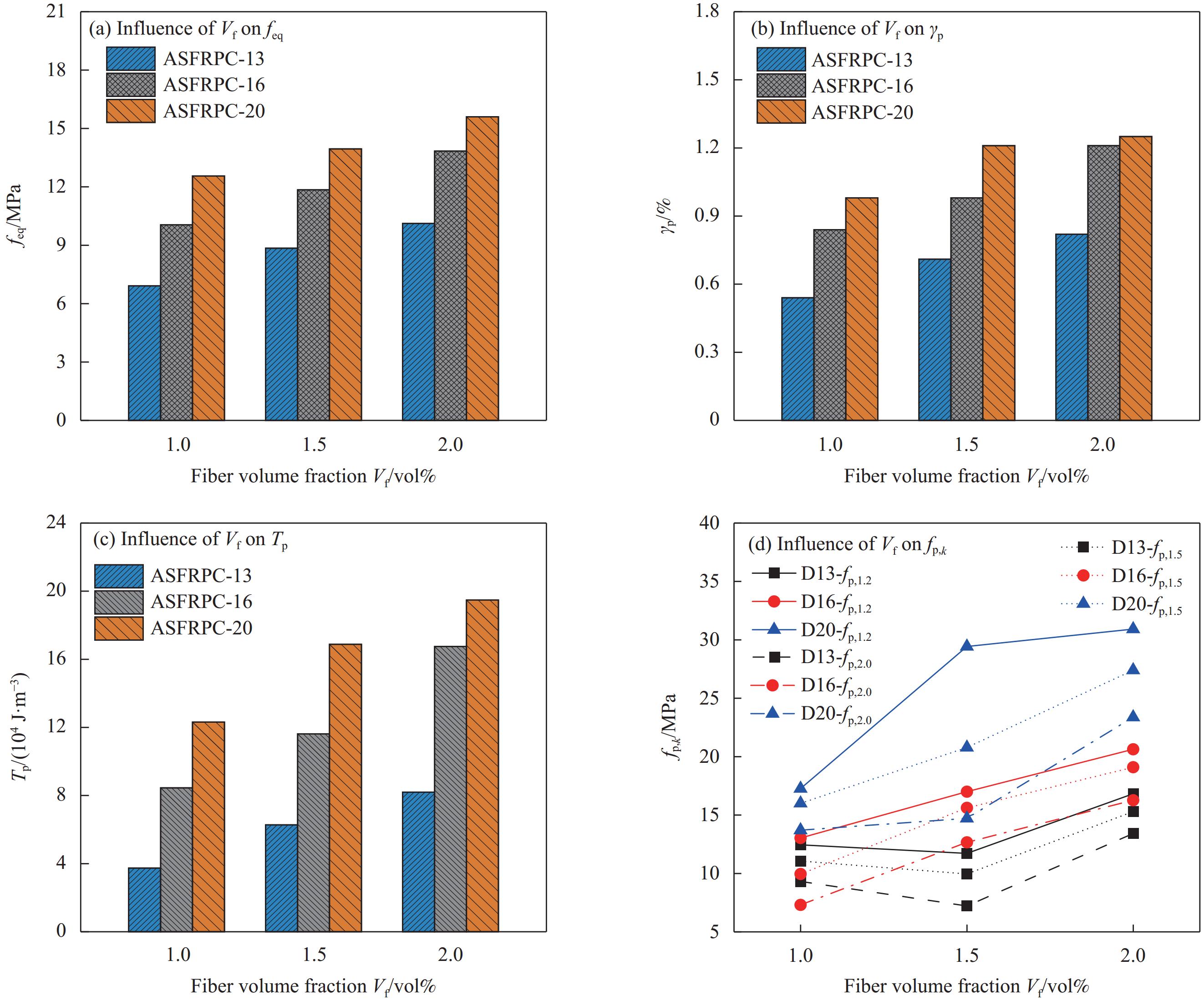
图18为纤维掺量对ASFRPC试件韧性参数的影响曲线。由表5和图18可知，随着纤维掺量的增加，同一纤维长度的ASFRPC试件的各项峰值前剪切韧性指标均显著提高，当纤维长度为13 mm时，纤维掺量为2vol%的ASFRPC试件的等效初始强度feq、峰值剪切应变γp及初始能量密度相比纤维掺量1vol%、1.5vol%的ASFRPC试件分别提高28.08%、14.35%；31.28%、15.5%；68.46%、30.57%，当纤维长度为16 mm时，纤维掺量为2vol%的ASFRPC试件的等效初始强度、峰值剪切应变及初始能量密度相比纤维掺量1vol%、1.5vol%的ASFRPC试件分别提高17.86%、16.8%；16.67%、23.45%；37.51%、44.14%，当纤维长度为20 mm时，纤维掺量为2vol%的ASFRPC试件的等效初始强度、峰值剪切应变及初始能量密度相比纤维掺量1vol%、1.5vol%的ASFRPC试件分别提高11.07%、11.83%；23.47%、10.74%；37.12%、15.4%。另一方面，纤维掺量在一定范围内(1vol%、1.5vol%、2vol%)，纤维长度为13 mm时，ASFRPC试件的等效残余剪切强度fp,1.2、fp,1.5、fp,2.0增幅为−6%、43.64%；−10%、53.51%；−22.56%、86%，纤维长度为16 mm时，ASFRPC试件的等效残余剪切强度fp,1.2、fp,1.5、fp,2.0增幅为30.47%、21.35%；56.98%、22.21%；73.42%、28.52%，纤维长度为20 mm时，ASFRPC试件的等效残余剪切强度fp,1.2、fp,1.5、fp,2.0增幅为70.51%、5.1%；29.88%、31.91%；7.37%、58.94%。
![]()
图 18 纤维掺量对ASFRPC试件韧性参数的影响Figure 18. Effects of Vf on toughness parameters of ASFRPC specimens2.4.3 钢纤维长度对剪切韧性的影响
图19为纤维长度对ASFRPC试件峰值韧性参数的影响曲线。由表5和图19可知，纤维掺量为1vol%的ASFRPC的试件，当纤维长度由13 mm增加至16 mm和20 mm时，其等效初始强度feq、峰值剪切应变γp及初始能量密度Tp的提高幅度分别为45.44%、24.98%；55.56%、16.67%；125.94%、45.68%；纤维掺量为1.5vol%的ASFRPC的试件，当纤维长度由13 mm变化至16 mm和20 mm时，其等效初始强度feq、峰值剪切应变γp及初始能量密度Tp的提高幅度分别为33.4%、17.72%；38.03%、23.47%；85.03%、45.27%；纤维掺量为2vol%的ASFRPC的试件，当纤维长度由13 mm增加至16 mm和20 mm时，其等效初始强度feq、峰值剪切应变γp及初始能量密度Tp的提高幅度分别为36.76%、12.71%；47.56%、3%；104.26%、16.3%。另一方面，除纤维掺量为1vol%的ASFRPC试件，其他试件的等效残余剪切强度fp,k均随纤维长度的增加而增大。当纤维掺量为1.5vol%时，纤维长度由13 mm增加至16 mm和20 mm，其等效残余剪切强度fp,1.2、fp,1.5、fp,2.0增幅分别为45.17%、73.12%；56.83%、33.03%；75.6%、16.2%，当纤维掺量为2vol%时，纤维长度由13 mm增加至16 mm和20 mm，其等效残余剪切强度fp,1.2、fp,1.5、fp,2.0增幅分别为22.65%%、49.88%；24.85%、43.58%；21.32%、43%。
![]()
图 19 纤维长度对ASFRPC试件峰值韧性参数的影响Figure 19. Effects of Lf on toughness parameters of ASFRPC specimens3. 结 论
通过对不同纤维掺量和纤维长度的定向分布钢纤维活性粉末混凝土(ASFRPC)和乱向分布钢纤维活性粉末混凝土(SFRPC)构件开展直剪试验，并在试验基础上进行了韧性指标分析，得到主要结论如下：
(1) ASFRPC试件的直剪承载力和变形能力均高于SFRPC试件，纤维长度20 mm，纤维掺量为1vol%时，提高幅度最大为36.43%。承载力和变形能力也随着纤维长度和纤维掺量的增加而增加；
(2) ASFRPC双面剪切试件的等效初始剪切强度feq、峰值剪应变γp、初始能量密度Tp及等效残余强度fp,k较SFRPC试件有显著的提升，其中初始能量密度提升幅度最高可达200.41%。各参数随钢纤维长度的增加而增加，且提高幅度随纤维长度增加逐渐降低；
(3)残余剪切韧度比Rp,k是个相对参数，反映了曲线峰值后的形状变化，由于ASFRPC和SFRPC试件的受剪荷载-位移曲线形状受纤维掺量、分布以及长度的影响规律不明显，因而基于此曲线计算的残余剪切韧度没有显著规律性；
(4)其他条件相同，随着钢纤维掺量的提高，等效初始剪切强度feq、峰值剪应变γp、初始能量密度Tp都呈现不同幅度的增加，其中纤维长度13 mm，掺量从1vol%增加到2vol%时，初始能量密度提升幅度高达68.46%。在相同条件下，剪切韧性随钢纤维长度增加而增加。跨越裂缝的钢纤维通过粘结横贯裂缝传递应力，钢纤维长度越大，纤维与基体间的粘结应力越大；
(5)纤维掺量和长度的进一步增加都会给钢纤维转向造成困难，在本试验参数范围内，通过综合对比纤维方向、纤维掺量和纤维长度，当纤维掺量为2vol%，纤维长度为20 mm时，ASFRPC试件剪切性能最优。
-
![]()
图 1 镀铜微丝钢纤维
Figure 1. Copper coated microfilament steel fiber
df—Steel fiber diameter; Lf—Steel fiber length
![]()
图 4 裂缝处定向分布钢纤维RPC (ASFRPC)与乱向分布钢纤维RPC (SFRPC)纤维分布对比
Figure 4. Fiber distribution at the crack of aligned steel fiber RPC (ASFRPC) and randomly distributed steel fiber RPC (SFRPC) specimens
![]()
图 5 双面剪切试验装置图
Figure 5. Schematic of the double shear test setup
a—Width of the cutting line; h—Height of the shear plane; F—Shear load
![]()
图 7 剪切韧性计算参数
Figure 7. Definitions for shear toughness indexes
δp is the deflection at the peak load of the shear deformation curve; Ωp is the area under the load shear deformation curve before the peak load; Ωp,k is the area under the load shear deformation curve from δp to δk; δp,k is the deformation difference of the corresponding δp to δk segment on the curve; k is the ratio of δk to the deflection δp at the peak load
![]()
图 8 SFRPC试件直剪失效模式和裂纹形态(以L20-1%为例)
Figure 8. Failure mode and crack morphology of SFRPC specimen (Take L20-1% as an example)
![]()
图 9 ASFRPC和SFRPC试件直剪失效模式和裂纹形态
Figure 9. Failure mode and crack morphology of the ASFRPC and SFRPC specimens
![]()
图 10 SFRPC试件和ASFRPC试件剪切荷载/应力-位移关系曲线
Figure 10. Shear load/stress-deformation curves of SFRPC specimens and ASFRPC specimens
![]()
图 11 纤维长度对ASFRPC试件抗剪强度与峰值变形的影响
Figure 11. Effect of fiber length on shear strength and peak deformation of ASFRPC specimens
![]()
图 12 纤维方向对SFRPC-13试件峰值前剪切韧性的影响
Figure 12. Effects of fiber orientation on toughness parameters pre-peak load of SFRPC-13 specimens
![]()
图 13 钢纤维方向对SFRPC-13试件峰值后剪切韧性的影响
Figure 13. Effects of fiber orientation on toughness parameters post-peak load of SFRPC-13 specimens
![]()
图 14 纤维方向对SFRPC-16试件峰值前剪切韧性指标的影响
Figure 14. Effects of fiber orientation on toughness parameters pre-peak load of SFRPC-16 specimens
![]()
图 15 钢纤维方向对SFRPC-16试件峰值后剪切韧性指标的影响
Figure 15. Effects of fiber orientation on toughness parameters postpeak load of SFRPC-16 specimens
![]()
图 16 纤维方向对SFRPC-20试件峰值前剪切韧性指标的影响
Figure 16. Effects of fiber orientation on toughness parameters prepeak load of SFRPC-20 specimens
![]()
图 17 纤维方向对SFRPC-20试件峰值后剪切韧性指标的影响
Figure 17. Effects of fiber orientation on toughness parameters post-peak load of SFRPC-20 specimens
![]()
图 18 纤维掺量对ASFRPC试件韧性参数的影响
Figure 18. Effects of Vf on toughness parameters of ASFRPC specimens
![]()
图 19 纤维长度对ASFRPC试件峰值韧性参数的影响
Figure 19. Effects of Lf on toughness parameters of ASFRPC specimens
表 1 活性粉末混凝土(RPC)配合比
Table 1 Mix proportion of reactive powder concrete (RPC)
W/B/% Unit weight/(kg·m−3) Water Cement Sand Silica fume SP 26 244.4 710.0 1266.0 230.0 3.6 Notes: W/B—Water binder ratio; SP—Super plasticizer. 
下载: 导出CSV
表 2 钢纤维的各项性能
Table 2 Properties of steel fiber
Type Diameter df/mm Length Lf/mm Aspect ratio Lf/df Density/(g·cm−3) Tensile strength/MPa Elastic modulus/GPa S13 0.2 13 65 7.8 2900 200 S16 0.2 16 80 S20 0.2 20 100
下载: 导出CSV
表 3 试件编号
Table 3 Specimen number
Specimen number Fiber length/mm Fiber content/vol% Fiber distribution L13-1% 13 1 Randomly L13-1.5% 13 1.5 Randomly L13-2% 13 2 Randomly L16-1% 16 1 Randomly L16-1.5% 16 1.5 Randomly L16-2% 16 2 Randomly L20-1% 20 1 Randomly L20-1.5% 20 1.5 Randomly L20-2% 20 2 Randomly D13-1% 13 1 Aligned D13-1.5% 13 1.5 Aligned D13-2% 13 2 Aligned D16-1% 16 1 Aligned D16-1.5% 16 1.5 Aligned D16-2% 16 2 Aligned D20-1% 20 1 Aligned D20-1.5% 20 1.5 Aligned D20-2% 20 2 Aligned
下载: 导出CSV
表 4 SFRPC、ASFRPC和RPC试件试验测量结果
Table 4 Test measurements of SFRPC, ASFRPC and RPC specimens
Specimen type Group fcu/MPa Fmax/kN △p/mm SFRPC L13-1% 87.33 200.4 0.49 L13-1.5% 89.78 243.2 0.53 L13-2% 95.04 302.6 0.82 L16-1% 93.31 241.4 0.53 L16-1.5% 95.96 301.2 0.67 L16-2% 103.52 358.8 0.8 L20-1% 93.63 300.8 0.75 L20-1.5% 95.45 390.6 0.89 L20-2% 98.22 444.2 0.98 ASFRPC D13-1% 87.33 254.6 0.54 D13-1.5% 89.78 305.8 0.71 D13-2% 95.04 353.4 0.83 D16-1% 93.31 318.8 0.84 D16-1.5% 95.96 384.4 0.98 D16-2% 103.52 442.2 1.2 D20-1% 93.63 422.4 0.95 D20-1.5% 95.45 520 1.21 D20-2% 98.22 549.2 1.25 RPC L0-0 79.91 138.8 0.31 Notes: fcu—Cube compressive strength; Fmax—Peak shear load; △p—Peak deformation; L13-1% represents SFRPC specimens with a fiber length of 13 mm and a fiber content of 1vol%; D13-1% represents ASFRPC specimens with a fiber length of 13 mm and a fiber content of 1vol%, and the rest are the same.
下载: 导出CSV
表 5 RPC试件剪切荷载-变形曲线峰值前及峰值后的韧性指标
Table 5 Toughness index evaluation pre-peak and post-peak load of shear load-deformation curves of RPC specimen
Specimen type Group feq/MPa γp/% Tp/(104 J·m−3) fp,k/MPa Rp,k/% fp,1.2 fp,1.5 fp,2.0 Rp,1.2 Rp,1.5 Rp,2.0 RPC L0-0 3.13 0.31 0.97 — — — — — — SFRPC L13-1% 5.56 0.49 2.73 9.61 9.17 8.17 0.96 0.92 0.82 L13-1.5% 6.49 0.53 3.44 9.93 10.04 7.90 0.82 0.83 0.65 L13-2% 9.47 0.8 7.06 11.7 8.76 6.39 0.77 0.58 0.42 L16-1% 6.67 0.515 3.54 9.88 7.94 6.00 0.82 0.66 0.50 L16-1.5% 8.40 0.67 5.63 14.11 13.38 11.30 0.94 0.89 0.75 L16-2% 10.6 0.8 8.48 16.09 14.40 12.96 0.9 0.80 0.72 L20-1% 9.42 0.75 7.07 14.68 12.85 9.86 0.98 0.85 0.66 L20-1.5% 11.74 0.89 10.45 18.71 16.65 15.30 0.96 0.85 0.78 L20-2% 12.44 0.98 12.2 22.28 20.19 17.74 1.00 0.91 0.8 ASFRPC D13-1% 6.91 0.54 3.74 12.44 11.06 9.31 0.98 0.87 0.73 D13-1.5% 8.85 0.71 6.28 11.71 9.96 7.21 0.76 0.65 0.47 D13-2% 10.12 0.82 8.2 16.82 15.29 13.41 0.95 0.87 0.76 D16-1% 10.05 0.84 8.45 13.03 9.95 7.30 0.82 0.62 0.46 D16-1.5% 11.85 0.98 11.62 17.00 15.62 12.66 0.88 0.76 0.66 D16-2% 13.84 1.21 16.75 20.63 19.09 16.27 0.93 0.86 0.74 D20-1% 12.56 0.98 12.31 17.26 16.00 13.70 0.82 0.76 0.65 D20-1.5% 13.95 1.21 16.88 29.43 20.78 14.71 1.13 0.80 0.57 D20-2% 15.6 1.25 19.48 30.92 27.41 23.38 1.13 1.00 0.85 Notes: feq—Initial equivalent shear strength; γp—Peak shear strain; Tp—Initial energy density; fp,k—Equivalent residual shear strength; Rp,k—Residual shear toughness ratio.
下载: 导出CSV
-
[1] 童良玉, 刘清风. 纤维增强混凝土氯离子扩散系数的多尺度预测模型[J]. 复合材料学报, 2022, 39(11): 5181-5191. TONG Liangyu, LIU Qingfeng. Multi-scale prediction model of chloride diffusivity of fiber reinforced concrete[J]. Acta Materiae Compositae Sinica, 2022, 39(11): 5181-5191(in Chinese).
[2] ROMUALDI J P, BATSON G B. Mechanics of crack arrest in concrete[J]. Journal of the Engineering Mechanics, 1963, 89(3): 147-168. DOI: 10.1061/JMCEA3.0000214
[3] MALVAR L J. Bond stress-slip characteristics of FRP rebar: Report TR-2013-SHR[R]. California: Naval Facilities Engineering Service Center, 1994.
[4] 高丹盈, 朱海堂, 谢晶晶. 纤维增强塑料筋混凝土粘结滑移本构模型[J]. 工业建筑, 2003, 33(7): 41-43, 82. DOI: 10.3321/j.issn:1000-8993.2003.07.011 GAO Danying, ZHU Haitang, XIE Jingjing. The constitutive models for bond slip relation between FRP rebars and concrete[J]. Industrial Construction, 2003, 33(7): 41-43, 82(in Chinese). DOI: 10.3321/j.issn:1000-8993.2003.07.011
[5] 李春蕊, 王学志, 李根, 等. 纤维混凝土梁研究综述[J]. 硅酸盐通报, 2018, 37(4): 1255-1265. LI Chunrui, WANG Xuezhi, LI Gen, et al. Review of research on fiber reinforced concrete beams[J]. Bulletin of the Chinese Ceramic Society, 2018, 37(4): 1255-1265(in Chinese).
[6] WU H S, ZANG Z S, DENG S Y, et al. Recent developments in pullout behaviors and tensile properties of ultra-high-performance concrete reinforced with steel fiber[J]. Archives of Civil and Mechanical Engineering, 2023, 23(3): 216. DOI: 10.1007/s43452-023-00761-0
[7] ROSSI P, ACKER P, MALIER Y. Effect of steel fiber at two different stages: The material and the structure[J]. Materials and Structure, 1987, 20(6): 436-439. DOI: 10.1007/BF02472494
[8] 高丹盈, 刘建秀. 钢纤维混凝土基本理论[M]. 北京: 科学技术出版社, 1994. GAO Danying, LIU Jianxiu. Basic theory of steel fiber reinforced concrete[M]. Beijing: Science and Technology Press, 1994(in Chinese).
[9] BRANDT A M. Fiber reinforced cement-based (FRC) composites after over 40 years of development in building and civil engineering[J]. Composite Structures, 2008, 86(1): 3-9.
[10] ZOLLO R F. Fiber-reinforced concrete: An overview after 30 years of development[J]. Cement Concrete Composites, 1997, 19(2): 107-122. DOI: 10.1016/S0958-9465(96)00046-7
[11] RICHARD P, CHEYREZY M. Composition of reactive power concretes[J]. Cement and Concrete Research, 1995, 25(7): 1501-1511. DOI: 10.1016/0008-8846(95)00144-2
[12] KANG S, KIM J. The relation between fiber orientation and tensile behavior in an ultra-high performance fiber reinforced cementitious composites (UHPFRCC)[J]. Cement and Concrete Research, 2011, 41(10): 1001-1014. DOI: 10.1016/j.cemconres.2011.05.009
[13] STAHLI P, SUTTER M, VAN MIER J G M. Improving the mechanical properties of HFC by adjusting the filling method[C]//Proceedings of the Fifth International Workshop on High Performance Fiber Reinforced Cement Composites. Mainz, Germany: RILEM Publications, 2007: 23-30.
[14] POITOU A, CHINESTA F, BERNIER G. Orienting fibers by extrusion in reinforced reactive powder concrete[J]. Journal of Engineering Mechanics, 2001, 127(6): 593-598. DOI: 10.1061/(ASCE)0733-9399(2001)127:6(593)
[15] KANG S T, PARK J J, RYU G S, et al. Fiber alignment of steel fiber reinforced high strength concrete (SFR-HSC) in flexural members and its effect on the flexural strength[J]. Key Engineering Materials, 2008, 385-387: 789-792.
[16] 慕儒, 邱欣, 赵全明, 等. 单向分布钢纤维增强水泥基复合材料(I): 钢纤维方向控制[J]. 建筑材料学报, 2015, 18(2): 208-213. MU Ru, QIU Xin, ZHAO Quanming, et al. Aligned steel fibre reinforced cement based composites (I): Orientation control of steel fibres[J]. Journal of Building Materials, 2015, 18(2): 208-213(in Chinese).
[17] 慕儒, 李辉, 王晓伟, 等. 单向分布钢纤维增强水泥基复合材料(II): 制备及钢纤维增强作用[J]. 建筑材料学报, 2015, 18(3): 387-392. MU Ru, LI Hui, WANG Xiaowei, et al. Aligned steel fibre reinforced cement based composites (II): Preparation and reinforcement of aligned steel fibres[J]. Journal of Building Materials, 2015, 18(3): 387-392(in Chinese).
[18] 慕儒, 王成, 李辉, 等. 单向分布钢纤维增强水泥基复合材料(III): 断裂性能[J]. 建筑材料学报, 2016, 19(1): 78-82. MU Ru, WANG Cheng, LI Hui, et al. Aligned steel fiber reinforced cement-based composites (III): Fracture properties[J]. Journal of Building Materials, 2016, 19(1): 78-82(in Chinese).
[19] MU R, LI H, QING L B. Aligning steel fiber in cement mortar using electro-magnetic field[J]. Construction and Building Materials, 2017, 131: 309-316. DOI: 10.1016/j.conbuildmat.2016.11.081
[20] MU R, DIAO C, LIU H, et al. Design, preparation and mechanical properties of full-field aligned steel fiber reinforced cementitious composite[J]. Construction and Building Materials, 2021, 272(3): 121631.
[21] YANG K, SU H, DAI T, et al. Experimental study on the flexural tensile properties of aligned steel fiber reinforced reactive powder concrete members[J]. Structural Concrete, 2023, 24(1): 1486-1502. DOI: 10.1002/suco.202200172
[22] 李坤坤, 杨克家, 李坤梁, 等. 纤维分布对活性粉末混凝土构件力学性能的影响[J]. 土木与环境工程学报(中英文), 2022, 44(5): 197-204. LI Kunkun, YANG Kejia, LI Kunliang, et al. Effect of fiber orientation on the mechanical properties of reactive powder concrete members[J]. Journal of Civil and Environmental Engineering (Chinese and English), 2022, 44(5): 197-204(in Chinese).
[23] YANG K J, LI K L, LIN Y W. Influence of fiber orientation on the shear properties of steel fiber-reinforced reactive powder concrete beams[J]. Advances in Civil Engineering, 2023, 9: 9953966.
[24] MINELLI F, PLIZZARI G. On the effectiveness of steel fibers as shear reinforcedment[J]. ACI Structural Journal, 2013, 110: 379-389.
[25] BOULEKBACHE B, HAMRAT M, CHEMROUK M, et al. Influence of yield stress and compressive strength on direct behavior of steel fiber-reinforced concrete[J]. Construction and Building Materials, 2012, 27(1): 6-14. DOI: 10.1016/j.conbuildmat.2011.07.015
[26] AVESTON J, COOPER G A, KELLY A. Single and multiple fracture, the properties of fiber composites[C]//Conference Proceedings on Properties of Fiber Composites, National Physical Laboratory. Guildford, UK: IPC Science and Technology Press Ltd., 1971: 15-26.
[27] SOETENS T, MATTYS S. Shear-stress transfer across a crack in steel fiber-reinforced concrete[J]. Cement and Concrete Composite, 2017, 82: 1-13. DOI: 10.1016/j.cemconcomp.2017.05.010
[28] 邓明科, 刘华政, 马福栋, 等. 聚乙烯醇纤维改性高延性混凝土双面剪切试验及剪切韧性评价方法[J]. 复合材料学报, 2020, 37(2): 461-471. DENG Mingke, LIU Huazheng, MA Fudong, et al. Double shear experiment of highly ductile concrete modified by polyvingl alcohol and shear toughness evaluation method[J]. Acta Materiae Compositae Sinica, 2020, 37(2): 461-471(in Chinese).
[29] MU R, WANG Z D, WANG X W. Experimental study on shear properties of aligned steel fiber reinforced cement-based composites[J]. Construction and Building Materials, 2018, 184: 27-33. DOI: 10.1016/j.conbuildmat.2018.06.026
[30] 中国工程建设标准化协会. 纤维混凝土试验方法标准: CECS13: 2009[S]. 北京: 中国计划出版社, 2010. China Association for Engineering Construction Standardization. Standard test methods for fiber reinforced concrete CECS13: 2009[S]. Beijing: China Planning Press, 2010(in Chinese).
-
其他相关附件
-
目的
通过磁场控制混凝土基体中的钢纤维分布，使其与主拉应力方向平行，可以有效提高钢纤维混凝土的抗弯、拉性能，但在与纤维分布方向垂直的剪切力作用下的性能存疑。本文以活性粉末混凝土(Reactive Powder Concrete，RPC)为基体，采用镀铜微丝钢纤维作为增强材料，制作定向分布钢纤维活性粉末混凝土(Aligned Steel Fiber RPC，ASFRPC)试件和乱向分布钢纤维活性粉末混凝土(Steel Fiber Reinforced RPC，SFRPC)试件，对其施加与纤维方向垂直的直剪荷载，研究ASFRPC的直剪性能，并对其韧性进行分析探讨。
方法试件振捣过程中施加不低于250高斯的电磁场作用，实现纤维定向分布。考虑三种纤维体积掺量(=1.0%、1.5%、2%)，三种纤维长度(=13mm、16mm、20mm)制作了ASFRPC试件和SFRPC试件，采用《纤维混凝土试验方法标准》(CECS13: 2009)中的规定对各试件开展直剪试验。通过对比ASFRPC和SFRPC试件的剪切荷载—位移曲线，分析纤维定向后试件直剪承载力和变形能力的变化特征。在现有弯曲韧性评价方法的基础上，采用初始能量密度与残余剪切韧度比作为剪切韧性评价指标对试件剪切韧性开展评价，避免了初裂点确定的困难，也适用于不同尺寸构件的对比。
结果ASFRPC试件的直剪承载力和变形能力均高于SFRPC试件，纤维长度20mm，纤维掺量为1%时，提高幅度最大为36.43%。承载力和变形能力也随着纤维长度和纤维掺量的增加而增加；ASFRPC双面剪切试件的等效初始剪切强度、峰值剪应变、初始剪切能量密度及等效残余强度较SFRPC试件有显著的提升，其中初始剪切能量密度提升幅度最高可达200.41%。各参数随钢纤维长度的增加而增加，且提高幅度随纤维长度增加逐渐降低；残余剪切韧度比是个相对参数，反映了曲线峰值后的形状变化，由于ASFRPC和SFRPC试件的受剪荷载-位移曲线形状受纤维掺量、分布以及长度的影响规律不明显，因而基于此曲线计算的残余剪切韧度没有显著规律性；其他条件相同，随着钢纤维掺量的提高，等效初始剪切强度、峰值剪应变、初始剪切能量密度都呈现不同幅度的增加，其中纤维长度13mm，掺量从1%增加到2%时，初始剪切能量密度提升幅度高达68.46%。在相同条件下，剪切韧性随钢纤维长度增加而增加。跨越裂缝的钢纤维通过粘结横贯裂缝传递应力，钢纤维长度越大，纤维与基体间的粘结应力越大；纤维掺量和长度的进一步增加都会给钢纤维转向造成困难，在本文试验参数范围内，通过综合对比纤维方向，纤维掺量和纤维长度，当纤维掺量为2%，纤维长度为20mm时，ASFRPC试件剪切性能最优。
结论电磁场可以对RPC基体中的钢纤维进行有效定向，定向后ASFRPC的直剪承载力和变形能力均得到显著提升。论文工作验证了RPC基体中镀铜微丝钢纤维定向的可行性，以及定向钢纤维试件在垂直纤维方向的力学性能。韧性评价中，剪切荷载峰值前采用初始能量密度进行韧性评价，可以综合反映峰值前抗剪强度与剪切变形能力，荷载峰值后采用残余剪切韧度比进行韧性评价可以满足不同变形需求对材料残余韧性的要求。韧性评价结果表明，总体上ASFRPC试件的剪切韧性优于SFRPC试件。
-
通过磁场控制钢纤维在混凝土基体中的分布，可以获得方向效应系数(纤维在给定方向投影长度总和与实际长度总和之比，随机分布钢纤维约为0.4)达0.9的定向分布钢纤维混凝土。钢纤维定向后混凝土顺纤维方向的受拉和受弯强度、变形能力及断裂韧性等均显著提升，但垂直纤维方向的力学性能鲜有关注。
为了进一步研究定向分布钢纤维的在垂直纤维方向的力学性能，本文选用镀铜微丝钢纤维，以无粗骨料的活性粉末混凝土(Reactive Powder Concrete，RPC)为基体，利用电磁场定向装置制备了3种不同纤维长度(13mm、16mm、20mm)和体积掺量(1%、1.5%、2%)的定向分布钢纤维RPC(Alinged Steel Fiber Reinforced RPC, ASFRPC)和随机分布钢纤维RPC(Steel Fiber Reinforced RPC, SFRPC)试件。通过双面直剪试验，获得其剪切荷载-位移曲线，选取全曲线上的初裂点、峰值点及其他几个特征点，定量地分析了试件的剪切性能与钢纤维方向、钢纤维掺量和钢纤维长度的关系。分析结果表明：ASFRPC试件的抗剪强度、峰值变形、剪切韧性相比于SFRPC试件均得到了显著提高。研究工作证实了ASFRPC试件垂直纤维方向的直剪力学性能。
磁场定向示意图
SFRPC试件和ASFRPC试件荷载-剪切变形曲线
纤维方向对SFRPC-20试件剪切韧性指标的影响
计量
- 文章访问数: 43
- HTML全文浏览量: 18
- PDF下载量: 4
