由于独特的结构，金属玻璃(Metallic glass，MG)拥有特别的物理和力学性能。与传统晶体合金相比，金属玻璃具有高强度、高硬度、高耐磨性、高耐腐蚀性等优点，目前已被应用在电子信息、医疗、航天等多个领域^[1–3]。然而，金属玻璃在室温下加载容易发生变形失稳而屈服，缺乏塑性变形的能力，这种变形失稳是由单个或几个剪切带的迅速扩展引起的。将第二相颗粒添加到金属玻璃中，形成金属玻璃基复合材料(Metallic glass matrix composites，MGMCs)以阻碍剪切带扩展或促进剪切带分散分布是金属玻璃增韧的有效方法。

实验发现，第二相的存在能有效地阻碍剪切带的快速发展，从而增强材料塑性^[4–7]。除开X射线衍射、扫描电子显微镜(SEM)和透射电子显微镜(TEM)等实验方法，有限元分析和大规模分子动力学(Molecular dynamics，MD)模拟等数值方法也可以在宏观和微观尺度上提供帮助。Jiang等^[8-9]利用基于自由体积理论和基于位错机制的应变梯度(MSG)塑性理论的数值方法，分析了金属玻璃基复合材料中剪切带与位错滑移之间的相互作用，阐明了剪切带起始于高位错密度区，并且拉伸延展性随着塑性颗粒的细化而提高。Li等^[10-11]采用热-力耦合本构模型描述了金属玻璃基体的力学行为，建立了金属玻璃基体复合材料的几何模型，并对各种变形条件进行了系统的有限元模拟，分析了颗粒增强金属玻璃基复合材料的力学性能。他们发现，增强颗粒的体积分数和强度都会影响复合材料的塑性。Fan等^[12]通过实验和理论计算研究了孪晶塑性效应引起的拉伸变形微观机制和加工硬化行为。他们在有限元模型中将椭圆颗粒假设为复合材料中原位枝晶，模拟结果表明基体中的枝晶改变了应力分布，阻碍了剪切带的快速扩展。Shete等^[13]基于Thamburaja^[14]提出的非局部塑性理论，使用有限元模拟来研究枝晶的几何参数，如纵横比、间距、取向和空间分布对金属玻璃基复合材料力学响应的影响。邱昆等^[15]基于自由体积模型编写ABAQUS子程序，分析了颗粒体积分数、颗粒应变硬化指数、颗粒间距、网状结构对金属玻璃基复合材料拉伸塑性的影响。他们的模拟结果显示，网状枝晶结构更能引起复合材料的均匀变形，进而增大复合材料的强度和韧性。Zhou等^[16]应用大规模分子动力学模拟，通过调整几何参数，包括晶相的形状、体积分数和取向，优化复合材料中塑性应变的分布。他们证明了具有适当几何形状(例如足够大的长宽比)的第二相纳米晶体能形成对剪切带扩展的有效屏障，第二相晶体的体积分数越大，材料整体塑性越好，并且平行或垂直载荷方向的纳米晶体能更好地阻碍局部剪切带扩展。Song等^[17-18]采用MD方法研究了圆柱形Cu晶体插入${\mathrm{C}\mathrm{u}}_{50}{\mathrm{Z}\mathrm{r}}_{50}$玻璃基体中构建的金属玻璃基复合材料试样的力学性能。他们也得出晶相的引入可以提高金属玻璃塑性的结论。Feng等^[19]从MD模拟中发现，非晶-晶体界面的引入可以显著改变屈服应力和流动应力。

然而，尽管这些研究深入了解了金属玻璃基复合材料延展性增强的机制，并讨论了晶体枝晶的几何参数对剪切带演化的影响，但大多数研究都假设枝晶形状是简单圆形或椭圆形以及它们的阵列，缺乏对复杂枝晶结构影响的深入探讨。在实际结构中，枝晶无论是纳米晶还是树状枝晶，在大多数情况下都以弥散分布的形式出现在金属玻璃基复合材料中。为了更加贴近真实情况，同时降低模拟的复杂性，我们将这种弥散分布的枝晶结构抽象为均匀的网状结构。本文采用MD数值模拟方法，研究含有弥散分布枝晶结构的金属玻璃基复合材料在单轴拉伸下的力学行为以及微结构演化，系统地探讨了枝晶聚集程度对材料中剪切转换区(STZ)原子萌生及剪切带发展的影响，并结合位错与剪切带耦合作用解释材料的塑性变形过程。模拟结果为理解金属玻璃材料中枝晶改性效应的微观机制提供帮助，并为制备具有良好拉伸延展性的金属玻璃材料提供参考。

1.   模型的建立与模拟过程

本文使用开源软件LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)进行MD模拟。二元合金Cu-Zr因其高的玻璃态形成能力和优异的热稳定性被选为本工作中的金属玻璃研究对象^[20–22]。Cu-Zr二元合金体系的势函数相对成熟，应用广泛^[23-24]。本文采用Mendelev等^[23]开发的嵌入原子势(EAM)方法来模拟铜锆原子间的相互作用。

1.1   MD数值试件的生成

采用了常规的熔融-淬火方法制备了${\mathrm{C}\mathrm{u}}_{64}{\mathrm{Z}\mathrm{r}}_{36}$玻璃试样。首先，用FCC Cu原子填充尺寸为21 (x) ×21 (y) ×5 (z) nm³的盒子，并将其中36%的Cu原子替换为Zr原子。其次，将合金试样在2000 K下弛豫600 ps后，在零压强下以0.1 K/ps (10¹¹ K/s)的速率冷却至50 K。实验中常用的降温速率通常在10³~10⁶ K/s之间，由于冷却率会对金属玻璃原子结构中的中、短程有序产生影响，进而影响到材料的力学性能，模拟设定的冷却速度应当尽可能地贴近实验。但受限于计算成本，大多数MD模拟中使用的降温速率通常在10¹⁰~10¹³ K/s之间^{[16-17, 24]}。现有模拟采用的冷却速率尽管不能捕获原子结构中的所有细节，但也能较好地体现金属玻璃中的结构特质^[25]。接着弛豫一段时间后，得到尺寸为23.5 (x)×23.5 (y)×5.4 (z) nm³的基体试样，其中含有~190000个原子。然后，在x和y方向复制试样，并经过一段时间的热力学弛豫，最终形成尺寸为47.0 (x)×70.6 (y)×5.6 (z) nm³含有~1150000个原子的更大试样。在熔化、淬火和弛豫的整个模拟过程中，试样的3个方向上都施加了PBC边界条件。积分时间步长设置为2 fs，温度和压力由Nose-Hoover恒温器^[26]和等压等温系综(NPT)控制。

随后，沿着Z轴方向按照特定形状柱状区域挖去部分${\mathrm{C}\mathrm{u}}_{64}{\mathrm{Z}\mathrm{r}}_{36}$基体原子，然后填充进FCC Cu原子，生成具有第二相颗粒的金属玻璃基复合材料试样。

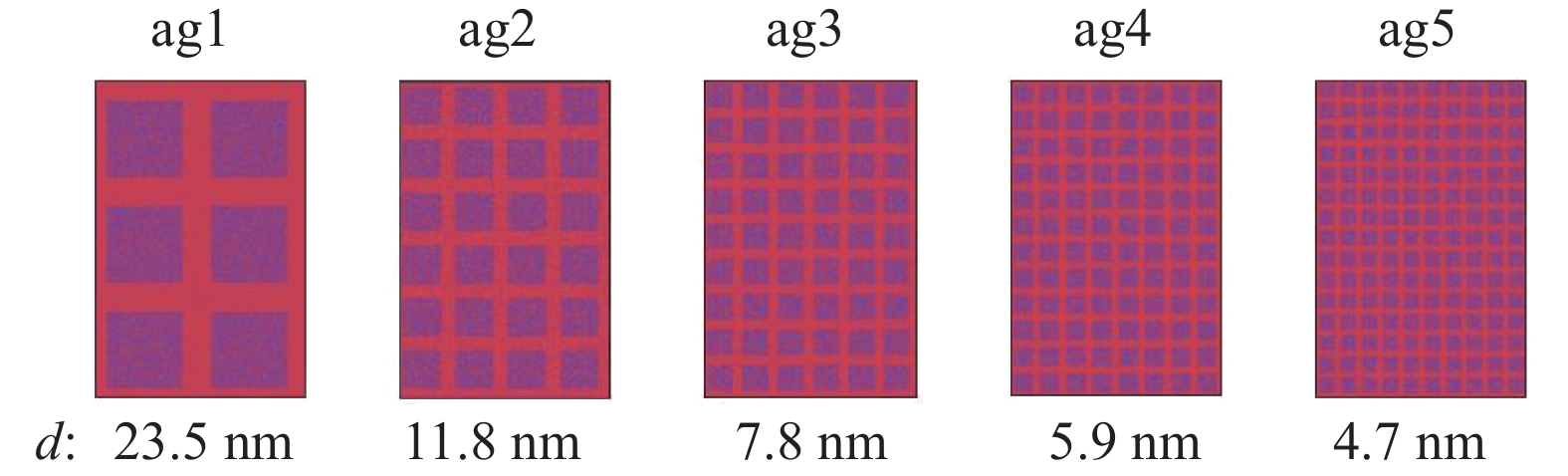
为了研究枝晶的聚集程度对金属玻璃基复合材料力学行为的影响，我们选取了阻碍剪切带效果较好的竖直-水平交错构型作为枝晶结构构型。通过调整枝晶间距d与枝晶宽度L，并控制枝晶的体积分数为恒定值，来表现不同的枝晶聚集程度。图1给出了具有不同枝晶聚集程度的试样的编号及对应的枝晶间距d。在枝晶体积分数相同和枝晶宽度/间距比例相同的情况下，枝晶间间距越大，枝晶聚集程度越大。

图  1  枝晶聚集程度不同的金属玻璃(MG)基复合材料的分子动力学(MD)试样模型(灰色区域代表由FCC Cu原子组成的枝晶，其余浅灰色区域代表金属玻璃基体)

Figure  1.  Molecular dynamics (MD) models of metallic glass (MG) matrix composites employed in tension simulation containing dendrites with different degree of aggregation (The prominent gray regions representing dendrites consisting of FCC Cu atoms and the rest light gray regions representing the glass matrix)

ag—Models containing dendrites with different degree of aggregation; d—Interdendritic spacing

下载: 全尺寸图片 幻灯片

1.2   拉伸模拟

在50 K下以1×10⁹ s⁻¹的恒定应变率沿Y方向对MD试样进行单轴拉伸，拉伸的最大应变为25%。Y方向和Z方向施加周期性边界条件，X方向施加自由边界条件。需要注意的是，具有第二相颗粒的复合材料试样需要在加载前进行退火。在退火过程中，先将复合材料试样加热至300 K，然后弛豫0.5 nm，再冷却至50 K。在此过程中，模拟区域沿X轴、Y轴和Z轴方向的边界均设置为周期性边界条件，因此原子可能出现一定程度的整体偏移，如图1所示。由于这种偏移不影响试样最终的枝晶体积分数以及聚集程度，本文忽略了这种偏移对材料变形行为的影响。

1.3   后处理

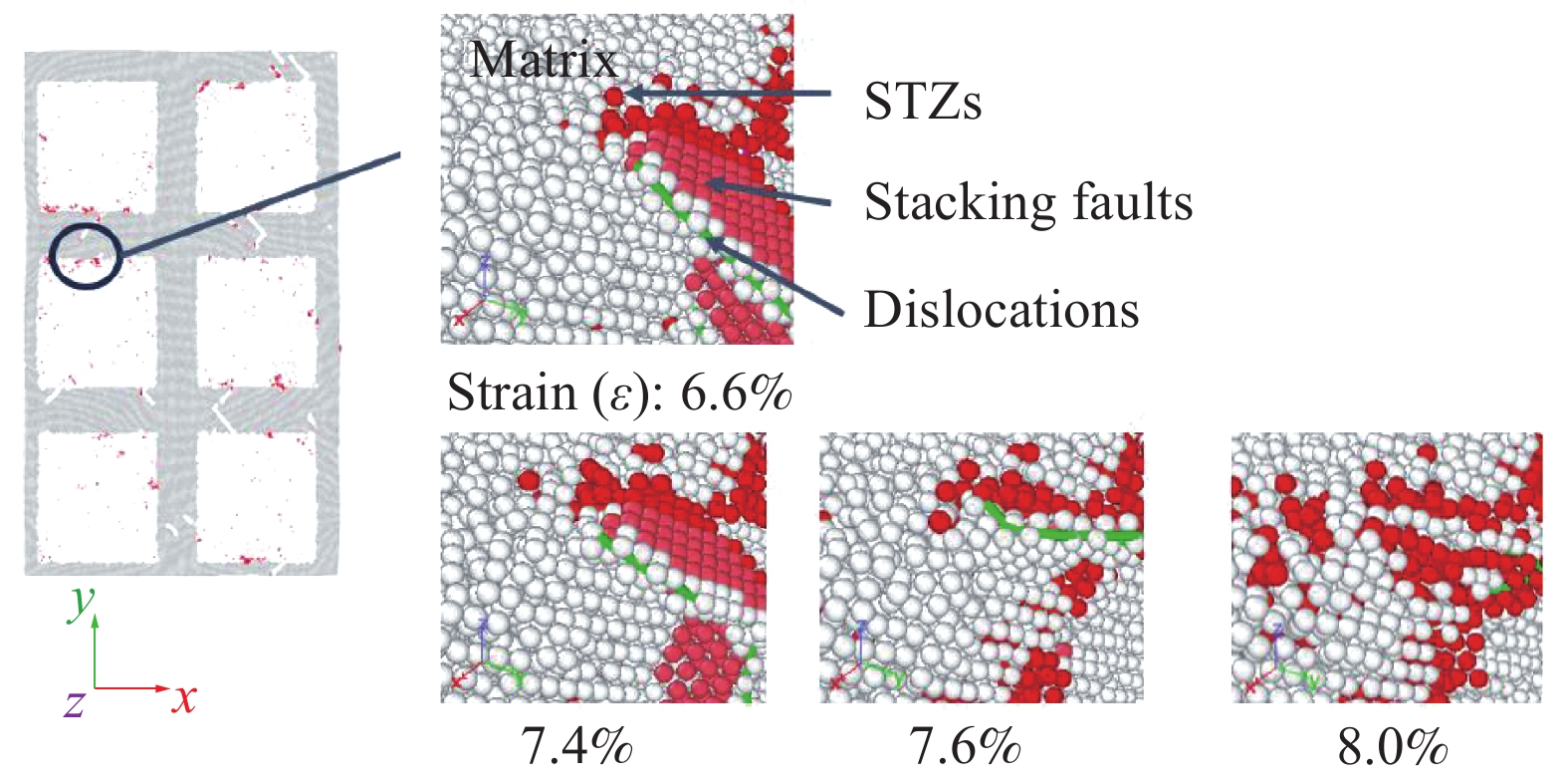
为了观察剪切带萌生和演化，我们使用von Mises局部剪切不变量$\eta\mathit{_{\mathrm{\mathit{ }}}^{\mathit{\mathrm{M}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{s}}}}$^[27]来识别剪切转换区(STZ)原子。$\eta_{ }^{{\mathrm{Mises}}}$经由以下公式得到：

式中，η表示原子的拉格朗日应变张量，下标xx、yy、zz分别表示沿x、y、z方向上的正应变，xy、xz、yz分别表示xy、xz、yz平面内的切应变。

该方法可以在可视化软件(Open visualization tool，OVITO)^[28]中轻松实现。$\eta_{ }^{\mathrm{M}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{s}}$值大于0.3的原子被视为STZ原子。该方法广泛用于金属玻璃MD模拟中的剪切带识别^[29]。

2.   结果与讨论

为了分离枝晶聚集程度和枝晶体积分数两个参数的影响，通过固定枝晶体积分数，来研究枝晶聚集程度对材料力学行为的影响。为此，我们选取了3种枝晶体积分数32.1vol%、54.2vol%和72.4vol%，代表枝晶比例由少到多的3种情况。为方便机制阐述，首先展示枝晶体积分数为32.1vol%和72.4vol%的结果。

2.1   枝晶体积分数为32.1vol%的试样

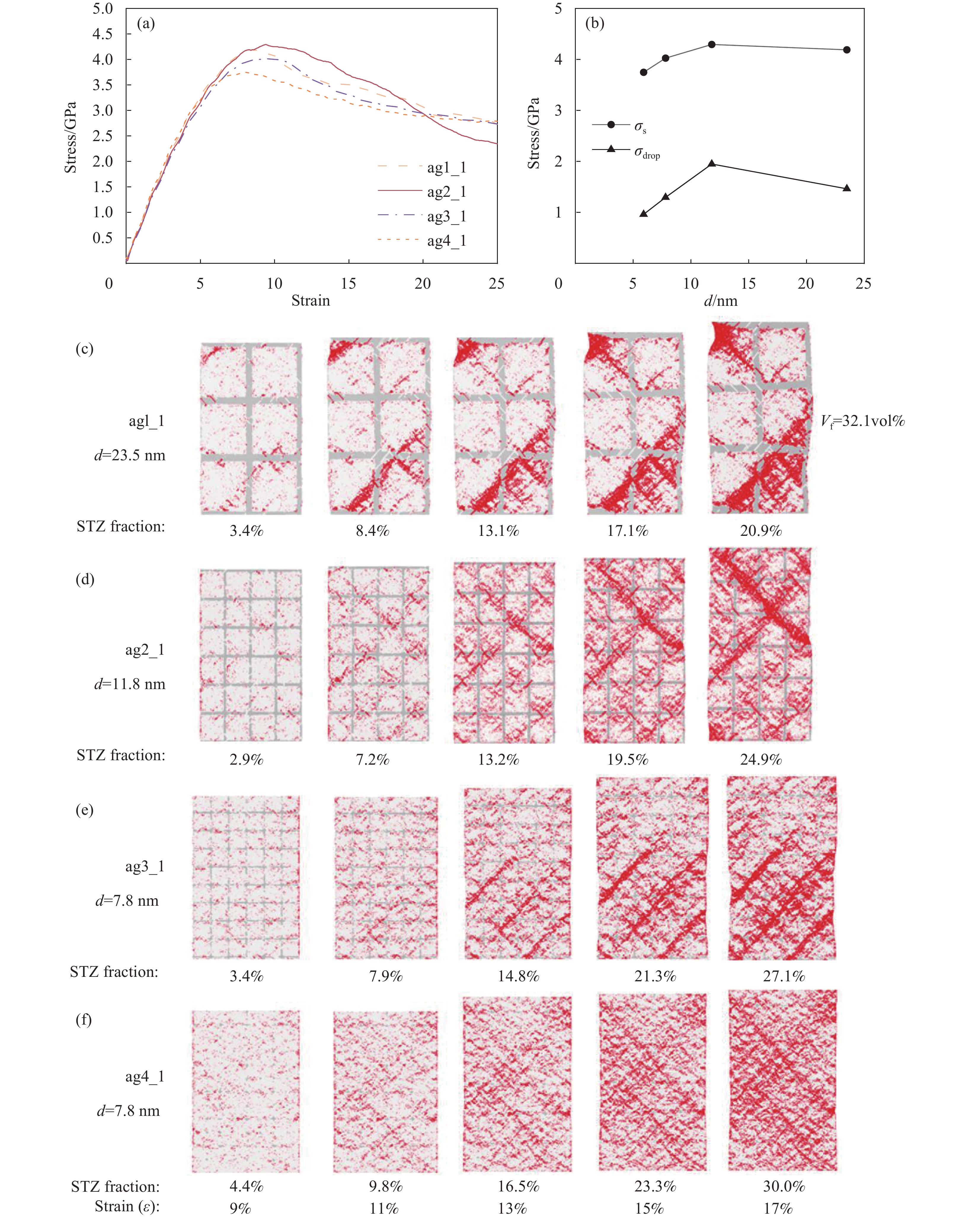
图2展示了枝晶体积分数为32.1vol%，枝晶聚集程度由高到低的金属玻璃基复合材料的模拟结果。图2(a)为试样的拉伸应力-应变曲线。在弹性阶段，材料展现出较为接近的弹性模量。屈服应力以及峰值过后的应力下降随聚集程度的变化趋势如图2(b)所示，其中试样的屈服应力随着聚集程度的降低，呈现先略微上升后下降的趋势，应力降随聚集程度的降低呈现先增大后下降的变化趋势。在枝晶体积分数较小的情况下，随着聚集程度的降低，界面面积增大，自由体积的含量随之增大，剪切带更容易多点萌发和分散分布，材料的屈服应力总体上呈下降的趋势。

图  2  枝晶体积分数32.1vol%的金属玻璃基复合材料的力学行为：(a)不同枝晶聚集程度下的拉伸应力-应变曲线；(b)材料屈服应力σ_s、应力峰值后应力降σ_drop与枝晶间间距d之间的关系；((c)~(f))各试样在不同应变下的剪切带演化 (图中深色区域代表STZ原子，灰色区域代表枝晶，其余浅灰色区域代表金属玻璃基体。金属玻璃基体中STZ原子的占比分数、枝晶间距d以及枝晶的体积分数V_f均在对应的快照旁标注)

Figure  2.  Mechanical behavior of MG matrix composites with 32.1vol% dendrite fraction: (a) Stress-strain curves of the simulated samples of with different degree of dendrite aggregation; (b) The yield stress σ_s, the stress drop after the peak stress σ_drop curves of the simulated samples of with different interdendritic spacing d; ((c)-(f)) Shear band evolution in the samples at different strains (The prominent dark regions represent STZ atoms, the gray regions represent dendrites, and the rest light gray regions represent the glass matrix. The fraction of STZ atoms in the glass matrix, interdendritic spacing d and the volume fraction of dendrites V_f are marked near the snapshots)

V_f—Dendrite volume fraction; STZ fraction—The fraction of STZ atoms in the glass matrix

下载: 全尺寸图片 幻灯片

如图2(c)~2(f)所示，在枝晶体积分数较低的情况下，枝晶的聚集程度对应力降有较大的影响。试样ag2_1中形成了狭窄的主剪切带，这对应了应力-应变曲线中最大的应力降。试样ag1_1中也形成了一条明显的贯穿剪切带，但宽度较大(~15 nm)，代表试样中用于承担宏观塑性变形的区域较大，因此应力的下降相较于试样ag2_1要缓和。试样ag3_1中出现了多条狭窄剪切带，对应于更缓和的应力下降趋势。随着枝晶聚集程度的进一步降低，试样ag4_1中的STZ原子分布更加分散，对应着相对最缓和的应力下降趋势。对于枝晶聚集程度小的试件ag4_1，由于枝晶的隔断，剪切带弥散分布，不易扩展形成贯穿整个试件的剪切带。

从以上结果可以看出，枝晶体积分数较小的金属玻璃基复合材料的塑性变形主要由基体中STZ原子及其产生的剪切带机制主导。在枝晶体积分数较小的情况下，材料的塑性变形能力通常较差，但可以通过调整枝晶的聚集程度获得更好的力学性能。当枝晶聚集程度较大时，在枝晶/非晶界面附近萌生的STZ原子会快速发展出较宽的主剪切带；随着聚集程度变小，剪切带会开始变窄，材料的塑性变形能力因此会有所波动；随着聚集程度的进一步变小，在到达某一特定范围时，STZ原子将在枝晶划分出的非晶子区域内均匀地弥散分布，此时枝晶结构对剪切带有着最好的阻碍作用。减小枝晶聚集程度总体有利于改善材料塑性变形能力。

2.2   枝晶体积分数为72.4vol%的试样

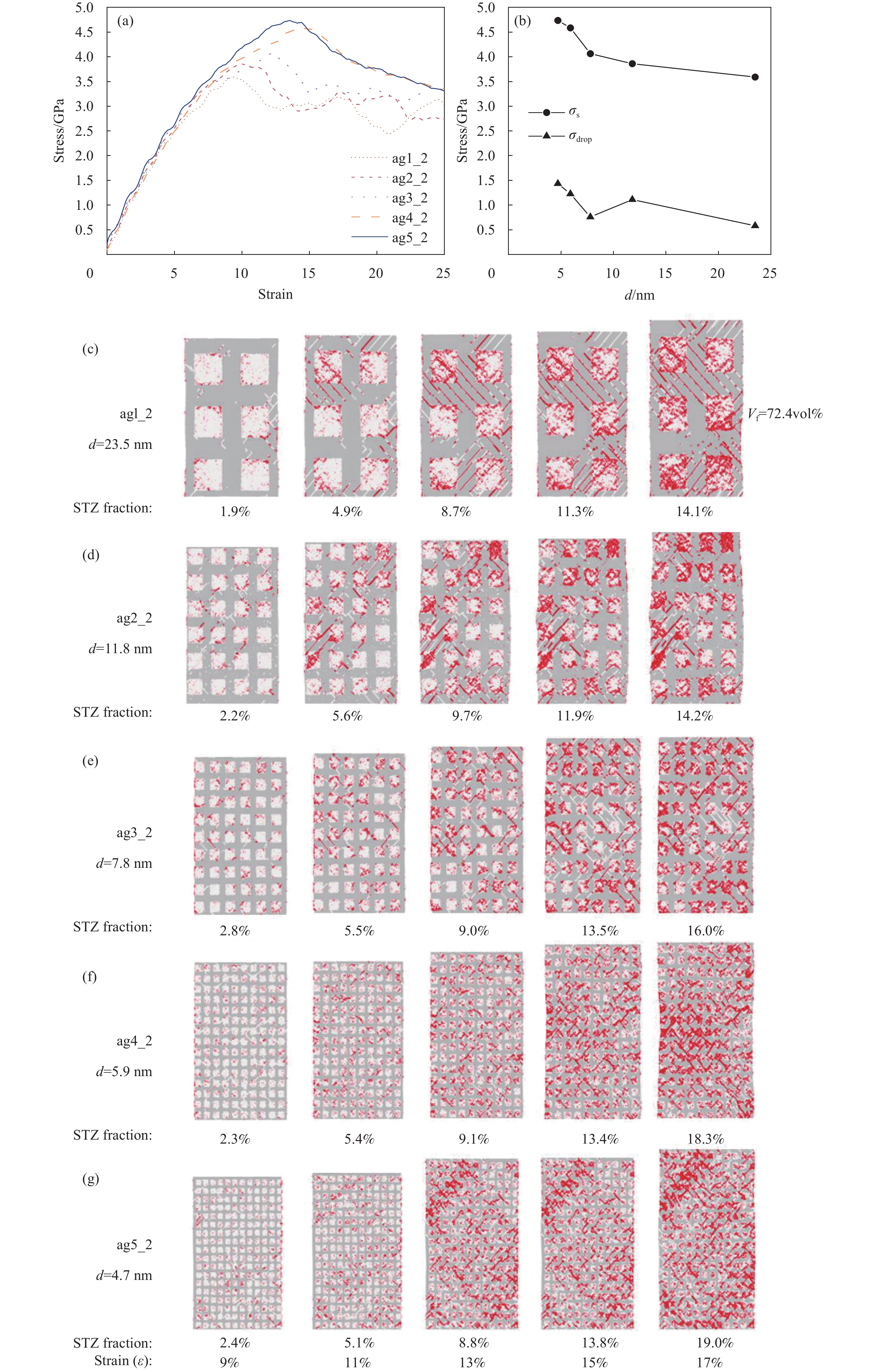
图3展示了枝晶体积分数为72.4vol%，枝晶聚集程度由高到低的金属玻璃基复合材料的模拟结果。图3(a)为试样的拉伸应力-应变曲线。在弹性阶段，材料展现出较为接近的弹性模量。如图3(b)所示，在塑性阶段，各试样的屈服应力有较大差别，随着枝晶聚集程度的降低，试样的屈服应力逐渐增大，这和枝晶体积分数较小的情况完全不同。在枝晶体积分数较小的试样中(图2)，非晶区域中STZ原子的比例通常能够代表材料的局部屈服程度。在相同的屈服应变下，样品中STZ原子的比例越低，整体屈服应变和应力-应变曲线上的峰值越大。但在枝晶体积分数较大的情况下，各试样屈服时的STZ原子数量越多，试样的屈服应力越大。这说明，枝晶内部的微结构演化在材料拉伸过程中起到了关键的作用，枝晶中的位错机制在材料塑性变形中发挥了更加主导的作用。枝晶聚集程度大的试样，虽然STZ原子数少，但枝晶宽度大，对位错塑性变形的约束小，即位错滑移充分，对应着较小的屈服应力。在应变软化阶段，不同试样有着较为接近的应力下降速率。尽管如此，试样ag1_2，ag2_2，ag3_2在持续了5%应变的应力下降阶段之后，应力响应进入了振荡的平台阶段，而试样ag4_2，ag5_2在应变截止至25%时应力都保持着下降的趋势。

图  3  枝晶体积分数72.4vol%的金属玻璃基复合材料的力学行为：(a)不同枝晶聚集程度下的拉伸应力-应变曲线；(b)材料屈服应力σ_s、应力峰值后应力降σ_drop与枝晶间间距d之间的关系；((c)~(g))各试样在不同应变下的剪切带演化

Figure  3.  Mechanical behavior of MG matrix composites with 72.4vol% dendrite fraction: (a) Stress-strain curves of the simulated samples of with different degree of dendrite aggregation; (b) The yield stress σ_s, the stress drop after the peak stress σ_drop curves of the simulated samples of with different interdendritic spacing d; ((c)-(g)) Shear band evolution in the samples at different strains

下载: 全尺寸图片 幻灯片

如图3(c)~3(g)所示，在枝晶体积分数较大情况下，枝晶的聚集程度对材料力学行为影响趋势与枝晶体积分数较小情况有很大不同。聚集程度大的试样ag1_2、ag2_2、ag3_2没有形成明显的剪切带。随着枝晶聚集程度的下降，材料的变形模式开始发生转变，ag4_2、ag5_2中STZ开始集中在局部区域，形成较为明显的剪切带，这对应着相对较大的应力降。

在枝晶体积分数较大的情况下，材料的强度和塑性变形能力有较大变化区间，可以通过调整枝晶的聚集程度获得更好的力学性能。当枝晶聚集程度较大时，材料的塑性变形由位错机制主导，枝晶结构贡献了主要的变形，材料的屈服应力较低；随着聚集程度变小，材料的屈服应力逐渐增大并延迟发生，STZ原子开始集中至局部区域，形成较为明显的剪切带。总体而言，对枝晶体积分数较大的金属玻璃基复合材料，塑性变形主要由枝晶的位错机制主导，减小枝晶聚集程度反而不利于提高材料的塑性变形能力。

2.3   枝晶体积分数为54.2vol%的试样

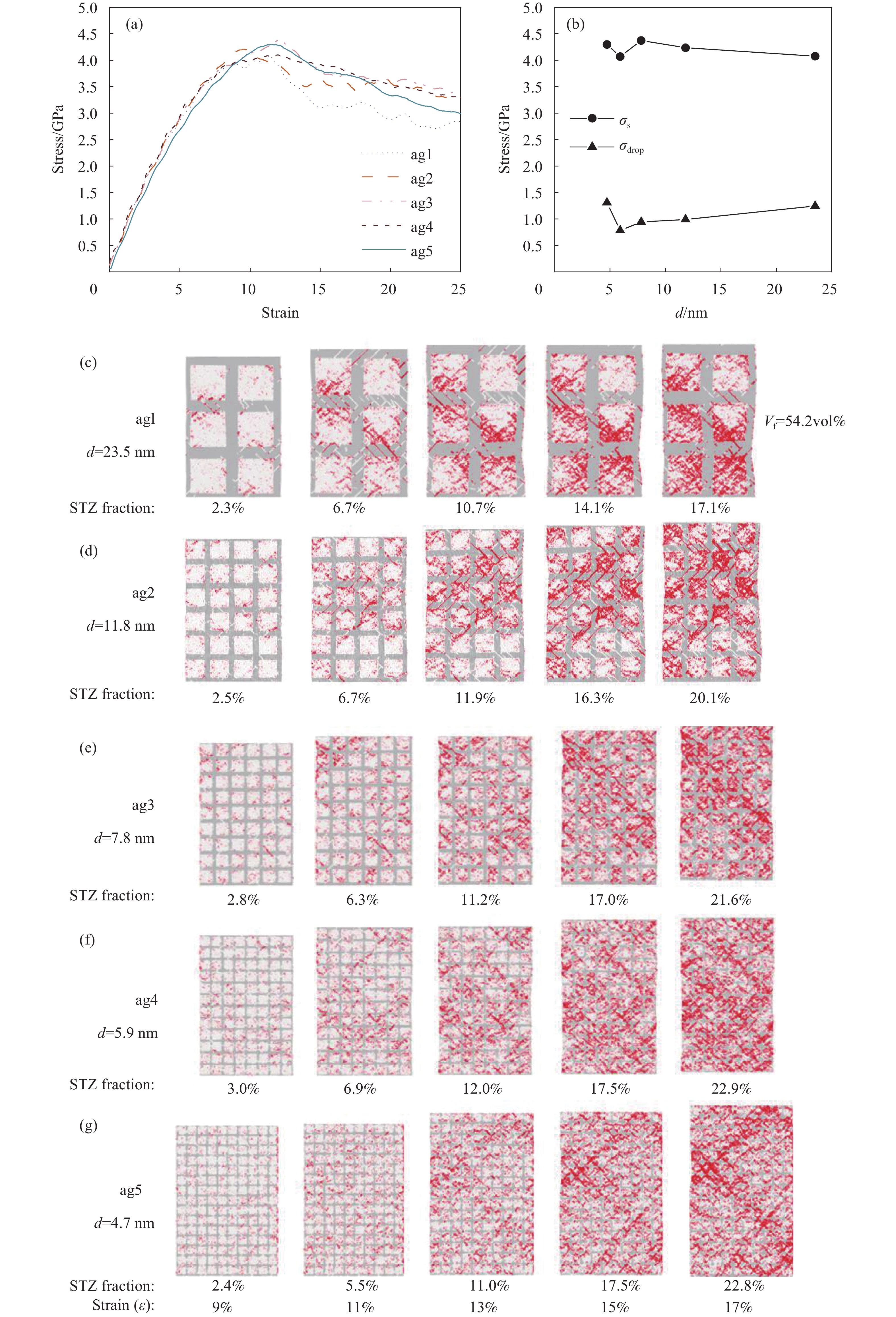
图4展示了枝晶体积分数为54.2vol%时，枝晶的聚集程度对材料的力学行为的影响。在弹性阶段，材料展现出较为接近的弹性模量。屈服应力以及峰值过后的应力下降随聚集程度的变化趋势如图4(b)所示，从中可见枝晶体积分数为54.2vol%时材料力学性能随枝晶聚集程度呈现明显非单调变化。其中试样的屈服应力随着聚集程度的降低，首先呈现上升的趋势，在枝晶间距为5.9 nm (对应试样ag4)时发生突然降低，之后4.7 nm时又有所升高。峰值过后的应力降随聚集程度的降低总体呈现下降趋势，但在枝晶间距为4.7 nm (对应试样ag5)时又明显增加。

图  4  枝晶体积分数52.4vol%的金属玻璃基复合材料的力学行为：(a)不同枝晶聚集程度下的拉伸应力-应变曲线；(b)材料屈服应力σ_s、应力峰值后应力降σ_drop与枝晶间间距d之间的关系；((c)~(g))各试样在不同应变下的剪切带演化

Figure  4.  Mechanical behavior of MG matrix composites with 52.4vol% dendrite fraction: (a) Stress-strain curves of the simulated samples with different degrees of dendrite aggregation; (b) The yield stress σ_s, the stress drop after the peak stress σ_drop curves of the simulated samples with different interdendritic spacing d; ((c)-(g)) Shear band evolution in the samples at different strains

下载: 全尺寸图片 幻灯片

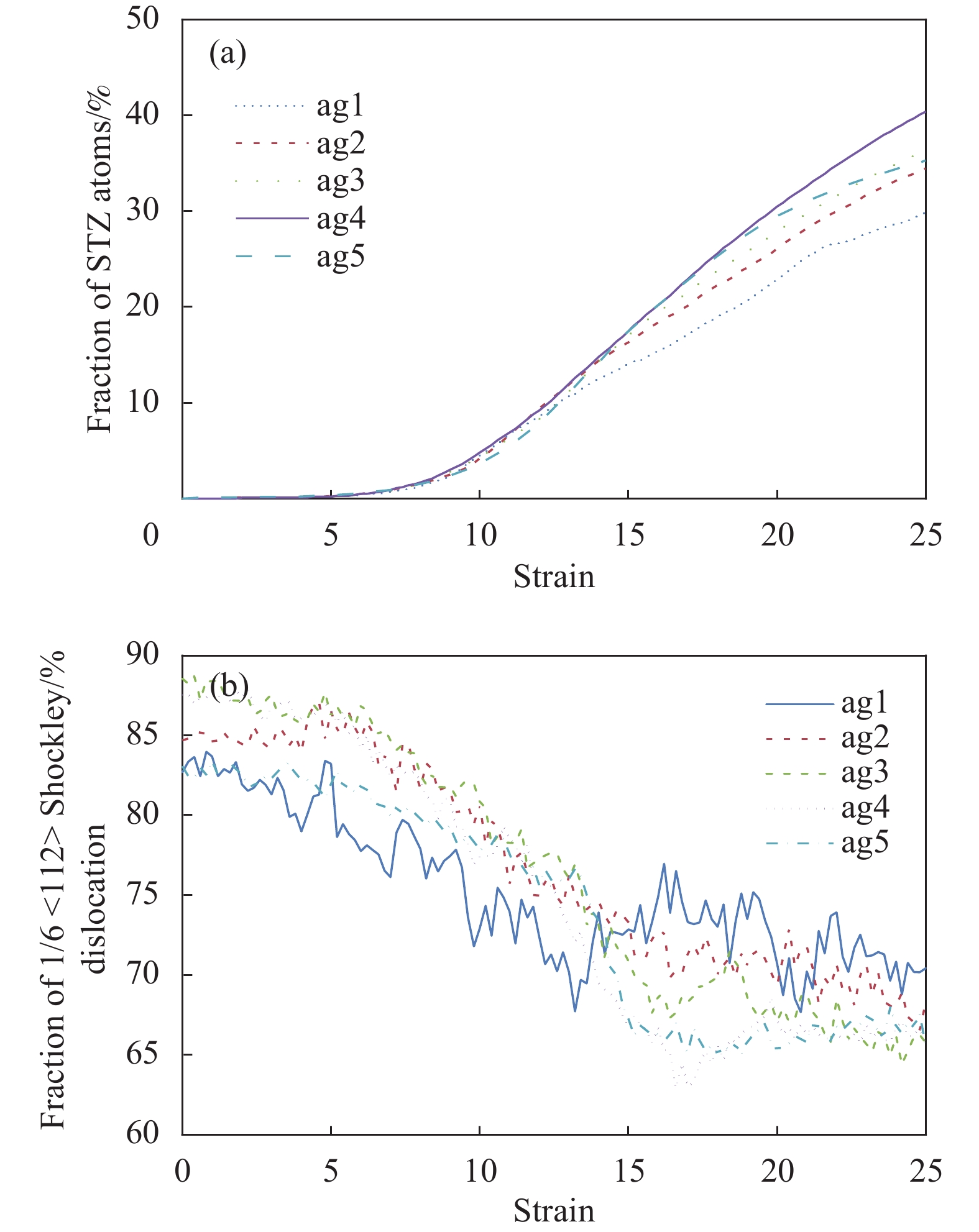
为了解释枝晶聚集程度对材料力学行为的影响，观察材料在变形过程中的微观结构演化。如图4(c)~4(g)所示，在枝晶结构中存在大量局部剪切变形，说明枝晶承担了相当一部分应力，并且在变形过程中，枝晶中部分原子开始发生相对滑移，形成位错。由图4(b)可知，试样的屈服应力随着聚集程度的降低，首先呈现上升的趋势，在枝晶间距为5.9 nm时发生转变。结合图4(c)~4(g)中试样的微观结构演化图，试样ag1、ag2、ag3中生成了较为明显的剪切带，而ag4中的STZ原子呈现了更加分散的分布特点，说明随着枝晶聚集程度的降低，材料的变形机制可能发生了转变，枝晶中的位错机制不再在材料塑性变形中占据主导作用。随着枝晶聚集程度降低(枝晶分布更分散)，试样中晶体/非晶界面面积增大，使自由体积增多。ag4的晶体/非晶界面产生的大量自由体积可能超过了某一阈值，使基体的STZ塑性变形机制得以充分开动，导致了试样ag4低的屈服应力。相对于ag4，试样ag5中过窄的枝晶间距限制了自由体积的数量，导致屈服应力有所回升。这点从图5(a)可以得到印证。该图展示了STZ原子数比例随加载应变的变化，可以看出各试样中STZ原子比例均随加载应变而增加，但增加速度不同。枝晶聚集程度越小的试样STZ原子比例增加得越快，在ag4试样中达到最快，但在ag5试样中又反而减小，反映出ag4试样拥有最多的自由体积。图5(b)展示了1/6 <112> Shockley位错比例的变化。如图所示，1/6 <112> Shockley位错是枝晶中主要的位错类型，这说明枝晶材料在变形过程中主要依赖于Shockley偏位错的滑移来容纳应变。随着应变的增加，Shockley位错线长度占位错线总长的比例大致呈现逐渐下降的趋势，然后在应变到达~17%以后变化较为平缓。这意味着在材料变形过程中，枝晶内部存在持续的原子重排。通过观察材料的微结构演化，以图6为例，观察到枝晶中的部分位错在枝晶/非晶界面处消失，同时在靠近界面的基体中萌生了STZ原子。

图  5  (a) STZ原子数比例随拉伸应变变化的曲线；(b) 1/6 <112> Shockley位错占比随拉伸应变变化的曲线

Figure  5.  (a) Fraction of STZ atoms as a function of tensile strain; (b) Fraction of 1/6 <112> Shockley dislocations as a function of tensile strain

下载: 全尺寸图片 幻灯片

图  6  单轴拉伸载荷下枝晶与基体的耦合变形

Figure  6.  Coupling deformation between dendrites and matrix under uniaxial tension loading

下载: 全尺寸图片 幻灯片

相比于体积分数对于应力降的剧烈影响，枝晶的聚集程度对应力降的影响相对小一些，所有试样截止至应变25%的应力降均不超过1 GPa。当然，试样间仍存在一定程度的区别，总体呈现随着聚集程度的降低而降低的趋势，但在枝晶间距小到4.7的ag5试样中发生了明显升高。如图4所示，试样ag1与试样ag3中形成了较宽的主剪切带，对应着应力-应变曲线应力峰值过后较大的应力降。试样ag4的STZ原子呈现出最为分散的分布特点，因此ag4有着最为缓和的应力降。随着聚集程度的进一步减小，试样ag5再次形成了两条较窄的剪切带，但枝晶较低的聚集程度有效地延迟了剪切带的形成，使得应力不会在较小的应变范围(~5%)内下降得过快。同时，试样ag5的位错总长以及1/6 <112> Shockley位错占比在应变到达~15%时便进入了平稳期。因此，剪切带主导了该试样的应变软化。当枝晶聚集程度较大时，STZ原子会在枝晶/非晶界面附近的基体中大量萌生，并在较大的非晶区域中快速发展成主剪切带，主导材料的应力软化；随着聚集程度变小，在达到某一特定范围时，STZ原子将在枝晶划分出的非晶子区域内较为均匀地分布，此时枝晶结构对剪切带有着最好的阻碍作用；随着聚集程度的进一步减小，枝晶的数量进一步增多，虽然对剪切带的成核起到了一定的抑制作用，但由于每条枝晶宽度过小，容易被剪切带穿透，使得变形集中在较少几条贯穿试件的剪切带中，应力降反而变大，如ag5试样的应力-应变曲线所示。

总体而言，对于枝晶体积分数居中的金属玻璃基复合材料，枝晶内部的位错塑性变形机制和基体中的STZ原子剪切带机制共同对塑性变形起作用，使得材料屈服应力和塑性变形能力随枝晶聚集程度呈现复杂非单调的变化趋势。可以利用两种机制的相互耦合作用来提高金属玻璃基复合材料的力学性能。

3.   结 论

为了研究枝晶的聚集程度对金属玻璃基复合材料力学行为的影响，构建并模拟了一系列具有不同聚集程度枝晶的复合材料试样。通过对比应力-应变曲线以及剪切带形成及演化特征，得出以下结论：

(1)金属玻璃基复合材料的屈服应力、屈服后的应力降受枝晶聚集程度的影响较大，而模量相对受影响较小；

(2)在枝晶体积分数较小时(~30vol%)，材料的屈服应力和峰值后应力降总体随枝晶聚集程度的减小而减小，在枝晶体积分数较大的情况下(~70vol%)，材料的屈服强度和峰值后应力降总体随枝晶聚集程度的减小而增大；

(3)在晶相体积分数居中的试样中，当枝晶聚集程度较大时，剪切转换区(STZ)原子会在枝晶/非晶界面附近的基体中大量萌生，并在较大的非晶区域中快速发展成主剪切带，主导材料的应力软化；随着聚集程度变小，剪切带变窄但数量增多，在到达某一特定聚集程度范围时，STZ原子将开始在枝晶划分出的众多非晶子区域内均匀地分布，此时枝晶结构对剪切带演化有着最强的阻碍作用；随着聚集程度的进一步变小，剪切带的成核依旧受到了一定的阻碍，延缓了应力下降，但最终形成了较少且狭窄的贯穿剪切带，总体应力降反而增大；

(4)枝晶体积分数较小时，金属玻璃基复合材料的塑性变形由STZ原子形成剪切带机制占主导；枝晶体积分数较大时，材料塑性变形由枝晶内位错滑移机制占主导；在枝晶体积分数中等的情况下，两种机制同时起作用且互相影响，使材料屈服应力和塑性变形能力随枝晶聚集程度变化而呈现复杂非单调的变化趋势。