近年来，轻量化与高承载是航空航天发展的永恒主题，先进复合材料以其质量轻、性能好而广泛应用于航空航天结构中，而复合材料网格回转体结构不仅具备先进复合材料的优点，同时还具备网格结构的结构效率高、可设计性强等优良性能^[1-3]。早在上世纪80年代起，美、俄、日等国家就已开始在航天领域复合材料回转体网格结构的设计、制造、评价及应用等方面开展了大量工作^[4-8]，并广泛应用于火箭整流罩、级间段及有效载荷支架。在国内，熊健等^[9]总结了轻质复合材料壳体结构研究进展，指出夹芯壳体结构具有优越的力学性能，但目前制备工艺还不成熟，并对轻质复合材料壳体结构未来发展方向进行预测。祖磊等^[10]基于非线性有限元理论，对承受内压载荷的复合材料壳体进行缠绕参数优化设计。陈小平等^[11]和王世勋等^[12]主要针对复合材料网格结构的设计及制备工艺进行综述，指出应在高质量复合材料网格结构制备工艺以及格栅结构强度理论方面开展深入的研究工作。韩振宇等^[13]指出复合材料网格结构在成型过程中纤维在交叉点处存在堆积和架空缺陷，揭示网格结构成型过程中工艺-结构-性能的关系，对准确预测结构承载效率和破坏形式有着重要作用。

目前国内外学者采用多种矫形方法修正变形^[14]，电磁校形^[15-16]适用于良好导电性材料，矫形精度高，同时可以很好地改善材料内部应力状态；激光校形技术^[17]是一种新型柔性校形工艺方法，通过一定强度的激光束可提高变形的形状精度；超声波喷丸校形技术^[18]可利用超声波产生的高频冲击波，通过弹丸或撞针等介质作用于金属材料表面变形区域，校正成形误差的技术。姚少非等^[19]对TC4钛合金筒形件进行热矫形仿真分析，证明温度对于筒形件内应力的消除及校形尺寸精度的提高起着主导作用。Lu等^[20]基于蠕变机制对钛合金薄壁构件开展热矫形工艺研究。金属的热矫形研究表明，零件在热矫形前后形状变化的原因主要是高温软化和应力松弛。罗玲^[21]对比研究线弹性固化变形模型和CHILE非线性固化模型，线弹性固化变形模型计算过程针对凝胶后的固化历程，工艺变形数值模拟精度同CHILE非线性固化模型差别不大。以上方法在矫形方面的应用越来越广泛，但对于机制分析还不明确，还有很多技术难题需要攻破。对于复合材料结构而言，由于材料各向异性及粘弹性特征复杂，为深入研究机制问题，本文基于材料粘弹性^[22-23]属性，在高温条件下用形状矫正模具对大型复合材料舱段进行热矫形，从热固性树脂角度出发阐述热矫形机制问题。该矫形方法可使内应力分布均匀，提高构件尺寸稳定性，降低后续的加工，是解决舱段工艺变形问题的有效途径。

大型复合材料网格回转体舱段在固化成型后主要变形特征为舱段横截面呈现椭圆特征。如借鉴传统的解决方案，在工艺试验的基础上凭经验对零件的固化工艺规范进行反复调整、对模具型面进行补偿性修正，会消耗大量的时间和原料，进一步增加了复合材料的制造成本。许英杰等^[24]验证了复合材料加筋壁板在强度提高的同时，固化变形显著降低。王浩军等^[25]、王海雷^[26]分别对C形、翼面类结构采用常用的“模具补偿修正”的方法，实现了固化变形控制。Liu等^[27]开展了碳纤维/环氧复合材料L型梁构件热矫形研究，采用复合材料粘弹性理论，发现高温蠕变后发生回弹，最终轮廓且与初始构件角度不同。但对于大型回转体舱段而言，因其多特征的复杂结构，结构工艺热矫形计算分析时间长，叠加粘弹性非线性本构关系，已有模型方法难以有效开展矫形数值仿真计算。

因此，本研究针对航天802双马树脂，开展太钢TG800碳纤维/802双马树脂复合材料网格结构的热矫形机制与模型研究。测试航天802双马树脂蠕变及卸载规律，验证双马树脂基复合材料热矫形机制；基于多层级固化变形仿真结果，通过应变能理论预报舱段热矫形过程，并分析复合材料网格结构热矫形内应力失效、基于时温等效的工艺条件等影响因素，形成复合材料网格舱段结构热矫形变形控制工艺变形仿真方法。

1.   复合材料网格舱段结构热矫形机制研究

关于热矫形机制研究，国内外很多学者在早期发现金属热矫形机制的本质是应力松弛或高温软化^[28-31]。而对于树脂基复合材料结构而言，高温下同样会发生蠕变或者应力松弛^[32-33]。因此，树脂基复合材料热矫形可借鉴金属热矫形。本文在热矫形机制上主要创新点为：从热固性树脂分子链角度出发，结合802双马树脂高温蠕变试验及四元件粘弹性模型，验证复合材料网格结构可进行矫形的微观材料机制为蠕变卸载后黏性流动应变的不可恢复，并推导建立应变能增量理论作为热矫形的理论模型。

1.1   聚合物基复合材料高温蠕变

热固性树脂基复合材料热矫形的原理是树脂基体的高温蠕变。聚合物蠕变本质上是分子链运动在不同时间尺度上先后体现的结果。一般而言，聚合物所处温度越高，或者承受应力(应变)越大、蠕变速率越快，发生蠕变现象越明显^[34]。值得指出的是：对于真实交联的热固性树脂中，往往会存在封闭链圈、端链等局部缺陷，会在较小范围内发生黏性流动形变，卸载后会产生长时间不可恢复的变形。热固性树脂蠕变及卸载过程可用四元器件模型^[35-36]描述。

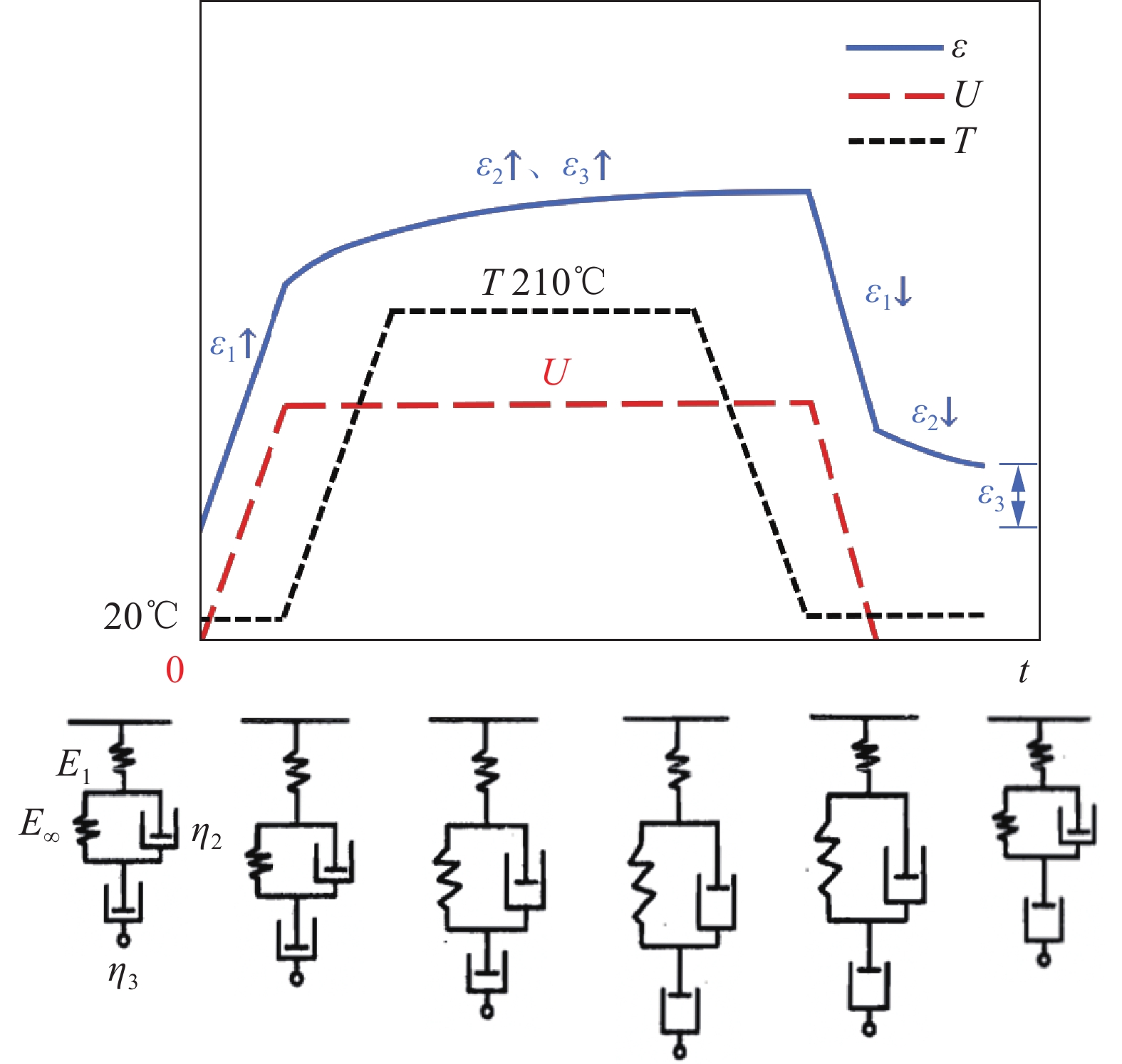
如图1所示，${ \varepsilon }$为蠕变过程中的应变，U为矫形位移，T为矫形温度，热矫形工艺温度控制在210℃。${{E}}_{\text{1}}$为普弹模量，${{E}}_{\text{∞}}$为高弹模量，$\eta _{\text{2}}$、$\eta_{\text{3}}$为黏性流动系数。在拉伸外力作用下，蠕变关系式可写为

式中：D为柔量(模量的倒数)；t为松弛时间；$\tau=\eta_2 / E_{\infty}$为推迟时间；$\text{(1}-\mathrm{e}^{-t/\tau}\text{)}$称为蠕变函数；t时刻的蠕变柔量由普弹柔量${{D}}_{\text{1}}$、高弹柔量$D_{\infty}\left(1-\mathrm{e}^{-t / \tau}\right)$和黏性流动导致的柔量${t}/\eta _{\text{3}\text{}}$三部分构成。

外力去除后，聚合物会发生蠕变恢复。如图1应变曲线所示，蠕变发生时，首先产生普弹应变，然后是高弹应变，最终是黏性流动应变；而卸载时，蠕变首先恢复的是普弹应变${{ \varepsilon }}_{\text{1}}$，高弹应变${{ \varepsilon }}_{\text{2}}$随时间逐渐衰减至0，而黏性流动应变${{ \varepsilon }}_{\text{3}}$因不可恢复而残留下来。这是非理想交联热固性树脂基复合材料结构能够通过高温蠕变/应力松弛及恢复过程，从而进行复合材料热矫形的微观组分材料机制。

图  1  树脂基复合材料结构热矫形机制

Figure  1.  Mechanism of hot sizing of polymer matrix composite structures

U—Displacement imposed by the correction; T—Temperature imposed by the correction; ${{ \varepsilon }}_{\text{1}}$—General elastic deformation; ${{ \varepsilon }}_{\text{2}}$—High elastic deformation; ${{ \varepsilon }}_{\text{3}}$—Viscous flow deformation; E—Modulus of elasticity; $\eta$—Coefficient of viscous flow

下载: 全尺寸图片 幻灯片

1.2   结构应变能增量理论

根据复合材料广义层合板理论^[37]，模拟板的运动行为的近似位移场可表示为

其中：${{x}}_{\text{1}}$、${{x}}_{\text{2}}$代表面内方向；${{x}}_{\text{3}}$代表板厚度方向；${{u}}_{{i}}$、${\beta }_{{i}}$、${\gamma }_{{i}}$是一组广义坐标，表示板的构型。直角坐标系中，根据几何方程，应变张量${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\varepsilon } _{ij}}$为位移的一阶偏导数，张量表达形式为

各向异性材料第k层本构关系用张量表示为

其中：$\sigma_{i j}^k$是应力分量；${{C}}_{{ij}}$为刚度系数，由基本弹性参数组成。将式(2)代入式(3)中，得到广义位移形式下的应变：

其中，${\kappa }_{{ij}}$、${\theta }_{{ij}}$为包含${\beta }_{{i}}$、${\gamma }_{{i}}$的应变。单位体积下的拉伸应力${{N}}_{{ij}}$、弯曲应力${{M}}_{{ij}}$、扭转应力${{R}}_{{ij}}$为

其中，${i,}{j=}{1,2,3}$。第k层的应变能密度${{U}}^{{k}}$表达式为

层合板应变能E可由应变能密度${{U}}^{{k}}$积分得到：

借助式(5)和式(6)将式(7)代入式(8)可得：

式中，${i}{,}{j=}{1,2,3}$、${r}{,}{s}{=}{1,2}$。经过复合材料网格舱段热矫形松弛以及回弹过程，黏性流动应变不可恢复而残留下来，确定复合材料舱段热矫形后的最终变形，结合热矫形后最终轮廓，可分析对固化变形的矫正效果。可以采用细观力学模型预报复合材料粘弹性属性^[38]，在舱段变形仿真基础上，进行热矫形模拟。具体来说，热矫形模型的理论假设是：

①室温加载时，矫形载荷所做的总功全部转化为舱段应变能${\text{d}{E}}_{\text{total}}$；

②卸载后，驱动舱段回弹的应变能为弹性应变能${\text{d}{E}}_{\text{elastic}}$，包括普弹应变能和高弹应变能；

③在高温矫形载荷作用下，导致舱段发生高温蠕变，形成额外的舱段不可恢复的应变能${\text{d}{E}}_{\text{creep}}$。

3种应变能增量表达式为

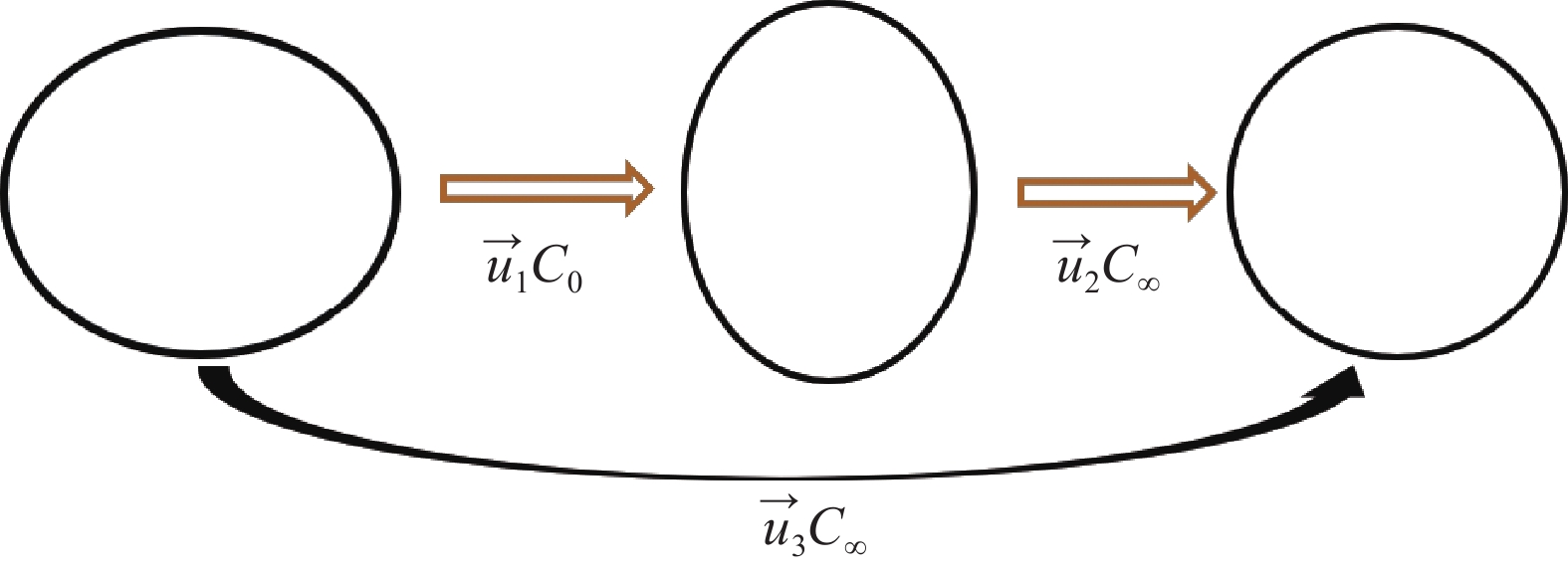
网格舱段在整个矫形过程中的轮廓如图2所示。其中，${{C}}_{\text{0}}$和${{C}}_{\text{∞}}$分别是复合材料矫形前的刚度和松弛后的刚度。${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _{1}}$为施加的矫形荷载位移变化场，${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _2}$为舱段发生变形回弹时的位移变化场，${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _3}$为舱段发生蠕变后残留变形与初始变形位移场的差。不同阶段的位移场可根据式(9)得到不同的应变能，并代入最终式(10)。

图  2  复合材料网格结构热矫形全过程轮廓变化

Figure  2.  Profile changes throughout the entire process of hot sizing of composite gird structures

${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _1}$—Field of change of applied corrective displacement; ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _2}$—Field of displacement change when deformation rebound occurs in the interstage segment; ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _3}$—Difference between the residual deformation and the initial deformation displacement field after the cabin segment has undergone creep

下载: 全尺寸图片 幻灯片

若舱段可进行热矫形，则${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _3}\text{≠}\text{0}$。若${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u } _3}\text{=}\text{0}$，这说明施加的矫形位移载荷增量${{{\mathrm{d}}E}}_{\text{total}}$等于舱段卸载回弹产生的位移载荷增量${\text{d}{E}}_{\text{elastic}}$，这就导致矫形后最终轮廓与固化变形后轮廓并无区别，矫形没有意义，也就是形状不可矫正，对应理想热固性树脂的蠕变粘弹性情形(黏性流动应变为0)。

2.   TG800/802双马树脂复合材料网格舱段结构热矫形

2.1   802双马树脂高温蠕变测试

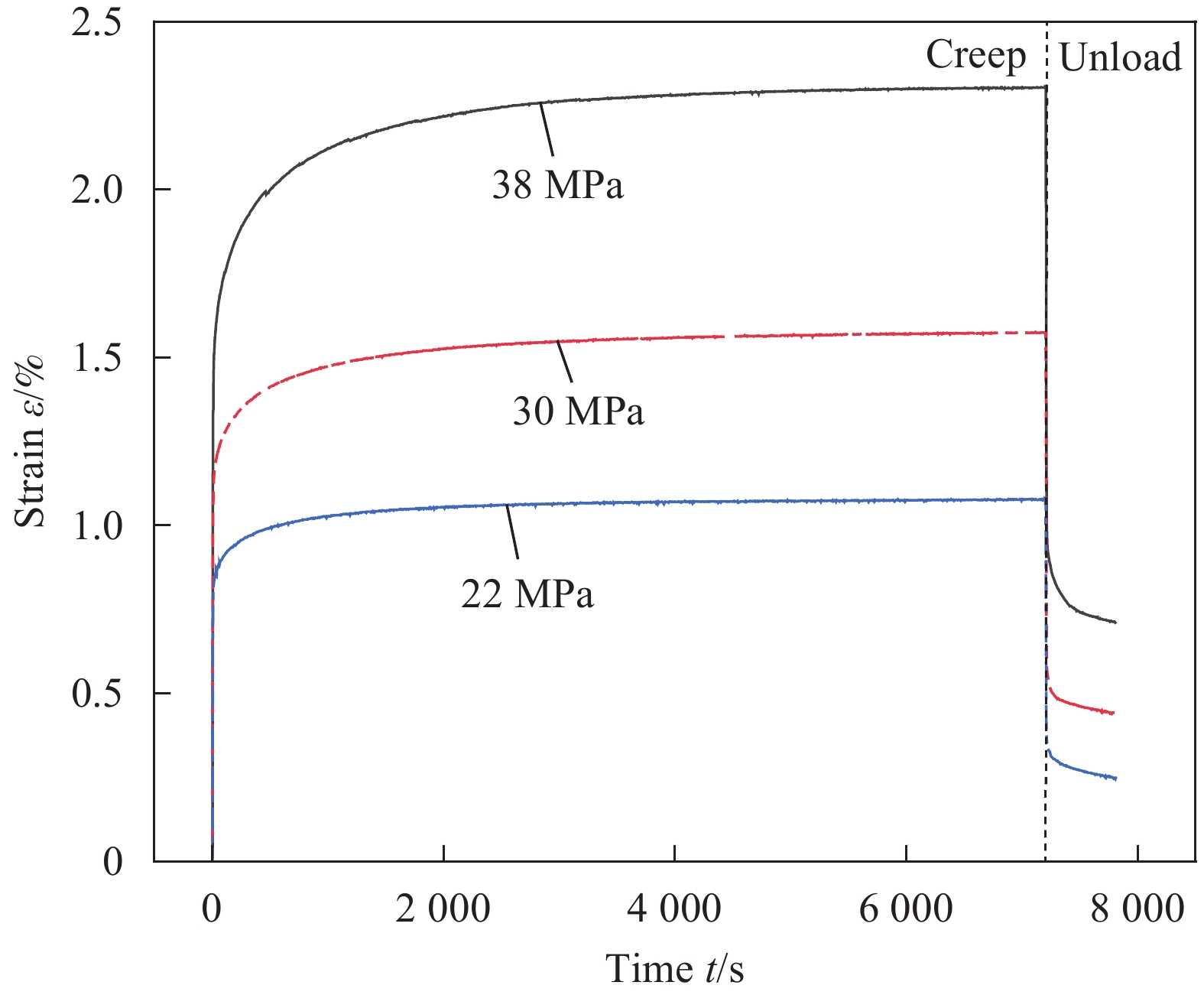
802双马树脂在210℃高温蠕变关系如图3所示。试验标准参考ISO 899-1^[39]拉伸蠕变性能的测定，初始加载拉伸应力选取了38 MPa、30 MPa和22 MPa。蠕变加载卸载速率均为20 mm/min，保证迅速平稳不出现瞬间过载。

图  3  802双马树脂在210℃不同应力水平下的高温蠕变及恢复过程中的应变-时间关系

Figure  3.  Strain and time relationships of 802 bismaleimide resin during high temperature creep and recovery under different stresses at 210℃

下载: 全尺寸图片 幻灯片

在210℃高温下，2 h内基本都达到蠕变平衡态，卸载后应变随时间变化。根据蠕变关系式(1)可写为应变形式为

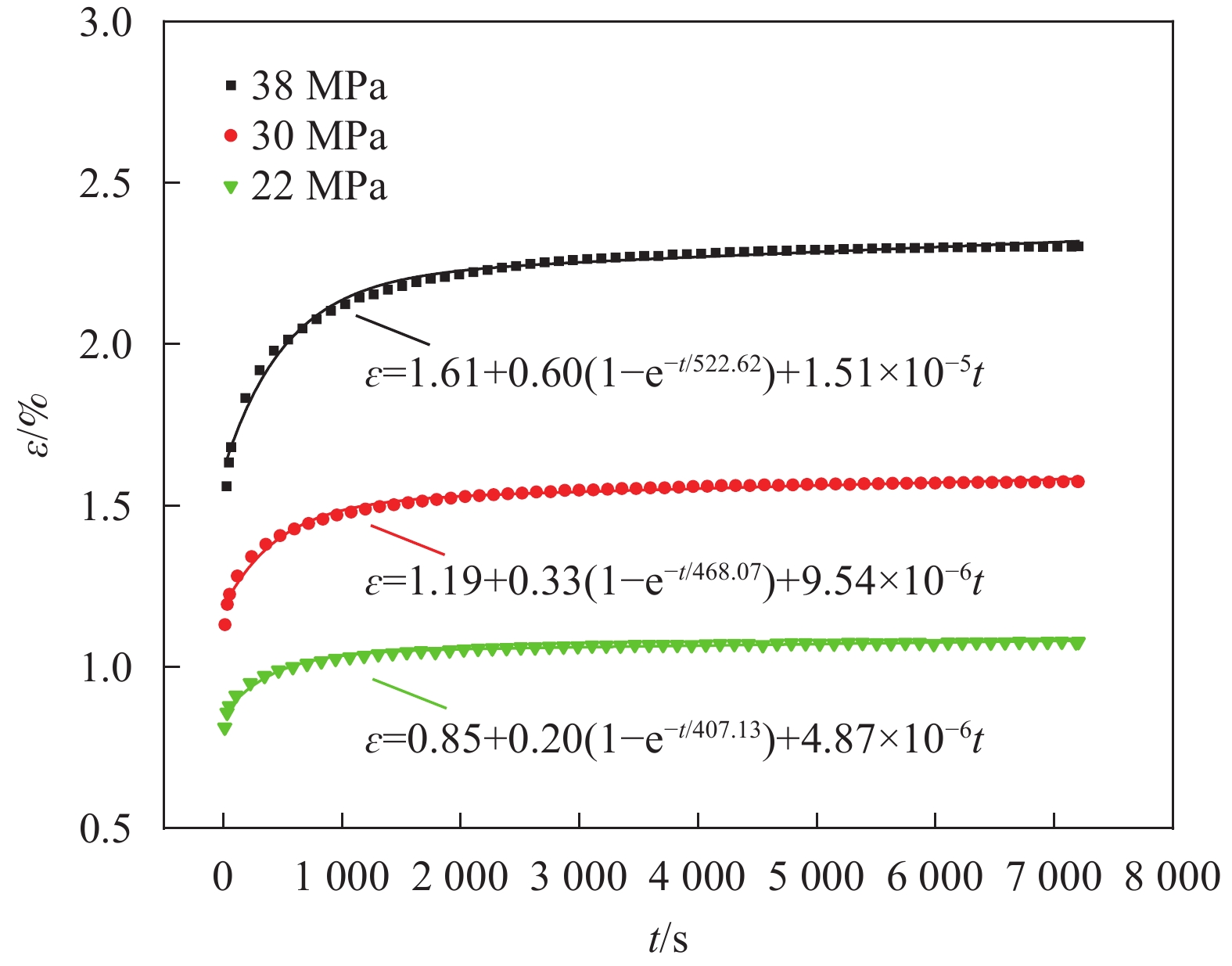
其中：$\varepsilon\left(t\right)$为蠕变应变；$\sigma$为初始应力。根据802双马树脂蠕变试验，普弹应变${{ \varepsilon }}_{\text{1}}$与时间成线性关系，高弹应变${{ \varepsilon }}_{\text{2}}$与黏性流动应变${{ \varepsilon }}_{\text{3}}$成非线性关系，对试验数据进行曲线拟合，拟合结果如图4所示。

图  4  802双马树脂高温蠕变应变曲线拟合

Figure  4.  Strain curve fitting of 802 bismaleimide resin for high temperature creep

下载: 全尺寸图片 幻灯片

根据蠕变关系式(11)可知，普弹应变只与初始应力有关，与时间无关，拟合时为保证拟合准确性，去除普弹直线段并用常数A代替。根据图4中蠕变曲线拟合结果，拟合方程为

式中：A代表普弹应变${{ \varepsilon }}_{\text{1}}$，与初始应力成正比例关系，与时间无关；B中的高弹模量${{E}}_{\text{∞}}$随时间变化，高弹应变${{ \varepsilon }}_{\text{2}}$与时间成指数曲线关系；C为$\tau$，即为推迟时间，与初始应力和高弹模量有关，并随着初始应力增加而增加；D表示初始应力与黏度${\eta }_{\text{3}}$的比值，随着初始应力增加而增加，黏性流动应变${{ \varepsilon }}_{\text{3}}$与时间成线性关系。

双马树脂在蠕变卸载瞬间，普弹应变消失，高弹应变15 min基本恢复，曲线区域平缓，黏性流动应变残留。在相同时间和温度残留应变，随初始应力施加而增加。蠕变卸载15 min后，38 MPa、30 MPa和22 MPa初始应力对应的残留应变分别为0.69%、0.42%和0.22%。至此，已通过试验验证热固性双马树脂体系存在明显的高温蠕变残留变形，该变形在长时间尺度内是不可恢复的，正因为黏性流动应变的残留，所以网格结构是可进行矫形的。

2.2   TG800/802双马树脂复合材料回转体舱段结构热矫形模拟

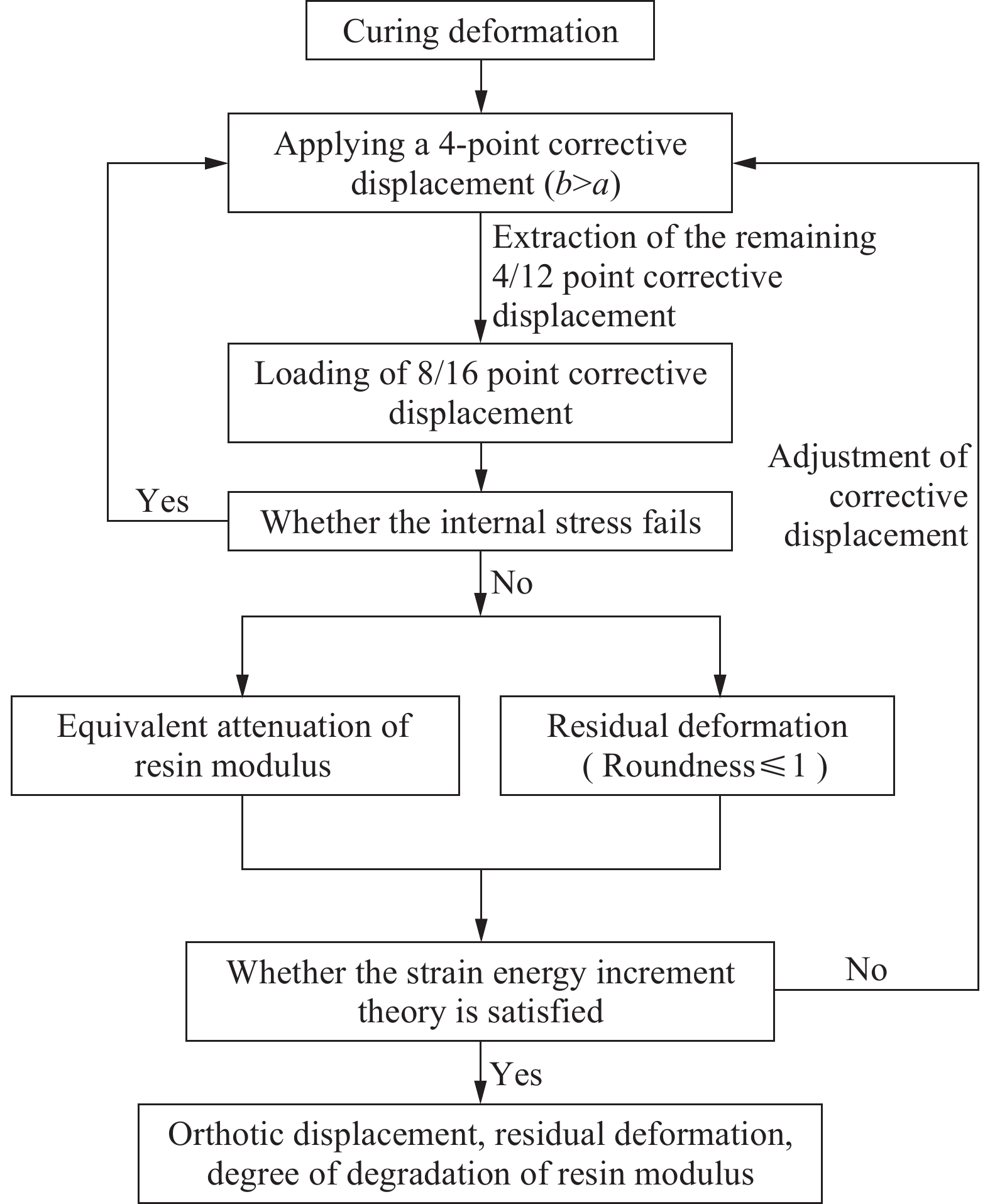
复合材料网格结构热矫形流程如图5所示，热矫形模拟开始前需对复合网格结构进行固化变形预报，在固化变形预报值与试验值达到工艺要求后进行热矫形模拟。通过有限元软件Abaqus，设置不同分析步模拟网格结构固化变形后施加矫形位移荷载、普弹及高弹变形回弹与最终黏性残留变形状态。并根据应变能理论与内应力失效分析调整结构所施加的机械矫形位移荷载，并结合热矫形过程中的轮廓变化验证热矫形应变能增量理论。

图  5  TG800碳纤维/802双马树脂复合材料网格结构热矫形模拟流程图

Figure  5.  Flow chart for hot sizing simulation of TG800 carbon fiber/802 bismaleimide resin composite grid structures

下载: 全尺寸图片 幻灯片

2.2.1   网格舱段固化变形预报

变形舱段轮廓是舱段矫形的理论基础，本研究通过基于逐级试验验证的思路建立多层级复合材料固化变形预报模型^[40-41]，确定舱段固化变形轮廓，并与试验结果对比验证。复合材料固化变形预报属性采用太钢TG800碳纤维/802双马树脂复合材料体系，属性参数由制造商提供，见表1。

表  1  TG800/802双马树脂复合材料室温力学性能

Table  1.  Mechanical properties of TG800/802 bismaleimide resin composite at room temperature

E11/MPa	E22/MPa	G12/MPa	G23/MPa	${\mu }_{\text{12}}$	${\sigma }_{\text{11}}\text{/MPa}$	${\sigma}_{\text{22}}\text{/MPa}$	ILSS/MPa	${\sigma}_{\text{12}}\text{/MPa}$
164000	9310	5690	3280	0.38	2482	59	101	88
Notes: E—Modulus of elasticity; G—Modulus of shear; μ—Poisson's ratio; σ—Intensity of stress; ILSS—Interlaminar shear strength.

下载: 导出CSV 

| 显示表格

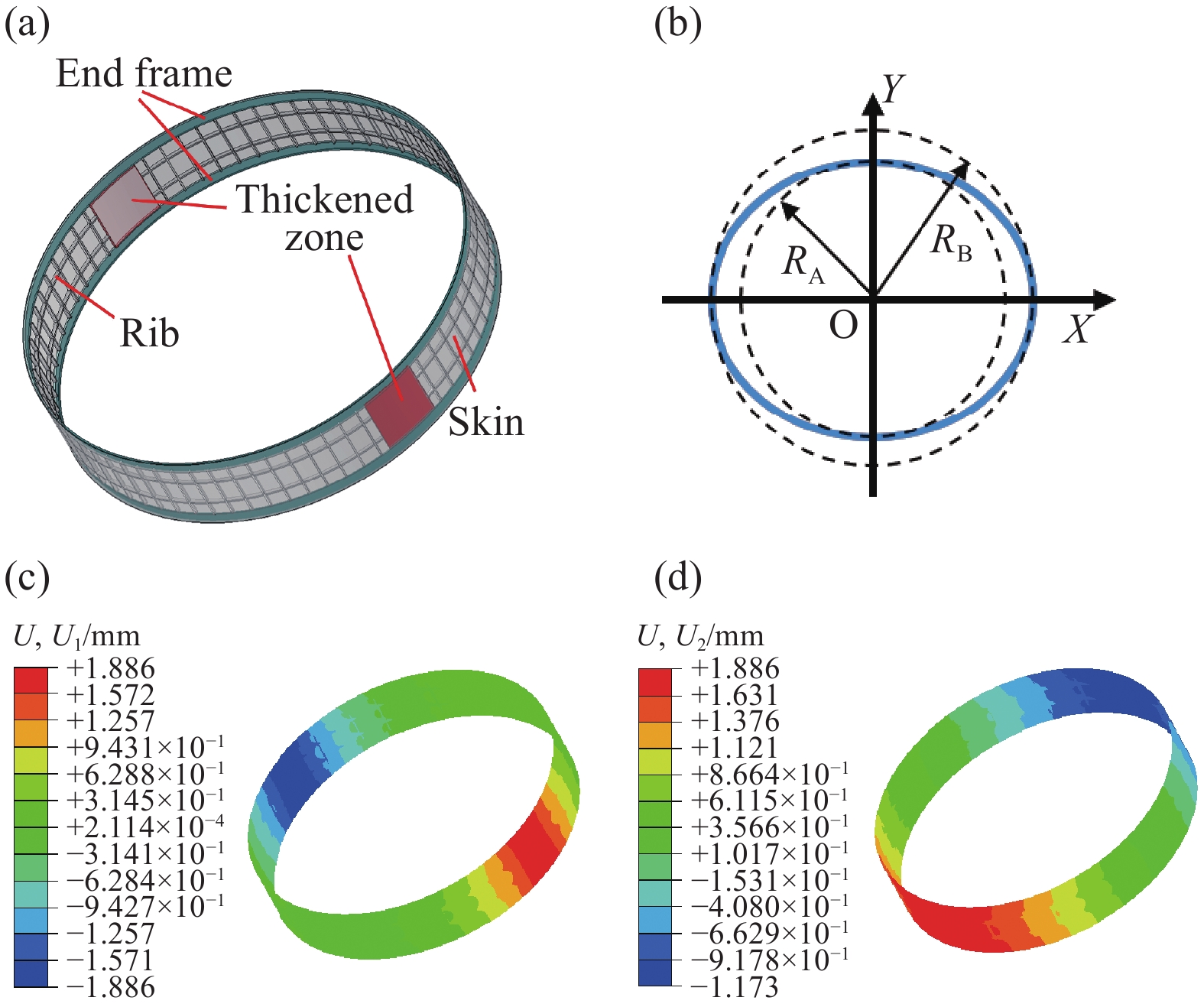
TG800/802复合材料网格舱段结构如图6(a)所示，结构高度为220 mm，最大直径为1100 mm，包括蒙皮、上下端框、横纵网格筋条以及两个对称加厚区。单层铺层厚度0.15 mm，各组分铺层见表2。

图  6  TG800/802双马树脂复合材料网格舱段结构(a)、圆度定义(b)、TG800/802双马树脂复合材料网格舱段固化变形预报结果((c), (d))

Figure  6.  TG800/802 bismaleimide resin composite grid interstage segment (a), definition of roundness (b), predicted results of curing deformation of TG800/802 bismaleimide resin composite grid interstage segment ((c), (d))

R_A—; R_B—; U—; U₁—

下载: 全尺寸图片 幻灯片

表  2  TG800/802复合材料平板及舱段结构铺层

Table  2.  Plying of TG800/802 composite laminate and grid interstage segment

Composite	Ply
Skin	[45/−45/0/90/0/0/90/0/−45/45]
End frame	[45/−45/0/90/0/0/90/0/−45/45]3
Thickened zone	[45/0/−45/0/15/0/−15/0/15/90]6

下载: 导出CSV 

| 显示表格

舱段变形模拟复合材料后固化温度平台(210℃)降温至室温过程，边界条件为约束结构下端框底端轴向变形(U₃)为0。采用Abaqus软件进行模拟，网格单元类型为C3D8R。图6(b)为结构的圆度定义(R_B-R_A)，用以表征工艺变形。舱段固化变形预报结果如图6(c)、图6(d)所示，加厚区的非对称铺层对圆度结果产生很大影响，两个加厚区向外扩张，从而导致与其垂直方向向内收缩，固化变形后结构呈椭圆状。确定固化变形后的圆度为3.04 mm，与实验所制造的网格舱段实验圆度3.22 mm进行对比，固化变形预报误差为5.6%。因此，舱段变形后的模型为结构热矫形提供了准确的初始轮廓。

2.2.2   网格舱段热矫形方案设计

将不同矫形工艺参数等效为双马树脂蠕变卸载后的模量衰减程度，利用Haipin-tsai细观力学方法^[42]，基于约束均匀应变条件和转动约束的假设，关联宏观应力和纤维材料性质并结合应变能增量理论方法模拟热矫形过程。复合材料网格结构在施加矫形荷载时，若施加的矫形位移过小，则会导致矫形荷载引起的应变能增量不足以满足网格结构卸载后回弹变形引起的应变能增量，很难达到预期矫形效果；若矫形荷载过大则会导致在热矫形过程中网格结构内部发生破坏，造成不必要的损失。因此，施加矫形荷载时必须选择合适的矫形位移大小。

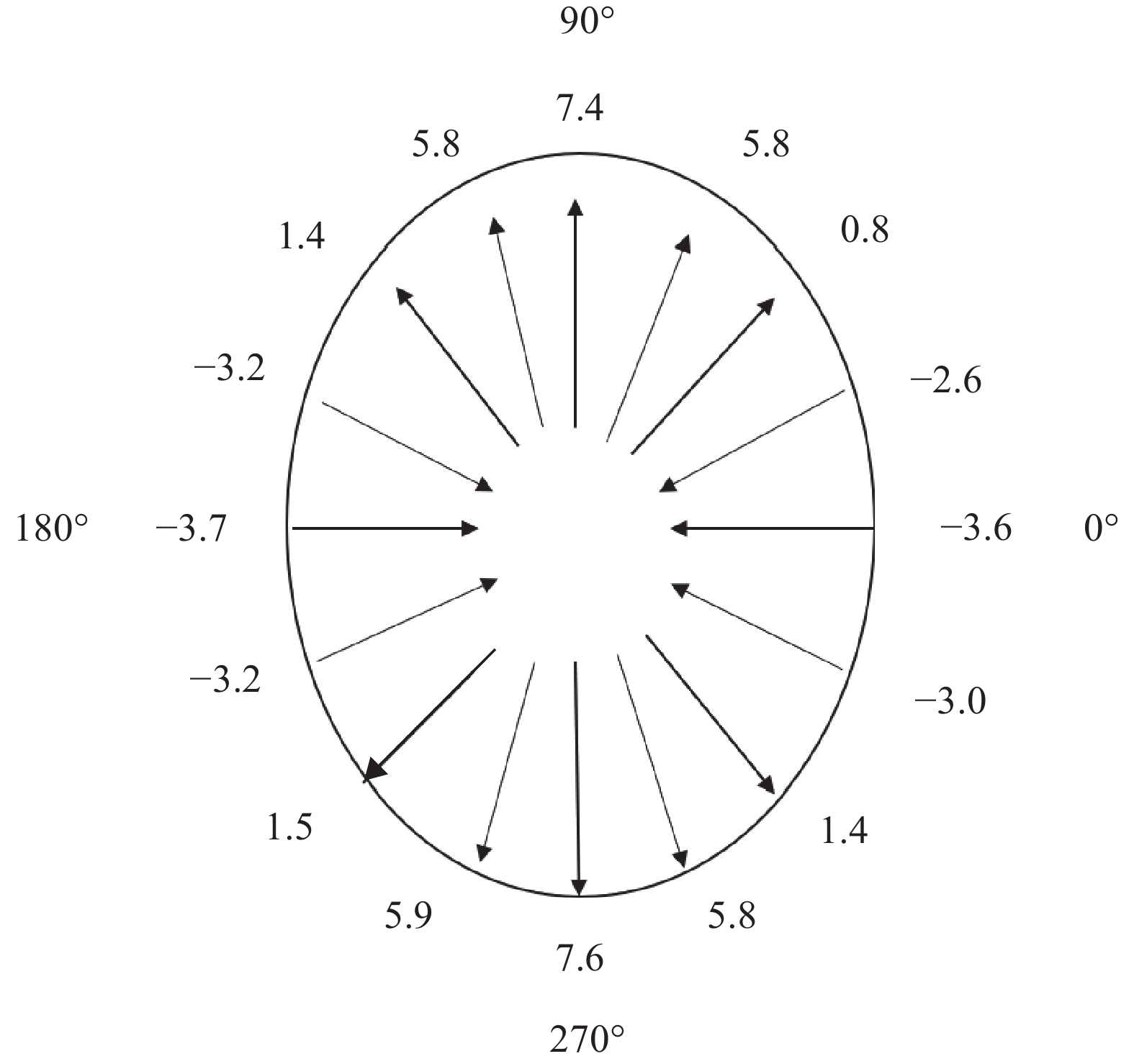
根据舱段结构固化变形轮廓，采取16个矫形点施加矫形位移荷载，如图7所示。图中数字表示各矫形点施加矫形位移后与固化变形后的前后位置变化值，整体轮廓呈椭圆状。椭圆竖直长轴b大于水平长轴a，因此90°、270°施加矫形位移值约为+7 mm，0°、180°(加厚区所在位置)施加矫形位移值约为−5 mm，其余各矫形点矫形位移大小根据内应力大小与应变能协调。

图  7  TG800/802双马树脂复合材料网格舱段16点矫形位移载荷大小

Figure  7.  Magnitude of displacement loads at 16 sizing points in the TG800/802 bismaleimide resin composite grid interstage segment

下载: 全尺寸图片 幻灯片

2.2.3   网格舱段热矫形模拟

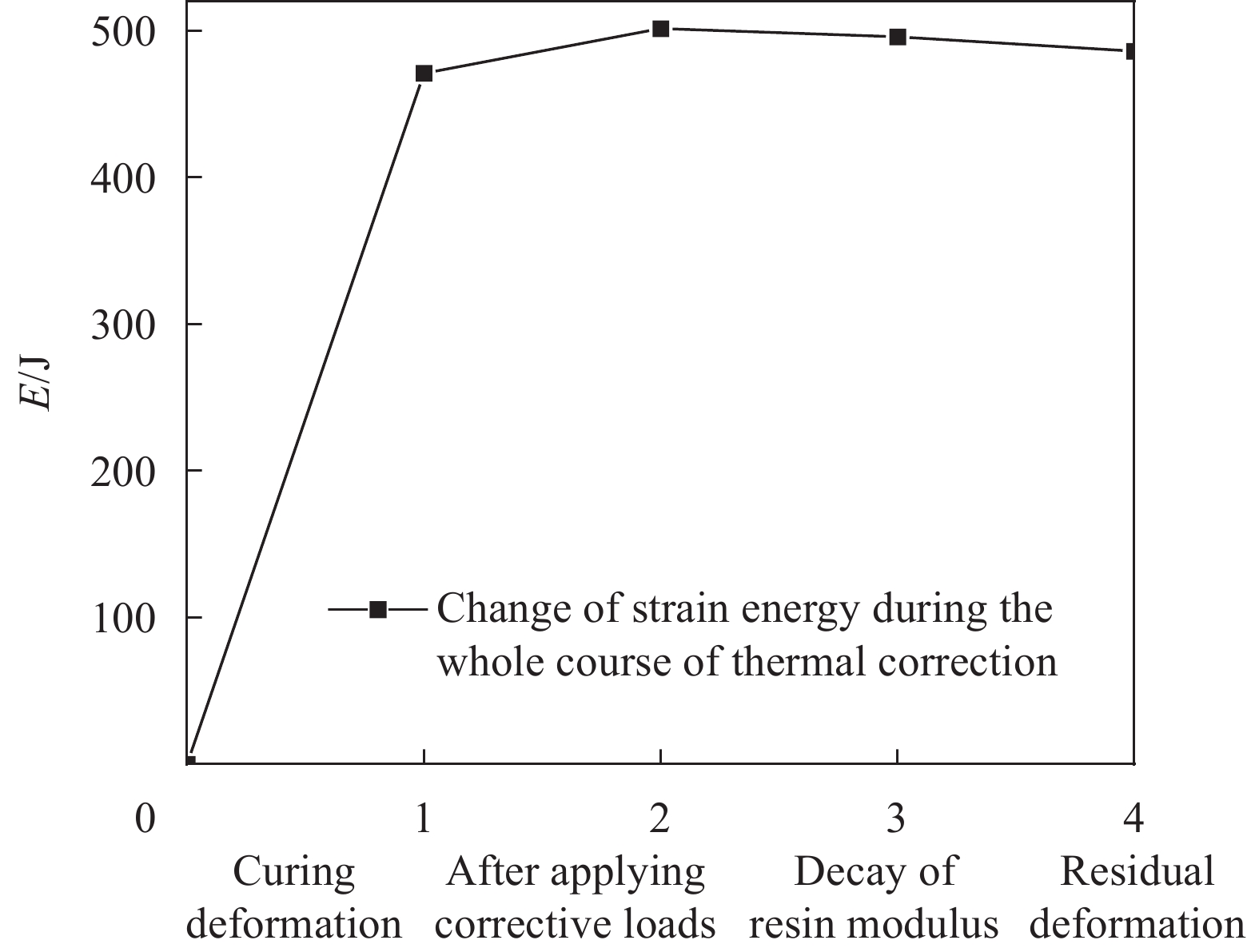
热矫形过程中施加矫形荷载后，将温度升温到210℃，然后先降温后卸载，结构松弛回弹。约束条件为下端框底端轴向变形(U₃)为0。热矫形过程中各阶段应变能如图8所示，矫形载荷引起的应变能增量等于矫形载荷卸载后回弹变形引起的应变能增量和最终矫形状态与初始变形状态之间的应变能增量之和并满足式(10)应变能增量理论。

图  8  TG800/802双马树脂复合材料网格舱段热矫形全过程应变能变化

Figure  8.  Changes in strain energy during hot sizing of TG800/802 bismaleimide resin composite grid interstage segment

下载: 全尺寸图片 幻灯片

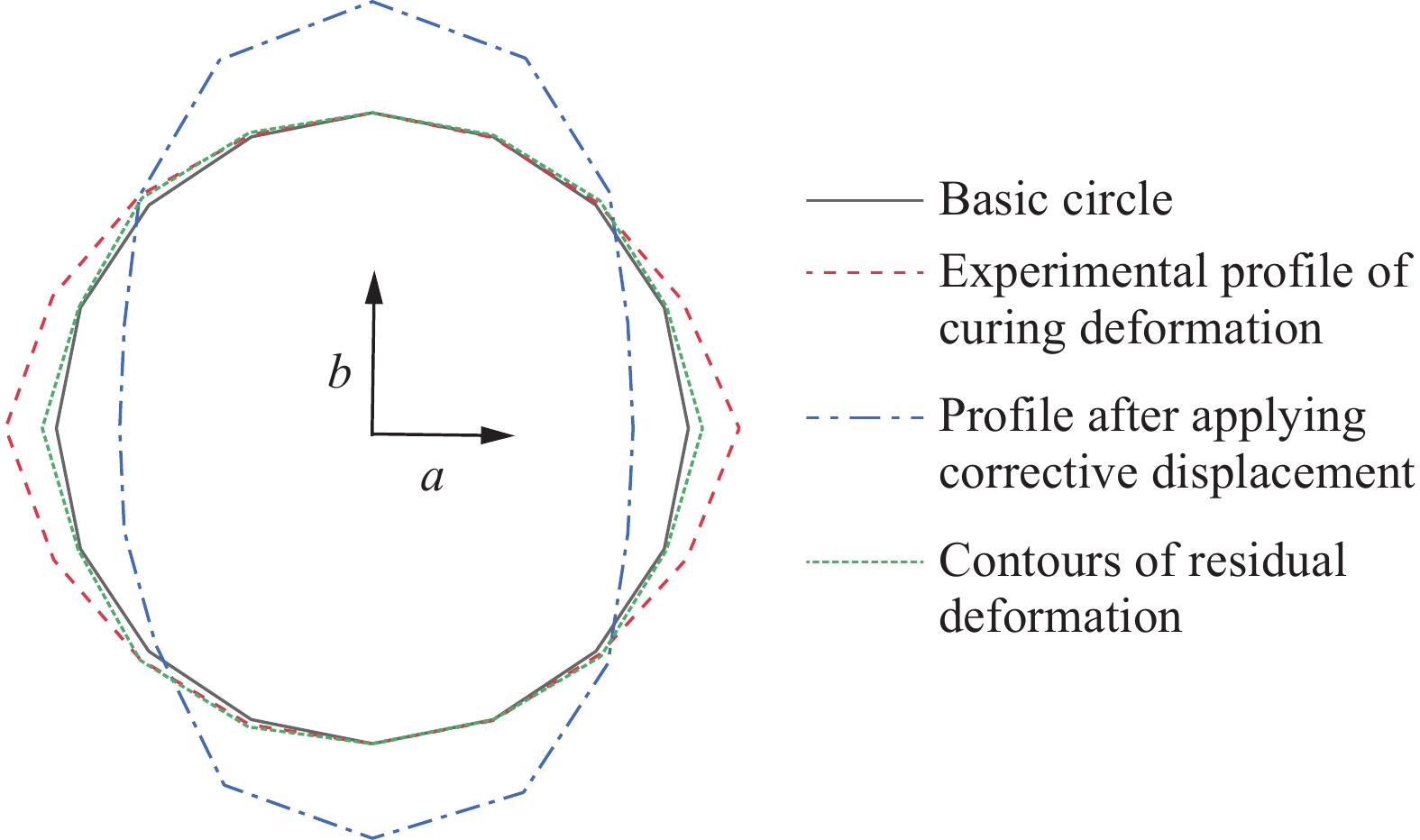
拟合得到“固化变形-热矫形”全过程轮廓如图9所示。固化变形后结构呈椭圆状，椭圆水平长轴a大于竖直短轴b。针对变形舱段，采用16个接触面尺寸为65 mm×35 mm的铝合金块，矫形位移施加在舱段下端框位置，将产品进行矫形试验验证。通过Abaqus设置不同分析步方法模拟舱段矫形过程中加载、卸载及回弹过程以及最终残留变形轮廓。施加矫形位移后，椭圆竖直轴b变为长轴。最后舱段结构残留轮廓回弹为圆，残留变形圆度预测值为0.87 mm。试验中网格舱段产品热矫形的试验轮廓圆度结果0.9 mm，证明该应变能理论仿真结果与试验结果相符合。

2.3   TG800/802双马树脂复合材料网格舱段热矫形工艺条件影响规律分析

2.3.1   网格舱段矫形内应力分析

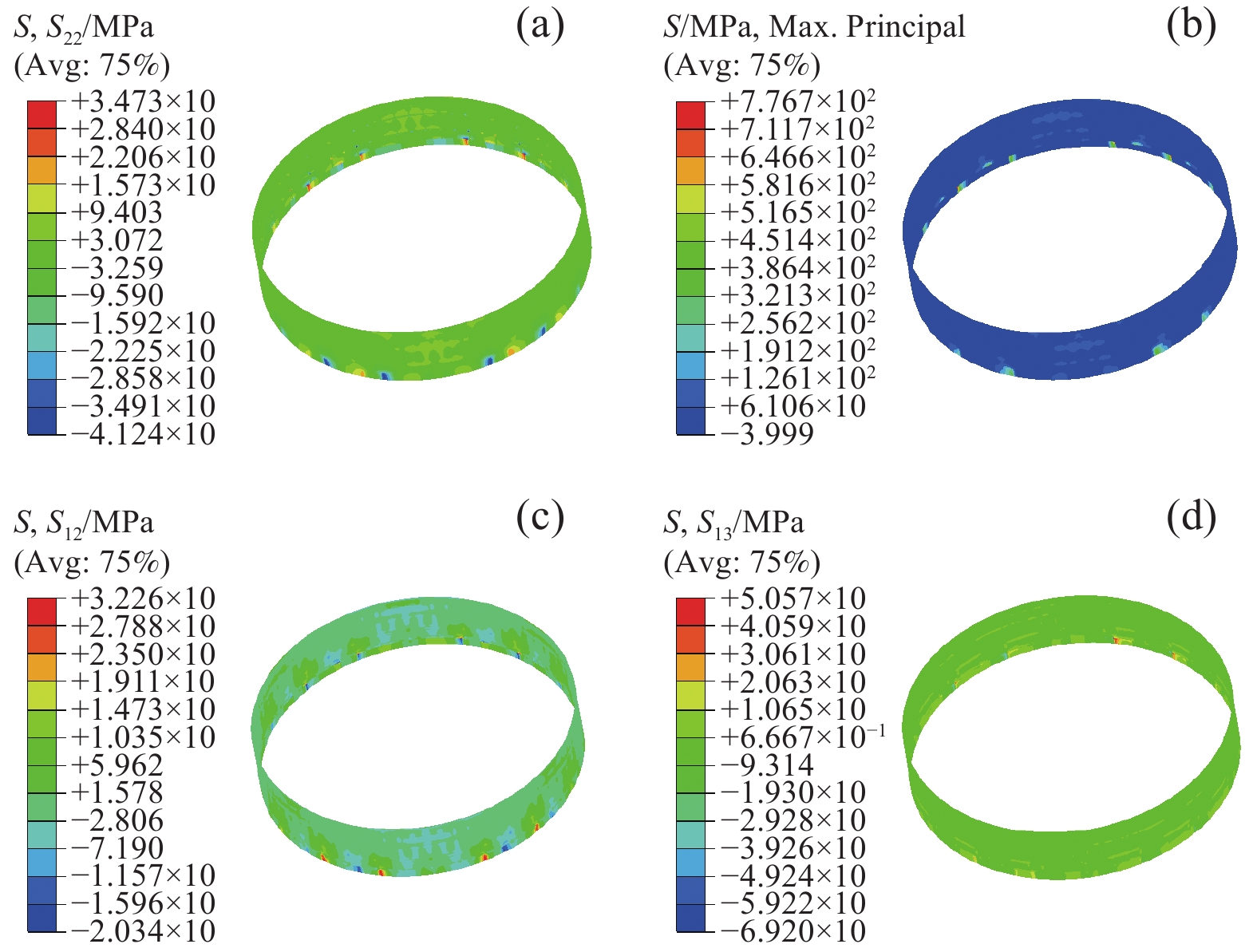
施加矫形位移过程中，需施加的矫形位移一般较高，以保证足够的残留变形量，但同时需注意避免施加矫形位移过大导致内应力过大，致使舱段结构发生破坏。如图10所示，内应力最值均发生在矫形点处。舱段内应力在铺层第3层上横向拉应力S₂₂达到最大值约为34.73 MPa，最大值位于舱段环向315°矫形位移施加点，达到横向拉伸强度的58.60%，易发生树脂拉伸损伤。纵向拉伸应力776.70 MPa，为拉伸强度的31.29%；面内剪切应力S₁₂最大值约为32.26 MPa，为剪切强度的36.79%；面外剪切应力S₁₃最大值为50.57 MPa，为剪切强度的50.07%。

将S₂₂应力危险单元应力值代入Hashin失效准则^[43]计算舱段矫形位移载荷对应的损伤状态。结果如表3所示，易发生树脂拉伸损伤，将横向拉应力S₂₂最大值所在单元其余应力值判断内应力并未达到失效条件，舱段结构未发生损伤。

图  9  TG800/802双马树脂复合材料网格舱段“固化变形-矫形荷载施加后-残留变形”轮廓

Figure  9.  Profiles of "curing deformation, application of corrective load, and residual deformation" of TG800/802 bismaleimide resin composite grid interstage segment

b—; a—

下载: 全尺寸图片 幻灯片

图  10  TG800/802双马树脂复合材料网格舱段热矫形内应力云图：(a)横向拉应力S₂₂；(b)最大主应力；(c)面内剪切应力S₁₂；(d)面外剪切应力S₁₃

Figure  10.  Internal stress distribution of hot sizing of TG800/802 bismaleimide resin composite grid interstage segment: (a) Transverse tensile stress S₂₂; (b) Max principle stress; (c) S₁₂; (d) S₁₃

下载: 全尺寸图片 幻灯片

表  3  网格舱段层合板单元失效指数

Table  3.  Failure index of grid interstage segment laminate unit

Failure mode	Hashin
Fiber tensile failure	0.008
Fiber compression failure	0.000
Matrix tension failure	0.889
Matrix compression failure	0.157

下载: 导出CSV 

| 显示表格

2.3.2   矫形点个数影响

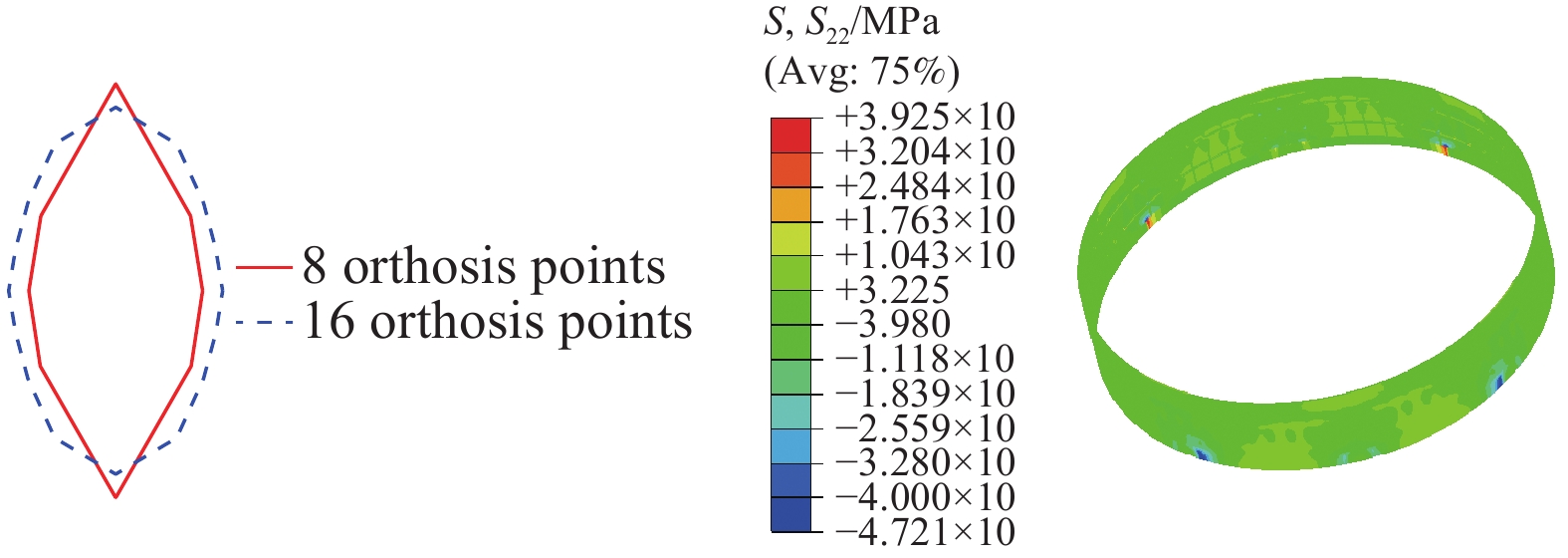
在工程实际加载过程中并非16个矫形点同时加载，且并无固定次序。计算时采用90°、270°先施加矫形位移，由2矫形点、4矫形点、8矫形点、16矫形点逐步施加矫形位移。2矫形点及4矫形点个数较少，同时需要施加比较大的矫形位移，并且加载后产生的应变能增量很小，不足以保证舱段轮廓回弹为圆。如图11所示，8矫形点相比于16矫形点加载时均可满足应变能增量理论，但通过8矫形点施加矫形位移荷载时，矫形点之间相距较远，很难保证舱段结构加载后轮廓为椭圆，并且加载时易产生更大的内应力，横向拉应力S₂₂最大值为39.25 MPa，相比于16点矫形应力值增加13.01%，结构易发生破坏。

图  11  不同矫形点个数下的TG800/802双马树脂复合材料网格舱段轮廓

Figure  11.  Contours of TG800/802 bismaleimide resin composite grid interstage segment with different number of corrective points

下载: 全尺寸图片 幻灯片

2.3.3   802双马树脂模量等效衰减

矫形位移确定后，满足应变能增量理论前提下，黏性流动导致的变形残留部分由外加载荷和时间/温度(时温等效原理)共同确定，矫形的温度、时间和位移可以通过树脂模量等效衰减表示。

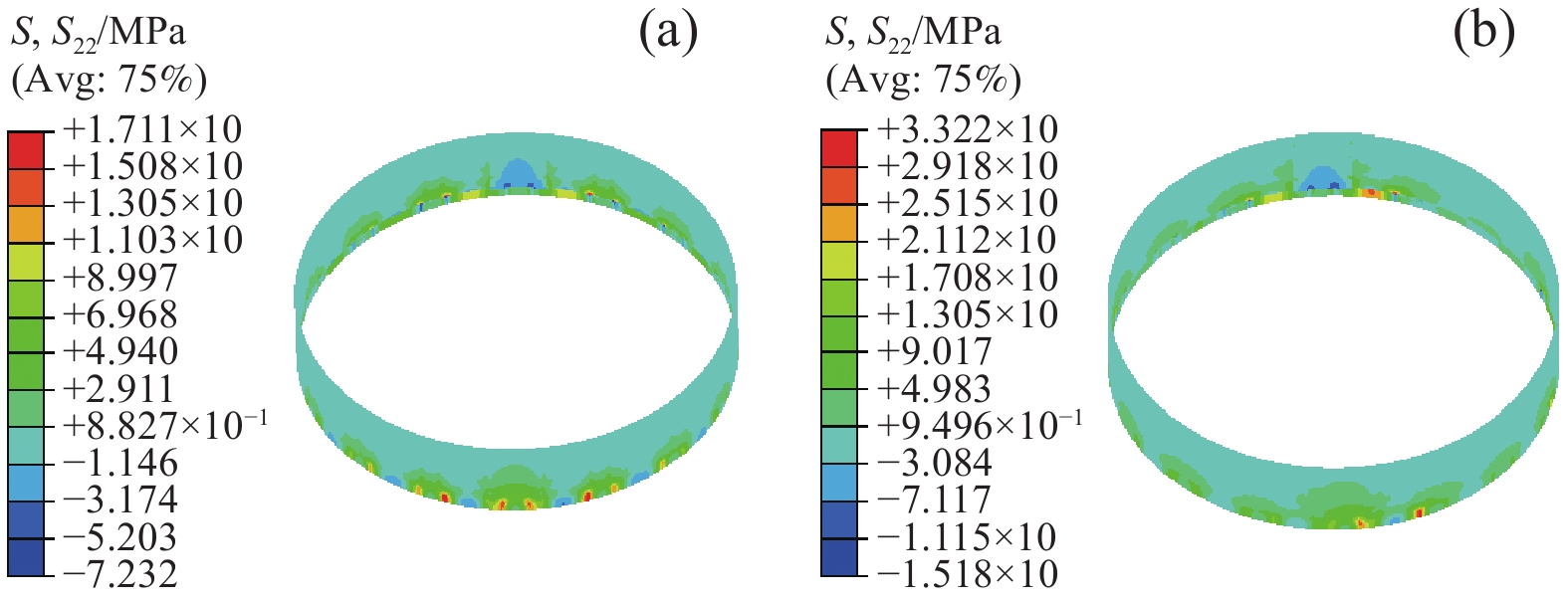
分别计算了树脂模量分别衰减5%、6%、9%时的残留应力，通过两种树脂模量等效衰减后的残留应力对比，分析舱段矫形工艺条件的影响规律。根据图12、表4所示结果，高温蠕变卸载后树脂模量等效衰减的越多，残留矫形应力越大。树脂模量等效衰减由5%衰减至9%时，应力最值均发生在矫形点处，纵向拉应力增加216.1 MPa，横向拉应力增加16.1 MPa。树脂模量衰减的越多，说明时间越长或温度越高，则会导致热矫形过程中的残留应力水平增加，矫形难度增大。

通过对施加矫形荷载后的舱段内应力失效分析、矫形点个数以及树脂模量等效衰减工艺条件影响规律分析，网格舱段热矫形过程中施加的矫形位移过大、矫形时间越长及温度越高都会增加结构的内应力，结构易发生破坏。因此在热矫形过程关于工艺条件影响规律的分析至关重要，可缩短制造周期，降低制造成本。

图  12  TG800/802双马树脂复合材料网格舱段热矫形后残留S₂₂：(a)树脂模量衰减5%；(b)树脂模量衰减9%

Figure  12.  Residual S₂₂ after hot sizing of TG800/802 bismaleimide resin composite grid interstage segment: (a) Resin modulus attenuation by 5%; (b) Resin modulus attenuation by 9%

下载: 全尺寸图片 幻灯片

表  4  树脂模量等效衰减程度对应残留应力水平

Table  4.  Equivalent attenuation degree of resin modulus corresponding to residual stress

Decay of resin modulus	Internal stress/MPa
	Maximum principal stress	S22	S12	S13
5%	194.7	17.1	6.9	19.6
6%	227.4	19.8	8.1	22.9
9%	410.8	33.2	18.6	40.5

下载: 导出CSV 

| 显示表格

3.   结 论

通过对复合材料回转体网格结构热矫形机制研究与有限元模拟，主要取得以下结论：

(1)复合材料网格结构热矫形机制根本原因是热固性树脂高温蠕变，802双马树脂在降温卸载回弹后，普弹应变及高弹应变会逐渐恢复，黏性流动应变不可恢复而残留下来，故而可对网格结构进行形状矫正；

(2)矫形位移载荷大小的选择决定网格结构卸载后回弹轮廓，施加较大矫形荷载时应避免内应力过大导致结构破坏；施加载荷过小则会导致蠕变卸载后结构应变能增量变化小，网格结构最终轮廓达不到预期矫形效果；

(3)通过有限元模拟设计矫形位移，在保证最终残留变形轮廓相同的情况下，8矫形点时会导致结构产生更大的内应力，易发生树脂拉伸损伤；外加载荷和时间/温度(时温等效)可通过树脂模量等效衰减体现，树脂模量等效衰减越多，残留应力越高。