Numerical investigation on dynamic response of bio-inspired bi-directional corrugated lattice structure under impact loading
-
摘要:
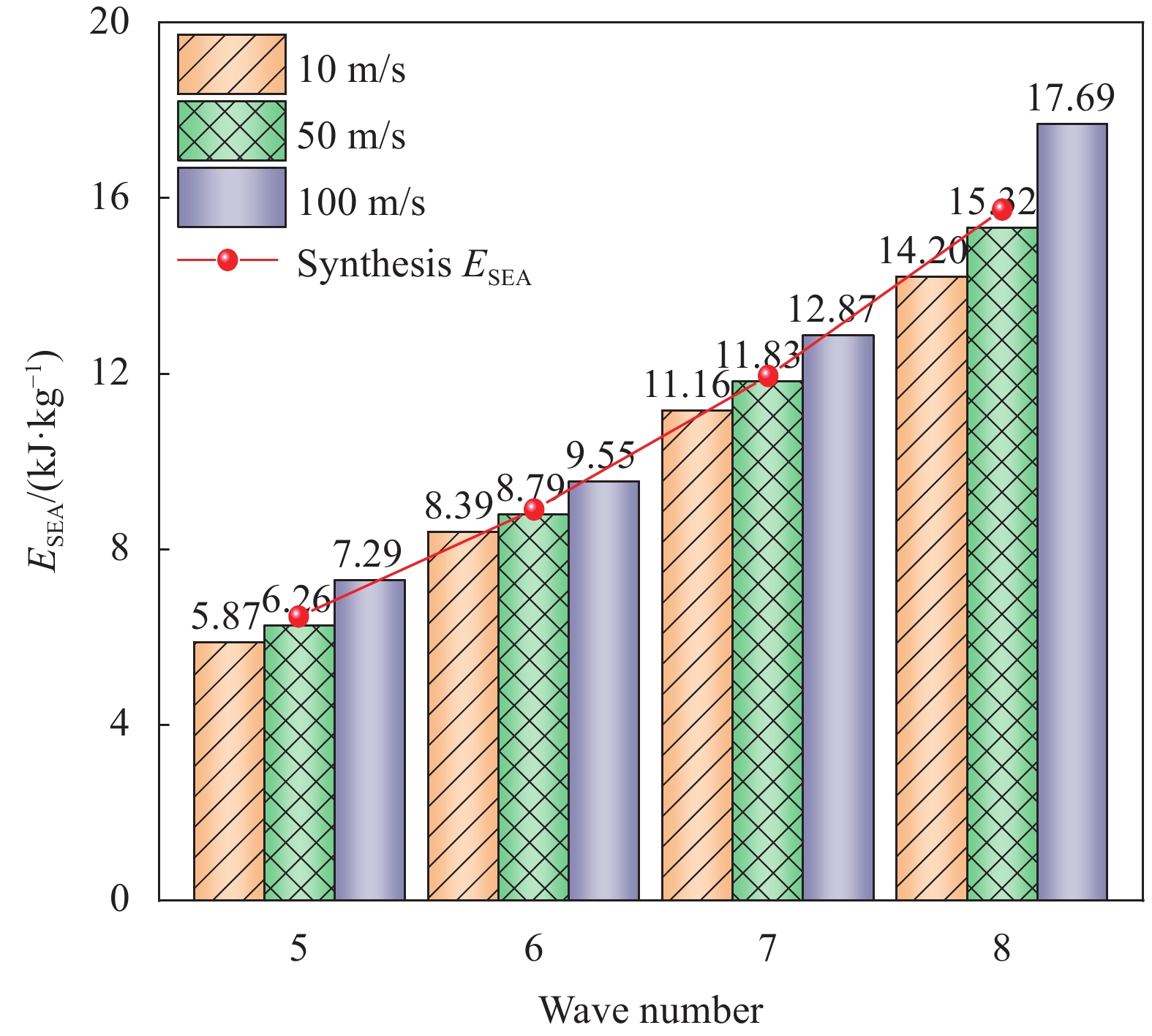
为了探究仿生双正弦波纹点阵结构(Bio-inspired bi-directional corrugated lattice structure，BBCLS)的抗冲击性能，采用ANSYS/LSDYNA有限元分析软件建立了其在冲击荷载作用下的有限元数值模型，并基于已有的试验结果与数值模拟结果进行了对比，验证了该模型的有效性。在此基础上，研究了不同冲击速度对BBCLS的应力分布、变形模式、承载能力以及能量吸收特性的影响，并与传统体心立方点阵结构(BCC)进行了对比。同时利用该数值模型进一步分析了振幅、波纹数和胞壁厚度等微结构几何参数对BBCLS抗冲击性能的影响。研究结果表明：BBCLS在冲击荷载作用下的承载能力、吸能总量及比吸能均明显优于传统的BCC点阵结构。BBCLS的冲击动力学响应主要与冲击速度和微结构几何参数有关。在低速冲击时，BBCLS呈现整体变形模式；中高速冲击时，结构向局部变形模式转换。随着冲击速度的提高，增大振幅、波纹数、胞壁厚度均使结构在受到冲击载荷时应力分布均匀，有效增加了冲击端的平台应力。此外，微结构几何参数的改变对结构比吸能以及综合比吸能有显著影响。由于波纹数的增大，BBCLS的承载能力、刚度和吸能性均大幅度提高，当波纹数为8，冲击速度达到100 m/s，相比于波纹数为5，冲击速度为10 m/s比吸能提高201.36%。研究结果为研究仿生点阵结构的冲击变形失效和吸能效果提供了力学依据。
Abstract:In order to explore the impact resistance of bio-inspired bi-directional corrugated lattice structure (BBCLS), ANSYS/LSDYNA finite element analysis software was used to establish the finite element numerical model under the impact load, and the existing test results were compared with the numerical simulation results to verify the effectiveness of the model. On this basis, the effects of different impact velocities on the stress distribution, deformation mode, bearing capacity and energy absorption characteristics of BBCLS were studied, and compared with the traditional body-centered cubic lattice structure (BCC). The effects of the geometric parameters such as amplitude, ripple number and cell wall thickness on the impact resistance of BBCLS were further analyzed using the numerical model. The results show that the carrying capacity, total energy absorption and specific energy of BBCLS under impact load are obviously superior to the traditional BCC lattice structure. The impact dynamic response of BBCLS is mainly related to impact velocity and microstructure geometry parameters. At low speed impact, BBCLS presents an overall deformation pattern. The structure changes to the local deformation mode during the impact of medium and high speed. With the increase of impact velocity, the increase of amplitude, ripple number and cell wall thickness can make the stress distribution of the structure under impact load uniform, and effectively increase the platform stress at the impact end. In addition, the change of microstructure geometric parameters has a significant effect on the specific absorption energy of the structure and the overall specific absorption energy. As the number of ripples increases, the bearing capacity, stiffness and energy absorption of BBCLS are greatly improved. When the number of ripples is 8, the impact velocity reaches 100 m/s. Compared with the number of ripples, the impact velocity is 10 m/s, which is 201.36% higher than the energy absorption. The results provide a mechanical basis for the study of impact deformation failure and energy absorption effects of bionic lattice structures.
-
PPCPs (Pharmaceuticals and Personal Care Products)，即药品及个人护理用品，是水体中普遍存在的痕量有机物，与人类的生产活动密切相关。虽然PPCPs类物质在环境中检测到的浓度较低，但由于其持久性、生物累积性和远距离迁移性等特征，对生态系统和人类健康的潜在风险不容忽视[1, 2]。PPCPs种类繁多，在疾病预防与治疗等方面主要包括处方类和非处方类药品，如抗生素、β受体阻滞剂、抗癫痫药等[3]。其中，卡马西平(Carbamazepine，CBZ)是一种常见的抗癫痫和精神类药物，因其在废水中检出频率较高，是具有代表性的PPCPs类物质[4]。传统生物法对卡马西平的去除率较低[5, 6]，因此开发一种经济高效的处理技术刻不容缓。
高级氧化技术(Advance Oxidation Process，AOPs)是处理水中难降解有机污染物最具有应用前景的方法之一。其中，经典芬顿氧化法是在酸性(pH=2~4)条件下，Fe(II)催化H2O2产生羟基自由基(·OH)，可将目标污染物快速分解成小分子物质，甚至达到完全矿化的目标[7]。然而，该反应过程存在pH适用范围窄、H2O2利用率低、处理含铁污泥成本高、易产生二次污染等缺点[8, 9]。因此，开发金属固体催化剂应用于非均相类芬顿反应是目前的研究热点和难点。
以金属Fe为核心的催化剂，如零价铁/Fe3O4复合催化剂[10]、Fe3O4负载活性炭[11]、Fe-金属有机框架[12, 13]、Fe掺杂氮化碳材料等[14, 15]，具有良好的稳定性和循环利用效率，并能有效提高Fenton反应速率，但该体系仍需在酸性条件下进行(pH=2~4)。以金属Cu替代Fe频繁出现在近年来的研究中。Sun等人制备Cu@SiO2催化剂活化H2O2降解多种持久性有机物，在中性条件下均能达到较好的去除和矿化效果[16]。Zhang等人合成CuCN催化剂应用于光-Fenton体系，在pH=4~8的条件下，60 min内对四环素的去除率达93.60%[17]。杨露等人设计含双功能区(零价铜(Cu0)和氧空位(OVs))的铜基催化剂，在仅投加5 mmol/L H2O2和不调节溶液pH的条件下，90 min 内土霉素的去除率便达到89.2%[18]。大量的研究结果表明，Cu0，Cu(I)和Cu(II)均可与H2O2构成类芬顿体系，且铜基催化剂具有反应速率快、pH适应范围广、矿化能力强等优点[19, 20]。
铜基催化剂常用的载体包括金属氧化物[21]、二氧化硅[22]、分子筛[23]和碳材料[24, 25]等。其中，石墨相氮化碳，简称g-C3N4，具备禁带宽度窄(约2.7 eV)、合成方法简单、物化性质稳定、环境友好等优点[26, 27]。g-C3N4结构中的C原子和N原子以sp2杂化形成高度离域的π电子共轭体系，其丰富的π电子可促进芬顿反应中的电子转移[28]。同时，高密度的N基大环单元包含六个孤立电子对，可提供更多的金属配位点作为催化活性中心[29]。因此g-C3N4被认为是极具潜力的类芬顿催化剂载体。CuO是一种带隙范围在1.3~1.6 eV的p型窄带隙半导体，与g-C3N4的能级结构匹配。二者复合形成CuO/g-C3N4异质结，不仅可提高CuO的稳定性，减少溶液中Cu(II)的溶出，同时能提高Cu的电子传递效率，优化材料的催化性能[30~32]。
基于此，本研究拟制备CuO/g-C3N4复合材料构建非均相类芬顿体系，选择卡马西平(Carbamazepine，CBZ)为处理对象，考察铜的复合量、CuO/g-C3N4投加量、双氧水投加量以及溶液pH对CBZ去除效果的影响。测试材料的稳定性和循环利用效率。结合反应动力学、自由基淬灭实验和密度泛函理论(Density Function Theory，DFT)计算，探讨催化降解机制。
1. 材料与方法
1.1 实验试剂
卡马西平 (Carbamazepine，CBZ)购自阿拉丁试剂(上海)有限公司，过氧化氢(H2O2，30%)、尿素(CH4N2O)、无水乙醇(C2H6O)、六水合硝酸铜(Cu(NO3)2•6H2O)、NaOH、HCl等购于成都市科隆化学品有限公司。所有实验用水均为超纯水(UPT-I-10T，四川优普)。
1.2 催化剂的制备
g-C3N4通过煅烧法制得[33, 34]。即称取一定量的尿素置于坩埚中，在马弗炉中以550℃高温煅烧4 h后便得到淡黄色粉末状的g-C3N4样品。CuO/g-C3N4复合材料的制备方法则是将一定量的g-C3N4超声分散1 h后，加入一定量的Cu(NO3)2•6H2O再超声处理2 h。将混合液过滤，滤渣烘干、研磨后转移到坩锅中，在500℃马弗炉中焙烧4 h，便得到固体样品，表示为CuO/g-C3N4。该样品用去离子水、无水乙醇分别洗涤三次后烘干备用。调节Cu的复合量(铜元素质量占催化剂总质量的百分比)，制备了复合量分别1%、3%、5%、7%的催化剂。
1.3 实验方法
将一定量的CuO/g-C3N4复合材料和 H2O2 加入100 mL、20 mg/L的CBZ溶液中，在20℃恒温条件下震荡反应，收集不同时间段的液体样品，测定CBZ浓度，考察材料的催化降解性能。将反应后的催化剂经醇洗和烘干后，进行重复实验，考察材料的稳定性和重复利用效率。
采用自由基淬灭实验确定该类芬顿体系的活性物种。在H2O2 投加前，分别加入50 mmol/L异丙醇(IPA)、0.15 mmol/L乙二胺四乙酸二钠(EDTA-2 Na)和5 mmol/L L-组氨酸(L-His)作为∙OH、h+和1O2的淬灭剂。
1.4 分析表征方法
CBZ浓度采用高效液相色谱(安捷伦1200型)测定。选择C18 (5 μm×4.6 mm×150 mm)柱，流动相采用甲醇/水(体积比为6∶4)，设定检测波长为262 nm，流速0.8 mL/min，进样量为10 μL。采用扫描电子显微镜(Scanning Electron Microscope，SEM，日本电子 JEOL，JSM-7800F Prime 型)、能谱仪(Energy Dispersive Spectrometer，EDS，牛津仪器Ultim MAX 型) 、氮气等温吸附/脱附曲线(康塔Autosorb EVO型)、傅里叶变换红外光谱仪(Fourier Transform Infrared Spectroscopy，FT-IR，赛默飞Nicolet 670型)、X射线衍射(X-Ray Diffraction，XRD，赛默飞Smartlab 9型)、X射线光电子能谱仪(X-ray Photoelectron Spectroscopy，XPS，赛默飞Escalab 250Xi型)，对催化剂的表面形貌、孔径结构、表面官能团、晶形结构及元素价态进行分析。
1.5 密度泛函理论计算
使用Materials Studio软件中的DMol3模块进行计算。选择Perdew-Burke-Ernzerhof (PBE)函数和广义梯度近似(Generalized Gradient Approximation，GGA)处理体系的交互关联能[35, 36]。采用双数值极化(DNP+)为计算机组，TS方法考虑体系中的范德华力。为了减少层间的相互作用，模型真空层设置为20 Å。所有计算使用自旋杂化，smearing使用0.005 Ha。能量收敛限制设置为1.0 × 10−5 Ha，最大应力和位移分别设置为0.002 Ha/Å和0.005 Å，混合电荷密度设置为0.2。未勾选使用COSMO。
2. 结果与讨论
2.1 CuO/g-C3N4复合材料的表征分析
CuO/g-C3N4复合材料的SEM图像如图1(a)所示。从中可观察到多孔堆叠的层状结构，较蓬松，表面粗糙且有部分小粒径颗粒物，推测可能是铜的氧化物。对其所含元素及分布情况进行能谱分析，如图1(b)所示，材料中含有C、N、O、Cu等元素，且各元素分布均匀。此外，通过N2等温吸附/脱附曲线拟合可知，g-C3N4和CuO/g-C3N4的比表面积和孔容积分别为10.46 m2/g、0.028 cm3/g和26.12 m2/g、0.071 cm3/g。显著增大的比表面积和孔结构可为催化反应提供更多的电荷转移通道和活性点位。
![]()
图 1 (a) CuO/g-C3N4材料的SEM图；(b) CuO/g-C3N4材料的EDS图Figure 1. (a) Scanning Electron Microscope of CuO/g-C3N4 composites; (b) Energy Dispersive Spectrometer diagram of CuO/g-C3N4 composites采用FT-IR分析材料的分子结构，其结果如图2(a)所示。g-C3N4和CuO/g-C3N4的吸附峰位置基本一致，说明复合CuO对g-C3N4的分子结构没有影响。图中出现三处明显的吸收区域，其中810 cm−1的吸收峰归属于氮化碳七嗪结构的面外弯曲振动[37]，
1100 ~1700 cm−1范围的峰属于杂环芳香族C–N的伸缩振动，3000 ~3500 cm−1范围的峰为仲胺或伯胺的伸缩振动[38]。材料的晶体结构表征结果如图2(b)所示。g-C3N4的XRD图谱在12.8°和27.6°出现两个明显的衍射峰，分别对应石墨相氮化碳的(1 0 0)晶面和(0 0 2)晶面[39]。上述衍射峰在CuO/g-C3N4的XRD图谱上的强度变弱，特别是2θ=12.8°的衍射峰，说明CuO的引入对g-C3N4石墨层间的范德华力和π–π 堆积力有一定程度的影响。此外，在35.5°和38.7°观察到CuO的(1 1 −1)和(1 1 1)晶面(JCPDS 80-1917)[40, 41]。![]()
图 2 (a) g-C3N4和CuO/g- C3N4的FT-IR谱图；(b) XRD谱图Figure 2. (a) Fourier Transform Infrared Spectroscopy spectra; (b) X-ray Diffraction pattern of g-C3N4 and CuO/g-C3N4为了进一步探索材料中元素的化学价态，对CuO/g-C3N4进行XPS光谱分析。图3(a)检测到C、N、O和Cu元素信号，与制备的复合材料构成一致。在O1 s谱图中(图3(b) )，可拟合为两处特征峰，分别对应材料表面的—OH(531.5 eV)和C—O (532.7 eV)[42, 43]。从图3(c)可以看出，Cu 2p谱图在932.4 eV和934.8 eV处的峰分别归属于Cu(I)(2p 3/2轨道)和Cu(II)(2p 3/2轨道) [40, 44]。Cu(II)的强卫星峰位于941.0 eV，表明铜原子以CuO形式存在[45]。
2.2 CuO/g-C3N4催化H2O2降解CBZ的效能研究
2.2.1 Cu的复合量对CBZ去除率的影响
图4展示了Cu复合量对CBZ去除率的影响。从图可以看出，单独的g-C3N4材料很难催化H2O2降解CBZ，其去除率仅为24.54%，主要取决于H2O2的氧化作用。当Cu复合量由1%增加到7%时，CBZ的去除率从70.95%增加到96.59%。该结果表明g-C3N4材料中Cu含量的增加可提供更多的活性位点与H2O2反应，进而产生更多的自由基攻击CBZ分子。考虑到材料制备的可行性和经济性，Cu的最佳复合量设置为7%。
![]()
图 4 Cu复合量对CBZ去除率的影响Figure 4. The effect of Cu composite amount on the removal rate of CBZ(Experimental condition: CBZ: 20 mg/L; CuO/g-C3N4 dosage: 2 g/L; H2O2 dosage: 147 mmol/L; solution pH: unadjusted; reaction time: 60 min)2.2.2 CuO/g-C3N4投加量对CBZ去除率的影响
不同CuO/g-C3N4投加量对CBZ的去除率如图5所示。当材料投加量为0时，H2O2对CBZ的氧化率为20.03%。当CuO/g-C3N4投加量由0.5 g/L增加到2 g/L，CBZ去除率由55.89%提高到96.59%。由此可见，催化剂投加量的增加能增大H2O2与Cu的接触，进而提高自由基的产生量，促进CBZ的降解[46]。当CuO/g-C3N4投加量进一步增大到3 g/L时，CBZ去除率的提升并不明显，仅为1.41%，这是因为过量的催化剂在溶液中分散不均导致利用率降低[47]。考虑到工程应用上的经济性，CuO/g-C3N4的最佳投加量确定为2 g/L。
![]()
图 5 CuO/g-C3N4投加量对CBZ去除率的影响Figure 5. The effect of CuO/g-C3N4 dosage on the removal rate of CBZ(Experimental condition: CBZ: 20 mg/L; H2O2 dosage: 147 mmol/L; solution pH: unadjusted; reaction time: 60 min)2.2.3 H2O2投加量对CBZ去除率的影响
H2O2的投加量对CBZ去除效果的影响如图6所示。单独的CuO/g-C3N4对CBZ的吸附能力较弱，仅为2.60%。当H2O2投加量从49 mmol/L增加到147 mmol/L时，CBZ去除率由85.65%增加到96.59%。这是由于溶液中H2O2浓度增加提高了对表面活性点位的暴露， CuO/g-C3N4活化分解H2O2产生更多的自由基用以降解CBZ。但随着H2O2投加量的进一步增加，CBZ的去除率没有显著提高，其原因可能是过多的H2O2会与自由基反应，从而造成H2O2的浪费。具体的反应方程式如下：∙OH+H2O2→∙HO2+H2O,∙HO2+∙OH→O2+H2O[48]。因此，H2O2的最佳投加量为147 mmol/L。
![]()
图 6 H2O2投加量对CBZ去除率的影响Figure 6. The effect of H2O2 dosage on the removal rate of CBZ(Experimental condition: CBZ: 20 mg/L; CuO/g-C3N4 dosage: 2 g/L; solution pH: unadjusted; reaction time: 60 min)2.2.4 溶液pH对CBZ去除率的影响
不同溶液pH条件下CuO/g-C3N4催化H2O2降解CBZ的效果如图7所示。当溶液初始pH值为2时，CBZ的去除率仅为52.38%。这是由于H2O2在极酸条件下(pH＜3)稳定性较差，会被快速分解成水[49]；在 pH=3~9的范围内，CBZ的去除率均在96%以上，说明该催化体系具有较好的pH适应性。
![]()
图 7 溶液pH对CBZ去除率的影响Figure 7. The effect of solution pH on the removal rate of CBZ(Experimental condition: CBZ: 20 mg/L; CuO/g-C3N4 dosage: 2 g/L; H2O2 dosage: 147 mmol/L; reaction time: 60 min)2.2.5 CuO/g-C3N4材料的稳定性
催化剂的稳定性是评价其性能的主要指标。如图8所示，CuO/g-C3N4复合材料重复使用5次后，反应60 min后CBZ去除率仅由96.59%降低到94.23% (图8)，说明该材料具有较好的稳定性。其中，CBZ去除率的降低可能与CBZ及其降解的中间产物被吸附在催化剂表面、少量Cu被浸出到溶液中等原因所导致的孔隙堵塞、活性位点和表面积下降有关。此外，检测到反应溶液中铜的浓度为0.7~4.95 μg/L，远低于欧盟发布委员会条例(EU)中规定浓度(＜2 mg/L)。
![]()
图 8 CuO/g-C3N4复合材料的稳定性Figure 8. Stability of CuO/g-C3N4 composites(Experimental condition: CBZ: 20 mg/L; CuO/g-C3N4 dosage: 2 g/L; H2O2 dosage: 147 mmol/L; solution pH: unadjusted; reaction time: 60 min)2.3 CuO/g-C3N4催化H2O2降解CBZ的机制研究
2.3.1 CBZ的降解动力学研究
在Cu的复合量为7%，CuO/g-C3N4投加量为2 g/L，H2O2投加量为147 mmol/L的条件下，溶液中CBZ的浓度随时间的变化如图9(a)所示。通过伪一级动力学模型的拟合，CBZ的降解速率常数为
0.0053 min−1，高于已有的部分研究[50, 51]。溶液TOC的变化如图9(b)所示。TOC的初始浓度为15 mg/L，与20 mg/L CBZ溶液所对应的TOC浓度接近。在反应15 min、30 min和60 min时溶液中TOC浓度分别为9.0 mg/L、8.83 mg/L、6.96 mg/L，CBZ的矿化率约为53.66%。![]()
图 9 (a) CuO/g-C3N4的降解动力学曲线；(b) CuO/g-C3N4的TOC测试浓度Figure 9. (a) Kinetics of CBZ degradation of CuO/g-C3N4; (b) TOC concentration of CuO/g-C3N42.3.2 自由基捕获
添加三种不同的自由基淬灭剂后，CBZ的去除率如图10所示。当反应体系中加入50 mmol/L异丙醇，CBZ的去除率为45.68%，说明·OH对CBZ的降解具有重要的作用。EDTA-2 Na的添加对CBZ的降解也存在一定程度的抑制作用，90 min后CBZ的去除率为84.15%。当L-组氨酸的投加浓度为5 mmol/L，CBZ的去除率由96.59%降低到56.44%，说明该系统还存在1O2的氧化作用。综上所述，·OH和1O2是CuO/g-C3N4非均相类Fenton催化体系中主要的活性物种，h+对体系贡献较少。
2.3.3 DFT理论计算结果
CBZ和H2O2分子在CuO/g-C3N4上的最佳模拟吸附位如图11(a)和(b)所示。当仅有CBZ分子吸附时，CBZ上的酰胺基与Cu−O的距离为1.962 Å, 说明氢键的形成(图11(a))。而在CBZ水溶液中，CBZ与水分子在CuO/g-C3N4上形成竞争吸附，Cu−O优先与H2O上的氢原子结合形成氢键，键长为1.472 Å。而CBZ的酰胺基与H2O上的氧原子连接，键长为1.759 Å(图11(b))。CuO/g-C3N4上的金属氧化物更容易与极性的水分子结合，从而阻止CBZ的吸附，该结果也解释了CuO/g-C3N4对CBZ较弱的吸附能力。
![]()
图 11 (a) CBZ (b) CBZ水溶液 (c) H2O2、CBZ水溶液在CuO/g-C3N4上的模拟吸附位图Figure 11. Simulated adsorption bitmap on CuO/g-C3N4 of (a) CBZ (b) CBZ aqueous solution (c) H2O2 and CBZ aqueous solutionH2O2投加后主要通过三个步骤激发类Fenton反应：1) H2O2将取代之前吸附的H2O而优先吸附在CuO/g-C3N4表面，其氢键键长为1.004 Å(图11(c))；2) CuO/g-C3N4与H2O2发生电子交换；3) H2O2 分子O−O键长度由1.453 Å 增加到1.509 Å，O−O键电子密度降低将促进其断裂并分解产生∙OH。CuO/g-C3N4与H2O2之间的电子交换导致Cu(II)/ Cu(I)氧化还原过程的持续发生，进而分解H2O2产生大量的活性基团攻击CBZ分子，促进CBZ的降解。该催化反应过程如下[52, 53]:
Cu(II)+H2O2→Cu(I)+O2−+H+ O−2+H+→1O2+H2O2 Cu(I)+H2O2→Cu(II)+⋅OH+OH− 3. 结 论
(1)通过煅烧法制备CuO/g-C3N4复合材料,其中Cu主要以氧化铜形式存在；
(2)以CuO/g-C3N4复合材料构建非均相类芬顿体系，对卡马西平的去除率达96.59%，∙OH和1O2是反应主要的活性物种；
(3) CuO/g-C3N4复合材料具有较好的稳定性，重复使用5次后对CBZ的去除率仍高达94.23%。
-
![]()
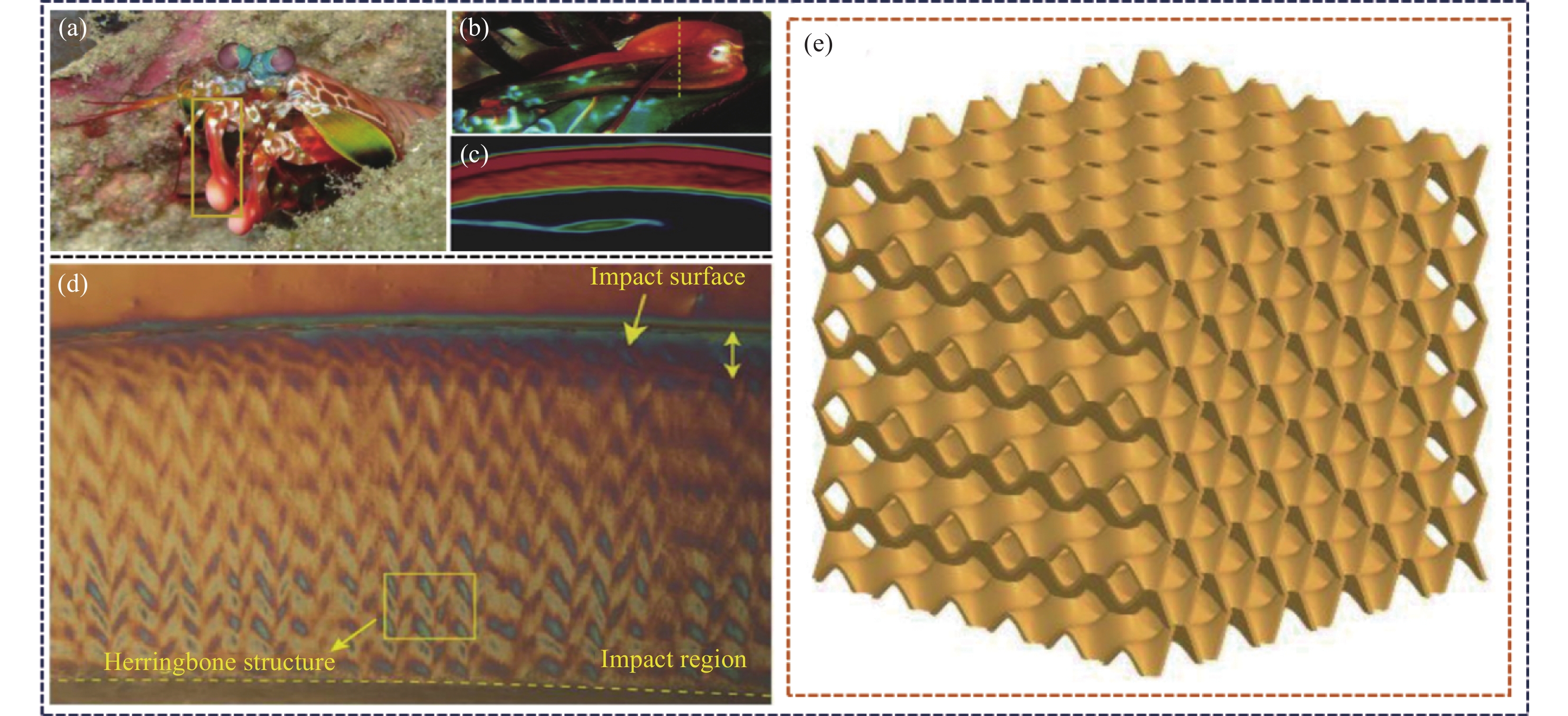
图 1 仿生双正弦波纹点阵结构(BBCLS)示意图：(a)雀尾螳螂虾[25]；(b)虾鳌[27]；(c)抗冲击区域[27]；(d)虾螯抗冲击区域微观结构[27]；(e) BBCLS[32]
Figure 1. Schematic diagram of bio-inspired bi-directional corrugated lattice structure (BBCLS): (a) Odontodactylus scyllarus[25]; (b) Shrimp chela[27];(c) Impact zone[27]; (d) Macro-microstructure of shrimp chela[27]; (e) BBCLS[32]
![]()
图 2 BBCLS有限元模型：(a)准静态压缩荷载下BBCLS计算模型；(b) BBCLS单层模型；(c) BBCLS胞元模型
Figure 2. BBCLS finite element model: (a) Computational model of BBCLS under quasi-static compression loading; (b) BBCLS single-layer model; (c) BBCLS single cell model
A—Amplitude; N—Wave number; t—Cell wall thickness
![]()
图 3 BBCLS试验与模拟破坏形态对比图
Figure 3. Comparison between experimental and simulated failure state of BBCLS
![]()
图 4 BBCLS的力-位移曲线试验与模拟结果对比
Figure 4. Comparison of experimental and simulated force-displacement curves of BBCLS
FEM—Finite element model; EXP—Experiment
![]()
图 5 不同冲击速度下的BBCLS在典型应变水平下的变形图
Figure 5. Deformation diagram of BBCLS under typical strain levels at different impact velocities
![]()
图 6 不同冲击速度下的BBCLS在冲击端和固定端的名义应力-应变曲线
Figure 6. Nominal stress-strain curves on impact end and fixed end of BBCLS under different impact velocities
![]()
图 7 不同冲击速度下的BBCLS能量吸收效率
Figure 7. Energy absorption efficiency of BBCLS at different impact velocities
![]()
图 8 不同冲击速度下的BBCLS平台应力及密实化应变
Figure 8. Plateau stress and densification strain curves of BBCLS at different impact velocities
![]()
图 9 不同冲击速度下BBCLS的比吸能ESEA对比
Figure 9. Comparison of specific energy absorption ESEA of BBCLS at different impact velocities
![]()
图 10 静态荷载与冲击荷载下BBCLS比吸能对比
Figure 10. Comparison of BBCLS ESEA under static load and dynamic load
![]()
图 11 体心立方点阵结构(BCC)有限元模型：(a) 冲击荷载作用下BCC计算模型；(b) BCC三维模型；(c) BCC胞元模型
Figure 11. Body-centered cubic lattice structure (BCC) finite element model: (a) Computational model of BCC under impact load; (b) BCC three-dimensional model; (c) BCC single cell model
H—; L—; W—; h—; d—; l—; w—;
![]()
图 13 两种点阵结构在冲击荷载下的力-位移曲线
Figure 13. Force-displacement curves of two lattice structure under impact loading
![]()
图 14 两种点阵结构在冲击荷载下的能量吸收指标
Figure 14. Energy absorption indicators of two lattice structure under impact loading
![]()
图 15 两种点阵结构的应力云图：(a) BCC；(b) BBCLS
Figure 15. Stress cloud of two lattice structures: (a) BCC; (b) BBCLS
![]()
图 16 不同振幅A下BBCLS固定端的名义应力-应变曲线
Figure 16. Nominal stress-strain curves on fixed end of BBCLS under different amplitudes A
![]()
图 19 不同振幅的BBCLS在0.6应变下的比吸能
Figure 19. ESEA at 0.6 strain of BBCLS under different amplitudes
![]()
图 17 不同振幅下BBCLS冲击端的名义应力-应变曲线
Figure 17. Nominal stress-strain curves on impact end of BBCLS under different amplitudes
![]()
图 18 不同振幅的BBCLS比吸能对比
Figure 18. Comparison of ESEA of BBCLS under different amplitudes
![]()
图 20 不同波纹数N下BBCLS在固定端的名义应力-应变曲线
Figure 20. Nominal stress-strain curves on fixed end of BBCLS under different wave number N
![]()
图 23 不同波纹数的BBCLS在0.6应变下的比吸能
Figure 23. ESEA at 0.6 strain of BBCLS under different wave number
![]()
图 21 不同波纹数下BBCLS在冲击端的名义应力-应变曲线
Figure 21. Nominal stress-strain curves on impact end of BBCLS under different wave number
![]()
图 22 不同波纹数的BBCLS比吸能对比
Figure 22. Comparison of ESEA of BBCLS under different wave number
![]()
图 24 不同厚度t下BBCLS在固定端的名义应力-应变曲线
Figure 24. Nominal stress-strain curves on fixed end of BBCLS under different thicknesses t
![]()
图 27 不同厚度的BBCLS在0.6应变下的比吸能
Figure 27. ESEA at 0.6 strain of BBCLS under different thicknesses
![]()
图 25 不同厚度下BBCLS在冲击端的名义应力-应变曲线
Figure 25. Nominal stress-strain curves on impact end of BBCLS under different thicknesses
![]()
图 26 不同厚度的BBCLS比吸能对比
Figure 26. Comparison of ESEA of BBCLS under different thicknesses
表 1 BBCLS初始峰值力仿真与试验误差对比
Table 1 Comparison between simulation and test error of BBCLS contact force peak value
Sample name Wave number Relative
densityTest
value [32]/kNSimulated
value/kNAbsolute
error/kNRelative
error/%1 5 0.13303 2.97 2.84 0.13 4.38 2 6 0.14662 4.25 4.17 0.08 1.88 3 7 0.16201 5.65 5.46 0.19 3.36 
下载: 导出CSV
-
[1] BAROUTAJI A, SAJJIA M, OLABI A G. On the crashworthiness performance of thin-walled energy absorbers: Recent advances and future developments[J]. Thin-Walled Structures, 2017, 118: 137-163. DOI: 10.1016/j.tws.2017.05.018
[2] QIU X M, YU T X. Some topics in recent advances and applications of structural impact dynamics[J]. Applied Mechanics Reviews, 2011, 64(3): 1-12.
[3] 余同希, 朱凌, 许骏. 结构冲击动力学进展(2010~2020)[J]. 爆炸与冲击, 2021, 41(12): 4-64. YU Tongxi, ZHU Ling, XU Jun. Progress of structural impact dynamics (2010—2020)[J]. Explosion and Shock Waves, 2021, 41(12): 4-64(in Chinese).
[4] YANG J, CHEN X, SUN Y, et al. Compressive properties of bidirectionally graded lattice structures[J]. Materials & Design, 2022, 218: 110683.
[5] YE J, SUN Z, DING Y, et al. The deformation mechanism, energy absorption behavior and optimal design of vertical-reinforced lattices[J]. Thin-Walled Structures, 2023, 190: 110988. DOI: 10.1016/j.tws.2023.110988
[6] 张武昆, 谭永华, 高玉闪, 等. 周期性轻质多孔结构在能量吸收和振动方面的研究进展[J]. 振动与冲击, 2023, 42(8): 1-19. ZHANG Wukun, TAN Yonghua, GAO Yushan, et al. Research progress on energy absorption and vibration of periodic lightweight porous structures[J]. Journal of Vibration and Shock, 2023, 42(8): 1-19(in Chinese).
[7] XU P, GUO W, YANG L, et al. Crashworthiness analysis of the biomimetic lotus root lattice structure[J]. International Journal of Mechanical Sciences, 2024, 263: 108774. DOI: 10.1016/j.ijmecsci.2023.108774
[8] 韩剑, 孙士勇, 牛斌, 等. 树脂基复合材料点阵结构的制造技术研究进展[J]. 航空学报, 2023, 44(9): 47-67. HAN Jian, SUN Shiyong, NIU Bin, et al. Research progress in manufacturing technology of resin matrix composites with lattice structure[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(9): 47-67(in Chinese).
[9] XU Z, RAZAVI S M J, AYATOLLAHI M R. Functionally graded lattice structures: Fabrication methods, mechanical properties, failure mechanisms and applications[M]. Comprehensive Structural Integrity, 2022: 433-466.
[10] DONG G, WIJAYA G, TANG Y, et al. Optimizing process parameters of fused deposition modeling by Taguchi method for the fabrication of lattice structures[J]. Additive Manufacturing, 2018, 19: 62-72. DOI: 10.1016/j.addma.2017.11.004
[11] CUI Z, ZHAO J, XU R, et al. Mechanical design and energy absorption performances of novel plate-rod hybrid lattice structures[J]. Thin-Walled Structures, 2023, 194(10): 111349.
[12] YANG J, CHEN X, SUN Y, et al. Rational design and additive manufacturing of grain boundary-inspired, multi-architecture lattice structures[J]. Materials & Design, 2023, 235: 112448.
[13] XIAO L, FENG G, LI S, et al. Mechanical characterization of additively-manufactured metallic lattice structures with hollow struts under static and dynamic loadings[J]. International Journal of Impact Engineering, 2022, 169: 104333. DOI: 10.1016/j.ijimpeng.2022.104333
[14] MA X, ZHANG N, CHANG Y, et al. Analytical model of mechanical properties for a hierarchical lattice structure based on hierarchical body-centered cubic unit cell[J]. Thin-Walled Structures, 2023, 193: 111217. DOI: 10.1016/j.tws.2023.111217
[15] LEE J J, MOHAMMED A A, PULLEN A, et al. Mechanical characterisation of 3D printed lightweight lattice structures with varying internal design alterations[J]. Materials Today Communications, 2023, 36: 106456. DOI: 10.1016/j.mtcomm.2023.106456
[16] XIAO L, SONG W. Additively-manufactured functionally graded Ti-6Al-4V lattice structures with high strength under static and dynamic loading: Experiments[J]. International Journal of Impact Engineering, 2018, 111: 255-272. DOI: 10.1016/j.ijimpeng.2017.09.018
[17] HA N S, LU G. A review of recent research on bio-inspired structures and materials for energy absorption applications[J]. Composites Part B: Engineering, 2020, 181: 107496. DOI: 10.1016/j.compositesb.2019.107496
[18] PLESSIS A, BROECKHOVEN C, YADROITSAVA I, et al. Beautiful and functional: A review of biomimetic design in additive manufacturing[J]. Additive Manufacturing, 2019, 27: 408-427. DOI: 10.1016/j.addma.2019.03.033
[19] AHAMED M K, WANG H, HAZELL P J. From biology to biomimicry: Using nature to build better structures—A review[J]. Construction and Building Materials, 2022, 320: 126195. DOI: 10.1016/j.conbuildmat.2021.126195
[20] SIDDIQUE S H, HAZELL P J, WANG H, et al. Lessons from nature: 3D printed bio-inspired porous structures for impact energy absorption—A review[J]. Additive Manufacturing, 2022, 58: 103051. DOI: 10.1016/j.addma.2022.103051
[21] ZHANG W, YIN S, YU T X, et al. Crushing resistance and energy absorption of pomelo peel inspired hierarchical honeycomb[J]. International Journal of Impact Engineering, 2019, 125: 163-172. DOI: 10.1016/j.ijimpeng.2018.11.014
[22] 冀旭晖. 仿生蜘蛛网点阵结构设计及其吸能效果研究[D]. 哈尔滨: 哈尔滨理工大学, 2022. JI Xuhui. Study on bionic spider web lattice structure design and Energy absorption effect[D]. Harbin: Harbin University of Science and Technology, 2022(in Chinese).
[23] MENG L, SHI J, YANG C, et al. An emerging class of hyperbolic lattice exhibiting tunable elastic properties and impact absorption through chiral twisting[J]. Extreme Mechanics Letters, 2020, 40: 100869. DOI: 10.1016/j.eml.2020.100869
[24] PATEK S N, KORFF W L, CALDWELL R L. Deadly strike mechanism of a mantis shrimp[J]. Nature, 2004, 428(6985): 819-820. DOI: 10.1038/428819a
[25] WEAVER J C M G W, MISEREZ A, EVANS-LUTTERODT K, et al. The stomatopod dactyl club: A formidable damage-tolerant biological hammer[J]. Science, 2012, 336(6086): 1275-1280. DOI: 10.1126/science.1218764
[26] PATEK S N, CALDWELL R L. Extreme impact and cavitation forces of a biological hammer: Strike forces of the peacock mantis shrimp Odontodactylus scyllarus[J]. Journal of Experimental Biology, 2005, 208(19): 3655-3664. DOI: 10.1242/jeb.01831
[27] YARAGHI N A, GUARÍN-ZAPATA N, GRUNENFELDER L K, et al. A sinusoidally architected helicoidal biocomposite[J]. Advanced Materials, 2016, 28(32): 6835-6844. DOI: 10.1002/adma.201600786
[28] YANG X, MA J, SHI Y, et al. Crashworthiness investigation of the bio-inspired bi-directionally corrugated core sandwich panel under quasi-static crushing load[J]. Materials & Design, 2017, 135: 275-290.
[29] HAN Q, SHI S, LIU Z, et al. Study on impact resistance behaviors of a novel composite laminate with basalt fiber for helical-sinusoidal bionic structure of dactyl club of mantis shrimp[J]. Composites Part B: Engineering, 2020, 191: 107976. DOI: 10.1016/j.compositesb.2020.107976
[30] HUANG H, YANG X, YAN Q, et al. Crashworthiness analysis and multiobjective optimization of bio-inspired sandwich structure under impact load[J]. Thin-Walled Structures, 2022, 172(3): 108840.
[31] CUI C Y, CHEN L, FENG S, et al. Novel cuttlebone-inspired hierarchical bionic structure enabled high energy absorption[J]. Thin-Walled Structures, 2023, 186: 110693. DOI: 10.1016/j.tws.2023.110693
[32] LI B, LIU H, ZHANG Q, et al. Crushing behavior and energy absorption of a bio-inspired bi-directional corrugated lattice under quasi-static compression load[J]. Composite Structures, 2022, 286: 115315. DOI: 10.1016/j.compstruct.2022.115315
[33] HUNT C J, MORABITO F, GRACE C, et al. A review of composite lattice structures[J]. Composite Structures, 2022, 284: 115120. DOI: 10.1016/j.compstruct.2021.115120
[34] ZHU J, ZHOU H, WANG C, et al. A review of topology optimization for additive manufacturing: Status and challenges[J]. Chinese Journal of Aeronautics, 2021, 34(1): 91-110. DOI: 10.1016/j.cja.2020.09.020
[35] CLAVERIE T, CHAN E, PATEK S N. Modularity and scaling in fast movements: Power amplification in mantis shrimp[J]. Evolution, 2011, 65(2): 443-461. DOI: 10.1111/j.1558-5646.2010.01133.x
[36] 黄晗, 许述财, 陈姮. 仿生波纹夹层结构耐撞性分析及优化[J]. 爆炸与冲击, 2021, 41(8): 36-46. DOI: 10.11883/bzycj-2020-0275 HUANG Han, XU Shucai, CHEN Heng. Impact resistance analysis and optimization of biomimetic corrugated sandwich structures[J]. Explosion and Shock Waves, 2021, 41(8): 36-46(in Chinese). DOI: 10.11883/bzycj-2020-0275
[37] 魏路路, 余强, 赵轩, 等. 内凹-反手性蜂窝结构的面内动态压溃性能研究[J]. 振动与冲击, 2021, 40(4): 261-269. WEI Lulu, YU Qiang, ZHAO Xuan, et al. Research on in-plane dynamic crushing behavior of concave and backhanded honeycomb structures[J]. Journal of Vibration and Shock, 2021, 40(4): 261-269(in Chinese).
[38] GIBSON L J, ASHBY M F. Cellular solids[M]. Cambridge: Cambridge University Press, 1997.
[39] 刘伟洛. 增材制造三周期极小曲面结构的力学性能研究[D]. 广州: 广州大学, 2021. LIU Weiluo. Research on mechanical properties of additive manufacturing three-period minimal curved surface structures[D]. Guangzhou: Guangzhou University, 2021(in Chinese).
[40] 徐向聪, 高佳丽, 郝云波. 304不锈钢多层梯度点阵结构压缩性能及梯度率影响研究[J]. 机械强度, 2023, 45(6): 1318-1325. XU Xiangcong, GAO Jiali, HAO Yunbo. Research on compression properties and influence of gradient rate of 304 stainless steel multilayer gradient lattice structure[J]. Mechanical Strength, 2023, 45(6): 1318-1325(in Chinese).
[41] MASKERY I, ABOULKHAIR N T, AREMU A O, et al. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting[J]. Materials Science and Engineering: A, 2016, 670: 264-274. DOI: 10.1016/j.msea.2016.06.013
[42] 李晓丹, 朱庆丰, 孔淑萍, 等. 3D打印AlSi10Mg合金组织性能研究[J]. 材料科学与工艺, 2019, 27(2): 16-21. DOI: 10.11951/j.issn.1005-0299.20180138 LI Xiaodan, ZHU Qingfeng, KONG Shuping, et al. Study on microstructure and properties of 3D printed AlSi10Mg alloy[J]. Materials Science and Technology, 2019, 27(2): 16-21(in Chinese). DOI: 10.11951/j.issn.1005-0299.20180138
[43] 陈剑勇. 静动态载荷下三周期极小曲面多孔结构响应特性研究[D]. 武汉: 华中科技大学, 2023. CHEN Jianyong. Study on response characteristics of three-period minimal curved porous structures under static and dynamic loads[D]. Wuhan: Huazhong University of Science and Technology, 2023(in Chinese).
[44] MACONACHIE T, LEARY M, TRAN P, et al. The effect of topology on the quasi-static and dynamic behaviour of SLM AlSi10Mg lattice structures[J]. The International Journal of Advanced Manufacturing Technology, 2021, 118(11-12): 4085-4104.
[45] 厉雪, 肖李军, 宋卫东. 3D打印梯度Gyroid结构的动态冲击响应[J]. 高压物理学报, 2021, 35(3): 90-99. DOI: 10.11858/gywlxb.20210701 LI Xue, XIAO Lijun, SONG Weidong. Dynamic impact response of 3D printed gradient gyroid structure[J]. Journal of High Pressure Physics, 2021, 35(3): 90-99(in Chinese). DOI: 10.11858/gywlxb.20210701
[46] 卢子兴, 王欢, 杨振宇, 等. 星型-箭头蜂窝结构的面内动态压溃行为[J]. 复合材料学报, 2019, 36(8): 1893-1900. LU Zixing, WANG Huan, YANG Zhenyu, et al. In-plane dynamic crushing behavior of star-arrow honeycomb structures[J]. Acta Materiae Compositae Sinica, 2019, 36(8): 1893-1900(in Chinese).
[47] 张晓楠, 晏石林, 欧元勋, 等. 负泊松比内凹蜂窝结构梯度设计与动态冲击响应[J]. 振动与冲击, 2023, 42(3): 193-198. ZHANG Xiaonan, YAN Shilin, OU Yuanxun, et al. Gradient design and dynamic shock response of concave honeycomb structures with negative Poisson's ratio[J]. Journal of Vibration and Shock, 2023, 42(3): 193-198(in Chinese).
[48] 李成兵, 李锐, 张吉涛, 等. 多阶式层级梯度蜂窝结构的共面冲击响应[J]. 高压物理学报, 2023, 37(3): 121-132. LI Chengbing, LI Rui, ZHANG Jitao, et al. Coplanar shock response of multistage hierarchical gradient honeycomb structures[J]. Journal of High Pressure Physics, 2023, 37(3): 121-132(in Chinese).
[49] 纪小刚, 张建安, 栾宇豪, 等. 仿皮肤三维多孔点阵结构压缩吸能性能研究[J]. 机械工程学报, 2021, 57(15): 222-230. DOI: 10.3901/JME.2021.15.222 JI Xiaogang, ZHANG Jian'an, LUAN Yuhao, et al. Study on compressive energy absorption performance of three-dimensional porous lattice structure modeled on skin[J]. Chinese Journal of Mechanical Engineering, 2021, 57(15): 222-230(in Chinese). DOI: 10.3901/JME.2021.15.222
[50] 李心远, 宋卫东, 陈键. 3D打印TPMS多孔材料力学性能数值仿真[J]. 太原理工大学学报, 2019, 50(3): 386-393. LI Xinyuan, SONG Weidong, CHEN Jian. Numerical simulation of mechanical properties of 3D printed TPMS porous materials[J]. Journal of Taiyuan University of Technology, 2019, 50(3): 386-393(in Chinese).
[51] 肖江海, 侯俊玲, 李群. 基于MJF的极小曲面结构力学行为及吸能特性研究[J]. 固体力学学报, 2024, 45(2): 201-212. XIAO Jianghai, HOU Junling, LI Qun. Study on mechanical behavior and energy absorption characteristics of minimal surface structures based on MJF[J]. Journal of Solid Mechanics, 2024, 45(2): 201-212(in Chinese).
[52] 赵众豪, 池瑜莉, 冯峻良, 等. 新型CFCB点阵夹芯结构面外压缩载荷下能量吸收特性研究[J]. 振动与冲击, 2023, 42(17): 166-174. ZHAO Zhonghao, CHI Yuli, FENG Junliang, et al. Study on energy absorption characteristics of novel CFCB lattice sandwich structures under out-of-plane compression loads[J]. Journal of Vibration and Shock, 2023, 42(17): 166-174(in Chinese).
[53] 虞科炯, 徐峰祥, 华林. 正弦曲边负泊松比蜂窝结构面内冲击性能研究[J]. 振动与冲击, 2021, 40(13): 51-59. YU Kejiong, XU Fengxiang, HUA Lin. Research on in-plane impact performance of sinusoidal curved curved negative Poisson's ratio honeycomb[J]. Journal of Vibration and Shock, 2021, 40(13): 51-59(in Chinese).
-
其他相关附件
-
目的
点阵结构作为一种新型轻质多功能结构，因其具有能量吸收能力好、比强度和比刚度高等诸多优异的性能，常被用于保护人员或结构免受冲击载荷的影响。与准静态荷载下的失效模式不同，在冲击荷载作用下，点阵结构一般会发生动态失稳，结构内部发生大的塑性/弹性变形。此外，点阵结构在空间上有材料与结构双重多尺度特征，冲击载荷作用又增加了时间多尺度特征。本研究旨在探究一种新型仿生双正弦波纹点阵结构(Bio-inspired bi-directional corrugated lattice structure, BBCLS)在冲击荷载作用下的力学性能和吸能特性。
方法首先采用ANSYS/LSDYNA有限元分析软件建立了其在冲击荷载作用下的有限元数值模型，并基于已有的试验结果与数值模拟结果进行了对比，验证了该模型的有效性。在此基础上，研究了不同冲击速度对BBCLS的应力分布、变形模式、承载能力以及能量吸收特性的影响，并与传统体心立方点阵结构(BCC)进行了对比。此外，系统探究了冲击速度及振幅、波纹数、胞壁厚度等微结构几何参数对BBCLS抗冲击特性的影响规律。
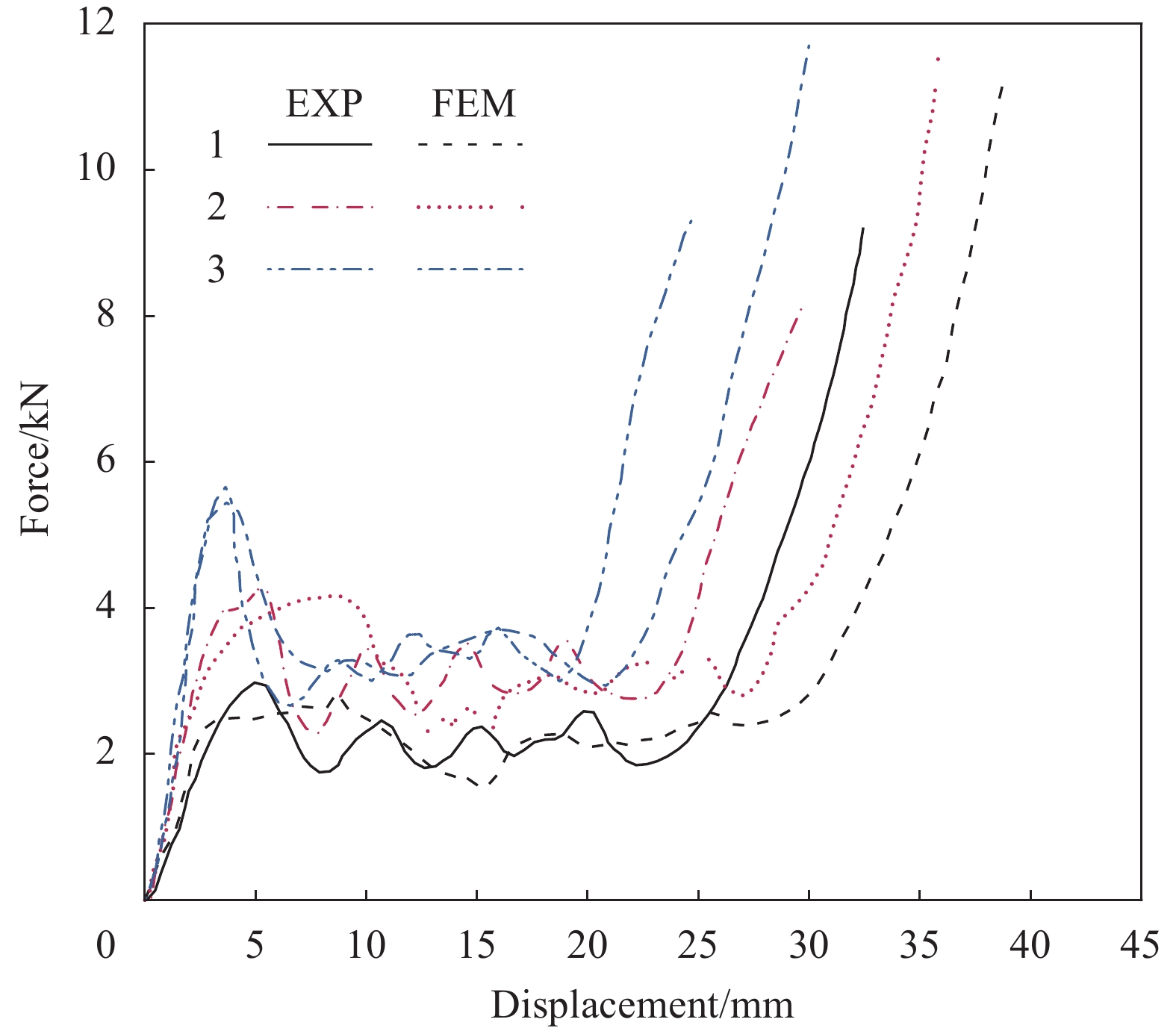
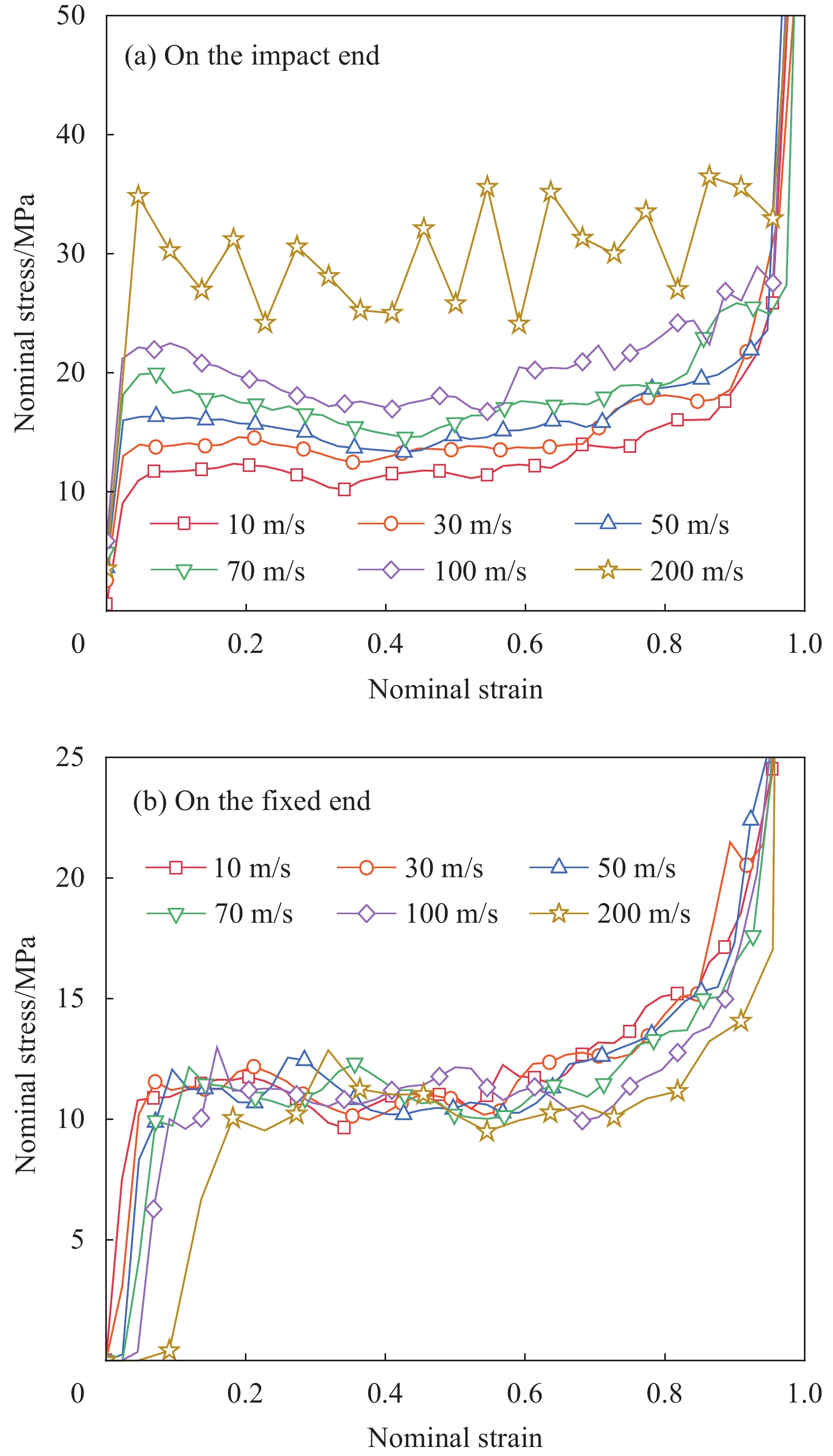
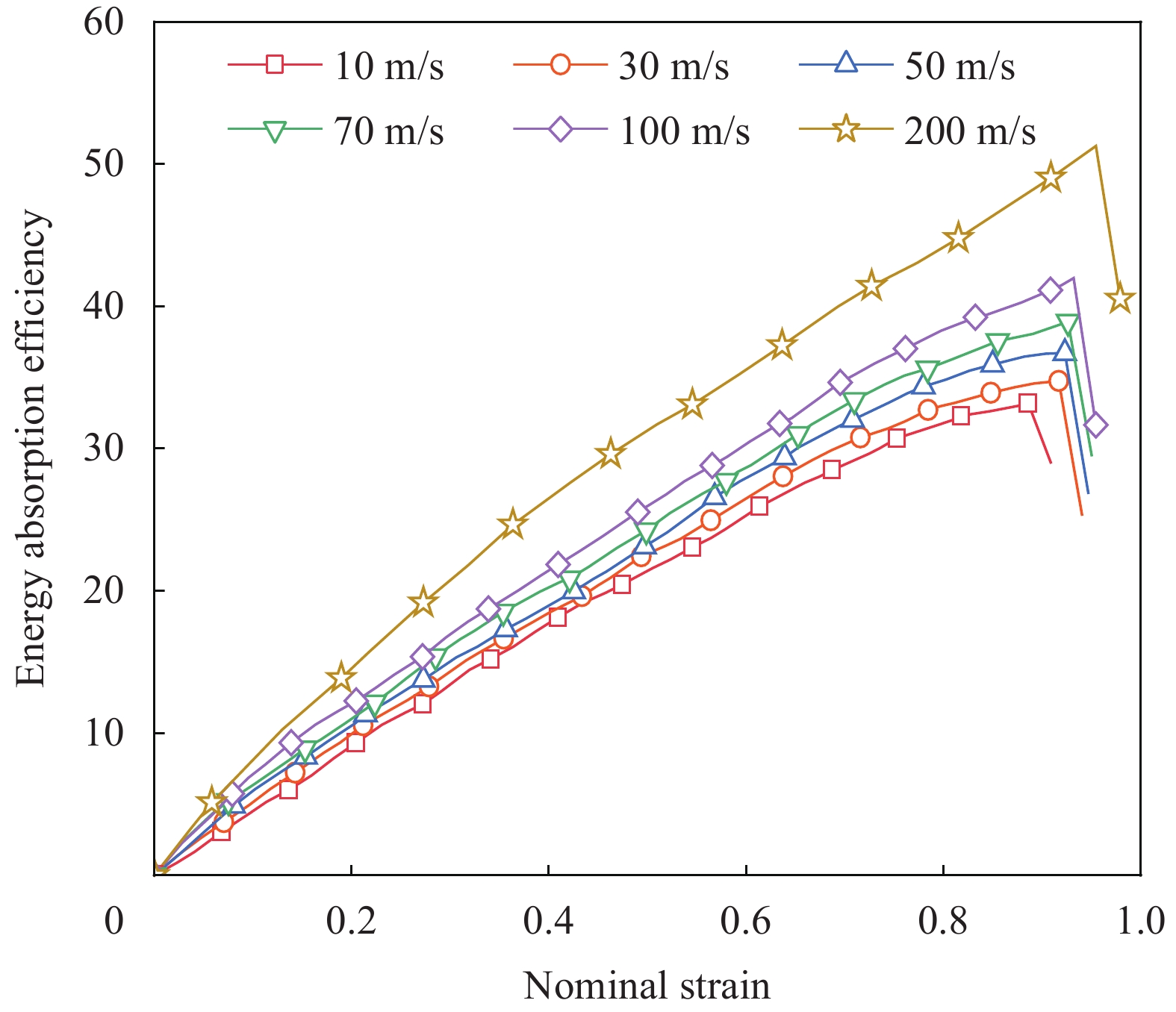
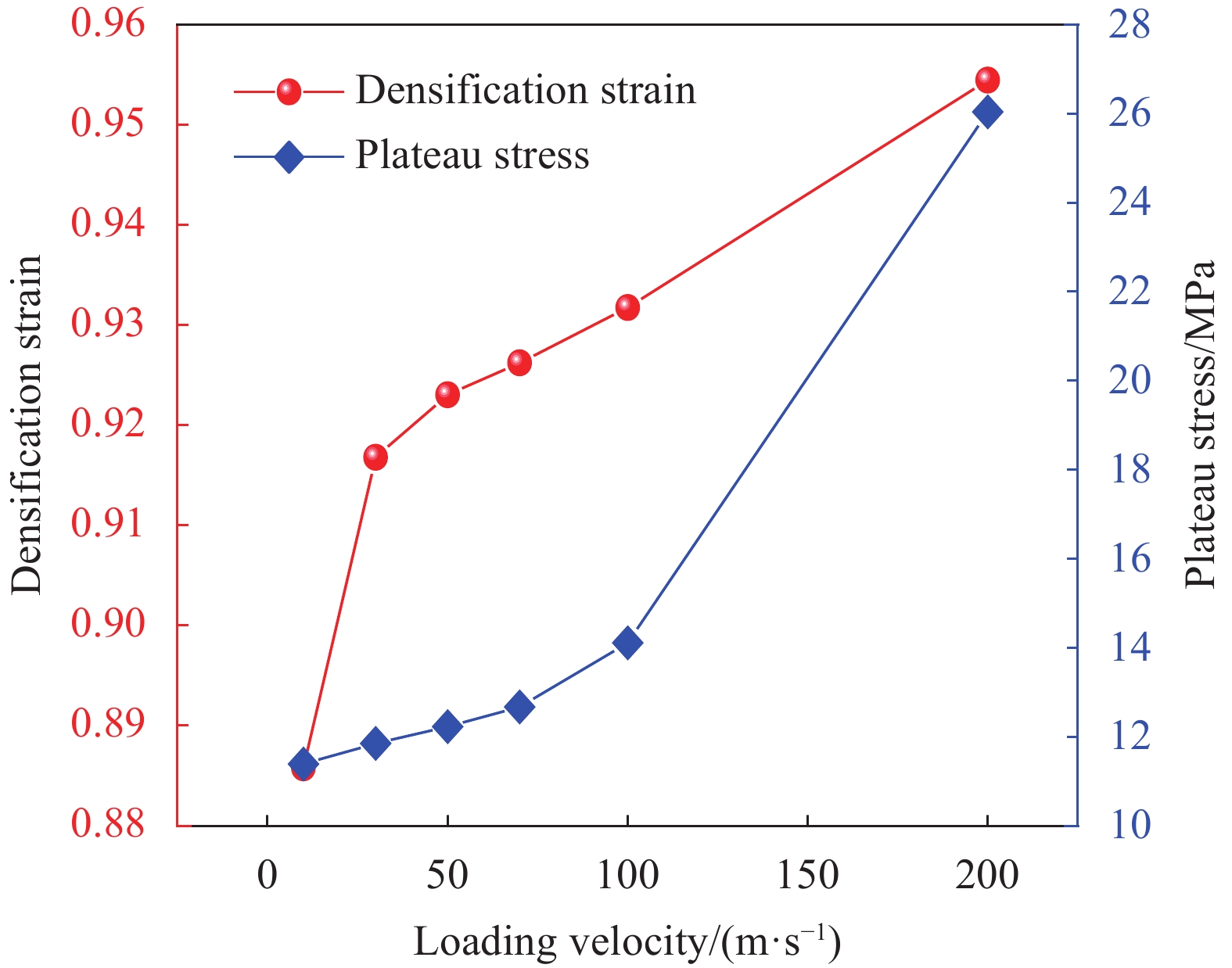
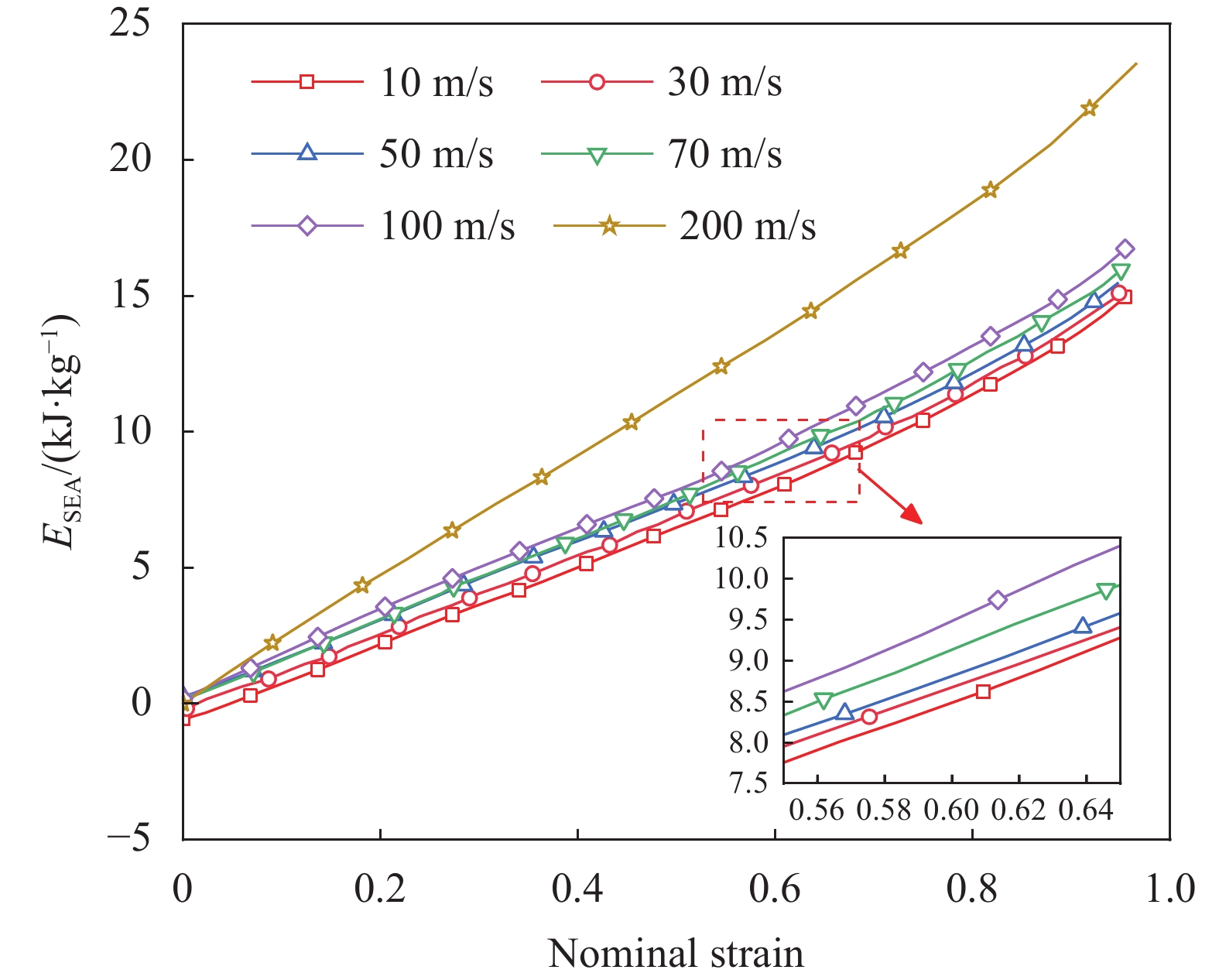
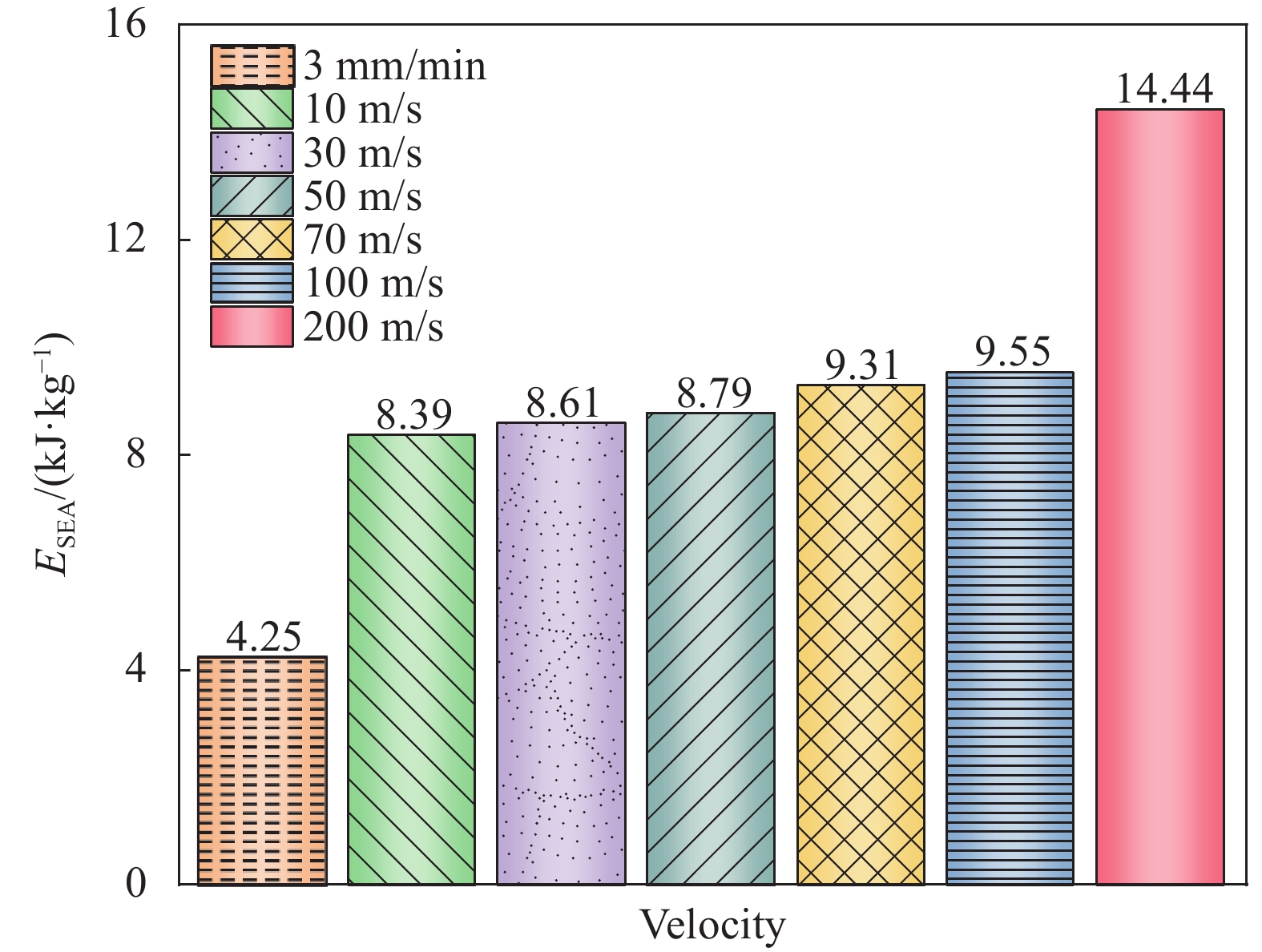
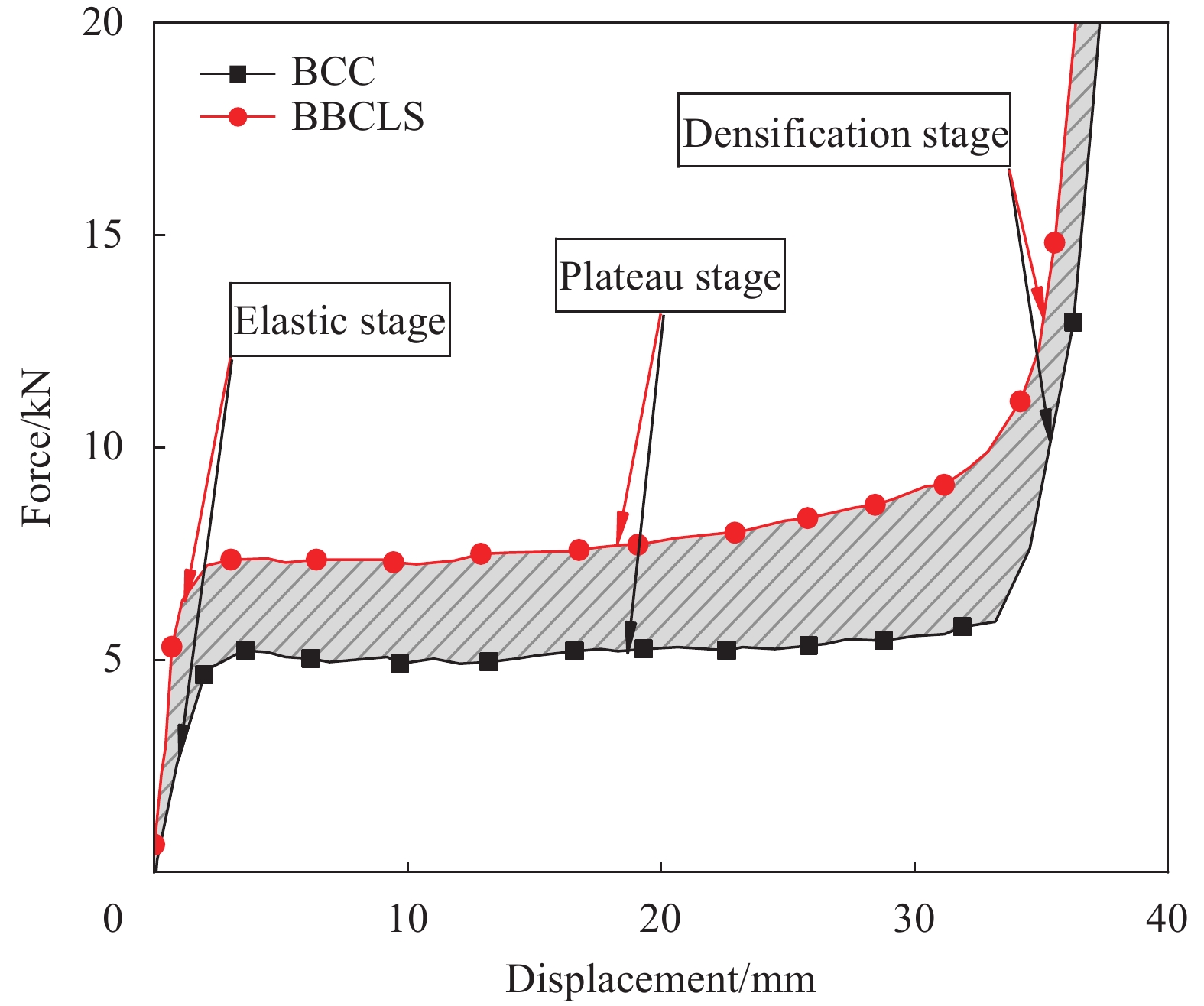
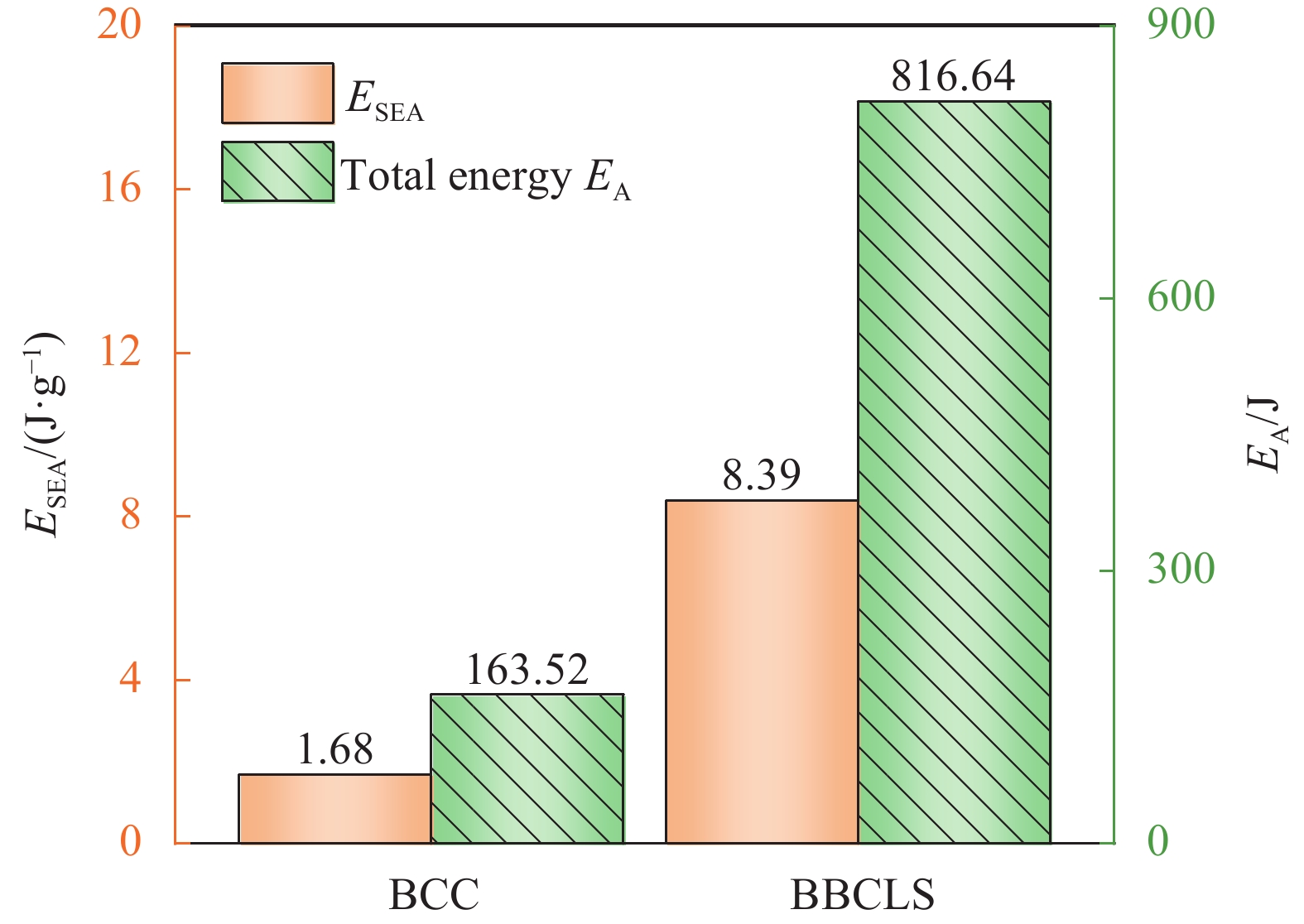
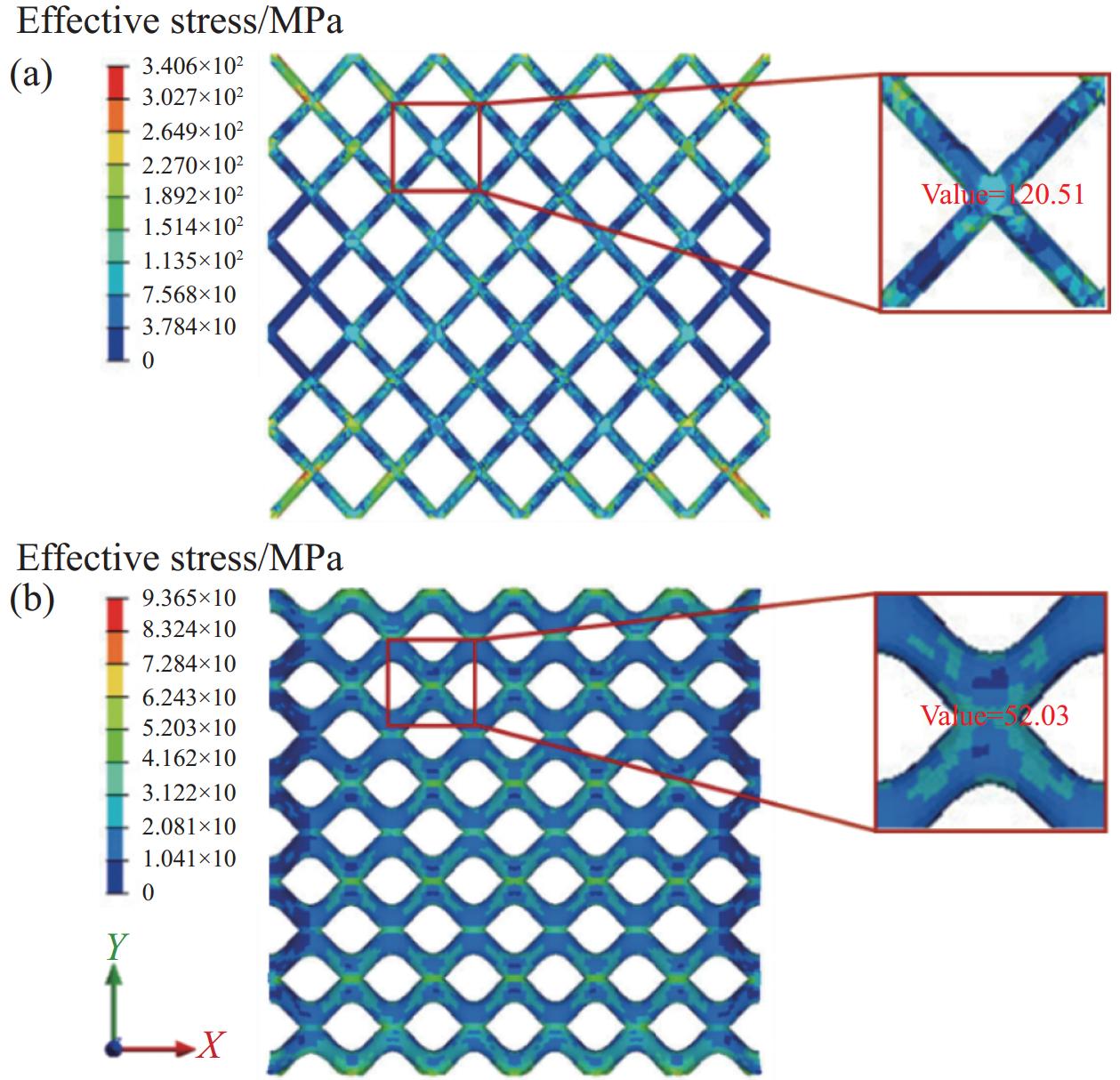
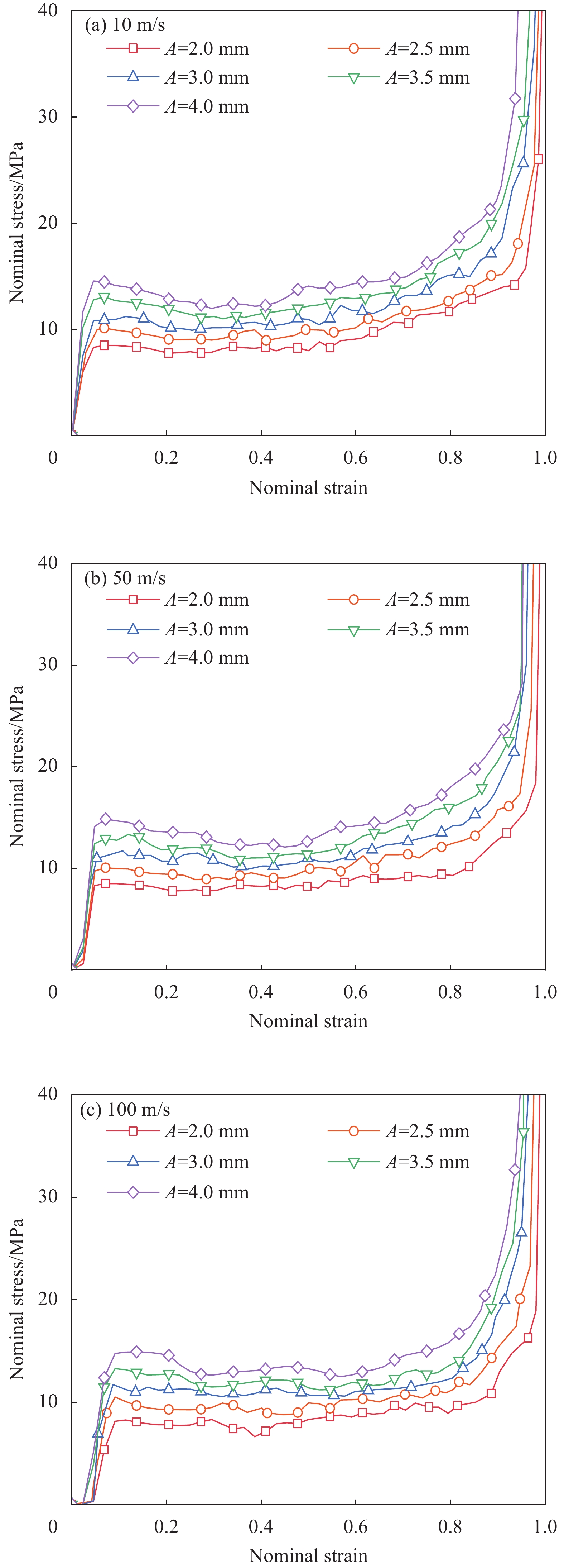
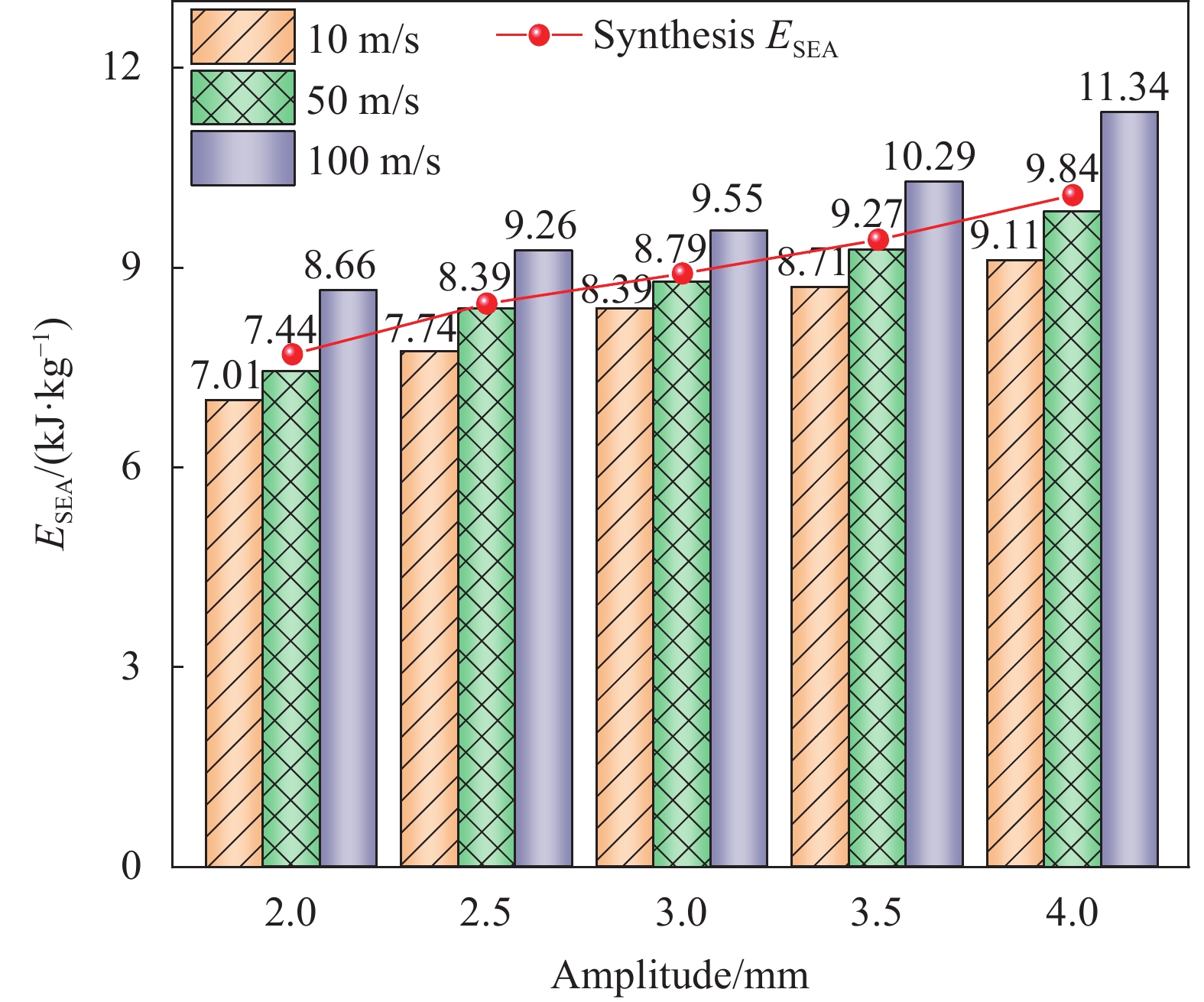
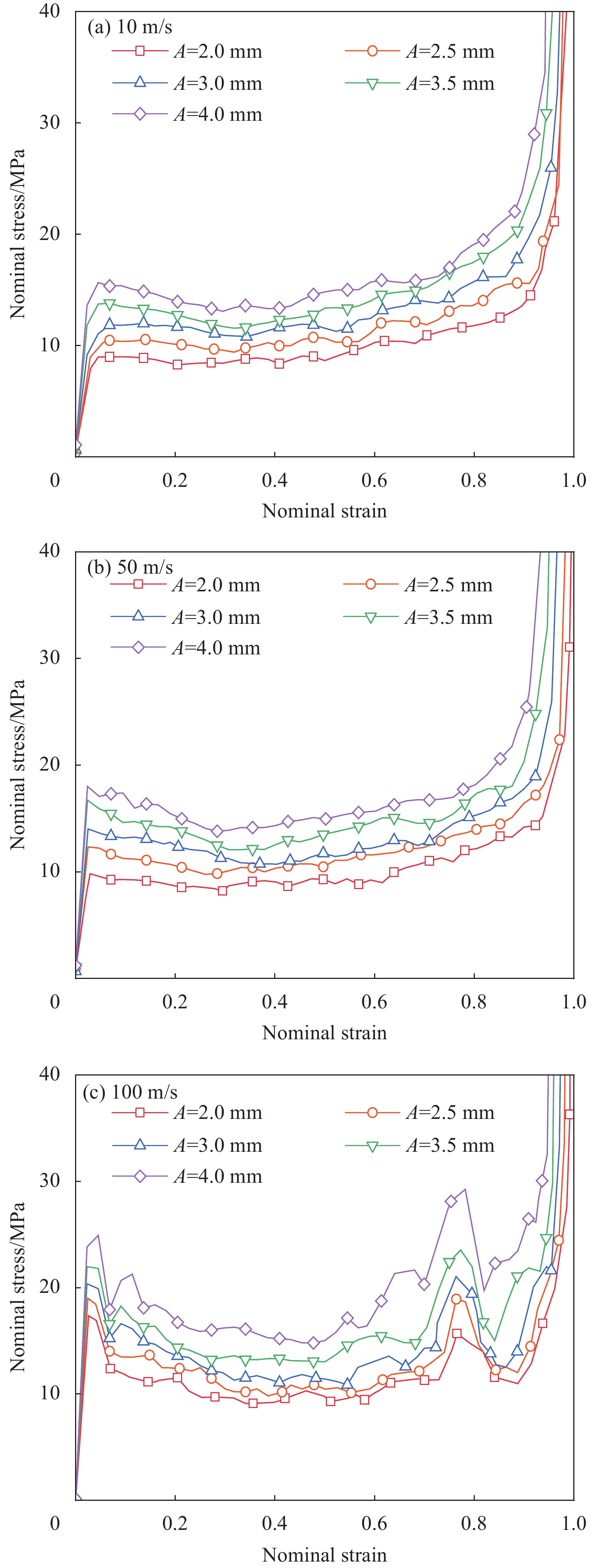
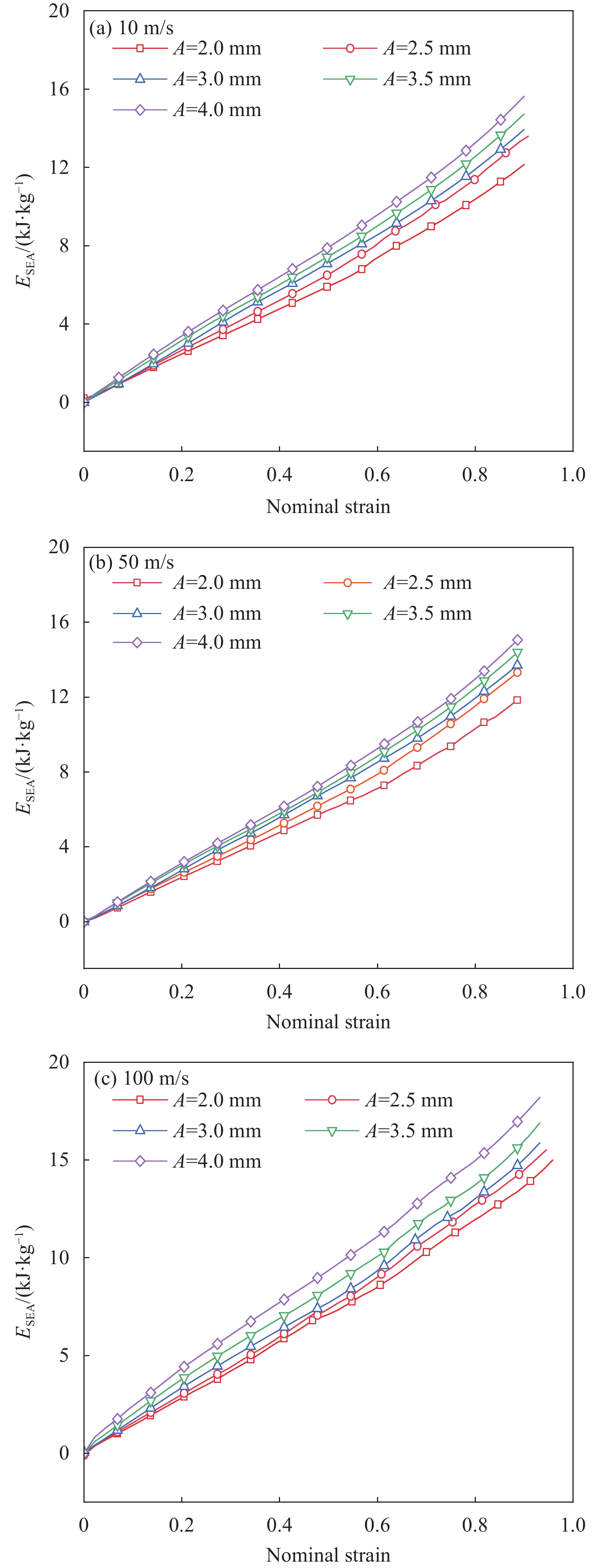
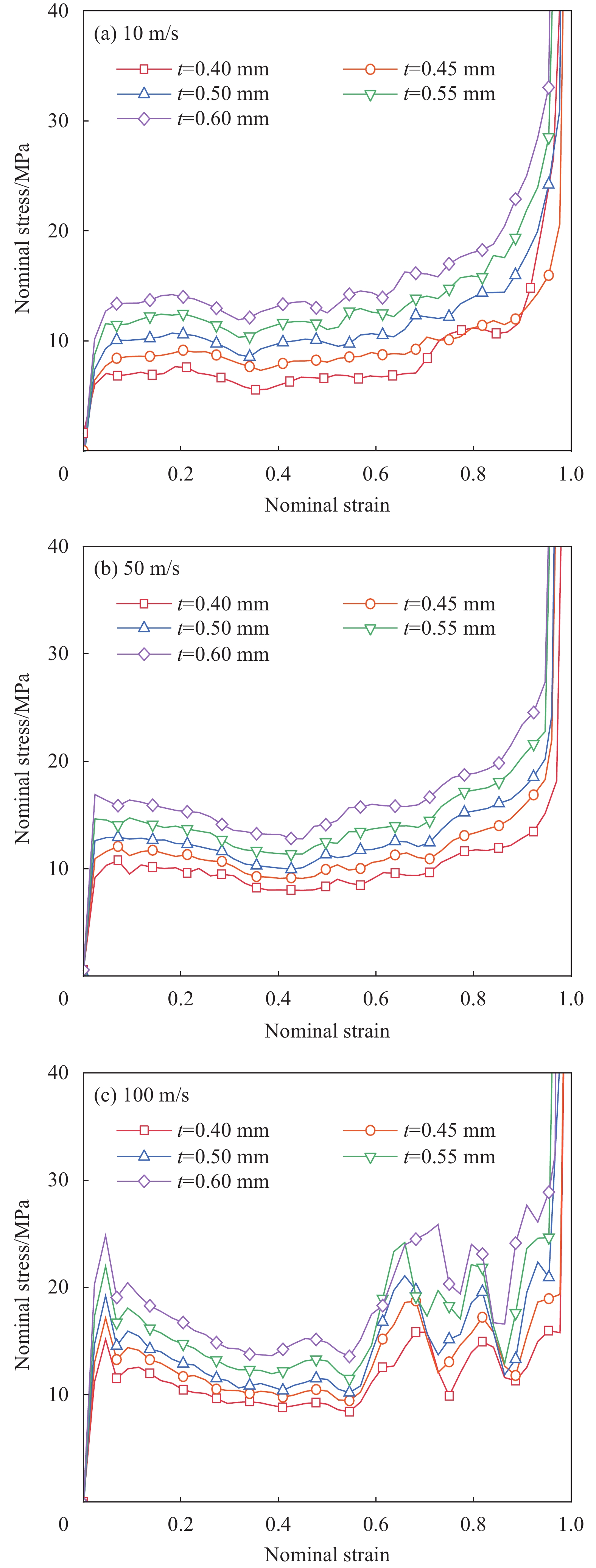
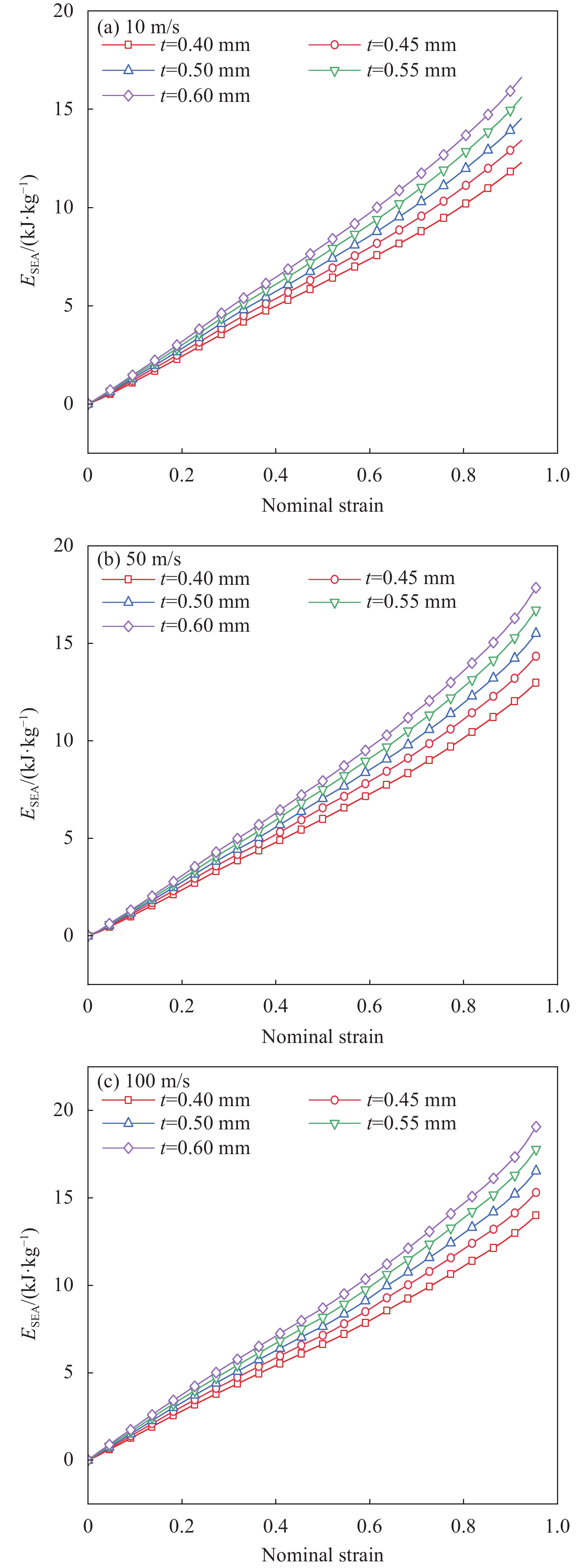
结果①数值模拟得到的压缩荷载作用下BBCLS整体变形模式与试验结果基本一致；同时从BBCLS力-位移曲线的试验和模拟对比结果，可以看出数值模拟结果变化趋势与试验结果吻合较好，其中初始峰值力与试验结果误差较小，为1.88%~4.38%，这也验证了数值模拟的可靠性。②BBCLS的动态吸能性能要优于其准静态压缩，这主要由于BBCLS的变形模式与冲击速度密切相关，随着冲击速度增加，惯性效应逐渐增强，更多胞元均匀协调地参与变形，使BBCLS抗压溃能力更强，同时更早到达密实阶段。此外，通过对BBCLS在不同冲击速度下冲击端及固定端名义应力-应变曲线的分析可知，BBCLS可以降低传递到被保护件的应力值，从而有效地保护结构不被破坏。冲击速度对于BBCLS平台应力有显著影响，冲击速度越大，冲击端平台应力越大，BBCLS受到冲击时吸能效果更好。与平台应力的变化相同，密实化应变与冲击速度的变化呈线性增大关系。然而，不同冲击速度作用下BBCLS的密实化应变相差不大(10m/s与200m/s冲击时仅差0.068)。这表明冲击速度对于BBCLS密实应变没有影响，而密实应变主要受结构内部胞元的影响。此外，不同冲击载荷下BBCLS均呈现出比准静态载荷下更优异的能量吸收能力，说明BBCLS更加适用于冲击载荷下的能量吸收。③通过与冲击荷载作用下传统的BCC对比发现，BBCLS表现出了优越的吸收能量特性，BBCLS的能量吸收总量与比能量吸收均为BCC型的5倍左右，显著优于BCC，且极大的缓解了BCC点阵结构节点处应力集中问题，这是由于BBCLS为曲面型结构，胞元之间由连续且光滑的表面过渡和连接，有效增加了结构实体部分应力分布的面积，使得应力可以迅速均匀地分布到结构内部，并且由于BBCLS内部存在孔隙，使得结构充分发挥出减震抗冲击性能。④随着冲击速度的提高，增大振幅、波纹数、胞壁厚度等微结构几何参数均使结构在受到冲击载荷时应力分布均匀，有效增加了冲击端的平台应力。此外，微结构几何参数的改变对结构比吸能以及综合比吸能有显著影响。
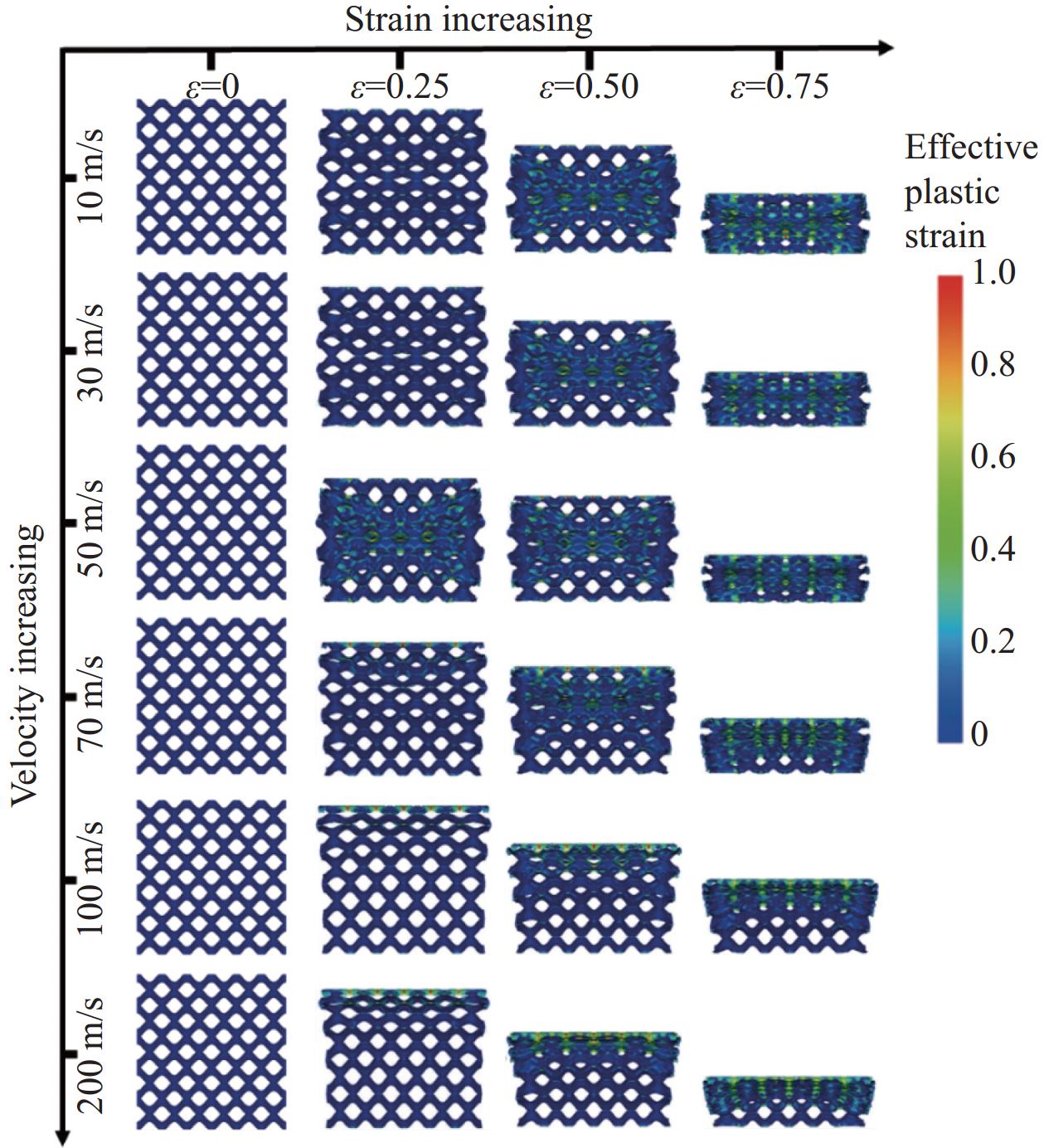
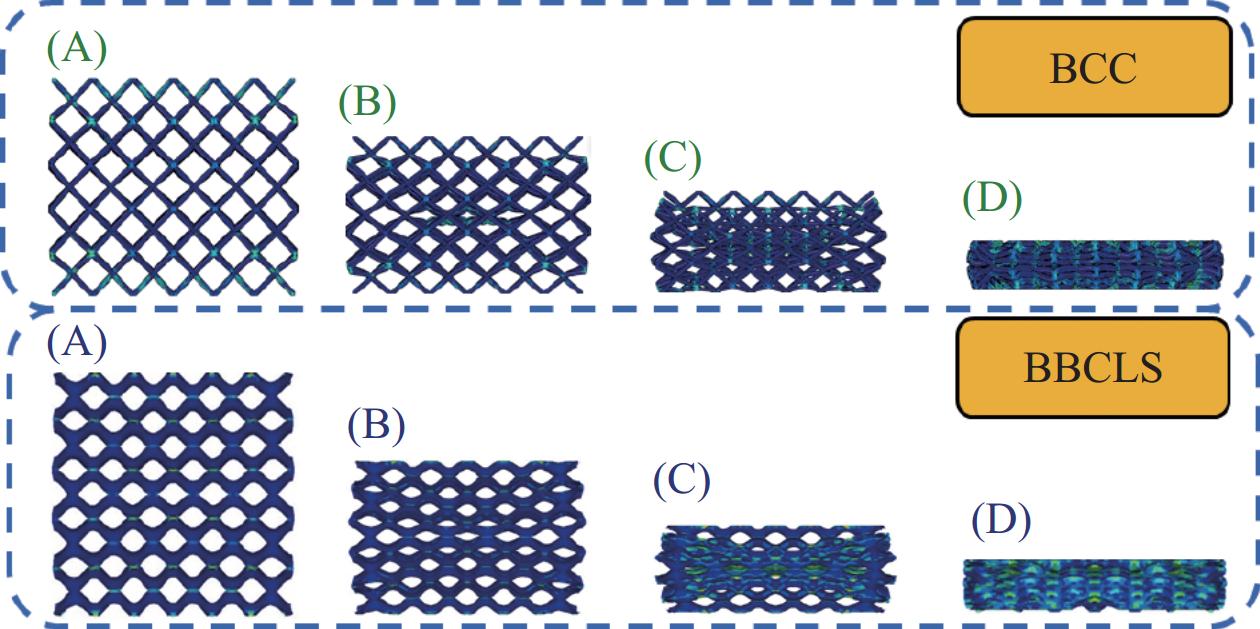
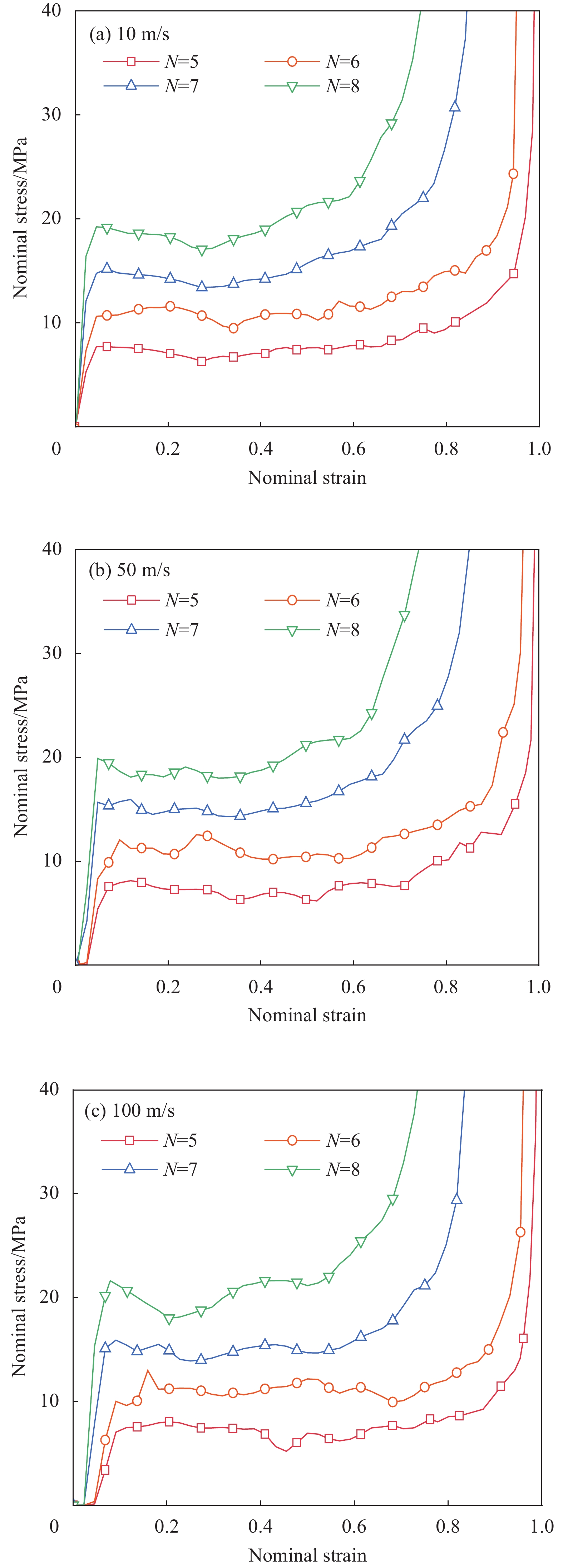
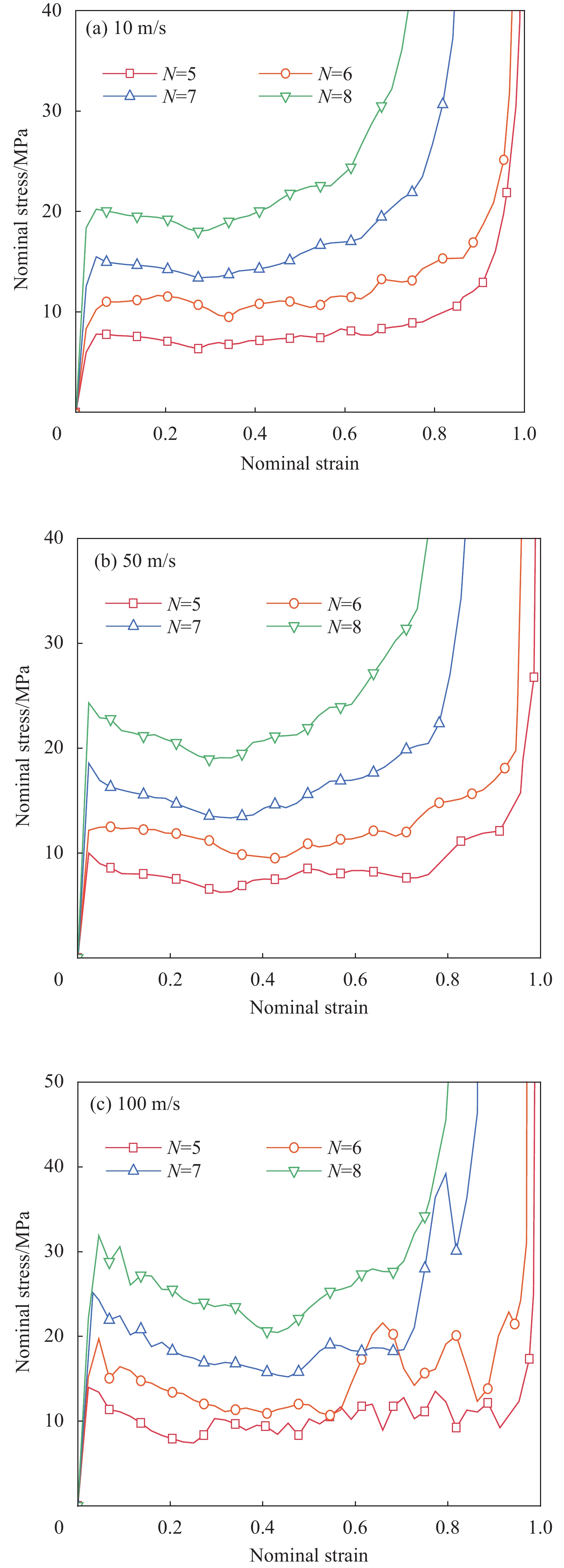
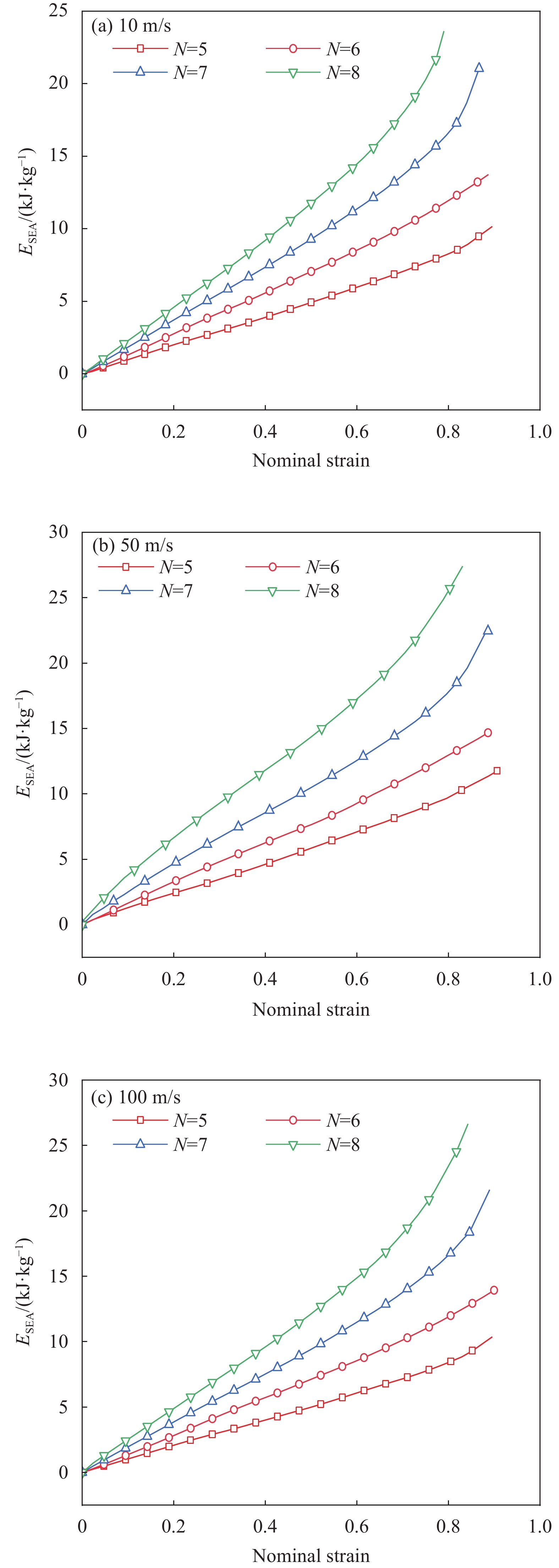
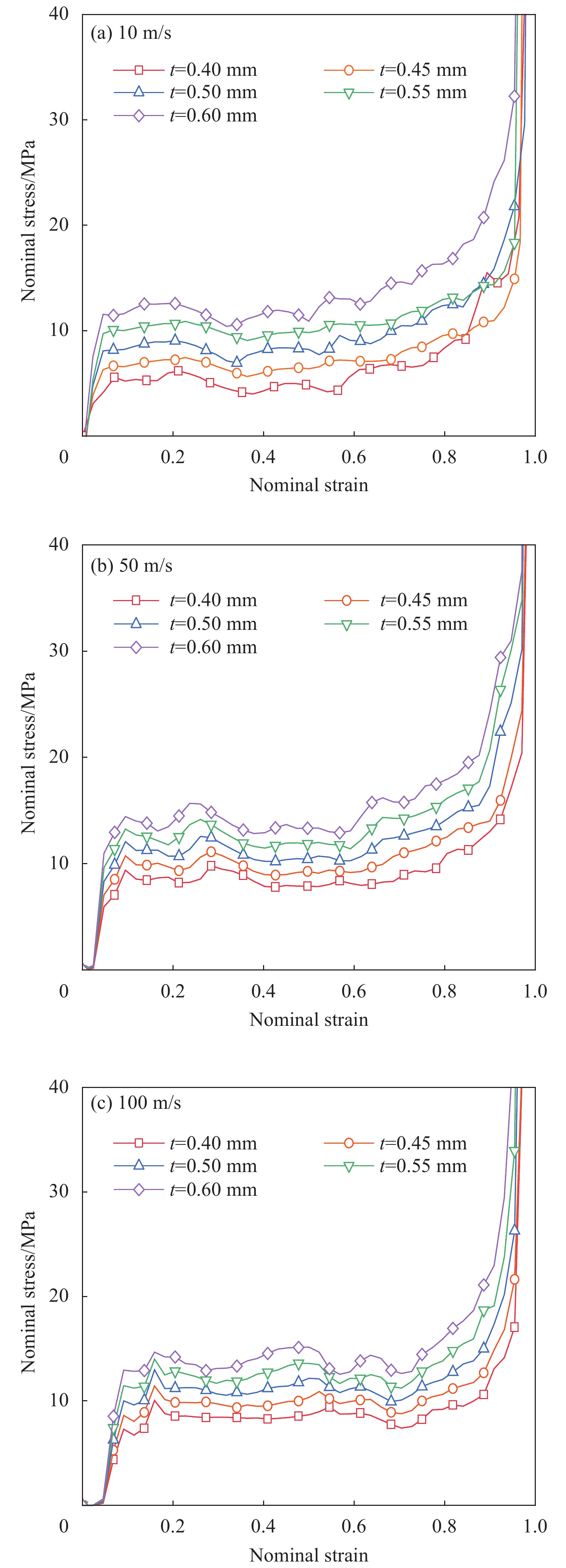
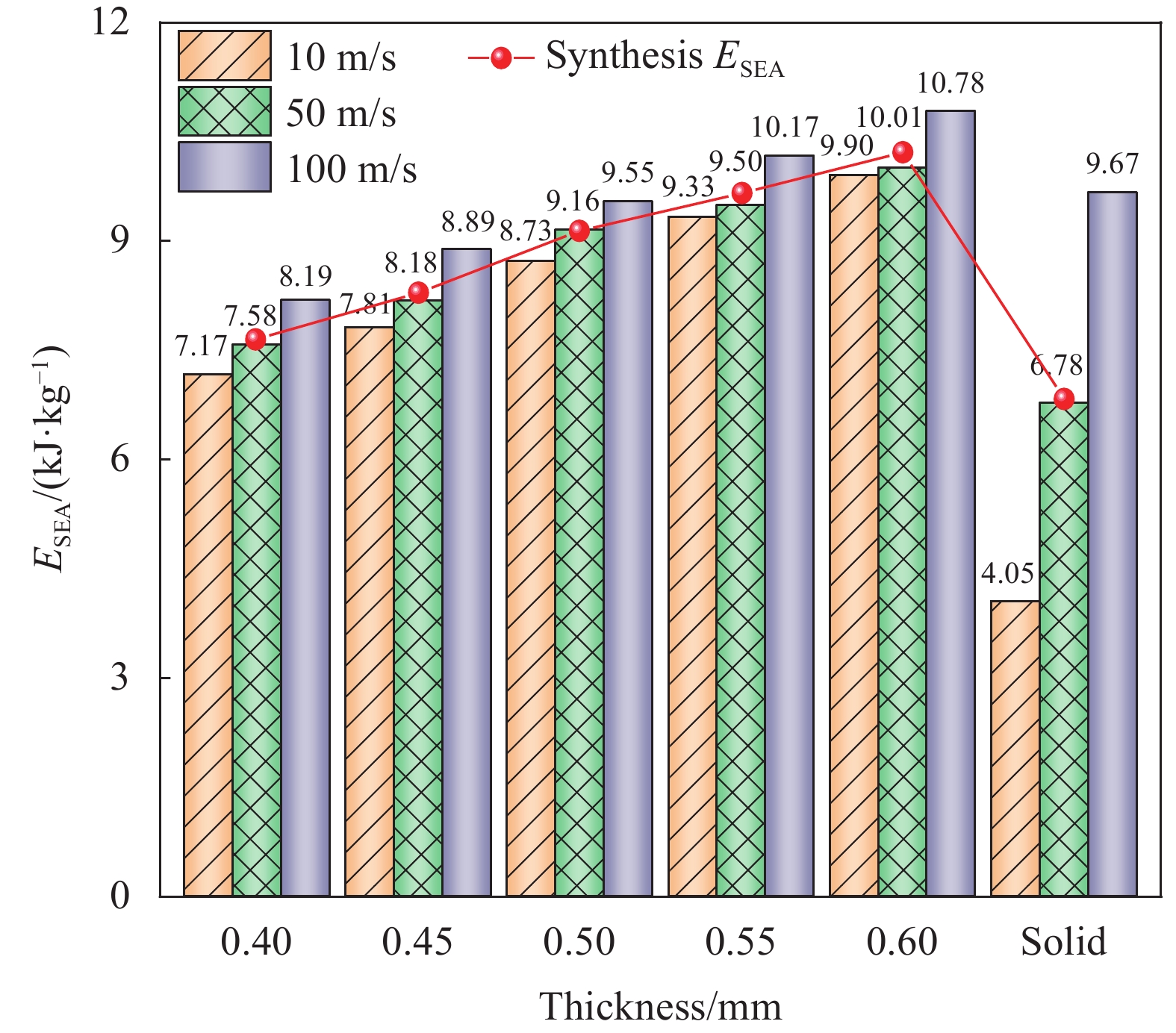
结论①与准静态压缩荷载变形模式不同，BBCLS在冲击载荷作用下的冲击过程可分为三种模式：低速冲击荷载下的均匀变形模式；中速冲击荷载下的过渡变形模式；高速冲击荷载下的动态变形模式。随着冲击速度的增大，BBCLS的初始应力峰值、平台应力和密实应变越大，能量吸收能力越强。②BBCLS在冲击荷载作用下的承载能力、吸能总量及比吸能均明显优于传统的BCC点阵结构，BBCLS不仅改善了传统BCC点阵结构在节点处应力集中的问题，且在承载能力与能量吸收性能方面表现出明显的优势。③随着冲击速度的增大，相同振幅的BBCLS冲击端平台应力会随着冲击速度提升而增大，且速度越高增幅越明显。④由于波纹数的增大，BBCLS的承载能力、刚度和吸能性均大幅度提高，BBCLS在相同冲击速度下的平台应力逐渐升高，波纹数为8时结构的平台应力最大。当波纹数为8时，冲击速度达到100m/s，相比于波纹数为5，冲击速度为10m/s结构在应变达到0.6的SEA提高201.36%。⑤随着胞壁厚度和冲击速度的增大，BBCLS的比吸能明显增大。其中胞壁厚度对BBCLS比吸能的增大作用更为显著。在一定程度上增大胞壁厚度可使结构冲击变形更加均匀，能够有效地提高BBCLS在不同冲击载荷作用下的吸能能力。在实际应用中，需要综合考虑结构轻量化设计不可盲目增大相对密度以达到更强的承载效果。
-
点阵结构具有良好抗冲击能力和能量吸收能力，在工程领域具有广泛的应用前景。尽管目前有关点阵结构的制备、设计和力学性能等方面取得了一定的研究进展，但是研究人员仍在不断探索结构更加复杂、抗冲击性能更加优越的点阵结构。近年来，仿生结构因在能量吸收能力上表现出比传统结构更加优异的性能，引起国内外学者广泛关注。其中，受雀尾螳螂虾螯抗冲击区域微观结构启发而提出的仿生双正弦波纹点阵结构(Bio-inspired bi-directional corrugated lattice structure，BBCLS)，在静态压缩性能和吸能方面展现出独特的优势。但是，目前对于其在冲击载荷下的变形失效机理尚不清楚。为了探究BBCLS的抗冲击性能，本文采用ANSYS/LSDYNA有限元分析软件建立了其在冲击荷载作用下的有限元数值模型，并基于已有的试验结果与数值模拟结果进行了对比，验证了该模型的有效性。在此基础上，研究了不同冲击速度对BBCLS的应力分布、变形模式、承载能力以及能量吸收特性的影响，并与传统体心立方点阵结构(BCC)进行了对比。同时利用该数值模型进一步分析了振幅、波纹数和胞壁厚度等微结构几何参数对BBCLS抗冲击性能的影响。研究结果表明：BBCLS在冲击荷载作用下的承载能力、吸能总量及比能量均明显优于传统的BCC点阵结构。BBCLS的冲击动力学响应主要与冲击速度和微结构几何参数有关。在低速冲击时，BBCLS呈现整体变形模式；中高速冲击时，结构向局部变形模式转换。随着冲击速度的提高，增大振幅、波纹数、胞壁厚度均使结构在受到冲击载荷时应力分布均匀，有效增加了冲击端的平台应力。研究结果为研究仿生点阵结构的冲击变形失效和吸能效果提供了力学依据。
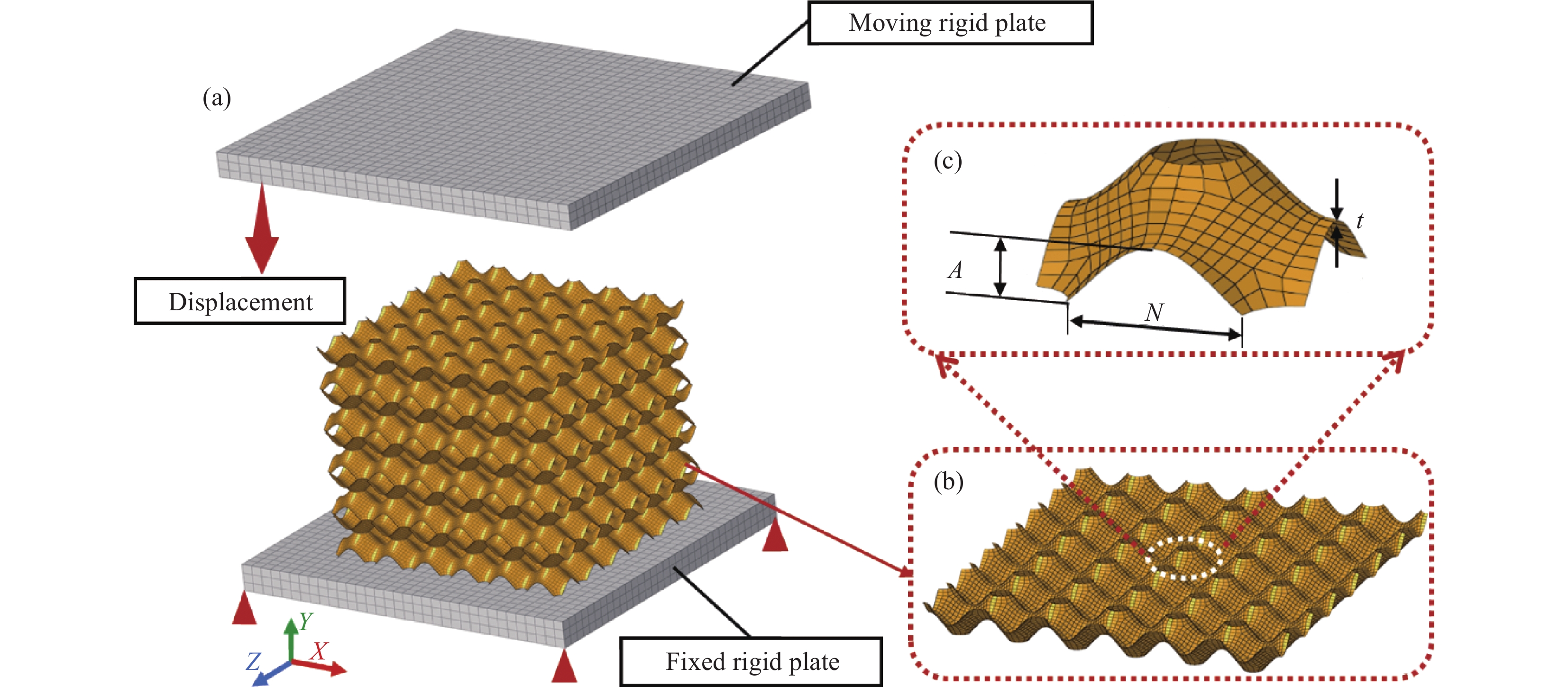
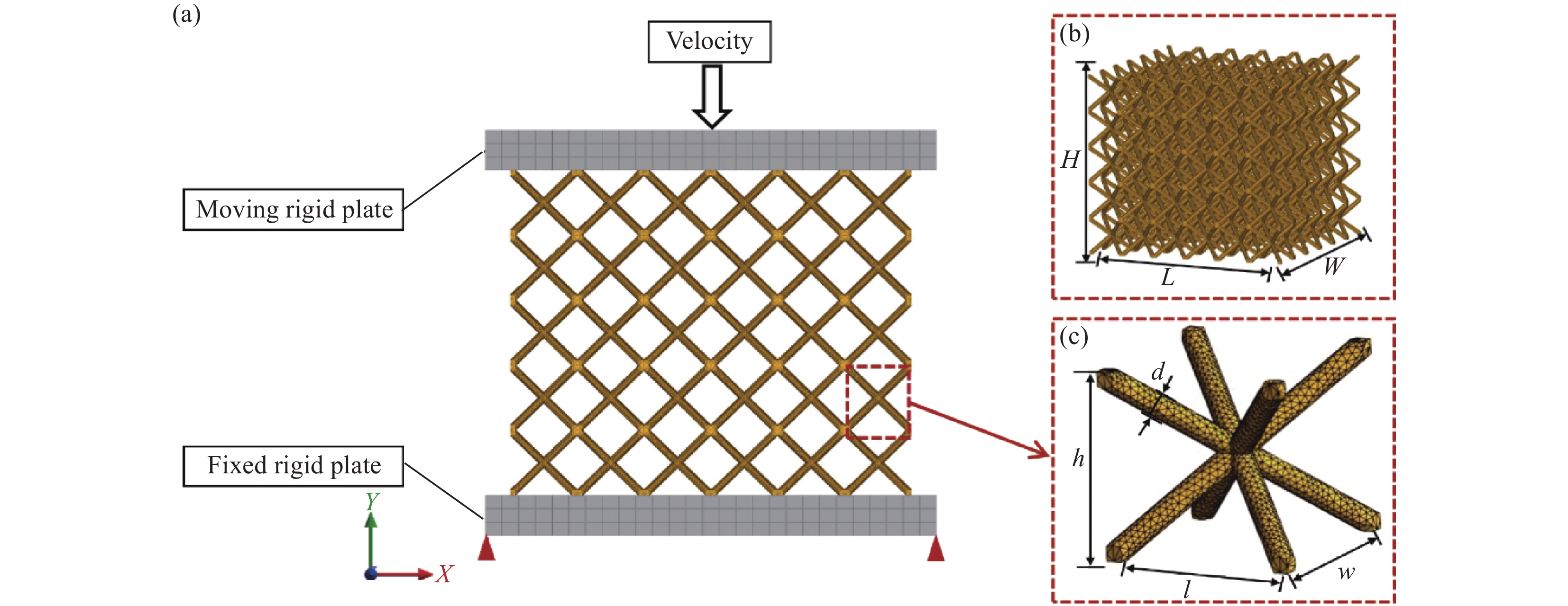
BBCLS有限元模型
不同冲击速度下的BBCLS在典型应变水平下的变形图
计量
- 文章访问数: 224
- HTML全文浏览量: 109
- PDF下载量: 9
