Analysis on pore characteristics of hybrid basalt-polypropylene fiber-reinforced concrete based on nuclear magnetic resonance technology
-
摘要:
采用核磁共振(Nuclear magnetic resonance，NMR)测试了玄武岩-聚丙烯混杂纤维混凝土(HBPRC)的孔隙特征，对比分析了玄武岩纤维(BF)和聚丙烯纤维(PF)及二者混杂对HBPRC的抗压强度、孔隙率、孔径分布和曲折度的影响，并基于核磁共振T2谱和孔隙结构分形理论对4个孔径区域的孔隙结构分形维数进行了量化。结果表明：随着BF的添加，T2谱反映出适量的BF可以减小混凝土的孔隙率，而且有利于减小大孔体积占比；而随着PF含量增加，T2谱面积增加，且混凝土内部孔隙有变大的趋势。掺入BF-PF混杂纤维对混凝土的孔隙特征会产生正协同作用，当BF和PF掺量均为0.05vol%时，协同作用最佳，与普通混凝土相比，抗压强度提高了3.52%、孔隙率降低了1.47%、曲折度提高了8.20%。凝胶孔体积占比增大了8.76%，大孔体积占比降低了5.30%，孔径分布得到优化。HBPRC的孔隙结构具有明显的分形特征，孔隙结构分形维数在过渡孔、毛细孔和大孔区域依次增加，此外，分形维数越大，抗压强度越大。通过微观分析认为，纤维在混凝土基体中的粘结状态和分布是影响HBPRC孔隙分形特征的主要原因。
-
关键词:
- 玄武岩-聚丙烯混杂纤维混凝土 /
- 核磁共振 /
- 孔隙特征 /
- 抗压强度 /
- 孔隙结构分形维数
Abstract:The pore characteristics of hybrid basalt-polypropylene fiber-reinforced concrete (HBPRC) was tested by nuclear magnetic resonance (NMR). The effects of basalt fiber (BF) and polypropylene fiber (PF) as well as their blends on the compressive strength, porosity, pore size distribution and tortuosity of HBPRC were analyzed comparatively. The fractal dimensions of the pore structure in four pore-size regions were quantified based on the T2 spectra of NMR and pore structure fractal theory. The results show that with the addition of BF, the T2 spectrum reflects that the appropriate amount of BF can reduce the porosity of concrete, and it is beneficial to reduce the percentage of large pore volume. But as the PF content increases, the T2 spectral area increases and there is a tendency for the pores of the concrete to become larger. Incorporation of BF-PF hybrid fibers produces a positive synergistic effect on the pore characteristics of concrete. The synergistic effect is optimal when the dosage of both BF and PF is 0.05vol%, which improves the compressive strength by 3.52%, reduces the porosity by 1.47%, increases the volume percentage of gel pores by 8.76%, increases the tortuosity by 8.20%, and reduces the volume percentage of large pores by 5.30%, and optimizes the distribution of pore size, as compared with ordinary concrete. There are obvious fractal characteristics in the pore structure of HBPRC, and the fractal dimensions of the pore structure of HBPRC increases sequentially in the region of transition pores, capillary pores, and large pores. In addition, the larger the fractal dimension, the greater the compressive strength. It is concluded from the microscopic analysis that the bonding state and distribution of fibers in the concrete matrix are the main reasons affecting the pore fractal characteristics of HBPRC.
-
超材料[1-3]是一类由阵列化的人工微结构单元构成的复合结构。通过对超材料中的微结构单元及其排布方式进行调控设计，可产生低频弹性波带隙、负等效质量密度、负弹性模量、负折射等一系列超常效应[1]，因而在航空航天、工程建筑、轨道交通等[4-6]工程领域具有广泛的应用前景。声学超材料按照带隙形成的机制不同可以分为布拉格散射型和局域共振型[7]。布拉格散射起主导性作用的是周期性的材料特性与弹性波之间的相互作用；局域共振型起主导作用的是散射体的振动特性与基体中长波行波之间的耦合作用，从而抑制弹性波的传播[8]。
近年来，一些学者结合带隙形成机制，在低频范围内获得了较宽的带隙，并通过改变几何参数对带隙进行优化[9-13]。张思文等[14]提出了一种新型局域共振复合结构，实现了声子晶体的多重共振，在低频范围能打开多条共振带隙；Li等[15]研究了振动形式对韧带结构带隙的影响，通过拓扑优化提高了带隙的覆盖范围；Coffy等[16]设计了一种新型声子晶体，有效增加了带隙宽度；李孟昶等[17]设计了一种新型管道超结构构型，该结构在
2500 Hz内产生了两条完全带隙。传统超材料设计方法无法实现参数连续控制。实际工程中，结构随不同工况动态特性相应发生变化，可控超结构可根据目标需求调节结构的带隙特性，实现对不同工况下结构减振的可控调节。近年来，可控超结构日益受到学者们的广泛关注[18-20]。Yao等[21]研究了温度对不同晶格类型声子晶体的带隙调控机制；Geng等[22]研究了不同缺陷态声子晶体几何参数对弯曲波带隙的可控性，结果表明温度升高会造成带隙的频率范围减小；Dai等[23]结合声学拓扑绝缘体，利用温控可调拓扑声子晶体控制和引导水声，但调控范围比较有限。一些学者开展了通过外部激励实现带隙调控的研究。Li等[24-25]分别提出了一种衍生结构和混合声学超结构，可通过施加主动应变调控结构的带隙特性；Bertoldi和Boyce[26]研究了有限形变对周期性超弹性材料中弹性波传播的影响；Shan等[27]研究了周期性多孔超弹性声子晶体在施加载荷后的带隙特性，并分析了不同屈曲模式对带隙的调节效果；Li等[28]研究了结构不同屈曲模式对带隙的影响；Gei[29]研究了准无限周期梁的轴向波和弯曲波的能带结构，分析了轴向拉伸预应力调节结构弯曲波的特性；Huang等[30-32]研究了大形变和预拉伸应变对由超弹性材料制成的声子晶体板带隙的影响。目前已开展的可控超结构研究相对较少，且大多针对结构特定频率范围(低频或中高频)。本文提出一种复合带隙可控超结构构型，可同时产生低频的局域共振型带隙和较高频的布拉格散射型带隙，且通过调节振子位置和施加可控位移，可实现对结构复合带隙的有效调控。采用有限元法研究了4种不同复合带隙可控超结构的带隙特性及其在外加激励作用下的带隙调控规律，计算了该结构的振动传输特性曲线，并与实验结果进行了对比验证。
1. 构型设计及带隙特性
1.1 复合带隙可控超结构构型及其带隙计算
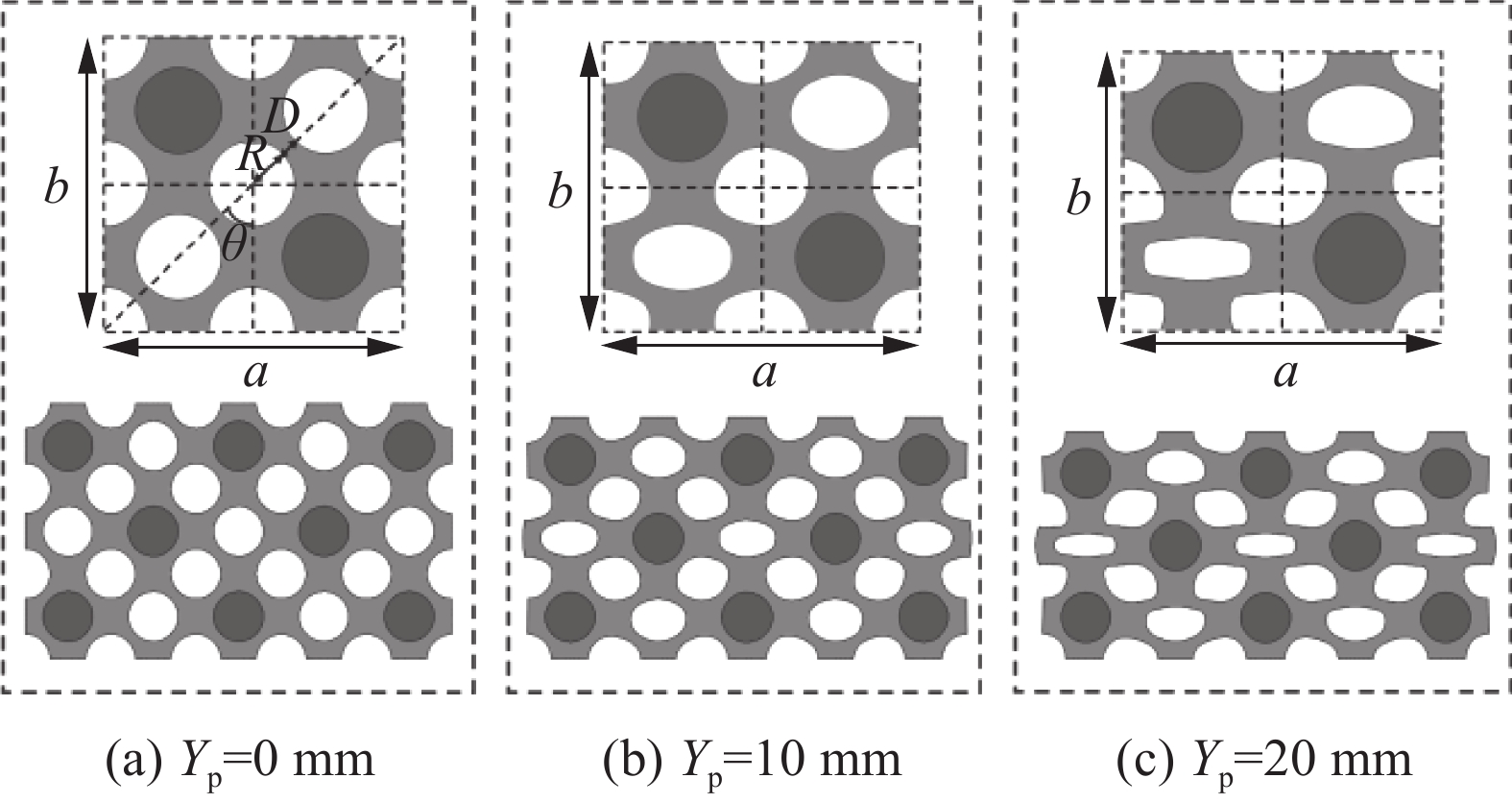
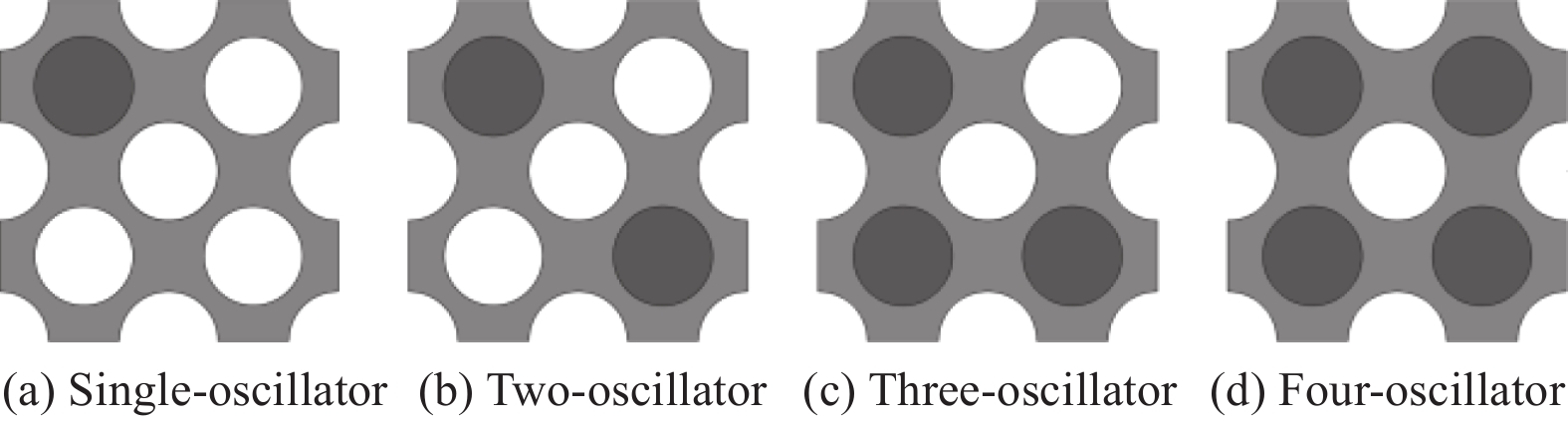
本文提出的复合带隙可控超结构的元胞构型如图1所示，该结构由多孔软材料及内部嵌入的局域共振振子构成。根据振子分布位置不同，分别有单振子、二振子、三振子及四振子4种构型，如图1所示。当对该结构施加可控轴向压缩时(图2)，结构逐渐发生变形，带隙结构分布随之改变，实现带隙的可调可控。
![]()
图 1 不同构型复合带隙可控超结构元胞Figure 1. Composite band gap controllable metastructure cells with different configurations![]()
图 2 不同轴向压缩下二振子构型超结构元胞及试件示意图Figure 2. Schematic diagram of the metastructure cells and specimens of two-oscillator configurations under different axial compressionsYp—Axial compression of the structure; a, b—Lattice constant; R—Radius of the hole; θ—Angle of the diagonal of the cell; D—Distance between the holes本文采用有限元法计算该结构在{\boldsymbol{{ M}\varGamma}} 、{\boldsymbol{\varGamma { X}}}、{\boldsymbol{{ X}{ M}}}方向上的能带分布。在忽略介质阻尼的影响下，弹性波在线弹性非均匀介质中的波动方程可以写为
\nabla \cdot \left[ {{\boldsymbol{C}}\left( {\boldsymbol{r}} \right):\nabla {\boldsymbol{u}}\left( {{\boldsymbol{r}},t} \right)} \right] = {\boldsymbol{\rho}} \left( {\boldsymbol{r}} \right)\frac{{{\partial ^2}{\boldsymbol{u}}\left( {{\boldsymbol{r}},t} \right)}}{{{\partial ^2}t}} (1) 式中：{\boldsymbol{ r}} 为位置矢量，{\boldsymbol{r}} = \left( {x,y,{\textit{z}}} \right)；{\boldsymbol{u}}\left( {\boldsymbol{r}} \right)为位移矢量，{\boldsymbol{u}}\left( {\boldsymbol{r}} \right) = \left( {{u_x},{u_y},{u_{\textit{z}}}} \right)；t为时间； {\boldsymbol{C}}\left({\boldsymbol{ r }}\right) 和{\boldsymbol{ \rho}} \left( {\boldsymbol{r}} \right) 分别为材料的弹性张量及密度张量。
由于波动方程中的系数具有周期性，因此根据Bloch-Floquet周期性边界条件，单胞离散形式的特征值方程及边界条件可表示为
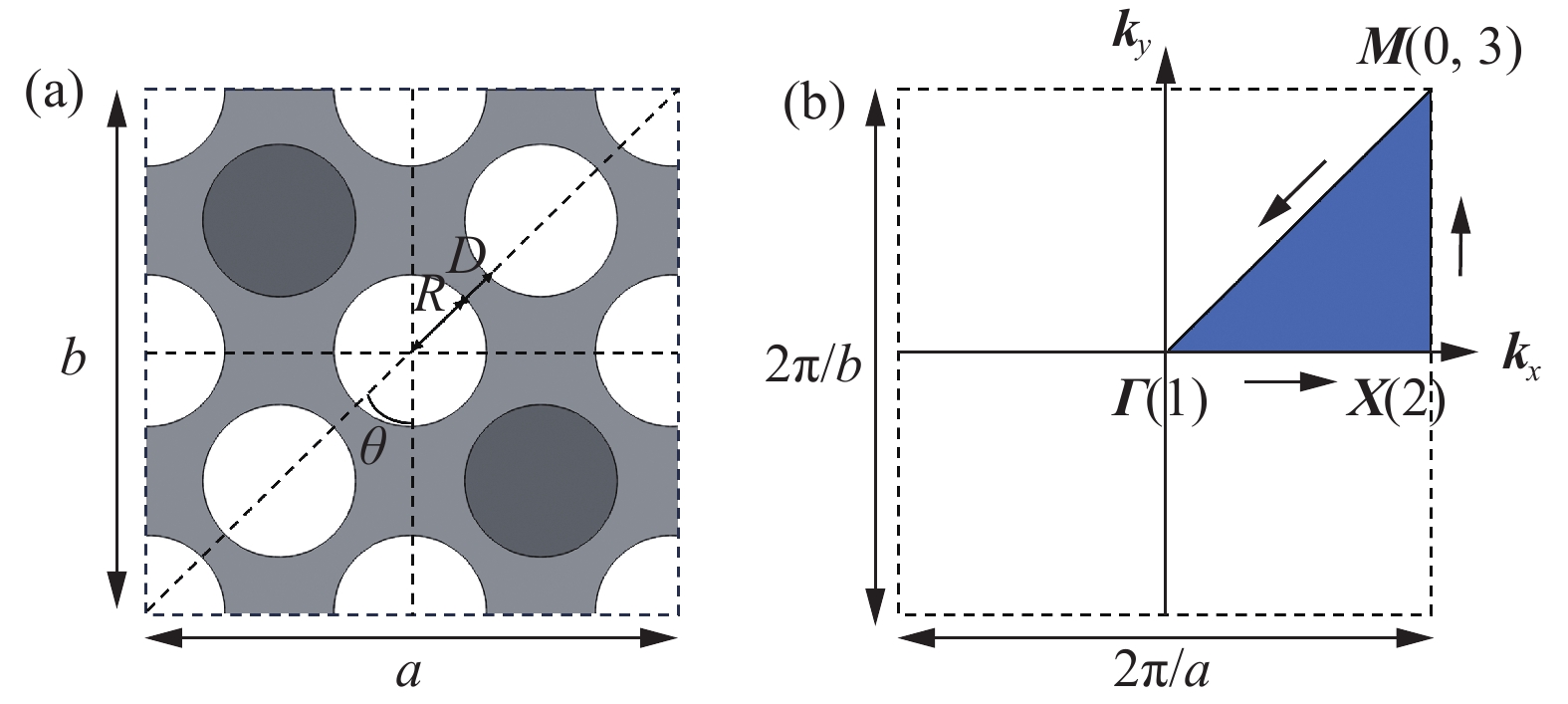
{\boldsymbol{KU}} = {\omega _n^2}{\boldsymbol{MU}} (2) \boldsymbol{u}\left(\boldsymbol{r},t\right)={\mathrm{e}}^{\mathrm{i}\left({\boldsymbol{k}} \, \cdot \,{\boldsymbol{r}}-\omega t\right)}\boldsymbol{u}_{\boldsymbol{k}}\left(\boldsymbol{r}\right) (3) 式中： {\boldsymbol{K}} 为结构的刚度矩阵；{\boldsymbol{M}}为质量矩阵；{\boldsymbol{U}}为单元节点位移矩阵；{\omega _n}为声子晶体的固有频率； {{\boldsymbol{u}}_{\boldsymbol{k}}}\left({\boldsymbol{ r}} \right) 是周期性边界源面的位移向量；i为虚数单位；ω为频率；{\boldsymbol{k}}为限制在第一布里渊区内的Bloch波矢，布里渊区示意图如图3所示。
![]()
图 3 Y_{\mathrm{p}}=0\; \mathrm{mm} 时二振子构型超结构元胞(a)及其第一不可约布里渊区(阴影区域) (b)M, Γ and X are the high symmetry points of the first irreducible Brillouin zone, respectively; kx and ky are the components of wave vector k in x and y directions, respectivelyFigure 3. Two-oscillator configuration metastructure cell (a) and its first irreducible Brillouin zone (Shaded region) (b) in Y_{\mathrm{p}}=0\; \mathrm{mm}联立式(2)与式(3)，令波矢{\boldsymbol{k}}扫略第一不可约布里渊区的边界，可得到一系列特征频率{\omega ^2}。在本文中选择波矢{\boldsymbol{k}}前50阶特征频率在第一布里渊区的变化来计算能带结构。对 {{\boldsymbol{k}}_x} 、 {{\boldsymbol{k}}_y} 的扫描路径进行设计，使波矢{\boldsymbol{k}}能够取到第一不可约布里渊区的所有值，其中波矢{\boldsymbol{k}}的方向及取值范围如图3中第一不可约布里渊区示意图所示，Bloch波矢{\boldsymbol{k}}的方向及 {{\boldsymbol{k}}_x} 、 {{\boldsymbol{k}}_y} 的关系如下：
{{\boldsymbol{k}}_x} = \left\{ {\begin{array}{l} {(1 - k)\dfrac{{\text{π}} }{a},0 < k < 1} \\ {(k - 1)\dfrac{{\text{π}} }{a},1 < k < 2} \\ {\dfrac{{\text{π}} }{a},2 < k < 3} \end{array}} \right.{\text{ }}{{\boldsymbol{k}}_y} = \left\{ {\begin{array}{l} {(1 - k)\dfrac{{\text{π}} }{a},0 < k < 1} \\ {0,1 < k < 2} \\ {(k - 2)\dfrac{{\text{π}} }{a},2 < k < 3} \end{array}} \right. (4) 进而可得到波矢k与频率\omega 的色散关系。
1.2 带隙特性分析
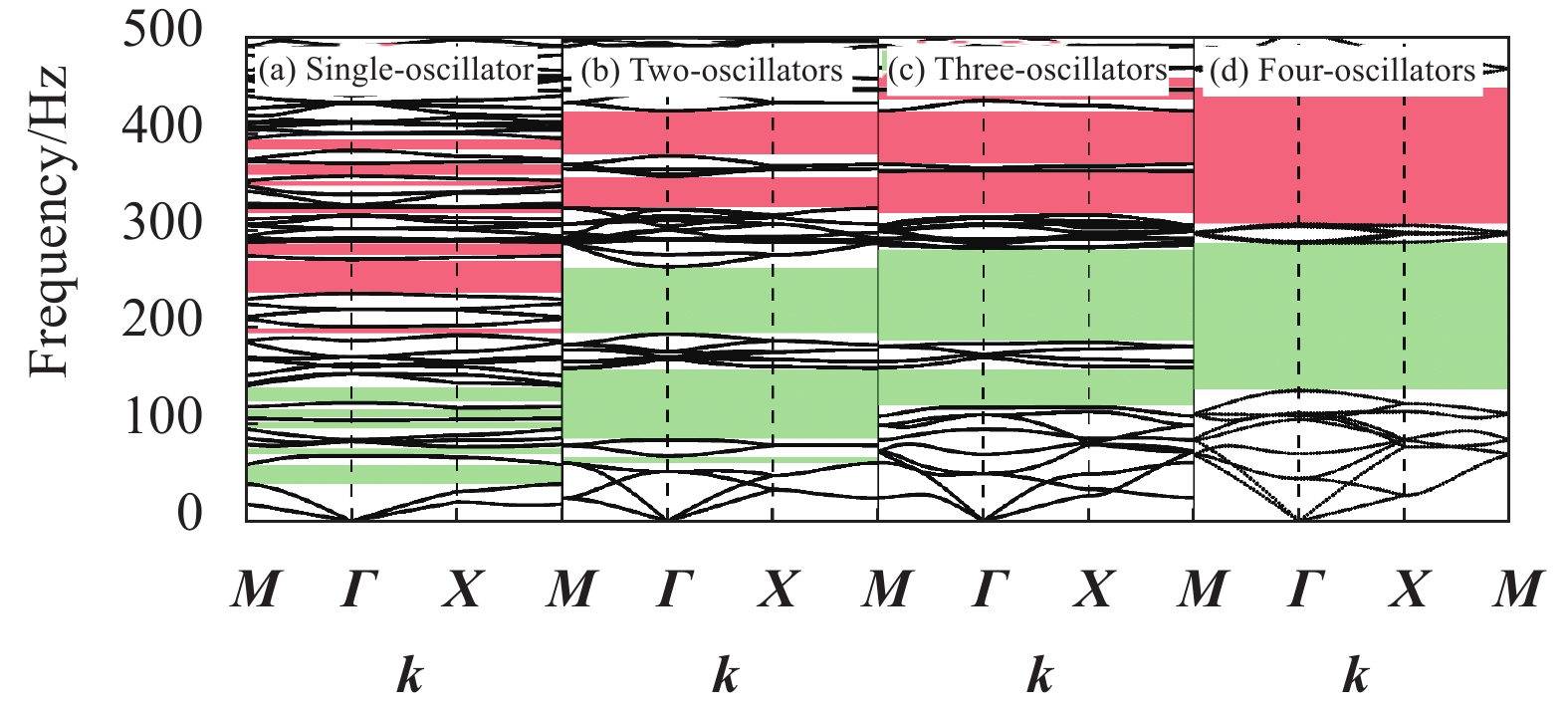
本文设计的复合带隙可控超结构采用硅橡胶材料制成，内部嵌入铅块作为其局域共振振子，其几何参数和材料参数如表1所示，未压缩情况下的晶格常数为a = b = 120\;{{\mathrm{mm}}} 。应用COMSOL软件建立了图1中4个元胞结构的有限元模型，并在相应位置施加Floquet周期性边界条件，应用特征频率求解器对布里渊区边界进行波矢扫描计算，可以得到元胞振动的能带结构图，并将它们进行对比，如图4所示。
表 1 几何参数和材料参数Table 1. Geometric parameters and material parametersGeometric parameters Value Material Material parameters Value R/mm 17.5 Silicon rubber E/MPa 0.870 ρ/(kg·m−3) 1230 D/mm 7.426 ν 0.499 Lead E/MPa 40.8 θ/(°) 45 ρ/(kg·m−3) 11340 ν 0.37 Notes：E—Elastic modulus；ρ—Density；ν—Poisson's ratio. ![]()
图 4 不同元胞构型 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构对比图Figure 4. Energy band structure comparison diagram of different cell configurations Y_{\mathrm{p}}=0\; \mathrm{mm}从图4可以看出，中间孔无填充情况下，局域共振振子规律排列在中间孔的四周，随局域共振振子数量增加，300 Hz内的低阶带隙宽度增加，结构中带隙数量逐渐减少，带隙位置逐渐上移；且随着振子数量增加，结构刚度逐渐增大进而导致了带隙中心频率增加。
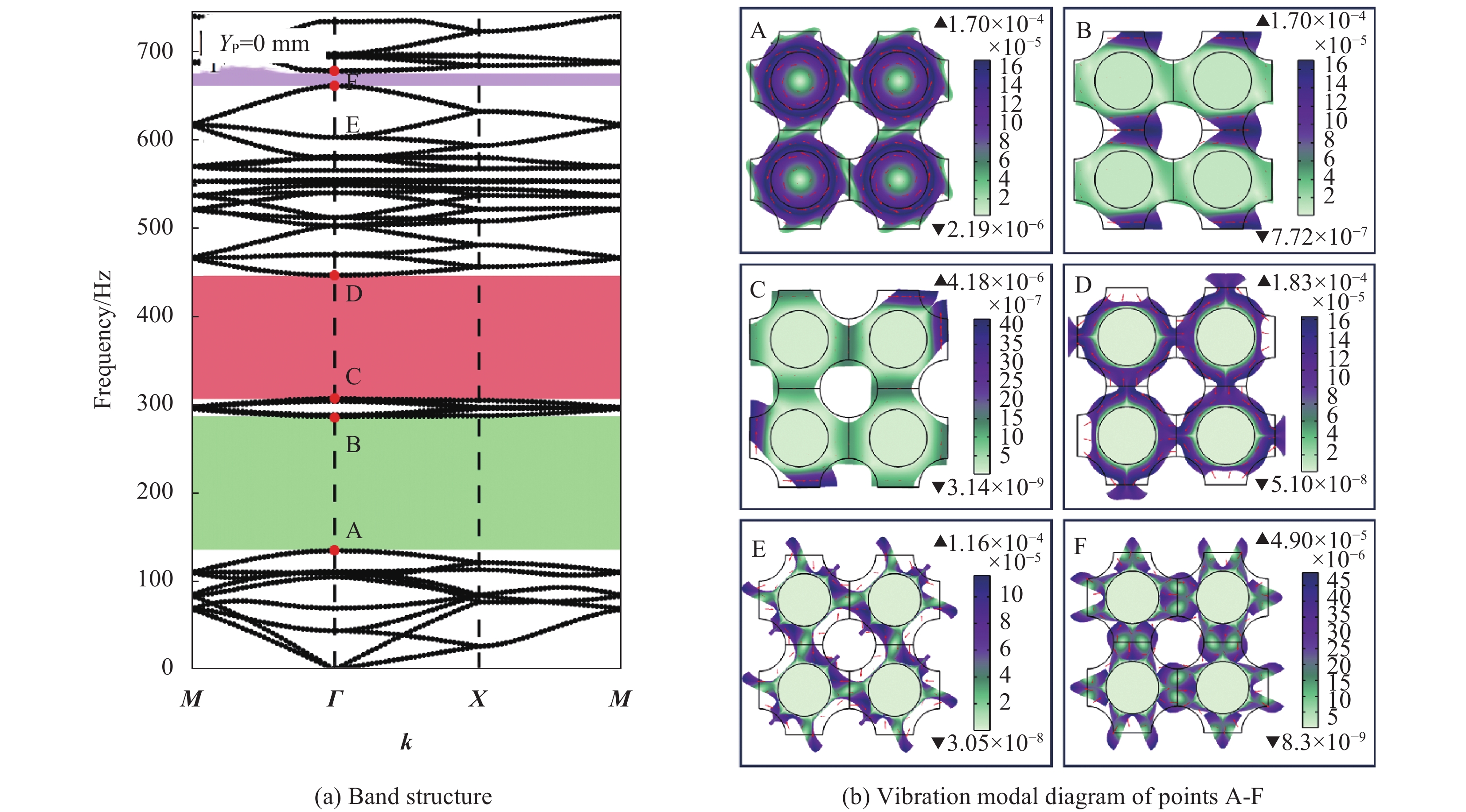
图5(a)给出了有限元法计算得到的四振子结构的能带结构图。可以看出，当结构的轴向压缩值 Y_{\mathrm{p}}=0\; \mathrm{mm} 时，前50阶特征频率形成了两条较宽的完全带隙和一条较窄的完全带隙，由低到高的频率范围分别为134.48~287.53 Hz、307.26~447.81 Hz和662.44~679.43 Hz。
![]()
图 5 四振子复合带隙可控超结构 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构及振动模态Figure 5. Band structure and vibration mode of the four-oscillator composite band gap controllable metastructure Y_{\mathrm{p}}=0\; \mathrm{mm}为进一步分析复合带隙可控超结构的带隙类型，图5(b)给出了A~F这6个点的振动模态图。可以看出，在A点，振动主要集中在散射体上，基体与散射体同向振动；B点散射体的振动降低。当波的频率接近散射体的固有频率时，基体与散射体发生共振，从而抑制了振动在特定方向上的传播。因此，图5(a)中的第一阶带隙为局域共振带隙。而对应C、D、E、F点振动模态为结构整体振动，因此第二阶带隙与第三阶带隙为布拉格散射型带隙。同理，图4所示能带结构中的带隙可根据高对称点的振动模态图来判断：第一阶带隙为局域共振型带隙，第二阶带隙为布拉格散射型带隙。
2. 复合带隙可控超结构带隙调控
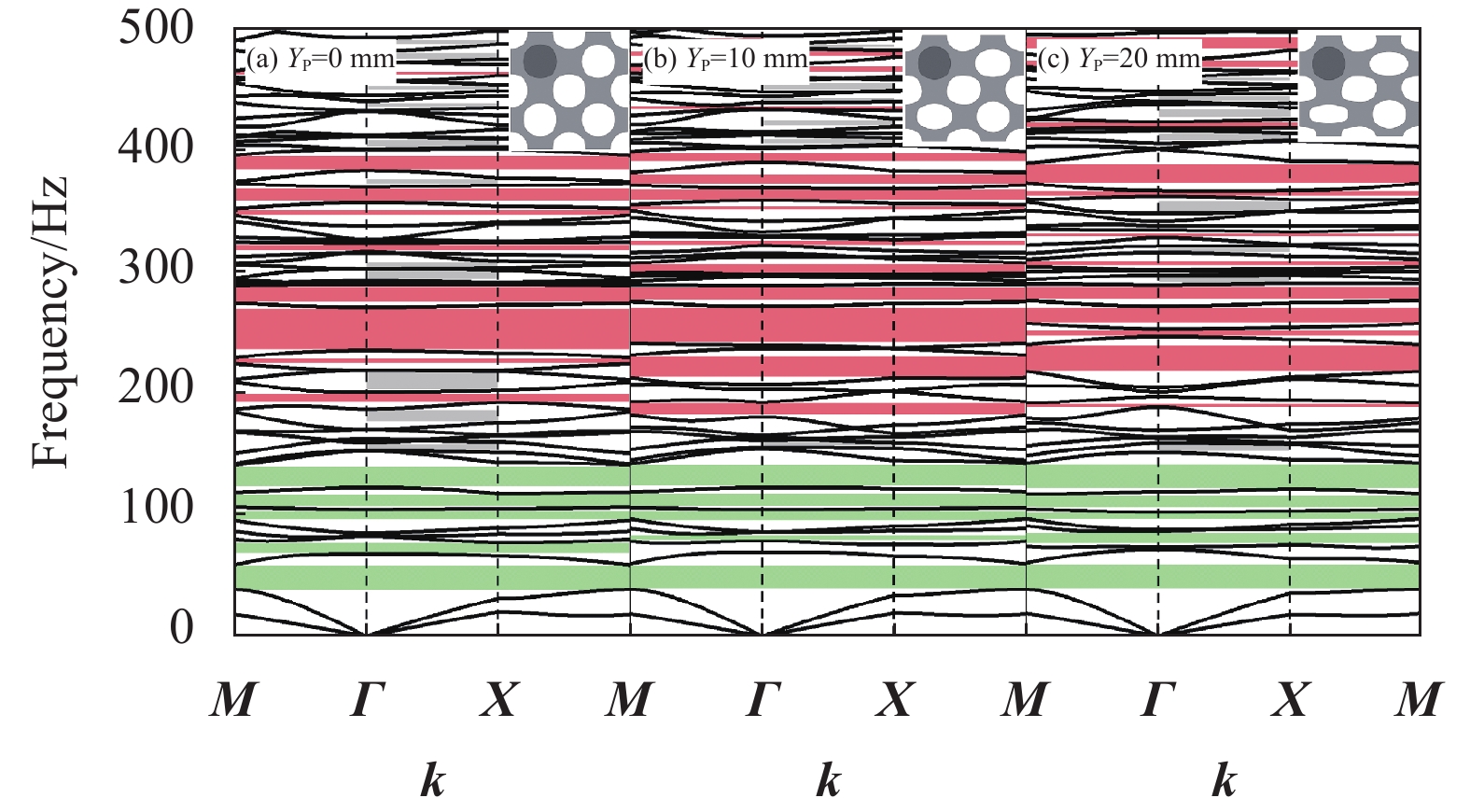
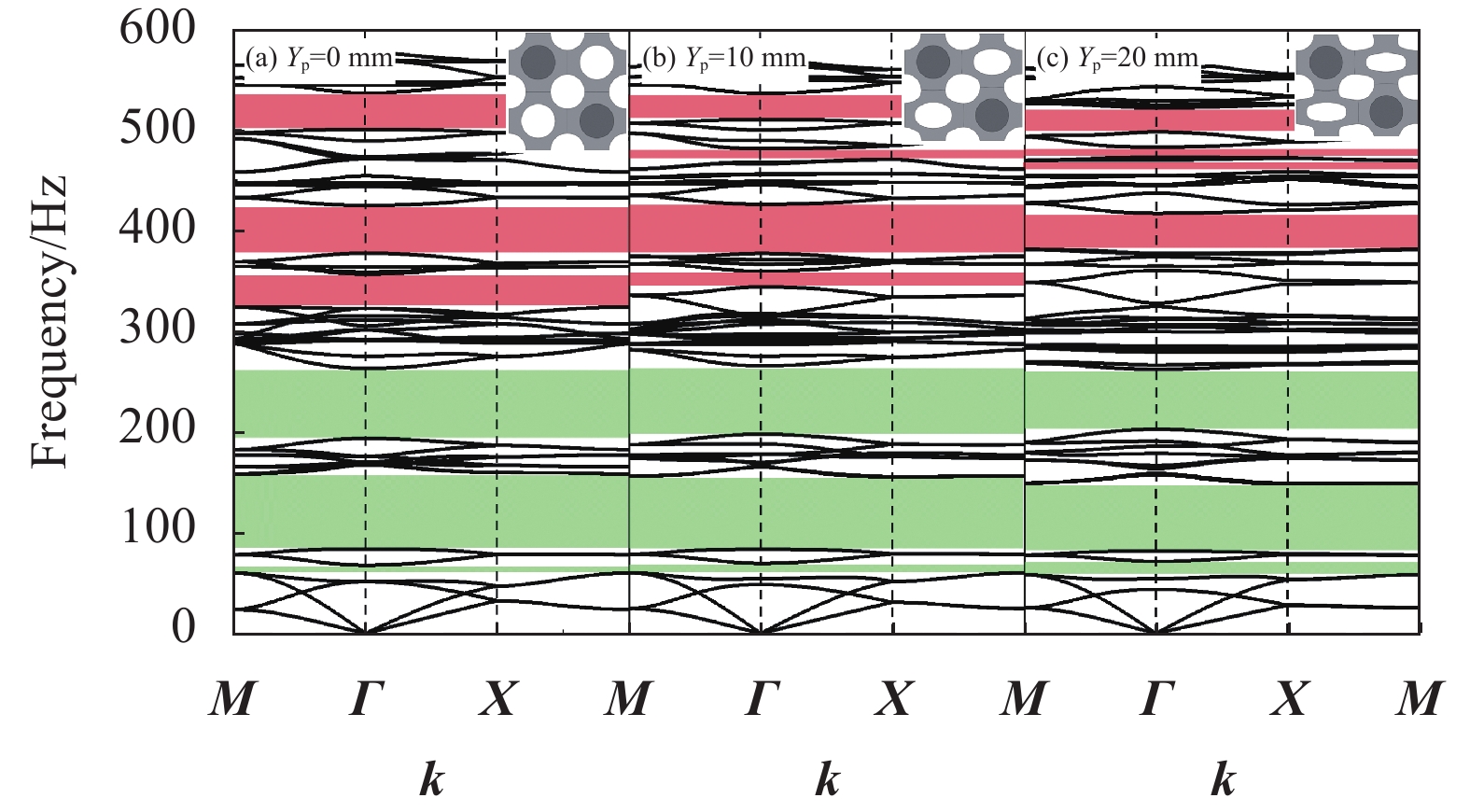
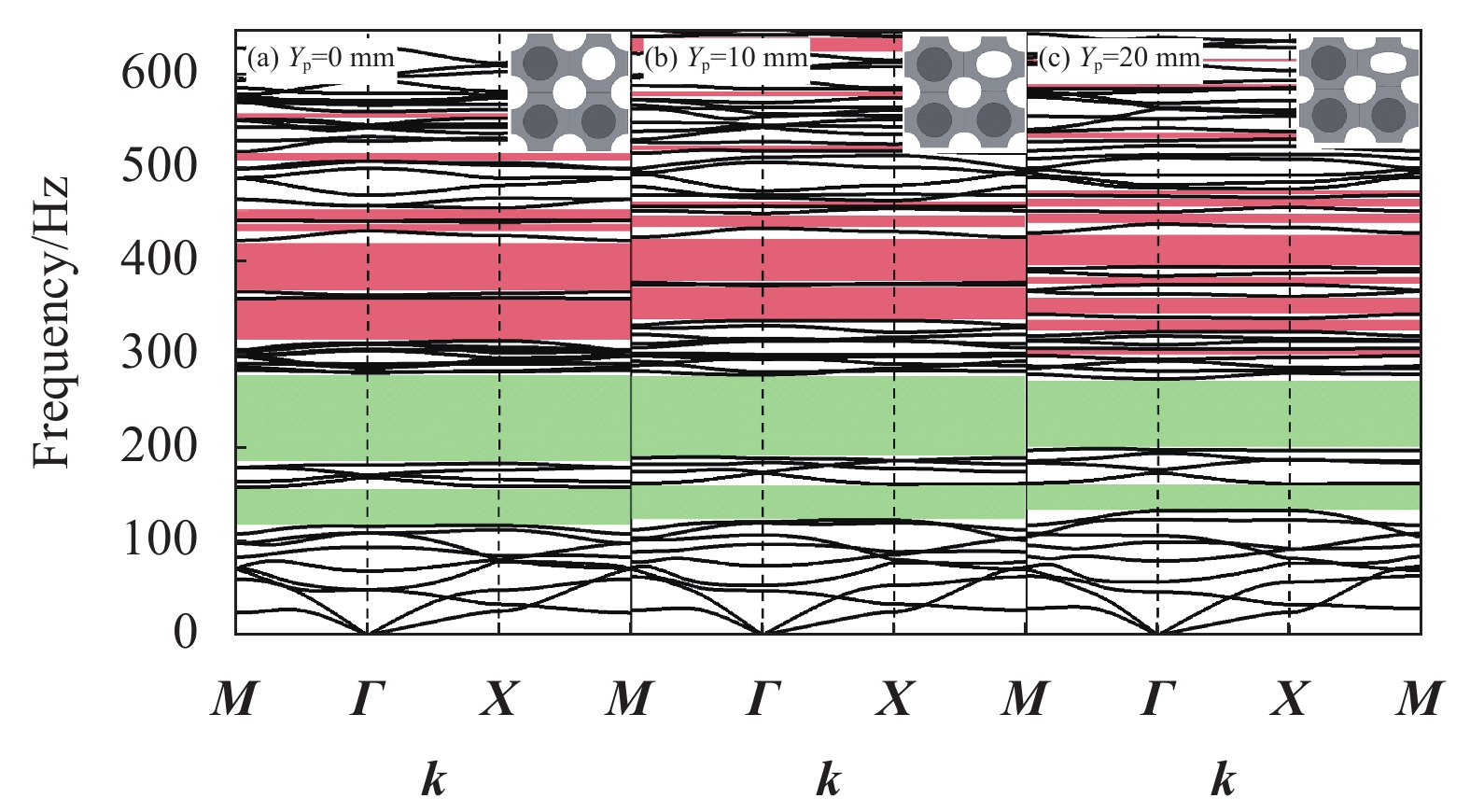
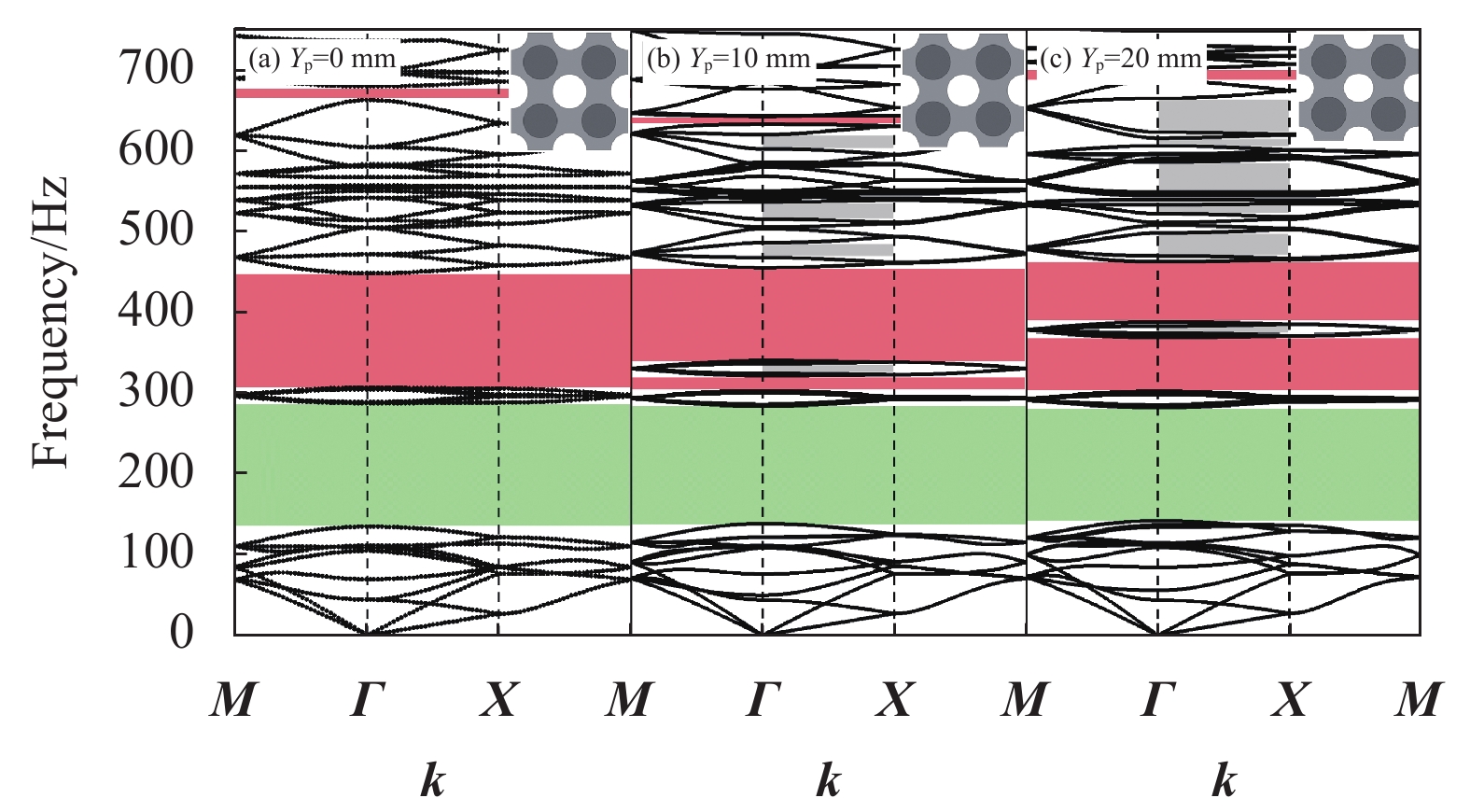
为了进一步分析轴向压缩对结构带隙调控的机制，对结构施加竖向位移量 Y_{\mathrm{p}} 。考虑到结构在较大变形下会发生屈曲，将应用COMSOL软件对结构的屈曲临界载荷和相应变形进行分析，计算得到各元胞发生屈曲的临界变形量在22.378~39.682 mm之间。因此，计算中在保证所有结构不发生屈曲的前提下，将图1中单振子、二振子、三振子、四振子元胞分别从0 mm开始依次增加10 mm进行轴向压缩，然后计算它们的能带结构图并分析带隙变化的规律，如图6~图9所示。
对比图6~图9中各阶带隙可以看出，随着竖向位移量 Y_{\mathrm{p}} 的增大，第一阶局域共振带隙变化较小，高阶的布拉格散射带隙中心频率逐渐向上移动，并在较高频率范围内出现了新的布拉格带隙，且单振子元胞和四振子元胞构型出现多条方向带隙(灰色部分)。这是由于轴向压缩对局域共振型带隙参数影响较小，但随着轴向位移 Y_{\mathrm{p}} 的增加，元胞晶格尺寸发生了变化，x方向尺寸a逐渐变大，y方向尺寸b逐渐变小，弹性波在晶格之间的传播与反射波的叠加发生了变化，色散曲线中心频率上移。可以发现，轴向压缩对不同构型复合带隙可控超结构具有较一致的调控机制，带隙调控的规律与局域共振振子的数量之间没有明显的关系。
![]()
图 6 单振子元胞在不同轴向压缩值下的能带结构对比图Figure 6. Energy band structure comparison diagram of single-oscillator cell under different axial compression values![]()
图 7 二振子元胞在不同轴向压缩值下的能带结构对比图Figure 7. Energy band structure comparison diagram of two-oscillator cell under different axial compression values![]()
图 8 三振子元胞在不同轴向压缩值下的能带结构对比图Figure 8. Energy band structure comparison diagram of three-oscillator cell under different axial compression values![]()
图 9 四振子元胞在不同轴向压缩值下的能带结构对比图Figure 9. Energy band structure comparison diagram of four-oscillator cell under different axial compression values3. 复合带隙可控超结构振动传输特性
3.1 有限周期结构的振动传输特性
为了进一步研究复合带隙可控超结构的实际工程应用效果，本文分别采用数值计算和实验方法对其进行了有限周期结构的振动传输特性研究。结构振动衰减情况常用传输损失{T_{\mathrm{L}}}来描述，传输损失 {T_{\mathrm{L}}} 计算式为[33]
T_{\mathrm{L}}=20\mathrm{lg}\left(\frac{a_{\mathrm{out}}}{a_{\mathrm{in}}}\right) (5) 式中，{a_{{\mathrm{in}}}}和{a_{{\mathrm{out}}}}分别为输入点和输出点处的加速度响应。
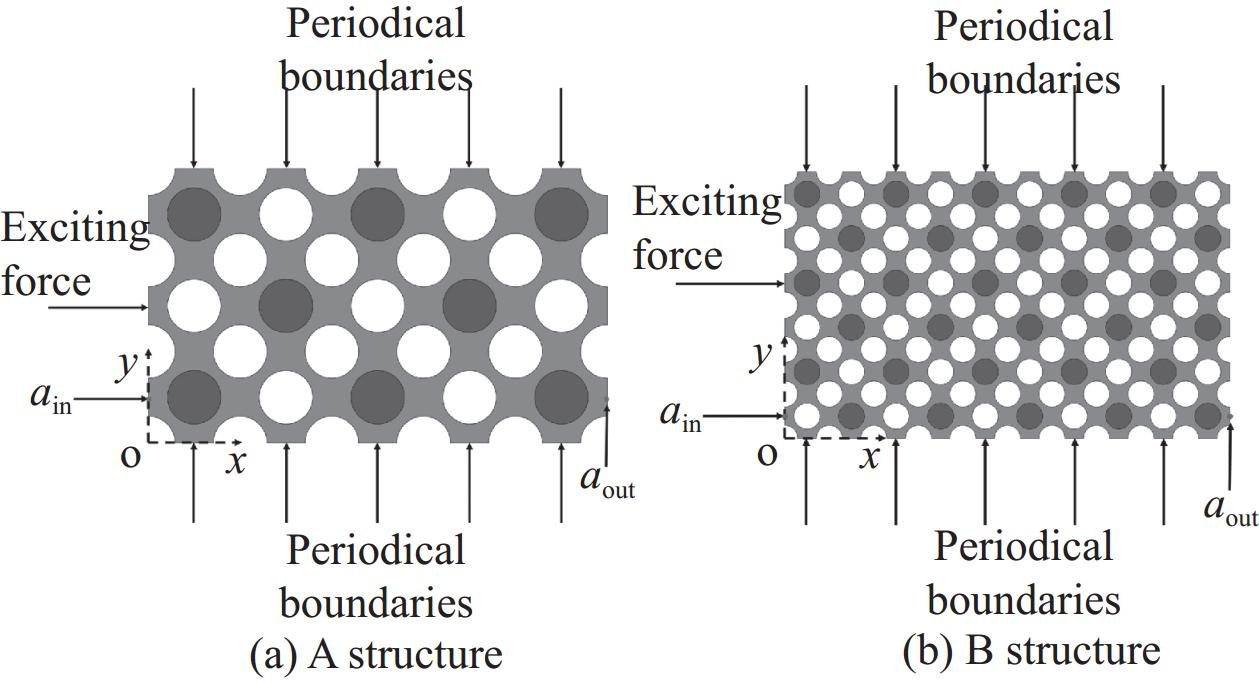
为了对比不同数量周期结构对振动传输特性结果的影响，开展了图10中有限周期二振子构型A、B结构的传输特性计算。应用COMSOL软件建立了两个结构的模型，在其左端处施加轴向单位激振力，限制结构y方向的刚体位移，在结构左右两端施加了自由边界条件，并在另一端{a_{{\mathrm{out}}}}处计算得到输出振动响应。
![]()
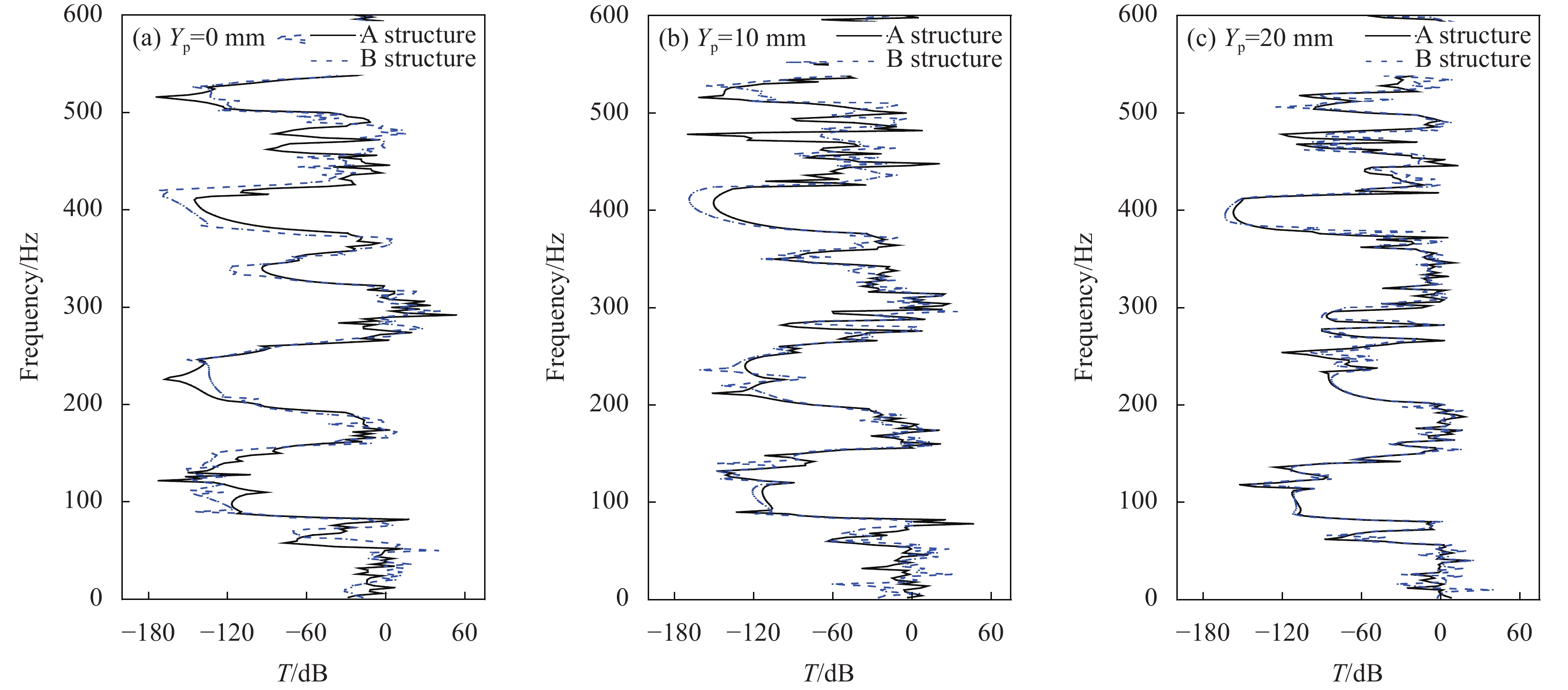
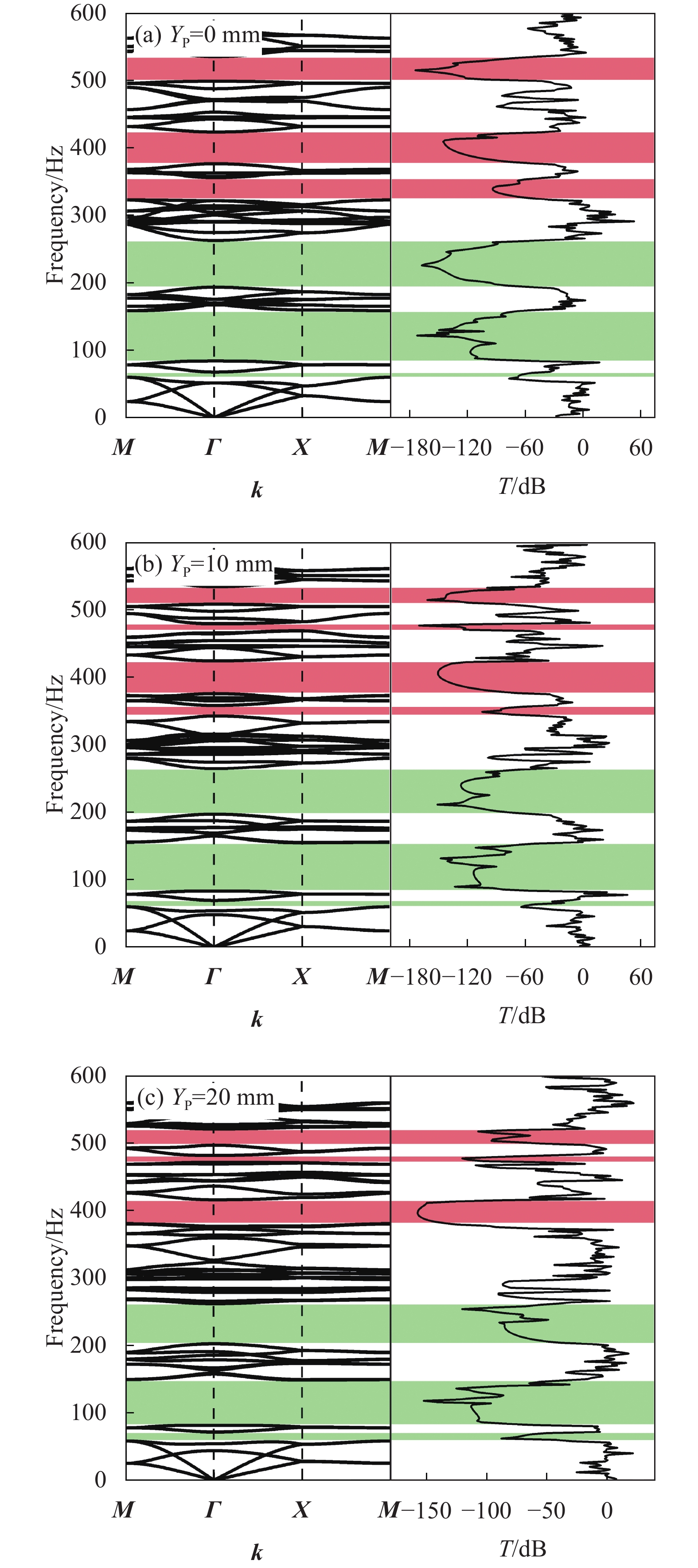
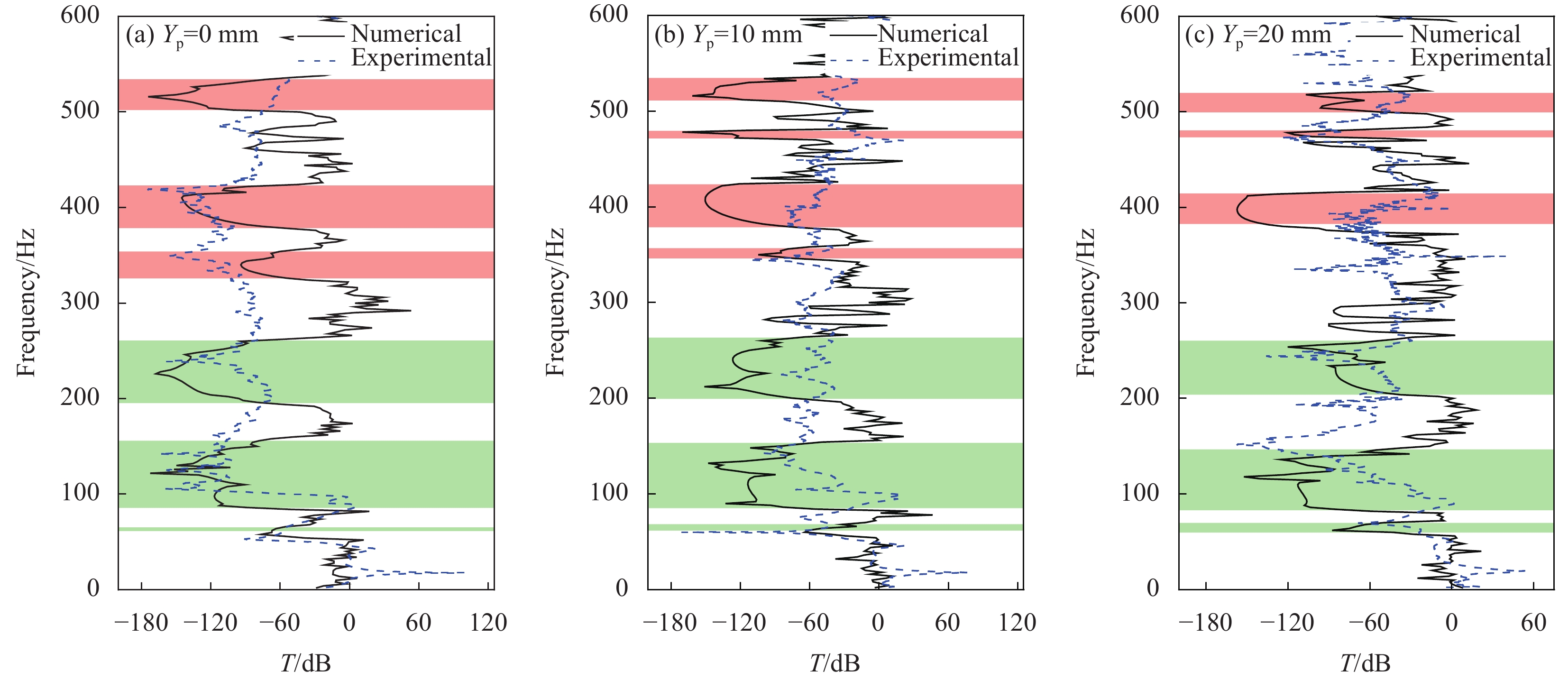
图 10 有限周期二振子超结构振动传输特性分析示意图ain and aout are the signal acquisition points of the input end and the output end, respectivelyFigure 10. Analysis diagram of vibration transmission characteristics of finite period two-oscillator metastructure图11给出了不同轴向压缩值下两个结构的振动传输特性曲线，可以看出尺寸较小的A结构与尺寸较大的B结构的振动传输特性具有较好的一致性。考虑到本文制作的实验试件尺寸有限，为便于与实验结果对比分析，选取周期结构数量与试验件相一致的A结构进行研究。图12(a)~图12(c)分别给出了二振子构型A结构在 Y_{\mathrm{p}}=0\; \mathrm{mm} 、 Y_{\mathrm{p}}=10\; \mathrm{mm} 、 Y_{\mathrm{p}}=20\; \mathrm{mm} 时的能带结构及振动传输特性曲线对比图。
![]()
图 11 不同轴向压缩值下两种尺寸有限周期二振子超结构振动传输特性曲线对比T—Structural vibration attenuationFigure 11. Comparison of vibration transmission characteristics curves of finite-period two-oscillator metastructures with two different sizes under different axial compression values![]()
图 12 不同轴向压缩值二振子构型超结构的能带结构及振动传输特性曲线Figure 12. Energy band structure and vibration transmission characteristic curves of two-oscillator configuration metastructures with different axial compression values从图12中的数值结果可以看出，传输特性曲线中振动衰减部分的频率范围与计算得到的能带结构中的带隙频率范围基本一致。另外，传输特性曲线中，除完全带隙对应的衰减，其余的衰减部分对应于方向带隙。在带隙范围内，结构的传输特性衰减明显，未压缩结构与轴向压缩结构的最大衰减均可达到150 dB。由此可见，弹性波在带隙频率范围内会出现明显的衰减。
3.2 实验研究
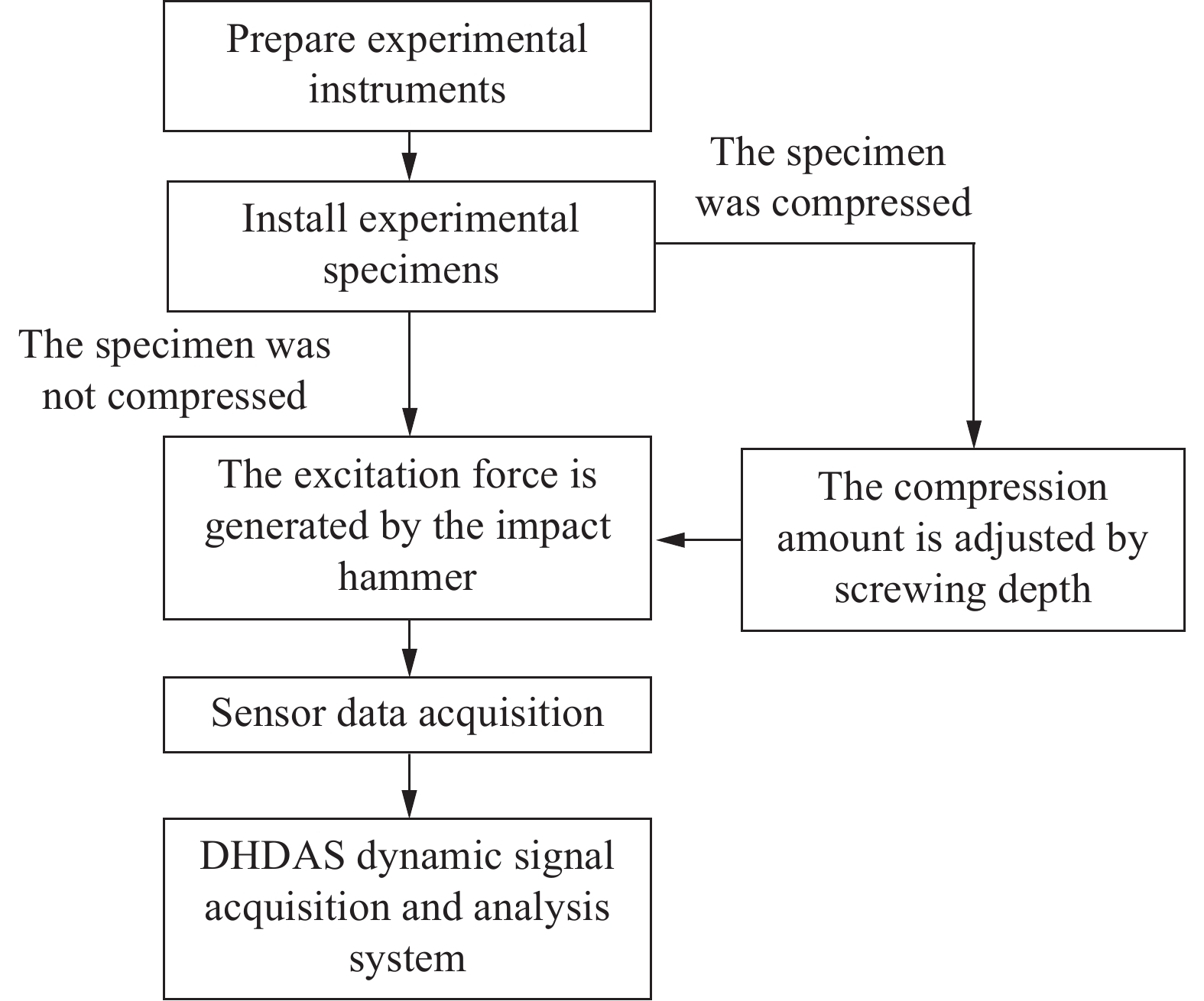
为研究有限周期二振子超结构振动传输特性，制作了二振子元胞结构试件，如图13所示。该试件由多孔硅橡胶构成，长度为300 mm，宽度为180 mm，厚度为50 mm，在橡胶孔内规律嵌入铅块构成局域共振振子。实验中，通过螺栓、螺母固定夹具，同时可调节控制其整体竖向位移。加速度传感器(352 C33，PCB)设置在图10中输入点{a_{{\mathrm{in}}}}与拾取点{a_{{\mathrm{out}}}}对应位置，使用力锤(CL-YD-303，江苏联能电子技术有限公司)沿水平方向冲击产生激励，通过DHDAS动态信号采集分析系统(DH8303，江苏东华测试技术股份有限公司)采集输入、输出端的加速度响应，实验装置如图14所示，实验流程如图15所示。将采集的数据利用式(5)进行计算，即可得到结构的振动传输特性曲线。
3.3 结果分析
将实验测得的加速度响应通过式(5)进行计算，所得到的数据经归一化处理后可获得二振子结构的振动传输特性曲线，如图16虚线所示。可以看出，带隙所在范围内(阴影区域)弹性波发生了衰减，这与有限元计算得到的结果比较一致，并且振动传输特性曲线的实验结果与数值结果也得到了较好的一致性。从图16可以看出：当 Y_{\mathrm{p}}=0\; \mathrm{mm} 与 Y_{\mathrm{p}}=10\; \mathrm{mm} 时，实验得到的振动传输特性曲线的衰减峰值与数值结果中的衰减峰值比较吻合；当 Y_{\mathrm{p}}=20\; \mathrm{mm} 时，部分低阶带隙的结果存在一定差异。这主要是由于：实验中结构通过夹具施加轴向压缩值，而相应的计算分析过程中，忽略了夹具和结构自重的影响，同时随着轴向压缩值的增加，结构内部产生的应力及自身的结构阻尼对其带隙亦有影响，因此两者有一定的误差。
![]()
图 16 不同轴向压缩值下二振子构型超结构的实验、数值振动传输特性曲线对比Figure 16. Comparison of experimental and numerical vibration transmission characteristic curves of two-oscillator configuration metastructure under different axial compression values4. 结 论
本文提出一种复合带隙可控超结构构型，该结构由多孔软材料和局域共振振子组成，可同时产生局域共振和布拉格散射两种带隙，通过施加轴向位移可实现对带隙的有效调控。采用有限元法研究了该结构在不同构型下的带隙特性及轴向压缩对带隙的调控规律，计算了二振子结构的振动传输特性并与带隙分布进行了对比验证。搭建了二振子结构振动特性实验平台，测得了该结构的传输特性曲线，与实验结果相对比，两者取得了较好的一致性。主要结论如下：
(1)对比分析了复合带隙可控超结构的4种不同构型带隙特性，数值结果表明该结构可产生局域共振型和布拉格散射型两种带隙分布；随局域共振振子数量增加，一定频率范围内，结构中带隙宽度增加，数量减少，且带隙中心频率上移；
(2)轴向压缩对该结构带隙分布具有一定的调控作用，随着轴向压缩值的增加，布拉格带隙中心频率逐渐上移，同时出现更多的完全带隙和方向带隙，局域共振型带隙变化较小，4种复合带隙可控超结构带隙调控规律基本一致；
(3)复合带隙可控超结构在带隙范围内具有较好的减振效果，振动传输特性曲线的实验结果与数值结果中衰减部分基本吻合。因此，弹性波在带隙频率范围内会出现明显的衰减。
本文提出的复合带隙可控超结构可以实现结构在不同工况下的带隙调控，在航空航天、轨道交通等领域有广阔的应用前景。结构由软材料组成，理论分析存在一定难度，且变形较大时出现非线性特性，在未来工作中将开展内在机制的理论分析及非线性特性研究。
-
![]()
图 2 MesoMR12-060H-I 岩石微观孔隙结构分析与成像系统
Figure 2. MesoMR12-060H-I rock microscopic pore structure analysis and imaging system
![]()
图 6 (a) PF断裂形貌；(b) 纤维搭接；(c) BF-PF三维纤维网
Figure 6. (a) PF fracture morphology; (b) Fibers overlap; (c) Three-dimensional bearing fiber mesh of BF-PF
![]()
图 7 单掺BF试件横向弛豫时间分布
Figure 7. Transverse relaxation-time distribution of single doped BF specimen
![]()
图 8 单掺PF试件弛豫时间分布
Figure 8. Transverse relaxation-time distribution of single doped PF specimen
![]()
图 13 HBPRC横向弛豫时间与分形特征的关系
Sv—Cumulative pore volume fraction; T2—Transverse relaxation time
Figure 13. Relationship between transverse relaxation time and fractal characteristics of HBPRC
![]()
图 14 不同孔隙的HBPRC的孔隙结构分形维数
Figure 14. Fractal dimension of pore structure of HBPRC with different pores
![]()
图 15 纤维与混凝土基体粘结
ITZ—Interfacial transition zone; CH—Ca(OH)2
Figure 15. Bonding between fibers and concrete matrix
![]()
图 17 HBPRC抗压强度与孔隙结构分形维数的关系
R2—Goodness of fit
Figure 17. Relationship between compressive strength and fractal dimension of pore structure of HBPRC
表 1 胶凝材料和玄武岩纤维(BF)的化学组成(wt%)
Table 1 Chemical composition of cementitious materials and basalt fiber (BF) (wt%)
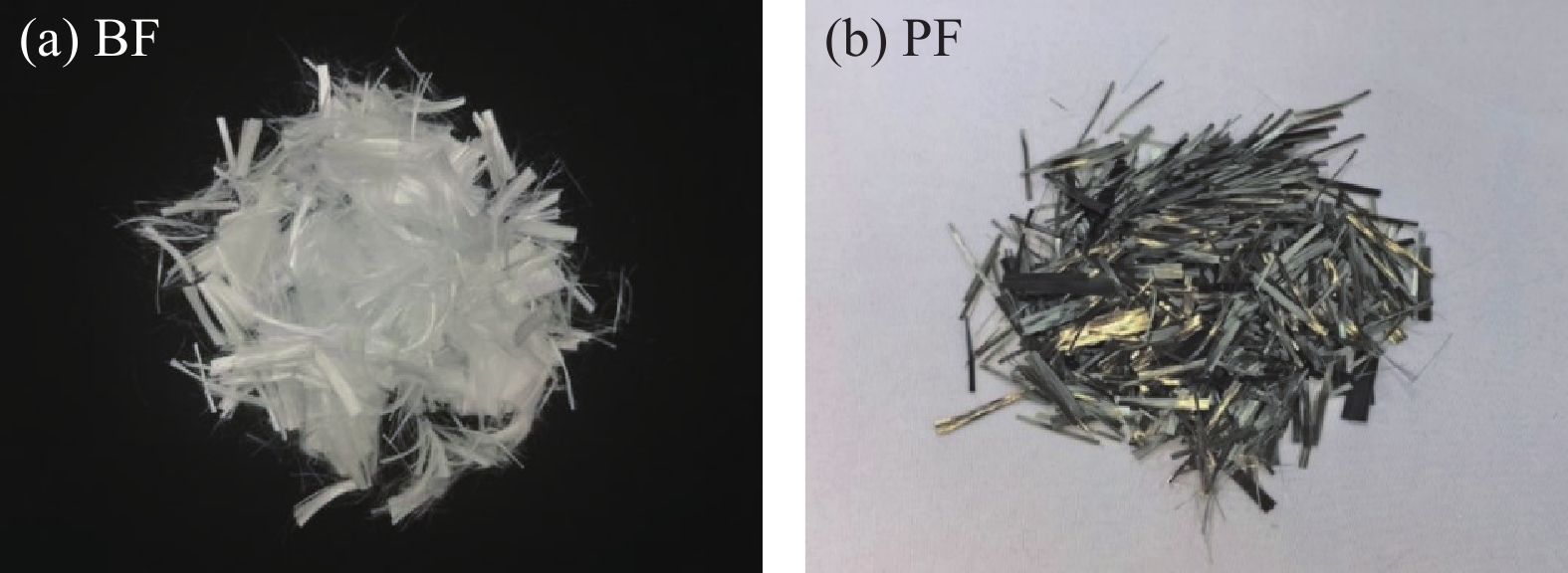
Composition SiO2 Al2O3 Fe2O3 CaO MgO Cement 34.67 7.90 2.93 35.50 1.77 Fly ash 50.77 22.68 5.64 5.98 1.74 BF 51.40 15.40 9.80 9.00 5.70 
下载: 导出CSV
表 2 BF和聚丙烯纤维(PF)的物理力学性能
Table 2 Physical and mechanical of BF and polypropylene fiber (PF)
Type Density/(kg·m−3) Tensile strength/MPa Elastic modulus/GPa Diameter/μm Length/mm BF 2.65 ≥ 2400 ≥40 15 18 PF 0.91 270 0.3 30 19
下载: 导出CSV
表 3 玄武岩-聚丙烯混杂纤维混凝土(HBPRC)配合比
Table 3 Mix proportions of hybrid basalt-polypropylene fiber-reinforced concrete (HBPRC)
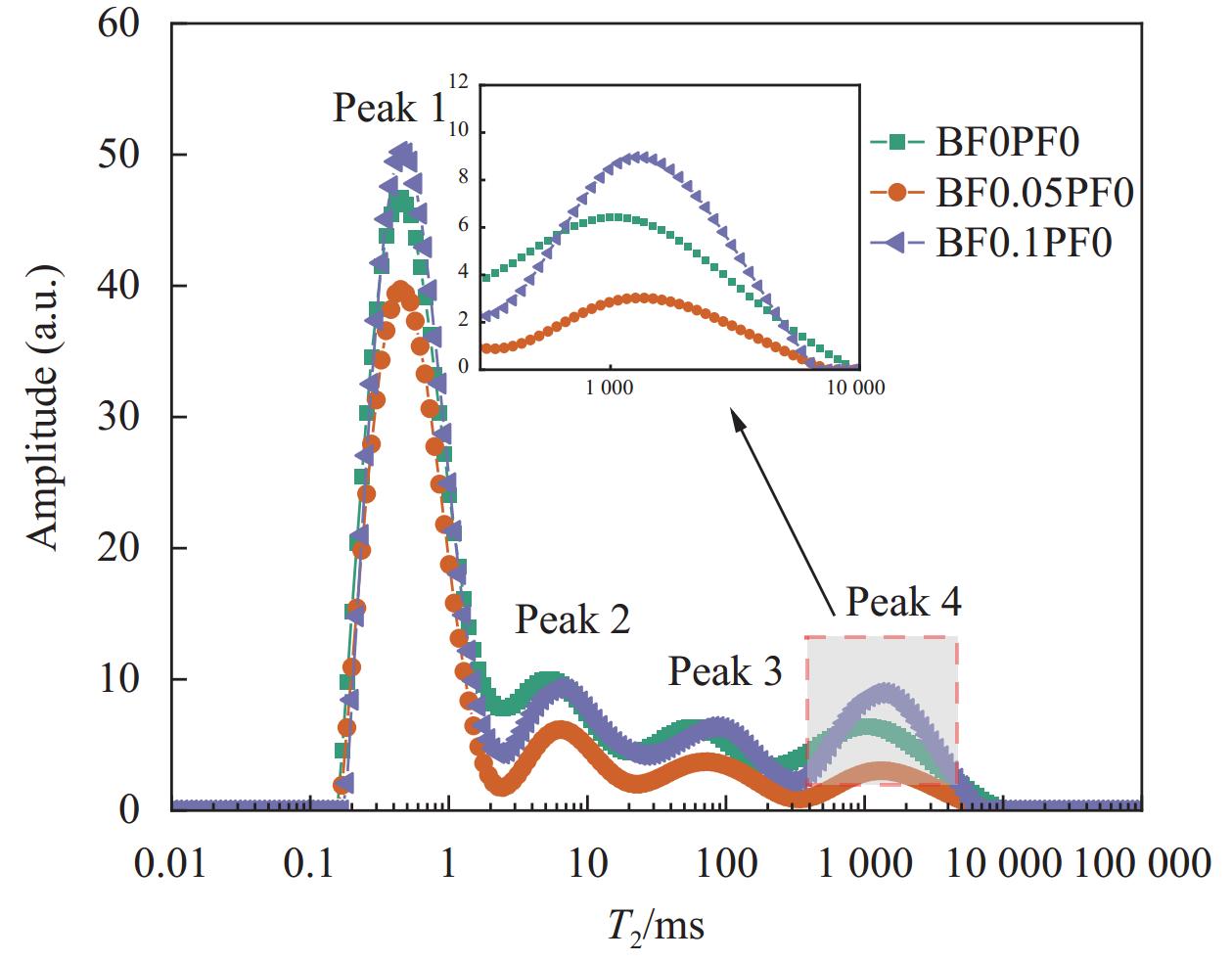
Mixture Mixture composition/(kg·m−3) C W CA S FA PBS BF PF BF0PF0 320 160 1068 712 100 6.3 0 0 BF0.05PF0 320 160 1068 712 100 6.3 1.3 0 BF0.1PF0 320 160 1068 712 100 6.3 2.6 0 BF0PF0.05 320 160 1068 712 100 6.3 0 0.5 BF0PF0.1 320 160 1068 712 100 6.3 0 0.9 BF0.05PF0.05 320 160 1068 712 100 6.3 1.3 0.5 BF0.1PF0.05 320 160 1068 712 100 6.3 2.6 0.5 BF0.05PF0.1 320 160 1068 712 100 6.3 1.3 0.9 BF0.1PF0.1 320 160 1068 712 100 6.3 2.6 0.9 Notes: "C" refers to cement; "W" refers to water; "CA" refers to coarse aggregate; "S" refers to river sand; "FA" refers to fly ash; "PBS" refers to performance water reducer; "0", "0.05", "0.1" represent the fiber volume content of 0vol%, 0.05vol%, 0.1vol%, respectively.
下载: 导出CSV
表 4 HBPRC的横向弛豫T2谱峰面积比例
Table 4 Transverse relaxation-time T2 spectral peak area percentage of HBPRC
Mixture Peak 1/% Peak 2/% Peak 3/% Peak 4/% BF0PF0 62.60 13.91 10.18 13.28 BF0.05PF0 72.54 11.55 8.70 7.19 BF0.1PF0 61.79 13.66 10.07 14.46 BF0PF0.05 51.43 13.69 12.42 22.44 BF0PF0.1 56.05 13.77 10.25 19.92 BF0.05PF0.05 69.48 12.72 10.97 6.81 BF0.1PF0.05 64.08 13.52 9.44 12.94 BF0.05PF0.1 55.91 15.72 10.96 17.39 BF0.1PF0.1 65.80 14.44 12.14 7.60
下载: 导出CSV
-
[1] LEE J H, CHO B, CHOI E. Flexural capacity of fiber reinforced concrete with a consideration of concrete strength and fiber content[J]. Construction and Building Materials, 2017, 138: 222-231. DOI: 10.1016/j.conbuildmat.2017.01.096
[2] DIAMOND S. Aspects of concrete porosity revisited[J]. Cement and Concrete Research, 1999, 29(8): 1181-1188. DOI: 10.1016/S0008-8846(99)00122-2
[3] 黄东明, 宗帅, 刘真真, 等. PVA纤维地聚合物再生混凝土轴拉性能研究[J]. 内蒙古工业大学学报(自然科学版), 2023, 42(3): 265-272. HUANG Dongming, ZONG Shuai, LIU Zhenzhen, et al. Axial tensile properties of PVA fiber reinforced recycled geopolymer concrete[J]. Journal of Inner Mongolia University of Technology, 2023, 42(3): 265-272(in Chinese).
[4] SIDDIKA A, AL MAMUN M A, ALYOUSEF R, et al. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review[J]. Journal of Building Engineering, 2019, 25: 100798. DOI: 10.1016/j.jobe.2019.100798
[5] ZHANG J, BIAN F, ZHANG Y, et al. Effect of pore structures on gas permeability and chloride diffusivity of concrete[J]. Construction and Building Materials, 2018, 163: 402-413. DOI: 10.1016/j.conbuildmat.2017.12.111
[6] JIANG C, FAN K, WU F, et al. Experimental study on the mechanical properties and microstructure of chopped basalt fibre reinforced concrete[J]. Materials & Design, 2014, 58: 187-193.
[7] 孙伟, 钱红萍, 陈惠苏. 纤维混杂及其与膨胀剂复合对水泥基材料的物理性能的影响[J]. 硅酸盐学报, 2000(2): 95-99, 104. DOI: 10.3321/j.issn:0454-5648.2000.02.001 SUN Wei, QIAN Hongping, CHEN Huisu. The effect of the combination of hybrid fibers and expansive agent on the physical properties of cementitious composities[J]. Chinese Journal of Ceramics, 2000(2): 95-99, 104(in Chinese). DOI: 10.3321/j.issn:0454-5648.2000.02.001
[8] 刘洋. 纤维对筋材与自密实混凝土的粘结性能的影响[D]. 大连: 大连理工大学, 2010. LIU Yang. Fiber effect on bond behaviour between bars and self-compacting concrete matrix[D]. Dalian: Dalian University of Technology, 2010(in Chinese).
[9] 张兰芳, 尹玉龙, 刘晶伟, 等. 玄武岩纤维增强混凝土力学性能的研究[J]. 硅酸盐通报, 2014, 33(11): 2834-2837. ZHANG Lanfang, YIN Yulong, LIU Jingwei, et al. Mechanical properties study on basalt fiber reinforced concrete[J]. Bulletin of the Chinese Ceramic Society, 2014, 33(11): 2834-2837(in Chinese).
[10] 王嘉旋. 高性能纤维喷射混凝土力学性能试验研究[D]. 北京: 北京交通大学, 2021. WANG Jiaxuan. Experimental study on mechanical properties of high performance fiber reinforced shotcrete[D]. Beijing: Beijing Jiaotong University, 2021(in Chinese).
[11] 翟荃. 玄武岩-聚丙烯纤维陶粒混凝土力学性能及耐久性研究[D]. 荆州: 长江大学, 2023. ZHAI Quan. Study on mechanics and durability of basalt-polypropylene hybrid fiber lightweight aggregate concrete[D]. Jingzhou: Yangtze University, 2023(in Chinese).
[12] 张克纯. 聚丙烯-玄武岩混杂纤维混凝土的耐久性能研究[J]. 非金属矿, 2020, 43(5): 45-47, 51. DOI: 10.3969/j.issn.1000-8098.2020.05.014 ZHANG Kechun. Study on the durability of polypropylene-basalt fiber concrete[J]. Non-Metallic Mines, 2020, 43(5): 45-47, 51(in Chinese). DOI: 10.3969/j.issn.1000-8098.2020.05.014
[13] 刘大昌. 玄武岩聚丙烯混杂纤维混凝土性能试验研究[D]. 重庆: 重庆交通大学, 2018. LIU Dachang. Study on the properties of basalt and polypropylene mixed fiber concrete[D]. Chongqing: Chongqing Jiaotong University, 2018(in Chinese).
[14] 骆冰冰, 毕巧巍. 混杂纤维自密实混凝土孔结构对抗压强度影响的试验研究[J]. 硅酸盐通报, 2012, 31(3): 626-630. LUO Bingbing, BI Qiaowei. Experimental study on the influence of pore structure of hybrid fibers self-compacting concrete on compressive strength[J]. Bulletin of the Chinese Ceramic Society, 2012, 31(3): 626-630(in Chinese).
[15] CHEN Y, AL-NESHAWY F, PUNKKI J. Investigation on the effect of entrained air on pore structure in hardened concrete using MIP[J]. Construction and Building Materials, 2021, 292: 123441. DOI: 10.1016/j.conbuildmat.2021.123441
[16] ZHU Z, HUO W, SUN H, et al. Correlations between unconfined compressive strength, sorptivity and pore structures for geopolymer based on SEM and MIP measurements[J]. Journal of Building Engineering, 2023, 67: 106011. DOI: 10.1016/j.jobe.2023.106011
[17] TANG S W, HE Z, CAI X H, et al. Volume and surface fractal dimensions of pore structure by NAD and LT-DSC in calcium sulfoaluminate cement pastes[J]. Construction and Building Materials, 2017, 143: 395-418. DOI: 10.1016/j.conbuildmat.2017.03.140
[18] VÖLKL J J, BEDDOE R E, SETZER M J. The specific surface of hardened cement paste by small-angle X-ray scattering effect of moisture content and chlorides[J]. Cement and Concrete Research, 1987, 17(1): 81-88. DOI: 10.1016/0008-8846(87)90062-7
[19] FORSE A C, MERLET C, GREY C P, et al. NMR studies of adsorption and diffusion in porous carbonaceous materials[J]. Progress in Nuclear Magnetic Resonance Spectroscopy, 2021, 124: 57-84.
[20] ZENG Q, LUO M, PANG X, et al. Surface fractal dimension: An indicator to characterize the microstructure of cement-based porous materials[J]. Applied Surface Science, 2013, 282: 302-307. DOI: 10.1016/j.apsusc.2013.05.123
[21] FU H, WANG X, ZHANG L, et al. Investigation of the factors that control the development of pore structure in lacustrine shale: A case study of block X in the Ordos Basin, China[J]. Journal of Natural Gas Science and Engineering, 2015, 26: 1422-1432. DOI: 10.1016/j.jngse.2015.07.025
[22] MA X, WANG H, ZHOU S, et al. Insights into NMR response characteristics of shales and its application in shale gas reservoir evaluation[J]. Journal of Natural Gas Science and Engineering, 2020, 84: 103674. DOI: 10.1016/j.jngse.2020.103674
[23] ZHANG S, ZHENG S, WANG E, et al. Grey model study on strength and pore structure of self-compacting concrete with different aggregates based on NMR[J]. Journal of Building Engineering, 2023, 64: 105560. DOI: 10.1016/j.jobe.2022.105560
[24] FLEURY M, CHEVALIER T, BERTHE G, et al. Water diffusion measurements in cement paste, mortar and concrete using a fast NMR based technique[J]. Construction and Building Materials, 2020, 259: 119843. DOI: 10.1016/j.conbuildmat.2020.119843
[25] HAN X, FENG J J, WANG B M. Relationship between fractal feature and compressive strength of fly ash-cement composite cementitious materials [J]. Cement and Concrete Composites, 2023, 139: 105052.
[26] 谢恩慧, 周春圣. 利用低场磁共振弛豫测孔技术预测水泥基材料的水分渗透率[J]. 硅酸盐学报, 2020, 48(11): 1808-1816. XIE Enhui, ZHOU Chunsheng. Prediction of water permeability for cement-based material from the pore size distribution achieved by low-field nuclear magnetic resonance relaxation technique [J]. Chinese Journal of Ceramics, 2020, 48(11): 1808-1816(in Chinese).
[27] LAN X, ZENG X, ZHU H, et al. Experimental investigation on fractal characteristics of pores in air-entrained concrete at low atmospheric pressure[J]. Cement and Concrete Composites, 2022, 130: 104509. DOI: 10.1016/j.cemconcomp.2022.104509
[28] FAN J, ZHANG B. Study on freeze-thaw deterioration model of new-to-old concrete based on pore surface fractal characteristics[J]. Construction and Building Materials, 2024, 421: 135757. DOI: 10.1016/j.conbuildmat.2024.135757
[29] MA H, SUN J, WU C, et al. Study on the pore and microstructure fractal characteristics of alkali-activated coal gangue-slag mortars[J]. Materials, 2020, 13(11): 2442. DOI: 10.3390/ma13112442
[30] MAHAMUD M, LÓPEZ Ó, PIS J J, et al. Textural characterization of chars using fractal analysis[J]. Fuel Processing Technology, 2004, 86(2): 135-149.
[31] 中华人民共和国住房和城乡建设部. 混凝土力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for test methods of concrete physical and mechanical properties: GB/T 50081—2019[S]. Beijing: China Architecture and Building Press, 2019(in Chinese).
[32] 薛慧君, 申向东, 邹春霞, 等. 基于NMR的风积沙混凝土冻融孔隙演变研究[J]. 建筑材料学报, 2019, 22(2): 199-205. XUE Huijun, SHEN Xiangdong, ZOU Chunxia, et al. Freeze-thaw pore evolution of aeolian sand concrete based on nuclear magnetic resonance[J]. Journal of Building Materials, 2019, 22(2): 199-205(in Chinese).
[33] 朱翔琛, 张云升, 刘志勇, 等. 基于核磁共振技术的硫酸盐冻融下机制骨料混凝土孔结构演变规律研究[J]. 复合材料学报, 2024, 41(10): 5478-5491. ZHU Xiangchen, ZHANG Yunsheng, LIU Zhiyong, et al. Study on the evolution of pore structure of manufactured aggregate concrete under sulfate freeze-thaw based on nuclear magnetic resonance technology[J]. Acta Materiae Compositae Sinica, 2024, 41(10): 5478-5491(in Chinese).
[34] ZHAO K, MA C, YANG J, et al. Pore fractal characteristics of fiber-reinforced backfill based on nuclear magnetic resonance[J]. Powder Technology, 2023, 426: 118678. DOI: 10.1016/j.powtec.2023.118678
[35] 高真, 曹鹏, 孙新建, 等. 玄武岩纤维混凝土抗压强度分析与微观表征[J]. 水力发电学报, 2018, 37(8): 111-120. DOI: 10.11660/slfdxb.20180812 GAO Zhen, CAO Peng, SUN Xinjian, et al. Compressive strength analysis and microscopic characterization of basalt fiber reinforced concrete[J]. Journal of Hydroelectric Engineering, 2018, 37(8): 111-120(in Chinese). DOI: 10.11660/slfdxb.20180812
[36] 刘卫东, 苏文悌, 王依民. 冻融循环作用下纤维混凝土的损伤模型研究[J]. 建筑结构学报, 2008(1): 124-128. DOI: 10.3321/j.issn:1000-6869.2008.01.018 LIU Weidong, SU Wenti, WANG Yimin. Research on damage model of fiber concrete under action of freeze-thaw cycle[J]. Journal of Building Strucures, 2008(1): 124-128(in Chinese). DOI: 10.3321/j.issn:1000-6869.2008.01.018
[37] HUO L, BI J, ZHAO Y, et al. Constitutive model of steel fiber reinforced concrete by coupling the fiber inclining and spacing effect[J]. Construction and Building Materials, 2021, 280: 122423. DOI: 10.1016/j.conbuildmat.2021.122423
[38] 焦华喆, 韩振宇, 陈新明, 等. 玄武岩纤维对喷射混凝土力学性能及微观结构的影响机制[J]. 复合材料学报, 2019, 36(8): 1926-1934. JIAO Huazhe, HAN Zhenyu, CHEN Xinming, et al. Influence mechanism of basalt fibers on the toughness and microstructure of spray concrete[J]. Acta Materiae Compositae Sinica, 2019, 36(8): 1926-1934(in Chinese).
[39] WANG D, JU Y, SHEN H, et al. Mechanical properties of high performance concrete reinforced with basalt fiber and polypropylene fiber[J]. Construction and Building Materials, 2019, 197: 464-473. DOI: 10.1016/j.conbuildmat.2018.11.181
[40] CHEN F, XU B, JIAO H, et al. Fiber distribution and pore structure characterization of basalt fiber reinforced concrete[J]. Journal of China University of Mining and Technology, 2021, 2: 273-280.
[41] GUO Y, HU X, LYU J. Experimental study on the resistance of basalt fibre-reinforced concrete to chloride penetration[J]. Construction and Building Materials, 2019, 223: 142-155. DOI: 10.1016/j.conbuildmat.2019.06.211
[42] NIU D T, SU L, LUO Y, et al. Experimental study on mechanical properties and durability of basalt fiber reinforced coral aggregate concrete[J]. Construction and Building Materials, 2020, 237: 117628. DOI: 10.1016/j.conbuildmat.2019.117628
[43] XU L, DENG F, CHI Y. Nano-mechanical behavior of the interfacial transition zone between steel-polypropylene fiber and cement paste[J]. Construction and Building Materials, 2017, 145: 619-638. DOI: 10.1016/j.conbuildmat.2017.04.035
[44] 薛翠真, 申爱琴, 郭寅川. 基于孔结构参数的掺CWCPM混凝土抗压强度预测模型的建立[J]. 材料导报, 2019, 33(8): 1348-1353. XUE Cuizhen, SHEN Aiqin, GUO Yinchuan. Prediction model for the compressive strength of concrete mixed with CWCPM based on pore structure parameters [J] Materials Reports, 2019, 33(8): 1348-1353(in Chinese).
[45] XIONG Q X, TONG L Y, ZHANG Z D, et al. A new analytical method to predict permeability properties of cementitious mortars: The impacts of pore structure evolutions and relative humidity variations[J]. Cement and Concrete Composites, 2023, 137: 104912. DOI: 10.1016/j.cemconcomp.2022.104912
[46] TONG L Y, XIONG Q X, ZHANG Z D, et al. A novel lattice model to predict chloride diffusion coefficient of un-saturated cementitious materials based on multi-typed pore structure characteristics[J]. Cement and Concrete Research, 2024, 176: 107351.
[47] YU B M, LI J H. A geometry model for tortuosity of flow path in porous media[J]. Chinese Physics Letters, 2004, 21(8): 1569. DOI: 10.1088/0256-307X/21/8/044
[48] 罗祥. 引气剂低温作用效果及其温度敏感性机理[D]. 北京: 中国建筑材料科学研究总院, 2023. LUO Xiang. Performance of air-entraining agents at low temperature and its temperature sensitivity mechanism[D]. Beijing: China Building Materials Academy, 2023(in Chinese).
[49] LAI J, WANG G, FAN Z, et al. Fractal analysis of tight shaly sandstones using nuclear magnetic resonance measurements[J]. AAPG Bulletin, 2018, 102(2): 175-193. DOI: 10.1306/0425171609817007
[50] 张金喜, 金珊珊. 水泥混凝土微观孔隙结构及其作用[M]. 北京: 中国科学技术出版社, 2014: 46-48. ZHANG Jinxi, JIN Shanshan. Cement concrete microscopic pore structure and its role[M]. Beijing: Science and Technology of China press, 2014: 46-48(in Chinese).
[51] ZHANG B, LI S. Determination of the surface fractal dimension for porous media by mercury porosimetry[J]. Industrial & Engineering Chemistry Research, 1995, 34(4): 1383-1386.
[52] LI Y, ZHANG J, HE Y, et al. A review on durability of basalt fiber reinforced concrete[J]. Composites Science and Technology, 2022, 225: 109519. DOI: 10.1016/j.compscitech.2022.109519
[53] ZHANG W, SHI D, SHEN Z, et al. Reduction of the calcium leaching effect on the physical and mechanical properties of concrete by adding chopped basalt fibers[J]. Construction and Building Materials, 2023, 365: 130080. DOI: 10.1016/j.conbuildmat.2022.130080
[54] LI J J, NIU J G, WAN C J, et al. Investigation on mechanical properties and microstructure of high performance polypropylene fiber reinforced lightweight aggregate concrete[J]. Construction and Building Materials, 2016, 118: 27-35. DOI: 10.1016/j.conbuildmat.2016.04.116
[55] ZAMBRANO O A, CORONADO J J, RODRÍGUEZ S A. Mechanical properties and phases determination of low carbon steel oxide scales formed at 1200℃ in air[J]. Surface and Coatings Technology, 2015, 282: 155-162. DOI: 10.1016/j.surfcoat.2015.10.028
[56] 本斯迪德. 水泥的结构和性能[M]. 北京: 化学工业出版社, 2008: 113-114. BENSTED J. Structure and properties of cement[M]. Beijing: Chemical Industry Press of China, 2008: 113-114(in Chinese).
[57] HAN X, WANG B M, FENG J J. Relationship between fractal feature and compressive strength of concrete based on MIP[J]. Construction and Building Materials, 2022, 322: 126504. DOI: 10.1016/j.conbuildmat.2022.126504
-
其他相关附件
-
目的
研究不同掺量的玄武岩-聚丙烯混杂纤维增强混凝土(HBPRC)的谱分布、孔隙率、孔径分布、曲折度等孔隙特征以及孔隙结构分形维数与抗压强度的关系。
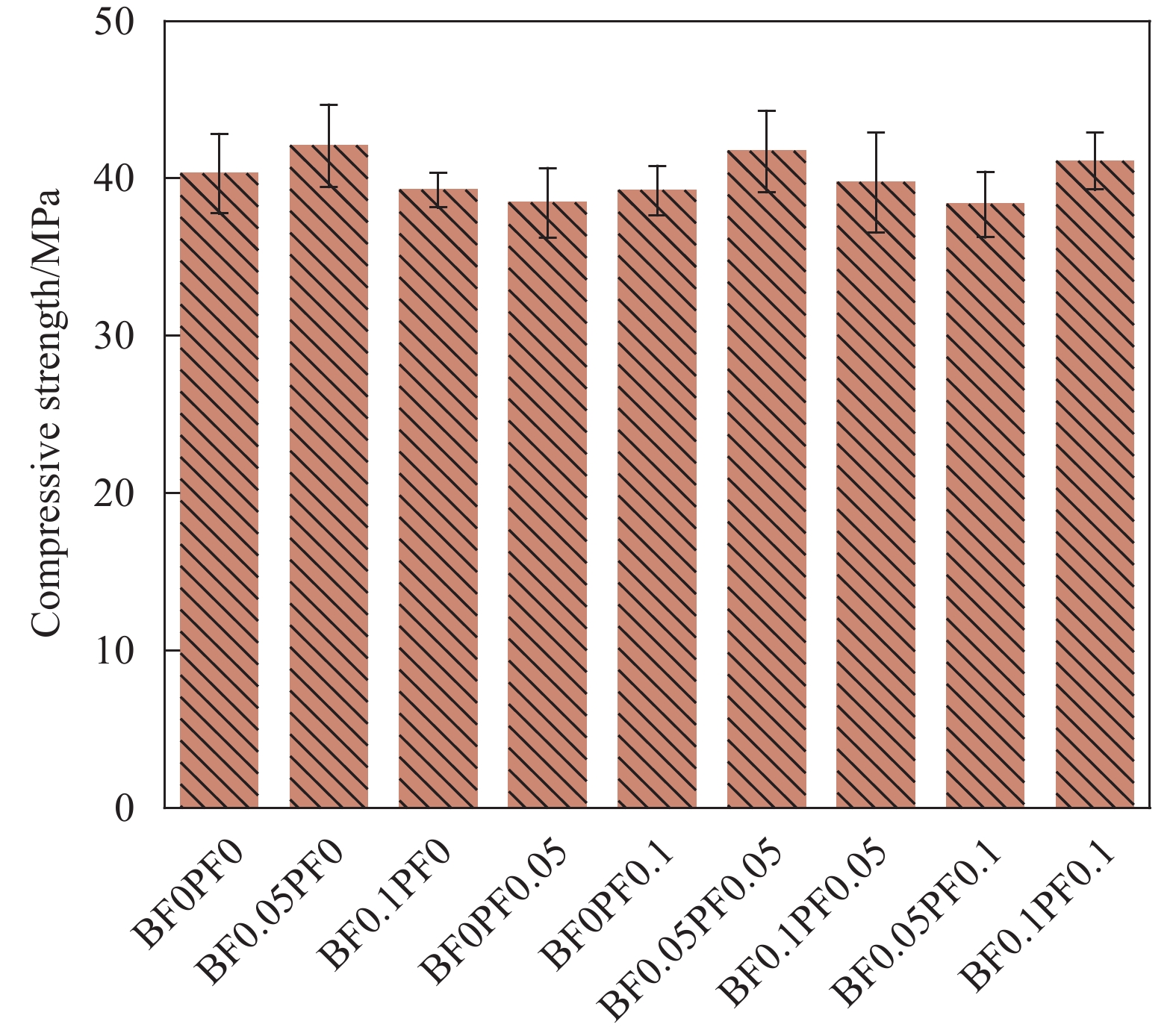
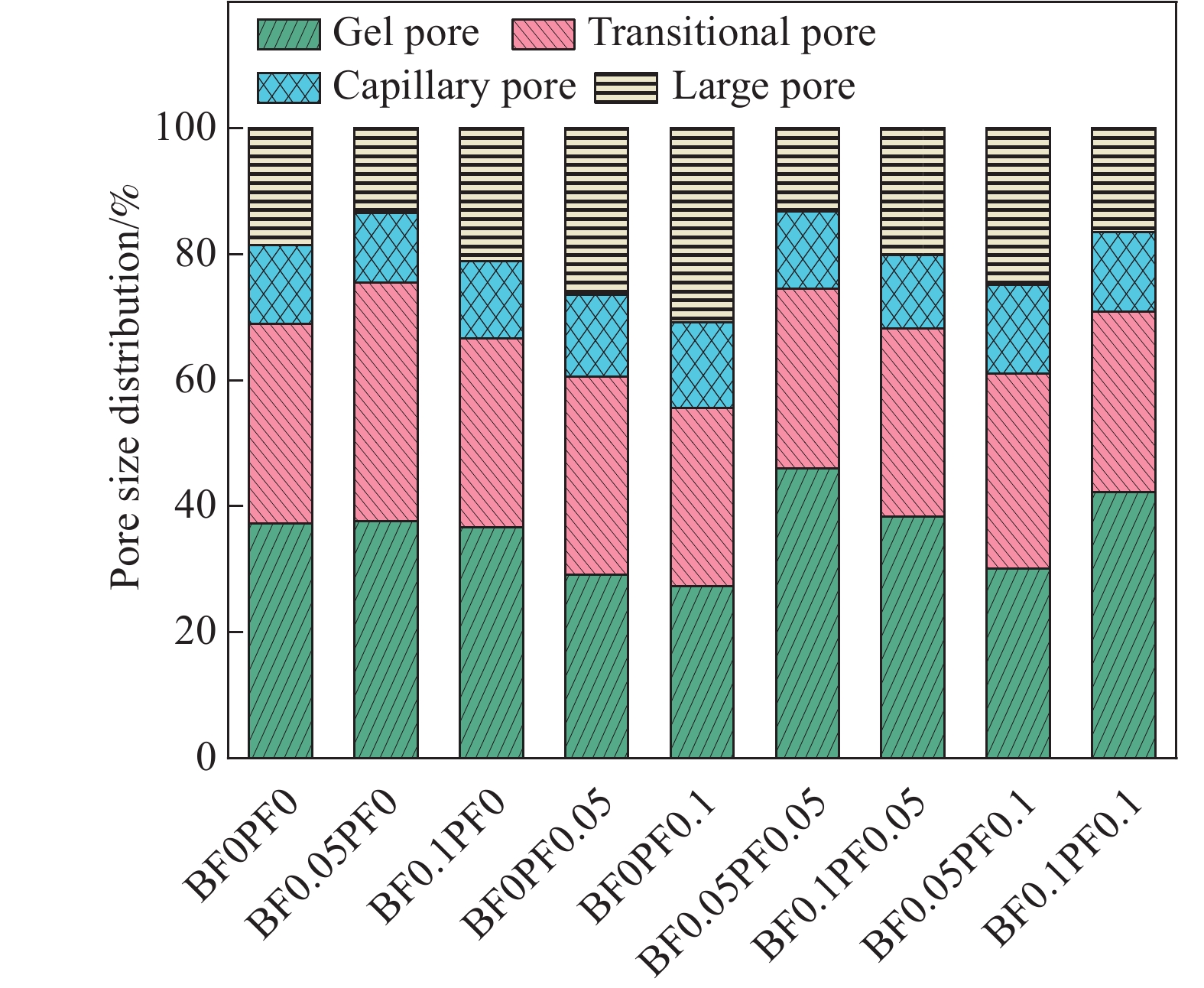
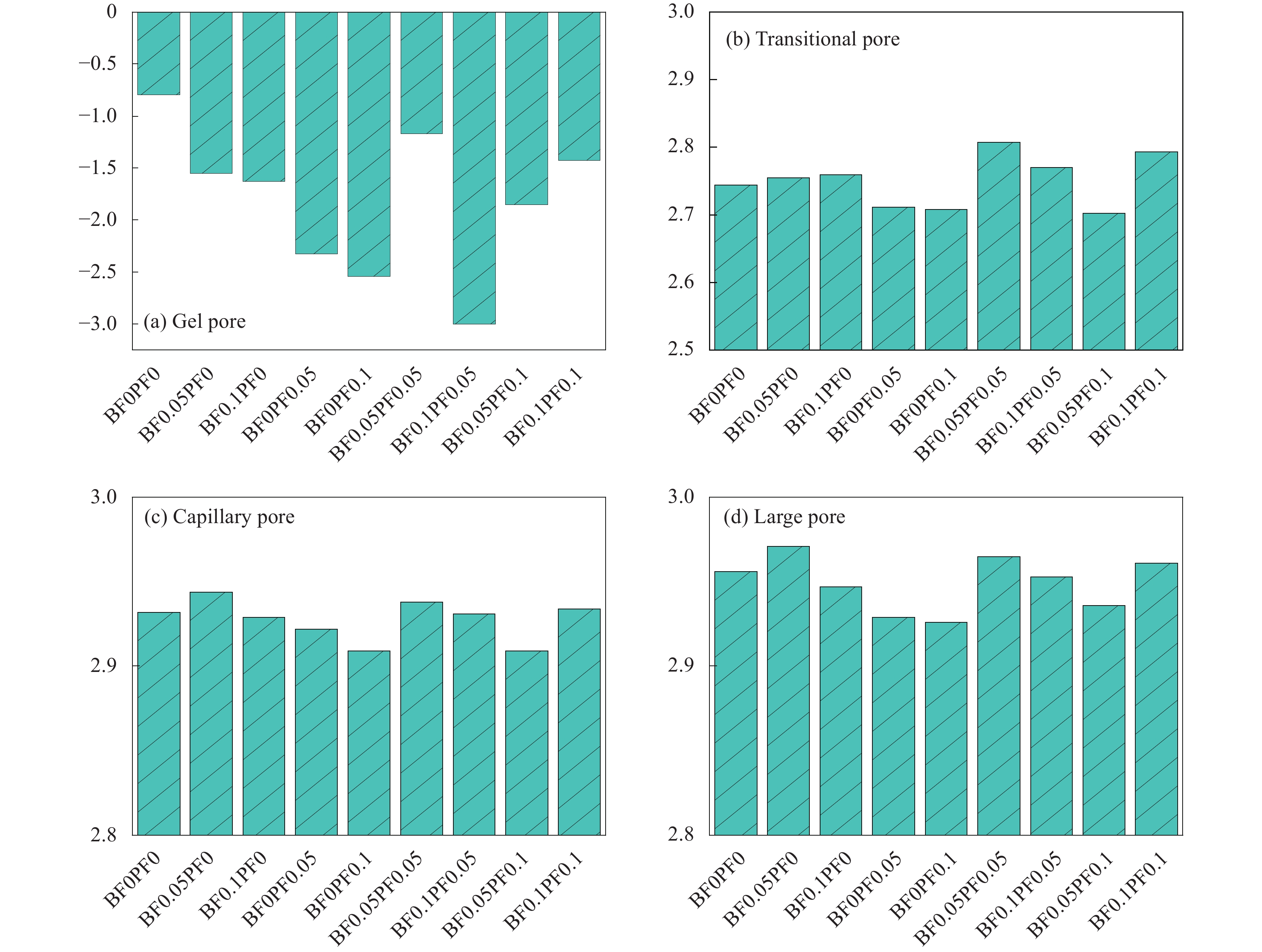
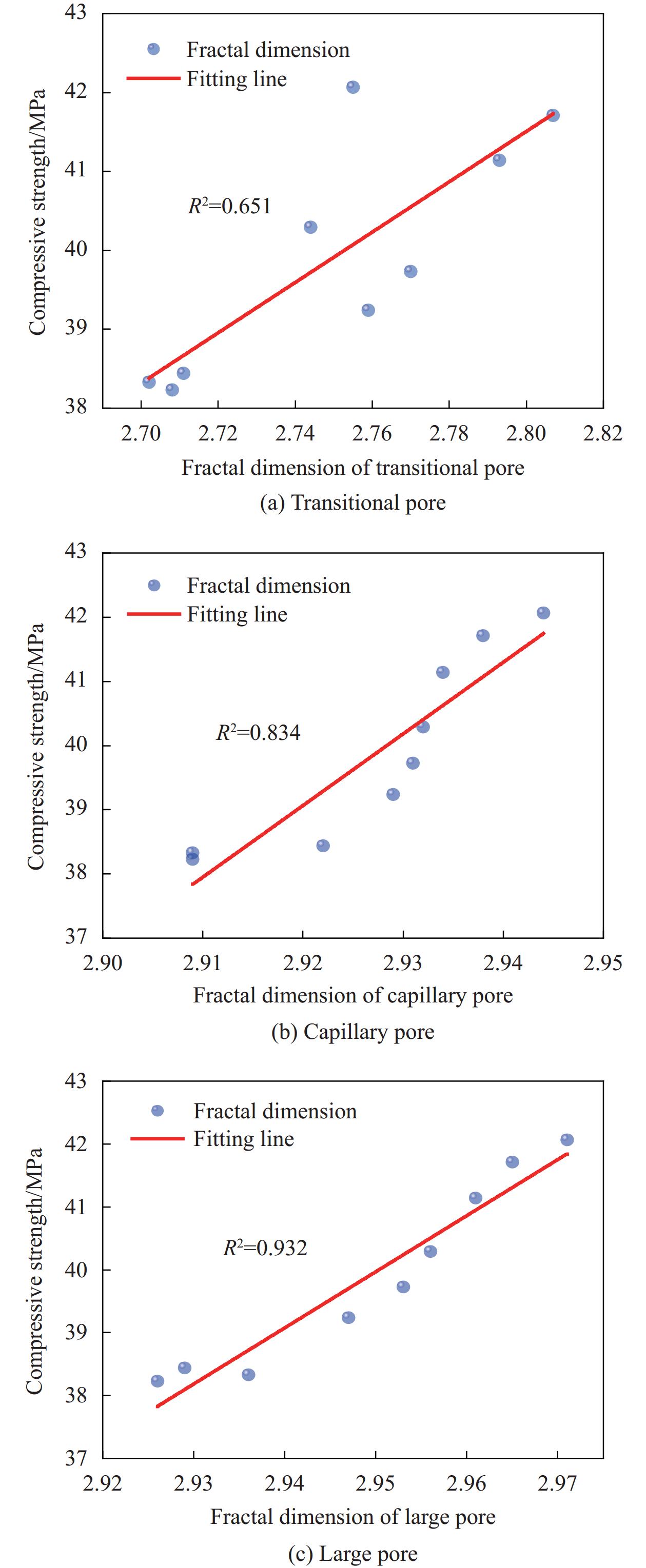
方法采用核磁共振技术、SEM微观形貌分析及分形理论共同揭示了BF、PF及BF-PF混杂对混凝土孔隙特征和抗压强度的影响。结果表明：适量的BF可以减小混凝土的孔隙率，随着PF含量增加，混凝土内部孔隙有扩大的趋势。BF和PF分别为0.05%混杂时可在混凝土内部形成均匀分布的三维纤维网，在混凝土中发挥出正协同作用。BF0.05PF0.05较普通混凝土孔隙率降低了1.47%，凝胶孔占比增大了8.76%，大孔占比降低了5.30%，混凝土的孔径分布得到优化，同时抗压强度和曲折度得到提高；通过分形理论表明HBPRC的孔隙结构具有明显的分形特征，孔隙结构分形维数随着孔径增大而减小，且与抗压强度有相关关系；通过微观分析认为，纤维在混凝土基体中的粘结状态和分布是影响HBPRC孔隙分形特征的主要原因。
结论综上，BF-PF混杂可以减小混凝土的孔隙率、优化孔径分布、提高孔隙的曲折度，使混凝土具有更好的孔隙特征，同时得出HBPRC的孔隙结构具有明显的分形特征，而且孔隙结构分形维数既可以作为其孔隙分形特征的定量表达，也可以客观反应其抗压强度。
-
混杂纤维可以在混凝土发挥各自的纤维优势，相互激发、相互补充，达到取长补短的效果，有利于减少混凝土的固有缺陷，提升混凝土的性能，在纤维混凝土领域吸引了越来越多的研究。玄武岩-聚丙烯混杂纤维增强混凝土(HBPRC)作为一种新型的建筑材料尚处于一个初期的探索阶段，明晰两种纤维及其混杂对混凝土孔隙结构的影响可助力HBPRC的推广及应用。
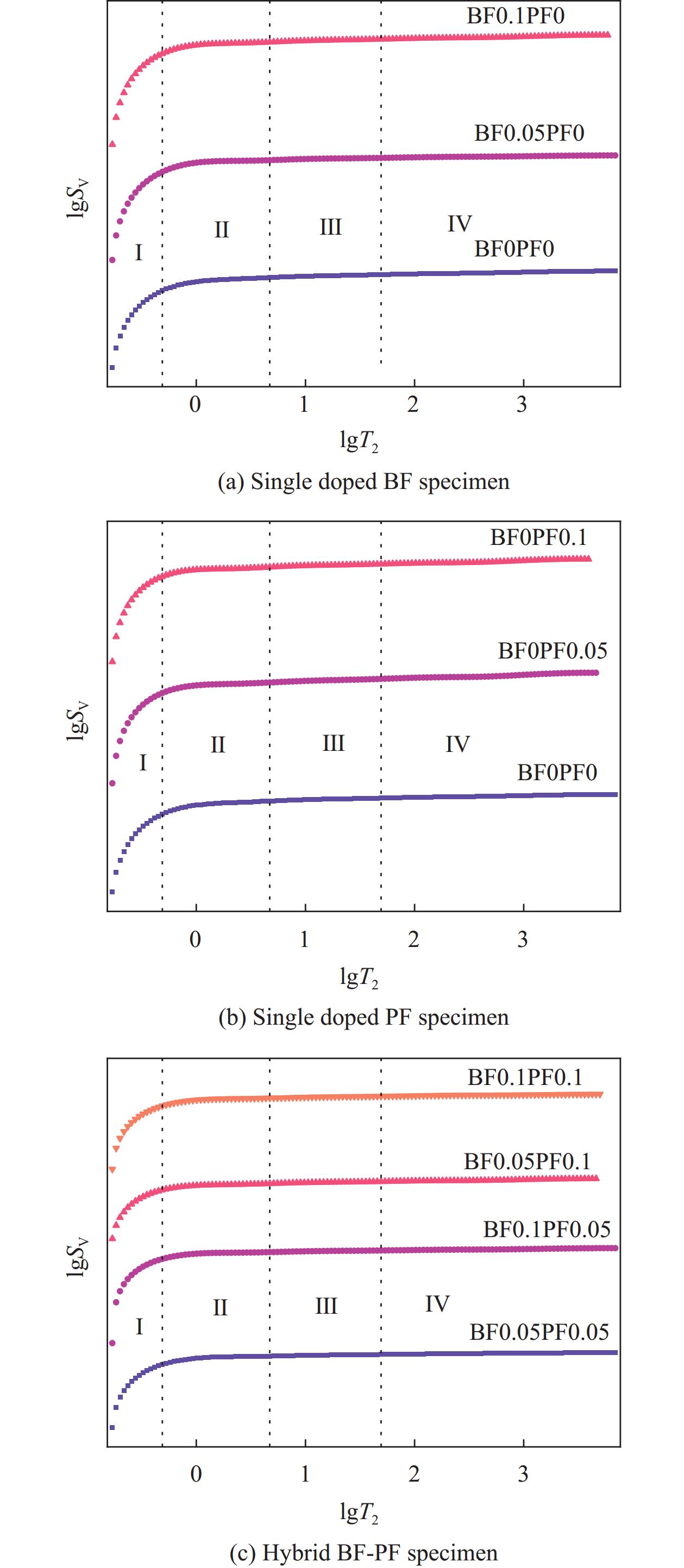
采用核磁共振(Nuclear Magnetic Resonance，NMR)测试了HBPRC的孔隙特征，对比分析了玄武岩纤维(BF)和聚丙烯纤维(PF)以及二者混杂对HBPRC的抗压强度、孔隙率、孔径分布和曲折度的影响，并基于核磁共振T2谱和孔隙结构分形理论对4个孔径区域的孔隙结构分形维数进行了量化。结果表明：随着BF的添加，T2谱反映出适量的BF可以减小混凝土的孔隙率，而且有利于减小大孔体积占比；而随着PF含量增加，T2谱面积增加，且混凝土内部孔隙有变大的趋势。掺入BF-PF混杂纤维对混凝土的孔隙特征会产生正协同作用，当BF和PF掺量均为0.05%时，协同作用最佳，与普通混凝土相比，抗压强度提高了3.52%、孔隙率降低了1.47%、曲折度提高了8.20%。凝胶孔体积占比增大了8.76%，大孔体积占比降低了5.30%，孔径分布得到优化。HBPRC的孔隙结构具有明显的分形特征，孔隙结构分形维数在过渡孔、毛细孔和大孔区域依次增加，此外，分形维数越大，抗压强度越大。通过微观分析认为，纤维在混凝土基体中的粘结状态和分布是影响HBPRC孔隙分形特征的主要原因。
计量
- 文章访问数: 252
- HTML全文浏览量: 104
- PDF下载量: 21
