Study on the complex band gap characteristic of controllable metastructure
-
摘要:
可控超结构可根据目标需求调节结构的带隙特性，实现对不同工况下结构减振的可控调节，在航空航天、轨道交通等工程领域具有广泛的应用前景。本文提出一种新型可控超结构构型，可同时产生局域共振和布拉格散射两种带隙，通过施加位移可实现对带隙的有效调控。应用COMSOL软件建立了该结构的有限元模型，研究了4种可控超结构构型的能带分布及其在外加位移激励作用下的带隙特性调控规律，开展了该结构的振动传输特性实验，并与数值结果进行对比验证。研究结果表明：四振子复合带隙可控超结构在0~800 Hz范围内共有3条完全带隙，第一阶带隙范围低至134.48~287.53 Hz，第二阶带隙范围为307.26~447.81 Hz，第三阶带隙范围为662.44~679.43 Hz。对比分析4种元胞构型带隙特性，在一定频率范围内，随着振子数量增加，带隙数量减少，带宽增加，带隙位置逐渐上移；施加结构位移可有效调控结构带隙，随着位移值增加，结构中低频局域共振带隙变化较小，布拉格带隙中心频率逐渐上移，并出现新带隙。本文的研究表明该结构在带隙范围内具有良好的减振特性，所设计的复合带隙可控超结构可实现对复合带隙的调控，为超结构减振设计研究提供有益的参考。
Abstract:The controllable metastructure can adjust the band gap characteristic of the structure according to the target requirements, and realize the controllable adjustment of structural vibration reduction under different working conditions. It has a wide application prospect in aerospace, rail transit and other engineering fields. A new controllable metastructure configuration was proposed, which can simultaneously generate two kinds of band gaps, local resonance and Bragg scattering. The band gap can be effectively controlled by applying displacement. The finite element model of the structure was established by COMSOL software. The energy band distribution of four controllable metastructure configurations and the regulation of band gap characteristics under external displacement excitation were studied. The vibration transmission characteristics of the structure were tested and compared with the numerical results. The results show that the four-oscillator composite band gap controllable metastructure has three complete band gaps in the range of 0-800 Hz. The first-order band gap range is as low as 134.48-287.53 Hz, the second-order band gap range is 307.26-447.81 Hz, and the third-order band gap range is 662.44-679.43 Hz. The band gap characteristics of four cell configurations were compared and analyzed. In a certain frequency range, as the number of oscillators increases, the number of band gaps decreases, the bandwidth increases, and the band gap position gradually moves up. The application of structural displacement can effectively control the structural band gap. As the displacement value increases, the low-frequency local resonance band gap in the structure changes little, and the center frequency of the Bragg band gap gradually moves up, and a new band gap appears. This study shows that the structure has good vibration reduction characteristics in the band gap range. The results show that the designed composite band gap controllable metastructure can realize the regulation of the composite band gap, which provides a useful reference for the research of metastructure vibration reduction design.
-
超材料[1-3]是一类由阵列化的人工微结构单元构成的复合结构。通过对超材料中的微结构单元及其排布方式进行调控设计，可产生低频弹性波带隙、负等效质量密度、负弹性模量、负折射等一系列超常效应[1]，因而在航空航天、工程建筑、轨道交通等[4-6]工程领域具有广泛的应用前景。声学超材料按照带隙形成的机制不同可以分为布拉格散射型和局域共振型[7]。布拉格散射起主导性作用的是周期性的材料特性与弹性波之间的相互作用；局域共振型起主导作用的是散射体的振动特性与基体中长波行波之间的耦合作用，从而抑制弹性波的传播[8]。
近年来，一些学者结合带隙形成机制，在低频范围内获得了较宽的带隙，并通过改变几何参数对带隙进行优化[9-13]。张思文等[14]提出了一种新型局域共振复合结构，实现了声子晶体的多重共振，在低频范围能打开多条共振带隙；Li等[15]研究了振动形式对韧带结构带隙的影响，通过拓扑优化提高了带隙的覆盖范围；Coffy等[16]设计了一种新型声子晶体，有效增加了带隙宽度；李孟昶等[17]设计了一种新型管道超结构构型，该结构在
2500 Hz内产生了两条完全带隙。传统超材料设计方法无法实现参数连续控制。实际工程中，结构随不同工况动态特性相应发生变化，可控超结构可根据目标需求调节结构的带隙特性，实现对不同工况下结构减振的可控调节。近年来，可控超结构日益受到学者们的广泛关注[18-20]。Yao等[21]研究了温度对不同晶格类型声子晶体的带隙调控机制；Geng等[22]研究了不同缺陷态声子晶体几何参数对弯曲波带隙的可控性，结果表明温度升高会造成带隙的频率范围减小；Dai等[23]结合声学拓扑绝缘体，利用温控可调拓扑声子晶体控制和引导水声，但调控范围比较有限。一些学者开展了通过外部激励实现带隙调控的研究。Li等[24-25]分别提出了一种衍生结构和混合声学超结构，可通过施加主动应变调控结构的带隙特性；Bertoldi和Boyce[26]研究了有限形变对周期性超弹性材料中弹性波传播的影响；Shan等[27]研究了周期性多孔超弹性声子晶体在施加载荷后的带隙特性，并分析了不同屈曲模式对带隙的调节效果；Li等[28]研究了结构不同屈曲模式对带隙的影响；Gei[29]研究了准无限周期梁的轴向波和弯曲波的能带结构，分析了轴向拉伸预应力调节结构弯曲波的特性；Huang等[30-32]研究了大形变和预拉伸应变对由超弹性材料制成的声子晶体板带隙的影响。目前已开展的可控超结构研究相对较少，且大多针对结构特定频率范围(低频或中高频)。本文提出一种复合带隙可控超结构构型，可同时产生低频的局域共振型带隙和较高频的布拉格散射型带隙，且通过调节振子位置和施加可控位移，可实现对结构复合带隙的有效调控。采用有限元法研究了4种不同复合带隙可控超结构的带隙特性及其在外加激励作用下的带隙调控规律，计算了该结构的振动传输特性曲线，并与实验结果进行了对比验证。
1. 构型设计及带隙特性
1.1 复合带隙可控超结构构型及其带隙计算
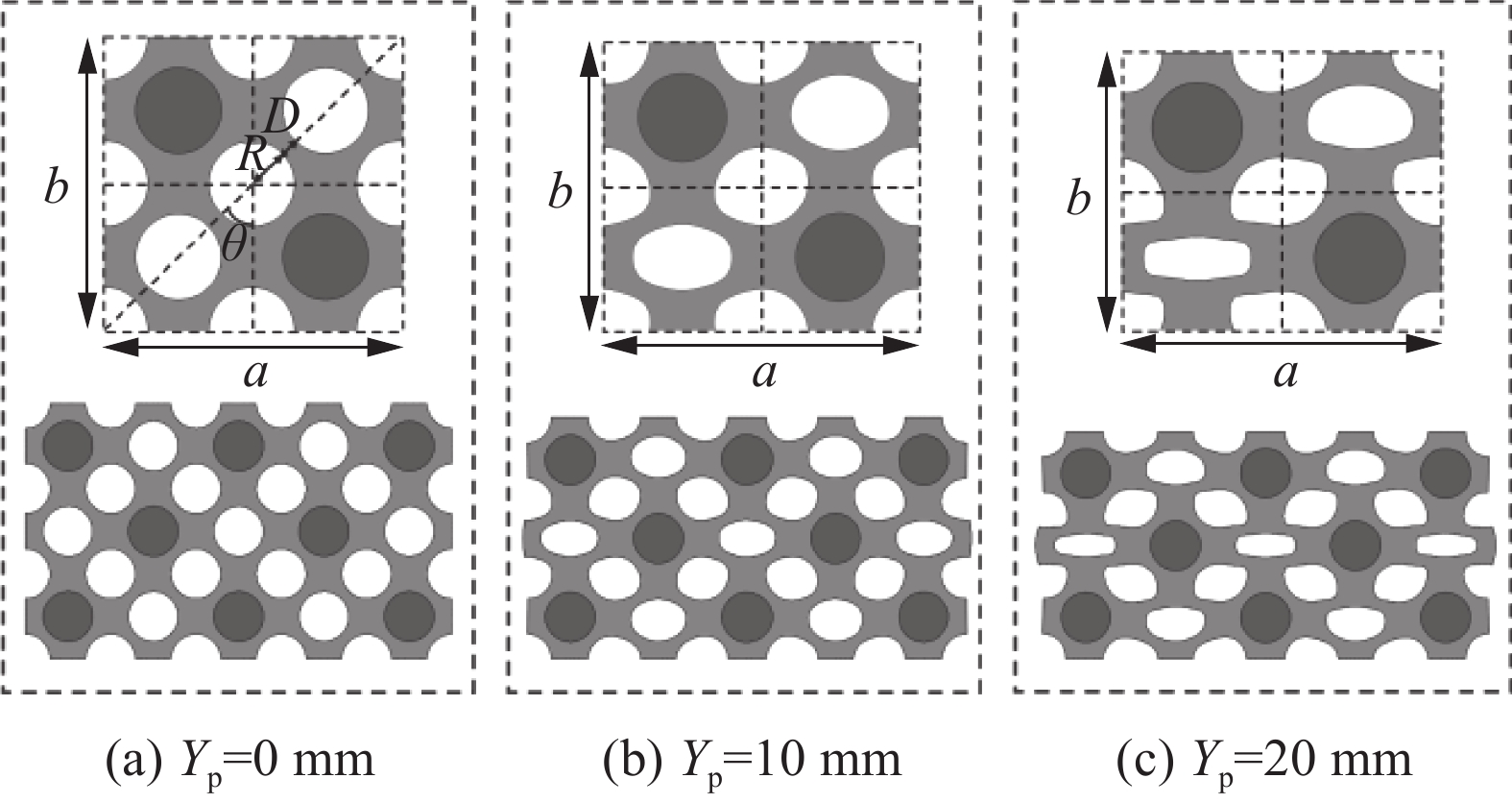
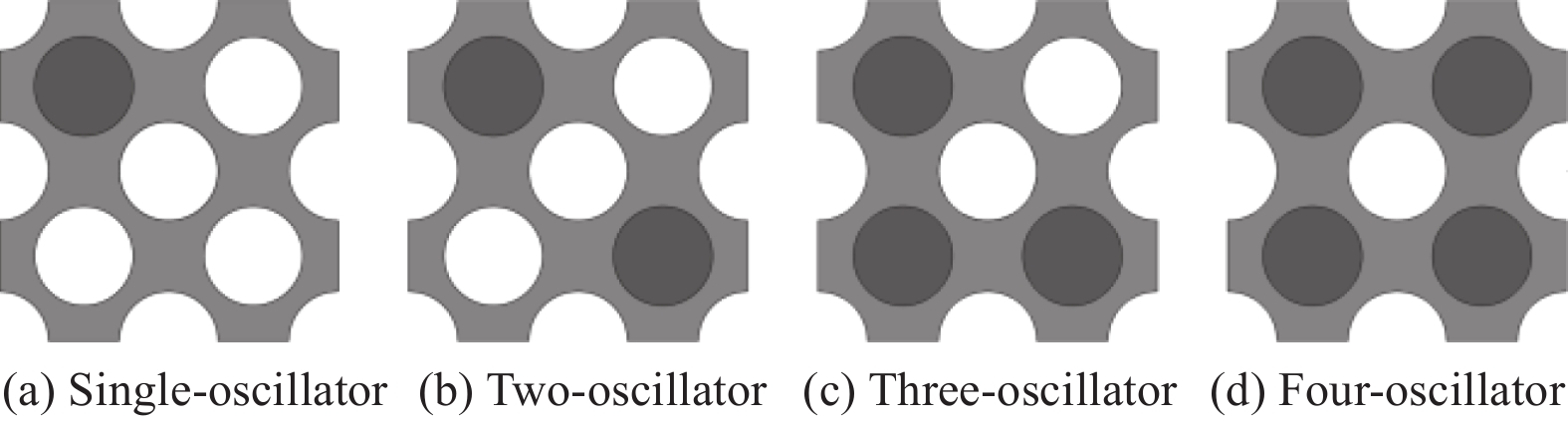
本文提出的复合带隙可控超结构的元胞构型如图1所示，该结构由多孔软材料及内部嵌入的局域共振振子构成。根据振子分布位置不同，分别有单振子、二振子、三振子及四振子4种构型，如图1所示。当对该结构施加可控轴向压缩时(图2)，结构逐渐发生变形，带隙结构分布随之改变，实现带隙的可调可控。
![]()
图 1 不同构型复合带隙可控超结构元胞Figure 1. Composite band gap controllable metastructure cells with different configurations![]()
图 2 不同轴向压缩下二振子构型超结构元胞及试件示意图Figure 2. Schematic diagram of the metastructure cells and specimens of two-oscillator configurations under different axial compressionsYp—Axial compression of the structure; a, b—Lattice constant; R—Radius of the hole; θ—Angle of the diagonal of the cell; D—Distance between the holes本文采用有限元法计算该结构在{\boldsymbol{{ M}\varGamma}} 、{\boldsymbol{\varGamma { X}}}、{\boldsymbol{{ X}{ M}}}方向上的能带分布。在忽略介质阻尼的影响下，弹性波在线弹性非均匀介质中的波动方程可以写为
\nabla \cdot \left[ {{\boldsymbol{C}}\left( {\boldsymbol{r}} \right):\nabla {\boldsymbol{u}}\left( {{\boldsymbol{r}},t} \right)} \right] = {\boldsymbol{\rho}} \left( {\boldsymbol{r}} \right)\frac{{{\partial ^2}{\boldsymbol{u}}\left( {{\boldsymbol{r}},t} \right)}}{{{\partial ^2}t}} (1) 式中：{\boldsymbol{ r}} 为位置矢量，{\boldsymbol{r}} = \left( {x,y,{\textit{z}}} \right)；{\boldsymbol{u}}\left( {\boldsymbol{r}} \right)为位移矢量，{\boldsymbol{u}}\left( {\boldsymbol{r}} \right) = \left( {{u_x},{u_y},{u_{\textit{z}}}} \right)；t为时间； {\boldsymbol{C}}\left({\boldsymbol{ r }}\right) 和{\boldsymbol{ \rho}} \left( {\boldsymbol{r}} \right) 分别为材料的弹性张量及密度张量。
由于波动方程中的系数具有周期性，因此根据Bloch-Floquet周期性边界条件，单胞离散形式的特征值方程及边界条件可表示为
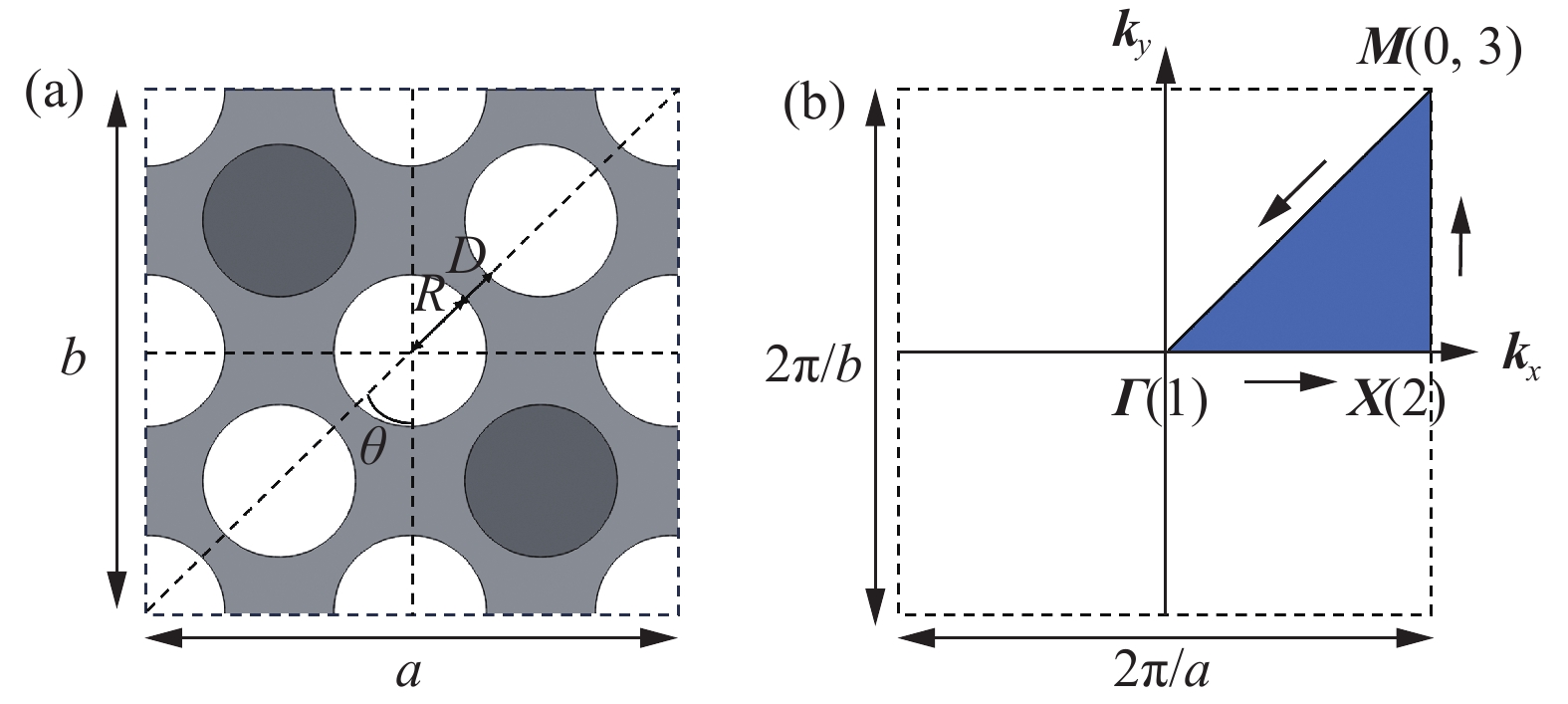
{\boldsymbol{KU}} = {\omega _n^2}{\boldsymbol{MU}} (2) \boldsymbol{u}\left(\boldsymbol{r},t\right)={\mathrm{e}}^{\mathrm{i}\left({\boldsymbol{k}} \, \cdot \,{\boldsymbol{r}}-\omega t\right)}\boldsymbol{u}_{\boldsymbol{k}}\left(\boldsymbol{r}\right) (3) 式中： {\boldsymbol{K}} 为结构的刚度矩阵；{\boldsymbol{M}}为质量矩阵；{\boldsymbol{U}}为单元节点位移矩阵；{\omega _n}为声子晶体的固有频率； {{\boldsymbol{u}}_{\boldsymbol{k}}}\left({\boldsymbol{ r}} \right) 是周期性边界源面的位移向量；i为虚数单位；ω为频率；{\boldsymbol{k}}为限制在第一布里渊区内的Bloch波矢，布里渊区示意图如图3所示。
![]()
图 3 Y_{\mathrm{p}}=0\; \mathrm{mm} 时二振子构型超结构元胞(a)及其第一不可约布里渊区(阴影区域) (b)M, Γ and X are the high symmetry points of the first irreducible Brillouin zone, respectively; kx and ky are the components of wave vector k in x and y directions, respectivelyFigure 3. Two-oscillator configuration metastructure cell (a) and its first irreducible Brillouin zone (Shaded region) (b) in Y_{\mathrm{p}}=0\; \mathrm{mm}联立式(2)与式(3)，令波矢{\boldsymbol{k}}扫略第一不可约布里渊区的边界，可得到一系列特征频率{\omega ^2}。在本文中选择波矢{\boldsymbol{k}}前50阶特征频率在第一布里渊区的变化来计算能带结构。对 {{\boldsymbol{k}}_x} 、 {{\boldsymbol{k}}_y} 的扫描路径进行设计，使波矢{\boldsymbol{k}}能够取到第一不可约布里渊区的所有值，其中波矢{\boldsymbol{k}}的方向及取值范围如图3中第一不可约布里渊区示意图所示，Bloch波矢{\boldsymbol{k}}的方向及 {{\boldsymbol{k}}_x} 、 {{\boldsymbol{k}}_y} 的关系如下：
{{\boldsymbol{k}}_x} = \left\{ {\begin{array}{l} {(1 - k)\dfrac{{\text{π}} }{a},0 < k < 1} \\ {(k - 1)\dfrac{{\text{π}} }{a},1 < k < 2} \\ {\dfrac{{\text{π}} }{a},2 < k < 3} \end{array}} \right.{\text{ }}{{\boldsymbol{k}}_y} = \left\{ {\begin{array}{l} {(1 - k)\dfrac{{\text{π}} }{a},0 < k < 1} \\ {0,1 < k < 2} \\ {(k - 2)\dfrac{{\text{π}} }{a},2 < k < 3} \end{array}} \right. (4) 进而可得到波矢k与频率\omega 的色散关系。
1.2 带隙特性分析
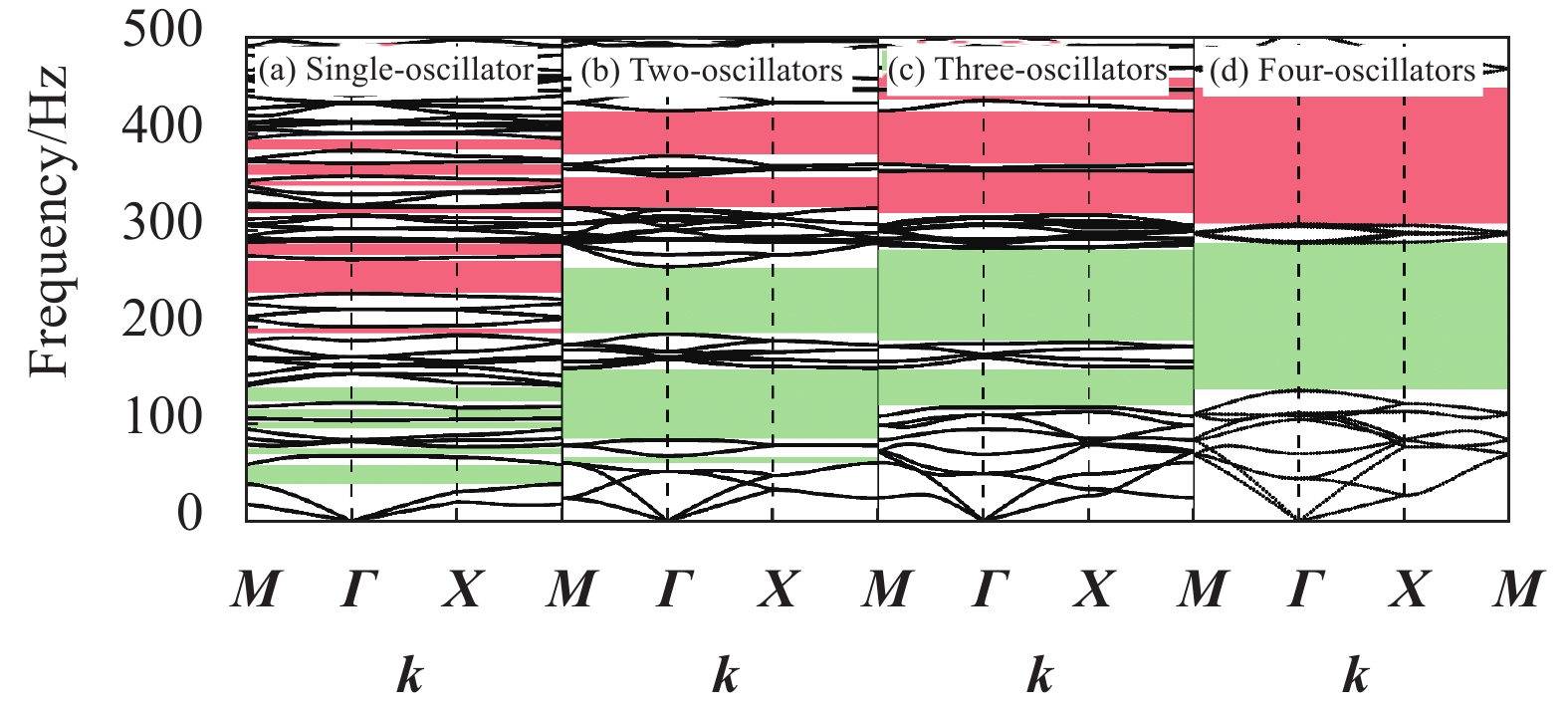
本文设计的复合带隙可控超结构采用硅橡胶材料制成，内部嵌入铅块作为其局域共振振子，其几何参数和材料参数如表1所示，未压缩情况下的晶格常数为a = b = 120\;{{\mathrm{mm}}} 。应用COMSOL软件建立了图1中4个元胞结构的有限元模型，并在相应位置施加Floquet周期性边界条件，应用特征频率求解器对布里渊区边界进行波矢扫描计算，可以得到元胞振动的能带结构图，并将它们进行对比，如图4所示。
表 1 几何参数和材料参数Table 1. Geometric parameters and material parametersGeometric parameters Value Material Material parameters Value R/mm 17.5 Silicon rubber E/MPa 0.870 ρ/(kg·m−3) 1230 D/mm 7.426 ν 0.499 Lead E/MPa 40.8 θ/(°) 45 ρ/(kg·m−3) 11340 ν 0.37 Notes：E—Elastic modulus；ρ—Density；ν—Poisson's ratio. ![]()
图 4 不同元胞构型 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构对比图Figure 4. Energy band structure comparison diagram of different cell configurations Y_{\mathrm{p}}=0\; \mathrm{mm}从图4可以看出，中间孔无填充情况下，局域共振振子规律排列在中间孔的四周，随局域共振振子数量增加，300 Hz内的低阶带隙宽度增加，结构中带隙数量逐渐减少，带隙位置逐渐上移；且随着振子数量增加，结构刚度逐渐增大进而导致了带隙中心频率增加。
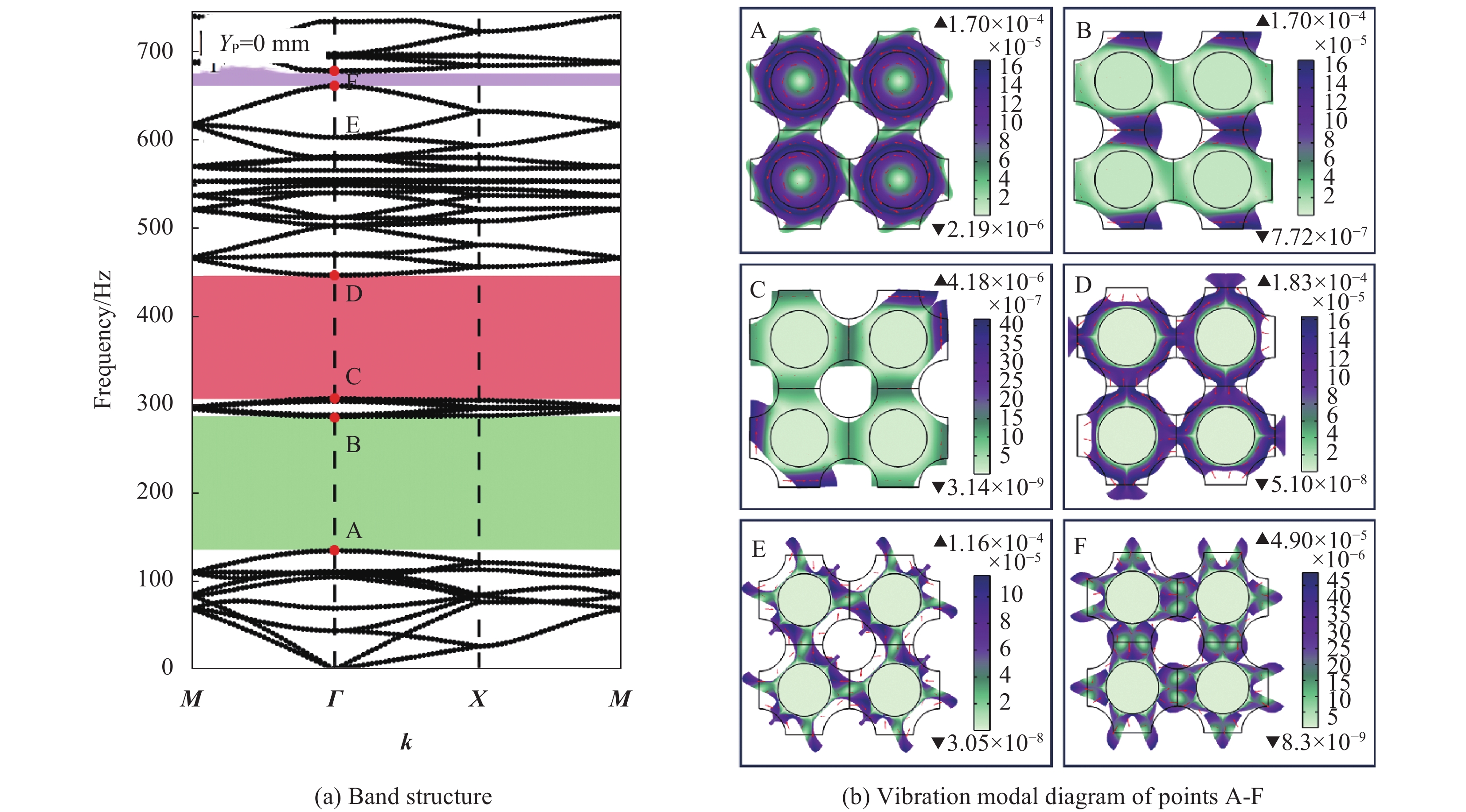
图5(a)给出了有限元法计算得到的四振子结构的能带结构图。可以看出，当结构的轴向压缩值 Y_{\mathrm{p}}=0\; \mathrm{mm} 时，前50阶特征频率形成了两条较宽的完全带隙和一条较窄的完全带隙，由低到高的频率范围分别为134.48~287.53 Hz、307.26~447.81 Hz和662.44~679.43 Hz。
![]()
图 5 四振子复合带隙可控超结构 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构及振动模态Figure 5. Band structure and vibration mode of the four-oscillator composite band gap controllable metastructure Y_{\mathrm{p}}=0\; \mathrm{mm}为进一步分析复合带隙可控超结构的带隙类型，图5(b)给出了A~F这6个点的振动模态图。可以看出，在A点，振动主要集中在散射体上，基体与散射体同向振动；B点散射体的振动降低。当波的频率接近散射体的固有频率时，基体与散射体发生共振，从而抑制了振动在特定方向上的传播。因此，图5(a)中的第一阶带隙为局域共振带隙。而对应C、D、E、F点振动模态为结构整体振动，因此第二阶带隙与第三阶带隙为布拉格散射型带隙。同理，图4所示能带结构中的带隙可根据高对称点的振动模态图来判断：第一阶带隙为局域共振型带隙，第二阶带隙为布拉格散射型带隙。
2. 复合带隙可控超结构带隙调控
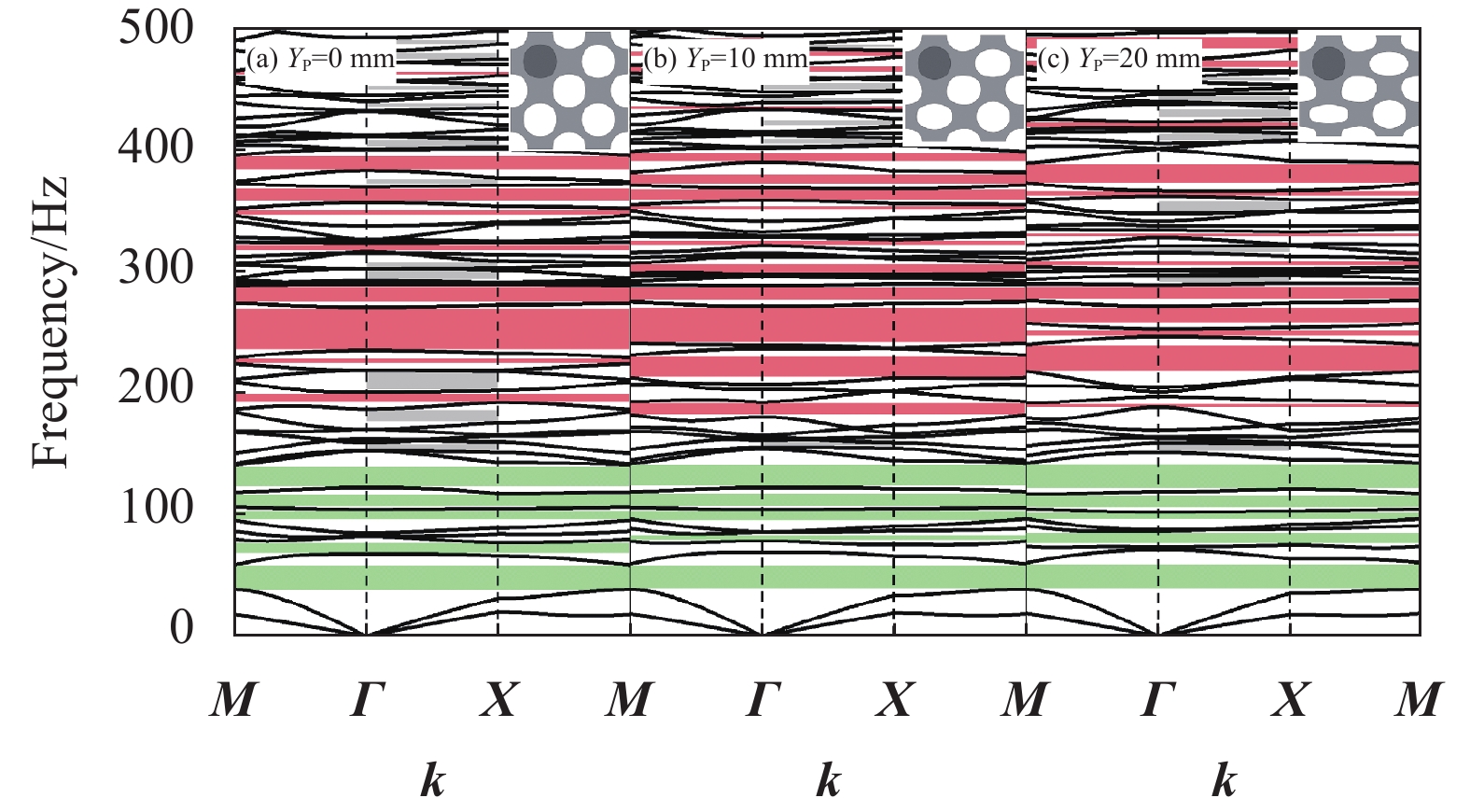
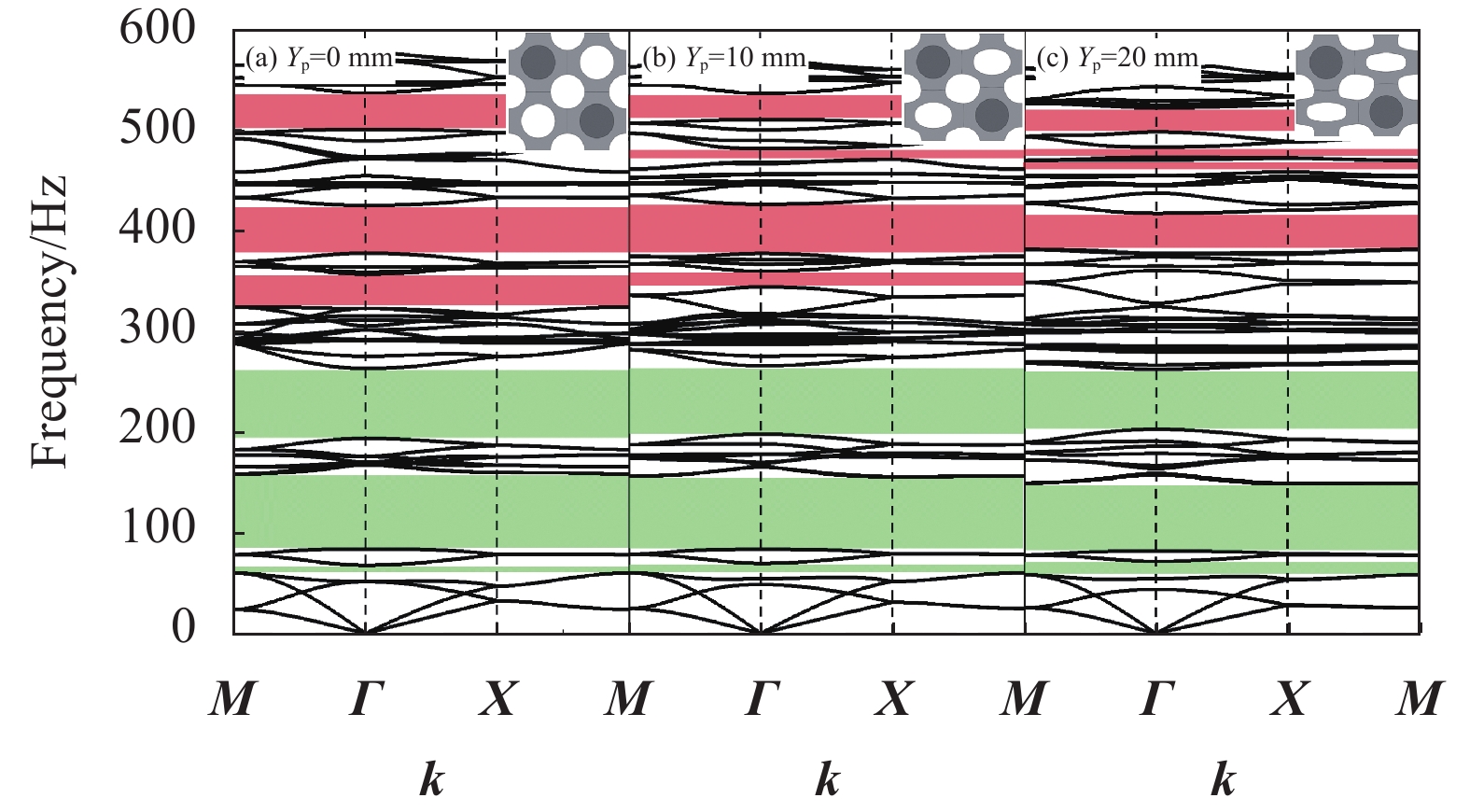
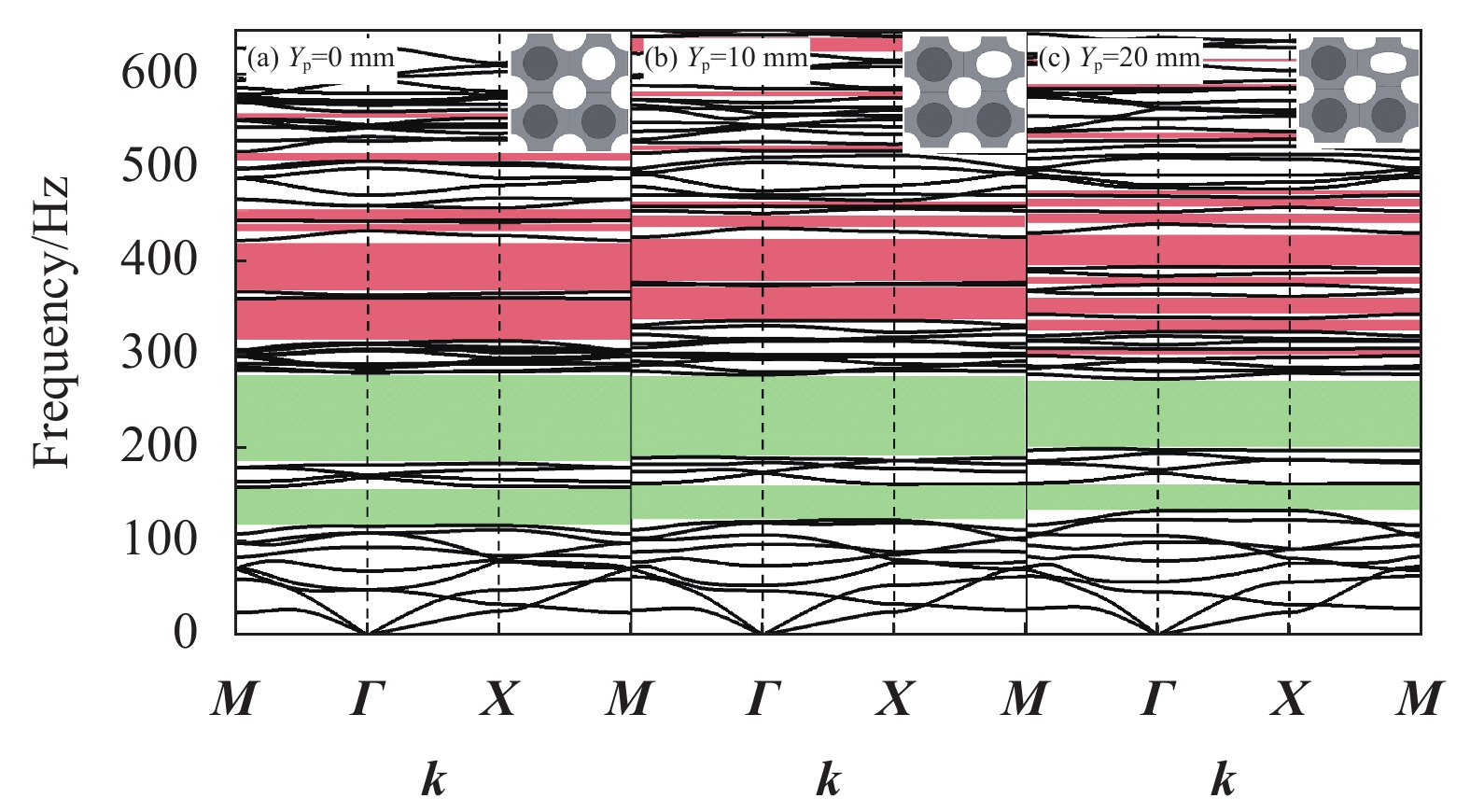
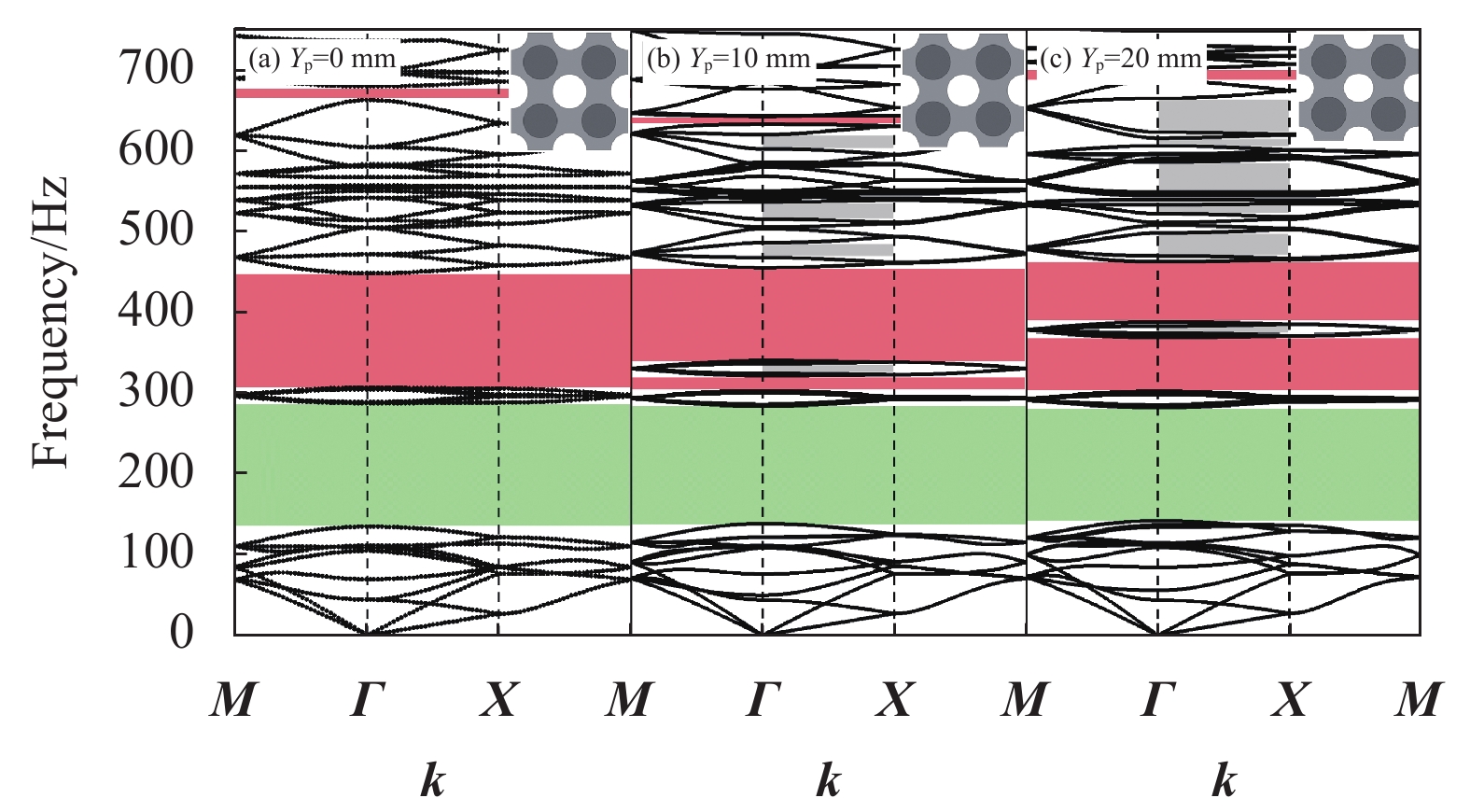
为了进一步分析轴向压缩对结构带隙调控的机制，对结构施加竖向位移量 Y_{\mathrm{p}} 。考虑到结构在较大变形下会发生屈曲，将应用COMSOL软件对结构的屈曲临界载荷和相应变形进行分析，计算得到各元胞发生屈曲的临界变形量在22.378~39.682 mm之间。因此，计算中在保证所有结构不发生屈曲的前提下，将图1中单振子、二振子、三振子、四振子元胞分别从0 mm开始依次增加10 mm进行轴向压缩，然后计算它们的能带结构图并分析带隙变化的规律，如图6~图9所示。
对比图6~图9中各阶带隙可以看出，随着竖向位移量 Y_{\mathrm{p}} 的增大，第一阶局域共振带隙变化较小，高阶的布拉格散射带隙中心频率逐渐向上移动，并在较高频率范围内出现了新的布拉格带隙，且单振子元胞和四振子元胞构型出现多条方向带隙(灰色部分)。这是由于轴向压缩对局域共振型带隙参数影响较小，但随着轴向位移 Y_{\mathrm{p}} 的增加，元胞晶格尺寸发生了变化，x方向尺寸a逐渐变大，y方向尺寸b逐渐变小，弹性波在晶格之间的传播与反射波的叠加发生了变化，色散曲线中心频率上移。可以发现，轴向压缩对不同构型复合带隙可控超结构具有较一致的调控机制，带隙调控的规律与局域共振振子的数量之间没有明显的关系。
![]()
图 6 单振子元胞在不同轴向压缩值下的能带结构对比图Figure 6. Energy band structure comparison diagram of single-oscillator cell under different axial compression values![]()
图 7 二振子元胞在不同轴向压缩值下的能带结构对比图Figure 7. Energy band structure comparison diagram of two-oscillator cell under different axial compression values![]()
图 8 三振子元胞在不同轴向压缩值下的能带结构对比图Figure 8. Energy band structure comparison diagram of three-oscillator cell under different axial compression values![]()
图 9 四振子元胞在不同轴向压缩值下的能带结构对比图Figure 9. Energy band structure comparison diagram of four-oscillator cell under different axial compression values3. 复合带隙可控超结构振动传输特性
3.1 有限周期结构的振动传输特性
为了进一步研究复合带隙可控超结构的实际工程应用效果，本文分别采用数值计算和实验方法对其进行了有限周期结构的振动传输特性研究。结构振动衰减情况常用传输损失{T_{\mathrm{L}}}来描述，传输损失 {T_{\mathrm{L}}} 计算式为[33]
T_{\mathrm{L}}=20\mathrm{lg}\left(\frac{a_{\mathrm{out}}}{a_{\mathrm{in}}}\right) (5) 式中，{a_{{\mathrm{in}}}}和{a_{{\mathrm{out}}}}分别为输入点和输出点处的加速度响应。
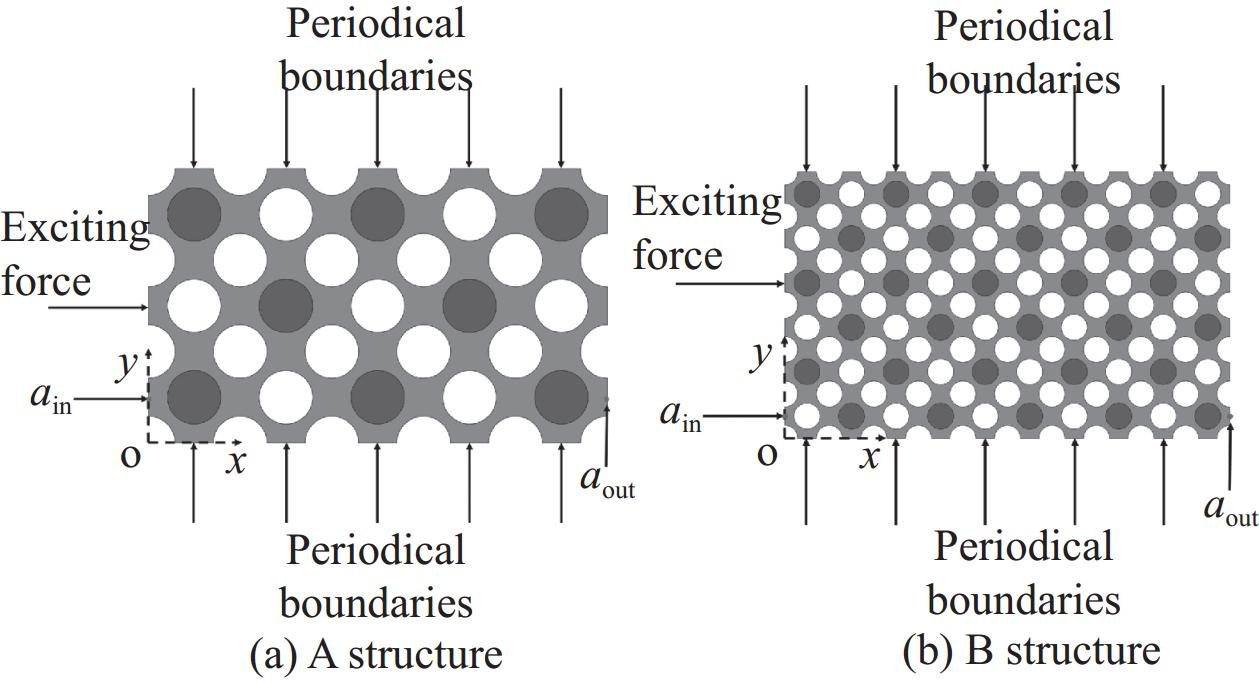
为了对比不同数量周期结构对振动传输特性结果的影响，开展了图10中有限周期二振子构型A、B结构的传输特性计算。应用COMSOL软件建立了两个结构的模型，在其左端处施加轴向单位激振力，限制结构y方向的刚体位移，在结构左右两端施加了自由边界条件，并在另一端{a_{{\mathrm{out}}}}处计算得到输出振动响应。
![]()
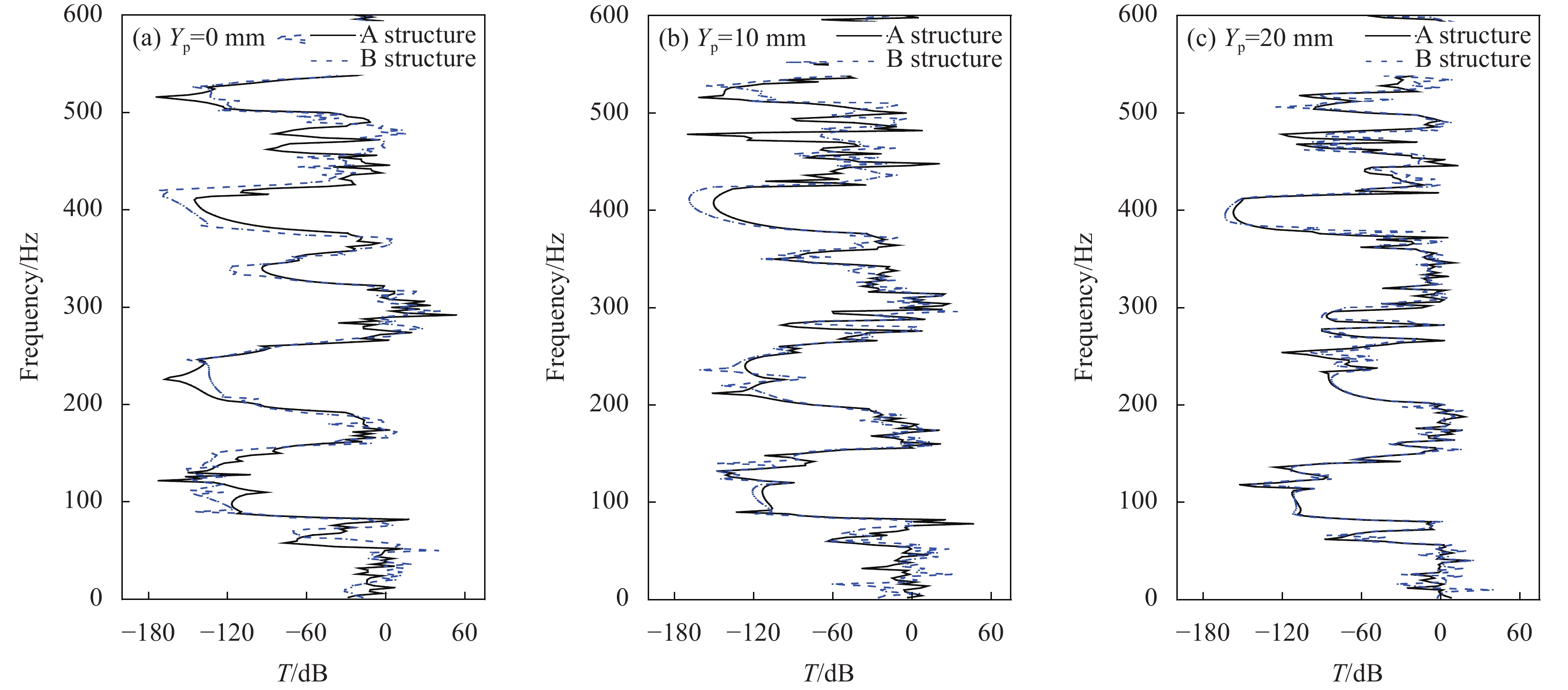
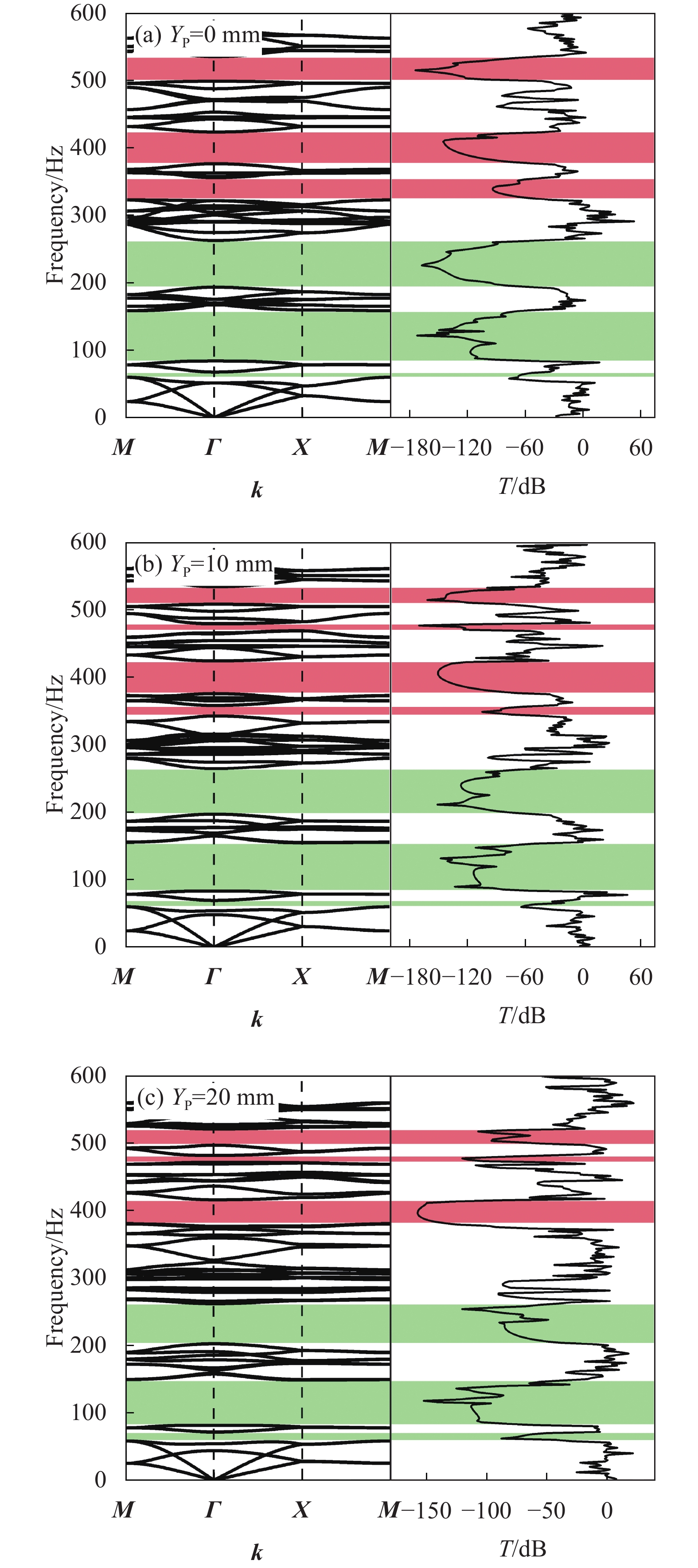
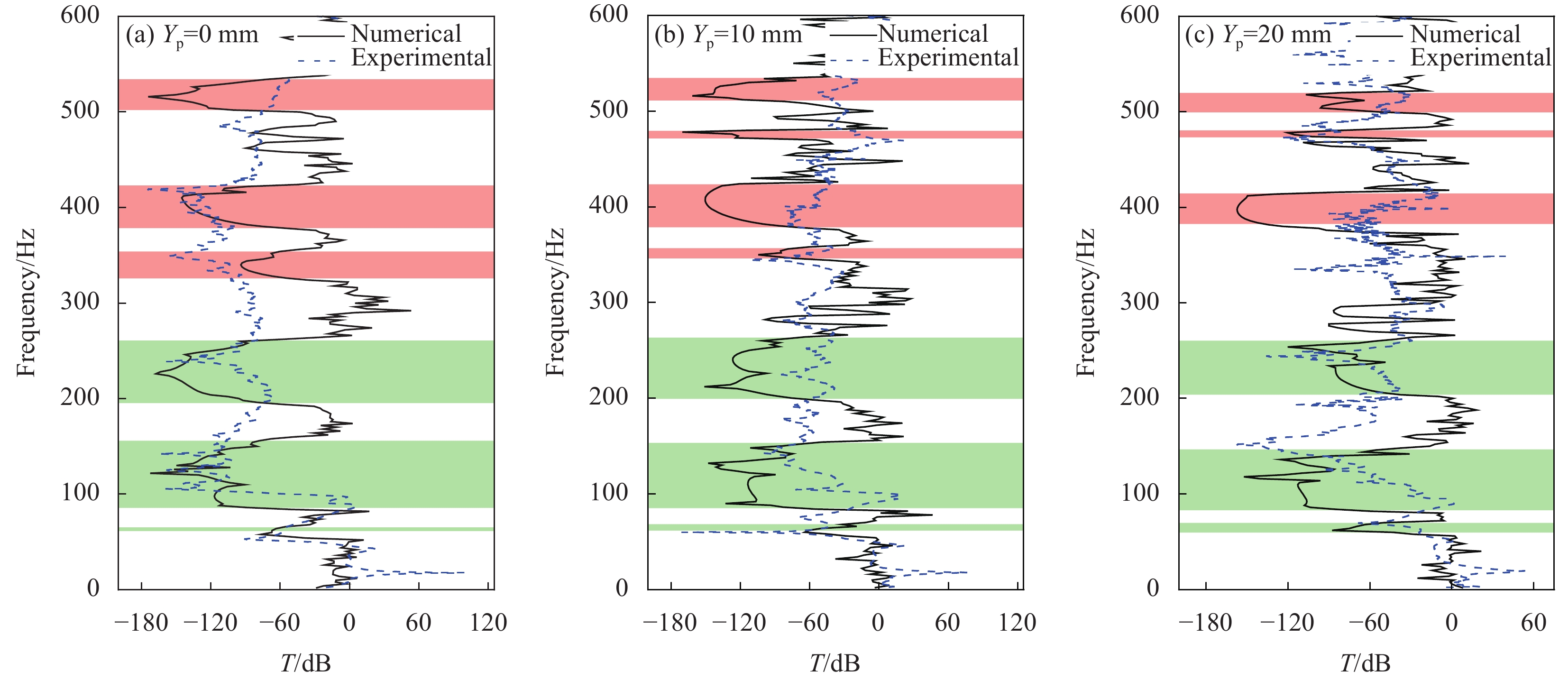
图 10 有限周期二振子超结构振动传输特性分析示意图ain and aout are the signal acquisition points of the input end and the output end, respectivelyFigure 10. Analysis diagram of vibration transmission characteristics of finite period two-oscillator metastructure图11给出了不同轴向压缩值下两个结构的振动传输特性曲线，可以看出尺寸较小的A结构与尺寸较大的B结构的振动传输特性具有较好的一致性。考虑到本文制作的实验试件尺寸有限，为便于与实验结果对比分析，选取周期结构数量与试验件相一致的A结构进行研究。图12(a)~图12(c)分别给出了二振子构型A结构在 Y_{\mathrm{p}}=0\; \mathrm{mm} 、 Y_{\mathrm{p}}=10\; \mathrm{mm} 、 Y_{\mathrm{p}}=20\; \mathrm{mm} 时的能带结构及振动传输特性曲线对比图。
![]()
图 11 不同轴向压缩值下两种尺寸有限周期二振子超结构振动传输特性曲线对比T—Structural vibration attenuationFigure 11. Comparison of vibration transmission characteristics curves of finite-period two-oscillator metastructures with two different sizes under different axial compression values![]()
图 12 不同轴向压缩值二振子构型超结构的能带结构及振动传输特性曲线Figure 12. Energy band structure and vibration transmission characteristic curves of two-oscillator configuration metastructures with different axial compression values从图12中的数值结果可以看出，传输特性曲线中振动衰减部分的频率范围与计算得到的能带结构中的带隙频率范围基本一致。另外，传输特性曲线中，除完全带隙对应的衰减，其余的衰减部分对应于方向带隙。在带隙范围内，结构的传输特性衰减明显，未压缩结构与轴向压缩结构的最大衰减均可达到150 dB。由此可见，弹性波在带隙频率范围内会出现明显的衰减。
3.2 实验研究
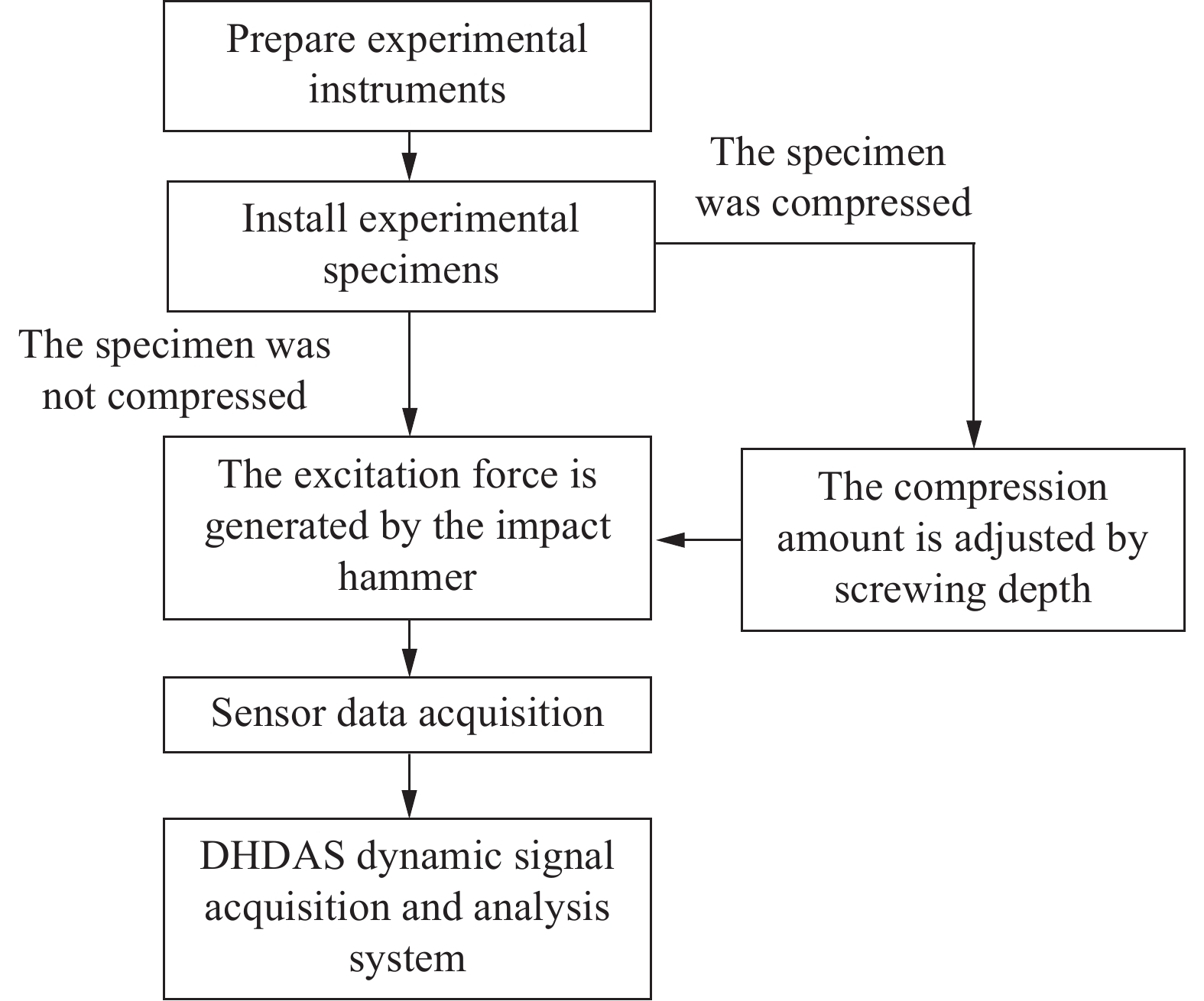
为研究有限周期二振子超结构振动传输特性，制作了二振子元胞结构试件，如图13所示。该试件由多孔硅橡胶构成，长度为300 mm，宽度为180 mm，厚度为50 mm，在橡胶孔内规律嵌入铅块构成局域共振振子。实验中，通过螺栓、螺母固定夹具，同时可调节控制其整体竖向位移。加速度传感器(352 C33，PCB)设置在图10中输入点{a_{{\mathrm{in}}}}与拾取点{a_{{\mathrm{out}}}}对应位置，使用力锤(CL-YD-303，江苏联能电子技术有限公司)沿水平方向冲击产生激励，通过DHDAS动态信号采集分析系统(DH8303，江苏东华测试技术股份有限公司)采集输入、输出端的加速度响应，实验装置如图14所示，实验流程如图15所示。将采集的数据利用式(5)进行计算，即可得到结构的振动传输特性曲线。
3.3 结果分析
将实验测得的加速度响应通过式(5)进行计算，所得到的数据经归一化处理后可获得二振子结构的振动传输特性曲线，如图16虚线所示。可以看出，带隙所在范围内(阴影区域)弹性波发生了衰减，这与有限元计算得到的结果比较一致，并且振动传输特性曲线的实验结果与数值结果也得到了较好的一致性。从图16可以看出：当 Y_{\mathrm{p}}=0\; \mathrm{mm} 与 Y_{\mathrm{p}}=10\; \mathrm{mm} 时，实验得到的振动传输特性曲线的衰减峰值与数值结果中的衰减峰值比较吻合；当 Y_{\mathrm{p}}=20\; \mathrm{mm} 时，部分低阶带隙的结果存在一定差异。这主要是由于：实验中结构通过夹具施加轴向压缩值，而相应的计算分析过程中，忽略了夹具和结构自重的影响，同时随着轴向压缩值的增加，结构内部产生的应力及自身的结构阻尼对其带隙亦有影响，因此两者有一定的误差。
![]()
图 16 不同轴向压缩值下二振子构型超结构的实验、数值振动传输特性曲线对比Figure 16. Comparison of experimental and numerical vibration transmission characteristic curves of two-oscillator configuration metastructure under different axial compression values4. 结 论
本文提出一种复合带隙可控超结构构型，该结构由多孔软材料和局域共振振子组成，可同时产生局域共振和布拉格散射两种带隙，通过施加轴向位移可实现对带隙的有效调控。采用有限元法研究了该结构在不同构型下的带隙特性及轴向压缩对带隙的调控规律，计算了二振子结构的振动传输特性并与带隙分布进行了对比验证。搭建了二振子结构振动特性实验平台，测得了该结构的传输特性曲线，与实验结果相对比，两者取得了较好的一致性。主要结论如下：
(1)对比分析了复合带隙可控超结构的4种不同构型带隙特性，数值结果表明该结构可产生局域共振型和布拉格散射型两种带隙分布；随局域共振振子数量增加，一定频率范围内，结构中带隙宽度增加，数量减少，且带隙中心频率上移；
(2)轴向压缩对该结构带隙分布具有一定的调控作用，随着轴向压缩值的增加，布拉格带隙中心频率逐渐上移，同时出现更多的完全带隙和方向带隙，局域共振型带隙变化较小，4种复合带隙可控超结构带隙调控规律基本一致；
(3)复合带隙可控超结构在带隙范围内具有较好的减振效果，振动传输特性曲线的实验结果与数值结果中衰减部分基本吻合。因此，弹性波在带隙频率范围内会出现明显的衰减。
本文提出的复合带隙可控超结构可以实现结构在不同工况下的带隙调控，在航空航天、轨道交通等领域有广阔的应用前景。结构由软材料组成，理论分析存在一定难度，且变形较大时出现非线性特性，在未来工作中将开展内在机制的理论分析及非线性特性研究。
-
![]()
图 1 不同构型复合带隙可控超结构元胞
Figure 1. Composite band gap controllable metastructure cells with different configurations
![]()
图 2 不同轴向压缩下二振子构型超结构元胞及试件示意图
Figure 2. Schematic diagram of the metastructure cells and specimens of two-oscillator configurations under different axial compressions
Y_{\mathrm{p}} —Axial compression of the structure; a, b—Lattice constant; R—Radius of the hole; θ—Angle of the diagonal of the cell; D—Distance between the holes
![]()
图 3 Y_{\mathrm{p}}=0\; \mathrm{mm} 时二振子构型超结构元胞(a)及其第一不可约布里渊区(阴影区域) (b)
M, Γ and X are the high symmetry points of the first irreducible Brillouin zone, respectively; kx and ky are the components of wave vector k in x and y directions, respectively
Figure 3. Two-oscillator configuration metastructure cell (a) and its first irreducible Brillouin zone (Shaded region) (b) in Y_{\mathrm{p}}=0\; \mathrm{mm}
![]()
图 4 不同元胞构型 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构对比图
Figure 4. Energy band structure comparison diagram of different cell configurations Y_{\mathrm{p}}=0\; \mathrm{mm}
![]()
图 5 四振子复合带隙可控超结构 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构及振动模态
Figure 5. Band structure and vibration mode of the four-oscillator composite band gap controllable metastructure Y_{\mathrm{p}}=0\; \mathrm{mm}
![]()
图 6 单振子元胞在不同轴向压缩值下的能带结构对比图
Figure 6. Energy band structure comparison diagram of single-oscillator cell under different axial compression values
![]()
图 7 二振子元胞在不同轴向压缩值下的能带结构对比图
Figure 7. Energy band structure comparison diagram of two-oscillator cell under different axial compression values
![]()
图 8 三振子元胞在不同轴向压缩值下的能带结构对比图
Figure 8. Energy band structure comparison diagram of three-oscillator cell under different axial compression values
![]()
图 9 四振子元胞在不同轴向压缩值下的能带结构对比图
Figure 9. Energy band structure comparison diagram of four-oscillator cell under different axial compression values
![]()
图 10 有限周期二振子超结构振动传输特性分析示意图
ain and aout are the signal acquisition points of the input end and the output end, respectively
Figure 10. Analysis diagram of vibration transmission characteristics of finite period two-oscillator metastructure
![]()
图 11 不同轴向压缩值下两种尺寸有限周期二振子超结构振动传输特性曲线对比
T—Structural vibration attenuation
Figure 11. Comparison of vibration transmission characteristics curves of finite-period two-oscillator metastructures with two different sizes under different axial compression values
![]()
图 12 不同轴向压缩值二振子构型超结构的能带结构及振动传输特性曲线
Figure 12. Energy band structure and vibration transmission characteristic curves of two-oscillator configuration metastructures with different axial compression values
![]()
图 16 不同轴向压缩值下二振子构型超结构的实验、数值振动传输特性曲线对比
Figure 16. Comparison of experimental and numerical vibration transmission characteristic curves of two-oscillator configuration metastructure under different axial compression values
表 1 几何参数和材料参数
Table 1 Geometric parameters and material parameters
Geometric parameters Value Material Material parameters Value R/mm 17.5 Silicon rubber E/MPa 0.870 ρ/(kg·m−3) 1230 D/mm 7.426 ν 0.499 Lead E/MPa 40.8 θ/(°) 45 ρ/(kg·m−3) 11340 ν 0.37 Notes：E—Elastic modulus；ρ—Density；ν—Poisson's ratio. 
下载: 导出CSV
-
[1] 肖勇, 王洋, 赵宏刚, 等. 面向减振降噪应用的声学超构材料研究进展[J]. 机械工程学报, 2023, 59(19): 277-298. DOI: 10.3901/JME.2023.19.277 XIAO Yong, WANG Yang, ZHAO Honggang, et al. Research progress of acoustic metamaterials for vibration and noise reduction applications[J]. Journal of Mechanical Engineering, 2023, 59(19): 277-298(in Chinese). DOI: 10.3901/JME.2023.19.277
[2] 代洪庆. 基于声学超材料的声场调控及微粒操控研究[D]. 长沙: 湖南大学, 2022. DAI Hongqing. Research on sound field control and particle manipulation based on acoustic metamaterials [D]. Changsha: Hunan University, 2022(in Chinese).
[3] LIU Z Y, ZHANG X X, MAO Y W, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736. DOI: 10.1126/science.289.5485.1734
[4] AMER Y A, EL-SAYED A T, AHMED E E. Vibration reduction of a non-linear ship model using positive position feedback controllers[J]. International Journal of Dynamics and Control, 2022, 10(2): 409-426. DOI: 10.1007/s40435-021-00801-8
[5] RUI J F, WANG L, LU P. Summary of research on supporting facilities and structure vibration and noise reduction of high-rise buildings[C]//IOP Conference Series: Earth and Environmental Science. Bristol: IOP Publishing, 2021, 791(1): 012023.
[6] DESAI R, GUHA A, SESHU P. Modelling and simulation of active and passive seat suspensions for vibration attenuation of vehicle occupants[J]. International Journal of Dynamics and Control, 2021, 9(4): 1423-1443.
[7] 郁殿龙. 基于声子晶体理论的梁板类周期结构振动带隙特性研究[D]. 长沙: 国防科学技术大学, 2007. YU Dianlong. Research on the vibration band gap characteristics of beam-plate periodic structures based on phononic crystal theory [D]. Changsha: National University of Defense Science and Technology, 2007(in Chinese).
[8] 王刚. 声子晶体局域共振带隙机理及减振特性研究[D]. 长沙: 国防科学技术大学, 2007. WANG Gang. Study on the local resonance band gap mechanism and vibration reduction characteristics of phononic crystals [D]. Changsha: University of Defense Science and Technology, 2007(in Chinese).
[9] LEE T, IIZUKA H. Bragg scattering based acoustic topological transition controlled by local resonance[J]. Physical Review B, 2019, 99(6): 064305. DOI: 10.1103/PhysRevB.99.064305
[10] ZHOU X, WANG L. Opening complete band gaps in two dimensional locally resonant phononic crystals[J]. Journal of Physics and Chemistry of Solids, 2018, 116: 174-179. DOI: 10.1016/j.jpcs.2018.01.025
[11] 肖鹏, 缪林昌, 郑海忠, 等. 一种新型二维三组元水泥基拟声子晶体复合材料的低频带隙特性与应用[J]. 复合材料学报, 2024, 41(10): 5607-5621. XIAO Peng, MIAO Linchang, ZHENG Haizhong, et al. Low-frequency band gap properties and applications of a new two-dimensional three-component cement-based phononic crystal composite [J]. Acta Materiae Compositae Sinica, 2024, 41(10): 5607-5621(in Chinese).
[12] GAO N, HOU H, WU J H, et al. Low frequency band gaps below 10 Hz in radial flexible elastic metamaterial plate[J]. Journal of Physics D: Applied Physics, 2016, 49(43): 435501. DOI: 10.1088/0022-3727/49/43/435501
[13] ZHOU X, XU Y, LIU Y, et al. Extending and lowering band gaps by multilayered locally resonant phononic crystals[J]. Applied Acoustics, 2018, 133: 97-106. DOI: 10.1016/j.apacoust.2017.12.012
[14] 张思文, 吴九汇. 局域共振复合单元声子晶体结构的低频带隙特性研究[J]. 物理学报, 2013, 62(13): 134302. DOI: 10.7498/aps.62.134302 ZHANG Siwen, WU Jiuhui. Low-frequency band gap characteristics of phononic crystal structure of locally resonant composite unit[J]. Physical Journal, 2013, 62(13): 134302(in Chinese). DOI: 10.7498/aps.62.134302
[15] LI X F, CHENG S L, YANG H Y, et al. Optimization of vibration characteristics and directional propagation of plane waves in branching ligament structures of wind models[J]. Results in Physics, 2023, 47: 106345. DOI: 10.1016/j.rinp.2023.106345
[16] COFFY E, LAVERGNE T, ADDOUCHE M, et al. Ultra-wide acoustic band gaps in pillar-based phononic crystal strips[J]. Journal of Applied Physics, 2015, 118(21): 214902. DOI: 10.1063/1.4936836
[17] 李孟昶, 郭少杰, 张红艳. 管道超结构轴向带隙特性分析及实验研究[J]. 人工晶体学报, 2023, 52(1): 65-72. DOI: 10.3969/j.issn.1000-985X.2023.01.009 LI Mengchang, GUO Shaojie, ZHANG Hongyan. Analysis and experimental study on axial band gap characteristics of pipe metastructure[J]. Journal of Artificial Crystallography, 2023, 52(1): 65-72(in Chinese). DOI: 10.3969/j.issn.1000-985X.2023.01.009
[18] 李潘玉, 游世辉, 李维, 等. 磁流变弹性体基拓扑声子晶体弹性波传输可调性研究[J]. 功能材料, 2021, 52(5): 5151-5158. DOI: 10.3969/j.issn.1001-9731.2021.05.023 LI Panyu, YOU Shihui, LI Wei, et al. Study on the tunability of elastic wave transmission in magnetorheological elastomer-based topological phononic crystals[J]. Functional Materials, 2021, 52(5): 5151-5158(in Chinese). DOI: 10.3969/j.issn.1001-9731.2021.05.023
[19] 王婷英, 柴怡君, 耿谦, 等. 力-压电混合弹性超材料梁的带隙调节特性[J]. 固体力学学报, 2022, 43(4): 406-418. WANG Tingying, CHAI Yijun, GENG Qian, et al. Band gap tuning properties of force-piezoelectric hybrid elastic metamaterial beams[J]. Journal of Solid Mechanics, 2022, 43(4): 406-418(in Chinese).
[20] WU Y, YU K P, YANG L Y, et al. Effect of thermal stresses on frequency band structures of elastic metamaterial plates[J]. Journal of Sound and Vibration, 2018, 413: 101-119. DOI: 10.1016/j.jsv.2017.10.014
[21] YAO Y W, WU F G, ZHANG X, et al. Thermal tuning of lamb wave band structure in a two-dimensional phononic crystal plate[J]. Journal of Applied Physics, 2011, 110(12): 123503. DOI: 10.1063/1.3669391
[22] GENG Q, CAI T, LI Y. Flexural wave manipulation and energy harvesting characteristics of a defect phononic crystal beam with thermal effects[J]. Journal of Applied Physics, 2019, 125(3): 035103. DOI: 10.1063/1.5063949
[23] DAI H, XIA B, YU D. Temperature-controlled tunable underwater acoustic topological insulators[J]. Journal of Applied Physics, 2019, 125(23): 235105. DOI: 10.1063/1.5090789
[24] LI X F, CHENG S L, YANG H Y, et al. Integrated analysis of bandgap optimization regulation and wave propagation mechanism of hexagonal multi-ligament derived structures[J]. European Journal of Mechanics-A/Solids, 2023, 99: 104952. DOI: 10.1016/j.euromechsol.2023.104952
[25] LI X F, CHENG S L, YANG H Y, et al. Bandgap tuning and in-plane wave propagation of chiral and anti-chiral hybrid metamaterials with assembled six oscillators[J]. Physica A: Statistical Mechanics and Its Applications, 2023, 615: 128600. DOI: 10.1016/j.physa.2023.128600
[26] BERTOLDI K, BOYCE M C. Wave propagation and instabilities in monolithic and periodically structured elastomeric materials undergoing large deformations[J]. Physical Review B, 2008, 78(18): 184107. DOI: 10.1103/PhysRevB.78.184107
[27] SHAN S, KANG S H, WANG P, et al. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves[J]. Advanced Functional Materials, 2014, 24(31): 4935-4942. DOI: 10.1002/adfm.201400665
[28] LI J, WANG Y S, CHEN W Q, et al. Harnessing inclusions to tune post-buckling deformation and bandgaps of soft porous periodic structures[J]. Journal of Sound and Vibration, 2019, 459: 114848. DOI: 10.1016/j.jsv.2019.114848
[29] GEI M. Wave propagation in quasiperiodic structures: Stop/pass band distribution and prestress effects[J]. International Journal of Solids and Structures, 2010, 47(22): 3067-3075.
[30] 黄屹澜. 软材料周期结构中波传播行为主动调控[D]. 杭州: 浙江大学, 2020. HUANG Yilan . Active control of wave propagation behavior in periodic structures of soft materials [D]. Hangzhou: Zhejiang University, 2020(in Chinese).
[31] HUANG Y, LI J, CHEN W Q, et al. Tunable bandgaps in soft phononic plates with spring-mass-like resonators[J]. International Journal of Mechanical Sciences, 2019, 151: 300-313. DOI: 10.1016/j.ijmecsci.2018.11.029
[32] HUANG Y, GAO N, CHEN W Q, et al. Extension/compression-controlled complete band gaps in 2D chiral square-lattice-like structures[J]. Acta Mechanica Solida Sinica, 2018, 31(1): 51-65.
[33] 付强, 姚飞, 张红艳. 局域共振夹芯超结构梁带隙特性及实验研究[J]. 人工晶体学报, 2024, 53(1): 65-72. DOI: 10.3969/j.issn.1000-985X.2024.01.007 FU Qiang, YAO Fei, ZHANG Hongyan. Band gap characteristics and experimental study of locally resonant sandwich metastructure beams[J]. Journal of Artificial Crystallography, 2024, 53(1): 65-72(in Chinese). DOI: 10.3969/j.issn.1000-985X.2024.01.007
-
目的
传统超结构设计方法无法实现参数连续控制，实际工程中结构随不同工况动态特性相应发生变化，可控超结构可根据目标需求调节结构的带隙特性，实现对不同工况下结构减振的可控调节。通过在超结构中引入外部激励(例如机械载荷、电场、磁场和温度场等外部条件)可以改变结构的能带结构从而达到实时调控带隙的目的。本文提出一种新型可控超结构构型，该结构由多孔软材料和局域共振振子组成，可同时产生局域共振和布拉格散射两种带隙，通过施加位移可实现对带隙的有效调控。该结构可以实现结构在不同工况下的带隙调控，在航空航天、轨道交通等领域有广阔的应用前景。
方法应用COMSOL软件建立了4种可控超结构的有限元模型，施加周期性边界条件。令波矢扫略第一不可约布里渊区的边界、、，计算得到结构的前50阶特征频率，进而可得到波矢与频率的色散曲线。研究了4种可控超结构构型的能带分布及其在外加位移激励作用下的带隙特性调控规律。制作了二振子元胞结构试件，搭建了有限周期结构的振动传输特性实验平台，使用力锤沿水平方向冲击产生激励，采集输入、输出端的加速度响应，得到该结构的振动传输特性曲线，并与数值结果进行对比验证。
结果复合带隙可控超结构的4种构型均可产生局域共振型和布拉格散射型两种带隙。四振子构型在0~800Hz范围内共有3条完全带隙，第一阶带隙范围低至134.48~287.53Hz，第二阶带隙范围为307.26~447.81Hz，第三阶带隙范围为662.44~679.43Hz。对比分析4种构型的带隙特性，随着元胞中局域共振振子数量增加，300Hz内的低阶带隙宽度增加，结构中带隙数量逐渐减少，且振子数量的增加使结构刚度逐渐增大进而导致了带隙中心频率增加，带隙位置逐渐上移。轴向压缩对该结构带隙分布具有一定的调控作用，随着竖向位移量的增大，局域共振带隙变化较小，布拉格散射带隙中心频率逐渐向上移动，并在较高频率范围内出现了新的完全带隙和方向带隙，且轴向压缩对4种复合带隙可控超结构具有相同的带隙调控规律。计算了二振子复合带隙可控超结构传输特性，数值结果表明其在带隙范围内具有较好的减振效果，未压缩结构与轴向压缩结构的最大衰减均可达到150dB，且振动传输特性曲线实验结果与数值结果中衰减部分基本吻合，因此，弹性波在带隙频率范围内会出现明显的衰减。
结论本文提出的复合带隙可控超结构，由多孔软材料及内部嵌入的局域共振振子构成，根据振子分布位置不同，分别有单振子、二振子、三振子及四振子四种构型。该结构均可同时产生低频的局域共振型带隙和较高频的布拉格散射型带隙。通过调节振子位置可以实现对低频局域共振带隙的调控，施加可控位移可调节较高频的布拉格散射带隙。该结构在带隙范围内具有良好的减振特性。复合带隙可控超结构可实现对复合带隙的调控，为超结构减振设计研究提供有益的参考，在航空航天、轨道交通等领域有广阔的应用前景。
计量
- 文章访问数: 243
- HTML全文浏览量: 105
- PDF下载量: 26
