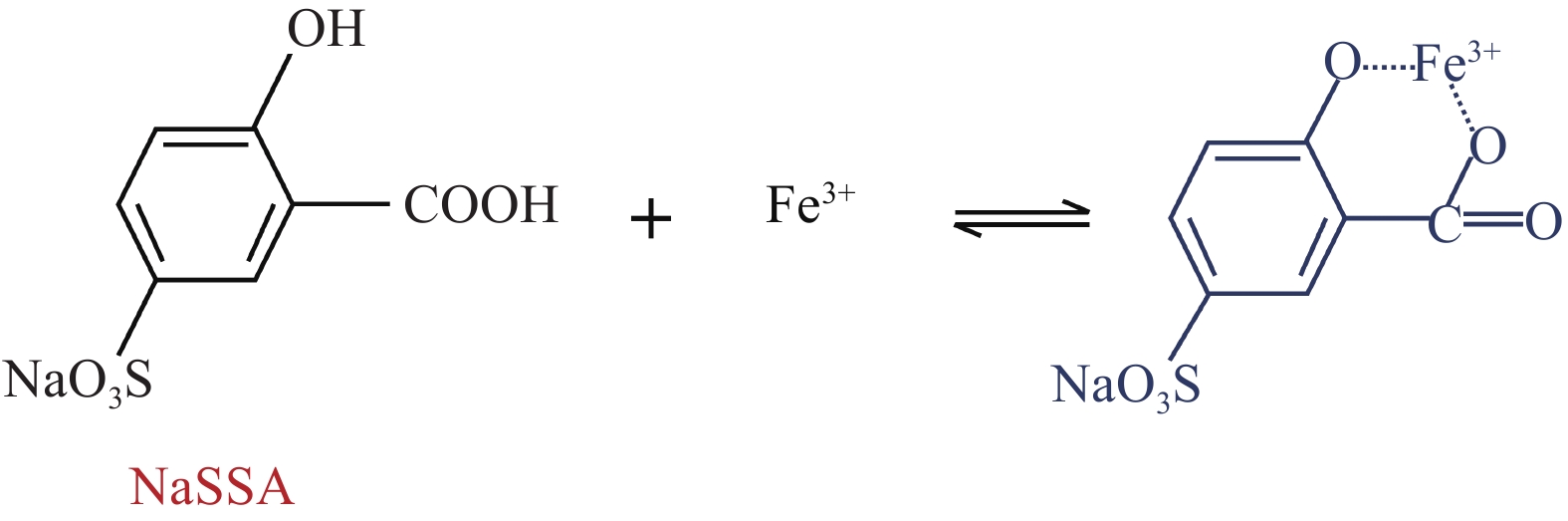基于声发射和蝙蝠算法的三点弯曲作用下CFRP加固钢管的损伤性能

周灵杰; 佘艳华; 何佳明; 黄俊杰; 谢玉强

doi:10.13801/j.cnki.fhclxb.20240513.003

基于声发射和蝙蝠算法的三点弯曲作用下CFRP加固钢管的损伤性能

长江大学　城市建设学院，荆州 434023

基金项目: 国家自然科学基金(51408057)；住房与城乡建设部科学技术项目(2021-K-086)

详细信息

通讯作者:
佘艳华，博士，副教授，硕士生导师，研究方向为工程材料和结构检测　E-mail: syh916@126.com

中图分类号: TB333
计量
- 文章访问数: 185
- HTML全文浏览量: 85
- PDF下载量: 23
出版历程
- 收稿日期: 2024-03-12
- 修回日期: 2024-04-15
- 录用日期: 2024-04-30
- 网络出版日期: 2024-06-04
- 发布日期: 2024-05-13
- 刊出日期: 2024-11-26

Research on damage performance of steel tube reinforced by CFRP under three-point bending loads based on acoustic emission and bat algorithm

School of Urban Construction, Yangtze University, Jingzhou 434023, China

Funds: National Natural Science Foundation of China (51408057); Ministry of Housing and Urban Rural Development Science and Technology Project (2021-K-086)

施引文献

摘要

摘要:
研究了碳纤维增强树脂复合材料(Carbon fiber reinforced polymer，CFRP)加固Q345钢管在弯曲负荷下的损伤性能。通过三点弯曲试验，采用吸能特性分析方法评估不同加固方式下的抗弯强度和能量吸收性能。采用声发射(Acoustic emission，AE)技术，对比分析了不同CFRP铺层方式对钢管的加固效果及探究结构内部损伤和弯曲破坏的声学特征演化规律。最后提出了蝙蝠算法(Bat algorithm，BA)优化最小二乘支持向量机(Least squares support vector machine，LSSVM)的损伤分类预测模型。研究发现，增加CFRP缠绕层数可以显著提升钢管的抗弯强度和吸能能力，但增大缠绕角度会降低结构性能。通过对比分析不同加固方式下试件的声发射信号，证实了声发射技术在揭示碳纤维复合材料钢管弯曲过程中的损伤模式方面的有效性。能量概率密度的分析和最大似然评估显示，无论加固方式如何，复合管在不同能量级别上均遵循幂律分布，且能量分布指数随着CFRP缠绕层数增加而增大、随着缠绕角度增加而减小。所建立的BA-LSSVM损伤分类模型对试件损伤过程中的损伤程度分类准确性高达98%以上。
- CFRP加固钢管 /
- 三点弯曲 /
- 损伤性能 /
- 声发射 /
- BA优化LSSVM
Abstract:
In this study, the damage performance of carbon fiber reinforced polymer (CFRP) strengthened Q345 steel tubes under bending loads was researched. Through three-point bending tests, the bending strength and energy absorption performance under different reinforcement methods were evaluated using energy characteristic analysis. Additionally, using acoustic emission (AE) techniques, the reinforcement effects of different CFRP layup methods on steel tubes were comparatively analyzed, as well as exploring the evolution of acoustic characteristics of internal damage and bending failure. Finally, a damage classification model optimized by the bat algorithm (BA) for the least squares support vector machine (LSSVM) was proposed. The study finds that CFRP winding layers increasing can significantly enhance the bending strength and energy absorption capacity of the steel tubes, but increasing the winding angle will reduce the structural performance. By comparing the acoustic emission signals of specimens under different reinforcement methods, the effectiveness of acoustic emission technology in revealing the damage modes of carbon fiber reinforced steel tubes during bending was confirmed. Analysis of energy probability density and maximum likelihood estimation shows that, the composite tubes acoustic emission energy follow a power-law distribution at different energy levels, with the energy distribution exponent increasing with the increase of CFRP winding layers and decreasing with the increase of winding angle. The BA-LSSVM model was established to classify the degree of damage during the specimens damage process, with an accuracy of over 98%.
- CFRP reinforced steel tube /
- three-point bending /
- damage performance /
- acoustic emission /
- BA optimized LSSVM

HTML全文

玄武岩纤维是以玄武岩矿石为原材料，将矿石破碎后，加入熔窑中，在1450~1700℃下进行熔融，生成玻璃状熔融液体，通过铂铑合金拉丝漏板拉制而成的连续纤维^[1-4]。玄武岩纤维在整个生产过程中，不会析出任何有毒有害物质，不会释放任何有害气体，因此，玄武岩纤维的生产制造不会造成环境污染，被誉为“21世纪的新型环保纤维” ^[5]。另一方面，随着纤维增强复合材料在土木工程、交通运输、航空航天等领域中的广泛应用，纤维的可回收性逐渐引起了重视。相比于回收困难的碳纤维，玄武岩纤维原材料本身是天然的玄武岩石，因此，废弃的玄武岩纤维可以直接进行回炉再生，具有较高的回收利用率，这有助于材料的可持续发展。此外，玄武岩纤维拥有许多优异的性能，例如，优异的拉伸性能(拉伸强度可达到4840 MPa)、较强的耐腐蚀性能和化学稳定性、良好的热稳定性能等^[6-8]。玄武岩纤维增强复合材料已经广泛地运用在航空航天、汽车船舶、建筑、石油化工、体育器材等领域。

随着能源电子、空间技术等尖端科学领域的快速发展，材料的电磁性能愈发重要^[9]。然而，玄武岩纤维是一种绝缘材料，其电阻率达到10¹¹ Ω·cm，限制了玄武岩纤维在电磁屏蔽、静电防护等领域的运用，因此实现玄武岩纤维的导电性能够扩宽玄武岩纤维的应用领域，提高材料的附加值。另一方面，多功能复合材料成为目前研究热点。碳纤维增强复合材料(CFRP)由于碳纤维的导电性使CFRP在作为承载构件的同时，也能够实现自感知。而玄武岩纤维增强复合材料(BFRP)由于玄武岩纤维和数值的绝缘性，无法实现自感知。因此，导电玄武岩纤维有望能开发BFRP的自感知性能。目前，开发实现玄武岩纤维导电性的研究较少。谭文军等^[10]以过硫酸铵(APS)作为氧化剂，酸性条件下在玄武岩纤维布表面原位生长聚苯胺(PANI)，所制的导电玄武岩纤维的电导率可达4 S/cm，但实验过程使用浓硝酸、高氯酸等具有强腐蚀性的强酸，制备方法不够友好。冯倩倩等^[11]采用金属沉积法在玄武岩纤维表面镀镍金属层制备导电玄武岩纤维，纤维的平均电阻值为14.2 Ω/cm，电阻率为1.9×10⁻³ Ω·cm，具有良好的导电性，但制备方法采用重金属，价格昂贵，成本高。马鹏程等^[12]提出通过化学气相沉积法，在玄武岩纤维表面沉积碳纳米材料，从而实现玄武岩纤维的导电性。该方法可获得均匀沉积在纤维表面的碳纳米层，但气相沉积法在500~1000℃温度下进行，对玄武岩纤维结构可能会造成一定破坏，从而降低玄武岩纤维的力学性能，有必要提供一种在不损伤玄武岩纤维机械性能的前提下高效、友好的实现玄武岩纤维导电性的改性方法。

聚吡咯是由共轭单双键结构排列而成的导电高分子聚合物，具有易于合成、成本低、无毒、导电性和氧化还原性好等优点^[13-16]。目前，合成聚吡咯的方法主要有化学氧化剂的化学聚合法和阳极氧化的电聚合法。然而，聚吡咯一般以颗粒状存在，不溶也不融，这限制了聚吡咯的进一步应用。如果将聚吡咯通过原位聚合法沉积在玄武岩纤维上，制备出导电玄武岩纤维，一方面能够赋予玄武岩纤维良好的导电性，且避免高温、酸碱刻蚀等会对纤维造成伤害的工艺，保护纤维的机械性能^[17-19]，另一方面，也能解决聚吡咯应用难的问题。通过研究^[13]发现，无缺陷共轭结构的聚吡咯的导电性较差，因此，需要通过加入合适的掺杂剂来构建具有缺陷的共轭结构，来提高聚吡咯的导电性。掺杂剂在吡咯发生氧化还原反应过程中，在聚吡咯共轭长分子链嵌入/移出电子，形成电荷载体，电荷载体能够沿着聚吡咯长链运动，提高聚吡咯的导电性^[20]。Varesano等^[21]发现在吡咯聚合过程中，当加入芳香族磺酸盐类的化合物作为掺杂剂时，聚吡咯的导电性明显提升。彭章^[22]对比了不同氧化剂和不同掺杂剂对聚吡咯导电性的影响。当分别使用过硫酸铵(APS)、氯化铁(FeCl₃)、过氧化氢(H₂O₂)作为氧化剂，使用FeCl₃制备的聚吡咯的电导率具有明显优势，是APS和H₂O₂的800多倍；当分别用十二烷基苯磺酸钠(SDBS)、5-磺基水杨酸钠(NaSSA)作为掺杂剂对聚吡咯导电性的影响，发现NaSSA的掺杂效果优于SDBS。何青青^[23]对比了相同浓度下甲基苯磺酸(PTS)、5-磺基水杨酸钠、蒽醌-2-磺酸钠盐(NaAQSA)作为掺杂剂对聚吡咯导电性影响，发现NaSSA作为掺杂剂时，导电性能最为优异，掺杂效果最好。因此，基于已有研究结论，本文中使用FeCl₃作为吡咯单体聚合的氧化剂，NaSSA作为合成聚吡咯的掺杂剂。

本文开发了一种实现玄武岩纤维导电性的改性方法。该方法在实现玄武岩纤维高导电性的同时，提高了玄武岩纤维的拉伸强度。该方法成本低，制备过程简单、高效、友好，是一种适合于大量生产的改性方法。本文以吡咯单体、氧化剂氯化铁和掺杂剂5-磺基水杨酸钠为原料，通过原位聚合法在玄武岩纤维表面沉积导电聚合物聚吡咯，通过调整吡咯单体、氧化剂和掺杂剂的浓度来调控和研究玄武岩纤维上导电聚合物的结构、颗粒大小、涂层厚度及玄武岩纤维的导电性。此外，本文通过纤维单丝拉伸强度来研究改性过程对纤维自身结构造成的影响。该研究实现了在不损伤纤维结构的基础上显著降低玄武岩纤维电阻率，扩宽了玄武岩纤维的应用领域，为玄武岩纤维复合材料实现结构-功能一体化提供了新的方案，具有广阔的运用前景。

1. 试验材料与方法

1.1 原材料

玄武岩纤维布(直径d 约为 13 μm)，购自江苏绿材谷新材料科技发展有限公司；无水乙醇、吡咯(Py，AR)、无水三氯化铁(FeCl₃，AR)、5-磺基水杨酸钠(NaSSA，AR)均购自上海麦克林生化科技有限公司，所有化学试剂均未做进一步处理。对吡咯单体进行冷藏保存，并在使用前观察吡咯单体颜色，确保使用时吡咯单体为白色而非黄色，从而避免由于保存时间过久和保存条件不当使吡咯自身发生氧化形成二聚体。

1.2 聚吡咯改性玄武岩纤维制备方法

将2 cm×2 cm的玄武岩纤维布用无水乙醇和去离子水洗涤3~5次，去除表面杂质。将其浸泡于一定浓度的吡咯单体溶液中进行吸附30 min，控制温度为0~2℃。配制一定量的氧化剂FeCl₃和掺杂剂NaSSA的混合液，将混合液缓慢加入到浸泡玄武岩纤维的吡咯单体溶液中，进行聚合反应5 h，控制聚合反应体系温度为0~2℃。取出玄武岩纤维，用无水乙醇和去离子水洗涤3~5次，洗去未附着的聚吡咯颗粒。最后，将改性后的玄武岩纤维在60℃下烘干至恒重，得到聚吡咯改性的导电玄武岩纤维，记为PPy/BF。主要的制备流程如图1所示。

图 1 导电玄武岩纤维的制备流程图

Py—Pyrrole; NaSSA—Sodium 5-sulfosalicylate; PPy—Polypyrrole

Figure 1. Flow chart for the preparation of conductive basalt fiber fabric

下载: 全尺寸图片幻灯片

为了研究吡咯单体浓度对玄武岩纤维导电性和聚吡咯结构的影响，设计了4种浓度的吡咯单体溶液，吡咯单体与氧化剂FeCl₃的摩尔比分别为0.5、1、2、3。其中FeCl₃的浓度固定为1 mol/L。将4种摩尔比下原位聚合得到的PPy/BF分别记为PPy/BF-0.5、PPy/BF-1、PPy/BF-2、PPy/BF-3。为了研究掺杂剂NaSSA的浓度对玄武岩纤维导电性和聚吡咯结构的影响，在上述导电性最优的PPy/BF的吡咯单体浓度的基础上，选取了5种NaSSA溶液的浓度。其分别与吡咯单体的摩尔比为0、0.05、0.1、0.5、1，将不同NaSSA浓度下原位聚合得到的PPy/BF分别记为PPy/BF(0)、PPy/BF(0.05)、PPy/BF(0.1)、PPy/BF(0.5)、PPy/BF(1) (表1)。

表 1 不同聚吡咯/玄武岩纤维复合材料的合成条件

Table 1. Synthesis conditions of different polypyrrole/basalt fiber composites

Sample	Py/ (mol·L⁻¹)	FeCl₃/ (mol·L⁻¹)	NaSSA/ (mol·L⁻¹)	Temperature/ ℃	Polymerization time/h
PPy/BF-0.5	0.5	1	0	0-2	5
PPy/BF-1	1	1	0	0-2	5
PPy/BF-2	2	1	0	0-2	5
PPy/BF-3	3	1	0	0-2	5
PPy/BF(0)	3	1	0	0-2	5
PPy/BF(0.05)	3	1	0.15	0-2	5
PPy/BF(0.1)	3	1	0.3	0-2	5
PPy/BF(0.5)	3	1	1.5	0-2	5
PPy/BF(1)	3	1	3	0-2	5
Notes: Py—Concentration of pyrrole monomer solution; FeCl₃—Concentration of ferric chloride solution; NaSSA—Concentration of sodium 5-sulfosalicylate; BF—Basalt fibers.

下载: 导出CSV

| 显示表格

1.3 材料表征与性能测试

1.3.1 材料表征

使用场发射扫描电子显微镜(FESEM，JSM-7610 F Plus)来表征聚吡咯改性前后玄武岩纤维的表面形态和微观结构；使用X射线光电子能谱(XPS，Thermo Scientific Escalab 250 Xi)以单色Al K_α射线源测试改性前后玄武岩纤维表面的元素种类和相对含量及各成分的化学状态，分析图谱前将N1s峰位校准至400 eV；使用拉曼光谱(Raman spectra，Thermo Fisher DXRxi)来分析聚吡咯涂层的化学结构，测试光源的激发波长为532 nm。

活性物质聚吡咯的负载量通过以下方式表征。使用聚吡咯改性前的玄武岩纤维布的质量为m₀，使用聚吡咯改性后的玄武岩纤维布的质量为m₁，因此，活性物质聚吡咯的负载量 $\lambda$ 通过下式计算：

$\lambda=\frac{m_1-m_0}{m_0}\times100\text{%}$

(1)

1.3.2 导电性能测试

采用四探针法(HPS2662，精密四探针电阻率测试仪，常州海尔帕电子科技有限公司)测量玄武岩纤维布表面的方阻值，如图2所示，探针间距为1 mm，对玄武岩纤维布正反面分别测量5次，取平均值，得到表面方阻(R)；使用游标卡尺测量玄武岩纤维布的厚度，分别测量5次，取平均值，得到玄武岩纤维布的厚度(d，cm)，通过公式(2)计算得到玄武岩纤维布的电阻率(ρ，Ω·cm)，并通过公式(3)计算电阻率的标准差(Standard deviation，s)来反映纤维布上负载聚吡咯的均匀性。

图 2 四探针法测电阻实验

Figure 2. Schematic diagram of four-probe method for resistance measurement experiment

下载: 全尺寸图片幻灯片

$\rho=Rd$

(2)

$s = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^N {{{({X_i} - \mu )}^2}} }}{N}}$

(3)

其中：N为测试的纤维单丝的总数；X_i为第i根纤维的拉伸强度；μ为纤维单丝拉伸强度的平均值。

1.3.3 纤维单丝拉伸性能测试

采用XQ-2型纤维强伸度仪(上海新纤仪器公司)测量改性前后玄武岩纤维的拉伸强度和模量来表征纤维机械性能，如图3所示。将纤维单丝粘贴于U形纸片上。将U形纸片放置在仪器上，剪断纸框，设置参数为预张力0 cN、加持距离20 mm、拉伸速度10 mm/min，测试得到纤维的单丝强力(P， cN)。选取纤维单丝位于中部断裂的作为有效数据样本，舍弃在根部断裂的样本。采用XY-MRT反式金相显微镜(中国舜宇)测试相应纤维单丝的直径(d，μm)，根据公式(4)，计算得到纤维的单丝拉伸强度(σ，MPa)。根据GB/T 31290—2022^[24]，利用公式(5)计算纤维的弹性模量(E，MPa)。通过公式(6)计算离散系数(C_v)来反映拉伸强度和弹性模量的离散性。

图 3 纤维单丝拉伸实验：(a) 纤维单丝样品；(b) XQ-2纤维强伸度仪进行拉伸试验

Figure 3. Schematic diagram of single fiber tensile experiment: (a) Single fiber sample; (b) Tensile test with XQ-2 fiber strength instrumentation

下载: 全尺寸图片幻灯片

$\sigma = \frac{P}{{\text{π} {{\left({d}/{2}\right)}^2}}} \times 10000$

(4)

$E = \frac{{{\sigma _1} - {\sigma _2}}}{{{\varepsilon _1} - {\varepsilon _2}}}$

(5)

式中：根据规范，应变ε₁=0.1%，ε₂=0.3%；σ₁为应变为ε₁对应的应力，σ₂为应变为ε₂对应的应力。

${C_{\text{v}}} = \frac{s}{\mu }$

(6)

式中，s和μ分别为拉伸强度和模量的标准差和平均值。

2. 结果与讨论

本文通过原位聚合法使用PPy对玄武岩纤维进行改性，在不牺牲机械性能的基础上实现了玄武岩纤维的高导电性，也为PPy提供了新的应用方向。PPy作为导电聚合物的一种，具有优异的导电性。玄武岩纤维通过吸附Py单体，在氧化剂和掺杂剂的作用下，在表面原位生长PPy，形成厚实稳定的PPy涂层。如图4所示，玄武岩纤维表面的颜色由褐色逐渐变成黑色。通过研究吡咯单体和氧化剂的比例及掺杂剂NaSSA与吡咯单体的比例，得到了导电性能较好的PPy/BF。PPy在玄武岩纤维表面形成了连续有效的导电网络，使玄武岩纤维的电阻大幅度下降，实现了玄武岩纤维的高导电性。在制备过程中，通过原位生长的方法，避免了对纤维造成伤害的高温、酸碱处理等工艺，很好地保护了玄武岩纤维的结构，保护了玄武岩纤维优异的拉伸性能。

图 4 聚吡咯/玄武岩纤维(PPy/BF)宏观形貌及形成过程示意图

Figure 4. Schematic diagram of polypyrrole/basalt fibers (PPy/BF) macroscopic morphology and formation process

下载: 全尺寸图片幻灯片

2.1 PPy/BF微观形貌和结构组成

图5(a)为未改性的玄武岩纤维的扫描电镜图，玄武岩纤维呈现圆柱状，表面平整光滑，含有少量的杂质。当使用浓度较低的吡咯单体溶液对玄武岩纤维进行改性时(PPy/BF-0.5)，从图5(b)中可以看出，聚吡咯颗粒成功负载在玄武岩纤维表面，纤维表面变得粗糙，但由于聚吡咯的负载量较小，聚吡咯颗粒分布不均匀，离散性较大。因此，当吡咯浓度较小时，在玄武岩纤维表面拥有较少的连续导电网络，导致玄武岩纤维的导电性较差。当吡咯浓度较大且引入掺杂剂NaSSA后，聚吡咯在玄武岩纤维上的负载量较大。图5(c)为PPy/BF(1) 的FESEM图，从图中可以看出，玄武岩纤维表面附着上了较厚的聚吡咯涂层，很大地提升了玄武岩纤维表面的粗糙度，有利于玄武岩纤维与树脂基体之间的粘结，可能能够在一定程度上提升了玄武岩纤维增强复合材料的界面性能。相比于PPy/BF-0.5 (图5(b))，聚吡咯涂层均匀稳定地附着在玄武岩纤维表面，在玄武岩纤维表面构建了连续有效的导电网络，因此具有更良好的导电性能。对比PPy/BF-0.5和PPy/BF(1)上的PPy颗粒(图5(d)~图5(f))，可以看出二者所生长的PPy颗粒均呈现“花菜状” ^[25]，PPy/BF(1)上生长的PPy颗粒具有更小的直径，分布更加均一。结合图5(b)和图5(c)，PPy的团聚程度也进一步减小，说明掺杂剂NaSSA能够有效地控制PPy分子链有序缓慢地增长，聚吡咯具有更优异的颗粒形貌，进一步实现了PPy颗粒纳米化。

图 5 FESEM图：(a)未处理的玄武岩纤维；((b), (c)) PPy/BF-0.5和PPy/BF(1)；(d) PPy/BF-0.5上聚合生长的PPy颗粒；((e), (f)) PPy/BF(1)上聚合生长的PPy颗粒

Figure 5. FESEM images: (a) Untreated basalt fibers; ((b), (c)) PPy/BF-0.5 and PPy/BF(1); (d) PPy particles polymerized on PPy/BF-0.5; ((e), (f)) PPy particles polymerized on PPy/BF(1)

下载: 全尺寸图片幻灯片

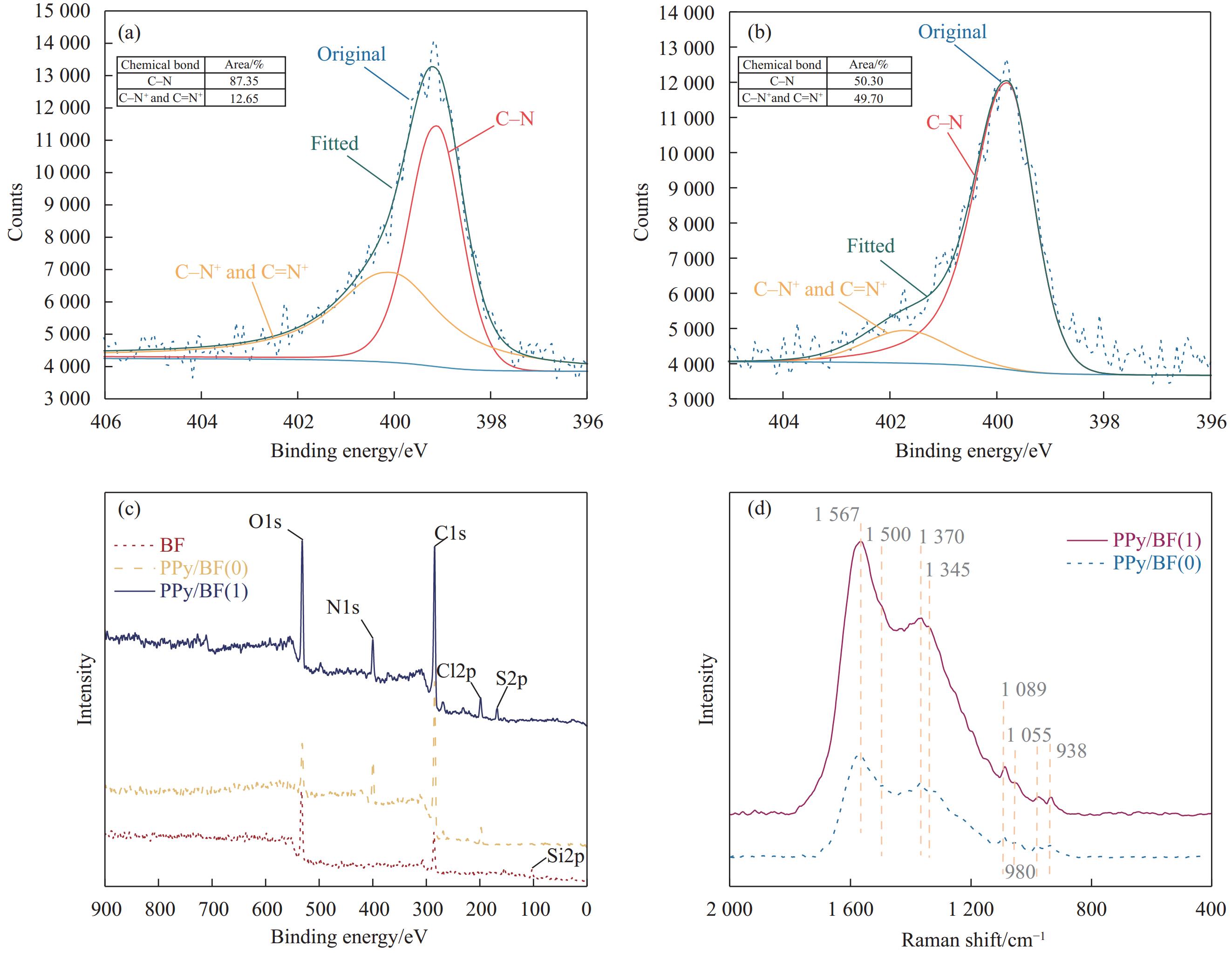
采用XPS对改性前后的玄武岩纤维表面元素变化及元素相对含量进行表征和分析。图6(c)为采用聚吡咯改性玄武岩纤维前后的BF、PPy/BF(0)、PPy/BF(1)的XPS全谱图。通过XPS全谱图中可以看出，玄武岩纤维表面主要含有C、O、Si元素，其中O1s的谱峰位于531.95 eV，C1s的谱峰位于284.80 eV，Si2p的谱峰位于102.35 eV^[26]。PPy/BF相比于BF多了N1s、Cl2p和S2p谱峰，其中，N1s、Cl2p和S2p谱峰分别位于400 eV、199 eV和169 eV位置。其中，N元素主要来源于PPy，Cl元素主要来源于氧化剂FeCl₃，S元素主要来源于掺杂剂NaSSA。结合XPS全谱图和表2，未改性的玄武岩纤维表面C元素含量最高，O元素和Si元素次之。玄武岩纤维表面含有大量的Si—OH活性官能团，有利于提高玄武岩纤维的表面活性，从而提高涂敷上浆剂的均匀性和复合材料的界面性能。聚吡咯涂层形成过程一般含有C、O、N、Cl、S等元素，通过聚吡咯改性玄武岩纤维后，XPS全谱图中出现了N1s峰，说明聚吡咯成功附着在了玄武岩纤维表面。PPy/BF(1)相比于PPy/BF(0)表面增加了S元素，这是由于在改性过程中，加入了掺杂剂NaSSA。

图 6 PPy/BF(0) (a)和PPy/BF(1) (b)的N1s分峰拟合图；(c) BF、PPy/BF(0)和PPy/BF(1)的XPS全谱图；(d) PPy/BF(0)和PPy/BF(1)的Raman图谱

Figure 6. N1s region spectra of PPy/BF(0) (a) and PPy/BF(1) (b); (c) XPS full spectra of BF, PPy/BF(0) and PPy/BF(1); (d) Raman spectra of PPy/BF(0) and PPy/BF(1)

下载: 全尺寸图片幻灯片

表 2 XPS全谱图中BF、PPy/BF(0)和PPy/BF(1)表面元素及其原子分数(at%)

Table 2. Surface elements and atomic fractions (at%) of BF, PPy/BF(0) and PPy/BF(1) by the XPS spectra

Sample	C	O	N	Cl	S	Si	(Cl+S)/N
BF	48.81	39.61	–	–	–	11.58	–
PPy/BF(0)	71.16	11.76	12.72	2.89	–	1.47	0.23
PPy/BF(1)	63.51	20.36	9.50	3.09	2.34	1.21	0.57

下载: 导出CSV

| 显示表格

对PPy/BF(0)和PPy/BF(1)的N1s图谱进行分峰拟合，结果如图6(a)、所示。聚吡咯的N元素可以分出3种波峰，其相应的结合能分别位于402.3 eV、401.0 eV和399.8 eV，对应于质子化醌类亚胺(—N⁺=)、质子化亚胺(—N⁺H—)和亚胺(—NH—)。含有质子化氮说明聚吡咯是掺杂态的，可以用质子化氮和氮的比值来反映聚吡咯的掺杂程度( $\mathrm{[N^+]/[N]}$ )^[27-28]，该比值可通过N1s分峰拟合图中曲线的面积来计算。通过计算，得到PPy/BF(0)的 $\mathrm{[N^+]/[N]}$ =12.65%，而PPy/BF(1)的 $\mathrm{[N^+]/[N]}$ =49.70%，因此，PPy/BF(1)具有更高的质子化程度，其纤维表面的聚吡咯也就拥有更高的掺杂水平，这归因于PPy/BF(1)加入了掺杂剂 NaSSA。此外，也可以通过XPS全谱图来反映聚吡咯的掺杂水平。Cl和S元素分别来自于氧化剂FeCl₃ 和掺杂剂NaSSA，氯离子和磺酸根阴离子都可以作为反离子起到对聚吡咯的掺杂作用，基于此，可以使用 $\mathrm{(Cl+S)/N}$ 来表征聚吡咯的掺杂程度^[29]。根据计算，如所示，PPy/BF(0)的 $\mathrm{(Cl+S)/N}$ = 0.23，而PPy/BF(1)的 $\mathrm{(Cl+S)/N}$ =0.57，这也说明了PPy/BF(1)表面的聚吡咯拥有更高的掺杂水平。而掺杂水平影响着聚吡咯的导电性、氧化还原性、柔韧性及微观结构等。由于掺杂剂的加入会显著增加聚吡咯链上电荷的载体数量，因此，更高的掺杂水平意味着聚吡咯具有更优异的导电性能。通过PPy/BF(0)和PPy/BF(1)的Raman图谱来对比其上负载的聚吡咯分子的结构差异。如图6(d)所示，PPy/BF(0)和PPy/BF(1)展现出一致的Raman光谱特征峰。其中，1567 cm⁻¹处为PPy骨架中C=C键的伸缩振动，1500 cm⁻¹处为骨架光带，1370 cm⁻¹处是C—N键的反对称伸缩，1345 cm⁻¹处为吡咯环中C—C键的伸缩振动，1089 cm⁻¹处代表双极化子C—H的对称面内弯曲振动，1055 cm⁻¹处代表极化子C—H的对称面内弯曲振动，980 cm⁻¹处为形成极化子时吡咯环的变形振动，938 cm⁻¹处为形成双极化子时吡咯环的变形振动^[30-31]。

其中，聚吡咯共轭分子链中产生的可移动的自由基阳离子，称为极化子；当失去两个电子，产生的是双阳离子，称为双极化子。双极化子和极化子在电流作用下移动，为聚吡咯提供导电性，双极化子比极化子对于提高聚吡咯导电性更有利。Dauginet-De Pra等^[32]提出可以通过Raman光谱中R₁= $\dfrac{{I(938 \,\,{{\mathrm{cm}}^{ - 1}})}}{{I(980 \,\, {{\mathrm{cm}}^{ - 1}})}}$ 、R₂= $\dfrac{{I(1\,089 \,\,{{\mathrm{cm}}^{ - 1}})}}{{I(1\,055 \,\, {{\mathrm{cm}}^{ - 1}})}}$ 、R₃= $\dfrac{{I(938 \,\,{{\mathrm{cm}}^{ - 1}}) + I(1\,089 \,\,{{\mathrm{cm}}^{ - 1}})}}{{I(980\,\, {{\mathrm{cm}}^{ - 1}}) + I(1\,055\,\, {{\mathrm{cm}}^{ - 1}})}}$ 3个值的大小来反映聚吡咯分子中双极化子和极化子的比例(I表示特征峰强度)，其结果如表3，通过对比可以看出，PPy/BF(1)的R₁、R₂、R₃值均大于PPy/BF(0)，说明PPy/BF(1)具有更高的双极化子比例，说明形成的聚吡咯结构更优异，导电性能更好。此外，Dauginet-De Pra等^[32]还提出可以使用 $L = \dfrac{{I(1\,568 \,\,{{\mathrm{cm}}^{ - 1}})}}{{I(1\,500 \,\,{{\mathrm{cm}}^{ - 1}})}}$ 来表征聚吡咯共轭链的长度，通过可以看出，PPy/BF(1)具有比PPy/BF(0)更大的L值。共轭链长度影响着聚吡咯的导电性。由于聚吡咯是一种含有大 $\text{π}$ 键的共轭高分子，其电导率主要受到载流子迁移率的影响，而载流子迁移率主要取决于聚吡咯分子链的链距和载流子在聚吡咯分子链上跃迁的频率。聚吡咯分子链有效共轭长度和取向影响着跃迁频率。因此，由于PPy/BF(1)的有效共轭链长度大于PPy/BF(0)，共轭体系更完善，其电导率也更高。

表 3 Raman光谱中不同特征峰强度比

Table 3. Intensity ratios of different characteristic peaks in Raman spectra

Sample	R₁	R₂	R₃	L
PPy/BF(0)	0.93	1.07	1.02	1.39
PPy/BF(1)	1.17	1.23	1.21	1.64
Notes: R₁= $\frac{I(938\, \, \rm{cm}^{-1})}{I(980\, \, \rm{cm}^{-1})}$ , R₂ = $\frac{I(1\, 089\, \, \rm{cm}^{-1})}{I(1\, 055\, \, \rm{cm}^{-1})}$ , R₃ = $\frac{I(938\, \, {\rm cm}^{-1})+I(1\, 089\, \, \rm{cm}^{-1})}{I(980\, \, {\rm cm}^{-1})+I(1\, 055\, \, \rm{cm}^{-1})}$ , L = $\frac{I(1\, 568\, \, {\rm cm}^{-1})}{I(1\, 500\, \, \rm{cm}^{-1})}$ ; I—Intensity of a characteristic peak at a specific position in the Raman spectrum.

下载: 导出CSV

| 显示表格

2.2 PPy/BF导电性能研究

基于SEM、XPS和Raman光谱的结果，PPy/BF(1)上的聚吡咯具有最优异的结构，因此也具有最好的导电性。以下使用PPy的负载量及电阻率的平均值和方差来量化不同参数下PPy/BF的电阻率，并具体分析机制。

2.2.1 吡咯单体浓度对PPy/BF导电性影响

展示了吡咯单体浓度对PPy/BF电阻率的影响。从图中可以看出，随着吡咯单体浓度的增大，聚吡咯的负载量逐渐增加，PPy/BF的电阻率逐渐下降而趋于稳定。当吡咯单体浓度为0.5、1、2、3 mol/L时(即 $\dfrac{C(\mathrm{Py)}}{C(\mathrm{FeCl_3)}}$ = 0.5、1、2、3)，聚吡咯的负载量分别为12.93wt%、14.24wt%、17.43wt%、21.19wt%，PPy/BF的电导率分别为0.254、0.205、0.148、0.125 Ω·cm。在不添加掺杂剂的条件下，PPy/BF上聚吡咯的负载量能达到20wt%，电阻率能达到0.125 Ω·cm，具有良好的导电性。

图 7 不同制备参数下PPy/BF的电阻率：(a) Py与FeCl₃不同摩尔比(C(Py) : C(FeCl₃))的影响；(b) NaSSA与Py不同摩尔比(C(NaSSA) : C(Py))的影响

Figure 7. Resistivity of PPy/BF under different preparation parameters: (a) Effect of different molar ratios (C(Py) : C(FeCl₃)) of Py to FeCl₃; (b) Effect of different molar ratios (C(NaSSA) : C(Py)) of NaSSA to Py

下载: 全尺寸图片幻灯片

当吡咯浓度较低时，合成的聚吡咯较少，聚吡咯在玄武岩纤维布上无法形成较多连续有效的导电通路，且聚吡咯共轭链长度较短，加上玄武岩纤维自身的电绝缘性，导致PPy/BF-0.5的电阻率较高。当吡咯浓度较大时，聚吡咯的负载量提升，玄武岩纤维布上拥有了较多聚吡咯颗粒，聚吡咯共轭链长度增大，此时PPy/BF的电阻率下降。但由于氧化剂的量是固定的，随着聚合反应的进行，氧化剂的量逐渐减少，聚合反应速度逐渐减缓，聚吡咯的负载量和PPy/BF的电导率均逐渐趋于稳定。对所测试的10个不同位置的电阻率进行标准差分析，从图7(a)中可以看出，由于吡咯浓度较小，在玄武岩纤维表面聚合生长的离散性较大，聚合生长均一性差，因此在不同位置的电阻率差异也较大。随着吡咯浓度的增加，聚吡咯在玄武岩纤维表面稳定且均一地生长，因此标准差逐渐减小且趋于稳定。

2.2.2 掺杂剂NaSSA浓度对PPy/BF导电性影响

图7(b)展示了掺杂剂NaSSA的浓度对PPy/BF电阻率的影响。曲线的变化趋势可以看出，随着NaSSA浓度的增大，聚吡咯的负载量逐渐增加，PPy/BF的电阻率逐渐下降而趋于稳定。当掺杂剂NaSSA与吡咯单体的摩尔比为0、0.05、0.1、0.5、1时，相应地，聚吡咯的负载量分别为21.19wt%、24.02wt%、27.47wt%、30.45wt%、31.92wt%，PPy/BF的电导率分别为0.125、0.0878、0.0278、0.0106、0.00785 Ω·cm。因此，在加入掺杂剂NaSSA之后，PPy/BF的电阻率有了很明显的下降，能达到8×10⁻³ Ω·cm，聚吡咯的负载量能达到32wt%。相比于未加入掺杂剂的PPy/BF(0)，PPy/BF(1)的电阻率下降了94%，负载量提升了51%。

氧化剂FeCl₃和掺杂剂NaSSA会发生络合反应，Fe³⁺和SSA⁻上的羧基和羟基形成紫红色的络合物，隐藏了部分Fe³⁺，如图8所示。使吡咯单体不容易接近Fe³⁺，吡咯被氧化的速率得到了减缓，相当于得到了一种温和的氧化剂，防止吡咯被过氧化，控制聚吡咯共轭链缓慢有序地生长，形成有效连通的导电网络。另一方面，在聚合反应的过程中，由于Cl⁻和SSA⁻阴离子的存在，聚吡咯的分子链产生正电荷后，Cl⁻和SSA⁻阴离子在正电荷附近沉积，并形成掺杂态的聚吡咯，具有较高的导电性^[33]。

图 8 NaSSA与Fe³⁺反应生成紫色络合物方程式示意图

Figure 8. Schematic diagram of the equation for the reaction of NaSSA with Fe³⁺ to form a purple complex

下载: 全尺寸图片幻灯片

2.3 纤维单丝拉伸性能

2.3.1 纤维单丝拉伸强度分析

图9和表4展示了玄武岩纤维在改性前后的拉伸性能。玄武岩纤维在改性前强度为2203 MPa，改性之后玄武岩纤维强度为2657 MPa，相比于未改性前提升了20.6%，改性前后弹性模量几乎保持不变。分析单丝强度的提升原因在于：(1) 改性过程中没有使用到会对玄武岩纤维结构造成伤害的例如高温、酸碱腐蚀等技术方法，因此不会造成纤维结构的破坏和力学强度的下降；(2) 聚吡咯颗粒粒径较小，能够对玄武岩纤维制造过程所产生的表面缺陷和孔洞具有一定的填充和桥接作用，因此提升了玄武岩纤维的单丝拉伸强度。此外，复合材料的破坏很大一部分是由于纤维与基体的界面所引起的。从FESEM图中可以看出，经过聚吡咯改性后，玄武岩纤维表面的粗糙度明显增大，可能能够在一定程度上提升纤维与基体的粘结性能，从而进一步提升复合材料的力学性能。

图 9 BF和PPy/BF(1) 纤维单丝拉伸应力-应变曲线

Figure 9. Single fiber tensile stress-strain curves of BF and PPy/BF(1)

下载: 全尺寸图片幻灯片

表 4 PPy改性前后玄武岩纤维单丝拉伸强度

Table 4. Monofilament tensile strength of basalt fiber before and after PPy modification

Sample	Monofilament tensile strength/ MPa	Dispersion coefficient/%	Elastic modulus/GPa	Dispersion coefficient/%
BF	2203	6.5	72.91	4.9
PPy/BF(1)	2657	7.1	74.85	5.2

下载: 导出CSV

| 显示表格

2.3.2 纤维单丝拉伸强度差异性分析

利用统计学方法对单丝拉伸的试验结果进行检验，使用独立样本T检验得到PPy改性后玄武岩纤维拉伸强度的变化情况。首先，对BF和PPy/BF的拉伸强度进行正态性检验。若BF和PPy/BF的拉伸强度符合正态性分布，则对BF和PPy/BF的拉伸强度进行方差齐次性检验，若能通过方差齐次性检验，则可采用独立样本T检验来对比BF和PPy/BF的拉伸强度是否存在显著性差异，验证PPy改性是否保护了纤维结构和一定程度上提升了纤维的单丝拉伸强度。

BF和PPy/BF的正态性检验采用夏皮洛-威尔克(Shapiro-Wilk，S-W)检验方法，这是由于S-W检验方法适合于对小样本数据进行正态性检验，具体如下式所示：

$w=\frac{\left(\displaystyle\sum\limits_{i=1}^l\alpha_ix_i^{ }\right)^2}{\displaystyle\sum\limits_{i=1}^n\left(x_i-\overline{x}\right)^2}$

(7)

式中： $\alpha_i$ 为权重系数； $x_i$ 表示第i个排列后的数据； $\overline{x}$ 为平均值。

根据α=0.05，查表可得w的临界值为w'= 0.927。如果w > w'，则接受原假设，即纤维拉伸强度分布呈现正态分布，通过计算，得到BF和PPy/BF(1)的w统计量和P值，其结果如表5所示。从表中可以看出，BF和PPy/BF(1)的w值均大于临界值0.927，P值均大于0.05，水平不呈现显著性，接受原假设，因此符合正态性检验，满足独立同分布的条件。

表 5 BF和PPy/BF单丝拉伸强度Shapiro-Wilk检验

Table 5. Shapiro-Wilk test of BF and PPy/BF monofilament tensile strength

Sample	w statistical indicator	P value
BF	0.943	0.213
PPy/BF(1)	0.969	0.672

下载: 导出CSV

| 显示表格

在进行独立样本T检验之前，需要对BF和PPy/BF进行方差齐次性检验，这是使用独立样本T检验需满足的前提。方差齐次性检验采用F检验的方法，采用P值对结果进行表征，如果P值大于显著性水平0.05，则接受原假设，BF和PPy/BF的单丝拉伸强度满足方差齐次性。方差齐次性检验结果如表6所示，从表中可以看出，F统计量为2.63，P值大小为0.112，水平上呈现不显著，因此，BF和PPy/BF的单丝拉伸强度满足方差齐次性。

表 6 BF和PPy/BF单丝拉伸强度方差齐次性检验

Table 6. F-test of BF and PPy/BF monofilament tensile strength

Sample	F statistical indicator	P value
BF and PPy/BF(1)	2.63	0.112

下载: 导出CSV

| 显示表格

因此，基于BF和PPy/BF满足正态性检验和方差齐次性检验，采用独立样本T检验的方法来判断BF和PPy/BF的单丝拉伸强度是否存在显著性差异，结果如表7所示。从表中可以看出，独立样本T检验的P值为0.001，统计结果显著，拒绝原假设，说明BF和PPy/BF的单丝拉伸强度存在明显差异，这证明PPy能够在一定程度上提升玄武岩纤维的单丝拉伸强度。此外，采用Cohen's d效应值来反映差异性程度。Cohen's d效应值为0.2、0.5和0.8分别是显著性差异小、中、大的临界值。从表中可以看出，Cohen's d效应值为1.053，说明BF和PPy/BF(1)的单丝拉伸强度显著性差异明显。这不仅证明了独立样本T检验的结果，也证明了PPy在保护纤维强度、弥补纤维缺陷、提升纤维单丝拉伸强度上的作用。

表 7 BF和PPy/BF单丝拉伸强度独立样本T检验

Table 7. Independent samples T-test of BF and PPy/BF monofilament tensile strength

Sample	T statistical indicator	P value	Cohen's d value
BF and PPy/BF(1)	−3.571	0.001	1.053

下载: 导出CSV

| 显示表格

2.3.3 纤维单丝拉伸强度Weibull分布模型

纤维本身是一种脆性材料，纤维表面的缺陷会对纤维的单丝拉伸强度产生影响。因此，仅使用离散系数来反映离散性不够全面和客观。基于以上的实验结果和差异性分析，下面使用Weibull分布来对BF和PPy/BF的离散性进行分析。

Weibull分布以“最弱链”理论为基础^[34-36]，认为纤维束长度方向的缺陷是随机分布的，当其中最大的缺陷发生破坏时，整个结构发生失效。Weibull统计模型的密度函数 $f\left(\sigma,\beta,\eta\right)$ 和累积分布函数 $F\left(\sigma,\beta,\eta\right)$ 如公式(8)和公式(9)所示：

$f(\sigma ,\beta ,\eta ) = \frac{\beta }{{{\eta ^\beta }}}{\sigma ^{\beta - 1}}\exp \left[ - {\left( {\frac{\sigma }{\eta }} \right)^\beta }\right]$

(8)

$F(\sigma ,\beta ,\eta ) = 1 - \exp \left[ - {\left( {\frac{\sigma }{\eta }} \right)^\beta }\right]$

(9)

式中： $F(\sigma ,\beta ,\eta )$ 表示在应力≤σ时的破坏概率；β为形状参数；η为位置参数。移项后，对两边取对数，得到下式：

$\ln \ln \frac{1}{{1 - F}} = \beta \ln \sigma - \beta \ln \eta$

(10)

通过 $\ln \ln \dfrac{1}{{1 - F}}$ 对 $\ln \sigma$ 作图后进行线性拟合，如果线性拟合效果好，即相关系数R²接近于1，则证明纤维拉伸强度数据符合Weibull分布，根据线性拟合方程 $y = wx + b$ 的w和b来求解形状系数和位置系数。公式中F根据下式计算：

$F = \frac{n}{{1 + N}}$

(11)

式中：N为纤维单丝总数；n为强度低于σ的纤维单丝的数量。

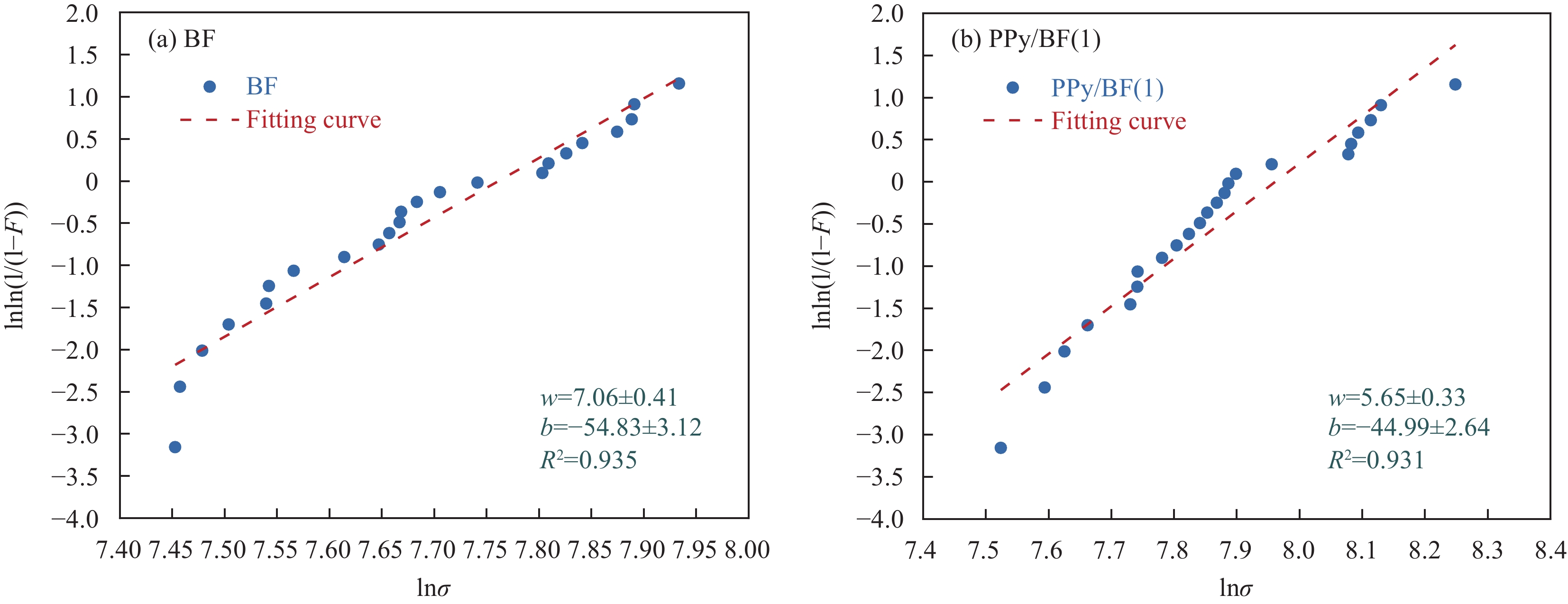
图10为基于公式(10)的BF和PPy/BF(1)单丝拉伸强度的Weibull分布双对数图，图中w、b和R²分别代表拟合直线的斜率，截距和决定系数。表8为Weibull分布线性拟合的相关系数、形状参数和位置参数。从图中可以看出，线性拟合的结果很好，相关系数R分别为0.967、0.965，均大于0.95，说明BF和PPy/BF(1)的纤维单丝拉伸强度分布均符合Weibull分布。

图 10 BF (a)和PPy/BF(1) (b)纤维单丝拉伸强度Weibull双对数图

σ—Tensile strength of a single fiber; F—Failure probability when the stress is less than or equal to σ; w, b—Slope and intercept of the fitted line, respectively; R²—Coefficient of determination

Figure 10. Weibull double logarithmic plot of monofilament fiber tensile strength of BF (a) and PPy/BF(1) (b)

下载: 全尺寸图片幻灯片

根据“最弱链“理论，形状参数β与材料缺陷分布的均匀性有关，形状参数越大，意味着纤维的缺陷分布越均匀，纤维单丝拉伸强度的离散性越小。因此，从中可以看出，BF和PPy/BF(1)的形状系数分别为7.06和5.65，说明了PPy/BF(1)的离散性较大，这与的离散系数结果一致。PPy/BF(1)相比于BF的离散性较大可能是由于PPy在BF上是随机分布的。从离散系数和形状参数的结果来看，PPy/BF(1)相比于BF离散性虽然增大，但在可接受的范围内。位置参数η用来表示纤维强度的统计值大小。根据 $\ln \ln (1/(1 - F(\sigma ,\beta ,\eta )) = 0$ ，求得η表示破坏概率为63.21%的纤维单丝拉伸强度。根据表8，BF和PPy/BF(1)的η分别为2359.70和2872.20，说明PPy/BF(1)的拉伸强度比BF高，这与表4的结果一致。

表 8 Weibull分布线性拟合结果

Table 8. Linear fitting results for the Weibull distribution

Sample	Correlation coefficient (R)	Shape parameter (β)	Position parameter (η)
BF	0.967	7.06	2359.70
PPy/BF	0.965	5.65	2872.20

下载: 导出CSV

| 显示表格

3. 结论

本文开发了一种具有高导电性且同时保护纤维机械性能的低成本、高效、友好的导电玄武岩纤维制备方法。研究了吡咯单体和掺杂剂5-磺基水杨酸钠(NaSSA)浓度的不同对玄武岩纤维导电性的影响及改性前后玄武岩纤维单丝拉伸强度的变化，并通过FESEM、XPS、Raman光谱等方法探究了不同参数对聚吡咯/玄武岩纤维(PPy/BF)导电性能影响的机制，得出以下结论：

(1) 通过对比聚吡咯改性玄武岩纤维前后的FESEM，得到聚吡咯均匀稳定且厚实地附着在玄武岩纤维上，增大了玄武岩纤维表面的粗糙度。对比XPS全谱图和N1s分峰拟合图，PPy/BF(1)的 $\mathrm{[N^+]/[N]}$ 和 $\mathrm{(Cl+S)/N}$ 值均大于PPy/BF(0)，说明PPy/BF(1)上的聚吡咯具有更高的掺杂水平。通过Raman光谱分析了PPy/BF上的化学结构，得出PPy/BF(1)上的聚吡咯具有比PPy/BF(0)更高的双极化子比例和共轭链长度；

(2) 吡咯单体浓度和掺杂剂NaSSA的浓度均对PPy/BF的导电性和PPy的负载量有很大的影响。随着浓度的增大，PPy的负载量不断增大，PPy/BF的电阻率均表现出先下降而后趋于稳定。特别地，掺杂剂NaSSA对于降低PPy/BF电阻率具有显著作用，相比于未加入掺杂剂的PPy/BF，其电阻率下降了94%，负载量提升了51%。所制备的导电玄武岩纤维(PPy/BF)电阻率可下降至8×10⁻³Ω·cm，导电性能良好。这为玄武岩纤维及其复合材料作为优异结构材料的同时，发展成为具有电磁屏蔽、静电防护或自感知等功能的结构-功能一体化复合材料提供了可能；

(3) PPy/BF单丝拉伸强度比BF提升了20.6%。独立样本T检验结果证明PPy/BF(1) 提升玄武岩纤维单丝拉伸强度具有显著性和可靠性。并且，纤维单丝拉伸强度符合Weibull分布。这证明了本文采用的改性方法不破坏玄武岩纤维自身结构，保留了玄武岩纤维作为结构材料优异的机械性能。由于聚吡咯对于玄武岩制造过程表面产生的孔洞和缺陷具有填充和桥接作用，一定程度上提升了玄武岩纤维的单丝拉伸强度。

图 1 碳纤维增强树脂复合材料(CFRP)-钢复合管的制备

θ—Winding angle

Figure 1. Preparation of carbon fiber reinforced polymer (CFRP)-steel composite tube

下载: 全尺寸图片幻灯片

图 2 加载装置图

AE—Acoustic emission; ϕ—Diameter

Figure 2. Loading device diagram

下载: 全尺寸图片幻灯片

图 3 声发射(AE)传感器布置位置

Figure 3. Location of the acoustic emission (AE) sensor arrangement

下载: 全尺寸图片幻灯片

图 4 CFRP增强钢管的破坏形式

Figure 4. Failure forms of CFRP-reinforced tube components

下载: 全尺寸图片幻灯片

图 5 ST和C2T0的荷载-位移曲线

Figure 5. Load-displacement curves of ST and C2T0

下载: 全尺寸图片幻灯片

图 6 CFRP加固钢管的荷载-位移曲线

Figure 6. Load-displacement curves of CFRP-reinforced steel tubes

下载: 全尺寸图片幻灯片

图 7 CFRP加固钢管的吸能特性参数对比

F_max—Peak load; F_mean—Mean load; C_FE—Crushing force efficiency; S_EA—Specific energy absorption

Figure 7. Comparison of energy absorption characteristic parameters of CFRP-reinforced steel tubes

下载: 全尺寸图片幻灯片

图 8 CFRP加固钢管的声发射信号特征参数图

Figure 8. Acoustic emission signal characteristic parameter diagram of CFRP-reinforced steel tubes

下载: 全尺寸图片幻灯片

图 9 CFRP加固钢管的能量释放特征

Figure 9. Energy release characteristics of CFRP reinforced steel tubes

下载: 全尺寸图片幻灯片

图 10 CFRP加固钢管的声发射能量概率密度分布图

P/E—Energy probability density; E_min—Lower limit of energy normalisation; k₁-k₆—Critical indices of AE absolute energy distribution

Figure 10. Probability density distribution of AE energy of CFRP-reinforced steel tubes

下载: 全尺寸图片幻灯片

图 11 CFRP加固钢管的声发射能量临界指数最大似然估计曲线

Figure 11. Maximum likelihood estimation curves of AE energy critical index of CFRP-reinforced steel tubes

下载: 全尺寸图片幻灯片

图 12 蝙蝠算法(BA)流程图

r_j—Transmitting frequency; A_j—Sound intensity

Figure 12. Bat algorithm (BA) flowchart

下载: 全尺寸图片幻灯片

图 13 蝙蝠算法优化最小二乘支持向量机(BA-LSSVM)流程图

Figure 13. Bat algorithm for the least squares support vector machine (BA-LSSVM) flowchart

下载: 全尺寸图片幻灯片

图 14 CFRP加固钢管的预测损伤类型与实际损伤类型对比图

Figure 14. Comparison chart of predicted damage types and actual damage types of CFRP-reinforced steel tubes

下载: 全尺寸图片幻灯片

表 1 钢管及碳纤维性能参数

Table 1 Performance parameters of steel pipe and carbon fiber

Steel tube			Carbon fiber
Tensile strength/ MPa	Yield strength/ MPa	Extension rate	Gram weight/ (g·m⁻²)	Tensile strength/ MPa	Elastic modulus/ GPa	Elongation rate
670	409	16	300	3870	2.45	1.74

下载: 导出CSV

表 2 试件名称及参数

Table 2 Specimen name and parameters

Test specimen	CFRP winding layer	CFRP winding angle/(°)	Quality/g
ST	–	–	1651
C2T0	2	0	1799
C4T0	4	0	1953
C2T30	2	30	1798
C2T60	2	60	1801
C2T90	2	90	1800
Note: ST—Steel tube.

下载: 导出CSV

参考文献(39)

[1]	高小育, 段海, 杨正朴, 等. CFRP加固圆形钢管抗压承载力研究[J]. 建筑科学与工程学报, 2020, 37(6): 55-63. GAO Xiaoyu, DUAN Hai, YANG Zhengpu, et al. Research on the compressive capacity of circular steel pipe reinforced by CFRP[J]. Journal of Building Science and Engineering, 2020, 37(6): 55-63(in Chinese).
[2]	阳涛, 胡乔, 陈小兵, 等. 碳纤维布加固带缺陷的三层聚乙烯防腐涂层钢管及聚乙烯管道的试验研究[J]. 工业建筑, 2018, 48(12): 169-173, 180. YANG Tao, HU Qiao, CHEN Xiaobing, et al. Experimental study on carbon fiber cloth reinforced three-layer polyethylene anticorrosive coated steel pipe and polyethylene pipe with defects[J]. Industrial Architecture, 2018, 48(12): 169-173, 180(in Chinese).
[3]	代岩, 赵均海, 张常光. CFRP和角钢复合加固钢管混凝土叠合柱轴心受压承载力分析[J]. 建筑结构, 2018, 48(17): 96-103. DAI Yan, ZHAO Junhai, ZHANG Changguang. Analysis of axial compression capacity of CFRP and angle steel composite reinforced concrete filled steel tube composite column[J]. Architectural Structure, 2018, 48(17): 96-103(in Chinese).
[4]	黄辉, 路四方, 张祥, 等. 碳纤维复材加固钢管的抗内爆性能[J]. 工业建筑, 2022, 52(1): 211-215. HUANG Hui, LU Sifang, ZHANG Xiang, et al. Implosion resistance of carbon fiber reinforced steel pipe[J]. Industrial Building, 2022, 52(1): 211-215(in Chinese).
[5]	颜宇鸿, 卢亦焱, 李杉, 等. 碳纤维编织网增强ECC加固钢管混凝土短柱压弯承载力计算方法[J]. 建筑结构学报, 2023, 44(10): 178-187. YAN Yuhong, LU Yiyan, LI Shan, et al. Calculation method of compressive bending capacity of ECC reinforced concrete filled steel tube short column reinforced by carbon fiber braided mesh[J]. Journal of Building Structures, 2019, 44(10): 178-187(in Chinese).
[6]	LI Z B, GAO Y, WANG Y, et al. Failure mechanisms and acoustic emission pattern recognition of all-CFRP cylindrical honeycomb sandwich shell under three-point bending[J]. Composites Science and Technology, 2023, 237: 1-13.
[7]	LAVAYEN F D, BUTENEGRO G J A, BOADA M J S, et al. Theoretical and experimental study of the bending collapse of partially reinforced CFRP-steel square tubes[J]. Thin-Walled Structures, 2022, 177: 1-13.
[8]	黄俊杰, 佘艳华, 李猛, 等. 不同碳纤维布加固方式的木构件损伤演化规律[J]. 东北林业大学学报, 2024, 52(1): 115-123. HUANG Junjie, SHE Yanhua, LI Meng, et al. Damage evolution of wood parts with different reinforcement methods of carbon fiber sheet[J]. Journal of Northeast Forestry University, 2024, 52(1): 115-123(in Chinese).
[9]	邵家儒, 刘牛, 杨瑜, 等. CFRP复合材料构件胶接特性及失效规律研究[J]. 应用力学学报, 2023, 40(5): 1058-1067. SHAO Jiaru, LIU Niu, YANG Yu, et al. Study on bonding characteristics and failure rules of CFRP composite components[J]. Chinese Journal of Applied Mechanics, 2023, 40(5): 1058-1067(in Chinese).
[10]	黄书峰, 陈晓周, 刘东, 等. 碳纤维增强复合材料力学性能退化及失效过程的研究进展[J]. 宇航材料工艺, 2022, 52(5): 14-20. DOI: 10.12044/j.issn.1007-2330.2022.05.003 HUANG Shufeng, CHEN Xiaozhou, LIU Dong, et al. Research progress on mechanical degradation and failure processes of carbon fiber reinforced composites[J]. Aerospace Materials & Technology, 2022, 52(5): 14-20(in Chinese). DOI: 10.12044/j.issn.1007-2330.2022.05.003
[11]	ALI Z A, TIAN X Y, LIU T F, et al. Mechanical and energy absorption behaviors of 3D printed continuous carbon/Kevlar hybrid thread reinforced PLA composites[J]. Composite Structures, 2023, 303: 1-12.
[12]	WANG H, PEI Z, CONG W. A mechanistic cutting force model based on ductile and brittle fracture material removal modes for edge surface grinding of CFRP composites using rotary ultrasonic machining[J]. International Journal of Mechanical Sciences, 2020, 176: 105551.
[13]	YU J G, ZHU S Q, FENG X T. Seismic behavior of CFRP-steel composite plate shear wall with edge reinforcement[J]. Journal of Constructional Steel Research, 2023, 203: 1-23.
[14]	陈卓异, 曾剑波, 彭岚, 等. 考虑缺陷位置和CFRP粘贴方式的钢板疲劳性能[J]. 中国公路学报, 2022, 35(2): 212-222. DOI: 10.3969/j.issn.1001-7372.2022.02.019 CHEN Zhuoyi, ZENG Jianbo, PENG Lan, et al. Fatigue properties of steel plate considering defect location and CFRP bonding[J]. China Journal of Highway and Transport, 2022, 35(2): 212-222(in Chinese). DOI: 10.3969/j.issn.1001-7372.2022.02.019
[15]	余海燕, 吴航宇. 碳纤维复合材料/钢的胶铆连接失效机理和选材方法[J]. 上海交通大学学报, 2023, 57(2): 230-240. YU Haiyan, WU Hangyu. Failure mechanism and material selection method of riveted joint of carbon fiber composite/steel[J]. Journal of Shanghai Jiao Tong University, 2023, 57(2): 230-240(in Chinese).
[16]	王庆松, 张玉, 张洪雨, 等. 基于改进Elman神经网络的CFRP补强钢板界面脱粘预测研究[J]. 振动与冲击, 2024, 43(3): 120-127. WANG Qingsong, ZHANG Yu, ZHANG Hongyu, et al. Prediction of interface desticking of CFRP reinforced steel plate based on improved Elman neural network[J]. Journal of Vibration and Shock, 2024, 43(3): 120-127(in Chinese).
[17]	ZHANG Y, LIU Z Z, XIN J H, et al. The attenuation mechanism of CFRP repaired corroded marine pipelines based on experiments and FEM[J]. Thin-Walled Structures, 2021, 169: 1-11.
[18]	谢玉强, 佘艳华, 黄俊杰, 等. 碳纤维增强复合材料加固柏木轴压裂纹演化规律的研究[J]. 森林工程, 2024, 40(2): 102-116. DOI: 10.3969/j.issn.1006-8023.2024.02.012 XIE Yuqiang, SHE Yanhua, HUANG Junjie, et al. Study on axial compression crack evolution of cypress wood reinforced by carbon fiber reinforced composites[J]. Forest Engineering, 2024, 40(2): 102-116(in Chinese). DOI: 10.3969/j.issn.1006-8023.2024.02.012
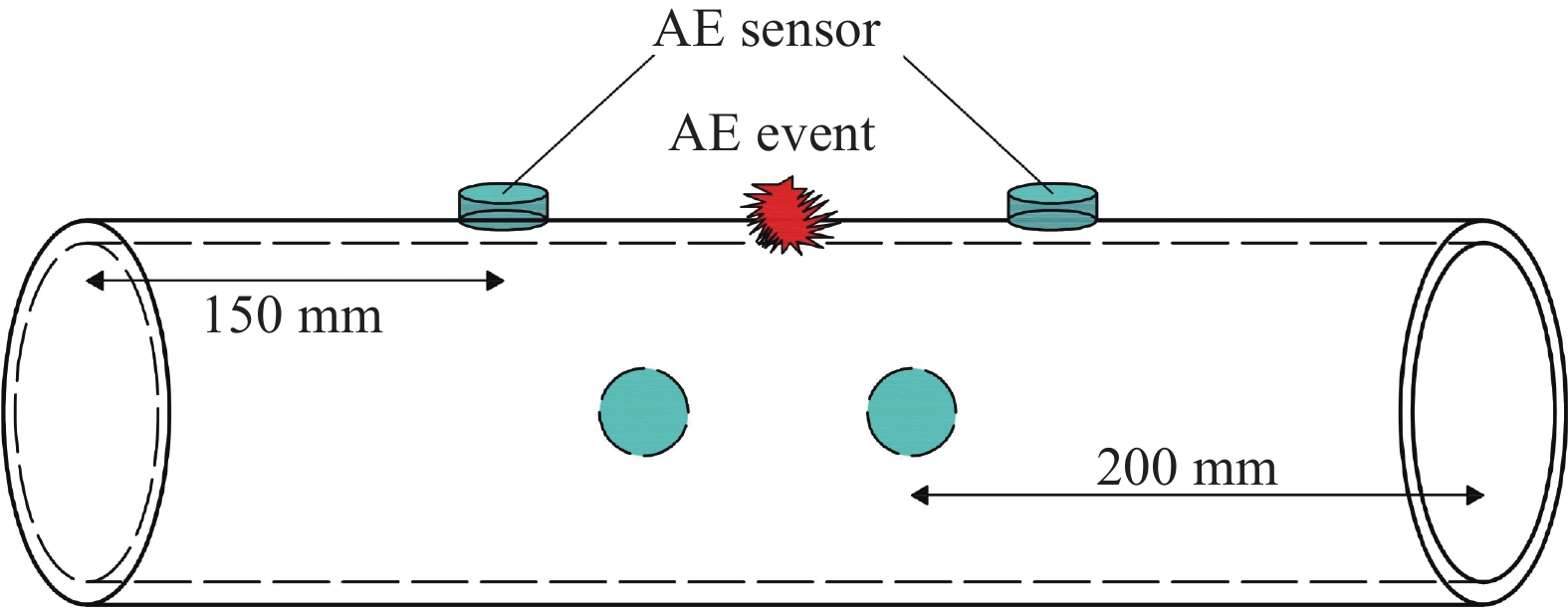
[19]	田宝柱, 徐文涛, 梁鹏, 等. 基于多传感器融合的埋地输水管道泄漏声发射定位方法[J]. 科学技术与工程, 2023, 23(24): 10307-10316. DOI: 10.12404/j.issn.1671-1815.2023.23.24.10307 TIAN Baozhu, XU Wentao, LIANG Peng, et al. Acoustic emission location method for buried water pipeline leakage based on multi-sensor fusion[J]. Science Technology and Engineering, 2023, 23(24): 10307-10316(in Chinese). DOI: 10.12404/j.issn.1671-1815.2023.23.24.10307
[20]	王青原, 许颖, 钱胜. 基于机器视觉和数字图像相关技术的混凝土损伤演化研究[J]. 湖南大学学报(自然科学版), 2023, 50(11): 169-180. WANG Qingyuan, XU Ying, QIAN Sheng. Research on concrete damage evolution based on machine vision and digital image correlation technology[J]. Journal of Hunan University (Natural Science Edition), 2023, 50(11): 169-180(in Chinese).
[21]	许颖, 樊悦, 王青原, 等. 基于DIC的聚丙烯纤维增强混凝土断裂过程分析[J]. 华中科技大学学报(自然科学版), 2024, 52(2): 103-111. XU Ying, FAN Yue, WANG Qingyuan, et al. Fracture process analysis of polypropylene fiber reinforced concrete based on DIC[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2024, 52(2): 103-111(in Chinese).
[22]	袁逸齐, 兰恒星, 刘世杰, 等. 砂岩石窟热诱导裂纹损伤时空特征与分析[J]. 岩石力学与工程学报, 2022, 41(12): 2530-2542. YUAN Yiqi, LAN Hengxing, LIU Shijie, et al. Spatiotemporal characteristics and analysis of heat-induced crack damage in sandstone grottoes[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(12): 2530-2542(in Chinese).
[23]	许鑫浩, 徐福泉, 刘英利, 等. 红外热成像法检测预制混凝土构件外饰面内部缺陷试验研究[J]. 建筑科学, 2021, 37(7): 52-59. XU Xinhao, XU Fuquan, LIU Yingli, et al. Experimental study on detection of internal defects of precast concrete members by infrared thermal imaging[J]. Building Science, 2021, 37(7): 52-59(in Chinese).
[24]	LIU Y H, ZHANG L, LI Z X, et al. Investigation on damage evolution of open-hole plain woven composites under tensile load by acoustic emission signal analysis[J]. Composite Structures, 2023, 305: 1-12.
[25]	PEI N, XIANG Y X. Torsional damage analysis for pre-delaminated carbon/glass fiber-reinforced hybrid laminates based on acoustic emission[J]. Applied Acoustics, 2023, 202: 1-9.
[26]	ZHAO W Z, PEI N, XU C G. Experimental study of carbon/glass fiber-reinforced hybrid laminate composites with torsional loads by using acoustic emission and micro-CT[J]. Composite Structures, 2022, 290: 1-9.
[27]	ZHOU J, MATHEWS J V, ADAMS O D. Acoustic emission-based impact location estimation on composite structures[J]. Structural Health Monitoring, 2019, 18(5-6): 1652-1668.
[28]	林俊亭, 王帅. 基于DBN-MPA-LSSVM的无绝缘轨道电路故障诊断研究[J]. 电子测量与仪器学报, 2022, 36(9): 37-44. LIN Junting, WANG Shuai. Research on uninsulated track circuit fault diagnosis based on DBN-MPA-LSSVM[J]. Journal of Electronic Measurement and Instrumentation, 2022, 36(9): 37-44(in Chinese).
[29]	杨兴武, 王江, 孟致丞, 等. 基于电容电流状态估计的MMC多管开路故障诊断方法[J]. 中国电机工程学报, 2023, 43(23): 9297-9310. YANG Xingwu, WANG Jiang, MENG Zhicheng, et al. MMC multi-tube open-circuit fault diagnosis method based on capacitor current state estimation[J]. Proceedings of the CSEE, 2023, 43(23): 9297-9310(in Chinese).
[30]	李云淏, 咸日常, 张海强, 等. 基于改进灰狼算法与最小二乘支持向量机耦合的电力变压器故障诊断方法[J]. 电网技术, 2023, 47(4): 1470-1478. LI Yunhao, XIAN Richang, ZHANG Haiqiang, et al. Power transformer fault diagnosis method based on improved gray wolf algorithm coupled with least squares support vector machine[J]. Power Grid Technology, 2023, 47(4): 1470-1478(in Chinese).
[31]	杨海柱, 石剑, 江昭阳, 等. 基于CEEMD-SSA-LSSVM短期电力负荷预测模型[J]. 武汉大学学报(工学版), 2022, 55(6): 609-616. YANG Haizhu, SHI Jian, JIANG Zhaoyang, et al. Short-term power load forecasting model based on CEEMD-SSA-LSSVM[J]. Journal of Wuhan University (Engineering and Technology Edition), 2022, 55(6): 609-616(in Chinese).
[32]	GUAN S Y, HUANG D, GUO S G, et al. An improved fault diagnosis approach using LSSVM for complex industrial systems[J]. Machines, 2022, 10(6): 443.
[33]	MENG Q C, CHEN X M, ZHU Y L, et al. Communication signal classification and recognition method based on GA-LSSVM classifier[J]. Journal of Physics: Conference Series, 2019, 1345(2): 1-8.
[34]	MA Q, DONG B, ZHA Y, et al. Multi-objective optimization for energy absorption of carbon fiber-reinforced plastic/aluminum hybrid circular tube under both transverse and axial loading[J]. Journal of Materials Engineering and Performance, 2020, 29(9): 1-16.
[35]	中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料弯曲试验方法: GB/T 232—2010[S]. 北京: 中国标准出版社, 2010. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Bending test method for metal materials: GB/T 232—2010[S]. Beijing: Standards Press of China, 2010(in Chinese).
[36]	LIU Y S, CHEN X H, WU Z Y, et al. Effect of axial yarn distribution on the progressive damage behavior of braided composite tube subjected to three-point bending[J]. Thin-Walled Structures, 2022, 181: 1-12.
[37]	任松, 赵云峰, 张军伟, 等. 煤样巴西劈裂试验声发射能量幂律分布规律[J]. 东北大学学报(自然科学版), 2017, 38(4): 581-585. DOI: 10.3969/j.issn.1005-3026.2017.04.026 REN Song, ZHAO Yunfeng, ZHANG Junwei, et al. Power law distribution of acoustic emission energy in brazil splitting test of coal sample[J]. Journal of Northeastern University (Natural Science Edition), 2017, 38(4): 581-585(in Chinese). DOI: 10.3969/j.issn.1005-3026.2017.04.026
[38]	CLAUSET A, SHALIZI C R, NEWMAN M E J. Power-law distributions in empirical data[J]. SIAM Review, 2009, 51(4): 661-703. DOI: 10.1137/070710111
[39]	HOSSEIN N, POOYA R. Development of a probability distribution model for the SCFs in tubular X-connections retrofitted with FRP[J]. Structures, 2022, 36: 233-247.

施引文献

资源附件(4)

其他相关附件
- 本文图文摘要
  10.13801-j.cnki.fhclxb.20240513.003-GA3 点击下载
- 本文图文摘要
  10.13801-j.cnki.fhclxb.20240513.003-GA4 点击下载
- 本文图文摘要
  10.13801-j.cnki.fhclxb.20240513.003-GA2 点击下载
- 本文图文摘要
  10.13801-j.cnki.fhclxb.20240513.003-GA1 点击下载

长摘要

目的
碳纤维增强树脂复合材料(Carbon fiber reinforced polymer, CFRP)因其高强度、轻质和优异的耐腐蚀性能而成为薄壁钢管结构的重要加固材料。然而，现有研究大多聚焦于观察CFRP加固钢管后的宏观力学性能和损伤表现，对加固钢管内部裂纹扩展规律与整体损伤的联系缺乏深入探究。为了研究不同CFRP加固方式对钢管内部损伤程度和裂纹发展规律的影响，揭示CFRP加固钢管的损伤机制，本文对6组不同CFRP铺层方式的钢管开展三点弯曲损伤监测试验。
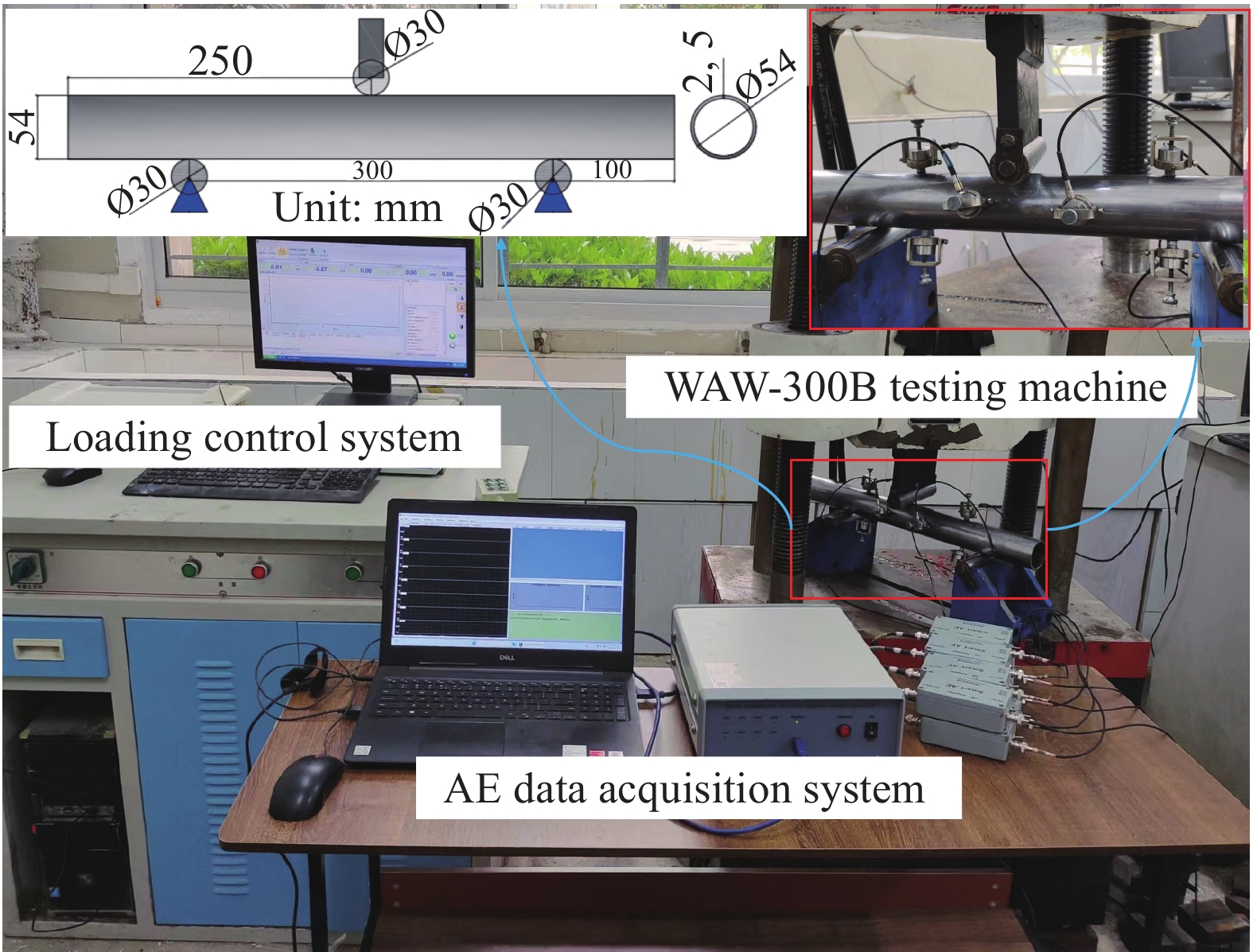
方法
试验以缠绕层数(0、2、4)和缠绕角度(0°、30°、60°、90°)为主要变量，设计了6组不同CFRP铺层方式的钢管。试验采用WAW-300B微机伺服控制液压万能试验机对CFRP加固木柱进行三点弯曲加载试验，其加载速率为2 mm/s，加载控制位移设置为60 mm。采用声发射技术(Acoustic emission, AE)实时监测CFRP加固钢管的三点弯曲损伤情况，通过采集的声发射信号，研究了CFRP加固钢管的力学性能、吸能性能和声发射参数特征，并提出了蝙蝠算法(Bat algorithm, BA)优化最小二乘支持向量机(Least squares support vector machine, LSSVM)的损伤分类预测模型。
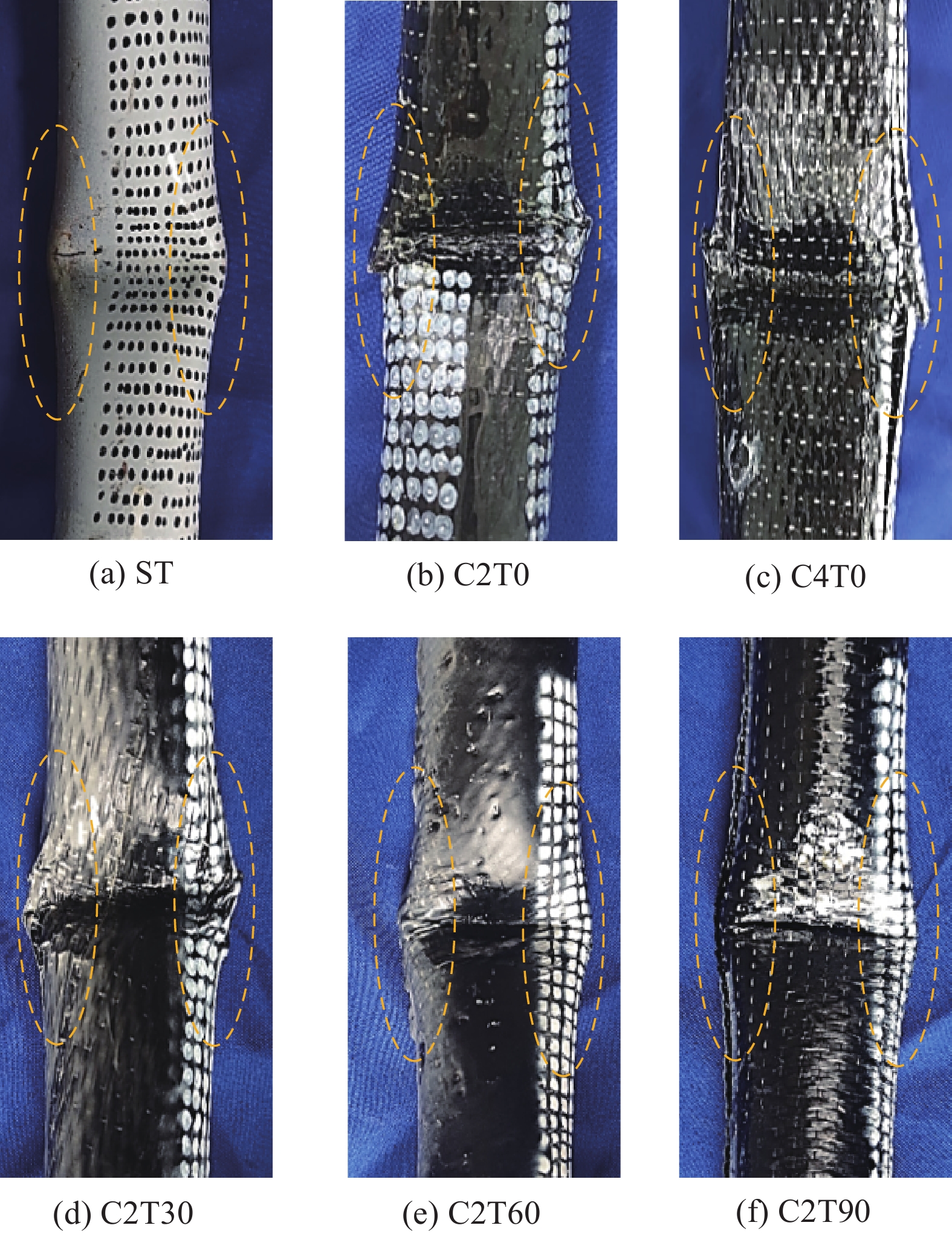
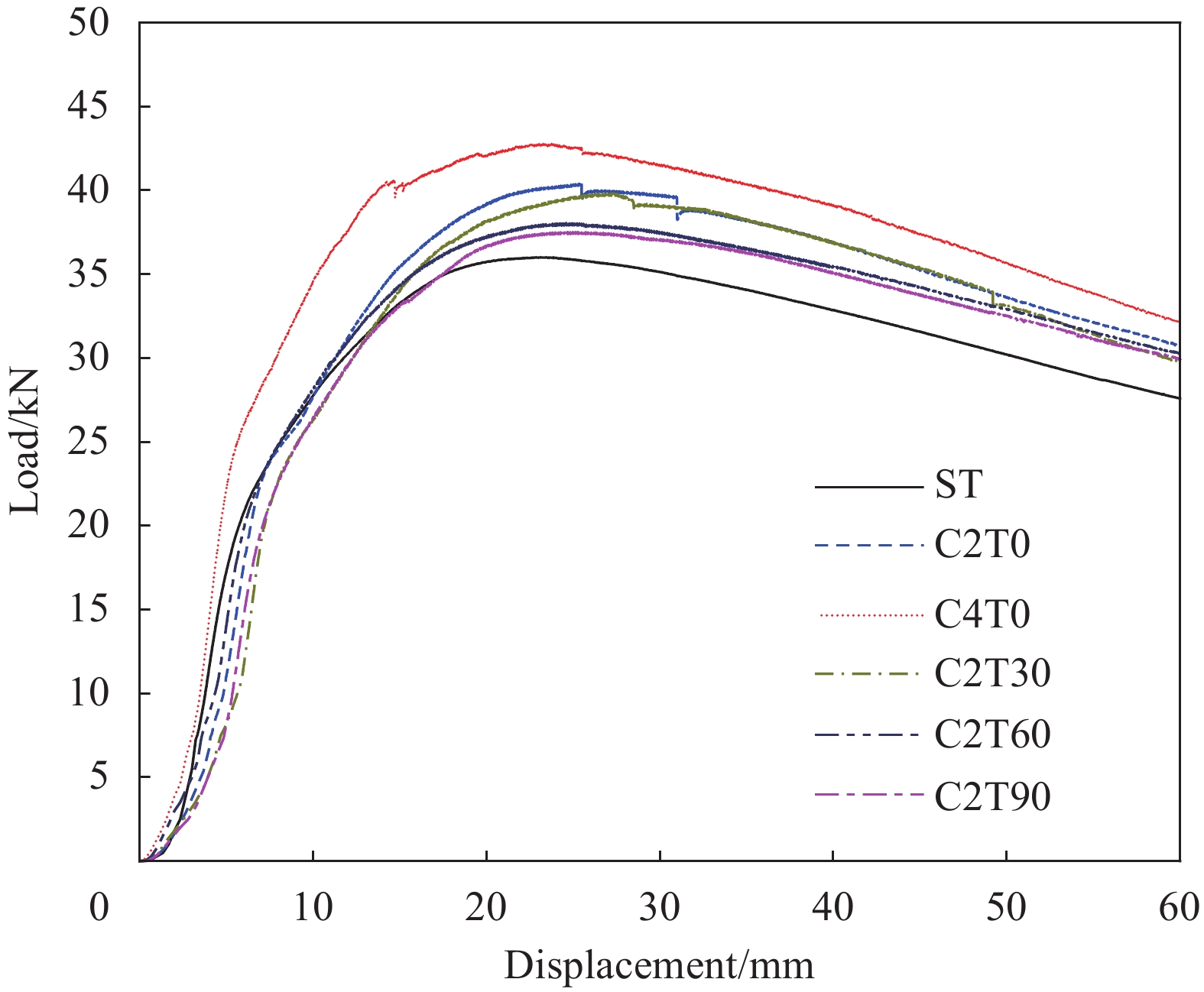
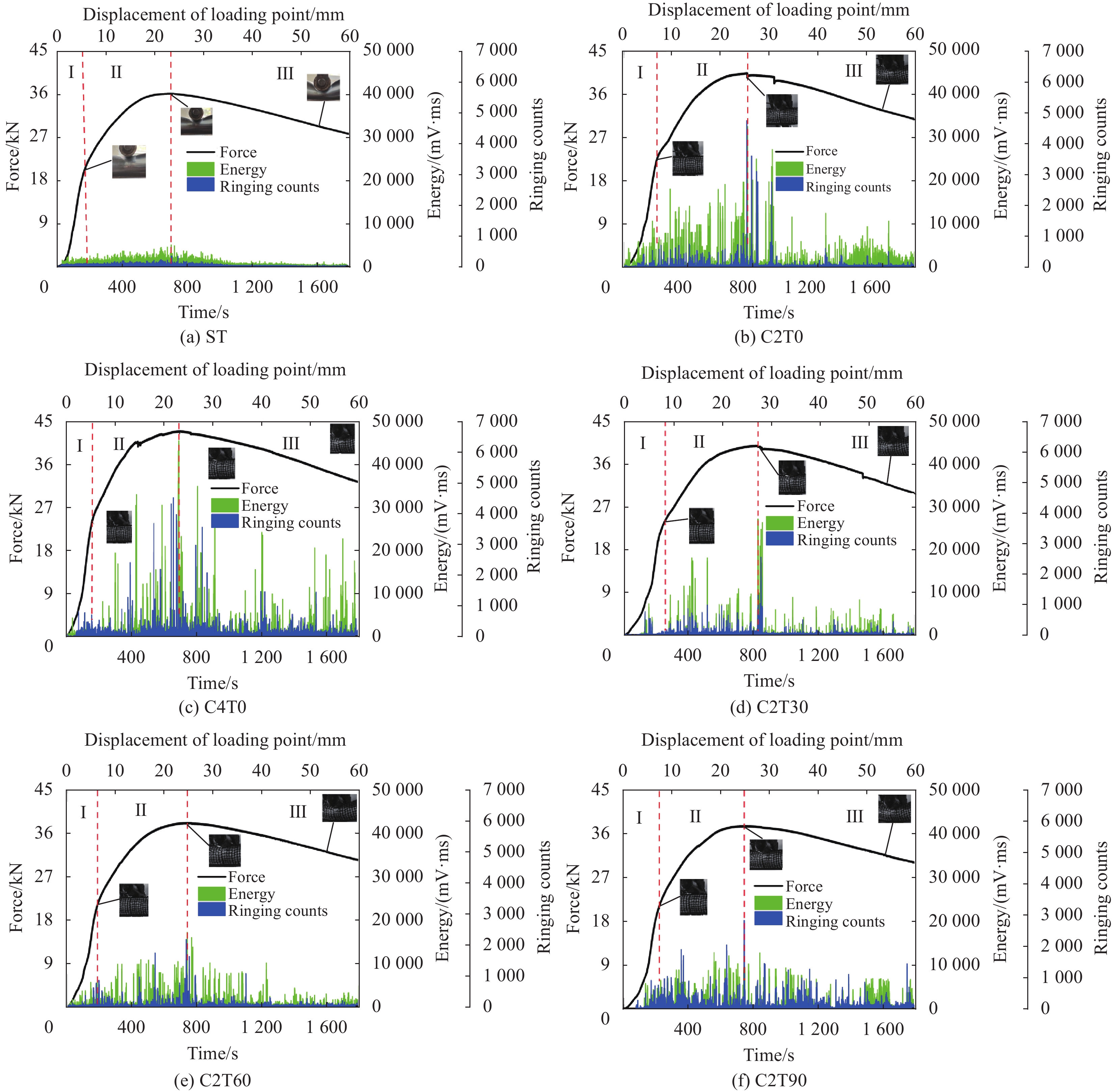
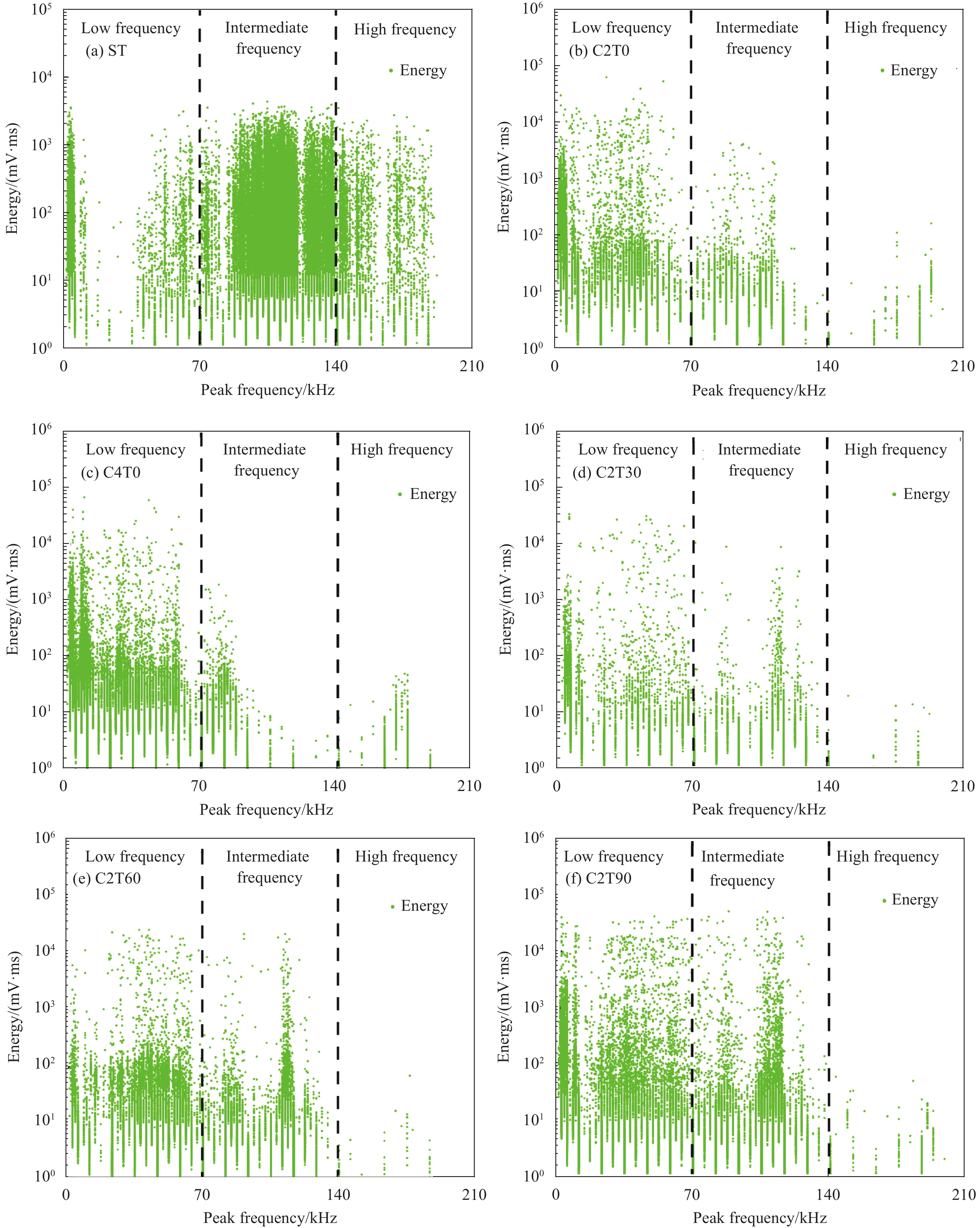
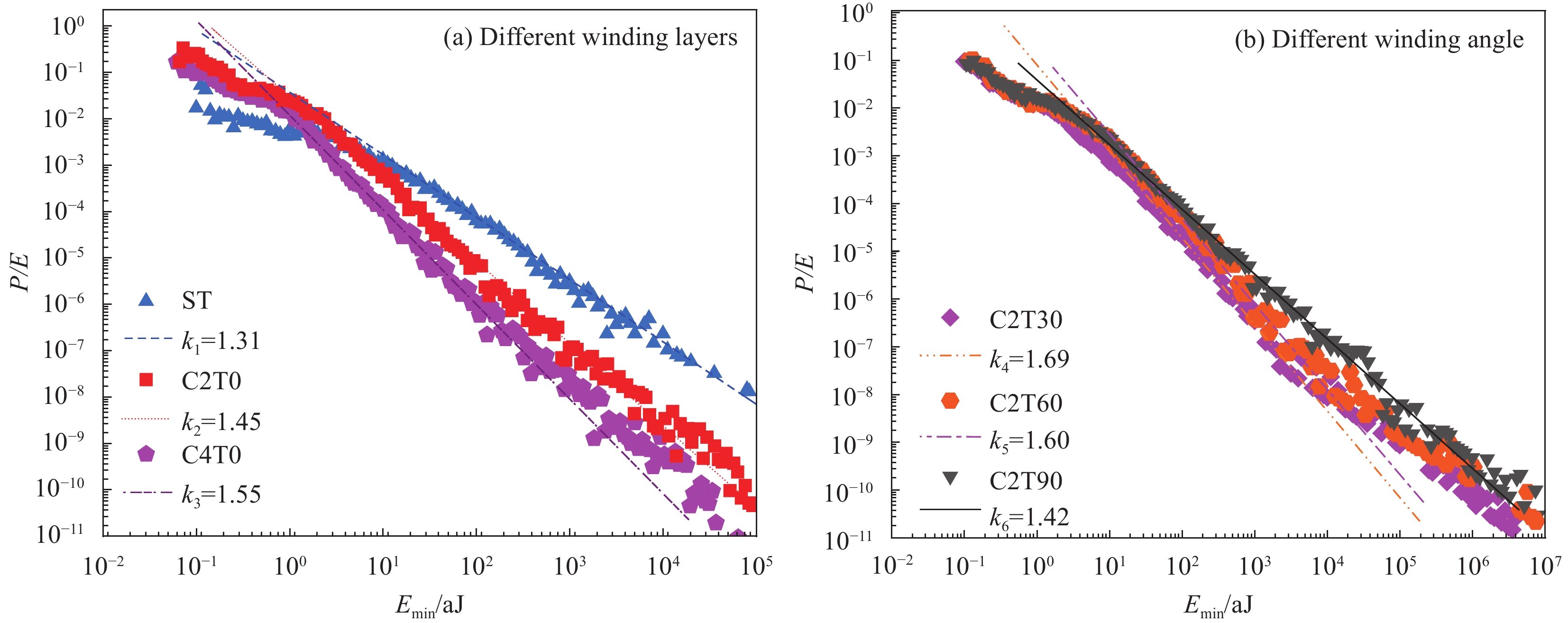
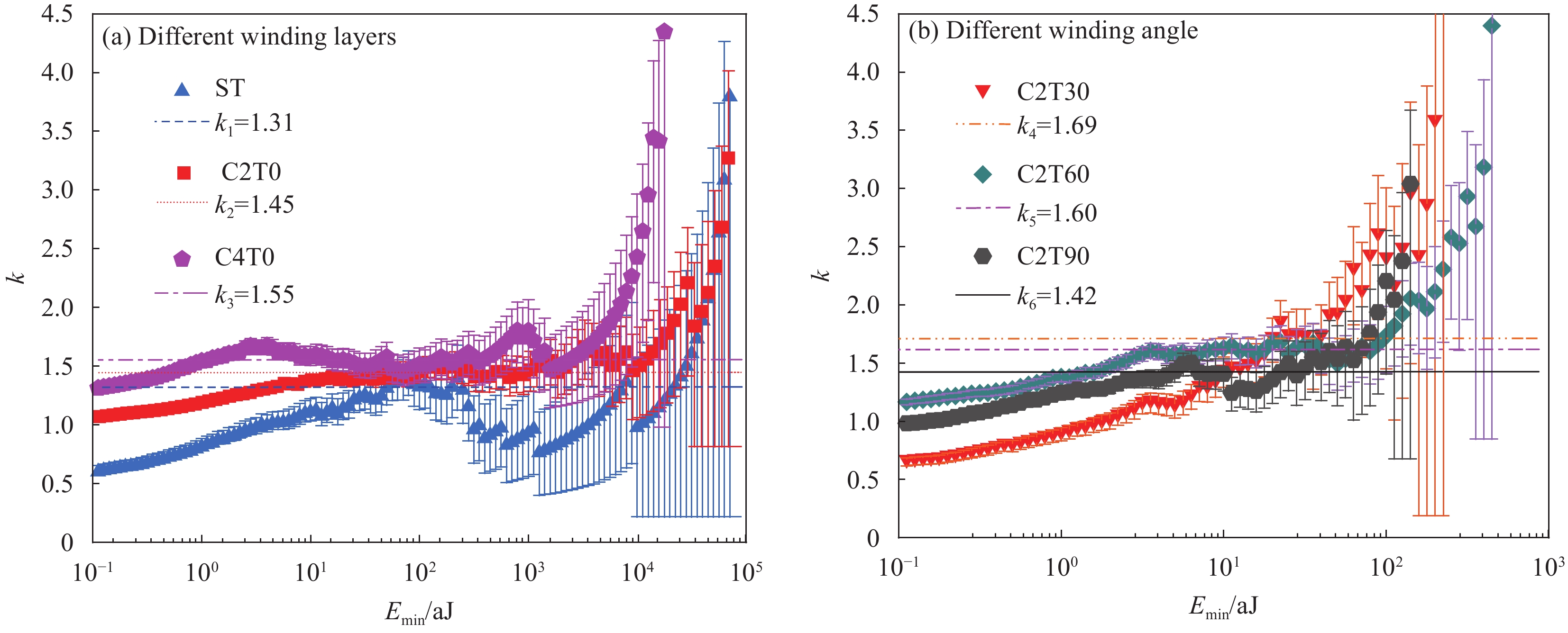
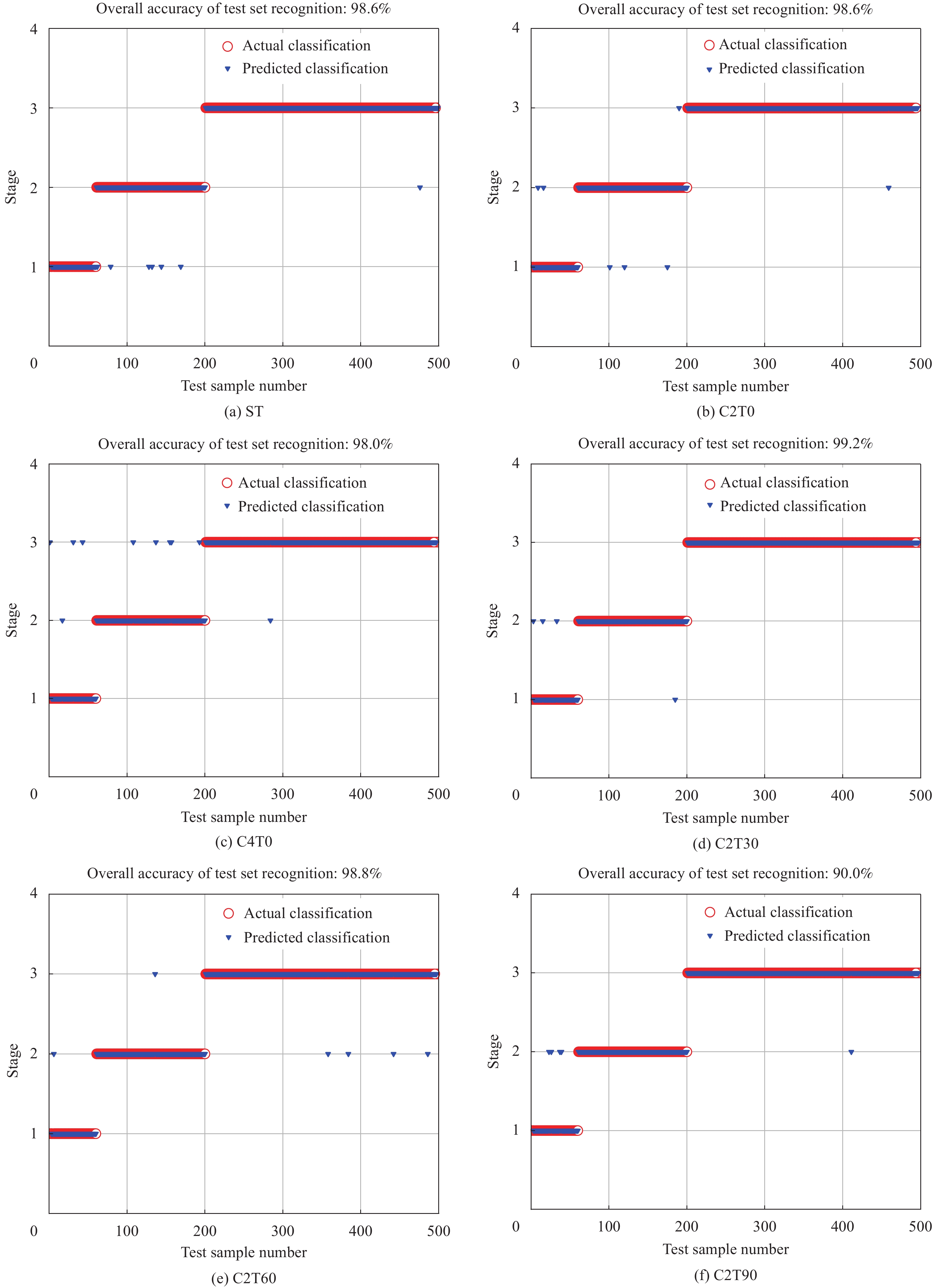
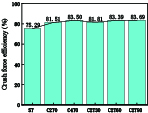
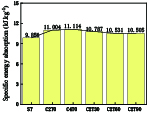
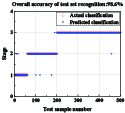
结果
从CFRP加固钢管的三点弯曲-声发射试验中得到了不同CFRP铺层方式下钢管的破坏形式、荷载-位移曲线和声发射特征参数。结果表明：①随着缠绕层数增加，复合管抗弯性能提高，峰值、平均载荷和比吸能均增强。与未加固钢管相比，2层、4层CFRP复合管峰值载荷分别提升12.19%、18.8%。②通过分析声发射信号能量的分布和强度，可以追踪弯曲破坏的累积过程，而通过分析CFRP加固钢管的声发射振铃计数可以评估破坏的程度。③随着CFRP缠绕角度的增加，各试件的AE信号值呈现下降趋势。这一变化表明CFRP的缠绕角度显著影响了AE的分布特征。在不同的缠绕角度下，C2T0试件显示出最高的损伤程度，而C2T90试件则表现出最低的损伤程度和最好的结构完整性。④CFRP加固钢管在三点弯曲载荷作用下，其损伤模式演变主要受CFRP缠绕层数和角度的影响。随着层数的增加，大尺度损伤如纤维断裂、基体剥离等占主导地位；随着缠绕角度的增加，小尺度损伤如界面剥离、基体微裂纹等所占比重逐渐增大。⑤利用直方图法和最大似然估计法得到的声发射能量概率密度临界指数相同，6种加固方式下，临界指数分别为1.31、1.45、1.55、1.69、1.60、1.42。⑥使用蝙蝠算法优化最小二乘支持向量机能够有效防止算法陷入局部最优解，显著加快了算法的收敛速度。建立的BA-LSSVM损伤分类模型对不同加固方式下钢管的损伤程度识别准确率达到98%以上。
结论
①CFRP加固钢管在整个弯曲损伤过程中抗弯性能及吸能能力明显优于未加固试件。钢管的吸能性能随着CFRP缠绕层数增大而提升，而随着CFRP缠绕角度的增大而减少。缠绕角度从0°增加至90°时，峰值载荷和平均载荷均表现出下降趋势。②通过分析CFRP加固钢管的声发射振铃计数演化，可将其损伤破坏过程细分为弹性变形、渐进弯曲变形以及结构塌陷三个阶段。③声发射峰值频率的分布区间能够反映CFRP加固钢管的破坏尺度，随着碳纤维缠绕层数增大和角度的减小，CFRP加固钢管的损伤形式从大尺度损伤逐渐转变为小尺度损伤。④不同的缠绕层数和角度对应的复合管试件在声发射能量信号中遵循幂律分布，符合无尺度分布特征。由幂律方法确定的临界指数，能够反映不同缠绕方式下复合管的损伤性能及受弯破坏机理。⑤建立的BA-LSSVM损伤分类预测模型能够地对CFRP不同加固方式下钢管的损伤程度进行识别分类预测。

创新点

薄壁钢管在航天、公共交通和基础设施等行业中充当重要的缓冲与能量吸收角色。然而，长期的环境暴露和负载作用往往导致钢管结构的损伤和劣化。近年来，碳纤维增强树脂复合材料(CFRP)因其高强度、轻质和优异的耐腐蚀性能而成为薄壁钢管结构中的重要加固材料。然而，现有研究大多聚焦于观察CFRP加固后的宏观力学性能和损伤表现，对加固钢管内部裂纹扩展时声发射信号与整体损伤的联系缺乏深入探究。
本实验通过声发射技术，对六组CFRP加固钢管的弯曲损伤过程进行实时监测，研究了CFRP加固钢管在弯曲负荷下的损伤性能，揭示了CFRP增强钢管的破坏机制，试验结果可为CFRP加固钢管的损伤评估提供一定的依据。通过对比各组试件的压溃效率和比吸能发现，增加CFRP缠绕层数可以显著提升钢管的抗弯强度和吸能能力，但增大缠绕角度会降低结构性能。对声发射信号进行去噪处理提取到的峰值频率可以很好地表征钢管的损伤尺度。随着CFRP缠绕角度增加，低频和高频能量信号差别不大，但中频区的能量信号逐渐增多。这表明缠绕角度增加时，复合管试件的小尺度损伤加重，所占比重增大。不同缠绕层数和角度的复合管试件的声发射能量信号遵循幂律分布，符合无尺度分布特性，同时临界指数k也能反映材料的损伤程度。为了进一步对CFRP加固钢管在弯曲荷载作用下的损伤模式进行识别研究，采用机器学习对声发射数据进行分析，建立了蝙蝠算法优化最小二乘向量机模型，对钢管实际损伤进行分类识别。所建立的BA-LSSVM损伤分类模型对试件损伤过程中的损伤程度分类准确性高达98%以上。
1
CFRP增强钢管的压溃效率
2
CFRP增强钢管的比吸能
3
C2T0预测分类对比图
4
不同CFRP缠绕层数的声发射能量概率密度分布图(a)和最大似然估计曲线(b)