Effect of hot drawing on the properties of three-dimensional braided polylactic acid composites
-
摘要:
三维编织热塑性复合材料有着更易回收、生产周期短的特点。其中，聚乳酸(Polylactic acid，PLA)的生物相容性较好，且成本较低，得到广泛关注。热压成型(Hot pressing，HP)工艺有着较高的设计自由度，然而，采取HP工艺制备三维编织聚乳酸复合材料因模具合模时对预制体挤压，可能会破坏编织结构，造成纤维分布不匀，破坏界面性能，导致力学性能下降。热拉伸成型工艺(Hot drawing，HD)作为一种自增强技术，在HP工艺的基础上于三维编织预制体的轴向施以拉伸力，可以有效提高PLA的结晶度和复合材料的力学性能。本实验分别采取HD和HP两种成型工艺制备玻璃纤维(Glass fiber，GF)增强PLA复合材料并进行测试，发现HD复合材料较HP复合材料的剪切强度高出了33.03%，弯曲强度高出了26.92%，拉伸强度高出了39.67%，结晶度提高了20.03%，并略微提升热稳定性。热拉伸工艺促进了PLA分子晶体沿轴向有序排列和晶核的生长，使PLA分子链排列更加简单，提高了PLA的结晶度，同时提高了复合材料的力学性能。结合宏观及3D轮廓观察，发现HD工艺改善了编织结构遭到破坏的问题，保证了三维编织花节的完整性，GF纤维束排列有序，有利于复合材料整体性能的提升。
Abstract:Three-dimensional braided thermoplastic composites are characterized by easier recycling and shorter production cycles. Among them, polylactic acid (PLA) has received wide attention for its better biocompatibility and lower cost. The hot pressing (HP) process has a high degree of design freedom, however, the adoption of the HP process for the preparation of three-dimensional braided PLA composites may destroy the braided structure due to the extrusion of the preform during mold closure, resulting in the uneven distribution of the fibers, destroying the interfacial properties, and leading to the degradation of the mechanical properties. As a self-reinforcing technology, hot drawing (HD) can effectively improve the crystallinity of PLA and the mechanical properties of composites by applying a tensile force in the axial direction of the three-dimensional braided preforms based on the HP process. In this experiment, the glass fiber (GF) reinforced PLA composites were prepared and tested by two molding processes, HD and HP, respectively, and it was found that: The shear strength of HD composites compared with HP composites was 33.03% higher, the bending strength was 26.92% higher, the tensile strength was 39.67% higher, and the degree of crystallinity was increased by 20.03%, and the thermal stability was slightly improved. The hot drawing process promoted the orderly arrangement of PLA molecular crystals along the axial direction and the growth of nuclei, which led to a simpler arrangement of PLA molecular chains and improved the crystallinity of PLA, as well as the mechanical properties of the composites. Combining macroscopic as well as 3D profile observation, it is found that the HD process improves the problem of damage to the braided structure, ensures the integrity of the three-dimensional braided knots, and arranges the GF fiber bundles in an orderly manner, which is conducive to the improvement of the overall performance of the composites.
-
Keywords:
- hot drawing /
- hot pressing /
- three-dimensional braiding /
- polylactic acid /
- thermoplastic composite
-
超材料[1-3]是一类由阵列化的人工微结构单元构成的复合结构。通过对超材料中的微结构单元及其排布方式进行调控设计，可产生低频弹性波带隙、负等效质量密度、负弹性模量、负折射等一系列超常效应[1]，因而在航空航天、工程建筑、轨道交通等[4-6]工程领域具有广泛的应用前景。声学超材料按照带隙形成的机制不同可以分为布拉格散射型和局域共振型[7]。布拉格散射起主导性作用的是周期性的材料特性与弹性波之间的相互作用；局域共振型起主导作用的是散射体的振动特性与基体中长波行波之间的耦合作用，从而抑制弹性波的传播[8]。
近年来，一些学者结合带隙形成机制，在低频范围内获得了较宽的带隙，并通过改变几何参数对带隙进行优化[9-13]。张思文等[14]提出了一种新型局域共振复合结构，实现了声子晶体的多重共振，在低频范围能打开多条共振带隙；Li等[15]研究了振动形式对韧带结构带隙的影响，通过拓扑优化提高了带隙的覆盖范围；Coffy等[16]设计了一种新型声子晶体，有效增加了带隙宽度；李孟昶等[17]设计了一种新型管道超结构构型，该结构在
2500 Hz内产生了两条完全带隙。传统超材料设计方法无法实现参数连续控制。实际工程中，结构随不同工况动态特性相应发生变化，可控超结构可根据目标需求调节结构的带隙特性，实现对不同工况下结构减振的可控调节。近年来，可控超结构日益受到学者们的广泛关注[18-20]。Yao等[21]研究了温度对不同晶格类型声子晶体的带隙调控机制；Geng等[22]研究了不同缺陷态声子晶体几何参数对弯曲波带隙的可控性，结果表明温度升高会造成带隙的频率范围减小；Dai等[23]结合声学拓扑绝缘体，利用温控可调拓扑声子晶体控制和引导水声，但调控范围比较有限。一些学者开展了通过外部激励实现带隙调控的研究。Li等[24-25]分别提出了一种衍生结构和混合声学超结构，可通过施加主动应变调控结构的带隙特性；Bertoldi和Boyce[26]研究了有限形变对周期性超弹性材料中弹性波传播的影响；Shan等[27]研究了周期性多孔超弹性声子晶体在施加载荷后的带隙特性，并分析了不同屈曲模式对带隙的调节效果；Li等[28]研究了结构不同屈曲模式对带隙的影响；Gei[29]研究了准无限周期梁的轴向波和弯曲波的能带结构，分析了轴向拉伸预应力调节结构弯曲波的特性；Huang等[30-32]研究了大形变和预拉伸应变对由超弹性材料制成的声子晶体板带隙的影响。目前已开展的可控超结构研究相对较少，且大多针对结构特定频率范围(低频或中高频)。本文提出一种复合带隙可控超结构构型，可同时产生低频的局域共振型带隙和较高频的布拉格散射型带隙，且通过调节振子位置和施加可控位移，可实现对结构复合带隙的有效调控。采用有限元法研究了4种不同复合带隙可控超结构的带隙特性及其在外加激励作用下的带隙调控规律，计算了该结构的振动传输特性曲线，并与实验结果进行了对比验证。
1. 构型设计及带隙特性
1.1 复合带隙可控超结构构型及其带隙计算
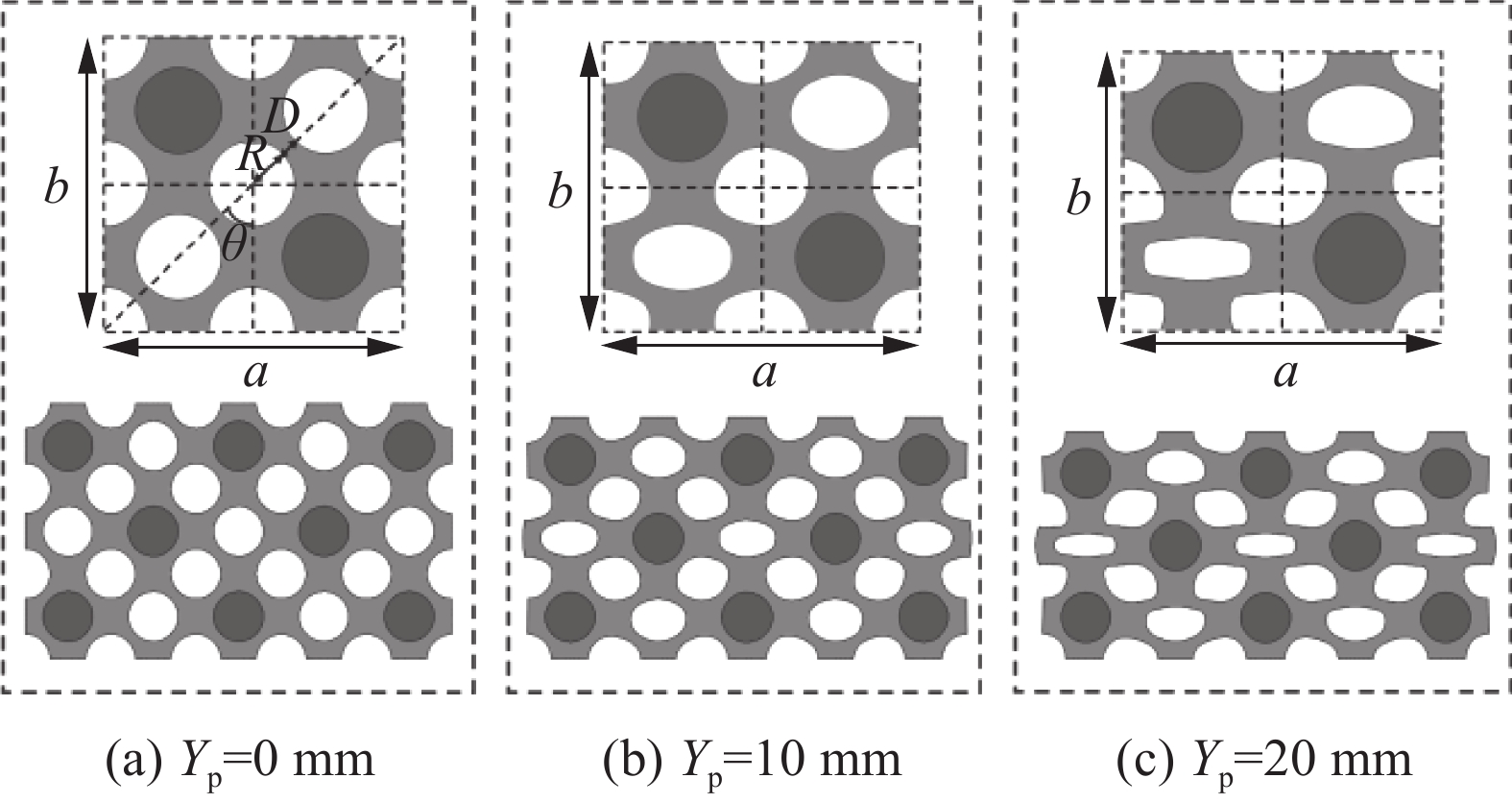
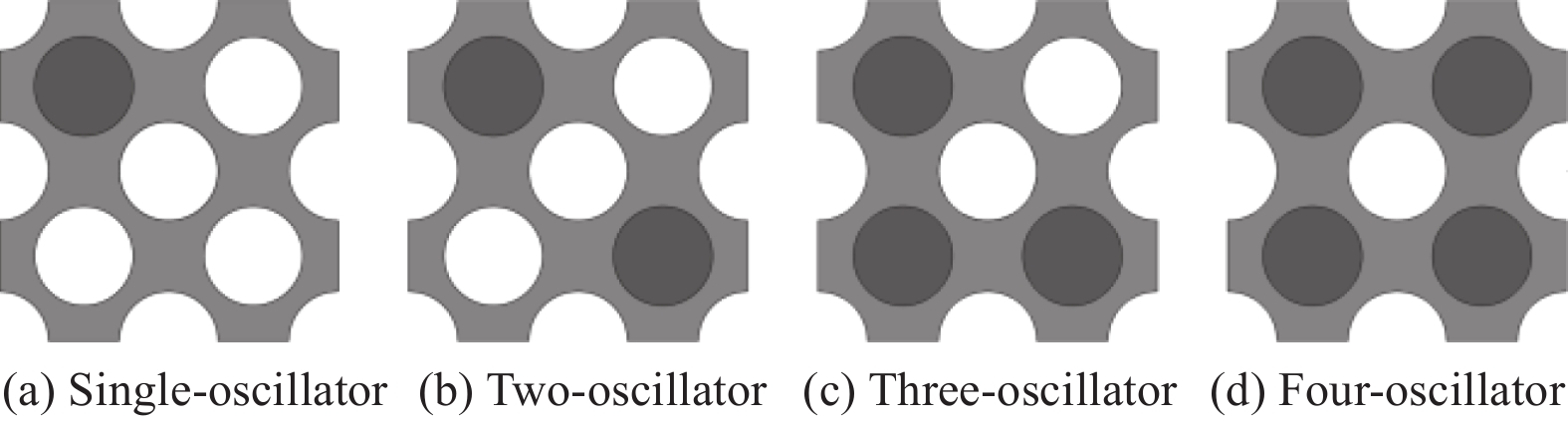
本文提出的复合带隙可控超结构的元胞构型如图1所示，该结构由多孔软材料及内部嵌入的局域共振振子构成。根据振子分布位置不同，分别有单振子、二振子、三振子及四振子4种构型，如图1所示。当对该结构施加可控轴向压缩时(图2)，结构逐渐发生变形，带隙结构分布随之改变，实现带隙的可调可控。
![]()
图 1 不同构型复合带隙可控超结构元胞Figure 1. Composite band gap controllable metastructure cells with different configurations![]()
图 2 不同轴向压缩下二振子构型超结构元胞及试件示意图Figure 2. Schematic diagram of the metastructure cells and specimens of two-oscillator configurations under different axial compressionsYp—Axial compression of the structure; a, b—Lattice constant; R—Radius of the hole; θ—Angle of the diagonal of the cell; D—Distance between the holes本文采用有限元法计算该结构在{\boldsymbol{{ M}\varGamma}} 、{\boldsymbol{\varGamma { X}}}、{\boldsymbol{{ X}{ M}}}方向上的能带分布。在忽略介质阻尼的影响下，弹性波在线弹性非均匀介质中的波动方程可以写为
\nabla \cdot \left[ {{\boldsymbol{C}}\left( {\boldsymbol{r}} \right):\nabla {\boldsymbol{u}}\left( {{\boldsymbol{r}},t} \right)} \right] = {\boldsymbol{\rho}} \left( {\boldsymbol{r}} \right)\frac{{{\partial ^2}{\boldsymbol{u}}\left( {{\boldsymbol{r}},t} \right)}}{{{\partial ^2}t}} (1) 式中：{\boldsymbol{ r}} 为位置矢量，{\boldsymbol{r}} = \left( {x,y,{\textit{z}}} \right)；{\boldsymbol{u}}\left( {\boldsymbol{r}} \right)为位移矢量，{\boldsymbol{u}}\left( {\boldsymbol{r}} \right) = \left( {{u_x},{u_y},{u_{\textit{z}}}} \right)；t为时间； {\boldsymbol{C}}\left({\boldsymbol{ r }}\right) 和{\boldsymbol{ \rho}} \left( {\boldsymbol{r}} \right) 分别为材料的弹性张量及密度张量。
由于波动方程中的系数具有周期性，因此根据Bloch-Floquet周期性边界条件，单胞离散形式的特征值方程及边界条件可表示为
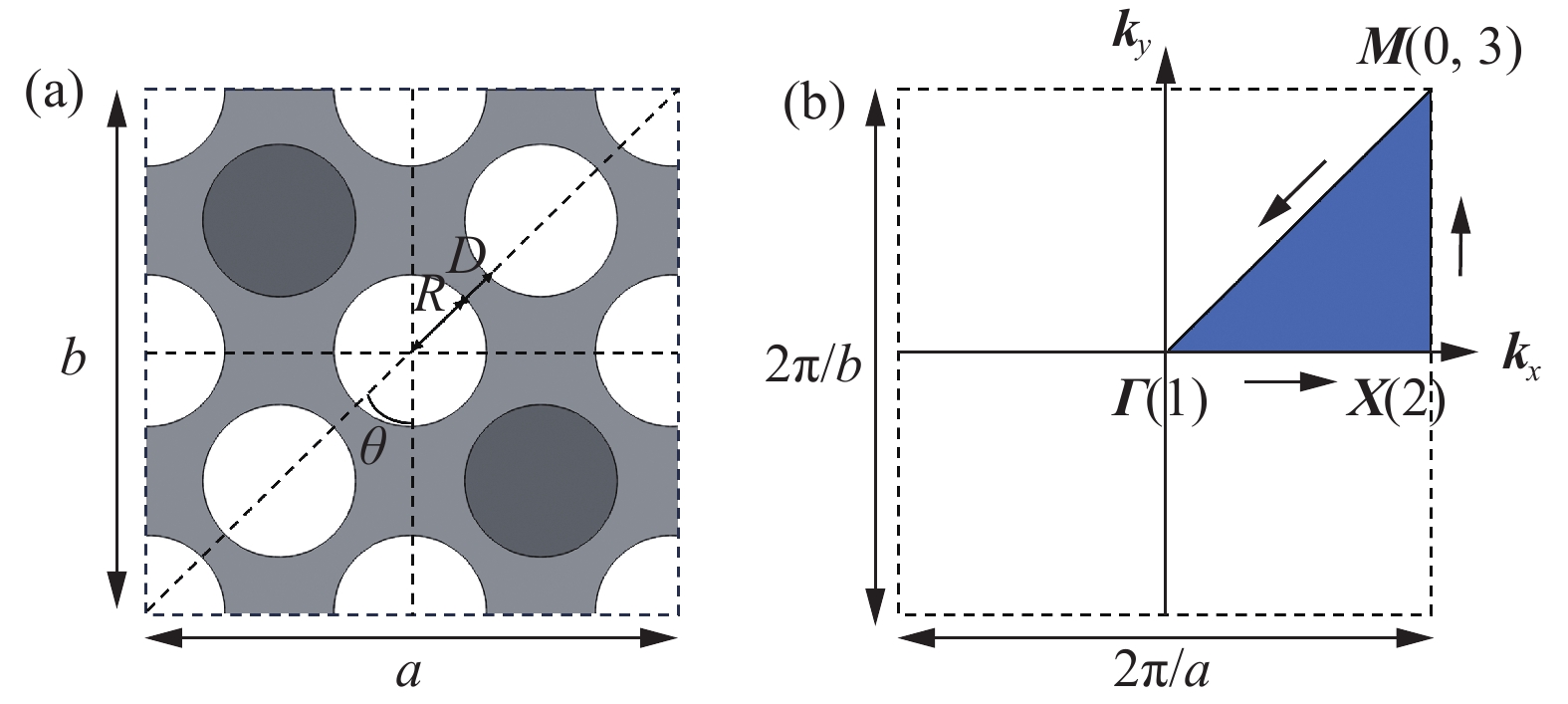
{\boldsymbol{KU}} = {\omega _n^2}{\boldsymbol{MU}} (2) \boldsymbol{u}\left(\boldsymbol{r},t\right)={\mathrm{e}}^{\mathrm{i}\left({\boldsymbol{k}} \, \cdot \,{\boldsymbol{r}}-\omega t\right)}\boldsymbol{u}_{\boldsymbol{k}}\left(\boldsymbol{r}\right) (3) 式中： {\boldsymbol{K}} 为结构的刚度矩阵；{\boldsymbol{M}}为质量矩阵；{\boldsymbol{U}}为单元节点位移矩阵；{\omega _n}为声子晶体的固有频率； {{\boldsymbol{u}}_{\boldsymbol{k}}}\left({\boldsymbol{ r}} \right) 是周期性边界源面的位移向量；i为虚数单位；ω为频率；{\boldsymbol{k}}为限制在第一布里渊区内的Bloch波矢，布里渊区示意图如图3所示。
![]()
图 3 Y_{\mathrm{p}}=0\; \mathrm{mm} 时二振子构型超结构元胞(a)及其第一不可约布里渊区(阴影区域) (b)M, Γ and X are the high symmetry points of the first irreducible Brillouin zone, respectively; kx and ky are the components of wave vector k in x and y directions, respectivelyFigure 3. Two-oscillator configuration metastructure cell (a) and its first irreducible Brillouin zone (Shaded region) (b) in Y_{\mathrm{p}}=0\; \mathrm{mm}联立式(2)与式(3)，令波矢{\boldsymbol{k}}扫略第一不可约布里渊区的边界，可得到一系列特征频率{\omega ^2}。在本文中选择波矢{\boldsymbol{k}}前50阶特征频率在第一布里渊区的变化来计算能带结构。对 {{\boldsymbol{k}}_x} 、 {{\boldsymbol{k}}_y} 的扫描路径进行设计，使波矢{\boldsymbol{k}}能够取到第一不可约布里渊区的所有值，其中波矢{\boldsymbol{k}}的方向及取值范围如图3中第一不可约布里渊区示意图所示，Bloch波矢{\boldsymbol{k}}的方向及 {{\boldsymbol{k}}_x} 、 {{\boldsymbol{k}}_y} 的关系如下：
{{\boldsymbol{k}}_x} = \left\{ {\begin{array}{l} {(1 - k)\dfrac{{\text{π}} }{a},0 < k < 1} \\ {(k - 1)\dfrac{{\text{π}} }{a},1 < k < 2} \\ {\dfrac{{\text{π}} }{a},2 < k < 3} \end{array}} \right.{\text{ }}{{\boldsymbol{k}}_y} = \left\{ {\begin{array}{l} {(1 - k)\dfrac{{\text{π}} }{a},0 < k < 1} \\ {0,1 < k < 2} \\ {(k - 2)\dfrac{{\text{π}} }{a},2 < k < 3} \end{array}} \right. (4) 进而可得到波矢k与频率\omega 的色散关系。
1.2 带隙特性分析
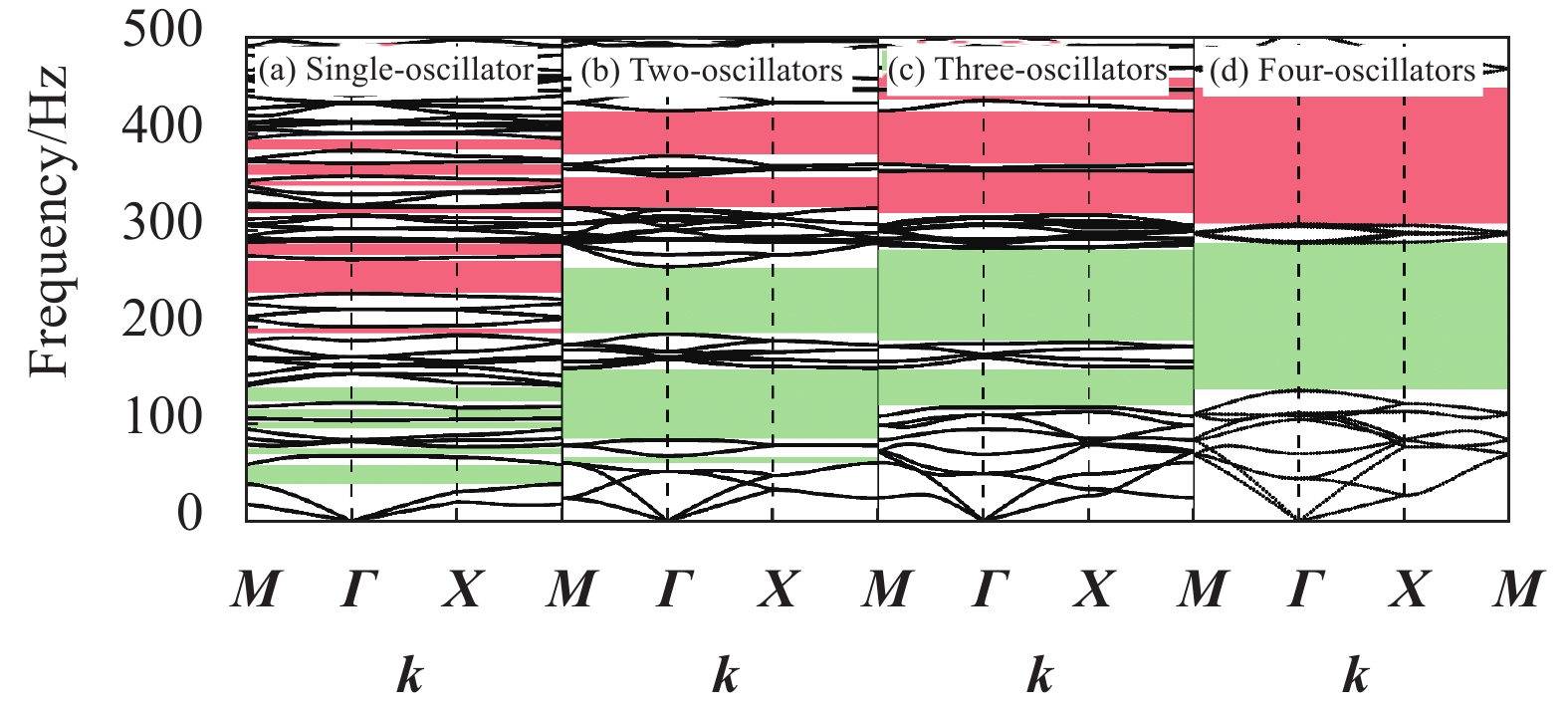
本文设计的复合带隙可控超结构采用硅橡胶材料制成，内部嵌入铅块作为其局域共振振子，其几何参数和材料参数如表1所示，未压缩情况下的晶格常数为a = b = 120\;{{\mathrm{mm}}} 。应用COMSOL软件建立了图1中4个元胞结构的有限元模型，并在相应位置施加Floquet周期性边界条件，应用特征频率求解器对布里渊区边界进行波矢扫描计算，可以得到元胞振动的能带结构图，并将它们进行对比，如图4所示。
表 1 几何参数和材料参数Table 1. Geometric parameters and material parametersGeometric parameters Value Material Material parameters Value R/mm 17.5 Silicon rubber E/MPa 0.870 ρ/(kg·m−3) 1230 D/mm 7.426 ν 0.499 Lead E/MPa 40.8 θ/(°) 45 ρ/(kg·m−3) 11340 ν 0.37 Notes：E—Elastic modulus；ρ—Density；ν—Poisson's ratio. ![]()
图 4 不同元胞构型 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构对比图Figure 4. Energy band structure comparison diagram of different cell configurations Y_{\mathrm{p}}=0\; \mathrm{mm}从图4可以看出，中间孔无填充情况下，局域共振振子规律排列在中间孔的四周，随局域共振振子数量增加，300 Hz内的低阶带隙宽度增加，结构中带隙数量逐渐减少，带隙位置逐渐上移；且随着振子数量增加，结构刚度逐渐增大进而导致了带隙中心频率增加。
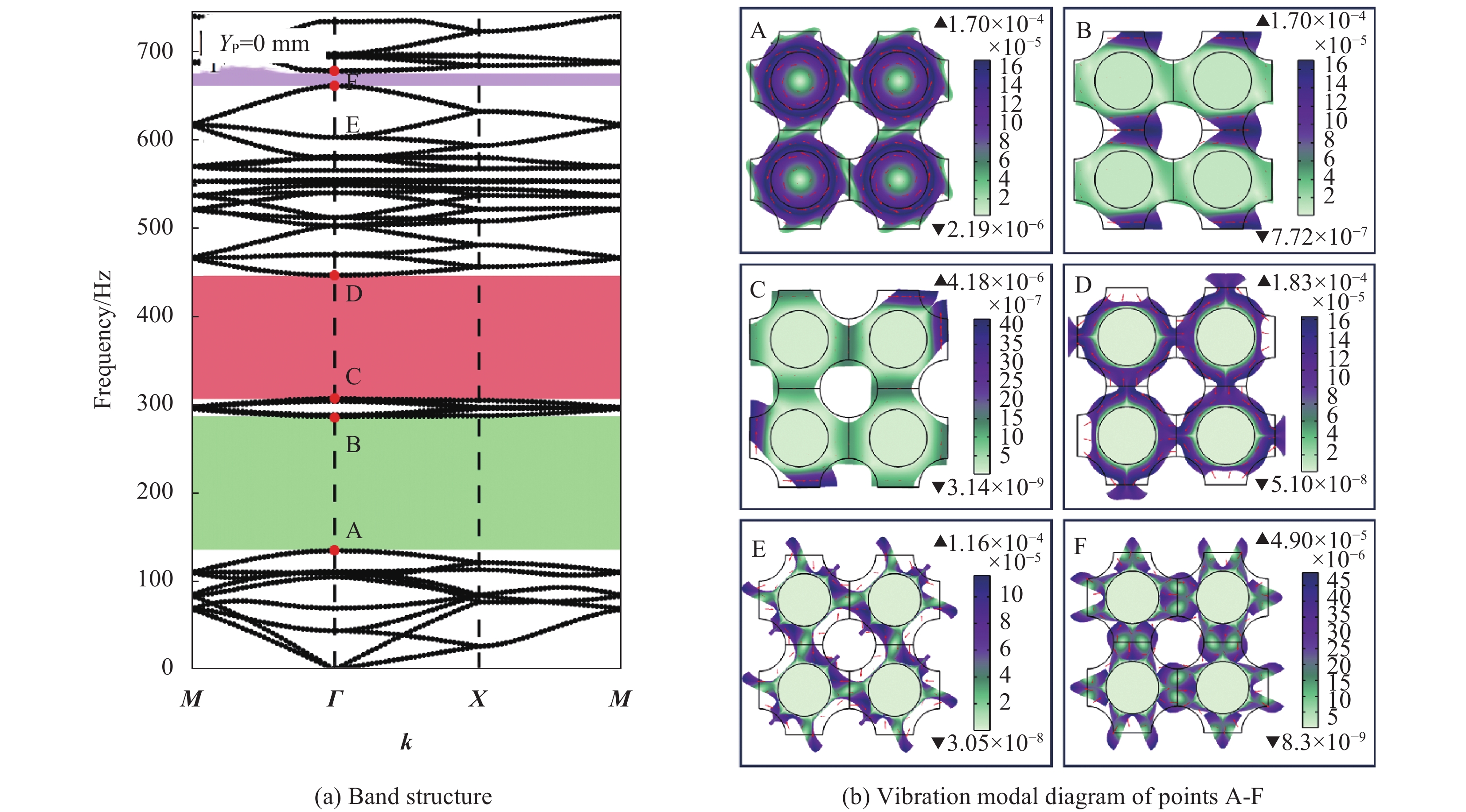
图5(a)给出了有限元法计算得到的四振子结构的能带结构图。可以看出，当结构的轴向压缩值 Y_{\mathrm{p}}=0\; \mathrm{mm} 时，前50阶特征频率形成了两条较宽的完全带隙和一条较窄的完全带隙，由低到高的频率范围分别为134.48~287.53 Hz、307.26~447.81 Hz和662.44~679.43 Hz。
![]()
图 5 四振子复合带隙可控超结构 Y_{\mathrm{p}}=0\; \mathrm{mm} 时能带结构及振动模态Figure 5. Band structure and vibration mode of the four-oscillator composite band gap controllable metastructure Y_{\mathrm{p}}=0\; \mathrm{mm}为进一步分析复合带隙可控超结构的带隙类型，图5(b)给出了A~F这6个点的振动模态图。可以看出，在A点，振动主要集中在散射体上，基体与散射体同向振动；B点散射体的振动降低。当波的频率接近散射体的固有频率时，基体与散射体发生共振，从而抑制了振动在特定方向上的传播。因此，图5(a)中的第一阶带隙为局域共振带隙。而对应C、D、E、F点振动模态为结构整体振动，因此第二阶带隙与第三阶带隙为布拉格散射型带隙。同理，图4所示能带结构中的带隙可根据高对称点的振动模态图来判断：第一阶带隙为局域共振型带隙，第二阶带隙为布拉格散射型带隙。
2. 复合带隙可控超结构带隙调控
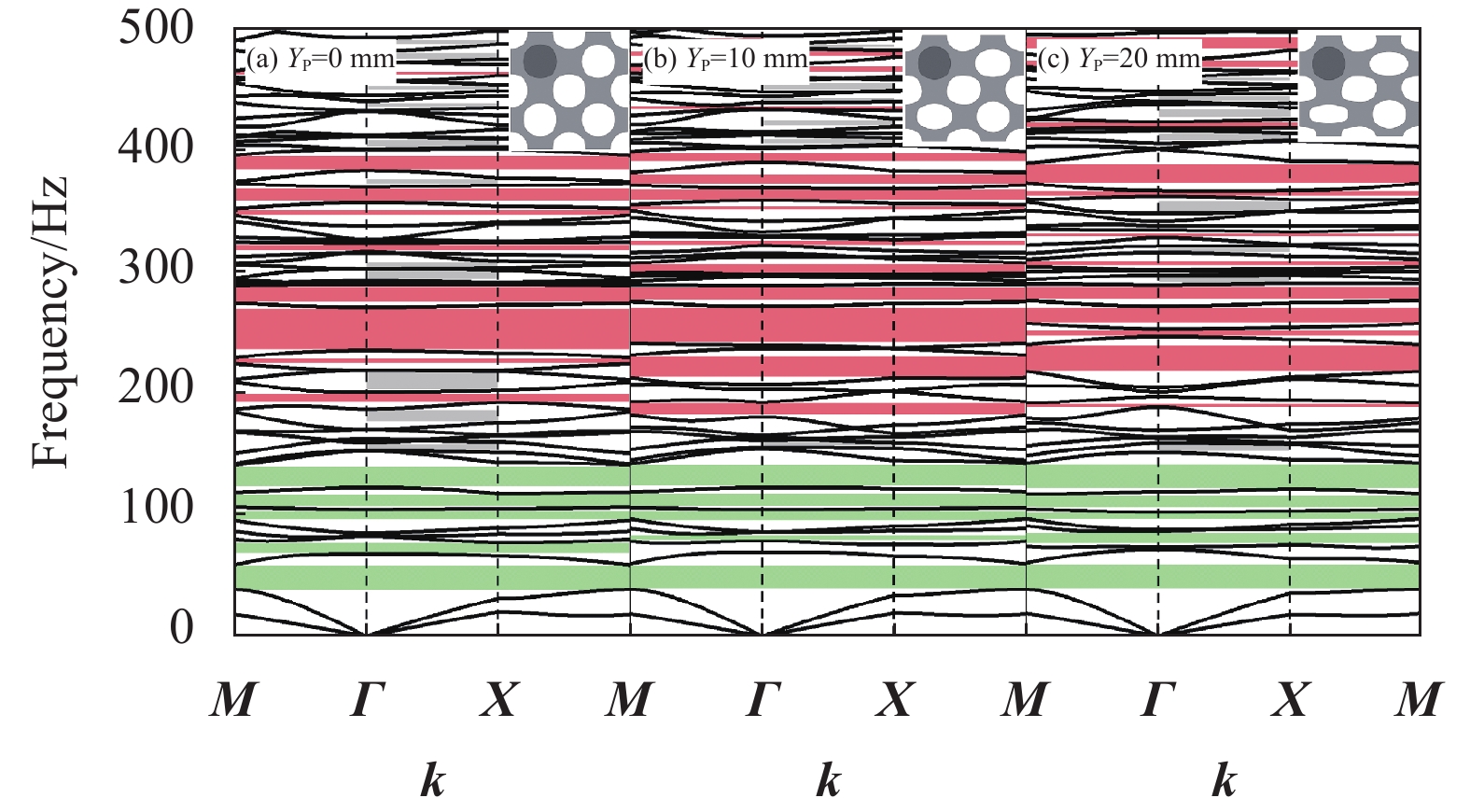
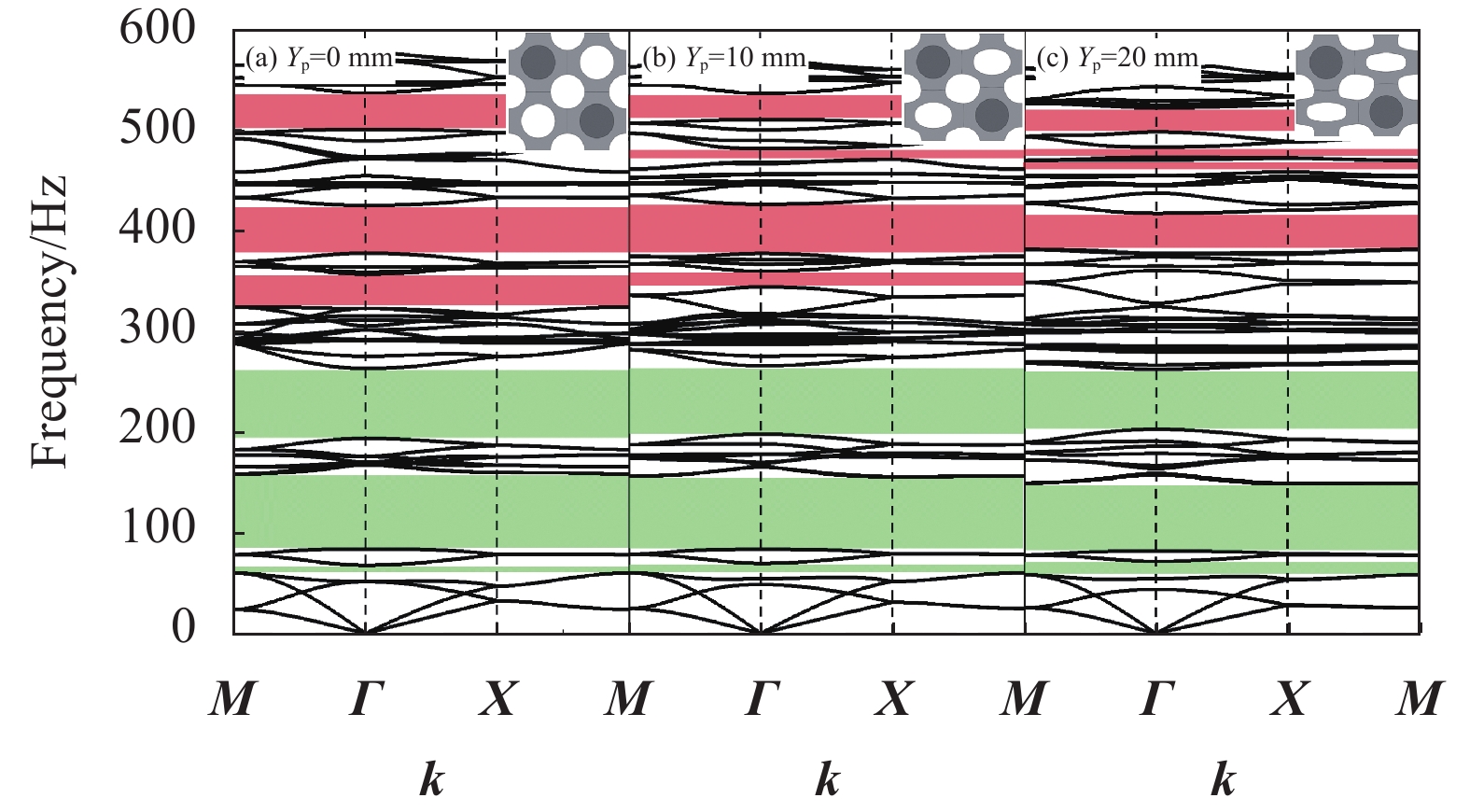
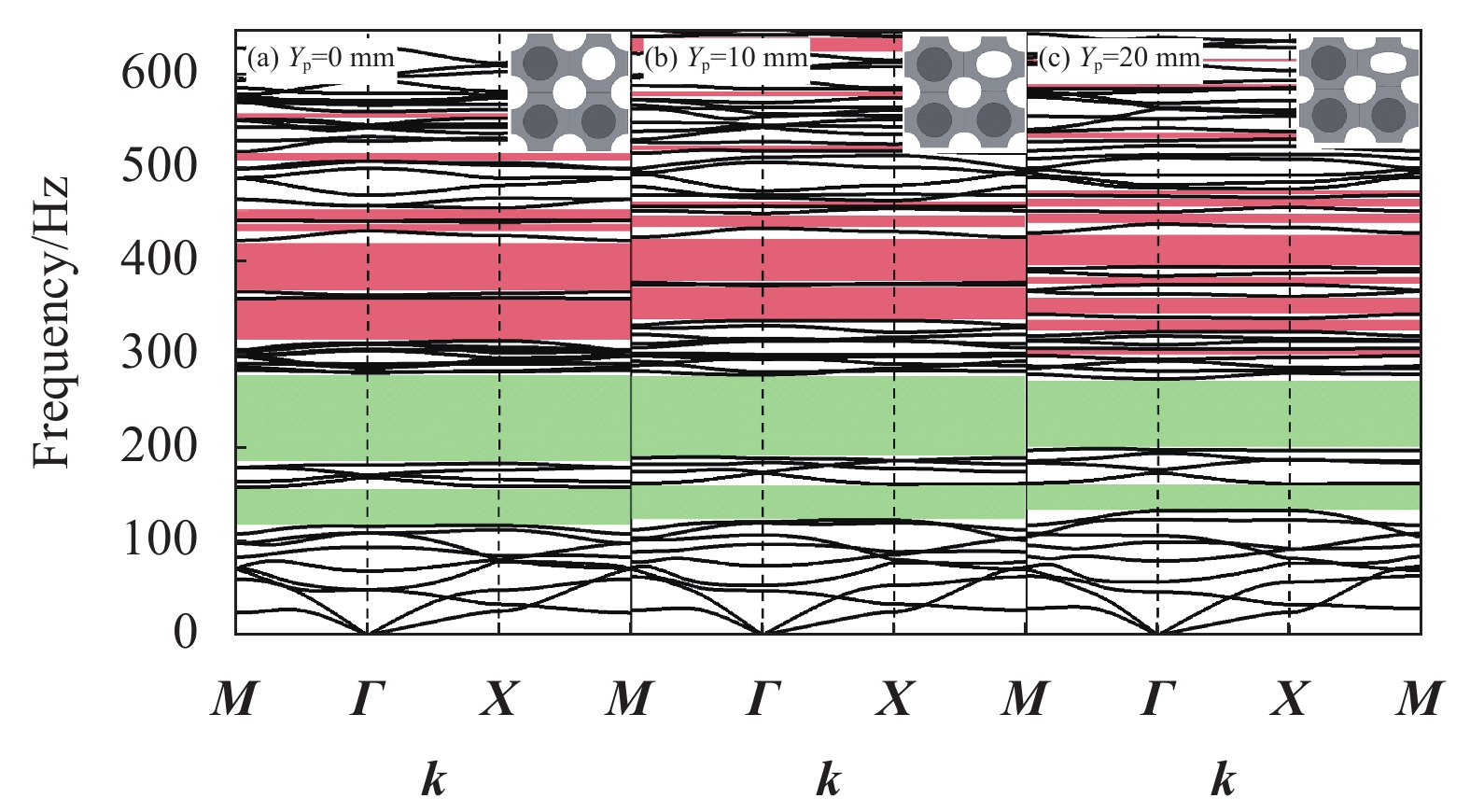
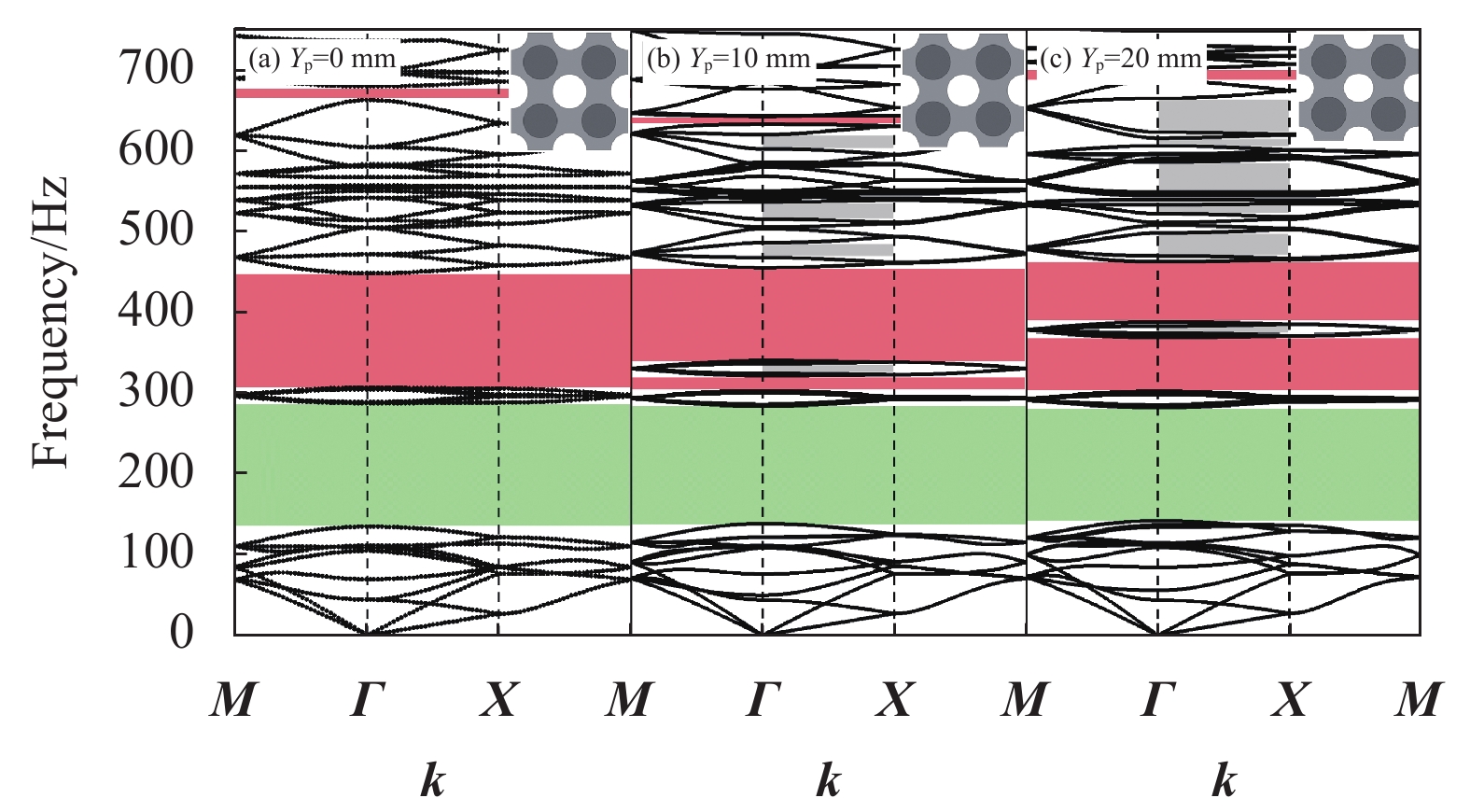
为了进一步分析轴向压缩对结构带隙调控的机制，对结构施加竖向位移量 Y_{\mathrm{p}} 。考虑到结构在较大变形下会发生屈曲，将应用COMSOL软件对结构的屈曲临界载荷和相应变形进行分析，计算得到各元胞发生屈曲的临界变形量在22.378~39.682 mm之间。因此，计算中在保证所有结构不发生屈曲的前提下，将图1中单振子、二振子、三振子、四振子元胞分别从0 mm开始依次增加10 mm进行轴向压缩，然后计算它们的能带结构图并分析带隙变化的规律，如图6~图9所示。
对比图6~图9中各阶带隙可以看出，随着竖向位移量 Y_{\mathrm{p}} 的增大，第一阶局域共振带隙变化较小，高阶的布拉格散射带隙中心频率逐渐向上移动，并在较高频率范围内出现了新的布拉格带隙，且单振子元胞和四振子元胞构型出现多条方向带隙(灰色部分)。这是由于轴向压缩对局域共振型带隙参数影响较小，但随着轴向位移 Y_{\mathrm{p}} 的增加，元胞晶格尺寸发生了变化，x方向尺寸a逐渐变大，y方向尺寸b逐渐变小，弹性波在晶格之间的传播与反射波的叠加发生了变化，色散曲线中心频率上移。可以发现，轴向压缩对不同构型复合带隙可控超结构具有较一致的调控机制，带隙调控的规律与局域共振振子的数量之间没有明显的关系。
![]()
图 6 单振子元胞在不同轴向压缩值下的能带结构对比图Figure 6. Energy band structure comparison diagram of single-oscillator cell under different axial compression values![]()
图 7 二振子元胞在不同轴向压缩值下的能带结构对比图Figure 7. Energy band structure comparison diagram of two-oscillator cell under different axial compression values![]()
图 8 三振子元胞在不同轴向压缩值下的能带结构对比图Figure 8. Energy band structure comparison diagram of three-oscillator cell under different axial compression values![]()
图 9 四振子元胞在不同轴向压缩值下的能带结构对比图Figure 9. Energy band structure comparison diagram of four-oscillator cell under different axial compression values3. 复合带隙可控超结构振动传输特性
3.1 有限周期结构的振动传输特性
为了进一步研究复合带隙可控超结构的实际工程应用效果，本文分别采用数值计算和实验方法对其进行了有限周期结构的振动传输特性研究。结构振动衰减情况常用传输损失{T_{\mathrm{L}}}来描述，传输损失 {T_{\mathrm{L}}} 计算式为[33]
T_{\mathrm{L}}=20\mathrm{lg}\left(\frac{a_{\mathrm{out}}}{a_{\mathrm{in}}}\right) (5) 式中，{a_{{\mathrm{in}}}}和{a_{{\mathrm{out}}}}分别为输入点和输出点处的加速度响应。
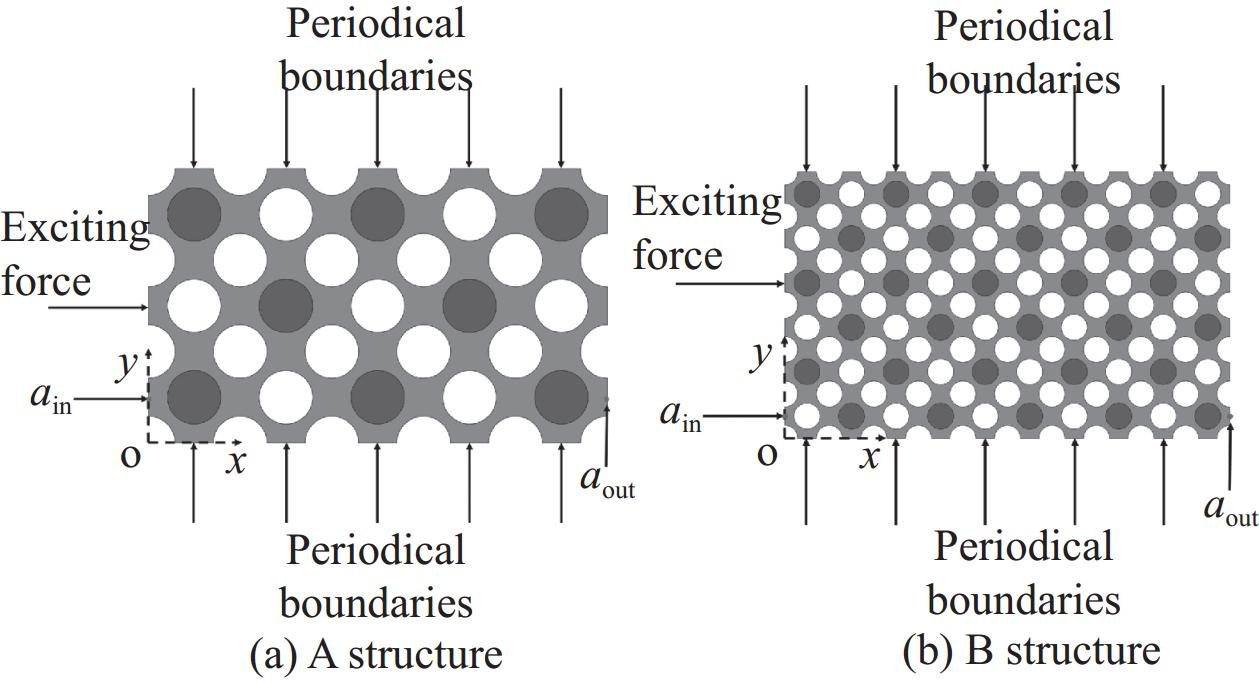
为了对比不同数量周期结构对振动传输特性结果的影响，开展了图10中有限周期二振子构型A、B结构的传输特性计算。应用COMSOL软件建立了两个结构的模型，在其左端处施加轴向单位激振力，限制结构y方向的刚体位移，在结构左右两端施加了自由边界条件，并在另一端{a_{{\mathrm{out}}}}处计算得到输出振动响应。
![]()
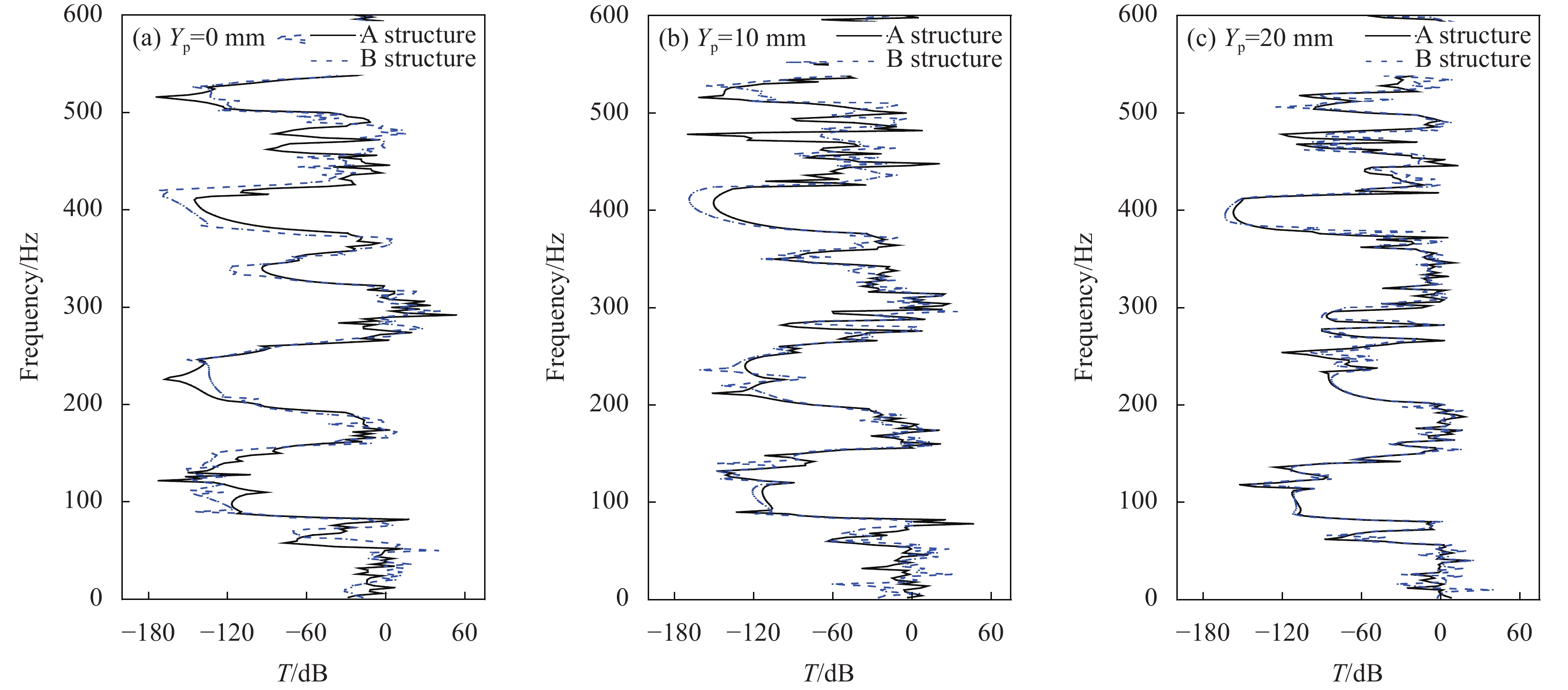
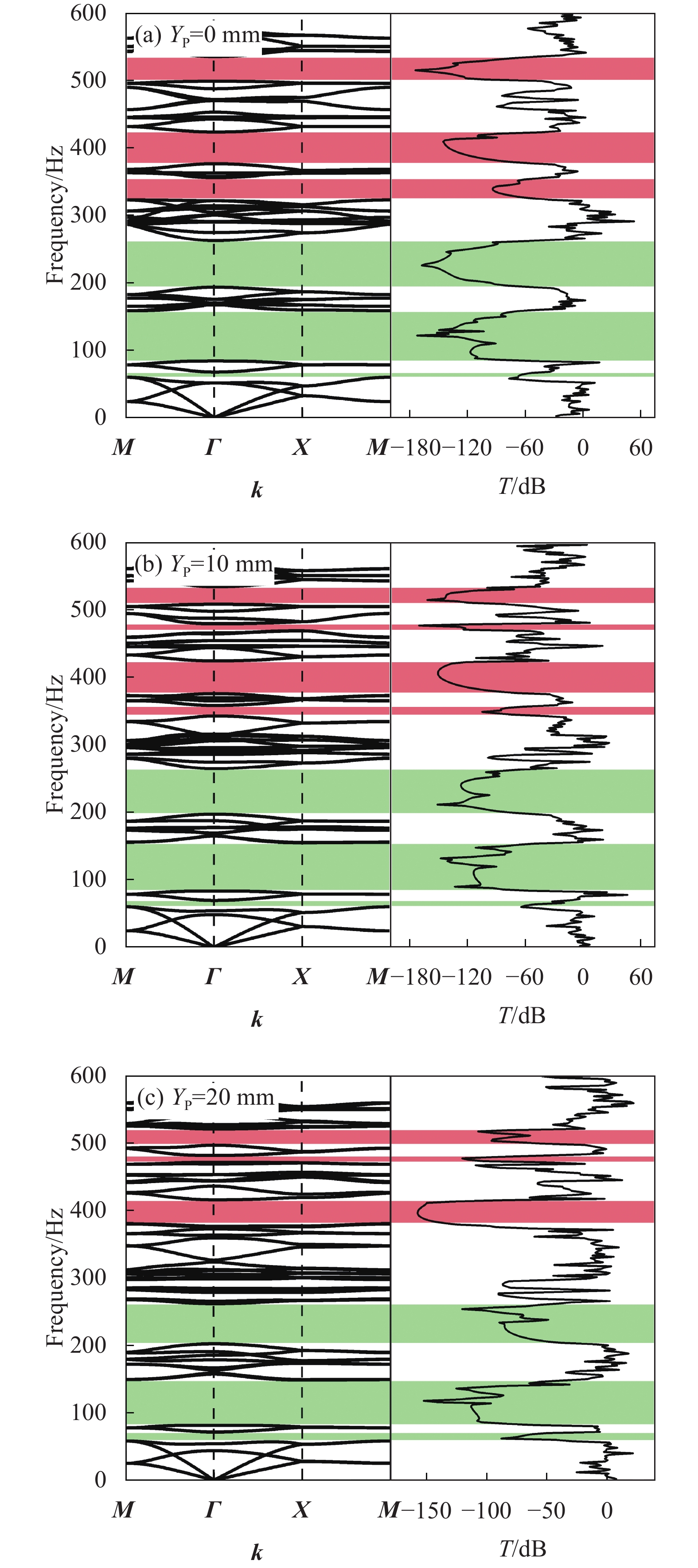
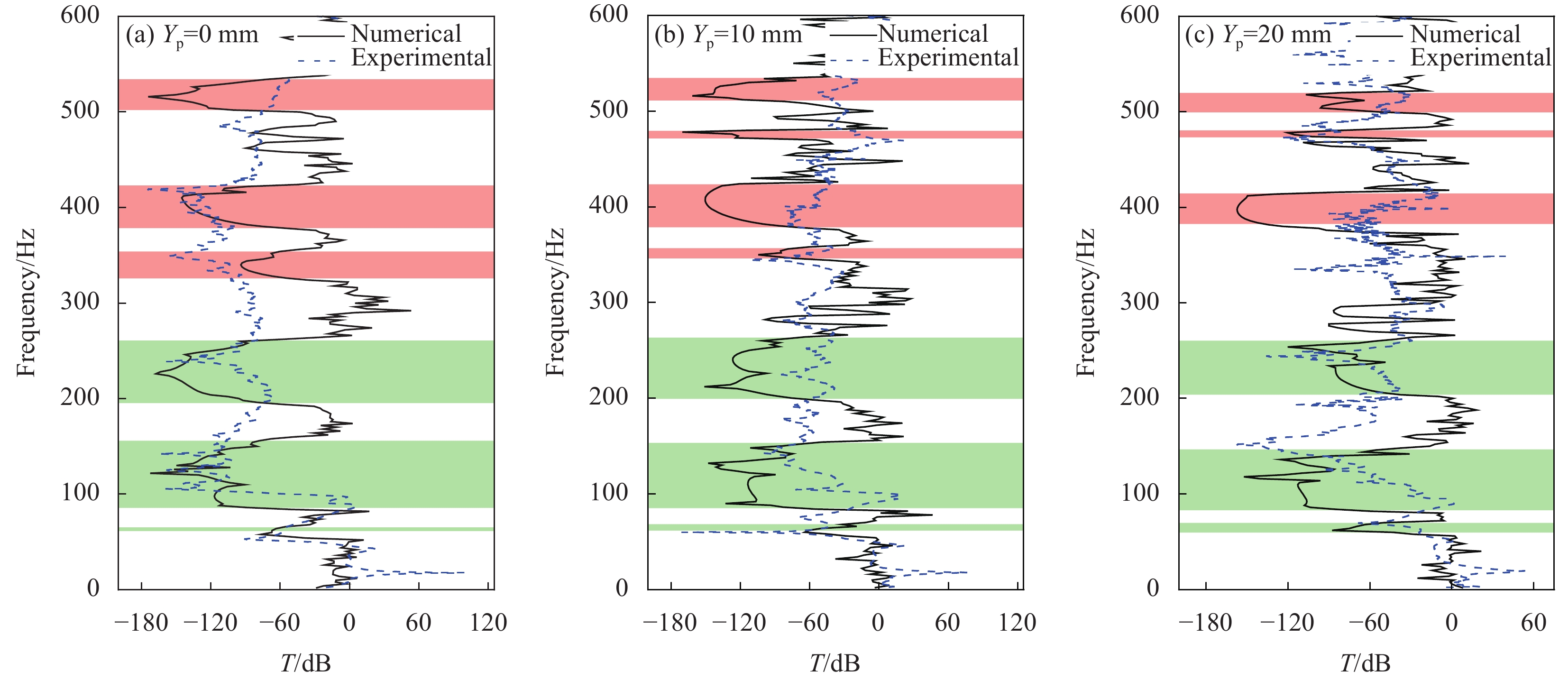
图 10 有限周期二振子超结构振动传输特性分析示意图ain and aout are the signal acquisition points of the input end and the output end, respectivelyFigure 10. Analysis diagram of vibration transmission characteristics of finite period two-oscillator metastructure图11给出了不同轴向压缩值下两个结构的振动传输特性曲线，可以看出尺寸较小的A结构与尺寸较大的B结构的振动传输特性具有较好的一致性。考虑到本文制作的实验试件尺寸有限，为便于与实验结果对比分析，选取周期结构数量与试验件相一致的A结构进行研究。图12(a)~图12(c)分别给出了二振子构型A结构在 Y_{\mathrm{p}}=0\; \mathrm{mm} 、 Y_{\mathrm{p}}=10\; \mathrm{mm} 、 Y_{\mathrm{p}}=20\; \mathrm{mm} 时的能带结构及振动传输特性曲线对比图。
![]()
图 11 不同轴向压缩值下两种尺寸有限周期二振子超结构振动传输特性曲线对比T—Structural vibration attenuationFigure 11. Comparison of vibration transmission characteristics curves of finite-period two-oscillator metastructures with two different sizes under different axial compression values![]()
图 12 不同轴向压缩值二振子构型超结构的能带结构及振动传输特性曲线Figure 12. Energy band structure and vibration transmission characteristic curves of two-oscillator configuration metastructures with different axial compression values从图12中的数值结果可以看出，传输特性曲线中振动衰减部分的频率范围与计算得到的能带结构中的带隙频率范围基本一致。另外，传输特性曲线中，除完全带隙对应的衰减，其余的衰减部分对应于方向带隙。在带隙范围内，结构的传输特性衰减明显，未压缩结构与轴向压缩结构的最大衰减均可达到150 dB。由此可见，弹性波在带隙频率范围内会出现明显的衰减。
3.2 实验研究
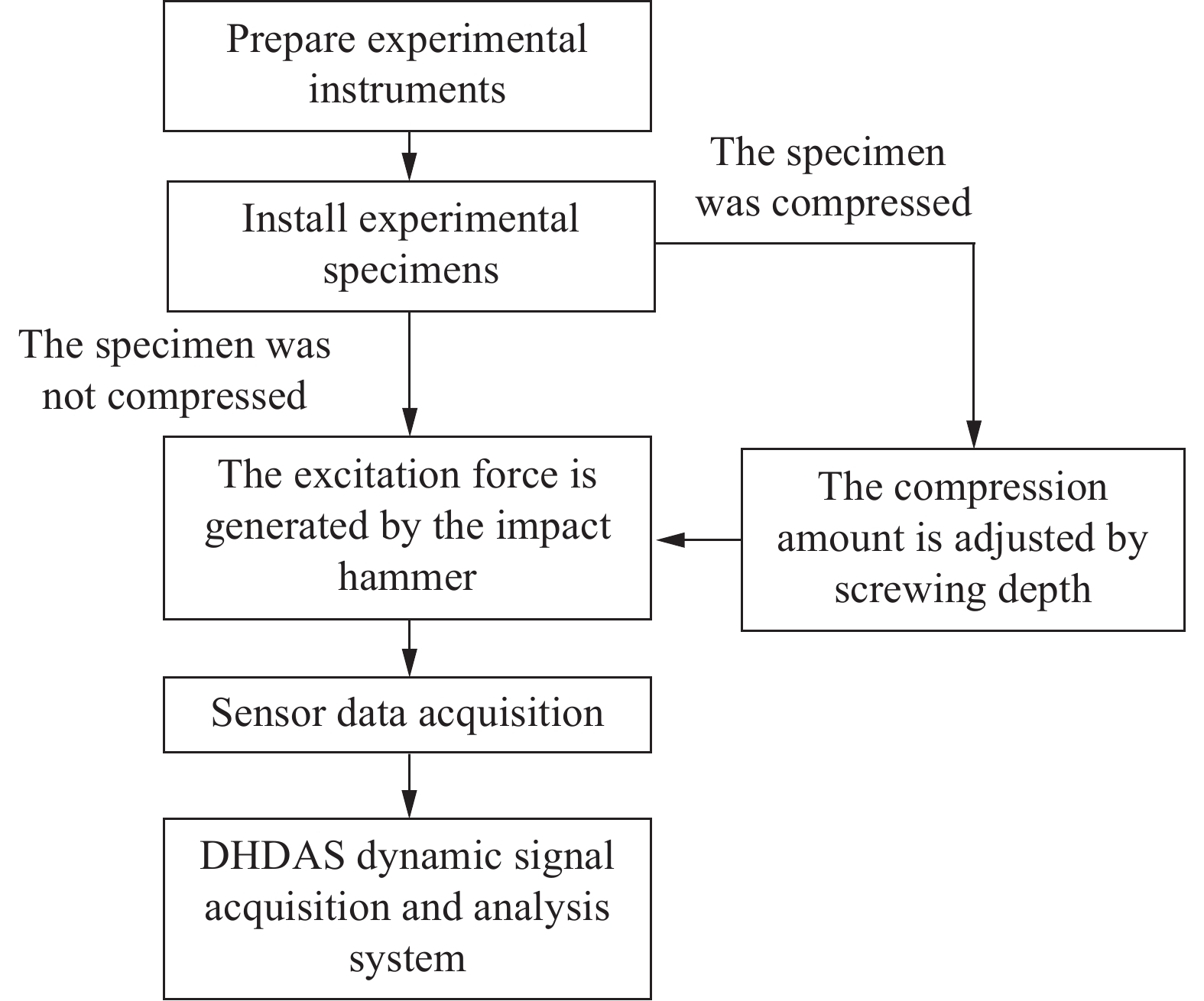
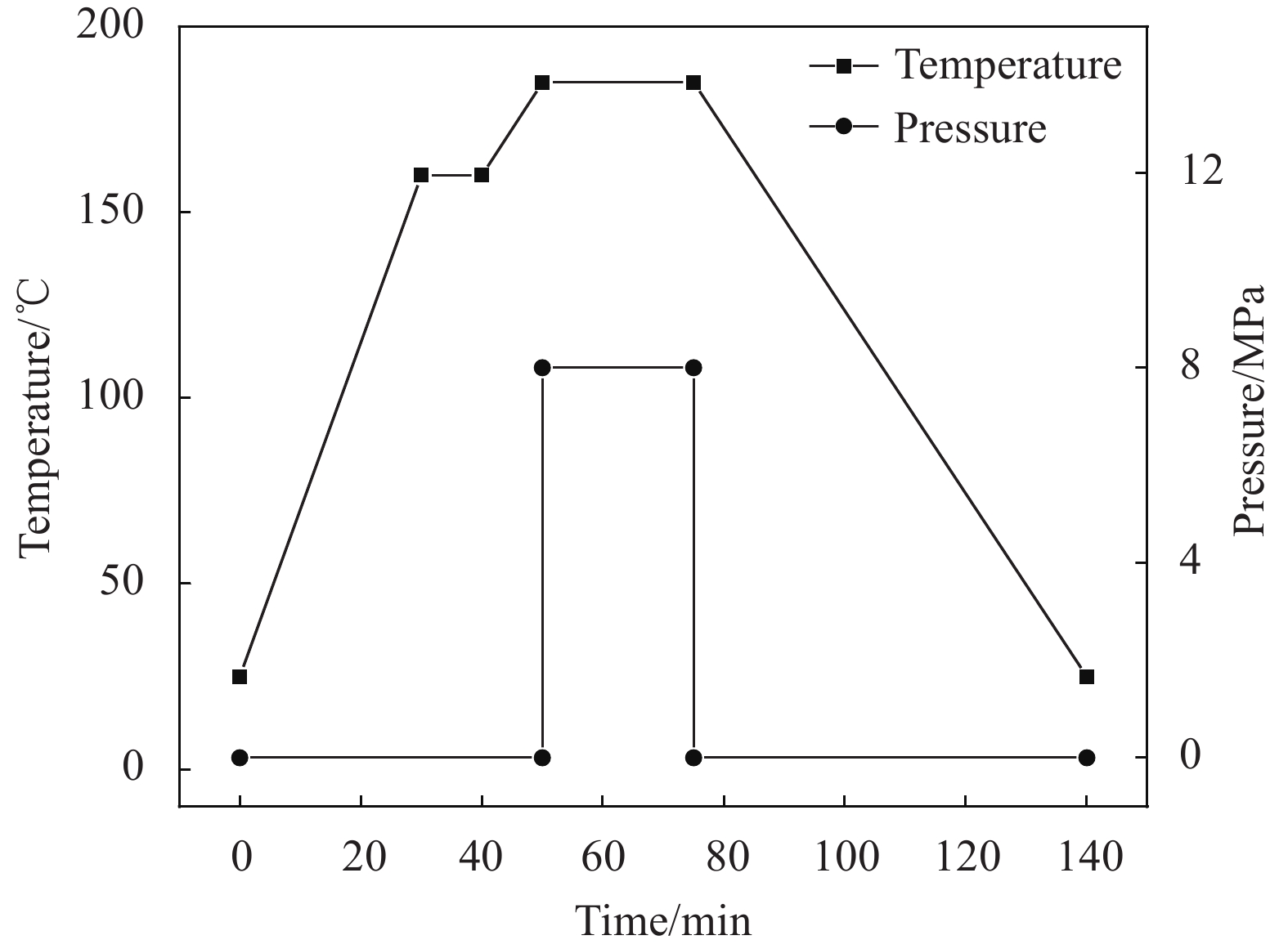
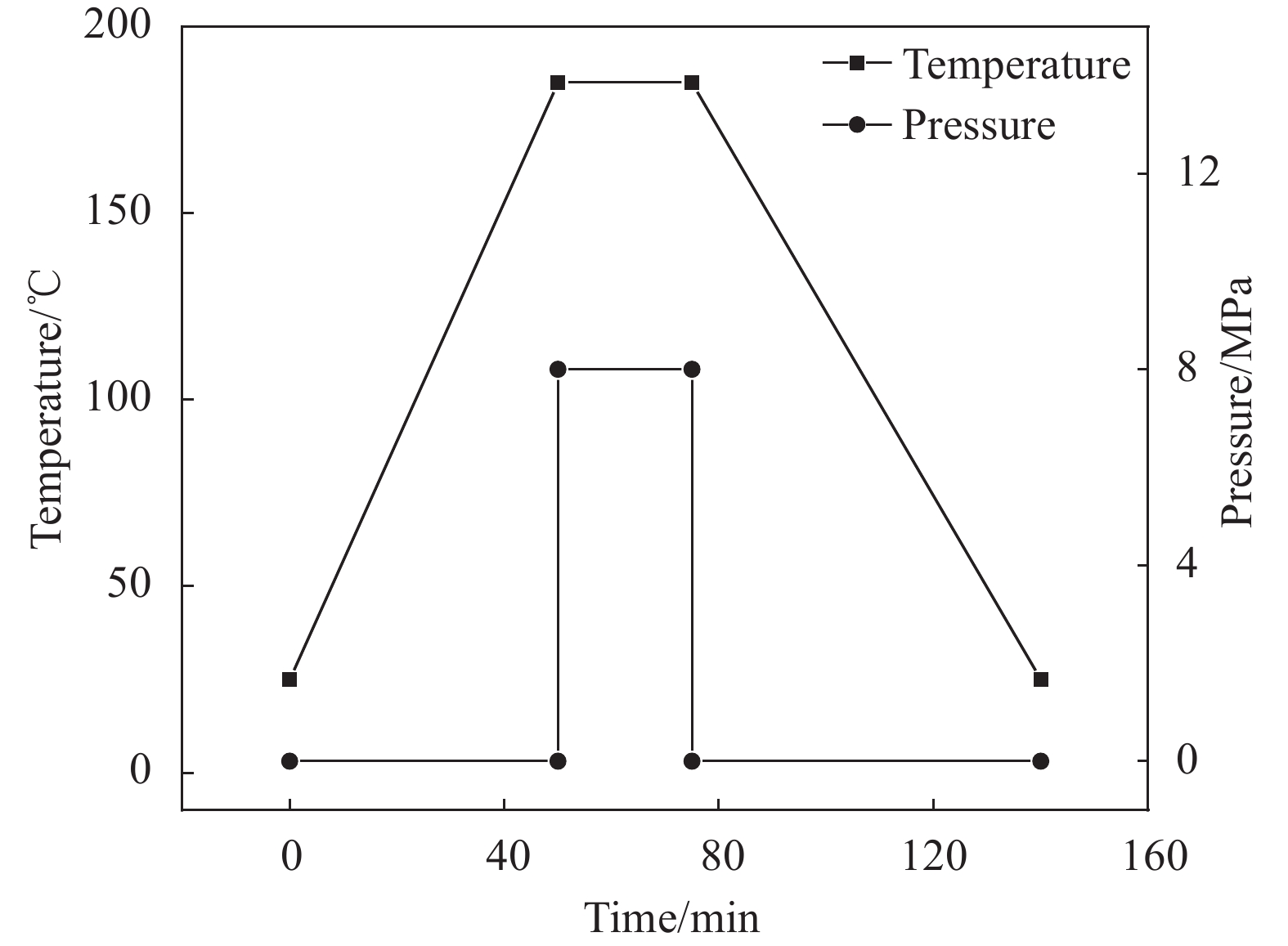
为研究有限周期二振子超结构振动传输特性，制作了二振子元胞结构试件，如图13所示。该试件由多孔硅橡胶构成，长度为300 mm，宽度为180 mm，厚度为50 mm，在橡胶孔内规律嵌入铅块构成局域共振振子。实验中，通过螺栓、螺母固定夹具，同时可调节控制其整体竖向位移。加速度传感器(352 C33，PCB)设置在图10中输入点{a_{{\mathrm{in}}}}与拾取点{a_{{\mathrm{out}}}}对应位置，使用力锤(CL-YD-303，江苏联能电子技术有限公司)沿水平方向冲击产生激励，通过DHDAS动态信号采集分析系统(DH8303，江苏东华测试技术股份有限公司)采集输入、输出端的加速度响应，实验装置如图14所示，实验流程如图15所示。将采集的数据利用式(5)进行计算，即可得到结构的振动传输特性曲线。
3.3 结果分析
将实验测得的加速度响应通过式(5)进行计算，所得到的数据经归一化处理后可获得二振子结构的振动传输特性曲线，如图16虚线所示。可以看出，带隙所在范围内(阴影区域)弹性波发生了衰减，这与有限元计算得到的结果比较一致，并且振动传输特性曲线的实验结果与数值结果也得到了较好的一致性。从图16可以看出：当 Y_{\mathrm{p}}=0\; \mathrm{mm} 与 Y_{\mathrm{p}}=10\; \mathrm{mm} 时，实验得到的振动传输特性曲线的衰减峰值与数值结果中的衰减峰值比较吻合；当 Y_{\mathrm{p}}=20\; \mathrm{mm} 时，部分低阶带隙的结果存在一定差异。这主要是由于：实验中结构通过夹具施加轴向压缩值，而相应的计算分析过程中，忽略了夹具和结构自重的影响，同时随着轴向压缩值的增加，结构内部产生的应力及自身的结构阻尼对其带隙亦有影响，因此两者有一定的误差。
![]()
图 16 不同轴向压缩值下二振子构型超结构的实验、数值振动传输特性曲线对比Figure 16. Comparison of experimental and numerical vibration transmission characteristic curves of two-oscillator configuration metastructure under different axial compression values4. 结 论
本文提出一种复合带隙可控超结构构型，该结构由多孔软材料和局域共振振子组成，可同时产生局域共振和布拉格散射两种带隙，通过施加轴向位移可实现对带隙的有效调控。采用有限元法研究了该结构在不同构型下的带隙特性及轴向压缩对带隙的调控规律，计算了二振子结构的振动传输特性并与带隙分布进行了对比验证。搭建了二振子结构振动特性实验平台，测得了该结构的传输特性曲线，与实验结果相对比，两者取得了较好的一致性。主要结论如下：
(1)对比分析了复合带隙可控超结构的4种不同构型带隙特性，数值结果表明该结构可产生局域共振型和布拉格散射型两种带隙分布；随局域共振振子数量增加，一定频率范围内，结构中带隙宽度增加，数量减少，且带隙中心频率上移；
(2)轴向压缩对该结构带隙分布具有一定的调控作用，随着轴向压缩值的增加，布拉格带隙中心频率逐渐上移，同时出现更多的完全带隙和方向带隙，局域共振型带隙变化较小，4种复合带隙可控超结构带隙调控规律基本一致；
(3)复合带隙可控超结构在带隙范围内具有较好的减振效果，振动传输特性曲线的实验结果与数值结果中衰减部分基本吻合。因此，弹性波在带隙频率范围内会出现明显的衰减。
本文提出的复合带隙可控超结构可以实现结构在不同工况下的带隙调控，在航空航天、轨道交通等领域有广阔的应用前景。结构由软材料组成，理论分析存在一定难度，且变形较大时出现非线性特性，在未来工作中将开展内在机制的理论分析及非线性特性研究。
-
![]()
图 1 聚乳酸(PLA)纤维的DSC曲线
Tg—Glass transition temperature; Tm—Melting point
Figure 1. DSC curve of polylactic acid (PLA) fibers
![]()
图 5 热拉伸成型工艺(HD)和热压成型(HP)复合材料的剪切载荷-位移曲线对比
Figure 5. Comparison of shear load-displacement curves for hot drawing (HD) and hot pressing (HP) composites
![]()
图 7 HD和HP复合材料的弯曲载荷-位移曲线对比
Figure 7. Comparison of bending load-displacement curves for HD and HP composites
![]()
图 9 HD和HP复合材料的拉伸载荷-位移曲线对比
Figure 9. Comparison of tensile load-displacement curves for HD and HP composites
![]()
图 10 HD和HP复合材料的拉伸强度对比
Figure 10. Comparison of tensile strength of HD and HP composites
![]()
图 12 HD和HP复合材料TG (a)和DTG (b) 曲线对比
Figure 12. Comparison of TG (a) and DTG (b) curves of HD and HP composites
![]()
图 13 HD (a) 和HP (b) 复合材料的宏观形貌对比
Figure 13. Comparison of macroscopic morphology of HD (a) and HP (b) composites
![]()
图 14 HD复合材料的表面形貌(a) 和3D扫描轮廓图(b)
Figure 14. Surface morphology (a) and 3D scanning contour (b) of HD composites
-
[1] PUGLIA D, LUZI F, TORRE L. Preparation and applications of green thermoplastic and thermosetting nanocomposites based on nanolignin[J]. Polymers, 2022, 14(24): 5470.
[2] CAMPOS B M, BOURBIGOT S, FONTAINE G, et al. Thermoplastic matrix-based composites produced by resin transfer molding: A review[J]. Polymer Composites, 2022, 43(5): 2485-2506.
[3] ALSHAMMARI B A, ALSUHYBANI M S, ALMUSHAIKEH A M, et al. Comprehensive review of the properties and modifications of carbon fiber-reinforced thermoplastic composites[J]. Polymers, 2021, 13(15): 2474.
[4] ALMUSHAIKEH A M, ALASWAD S O, ALSUHYBANI M S, et al. Manufacturing of carbon fiber reinforced thermoplastics and its recovery of carbon fiber: A review[J]. Polymers Testing, 2023, 122: 108029.
[5] AN W L, WANG X L, LIU X H, et al. Chemical recovery of thermosetting unsaturated polyester resins[J]. Green Chemistry, 2022, 24(2): 701-712. DOI: 10.1039/D1GC03724B
[6] KORKMAZ M, OKUR A. The review about the numerical modelling and analysis of 3D woven fabrics[J]. Journal of the Textile Institute, 2022, 114(3): 496-522.
[7] GRIES T, BETTERMANN I, BLAUROCK C, et al. Aachen technology overview of 3D textile materials and recent innovation and applications[J]. Applied Composite Materials, 2022, 29(1): 43-64. DOI: 10.1007/s10443-022-10011-w
[8] 李紫伦, 杨安坤, 覃小红, 等. 三维编织玻璃纤维/环氧树脂复合材料薄壁管轴向压缩性能的温度效应[J]. 复合材料学报, 2023, 40(10): 5588-5600. LI Zilun, YANG Ankun, QIN Xiaohong, et al. Temperature effect on axial compressive properties of three-dimensional glass fiber/epoxy resin braided composite thin-walled tubes[J]. Acta Materiae Compositae Sinica, 2023, 40(10): 5588-5600(in Chinese).
[9] GU Q J, QUAN Z Z, SHEN M D, et al. Fabrication and braiding angle effect on the improved interlaminar shear performances of 3D braided sandwich hybrid composites[J]. Journal of Materials Research and Technology, 2023, 25: 5795-5806.
[10] ZHANG D, ZHENG X T, WANG Z B, et al. Effects of braiding architectures on damage resistance and damage tolerance behaviors of 3D braided composites[J]. Composite Structures, 2020, 232: 111565.
[11] KANAKANNAVAR S, PITCHAIMANI J, RAMESH M R. Tribological behaviour of natural fibre 3D braided woven fabric reinforced PLA composites[J]. Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology, 2021, 235(7): 1353-1364. DOI: 10.1177/1350650120954949
[12] 俞锐晨, 姜金华, 朱晓锦, 等. 航空发动机复合材料叶片先进制造技术研究进展[J]. 科技导报, 2023, 41(5): 27-33. YU Ruichen, JIANG Jinhua, ZHU Xiaojin, et al. Research progress on advanced manufacturing technology of aero-engine composite blades[J]. Science & Technology Review, 2023, 41(5): 27-33(in Chinese).
[13] EL-DESSOUKY H M, LIU B, SALEH M N, et al. Co-woven carbon and nylon fibres for manufacturing thermoplastic composite plaques[C]. 2nd Cirp Conference on Composite Material Parts Manufacturing, 2019, 85: 272-276.
[14] MA J, XUE Y B, LIANG X Y, et al. Bi-directional regulatable mechanical properties of 3D braided polyetheretherketone (PEEK)[J]. Materials Science & Engineering C-Materials for Biological Applications, 2019, 103: 109811.
[15] GHAEDSHARAF M, BRUNEL J, LEBEL L L. Multiscale numerical simulation of the forming process of biaxial braids during thermoplastic braid-trusion: Predicting 3D and internal geometry and fiber orientation distribution[J]. Composites Part A: Applied Science and Manufacturing, 2021, 150: 106637.
[16] WU S H, LIU J, CAI J Y, et al. Combining electrospinning with hot drawing process to fabricate high performance poly (L-lactic acid) nanofiber yarns for advanced nanostructured bio-textiles[J]. Biofabrication, 2021, 13(4): 045018.
[17] DEBBABI F, ABDESSALEM S B. Impact of hot-stretching treatment on physical and mechanical properties of braided polyamide suture[J]. Textile Research Journal, 2016, 86(7): 696-709. DOI: 10.1177/0040517514566108
[18] CAI H, MENG J, LI X, et al. In vitro degradation behavior of Mg wire/poly(lactic acid ) composite rods prepared by hot pressing and hot drawing[J]. Acta Biomaterialia, 2019, 98: 125-141. DOI: 10.1016/j.actbio.2019.05.059
[19] HUANG T, WANG Y L, WANG G. Review of the mechanical properties of a 3D woven composite and its applications[J]. Polymer-Plastics Technology and Engineering, 2018, 57(8): 740-756. DOI: 10.1080/03602559.2017.1344857
[20] American Society for Testing Materials. Standard test method for short beam shear strength of polymer matrix composites and their laminates: ASTM/D 2344—2016[S]. West Conshohocken: ASTM International, 2016.
[21] American Society for Testing Materials. Standard test method for flexural properties of polymer matrix composite materials: ASTM/D 7264—2015[S]. West Conshohocken: ASTM International, 2015.
[22] American Society for Testing Materials. Standard test method for tensile properties of polymer matrix composite materials: ASTM/D 3039[S]. West Conshohocken: ASTM International, 2017.
[23] KASHIF M, HAMDANI S T, ZUBAIR M, et al. Effect of interlocking pattern on short beam strength of 3D woven composites[J]. Journal of Composite Materials, 2018, 53(20): 2789-2799.
[24] LI Z X, GUO L C, ZHANG L, et al. In situ experimental investigation on the out-plane damage evolution of 3D woven carbon-fiber reinforced composites[J]. Composites Science and Technology, 2018, 162: 101-109. DOI: 10.1016/j.compscitech.2018.04.024
[25] ZHU L, LYU L, ZHANG X, et al. Bending properties of zigzag-shaped 3D woven spacer composites: Experiment and FEM simulation[J]. Materials, 2019, 12(7): 1075. DOI: 10.3390/ma12071075
[26] LI P, MA J, HE L, et al. Pultrusion preparation and properties of continuous glass fiber reinforced polylactic acid thermoplastic composites[J]. Journal of Applied Polymer Science, 2023, 140(33): e54292.
[27] YILMAZ E, ALTAS S. Development of 3D hollow woven fabrics with superior mechanical properties by using nitinol and steel wire core hybrid yarns[J]. Journal of Industrial Textiles, 2020, 53: 1-38
[28] JAYSWAL A, ADANUR S. Characterization of PLA/TPU composite filaments manufactured for 3D printing with FDM[J]. Journal of Thermoplastic Composite Materials, 2023, 36(4): 1450-1471. DOI: 10.1177/08927057211062561
[29] JAYSWAL A, ADANUR S. Effect of heat treatment on crystallinity and mechanical properties of flexible structures 3D printed with fused deposition modeling[J]. Journal of Industrial Textiles, 2022, 51(2S): 2616S-2641S.
[30] ZHANG M, SUN S, LIU J, et al. Recycling polypropylene from non-woven disposable masks in developing a three-dimensional printing filament[J]. Textile Research Journal, 2023, 93(11-12): 2789-2808. DOI: 10.1177/00405175221147722
-
其他相关附件
-
目的
聚乳酸(polylactic acid, PLA)的生物相容性较好，且成本较低，适用于制备三维编织复合材料，然而通过热压成型(hot pressing, HP)工艺制备会造成编织结构破坏，导致纤维分布不匀，可能导致力学性能下降。本文采取热拉伸成型工艺(hot drawing, HD)制备玻璃纤维(glass fiber, GF)增强PLA复合材料，以期对三维编织聚乳酸复合材料成型方式提供理论参考。
方法本实验采取四步法三维四向编织工艺，将连续GF和PLA纤维复合制备成预制体。分别采取HD和HP工艺制备复合材料。探究不同成型工艺对GF/PLA复合材料性能的影响，采取万能材料试验机对弯曲、剪切和拉伸性能进行测试，采取差示扫描量热仪对复合材料进行结晶度测试，采取热分析仪对复合材料进行热稳定性的测试，采取3D轮廓测量仪进行3D形貌观察。
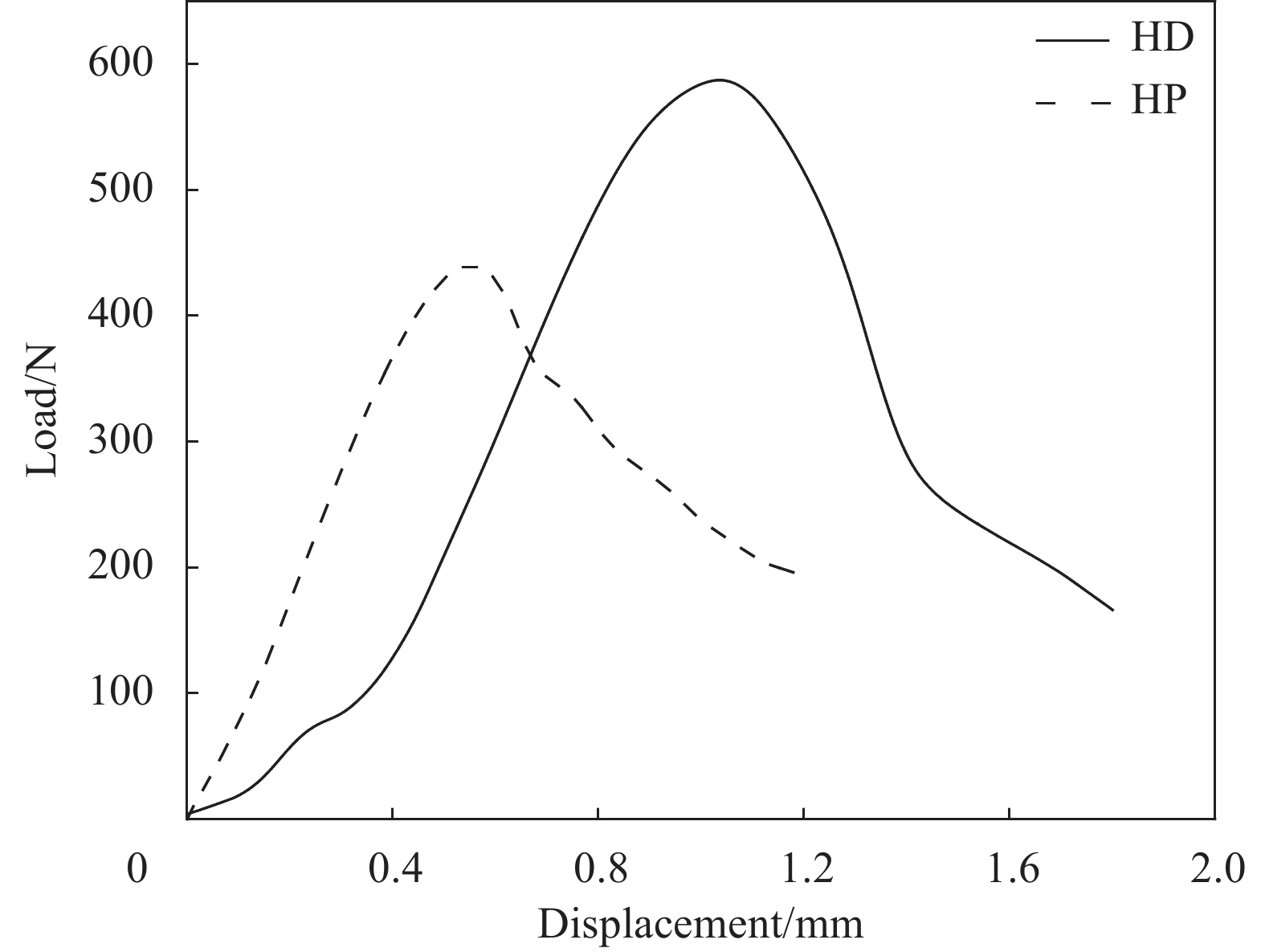
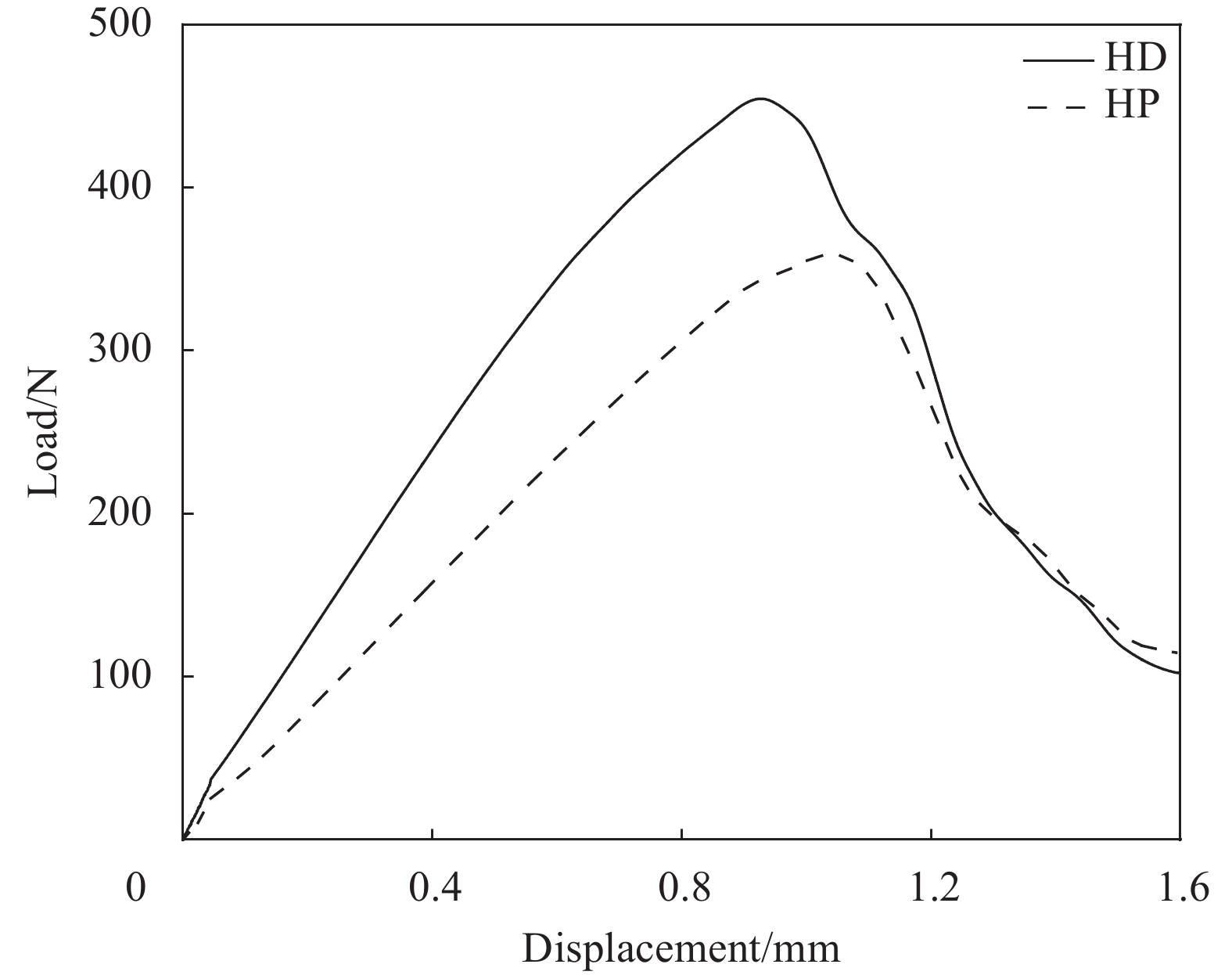
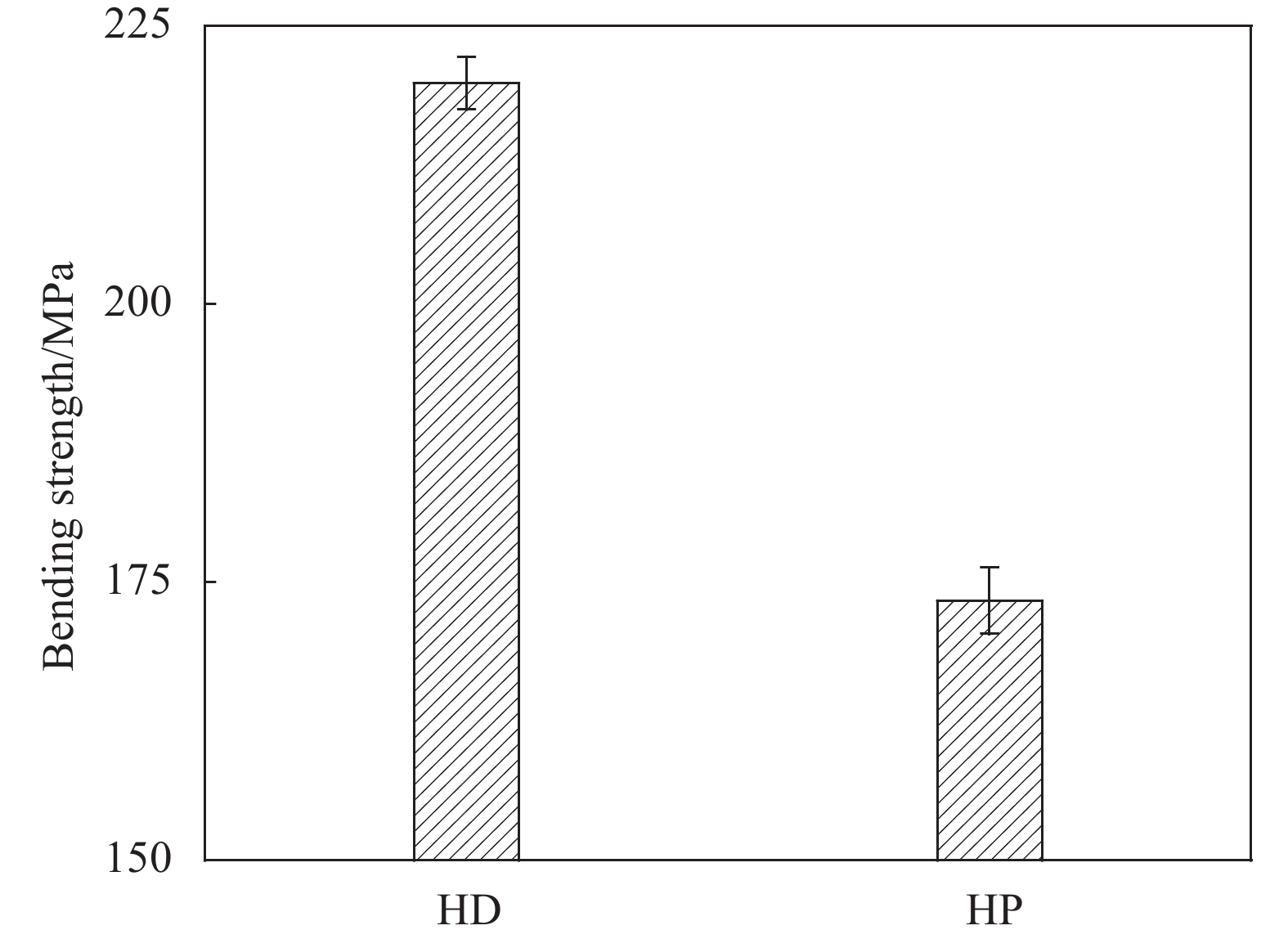
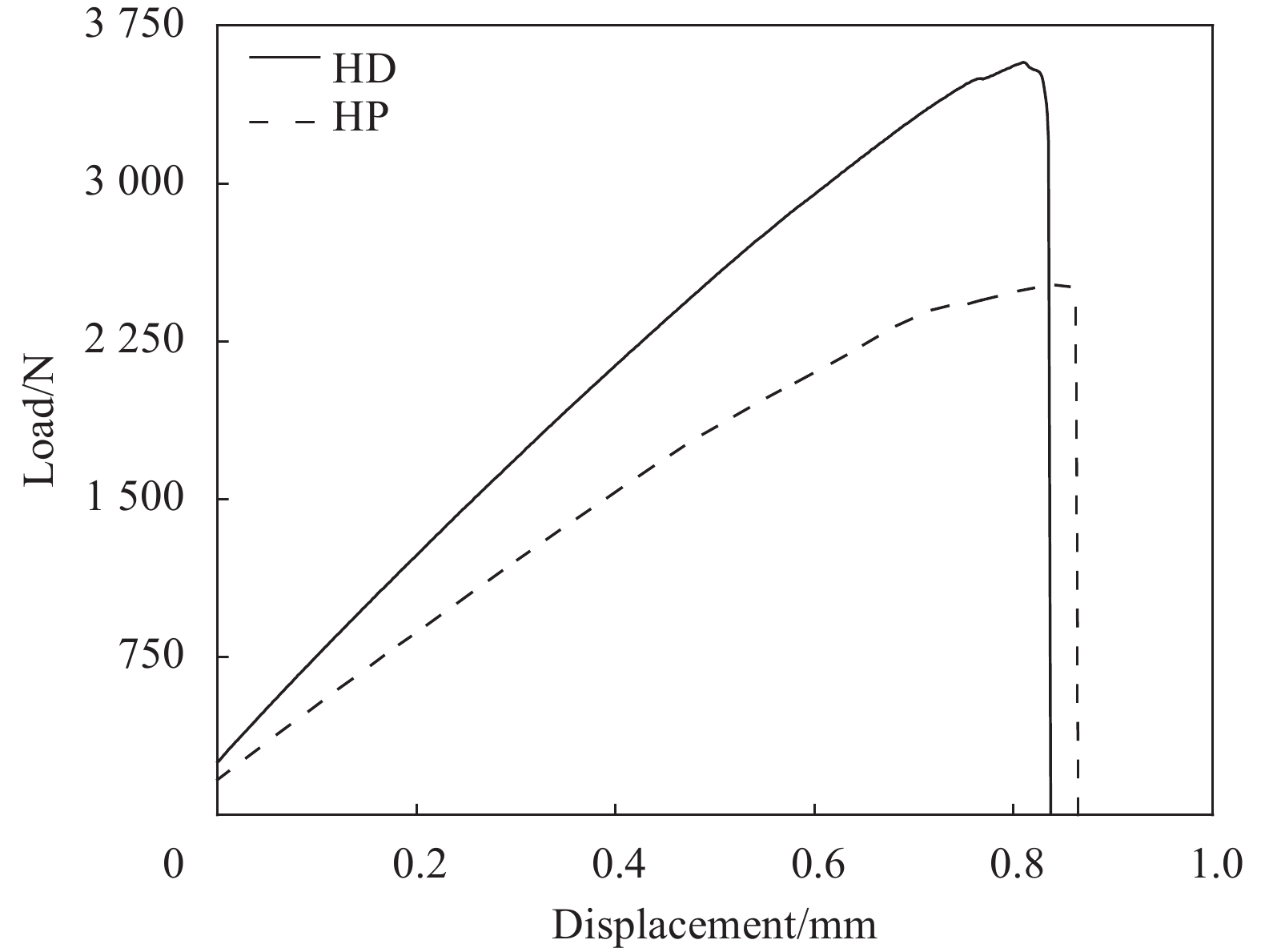
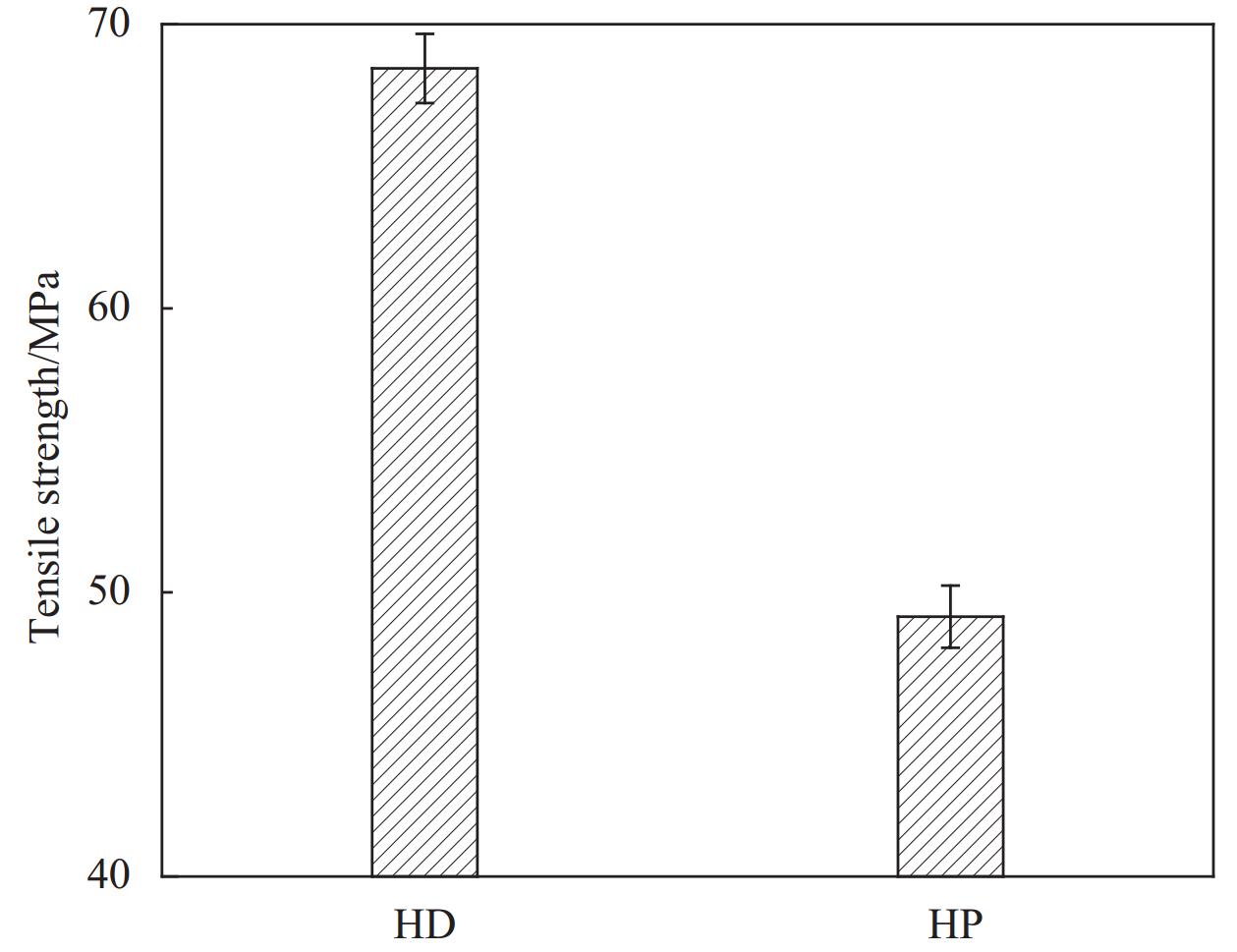
结果本文采取四步法三维编织工艺制备GF/PLA预制体，并分别采用HD和HP两种工艺制备复合材料，并分别测试其性能，结果如下：ϕHD复合材料较HP复合材料的剪切性能高出了33.03%，弯曲性能高出了26.92%，拉伸性能高出了39.67%。HD工艺有助于复合材料力学性能的提高，缓解了HP工艺造成的编织结构损伤问题，提高了PLA分子链的取向度，GF和PLA之间的界面机械强度有所增加，提升复合材料整体力学性能。‚HD复合材料较HP复合材料的结晶度高出了20.03%。结晶度的提高有助于提升复合材料的力学性能和热稳定性，拉伸工序促进了PLA晶体的有序排列，使得PLA分子链结构更加简单，提升了GF和PLA之间的界面性能，结晶度有所增加，并略微提升了热稳定性。ƒ结合HD和HP复合材料宏观形貌和3D轮廓观察，HD工艺作为自增强技术，在保证三维编织的花节结构完整的同时，提升了PLA复合材料的结晶度和力学性能。结合3D扫描轮廓图，可见HD复合材料，纤维的交错结构完整，而HP复合材料，纤维排列散乱导致纤维断裂，产生分界现象，影响力学性能，这与弯曲、剪切以及拉伸强度的测试结果一致。
结论HD工艺维持了三维编织结构，提高了复合材料的弯曲、剪切和拉伸性能，同时提高了结晶度，并略微提升热稳定性。从宏观和3D轮廓扫描结果来看，HP复合材料的结构遭到破坏，纤维分布不匀，而HD复合材料的结构保存完整，印证了力学测试结果。
-
三维编织热塑性复合材料由于有着独特的编织结构，可以显著提升材料在受到外部作用力时的抵抗性，但通过热压成型(hot pressing, HP)工艺制备三维编织热塑性复合材料存在着编织结构遭到破坏，从而导致纤维之间分布不匀的问题。本文采用热拉伸成型(hot drawing, HD)工艺改善此问题，HD工艺作为自增强技术，可以提升树脂的结晶度，从而提高复合材料的力学性能。
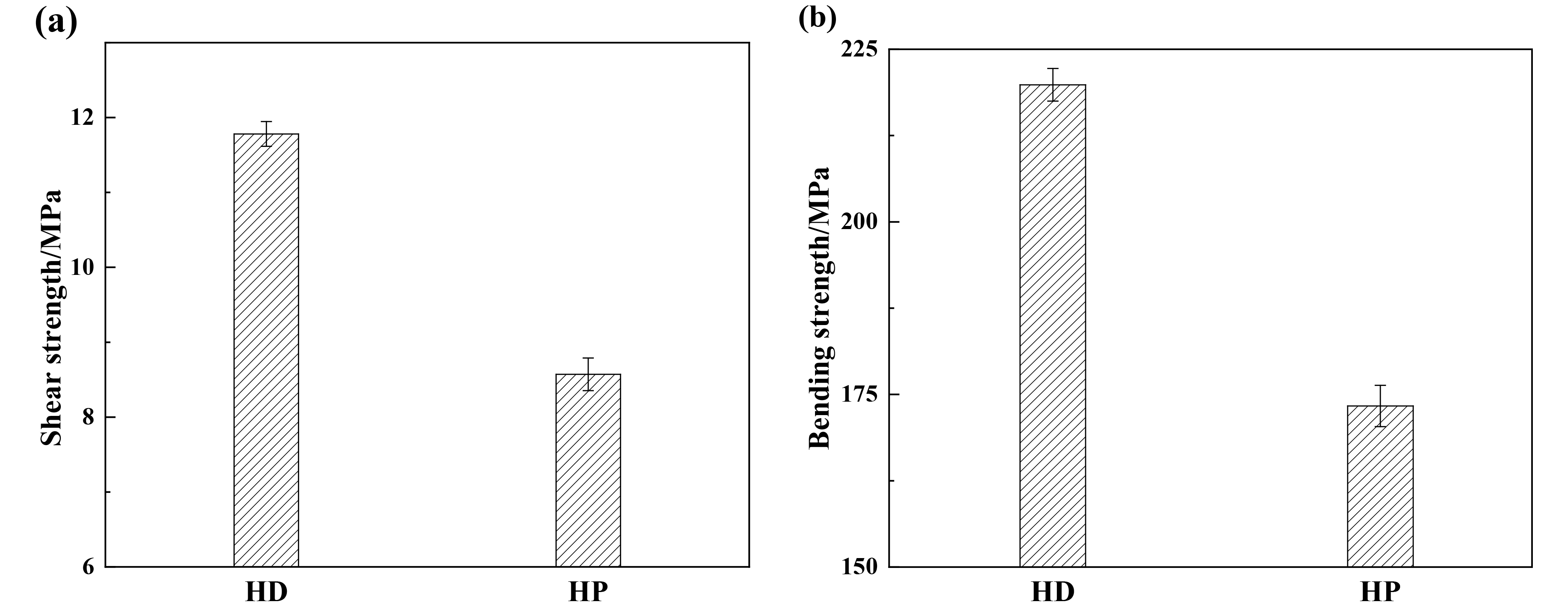
本研究采用三维编织工艺制备了玻璃纤维(glass fiber, GF)增强聚乳酸(polylactic acid, PLA)预制体，并分别通过HD和HP成型工艺制备复合材料。分析了拉伸工序对于复合材料性能的影响，发现，HD复合材料较HP复合材料的剪切强度高出了33.03%，弯曲强度高出了26.92%，拉伸强度高出了39.67%，结晶度提高了20.03%，且略微提升热稳定性。热拉伸促进了PLA分子沿着轴向有序排列，同时促进晶核生长，提高了结晶度，对于复合材料的抗弯抗剪性起到正向作用。对材料表面进行宏观形貌及3D轮廓观察，发现HD工艺改善了编织结构遭到破坏的问题，编织花节完整，而HP复合材料的结构散乱，GF纤维因摩擦产生断裂，力学性能下降。图1为HD和HP复合材料宏观形貌对比，图2(a)为HD和HP复合材料剪切强度对比，图2(b)为HD和HP复合材料弯曲强度对比。
HD和HP复合材料宏观形貌对比
HD和HP复合材料的(a)剪切强度对比, (b)弯曲强度对比
下载:
计量
- 文章访问数: 277
- HTML全文浏览量: 117
- PDF下载量: 31
