Experimental study on the flexural behavior of textile/steel wire strand mesh reinforced ECC-RC composite beam
-
摘要:
为探究不同类型网格增强工程水泥基复合材料(ECC)层加固钢筋混凝土梁的抗弯性能，通过四点弯曲试验，分析了纤维网格和钢绞线网格对复合梁承载力、控裂能力、延性和刚度等抗弯性能的影响。研究结果表明：与ECC-钢筋混凝土(RC)梁相比，采用纤维网格和钢绞线网格增强ECC-RC复合梁裂缝宽度减小，裂缝数量增加25%~70%，纤维网格和钢绞线网格增强ECC层可提高复合梁的控裂能力，抑制裂缝扩展；纤维网格和钢绞线网格增强ECC层可提高复合梁的开裂荷载、屈服荷载、极限荷载、延性及刚度；受弯过程中，所有ECC-RC复合梁截面满足平截面假设，纤维网格和钢绞线网格增强ECC层与混凝土粘结良好；基于理论分析与试验结果，考虑纤维网格利用率，建立了纤维网格和高强钢绞线网格增强ECC-RC复合梁抗弯承载力计算公式，计算结果与试验结果吻合良好。钢绞线网格增强ECC层对ECC-RC复合梁抗弯性能加固效果最佳，可显著提高复合梁承载力、延性及抗裂性。
Abstract:In order to explore the flexural performance of reinforced concrete beams strengthened with different types of grid reinforced engineered cementitious composites (ECC) layer, the effects of textile and steel wire strand mesh on the bearing capacity, crack control ability, ductility and stiffness of composite beams were analyzed by four-point bending test. The experimental results show that compared with ECC-RC beam, the crack width of ECC-RC composite beams reinforced by textile or steel wire strand mesh decreases, and the number of cracks increases by 25%-70%. The textile-reinforced ECC layer can improve the crack control ability of composite beams and inhibit crack propagation. The textile or steel wire strand mesh reinforced ECC layer can improve the cracking load, yield load, ultimate load, ductility and stiffness of the composite beam. During the bending loading, the section of textile or steel wire strand mesh rein-forced ECC-reinforced concrete (RC) composite beam meets the plane section assumption, and the textile-reinforced ECC layer is well bonded to concrete. Based on theoretical analysis and the experimental results and considering the utilization rate of textile, the calculation formula of the flexural capacity of textile or steel wire strand mesh reinforced ECC-RC composite beams is established. The calculation results are in good agreement with the experimental results. The high-strength-reinforced ECC layer has the best reinforcement effect on the flexural performance of ECC-RC composite beams, which can significantly improve the bearing capacity, ductility and crack resistance of composite beams.
-
Keywords:
- bridge engineering /
- flexural performance /
- ECC /
- textile /
- high-strength steel wire strand mesh
-
双稳态复合材料层板具有两种稳定状态，两种稳定状态之间的转换只需要一个较小激励便可获得较大变形，且无需持续的能量输入维持其稳定构型，在可变形结构和能量收集领域得到了高度关注。
Hyer[1]首次在实验中发现了非对称铺层的复合材料层板在固化后会呈现两个圆柱形稳定状态，与经典层板理论获得的马鞍形构型不同，随后建立了双稳态层板理论预报模型[2-3]，开始了双稳态层板研究的先河。目前，国内外研究学者在双稳态层板的改进理论预报模型[4-6]、跳变过程分析[7-10]、驱动方法[11-14]与可变形结构应用[15-17]等方面展开了大量的研究。
在双稳态层板的基础上，发展复合材料层板的多稳态特性可以拓宽其在可变形结构中的应用范围。目前主要的实现途径分为两类，一类是分段铺层的变刚度设计，Mattioni等[18]提出了一种由对称与非对称两种不同铺层顺序组成的变刚度层板，并建立了层板的数值计算模型，验证了多稳态铺层设计。Sousa等[19]针对对称与非对称铺层区域相交处纤维不连续性所产生的应力集中问题，引入弯曲纤维来提高结构的稳定性。Arrieta等[20]提出了分段式铺层的多稳态结构，通过串联连续的复合铺层，在机翼结构中嵌入可变形单元来获得变刚度特性。Cui等[21]将多稳态层板的应用扩展至二维空间，设计了一种由9个双稳态方形单元组合而成的曲面层板，运用特定的铺层顺序减小变形单元连接处由于弯曲方向不一致而产生的几何不兼容现象。Wang等[22]引入了对称铺层的过渡单元设计来缓解各变形单元之间的几何兼容问题，提高了多稳态层板的可设计性与可变形性。Zhang等[23]受此启发，将不对称铺层层板应用于过渡单元，发现该方法不仅能减小过渡单元的面积，并且对各类变形单元都有较好的适应性。Annamalai[24]运用分布式铺层方法，对如十字形等各类不同几何外形的层板进行了多稳态结构的有限元设计，但该方法仍存在几何不兼容的问题。
第二类是使用组合叠加的方法，该方法能够优化分段铺层的几何兼容性问题，同时具有大变形与可设计性等优势。Dai等[25]采用螺栓固定的方法制备了一种多稳态晶格结构，利用刚性连接来获得相交处的几何兼容性，并且通过拼接可以使该结构具有各种变形形状。Zhang等[26]以机械连接形式将双稳态层板进行组合获得了具有多种稳态的捕蝇草结构系统。Panesar等[27]利用丝束转向技术制造了一种多稳态混合襟翼，确保了纤维在层板面内的连续性。Algmuni等[28]通过在变形单元之间连接柔性带，以提高周期性结构的稳定性。Risso等[29]提出了一种将预拉伸薄膜与条带状复合材料层板相结合的多稳态结构，通过条带状层板的调整，能够实现正多边形的多稳态结构设计。Phanendra等[30]从理论与仿真两方面对由多个矩形层板叠加铺层得到的星形多稳态层板进行了研究，但是没有考虑制备的可行性。组合叠加得到的层板，结构较复杂且需要额外的机械紧固件连接。
本文通过将两块矩形层板以交叉铺设的形式连接并采用热压罐共固化成型，期望获得多稳态层板。然而这种交叉连接的方式会引起中心胶接区域产生较大刚度，从而导致结构失去多稳态特性。因此，本文对十字形层板引入切口设计的方法削弱中心区域刚度，并获得层板的多稳态特性。通过有限元和试验手段研究了胶接面积、切口角度和层板纵横比等参数对新型十字形多稳态层板稳定构型的影响规律，并根据层板的跳变行为揭示其影响机制，为含切口十字形多稳态层板的构型调控奠定基础。
1. 含切口矩形非对称层板的双稳态特性
选用S4C9/SY-24型玻璃纤维增强环氧树脂复合材料(中航复合材料有限公司)，材料属性如表1所示。对矩形层板进行切口设计，如图1所示，采用[902/02]非对称铺层，单层厚度为0.11 mm，固化温度135℃。令层板总长L=250 mm、宽度W=75 mm，中心区域边长a=25 mm、切口角度θ=45°，首先从仿真与实验两方面分析该切口设计对矩形层板稳定构型的影响情况。
表 1 S4C9/SY-24型玻璃纤维增强环氧树脂复合材料的材料属性Table 1. Material properties of S4C9/SY-24 glass fiber reinforced polymer compositeMaterial property E1/GPa E2/GPa ν12 G12/GPa G13/GPa G23/GPa α11/℃−1 α12/℃−1 α13/℃−1 Value 54.6 10.5 0.33 5.5 5.5 3.9 6.7×10−6 2.9×10−5 2.9×10−5 Notes: E1—Longitudinal modulus; E2—Transverse modulus; ν12—Poisson's ratio; G12—In-plane shear modulus; G13, G23—Inter-laminar shear modulus; α11—Longitudinal thermal expansion coefficient; α12, α13—Transverse thermal expansion coefficient. ![]()
图 1 矩形双稳态层板切口设计L—Total length; W—Width; L1—Length of single-petal; a—Edge length of central area; θ—Notch angleFigure 1. Notch design of rectangular bistable laminate在ABAQUS中采用隐式静态几何非线性分析方法，对矩形层板的几何中心点施加一个固定约束，并在设定的固化温度条件下获得层板的第一稳态，随后在矩形的四角点上添加方向与第一稳态弯曲方向相反的位移载荷，以获得其第二稳态。在网格划分中，主要选取SR4缩减积分壳单元，切口处填充S3单元，划分完成后得到
2673 个单元网格。仿真结果如图2(a)所示，矩形层板具有传统的双稳态变形特点，在第一稳态中，矩形层板首先沿长度方向发生变形，向90°铺层面进行弯曲(沿z轴正向)，宽度方向上的纤维基本不发生改变，维持直线状态。在施加位移载荷后获得的第二稳态中，层板沿宽度方向发生反向弯曲(沿z轴反向)，在长度方向上发生回弹。在图2(b)中，含切口层板的第一稳态与矩形层板具有几乎相同的弯曲变形，但是其第二稳态构型发生了不同的变形情况，层板发生了翘曲现象，最大翘曲位置出现在层板两端中点处，如图中红色标点所示。
![]()
图 2 矩形及含切口矩形双稳态层板稳定构型Figure 2. Stable configurations of rectangular and notched rectangular bistable composite laminates采用热压罐成型工艺制备了普通及含切口的矩形非对称铺层层板，如图3所示。为获得层板的稳态构型及其面外最大位移值，使用示波器(美国Tektronix，MDO3024数字混合域示波器)、滑台、滑轨与激光测距仪(日本KEYENCE，IL-100)等搭建了双稳态试件稳定构型测量平台，如图4所示。将试件放置于平整表面，操纵滑台与滑轨以控制试件在水平面内的匀速平移，采用激光测距仪沿层板对称轴连续测量试件各点的面外相对位移，并通过示波器绘制构型曲线，曲线拐点所对应的值即面外最大位移。
![]()
图 3 矩形及含切口矩形双稳态层板试件Figure 3. Specimens of rectangular and notched rectangular bistable laminates![]()
图 4 面外相对位移(a)及构型曲线(b)测量平台Figure 4. Measurement platform for out-of-plane displacement (a) and configuration curve (b)为提高实验数据的准确性，对矩形及含切口矩形层板均制备了至少3个有效试件，实验结果通过计算均值与添加误差棒的形式表现。仿真与实验结果对比显示：矩形层板与含切口矩形层板的第一稳定构型几乎完全一致，如图5所示，切口设计对矩形层板的第一稳态影响甚微。第二稳态则出现了明显的差异，含切口矩形层板的两端出现了翘曲现象，通过对面外最大位移进行测量，得到矩形层板的面外最大位移均值仅为4.39 mm，含切口矩形层板的面外最大翘曲高度均值为11.96 mm，翘曲高度远大于纤维弯曲变形所产生的位移变化量，如图6所示。
![]()
图 5 矩形及含切口矩形层板第一稳态稳定构型Figure 5. Stable configurations of configuration I of rectangular and notched rectangular laminates![]()
图 6 矩形及含切口矩形层板双稳态面外最大位移Con.—Configuration; Sim—Simulative; Exp—ExperimentalFigure 6. Max out-of-plane displacement of bistable configurations of rectangular and notched rectangular laminates2. 含切口十字形非对称层板的多稳态特性
2.1 十字形层板多稳态特性
将两块尺寸为250 mm×75 mm，铺层均为[902/02]的矩形层板在几何中心处交叉铺设，采用共固化成型工艺，预期获得的十字形层板具有多种稳态，且相较于传统的采用机械连接的双稳态层板组合叠加设计方案，简化了工艺步骤，降低了结构的复杂程度，拓展了多稳态层板在结构可重构领域内的实际应用价值。
然而通过实验发现，交叉铺设得到的十字形结构仅能获得第一稳态，层板跳变无法得到第二稳态。一是由于层板第二稳态以交叉形式连接时，上下胶接面的变形方向不同造成了几何不兼容问题，使共固化后胶接区域内会产生较大约束力；二是共固化引起胶接区域内的铺层厚度增大，并且铺层顺序改变为对称铺层[902/02]S，使中心区域刚度加强，二者阻碍了跳变发生，导致第二稳态失去稳定性。这一现象在仿真中表现为获得的第二稳态稳定性极差，施加的位移载荷发生微小改变就会大幅影响最终的计算结果。因此，对矩形层板进行切口设计，通过削弱中心区域的刚度减少胶接区域对第二稳态产生的影响，如图7所示。
在ABAQUS中对两个非对称矩形层板进行单独建模，在胶接区域内施加TIE约束条件连接层板模拟共固化成型，获得含切口设计的十字形多稳态层板结构，如图8所示。在图8(a)中，第一稳态发生了较大变形，随后在十字形四边的8个角点上施加垂直向下的位移载荷，层板发生跳变并获得了如图8(b)中所示的第二稳态，十字形层板的四边都发生了一定程度的翘曲现象，且翘曲高度大于矩形层板自身第二稳态发生的弯曲变形，这与含切口矩形层板第二稳态的变化情况具有相似性。此时十字形层板第二稳态的面外最大位移不再取决于宽度方向上纤维产生的弯曲变形，而是由四边翘曲高度决定。此外，单独对十字形四瓣中的其中一瓣或多瓣施加位移载荷，能够使十字形层板出现多种不同的稳定状态，将双稳态特性进一步拓展至多稳态的特性研究，如图8(c)所示。同时对含切口设计的十字形层板进行实验制备，获得的试件具有与仿真结果相同的多稳态特性，证明了通过切口设计实现十字形多稳态复合材料层板的可行性。
![]()
图 8 十字形非对称层板的多稳态特性Figure 8. Multistable characteristics of cruciform unsymmetric laminate在多稳态层板的有限元研究中，通常使用外力加载的方式实现层板构型变换的表征，但在实际应用中，则需要通过驱动方法来实现层板多稳态构型的转变。为此，本文设计了一种基于形状记忆合金(SMA)的多稳态驱动方案，利用形状记忆合金在温度作用下形状收缩的特点实现层板多稳态构型的转变。
在ABAQUS中，由于仅利用了形状记忆合金的形状收缩特性，因此可以对仿真模型进行简化，将形状记忆合金的形状收缩等效为热膨胀材料由于温度降低引起的形状收缩，赋予材料热膨胀系数α=
0.0008 ，其余材料属性取母相奥氏体，弹性模量E=81 GPa，泊松比ν=0.3。采用片状SMA驱动器，其厚度为0.05 mm，宽度为1 mm，加载方式如图9(a)所示，驱动元件与层板之间使用TIE刚性连接，驱动元件SMA1加载于90°铺层面上，控制层板由第二稳态向第一稳态发生转变，SMA2则加载于0°铺层面上，控制层板由第一稳态向第二稳态发生转变。在网格划分中，对驱动元件进行网格加密，最终得到9893 个单元网格，如图9(b)所示。![]()
图 9 形状记忆合金(SMA)驱动元件加载方案Figure 9. Loading method of shape memory alloy (SMA) actuations仿真结果如图10所示，对于形状记忆合金驱动的十字形多稳态层板，通过控制SMA2的形状收缩，能够实现单瓣或多瓣的跳变驱动，使层板从第一稳态向第二稳态发生转变；同样，通过控制SMA1，也可以使层板由第二稳态向第一稳态发生单瓣或多瓣的跳回现象。通过对形状记忆合金的调控，实现了对十字形多稳态层板结构变形的主动控制。同时，对比形状记忆合金加载前后十字形层板多种稳态的稳定构型与面外位移，可以发现，由于采用的片状SMA驱动器尺寸很小，因此驱动元件的加载对十字形层板的构型影响甚微。
![]()
图 10 十字形多稳态层板形状记忆合金驱动方法U, U3—Out-of-plane displacement (mm)Figure 10. Cruciform multistable laminate actuating method through SMA此外，研究发现，外力施加与形状记忆合金驱动下的十字形多稳态层板，单瓣片均具有独立变形能力，即对于未施加位移扰动的瓣片，其面外位移保持相对稳定，相较于第一稳态没有显著变化。而对于已经施加了位移扰动并完成了跳变的瓣片，其最大翘曲程度又与第二稳态具有的翘曲现象相当。
这一多稳态变形特点取决于胶接区域的大刚度特性。胶接区域的较大刚度导致了当一部分瓣片受到载荷作用时，其变形不会对其他未受载荷的瓣片产生显著影响，这种变形独立性体现了含切口十字形层板在设计上的优势，尤其是在需要精确控制局部变形的应用场景中。
2.2 胶接面积影响
对含切口十字形多稳态层板进行参数影响研究。保持层板尺寸L=250 mm、W=75 mm不变，当中心胶接区域为正方形(θ=45°)时，就能够在不改变几何外形为十字形的前提下，通过改变胶接区域边长a，研究不同胶接面积对十字型多稳态层板稳定构型的影响规律。
令胶接区域边长a在10~60 mm范围内逐渐增大，单次增幅∆a为5 mm，不同胶接面积与层板面外最大位移之间的变化关系曲线，如图11所示。由图可知，第一稳态面外位移大小随胶接面积的增大而减小，且呈线性关系，这是由于胶接面积的增大使层板参与弯曲变形的长度缩小导致的。而第二稳态中面外最大位移的变化情况较复杂，如图11(b)所示，首先当a在10~40 mm的范围内增大时，面外最大位移减小，随后a继续在40~60 mm区间内增大时，面外最大位移则出现上升趋势。
![]()
图 11 胶接面积对十字形多稳态层板面外最大位移的参数影响分析Figure 11. Parametric analysis of co-curing area on the max out-of-plane displacement of cruciform multistable laminates依次选择参数a=10、20、30、40、50 mm，研究不同胶接面积对层板跳变行为的影响情况，如图12所示。将仿真中层板固定端支反力，等效为十字形层板跳变所需的外部加载，获得了位移-载荷曲线图。从图中能够观察到层板的跳变行为：载荷首先随层板面外位移的增大线性增加，层板发生弹性形变；当载荷上升至峰值时，层板开始跳变，曲线的最大值即跳变载荷大小；随后载荷迅速降低，载荷的减小量随胶接面积的增大而增大。当a=30 mm时，维持层板变形所需的载荷大小降为0。这意味着对于a=30 mm的含切口十字形层板，当施加的外部载荷达到结构的跳变载荷后无需继续加载，即可使层板完成向第二稳态的转变。对于a=40 mm、50 mm的十字形层板，则表现出负刚度行为，载荷出现了回升，对应着图11(b)中a=40 mm处曲线出现拐点的现象，第二稳态的面外最大位移变化趋势发生改变。
![]()
图 12 不同胶接面积的十字形多稳态层板跳变行为分析Figure 12. Snap-through behavior of cruciform multistable laminates with different co-curing area试验验证了不同胶接面积对十字形层板稳定构型的影响规律，如表2所示，分别制备了边长a=10、25、50 mm的3种十字形层板(红色框选表示实际的胶接区域)，层板的两种稳态均具有良好的稳定性，且与仿真中两种稳定构型的变形情况吻合，第一稳态发生较大变形，第二稳态产生了四边翘曲现象，翘曲高度决定了层板的面外最大位移。同时，结构的稳定性还体现在，重复变换不同稳态多次后，结构仍然可以使用，层板的稳定构型与多稳态特性几乎不受到影响。
表 2 不同胶接面积下十字形多稳态层板的两种稳定构型Table 2. Two stable configurations of cruciform multistable laminates with different co-curing areaCo-curing area/(mm×mm) Configuration I Configuration II 10×10 
25×25 
50×50 
采用激光测距仪对层板的稳定构型与面外最大位移进行测量，如图13、图14所示，实验结果与有限元结果之间吻合良好，最大误差不超过5%。对比图13中所示的层板第一稳态构型情况，可以发现：虽然层板第一稳态的面外最大位移会随着胶接面积的改变发生线性变化，但层板在胶接区域外发生的弯曲变形曲率基本一致，胶接面积的改变对构型曲率产生较小影响。
![]()
图 13 不同胶接面积十字形多稳态层板第一稳态稳定构型Figure 13. Stable configurations of configuration I of cruciform multistable laminates with different co-curing area![]()
图 14 十字形多稳态层板两种稳态的面外最大位移Figure 14. Max out-of-plane displacement of two stable configurations of cruciform multistable laminates2.3 切口角度影响
为了获得在相同胶接面积下不同切口角度对十字形多稳态层板稳定构型的影响情况，保持胶接区域边长a=10 mm不变，改变切口角度θ。为了保证结构的稳定性，结构参数需要满足W≤L1及防止过度胶接切口角度需小于45°。
令切口角度分别为θ=35°、37.5°、40°、42.5°和45°，切口角度对面外最大位移的影响情况如图15所示。可知：随着切口角度θ的改变，第一稳态的面外最大位移基本不受影响，改变量仅为0.38 mm，百分比变化仅为0.8%；第二稳态的面外最大位移则随θ的减小而增大，总增量为2.32 mm，百分比变化为21.6%。
![]()
图 15 切口角度θ对十字形多稳态层板面外最大位移的参数影响分析Figure 15. Parametric analysis of notch angle θ on the max out-of-plane displacement of cruciform multistable laminates切口角度θ的减小，使胶接区域周边的纤维面积缩减。十字形层板第二稳态的面外最大位移受到中心区域内作用力影响，作用力主要取决于胶接区域内阻碍跳变发生的约束力及层板内部激发双稳态变形的热残余应力。在胶接面积不发生改变的条件下，引起层板四边翘曲的约束力大小保持不变，但切口角度与纤维面积的缩减减小了参与矩形层板第二稳态弯曲变形的热应力大小，在二者的相互作用下，导致翘曲现象更加明显，第二稳态面外最大位移增大。
2.4 纵横比影响
改变矩形层板纵横比，由于矩形宽度的改变会带动切口角度发生变化，因此保持宽度不变，令层板长度逐渐增大(L=220、230、240、250、260、270、280 mm)，参数对面外最大位移的影响如图16所示。可知：随着长度L增大，第一稳态与第二稳态的面外最大位移均随之增大，并且L对第一稳态构型的影响远大于第二稳态，第一稳态的面外最大位移总增量为19.96 mm，百分比变化为46.7%；而第二稳态总增量仅为2.83 mm，百分比变化为26.4%。
十字形层板两种稳态的构型变化规律与矩形层板基本相同，长度L与面外最大位移呈线性关系，这是由于纵横比L/W的增大，使层板内部沿长度方向上的纤维长度增加，结构发生了更大的弯曲变形。
![]()
图 16 长度L对十字形多稳态层板面外最大位移的参数影响分析Figure 16. Parametric analysis of length L on the max out-of-plane displacement of cruciform multistable laminates3. 结 论
(1)通过仿真与试验手段研究了普通及含切口矩形双稳态层板的稳定构型，获得了二者的稳定构型与变形规律。结果表明切口设计对层板第二稳定构型影响较大，含切口的矩形层板第二稳定状态两边产生了翘曲现象，且翘曲高度大于纤维自身所产生的弯曲变形量，面外最大位移变为由翘曲高度决定。
(2)通过将两块矩形双稳态层板交叉铺设共固化成型并引入切口设计，提出了一种新的十字形多稳态复合材料层板，通过有限元和试验验证了切口设计的可行性。
(3)胶接面积与十字形层板第一稳定构型面外最大位移呈线性减小关系；第二稳定构型面外最大位移随胶接面积的增加呈现出先减小后增大的趋势。
(4)研究了相同胶接面积下不同切口角度与纵横比对十字形层板稳定构型的影响规律，切口角度主要影响十字形层板的第二稳态，而纵横比则对第一稳态起重要作用。
-
![]()
图 10 试验梁截面刚度-挠度曲线对比
Figure 10. Comparison of section stiffness-deflection curves of test beams
![]()
图 11 试验梁跨中截面的应变分布
Figure 11. Strain distribution along mid-span cross-section of test beams
Pmax—Ultimate load
![]()
图 12 试验梁正截面应力分布简图
Figure 12. Distribution of stresses and strains along cross-section of test beam
h—Height of beam; b—Width of beam; htg— Distance from the grid to the top of the composite beam; as—The distance from the tensile steel bar to the bottom of the composite beam; h0—Effective height of composite beam; he—ECC thickness; As—The cross section area of tensile reinforcement; A′s—The cross section area of compressive steel bar; εcu—Concrete ultimate compressive strain; ε's—Compressive steel bar strain; εs—Tensile steel bar strain; εe—ECC tensile strain; εtg—Textile or the high-strength steel wire strand mesh strain; xc—Compression zone height; yc—The distance from the concrete resultant point to the top of the composite beam; σc—Concrete compressive stress; σec—ECC tensile stress; Cc—Concrete resultant force; T′s—Compressed steel bar resultant force; Ts—Tensile steel bar resultant force; Ttg—Grid resultant force.
表 1 试件设计参数
Table 1 Design parameters of specimens
Specimen number Thickness of
ECC/mmDistance from
grid to beam
bottom/mmGrid type RC 0 — — ECC-RC 60 — — CFRP/ECC-RC 60 10 CFRP textile BFRP/ECC-RC 60 10 BFRP textile HSSWS/ECC-RC 60 10 High-strength steel wire strand mesh Notes: ECC—Engineered cementitious composite; RC—Reinforced concrete; CFRP—Carbon fiber reinforced polymer; BFRP—Basalt fiber reinforced polymer; HSSWS—High strength steel wire strand. 
下载: 导出CSV
表 2 ECC的配合比(单位：kg/m3)
Table 2 Mix proportion of ECC (Unit: kg/m3)
Material Fumed silica/mm P·O 52.5 Sand Water Water
reducerExpansion agent Fiber Silica
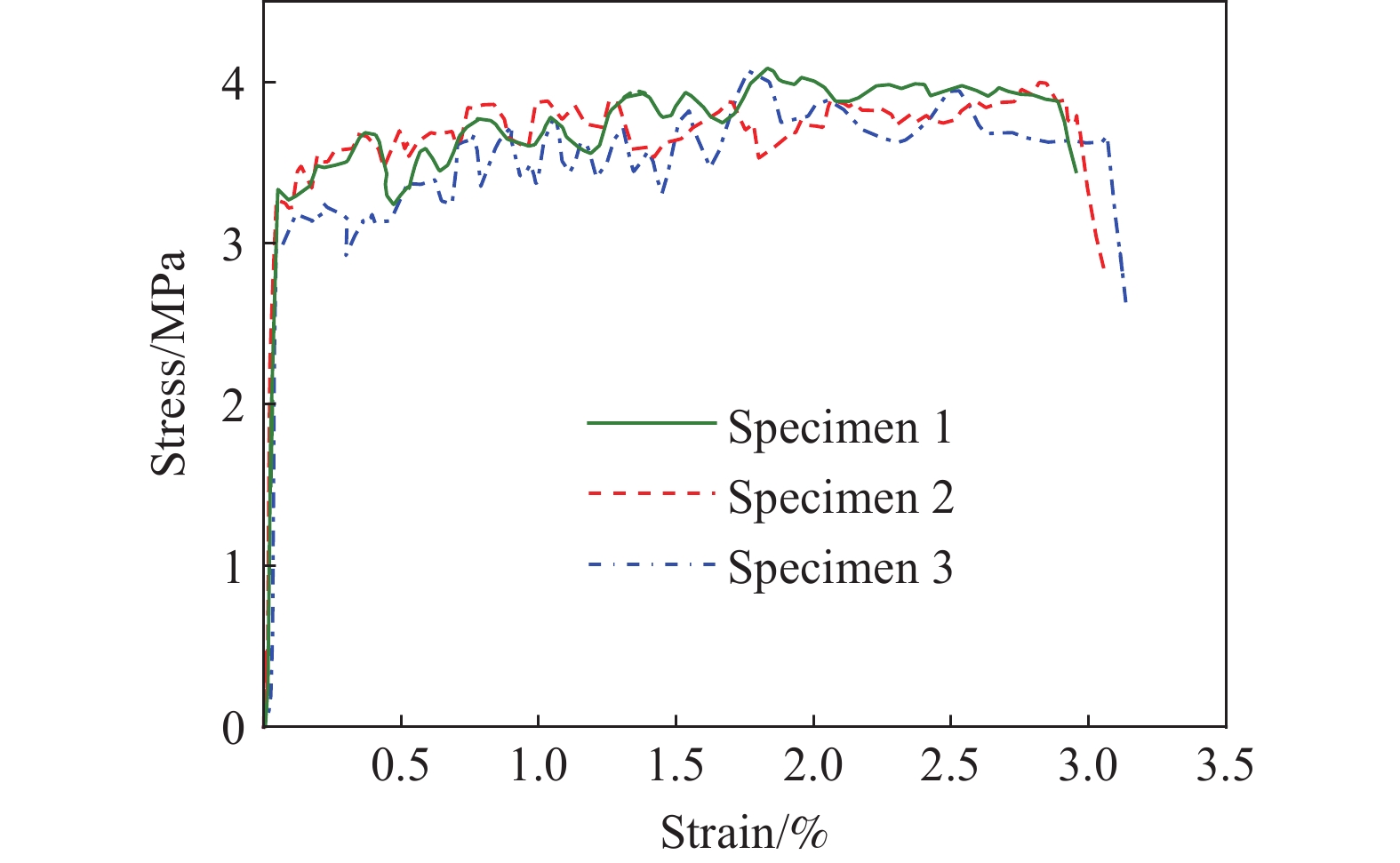
fume5-16 16-32.5 C50 471 706 520 706 161 7.8 — — — ECC — — 500 600 190 3 25 23 25
下载: 导出CSV
表 3 纤维网格和高强钢绞线网格力学性能
Table 3 Mechanical properties of textile and high-strength steel wire strand mesh
Grid type Ultimate tensile strength/MPa Elastic modulus/GPa Ultimate tensile strain/% Cross-sectional area/mm2 CFRP textile 4815 252 1.90 0.89 BFRP textile 3330 90 3.70 0.89 High-strength steel wire strand mesh 1845 180 2.96 4.71
下载: 导出CSV
表 4 试验梁特征数据结果
Table 4 Characteristic data results of test beams
Specimen number Pcr/kN Mcr/(kN·m) Dcr/% Py/kN My/(kN·m) Dy/% Pu/kN Mu/(kN·m) Du/% Δy/mm Δu/mm DΔu/% RC 14 5.25 — 104 39.00 — 121 45.38 — 9.99 25.51 — ECC-RC 16 6.00 — 113 42.38 — 127 47.63 — 10.05 27.77 — CFRP/ECC-RC 27 10.13 68.83 125 46.88 10.62 141 52.88 11.02 10.46 29.39 5.83 BFRP/ECC-RC 22 8.25 37.50 122 45.75 7.95 139 52.13 9.45 9.78 31.97 15.12 HSSWS/ECC-RC 28 10.50 75.00 143 53.62 26.52 170 63.75 33.84 10.28 34.36 23.73 Notes: Pcr—Cracking load; Mcr—Cracking moment; Py—Yielding load; My—Yielding moment; Pu—Ultimate load; Mu—Ultimate moment; Δy—Deflection of the specimen at My; Δu—Deflection of the specimen at Mu; Dcr, Dy, Du, DΔu represent the increase of cracking load, yield load, ultimate load and ultimate deflection compared with ECC-RC beam, respectively.
下载: 导出CSV
表 5 试验梁受弯承载力计算值和试验值对比
Table 5 Comparison of flexural bearing capacity between experimental and theoretical results of test beams
Specimen number Muc/(kN·m) Mut/(kN·m) Muc/Mut Error/% CFRP/ECC-RC 52.00 52.88 0.98 1.7 BFRP/ECC-RC 51.40 52.13 0.99 1.4 HSSWS/ECC-RC 61.85 63.75 0.97 3.0 ECC-RC 49.96 47.63 1.05 4.9 BA-1[23] 15.75 14.80 1.06 5.7 BB-1[23] 16.66 15.70 1.06 5.5 BC-1[23] 17.46 16.60 1.05 4.9 Notes: Muc—Calculated value of ultimate bending moment of composite beam; Mut—Experimental value of ultimate bending moment of composite beam; BA-1, BB-1, BC-1—Specimen name from literature[23].
下载: 导出CSV
-
[1] LI V C, STANG H, KRENCHEL H. Micromechanics of crack bridging in fiber-reinforced concrete[J]. Materials and Structures, 1993, 26(8): 486-494.
[2] LI V C, LEUNG C K Y. Steady state and multiple cracking of short random fiber composites[J]. Journal of Engineering Mechanics, 1992, 188(11): 2246-2264.
[3] SHANOUR A S, SAID M, ARAFA A I, et al. Flexural performance of concrete beams containing engineered cementitious composites[J]. Construction and Building Materials, 2018, 180: 23-34. DOI: 10.1016/j.conbuildmat.2018.05.238
[4] 崔涛, 何浩祥, 闫维明, 等. 带ECC底板的装配式梁受弯性能及损伤分析[J]. 哈尔滨工业大学学报, 2019, 51(12): 104-112. DOI: 10.11918/j.issn.0367-6234.201812126 CUI Tao, HE Haoxiang, YAN Weiming, et al. Bending performance test and damage analysis of precast beams with ECC plate[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 104-112(in Chinese). DOI: 10.11918/j.issn.0367-6234.201812126
[5] 王新玲, 罗鹏程, 钱文文, 等. 高强不锈钢绞线网增强工程水泥基复合材料薄板受弯承载力研究[J]. 建筑结构学报, 2022, 43(1): 164-172. WANG Xinling, LUO Pengcheng, QIAN Wenwen, et al. Study on flexural bearing capacity of high-strength stainless steel wire mesh reinforced ECC thin plate[J]. Journal of Building Structures, 2022, 43(1): 164-172(in Chinese).
[6] 朱俊涛, 张凯, 王新玲, 等. 高强不锈钢绞线网与ECC粘结-滑移关系模型[J]. 土木工程学报, 2020, 53(4): 83-92. ZHU Juntao, ZHANG Kai, WANG Xinling, et al. Bond-slip relational model between high-strength stainless steel wire mesh and ECC[J]. China Civil Engineering Journal, 2020, 53(4): 83-92(in Chinese).
[7] 王新玲, 陈永杰, 钱文文, 等. 高强不锈钢绞线网增强工程水泥基复合材料弯曲性能试验[J]. 复合材料学报, 2021, 38(4): 1292-1301. WANG Xinling, CHEN Yongjie, QIAN Wenwen, et al. Experiment on bending performance of engineered cementitious composites reinforced by high-strength stainless steel wire strand mesh[J]. Acta Materiae Compositae Sinica, 2021, 38(4): 1292-1301(in Chinese).
[8] 李传秀, 尹世平, 赵俊伶. 纤维编织网增强ECC的拉伸和弯曲性能[J]. 建筑材料学报, 2021, 24(4): 736-741. DOI: 10.3969/j.issn.1007-9629.2021.04.009 LI Chuanxiu, YIN Shiping, ZHAO Junling. Tensile and bending properties of textile reinforced ECC[J]. Journal of Building Materials, 2021, 24(4): 736-741(in Chinese). DOI: 10.3969/j.issn.1007-9629.2021.04.009
[9] 徐世烺, 李庆华, 李贺东. 碳纤维编织网增强超高韧性水泥基复合材料弯曲性能的试验研究[J]. 土木工程学报, 2007, 40(12): 69-76. DOI: 10.3321/j.issn:1000-131x.2007.12.009 XU Shilang, LI Qinghua, LI Hedong. An experimental study on the flexural properties of carbon textile reinforced ECC[J]. China Civil Engineering Journal, 2007, 40(12): 69-76(in Chinese). DOI: 10.3321/j.issn:1000-131x.2007.12.009
[10] 王新玲, 苏会晓, 李可, 等. FRP网格增强ECC加固素混凝土柱受压性能数值分析[J]. 建筑科学, 2018, 34(3): 22-29. WANG Xinling, SU Huixiao, LI Ke, et al. Numerical analysis of compressive performance of plain concrete columns strengthened with FRP-grid and ECC[J]. Building Science, 2018, 34(3): 22-29(in Chinese).
[11] 郭瑞, 任宇, 顾天宇. 纤维增强复材网格-工程水泥基复合材料加固钢筋混凝土梁的抗剪性能试验研究[J]. 工业建筑, 2019, 49(9): 145-151. GUO Rui, REN Yu, GU Tianyu. Experimental research on shear behavior of RC beams reinforced with FRP grid-ECC[J]. Cement Science & Concrete Technology, 2019, 49(9): 145-151(in Chinese).
[12] ZHENG Y Z, WANG W W, MOSALAM K M, et al. Experimental investigation and numerical analysis of RC beams shear strengthened with FRP/ECC composite layer[J]. Composite Structures, 2020, 246: 112436. DOI: 10.1016/j.compstruct.2020.112436
[13] GUO R, REN Y, LI M Q, et al. Experimental study on flexural shear strengthening effect on low-strength RC beams by using FRP grid and ECC[J]. Engineering Structures, 2021, 227: 111434. DOI: 10.1016/j.engstruct.2020.111434
[14] ZHENG A H, LIU Z Z, LI F P, et al. Experimental investigation of corrosion-damaged RC beams strengthened in flexure with FRP grid-reinforced ECC matrix composites[J]. Engineering Structures, 2021, 244: 112779. DOI: 10.1016/j.engstruct.2021.112779
[15] YANG X, GAO W Y, DAI J G. Flexural strengthening of RC beams with CFRP grid-reinforced ECC matrix[J]. Composite Structures, 2018, 189: 9-26. DOI: 10.1016/j.compstruct.2018.01.048
[16] ZHENG Y Z, WANG W W, BRIGHAM J C. Flexural behaviour of reinforced concrete beams strengthened with a composite reinforcement layer: BFRP grid and ECC[J]. Construction and Building Materials, 2016, 115: 424-437. DOI: 10.1016/j.conbuildmat.2016.04.038
[17] 郑宇宙. FRP格栅增强ECC复合加固混凝土梁试验与计算方法研究[D]. 南京: 东南大学, 2018. ZHENG Yuzhou. Experimental and calculation method research on reinforced concrete (RC) beams strengthened with the composite of FRP grid and ECC[D]. Nanjing: Southeast University, 2018(in Chinese).
[18] 郑宇宙, 王文炜. 复材网格-UHTCC复合增强钢筋混凝土梁抗弯性能试验研究[J]. 土木工程学报, 2017, 50(6): 23-32. ZHENG Yuzhou, WANG Wenwei. Experimental research on flexural behavior of RC beams strengthened with FRP grid-UHTCC composite[J]. China Civil Engineering Journal, 2017, 50(6): 23-32(in Chinese).
[19] 张振. 玄武岩纤维网-ECC复合材料加固RC梁抗弯性能研究[D]. 长春: 吉林建筑大学, 2022. ZHANG Zhen. Study on flexural behavior of RC beams strengthened by basalt fiber grid-ECC composite material[D]. Changchun: Jilin Jianzhu University, 2022(in Chinese).
[20] 李可, 赵佳丽, 李志强, 等. 高强钢绞线网增强ECC抗弯加固无损RC梁试验[J]. 复合材料学报, 2022, 39(7): 3428-3440. LI Ke, ZHAO Jiali, LI Zhiqiang, et al. Experiment on non-damaged RC beams strengthened by high-strength steel wire strand meshes reinforced ECC in bending[J]. Acta Materiae Compositae Sinica, 2022, 39(7): 3428-3440(in Chinese).
[21] 李可, 王宇, 李志强, 等. 高强钢绞线网增强ECC加固无损RC梁受弯承载力研究[J]. 建筑结构学报, 2022, 43(12): 82-90. LI Ke, WANG Yu, LI Zhiqiang, et al. Research on flexural bearing capacity of non-damaged RC beams strengthened by high-strength steel wire strand mesh-reinforced ECC[J]. Journal of Building Structures, 2022, 43(12): 82-90(in Chinese).
[22] 李可, 任魁, 李志强, 等. 高强钢绞线网增强ECC加固无损RC梁截面刚度计算[J]. 铁道科学与工程学报, 2022, 19(10): 3046-3054. LI Ke, REN Kui, LI Zhiqiang, et al. Calculation of section rigidity of non-damaged RC beams strengthened by high-strength steel wire strand meshes reinforced ECC[J]. Journal of Railway Science and Engineering, 2022, 19(10): 3046-3054(in Chinese).
[23] 盛杰, 尹世平, 裴浩. 纤维编织网-ECC加固RC梁受弯性能试验[J]. 中国公路学报, 2022, 35(9): 287-297. DOI: 10.3969/j.issn.1001-7372.2022.09.022 SHENG Jie, YIN Shiping, PEI Hao. Experimental study on flexural behavior of RC beams strengthened with textile and ECC[J]. China Journal of Highway and Transport, 2022, 35(9): 287-297(in Chinese). DOI: 10.3969/j.issn.1001-7372.2022.09.022
[24] 葛文杰, 宗耀锋, 仇胜伟, 等. 碳纤维布粘贴加固BFRP筋-ECC-混凝土组合梁受弯性能研究[J]. 建筑结构学报, 2021, 42(S1): 302-311. GE Wenjie, ZONG Yaofeng, QIU Shengwei, et al. Study on flexural behavior of BFRP reinforced-ECC-concrete composite beams strengthened with carbon fiber sheets[J]. Journal of Building Structures, 2021, 42(S1): 302-311(in Chinese).
[25] 高培琦, 葛文杰, 虞佳敏, 等. 碳纤维布加固钢筋ECC/混凝土复合梁受弯性能试验研究[J]. 建筑科学, 2019, 35(11): 103-110. GAO Peiqi, GE Wenjie, YU Jiamin, et al. Experimental study on flexural behavior of ECC/concrete composite beams strengthened with carbon fiber sheets[J]. Building Science, 2019, 35(11): 103-110(in Chinese).
[26] 黄华. 高强钢绞线网—聚合物砂浆加固混凝土梁式桥试验研究与机理分析[D]. 西安: 长安大学, 2008. HUANG Hua. Experimental study and theoretical analysis on strengthening RC girder bridge with steel wire mesh and polymer mortar[D]. Xi'an: Chang'an University, 2008(in Chinese).
[27] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2015(in Chinese).
[28] 董志芳, 邓明科, 张聪. 纤维织物增强高延性混凝土单轴拉伸性能试验研究[J]. 土木工程学报, 2020, 53(10): 13-25. DONG Zhifang, DENG Mingke, ZHANG Cong. Experimental investigation on uniaxial tension behavior of textile-reinforced highly ductile concrete[J]. China Civil Engineering Journal, 2020, 53(10): 13-25(in Chinese).
-
期刊类型引用(2)
1. 郭小杰，杜丽勇. 尿素掺杂CH_3NH_3PbI_3薄膜及其钙钛矿太阳能电池性能研究. 功能材料. 2024(01): 1086-1091 . 
百度学术
2. 张晨亮. 溴化锂材料浓度对太阳能电池蓄能力影响的计算机动态分析. 信息记录材料. 2023(02): 158-160 . 百度学术
其他类型引用(5)
-
其他相关附件
-
目的
ECC因其具有应变硬化特征及优异的裂缝分散能力和控制力，被广泛用于混凝土结构加固领域。本文探究CFRP网格、BFRP网格、高强钢绞线网格增强ECC层对钢筋混凝土梁抗弯性能的影响，以及对钢筋混凝土加固效果最优的网格增强ECC层。
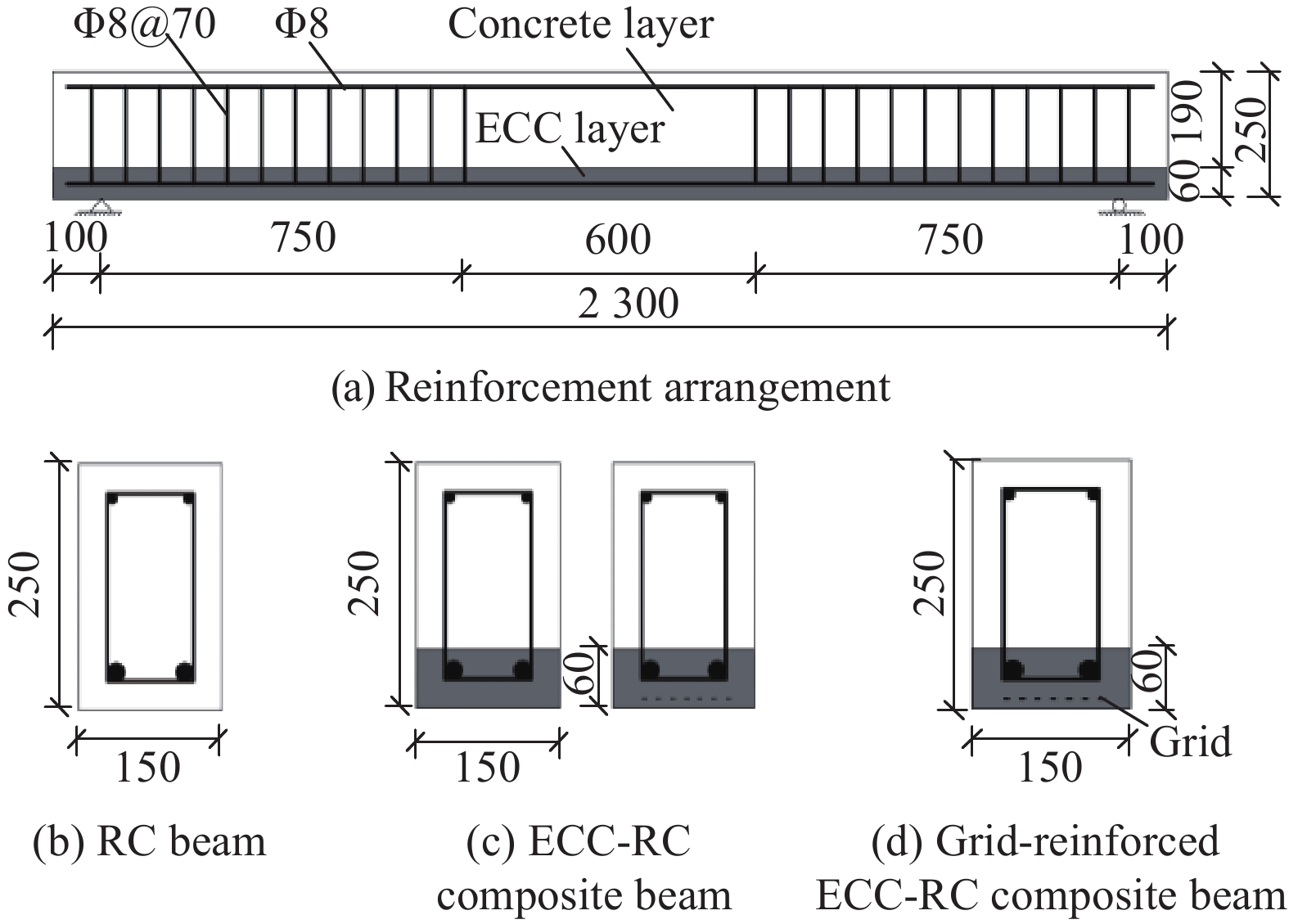
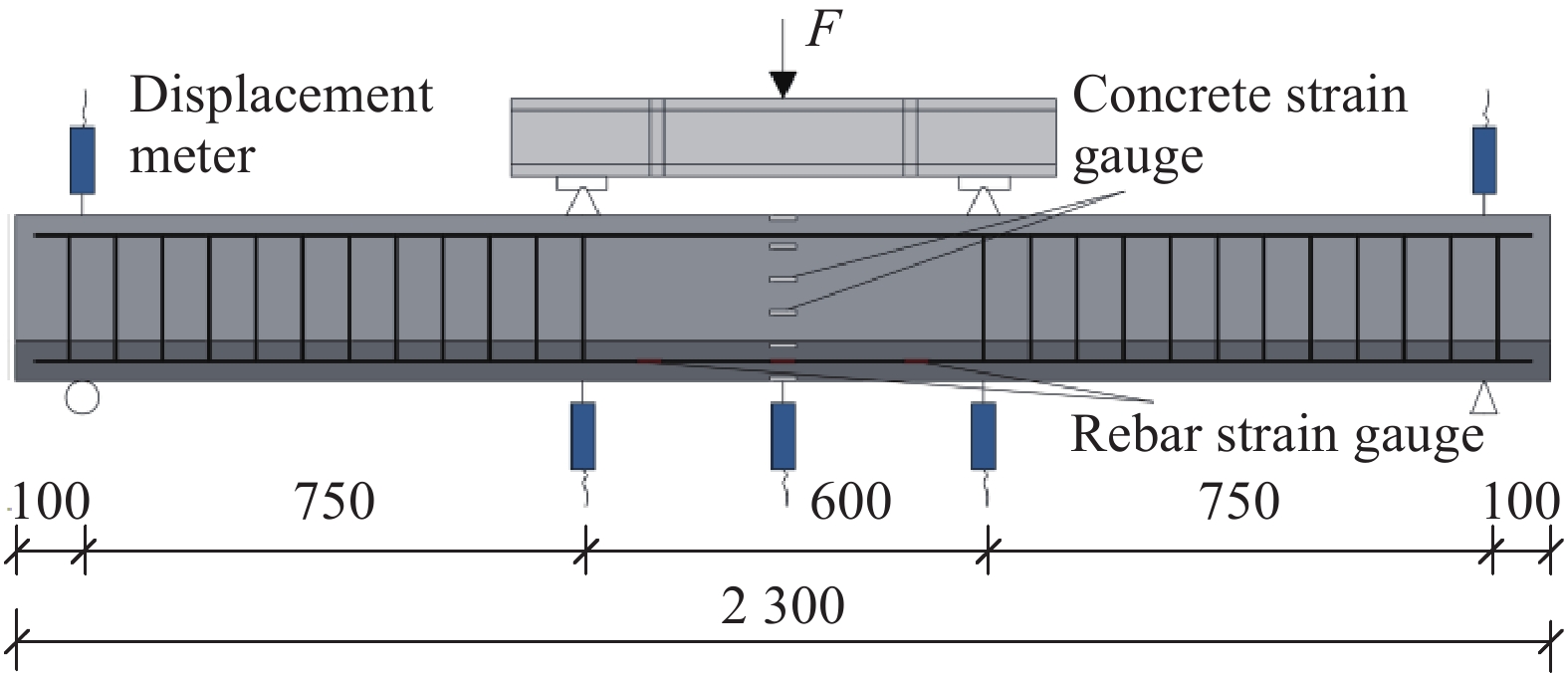
方法本文采用了一种新的钢筋混凝土梁加固方式，采用网格增强ECC层替换受拉区混凝土的加固方式，形成ECC-RC复合梁。本文主要采用试验对比方法，一共设置了两片对比梁，一片钢筋混凝土梁，一片不含网格的ECC-RC复合梁；三片不同类型网格增强ECC-RC复合梁。结合四点弯曲加载试验和数字图像技术，收集试验梁支座两端位移、跨中挠度、混凝土/钢筋应变以及荷载等级等数据，采用Origin软件对相对数据进行分析；依据钢筋混凝土正截面抗弯承载能力计算公式，在考虑纤维网格利用率的基础上，推导网格增强ECC-RC复合梁正截面抗弯承载能力计算公式。
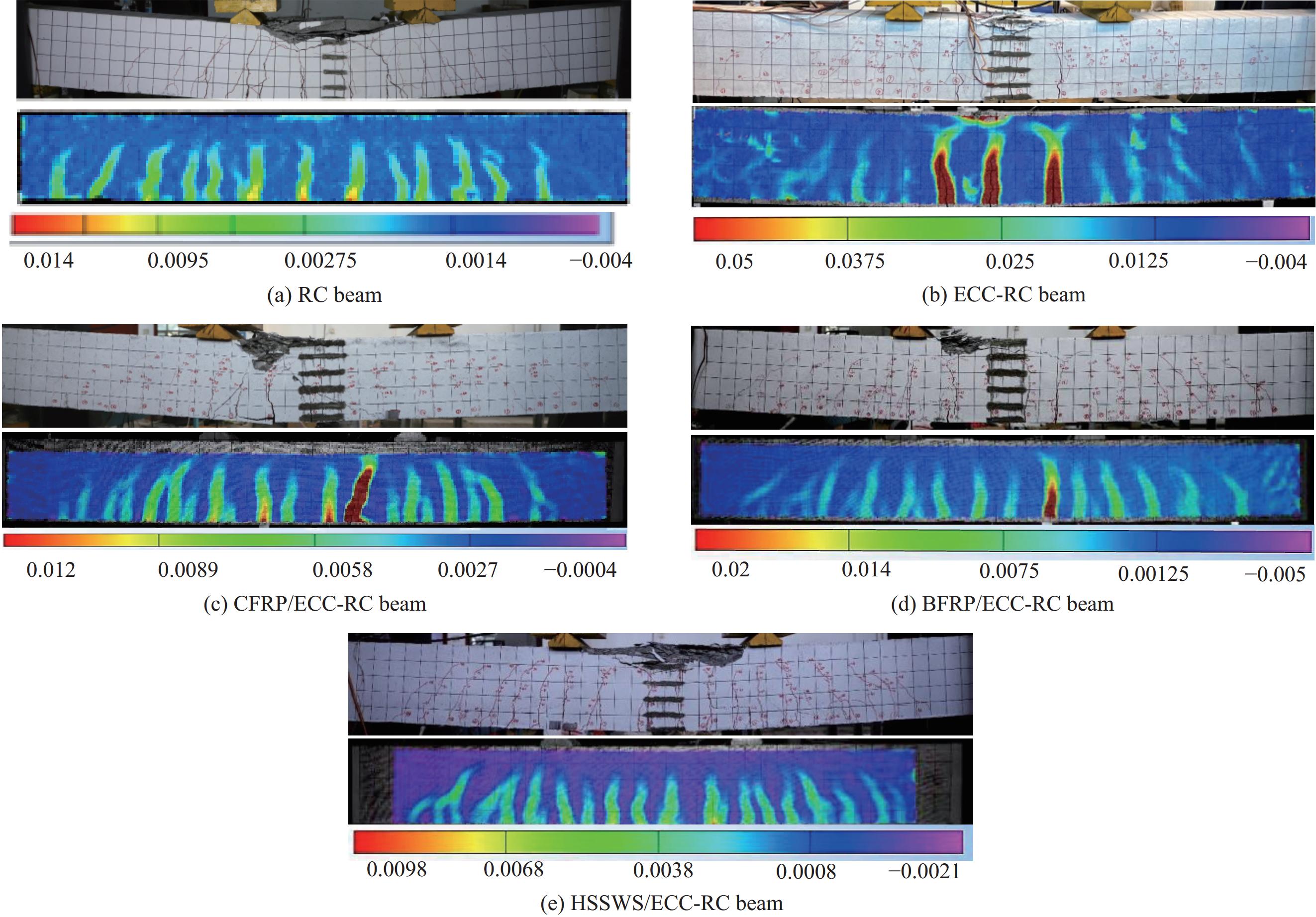
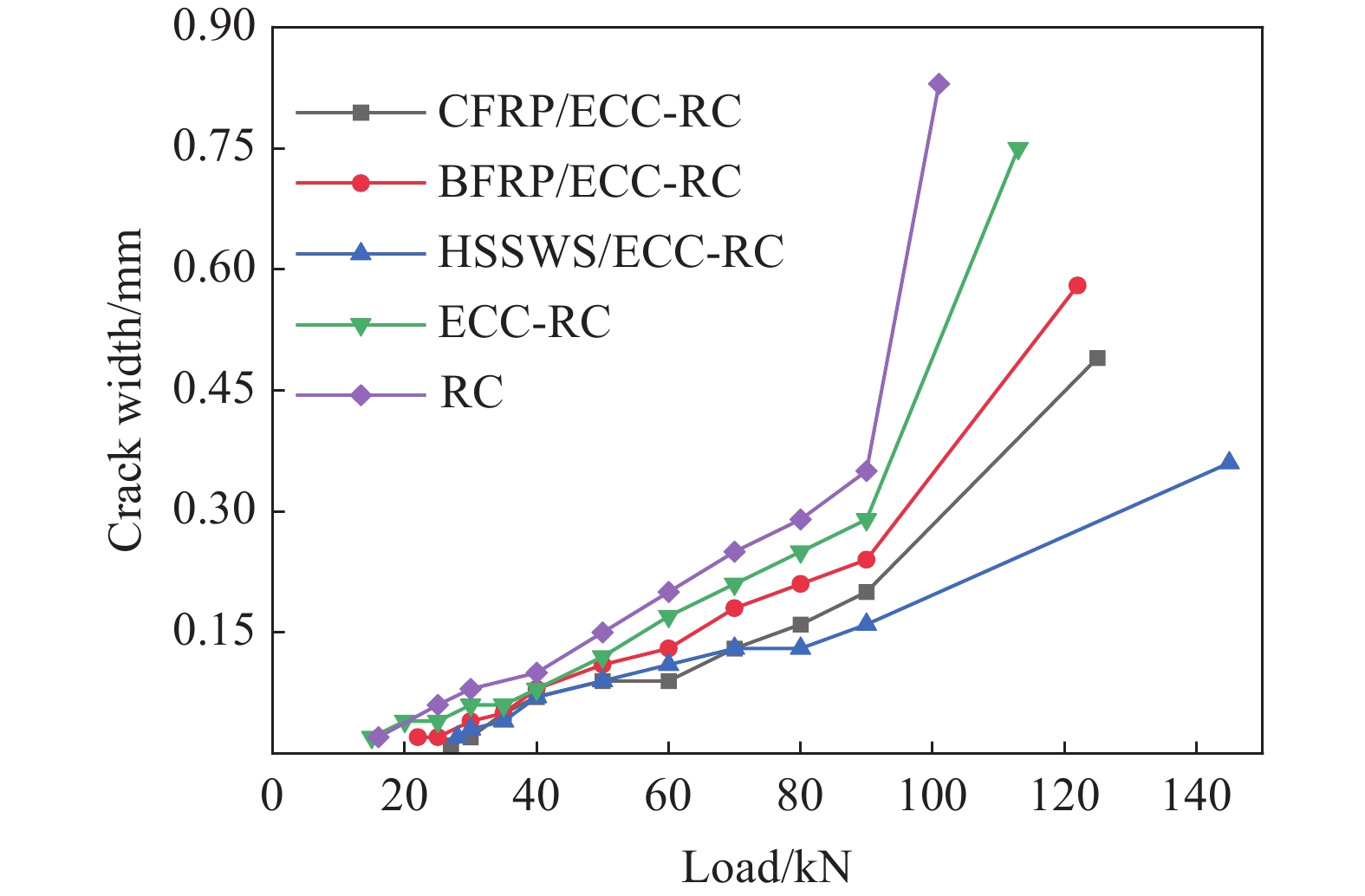
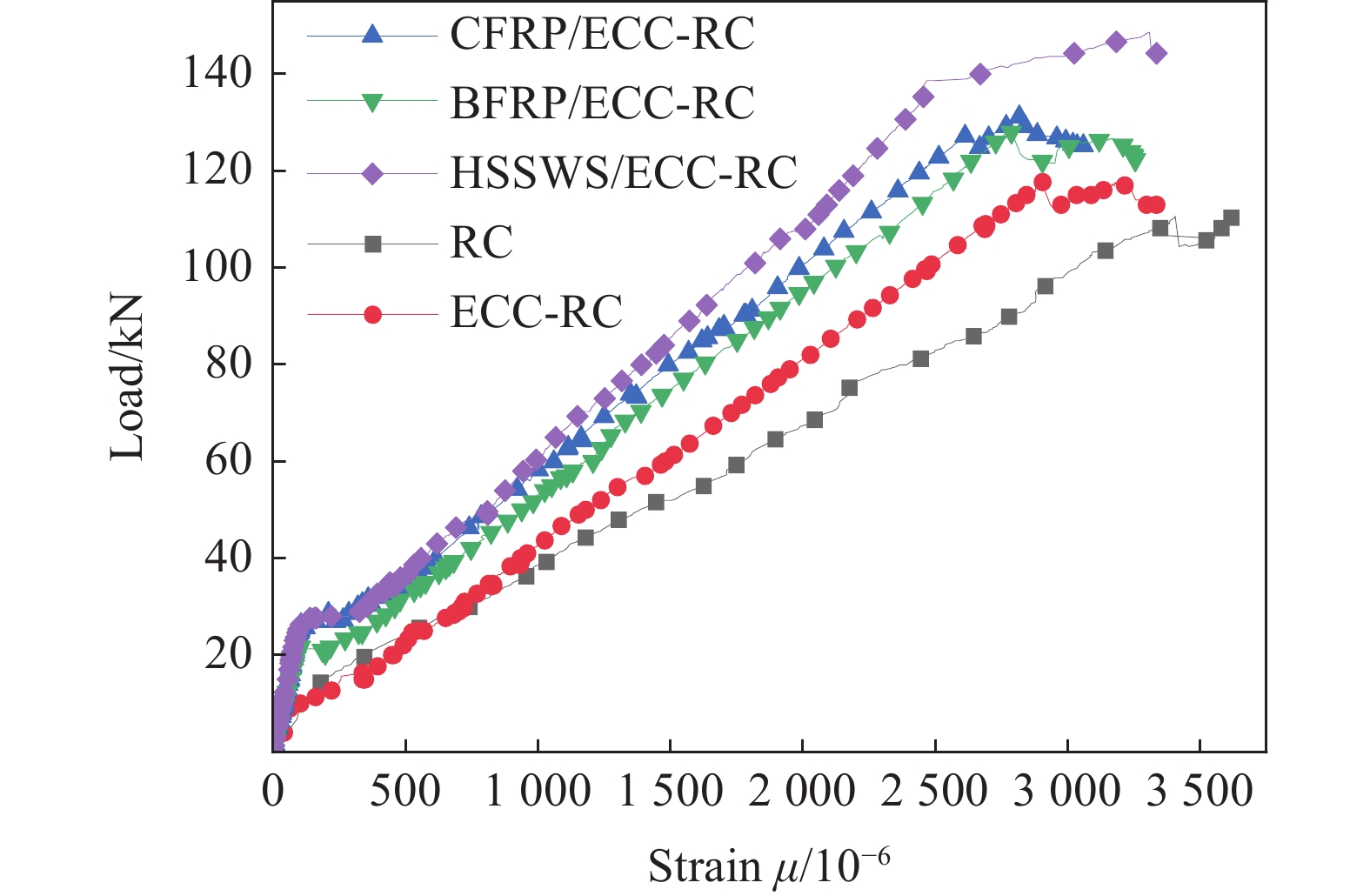
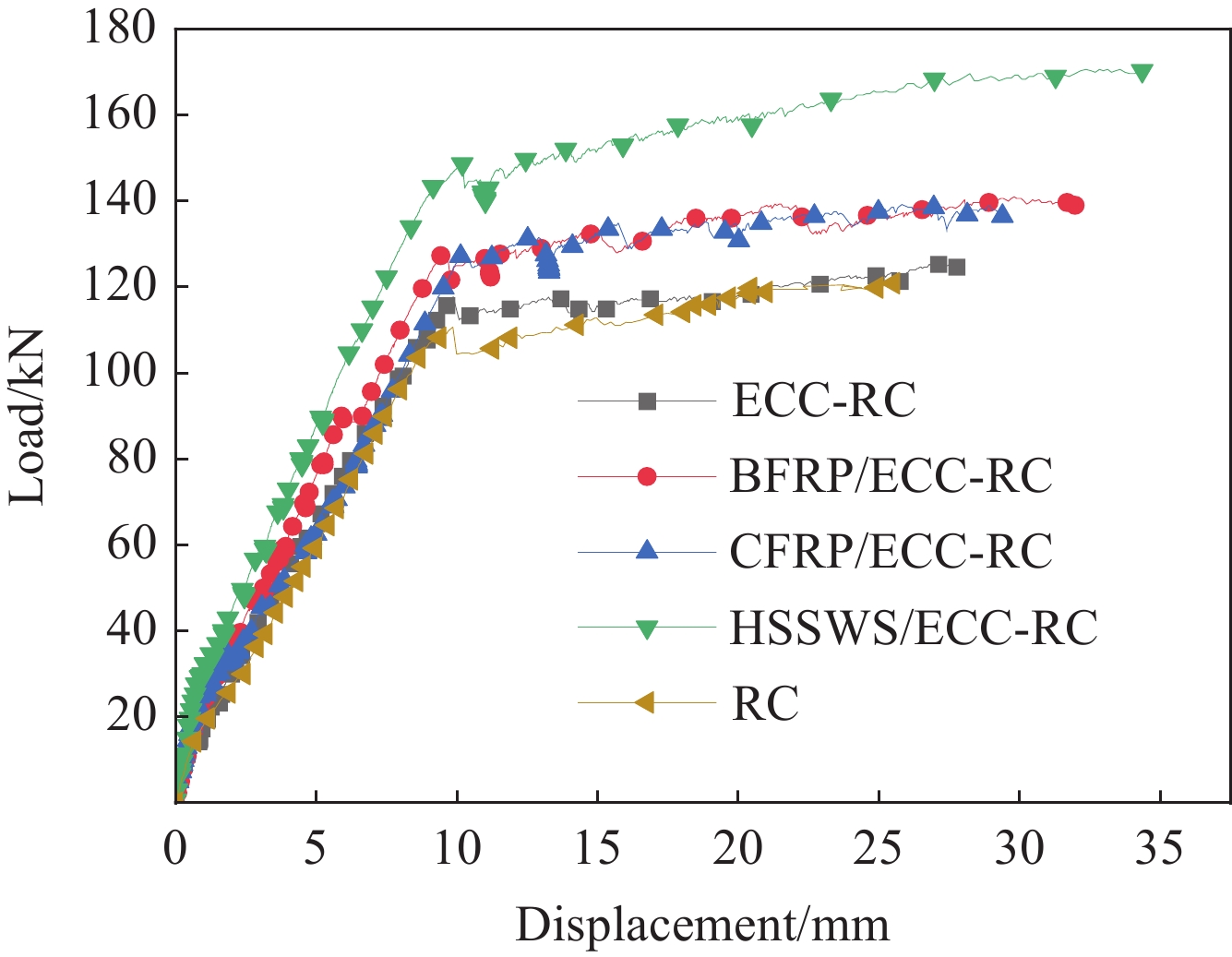
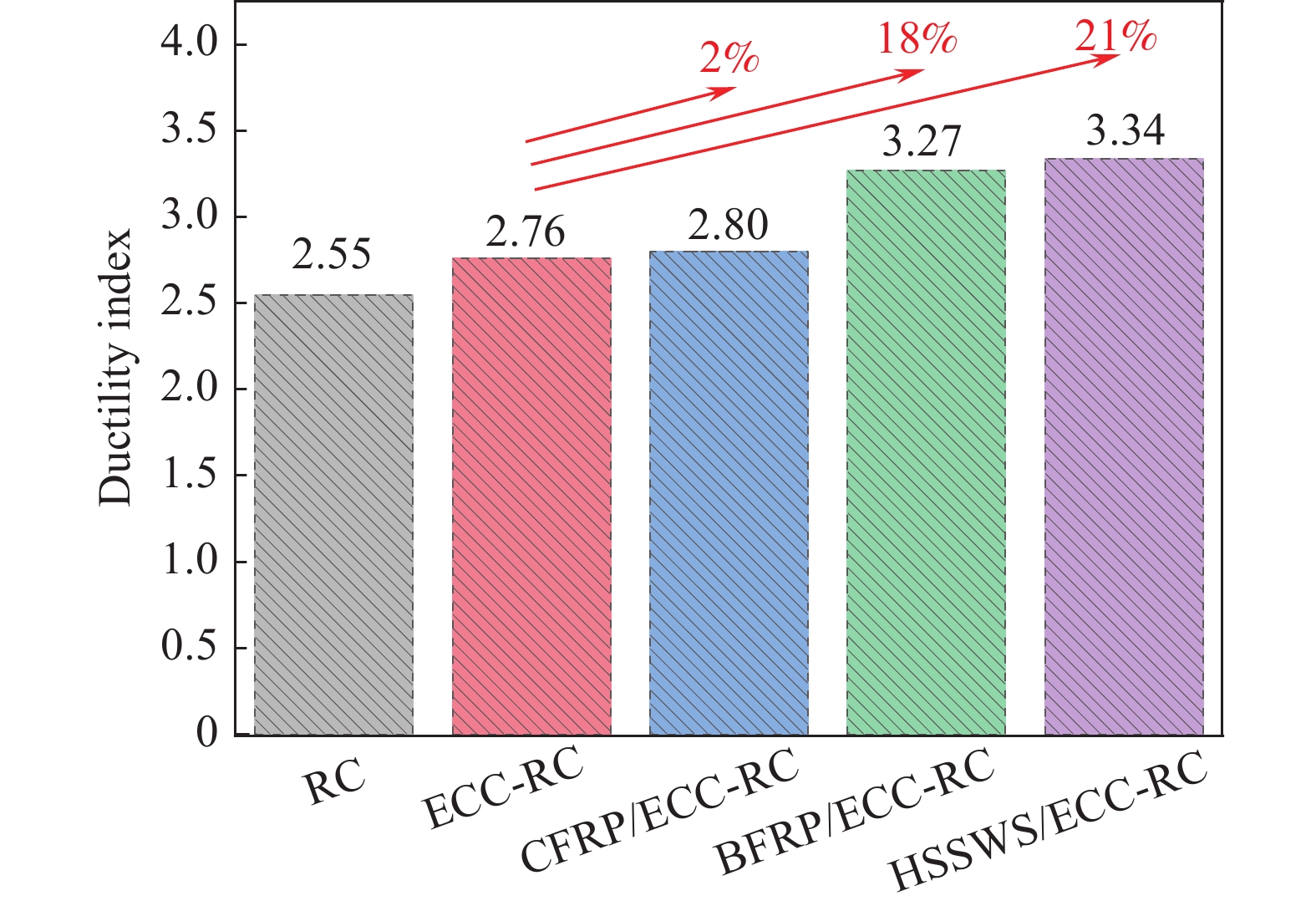
结果从根据四点弯曲加载试验，所有网格增强ECC-RC试验梁破坏过程为受拉钢筋先屈服，随着荷载等级增加，受压区混凝土压碎，随即试验梁破坏；纤维网格增强ECC-RC梁在加载过程中存在纤维网格受力不均导致断裂的现象。根据混凝土跨中截面不同高度处的混凝土应变分析可知，沿截面高度平行于梁中和轴的各纵向混凝土应变与其到中和轴的距离大致成线性分布。相对不含网格增强ECC-RC复合梁，CFRP网格增强ECC-RC梁、BFRP网格增强ECC-RC梁、高强钢绞线网格增强ECC-RC复合梁裂缝数量分别增加了25%、70%和40%，同时网格增加ECC-RC最大裂缝宽度均减小。从极限荷载分析，相对不含网格增强ECC-RC复合梁，CFRP网格增强ECC-RC梁、BFRP网格增强ECC-RC梁、高强钢绞线网格增强ECC-RC复合梁分别提高11.02%、9.45%和33.84%。从极限荷载对应的跨中挠度分析，相对不含网格增强ECC-RC复合梁，CFRP网格增强ECC-RC梁、BFRP网格增强ECC-RC梁、高强钢绞线网格增强ECC-RC复合梁分别提高5.83%、15.12%和23.73%。采用位移延性系数评价试验梁的延性，相对不含网格增强ECC-RC复合梁，CFRP网格增强ECC-RC梁、BFRP网格增强ECC-RC梁、高强钢绞线网格增强ECC-RC复合梁分别提高2%、18%和21%。采用黄华定义的截面刚度，即跨中弯矩与挠度的比值，分析各试验梁刚度。在受力全过程中，CFRP网格增强ECC-RC梁、BFRP网格增强ECC-RC梁、高强钢绞线网格增强ECC-RC复合梁的刚度较对比梁更大。此外，本文依据试验结果和理论分析，建立网格增强ECC-RC复合梁正截面抗弯承载能力计算公式。
结论网格增强ECC-RC复合梁破坏形态为延性破坏，在加载全过程中满足平截面假定，ECC与纤维网格或高强钢绞线网格、ECC层和混凝土黏结性能良好，二者能协调变形，且网格增强ECC层显著提高ECC-RC复合梁的裂缝分散能力和抗裂性。CFRP/BFRP/高强钢绞线网格增强ECC层对ECC-RC复合梁受弯承载力、变形能力、延性及刚度有不同程度的提升，对受弯承载力、刚度提升效果：高强钢绞线网格>CFRP网格>BFRP网格；对变形能力和延性的提高效果：高强钢绞线网格>BFRP网格>CFRP网格。在考虑纤维网格利用率基础上，建立网格增强ECC-RC复合梁正截面抗弯承载能力计算公式，且与试验结果吻合良好。
-
工程水泥基材料(ECC)因其应变硬化和多缝开裂的特点被广泛用于钢筋混凝土梁加固领域，主要加固方式为在混凝土梁底部外粘贴ECC层。但在外荷载作用下加固梁会发生剥离破坏，且承载能力、变形、延性等抗弯性能提升有限。
本文采用纤维网格和钢绞线网格增强ECC层替换受拉区混凝土层的加固方式，分析了CFRP网格、BFRP网格替换层以及钢绞线网格替换层替换层对ECC-RC复合梁承载能力、变形、延性等抗弯性能和抗裂性能的影响。经试验结果分析，纤维网格和钢绞线网格增强ECC-RC复梁中ECC层的网格可以承担部分拉应力，延缓受拉钢筋的屈服，故ECC-RC复合梁的承载能力均提高。其次，RC梁受拉区ECC层中PVA纤维通过桥联作用，在裂缝处可以有效地向未开裂ECC层区域传递拉应力，限制裂缝宽度的扩展，在复合梁受拉区裂缝细密分布，其抗裂性得到显著提高。
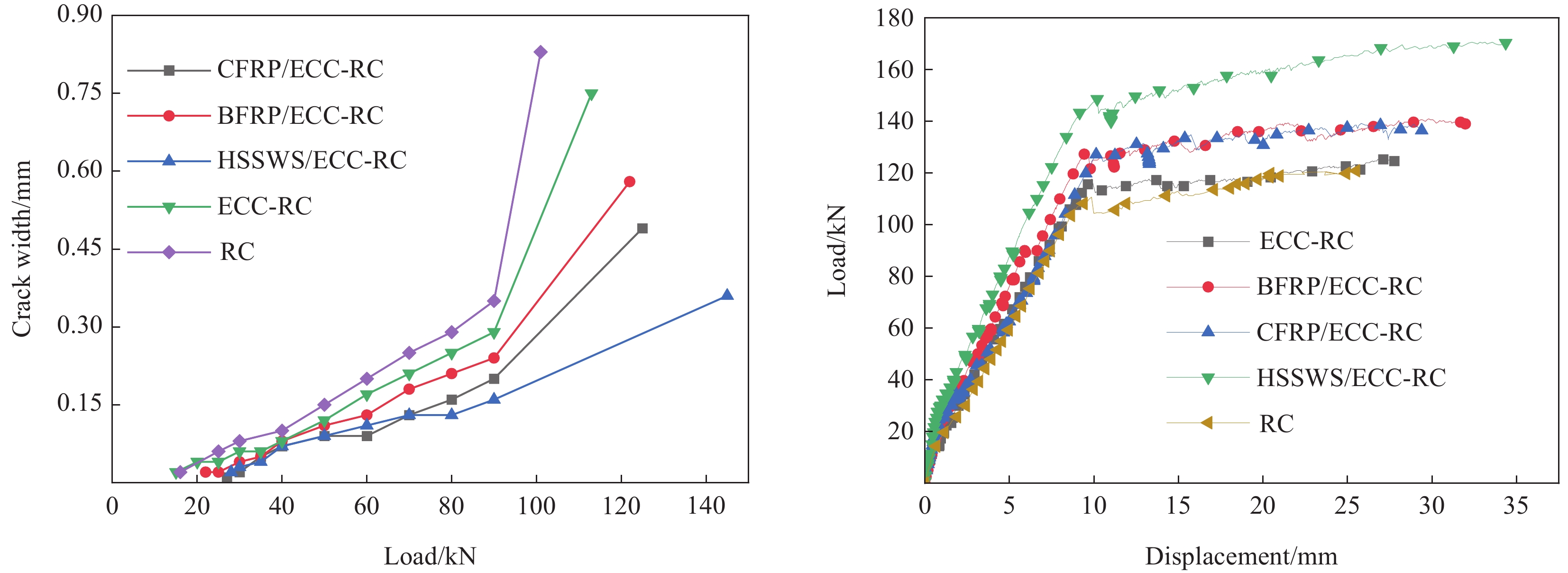
网格增强ECC-RC复合梁荷载-裂缝宽度曲线和荷载挠度曲线
计量
- 文章访问数: 283
- HTML全文浏览量: 104
- PDF下载量: 25
- 被引次数: 7
