Static strength reliability and sensitivity analysis of large composite structures based on surrogate models
-
摘要:
基于代理模型的结构可靠性分析方法目前已有多种代理模型和多种失效概率计算方法,参数灵敏度分析也存在多种灵敏度指标,为探讨大尺寸复合材料结构可靠性分析方法,并研究不同代理模型和计算方法对民机复合材料结构静强度预测结果的差异性,以某型飞机碳纤维复合材料升降舵结构为研究对象,考虑单层板力学性能、厚度、密度和不同部位铺层角度等17种输入变量的不确定性,利用Matlab和Optistruct仿真软件,构建Kriging、PC-Kriging和支持向量回归机(SVR) 3种代理模型,结合蒙特卡洛法(MCS)和Subset两种方法求解结构失效概率,根据代理模型验证误差选取最准确的代理模型计算Morris基本效应筛选指标和Sobol指标,从而获得关键设计参数排序,为民机复合材料结构可靠性设计提供参考。
Abstract:Multiple surrogate models and multiple calculation methods of structural probability of failure are proposed for the structural reliability analysis based on surrogate model. Multiple sensitivity indices are also proposed for the sensitivity analysis of input variables. For the purpose of studying the reliability analysis methods for large composite structures, and studying the differences among different surrogate models and methods to predict the static strength of composite structures of civil aircrafts, a composite elevator of a certain aircraft was taken as an example. The uncertainty of 17 input variables were considered, including mechanical properties, thickness, density and ply angles. Matlab and Optistruct softwares were used to obtain three surrogate models, including Kriging, PC-Kriging and support vector machine for regression (SVR) models. Monte Carlo simulation (MCS) and Subset simulate methods were applied to calculate the structural probability of failure. The best surrogate model can be obtained by comparing validation errors. The critical design parameters can be obtained by the importance ranking based on Morris elementary effects and Sobol indices, which is useful for the design of civil aircraft composite structures.
-
国内外民用飞机的主承力和次承力结构广泛应用碳纤维复合材料(CFRP),期望利用其轻质高强的特性,使得民机结构不仅满足结构强度和刚度要求,更重要的是能够提升结构效率。然而,民机结构高可靠性的要求,使得复合材料结构在进行传统确定性的安全系数设计时易产生裕度冗余[1],导致结构效率的提升效果有限,例如由于材料本身的性能分散性和制造过程中引入的缺陷或误差,在开展静强度分析和校核时,材料许用值和设计许用值通常保守取值,使得裕度结果同样保守。将材料性能和铺层参数等设计变量作为符合一定统计分布的随机变量,开展基于概率的复合材料结构可靠性优化设计已成为近年来的研究热点。
由于大尺寸复合材料结构设计变量繁杂,包括单层材料性能、铺层、几何尺寸、外载荷等多种变量;且其极限状态函数通常为非线性、隐式函数,通常由有限元模型等数值模型和极限状态确定;此外,民机结构失效概率为极小概率,通过直接蒙特卡洛抽样方法所需样本量过大。因此,目前研究人员更多地采用代理模型(或元模型),即通过对较小样本量和响应值进行学习所形成可近似替代原复杂物理模型的代理模型,基于生成的代理模型开展复合材料结构的可靠性和参数灵敏度分析,可简化分析和缩短计算时间[2]。常用的代理模型有Kriging、多项式混沌展开(Polynomial chaos expansions,PCE)、多项式混沌Kriging (Polynomial chaos-Kriging,PC-Kriging)、支持向量机(Support vector machine,SVM)、人工神经网络(Artificial Neutral Network,ANN)、卷积神经网络(convolutional neural network,CNN)[3]等。常用的可靠性分析方法包括直接蒙特卡洛法(Crude Monte Carlo simulation,Crude MCS)、重要性采样(Importance sampling)和子集模拟(Subset simulation)等,常用的灵敏度分析方法包括局部和全局两种,前者通常针对简单模型和线性模型,本文不做讨论,常用的全局灵敏度指标包括Morris基本效应(Morris' elementary effects)、Borgonovo指标、Sobol指标、ANCOVA指标等。Zhang等[4]对金属复合材料混杂连接的单搭接接头构建PCE代理模型,通过留一法交叉验证(Leave-one-out cross-validation,LOOCV)检验模型准确度,并开展Sobol灵敏度分析。Balokas等[5]对单向复合材料横向拉伸刚度和强度构建PCE代理模型,并开展全局灵敏度分析。Reiner等[6]建立神经网络代理模型用于含开孔层合板拉伸载荷下渐进损伤分析和参数估计。阮文斌等[7]对复合材料工字梁结构进行全局灵敏度分析。Sharma等[8]基于PCE建立代理模型,对夹芯复合材料梁结构开展可靠性分析和Sobol灵敏度计算。丁振东等[9]对机身蒙皮复合材料夹层结构的静强度失效模式建立Kriging代理模型,通过检验样本集对代理模型预测结果进行检验,并结合Subset模拟方法计算结构失效概率。可以发现,文献主要集中于针对复合材料板、梁结构的可靠性分析,对于大尺寸复合材料结构的可靠性分析较少。此外,不同代理模型、可靠性分析方法和灵敏度指标的选取,均可能影响最终的分析结果。Zhou等[10]和周春苹等[11]基于Matlab和Nastran对石英纤维复合材料结构构造自适应Kriging模型计算结构静强度失效概率,并与MCS、Kriging、SVM和径向基神经网络(RBFnn)对比,所提模型与MCS结果最为接近,其次为Kriging模型,RBFnn误差最大,并开展局部和全局灵敏度分析。龚煜廉等[12]提出一种主动学习基自适应PC-Kriging模型的可靠度算法,对复合材料机翼结构开展随机固有频率可靠性分析,并与MCS、PCE、SVM、Kriging结果对比,所提出的算法模型调用次数虽有所增加,但计算结果与MCS结果更为接近。然而,多次调用有限元分析软件获得响应值以迭代代理模型的主动学习自适应方法(如前文提到的石英纤维复合材料结构,需额外依次调用有限元模型计算76次[10]),虽在计算精度上有一定优势,但对于大型复杂模型相关的工程应用而言,其计算效率显然不如并行计算,因此本文构建代理模型时,采用并行计算批量得到响应值,通过检验代理模型准确度,视情迭代。由于前述文献显示人工神经网络方法生成代理模型的预测准确度还有待提升,本文暂不考虑该类代理模型。
为探索大尺寸复合材料结构的可靠性分析方法,并研究不同代理模型、可靠性方法和灵敏度指标对预测结果带来的差异性,本研究以某型飞机碳纤维复合材料升降舵结构为研究对象,在考虑复合材料单层材料力学性能、单层厚度、密度和铺层角度等参数不确定性基础上,通过构建Kriging、PC-Kriging和支持向量回归机(SVM for regression,SVR) 3种代理模型,并结合MCS和Subset模拟方法开展可靠性分析,最后选取预测最为准确的代理模型计算Morris基本效应筛选指标和Sobol指标两种灵敏度指标,获得关键设计参数,为民机大尺寸复合材料结构可靠性设计提供参考。
1. 可靠性及灵敏度分析方法
1.1 代理模型介绍
通过直接MCS方法预测失效概率时,需计算大量有限元模型,比如对于失效概率为10−5,为保证计算精度,应至少计算106个有限元模型,导致即使是简单模型,也会占用大量时间,因此直接MCS方法不适用于小概率的可靠性分析。代理模型(或元模型)对计算过程进行简化,仅需批量计算少量有限元模型,通过Kriging、PC-Kriging和SVR等算法生成近似取代原复杂模型的代理模型,吸引了学术界和工程界的广泛兴趣。
1.1.1 Kriging
Kriging[13]也称高斯过程回归,是一种无偏估计模型,适用于非线性分析。Kriging代理模型的一般形式为
\hat{\mathcal{M}}_{\mathrm{K}}(\boldsymbol{x})=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{f}(\boldsymbol{x})+\sigma^2 Z(\boldsymbol{x}, \omega) (1) 式中:{\boldsymbol{x}}为任意模型输入; \hat{\mathcal{M}}_{\mathrm{K}}({\boldsymbol{x}}) 为对于输入的模型输出;第一项 {{\boldsymbol{\beta }}^{\text{T}}}{\boldsymbol{f}}({\boldsymbol{x}}) 为趋势函数,是高斯过程的均值,包括基函数向量 {\boldsymbol{f}}({\boldsymbol{x}}) 和回归系数向量 {\boldsymbol{\beta }} ,一般认为趋势函数的形式对整个模型的拟合精度影响不大,因此采用普通Kriging (Ordinary Kriging),即认为趋势函数为一个未知的常数{\beta _0};第二项 {\sigma ^2}Z({\boldsymbol{x}},\omega ) 包括高斯过程的方差 {\sigma ^2} 和零均值单位方差的稳定高斯过程 Z({\boldsymbol{x}},\omega ) ; \omega 为概率空间,通过相关函数R定义输出空间内两个样本点之间的相关性。
相关函数也称核函数,与x、x'和超参数θ有关,本文采用Matérn核函数[14],通过平滑因子\nu (通常取值为3/2或5/2,本文取5/2)控制学习函数的平滑程度,避免高斯核函数的过平滑情况,是高斯核函数的泛化形式。当\nu =5/2时,其核函数为
\begin{gathered} R\left( {{\boldsymbol{x}},{\boldsymbol{x}}';{\boldsymbol{\theta}} ,v = 5/2} \right) = \\ \quad \left( {1 + \sqrt 5 \frac{{\left| {{\boldsymbol{x}} - {\boldsymbol{x}}'} \right|}}{{\boldsymbol{\theta}} } + \frac{5}{3}{{\left( {\frac{{\left| {{\boldsymbol{x}} - {\boldsymbol{x}}'} \right|}}{{\boldsymbol{\theta}} }} \right)}^2}} \right)\exp \left[ { - \sqrt 5 \frac{{\left| {{\boldsymbol{x}} - {\boldsymbol{x}}'} \right|}}{{\boldsymbol{\theta}} }} \right] \\ \end{gathered} (2) 对于参数估计,采用遗传算法(GA)、混合算法等进行优化,对于初始样本Xexp和真实响应值 {{\boldsymbol{Y}}_{\exp }} = \mathcal{M}\left( {{{\boldsymbol{X}}_{\exp }}} \right) ,计算留一法交叉验证(LOOCV)误差:
{e_{{\text{LOO}}}} = \frac{1}{N}\left[ {\frac{{\displaystyle\sum\limits_{i = 1}^N {{{\left( {\mathcal{M}\left( {{{\boldsymbol{x}}_i}} \right) - {\mu _{\hat Y,( - i)}}\left( {{{\boldsymbol{x}}_i}} \right)} \right)}^2}} }}{{{{\mathrm{Var}}} [{{\boldsymbol{Y}}_{{\text{exp}}}}]}}} \right] (3) 式中: {\mu _{\hat Y,( - i)}}\left( {{{\boldsymbol{x}}_i}} \right) 对应除xi之外的其他样本点预测结果均值;N为数据集的数据量; \mathrm{Var}[\boldsymbol{Y}_{\text{exp}}] 为真实响应值的方差。迭代得到LOOCV最小的代理模型作为最优Kriging模型。
1.1.2 PC-Kriging
Schobi等[15]提出综合PCE和Kriging分别在全局精度和局部精度方面的优势,即将Kriging的趋势函数替换为混沌多项式展开,形成PC-Kriging代理模型,可得到更为准确的近似,其一般形式为
\hat{\mathcal{M}}_{\mathrm{PCK}}(\boldsymbol{x})=\sum_{\alpha \in A} \beta_\alpha \varPsi_\alpha(\boldsymbol{x})+\sigma^2 Z(\boldsymbol{x}, \omega) (4) 式中:第一项\displaystyle\sum_{\alpha \in A} \beta_\alpha \varPsi_\alpha(\boldsymbol{x}) 同样为趋势函数,\alpha 为一组自然数向量,A为多项式集, {\beta _\alpha } 为相关回归系数, \varPsi_\alpha(\boldsymbol{x}) 为一组多元标准正交多项式;第二项即Kriging模型第二项,核函数同样采用Matérn核函数。
对于多项式集和参数估计,采用最小角回归筛选(LARS)获得多项式集排序,再将每个多项式代入PC-Kriging模型中的趋势函数,迭代得到LOOCV最小的代理模型作为最优PC-Kriging模型。
1.1.3 SVR
SVR是SVM[16]对回归分析问题的一种应用,对于非线性问题,其一般形式为
\hat{\mathcal{M}}_{\mathrm{SVR}}(\boldsymbol{x})=\sum_{i=1}^N\left(\alpha_i-\alpha_i^*\right) k\left(\boldsymbol{x}_i, \boldsymbol{x}\right)+b (5) 式中: {\alpha _i} 和 \alpha _i^* 为拉格朗日乘子; k({{\boldsymbol{x}}_i},{\boldsymbol{x}}) 为核函数,本文同样采用Matérn核函数,与式(2)右侧类似,此时\theta 为特征长度尺度。
对于参数估计,与Kriging类似,优化迭代得到LOOCV最小的代理模型作为最优SVR模型。
最后,关于不同代理模型预测准确度对比,可参考LOOCV最小值,也可通过与初始样本集不同的同一组检验样本集Xval和真实响应Yval,得到验证误差
{e_{{\text{val }}}} = \frac{{{N_{{\text{val }}}} - 1}}{{{N_{{\text{val }}}}}}\left[ {\frac{{{{\displaystyle\sum\limits_{i = 1}^{{N_{{\text{val }}}}} {\left( {\mathcal{M}\left( {{\boldsymbol{x}}_{{\text{val }}}^{(i)}} \right) - {\mathcal{M}_{{\text{Metamodel}}}}\left( {{\boldsymbol{x}}_{{\text{val }}}^{(i)}} \right)} \right)} }^2}}}{{\displaystyle\sum\limits_{i = 1}^{{N_{{\text{val }}}}} {{{\left( {\mathcal{M}\left( {{\boldsymbol{x}}_{{\text{val }}}^{(i)}} \right) - {{\hat \mu }_{{Y_{{\text{val }}}}}}} \right)}^2}} }}} \right] (6) 式中, {\hat \mu _{{Y_{{\text{val }}}}}} 为检验样本集响应值的均值。本文采用验证误差 {e_{{\text{val }}}} 对比不同代理模型预测效果。
1.2 可靠性分析方法
结构可靠性分析中,定义极限状态函数g(x)将模型定义域分为安全集和失效集,其中失效集由g(x)≤0给出,则失效概率为
{P_{\text{f}}} = \int_{\{ {\boldsymbol{x}}:\;g({\boldsymbol{x}}) \leqslant 0\} } {{f_{\boldsymbol{X}}}({\boldsymbol{x}}){\text{d}}{\boldsymbol{x}}} (7) 式中, {f_{{X}}} 为输入变量的概率密度函数。工程上难以对该积分直接求解,本节简述包括MCS方法和Subset模拟方法。
1.2.1 MCS
MCS方法通过直接对输入变量进行大量采样,样本量为N,计算相应响应值,从而评估失效概率为
{P_{{\text{f}},{\text{MCS}}}} = \frac{{{N_{{\text{fail}}}}}}{N} (8) 式中, {N_{{\text{fail}}}} 为使得g(x)≤0的样本量。MCS方法简单方便,但计算成本随失效概率降低而大幅增加。
1.2.2 Subset模拟
Subset模拟方法[17]继承了MCS方法解决高维度、非线性问题的优势,采用马尔科夫链蒙特卡罗方法 MCMC (Markov chain Monte Carlo)高效生成中间失效域样本以估计中间失效概率,由一系列中间失效概率的乘积计算得到失效概率,尤其对于小失效概率问题,可减少总样本量,提高计算效率。
引入一系列临界值{b_1} > {b_2} > \cdots > {b_m} = 0,构成中间失效事件{F_k} = \{ {\boldsymbol{x}}:g({\boldsymbol{x}}) \leqslant {b_k}\} (k = 1,2, \cdots ,m),有{F_1} \supset {F_2} \supset \cdots {F_m} = F,且{F_k} = \bigcap\limits_{i = 1}^k {{F_i}} ,则采用Subset模拟方法的失效概率可写为[17]
{P_{{\text{f}},{\text{Subset}}}} = \prod\limits_{i = 1}^m {{P_i}} (9) 式中:{P_1} = P({F_1});{P_i} = P({F_i}|{F_{i - 1}})(i = 2, \cdots ,m)。
1.3 灵敏度分析方法
开展灵敏度分析主要是为了评估模型输入变量X对输出响应Y的影响程度,从而识别出对模型输出最为重要的关键变量。目前已有多种全局灵敏度分析方法,即考虑整个不确定性范围的输入变量对输出响应统计特征的影响程度,包括Morris基本效应筛选和Sobol指标等。
1.3.1 Morris基本效应筛选
Morris方法[18] 计算量小,通过对输入变量进行排序来进行定性度量,无法量化其对输出的影响。对于包含M个变量的模型,随机生成多组初始变量向量,分别计算第i个输入变量的基本效应指数
d_i^*({\boldsymbol{x}}) = \left| {\frac{{\mathcal{M}({x_1}, \cdots ,{x_i} + \Delta , \cdots ,{x_M}) - \mathcal{M}({\boldsymbol{x}})}}{\Delta }} \right| (10) 式中,\Delta 为设定的变化量。接着得到基本效应指数的均值和标准差,其中均值用于衡量该变量对模型输出的重要性,均值越大,该变量越重要;标准差用于衡量该变量对模型的非线性和变量间的相互作用,该值越大,则该变量的非线性或与其他变量间的相互作用越强。
1.3.2 Sobol指标
Sobol方法[19-20]基本思想是方差分解,是一种基于方差的蒙特卡洛法,通过将模型分解为单输入变量以及多输入变量相互组合构成的函数,并计算单或多输入变量的方差对总输出方差的影响得到其对应的灵敏度指标。一般考虑一阶指数和总效应指数来衡量输入变量的重要程度:一阶指数是衡量单个变量对输出方差贡献的指标,一阶指数越大,则意味着该参数对输出的贡献越大,其变化会显著影响到输出的波动性;总效应指数是衡量单变量以及该变量与其他变量的相互作用对输出方差贡献的指标,总效应指数与一阶指数之间差距越大,表示该变量与其他变量的相互作用对输出的贡献越大,其变化会显著影响到输出的波动性,可识别出参数间的非线性关系和系统中的重要交互作用。输入变量Xi的总效应指数为
\begin{gathered} S_i^{\text{T}} = \sum\limits_{i \subset \{ {i_1}, \cdots ,{i_s}\} } {{S_{{i_1}, \cdots ,{i_s}}}}= 1 - {S_{ \sim i}}, \\ \quad 1 \leqslant {i_1} < \cdots < {i_s} \leqslant M;\;s = 1, \cdots ,M \\ \end{gathered} (11) 式中:M为输入变量数;Si为变量Xi的一阶指数, {S_{1,2, \cdots ,k}} 为k阶指数,表示k个变量之间的交叉影响; \sim i 表示排除i。
2. 复合材料升降舵结构静强度可靠性分析模型
2.1 有限元模型和参数化建模
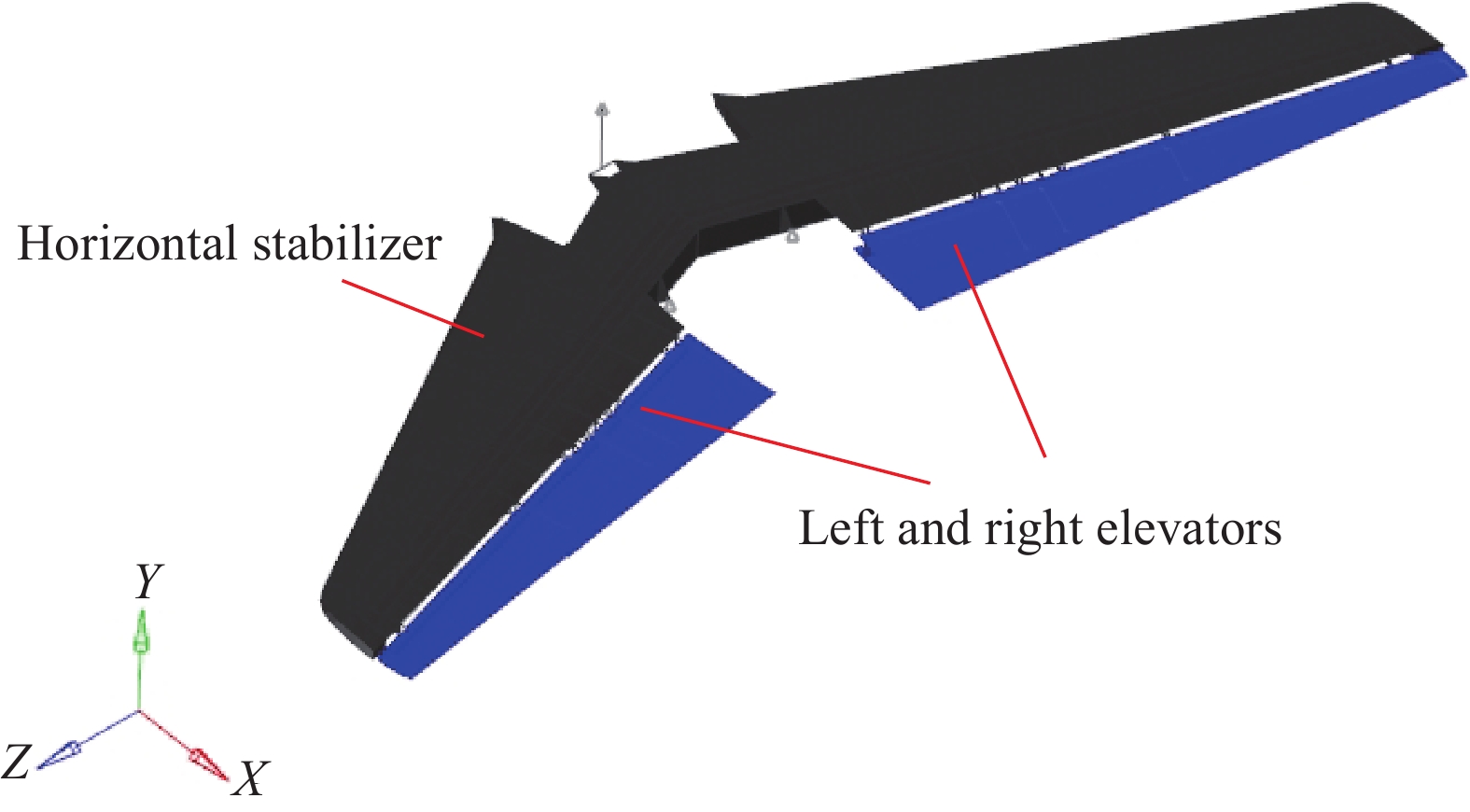
本文计算采用的某型飞机碳纤维/环氧树脂复合材料升降舵结构如图1所示(下方蓝色部分),对平尾前操纵接头、平尾后铰链接头三点静定约束,在下壁板表面施加集中力载荷,左右升降舵结构和载荷完全对称。可靠性分析中考虑输入变量包括材料弹性模量和强度性能、密度、单层厚度和铺层角,共17个变量,假设满足正态分布,变量名称、均值及标准差见表1。
表 1 复合材料升降舵结构随机输入变量正态分布Table 1. Normal distribution of random input variables of the composite elevator structureVariable Mean Standard deviation Description E11/GPa 60 6.0 Elastic modulus in 11 direction E22/GPa 54 5.4 Elastic modulus in 22 direction G12/GPa 3.7 0.37 Elastic modulus in 12 direction G13/GPa 3.0 0.30 Elastic modulus in 13 direction G23/GPa 3.0 0.30 Elastic modulus in 23 direction ρ/(kg·m−3) 1440 144.0 Density Xt/MPa 830 83.0 Longitudinal tensile strength Xc/MPa 650 65.0 Longitudinal compressive strength Yt/MPa 250 25.0 Transverse tensile strength Yc/MPa 230 23.0 Transverse compressive strength S12/MPa 100 10.0 In-plane shear strength t/mm 0.216 0.0216 Thickness of a lamina α1/(°) 0 4.5 (0°, 90°) ply angle for skin panel α2/(°) 45 4.5 (±45°) ply angle for skin panel α3/(°) 0 4.5 (0°, 90°) ply angle for spar α4/(°) 45 4.5 (±45°) ply angle for spar α5/(°) 45 4.5 (±45°) ply angle for ribs 2.2 失效准则
采用经典的Tsai-Wu失效准则和首层失效假设研究升降舵复合材料面板的静强度可靠性。对于平面应力状态,Tsai-Wu失效准则表示为
\begin{split} &{F_1}{\sigma _1} + {F_2}{\sigma _2} + 2{F_{12}}{\sigma _1}{\sigma _2} + {F_{11}}\sigma _1^2 +\\ &\quad{F_{22}}\sigma _2^2 + {F_6}{\tau _{12}} + {F_{66}}\tau _{12}^2 = 1 \end{split} (12) 式中:F_1={1}/{X_{\text{t}}}-{1}/{X_{\text{c}}};\; F_2={1}/{Y_{\text{t}}}-{1}/{Y_{\text{c}}} ;F_{12}= -{1}/{2}\sqrt{{1}/{X_{\text{t}}X_{\text{c}}Y_{\text{t}}Y_{\text{c}}}}, F_{11} = {1}/{X_{\text{t}}X_{\text{c}}};F_{22} = {1}/{Y_{\text{t}}Y_{\text{c}}};F_6 = \text{0} ;F_{66}={1}/{S_{\text{12}}^{\text{2}}} ; \sigma_1 和 \sigma_2 分别为1方向和2方向拉应力; \tau_{12} 为12方向切应力。
采用Tsai-Wu强度比(RS):
{R_{\text{S}}} = \frac{{ - {C_1} + \sqrt {\left| {C_1^2 + 4{C_2}} \right|} }}{{2{C_2}}} (13) 式中:C_1 = F_1\sigma_1 + F_2\sigma_2 + F_6\tau_{12} ;C_2 = F_{11}\sigma_1^2+F_{22}\sigma_2^2+ F_{66}\tau_{12}^2+2F_{12}\sigma_1\sigma_2 。
作为失效判据,当RS>1时,结构安全,当RS≤1时,结构失效。
2.3 可靠性和灵敏度分析流程
基于代理模型的结构可靠性及灵敏度分析流程图如图2所示,本文采用的计算软件为Matlab和Optistruct。分析流程包括:
(1)梳理和定义随机变量的统计特征,见2.1节;
(2)采用超立方抽样方法对输入变量进行采样,获取试验样本集和验证样本集,批量生成有限元计算文件,调用Optistruct进行批量计算,获取对应于每组样本的最小强度比({R_{\text{S}}}_{{\text{min}}} )响应值;
(3)定义极限状态函数g(x) = {R_{\text{S}}}_{{\text{min}}} - 1 = 0,采用试验样本集和对应响应值分别训练代理模型:Kriging、PC-Kriging和SVR代理模型,分别迭代计算LOOCV误差,若3种模型之间 {e_{{\text{LOO}}}} 最小值仍不小于0.05,则扩大试验样本集,重复第(2)步,直到 {e_{{\text{LOO}}}} 最小值小于0.05,同时基于相同的验证样本集获得验证误差 {e_{{\text{val }}}} ;
(4)对比3种模型的验证误差 {e_{{\text{val }}}} ,选择最小值对应的代理模型进行失效概率和灵敏度求解;
(5)采用MCS和Subset等方法计算失效概率,采用Morris基本效应筛选法进行变量重要性定性排序,采用Sobol指标进行定量灵敏度分析,最后获得关键变量。
3. 复合材料升降舵结构静强度可靠性及灵敏度分析结果
3.1 复合材料升降舵结构静强度确定性分析结果
本工况为对称下弯工况,进行确定性分析时,输入参数取值为表1各变量均值,得到全局坐标系下,左升降舵Y向位移云图如图3所示,复合材料板强度比(RS)如图4所示,最小强度比为1.657,即安全裕度为0.657。
3.2 复合材料升降舵结构静强度可靠性分析结果
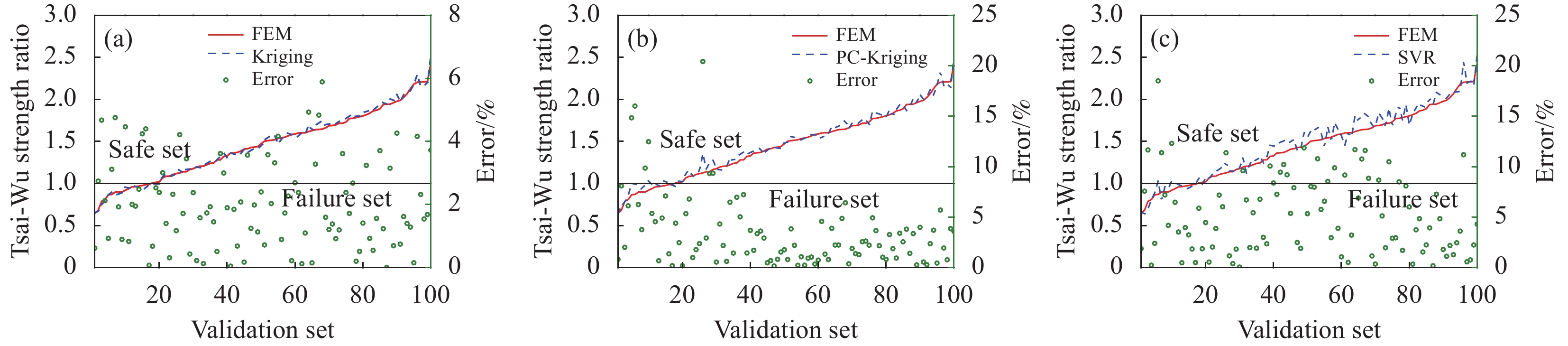
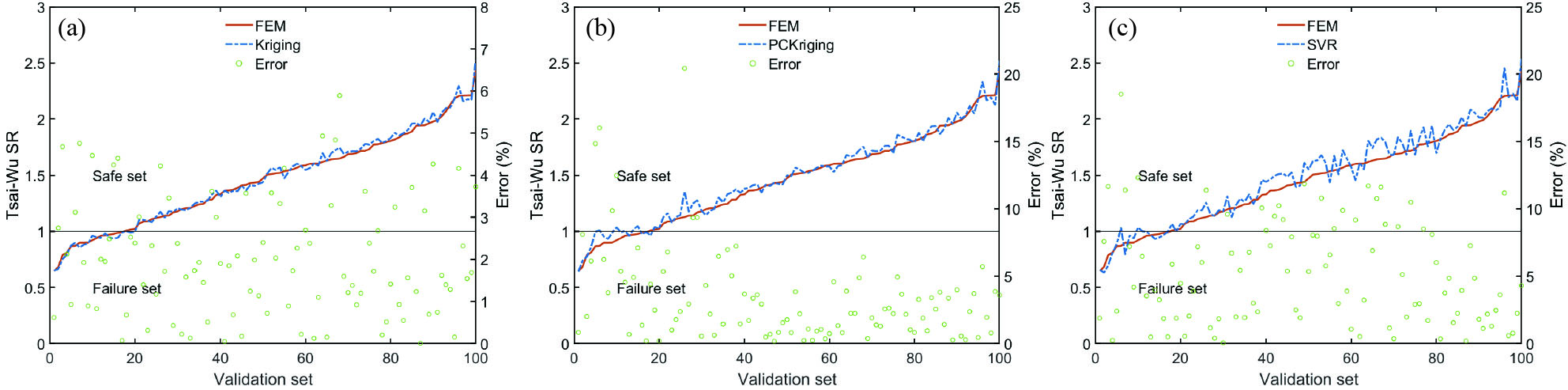
表2为复合材料升降舵结构静强度可靠性分析所用3种代理模型的误差及失效概率计算结果对比,从验证误差 {e_{{\text{val }}}} 来看,Kriging模型的验证误差低于0.01,3种代理模型的验证误差由低到高排序为:Kriging、PC-Kriging和SVR。将验证样本集的100组样本按最小强度比有限元计算结果从小到大排序,形成折线图为图5中的实线,每组样本对应的代理模型预测结果为图5中的虚线,每组样本有限元结果和代理模型结果的相对误差为图5中的圆圈,RS =1为安全域和失效域之间的临界线,可以看出Kriging代理模型的相对误差99%在5%以内。因此,在本分析中,Kriging代理模型的预测最准确。虽然PC-Kriging代理模型在提出之初是为了在Kriging模型局部精度优势基础上结合PCE在全局精度上的优势,但对于不同的复杂模型,该代理模型可能并不一定优于Kriging模型,因此也有学者[21]提出基于自适应集成学习代理模型(Kriging模型与PC-Kriging模型)的结构可靠性分析方法,综合这两种模型的优势进行可靠性分析,准确性优于单一代理模型分析。
表 2 基于不同代理模型的模型误差和失效概率结果对比Table 2. Comparison of errors and failure probability results based on different surrogate modelsMetamodel {e_{{\text{LOO}}}} {e_{{\text{val }}}} P_{\text{f}}^{{{\mathrm{MCS}}} }(Evaluations) P_{\text{f}}^{{\mathrm{Subset}}}(Evaluations) Kriging 4.56×10−2 8.00×10−3 7.02×10−4 (106) 7.66×10−4 ( 25900 )PC-Kriging 3.61×10−2 2.04×10−2 6.78×10−4 (106) 5.27×10−4 ( 25900 )SVR 1.22×10−1 5.08×10−2 1.60×10−4 (106) 1.18×10−4 ( 25900 )Notes: {e_{{\text{LOO}}}} and {e_{{\text{val }}}} are leave-one-out cross-validation error and validation error, respectively; P_{\text{f}}^{{{\mathrm{MCS}}} } and P_{\text{f}}^{{\mathrm{Subset}}} are failure probability based on MCS and Subset methods, respectively. 表2后两列为基于不同代理模型的失效概率计算结果,其中采用MCS方法需要调用模型次数较多,失效概率收敛性见图6,可以看出,5万次计算后失效概率基本收敛,对于Kriging代理模型,10万次计算结果为7.02×10−4;采用Subset方法可大幅降低调用模型次数(
25900 次),计算结果与MCS方法接近,说明了Subset方法在小失效概率问题上的优势。![]() 图 6 基于不同代理模型的复合材料升降舵结构失效概率收敛性:(a) Kriging;(b) PC-Kriging;(c) SVR (失效概率计算方法均为MCS)Figure 6. Convergence of failure probability of the composite elevator structure based on different metamodels: (a) Kriging; (b) PC-Kriging; (c) SVR (MCS has been applied for the evaluation of failure probability)CI—Confidence interval; N—Numbers of calculations
图 6 基于不同代理模型的复合材料升降舵结构失效概率收敛性:(a) Kriging;(b) PC-Kriging;(c) SVR (失效概率计算方法均为MCS)Figure 6. Convergence of failure probability of the composite elevator structure based on different metamodels: (a) Kriging; (b) PC-Kriging; (c) SVR (MCS has been applied for the evaluation of failure probability)CI—Confidence interval; N—Numbers of calculations3.3 复合材料升降舵结构灵敏度分析结果
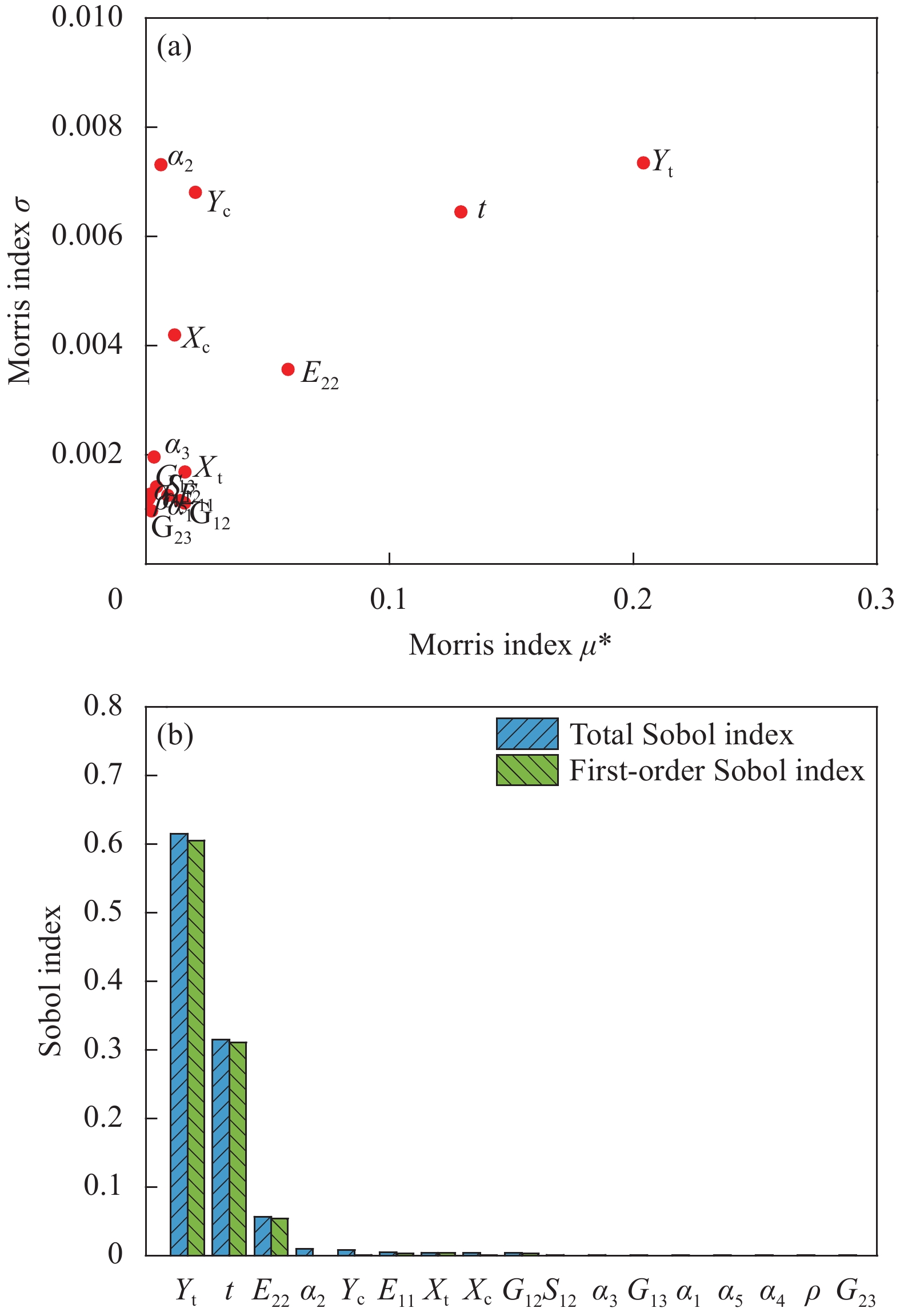
图7(a)为各输入随机变量的Morris基本效应指数的均值μ*和标准差σ,可筛选出均值较大的随机变量排序(从大到小)为横向拉伸强度Yt、单层厚度t和横向弹性模量E22,标准差较大的随机变量排序(从大到小)为Yt、壁板面板(±45°)铺层角α2、横向压缩强度Yc、t、纵向压缩强度Xc和E22。图7(b)为各输入随机变量的Sobol总效应指数和一阶指数,按总效应指数排序,可以看出Yt和t的总效应指数远大于其他变量,E22排第三位,以上三者的一阶指数占总效应指数百分比均超过94%,说明这三者对输出响应影响最大,且均以线性影响为主,或与其他变量的相互关系较弱。综合两种灵敏度分析,按Morris基本效应指数的均值μ*排序,并同时列出Sobol一阶指数排序对比如图8所示,可以看出二者对前三位排序一致,对最小强度比输出响应影响最大的为Yt,其次为t和E22,进行优化设计时应重点关注这3个随机变量。此外,对于输出响应结果稳定性而言,也应重点关注Yt和t的分散性,还应关注α2和横向压缩强度Yc的分散性。
4. 结 论
(1)以民机复合材料升降舵结构为例,建立复合材料结构可靠性分析流程,包括结合参数化、自动化有限元分析前/后处理开展结构有限元分析,生成代理模型和失效概率计算等,适用于大尺寸复合材料结构的可靠性分析。
(2)对于代理模型预测准确性评估,可采用留一法交叉验证(LOOCV)误差和验证误差两种方式,其中后者适用于不同代理模型之间的对比。通过对比Kriging、PC-Kriging和支持向量回归机(SVR) 3种代理模型对于同一验证样本集的验证误差,可得到适用于特定问题的最优代理模型。在本算例中,Kriging代理模型的验证误差为0.008,相对误差99%在5%以内,表明了其预测准确性。
(3)对于可靠性分析方法,针对小失效概率问题,Subset方法相比于蒙特卡洛法(MCS)方法可减少失效概率计算时模型调用次数,减少计算工作量。
(4)综合Morris基本效应筛选和Sobol总/一阶效应指数进行全局灵敏度分析,可筛选对于输出响应及结果稳定性影响最大的关键输入随机变量,用于指导优化设计和过程控制等。
-
图 6 基于不同代理模型的复合材料升降舵结构失效概率收敛性:(a) Kriging;(b) PC-Kriging;(c) SVR (失效概率计算方法均为MCS)
Figure 6. Convergence of failure probability of the composite elevator structure based on different metamodels: (a) Kriging; (b) PC-Kriging; (c) SVR (MCS has been applied for the evaluation of failure probability)
CI—Confidence interval; N—Numbers of calculations
表 1 复合材料升降舵结构随机输入变量正态分布
Table 1 Normal distribution of random input variables of the composite elevator structure
Variable Mean Standard deviation Description E11/GPa 60 6.0 Elastic modulus in 11 direction E22/GPa 54 5.4 Elastic modulus in 22 direction G12/GPa 3.7 0.37 Elastic modulus in 12 direction G13/GPa 3.0 0.30 Elastic modulus in 13 direction G23/GPa 3.0 0.30 Elastic modulus in 23 direction ρ/(kg·m−3) 1440 144.0 Density Xt/MPa 830 83.0 Longitudinal tensile strength Xc/MPa 650 65.0 Longitudinal compressive strength Yt/MPa 250 25.0 Transverse tensile strength Yc/MPa 230 23.0 Transverse compressive strength S12/MPa 100 10.0 In-plane shear strength t/mm 0.216 0.0216 Thickness of a lamina α1/(°) 0 4.5 (0°, 90°) ply angle for skin panel α2/(°) 45 4.5 (±45°) ply angle for skin panel α3/(°) 0 4.5 (0°, 90°) ply angle for spar α4/(°) 45 4.5 (±45°) ply angle for spar α5/(°) 45 4.5 (±45°) ply angle for ribs 表 2 基于不同代理模型的模型误差和失效概率结果对比
Table 2 Comparison of errors and failure probability results based on different surrogate models
Metamodel {e_{{\text{LOO}}}} {e_{{\text{val }}}} P_{\text{f}}^{{{\mathrm{MCS}}} }(Evaluations) P_{\text{f}}^{{\mathrm{Subset}}}(Evaluations) Kriging 4.56×10−2 8.00×10−3 7.02×10−4 (106) 7.66×10−4 ( 25900 )PC-Kriging 3.61×10−2 2.04×10−2 6.78×10−4 (106) 5.27×10−4 ( 25900 )SVR 1.22×10−1 5.08×10−2 1.60×10−4 (106) 1.18×10−4 ( 25900 )Notes: {e_{{\text{LOO}}}} and {e_{{\text{val }}}} are leave-one-out cross-validation error and validation error, respectively; P_{\text{f}}^{{{\mathrm{MCS}}} } and P_{\text{f}}^{{\mathrm{Subset}}} are failure probability based on MCS and Subset methods, respectively. -
[1] 李志远, 原崇新. 可靠性分析在航空复合材料结构上的应用及展望[J]. 民用飞机设计与研究, 2023(2): 145-152. LI Zhiyuan, YUAN Chongxin. Application and future of probabilistic analysis on aeronautical composite structures[J]. Civil Aircraft Design and Research, 2023(2): 145-152(in Chinese).
[2] MOUSTAPHA M, SUDRET B. Surrogate-assisted reliability-based design optimization: A survey and a unified modular framework[J]. Structural and Multidisciplinary Optimization, 2019, 60(5): 2157-2176. DOI: 10.1007/s00158-019-02290-y
[3] 闫海, 邓忠民. 基于深度学习的短纤维增强聚氨酯复合材料性能预测[J]. 复合材料学报, 2019, 36(6): 1413-1420. YAN Hai, DENG Zhongmin. Prediction of properties of short fiber reinforced urethane polymer composites based on deep learning[J]. Acta Materiae Compositae Sinica, 2019, 36(6): 1413-1420(in Chinese).
[4] ZHANG H Y, ZHANG L, XU C, et al. Global sensitivity analysis of mechanical properties in hybrid single lap aluminum-CFRP (plain woven) joints based on uncertainty quantification[J]. Composite Structures, 2022, 280: 114841. DOI: 10.1016/j.compstruct.2021.114841
[5] BALOKAS G, KRIEGESMANN B, ROLFES R. Data-driven inverse uncertainty quantification in the transverse tensile response of carbon fiber reinforced composites[J]. Composites Science and Technology, 2021, 211: 108845. DOI: 10.1016/j.compscitech.2021.108845
[6] REINER J, LINDEN N, VAZIRI R, et al. Bayesian parameter estimation for the inclusion of uncertainty in progressive damage simulation of composites[J]. Composite Structures, 2023, 321: 117257.
[7] 阮文斌, 吕震宙, 安军, 等. 不确定条件下复合材料结构的全局灵敏度分析[J]. 复合材料学报, 2014, 31(3): 699-706. RUAN Wenbin, LYU Zhenzhou, AN Jun, et al. Global sensitivity analysis for composite structures with uncertainties[J]. Acta Materiae Compositae Sinica, 2014, 31(3): 699-706(in Chinese).
[8] SHARMA H, GANGULI R. Optimization of a higher-order sandwich composite beam under uncertainties[J]. Composite Structures, 2021, 269: 114003.
[9] 丁振东, 李洪双, 管晓乐. 基于代理模型的机身蒙皮复合材料夹层结构可靠性分析[J]. 西北工业大学学报, 2022, 40(2): 360-368. DOI: 10.3969/j.issn.1000-2758.2022.02.016 DING Zhendong, LI Hongshuang, GUAN Xiaole. Reliability analysis of composite sandwich structure for fuselage skin based on surrogate model[J]. Journal of Northwestern Polytechnical University, 2022, 40(2): 360-368(in Chinese). DOI: 10.3969/j.issn.1000-2758.2022.02.016
[10] ZHOU C C, LI C, ZHANG H L, et al. Reliability and sensitivity analysis of composite structures by an adaptive Kriging based approach[J]. Composite Structures, 2021, 278: 114682. DOI: 10.1016/j.compstruct.2021.114682
[11] 周春苹, 刘付超, 周长聪, 等. 石英纤维/环氧树脂复合材料结构静强度的可靠度计算及全局灵敏度分析[J]. 复合材料学报, 2020, 37(7): 1611-1618. ZHOU Chunping, LIU Fuchao, ZHOU Changcong, et al. Reliability and global sensitivity analysis for static strength of quartz/epoxy composite[J]. Acta Materiae Compositae Sinica, 2020, 37(7): 1611-1618(in Chinese).
[12] 龚煜廉, 张建国, 吴志刚, 等. 主动学习基自适应PC-Kriging模型的复合材料结构可靠度算法[J]. 航空学报, 2024, 45(8): 181-191. GONG Yulian, ZHANG Jianguo, WU Zhigang, et al. Reliability algorithm of composite structure based on active learning basis-adaptive PC-Kriging model[J]. Acta Aeronautica et Astronautica Sinica, 2024, 45(8): 181-191(in Chinese).
[13] KRIGE D G. A statistical approach to some mine valuation and allied problems on the Witwatersrand [D]. Johannesburg: University of the Witwatersrand, 1951.
[14] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge: MIT Press, 2006: 82-89.
[15] SCHOBI R, SUDRET B, WIART J. Polynomial-chaos-based Kriging[J]. International Journal for Uncertainty Quantification, 2015, 5(2): 171-193. DOI: 10.1615/Int.J.UncertaintyQuantification.2015012467
[16] VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer, 1995: 133-140.
[17] AU S K, BECK J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001, 16(4): 263-277. DOI: 10.1016/S0266-8920(01)00019-4
[18] MORRIS M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991, 33(2): 161-174. DOI: 10.1080/00401706.1991.10484804
[19] MARELLI S, SUDRET B. UQLab user manual—Polynomial chaos expansions[Z]. Zurich, Switzerland: ETH Zurich, 2021.
[20] SOBOL' I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1-3): 271-280. DOI: 10.1016/S0378-4754(00)00270-6
[21] 李宁, 潘慧雨, 李忠献. 一种基于自适应集成学习代理模型的结构可靠性分析方法[J]. 工程力学, 2023, 40(3): 27-35. DOI: 10.6052/j.issn.1000-4750.2021.09.0708 LI Ning, PAN Huiyu, LI Zhongxian. Structural reliability analysis method based on adaptive ensemble learning-surrogate model[J]. Engineering Mechanics, 2023, 40(3): 27-35(in Chinese). DOI: 10.6052/j.issn.1000-4750.2021.09.0708
-
其他相关附件
-
目的
基于代理模型的结构可靠性分析方法目前已有多种代理模型和多种失效概率计算方法,参数灵敏度分析也存在多种灵敏度指标,为探讨大尺寸复合材料结构可靠性分析方法,并研究不同代理模型和计算方法对民机复合材料结构静强度预测结果的差异性,以某型飞机碳纤维复合材料升降舵结构为研究对象,探索大尺寸复合材料结构可靠性分析流程和方法。
方法建立大尺寸复合材料结构可靠性分析流程,包括定义随机变量;获取试验及验证样本集、采用有限元批量获得响应值;定义极限状态函数,采用试验样本集和对应响应值训练代理模型,迭代计算留1法交叉验证误差(LOOCV),若其大于设定的阈值,则扩大试验样本集,重新训练模型直到该值满足要求;基于验证样本集获得验证误差,对比选择最小值对应的代理模型;最后计算失效概率,开展灵敏度计算以获得关键变量。以某型飞机碳纤维复合材料升降舵结构为研究对象,考虑单层板力学性能、厚度、密度和铺层角等17种输入变量的不确定性。利用Matlab和Optistruct仿真软件,分别构建Kriging、PCKriging和支持向量回归机(SVR)三种代理模型,结合蒙特卡洛模拟(MCS)和子集模拟法两种方法求解结构失效概率,根据代理模型验证误差选取最准确的代理模型计算Morris基本效应筛选指标和Sobol指标,从而获得关键设计参数排序。
结果三种代理模型的验证误差由低到高排序为:Kriging、PCKriging和SVR,对比验证样本集有限元结果和代理模型预测结果,可以看出Kriging模型的相对误差99%在5%以内。因此,在本分析中,Kriging模型预测最准确。对于失效概率计算,采用MCS方法需要调用模型次数较多,5万次计算后失效概率基本收敛;采用子集模拟法可大幅降低调用模型次数,计算结果与MCS方法接近,说明子集模拟法在小失效概率问题上的优势。对于灵敏度分析,从各输入随机变量的Morris基本效应指数的均值和标准差来看,均值较大的随机变量排序(从大到小)为横向拉伸强度、单层厚度和横向拉伸模量,标准差较大的随机变量排序(从大到小)为横向拉伸强度、壁板面板(±45°)铺层角、横向压缩强度、单层厚度、纵向压缩强度和横向拉伸模量。从各输入随机变量的Sobol总效应指数和一阶指数来看,横向拉伸强度和单层厚度的总效应指数远大于其他变量,横向拉伸模量排第三位,以上三者的一阶指数占总效应指数百分比均超过94%,说明这三者对输出响应影响最大,且均以线性影响为主,或与其他变量的相互关系较弱。综合两种灵敏度分析,可以看出二者对前三位排序一致,对最小强度比输出响应影响最大的为横向拉伸强度,其次为单层厚度和横向弹性模量,进行优化设计时应重点关注这三个随机变量。此外,对于输出响应结果稳定性而言,也应重点关注横向拉伸强度和单层厚度的分散性,还应关注壁板面板(±45°)铺层角和横向压缩强度的分散性。
结论建立的分析流程适用于大尺寸复合材料结构的可靠性分析。对于代理模型预测准确性评估,可采用LOOCV和验证误差两种方式,其中后者适用于不同代理模型之间对比。通过对比Kriging、PCKriging和SVR三种代理模型对于同一验证样本集的验证误差,可得到适用于特定问题的最优代理模型。对于可靠性分析方法,针对小失效概率问题,子集模拟法相比于MCS方法可减少失效概率计算时模型调用次数,减少计算工作量。综合Morris基本效应筛选和Sobol总/一阶效应指数进行全局灵敏度分析,可筛选对于输出响应及结果稳定性影响最大的关键输入随机变量,用于指导优化设计和过程控制等,为民机复合材料结构可靠性设计提供参考。
-
复合材料结构力学性能和几何尺寸等不确定性,为结构设计与航空应用带来挑战。代理模型在解决多变量、隐式极限状态函数上的优势,吸引了航空复合材料结构设计领域越来越多的关注和研究,但目前研究较为分散,仍处于初步阶段,缺少基于不同代理模型的结构可靠性分析之间的对比。本文针对大尺寸复合材料结构,以某型飞机碳纤维复合材料升降舵结构为研究对象,考虑单层板力学性能、厚度、密度和不同部位铺层角度等17种输入变量的不确定性,利用Matlab和Optistruct仿真软件,首先构建目前主流的Kriging、PCKriging和支持向量回归机(SVR)三种代理模型,对比三种代理模型的预测误差。同时,对比MCS和Subset两种求解结构失效概率的方法,根据代理模型验证误差选取最准确的代理模型,综合Morris基本效应筛选和Sobol总/一阶效应指数进行全局灵敏度分析,筛选对于输出响应及结果稳定性影响最大的关键输入随机变量,为民机复合材料结构可靠性设计提供参考。
基于不同代理模型的复合材料升降舵结构最小Tsai-Wu强度比预测结果与有限元计算结果对比:(a) Kriging、(b) PCKriging和(c) SVR




 下载:
下载: