Effect of SMA laying configuration in GFRP patch on thermal vibration characteristics of repair laminate
-
摘要: 在复合材料中加入形状记忆合金(SMA)制成的纤维增强材料具有高强度、高阻尼与良好的自修复性等优点，可明显提高修理结构刚度及抗剥离性。为了探究热环境下玻璃纤维补片内嵌不同铺设数量与方式的SMA修理板的振动特性，基于Liang-Rogers的SMA本构模型编制用户自定义材料子程序(UMAT)，实现有限元精确求解。对比传统修理板与本文制备的SMA修理板的振型、固有频率及阻尼比变化情况，探究不同温度下SMA铺设构型对双面贴补修理玻璃纤维层合板振动特性的影响。实验与仿真结果表明：相较于单线型(D)与垂直交叉型(C)，斜铺交叉型(X) SMA修理板前三阶振型更接近传统修理板(Q0)，且振型与嵌入的SMA数量无关。SMA相变时，内嵌SMA使修理板前二阶固有频率上升且上升率与SMA数量呈正相关，与SMA铺设方式关系如下：C型>D型>X型。内嵌SMA使修理板耗能能力及阻尼性优于Q0板，与SMA数量呈正相关，与SMA铺设方式关系如下：X型>C型>D型。本文研究的铺设构型中，X24型修理效果最优，其一、二阶固有频率最高可恢复至Q0板的108.47%与112.26%，阻尼比相较于Q0板增大了5.19倍。该工作可以为现有传统复合材料修理向智能复合材料修理技术转变提供参考。
-
关键词:
- SMA /
- 编织玻璃纤维复合材料 /
- 振动特性 /
- 双面贴补修理 /
- 智能材料
Abstract: Fiber reinforced materials made by adding shape memory alloy (SMA) to composite materials have the advantages of high strength, high damping and good self-repair, which can significantly improve the rigidity and peel resistance of repair structures. In order to explore the vibration characteristics of SMA repair plates with different laying quantities and methods embedded in glass fiber patches under thermal environment, a user-defined material subprogram (UMAT) was developed based on Liang-Rogers' SMA constitutive model to achieve accurate finite element solving. The changes of mode shape, natural frequency and damping ratio of traditional repair plate and SMA repair plate prepared in this paper were compared, and the influence of SMA laying configuration on the vibration characteristics of double-sided patch repair fiberglass laminate was explored at different temperatures. Experimental and simulation results show that compared with single-line (D) and vertical cross (C), the first three-order mode shape of the diagonal cross (X) SMA repair plate is closer to the traditional repair plate (Q0), and the mode shape is independent of the number of embedded SMAs. When the SMA phase changes, the embedded SMA increases the natural frequency of the first second order of the repair plate, and the rise rate is positively correlated with the number of SMA, which is related to the SMA laying mode as follows: C-type> D-type> X-type. The embedded SMA makes the energy dissipation capacity and damping of the repair board better than that of the Q0 board, which is positively correlated with the number of SMA, and the relationship with the SMA laying method is as follows: X-type> C-type> D-type. In the laying configuration studied in this paper, the X24 type has the best repair effect, and its natural frequency of the first and second orders can be restored to 108.47% and 112.26% of the Q0 plate, and the damping ratio is 5.19 times higher than that of the Q0 plate. This work can provide a reference for the technical transformation of existing traditional composite repair to intelligent composite material repair. -
-
![]()
图 1 MTS Landmark伺服测试系统对形状记忆合金(SMA)进行拉伸实验
DC—Direct current
Figure 1. MTS Landmark servo test system performs shape memory alloy (SMA) tensile experiments
![]()
图 2 SMA纤维超弹性和形状记忆效应的应力-应变曲线
Figure 2. Stress-strain curves for SMA fiber hyper elasticity and shape memory effects
![]()
图 3 含SMA补片双面贴补修理玻璃纤维层合板
Figure 3. Fiberglass laminate with SMA patch double-sided patch repair
![]()
图 7 常温状态下(25℃) ((a)~(c))和高温状态下(100℃) ((d)~(f))玻璃纤维层合板的微观组织形貌
Figure 7. Microstructure morphology of glass fiber laminate at room temperature (25℃) ((a)-(c)) and at high temperature (100℃) ((d)-(f))
![]()
图 8 模态测试装置连接示意图
FFT—Fast fourier transform
Figure 8. Schematic diagram of modal test device connection
![]()
图 10 补片内嵌SMA纤维双面贴补修理损伤层合板分体图
Figure 10. Split diagram of SMA fiber embedded in the patch double-sided patch repair of damaged laminate
![]()
图 12 修理板的实验解与有限元数值解对比
Figure 12. Comparison of experimental solutions and finite element numerical solutions of repair plates
![]()
图 13 不同铺设数量的SMA纤维修理损伤板的前三阶振型
Figure 13. First three-order mode shape of the SMA fiber repair damaged plate with different laying quantities
![]()
图 14 不同铺设方式的SMA纤维修理损伤板前三阶振型
Figure 14. First three-order mode shape diagram of SMA fiber repair damage plate with different laying methods
![]()
图 15 不同铺设方式的SMA纤维修理损伤板第一阶固有频率
FEM—Finite element method; As—Temperature at which the austenite phase transition begins; Af—Temperature at which the austenite phase transition ends
Figure 15. First-order natural frequencies of SMA fiber repair damage plate with different laying methods
![]()
图 16 不同铺设方式的SMA纤维修理损伤板第二阶固有频率
Figure 16. Second-order natural frequency of SMA fiber repair damage plate with different laying methods
![]()
图 17 不同铺设数量的SMA纤维修理损伤板第一阶固有频率
Figure 17. First-order natural frequencies of the SMA fiber repair damaged plate with different laying quantities
![]()
图 18 不同铺设数量的SMA纤维修理损伤板第二阶固有频率
Figure 18. Second-order natural frequency of the SMA fiber repair damaged plate with different laying quantities
![]()
图 19 不同铺设方式的SMA纤维修理损伤板前四阶阻尼比
Figure 19. First four-order damping ratio of SMA fiber repair damage plate with different laying methods
![]()
图 20 不同铺设数量的SMA纤维修理损伤板前四阶阻尼比
Figure 20. First four-order damping ratio of the SMA fiber repair damaged plate with different laying quantities
表 1 SMA纤维性能参数
Table 1 SMA fiber performance parameters
Property Value Modulus of elasticity of martensite EM/GPa 21.36 Modulus of elasticity of austenitic EA/GPa 38.47 Modulus of martensite thermoelasticity ΘM/(MPa·℃−1) 0.102 Austenitic thermoelastic modulus ΘA/(MPa·℃−1) 0.567 Martensitic phase transition start temperature Ms/℃ 34.3 Martensite phase transition end temperature Mf/℃ 26.1 Austenite phase transition start temperature As/℃ 57.3 Austenite phase transition end temperature Af/℃ 74.1 Martensite critical phase change stress coefficient CM/(MPa·℃−1) 10.81 Austenite critical phase change stress coefficient CA/(MPa·℃−1) 6.228 Critical phase transition begins stress σcrs/MPa 73.21 Critical phase transition end stress σcrf/MPa 87.63 Coefficient of thermal expansion of austenite αA/(10−6 ℃−1)[5] 10.26 Coefficient of thermal expansion of martensite αM/(10−6 ℃−1)[5] 6.60 Poisson's ratio υS[5] 0.33 Density ρ/(kg·m−3)[5] 6450 Maximum residual strain εL/% 7.0 Note：Data are from reference [5] and manufacturer. 
下载: 导出CSV
表 2 Hansort 8313预浸料的性能参数
Table 2 Performance parameters of Hansort 8313 prepreg
Elastic modulus
E12, E23, E31/GPaShear modulus
G12, G23, G31/GPaPoisson's ratio
μ12, μ23, μ31Density
ρ/(kg·m−3)Coefficient of thermal Humidity expansion α1 α2 β1 β2 15.4 4.47 0.43 1660 −0.3×10−6 28.1×10−6 0 0.44
下载: 导出CSV
表 3 SMA纤维铺设参数及修理板分组编号
Table 3 SMA fiber laying parameters and repair plate group number
No. SMA fiber laying method Number of SMA fibers laid/root Fiber spacing/mm D6 Single-lined (D) 6 16.67 D12 12 8.33 D24 24 4.17 C6 Vertically crossed type (C) 6 23.57 C12 12 11.79 C24 24 5.89 X6 Diagonal cross type (X) 6 23.57 X12 12 11.79 X24 24 5.89 Q0 Traditional patching 0 —
下载: 导出CSV
-
[1] 孔方昀, 常孟周, 王振清, 等. 形状记忆合金-玻璃纤维/环氧树脂复合材料在振动边界条件下的低速冲击数值模拟[J]. 复合材料学报, 2019, 36(10): 2316-2329. DOI: 10.13801/j.cnki.fhclxb.20181119.006 KONG Fangyun, CHANG Mengzhou, WANG Zhenqing, et al. Numerical simulation of low-velocity shock of shape memory alloy-glass fiber/epoxy resin composites under vibration boundary conditions[J]. Acta Materiae Compositae Sinica, 2019, 36(10): 2316-2329(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20181119.006
[2] 陈邵杰. 复合材料结构修理指南[M]. 北京: 航空工业出版社, 2001: 42-43. CHEN Shaojie. Repair guide of composite structure[M]. Beijing: Aviation Industry Press, 2001: 42-43(in Chinese).
[3] ZHOU W, JI X, YANG S, et al. Review on the performance improvements and non-destructive testing of patches repaired composites[J]. Composite Structures, 2021, 263: 113659. DOI: 10.1016/j.compstruct.2021.113659
[4] 刘兵飞, 刘亚冬, 张亚楠. 形状记忆合金在复合材料损伤修复中的应用[J]. 复合材料学报, 2022, 39(4): 1834-1846. DOI: 10.13801/j.cnki.fhclxb.20210608.004 LIU Bingfei, LIU Yadong, ZHANG Yanan. Application of shape memory alloy in damage repair of composite materials[J]. Acta Materiae Compositae Sinica, 2022, 39(4): 1834-1846(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20210608.004
[5] NASSHO Y, SANADA K. Microstructure optimizations for improving interlaminar shear strength and self-healing efficiency of spread carbon fiber/epoxy laminates containing microcapsules[J]. Journal of Composite Materials, 2021, 55(1): 27-38. DOI: 10.1177/0021998320943941
[6] KAMARIAN S, SONG J. A comparative study on the effect of SMAs and CNTs on the vibration of composite plates exposed to thermal environments[J]. Case Studies in Thermal Engineering, 2022, 36: 102121. DOI: 10.1016/j.csite.2022.102121
[7] NEKOUEI M, RAGHEBI M, MOHAMMADI M. Free vibration analysis of hybrid laminated composite cylindrical shells reinforced with shape memory alloy fibers[J]. Journal of Vibration and Control, 2020, 26(7-8): 610-626. DOI: 10.1177/1077546319889857
[8] VERMA L, ANDREW J J, SIVAKUMAR S M, et al. Compression after high-velocity impact behavior of pseudo-elastic shape memory alloy embedded glass/epoxy composite laminates[J]. Composite Structures, 2021, 259: 113519. DOI: 10.1016/j.compstruct.2020.113519
[9] ROGERS C, LIANG C, JIA J. Behavior of shape memory alloy reinforced composite plates. I-Model formulations and control concepts[C]//30th Structures, Structural Dynamics and Materials Conference. Alabama, 1989: 1389.
[10] PARHI A, SINGH B N. Nonlinear free vibration analysis of shape memory alloy embedded laminated composite shell panel[J]. Mechanics of Advanced Materials and Structures, 2017, 24(9): 713-724. DOI: 10.1080/15376494.2016.1196777
[11] SHIAU L C, KUO S Y, CHANG S Y. Free vibration of buckled SMA reinforced composite laminates[J]. Composite Structures, 2011, 93(11): 2678-2684. DOI: 10.1016/j.compstruct.2011.06.008
[12] NEKOUEI M, RAGHEBI M, MOHAMMADI M. Free vibration analysis of laminated composite conical shells reinforced with shape memory alloy fibers[J]. Acta Mechanica, 2019, 230: 4235-4255. DOI: 10.1007/s00707-019-02501-z
[13] MALEKZADEH K, MOZAFARI A, GHASEMI F A. Free vibration response of a multilayer smart hybrid composite plate with embedded SMA wires[J]. Latin American Journal of Solids and Structures, 2014, 11: 279-298. DOI: 10.1590/S1679-78252014000200008
[14] MAHABADI R K, SHAKERI M, PAZHOOH M D. Free vibration of laminated composite plate with shape memory alloy fibers[J]. Latin American Journal of Solids and Structures, 2016, 13: 314-330. DOI: 10.1590/1679-78252162
[15] KARIMIASL M, EBRAHIMI F, AKGOZ B. Buckling and post-buckling responses of smart doubly curved composite shallow shells embedded in SMA fiber under hygro-thermal loading[J]. Composite Structures, 2019, 223: 110988. DOI: 10.1016/j.compstruct.2019.110988
[16] LI W, STACHIV I. Computational modeling and parametric analysis of SMA hybrid composite plates under thermal environment[J]. Sensors, 2023, 23(3): 1344. DOI: 10.3390/s23031344
[17] TANAKA K. Thermomechanical sketch of shape memory effect: One-dimensional tensile behavior[J]. Res Mechanica, 1986, 18(3): 251-263. TANAKA K. Thermomechanical sketch of shape memory effect: One-dimensional tensile behavior[J]. Res Mechanica, 1986, 18(3): 251-263.
[18] LIANG C, ROGERS C A. One-dimensional thermomechanical constitutive relations for shape memory materials[J]. Journal of Intelligent Material Systems and Structures, 1990, 1(2): 207-234.
[19] American Society for Testing and Materials. Standard test method for tension testing of nickel-titanium superelastic materials: ASTM F2516-07e2[S]. West Conshohocken: ASTM International, 2007.
[20] KIM Y J, JEONG J W, LIM J H, et al. An enhanced Brinson model with modified kinetics for martensite transformation[J]. Journal of Mechanical Science and Technology, 2017, 31: 1157-1167. DOI: 10.1007/s12206-017-0214-1
[21] SONG J J, CHEN Q, NAGUIB H E. Constitutive modeling and experimental validation of the thermo-mechanical response of a shape memory composite containing shape memory alloy fibers and shape memory polymer matrix[J]. Journal of Intelligent Material Systems and Structures, 2016, 27(5): 625-641. DOI: 10.1177/1045389X15575086
[22] KARIMI M R, DANESH P M, SHAKERI M. On the free vibration and design optimization of a shape memory alloy hybrid laminated composite plate[J]. Acta Mechanica, 2021, 232: 323-343. DOI: 10.1007/s00707-020-02824-2
[23] American Society for Testing and Materials. Standard test method for moisture absorption properties and equilibrium conditioning of polymer matrix composite materials: ASTM D5229/D5229M—20[S]. West Conshohocken: ASTM International, 2020.
[24] 谢军伟, 刘维国, 詹国宁. 复合材料开孔层合板有限元网格划分方法研究[J]. 机械设计与制造, 2020, 49(4): 228-231. DOI: 10.19356/j.cnki.1001-3997.2013.04.072 XIE Junwei, LIU Weiguo, ZHAN Guoning. Study on finite element meshing method of composite open-cell laminate[J]. Mechanical Design and Manufacturing, 2020, 49(4): 228-231(in Chinese). DOI: 10.19356/j.cnki.1001-3997.2013.04.072
[25] 万小朋, 李小聪, 鲍凯, 等. 利用振型变化进行结构损伤诊断的研究[J]. 航空学报, 2003, 24(5): 422-426. WAN Xiaopeng, LI Xiaocong, BAO Kai, et al. Research on structural damage diagnosis using mode shape change[J]. Journal of Aeronautics, 2003, 24(5): 422-426(in Chinese).
[26] 胡成宝, 王云岗, 凌道盛. 瑞利阻尼物理本质及参数对动力响应的影响[J]. 浙江大学学报, 2017, 51(7): 1284-1290. HU Chengbao, WANG Yungang, LING Daosheng. Influence of physical nature and parameters of Rayleigh damping on dynamic response[J]. Journal of Zhejiang University, 2017, 51(7): 1284-1290(in Chinese).
[27] 张景业. 超弹性形状记忆合金混杂复合材料振动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. ZHANG Jingye. Study on vibration characteristics of superelastic shape memory alloy hybrid composites[D]. Harbin: Harbin Institute of Technology, 2016(in Chinese).
[28] 杨海如. 基于材料与结构阻尼的CFRP筏架阻尼性能研究[D]. 武汉: 武汉理工大学, 2021. YANG Hairu. Study on damping performance of CFRP raft frame based on material and structural damping[D]. Wuhan: Wuhan University of Technology, 2021(in Chinese).
-
目的
在复合材料中加入形状记忆合金(SMA)制成的纤维增强材料具有高强度、高阻尼与良好的自修复性等优点，可明显提高修理结构刚度及抗剥离性。而温度增加会导致SMA发生相变，以及复合材料内部产生热膨胀，使结构刚度与模量均发生改变。为了探究热环境下玻璃纤维补片内嵌不同铺设构型的SMA修理层合板的振动特性，通过制备不同铺设构型的SMA补片，并对中心穿透损伤的层合板进行双面贴补修理，通过模态实验与数值分析方式研究修理板的振动特性随温度的变化规律。
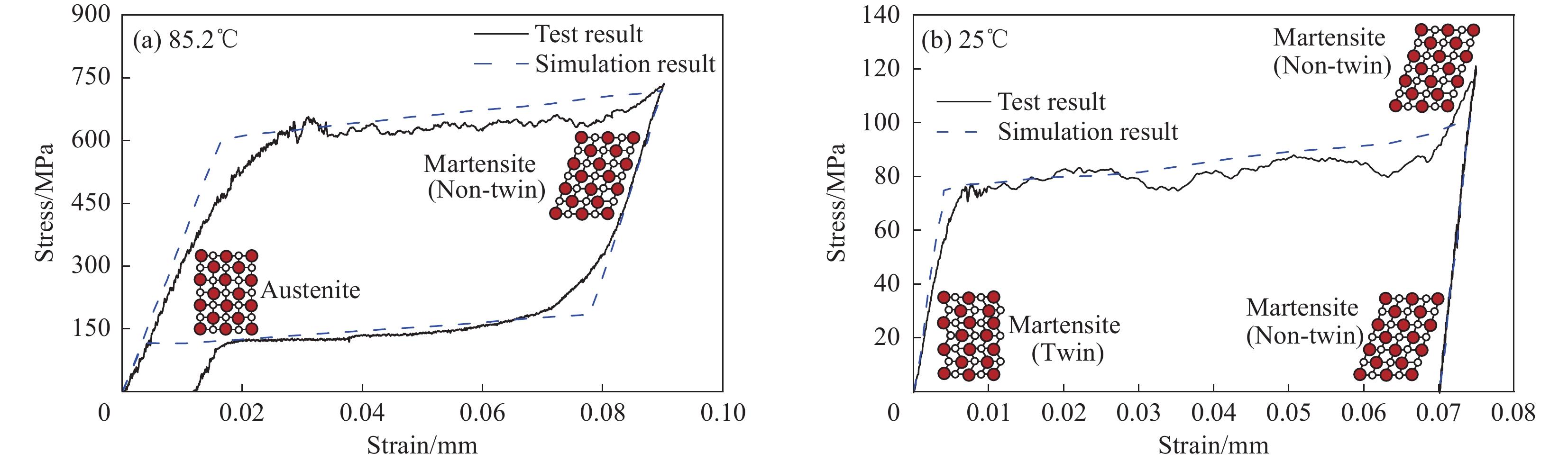
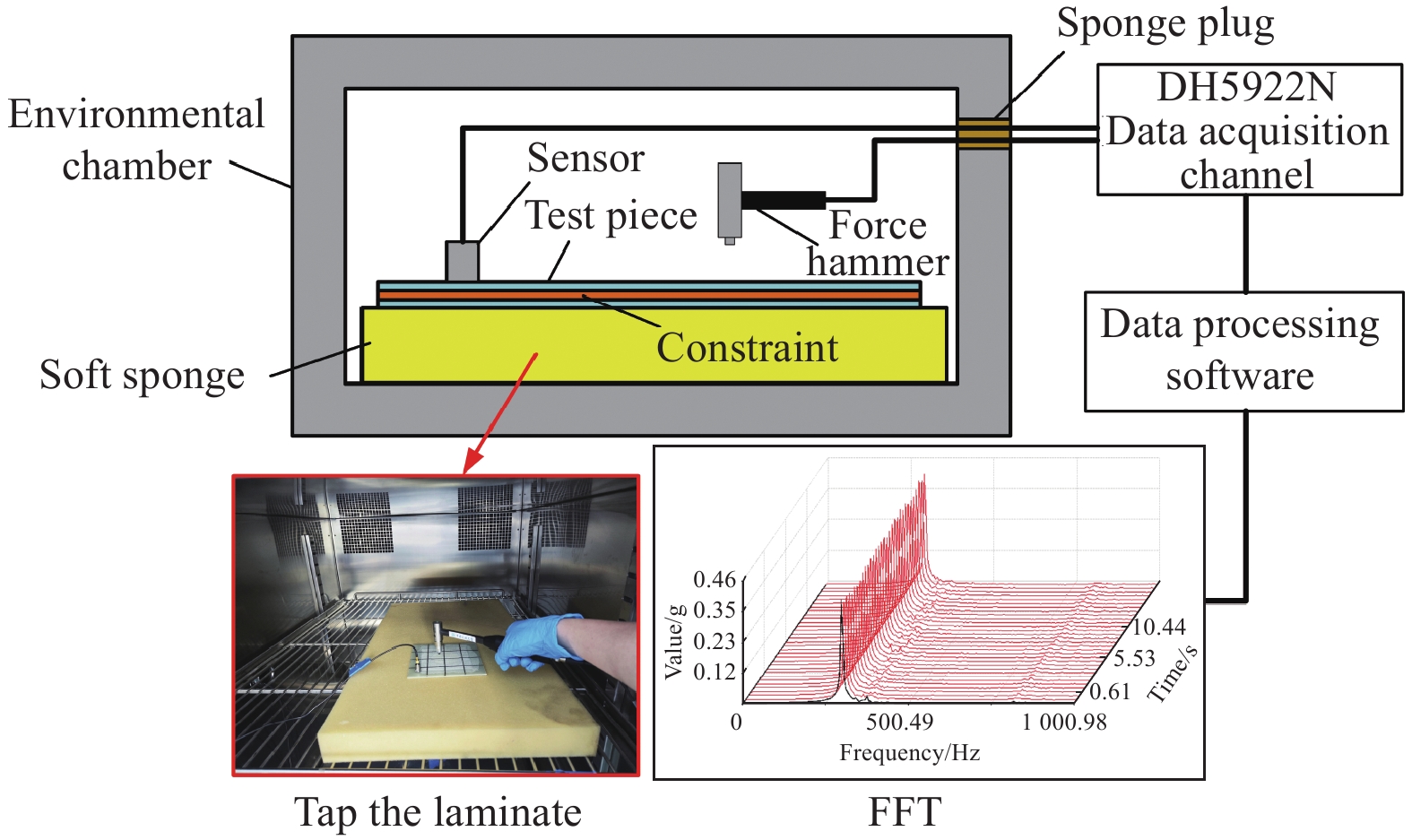
方法首先，利用Tanaka在热力学、热动力学以及相变动力学基础上建立的以马氏体为单一内变量的导数形式的一维SMA本构模型。Liang-Rogers根据SMA纤维在自由恢复过程中的变形特点，对Tanaka本构模型进行积分，推导出全量形式的SMA本构方程。其次，通过将上述所构建的SMA本构模型编入用户自定义材料子程序(User-defined Material Mechanical Behavior，UMAT)，使用ABAQUS软件实现SMA材料力学本构行为的表征，从而进行相应的结构数值计算。然后，根据ASTM F2516:2007e1试验标准，使用MTS工业系统(中国)有限公司制造的MTS Landmark伺服测试系统对SMA纤维分别在恒温85.2℃、室温(25℃)下进行拉伸试验，得到SMA超弹性与形状记忆效应曲线，并与UMAT子程序计算结果进行对比，验证自定义材料子程序(UMAT)的有效性。最后，通过模态实验与数值分析相结合方式研究不同铺设方式和数量的SMA纤维修理层合板在自由边界条件下的固有频率、模态振型和阻尼比随温度的变化规律。
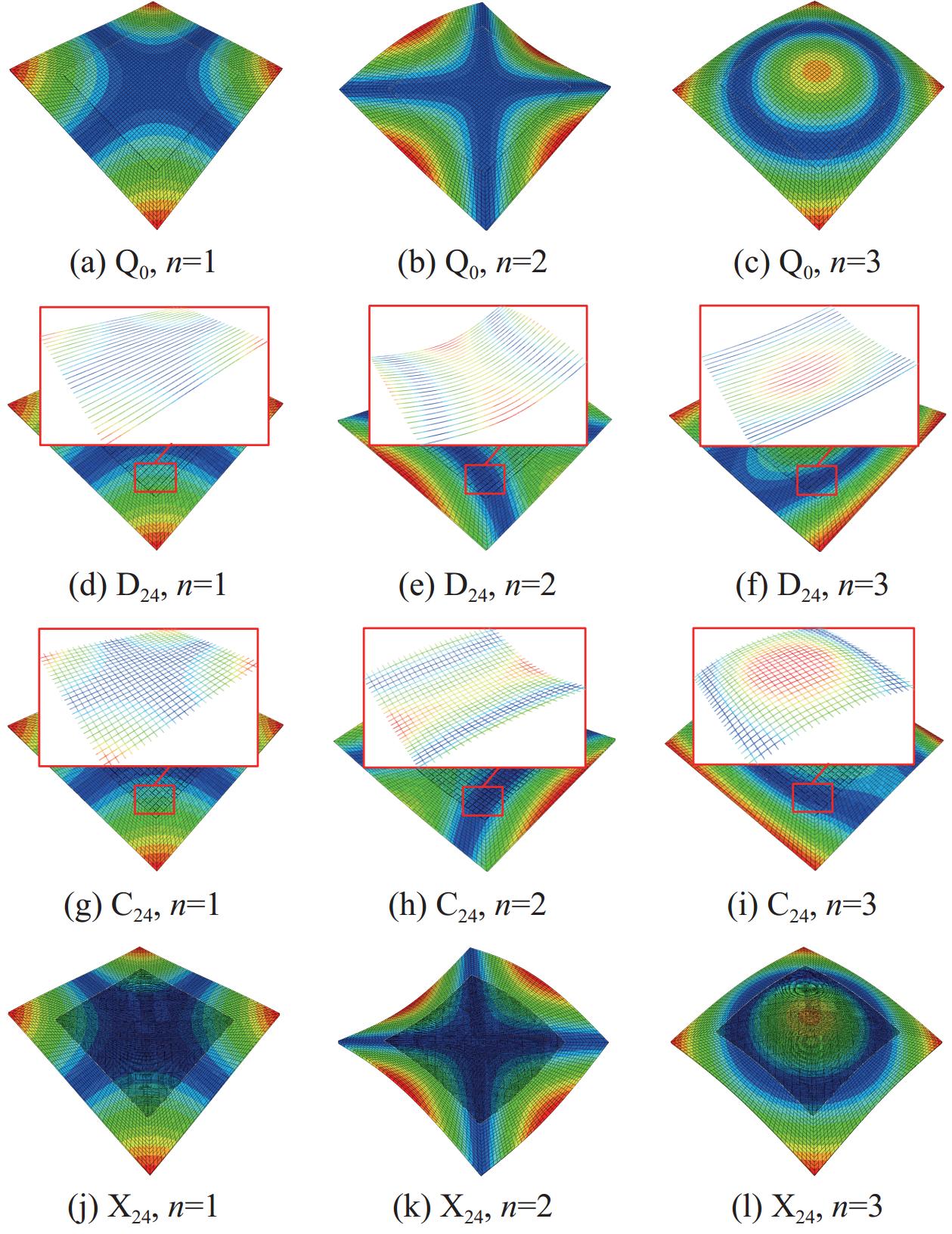
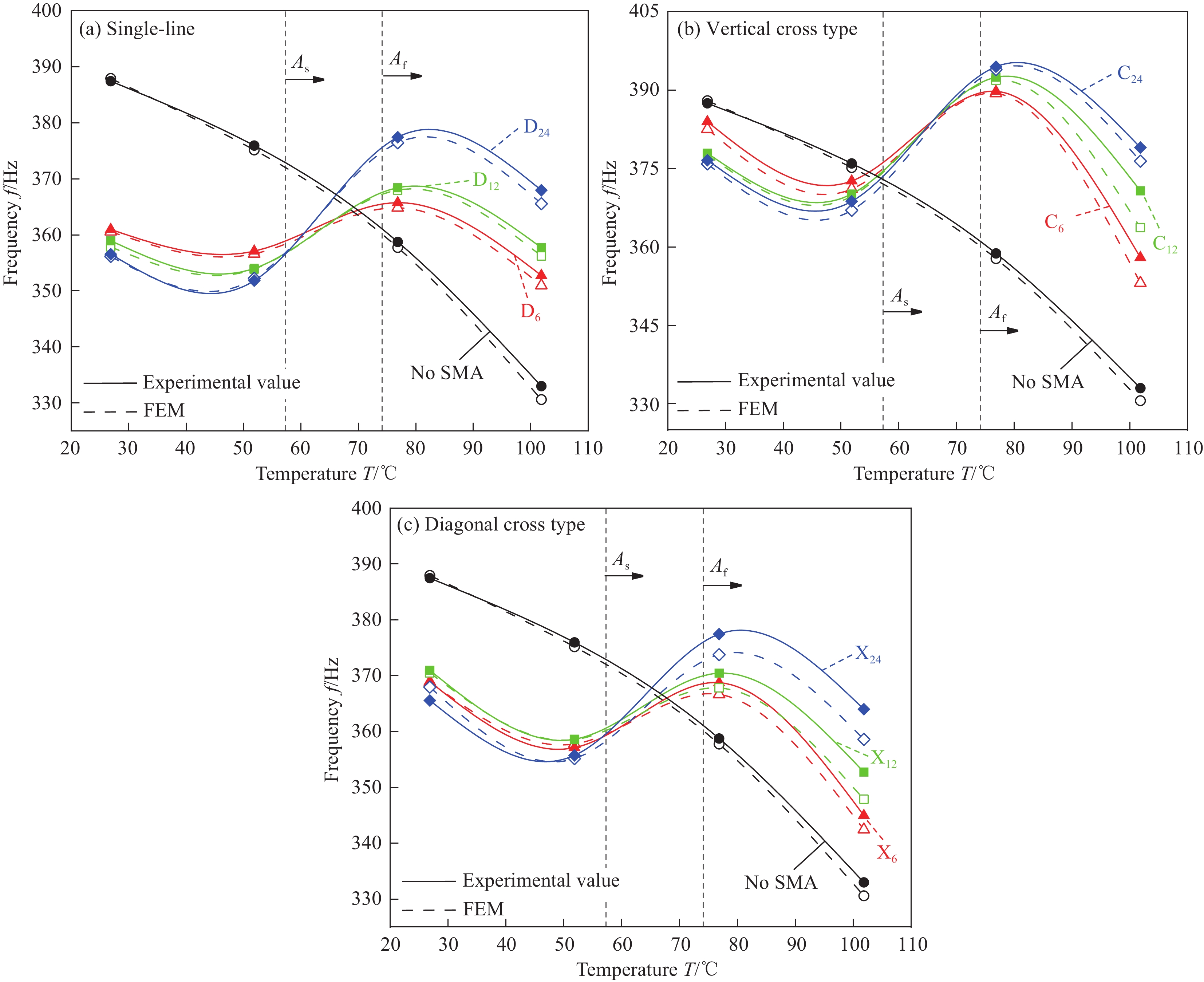
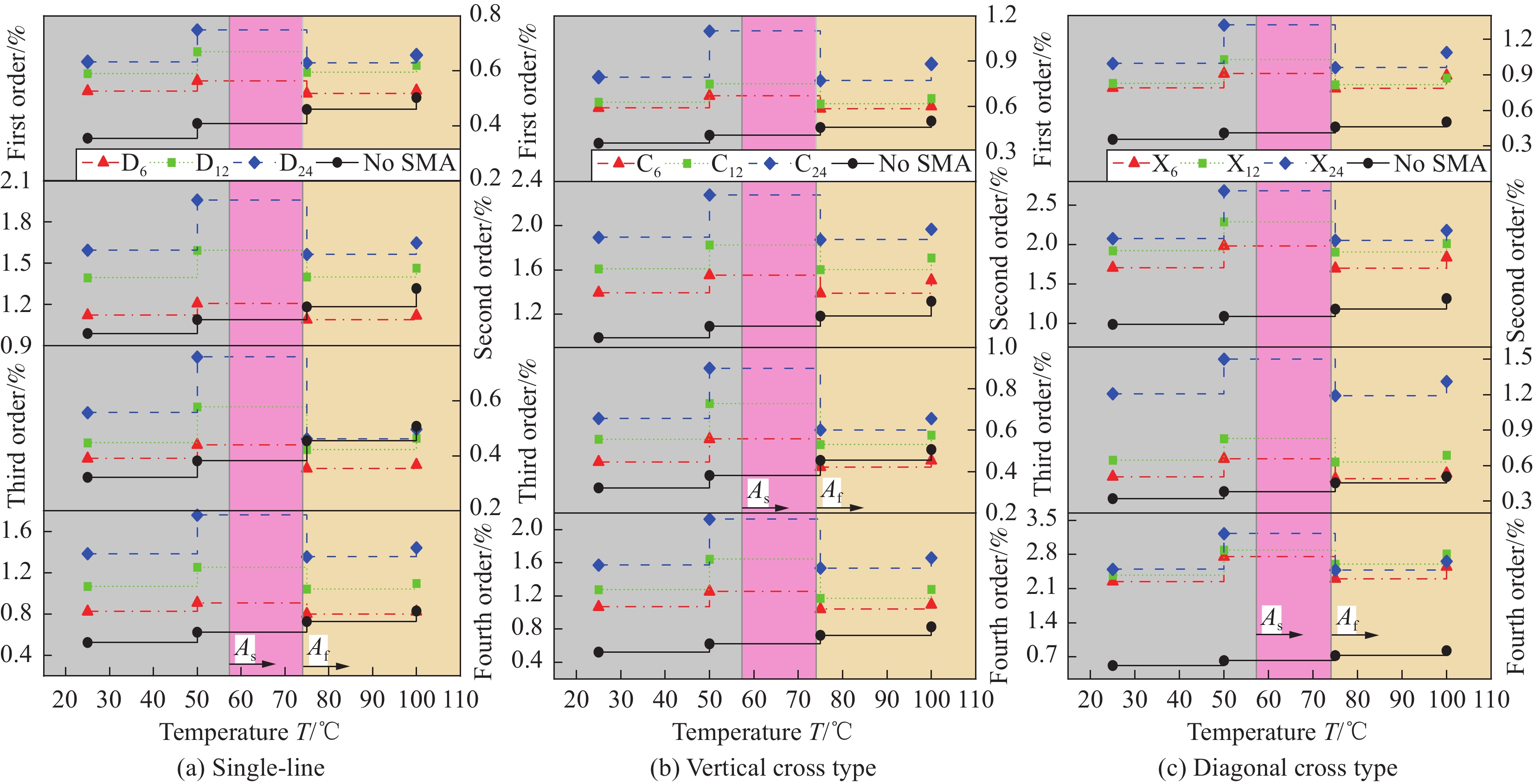
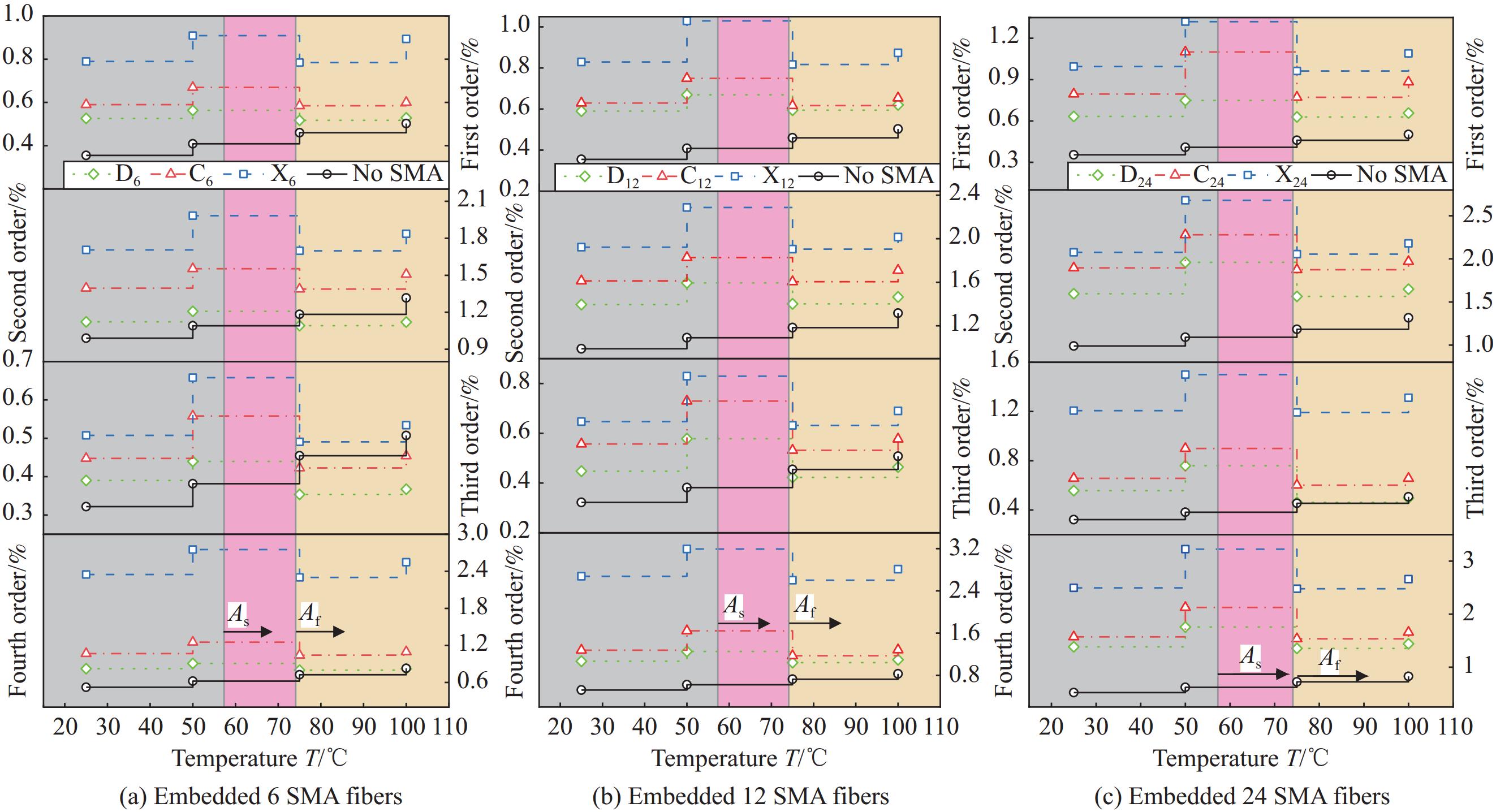
结果①内嵌斜铺交叉型(X)SMA纤维的修理板前三阶振型更为接近传统修理板(Q)，而单线铺设(D)与垂直交叉铺设(C)两种构型的二三阶振型与Q修理板存在较大差异。此外，当修理板处于高温环境下，斜铺交叉型(X)的SMA纤维可以产生较大回复应力来减缓高温对复材树脂基体软化产生的链段运动，达到保持层合板原有结构形状的目的。因此当补片采用斜铺交叉型(X)的SMA纤维进行铺设时更能满足对耐久性的要求。②随着温度上升，内嵌SMA使修理板的前二阶固有频率及其上升率升高，且与嵌入SMA数量呈正相关，与铺设构型有如下关系：垂直交叉型(C)>直线型(D)>斜铺交叉型(X)，其中C、C、C的第一阶固有频率的上升率分别为4.93%、6.01%、7.32%，D、D、D分别为2.30%、3.98%、6.88%，X、X、X分别为2.48%、2.57%、5.23%，这种增加趋势一直持续到奥氏体相变结束温度。③内嵌SMA使修理板耗能能力及阻尼性优于Q板，与SMA数量呈正相关，对于阻尼比增幅较大的斜铺交叉型(X)，X、X、X的上升率分别为0.15%、0.24%、0.33%；与SMA铺设方式有如下关系：X型>C型>D型，温度为50℃时，内嵌D、C、X型SMA修理板的第四阶阻尼比分别是Q板的2.82、3.42、5.19倍。④在本文所研究的温度范围内，X型修理板的一阶与二阶固有频率最高可恢复至Q板的108.47%与112.26%，其一阶阻尼比是Q板的5.19倍。当SMA以X构型嵌入补片时修理层合板的综合效果最优。
结论通过将Liang-Rogers构建的全量形式的SMA本构模型编入UMAT子程序可以实现SMA材料力学本构行为的表征，进行SMA修理板振动性能的结构数值计算。SMA相变时，内嵌SMA使修理板前二阶固有频率上升且上升率与SMA数量呈正相关，与SMA铺设方式关系如下：C型>D型>X型。内嵌SMA可以使修理板耗能能力及阻尼性优于Q板，且与SMA数量呈正相关，与SMA铺设方式关系如下：X型>C型>D型。此外，SMA纤维以斜铺交叉型(X)嵌入补片时，一定程度上可以提高修理结构的整体刚度与承载能力，以及修理区域的抗剥离性。当补片中内嵌SMA双面贴补修理损伤层合板时，可优先考虑SMA以X型嵌入层合板，其修理效果最优。
-
在服役环境作用下，复合材料因冲击载荷造成的内部裂纹常采用操作简单的贴补修理，其优点是可以降低修理区的应力集中，提高修理结构的残余比强度和刚度，而传统的贴补修理技术很难达到复合材料对刚度的恢复指标要求(原件的60%~80%)，因此对复合材料自修复技术成为研究的热点。
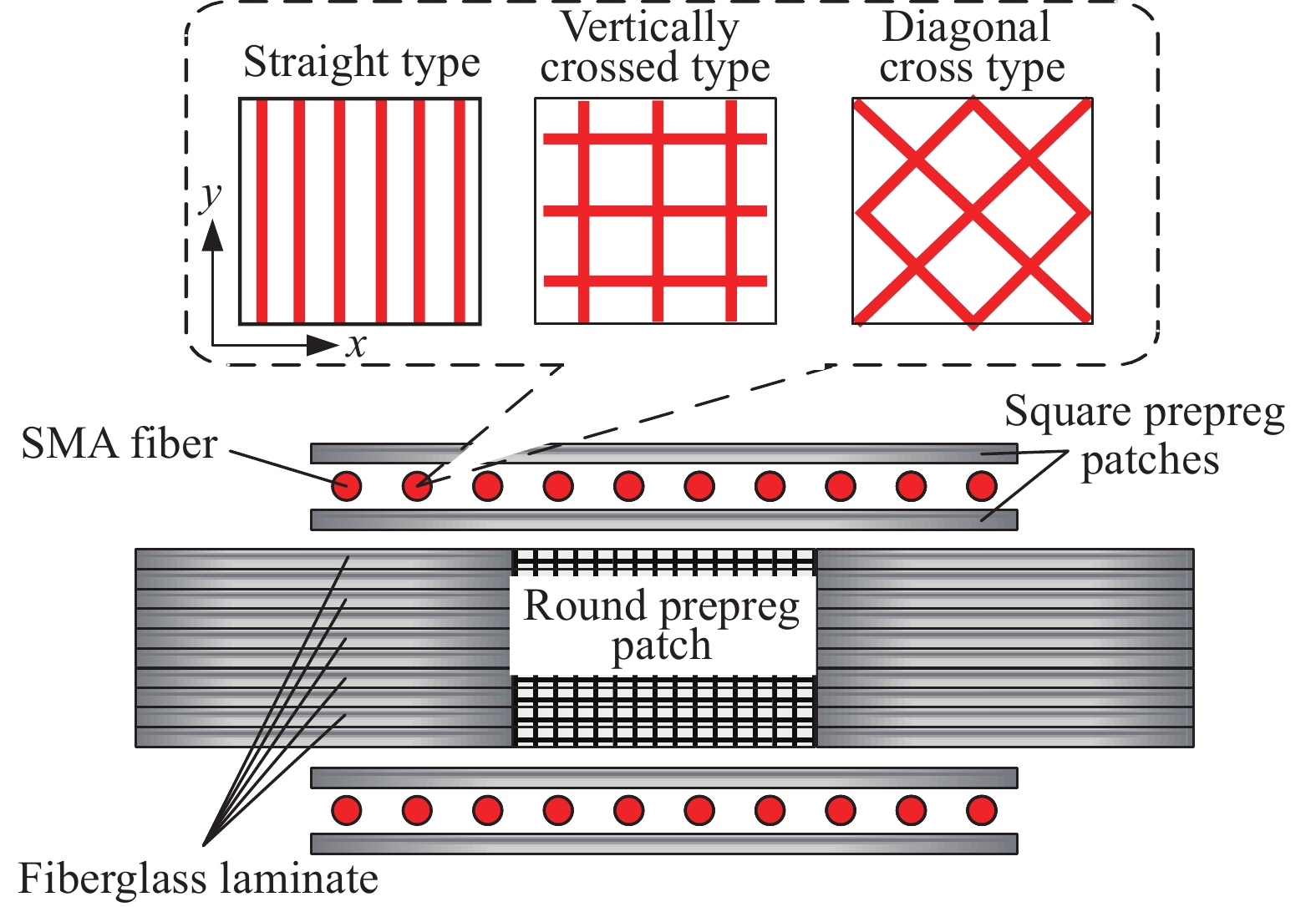
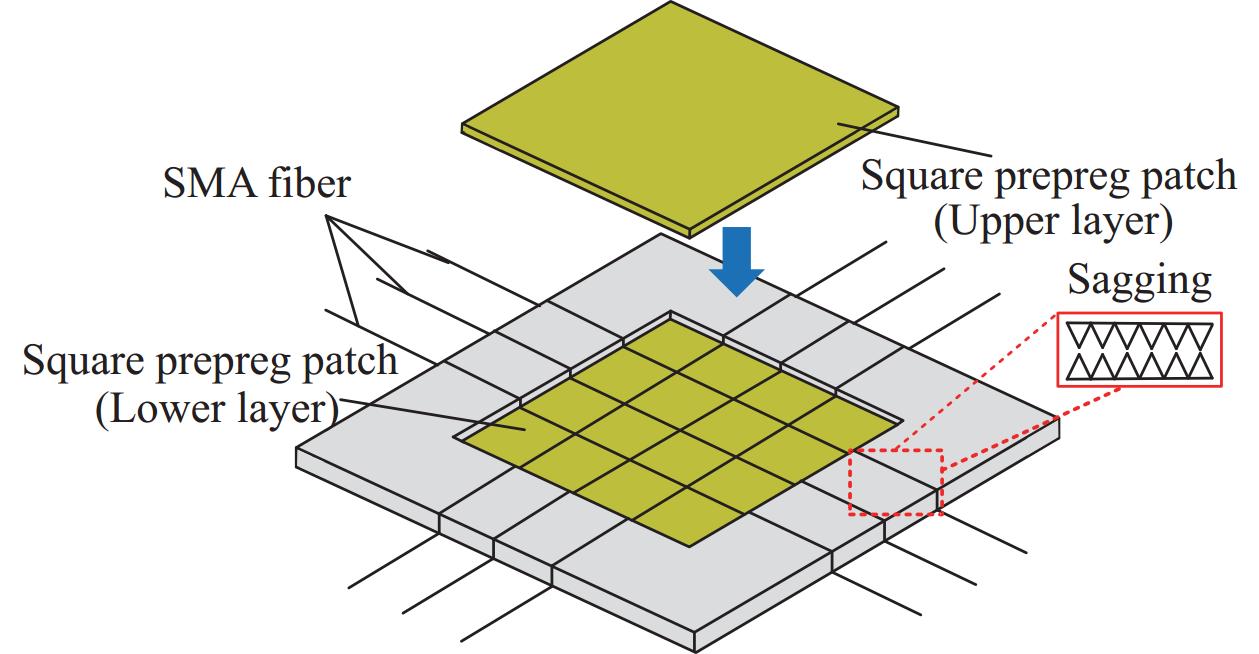
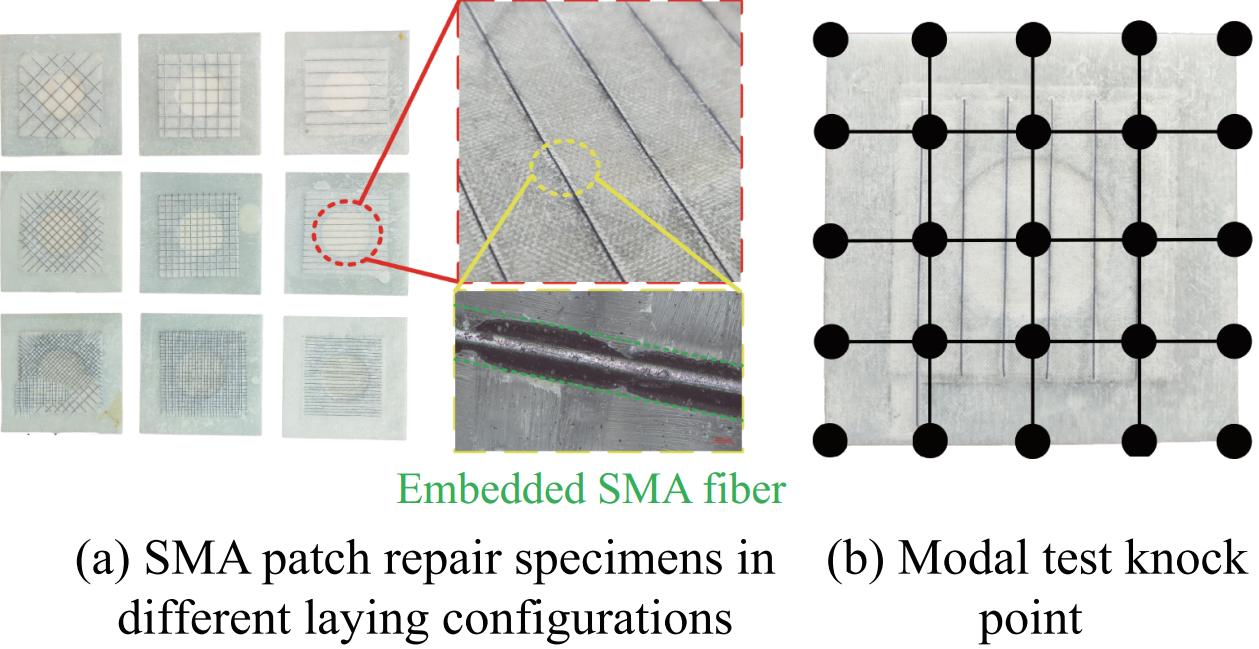
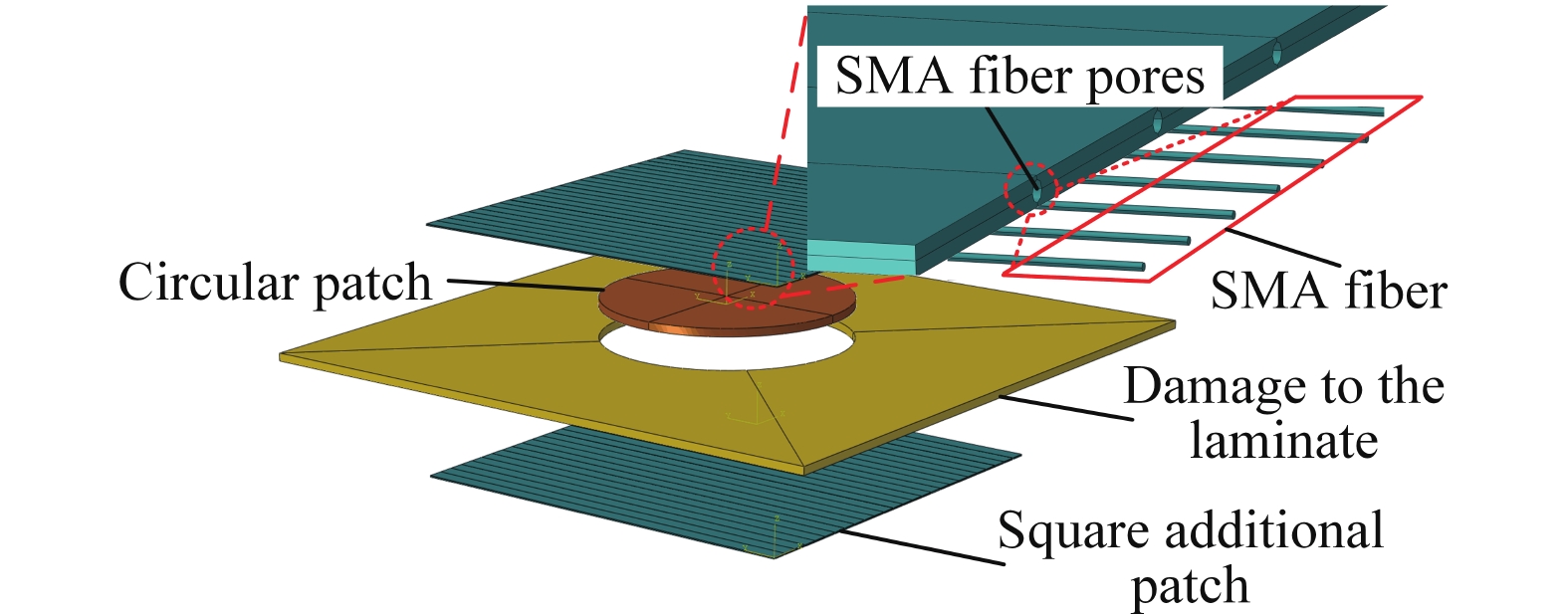
形状记忆合金(Shape Memory Alloy，SMA)是一种新型智能材料，具有高强度、高阻尼与良好的自修复性等优点。本文通过将不同铺设方式(单线型-D、垂直交叉型-C、斜铺交叉型-X)与数量(6根、12根、24根)的SMA纤维内嵌到编织玻璃纤维补片中对损伤层合板进行双面贴补修理，制备了不同构型的SMA纤维增强复合材料修理板。相较于传统的修理板(Q0)，不仅可明显提高修理结构的刚度及抗剥离性，提高修理结构的残余比强度与刚度，而且此结构具有较高的结构抗损伤能力与高阻尼响应特性等。其中所制备的不同构型的SMA修理板中，X24构型的修理板综合效果最优，在本文所研究的温度范围内，其一阶与二阶固有频率最高可恢复至Q0板的108.47%与112.26%，四阶阻尼比是Q0板的5.19倍。
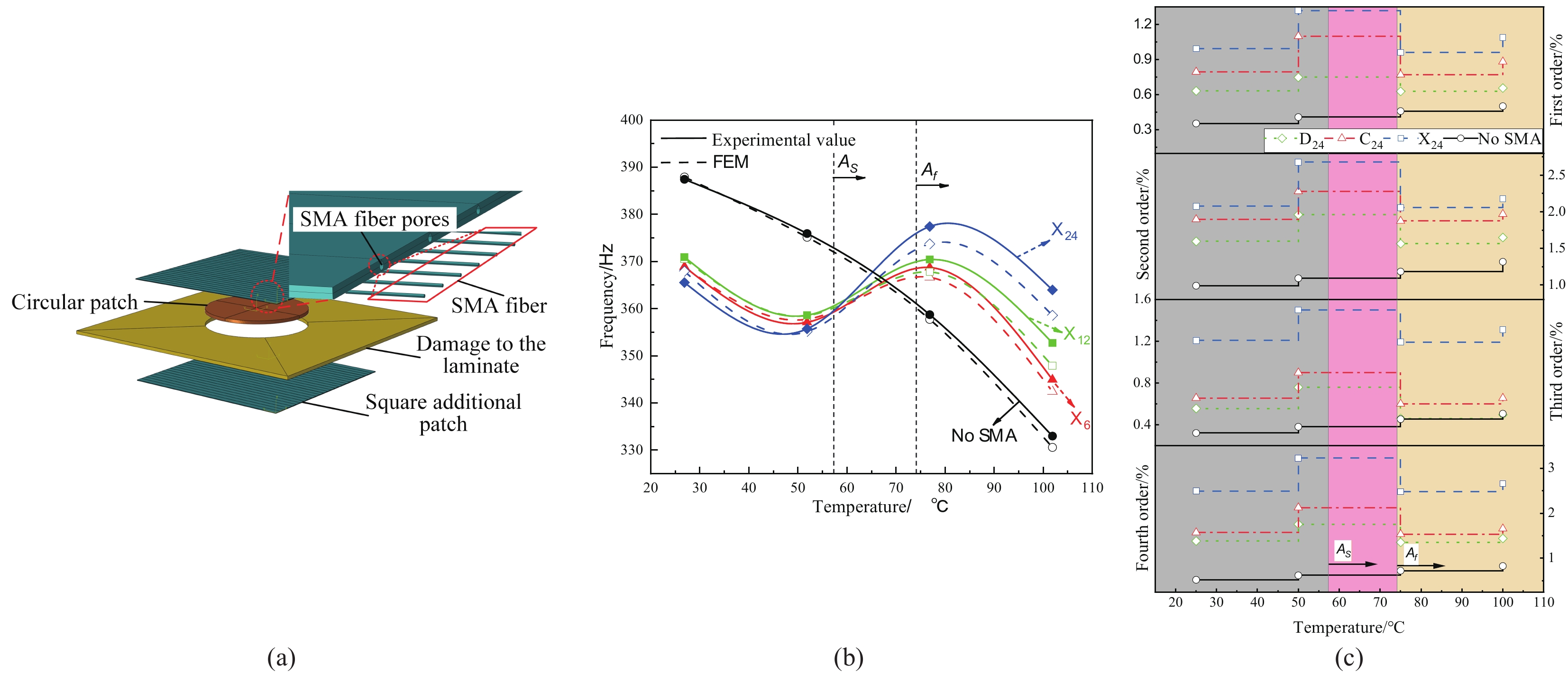
(a) 补片内嵌SMA纤维双面贴补修理损伤层合板分体图(b) 热效应作用下X6、X12、X24型修理板与传统型修理板的一阶固有频率对比(c) 内嵌不同铺设方式(D、C、X)的SMA双面贴补修理层合板前四阶阻尼比随温度的变化情况
计量
- 文章访问数: 430
- HTML全文浏览量: 291
- PDF下载量: 22
