Impact localization on stiffened composite plate based on adaptive time reversal focusing
-
摘要: 复合材料结构在航空航天、海洋工程和轨道交通等领域中占有重要地位。但由于复合材料在抗冲击性能方面存在缺陷，实时在线的冲击监测技术越来越受到关注。本文提出了基于自适应时间反转聚焦的加筋复材板冲击定位方法。首先，利用结构表面布置的压电传感器网络接收冲击响应信号；然后，利用连续小波变换提取冲击响应信号的窄带Lamb波信号，使用窄带Lamb波信号的包络特征，根据时间反转聚焦原理，构建以冲击位置坐标和窄带Lamb波群速度为变量的虚拟时间反转成像函数；最后，迭代计算不同群速度下对应的虚拟时间反转成像结果，根据不同群速度对应的图像最大像素曲线获得自适应时间反转聚焦图像，从而实现冲击定位。利用尺寸为800 mm×400 mm (长×宽)的加筋编织复材板进行落球冲击实验，验证该方法的有效性。结果表明该方法可以准确的识别冲击位置，且在引入噪声、传感器数量减少和变温情况下仍然具有较好的精度。Abstract: Composite structures play an important role in the fields of aerospace, ocean engineering and rail transit. Due to their defects in impact resistance, real-time on-line impact monitoring technology has attracted more and more attention. In this paper, an impact localization method for stiffened composite plates based on adaptive time reversal focusing imaging was proposed. Firstly, the impact response signal was received by piezoelectric sensor network arranged on the surface of the structure. Then, the narrowband Lamb wave signal of impact response signal was extracted by continuous wavelet transform. And a virtual time-reversal imaging function with impact position coordinates and narrowband Lamb wave group velocity as variables was constructed according to the time-reversal focusing principle. Finally, the virtual time reversal imaging results corresponding to different group velocities were iteratively calculated, and the adaptive time reversal focusing image was obtained according to the maximum pixel curve corresponding to different group velocities to realize impact localization. Drop ball impact experiments were carried out on a stiffened braided composite plate of 800 mm×400 mm (length×width) to verify the effectiveness of the method. The results show that this method can accurately identify the impact location and has a good accuracy in the cases of noise, reducing the number of sensors, and changing temperature.
-
复合材料由于具有高比强度、高比刚度、可设计性强等优点，被广泛应用于航空航天、海洋工程和轨道交通等领域[1]。其中，编织复材板因其成型便捷、抗损伤扩展性能优异，及相比传统层合板更具优势的抗冲击性能，近年来在工程领域扮演着十分重要的角色[2]。然而，复合材料在制造、运输和服役过程中不可避免地会受到外界低速冲击载荷的作用，可能产生目不可见的“内伤”(包括基体开裂、分层和纤维断裂等)，严重威胁结构的健康安全[3]。冲击监测技术可以实时在线监测复合材料结构的冲击事件，对于复合材料结构的安全维护和服役稳定具有重要意义，因此受到广泛关注[4]。
冲击监测技术首要任务是确定冲击位置。在结构上布置传感器(一般为压电、应变或加速度传感器)网络接收冲击响应信号，通过信号处理和特征提取结合特定的算法可以实现结构的冲击定位[5-7]。国内外研究人员提出了大量的结构冲击定位方法，具有代表性的包括几何方法[8]、时间反转方法[9]、参考数据库方法[10]和机器学习方法[11]等。
几何方法因简单易行，且效率高，最早得到发展。它一般根据传感器和冲击位置的几何关系建立非线性方程组并利用优化算法进行求解得到冲击位置。Tobias[12]提出经典的三角测量方法，利用3个传感器在各向同性结构上就能够识别冲击位置。Ciampa等[13]提出改进的三角测量方法，采用牛顿迭代优化算法求解非线性方程确定铝板上的冲击位置，且不依赖于波速。Gorgin等[14]提出基于误差指数的概率成像算法，在各向异性的复材板上同样不依赖于波速也能实现冲击定位。然而，几何方法的关键是获取准确的波达时间，受到操作环境噪声、边界反射和加强筋等影响，往往难以获取准确的波达时间差[15]。这表明几何方法在含有加强筋的复杂结构上难以获得较高的冲击定位精度。
基于互易性原理的时间反转方法由于不需要结构的先验信息而被广泛用于各领域的位置识别研究当中。它对传感器接收到的信号根据“后至先发，先至后发”的原则通过信号时间反转聚焦来确定冲击位置，一般分为信号后处理的虚拟时间反转方法和基于全波场测量的时间反转方法。Qiu等[16]采用香农复数小波变换计算Lamb波的相速度，提出基于相位合成的虚拟时间反转聚焦方法，在飞机翼盒上进行冲击概率成像来确定冲击位置。Miniaci等[17]发展了基于时间反转和激光测振的冲击定位方法来预测加筋铝板的冲击位置，该算法对波速及几何特征不敏感。然而上述时间反转方法要么需要测定波速，要么依赖于全波场测量设备，从而不利于这类方法在结构冲击监测领域的工程应用。
参考数据库方法因其在传感器较少的情况下可获得满意的定位精度而得到应用。这类方法将冲击响应信号的当前特征与在所有训练网格点预先存储的冲击响应信号特征参考数据库进行匹配，将相似匹配度最高的网格点作为预测的冲击位置。Kim等[18]提出了一种基于修正误差-离群值的算法，可以识别不同温度下复合材料板上的冲击位置。Wu等[19]在不考虑冲击应力波波速的情况下，采用包含信号功率和到达时间的位置基向量来确定冲击位置。然而，这些方法需要花费大量时间成本来建立参考数据库。此外，在训练点数较少的情况下，算法性能表现较差。
近年来，随着人工智能技术的发展，机器学习方法因其能够适应具有复杂波场的结构也被引入到冲击定位当中。它通常把冲击定位看作是回归问题，在模型中将冲击响应信号的特征作为输入，将冲击位置坐标作为输出，训练神经网络即可预测冲击位置。早期，研究人员一般输入冲击响应信号单个域上的特征信息训练神经网络，导致网络的预测性能较差[20]。最近，Liu等[21]提出了一种基于多域特征的支持向量机(SVR)回归方法，提高了复合材料结构中冲击定位的精度。但是，该类方法对于包含众多组分的真实结构件需要建立庞大的数据库，十分耗时且占据大量的计算资源，使该方法目前难以实现工程应用。
针对上述存在的问题，本文提出一种基于自适应时间反转聚焦的冲击定位方法。利用连续小波变换提取冲击响应信号中的窄带Lamb波信号，使用窄带Lamb波信号在监测区域内进行信号合成，利用合成信号包络特征根据时间反转聚焦原理构建以冲击位置和窄带Lamb波群速度为变量的虚拟时间反转成像函数，最后迭代计算不同波速下对应的虚拟时间反转成像结果，根据不同群速度对应的最大像素曲线获得自适应时间反转聚焦图像从而实现冲击定位。该方法不需要波速和结构的先验知识，且具有良好的抗噪性，在加筋复合材料结构的冲击监测方面具有较好的应用前景。
1. 原理及方法
1.1 时间反转聚焦原理
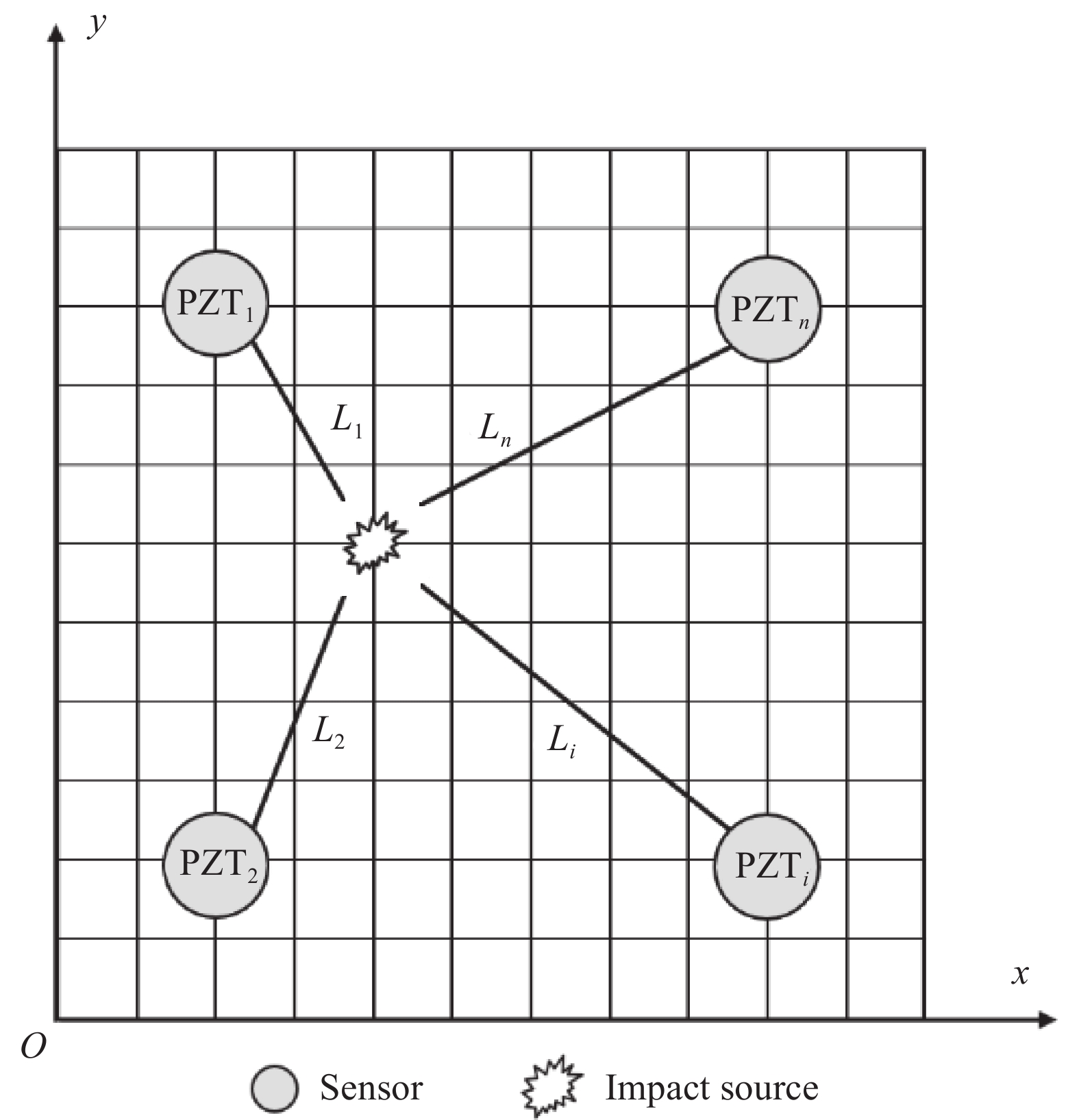
图1为时间反转聚焦原理示意图。在监测结构表面布置了总数为n的压电传感器网络，传感器编号记为PZTi，i = 1, 2, ···, n。在某个位置发生冲击事件时，传感器PZTi接收到的信号频谱Ei(ω)可以表示为
Ei(ω)=Hi(r,ω)S(ω) (1) 其中：S(ω)为冲击源激励信号的频谱；r为冲击源到传感器的距离；ω为角频率；Hi(r, ω)为冲击源激励信号至传感器PZTi接收到的冲击响应信号的传递函数。
![]()
图 1 时间反转聚焦原理示意图Figure 1. Schematic diagram of time reversal focusing principlePZTi—Sensor number; Hi—Transfer function of impact signal from impact source to sensor PZTi; HTR-i—Transfer function of time reversal signal from sensor PZTi to the impact source将传感器接收到的时域冲击响应信号进行时间反转(频域中即为复共轭)，可以得到：
E∗i(ω)=H∗i(r,ω)S∗(ω) (2) 其中，“*”表示对信号取复共轭。
对所有传感器激励时间反转后的冲击响应信号，则在冲击源位置处接收到的合成信号的频谱为
C(ω)=n∑i=1HTR-i(r,ω)H∗i(r,ω)S∗(ω) (3) 式中：HTR-i (r, ω)表示传感器激励的时间反转信号到冲击源接收信号的传递函数。
令
\sum\limits_{i = 1}^n {H_i^*(r,\omega )} = {{\boldsymbol{H}}^*} (4) 根据弹性波传播的互易性原理可知：
{H_{{\rm{TR }}{\text{-}} i}} = {H_i} (5) 则
\sum\limits_{i = 1}^n {{H_{{\rm{TR}} {\text{-}} i}}(r,\omega )} = {\boldsymbol{H}} (6) 式(3)可化简为
C(\omega ) = ({\boldsymbol{H}} \cdot {{\boldsymbol{H}}^ * }) {S^ * }(\omega ) = {\left| {\boldsymbol{H}} \right|^2} {S^ * }(\omega ) (7) 对C(ω)进行傅里叶逆变换得到时域表示：
C(t) = \frac{1}{{2{\text{π }}}}\int_{ - \infty }^\infty {{{\left| {\boldsymbol{H}} \right|}^2}{S^*}(\omega )} {{\text{e}}^{{\rm{j}}\omega t}}{\text{d}}\omega = \frac{{{{\left| {\boldsymbol{H}} \right|}^2}}}{{2{\text{π }}}}C( - t) (8) 从式(8)可以看出，冲击源接收到的时域信号相对于初始的冲击源激励的信号而言，幅值得到了放大，时间相对于零点对称。因此，当传感器接收到冲击源激励的信号，对传感器接收的信号进行时间反转并激励给传感器，信号可以在冲击源发生聚焦效果。而在非冲击源处：
{H_{{\rm{TR}} {\text{-}} i}} \ne {H_i} (9) 则不能发生信号聚焦。
1.2 信号处理
板状结构上的冲击响应信号是Lamb波信号[22]。由于Lamb波的频散性，对于原始冲击响应信号难以分析。小波变换被称为“数学上的显微镜”，是一种在结构健康监测应用十分广泛的时频分析工具[23]，可以提取冲击响应信号中的窄带Lamb波信号，能够减弱冲击响应信号的频散效应，有助于冲击响应信号的分析。对于一个冲击响应信号y(t)的小波变换定义如下：
{y_{{\text{CWT}}}}\left( {a,b} \right) = \left\langle {y(t),{\psi _{a,b}}(t)} \right\rangle = \frac{1}{{\sqrt a }}\int\limits_R {y\left( t \right){\psi ^*}\left( {\frac{{t - b}}{a}} \right)} {\text{d}}t (10) 其中：a是小波变换的伸缩尺度参数；b是小波变换的平移尺度参数；“< >”表示内积；“*”表示共轭；ψ(t)为小波函数，本文选取Morlet小波函数：
\psi \left( t \right) = \frac{1}{{\sqrt {{\text{π }}{f_{\text{b}}}} }}{{\text{e}}^{ - \frac{{{t^2}}}{{{f_{\text{b}}}}}}}[\cos (2{\text{π}}{f_{\text{c}}}t) + {\rm{j}}\sin (2{\text{π}}{f_{\text{c}}}t)] (11) 式中： {f_{\text{b}}} 为小波带宽； {f_{\text{c}}} 为小波中心频率。
利用小波变换提取的窄带Lamb波信号的中心频率与伸缩尺度参数之间的关系如下：
{f_{{\text{req}}}} = \frac{{{f_{\text{c}}}}}{{aT}} (12) 其中：freq为想要提取的窄带Lamb波信号的中心频率；T为冲击响应信号的采样周期。
因此，通过调节伸缩尺度参数a、小波中心频率fc和小波带宽fb，可以提取冲击响应信号中感兴趣的特定中心频率窄带Lamb波信号。
1.3 冲击定位方法
由于在现实情况中很难在监测区域内所有位置接收传感器激励的信号，然后判定时间反转信号聚焦的位置，从而实现冲击定位。本文通过信号处理方法实现自适应虚拟时间反转聚焦成像。
对于板状结构，考虑冲击响应信号为低频动态响应信号，Lamb波存在A0和S0两种模式，但以A0模态为主[24]，因此，其传递函数可以近似写为
H\left( {r,\omega } \right) \approx A\left( {r,\omega } \right){{\text{e}}^{ - {\rm{j}}\omega r/c}} (13) 其中： A\left( {r,\omega } \right) 为A0模式信号的幅值；r和c为其传播距离和传播速度。
由式(13)可知，结构传递函数主要存在幅值项 A\left( {r,\omega } \right) 和相位项 {{\rm{e}}^{ -{\rm{ j}}\omega r/c}} ，幅值项只对时间反转聚焦信号的幅度大小起作用，信号时间反转后能否产生聚焦效果与相位项相关。假设由冲击产生的信号频率响应为G，第i号传感器接收到的冲击响应信号可以表示为
V({r_i}) = A\left( {{r_i},\omega } \right){{\text{e}}^{ - {\rm{j}}\omega {r_i}/c}}G (14) 将n个传感器的冲击响应信号时间反转后在传播到距离处 r_i' 进行信号合成可以表示为
V' = \sum\limits_{i = 1}^n {A\left( {{r_i},\omega } \right)A\left( {r_i',\omega } \right){{\text{e}}^{ - {\rm{j}}\omega ({r_i} - r_i')/c}}{G^*}} (15) 在式(15)中，c为监测环境下的正确波速，如果 {r_i} = r_i' ， \left| {V'} \right| 将取得最大值。也就是说如果距离各个传感器的位置为实际冲击源所在位置，且c为监测环境下正确的波速，合成信号的幅度将会聚焦。因此在合理的波速区间内对监测区域各点进行信号合成，根据不同波速下信号合成的最大幅度可以确定监测环境下正确的波速，正确的波速下合成信号会发生聚焦，即不需要预先进行测定就能反演出监测环境下的波速。将正确波速下监测区域信号合成幅度图像称为“自适应虚拟时间反转聚焦图像”。根据聚焦位置即可确定冲击位置。
图2为冲击定位方法示意图。对结构监测区域进行网格划分，建立笛卡尔坐标系，假定网格点(x, y)为冲击源的位置，它至传感器PZTi的距离为Li (x, y)：
![]()
图 2 冲击定位方法示意图Figure 2. Schematic diagram of the impact localization methodLi—Distance from the assumed impact source to sensor PZTi{L_i}(x,y) = \sqrt {{{(x - {S_{ xi}})}^2} + {{(y - {S_{ yi}})}^2}} (16) 其中，(Sxi, Syi)为传感器PZTi的坐标。
传感器PZTi与PZT1到网格点(x, y)的距离之差为Di (x, y)：
{D_i}(x,y) = {L_i}(x,y) - {L_1}(x,y) (17) 利用小波变换提取所有传感器冲击响应信号的窄带Lamb波信号Vi，i = 1、2、···、n。
对于网格点(x, y)，窄带Lamb波信号传播至传感器PZTi和PZT1的时间差τi为
{\tau _i} = \frac{{{D_i}(x,y)}}{{{C_{\rm{g}}}}} (18) 其中，Cg为窄带Lamb波的传播速度。
取包含直达波的时间长度Δ，将所有传感器窄带Lamb波信号进行时间反转，按照“先至后发，后至先发”原则，在网格点合成信号P(t)：
P(t) = \sum\limits_{i = 1}^n {V_i^{{\text{TR}}}(\Delta - t - {\tau _i})} (19) 其中， V_i^{{\text{TR}}}(\Delta - t) 为传感器PZTi窄带Lamb波信号的时间反转信号。
波的传播速度受到温度变化因素影响也会发生变化，如果通过预先进行实验测量或者根据弹性波理论计算获取窄带Lamb波的群速度[25]，在变温度的环境下不具有自适应性。而通过力学理论建模获取信号传递函数然后进行时间反转成像[26]，对于加筋复合材料结构而言，建模过程复杂，获取的信号传递函数可能误差较大，甚至很难得到其传递函数。因此，本文采取迭代的方法实现自适应时间反转聚焦。首先设置合理的迭代区间[ C_{\rm{g}}^{\min } , C_{\rm{g}}^{\max } ]，以 C_{\rm{g}}^{\min } 为初始值，以 \Delta {C_{\rm{g}}} 为步长，确定迭代群速度 {C_{\rm{g}}} ：
{C_{\rm{g}}} = C_{\rm{g}}^{\min } + (k - 1) \Delta {C_{\rm{g}}} (20) 然后以合成信号的包络幅值最大值作为网格点的像素，迭代计算不同群速度对应的虚拟时间反转成像结果 I({C_{\rm{g}}},x,y) ：
I\left(C_{\rm{g}}, x, y\right)=\max (\tilde{P}(t)) (21) 其中，“~”表示为信号取包络。
当 {C_{\rm{g}}} = C_{\rm{g}}^{\max } ，迭代终止。根据前面所述的自适应时间反转聚焦机制可知，只有在真正的冲击源位置和窄带Lamb波的群速度条件下，合成信号才能发生聚焦。因此，根据不同群速度对应的虚拟时间反转成像的最大像素曲线，即可确定窄带Lamb的群速度 \mathop {{C_{\rm{g}}}}\limits^ \wedge ：
\hat{C}_{\rm{g}}=\underset{C_{\rm{g}}}{\arg \max }\left(I\left(C_{\rm{g}}, x, y\right)\right) (22) 自适应时间反转聚焦图像为\hat{I}(x, y) ：
\hat{I}(x, y)=I\left(C_{\rm{g}}=\hat{C}_{\rm{g}}, x, y\right) (23) 图像中像素最大的网格点位置代表概率最大的冲击源位置，将其作为预测的冲击位置。
1.4 方法实施流程
基于自适应虚拟时间反转聚焦成像的冲击定位流程如图3所示，具体实施步骤如下：
![]()
图 3 冲击定位算法流程图Figure 3. Flow chart of impact localization algorithmk—Iteration step number; Cg—Group velocity; Cg min and Cg max—Minimum and maximum values of the iteration group velocity; ΔCg—Iteration step size; (x, y)—Coordinates of the pixel point assumed to be the position of the impact source; (Sxi, Syi)—Coordinates of the sensor PZTi ; Vi—Narrowband Lamb wave signal of the impact signal; P(t)—Synthesized signal at the pixel poin; "~" indicates that the signal is taken as an envelope; \mathop {{C_{\rm{g}}}}\limits^ \wedge —Determined group velocity of the narrowband Lamb; \hat{I}(x, y)—Adaptive time reversal focusing image(1) 对结构监测区域进行网格划分，建立直角坐标系，标记传感器坐标(Sxi, Syi)，i = 1、2、 ···、n，网格点坐标记为(x, y)；
(2) 采用小波变换提取冲击响应信号特定中心频率下的窄带Lamb波信号；
(3) 对窄带Lamb波信号进行时间反转，根据“先至后发，后至先发”原则，按式(19)在所有网格点进行信号合成；
(4) 以合成信号的包络幅值最大值作为网格点的像素，根据式(20)和式(21)迭代计算不同群速度对应的虚拟时间反转成像结果；
(5) 按式(22)确定窄带Lamb的群速度，按式(23)得到自适应时间反转聚焦图像，图像最大像素值所在的网格点位置为预测的冲击位置。
2. 实验验证
2.1 实验设置
如图4所示，在一块加筋编织复合材料板上进行实验验证本文方法的有效性。加筋编织复材板的尺寸为800 mm × 400 mm (长×宽)，包含两根L型加强筋，加强筋的底宽为30 mm，长为400 mm，腹部高为30 mm，跨距300 mm。结构材料为威海光威复合材料股份有限公司生产的T700 SC-12 k碳纤维织物，层合板和加强筋的铺层均为[0/90]3，需要指出的是A0模态Lamb波的波速分布在正交铺层上几乎各向同性[27]。在结构表面粘贴了12个直径为16 mm、厚度为0.5 mm的 P-51型压电陶瓷圆片。以板左下角为原点建立笛卡尔坐标系，传感器的编号及坐标如表1所示。结构的两端用夹具进行固支，由钢球自由下落来激发冲击事件，采用大连君晟科技有限公司研发的动态数据采集系统对传感器接收到的冲击响应信号进行采集，采样率为200 kHz。
表 1 传感器的位置坐标Table 1. Position coordinates of the sensorsNumber Coordinate/mm Number Coordinate/mm P1 (100, 50) P7 (500, 200) P2 (300, 50) P8 (700, 200) P3 (500, 50) P9 (100, 350) P4 (700, 50) P10 (300, 350) P5 (100, 200) P11 (500, 350) P6 (300, 200) P12 (700, 350) 2.2 冲击响应信号处理
在板上坐标为(300 mm, 275 mm)的位置进行冲击，采集得到的压电传感器P6的冲击响应信号如图5(a)所示，图5(b)为冲击响应信号的频谱。从频谱中可知冲击响应信号的能量主要集中在0~5 kHz这个区间范围内，大于5 kHz的信号能量非常小。对小波变换而言，频率越高，得到的信号时间分辨率越高。但对于Lamb波信号的模式而言，频率越高的信号，信号模态也越复杂。一般在100 kHz以下，Lamb波主要为A0和S0这两种模态，并且A0模态占主导地位[28]。综合考虑，利用小波变换从冲击响应信号中提取中心频率为5 kHz的窄带Lamb波信号，如图5(c)所示。在提取的窄带Lamb波中可以很明显地看到第一个直达波。此外，图5(c)还给出了根据希尔伯特变换计算得到的窄带Lamb波的包络信号，可以看出窄带Lamb波信号的包络在直达波的位置有明显的峰值。对窄带Lamb信号进行时间反转，如图5(d)所示，下面将利用时间反转信号在结构监测区域进行信号合成，利用包络特征进行虚拟时间反转聚焦成像。
![]()
图 5 (a) 冲击响应时域信号；(b) 冲击响应频谱；(c) 中心频率5 kHz的窄带Lamb波信号及其包络；(d) 时间反转信号及包络Figure 5. (a) Impact response time domain signal; (b) Impact response frequency spectrum; (c) Narrowband Lamb wave signal with center frequency of 5 kHz and its envelope; (d) Time reversal signal and envelope2.3 结果与讨论
按照图3的冲击定位流程，对发生在复合材料加筋板(300 mm, 275 mm)位置的冲击事件进行自适应时间反转聚焦冲击定位，其结果如图6所示。
![]()
图 6 复合材料加筋板冲击定位结果： (a) 不同群速度的虚拟时间反转成像结果；(b) 不同群速度对应的最大图像像素曲线；(c) 自适应时间反转聚焦图像Figure 6. Impact localization results of the stiffened composite plate: (a) Virtual time reversal imaging results corresponding to different group velocities; (b) The curve of different group velocity and their corresponding maximum image pixel values; (c) Adaptive time reversal focusing image图6(a)为不同群速度迭代计算的虚拟时间反转成像结果，可以看出不同群速度对应的虚拟时间反转成像结果聚焦程度不同。由自适应虚拟时间反转聚焦机制(见1.3节)可知，在真正的窄带Lamb波的群速度和冲击源位置条件下，合成信号包络幅值会发生最佳的聚焦效果，因此根据不同群速度对应的最大图像像素曲线(图6(b))，最大像素对应的虚拟时间反转成像结果即为自适应时间反转聚焦图像，如图6(c)所示。图中黑色的“×”表示实际冲击位置，红色的“×”表示预测的冲击位置，可以看到预测的冲击位置和实际的冲击位置十分吻合，从而验证了该方法的有效性。
为了验证本文算法在结构不同区域的冲击定位性能，在位置分别为(150 mm, 150 mm)、(400 mm, 50 mm)、(400 mm, 275 mm)和(600 mm, 270 mm)的4个位置重复自适应时间反转聚焦成像冲击定位流程，成像结果如图7所示。可以看出在不同位置，算法预测的冲击位置都与实际冲击位置吻合的较好，但在靠近边界处的冲击定位效果要稍差。这是由于冲击离边界较近时一些传感器接收到的直达波和边界反射波混叠在一起，造成信号相对比较复杂。
![]()
图 7 复合材料加筋板不同位置的冲击成像定位结果：(a) (150, 150)；(b) (400, 50)；(c) (400, 275)；(d) (650, 270)Figure 7. Impact localization results at different positions of the stiffened composite plate: (a) (150, 150); (b) (400, 50); (c) (400, 275); (d) (650, 270)为了进一步评估本文所提算法的定位精度，按下式定义冲击定位误差：
e = \sqrt {{{({x_{\text{p}}} - {x_{\text{r}}})}^2} + {{({y_{\text{p}}} - {y_{\text{r}}})}^2}} (24) 其中：xp和yp分别为预测冲击位置的横坐标和纵坐标；xr和yr分别为真实冲击位置的横坐标和纵坐标。
统计10次不同冲击位置的定位误差，冲击事件的实际位置与预测位置如表2所示。可以看到，所有冲击事件的定位误差均不超过3 cm，10次冲击事件的平均定位误差仅为1.02 cm。说明本文提出的基于自适应虚拟时间反转聚焦成像的算法具有很好的定位精度。
表 2 复合材料加筋板预测冲击位置与实际冲击位置比较Table 2. Comparison of predicted and actual impact positions of the stiffened composite plateNumber Actual impact position/mm Predicted impact position/mm Error/mm 1 (150, 150) (146, 160) 10.7 2 (150, 300) (148, 310) 10.2 3 (300, 275) (295, 270) 7.1 4 (400, 50) (402, 22) 28.1 5 (400, 275) (402, 280) 5.4 6 (500, 275) (506, 270) 7.8 7 (550, 300) (538, 310) 15.6 8 (600, 200) (590, 198) 10.2 9 (650, 270) (646, 266) 5.7 10 (700, 125) (714, 130) 14.9 图8是加筋面板上的冲击定位误差分布图，黑色的O表示实际冲击位置，红色的☆表示预测的冲击位置。对加筋板面板上的冲击定位误差分布进行分析可以发现，一般地，当冲击位于两根加强筋的内部误差一般较小，而对于加强筋外侧定位误差要稍大一些。这主要是由于加强筋对波传播存在影响，当冲击位于加强筋及加强筋外侧，过筋的传感器路径更多，从而影响冲击定位精度。
上述对单个冲击的冲击成像定位情况进行了讨论，对于多个冲击而言，绝对同时发生多个冲击的情况概率较低。下面进一步考虑时间间隔较短内发生的近似为同时发生的两点冲击。用两个小球同时对结构施加冲击，但由于人为操作的因素，无法实现两个冲击的绝对同时刻发生，图9为两点冲击传感器接收到的响应信号，从图中的信号看到两个冲击发生的时间间隔较短，约为5 ms。利用本文方法对两点冲击的成像定位结果如图10所示，定位误差如表3所示。根据冲击成像结果和统计的定位误差结果可以看出，本文方法能够对两点冲击进行成像定位，最大误差在3.5 cm左右。相对于单点冲击，两点冲击中后发生的冲击定位误差有所增加，主要是由于后发生的冲击响应信号与前面发生的冲击引起的边界反射信号有小部分混叠在一起，由此会引入了一定的误差。
![]()
图 8 复合材料加筋板冲击定位误差分布图Figure 8. Impact localization error distribution of the stiffened composite plate![]()
图 9 两个小球同时对复合材料加筋板冲击的响应信号Figure 9. Impact response signals of two balls on the stiffened composite plate at the same time![]()
图 10 复合材料加筋板两点冲击的成像定位结果：(a) (250, 150), (400, 275)；(b) (500, 125), (650, 270)Figure 10. Imaging localization results of two-point impact on the stiffened composite plate: (a) (250, 150), (400, 275); (b) (500, 125), (650, 270)表 3 复合材料加筋板两点冲击定位误差Table 3. Impact localization error of two-point impact on the stiffened composite plateNumber Actual impact position/mm Predicted impact position/mm Error/
mmFig. 10(a) Impact 1 (250, 150) (250, 160) 10.0 Impact 2 (400, 275) (390, 305) 31.6 Fig. 10(b) Impact 1 (500, 125) (490, 130) 11.2 Impact 2 (650, 270) (675, 245) 35.4 考虑到在实际情况中必然存在噪声因素的影响，因此有必要研究在噪声情况下算法的性能。在Matlab软件中给传感器信号施加20 dB的噪声，图11为增加噪声后的传感器信号。在噪声情况下，根据本文提出的算法得到上述4个冲击位置的自适应时间反转聚焦成像结果如图12所示。可以看到，在引入噪声后，定位成像分辨率仍然较好。
![]()
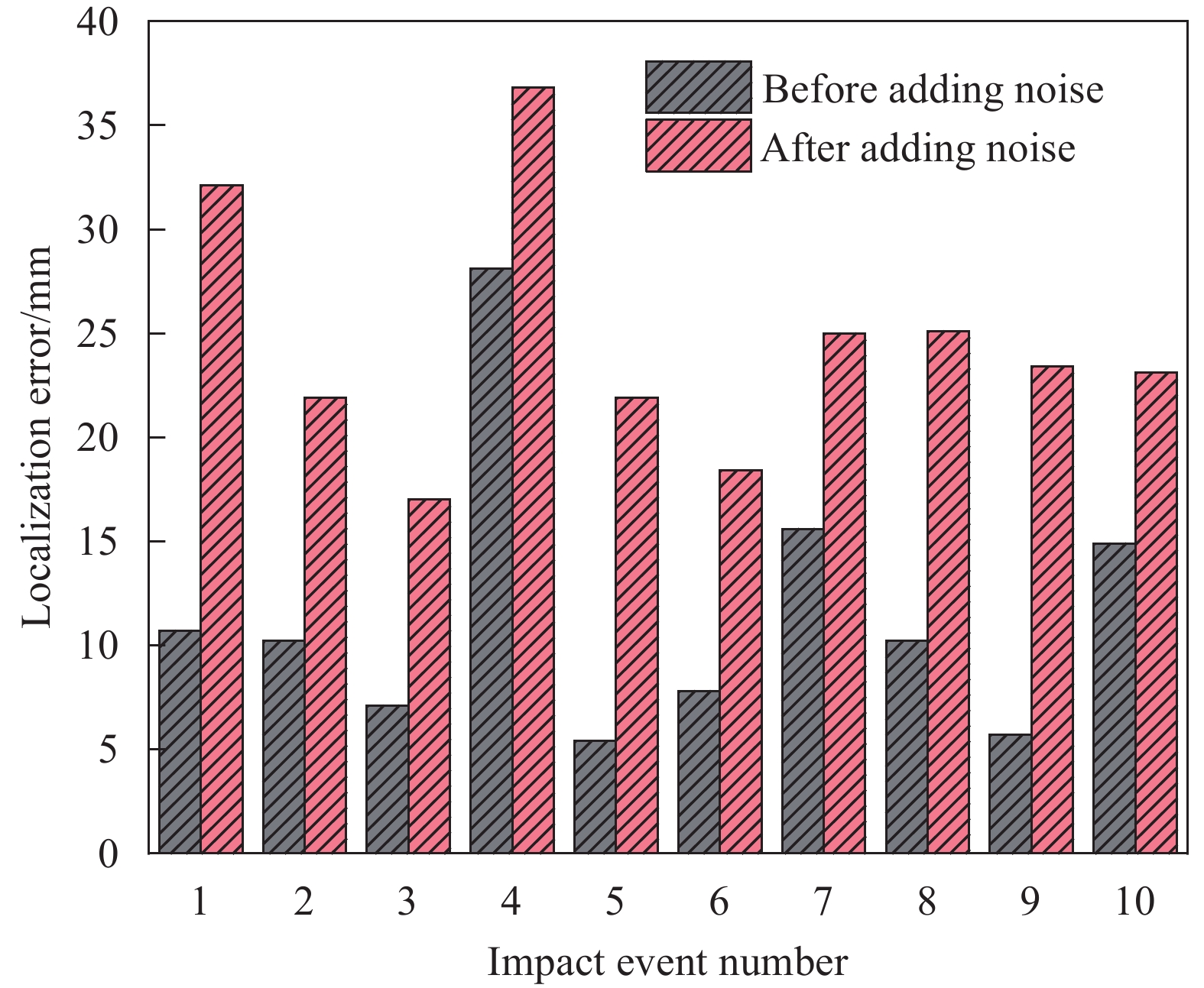
图 12 噪声情况下复合材料加筋板不同位置冲击成像定位结果：(a) (150, 150)；(b) (400, 50)；(c) (400, 275)；(d) (650, 270)Figure 12. Impact localization results of different positions on the stiffened composite plate under noise conditions: (a) (150, 150); (b) (400, 50); (c) (400, 275); (d) (650, 270)对10次冲击事件的预测冲击位置与实际冲击位置比较如表4所示，平均定位误差为2.39 cm。图13是施加噪声前后冲击定位误差的对比。总体而言，施加噪声后，本文提出的冲击定位算法的定位误差有所增加，但依然拥有较好的定位精度和成像分辨率，这非常有益于实际工程应用。
此外，在实际情况应用中由于一些不可预测的因素，参与定位的有效传感器数量会减少。还有必要研究减少传感器数量情况下算法的性能。减少1/3的传感器数量后，根据本文提出的算法得到上述4个冲击位置的冲击成像结果如图14所示。可以看到，减少传感器数量后，本文所提出算法的总体冲击定位精度虽然有所降低，但对监测区域内部的冲击事件仍然具有较高的定位精度，只是对靠近边界位置的冲击事件的定位精度下降比较明显。
表 4 考虑噪声情况下复合材料加筋板预测冲击位置与实际冲击位置比较Table 4. Comparison between predicted and actual impact position of the stiffened composite plate under noise conditionsNumber Actual impact position/mm Predicted impact position/mm Error/mm 1 (150, 150) (182, 148) 32.1 2 (150, 300) (141, 320) 21.9 3 (300, 275) (287, 264) 17.0 4 (400, 50) (366, 36) 36.8 5 (400, 275) (384, 290) 21.9 6 (500, 275) (513, 262) 18.4 7 (550, 300) (530, 315) 25.0 8 (600, 200) (577, 190) 25.1 9 (650, 270) (628, 262) 23.4 10 (700, 125) (722, 118) 23.1 ![]()
图 13 施加噪声前后复合材料加筋板冲击定位误差对比Figure 13. Comparison of impact localization error of the stiffened composite plate before and after adding noise![]()
图 14 减少传感器数量后复合材料加筋板冲击定位结果：(a) (150, 150)；(b) (400, 50)；(c) (400, 275)；(d) (650, 270)Figure 14. Impact localization results of the stiffened composite plate after reducing the number of sensors: (a) (150, 150); (b) (400, 50); (c) (400, 275); (d) (650, 270)减少传感器数量后，基于本文算法对10次冲击事件的预测冲击位置与实际冲击位置对比如表5所示。可以看到，对于大部分冲击事件的定位误差都不超过3 cm，平均定位误差为1.9 cm。图15是本文算法减少传感器数量前后冲击定位误差的对比。总的来说，传感器数量减少后，本文提出的冲击定位算法的定位误差有所增加，但依然拥有较好的精度和成像分辨率。
冲击监测技术在实际运用中还要面临温度变化环境的影响。因此还需要在不同温度环境下对算法的性能进行评估。通过在板的两侧使用两个卤素灯照射来增加结构的温度。图16为升温前后相同冲击下传感器的响应信号。可以看到，温度变化引起冲击响应信号的振幅和相位发生了变化。图17为本文方法与传统虚拟时间反转方法[25]在温度变化环境下的相同冲击位置的成像定位对比结果。可以看出，温度变化下本文方法相比于传统方法冲击成像定位精度更高，能够更加适应于温度变化环境。
表 5 减少传感器数量后复合材料加筋板预测冲击位置与实际冲击位置比较Table 5. Comparison between predicted and actual impact position of the stiffened composite plate after reducing the number of sensorsNumber Actual impact position/mm Predicted impact position/mm Error/mm 1 (150, 150) (135, 155) 15.8 2 (150, 300) (140, 310) 14.1 3 (300, 275) (290, 265) 14.1 4 (400, 50) (395, 90) 40.3 5 (400, 275) (410, 270) 11.1 6 (500, 275) (515, 260) 18.0 7 (550, 300) (545, 325) 25.5 8 (600, 200) (615, 200) 15.0 9 (650, 270) (660, 282) 15.6 10 (700, 125) (740, 120) 40.3 ![]()
图 15 减少传感器数量前后复合材料加筋板冲击定位误差对比Figure 15. Comparison of impact localization error of the stiffened composite plate before and after reducing the number of sensors![]()
图 16 不同温度下复合材料加筋板的冲击响应信号Figure 16. Imapct response signals of the stiffened composite plate at different temperatures3. 结 论
(1) 本文提出的基于自适应虚拟时间反转聚焦的冲击定位方法，适用于各向异性不强的含加强筋的复合材料板结构，无需测量波速，也无需结构的先验知识，实施过程简单，有助于复合材料结构冲击监测技术的工程应用。
(2) 采用连续小波变换可以提取特定中心频率的窄带Lamb波信号，使用窄带Lamb波信号在监测区域内进行信号合成，利用合成信号的包络特征可以进行虚拟时间反转成像。
![]()
图 17 不同温度下复合材料加筋板冲击成像定位结果：(a) 本文方法25℃；(b) 本文方法55℃；(c) 传统方法25℃；(d) 传统方法55℃Figure 17. Impact localization results of the stiffened composite plate at different temperatures: (a) Proposed method at 25℃; (b) Proposed method at 55℃; (c) Traditional method at 25℃; (d) Traditional method at 55℃(3) 在总体尺寸为800 mm×400 mm (长×宽)的加筋编织复合材料板上验证了本文所提出算法的有效性，对10个不同冲击位置的平均定位误差仅为1.02 cm。此外，可以对两个冲击源进行定位。
(4) 减少传感器数量或引入噪声后，本文所提出算法的冲击定位误差有所增大，但仍然拥有可观的定位精度和成像分辨率。在温度变化环境下具有自适应性，成像定位精度优于传统方法。
(5) 在后续研究中将考虑利用时间反转聚焦原理对结构的冲击载荷重构方法进行研究。
-
![]()
图 1 时间反转聚焦原理示意图
Figure 1. Schematic diagram of time reversal focusing principle
PZTi—Sensor number; Hi—Transfer function of impact signal from impact source to sensor PZTi; HTR-i—Transfer function of time reversal signal from sensor PZTi to the impact source
![]()
图 2 冲击定位方法示意图
Figure 2. Schematic diagram of the impact localization method
Li—Distance from the assumed impact source to sensor PZTi
![]()
图 3 冲击定位算法流程图
Figure 3. Flow chart of impact localization algorithm
k—Iteration step number; Cg—Group velocity; Cg min and Cg max—Minimum and maximum values of the iteration group velocity; ΔCg—Iteration step size; (x, y)—Coordinates of the pixel point assumed to be the position of the impact source; (Sxi, Syi)—Coordinates of the sensor PZTi ; Vi—Narrowband Lamb wave signal of the impact signal; P(t)—Synthesized signal at the pixel poin; "~" indicates that the signal is taken as an envelope; \mathop {{C_{\rm{g}}}}\limits^ \wedge —Determined group velocity of the narrowband Lamb; \hat{I}(x, y)—Adaptive time reversal focusing image
![]()
图 5 (a) 冲击响应时域信号；(b) 冲击响应频谱；(c) 中心频率5 kHz的窄带Lamb波信号及其包络；(d) 时间反转信号及包络
Figure 5. (a) Impact response time domain signal; (b) Impact response frequency spectrum; (c) Narrowband Lamb wave signal with center frequency of 5 kHz and its envelope; (d) Time reversal signal and envelope
![]()
图 6 复合材料加筋板冲击定位结果： (a) 不同群速度的虚拟时间反转成像结果；(b) 不同群速度对应的最大图像像素曲线；(c) 自适应时间反转聚焦图像
Figure 6. Impact localization results of the stiffened composite plate: (a) Virtual time reversal imaging results corresponding to different group velocities; (b) The curve of different group velocity and their corresponding maximum image pixel values; (c) Adaptive time reversal focusing image
![]()
图 7 复合材料加筋板不同位置的冲击成像定位结果：(a) (150, 150)；(b) (400, 50)；(c) (400, 275)；(d) (650, 270)
Figure 7. Impact localization results at different positions of the stiffened composite plate: (a) (150, 150); (b) (400, 50); (c) (400, 275); (d) (650, 270)
![]()
图 8 复合材料加筋板冲击定位误差分布图
Figure 8. Impact localization error distribution of the stiffened composite plate
![]()
图 9 两个小球同时对复合材料加筋板冲击的响应信号
Figure 9. Impact response signals of two balls on the stiffened composite plate at the same time
![]()
图 10 复合材料加筋板两点冲击的成像定位结果：(a) (250, 150), (400, 275)；(b) (500, 125), (650, 270)
Figure 10. Imaging localization results of two-point impact on the stiffened composite plate: (a) (250, 150), (400, 275); (b) (500, 125), (650, 270)
![]()
图 12 噪声情况下复合材料加筋板不同位置冲击成像定位结果：(a) (150, 150)；(b) (400, 50)；(c) (400, 275)；(d) (650, 270)
Figure 12. Impact localization results of different positions on the stiffened composite plate under noise conditions: (a) (150, 150); (b) (400, 50); (c) (400, 275); (d) (650, 270)
![]()
图 13 施加噪声前后复合材料加筋板冲击定位误差对比
Figure 13. Comparison of impact localization error of the stiffened composite plate before and after adding noise
![]()
图 14 减少传感器数量后复合材料加筋板冲击定位结果：(a) (150, 150)；(b) (400, 50)；(c) (400, 275)；(d) (650, 270)
Figure 14. Impact localization results of the stiffened composite plate after reducing the number of sensors: (a) (150, 150); (b) (400, 50); (c) (400, 275); (d) (650, 270)
![]()
图 15 减少传感器数量前后复合材料加筋板冲击定位误差对比
Figure 15. Comparison of impact localization error of the stiffened composite plate before and after reducing the number of sensors
![]()
图 16 不同温度下复合材料加筋板的冲击响应信号
Figure 16. Imapct response signals of the stiffened composite plate at different temperatures
![]()
图 17 不同温度下复合材料加筋板冲击成像定位结果：(a) 本文方法25℃；(b) 本文方法55℃；(c) 传统方法25℃；(d) 传统方法55℃
Figure 17. Impact localization results of the stiffened composite plate at different temperatures: (a) Proposed method at 25℃; (b) Proposed method at 55℃; (c) Traditional method at 25℃; (d) Traditional method at 55℃
表 1 传感器的位置坐标
Table 1 Position coordinates of the sensors
Number Coordinate/mm Number Coordinate/mm P1 (100, 50) P7 (500, 200) P2 (300, 50) P8 (700, 200) P3 (500, 50) P9 (100, 350) P4 (700, 50) P10 (300, 350) P5 (100, 200) P11 (500, 350) P6 (300, 200) P12 (700, 350) 
下载: 导出CSV
表 2 复合材料加筋板预测冲击位置与实际冲击位置比较
Table 2 Comparison of predicted and actual impact positions of the stiffened composite plate
Number Actual impact position/mm Predicted impact position/mm Error/mm 1 (150, 150) (146, 160) 10.7 2 (150, 300) (148, 310) 10.2 3 (300, 275) (295, 270) 7.1 4 (400, 50) (402, 22) 28.1 5 (400, 275) (402, 280) 5.4 6 (500, 275) (506, 270) 7.8 7 (550, 300) (538, 310) 15.6 8 (600, 200) (590, 198) 10.2 9 (650, 270) (646, 266) 5.7 10 (700, 125) (714, 130) 14.9
下载: 导出CSV
表 3 复合材料加筋板两点冲击定位误差
Table 3 Impact localization error of two-point impact on the stiffened composite plate
Number Actual impact position/mm Predicted impact position/mm Error/
mmFig. 10(a) Impact 1 (250, 150) (250, 160) 10.0 Impact 2 (400, 275) (390, 305) 31.6 Fig. 10(b) Impact 1 (500, 125) (490, 130) 11.2 Impact 2 (650, 270) (675, 245) 35.4
下载: 导出CSV
表 4 考虑噪声情况下复合材料加筋板预测冲击位置与实际冲击位置比较
Table 4 Comparison between predicted and actual impact position of the stiffened composite plate under noise conditions
Number Actual impact position/mm Predicted impact position/mm Error/mm 1 (150, 150) (182, 148) 32.1 2 (150, 300) (141, 320) 21.9 3 (300, 275) (287, 264) 17.0 4 (400, 50) (366, 36) 36.8 5 (400, 275) (384, 290) 21.9 6 (500, 275) (513, 262) 18.4 7 (550, 300) (530, 315) 25.0 8 (600, 200) (577, 190) 25.1 9 (650, 270) (628, 262) 23.4 10 (700, 125) (722, 118) 23.1
下载: 导出CSV
表 5 减少传感器数量后复合材料加筋板预测冲击位置与实际冲击位置比较
Table 5 Comparison between predicted and actual impact position of the stiffened composite plate after reducing the number of sensors
Number Actual impact position/mm Predicted impact position/mm Error/mm 1 (150, 150) (135, 155) 15.8 2 (150, 300) (140, 310) 14.1 3 (300, 275) (290, 265) 14.1 4 (400, 50) (395, 90) 40.3 5 (400, 275) (410, 270) 11.1 6 (500, 275) (515, 260) 18.0 7 (550, 300) (545, 325) 25.5 8 (600, 200) (615, 200) 15.0 9 (650, 270) (660, 282) 15.6 10 (700, 125) (740, 120) 40.3
下载: 导出CSV
-
[1] 杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1):1-12. DU Shanyi. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica,2007,24(1):1-12(in Chinese).
[2] 鲍益东, 何瑞, 宋云鹤, 等. 二维编织碳纤维增强树脂复合材料一步法铺层展开[J]. 复合材料学报, 2022, 39(7):3144-3155. BAO Yidong, HE Rui, SONG Yunhe, et al. One-step spreading for 2D woven carbon fiber reinforced plastics[J]. Acta Materiae Compositae Sinica,2022,39(7):3144-3155(in Chinese).
[3] SIKDAR S, KUDELA P, RADZIENSKI M, et al. Online detection of barely visible low-speed impact damage in 3D-core sandwich composite structure[J]. Composite Structures,2018,185:646-655. DOI: 10.1016/j.compstruct.2017.11.067
[4] DIAMANTI K, SOUTIS C. Structural health monitoring techniques for aircraft composite structures[J]. Progress in Aerospace Sciences,2010,46(8):342-352. DOI: 10.1016/j.paerosci.2010.05.001
[5] SIKDAR S, MIRGAL P, BANERJEE S. Low-velocity impact source localization in a composite sandwich structure using a broadband piezoelectric sensor network[J]. Composite Structures,2022,291:115619. DOI: 10.1016/j.compstruct.2022.115619
[6] KIRKBY E, OLIVEIRA R, MICHAUD V, et al. Impact localisation with FBG for a self-healing carbon fibre composite structure[J]. Composite Structures,2011,94(1):8-14. DOI: 10.1016/j.compstruct.2011.07.030
[7] GOUTAUDIER D, OSMOND G, GENDRE D. Impact localization on a composite fuselage with a sparse network of accelerometers[J]. Comptes Rendus Mecanique,2020,348:191-209. DOI: 10.5802/crmeca.12
[8] SIMONE M E, CIAMPA F, BOCCARDI S, et al. Impact source localisation in aerospace composite structures[J]. Smart Materials and Structures,2017,26(12):125026. DOI: 10.1088/1361-665X/aa973e
[9] COLES A, CASTRO B A, ANDREADES C, et al. Impact localization in composites using time reversal, embedded PZT transducers, and topological algorithms[J]. Frontiers in Built Environment,2020,6:27. DOI: 10.3389/fbuil.2020.00027
[10] SHRESTHA P, KIM J H, PARK Y, et al. Impact localization on composite wing using 1D array FBG sensor and RMS/correlation based reference database algorithm[J]. Composite Structures,2015,125:159-169. DOI: 10.1016/j.compstruct.2015.01.029
[11] DIPIETRANGELO F, NICASSIO F, SCARSELLI G. Structural health monitoring for impact localisation via machine learning[J]. Mechanical Systems and Signal Processing,2023,183:109621. DOI: 10.1016/j.ymssp.2022.109621
[12] TOBIAS A. Acoustic-emission source location in two dimensions by an array of three sensors[J]. Non-Destructive Testing,1976,9(1):9-12. DOI: 10.1016/0029-1021(76)90027-X
[13] CIAMPA F, MEO M. Acoustic emission source localization and velocity determination of the fundamental mode A0 using wavelet analysis and a newton-based optimization technique[J]. Smart Materials and Structures,2010,19(4):045027. DOI: 10.1088/0964-1726/19/4/045027
[14] GORGIN R, WANG Z, WU Z, et al. Probability based impact localization in plate structures using an error index[J]. Mechanical Systems and Signal Processing,2021,157:107724. DOI: 10.1016/j.ymssp.2021.107724
[15] MARINO M, ANDREA B, PIETRO G, et al. A novel differential time-of-arrival estimation technique for impact localization on carbon fiber laminate sheets[J]. Sensors,2017,17(10):2270. DOI: 10.3390/s17102270
[16] QIU L, YUAN S, ZHANG X, et al. A time reversal focusing based impact imaging method and its evaluation on complex composite structures[J]. Smart Materials and Structures,2011,20(10):105014. DOI: 10.1088/0964-1726/20/10/105014
[17] MINIACI M, MAZZOTTI M, RADZIEŃSKI M, et al. Application of a laser-based time reversal algorithm for impact localization in a stiffened aluminum plate[J]. Frontiers in Materials,2019,6:30. DOI: 10.3389/fmats.2019.00030
[18] KIM M G, KIM S W. Impact localization for composite plate using the modified error-outlier algorithm with Pugh's concept selection under various temperatures[J]. Compo-site Structures,2021,272:114226. DOI: 10.1016/j.compstruct.2021.114226
[19] WU Z, XU L, WANG Y, et al. Impact energy identification on a composite plate using basis vectors[J]. Smart Materials and Structures,2015,24(9):095007. DOI: 10.1088/0964-1726/24/9/095007
[20] MASERAS-GUTIERREZ M A, STASZEWSKI W J, FOUND M S, et al. Detection of impacts in composite materials using piezoceramic sensors and neural networks[J]. Smart Structures,1998,3329:491-497.
[21] LIU Q, WANG F, LI J, et al. A hybrid support vector regression with multi-domain features for low-velocity impact localization on composite plate structure[J]. Mechanical Systems and Signal Processing,2021,154:107547. DOI: 10.1016/j.ymssp.2020.107547
[22] YAN G. A bayesian approach for damage localization in plate-like structures using Lamb waves[J]. Smart Materials & Structures,2013,22(3):035012.
[23] CIAMPA F, MEO M, BARBIERI E. Impact localization in composite structures of arbitrary cross section[J]. Structural Health Monitoring—An International Journal,2012,11(6):643-655. DOI: 10.1177/1475921712451951
[24] GIURGIUTIU V, SANTONI-BOTTAI G. Structural health monitoring of composite structures with piezoelectric-wafer active sensors[J]. AIAA Journal,2011,49(3):565-581. DOI: 10.2514/1.J050641
[25] WANG S, WANG H, WANG D, et al. AE source localization and imaging on cylindrical shell structures based on six-AE-sensor monitoring network and VTR focusing imaging[J]. Nondestructive Testing and Evaluation,2021,36(1):35-61. DOI: 10.1080/10589759.2019.1692012
[26] CHEN C, YUAN F. Impact source identification in finite isotropic plates using a time-reversal method: Theoretical study[J]. Smart Materials & Structures,2010,19(10):105028.
[27] YANG Z, YANG L, ZHANG J, et al. Damage shape recognition algorithm of composite woven fabric plate based on guided waves[J]. Composite Structures, 2023, 303: 116351.
[28] 胡宁, 刘瑶璐, 赵友选, 等. 基于低频动态信息和超声导波的复杂结构损伤的在线诊断技术[J]. 固体力学学报, 2017, 38(4):312-347. HU Ning, LIU Yaolu, ZHAO Youxuan, et al. On-line monitoring technologies for complex structural damage identification based on low-frequency structural dynamic signals and ultrasonic guided waves[J]. Chinese Journal of Solid Mechanics,2017,38(4):312-347(in Chinese).
-
期刊类型引用(2)
1. 田童，李建乐，邓德双，曾旭，林奎旭，董珊珊，杨雷，徐浩，杨正岩，武湛君. 飞行器结构健康监测技术研究进展. 航空制造技术. 2024(13): 41-67+98 . 
百度学术
2. 曾旭，邓德双，杨红娟，杨正岩，马书义，杨雷，武湛君. 航空结构低速冲击监测技术研究进展. 航空学报. 2024(23): 100-127 . 百度学术
其他类型引用(0)
-
目的
复合材料结构在航空航天、海洋工程和轨道交通等领域中占有重要地位。但由于复合材料在抗冲击性能方面存在缺陷，实时在线的冲击监测技术越来越受到关注。本文提出了基于自适应时间反转聚焦的加筋复材板冲击定位方法。
方法首先，利用结构表面布置的压电传感器网络接收冲击响应信号；然后，利用连续小波变换提取冲击响应信号的窄带Lamb波信号，使用窄带Lamb波信号的包络特征，根据时间反转聚焦原理对窄带Lamb波信号进行时间反转，以合成信号的包络幅值最大值作为网格点的像素，构建以冲击位置坐标和窄带Lamb波群速度为变量的虚拟时间反转成像函数。最后，迭代计算不同群速度下对应的虚拟时间反转成像结果，根据不同群速度对应的图像最大像素曲线获得自适应时间反转聚焦图像，从而实现冲击定位。利用尺寸为800 mm × 400 mm(长×宽)的加筋编织复材板进行落球冲击实验，验证该方法的有效性。并探究了在多源冲击、噪声环境、减少传感器数量以及不同温度的情况下本文方法的有效性。
结果采用本文的方法在总体尺寸为800 mm × 400 mm(长×宽)的加筋编织复合材料板上进行冲击实验，从不同群速度迭代计算的虚拟时间反转成像结果，可以看出不同群速度对应的虚拟时间反转成像结果聚焦程度不同。所有冲击事件的定位误差均不超过3 cm，10次冲击事件的平均定位误差仅为1.02 cm。此外，本文方法能够对两点冲击进行成像定位，最大误差在3.5 cm左右。相对于单点冲击，两点冲击中，相对时间后发生的冲击定位误差有所增加，主要是由于后发生的冲击响应信号与前面发生的冲击引起的边界反射信号有小部分混叠在一起，由此会引入了一定的误差。研究了减少传感器数量和引入噪声的条件下本文方法的定位效果。在减少1/3的传感器数量后，对于大部分冲击事件的定位误差都不超过3 cm，平均定位误差为1.9 cm。在引入噪声后，定位成像分辨率仍然较好，对10次冲击事件的平均定位误差为2.39 cm。比较了在不同温度环境下对算法的自适应性能，温度变化下本文方法相比于传统方法冲击成像定位精度更高，能够更加适应于温度变化环境。
结论本文提出的基于自适应虚拟时间反转聚焦的冲击定位方法，适用于各向异性不强的含加强筋的复合材料板结构，无需测量波速，也无需结构的先验知识，实施过程简单，有助于复合材料结构冲击监测技术的工程应用。减少传感器数量或引入噪声后，本文所提出算法的冲击定位误差有所增大，但仍然拥有可观的定位精度和成像分辨率。在温度变化环境下具有自适应性，成像定位精度优于传统方法。在后续研究中将考虑利用时间反转聚焦原理对结构的冲击载荷重构方法进行研究。
-
复合材料因其比强度高、比刚度大，可设计性强等优点，被广泛应用于航空航天、船舶海洋和轨道交通等工程领域。然而，复合材料结构在制造、运输和服役过程中不可避免地受到低速冲击载荷的作用，可能产生目不可见的“内伤”(包括基体开裂、分层和纤维断裂等)，严重威胁结构的健康安全。冲击监测技术可以实时在线地监测复合材料结构的冲击事件，对于复合材料结构的健康安全维护具有重要意义，因此受到广泛关注。
本文提出一种基于自适应时间反转聚焦的加筋复材板冲击定位方法，根据时间反转聚焦原理构建以冲击位置和窄带Lamb波群速度为变量的虚拟时间反转成像函数，迭代计算不同群速度下对应的虚拟时间反转成像结果，根据不同群速度对应的图像最大像素曲线获得自适应时间反转聚焦图像，从而实现冲击定位。该算法具有以下优点：(a) 无需知道结构的波速分布和先验知识，也无需建立数据库，实施过程简单；(b) 对加筋复材板具有很好的冲击成像分辨率和冲击定位精度；(c) 减少传感器数量，在低信噪比情况及变温度环境下依然拥有可观的冲击定位精度。
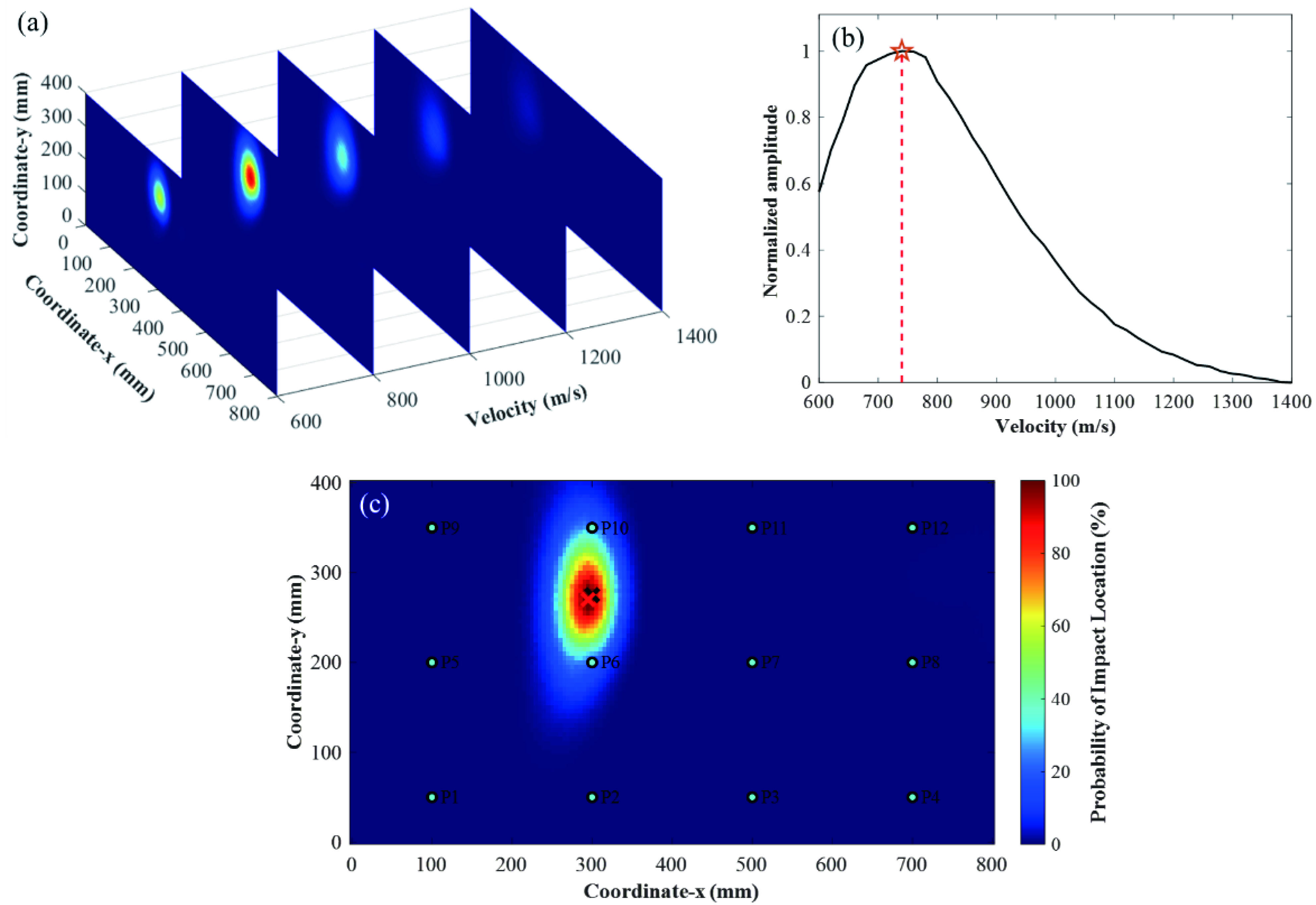
(a) 不同群速度迭代计算的虚拟时间反转成像结果； (b) 不同群速度对应的最大图像像素曲线； (c) 自适应时间反转聚焦成像冲击定位结果
计量
- 文章访问数: 665
- HTML全文浏览量: 234
- PDF下载量: 54
- 被引次数: 2
