CFRP薄壁结构多尺度建模及耐撞性分析

朱国华; 竺森森; 胡珀; 王振; 赵轩

doi:10.13801/j.cnki.fhclxb.20220720.002

CFRP薄壁结构多尺度建模及耐撞性分析

长安大学　汽车学院，西安 710064

基金项目: 国家重点研发计划(2021 YFB2501705)；国家自然科学基金 (51905042)；长安大学中央高校基础研究基金 (300102221201)National Key R&D Program of China (2021YFB2501705); National Natural Science Foundation of China (51905042); The Fundamental Research Funds for the Central Universities, CHD (300102221201)

详细信息

通讯作者:
朱国华，博士，副教授，硕士生导师，研究方向为汽车轻量化　 E-mail: guohuazhu@chd.edu.cn

中图分类号: TB332
计量
- 文章访问数: 1067
- HTML全文浏览量: 726
- PDF下载量: 148
出版历程
- 收稿日期: 2022-06-06
- 修回日期: 2022-06-22
- 录用日期: 2022-07-06
- 网络出版日期: 2022-07-21
- 刊出日期: 2023-06-14

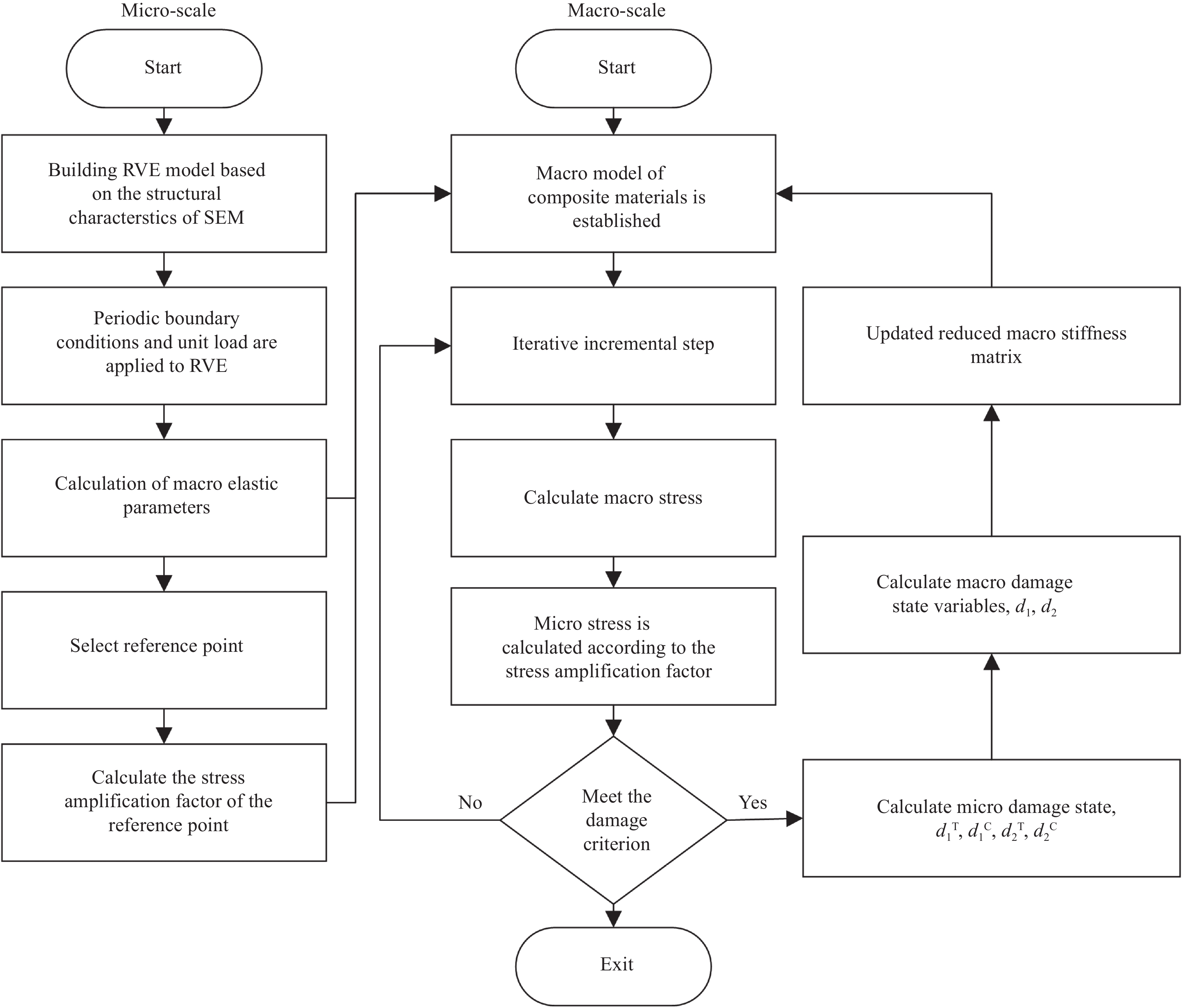
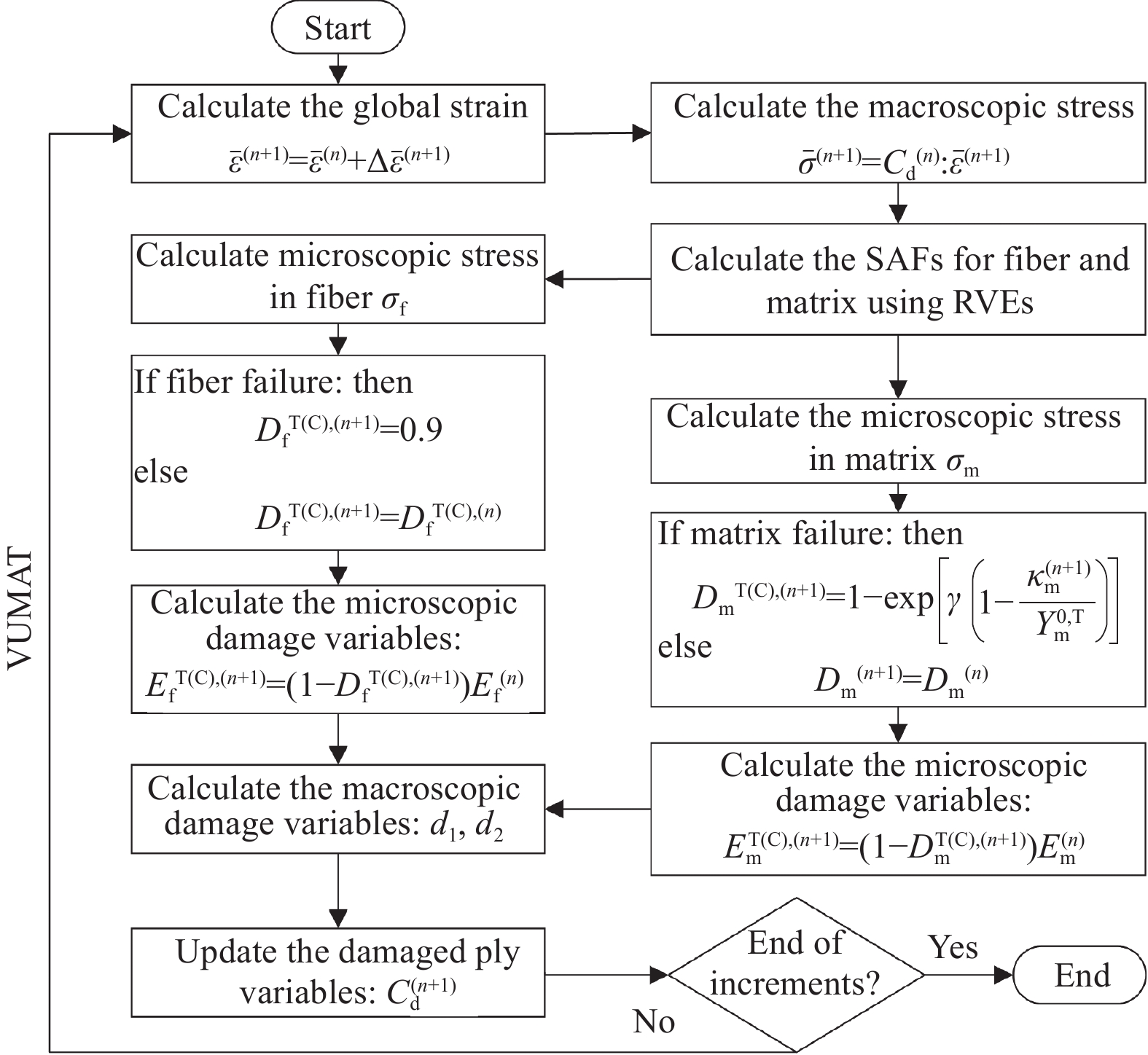
Multi-scale modeling and crashworthiness analysis of CFRP thin-walled structures

School of Automobile, Chang'an University, Xi'an 710064, China

HTML全文

摘要

摘要: 碳纤维增强树脂基复合材料(CFRP)具有较高的比强度、比刚度及显著的轻量化效果，因此CFRP薄壁结构被作为能量吸收装置广泛应用于工程领域。以单向碳纤维复合材料为研究对象，利用扫描电镜获取其微观胞元结构参数及纤维体积分数，构建能够准确反映其微观形态的代表性体积单元(Representative volume element，RVE)，通过加载周期性边界条件及单位载荷，获取材料宏观等效弹性参数，并开展实验验证。随后，开发基于微观力学的失效准则及损伤演化方程，并结合材料力学特点，构建CFRP宏观损伤模型，最终形成一套基于微观失效的多尺度损伤模型。在此基础上，对CFRP薄壁圆管在轴向准静态载荷下的压溃性能进行数值仿真，并与实验结果进行对比，验证了多尺度模型的仿真精度。最后，基于验证后的多尺度有限元模型，研究了碳纤维铺层角度及碳纤维体积分数对CFRP薄壁结构耐撞性的影响。结果表明：铺层角度和碳纤维体积分数对CFRP圆管耐撞性能具有较大影响。
- 碳纤维增强树脂基复合材料 /
- 耐撞性 /
- 多尺度分析 /
- 多尺度损伤模型 /
- 微观失效准则
Abstract: Carbon fiber reinforced plastics (CFRP) are of high specific strength, specific stiffness and significant lightweight effect. Therefore, CFRP thin-walled structures are widely used as energy-absorbing devices in engineering fields. This paper took unidirectional CFRP as research object. The micro-scale structural parameters and fiber volume fraction were obtained by using scanning electron microscope. Then, a representative volume element (RVE) was established, which was capable to accurately reflect its micro morphology. By applying periodic boundary conditions and unit load, the macro equivalent elastic parameters were acquired and then verified by experimental tests. Subsequently, the failure criterion and damage evolution equation based on micromechanics were developed. Combined with the mechanical characteristics of unidirectional CFRP, the macro damage model was developed, and finally forming a set of multi-scale damage model based on micro failure. On this basis, the crashworthiness performance of CFRP thin-walled circular tube under axial quasi-static load was numerically explored, and the numerical results were verified through the crushing test. Based on the verified multi-scale finite element model, the effects of carbon fiber ply angle and carbon fiber volume fraction on the crashworthiness were investi-gated. The results show that the ply angle and carbon fiber volume fraction have great impact on the crashworthiness characteristics of CFRP thin-walled structures.
- carbon fiber reinforced plastics /
- crashworthiness /
- multi-scale analysis /
- multi-scale damage model /
- micromechanics of failure

HTML全文

世界环境污染问题日趋严重，其中有机废水污染对人类健康和环境构成了极大的威胁^[1-2]。光催化技术作为一种高效、安全的环境友好型净化技术，被广泛应用于降解环境中的有机污染物，具有广阔的应用前景^[3-6]。

TiO₂是众多光催化材料中最具有潜力的，因其无毒、稳定、廉价、可循环利用等优点而得到广泛的研究和商业应用^[7-9]，但是TiO₂存在低表面积、禁带宽、电子空穴对复合率高、光吸收能力低等问题限制了它的光催化性能^[10-11]。为此，研究者们提出了多种方法来提高TiO₂的光催化性能，如贵金属掺杂^[12]、非金属元素掺杂^[13-14]、稀土或过渡金属掺杂、构建异质结等^[15-16]。结果表明，经复合改性后的TiO₂催化效率均有不同程度的提高^[17]。但是，制备一种禁带宽度小、光吸收范围大、光生电子还原能力强的基于TiO₂的光催化复合材料仍然是一个关键挑战^[18]。在众多改性方法中，构建异质结是较有效的方法^[19]。相比于成本较高的贵金属等催化材料，碳材料具有特殊的结构和形态，而在不同结构的碳材料中，空心碳球(HCS)为独特的中空结构^[20]，具有比表面积大、亲水性好、化学稳定性高、热稳定性高、密度低等特点^[21]。

本文基于HCS与TiO₂两者之间可以通过氢键和范德华力，形成HCS@TiO₂范德华异质结，HCS作为导电基板的引入，提高了光生电子对从TiO₂中的分离效率^[22]，高比表面积和良好的亲水性增大了TiO₂与染料的接触面积^[23]及对染料颗粒的吸附性能，使染料被高效地光催化降解，同时具有优异的重复使用性和广谱性，为光催化降解有机染料的复合材料的设计和制备提供了一条新的途径。通过简单的湿化学法制备了HCS@TiO₂光催化复合材料，探索了在模拟太阳光下光催化降解活性红195 (RR195)的光催化性能。通过SEM、TEM、XRD、XPS、TG、N₂吸附-脱附曲线、接触角测试对其进行形貌与结构的表征；通过紫外-可见吸收光谱(UV-Vis DRS)、Mott-Schottky测试分析其光学特性；通过UV-Vis DRS、电化学阻抗谱(EIS)测试、瞬态光电流响应图和循环降解试验分析其光催化降解性能，同时对HCS@TiO₂光催化复合材料的光催化机制进行了探究，结合自由基捕获实验、电子顺磁共振波谱(ESR)表征的方法提出了HCS@TiO₂光催化复合材料的光催化降解机制。

1. 实验材料及方法

1.1 原材料

活性红195，工业级，浙江龙盛化工研究有限公司；乙酰丙酮钛、吡咯、过硫酸铵、硝酸、氢氧化钠、硫酸、无水乙醇，分析纯，均购自国药集团化学试剂有限公司。

1.2 HCS@TiO₂复合材料的合成

HCS的制备：采用乳液聚合法^[24]合成了聚苯乙烯(PS)纳米球。PS母液(1 mg·mL⁻¹，2 mL)作为模板，分散在去离子水(100 mL)中，搅拌10 min，然后，向溶液中加入吡咯单体(0.2 mL)的同时逐滴添加过硫酸铵(0.13 g，30 mL)，反应4 h，将沉淀物过滤并用水和乙醇洗涤数次，所得产物记为PS@聚吡咯(PPy)。最后，将PS@PPy在5℃·min⁻¹的加热速率下从20℃碳化至850℃，并在氩气(Ar)流下保持2 h，得到HCS。

HCS的酸化处理：将制备的HCS加入体积比为1∶3的H₂SO₄/HNO₃混合物中，在60℃下搅拌24 h。然后过滤沉淀用水和乙醇洗涤数次，直至pH值达到7.0。接着在70℃下真空干燥酸化的HCS。

HCS@TiO₂复合材料的制备：将HCS (5 mg)加入到无水乙醇(4 mL)和去离子水(1 mL)的混合物中。在超声波作用下持续振荡0.5 h至形成黑色悬浮液。然后，在HCS悬浮液中加入乙酰丙酮钛(50 mg)，搅拌24 h，去除残留溶剂；所得产物记为HCS@二氧化钛前驱体(TOAC)。然后，将一定数量的HCS@TOAC (质量比1∶10)在空气气流下以350℃碳化1 h，然后在Ar气流下以5℃·min⁻¹的加热速率加热至650℃，保温2 h。冷却至室温后，经后处理得到HCS@TiO₂。采用不同煅烧温度(250℃、300℃、350℃、550℃、650℃)可制备不同煅烧温度下的HCS@TiO₂复合材料。图1为HCS@TiO₂复合材料的合成示意图。

图 1 空心碳球(HCS)@TiO₂的合成示意图

PPy—Polypyrrole; TOAC—Titanium oxide precursor

Figure 1. Composite diagram of hollow carbon sphere (HCS)@TiO₂

下载: 全尺寸图片幻灯片

1.3 样品表征

采用Gemini 300扫描电镜(德国蔡司)、Tecnai G2F20 200 kV场发射透射电子显微镜(美国FEI公司)分析光催化复合材料的整体形貌和结构。利用Philips X'pert PRO X射线衍射仪(荷兰帕纳科公司)分析了煅烧温度和煅烧气流对TiO₂结晶度的影响。以MgK_α为X射线源在Shimadzu ESCA-3400型 X 射线光电子能谱仪(宁波欧普仪器有限公司)上对样品进行XPS测量。采用ASAP 2020 比表面与孔隙度分析仪(麦克仪器)，在77 K下以N₂为吸附剂测得样品的N₂吸附-脱附等温线，并利用BET方程计算其表面积。采用TGA400型热重分析仪(珀金埃尔默)，在空气下，温度范围为30~650℃，对样品进行热重(TG)分析，加热速率为10℃·min⁻¹。通过接触角测试分析样品的亲疏水性能。采用TU-1901 UV-Vis 分光光度计(普析)测试样品的漫反射光谱，以BaSO₄为参比，扫描范围为200~600 nm。在上海辰华CHI660 E 电化学工作站上测量制备的复合材料的电化学阻抗谱、瞬态光电流响应图和Mott-Schottky曲线，测试条件：三电极系统(对电极：铂电极；参比电极：银/氯化银电极；工作电极：氧化铟锡(Indium tin oxide，ITO)；底液：0.1 mol/L硫酸钠溶液；偏压：0 V；光源：氙灯(> 420 nm)，光电流测试光照时间间隔为5 s (开灯5 s，关灯5 s)，进行14个循环，EIS测试频率范围为0.1 Hz~100 kHz，Mott-Schottky曲线测试范围为−0.4~0.8 V，频率为500、1000、1500 Hz。采用EMX-8 spectrometer电子顺磁共振波谱仪(德国布鲁克公司)测试反应体系中自由基和光生电子空穴。测试方法：取适量光催化剂分散到含有四甲基哌啶(TEMPO)的甲醇溶液中，超声3 min使其均匀分散，然后打开氙灯，光照2 min后，放入仪器中进行检测e⁻。

1.4 光催化性能测试

以RR195为实验对象，测试制备的HCS@TiO₂复合材料的光催化性能，同时分析各种样品对浓度为20 mg/L (100 mL)的RR195溶液的降解率，验证HCS和TiO₂之间是否存在协同效应。另外，利用HCS@TiO₂复合材料分别对RR195、活性黑5 (RB5)和碱性蓝9 (MB)进行光催化降解，验证复合材料的广谱性。在进行光催化降解RR195的实验之前，使用H₂SO₄/NaOH ±(0.5 mol/L)将染料废水的pH调整到3~11 (±0.1)。然后，将复合材料(10 mg)加入到100 mL的RR195溶液中。超声分散后，在黑暗中搅拌30 min达到吸附平衡。然后打开氙气灯(250 W，输出波长290~800 nm)，开始光催化反应。光反应开始后，以给定的时间间隔，取约4 mL的悬浮液，离心(4000 r/ min，3 min)去除光催化剂，然后使用UV-Vis分光光度计进行测试，在543 nm处分析残留染料浓度，计算其降解率，如下式所示：

$D=\frac{C_0-C\mathit{\mathit{\mathit{_{\rm{\mathit{t}}}}}}}{C_0}\times100\%$

(1)

其中： $D$ 为降解率； ${C}_{0}$ 为染料初始浓度； $C\mathit{\mathit{\mathit{_{\rm{\mathit{t}}}}}}$ 为时间t的染料浓度。

2. 结果与讨论

2.1 HCS@TiO₂的形貌和结构分析

为了观察光催化复合材料的形貌，通过SEM、TEM对TiO₂和HCS@TiO₂进行表征，结果如图2所示。由图2(a)和图2(b)可以看出，HCS为规整光滑、尺寸均匀的中空球体，粒径约为200 nm。图2(c)可以看出TiO₂ 均匀地负载在HCS上，且HCS负载TiO₂后仍保持球形结构，稳定性好。图2(d)可以看出该材料没有出现TiO₂纳米颗粒聚集的现象。图2(e)的C、N (来自吡咯衍生物)、O、Ti元素的映射图说明TiO₂纳米颗粒分布在HCS表面。图2(f)可以观察到无定形碳包围着TiO₂晶格条纹，其晶格间距为0.352 nm，对应锐钛矿型TiO₂的(101)晶面^[25]，图2(g)也证实了晶面间距为0.352 nm。

图 2 HCS ((a), (b)) 和HCS@TiO₂((c), (d))的SEM、TEM图像；(e) HCS@TiO₂的EDS元素分布图； HCS@TiO₂的HRTEM图像(f)和快速傅里叶变换(FFT)图(g)

d—Distance

Figure 2. SEM and TEM images of HCS ((a), (b)) and HCS@TiO₂ ((c), (d)); (e) EDS images of HCS@TiO₂; HRTEM image (f) and fast Fourier transform (FFT) image (g) of HCS@TiO₂

下载: 全尺寸图片幻灯片

通过XRD分析煅烧温度和煅烧气流对TiO₂结晶度的影响，结果如图3和图4所示。图3为Ar气流下650℃煅烧制备HCS@TiO₂的XRD图谱，其中TiO₂的衍射峰不尖锐，晶体结构不够规整。图4为不同煅烧温度下制备HCS@TiO₂的XRD图谱，TiO₂的衍射峰与锐钛矿型TiO₂ (JCPDS No. 21-1272) 和金红石型TiO₂ (JCPDS No. 21-1276)相匹配良好，表明在空气中650℃煅烧得到的TiO₂是一种双晶结构^[26-27]。HCS在空气气流下400℃左右碳化时，其骨架开始坍塌，HCS@TiO₂需先在O₂气流中煅烧，后在Ar气流下进行煅烧。将不同煅烧温度下的HCS@TiO₂的XRD进行分析对比，可得HCS@TiO₂ 350℃(O₂)-650℃(Ar)的锐钛矿型衍射峰最强，说明晶体结构最规整，在2θ=25.2°、37.8°、48.0°、53.8°、55.0°和62.6°处的特征衍射峰与锐钛矿相的(101)、(004)、(200)、(105)、(211)、(204)晶面对应，而锐钛矿型TiO₂具有比金红石型TiO₂更优异的光催化性能^[28]。

图 3 Ar气流下煅烧制备HCS@TiO₂的XRD图谱

Figure 3. XRD pattern of HCS@TiO₂ prepared by calcination under Ar flow

下载: 全尺寸图片幻灯片

图 4 不同煅烧温度下制备HCS@TiO₂的XRD图谱

Figure 4. XRD patterns of HCS@TiO₂ prepared at different calcination temperatures

下载: 全尺寸图片幻灯片

此外，在不同热解温度(O₂和Ar气流)下制备的HCS@TiO₂在TiO₂相同的2θ位置上出现衍射峰，表明HCS对TiO₂晶体结构的影响可以忽略不计。

图5为TiO₂、HCS及HCS@TiO₂的XPS全谱图，可以看出HCS@TiO₂在284.8 eV、459.4 eV和530.0 eV的位置存在C1s峰、Ti2p峰和O1s峰，表明HCS@TiO₂中仅存在C、O和Ti元素，没有被污染。

图 5 TiO₂、HCS、HCS@TiO₂的XPS图谱

Figure 5. XPS spectra of TiO₂, HCS and HCS@TiO₂

下载: 全尺寸图片幻灯片

图6为样品不同元素的高分辨XPS光谱。图6(a)和图6(b)分别为HCS和HCS@TiO₂在C1s区域的高分辨XPS光谱，可以看出HCS的C1s XPS有3个特征峰，对应C=C、C—C和O—C=O键，分别位于284.4 eV、285.2 eV和288.3 eV处，而在HCS@TiO₂中观察到两个处于283.3 eV(C—Ti)和286.1 eV(C=O)的新峰，说明HCS和TiO₂之间有很强的相互作用，且前3个峰均呈轻微的负位移。由TiO₂和HCS@TiO₂的O1s高分辨XPS光谱(图6(c)、图6(d))可以看出，TiO₂在529.5 eV和530.8 eV处显示的两个特征峰，属于Ti—O—Ti和Ti—OH键。与TiO₂相比，HCS@TiO₂的O1s XPS中的两个特征峰发生了负位移。在TiO₂和HCS@TiO₂的Ti2p高分辨XPS光谱(图6(e)、图6(f))中，TiO₂的Ti2p_3/2和Ti2p_1/2^[29]的结合能分别为458.2 eV和463.9 eV，而HCS@TiO₂的Ti2p_3/2和Ti2p_1/2峰值信号与TiO₂相比，向上移动了约0.5 eV，可能是TiO₂和HCS之间形成C—Ti的原因。基于上述说明TiO₂成功锚定在HCS上。

图 6 HCS和HCS@TiO₂的C1s高分辨XPS图谱((a), (b)) 、O1s高分辨XPS图谱((c), (d))及Ti2p高分辨XPS图谱((e), (f))

Figure 6. C1s high-resolution XPS spectra ((a), (b)), O1s high-resolution XPS spectra ((c), (d)) and Ti2p high-resolution XPS spectra ((e), (f)) of TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

TiO₂和HCS@TiO₂的N₂吸附-脱附等温线如图7所示，两种材料均为IV型等温线，表明两种材料中均存在大孔或介孔，TiO₂等温线中存在H3型磁滞回环，而HCS@TiO₂的滞回环类型变为H1型，这归功于HCS具有大量孔隙。根据BET方程计算得出，TiO₂和HCS@TiO₂的比表面积分别为19.6 m²/g和91.1 m²/g，表明HCS的加入，大大增加了HCS@TiO₂的比表面积，减少了TiO₂的团聚。

图 7 TiO₂和 HCS@TiO₂的N₂吸附-解吸等温线

V—Adsorption capacity; STP—Standard temperature and pressure

Figure 7. N₂ adsorption/desorption isotherms of TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

为了测试HCS@TiO₂的定量组分和热稳定性，采用TGA对HCS@TiO₂的热稳定性进行了研究，结果如图8所示。

可以看出，样品发生两次明显的质量损失。第一次质量损失是样品在100℃以下损失2.4wt%，主要归因于物理吸附和水的蒸发；第二次质量损失是样品在400℃以上损失17.2wt%，主要归因于燃烧HCS去除碳框架。最后，在600℃以上保持在80wt%不变。因此，确定HCS@TiO₂中TiO₂的质量分数为80wt%，具有优异的热稳定性。

图 8 HCS@TiO₂的热重分析图

Figure 8. Thermalgravimetric curves of HCS@TiO₂

下载: 全尺寸图片幻灯片

通过接触角测试，分析HCS、酸化后的HCS、TiO₂、HCS@TiO₂的亲疏水性能，测试结果如图9所示，HCS、酸化后的HCS、TiO₂、HCS@TiO₂的接触角分别为135°、38°、85°和55°。HCS为疏水性材料，经过强酸酸化后，接触角明显减小了，说明酸化使HCS表面引入了大量极性基团，使其具有优异的亲水性和分散性。TiO₂的接触角为85°，易发生团聚现象。与TiO₂相比，HCS@TiO₂的亲水性得到了明显提升，利于染料的吸附。

图 9 HCS、酸化后的HCS、TiO₂、HCS@TiO₂的接触角分析

Figure 9. Contact angle analysis diagram of HCS, acidified HCS, TiO₂, HCS@TiO₂

下载: 全尺寸图片幻灯片

2.2 HCS@TiO₂的光学特性

TiO₂和HCS@TiO₂的紫外-可见吸收光谱如图10(a)所示。可以看出，TiO₂的吸收边带在390 nm左右，而HCS@TiO₂的吸收边带发生了红移，在450 nm左右。

采用公式

${\left(\alpha hv\right)}^{n}=A\left(hv-{E}_{\mathrm{g}}\right)$

(2)

其中：α为吸光度；h为普朗克常数；v为频率；指数n与半导体类型直接相关；A为比例常数；E_g为半导体的能隙，可以计算得到TiO₂和HCS@TiO₂的能量间隙图，利用切线法较精确地得到TiO₂和HCS@TiO₂复合材料的带隙能图，如图10(b)所示，TiO₂的带隙能为3.13 eV，而HCS@TiO₂的带隙能为2.83 eV，即HCS@TiO₂的带隙能降低了，对光吸收范围更大了。

图 10 TiO₂和 HCS@TiO₂的UV-Vis DRS光谱(a) 和能隙图(b)

α—Absorption coefficient; h—Planck's constant; ν—Frequency

Figure 10. UV-visible diffuse reflectance spectra (a) and energy gap diagram (b) of TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

对TiO₂和HCS@TiO₂进行了Mott-Schottky测试，结果如图11所示。样品的曲线斜率均为正，这说明TiO₂和HCS@TiO₂均为n型半导体；且HCS@TiO₂的斜率明显小于TiO₂的斜率，表明HCS@TiO₂的载流子浓度比TiO₂的载流子浓度高。

图 11 TiO₂和HCS@TiO₂的Mott-Schottky 曲线

C—Interfacial capacitance

Figure 11. Mott-Schottky curves of TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

2.3 HCS@TiO₂复合材料的光催化降解染料性能

通过EIS研究TiO₂和HCS@TiO₂的电荷转移效率，结果如图12(a)所示。可以看出，HCS@TiO₂的圆弧半径明显小于TiO₂，说明其电荷转移电阻较低，促进电荷转移的同时抑制光生电子空穴对的复合，有利于光催化性能的提高^[30]。图12(b)展示了HCS@TiO₂和TiO₂在可见光下反复开/关时的瞬态光电流，两种材料均展示出快速可逆的瞬态光电流响应，且随着光照时间的增强，光电流密度没有明显的衰减，同时，HCS@TiO₂的光电流密度明显高于TiO₂。表明HCS@TiO₂的光生电子空穴对复合率更低，为光催化过程中提供稳定数量的光生电子^[6]。

图 12 TiO₂和HCS@TiO₂的电化学阻抗谱(a)及瞬态光电流响应图(b)

Figure 12. Electrochemical impedance spectra (a) and transient photocurrent response diagram (b) of TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

图13为HCS、TiO₂ 和HCS@TiO₂这3种材料对RR195的降解曲线图，图14为HCS@TiO₂光催化降解RR195、RB5和MB的曲线图。由图13可以看出，在暗箱吸附30 min 后，HCS的吸附达到平衡，之后一直保持不变；光照120 min后，TiO₂降解率为62.93%，而HCS@TiO₂降解率为95.36%，这是由于HCS和TiO₂之间存在协同效应，提高了光生电子空穴对的分离效率，加速了污染物的降解。由图14可以看出，HCS@TiO₂在光照120 min内对3种不同结构染料的降解率均高达95.00%，故HCS@TiO₂具有广谱性。

图 13 HCS、TiO₂和HCS@TiO₂对活性红195 (RR195)的降解曲线

D—Degradation

Figure 13. Degradation curves of Reactive Red 195 (RR195) using HCS, TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

图 14 HCS@TiO₂对RR195、活性黑5 (RB5)和碱性蓝9 (MB)的降解曲线

Figure 14. Degradation curves of RR195 and Reactive Black 5 (RB5) and Alkaline Blue 9 (MB) using HCS@TiO₂

下载: 全尺寸图片幻灯片

图15为HCS@TiO₂降解RR195的紫外-可见光吸收光谱图及降解过程中的染液颜色变化图。可以看出，反应初始，RR195在510 nm和543 nm处均出现了吸收峰，对应—N=N—。随着反应的进行，RR195的颜色由艳红逐渐变为无色，最大吸收峰逐渐降低，说明其发色基团被有效降解。另外，为了考察HCS@TiO₂的可重复利用性，进行了5次降解RR195的循环实验，每个循环周期都要进行30 min的暗箱吸附和120 min的光降解，结果如图16所示。可以看出，该复合材料5次循环后，降解率为93.34%，依旧保持很高的光催化活性，这归因于其本身独特的3D球形结构，可以防止负载在HCS上的TiO₂掉落。另外，降解后，HCS@TiO₂的回收率可达91.30%。

图 15 HCS@TiO₂降解RR195的紫外-可见光吸收光谱图(插图为RR195的颜色变化图)

Figure 15. UV-vis adsorption spectra of RR195 by HCS@TiO₂ degradation(Illustrated with the color change of RR195)

下载: 全尺寸图片幻灯片

图 16 HCS@TiO₂降解RR195的循环测试性能

Figure 16. Recycling test for the removal of RR195 using HCS@TiO₂

下载: 全尺寸图片幻灯片

2.4 HCS@TiO₂的光催化降解机制

为了研究光催化降解中起主要作用的活性物质，采用苯醌(BQ)、乙二胺四乙酸钠(EDTA-2Na)和异丙醇(IPA)分别作为 ${\text{•}}{\rm{O}}_2^ -$ 、h⁺和•OH的捕获试剂，结果如图17所示。

图 17 利用各种捕获剂与HCS@TiO₂光催化降解RR195

BQ—Benzoquinone; EDTA-2 Na—Ethylenediamine tetraacetate sodium; IPA—Isopropyl alcohol

Figure 17. Photocatalytic degradation of RR195 using HCS@TiO₂ of with various radical scavengers

下载: 全尺寸图片幻灯片

可以看出，在反应体系中加入捕获试剂后，光催化降解效率都会受到不同程度的抑制。其中加入BQ后，光催化效率下降最明显，降解率为49.83%，说明 ${\text{•}}{\rm{O}}_2^ -$ 在光催化反应体系中起主要作用；而加入EDTA-2Na和IPA，降解率分别为83.50%和89.67%，说明h⁺和•OH在光催化反应体系中起次要作用，由此说明3种自由基的降解效率， ${\text{•}}{\rm{O}}_2^ -$ 最高，h⁺次之，•OH最低。可以推断，RR195可能在紫外照射下主要被•O₂ ⁻和h⁺分解。

为了进一步探究光催化机制，通过ESR研究了自由基产生和转移机制，结果如图18所示。由于四甲基哌啶(TEMPO)作为电子e⁻的自旋标记分子，能够被检测到信号强度为1∶1∶1的信号峰，信号峰越弱，表明该样品生成的光生电子越多。可以看出，0 min即不光照时，TiO₂的信号强度低于HCS@TiO₂的信号强度；辐照10 min后，TiO₂和HCS@TiO₂的信号强度均有所减弱，且HCS@TiO₂信号强度明显低于TiO₂的信号强度，这是由于HCS作为电子陷阱促进了电子的转移，提高了光生电子空穴对的分离效率，因而HCS@TiO₂相比于TiO₂可以生成更多的光生电子。

图 18 TiO₂和HCS@TiO₂的四甲基哌啶(TEMPO)-e^–电子顺磁共振波谱(ESR)

Figure 18. Tetramethylpiperidine (TEMPO)-e^– electron paramagnetic resonance spectroscopy (ESR) of TiO₂ and HCS@TiO₂

下载: 全尺寸图片幻灯片

基于上述实验结果与分析，提出了HCS@TiO₂复合材料光催化活性增强机制，如图19所示。由图可以看出：在光照下，e⁻从TiO₂的价带(VB)跃迁到导带(CB)上，HCS功函高于TiO₂，e⁻从TiO₂的CB转移到HCS表面；TiO₂上的h⁺会与H₂O发生反应生成•OH；HCS表面的e⁻会与O₂发生反应，使其生成 ${\text{•}}{\rm{O}}_2^ -$ ， ${\rm{O}}_2^ -$ 还会与H⁺反应，生成过氧化氢自由基(H₂O•)，H₂O•是H₂O₂的前躯体，后续反应生成H₂O₂，氧化反应和还原反应分别在TiO₂和HCS上进行。此外，HCS的高比表面积可以使TiO₂均匀负载，改善TiO₂团聚现象，增加吸附点和活性位点，提高反应体系的降解速率。

图 19 HCS@TiO₂光催化降解RR195机制

VB—Valence band; CB—Conduction band

Figure 19. Mechanism diagram of photocatalytic degradation of RR195 by HCS@TiO₂

下载: 全尺寸图片幻灯片

3. 结论

(1)利用简单的湿化学法可以制备空心碳球(HCS)@TiO₂光催化复合材料，且TiO₂均匀负载在HCS上，形成亲水性强、比表面积大、热稳定性优异的球形复合材料。

(2)光电化学性质分析表明，HCS@TiO₂比TiO₂禁带宽度更小，光响应范围更大，光生电子还原能力更强。

(3) HCS和TiO₂之间的协同效应，提高了光生电子空穴对的分离效率，加速了污染物的降解。相同条件下，TiO₂降解率仅为62.93%，而HCS@TiO₂的降解率为95.36%，5次循环后降解率为93.34%，回收率为91.30%，且具有广谱性。

(4) 结合自由基捕获实验及电子顺磁共振光谱，提出了HCS@TiO₂光催化复合材料的光催化降解机制，证实了 ${\text{•}}{\rm{O}}_2^ -$ 在光催化反应体系中起主要作用。

图 1 碳纤维增强树脂基复合材料(CFRP)薄壁管制造工艺流程图

Figure 1. Manufacturing process of carbon fiber reinforced plastics (CFRP) thin-walled tubes

下载: 全尺寸图片幻灯片

图 2 试验现场布置图

Figure 2. Experimental setup

下载: 全尺寸图片幻灯片

图 3 CFRP的截面SEM图像

Figure 3. SEM images of cross section for CFRP

下载: 全尺寸图片幻灯片

图 4 (a) 单向碳纤维复合材料六面体代表性体积单元(RVE)模型；(b) RVE参考点

Figure 4. (a) Hexagonal representative volume element (RVE) model of UD-CFRP; (b) Reference points at RVE

F, M—Fiber and matrix, respectively; Number—Selection order of reference points; a=c=1; b= $\sqrt 3$

下载: 全尺寸图片幻灯片

图 5 多尺度分析框架

Figure 5. Multiscale analysis framework

下载: 全尺寸图片幻灯片

图 6 多尺度模型的数值算法流程

Figure 6. Numerical calculation procedure for the multi-scale model

SAFs—Stress amplification factors; RVEs—Representative volume elements

下载: 全尺寸图片幻灯片

图 7 CFRP薄壁结构单位应力施加

Figure 7. Application of unit macro stress for CFRP thin-walled structure

下载: 全尺寸图片幻灯片

图 8 CFRP薄壁结构RVE模型在宏观六工况下的微观应力分布

Figure 8. Microscopic stress distribution for RVEs of CFRP thin-walled structure under six loading cases

下载: 全尺寸图片幻灯片

图 9 CFRP薄壁结构0°拉伸试件试验结果

Figure 9. Experimental results of 0° samples of CFRP thin-walled structure

下载: 全尺寸图片幻灯片

图 10 CFRP薄壁结构90°拉伸试件试验结果

Figure 10. Experimental results of 90 ° samples of CFRP thin-walled structure

下载: 全尺寸图片幻灯片

图 11 CFRP薄壁结构有限元模型

Figure 11. Finite element model of CFRP thin-walled structure

下载: 全尺寸图片幻灯片

图 12 网格大小敏感性分析

Figure 12. Mesh size sensitivity analysis

下载: 全尺寸图片幻灯片

图 13 CFRP薄壁结构实验与仿真载荷-位移对比曲线

Figure 13. Comparison of load-displacement curves between experiment and simulation for CFRP thin-walled structure

下载: 全尺寸图片幻灯片

图 14 CFRP薄壁结构变形结果对比

Figure 14. Comparison of deformation modes for CFRP thin-walled structure

下载: 全尺寸图片幻灯片

图 15 不同铺层角度的CFRP圆管载荷-位移曲线

Figure 15. Comparison of load-displacement curves for CFRP tubes with different fiber orientations

下载: 全尺寸图片幻灯片

图 16 不同铺层角度CFRP薄壁圆管轴向压溃后的变形结果

Figure 16. Crushing process of CFRP tubes with different fiber orientations

下载: 全尺寸图片幻灯片

图 17 不同体积分数的CFRP薄壁圆管载荷-位移曲线

Figure 17. Comparison of load-displacement curves for CFRP tubes with different fiber volume fractions

下载: 全尺寸图片幻灯片

图 18 不同纤维体积分数CFRP薄壁圆管的变形过程

Figure 18. Deformation process of CFRP thin-walled circular tubes with different fiber volume fractions

下载: 全尺寸图片幻灯片

表 1 T300碳纤维力学性能

Table 1 Mechanical properties of T300 carbon fiber

Mechanical property	Value
$E_{\text{f}\text{1}}$ /GPa	185
$E_{\text{f}\text{2}}\text{=}E_{\text{f}\text{3}}$ /GPa	13
${G}_{\text{f}\text{12}}\text{=}{G}_{\text{f}\text{13}}$ /GPa	15
${G}_{\text{f}\text{23}}$ /GPa	9
${\nu}_{\text{f}\text{12}}\text{=}{\nu}_{\text{f}\text{13}}$	0.28
${\nu}_{\text{f}\text{23}}$	0.35
Notes: E_f1, E_f2, E_f3, G_f12, G_f13, and G_{—Elastic moduli of T300 carbon fiber fibers in the 1, 2, 3, 12, 13, and 23 directions, respectively; v_f12, v_f13, and v_f23—Poisson's ratios in the 12, 13, and 23 directions, respectively.}

下载: 导出CSV

表 2 基体力学性能

Table 2 Mechanical properties of matrix

Mechanical property	Value
${E}_{\mathrm{m}}$ /GPa	2.6
$\nu$	0.33
Note: E_m and v—Micro elastic modulus and Poisson's ratio of the matrix, respectively.

下载: 导出CSV

表 3 CFRP薄壁结构宏观单位应力加载

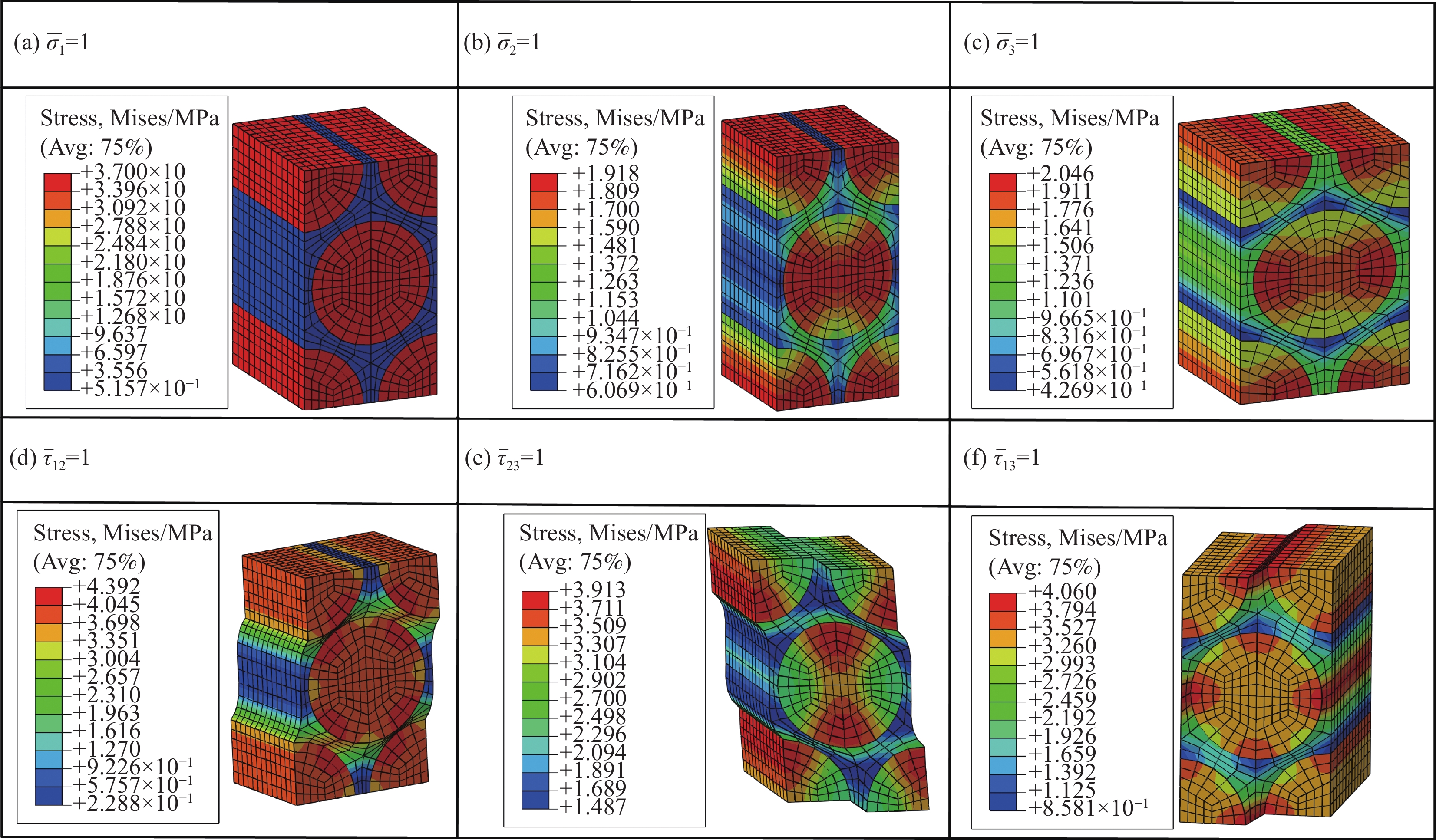
Table 3 Appling macro unit stress of CFRP thin-walled structure

n	${\overline{\sigma} }_{\text{1}}$	${\overline{\sigma} }_{\text{2}}$	${\overline{\sigma} }_{\text{3}}$	${\overline{\tau} }_{\text{12}}$	${\overline{\tau} }_{\text{23}}$	${\overline{\tau} }_{\text{13}}$
1	1	0	0	0	0	0
2	0	1	0	0	0	0
3	0	0	1	0	0	0
4	0	0	0	1	0	0
5	0	0	0	0	1	0
6	0	0	0	0	0	1
Notes: ${\overline{\sigma} }_{\text{1}}$ , ${\overline{\sigma} }_{\text{2}}$ and ${\overline{\sigma} }_{\text{3}}$ —Macro-stress in the 1, 2 and 3 direction of CFRP, respectively; ${\overline{\tau} }_{\text{12}}$ , ${\overline{\tau} }_{\text{23}}$ , ${\overline{\tau} }_{\text{13}}$ —Macro shear stress in the 12, 23 and 13 direction of CFRP, respectively.

下载: 导出CSV

表 4 CFRP薄壁结构宏观弹性参数计算方法

Table 4 Calculation method of macro elastic parameters for CFRP thin-walled structure

Loading case	Loading condition	Calculation formula
1	${\overline{\sigma }}_{{1}}$ =1	${{E}}_{{1}}=\dfrac{{\overline{\sigma }}_{{1}}}{{}{\bar{{ \varepsilon }}}_{{1}}} ， {\upsilon }_{{12}} =−\dfrac{{\bar{{ \varepsilon }}}_{{2}}}{{}{\bar{{ \varepsilon }}}_{{1}}} ， {\upsilon }_{{13}} =−\dfrac{{\bar{{ \varepsilon }}}_{{3}}}{{}{\bar{{ \varepsilon }}}_{{1}}}$
2	${\overline{\sigma }}_{{2}}$ =1	${{E}}_{{2}}=\dfrac{{\overline{\sigma }}_{{2}}}{{\bar{{ \varepsilon }}}_{{2}}} ， {\upsilon }_{{21}} =−\dfrac{{\bar{{ \varepsilon }}}_{{1}}}{{}{\bar{{ \varepsilon }}}_{{2}}} ， {\upsilon }_{{23}} =− \dfrac{{\bar{{ \varepsilon }}}_{{3}}}{{}{\bar{{ \varepsilon }}}_{{2}}}$
3	${\overline{\sigma }}_{{3}}$ =1	${{E}}_{{3}} =\dfrac{{\overline{\sigma }}_{{3}}}{{}{\bar{{ \varepsilon }}}_{{3}}}，{\upsilon }_{{31}} =− \dfrac{{}{\bar{{ \varepsilon }}}_{{1}}}{{}{\bar{{ \varepsilon }}}_{{3}}} ，{\upsilon }_{{32}}=− \dfrac{{\bar{{ \varepsilon }}}_{{2}}}{{}{\bar{{ \varepsilon }}}_{{3}}}$
4	${\overline{\tau }}_{{12}}$ =1	${{G}}_{{12}}=\dfrac{{\overline{\tau }}_{{12}}}{{\bar{\gamma }}_{{12}}}$
5	${\overline{\tau }}_{{23}}$ =1	${{G}}_{{23}}=\dfrac{{\overline{\tau }}_{{23}}}{{\bar{\gamma }}_{{23}}}$
6	${\overline{\tau }}_{{13}}=1$	${{G}}_{{13}} = \dfrac{{\overline{\tau }}_{{13}}}{{\bar{\gamma }}_{{13}}}$
Notes: E₁, E₂ and E₃—Macroscopic elastic modulus in the 1, 2 and 3 direction of CFRP, respectively; G₁₂, G₂₃ and G₁₃—Macroscopic shear modulus in the 12, 23 and 13 direction of CFRP, respectively; ${\bar \upsilon} _{ij}$ (i, j=1, 2, 3)—Poisson's ratio of CFRP in the ij direction; ${\bar\varepsilon} _i$ (i=1, 2, 3)—Strain of CFRP in the i direction; ${\bar \gamma} _{ij}$ (i, j=1, 2, 3)—Strain of CFRP in the ij direction.

下载: 导出CSV

表 5 CFRP弹性参数预测结果与试验结果对比

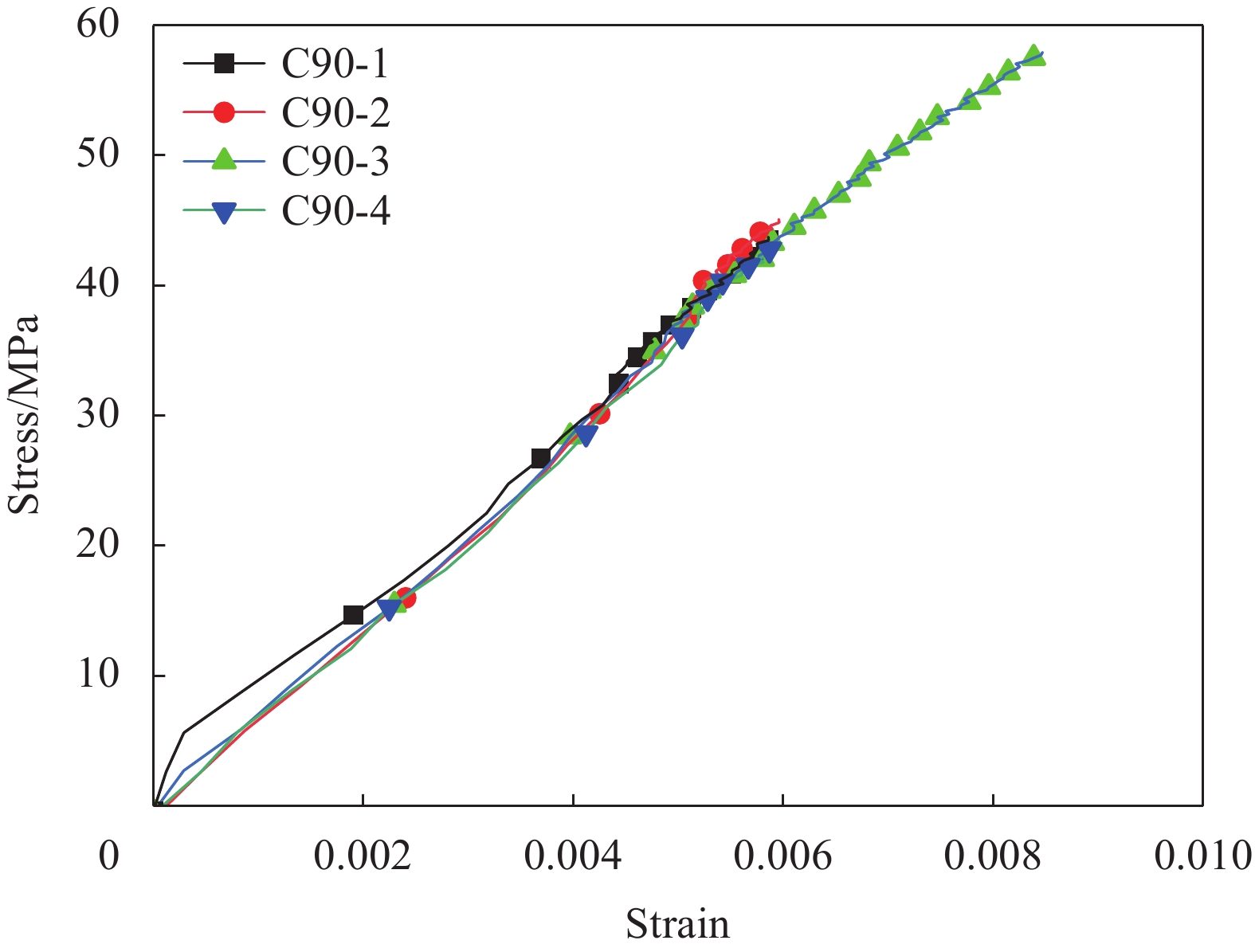
Table 5 Comparison of CFRP elastic parameters between numerical and experimental results

Property	${ {E} }_{ {1} }$ /GPa	${ {E} }_{ {2} }$ = ${ {E} }_{ {3} }$ /GPa	${{G}}_{{12}}={{G}}_{{13}}$ /GPa	${{G}}_{{23}}$ /GPa	${\upsilon }_{{12}}{=}{\upsilon }_{{13}}$	${\upsilon }_{{23}}$
Test	131.5	7.6	—	—	0.29	—
RVE	132.6	7.5	4.3	3.5	0.29	0.39
Error/%	2.13	9.21	—	—	0	—

下载: 导出CSV

表 6 CFRP多尺度损伤模型输入参数

Table 6 Input parameters of CFRP multi-scale damage model

Parameter	Value	Parameter	Value
${E}_{\text{1} }$ /MPa	132600	${E}_{\text{f}\text{1}}$ /MPa	185000
${E}_{\text{2} }$ /MPa	7500	${E}_{\text{f}\text{2}}$ /MPa	13000
${E}_{\text{3} }$ /MPa	7500	${\text{X}}_{\text{f}}^{\text{0,}\text{T}}$ /MPa	3470
${\nu}_{\text{12}}$	0.29	${\text{X}}_{\text{f}}^{\text{0,}\text{C}}$ /MPa	2100
${\nu}_{\text{13}}$	0.29	${E}_{\text{m}}$ /MPa	2600
${\nu}_{\text{23}}$	0.39	${\text{Y}}_{\text{m}}^{\text{0,}\text{T}}$ /MPa	77
${G}_{\text{12}}$ /MPa	4300	${\text{Y}}_{\text{m}}^{\text{0,}\text{C}}$ /MPa	121
${G}_{\text{13}}$ /MPa	4300	$\text{γ}$	1.5
${G}_{\text{23}}$ /MPa	3500	$\rho$ /(t·mm⁻³)	1.4×10⁻⁹
Notes: $\rm X_f^{0,T}$ and $\rm X_f^{0,C}$ —Longitudinal tensile strength and compressive strength of T300 fiber, respectively; $\rm Y_m^{0,T}$ and $\rm Y_m^{0,C}$ —Final tensile strength and compressive strength of matrix, respectively; $\gamma$ —Damage shape parameter of matrix; p—Beta damping parameter of CFRP.

下载: 导出CSV

表 7 CFRP层间失效模型输入参数

Table 7 Input parameters of CFRP inter-laminar failure model

Description	Variable	Value
Damage initiation/MPa	${{t}}_{\text{n}}^{\text{0}}$	49.2
	${{t}}_{\text{s}}^{\text{0}}$	59.5
	${{t}}_{\text{t}}^{\text{0}}$	59.5
Fracture energies/(J·m⁻²)	${{G}}_{\text{n}}^{\text{C}}$	490
	${{G}}_{\text{s}}^{\text{C}}$	1060
	${{G}}_{\text{t}}^{\text{C}}$	1060
BK	${\eta}$	2.284
Notes: ${{t}}_{\text{n}}^{\text{0}}$ —Maximum nominal stress in the normal-only mode; ${{t}}_{\text{s}}^{\text{0}}$ —Maximum nominal stress in the first shear direction (for a mode that involves separation only in this direction); ${{t}}_{\text{t}}^{\text{0}}$ —Maximum nominal stress in the second shear direction (for a mode that involves separation only in this direction); ${{G}}_{\text{n}}^{\text{C}}$ —Ttype I critical fracture energies in n direction; ${{G}}_{\text{s}}^{\text{C}}$ — Type II critical fracture energies in n direction; ${{G}}_{\text{t}}^{\text{C}}$ —Critical fracture energies in t direction; $\eta$ —A bonding attribute parameter.

下载: 导出CSV

表 8 CFRP薄壁结构耐撞性能指标结果对比

Table 8 Comparison of crashworthiness index results for CFRP thin-walled structure

Property	F_p/kN	W_e/kJ	W_s/(J·g⁻¹)	F_m/kN	E_c
Experimental	35.0	2.230	48.02	27.88	0.80
Simulation	37.8	2.218	47.76	27.73	0.73
Error/%	8	0.54	0.54	0.5	7.9
Notes: F_p—Maximum peak force that occurs during the entire crushing process; W_e—Total energy absorbed by the structural component during the impact process; W_s—Amount of energy absorbed by energy absorbing structure per unit mass; F_m—Average force is the energy absorbed during the impact process per unit distance; E_c—Ratio of the average force to the maximum peak force.

下载: 导出CSV

表 9 不同铺层角度的CFRP薄壁圆管耐撞性能指标结果

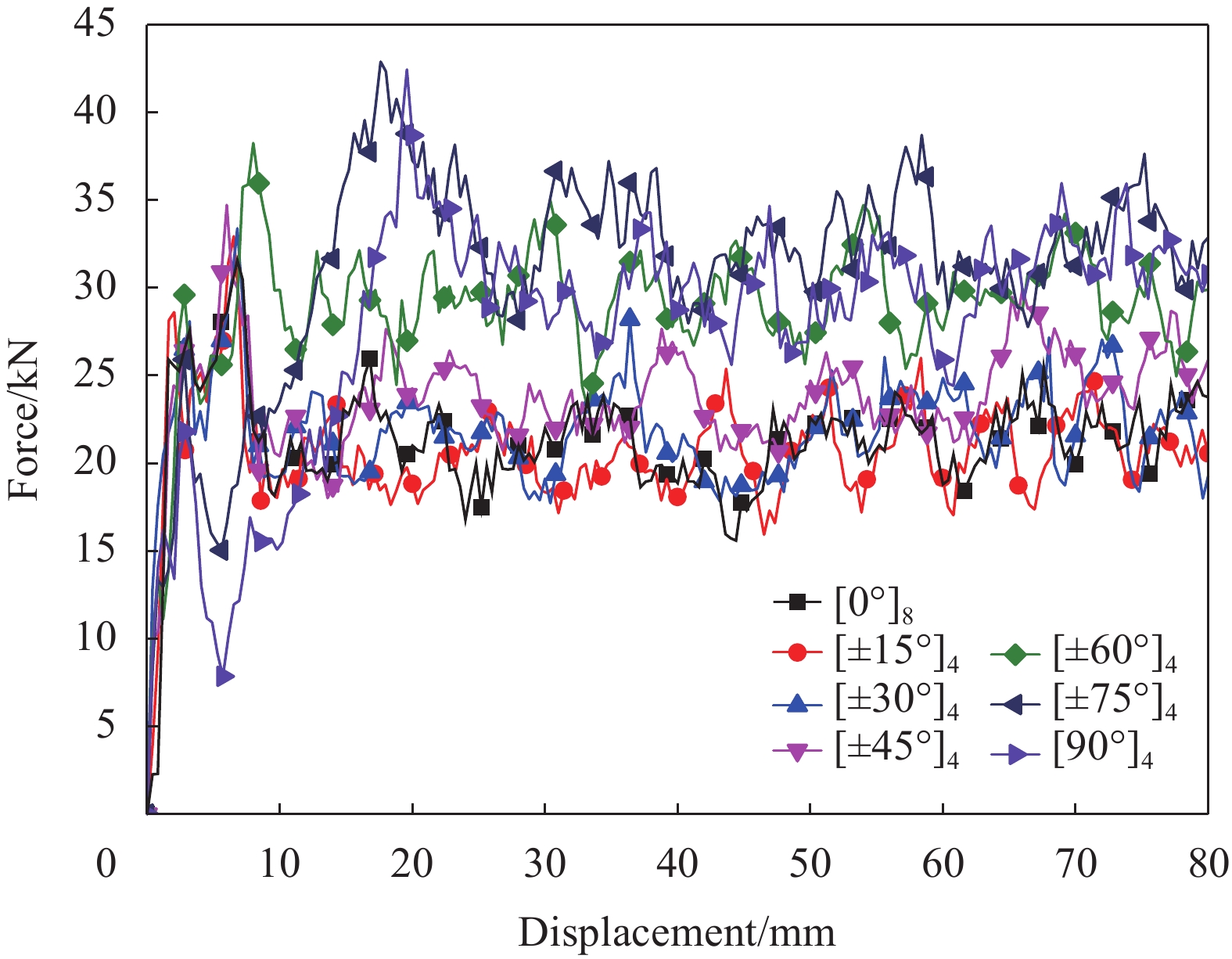
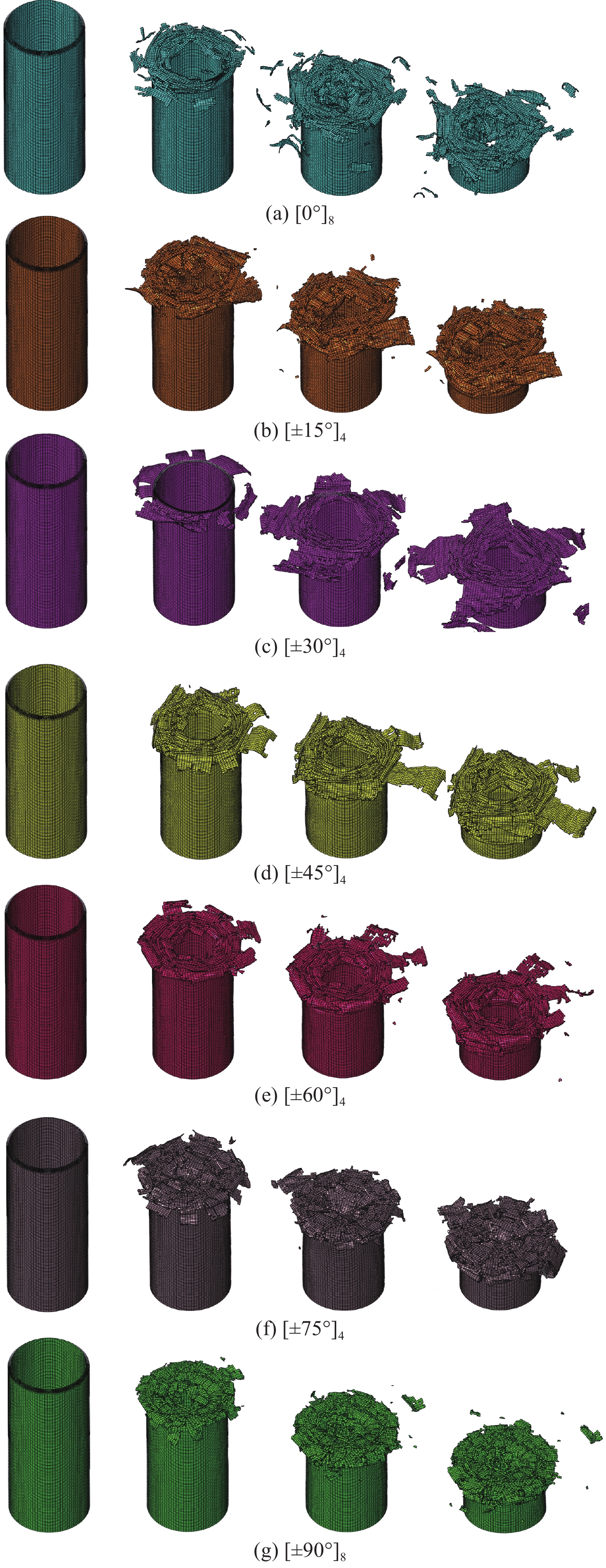
Table 9 Crashworthiness index results of CFRP tubes with different fiber orientations

Ply angle	F_p/kN	W_e/J	W_s/(J·g⁻¹)	F_m/kN	E_c
[0°]₈	31.6	1703	36.7	21.3	0.674
[±15°]₄	32.9	1653	35.6	20.7	0.629
[±30°]₄	33.4	1754	37.8	21.9	0.656
[±45°]₄	34.7	1899	40.9	23.7	0.683
[±60°]₄	38.3	2316	49.9	29.0	0.757
[±75°]₄	42.9	2496	53.7	31.2	0.727
[90°]₈	42.4	2236	48.1	28.0	0.660

下载: 导出CSV

表 10 不同体积分数的CFRP薄壁圆管耐撞性能指标结果

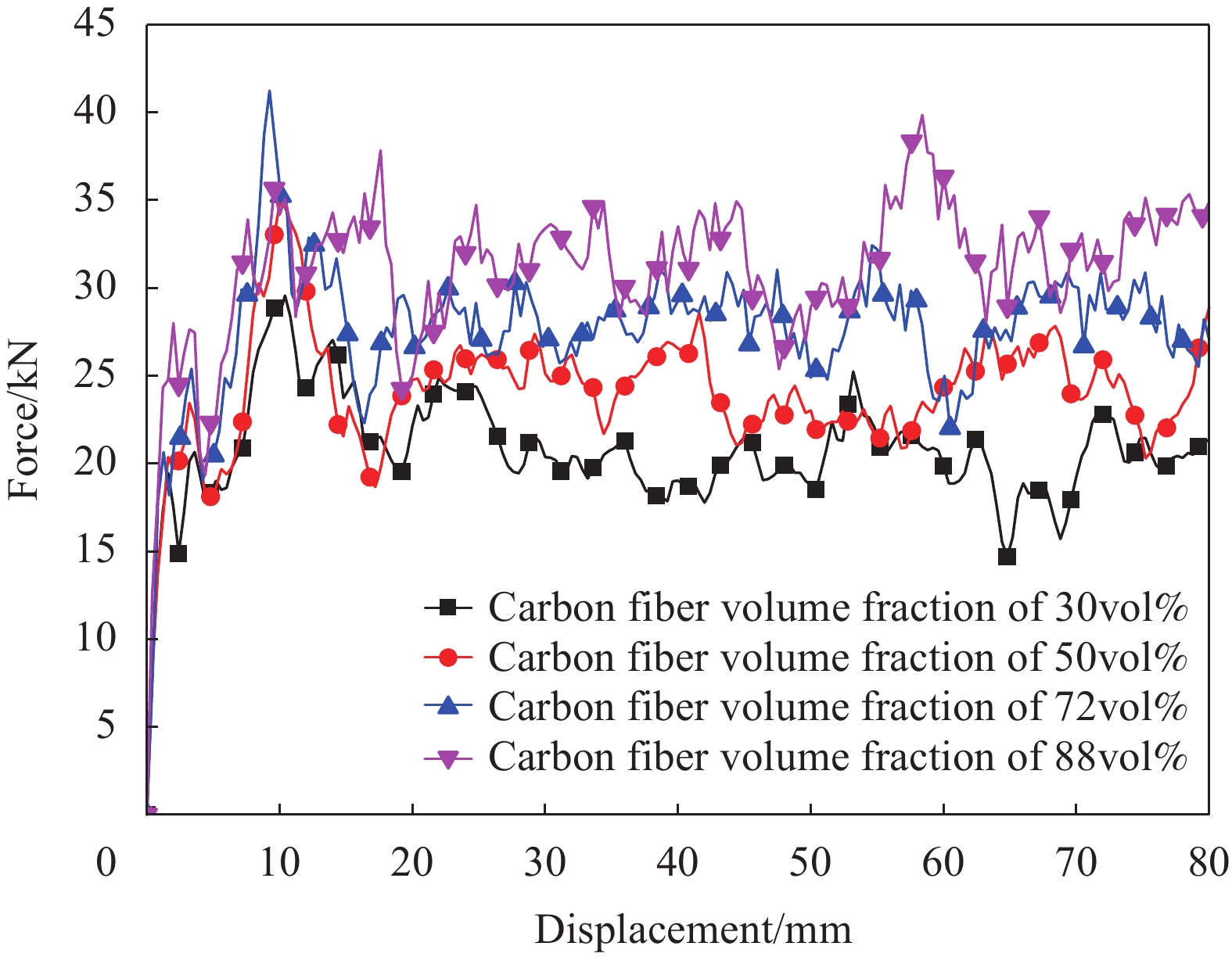
Table 10 Crashworthiness indicators of CFRP tubes with different volume fractions

Volume fraction/vol%	m/g	F_p/kN	W_e/J	W_s/(J·g⁻¹)	F_m $/$ kN	E_c
30	38.95	29.8	1649	42.3	20.6	0.692
50	42.52	34.8	1933	45.5	24.2	0.694
72	46.44	37.8	2218	47.8	27.7	0.733
88	49.56	39.9	2494	50.3	31.2	0.781
Note: m—Mass of carbon fiber.

下载: 导出CSV

参考文献(26)

[1]	HA N S, LU G. A review of recent research on bio-inspired structures and materials for energy absorption applications[J]. Composites Part B: Engineering,2020,181:107496. DOI: 10.1016/j.compositesb.2019.107496
[2]	HA N S, LU G. Thin-walled corrugated structures: A review of crashworthiness designs and energy absorption characteristics[J]. Thin-Walled Structures,2020,157:106995. DOI: 10.1016/j.tws.2020.106995
[3]	ZHU G, LIAO J, SUN G, et al. Comparative study on metal/CFRP hybrid structures under static and dynamic loading[J]. International Journal of Impact Engineering,2020,141:103509.
[4]	MAMALIS A G, MANOLAKOS D E, IOANNIDIS M B, et al. On the response of thin-walled CFRP composite tubular components subjected to static and dynamic axial compressive loading: Experimental[J]. Composite Structures,2005,69(4):407-420. DOI: 10.1016/j.compstruct.2004.07.021
[5]	ZHU G, SUN G, LI G, et al. Modeling for CFRP structures subjected to quasi-static crushing[J]. Composite Structures,2018,184:41-55. DOI: 10.1016/j.compstruct.2017.09.001
[6]	LIU Q, OU Z, MO Z, et al. Experimental investigation into dynamic axial impact responses of double hat shaped CFRP tubes[J]. Composites Part B: Engineering,2015,79(15):494-504.
[7]	GRECO F, LUCIANO R. A theoretical and numerical stability analysis for composite micro-structures by using homogenization theory[J]. Composites Part B: Engineering,2011,42(3):382-401. DOI: 10.1016/j.compositesb.2010.12.006
[8]	ZHAO Z, DANG H, ZHANG C, et al. A multi-scale modeling framework for impact damage simulation of triaxially braided composites[J]. Composites Part A: Applied Science and Manufacturing,2018,110:113-125. DOI: 10.1016/j.compositesa.2018.04.020
[9]	MELRO A R, CAMANHO P P, ANDRADE P F M, et al. Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part I–Constitutive modelling[J]. International Journal of Solids and Structures,2013,50:1897-1905. DOI: 10.1016/j.ijsolstr.2013.02.009
[10]	GE L, LI H, LIU B, et al. Multi-scale elastic property prediction of 3D five-directional braided composites considering pore defects[J]. Composite Structures,2020,244:112287. DOI: 10.1016/j.compstruct.2020.112287
[11]	XIONG X, HUA L, MIAO M, et al. Multi-scale constitutive modeling of natural fiber fabric reinforced composites[J]. Composites Part A: Applied Science & Manufacturing,2018,115:383-396.
[12]	CALNERYTE D, BARAUSKAS R. Multi-scale evaluation of the linear elastic and failure parameters of the unidirectional laminated textiles with application to transverse impact simulation[J]. Composite Structures,2016,142:325-334. DOI: 10.1016/j.compstruct.2016.01.104
[13]	TAO W, LIU Z, ZHU P, et al. Multi-scale design of three dimensional woven composite automobile fender using modified particle swarm optimization algorithm[J]. Composite Structures,2017,181:73-83. DOI: 10.1016/j.compstruct.2017.08.065
[14]	HA S K, JIN K K, HUANG Y. Micro-mechanics of failure (MMF) for continuous fiber reinforced composites[J]. Journal of Composite Materials,2008,42(18):1873-1895. DOI: 10.1177/0021998308093911
[15]	JIN K K, HWAN Y C, LEE Y H, et al. Distribution of micro stresses and interfacial tractions in unidirectional compo-sites[J]. Journal of Composite Materials,2008,42(18):1825-1849. DOI: 10.1177/0021998308093909
[16]	LIAO B, TAN H, ZHOU J, et al. Multi-scale modelling of dynamic progressive failure in composite laminates subjected to low velocity impact[J]. Thin-Walled Structures,2018,131:695-707. DOI: 10.1016/j.tws.2018.07.047
[17]	LANGSETH M, HOPPERSTAD O S. Static and dynamic axial crushing of square thin-walled aluminium extrusions[J]. International Journal of Impact Engineering,1996,18(7-8):949-968. DOI: 10.1016/S0734-743X(96)00025-5
[18]	ASTM. Standard test method for tensile properties of polymer matrix composite materials: ASTM D3039[S]. West Conshohcken: ASTM, 2000.
[19]	李星, 关志东, 刘璐, 等. 复合材料跨尺度失效准则及其损伤演化[J]. 复合材料学报, 2013, 30(2):152-158. DOI: 10.13801/j.cnki.fhclxb.2013.02.003 LI Xing, GUAN Zhidong, LIU Lu, et al. Composite multiscale failure criteria and damage evolution[J]. Acta Materiae Compositae Sinica,2013,30(2):152-158(in Chinese). DOI: 10.13801/j.cnki.fhclxb.2013.02.003
[20]	LI S, WONGSTO A. Unit cells for micromechanical analyses of particle-reinforced composites[J]. Mechanics of Materials,2004,36(7):543-572. DOI: 10.1016/S0167-6636(03)00062-0
[21]	赖卫清, 王秀梅, 辛亮亮, 等. 基于RVE方法的二维机织复合材料弹性性能预测[J]. 玻璃钢/复合材料, 2019(6):64-72. LAI Weiqing, WANG Xiumei, XIN Liangliang, et al. Prediction of elastic properties of 2D woven composites based on RVE method[J]. Composites Science and Engineering,2019(6):64-72(in Chinese).
[22]	王新峰. 机织复合材料多尺度渐进损伤研究[D]. 南京: 南京航空航天大学, 2007. WANG Xinfeng. Multi-scale analyses of damage evolution in woven composite materials[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007(in Chinese).
[23]	HUANG Y, XU L, HA S K. Prediction of three-dimensional composite laminate response using micromechanics of failure[J]. Journal of Composite Materials,2012,46(19-20):2431-2442. DOI: 10.1177/0021998312449888
[24]	XU L, JIN C Z, HA S K. Ultimate strength prediction of braided textile composites using a multi-scale approach[J]. Journal of Composite Materials,2015,49(4):477-494. DOI: 10.1177/0021998314521062
[25]	WANG L, WANG B, WEI S, et al. Prediction of long-term fatigue life of CFRP composite hydrogen storage vessel based on micromechanics of failure[J]. Composites Part B: Engineering,2016,97:274-281.
[26]	薛亚红, 陈继刚, 闫世程, 等. 二维机织复合材料力学分析中的周期性边界条件研究[J]. 纺织学报, 2016, 37(9):70-77. DOI: 10.13475/j.fzxb.20150800808 XUE Yahong, CHEN Jigang, YAN Shicheng, et al. Periodic boundary conditions for mechanical property analysis of 2D woven fabric composite[J]. Journal of Textile Research,2016,37(9):70-77(in Chinese). DOI: 10.13475/j.fzxb.20150800808

施引文献(4)

期刊类型引用(3)

1.	李梦涵，魏娜，徐瑞琪，杨泽钰，崔洪芝. 三维碳纳米管/硅藻土基多孔陶瓷复合材料的制备及其光热水蒸发性能. 复合材料学报. 2023(08): 4577-4586 . 本站查看
2.	吴玉萍，王乾廷，孙炜，周忠华，谢宗丽，宋铭雨. 含椭圆叶片状SiO_2/聚乙烯醇渗透汽化复合膜的制备与性能. 复合材料学报. 2022(06): 2783-2791 . 本站查看
3.	赵士雄. 反渗透复合膜制备及其改性方法研究进展. 云南化工. 2022(06): 20-21+38 . 百度学术