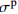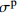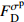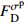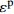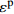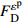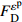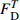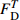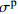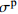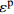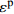钢-塑钢混杂纤维再生混凝土单轴压缩动态力学性能试验

冯俊杰; 尹冠生; 刘柱; 梁建红; 张云杰; 牛志强; 王鹏博

doi:10.13801/j.cnki.fhclxb.20211221.002

钢-塑钢混杂纤维再生混凝土单轴压缩动态力学性能试验

1.
长安大学　理学院，西安 710064
2.
陕西铁投工程检测科技有限公司，西安 710304
3.
郑州科技学院　土木建筑工程学院，郑州 450064

基金项目: 长安大学博士研究生创新能力培养资助项目(300203211121)；陕西省交通运输厅交通科研项目(21-67K)；长安大学相变蓄能建筑材料创新开放实验室项目(2018CXSY06)；河南省科技厅科技攻关项目(182102311091)；郑州科技学院自然科学项目(2017-XYZK-002)

详细信息

通讯作者:
尹冠生，博士，教授，博士生导师，研究方向为混凝土结构　E-mail: yings@chd.edu.cn

中图分类号: TV431
计量
- 文章访问数: 0942
- HTML全文浏览量: 0477
- PDF下载量: 063
出版历程
- 收稿日期: 2021-10-14
- 修回日期: 2021-12-09
- 录用日期: 2021-12-12
- 网络出版日期: 2021-12-21
- 刊出日期: 2022-10-31

Experiment on dynamic mechanical properties of steel and macro-polypropylene hybrid fibers reinforced recycled aggregate concrete under uniaxial compression

1.
School of Science, Chang’an University, Xi’an 710064, China
2.
Shaanxi Tietou Engineering Testing Technology CO., LTD., Xi’an 710304, China
3.
School of Civil Engineering and Architecture, Zhengzhou University of Science and Technology, Zhengzhou 450064, China

摘要

摘要: 为探究钢-塑钢混杂纤维再生混凝土的压缩动态力学性能，设计了A、B和C 3个系列混杂纤维再生混凝土包含3种再生粗骨料取代率和5种体积分数1.5vol%的钢纤维和塑钢混掺纤维组合，采用了4种加载应变率。试验表明：随应变率增加，混杂纤维再生混凝土峰值应力、弹性模量和压缩韧性增大，峰值应变减小。相较于基准组，在相同应变率下3个系列中的含纤维组峰值应力最大增幅分别为23%、16%和16%；峰值应变最大增幅分别为19%、12%和13%；弹性模量最大增幅分别为15%、14%和35%；压缩韧性最大增幅分别为46%、32%和37%。在试验应变率范围内，再生粗骨料显著提高峰值应力、弹性模量和压缩韧性的应变率敏感性，对峰值应变的应变率敏感性并无明显影响；掺入纤维降低混凝土峰值应变和弹性模量的应变率敏感性，提高普通混凝土峰值应力和压缩韧性的应变率敏感性，降低再生混凝土峰值应力和压缩韧性的应变率敏感性。提出的动态损伤本构模型考虑了纤维增强系数、再生粗骨料取代率和应变率，计算结果与试验结果吻合较好。
- 混杂纤维再生混凝土 /
- 单轴压缩 /
- 动态力学性能 /
- 动态增长因子 /
- 应变率敏感性 /
- 动态损伤本构模型
Abstract: The dynamic compressive behavior of hooked-end steel (HES) and macro-polypropylene (MPP) hybrid fibers reinforced recycled aggregate concrete (HyF/RAC) was studied. Three series (A, B and C) of HyF/RAC specimens were designed, which include three different recycled coarse aggregates (RCA) replacement ratios and five combinations of hybrid fibers at the total volume fraction of 1.5vol%, and four different strain rates were conducted. The results show that with the increase of strain rate, the peak stress, elastic modulus and compressive toughness increase, while the peak strain decreases. Compared with control groups in three series under the same strain rate, the largest increases of peak stress for specimens with fibers are 23%, 16% and 16%, respectively. The largest increases of peak strain are 19%, 12% and 13%, respectively. The largest increases of elastics modulus are 15%, 14% and 35%, respectively. The largest increases of compressive toughness are 46%, 32% and 37%, respectively. In the strain rate range, the strain rate sensitivity of peak stress, elastic modulus and compressive toughness increase with the RCA, and the RCA replacement ratio does not affect the strain rate sensitivity of peak strain. The strain rate sensitivity of peak strain and elastics modulus decrease with the addition of fiber. The addition of fibers enhances the strain rate sensitivity of peak stress and compressive toughness for natural aggregate concrete (NAC). While the strain rate sensitivity of peak stress and compressive toughness decrease for recycled aggregate concrete (RAC). The dynamic constitutive damage model was proposed considering the reinforcing index of fibers, RCA replacement ratio and strain rates. And all the models agree well with the experimental curves.
- hybrid fibers reinforced recycled aggregate concrete /
- uniaxial compression /
- dynamic mechanical properties /
- dynamic increase factor /
- strain rate sensitivity /
- dynamic damage constitutive model

HTML全文

图 1 压缩试验加载装置(单位：mm)

Figure 1. Loading setup for compressive test (Unit: mm)

下载: 全尺寸图片幻灯片

图 2 不同应变率下HyF/RAC(C0和C3组)试件破坏形态

Figure 2. Failure modes of C0 and C3 specimens for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 3 不同应变率下HyF/RAC(C0和C3组)试件应力-应变曲线

Figure 3. Stress-strain curve of C0 and C3 specimens for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 4 不同应变率下HyF/RAC峰值应力 $\sigma^{\rm{p}}$

Figure 4. Peak stress $\sigma^{\rm{p}}$ of HyF/RAC at different strain rates

$\dot \varepsilon$ —Strain rate; ${\dot \varepsilon _{\text{s}}}$ —Quasi-static strain rate

下载: 全尺寸图片幻灯片

图 5 不同应变率下HyF/RAC峰值应力动态增长因子 $F^{{\sigma}^{\rm{p}}}_{\rm{D}}$

Figure 5. Dynamic increase factor $F^{{\sigma}^{\rm{p}}}_{\rm{D}}$ of peak stress of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 6 不同应变率下HyF/RAC峰值应变 $\varepsilon^{\rm{p}}$

Figure 6. Peak strain $\varepsilon^{\rm{p}}$ of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 7 不同应变率下HyF/RAC峰值应变动态增长因子 $F^{{\varepsilon}^{\rm{p}}}_{\rm{D}}$

Figure 7. Dynamic increase factor $F^{{\varepsilon}^{\rm{p}}}_{\rm{D}}$ of peak strain of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 8 不同应变率下HyF/RAC弹性模量 E

Figure 8. Elastic modulus E of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 9 不同应变率下HyF/RAC弹性模量动态增长因子 $F^E_{\rm{D}}$

Figure 9. Dynamic increase factor $F^E_{\rm{D}}$ of elastic modulus of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 10 不同应变率下HyF/RAC压缩韧性T

Figure 10. Compressive toughness T of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 11 不同应变率下HyF/RAC压缩韧性动态增长因子 $F^T_{\rm{D}}$

Figure 11. Dynamic increase factor $F^T_{\rm{D}}$ of compressive toughness of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 12 HyF/RAC应力-应变曲线特征参数预测模型性能

SD—Standard deviation; Err—Mean relative error

Figure 12. Performance of prediction models for characteristic indices of HyF/RAC stress-strain curves

下载: 全尺寸图片幻灯片

图 13 不同应变率下HyF/RAC(C0组)试验曲线与各模型曲线对比

Figure 13. Comparison of experimental and theoretical stress-strain curves of C0 for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 14 不同应变率下HyF/RAC(C3组)试验曲线与各模型曲线对比

Figure 14. Comparison of experimental and theoretical stress-strain curves of C3 for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 15 不同应变率下HyF/RAC(C0和C3组)损伤演化

Figure 15. Damage evolution curves of C0 and C3 for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

表 1 端钩钢纤维(HES)和塑钢纤维(MPP)属性

Table 1 Properties of hooked-end steel fiber (HES) and macro-polypropylene fiber (MPP)

Fiber type	Equivalent diameter/mm	Length/mm	Aspect ratio	Density/(kg·m⁻³)	Tensile strength/MPa	Young’s modulus/GPa
HES	0.75	35	47	7800	1120	200.0
MPP	0.94	28	30	910	580	5.5

下载: 导出CSV

表 2 钢-塑钢混杂纤维再生混凝土(HyF/RAC)配合比设计

Table 2 Designed mix proportions of hybrid fiber reinforced recycled aggregate concrete (HyF/RAC) kg/m³

Mix	Notation	Water	Cement	Sand	RCA	NCA	HES	MPP	AW
A0	NAC	251	467	639	0	1044	0	0.00	0
A1	1.5%HES/NAC	251	467	639	0	1044	117	0.00	0
A2	1.25%HES-0.25%MPP/NAC	251	467	639	0	1044	98	2.28	0
A3	1.0%HES-0.5%MPP/NAC	251	467	639	0	1044	78	4.55	0
A4	0.75%HES-0.75%MPP/NAC	251	467	639	0	1044	59	6.83	0
A5	0.5%HES-1.0%MPP/NAC	251	467	639	0	1044	39	9.10	0
B0	RAC(50%)	251	467	639	522	522	0	0.00	20
B1	1.5%HES/RAC(50%)	251	467	639	522	522	117	0.00	20
B2	1.25%HES-0.25%MPP/RAC(50%)	251	467	639	522	522	98	2.28	20
B3	1.0%HES-0.5%MPP/RAC(50%)	251	467	639	522	522	78	4.55	20
B4	0.75%HES-0.75%MPP/RAC(50%)	251	467	639	522	522	59	6.83	20
B5	0.5%HES-1.0%MPP/RAC(50%)	251	467	639	522	522	39	9.10	20
C0	RAC(100%)	251	467	639	1044	0	0	0.00	40
C1	1.5%HES/RAC(100%)	251	467	639	1044	0	117	0.00	40
C2	1.25%HES-0.25%MPP/RAC(100%)	251	467	639	1044	0	98	2.28	40
C3	1.0%HES-0.5%MPP/RAC(100%)	251	467	639	1044	0	78	4.55	40
C4	0.75%HES-0.75%MPP/RAC(100%)	251	467	639	1044	0	59	6.83	40
C5	0.5%HES-1.0%MPP/RAC(100%)	251	467	639	1044	0	39	9.10	40
Notes: NAC—Natural aggregate concrete; RAC—Recycled aggregate concrete; RCA—Recycled coarse aggregate; NCA—Natural coarse aggregate; AW—Absorbed water; In iHES-jMPP/RAC(k), i—Volume fraction of HES, j—Volume fraction of MPP, k—Replacement ratio by mass of RCA.

下载: 导出CSV

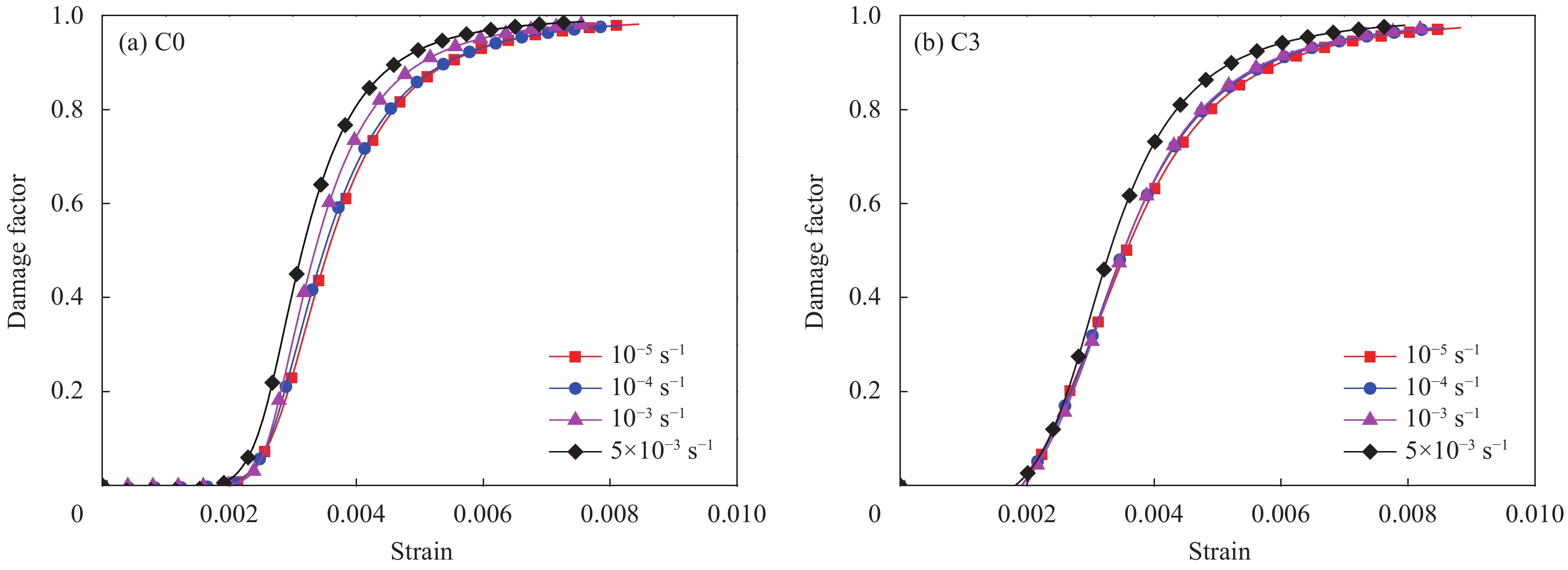
表 3 不同应变率下HyF/RAC峰值应力 ${\sigma ^{\text{p}}}$

Table 3 Results of peak stress ${\sigma ^{\text{p}}}$ of HyF/RAC at different strain rates

Mix	10⁻⁵ s⁻¹		10⁻⁴ s⁻¹		10⁻³ s⁻¹		5×10⁻³ s⁻¹
Mix	${\sigma ^{\text{p}}}$ /MPa	C_V/%	${\sigma ^{\text{p}}}$ /MPa	C_V/%	${\sigma ^{\text{p}}}$ /MPa	C_V/%	${\sigma ^{\text{p}}}$ /MPa	C_V/%
A0	31.3	1.58	32.4	2.84	33.7	3.15	34.7	0.00
A1	32.4	2.53	34.0	2.72	38.8	4.01	39.3	1.03
A2	32.9	4.31	36.3	0.98	39.1	1.27	40.1	5.14
A3	34.9	0.17	39.0	2.90	41.3	0.34	41.9	0.84
A4	31.5	3.59	32.8	5.40	35.2	4.22	36.9	4.41
A5	32.7	5.19	34.4	3.29	36.6	2.61	37.3	5.13
B0	28.3	1.00	29.1	3.87	32.4	1.46	34.0	2.29
B1	29.6	2.15	30.8	1.15	34.6	4.71	35.7	4.56
B2	31.9	1.30	33.6	5.27	34.2	3.93	36.1	3.73
B3	31.2	0.23	32.4	1.97	35.7	1.98	37.2	6.84
B4	30.4	1.51	32.3	1.99	35.3	3.13	36.1	0.78
B5	31.6	1.59	33.7	1.70	37.3	0.57	38.3	2.22
C0	24.6	8.57	26.9	2.74	30.6	4.48	32.5	0.22
C1	26.2	4.04	27.8	3.89	31.6	1.14	32.4	3.45
C2	26.8	2.24	28.8	0.72	32.2	2.64	32.8	1.72
C3	28.4	2.69	31.1	0.68	33.0	2.69	34.4	3.63
C4	27.8	0.95	30.0	6.21	32.7	2.60	33.1	5.32
C5	26.3	0.79	27.3	2.23	30.6	5.46	32.7	0.43
Note: C_V—Coefficients of variation.

下载: 导出CSV

表 4 不同应变率下HyF/RAC峰值应变 ${\varepsilon ^{\text{p}}}$

Table 4 Results of peak strain ${\varepsilon ^{\text{p}}}$ of HyF/RAC at different strain rates

Mix	10⁻⁵ s⁻¹		10⁻⁴ s⁻¹		10⁻³ s⁻¹		5×10⁻³ s⁻¹
Mix	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%
A0	2.376	4.73	2.330	8.37	2.224	1.67	2.101	9.02
A1	2.410	2.87	2.340	7.71	2.256	10.77	2.199	11.43
A2	2.413	1.55	2.390	0.74	2.378	11.52	2.321	6.02
A3	2.599	8.68	2.555	3.18	2.528	3.98	2.500	3.42
A4	2.419	2.70	2.425	6.95	2.413	10.11	2.312	11.72
A5	2.443	6.27	2.432	8.62	2.330	6.22	2.254	1.68
B0	2.593	3.67	2.469	0.79	2.370	3.18	2.325	6.08
B1	2.651	9.27	2.631	6.65	2.620	6.75	2.510	6.20
B2	2.673	3.61	2.645	9.62	2.592	5.28	2.481	9.76
B3	2.760	5.68	2.708	7.48	2.631	7.32	2.610	5.55
B4	2.583	0.39	2.544	2.43	2.544	7.28	2.533	8.45
B5	2.666	2.41	2.658	6.79	2.630	4.84	2.591	2.11
C0	2.814	4.46	2.726	3.44	2.621	2.51	2.524	2.73
C1	2.933	1.81	2.815	11.43	2.708	5.28	2.694	0.33
C2	2.950	1.47	2.813	1.33	2.769	2.75	2.733	2.20
C3	2.941	1.62	2.853	0.99	2.845	6.83	2.648	3.47
C4	3.041	3.67	2.996	4.01	2.891	0.79	2.861	9.33
C5	2.981	3.50	2.859	1.67	2.754	7.66	2.701	0.46

下载: 导出CSV

表 5 不同应变率下HyF/RAC弹性模量E

Table 5 Results of elastic modulus E of HyF/RAC at different strain rates

Mix	10⁻⁵s⁻¹		10⁻⁴s⁻¹		10⁻³s⁻¹		5×10⁻³s⁻¹
Mix	E/GPa	C_V/%	E/GPa	C_V/%	E/GPa	C_V/%	E/GPa	C_V/%
A0	29.5	3.86	33.2	9.20	37.6	9.87	41.2	2.37
A1	31.8	8.13	35.3	1.34	38.6	3.95	42.0	9.60
A2	32.1	7.05	34.3	1.09	38.3	4.35	41.4	4.92
A3	34.1	7.30	34.1	2.88	34.7	0.61	38.1	10.65
A4	32.5	7.19	33.7	5.58	35.7	4.14	37.4	11.49
A5	33.9	4.75	34.0	5.06	35.0	3.23	38.2	2.85
B0	24.8	7.61	26.2	8.55	28.6	3.24	30.8	2.69
B1	25.6	9.08	26.2	0.91	28.6	5.58	30.8	9.23
B2	27.1	0.22	28.1	11.70	29.4	8.73	33.9	8.52
B3	27.3	0.70	28.7	9.85	31.0	6.90	31.7	1.92
B4	28.2	1.65	29.9	3.60	33.2	0.66	33.6	6.38
B5	27.2	4.70	27.8	11.33	28.9	9.67	32.9	11.19
C0	18.7	3.06	21.9	11.63	24.9	6.18	26.7	9.24
C1	20.7	8.05	22.8	11.44	26.3	11.54	27.8	7.55
C2	23.2	7.56	24.3	2.31	26.1	1.54	29.5	10.99
C3	25.1	6.06	26.3	4.08	28.0	11.09	28.1	2.47
C4	22.9	0.56	23.3	2.43	25.2	4.69	28.3	9.75
C5	22.7	0.56	24.4	9.26	27.9	3.17	29.2	9.11

下载: 导出CSV

表 6 不同应变率下HyF/RAC压缩韧性T

Table 6 Results of compressive toughness T of HyF/RAC at different strain rates

Mix	10⁻⁵ s⁻¹	10⁻⁴ s⁻¹	10⁻³ s⁻¹	5×10⁻³ s⁻¹
Mix	T/MPa	T/MPa	T/MPa	T/MPa
A0	0.042	0.044	0.046	0.043
A1	0.047	0.049	0.051	0.050
A2	0.047	0.051	0.053	0.047
A3	0.055	0.058	0.060	0.062
A4	0.047	0.048	0.052	0.053
A5	0.047	0.049	0.047	0.051
B0	0.041	0.043	0.043	0.045
B1	0.046	0.048	0.050	0.052
B2	0.049	0.051	0.053	0.056
B3	0.051	0.051	0.055	0.057
B4	0.048	0.050	0.054	0.057
B5	0.050	0.051	0.057	0.058
C0	0.038	0.040	0.043	0.045
C1	0.043	0.046	0.050	0.053
C2	0.048	0.049	0.051	0.057
C3	0.052	0.053	0.055	0.052
C4	0.051	0.054	0.054	0.057
C5	0.047	0.047	0.047	0.052

下载: 导出CSV

表 7 现有压缩动态本构模型

Table 7 Review of dynamic constitutive models under compression

Reference	Model	Parameter	Application range
Ibrahim et al^[21]	$\begin{gathered} y = \frac{{Ax + \left( {B - 1} \right){x^2}}}{{1 + \left( {A - 2} \right)x + B{x^2}}} \\ A\left( {A - 2} \right) - B + 1 \geqslant 0 \\ A + B > 1 \\ \end{gathered}$	$\begin{gathered} A = 3.6\exp \left( {9.0 \times {{10}^{ - 8}}\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\text{s}}}}}} \right)\left( {1 + 0.01R_V^{0.82}} \right)} \right) \\ B = 0.22\exp \left( {3.8 \times {{10}^{ - 7}}\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\text{s}}}}}} \right)\left( {1 + 0.002R_V^{0.82}} \right)} \right) \\ \end{gathered}$	$\begin{gathered} 25{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 125{\text{ }}{{\text{s}}^{ - 1}} \\ 1.2{\text{% }} \leqslant V \leqslant 1.4\% \\ \end{gathered}$
Zhou et al^[22]	$\begin{gathered} \sigma = {\sigma _{\text{m}}}\left( {1 - D} \right) = E\varepsilon \left( {1 - D} \right) \\ D = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{{{F_0}}}} \right)}^m}} \right] \\ \end{gathered}$	$\begin{gathered} {F_0} = 3.3578\ln \dot \varepsilon - 10.6562 \\ m = 1.2804\ln \dot \varepsilon - 1.8711 \\ \end{gathered}$	$19.8{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 281{\text{ }}{{\text{s}}^{ - 1}}$
Hou et al^[23]	$\begin{gathered} \sigma = {\sigma _{\text{m}}}\left( {1 - {C_{\text{n}}}D} \right) = E\varepsilon \left( {1 - {C_{\text{n}}}D} \right) \\ D = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{{{F_0}}}} \right)}^m}} \right] \\ \end{gathered}$	$\begin{gathered} {F_0} = 0.0062 + 0.31{V^{1.7}} - 0.00167\left( {0.1 + V} \right)\ln \dot \varepsilon \\ m = - 0.56 + 3V + \left( {0.35 - 2V} \right)\ln \dot \varepsilon \\ {C_{\text{n}}} = 0.977 - 1.4V + \left( {0.004 + 0.25V} \right)\ln \dot \varepsilon \\ \end{gathered}$	$\begin{gathered} \dot \varepsilon \leqslant 294{\text{ }}{{\text{s}}^{ - 1}} \\ V \leqslant 5\% \\ \end{gathered}$
Sun et al^[25]	$\begin{gathered} \sigma = {\sigma _{\text{m}}}\left( {1 - D} \right) = E\varepsilon \left( {1 - D} \right) \\ \dot D = AD\left( {1 - D} \right) \\ \end{gathered}$	$\begin{gathered} {D} = 0.35 - 8.2 \times {10^{ - 9} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right) - \\ \qquad 4.4V + 1.3 \times {10^{ - 7} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right)V \\ A = 234 + 1.3 \times {10^{ - 7} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right) + \\ \qquad 1718V - 8.6 \times {10^{ - 5} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right)V \\ \end{gathered}$	$\begin{gathered} 53{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 152{{\text{s}}^{ - 1}} \\ V \leqslant 6.0\% \\ \end{gathered}$
Zhang et al^[26]	$\begin{gathered} \sigma = \left( {1 - D} \right){\sigma _{\text{m}}} \\ {\sigma _{\text{m}}} = {\sigma _{\text{e}}}\left( \varepsilon \right) + {E_1}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _1}}}} \right){\rm{d}}\tau } + \\ \qquad {E_2}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _2}}}} \right){\rm{d}}\tau } \\ {\sigma _{\text{e}}}\left( \varepsilon \right) = E\varepsilon + \alpha {\varepsilon ^2} + \beta {\varepsilon ^3} \\ D = \left\{ \begin{gathered} 0{\text{ }}\qquad(\varepsilon \leqslant {\varepsilon ^{{\text{th}}}}) \\ 1 - \exp \left[ { - {{\left( {\frac{{\varepsilon - {\varepsilon ^{{\text{th}}}}}}{{{F_0}}}} \right)}^m}} \right]{\text{ }}\qquad(\varepsilon > {\varepsilon ^{{\text{th}}}}) \\ \end{gathered} \right. \\ \end{gathered}$	No fitting equation	$\begin{gathered} 27{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 94{\text{ }}{{\text{s}}^{ - 1}} \\ V \leqslant 0.2\% \\ \end{gathered}$
Wang et al^[27]	$\begin{gathered} \sigma = \left( {1 - D} \right)\sigma \\ {\sigma _{\text{m}}} = {\sigma _{\text{e}}}\left( \varepsilon \right) + {E_1}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _1}}}} \right){\rm{d}}\tau } + \\ \qquad {E_2}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _2}}}} \right){\rm{d}}\tau } \\ D = \left\{ \begin{gathered} 0{\text{ }}\qquad(\varepsilon \leqslant {\varepsilon ^{{\text{th}}}} ) \\ {K_D}{{\dot \varepsilon }^{\lambda - 1}}{\left( {\varepsilon - {\varepsilon ^{{\text{th}}}}} \right)^\kappa }{\text{ }}\qquad(\varepsilon > {\varepsilon ^{{\text{th}}}} ) \\ \end{gathered} \right. \\ \end{gathered}$	No fitting equation	${10^{ - 4}}{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant {10^3}{\text{ }}{{\text{s}}^{ - 1}}$
Notes: $y = {\sigma \mathord{\left/ {\vphantom {\sigma { {\sigma ^{\text{p} } } } } } \right. } { {\sigma ^{\text{p} } } }}, x = {\varepsilon \mathord{\left/ {\vphantom {\varepsilon { {\varepsilon ^{\text{p} } } } } } \right. } { {\varepsilon ^{\text{p} } } }}$ , $\sigma$ —Stress, ${\sigma ^{\text{p}}}$ —Peak stress, $\varepsilon$ —Strain, ${\varepsilon ^{\text{p}}}$ —Peak strain; R_V—Reinforcing index of hybrid fibers; D—Damage parameter; t—Loading time; τ—Delay time of stress; E₁, ${\varphi _1}$ —Elastic modulus and relaxation time at a low strain rate and frequency; E₂, ${\varphi _2}$ —Elastic modulus and relaxation time at a high strain rate and frequency; α, β—Elastic constant; ${K_D},{\text{ }}\lambda ,{\text{ }}\kappa$ —Material parameter; ${\varepsilon ^{{\text{th}}}}$ —Strain threshold.

下载: 导出CSV

表 8 HyF/RAC修正模型参数 $\alpha$ 拟合值

Table 8 Fitted results of parameter $\alpha$ in modified constitutive models for HyF/RAC

Mix	$\dot \varepsilon$
	10⁻⁵s⁻¹		10⁻⁴s⁻¹		10⁻³s⁻¹		5×10⁻³s⁻¹
	Fitted value	R²	Fitted value	R²	Fitted value	R²	Fitted value	R²
A0	3.434	0.991	3.399	0.946	2.597	0.953	2.285	0.940
A1	1.882	0.978	1.175	0.998	1.699	0.986	1.352	0.973
A2	1.386	0.999	1.401	0.997	1.020	0.981	1.039	0.994
A3	1.442	0.997	1.912	0.992	1.607	0.965	1.650	0.974
A4	2.219	0.994	2.431	0.970	2.057	0.965	1.466	0.984
A5	2.600	0.998	2.633	0.984	2.288	0.971	1.757	0.992
B0	3.524	0.991	3.742	0.994	2.589	0.942	3.053	0.997
B1	1.440	0.976	1.125	0.983	1.225	0.997	1.873	0.996
B2	1.932	0.985	2.124	0.991	2.001	0.996	1.583	0.979
B3	2.026	0.994	1.636	0.999	2.274	0.988	2.297	0.984
B4	1.876	0.990	2.683	0.992	2.305	0.994	2.613	0.935
B5	2.457	0.994	3.036	0.997	2.873	0.940	2.496	0.984
C0	3.173	0.978	2.958	0.978	3.609	0.986	4.137	0.954
C1	1.552	0.993	1.657	0.976	2.280	0.976	2.749	0.993
C2	1.673	0.975	2.013	0.999	2.259	0.999	2.364	0.953
C3	2.059	0.998	2.149	0.999	2.278	0.998	2.732	0.996
C4	1.868	0.976	2.174	0.997	3.339	0.968	2.842	0.934
C5	2.218	0.971	2.859	0.990	3.483	0.964	3.394	0.993

下载: 导出CSV

参考文献(35)

[1]	高光发. 混凝土材料动态压缩强度的应变率强化规律[J]. 高压物理学报, 2017, 31(3):261-270. GAO Guangfa. Effect of strain-rate hardening on dynamic compressive strength of plain concrete[J]. Chinese Jour-nal of High Pressure Physics,2017,31(3):261-270(in Chinese).
[2]	王国盛, 路德春, 杜修力, 等. 混凝土材料真实动态强度及率效应机理研究[J]. 工程力学, 2018, 35(6):58-67. WANG Guosheng, LU Dechun, DU Xiuli, et al. Research on the actual dynamic strength and the rate effect mecha-nisms for concrete materials[J]. Engineering Mechanics,2018,35(6):58-67(in Chinese).
[3]	艾思平, 唐鹏. 考虑地震量级作用下橡胶纤维混凝土受压动力性能试验研究[J]. 建筑材料学报, 2021, 24(5): 1002-1010. AI Siping, TANG Peng. Experimental study on the dynamic behavior of rubber fiber reinforced concrete under the action of earthquake magnitude[J]. Journal of Building Material, 2021, 24(5): 1002-1010(in Chinese).
[4]	白卫峰, 李思蕾, 管俊峰, 等. 再生混凝土单轴压缩动态力学性能试验研究[J]. 建筑材料学报, 2022, 25(5): 498-508. BAI Weifeng, LI Silei, GUAN Junfeng, et al. Study on dynamic mechanical properties of recycled concrete under uniaxial compression[J]. Journal of Building Materials,2022, 25(5): 498-508(in Chinese).
[5]	XIAO J, ZHANG K, ZHANG Q. Strain rate effect on compres-sive stress-strain curves of recycled aggregate concrete with seawater and sea sand[J]. Construction and Building Materials,2021,300:124014. DOI: 10.1016/j.conbuildmat.2021.124014
[6]	董海龙, 彭有开, 骆开静, 等. 粗骨料取代下的高性能再生混凝土率敏性研究[J]. 实验力学, 2019, 34(2):249-257. DONG Hailong, PENG Youkai, LUO Kaijing, et al. Study on rate sensitivity of high performance recycled concrete with different coarse aggregate replacement ratios[J]. Journal of Experimental Mechanics,2019,34(2):249-257(in Chinese).
[7]	TANG Z, LI W, TAM V W Y, et al. Investigation on dynamic mechanical properties of fly ash/slag-based geopolymeric recycled aggregate concrete[J]. Composites Part B: Engi-neering,2020,185:107776. DOI: 10.1016/j.compositesb.2020.107776
[8]	FENG J, YIN G, TUO H, et al. Parameter optimization and regression analysis for multi-index of hybrid fiber-reinforced recycled coarse aggregate concrete using orthogonal experimental design[J]. Construction and Building Materials,2021,267:121013. DOI: 10.1016/j.conbuildmat.2020.121013
[9]	陈宇良, 吉云鹏, 陈宗平, 等. 钢纤维再生混凝土三轴受压力学性能试验[J]. 复合材料学报, 2022, 39(8): 4005-4016. CHEN Yuliang, JI Yunpeng, CHEN Zongping, et al. Experiment on mechanical properties of steel fiber recycled aggregate concrete under triaxial compression[J]. Acta Materiae Compositae Sinica, 2022, 39(8): 4005-4016(in Chinese).
[10]	丁亚红, 郭书奇, 张向冈, 等. 玄武岩纤维对再生混凝土抗碳化性能的影响[J]. 复合材料学报, 2022, 39(3): 1228-1238. DING Yahong, GUO Shuqi, ZHANG Xianggang, et al. Influence of basalt fiber on the anti-carbonation performance of recycled aggregate concrete[J]. Acta Materiae Compositae Sinica, 2022, 39(3): 1228-1238(in Chinese).
[11]	XIE J, KOU S, MA H, et al. Advances on properties of fiber reinforced recycled aggregate concrete: Experiments and models[J]. Construction and Building Materials,2021,277:122345. DOI: 10.1016/j.conbuildmat.2021.122345
[12]	王兴国, 姜茂林, 陈旭, 等. 不同预浸骨料-PVA纤维对再生混凝土力学性能影响[J]. 复合材料学报, 2022, 39(3): 1205-1214. WANG Xingguo, JIANG Maolin, CHEN Xu, et al. Effect of different pre-soaked aggregate-PVA fiber on the mechani-cal properties of recycled aggregate concrete[J]. Acta Materiae Compositae Sinica, 2022, 39(3): 1205-1214(in Chinese).
[13]	孔祥清, 何文昌, 周聪, 等. 混杂掺入钢/聚丙烯纤维再生混凝土力学性能及抗冲击性能试验研究[J]. 建筑科学, 2020, 36(3):94-99. KONG Xiangqing, HE Wenchang, ZHOU Cong, et al. Experimental investigation on the mechanical properties and impact resistance of steel and polypropylene hybrid fiber reinforced recycled aggregates concrete[J]. Building Science,2020,36(3):94-99(in Chinese).
[14]	FENG J, YIN G, TUO H, et al. Uniaxial compressive behavior of hook-end steel and macro-polypropylene hybrid fibers reinforced recycled aggregate concrete[J]. Construction and Building Materials,2021,304:124559. DOI: 10.1016/j.conbuildmat.2021.124559
[15]	周宏宇, 麻全周, 赵晓花, 等. 考虑应变率效应的混凝土材料单轴压缩特性尺寸效应研究[J]. 混凝土, 2021(1):61-65, 69. DOI: 10.3969/j.issn.1002-3550.2021.01.015 ZHOU Hongyu, MA Quanzhou, ZHAO Xiaohua, et al. Experimental study on dynamic rate relevance of concrete size effect[J]. Concrete,2021(1):61-65, 69(in Chinese). DOI: 10.3969/j.issn.1002-3550.2021.01.015
[16]	肖诗云, 张剑. 不同应变率下混凝土受压损伤试验研究[J]. 土木工程学报, 2010, 43(3):40-45. XIAO Shiyun, ZHANG Jian. Compressive damage experiment of concrete at different strain rates[J]. China Civil Engineering Journal,2010,43(3):40-45(in Chinese).
[17]	焦楚杰, 孙伟, 张亚梅, 等. 钢纤维高强混凝土在不同应变率时的单轴受压性能[J]. 建筑结构, 2004, 34(8):65-67. JIAO Chujie, SUN Wei, ZHANG Yamei, et al. Mechanical properties of SFRHSC under uniaxial compression with different strain rates[J]. Building Structure,2004,34(8):65-67(in Chinese).
[18]	梁宁慧, 杨鹏, 刘新荣, 等. 高应变率下多尺寸聚丙烯纤维混凝土动态压缩力学性能研究[J]. 材料导报, 2018, 32(2):288-294. LIANG Ninghui, YANG Peng, LIU Xinrong, et al. A study on dynamic compressive mechanical properties of multi-size polypropylene fiber concrete under high strain rate[J]. Materials Reports,2018,32(2):288-294(in Chinese).
[19]	沈才华, 钱晋, 陈晓峰, 等. 纤维掺量对PVA纤维混凝土力学参数的影响及压缩韧性指标的计算方法[J]. 硅酸盐通报, 2020, 39(10):3152-3160. SHEN Caihua, QIAN Jin, CHEN Xiaofeng, et al. Influence of fiber content on mechanical parameters of PVA fiber concrete and method for calculating compression toughness index[J]. Bulletin of the Chinese Ceramic Society,2020,39(10):3152-3160(in Chinese).
[20]	HE W, KONG X, FU Y, et al. Experimental investigation on the mechanical properties and microstructure of hybrid fiber reinforced recycled aggregate concrete[J]. Construction and Building Materials,2020,261:120488. DOI: 10.1016/j.conbuildmat.2020.120488
[21]	IBRAHIM S M, ALMUSALLAM T H, AL-SALLOUM Y A, et al. Strain rate dependent behavior and modeling for compression response of hybrid fiber reinforced concrete[J]. Latin American Journal of Solids and Structures,2016,13:1695-1715. DOI: 10.1590/1679-78252717
[22]	ZHOU J, CHEN X. Stress-strain behavior and statistical continuous damage model of cement mortar under high strain rates[J]. Journal of Materials in Civil Engineering,2013,25(1):120-130. DOI: 10.1061/(ASCE)MT.1943-5533.0000570
[23]	HOU X, CAO S, RONG Q, et al. Effects of steel fiber and strain rate on the dynamic compressive stress-strain relationship in reactive powder concrete[J]. Construction and Building Materials,2018,170:570-581. DOI: 10.1016/j.conbuildmat.2018.03.101
[24]	CUI T, HE H, YAN W, et al. Compression damage constitutive model of hybrid fiber reinforced concrete and its experimental verification[J]. Construction and Building Materials,2020,264:120026. DOI: 10.1016/j.conbuildmat.2020.120026
[25]	SUN X, ZHAO K, LI Y, et al. A study of strain-rate effect and fiber reinforcement effect on dynamic behavior of steel fiber-reinforced concrete[J]. Construction and Building Materials,2018,158:657-669. DOI: 10.1016/j.conbuildmat.2017.09.093
[26]	ZHANG H, WANG B, XIE A, et al. Experimental study on dynamic mechanical properties and constitutive model of basalt fiber reinforced concrete[J]. Construction and Building Materials,2017,152:154-167. DOI: 10.1016/j.conbuildmat.2017.06.177
[27]	王礼立, 胡时胜, 杨黎明, 等. 聊聊动态强度和损伤演化[J]. 爆炸与冲击, 2017, 37(2):169-179. WANG Lili, HU Shisheng, YANG Liming, et al. Talk about dynamic strength and damage evolution[J]. Explosion and Shock Waves,2017,37(2):169-179(in Chinese).
[28]	CAO S, HOU X, RONG Q. Dynamic compressive properties of reactive powder concrete at high temperature: A review[J]. Cement and Concrete Composites,2020,110:103568. DOI: 10.1016/j.cemconcomp.2020.103568
[29]	中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB/T 50010—2010[S]. 北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures: GB/T 50010—2010[J]. Beijing: China Architecture and Building Press, 2015(in Chinese).
[30]	张聪, 余志辉, 韩世诚, 等. 混杂纤维增强应变硬化水泥基复合材料的压缩本构关系[J]. 复合材料学报, 2020, 37(5):1221-1226. ZHANG Cong, YU Zhihui, HAN Shicheng, et al. Compression constitutive relation of hybrid fiber reinforced strain hardening cementitous composites[J]. Acta Materiae Compositae Sinica,2020,37(5):1221-1226(in Chinese).
[31]	SHI X, PARK P, REW Y, et al. Constitutive behaviors of steel fiber reinforced concrete under uniaxial compression and tension[J]. Construction and Building Materials,2020,233:117316. DOI: 10.1016/j.conbuildmat.2019.117316
[32]	ABADEL A, ABBAS H, ALMUSALLAM T, et al. Mechanical properties of hybrid fibre-reinforced concrete-analytical modelling and experimental behaviour[J]. Magazine of Concrete Research,2016,68:823-843. DOI: 10.1680/jmacr.15.00276
[33]	施林林, 宋玉普, 沈璐. 不同应变率下大骨料及湿筛混凝土单轴受压试验研究[J]. 世界地震工程, 2016, 32(2):270-276. SHI Linlin, SONG Yupu, SHEN Lu. Experimental study on uniaxial compression properties of large aggregate and wet-screened concrete at different strain rates[J]. World Earthquake Engineering,2016,32(2):270-276(in Chinese).
[34]	李庆斌, 邓宗才, 张立翔. 考虑初始弹模变化的混凝土动力损伤本构模型[J]. 清华大学学报(自然科学版), 2003(8):1088-1091. DOI: 10.3321/j.issn:1000-0054.2003.08.025 LI Qingbin, DENG Zongcai, ZHANG Lixiang. Dynamic damage constitutive model for concrete accounting for the difference of the initial elastic modulus[J]. Journal of Tsinghua University (Science and Technology),2003(8):1088-1091(in Chinese). DOI: 10.3321/j.issn:1000-0054.2003.08.025
[35]	DONG S, HAN B, YU X, et al. Dynamic impact behaviors and constitutive model of super-fine stainless wire reinforced reactive powder concrete[J]. Construction and Building Materials,2018,184:602-616. DOI: 10.1016/j.conbuildmat.2018.07.027

施引文献(6)

期刊类型引用(2)

1.	李滋阳，王思佳，邓文举. 陶瓷颗粒增强金属基复合材料研究进展. 轻工科技. 2021(04): 41-44 . 百度学术
2.	陈亚楠，金云学，牛牧野，陈洪美，杜文栋. Ni_3Al(Cr)合金室温干滑动摩擦磨损性能研究. 江苏科技大学学报(自然科学版). 2019(05): 18-26 . 百度学术