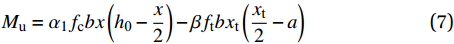Flexural properties of ultra high performance concrete reinforced with steel wire mesh or fiber mesh
-
摘要: 为研究钢丝网或纤维网对混杂纤维超高性能混凝土(Ultra-high performance concrete，UHPC)板弯曲性能的影响，进行了四边简支双向板弯曲试验。UHPC中短切纤维为：单掺钢纤维、钢纤维分别与聚乙烯醇纤维、玻璃纤维、玄武岩纤维混掺等。研究参数为：钢丝网与玻璃纤维网层数、孔径、混掺纤维比例等。结果表明，单掺体积分数为1.5vol%的钢纤维时，铺设3层和4层钢丝网的UHPC板的极限承载力和25 mm挠度处的能量吸收值较2层分别提升14.9%、32.3%和14.1%、25.2%；孔径较小的钢丝网对UHPC板承载力和韧性提升明显。当混杂纤维总体积分数为1.5vol%且钢丝网2层时，混掺1.0vol%钢纤维和0.5vol%聚乙烯醇纤维对UHPC板增强增韧效果更好，0.5vol%钢纤维与1.0vol%玻璃纤维或玄武岩纤维混掺较0.5vol%钢纤维与1.0vol%聚乙烯醇纤维混掺对改善板峰后持荷能力更有利，即钢纤维与较高弹性模量非金属纤维混掺有利于提高裂后承载力。与玻璃纤维网相比，铺设钢丝网的UHPC板在峰后延性更好。提出了以素UHPC板峰值荷载挠度作为初裂挠度的韧性指标评定方法，该方法可表征网格和纤维对UHPC板裂后韧性的贡献。基于网格有效利用率概念，建立了板抗弯承载力计算方法，理论值与试验值吻合良好。Abstract: To study the influence of steel wire mesh on the bending properties of ultra-high performance concrete (UHPC) slabs, a bending test of simply supported two-way slabs with four sides was carried out. The chopped fibers in UHPC ware: Steel fiber and steel fiber were mixed with polyvinyl alcohol fiber, glass fiber and basalt fiber, respectively. The research parameters were: Number of layers of wire mesh and glass fiber mesh, pore size and proportion of blended fibers. The results show that when UHPC is single-doped with 1.5vol% steel fiber, the ultimate bearing capacity and energy absorption at 25 mm deflection of UHPC slabs with 3 layers and 4 layers are increased by 14.9%, 32.3% and 14.1%, 25.2%, respectively compared with UHPC slabs with 2 layers of steel wire mesh. When the total volume fraction of hybrid fibers is 1.5vol% and the steel wire mesh is 2 layers, the blending of 1.0vol% steel fiber and 0.5vol% polyvinyl alcohol fiber has better reinforcing and toughening effect on UHPC slabs, and the UHPC slab mixed with 0.5vol% steel fiber and 1.0vol% glass fiber or basalt fiber has a stronger ability to maintain load after peak load than 1.0vol% polyvinyl alcohol fiber, namely the mixing of steel fiber with higher modulus of elasticity non-metallic fiber is advantageous to increase the post-cracking bearing capacity. Compared with glass fiber mesh, UHPC slabs with steel mesh have better ductility after peak load. A method for evaluating the flexibility of UHPC slabs with peak load deflection as initial cracking parameter was proposed, which can characterize the contribution of mesh and fibers to the post-crack toughness of UHPC slabs. Based on the concept of effective utilization of mesh, the theoretical value is in good agreement with the experimental value by calculating the bending capacity.
-
Keywords:
- steel mesh /
- two-way slab /
- hybrid fiber /
- hardening index /
- toughness index /
- bending capacity
-
超高性能混凝土(Ultra-high performance concrete，UHPC)是一种新型水泥基复合材料，由于致密的微观结构，使其具有优异的强度、延展性和耐久性，能够有效减轻结构自重，延长使用寿命等，是未来工程材料重要的发展方向[1-5]。
大量研究发现，钢纤维能够有效地抑制宏观和微观裂缝，从而显著提高了UHPC的弯曲性能及抗裂能力[6-8]。邵旭东等[8]进行了轴拉和四点弯曲试验研究，结果表明同一体积掺量下不同长径比、不同形状的钢纤维混掺能显著提高UHPC的拉伸强度和弯曲韧性。但高掺量钢纤维成本过高，低掺量钢纤维增强增韧效果有限，因此一些学者将不同弹性模量、形状的纤维混杂，制备出性能良好、成本较低的混杂纤维UHPC[9-11]。同时研究发现由于短切纤维乱向分布于UHPC中，其工作效率只有40%~70%，纤维作用不能充分发挥，因此在混凝土、UHPC构件中铺设双向均有良好抗拉强度及抗开裂性能的纤维网格成为新的研究方向[12-13]。与传统钢筋混凝土相比，纤维网格具有种类多、材质轻、抗拉强度高、耐腐蚀性能好等优点。李冬等[14]、丁一宁等[15]和Li等[16]通过试验表明，铺设玻璃纤维网格和玄武岩纤维网格显著提高了混凝土双向板的承载力和弯曲韧性，但峰值荷载后，试件呈现显著的脆性破坏。这是由于玻璃纤维、玄武岩纤维网格呈现脆性破坏特征引起的。为了充分降低纤维网格混凝土的脆性，赵国藩等[17]用钢丝网增强混凝土T形梁，试验结果表明短的钢纤维与钢丝网的复合能起到显著的增强效果，可有效提高混凝土梁的抗弯承载力和延性。
由于UHPC具有高强度，在制作薄板构件或者进行结构加固时，采用高强度钢丝网作为增强材料，让UHPC充分嵌入网孔中，使钢丝网与UHPC充分握裹，形成受力整体。与乱向分布的钢纤维相比，钢丝网增强UHPC显著提高了钢丝利用率和增强效果，有利于发展新型的钢丝网-UHPC材料及其结构体系。
目前关于网格增强混凝土的试验研究主要局限于纤维网格和普通混凝土，对钢丝网增强UHPC构件研究鲜有报道。本文借鉴欧洲EFNARC规范 ISBN 0-952-24831-X[18]，采用四边简支双向板试验，研究不同钢丝网格层数、孔径等参数变化对UHPC板增强增韧效果的影响规律，分析钢丝网与玻璃纤维网UHPC板力学性能的差异，研究结果将为工程应用提供参考。
1. 试验概括
1.1 原材料
试验使用的钢丝网(Steel wire mesh，SWM)由河北安平县丝网有限公司提供，孔径分别为12 mm×12 mm和20 mm×20 mm，单根钢丝直径均为1.0 mm，如图1(a)所示；玻璃纤维网格(Glass fiber mesh，GFM)由山东泰山玻璃纤维有限公司提供，网孔尺寸为5 mm×5 mm，单束玻璃纤维等效直径为0.3 mm，如图1(b)所示。钢丝及玻璃纤维丝的力学性能参数见表1。UHPC基体配合比见表2。其中水泥为P·Ⅱ·52.5R；硅灰中SiO2含量不小于95wt%，950℃烧失量不大于1%；矿粉为S95级粒化高炉矿渣粉；细骨料为3种不同目数的河砂。
表 1 钢丝网和玻璃纤维网力学性能参数Table 1. Mechanical property parameters of steel wire mesh and glass fiber meshMesh name Tensile strength/MPa Elastic modulus/GPa Monofilament area/mm2 Elongation/
%SWM 582 200 0.785 2.6 GFM 2200 79 0.290 3.0 表 2 超高性能混凝土(UHPC)基体配合比Table 2. Composition ratio of ultra-high performance concrete (UHPC)Matrix type Cement Silica Mineral powder River sand Water
consumptionUHPC 1.000 0.182 0.621 2.182 0.327 1.2 双向板设计及制备
试验共制备11个500 mm×500 mm×50 mm的UHPC双向板，试验参数为网格层数、孔径、网格品种及混杂纤维的品种及其掺率。根据研究参数不同，将试件分为四组：第一组试件钢纤维体积分数为1.5vol%，SWM层数分别为2、3和4层，孔径均为12 mm，以研究SWM层数变化对UHPC板抗弯性能的影响；第二组试件钢纤维体积分数为1.5vol％，SWM层数分别为2、3和4层，分别研究SWM孔径由12 mm变为20 mm时对UHPC板抗弯性能的影响；第三组研究SWM层数均为2层时，UHPC中混杂纤维品种及其掺率变化对UHPC板力学性能的影响；第四组比较SWM与GFM增强UHPC板抗弯性能的差异。试件编号及分组见表3，Un代表UHPC种类，Sn/Gn代表SWM或GFM种类及层数，其后数字代表网格孔径。根据掺入混杂纤维的品种及掺率将UHPC材料分为5种，U1为单掺体积分数为1.5vol%钢纤维(Steel fiber，SF)，U2为混掺体积分数为1.0vol%钢纤维和0.5vol%聚乙烯醇纤维(Polyvinyl alcohol，PVA)，U3为混掺体积分数为0.5vol%钢纤维和1.0vol%聚乙烯醇纤维，U4为混掺体积分数为0.5vol%钢纤维和1.0vol%玻璃纤维(Glass fiber，GF)，U5为混掺体积分数为0.5vol%钢纤维和1.0vol%玄武岩纤维(Basalt fiber，BF)。各短切纤维性能参数见表4。
表 3 SWM或GFM增强UHPC双向板试件编号与分组方案Table 3. Specimen number and grouping scheme of UHPC reinforced with SWM or GFMGroup category Specimen number Dosage and type
of fiberNumber of mesh layers The first
groupU1-S2-12 1.5vol% SF 2 U1-S3-12 1.5vol% SF 3 U1-S4-12 1.5vol% SF 4 The second group U1-S2-12 1.5vol% SF 2 U1-S2-20 1.5vol% SF 2 U1-S3-12 1.5vol% SF 3 U1-S3-20 1.5vol% SF 3 U1-S4-12 1.5vol% SF 4 U1-S4-20 1.5vol% SF 4 The third group U1-S2-20 1.5vol% SF 2 U2-S2-20 1.0vol% SF+0.5vol% PVA 2 U3-S2-20 0.5vol% SF+1.0vol% PVA 2 U4-S2-20 0.5vol% SF+1.0vol% GF 2 U5-S2-20 0.5vol% SF+1.0vol% BF 2 The fourth
groupU1-S2-12 1.5vol% SF 2 U1-S2-20 1.5vol% SF 2 U1-G2-5 1.5vol% SF 2 Notes: In specimen number, Un represent UHPC types; Sn/Gn represent SWM or GFM types and number of mesh layers; The next number represents the mesh aperture. Such as, U1-S2-12 represents UHPC slab with 2 layers of steel wire mesh with 12 mm aperture and 1.5vol% steel fiber volume fraction. 表 4 短切纤维性能参数Table 4. Performance parameters of chopped fibersFiber type Diameter/µm Tensile strength/MPa Density/(g·cm−3) Elastic modulus/GPa Length/mm Steel fiber 200 2950 78 205 13 Polyvinyl alcohol 40 1600 1.3 35-40 12 Glass fiber 18 1700 2.68 72 18 Basalt fiber 20 3200 2.6 90-110 20 试件采用分层浇筑法成型[19]，对于铺设多层网格的UHPC板，相邻网格间距为3 mm。以2层钢丝网UHPC板为例说明浇筑过程：(1)将500 mm×500 mm×50 mm木模具放平，在模板底部四周放置3 mm厚UHPC垫块，将第一层SWM水平放置上去(SWM厚度为2 mm，铺设时确保SWM平展性良好)，然后在网格表面四周继续放置3 mm厚垫块，浇筑8 mm UHPC，如图2(a)和图2(b)；(2) 将第二层SWM水平放置上去，浇筑42 mm UHPC，如图2(c)和图2(d)。浇筑完成后标准养护28天，试验前取出晾干。3层与4层网格试件浇筑过程相似，不同层数网格在板内的位置见图3。
![]()
图 3 不同层数网格在UHPC双向板内的高度示意图Figure 3. Schematic diagram of height of mesh with different layers in the UHPC two-way slabs1.3 双向板加载方案
试验时将双向板置于正方形刚性底座上，板顶中心通过80 mm×80 mm×100 mm预制钢块和150 mm×150 mm钢板传递集中荷载，在两侧的刚性支架上安装两个位移计，同时在板底中心和板顶钢板四周的UHPC表面各粘贴两个应变片以测量应变变化，用力传感器测量荷载，数据采集仪同步采集力、挠度及应变等数据，加载过程采用微机控制的MTS电液伺服实验机，加载速率为0.5 mm/min，加载装置及示意图见图4和图5。
![]()
图 4 试验加载和测量装置Figure 4. Loading and measuring arrangementLVDT—Linear variable displacement transducer2. 结果与讨论
2.1 UHPC板弯曲破坏过程及破坏形态
2.1.1 UHPC板弯曲破坏过程
图6为典型的铺设SWM的UHPC双向板荷载-挠度曲线。可知双向板从加载至完全破坏主要经历了三个阶段。
第一阶段为线弹性阶段：该阶段初始荷载较小，混凝土未开裂，曲线近似为直线，可认为处于弹性阶段，随着荷载持续增大，板底出现第1条裂缝，刚度下降，标志该阶段结束；
第二阶段为应变硬化阶段：初始裂缝出现后，板微裂缝处乱向分布的短切纤维的桥联作用显著。随着荷载增加，裂缝宽度不断增大，部分短切纤维不断被拉断或拔出，荷载由网格和未拔出的短切纤维共同承担，曲线表现为持续、波动上升。随着变形继续增大，应力主要由网格承担，直至承载力开始下降，标志该阶段结束；
第三阶段为应变软化阶段：在该阶段不再出现新的裂缝，细裂缝开始逐步扩展成主裂缝，随着挠度的增大，主裂缝宽度快速扩展，裂缝截面处网格不断被拉断，荷载缓慢降低，直至丧失承载能力。
2.1.2 UHPC板弯曲破坏形态
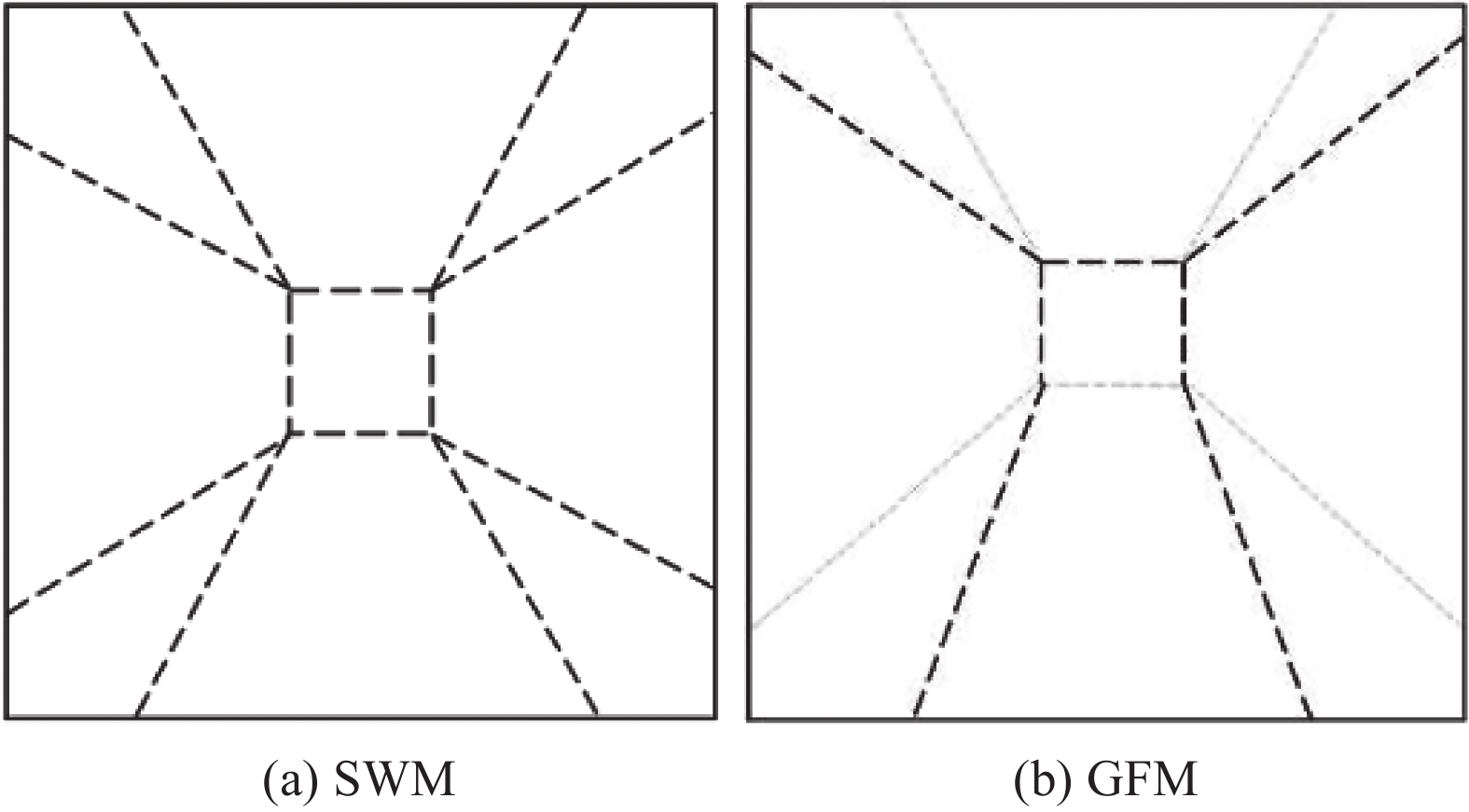
图7为铺设不同网格层数的UHPC板破坏形态。图8为铺设SWM或者GFM的UHPC板破坏形态示意图。由图7可知，第一组和第二组试件中，随着SWM层数增加或者孔径减小，UHPC板底中心处微裂缝数量显著增加，主裂缝宽度逐渐变小。第三组试件中，所有试件微裂缝数量较少，主裂缝数量相当，表明纤维种类的变化对铺设SWM的UHPC板的破坏形态影响较小。由图7和图8可知，第四组试件中，铺设SWM或GFM的UHPC板在板底中心处均会形成一个大致方形的裂缝圈，各裂缝圈角部基本都会产生2条主裂缝，并沿着双向板对角线向四周延伸，但GFM较SWM在破坏时环形裂缝不显著，其主裂缝数量较少，微裂缝数量较多，表明GFM能增加微裂缝数量，延缓或抑制主裂缝的扩展，实现增强增韧的效用。
![]()
图 8 SWM或GFM增强UHPC板破坏形态示意图Figure 8. Schematic diagram of failure modes of UHPC slabs with SWM or GFM2.2 影响UHPC板承载力和变形的主要因素
2.2.1 钢丝网层数的影响
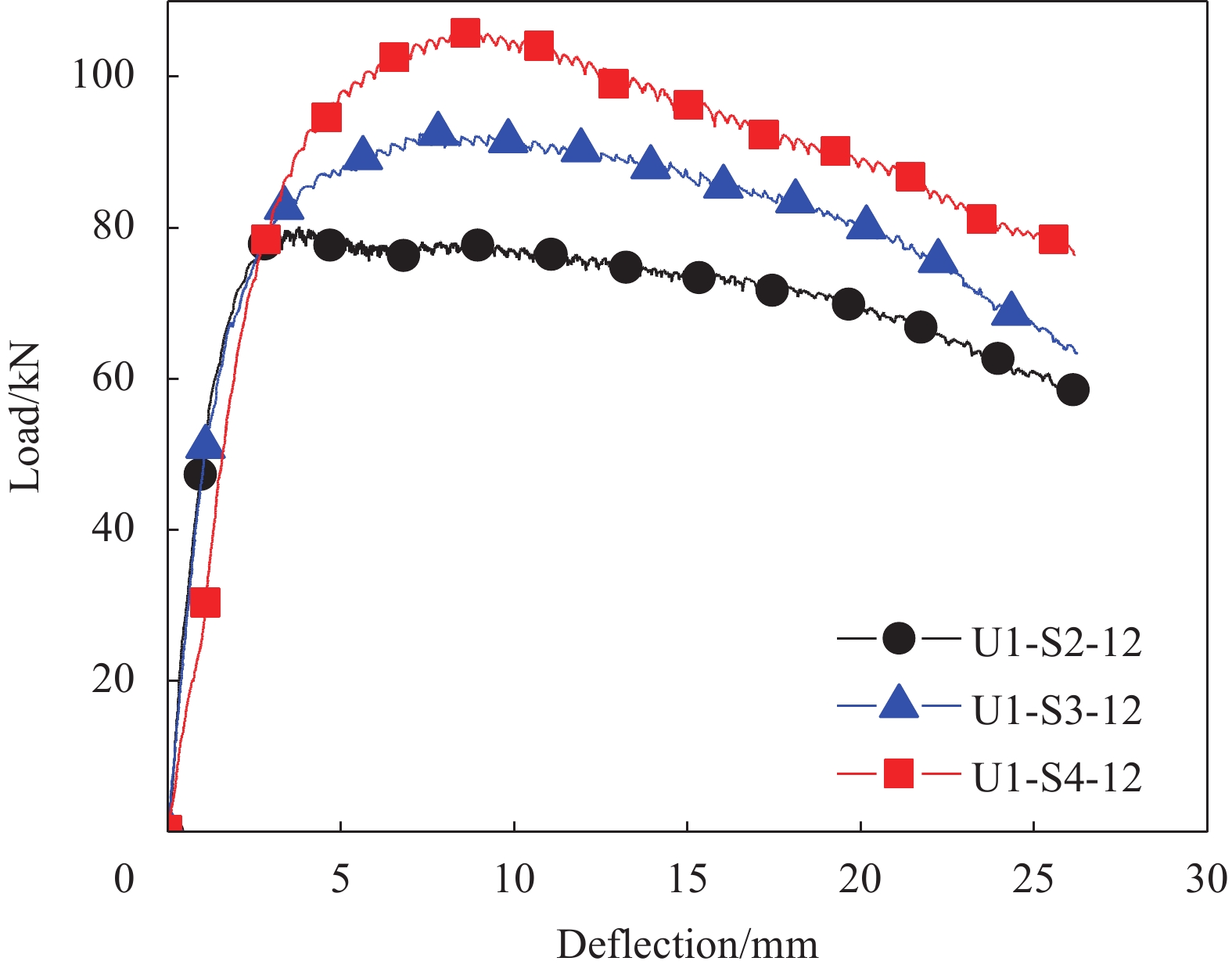
图9为不同SWM层数的UHPC板荷载-挠度曲线。表5为试验测得的板初裂荷载、峰值荷载及其挠度值。可知，第一组试件U1-S3-12、U1-S4-12峰值荷载分别为92.06 kN、106.05 kN，较试件U1-S2-12分别提升14.9%和32.3%，对应的挠度分别增加2.43倍和2.67倍，表明铺设SWM的UHPC板承载力随网格层数的增加而增大，这是由于随着板底层SWM不断被拉断，板发生内力重分布，荷载由基体传至上一层网格，层数越多承担荷载越大。
![]()
图 9 不同SWM层数UHPC板荷载-挠度曲线Figure 9. Load-deflection curves of UHPC slabs with different SWM layers2.2.2 钢丝网孔径的影响
图10为不同孔径SWM的UHPC板荷载-挠度曲线。结合表5可知，第二组孔径较小的试件U1-S2-12、U1-S3-12、U1-S4-12峰值荷载分别为80.15 kN、92.06 kN、106.05 kN，较孔径大的试件U1-S2-20、U1-S3-20、U1- S4-20分别提升10.2%、14.6%、19.5%。表明相同层数下，孔径较小的SWM试件峰值荷载高于孔径大的试件，这是由于网格孔径较小时，相同单位宽度板下网格截面面积更大，承担的荷载更高。
![]()
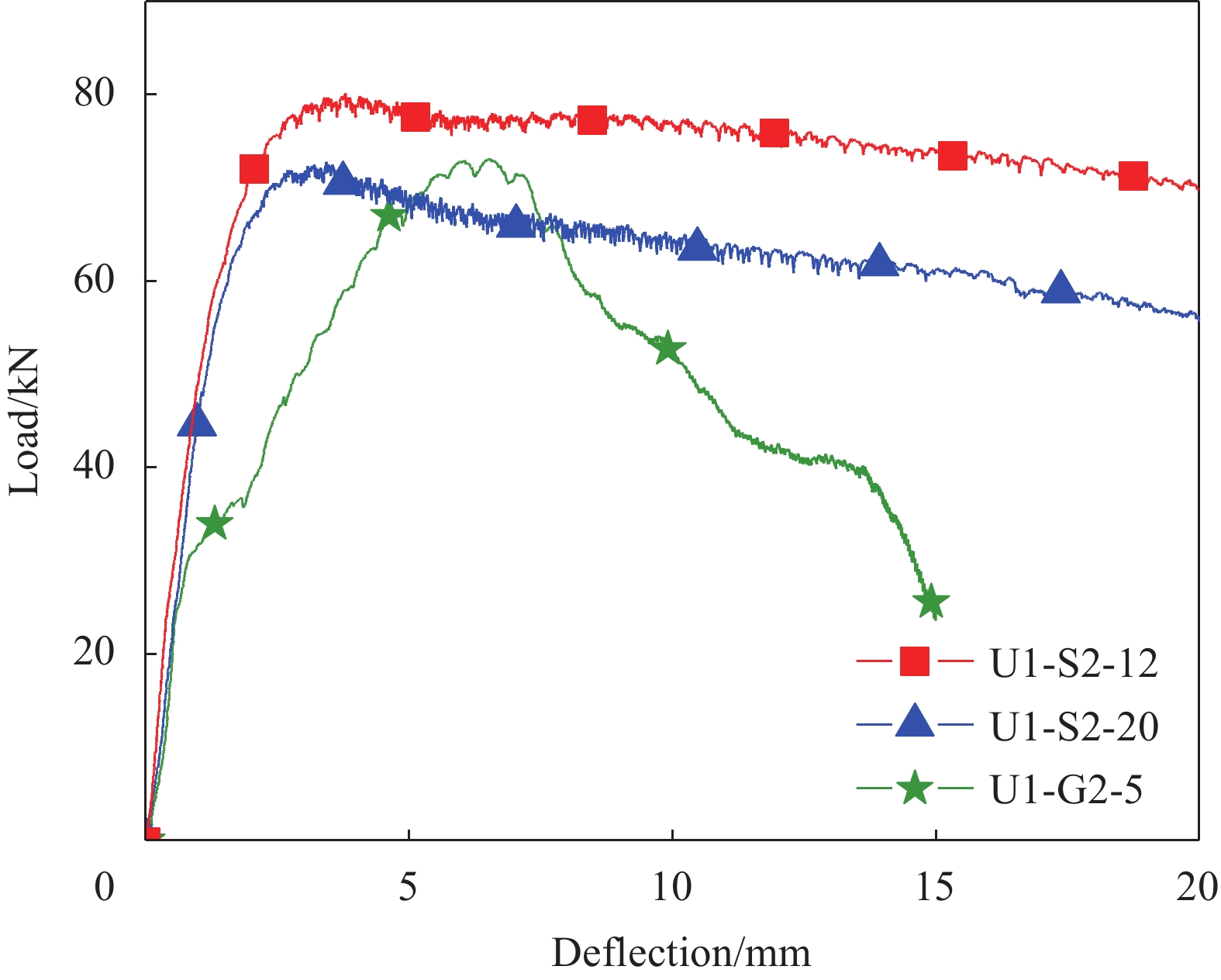
图 10 不同SWM孔径UHPC板荷载-挠度曲线Figure 10. Load-deflection curves of UHPC slabs with different SWM aperture表 5 SWM或GFM增强UHPC板初裂、峰值荷载及其挠度Table 5. Initial crack, peak load and deflection of UHPC slabs with SWM or GFMSpecimen number Pcr/kN δcr/mm Pm/kN δm/mm U1-S2-12 61.76 1.50 80.15 3.79 U1-S3-12 64.88 1.84 92.06 7.76 U1-S4-12 72.95 2.50 106.05 8.53 U1-S2-20 57.93 1.44 72.79 3.43 U1-S3-20 61.15 1.64 80.30 7.32 U1-S4-20 68.35 2.05 88.73 8.86 U2-S2-20 51.34 1.48 77.08 3.49 U3-S2-20 52.72 1.53 65.59 3.47 U4-S2-20 45.97 1.57 60.73 13.02 U5-S2-20 43.15 1.39 57.62 11.93 U1-G2-5 30.56 0.85 73.14 6.53 Notes: Pcr—Initial crack load；δcr—Deflection at initial crack load；Pm—Peak load；δm—Deflection at peak load. 2.2.3 纤维种类的影响
图11为不同纤维种类UHPC板荷载-挠度曲线。结合表5可知，第三组试件U2-S2-20峰值荷载为77.08 kN，较U1-S2-20、U3-S2-20、U4-S2-20、U5-S2-20分别提升5.9%、17.5%、26.9%、33.8%，表明混掺1.0vol% SF与0.5vol% PVA对铺设SWM的板承载力提升最显著。
![]()
图 11 不同纤维种类UHPC板荷载-挠度曲线Figure 11. Load-deflection curves of UHPC slabs with different fiber types当混杂纤维总体积分数为1.5vol%时，试件U1-S2-20、U2-S2-20、U3-S2-20随着SF掺率的减小和PVA掺率的增加，UHPC板峰值荷载表现出先升后降的趋势，这是由于当混掺少量PVA时，PVA的亲水特性使其与胶凝材料的水化产物充分粘结，增强了界面粘结力，从而增大了板的承载力；但当PVA体积分数增加到1.0vol%，SF体积分数降为0.5vol%时，承载力略有下降，是由于PVA的弹性模量远小于SF，其“销栓”作用也低于SF，较高的SF代替率，导致承载力降低。
钢纤维体积分数为1.0vol%时，试件U3-S2-20峰值荷载较U4-S2-20、U5-S2-20分别提升8.0%和13.8%，但挠度分别降低了3.75倍和3.44倍，表明纤维种类对铺设2层SWM的UHPC板承载力影响较小，对峰值荷载处的挠度影响较大，这是由于长度较短的PVA较GF或BF对微裂缝的桥接能力更强，混掺PVA的UHPC板初裂后的曲线斜率大于混掺GF或BF，相同荷载时后者挠度更大。挠度25 mm处，试件U3-S2-20、U4-S2-20、U5-S2-20残余荷载分别为26.21 kN、33.25 kN、34.02 kN，混掺GF和BF板峰后持荷能力强于PVA，这是由于长度较大的GF、BF桥接宏观裂缝能力更强，峰后能承受更高荷载。
2.2.4 网格种类的影响
图12为不同网格种类UHPC板荷载-挠度曲线。结合表5可知，SWM与GFM层数相同时，试件U1-G2-5的峰值荷载较U1-S2-20、U1-S2-12分别提升0.5%、−8.7%，三者相差较小；挠度15 mm处的残余荷载分别降低68.1%、61.5%，表明铺设GFM的UHPC板曲线下降更快，这是由于GFM弹性模量远小于SWM，具有一定脆性特征，达到极限抗拉强度后网格易突然断裂，承载力突降。
![]()
图 12 不同网格种类UHPC板荷载-挠度曲线Figure 12. Load-deflection curves of UHPC slabs with different mesh types3. 现有混凝土板弯曲韧性评价方法
弯曲韧性是用来表征纤维和钢丝网等材料对混凝土开裂后的增韧效果，板的韧性一般用破坏过程中的能量吸收值来评价，由下式计算[20]：
Q=∫a0F(x)dx (1) 式中：Q为能量吸收值；a为板中心挠度；F(x)是挠度为x时的荷载值。表6为不同挠度处的能量吸收值。
表 6 SWM或GFM增强UHPC板不同挠度处能量吸收计算值Table 6. Calculated values of energy absorption for different deflections of UHPC slabs with SWM or GFMSpecimen
numberQcr/J Qm/J Q2/J Q5/J Q15/J Q25/J U1-S2-12 54.78 226.42 88.71 321.55 1084.37 1769.73 U1-S3-12 74.39 578.58 84.55 329.84 1229.86 2019.31 U1-S4-12 94.82 676.10 60.43 315.28 1332.85 2215.37 U1-S2-20 44.57 180.36 80.03 290.77 934.06 1480.90 U1-S3-20 61.06 490.54 83.62 306.65 1087.16 1762.61 U1-S4-20 82.41 656.36 79.01 320.16 1181.46 1965.45 U2-S2-20 41.32 178.87 71.49 292.22 959.04 1501.36 U3-S2-20 40.85 156.78 66.52 254.19 805.11 1139.25 U4-S2-20 36.30 673.04 56.85 213.34 785.48 1206.25 U5-S2-20 36.15 578.58 63.19 211.76 759.31 1191.33 U1-G2-5 12.83 327.61 52.35 218.20 744.56 − Notes: Qcr and Qm—Energy absorption values at the initial crack and peak load deflection of UHPC slabs, respectively; Q2, Q5, Q15, Q25—Energy absorption value of UHPC slabs with deflection of 2 mm, 5 mm, 15 mm and 25 mm, respectively. 3.1 网格层数对UHPC弯曲韧性的影响
图13为不同SWM层数的UHPC板能量吸收值。结合表6可知，试件U1-S3-12、U1-S4-12峰值荷载挠度处的能量吸收值较试件U1-S2-12分别提升155.5%、198.6%，挠度25 mm处分别提升14.1%、25.2%，表明UHPC板弯曲韧性随着SWM层数增加而增大。
![]()
图 13 不同SWM层数UHPC板能量吸收值Figure 13. Energy absorption value of UHPC slabs with different SWM layers3.2 孔径对UHPC弯曲韧性的影响
图14为不同SWM孔径的UHPC板能量吸收值。结合表6可知，试件U1-S2-12、U1-S3-12、U1-S4-12峰值荷载挠度处能量吸收值较试件U1-S2-20、U1-S3-20、U1-S4-20分别提升25.5%、17.9%、3.0%，挠度25 mm处分别提升19.5%、14.6%、12.7%，表明UHPC板的弯曲韧性随着SWM孔径的减小而增大，增韧幅度随着层数的增加而降低。
![]()
图 14 不同SWM孔径UHPC板能量吸收值Figure 14. Energy absorption value of UHPC slabs with different SWM aperture3.3 纤维种类对UHPC弯曲韧性的影响
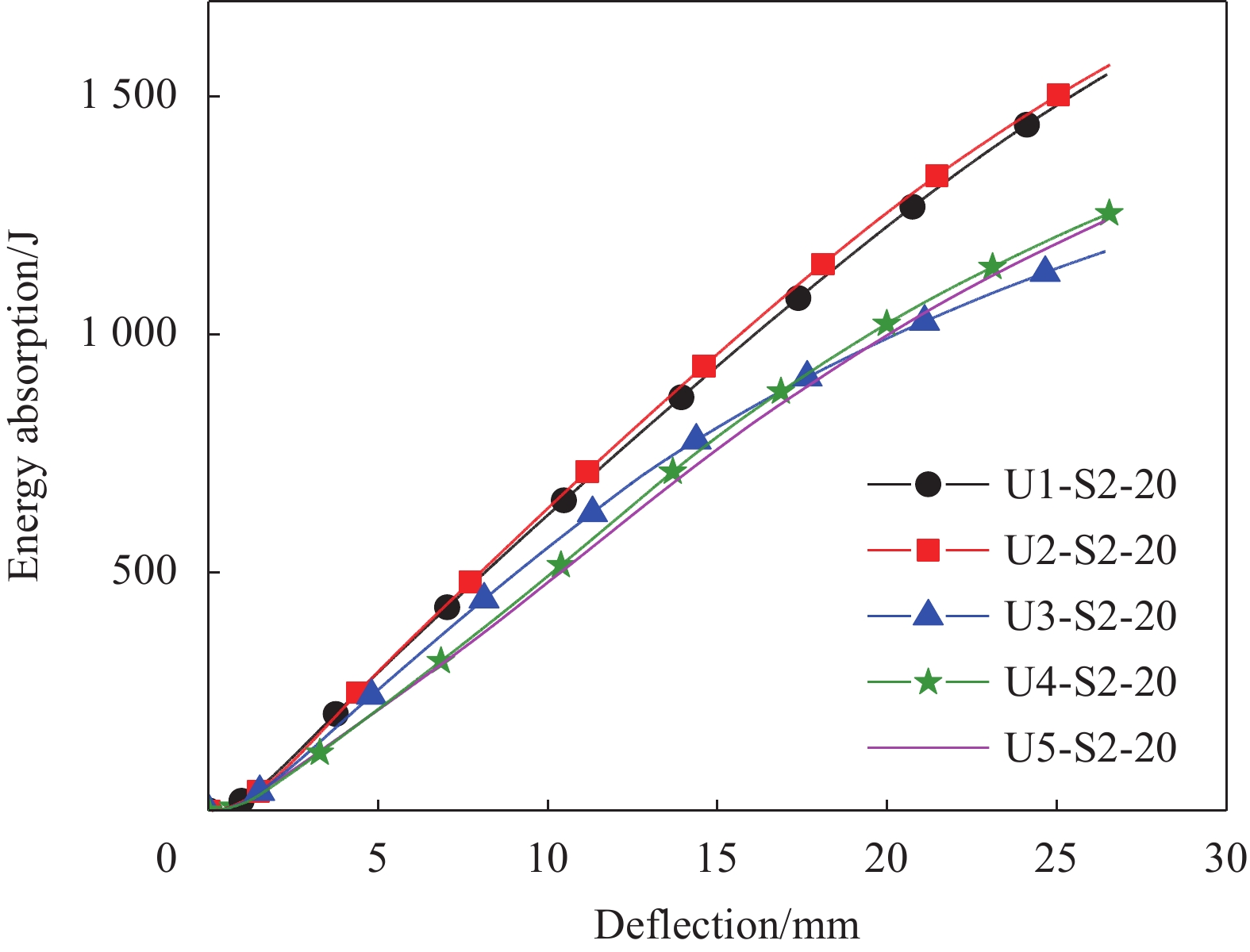
图15为不同纤维种类UHPC板能量吸收值。结合表6可知，试件U1-S2-20、U2-S2-20挠度25 mm处能量吸收值较U3-S2-20、U4-S2-20、U5-S2-20增加1.23~1.32倍，其中混掺1.0vol%SF和0.5vol%PVA纤维对铺设2层SWM的UHPC板增韧效果最好，表明在加载阶段，SF掺率较高对铺设2层SWM的UHPC板增韧效果更好，这是由于SF较非金属纤维弹性模量大，与基体机械咬合力更强，耗能能力更优越。
![]()
图 15 不同纤维种类UHPC板能量吸收值Figure 15. Energy absorption value of UHPC slabs with different fiber types3.4 网格种类对UHPC弯曲韧性的影响
图16为不同网格种类的UHPC板能量吸收值。结合表6可知，试件U1-G2-5峰值荷载挠度处的能量吸收值较U1-S2-20、U1-S2-12分别提升81.3%、44.7%，表明相较SWM，铺设GFM对UHPC板峰值荷载前的增韧效果更好。挠度15 mm处，试件U1-S2-20、U1-S2-12较U1-G2-5分别提升25.5%、45.6%，表明板变形较大时，铺设SWM有利于提高板峰后承载力。
![]()
图 16 不同网格种类UHPC板能量吸收值Figure 16. Energy absorption value of UHPC slabs with different mesh types4. 改进的UHPC弯曲韧性评价方法
前述的弯曲韧性评价方法是根据加载过程中板吸收的能量大小进行评价，无法直观地评估网格和纤维对UHPC板增强增韧的贡献。网格和纤维增强UHPC板开裂后具有显著的应变硬化特征，即板开裂后承载力仍继续增大，峰值荷载后，网格和纤维增强UHPC板具有良好的变形能力。因此为了更全面评估网格和纤维对UHPC板的增强和增韧作用，采用下面分段评估的方法。
4.1 UHPC硬化指数
用应变硬化指数ISh(Strain hardening index，Sh)来表征UHPC板从初裂到峰值荷载这一段承载力继续增加的特征，其增强效应的计算公式如下：
ISh=PmPcr (2) 式中：Pcr为初裂点对应荷载；Pm为峰值点对应荷载。
4.2 UHPC韧性指数
由荷载-挠度曲线可知，当试件尺寸和加载方式一定时，网格UHPC板的初裂荷载、峰值荷载及其增幅随纤维和网格的变化而变化，而素UHPC板的初裂荷载与峰值荷载几乎相等，且比较稳定。因此将素UHPC板峰值荷载时的挠度作为网格UHPC板基体的初裂挠度，网格和纤维的增韧贡献主要体现在基体裂后的贡献。用韧性指数Tk来评价UHPC板不同挠度处的弯曲韧性。网格增强UHPC板基体开裂后网格和纤维的增韧贡献Tk根据下式计算：
Tk=Qk−Q0Q0 (3) 式中：Q0为素UHPC板荷载-挠度曲线峰值荷载挠度处所包的面积，即素UHPC板完全破坏时需要吸收的能量，试验测得Q0为7.6 J；Qk表示超过峰值荷载后挠度为δk时的能量吸收值，本文k分别取15 mm和25 mm。UHPC板的硬化指数ISh和韧性指数Tk计算值列于表7。
表 7 SWM或GFM增强UHPC板硬化指数和韧性指标Table 7. Hardening index and toughness index of UHPC slabs with SWM or GFMSpecimen number ISh T15 T25 U1-S2-12 1.30 141.68 231.86 U1-S3-12 1.42 160.82 264.70 U1-S4-12 1.45 174.38 290.50 U1-S2-20 1.26 121.90 193.86 U1-S3-20 1.31 142.05 230.92 U1-S4-20 1.30 154.46 257.61 U2-S2-20 1.50 125.19 196.55 U3-S2-20 1.24 104.94 148.90 U4-S2-20 1.32 102.35 157.72 U5-S2-20 1.34 98.91 155.75 U1-G2-5 2.39 96.97 − Notes: ISh—Hardening index; T15—Toughness index at 15 mm deflection; T25—Toughness index at 25 mm deflection. 与前面的方法相比，该方法具有以下优点：(1) 可以全面评价UHPC板峰前应变硬化特征和初裂后的弯曲韧性；(2) 采用强度比值法和能量比值法，具有无量纲形式，不受试件尺寸和加载方式的影响；(3) 物理意义明确，ISh越大，应变硬化越显著；Tk越大，网格和纤维对UHPC板开裂后增韧效果越好。
4.3 网格层数对UHPC硬化指数和韧性指数的影响
由表7可知，第一组试件U1-S3-12、U1-S4-12硬化指标ISh较试件U1-S2-12分别提升9.2%、11.5%，韧性指标T25分别提升9.3%、25.3%，表明硬化指数和韧性指数随着层数增加而增大，铺设3层和4层SWM的UHPC板的应变硬化较2层显著，UHPC板初裂后的弯曲韧性随着层数增加而增大。
4.4 网格孔径对UHPC硬化指数和韧性指数的影响
由表7可知，第二组孔径小的试件U1-S2-12、U1-S3-12、U1-S4-12硬化指数ISh分别较孔径大的试件U1-S2-20、U1-S3-20、U1-S4-20提升3.2%、8.4%、11.5%，韧性指数T25分别提升19.6%、14.6%、12.8%，表明UHPC板的硬化指数和韧性指数随着SWM孔径的减小逐渐增大。
4.5 纤维种类对UHPC硬化指数和韧性指数的影响
由表7可知，第三组试件U1-S2-20、U2-S2-20、U3-S2-20中，随着SF掺率减少和PVA掺率增加，硬化指数ISh和韧性指数T25均表现出先增后减的趋势，当SF体积分数高于1.0vol%时，SF对铺设SWM的UHPC板贡献最大，其中混掺1.0vol% SF和0.5vol% PVA纤维的UHPC板在开裂后应变硬化最显著，且增韧最好。SF体积分数为0.5vol%时，混掺1.0vol% GF或BF的UHPC板的硬化指数ISh和韧性指数T25高于混掺1.0vol% PVA的UHPC板，这是由于GF和BF弹性模量高于PVA纤维，在桥接宏观裂缝和增韧方面均更好；但三者相较单掺体积分数为1.5vol% SF的UHPC板韧性指数T25显著降低，表明较高SF代替率，降低了UHPC板增韧效果。
4.6 网格种类对UHPC硬化指数和韧性指数的影响
由表7可知，第四组试件U1-S2-12、U1-S2-20韧性指数T15较U1-G2-5分别提升46.1%、25.7%，硬化指数ISh分别降低83.8%、89.7%，表明相较GFM，铺设SWM显著增加UHPC板开裂后的弯曲韧性，且SWM孔径越小增韧越显著；从初裂到峰值荷载阶段，铺设孔径较小的GFM的UHPC板应变硬化特征较SWM显著。
5. UHPC板承载力计算
计算网格增强UHPC板抗弯承载力时，其截面的实际应力分布图呈现非线性，为了简化计算，将截面受拉、受压应力曲线图等效为矩形应力图，确保等效矩形应力图与实际应力图受压区合力大小和作用点不变，其结果如图17所示。混凝土受拉区等效高度按下式计算：
xt=h−xk (4) 其中，
xc=xk (5) ![]()
图 17 UHPC双向板矩形截面受弯承载力计算图Figure 17. Calculation diagram of bending capacity of rectangular section of UHPC two-way slabsfc—Axial compressive strength; ft—Axial tensile strength; h0—Effective height of section; Mu−Theoretical bending capacity; a—Distance from the mesh resultant point in the tension zone to the edge of the bottom section of the slab; b—Calculated width of the slab; α1—Equivalent rectangular stress diagram coefficient of compression zone, take 0.88; β—Equivalent rectangular stress diagram coefficient of tensile zone, take 0.35; xc—Height of compression zone; xt—Equivalent rectangular stress height of tension zone; fte—Mesh effective stress; k—Ratio of x to xc; Af—Total section area of grid; h—Height of slab; x—Equivalent rectangular stress height of compression zone式中：xc为UHPC受压区高度；xt为受拉区等效矩形应力图高度；h为板的截面高度；x为UHPC板受压区等效矩形应力图高度；k为UHPC板受压区矩形应力图高度x与按平截面假定确定的中和轴高度xc的比值，根据文献[21]，取0.72。根据平衡条件，轴向力计算公式为
α1fcbx=fteAf+βftbxt (6) 抗弯承载力计算公式为
Mu=α1fcbx(h0−x2)−βftbxt(xt2−a) (7) 式中：fc、ft分别为UHPC轴心抗压、抗拉强度平均值；α1、β分别为fc、ft等效应力值影响系数，分别取0.88和0.35[21]；b为板计算宽度；Af为网格总截面面积；a为受拉区网格合力点至板底截面边缘的距离；fte为网格在基体中发挥的有效应力值，其计算公式如下：
fte = Etεte (8) 式中：Et为网格弹性模量；εte为网格有效应变，其计算公式为
εte = λεtu (9) 式中：λ为网格利用率；εtu为网格极限拉应变。
在网格破坏前，由于混凝土拉应变小，因此不考虑混凝土拉应变影响，混凝土压应变和网格的有效拉应变符合平截面假定，其关系为：
εcxc = εteh0−xc (10) 式中：εc为极限荷载时的混凝土受压区压应变；h0为UHPC板跨中截面的有效高度，多层网格为纤维束形心到板顶边缘距离。
其中混凝土受压区高度按照下列步骤进行计算：先假定混凝土受压区高度xc1，然后代入式(10)计算出网格有效拉应变εte，再由力平衡公式(6)计算出x1，将x1代入式(5)计算出xc2，用xc2替代xc1重复上述步骤，直至xc1和xc2误差小于1%时，所得xc2即为混凝土受压区高度。
各UHPC板的计算结果见表8。可见，第一组试件U1-S2-12、U1-S3-12、U1-S4-12的抗弯承载力分别为9.96 kN·m、10.95 kN·m、11.54 kN·m，利用率分别为82.0%、64.9%和55.0%，表明抗弯承载力随网格层数增加而增大，利用率随网格层数增加而逐渐减小。试件U1-S2-12、U1-S3-12、U1-S4-12的抗弯承载力较第二组试件U1-S2-20、U1-S3-20、U1-S4-20分别提升27.5%、24.1%、22.9%，利用率分别降低16.1%、19.0%、19.7%，表明抗弯承载力随孔径增大而减小，利用率随孔径增大而增大。第三组试件中2层钢丝网利用率均在87%以上，这是由于短切纤维斜插入网格，与网格形成“销栓”作用，能够在一定程度上阻止网格与基体间的滑移，进而提高了网格利用效率；同时随着SF掺率减少，网格利用率降低，表明用非金属纤维代替SF不能提高钢丝网利用率。第四组试件U1-S2-12、U1-S2-20抗弯承载力较U1-G2-5分别提高37.6%、7.9%，铺设SWM的UHPC板抗弯承载能力高于GFM。根据塑性铰线理论，运用虚功原理将计算出的试验弯矩Me与理论计算值Mu进行比较，发现试验值与理论计算值吻合良好。
表 8 各UHPC板抗弯承载力计算结果Table 8. Calculation results of bending capacity of UHPC slabsSpecimen
numberfc/MPa ft/MPa h0/mm εc fte/MPa λ/% Mu
/(kN·m)Me
/(kN·m)Me/Mu U1-S2-12 98.81 6.37 43.5 0.00391 3279.73 82.0 9.96 10.02 1.006 U1-S3-12 98.81 6.37 41.0 0.00397 2595.67 64.9 10.95 11.13 1.017 U1-S4-12 98.81 6.37 38.5 0.00401 2199.33 55.0 11.54 13.26 1.198 U1-S2-20 98.81 6.37 43.5 0.00353 3908.73 97.7 7.81 9.10 1.165 U1-S3-20 98.81 6.37 41.0 0.00365 3205.44 80.1 8.82 10.04 1.138 U1-S4-20 98.81 6.37 38.5 0.00385 2740.10 68.5 9.39 11.09 1.227 U2-S2-20 91.12 6.49 43.5 0.00353 3871.35 96.3 7.73 9.64 1.247 U3-S2-20 90.78 6.11 43.5 0.00341 3681.44 92.0 7.36 8.20 1.114 U4-S2-20 86.52 5.95 43.5 0.00339 3570.49 89.3 7.14 7.59 1.064 U5-S2-20 83.06 5.89 43.5 0.00338 3480.91 87.0 6.97 7.20 1.034 U1-G2-5 98.81 6.37 45.0 0.00409 2027.73 78.0 7.24 8.62 1.191 Notes：fc—Axial compressive strength; ft—Axial tensile strength; h0—Effective height of section; εc—Compressive strain of concrete; fte—Mesh effective stress; λ—Effective utilization of mesh; Mu—Theoretical bending capacity; Me—Experimental bending capacity. 6. 结 论
(1) 铺设钢丝网的超高性能混凝土(UHPC)板荷载-挠度曲线下降平缓，应变硬化现象明显，试件呈现多条主裂缝破坏形态，承载能力和弯曲韧性随着网格层数增加和孔径的减小而增大。
(2) 钢丝网层数2层时，1.0vol%钢纤维和0.5vol%聚乙烯醇纤维混掺使UHPC板承载力和韧性的提升最显著；0.5vol%钢纤维与1.0vol%玻璃纤维或1.0vol%玄武岩纤维混掺UHPC板在25 mm挠度处的残余承载力较0.5vol%钢纤维与1.0vol%聚乙烯醇纤维混掺分别提升26.9%和29.8%，钢纤维与较高弹性模量非金属纤维混掺有利于提高峰后承载力。
(3) 与玻璃纤维网格相比，铺设钢丝网的UHPC板增韧效果更显著，峰后挠度15 mm处的残余承载力提高150%以上。
(4) 提出基于强度比和能量比的分阶段韧性评价方法，即分别用硬化指数表征峰前应变硬化效应，用韧性指数表征网格和纤维对板峰后软化段的增韧贡献；硬化指数和韧性指数与网格层数增加和孔径减小呈正相关，且对纤维种类及掺率变化敏感。
(5) 考虑网格有效利用率，建立了网格增强UHPC板抗弯承载力计算方法，理论计算值与试验值吻合良好。
-
![]()
图 3 不同层数网格在UHPC双向板内的高度示意图
Figure 3. Schematic diagram of height of mesh with different layers in the UHPC two-way slabs
![]()
图 4 试验加载和测量装置
Figure 4. Loading and measuring arrangement
LVDT—Linear variable displacement transducer
![]()
图 8 SWM或GFM增强UHPC板破坏形态示意图
Figure 8. Schematic diagram of failure modes of UHPC slabs with SWM or GFM
![]()
图 9 不同SWM层数UHPC板荷载-挠度曲线
Figure 9. Load-deflection curves of UHPC slabs with different SWM layers
![]()
图 10 不同SWM孔径UHPC板荷载-挠度曲线
Figure 10. Load-deflection curves of UHPC slabs with different SWM aperture
![]()
图 11 不同纤维种类UHPC板荷载-挠度曲线
Figure 11. Load-deflection curves of UHPC slabs with different fiber types
![]()
图 12 不同网格种类UHPC板荷载-挠度曲线
Figure 12. Load-deflection curves of UHPC slabs with different mesh types
![]()
图 13 不同SWM层数UHPC板能量吸收值
Figure 13. Energy absorption value of UHPC slabs with different SWM layers
![]()
图 14 不同SWM孔径UHPC板能量吸收值
Figure 14. Energy absorption value of UHPC slabs with different SWM aperture
![]()
图 15 不同纤维种类UHPC板能量吸收值
Figure 15. Energy absorption value of UHPC slabs with different fiber types
![]()
图 16 不同网格种类UHPC板能量吸收值
Figure 16. Energy absorption value of UHPC slabs with different mesh types
![]()
图 17 UHPC双向板矩形截面受弯承载力计算图
Figure 17. Calculation diagram of bending capacity of rectangular section of UHPC two-way slabs
fc—Axial compressive strength; ft—Axial tensile strength; h0—Effective height of section; Mu−Theoretical bending capacity; a—Distance from the mesh resultant point in the tension zone to the edge of the bottom section of the slab; b—Calculated width of the slab; α1—Equivalent rectangular stress diagram coefficient of compression zone, take 0.88; β—Equivalent rectangular stress diagram coefficient of tensile zone, take 0.35; xc—Height of compression zone; xt—Equivalent rectangular stress height of tension zone; fte—Mesh effective stress; k—Ratio of x to xc; Af—Total section area of grid; h—Height of slab; x—Equivalent rectangular stress height of compression zone
表 1 钢丝网和玻璃纤维网力学性能参数
Table 1 Mechanical property parameters of steel wire mesh and glass fiber mesh
Mesh name Tensile strength/MPa Elastic modulus/GPa Monofilament area/mm2 Elongation/
%SWM 582 200 0.785 2.6 GFM 2200 79 0.290 3.0 
下载: 导出CSV
表 2 超高性能混凝土(UHPC)基体配合比
Table 2 Composition ratio of ultra-high performance concrete (UHPC)
Matrix type Cement Silica Mineral powder River sand Water
consumptionUHPC 1.000 0.182 0.621 2.182 0.327
下载: 导出CSV
表 3 SWM或GFM增强UHPC双向板试件编号与分组方案
Table 3 Specimen number and grouping scheme of UHPC reinforced with SWM or GFM
Group category Specimen number Dosage and type
of fiberNumber of mesh layers The first
groupU1-S2-12 1.5vol% SF 2 U1-S3-12 1.5vol% SF 3 U1-S4-12 1.5vol% SF 4 The second group U1-S2-12 1.5vol% SF 2 U1-S2-20 1.5vol% SF 2 U1-S3-12 1.5vol% SF 3 U1-S3-20 1.5vol% SF 3 U1-S4-12 1.5vol% SF 4 U1-S4-20 1.5vol% SF 4 The third group U1-S2-20 1.5vol% SF 2 U2-S2-20 1.0vol% SF+0.5vol% PVA 2 U3-S2-20 0.5vol% SF+1.0vol% PVA 2 U4-S2-20 0.5vol% SF+1.0vol% GF 2 U5-S2-20 0.5vol% SF+1.0vol% BF 2 The fourth
groupU1-S2-12 1.5vol% SF 2 U1-S2-20 1.5vol% SF 2 U1-G2-5 1.5vol% SF 2 Notes: In specimen number, Un represent UHPC types; Sn/Gn represent SWM or GFM types and number of mesh layers; The next number represents the mesh aperture. Such as, U1-S2-12 represents UHPC slab with 2 layers of steel wire mesh with 12 mm aperture and 1.5vol% steel fiber volume fraction.
下载: 导出CSV
表 4 短切纤维性能参数
Table 4 Performance parameters of chopped fibers
Fiber type Diameter/µm Tensile strength/MPa Density/(g·cm−3) Elastic modulus/GPa Length/mm Steel fiber 200 2950 78 205 13 Polyvinyl alcohol 40 1600 1.3 35-40 12 Glass fiber 18 1700 2.68 72 18 Basalt fiber 20 3200 2.6 90-110 20
下载: 导出CSV
表 5 SWM或GFM增强UHPC板初裂、峰值荷载及其挠度
Table 5 Initial crack, peak load and deflection of UHPC slabs with SWM or GFM
Specimen number Pcr/kN δcr/mm Pm/kN δm/mm U1-S2-12 61.76 1.50 80.15 3.79 U1-S3-12 64.88 1.84 92.06 7.76 U1-S4-12 72.95 2.50 106.05 8.53 U1-S2-20 57.93 1.44 72.79 3.43 U1-S3-20 61.15 1.64 80.30 7.32 U1-S4-20 68.35 2.05 88.73 8.86 U2-S2-20 51.34 1.48 77.08 3.49 U3-S2-20 52.72 1.53 65.59 3.47 U4-S2-20 45.97 1.57 60.73 13.02 U5-S2-20 43.15 1.39 57.62 11.93 U1-G2-5 30.56 0.85 73.14 6.53 Notes: Pcr—Initial crack load；δcr—Deflection at initial crack load；Pm—Peak load；δm—Deflection at peak load.
下载: 导出CSV
表 6 SWM或GFM增强UHPC板不同挠度处能量吸收计算值
Table 6 Calculated values of energy absorption for different deflections of UHPC slabs with SWM or GFM
Specimen
numberQcr/J Qm/J Q2/J Q5/J Q15/J Q25/J U1-S2-12 54.78 226.42 88.71 321.55 1084.37 1769.73 U1-S3-12 74.39 578.58 84.55 329.84 1229.86 2019.31 U1-S4-12 94.82 676.10 60.43 315.28 1332.85 2215.37 U1-S2-20 44.57 180.36 80.03 290.77 934.06 1480.90 U1-S3-20 61.06 490.54 83.62 306.65 1087.16 1762.61 U1-S4-20 82.41 656.36 79.01 320.16 1181.46 1965.45 U2-S2-20 41.32 178.87 71.49 292.22 959.04 1501.36 U3-S2-20 40.85 156.78 66.52 254.19 805.11 1139.25 U4-S2-20 36.30 673.04 56.85 213.34 785.48 1206.25 U5-S2-20 36.15 578.58 63.19 211.76 759.31 1191.33 U1-G2-5 12.83 327.61 52.35 218.20 744.56 − Notes: Qcr and Qm—Energy absorption values at the initial crack and peak load deflection of UHPC slabs, respectively; Q2, Q5, Q15, Q25—Energy absorption value of UHPC slabs with deflection of 2 mm, 5 mm, 15 mm and 25 mm, respectively.
下载: 导出CSV
表 7 SWM或GFM增强UHPC板硬化指数和韧性指标
Table 7 Hardening index and toughness index of UHPC slabs with SWM or GFM
Specimen number ISh T15 T25 U1-S2-12 1.30 141.68 231.86 U1-S3-12 1.42 160.82 264.70 U1-S4-12 1.45 174.38 290.50 U1-S2-20 1.26 121.90 193.86 U1-S3-20 1.31 142.05 230.92 U1-S4-20 1.30 154.46 257.61 U2-S2-20 1.50 125.19 196.55 U3-S2-20 1.24 104.94 148.90 U4-S2-20 1.32 102.35 157.72 U5-S2-20 1.34 98.91 155.75 U1-G2-5 2.39 96.97 − Notes: ISh—Hardening index; T15—Toughness index at 15 mm deflection; T25—Toughness index at 25 mm deflection.
下载: 导出CSV
表 8 各UHPC板抗弯承载力计算结果
Table 8 Calculation results of bending capacity of UHPC slabs
Specimen
numberfc/MPa ft/MPa h0/mm εc fte/MPa λ/% Mu
/(kN·m)Me
/(kN·m)Me/Mu U1-S2-12 98.81 6.37 43.5 0.00391 3279.73 82.0 9.96 10.02 1.006 U1-S3-12 98.81 6.37 41.0 0.00397 2595.67 64.9 10.95 11.13 1.017 U1-S4-12 98.81 6.37 38.5 0.00401 2199.33 55.0 11.54 13.26 1.198 U1-S2-20 98.81 6.37 43.5 0.00353 3908.73 97.7 7.81 9.10 1.165 U1-S3-20 98.81 6.37 41.0 0.00365 3205.44 80.1 8.82 10.04 1.138 U1-S4-20 98.81 6.37 38.5 0.00385 2740.10 68.5 9.39 11.09 1.227 U2-S2-20 91.12 6.49 43.5 0.00353 3871.35 96.3 7.73 9.64 1.247 U3-S2-20 90.78 6.11 43.5 0.00341 3681.44 92.0 7.36 8.20 1.114 U4-S2-20 86.52 5.95 43.5 0.00339 3570.49 89.3 7.14 7.59 1.064 U5-S2-20 83.06 5.89 43.5 0.00338 3480.91 87.0 6.97 7.20 1.034 U1-G2-5 98.81 6.37 45.0 0.00409 2027.73 78.0 7.24 8.62 1.191 Notes：fc—Axial compressive strength; ft—Axial tensile strength; h0—Effective height of section; εc—Compressive strain of concrete; fte—Mesh effective stress; λ—Effective utilization of mesh; Mu—Theoretical bending capacity; Me—Experimental bending capacity.
下载: 导出CSV
-
[1] GUO Z W, DUAN X Z, WANG Q, et al. Development on the corrosion of steel fiber and prevention in the ultra-high performance concrete (UHPC)[J]. Materials Science Forum,2021,1036:358-370. DOI: 10.4028/www.scientific.net/MSF.1036.358
[2] NIU Y F, WEI J X, JIAN C J. Crack propagation behavior of ultra-high-performance concrete (UHPC) reinforced with hybrid steel fibers under flexural loading[J]. Construction and Building Materials,2021,294:123510. DOI: 10.1016/j.conbuildmat.2021.123510
[3] FAN W, SHEN D J, ZHANG Z Y, et al. A novel UHPFRC-based protective structure for bridge columns against vehicle collisions: Experiment, simulation, and optimization[J]. Engineering Structures,2020,207:110247. DOI: 10.1016/j.engstruct.2020.110247
[4] 邵旭东, 樊伟, 黄政宇. 超高性能混凝土在结构中的应用[J]. 土木工程学报, 2021, 54(1):1-13. SHAO Xudong, FAN Wei, HUANG Zhengyu. Application of ultra-high performance concrete in engineering structures[J]. China Civil Engineering Journal,2021,54(1):1-13(in Chinese).
[5] 陈宝春, 韦建刚, 苏家战, 等. 超高性能混凝土应用进展[J]. 建筑科学与工程学报, 2019, 36(2):10-20. DOI: 10.3969/j.issn.1673-2049.2019.02.003 CHEN Baochun, WEI Jian'gang, SU Jiazhan, et al. State-of-the-art progress on application of ultra-high performance concrete[J]. Journal of Architecture and Civil Engineering,2019,36(2):10-20(in Chinese). DOI: 10.3969/j.issn.1673-2049.2019.02.003
[6] FERDOSIAN I, CAMOES A. Mechanical performance and post-cracking behavior of self-compacting steel-fiber reinforced eco-efficient ultra-high performance concrete[J]. Cement and Concrete Composites,2021,121:104050. DOI: 10.1016/j.cemconcomp.2021.104050
[7] 梁兴文, 胡翱翔, 于婧, 等. 钢纤维对超高性能混凝土抗弯力学性能的影响[J]. 复合材料学报, 2018, 35(3):722-731. LIANG Xingwen, HU Aoxiang, YU Jing, et al. Effect of steel fibers on the flexural response of ultra-high performance concrete[J]. Acta Materiae Compositae Sinica,2018,35(3):722-731(in Chinese).
[8] 邵旭东, 李芳园, 邱明红, 等. 钢纤维特性对UHPC轴拉性能与弯拉性能的影响及对比研究[J]. 中国公路学报, 2020, 33(4):51-64. DOI: 10.3969/j.issn.1001-7372.2020.04.006 SHAO Xudong, LI Fangyuan, QIU Minghong, et al. Influential and comparative research on the effects of steel fiber properties on the axial tensile and bending tensile properties of UHPC[J]. China Journal of Highway and Transport,2020,33(4):51-64(in Chinese). DOI: 10.3969/j.issn.1001-7372.2020.04.006
[9] KIM D J, PARK S H, RYU G S, et al. Comparative flexural behavior of hybrid ultra high performance fiber reinforced concrete with different macro fibers[J]. Construction and Building Materials,2011,25(11):4144-4155. DOI: 10.1016/j.conbuildmat.2011.04.051
[10] SU T K, JEONG I C, KYUNG T K, et al. Hybrid effects of steel fiber and microfiber on the tensile behavior of ultra-high performance concrete[J]. Composite Structures,2016,145:37-42. DOI: 10.1016/j.compstruct.2016.02.075
[11] YAN P, CHEN B, AFGAN S, et al. Experimental research on ductility enhancement of ultra-high performance concrete incorporation with basalt fiber, polypropylene fiber and glass fiber[J]. Construction and Building Materials,2021,279:122489. DOI: 10.1016/j.conbuildmat.2021.122489
[12] 朱江. 纤维增强钢丝网混凝土构件抗弯性能试验研究[D]. 大连: 大连理工大学, 2007. ZHU Jiang. Experimental study on flexural behavior of fiber reinforced ferroconcrete member[D]. Dalian: Dalian University of Technology, 2007(in Chinese).
[13] 周臻, 张逸, 王永泉, 等. 网格增强UHPC薄板拉伸力学性能试验研究[J]. 东南大学学报(自然科学版), 2019, 49(4):611-617. ZHOU Zhen, ZHANG Yi, WANG Yongquan, et al. Experimental study on tensile mechanical property of grid reinforced UHPC plates[J]. Journal of Southeast University (Natural Science Edition),2019,49(4):611-617(in Chinese).
[14] 李冬, 丁一宁. 钢纤维对玄武岩纤维编织网增强混凝土板双向弯曲性能的影响[J]. 复合材料学报, 2019, 36(2):482-490. LI Dong, DING Yining. Effect of steel fiber on biaxial flexural property of TRC with basalt fiber mesh in slab test[J]. Acta Materiae Compositae Sinica,2019,36(2):482-490(in Chinese).
[15] 丁一宁, 菅淑敏, 李冬. 玻璃纤维网格布的耐碱性能及其对混凝土板双向受弯性能的影响[J]. 复合材料学报, 2019, 36(4):954-963. DING Yining, JIAN Shumin, LI Dong. Alkaline resistance of glass fiber meshes and its effect on biaxial flexural behavior of concrete slabs[J]. Acta Materiae Compositae Sinica,2019,36(4):954-963(in Chinese).
[16] LI D, DING Y N, WANG Q, et al. Hybrid effect of fiber mesh and short fibers on the biaxial bending behavior of TRC[J]. Magazine of Concrete Research,2018,71(16):869-880. DOI: 10.1680/jmacr.17.00284
[17] 赵国藩, 李士恩, 李丽娟, 等. 钢纤维增强钢丝网混凝土T形梁的抗弯试验研究[J]. 华南理工大学学报(自然科学版), 2008, 36(1):117-121, 127. ZHAO Guofan, LI Shien, LI Lijuan, et al. Experimental investigation into flexural behavior of steel fiber-reinforced ferroconcrete T-shape beam[J]. Journal of South China University of Technology (Natural Science Edition),2008,36(1):117-121, 127(in Chinese).
[18] European Federation of National Associations Representing for Concrete. European specification for sprayed concrete: ISBN 0-952-24831-X[S]. Loughborough: Loughborough University, 1996.
[19] KONG K, MESTICOU Z, MICHEL M, et al. Comparative characterization of the durability behaviour of textile-reinforced concrete (TRC) under tension and bending[J]. Composite Structures,2017,179:107-123. DOI: 10.1016/j.compstruct.2017.07.030
[20] SOLEIMANI M S, BANTHIN N. Flexural response of hybrid fiber-reinforced cementitious composites[J]. ACI Materials Journal, 2005, 102(6): 382-389.
[21] 王志成. 超高性能混凝土结构抗弯性能试验研究[D]. 成都: 西南交通大学, 2017. WANG Zhicheng. Experimental study on flexural perfor-mance of ultra high performance concrete structure[D]. Chengdu: Southwest Jiaotong University, 2017(in Chinese).
-
期刊类型引用(3)
1. 邓宗才，李倩. 混杂网格增强超高性能混凝土双向板的弯曲性能. 天津大学学报(自然科学与工程技术版). 2024(03): 301-310 . 
百度学术
2. 王卓群，宗钟凌，谢青海，骆辉，卢浩宇，赖斌，高子晴. 掺磷尾矿砂的UHPC板抗弯性能试验研究. 混凝土与水泥制品. 2024(04): 42-47 . 百度学术
3. 谢剑，刘家旺，李伟，金凌翼. 玄武岩纤维网格增强磷酸镁水泥砂浆复合材料力学性能. 复合材料学报. 2024(10): 5492-5503 . 本站查看
其他类型引用(8)
-
计量
- 文章访问数: 1261
- HTML全文浏览量: 628
- PDF下载量: 58
- 被引次数: 11
