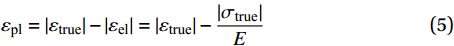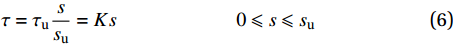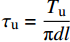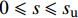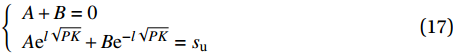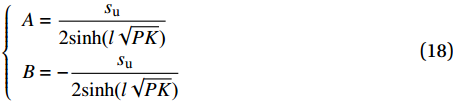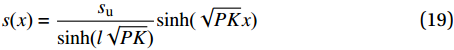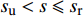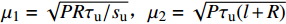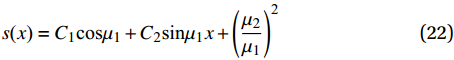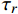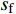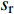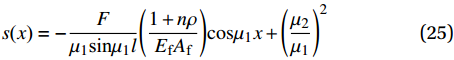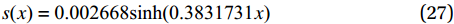Bond-slip constitutive relation between FRP bars and coral aggregate seawater concrete
-
摘要: 纤维增强树脂复合材料(Fiber reinforced polymer,FRP)具有优良的抗腐蚀性能,用其代替普通钢筋能够很好地解决钢筋锈蚀问题。同时我国的珊瑚和海水资源丰富,用其代替传统砂石骨料是解决海岛建设中传统材料稀缺问题的有效方法之一。FRP筋与珊瑚骨料海水混凝土之间的粘结性能是决定其是否能像普通钢筋混凝土一样在实际工程中应用的重要因素之一。目前,关于FRP筋全珊瑚骨料海水混凝土结构的界面粘结性能研究很少,尤其是理论方面。于是,通过试验和数值模拟验证了简化双线性模型的合理性,并在此基础上推导了FRP筋全珊瑚骨料海水混凝土的界面粘结应力τ(x)和相对滑移量s(x)表达式,绘制了界面相对滑移和界面粘结应力的分布图。将采用表达式所得到的理论解与试验和模拟结果进行对比分析,其结果表明:通过理论计算所得的理论解与试验结果吻合度较高;FRP筋直径和粘结长度的增加会导致界面粘结应力和相对滑移的分布更加不均匀;珊瑚骨料混凝土强度的改变对界面粘结应力和相对滑移的分布影响不大;玻璃纤维增强树脂复合材料(GFRP)筋和玄武岩纤维增强树脂复合材料(BFRP)筋珊瑚骨料海水混凝土的界面粘结应力和相对滑移的分布相类似,与碳纤维增强树脂复合材料(CFRP)筋珊瑚骨料海水混凝土相比,前者的分布更加均匀。
-
关键词:
- 全珊瑚骨料海水混凝土 /
- FRP筋 /
- 粘结性能 /
- 本构模型 /
- 理论计算方法
Abstract: Since fiber reinforced polymer (FRP) has excellent corrosion resistance, it can be used to replace ordi-nary steel bars to solve the problem of steel corrosion. Because of the abundant coral and seawater resources in China, using coral instead of traditional sand aggregate is one of the effective methods to solve the problem of scarcity of traditional materials in island construction. Bonding property between FRP bars and coral aggregate seawater concrete is one of the important factors to determine whether FRP reinforced coral aggregate seawater concrete structure can be applied in practical engineering like ordinary reinforced concrete structure. At present, there is little research on the interfacial bonding property of FRP reinforced coral aggregate seawater concrete structure, especially in theory. Therefore, the rationality of the simplified bilinear model will be verified by experiments and numerical simulation. Based on the experiments and numerical simulation, the expressions of interfacial bonding stress and relative slip of FRP reinforced coral aggregate seawater concrete will be derived, and then the distribution maps of interfacial bonding stress and relative slip will be plotted. The theoretical solution obtained by the expression will be compared with the experimental and numerical simulation solution. The results show that the theoretical solution obtained by theoretical calculation is in good agreement with the experimental results. The increase of FRP bar diameter and bonding length will lead to more non-uniform distribution of interfacial bonding stress and relative slip. The change of coral aggregate concrete strength has little effect on the distribution of interfacial bonding stress and relative slip. The interfacial bond stress and relative slip distribution of glass fiber reinforced polymer (GFRP) and basalt fiber reinforced polymer (BFRP) reinforced coral aggregate seawater concrete are similar, and are more uniform than that of carbon fiber reinforced polymer (CFRP) coral aggregate concrete. -
随着国家社会经济的发展,海岛基础设施的建设对于海洋资源的发掘及我国合法权益的维护具有重大意义[1-2]。但是由于岛礁上的传统建筑材料稀缺,将其用于海岛建设不仅成本较高,还会造成自然环境的破坏[3-5]。我国珊瑚及海水资源丰富,利用珊瑚替代传统砂石和海水替代淡水来制备混凝土恰好可以解决资源稀缺和环境破坏的问题。可是珊瑚混凝土及海水中含有大量的氯离子,对普通钢筋具有加速腐蚀作用,严重阻碍了钢筋珊瑚混凝土结构的发展[6]。纤维增强树脂复合材料(FRP)具有良好的抗腐蚀性能,将其替代普通钢筋能够很好地解决钢筋锈蚀问题。因此,采用FRP筋珊瑚混凝土结构代替普通钢筋混凝土结构具有广泛的应用前景[7-9]。
在钢筋混凝土结构中,钢筋与混凝土良好的粘结性能是其能够充分发挥各自优势并广泛应用于实际工程中的基础。同理,FRP筋与全珊瑚骨料海水混凝土之间的粘结性能决定了其是否能够在实际工程中得到应用。由于FRP筋是由纤维与聚合物树脂制作而成,其所用的材料与制作工艺都不同于普通钢筋,因此其材料属性与普通钢筋不同[10]。同时,珊瑚骨料海水混凝土的组成成分、强度分布及材料属性都与普通混凝土有所差别[11]。因此,FRP筋与全珊瑚骨料海水混凝土的粘结性能与普通钢筋混凝土不同,因此需要对其展开相关研究以验证FRP筋全珊瑚骨料海水混凝土结构在实际工程中的适用性。
基于上述背景,国内外已有部分学者就FRP筋珊瑚骨料混凝土构件的界面粘结性能开展了试验研究,主要从珊瑚骨料混凝土强度、粘结长度、FRP筋直径、FRP筋类型及表面形式等方面研究了各因素对FRP筋珊瑚骨料混凝土界面粘结性能的影响。胡长顺[12]、Yin等[13]研究了FRP筋类型和表面形式对FRP筋珊瑚骨料混凝土粘结性能的影响,发现改变筋材表面形式能够有效提高构件的粘结性能,玄武岩纤维增强树脂复合材料(BFRP)筋珊瑚骨料混凝土与玻璃纤维增强树脂复合材料(GFRP)筋珊瑚骨料混凝土的粘结强度相近且约为碳纤维增强树脂复合材料(CFRP)筋珊瑚骨料混凝土的3倍。王磊等[14-15]、杨超等[16]分别对CFRP筋珊瑚骨料混凝土、GFRP筋珊瑚骨料混凝土和BFRP筋珊瑚骨料混凝土构件的粘结性能进行了研究,结果表明,筋材直径的增大及粘结长度的增加都会导致构件的粘结强度降低,并且破坏模式也会受到很大的影响。胡长顺[12]、吴翔[17]分别研究了珊瑚混凝土强度对BFRP筋珊瑚骨料混凝土和CFRP筋珊瑚骨料混凝土构件粘结性能的影响,发现提高混凝土强度能够增强构件的界面粘结性能,并且在强度较低时这种增强效果更加明显。
试验研究可以较好地反应试件的破坏模式和极限承载力,但无法描述在拉拔过程中FRP筋与珊瑚骨料混凝土界面的真实应力和应变的分布情况。对此,部分学者通过有限元模拟对FRP筋普通混凝土结构和FRP筋珊瑚骨料混凝土结构的粘结性能进行了分析。王召[18]分别采用弹簧模型和接触模型建立了FRP筋普通混凝土界面有限元模型,发现接触模型的计算结果与试验结果吻合度更高,但建模所需的参数较多,没有弹簧模型简便。陈爽[19]采用有限元模型分析了CFRP筋和GFRP筋珊瑚骨料混凝土梁的粘结性能,发现CFRP筋珊瑚骨料混凝土梁的粘结强度较GFRP筋珊瑚骨料混凝土梁大,滑移量较小,并且有限元计算结果与试验结果基本一致。Arnaud等[20]通过有限元模型分析了FRP筋与普通混凝土的粘结性能,提出了基于Cosenza-Manfredi-Realfonzo (CMR)模型变体的解析粘结滑移模型,并对有限元计算结果和试验结果进行了对比,发现其提出的模型能够很好地模拟高荷载水平下的粘结性能,而在低、中荷载水平下的拟合性较差。
采用有限元模型进行计算时,选用适用性较强的界面粘结-滑移本构模型是保证有限元计算准确性的重要前提。Eligehausen等[21]于1982年提出了钢筋与混凝土的界面粘结-滑移本构(BPE)模型,其关系曲线包括上升段、水平段、下降段及残余应力段四个部分。然而由于FRP筋与钢筋材料属性的不同,BPE模型不能准确地表达FRP筋普通混凝土构件的界面粘结-滑移关系。对此Cosenza等[22]在大量的试验基础上对BPE模型进行了改进,认为FRP筋普通混凝土构件的界面粘结-滑移关系曲线不应包含水平段,于是将其除去后得到了修正的界面粘结-滑移本构(MBPE)模型。Malvar[23]对不同表面形式的GFRP筋普通混凝土构件进行了研究,提出了一种新的界面粘结-滑移本构模型(Malvar模型),但是该模型较复杂,与试验结果的吻合度较低,因此很少被使用。之后,Cosenza等[24]针对实际使用情况建立了能够准确反映FRP筋普通混凝土构件界面粘结-滑移关系的CMR模型,该模型表达式较简洁,与实际的吻合度较高,但仅仅考虑了结构在正常使用阶段的计算过程。基于上述模型的不足,高丹盈等[25]提出了连续曲线模型,即在最大粘结应力处曲线应该是连续的并且下降段不应是直线,该模型与实际状况相符,适用性较强。
综上所述,目前国内外对FRP筋普通混凝土结构粘结性能的研究已取得了较多的成果,但对于FRP筋珊瑚骨料海水混凝土结构的研究较少,并且大多都是对其进行试验方面的研究。可是在试验研究中,难以通过试验结果来描述FRP筋与珊瑚骨料海水混凝土界面粘结应力的分布情况,因此基于试验研究和数值模拟得到的结果,对FRP筋珊瑚骨料混凝土界面粘结应力和相对滑移的分布进行了理论推导,并采用试验结果来验证计算公式的可行性,进而对FRP筋珊瑚骨料混凝土界面的粘结应力和相对滑移量沿界面的分布进行分析。
1. FRP筋全珊瑚骨料混凝土粘结性能试验研究
1.1 试验概况
试验研究考虑了FRP筋直径d、FRP筋种类、粘结长度l和珊瑚混凝土强度对FRP筋全珊瑚骨料混凝土界面粘结性能的影响。本次试验共设置了14组,每组5个试件,构件的详细构造如表1所示。试验采用中心拉拔试验方法,试件设计具体构造情况如图1所示。
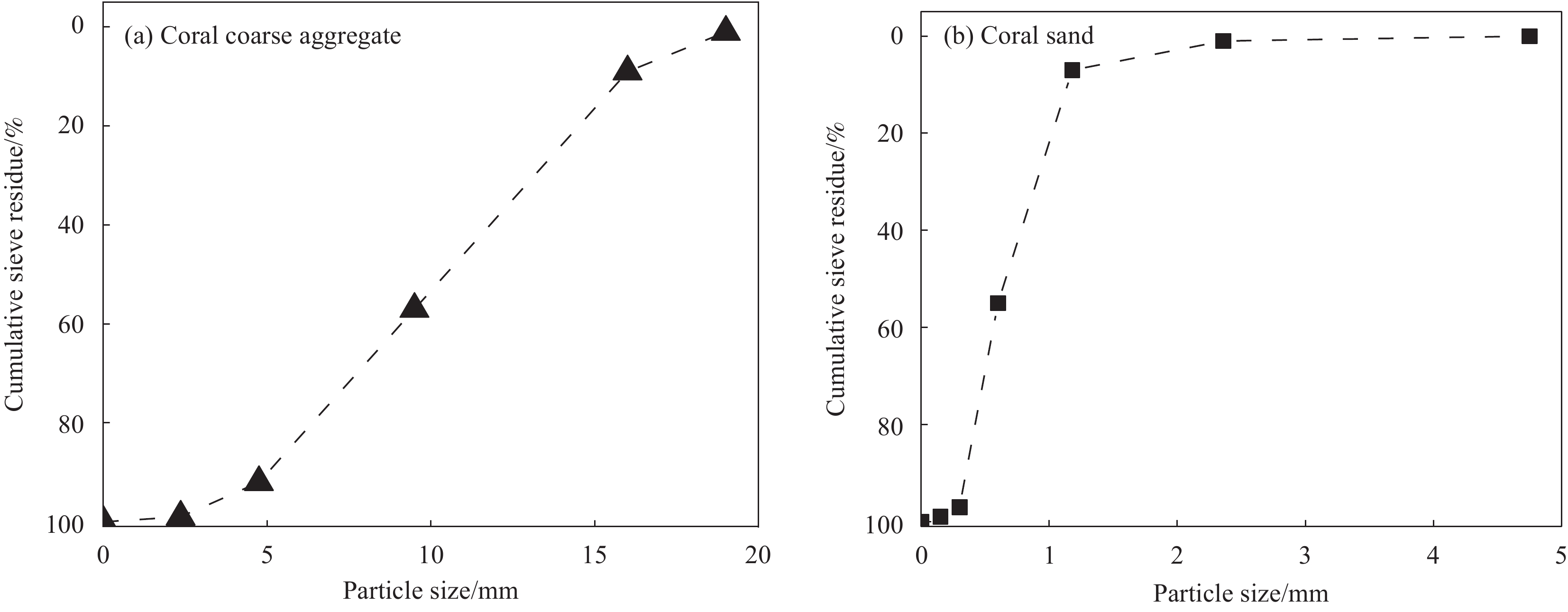
表 1 纤维增强树脂复合材料(FRP)筋全珊瑚骨料海水混凝土构件参数Table 1. Parameters of fiber reinforced polymer (FRP) reinforced full coral aggregate seawater concreteSpecimen number d/mm Fiber reinforced polymer (FRP) l/mm Coral concrete strength BFRP(d8)/C40-2.5d 8 BFRP 2.5d C40 BFRP(d8)/C40-5d 8 BFRP 5.0d C40 BFRP(d8)/C40-7.5d 8 BFRP 7.5d C40 BFRP(d10)/C40-2.5d 10 BFRP 2.5d C40 BFRP(d10)/C40-5d 10 BFRP 5.0d C40 BFRP(d10)/C40-7.5d 10 BFRP 7.5d C40 BFRP(d12)/C40-2.5d 12 BFRP 2.5d C40 BFRP(d12)/C40-7.5d 12 BFRP 7.5d C40 CFRP(d12)/C40-5d 12 CFRP 5.0d C40 BFRP(d12)/C40-5d 12 BFRP 5.0d C40 GFRP(d12)/C40-5d 12 GFRP 5.0d C40 BFRP(d12)/C30-5d 12 BFRP 5.0d C30 BFRP(d12)/C35-5d 12 BFRP 5.0d C35 Notes: d—Diameter of FRP bars; C—Coral concrete strength grade; l—Bond length; BFRP—Basalt fiber reinforced polymer; CFRP—Carbon fiber reinforced polymer; GFRP—Glass fiber reinforced polymer. 试验采用的FRP筋为江苏绿材谷新材料科技发展有限公司生产的CFRP筋、GFRP筋和BFRP筋,实测各类FRP筋的力学性能如表2所示。珊瑚骨料取自南海,原状的珊瑚礁、破碎后的珊瑚和珊瑚砂的形状如图2所示,珊瑚粗骨料的粒径分布为5~20 mm,含水率为0.40%,容重为964.52 kg/m3,表观密度为2008.67 kg/m3,孔隙率为51.7%,1 h内吸水率为10.1%。珊瑚砂的含水率为0.45%,珊瑚粗骨料和珊瑚砂的级配曲线如图3所示。水泥采用P.O.42.5硅酸盐水泥,海水采用按照南海海水组成配制的人工海水[26],具体化学组成成分如表3所示。混凝土采用抗压强度不低于40 MPa的全珊瑚骨料海水混凝土,混凝土配合比及标准养护28天后的实测抗压强度如表4所示。
表 2 变形FRP筋材料性能参数Table 2. Performance parameters of deformed FRP barsReinforcement
typeDiameter/
mmYield strength/
MPaStandard value of ultimate
strength/MPaElastic modulus/
GPaElongation/
%BFRP 12 – 1405 53.6 2.63 GFRP 12 – 1021 54.8 1.87 CFRP 12 – 1815 104.5 1.78 表 3 人工海水化学成分(g/L)Table 3. Chemical composition of artificial seawater (g/L)NaCl MgCl2 Na2SO4 CaCl2 KCl NaHCO3 22.16 5.265 3.861 1.082 0.745 0.207 表 4 全珊瑚骨料海水混凝土配合比设计Table 4. Full coral aggregate seawater concrete mix designConcrete
typeCement/
(kg·m−3)Coarse aggregate/
(kg·m−3)Fine aggregate/
(kg·m−3)Water consumption/
(kg·m−3)Water reducing
agent/(kg·m−3)28-day cube compressive
strength/MPaCoral concrete 540 560 710 220 7.5 41.2 1.2 试验结果
将试件以筋材种类(筋材直径)/珊瑚骨料混凝土强度-粘结长度方式进行命名。试验采用位移控制的万能试验机对构件进行加载,加载速率为0.5 mm/min,当试件破坏或FRP筋被拉出35 mm时,终止试验。同时采用荷载传感器、位移计及数据采集仪对自由端和加载端FRP筋的位移进行测量采集。试验结果如表5所示,由于自由端的滑移量分布较加载端更加均匀,因此峰值荷载滑移量采用自由端的滑移量。
表 5 FRP筋全珊瑚骨料海水混凝土试件拉拔试验结果Table 5. Drawing test results of FRP reinforced full coral aggregate seawater concrete specimenGroup
numberSpecimen
numberAverage value
of ultimate
load/kNUltimate load slip amount/mm Average value
of ultimate bond
strength/MPaFailure
modeLa1 BFRP(d8)/C40-2.5d 21.77 2.84 43.32 Pulling-out failure La2 BFRP(d8)/C40-5d 34.68 2.62 34.51 Pulling-out failure La3 BFRP(d8)/C40-7.5d 39.48 2.96 26.19 Pulling-out failure
(one pulling-out-splitting failure)Lb1 BFRP(d10)/C40-2.5d 28.39 3.75 36.16 Pulling-out failure Lb2 BFRP(d10)/C40-5d 44.05 3.51 28.06 Pulling-out failure
(one splitting failure)Lb3 BFRP(d10)/C40-7.5d 45.88 2.03 19.48 Splitting failure Lc1 BFRP(d12)/C40-2.5d 40.12 4.19 35.49 Pulling-out failure
(two splitting failure)Lc3 BFRP(d12)/C40-7.5d 48.93 — 14.43 Splitting failure Ld1 CFRP(d12)/C40-5d 10.48 1.30 4.64 Pulling-out failure Ld2 BFRP(d12)/C40-5d 30.52 1.81 13.50 Pulling-out failure Ld3 GFRP(d12)/C40-5d 29.57 2.03 13.08 Pulling-out failure Le1 BFRP(d12)/C30-5d 49.39 3.86 21.85 Pulling-out failure
(one splitting failure)Le2 BFRP(d12)/C35-5d 61.00 5.00 26.98 Splitting failure
(one pulling-out failure)由表5可知,试件的破坏模式主要有拔出破坏、劈裂破坏和拔出-劈裂破坏三种。如图4(a)所示,大多数拔出破坏表现为FRP筋表面被磨损变得光圆,使界面的摩擦力和机械咬合力减小,导致FRP筋被拔出,混凝土界面未发生破坏;部分拔出破坏则表现为混凝土界面附近被FRP筋的横肋拉坏,FRP筋被拔出。如图4(c)所示,由于FRP筋与珊瑚混凝土之间存在相互作用,使两者接触面处的应力方向并不与接触面平行,而是与接触面形成一定的角度,导致接触处的应力既存在平行于接触面的分力也存在垂直于接触面的分力,这一垂直方向的分力会使混凝土内产生拉应力,在混凝土保护层厚度较小时,由拉应力引起的裂纹向混凝土表面扩展,混凝土发生劈裂破坏。如图4(b)所示,拔出-劈裂破坏主要表现为混凝土界面的裂缝向表面扩展,在混凝土表面出现裂纹后FRP筋被拔出,试件未发生破裂。
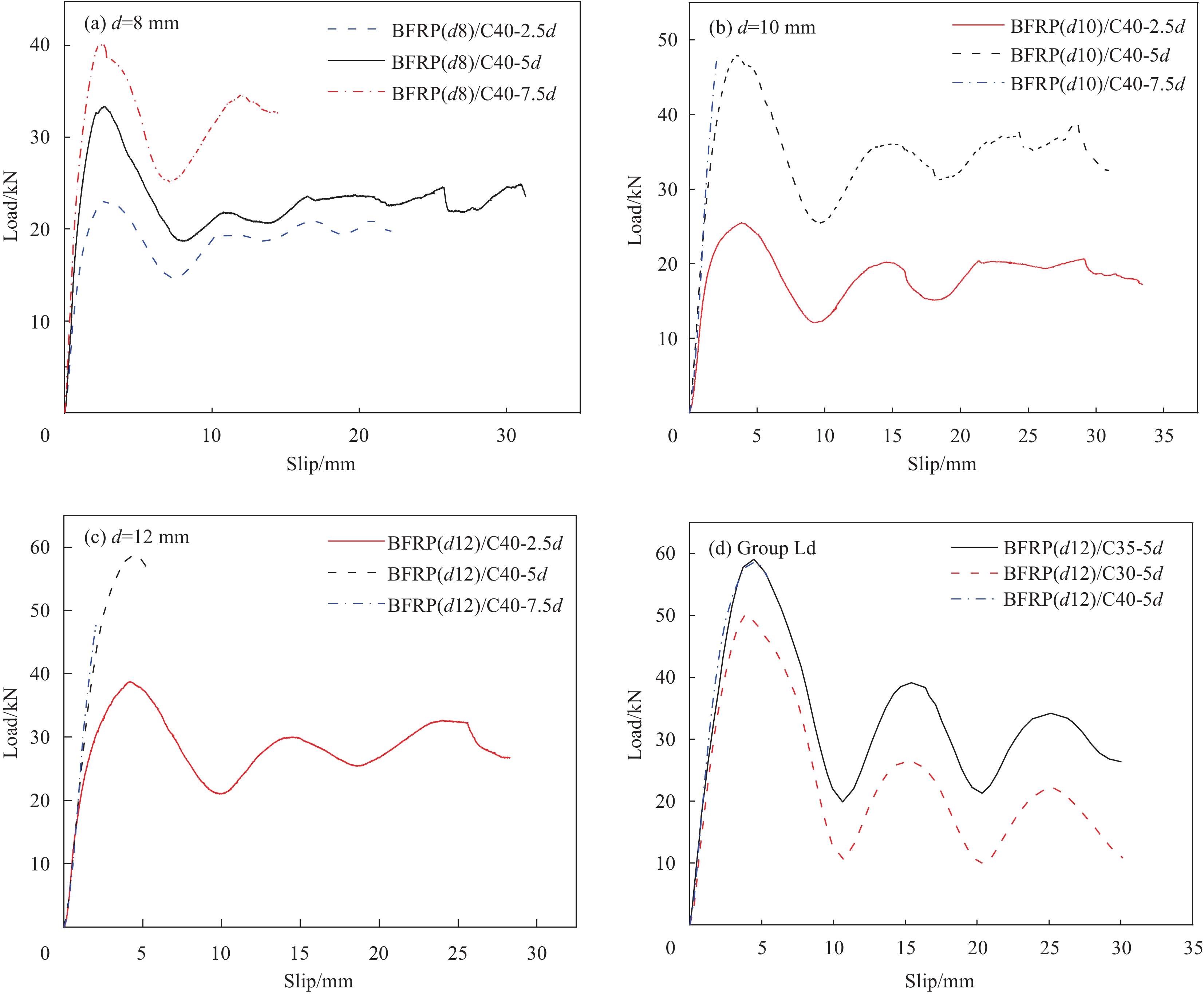
图5为不同FRP筋直径和珊瑚骨料混凝土强度条件下BFRP筋珊瑚混凝土构件的荷载-滑移曲线。可以看出,粘结滑移过程主要分为滑移段、下降段和残余段三个阶段。在滑移段初期,构件处于弹性阶段,滑移量随着荷载的提升而缓慢增加,此时曲线的变化为一倾斜直线,之后随着荷载的继续增大,化学胶着作用开始失效,界面粘结作用也随之减弱,此时曲线的斜率逐渐降低,滑移量继续增大。在下降段,由于FRP筋表面受到磨损,FRP筋与珊瑚混凝土之间的摩擦力和机械咬合力减小,界面粘结作用继续降低,此时曲线在达到峰值荷载后开始回落,滑移量明显增大。在残余段,随着FRP筋表面磨损程度的增大,二者之间仅存在部分摩擦力和机械咬合力,粘结荷载较小,此时曲线为波动形式,并且越往后波动幅度越小,可能是机械咬合作用逐渐完全失效所致。
结合表5和图5可以看出,随着FRP筋直径的增加,构件的极限拉拔承载力和相对滑移量增大,随着粘结长度的增加,构件的极限拉拔承载力增大,而相对滑移量减小。此外,FRP筋直径和粘结长度的增加均会导致极限粘结强度降低,这是由于随着FRP筋直径和粘结长度的增大,FRP筋的剪力滞后现象越明显,界面粘结应力分布不均匀现象也越显著,从而导致FRP筋与珊瑚骨料混凝土之间的粘结性能变差。在相同粘结长度、筋材直径和珊瑚混凝土强度条件下,BFRP筋和GFRP筋珊瑚骨料混凝土构件的极限粘结强度相近,大约是CFRP筋试件的3倍,这是由于施工工艺的不同导致CFRP筋表面的抗剪能力较差。由于提升珊瑚混凝土强度对试件的粘结性能影响不大,因此不再对其进行具体分析。
2. FRP筋全珊瑚骨料混凝土粘结性能的数值模拟计算
2.1 有限元模型的建立
采用ABAQUS软件来建立FRP筋珊瑚骨料混凝土界面的有限元模型。首先需要在材料属性赋予模块中输入珊瑚混凝土的单轴应力-应变曲线,该曲线参考标准GB50010—2010[27]可得到单轴拉压的名义应力与应变的关系,如下列公式所示:
单轴受压:
σnom=(1−dc)Ecεnom (1) 单轴受拉:
σnom=(1−dt)Ecεnom (2) 其中:Ec为全珊瑚骨料混凝土弹性模量;σnom
为珊瑚混凝土的名义应力;εnom为珊瑚混凝土的名义应变;dc为混凝土单轴受压损伤演化参数;dt为混凝土单轴受拉损伤演化参数。 然而模拟计算需要的是构件的真实应力和塑性应变曲线作为本构关系,因此需要对材料受压和受拉得到的名义应力σnom和名义应变εnom进行转化,转化方式采用规范中建议的转化方法,如下列公式所示:
真实应力:
σture=σnom(1+εnom) (3) 真实应变:
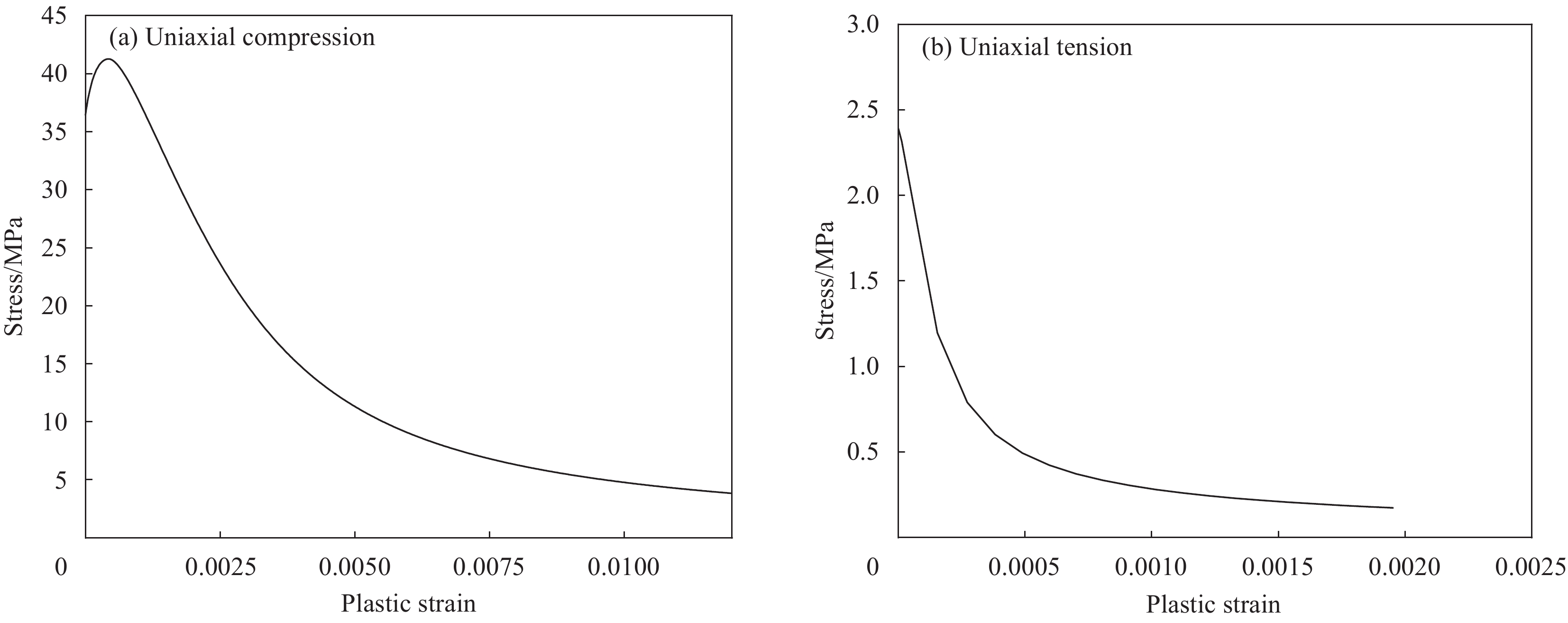
εture=ln(1+εnom) (4) εpl=|εtrue|−|εel|=|εtrue|−|σtrue|E (5) 根据真实应变εture与名义应变εnom之间的关系及真实应力σture与名义应力σnom之间的关系,并根据塑性应变和弹性应变共同组成真实应变的关系得到了全珊瑚骨料混凝土单轴受压和受拉的真实应力-塑性应变曲线,如图6所示。
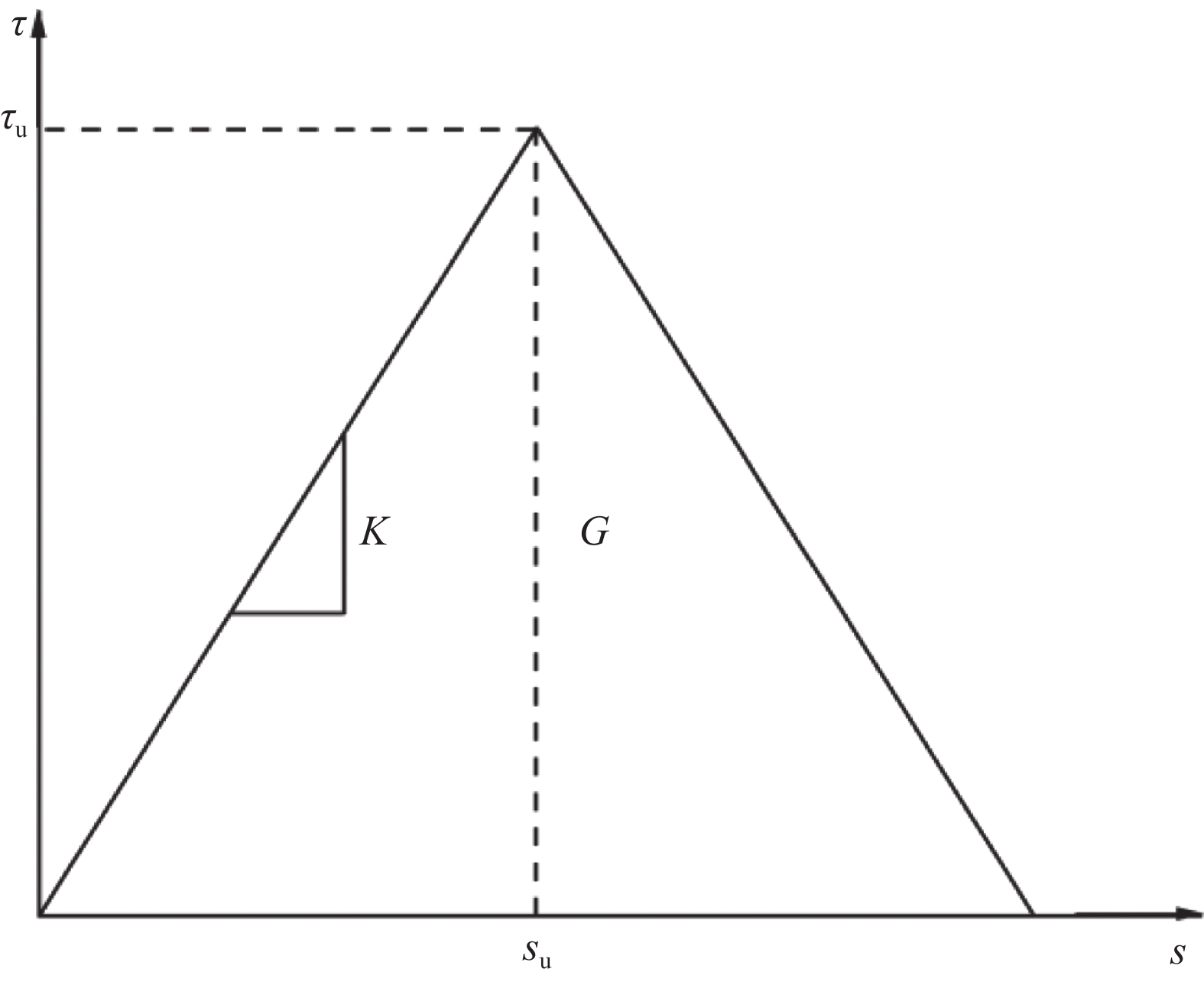
将FRP筋的材料属性定义为弹性材料,并根据表2输入材料的相关数据。界面粘结单元的粘结-滑移本构关系采用简化双线性模型,本构关系如图7所示,并采用上述试验中得到的界面粘结强度和断裂能作为界面粘结滑移的控制参数。同时,当粘结单元完全失效时结束试验。
在接触关系和边界条件上,将FRP筋与珊瑚混凝土粘结层上下表面之间设置成表面对表面的接触,自由端设置成完全固定,加载过程采用位移控制,以2 mm法向位移为边界条件分级加载。在网格划分和单元选择上,采用边缘布种的方法将珊瑚混凝土部分网格划分为20 mm等级,FRP筋网格尺寸为1 mm,二者均采用C3D8R八节点六面体单元模拟。最后采用线性损伤演化模型描述FRP筋全珊瑚骨料混凝土构件的界面损伤演变过程。
2.2 有限元计算结果
数值模拟方案的设计与试验方案相同,即分别对不同FRP筋直径d(8 mm、10 mm、12 mm)、珊瑚骨料混凝土强度fc(C30、C35、C40)、粘结长度l(2.5d、5d、7.5d)、FRP筋种类(CFRP、GFRP、BFRP)的FRP筋珊瑚混凝土构件进行了分析,构件具体构造如表1所示。
将数值计算所得到的结果与试验结果进行对比,如表6所示。数值模拟结果与试验结果吻合度较高,FRP筋珊瑚骨料混凝土构件的极限拉拔承载力和峰值荷载滑移量模拟结果与试验结果的误差均小于10%。这表明有限元分析采取的参数和模型能够较准确地模拟FRP筋珊瑚骨料混凝土构件的粘结性能。同时也说明了可以采用简化双线性本构模型粘结单元对FRP筋珊瑚骨料海水混凝土结构的粘结性能进行模拟计算。
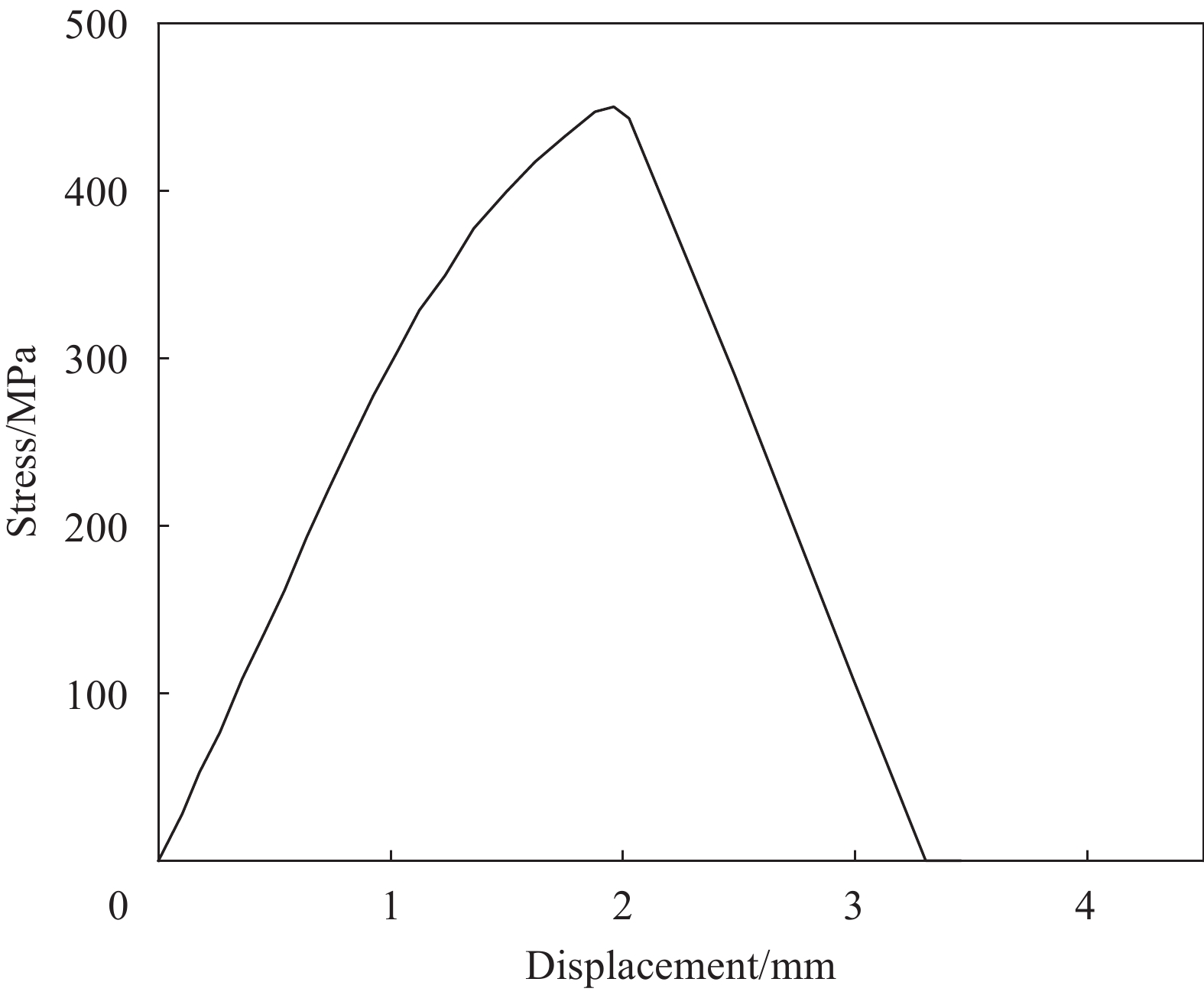
表 6 FRP筋全珊瑚骨料海水混凝土试件的计算值与试验值对比Table 6. Comparison of calculated and experimental values of FRP reinforced full coral aggregate seawater concrete specimensGroup number Ptest/kN Pcal/kN Error/% δtest/mm δcal/mm Error/% La1 21.77 21.44 1.53 2.84 2.60 8.51 La2 34.68 33.84 2.42 2.62 2.40 8.32 La3 39.48 38.83 1.64 2.96 2.82 4.61 Lb1 28.39 27.94 1.57 3.75 3.47 7.54 Lb2 44.05 43.49 1.26 3.51 3.20 8.76 Lb3 45.88 43.23 5.77 2.03 1.87 8.12 Lc1 40.12 39.31 2.01 4.19 3.92 6.48 Lc3 57.87 54.67 5.53 – 2.30 – Ld1 10.84 10.64 1.86 1.30 1.20 7.64 Ld2 29.57 28.29 4.32 1.81 1.71 5.34 Ld3 30.52 29.47 3.41 2.03 1.96 3.21 Le1 49.39 46.31 6.23 3.86 3.61 6.52 Le2 55.23 51.30 7.12 5.00 4.76 4.87 Notes: Ptest—Average value of the ultimate load obtained from the test; δtest—Slip value corresponding to the ultimate load obtained in the test; δcal—Slip value corresponding to the ultimate load obtained by numerical simulation. 试件La2的粘结应力-滑移曲线如图8所示。可以看出,在初始加载阶段,粘结应力随着滑移量的增大而增加,当滑移量达到2 mm时,粘结应力达到最大,此时界面开始发生破坏。随着滑移量的继续增大,界面的破坏程度也更加严重,因此在达到峰值粘结应力后FRP筋的应力随着滑移量的增大而减小,直至降低为零,界面粘结作用完全失效。
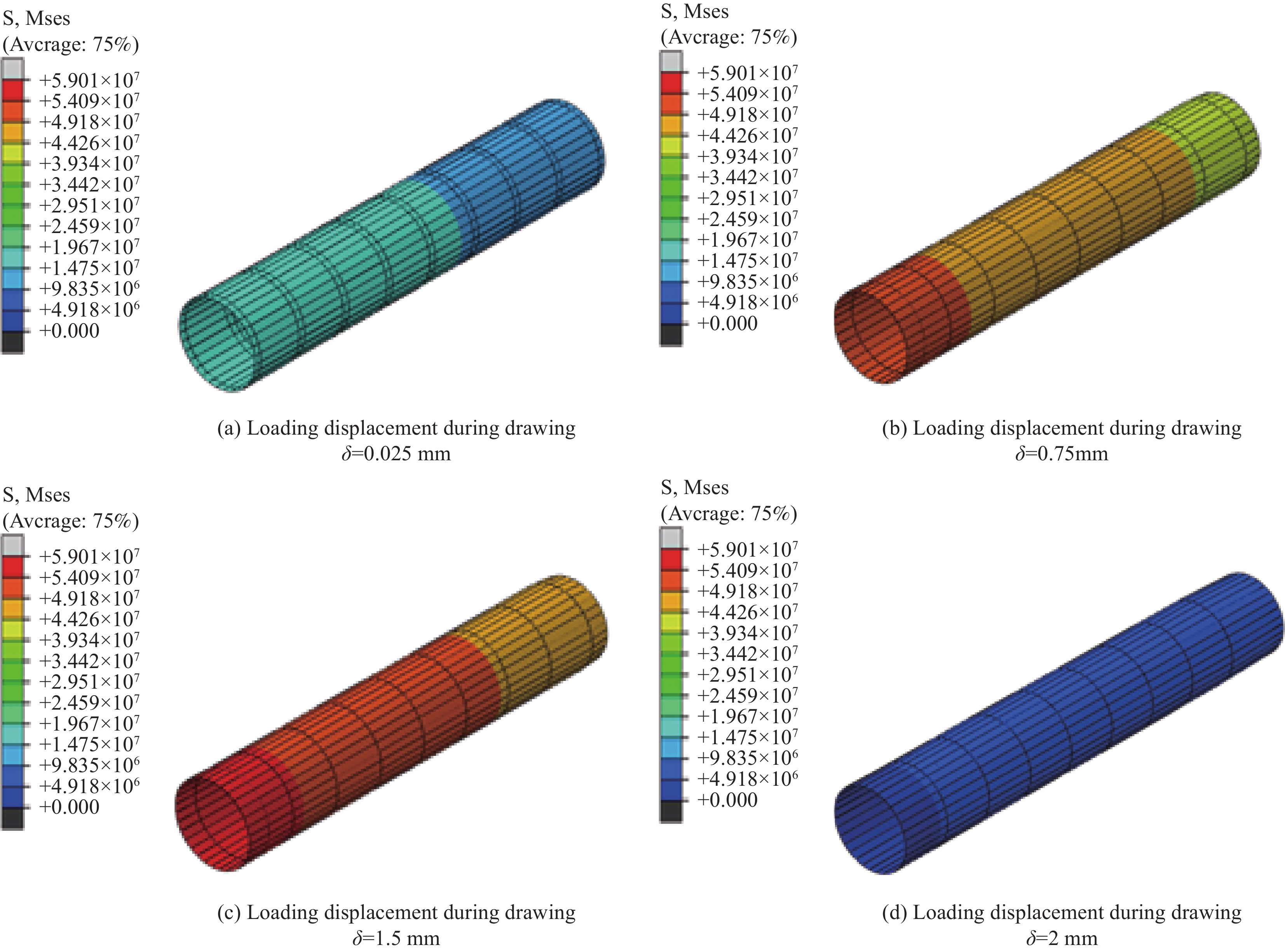
图9为试件La2在加载过程中FRP筋与珊瑚骨料混凝土之间界面粘结层的应力分布情况。在加载初期,加载端的界面粘结应力要高于自由端,随着加载过程的进行,界面平均粘结应力不断提高,加载端的粘结应力先达到最大,粘结单元开始发生破坏,之后最大粘结应力向自由端移动,直至界面完全破坏,此时粘结单元的应力降为零,界面粘结作用失效,FRP筋与珊瑚骨料混凝土完全分离。
3. FRP筋珊瑚骨料混凝土界面粘结-滑移理论分析
FRP筋珊瑚骨料混凝土界面粘结-滑移本构模型的建立不仅可以表征二者之间界面粘结作用,还可为试验研究和数值模拟提供理论基础。同时,试验只能了解到结构的破坏模式,无法确定应力和滑移沿着界面的分布情况。因此在试验与数值计算结果及现有模型的基础上对FRP筋珊瑚骨料海水混凝土的界面粘结应力和相对滑移量表达式进行了推导并分析二者沿界面的分布情况。
3.1 简化双线性粘结滑移模型
现有的模型大多都能够很好地模拟FRP筋混凝土构件的界面粘结行为,但是Malvar模型[23]、连续曲线模型及薛伟辰模型[28]都是根据试验结果拟合而成,表达形式较复杂,部分控制点参数难以确定,不便用于理论推导和数值模拟计算。CMR模型[24]的表达形式虽然比较简便,但该模型只给出了上升段的表达式,无法全面地描述FRP筋混凝土构件的界面粘结行为。修正的BPE模型[22]比较简便,与试验所得结果的吻合度较高,在一定程度上能够满足FRP筋混凝土构件本构模型研究的需要。
为了能够更加简便又较准确地模拟FRP筋珊瑚骨料混凝土的界面粘结滑移机制,采用简化的双线性粘结滑移模型来描述FRP筋珊瑚骨料混凝土的粘结-滑移关系。这种模型包括两个阶段:第一阶段是将现有模型中的微滑移段和滑移段结合成线性上升段,第二阶段是界面粘结应力在达到峰值应力后因刚度变小而进入线性下降段。在残余段,由于FRP筋与珊瑚混凝土之间的化学胶着作用已经失效,二者间仅存在部分的摩擦力和机械咬合力,粘结作用较小,而且残余强度对粘结滑移的影响不大,同时残余段的理论公式推导较复杂并且所需参数较多,不便于应用,因此不考虑残余段。本构模型曲线如图7所示。
简化双线性粘结滑移本构关系可用公式表示为
上升阶段:
τ=τussu=Ks0⩽ (6) 下降阶段:
\tau = -\frac{{{\tau _{\text{u}}}}}{{{s_{\text{r}}} - {s_{\text{u}}}}}{\text{(}}s - {s_{\text{u}}}{\text{)}}\qquad\qquad\qquad s < s \leqslant {s_{\text{r}}} (7) 其中:
{\tau _{\text{u}}} = \dfrac{{{T_{\text{u}}}}}{{{\text{π}} {d}l}} 为界面最大粘结强度;Tu是极限拉拔承载力;d是FRP筋直径;l为构件锚固长度;su是达到最大粘结应力对应的滑移量;K为起裂粘结刚度;τu为峰值粘结强度; s为拉拔过程中的滑移量; sr为残余粘结应力对应的滑移量。3.2 界面粘结滑移理论
首先假设FRP筋珊瑚骨料混凝土试件的横截面满足平截面假定,并且两种材料均为线弹性材料。取出构件一微分单元,其受力情况如图10所示。
根据图10中的受力情况,可知受力平衡方程为
{A_{\text{c}}}{\text{d}}{\sigma _{\text{c}}} + {A_{\text{f}}}{\text{d}}{\sigma _{\text{f}}} = 0 (8) \frac{{{\text{π}} d^2}}{4}{\text{d}}{\sigma _{\text{f}}} = {\text{π}} {d}\tau {\text{d}}x (9) 式中:τ为粘结应力;σf为FRP筋拉应力;σc为珊瑚混凝土应力;d为FRP筋直径;Af为FRP筋截面面积;Ac全珊瑚骨料混凝土截面面积。
两种材料间的相对滑移量可通过FRP筋的滑移量减去珊瑚骨料混凝土的滑移量得到,其计算式为
s{\text{(}}x{\text{)}} = {s_{\text{f}}}{\text{(}}x{\text{)}} - {s_{\text{c}}}{\text{(}}x{\text{)}} (10) 对式(10)进行求导,可得:
\frac{{{\text{d}}s}}{{{\text{d}}x}} = \frac{{{\text{d}}{s_{\text{f}}}}}{{{\text{d}}x}} - \frac{{{\text{d}}{s_{\text{c}}}}}{{{\text{d}}x}} = {\varepsilon _{\text{f}}}{\text{(}}x{\text{)}} - {\varepsilon _{\text{c}}}{\text{(}}x{\text{)}} (11) 根据胡克定律,FRP筋与珊瑚骨料混凝土的应力-应变关系如下:
{\sigma _{\text{f}}} = {E_{\text{f}}}{\varepsilon _{\text{f}}} {\sigma _{\text{c}}} = {E_{\text{c}}}{\varepsilon _{\text{c}}} (12) 式中:Ef为FRP筋弹性模量;Ec为全珊瑚骨料混凝土弹性模量;εf为FRP筋应变;εc为全珊瑚骨料混凝土应变。
联立式(8)~(12) 并进行代数变换后可得到FRP筋珊瑚骨料混凝土界面粘结应力与相对滑移量的微分方程:
\frac{{{{\text{d}}^2}s{\text{(}}x{\text{)}}}}{{{\text{d}}{x^2}}} - P\tau {\text{(}}x{\text{)}} = {\text{0}} (13) 其中,P为与曲线下降段有关的参数:
P = \frac{4}{{{E_{\text{f}}}{d_{\text{f}}}}}{{\Bigg(}}1 + \frac{{{E_{\text{f}}}{A_{\text{f}}}}}{{{E_{\text{c}}}{A_{\text{c}}}}}{{\Bigg)}} (14) 将上述的简化双线性粘结滑移模型作为FRP筋珊瑚骨料混凝土界面粘结应力与相对滑移量微分方程的边界条件,可得到FRP筋与珊瑚骨料混凝土界面的粘结应力τ与相对滑移量s之间的关系,具体计算过程如下所示:
(1)当
{\text{0}} \leqslant s \leqslant {s_{\text{u}}} 时 (上升段):将式(6)代入式(13)可得:
\frac{{{{\text{d}}^2}s{\text{(}}x{\text{)}}}}{{{\text{d}}{x^2}}} - PKs{\text{(}}x{\text{)}} = 0 (15) 求解上述微分方程,可得通解为
s{\text{(}}x{\text{)}} = A{{\rm{e}}^{\sqrt {PK} x}} + B{{\rm{e}}^{ - \sqrt {PK} x}} (16) 以峰值荷载对应的滑移量为边界条件,代入式(13)可得系数A、B的值及二者的关系为
\left\{ {\begin{array}{*{20}{l}} {A + B = 0} \\ {A{{\rm{e}}^{l\sqrt {PK} }} + B{{\rm{e}}^{ - l\sqrt {PK} }} = {s_{\text{u}}}} \end{array}} \right. (17) \left\{ {\begin{array}{*{20}{l}} {A = \dfrac{{{s_{\text{u}}}}}{{2{\rm{sinh}}{\text{(}}l\sqrt {PK} {\text{)}}}}} \\ {B = - \dfrac{{{s_{\text{u}}}}}{{2{\rm{sinh}}{\text{(}}l\sqrt {PK} {\text{)}}}}} \end{array}} \right. (18) 通过联立式(6)、(16)和(18)可得上升段粘结应力τ与滑移量s沿着界面的分布关系:
s{\text{(}}x{\text{)}} = \frac{{{s_{\text{u}}}}}{{{\rm{sinh}}{\text{(}}l\sqrt {PK} {\text{)}}}}{\rm{sinh}}{\text{(}}\sqrt {PK} x{\text{)}} (19) \tau {\text{(}}x{\text{)}} = \frac{{{s_{\text{u}}}K}}{{{\rm{sinh}}{\text{(}}l\sqrt {PK} {\text{)}}}}{\rm{sinh}}{\text{(}}\sqrt {PK} x{\text{)}} (20) (2)当
{s_{\text{u}}} < s \leqslant {s_{\text{r}}} 时 (下降段):将式(13)转变为
\frac{{{{\text{d}}^2}s}}{{{\text{d}}{x^2}}} + \mu _1^2s = \mu _1^2 (21) 其中,
{\mu }_{1}=\sqrt{PR{\tau }_{\text{u}}/{s}_{\text{u}}},{\mu }_{2}=\sqrt{P{\tau }_{\text{u}}(l+R)} ,R是与下降段有关的参数。其解为
s{\text{(}}x{\text{)}} = {C_1}{\text{cos}}{\mu _1} + {C_2}{\text{sin}}{\mu _1}x + {{{\Bigg(}}\frac{{{\mu _2}}}{{{\mu _1}}}{{\Bigg)}}^{\text{2}}} (22) 其中,μ1、 μ2、 C1和 C2均为系数。边界条件为粘结应力达到
{\tau _r} 时,自由端滑移量{s_{\rm{f}}} 和加载端滑移量{s_{\rm{r}}} ,即\left\{ {\begin{array}{*{20}{c}} {s{\text{(}}x{\text{)}}\left| {_{x = 0} = {s_{\text{f}}}} \right.} \\ {s{\text{(}}x{\text{)}}\left| {_{x = l} = {s_{\text{r}}}} \right.} \end{array}} \right. (23) 联立式(22)和(23)可得:
{C_1} = - \frac{F}{{{\mu _1}{\text{sin}}{\mu _1}l}}{{\Bigg(}}\frac{{1 + n\rho }}{{{E_{\text{f}}}{A_{\text{f}}}}}{{\Bigg)}},{C_2} = 0 (24) 其中:F为拉拔荷载;ρ为由实验确定的参数。因此,下降段粘结应力τ与滑移量s沿着界面的分布关系为
s{\text{(}}x{\text{)}} = - \frac{F}{{{\mu _1}{\text{sin}}{\mu _1}l}}{{\Bigg(}}\frac{{1 + n\rho }}{{{E_{\text{f}}}{A_{\text{f}}}}}{{\Bigg){\rm{cos}}}}{\mu _1}x + {{{\Bigg(}}\frac{{{\mu _2}}}{{{\mu _1}}}{{\Bigg)}}^2} (25) \tau {\text{(}}x{\text{)}} = \frac{{{\mu _1}F}}{{{\text{π}} {d_{\text{f}}}{\text{sin}}{\mu _1}l}}{\text{cos}}{\mu _1}x (26) 由于残余强度在实际工程应用中影响较小,故不考虑残余段的影响。
3.3 界面粘结滑移理论公式应用
采用上述的试验数据对不同影响因素条件下FRP筋珊瑚骨料混凝土构件的界面粘结应力和相对滑移量进行分析。将试验得到的各类参数代入到式(19)~(20)中,便可得到界面粘结应力和相对滑移量的函数表达式。以试件La1为例,参数d=8 mm、Ef=52.1 GPa、l=20 mm、τu=43.33 MPa、su=2.84 mm,则试件的界面粘结应力和相对滑移量的分布函数式如下所示:
s{\text{(}}x{\text{)}} = {\text{0}}{\text{.002668sinh(0}}{\text{.3831731}}x{\text{)}} (27) \tau {\text{(}}x{\text{)}} = 0.001022{\text{sinh(}}0.3831731x{\text{)}} (28) 根据式(27)~(28)便可绘制出试件达到极限拉拔承载力Tu时界面粘结应力和相对滑移量沿界面的分布情况。
(1) FRP筋珊瑚骨料混凝土界面粘结应力分布理论解
各影响因素下峰值荷载时试件的界面粘结应力分布如图11所示。可以看出,在任何影响因素下,FRP筋珊瑚骨料混凝土构件的界面粘结应力沿界面由自由端向加载端递增,同时FRP筋珊瑚骨料混凝土构件的粘结强度随着粘结长度和FRP筋直径的增加而减小,这与试验和数值模拟得到的结果一致。如图11(a)~11(c)所示,界面粘结长度和FRP筋直径越大,FRP筋珊瑚骨料混凝土构件的界面粘结应力分布越不均匀。如图11(e)所示,随着珊瑚骨料混凝土强度的提高,试件的界面粘结强度也增大,这是由于珊瑚混凝土强度越高,对FRP筋的握裹能力越好,两者间的摩檫作用和机械咬合作用就越强,因此能够更好地抑制裂纹的扩展,减少试件劈裂的可能。同时也可以看出,混凝土强度的提高对粘结应力分布的影响较小,这也与试验和模拟结果一致。在相同的FRP筋直径,粘结长度和珊瑚骨料混凝土强度条件下,GFRP筋和BFRP筋珊瑚骨料混凝土的界面粘结应力分布相似,并且与CFRP筋珊瑚骨料混凝土相比更加均匀。通过分析界面粘结应力分布的理论计算结果并与试验和模拟结果进行对比可以看出,采用上述粘结应力分布表达式求得的计算结果与试验和模拟结果相符,可以将其用于对FRP筋珊瑚骨料混凝土构件的界面粘结应力理论计算。
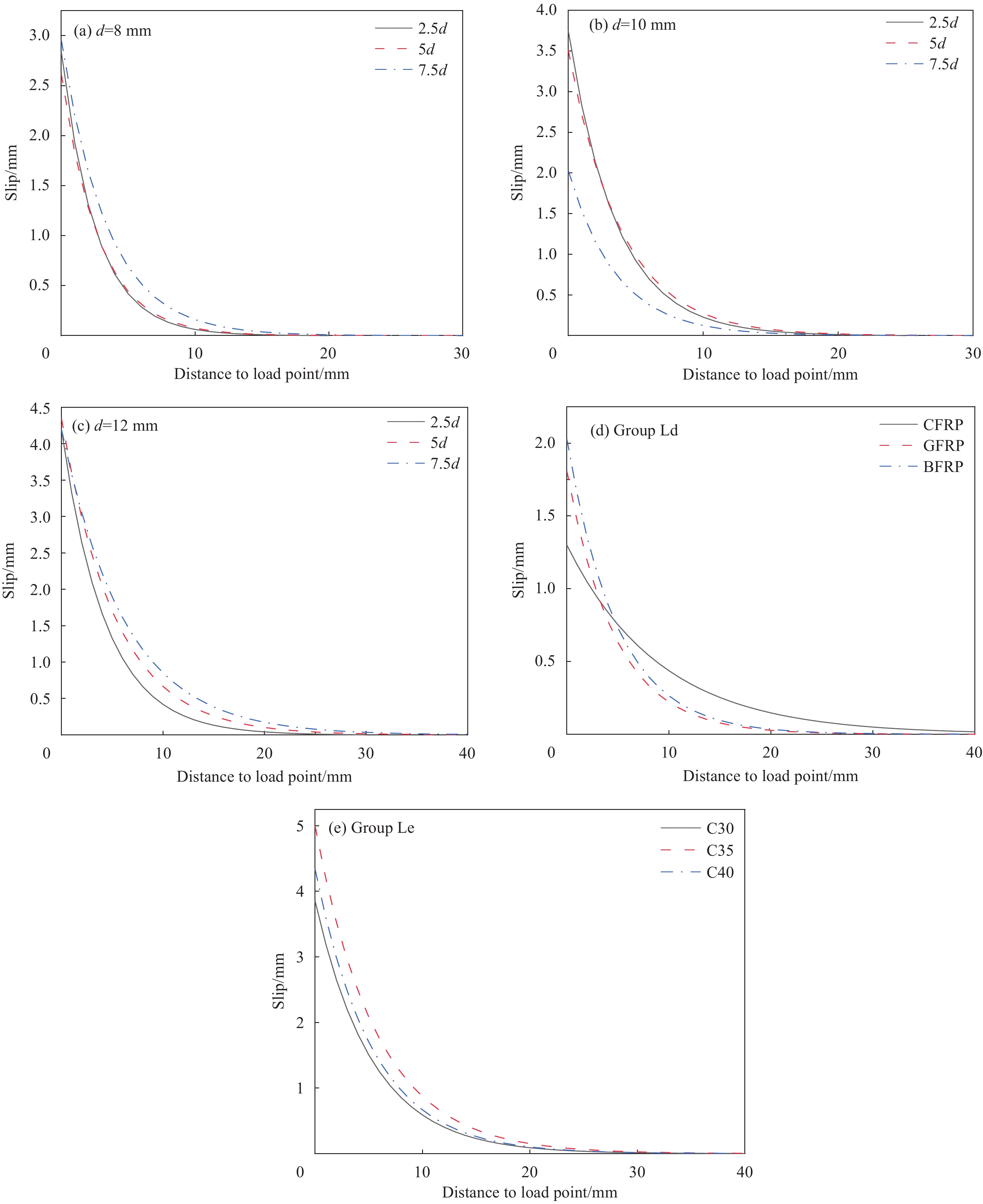
(2) FRP筋珊瑚骨料混凝土界面相对滑移分布理论解
各影响因素下峰值荷载时试件的界面相对滑移量分布如图12所示。FRP筋珊瑚骨料混凝土界面相对滑移量的分布由自由端向加载端递增。由图12(a)~12(c)可以看出,粘结长度对界面相对滑移量的影响较小,但基本遵循粘结长度越短界面相对滑移量分布越均匀的规律,并且随着粘结长度的增加相对滑移量逐渐减小,这主要与破坏模式有关,由试验和模拟结果发现,粘结长度较短的试件更容易发生拔出破坏,相对滑移量也就更大。对于图12(d)中粘结长度为7.5d时的滑移量要比其他滑移量小得多的情况,可能是由于试验误差导致参数有误对理论计算造成了影响。在FRP筋直径、粘结长度和珊瑚骨料混凝土强度相同的条件下,GFRP筋和BFRP筋珊瑚骨料混凝土界面相对滑移量的分布相似,并且比CFRP筋珊瑚骨料混凝土界面相对滑移量的分布均匀。由图12(e)可以看出,界面相对滑移量随着珊瑚骨料混凝土强度的增大而有所降低,这是由于提高混凝土强度可以增强珊瑚混凝土对FRP筋的握裹力和机械咬合作用,使界面粘结作用增大。
虽然界面粘结滑移理论计算公式是在FRP筋和珊瑚混凝土完全弹性的条件下建立的,而FRP筋和珊瑚混凝土并非理想弹性材料,对FRP筋珊瑚骨料混凝土构件不能完全适用,但通过理论公式应用分析可以看出,该计算公式在一定程度上能够为FRP筋珊瑚骨料混凝土结构的研究提供理论依据。
4. 结 论
在纤维增强树脂复合材料(FRP)筋珊瑚骨料混凝土拉拔试验和数值模拟的基础上,以简化双线性本构模型为边界条件,通过弹性理论分析,推导了FRP筋珊瑚骨料混凝土界面粘结应力和相对滑移量的微分方程,进而得到了粘结应力τ和相对滑移量s沿界面分布的表达式。基于以上研究,得到了以下结论:
(1) 采用简化双线性模型作为粘结单元本构模型进行数值模拟分析所得到的结果与试验结果的吻合度很高,因此可以用简化双线性本构模型粘结单元来对FRP筋珊瑚骨料海水混凝土结构的粘结性能进行数值模拟分析;
(2) 粘结应力分布和相对滑移量分布的理论解与试验结果一致。因此可以采用简化双线性模型作为边界条件推导的FRP筋珊瑚混凝土界面粘结应力与相对滑移量表达式来分析二者沿FRP筋与珊瑚混凝土界面的分布情况;
(3) FRP筋珊瑚骨料混凝土构件的界面粘结应力分布由自由端向加载端逐渐递增,界面粘结应力分布的不均匀程度随着粘结长度和FRP筋直径的增加而增大,玄武岩纤维增强树脂复合材料(BFRP)筋和玻璃纤维增强树脂复合材料(GFRP)筋珊瑚骨料混凝土界面粘结应力分布的不均匀程度相类似且比碳纤维增强树脂复合材料(CFRP)筋均匀,珊瑚骨料混凝土强度的变化对FRP筋珊瑚骨料混凝土界面粘结应力分布的影响不大;
(4) FRP筋珊瑚骨料混凝土界面相对滑移量的分布由自由端向加载端逐渐递增,粘结长度对相对滑移量的分布影响不大,FRP筋珊瑚骨料混凝土界面相对滑移量的分布随着珊瑚骨料混凝土强度的增大而有所减小,BFRP筋和GFRP筋珊瑚骨料混凝土界面相对滑移量的分布不均匀程度相类似且比CFRP筋均匀。
-
表 1 纤维增强树脂复合材料(FRP)筋全珊瑚骨料海水混凝土构件参数
Table 1 Parameters of fiber reinforced polymer (FRP) reinforced full coral aggregate seawater concrete
Specimen number d/mm Fiber reinforced polymer (FRP) l/mm Coral concrete strength BFRP(d8)/C40-2.5d 8 BFRP 2.5d C40 BFRP(d8)/C40-5d 8 BFRP 5.0d C40 BFRP(d8)/C40-7.5d 8 BFRP 7.5d C40 BFRP(d10)/C40-2.5d 10 BFRP 2.5d C40 BFRP(d10)/C40-5d 10 BFRP 5.0d C40 BFRP(d10)/C40-7.5d 10 BFRP 7.5d C40 BFRP(d12)/C40-2.5d 12 BFRP 2.5d C40 BFRP(d12)/C40-7.5d 12 BFRP 7.5d C40 CFRP(d12)/C40-5d 12 CFRP 5.0d C40 BFRP(d12)/C40-5d 12 BFRP 5.0d C40 GFRP(d12)/C40-5d 12 GFRP 5.0d C40 BFRP(d12)/C30-5d 12 BFRP 5.0d C30 BFRP(d12)/C35-5d 12 BFRP 5.0d C35 Notes: d—Diameter of FRP bars; C—Coral concrete strength grade; l—Bond length; BFRP—Basalt fiber reinforced polymer; CFRP—Carbon fiber reinforced polymer; GFRP—Glass fiber reinforced polymer. 表 2 变形FRP筋材料性能参数
Table 2 Performance parameters of deformed FRP bars
Reinforcement
typeDiameter/
mmYield strength/
MPaStandard value of ultimate
strength/MPaElastic modulus/
GPaElongation/
%BFRP 12 – 1405 53.6 2.63 GFRP 12 – 1021 54.8 1.87 CFRP 12 – 1815 104.5 1.78 表 3 人工海水化学成分(g/L)
Table 3 Chemical composition of artificial seawater (g/L)
NaCl MgCl2 Na2SO4 CaCl2 KCl NaHCO3 22.16 5.265 3.861 1.082 0.745 0.207 表 4 全珊瑚骨料海水混凝土配合比设计
Table 4 Full coral aggregate seawater concrete mix design
Concrete
typeCement/
(kg·m−3)Coarse aggregate/
(kg·m−3)Fine aggregate/
(kg·m−3)Water consumption/
(kg·m−3)Water reducing
agent/(kg·m−3)28-day cube compressive
strength/MPaCoral concrete 540 560 710 220 7.5 41.2 表 5 FRP筋全珊瑚骨料海水混凝土试件拉拔试验结果
Table 5 Drawing test results of FRP reinforced full coral aggregate seawater concrete specimen
Group
numberSpecimen
numberAverage value
of ultimate
load/kNUltimate load slip amount/mm Average value
of ultimate bond
strength/MPaFailure
modeLa1 BFRP(d8)/C40-2.5d 21.77 2.84 43.32 Pulling-out failure La2 BFRP(d8)/C40-5d 34.68 2.62 34.51 Pulling-out failure La3 BFRP(d8)/C40-7.5d 39.48 2.96 26.19 Pulling-out failure
(one pulling-out-splitting failure)Lb1 BFRP(d10)/C40-2.5d 28.39 3.75 36.16 Pulling-out failure Lb2 BFRP(d10)/C40-5d 44.05 3.51 28.06 Pulling-out failure
(one splitting failure)Lb3 BFRP(d10)/C40-7.5d 45.88 2.03 19.48 Splitting failure Lc1 BFRP(d12)/C40-2.5d 40.12 4.19 35.49 Pulling-out failure
(two splitting failure)Lc3 BFRP(d12)/C40-7.5d 48.93 — 14.43 Splitting failure Ld1 CFRP(d12)/C40-5d 10.48 1.30 4.64 Pulling-out failure Ld2 BFRP(d12)/C40-5d 30.52 1.81 13.50 Pulling-out failure Ld3 GFRP(d12)/C40-5d 29.57 2.03 13.08 Pulling-out failure Le1 BFRP(d12)/C30-5d 49.39 3.86 21.85 Pulling-out failure
(one splitting failure)Le2 BFRP(d12)/C35-5d 61.00 5.00 26.98 Splitting failure
(one pulling-out failure)表 6 FRP筋全珊瑚骨料海水混凝土试件的计算值与试验值对比
Table 6 Comparison of calculated and experimental values of FRP reinforced full coral aggregate seawater concrete specimens
Group number Ptest/kN Pcal/kN Error/% δtest/mm δcal/mm Error/% La1 21.77 21.44 1.53 2.84 2.60 8.51 La2 34.68 33.84 2.42 2.62 2.40 8.32 La3 39.48 38.83 1.64 2.96 2.82 4.61 Lb1 28.39 27.94 1.57 3.75 3.47 7.54 Lb2 44.05 43.49 1.26 3.51 3.20 8.76 Lb3 45.88 43.23 5.77 2.03 1.87 8.12 Lc1 40.12 39.31 2.01 4.19 3.92 6.48 Lc3 57.87 54.67 5.53 – 2.30 – Ld1 10.84 10.64 1.86 1.30 1.20 7.64 Ld2 29.57 28.29 4.32 1.81 1.71 5.34 Ld3 30.52 29.47 3.41 2.03 1.96 3.21 Le1 49.39 46.31 6.23 3.86 3.61 6.52 Le2 55.23 51.30 7.12 5.00 4.76 4.87 Notes: Ptest—Average value of the ultimate load obtained from the test; δtest—Slip value corresponding to the ultimate load obtained in the test; δcal—Slip value corresponding to the ultimate load obtained by numerical simulation. -
[1] 王芳. 新时代海洋强国建设必须走陆海统筹之路[J]. 中国国土资源经济, 2021, 34(2):1. WANG Fang. The construction of a maritime power in the new era must take the road of land and sea coordination[J]. China's Land and Resources Economy,2021,34(2):1(in Chinese).
[2] 廖维晓, 李督. 南海海岛资源开发研究[J]. 潍坊工程职业学院学报, 2020, 33(3):73-76. DOI: 10.3969/j.issn.1009-2080.2020.03.015 LIAO Weixiao, LI Du. Research on the development of south China sea island resources[J]. Journal of Weifang Engineering Vocational College,2020,33(3):73-76(in Chinese). DOI: 10.3969/j.issn.1009-2080.2020.03.015
[3] LYU B, WANG A, ZHANG Z, et al. Coral aggregate concrete: Numerical description of physical, chemical and morphological properties of coral aggregate[J]. Cement and Concrete Composites,2019,100:25-34. DOI: 10.1016/j.cemconcomp.2019.03.016
[4] LI Y L, ZHAO X L, RAMAN R K S. Behavior of seawater and sea sand concrete filled FRP square hollow sections[J]. Thin-Walled Structures,2020,148:20-30.
[5] ZHANG B, ZHU H, SHAH K W, et al. Performance evaluation and microstructure characterization of seawater and coral/sea sand alkali-activated mortars[J]. Construction and Building Materials,2020,259:120403.
[6] SUN Z, ZHANG L, NIU D, et al. Time-varying model for predicting the resistivity of coral aggregate concrete[J]. Construction and Building Materials,2020,265(4):120588. DOI: 10.1016/j.conbuildmat.2020.120588
[7] 洪乃丰. 混凝土中氯盐与钢筋腐蚀的几个相关问题[J]. 工业建筑, 2003(11):39-42. DOI: 10.3321/j.issn:1000-8993.2003.11.011 HONG Naifeng. Several related problems of chloride in concrete and corrosion of steel bars[J]. Industrial Building,2003(11):39-42(in Chinese). DOI: 10.3321/j.issn:1000-8993.2003.11.011
[8] 吴敬宇. 玄武岩纤维复合筋高温性能研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2011. WU Jingyu. Study on high temperature performance of basalt fiber composite reinforcement[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2011(in Chinese).
[9] DONG Z, WU G, XU B, et al. Bond durability of BFRP bars embedded in concrete under seawater conditions and the long-term bond strength prediction[J]. Materials & Design,2016,92:552-562.
[10] 陈爽. 湿热海洋环境下FRP筋-珊瑚混凝土粘结滑移性能研究[D]. 南宁: 广西大学, 2019. CHEN Shuang. Study on the bond-slip performance of FRP bar-coral concrete under humid and hot ocean environment[D]. Nanning: Guangxi University, 2019(in Chinese).
[11] 中国冶金建设协会. 纤维增强复合材料建设工程应用技术规范: GB 50608—2010[S]. 北京: 中国计划出版社, 2010. China Metallurgical Construction Association. Technical specification for fiber-reinforced composite material construction engineering application: GB 50608—2010[S]. Beijing: China Planning Press, 2010(in Chinese).
[12] 胡长顺. 全珊瑚骨料海水混凝土与FRP筋粘结性能试验研究[D]. 徐州: 中国矿业大学, 2020. HU Changshun. Experimental study on the bonding pro-perties of all-coral aggregate seawater concrete and FRP bars[D]. Xuzhou: China University of Mining and Technology, 2020(in Chinese).
[13] YIN S, HU C, LIANG X. Bonding properties of different kinds of FRP bars and steel bars with all-coral aggregate seawater concrete[J]. Journal of Materials in Civil Engi-neering,2020,32(10):04020282. DOI: 10.1061/(ASCE)MT.1943-5533.0003378
[14] 王磊, 吴翔, 曾榕, 等. CFRP筋与珊瑚混凝土的黏结性能试验研究[J]. 中国农村水利水电, 2016(7):127-131. DOI: 10.3969/j.issn.1007-2284.2016.07.031 WANG Lei, WU Xiang, ZENG Rong, et al. Experimental study on the bonding performance of CFRP bars and coral concrete[J]. China Rural Water and Hydropower,2016(7):127-131(in Chinese). DOI: 10.3969/j.issn.1007-2284.2016.07.031
[15] 王磊, 李威, 陈爽, 等. 海水浸泡对FRP筋-珊瑚混凝土粘结性能的影响[J]. 复合材料学报, 2018, 35(12):3458-3465. WANG Lei, LI Wei, CHEN Shuang, et al. The effect of seawater immersion on the bonding properties of FRP tendons and coral concrete[J]. Journal of Composite Materials,2018,35(12):3458-3465(in Chinese).
[16] 杨超, 杨树桐, 戚德海. BFRP筋与珊瑚混凝土粘结性能试验研究[J]. 工程力学, 2018, 35(S1):172-180. DOI: 10.6052/j.issn.1000-4750.2017.06.S034 YANG Chao, YANG Shutong, QI Dehai. Experimental study on the bond performance of BFRP bars and coral concrete[J]. Engineering Mechanics,2018,35(S1):172-180(in Chinese). DOI: 10.6052/j.issn.1000-4750.2017.06.S034
[17] 吴翔. 碳纤维筋与珊瑚混凝土粘结性能试验研究[D]. 桂林: 桂林理工大学, 2016. WU Xiang. Experimental study on the bonding perfor-mance of carbon fiber reinforcement and coral concrete[D]. Guilin: Guilin University of Technology, 2016(in Chinese).
[18] 王召. FRP筋混凝土界面粘结性能的研究[D]. 大连: 大连理工大学, 2015. WANG Zhao. Study on the bonding properties of FRP bars in concrete interface[D]. Dalian: Dalian University of Technology, 2015(in Chinese).
[19] 陈爽. 湿热海洋环境下FRP筋-珊瑚混凝土粘结滑移性能研究[D]. 南宁: 广西大学, 2019. CHEN Shuang. Study on the bond-slip properties of FRP bar-coral concrete in hot and humid marine environment[D]. Nanning: Guangxi University, 2019(in Chinese).
[20] ARNAUD R, PIERRE A, KARIM B, et al. Analytical and numerical modeling of the bond behavior between FRP reinforcing bars and concrete[J]. Construction and Building Materials,2020,231:117160. DOI: 10.1016/j.conbuildmat.2019.117160
[21] ELIGEHAUSEN R, POPOV E P, BERTERO V V. Local bond stress-slip relationships of deformed bars under genera-lized excitations[M]. California: University of California Press, 1982.
[22] COSENZA E, MANFREDI G, REALFONZO R. Analytical modelling of bond between FRP reinforcing bars and concrete[C]//Non-Metallic (FRP) Reinforcement for Concrete Structures Proceedings of the Second International RILEM Symposium. London, 1995: 164-171.
[23] MALVAR L J. Bond stress-slip characteristics of FRP rebar[R]. Naval Facilities Engineering Service Center Port Hueneme CA, 1994.
[24] COSENZA E, MANFREDI G, REALFONZO R. Behavior and modeling of bond of frp rebars to concrete[J]. Journal of Composites for Construction,1997,1(2):40-51. DOI: 10.1061/(ASCE)1090-0268(1997)1:2(40)
[25] 高丹盈, 朱海堂, 谢晶晶. 纤维增强塑料筋混凝土粘结滑移本构模型[J]. 工业建筑, 2003, 33(7):41-43. DOI: 10.3321/j.issn:1000-8993.2003.07.011 GAO Danying, ZHU Haitang, XIE Jingjing. The constitutive model of fiber reinforced plastic bar concrete bond-slip[J]. Industrial Construction,2003,33(7):41-43(in Chinese). DOI: 10.3321/j.issn:1000-8993.2003.07.011
[26] YANG S, YU M, DONG K, et al. Properties of alkali-resistant glass fiber reinforced coral aggregate concrete[J]. Materials,2020,13(16):220-230.
[27] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Design code for concrete structures: GB 50010—2010[S]. Beijing: China Building Industry Press, 2010(in Chinese).
[28] 薛伟辰, 刘华杰, 王小辉. 新型FRP筋粘结性能研究[J]. 建筑结构学报, 2004, 25(2):104-109. DOI: 10.3321/j.issn:1000-6869.2004.02.017 XUE Weichen, LIU Huajie, WANG Xiaohui. Study on the bonding properties of new FRP bars[J]. Journal of Building Structures,2004,25(2):104-109(in Chinese). DOI: 10.3321/j.issn:1000-6869.2004.02.017
-
期刊类型引用(8)
1. 李文龙,黄伟,方圆,张苛,谢巍. 纤维增强聚合物筋混凝土梁力学性能研究进展. 建筑结构. 2025(02): 116-125 .  百度学术
百度学术
2. 张振雷,刘华新,徐佳宁. BFRP筋与再生骨料混凝土粘结性能试验研究. 建筑结构. 2024(10): 100-105 .  百度学术
百度学术
3. 尹世平,李雨珊,刘运超. FRP筋与全珊瑚骨料海水混凝土粘结性能数值模拟. 应用基础与工程科学学报. 2023(01): 210-223 .  百度学术
百度学术
4. 姜天华,万聪聪,颜斌. BFRP筋与钢-PVA混杂ECC粘结性能. 复合材料学报. 2023(06): 3499-3512 .  本站查看
本站查看
5. 毕涵喆,韩天宇,刘年增,郑鹏,聂明月. H型钢柱-钢筋混凝土底梁支护结构柱脚节点力学性能数值分析. 建筑结构. 2023(S1): 1825-1833 .  百度学术
百度学术
6. 陈宇良,刘志华,叶培欢,陈宗平. 高温后珊瑚海水海砂混凝土直剪力学性能及损伤演化. 复合材料学报. 2023(07): 4128-4138 .  本站查看
本站查看
7. 杨树桐,孙忠科,蒋济同,范国玺,董坤,杨天戈. 海洋骨料混凝土材料与结构性能研究进展. 中国海洋大学学报(自然科学版). 2023(10): 11-19 .  百度学术
百度学术
8. 张众,蔡斌. 钢筋与火山渣混凝土粘结滑移性能有限元分析. 吉林建筑大学学报. 2022(03): 25-30 .  百度学术
百度学术
其他类型引用(10)
-




 下载:
下载: