Experiment on seismic performance of prestressed CFRP tendons and rebars-steel reinforced concrete eccentrically tensioned members
-
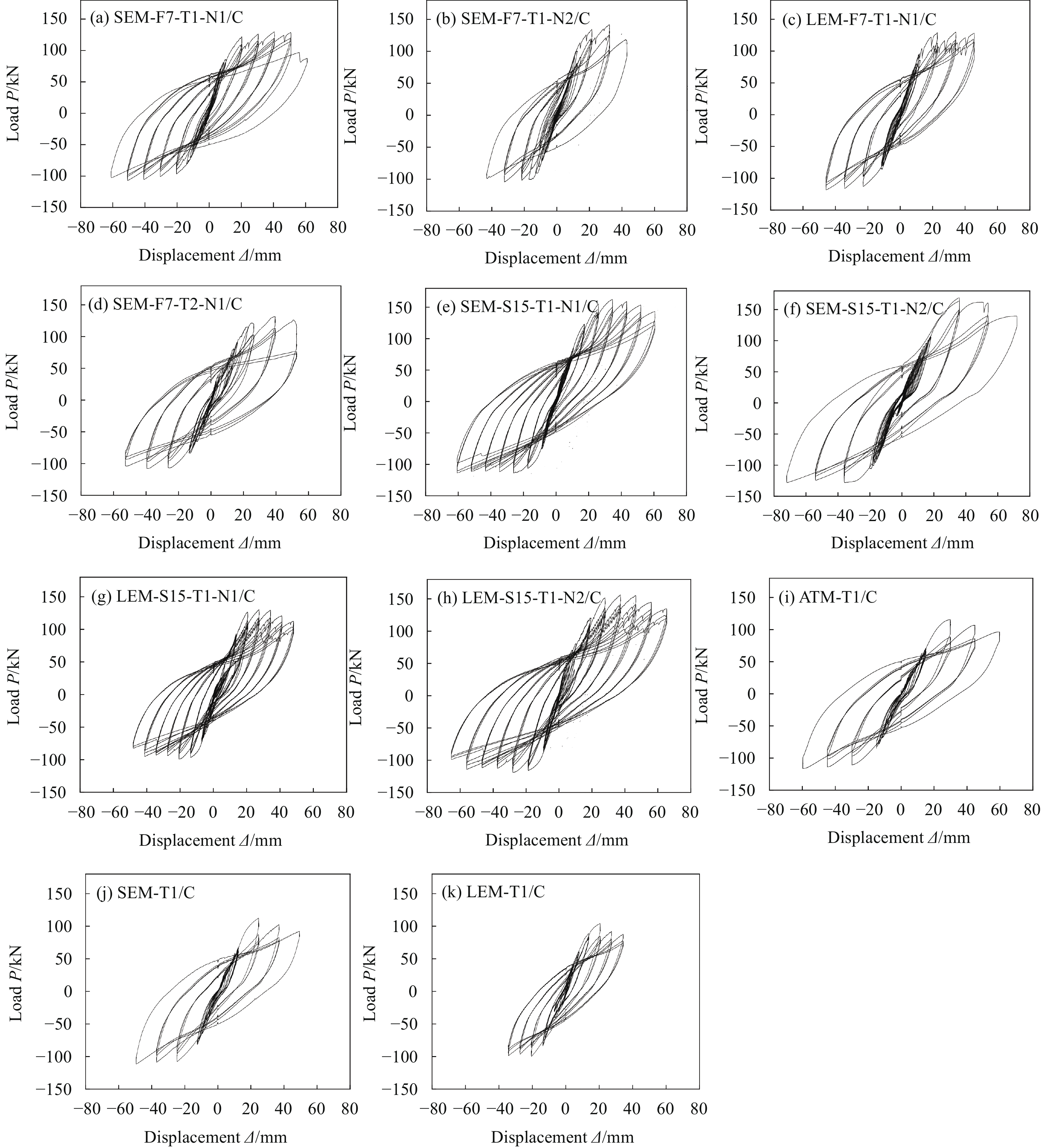
摘要: 为研究预应力碳纤维增强树脂复合材料(CFRP)筋-螺纹钢筋-型钢/混凝土(SRC)偏拉构件的抗震性能，对4根预应力CFRP筋-SRC偏拉构件、4根预应力螺纹钢筋-SRC偏拉构件和3根普通SRC受拉构件进行了低周反复荷载对比试验，试验参数包括偏心距、预应力张拉水平、竖向拉力、预应力筋类型。研究结果表明：所有构件的破坏形态均为弯剪破坏，构件滞回曲线均较饱满，延性较好。随着偏心距的增大，各构件承载力、延性及耗能能力均相应降低；随着预应力张拉水平的增大，构件承载力有一定提高，但耗能能力降低，延性系数先增后降，且增加幅度大于降低幅度；随着竖向拉力的增大，预应力CFRP筋-SRC偏拉构件的承载力、延性及耗能能力均相应降低。相较于普通SRC受拉构件，预应力CFRP筋-SRC偏拉构件具有更好的承载力、刚度、延性和抗裂能力，但耗能能力低；相较于预应力螺纹钢筋-SRC偏拉构件，预应力CFRP筋-SRC偏拉构件的承载力和延性较低，但耗能能力强。Abstract: In order to investigate the seismic performance of prestressed carbon fiber reinforced polymer (CFRP) tendons and rebars-steel reinforced concrete (SRC) eccentrically tensioned member, the low reversed cyclic loading tests of four members of prestressed CFRP tendons-SRC eccentric tension, 4 members of prestressed rebar-SRC eccentric tension and 3 members of ordinary SRC tension were conducted. The test parameters include eccentricity, prestressed tension level, vertical force and the types of prestressed tendon. The results show that the failure modes of all the members are bending shear failure, and the hysteretic curves of all the members are full and the ductility is good. With the increase of eccentricity, the bearing capacity, ductility and energy dissipation capacity of each component decrease accordingly. With the increase of the prestress tensile level, the bearing capacity of the component increases to a certain extent, but the energy dissipation capacity decreases, and the ductility coefficient increases first and then decreases, and the increase range is greater than the decrease range. With the increase of vertical tensile force, the bearing capacity, ductility and energy dissipation capacity of the prestressed CFRP tendons-SRC eccentric tensile member decrease correspondingly. Compared with the ordinary SRC tensile member, the prestressed CFRP tendons-SRC eccentric tensile member has better bearing capacity, stiffness, ductility and crack resistance, but lower energy consumption capacity. Compared with the prestressed rebar-SRC eccentric tensile member, the prestressed CFRP tendons-SRC eccentric tensile member has lower bearing capacity and ductility, but higher energy dissipation capacity.
-
碳化钨颗粒增强钢铁基(WCP/Fe)复合材料因兼顾金属基体的良好韧性与陶瓷增强颗粒的高强度、高硬度、高模量而广泛应用于机械制造、能源开发、交通运输等领域，但基体与增强颗粒间热物理性能差异过大使复合材料在激冷激热环境下服役时产生热应力，诱发界面处裂纹的萌生与扩展[1-4]。而将WC充分溶解，W在熔体中均匀扩散形成合金化复合层能有效解决该问题，故研究WC/Fe复合材料中W扩散均匀性十分必要[5-7]。
蜂窝结构因形状连续、比强度高等特性而对复合材料的综合性能产生重要影响[8-10]。Magotteaux公司发明X-win蜂窝结构ZTAP/Fe复合材料技术，制造的磨辊使用寿命提高两倍以上[11]；WU等[12]从模拟与实验角度出发，揭示预制体孔径与孔距作为蜂窝结构重要参数对复合材料力学性能的影响；SONG等[13]成功制备蜂窝结构还原氧化石墨烯增强环氧树脂(rGH/EP)复合材料，电磁屏蔽效能与导电性明显提升。但对蜂窝预制体结构与元素扩散均匀性间的关联机制仍研究较少。
本文采用真空消失模铸渗(V-EPC)工艺制备WC/Fe复合材料[14-15]，选取孔径孔距比相同孔径不同的蜂窝预制体，并将W质量分数最高与最低的预制体原孔壁与原孔心处W质量分数作为W扩散均匀性的判断条件[16-17]。表征复合层的显微组织、物相组成、元素分布，并检测预制体原孔壁与原孔心处W质量分数、硬度及复合层耐磨性，揭示其孔径对W质量分数分布的影响规律。通过求解非稳态扩散方程得解析解，对预制体孔内熔体凝固时的热物理场进行有限元模拟，并通过二次开发程序对其原孔内W质量分数分布进行数值模拟，揭示其孔径对W扩散均匀性的影响机制；提出W扩散均匀性与复合层耐磨性间的关联机制，为工程应用提供理论依据。
1. 实验材料与方法
为避免铸渗时W粉因粒径过小而大量烧损，选取铸造WC颗粒(WC/W2CP)为合金化提供W；表1为WC/Fe复合材料中预制体的成分组成，配置预制体粉末300 g，与5wt%水玻璃粘结剂均匀混合；表2为WC/Fe复合材料中预制体的结构参数，填充到预制体孔径孔距比相同孔径不同的蜂窝模具内，其轮廓为50 mm×100 mm×6 mm；采用CO2硬化与微波烧结方法，得最终预制体。
表3为WC/Fe复合材料中基体的成分组成。配置基体并采用中频感应炉熔炼20 kg。图1为WC/Fe复合材料的制备过程，采用V-EPC工艺成型，浇注温度为1 500℃，型腔负压为0.05 MPa。
表 1 WC/Fe复合材料中预制体的成分Table 1. Composition of preform in WC/Fe compositesComposition Mass fraction/wt% Size/μm WC 40 150-200 Ni60 30 60-90 FeCr55C6.0 30 150-200 表 2 WC/Fe复合材料中预制体的结构参数Table 2. Structure parameters of preform in WC/Fe compositesDiameter R/mm Distance d/mm Number n 3 6 63 6 12 16 9 18 7 表 3 WC/Fe复合材料中基体的成分Table 3. Composition of matrix in WC/Fe compositesComposition C Cr Mn Si Fe Mass fraction/wt% 1.2-1.3 18.0-20.0 0.4-0.6 1.0-1.2 Balance ![]()
图 1 WC/Fe复合材料的制备过程Figure 1. Preparation process of WC/Fe composites ((a)V-EPC (Vacuum-expendable pattern casting); (b)Honeycomb preform; (c)Transformation between preform and layer)采用尼康MA200型OM表征复合层显微组织，并统计预制体原孔壁与原孔心处平均晶粒尺寸分布。采用岛津7000S/L型XRD、牛津仪器Ultim Extreme型EDS面扫描表征复合层物相组成、元素分布。采用牛津仪器Ultim Extreme型EDS点扫描、上海光学仪器厂HX1000型显微硬度计表征复合层预制体原孔壁与原孔心处元素质量分数、硬度。采用广州试验仪器厂MS-5E型三体磨料磨损机表征复合层耐磨性，载荷为2 kg、转速为40 r/min、预磨时间为30 min、磨粒粒径为200~550 μm，并采用蔡司EVO18型SEM表征预制体原孔心处磨损形貌。采用COMSOL Multiphysics 5.4有限元模拟预制体孔内熔体凝固时的热物理场。采用MATLAB R2015b通过二次开发程序数值模拟预制体原孔内W质量分数分布。
2. 结果与分析
2.1 WC/Fe复合材料复合层的显微组织与元素分布
图2为不同预制体孔径下WC/Fe复合材料复合层的显微组织。熔体填充预制体孔洞，WC高温下分解，W由其孔壁扩散至孔心处，形成复合层。图3为不同预制体孔径下WC/Fe复合材料复合层原孔内的平均晶粒尺寸分布，随预制体孔径增加，其原孔壁处晶粒尺寸基本不变，而在其原孔心处先减小后增大。
![]()
图 3 不同预制体孔径下WC/Fe复合材料复合层原孔内的平均晶粒尺寸分布Figure 3. Average grain size distribution into initial hole of layer in WC/Fe composites with different hole diameters of preform图4为不同预制体孔径下WC/Fe复合材料复合层原孔内的平均晶粒尺寸分布。表明复合层中均形成W2C、WC、Ni17W3、Fe3W3C、(Fe,Cr)3C。根据W-C相图，WC/W2CP中WC分解形成W2C、C，而C扩散到熔体中使(Fe,Cr)3C增多；根据Fe-W-C相图，熔体与W2C发生包晶反应形成Fe3W3C；WC、Ni60分解使W、Ni质量分数增加，形成镍钨化合物Ni17W3。
![]()
图 2 不同预制体孔径下WC/Fe复合材料复合层的显微组织Figure 2. Microstructure of layer in WC/Fe composites with different hole diameters of preform![]()
图 4 不同预制体孔径下WC/Fe复合材料复合层的物相组成Figure 4. Phase composition of layer in WC/Fe composites with different hole diameters of preform根据Fe-Cr-C相图[18-19]，推测熔体(Cr：18.0wt%~20.0wt%，C：1.2wt%~1.3wt%)为典型亚共晶成分合金(Cr：11.0wt%~30.0wt%，C：<2.8wt%)，凝固时先析出一次奥氏体枝晶，待温度降至共晶点发生共晶转变形成共晶奥氏体与二次碳化物的混合共晶组织，而复合层为网状形貌的M3C型碳化物[7,20]。图5为不同预制体孔径下WC/Fe复合材料复合层的元素分布。Cr分布在共晶奥氏体与二次碳化物中，W、Ni弥散分布在一次奥氏体枝晶内。
![]()
图 5 不同预制体孔径下WC/Fe复合材料复合层的元素分布Figure 5. Element distribution of layer in WC/Fe composites with different hole diameters of preform图6为不同预制体孔径下WC/Fe复合材料复合层原孔内的W质量分数分布。其原孔壁处W质量分数较高，而在其原孔心处较低。与晶粒尺寸的变化相反，随预制体孔径增加，其原孔壁处W质量分数基本不变，而在其原孔心处先增大后减小。为进一步表征W扩散均匀性，通过计算得不同预制体孔径下W扩散均匀性分别为84.1%、88.7%、86.9%，表明W扩散均匀性随其孔径增加而先增大后减小，W扩散均匀性的表达式为
![]()
图 6 不同预制体孔径下WC/Fe复合材料复合层原孔内的W质量分数分布Figure 6. W mass fraction distribution into initial hole of layer in WC/Fe composites with different hole diameters of preformδ=1−2√3πR2C(0,tmax (1) 式中：δ为W扩散均匀性；C(0,tmax)、C(R/2,tmax)分别为预制体原孔壁、原孔心处W质量分数。
2.2 WC/Fe复合材料复合层的硬度分布与耐磨性
图7为不同预制体孔径下WC/Fe复合材料复合层原孔内的硬度分布。其原孔壁处硬度较高，而在其原孔心处较低。与W质量分数的变化相同，随预制体孔径增加，其原孔壁处硬度基本不变，而在其原孔心处先增大后减小。图8为不同预制体孔径下WC/Fe复合材料复合层原孔心处的磨损形貌。R=3 mm时其原孔心处犁沟最明显，R=9 mm时次之，R=6 mm时最不明显。图9为不同预制体孔径下WC/Fe复合材料复合层的磨损量。表明复合层耐磨性随其孔径增加而先增大后减小。
![]()
图 7 不同预制体孔径下WC/Fe复合材料复合层原孔内的硬度分布Figure 7. Hardness distribution into initial hole of layer in WC/Fe composites with different hole diameters of preform![]()
图 8 不同预制体孔径下WC/Fe复合材料复合层原孔心处的磨损形貌Figure 8. Wear morphologies at initial hole center of layer in WC/Fe composites with different hole diameters of preform![]()
图 9 不同预制体孔径下WC/Fe复合材料复合层的磨损量Figure 9. Wear amount of layer in WC/Fe composites with different hole diameters of preform2.3 WC/Fe复合材料复合层的W扩散均匀性机制
为进一步探究影响W扩散均匀性的因素，对预制体原孔内W质量分数分布进行数值模拟。将W扩散区看作受固液界面移动驱动的半无限大物体，且扩散时间近似为预制体孔内熔体凝固时间[21-22]。下式为W扩散区边界条件的表达式：
\left\{ \begin{array}{l} C\left( {x,t} \right) = {C_{{\rm{SL}}}},x = x\left( t \right) \\ C\left( {x,t} \right) = {C_{{\rm{LS}}}},x < x\left( t \right) \end{array}\right. (2) 式中，CSL、CLS分别为固液界面固、液相侧W质量分数。根据Arrhenius方程，W质量分数分布为
\left\{ \begin{array}{l} C\left( {x,t} \right) = \dfrac{{{C_{{\rm{SL}}}}}}{{{\rm{erf}}\left( k \right) - 1}}\left( {{\rm{erf}}\left( {\dfrac{x}{{2\sqrt {Dt} }}} \right) + 1} \right) \\ D = {D_0}{\rm{exp}}\left( { - \dfrac{{{E_{\rm{A}}}}}{{{k_{\rm{B}}}T}}} \right) \end{array} \right. (3) 式中：x为W扩散距离；t为W扩散时间；T为W扩散温度；D为W扩散系数；k为常数；EA为W元素扩散激活能；kB为玻尔兹曼常数[22]。W扩散总时间为
{t_{{\rm{max}}}} = \frac{{{R^2}}}{{64{k^2}D}} (4) 通过解析解得W扩散过程同时受温度与固液界面移动影响。故先采用有限元模拟软件COMSOL Multiphysics 5.4模拟预制体孔内熔体凝固时的温度场与相场，表4为预制体孔内熔体凝固时热物理场模拟的参数设置。图10为预制体孔内熔体凝固时热物理场的有限元模拟。发现固液界面明显存在，且其左侧温度较高，熔体为液相，而其右侧温度较低，熔体为固相，即其孔壁处熔体先凝固，且固液界面移动驱动W扩散。此外，随预制体孔径增加，其孔内熔体高温区增多，使其平均温度增高，W扩散系数受W扩散温度影响，扩散温度越高扩散系数越大，其原孔内W质量分数分布曲线斜率绝对值越大；图11为不同预制体孔径下WC/Fe复合材料复合层原孔内W质量分数分布的数值模拟。再将该有限元模拟结果代入数学分析软件MATLAB R2015b的二次开发程序中进行数值模拟，最终得其原孔内W质量分数分布曲线，发现其原孔内W质量分数为W扩散距离的单调递减函数。因预制体孔径孔距比相同且W扩散区为受固液界面移动驱动的半无限大物体，故设置W初始质量分数相同。随预制体孔径增加，其原孔内W质量分数分布曲线斜率绝对值增大，故R=3 mm时其原孔心处W质量分数较R=6 mm时低，但R=6 mm时W扩散距离较R=9 mm时短，故其原孔心处W质量分数R=6 mm时最高，R=9 mm时次之，R=3 mm时最低，即该数值模拟与实验结果相符。
表 4 预制体孔内熔体凝固时热物理场模拟的参数设置Table 4. Parameters setting of thermal physical field simulation when internal matrix of preform solidifiesPhase Density/(kg·m−3) Thermal conductivity/(W·m−1·K−1) Heat capacity/(J·kg−1·K−1) Fe(s) 8 500 200 400 Fe(l) 7 800 450 550 Inlet temperature/°C Melting temperature/°C Temperature transition half width/K Surface emissivity 1 500 1 100 50 0.8 Specific heat/(J·kg−1·K−1) Solidification latent heat/(kJ·kg−1) Heat transfer coefficient/(W·m−2·K−1) 60 200 800 ![]()
图 10 不同预制体孔径下孔内熔体凝固时热物理场的有限元模拟Figure 10. Finite element simulation of thermal physical field when internal matrix solidifies with different hole diameters of preform![]()
图 11 不同预制体孔径下WC/Fe复合材料复合层原孔内W质量分数分布的数值模拟Figure 11. Numerical simulation of W mass fraction distribution in initial hole in WC/Fe composites with different hole diameters of preform预制体孔径较大时，其孔内熔体较多，温度也较高。一方面扩散时间较长，有利于W扩散；另一方面扩散距离较长，不利于W扩散均匀，使预制体原孔心处W质量分数降低。同理，预制体孔径较小时，扩散距离虽短，但扩散时间较短，使W扩散不充分，其原孔心处W质量分数较低，故W扩散均匀性也较低；故预制体孔径适中时，因兼顾扩散距离与扩散时间而使W扩散均匀性最高。综上所述，W扩散过程同时受扩散距离与扩散时间的影响。
2.4 WC/Fe复合材料复合层的耐磨性与W扩散均匀性间关联机制
亚共晶Fe-Cr-C系合金中含大量低硬度、高韧性的一次奥氏体，硬度、耐磨性较低，而W弥散分布在一次奥氏体枝晶内形成M6C型碳化物Fe3W3C，细化晶粒使复合层冲击韧性未明显降低，且引入硬质相使其硬度明显提高[20,23]，一定范围内也提高其耐磨性[24]。W扩散均匀性越高，预制体原孔心处W质量分数越高，形成硬质相越多，硬度也越高，最终提高复合层耐磨性。
3. 结 论
采用真空消失模铸渗(V-EPC)工艺制备WC/Fe复合材料，选取预制体孔径孔距比相同孔径不同的蜂窝预制体，并将其原孔壁与原孔心处W质量分数作为W扩散均匀性的判断条件，得如下结论。
(1) WC高温下分解，W由预制体孔壁至孔心处扩散，形成弥散分布的硬质相Fe3W3C。
(2)预制体原孔壁与原孔心处W质量分数与硬度相差随孔径增加而先增大后减小，复合层耐磨性的变化亦然。
(3) W扩散均匀性同时受扩散距离与扩散时间的影响。预制体孔径较小时，扩散距离虽短，但扩散时间较短，不利于W扩散；预制体孔径较大时，扩散时间虽长，但扩散距离增长，仍不利于W扩散；预制体孔径适中时，因兼顾扩散距离与扩散时间，利于W扩散。
(4)耐磨性与W扩散均匀性间存在关联，W扩散均匀性越高，预制体原孔心处W质量分数越高，形成硬质相越多，硬度也越高，一定范围内复合层耐磨性也越高。
-
![]()
图 1 预应力碳纤维增强树脂复合材料(CFRP)筋-螺纹钢筋-型钢/混凝土试件几何尺寸及配筋图
Figure 1. Geometry size and reinforcing bars of prestressed carbon fiber reinforced polymer (CFRP) tendons and rebars-steel reinforced concrete specimens
![]()
图 2 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件加载端头示意图
Figure 2. Schematic diagram of loading end of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
![]()
图 5 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件测点布置
Figure 5. Measuring points layout of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
![]()
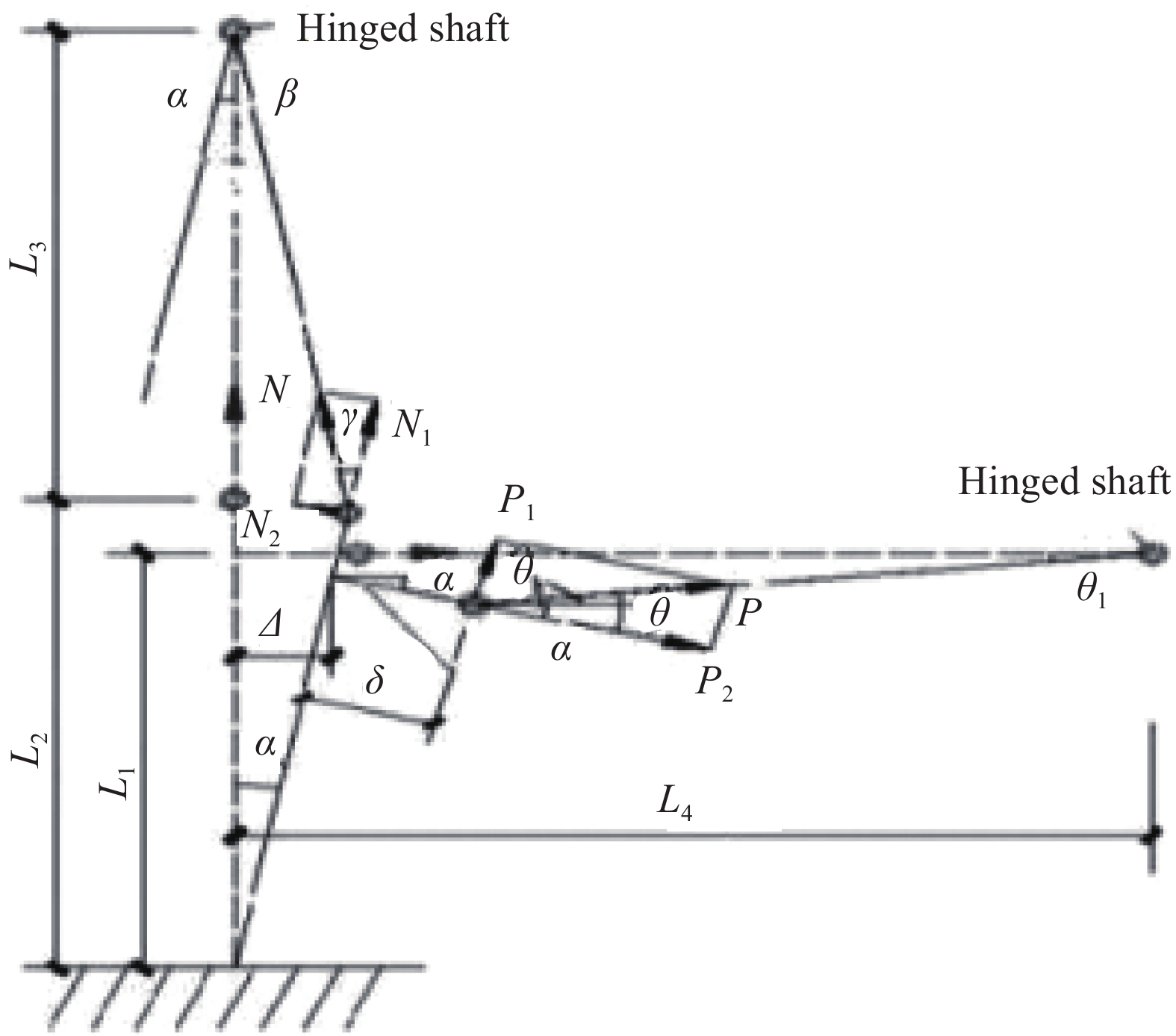
图 6 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件变形下受力示意图
Figure 6. Force schematic of prestressed CFRP tendons and rebars-steel reinforced concrete specimens under deformation
L1—Distance from the point of horizontal force to the bottom of the component; L2—Distance from the point of vertical force to the bottom of the specimen; L3—Distance between the point of vertical force operation and the vertical hinge shaft; L4—Distance from the specimen axis to the horizontal hinge axis; P—Actual horizontal tension; P1—Component of horizontal force perpendicular to the direction of the specimen; P2—Component of the horizontal force along the direction of the specimen; N—Actual vertical tension; N1—Component of vertical tension along the direction of the specimen; N2—Component of the vertical tension perpendicular to the direction of the specimen; θ1—Deviation angle between the horizontal hinge axis and the horizontal plane; α—Rotation angle between axis and vertical direction; β—Deflection angle between the direction of vertical tension and the vertical direction; δ—Distance between the point of horizontal force and the specimen axis; Δ—Horizontal displacement at the point of horizontal force
![]()
图 7 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件破坏形态
Figure 7. Failure patterns of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
![]()
图 8 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件滞回曲线
Figure 8. Hysteretic loops of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
![]()
图 9 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件骨架曲线
Figure 9. Skeleton curves of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
![]()
图 10 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件刚度退化曲线
Figure 10. Stiffness degradation curves of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
表 1 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件主要设计参数
Table 1 Main design parameters of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
Specimen e/mm Lp/% T
/kNType of prestressed tendon SEM-F7-T1-N1/C 50 40 30 CFRP SEM-F7-T1-N2/C 50 60 30 CFRP LEM-F7-T1-N1/C 150 40 30 CFRP SEM-F7-T2-N1/C 50 40 50 CFRP SEM-S15-T1-N1/C 50 40 30 Rebar SEM-S15-T1-N2/C 50 60 30 Rebar LEM-S15-T1-N1/C 150 40 30 Rebar LEM-S15-T1-N2/C 150 60 30 Rebar ATM-T1/C 0 0 30 － SEM-T1/C 50 0 30 － LEM-T1/C 150 0 30 － Notes: ATM—Axial tension member; SEM—Small eccentric member; LEM—Large eccentric member; F7—CFRP tendons; S15—Finely-rolled threaded bars; T1 and T2—Eccentric tension of the specimens, which are 30kN and 50kN; N1 and N2—Tensioning level of the prestressed tendons, which are 40%fptk and 60%fptk; C—C40 concrete; e—Eccentricity; Lp—Prestressed tension level; T—Vertical pull. 
下载: 导出CSV
表 2 钢材力学性能指标
Table 2 Mechanical properties of steel
Type Yield
strength/MPaUltimate
strength/MPaModulus of
elasticity/105MPaSteel Q235 312.5 447.5 2.0 Q345 395.6 556.6 2.0 Grade HRB400 reinforced C6 492 608 2.1 C10 475 690 2.1 C12 438 618 2.0
下载: 导出CSV
表 3 预应力筋力学性能指标
Table 3 Mechanical properties of prestressed tendons
Type Diameter
/mmUltimate
strength/MPaModulus of
elasticity/105MPaCFRP 7 1 910 1.54 Rebar 15 1026 2.10
下载: 导出CSV
表 4 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件主要实验结果
Table 4 Main experimental results of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
Specimen Loading direction Cracking point
Pcr/kNYield point Peak point Ultimate point μ Py/kN Δy/mm Pm/kN Δm/mm Pu/kN Δu/mm SEM-F7-T1-N1/C + 24.2 85.4 10.17 128.1 40.72 84.1 61.08 5.43 − 12.1 75.3 12.56 104.2 40.70 99.0 61.05 SEM-F7-T1-N2/C + 32.1 100.2 12.19 141.1 32.31 116.3 43.07 3.77 − 10.2 80.3 10.76 104.1 32.30 88.2 43.10 LEM-F7-T1-N1/C + 18.1 85.6 12.08 118.2 34.36 104.2 57.24 4.87 − 14.0 85.2 11.44 110.1 34.35 100.0 57.21 SEM-F7-T2-N1/C + 21.1 84.0 12.12 116.0 39.48 98.1 65.81 3.99 − 18.1 74.1 13.16 104.1 39.52 88.5 65.72 SEM-S15-T1-N1/C + 26.2 84.0 10.53 155.7 34.66 137.7 60.65 6.38 − 13.8 75.2 8.66 110.0 34.65 106.1 60.63 SEM-S15-T1-N2/C + 30.0 105.3 18.01 161.1 54.01 134.1 72.05 3.99 − 12.1 100.3 18.14 121.6 54.06 110.2 72.06 LEM-S15-T1-N1/C + 23.0 91.9 13.74 130.4 29.13 108.1 48.17 5.76 − 15.1 66.0 6.02 114.4 29.10 96.8 48.19 LEM-S15-T1-N2/C + 26.1 120.2 28.88 154.1 39.27 132.1 65.42 3.63 − 13.7 80.0 13.09 110.3 39.26 94.3 65.42 ATM-T1/C + 8.8 70.4 12.1 110.3 36.30 93.0 60.50 4.94 − 10.0 80.0 12.4 106.9 36.28 90.9 60.52 SEM-T1/C + 4.27 65.9 12.34 103.3 24.69 87.1 49.38 4.21 − 12.10 73.0 11.16 100.1 24.70 86.1 49.38 LEM-T1/C + 2.01 48.1 6.85 96.2 20.56 82.3 34.28 3.89 − 13.23 70.0 12.36 93.71 20.60 80.9 34.25 Notes: Pcr —Specimen cracking load; Py—Yield load at the end of specimen; Δy—Specimen yield displacement; Pm—Peak load; Δm—Displacement when the specimen reached peak load; Pu—Ultimate load of the specimen at failure; Δu—Displacement when the specimen reached ultimate load; µ−Ductility factor which is the ratio of Δu to Δy and the ductility factor is the average of the positive and negative values.
下载: 导出CSV
表 5 预应力CFRP筋-螺纹钢筋-型钢/混凝土试件等效粘滞阻尼系数
Table 5 Equivalent viscous damping coefficients of prestressed CFRP tendons and rebars-steel reinforced concrete specimens
Specimen hey hem heu SEM-F7-T1-N1/C 0.056 0.191 0.265 SEM-F7-T1-N2/C 0.043 0.188 0.229 LEM-F7-T1-N1/C 0.052 0.183 0.239 SEM-F7-T2-N1/C 0.049 0.189 0.240 SEM-S15-T1-N1/C 0.067 0.173 0.255 SEM-S15-T1-N2/C 0.045 0.162 0.215 LEM-S15-T1-N1/C 0.059 0.167 0.232 LEM-S15-T1-N2/C 0.031 0.154 0.207 ATM-T1/C 0.063 0.228 0.295 SEM-T1/C 0.061 0.166 0.282 LEM-T1/C 0.060 0.156 0.247 Notes: hey—Equivalent damping coefficient of yield point; hem—Equivalent damping coefficient of peak point; heu—Equivalent damping coefficient of ultimate point.
下载: 导出CSV
-
[1] 张书强, 苏小卒. 预应力型钢混凝土结构抗震性能研究综述[J]. 江西科学, 2013, 31(1):63-66, 89. DOI: 10.3969/j.issn.1001-3679.2013.01.017 ZHANG Shuqiang, SU Xiaozu. A review on seismic performance of prestressed steel reinforced concrete structures[J]. Jiangxi Science,2013,31(1):63-66, 89(in Chinese). DOI: 10.3969/j.issn.1001-3679.2013.01.017
[2] 熊学玉, 高峰, 徐晓明. 预应力型钢混凝土结构理论研究[J]. 工业建筑, 2012, 42(4):113-117. XIONG Xueyu, GAO Feng, XU Xiaoming. Theoretical research on prestressed steel concrete structure[J]. Industrial Building,2012,42(4):113-117(in Chinese).
[3] 董石麟, 邢栋, 赵阳. 现代大跨空间结构在中国的应用与发展[J]. 空间结构, 2012, 18(1):3-16. DONG Shilin, XING Dong, ZHAO Yang. Application and development of modern large-span spatial structure in China[J]. Spatial Structure,2012,18(1):3-16(in Chinese).
[4] 尹世平, 华云涛, 徐世烺. FRP配筋混凝土结构研究进展及其应用[J]. 建筑结构学报, 2021, 42(1):134-150. YIN Shiping, HUA Yuntao, XU Shilang. Research progress and application of FRP reinforced concrete structures[J]. Journal of Building Structures,2021,42(1):134-150(in Chinese).
[5] SELVACHANDRAN P, ANANDAKUMAR A, MUTHURAMU K L. Modified frosch crack width model for concrete beams prestressed with CFRP bars[J]. Polymers and Polymer Composites,2016,24(7):587-596. DOI: 10.1177/096739111602400719
[6] CAO Qi, ZHOU Jianpu, WU Zhimin, et al. Flexural behavior of prestressed CFRP reinforced concrete beams by two different tensioning methods[J]. Engineering Structures,2019,189:411-422.
[7] 程东辉, 郑文忠. 无粘结CFRP筋部分预应力混凝土连续梁试验与分析[J]. 复合材料学报, 2008(5):104-113. DOI: 10.3321/j.issn:1000-3851.2008.05.018 CHENG Donghui, ZHENG Wenzhong. Test and analysis of unbonded CFRP bars partially prestressed concrete continuous beams[J]. Acta Materiae Compositae Sinica,2008(5):104-113(in Chinese). DOI: 10.3321/j.issn:1000-3851.2008.05.018
[8] UY B, CRAINE S. Static flexural behaviour of externally post-tensioned steel-concrete composite beams[J]. Advances in Structural Engineering,2004,7(1):1-20. DOI: 10.1260/136943304322985729
[9] 王琨, 智海祥, 曹大富, 等. 预应力型钢混凝土梁-钢管混凝土叠合柱框架节点抗震性能试验研究[J]. 建筑结构学报, 2018, 39(12):29-38. WANG Kun, ZHI Haixiang, CAO Dafu, et al. Experimental study on seismic performance of prestressed steel-concrete beam and concrete-filled steel T-ubular composite column frame joints[J]. Journal of Building Structures,2018,39(12):29-38(in Chinese).
[10] 李世平. 考虑核心约束的大尺度预应力H型钢—混凝土组合梁受力性能研究[D]. 哈尔滨: 东北林业大学, 2019. LI Shiping. Study on mechanical behavior of large-scale prestressed H-beam with core constrains[D]. Harbin: Northeast Forestry University, 2019(in Chinese).
[11] 邓宇, 武晓彤, 张鹏. 预应力型钢混凝土柱偏心受拉性能试验研究[J]. 建筑结构学报, 2019, 40(5):115-123. DENG Yu, WU Xiaotong, ZHANG Peng. Experimental study on eccentric tensile behavior of prestressed SRC columds[J]. Journal of Building Structure,2019,40(5):115-123(in Chinese).
[12] 郑文忠, 王琨. 型钢混凝土梁-角钢混凝土柱框架抗震性能试验研究[J]. 土木工程学报, 2011, 44(3):49-60. ZHENG Wenzhong, WANG Kun. Experimental study on seismic performance of shaped steel concrete beam-angle steel concrete column frame[J]. Chinese Journal of Civil Engineering,2011,44(3):49-60(in Chinese).
[13] 杨勇, 薛亦聪, 于云龙. 部分预制装配型钢混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2019, 40(8):42-50. YANG Yong, XUE Yicong, YU Yunlong. Experimental study on seismic performance of partially precast steel concrete columns[J]. Journal of Building Structures,2019,40(8):42-50(in Chinese).
[14] 薛建阳, 马辉. 低周反复荷载下型钢再生混凝土短柱抗震性能试验研究[J]. 工程力学, 2013, 30(12):123-131. DOI: 10.6052/j.issn.1000-4750.2012.08.0571 XUE Jianyang, MA Hui. Experimental study on seismic performance of shaped steel recycled concrete short columned under low cyclic repeated load[J]. Engineering Mechanics,2013,30(12):123-131(in Chinese). DOI: 10.6052/j.issn.1000-4750.2012.08.0571
[15] 陈小刚, 牟在根, 张举兵. 型钢混凝土柱抗震性能实验研究[J]. 北京科技大学学报, 2009, 31(12):1516-1524. DOI: 10.3321/j.issn:1001-053X.2009.12.006 CHEN Xiaogang, MOU Zaigen, ZHANG Jubing. Experimental study on seismic performance of steel reinforced concrete columns[J]. Journal of University of Science and Technology Beijing,2009,31(12):1516-1524(in Chinese). DOI: 10.3321/j.issn:1001-053X.2009.12.006
[16] 李俊华, 王新堂, 薛建阳. 低周反复荷载下型钢高强混凝土柱受力性能试验研究[J]. 土木工程学报, 2007(7):11-18. DOI: 10.3321/j.issn:1000-131x.2007.07.003 LI Junhua, WANG Xintang, XUE Jianyang. Experimental study on mechanical behavior of steel high-strength concrete column under low cyclic cyclic load[J]. China Civil Engineering Journal,2007(7):11-18(in Chinese). DOI: 10.3321/j.issn:1000-131x.2007.07.003
[17] 高峰, 熊学玉. 预应力型钢混凝土框架结构竖向反复荷载作用下抗震性能试验研究[J]. 建筑结构学报, 2013, 34(7):62-71. GAO Feng, XIONG Xueyu. Experimental study on seismic performance of prestressed SRC frame structures under vertical repeated loading[J]. Journal of Building Structures,2013,34(7):62-71(in Chinese).
[18] 金怀印, 薛伟辰, 杨晓, 等. 预应力型钢混凝土梁-钢管混凝土柱节点抗震性能试验研究[J]. 建筑结构学报, 2012, 33(8):66-74. JIN Huaiyin, XUE Weichen, YANG Xiao, et al. Experimental study on seismic performance of prestressed steel-concrete beam and concrete-filled steel tubular column joints[J]. Journal of Building Structures,2012,33(8):66-74(in Chinese).
[19] 傅传国, 李玉莹, 孙晓波, 等. 预应力及非预应力型钢混凝土框架受力及抗震性能试验研究[J]. 建筑结构学报, 2010, 31(8):15-21. FU Chuanguo, LI Yuying, SUN Xiaobo, et al. Experimental study on stress and seismic performance of prestressed and unprestressed steel concrete frame[J]. Journal of Building Structures,2010,31(8):15-21(in Chinese).
[20] 中华人民共和国住房和城乡建设部. 混凝土结构试验方法标准: GB/T 50152—2012[S]. 北京: 中国建筑工业出版社, 2012. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for test method of concrete structures: GB/T 50152—2012[S]. Beijing: China Architecture and Building Press, 2012(in Chinese).
-
期刊类型引用(0)
其他类型引用(1)
-
计量
- 文章访问数: 895
- HTML全文浏览量: 514
- PDF下载量: 73
- 被引次数: 1
