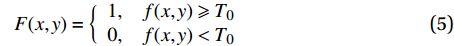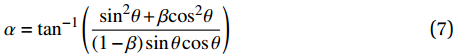In-plane permeability characterization of fiber fabric based on digital image technology
-
摘要: 材料渗透率的表征受其结构空间离散性和求解方式准确性的严重影响。基于数字图像技术，评估了纤维织物渗透率的空间分布，并探讨了阶梯铺层对灌注工艺的影响。首先，从恒压单向注射实验的视频流中动态提取了流动前沿的流速分布和流动前沿角，通过织物渗透率与结构的关系仅一次实验便可求得纤维织物的面内局部渗透率分布；其次，利用正态分布函数拟合，建立了基于数字图像技术的纤维织物面内主方向渗透率张量的求解方法，并利用该方法研究了编织形式对渗透率的影响；最后，研究了阶梯铺层和恒定铺层对灌注过程的影响。结果表明：建立的基于数字图像技术的渗透率表征方法可以通过一次实验同时获取面内主方向上的渗透率及其空间离散型；在恒定铺层下缎纹织物渗透率随着纤维层数增大而增大，从厚铺层向薄铺层的灌注方式可以达到最优的灌注时间。Abstract: The spatial discretization of the structure and the method’s accuracy have profoundly affected the characterization of material permeability. The spatial distribution of fabrics’ permeability was evaluated based on digital image technology, and the effect of step layup sequence on the infusion process was discussed. Firstly, the flow velocity distribution and the flow front angle of the flow front were dynamically extracted from the video stream of the constant pressure unidirectional injection experiments. The in-plane local permeability distribution of the fiber fabric can be obtained through only an experiment by the relationship between fabric permeability and structure. Secondly, solving method of the permeability tensor in the main direction of the fiber fabric based on digital image technology was established by fitting the normal distribution function and was used to study the influence of the weaving form on the permeability. Finally, the step layup sequence and constant layup sequence on the infusion process were studied. The results show that the in-plane permeability characterization method established based on digital image technology could simultaneously obtain the permeability in the main direction of the plane and its spatial discretization through only one experiment. The permeability of satin fabric increases with the increase of the number of fiber layers. The infusion method from thicker region to the thin region can achieve the optimal infusion time.
-
Keywords:
- vacuum infusion /
- fiber fabric /
- permeability /
- flow front /
- digital image technology
-
液体模塑成型工艺(Liquid composite molding，LCM)具有可重复性好、制备周期短、制作复杂构件成本相对较低等优势，被广泛应用于航空航天、汽车、风电叶片、船舶等领域[1-3]。渗透率作为LCM工艺中衡量树脂在纤维织物流动的难易程度，其值越小，表明树脂流动所受到的阻力越大，浸润纤维织物越困难。因此，通过对纤维织物渗透率的求解与分析，结合数值仿真技术，可以预测充模时间，优化工艺参数，对大型复杂构件的成型工艺设计提供指导，从而降低传统“试错法”带来的经济成本。因此，纤维织物渗透率的研究尤为重要[4-5]。
目前常用的渗透率测试方法包括径向法和单向法[6]。径向法的优势在于可避免边缘效应对渗透率的干扰，但流体浸润纤维时流动前沿形状复杂，难以精确分析面内渗透率；而单向法的优势在于一次实验只用考虑一个方向的流动状况，重现性好，然而一次实验仅能获取一个方向的渗透率。国内外针对这两种方法做了大量研究，但由于测试过程中采用的模具及流体等差异，导致织物渗透率的测试结果偏差大，不利于对纤维织物渗透率的表征。因此，众多科研机构采用相同的材料与测试手段进行实验，评估了渗透率测试结果的差异性，致力于建立渗透率测试的标准[7-8]。
除了以上两种传统方法，Demaria C等[9]利用单向法测出织物0°、45°、90°三个方向的渗透率，用迭代法求解织物面内主方向的渗透率及其各向异性程度。Fauster E等[10]通过建立三维空间坐标系，将采集到的二维流动前沿与时间构建椭圆抛物面，用平面去截取抛物面求解出不同方向上的面内渗透率。
渗透率一般是通过获取流动前沿的位置和时间参数，经过线性拟合求解。常见的参数获取方式是记录流体流至等间距位置处的时间，但该方法可采集的数据点有限，无法分析由于材料离散性导致的渗透率局部突变，而其突变可能导致流动前锋交汇、出现空气被包裹的情况，导致构件产生制造缺陷，即空隙[11-12]。Pierce R S等[13]探索了图像技术在径向法渗透率测试中的应用，并求解了织物的面内渗透率，然而未对纤维织物的局部渗透率进行求解。Cosson B等[14]采用光学方法将纤维的局部区域灰度图转化为面积权重图，以此确定纤维孔隙分布，表明了采用数字图像技术评价材料空间离散型的可能性。纤维织物的多尺度结构特征导致流体浸润纤维的过程难以监测，为了能获取材料的空间离散型，也需要可靠的高通量方法对其进行监测和调控。
在真空灌注工艺中，纤维织物层数的改变会影响纤维厚度及预成型体的孔隙率，进而影响织物的渗透率。耿奕等[15]通过研究经编四轴向织物不同层数的渗透率，发现低铺层数下织物的渗透率随着纤维层数增加而增加。方良超[16]通过研究无卷曲(NCF)织物的压缩性能，发现随着纤维层数增加，纤维出现层间嵌套，平均单层厚度减少，纤维体积分数增加，渗透率减小。而Pearce N等[17]通过研究平纹织物的压缩性能得到相反结论，由于纤维层间和纤维-模具间受力状态不同，抑制了纤维织物的层间嵌套，纤维织物的平均单层厚度随层数增加而增加。然而，梯度铺层预成型体铺层变化区域的变异性影响尚未见报道。在使用真空灌注工艺生产构件时，从不同厚度铺层区域间进行灌注十分常见，因此，本文通过阶梯铺层改变纤维层数，研究其过程中渗透率的变化情况。
在面内渗透率测试过程中，常用传感器、光纤、导线[18]等方式监测流体流动，但由于监测材料与纤维会有一定接触，通常会对流动前沿的获取有所影响，故应采用非侵入式的方法对流动前沿进行监测，降低监测装置带来的干扰，使数据更加准确可靠。另外，虽然传统的单向法具有重现性好的优势，但通常需要测面内三个不同方向上的渗透率才可求解出织物面内主方向上的渗透率，测试次数较多。因此，本文利用数字图像技术对流动前沿进行监测，通过一次单向法实验即可求解出织物面内主方向上的渗透率。
本文在传统单向法的基础上提出面内渗透率的联动测试方法，基于数字图像技术对流动前沿的监测，实现了面内渗透率分布的精确评估。其次，建立了纤维织物面内主方向渗透率的测试方法，并研究了纤维编织形式对渗透率的影响。最后，通过改变纤维织物的铺层方式，研究了阶梯铺层和恒定铺层对灌注工艺的影响。
1. 理论基础
在LCM工艺中，流体浸润纤维织物可视为流体在多孔介质中的层流流动，故其流动行为可用达西定律来描述：
v=−Kμ∇P (1) 式中：v为平均体积速度(m/s)；
∇ P为压力梯度(Pa/m)；μ为流体黏度(Pa·s)；K为预成形体织物渗透率(m2)。假设在一维流动中沿灌注方向的压力差ΔP为定值，通过式(1)可得到微分表达式：
dxdt=−KΔPμφx (2) 通过对式(2)在充分小的时间区间[t1, t2]上积分，便近似得到局部区域内的瞬态渗透率解析方程，其渗透率表达式为
K=μφ2ΔPx22−x21t2−t1 (3) 式中：ΔP为流动方向上的压力差(Pa)；x1、x2分别为t1、t2时刻对应流动前沿的位置(m)。
根据式(3)可研究纤维织物空间离散性导致的渗透率分布。纤维织物的孔隙率
φ 可表示为φ=1−Vf=1−nρahρf (4) 式中：n为纤维织物的层数；h为纤维织物的总厚度(m)；Vf为纤维织物的纤维体积分数；ρa为纤维织物的面密度(kg/m2)；ρf为纤维织物的体密度(kg/m3)。
2. 实验部分
2.1 原材料及设备
实验材料：采用乙烯基树脂(颜色呈淡黄色，便于对已浸润部分与未浸润部分的区分)和4种不同编织形式的玻璃纤维织物，如图1所示。相关参数见表1。上模具选用柔性真空袋，下模具选用透明玻璃板。其他辅材有导流网、吸胶毡、空压软管。
表 1 实验材料的相关参数Table 1. Related parameters of experimental materialsMaterial Type Areal weight/(g·m−2) Density/(kg·m−3) Vinyl resin ATLAC 430 LV − 1100 Satin fabric − 220 2550 Twill fabric 2/2 Twill 327 2550 Biaxial fabric EKB450 455 2550 Biaxial fabric EKB424 424 2550 实验设备：2XZ-2型真空泵，浙江台州有限公司；DV2T黏度计，美国BROOKFIELD博勒飞公司；摄像机(帧速：60帧/s)。
2.2 实验方法
所述实验均采用恒压真空灌注的方式，真空压力为9.2×104 Pa，注射方式与传统单向法一致，通过测出流动方向上的流动前沿角和渗透率，求解出织物主方向上的渗透率。将纤维织物沿经纬45°方向裁剪成400 mm×100 mm大小的试样，层数为2层。如图2所示，流体从右侧注入，在织物与注胶管间铺设导流网，保证灌注方式为线注入，并将纤维另一侧与吸胶毡搭接，用来保证抽气的稳定性。在实验装置正上方放置摄像机来采集流动前沿的位置数据。
阶梯铺层实验：选用缎纹织物(Satin fabric，SF)为研究对象，分别铺设2、3、4、5层纤维织物进行0°方向单向渗透率测试；然后采取阶梯铺层方式进行渗透率测试，研究纤维织物阶梯铺层对灌注工艺的影响。图3为纤维织物阶梯铺层示意图，纤维织物的层数从入口向出口由5层等间距逐层递减至2层，间距为100 mm，与均一铺层下的树脂流动行为进行对比。
2.3 基于数字图像技术的全局与局部渗透率提取
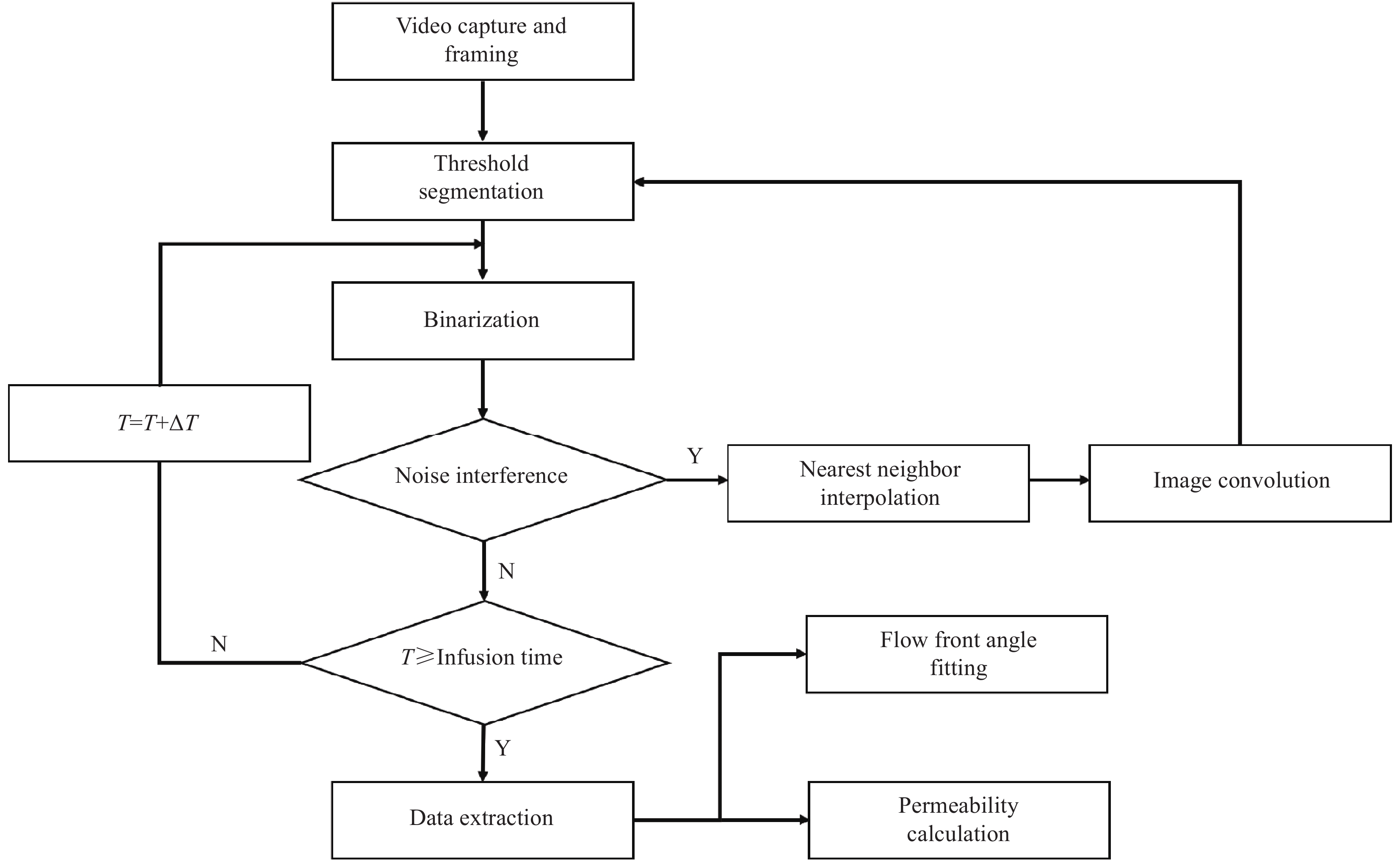
图4为构建的基于数字图像技术的渗透率计算流程。首先，用MATLAB自编程序对实验采集的流动前沿视频流按等时间间隔进行动态提取，并对目标矩形区域(纤维织物的占有位置Ω：400 mm×100 mm)进行畸形矫正，去除非纤维织物区域。然后，将彩色图图像转化为灰度值介于0~255之间的灰度图，便于流动前沿的提取。其中，已浸润区域和未浸润区域在灰度上的差别可导致其灰度直方图呈现出双峰分布[19]。最后，将灰度直方图中波谷处的灰度值设定为初始阈值T0，对图像进行阈值分割。
然后，利用下式所示的阶跃函数将灰度图转化成二值化图像，将原始像素矩阵转化0或1分布的二值化矩阵[M×N]，M、N分别对应模腔400 mm、100 mm方向的像素点长度：
F(x,y)={1,f(x,y)⩾ (5) 式中：(x, y)为像素点位置坐标，1≤x≤N，1≤y≤M；f (x, y)为输入图像；F (x, y)为输出图像；T0为阈值分割特征值。
由于纤维织物局部区域会因光线变化等原因使二值化图像出现紊乱的噪点，直接进行图像二值化处理会对流动前沿的数据提取产生干扰导致误差。因此，采用迭代法对二值化图像进行最近邻域卷积处理[20]，从而精确实现已浸润区域与未浸润区域的分割和流动前沿的识别。具体的卷积操作是：计算二值化矩阵中任意元素与其邻域8个元素的均值，若其均值小于0.5，则该元素值确定为0，反之确定为1，从而实现像素值的再次变换，降低了噪点的权重。
最后，对识别的流动前沿数据进行提取并计算渗透率。通过计算已浸润区域长度相对于初始标定的模腔长度的比例求解出流动前沿的位置，故模腔中不同位置处的流动前沿f可表示为
f = L \times \left(1 - \frac{s}{M}\right) (6) 式中：L为标定模腔长度(m)；s为二值化矩阵各列向量元素之和；M为二值化矩阵总行数。
根据时间线循环遍历视频流图片，若部分图片帧处理后仍存在局部干扰点，则调整阈值再次重复上述操作，直至所有图片已浸润区域和未浸润区域被完全区分。最终获取不同时刻的流动前沿，通过式(3)的差值运算得到全场域的局部渗透率及其分布，并根据正态分布拟合求解出全局渗透率。
3. 结果与分析
3.1 纤维织物流动前沿角
如图5所示，在单向法测渗透率实验中，当灌注方向与纤维织物的主方向不同时，会导致瞬态压力梯度与速度梯度不平行，从而导致流动前沿角α小于90°，其中流动前沿角的余角δ可定义为流动拟合角，用于对后续数据的拟合分析。对于各向异性材料而言，流动前沿会在径向法测渗透率实验中呈现出椭圆状，且织物面内渗透率主方向会与编织经向方向呈现夹角θ，称为纤维织物渗透率的各向异性角。α与θ有以下关系[21]：
![]()
图 5 纤维织物流动前沿示意图Figure 5. Schematic diagram of the flow front of fiber fabricα—Flow front angle; δ—Complementary angle of the flow front angle; \nabla P—Pressure gradient\alpha = {\tan ^{ - 1}}\left( {\frac{{{{\sin }^2}\theta + \beta {{\cos }^2}\theta }}{{\left( {1 - \beta } \right)\sin \theta \cos \theta }}} \right) (7) 式中：K2、K1分别为流体浸润纤维织物最慢与最快方向上的渗透率(m2)；α为流体流动方向与流动前沿的夹角；θ为纤维织物渗透率的各向异性角；β为各向异性程度，β=K2/K1。
以SF在572 s时刻对应的图片为例具体分析流动过程。图6(a)为该时刻下的灰度直方图，横坐标为图片的像素值，纵坐标为像素值的统计次数，波谷出现在140~180范围内，将其区域中值160设定为初始阈值。经过阈值分割、迭代优化等图像处理操作，对所有图片循环遍历后，确定阈值为168时，所有图片已浸润区域和未浸润区域被完全区分。
![]()
图 6 缎纹织物(SF)在572 s时刻对应的灰度直方图 (a) 和流动前沿拟合图 (b)Figure 6. Gray histogram (a) and fitting of flow front (b) of satin fabric (SF) at time 572 s图6(b)为SF在572 s时刻的流动前沿拟合图。流体浸润纤维的状况与纤维结构、铺设工艺有关，不同位置处的流动前沿不同，通过不同位置相对于标定尺寸(0.4 m)的比例计算出对应的流动前沿。通过线性拟合得到线性回归方程为：y=0.0851x+0.2062。对直线斜率求反正切值得到流动前沿拟合角为4.87°，流动前沿角和拟合角互余，故将该时刻的流动前沿角确定为85.13°。
图7为SF部分时刻所呈现的实验流动前沿位置及其数据结果提取图，经优化后的图像满足渗透率计算的需求。
![]()
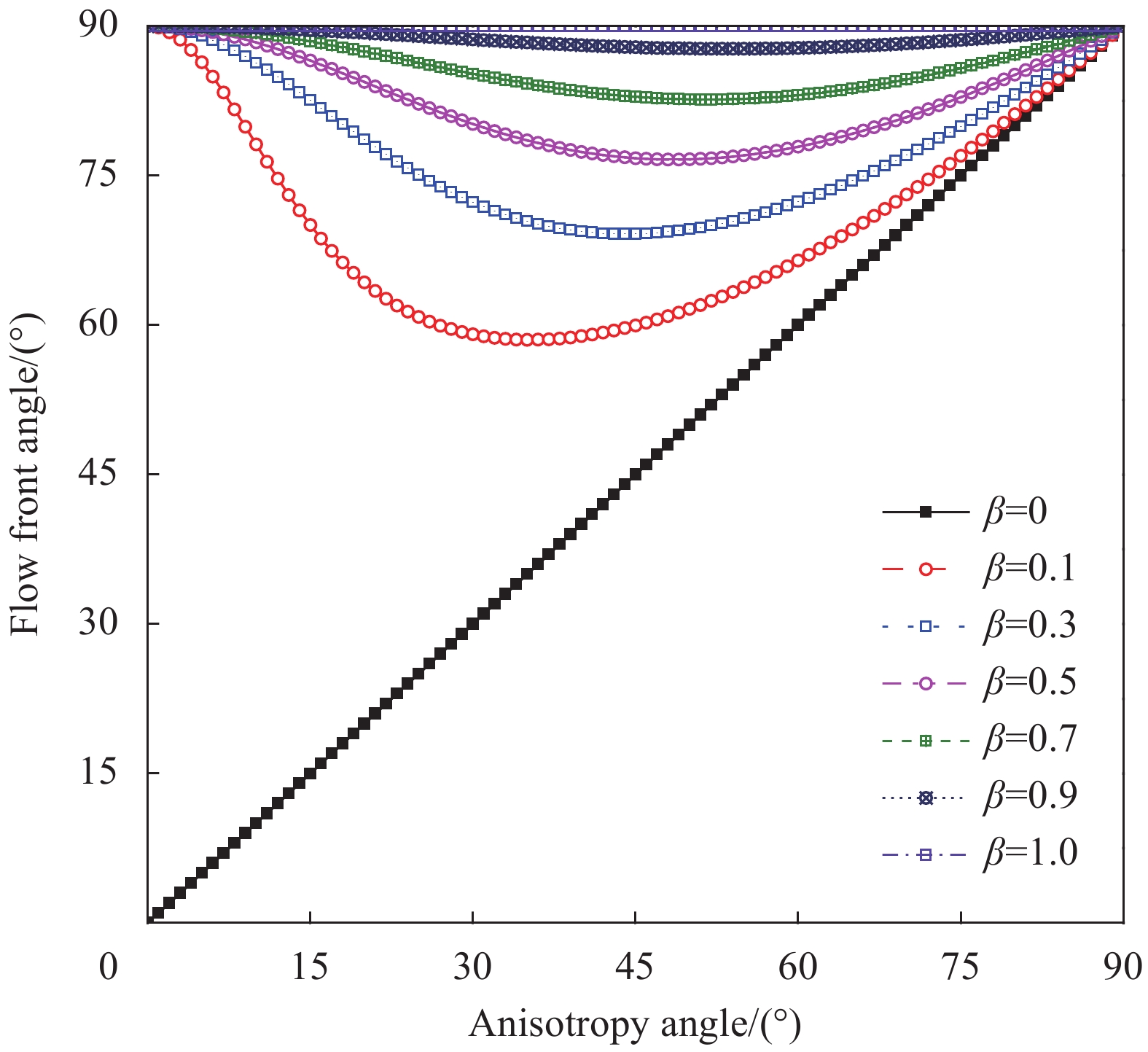
图 7 SF部分时刻下的实验流动前沿及数据提取结果Figure 7. Experimental flow front and data extraction results of SF at some moments图8为根据式(7)计算得到的不同各向异性程度下α与θ间的关系，当θ为0°时，流动前沿角α恒为90°；当0°<θ<90°时，θ≤α≤90°。当β→0时，α≈θ；而当β=1时，α恒为90°；当0<β<1时，α随着θ先减小后增大，β值越大，α随θ可变化的范围越小。当灌注方向确定后，便可通过稳态下的流动前沿角推导出主方向上的渗透率。将沿纤维织物经纬45°方向设定为灌注方向，则流动前沿角α与渗透率K的关系如下：
![]()
图 8 不同各向异性程度下纤维织物流动前沿角与各向异性角关系Figure 8. Relationship between flow front angle and anisotropy angle of fiber fabric under different degrees of anisotropyP = \tan {\alpha _{{{45}^ \circ }}} = \frac{{1{\rm{ + }}\beta }}{{1 - \beta }} (8) \begin{split} &{}\\ & Q = {K_{{{45}^ \circ }}} = \frac{{2{K_1}\beta }}{{1{\rm{ + }}\beta }} \end{split} (9) 因此，一次单向法实验便可以同时求得P和Q，进而联立式(8)和式(9)即可解出K1、K2、β：
\beta = \frac{{P - 1}}{{P{\rm{ + }}1}} (10) {K_1} = \frac{Q}{2}\left( {1 + \frac{1}{\beta }} \right) = \frac{{PQ}}{{P - 1}} (11) {K_2} = {K_1}\beta = \frac{{PQ}}{{P + 1}} (12) 图9为不同编织形式织物在45°方向灌注下的流动拟合角随时间变化图。可知，流动拟合角基本上随时间先增大后趋于稳定。由于灌注初期压力梯度大，流体流速相对较快，导致流体在灌注过程中出现非稳态流动，流动拟合角的变化相对较大；灌注中后期速度逐渐变慢，流体随着纤维织物的编织方式稳定流动，故流动拟合角逐渐趋于稳定。
![]()
图 9 不同编织形式织物在45°方向灌注下流动拟合角随时间变化Figure 9. Flow fitting angle change with time of different textiles under 45° infusion其中，由于实验中SF铺放误差导致的局部边缘效应，加速了流体浸润原本灌注较慢的一侧，导致拟合角从负值向正值转变，但由于流体在灌注中后期下逐渐达到稳态，流动前沿角逐渐趋于稳定。另外，由于EKB424织物纤维束间空隙尺寸较大，流体优先充满纤维束间空隙，流动前沿边界经图像处理后会存在误差，因此在灌注后期流动拟合角仍存在小幅度的波动，但流动拟合角基本趋于稳定状态。
由图9还可知，稳态下SF、斜纹织物(Twill)、EKB450织物、EKB424织物的流动拟合角分别为4°、12°、16°、32°，故对应的流动前沿角分别为86°、78°、74°、58°。流动前沿角与纤维织物的编织方式有关，SF缎纹织物基本为各向同性材料，导致流动前沿角接近90°。由于EKB450织物缝线与经纬交织点处存在不规则束间孔隙，同时缝线会有一定的阻碍作用，导致两主方向的渗透率不同，流动前沿角偏离90°。而EKB424织物不仅在纤维束经纬方向上存在差异，而且织物的束间空隙在经纬方向上的尺寸不同，同时缝线在束间空隙和纬向纤维束交错穿过，导致两主方向上渗透率差异更大，其流动前沿角严重偏离90°。因此，织物的编织形式会影响流体流动状态，进而影响流体的流动前沿角。
3.2 纤维织物面内渗透率的空间分布
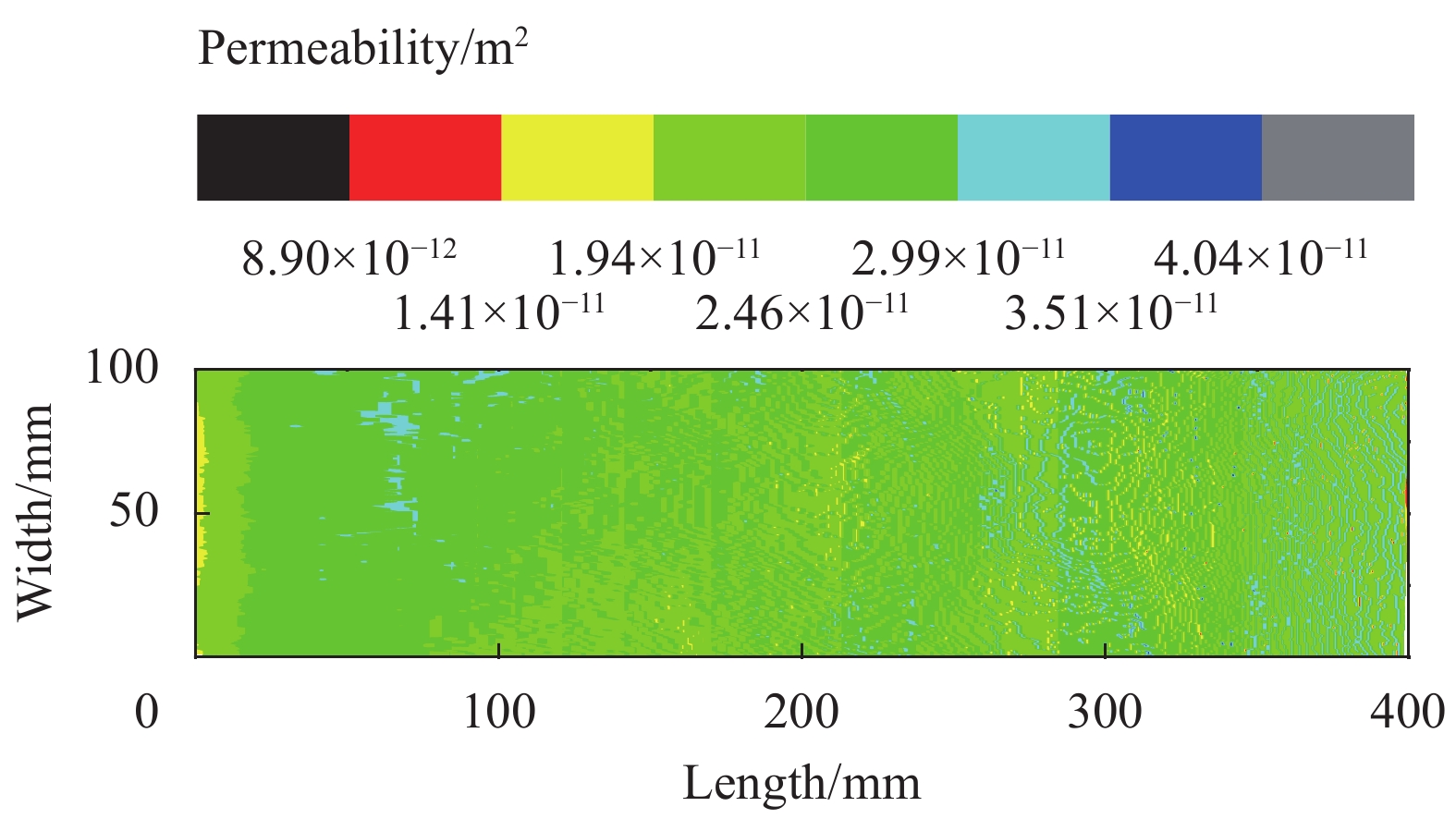
图10为SF在0°方向上的渗透率-位置云图。可知，由于织物局部区域存在剪切变形阻碍流体流动，会延缓流体浸润纤维，故渗透率会出现局部下降的趋势。故由于织物的材料属性的离散性及制样过程可能产生的影响，导致渗透率在空间上具有分布性，即随着织物自身区域结构差异变化。
图11为SF在0°方向上流动前沿与时间的关系。可知L2-t线性拟合效果良好，通过拟合法计算得到0°方向上的全局渗透率为2.50×10−11 m2。
![]()
图 11 SF在0°方向上流动前沿与时间拟合图Figure 11. Fitting diagram of flow front and time of SF in 0° direction以微小时间段用差分计算渗透率，可近似获得纤维织物的局部渗透率。图12为SF在0°方向上的局部渗透率频数分布直方图。可知，局部渗透率分布在1.0×10−11~4.0×10−11 m2之间。用正态分布函数对渗透率频数分布直方图进行拟合，可得正态均值X (全局渗透率)为2.490×10−11 m2，标准差σ为4.515×10−12，与拟合法求得的渗透率保持一致。(X±3σ)的区间范围为[1.1355×10−11，3.8445×10−11] m2，包含了所有实测渗透率的分布值，故可用(X±3σ)代表纤维织物的渗透率及波动。
对比两种方法可知：均可得到纤维织物的全局渗透率，但差分法体现出织物渗透率在不同区域存在波动，受纤维织物实际结构的影响。
通过正态拟合求解的全局渗透率及稳态流动前沿角，可计算出不同织物主方向上的渗透率K1、K2和各向异性程度β，计算结果见表2。可知，β值的相对大小：SF＞Twill＞EKB450＞EKB424；渗透率的相对大小：EKB424＞SF＞EKB450＞Twill。β为织物结构参数，β越大，织物结构越规整，相对于双轴向织物而言，SF和Twill结构规整，故β值相对较大。与Twill相比，SF面密度小，单位面积下经纬向交织点多，流道产生的几率增加，故其渗透率相较于Twill大。EKB450与EKB424同为双轴向织物，EKB424织物的束间尺寸大致在0.75~1.5 mm，而纤维束宽度在2 mm左右，束间尺寸较大易产生流道，导致织物更容易被渗透，表现为织物渗透率较大；而EKB450织物束间空隙较小，结构相对于EKB424织物更致密，流体基本在纤维束内流动，故该织物渗透率较小。同时，由于EKB424织物束间空隙长宽比约为1∶2，导致两主方向上渗透率相差较大，β值较小。因此，纤维织物的束间空隙越大，织物的渗透率相对较高。
表 2 纤维织物的面内渗透率结果Table 2. In-plane permeability results of fiber fabricTextile α/(°) K45°/10−11 m2 K1/10−11 m2 K2/10−11 m2 β SF 86 2.386 2.565 2.230 0.869 Twill 78 0.521 0.662 0.430 0.649 EKB450 74 0.990 1.387 0.769 0.554 EKB424 58 9.544 25.442 5.874 0.231 Notes: K45°—Permeability of the fabric in 45° direction; K1—Permeability of the fabric in the fastest direction; K2—Permeability of fabric in the slowest direction; β—Degree of anisotropy. 3.3 纤维织物阶梯铺层对灌注的影响
表3为SF在均一铺层与阶梯铺层下对应的渗透率。可知：在均一铺层条件下，纤维织物的渗透率随着纤维层数增加而递增。由图13中SF的微观结构图可知，SF纤维束尺寸较小，纤维表面平整且结构相对密实，在压缩状态下嵌套效应的作用不明显，而织物间力的传递起着主导作用。在均一铺层条件时，压实状态下力的传递依靠相邻纤维之间的表面接触，随着SF层数增加，纤维压实率递减，平均单层厚度递增，纤维体积分数递减，纤维织物的几何造型在内部出现了更多的空隙，因此渗透率呈现递增的趋势。另外，织物渗透率K与纤维体积分数Vf可用经验公式K=AebVf拟合[22]，拟合结果为：A=6.436×10−11，b=−1.829。
表 3 SF在均一铺层与阶梯铺层下渗透率对比Table 3. Comparison of permeability of SF under uniform ply and step plyTextile Number of
layersThickness/
mmAverage layer
thickness/mmVf/% KU/(10−11 m2) σ/(10−11 m2) KS/(10−11 m2) σ/(10−11 m2) SF 2 0.331 0.1655 52.13 2.490 0.451 4.363 0.829 3 0.525 0.1750 49.30 2.613 0.424 3.586 0.663 4 0.723 0.1808 47.73 2.691 0.487 2.998 0.874 5 0.922 0.1844 46.79 2.773 0.513 2.775 0.730 Notes: Vf—Fiber volume fraction; KU—Permeability under uniform ply; KS—Permeability under step ply; σ—Standard deviation. 由表3可知，在阶梯铺层条件下，第一段区域5层纤维织物的渗透率基本无变化，均为2.77×10−11 m2，而随着灌注方向纤维织物层数的减少，渗透率呈现递增的趋势，与均一铺层的渗透率规律相反。
在阶梯铺层中，由于5层纤维织物位于第一段区域，与均一铺设5层织物保持一致，故渗透率基本不变。在流体从5层织物向4层织物方向浸润的交界处，纤维织物的厚度由0.922 mm变为0.723 mm，此时模腔截面积变小，而流量基本不变，导致流动速度跃迁至极大值V0，在该时刻后速度开始连续下降，但在第二段区域的速度仍高于均一铺设4层织物的速度，故灌注时间缩短。同理，流体在向3层及2层织物浸润时，流体流至阶梯交界处时，速度再次跃迁至极大值V1、V2，同样缩短了灌注时间。
本实验中阶梯铺层方案灌注耗时2996 s，而按照5或2层织物均一铺层，灌注耗时分别为4218 s和4236 s，故流体从厚铺层向薄铺层灌注可显著缩短灌注时长，即阶梯铺层表观渗透率显著增大。由此可知，厚铺层向薄铺层灌注的灌注方式可加快流体对纤维的浸润，有助于提高大型构件的生产效率。
4. 结 论
在传统单向法测渗透率的基础上，采用数字图像技术，实现了一次测试获取织物全局渗透率和局部渗透率及其分布。考察了编织形式对流体流动和织物的渗透率影响，并用正态分布函数对局部渗透率进行拟合。基于纤维层数对纤维体积分数的影响，研究了面内渗透率与其关系，得到以下结论：
(1) 数字图像技术的应用改善了纤维织物渗透率测试的精度和数据处理效率，极大地增加了单次实验数据获取量，通过该技术既可研究纤维织物的局部渗透率突变，也可利用正态分布函数求解全局渗透率，结果吻合度高。
(2) 通过一次单向渗透率实验可求解出面内两个主方向上的渗透率，提高了实验效率。织物渗透率与编织形式有关，若纤维织物束间尺寸较大，渗透率会较大程度地提高；EKB424织物渗透率比EKB450织物大一个数量级，缎纹织物(SF)的渗透率大于斜纹织物(Twill)。
(3) 均一铺层下，SF渗透率随层数增大而增大。阶梯铺层会导致区域交界处流动速度产生突变，改变区域初始流动，影响表观渗透率。厚铺层向薄铺层灌注会缩短灌注时间，可指导实际宏观多尺度构件在真空灌注下的工艺。
建立的基于数字图像技术的面内渗透率测试方法可以更精确地获取不同结构织物的面内渗透率及其分布，可用来研究边缘效应、纤维体积分数分布等因素对渗透率的影响，将获得的参数输入至仿真软件中，以提高仿真精度，为实际工艺路线提供指导。
-
![]()
图 5 纤维织物流动前沿示意图
Figure 5. Schematic diagram of the flow front of fiber fabric
α—Flow front angle; δ—Complementary angle of the flow front angle; \nabla P—Pressure gradient
![]()
图 6 缎纹织物(SF)在572 s时刻对应的灰度直方图 (a) 和流动前沿拟合图 (b)
Figure 6. Gray histogram (a) and fitting of flow front (b) of satin fabric (SF) at time 572 s
![]()
图 7 SF部分时刻下的实验流动前沿及数据提取结果
Figure 7. Experimental flow front and data extraction results of SF at some moments
![]()
图 8 不同各向异性程度下纤维织物流动前沿角与各向异性角关系
Figure 8. Relationship between flow front angle and anisotropy angle of fiber fabric under different degrees of anisotropy
![]()
图 9 不同编织形式织物在45°方向灌注下流动拟合角随时间变化
Figure 9. Flow fitting angle change with time of different textiles under 45° infusion
![]()
图 11 SF在0°方向上流动前沿与时间拟合图
Figure 11. Fitting diagram of flow front and time of SF in 0° direction
表 1 实验材料的相关参数
Table 1 Related parameters of experimental materials
Material Type Areal weight/(g·m−2) Density/(kg·m−3) Vinyl resin ATLAC 430 LV − 1100 Satin fabric − 220 2550 Twill fabric 2/2 Twill 327 2550 Biaxial fabric EKB450 455 2550 Biaxial fabric EKB424 424 2550 
下载: 导出CSV
表 2 纤维织物的面内渗透率结果
Table 2 In-plane permeability results of fiber fabric
Textile α/(°) K45°/10−11 m2 K1/10−11 m2 K2/10−11 m2 β SF 86 2.386 2.565 2.230 0.869 Twill 78 0.521 0.662 0.430 0.649 EKB450 74 0.990 1.387 0.769 0.554 EKB424 58 9.544 25.442 5.874 0.231 Notes: K45°—Permeability of the fabric in 45° direction; K1—Permeability of the fabric in the fastest direction; K2—Permeability of fabric in the slowest direction; β—Degree of anisotropy.
下载: 导出CSV
表 3 SF在均一铺层与阶梯铺层下渗透率对比
Table 3 Comparison of permeability of SF under uniform ply and step ply
Textile Number of
layersThickness/
mmAverage layer
thickness/mmVf/% KU/(10−11 m2) σ/(10−11 m2) KS/(10−11 m2) σ/(10−11 m2) SF 2 0.331 0.1655 52.13 2.490 0.451 4.363 0.829 3 0.525 0.1750 49.30 2.613 0.424 3.586 0.663 4 0.723 0.1808 47.73 2.691 0.487 2.998 0.874 5 0.922 0.1844 46.79 2.773 0.513 2.775 0.730 Notes: Vf—Fiber volume fraction; KU—Permeability under uniform ply; KS—Permeability under step ply; σ—Standard deviation.
下载: 导出CSV
-
[1] 武卫莉, 陈丰雨. 真空辅助树脂灌注法制备风电叶片树脂的渗透及缺陷[J]. 复合材料学报, 2019, 36(12):2779-2785. WU Weili, CHEN Fengyu. Resin permeation and defects of wind turbine blades prepared by vacuum assisted resin infusion method[J]. Acta Materiae Compositae Sinica,2019,36(12):2779-2785(in Chinese).
[2] 赵安安, 王林文, 王浩军, 等. 复合材料液体成型技术的航空应用[J]. 工程塑料应用, 2018, 46(4):145-150. ZHAO Anan, WANG Linwen, WANG Haojun, et al. Application of liquid composite molding technology on aeronautics[J]. Engineering Plastics Applications,2018,46(4):145-150(in Chinese).
[3] KONSTANTOPOULOS S, HUEBER C, ANTONIADIS I, et al. Liquid composite molding reproducibility in real-world production of fiber reinforced polymeric composites: A review of challenges and solutions[J]. Advanced Manufacturing: Polymer & Composites Science,2019,5(3):85-99.
[4] 杨旭静, 王跃飞, 韦凯, 等. 基于孔隙控制的车身结构树脂传递模塑成型工艺设计[J]. 复合材料学报, 2017, 34(5):970-977. YANG Xujing, WANG Yuefei, WEI Kai, et al. Design of resin transfer molding process for vehicle body structure based on porosity control[J]. Acta Materiae Compositae Sinica,2017,34(5):970-977(in Chinese).
[5] SIRTAUTAS J, PICKETT A K, GEORGE A. Materials characterisation and analysis for flow simulation of liquid resin infusion[J]. Applied Composite Materials,2014,22(3):1-19.
[6] NAIK N K, SIRISHA M, INANI A. Permeability characterization of polymer matrix composites by RTM/VARTM[J]. Progress in Aerospace Sciences, 2014, 65: 22-40.
[7] MAY D, AKTAS A, ADVANI S G, et al. In-plane permeability characterization of engineering textiles based on radial flow experiments: A benchmark exercise[J]. Composites Part A: Applied Science and Manufacturing,2019,121:100-114. DOI: 10.1016/j.compositesa.2019.03.006
[8] RUIZ E, VERNET N, ADVANI S. Experimental determination of the permeability of engineering textiles: Benchmark II[J]. Composites Part A: Applied Science and Manufacturing,2014,61:172-184. DOI: 10.1016/j.compositesa.2014.02.010
[9] DEMARIA C, RUIZ E, TROCHU F. In-plane anisotropic permeability characterization of deformed woven fabrics by unidirectional injection. Part I: Experimental results[J]. Polymer Composites,2007,28(6):797-811. DOI: 10.1002/pc.20107
[10] FAUSTER E, BERG D C, MAY D, et al. Robust evaluation of flow front data for in-plane permeability characterization by radial flow experiments[J]. Advanced Manufacturing: Polymer & Composites Science,2018,4(1):24-40.
[11] 张嘉阳, 刘刚, 李龙, 等. 国产CCF300碳纤维单向织物液体成型工艺性及其复合材料力学性能[J]. 复合材料学报, 2016, 33(1):17-26. ZHANG Jiayang, LIU Gang, LI Long, et al. Processability of domestic CCF300 carbon fiber unidirectional fabrics for liquid molding and mechanical properties of their compo-sites[J]. Acta Materiae Compositae Sinica,2016,33(1):17-26(in Chinese).
[12] FERLAND P, GUITTARD D, TROCHU F. Concurrent methods for permeability measurement in resin transfer molding[J]. Polymer Composites, 1996, 17(1): 149-158.
[13] PIERCE R S, FALZON B G, THOMPSON M C. Permeability characterization of sheared carbon fiber textile preform[J]. Polymer Composites,2018,39(7):2287-2298. DOI: 10.1002/pc.24206
[14] COSSON B. Optical measurement of local permeability of flax fiber fabrics before liquid composite molding[J]. Journal of Composite Materials,2018,52(24):3289-3297. DOI: 10.1177/0021998318764579
[15] 耿奕, 蒋金华, 陈南梁. 经编四轴向玻璃纤维织物的渗透行为和渗透率[J]. 纺织学报, 2017, 38(10):49-56. GENG Yi, JIANG Jinhua, CHEN Nanliang. Permeation behavior and permeability of warp-knitted quadri-axial glass fiber fabric[J]. Journal of Textile Research,2017,38(10):49-56(in Chinese).
[16] 方良超. 嵌套效应对织物压缩性及渗透性的影响研究[D]. 西安: 西北工业大学, 2016. FANG Liangchao. Effect of nesting on compaction and permeability properties of fabrics[D]. Xi’an: Northwestern Polytechnical University, 2016(in Chinese).
[17] PEARCE N, SUMMERSCALES J. The compressibility of a reinforcement fabric[J]. Composites Manufacturing,1995,6(1):15-21. DOI: 10.1016/0956-7143(95)93709-S
[18] 周莉莉. 实时监测技术在LCM工艺上的应用研究[D]. 上海: 东华大学, 2009. ZHOU Lili. Application of real-time sensing and monitoring in LCM process[D]. Shanghai: Donghua University, 2009(in Chinese).
[19] 武红玉. 阈值分割算法在图像处理中的应用[J]. 科技信息, 2012(27):201-202. WU Hongyu. Application of threshold segmentation algorithm in image processing[J]. Science and Technology Information,2012(27):201-202(in Chinese).
[20] 孔凡胜, 王竹林, 高伟伟. 某型检测系统图像信息噪声处理研究[J]. 计算机与数字工程, 2014, 42(8):1484-1487. KONG Fansheng, WANG Zhulin, GAO Weiwei. Noise information processing of some detection system[J]. Computer and Digital Engineering,2014,42(8):1484-1487(in Chinese).
[21] FRATTA C D, KOUTSOUKIS G, KLUNKER F, et al. Characterization of anisotropic permeability from flow front angle measurements[J]. Polymer Composites,2016,37(7):2037-2052. DOI: 10.1002/pc.23382
[22] BARIS C, DAMIANO S, MURAT S E, et al. In-plane permeability distribution mapping of isotropic mats using flow front detection[J]. 2018, 113: 275-286.
-
期刊类型引用(6)
1. 付硕，许一虎，孙治博. 汽车空气悬架系统及精准控制技术发展综述. 液压与气动. 2023(04): 107-114 . 
百度学术
2. 陈俊杰，谭月玲，康盛，邱光琦. 膜式空气弹簧帘子线铺设角-承载力映射模型研究. 振动与冲击. 2023(21): 291-297 . 百度学术
3. 中国汽车工程学术研究综述·2023. 中国公路学报. 2023(11): 1-192 . 百度学术
4. 王相平，李星，王剑锋，吴少培，丁旺才，李国芳. 中低速磁浮车辆空气弹簧动力学建模及其应用研究. 振动工程学报. 2023(06): 1527-1538 . 百度学术
5. 刘琼，杨纪远，张磊，商涛，谢济兴. 帘线参数对单囊空气弹簧垂向刚度的影响研究. 三明学院学报. 2023(06): 117-124 . 百度学术
6. 孙文，李晨阳，王军年，钱灏喆，张文通. 越野车复合型悬架平顺性的研究. 汽车工程. 2022(01): 105-114+122 . 百度学术
其他类型引用(8)
-
计量
- 文章访问数: 1299
- HTML全文浏览量: 573
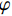
- PDF下载量: 95
- 被引次数: 14
