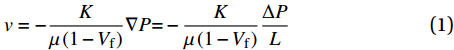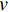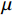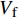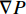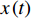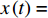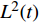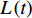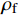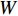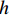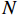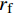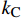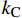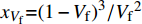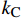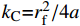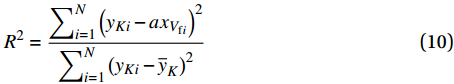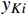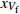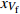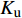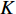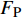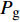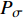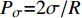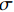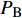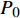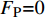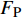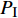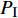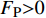Impregnation characteristics of carbon fiber composite during ultrasonic vibration assisted RTM process
-
摘要: 研究了织物类型、纤维体积分数和超声振动对树脂在碳纤维织物中流动特性的影响规律,设计了超声振动辅助RTM工艺过程中单向渗透率测量装置,开展了16组渗透率测试实验,并结合COMSOL软件仿真分析了织物中的树脂流动特性。研究表明,在相同纤维体积分数水平下,斜纹编织物的纤维束间隙通道比平纹织物的更宽,2/2斜纹编织织物渗透率比平纹织物提高了约21.5%。纤维体积分数与织物渗透率呈负相关,其函数关系与半经验公式Kozeny-Carman(KC)方程吻合较好。树脂流动过程中加入超声振动,其超声空化效应、加速度效应和微射流效应作用于纤维丝束表面,提高了织物渗透率约58.2%。有限元仿真模拟了椭圆形和近矩形纤维束截面设计的织物模型的流动过程,结果发现近矩形纤维束截面高流速区域范围更广,流体向纤维布夹层浸渍的速度分量更大。超声作用于织物纤维可能带动纤维丝束蠕动,使纤维束截面趋于近矩形状,从而提高了树脂对纤维织物的浸润性。上述研究结果对优化碳纤维复合材料成型工艺和成型性能具有一定的指导意义。Abstract: The flow characteristics of carbon fiber fabric was studied under different forming conditions, including fabric type, fiber volume fraction and ultrasonic vibration. The unidirectional permeability measurement device of ultrasonic vibration assisted RTM was newly designed. Permeability testing experiment including 16 trials was carried out, and the resin flow characteristics in the fabric were analyzed using COMSOL simulation. Results show that with the same fiber volume fraction, the fiber bundle gap channel of 2/2 twill weave fabric is wider than that of plain weave fabric, and the permeability of twill weave fabric is averagely 21.5% higher than result from plain weave fabric. The fiber volume fraction is negatively correlated with fabric permeability, and the functional relationship is in good agreement with the semi-empirical Kozeny-Carman (K-C) equation. The ultrasonic vibration is introduced into the resin flow process, and the ultrasonic cavitation effect, acceleration effect and micro-jet effect acted on the surface of fiber bundle, which significantly improves the permeability of fiber fabric about 58.2%. The flow process of fabric model, which is designed with elliptic and nearly rectangular fiber bundle section, was simulated by finite element model, and results show that the high velocity area of near rectangular fiber bundle section is relatively wider, and the velocity component of fluid impregnation to the interlayer of fiber cloth is larger. Ultrasonic acting on the fabric fibers probably drives the fiber bundle peristalsis, making the fiber bundle cross section tend to be nearly rectangular, subsequently improving the resin infiltration of the fiber fabric. Experimental results from this work have certain guiding significance to optimize the forming process of composites.
-
Keywords:
- flow characteristic /
- fabric type /
- resin impregnation /
- ultrasonic vibration /
- permeability
-
复合材料液态成型技术是连续纤维增强复合材料的关键制造工艺,主要包括树脂传递模塑(RTM)、真空辅助RTM (VARTM)、真空注塑工艺(VI)和柔性工具下的树脂注塑技术(RIFT)[1-2]。在传统RTM工艺中,成型步骤包括纤维铺层、树脂注入和固化。铺层设计决定了织物的多孔质几何结构,需要综合考虑纤维布铺层角度、层数、轴向-径向纤维的合理搭接方式和铺层对称性。树脂在外部压力驱动下浸渍模具内织物,而后施加一定外部压力或温度,待其完全固化后,即可取模得到一块复合层压板。通常,制造过程中伴随着缺陷的存在,例如织物未完全浸渍出现的干斑和空隙会降低复合材料成型产品的力学性能[3]。因此有必要提高树脂在浸渍过程中的浸渍平稳性,减少浸渍缺陷。考虑到浸润过程的效率来缩短制造周期,在保证树脂渗透质量的前提下,浸润时间需尽可能短[4]。
树脂浸润过程涉及多因素综合影响,常用流体动力学理论进行模拟分析。一些学者[5-7]提出了不同的理论模型来预测树脂填充过程,并进行有限元仿真模拟,其仿真得到的渗透率与文献中验证实验测量渗透率基本吻合。渗透率被用来评估流体通过多孔质织物的难易程度,其主要与纤维织物的空隙率、铺层结构和纤维束横截面形状等有关[8]。平面渗透率常被用于表征织物的宏观流动性,可通过单向或径向流实验确定[9-10]。织物渗透率的主要影响因素是流体流动特性和纤维织物几何结构,包括纤维布铺层、纤维束截面形状和编织方式、纤维弯曲度及纤维束间的间隙[11-14]。
编织型织物由纤维束编织而成,束间间隙是毫米级,而纤维束是由大量纤维丝组成,其间隙是微米级,束间和丝间间隙的浸渍流动表现出双尺度流动现象[15]。束间通道流动主要受流体黏度影响,而丝间通道主要受毛细管力驱动,丝间通道狭小,其流量远低于束间通道。因此,研究纤维束间的间隙流动可较好评估树脂在织物间的整个流动过程[16-17]。Endruweit等[18]研究发现在相同等效渗透性的织物模型中,不同纱线截面形状的织物渗透率差异最大可达3.3倍,管道宽高比接近1时,管道渗透率最大。这意味着,改变管道形状来增加管道面积并不一定导致织物渗透率增加。
近年来,超声振动逐渐被应用于复合材料成型工艺中。刘丽等[19-20]采用超声波分别处理环氧树脂体系和芳纶纤维,研究了超声振幅和超声作用时间对树脂黏度、表面张力及纤维表面特性的影响。研究表明,超声场空化效应导致树脂体系交替生成大量小气泡,释放出大量空化能,降低了树脂的黏度和表面张力及芳纶纤维和环氧树脂之间的浸润角,从而促进树脂对纤维的浸润性。另一方面,超声的声流作用可能使树脂组分进入纤维表面微孔,增加了纤维表面氧含量,从而提高了纤维表面极性。当超声能量较大时,树脂嵌入纤维表面形成微纤,使纤维表面粗糙度增大,易形成微观机械啮合结构,从而提高增强材料的界面性能,而超声功率过大时,纤维表面皮质几乎完全脱落,纤维本体受到破坏,最终使复合材料界面强度降低。姜开宇等[21]研究超声功率对纤维增强复合材料注射成型特性的影响,结果发现纤维含量较低时,超声作用诱导基体分子链缠结与解缠,引起织物流动性变化;而纤维含量较高时,声流促进纤维移动,使玻璃纤维取向度下降。
本文以平纹和斜纹两种编织类型、四种纤维体积分数的碳纤维织物为研究对象,开展了16组单向渗透率测试实验,并结合COMSOL软件仿真分析了树脂浸渍过程,获得了织物编制类型和纤维体积分数与织物渗透率的变化规律,同时探讨了超声振动辅助成型工艺下树脂浸渍过程的变化规律。
1. 实验材料及方法
1.1 原材料
采用两种不同编织方式的纤维布,即平纹和斜纹(由思维奇碳纤维产品制造有限公司生产)。如图1所示。纤维布的大小与渗透率测试模具空腔尺寸一致,为350 mm×100 mm。纤维布是使用同一种纤维丝束编织而成,在径向和纬向上具有相同的宏观物理性能,其相关参数列于表1。实验中使用的测试流体是2%浓度聚乙二醇(PEG)的水溶液(由Sigma Aldrich公司提供的,Mw=35 kDa)。其密度为1001 kg/m3,在20℃室温条件下测得黏度为0.0028 Pa·s。所有实验都是在20℃的室温条件下进行。
表 1 碳纤维布的主要参数Table 1. Main parameters of carbon fiber fabricρs/(g·m−2) ft/K rf/μm h/mm 480 12 3.4 0.52 Notes: ρs—Area density; ft—Fiber tow type; rf —Radius of a single fiber filament; h—Thickness of fabric. 1.2 单向非饱和渗透率测试方法
在树脂浸渍织物的流动过程中,假设流体是不可压缩的牛顿流体,纤维织物是不可压缩多孔介质,流体在压力梯度驱动下流经多孔介质,该过程通常可用达西定律和质量守恒方程来描述。如图2所示,在出入口压力差作用下,流体流动前沿沿着流动方向蔓延。此时流体动力学可描述为
v=−Kμ(1−Vf)∇P=−Kμ(1−Vf)ΔPL (1) 式中:
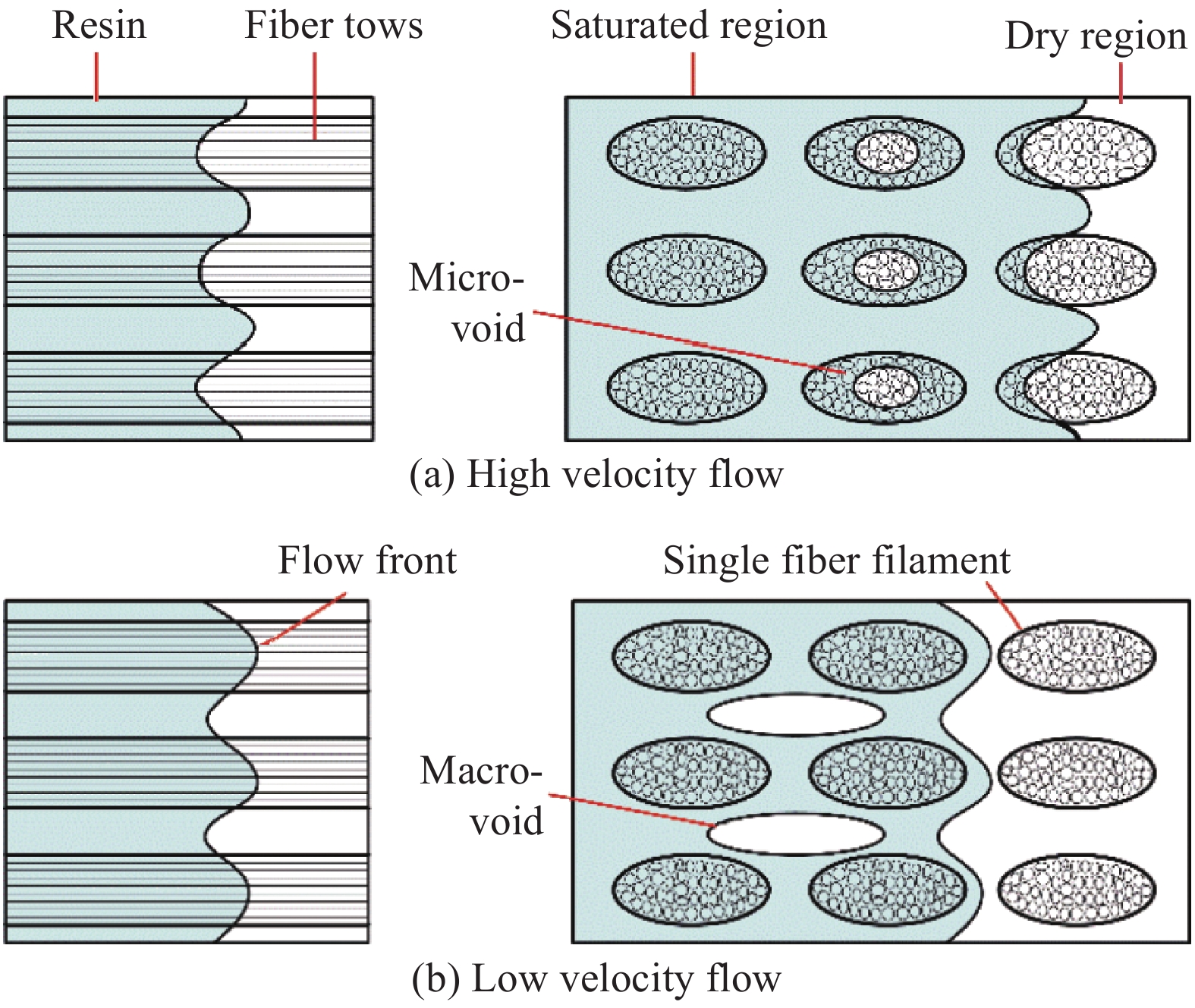
v 是流速;μ 是流体黏度;Vf 是纤维体积分数;K 是织物渗透率;∇P 是流动前沿的压力梯度。树脂流动过程简化为一维流动,在非饱和流动过程中,纤维束内的毛细管效应作用于流动前沿,使出入口的实际压力差低于出入口处的压力差值。双尺度流动模型用于描述树脂的微观流动过程。纤维布在微观上是若干纤维束排列组成的宏观结构。在纤维束间隙通道中,树脂主要受到压力差形成的驱动力;在纤维束内部的丝间通道流动中,主要受到由纤维丝表面张力对流体形成的毛细管力。当流速较大时,压差驱动力占主导地位,流体在纤维束间流动快于纤维丝间流动,最终形成微观空隙,如图3(a)所示;当流速较低时,树脂由于自身黏度特性,纤维束内存在的毛细管力占主导作用,最终形成宏观孔隙,如图3(b)所示。Pucci等[4]发现在织物具有极低渗透率时毛细管压差作用主导树脂流动。因此,在不考虑微观结构的宏观渗透率测试过程中,可以忽略毛细管作用。流动前沿处的压降可简化为:
ΔP=Pin−P0 (2) 在保持出入口恒定压力下,树脂流动模型将简化为一维非压缩流体的层间流动模型,其流动方程为[22]
x(t)=2KΔPμ(1−Vf)⋅t (3) 式中:
x(t) 是流动前沿移动距离的平方,即x(t)= L2(t) ;L(t) 是在t时刻流动前沿位置。不饱和渗透率可以使用平方流动前沿方法(Squared flow front method,SFF)来计算。在流体浸润纤维织物的过程中,用数码相机记录流动前沿的浸渍过程,以获取不同时刻的流动前沿位移数据集。流动前沿位置与时间的斜率s通过线性拟合流动前沿位移数据集计算得出。从而,渗透率测量的计算表达式为
K=μ2ΔP(1−Vf)s (4) 1.3 渗透率测试实验
实验使用的单向非饱和渗透率测试装置如图4所示。该装置主要构成包括存放树脂的树脂罐、易于观测的透明模具、提供进出口压力差的真空泵和超声生成辅助设备。纤维布被水平地铺放在模具内,上模具是透明玻璃材质,其正上方安装了数码相机,便于记录流体的浸渍过程。
在渗透率测试中,树脂冲刷、纤维布铺层缺陷和模具的边缘效应会影响流动前沿平整性,从而使前沿位移难以确定、降低渗透率测量精度。本渗透测量装置在出入口处分别设计一个缓冲槽,以减少树脂冲刷力对流动前沿的影响。模具两侧设计的螺柱被用于调节上模具的上下位置,以改变模具内腔的高度,从而控制内置织物的纤维体积分数。每组渗透率测试实验都铺放6层纤维,其纤维体积分数可以根据下式计算:
Vf=NW/(hρf) (5) 式中:
ρf 是纤维密度;W 是织物面密度;h 是模具内腔高度;N 纤维铺层层数,其值为6。在渗透率测试过程中,先调整真空泵功率,使出口处的压力保持恒定预设值(P0=0.404×105 Pa)。打开入口阀门后,连接大气的树脂罐液面与出口处的压力差驱动树脂浸润模具中的纤维织物,其浸渍过程被数码相机记录。超声波振动辅助装置由超声波发生器和两个超声波机械振头构成,如图4所示。超声发生器型号是DW-S20-1000 (由杭州钛威超声波科技有限公司提供),其输出频率恒定为20 kHz,输出功率调节范围是0~1000 W。两个机械振头被固定在模具正下方。超声波发生器功率设置为100 W。超声系统在树脂流动过程中一直运行,渗透率测量实验中每次测量时间都不超过1 min。
基于全因子实验法设计16组实验,研究不同成型条件下的浸润情况。本文研究的成型条件包括:纤维体积分数、织物类型和流动过程的有无超声振动。实验中通过改变模具内腔高度设置了4组不同纤维体积分数,分别为41.1vol%、47vol%、54.9vol%和60.9vol%。两种织物类型分别为平纹和斜纹。并且在浸润过程中引入超声波。开展的实验组见表2。
表 2 实验设计组及详细参数Table 2. Experimental design group and detailed parametersParameter Level Fabric type Plain Twill Ultrasonic vibration Yes No Fiber volume fraction/vol% 41.1, 47.0, 54.9, 60.9 1.4 流动仿真分析
本文开展流体流动过程的仿真分析,分析在不同织物中流场的压力分布和流速分布。Endruweit等[18]用幂椭圆描述定向直丝的纤维束截面形状,并对纤维束间隙的轴向流动进行了数值分析。织物的纤维体积分数与纤维束间距相关,但是纤维束的排列和横截面形状是保持恒定的。在流动过程仿真中,纤维束的横截面形状可由幂椭圆函数来描述,即
(xR)2+(yh/2)2/n=1 (6) 式中:n是幂椭圆的形状因子;x是长轴方向;y是短轴方向;R是纤维束宽度的一半;h是纤维束的高度。
如图5所示,随着形状因子n增大,界面形状从近矩形、椭圆形,最后演变成透镜形。通常纤维束横截形状被认为是椭圆形,即截面形状因子n=1。
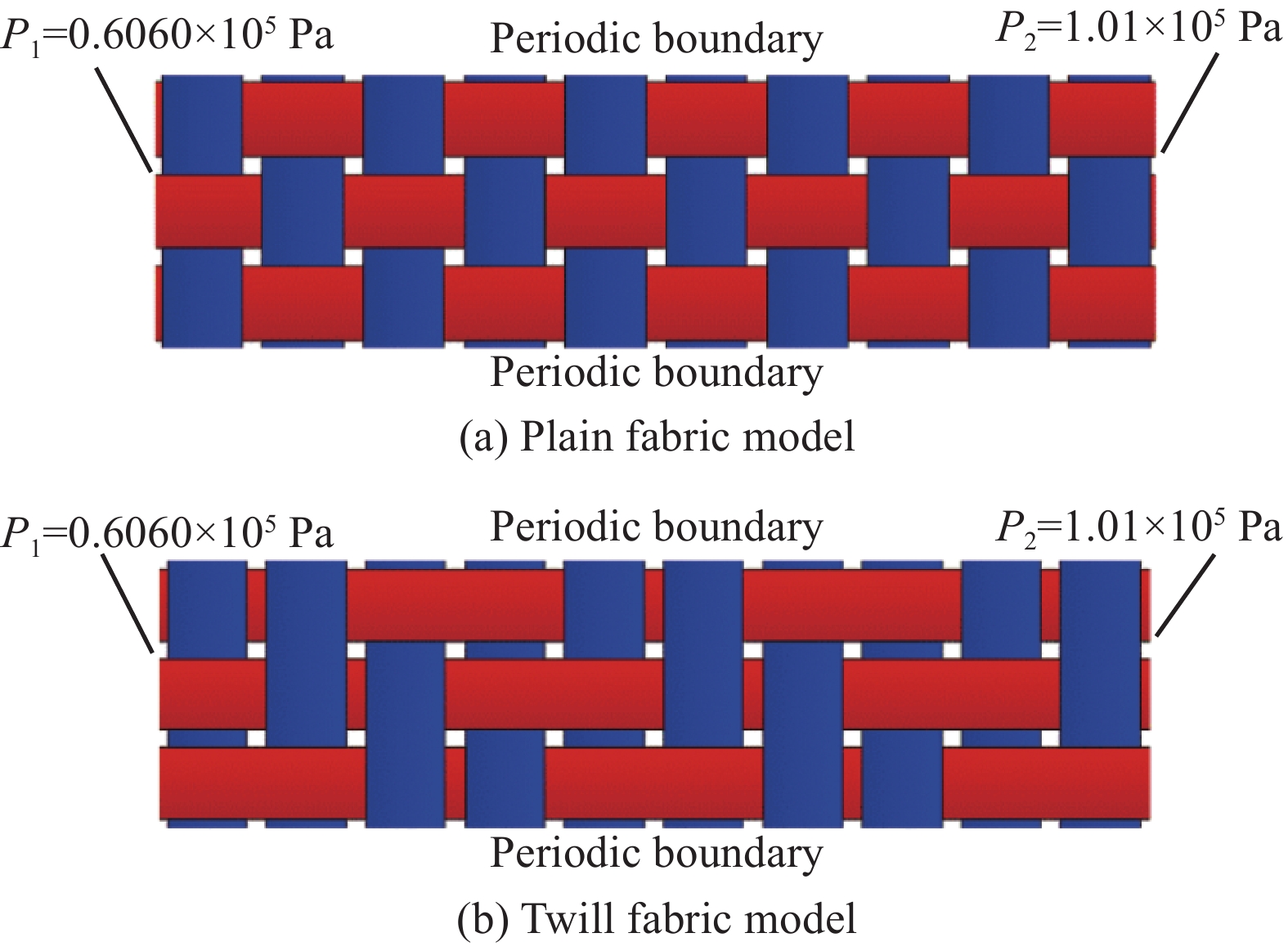
在TexGen中,可以快速精确地创建出椭圆形纤维束的织物模型。实际织物中每层纤维布的参数性能是相同的。假设织物中的纤维布是均匀铺层的,那么纤维织物每层和每个区域的流动特性是一致的。取纤维织物中单层的部分区域即可代表该织物的流动特性,以此减少计算开销。织物仿真模型仅建立一层纤维布,该模型的长和宽尺寸取实际尺寸的1/10左右,其经纱数量(Warp yarns)为3,纬纱数量(Weft yarns)为10。纤维束的截面尺寸与实际一致,纱线间距L为4.5 mm;纱线宽度2R统一设为4.0 mm。纤维织物模型的高度根据对应的纤维体积分数来确定。将建立的织物模型导入COMSOL软件中进行仿真计算。采用不可压缩粘性流体稳态流动下的纳维-斯托克斯方程和质量方程描述流体动力学。在该仿真中,忽略纤维束内的微观流动,即纤维束是不可渗透的,流体只流经纤维束间的空腔通道。因此,纤维束表面设置为无滑移边界条件,即u=0。织物模型两侧分别代表织物进出口面,入口处施加压力P1=0.606×105 Pa以驱动流体流入织物,出口处与大气相连压力为P2=1.01×105 Pa。纤维织物模型的边界条件布局如图6所示。
2. 结果与讨论
2.1 织物类型对织物渗透性的影响
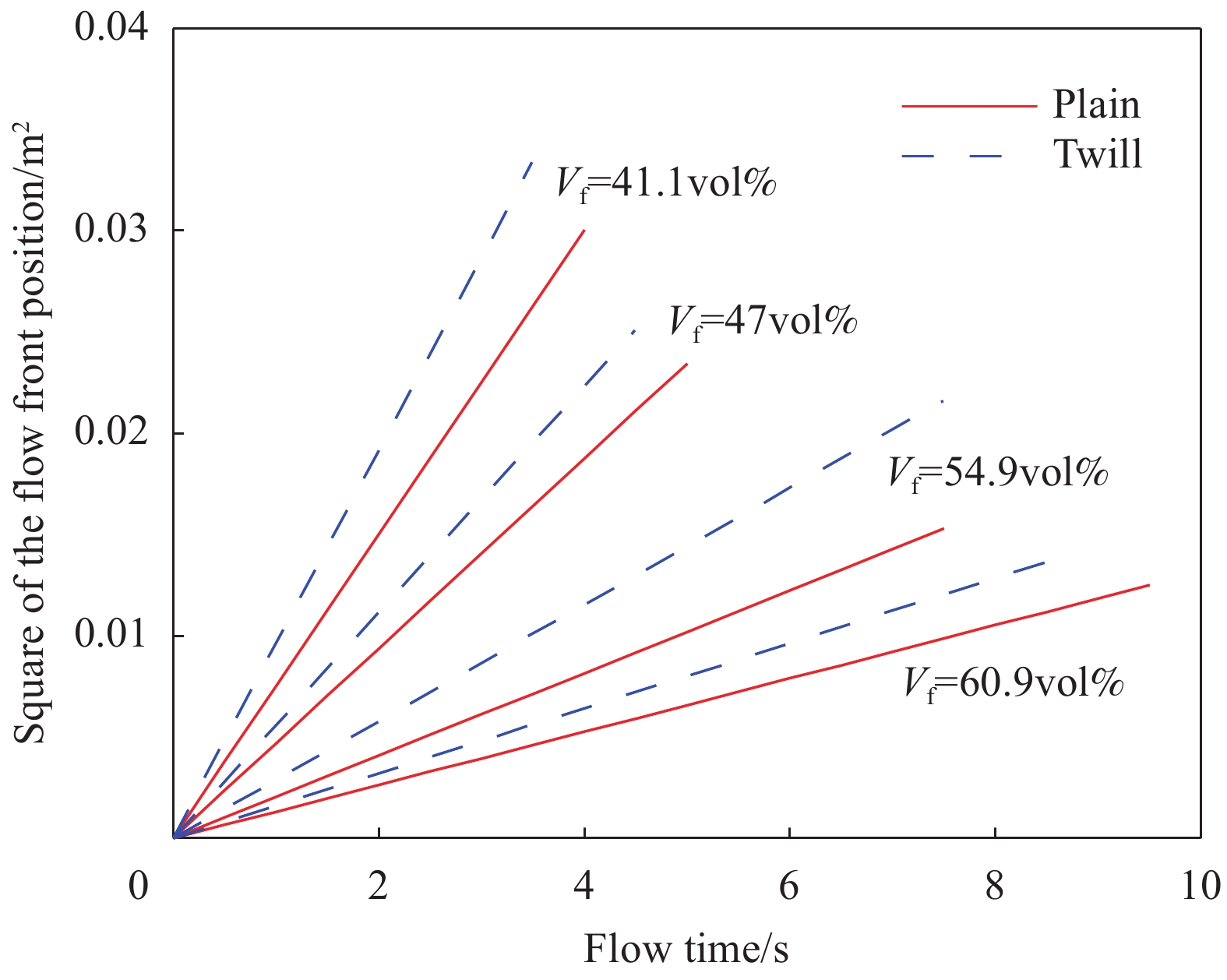
平纹和斜纹织物在4组不同纤维体积分数下的流动前沿数据集如图7所示。流体浸渍时间与流动前沿距离平方呈线性关系,这说明简化毛细管效应的假设几乎不影响渗透率测试。表3为编织物不同纤维体积分数下的平方流动前沿(SFF)曲率。在纤维体积分数相同时,斜纹织物的曲线斜率s比平纹的高,平均提高了约21.5%。这是由于斜纹织物编织的纤维束间隙更大,流体更容易在束间间隙中流动。而且平纹织物的编织节点多,纤维渗透阻力更大,因此,相同纤维体积分数下的平纹织物渗透性普遍低于对应的斜纹织物。
表 3 编织物不同纤维体积分数下的平方流动前沿(SFF)曲率Table 3. Squared flow front (SFF) curvature of fabrics with different fiber volume fractionsVf/vol% splain stwill rg/% 41.1 0.00751 0.00957 21.53 47.0 0.00469 0.00558 15.95 54.9 0.00204 0.00294 30.61 60.9 0.00132 0.00161 18.01 Notes: Vf—Fiber volume fraction; splain—Slope of plain fabric; stwill—Slope of twill fabric; rg—Relative growth rate of twill fabrics relative to plain weave fabrics. 2.2 纤维体积分数对织物渗透性的影响
2.2.1 织物结构
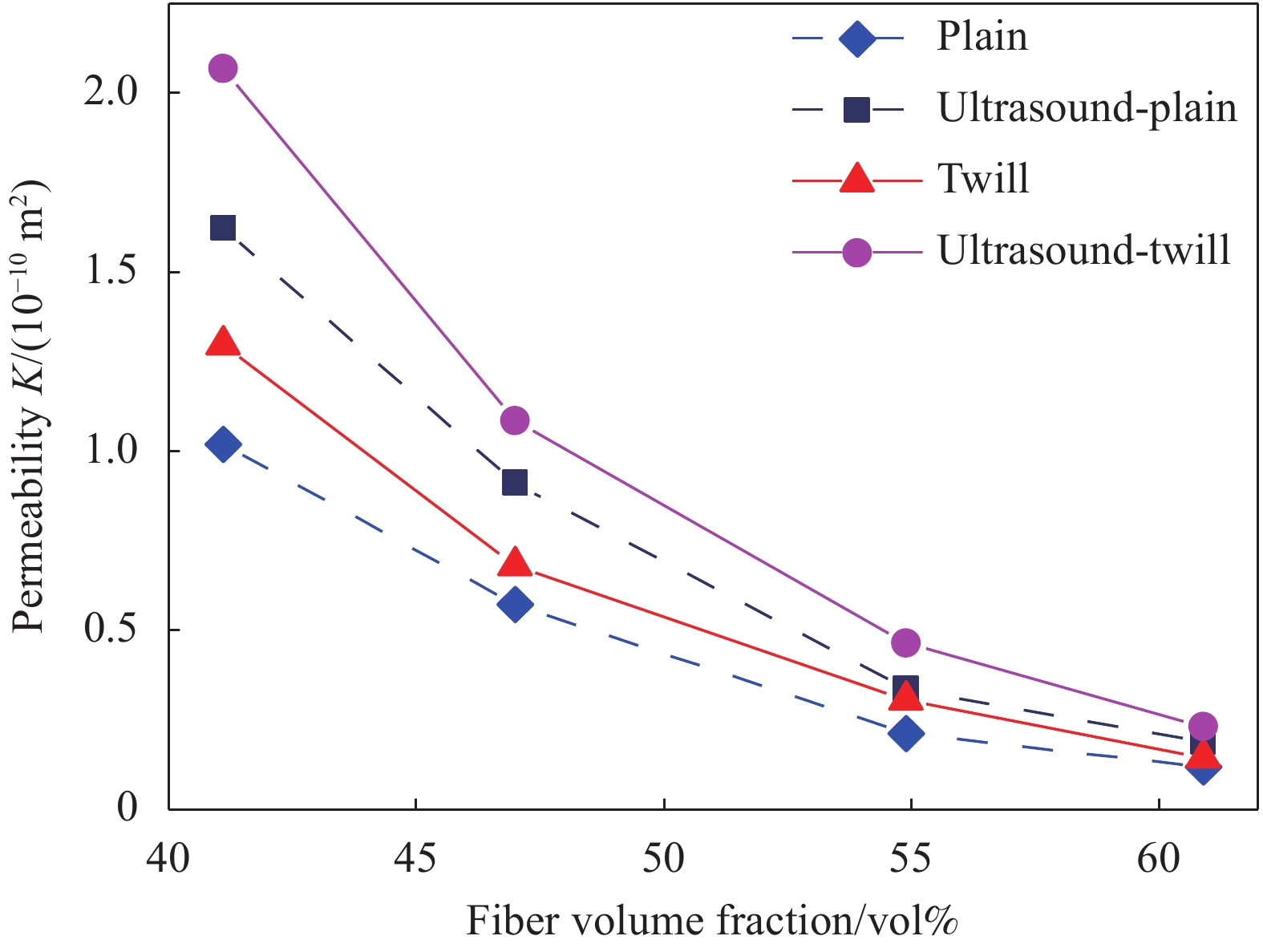
根据SSF法,计算出不同纤维体积分数(41.1vol%、 47vol%、54.9vol%、60.9vol%)下的织物渗透率,如图8所示。相同织物类型和成型处理方式下,织物渗透率与纤维体积分数是负相关关系。流体浸润纤维体积分数为41.1vol%的织物时浸润时间最短,其中,超声处理下的斜纹织物渗透率达到2.07×10−10 m2,比Vf=60.9vol%的斜纹织物渗透率高8倍。
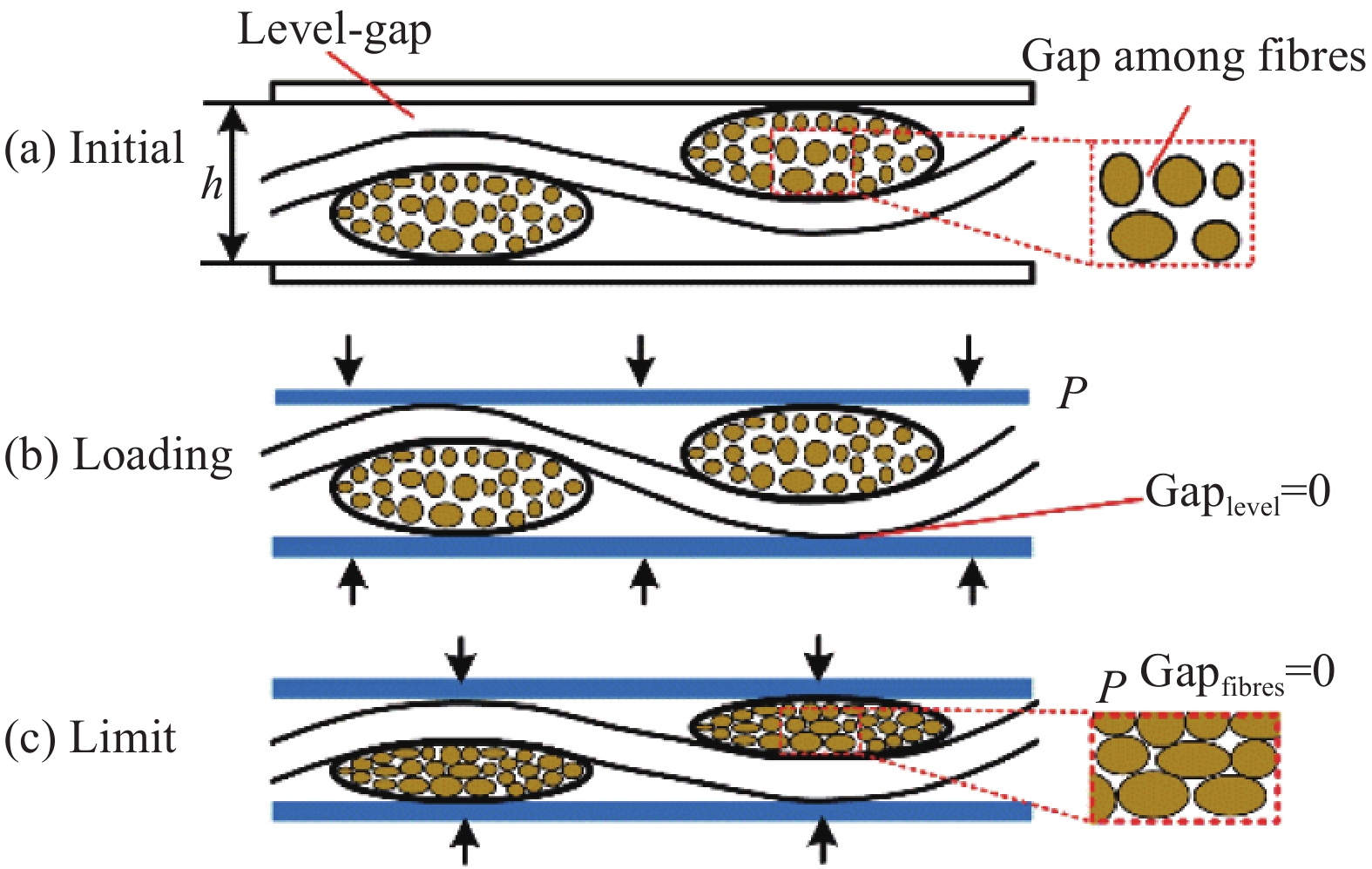
织物纤维体积分数的变化可用织物压缩过程来描述,如图9所示。织物压缩过程分为三个阶段[8]。在纤维布铺层之后,层间存在一定的间隙,此时为压缩初始状态,如图9(a)所示。纤维织物受到一个铅垂力的压缩,使各层纤维布的间距逐步减少。如图9(b)所示,此时各层纤维布之间刚好不存在间隙,纤维束之间开始形成摩擦阻力。继续施加的压力克服纤维束间和层间的摩擦阻力,进一步加强纤维丝的排列紧凑度,如图9(c)所示。随着压缩的进行,纤维丝中间隙越小时,需要施加的压缩力将进一步增大。理论上,当纤维丝间无间隙时,可认为是织物的压缩极限状态,此时需要施加的压力等于纤维压缩强度。不同纤维体积分数的织物是通过控制织物高度h来获取的。织物高度h越小,说明织物压缩程度越深,纤维布和纤维丝的排列更紧凑,层间间距和纤维束间间距变小,同时纤维束间的摩擦力也会增大。因此,在高纤维体积分数的织物中,树脂流入多孔介质的空隙通道面积变小,流体浸润到纤维布内,需要克服较大的阻力,从而延长了流体浸润时间,减少了织物渗透率。更严重的是织物可能存在部分区域未完全浸润,从而影响成型件的力学性能,这在成型工艺是应该要避免的。
2.2.2 纤维体积分数与渗透率的函数关系
学者针对织物渗透率与其纤维体积分数进行了大量的研究,提出许多半经验模型用来描述织物渗透率与纤维体积分数之间的函数关系。其中,Kozeny-Carman (K-C)方程最普遍,其表达式如下:
K=r2f4kC⋅(1−Vf)3Vf2 (7) 式中:
rf 是碳纤维单丝半径(rf=3.4 μm);kC 是Kozeny常数。假设每层纤维布中的纤维束是彼此平行小管道。
kC 常数可以使用最小二乘法拟合纤维体积分数与渗透率的函数关系来获取。将K-C方程简化成线性形式:yK=axVf (8) 式中:
xVf=(1−Vf)3/Vf2 是纤维体积分数的换元因子;a是线性拟合参数。此时,
kC 常数即为kC=r2f/4a 。采用最小二乘法,可以得到线性拟合参数a和拟合优度R2的计算式a=∑Ni=1xVfiyKi∑Ni=1x2Vfi (9) R2=∑Ni=1(yKi−axVfi)2∑Ni=1(yKi−¯yK)2 (10) 将图8中两种织物不同纤维体积分数下的渗透率值
yKi 代入式(9)和式(10)中,数值计算结果列于表4中。拟合计算出的拟合优度R2都超过了99%,这说明织物渗透率与纤维体积分数的曲线拟合效果很好,拟合曲线如图10所示,从而验证了实验测得渗透率数据的准确性。表 4 拟合参数a的数值计算结果Table 4. Numerical results of the fitting parameter aPlain Ultrasound-plain Twill Ultrasound-twill a 0.8356 1.3305 1.0535 1.6749 R2 0.9956 0.9956 0.9972 0.9963 2.3 超声振动对织物渗透性的影响
在之前8种成型参数的织物上加入超声激励,超声辅助下的非饱和渗透率记录在图10中。加入超声处理后的织物渗透率与织物纤维体积分数依然符合KC方程,这说明超声处理并不影响织物纤维的铺层结构。同类型织物加入超声激励后,其渗透率均大大增加。这说明超声波可以促进流体更好地浸润到模具中的纤维织物中。为了量化超声作用对织物渗透率的正向影响效果,引入渗透相对增长率的概念:
rp=Ku−KK (11) 式中:
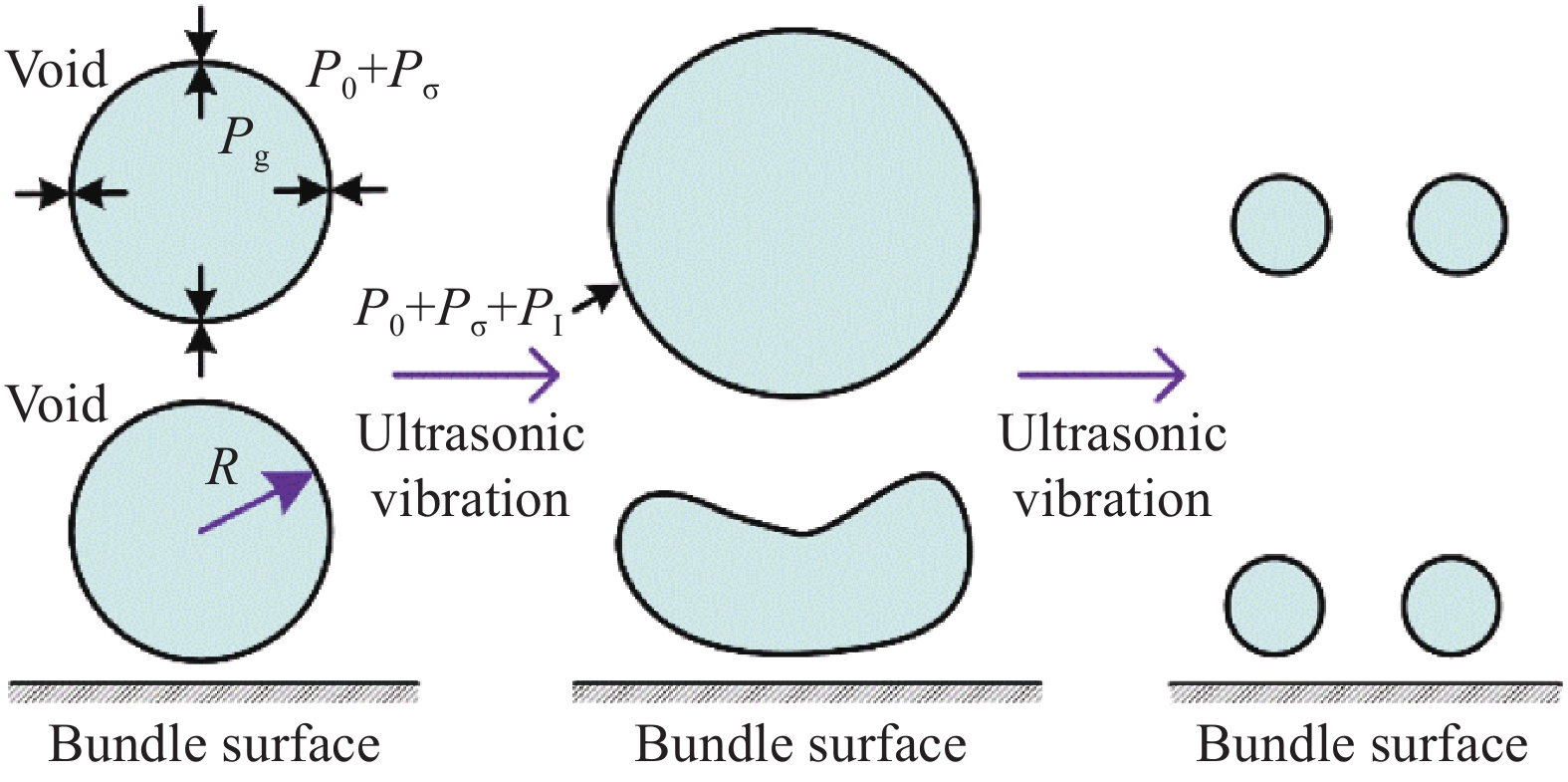
rp 是渗透相对增长率;Ku 是加入超声振动测得的织物渗透率;K 是未引入超声振动测得的织物渗透率。统计8组织物渗透相对增长率,渗透相对增长率关于编织类型和纤维体积分数基本恒定,平均取值为58.2%。这说明超声激励作用不受织物纤维体积分数和织物编织类型的影响,对树脂浸润织物的激励效果稳定,平均提高织物渗透率约为58.2%。超声波在流体中会出现大量小气泡涨落,这是超声场引起的空化效应。气泡内外侧的压强变化主导其生长和坍塌,气泡在超声空化效应下的演变,如图11所示。气泡内外侧压强差
FP 可表示为[23]FP=Pg−(PB+Pσ) (12) 式中:
Pg 是气泡内的气体压强;Pσ 是表面张力引起的附加压强,其值为Pσ=2σ/R ;σ 是表面张力;PB 是气泡外侧的液体压强,当流体中没有超声振动时,其值等于大气压强P0 。当
FP=0 时,气泡内外侧压强相等,气泡形成后在流体中稳定存在。当流体中加入超声振动后,气泡内外侧的总压强FP 为FP=Pg−(P0+PI+Pσ) (13) 式中:
PI 是超声波的声压,可用正弦函数表示:PI=Asin(ωt+φ) (14) 超声振动的声压
PI 波动,导致气泡内外侧压强失衡。当FP>0 时,气泡内侧压强大于外侧压强,促进气泡生长,半径R变大,导致气泡生长的额外压力增大,进而发生破裂。气泡破裂和微振动作用于纤维束表面,可移除纤维表面的杂质,提高纤维表面氧化极性[20],从而促进流体更好地渗入纤维中。例如,在有超声和无超声的浸润条件下,纤维体积分数为54.9vol%的平纹织物在同一时刻的流动前沿位置,如图12所示。超声激励下流体流动距离比无超声激励下的流动前沿距离长32%。但超声激励下的流动前沿更不平齐,这是由于超声振动可以提高模具两侧的流体流动[24]。2.4 流动过程仿真与场分布
流体在椭圆形和近矩形纤维束编织而成的平纹织物模型中饱和稳态流动过程的流体压力在织物模型的流动方向上线性递减,如图2所示。流体在多孔介质中的流动特性与多孔介质的几何结构有密切的关系。在仿真分析中最主要的流动特性是流体的流速分布和织物渗透率。如图13所示,选取两种不同截面纤维束形状的同参数平纹织物模型中3个位置处的横截面速度分布:入口处(Entrance)、流动方向上的中部(Middle)、出口处(Exit)。图中黑色椭圆标记区域代表树脂流速大于1~1.5 m/s的主流通道区域,横向黑色箭头代表树脂在该域横向速度分量(大于0.1 m/s)的流向,纵向黑色箭头代表树脂在该域纵向速度分量(大于0.1 m/s)的流向。无论纤维束形状,流体在两束之间的流速明显高于其他截面区域,这说明流体在织物结构中主要从纤维束间通道流入。在无纤维布铺层缺陷时,低纤维体积分数的织物容易在纤维束间形成树脂富余区。而高纤维体积分数织物的纤维布层间易出现纤维未完全浸渍现象。在相同尺寸下,纤维布编织节点密度越大,其纤维束间通道越多,从而使编织的织物渗透率更高。
树脂在入口处以平面边界条件进入,横纵向分量远低于0.1 m/s,树脂主流通道聚集于纤维束间间隙,两种织物模型的速度云图分布基本一致。树脂进入到织物模型中,沿着不同模型的间隙通道流动,在相同的织物纤维体积分数(Vf=41.1vol%)下,近矩形纤维束织物模型中部的主流通道范围明显大于椭圆状纤维束织物的,并且近矩形纤维束织物模型中部的树脂横向分量明显高于椭圆形纤维束织物模型。这说明在近矩形纤维束织物模型中树脂能以较快的速度向纤维布夹层渗透,从而促进了树脂对纤维织物的浸渍。树脂达到平面出口边界时,流道变宽,树脂向四周扩散,两种织物模型的速度云图和流向箭头分布基本一致。
图14为在4种纤维体积分数(41.1vol%、47vol%、54.9vol%、60.9vol%)下的平纹和斜纹织物的实测渗透率和仿真渗透率及对应的KC线性拟合线。仿真渗透率是对稳态流动过程使用达西公式计算出来的。图14中所有渗透率的KC拟合优度均高达99%。这说明建立的纤维织物模型和流动仿真结果是可靠的。椭圆纤维束模型的仿真渗透率与无超声振动的实测渗透率基本一致,如图14(a)和图14(c)所示。近矩形纤维束模型的仿真渗透率与有超声振动的实测织物渗透率基本吻合,如图14(b)和图14(d)所示。这说明超声微射流效应作用于纤维束表面,可能诱导纤维束截面形状趋于近矩形状,增大了纤维束间的主流管道(高流速)区域面积,使树脂更易向纤维布夹层浸渍,从而提高了树脂对织物的浸润性。纤维束形状对织物的流动仿真影响较大,实际织物纤维束模型与实际形状越精确,其流动过程的仿真结果误差越小[18]。而实际织物的纤维束形状难以精准预测和模拟,这也是图14(a)~14(d)中两条KC线性拟合存在误差的原因之一。
3. 结 论
(1) 同种编织类型的织物,其纤维体积分数与织物渗透是负相关的,其关系可以用KC方程来描述。由于纤维体积分数越大,纤维布层间间隙越小,流动通道变窄,流动阻力增大,减少了流体流量从而降低了织物渗透率。
(2) 在相同纤维体积分数下,平纹织物的渗透率低于斜纹织物21.5%。斜纹编织布的纤维束间间隙比平纹编织布的要大,从仿真模型的流速分布可知,流体主要从束间间隙通过,因此斜纹中更宽的间隙有利于流体的浸渍。但是在相同尺寸下,平纹织物的编织节点是斜纹织物的2倍,即平纹织物中的纤维束间隙通道更多,这促进了流体流动,因此编织类型对织物渗透率的综合影响有限。
(3) 在织物流动过程中加入超声激励,超声波在流体中的空化效应、加速度效应和微射流作用于纤维束,清除了纤维丝表面杂质,提高了纤维表面极性,从而使其渗透率明显有了很大的提升。两种纤维束模型的仿真渗透率结果显示,纤维束截面形状对织物渗透率的影响很大。这也暗示着超声波的综合作用也可能是通过改变纤维束截面形状从而提高织物的渗透率。
-
表 1 碳纤维布的主要参数
Table 1 Main parameters of carbon fiber fabric
ρs/(g·m−2) ft/K rf/μm h/mm 480 12 3.4 0.52 Notes: ρs—Area density; ft—Fiber tow type; rf —Radius of a single fiber filament; h—Thickness of fabric. 表 2 实验设计组及详细参数
Table 2 Experimental design group and detailed parameters
Parameter Level Fabric type Plain Twill Ultrasonic vibration Yes No Fiber volume fraction/vol% 41.1, 47.0, 54.9, 60.9 表 3 编织物不同纤维体积分数下的平方流动前沿(SFF)曲率
Table 3 Squared flow front (SFF) curvature of fabrics with different fiber volume fractions
Vf/vol% splain stwill rg/% 41.1 0.00751 0.00957 21.53 47.0 0.00469 0.00558 15.95 54.9 0.00204 0.00294 30.61 60.9 0.00132 0.00161 18.01 Notes: Vf—Fiber volume fraction; splain—Slope of plain fabric; stwill—Slope of twill fabric; rg—Relative growth rate of twill fabrics relative to plain weave fabrics. 表 4 拟合参数a的数值计算结果
Table 4 Numerical results of the fitting parameter a
Plain Ultrasound-plain Twill Ultrasound-twill a 0.8356 1.3305 1.0535 1.6749 R2 0.9956 0.9956 0.9972 0.9963 -
[1] MATSUZAKI R, KOBAYASHI S, TODOROKI A, et al. Full-field monitoring of resin flow using an area-sensor array in a VARTM process[J]. Composites Part A: Applied Science and Manufacturing,2011,42(5):550-559. DOI: 10.1016/j.compositesa.2011.01.014
[2] BODAGHI M, LOMOV S V, SIMACEK P, et al. On the variability of permeability induced by reinforcement distortions and dual scale flow in liquid composite moulding: A review[J]. Composites Part A: Applied Science and Manufacturing,2019,120:188-210. DOI: 10.1016/j.compositesa.2019.03.004
[3] BODAGHI M, CRISTÓVÃO C, GOMES R, et al. Experimental characterization of voids in high fibre volume fraction composites processed by high injection pressure RTM[J]. Composites Part A: Applied Science and Manufacturing,2016,82:88-99. DOI: 10.1016/j.compositesa.2015.11.042
[4] PUCCI M F, LIOTIER P J, DRAPIER S. Capillary wicking in a fibrous reinforcement-Orthotropic issues to determine the capillary pressure components[J]. Composites Part A: Applied Science and Manufacturing,2015,77:133-141. DOI: 10.1016/j.compositesa.2015.05.031
[5] NABOVATI A, LLEWELLIN E W, SOUSA A C M. A general model for the permeability of fibrous porous media based on fluid flow simulations using the lattice Boltzmann method[J]. Composites Part A: Applied Science and Manufacturing,2009,40(6):860-869.
[6] GERVAIS P C, BARDIN-MONNIER N, THOMAS D. Permeability modeling of fibrous media with bimodal fiber size distribution[J]. Chemical Engineering Science,2012,73:239-248. DOI: 10.1016/j.ces.2012.01.040
[7] WOUDBERG S. Permeability prediction of an analytical pore-scale model for layered and isotropic fibrous porous media[J]. Chemical Engineering Science,2017,164:232-245. DOI: 10.1016/j.ces.2017.01.061
[8] POTLURI P, SAGAR T V. Compaction modelling of textile preforms for composite structures[J]. Composite Structures,2008,86(1):177-185.
[9] HAN S H, CHO E J, LEE H C, et al. Study on high-speed RTM to reduce the impregnation time of carbon/epoxy composites[J]. Composite Structures,2015,119:50-58. DOI: 10.1016/j.compstruct.2014.08.023
[10] AMERI E, LEBRUN G, LAPERRIÈRE L. In-plane permeability characterization of a unidirectional flax/paper reinforcement for liquid composite molding processes[J]. Composites Part A: Applied Science and Manufacturing,2016,85:52-64. DOI: 10.1016/j.compositesa.2016.03.002
[11] PEARCE N R L, SUMMERSCALES J, GUILD F J. Improving the resin transfer moulding process for fabric-reinforced composites by modification of the fabric architecture[J]. Composites Part A: Applied Science and Manufacturing,2000,31(12):1433-1441. DOI: 10.1016/S1359-835X(00)00140-8
[12] RIEBER G, JIANG J, DETER C, et al. Influence of textile parameters on the in-plane permeability[J]. Composites Part A: Applied Science and Manufacturing,2013,52:89-98. DOI: 10.1016/j.compositesa.2013.05.009
[13] MARTIN B, COMAS-CARDONA S, BINETRUY C, et al. Influence of fabrics’ design parameters on the morphology and 3D permeability tensor of quasi-unidirectional non-crimp fabrics[J]. Composites Part A: Applied Science and Manufacturing,2016,90:470-479. DOI: 10.1016/j.compositesa.2016.08.013
[14] SYERKO E, BINETRUY C, COMAS-CARDONA S, et al. A numerical approach to design dual-scale porosity composite reinforcements with enhanced permeability[J]. Materials & Design,2017,131:307-322.
[15] GODBOLE M G, PURANDARE R, HARSHE R, et al. Influence of filament distribution on transverse tow permeability: Model predictions and experimental validation[J]. Composites Part A: Applied Science and Manufacturing,2019,118:150-161. DOI: 10.1016/j.compositesa.2018.12.024
[16] BODAGHI M, VANAERSCHOT A, LOMOV S V, et al. On the variability of mesoscale permeability of a 2/2 twill carbon fabric induced by variability of the internal geometry[J]. Composites Part A: Applied Science and Manufacturing,2017,101:394-407. DOI: 10.1016/j.compositesa.2017.05.030
[17] BODAGHI M, VANAERSCHOT A V, LOMOV S, et al. On the stochastic variations of intra-tow permeability induced by internal geometry variability in a 2/2 twill carbon fabric[J]. Composites Part A: Applied Science and Manufacturing,2017,101:444-458. DOI: 10.1016/j.compositesa.2017.07.008
[18] ENDRUWEIT A, ZENG X, MATVEEV M, et al. Effect of yarn cross-sectional shape on resin flow through inter-yarn gaps in textile reinforcements[J]. Composites Part A: Applied Science and Manufacturing,2018,104:139-150. DOI: 10.1016/j.compositesa.2017.10.020
[19] 刘丽, 张志谦, 黄玉东, 等. 超声作用对芳纶/环氧浸润行为的影响[J]. 材料科学与工艺, 2002, 10(1):69-72. LIU Li, ZHANG Zhiqian, HUANG Yudong, et al. Effect of ultrasound on wetting behavior between aramid fiber and epoxy resin[J]. Materials Science & Technology,2002,10(1):69-72(in Chinese).
[20] 刘丽, 张翔, 黄玉东, 等. 超声作用对芳纶纤维表面性质的影响[J]. 复合材料学报, 2003, 20(2):35-40. LIU Li, ZHANG Xiang, HUANG Yudong, et al. Effect of ultrasonic treatment on surface characteristics of aramid[J]. Acta Materiae Compositae Sinica,2003,20(2):35-40(in Chinese).
[21] 姜开宇, 李豪, 左军超, 等. 超声振动对玻纤增强聚丙烯复合材料注射成型特性的影响[J]. 复合材料学报, 2015, 32(5):1330-1340. JIANG Kaiyu, LI Hao, ZUO Junchao, et al. Effects of ultrasonic vibration on injection molding characteristics of glass fiber reinforced polypropylene composites[J]. Acta Materiae Compositae Sinica,2015,32(5):1330-1340(in Chinese).
[22] SALVATORI D, CAGLAR B, TEIXIDÓ H, et al. Permeability and capillary effects in a channel-wise non-crimp fabric[J]. Composites Part A: Applied Science and Manufacturing,2018,108:41-52. DOI: 10.1016/j.compositesa.2018.02.015
[23] ZHANG D, JIANG E, ZHOU J, et al. Investigation on enhanced mechanism of heat transfer assisted by ultrasonic vibration[J]. International Communications in Heat and Mass Transfer,2020,115:104523.
[24] 吉智. 超声辅助注射成型充模流动特性的可视化研究[D]. 大连: 大连理工大学, 2014. JI Zhi. Visualization research on polymer filling flow characteristics of ultrasonic assisted injection molding[D]. Dalian: Dalian University of Technology, 2014(in Chinese).
-
期刊类型引用(6)
1. 张前 ,谭艳 ,廖庆华 ,益小苏 . 基于“离位”点阵预成型体ES-T300/GT910复合材料的工程化制备及性能研究. 广州化工. 2024(04): 66-69 .  百度学术
百度学术
2. 周钰博,李敏,王绍凯,顾轶卓,陶飞,陈祥宝,张佐光. 面向AI时代的纤维增强树脂基复合材料工艺仿真. 航空材料学报. 2024(05): 17-36 .  百度学术
百度学术
3. 王旭东. 碳纤维复合材料在体育器械中的应用. 塑料助剂. 2024(06): 87-90+113 .  百度学术
百度学术
4. 黄飞,夏露,张友寿,任彦臻. 超声波用于制备复合磷酸盐粘结剂的研究. 特种铸造及有色合金. 2023(02): 284-288 .  百度学术
百度学术
5. 张金童,杨涛,杜宇,张林涛. 超声振动对手糊成型碳纤维复合材料力学性能的影响. 复合材料科学与工程. 2023(12): 38-43+62 .  百度学术
百度学术
6. 王佳明,贾明印,董贤文,陈轲. 树脂传递模塑成型工艺研究进展. 塑料工业. 2021(11): 9-14+43 .  百度学术
百度学术
其他类型引用(5)
-





 下载:
下载: