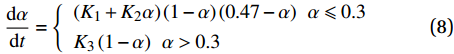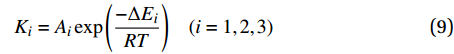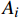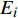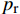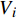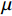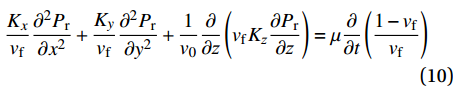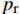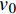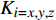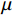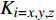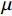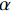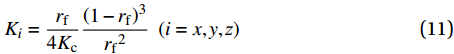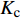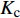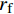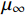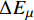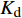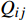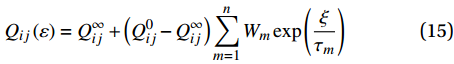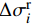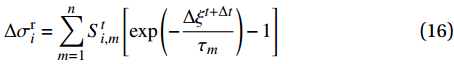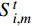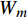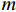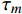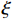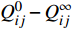Simulation of manufacture of the hat-stiffened composite plate based on multidisciplinary coupling
-
摘要: 民机复合材料帽型壁板自动化制造包含自动铺丝(AFP)和热压罐固化过程,工艺复杂,故有必要对其进行理论研究和建模。分别建立粘弹性力学和多孔渗流耦合模型对铺丝过程进行仿真;建立复合材料热传导、化学交联反应、固化动力学、多孔介质渗流和材料性能时变性耦合模型对固化过程进行仿真。应用所建立的耦合模型对AS4/3051-6系列碳纤维/环氧树脂(CFRP)预浸料热压罐固化制备复合材料平板工艺进行仿真,并将其结果与实验结果对比,验证了此方法的有效性。随后,将此方法应用于大型复合材料帽型壁板制造过程仿真,仿真结果表明:(1) AFP头在经过帽型腔体时存在下陷,下陷量与硅橡胶气囊支撑性能相关,应用本文设计芯模下陷量仿真值为原先的38%,铺丝头对蒙皮的影响面积仿真值为原先的30%;(2) 帽型加筋板内部温度与工艺温度不同,其最高温度出现在保温过程结束后升温阶段初期,预测值为工艺温度的106%,且接合处内外层温度差别明显;(3) 帽型加筋壁板内部黏度随时间先减小后急剧上升,内层黏度较外层黏度变化速率更大;(4) 帽型加筋板蒙皮平均厚度预测值由成型前的4.5 mm减少至4 mm,测量厚度为3.88 mm,仿真误差为3.1%。
-
关键词:
- 多学科耦合 /
- CFRP复合材料帽型加筋板 /
- 过程仿真 /
- 自动化制造 /
- 芯模
Abstract: The carbon fiber reinforced polymer (CFRP) hat-stiffened plate which is fabricated in wide-bodied airplane is concluded in line with manufacturing crafts of automatic fiber placement (AFP) and autoclave forming that is very complex, so it is necessary to make theoretical research and modeling. Viscoelastic mechanics and percolation model were used to simulate the AFP process, while the composite material heat conduction, curing crosslinking chemical reaction, curing dynamics and porous media percolation model were employed in the simulation of the autoclave process, every multidisciplinary model sharing coupling relationship. On this base, numerical simulation of curing process of manufacturing simple carbon fiber reinforced epoxy resin multilayer under the AS4/3501-6 resin system was carried out. The consequences of simulation were verified when compared with the experimental results. Applying this approach of simulation in CFRP hat-stiffened plate, the results manifest that: (1) The operating head of the AFP equipment can generate a sag whose extend is related to the mandrel’s supporting property, after adding the supporting structure, the simulated sag value and the affecting area value decreases to 38% and 30% compared with the original mandrel; (2) The internal temperature of the hat-stiffened plate is different from the setting process temperature, and the maximum temperature appears in the early heating stage after the end of the insulation process, the predicted value is 106% of the process temperature, and the temperature difference between the inner and outer layers at the joint is obvious; (3) The internal viscosity of the hat-stiffened panels decreases first and then increases sharply, and the change rate of the inner layer viscosity is greater than that of the outer layer; (4) The predicted average skin thickness of the hat-stiffened plate reduces from 4.5 mm before forming to 4 mm, the measured thickness is 3.88 mm, the simulation error is 3.1%. -
复合材料加筋板被大量应用于航空航天结构中[1]。又因扭转刚度高,该结构在民机大型承力壁板设计中被广泛采用[2]。复合材料帽型加筋板截面形状复杂、帽腔狭长,其制造过程复杂、工序繁多且成型质量不稳定,导致其生产效率低下。而随着复合材料帽型壁板尺寸的增大和自动化制造程度的提高,其制造周期长、制造成本高,故目前依靠经验和试制来确定成型方法、分析成型质量、改进工艺参数的方法已不能满足自动化制造需求。同时,对复合材料复杂结构制造工艺参数监测较复杂,尤其对于固化工艺,其不同部位黏度、固化度、厚度的全过程监测基本无法实现,故通过理论方法研究其制造工艺过程、通过多学科耦合模型对其工艺进行数字孪生十分必要,有利于获得更准确地预测结果,为自动化制造过程中的工艺参数优化提供支持。
Kim等[3]通过实验方法研究了共固化、共胶接、二次胶接工艺下复合材料帽型加筋板几何及力学性能的差异,发现共固化工艺制件几何分散性较小,力学性能优异。姜茂川等[4]通过真空辅助注塑(VARI)成型技术制备复合材料帽型加筋板,证明了该技术的可行性。复合材料帽型加筋板帽腔芯模的材料与芯模结构决定了帽型加筋板成型质量[5],芯模为自动铺丝提供支撑,并在固化过程中提供成型压力。对于展向长度大或者带曲率的复合材料帽型壁板,需同时满足保形、传压、脱模三方面的技术需求。蒲永伟、湛丽华[6]使用预制孔硅橡胶充当芯模,以硅橡胶的热胀效应提供成型压力,发现预制孔在12 mm时成型质量较好。Kim等[3]将金属、气囊、预制孔硅橡胶芯模进行比较,认为气囊芯模压力可达性最好而金属芯模成型质量最佳。由于实验全过程监测十分困难,Springer使用二维数值模拟分析了制造过程[7-9],将两个物理场进行耦合,并应用所建立双场耦合模型对简单平板的成型过程进行仿真。Costa等[10]建立了热传导和固化动力学相耦合的平板三维固化模型,发现厚板的固化行为与压力有密切关系。Li等[11]采用ABAQUS软件研究了成型温度对平板成型变形的影响。近期有学者建立了更全面的多物理场平板模型,将热-化学场,固化动力学及树脂流动场相耦合[12-17],其仿真结果更准确。随着分析的深入,发现材料的物理性能为时变量,会随着反应进行发生改变。元振毅等[18]基于材料时变性对复合材料平板进行了多学科建模,使用COMSOL多物理场软件对复合材料平板的固化过程进行仿真,同时研究了模具与制件间的摩擦效应对成型的影响。发现在考虑材料性能时变性和模具/制件相互作用后,成型过程中温度、压力、形变等过程量与试验数据更吻合。
本文研究帽型壁板自动化制造工艺,其工序为在厚气囊芯模的辅助下直接铺放壁板蒙皮,铺叠完毕后选择复合材料成型中普遍使用的热压罐共固化工艺进行成型。该工艺涉及多个学科和物理场,故本文对自动铺丝过程建立了黏弹性力学[19]与多孔介质渗流[20]耦合模型,使用此模型分析了铺丝过程中蒙皮的下陷量,并讨论在使用两种不同芯模结构时,下陷量的变化情况。对热压罐成型过程,本文将复合材料看作和“挤压海绵”类似的多孔结构[21],分别应用各向异性三维傅里叶热传导方程[22]、化学交联反应方程[23]、固化动力学方程、基于达西定律的多孔介质渗流方程[24-25]和材料时变性方程,建立了多物理场耦合模型。应用此模型先对复合材料厚板进行仿真,将预测结果与实验数据对比,验证了模型的可行性。后将此模型应用到复合材料帽型加筋板的热压罐制造过程仿真中,得到固化过程温度变化曲线、固化度曲线、黏度曲线、成型压力分布曲线和工艺过程减薄量曲线,实现了对复合材料帽型加筋板自动化制造过程的多场耦合仿真。
1. 多学科模型
1.1 传热模型
复合材料帽型加筋板固化过程中,温度场决定了其化学反应的程度、固化度及树脂黏度,故传热模型与其余模型间存在耦合关系。考虑复合材料的各向异性与成型过程中的树脂流动对热量的影响,使用加入流动传热项的三维傅里叶瞬态热传导定律[23]:
ρCpdTdt+ρrCrVxdTdx+ρrCrVydTdy+ρrCrVzdTdz=∂∂x(Kx∂T∂x)+∂∂y(Ky∂T∂y)+∂∂z(Kz∂T∂z)+∂Q∂t (1) 其中:
ρ 、Cp 、T、t分别为复合材料的密度、比热容、内部瞬时温度及时间;Kx 、Ky 、Kz 分别为复合材料在x、y、z 坐标轴方向的导热系数;ρr 、Cr 分别为树脂的密度和比热容;Vx 、Vy 、Vz 为x、y、z 方向树脂流动速率;Q为化学反应产生的内热源。复合材料密度和比热容可由混合律计算:ρ=vfρf+(1−vf)ρr (2) Cp=(1−vf)ρrCr+vfρfCfρ (3) 式中:
ρf 为碳纤维密度,为1790kg⋅m−3 ;Cf 、vf 分别为碳纤维比热容和纤维体积分数。复合材料各方向导热系数可使用Springer-Tsai模型[26]计算:Kx=Kr(1−vf)+KLfvf (4) Ky=(1−2√vfπ)Kr+1Dπ−4D√1−D2vfπarctan√1−D2vfπ1+D√vfπKr (5) D=2(KrKTf−1) (6) 其中,
Kr 、KLf 、KTf 分别为树脂导热系数、碳纤维沿纤维方向和垂直于纤维方向的导热系数。1.2 化学模型及材料时变性模型
复合材料板被热压罐加热,触发树脂的交联化学反应。此反应放热量与固化反应中固化度的边际相关,公式如下:
∂Q∂t=ρr(1−vf)Hrdαdt (7) 其中:
α 为固化反应的固化度;Hr 为固化完成时的总放热。除考虑复合材料整体物理性能随纤维体积分数
vf 而变化外,还考虑了纤维和树脂的物理性能的时变性,以进一步提高预测精度。在实验参数拟合的基础上,以传热模型输出温度T及固化动力学模型所输出固化度α 的一阶函数描述材料物理量的时变性,因材料性能时变性公式包含了重要工艺参数T与固化过程参数α 所产生的影响,且包含了对实验数据的拟合,其在减小计算量的同时仍可保持较高精度。对于AS4/3501-6体系,各时变性参数如表1所示。表 1 AS4/3501-6碳纤维/环氧树脂复合材料时变性性能Table 1. Time-dependent property of AS4/3501-6 carbon fiber/epoxy compositesParameter Linear time-varying description ρr/(kg⋅m−3) ρr={90α+1232α⩽ {C_{\rm{r}}}/({\rm{J}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) {C_{\rm{r} } } = 4\;184\left( {0.47 + 6 \times { {10}^{ - 4} }T - 0.14\alpha } \right) {C_{\rm{f}}}/({\rm{J}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) {C_{\rm{f} } } = 1\;390 + 4.5T {K_{\rm{r}}}/({\rm{W}} \cdot {{\rm{m}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) {K_{\rm{r}}} = 0.042\left[ {3.85 + \left( {0.035T - 0.14} \right)\alpha } \right] {K_{\rm{f}}}/({\rm{W}} \cdot {{\rm{m}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) K_{\rm{f}}^{\rm{L}} = 0.742 + 9.02 \times {10^{ - 4}}T Notes: {\rho _{\rm{r}}}—Density of resin; {C_{\rm{r}}} and {C_{\rm{f}}}—Specific heat capacity of resin and fibers; {K_{\rm{r}}} and {K_{\rm{f}}}—Heat conductivity coefficient of resin and fibers; \alpha —Curing degree; T—Internal instantaneous temperature. 1.3 固化动力学模型
树脂的固化反应是一个热激活的复杂交联反应,大多数动力学模型以经验或线性拟合公式为基础。采用唯象动力学模型,该模型不考虑固化反应过程中的动力学机制,只用简单的回归公式表述反应过程中各参数的相互影响[8]。将此模型应用到复合材料帽型壁板制造过程中,其方程为
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = \left\{ \begin{array}{l} \left( {{K_1} + {K_2}\alpha } \right)\left( {1 - \alpha } \right)\left( {0.47 - \alpha } \right)\;\;\alpha \leqslant 0.3\\ {K_3}\left( {1 - \alpha } \right)\;\;\alpha >0.3 \end{array} \right. (8) 其中,Ki (i = 1,2,3)为反应速率常数,如下式:
\begin{array}{*{20}{c}} {{K_i} = {A_i}\exp \left( {\dfrac{{ - \Delta {E_i}}}{{{{R}}T}}} \right)}&{(i = 1,2,3} ) \end{array} (9) 式中:
{A}_{i} 为频率因子;{E}_{i} 为化学反应活化能;R为普适气体常数。1.4 多孔渗流模型
在假设(a) 纤维伸展与压缩受限、(b) 树脂在纤维孔隙中为饱和连续流动、(c) 纤维质量不发生变化的前提下,复合材料固化成型过程中的树脂溢出可看作纤维床“压缩海绵”[21],此过程基于Biot固结原理的多孔渗流建立模型,使用三维Darcy定律来描述渗流过程中的压力分布、流速和黏度,得到影响材料时变性模型的树脂压力
{p_{\rm{r}}} 、影响传热模型的流动速率{V_i} 和工艺参数\mu ,各方程如下:\begin{split} \frac{{{K_x}}}{{{v_{\rm{f}}}}}\frac{{{\partial ^2}{P_{\rm{r}}}}}{{\partial {x^2}}} + \frac{{{K_y}}}{{{v_{\rm{f}}}}}\frac{{{\partial ^2}{P_{\rm{r}}}}}{{\partial {y^2}}} + \frac{1}{{{v_0}}}\frac{\partial }{{\partial {\textit{z}}}}\left( {{v_{\rm{f}}}{K_{\textit{z}}}\frac{{\partial {P_{\rm{r}}}}}{{\partial {\textit{z}}}}} \right) = \mu \frac{\partial }{{\partial t}}\left( {\frac{{1 - {v_{\rm{f}}}}}{{{v_{\rm{f}}}}}} \right) \end{split} (10) 其中:
{p_{\rm{r}}} 为树脂压力;{v_0} 为反应开始前纤维体积分数;{K_{i{\rm{ = }}x,y,{\textit{z}}}} 为复合材料渗透率;\mu 为树脂黏度。{K_{i{\rm{ = }}x,y,{\textit{z}}}} 、\mu 与其化学、物理性质和固化动力学模型的输出固化度\alpha 有关,公式分别为{{K_i} = \dfrac{{{{{r}}_{\rm{f}}}}}{{4{K_{\rm{c}}}}}\dfrac{{{{\left( {1 - {{{r}}_{\rm{f}}}} \right)}^3}}}{{{{{r}}_{\rm{f}}}^2}}}\;\;{(i = x,y,{\textit{z}})} (11) \mu = {\mu _\infty }\exp \left( {\frac{{\Delta {E_\mu }}}{{{{R}}T}} + {K_{\rm{d}}}\alpha } \right) (12) 式中:
{K_{\rm{c}}} 为Kozeny-Carman常数,其与纤维结构和树脂流动方向有关,具有各向异性特性,平行于纤维方向的{K_{\rm{c}}} 值为0.6,垂直于纤维方向为14.2;{r_{\rm{f}}} 为纤维半径;{\mu _\infty } 为指前常数;\Delta {E_\mu } 为黏流活化能;{K_{\rm{d}}} 为温度独立常数。应用Darcy定律所表示的树脂在纤维丛中的流速如下:
{{V_i} = - \dfrac{{{K_i}}}{\mu }\dfrac{{{\rm{d}}{p_{\rm{r}}}}}{{{\rm{d}}i}}}{\left( {i = x,y,{\textit{z}}} \right)} (13) 1.5 黏弹性力学模型
假设复合材料有简单热流变材料性质(LSMs),则各向异性黏弹性增量本构[19]方程为
\Delta \sigma _i^{t + \Delta t} = {Q_{ij}}\Delta \varepsilon _j^{t + \Delta t} + \Delta \sigma _i^{\rm{r}} (14) {Q}_{ij} 为复合材料松弛刚度,广义Maxwell模型为{Q_{ij}}\left( \varepsilon \right) = Q_{ij}^\infty + \left( {Q_{ij}^0 - Q_{ij}^\infty } \right)\sum\limits_{m = 1}^n {{W_m}\exp \left( {\frac{\xi }{{{\tau _m}}}} \right)} (15) 本构方程中的
\Delta {\sigma }_{i}^{\mathrm{r}} 可表示为\Delta \sigma _i^{\rm{r}} = \sum\limits_{m = 1}^n {S_{i,m}^t\left[ {\exp \left( { - \frac{{\Delta {\xi ^{t + \Delta t}}}}{{{\tau _m}}}} \right) - 1} \right]} (16) 式中:
S_{i,m}^t 是历史变量,初始值取0;{W_m} 为第m 个麦克斯韦权衡因子;{\tau _m} 是第m个麦克斯韦松弛时间;\xi 为缩减时间。Q_{ij}^0 - Q_{ij}^\infty 为平衡状态与初始状态的刚度差。麦克斯韦方程原理图如图1所示。1.6 各模型耦合关系
在不做任何简化的前提下,制造工艺过程所涉及物理场存在耦合关系。耦合分为强耦合和弱耦合,强耦合为两个模型之间存在双向数据交换,互相影响;弱耦合为两模型间单向影响,数据单向交换。
各模型耦合关系、方程及传递参数如表2所示。
表 2 多学科模型及耦合关系Table 2. Multi-disciplinary model and coupling connectionsDisciplinary model Equation Coupling object Mode Output/Input parameter Thermal conduction Fourier heat equation Chemical reaction & Curing kinetic Bi-direction T Chemical reaction Crosslinking equation Thermal conduction & Curing kinetic Bi-direction Q Curing kinetic Partial differential equation Porous filtration & Chemical reaction Bi-direction dα/dt, α Porous filtration Darcy’s law Thermal conduction Uni-direction P, {V_i}, h Time-varying behavior Linear equation All models Bi-direction K, C, \rho Viscoelastic mechanics Constitutive equation Filtration in AFP Uni-direction \sigma Notes: AFP—Automatic fiber placement; Q—Chemical reaction heat; P—Tnner forming pressure; Vi—Flow rate during curing process; h—Thickness of the plate or the hat; K—Heat conductivity coefficient; C—Specific heat; ρ—Density of the composite; σ—Stress in AFP. 具体耦合关系如下:(1) 自动铺丝过程:黏弹性力学模型与多孔渗流模型存在弱耦合,后者为前者提供以“压力井”形式分布的载荷;(2) 复合材料热压罐固化成型过程中,各模型之间耦合关系复杂,下文进行详细分析。
(a) 传热模型与化学反应模型、固化动力学模型之间存在强耦合关系,且为化学反应模型及固化动力学模型提供温度场,而化学反应模型中的放热项和固化动力学模型中的固化度场又影响传热模型。
(b) 材料时变性与其余模型均存在强耦合关系,随反应的进行,树脂及纤维属性受其余模型输出量的影响,而这些模型的输入量有赖于通过时变性模型对材料物理属性进行更新。
(c) 多孔渗流模型与传热模型间为弱耦合关系,多孔渗流模型输出的复合材料厚度和树脂流动速率为传热模型的输入量。
(d) 固化动力学模型与多孔渗流模型为弱耦合关系,且与化学反应模型存在强耦合关系,固化动力学模型输出的固化率为渗流模型的输入量,而渗流过程亦会影响固化率的大小。
2. CFRP平板成型有限元仿真方法及验证
2.1 CFRP平板有限元仿真方法介绍
本节采用上述多学科耦合模型对复合材料平板成型进行仿真,并与复合材料板成型实验数据对比,证明所建立模型的正确性。
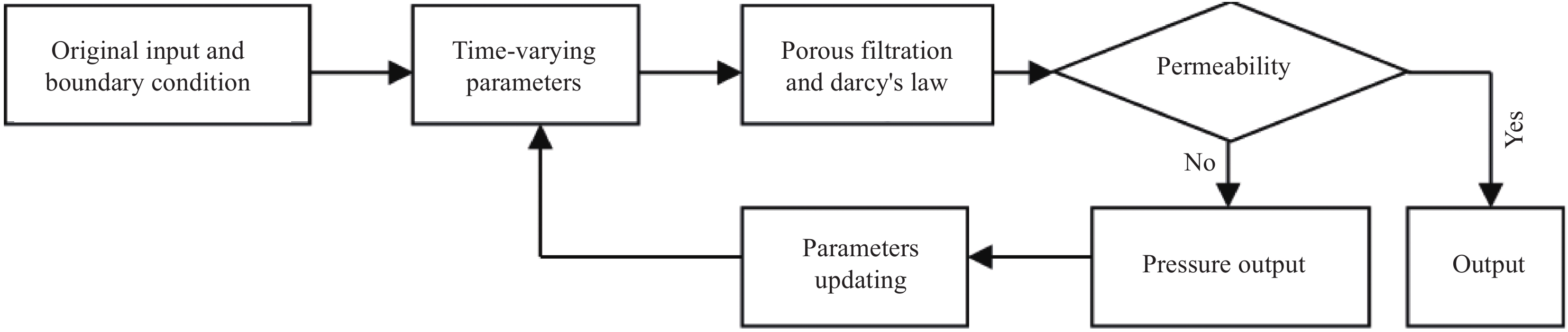
应用多物理场有限元分析软件COMSOL对复合材料板的制造进行有限元数值仿真。采用全局变量描述固化过程中复合材料性能发生的变化。根据上述理论模型,采用COMSOL软件流体流动模块中的多孔介质和地下水流模块、固体传热模块、流体模块、自定义系数型偏微分方程模块,将各模块耦合并进行仿真,得到复合材料板各处树脂黏度、工艺温度、固化度、态纤维体积分数等关键量的变化情况,并根据下式得到复合材料板的减薄量:
- \frac{{{\rm{d}}\left( {hA} \right)}}{{{\rm{d}}t}} = \frac{{{K_{\textit{z}}}{p_{\rm{r}}}}}{{\mu h}} (17) 其中,h为预测工艺过程瞬时厚度,其余参数可由多孔渗流模型得到。
仿真原理图如图2所示。
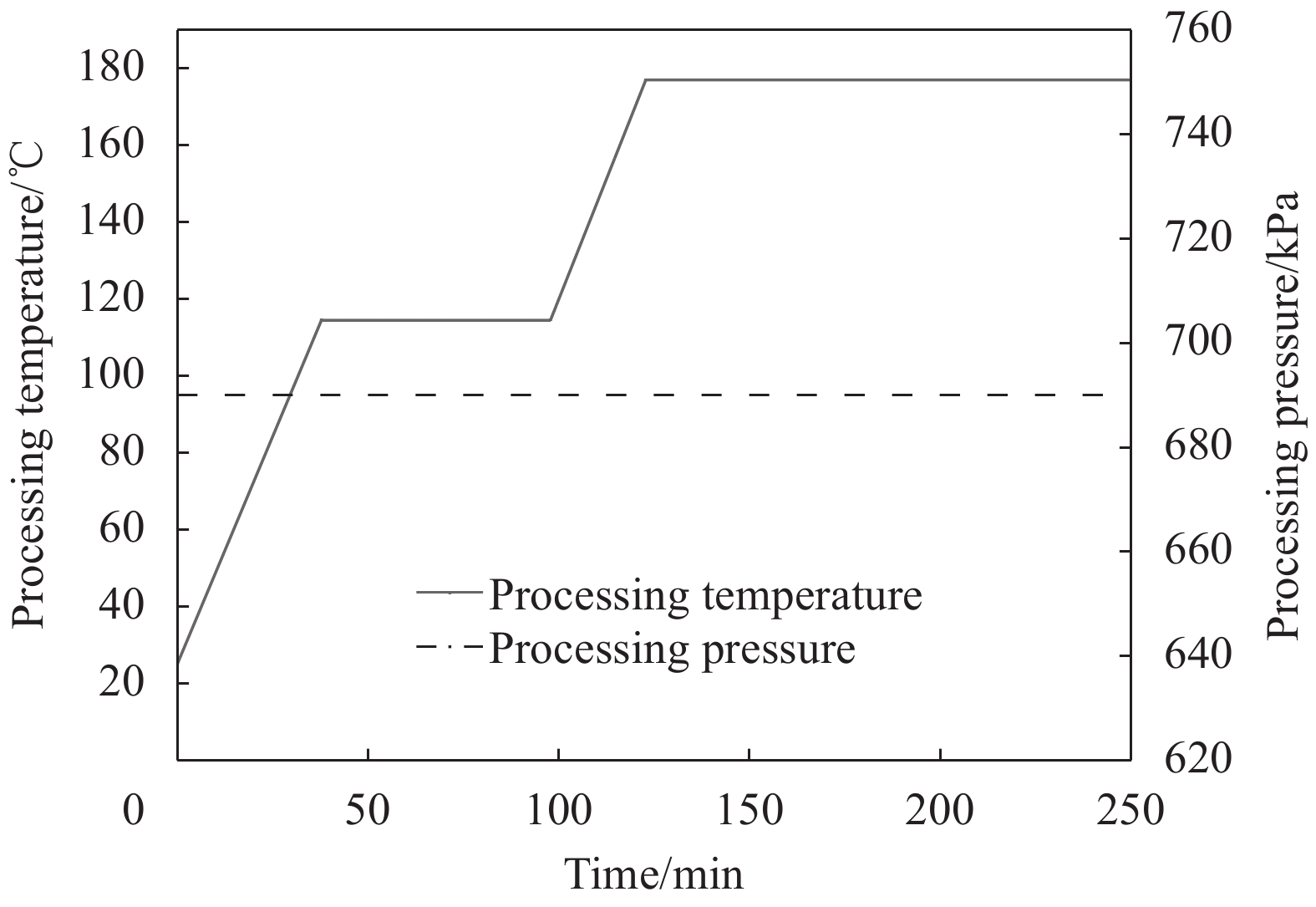
复合材料板铺层方式为[0°/90°/90°/0°],尺寸为10 cm×10 cm,单层厚度为0.625 cm,总厚度为2.5 cm,其余化学参数如表3所示。固化过程热压罐工艺温度及压力曲线如图3所示。
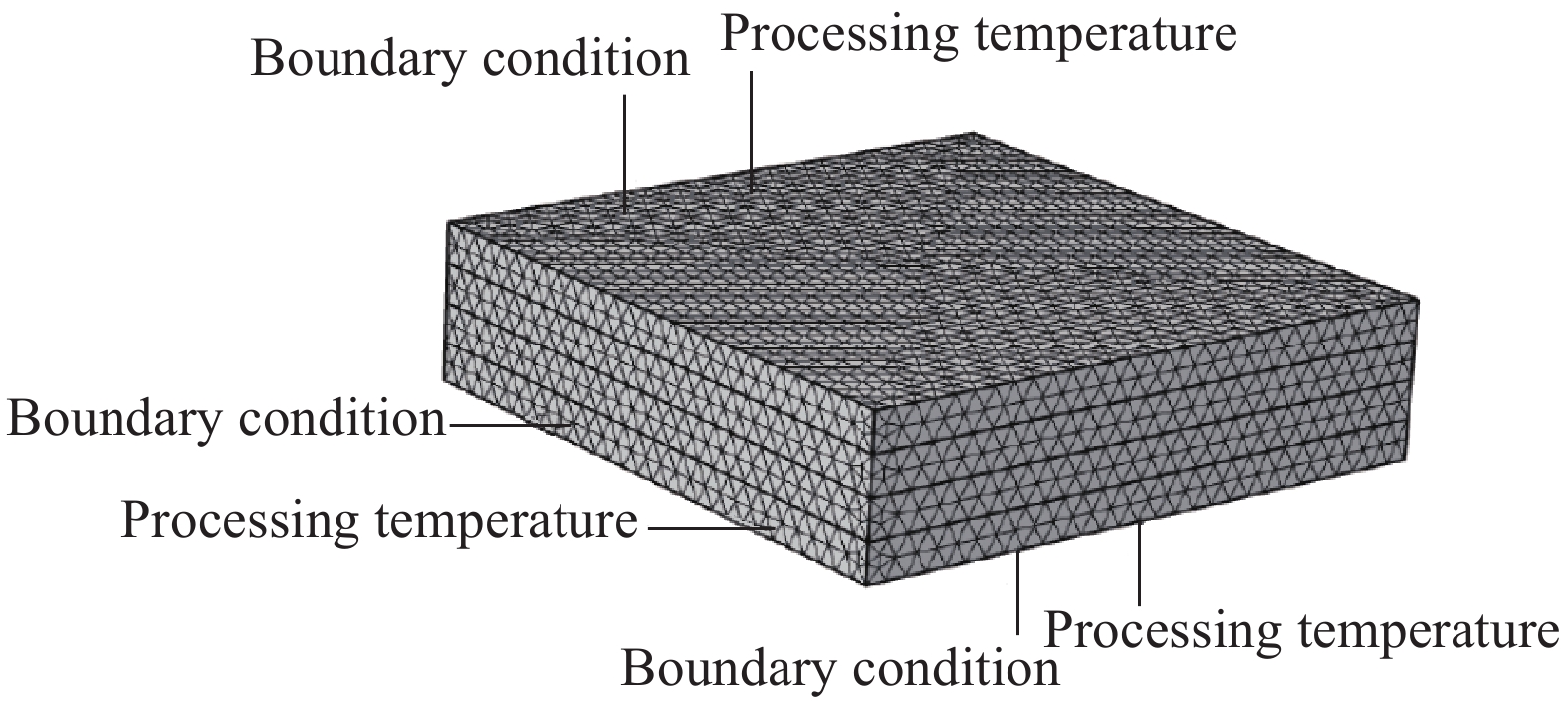
表 3 CFRP复合材料板多学科性能Table 3. Multi-disciplinary behavior of CFRP plateParameter Value Parameter Value {A_1}/{\min ^{ - 1}} 2.102×109 \Delta {E_\mu }/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 9.43×104 {A_2}/{\min ^{ - 1}} −2.014×109 {{R/} }\left( { {\rm{J} } \cdot {\rm{mo} }{ {\rm{l} }^{ - 1} } \cdot { {\rm{K} }^{ - 1} } } \right) 8.3143 {A_3}/{\min ^{ - 1}} 1.96×105 {\mu _\infty }/\left( {{\rm{Pa}} \cdot {\rm{s}}} \right) 7.93×10−14 \Delta {E_1}/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 8.07×104 {r_{\rm{f}}}/m 4×10−6 \Delta {E_2}/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 7.78×104 {K_{\rm{c}}}(Parallel to fiber) 0.6 \Delta {E_3}/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 5.66×104 {K_{\rm{c}}}(Vertical to fiber) 14.2 Notes: A1, A2, A3—Frequency factors; ∆E1, ∆E2, ∆E3—Activation energy; \Delta {E_\mu }—Activation energy of viscous; {\mu _\infty }—Constant; R—Universal gas constant; {r_{\rm{f}}}—Radius of carbon fiber; {K_{\rm{c}}}—Kozeny constant. 热压罐固化工艺包括以下阶段:第一阶段以2.5℃/min的速率由室温上升至116℃,恒温保持1 h以促进其化学交联反应进行。后以相同速率加热25 min,并保持177℃的罐内温度直至工艺结束进行降温。工艺压力始终为690 kPa。据此设定边界条件,采用自适应网格对模型进行网格划分,如图4所示。
2.2 CFRP平板成型实验数据验证
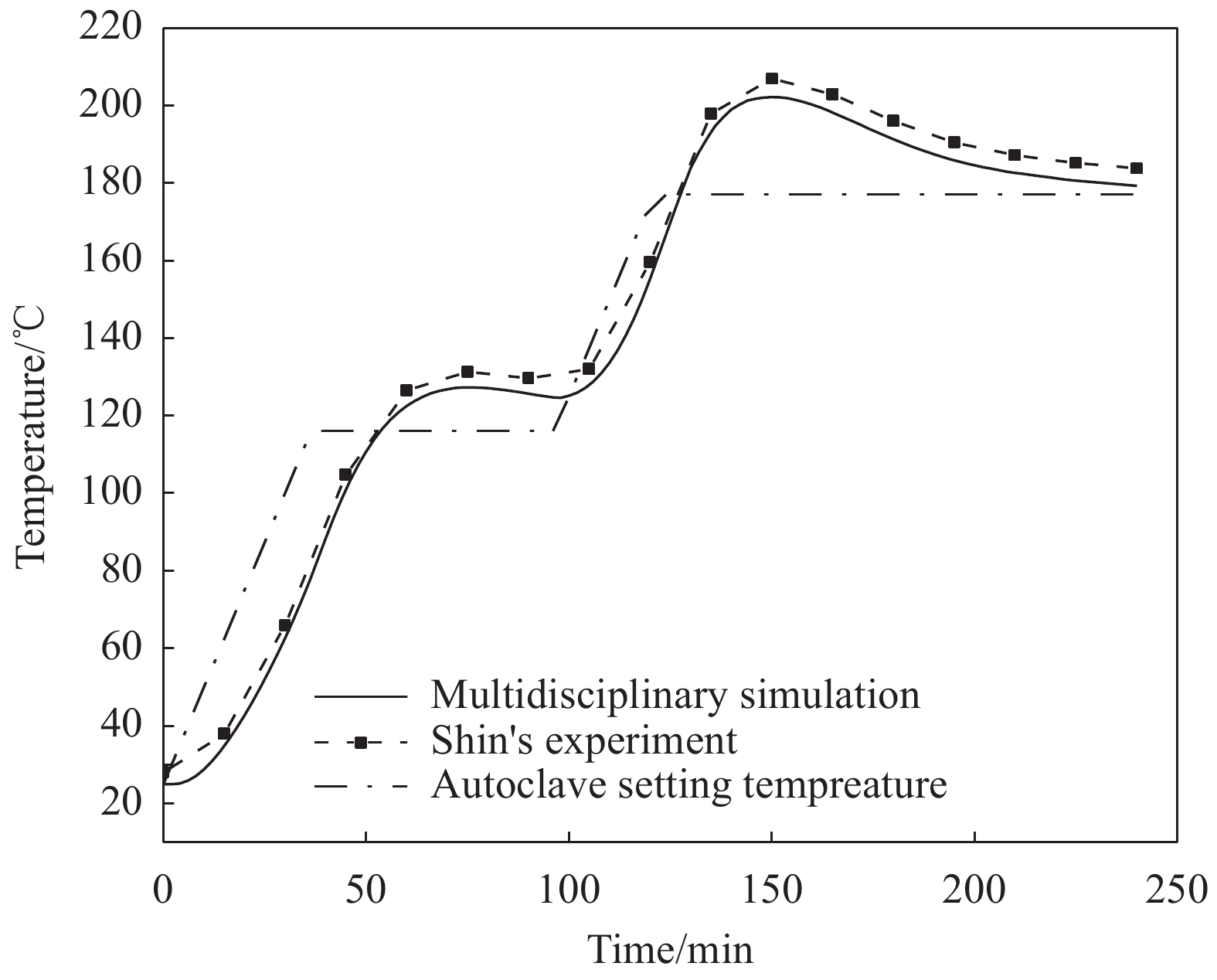
基于上述多学科仿真方法,应用软件COMSOL进行仿真,得到了平板内部各点温度变化、固化度与成型过程减薄量曲线,与Daniel等[16]和Kim等[17]试验结果进行对比。考虑到制造过程在线监测技术的复杂性和局限性,其对比结果一致性良好,最大误差控制在10%以内,如图5、图6、图7所示,由此说明此仿真方法的正确性。
2.3 CFRP平板成型其他物理量仿真分析
应用经过验证的仿真方法,可得出平板固化过程中其他影响成型质量的物理量变化情况。
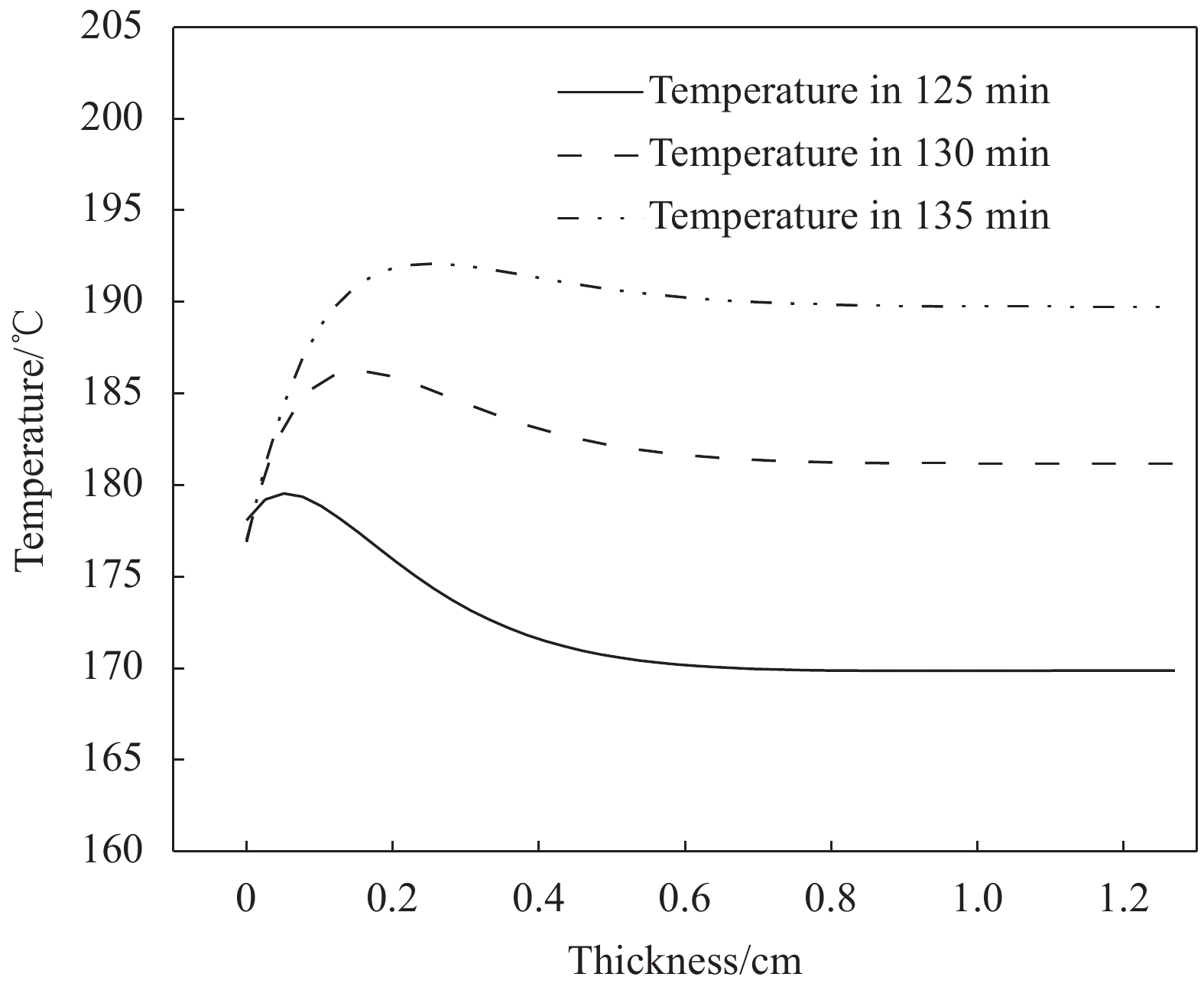
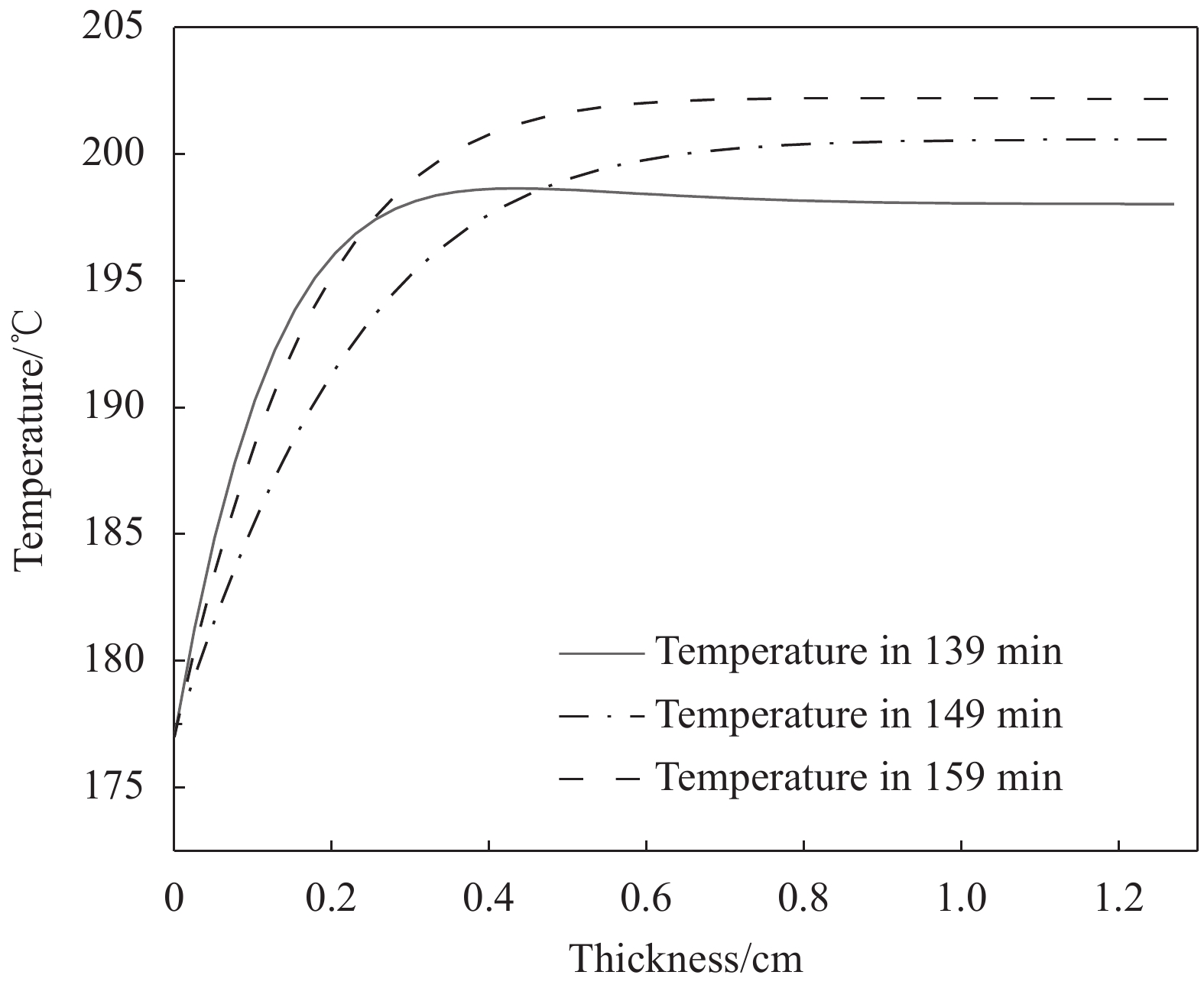
复合材料板各点温度随时间变化曲线如图8所示。由于复合材料传热较差且具有各向异性,其厚度方向温度分布较复杂,图9、图10、图11为三个典型阶段面内温度分布曲线。
图9为加热刚开始阶段,由于复合材料热导系数较小且厚度较大,温度外高内低,平板中心温度显著低于热压罐工艺温度。随着表面温度上升,靠外侧树脂先发生化学反应,导致从边缘至中心的温度先增后减(图10)。最后随着化学交联反应剧烈进行而内部散热不佳,温度为内高外低,内部层温度显著高于外部,如图11所示。
同时可得到树脂黏度在纤维网中的变化曲线(图12),其黏度先减小,后随着化学交联反应进行而迅速增加。
3. 帽型加筋板制造过程仿真
3.1 自动铺丝工序仿真
帽型加筋板自动铺丝工艺可分为五步,分别为外部模具准备、帽型筋条铺放、薄层硅橡胶气囊芯模放置、上层蒙皮铺放、合模后热压罐固化成型,本文研究的铺丝工艺如图13所示,机器人辅助铺丝过程如图14所示。
由于帽型腔内气囊芯模支撑能力不足,在芯模中增加了快卸机械结构[27]来减少铺丝头的下陷。
通过对复合材料帽型加筋板自动化制造过程的研究分析,发现其自动铺丝过程与黏弹性力学模型和多孔介质渗流模型相关。由于铺丝过程中丝束带并未固化,其受压行为可采用黏弹性力学模型进行描述,而自动铺丝机压力头所引起的树脂在纤维丛中的流动可用多孔介质渗流模型进行描述,因此将铺丝机压力头简化为渗流模型中的压力井,与传统固体力学中将铺丝头简化为点压力的方法对比,其预测的蒙皮自动铺丝下陷量更准确。
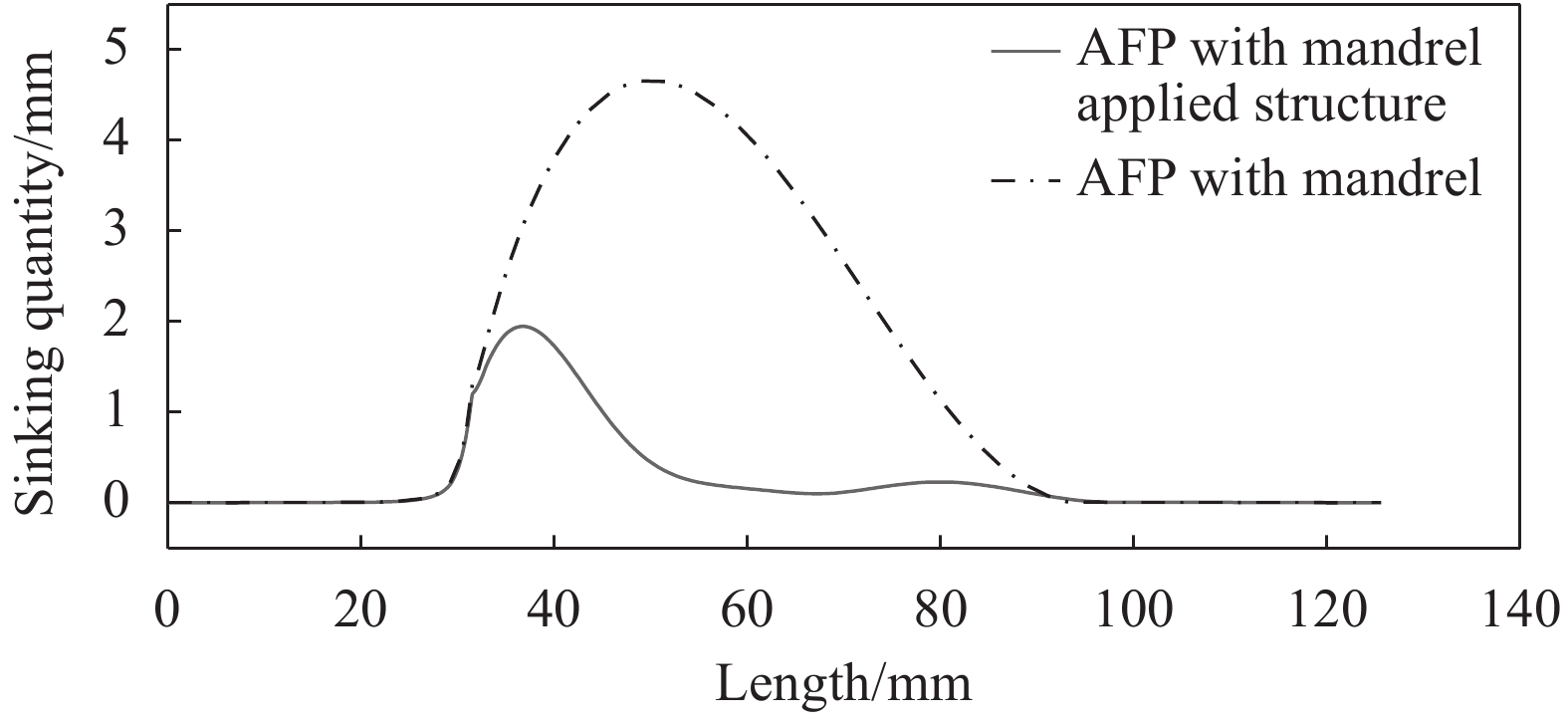
应用此模型仿真得到自动铺丝时的下陷量,对比两种模具下由于自动铺丝头压力造成的下陷量,若为硅橡胶气囊芯模,铺丝头压力造成的下陷量达到4.7 mm,且铺丝头压力影响面较大,因此可能造成丝束弯曲及内部缺陷。采用第二种芯模的制造流程如图15所示,在不影响脱模的前提下改善了芯模支撑性能,其下陷量为原先下陷量的38%,对蒙皮影响面面积为原先影响面面积的30% (图16)。
3.2 热压罐固化工艺仿真
帽型复合材料壁板热压罐成型全过程监测技术十分复杂,故使用经过复合材料板验证的上述多学科耦合模型对体系为AS4/3501-6的帽型壁板成型过程物理量进行模拟,尺寸参数及铺层顺序如图17所示,热压罐固化工艺与复合材料板固化工艺相同。
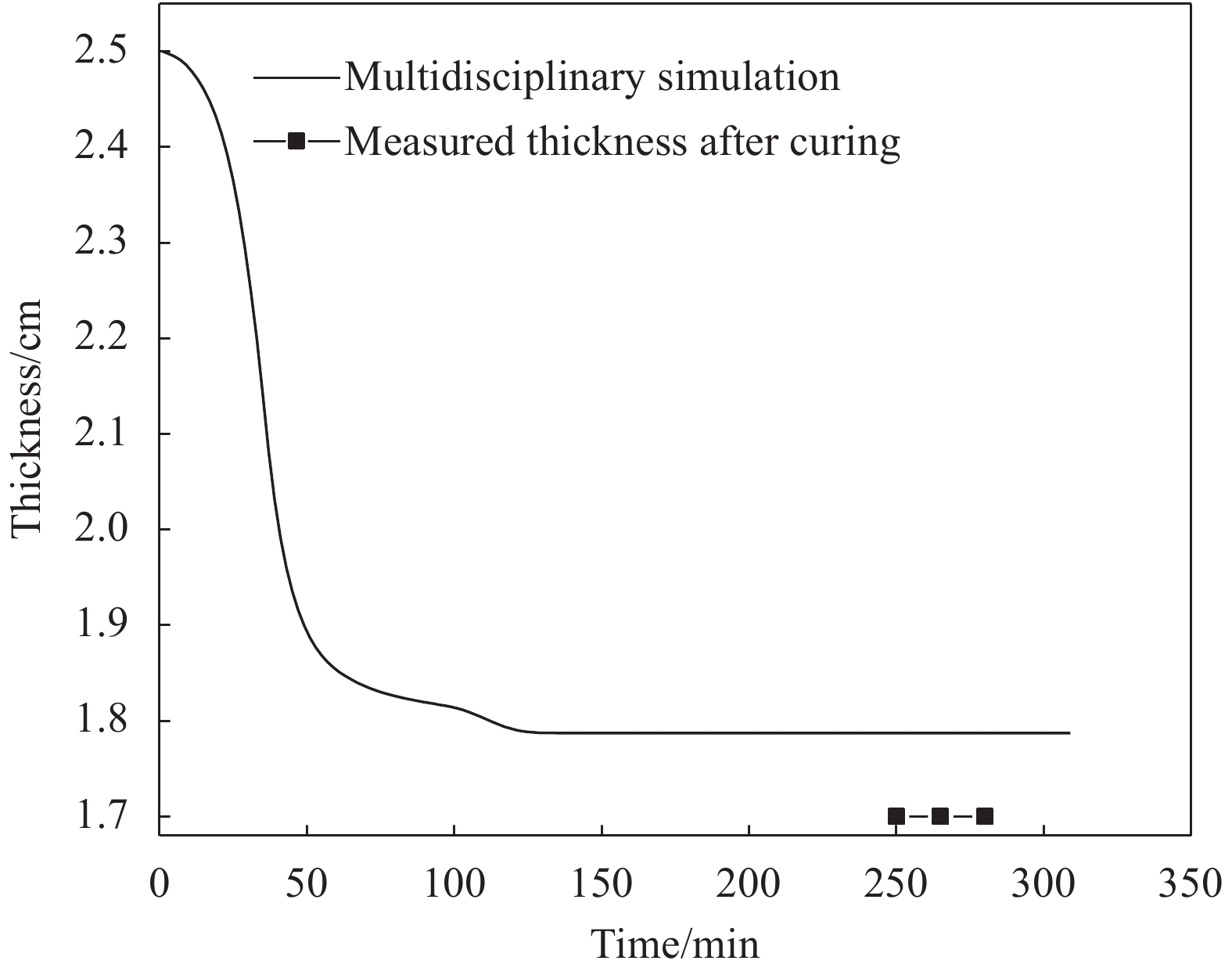
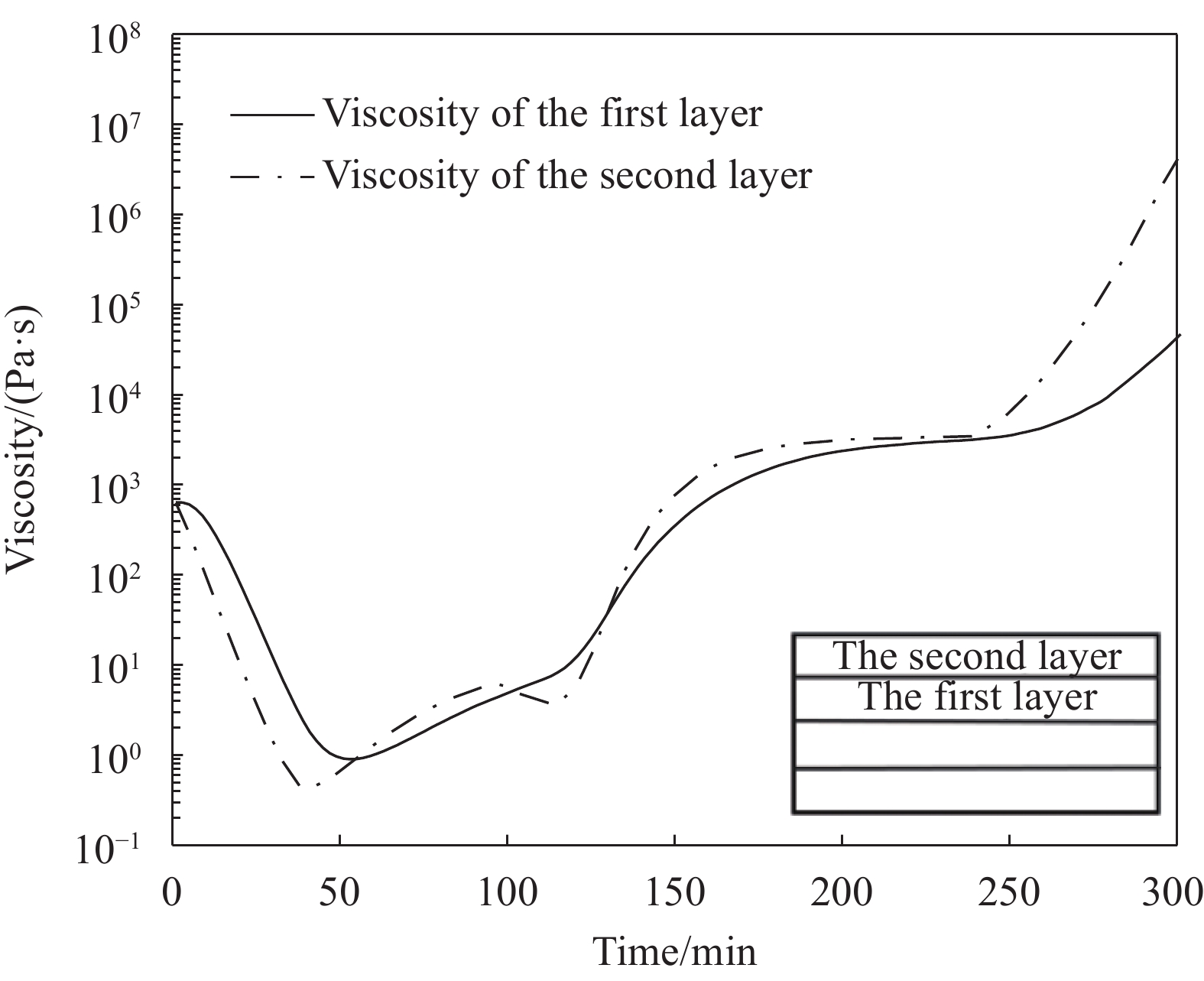
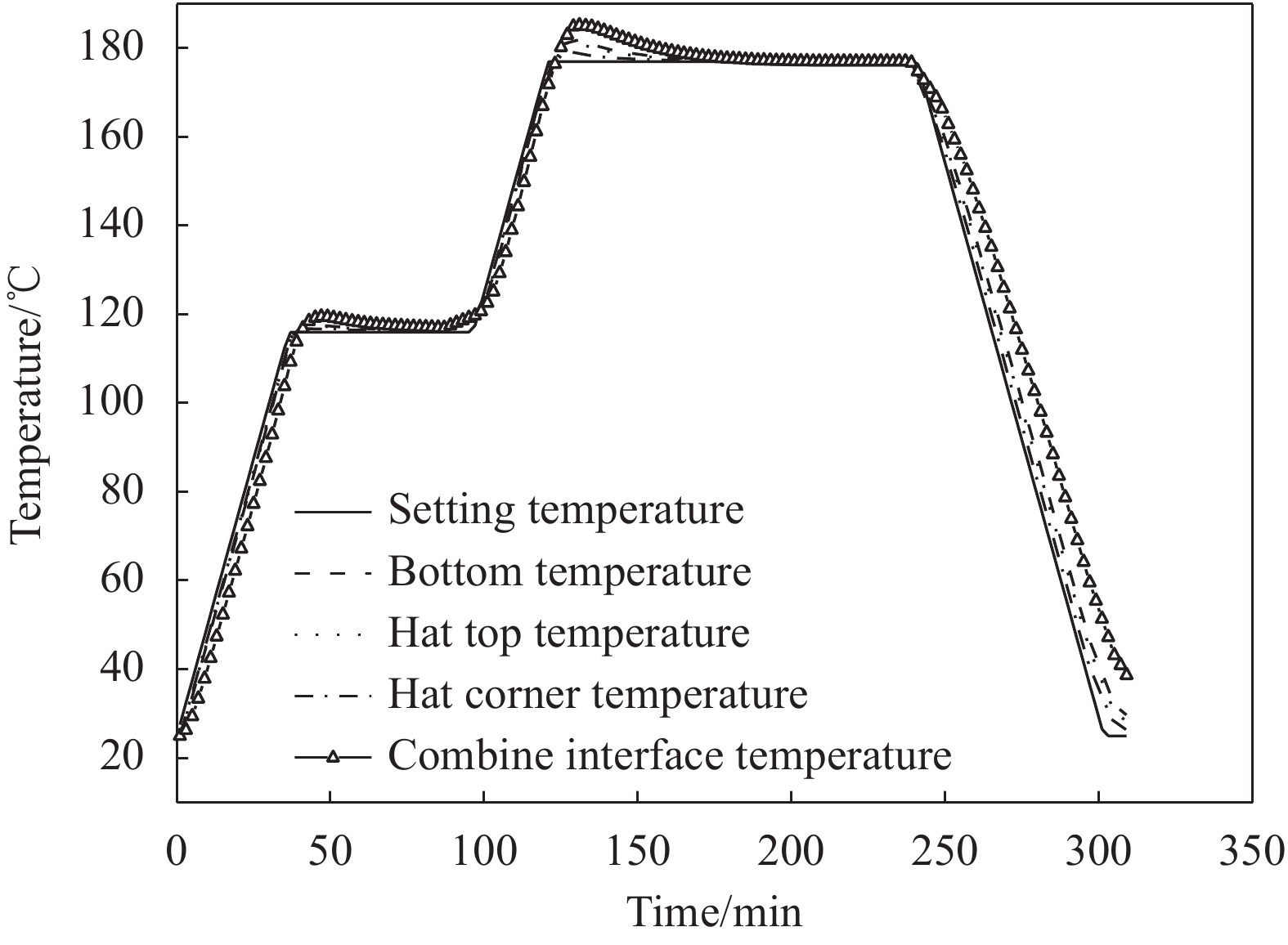
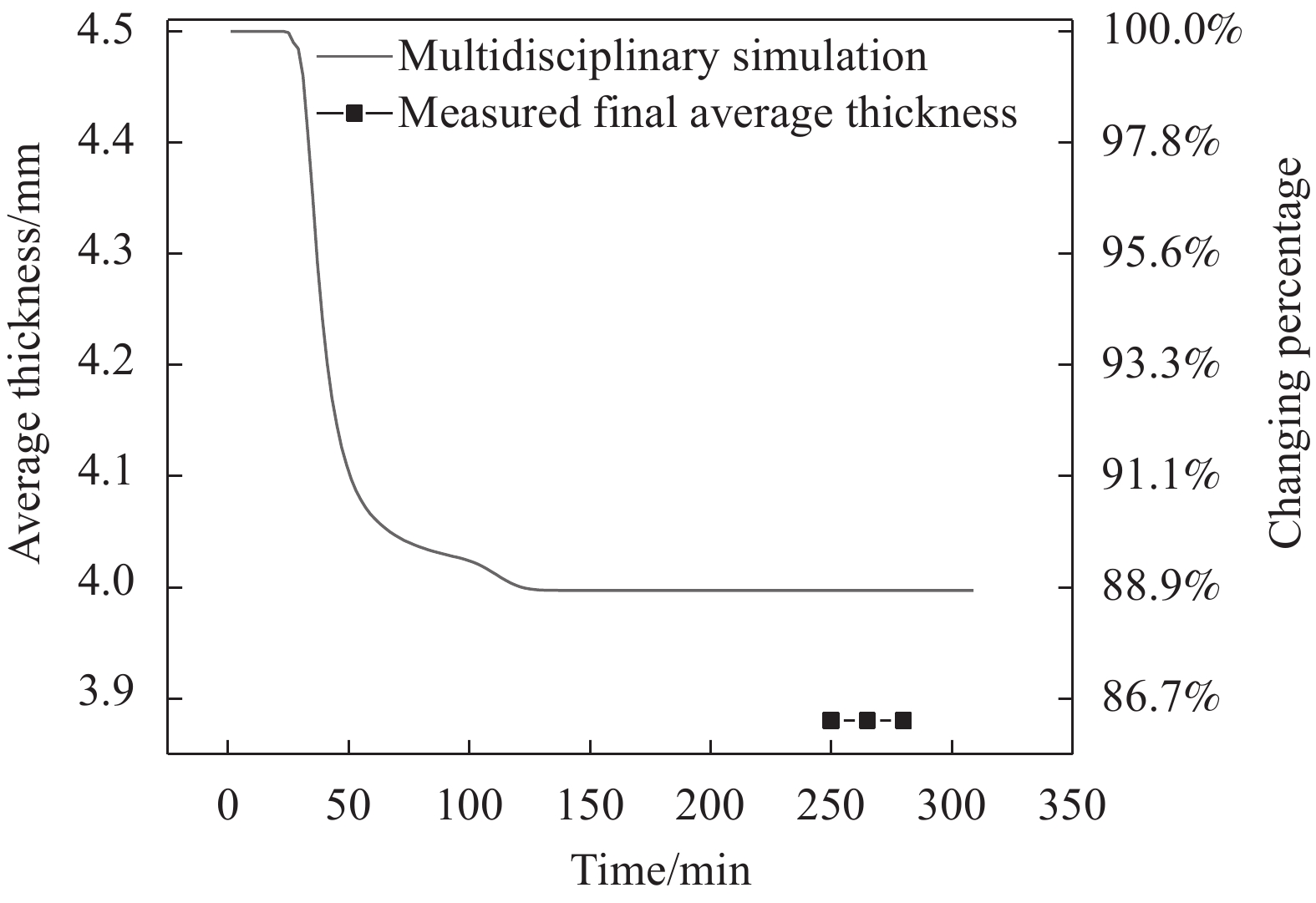
应用上述方法,对复合材料帽型加筋板固化过程进行仿真,得到蒙皮与筋条结合面的温度分布曲线(图18),固化度曲线(图19)与黏度曲线(图20)。成型过程厚度减薄量如图21所示,将成型后的帽型加筋板蒙皮厚度与商飞复材中心所提供的测量值进行比较,误差在8%以内。
4. 结 论
(1) 采用黏弹性力学与多孔渗流耦合模型,对复合材料帽型加筋板蒙皮铺丝下陷量进行仿真,发现在使用硅橡胶气囊芯模时铺丝下陷量达到4.7 mm,且铺丝头压力影响面积较大,故可能造成丝束弯曲及内部缺陷。采用本文设计的带有内部结构的芯模,在不影响脱模的前提下改善了芯模支撑性能,其下陷量仿真值仅为原先下陷量的38%,影响面积为原先的30%。
(2) 采用传热、固化动力学、化学交联反应、多孔渗流和材料性能时变性模型描述热压罐固化过程,分析各学科耦合关系,建立多学科耦合仿真方法。应用此方法对复合材料平板工艺参数进行预测,并与复合材料平板实验数据进行对比,结果表明:(a) 内部中心点预测温度与实验数据基本一致,仅在第一段加热末期存在误差,误差在10%以内;(b) 内部中心点固化度仿真结果与实验结果吻合,对树脂固化机制定性分析后发现,较实验曲线更能反映实际固化度变化情况;(c) 成型后平板厚度预测值为1.8 cm,厚度减小27%,与测量值较一致。
(3) 复合材料平板成型过程中,在加热开始阶段,复合材料热导系数较小且厚度较大,温度为外高内低,平板中心温度显著低于热压罐工艺温度,为工艺温度的60%~78%。随着表面温度上升,靠外侧树脂先发生化学反应,导致从边缘至中心的温度先增后减。最后随着化学交联反应剧烈进行而内部散热不佳,温度为内高外低,内部层温度高于外部10%~15%。
(4) 应用该多场耦合仿真方法对复合材料帽型加筋板固化工艺开展仿真分析,研究结果表明:(a) 帽型加筋板内部温度与工艺温度不同,其最高温度出现在保温过程结束后升温阶段初期,预测值为工艺温度的106%,且接合处内外层温度差别明显;(b) 帽型加筋壁板内部黏度随时间先减小后急剧上升,内层黏度较外层黏度变化速率更大;(c) 蒙皮平均厚度由成型前的4.5 mm减小至4 mm,减薄量为11%,测量厚度为3.88 mm,减薄量为13%,仿真误差为3.1%。
致谢:感谢上海商用飞机制造有限责任公司复材中心的数据支持。
-
表 1 AS4/3501-6碳纤维/环氧树脂复合材料时变性性能
Table 1 Time-dependent property of AS4/3501-6 carbon fiber/epoxy composites
Parameter Linear time-varying description {\rho _{\rm{r}}}/({\rm{kg}} \cdot {{\rm{m}}^{ - 3}}) {\rho _{\rm{r} } } = \left\{ \begin{array}{l}90\alpha + 1\;232\quad \alpha \leqslant0.45\\1\;272\qquad \quad \;\;\alpha \geqslant0.45\end{array} \right. {C_{\rm{r}}}/({\rm{J}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) {C_{\rm{r} } } = 4\;184\left( {0.47 + 6 \times { {10}^{ - 4} }T - 0.14\alpha } \right) {C_{\rm{f}}}/({\rm{J}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) {C_{\rm{f} } } = 1\;390 + 4.5T {K_{\rm{r}}}/({\rm{W}} \cdot {{\rm{m}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) {K_{\rm{r}}} = 0.042\left[ {3.85 + \left( {0.035T - 0.14} \right)\alpha } \right] {K_{\rm{f}}}/({\rm{W}} \cdot {{\rm{m}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}) K_{\rm{f}}^{\rm{L}} = 0.742 + 9.02 \times {10^{ - 4}}T Notes: {\rho _{\rm{r}}}—Density of resin; {C_{\rm{r}}} and {C_{\rm{f}}}—Specific heat capacity of resin and fibers; {K_{\rm{r}}} and {K_{\rm{f}}}—Heat conductivity coefficient of resin and fibers; \alpha —Curing degree; T—Internal instantaneous temperature. 表 2 多学科模型及耦合关系
Table 2 Multi-disciplinary model and coupling connections
Disciplinary model Equation Coupling object Mode Output/Input parameter Thermal conduction Fourier heat equation Chemical reaction & Curing kinetic Bi-direction T Chemical reaction Crosslinking equation Thermal conduction & Curing kinetic Bi-direction Q Curing kinetic Partial differential equation Porous filtration & Chemical reaction Bi-direction dα/dt, α Porous filtration Darcy’s law Thermal conduction Uni-direction P, {V_i}, h Time-varying behavior Linear equation All models Bi-direction K, C, \rho Viscoelastic mechanics Constitutive equation Filtration in AFP Uni-direction \sigma Notes: AFP—Automatic fiber placement; Q—Chemical reaction heat; P—Tnner forming pressure; Vi—Flow rate during curing process; h—Thickness of the plate or the hat; K—Heat conductivity coefficient; C—Specific heat; ρ—Density of the composite; σ—Stress in AFP. 表 3 CFRP复合材料板多学科性能
Table 3 Multi-disciplinary behavior of CFRP plate
Parameter Value Parameter Value {A_1}/{\min ^{ - 1}} 2.102×109 \Delta {E_\mu }/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 9.43×104 {A_2}/{\min ^{ - 1}} −2.014×109 {{R/} }\left( { {\rm{J} } \cdot {\rm{mo} }{ {\rm{l} }^{ - 1} } \cdot { {\rm{K} }^{ - 1} } } \right) 8.3143 {A_3}/{\min ^{ - 1}} 1.96×105 {\mu _\infty }/\left( {{\rm{Pa}} \cdot {\rm{s}}} \right) 7.93×10−14 \Delta {E_1}/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 8.07×104 {r_{\rm{f}}}/m 4×10−6 \Delta {E_2}/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 7.78×104 {K_{\rm{c}}}(Parallel to fiber) 0.6 \Delta {E_3}/\left( {{\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) 5.66×104 {K_{\rm{c}}}(Vertical to fiber) 14.2 Notes: A1, A2, A3—Frequency factors; ∆E1, ∆E2, ∆E3—Activation energy; \Delta {E_\mu }—Activation energy of viscous; {\mu _\infty }—Constant; R—Universal gas constant; {r_{\rm{f}}}—Radius of carbon fiber; {K_{\rm{c}}}—Kozeny constant. -
[1] 杜善义, 关志东. 我国大型客机先进复合材料技术应对策略思考[J]. 复合材料学报, 2008, 25(1):1-10. DOI: 10.3321/j.issn:1000-3851.2008.01.001 DU Shanyi, GUAN Zhidong. Strategy consideration for development of advanced technology for large commercial aircraft in China[J]. Acta Materiae Compositae Sinica,2008,25(1):1-10(in Chinese). DOI: 10.3321/j.issn:1000-3851.2008.01.001
[2] PRUSTY B G. Free vibration and bulking response of hat-stiffened composite plate under general loading[J]. International Journal of Mechanical Science,2008,50(8):1326-1333. DOI: 10.1016/j.ijmecsci.2008.03.003
[3] KIM G H, CHOI J H, KWEON J H. Manufacture and performance evaluation of the composite hat-stiffened plate[J]. Composite Structures,2010,92(9):2276-2284. DOI: 10.1016/j.compstruct.2009.07.019
[4] 姜茂川, 赵龙, 刘强, 等. VARI液体成型工艺制备复合材料帽型泡沫夹心构件的工艺模拟及验证[J]. 复合材料学报, 2013(S1):266-272. JIANG Maochuan, ZHAO Long, LIU Qiang, et al. Process simulation of composite cap sharped foam core sandwich structure by VAIR process[J]. Acta Materiae Compositae Sinica,2013(S1):266-272(in Chinese).
[5] LI Shujian, PU Yongwei. Effect of mandrel structures on co-curing quality for polymer composite hat stiffened structures[J]. Fiber and Polymers,2015,16(9):1898-1907. DOI: 10.1007/s12221-015-5051-1
[6] 蒲永伟, 湛利华. 复合材料帽型结构热压共固化成型质量研究[J]. 航空材料学报, 2015, 35(5):75-81. PU Yongwei, ZHAN Lihua, et al. Research on quality of autoclave co-curing manufacture of composite hat stiffened structure[J]. Journal of Aeronautical Materials,2015,35(5):75-81(in Chinese).
[7] 马成, 赵聪, 王显峰. 气囊硬度对固化后帽型长桁厚度的影响[J]. 航空学报, 2018, 35(6):162-170. MA Cheng, ZHAO Cong, WANG Xianfeng. Effect of thickness of stringer with the hardness of airbag[J]. Acta Aeronautica et Astronautica Sinica,2018,35(6):162-170(in Chinese).
[8] LOOS A C, SPRINGER G S. Curing of epoxy matrix compo-site[J]. Journal of Composite Materials,1983,17(2):135-169. DOI: 10.1177/002199838301700204
[9] 唐占文, 张博明. 复合材料设计制造一体化技术中的固化变形预测技术[J]. 航空制造技术, 2014(15):32-37. DOI: 10.3969/j.issn.1671-833X.2014.15.003 TANG Zhanwen, ZHANG Boming. The prediction technique of curing deformation in manufacture-design integration of composite material[J]. Aeronautical Manufacturing Technology,2014(15):32-37(in Chinese). DOI: 10.3969/j.issn.1671-833X.2014.15.003
[10] COSTA V A F, SOUSA A C M. Modeling of flow thermo-kinetics during the cure of thick laminated composites[J]. International Journal of Thermal Sciences,2003,42(1):15-22. DOI: 10.1016/S1290-0729(02)00003-0
[11] LI J, YAO X, LIU Y., et al. A study of integrated composite material structure under different fabrication processing[J]. Composite Part A: Applied Science and Manufacturing,2009,40(4):455-462. DOI: 10.1016/j.compositesa.2008.10.022
[12] WANG C, YUE G, BAI G, et al. Compaction behavior and permeability property tests of preforms in vacuum-assisted resin transfer molding using a combined device[J]. Measurement,2016,90:357-364. DOI: 10.1016/j.measurement.2016.04.058
[13] SIMACEK P, SINHA S, et al. A process model for the compaction and saturation of partially impregnated thermoset prepreg tapes[J]. Composites Part A: Applied Science and Manufacturing,2014,64(21):234-244.
[14] 刘勇, 吴颂平. 热压工艺热-化学-应力三维数值模型及有限元分析[J]. 复合材料学报, 2009, 26(1):134-139. DOI: 10.3321/j.issn:1000-3851.2009.01.023 LIU Yong, WU Songpin. Three dimensional thermol-chemical-stress numerical model and finite element analysis for hot pressing process[J]. Acta Materiae Compositae Sinica,2009,26(1):134-139(in Chinese). DOI: 10.3321/j.issn:1000-3851.2009.01.023
[15] KIM Y K, WHITE S R. Process-induced stress relation analysis of AS4/3501-6 laminate[J]. Journal of Reinforced Plastics and Composites,1997,16(1):2-16. DOI: 10.1177/073168449701600102
[16] DANIEL D, SHIN H, THOMAS H. Compaction of thick composites: Simulation and experiment[J]. Polymer Compo-sites,2004,25(1):49-59. DOI: 10.1002/pc.20004
[17] KIM Y K, SCOTT R W. Viscoelastic analysis of processing-induced residual stresses in thick composite laminates[J]. Mechanics of Advanced Materials and Structures,1997,4(4):361-387. DOI: 10.1080/10759419708945889
[18] 元振毅, 王永军, 王俊彪. 基于材料性能时变性的复合材料固化过程多场耦合数值模拟[J]. 复合材料学报, 2015, 32(1):167-175. YUAN Zhenyi, WANG Yongjun, WANG Junbiao. Multi-field coupled numerical simulation for curing process of composite with time-depended properties of materials[J]. Acta Materiae Compositae Sinica,2015,32(1):167-175(in Chinese).
[19] ZOCHER M A, GROVES S E, ALLEN D H. A three-dimensional finite element formulation for thermoviscoelastic orthotropic media[J]. International Journal for Numerical Methods in Engineering,1997,40(12):2267-2288. DOI: 10.1002/(SICI)1097-0207(19970630)40:12<2267::AID-NME156>3.0.CO;2-P
[20] 谢福原, 王雪明, 李敏, 等. T形加筋板热压罐成型过程压力分布与树脂流动实验研究[J]. 复合材料学报, 2009, 26(6):66-71. XIE F Y, WANG X M, LI M, et al. Experimental research on pressure distribution and resin flow of T-stiffened skins in autoclave process[J]. Acta Materiae Compositae Sinica,2009,26(6):66-71(in Chinese).
[21] GUTOWSKI T G, DILLON G. The elastic deformation of lubricated carbon fiber bundles: Comparison of theory and experiments[J]. Journal of Composite Materials,1992,26(16):2330-2347. DOI: 10.1177/002199839202601601
[22] 胡汉平. 热传导理论[M].北京: 中国科学技术大学出版社, 2010. HU Hanping. Heat transport theory[M]. Beijing: University of Science and Technology of China Press, 2010(in Chinese).
[23] TWARDOWSKI T E, LIN S E, GEIL P H. Curing in thick composite laminates: Experiments and simulation[J]. Journal of Composite Materials,1993,27(3):216-250. DOI: 10.1177/002199839302700301
[24] WALCZYK D, KUPPERS J. Thermal press curing of advanced thermoset composite laminate parts[J]. Compo-sites Part A: Applied Science and Manufacturing,2012,43(4):635-646. DOI: 10.1016/j.compositesa.2011.12.008
[25] GOURICHON B, BINETRUY C, KRAWCZAK P. A new numerical procedure to predict dynamic void content in liquid composite molding[J]. Composites Part A: Applied Science and Manufacturing,2006,37(11):1961-1969. DOI: 10.1016/j.compositesa.2005.12.017
[26] SPRINGER G S, TSAI S W. Thermal conductivities of unidirectional materials[J]. Journal of Composite Materials,1979,1(2):166-173.
[27] 史明. 航空复合材料帽型加筋板热压罐成型芯模及包含此芯模的热压罐成型全套模具: 中国, CN111572058A[P]. 2020-08-25. SHI Ming. The autoclave curing mandrel and the whole set of the mold including the mandrel using to manufacture the composite hat-stiffened plate that use in aeronautics, China, CN111572058A[P]. 2020-08-25(in Chinese).
-




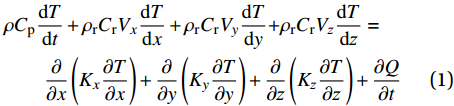
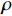
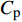
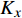
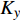
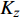

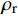
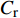
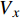
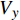
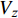


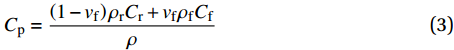
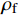
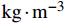
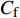
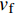

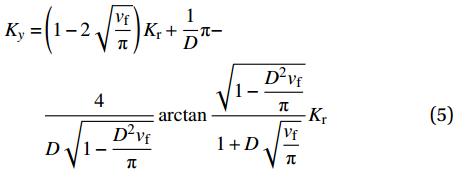

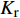
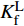
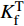

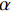
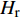
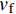
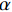
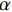
 下载:
下载: