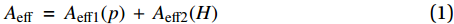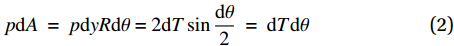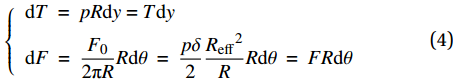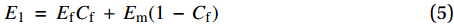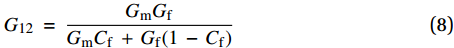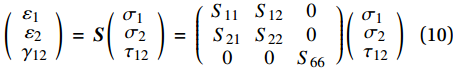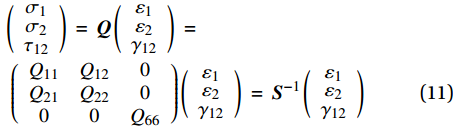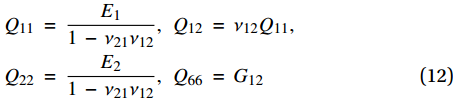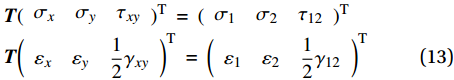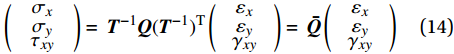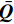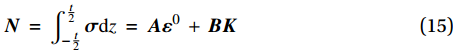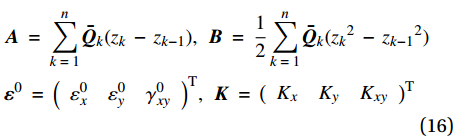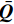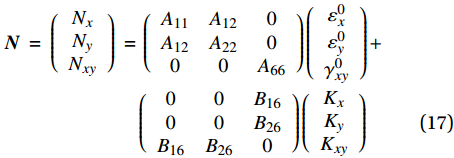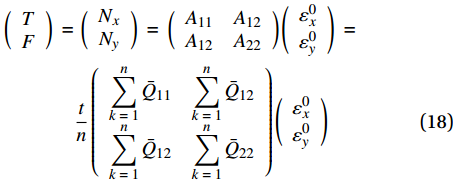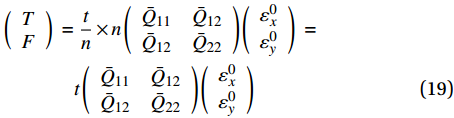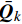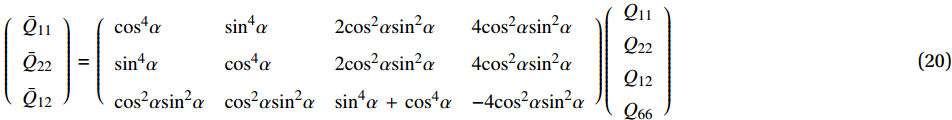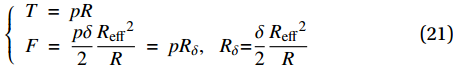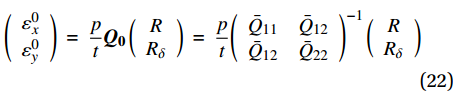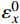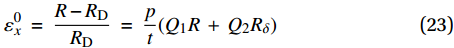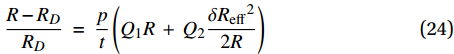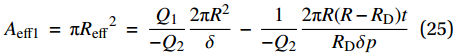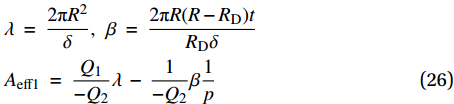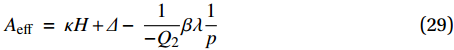A predictive method of effective area of rolling lobe air spring for vehicles
-
摘要: 空气弹簧帘线-橡胶复合材料结构具有刚度可变、轻量化、高度可调、隔振效果好等优势，在汽车“新四化”的发展趋势下，车用空气弹簧力学成为学术和工程研究热点。但其受力的“有效面积”这一重要参数还未建立完善理论模型。结合复合材料力学特性与几何学特征，提出一种车用膜式空气弹簧有效面积理论分析与预测方法。给出了空气弹簧有效面积理论预测表达式，体现了空气弹簧气囊内压强、空气弹簧高度等因素对有效面积的综合影响。利用力学综合实验台架设计实验，对某型号空气弹簧进行有效面积测量，实验结果与理论分析的对比显示在实验测量的范围内，理论预测的有效面积误差在1%以内，表明了这种理论分析方法的合理性。这种方法对进行有效面积的预测、空气弹簧的准确建模及进一步进行高精度的车高控制具有一定的指导意义。Abstract: Air springs with cord-rubber structure have the advantages of variable stiffness, lightweighting and better isolating effect, which have become the highlights of vehicle research in the current of new developing trends of automobile. However, as an important parameter, the effective area of air spring is lack of thorough predictive theory. A predictive analytical method for effective area of rolling lobe air spring for vehicles was put forward based on composite material mechanics and the geometrical characteristics of air spring bellow. A predictive formula of air spring effective area was given manifesting the influence of various parameters especially pressure inside bellow and air spring height on effective area. Experiments were conducted using mechanical test rig with certain air spring and the results of test fit the theory well. The errors of theoretical prediction can be less than 1% compared with experiment data. The method is useful for effective area prediction and accurate modeling as well as the height control of air suspension.
-
空气悬架作为一种可实现高度调节的车辆半主动悬架，越来越受到关注。空气悬架的核心是可通过充放气调节高度和刚度的空气弹簧(下简称空簧)。空簧的有效面积被定义为空簧支承力与内部气体相对压强的比值，其特性对于空气悬架的准确建模与控制设计十分关键。然而，这是一个等效物理量，无法直接测量得到。
在实际中，空簧有效面积主要是空簧高度和内部压强的函数，且存在一定的非线性特征。文献中研究有效面积主要采用有限元仿真[1-4]、几何图解[5-14]、实验拟合[15-20]等手段。成小霞等[3]、胡德安等[4]提出的有效面积确定方法结合有限元工具进行了验证。杨泽彪[7]给出一种几何意义上的有效面积定义，确定了有效面积及其随高度的变化率。其他几何图解方法也沿用了文献[7]中的一些变形规律假设。罗贤光[10]分析了不同受力状态下的囊式空簧有效面积情况。Li等[13-14]在对轨道车辆空簧刚度的分析中给出了有效面积变化率的图解公式。不同形式的空簧有效面积变化规律也有差异[17]。部分空气悬架设计与建模工作采用空簧活塞面积或最大外径面积[16]代替有效面积，精度不高。采用实验拟合方法确定的有效面积规律一般随高度以线性[19-20]或多项式[15]规律变化。
文献中大多仅考虑空簧有效面积与高度的关系[18-21]，对其随压强变化规律研究相对较少。在不同车辆载荷下，即使空簧处于同一高度，其内部压强也会变化，进而显著影响有效面积和悬架动力学性能。本文结合复合材料力学与几何学分析，提出一种新的车用膜式空簧的有效面积预测方法，探究空簧各参量(尤其是压强)对有效面积变化的影响，并与实验结果进行比对以验证其合理性。
1. 空气弹簧有效面积计算的理论分析
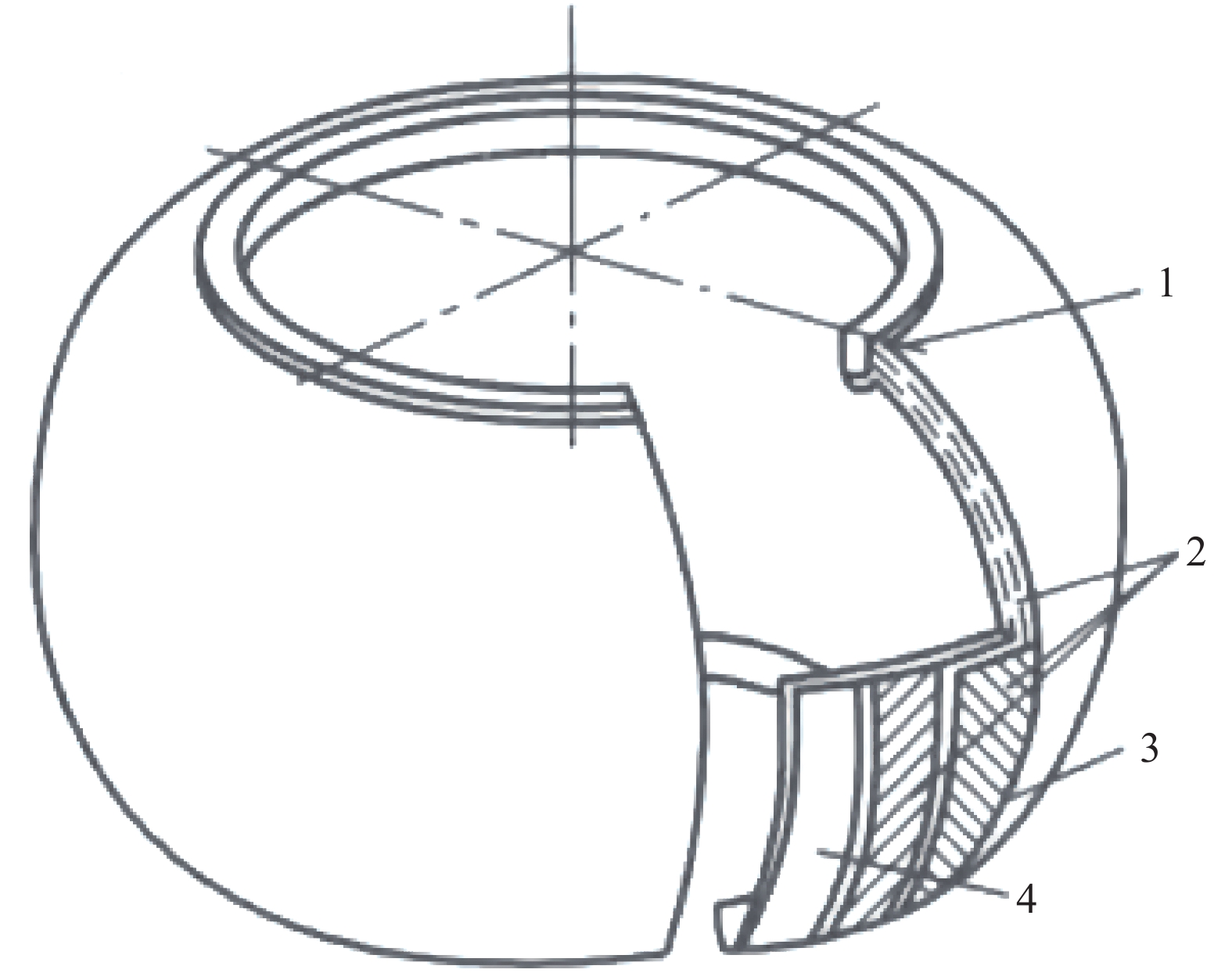
空簧气囊结构一般如图1所示，通过钢丝圈紧箍密闭，以中心帘线-橡胶层为主要承力部位，内外涂以胶层。常用于乘用车的空簧一般为膜式空簧，活塞上下移动时通过气囊壁垂耳在活塞边缘翻卷以改变空簧高度。一般来说，空簧有效面积Aeff与其高度和内部压强相关：
![]()
图 1 空簧气囊的典型结构Figure 1. Structure of air spring rubber reservoir1—Bead wire; 2—Cord-rubber ply; 3—Outer layer; 4—Inner layerAeff=Aeff1(p)+Aeff2(H) (1) 式中：p为气囊内部的相对压强；H为空簧气囊高度。
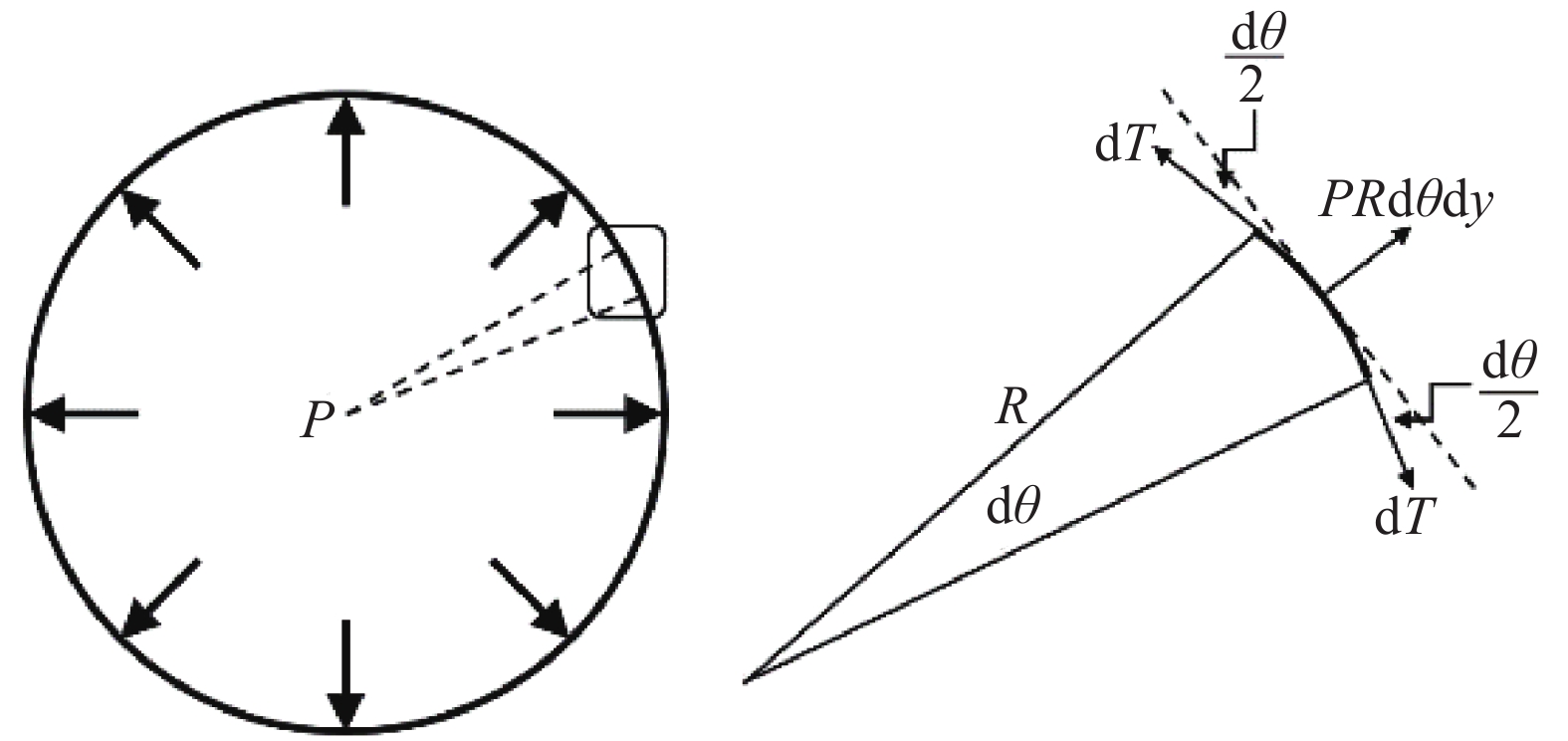
在气囊工作范围内可视其横截面为圆形，其纵截面如图2所示。这里取远离上下盖板及垂耳处、高度为dy的微元高度横切气囊壁进行分析，横切气囊壁微元段在径向和周向的受力情况如图3、图4所示。
![]()
图 2 膜式空簧纵截面示意Figure 2. Longitudinal section of rolling lobe air springR—Radius of cross sectional bellow; Reff—Radius of effective area![]()
图 3 微元高度横切气囊壁的受力分析Figure 3. Mechanical analysis of cross sectional bellow wall with infinitesimal heightP—Inner pressure of air spring; dT—Vertical force in infinitesimal circumferential length; dθ—Infinitesimal central angle; dy—Infinitesimal height![]()
图 4 气囊壁微元体平面内受力状态Figure 4. Stress diagram of bellow wall microbody in planedF—Circumferential force in infinitesimal circumferential length在图3中，dθ为横切气囊壁微元段沿经线方向分割后对应的微元圆心角。由受力平衡，有：
pdA=pdyRdθ=2dTsindθ2=dTdθ (2) 式中：dA为微元面积；R为横切面的半径；dT为垂向的微元力。假定横切面在垂向上受到的与有效面积相关的拉力F0为
F0=δpπReff2 (3) 式中：δ为形状参数；Reff为有效面积对应的半径。
进一步进行经线方向和纬线方向的受力分析：
{dT=pRdy=TdydF=F02πRRdθ=pδ2Reff2RRdθ=FRdθ (4) 式中：dF为周向的微元力；T、F分别为垂向与周向单位长度上产生的力。由于取的微元体很小，近似符合平面应力条件，可将圆柱坐标系转化为随体直角坐标系。在该直角坐标系中，忽略内外气压差对垂直于平面方向应变的影响，结合转换关系dx=Rdθ，该微元体在随体坐标系下平面内受力状态如图4所示。
下面对微元体的材料结构进行分析。忽略内外胶层对气囊力学特性的影响，假定完全由帘线-橡胶层承载气囊所受的力。橡胶在大变形情况下具有非线性力学特性，但考虑到气囊是帘线增强的复合材料结构，在力学分析时为简化起见用线弹性材料描述橡胶基体行为。基于此假设，将帘线-橡胶看作正交各向异性复合材料，其中，橡胶作为基体提供支撑，尼龙帘线作为增强体起主要承力作用。
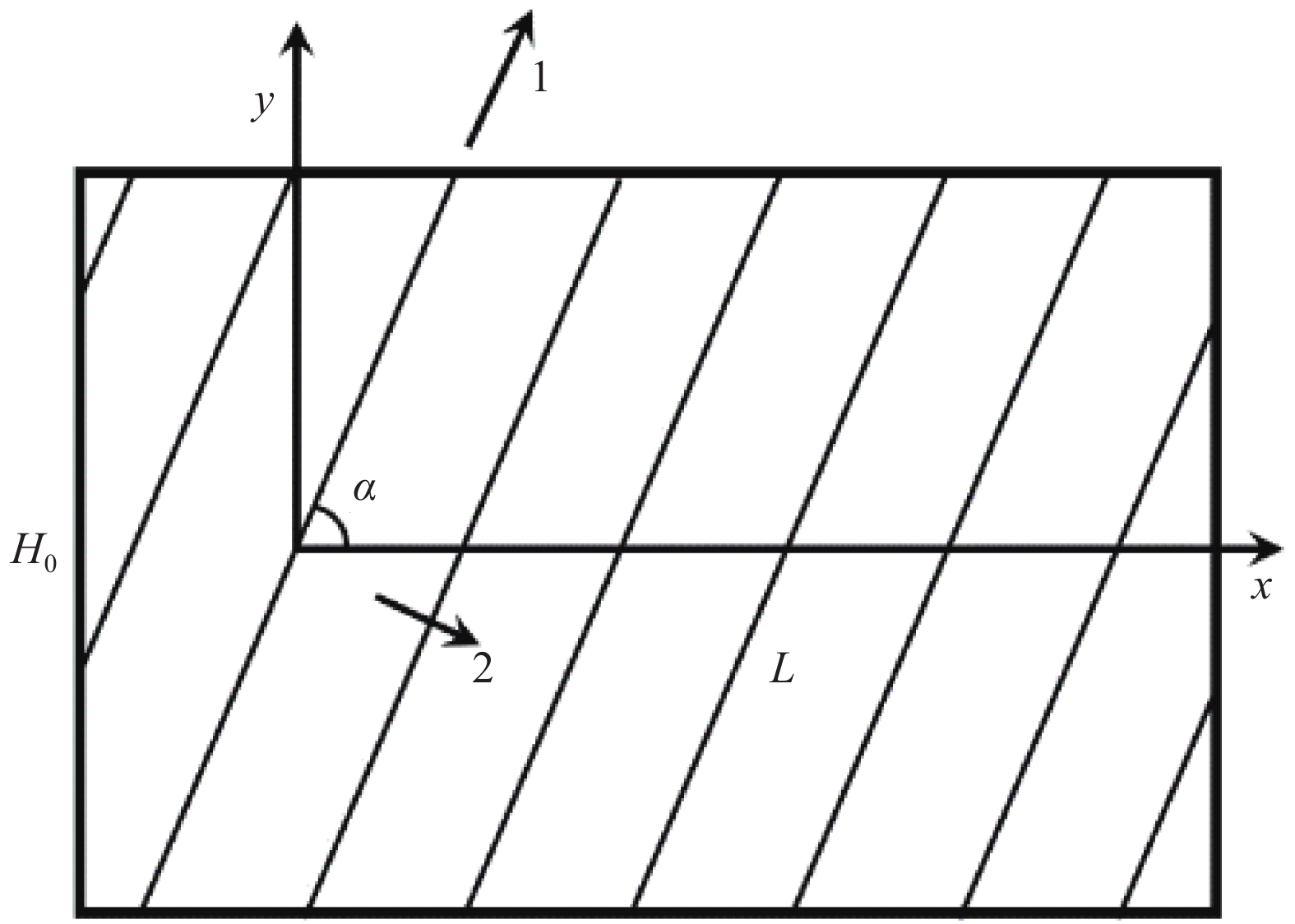
单层帘线-橡胶材料的帘线铺层随体坐标与主方向定义如图5所示。图中的x、y随体坐标轴方向分别对应于前述的空簧气囊的纬线方向与经线方向，1、2分别对应平行与垂直帘线的主方向。
![]()
图 5 微元体随体坐标与主方向定义Figure 5. Definition of local coordinate and principle direction of microbodyH0—Initial height of air spring; α—Ply angle; L—Length of cords结合上述假设，利用复合材料单层板理论[22]，单层板1号主方向上的弹性模量E1、2号主方向的弹性模量E2、复合材料2-1方向泊松比ν21与1-2方向剪切模量G12的表达式分别为
E1=EfCf+Em(1−Cf) (5) E2=EfEmCmEf+CfEm (6) ν21=Cfνf+νm(1−Cf) (7) G12=GmGfGmCf+Gf(1−Cf) (8) 式中，Ef、Cf、νf和Gf分别表示帘线的弹性模量、相对体积含量、泊松比和剪切模量，与之相对应的m下标四个参量均为橡胶的等效材料参量。采用线弹性小变形的假设，存在如下关系[23]：
Em=9KG3K+G (9) 其中，K、G分别为橡胶材料等效的体积模量与剪切模量。值得注意的是，不同理论可对复合材料参数给予不同的预报，这里选择了较通用的一种，暂不研究参数预报方法的准确性。
根据前述假设得到的简化本构方程为
\left( {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ {{\gamma _{12}}} \end{array}} \right)\; = \;{\boldsymbol{S}}\left( {\begin{array}{*{20}{c}} {{\sigma _1}} \\ {{\sigma _2}} \\ {{\tau _{12}}} \end{array}} \right)\; = \;\left( {\begin{array}{*{20}{c}} {{S_{11}}}&{{S_{12}}}&0 \\ {{S_{21}}}&{{S_{22}}}&0 \\ 0&0&{{S_{66}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\sigma _1}} \\ {{\sigma _2}} \\ {{\tau _{12}}} \end{array}} \right)\; (10) 其中：σ1、ε1、σ2、ε2、γ12与τ12分别为面内1方向、2方向和1-2切向的应力与应变；S为柔度矩阵。进一步利用折减刚度矩阵Q表示本构方程：
\begin{split} &\left( {\begin{array}{*{20}{c}} {{\sigma _1}} \\ {{\sigma _2}} \\ {{\tau _{12}}} \end{array}} \right)\; = \;{\boldsymbol{Q}}\left( {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ {{\gamma _{12}}} \end{array}} \right)\; =\\ &\;\left( {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}&0 \\ {{Q_{21}}}&{{Q_{22}}}&0 \\ 0&0&{{Q_{66}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ {{\gamma _{12}}} \end{array}} \right)\; = \;{{\boldsymbol{S}}^{ - 1}}\left( {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ {{\gamma _{12}}} \end{array}} \right) \end{split} (11) 其中：
\begin{split} &{Q_{11}}\; = \;\frac{{{E_1}}}{{1\; - \;{\nu _{21}}{\nu _{12}}}},\;\;{Q_{12}}\; = \;{\nu _{12}}{Q_{11}},\\ &{Q_{22}}\; = \;\frac{{{E_2}}}{{1\; - \;{\nu _{21}}{\nu _{12}}}},\;\;{Q_{66}}\; = \;{G_{12}} \end{split} (12) 本构方程(11)中存在的四个独立的弹性常数，可利用前述预报公式求得，式(12)中1-2方向的泊松比ν12利用麦克斯韦方程式计算。进一步结合转移矩阵T进行复合材料的转轴转化：
\begin{split} & {\boldsymbol{T}}{\left( {\begin{array}{*{20}{c}} {{\sigma _x}}&{{\sigma _y}}&{{\tau _{xy}}} \end{array}} \right)^{\rm{T}}}\; = \;{\left( {\begin{array}{*{20}{c}} {{\sigma _1}}&{{\sigma _2}}&{{\tau _{12}}} \end{array}} \right)^{\rm{T}}} \\ & {\boldsymbol{T}}{\left( {\begin{array}{*{20}{c}} {{\varepsilon _x}}&{{\varepsilon _y}}&{\dfrac{1}{2}{\gamma _{xy}}} \end{array}} \right)^{\rm{T}}}\; = \;{\left( {\begin{array}{*{20}{c}} {{\varepsilon _1}}&{{\varepsilon _2}}&{\dfrac{1}{2}{\gamma _{12}}} \end{array}} \right)^{\rm{T}}} \end{split} (13) \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\sigma _x}} \\ {{\sigma _y}} \end{array}} \\ {{\tau _{xy}}} \end{array}} \right) = \;{{\boldsymbol{T}}^{ - 1}}{\boldsymbol{Q}}{({{\boldsymbol{T}}^{ - 1}})^{\rm{T}}}\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\varepsilon _x}} \\ {{\varepsilon _y}} \end{array}} \\ {{\gamma _{xy}}} \end{array}} \right) = \;{\boldsymbol{\bar Q}}\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\varepsilon _x}} \\ {{\varepsilon _y}} \end{array}} \\ {{\gamma _{xy}}} \end{array}} \right) (14) 式中：σx、εx、σy、εy、γxy与τxy分别为面内x方向、y方向和x-y切向的应力与应变；
\bar{\boldsymbol{Q}} 为转轴折减刚度矩阵。下面对多层帘线-橡胶增强复合材料特性进行分析。当前用于乘用车的空簧帘线铺层一般采用偶数反对称铺设，帘线角度铺设形式类似于[+α/…/−α/+α/…/−α]，α为正值帘线铺层角。图6为四层反对称层合板的示意，t为总厚度。根据复合材料宏观力学理论[22]，层合板边缘单位长度受力向量N为
{\boldsymbol{N}}\; = \;\int_{ - \frac{t}{2}}^{\frac{t}{2}} {{\boldsymbol{\sigma }}{\rm{d}}z} \; = \;{\boldsymbol{A}}{{\boldsymbol{\varepsilon }}^0}\; + \;{\boldsymbol{BK}} (15) \begin{split} & {\boldsymbol{A}}\; = \;\displaystyle\sum\limits_{k\; = \;1}^n {{{{\boldsymbol{\bar Q}}}_k}({z_k}\; - \;{z_{k - 1}})} ,\;\;{\boldsymbol{B}}\; = \;\dfrac{1}{2}\displaystyle\sum\limits_{k\; = \;1}^n {{{{\boldsymbol{\bar Q}}}_k}({z_k}^2\; - \;{z_{k - 1}}^2)} \\ & {{\boldsymbol{\varepsilon }}^0}\; = \;{\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0}&{\varepsilon _y^0}&{\gamma _{xy}^0} \end{array}} \right)^{\rm{T}}},\;\;{\boldsymbol{K}}\; = \;{\left( {\begin{array}{*{20}{c}} {{K_x}}&{{K_y}}&{{K_{xy}}} \end{array}} \right)^{\rm{T}}} \end{split} (16) 其中：A、B分别为拉伸、耦合刚度矩阵；ε0、K分别为中面应变向量、中面曲率向量；
\bar{\boldsymbol{Q}} k为第k层的转轴折减刚度矩阵。偶数层反对称层合板的A、B矩阵有恒零项，且存在拉扭耦合。进一步将式(15)中A、B展开，写为\begin{split} {\boldsymbol{N}}\; = \;\left( {\begin{array}{*{20}{c}} {{N_x}} \\ {{N_y}} \\ {{N_{xy}}} \end{array}} \right)\; = &\;\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&0 \\ {{A_{12}}}&{{A_{22}}}&0 \\ 0&0&{{A_{66}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0} \\ {\varepsilon _y^0} \\ {\gamma _{xy}^0} \end{array}} \right) + \\ &\left( {\begin{array}{*{20}{c}} 0&0&{{B_{16}}} \\ 0&0&{{B_{26}}} \\ {{B_{16}}}&{{B_{26}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{K_x}} \\ {{K_y}} \\ {{K_{xy}}} \end{array}} \right) \end{split} (17) 考虑到本文主要关注气囊x、y方向上的宏观作用力产生的应变，忽略层合板的扭曲率，即Kxy = 0，结合式(4)，简化式(17)为
\begin{split} \left( {\begin{array}{*{20}{c}} T \\ F \end{array}} \right)\; =& \;\left( {\begin{array}{*{20}{c}} {{N_x}} \\ {{N_y}} \end{array}} \right)\; = \;\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}} \\ {{A_{12}}}&{{A_{22}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0} \\ {\varepsilon _y^0} \end{array}} \right)\; = \\ &\frac{t}{n}\left( {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{k\; = \;1}^n {{{\bar Q}_{11}}} }&{\displaystyle\sum\limits_{k\; = \;1}^n {{{\bar Q}_{12}}} } \\ {\displaystyle\sum\limits_{k\; = \;1}^n {{{\bar Q}_{12}}} }&{\displaystyle\sum\limits_{k\; = \;1}^n {{{\bar Q}_{22}}} } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0} \\ {\varepsilon _y^0} \end{array}} \right) \end{split} (18) 其中，n为层数。由上文的简化可见，拉扭耦合矩阵B对有效面积计算没有影响。结合层合板的反对称性，式(18)进一步可以简化为
\begin{split} \left( {\begin{array}{*{20}{c}} T \\ F \end{array}} \right)\; = &\;\frac{t}{n} \times n\left( {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&{{{\bar Q}_{12}}} \\ {{{\bar Q}_{12}}}&{{{\bar Q}_{22}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0} \\ {\varepsilon _y^0} \end{array}} \right)\; = \\ &t\left( {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&{{{\bar Q}_{12}}} \\ {{{\bar Q}_{12}}}&{{{\bar Q}_{22}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0} \\ {\varepsilon _y^0} \end{array}} \right) \end{split} (19) 注意到转轴折减刚度矩阵中并非所有项都需要经过计算得出，可得
{\bar{\boldsymbol{Q}}}_{k} 部分项的表达式为\left( {\begin{array}{*{20}{c}} {{{\bar Q}_{{\rm{11}}}}} \\ {{{\bar Q}_{{\rm{22}}}}} \\ {{{\bar Q}_{{\rm{12}}}}} \end{array}} \right)\;{\rm{ = }}\;\left( {\begin{array}{*{20}{l}} {{{\cos }^4}\alpha }&{{{\sin }^4}\alpha }&{2{{\cos }^2}\alpha {{\sin }^2}\alpha }&{4{{\cos }^2}\alpha {{\sin }^2}\alpha } \\ {{{\sin }^4}\alpha }&{{{\cos }^4}\alpha }&{2{{\cos }^2}\alpha {{\sin }^2}\alpha }&{4{{\cos }^2}\alpha {{\sin }^2}\alpha } \\ {{{\cos }^2}\alpha {{\sin }^2}\alpha }&{{{\cos }^2}\alpha {{\sin }^2}\alpha }&{{{\sin }^4}\alpha \; + \;{{\cos }^4}\alpha }&{ - 4{{\cos }^2}\alpha {{\sin }^2}\alpha } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{Q_{11}}} \\ {{Q_{22}}} \\ {{Q_{12}}} \\ {{Q_{66}}} \end{array}} \right) (20) 对微元体受力平衡方程式(4)进行转化：
\left\{ \begin{array}{l} T\; = \;pR \\ F\; = \;\dfrac{{p\delta }}{2}\dfrac{{{R_{{\rm{eff}}}}^2}}{R}\; = \;p{R_\delta },\;\;\;{R_\delta }{\rm{ = }}\dfrac{\delta }{2}\dfrac{{{R_{{\rm{eff}}}}^2}}{R} \\ \end{array} \right. (21) 由(19)可得：
\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0} \\ {\varepsilon _y^0} \end{array}} \right)\; = \;\dfrac{p}{t}{{\boldsymbol{Q}}_{\boldsymbol{0}}}\left( {\begin{array}{*{20}{c}} R \\ {{R_\delta }} \end{array}} \right)\; = \;\dfrac{p}{t}{\left( {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&{{{\bar Q}_{12}}} \\ {{{\bar Q}_{12}}}&{{{\bar Q}_{22}}} \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} R \\ {{R_\delta }} \end{array}} \right) (22) 此处主要关心
\varepsilon _x^0 ，即与气囊半径变化相关的中面横向应变：\varepsilon _x^0\; = \;\frac{{R - {R_{\rm{D}}}}}{{{R_{\rm{D}}}}}\; = \;\frac{p}{t}({Q_1}R\; + \;{Q_2}{R_\delta }) (23) 其中：Q1、Q2为式(22)中定义的Q0矩阵第一行第一列和第二列的元素，材料特性确定后，为α的函数，且有Q1 > 0、Q2 < 0；R为压强变化后的气囊半径；RD为气囊内压强较小时，随压强变化不再发生明显径向形变的初始半径，经实验确定为内部相对压强为0.2 MPa时的气囊外半径。式(23)进一步转化为
\frac{{R - {R_D}}}{{{R_D}}}\; = \;\frac{p}{t}\left({Q_1}R\; + \;{Q_2}\frac{{\delta {R_{{\rm{eff}}}}^2}}{{2R}}\right) (24) 根据式(24)可得有效面积随压强变化部分的表达式为
{A_{{\rm{eff1}}}}\; = \;{\rm{{\text{π}} }}{R_{{\rm{eff}}}}^2\; = \;\frac{{{Q_1}}}{{ - {Q_2}}}\frac{{2{\rm{{\text{π}} }}{R^2}}}{\delta }\; - \;\frac{1}{{ - {Q_2}}}\frac{{2{\rm{{\text{π}} }}R(R - {R_{\rm{D}}})t}}{{{R_{\rm{D}}}\delta p}} (25) 这里假设空簧气囊壁在经线方向长度不变，铺层角α不随空簧高度发生变化[13]。引入新的参数λ、β，并将式(25)进行转化：
\begin{split} &\lambda \; = \;\dfrac{{2{\rm{{\text{π}} }}{R^2}}}{\delta },\;\;\beta \; = \;\dfrac{{2{\rm{{\text{π}} }}R(R - {R_{\rm{D}}})t}}{{{R_{\rm{D}}}\delta }} \\ & {A_{{\rm{eff1}}}}\; = \;\dfrac{{{Q_1}}}{{ - {Q_2}}}\lambda \; - \;\dfrac{1}{{ - {Q_2}}}\beta \dfrac{1}{p} \end{split} (26) 空簧气囊的高度主要由气囊壁垂耳的翻卷改变，前述分析没有考虑到这一高度变化的影响。基于实验[19]与几何图解[3]的方法均指出有效面积随高度的近似线性变化规律。这里设定高度对有效面积的影响为线性，由根据实验确定的参量κ表征[20]。这一部分对有效面积的影响写为
{A_{{\rm{eff2}}}}\; = \;\kappa (H - {H_0}) (27) 其中，H0为实验中空簧的初始工作高度。结合式(26)~(27)，进一步定义参数Δ：
\varDelta \; = \; - \kappa {H_0} + \frac{{{Q_1}}}{{ - {Q_2}}}\lambda (28) 最终有效面积预测公式写为
{A_{{\rm{eff}}}}\; = \;\kappa H + \varDelta - \;\frac{1}{{ - {Q_2}}}\beta \lambda \frac{1}{p} (29) 根据相应国家标准GB/T 9101—2017[24]，采用的帘线-橡胶力学参数[25-26]如表1所示。根据式(5)~(8)计算出的复合材料表观力学参数如表2所示，参数Q1、Q2随铺层角α的变化规律如图7所示。
表 1 橡胶和帘线力学参数Table 1. Mechanical parameters of rubber and cordParameter Value Ef/MPa 2700 νf 0.3 Cf/% 33.2 Gf/MPa 1038 Em/MPa 2.0 νm 0.497 Cm/% 66.8 Gm/MPa 0.667 Notes: Ef, νf, Cf and Gf —Young’s modulus, Poisson’s ratio, volume fraction and shear modulus of cord material in composite; Em, νm, Cm and Gm—Equivalent Young’s modulus, Poisson’s ratio, volume fraction and shear modulus of rubber material in composite. 表 2 计算得到的帘线-橡胶复合材料表观力学值Table 2. Apparent mechanical value of cord-rubber composite via computationParameter Value E1/MPa 897.7 E2/MPa 2.993 ν21 0.432 ν12 1.439×10−3 G12/MPa 0.998 Q11/MPa 898.3 Q12/MPa 1.293 Q22/MPa 2.995 Q66/MPa 0.998 Notes: E1, E2—Elastic modulus of laminate in 1st and 2nd principle direction; ν21, ν12—Poisson’s ratios of laminate; G12—Shear modulus of laminate in plane; Q11, Q12, Q21, Q22 and Q66—Elements in matrix Q in Eq.(11). 2. 实验对比与验证
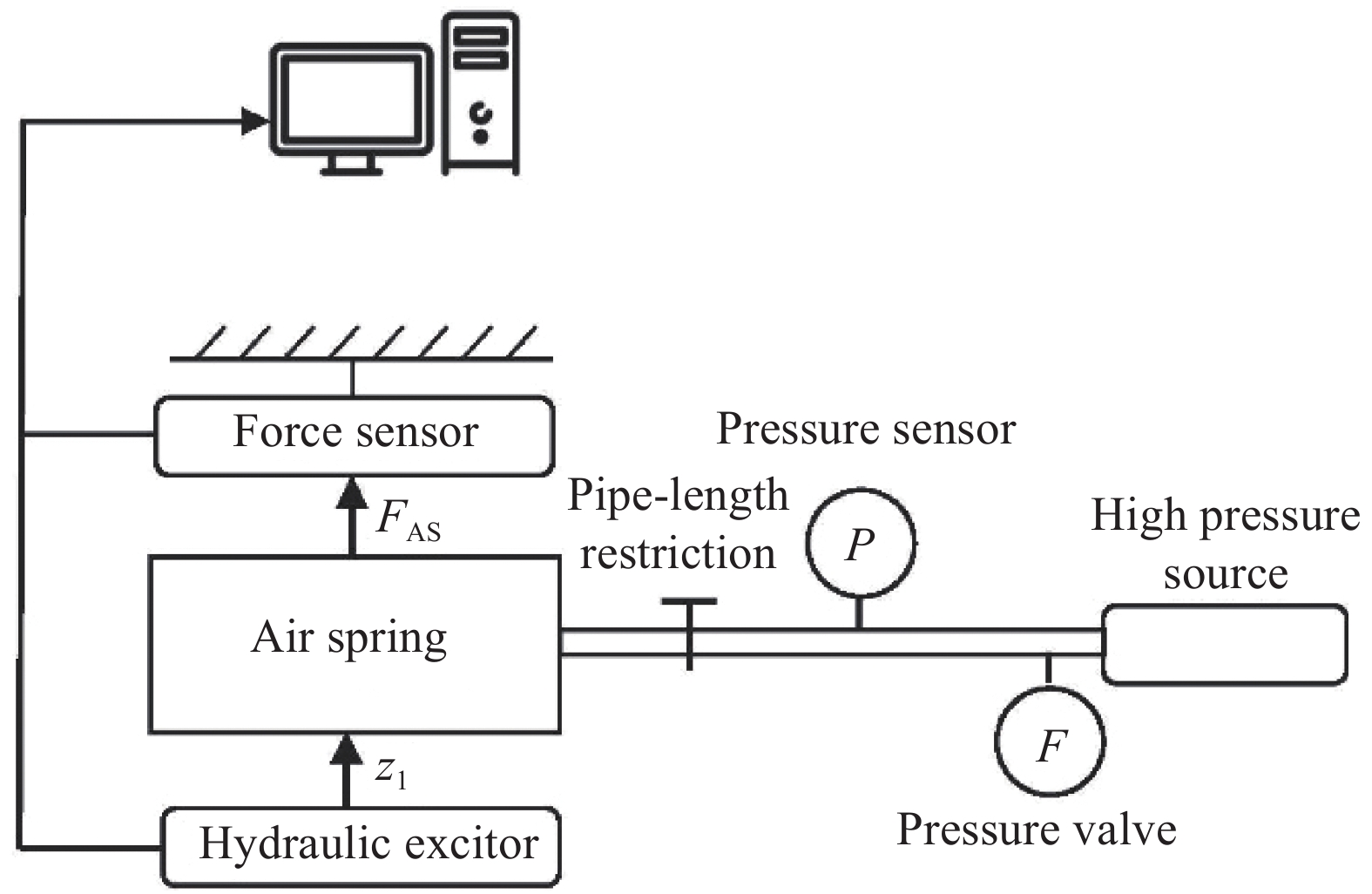
在上述理论分析基础上，利用Mechanical Testing & Simulation公司生产的力学性能测试平台对某型号后空簧进行了实验，图8和图9分别为实验台架设备及实验原理。台架下端的液压作动器可产生给定位移，台架上端的力传感器可以测量产生的力并传输至计算机进行采集分析。
![]()
图 9 实验原理Figure 9. Experimental principleFAS—Force produced by air spring; z1—Unsprung displacement在实验中，首先将空簧上端固定，调节下端位置到一定高度并充气至较低的初始压强。保持空簧高度不变，利用减压阀改变空簧内的气体压强，其值通过与管路相连的压强传感器读出。在不同压强下，当力传感器、压强传感器测得的数据基本保持稳定时，记录对应的力与压强。在同一高度下完成不同充气压强的实验测量后，再调整台架至另一实验高度，重复上述过程。最终根据测得的力与压强的比值作为各测量工况下的有效面积。为保证数据的准确性，同一高度的实验中先逐步升压至最大测量压强，再逐步减压至初始压强，每一个压强测量点在升降压过程中均进行数据采集并求平均以减小误差。实验选择了230 mm、250 mm、270 mm和290 mm的空簧高度进行实验，压强变化范围为0.3~0.8 MPa，这基本覆盖了该空簧的实际工况。
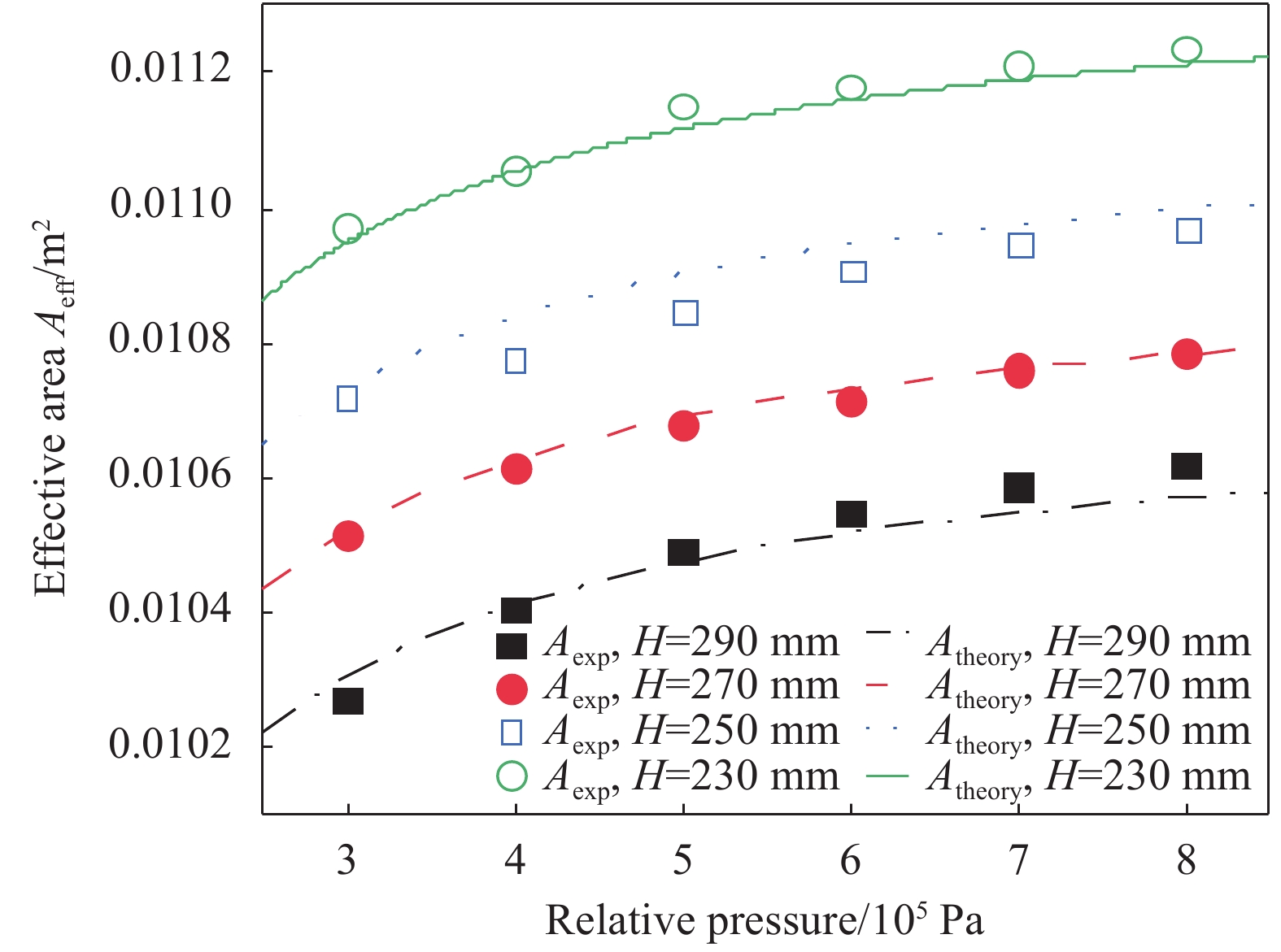
根据上节所述的理论分析方法，结合空簧的基本参数，对该空簧的有效面积计算公式进行了拟合，部分参数取值如表3所示，实验数据与理论预测数据如图10所示，理论与实验的误差情况如表4所示。由图10可知，随高度减小、压强增大，有效面积有变大的趋势，此时经线方向上卷耳部分的长度增加，导致空簧气囊整体有变得矮粗的趋势。由表4可以看出，在实验对应的测量范围中，理论预测的有效面积误差都小于1%，这表明上述空簧有效面积的理论分析方法能很好地与实验数据相符合，对进行空簧有效面积的预测具有一定的指导意义。
表 3 用于空气弹簧有效面积计算的参数取值Table 3. Parameter values in effective area computation for air springParameter Value α/(°) 50 R/10−2m 7.50 RD /10−2m 7.32 t/10−3m 2.00 δ 0.8 κ/10−2m −1.069 Δ/m2 0.01383 Notes: R—Bellow radius after pressure variation; RD —Initial bellow radius without obvious radial deformation; δ, κ and Δ—Experimental parameters defined in Eq.(27) and Eq.(29). ![]()
图 10 空气弹簧实验数据与理论预测对比Figure 10. Comparison of experimental data and theoretical prediction of air spring表 4 空气弹簧理论预测与实验数据的误差Table 4. Errors between experimental data and theoretical prediction of air springPressure/
105 Pae23/% e25/% e27/% e29/% 3 0.20 0.11 <0.01 0.39 4 0.04 0.56 0.11 0.03 5 0.31 0.51 0.10 0.16 6 0.18 0.35 0.14 0.29 7 0.22 0.25 <0.01 0.38 8 0.23 0.26 <0.01 0.46 Notes: e23, e25, e27 and e29—Errors between experimental data and theoretical prediction when height of air spring are 230 mm, 250 mm, 270 mm and 290 mm, respectively. 3. 结 论
(1) 提出一种车用膜式空簧的有效面积理论分析与预测方法，给出了与空簧高度和内部压强相关的空簧有效面积理论预测表达式。
(2) 利用实验台架对某型号空簧进行有效面积测量实验，实验与理论预测的结果的对比验证了这种理论分析方法的合理性。
-
![]()
图 1 空簧气囊的典型结构
Figure 1. Structure of air spring rubber reservoir
1—Bead wire; 2—Cord-rubber ply; 3—Outer layer; 4—Inner layer
![]()
图 2 膜式空簧纵截面示意
Figure 2. Longitudinal section of rolling lobe air spring
R—Radius of cross sectional bellow; Reff—Radius of effective area
![]()
图 3 微元高度横切气囊壁的受力分析
Figure 3. Mechanical analysis of cross sectional bellow wall with infinitesimal height
P—Inner pressure of air spring; dT—Vertical force in infinitesimal circumferential length; dθ—Infinitesimal central angle; dy—Infinitesimal height
![]()
图 4 气囊壁微元体平面内受力状态
Figure 4. Stress diagram of bellow wall microbody in plane
dF—Circumferential force in infinitesimal circumferential length
![]()
图 5 微元体随体坐标与主方向定义
Figure 5. Definition of local coordinate and principle direction of microbody
H0—Initial height of air spring; α—Ply angle; L—Length of cords
![]()
图 9 实验原理
Figure 9. Experimental principle
FAS—Force produced by air spring; z1—Unsprung displacement
![]()
图 10 空气弹簧实验数据与理论预测对比
Figure 10. Comparison of experimental data and theoretical prediction of air spring
表 1 橡胶和帘线力学参数
Table 1 Mechanical parameters of rubber and cord
Parameter Value Ef/MPa 2700 νf 0.3 Cf/% 33.2 Gf/MPa 1038 Em/MPa 2.0 νm 0.497 Cm/% 66.8 Gm/MPa 0.667 Notes: Ef, νf, Cf and Gf —Young’s modulus, Poisson’s ratio, volume fraction and shear modulus of cord material in composite; Em, νm, Cm and Gm—Equivalent Young’s modulus, Poisson’s ratio, volume fraction and shear modulus of rubber material in composite. 
下载: 导出CSV
表 2 计算得到的帘线-橡胶复合材料表观力学值
Table 2 Apparent mechanical value of cord-rubber composite via computation
Parameter Value E1/MPa 897.7 E2/MPa 2.993 ν21 0.432 ν12 1.439×10−3 G12/MPa 0.998 Q11/MPa 898.3 Q12/MPa 1.293 Q22/MPa 2.995 Q66/MPa 0.998 Notes: E1, E2—Elastic modulus of laminate in 1st and 2nd principle direction; ν21, ν12—Poisson’s ratios of laminate; G12—Shear modulus of laminate in plane; Q11, Q12, Q21, Q22 and Q66—Elements in matrix Q in Eq.(11).
下载: 导出CSV
表 3 用于空气弹簧有效面积计算的参数取值
Table 3 Parameter values in effective area computation for air spring
Parameter Value α/(°) 50 R/10−2m 7.50 RD /10−2m 7.32 t/10−3m 2.00 δ 0.8 κ/10−2m −1.069 Δ/m2 0.01383 Notes: R—Bellow radius after pressure variation; RD —Initial bellow radius without obvious radial deformation; δ, κ and Δ—Experimental parameters defined in Eq.(27) and Eq.(29).
下载: 导出CSV
表 4 空气弹簧理论预测与实验数据的误差
Table 4 Errors between experimental data and theoretical prediction of air spring
Pressure/
105 Pae23/% e25/% e27/% e29/% 3 0.20 0.11 <0.01 0.39 4 0.04 0.56 0.11 0.03 5 0.31 0.51 0.10 0.16 6 0.18 0.35 0.14 0.29 7 0.22 0.25 <0.01 0.38 8 0.23 0.26 <0.01 0.46 Notes: e23, e25, e27 and e29—Errors between experimental data and theoretical prediction when height of air spring are 230 mm, 250 mm, 270 mm and 290 mm, respectively.
下载: 导出CSV
-
[1] 郑明军, 林逸, 王海花, 等. 多曲囊式空簧非线性弹性特性研究[J]. 振动与冲击, 2009, 28(8):11-15. DOI: 10.3969/j.issn.1000-3835.2009.08.003 ZHENG Mingjun, LIN Yi, WANG Haihua, et al. Nonlinear stiffness characteristics of multilayer cystiform air spring[J]. Journal of Vibration and Shock,2009,28(8):11-15(in Chinese). DOI: 10.3969/j.issn.1000-3835.2009.08.003
[2] 叶珍霞, 朱海潮, 鲁克明, 等. 囊式空簧刚度特性的非线性有限元法研究[J]. 振动与冲击, 2006(4):94-97. DOI: 10.3969/j.issn.1000-3835.2006.04.026 YE Zhenxia, ZHU Haichao, LU Keming, et al. Study on stiffness characteristics of air spring with nonlinear finite element method[J]. Journal of Vibration and Shock,2006(4):94-97(in Chinese). DOI: 10.3969/j.issn.1000-3835.2006.04.026
[3] 成小霞, 李宝仁, 杨钢, 等. 囊式空簧载荷建模与实验研究[J]. 振动与冲击, 2014, 33(17):80-84. CHENG Xiaoxia, LI Baoren, YANG Gang, et al. Modeling and tests for load of a cystiform air spring[J]. Journal of Vibration and Shock,2014,33(17):80-84(in Chinese).
[4] 胡德安, 甘亮亮, 丁飞, 等. 基于活塞形状改变的空簧特性仿真研究[J]. 计算机仿真, 2012, 29(1):331-334. DOI: 10.3969/j.issn.1006-9348.2012.01.084 HU De’an, GAN Liangliang, DING Fei, et al. Simulation of stiffness character of diaphragm air spring based on change piston contour[J]. Computer Simulation,2012,29(1):331-334(in Chinese). DOI: 10.3969/j.issn.1006-9348.2012.01.084
[5] 夏仕朝. 空簧隔振系统载荷分配优化研究[D]. 西安: 西安科技大学, 2008. XIA Shichao. Optimization of load distribution of vibration isolation system of air spring[D]. Xi’an: Xi’an University of Science and Technology, 2008(in Chinese).
[6] CHEN J J, YIN Z H, RAKHEJA S, et al. Theoretical modelling and experimental analysis of the vertical stiffness of a convoluted air spring including the effect of the stiffness of the bellows[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2018,232(4):547-561. DOI: 10.1177/0954407017704589
[7] 杨泽彪. 车用膜式空簧承载特性建模与试验研究[D]. 广州: 华南理工大学, 2018. YANG Zebiao. Research on modeling and testing of bearing characteristics of vehicular rolling lobe air spring[D]. Guangzhou: South China University of Technology, 2018(in Chinese).
[8] 冯元元. 半挂车电控空气悬架系统的建模与控制研究[D]. 广州: 华南理工大学, 2011. FENG Yuanyuan. Research on modeling and control of electrically controlled air suspension for semi-trailer[D]. Guangzhou: South China University of Technology, 2011(in Chinese).
[9] PRASIL L, KRACIK V, FRYDRYCH D. Shape modelling of air bellows springs[C]//Proceedings of Algoritmy. Bratislava: Publishing House of STU, 2005: 142–149.
[10] 罗贤光. 曲囊式橡胶空簧的一些力学问题[J]. 橡胶工业, 1997(4):36-40. LUO Xianguang. Mechanical problems of bellow-type rubber spring[J]. China Rubber Industry,1997(4):36-40(in Chinese).
[11] 李滨, 陈无畏. 汽车膜式空簧的分析与计算[J]. 合肥工业大学学报(自然科学版), 2004, 27(10):1191-1195. LI Bin, CHEN Wuwei. Analysis and calculation of diaphragm air spring of an automobile[J]. Journal of Hefei University of Technology (Natural Science),2004,27(10):1191-1195(in Chinese).
[12] QUAGLIA G, GUALA A. Evaluation and validation of an air spring analytical model[J]. International Journal of Fluid Power,2003,4(2):43-54. DOI: 10.1080/14399776.2003.10781165
[13] LI X B, LI T. Research on vertical stiffness of belted air springs[J]. Vehicle System Dynamics,2013,51(11):1655-1673. DOI: 10.1080/00423114.2013.819984
[14] LI X B, HE Y, LIU W Q, et al. Research on the vertical stiffness of a rolling lobe air spring[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit,2016,230(4):1172-1183.
[15] 汪少华. 半主动空气悬架混杂系统的多模式切换控制研究[D]. 镇江: 江苏大学, 2013. WANG Shaohua. Research on multi-mode switching control of semi-active air suspension hybrid system[D]. Zhen-jiang: Jiangsu University, 2013(in Chinese).
[16] FOX M N, ROEBUCK R L, CEBON D, et al. Modelling rolling-lobe air springs[J]. International Journal of Heavy Vehicle Systems,2007,14(3):254-270. DOI: 10.1504/IJHVS.2007.015603
[17] CHANG F. LU Z H. Air suspension performance analysis using nonlinear geometrical parameters model[J]. SAE Technical Paper,2007,1:9.
[18] ZHU H, YANG J, ZHANG Y, et al. Nonlinear dynamic model of air spring with a damper for vehicle ride comfort[J]. Nonlinear Dynamics,2017,89(2):1545-1568. DOI: 10.1007/s11071-017-3535-9
[19] QUAGLIA G, SORLI M. Air suspension dimensionless analysis and design procedure[J]. Vehicle System Dynamics,2001,35(6):443-475. DOI: 10.1076/vesd.35.6.443.2040
[20] NIETO A J, MORALES A L, GONZÁLEZ A, et al. An analytical model of pneumatic suspensions based on an experimental characterization[J]. Journal of Sound& Vibration,2008,313(1-2):290-307.
[21] 曾亮铭. 基于主动悬架的汽车平顺性与操纵稳定性协调控制[D]. 长沙: 湖南大学, 2017. ZENG Liangming. Coordinated control of vehicle ride comfort and handling stability based on active suspension[D]. Changsha: Hunan University, 2017(in Chinese).
[22] 沈观林, 胡更开. 复合材料力学[M]. 2版. 北京: 清华大学出版社, 2013. SHEN Guanlin, HU Gengkai. Mechanics of composite materials[M]. 2nd edition. Beijing: Tsinghua University Press, 2013(in Chinese).
[23] 徐芝纶. 弹性力学[M]. 5版. 北京: 高等教育出版社, 2016. XU Zhilun. Elasticity[M]. 5th edition. Beijing: Higher Education Press, 2016(in Chinese).
[24] 中国国家标准化管理委员会. 锦纶66浸胶帘子布: GB/T 9101—2017[S]. 北京: 中国标准出版社, 2017. Standardization Administration of the People’s Republic of China. Polyamide 66 dipped tyre cord fabric: GB/T 9101—2017[S]. Beijing: China Standards Press, 2017(in Chinese).
[25] 李雪冰. 空簧刚度的精确仿真与解析计算研究[D]. 北京: 清华大学, 2020. LI Xuebing. Research on accurate simulation and analytical calculation of air spring stiffness[D]. Beijing: Tsinghua University, 2020(in Chinese).
[26] 李雪冰, 曹金凤, 危银涛. 空簧多变过程的有限元模拟[J]. 工程力学, 2019, 36(2):224-228. DOI: 10.6052/j.issn.1000-4750.2017.12.0925 LI Xuebing, CAO Jinfeng, WEI Yintao. Finite element modelling on polytropic process of air springs[J]. Engineering Mechanics,2019,36(2):224-228(in Chinese). DOI: 10.6052/j.issn.1000-4750.2017.12.0925
-
期刊类型引用(6)
1. 付硕，许一虎，孙治博. 汽车空气悬架系统及精准控制技术发展综述. 液压与气动. 2023(04): 107-114 . 
百度学术
2. 陈俊杰，谭月玲，康盛，邱光琦. 膜式空气弹簧帘子线铺设角-承载力映射模型研究. 振动与冲击. 2023(21): 291-297 . 百度学术
3. 中国汽车工程学术研究综述·2023. 中国公路学报. 2023(11): 1-192 . 百度学术
4. 王相平，李星，王剑锋，吴少培，丁旺才，李国芳. 中低速磁浮车辆空气弹簧动力学建模及其应用研究. 振动工程学报. 2023(06): 1527-1538 . 百度学术
5. 刘琼，杨纪远，张磊，商涛，谢济兴. 帘线参数对单囊空气弹簧垂向刚度的影响研究. 三明学院学报. 2023(06): 117-124 . 百度学术
6. 孙文，李晨阳，王军年，钱灏喆，张文通. 越野车复合型悬架平顺性的研究. 汽车工程. 2022(01): 105-114+122 . 百度学术
其他类型引用(8)
-
计量
- 文章访问数: 1596
- HTML全文浏览量: 549
- PDF下载量: 89
- 被引次数: 14
