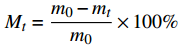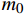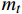Stacking sequence optimization of composite stiffened panel considering buckling
-
摘要: 提出了一种考虑屈曲的复合材料加筋壁板铺层顺序优化方法。基于复合材料加筋壁板屈曲载荷求解的能量法，系统推导了轴压载荷作用下复合材料加筋壁板蒙皮、筋条局部屈曲载荷的显示表达式，考虑了加筋壁板各板元之间的弹性支持作用及筋条下缘条的影响，引入工程法求解了加筋壁板整体屈曲载荷。基于国产自主结构分析软件HAJIF中的复合材料铺层工程数据库，以铺层参数为中间变量，利用本文提出的复合材料加筋壁板屈曲载荷求解方法，构建了考虑屈曲的复合材料加筋壁板铺层顺序优化设计流程并完成程序实现，将最小二乘法用于最优铺层顺序与工程铺层数据库的匹配。相比于传统有限元计算方法，本文提出的复合材料加筋壁板屈曲载荷求解方法具备较好的求解精度及求解效率。复合材料加筋壁板优化算例表明，采用本文提出的加筋壁板屈曲载荷分析及其优化方法，在结构重量不变的前提下，屈曲载荷提高约17%，且铺层顺序优化结果可直接从铺层工程数据库中提取并用于工程实际。Abstract: A method dealing with stacking sequence optimization of composite stiffened panel considering buckling was proposed. Based on the energy-based method in calculating buckling loads of composite stiffened panels, the explicit formulations in calculating local buckling loads of skin and stiffener of composite stiffened panel were proposed systematically. The influences of each elastic supporting panel element and stiffener’s foot were taken into account during the calculation of the local buckling loads of skin and stiffener. Engineering method was introduced to calculate the global buckling load. Based on the homemade HAJIF’s composite stacking engineering library, the stacking parameters were regarded as design variables and the proposed explicit formulations in calculating buckling loads were used to build an optimization progress of composite stiffened panels’ stacking sequence and its program implementation. The least square method was applied to choose the most closed staking parameter of optimized and engineering-library laminates automatically. A higher accuracy and efficiency of the proposed formulations in calculating the buckling loads of composite stiffened panels was obtained in comparison with the traditional FEA method. The numerical optimization examples of the composite stiffened panel show that the stiffened panel’s buckling load increases by 17% with an almost unchanged weight. And the optimal stacking sequence results can be extracted from the composite stacking engineering library and be used in practical structure directly.
-
纤维增强聚合物基复合材料(Fiber reinforced polymer，FRP)具有高比强度、高比刚度、耐腐蚀性能好、可设计性强等一系列独特的优点[1]，使其集结构、承载和功能于一身，在航空航天领域得到广泛应用[2-3]。碳纤维(CF)和玻璃纤维(GF)因其优势(高强度、高刚度)广泛应用于FRP增强体，是目前使用最多的两种无机纤维[4]。由CF和GF制成的CF-GF混杂增强聚合物基复合材料通过GF和CF的混杂排列、编织，使之具有优异的力学性能，是一种典型的结构-功能一体化复合材料[5]。
随着作战飞机的快速发展，FRP被期望用于非常恶劣的高温环境中。例如：在飞行过程中，高速战机与大气摩擦，其机翼表面温度升至177℃以上[6]，长期暴露于这样的环境下，FRP会发生化学物理变化，即老化，材料发生老化会引起其结构的尺寸变化，其性能也会逐渐降低，进而飞行器服役的可靠性与寿命会受到影响[7]。且由于混杂纤维层的存在，在受到热氧环境考验后其力学性能或许恶化的更快。然而，目前关于FRP的热氧老化研究已有几十年的历史，但对混杂编织复合材料的研究甚少[8-9]。因此，CF-GF混杂增强聚合物基复合材料在热氧环境下的老化和可靠性问题广受关注。
热氧老化导致纤维与基体之间脱粘，产生的微裂纹非常容易在层合复合材料的层与层之间扩展，为其后续的使用埋下了隐患[10]，尤其在遭受外部作用力时，分层破坏容易被诱发，其使用寿命也会大大降低[11-12]。而三向正交复合材料中沿厚度方向的Z向纱线将其他所有纱线捆绑为一个整体结构，能有效克服工程中容易出现分层破坏的现象，其厚度方向的强度和抗冲击损伤的性能显著提升，因而广受关注并得到飞速发展[13]。此外，复合材料在一些实际工程应用中，往往要承受多方向的应力。例如，飞机机翼在飞行时承受不断变化的交变载荷，为了解决这一问题，准各向同性层合板被开发出来，通过在预制体中定向纤维来改善面内性能[14-15]。因此，本研究在三向正交CF-GF混杂复合材料中加入±45°纱线，制备成三维编织CF-GF/双马来酰亚胺树脂复合材料(简称为编织复合材料)，并以层合CF-GF/双马来酰亚胺树脂复合材料(简称为层合复合材料)为参照对象，研究热氧老化对其二者力学性能的影响。
弯曲实验不仅是一种制样简单、容易操作的实验方法，且复合材料内部任何一个环节薄弱，其弯曲性能都会降低，因此在复合材料的工艺控制、质量检验等方面被广泛应用[16-17]。而且复合材料的弯曲强度对基体强度和纤维/基体界面强度非常敏感，基体和界面的轻微氧化降解都能通过弯曲强度体现出来[18]。短梁剪切是表征复合材料层间性能的一种方法，但是Akay等[19]认为采用短梁剪切进行实验，材料常常会有多种破坏模式，并不是真正的剪切破坏。而双切口剪切测试的主要优点是层间剪切破坏是持续的，且制样容易，测试装备简单[20]。因此，本研究采用弯曲试验和双切口剪切试验来探究热氧老化对三维CF-GF/双马来酰亚胺树脂复合材料力学性能的影响。
1. 试验过程
1.1 原材料和复合材料的制备
复合材料由日本TORAY公司生产的T700-12K碳纤维(CF)和陕西华特新材料有限公司生产的400 tex的E型玻璃纤维(E-GF)形成增强体，江苏恒神股份有限公司的型号为BH301的双马来酰亚胺树脂(BMI)作为基体。CF、E-GF和BMI的性能如表1所示。三维编织CF-GF混杂织物(简称为编织织物)和层合CF-GF混杂织物(简称为层合织物)织造工艺参数如表2所示。另外，两种织物中间四层0°/90°纱线均为CF，上下各两层的±45°纱线和Z向纱为E-GF。
表 1 组成材料的性能参数Table 1. Properties of constituent materialsMaterial Type Tensile strength/MPa Tensile modulus/GPa Elongation at break/% Density/(g·cm−3) Carbon fiber T700 4 900 240 2.1 1.80 Glass fiber E 3 430 73 4.8 2.54 Bismaleimide BH301 92 4.5 2.4 1.25 表 2 三维编织碳纤维(CF)-玻璃纤维(GF)混杂织物和层合CF-GF混杂织物的织造工艺参数Table 2. Technological parameters of the three-dimensional braided carbon fiber(CF)-glass fibers (GF) hybrid fabric and the laminated CF-GF hybrid fabricReinforced
structureYarns liner density/tex Preformed unit density/(yarn·cm−1) Layers Fiber volume
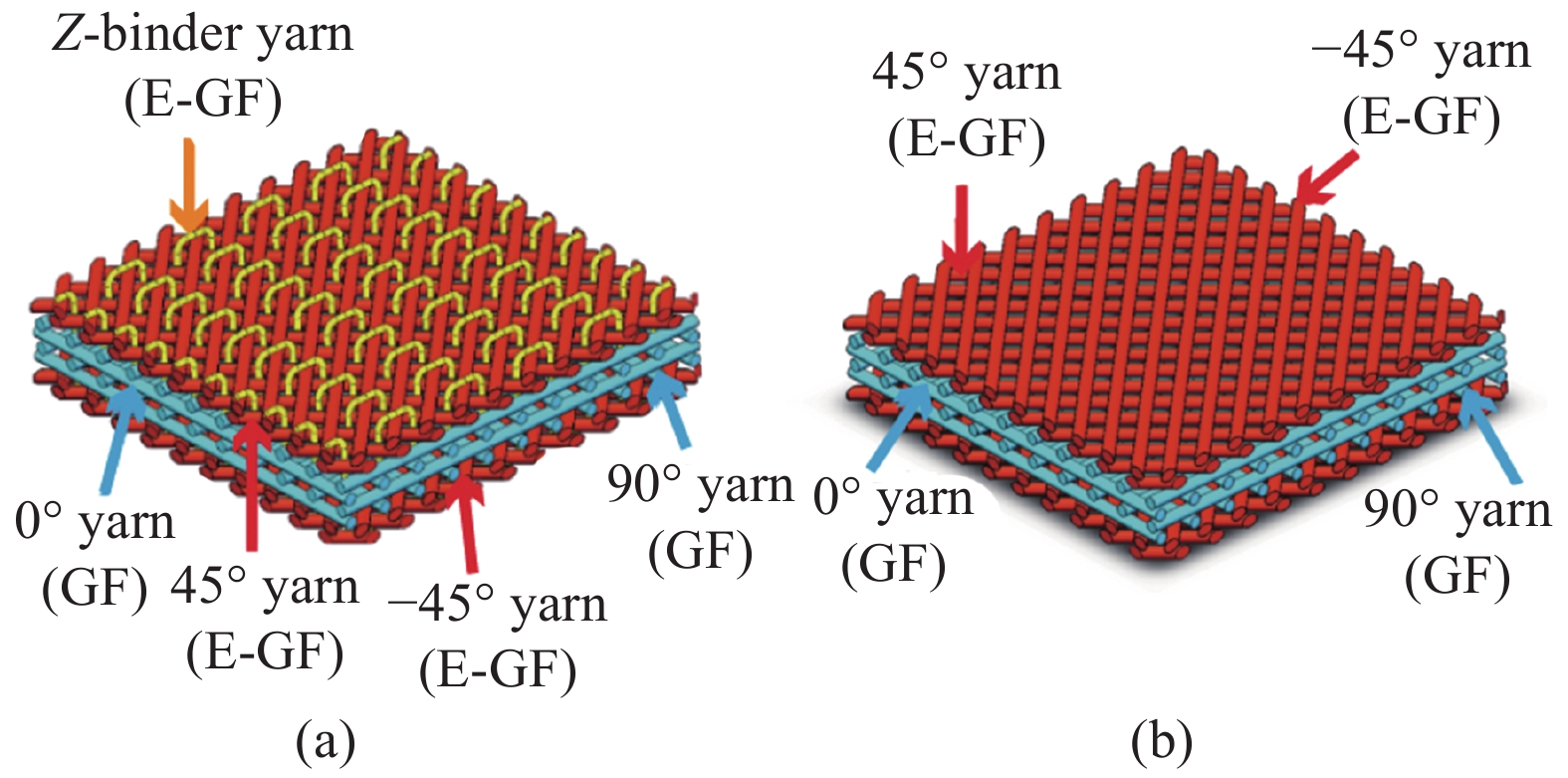
fraction/vol%0°/90° ±45° Z-binder yarns 0°/90° ±45° Z-binder yarns Braided fabric 800 400×2 400 5 6 5 8 47.74±1.16 Laminated fabric 800 400×2 — 6 6 — 8 46.23±1.42 图1为编织织物与层合织物的结构示意图。其中，编织织物采用置换法来制备[21]。层合织物由经密为6根/cm的CF单向带和E-GF单向带，按照设计要求铺层形成。
![]()
图 1 编织织物 (a) 和层合织物 (b) 的结构示意图Figure 1. Schematics of the braided fabric (a) and the laminated fabric (b)E-GF—E-glass fiber树脂传递模塑成型工艺被用于制备两种复合材料，将编织织物(250 mm×180 mm×4 mm)和层合织物(250 mm×180 mm×4 mm)放到模具中，合模，检查模具是否漏气后放入烘箱中加热到130℃。将BMI注入反应釜中，并加热到130℃，静置5 min。然后将模具和反应釜用导管相连，并用真空泵将模具抽真空，然后给反应釜加0.6 MPa的压强使树脂注入模具，直到在树脂收集器中看到足够量的树脂，表明模具已经被树脂完全填满。之后将导管拆除，把模具放在烘箱内使树脂加热固化。固化工艺为：180℃-3 h、230℃-3 h。固化完毕后，让模具在烘箱内自然冷却至室温后方可取出模具，防止快速冷却造成热应力。然后进行拆模，取出固化完全的复合材料。最后按照各实验用样尺寸要求将大块三维面内准各向同性CF-GF混杂编织/BMI复合材料和面内准各向同性CF-GF混杂层合/BMI复合材料在水切割机上切割成所需大小即可。
1.2 热氧老化试验
本研究选用的BMI的玻璃化转变温度为230℃，因此，200℃和高于玻璃化转变温度的250℃被选定作为老化温度来进行老化实验。老化时间为10、30、90、120和180天。为消除固化差异对复合材料性能产生的影响，本研究将所有试样均匀混合在一起采取随机抽取的方法将试样分配到每个老化条件下。为了减少试样离散性带来的误差，每个老化条件下安排3个试样，进行独立重复试验。
将每个温度的试样按照倒序的顺序放入由北京中科环试股份有限公司生产的HQL-50高温换气老化试验箱，即先放老化时间为180天的试样，过60天后放入老化时间为120天的试样，再过30天放入老化时间为90天的试样，以此类推，直到按照设定的老化时间将所有试样放入老化箱。目的是让所有试样可以在同一天取出，可以有效避免测量环境造成的影响。取出来的试样需要放入干燥的密闭容器内至少24 h后方可进行性能测试。
1.3 测试表征
1.3.1 红外光谱测试
德国PerkinElmer公司生产的Spotlight 400 & Frontier型傅里叶变换红外光谱仪(FTIR)被用来观测老化前后复合材料试样表面波长在4000~400 cm−1范围内官能团的变化。FTIR只能记录从样品表面到内部500 μm深度范围内的官能团的变化，因此测试得到的主要是表面官能团的变化。样品用酒精擦洗干净并放入70℃的恒温干燥箱内干燥24 h后方可进行测试。
1.3.2 失重测试
使用精度为0.01 mg的日本岛津AUW120D型电子分析天平获得两种复合材料的弯曲试样在200℃和250℃下老化前后的质量，老化失重率按下式进行计算：
Mt=m0−mtm0×100% 式中：
Mt 表示失重率；m0 和mt 分别为试样的初始质量(g)与老化t天后的质量(g)。1.3.3 形貌表征
使用基恩士VHX-5000三维显微系统对老化前后试样的裂纹和断裂形貌进行观测，同时得到其深度合成图像。深度合成图是通过改变焦距，从而获得凹凸不平表面的深度信息。采用美国FEI公司生产的Quanta-450-FEG场发射扫描电子显微镜(FESEM)和X-MAX50能谱仪(EDS)对样品老化前后的纤维/基体界面形貌和元素含量进行了表征。
1.3.4 力学性能测试
弯曲性能测试为三点弯曲实验，参考标准GB/T 1449—2005[22]在深圳三思纵横科技股份有限公司生产的UTM5205X型万能材料试验机上进行，加载速率为2 mm/min，试样大小为80 mm×15 mm×4 mm。
双切口剪切性能测试参考标准ASTM D3846[23]在UTM5205X型万能材料试验机上进行，加载速度为1.3 mm/min，试样尺寸如图2(a)所示，图2(b)为双切口剪切测试夹具。
![]()
图 2 双切口剪切试样尺寸图 (a) 与测试夹具图 (b)Figure 2. Size fabric picture (a) and test fixture picture (b) of the double-notch shear sample2. 结果与讨论
2.1 热氧老化对BMI化学结构的影响
图3为BMI分别在200℃和250℃条件下热氧老化不同时间前后的FTIR图谱。可以看出热氧老化对BMI的影响。此外，表3总结了老化前后BMI的特征峰。如图3所示，在200℃和250℃条件下老化180天(对比未老化试样)的BMI的FTIR图谱发生了明显的变化。首先，2922 cm−1和2851 cm−1的峰值与单体单元的C—H拉伸有关，它们的减少证实了BMI中易受影响的烃类单元经过长时间的热氧老化后会被严重氧化。此外，在1710 cm−1和1365 cm−1处的吸收峰减小是由于高温导致这些化学键的断裂[21]。然而，随着老化时间的延长，1602 cm−1处的吸收峰逐渐增加，这证实了固化后的BMI中的亚甲基基团(—CH2—)被氧化并与苯环结合形成了C=O[24-25]。1510 cm−1、1184 cm−1、1098 cm−1处的吸收峰都与热氧分解有关，934 cm−1处的吸收峰也明显减小，这些都说明了交联的马来酰亚胺环分解得越来越多。综上所述，BMI在高温下老化不同时间发生主要的变化是交联马来酰亚胺的氧化分解，这是BMI发生破坏的主要原因。此外对比图3(a)和图3(b)可以发现，BMI无论在200℃还是在250℃下热氧老化，其变化的吸收峰都是一致的，然而，在250℃条件下老化的BMI老化10天后就发生了明显破坏，大部分吸收峰已经变得不明显，这说明在高于玻璃化转变温度的250℃条件下进行热氧老化时，BMI在短时间内就会发生非常明显的破坏。
![]()
图 3 双马来酰亚胺树脂(BMI)在200℃ (a) 和250℃ (b) 下老化不同时间前后的FTIR图谱Figure 3. FTIR spectra of the bismaleimide (BMI) at 200℃ (a) and 250℃ (b) for different aging time表 3 老化BMI的红外特征峰位置对照Table 3. Comparison of infrared characteristic peak position of aged BMIWavenumber/cm−1 Characteristic peak Functional group 2922 Asymmetric CH2 —CH2— 2851 Symmetric CH3 —CH3— 1710 Asymmetric imides —C=O— 1602 Combined production of C=C and C=O —C=C–C=O 1510 C—C of the benzene ring —C—C— 1365 Aliphatic groups and imines CH, CH2, CH3 1180 Generated by C=C C—N—C 1098 Succinimide or ether —C—O—C— 934 Maleimide deformation C=C 为了进一步了解热氧化老化对复合材料中BMI的C、O元素的影响，分别对未老化和在200℃和250℃老化的BMI进行了能谱分析。图4列出了C、O的相对原子分数和O/C原子比的值。可以发现，随着老化时间的延长及老化温度的增加，O元素含量及O/C值在增加，在200℃和250℃热氧条件下老化180天后，O/C值分别达到了16.86%和23.89%，而C元素含量总体在减小，这一结果和FTIR图谱(图3)的分析结果是一致的。C元素相对含量减小有两方面原因，一方面是由于部分含C官能团被O2氧化，O元素的含量提高，相应的C元素含量就会降低；另一方面可能是试样中部分C元素和O元素结合生成CO2挥发了[26-27]。
![]()
图 4 200℃和250℃下老化前后BMI试样表面C (a)、O (b) 相对含量及O/C (c) 的值Figure 4. Change of C relative content (a), O relative content (b), and the value of O/C (c) of the BMI sample surface at 200℃ and 250℃ for different aging time2.2 热氧老化对复合材料外观形貌的影响
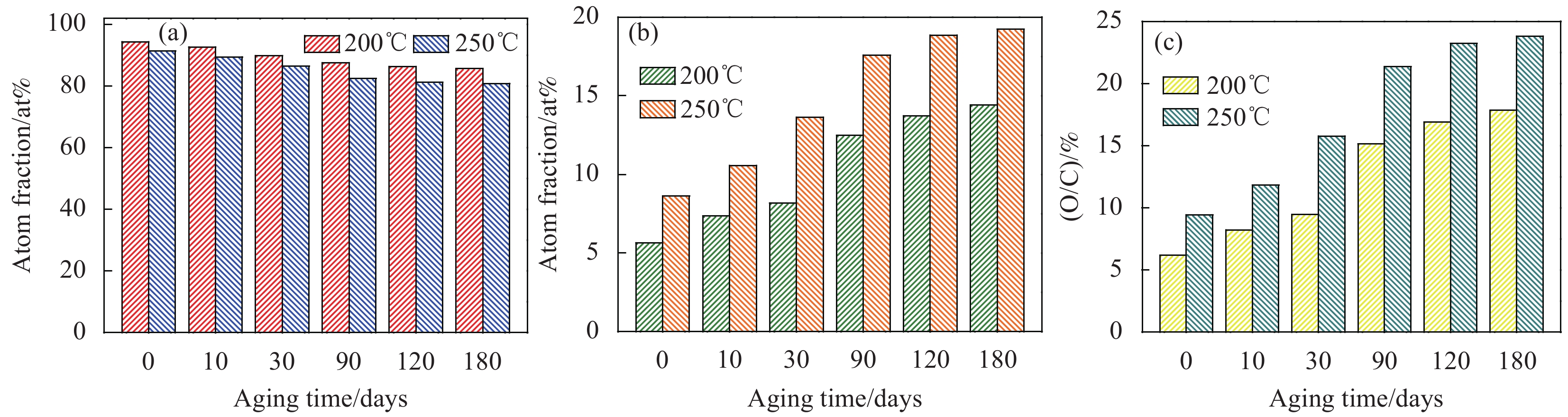
在250℃条件下老化不同时间(10天、30天、90天、120天、180天)的编织复合材料表面的光学显微图像和相应的实时深度合成图像如图5所示。可以发现，未老化的试样表面(图5(a))相对光滑，对应的实时深度合成图像(图5(b))可以更清楚地验证这一结果。经过250℃高温热氧老化后，试样表面开始变得凹凸不平(图5(c)~5(l))。且随着老化时间的延长，试样表面越来越不平。这是由于热氧老化导致BMI分解脱水，分子链断裂，然后树脂开始收缩并逐渐分解[26]。此外，CF和E-GF的热膨胀系数分别为−0.38×10−6℃−1和2.59×10−6℃−1(由制造商提供)，BMI的热膨胀系数为44×10−6℃−1[27]。因此，由于CF、E-GF和BMI三者的热膨胀系数的不匹配，纤维与BMI的界面处会产生局部热应力，容易造成裂纹的产生。另外，老化后的样品表面的裂纹为氧气进入复合材料内部提供了额外的通道，加速了BMI的氧化降解。因此可以认为，在热氧老化过程中，老化的样品表面变得越来越粗糙，并出现了大量的裂纹，这是由于热氧老化导致试样中大量BMI逐渐被氧化分解造成的。
![]()
图 5 三维编织CF-GF/BMI复合材料在250℃老化不同时间表面的显微照片和实时深度复合图像Figure 5. Micrographs and real-time depth composite images on the surface of the braided CF-GF/BMI composite at 250℃ for different aging time图6为编织复合材料和层合复合材料在250℃老化前后的侧面的显微照片。首先，可以清楚地看到，编织复合材料中存在沿厚度方向的Z向纱。其次可以看出，未经热氧老化的层合复合材料和编织复合材料的截面相对比较光滑(图6(a)和图6(c))。在250℃条件下老化180天后的试样表面出现了大量的裂纹(图6(b)和图6(d))。图6(e)和图6(f)为图6(d)裂纹的扫描电镜图，纤维束之间的裂缝清晰可见。
![]()
图 6 CF-GF/BMI复合材料试样在250℃老化前后的侧面的显微照片Figure 6. Photomicrographs of cross-section of the CF-GF/BMI composite sample before and after aging at 250℃((a), (b) Laminated composite; (c), (d) Braided composite; (e), (f) Zoom on cracks corresponding to (d))图7为编织复合材料在250℃老化不同时间SEM图像。可以看到大量的BMI覆盖在未老化试样的纤维表面(图7(a))，这说明纤维/基体间有良好的结合力。暴露在250℃高温环境后，随着老化时间的延长，附着在纤维上的树脂量逐渐减少(图7(b)~7(f))。样品在250℃老化120天后(图7(e))和180天后(图7(f))，纤维排列变得松散，表面逐渐光滑，BMI基体材料变少，这说明界面被严重破坏，BMI基体与纤维之间的弱界面附近出现明显的裂纹。
![]()
图 7 编织复合材料在250℃老化不同时间的SEM图像Figure 7. SEM images taken from the braided composite at 250℃ for different aging time2.3 热氧老化对复合材料质量的影响
图8为在200℃和250℃条件下老化后的编织复合材料和层合复合材料失重率与老化时间的关系。可以看到，两种试样老化后的失重率都逐渐增加。此外可以发现，在刚开始老化一段时间内，试样的质量损失很快，随着老化时间的继续延长，老化失重速率的增加逐渐减小。这是由于在老化开始阶段，存贮在复合材料内部的具有一定的初始湿含量的残余低分子物质迅速挥发，因此试样质量损失很快，且温度越高，质量损失越快。之后物理老化和化学老化协同作用，试样在长期的高温环境中开始分解产生低分子物质，这些低分子物质继续挥发，使老化失重率继续增加。此外，在两种温度下，编织复合材料的失重始终小于层合复合材料，这是由于纤维在热氧环境下具有稳定性，因此树脂基复合材料的失重只与基体有关[28]。编织复合材料的纤维体积含量(47.74 vol%)比层合复合材料的纤维体积含量(46.23 vol%)大，即层合复合材料的基体含量为53.77 vol%，编织复合材料为52.26 vol%，由于失重主要来自树脂基体的热氧分解，因此层合复合材料中有更多的树脂被氧化分解，造成编织复合材料的失重略低于层合复合材料。另外可以看到，在高于玻璃化转变温度的250℃下老化的试样失重率明显远高于200℃下老化的试样，这说明温度越高，树脂分解越严重。
![]()
图 8 层合复合材料和编织复合材料老化后失重率与老化时间的关系Figure 8. Relationship between weight loss rate and aging time of laminated composite and braided composites2.4 热氧老化对复合材料弯曲性能的影响
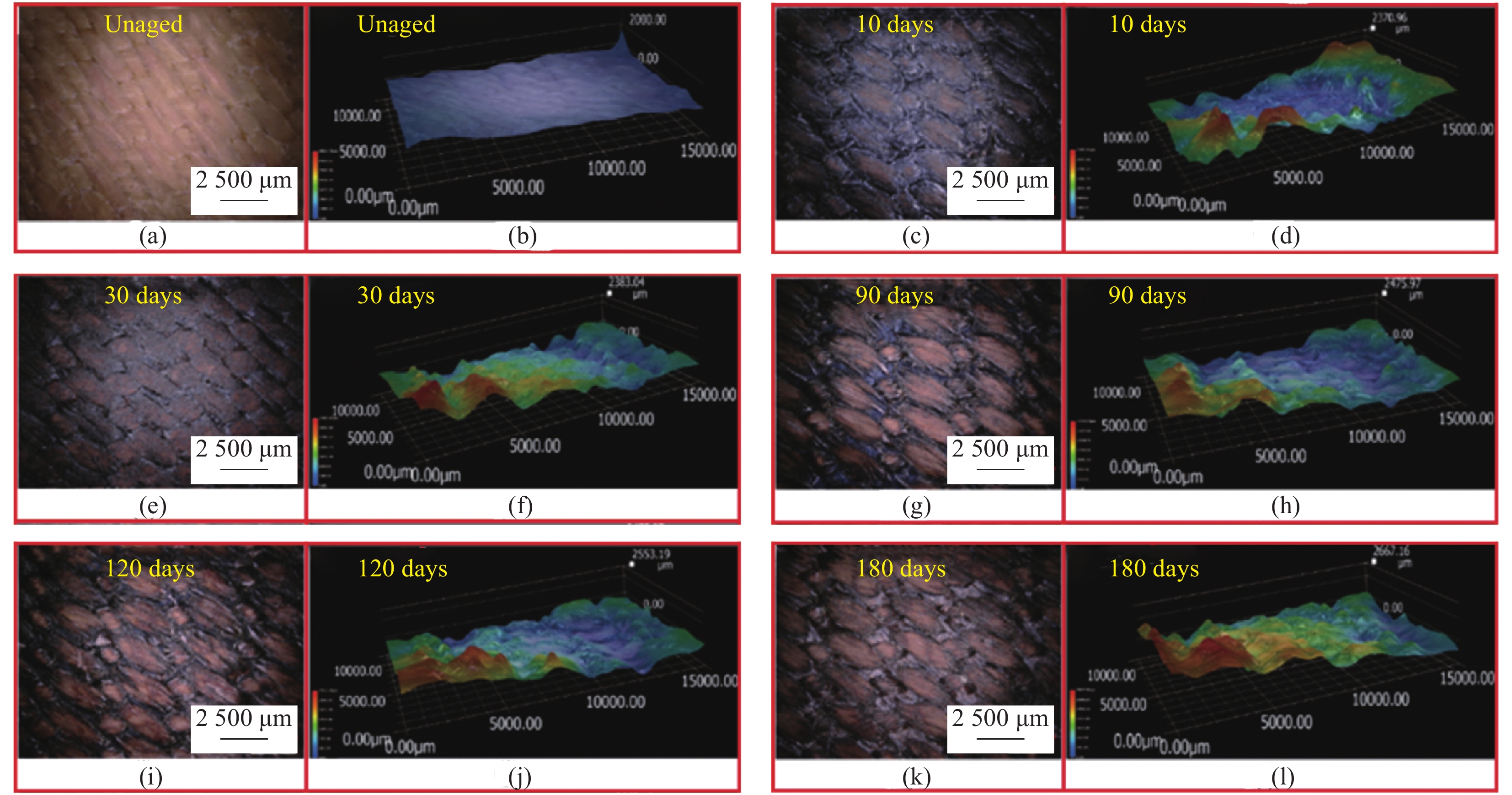
图9为编织复合材料和层合复合材料在不同温度下老化前后典型的三点弯曲载荷-位移曲线。由图9(a)可以发现，常温下层合复合材料在破坏初期表现出明显的线弹性行为，之后开始线性增加，达到最大载荷后开始急速下降，这是材料分层破坏迅速扩展导致的。而编织复合材料的曲线在初始阶段随着位移线性增加，在达到最大载荷前呈缓慢爬升趋势，然后开始下降，这是由于编织复合材料存在沿厚度方向的Z向纱线，Z向纱将其他所有的纱线都捆绑在一起，层间裂纹行进至Z向纱处被阻止，不能继续向前扩展，复合材料表现出渐进破坏特征。此外，相比于老化前，层合复合材料和编织复合材料在老化180天后的载荷均急速下降，在250℃老化后的载荷-位移曲线几乎为一条直线。结合前面的分析可以知道，弯曲断裂载荷的不断下降是老化导致的树脂基体不断降解和CF/BMI和E-GF/BMI界面性能不断下降协同作用的结果。
![]()
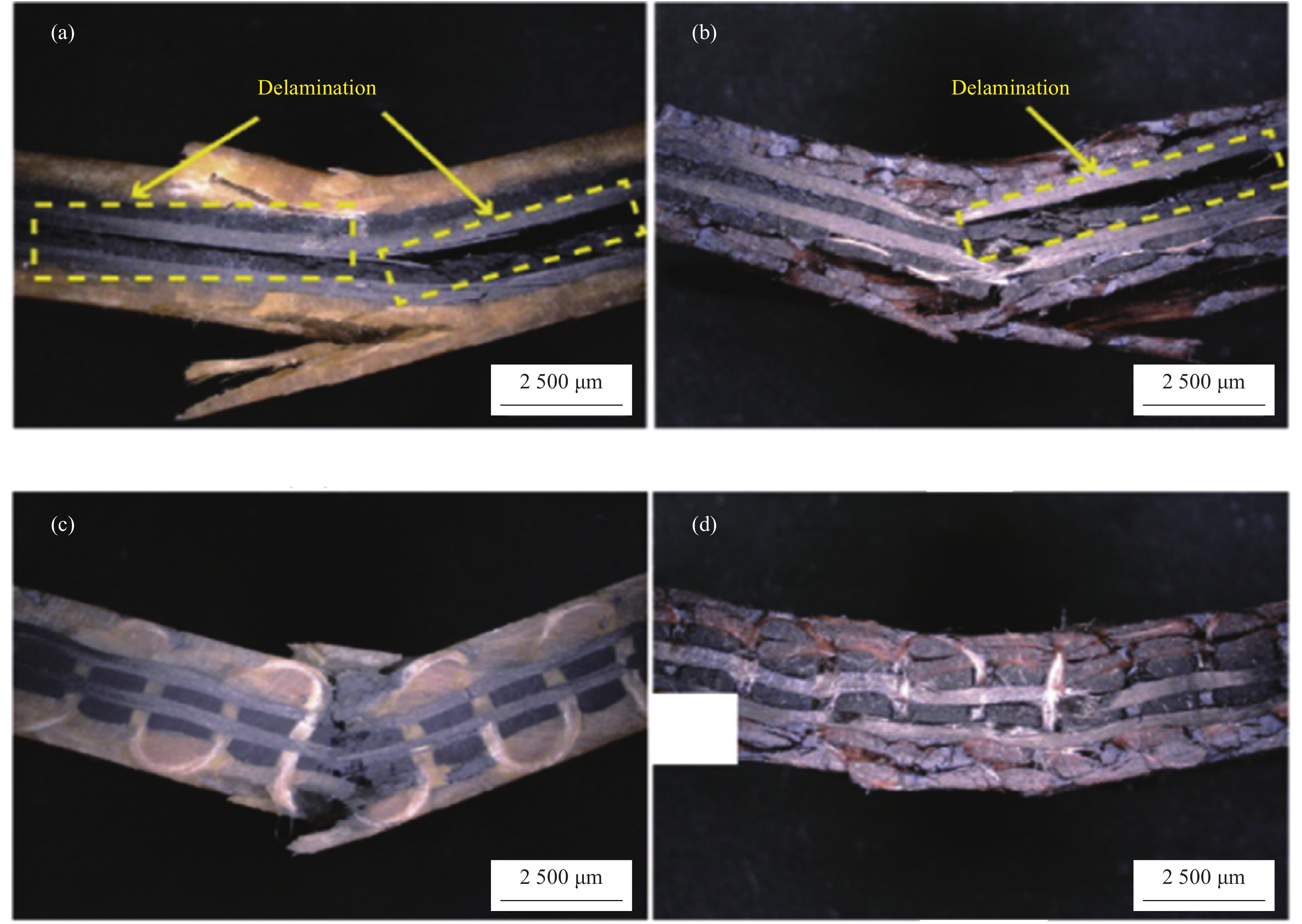
图 9 编织复合材料 (a) 和层合复合材料 (b) 在200℃和250℃老化不同时间前后的弯曲载荷-位移曲线Figure 9. Bending load-displacement curves of the braided composites (a) and laminated composites (b) at 200℃ and 250℃ for different aging time图10为250℃老化前后两种材料的试样在弯曲试验破坏后沿长度方向的侧面显微图像。可以清楚地看到，层合复合材料发生了明显的分层破坏(图10(a))，而编织复合材料没有出现此现象(图10(c))，这验证了对图9的解释。层合复合材料无论是否老化都出现了分层破坏(图10(a)和图10(b))，且试样经热氧老化后，分层破坏也更严重。另外，可以看到经过弯曲破坏后的试样侧面(相对于未老化试样)出现了更多的裂纹，这是由于老化导致纤维/基体结合性能下降。从图10(c)和图10(d)可以看到编织复合材料的裂纹大多都出现在纱线交汇的区域，而纤维很少断裂。且在250℃下老化180天后的编织复合材料也没有像层合复合材料那样出现分层现象，这是由于编织复合材料的增强体是由沿厚度方向的Z向纱线将所有纱线捆绑起来，因此即使在老化导致界面性能下降进而产生裂纹的情况下，Z向纱的存在仍可以有效阻碍裂纹的扩展，避免了编织复合材料发生分层现象。
![]()
图 10 CF-GF/BMI复合材料弯曲试样在250℃条件下老化前后的沿长度方向的破坏形貌Figure 10. Fracture morphologies of the bending CF-GF/BMI composite samples along the length direction before and after aging at 250℃((a) Unaged laminated composite; (b) Aged laminated composite; (c) Unaged braided composite; (d) Aged braided composite)![]()
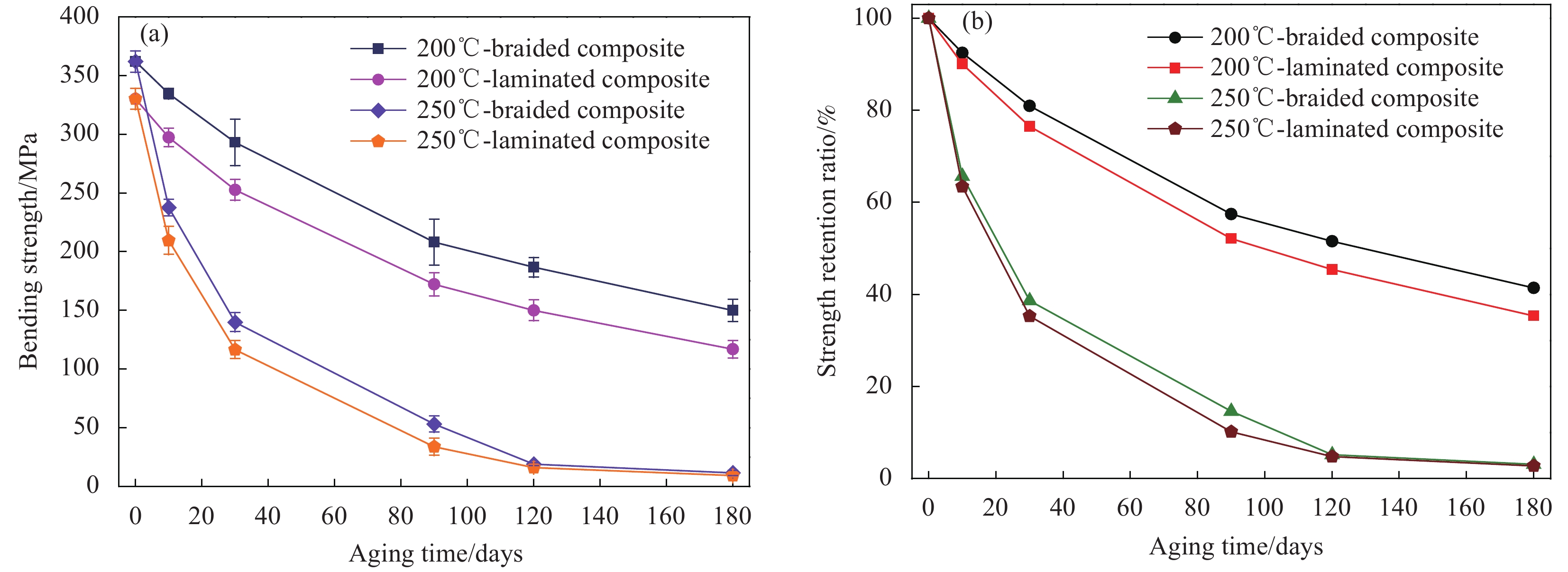
图 11 两种复合材料在200℃和250℃老化不同时间的弯曲强度 (a) 和弯曲强度保留率 (b)Figure 11. Bending strength (a) and bending strength retention rate (b) of two composites aged at 200℃ and 250℃ for different times图11(a)为弯曲平均强度随老化时间变化的趋势图。可以看到两种复合材料的弯曲强度都随老化时间的延长和老化温度的升高而下降。结合前面的化学结构分析、裂纹分析和界面结合情况分析得知，热氧老化导致的BMI出现氧化分解和纤维/基体界面结合性能退化是造成两种复合材料的弯曲性能都下降的原因。然而，两种复合材料的下降程度却并不相同。由图11(b)可以看到在不同的老化时间下编织复合材料的弯曲强度的保留率始终比层合复合材料大，由于两种复合材料都由相同的树脂和纤维构成，那么这种差异就只能归咎于增强体结构的差异。对于层合复合材料来说，沿厚度方向没有纤维的支撑，层与层之间只有树脂，当层合复合材料在遭受到弯曲破坏时，层与层之间非常容易产生裂纹，且裂纹一旦形成就容易沿着层间扩展，最终导致分层破坏的发生。而对于编织复合材料来说，沿厚度方向的Z向纱线的存在，使编织复合材料即使受到弯曲载荷作用后在试样表面产生了裂纹，Z向纱线也会阻碍这些裂纹的扩展，因此经过热氧老化的编织复合材料在纤维/基体界面性能下降的情况下也不会像层合复合材料那样发生分层破坏，而是所有的纱线抱合在一起共同承担外部的应力。因此，与层合复合材料相比，编织复合材料这种整体结构能够起到补偿由热氧老化导致的弯曲性能下降的作用。
2.5 热氧老化对复合材料层间性能的影响
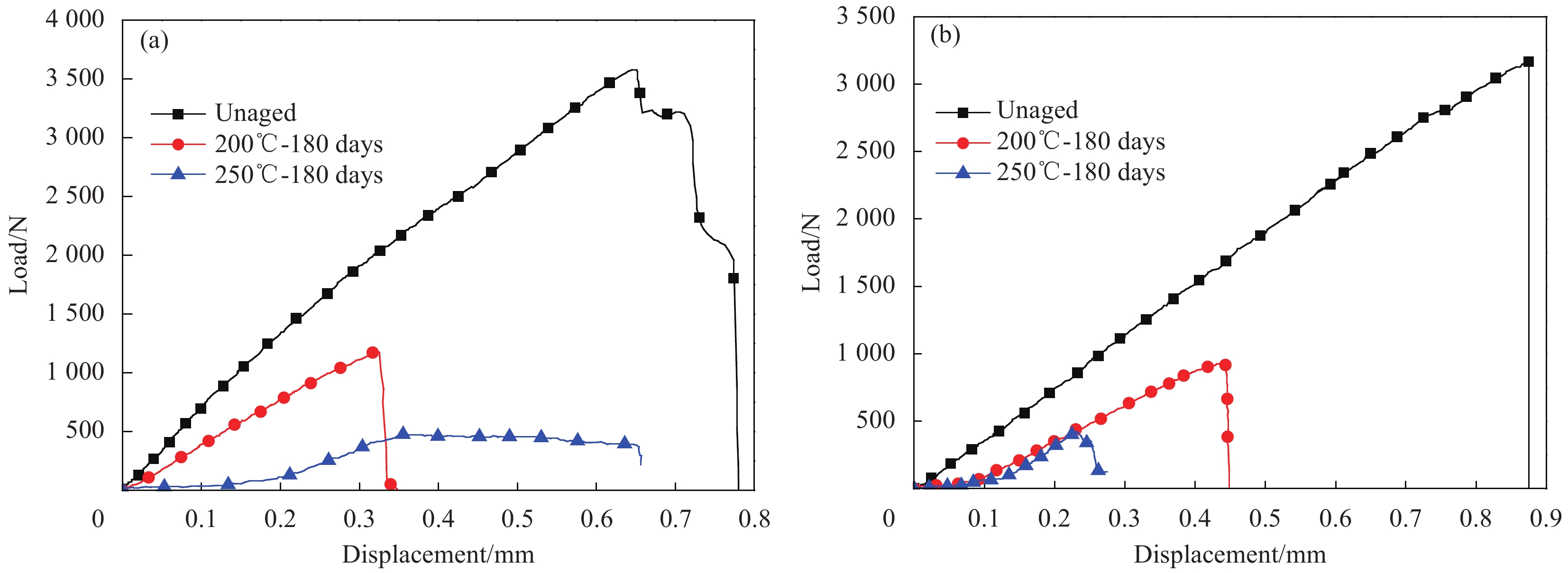
图12为层合复合材料和编织复合材料在200℃和250℃条件下老化180天前后典型的双切口剪切载荷-位移曲线。对比图12(a)和图12(b)，两种复合材料未老化时的剪切载荷-位移曲线在初始阶段表现出了线弹性现象。在达到峰值后，层合复合材料的载荷急剧下降，而编织复合材料在达到最大载荷后，出现了明显的平台。这是由于在编织复合材料在达到最大破坏载荷之后，大部分应力区域都发生了剪切破坏，然而，还有一些Z向纱线并没有完全断裂，并继续承受随后的剪切应力。图13是未老化的编织复合材料和层合复合材料试样在进行双切口剪切破坏后的断裂形貌图。很明显可以看到层合复合材料的断裂面只有交错的0°纱线和90°纱线(图13(c)和图13(d))。而编织复合材料中除了0°和90°纱线，还有大量的Z向纱线。此外可以发现两种复合材料承受剪切破坏的能力都随着老化时间的延长和老化温度的升高而降低。
![]()
图 12 编织复合材料 (a) 和层合复合材料 (b) 在200℃和250℃老化不同时间后的剪切载荷-位移曲线Figure 12. Shear load-displacement curves of the braided composite (a) and laminated composite (b) at 200℃ and 250℃ for different aging time![]()
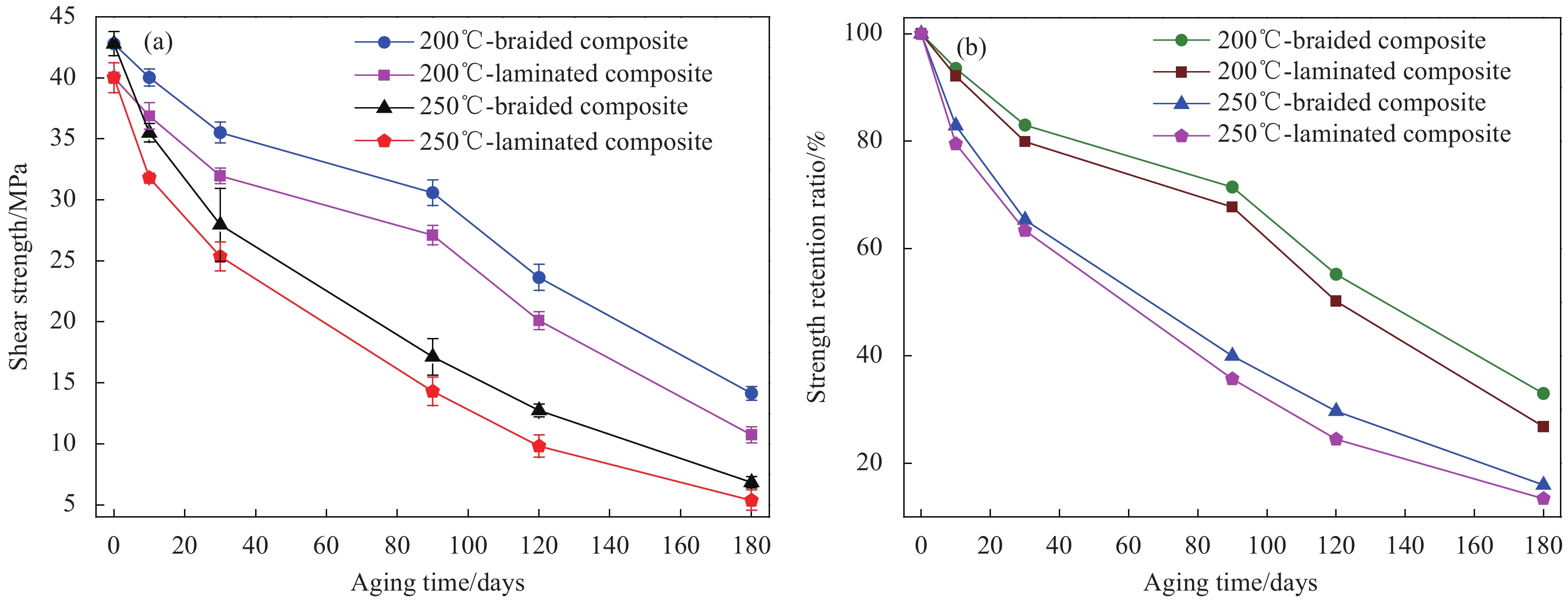
图 13 编织复合材料 (a) 和层合复合材料 (c) 未老化试样的双切口剪切破坏后的断裂形貌 ((b)和(d)分别为(a)和(c)对应的放大图)Figure 13. Fracture morphologies of braided composite (a) and laminated composite (c) after double-notch shear failure of unaged specimens ((b), (d) are enlarged images corresponding to (a) and (c), respectively)图14(a)是编织复合材料和层合复合材料在200℃和250℃条件下老化不同时间的平均剪切强度。可以看到未老化的编织复合材料的平均剪切强度为42.8 MPa，比未老化的层合试样的剪切强度(40.0 MPa)高了6.95%。这是由于层合复合材料在受到剪切破坏时，只有层与层之间的树脂基体承受力，而编织复合材料的增强体有沿厚度方向的Z向纱的存在，由于Z向纱比BMI能承受更大的力，因此编织复合材料可以承受更高的剪切应力。此外随着老化时间的延长，编织复合材料的平均剪切强度始终大于层合复合材料，而且相对于在200℃老化来说，在250℃老化的两种复合材料的层间剪切性能都下降得更严重。这是由热氧老化导致大量基体树脂的氧化分解和纤维/BMI基体界面性能的下降两方面原因造成的。
![]()
图 14 两种复合材料在200℃和250℃老化不同时间的剪切强度 (a) 和剪切强度保留率 (b)Figure 14. Shear strength (a) and shear strength retention rate (b) of two composites aged at 200℃ and 250℃ for different time为了比较两种材料的热氧稳定性，计算了两者的剪切强度保留率，图14(b)为剪切强度保留率与老化时间和老化温度的关系。可以看出，在相同的老化条件下编织复合材料的剪切强度保留率始终大于层合复合材料，这是由于编织复合材料是由沿厚度方向的Z向纱将所有纱线捆绑为一个整体结构，因此在热氧老化造成复合材料之间产生裂纹时，Z向纱的存在可以阻挡裂纹的扩展，减缓材料的老化速率。因此，与传统的层合复合材料相比，编织复合材料这种整体结构能够起到补偿由热氧老化导致纤维增强聚合物基复合材料的剪切性能下降的作用。
3. 结 论
(1) 热氧老化会导致复合材料表面产生大量裂纹，试样表面变得凹凸不平，且随着老化时间的延长和老化温度的增加，裂纹会变得越来越多，试样表面越来越粗糙。这一方面是由于热氧老化导致基体双马来酰亚胺树脂的氧化分解，另一方面是由于纤维与基体树脂的热膨胀系数不匹配，在纤维与基体的界面处产生局部热应力，导致纤维与基体之间界面结合性能下降，且下降程度随着老化时间的延长和老化温度的上升会变得愈发严重。
(2) 热氧老化导致两种复合材料的弯曲与剪切性能出现了不同程度的下降，然而在相同的热氧老化条件下编织复合材料的弯曲性能和剪切性能的保留率却始终大于层合复合材料。这是由两种材料的增强体结构不同造成的。编织复合材料由沿厚度方向的Z向纱将所有平面内纱线捆绑为一个整体结构，因此在热氧老化导致复合材料层间产生裂纹时，Z向纱线可以有效阻挡裂纹的扩展，减缓材料的老化速率。因此，与传统的层合复合材料相比，编织复合材料这种整体结构能够起到补偿由热氧老化导致纤维增强聚合物基复合材料的弯曲和剪切性能下降的作用。
-
![]()
图 1 蒙皮及其两侧筋条示意图
Figure 1. Illustration of skin with its siding ribs
kL—Elastic constraint stiffness on the left side of skin; kR—Elastic constraint stiffness on the right side of skin
![]()
图 3 帽型加筋壁板截面视图
Figure 3. Illustration of the section of cap-shape stiffened panel
b1—Distance between the adjacent stiffeners’ right and left side; b2—Width of the top end of stiffener; b3—Inner distance of the stiffener at its bottom end; bf—Width of stiffener’s foot; h—Height of the stiffener
![]()
图 4 两种方法下闭剖面蒙皮屈曲载荷对比
Figure 4. Buckling loads of the closed section shin with the two different methods
![]()
图 7 两种方法下开剖面蒙皮屈曲载荷对比
Figure 7. Buckling loads of the open section shin with the two different methods
![]()
图 8 Z型筋条板元分解
Figure 8. Partition Z-shape rib into plate elements
ba—Width of flange; bw—Width of web
![]()
图 9 帽型加筋壁板剖面示意图
Figure 9. Illustration of the section of plate with cap-shape ribs
Unit: mm
![]()
图 13 复合材料加筋壁板铺层顺序优化流程示意图
Figure 13. Sketch of the optimization process of stacking sequence optimization of composite stiffened panel
![]()
图 14 Z型复合材料加筋板结构剖面尺寸示意图
Figure 14. Cross-section size sketch of stiffened panel with Z-shape ribs
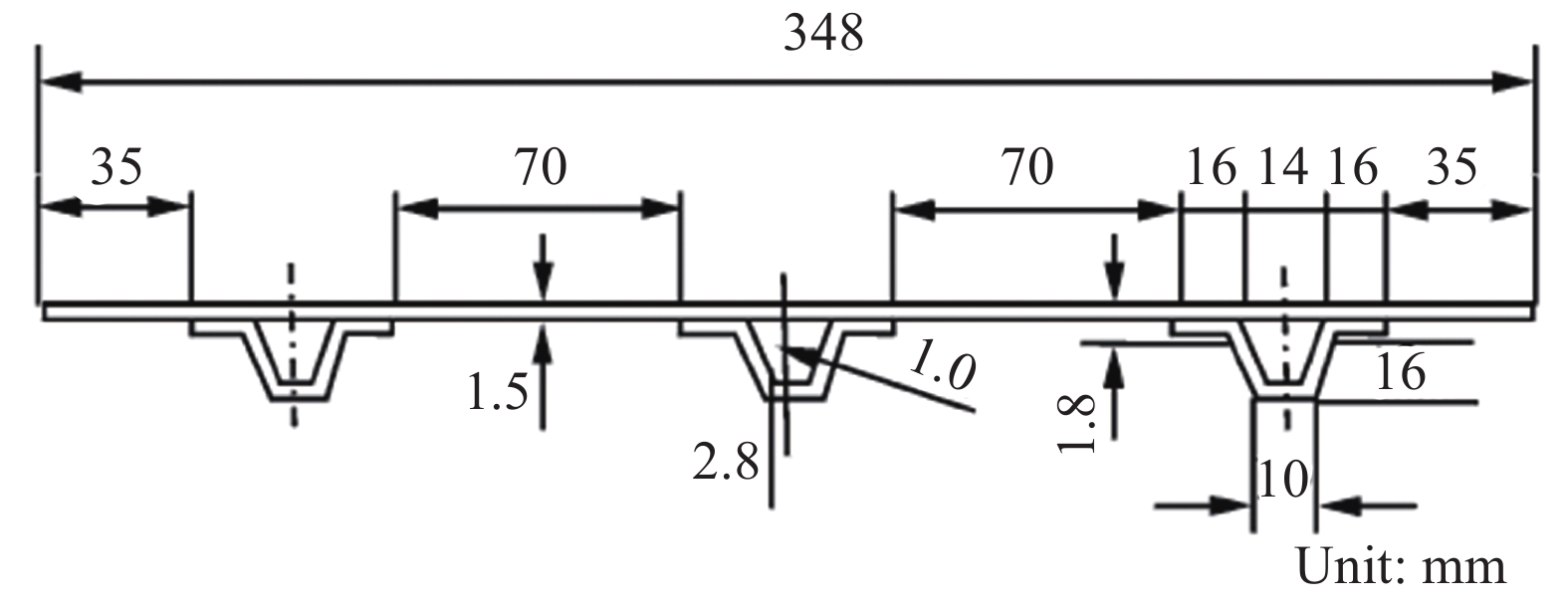
表 1 帽型加筋壁板单层材料属性
Table 1 Material property of laminate of cap-shape stiffened panel
Property E1/GPa E2/GPa G12/GPa ν12 Value 98 10.78 5.194 0.31 Notes: E1, E2,G12—Elastic constants of the material; ν12—Poisson's ratio. 
下载: 导出CSV
表 2 帽型加筋壁板基本参数
Table 2 Basic parameters of cap-shape stiffened panel
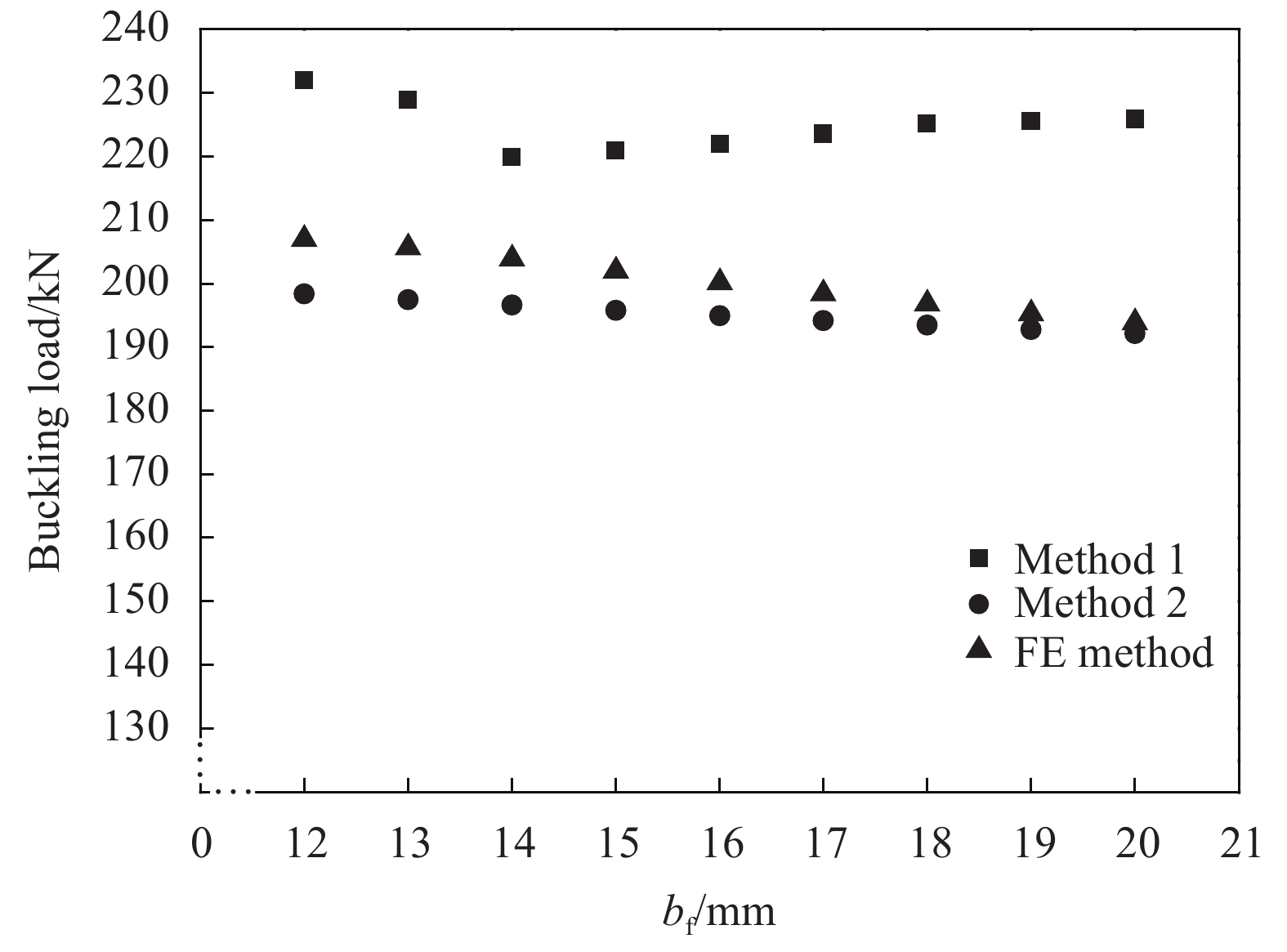
No. b2/mm b3/mm h/mm bf/mm 1 10 14 16 12 2 10 14 16 13 3 10 14 16 14 4 10 14 16 15 5 10 14 16 16 6 10 14 16 17 7 10 14 16 18 8 10 14 16 19 9 10 14 16 20
下载: 导出CSV
表 3 T型加筋壁板单层材料属性
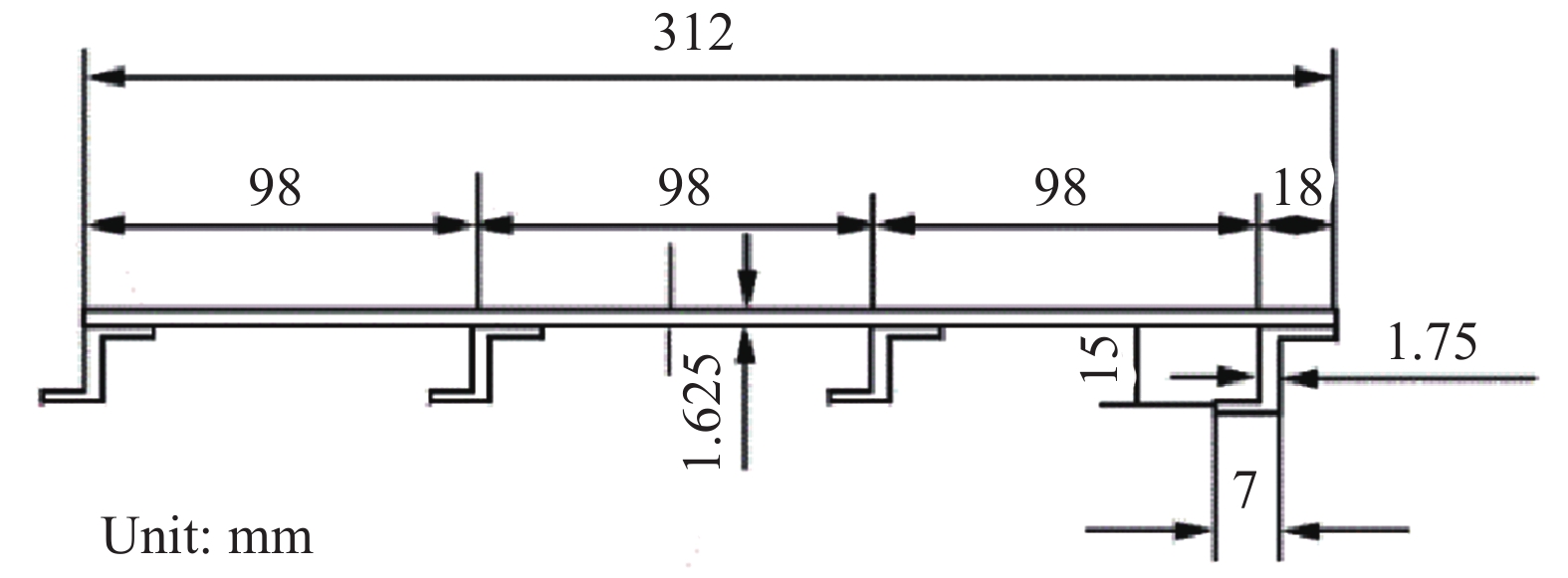
Table 3 Material property of laminate of T-shape stiffened panel
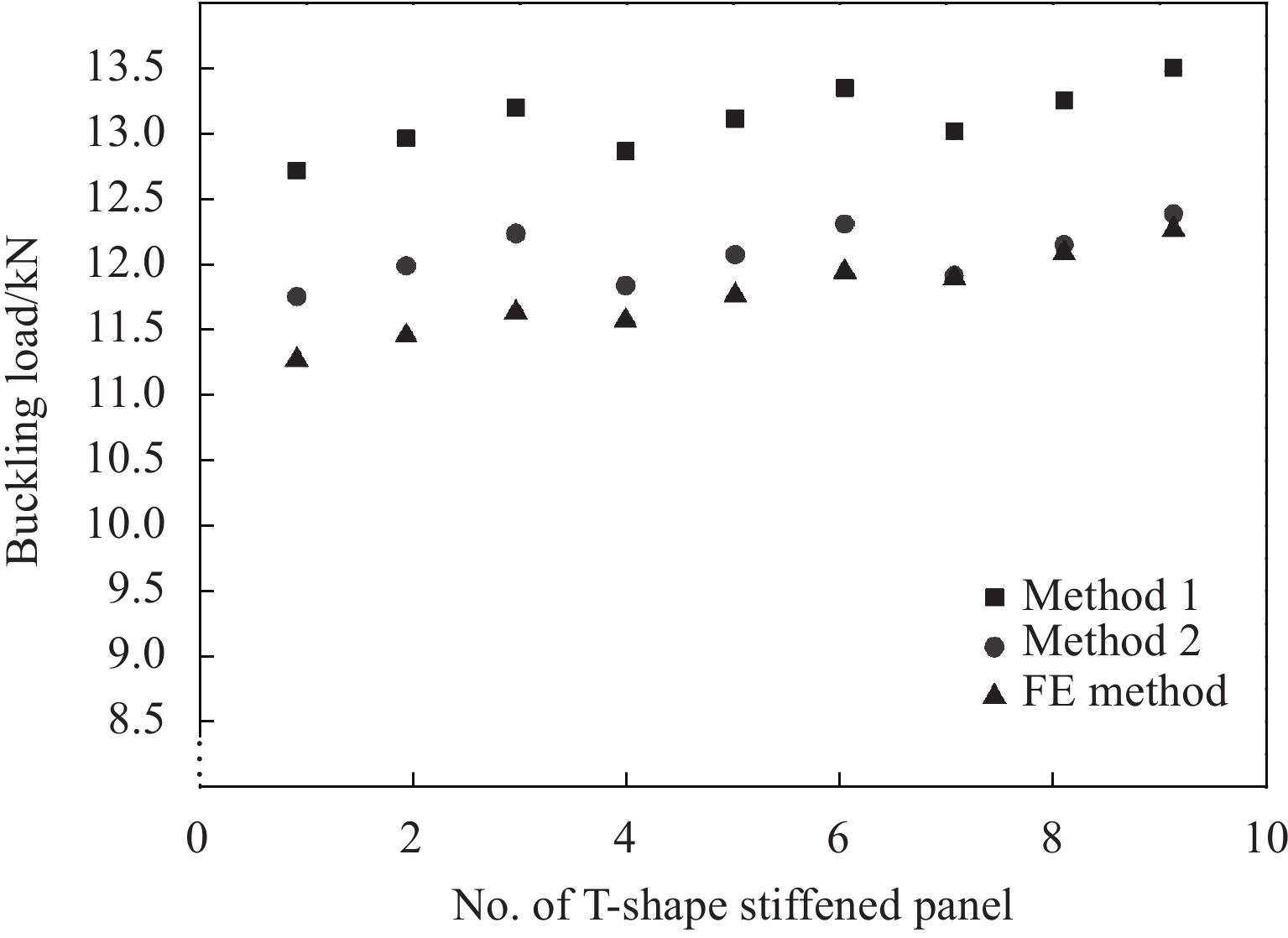
Property E1/GPa E2/GPa G12/GPa ν12 Value 59.2 58 3.77 0.32
下载: 导出CSV
表 4 T型加筋壁板基本参数
Table 4 Basic parameters of T-shape stiffened panel
No. b2/mm b3/mm 1 24 18 2 24 20 3 24 22 4 26 18 5 26 20 6 26 22 7 28 18 8 28 20 9 28 22
下载: 导出CSV
表 5 Z型加筋壁板单层材料属性
Table 5 Material property of laminate of Z-shape stiffened panel
Property E1/GPa E2/GPa G12/GPa ν12 Value 118 8.11 3.75 0.31
下载: 导出CSV
表 6 T型加筋壁板织物及单向带材料属性
Table 6 Woven and unidirectional fabric material property of laminate of Z-shape stiffened panel
Woven property Ex/GPa Ey/GPa Gxy/GPa νxy Value 50 50 4.8 0.3 Unidirectional fabric property E11/GPa E22/GPa G12/GPa ν12 Value 115.2 7.72 4.7 0.3 Notes: Ex, Ey and Gxy—Elastic constants of the woven fabric with νxy Poisson's ratio; E11, E22 and G12—Elastic constants of the unidirectional fabric with ν12 Poisson's ratio.
下载: 导出CSV
表 7 本文方法与参考书目提供的试验值、有限元方法计算值对比
Table 7 Results comparison of proposed formulation, experiments and FEA provided by reference book
下载: 导出CSV
表 8 Z型复合材料加筋板蒙皮铺层参数上下限
Table 8 Bounds of skin’s stacking parameters of sttiffened panel with Z-shape ribs
Stacking parameters ξ1Ask ξ2Ask ξ3Ask ξ1Dsk ξ2Dsk ξ3Dsk Lower bound 0.2308 0 0.6923 0.2198 0.1315 0.6240 Upper bound 0.4615 0.0769 0.0769 0.3195 0.2189 0.3609
下载: 导出CSV
表 9 Z型加筋板筋条铺层参数上下限
Table 9 Bounds of stiffener’s stacking parameters of sttifened panel with Z-shape ribs
Stacking parame-ters ξ1Ast ξ2Ast ξ3Ast ξ1Dst ξ2Dst ξ3Dst Lower bound 0.1429 0 0.7143 0.2303 0.1224 0.6443 Upper bound 0.4286 0 0.1429 0.3411 0.2099 0.3178
下载: 导出CSV
表 10 优化前后Z型加筋壁板屈曲载荷计算值
Table 10 Calculation values of buckling load of Z-shape stiffened panel before and after optimization
Method Buckling loads before
optimization/(N·m−1)Buckling loads after
optimization/(N·m−1)Improvement of
buckling loads/%Energy based method 268.84 314.25 16.90 Finite element method 259.03 304.02 17.37 Relative error/% 3.65 3.26 —
下载: 导出CSV
-
[1] NIKBAKT S, KAMARIAN S, SHAKERI M. A review on optimization of composite structures Part I: Laminated compo-sites[J]. Composite Structures,2018,195:158-185. DOI: 10.1016/j.compstruct.2018.03.063
[2] GUO M W, HARIK I E., REN W X. Buckling behavior of stiffened laminated plates[J]. International Journal of Solids and Structures,2002,39:3039-3055. DOI: 10.1016/S0020-7683(02)00232-9
[3] PERRET Adrien, MISTOU Sébastien, FAZZINI Marina. Global behaviour of a composite stiffened panel in buckling. Part 1: Numerical modeling[J]. Composite Structures,2011,93:2610-2618. DOI: 10.1016/j.compstruct.2011.04.026
[4] MO Yuming, GE Dongyun, ZHOU Jiangfan. Experiment and analysis of hat-stringer-stiffened composite curved panels under axial compression[J]. Composite Structures,2015,123:150-160. DOI: 10.1016/j.compstruct.2014.11.074
[5] LANZI Luca, GIAVOTTO Vittorio. Post-buckling optimization of composite stiffened panels: Computations and experiments[J]. Composite Structures,2006,73:208-220. DOI: 10.1016/j.compstruct.2005.11.047
[6] IRISARRI F, LAURIN F, LEROY F, et al. Computational strategy for multiobjective optimization of composite stiffened panels[J]. Composite Structures,2011,93:1158-1167. DOI: 10.1016/j.compstruct.2010.10.005
[7] 王燕, 李书, 许秋怡, 等. 复合材料加筋板剪切后屈曲分析及优化设计[J]. 航空学报, 2016, 37(5):1512-1525. WANG Y, LI S, XU Q Y, et al. Optimization design and analysis of stiffened composite panels in post-buckling under shear[J]. Acta Aeronautica et Astronautica Sinica,2016,37(5):1512-1525(in Chinese).
[8] NEMETH M P. Buckling behavior of long anisotropic plates subjected to combined loads: NASA TP-3568[R]. Washington: National Aeronautics and Space Administration, 1995.
[9] TARJÁN G, SAPKÁS Á, KOLLÁR L P. Stability analysis of long composite plates with restrained edges subjected to shear and linearly varying loads[J]. Journal of Reinforced Plastics and Composites,2010,29(9):1386-1398. DOI: 10.1177/0731684409105078
[10] QIAO Pizhong, SHAN Luyang. Explicit local buckling analysis and design of fiber-reinforced plastic composite structural shapes[J]. Composite Structure,2005,70(4):468-483. DOI: 10.1016/j.compstruct.2004.09.005
[11] HUO X P, QIAO P Z. Explicit local buckling analysis of rotationally and vertically restrained orthotropic plates under uniaxial compression[J]. International Journal of Structural Stability and Dynamics,2012,12(5):38-59.
[12] 余权舟, 乔丕忠, 祁洋, 等. 弹性约束正交各向异性板屈曲精度改进分析[J]. 力学季刊, 2016, 35(2):180-188. YU Quanzhou, QIAO Pizhong, QI Yang, et al. Precision improved local buckling analysis of elastically restrained orthotropic plates[J]. Chinese Quarterly of Mechanics,2016,35(2):180-188(in Chinese).
[13] BISAGN Chiara, VESCOVINI Riccardo. Analytical formulation for local buckling and post-buckling analysis of stiffened laminated panels[J]. Thin-Walled Structures,2009,47:318-334. DOI: 10.1016/j.tws.2008.07.006
[14] VESCOVINI Riccardo, BISAGN Chiara. Semi-analytical buckling analysis of omega stiffened panels under multi-axial loads[J]. Composite Structures,2015,120:285-299. DOI: 10.1016/j.compstruct.2014.10.003
[15] OMAR Bacarreza, ALIABADI M, APICELLA Alfonso. Robust design and optimization of composite stiffened panels in post-buckling[J]. Struct Multidisc Optim,2015,51:409-422. DOI: 10.1007/s00158-014-1136-5
[16] DE ALMEIDA F S. Stacking sequence optimization for maximum buckling load of composite plates using harmony search algorithm[J]. Composite Structures,2016,143:287-299. DOI: 10.1016/j.compstruct.2016.02.034
[17] AYMERICH F, SERRA M. Optimization of laminate stacking sequence for maximum buckling load using the ant colony optimization (ACO) metaheuristic[J]. Composites Part A: Applied Science and Manufacturing,2008,39(2):262-272. DOI: 10.1016/j.compositesa.2007.10.011
[18] 范志瑞, 杨世文, 金达锋, 刘哲. 基于分级优化的复合材料带加强筋板屈曲优化[J]. 复合材料学报, 2015, 32(3):797-804. FAN Zhirui, YANG Shiwen, JIN Dafeng, et al. Optimum buckling of composite stiffened panel based on hierarchy optimization[J]. Acta Materiae Composite Sinica,2015,32(3):797-804(in Chinese).
[19] 乔巍, 姚卫星. 复合材料加筋板铺层优化设计的等效弯曲刚度法[J]. 计算力学学报, 2011, 28(1):158-162. DOI: 10.7511/jslx201101028 QIAO Wei, YAO Weixing. Equivalent bending stiffness method for stacking sequence optimization of composite stiffened panel[J]. Chinese Journal of Computational Mechanic,2011,28(1):158-162(in Chinese). DOI: 10.7511/jslx201101028
[20] 冯玉龙, 程家林, 姚卫星. 复合材料加筋板结构的并行空间协同优化设计方法[J]. 南京航空航天大学学报, 2013, 45:360-366. DOI: 10.3969/j.issn.1005-2615.2013.03.011 FENG Yulong, CHENG Jialin, YAO Weixing. Concurrent subspace optimum design method for composite stiffened panel[J]. Journal of Nanjing University of Aeronautics & Astronautics,2013,45:360-366(in Chinese). DOI: 10.3969/j.issn.1005-2615.2013.03.011
[21] 吴莉莉, 姚卫星. 复合材料加筋板结构的二级协同优化设计方法[J]. 南京航空航天大学学报, 2011, 43(5):645-649. DOI: 10.3969/j.issn.1005-2615.2011.05.014 WU Lili, YAO Weixing. Two-level collaborative optimum design method for composite stiffened panel[J]. Journal of Nanjing University of Aeronautics & Astronautics,2011,43(5):645-649(in Chinese). DOI: 10.3969/j.issn.1005-2615.2011.05.014
[22] MIKI M. Optimum design of laminated composite plates using lamination parameters[J]. AIAA Journal,1993,31(5):275-283.
[23] LIU D Z, VASSILI V. A lamination parameter-based strategy for solving an integer-continuous problem arising in composite optimization[J]. Computers and Structures,2013,128:170-174. DOI: 10.1016/j.compstruc.2013.06.003
[24] DUTRA T A, ALMEIDA S D. Composite plate stiffness multicriteria optimization using lamination parameters[J]. Composite Structures,2015,133:166-177. DOI: 10.1016/j.compstruct.2015.07.029
[25] 刘哲, 金达锋, 范志瑞. 基于代理模型的复合材料带加强筋板铺层优化[J]. 清华大学学报(自然科学版), 2015, 55(7):782-789. LIU Zhe, JIN Dafeng, FAN Zhirui. Laminate optimization of a composite stiffened panel based on surrogate model[J]. Journal of Tsinghua University (Science and Technology),2015,55(7):782-789(in Chinese).
[26] 张长兴, 段世慧. 考虑稳定性的复合材料加筋板结构快速化铺层优化设计[J]. 玻璃钢/复合材料, 2018, 8:42-47. ZHANG Changxing, DUAN Shihui. Rapid stacking sequence optimization of composite stiffened panels considering stability[J]. Fiber Reinforced Plastics/Composites,2018,8:42-47(in Chinese).
[27] 中国航空研究院. 复合材料结构稳定性分析指南[M]. 北京: 航空工业出版社, 2002. Chinese Aeronautical Establishment. Guide for structural stability analysis of composite materials[M]. Beijing: Aviation industry Press, 2002(in Chinese).
[28] BISAGNI C, VESCOVINI R. Fast tool for buckling analysis and optimization of stiffened panels[J]. Journal of Aircraft, 2010, 46(6): 2041-2053.
[29] 沈观林, 胡更开, 刘彬, 等. 复合材料力学[M]. 北京: 清华大学出版社, 2013. SEHN Guanlin, HU Gengkai, LIU Bin, et al. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2013(in Chinese).
[30] CHRISTIAN M, MATTHIAS B. Closed-form buckling analysis of compressively loaded composite plates by omega-stringers[J]. Composite Structures,2009,88:424-435. DOI: 10.1016/j.compstruct.2008.05.021
[31] 陈金睿, 陈普会, 孔斌, 等. 考虑筋条弹性支持的轴压复合材料加筋板局部屈曲分析方法[J]. 南京航空航天大学学报, 2017, 49(1):76-82. CHEN J R, CHEN P H, KONG B, et al. Local buckling analysis of axially compressed stiffened laminated panels considering rotational restraint of stiffeners[J]. Journal of Nanjing University of Aeronautics & Astronautics,2017,49(1):76-82(in Chinese).
-
期刊类型引用(7)
1. 杨晨，姜亚明，项赫，李佳楠. 热氧老化对纬编双轴向多层衬纱织物增强复合材料力学性能的影响. 复合材料学报. 2023(01): 96-108 . 
本站查看
2. 张裕恒，王继辉，魏建辉，刘明，李旭，丁安心. 湿热环境下碳纤维增强乙烯基树脂复合材料长期力学性能. 复合材料学报. 2023(03): 1406-1416 . 本站查看
3. 魏建辉，刘明，高进城，张裕恒，丁安心. 吸湿老化后碳纤维增强乙烯基脂树脂复合材料高低温力学性能. 复合材料学报. 2023(06): 3279-3290 . 本站查看
4. 马琳梦，邹忠利，许满足，刘坤. 老化时间对AZ31B镁合金铁氰化钾转化膜耐蚀性的影响. 表面技术. 2022(01): 113-120+191 . 百度学术
5. 秦春丽，符浩，保安青. 碳纤维增强建筑用ZL109合金的组织及拉伸性能分析. 粉末冶金工业. 2022(02): 72-76 . 百度学术
6. 赵昌方，周志坛，张克斌，仲健林，任杰，乐贵高. 碳纤维复合材料燃气射流热冲击研究:冲蚀形貌及热力分析. 湘潭大学学报(自然科学版). 2022(03): 37-45+71 . 百度学术
7. 王志平，陈灏，路鹏程. 电-湿耦合作用下碳纤维增强树脂基复合材料损伤机制. 中国塑料. 2022(10): 39-45 . 百度学术
其他类型引用(2)
-
计量
- 文章访问数: 1263
- HTML全文浏览量: 658
- PDF下载量: 131
- 被引次数: 9
