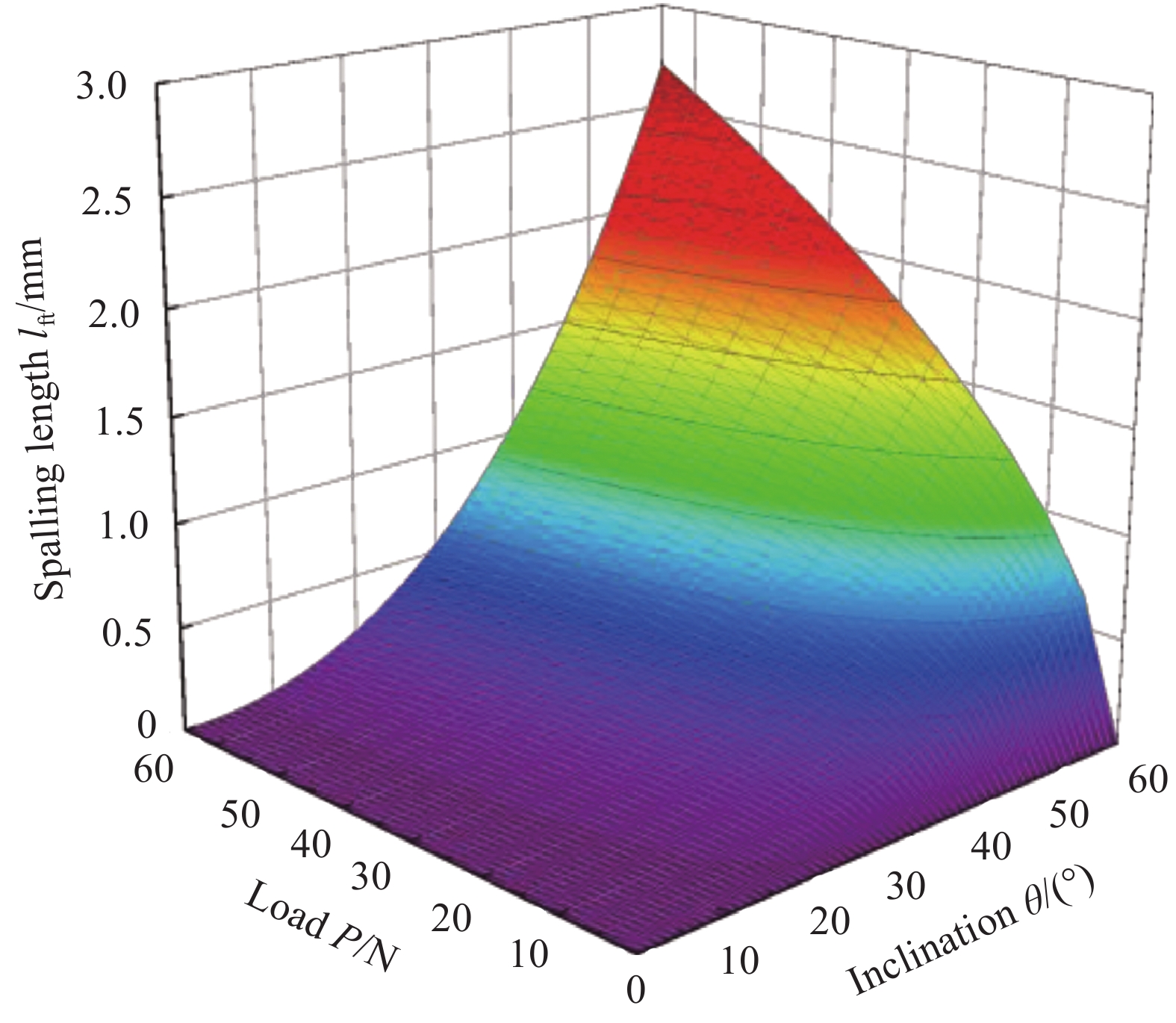
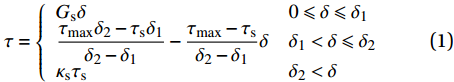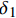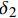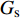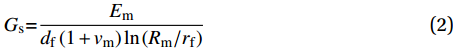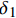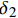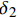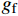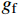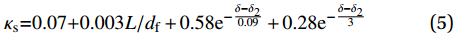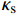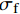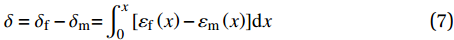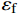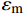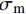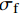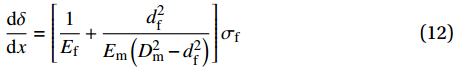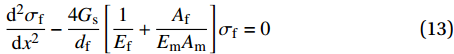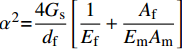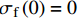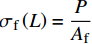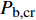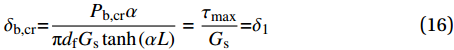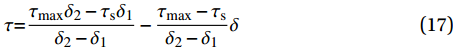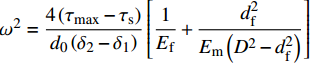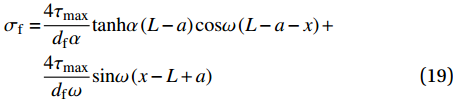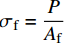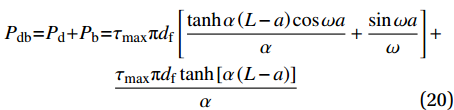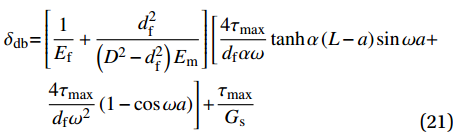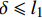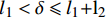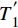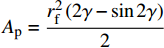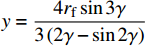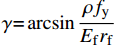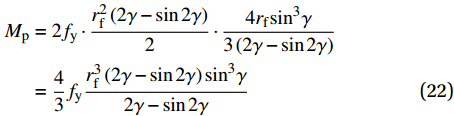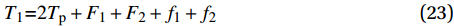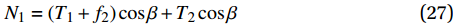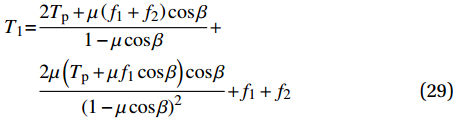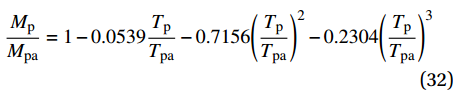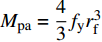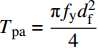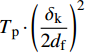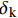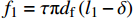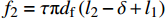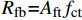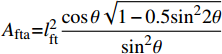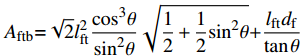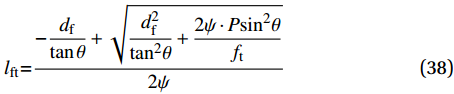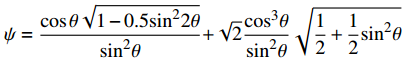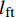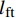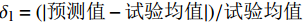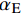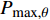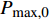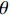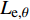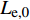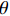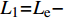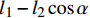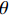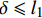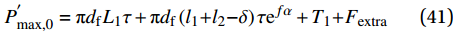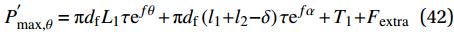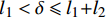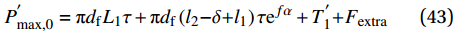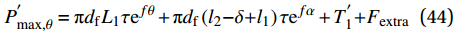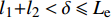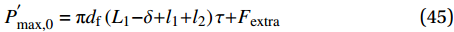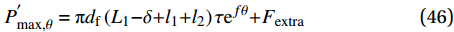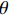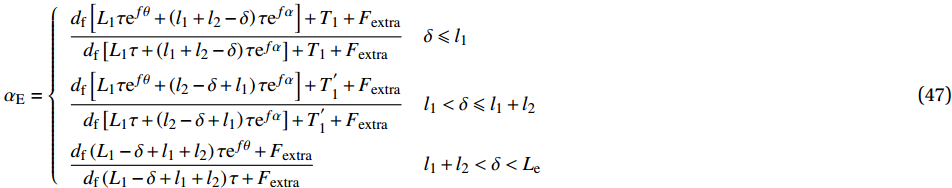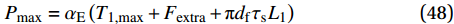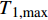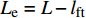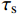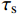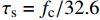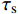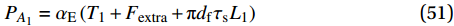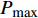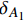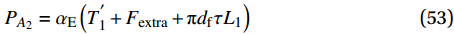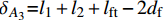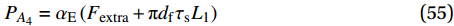Calculation model for pullout behavior of inclined hooked-end steel fiber in cement-based materials
-
摘要: 端钩型钢纤维是结构工程中应用最广泛的钢纤维品类之一,单根钢纤维拔出力学性能对于确定钢纤维混凝土的受拉本构及受拉韧性具有重要意义。为了得到能够有效预测倾斜端钩型钢纤维拔出荷载-端部位移曲线的理论模型,首先将倾斜端钩型钢纤维拔出过程分为完全黏结、脱黏和拔出滑移阶段三种受力状态,考虑不同拔出阶段及基体孔道损伤,建立了钢纤维黏结应力与纤维端部位移之间的关系,同时考虑钢纤维塑性变形、附加摩擦力及纤维拔出角度导致的基体剥落和挤压摩擦效应,建立了一种可以预测倾斜端钩型钢纤维拔出全过程的理论计算模型,在此基础上提出形式简单的简化模型,选取已有试验数据对提出的计算模型进行验证,结果表明:本文提出的两种模型均能够有效预测端钩型钢纤维拔出全过程,具有较高的计算精度且变异系数小,为进一步分析钢纤维对水泥基材料受拉性能的增强作用提供了理论依据。Abstract: It is well-known that the hooked-end steel fiber is one of the most widely-used type of steel fiber in structural engineering, and the pullout behavior of a single steel fiber is significant for determining the tensile constitutive and the tensile toughness of steel fiber reinforced concrete. In order to obtain a theoretical analysis method which can effectively predict the pullout load-end displacement curves of inclined hooked-end steel fiber, the inclined pullout process of the hooked-end steel fiber was divided into three states: fully bonding stage, debonding stage and pullout slipping stage. A novel bond shear stresses-end displacement model was established considering the different steel fiber pullout stages and the damage of the matrix hole. A theoretical analysis model that can predict the load-slip curve of the pullout behavior of inclined hooked-end steel fiber was proposed by considering the plastic deformation of the steel fiber, the additional friction, spalling and snubbing effects of the matrix caused by the fiber pullout inclination. A simplified model was also proposed based on the theoretical model. The existing experimental data were selected to verify and evaluate the proposed calculation model. The results show that the two models proposed in this paper can effectively predict the process of hooked-end steel fiber inclined pullout. And the two models have high calculation accuracy and low coefficient of variation, which provide a theoretical reference for further analysis of the effect of steel fiber on the enhancement of tensile properties of cement-based materials.
-
水泥基材料(如混凝土、水泥砂浆等)是目前结构工程中应用最广泛的建筑材料,由于其抗拉强度低,严重限制了其在实际工程中的应用。而在水泥基材料中加入钢纤维可以极大地改善其受拉性能,基体中随机分布的钢纤维可以通过桥接作用有效地限制裂缝的产生与发展[1]。
过去几十年研究者们对钢纤维混凝土(SFRC)进行了大量研究[2-3],包括SFRC材料的力学性能及其在结构中的应用,发现钢纤维与基体之间的黏结性能对于SFRC的力学性能有显著影响。工程中常用的钢纤维类型主要有:平直型、端钩型和波浪型;相同纤维体积掺量下加入平直型钢纤维对于混凝土和易性影响较小,不易出现纤维抱团等现象,可以进一步增加钢纤维体积掺量;而波浪型钢纤维由于其本身的机械变形可以显著增加其锚固性能,故可以增加钢纤维与基体之间的黏结性能;但是两者的缺点也很明显,端钩型钢纤维有效结合平直型钢纤维与波浪型钢纤维的优点,可以有效增强混凝土力学性能,对掺入不同形状钢纤维的混凝土进行试验也发现端钩型钢纤维对于提高混凝土力学性能是三者中最有效的[4-5],端钩型钢纤维也是实际工程中SFRC结构常用的钢纤维类型。研究端钩型钢纤维与混凝土基体之间的黏结-滑移性能可以为进一步明确钢纤维对SFRC抗拉性能的增强作用提供理论依据,尤其对于抗拉强度、受拉应力-应变曲线及韧性等具有重要意义。
研究者们对于钢纤维与混凝土基体之间的黏结性能进行了大量的试验研究[6-8],发现钢纤维与混凝土基体之间的黏结性能受多种因素的影响,包括纤维拔出角度、纤维埋置深度、基体强度及钢纤维形状等。平直型钢纤维的黏结性能主要由钢纤维与基体之间的化学胶着力和摩擦力组成[9-10];而端钩型钢纤维由于纤维变形会导致钢纤维拔出力学性能显著增强,需要在平直型钢纤维的基础上考虑纤维变形、附加摩擦等多种因素的影响[11-13],且在实际应用中纤维拔出角度对于钢纤维拔出力学性能影响较大,这也使分析端钩型钢纤维的拔出力学性能更加复杂。
目前对于平直型钢纤维的拔出力学模型的研究较多,但是不能将其直接应用于端钩型钢纤维,一些研究者在平直型钢纤维分析模型的基础上提出了端钩型钢纤维的拔出力学性能分析模型。Ghoddousi等[11]将钢纤维分为两部分,即平直部分和端钩部分,并将端钩部分等效为直径更大的平直钢纤维,以此来表现端钩部分的增强作用,从而提出一种简化的分析模型,该模型是在Naaman等[9]平直型钢纤维分析模型的基础上提出的,且将端钩部分等效为平直部分时简化较多,故其与试验结果相比误差很大。Soetens等[12]进行了一系列倾斜端钩型钢纤维拔出试验,根据试验结果确定了部分参数并得到端钩型钢纤维的拔出力学性能半经验计算方法。Laranjeira等[13]根据试验结果将倾斜端钩型钢纤维拔出全曲线分为多个控制点,根据端钩型钢纤维垂直拔出试验得到的荷载-位移全曲线来确定这些控制点的荷载和位移,该计算模型计算过程简便,但需要提前进行钢纤维拔出试验才能得到相应的数据。
可以看出目前对于端钩型钢纤维拔出力学性能的分析大多是基于试验结果拟合得到的经验计算模型,其力学概念不明确,很难适用于更大范围的应用。因此,提出一种端钩型钢纤维拔出力学性能理论计算模型具有重要意义。本文将钢纤维拔出过程分为三个阶段:完全黏结、脱黏和拔出滑移,考虑了纤维拔出角度、纤维变形及附加摩擦力等因素的影响,提出一种可以有效预测倾斜端钩型钢纤维拔出全过程的理论计算模型,并给出具体计算步骤。为了简化计算流程,在此基础上提出一种简化模型,采用提出模型对已有试验进行预测,并将试验结果与预测结果进行对比,验证了提出计算模型和简化模型的有效性和精确性。
1. 端钩型钢纤维拔出力学性能计算模型
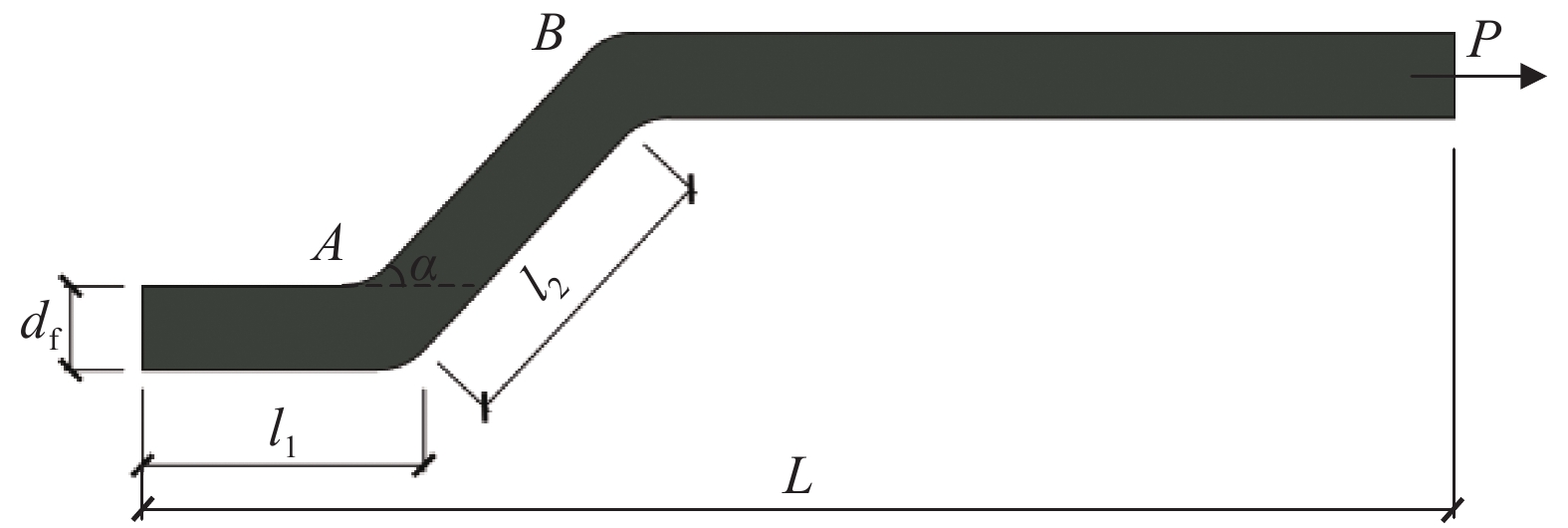
如图1所示,本文将钢纤维的拔出过程分为三个阶段,即完全黏结、脱黏和拔出滑移。端钩型钢纤维的几何尺寸如图2所示,其中L为钢纤维埋置长度,α为端钩倾角。
在加载初期,此时钢纤维与基体之间的黏结处于弹性阶段,对应图1(a);随着黏结应力超过最大黏结应力,沿钢纤维与混凝土基体的黏结部分开始由端钩部分向外逐渐脱黏,对应图1(b);在完全脱黏后钢纤维开始沿基体孔道向外侧拔出滑移,在滑移过程中会逐渐产生塑性变形,钢纤维端钩部分会逐渐被拉直,直至完全拔出,对应图1(c)。在完全黏结和脱黏阶段,由于端钩部分贡献较小,故在这两个阶段分析中将端钩部分看作平直部分进行分析。
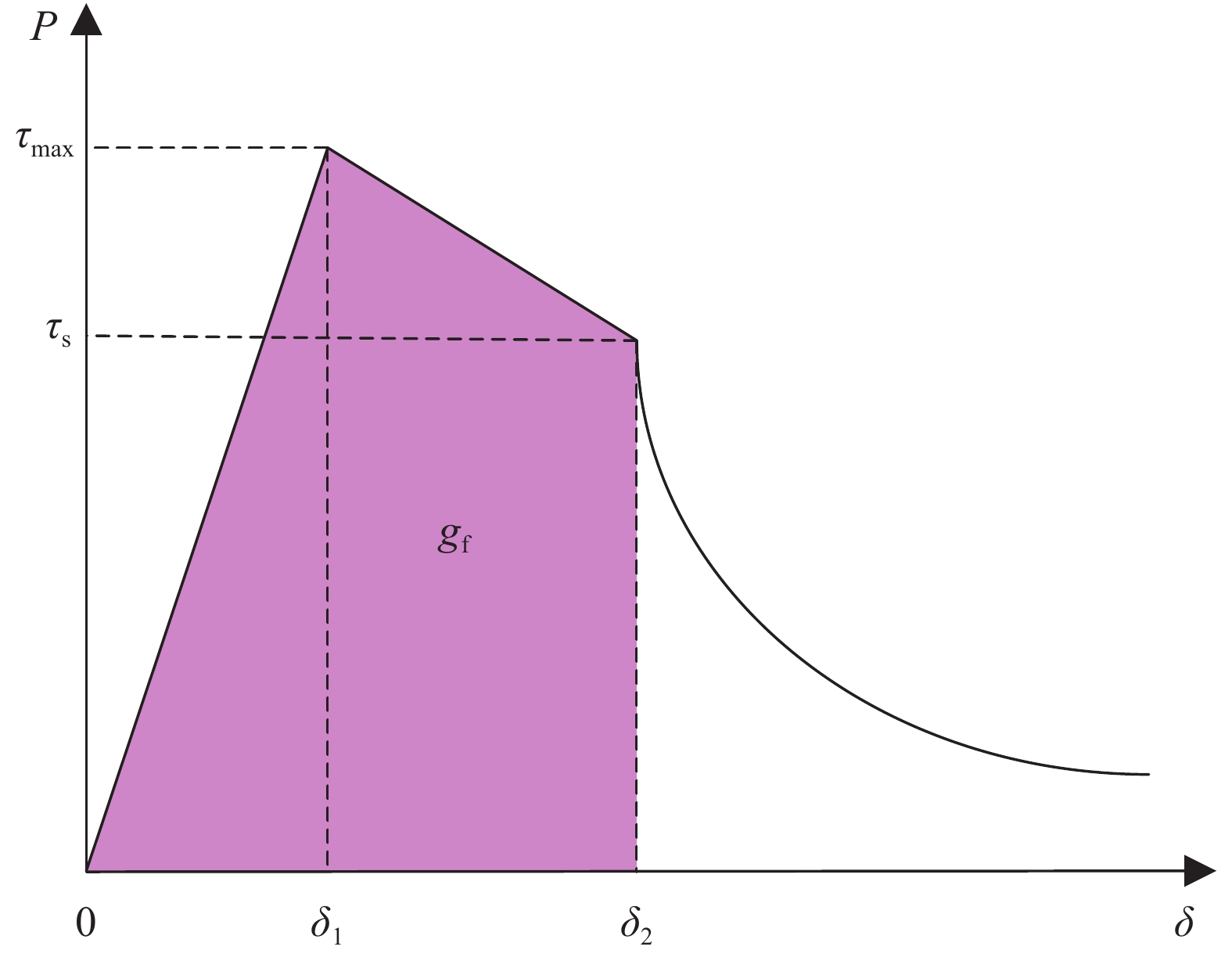
根据试验结果[8, 12-13],钢纤维与基体之间的黏结应力可以根据钢纤维端部位移的大小分为三种情况,完全黏结阶段时黏结应力处于弹性状态;当钢纤维处于脱黏阶段时,黏结应力会随着脱黏而线性减小;而当钢纤维产生滑移后,由于孔道损伤逐渐积累,导致钢纤维与基体间的黏结应力逐渐减小,如图3所示。本文根据不同拔出阶段提出的黏结应力计算公式为
![]() 图 3 钢纤维黏结应力-端部位移关系Figure 3. Relationship between fiber bond stress and end displacementδ1, δ2—Maximum end-displacement in the completely bonding stage and debonding stage, respectively; τmax—Bond shear strength; τs—Bond shear stress corresponding to the end of the debongding stage; gf—Interfacial shear fracture energy
图 3 钢纤维黏结应力-端部位移关系Figure 3. Relationship between fiber bond stress and end displacementδ1, δ2—Maximum end-displacement in the completely bonding stage and debonding stage, respectively; τmax—Bond shear strength; τs—Bond shear stress corresponding to the end of the debongding stage; gf—Interfacial shear fracture energyτ={Gsδ0⩽ (1) 其中:
{\delta _1} 和{\delta _2} 分别为完全黏结和脱黏阶段对应的最大位移,根据{\delta _1}{\rm{ = }}{\tau _{\max }}/{G_{\rm{s}}} 进行计算;{G_{\rm{s}}} 为黏结模量,根据下式[14]计算:{G_{\rm{s}}}{\rm{ = }}\dfrac{{{E_{\rm{m}}}}}{{{d_{\rm{f}}}\left( {1 + {v_{\rm{m}}}} \right)\ln \left( {{R_{\rm{m}}}/{r_{\rm{f}}}} \right)}} (2) 其中:Em为基体的弹性模量;df为钢纤维直径;rf为钢纤维半径;vm为基体泊松比;Rm为钢纤维对基体影响范围的半径。
{\delta _1} 和{\delta _2} 之间的下降段表示脱黏过程中钢纤维与基体之间黏结应力的减弱,Gao等[15]基于断裂力学对纤维混凝土的II型断裂能进行分析并提出相应的破坏准则,认为沿着钢纤维埋置深度的界面剪切断裂能基本保持不变,如图3所示,假定钢纤维的界面剪切断裂能为黏结应力曲线在纤维完全脱黏之前与横坐标轴之间区域的面积,则可以据此求得脱黏阶段的最大位移{\delta _2} 为{\delta _2}{\rm{ = }}\dfrac{{2{g_{\rm{f}}} + {\tau _{\rm{s}}}{\delta _{\rm{1}}}}}{{{\tau _{{\rm{max}}}} + {\tau _{\rm{s}}}}} (3) 其中,
{g_{\rm{f}}} 为界面剪切断裂能,根据试验结果[8]可以看出,界面黏结破坏发生在钢纤维与基体相邻界面上的一层厚度非常小的水泥砂浆薄层内,故认为{g_{\rm{f}}} 主要与水泥砂浆的断裂能相关,根据Yang等[16]对于水泥基材料界面断裂能的研究并考虑钢纤维表面相对光滑[12],{g_{\rm{f}}} 近似取为5 N/m。式(1)中系数
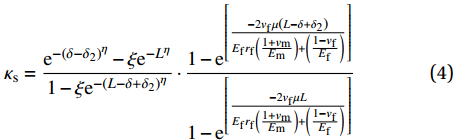
{\kappa _{\rm{s}}} 用来表示由于孔道损伤带来的黏结应力减小,Naaman等[9]根据大量试验研究,发现这一过程基本按照指数函数的下降规律,并提出了相应的计算公式:{\kappa _{\rm{s}}} = \frac{{{{\rm{e}}^{ - {{\left( {\delta - {\delta _{\rm{2}}}} \right)}^\eta }}} - \xi {{\rm{e}}^{{\rm{ - }}{L^\eta }}}}}{{1 - \xi {{\rm{e}}^{ - {{\left( {L - \delta {\rm{ + }}{\delta _{\rm{2}}}} \right)}^\eta }}}}} \cdot \frac{{1 - {{\rm{e}}^{\left[ {\frac{{ - 2{v_{\rm{f}}}\mu \left( {L - \delta {\rm{ + }}{\delta _{\rm{2}}}} \right)}}{{{E_{\rm{f}}}{r_{\rm{f}}}\left( {\frac{{1 + {v_{\rm{m}}}}}{{{E_{\rm{m}}}}}} \right) + \left( {\frac{{1 - {v_{\rm{f}}}}}{{{E_{\rm{f}}}}}} \right)}}} \right]}}}}{{1 - {{\rm{e}}^{\left[ {\frac{{ - 2{v_{\rm{f}}}\mu L}}{{{E_{\rm{f}}}{r_{\rm{f}}}\left( {\frac{{1 + {v_{\rm{m}}}}}{{{E_{\rm{m}}}}}} \right) + \left( {\frac{{1 - {v_{\rm{f}}}}}{{{E_{\rm{f}}}}}} \right)}}} \right]}}}} (4) 其中:μ为钢纤维与基体之间的摩擦系数;Ef为钢纤维的弹性模量;vf为钢纤维的泊松比;L为钢纤维埋置深度;η为下降指数,对于钢纤维取0.2;ξ为损伤因子,一般不大于0.5。由于式(4)形式过于复杂,在实际应用中非常困难,而通过分析可以发现
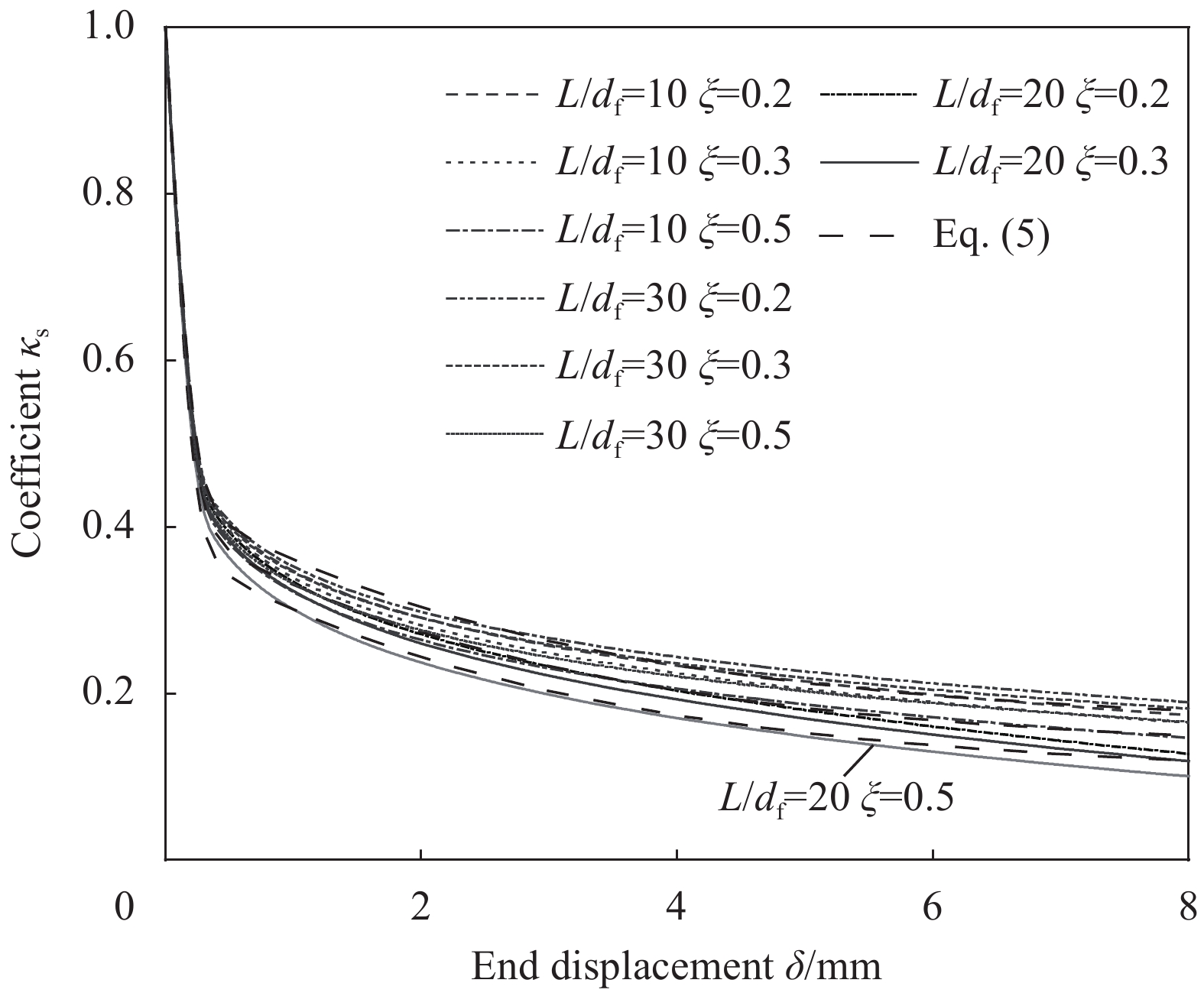
{\kappa _{\rm{s}}} 主要与L/df和δ相关,故本文在式(4)的基础上,提出了简化的两相指数衰减公式:{\kappa _{\rm{s}}}{\rm{ = }}0.07{\rm{ + 0}}{\rm{.003}}L/{d_{\rm{f}}} + 0.58{{\rm{e}}^{ - \frac{{\delta - {\delta _2}}}{{0.09}}}} + 0.28{{\rm{e}}^{ - \frac{{\delta - {\delta _2}}}{3}}} (5) 为了验证简化计算公式的有效性,将其与式(4)的计算结果进行比较,其中vf和vm分别取为0.3和0.2,Ef和Em分别取为2×105 MPa和3.2×104 MPa,μ 取为0.3,L/df分别取10、20和30,ξ分别取0.2、0.3和0.5,并令δ2为0。具体计算结果如图4所示,可以发现损伤因子对于
{\kappa _{\rm{s}}} 的影响很小,而简化计算公式与式(4)计算结果吻合良好,且不需要根据试验来确定损伤因子,故采用式(5)来表征纤维拔出时孔道损伤带来的黏结应力下降。取钢纤维上一个微单元进行受力分析,如图5所示,可以得到:
{\sigma _{\rm{f}}} + {\rm{d}}{\sigma _{\rm{f}}} = \dfrac{{4\tau {\rm{d}}x}}{{{d_{\rm{f}}}}} + {\sigma _{\rm{f}}} (6) 其中,
{\sigma _{\rm{f}}} 为钢纤维应力。钢纤维端部位移量δ根据下式定义并进行计算:
\delta = {\delta _{\rm{f}}} - {\delta _{\rm{m}}}{\rm{ = }}\int_0^x {\left[ {{\varepsilon _{\rm{f}}}\left( x \right) - {\varepsilon _{\rm{m}}}\left( x \right)} \right]} {\rm{d}}x (7) 其中:δf和δm分别是钢纤维和基体的位移;
{\varepsilon _{\rm{f}}} 和{\varepsilon _{\rm{m}}} 分别是钢纤维和基体的应变。为满足静力平衡方程,总的拔出荷载P由钢纤维和周围基体两者共同承担,即
P{\rm{ = }}{A_{\rm{f}}}{E_{\rm{f}}}{\varepsilon _{\rm{f}}} + {A_{\rm{m}}}{E_{\rm{m}}}{\varepsilon _{\rm{m}}} (8) 其中,Af和Am分别为钢纤维和基体的截面面积。
根据式(6)可以得到黏结应力表达式为
\tau {\rm{ = }}\dfrac{{{d_{\rm{f}}}}}{4}\dfrac{{{\rm{d}}{\sigma _{\rm{f}}}}}{{{\rm{d}}x}} (9) 对式(7)求导可得:
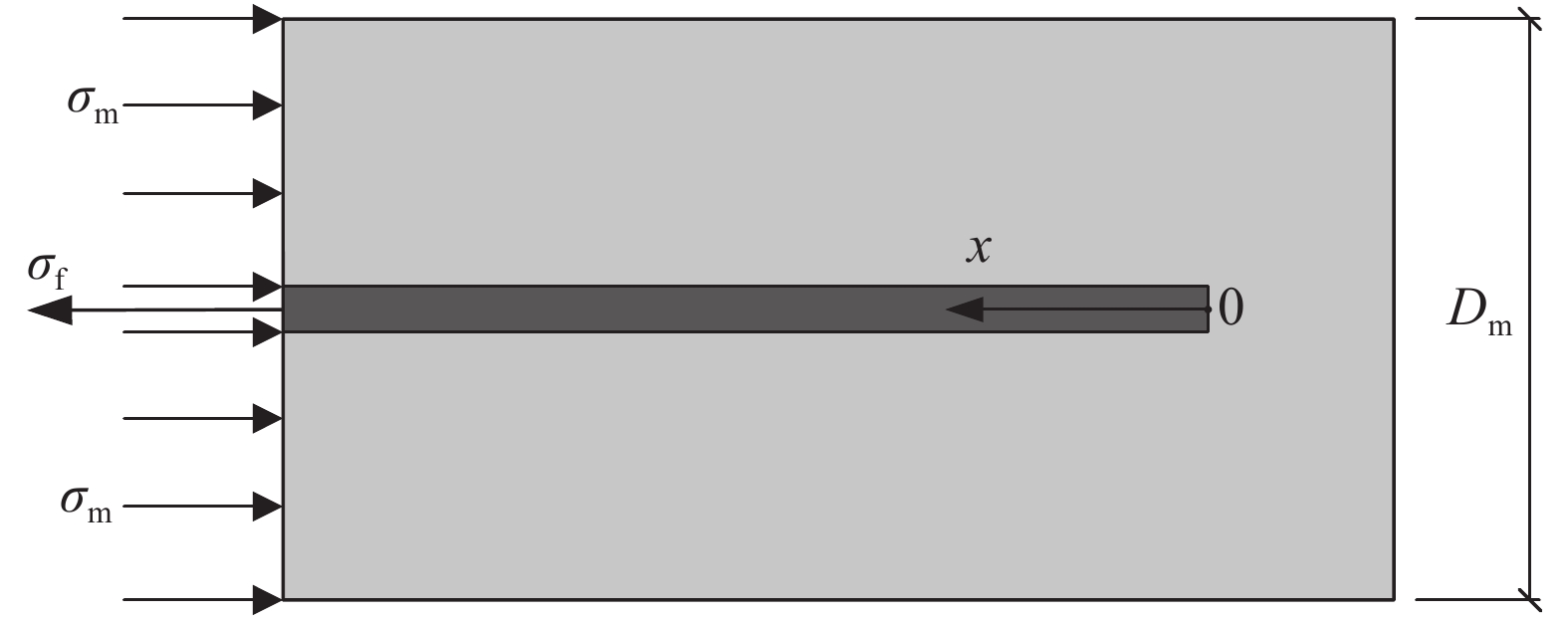
\dfrac{{{\rm{d}}\delta }}{{{\rm{d}}x}} = {\varepsilon _{\rm{f}}} - {\varepsilon _{\rm{m}}} (10) 钢纤维锚固端截面受力如图6所示,根据水平力平衡可得基体应力
{\sigma _{\rm{m}}} 和钢纤维应力{\sigma _{\rm{f}}} 的关系为{\sigma _{\rm{m}}}{\rm{ = }}\dfrac{{d_{\rm{f}}^2}}{{D_{\rm{m}}^2 - d_{\rm{f}}^2}}{\sigma _{\rm{f}}} (11) 其中,Dm为钢纤维对基体影响范围的直径。
将式(11)与式(10)结合可得:
\dfrac{{{\rm{d}}\delta }}{{{\rm{d}}x}} = \left[ {\dfrac{1}{{{E_{\rm{f}}}}} + \dfrac{{d_{\rm{f}}^2}}{{{E_{\rm{m}}}\left( {D_{\rm{m}}^2 - d_{\rm{f}}^2} \right)}}} \right]{\sigma _{\rm{f}}} (12) 1.1 完全黏结阶段
在加载初期,此时钢纤维受力如图1(a)所示,钢纤维与基体的黏结仍处于弹性阶段,直至达到最大黏结应力,由于端钩部分贡献非常小,该部分按照平直纤维进行计算,将式(8)与式(10)代入式(12)可得控制微分方程为
\dfrac{{{{\rm{d}}^2}{\sigma _{\rm{f}}}}}{{{\rm{d}}{x^2}}} - \dfrac{{4{G_{\rm{s}}}}}{{{d_{\rm{f}}}}}\left[ {\dfrac{1}{{{E_{\rm{f}}}}} + \dfrac{{{A_{\rm{f}}}}}{{{E_{\rm{m}}}{A_{\rm{m}}}}}} \right]{\sigma _{\rm{f}}} = 0 (13) 令
{\alpha ^2}{\rm{ = }}\dfrac{{4{G_{\rm{s}}}}}{{{d_{\rm{f}}}}}\left[ {\dfrac{1}{{{E_{\rm{f}}}}} + \dfrac{{{A_{\rm{f}}}}}{{{E_{\rm{m}}}{A_{\rm{m}}}}}} \right] ,并将边界条件{\sigma _{\rm{f}}}\left( 0 \right) = 0 及{\sigma _{\rm{f}}}\left( L \right) = \dfrac{P}{{{A_{\rm{f}}}}} 代入式(13)可得:{\sigma _{\rm{f}}} = \dfrac{{4P\sinh \left( {\alpha x} \right)}}{{{\rm{{\text{π}} }}d_{\rm{f}}^2\sinh \left( {\alpha L} \right)}} (14) 从上述钢纤维黏结应力-端部位移关系式(1)可知,在黏结应力达到
{\tau _{\max }} 后,钢纤维与基体之间的界面开始脱黏,则可以据此求得弹性阶段的最大荷载{P_{{\rm{b,cr}}}} 为{P_{{\rm{b,cr}}}} = \dfrac{{{\tau _{\max }}{\text{π}} {d_{\rm{f}}}\tanh \left( {\alpha L} \right)}}{\alpha } (15) 式(15)结合式(7)、式(8)及式(11)可以求得对应钢纤维端部的位移为
{\delta _{{\rm{b,cr}}}}{\rm{ = }}\dfrac{{{P_{{\rm{b,cr}}}}\alpha }}{{{\rm{{\text{π}} }}{d_{\rm{f}}}{G_{\rm{s}}}\tanh \left( {\alpha L} \right)}} = \dfrac{{{\tau _{\max }}}}{{{G_{\rm{s}}}}}{\rm{ = }}{\delta _1} (16) 1.2 脱黏阶段
如图1(b)所示,钢纤维脱黏过程中,部分钢纤维仍处于完全黏结状态,部分钢纤维已经脱黏,a为钢纤维的脱黏长度。分析可知,脱黏部分和弹性黏结部分相交界面的黏结应力为
{\tau _{\max }} 。脱黏部分的黏结应力根据式(1)可以得到,即
\tau {\rm{ = }}\dfrac{{{\tau _{{\rm{max}}}}{\delta _2} - {\tau _{\rm{s}}}{\delta _1}}}{{{\delta _2} - {\delta _1}}} - \dfrac{{{\tau _{{\rm{max}}}} - {\tau _{\rm{s}}}}}{{{\delta _2} - {\delta _1}}}\delta (17) 将式(17)及式(9)代入式(12)可得:
\dfrac{{{{\rm{d}}^2}{\sigma _{\rm{f}}}}}{{{\rm{d}}{x^2}}} + {\omega ^2}{\sigma _{\rm{f}}} = 0 (18) 其中,
{\omega ^2} = \dfrac{{4\left( {{\tau _{{\rm{max}}}} - {\tau _{\rm{s}}}} \right)}}{{{d_{\rm{0}}}\left( {{\delta _2} - {\delta _1}} \right)}}\left[ {\dfrac{1}{{{E_{\rm{f}}}}} + \dfrac{{d_{\rm{f}}^2}}{{{E_{\rm{m}}}\left( {{D^2} - d_{\rm{f}}^2} \right)}}} \right] 根据完全黏结部分与脱黏部分结合界面左右应力平衡及变形协调条件可以得到钢纤维的应力为
\begin{split} {\sigma }_{\rm{f}}=&\dfrac{4{\tau }_{\mathrm{max}}}{{d}_{\rm{f}}\alpha }\mathrm{tanh}\alpha \left(L-a\right)\mathrm{cos}\omega \left(L-a-x\right)+\\ &\dfrac{4{\tau }_{\mathrm{max}}}{{d}_{\rm{f}}\omega }\mathrm{sin}\omega \left(x-L+a\right)\end{split} (19) 代入
{\sigma _{\rm{f}}} = \dfrac{P}{{{A_{\rm{f}}}}} 可以求得总的纤维拔出力为\begin{split} {P_{{\rm{db}}}}{\rm{ = }} {P_{\rm{d}}}{\rm{ + }}{P_{\rm{b}}}{\rm{ = }}&{\tau _{\max }}{\rm{{\text{π}} }}{d_{\rm{f}}}\left[ {\dfrac{{\tanh \alpha \left( {L - a} \right)\cos \omega a}}{\alpha } + \dfrac{{\sin \omega a}}{\omega }} \right] + \\ & {\rm{ }}\dfrac{{{\tau _{\max }}{\rm{{\text{π}} }}{d_{\rm{f}}}\tanh \left[ {\alpha \left( {L - a} \right)} \right]}}{\alpha } \\[-12pt] \end{split} (20) 将上式结合式(7)~(8)及式(11)可以求得对应钢纤维端部的位移为
\begin{split} {\delta _{{\rm{db}}}}{\rm{ = }}&\left[ {\frac{1}{{{E_{\rm{f}}}}} + \frac{{d_{\rm{f}}^2}}{{\left( {{D^2} - d_{\rm{f}}^2} \right){E_{\rm{m}}}}}} \right]\left[ {\frac{{4{\tau _{\max }}}}{{{d_{\rm{f}}}\alpha \omega }}\tanh \alpha \left( {L - a} \right)\sin \omega a + } \right.\\ & \left. {\frac{{4{\tau _{\max }}}}{{{d_{\rm{f}}}{\omega ^2}}}\left( {1 - \cos \omega a} \right)} \right]{\rm{ + }}\frac{{{\tau _{\max }}}}{{{G_{\rm{s}}}}}\\[-12pt] \end{split} (21) 1.3 拔出滑移阶段
1.3.1 端钩部分的变形及摩擦
如图1(c)所示,钢纤维完全脱黏后,开始沿着原有的孔道向外拔出滑移,直线部分沿着水平孔道直接拔出,拔出过程中只承受钢纤维与基体界面产生的摩擦力,而端钩部分会在孔洞的两个转角处产生塑性变形,从而增加纤维拔出力的大小,如图7(a)所示,本文根据滑移量将端钩部分的受力分为两种情况进行分析,位移量
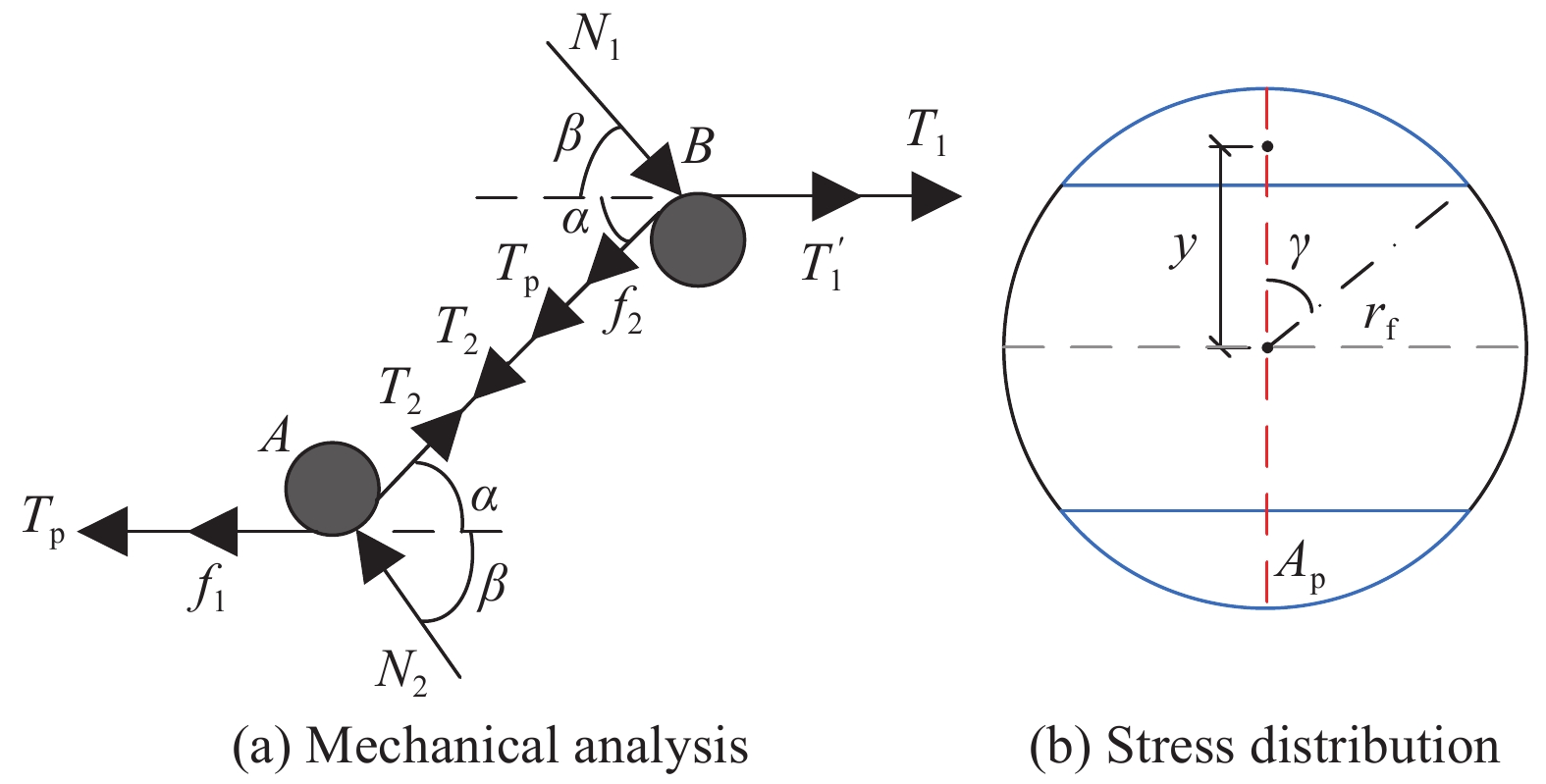
\delta \leqslant {l_1} 时,对应钢纤维同时在A、B两点产生塑性变形,此时A点的拔出力为T2,B点的拔出力为T1;当钢纤维的位移量{l}_{1} < \delta \leqslant {l}_{1}\rm{+}{l}_{2} 时,此时只有在B点产生塑性变形,对应的拔出力为T_1^{'} 。![]() 图 7 钢纤维端钩部分受力分析及截面应力分布Figure 7. Mechanical analysis and stress distribution of hooked-end of steel fiberT1, T2 and T1'—Tensile force for the end-hook; f1 and f2—Bond force of the end-hook; Tp—Tensile force required for plastic deformation; β—Angle of the normal force; N1 and N2—Normal force; rf—Radius of steel fiber; Ap—Area of the plastic region; y—Distance between the neutral axis and the plastic zone centroid; γ—Angle between the plastic zone and the vertical axis
图 7 钢纤维端钩部分受力分析及截面应力分布Figure 7. Mechanical analysis and stress distribution of hooked-end of steel fiberT1, T2 and T1'—Tensile force for the end-hook; f1 and f2—Bond force of the end-hook; Tp—Tensile force required for plastic deformation; β—Angle of the normal force; N1 and N2—Normal force; rf—Radius of steel fiber; Ap—Area of the plastic region; y—Distance between the neutral axis and the plastic zone centroid; γ—Angle between the plastic zone and the vertical axis当钢纤维在孔道转角处发生塑性变形时,钢纤维截面应力分布如图7(b)所示,截面顶部和底部区域进入塑性,而中间区域依然为弹性状态。塑性区域的面积为:
{A_{\rm{p}}} = \dfrac{{r_{\rm{f}}^2\left( {2\gamma - \sin 2\gamma } \right)}}{2} ,塑性区域形心距中性轴的距离为:y = \dfrac{{4{r_{\rm{f}}}\sin 3\gamma }}{{3\left( {2\gamma - \sin 2\gamma } \right)}} ,其中γ为塑性区域与竖轴之间的夹角,可以根据\gamma {\rm{ = }}\arcsin \dfrac{{\rho {f_{\rm{y}}}}}{{{E_{\rm{f}}}{r_{\rm{f}}}}} 进行计算,ρ为转角处的曲率半径;fy为钢纤维的屈服强度。根据钢纤维截面特性可以得到塑性弯矩Mp为\begin{split} {M_{\rm{p}}} & =2{f_{\rm{y}}} \cdot \dfrac{{r_{\rm{f}}^2\left( {2\gamma - \sin 2\gamma } \right)}}{2} \cdot \dfrac{{4{r_{\rm{f}}}{{\sin }^3}\gamma }}{{3\left( {2\gamma - \sin 2\gamma } \right)}} \\ & = \dfrac{4}{3}{f_{\rm{y}}}\dfrac{{r_{\rm{f}}^3\left( {2\gamma - \sin 2\gamma } \right){{\sin }^3}\gamma }}{{2\gamma - \sin 2\gamma }} \end{split} (22) 钢纤维在滑移时所需的荷载,采用如图7(a)所示的简化模型进行计算,根据力的平衡可以得到端钩部分的拔出力近似为
{T_1}{\rm{ = }}2{T_{\rm{p}}} + {F_1} + {F_2} + {f_1} + {f_2} (23) {T_2}{\rm{ = }}{T_{\rm{p}}} + {F_2}{\rm{ + }}{f_2} (24) 转角处的摩擦力分别为
{F_1}{\rm{ = }}\mu {N_1} (25) {F_2}{\rm{ = }}\mu {N_2} (26) 根据节点受力平衡可以求得法向压力N1和N2分别为
{N_1} = \left( {{T_1} + {f_2}} \right)\cos \beta + {T_2}\cos \beta (27) {N_2} = \left( {{T_2}{\rm{ + }}{f_1}} \right)\cos \beta (28) 从而可以求得两种情况下由于端钩部分塑性变形及界面摩擦产生的拔出力为
\begin{split} {T_1}{\rm{ = }}&\dfrac{{2{T_{\rm{p}}} + \mu \left( {{f_1} + {f_2}} \right)\cos \beta }}{{1 - \mu \cos \beta }} + \\ &\dfrac{{2\mu \left( {{T_{\rm{p}}} + \mu {f_1}\cos \beta } \right)\cos \beta }}{{{{\left( {1 - \mu \cos \beta } \right)}^2}}}{\rm{ + }}{f_1} + {f_2} \end{split} (29) T_1^{'}{\rm{ = }}\dfrac{{{T_{\rm{p}}} + \mu {f_2}\cos \beta }}{{1 - \mu \cos \beta }}{\rm{ + }}{f_2} (30) {T_2}{\rm{ = }}\dfrac{{{T_{\rm{p}}} + \mu {f_1}\cos \beta }}{{1 - \mu \cos \beta }}{\rm{ + }}{f_1} (31) 其中,Tp为钢纤维产生塑性变形所需的拉力,为了计算Tp,Chanvillard等[17]基于大量试验结果和理论分析,得到了钢纤维产生塑性变形时所承受拉力与弯矩之间的关系:
\dfrac{{{M_{\rm{p}}}}}{{{M_{{\rm{pa}}}}}} = 1 - 0.0539\dfrac{{{T_{\rm{p}}}}}{{{T_{{\rm{pa}}}}}} - 0.7156{\left( {\dfrac{{{T_{\rm{p}}}}}{{{T_{{\rm{pa}}}}}}} \right)^2} - 0.2304{\left( {\dfrac{{{T_{\rm{p}}}}}{{{T_{{\rm{pa}}}}}}} \right)^3} (32) 其中,Mpa和Tpa分别表示使钢纤维全截面进入塑性状态的弯矩和拉力,根据
{M_{{\rm{pa}}}} = \dfrac{4}{3}{f_{\rm{y}}}r_{\rm{f}}^3 和{T_{{\rm{pa}}}} = \dfrac{{{\text{π}} {f_{\rm{y}}}d_{\rm{f}}^2}}{4} 分别进行计算。由于式(32)形式复杂,为了避免繁琐的高阶计算,本文提出简化计算公式来计算钢纤维塑性变形所需要的拉力Tp,如下式所示:
\dfrac{{{M_{\rm{p}}}}}{{{M_{{\rm{pa}}}}}} = 1.18 - \dfrac{{{T_{\rm{p}}}}}{{{T_{{\rm{pa}}}}}} (33) 式(33)与式(32)的计算结果如图8所示,可以看出式(33)与式(32)的计算结果基本吻合,且形式简单,可以近似替代式(32)。
在计算过程中,使钢纤维产生塑性变形的拉力并不是直接达到最大值,而是有一个递增的过程,本文假定其在2df范围内从0增加至最大值,即按照
{T_{\rm{p}}} \cdot {\left( {\dfrac{{{\delta _{\rm{k}}}}}{{2{d_{\rm{f}}}}}} \right)^2} 进行计算,其中{\delta _{\rm{k}}} 为钢纤维开始产生塑性变形后的相对滑移量,同理,该力减小时在2df范围内由最大值降至0。式(23)和式(24)中的f1与f2表示钢纤维端钩部分向外拔出时与基体之间的摩擦力,根据上述给出的黏结应力计算公式可以求出,分别按照
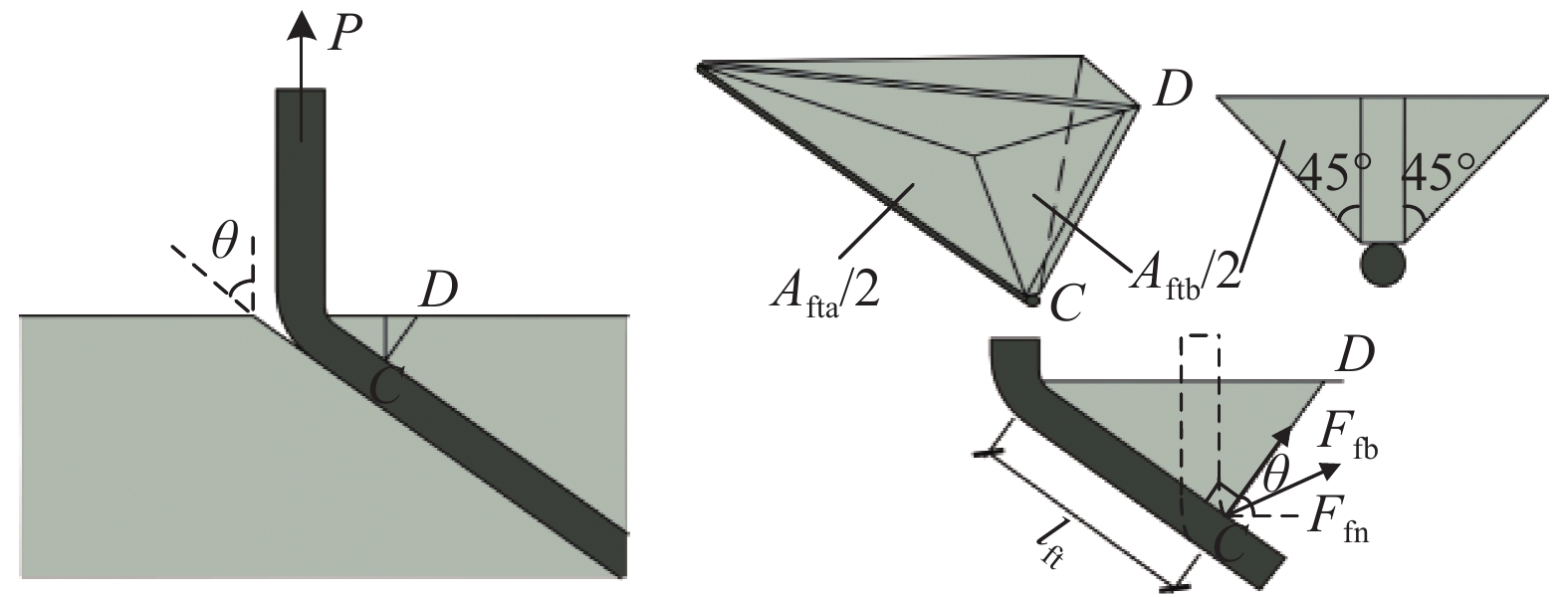
{f_1} = \tau {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{l_1} - \delta } \right) 和{f_2} = \tau {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{l_2} - \delta + {l_1}} \right) 进行计算。1.3.2 附加摩擦力
当钢纤维沿着基体中的孔道滑移时,端钩部分会产生塑性变形,而经过塑性变形后的钢纤维端钩部分不会变得完全平直,而是会存在一定的残余变形,这些残余变形会显著增加钢纤维与混凝土基体之间的摩擦作用,即附加摩擦力。由于附加摩擦力在试验中很难采用试验仪器进行测定,故目前还没有对于该参数的试验研究。
Georgiadis-Stefanidi等[18]对水泥基材料中端钩型钢纤维拔出力学性能进行了有限元分析,其中对附加摩擦力进行了全面的研究,结果表明,最大附加拔出力主要与基体抗压强度fc、钢纤维屈服强度fy和钢纤维直径df相关,且最大附加拔出力与这三个因素均成正比,本文根据量纲统一规则和反向分析得到最大附加拔出力计算公式为
F_{{\rm{extra}}}^{'} = 0.85\sqrt {{f_{\rm{c}}}{f_{\rm{y}}}} d_{\rm{f}}^2 (34) 而附加摩擦力的大小是随着钢纤维的拔出过程改变的,当纤维开始拔出滑移时附加摩擦力为0,随着滑移量增加,转角处均开始产生塑性变形,附加摩擦力也逐渐增加,当钢纤维拔出位移等于l1+l2时,附加摩擦力达到最大值,并一直到钢纤维完全被逐渐拔出时开始减小,对应的滑移量为Le-l1-l2。采用的附加摩擦力和钢纤维拔出位移之间的关系如图9所示。
2. 钢纤维拔出角度对拔出力学性能的影响
2.1 倾斜端钩型钢纤维拔出基体剥落
根据试验结果[8]可以发现,钢纤维的拔出角度对于钢纤维拔出力学性能具有显著影响,随着纤维拔出角度的增加,钢纤维的拔出峰值荷载会明显增大,但是当纤维拔出角度超过某一限值时,拔出峰值荷载相比于垂直拔出时的峰值荷载有所下降。通过分析可知,倾斜钢纤维拔出时,孔道出口部分的基体可能会挤碎剥落,进一步导致钢纤维的埋置长度变短。而基体的剥落是由于基体表面钢纤维的局部曲率变化和混凝土受拉等综合作用导致的一种极其复杂的现象,它和许多因素相关,比如钢纤维直径、钢纤维屈服强度及基体的抗拉强度等。而随着纤维拔出角度的增大,应力集中程度也有所增加,导致孔道出口处的基体被挤碎剥落的体积更大,使钢纤维的埋置长度更短,从而拔出荷载更小。
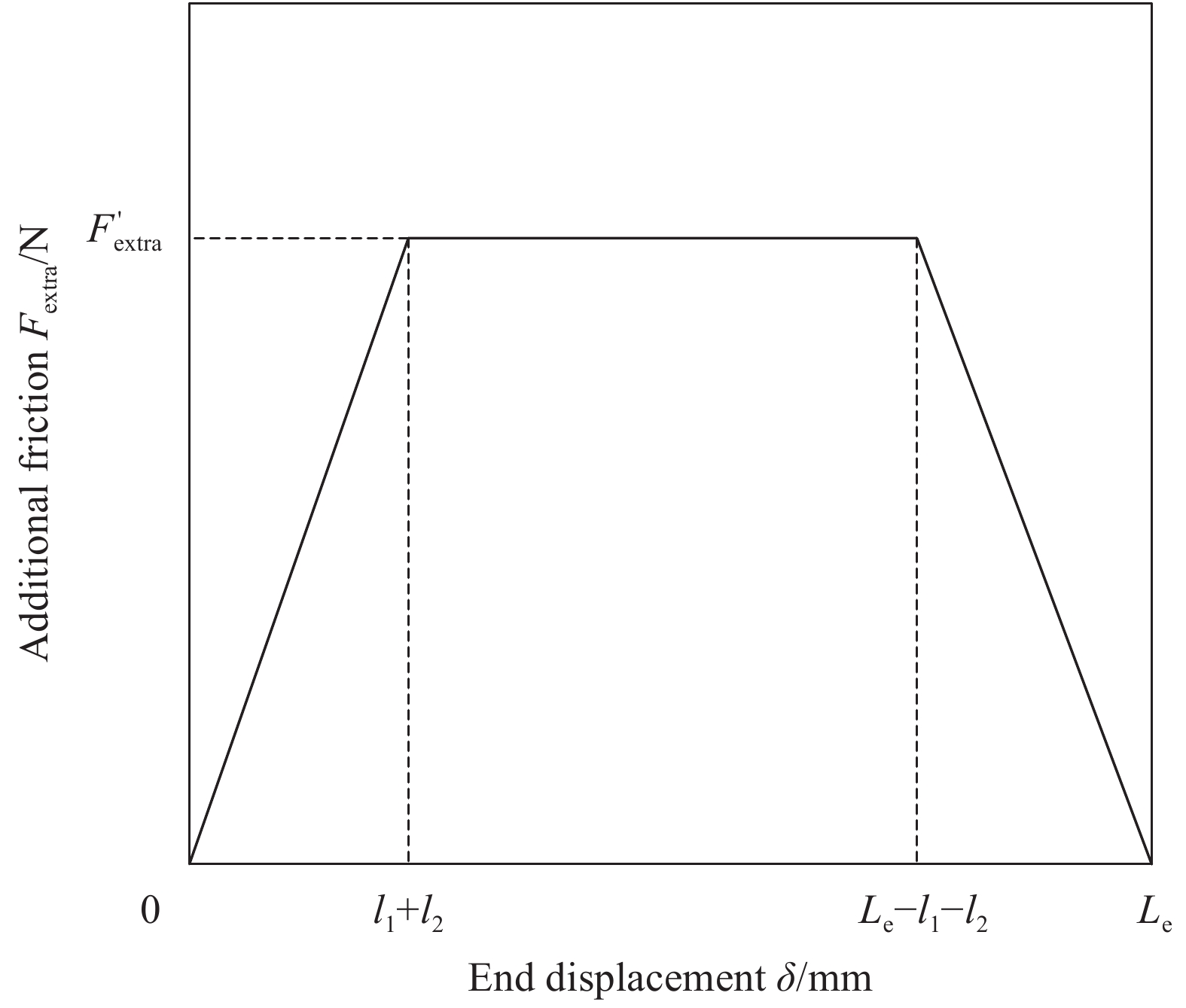
采用一种简化的多边几何体模型来计算剥落基体的长度,如图10所示,其中lft表示多边体在纤维主轴方向上的投影长度,θ表示钢纤维拔出角度。多边体受力较复杂,基体之间裂缝界面实际上处于一种拉-剪复合受力状态,其中剪力根据纤维拔出角度的变化而改变且承受剪力较小,故忽略裂缝界面剪力,基体的剥落采用Rankin破坏准则,即最大主应力准则,基体界面抗力和钢纤维所施加的使基体剥落的荷载之间的简化破坏准则如下式:
{F_{{\rm{fb}}}} \geqslant {R_{{\rm{fb}}}} (35) 其中:基体界面抗力近似按照
{R_{{\rm{fb}}}}{\rm{ = }}{A_{{\rm{ft}}}}{f_{{\rm{ct}}}} 进行计算,fct为基体抗拉强度;Aft为基体脱落界面的面积,如图10所示,分为两部分进行计算,即{A_{{\rm{ft}}}} = {A_{{\rm{fta}}}} + {A_{{\rm{ftb}}}} (36) 其中,
{A_{{\rm{fta}}}}{\rm{ = }}l_{{\rm{ft}}}^2\dfrac{{\cos \theta \sqrt {1 - 0.5{{\sin }^2}2\theta } }}{{{{\sin }^2}\theta }} {A_{{\rm{ftb}}}}{\rm{ = }}\sqrt 2 l_{{\rm{ft}}}^2\dfrac{{{{\cos }^3}\theta }}{{{{\sin }^2}\theta }}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}{{\sin }^2}\theta } {\rm{ + }}\dfrac{{{l_{{\rm{ft}}}}{d_{\rm{f}}}}}{{\tan \theta }} 如图10所示,使基体剥落的力Ffb平行于开裂面CD,而根据Cailleux等[19]的试验研究发现开裂面CD与纤维轴线方向基本垂直。根据图10所示的纤维孔道出口处受力,使基体剥落的荷载实际上是钢纤维对基体压力Ffn的分力,而压力Ffn并不是垂直于纤维轴向的,而是与纤维有一定的夹角,且随着基体与钢纤维接触部分的形状而改变;而压力Ffn的另外一个平行于钢纤维轴向的分力会增加CD面的摩擦力,从而也会减小基体剥落的荷载Ffb。故在受力平衡的基础上考虑各因素的折减,Ffb近似取为
{F_{{\rm{fb}}}} = \dfrac{1}{2}P {\sin ^2}\theta (37) 则根据式(35)可以求得脱落混凝土基体在钢纤维轴向的投影长度lft为
{l_{{\rm{ft}}}}{\rm{ = }}\dfrac{{ - \dfrac{{{d_{\rm{f}}}}}{{\tan \theta }} + \sqrt {\dfrac{{d_{\rm{f}}^2}}{{{{\tan }^2}\theta }} + \dfrac{{2\psi \cdot P{{\sin }^2}\theta }}{{{f_{\rm{t}}}}}} }}{{2\psi }} (38) 其中,
\psi =\dfrac{{\cos \theta \sqrt {1 - 0.5{{\sin }^2}2\theta } }}{{{{\sin }^2}\theta }}{\rm{ + }}\sqrt 2 \dfrac{{{{\cos }^3}\theta }}{{{{\sin }^2}\theta }}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}{{\sin }^2}\theta } 图11为基于式(38)计算出的基体剥落长度随不同荷载和纤维拔出角度的变化情况。可以看出荷载和纤维拔出角度的增加均会导致剥落长度的增加。当荷载确定而纤维拔出角度较小时,基体剥落长度
{l_{{\rm{ft}}}} 增长缓慢,但是当拔出角度大于40°时,基体剥落长度会随着加载角度快速增长;当加载角度确定时,在加载初期{l_{{\rm{ft}}}} 增长较快,而在荷载大于30 N时趋于平缓。为评估本文提出的基体剥落长度计算方法的有效性,按照本文计算方法对Leung等[20]的试验进行验证,该试验对5种不同平直型钢纤维进行斜向拔出试验,计算结果和试验结果的对比如图12所示,纤维拔出角度为60°,图中误差根据
{\delta }_{\rm{l}}=({|{\text{预测值}}-{\text{试验均值}}|})/{{\text{试验均值}}} 计算。可以看出本文计算方法可以有效预测基体剥落长度,并具有较高的计算精度。2.2 倾斜端钩型钢纤维拔出挤压摩擦效应
基体剥落长度增加会导致钢纤维埋置深度减小,从而降低拔出峰值荷载,这与试验结果有很大区别,这是由于倾斜钢纤维拔出时还存在增强效应,纤维在变角度处产生弯曲变形,从而会对周围混凝土基体造成挤压,使摩擦力显著增加,导致拔出力增加,即挤压摩擦效应。挤压摩擦效应与多种因素相关,如钢纤维直径、钢纤维屈服强度和基体强度等, Li等[21]和Xu等[22]对倾斜平直型钢纤维拔出导致的挤压摩擦效应已经进行了大量的试验及理论研究,但是平直型钢纤维与端钩型钢纤维拔出过程存在较大差异,故在已有研究基础上提出适用于倾斜端钩型钢纤维拔出挤压摩擦效应的计算方法。
挤压摩擦效应主要通过挤压摩擦系数来体现,挤压摩擦系数
{\alpha _{\rm{E}}} 定义为单位长度上倾斜钢纤维拔出荷载与平直纤维拔出荷载之比,即{\alpha _{\rm{E}}}{\rm{ = }}\dfrac{{{P_{{\rm{max,\theta }}}}/{L_{{\rm{e,\theta }}}}}}{{{P_{{\rm{max,0}}}}/{L_{{\rm{e,0}}}}}} (39) 其中:
{P_{{\rm{max,\theta }}}} 和{P_{{\rm{max,0}}}} 分别表示倾角为\theta 和垂直拔出时钢纤维拔出峰值荷载;{L_{{\rm{e,\theta }}}} 和{L_{{\rm{e,0}}}} 分别表示倾角为\theta 时和垂直拔出时钢纤维的有效埋置长度。根据Li等[21]及Xu等[22]的研究,倾斜平直型钢纤维拔出时挤压摩擦系数为{\alpha _{\rm{E}}}{\rm{ = }}\dfrac{{{P_{{\rm{max,\theta }}}}/{L_{{\rm{e,\theta }}}}}}{{{P_{{\rm{max,0}}}}/{L_{{\rm{e,0}}}}}}{\rm{ = }}{{\rm{e}}^{f\theta }} (40) 其中,f为挤压增强系数,根据不同的纤维类型确定,对于钢纤维取为0.6。
而对于端钩型钢纤维来说,平直型钢纤维的挤压摩擦系数不能直接应用,在钢纤维拔出的过程中,出现挤压摩擦的区域不仅仅在钢纤维孔道出口处,在钢纤维端钩部分的每个转角处都会产生挤压摩擦现象。故根据挤压摩擦系数的定义,当倾斜钢纤维拔出时,根据拔出长度的不同可以将挤压摩擦系数分为三种情况考虑,并令
{L_1}{\rm{ = }} {L_{\rm{e}}} - {l_1} - {l_2}\cos \alpha ,则可以得到对应的端钩型钢纤维垂直拔出时和拔出角度为\theta 时拔出峰值荷载分别为当
\delta \leqslant {l_1} 时:P_{\max ,0}^{'} = {\rm{{\text{π}} }}{d_{\rm{f}}}{L_1}\tau + {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{l_1}{\rm{ + }}{l_2}{\rm{ - }}\delta } \right)\tau {{\rm{e}}^{f\alpha }} + {T_1}{\rm{ + }}{F_{{\rm{extra}}}} (41) P_{\max ,\theta }^{'} = {\rm{{\text{π}} }}{d_{\rm{f}}}{L_1}\tau {{\rm{e}}^{f\theta }} + {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{l_1}{\rm{ + }}{l_2}{\rm{ - }}\delta } \right)\tau {{\rm{e}}^{f\alpha }} + {T_1}{\rm{ + }}{F_{{\rm{extra}}}} (42) 当
{l}_{1} < \delta \leqslant {l}_{1}{+}{l}_{2} 时:P_{\max ,0}^{'} = {\rm{{\text{π}} }}{d_{\rm{f}}}{L_1}\tau + {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{l_2}{\rm{ - }}\delta {\rm{ + }}{l_1}} \right)\tau {{\rm{e}}^{f\alpha }} + T_1^{'}{\rm{ + }}{F_{{\rm{extra}}}} (43) P_{\max ,\theta }^{'} = {\rm{{\text{π}} }}{d_{\rm{f}}}{L_1}\tau {{\rm{e}}^{f\theta }} + {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{l_2}{\rm{ - }}\delta {\rm{ + }}{l_1}} \right)\tau {{\rm{e}}^{f\alpha }} + T_1^{'}{\rm{ + }}{F_{{\rm{extra}}}} (44) 当
{l}_{1}{+}{l}_{2} < \delta \leqslant {L}_{\rm{e}} 时:P_{\max ,0}^{'} = {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{L_1}{\rm{ - }}\delta {\rm{ + }}{l_1}{\rm{ + }}{l_2}} \right)\tau {\rm{ + }}{F_{{\rm{extra}}}} (45) P_{\max ,\theta }^{'} = {\rm{{\text{π}} }}{d_{\rm{f}}}\left( {{L_1}{\rm{ - }}\delta {\rm{ + }}{l_1}{\rm{ + }}{l_2}} \right)\tau {{\rm{e}}^{f\theta }}{\rm{ + }}{F_{{\rm{extra}}}} (46) 将端钩型钢纤维拔出角度为
\theta 时和垂直拔出时的拔出峰值荷载代入挤压摩擦系数的定义式(39),则可以得到不同拔出长度时端钩型钢纤维的挤压摩擦系数为{\alpha }_{\rm{E}}=\left\{ {\begin{array}{ll}\dfrac{{π}{d}_{\rm{f}}\left[{L}_{1}\tau {\rm{e}}^{f\theta }+\left({l}_{1}+{l}_{2}-\delta \right)\tau {\rm{e}}^{f\alpha }\right]+{T}_{1}+{F}_{\rm{extra}}}{{π}{d}_{\rm{f}}\left[{L}_{1}\tau +\left({l}_{1}+{l}_{2}-\delta \right)\tau {\rm{e}}^{f\alpha }\right]+{T}_{1}+{F}_{\rm{extra}}} & \delta \leqslant {l}_{1} \\ \dfrac{{π}{d}_{\rm{f}}\left[{L}_{1}\tau {\rm{e}}^{f\theta }+\left({l}_{2}-\delta +{l}_{1}\right)\tau {\rm{e}}^{f\alpha }\right]+{T}_{1}^{\rm{'}}+{F}_{\rm{extra}}}{{π}{d}_{\rm{f}}\left[{L}_{1}\tau +\left({l}_{2}-\delta +{l}_{1}\right)\tau {\rm{e}}^{f\alpha }\right]+{T}_{1}^{\rm{'}}+{F}_{\rm{extra}}} & {l}_{1}<\delta \leqslant {l}_{1}+{l}_{2} \\ \dfrac{{π}{d}_{\rm{f}}\left({L}_{1}-\delta +{l}_{1}+{l}_{2}\right)\tau {\rm{e}}^{f\theta }+{F}_{\rm{extra}}}{{π}{d}_{\rm{f}}\left({L}_{1}-\delta +{l}_{1}+{l}_{2}\right)\tau +{F}_{\rm{extra}}} & {l}_{1}+{l}_{2}<\delta <{L}_{\rm{e}} \end{array}} \right. (47) 3. 倾斜端钩型钢纤维拔出力学性能计算步骤
将以上推导的纤维塑性变形、附加摩擦力和纤维与基体间摩擦力的计算公式进行叠加,并在此基础上考虑钢纤维拔出角度导致的基体剥落和挤压摩擦效应,则可以预测端钩型钢纤维倾斜拔出全过程,包括拔出峰值荷载和各个阶段荷载及纤维端部的位移,其中峰值荷载按照下式计算:
{P_{{\rm{max}}}} = {\alpha _{\rm{E}}}\left( {{T_{{\rm{1,max}}}} + {F_{{\rm{extra}}}} + {\rm{{\text{π}} }}{d_{\rm{f}}}{\tau _{\rm{s}}}{L_{\rm{1}}}} \right) (48) 其中,
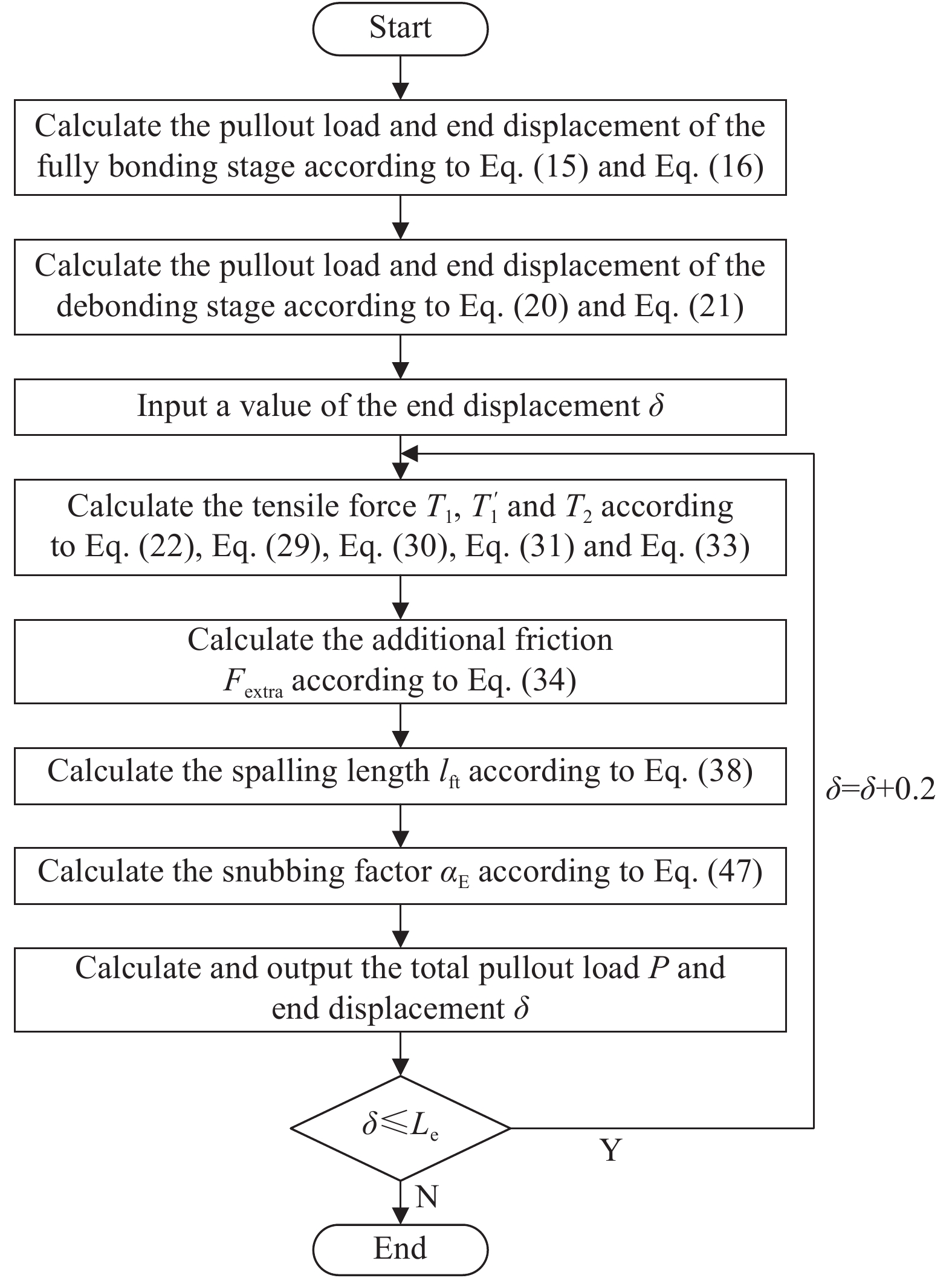
{T_{{\rm{1,max}}}} 为钢纤维端钩部分塑性变形及摩擦所需拉力的最大值。以纤维端部位移为主要变量,首先计算完全黏结阶段和脱黏阶段的荷载和钢纤维端部位移,然后以脱黏阶段的最大位移δdb为滑移阶段的位移初始值开始计算滑移阶段的荷载和端部位移,为了同时考虑计算精度及计算效率,滑移增量选择0.2 mm,计算中选取的重要参数取值如表1所示,具体的计算流程如图13所示。
表 1 用于预测端钩型钢纤维拔出力学性能的参数取值Table 1. Parameters used to predict the pullout behavior of hooked-end steel fiberParameter Value Elastic modulus of matrix Em/MPa 3.2×104 Elastic modulus of fiber Ef/MPa 2×105 Diameter of matrix Dm 10df Fiber Poisson's ratio vf 0.3 Matrix Poisson's ratio vm 0.2 Curvature radius of hooked fiber ρ 2df End hook angle α/(°) 50 上述表达式中Le均为钢纤维有效埋置深度,根据
{L_{\rm{e}}} = L - {l_{{\rm{ft}}}} 计算;根据平直钢纤维拔出试验可以确定最大黏结应力{\tau _{{\rm{max}}}} 和开始滑移时对应的黏结应力{\tau _{\rm{s}}} ,根据已有试验结果[12],发现{\tau _{\rm{s}}} 与基体轴心抗压强度存在明显的线性关系,采用{\tau _{\rm{s}}} = {f_{\rm{c}}}/32.6 来计算开始滑移时所对应的黏结应力{\tau _{\rm{s}}} ;而最大黏结应力{\tau _{{\rm{max}}}} 也主要与基体轴心抗压强度相关,目前对该强度的理论研究较少,本文根据搜集到的平直型钢纤维拔出力学性能试验结果[20, 23-27],其中轴心抗压强度fc的单位是MPa,拟合得到{\tau _{{\rm{max}}}} 的计算公式为{\tau _{{\rm{max}}}}{\rm{ = }}0.95\sqrt {{f_{\rm{c}}}} - 3.8 (49) 式(48)的计算结果与试验结果的对比如图14所示,可以看出式(49)计算结果与试验结果吻合良好,故采用式(49)计算最大黏结应力。
摩擦系数μ在计算过程中也是非常重要的一个参数,由于钢纤维拔出过程中的包兴格效应及孔道损伤,摩擦系数也会随着钢纤维拔出逐渐降低,根据Geng等[28]进行的大量试验研究,发现μ与黏结应力具有同样的变化规律,本文参考其提出的计算公式,采用下式计算摩擦系数μ:
\mu {\rm{ = }}{\mu _0}{\rm{ + }}\tau/{\tau _0} (50) 其中:μ0取为0.25;τ0取为21.28 MPa。
4. 倾斜端钩型钢纤维拔出力学性能简化计算模型及模型验证
4.1 简化计算模型
上述理论计算模型虽然具有较强的理论意义,力学概念明确,可以有效预测端钩型钢纤维拔出全过程,但是计算过程较复杂,尤其对于峰值荷载之前的部分,为了更好地将其推广到进一步的SFRC受拉性能研究中,在此基础上提出一种简化计算模型。
通过对大量倾斜端钩型钢纤维拔出试验进行分析可以发现其拔出荷载-位移全曲线的变化规律近似为如图15所示。
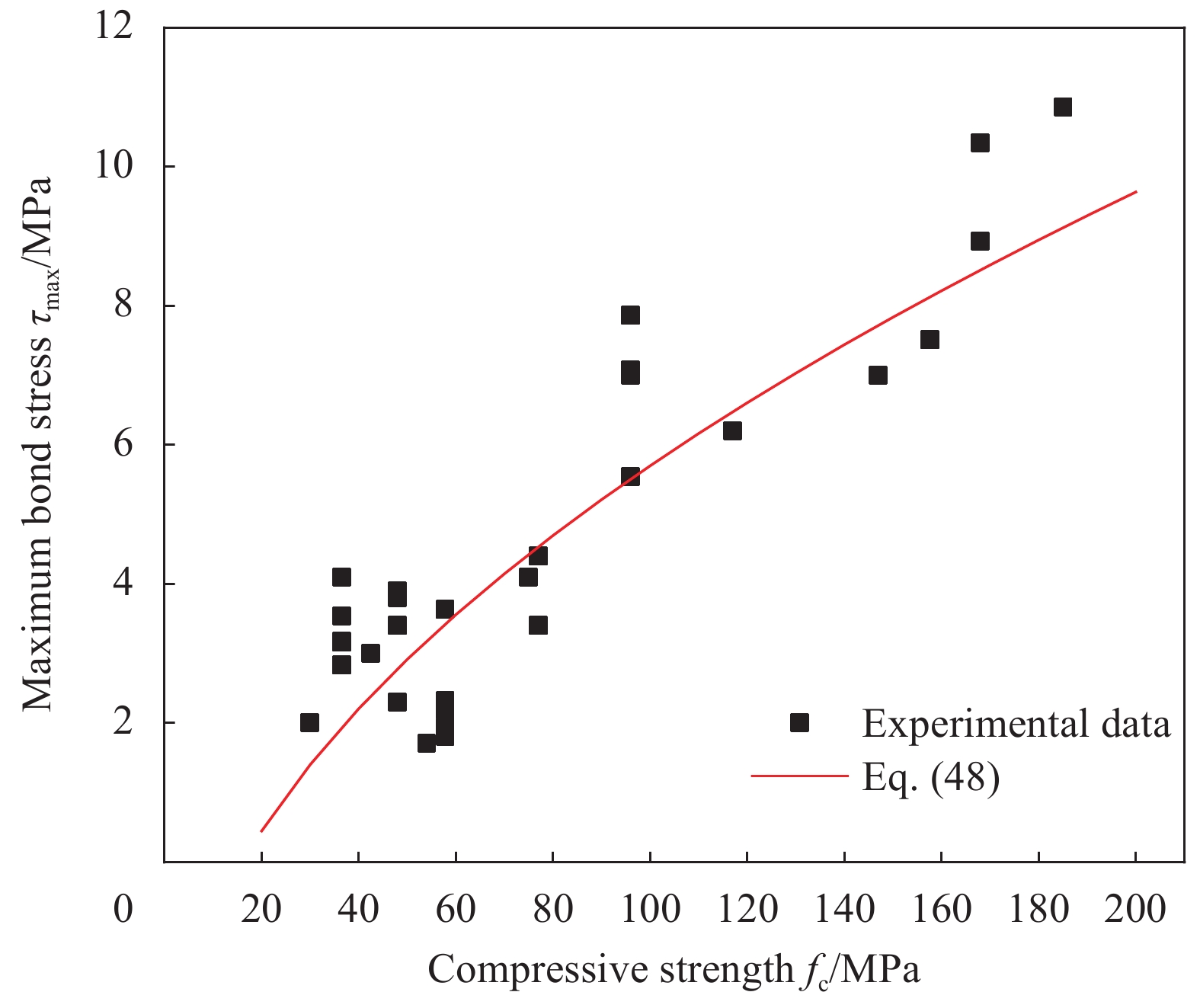
通过上述理论计算模型可以得到峰值点荷载计算公式为
{P_{{{A_1}}}} = {\alpha _{\rm{E}}}\left( {{T_{\rm{1}}} + {F_{{\rm{extra}}}} + {\rm{{\text{π}} }}{d_{\rm{f}}}{\tau _{\rm{s}}}{L_{\rm{1}}}} \right) (51) 通过分析可知,当T1达到最大值时,拔出荷载也达到
{P_{\max }} ,同时可以求得对应的位移为{\delta _{{{A_1}}}} 。为简化计算过程,荷载-位移全曲线的上升段的荷载按照下式进行计算:P{\rm{ = }}{P_{{{A}}_1}} {{\rm{e}}^{ - {{\left( {\frac{{{\delta _{\rm{s}}} - {\delta _{{{A_1}}}}}}{{{\delta _{{{A_1}}}}}}} \right)}^2}}} (52) 下降段分为5个部分进行计算,A1A2段为钢纤维从l1部分拔出所对应的荷载下降,A2点的荷载可以根据下式进行计算:
{P_{{{A}}_2}} = {\alpha _{\rm{E}}}\left( {T_1^{'} + {F_{{\rm{extra}}}} + {\rm{{\text{π}} }}{d_{\rm{f}}}\tau {L_{\rm{1}}}} \right) (53) {\delta _{{{A_2}}}}{\rm{ = }}{l_{\rm{1}}}{\rm{ + }}{l_{{\rm{ft}}}} (54) A3A4段为钢纤维从l2部分拔出对应的荷载下降,根据试验结果可以发现A2A3段较短且两点的荷载相差很小,故取A3对应的荷载与A2点相等,对应的位移为
{\delta _{{{A_3}}}}{\rm{ = }}{l_1} + {l_2} + {l_{{\rm{ft}}}} - 2{d_{\rm{f}}} 。同时可以求得A4对应的荷载与位移分别为{P_{{{A}}_4}} = {\alpha _{\rm{E}}}\left( {{F_{{\rm{extra}}}} + {\rm{{\text{π}} }}{d_{\rm{f}}}{\tau _{\rm{s}}}{L_{\rm{1}}}} \right) (55) {\delta _{{{A_4}}}}{\rm{ = }}{l_{\rm{1}}}{\rm{ + }}{l_{\rm{2}}}{\rm{ + }}{l_{{\rm{ft}}}} (56) A5A6段为钢纤维被完全拔出前的部分,此时附加摩擦力逐渐减小,直至降为0。故A5点的荷载近似取为最大附加摩擦力
{\alpha _{\rm{E}}}{F_{{\rm{extra}}}} ,对应的位移为{L_{\rm{e}}} - {l_1} - {l_2} 。A6点的位移为{\delta _{{{A_6}}}}{\rm{ = }}{L_{\rm{e}}} 。4.2 模型验证
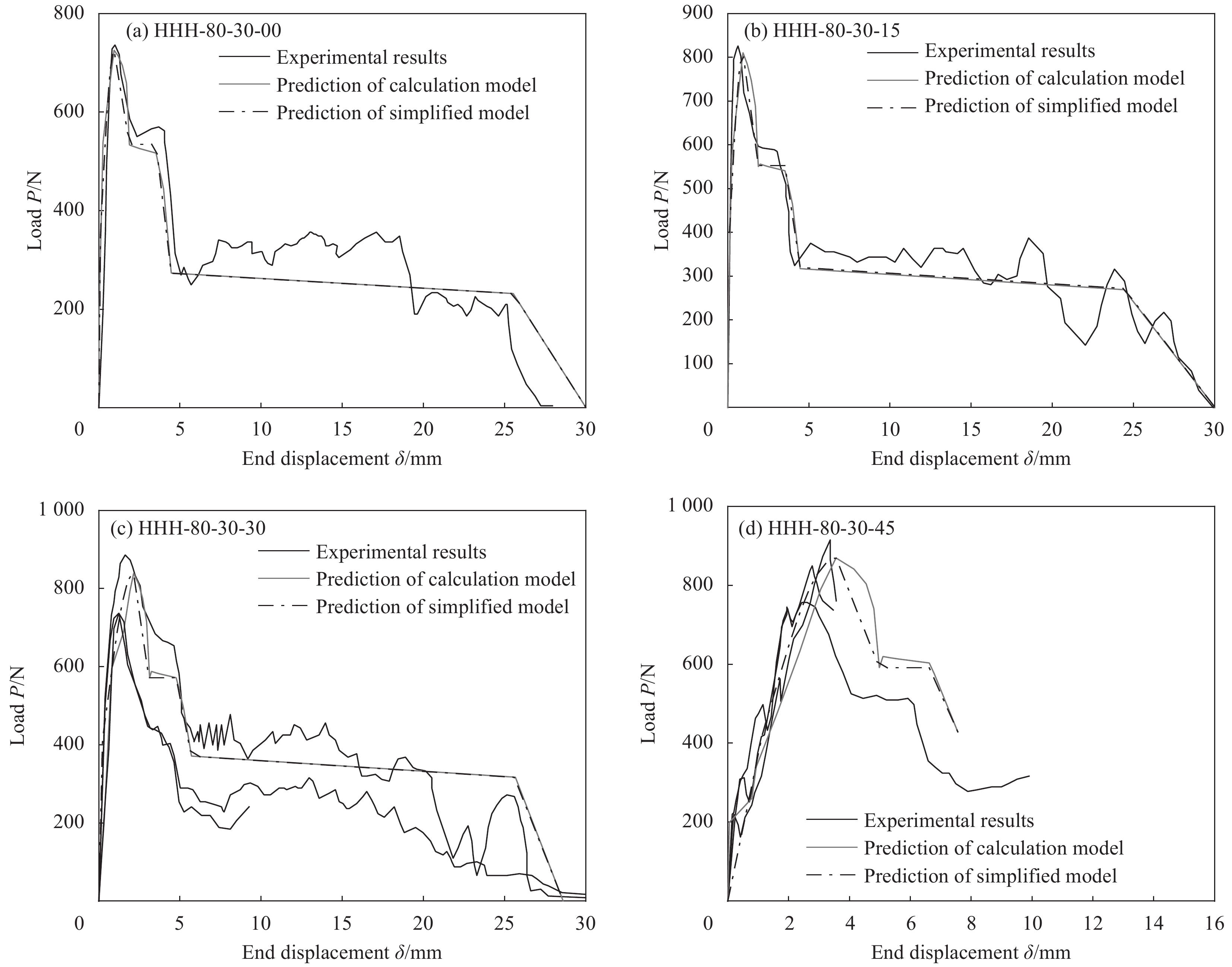
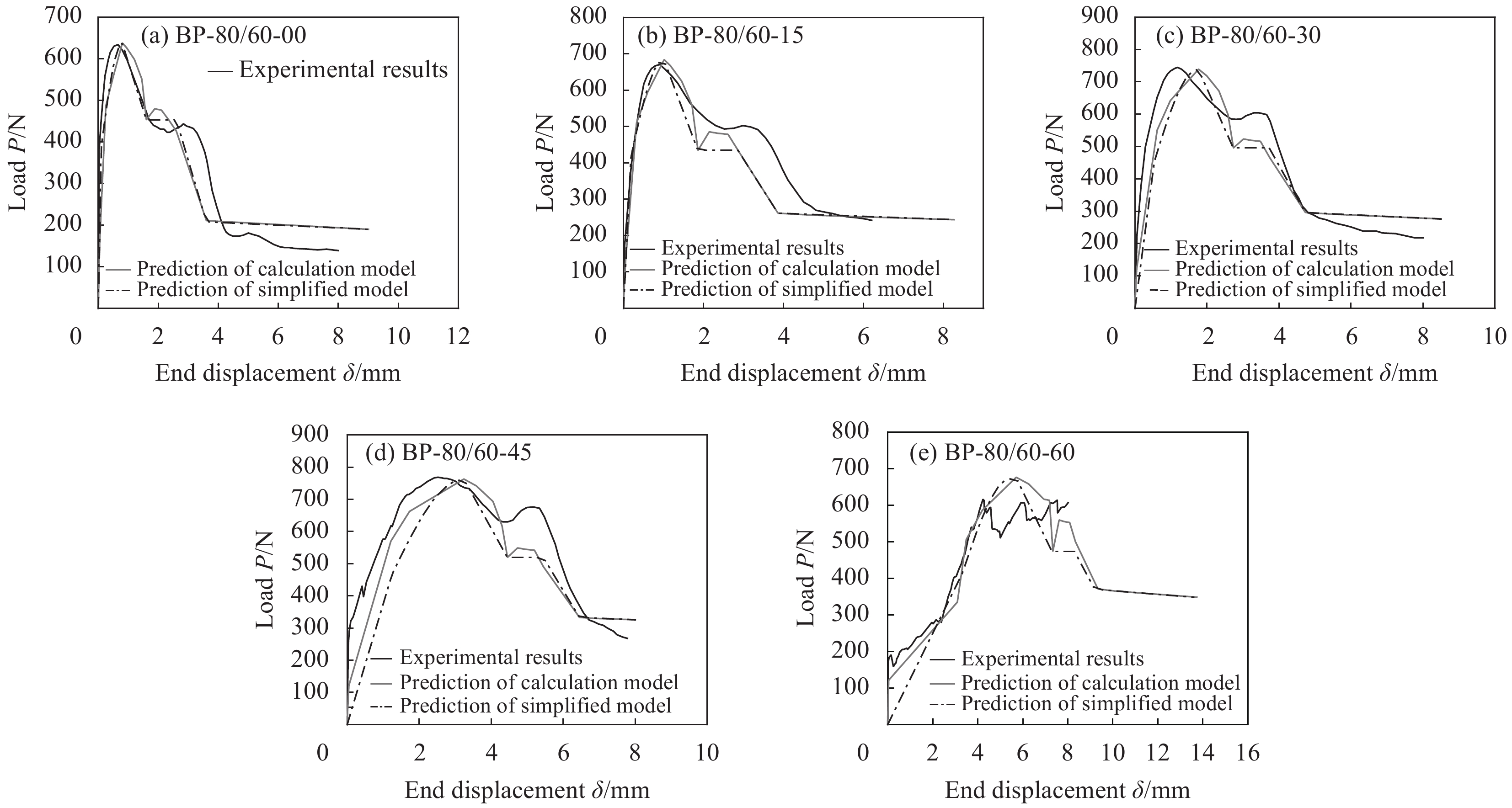
为了验证本文提出理论计算模型和简化模型的有效性及精确性,采用本文模型对Soetens等[12]和Breitenbücher等[29]的试验进行预测,纤维拔出角度在0°至60°之间,图16及图17为预测结果和试验结果的荷载-位移曲线对比,表2为预测的峰值荷载与试验结果的对比。
表 2 钢纤维拔出峰值荷载预测值与试验值对比Table 2. Comparison between predicted and experimental values of steel fiber pullout peak loadReference Specimen Ppre/N Pex/N Ppre/Pex Soetens et al[12] HHH-80-30-00 725.91 736.63 0.98 HHH-80-30-15 810.56 818.18 0.99 HHH-80-30-30 838.71 885.96 1.07 HHH-80-30-45 796.03 869.45 1.08 Breitenbücher et al[29] BP-80/60-00 637.51 633.88 1.01 BP-80/60-15 684.43 670.84 1.02 BP-80/60-30 739.01 744.76 0.99 BP-80/60-45 753.37 768.79 0.97 BP-80/60-60 675.96 615.40 1.10 μ 1.02 COV 0.05 Notes: Ppre and Pex—Predicted and the experimental value of the peak load, respectively; μ—Ratio of Ppre and Pex; COV—Coefficient of variation; “HHH” in notation system of the first series of tests represents the high strength matrix and hooked-end fiber with high carbon content. Figures in the second, third and fourth symbol represent fiber diameter (mm/100), embedded length (mm) and pullout inclination (°), respectively. For example, the notation of “HHH-80-30-30”—Pullout specimen with high strength matrix, 0.8 mm of fiber diameter, 30 mm of embedded length and 30° of pullout inclination. “BP” in notation system of the second series of tests represents a type of hooked-end fiber with tensile yield strength 2600 MPa. Figures in the second, third and fourth symbol represent fiber aspect ratio (-), fiber length (mm) and pullout inclination (°), respectively. For example, the notation of “BP-80/60-15”—Pullout specimen with 80 of fiber aspect ratio, 60 mm of fiber length and 15° of pullout inclination. 可以看出,本文提出的两种模型均可以准确地预测倾斜端钩型钢纤维拔出力学性能。理论计算模型预测的钢纤维拔出全过程荷载-位移曲线具有较高的计算精度,而简化模型对于拔出角度较小的钢纤维预测精度较高,这是由于简化模型不能有效模拟混凝土小块的剥落现象且上升段并没有分为三种拔出状态进行分析导致的,故当拔出角度较大时,预测的上升段拔出位移误差较大;对于下降段,由于简化模型将钢纤维从l2段拔出近似认为荷载不变,故不能有效预测钢纤维拔出的第二次峰值荷载。从表2可以得到本文模型预测的峰值荷载与试验值之比的平均值为1.02,变异系数为0.05,验证了理论模型的精确性。可以发现简化计算模型形式简单,计算过程便捷,且计算精度能够满足工程要求,故可以将其推广应用于进一步的SFRC受拉性能研究当中。
5. 结 论
(1) 考虑钢纤维滑移导致的孔道损伤,提出一种钢纤维与基体之间黏结应力-位移关系,可以有效表达钢纤维黏结应力随端部位移的变化,并基于已有试验数据确定了黏结应力关键指标与基体抗压强度之间的关系。
(2) 将端钩型钢纤维拔出过程分为完全黏结、脱黏和拔出滑移三个阶段分别进行受力分析和计算,考虑钢纤维塑性变形、附加摩擦力、基体剥落和挤压摩擦效应,推导了倾斜端钩型钢纤维拔出全过程理论计算模型,在此基础上提出一种形式简单的简化计算模型。
(3) 采用提出的理论计算模型和简化模型对试验进行预测,并将得到的荷载-位移全曲线及峰值荷载与试验结果进行对比,可以发现提出的两种计算模型均可以有效预测倾斜端钩型钢纤维拔出全过程,与试验结果吻合较好且变异系数小。
-
图 3 钢纤维黏结应力-端部位移关系
Figure 3. Relationship between fiber bond stress and end displacement
δ1, δ2—Maximum end-displacement in the completely bonding stage and debonding stage, respectively; τmax—Bond shear strength; τs—Bond shear stress corresponding to the end of the debongding stage; gf—Interfacial shear fracture energy
图 7 钢纤维端钩部分受力分析及截面应力分布
Figure 7. Mechanical analysis and stress distribution of hooked-end of steel fiber
T1, T2 and T1'—Tensile force for the end-hook; f1 and f2—Bond force of the end-hook; Tp—Tensile force required for plastic deformation; β—Angle of the normal force; N1 and N2—Normal force; rf—Radius of steel fiber; Ap—Area of the plastic region; y—Distance between the neutral axis and the plastic zone centroid; γ—Angle between the plastic zone and the vertical axis
表 1 用于预测端钩型钢纤维拔出力学性能的参数取值
Table 1 Parameters used to predict the pullout behavior of hooked-end steel fiber
Parameter Value Elastic modulus of matrix Em/MPa 3.2×104 Elastic modulus of fiber Ef/MPa 2×105 Diameter of matrix Dm 10df Fiber Poisson's ratio vf 0.3 Matrix Poisson's ratio vm 0.2 Curvature radius of hooked fiber ρ 2df End hook angle α/(°) 50 表 2 钢纤维拔出峰值荷载预测值与试验值对比
Table 2 Comparison between predicted and experimental values of steel fiber pullout peak load
Reference Specimen Ppre/N Pex/N Ppre/Pex Soetens et al[12] HHH-80-30-00 725.91 736.63 0.98 HHH-80-30-15 810.56 818.18 0.99 HHH-80-30-30 838.71 885.96 1.07 HHH-80-30-45 796.03 869.45 1.08 Breitenbücher et al[29] BP-80/60-00 637.51 633.88 1.01 BP-80/60-15 684.43 670.84 1.02 BP-80/60-30 739.01 744.76 0.99 BP-80/60-45 753.37 768.79 0.97 BP-80/60-60 675.96 615.40 1.10 μ 1.02 COV 0.05 Notes: Ppre and Pex—Predicted and the experimental value of the peak load, respectively; μ—Ratio of Ppre and Pex; COV—Coefficient of variation; “HHH” in notation system of the first series of tests represents the high strength matrix and hooked-end fiber with high carbon content. Figures in the second, third and fourth symbol represent fiber diameter (mm/100), embedded length (mm) and pullout inclination (°), respectively. For example, the notation of “HHH-80-30-30”—Pullout specimen with high strength matrix, 0.8 mm of fiber diameter, 30 mm of embedded length and 30° of pullout inclination. “BP” in notation system of the second series of tests represents a type of hooked-end fiber with tensile yield strength 2600 MPa. Figures in the second, third and fourth symbol represent fiber aspect ratio (-), fiber length (mm) and pullout inclination (°), respectively. For example, the notation of “BP-80/60-15”—Pullout specimen with 80 of fiber aspect ratio, 60 mm of fiber length and 15° of pullout inclination. -
[1] 韩嵘, 赵顺波, 曲福来. 钢纤维混凝土抗拉性能试验研究[J]. 土木工程学报, 2006, 39(11):63-67. DOI: 10.3321/j.issn:1000-131X.2006.11.010 HAN Rong, ZHAO Shunbo, QU Fulai. Experimental study on the tensile performance of steel flber reinforced concrete[J]. China Civil Engineering Journal,2006,39(11):63-67(in Chinese). DOI: 10.3321/j.issn:1000-131X.2006.11.010
[2] 卿龙邦, 聂雅彤, 慕儒. 钢纤维对水泥基复合材料抗起裂特性的影响[J]. 复合材料学报, 2017, 34(8):1862-1869. QING Longbang, NIE Yatong, MU Ru. Influence of steel fibres on the resistance to crack initiation of cementitious composites[J]. Acta Materiae Compositae Sinica,2017,34(8):1862-1869(in Chinese).
[3] 梁兴文, 胡翱翔, 于婧, 等. 钢纤维对超高性能混凝土抗弯力学性能的影响[J]. 复合材料学报, 2018, 35(3):722-731. LIANG Xingwen, HU Aoxiang, YU Jing, et al. Effect of steel fibers on the flexural response of ultra-high performance concrete[J]. Acta Materiae Compositae Sinica,2018,35(3):722-731(in Chinese).
[4] NAAMAN A E. Engineered steel fibers with optimal properties for reinforcement of cement composites[J]. Journal of Advanced Concrete Technology,2003,1(3):241-252. DOI: 10.3151/jact.1.241
[5] 秦鸿根, 刘斯凤, 孙伟, 等. 钢纤维掺量和类型对混凝土性能的影响[J]. 建筑材料学报, 2003(4):364-368. DOI: 10.3969/j.issn.1007-9629.2003.04.005 QIN Honggen, LIU Sifeng, SUN Wei, et al. Effect of types and volume percentage of steel fiber on properties of concrete[J]. Journal of Building Materials,2003(4):364-368(in Chinese). DOI: 10.3969/j.issn.1007-9629.2003.04.005
[6] 许碧莞, 施惠生, JU Jiannwen Woody. 水泥基体中弓形钢纤维拔出耗能模型[J]. 同济大学学报(自然科学版), 2010, 38(8):1194-1199. DOI: 10.3969/j.issn.0253-374x.2010.08.017 XU Biwan, SHI Huisheng, JU Jiannwen Woody. Modeling pullout energy of hooked end steel fiber in cementitious matrices[J]. Journal of Tongji University (Natural Science),2010,38(8):1194-1199(in Chinese). DOI: 10.3969/j.issn.0253-374x.2010.08.017
[7] 朱德举, 李向阳, 史才军, 等. 水泥基体中仿生钢纤维的拔出试验[J]. 湖南大学学报(自然科学版), 2018, 45(1):84-89. ZHU Deju, LI Xiangyang, SHI Caijun, et al. Pullout test of bio-inspired steel fiber from cementitious matrix[J]. Journal of Hunan University (Natural Sciences),2018,45(1):84-89(in Chinese).
[8] ROBINS P, AUSTIN S, JONES P. Pull-out behaviour of hooked steel fibres[J]. Materials and Structures,2002,35:434-442. DOI: 10.1007/BF02483148
[9] NAAMAN A E, NAMUR G G, ALWAN J M, et al. Fiber pullout and bond slip. I: Analytical study[J]. Journal of Structural Engineering,1991,117:2769-2790. DOI: 10.1061/(ASCE)0733-9445(1991)117:9(2769)
[10] SHANNAG M J, BRINCKER R, HANSEN W. Pullout behavior of steel fibers from cement-based composites[J]. Cement and Concrete Research,1997,27(6):925-936. DOI: 10.1016/S0008-8846(97)00061-6
[11] GHODDOUSI P, AHMADI R, SHARIFI M. Fiber pullout model for aligned hooked-end steel fiber[J]. Canadian Journal of Civil Engineering,2010,37:1179-1188. DOI: 10.1139/L10-053
[12] SOETENS T, VAN-GYSEL A, MATTHYS S, et al. A semi-analytical model to predict the pull-out behaviour of inclined hooked-end steel fibres[J]. Construction and Building Materials,2013,43(2):253-265.
[13] LARANJEIRA F, MOLINS C, AGUADO A. Predicting the pullout response of inclined hooked steel fibers[J]. Cement and Concrete Research,2010(40):1471-1487.
[14] KULLAA J. Dimensional analysis of bond modulus in fiber pullout[J]. Journal of Structural Engineering,1996,122(7):783-787. DOI: 10.1061/(ASCE)0733-9445(1996)122:7(783)
[15] GAO Y, MAI Y, COTTERELL B. Fracture of fiber-reinforced materials[J]. Journal of Applied Mathematics and Physics,1988,39(4):550-572.
[16] YANG S, HU X, LENG K, et al. Correlation between cohesive crack-tip local fracture energy and peak load in mortar beams[J]. Journal of Materials in Civil Engineering,2014,26(10):1-8.
[17] CHANVILLARD G. Modeling the pullout of wire-drawn steel fibers[J]. Cement and Concrete Research,1999,29(7):1027-1037. DOI: 10.1016/S0008-8846(99)00081-2
[18] GEORGIADIS-STEFANIDI K, MISTAKIDIS E, PANTOUSA D, et al. Numerical modelling of the pull-out of hooked steel fibers form high-strength cementitious matrix, supplemented by experimental results[J]. Construction and Building Materials,2010,24:2489-2506. DOI: 10.1016/j.conbuildmat.2010.06.007
[19] CAILLEUX E, CUTARD T, BERNHART G. Pullout of steel fibers from a refractory castable: Experiment and modelling[J]. Mechanics of Materials,2005,37(4):427-445. DOI: 10.1016/j.mechmat.2004.02.001
[20] LEUNG C K Y, SHAPIRO N. Optimal steel fiber strength for reinforcement of cementitious materials[J]. Journal of Materials in Civil Engineering,1999,11(2):116-123. DOI: 10.1061/(ASCE)0899-1561(1999)11:2(116)
[21] LI V C, WANG Y, BACKER S. Effect of inclining angle, bundling and surface treatment on synthetic fibre pull-out from a cement matrix[J]. Composites,1990,21(2):132-140. DOI: 10.1016/0010-4361(90)90005-H
[22] XU B W, JU J W, SHI H S. Progressive micromechanical modeling for pullout energy of hooked-end steel fiber in cement-based composites[J]. International Journal of Damage Mechanics,2011,20(6):922-938. DOI: 10.1177/1056789510385260
[23] PARK J K, NGO T T, KIM D J. Interfacial bond characteristics of steel fibers embedded in cementitious composites at high rates[J]. Cement and Concrete Research,2019,123:1-17.
[24] OUYANG C, PACIOS A, SHAH S P. Pullout of inclined fibers from cementitious matrix[J]. Journal of Engineering Mechanics,1994,120(12):2641-2659. DOI: 10.1061/(ASCE)0733-9399(1994)120:12(2641)
[25] ZHANG C, SHI C, WU Z, et al. Numerical and analytical modeling of fiber-matrix bond behaviors of high perfor-mance cement composite[J]. Cement and Concrete Research,2019,125:1-14.
[26] FENG J, SUN W, WANG X, et al. Mechanical analyses of hooked fiber pullout performance in ultra-high-perfor-mance concrete[J]. Construction and Building Materials,2014,69:403-410. DOI: 10.1016/j.conbuildmat.2014.07.049
[27] ABU-LEBDEH T, HAMOUSH S, HEARD W, et al. Effect of matrix strength on pullout behavior of steel fiber reinforced very-high strength concrete composites[J]. Construction and Building Materials,2011,25(1):39-46. DOI: 10.1016/j.conbuildmat.2010.06.059
[28] GENG Y P, LEUNG C K Y. Damage-based modeling of fiber pullout under variable compressive stress[J]. Journal of Engineering Mechanics,1997,123(4):342-349. DOI: 10.1061/(ASCE)0733-9399(1997)123:4(342)
[29] BREITENBUECHER R, MESCHKE G, SONG F, et al. Experimental, analytical and numerical analysis of the pullout behaviour of steel fibres considering different fibre types, inclinations and concrete strengths[J]. Structural Concrete,2014,15(2):126-135. DOI: 10.1002/suco.201300058
-
期刊类型引用(5)
1. 樊虎,王超,左小彪,周金岑,尚呈元. 高强中模碳纤维增强高耐热双马树脂复合材料性能. 宇航材料工艺. 2024(02): 89-93 .  百度学术
百度学术
2. 徐牛牛,杭传伟,张淑斌,彭飞. 纺丝工艺对T700级碳纤维及其复合材料性能的影响. 合成纤维. 2023(05): 29-33 .  百度学术
百度学术
3. 郭聪聪,尹国强,单瑞俊,胡啸天. 树脂分布设计对复合材料轴向压缩强度的影响. 高科技纤维与应用. 2023(03): 34-42 .  百度学术
百度学术
4. 符平坡,丁华,曾祥瑞,王纪,罗时清,魏宗来. 碳纤维复合材料-铝合金自冲铆接头成形规律及力学性能. 复合材料学报. 2023(08): 4517-4530 .  本站查看
本站查看
5. 胡丹丽,付大鹏,张越,甄金明,赵伟,张冉,贾正锋. 配副材料对碳纤维增强环氧树脂复合材料摩擦学性能的影响. 润滑与密封. 2022(07): 97-103 .  百度学术
百度学术
其他类型引用(7)
-





 下载:
下载: