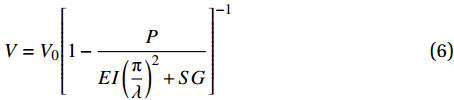碳纤维截面特性对碳纤维/环氧树脂复合材料压缩强度的影响

石佩洛; 尚呈元; 陈亮; 赵红燕; 周宇; 朱世鹏; 左小彪

doi:10.13801/j.cnki.fhclxb.20210203.001

碳纤维截面特性对碳纤维/环氧树脂复合材料压缩强度的影响

航天材料及工艺研究所，北京 100076

基金项目: 材料攻关项目(024)；国防青年基金 (2020-041)

详细信息

通讯作者:
左小彪，博士，研究员，研究方向为树脂基复合材料　E-mail：hotzuo1978@163.com

中图分类号: TB332；TQ327.3
计量
- 文章访问数: 2003
- HTML全文浏览量: 649
- PDF下载量: 248
出版历程
- 收稿日期: 2020-12-07
- 录用日期: 2021-01-21
- 网络出版日期: 2021-02-02
- 刊出日期: 2021-11-30

Compressive strength of carbon fiber reinforced epoxy composites with various carbon fiber cross section characteristics

Aerospace Research Institute of Materials and Processing Technology, Beijing 100076, China

HTML全文

摘要

摘要: 基于压拉平衡为特征的新一代先进复合材料的需求，开展了碳纤维截面形状和尺寸对碳纤维/环氧树脂复合材料压缩强度的影响研究。有限元模拟和试验结果均表明，增大碳纤维直径可以提高复合材料压缩强度。另外碳纤维截面形状也对复合材料压缩强度有影响，圆形截面优于椭圆形截面。
- 碳纤维增强树脂基复合材料 /
- 压缩强度 /
- 纤维直径 /
- 截面形状 /
- 有限元模拟
Abstract: Based on the demand of new generation advanced composites characterized by the balance of com-pressive and tensile strength, the compressive strength of carbon fiber/epoxy composites with various cross section characteristics of carbon fibers was studied by finite element simulation and experiment. Results show that the compressive strength of carbon fiber/epoxy composite increases with the increasing fiber diameter, and round is better than ellipse regarding to the fiber cross section shape.
- carbon fiber reinforced epoxy composites /
- compressive strength /
- fiber diameter /
- cross section shape /
- finite element simulation

HTML全文

碳纤维增强树脂基复合材料具有高比强度和高比模量，在航天航空等领域的应用日益广泛。新一代先进树脂基复合材料装备应用对材料的压拉平衡特性提出了强烈需求，然而通常情况下碳纤维单向复合材料的纵向压缩强度却远低于其纵向拉伸强度^[1-2]。T300级碳纤维增强树脂基复合材料的压拉强度比值为77%左右，T800级碳纤维增强树脂基复合材料的压拉强度比值为59%左右，随着碳纤维拉伸强度的不断提升，T1000级碳纤维增强树脂基复合材料的压拉强度比值进一步降低为52%左右，压拉强度不匹配成为碳纤维增强树脂基复合材料性能的短板，严重制约了整体性能的发挥。现有理论模型和试验研究结果表明，测试方法^[3-5]、碳纤维模量^[6-8]、碳纤维准直度^[9]、碳纤维表面状态^[10-12]、碳纤维毛丝状态^[13]、树脂模量^[14-16]、复合材料纤维含量^[17]、环境湿度^[18]、界面结合强度^[19-20]和复合材料破坏模式^[20-26]等多个影响因素都对复合材料压缩强度产生影响^[3-6]。

目前围绕碳纤维直径和截面形状对复合材料压缩强度影响方面的研究较少。一方面是由于碳纤维截面形状比较多元化，其整体形状包括圆形、椭圆形、腰形等；另一方面是由于碳纤维直径的变化往往会导致其本征结构及强度和模量等力学性能的显著变化，较难实现直径这个单一变量的变化。Xu等^[8]基于BOEF模型，计算发现碳纤维直径越大，复合材料纵向压缩强度越高，对于HTS碳纤维/环氧复合材料，碳纤维直径从3 μm增加到20 μm，对应的纵向压缩强度从1100 MPa提高到1620 MPa，提高了47%，该研究并没有实验数据的对比。李梦龙等^[27]利用拉伸回弹法测量了东丽T300、东丽T800H和5种国产T800级碳纤维的单丝压缩强度，发现国产T800级碳纤维由于石墨微晶基面宽度及取向度调控提升，单丝压缩强度可达2.8 GPa，显著高于东丽T800H的2.15 GPa，该研究没有考虑两种碳纤维截面形状因素引起的抗屈曲能力的差异。

本文选取了四种力学性能接近、直径和截面形状有显著差异的碳纤维，并制备了碳纤维/环氧树脂基复合材料，通过力学试验、理论模型和有限元计算，研究了碳纤维直径和截面形状对复合材料压缩强度的影响，可指导新一代压拉平衡先进树脂基复合材料的研制。

1. 材料与方法

12K规格碳纤维：T800H，日本东丽公司；TG800−1、TG800−2、TG800−3，山西钢科碳材料有限公司。耐高温环氧树脂体系：603B，航天材料及工艺研究所。上述碳纤维和树脂制备成热熔预浸料，180℃铺层固化4 h制备纤维体积分数为60%的碳纤维/环氧树脂复合材料单向板。

碳纤维当量直径的测试参考GB/T 3364—2008标准^[28]，取等面积圆的直径作为纤维的当量直径；碳纤维拉伸性能测试参照GB/T 3362—2005标准^[29]；复合材料拉伸性能测试参照GB/T3354—2014标准^[30]；复合材料压缩性能测试参照ASTM D3410—16标准^[31]，环境温度23℃，环境湿度40%。

4种碳纤维均采用湿法纺丝工艺制备，碳纤维表面沟槽明显，准直度较高，毛丝量较少，有利于压缩强度的发挥。4种复合材料界面结合强度较高(τ=100 MPa左右)，压缩破坏过程中界面未破坏，破坏模式为扭结带失效模式。

2. 结果与讨论

2.1 碳纤维性能

研究了1种进口和3种国产碳纤维的拉伸强度、拉伸模量、当量直径、截面形状和表面沟槽等性能，结果如表1所示。可以看出，国产TG800-1碳纤维与进口T800H碳纤维各项性能十分接近，当量直径5.0 μm，拉伸强度5800 MPa左右(实测值高于T800H官方报道值5490 MPa)，拉伸模量294 GPa左右。国产TG800-2和TG800-3碳纤维在保持强度和模量基本一致的前提下，当量直径与TG800-1相比显著提升，达到5.8 μm。

4种碳纤维的表观形貌SEM图像对比见图1。可以看出，4种碳纤维截面形貌差异较大：进口T800H碳纤维呈腰肾状接近椭圆形，虽然其当量直径为5.0 μm，但是长边直径达到6.0 μm，短边直径仅为约4.0 μm；3种国产TG800碳纤维截面均为较理想的圆形，当量直径分别为5.0 μm、5.3 μm和5.8 μm。4种碳纤维表面均有较明显沟槽。

表 1 4种碳纤维性能

Table 1. Properties of 4 types of carbon fibers

Type	Strength σ/MPa	Modulus E/GPa	Diameter/μm	Section shape	Surface roughness
T800H	5790	294	5.0	Ellipse	Obvious
TG800-1	5820	292	5.0	Round	Obvious
TG800-2	5860	292	5.3	Round	Obvious
TG800-3	5830	294	5.8	Round	Obvious

下载: 导出CSV

| 显示表格

图 1 4种碳纤维微观形貌SEM图像

Figure 1. SEM images of 4 types of carbon fibers

下载: 全尺寸图片幻灯片

综上，4种碳纤维强度、模量和表面沟槽状态十分接近，仅截面形状和直径大小不同，有利于研究碳纤维截面形状和直径大小等单一变量对复合材料性能的影响。

2.2 碳纤维/环氧树脂复合材料性能

4种碳/环氧复合材料的0°拉伸性能、0°压缩性能及压拉强度比值见表2。结果表明，4种复合材料的拉伸强度比较接近，介于2750~2820 MPa之间；3种圆形截面的国产碳纤维/环氧树脂复合材料压缩强度大于进口腰肾形截面碳纤维/环氧树脂复合材料，并且随着纤维直径的增大，压缩强度从1390 MPa逐渐增加到1660 MPa，压拉强度比值从0.50逐渐增加到0.60。

表 2 4种碳纤维/环氧复合材料力学性能

Table 2. Mechanical properties of 4 types of carbon fiber/epoxy composites

Type	0° tensile strength/MPa	0° compressive strength/MPa	Compressive/tensile strength ratio
T800H/603B	2770±180	1390±85	0.50
TG800-1/603B	2750±170	1505±71	0.55
TG800-2/603B	2805±210	1560±95	0.56
TG800-3/603B	2790±180	1660±93	0.60

下载: 导出CSV

| 显示表格

复合材料压缩失效的典型形貌如图2所示。可以看出，在压缩载荷下，碳纤维发生屈曲，并最终形成比较明显的的扭结带结构。

图 2 碳纤维/环氧树脂复合材料压缩失效宏观和微观形貌

Figure 2. Macroscopic and microscopic observations of carbon fiber/epoxy composites after compression

下载: 全尺寸图片幻灯片

2.3 欧拉屈曲模型

参考压杆失稳屈曲模型来分析压缩强度随截面形状和尺寸的变化规律。压杆由于加载偏心或外界干扰力等原因，导致在压缩状态下丧失自身平衡状态。欧拉屈曲临界应力如下式所示：

${\sigma }_{\mathrm{c}\mathrm{r}}=\frac{{\mathrm{{\text{π}} }}^{2}EI}{{SL}^{2}}$

(1)

式中：E为纵向压缩模量； S为横截面积；L为压杆长度；I为碳纤维横截面的最小惯性矩，其计算公式如下：

$I={\int }_{A}^{}{y}^{2}\mathrm{d}A$

(2)

可以看出，临界应力大小正比于I/S，即与最小惯性矩成正比，与截面积成反比。考虑图3所示3种典型截面形貌并计算欧拉屈曲临界应力：图3(a)为简单圆形，直径为d；图3(b)为椭圆形，长轴为a，短轴为b；图3(c)为有沟槽的圆形，直径为d，沟槽深度为t。模拟计算了三种典型截面形貌的最小惯性矩I及横截面积S。计算参数取值保证了3种形貌截面积完全相同，取值接近实际情况：圆形截面直径d=5 μm；椭圆形截面长轴为a=6.25 μm，短轴为b=4 μm；有沟槽的圆形，直径为d=5 μm，沟槽深度为t=0.5 μm。计算过程及结果见表3。

图 3 3种典型碳纤维截面形貌简化示意图

Figure 3. Schematic diagrams of 3 typical section shapes of carbon fibers

下载: 全尺寸图片幻灯片

表 3 3种典型碳纤维截面惯性矩计算

Table 3. Sectional inertia moments of 3 typical section shapes of carbon fibers

Shape	Round	Ellipse	Round with grooves
I (Equation)/μm⁴	${\mathrm{{\text{π}} }d}^{4}/64$	$\mathrm{{\text{π}} }a{b}^{3}/64$	${\mathrm{{\text{π}} }d}^{4}/64+{\mathrm{{\text{π}} }d}^{2}{t}^{2}/192$
S (Equation)/μm²	${\mathrm{{\text{π}} }d}^{2}/4$	$\mathrm{{\text{π}} }ab/4$	${\mathrm{{\text{π}} }d}^{2}/4$
Parameters/μm	d=5	a=6.25, b=4	d=5, t=0.5
S (Value)/μm²	6.25π	6.25π	6.25π
I (Value)/μm⁴	9.76π	6.25π	9.80π
Notes: I—Minimum moment of inertia; S—Section area d—Diameter for round section; a—Long axis of ellipse; b—Short axis of ellipse; t—Groove depth.

下载: 导出CSV

| 显示表格

表3中，最小惯性矩I根据式(2)计算得到。可以看出，计算参数的选择保证了三种形貌截面积S数值完全相同，均为6.25π μm²。对于圆形有无沟槽两种情况，有沟槽圆形的最小惯性矩为9.80π μm⁴，略高于普通圆形9.76π μm⁴，说明沟槽的存在有利于提高截面惯性矩和碳纤维弯曲刚度，但是提高幅度非常有限。

将表3中I和S的公式代入式(1)可以看出，对于圆形截面，欧拉屈曲临界应力与直径平方成正比，如下式：

${\sigma }_{\mathrm{c}\mathrm{r}}=\frac{{\mathrm{{\text{π}} }}^{2}E}{16{L}^{2}}{d}^{2}$

(3)

对于椭圆形截面，欧拉屈曲临界应力与短轴长度平方成正比，如下式：

${\sigma }_{\mathrm{c}\mathrm{r}}=\frac{{\mathrm{{\text{π}} }}^{2}E}{16{L}^{2}}{b}^{2}$

(4)

综上，纤维直径和截面形状对欧拉屈曲模型的临界应力影响较大。定义截面最小直径为d_m (对于圆形截面d_m为直径d；对于椭圆形截面d_m为短轴长度b)，则临界应力与最小直径平方成正比，与长轴或当量直径无关，如下式：

${\sigma }_{\mathrm{c}\mathrm{r}}=\frac{{\mathrm{{\text{π}} }}^{2}E}{16{L}^{2}}{d}_{\mathrm{m}}^{2}$

(5)

例如，对于截面形状近似椭圆形的进口T800H碳纤维，计算临界应力的最小直径为短轴长度4.0 μm，既不是等效直径5.0 μm，也不是长轴直径6.0 μm。这解释了与其等效直径相同的圆形截面TG800-1压缩强度实测结果更高的原因。

因此，模型结果表明碳纤维最小直径d_m代表了其抵抗弯曲变形的能力，碳纤维压缩失稳应力与碳纤维最小直径d_m的平方成正比例关系。将这一结论类比至复合材料，考察复合材料0°压缩强度与碳纤维最小直径的关系，图4为4种复合材料0°压缩强度与碳纤维最小直径的关系。其中圆点为试验数据，虚线为y=ax²+b关系式拟合，反映了复合材料压缩强度与碳纤维最小直径平方的正比例关系，模型与试验数据的拟合性较好，拟合因子R²=0.989。

图 4 4种碳纤维/环氧树脂复合材料0°压缩强度-纤维最小直径d_m的关系

Figure 4. 0° compressive strength-fiber minimum diameter d_m curve for 4 types of carbon fiber/epoxy composites

下载: 全尺寸图片幻灯片

将欧拉屈曲模型与其他纤维微屈曲模型对比可以发现其本质是一致的。例如Berbinau模型计算了纤维屈曲振幅V，如下式：

$V={V}_{0}{\left[1-\frac{P}{{EI\left(\dfrac{\mathrm{{\text{π}} }}{\lambda }\right)}^{2}+SG}\right]}^{-1}$

(6)

其中：V₀为初始振幅；P为试样两端压应力；λ为模型纤维的正弦波波长；G为材料响应函数。纤维发生失稳时，V迅速增大时对应的压缩应力即为纵向压缩强度，如下式：

${\sigma }_{\mathrm{c}\mathrm{r}}=\frac{P}{S}=\frac{{\mathrm{{\text{π}} }}^{2}EI}{{S\lambda }^{2}}+G$

(7)

对比式(6)和式(1)可以看出，两者是一致的。欧拉屈曲模型中的长度L即为Berbinau模型中的波长λ。Rosen模型和Xu-Reifsnider模型中计算使用的波长λ与纤维模量E和纤维惯性矩I成正比，与树脂刚度参数k成反比，如下式：

$\lambda =\sqrt[4]{\frac{EI}{k}}$

(8)

可见树脂刚度等特性也对压缩强度有影响。另外国内外普遍认为压缩过程由弹性屈曲和塑性扭结阶段组成，因此树脂和界面特性都对压缩强度有重要影响。本文重点研究碳纤维截面特性单一变量，认为树脂和界面特性为不变量，因此仅聚焦纤维屈曲过程开展了重点研究，对树脂和界面特性不展开进一步分析。

总之，通过欧拉屈曲模型计算并与试验数据拟合，可以看出圆形截面的国产TG800系列碳纤维与椭圆形截面的进口T800H碳纤维相比，碳纤维最小直径更大，因此截面惯性矩更大，碳纤维抗弯曲变形能力更强，复合材料压缩强度更高。另外，TG800系列碳纤维随着直径(同时也是最小直径)的提高，截面惯性矩更大，碳纤维抗弯曲变形能力更强，复合材料压缩强度更高。

2.4 有限元计算

通过ANSYS有限元软件建立了考虑纤维正弦初始位错的细观有限元模型，见图5(a)。模型长度L=2λ(λ为正弦周期的半波长，λ=150d_f，d_f为纤维直径)。综合考虑计算效率和准确性，模型宽度由纤维根数n_f=60及纤维体积分数v_f=60vol%决定，模型厚度等于纤维直径。

图 5 碳纤维/环氧树脂复合材料压缩有限元模型

Figure 5. Simulation model of compression for carbon fiber/epoxy composites

λ—Half wavelength of a sinusoidal period; d_f—Fiber diameter

下载: 全尺寸图片幻灯片

使用ANSYS软件的plane182单元的平面应力模式进行压实强度分析，综合考虑计算效率和准确性，有限元模型取104760个单元、105412个节点。对模型一端固定，另一端施加压缩位移载荷。

通过有限元模型可以看到：在压缩载荷作用下，由于正弦初始位错的存在，树脂基体会出现高剪应力集中，树脂基体开始发生屈服，如图5(b)所示。屈服经传播形成屈服带，当屈服带增加到一定宽度时，纤维由于失去基体的横向支撑，开始失稳。失稳破坏时的压缩应力被认为是材料的压缩强度。

计算得出复合材料压缩时应力与应变的关系曲线如图6所示。

图 6 有限元计算碳纤维/环氧树脂复合材料压缩应力-应变曲线

Figure 6. Compressive stress-strain curve of carbon fiber/epoxy composite by simulation

下载: 全尺寸图片幻灯片

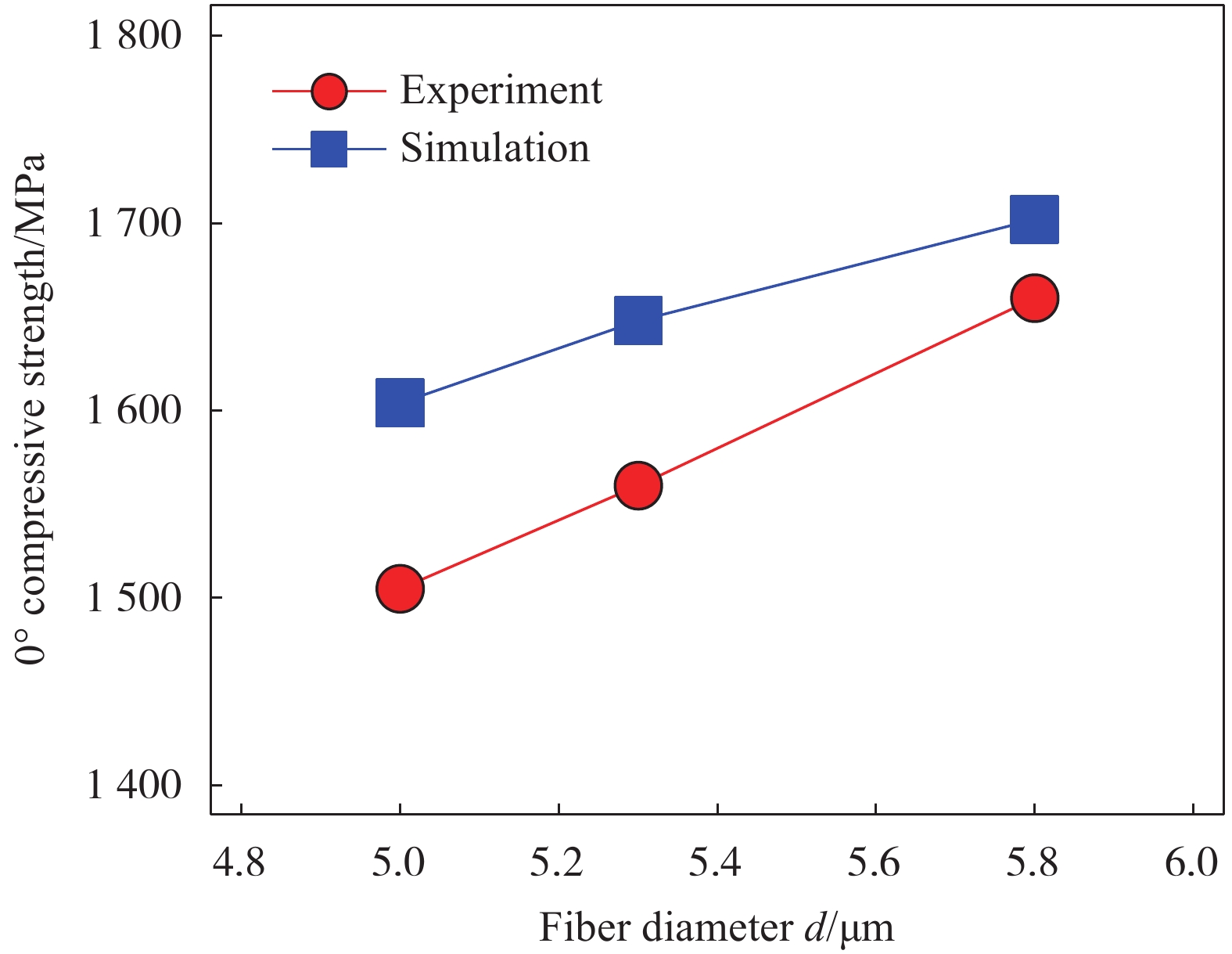
图7为纤维直径变化对复合材料压缩强度的影响。计算结果表明，5.0 μm、5.3 μm和5.8 μm三种纤维直径的复合材料的压缩强度分别为1604 MPa、1648 MPa和1702 MPa。碳纤维直径从5.0 μm增加到5.8 μm，复合材料有限元计算得到的压缩强度提高了6.1%，实验数据得到的压缩强度提高了10.3%。有限元计算、模型计算和实验数据都表明，随着纤维直径的增大，复合材料压缩强度更高。

图 7 碳纤维/环氧树脂复合材料压缩强度-纤维直径d的关系曲线

Figure 7. Compressive strength-fiber diameter d curves of carbon fiber/epoxy composites

下载: 全尺寸图片幻灯片

3. 结论

(1) 碳纤维截面形状影响碳纤维/环氧树脂复合材料压缩强度，由于截面最小惯性矩较大，碳纤维抗弯曲变形能力更强，因此圆形截面优于椭圆形截面。圆形截面国产TG800碳纤维与相同截面积的椭圆形进口T800H碳纤维相比，复合材料压缩强度实验数据从1390 MPa提高到1505 MPa，提高了8.3%。

(2) 碳纤维直径越大，碳纤维/环氧树脂复合材料压缩强度越高。TG800系列碳纤维直径从5.0 μm增加到5.8 μm，复合材料压缩强度实验数据从1505 MPa提高到1660 MPa，提高了10.3%；有限元模拟计算结果从1604 MPa提高到1702 MPa，提高了6.1%。

图 1 4种碳纤维微观形貌SEM图像

Figure 1. SEM images of 4 types of carbon fibers

下载: 全尺寸图片幻灯片

图 2 碳纤维/环氧树脂复合材料压缩失效宏观和微观形貌

Figure 2. Macroscopic and microscopic observations of carbon fiber/epoxy composites after compression

下载: 全尺寸图片幻灯片

图 3 3种典型碳纤维截面形貌简化示意图

Figure 3. Schematic diagrams of 3 typical section shapes of carbon fibers

下载: 全尺寸图片幻灯片

图 4 4种碳纤维/环氧树脂复合材料0°压缩强度-纤维最小直径d_m的关系

Figure 4. 0° compressive strength-fiber minimum diameter d_m curve for 4 types of carbon fiber/epoxy composites

下载: 全尺寸图片幻灯片

图 5 碳纤维/环氧树脂复合材料压缩有限元模型

Figure 5. Simulation model of compression for carbon fiber/epoxy composites

λ—Half wavelength of a sinusoidal period; d_f—Fiber diameter

下载: 全尺寸图片幻灯片

图 6 有限元计算碳纤维/环氧树脂复合材料压缩应力-应变曲线

Figure 6. Compressive stress-strain curve of carbon fiber/epoxy composite by simulation

下载: 全尺寸图片幻灯片

图 7 碳纤维/环氧树脂复合材料压缩强度-纤维直径d的关系曲线

Figure 7. Compressive strength-fiber diameter d curves of carbon fiber/epoxy composites

下载: 全尺寸图片幻灯片

表 1 4种碳纤维性能

Table 1 Properties of 4 types of carbon fibers

Type	Strength σ/MPa	Modulus E/GPa	Diameter/μm	Section shape	Surface roughness
T800H	5790	294	5.0	Ellipse	Obvious
TG800-1	5820	292	5.0	Round	Obvious
TG800-2	5860	292	5.3	Round	Obvious
TG800-3	5830	294	5.8	Round	Obvious

下载: 导出CSV

表 2 4种碳纤维/环氧复合材料力学性能

Table 2 Mechanical properties of 4 types of carbon fiber/epoxy composites

Type	0° tensile strength/MPa	0° compressive strength/MPa	Compressive/tensile strength ratio
T800H/603B	2770±180	1390±85	0.50
TG800-1/603B	2750±170	1505±71	0.55
TG800-2/603B	2805±210	1560±95	0.56
TG800-3/603B	2790±180	1660±93	0.60

下载: 导出CSV

表 3 3种典型碳纤维截面惯性矩计算

Table 3 Sectional inertia moments of 3 typical section shapes of carbon fibers

Shape	Round	Ellipse	Round with grooves
I (Equation)/μm⁴	${\mathrm{{\text{π}} }d}^{4}/64$	$\mathrm{{\text{π}} }a{b}^{3}/64$	${\mathrm{{\text{π}} }d}^{4}/64+{\mathrm{{\text{π}} }d}^{2}{t}^{2}/192$
S (Equation)/μm²	${\mathrm{{\text{π}} }d}^{2}/4$	$\mathrm{{\text{π}} }ab/4$	${\mathrm{{\text{π}} }d}^{2}/4$
Parameters/μm	d=5	a=6.25, b=4	d=5, t=0.5
S (Value)/μm²	6.25π	6.25π	6.25π
I (Value)/μm⁴	9.76π	6.25π	9.80π
Notes: I—Minimum moment of inertia; S—Section area d—Diameter for round section; a—Long axis of ellipse; b—Short axis of ellipse; t—Groove depth.

下载: 导出CSV

参考文献(31)

[1]	朱文墨, 李刚, 杨小平, 等. 连续纤维增强树脂复合材料纵向压缩强度预测模型的发展及其影响因素[J]. 复合材料学报, 2020, 37(1):1-15. ZHU W M, LI G, YANG X P, et al. Development of prediction model and influencing factors of longitudinal compressive strength for continuous fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica,2020,37(1):1-15(in Chinese).
[2]	张弥, 关志东, 黎增山, 等. 考虑纤维初始位错的复合材料轴向压缩性能[J]. 复合材料学报, 2017, 34(8):1754-1763. ZHANG M, GUAN Z D, LI Z S, et al. Longitudinal com-pressive properties of composites considering fiber initial misalignment[J]. Acta Materiae Compositae Sinica,2017,34(8):1754-1763(in Chinese).
[3]	ZHANG M, WANG X D, LI W D, et al. Compressive strength determined for ultrahigh modulus fiber reinforced composites by [90/0]ns laminates[J]. Composite Structures,2018,191:24-35. DOI: 10.1016/j.compstruct.2018.02.033
[4]	ROBINSON P, GREENHALGH E, PINHO S. Failure mechanisms in polymer matrix composites: Criteria, testing and industrial applications[M]. Sawston: Woodhead Publishing Limited, 2012.
[5]	BUDIANSKY B, FLECK N A. Compressive failure of fiber composites[J]. Journal of the Mechanics and Physics of Solids,1993,41(1):183-211. DOI: 10.1016/0022-5096(93)90068-Q
[6]	DE-MORAIS A B. Prediction of the layer longitudinal compression strength[J]. Journal of Composite Materials,2000,34(21):1808-1820. DOI: 10.1106/9XG6-F8T7-079T-YAHC
[7]	LO K H, CHIM E S M. Compressive strength of unidirectional composites[J]. Journal of Reinforced Plastics and Composites,1992,11(8):838-896. DOI: 10.1177/073168449201100801
[8]	XU Y L, REIFSNIDER K L. Micromechanical modeling of composite compressive strength[J]. Journal of Composite Materials,1993,27(6):572-588. DOI: 10.1177/002199839302700602
[9]	MAMALIS D, FLANAGAN T, CONCHÚR M O. Effect of fibre straightness and sizing in carbon fibre reinforced powder epoxy composites[J]. Composites Part A: Applied Science and Manufacturing,2018,110:93-105. DOI: 10.1016/j.compositesa.2018.04.013
[10]	GUO H, HUANG Y, LIU L, et al. Effect of epoxy coatings on carbon fibers during manufacture of carbon fiber reinforced resin matrix composites[J]. Materials & Design,2010,31(3):1186-1190.
[11]	SHARMA M, GAO S, MDER E, et al. Carbon fiber surfaces and composite interphases[J]. Composites Science and Technology,2014,102:35-50. DOI: 10.1016/j.compscitech.2014.07.005
[12]	SONG W, GU A, LIANG G, et al. Effect of the surface roughness on interfacial properties of carbon fibers reinforced epoxy resin composites[J]. Applied Surface Science,2011,257(9):4069-4074. DOI: 10.1016/j.apsusc.2010.11.177
[13]	李龙, 潘月秀, 朱世鹏, 等. 炭纤维毛丝评价表征研究[J]. 新型炭材料, 2018, 33(4):97-104. LI L, PAN Y X, ZHU S P, et al. A comparative study of the fuzz produced by friction and tension in China T800 and Toray T800H carbon fiber tows[J]. New Carbon Materials,2018,33(4):97-104(in Chinese).
[14]	ZHANG H J, SELLAIYAN S, KAKIZAKI T, et al. Effect of free-volume holes on dynamic mechanical properties of epoxy resins for carbon-fiber-reinforced polymers[J]. Macromolecules,2017,50:3933-3942. DOI: 10.1021/acs.macromol.7b00472
[15]	石佩洛, 王月友, 郭鸿俊, 等. 炭纤维/鳞片石墨/氰酸酯复合材料的导热和力学性能(英文)[J]. 新型炭材料, 2019, 34(1):110-114. DOI: 10.1016/S1872-5805(19)60005-3 SHI P L, WANG Y Y, GUO H J, et al. The thermal and mechanical properties of carbon fiber/flake graphite/cyanate ester composites[J]. New Carbon Materials,2019,34(1):110-114(in Chinese). DOI: 10.1016/S1872-5805(19)60005-3
[16]	BAZHENOV S L, KUPERMAN A M, ZELENSKII E S, et al. Compression failure of unidirectional glass-fibre-reinforced plastics[J]. Composites Science & Technology,1992,26(3):201-208.
[17]	BRUNBAUER J, STADLER H, PINTER G. Mechanical properties, fatigue damage and microstructure of carbon/epoxy laminates depending on fibre volume content[J]. International Journal of Fatigue,2015,70:85-92.
[18]	VERPOEST I, SPRINGER G S. Effects of moisture on the compressive and interlaminar shear strengths of aramid-epoxy composites[J]. Journal of Reinforced Plastics & Composites,1988,7(1):23-32.
[19]	XU P, YU Y, LIU D, et al. Enhanced interfacial and mechanical properties of high-modulus carbon fiber composites: Establishing modulus intermediate layer between fiber and matrix based on tailored-modulus epoxy[J]. Compo-sites Science and Technology,2018,163:26-33.
[20]	BERBINAU P, SOUTIS C, GUZ I A. Compressive failure of 0° unidirectional carbon-fibre-reinforced plastic (CFRP) laminates by fibre microbuckling[J]. Composites Science & Technology,1999,59(9):1451-1455.
[21]	NAIK N K, KUMAR R S. Compressive strength of unidirectional composites: Evaluation and comparison of prediction models[J]. Composite Structures,1999,46(3):299-308. DOI: 10.1016/S0263-8223(99)00098-7
[22]	CARLOS G, LORCA J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling[J]. Compo-sites Science and Technology,2007,67(13):2795-2806. DOI: 10.1016/j.compscitech.2007.02.001
[23]	VAUGHAN T J, MCCARTHY C T. Micromechanical modelling of the transverse damage behaviour in fibre reinforced composites[J]. Composites Science & Technology,2011,71(3):388-396.
[24]	YANG L, YAN Y, LIU Y, et al. Microscopic failure mechanisms of fiber-reinforced polymer composites under transverse tension and compression[J]. Composites Science & Technology,2012,72(15):1818-1825.
[25]	BRU T, ASP L E, OLSSON R, et al. Biaxial transverse compression testing for a fibre reinforced polymer material[C]. 18th European Conference on Composite Materials (ECCM18), 2018.
[26]	ZUMAQUERO P L, CORREA E, JUSTO J, et al. Microscopical observations of interface cracks from inter-fibre failure under compression in composite laminates[J]. Compo-sites Part A: Applied Science and Manufacturing,2018,110:76-83. DOI: 10.1016/j.compositesa.2018.04.004
[27]	李梦龙, 朱世鹏, 欧阳琴, 等. 不同直径国产高强中模型碳纤维结构及其轴向压缩强度关系的研究[J]. 高科技纤维与应用, 2018, 55(6):33-39. DOI: 10.3969/j.issn.1007-9815.2018.06.004 LI M L, ZHU S P, OUYANG Q. Structure and unidirectional compressive properties of fibres with different diameters[J]. HiTech Fiber Application,2018,55(6):33-39(in Chinese). DOI: 10.3969/j.issn.1007-9815.2018.06.004
[28]	中国国家标准化管理委员会. 碳纤维直径和根数试验方法: GB/T 3364—2008[S]. 北京: 中国标准出版社, 2005. Standardization Administration of the People’s Republic of China. Test methods for diameter of carbon fiber and filament number in carbon fiber strand: GB/T 3364—2008[S]. Beijing: China Standards Press, 2005(in Chinese).
[29]	中国国家标准化管理委员会. 碳纤维复丝拉伸性能试验方法: GB/T 3362—2005[S]. 北京: 中国标准出版社, 2005. Standardization Administration of the People’s Republic of China. Test methods for tensile properties of carbon fiber multifilament: GB/T 3362—2005[S]. Beijing: China Standards Press, 2005(in Chinese).
[30]	中国国家标准化管理委员会. 定向纤维增强聚合物基复合材料拉伸性能试验方法: GB/T 3354—2014[S]. 北京: 中国标准出版社, 2005. Standardization Administration of the People’s Republic of China. Test method for tensile properties of orientation fiber reinforced polymer matrix composite materials: GB/T 3354—2014[S]. Beijing: China Standards Press, 2005(in Chinese).
[31]	American Society for Testing and Materials. Standard test method for compressive properties of polymer matrix composite materials with unsupported gage section by shear loading: ASTM D3410—16[S]. West Conshohocken: ASTM, 2016.

施引文献(12)

期刊类型引用(5)

1.	樊虎，王超，左小彪，周金岑，尚呈元. 高强中模碳纤维增强高耐热双马树脂复合材料性能. 宇航材料工艺. 2024(02): 89-93 . 百度学术
2.	徐牛牛，杭传伟，张淑斌，彭飞. 纺丝工艺对T700级碳纤维及其复合材料性能的影响. 合成纤维. 2023(05): 29-33 . 百度学术
3.	郭聪聪，尹国强，单瑞俊，胡啸天. 树脂分布设计对复合材料轴向压缩强度的影响. 高科技纤维与应用. 2023(03): 34-42 . 百度学术
4.	符平坡，丁华，曾祥瑞，王纪，罗时清，魏宗来. 碳纤维复合材料-铝合金自冲铆接头成形规律及力学性能. 复合材料学报. 2023(08): 4517-4530 . 本站查看
5.	胡丹丽，付大鹏，张越，甄金明，赵伟，张冉，贾正锋. 配副材料对碳纤维增强环氧树脂复合材料摩擦学性能的影响. 润滑与密封. 2022(07): 97-103 . 百度学术