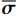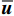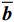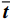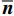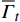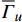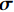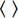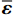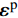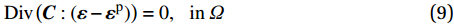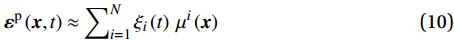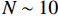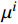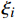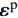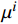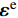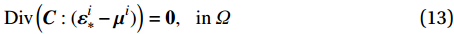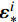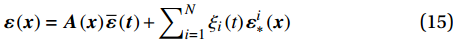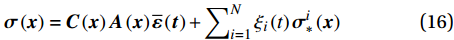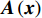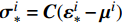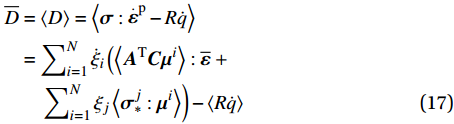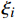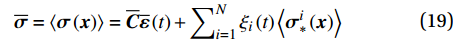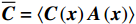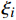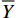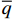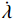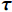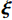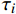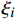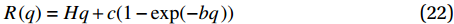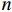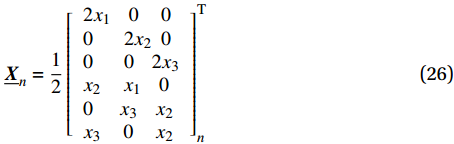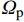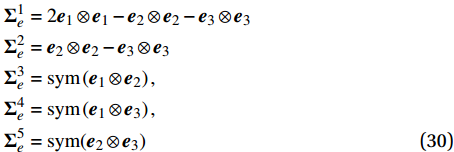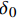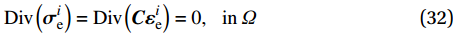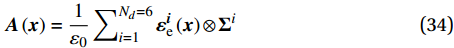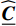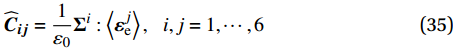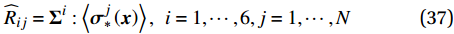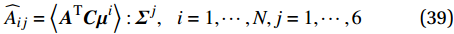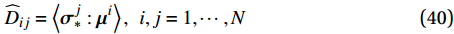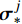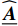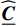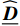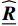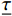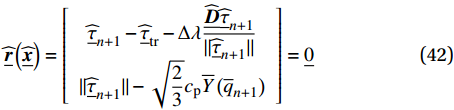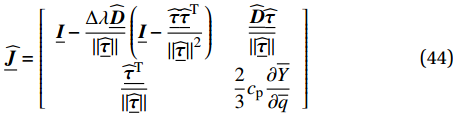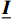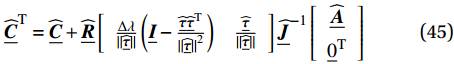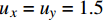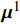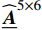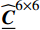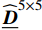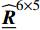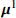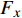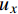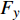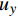Reduced order homogenization of graphene nanocomposites and its numerical implementation
-
摘要: 对石墨烯纳米复合材料进行三维有限元建模通常需极其精细的网格。在考虑塑性演变的情况下，细观代表性单元体模型的计算效率极其低下。为此，基于非均匀变换场分析理论，提出了石墨烯纳米复合材料的降阶均匀化方法。首先，针对不同加载路径进行预分析，提取细观塑性应变场信息；然后对这些信息进行本征正交分解，从而得到若干个塑性模态，用作降阶模型的基函数；基于宏、细观耗散功的等效原理，导出降阶变量的本构模型。该方法的离线分析部分通过MATLAB编程实现。为了便于工程计算，在线分析部分则由商业有限元软件ABAQUS的UMAT用户子程序接口实现。基于三维算例分析，验证了所提方法的有效性。结果显示，在保证较高精度的前提下，针对三维代表性单元体计算的加速率可达103~104量级。Abstract: A three-dimensional finite element modeling for graphene nanocomposites usually requires very fine meshes. In case of plasticity, the computational efficiency of a micro representative volume element model is extremely low. For a remedy, based on the theory of nonuniform transformation field analysis, a reduced order homogenization method for graphene nanocomposites was proposed. First, we performed a pre-analysis for different loading paths to extract micro plastic strain fields; then a proper orthogonal decomposition of those field information was performed to obtain several plastic modes, which were used as basis functions for model order reduction. A constitutive model of reduced variables was derived from the equivalence of macro and micro dissipation power. The offline analysis of this method was implemented in MATLAB. For engineering computations, the online analysis was implemented by the user subroutine interface UMAT of the commercial finite element software ABAQUS. The effectiveness of the proposed method was illustrated by three-dimensional numerical examples. The results show that the acceleration rate for 3D representative volume element computations is of the order of 103~104, while maintaining a sufficient accuracy level.
-
石墨烯因其卓越的力学性能(本征强度约130 GPa，杨氏模量约1 TPa)已发展成为备受瞩目的研究热点[1]。石墨烯纳米片(GPLs)作为石墨烯的一种衍生物，GPLs有着比碳纳米管大得多的比表面积，因此具有优越的界面力学性能，能够提供很好的载荷传递能力。另外，碳纳米管只在轴向有较高的强度，而GPLs则可在平面内任意方向保持较高的强度。大量研究表明，只需要在复合材料中加入很少量的GPLs就可以获得很大程度的力学性能提升，其在强度和刚度上的增强效果大约相当于十倍比重的碳纳米管[2]。GPLs自身出色的增强性能和较低的生产成本使其成为轻质复合结构的理想增强体[3]。在本质上，石墨烯纳米复合材料是一种非均质材料，具有复杂的细观结构(即在光学或常规电子显微镜下可见的材料细微结构)。
细观力学是固体力学的分支，用连续介质力学方法分析具有细观结构的材料(如复合材料)的力学问题[4]。均匀化方法是细观力学的基本方法，可从细观尺度推断出宏观尺度的行为[5-6]。早在六十年前，诺贝尔奖获得者Feynman就已经阐明了这类方法所蕴含的巨大潜能[7]。
随着计算机技术水平的提高，细-宏观耦合的双尺度数值方法[6, 8-9]得以发展，并在复杂问题(如复杂的细观结构和非线性力学行为)的分析中发挥出了高精度的优势，然而对于大型结构分析来说，其巨大的计算量和存储需求却令人望而却步。为此，Dvorak等[10]提出变换场分析(TFA)法。在此基础上，Michel和Suquet[11-12]提出了非均匀转换场分析(NTFA)法，考虑了细观场量的非均匀性分布。Fritzen和Leuschner[13]继而提出了基于增量形式的降阶均匀化方法。Yvonnet和He[14]提出了基于本征正交分解(POD)的R3M法，考虑了大形变问题。此外，Fish等[15]还提出基于混合型本征应变的降阶均匀化方法。Ju和Mahnken[16]扩展了NTFA法来考虑复合材料的损伤问题，并基于经验准则耦合了FE2法以提高计算精度。但是上述大部分工作，都是基于非商业化的有限元程序进行计算分析的，这就大大增加了该领域研究的门槛值，阻碍了该领域的迅速发展。目前针对石墨烯纳米复合材料的多尺度研究，主要集中在平均场方法[17]和数值方法[18-19]的应用方面，而在模型降阶方法的开发应用方面比较欠缺。针对这一现状，本文旨在于发展石墨烯纳米复合材料的降阶均匀化方法，并提出结合商业有限元软件的数值实现框架，为工程应用提供参考。
本文首先针对石墨烯纳米复合材料进行非均匀变换场分析，导出相应的降阶模型(NTFA)。然后，基于ABAQUS、MATLAB等软件平台，实现了代表性体积单元(RVE)模型的自动生成、边界条件的自动施加及降阶均匀化理论的离线分析，即RVE的预分析及系统矩阵(可看作等效参数)的计算。为了便于工程计算，在线分析部分通过ABAQUS的用户材料子程序(UMAT)接口实现，大幅度地提高了多尺度分析的计算效率。最后，通过算例分析验证了该降阶均匀化方法的有效性，并以此研究了石墨烯纳米复合材料的细观塑性演变对宏观力学性能的影响。
1. 理论基础
石墨烯纳米复合材料宏观尺度上呈现出均质材料特性，细观尺度上则包含石墨烯增强体、孔隙及材料界面等局部特征，呈现出明显的非均质特性。细观尺度与宏观尺度满足尺度分离条件，即
l≪L ，因此采用一阶均匀化理论。1.1 双尺度问题的基本提法
如图1所示，基于一阶均匀化理论，对非均质材料进行理想化，建立宏-细观耦合的双尺度分析框架。
![]()
图 1 宏-细观双尺度问题Figure 1. Illustration of a two scale (macro-micro) problemL—Macro characteristic length; l—Micro characteristic length;¯Ω—Macro domain; Ω—Micro domain; ¯σ—Macro stress tensor;σ—Micro stress tensor; ¯ε—Macro strain tensor; ε—Micro strain tensor材料在宏、细观尺度上都需要满足静态平衡条件。宏观问题的强形式为
\mathrm{D}\mathrm{i}\mathrm{v}\left(\overline{\boldsymbol{\sigma }}\right)+\overline{\boldsymbol{b}}={\bf{0}},\;\;\;\mathrm{i}\mathrm{n}\;\overline{\varOmega } (1) \overline{\boldsymbol{\sigma }}\overline{\boldsymbol{n}}=\overline{\boldsymbol{t}},\;\;\;\mathrm{o}\mathrm{n}\;{\overline{\varGamma }}_{t} (2) \overline{\boldsymbol{u}}={\overline{\boldsymbol{u}}}^{*},\;\;\;\mathrm{o}\mathrm{n}\;{\overline{\varGamma }}_{u} (3) 其中：
\overline{\boldsymbol{\sigma }} 为宏观应力张量；\overline{\boldsymbol{u}} 为宏观位移矢量；\overline{\boldsymbol{b}} 为体积力；\overline{\boldsymbol{t}} 为面力；\overline{\boldsymbol{n}} 为表面单位外法向量；{\overline{\varGamma }}_{t} 为Neumann边界；{\overline{\varGamma }}_{u} 为Dirichlet边界；\overline \varOmega 为宏观域。细观问题的强形式为\mathrm{D}\mathrm{i}\mathrm{v}\left({\boldsymbol{\sigma }}\right)={\bf{0}},\;\;\;\mathrm{i}\mathrm{n}\;{\varOmega } (4) 其中：
{\boldsymbol{\sigma }} 为细观应力张量；Ω为细观域。利用体积平均定理建立宏-细观尺度间的联系：\overline{\boldsymbol{\varepsilon }}=\left\langle {\boldsymbol{\varepsilon }} \right\rangle (5) \overline{\boldsymbol{\sigma }}=\left\langle {\boldsymbol{\sigma }} \right\rangle (6) 式中，
\left\langle {\;} \right\rangle 为体积平均算符。\overline{\boldsymbol{\varepsilon }} 和{\boldsymbol{\varepsilon }} 分别为宏观和细观应变张量。另外，宏-细观能量等效由Hill-Mandel条件[20]来保证：\overline{\boldsymbol{\sigma }}:\dot{\overline{\boldsymbol{\varepsilon }}}=\left\langle {{\boldsymbol{\sigma }}:\dot{\boldsymbol{\varepsilon }}} \right\rangle (7) 不同的边界条件可满足上述条件[21]。本文选用线性位移边界条件，其计算结果较保守，且不限于周期材料，并易于编程实现。
1.2 塑性应变场的时空分解
“变换场”的概念起源于变换场分析理论[22]，指的是本征应力及应变场。本文主要研究塑性变形所产生的变换场。塑性材料相的应力计算式为
{{\sigma }}={\boldsymbol{C}}:({\boldsymbol{\varepsilon }}-{\boldsymbol{\varepsilon }}^{\mathrm{p}}) (8) 其中：
{\boldsymbol{\varepsilon }}^{\mathrm{p}} 为细观塑性应变；{\boldsymbol{C}} 为细观弹性张量。将式(8)代入式(4)，得：\mathrm{D}\mathrm{i}\mathrm{v}\left({\boldsymbol{C}}:({\boldsymbol{\varepsilon }}-{\boldsymbol{\varepsilon }}^{\mathrm{p}})\right)={{0}},\;\;\;\mathrm{i}\mathrm{n}\;{\varOmega } (9) 非均匀变换场分析[11]的核心思想是细观塑性应变场的时空近似分解：
{\boldsymbol{\varepsilon }}^{\mathrm{p}}\left({\boldsymbol{x}},t\right)\approx \sum\nolimits_{i=1}^{N}{\xi }_{i}\left(t\right)\;{{\mu }}^{i}\left({\boldsymbol{x}}\right) (10) 用数量较少(
N\sim 10 )的塑性模态{{\mu }}^{i} 的线性组合来近似地表征{\boldsymbol{\varepsilon }}^{\mathrm{p}} 的空间分布。时间相关的系数{\xi }_{i} 被称为模态活化系数，用来表征{\boldsymbol{\varepsilon }}^{\mathrm{p}} 的演变过程。塑性模态{{\mu }}^{i} 需满足L2正交条件，用Karhunen-Loève分解法获得(详见2.3节)。由此可见，该方法是本征正交分解(POD)类方法。1.3 叠加原理和局部化准则
在小应变理论框架下，根据式(10)和式(5)，问题(9)化为1个弹性问题和N个本征应变问题的叠加。其中，弹性问题表述为
\mathrm{D}\mathrm{i}\mathrm{v}\left({\boldsymbol{C}}:{\boldsymbol{\varepsilon }}^{\mathrm{e}}\right)={\bf{0}},\;\;\;\mathrm{i}\mathrm{n}\;{\varOmega } (11) \left\langle {{\boldsymbol{\varepsilon }}^{\mathrm{e}}} \right\rangle=\overline{\boldsymbol{\varepsilon }} (12) 其中，
{\boldsymbol{\varepsilon }}^{\mathrm{e}} 为细观弹性应变张量。N个本征应变问题表述为\mathrm{D}\mathrm{i}\mathrm{v}\left({\boldsymbol{C}}:({\boldsymbol{\varepsilon }}_{*}^{i}-{\boldsymbol{\mu }}^{i})\right)={\bf{0}},\;\;\;\mathrm{i}\mathrm{n}\;{\varOmega } (13) \left\langle {{\boldsymbol{\varepsilon }}_{*}^{i}} \right\rangle={\bf{0}},\;\;i=\mathrm{1,2},\cdots ,N (14) 其中，
{\boldsymbol{\varepsilon }}_{*}^{i} 表示总应变张量。由上述N+1个子问题解的叠加，得：
{\boldsymbol{\varepsilon }}\left({\boldsymbol{x}}\right)={\boldsymbol{A}}\left({\boldsymbol{x}}\right)\overline{\boldsymbol{\varepsilon }}\left(\boldsymbol{t}\right)+\sum\nolimits_{i=1}^{N}{\xi }_{i}\left(t\right) {\boldsymbol{\varepsilon }}_{*}^{i}\left({\boldsymbol{x}}\right) (15) {\boldsymbol{\sigma }}\left({\boldsymbol{x}}\right)={\boldsymbol{C}}\left({\boldsymbol{x}}\right){\boldsymbol{A}}\left({\boldsymbol{x}}\right)\overline{\boldsymbol{\varepsilon }}\left(\boldsymbol{t}\right)+\sum\nolimits_{i=1}^{N}{\xi }_{i}\left(t\right) {\boldsymbol{\sigma }}_{*}^{i}\left({\boldsymbol{x}}\right) (16) 其中，
{\boldsymbol{A}}\left({\boldsymbol{x}}\right) 为细观力学中的应变局部化算子，本征应力张量为{\boldsymbol{\sigma }}_{*}^{i}={\boldsymbol{C}}({\boldsymbol{\varepsilon }}_{*}^{i}-{\boldsymbol{\mu }}^{i}) 。由上述局部化准则，可还原出相应的细观场信息。需要指出的是，上述叠加原理仅适用于小应变问题。1.4 降阶变量及其本构关系
由式(10)可见，降阶模型(NTFA)化为模态活化系数
{\xi }_{i} 的求解。基于热力学第二定律，从耗散机制出发，结合式(10)和式(16)，宏观耗散功率为\begin{split} \overline D &= \left\langle D \right\rangle = \left\langle {{\boldsymbol{\sigma }}:{{\mathop {\boldsymbol{\varepsilon }}\limits^. }^{\rm{p}}} - R\dot q} \right\rangle \\ & = \sum\nolimits_{i = 1}^N {{{\dot \xi }_i}} \left( {\left\langle {{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{C}}{{\boldsymbol{\mu }}^i}} \right\rangle :\overline {\boldsymbol{\varepsilon }} } \right.+\\ &\quad \left. { \sum\nolimits_{i = 1}^N {{\xi _j}} \left\langle {{\boldsymbol{\sigma }}_*^j:{{\boldsymbol{\mu }}^i}} \right\rangle } \right) - \left\langle {R\dot q} \right\rangle \end{split} (17) 由此可知，
{\xi }_{i} 的共轭力为{\tau }_{i}=\left\langle {{\boldsymbol{A}}^{\mathrm{T}}{\boldsymbol{C}}{\boldsymbol{\mu }}^{i}} \right\rangle:\overline{\boldsymbol{\varepsilon }}+\displaystyle\sum\nolimits_{i=1}^{N}{\xi }_{j} \left\langle {{{\boldsymbol{\sigma }}_{*}^{\boldsymbol{j}}:{\boldsymbol{\mu }}}^{i}} \right\rangle (18) 式(17)中：
R 为细观强化应力；q 为细观强化变量。对式(16)求体积平均值，得宏观应力张量：
\begin{array}{l} \overline{\boldsymbol{\sigma }}=\left\langle {{\boldsymbol{\sigma }}\left({\boldsymbol{x}}\right)} \right\rangle=\overline{\boldsymbol{C}}\overline{\boldsymbol{\varepsilon }}\left(t\right)+\displaystyle\sum\nolimits_{i=1}^{N}{\xi }_{i}\left(t\right)\left\langle {{\boldsymbol{\sigma }}_{*}^{i}\left({\boldsymbol{x}}\right)} \right\rangle \end{array} (19) 式中，
\overline{\boldsymbol{C}}=\left\langle {{\boldsymbol{C}}\left({\boldsymbol{x}}\right){\boldsymbol{A}}\left({\boldsymbol{x}}\right)} \right\rangle 恰好为细观力学中的等效弹性张量。活化系数
{\xi }_{i} 的演变规律取决于细观材料相的材料模型。对于具有等向强化的Mises塑性模型(对应第四强度理论)来说，宏观屈服方程为\overline{\phi }=||{\boldsymbol{\tau }}||-\sqrt{\frac{2}{3}}{c}_{\mathrm{p}}\overline{Y}\left(\overline{q}\right) (20) 其中：
{c}_{\mathrm{p}} 为塑性相的体积含量；\overline{Y} 为宏观屈服应力；\overline{q} 为宏观强化变量。由式(20)导出相关联的演化方程：\dot{\boldsymbol{\xi }}=\dot{\lambda }\frac{\partial \overline{\phi }}{\partial {\boldsymbol{\tau }}}=\dot{\lambda }\frac{\boldsymbol{\tau }}{||{\boldsymbol{\tau }}||} (21) 其中：
\dot{\lambda } 为塑性乘子；{\boldsymbol{\tau }} 和{\boldsymbol{\xi }} 分别为{\tau }_{i} 和{\xi }_{i} 的向量形式。1.5 降阶均匀化的基本流程
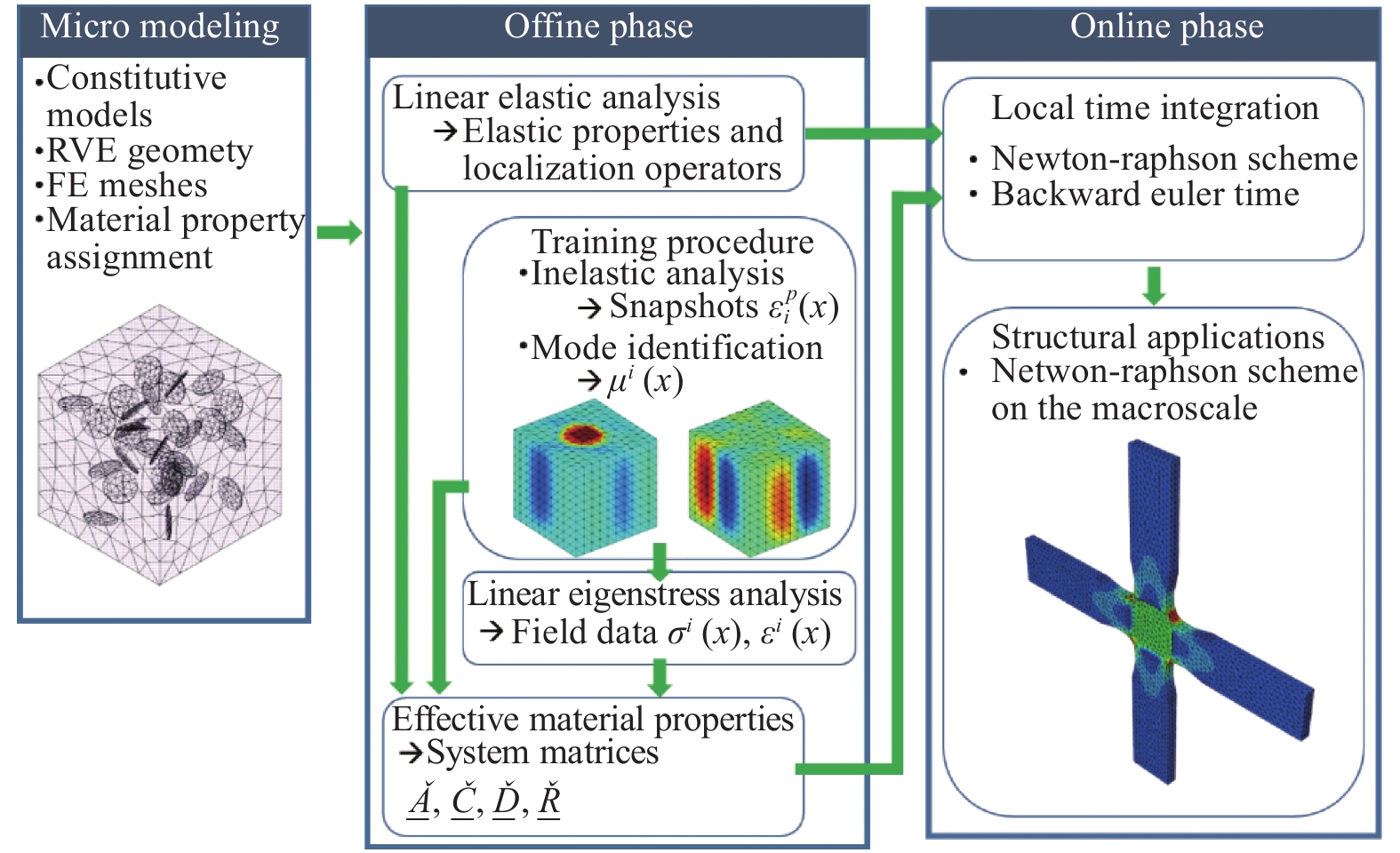
图2为石墨烯纳米复合材料的降阶均匀化流程。可以看出，在原模型(即细观有限元模型)的基础上，通过预分析来提取等效材料参数。这个过程是一次性的，被称为离线分析。如此，只需于在线分析中求解基于降阶变量的有效模型，从而大幅度地提高多尺度分析的计算效率。具体细节将于后续章节给出。
![]()
图 2 石墨烯纳米复合材料的降阶均匀化流程Figure 2. Flowchart of reduced order homogenization of graphene nano-composites2. 离线分析及其数值实现
2.1 石墨烯纳米复合材料代表性单元体(RVE)建模
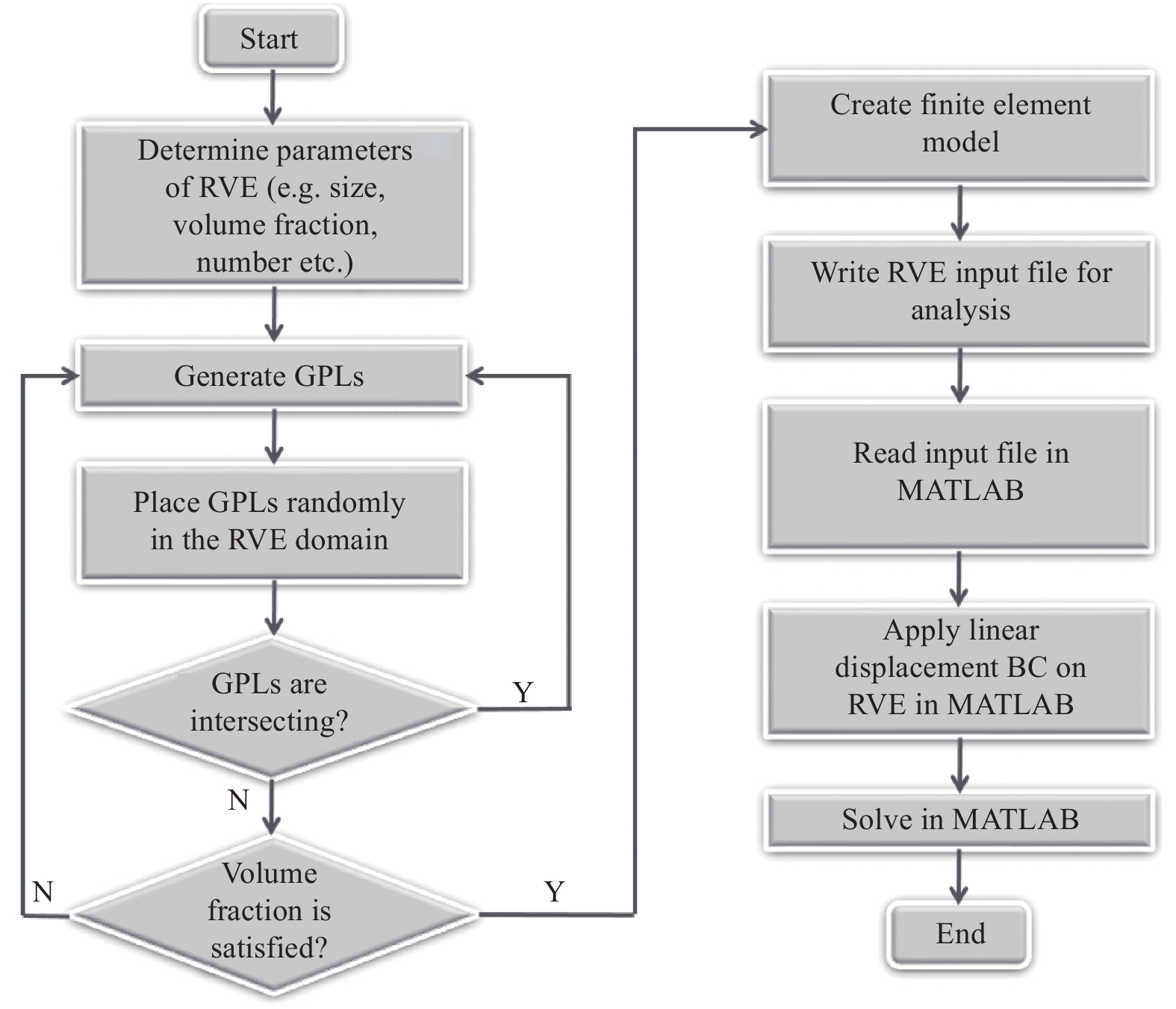
石墨烯纳米复合材料中石墨烯纳米片(GPLs)形状、大小和分布均具有很大的随机性。基于Fortran语言编写程序来自动生成三维RVE模型。GPLs在基体中呈随机、不定向分布。快速自动生成RVE的流程如图3所示。
![]()
图 3 石墨烯纳米复合材料代表性体积单元(RVE)建模和分析流程Figure 3. Flowchart of modeling and analyzing based on representative volume element (RVE) of graphene nanocomposites为描述塑性基体材料的等向强化，采用下述非线性强化方程：
R\left(q\right)=Hq+c(1-\mathrm{e}\mathrm{x}\mathrm{p}(-bq\left)\right) (22) 其中：H和c分别为线性和非线性部分的系数；b为指数系数，三者均为材料参数。该方程以线性和指数组合的方式，具有适应性强的优点[16, 23]。
所分析的石墨烯纳米复合材料由GPLs和基体组成。其相对应的材料属性如表1所示。GPLs被当成弹性材料来研究[24]。图4为构造的几种不同石墨烯含量的RVE模型，以作为本文多尺度研究的基础。假定GPLs的片径为200 nm。
表 1 石墨烯纳米复合材料的材料属性Table 1. Material properties of a graphene nanocompositeMaterial Young’s modulus/GPa Poisson's ratio Yield stress/MPa H/MPa b c/MPa Matrix 70 0.3 350 1500 25 360 GPLs 1050 0.186 — — — — Notes: H, b and c—Material parameters in Eq.(22); GPLs—Graphene nanoplates. ![]()
图 4 不同GPLs含量的石墨烯纳米复合材料RVE模型Figure 4. RVE models of graphene nanocomposites with different volume fractions of GPLs2.2 线性位移边界条件的施加
RVE边界
\varGamma 上的每个点{{x}} 都满足下述线性关系：{\boldsymbol{u}}({{x}},t)=\overline{\boldsymbol{\varepsilon }}\left(t\right){{x}},{{x}}\in \varGamma (23) 通过MATLAB编程，自动识别出RVE的边界，根据式(23)的矩阵形式：
{\underline{\boldsymbol{u}}}_{n}={\underline{\boldsymbol{X}}}_{n}\overline{\underline{\boldsymbol{\varepsilon }}} (24) 计算出边界上每个节点
n 的位移，并自动施加。式(24)中的量分别为{\underline{\boldsymbol{u}}}_{n}={\left[{u}_{1}{u}_{2}{u}_{3}\right]}_{n}^{\mathrm{T}} (25) {\underline {\boldsymbol{X}} _n} = \frac{1}{2}\left[ \begin{array}{l} 2{x_1}\;\;\;\;0\;\;\;\;\;0\\ 0\;\;\;\;\;\;\;2{x_2}\;\;0\\ 0\;\;\;\;\;\;\;0\;\;\;\;2{x_3}\\ {x_2}\;\;\;\;\;{x_1}\;\;\;\;0\\ 0\;\;\;\;\;\;{x_3}\;\;\;\;{x_2}\\ {x_3}\;\;\;\;\;0\;\;\;\;\;{x_2}\; \end{array} \right]_n^{\rm{T}} (26) \overline{\underline{\boldsymbol{\varepsilon }}}={\left[{\overline{\varepsilon }}_{11}\;{\overline{\varepsilon }}_{22}\;{\overline{\varepsilon }}_{33}\;2{\overline{\varepsilon }}_{12}\;2{\overline{\varepsilon }}_{23}\;2{\overline{\varepsilon }}_{13}\right]}^{\mathrm{T}} (27) 2.3 模态识别
模态识别的主要思路是通过在不同载荷情况下对RVE进行预分析(又称为应变路径计算)来收集一定量的塑性应变场信息，再对这些信息进行本征正交分解，以提取重要的特征信息，用作基函数。同时，塑性模态需满足归一化条件和L2正交性条件，即
{\left\langle {||{\boldsymbol{\mu }}^{i}||} \right\rangle}_{{\varOmega }_{{\rm{p}}}}=1 (28) \left\langle {{\boldsymbol{\mu }}^{i}:{\boldsymbol{\mu }}^{j}} \right\rangle=0,\;\;i\ne j (29) 值得注意的是，塑性模态只在塑性材料相区域
{\varOmega }_{\mathrm{p}} 内获得支持，式(28)只对{\varOmega }_{\mathrm{p}} 求体积平均值。在应变路径计算中，用下述五个相互正交的加载方向来构建加载路径：
\begin{split} &{\boldsymbol{\Sigma }}_{{e}}^{1}=2{\boldsymbol{e}}_{1}\otimes {\boldsymbol{e}}_{1}-{\boldsymbol{e}}_{2}\otimes {\boldsymbol{e}}_{2}-{\boldsymbol{e}}_{3}\otimes {\boldsymbol{e}}_{3}\\ & {\boldsymbol{\Sigma }}_{{e}}^{2}={\boldsymbol{e}}_{2}\otimes {\boldsymbol{e}}_{2}-{\boldsymbol{e}}_{3}\otimes {\boldsymbol{e}}_{3} \\ & {\boldsymbol{\Sigma }}_{{e}}^{3}=\mathrm{s}\mathrm{y}\mathrm{m}\left({\boldsymbol{e}}_{1}\otimes {\boldsymbol{e}}_{2}\right), \\ & {\boldsymbol{\Sigma }}_{{e}}^{4}=\mathrm{s}\mathrm{y}\mathrm{m}\left({\boldsymbol{e}}_{1}\otimes {\boldsymbol{e}}_{3}\right), \\ & {\boldsymbol{\Sigma }}_{{e}}^{5}=\mathrm{s}\mathrm{y}\mathrm{m}({\boldsymbol{e}}_{2}\otimes {\boldsymbol{e}}_{3}) \end{split} (30) 其中，e为基矢量。并在每个路径上都确保产生足够的塑性形变。每个路径都设有Nt个增量步，从而最终得到6·Nt个塑性应变场。这些场又被称为“Snapshots”，对其进行Karhunen–Loève分解分为两个步骤：(1)计算各场间的协方差，建立协方差矩阵，并对其特征值问题进行求解；(2)对所得特征值进行排序，略去较小的特征值，利用对应的特征向量构建塑性模态，详见文献[18]。该算法设有阈值
0<{\mathrm{\delta }}_{0}<1 ，该值越高，获得的模态数量就越多。本文取{\mathrm{\delta }}_{0} =0.999。2.4 系统矩阵
为了便于数值实现，需将式(18)和(19)化为矩阵形式。为此，引入6个正交基[25-26]：
\begin{split} &{\boldsymbol{\Sigma }}^{i}={\boldsymbol{e}}_{i}\otimes {\boldsymbol{e}}_{i},\;\;i=\mathrm{1,2},3,\\ & {\boldsymbol{\Sigma }}^{4}=\sqrt{2}\mathrm{s}\mathrm{y}\mathrm{m}\left({\boldsymbol{e}}_{1}\otimes {\boldsymbol{e}}_{2}\right),\\ & {\boldsymbol{\Sigma }}^{5}=\sqrt{2}\mathrm{s}\mathrm{y}\mathrm{m}\left({\boldsymbol{e}}_{1}\otimes {\boldsymbol{e}}_{3}\right),\\ & {\boldsymbol{\Sigma }}^{6}=\sqrt{2}\mathrm{s}\mathrm{y}\mathrm{m}({\boldsymbol{e}}_{2}\otimes {\boldsymbol{e}}_{3}) \end{split} (31) 对于三维问题来说，求解6个线弹性问题：
\mathrm{D}\mathrm{i}\mathrm{v}\left({\boldsymbol{\sigma }}_{\mathrm{e}}^{i}\right)=\mathrm{D}\mathrm{i}\mathrm{v}\left({{\boldsymbol{C}}{\boldsymbol{\varepsilon }}}_{\mathrm{e}}^{i}\right)=0,\;\;\;\mathrm{i}\mathrm{n}\;{\varOmega } (32) \left\langle {{\boldsymbol{\varepsilon }}_{\mathrm{e}}^{i}} \right\rangle={\varepsilon }_{0}{\boldsymbol{\Sigma }}^{i},\;\;i=1,\cdots ,6 (33) 其中，
{\varepsilon }_{0} 是一个正常数。式(15)中的应变局部化算子为{\boldsymbol{A}}\left({\boldsymbol{x}}\right)=\frac{1}{{\varepsilon }_{0}}\sum\nolimits_{i=1}^{{N}_{d}=6}{\boldsymbol{\varepsilon }}_{\mathrm{e}}^{\boldsymbol{i}}\left({\boldsymbol{x}}\right)\otimes {\boldsymbol{\Sigma }}^{i} (34) 其中，Nd为线弹性问题的数量。宏观弹性矩阵
\widehat{\underline{{\boldsymbol{C}}}} 的元素为{\widehat{{\boldsymbol{C}}}}_{{\boldsymbol{i}}{\boldsymbol{j}}}=\frac{1}{{\varepsilon }_{0}}{\boldsymbol{\Sigma }}^{i}:\left\langle {{\boldsymbol{\varepsilon }}_{\mathrm{e}}^{j}} \right\rangle,\;\;\;i,j=1,\cdots ,6 (35) 由此，式(19)可写作下述矩阵形式：
\widehat{\underline{\sigma }}=\widehat{\underline{\boldsymbol{C}}}\widehat{\underline{\varepsilon }}+\widehat{\underline{\boldsymbol{R}}}\widehat{\underline{\xi }} (36) {\widehat{R}}_{ij}={\boldsymbol{\Sigma }}^{i}:\left\langle {{\boldsymbol{\sigma }}_{*}^{j}\left({\boldsymbol{x}}\right)} \right\rangle,\;\;i=1,\cdots ,6,j=1,\cdots ,N (37) 同理，将式(18)记作：
\widehat{\underline{\tau }}=\widehat{\underline{\boldsymbol{A}}}\widehat{\underline{\varepsilon }}+\widehat{\underline{\boldsymbol{D}}}\widehat{\underline{\xi }} (38) {\widehat{A}}_{ij}=\left\langle {{\boldsymbol{A}}^{\mathrm{T}}{\boldsymbol{C}}{\boldsymbol{\mu }}^{i}} \right\rangle:{\boldsymbol{\varSigma }}^{j},\;\;\;i=1,\cdots ,N,j=1,\cdots ,6 (39) {\widehat{D}}_{ij}=\left\langle {{\boldsymbol{\sigma }}_{*}^{j}:{\boldsymbol{\mu }}^{i}} \right\rangle,\;\;i,j=1,\cdots ,N (40) 式(40)中的应力场
{\boldsymbol{\sigma }}_{*}^{j} 通过求解本征应变问题式(13)来得到。\widehat{\underline{\boldsymbol{A}}} 、\widehat{\underline{\boldsymbol{C}}} 、\widehat{\underline{\boldsymbol{D}}} 和\widehat{\underline{\boldsymbol{R}}} 被称为系统矩阵，可看作材料的等效宏观参数。本文中，RVE的预分析及系统矩阵的计算都是在MATLAB中编程实现的。3. 在线分析及其数值实现
在线分析过程中，需求解由式(20)和式(21)构成的NTFA。在数值上，对式(21)采用隐式欧拉积分求解。按照经典径向回归算法的思路，初步假定弹性状态，计算出共轭力
\underline{\tau } 的试验(Trial)态：{\underline{\widehat{\tau }}}_{\mathrm{t}\mathrm{r}}={\underline{\widehat{\tau }}}_{n}+\widehat{\underline{\boldsymbol{A}}}\mathrm{\Delta }\widehat{\underline{\varepsilon }} (41) 对式(20)~(21)进行离散化，得下述(N+1)维寻根问题：
\underline{\widehat{\boldsymbol{r}}}\left(\underline{\widehat{\boldsymbol{x}}}\right)=\left[\begin{array}{c}{\underline{\widehat{\tau }}}_{n+1}-{\underline{\widehat{\tau }}}_{\mathrm{t}\mathrm{r}}-\mathrm{\Delta }\mathrm{\lambda }\dfrac{\widehat{\underline{\boldsymbol{D}}}{\underline{\widehat{\tau }}}_{n+1}}{||{\underline{\widehat{\tau }}}_{n+1}||}\\ ||{\underline{\widehat{\tau }}}_{n+1}||-\sqrt{\dfrac{2}{3}}{c}_{\mathrm{p}}\overline{Y}\left({\overline{q}}_{n+1}\right)\end{array}\right]=\underline{0} (42) \underline{\widehat{\boldsymbol{x}}}=\left[\begin{array}{c}{\underline{\widehat{\tau }}}_{n+1}\\ \mathrm{\Delta }\lambda \end{array}\right] (43) 在此，采用Newton-Raphson迭代算法求解该非线性问题。该问题的雅可比矩阵形式如下：
\underline{\widehat{\boldsymbol{J}}}=\left[\begin{array}{cc}\underline{\boldsymbol{I}}-\dfrac{\mathrm{\Delta }\lambda \widehat{\underline{\boldsymbol{D}}}}{||\underline{\widehat{\boldsymbol{\tau }}}||}\left(\underline{\boldsymbol{I}}-\dfrac{\underline{\widehat{\boldsymbol{\tau }}}{\widehat{\underline{\boldsymbol{\tau }}}}^{\mathrm{T}}}{{||\underline{\widehat{\boldsymbol{\tau }}}||}^{2}}\right)& \dfrac{\widehat{\underline{\boldsymbol{D}}}\underline{\widehat{\boldsymbol{\tau }}}}{||\underline{\widehat{\boldsymbol{\tau }}}||}\\ \dfrac{\underline{{\widehat{\boldsymbol{\tau }}}^{\mathrm{T}}}}{||\underline{\widehat{\boldsymbol{\tau }}}||}& \dfrac{2}{3}{c}_{\mathrm{p}}\dfrac{\partial \overline{Y}}{\partial \overline{q}}\end{array}\right] (44) 其中，
\underline{\boldsymbol{I}} 为单位二次矩阵。求解式(42)后，便可根据式(36)计算宏观应力。另外，宏观结构问题的迭代求解还需要切线刚度矩阵：
{\underline{\widehat{\boldsymbol{C}}}}^{\mathrm{T}}=\widehat{\underline{\boldsymbol{C}}}+\widehat{\underline{\boldsymbol{R}}}\left[\begin{array}{cc}\frac{\mathrm{\Delta }\lambda }{||\underline{\widehat{\boldsymbol{\tau }}}||}\left(\underline{\boldsymbol{I}}-\frac{\underline{\widehat{\boldsymbol{\tau }}}{\widehat{\underline{\boldsymbol{\tau }}}}^{\mathrm{T}}}{{||\underline{\widehat{\boldsymbol{\tau }}}||}^{2}}\right)& \frac{\underline{\widehat{\boldsymbol{\tau }}}}{||\underline{\widehat{\boldsymbol{\tau }}}||}\end{array}\right]{\underline{\widehat{\boldsymbol{J}}}}^{-1}\left[\begin{array}{c}\widehat{\underline{\boldsymbol{A}}}\\ {\underline{0}}^{\mathrm{T}}\end{array}\right] (45) 尽管上述算法可以很容易地在MATLAB中实现，考虑到商业软件在有限元建模方面独到的优势，本文将该算法通过ABAQUS的UMAT子程序接口，基于Fortran语言编程实现。利用该子程序，能够对任意的复合材料结构进行宏-细观尺度耦合的力学分析。
由于系统矩阵的元素数量较多，在ABAQUS的inp文件中当做常规材料参数来读取十分不便。本文将系统矩阵写入独立的dat文件，并在UMAT中编写相对应的读取模块。如果每次调用UMAT子程序都需要读取一次数据，会严重影响计算效率。为此，通过UEXTERNALDB接口建立相应的公共变量，实现了数据的一次性读取，很好地解决了这一问题。
4. 石墨烯纳米复合材料的非线性多尺度分析
4.1 石墨烯纳米复合材料双向拉伸试验算例
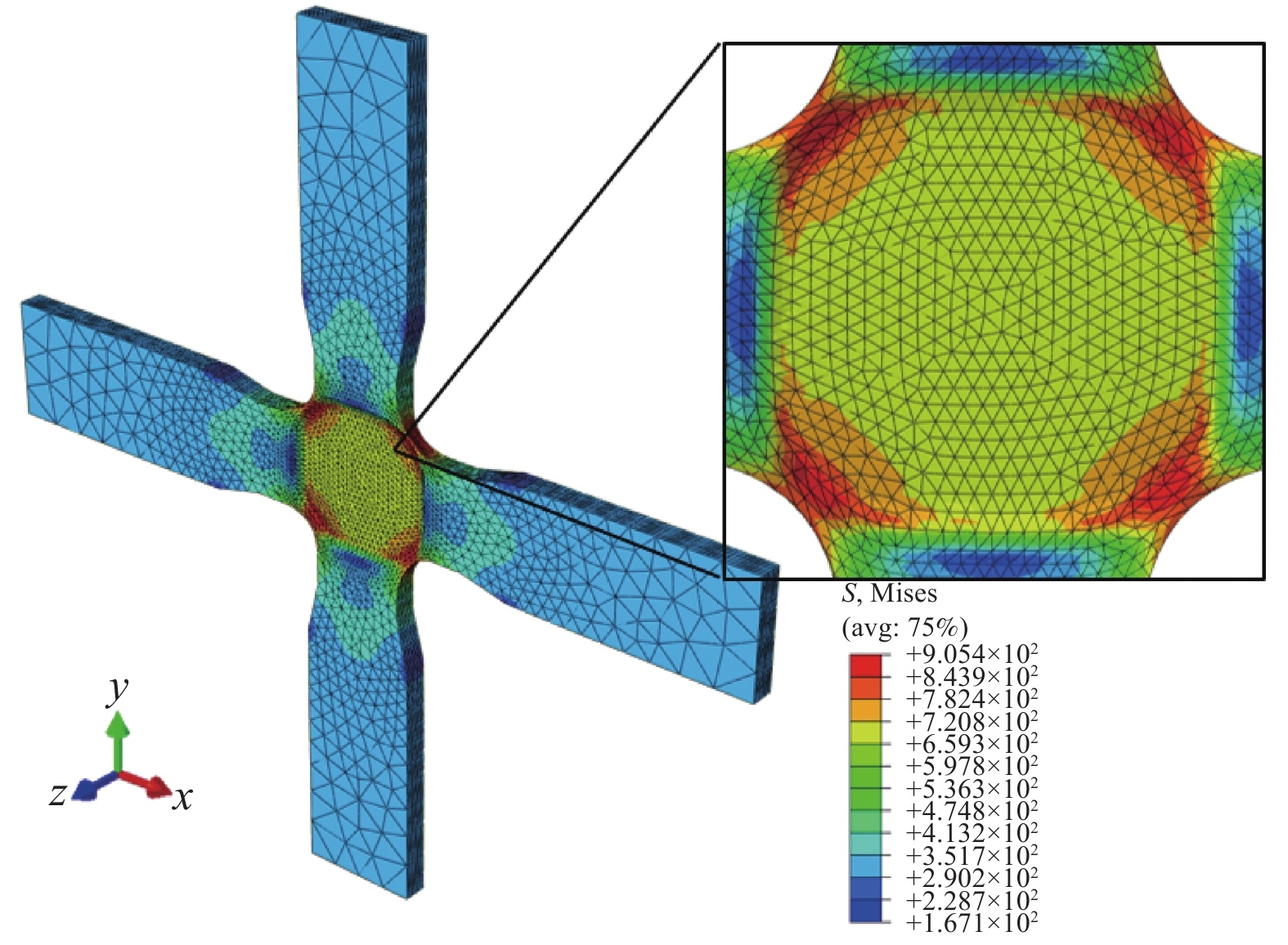
为了验证本文方法的有效性，在此进行石墨烯纳米复合材料双向拉伸试验的宏-细观双尺度模拟。如图5所示，采用Welsh型试样[27](长宽均为161.4 mm，厚度为5.1 mm)。采用位移控制进行均匀加载，即
{u}_{x}={u}_{y}=1.5 mm。宏观模型采用C3D10单元，共有33167个单元和53385个节点。考虑到该材料可能存在各向异性，采用完整模型进行计算。RVE模型中共包含32个不定向分布的GPLs(体积含量为1vol%)，采用C3D4单元，共计61185个单元和10441个节点。对此进行FE2模拟的惊人计算量不言而喻。![]()
图 5 石墨烯纳米复合材料双向拉伸试验宏-细观双尺度有限元模型(FEM)Figure 5. A two scale (macro-micro) finite element model (FEM) for a biaxial tensile test of a graphene nanocomposte4.2 石墨烯纳米复合材料塑性模态和系统矩阵
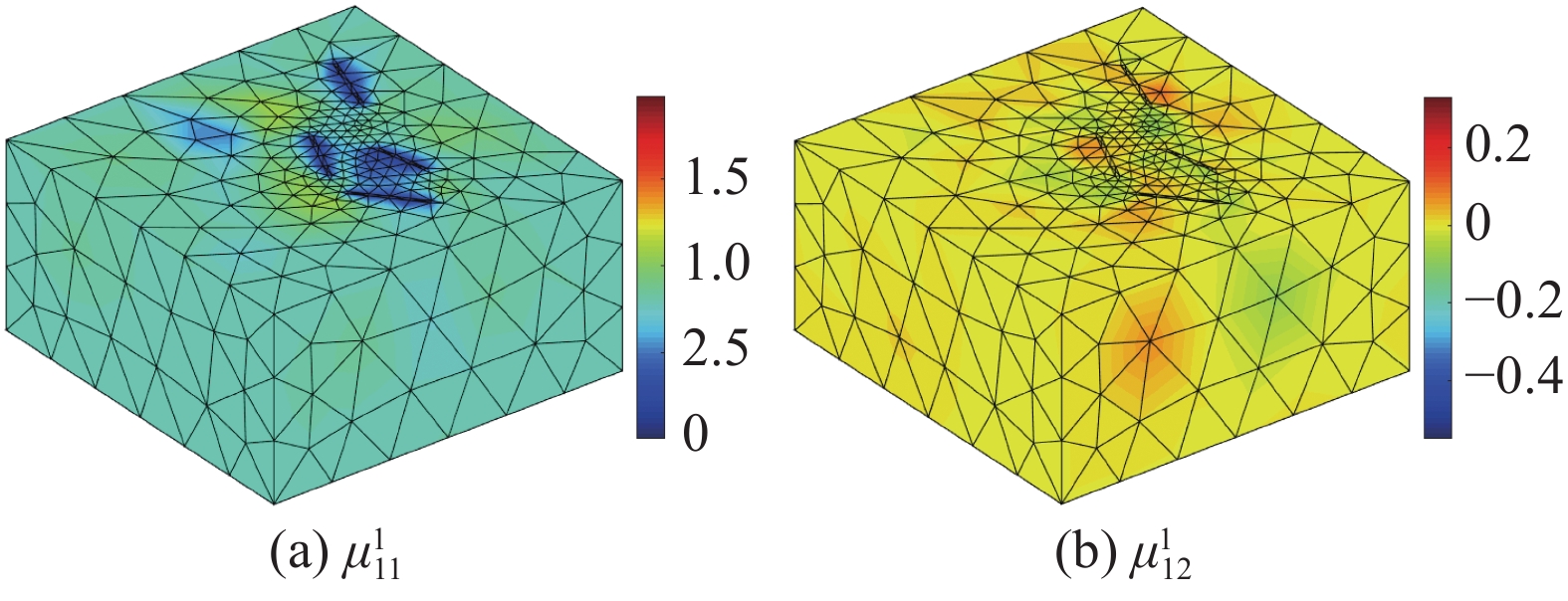
通过2.3节中所描述的方法对上述RVE模型进行预分析，得到了5个塑性模态。每个塑性模态包含6个不同的分量。图6象征性地展示了塑性模态
{\boldsymbol{\mu }}^{1} 的两个不同分量。可见，塑性模态本身具有很强的非均匀性，为表征实际塑性应变的非均匀分布提供基础。为了便于观测GPLs周围的情况，只对RVE模型的下半部分进行云图展示。由于GPLs为弹性材料，相应区域内的值为0。根据2.4节中的描述，计算得到四个系统矩阵{\widehat{\underline{\boldsymbol{A}}}}^{5\times 6} 、{\widehat{\underline{\boldsymbol{C}}}}^{6\times 6} 、{\widehat{\underline{\boldsymbol{D}}}}^{5\times 5} 和{\widehat{\underline{\boldsymbol{R}}}}^{6\times 5} 。由于篇幅限制，在此不予给出其具体值。![]()
图 6 石墨烯纳米复合材料塑性模态{\boldsymbol{\mu }}^{1} 的不同分量Figure 6. Different components of plastic mode{\boldsymbol{\mu }}^{1} for graphene nanocomposites4.3 石墨烯纳米复合材料降阶均匀化分析
在ABAQUS中建立图5中的宏观模型，并通过UMAT子程序完成了降阶均匀化分析。整个分析过程设有20个增量步，每个增量步都能够在4个迭代步内达到收敛，充分验证了式(45)给出的切线刚度矩阵的正确性。
图7为不同方向(试样右端和上端)的拉力-位移曲线。其中，
{F}_{x} 为试样左端所有节点在x方向上反力之和，与位移{u}_{x} 相对应；{F}_{y} 为试样上端所有节点在y方向上反力之和，与位移{u}_{y} 相对应。结果显示两者的吻合度非常高，特别是在弹性阶变形段。在塑性变形阶段，由于塑性演变的非均匀性，产生了轻微的差别。这也说明了2.1节中的RVE自动生成算法的有效性，能够再现GPLs在实际情况下的随机分布情况。![]()
图 7 石墨烯纳米复合材料双向拉伸试验的力(F) -位移 (u)曲线Figure 7. Force (F)-displacement (u) curve of a biaxial tension test for graphene nanocomposites图8为最后一个增量步中的Mises应力分布情况。在试样中间区域内，除了边缘区域出现应力集中现象外，中间大部分区域处于均匀的二向应力状态。模拟结果验证了该试样对石墨烯纳米复合材料的适用性。
![]()
图 8 石墨烯纳米复合材料宏观模型Mises应力云图Figure 8. Contour plot of von Mises stresses for the macro model of graphene nanocomposites4.4 计算精度与效率
由于三维模型单元数量过多，进行FE2模拟过于费时，采用下述方法来研究NTFA的计算精度与效率问题。
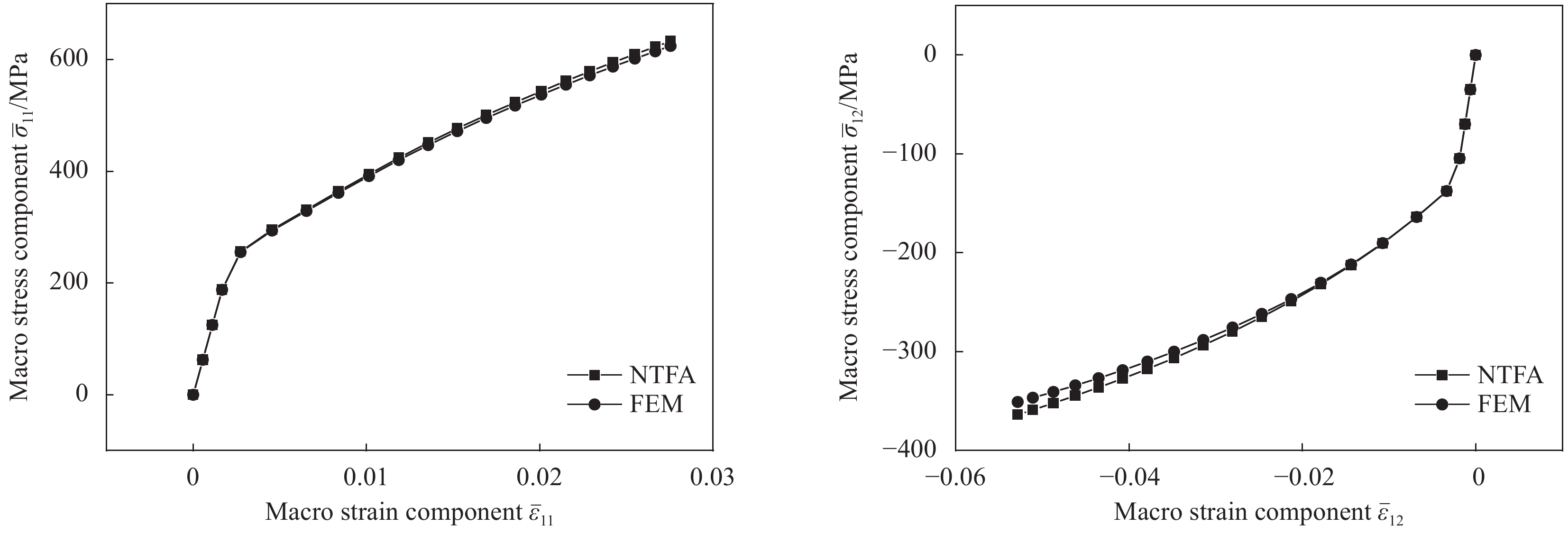
基于上述降阶均匀化分析结果，于图5中A点处提取应变历史，由此来定义一个真实且复杂的应变路径计算，分别求解NTFA和有限元模型(FEM)。结果显示，相较于FEM，NTFA的计算效率可以与现象学模型相媲美，加速约3082倍。
NTFA的宏观应力和FEM在各个分量上的匹配度都很高。图9为两者在两个不同应力应变分量上的对比。两者在线弹性阶段完美匹配，在塑性演化初期几乎重合，之后出现些许偏差。相比于NTFA极高的加速率，这样的偏差在很多情况下是可以接受的。
![]()
图 9 石墨烯纳米复合材料积分点A上的宏观应力-应变曲线Figure 9. Macro stress-strain curves at an integration point A of graphene nanocompositesNTFA—Nonuniform transformation field analysis降阶均匀化方法一般旨在计算宏观应力。通过本文方法，根据局部化准则式(15)和式(16)，能够通过后处理的方式还原出细观应力及应变场。图10为在最终加载状态下NTFA和FEM的细观Mises应力云图(RVE下半部分)对比。结果显示，NTFA可以完美再现GPLs周围的应力分布，在基体材料中的应力与有限元计算结果存在一些差异。另外，相较于宏观应力水平，RVE中存在显著的应力集中现象。应力峰值出现在GPLs中，由于插值效应，附近基体部分也显示出较高应力水平。另外需要指出的是，本文未考虑GPLs及界面的损伤问题，因此所得的应力值与真实情况相比肯定存在一定偏差。
![]()
图 10 石墨烯纳米复合材料降阶模型和有限元模型的Mises应力比较Figure 10. Comparison of Mises stress localization between reduced order model and FE model of graphene nanocomposites基于上述算例分析，本文所提出的降阶均匀化方法的有效性得以验证，为后续研究奠定了基础。
5. 结 论
(1) 基于非均匀变换场理论，提出了从构建代表性体积单元(RVE)到模型降阶及求解的一整套方法，能够合理、准确地表征石墨烯纳米复合材料的宏观等效性能。必要时，该法还可以还原出细观场信息，为材料在细观尺度上的损伤机制研究提供依据。该方法的局限性在于其对叠加原理的依赖，因此仅适用于小应变问题。
(2) 相较于FE2模拟，该法对计算效率的加速率可达惊人的103~104量级，使真实三维结构的多尺度分析成为可能。
(3) 基于ABAQUS的用户自定义子程序接口，实现了基于降阶均匀化理论的多尺度分析。编写的程序具有良好的通用性和可操作性。所提出的数值实现流程及方法，对降阶均匀化方法在实际工程问题中的应用具有重要的参考价值。
(4) 基于上述对石墨烯纳米复合材料的塑性演变进行了研究，揭示了其塑性演变的规律。但限于篇幅，只是较粗浅地从细观模型上研究了该材料的弹塑性演变行为。该方法和程序可以进一步地用来研究石墨烯纳米片(GPLs)的含量、分布及材料属性对材料和结构整体性能的影响，为优化石墨烯纳米复合材料的选材与结构设计提供依据。
-
![]()
图 1 宏-细观双尺度问题
Figure 1. Illustration of a two scale (macro-micro) problem
L—Macro characteristic length; l—Micro characteristic length;\overline{\varOmega } —Macro domain; {\varOmega } —Micro domain; \overline\sigma —Macro stress tensor;\sigma —Micro stress tensor; \overline\varepsilon —Macro strain tensor; \varepsilon —Micro strain tensor
![]()
图 2 石墨烯纳米复合材料的降阶均匀化流程
Figure 2. Flowchart of reduced order homogenization of graphene nano-composites
![]()
图 3 石墨烯纳米复合材料代表性体积单元(RVE)建模和分析流程
Figure 3. Flowchart of modeling and analyzing based on representative volume element (RVE) of graphene nanocomposites
![]()
图 4 不同GPLs含量的石墨烯纳米复合材料RVE模型
Figure 4. RVE models of graphene nanocomposites with different volume fractions of GPLs
![]()
图 5 石墨烯纳米复合材料双向拉伸试验宏-细观双尺度有限元模型(FEM)
Figure 5. A two scale (macro-micro) finite element model (FEM) for a biaxial tensile test of a graphene nanocomposte
![]()
图 6 石墨烯纳米复合材料塑性模态
{\boldsymbol{\mu }}^{1} 的不同分量Figure 6. Different components of plastic mode
{\boldsymbol{\mu }}^{1} for graphene nanocomposites![]()
图 7 石墨烯纳米复合材料双向拉伸试验的力(F) -位移 (u)曲线
Figure 7. Force (F)-displacement (u) curve of a biaxial tension test for graphene nanocomposites
![]()
图 8 石墨烯纳米复合材料宏观模型Mises应力云图
Figure 8. Contour plot of von Mises stresses for the macro model of graphene nanocomposites
![]()
图 9 石墨烯纳米复合材料积分点A上的宏观应力-应变曲线
Figure 9. Macro stress-strain curves at an integration point A of graphene nanocomposites
NTFA—Nonuniform transformation field analysis
![]()
图 10 石墨烯纳米复合材料降阶模型和有限元模型的Mises应力比较
Figure 10. Comparison of Mises stress localization between reduced order model and FE model of graphene nanocomposites
表 1 石墨烯纳米复合材料的材料属性
Table 1 Material properties of a graphene nanocomposite
Material Young’s modulus/GPa Poisson's ratio Yield stress/MPa H/MPa b c/MPa Matrix 70 0.3 350 1500 25 360 GPLs 1050 0.186 — — — — Notes: H, b and c—Material parameters in Eq.(22); GPLs—Graphene nanoplates. 
下载: 导出CSV
-
[1] LEE C, WEI X, KYSAR J, et al. Measurement of the elastic properties and intrinsic strength of monolayer graphene[J]. Science,2008,321(5887):385-388. DOI: 10.1126/science.1157996
[2] RAFIEE M A, RAFIEE J, WANG Z, et al. Enhanced mechanical properties of nanocomposites at low graphene content[J]. ACS Nano,2009,3(12):3884-3890. DOI: 10.1021/nn9010472
[3] HUANG X, QI X, BOEY F, et al. Graphene-based composites[J]. Chemical Society Reviews,2012,41(2):666-686. DOI: 10.1039/C1CS15078B
[4] 杨卫. 细观力学和细观损伤力学[J]. 力学进展, 1992, 22(1):1-9. DOI: 10.6052/1000-0992-1992-1-J1992-001 YANG W. Meso-mechanics and meso-damage mechanics[J]. Advances in Mechanics,1992,22(1):1-9(in Chinese). DOI: 10.6052/1000-0992-1992-1-J1992-001
[5] GEERS M G, KOUZNETSOVA V G, MATOUŠ K, et al. Homogenization methods and multiscale modeling: Nonlinear problems[J]. Encyclopedia of Computational Mechanics Second Edition,2017:1-34.
[6] GEERS M G D, KOUZNETSOVA V G, BREKELMANNS W A M. Multi-scale computational homogenization: Trends and challenges[J]. Journal of Computational and Applied Mathematics,2010,234:2175-2182. DOI: 10.1016/j.cam.2009.08.077
[7] FEYNMAN R P. There’s plenty of room at the bottom[data storage][J]. Journal of Microelectromechanical Systems,1992,1(1):60-66. DOI: 10.1109/84.128057
[8] FEYEL F, CHABOCHE J L. FE2 multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials[J]. Computer Methods in Applied Mechanics and Engineering,2000,183(3-4):309-330. DOI: 10.1016/S0045-7825(99)00224-8
[9] 许杨剑, 武鹏伟, 赵帅, 等. 弹塑性多尺度分析的实现及其在颗粒增强复合材料中的应用[J]. 复合材料学报, 2017, 34(9):1934-1943. XU Y J, WU P W, ZHAO S, et al. Implementation of elastic-plastic multi-scale analysis and application in particle reinforced composites[J]. Acta Materiae Compositae Sinica,2017,34(9):1934-1943(in Chinese).
[10] DVORAK G J, BENVENSITE Y. On transformation strains and uniform fields in multiphase elastic media[J]. Proceedings of the Royal Society of London,1992,437(A):291-310.
[11] MICHEL J C, SUQUET P. Nonuniform transformation field analysis[J]. International Journal for Solids and Structures,2003,40:6937-6955. DOI: 10.1016/S0020-7683(03)00346-9
[12] MICHEL J C, SUQUET P. Computational analysis of nonlinear composite structures using the nonuniform transformation field analysis[J]. Computer Methods in Applied Mechanics and Engineering,2004,193:5477-5502. DOI: 10.1016/j.cma.2003.12.071
[13] FRITZEN F, LEUSCHNER M. Reduced basis hybrid com-putational homogenization based on a mixed incremental formulation[J]. Computer Methods in Applied Mechanics and Engineering,2013,260:143-154. DOI: 10.1016/j.cma.2013.03.007
[14] YVONNET J, HE Q C. The reduced model multiscale method (R3M) for the non-linear homogenization of hyperelastic media at finite strains[J]. Journal of Computational Physics,2007,223(1):341-368. DOI: 10.1016/j.jcp.2006.09.019
[15] FISH J, FILONOVA V, YUAN Z. Hybrid impotent-incompatible eigenstrain based homogenization[J]. International Journal for Numerical Methods in Engineering,2013,95(1):1-32. DOI: 10.1002/nme.4473
[16] JU X, MAHNKEN R. An NTFA-based homogenization framework considering softening effects[J]. Mechanics of Materials,2016,96:106-125. DOI: 10.1016/j.mechmat.2016.01.007
[17] GAO C Y, ZHAN B, CHEN L, et al. A micromechanical model of graphene-reinforced metal matrix nanocomposites with consideration of graphene orientations[J]. Compo-sites Science and Technology,2017,152:120-128. DOI: 10.1016/j.compscitech.2017.09.010
[18] DAI G, MISHNAEVSKY L. Graphene reinforced nanocomposites: 3D simulation of damage and fracture[J]. Com-putational Materials Science,2014,95:684-692. DOI: 10.1016/j.commatsci.2014.08.011
[19] SPANOS K N, GEORGANTZINOS S K, ANIFANTIS N K. Mechanical properties of graphene nanocomposites: A multiscale finite element prediction[J]. Composite Structures,2015,132:536-544. DOI: 10.1016/j.compstruct.2015.05.078
[20] HILL R. Elastic properties of reinforced solids: Some theoretical principles[J]. Journal of the Mechanics and Physics of Solids,1963,11:357-372. DOI: 10.1016/0022-5096(63)90036-X
[21] KOCH A, MIEHE C. Computational micro-to-macro tran-sitions of discretized microstructures undergoing small strains[J]. Archive of Applied Mechanics,2002,72(2002):300-317.
[22] DVORAK G J, BAHEI-EL-DIN Y A, WAFA A M. The modeling of inelastic composite material with the transformation field analysis[J]. Modelling and Simulation in Materials Science and Engineering,1994,2:571-586. DOI: 10.1088/0965-0393/2/3A/011
[23] MAHNKEN R, SCHLIMMER M. Simulation of strength difference in elasto-plasticity for adhesive materials[J]. International Journal for Numerical Methods in Engineering,2005,63:1461-1477. DOI: 10.1002/nme.1315
[24] LIU F, MING P, LI J. Ab initio calculation of ideal strength and phonon instability of graphene under tension[J]. Physical Review B,2007,76:064120-1-7.
[25] FEDEROV F. Theory of elastic waves in crystals[M]. New York: Plenum Press, 1968.
[26] FRITZEN F, BÖHLKE T. Three-dimensional finite element implementation of the nonuniform transformation field analysis[J]. International Journal for Numerical Methods in Engineering,2010,84:803-829. DOI: 10.1002/nme.2920
[27] 肖瑞, 李晓星, 李荣锋, 等. 十字形试样双向拉伸试验[J]. 理化检验:物理分册, 2017, 53(8):538-543. XIAO R, LI X X, LI R F, et al. Biaxial tensile testing of cruciform specimens[J]. Physical Testing and Chemical Analysis Part A: Physical Testing,2017,53(8):538-543(in Chinese).
-
期刊类型引用(5)
1. 孙卫民，张振鹏，寇生中，何玲，杨小凤. Eu~(3+)/Tb~(3+)掺杂YAG-ZrO_2纤维增强铝基复合材料的应力-应变光谱响应. 复合材料学报. 2025(01): 537-547 . 
本站查看
2. 郝世明，刘鹏茹，刘欣欣，谢敬佩. 热处理对30%SiCp/Al复合材料阻尼性能的影响. 材料热处理学报. 2023(05): 39-46 . 百度学术
3. 伍潇，江鸿杰，成忠序，刘崇宇，刘淑辉. NiTip/5052 Al复合材料的制备及其阻尼行为. 复合材料学报. 2023(08): 4821-4830 . 本站查看
4. 苏宇辉，江鸿杰，张平，刘崇宇，黄宏锋. Cu含量对Al-Cu合金阻尼性能和储存模量的影响. 特种铸造及有色合金. 2023(12): 1688-1693 . 百度学术
5. 普丹丹，张富豪. 涤纶织物/PVC复合材料的动态机械性能及其在界面评价中的应用. 丝绸. 2021(10): 18-22 . 百度学术
其他类型引用(6)
-
计量
- 文章访问数: 1396
- HTML全文浏览量: 610
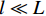
- PDF下载量: 111
- 被引次数: 11
