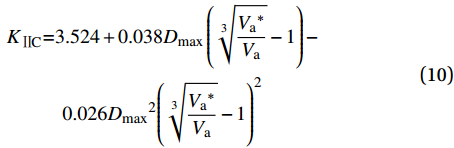Mode Ⅱ fracture parameters of concrete with different coarse aggregate volume fractions
-
摘要: 对不同粗骨料体积分数下的混凝土Ⅱ型断裂性能进行了研究。根据最大泥浆厚度(Maximum paste thickness, MPT)理论，给出了断裂韧度KⅡ C与粗骨料体积分数Va之间的经验关系式。通过对含有四种粗骨料体积分数(19%、25%、31%、37%)的无切口试件开展半边加载断裂试验，测得相应的峰值荷载、断裂韧度、能量释放率等断裂参数，并分析了断裂韧带表面的裂纹分布规律。试验结果表明：随着粗骨料体积分数的增加，混凝土的Ⅱ型断裂韧度KⅡ C和临界能量释放率GⅡ C明显增加，名义断裂韧带处的裂纹轮廓线更长、更曲折；各配比试件的开裂模式基本一致，剪切裂纹主要集中在名义断裂韧带区域。同时，利用数字图像相关技术(Digital image correlation, DIC)对试件表面的损伤演化进行分析，结果表明，试件表面的应变局部化能够较好地表征断裂过程区(Fracture process zone, FPZ)的形态特征及演化过程。随着粗骨料体积分数的增加，FPZ的形态更不规则，分支更多。Abstract: This paper focuses on the mode Ⅱ fracture behaviors of concrete with different coarse aggregate volume fractions by laboratory experiments. Based on the maximum paste thickness (MPT) theory, the empirical relationship between the fracture toughness KⅡ C and the coarse aggregate volume fraction Va was proposed. The mode Ⅱ fracture parameters including peak load, fracture toughness and energy release rate were determined by the compression on half part of the non-notched specimen with different coarse aggregate volume fractions of 19%, 25%, 31% and 37%. The crack distribution on the surface of the fracture ligaments was analyzed. The results show that both mode Ⅱ fracture toughness KⅡ C and the critical energy release rate GⅡ C enhance with the increase of coarse aggregate volume fraction from 19% to 37% while the crack paths become more tortuous and longer with the increase of coarse aggregate volume fraction. The fracture patterns of all specimens are basically identical, even if the coarse aggregate volume fractions are different. It is found that the shear crack propagation is mainly around the middle ligaments. Additionally, the technique of digital image correlation (DIC) was employed during the tests to track the fracture evolution and characterize the strain localization regions as well as fracture process zone (FPZ). It is also observed by the DIC technique that there are more branches in FPZ and their shapes are more irregular as the coarse aggregate volume fraction increases.
-
混凝土作为一种典型的复合材料，主要由砂浆、粗骨料以及它们之间的界面过渡区(Interfacial transition zone，ITZ)组成[1]。骨料作为混凝土的骨架，其体积往往能达到混凝土总体积的60%~70%[2]。因此，骨料的体积分数、粒径等性质对混凝土的力学性能有着重要的影响[1-5]。目前国内外学者针对粗骨料体积分数对混凝土断裂性能影响的研究主要集中于Ⅰ型断裂。而对于混凝土Ⅱ型断裂的关注相对较少，相关研究主要为基本理论分析及Ⅱ型断裂参数测定。在实际工程中，混凝土结构的开裂往往是既包含张拉又包含剪切的复合型断裂。Ⅱ型断裂作为三种基本的断裂模式之一[6]，是充分掌握混凝土复合断裂的基础和必要条件。探究骨料体积分数对混凝土Ⅱ型断裂参数的影响，对于揭示混凝土断裂机制，优化配合比设计，指导工程实践具有重要意义。因此有必要研究粗骨料体积分数对混凝土Ⅱ型断裂参数的影响。
国内外学者为了探究粗骨料体积分数和混凝土断裂参数之间的关系，做了大量的试验研究。Akcay等[1]的研究结果显示，提高粗骨料的体积分数将增强普通强度混凝土对开裂的抵抗能力。Chen等[2]发现，粗骨料体积分数从40%增加至80%，高强混凝土的I型断裂韧度KIC和断裂能GIF先增大后减小，在粗骨料体积分数为60%时，KIC和GIF达到峰值。韩宇栋等[3]利用预切口梁的三点弯试验，研究了不同水胶比下，粗骨料体积分数对混凝土I型断裂参数的影响。对于自密实混凝土，试验结果表明，增加粗骨料体积分数，KIC随之增加[4-5]。然而，这些研究大多是针对混凝土I型断裂，对于粗骨料体积分数与混凝土Ⅱ型断裂性能之间的关系仍缺少试验研究和理论分析，有待进一步研究。
为了测定混凝土Ⅱ型断裂参数，国内外学者曾先后提出多种试件形式及相应的加载构型。常见的Ⅱ型断裂试件有四点剪切梁[7]、双边切口剪切试件[8]、冲切剪切试件[9-10]以及双中心缺口剪切试件[11]等。但是，由于无法消除潜在断裂区内的Ⅰ型分量，利用上述试件进行的断裂测试，通常被认为是Ⅰ–Ⅱ混合型断裂[12-14]。为了研究纯Ⅱ型断裂，Xu等[12]提出一种两端切口单边对称加载的试件。许多学者运用该试件来测定混凝土Ⅱ型断裂能GIIF、断裂韧度KⅡ C[13-22]。值得注意的是，利用该方法测得的KⅡ C与名义断裂韧带的长度无关[13,15,22]。考虑到无切口试件几何形式简单、制作简便，且能得到同等精确的测试结果，徐世烺等[15,23]建议采用无切口Ⅱ型断裂试件进行混凝土Ⅱ型断裂测试。高洪波[15]利用无切口Ⅱ型断裂试件测定了混凝土的KⅡ C，李庆华等[24]对喷射UHTCC与混凝土界面的剪切断裂性能进行了研究。可见，无切口Ⅱ型断裂试件已被广泛用于混凝土Ⅱ型断裂测试。
本文采用无切口Ⅱ型断裂试件，通过半边加载，对含有4种粗骨料体积分数(19%、25%、31%、37%)的混凝土进行Ⅱ型断裂试验，讨论分析了粗骨料体积分数对混凝土Ⅱ型断裂性能的影响，并利用DIC技术分析了试件断裂韧带表面的断裂损伤演化过程。
1. 实验材料及方法
1.1 原材料及配合比设计
采用北京金隅水泥厂产P.O42.5普通硅酸盐水泥，其组成及物理性质分别见表1、表2。粗骨料为石灰石质碎石，粒径范围为5~16 mm，其粒径分布曲线见图1。细骨料(粒径为0~4 mm)为细度模量为2.34的天然河砂。超细石灰石粉的比重为2.69，主要成分为CaCO3。为提高混凝土和易性，采用了JFL-5萘系高效减水剂。
表 1 水泥组成Table 1. Composition of cementChemical composition/wt% SiO2 Fe2O3 Al2O3 CaO MgO Na2O K2O SO3 22.27 2.95 6.37 60.23 4.52 0.13 0.52 2.51 Mineral composition/wt% 3CaO·Al2O3 3CaO·SiO2 2CaO·SiO2 4CaO·Al2O3·Fe2O3 6.9 49.58 28.13 8.62 表 2 水泥力学性质Table 2. Physical properties of cementLoss on ignition/% Specific surface area /(m2·kg−1) fc/MPa ft/MPa Setting time/min 2.96 329 3d 28d 3d 28d Initial Final 23.5 50.3 5.6 8.8 196 258 Notes：fc is the compressive strength; ft is the tensile strength. 混凝土的配合比见表3。为研究粗骨料体积分数对混凝土Ⅱ型断裂参数的影响，设计了4种粗骨料体积分数，分别为19%、25%、31%和37%。所有配合比的水胶比均为0.31。
1.2 试件准备
本试验制作的试件主要包括无切口Ⅱ型断裂试件和立方体标准试件。其中，无切口Ⅱ型断裂试件用于剪切断裂测试，试件尺寸为200 mm×200 mm×100 mm，每个配合比10个，共40个；立方体标准试件用于测定抗压强度fc、弹性模量E和劈裂抗拉强度ft等常规力学参数，试件尺寸为150 mm×150 mm×150 mm，每个配合比10个，共40个。所有试件在浇筑后1天拆模，标准养护28天。
表 3 混凝土配合比Table 3. Compositions of concretesGroup Specimen Cement/
(kg·m−3)Sand/
(kg·m−3)Coarse aggregate/
(kg·m−3)Limestone powder/
(kg·m−3)Water/
(kg·m−3)Superplasticizer/
(kg·m−3)Va/% C19 C19-01—C19-10 490 1 167 500 96 179.3 5 19 C25 C25-01—C25-10 490 1 000 667 96 179.3 5.5 25 C31 C31-01—C31-10 490 834 833 96 179.3 6.1 31 C37 C37-01—C37-10 490 667 1 000 96 179.3 7.4 37 Note：Va—Volume fraction of coarse aggregate. 1.3 试验方法
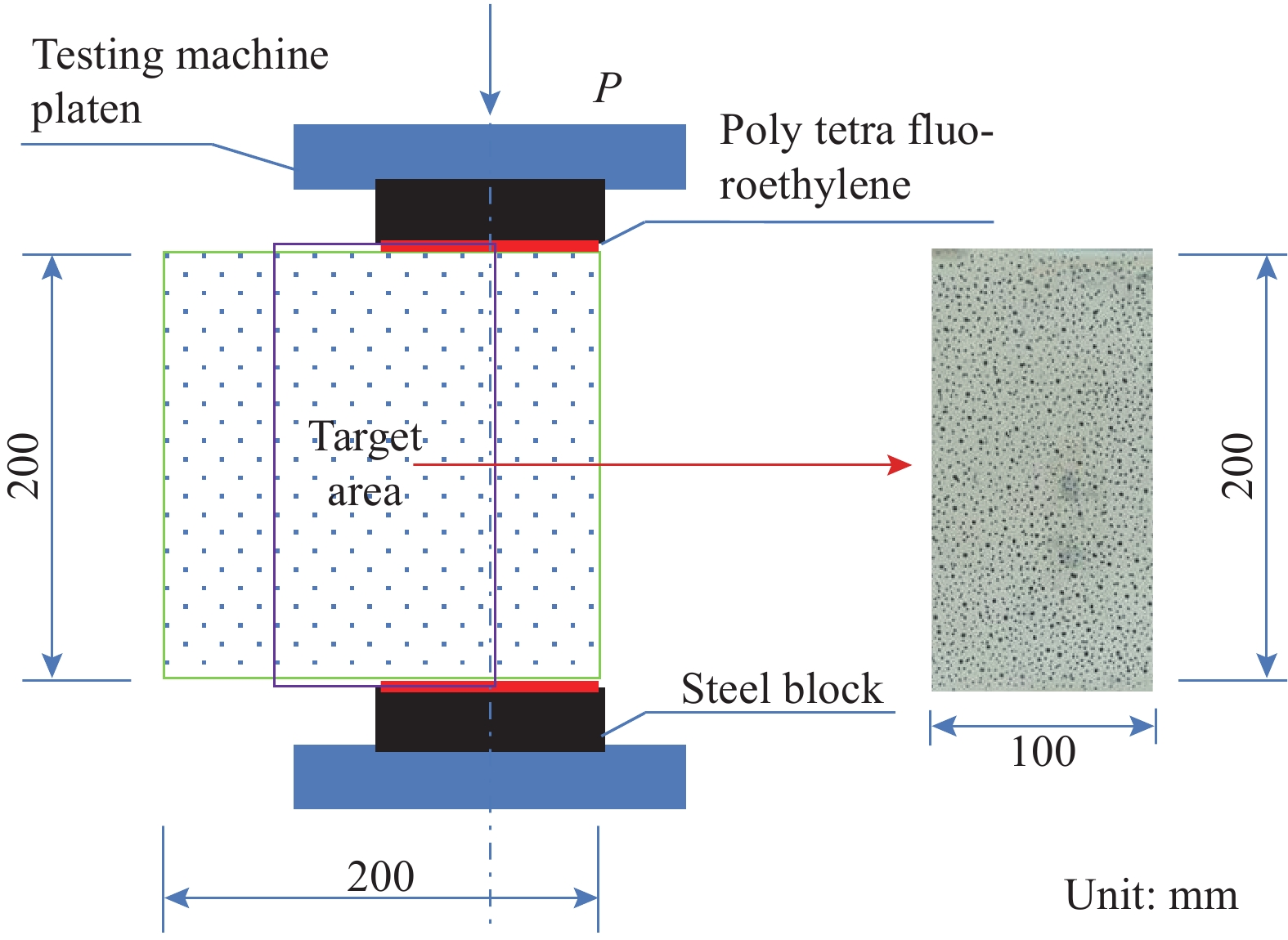
本次试验主要包括Ⅱ型断裂试验、单轴压缩试验和劈裂抗拉试验。所有试验均在深部岩土力学与地下工程国家重点实验室(北京) 200T电液伺服压力试验机上开展(图2)。图3为Ⅱ型断裂试验的加载示意图。其中，用于传递荷载的加载钢块的宽度为100 mm，即无切口Ⅱ型断裂试件宽度的1/2。因此，荷载经过钢块传递后，仅仅施加在试件上下表面的1/2上，以保证试件发生剪切断裂。另外，为了消除试件与加载钢块之间的横向摩擦，将试件表面打磨平整后，在试件的上下加载面各放置一层1 mm厚的聚四氟乙烯(Poly tetra fluoroethylene, PTFE)垫片。试件、加载钢块、压力试验机压头应仔细摆放，使其对齐。加载过程采用位移控制，加载速率为0.1 mm/min。整个试验过程中，对压力试验机上下加载板之间的压缩位移d、荷载值P进行了连续监测。
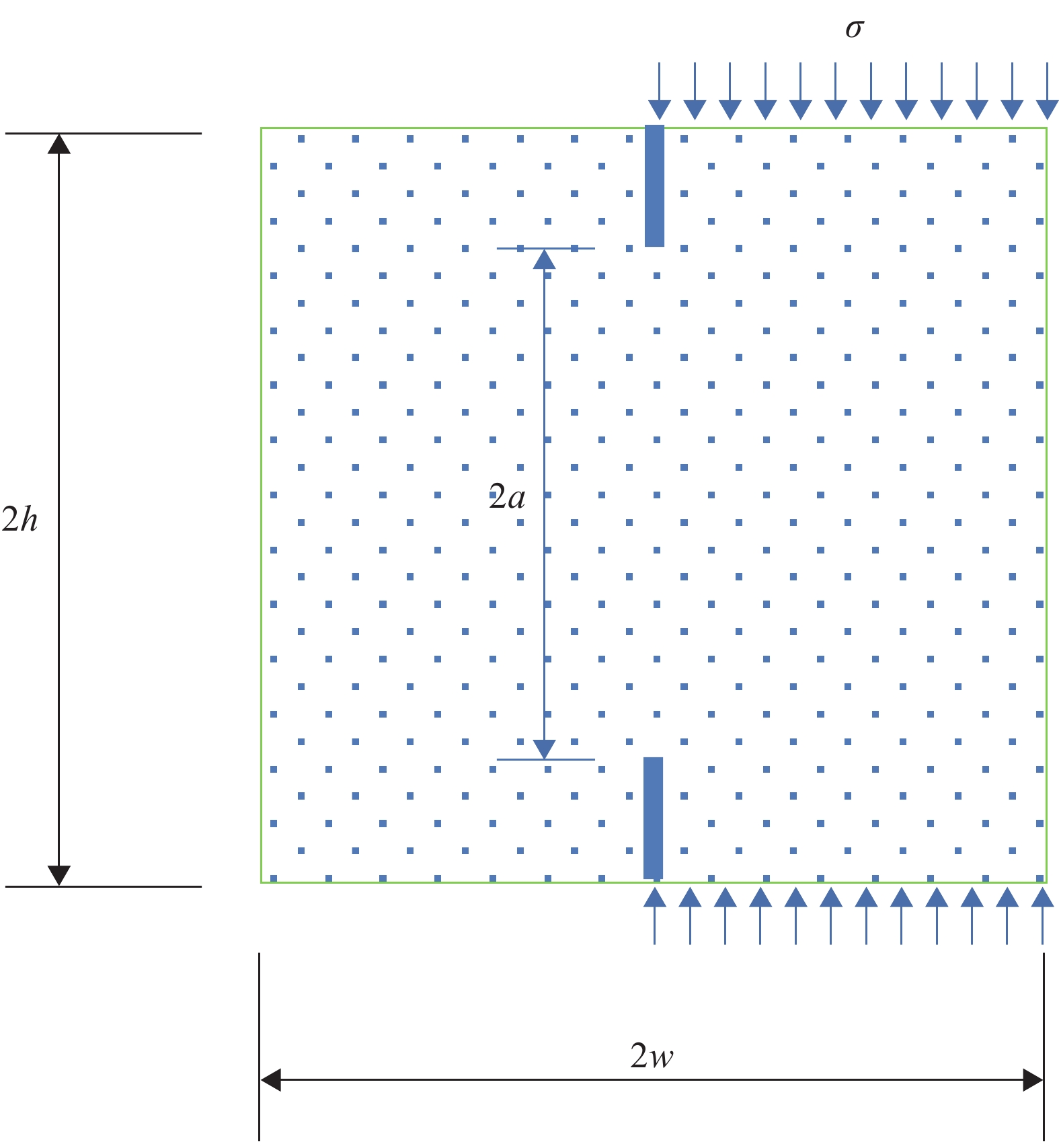
根据REINHARDT等[14]关于有限宽度的两端开口单边加载试件(图4)提出的断裂韧度计算方法，得到无切口Ⅱ型断裂试件的断裂韧度的计算表达式：
![]()
图 4 两端切口单边加载混凝土试件Figure 4. Illustration for the double-edge notched concrete specimenKⅡC=PC4b√w,h⩾ (1) 式中：PC为临界开裂荷载；w和h分别为试件宽度和高度的1/2；a为断裂韧带长度的1/2；b为试件的厚度。本次试验中，由于加载钢块的刚度足够大，使试件加载面上荷载均匀分布，因此h≥2a的限制条件可以放宽。将Ⅱ型断裂韧度KⅡ C代入下式，即可得到临界能量释放率GⅡ C：
{G_{{\rm{{\text{Ⅱ}}C}}}} = \frac{{{K_{{\rm{{\text{Ⅱ}}C}}}}^2}}{E} (2) 为了追踪剪切断裂过程中试件表面的断裂损伤演化过程，利用DIC技术对试件表面的变形场进行监测。DIC系统主要由CCD摄像机、LED补光灯和计算机组成(如图2所示)。选取名义断裂韧带周边区域(100 mm×200 mm)作为散斑观察区域，图3给出了观察区域的散斑图像。在整个加载过程中，CCD摄像机连续采集散斑图像，采集频率为50 Hz。
2. 结果与讨论
2.1 混凝土荷载-位移曲线
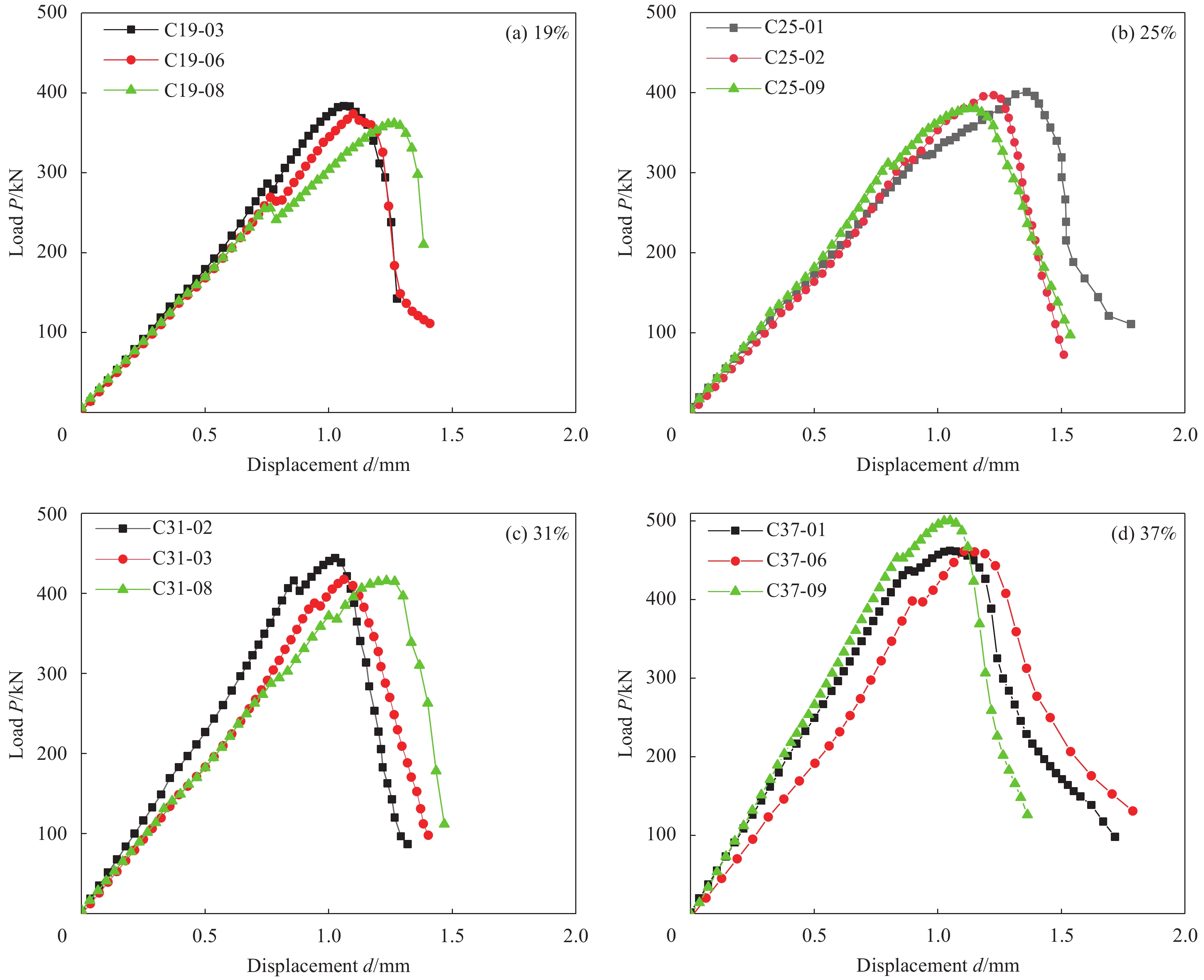
典型无切口Ⅱ型断裂试件(试件编号C37-09)的荷载-位移曲线、剪切断裂过程分别如图5、图6所示。在加载初期，原始的荷载-位移曲线(图5(a))呈现出明显的非线性，这是由于测得的竖向位移d包含PTFE垫片的非线性压缩变形。为了准确分析无切口Ⅱ型断裂试件的断裂力学响应，将PTFE垫片的变形从竖向位移中剔除[14]。随着加载水平提高，当压缩位移为1.0~1.5 mm之间时(即PTFE垫片的变形完成到裂纹萌生之前)荷载随位移线性增加(图5(a))，该阶段竖向位移中基本只包含试件的竖向压缩变形。因此，利用该阶段的荷载-位移曲线求出荷载与位移之间的近似线性关系式，将加载初期(初始非线性阶段)的位移代入该关系式，得到荷载为0时的位移(非0)，即PTFE垫片的变形，将总的竖向位移d减去该非0位移，得到试件的竖向位移，从而得到修正后的荷载-位移曲线(图5(b))。根据加载水平与断裂过程的对应关系，可将修正后的荷载-位移曲线分为三个阶段。
![]()
图 5 混凝土试件C37-09的原始和修正荷载-位移曲线Figure 5. Original and corrected load-displacement curves of C37-09 concrete specimen(1)第一阶段为荷载从0增加至457 kN。本阶段内，荷载基本随位移线性增加，试件处于近线弹性状态，试件表面未出现肉眼可观察到的裂纹(图6(a))。但是在该阶段将要结束时，试件内部可能出现局部损伤或微裂纹。因此，可运用线弹性本构方程来描述此阶段混凝土的力学行为。
(2)在第二阶段(荷载从457 kN增加至497 kN)的起始点附近，荷载-位移曲线出现轻微且快速的波动，即短暂卸荷后，荷载继续增加。该波动预示着宏观主裂纹的出现。由于半边加载，在试件上下表面与加载钢块边缘的接触位置(即名义断裂韧带的上、下端)形成应力集中，当荷载增加至一定值时，剪应力达到混凝土的抗剪强度，发生剪切断裂，开裂后裂纹沿着名义断裂韧带从两端向中部迅速扩展(图6(b))。因此，起始点对应的荷载，我们称为临界开裂荷载PC，可用来计算相应的断裂韧度KⅡ C。从起始点开始，荷载-位移曲线出现明显的非线性，这是由裂纹在试件中的快速扩展(图6(c))造成的。
(3)第三个部分为峰后软化阶段。在该阶段，随着裂纹的扩展，最终形成贯通整个名义断裂韧带的宏观裂缝，试件的自由端部分沿着名义断裂韧带从试件中脱离(图6(d))，受压部分继续承受单轴压缩，直至完全压溃。
图7给出了各配比试件的典型的荷载-位移曲线。所有的曲线形状基本相同，均包含了近线弹性、裂纹起裂及扩展、峰后软化，且均出现了用于确定临界开裂荷载PC的波动点。随着粗骨料体积分数的增加，起裂荷载、峰值荷载均明显增加。这说明增加粗骨料体积分数，将有助于提高混凝土对Ⅱ型断裂的抵抗能力。
![]()
图 7 含有不同骨料体积分数的混凝土试件的荷载-位移曲线Figure 7. Load-displacement curves of the concrete specimens with different volume fractions of aggregate2.2 混凝土断裂参数
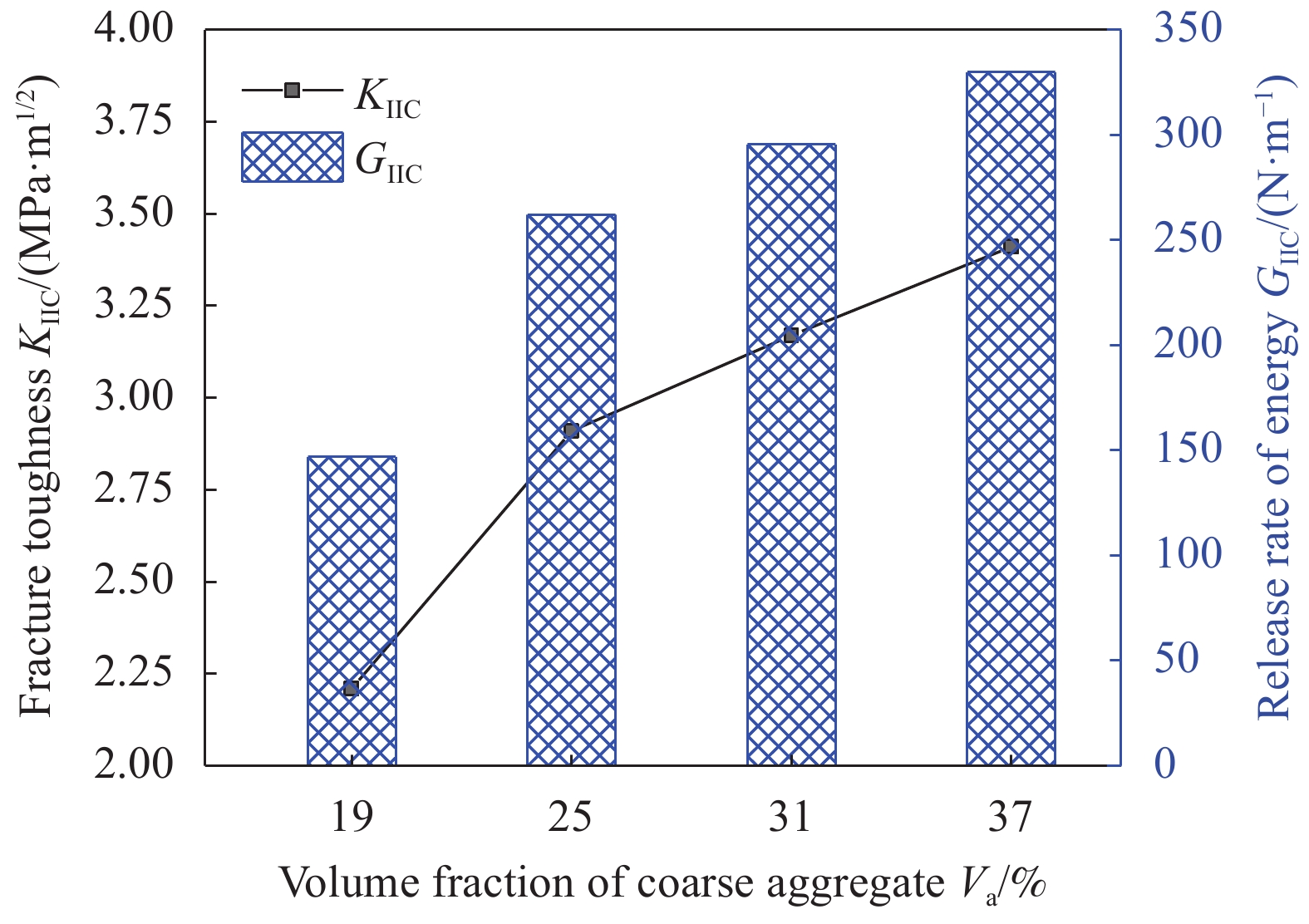
各配比试件的荷载-位移曲线的波动点对应的荷载即临界开裂荷载PC。将PC和相关试件尺寸代入式(1)和式(2)，计算得到Ⅱ型断裂韧度KⅡ C和临界能量释放率GⅡ C。表4给出了各配比混凝土试件的KⅡ C和GⅡ C的平均值。其中，测得的KⅡ C的变化范围为2.2~3.41 MPa·m1/2，这与许多学者已发表的试验结果基本一致[13-14,18,22]。
表 4 含有不同骨料体积分数的混凝土断裂参数Table 4. Fracture parameters of concretes with different volume fractions of aggregate measured from experimental testsVa/% fc/MPa ft/MPa E/GPa KⅡ C/(MPa·m1/2) GⅡ C/(N·m−1) 19 44.79 3.80 33.23 2.21 146.98 25 51.96 3.59 32.30 2.91 262.17 31 50.08 4.41 34.01 3.17 295.47 37 58.36 4.85 35.26 3.41 329.78 Notes：E is the modulus of elasticity; KⅡ C is the mode Ⅱ fracture toughness; GⅡ C is the mode Ⅱ critical energy release rate. 图8给出了KⅡ C和GⅡ C和粗骨料体积分数之间的关系。随着粗骨料体积分数的增加，KⅡ C和GⅡ C均显著地提高，且粗骨料体积分数从19%增加至25%对KⅡ C和GⅡ C的提高幅度明显高于粗骨料体积分数由25%增加至37%所引起的。KⅡ C和GⅡ C通常用以表征开裂过程中的能量耗散，而断裂路径、断裂面特征均与能量的耗散相关。通常，ITZ相对于周边的基质，具有较高的孔隙度和较弱的力学性能[25]。因此，当裂纹在混凝土中扩展时，往往沿着ITZ扩展，并且穿越水泥砂浆[26-28]，典型的无切口试件的裂纹扩展路径如图9所示。粗骨料体积分数较低时，被剥离的粗骨料的数量较少，断裂面轮廓线较为平直，且断裂面相对光滑；随着粗骨料体积分数的增加，骨料之间的桥联、互锁作用增强，且从水泥砂浆基质中剥离的骨料数量也随之增加，导致断裂面轮廓线更加曲折、更长(图10)，断裂面更粗糙，因此裂纹的扩展需要消耗更多的能量以克服粗骨料的阻碍效应。
![]()
图 8 混凝土KⅡ C和GⅡ C随粗骨料体积分数变化的关系Figure 8. KⅡ C and GⅡ C of concrete with different volume fractions of coarse aggregate![]()
图 10 含有不同骨料体积分数的混凝土试件的剪切裂纹形态Figure 10. Fracture patterns for concrete specimens with different volume fractions of coarse aggregate2.3 基于MPT理论的混凝土参数定量分析
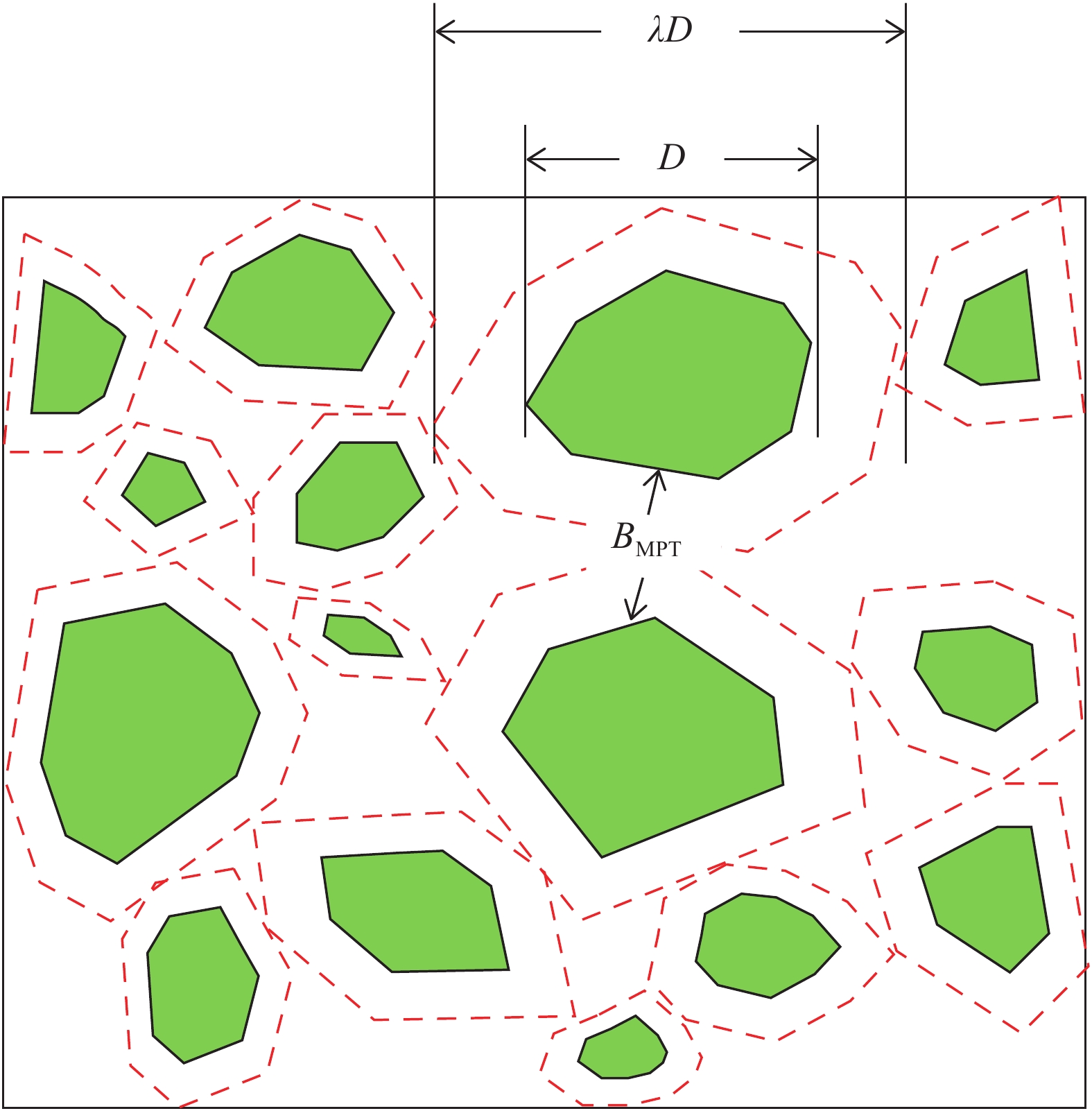
为了综合评价骨料体积分数、粒径对混凝土抗压强度的影响，Francois de Larrard等[29]提出了最大泥浆厚度(Maximum paste thickness, MPT)理论。其中，最大泥浆厚度为混凝土中相邻骨料之间的最大间距BMPT。在物理意义上，BMPT与ITZ相关联：随着BMPT的增大，ITZ在骨料之间的基质中的占比减小。图11给出了混凝土骨料充填示意图。假定通过一个均匀膨胀过程(x、y和z方向膨胀系数均为λ)，使相邻的堆积骨料互相接触且充满混凝土的体积。此时，骨料粒径D和骨料体积分数Va分别为
{D^*} = \lambda D (3) {V_{\rm{a}}}^* = {\lambda ^3}{V_{\rm{a}}} (4) 式中，D*和Va*分别为骨料膨胀后的粒径和骨料体积分数。膨胀系数λ可用下式进行计算：
\lambda {\rm{ = }}\frac{{{B_{{\rm{MPT}}}} + {D_{\max }}}}{{{D_{\max }}}} (5) 式中，Dmax为最大骨料粒径。因此，可推导出BMPT的表达式：
{B_{{\rm{MPT}}}} = {D_{\max }}\left(\sqrt[3]{{\frac{{{V_{\rm{a}}}^*}}{{{V_{\rm{a}}}}}}} - 1\right) (6) 对于碎石骨料，Va*可以用下式[29]进行计算：
{V_{\rm{a}}}^* = 1 - 0.45{\left(\frac{{{D_{\min }}}}{{{D_{\max }}}}\right)^{0.19}} (7) 基于上述理论，Francois de Larrard等[29]发现抗压强度fc和BMPT之间关系为幂函数形式：
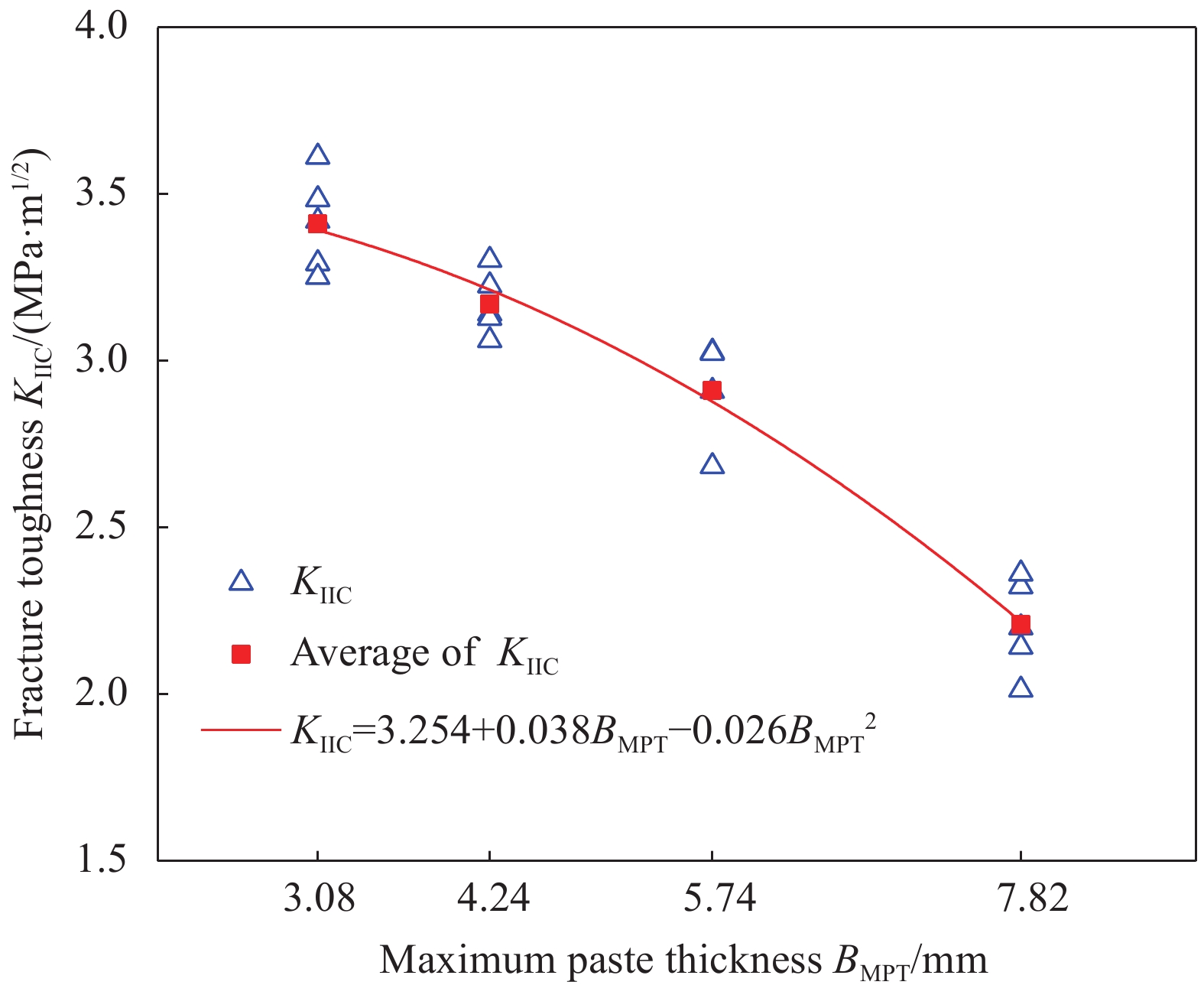
{f_{\rm{c}}}\infty {B_{{\rm{MPT}}}}^p (8) 类似的，试验数据显示，KⅡ C与BMPT之间具有相关性。通过对试验数据的分析、拟合，得到图12所示的关系。因此，KⅡ C与BMPT之间存在以下经验公式：
![]()
图 12 混凝土KⅡ C随最大泥浆厚度BMPT变化的关系Figure 12. Relationship between KⅡ C and maximum paste thickness BMPT of concrete{K_{{\rm{{\text{Ⅱ}}C}}}} = 3.254 + 0.038{B_{{\rm{MPT}}}} - 0.026{B_{{\rm{MPT}}}}^2 (9) 该经验公式的R2为0.988，试验值和预测值的符合性较好。同时，BMPT与骨料粒径和体积分数相关，将式(6)代入式(9)，可以得到KⅡ C与Va之间的经验关系为
\begin{gathered} {K_{{\rm{{\text{Ⅱ}}C}}}}{\rm{ = }}3.524 + 0.038{D_{\max }}\left(\sqrt[3]{{\frac{{{V_{\rm{a}}}^*}}{{{V_{\rm{a}}}}}}} - 1\right) - \\ 0.026{D_{\max }}^2{\left(\sqrt[3]{{\frac{{{V_{\rm{a}}}^*}}{{{V_{\rm{a}}}}}}} - 1\right)^2} \\ \end{gathered} (10) 经验式(10)综合反映了骨料粒径和体积分数Va对混凝土Ⅱ 型断裂韧度KⅡ C的影响，当骨料粒径一定时，随着Va增大，KⅡ C增大。混凝土Ⅱ 型断裂试验影响因素复杂、试验条件难控制[19]，使其断裂参数测定难度较大。因此，在不具备试验条件的情况下，可以根据骨料的粒径和体积分数推算混凝土的Ⅱ 型断裂韧度KⅡ C，为混凝土设计及工程实践提供可参考的断裂参数。
2.4 混凝土DIC变形场分析
DIC通过比较和分析变形前后的散斑图像，来解析试件表面的变形场。作为一种非接触和非破坏性测量方法，DIC可以用来分析断裂过程中混凝土表面位移、应变的演化过程。
利用DIC分析软件Davis 10，得到了各配比试件的位移以及应变场。对于混凝土断裂演化的分析，通常更关注断裂韧带的水平变形特征(即垂直于主裂纹方向的变形)[30]。图13给出了试件C37-09的不同加载水平的水平位移云图，位移指向图片的右边为正，左边为负。在加载初期，试件表面的水平位移均匀分布，且位移值较小，试件处于弹性状态。当荷载增加至457.68 kN (约为峰值荷载的92%)时，试件开始出现宏观裂纹，水平位移均匀分布，且位移值较小，试件处于弹性状态。当荷载增加至457.68 kN (约为峰值荷载的92%)时，试件开始出现宏观裂纹，位于左侧的自由端向左偏转，在韧带左下角形成了位移不连续分布，左侧位移绝对值大于右侧。在峰值荷载497.32 kN附近，裂缝迅速扩展，基本贯通断裂韧带，左侧位移明显增大，右侧位移基本无变化，位移不连续分布的分界线与裂纹轮廓线基本一致。此后荷载开始下降，当降至220.71 kN (约为峰值荷载的44%)，断裂韧带左下角位移不再增加，表明该位置裂纹扩展完成，此时分界线侵入韧带右侧，这主要是由于骨料对裂纹的阻碍使裂纹扩展路径发生偏移。
![]()
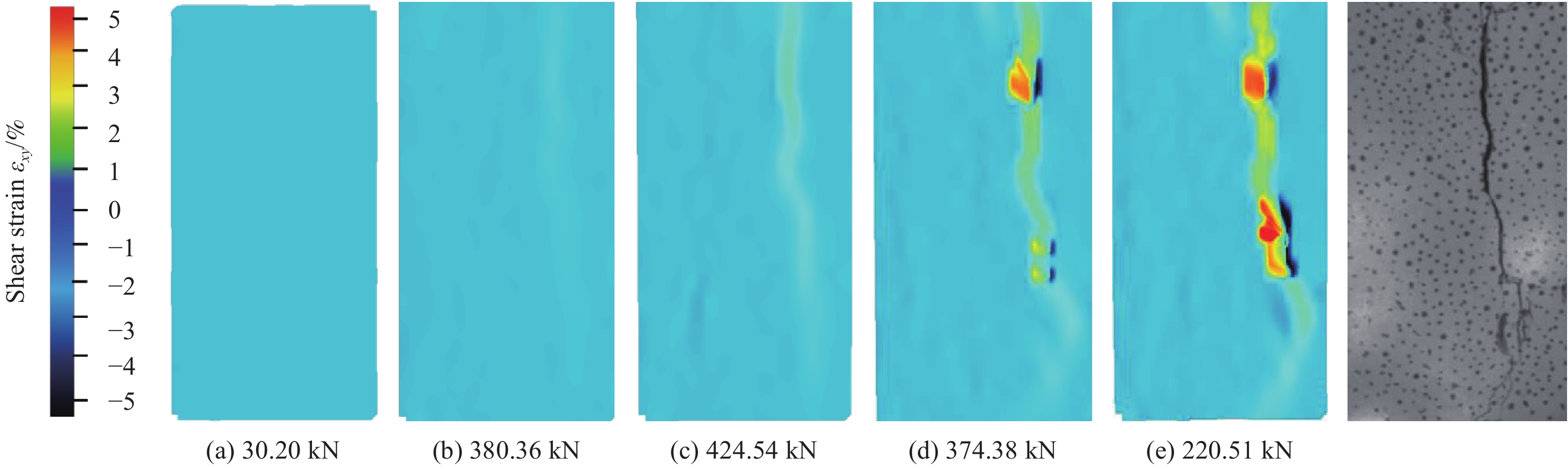
图 13 混凝土试件C37-09表面水平位移演化Figure 13. Evolution of x-displacement of concrete specimen C37-09图14给出了试件C31-08表面的剪切应变演化过程。在裂纹扩展的作用下，试件表面呈现出明显的应变局部化，而应变局部化的区域分布可用来表征FPZ的形态[31]。如图14所示，无切口Ⅱ断裂试件的典型FPZ为弯曲的条带状。与水平位移的演化过程类似，应变局部化区域并没有完全沿着名义断裂韧带区域规则分布，而是存在一定的偏差和一些分支，这是由于粗骨料之间的桥联互锁作用使得裂纹的扩展路径发生了偏移、错位。与水平位移的演化过程相比，剪切应变演化不仅能够精确识别裂纹的起裂、扩展及贯通的全过程，而且能反映出FPZ的真实形态。另外，通过分析断裂韧带的应变局部化演化特征，发现在不同的加载水平下，裂纹扩展具有不同的特征：当荷载增加至临界开裂荷载380.36 kN时，裂纹萌生并迅速扩展，此时裂纹主要分布在试件表面，裂纹宽度较小；在峰值荷载424.54 kN，裂纹基本联通整个断裂韧带的表面，随后裂纹开始向试件内部扩展，并且裂纹宽度迅速增大。
![]()
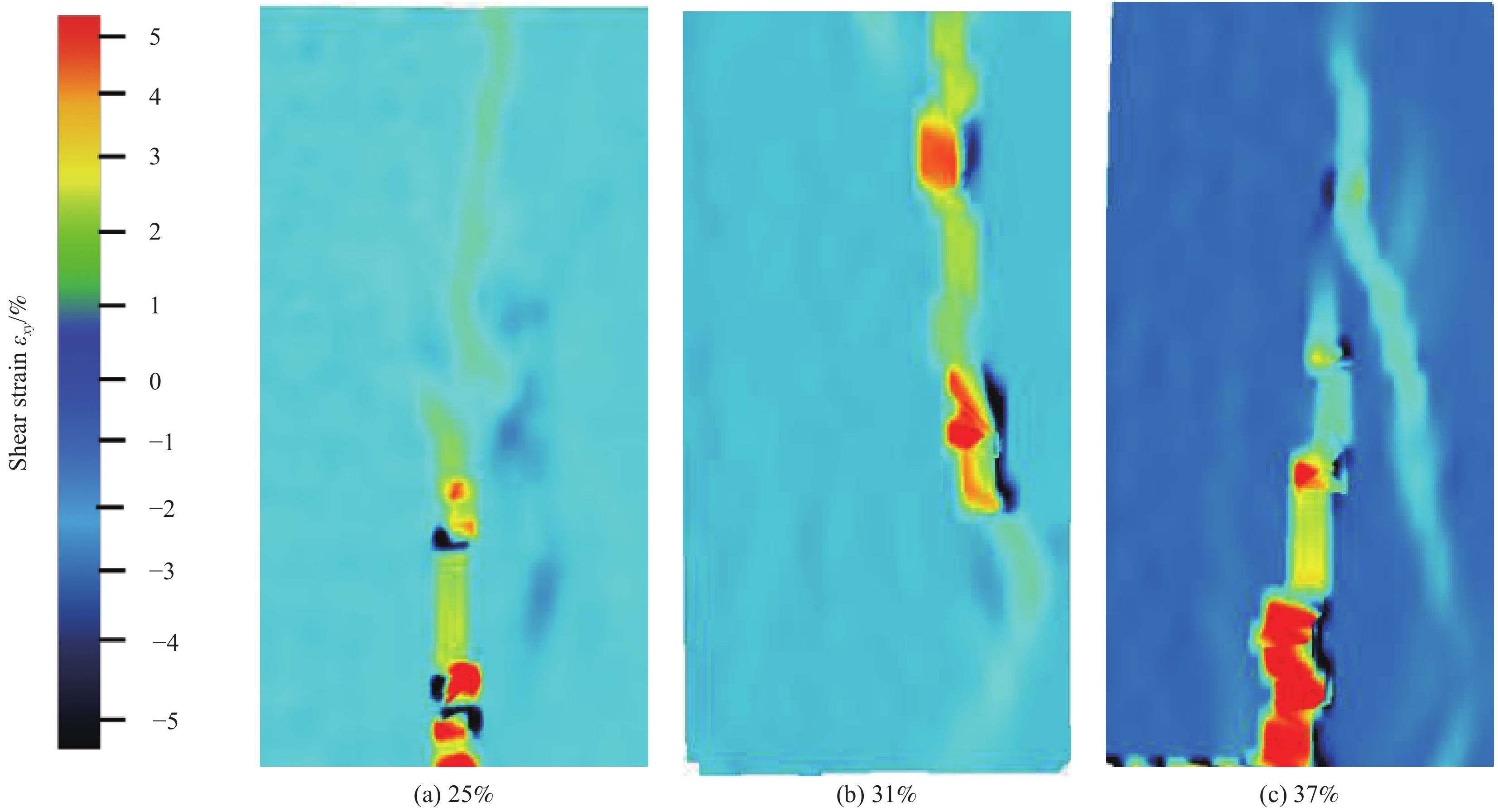
图 14 混凝土试件C31-08表面剪应变演化Figure 14. Evolution of shear strain of concrete specimen C31-08为了研究粗骨料体积分数对FPZ形态的影响，图15给出了粗骨料体积分数分别为25%、31%及37%的试件的典型FPZ形态图。随着粗骨料体积分数的增加，FPZ形态更不规则，分支更多，分布面积相对增大。通常，骨料的强度相对于周边的基质和ITZ要高很多，当裂纹扩展至骨料时，通常将沿着ITZ绕过骨料扩展，这就使裂纹的扩展路径发生了偏移。随着粗骨料含量的增加，骨料之间桥联、互锁能力增强，对裂纹的阻碍效应明显提高，导致裂纹发生较大偏移并产生更多的裂纹分支，进而使扩展面积增大。
![]()
图 15 含有不同骨料体积分数的混凝土试件FPZ形态Figure 15. Shape of FPZ for specimens with different volume fractions of coarse aggregate3. 结 论
通过对含有四种粗骨料体积分数的混凝土试件开展Ⅱ型断裂试验，对各配比试件的力学响应、断裂参数、断裂形态进行分析，并利用数字图像相关技术(Digital image correlation, DIC)对试件表面的断裂损伤过程进行分析，得到如下结论：
(1)随着粗骨料体积分数Va的增加，混凝土Ⅱ型断裂韧度KⅡ C和临界能量释放率GⅡ C均显著提高，且粗骨料体积分数Va从19%增加至25%对KⅡ C和GⅡ C的提高幅度明显高于粗骨料体积分数由25%增加至37%所引起的；
(2)各配比混凝土的开裂模式一致，剪切裂纹主要集中在名义断裂韧带区域；随着粗骨料体积分数的增加，裂纹轮廓线更长，更曲折；
(3)根据最大泥浆厚度 (Maximum paste thickness, MPT)理论，给出的断裂韧度KⅡ C和粗骨料体积分数Va之间的经验关系式预测值和试验值的符合性较好；
(4)在剪切断裂测试中，无切口Ⅱ型断裂试件的典型断裂过程区(Fracture process zone, FPZ)为弯曲的条带状；随着粗骨料体积分数的增加，FPZ的形态更不规则，分支更多，分布面积相对增大。
-
![]()
图 4 两端切口单边加载混凝土试件
Figure 4. Illustration for the double-edge notched concrete specimen
![]()
图 5 混凝土试件C37-09的原始和修正荷载-位移曲线
Figure 5. Original and corrected load-displacement curves of C37-09 concrete specimen
![]()
图 7 含有不同骨料体积分数的混凝土试件的荷载-位移曲线
Figure 7. Load-displacement curves of the concrete specimens with different volume fractions of aggregate
![]()
图 8 混凝土KⅡ C和GⅡ C随粗骨料体积分数变化的关系
Figure 8. KⅡ C and GⅡ C of concrete with different volume fractions of coarse aggregate
![]()
图 10 含有不同骨料体积分数的混凝土试件的剪切裂纹形态
Figure 10. Fracture patterns for concrete specimens with different volume fractions of coarse aggregate
![]()
图 12 混凝土KⅡ C随最大泥浆厚度BMPT变化的关系
Figure 12. Relationship between KⅡ C and maximum paste thickness BMPT of concrete
![]()
图 13 混凝土试件C37-09表面水平位移演化
Figure 13. Evolution of x-displacement of concrete specimen C37-09
![]()
图 14 混凝土试件C31-08表面剪应变演化
Figure 14. Evolution of shear strain of concrete specimen C31-08
![]()
图 15 含有不同骨料体积分数的混凝土试件FPZ形态
Figure 15. Shape of FPZ for specimens with different volume fractions of coarse aggregate
表 1 水泥组成
Table 1 Composition of cement
Chemical composition/wt% SiO2 Fe2O3 Al2O3 CaO MgO Na2O K2O SO3 22.27 2.95 6.37 60.23 4.52 0.13 0.52 2.51 Mineral composition/wt% 3CaO·Al2O3 3CaO·SiO2 2CaO·SiO2 4CaO·Al2O3·Fe2O3 6.9 49.58 28.13 8.62 
下载: 导出CSV
表 2 水泥力学性质
Table 2 Physical properties of cement
Loss on ignition/% Specific surface area /(m2·kg−1) fc/MPa ft/MPa Setting time/min 2.96 329 3d 28d 3d 28d Initial Final 23.5 50.3 5.6 8.8 196 258 Notes：fc is the compressive strength; ft is the tensile strength.
下载: 导出CSV
表 3 混凝土配合比
Table 3 Compositions of concretes
Group Specimen Cement/
(kg·m−3)Sand/
(kg·m−3)Coarse aggregate/
(kg·m−3)Limestone powder/
(kg·m−3)Water/
(kg·m−3)Superplasticizer/
(kg·m−3)Va/% C19 C19-01—C19-10 490 1 167 500 96 179.3 5 19 C25 C25-01—C25-10 490 1 000 667 96 179.3 5.5 25 C31 C31-01—C31-10 490 834 833 96 179.3 6.1 31 C37 C37-01—C37-10 490 667 1 000 96 179.3 7.4 37 Note：Va—Volume fraction of coarse aggregate.
下载: 导出CSV
表 4 含有不同骨料体积分数的混凝土断裂参数
Table 4 Fracture parameters of concretes with different volume fractions of aggregate measured from experimental tests
Va/% fc/MPa ft/MPa E/GPa KⅡ C/(MPa·m1/2) GⅡ C/(N·m−1) 19 44.79 3.80 33.23 2.21 146.98 25 51.96 3.59 32.30 2.91 262.17 31 50.08 4.41 34.01 3.17 295.47 37 58.36 4.85 35.26 3.41 329.78 Notes：E is the modulus of elasticity; KⅡ C is the mode Ⅱ fracture toughness; GⅡ C is the mode Ⅱ critical energy release rate.
下载: 导出CSV
-
[1] AKCAY B, AGAR-OZBEK A S, BAYRAMOV F, et al. Interpretation of aggregate volume fraction effects on fracture behavior of concrete[J]. Construction & Building Materials,2012,28(1):437-443.
[2] CHEN Bing, LIU Juanyu. Effect of aggregate on the fracture behavior of high strength concrete[J]. Construction & Building Materials,2004,18:585-590. DOI: 10.1016/j.conbuildmat.2004.04.013
[3] 韩宇栋, 张君, 高原. 粗骨料体积含量对混凝土断裂参数的影响[J]. 工程力学, 2013(3):201-207. HAN Yudong, ZHANG Jun, GAO Yuan. Effect of coarse aggregate content on fracture parameters of concrete[J]. Engineering Mechanics,2013(3):201-207(in Chinese).
[4] BEYGI M H A, KAZEMI M T, NIKBIN I M, et al. The influence of coarse aggregate size and volume on the fracture behavior and brittleness of self-compacting concrete[J]. Cement & Concrete Research,2014,66:75-90. DOI: 10.1016/j.cemconres.2014.06.008
[5] ALYHYJA W S, DHAHEER M S A, AL-RUBAYE M M, et al. Influence of mix composition and strength on the fracture properties of self-compacting concrete[J]. Construction and Building Materials,2016,110:312-322. DOI: 10.1016/j.conbuildmat.2016.02.037
[6] RAO Q H, SUN Z Q, STEPHANSSON O, et al. Shear fracture (Mode Ⅱ) of brittle rock[J]. International Journal of Rock Mechanics & Mining Sciences,2003,40(3):355-375.
[7] IOSIPESCU N. New accurate procedure for single shear testing of metals[J]. Journal of Materials,1967,2(3):537-566.
[8] BAZANT Z P, PFEIFFER P A. Shear fracture tests of concrete[J]. Materials and Structures,1986,19(110):111-121.
[9] DAVIES J. Numerical and experimental study of development of fracture path under mixed mode loading//VAN MIER J G M, ROTS J G, BAKKER A. Fracture processes in concrete, rock and ceramics[M]. London: E. &F. N. Spon, 1991: 717-726.
[10] DAVIES J, YIM C W A, MORGAN T G, et al. Determination of fracture parameters of a punch-through shear specimen[J]. International Journal of Cement Composites and Lightweight Concrete,1988,10(1):33-41.
[11] PRAKASH D, RAGHUPRASAD B K, DESAI V B. Mode-Ⅱ fracture of cementitious materials—Part I: Studies on specimens of some new geometries[J]. Journal of Structural Engineering,1999,26(1):11-18.
[12] XU S, REINHARDT H W, GAPPOEV M. Mode Ⅱ fracture testing method for highly orthotropic materials like wood[J]. International Journal of Fracture,1995,75(3):185-214.
[13] REINHARDT H W, OZBOLT J, XU S, et al. Shear of structural concrete members and pure mode Ⅱ testing[J]. Advanced Cement Based Materials,1997,5:75-85. DOI: 10.1016/S1065-7355(96)00003-X
[14] REINHARDT H W, XU S. Experimental determination of KⅡ C of normal strength concrete[J]. Materials and Structures,1998,31:296-302. DOI: 10.1007/BF02480670
[15] REINHARDT H W, XU S. A practical testing approach to determine mode Ⅱ fracture energy GⅡ F for concrete[J]. International Journal of Fracture,2000,105(2):107-125. DOI: 10.1023/A:1007649004465
[16] RAO T D G, KUMAR C N S. Fracture parameters of high-strength concrete-mode Ⅱ testing[J]. Magazine of Concrete Research,2010,62(3):157-162. DOI: 10.1680/macr.2010.62.3.157
[17] KUMAR C N S, RAO T D G. An empirical formula for mode-Ⅱ fracture energy of concrete[J]. KSCE Journal of Civil Engineering,2015,19(3):689-697. DOI: 10.1007/s12205-014-1148-0
[18] 高洪波, 徐世烺, 吴智敏, 等. 混凝土断裂韧度KⅡ C的试验研究[J]. 水力发电学报, 2006(5):68-73. DOI: 10.3969/j.issn.1003-1243.2006.05.015 GAO Hongbo, XU Shilang, WU Zhimin, et al. Experimental study on fracture toughness KⅡ C of concrete[J]. Journal of Hydroelectric Engineering,2006(5):68-73(in Chinese). DOI: 10.3969/j.issn.1003-1243.2006.05.015
[19] 覃茜, 徐千军. 成层混凝土的剪切强度和Ⅱ型断裂韧度[J]. 工程力学, 2019(9):188-196. QIN Xi, XU Qianjun. The shear strength and mode Ⅱ fracture toughness of layered concrete[J]. Engineering Mechanics,2019(9):188-196(in Chinese).
[20] 徐世烺, 喻常雄, 李庆华. 混凝土大坝接缝灌浆的剪切断裂过程及其断裂韧度测定[J]. 水利学报, 2007, 38(3):300-305. XU Shilang, YU Changxiong, LI Qinghua. Experimental study on shear fracture process and mode Ⅱ fracture toughness[J]. Journal of Hydraulic Engineering,2007,38(3):300-305(in Chinese).
[21] 邓爱民, 苟联盟, 徐道远. 2种Ⅱ型混凝土试件断裂韧度KⅡ C值的比较研究[J]. 防灾减灾工程学报, 2013(2):190-194. DENG Aimin, GOU Lianmeng, XU Daoyuan. Comparative research on fracture toughness KⅡ C of two types of mode Ⅱ concrete specimens[J]. Journal of Disaster Prevention and Mitigation Eengineering,2013(2):190-194(in Chinese).
[22] 高洪波. 混凝土Ⅰ型、Ⅱ型断裂参数确定的研究[D]. 大连: 大连理工大学, 2008. GAO Hongbo. Study on the determination of mode I and mode Ⅱ fracture parameters for concrete[D]. Dalian: Dalian University of Technology, 2008(in Chinese).
[23] 徐世烺, 赵艳华. 混凝土Ⅱ型断裂与破坏过程的三维非线性有限元数值模拟[J]. 水力发电学报, 2004, 23(5):15-21. DOI: 10.3969/j.issn.1003-1243.2004.05.004 XU Shilang, ZHAO Yanhua. Numerical simulation of mode Ⅱ fracture and failure processes in concrete by 3-dimensional nonlinear FEM[J]. Journal of Hydroelectric Engineering,2004,23(5):15-21(in Chinese). DOI: 10.3969/j.issn.1003-1243.2004.05.004
[24] 李庆华, 张逸风, 徐世烺, 等. 喷射UHTCC与混 凝土界面的Ⅱ型断裂试验研究[J]. 水利学报, 2018, 49(7):831-839. LI Qinghua, ZHANG Yifeng, XU Shilang, et al. Experimental study on mode Ⅱ fracture of interface between the UHTCC and concrete[J]. Journal of Hydraulic Engineering,2018,49(7):831-839(in Chinese).
[25] LI Guodong, YU Jiangjiang, CAO Peng, et al. Experimental and numerical investigation on Ⅰ-Ⅱ mixed-mode fracture of concrete based on the Monte Carlo random aggregate distribution[J]. Construction & Building Materials,2018,194:523-534.
[26] STRUBLE L, SKALNY J, MINDESS S. A review of the cement-aggregate bond[J]. Cement & Concrete Research,1980,10(2):277-286.
[27] TRENDE U, BÜYÜKÖZTÜRK O. Size effect and influence of aggregate roughness in interface fracture of concrete composites[J]. ACI Materials Journal,1998,95(4):331-338.
[28] MYONG L K, BUYUKOZTURK O, OUMERA A. Fracture analysis of mortar-aggregate interfaces in concrete[J]. Journal of Engineering Mechanics,1992,118(10):2031-2046. DOI: 10.1061/(ASCE)0733-9399(1992)118:10(2031)
[29] LARRARD F D, BELLOC A. Influence of aggregate on the compressive strength of normal and high-strength concrete[J]. ACI Materials Journal,1997,94(5):417-426.
[30] WU Zhimin, RONG Hua, ZHENG Jianjun, et al. An experimental investigation on the FPZ properties in concrete using digital image correlation technique[J]. Engineering Fracture Mechanics,2011,78(17):2978-2990. DOI: 10.1016/j.engfracmech.2011.08.016
[31] AL-SHAYEA N. Comparing reservoir and outcrop specimens for mixed mode Ⅰ-Ⅱ fracture toughness of a limestone rock formation at various conditions[J]. Rock Mechanics & Rock Engineering,2002,35(4):271-297.
-
期刊类型引用(7)
1. 黄志军，余震，孙志军，谭宗林，龙晨杰，许伟，沈卫国，王桂明. 正混凝土在路面工程中的应用研究. 硅酸盐通报. 2025(02): 756-764+784 . 
百度学术
2. 郑忠良，尤博，张兆彪，李宇翔，曹明莉. 不同水灰比条件下碳酸钙晶须对水泥净浆收缩性能的影响. 水利水电科技进展. 2024(01): 66-72 . 百度学术
3. 王骞，郑忠良，尤博，张兆彪，李宇翔，曹明莉. 基于综合性能试验的混凝土早期开裂行为研究. 大连理工大学学报. 2024(01): 82-89 . 百度学术
4. 陈徐东，吴朝国，黄业博，张伟，李升涛. 骨料粒径对混凝土Ⅰ型断裂裂缝扩展影响研究. 应用力学学报. 2024(02): 363-371 . 百度学术
5. 张正义，郑宇，肖海英，张笑瀛，彭航，陈俊翰. 骨料粒径对爆炸加载下混凝土破碎性的影响研究. 兵器装备工程学报. 2023(11): 84-89 . 百度学术
6. 陈燕伟，冯吉利，朱天宇，李凤晨. 不同骨料体积分数下混凝土增韧机制及细观断裂模拟. 复合材料学报. 2022(10): 4972-4987 . 本站查看
7. 童谷生，姚良发，徐攀. C40自密实混凝土II型断裂韧度的确定. 力学季刊. 2021(04): 800-810 . 百度学术
其他类型引用(6)
-
计量
- 文章访问数: 1176
- HTML全文浏览量: 640
- PDF下载量: 55
- 被引次数: 13
