电纺十二酸十二酯@聚乙烯醇蓄热调温纤维的制备及性能

石峰; 张国庆; 刘国金; 周岚

doi:10.13801/j.cnki.fhclxb.20201022.002

电纺十二酸十二酯@聚乙烯醇蓄热调温纤维的制备及性能

石峰^1,,
张国庆^{1, 2,},
刘国金^1,,
周岚^{1, 2, ,}

1.
浙江理工大学　纺织科学与工程学院(国际丝绸学院)，杭州 310018
2.
浙江理工大学　上虞工业技术研究院有限公司，绍兴 312300

基金项目: 国家自然科学基金 (22075252)；浙江省国际产业联合研发计划项目(2019C54003)

详细信息

通讯作者:
周岚，博士，副教授，硕士生导师，研究方向为功能性纺织品　 E-mail：lan_zhou330@163.com

中图分类号: TB34；TQ340.64
计量
- 文章访问数: 1390
- HTML全文浏览量: 503
- PDF下载量: 48
出版历程
- 收稿日期: 2020-08-26
- 录用日期: 2020-10-15
- 网络出版日期: 2020-10-21
- 刊出日期: 2021-08-14

Preparation and properties of the electrospun dodecanol dodecanoate@polyvinyl alcohol thermo-regulated fibers

SHI Feng^1,,
ZHANG Guoqing^{1, 2,},
LIU Guojin^1,,
ZHOU Lan^{1, 2, ,}

1.
College of Textile Science and Engineering (International Institute of Silk), Zhejiang Sci-tech University, Hangzhou 310018, China
2.
Shangyu Industrial Technology Research Institute CO. LTD., Zhejiang Sci-Tech University, Shaoxing 312300, China

摘要

摘要: 以十二酸十二酯作为相变材料(PCM)，以聚乙烯醇(PVA)作为支撑材料，通过乳液静电纺丝技术制备十二酸十二酯@PVA蓄热调温纤维。应用SEM、TEM、DSC、TGA、迷你温度记录仪和红外热成像仪等研究了纺丝液组成及静电纺纤维的表面形貌、潜热值、热稳定性、调温性能、力学性能和水溶性。结果表明，当PVA浓度为10.0wt%、十二酸十二酯∶PVA质量比为50%时，纺丝液具有较好的稳定性和可纺性。十二酸十二酯@PVA静电纺纤维具有明显的芯-鞘结构，纤维中PCM的热分解温度比纯PCM提高了20℃，具有良好的热稳定性。十二酸十二酯@PVA静电纺纤维的潜热值在63 J/g左右，在降温冷却和热红外成像测试中，显示出良好的蓄热调温性能。经戊二醛交联后，静电纺纤维中支撑材料的热稳定性显著增强，而且，纤维的力学性能和水溶解性得到明显改善。
- 聚乙烯醇 /
- 相变材料 /
- 十二酸十二酯 /
- 静电纺丝 /
- 蓄热调温纤维
Abstract: With dodecanol dodecanoate as the phase change material (PCM) and polyvinyl alcohol (PVA) as the supporting material, the dodecanol dodecanoate@PVA thermo-regulated fibers were prepared by emulsion electrospinning technology. The SEM, TEM, DSC, TGA, mini temperature recorder and infrared thermal imager were applied to study the composition of the spinning solution and the surface morphology, latent heat value, thermal stability, temperature regulating properties, mechanical property and water solubility of the electrospun fibers. The results show that with 10.0wt% of PVA and dodecanol dodecanoate∶PVA mass ratio of 50%, the spinning solution has better stability and spinnability. The dodecanol dodecanoate@PVA electrospun fibers have apparent core-sheath structure, and the thermal decomposition temperature of PCM in the fibers is 20℃ higher than the pure PCM, displaying good thermal stability. The latent heat value of dodecanol dodecanoate@PVA electrospun fibers is about 63 J/g, showing good heat storage and temperature regulation performance in cooling process and thermal infrared imaging test. After the crosslinking with glutaraldehyde, the thermal stability of the support material in the electrospun fibers is significantly enhanced, and the mechanical properties and water solubility of the fibers have notable improvement.
- polyvinyl alcohol /
- phase change materials /
- dodecanol dodecanoate /
- electrospinning /
- thermo-regulated fiber

HTML全文

随着经济和生活水平的提高，能源的消耗问题日益严重，尤其是建筑能耗。而在建筑能耗中，由于围护结构隔热性能的不足带来的能量消耗所占比例最大。因此，欧美国家提出了采用夹芯(Sandwich)结构墙体作为外围护结构来改善其隔热性能。该结构是将保温材料置于难燃材料中间，并使用连接件连接内外叶面层，从而形成一个集保温、装饰、隔声于一体的复合墙体结构^[1-2]。

传统的夹芯结构多采用普通混凝土材料作为面层，在实际使用中易出现面层较厚、整体质量较大、开裂、脱落等现象^[3]。同时，在建筑外墙保温所采用的做法中，外墙外保温是目前国内外应用最广泛、最成熟的保温形式^[4]。在使用这种做法时，外面层的开裂和脱落往往会加剧保温层与建筑主体结构或饰面层之间因光照、内外温差等原因产生的不同的收缩变形，从而降低了保温材料的保温效果。然而，作为一种有着显著的多缝开裂和应变硬化特征的材料，工程水泥基复合材料(Engineered cementitious composites，ECC)不仅具有卓越的抗拉性能，其裂缝宽度还可以控制在100 以下^[5-6]，同时还具有良好的韧性和耐久性^[7]。因此，将ECC作为夹芯结构的面层不仅可以解决传统夹芯结构面层厚度较厚、易开裂等问题，还可以解决因普通混凝土脆性带来的一系列问题。

夹芯结构的面层与保温层之间的粘结性能是决定二者能否协同工作，并充分发挥各自优势的重要因素。对此，学者们主要从保温材料种类、保温层厚度、表面处理形式及连接件的采用等方面对夹芯结构面层间的粘结性能进行了研究。Choi等^[8]、Tae等^[9]、Sopal^[10]通过试验研究发现保温材料为挤塑式聚苯乙烯(XPS)板试件的承载力比发泡式聚苯乙烯保温(EPS)板试件高，但EPS保温板与面层粘结性能和延性更好。宋小软等^[11]对由玻璃纤维增强水泥板和不同保温材料组成的试件进行了抗剪试验研究，结果表明，聚氨酯(PUR)材料与水泥板间的界面粘结性能较好，能够满足使用要求，而XPS与水泥板间的界面粘结性能相对较差，并且不建议在试件中只将XPS与混凝土表面进行单纯的自然粘结。Hodicky等^[12]通过试验研究发现，保温层厚度对界面粘结性能有很大影响，降低保温层厚度可以提高试件的界面粘结性能。高睿^[13]、Kazem等^[14]、Naito等^[15]通过试验研究发现，在界面处设置锚钉、在保温板表面预留沟槽及提高混凝土强度都能提高试件界面间的粘结强度，其中对保温板进行表面处理的效果最佳。Jang等^[16]和尹红宇等^[17]对混凝土与保温层之间的界面粘结性能进行了研究发现，在混凝土表面预留沟槽可以有效提高界面间的粘结性能。Teixeira等^[18]通过双面剪切试验研究了玄武岩纤维增强树脂复合材料(BFRP)筋直径和嵌入角度对试件的极限承载力和剪切刚度的影响，结果表明，增大连接件的嵌入角度和直径都能提高试件的极限荷载和刚度。

综上所述，EPS保温板与面层的粘结性能更好，因此本文仅对EPS保温板进行了研究。此外，由于BFRP筋具有耐腐蚀性、轻质高强、导热性低且低碳环保等特点^[19]，可用于替代普通钢筋作为夹芯结构墙板的连接件。但是，国内外只有少部分学者对采用BFRP筋作为连接件的夹芯结构的粘结性能进行了研究。同时，关于ECC作为面层、EPS作为保温层、BFRP筋作为连接件的夹芯结构的界面粘结性能研究较少，数据信息不够丰富。

因此，本文在前人研究的基础上，提出了将ECC与EPS相结合，并以BFRP筋作为夹芯墙板连接件，形成轻质、导热系数小、表层不易开裂的新型薄壁夹芯结构。同时，对夹芯结构进行了双面剪切试验，研究了制作方式、保温材料的厚度、有无连接件及其角度对ECC面层与保温材料间的界面粘结性能的影响，并推导了试件的抗剪承载力计算公式。

1. 试件设计与制备

1.1 原材料

试验采用EPS保温板的参数如表1所示。ECC的配合比如表2所示，该配合比下ECC材料在养护28天后的力学性能如表3所示，其中抗压试验采用70.7 mm×70.7 mm×70.7 mm的立方体试块，拉伸试验试件的总尺寸为32 mm×6 mm×13 mm、中间段长为8 mm、宽为30 mm，四点弯曲试验试件的尺寸为400 mm×100 mm×15 mm。聚乙烯醇(PVA)短切纤维的性能参数如表4所示。BFRP筋的直径及其力学性能如表5所示。

表 1 发泡式聚苯乙烯(EPS)性能参数

Table 1. Performance parameters of the expanded polystyrene (EPS)

Heat insulator	Thermal conductivity/(W·(m·K)⁻¹)	Density/(kg·m⁻³)	Tensile strength/MPa	Compressive strength/MPa
EPS	0.039	20	0.13	0.12

下载: 导出CSV

| 显示表格

表 2 工程水泥基复合材料(ECC)配合比

Table 2. Mix proportion of engineered cementitious composites (ECC) (kg/m³)

Material	Cement	Fly ash	Quartz sand	Water	Water reducing agent	PVA fiber
Mix proportion	379	885	455	379	17.4	26
Note: PVA—Polyvinyl alcohol.

下载: 导出CSV

| 显示表格

表 3 ECC力学性能

Table 3. Mechanical properties of ECC

Specimen number	Compressive strength/MPa	Ultimate tensile strength/MPa	Ultimate tensile strain/%	Ultimate bending load/kN	Ultimate mid-span deflection/mm
ECC-1	57.5	8.76	3.47	0.81	21.90
ECC-2	52.2	7.12	2.63	0.83	24.62
ECC-3	49.3	6.34	3.25	0.79	21.83
Average value	53.0	7.41	3.12	0.81	22.78
Standard deviation	3.40	1.01	0.36	0.02	1.30
Coefficient of variation	0.06	0.14	0.12	0.02	0.06

下载: 导出CSV

| 显示表格

表 4 聚乙烯醇(PVA)纤维性能参数

Table 4. Performance parameters of polyvinyl alcohol (PVA) fiber

Type	Length/mm	Diameter/mm	Tensile strength/MPa	Elastic modulus/GPa	Density/(g·cm⁻³)
PVA fiber	12	0.04	1600	42	1.3

下载: 导出CSV

| 显示表格

表 5 玄武岩纤维增强树脂复合材料(BFRP)筋的力学性能

Table 5. Mechanical properties of basalt fiber reinforced polymer (BFRP) bars

BFRP diameter/mm	Ultimate tensile strength/MPa	Elastic modulus/GPa	Percentage elongation/%
6	1279	60.12	2.13
8	1194	60.75	1.97
10	1066	55.84	1.91
12	1350	59.40	2.27

下载: 导出CSV

| 显示表格

1.2 试件设计

研究了不同制作方式、不同连接件角度及不同保温材料厚度对ECC面层与EPS保温层之间界面粘结性能的影响。试验共设置7组，每组试件各3个，共21个试件，试件的具体尺寸、配筋情况及制作方法如图1和表6所示。

图 1 ECC-EPS保温板双面剪切试验尺寸图

Figure 1. Size of ECC-EPS insulation board for double-sided shear test

下载: 全尺寸图片幻灯片

表 6 ECC-EPS保温板试验分组

Table 6. Test group of ECC-EPS insulation board

Specimen number	Type of insulation material	Production method	Insulating layer thickness/mm	BFRP connector or not	Connector insertion angle/(°)
ECC(X)-EPS(70)	EPS	Cast-in-site	70	Without	–
ECC(Y)-EPS(70)	EPS	Prefabrication	70	Without	–
ECC(X)-EPS(50)	EPS	Cast-in-site	50	Without	–
ECC(X)-EPS(100)	EPS	Cast-in-site	100	Without	–
ECC(X)-EPS(70)-BFRP(90)	EPS	Cast-in-site	70	Having	90
ECC(X)-EPS(70)-BFRP(60)	EPS	Cast-in-site	70	Having	60
ECC(X)-EPS(70)-BFRP(45)	EPS	Cast-in-site	70	Having	45
Notes: In specimen number, X—Cast-in-site; Y—Prefabrication; BFRP bar insertion angle refers to the angle between the bar and the specimen in the vertical direction; Insertion depth is 20 mm^[18].

下载: 导出CSV

| 显示表格

试件由三层ECC面板和两层EPS保温板交错分布而成，分布的顺序从左往右依次为ECC面层(厚度为25 mm)、EPS保温层(厚度分别为50 mm、70 mm、100 mm)、ECC面层(厚度为50 mm)、EPS保温层(厚度与前者保温层相同)、ECC面层(厚度为25 mm)。在本次试验中，由于保温层厚度的不同，试件的总体尺寸有三种，分别为400 mm×200 mm×150 mm(保温层厚度为50 mm)、400 mm×240 mm×150 mm(保温层厚度为70 mm)、400 mm×300 mm×150 mm(保温层厚度为100 mm)。同时，试件中共设置有两排连接件，其相对位置如图1的A-A剖面图所示，每一排连接件的布置情况如图1的B-B剖面图所示。最后，本试验中的连接件采用BFRP筋，其插入ECC面层中的深度为20 mm，插入角度分别45°、60°、90°。

试件按照ECC面层及制作方式、保温材料种类及厚度、连接件类型及角度的顺序进行命名。其中，第一项中的ECC(X)表示采用现浇ECC作为面层、ECC(Y)表示采用预制ECC作为面层，第二项中的EPS(50)、EPS(70)、EPS(100)分别表示采用50 mm、70 mm、100 mm厚的EPS保温层，第三项中的BFRP(45)、BFRP(60)、BFRP(90)分别表示插入BFRP连接件的角度为45°、60°、90°。对于无连接件的试件，不再写出第三项的组分信息。例如，表6中的ECC(X)-EPS(70)-BFRP(45)表示该试件的保温材料为EPS，制作方式为现浇，保温层厚度为70 mm，含有BFRP连接件并且连接件角度为45°。

1.3 试件制备

现浇试件的具体制作过程如下：首先，按照试件设计的尺寸制作木模板，同时用切割机将EPS保温板切割成指定尺寸；其次，在保温板表面标出连接件插入点的位置，然后根据定位点和指定的角度将BFRP筋插入保温板中(无连接件的试件省去此步骤)；在连接件插入后，将EPS保温板上不与ECC材料粘结的四个表面用透明胶带裹住；处理完EPS保温板后，在木模板内部涂抹脱模剂，并将EPS保温板放入木模板中，用小木块将EPS保温板按试件设计时的位置进行固定，如图2(a)所示；最后，按照表2所示的配合比制备ECC材料，并将其浇筑到木模板内剩余的空隙中，浇筑完成后振捣并抹平形成完整的试件。此外，在试件制作完成7天后拆除木模板，并持续养护28天以保证试件达到设计强度。最终的试件成型图如图2(b)所示。

图 2 ECC-EPS保温板制备过程

Figure 2. Preparation process of ECC-EPS insulation board

下载: 全尺寸图片幻灯片

预制试件的具体制作过程如下：首先，按照ECC面层的设计尺寸制作木模板；其次，在木模板内部涂抹脱模剂，同时按照表2所示的配合比制备ECC材料；制备好ECC后将其浇筑到木模板中，振捣并抹平；待ECC面层浇筑成型7天后拆除模板，并用粘结砂浆将脱模的ECC面层与保温材料粘结成整体，形成预制试件；最后需将试件养护28天以确保其达到设计强度。此外，需要注意的是，EPS保温板与ECC面板是直接粘结，未使用界面粘结剂。

1.4 试件加载设计

本试验采用双面剪切试验方法，试验中的试件均为对称试件。这种设计与传统的剪切试验相结合，试件推出量近似等于界面滑移量。

在试验过程中，为使试件所受荷载为均布荷载，在中间层ECC的正上方放置一个尺寸为150 mm×50 mm×20 mm的钢垫块。通过DDL-300电子万能试验机和钢垫块将垂直荷载施加到中间层ECC的顶面，以产生穿过界面的直接剪切力。同时，在试验机底座上面和试件底部外侧的两个ECC板下方分别放置钢板和高度为8 mm的钢垫块，以便双面剪切试验的正常进行，如图3(a)所示。

此外，双面剪切试验所用仪器为中国矿业大学力学教学实验室30 吨压力机，位移速率为0.2 mm/min。试件中间ECC层前后中点及试件两侧分别放置两个量程为100 mm和两个量程为30 mm的位移计，分别测量滑移量及偏移量。双面剪切试验示意图，如图3(b)所示。

图 3 ECC-EPS保温板双面剪切试验

Figure 3. Double-sided shear test of ECC-EPS insulation board

下载: 全尺寸图片幻灯片

2. ECC-EPS保温板试验结果与分析

2.1 ECC-EPS保温板双面剪切试验结果

试件的界面粘结性能可通过试件的破坏模式和抗剪强度进行评价。当界面结合面积相同时，抗剪强度由试件在加载过程中所受的荷载决定。由于界面剪切应力的分布是不均匀的，并且距离加载端较近的界面的剪切应力往往会大于距离加载端较远的界面，因此在加载过程中距离加载端较近的两个界面会率先达到极限强度。于是，本试验选用中间两个界面的抗剪强度作为本次双面剪切试验的抗剪强度，其计算公式如下：

${\tau _{{\text{max}}}}{\text{ = }}{P_{\text{m}}}/2A$

(1)

式中：τ_max为试件抗剪强度(MPa)；P_m为抗剪极限荷载值(N)；A为EPS保温板与ECC面层单个结合面的面积(mm²)。

图4为ECC-EPS 保温板破坏形态。可以看出，出现界面破坏的试件都是中间两个界面脱粘引起的，因此根据中间层ECC面板与保温材料粘结的两个界面会率先达到极限强度并发生破坏这一特征提出的抗剪强度计算公式，能够准确地得到试件的抗剪强度。

图 4 ECC-EPS保温板破坏形态

Figure 4. Failure mode of ECC-EPS insulation board

下载: 全尺寸图片幻灯片

双面剪切试验试件的极限荷载、抗剪强度、界面滑移量及破坏模式如表7所示。试件的破坏模式主要分为三种：ECC面层与EPS保温层界面脱粘，发生界面破坏；EPS保温层发生剪切破坏；两侧ECC面层发生受弯破坏。

表 7 ECC-EPS保温板双面剪切试验结果

Table 7. Results of double-sided shear test of ECC-EPS insulation board

Specimen number	Order number	Limit load/kN	Absolute deviation	Displacement/mm				Shear strength/ MPa	Mode of failure
Specimen number	Order number	Limit load/kN	Absolute deviation	Front displacement	Rear displacement	Average value	Absolute deviation	Shear strength/ MPa	Mode of failure
ECC(X)-EPS(70)	1	7.25	0.08	15.90	15.68	15.79	0.49	0.060
	2	7.43	0.10	17.60	17.86	17.73	1.45	0.062	Interfacial failure
	3	7.30	0.03	15.40	15.23	15.32	0.96	0.060
	Average value	7.33	–	–	–	16.28	–	0.060
ECC(Y)-EPS(70)	1	1.92	0.40	3.73	3.87	3.80	0.51	0.016
	2	2.87	0.55	5.73	4.20	4.97	0.66	0.024	Interfacial failure
	3	2.18	0.14	4.35	3.95	4.15	0.16	0.018
	Average value	2.32	–	–	–	4.31	–	0.020
ECC(X)-EPS(50)	1	8.50	0.16	16.41	16.55	16.48	1.49	0.070
	2	8.46	0.20	18.23	18.56	18.40	0.43	0.070	Shear failure of EPS and interfacial failure
	3	9.02	0.36	18.93	19.15	19.04	1.07	0.076
	Average value	8.66	–	–	–	17.97	–	0.072
ECC(X)-EPS(100)	1	6.07	0.00	13.12	15.27	14.20	1.36	0.050
	2	5.74	0.33	11.00	12.31	11.66	1.18	0.048	Interfacial failure
	3	6.39	0.32	11.24	14.10	12.67	0.17	0.054
	Average value	6.07	–	–	–	12.84	–	0.050
ECC(X)-EPS(70)-BFRP(90)	1	11.13	0.45	27.75	29.33	28.54	4.52	0.092
	2	11.89	0.31	19.49	20.38	19.94	4.08	0.100	Shear failure of EPS and BFRP bars splitting
	3	11.72	0.14	23.22	23.95	23.59	0.43	0.098
	Average value	11.58	–	–	–	24.02	–	0.096
ECC(X)-EPS(70)-BFRP(60)	1	20.53	1.07	12.81	13.64	13.23	0.01	0.172
	2	20.60	1.00	11.16	10.40	10.78	2.46	0.172	Bending failure of two ECC boards on the outside
	3	23.67	2.07	15.73	15.69	15.71	2.47	0.198
	Average value	21.60	–	–	–	13.24	–	0.181
ECC(X)-EPS(70)-BFRP(45)	1	47.74	5.33	18.90	20.80	19.85	2.35	0.398
	2	40.60	1.81	19.26	21.30	20.28	2.78	0.338	Interfacial failure
	3	38.90	3.51	12.67	12.05	12.36	5.14	0.324
	Average value	42.41	–	–	–	17.50	–	0.354

下载: 导出CSV

| 显示表格

由表7可知，大部分试件的破坏模式均为界面破坏，如图4(a)所示，并且即使试件未发生界面破坏，其界面处仍出现部分脱粘现象。这是由于在加载过程中，外荷载最先由ECC面层与EPS保温层之间的界面粘结作用来承担。随着荷载的增大，试件底部的中间ECC面层与两侧EPS保温层界面处开始出现裂缝，并向上延伸。对于无连接件的试件，荷载完全由界面粘结作用承担，随着荷载继续增大，裂缝迅速开展直至贯穿整个试件并发生破坏。对于采用BFRP筋作为连接件的试件，试件在出现裂缝后会进行内力重分布，从主要由界面粘结作用来承担外荷载转变为由连接件与界面粘结作用共同承担。因此破坏模式为界面破坏的情况主要发生在无连接件的试件中。

EPS保温层剪切破坏如图4(b)、图4(c)所示。这种破坏模式主要发生在无连接件且保温层厚度为50 mm的试件和有90°连接件的试件中，但是这两种试件发生破坏的原因和形态各不相同。对于无连接件且保温层厚度为50 mm的试件，由于保温层厚度和刚度较小，使EPS保温层随着荷载的增大产生较大的压缩变形。当试件的界面粘结作用和荷载大于EPS的剪切强度时，EPS保温层便会发生剪切破坏，如图4(b)所示。而有90°连接件的试件发生破坏的主要原因是剪切过程中中间层ECC面板中的BFRP连接件会受拉变形，使连接件位置处的保温层出现剪切裂缝，并且裂缝宽度随着变形的增大而增大，直至保温层发生剪切破坏，如图4(c)所示。同时，有90°连接件的试件在加载过程中还伴有BFRP连接件被拔出、拉断和劈裂现象，这是由于连接件在承担荷载时主要依靠其自身的拉拔强度及与ECC之间的的粘结力，当两者不能抵抗所承受的荷载时，便会出现连接件破坏的现象，如图4(e)所示。

ECC面层受弯破坏如图4(d)所示。这种破坏模式主要发生在保温层厚度为70 mm且连接角度为60°的试件中。这是由于ECC中60°的连接件不仅能够承担竖向剪力，还能加强中间层ECC与两侧ECC面层的连接。在加载过程中，BFRP连接件的角度会随着中间层ECC位移的增大而增大。由于嵌入角度为60°的连接件与ECC面层的粘结性能较好，不会发生BFRP连接件拔出现象，因此随着连接件角度的增大，BFRP筋在水平方向的长度也增大。由于连接件与ECC面层的粘结强度大于ECC面层与EPS保温板的粘结强度，因此连接件附近的外侧ECC面层与EPS保温板会首先发生脱粘，进而该处ECC面板会随着BFRP筋水平距离的增大而向外偏移，当ECC面板的横向位移达到其极限弯曲应变时，ECC面板发生破坏。此外，由于外侧ECC面层与EPS保温层的粘结界面仍有部分未发生脱粘，因此这一部分的粘结力会约束ECC面板的弯曲变形，从而导致外侧ECC面板直接断裂。

2.2 ECC-EPS保温板双面剪切试验结果与分析

2.2.1 制作方式的影响

比较图5(a)中的荷载-滑移曲线和表7可知，制作方式的不同不仅会严重影响界面粘结强度，还会改变其破坏模式。如表7所示，现浇试件的极限承载力和抗剪强度是预制试件的2.5倍，这表明采用预制ECC面层制作夹芯结构墙体会严重降低材料的界面粘结性能。由现浇试件和预制试件的荷载-滑移曲线可以看出，二者的荷载-滑移曲线均可大致分为两部分，即上升段和下降段。在上升段，两种试件在加载初期所承受的荷载与界面滑移均呈线性关系，而后随着界面粘结作用的损失，滑移量的增量增大。在下降段，现浇试件在达到峰值荷载后荷载缓慢下降，滑移量显著增大，并且出现多条剪切裂缝，最终发生界面剪切破坏并呈现出延性破坏特征。而预制试件在达到峰值荷载后迅速发生破坏，破坏时中间层ECC面板与EPS保温板完全剥离，呈脆性破坏特征。

图 5 ECC-EPS保温板的荷载-滑移曲线

Figure 5. Load-slip curves of ECC-EPS insulation board

下载: 全尺寸图片幻灯片

2.2.2 保温层厚度的影响

由图5(b)可以看出，EPS保温层厚度为50 mm、70 mm、100 mm试件的荷载-滑移曲线均呈现两个阶段，即线性上升阶段和缓慢下降阶段。在线性上升阶段，保温层厚度为50 mm和70 mm试件的荷载-滑移曲线基本重合，但保温层厚度为70 mm的试件的承载能力要低于50 mm的试件，而保温层厚度为100 mm的试件的承载力更低，曲线斜率也更大。这是由于当ECC面层厚度一定时，减小保温层厚度有助于提高试件的界面剪切刚度(如表7所示，保温层厚度为50 mm的试件相较于厚度为70 mm和100 mm的试件，平均抗剪强度分别提高了20%和44%，并且厚度为70 mm的试件平均抗剪强度比厚度为100 mm的试件提高了20%)，同时较大的保温层厚度还会导致试件的变形能力变差。

2.2.3 有无连接件的影响

由图5(c)可以看出，在荷载-滑移曲线的上升阶段，无连接件试件与连接件角度为90°的试件的斜率相近，但二者的极限承载力和抗剪强度相差很大。这是由于在加载初期，两种试件受到的荷载主要由ECC面层与EPS保温层之间的界面粘结作用承担。随着荷载的增加，无连接件试件承担荷载的方式不变，而嵌入连接件的试件承担荷载的方式从主要由界面粘结作用承担转变为由连接件和界面粘结作用共同承担。因此嵌入连接件的试件具有更高的极限承载力和抗剪强度，如表7所示，ECC(X)-EPS(70)-BFRP(90)试件的平均极限荷载值是ECC(X)-EPS(70)试件的1.6倍，平均抗剪强度提高了60.0%。在荷载滑移曲线的下降段，两种试件的承载力均逐渐降低，但是有连接件的试件承载力的下降较缓慢，并且在较长一段时间内仍保持有一定的承载力。而无连接件的试件在相对较短的时间内承载力会降至最小值。因此，连接件对与夹芯结构墙体的受力、变形等方面有着极其重要作用。

2.2.4 连接件角度的影响

由图5(d)可以看出，对于连接件角度为90°和60°的试件，荷载-滑移曲线可大致分为上升阶段和缓慢下降阶段，而对于连接件角度为45°的试件，荷载-滑移曲线较前者多了增强阶段。对于连接件角度为45°的试件，荷载在达到峰值后承载力仅有少量降低，并且后续还会出现承载力增强的现象。这是由于试件在承受荷载时，界面粘结作用对承载力的贡献逐渐降低，在加载后期主要由连接件来承担，因此45°的连接件在提高试件承载力方面发挥了重大作用。而由于连接件角度为60°的试件提前发生了ECC受弯破坏，其荷载-滑移曲线只有上升阶段和缓慢下降阶段两部分。对于连接件角度为90°的试件，由于连接件与ECC面层的粘结性能相对较弱，在发生破坏时，界面未出现较大的剥离，粘结力仍在发挥作用，并且出现BFRP筋被拔出等现象，这也导致了这种类型的试件未出现增强阶段。此外，连接件角度为45°的试件的承载能力和抗剪强度都要远高于连接件角度为60°和90°的试件，其试件的平均抗剪强度是60°和90°试件的2倍和3.7倍，极限承载力也分别提高了96.3%、266.2%。

2.3 ECC-EPS保温板韧性

为了进一步评价试件的界面粘结性能，采用Kim等^[20]提出的耗能理论，并引入韧性指数(Toughness index，α_S)来评价试件达到峰值后的耗能能力。韧性指数反映了试件加载后期界面粘结性能与试件破坏所需能量之间的转换关系，其数值越大，则试件在承载后期的抗剪性能越好：

${\alpha _{\text{S}}} = \frac{{E_{\text{post}}}}{{\left( {P_{\text{peak}} \delta_ {\text{peak}}} \right)/2}}$

(2)

式中：α_S为韧性指数；E_post为峰值荷载后的能量值(kN·mm)；P_peak为极限荷载值(kN)；δ_peak为极限荷载值时的界面滑移量(mm)。具有如下关系：

${E_{{\text{post}}}} = \int_{{\delta _{{\text{post-peak}}}}}^{{\delta _{{\text{peak}}}}} {P{\text{d}}\delta }$

(3)

式中：E_post取峰值荷载处到滑移量为20 mm时的荷载-滑移曲线下的面积。对于滑移量不够20 mm的试件曲线，终点为曲线终止处，峰值荷载后的能量值对应的界面滑移量δ_post-peak为20 mm。本文利用图6中网格分割法来估算E_post值。试件的E_post、P_peak、δ_peak及韧性指数值如表8所示。

图 6 峰值荷载后的能量E_post计算

P_peak—Limit load value (kN); δ_peak—Interface slip value at the limit load (mm); δ_post-peak—Interface slip corresponding to the energy value after the peak load

Figure 6. Calculation of energy value after peak load E_post

下载: 全尺寸图片幻灯片

由表8可知，有连接件的试件的韧性指数普遍较高，其中连接件角度为45°的试件的韧性指数最高，这表明了连接件的存在有助于提高试件的延性，避免发生脆性破坏。在无连接件试件中保温层厚度为50 mm的韧性指数最大，说明此类试件在加载后期界面间的粘结性能仍较好，延性较高，这与试验现象相吻合。

3. 夹芯结构墙体抗剪承载力计算

为了能够更加深入地了解夹芯结构墙体的破坏机制，基于Tomlinson等^[18]的分析理论提出了双面剪切试验抗剪承载力公式，预测了有连接件试件的抗剪承载力和结构中各因素对荷载值的贡献比例，并采用试验结果对计算公式进行了验证。

表 8 ECC-EPS保温板韧性指数

Table 8. Toughness index of ECC-EPS insulation board

Specimen number	E_post/(kN·mm)	P_peak/kN	δ_peak/mm	α_S
ECC(X)-EPS(70)	36.7	7.25	3.49	2.90
ECC(Y)-EPS(70)	2.4	2.87	1.51	1.09
ECC(X)-EPS(50)	78.8	9.02	4.46	3.92
ECC(X)-EPS(100)	25.8	6.07	6.68	1.27
ECC(X)-EPS(70)-BFRP(90)	124.2	11.89	5.90	3.54
ECC(X)-EPS(70)-BFRP(60)	142.0	23.67	1.88	6.38
ECC(X)-EPS(70)-BFRP(45)	425.0	47.74	2.55	6.98
Notes: E_post—Energy value after the peak load (kN·mm); α_S—Toughness index.

下载: 导出CSV

| 显示表格

由图4(d)可以看出，嵌入角度为60°BFRP连接件的试件均发生ECC面板受弯破坏，因此试件的抗剪强度应为ECC面板的弯曲破坏强度。然而，在加载过程中，ECC面板的受力较复杂，其不仅受到BFRP筋的横向推力，还受到界面粘结力的作用，这便导致了试验中ECC面板的弯曲破坏，但这种破坏与四点弯曲破坏并不完全相同。因此，在计算此类型试件的承载力时不能直接采用ECC材料的弯曲破坏强度作为试件的抗剪强度。于是，ECC面板对于抗剪承载力的贡献近似采用连接件和界面粘结作用对抗剪承载力的贡献之和来表示。因此在计算试件的抗剪承载力时，嵌入角度为45°和60°BFRP连接件的试件的抗剪承载力计算公式相同。

抗剪承载力主要有两个方面组成，分别为绝缘保温层与ECC面层间的界面粘结力F_in(N)和连接件的抗剪作用。其中，90°连接件的抗剪作用采用F_dw(N)来表示；45°、60°连接件的抗剪作用采用F_tr(N)来表示。因此，试件的抗剪承载力F值可用下式来表示，并作出四个假设，即梁理论适用于试件中连内外叶ECC面层的连接件；BFRP连接件为线弹性；保温板的破坏是由于对角拉伸分裂而失效的；在双面剪切试验过程中ECC面层不会发生挤压破碎：

$F=F_\text{in}+F_\text{dw}或F_\text{tr}$

(4)

3.1 夹芯结构中各因素对承载力的贡献

3.1.1 绝缘保温层对抗剪承载力的贡献

假设剪切变形很小，则剪切应变可用δ₁/L来表示。进而可得到绝缘保温层对抗剪承载力的贡献，其计算公式如下：

$F_{\text{in}} = \frac{{{G_{{\text{in}}}}{A_{{\text{in}}}}{\delta _{\text{1}}}}}{L}$

(5)

其中，F_in的最大值F_in,max为

$F_{\text{in,max}} = f_{\text{u,in}}A_{\text{in}}$

(6)

式中：G_in为保温材料的剪切模量(EPS材料为2.27 MPa)；A_in为保温受剪切面面积(等于bh，b为剪切面宽度，h为剪切面高度)(mm²)； $L$ 为保温层厚度(mm)；δ₁为相对滑移量(mm)，选荷载-滑移曲线中荷载首次突降时的滑移值；f_u,in为保温材料的抗拉强度(MPa)。

根据双面剪切试验结果，对保温层厚度为50 mm、70 mm、100 mm的试件的极限抗剪承载力进行拟合，将λ作为保温层厚度影响系数，则式(5)可调整为

$F_{\text{in}} = \lambda \frac{{{G_{{\text{in}}}}{A_{{\text{in}}}}\delta }}{L}$

(7)

其中， $\lambda = - {\text{5}}{\text{.411}} \times {10^{{{ - 4}}}}{L^2} + 0.080L - 1.922$ 。

3.1.2 嵌入90°的连接件对抗剪的贡献

由于嵌入90°连接件的销钉作用相当于结构中的固定梁，因此其对抗剪承载力的贡献可用下式表示：

$F_{\text{dw}} = \frac{{{\text{12}}E_{\text{sc}}I_{\text{sc}}\delta_ {\text{2}}}}{{\mathop L\nolimits^3 }}$

(8)

其中，F_dw的最大值F_{dw, max}为

$F_{\text{dw,max}} = \frac{{{\text{4}}f_{\text{u,sc}}I_{\text{sc}}}}{{L\phi }}$

(9)

式中：E_sc为连接件的弹性模量(MPa)；I_sc为连接件的转动惯量(mm⁴)；δ₂为相对滑移量(mm)，选取荷载-滑移曲线中荷载第二次突降时的滑移值；f_u,sc为连接件的抗压强度(MPa)，取其抗拉强度的30%^[21]； $\phi$ 为连接件直径(mm)。

3.1.3 嵌入角度为45°、60°的连接件对抗剪承载力的贡献

由于连接件的轴向分量决定了连接系统的性能，于是采用连接件的轴向应变ε_sc,a进行计算，其计算公式如下：

${\varepsilon }_{\text{sc,a}}=\frac{\Delta d_\text{ac}}{d_\text{ac}}=\frac{\sqrt{(L\mathrm{tan}\theta +\delta _\text{2}{)}^{2}+{L}^{2}}-d_\text{ac}}{d_\text{ac}}$

(10)

则连接件对抗剪性能的贡献F_tr可用下式表示：

$F_\text{tr}={F}_{\text{ac}}\mathrm{sin}\theta {'}=E_\text{sc}\varepsilon _\text{sc,a}A_\text{sc}{\mathrm{tan}}^{-1}\left(\frac{L\mathrm{tan}\theta +\delta_ \text{2}}{L}\right)$

(11)

式中：d_ac为连接件原始长度；F_ac为轴向力；A_sc为连接件的横截面面积(mm²)； $\theta '$ 为连接件在受力变形后与试件水平方向夹角(°)；θ为连接件与试件水平方向夹角(°)；E_sc为连接件弹性模量(MPa)。

当45°、60°连接件受到拉力而处于拉伸状态，并且杆所受的应力f_tr,strength超过BFRP的抗拉强度f_u,b时，连接件会发生断裂。此时，连接件发生拉伸破坏时的荷载值F_tr,strength应采用下式进行计算：

$F_{\text{tr,strength}} = f_{\text{tr,strength}}A_{\text{sc}}\sin \theta '$

(12)

其中：

${f}_{\text{tr,strength}}=\frac{\sqrt{(L\mathrm{tan}\theta +\delta {)}^{\text{2}}+{L}^{\text{2}}}-d_\text{ac}}{d_\text{ac}}E_\text{sc}+\frac{3E_\text{sc}\phi }{{L}^{2}}\delta _\text{2}$

(13)

当45°、60°连接件与ECC发生脱粘被拔出时，F_tr,strength应采用下式进行计算：

$F_{\text{tr,bond}} = f_{\text{tr,bond}}A_{\text{sc}}\sin \theta$

(14)

其中：

$f_\text{tr,bond}=\frac{0.083\sqrt{{f}_{\text{u,e}}}}{\alpha }\left(\text{13}\text{.6}\frac{d_\text{e}}{\phi }+\frac{C}{\phi }\frac{d_\text{e}}{\phi }+340\right)$

(15)

式中：f_u,e为ECC抗压强度(MPa)；d_e为连接件的嵌入长度(mm)；C 为BFRP筋中心位置到ECC面层边缘的最小保护层厚度(mm)； $\alpha$ 为连接件位置系数(当 $C/\phi$ 超过3.5时，取3.5，当嵌入深度小于 $20\phi$ 时， $\alpha$ 取值为 ${d}_{{\rm{e}}}/(20\phi )$ )；F_{tr, bond}为连接件发生脱粘破坏时的荷载值(N)。

最后，嵌入角度为45°和60°BFRP连接件的承受能力取式(12)和式(14)中的最小值。

3.2 理论值验证

对带有连接件且已画出荷载-滑移曲线图的EPS试件的极限承载力理论值和试验值进行对比分析，结果如表9所示。可以看出，采用上述计算公式计算得到的理论值与试验值的吻合度较高，因此采用上述公式来预测试件的抗剪承载力具有一定的可靠性。同时由计算结果还可以看出，对于连接件角度为90°的试件，保温材料对抗剪承载力的理论贡献值要大于连接件的理论贡献值。而对于连接件角度为45°和60°的试件，连接件对抗剪承载力的理论贡献值更大，并且对于发生ECC面板弯曲破坏的试件采用连接件与界面粘结作用对抗剪承载力的贡献来计算抗剪承载力能够满足实际需要。

表 9 ECC-EPS保温板计算荷载与实际荷载值对比

Table 9. Comparison of calculated load and actual load of ECC-EPS insulation board

Specimen number	Failure load/kN			Theoretical contribution value/%
Specimen number	Experimental value	Theoretical value	Experimental value/ Theoretical value	Thermal insulating material	Connectors
ECC(X)-EPS(70)-BFRP(90)	11.89	11.11	1.07	70.21	29.79
ECC(X)-EPS(70)-BFRP(60)	23.67	22.77	1.04	16.51	83.49
ECC(X)-EPS(70)-BFRP(45)	47.74	32.56	1.47	15.66	84.34

下载: 导出CSV

| 显示表格

4. 结论

(1) 由于预制夹芯结构墙板的粘结性能比现浇墙板差很多，因此在制备夹芯结构墙体时应尽可能采用现浇方式。

(2) 由于保温层厚度过小会导致保温层发生剪切破坏，而厚度过大会导致界面剪切刚度下降，因此在设计夹芯墙体时应合理选择保温层厚度。

(3) 为了提高试件的韧性和降低脆性破坏的可能性，夹芯结构墙体应该设置有连接件，同时为了保证连接件能够有效发挥作用，连接件应尽可能选择自身抗拉性能好、抗剪强度高且与工程水泥基复合材料(ECC)面层有良好粘结的材料。

(4) 不同处理方式下的夹芯墙体结构粘结性能优劣顺序为：嵌入连接件角度45°＞嵌入连接件角度60°＞嵌入连接件角度90°＞保温层厚50 mm＞保温层厚70 mm＞保温层厚100 mm＞预制。

(5) 综合比较各处理方式对夹芯结构粘结性能的影响，在设计夹芯墙体时应优先选用现浇方式，连接件的嵌入角度选为45°，保温层厚度选为70 mm。

(6) 基于Teixeira的分析理论推导的夹芯结构抗剪承载力与试验结果的吻合度较高，可以用于预测试件的抗剪承载力。

图 1 不同PVA浓度下PCM@PVA纺丝液静置24 h后的照片

Figure 1. Photos of the PCM@PVA solutions with different PVA concentrations after 24 h ((a) 6.0wt%; (b) 8.0wt%; (c) 10.0wt%; (d) 14.0wt%)

下载: 全尺寸图片幻灯片

图 2 不同PVA浓度所得PCM@PVA纤维的SEM图像

Figure 2. SEM images of PCM@PVA fibers prepared at different PVA concentrations ((a) 6.0wt%; (b) 8.0wt%; (c) 10.0wt%; (d) 14.0wt%)

下载: 全尺寸图片幻灯片

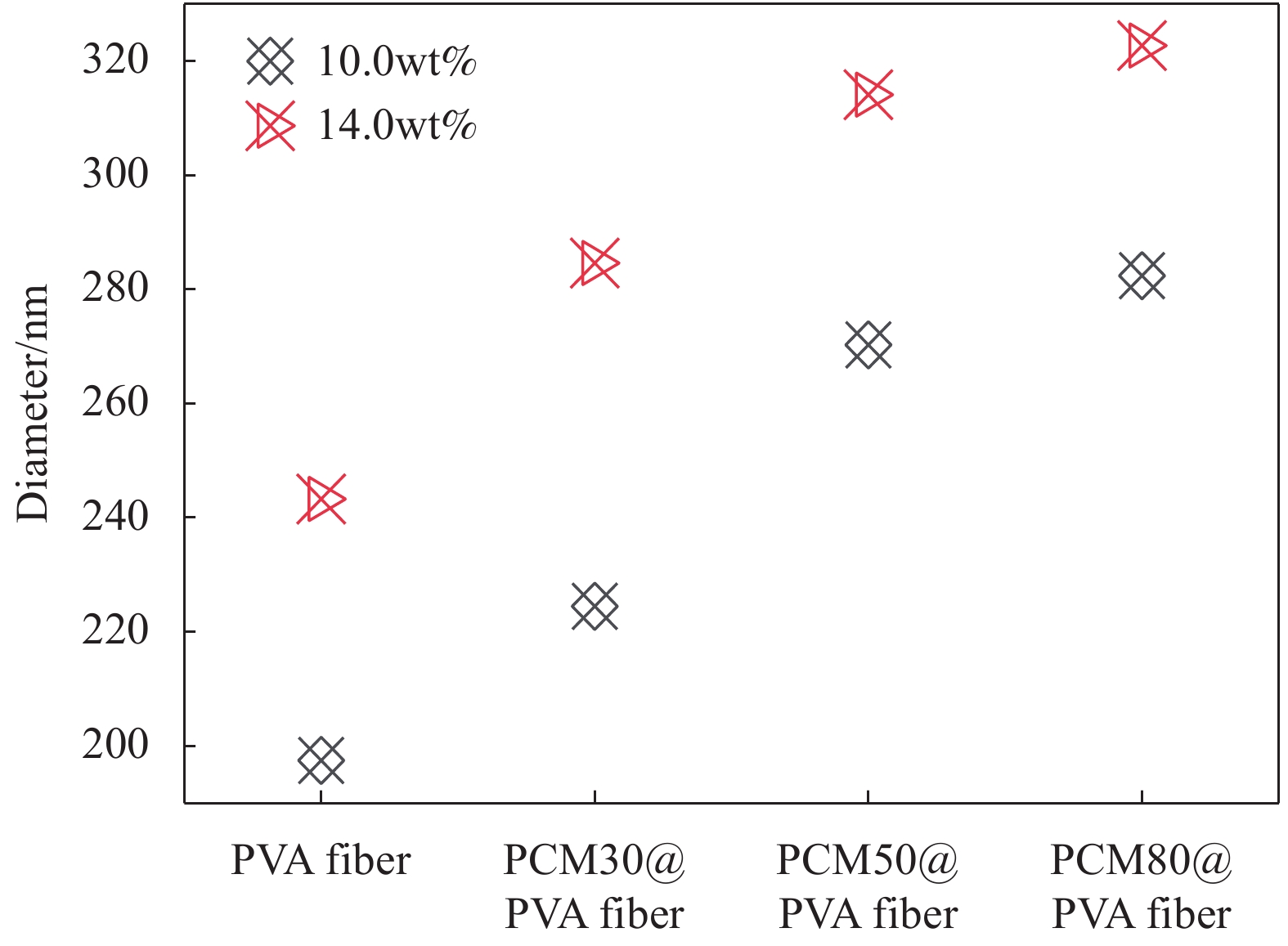
图 3 10.0wt%和14.0wt%PVA浓度制备的静电纺纤维的SEM图像

Figure 3. SEM images of electrospun fibers with 10.0wt% and 14.0wt% PVA concentrations ((a) PVA fiber (10.0wt%); (b) PCM30@PVA fiber (10.0wt%); (c) PCM50@PVA fiber (10.0wt%); (d) PCM80@PVA fiber (10.0wt%); (e) PVA fiber (14.0wt%); (f) PCM30@PVA fiber (14.0wt%); (g) PCM50@PVA fiber (14.0wt%); (h) PCM80@PVA fiber (14.0wt%))

下载: 全尺寸图片幻灯片

图 4 10.0wt%和14.0wt%PVA浓度制备的静电纺纤维的平均直径

Figure 4. Average diameter profile of electrospun fibers with 10.0wt% and 14.0wt% PVA concentrations

下载: 全尺寸图片幻灯片

图 5 10.0wt% (a) 和14.0wt% (b) PVA浓度制备的静电纺纤维及PCM的DSC曲线

Figure 5. DSC curves of PCM and electrospun fibers with 10.0wt% (a) and 14.0wt% (b) PVA concentrations

下载: 全尺寸图片幻灯片

图 6 10.0wt%和14.0wt%PVA制备的PCM@PVA纤维热处理后在吸油纸上的照片

Figure 6. Photos of PCM@PVA fibers prepared by 10.0wt% and 14.0wt% PVA on oil-absorbing sheet after heat treatment ((a) PCM30@PVA fiber (10.0wt%); (b) PCM50@PVA fiber (10.0wt%); (c) PCM80@PVA fiber (10.0wt%); (d) PCM30@PVA fiber (14.0wt%); (e) PCM50@PVA fiber (14.0wt%); (f) PCM80@PVA fiber (14.0wt%))

下载: 全尺寸图片幻灯片

图 7 不同样品的TEM图像

Figure 7. TEM images of different samples((a) PVA fiber; ((b), (c)) PCM@PVA fiber; (d) CPVA-PCM fiber)

下载: 全尺寸图片幻灯片

图 8 不同样品的TGA曲线

Figure 8. TGA curves of different samples

下载: 全尺寸图片幻灯片

图 9 PVA纤维和PCM@PVA纤维的降温曲线

Figure 9. Cooling curves of PVA fibers and PCM@PVA fibers

下载: 全尺寸图片幻灯片

图 10 PVA纤维和PCM@PVA纤维的热红外成像图

Figure 10. Thermal infrared images of PVA fibers and PCM@PVA fibers((a) PVA fiber; (b) PCM30@PVA fiber; (c) PCM50@PVA fiber; (d) PCM80@PVA fiber)

下载: 全尺寸图片幻灯片

图 11 不同样品的拉伸曲线

Figure 11. Tensile curves of different samples

下载: 全尺寸图片幻灯片

图 12 PCM@PVA纤维 (a) 和CPVA-PCM纤维 (b) 在不同时间的水溶解情况

Figure 12. Water solubility of PCM@PVA fiber (a) and CPVA-PCM fiber (b) at different time

下载: 全尺寸图片幻灯片

表 1 材料名称与缩写对应

Table 1 Corresponding of material name and abbreviation

Sample		Abbreviation
Fibers with different dodecanol dodecanoate∶PVA mass ratios	30%	PCM30@PVA fiber
	50%	PCM50@PVA fiber
	80%	PCM80@PVA fiber
Dodecanol dodecanoate@polyvinyl alcohol thermal storage solution		PCM@PVA solution
Dodecanol dodecanoate-polyvinyl alcohol thermal storage fiber		PCM@PVA fiber
Crosslinked polyvinyl alcohol/dodecanol dodecanoate thermal storage fiber		CPVA-PCM fiber
Notes: PCM—Phase change material; PVA—Polyvinyl alcohol; CPVA—Crosslinking PVA.

下载: 导出CSV

表 2 不同PCM@PVA纤维样品的热性能数据

Table 2 Thermal performance data of different PCM@PVA fiber samples

Sample	T_mo/℃	T_m/℃	ΔH_m/(J·g⁻¹)	T_co/℃	T_c1/℃	T_c2/℃	ΔH_c/(J·g⁻¹)
PCM	25.10	28.10	193.70	24.34	23.64	—	193.25
PVA fiber(10.0wt%)	—	—	—	—	—	—	—
PCM30@PVA fiber(10.0wt%)	25.96	28.72	26.91	24.81	23.99	8.51	26.99
PCM50@PVA fiber(10.0wt%)	26.30	29.71	63.18	25.11	24.88	14.63	62.52
PCM80@PVA fiber(10.0wt%)	26.69	29.07	72.48	25.07	25.01	14.29	72.32
PVA fiber(14.0wt%)	—	—	—	—	—	—	—
PCM30@PVA fiber(14.0wt%)	25.38	28.07	28.53	25.42	22.41	7.29	27.42
PCM50@PVA fiber(14.0wt%)	25.59	28.60	63.50	24.04	23.47	8.67	61.23
PCM80@PVA fiber(14.0wt%)	25.30	28.72	73.37	24.16	23.72	7.43	73.44
Notes: T_mo—Onset melting temperature; T_m—Melting temperature; ΔH_m—Melting enthalpy; T_co—Onest crystallizing temperature; T_c1—First crystallizing temperature; T_c2—Second crystallizing temperature; ΔH_c—Crystallization enthalpy.

下载: 导出CSV

表 3 不同样品的热分解数据

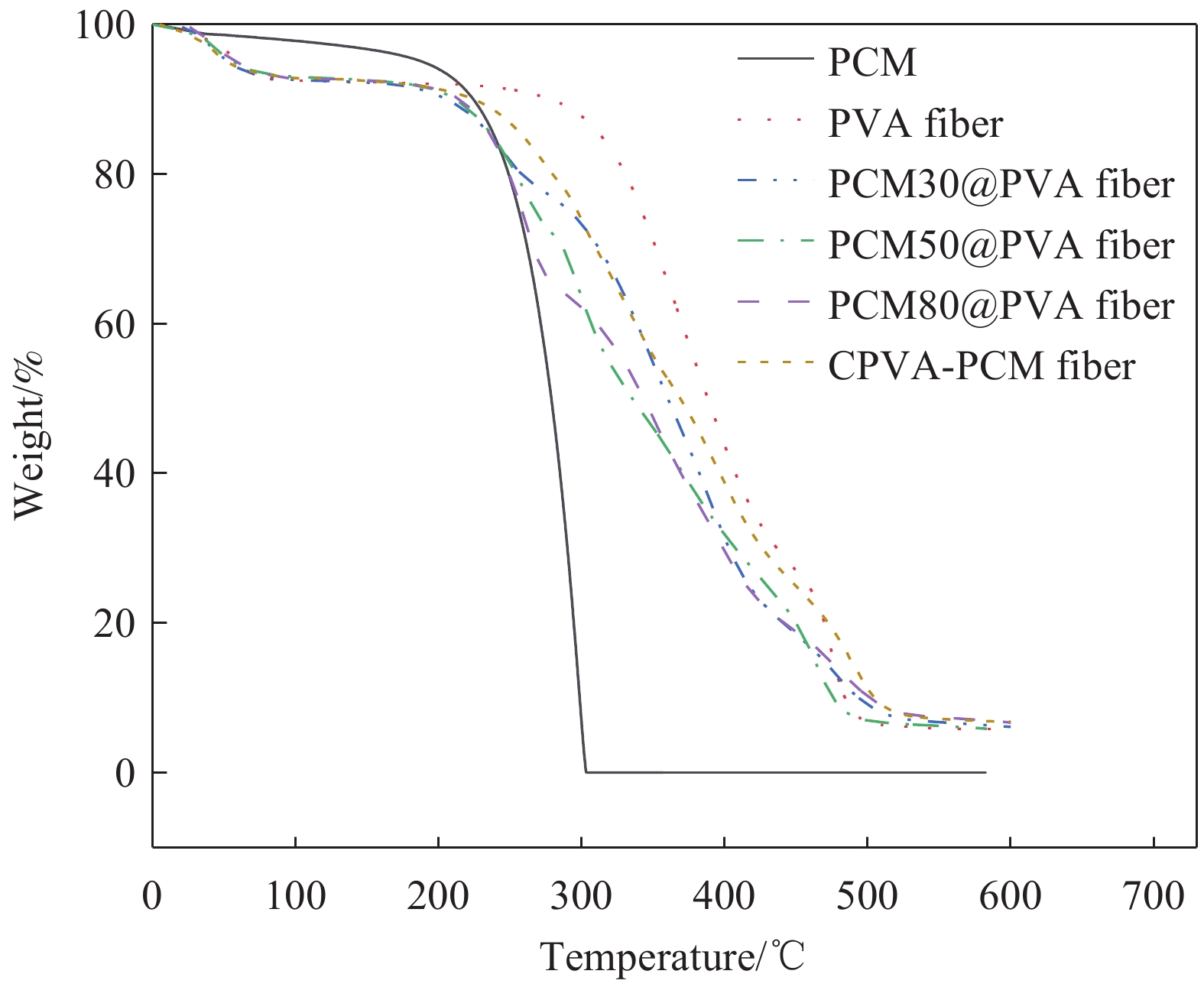
Table 3 Thermal decomposition data of different samples

Sample	T₁/℃	W₁/wt%	T₂/℃	W₂/wt%	T₃/℃	W₃/wt%	T₄/℃	W₄/wt%	W/wt%
PCM	190	100	—	—	—	—	—	—	100
PVA fiber	20	7.5	270	64.5	445	22	—	—	94
PCM30@PVA fiber	20	7.5	210	13.5	270	57	434	15	93
PCM50@PVA fiber	20	7.5	210	21	270	44.5	420	21	94
PCM80@PVA fiber	20	7.5	210	29	270	42	434	14.5	93
CPVA-PCM fiber	20	7.5	210	42.5	355	25	450	19	94
Notes: T₁, T₂, T₃, T₄—Initial degradation temperatures of the 1st, 2nd, 3rd and 4th stages; W₁, W₂, W₃, W₄—Mass loss fractions of the 1st, 2nd, 3rd and 4th stages; W—Final mass loss fraction.

下载: 导出CSV

参考文献(23)

[1]	张渤, 牟思阳, 李圣林, 等. 二元脂肪酸/生物基SiO₂复合相变材料的制备与性能[J]. 复合材料学报, 2016, 33(11):2674-2681. ZHANG B, MOU S Y, LI S L, et al. Preparation and properties of binary fatty acids/bio-based SiO₂ phase change composites[J]. Acta Materiae Compositae Sinica,2016,33(11):2674-2681(in Chinese).
[2]	李树芹, 陈赛, 王学晨, 等. 梳状相变聚合物为芯材的复合调温纤维的制备及热性能[J]. 复合材料学报, 2018, 35(1):8-15. LI S Q, CHEN S, WANG X C, et al. Fabrication and thermal properties of wet-spun thermo-regulating fibers with a novel comb-like phase change polymer core[J]. Acta Materiae Compositae Sinica,2018,35(1):8-15(in Chinese).
[3]	ZHOU D, ZHAO C Y, TIAN Y. Review on thermal energy storage with phase change materials (PCMs) in building applications[J]. Applied Energy,2012,92(4):593-605.
[4]	CHOI K, CHO G. Physical and mechanical properties of thermostatic fabrics treated with nanoencapsulated phase change materials[J]. Journal of Applied Polymer Science,2011,121(6):3238-3245. DOI: 10.1002/app.33870
[5]	BENMOUSSA D, MOLNAR K, HANNACHE H, et al. Novel thermo-regulating comfort textile based on poly(allyl ethylene diamine)/n-hexadecane microcapsules grafted onto cotton fabric[J]. Advances in Polymer Technology,2016,37(24):419-428.
[6]	WUTTIG M, YAMADA N. Phase-change materials for rewriteable data storage[J]. Nature materials,2007,6(11):824-832. DOI: 10.1038/nmat2009
[7]	BHARDWAJ N, KUNDU S C. Electrospinning: A fascinating fiberfabrication technique[J]. Biotechnology Advances,2010,28(3):325-347. DOI: 10.1016/j.biotechadv.2010.01.004
[8]	NASOURI K, SHOUSHTARI A M, MOJTAHEDI M R M. Effects of polymer/solvent systems on electrospun polyvinylpyrrolidone nanofiber morphology and diameter[J]. Polymer Science Series A,2015,57(6):747-755. DOI: 10.1134/S0965545X15060164
[9]	YUAN Y, ZHANG N, TAO W, et al. Fatty acids as phase change materials: A review[J]. Renewable and Sustainable Energy Reviews,2014,29:482-498. DOI: 10.1016/j.rser.2013.08.107
[10]	LIU C Z, RAO Z H, ZHAO J T, et al. Review on nanoencapsulated phase change materials: Preparation, characterization and heat transfer enhancement[J]. Nano Energy,2015,13:814-826.
[11]	DO C V, NGUYEN T T T, PARK J S. Fabrication of polyethylene glycol/polyvinylidene fluoride core/shell nanofibers via melt electrospinning and their characteristics[J]. Solar Energy Materials and Solar Cells,2012,104:131-139. DOI: 10.1016/j.solmat.2012.04.029
[12]	WU Y, CHEN C Z, JIA Y F, et al. Review on electrospun ultrafine phase change fibers (PCFs) for thermal energy storage[J]. Applied Energy,2018,210:167-181. DOI: 10.1016/j.apenergy.2017.11.001
[13]	蔡以兵, 孙桂岩, 刘盟盟, 等. 定形相变复合材料的研究进展—静电纺丝法[J]. 高分子通报, 2015(2):18-25. CAI Y B, SUN G Y, LIU M M, et al. The research progress of form-stable phase change composite marerials—electrospinning[J]. Polymer Bulletin,2015(2):18-25(in Chinese).
[14]	ZHANG C, FENG F Q, ZHANG H. Emulsion electrospinning: Fundamentals, food applications and prospects[J]. Trends in Food Science & Technology,2018,80:175-186.
[15]	ZHAO L, LUO J, LI Y, et al. Emulsion-electrospinning n-octadecane/silk composite fiber as environmental-friendly form-stable phase change materials[J]. Journal of Applied Polymer Science,2017,134(47):1-10.
[16]	ZDRAVEVA E, FANG J, MIJOVIC B, et al. Electrospun poly(vinyl alcohol)/phase change material fibers: Morphology, heat properties, and stability[J]. Industrial & Engineering Chemistry Research,2015,54(35):8706-8712.
[17]	ZHANG G Q, CAI C W, ZHU G C, et al. Preparation, properties and encapsulation of high thermostability phase-change material[J]. Journal of Fiber Bioengineering and Informatics,2019,12(1):43-54. DOI: 10.3993/jfbim00307
[18]	CAI C W, OUYANG X, ZHOU L, et al. Cosolvent free interfacial polycondensation and properties of polyurea PCM microcapsules with dodecanol dodecanoate as core material[J]. Solar Energy,2020,199:721-730. DOI: 10.1016/j.solener.2020.02.071
[19]	PAIPITAK K, PORNPRA T, MONGKONTALANG P, et al. Characterization of PVA-chitosan nanofibers prepared by electrospinning[J]. Procedia Engineering,2011,13(8):101-105.
[20]	ZHAO J H, SUN Z Y, SHAO Z B, et al. Effect of surface-active agent on morphology and properties of electrospun PVA nanofibres[J]. Fibers and Polymers,2016,17(6):896-901. DOI: 10.1007/s12221-016-6163-y
[21]	李珍, 王军. 静电纺丝可纺性影响因素的研究成果[J]. 合成纤维, 2008, 9:6-11. DOI: 10.3969/j.issn.1001-7054.2008.09.002 LI Z, WANG J. Studies on influential factors on nanofiber spinnability of electrospinning[J]. Synthetic Fiber in China,2008,9:6-11(in Chinese). DOI: 10.3969/j.issn.1001-7054.2008.09.002
[22]	WANG J, YAO H B, HE D, et al. Facile fabrication of gold nanoparticles-poly(vinyl alcohol) electrospun water-stable nanofibrous mats: Efficient substrate materials for biosensors[J]. ACS Applied Materials & Interfaces,2012,4(4):1963-1971.
[23]	PERESIN M S, HABIBI Y, ZOPPE J O, et al. Nanofiber composites of polyvinyl alcohol and cellulose nanocrystals: Manufacture and characterization[J]. Macromolecules,2010,11:674-681.

施引文献(15)

期刊类型引用(8)

1.	刘伟，杨继，袁春辉，夏旭，张锦光. 不同温度下碳纤维复合材料-钢胶接界面黏结性能研究. 复合材料科学与工程. 2025(03): 39-45+70 . 百度学术
2.	邵家儒，刘牛，杨瑜，郑子君. CFRP复合材料构件胶接特性及失效规律研究. 应用力学学报. 2023(05): 1058-1067 . 百度学术
3.	陈旭，曹亚周，崔健，葛继文. 碳纤维复合材料车体地板长大型材粘接工艺研究及装备设计. 机械. 2022(11): 63-69 . 百度学术
4.	陈卓异，彭彦泽，李传习，郭靖. 高温下双搭接钢-CFRP板胶粘界面力学性能试验. 复合材料学报. 2021(02): 449-460 . 本站查看
5.	李传习，李游，贺君，刘一鸣，彭彦泽. 固化剂对室温胶黏CFRP板/钢板界面性能的影响. 建筑材料学报. 2021(02): 339-347 . 百度学术
6.	杨峰，陈玉龙，罗旺，史剑，贾林江，陈子光. TG800碳纤维/聚酰亚胺树脂复合材料带翻边开口圆柱壳机匣件高温气动载荷下的承载性能. 复合材料学报. 2021(07): 2184-2195 . 本站查看
7.	桑海涛，周昕. 暖通空调胶接结构搭接接头承载力优化研究. 中国胶粘剂. 2021(11): 51-54+72 . 百度学术
8.	李传习，李游，高有为，胡正，刘一鸣. 纳米SiO_2质量分数对胶粘碳纤维增强树脂复合材料板-钢搭接界面黏结性能的影响. 复合材料学报. 2020(10): 2619-2635 . 本站查看