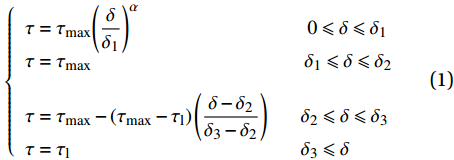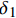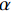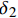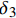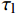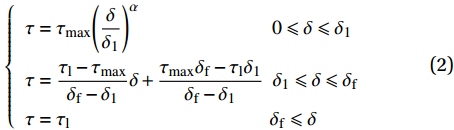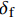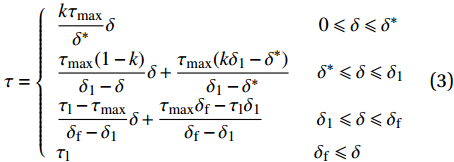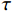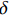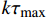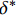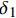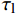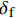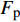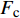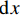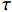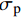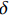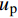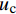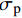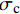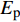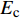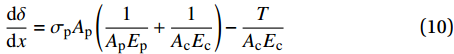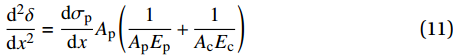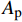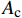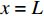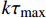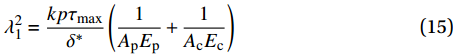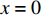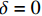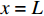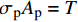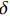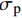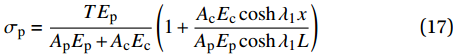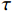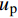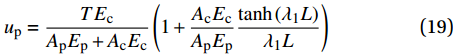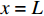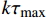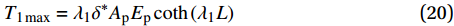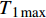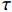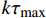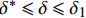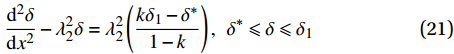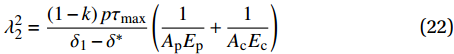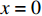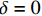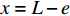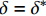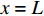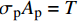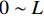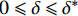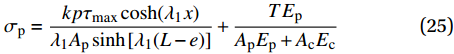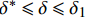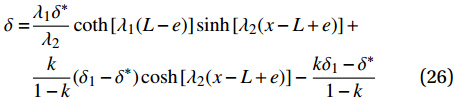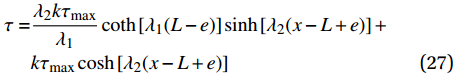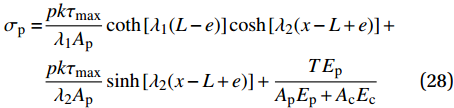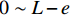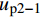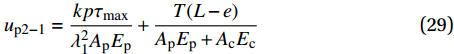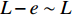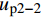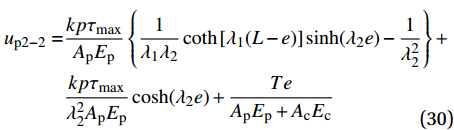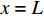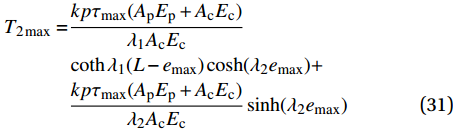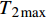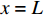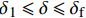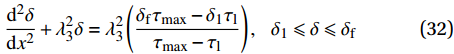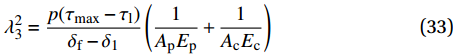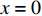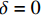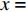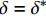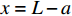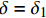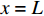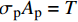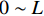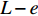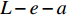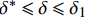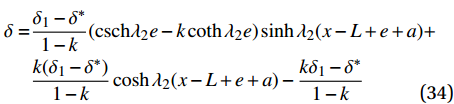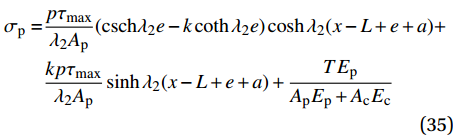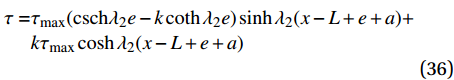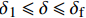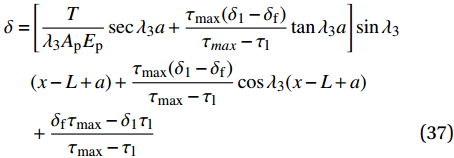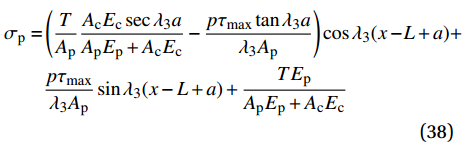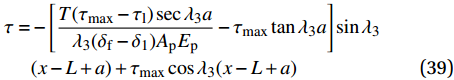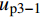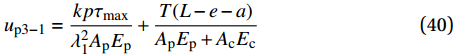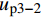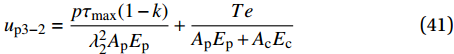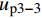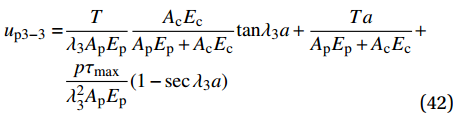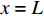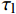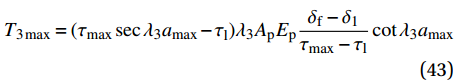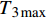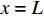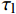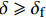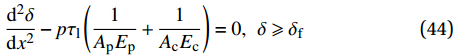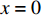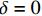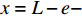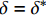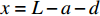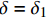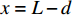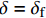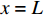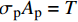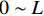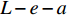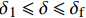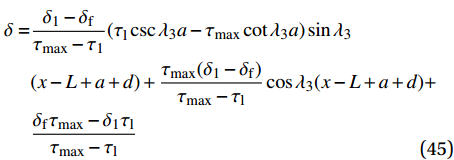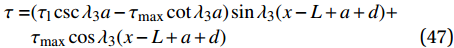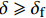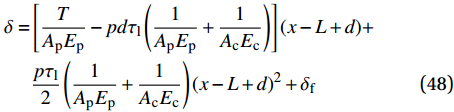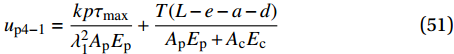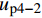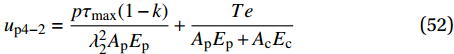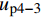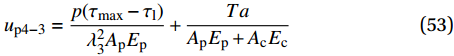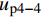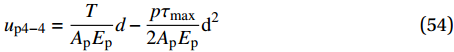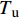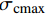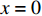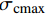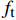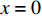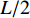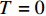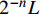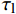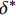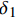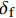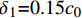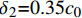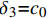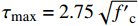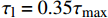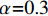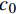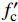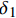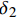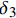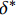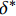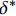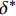Deformation analysis method of FRP bar/concrete tension members by considering tension stiffening effect
-
摘要: 考虑拉伸刚化效应是精确计算纤维增强树脂复合材料(FRP)筋/混凝土构件变形和裂缝的基础。提出了考虑拉伸刚化效应的FRP筋/混凝土拉伸构件变形计算的解析方法。首先,对修正Eligehausen黏结滑移模型(修正BPE模型)进行简化提出四线性黏结-滑移模型。根据该模型推导了拉伸构件在不同拉伸荷载阶段的FRP筋、混凝土应力和变形及黏结力和滑移量的分布表达式。结合混凝土开裂判别方法,提出了FRP筋/混凝土拉伸构件的全过程变形计算方法。通过与已有文献试验结果对比验证了本文方法的准确性。对影响拉伸刚化的一些参数进行了敏感性分析。结果表明,混凝土强度和配筋率对拉伸刚化效应影响不大,FRP筋弹性模量是影响拉伸刚化效应的主要因素。
-
关键词:
- 纤维增强树脂复合材料(FRP)筋 /
- 轴拉构件 /
- 拉伸刚化 /
- 黏结-滑移 /
- 配筋率
Abstract: The tension stiffening effect is the premise of accurate evaluation of the deformation and crack width of fiber reinforced polymer composite (FRP) bar/concrete members. An analytical method for determining the deformation of FRP bar/concrete tension member was proposed. A simplified four-linear model based on the modified Eligehausen model (modified BPE model) was presented. The distribution of stress, displacement of FRP bars and concrete and the distribution of bond force, slip between bars and concrete were established. By combining with the cracking criterion of concrete, an algorithm for the deformation of FRP reinforced tensive ties at different loading stages was proposed. After verification by comparing with experimental data in the literature, the effects of different parameters on the tension stiffening were analyzed. Parametric analysis results indicate that concrete strength and reinforcement ratio of FRP bars have a minor impact on the tension stiffening effect. However, the elastic modulus of FRP bars dominates the tension stiffening behavior of FRP reinforced concrete tensile elements. -
国内外大量理论和试验研究表明[1-2],服役条件下纤维增强树脂复合材料(FRP)筋/混凝土构件的变形和裂缝宽度均大于钢筋/混凝土构件,导致FRP筋/混凝土构件的设计经常是正常使用极限状态控制。因此,准确计算FRP筋/混凝土构件的刚度和裂缝宽度是进行FRP筋/混凝土结构设计的前提。FRP筋/混凝土构件开裂后,由于FRP筋与混凝土之间存在黏结作用,相邻裂缝间混凝土和FRP筋共同承受拉力,从而使构件裂缝间FRP筋的平均轴向刚度大于纯FRP筋的轴向刚度,这一现象称为拉伸刚化[3-4]。因此,为了精确计算FRP筋/混凝土构件的变形和裂缝宽度,必须考虑拉伸刚化效应。
目前对于FRP筋/混凝土刚化效应的理论和试验研究开展得均不多。理论方面,根据不同的目的可以将考虑拉伸刚化模型分为宏观模型和微观模型[5]。宏观模型主要包括有效模量模型和修正本构方程模型。杆系结构分析通常采用有效模量模型方法。该方法采用杆件未开裂截面和开裂截面的惯性矩的某种组合来表示杆件的有效惯性模量,主要用于计算杆件的变形。目前已有的FRP筋/混凝土构件有效模量模型主要在钢筋/混凝土构件模型的基础上修正得到,如ACI-440模型[6]和EC2模型[7]等;对于较为精细的分析,如二维、三维有限元分析,则采用修改钢筋或混凝土的应力-应变关系的方式考虑拉伸刚化效应。该方法在模型引入一些参数(如配筋率、FRP筋与混凝土的模量比)来控制相应材料应力-应变曲线的形状,常见的考虑拉伸刚化的混凝土本构方程有Bischoff混凝土模型[8]等。微观模型主要以FRP筋/混凝土拉伸试件为主要研究对象,通常以一维力学模型为基础,考虑FRP筋/混凝土之间的黏结-滑移关系,采用不同的解析和数值方法对该模型进行求解,并得到力和平均应变等关系,微观模型主要关注FRP筋/混凝土结构拉伸刚化机制,并用于校核宏观模型。Baena等[9]采用非线性有限差分法对FRP筋/混凝土拉伸构件变形过程分析。该研究采用实测黏结-滑移关系考虑拉伸刚化效应,计算结果与试验结果和EC2模型预测结果均吻合良好。Miglietta等[10]采用离散元-有限元混合法研究了玻璃纤维增强树脂复合材料(GFRP)筋/混凝土拉伸构件的拉伸刚化,并与已有试验结果进行对比。结果表明,离散元-有限元混合法能够对构件变形、裂缝间距和宽度及裂缝的扩展情况进行较为精确的模拟。Ghiassi等[11]对FRP布加固拉伸混凝土构件进行分析。研究考虑了混凝土开裂后裂缝间的桥联力、钢筋/混凝土间黏结力及FRP/混凝土间黏结力。研究结果用于确定裂缝间距、FRP布临界粘贴率、FRP布黏结强度及粘贴长度。Bischoff等[8]通过试验研究表明同等应变水平下,GFRP筋/混凝土构件的拉伸刚化效应大于钢筋/混凝土应变,认为拉伸刚化效应与配筋率无关,并基于此提出了拉伸刚化效应系数。Baena等[12]通过试验研究对比了ACI规范和EC2规范的刚度模型与裂缝宽度模型的预测精度。结果表明,ACI规范公式高估了构件的刚度,EC2规范公式计算结果与试验结果吻合良好。裂缝宽度预测方面则ACI规范公式优于EC2规范公式。Vilanova等[13]通过试验研究了持续荷载作用下GFRP筋的拉伸刚化效应。结果表明,持续荷载作用下GFRP筋与混凝土的黏结力发生退化,从而导致拉伸刚化效应退化。研究结果还表明,拉伸刚化效应损失率随混凝土强度的增大而减小。
综上可知,目前关于FRP筋构件拉伸刚化效应理论研究中,已有研究的数值解法尽管能得到拉伸构件的全程受力过程,但其缺点在于实现较为复杂,且不便于获取控制参数。为解决以上问题,本文在前人研究基础上,提出了基于简化四线性黏结-滑移模型的FRP筋/混凝土拉伸构件全过程分析解析解。在通过已有试验数据验证其正确性后,对控制其拉伸刚化效应的影响因素进行参数分析。
1. 纤维增强树脂复合材料(FRP)筋/混凝土黏结-滑移模型
国内外学者对FRP筋/混凝土的黏结-滑移关系进行了大量研究,并提出相应的黏结-滑移模型[14]。目前应用较广的主要有三个模型,分别为BPE模型、BPE改进模型和Harajli模型。
1.1 BPE模型
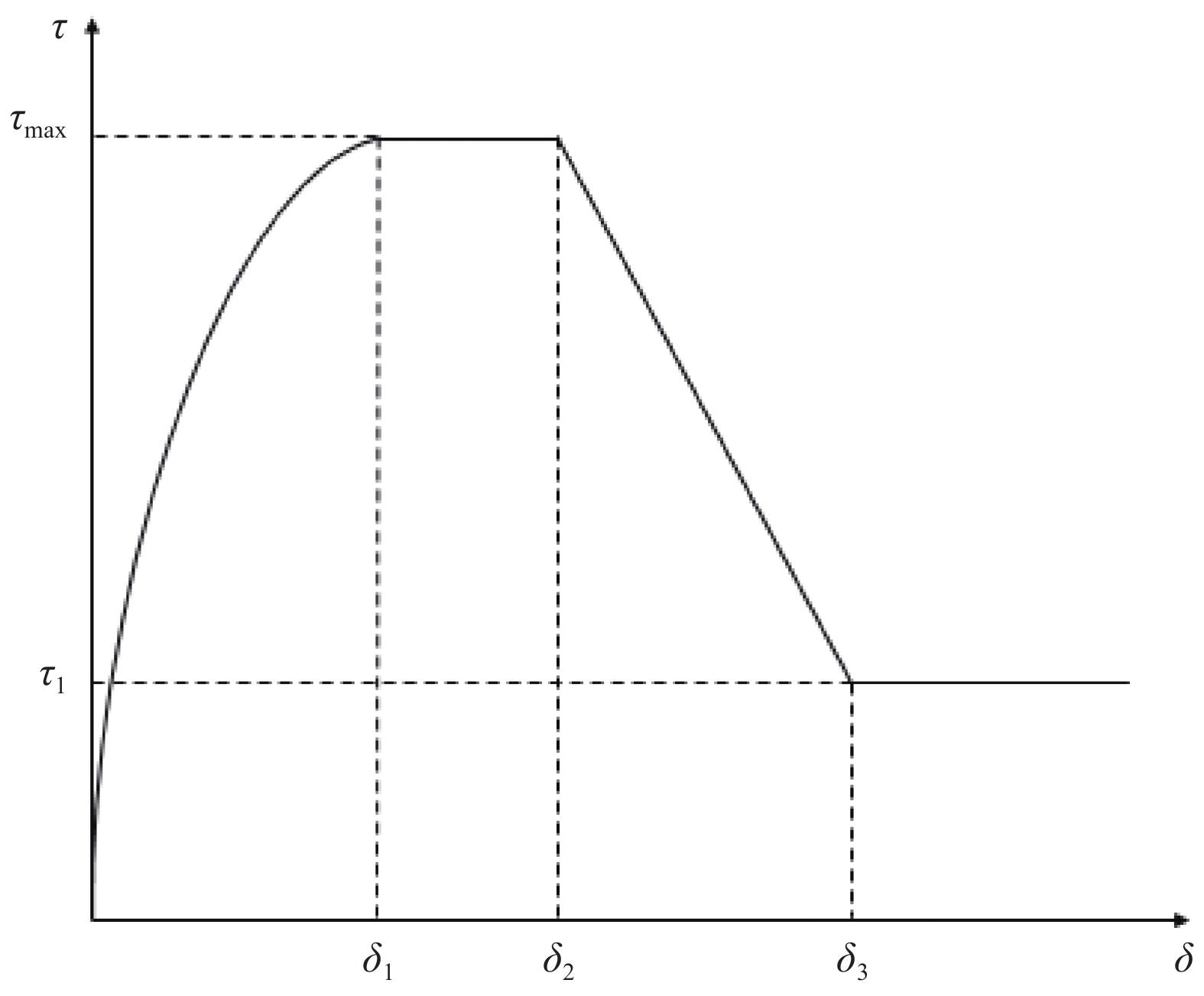
BPE模型由Eligehausen等[15]提出,该模型可分为四个阶段(如图1所示):(1)化学胶结力和机械咬合力逐渐发挥作用的非线性上升阶段;(2)最大切应力恒定阶段;(3)机械咬合力和化学胶结力逐渐失效的线性下降阶段;(4)表面摩擦力主导的摩擦切应力恒定阶段。
BPE模型的数学表达式为
{τ=τmax (1) 式中:
{\tau _{\max }} 为最大黏结应力;{\delta _1} 为达到{\tau _{\max }} 对应的滑移量;\alpha 为控制非线性上升阶段的曲率参数;{\delta _2} 为第二阶段结束时对应的滑移量;{\delta _3} 为第三阶段结束时滑移量;{\tau _{\rm{l}}} 为摩擦切应力恒定阶段大小。1.2 BPE改进模型
Cosenza等[16]通过对比试验曲线和数值分析曲线发现,对于FRP筋而言,并不需要考虑最大切应力恒定阶段,基于该事实,提出了BPE改进模型,如图2所示,其数学表达式为
\left\{ \begin{array}{l} \tau = {\tau _{\max }}{\left( {\dfrac{\delta }{{{\delta _1}}}} \right)^\alpha }\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \leqslant \delta \leqslant {\delta _1}\\ \tau = \dfrac{{{\tau _{\rm{l}}} - {\tau _{\max }}}}{{{\delta _{\rm{f}}} - {\delta _1}}}\delta + \dfrac{{{\tau _{\max }}{\delta _{\rm{f}}} - {\tau _{\rm{l}}}{\delta _1}}}{{{\delta _{\rm{f}}} - {\delta _1}}}\;\;{\delta _1} \leqslant \delta \leqslant {\delta _{\rm{f}}}\\ \tau = {\tau _{\rm{l}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\delta _{\rm{f}}} \leqslant \delta \end{array} \right. (2) 式中,
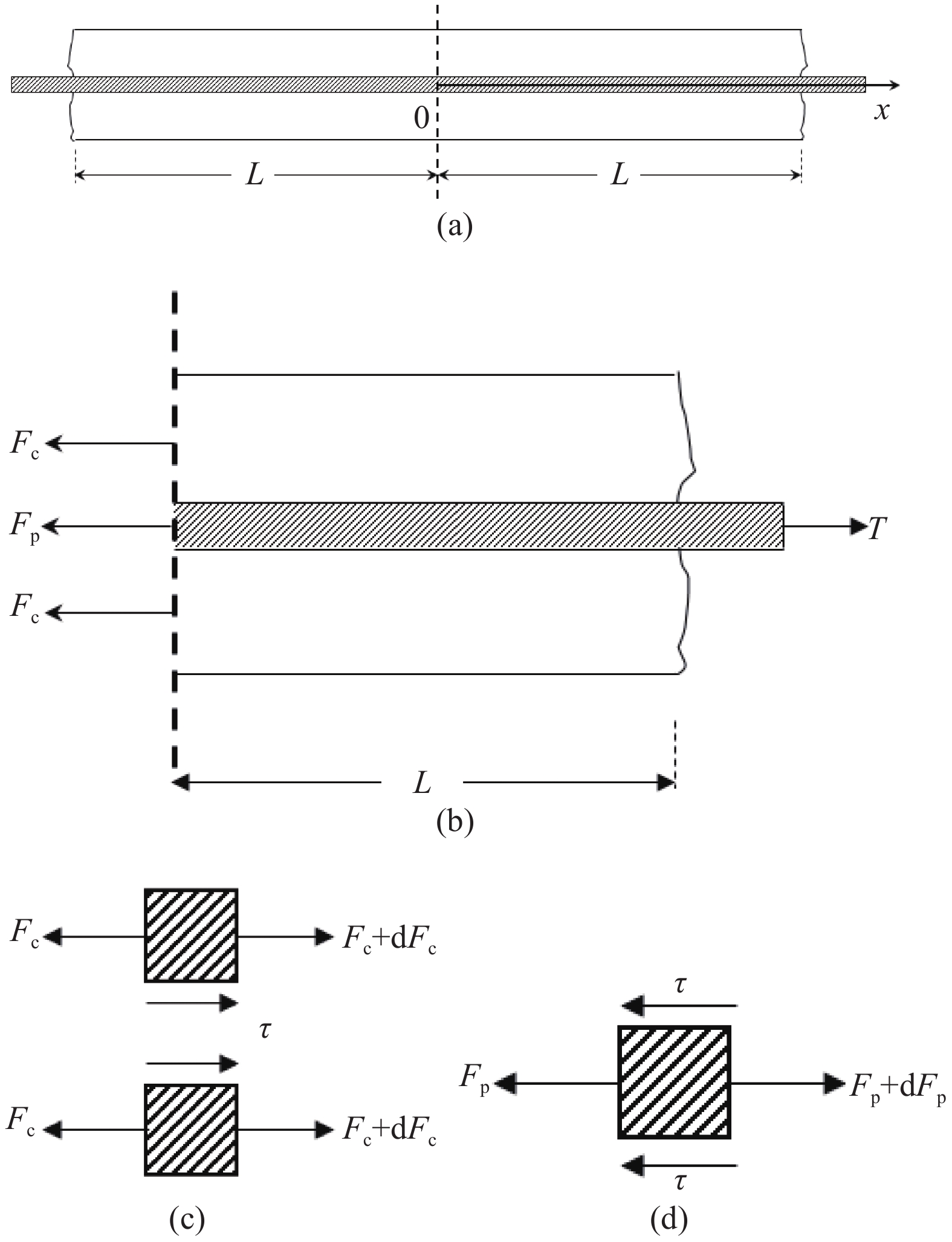
{\delta _{\rm{f}}} 为线性下降段结束时对应的滑移量。1.3 Harajli模型
Harajli等[17-19]根据不同的黏结破坏形式,提出了适用于普通变形钢筋和FRP筋的Harajli模型,如图3所示,该模型表达式与BPE模型相同,不同之处在于对模型参数的取值。
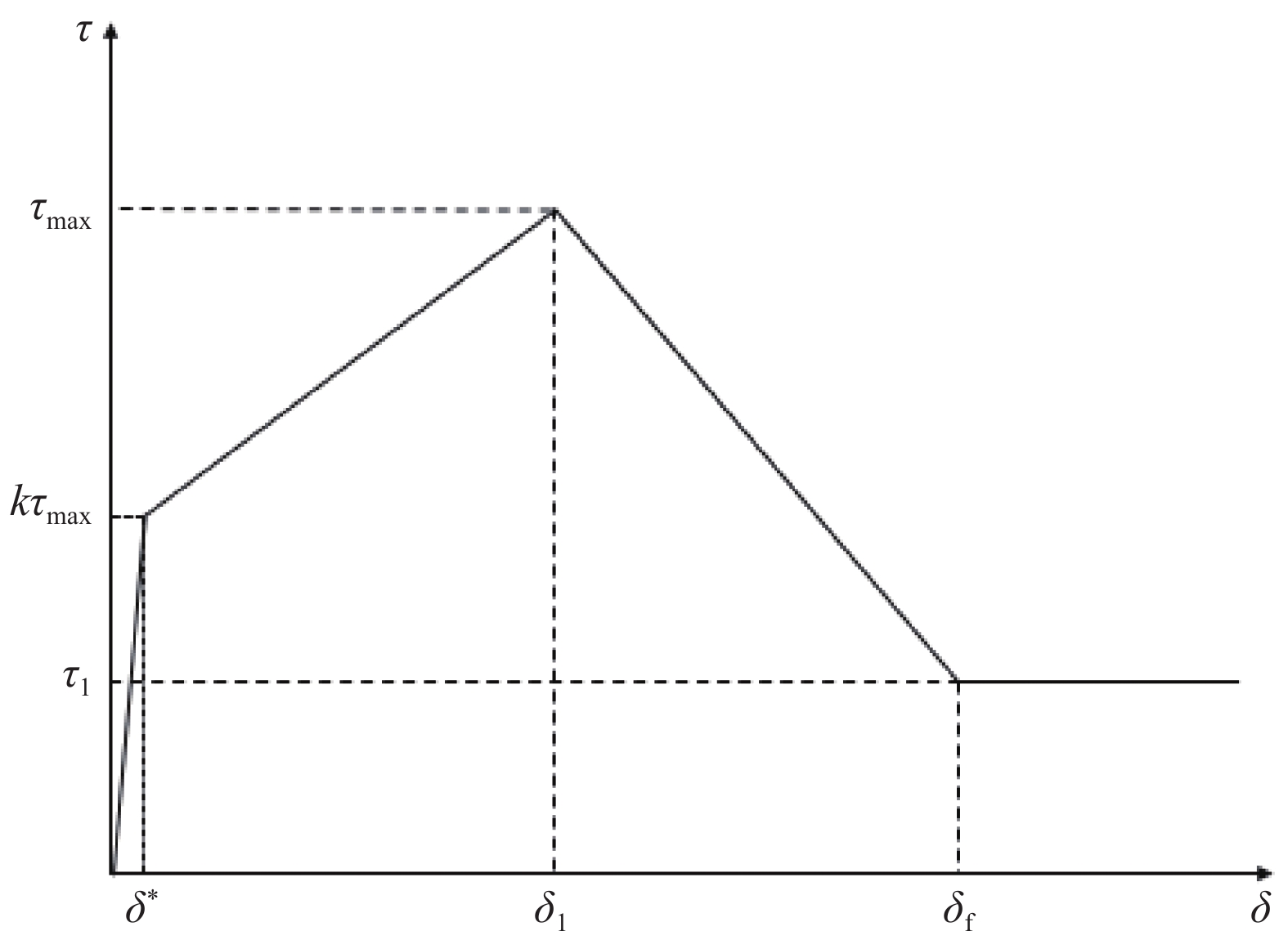
为了简化后续过程推导,本文在上述模型基础上,对BPE改进模型进行简化,提出四线性黏结-滑移模型,如图4所示,在保证黏结-滑移曲线面积不变的原则下,将BPE改进模型中的非线性上升段简化为两段斜率递减的上升段,线性下降阶段和摩擦切应力恒定阶段保持不变。其中参数取值结合三个模型,根据构件中的FRP筋类型和混凝土强度而定。因此,黏结-滑移关系可表示为
\tau = \left\{ \begin{array}{l} \dfrac{{k{\tau _{\max }}}}{{{\delta ^*}}}\delta \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \leqslant \delta \leqslant {\delta ^*}\\ \dfrac{{{\tau _{\max }}(1 - k)}}{{{\delta _1} - \delta }}\delta + \dfrac{{{\tau _{\max }}(k{\delta _1} - {\delta ^*})}}{{{\delta _1} - {\delta ^*}}}\;\;\;\;\;\;{\delta ^*} \leqslant \delta \leqslant {\delta _1}\\ \dfrac{{{\tau _{\rm{l}}} - {\tau _{\max }}}}{{{\delta _{\rm{f}}} - {\delta _1}}}\delta + \dfrac{{{\tau _{\max }}{\delta _{\rm{f}}} - {\tau _{\rm{l}}}{\delta _1}}}{{{\delta _{\rm{f}}} - {\delta _1}}}\;\;\;\;\;\;\;\;\;\;\;\;{\delta _1} \leqslant \delta \leqslant {\delta _{\rm{f}}}\\ {\tau _{\rm{l}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\delta _{\rm{f}}} \leqslant \delta \end{array} \right. (3) 式中:
\tau 为FRP筋和混凝土间的切应力;\delta 为FRP筋和混凝土间的相对滑移;k{\tau _{\max }} 为弹性阶段结束切应力大小,对应的滑移量为{\delta ^*} ;{\tau _{\max }} 为最大切应力,对应滑移量为{\delta _1} ;{\tau _{\rm{l}}} 为水平段切应力大小,对应滑移量为{\delta _{\rm{f}}} 。2. FRP筋/混凝土轴线拉伸控制方程
考虑一长度为2L的FRP筋/混凝土轴线拉伸构件,如图5(a)所示。设FRP筋轴线为x轴,以构件为原点建立坐标系,轴向拉力T沿x轴,直接作用于FRP筋。在推导过程中,采取如下假定:(1) FRP筋轴线必定与构件轴线重合,不存在偏心距;(2)混凝土截面各处变形相同,即不考虑应变梯度效应;(3) FRP筋和混凝土均为均匀材料,破坏前为线弹性材料,且其界面各点黏结-滑移关系一致。
由于对称性,以下仅取x轴正方向的一半构件作为研究对象[20]。由图5(b)所示单元体可以建立平衡方程如下:
{F_{\rm{p}}} + {F_{\rm{c}}} = T (4) 式中:
{F_{\rm{p}}} 为FPR筋所受轴力;{F_{\rm{c}}} 为混凝土所受轴力。在FRP筋与混凝土的接触面分别取出长度为
{\rm{d}}x 的FRP筋单元体与混凝土单元体,由图5(c)和图5(d)可得单元体平衡方程为\frac{{{\rm{d}}{F_{\rm{p}}}}}{{{\rm{d}}x}} = \tau p, \;\;\frac{{{\rm{d}}{F_{\rm{c}}}}}{{{\rm{d}}x}} = - \tau p (5) 式中:
\tau 为接触面的切应力;p为FRP筋截面周长。根据式(5)可以得到FRP筋应力为
\frac{{{\rm{d}}{\sigma _{\rm{p}}}}}{{{\rm{d}}x}} = \frac{{2\tau }}{r} (6) 式中:
{\sigma _{\rm{p}}} 为FRP筋正应力;r为FRP筋半径。根据定义相对滑移
\delta 可表示为\delta = {u_{\rm{p}}} - {u_{\rm{c}}} (7) 式中:
{u_{\rm{p}}} 为FRP筋的伸长量;{u_{\rm{c}}} 为混凝土的伸长量。根据假设(3),FRP筋与混凝土的本构方程可表式为
{\sigma _{\rm{p}}} = {E_{\rm{p}}}\frac{{{\rm{d}}{u_{\rm{p}}}}}{{{\rm{d}}x}} (8) {\sigma _{\rm{c}}} = {E_{\rm{c}}}\frac{{{\rm{d}}{u_{\rm{c}}}}}{{{\rm{d}}x}} (9) 式中:
{\sigma _{\rm{p}}} 和{\sigma _{\rm{c}}} 分别为FRP筋轴向应力和混凝土轴向应力;{E_{\rm{p}}} 和{E_{\rm{c}}} 分别为FRP筋和混凝土的弹性模量。对式(7)分别求一阶、二阶导数,并结合式(8)和式(9)可得
\frac{{{\rm{d}}\delta }}{{{\rm{d}}x}} = {\sigma _{\rm{p}}}{A_{\rm{p}}}\left( {\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}} \right) - \frac{T}{{{A_{\rm{c}}}{E_{\rm{c}}}}} (10) \frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{x^2}}} = \frac{{{\rm{d}}{\sigma _{\rm{p}}}}}{{{\rm{d}}x}}{A_{\rm{p}}}\left( {\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}} \right) (11) 式中,
{A_{\rm{p}}} 和{A_{\rm{c}}} 分别为FRP筋和混凝土的横截面积。将式(6)代入式(11)可得到控制方程如下:
\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{x^2}}} - {\lambda ^2}\tau = 0 (12) 其中,
{\lambda ^2} = p\left(\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}\right) (13) 3. FRP筋/混凝土拉伸过程计算
利用四线性黏结-滑移模型,并结合控制方程式(12),可以将FRP筋/混凝土构件拉伸过程划分为四个阶段。
3.1 弹性阶段
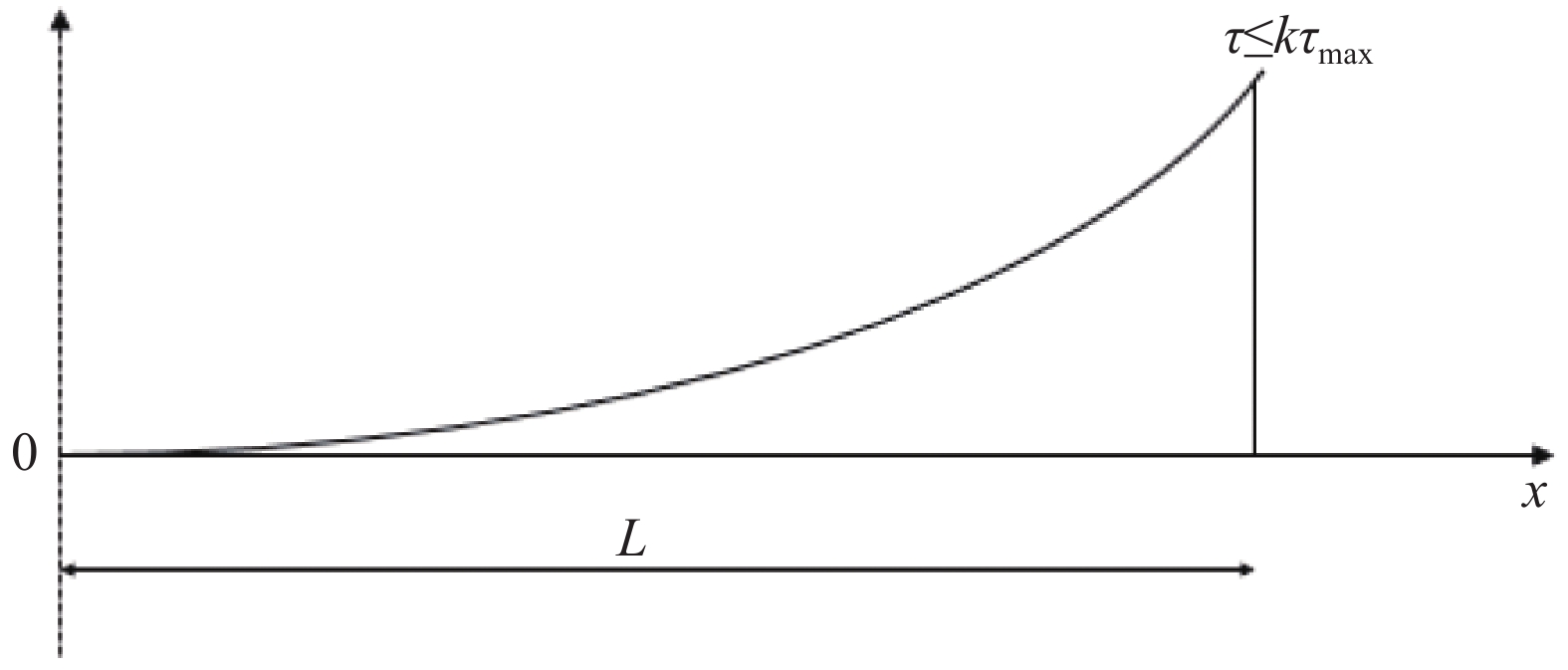
当轴向拉力T较小,在
x = L 处的\tau 小于k{\tau _{\max }} 时,组成黏结力的化学胶结力和机械咬合力随着拉力增大逐渐起作用,此时黏结-滑移处于弹性阶段,分离体内黏结应力分布如图6所示。将
0 \leqslant \delta \leqslant {\delta ^*} 时对应的式(3)代入式(12)可得:\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{x^2}}} - \lambda _1^2\delta = 0 (14) 其中,
\lambda _1^2 = \frac{{kp{\tau _{\max }}}}{{{\delta ^*}}}\left( {\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}} \right) (15) 该阶段的边界条件为:(1)
x = 0 ,\delta = 0 ;(2)x = L ,{\sigma _{\rm{p}}}{A_{\rm{p}}} = T 。根据上述边界条件可求得滑移量
\delta 为\delta = \frac{{T\sinh {\lambda _1}x}}{{{\lambda _1}{A_{\rm{p}}}{E_{\rm{p}}}\cosh {\lambda _1}L}} (16) 将式(16)代入式(10)可求得FRP筋应力
{\sigma _{\rm{p}}} 为{\sigma _{\rm{p}}} = \frac{{T{E_{\rm{p}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}}\left( {1 + \frac{{{A_{\rm{c}}}{E_{\rm{c}}}\cosh {\lambda _1}x}}{{{A_{\rm{p}}}{E_{\rm{p}}}\cosh {\lambda _1}L}}} \right) (17) 将式(16)代入式(12)可求得接触面切应力
\tau 为\tau = \frac{{Tk{\tau _{\max }}\sinh {\lambda _1}x}}{{{\lambda _1}{\delta ^*}{A_{\rm{p}}}{E_{\rm{p}}}\cosh {\lambda _1}L}} (18) 在0~L内对式(17)积分可得FRP筋伸长量
{u_{\rm{p}}} 为{u_{\rm{p}}} = \frac{{T{E_{\rm{c}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}}\left( {1 + \frac{{{A_{\rm{c}}}{E_{\rm{c}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}}}}\frac{{\tanh \left( {{\lambda _1}L} \right)}}{{{\lambda _1}L}}} \right) (19) 当
x = L 处的切应力等于k{\tau _{\max }} 时,该阶段结束,此时施加在构件上的轴向拉力大小为{T_{1\max }} = {\lambda _1}{\delta ^*}{A_{\rm{p}}}{E_{\rm{p}}}\coth \left( {{\lambda _1}L} \right) (20) 3.2 硬化阶段
当轴向拉力大于
{T_{1\max }} 时,在x=L处的\tau 逐渐大于k{\tau _{\max }} ,化学胶结力和机械咬合力伴随着微弱的失效继续增大,直到达到{\tau _{\max }} 。此时黏结-滑移处于硬化阶段,记硬化长度为e,分离体内黏结应力如图7所示,将对应的式(3)代入式(11),其中弹性段的方程同式(14)。求得{\delta }^{*}\leqslant \delta \leqslant {\delta }_{1} 时对应的方程为\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{x^2}}} - \lambda _2^2\delta = \lambda _2^2\left( {\frac{{k{\delta _1} - {\delta ^*}}}{{1 - k}}} \right), \;\;{\delta ^*} \leqslant \delta \leqslant {\delta _1} (21) 其中,
\lambda _2^2 = \frac{{\left( {1 - k} \right)p{\tau _{\max }}}}{{{\delta _1} - {\delta ^*}}}\left( {\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}} \right) (22) 该阶段的边界条件为:(1)
x = 0 ,\delta = 0 ;(2)x = L - e ,\delta = {\delta ^*} ;(3)x = L ,{\sigma _{\rm{p}}}{A_{\rm{p}}} = T ;(4)在0 \sim L 内,任意位置FRP筋应力连续可导。因此,可求出0 \leqslant \delta \leqslant {\delta ^*} 范围内的表达式为\delta = \frac{{{\delta ^*}\sinh \left( {{\lambda _1}x} \right)}}{{\sinh \left[ {{\lambda _1}\left( {L - e} \right)} \right]}} (23) \tau = \frac{{k{\tau _{{\rm{max}}}}\sinh ({\lambda _1}x)}}{{\sinh \left[ {{\lambda _1}(L - e)} \right]}} (24) {\sigma _{\rm{p}}} = \frac{{kp{\tau _{\max }}\cosh ({\lambda _1}x)}}{{{\lambda _1}{A_{\rm{p}}}\sinh \left[ {{\lambda _1}(L - e)} \right]}} + \frac{{T{E_{\rm{p}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (25) 求得
{\delta ^*} \leqslant \delta \leqslant {\delta _1} 范围内的表达式为\begin{split} \delta =& \dfrac{{{\lambda _1}{\delta ^*}}}{{{\lambda _2}}}\coth \left[ {{\lambda _1}(L - e)} \right]\sinh \left[ {{\lambda _2}(x - L + e)} \right] + \\& \dfrac{k}{{1 - k}}({\delta _1} - {\delta ^*})\cosh \left[ {{\lambda _2}(x - L + e)} \right] - \dfrac{{k{\delta _1} - {\delta ^*}}}{{1 - k}} \end{split} (26) \begin{split} \tau =& \frac{{{\lambda _2}k{\tau _{\max }}}}{{{\lambda _1}}}\coth \left[ {{\lambda _1}(L - e)} \right]\sinh \left[ {{\lambda _2}(x - L + e)} \right] +\\& k{\tau _{\max}}\cosh \left[ {{\lambda _2}(x - L + e)} \right] \end{split} (27) \begin{split} {\sigma _{\rm{p}}} =& \frac{{pk{\tau _{\max }}}}{{{\lambda _1}{A_{\rm{p}}}}}\coth \left[ {{\lambda _1}(L - e)} \right]\cosh \left[ {{\lambda _2}(x - L + e)} \right] + \\& \frac{{pk{\tau _{\max }}}}{{{\lambda _2}{A_{\rm{p}}}}}\sinh \left[ {{\lambda _2}(x - L + e)} \right] + \frac{{T{E_{\rm{p}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} \end{split} (28) 在
0 \sim L - e 内时,对式(25)换算成平均应变后进行积分可得弹性段FRP筋伸长量{u_{{\rm{p}}2 - 1}} 为{u_{{\rm{p}}2 - 1}} = \frac{{kp{\tau _{\max }}}}{{\lambda _1^2{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{{T(L - e)}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (29) 在
L - e \sim L 内时对式(28)换算成平均应变后进行积分可得硬化段FRP筋伸长量{u_{{\rm{p}}2 - 2}} 为\begin{split} {u_{{\rm{p}}2 - 2}} =& \frac{{kp{\tau _{\max }}}}{{{A_{\rm{p}}}{E_{\rm{p}}}}}\left\{ {\frac{1}{{{\lambda _1}{\lambda _2}}}\coth \left[ {{\lambda _1}(L - e)} \right]\sinh ({\lambda _2}e) - \frac{1}{{\lambda _2^2}}} \right\}+\\ & \frac{{kp{\tau _{\max }}}}{{\lambda _2^2{A_{\rm{p}}}{E_{\rm{p}}}}}\cosh ({\lambda _2}e) + \frac{{Te}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}}\\[-12pt] \end{split} (30) 当
x = L 的切应力达到{\tau _{\max }} 时,该阶段结束,硬化长度达到最大,记为{e_{\max }} 。此时施加在构件上的轴向拉力大小为\begin{split} {T_{2\max }} =& \frac{{kp{\tau _{\max }}({A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}})}}{{{\lambda _1}{A_{\rm{c}}}{E_{\rm{c}}}}}\\&\coth {\lambda _1}(L - {e_{\max }})\cosh ({\lambda _2}{e_{\max }})+\\ & \frac{{kp{\tau _{\max }}({A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}})}}{{{\lambda _2}{A_{\rm{c}}}{E_{\rm{c}}}}}\sinh ({\lambda _2}{e_{\max }}) \end{split} (31) 3.3 软化阶段
当轴向拉力大于
{T_{2\max }} 时,在x = L 处的τ逐渐小于{\tau _{\max }} ,化学胶结力和机械咬合力大部分开始失效,此时黏结-滑移处于软化阶段,记软化长度为a,分离体内黏结应力如图8所示,将对应的式(3)代入式(12),其中弹性段和硬化段的方程分别对应式(14)和式(21)。求得{\delta _1} \leqslant \delta \leqslant {\delta _{\rm{f}}} 时对应的方程为\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{x^2}}} + \lambda _3^2\delta = \lambda _3^2\left(\frac{{{\delta _{\rm{f}}}{\tau _{\max }} - {\delta _1}{\tau _{\rm{l}}}}}{{{\tau _{\max }} - {\tau _{\rm{l}}}}}\right), \;\;\;{\delta _1} \leqslant \delta \leqslant {\delta _{\rm{f}}} (32) 其中,
\lambda _3^2 = \frac{{p({\tau _{\max }} - {\tau _{\rm{l}}})}}{{{\delta _{\rm{f}}} - {\delta _1}}}\left(\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}\right) (33) 该阶段的边界条件为:(1)
x = 0 ,\delta = 0 ;(2)x = L - e - a ,\delta = {\delta ^*} ;(3)x = L - a ,\delta = {\delta _1} ;(4)x = L ,{\sigma _{\rm{p}}}{A_{\rm{p}}} = T ;(5)在0 \sim L 内,任意位置FRP筋应力连续可导。于是可求得各阶段公式,其中求解弹性段表达式时,采用的控制方程和边界条件与3.2节相同,因此只需将式(23)~式(25)中的L - e 替换成L - e - a 即可。求得{\delta ^*} \leqslant \delta \leqslant {\delta _1} 范围内的表达式为\begin{split}\delta =& \frac{{{\delta _1} - {\delta ^*}}}{{1 - k}}({\rm{csch}} {\lambda _2}e - k\coth {\lambda _2}e)\sinh {\lambda _2}(x - L + e + a) +\\ &\frac{{k({\delta _1} - {\delta ^*})}}{{1 - k}}\cosh {\lambda _2}(x - L + e + a) - \frac{{k{\delta _1} - {\delta ^*}}}{{1 - k}}\\[-12pt] \end{split} (34) \begin{split}{\sigma _{\rm{p}}} =& \frac{{p{\tau _{\max }}}}{{{\lambda _2}{A_{\rm{p}}}}}({\rm{csch}} {\lambda _2}e - k\coth {\lambda _2}e)\cosh {\lambda _2}(x - L + e + a) + \\ &\frac{{kp{\tau _{\max }}}}{{{\lambda _2}{A_{\rm{p}}}}}\sinh {\lambda _2}(x - L + e + a) + \frac{{T{E_{\rm{p}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} \end{split} (35) \begin{split} \tau =& {\tau _{\max }}({\rm{csch}} {\lambda _2}e - k\coth {\lambda _2}e)\sinh {\lambda _2}(x - L + e + a) + \\ &k{\tau _{\max }}\cosh {\lambda _2}(x - L + e + a) \end{split} (36) 求得
{\delta _1} \leqslant \delta \leqslant {\delta _{\rm{f}}} 范围内的表达式为\begin{split} \delta =& \left[ {\frac{T}{{{\lambda _3}{A_{\rm{p}}}{E_{\rm{p}}}}}\sec {\lambda _3}a + \frac{{{\tau _{\max }}({\delta _1} - {\delta _{\rm{f}}})}}{{{\tau _{max}} - {\tau _{\rm{l}}}}}\tan {\lambda _3}a} \right]\sin {\lambda _3}\\ & (x - L + a) + \frac{{{\tau _{\max }}({\delta _1} - {\delta _{\rm{f}}})}}{{{\tau _{\max }} - {\tau _{\rm{l}}}}}\cos {\lambda _3}(x - L + a)\\ & + \frac{{{\delta _{\rm{f}}}{\tau _{\max }} - {\delta _1}{\tau _{\rm{l}}}}}{{{\tau _{\max }} - {\tau _{\rm{l}}}}} \end{split} (37) \begin{split}{\sigma _{\rm{p}}} =& \left(\frac{T}{{{A_{\rm{p}}}}}\frac{{{A_{\rm{c}}}{E_{\rm{c}}}\sec {\lambda _3}a}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} - \frac{{p{\tau _{\max }}\tan {\lambda _3}a}}{{{\lambda _3}{A_{\rm{p}}}}}\right)\cos {\lambda _3}(x -\! L + a) + \\ &\frac{{p{\tau _{\max }}}}{{{\lambda _3}{A_{\rm{p}}}}}\sin {\lambda _3}(x - L + a) + \frac{{T{E_{\rm{p}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} \end{split} (38) \begin{split} \tau =& - \left[\frac{{T({\tau _{\max }} - {\tau _{\rm{l}}})\sec {\lambda _3}a}}{{{\lambda _3}({\delta _{\rm{f}}} - {\delta _1}){A_{\rm{p}}}{E_{\rm{p}}}}} - {\tau _{\max }}\tan {\lambda _3}a\right]\sin {\lambda _3}\\ &(x - L + a) + {\tau _{\max }}\cos {\lambda _3}(x - L + a) \end{split} (39) 根据式(8),代入各阶段FRP筋应力表达式,可求得弹性段FRP筋伸长量
{u_{{\rm{p}}3 - 1}} 为{u_{{\rm{p}}3 - 1}} = \frac{{kp{\tau _{\max }}}}{{\lambda _1^2{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{{T(L - e - a)}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (40) 硬化段FRP筋伸长量
{u_{{\rm{p}}3 - 2}} 为{u_{{\rm{p}}3 - 2}} = \frac{{p{\tau _{\max }}(1 - k)}}{{\lambda _2^2{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{{Te}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (41) 软化段FRP筋伸长量
{u_{{\rm{p}}3 - 3}} 为\begin{split} {u_{{\rm{p}}3 - 3}} =& \frac{T}{{{\lambda _3}{A_{\rm{p}}}{E_{\rm{p}}}}}\frac{{{A_{\rm{c}}}{E_{\rm{c}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}}{\rm{tan}}{\lambda _3}a + \frac{{Ta}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} + \\ &\frac{{p{\tau _{\max }}}}{{\lambda _3^2{A_{\rm{p}}}{E_{\rm{p}}}}}(1 - \sec {\lambda _3}a)\\[-12pt] \end{split} (42) 当
x = L 的切应力减小到{\tau _{\rm{l}}} 时,该阶段结束,软化长度达到最大,记为{a_{\max }} ,此时施加在构件上的轴向拉力大小为{T_{3\max }} = ({\tau _{\max }}\sec {\lambda _3}{a_{\max }} - {\tau _{\rm{l}}}){\lambda _3}{A_{\rm{p}}}{E_{\rm{p}}}\frac{{{\delta _{\rm{f}}} - {\delta _1}}}{{{\tau _{\max }} - {\tau _{\rm{l}}}}}\cot {\lambda _3}{a_{\max }} (43) 3.4 摩擦阶段
当轴向拉力大于
{T_{3\max }} 时,在x = L 处的切应力等于{\tau _{\rm{l}}} ,并向原点方向蔓延,此时化学胶结力和机械咬合力全部失效,只有界面摩擦力提供微弱的黏结力,此时黏结-滑移处于摩擦阶段,记摩擦长度为d,分离体内黏结应力如图9所示。将对应的式(3)代入弹性段、硬化段和软化段的方程式(14)、式(21)和式(32)。求得\delta \geqslant {\delta _{\rm{f}}} 对应的方程为\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{x^2}}} - p{\tau _{\rm{l}}}\left(\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}\right) = 0, \;\;\delta \geqslant {\delta _{\rm{f}}} (44) 该阶段的边界条件为:(1)
x = 0 ,\delta = 0 ;(2)x = L - e - a - d ,\delta = {\delta ^*} ;(3)x = L - a - d ,\delta = {\delta _1} ;(4)x = L - d ,\delta = {\delta _{\rm{f}}} ;(5)x = L ,{\sigma _{\rm{p}}}{A_{\rm{p}}} = T ;(6)在0\sim L 内,任意位置FRP筋应力连续可导。因此,可求得各阶段公式,其中求解弹性阶段采用的控制方程和边界条件与3.2节相同,只需将式(23)~式(25)中的L - e 替换成L - e - a - d ;同理,求解硬化段采用的控制方程和边界条件与3.3节相同,只需将式(34)~式(36)中的L - e - a 替换成L - e - a - d ,不再赘述。求得
{\delta _1} \leqslant \delta \leqslant {\delta _{\rm{f}}} 范围内的表达式为\begin{split} \delta =& \frac{{{\delta _1} - {\delta _{\rm{f}}}}}{{{\tau _{\max }} - {\tau _1}}}({\tau _{\rm{l}}}\csc {\lambda _3}a - {\tau _{\max }}\cot {\lambda _3}a)\sin {\lambda _3}\\ & (x - L + a + d) + \frac{{{\tau _{\max }}({\delta _1} - {\delta _{\rm{f}}})}}{{{\tau _{\max }} - {\tau _{\rm{l}}}}}\cos {\lambda _3}(x - L + a + d)+\\ & \frac{{{\delta _{\rm{f}}}{\tau _{\max }} - {\delta _1}{\tau _{\rm{l}}}}}{{{\tau _{\max }} - {\tau _{\rm{l}}}}}\\[-12pt] \end{split} (45) \begin{split} {\sigma _{\rm{p}}} =& \frac{p}{{{\lambda _3}{A_{\rm{p}}}}}({\tau _{\max }}\cot {\lambda _3}a - {\tau _{\rm{l}}}\csc {\lambda _3}a)\cos {\lambda _3}\\& (x - L + a + d) + \frac{{p{\tau _{\max }}}}{{{\lambda _3}{A_{\rm{p}}}}}\sin {\lambda _3}(x - L + a + d)+\\ & \frac{{T{E_{\rm{p}}}}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} \end{split} (46) \begin{split} \tau = &({\tau _{\rm{l}}}\csc {\lambda _3}a - {\tau _{\max }}\cot {\lambda _3}a)\sin {\lambda _3}(x - L + a + d) +\\ & {\tau _{\max }}\cos {\lambda _3}(x - L + a + d) \end{split} (47) 求得
\delta \geqslant {\delta _{\rm{f}}} 范围内的表达式为\begin{split} \delta = & \left[ {\frac{T}{{{A_{\rm{p}}}{E_{\rm{p}}}}} - pd{\tau _{\rm{l}}}\left( {\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}} \right)} \right](x - L + d)+\\ & \frac{{p{\tau _{\rm{l}}}}}{2}\left( {\frac{1}{{{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{1}{{{A_{\rm{c}}}{E_{\rm{c}}}}}} \right){(x - L + d)^2} + {\delta _{\rm{f}}} \end{split} (48) {\sigma _{\rm{p}}} = \frac{{p{\tau _{\rm{l}}}}}{{{A_{\rm{p}}}}}(x - L) + \frac{T}{{{A_{\rm{p}}}}} (49) \tau = {\tau _{\rm{l}}} (50) 根据式(8),代入各阶段钢筋应力表达式,可求得弹性段FRP筋伸长量为
{u_{{\rm{p}}4 - 1}} = \frac{{kp{\tau _{\max }}}}{{\lambda _1^2{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{{T(L - e - a - d)}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (51) 硬化段FRP筋伸长量
{u_{{\rm{p}}4 - 2}} 为{u_{{\rm{p}}4 - 2}} = \frac{{p{\tau _{\max }}(1 - k)}}{{\lambda _2^2{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{{Te}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (52) 软化段FRP筋伸长量
{u_{{\rm{p}}4 - 3}} 为{u_{{\rm{p}}4 - 3}} = \frac{{p({\tau _{\max }} - {\tau _{\rm{l}}})}}{{\lambda _3^2{A_{\rm{p}}}{E_{\rm{p}}}}} + \frac{{Ta}}{{{A_{\rm{p}}}{E_{\rm{p}}} + {A_{\rm{c}}}{E_{\rm{c}}}}} (53) 摩擦段FRP筋伸长量
{u_{{\rm{p}}4 - 4}} 为{u_{{\rm{p}}4 - 4}} = \frac{T}{{{A_{\rm{p}}}{E_{\rm{p}}}}}d - \frac{{p{\tau _{\max }}}}{{2{A_{\rm{p}}}{E_{\rm{p}}}}}{{\rm{d}}^2} (54) 当轴向拉力T达到FRP筋抗拉强度时,FRP筋被拉断,试件宣布破坏,拉伸过程计算结束。
需要指出的是,以上推导过程为基于构件混凝土拉伸过程中不发生开裂的情况进行。实际拉伸过程中,随着拉伸荷载的增大,混凝土会逐渐开裂。因此,将以上推导过程与混凝土开裂判别相结合。可以形成FRP筋/混凝土拉伸构件受力过程算法(如图10所示):(1) 构件初始化,给定混凝土、FRP筋几何尺寸,给定混凝土、FRP筋材料属性,给定FRP筋/混凝土黏结-滑移相应参数,根据FRP筋几何和材料参数确定构件最大拉伸荷载
{T_{\rm{u}}} 并将其分为n等分;(2) 分阶段加载过程,对每个荷载增量步,按照当前步拉伸荷载大小确定构件中黏结力、混凝土应力和FRP筋应力的分布,根据构件中部混凝土应力判断是否发生开裂,若发生开裂,则将构件长度减半,重复过程(2),若不发生开裂,计算构件相应力学量;(3) 进入下一个荷载增量步直至达到最大拉伸荷载{T_{\rm{u}}} 。需要指出的是,构件内混凝土最大拉应力
{\sigma _{{\rm{c}} {\rm{max}}}} 位于x=0 处。当{\sigma _{{\rm{c}}{\rm{max}}}} 等于混凝土抗拉强度{f_{\rm{t}}} 时,构件将在x=0 处发生开裂。开裂后重新选取相邻裂缝间的构件为研究对象,长度缩减为L/2 ,继续施加轴向拉力。此算法产生的裂缝间距按指数形式减小。当轴向拉力T = 0 时,裂缝间距2L的初始值取整个受拉构件的长度,随着开裂次数的增加,L的值将发生离散变化,大小为{2^{ - n}}L ,n为开裂次数。4. 结果与讨论
4.1 试验验证
为了对所提出的FRP筋/混凝土轴拉构件变形计算方法进行评估,本文收集国内外文献中8组FRP筋/混凝土拉伸试验数据进行对比。试件中FRP筋分为带肋型和不带肋型。试件的详细几何参数和材料参数如表1所示。
表 1 FRP筋/混凝土轴拉试件几何及材料参数Table 1. Geometric and material parameters of FRP bars/concrete axial tensile specimensReference Specimen 2L/mm b/mm h/mm d/mm {f'_{\rm{c}}}/MPa {f_{\rm{t}}}/MPa {E_{\rm{c}}}/GPa {f_{{\rm{fu}}}}/MPa {E_{\rm{p}}}/GPa {\delta _1}/mm {\delta _{\rm{f}}}/mm [12] 13-170 1200 170 170 13.7 48.1 1.8 27.4 770 37.6 0.29 2.83 16-170 1200 170 170 16.9 46.6 2.6 34.6 1030 41.7 0.29 2.83 19-170 1200 170 170 19.1 56.2 2.1 33.3 637 40.8 0.29 2.83 [21] C30-12A-100(1) 1000 100 100 13.0 37.7 2.8 34.8 983 50.3 0.29 2.83 C85-16C-100(1) 1000 100 100 20.0 116.4 4.1 54.1 1236 63.8 1.50 10.00 [22] C50/13/100 1500 100 100 12.7 52.0 2.9 36.2 792 42.9 1.50 10.00 C50/19/150 1300 150 150 19.1 52.0 2.9 36.2 715 41.9 1.50 10.00 C90/19/150 1300 200 200 19.1 91.0 5.2 48.3 715 41.9 1.50 10.00 Notes:2L—Effective length of specimens; b, h—Width and height of cross sections, respectively; d—Perimeter of FRP bars; {f'_{\rm{c}}}—Compressive strength of concrete; {f_{\rm{t}}}—Tensile strength of concrete; {E_{\rm{c}}}, {E_{\rm{p}}}—Elastic modulus of concrete and FRP bars, respectively; {f_{\rm{fu}}}—Ultimate tensile strength of FRP bars; {\delta _1}, {\delta _{\rm{f}}}—Maximum slip in hardening stage and softening stage, respectively. 4.2 参数取值
本文提出的简化模型涉及到切应力参数
{\tau _{\max }} 和{\tau _{\rm{l}}} 及滑移参数{\delta ^*} 、{\delta _1} 和{\delta _{\rm{f}}} 。该模型通过将BPE修正模型中的非线性上升段简化为两个线性上升段得到。Rossetti等[23]对不同混凝土强度、纵筋表面光滑程度不同的非变形FRP筋进行拉拔试验,通过试验数据对BPE模型中参数进行标定,如表2所示。
表 2 BPE模型黏结-滑移参数Table 2. Bond-slip parameters for BPE modelParameter Rough surface and medium strength concrete Smooth surface and medium strength concrete Rough surface and low strength concrete Rough surface and high strength concrete α 0.25 0.16 0.39 0.12 { {\delta } }_{ {{1} } }/mm 0.29 0.42 0.61 0.24 { {\delta } }_{ {{2} } }/mm 0.76 2.54 1.18 0.37 { {\delta } }_{ {{3} } }/mm 2.83 4.23 3.74 3.79 { {\tau } }_{ {{\rm{max}}} }/MPa 0.93 0.50 0.78 3.13 Notes: \alpha —A constant which controls initial nonlinear curvature; {\delta _1}, {\delta _2}, {\delta _3}— Maximum slip at nonlinear ascent stage, constant maximum bond stress stage and linear descent stage, respectively; {\tau _{\max }}— Maximum bond stress. 已有试验结果[19]表明,FRP筋是否带肋对整体黏结-滑移影响较大,表2中未具体给出当FRP筋带肋时参数的取值方法。Harajli模型中的参数取值考虑了变形纵筋肋间距的影响:
{\delta _1}{\rm{ = }} 0.15{c_0} ,{\delta _2}{\rm{ = }}0.35{c_0} ,{\delta _3}{\rm{ = }}{c_0} ,{\tau _{\max }} = 2.75\sqrt {{{f'}_{\rm{c}}}} ,{\tau _{\rm{l}}} = 0.35{\tau _{\max }} ,\alpha {\rm{ = }}0.3 ,式中:{c_0} 为变形钢筋肋间净距;{f'_{\rm{c}}} 为圆柱体混凝土抗压强度。若没有详细肋间净距,Harajli统一了取值方法,{\delta _1} 、{\delta _2} 和{\delta _3} 分别取1.5 mm、3.5 mm和10.0 mm。在确定黏结-滑移参数时,本文综合考虑了上述研究结果,若FRP筋带肋,则参考Harajli取值方法;若FRP筋不带肋,则采用表2标定值。在选取的试件中,前4个试件为表面磨砂的FRP筋,后4个试件为带肋FRP筋。
参数
{\delta ^*} 是本文为将非线性上升段简化为两个线性上升段设置的折点,已有文献中并没有该参数的取值建议。在黏结-滑移初期,由于筋材与混凝土黏结性能良好,其初始刚度较大,随着滑移不断进行,刚度也逐渐退化,因此参数{\delta ^*} 应足够小以适应滑移阶段初期刚度大的要求。实际计算表明,当参数{\delta ^*} 在0.005~0.05 mm内时,与试验结果均能吻合良好。在与试验结果比较和参数分析时,本文均选取{\delta ^*} =0.005 mm进行计算。4.3 计算结果及对比
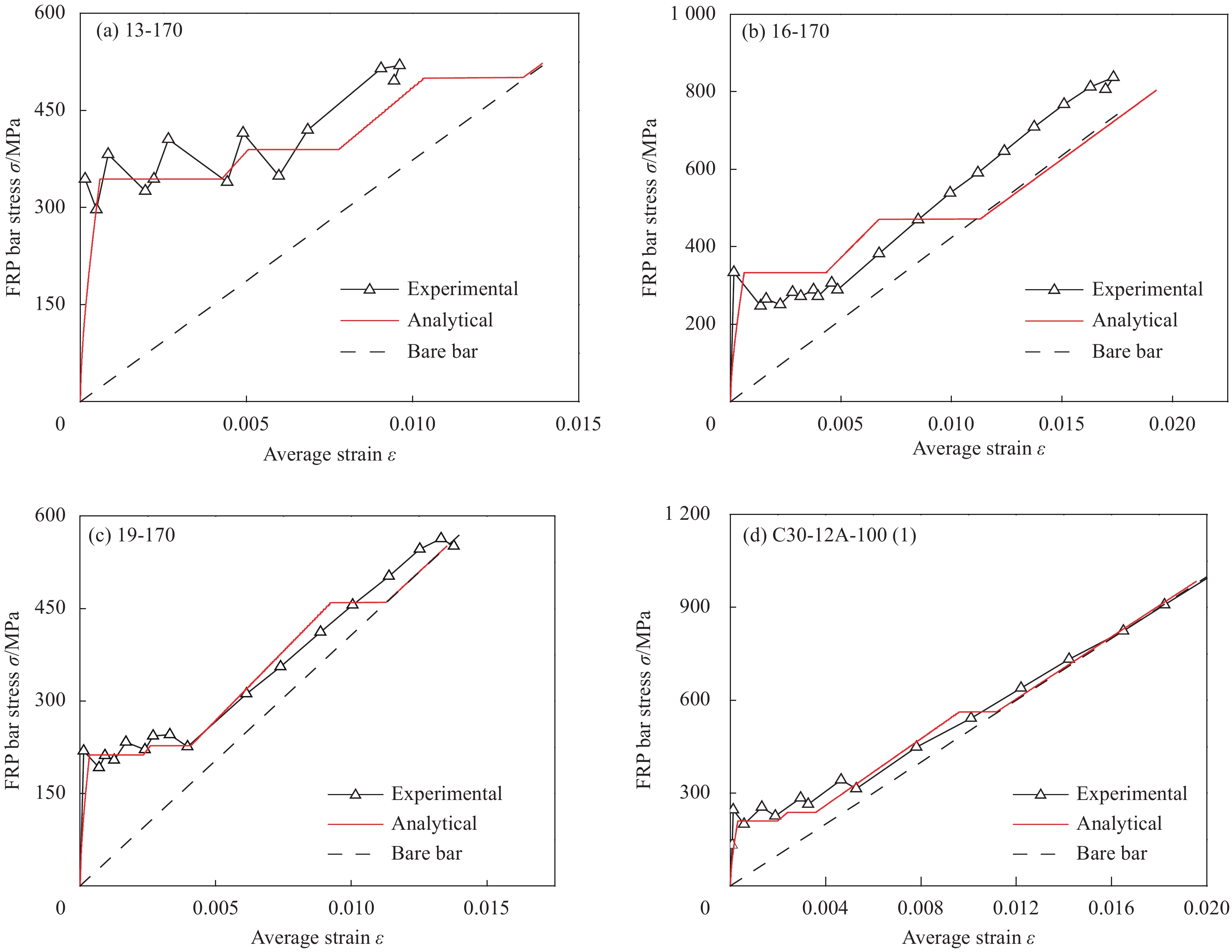
图11为采用本文方法计算与表1中试件的试验轴力-平均应变曲线的对比。文献中并未给出详细的肋间净距,因此采用Harajli取值方法。另外在多数情况下,由于环境和材料等各种因素,混凝土轴拉构件在施加荷载前已产生部分收缩应变,使实际测得的构件第一次开裂拉力低于预期。本文根据Bischoff[24]提出的理论,将试验曲线中的收缩应变扣除,还原成无收缩试验曲线,方便系统比较。可以看出,本文计算结果与试验结果在初次开裂对应的轴向拉力和后续刚度变化方面均吻合良好,因此验证了本文方法的有效性。
4.4 参数分析
对影响拉伸刚化效应的一些参数进行敏感性分析,包括混凝土强度、配筋率和FRP筋弹性模量。以表1中试件C50/13/100试件的参数作为基准。
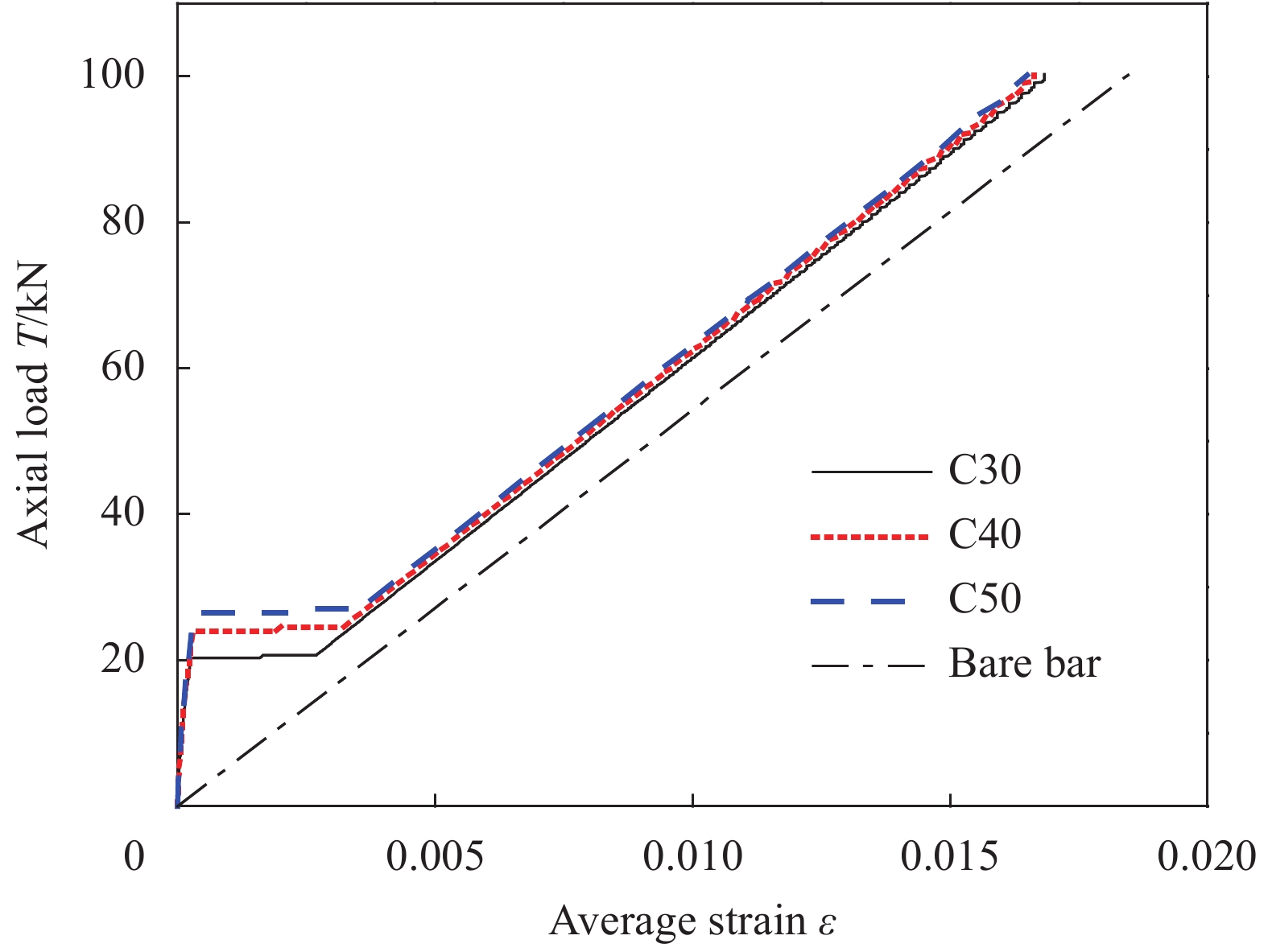
图12为混凝土强度对FRP筋/混凝土拉伸刚化的影响。可以看出,混凝土强度增大时,FRP筋/混凝土构件初次开裂荷载相应增大,但与FRP筋之间的黏结效果没有显著提高,因此对拉伸刚化效应并不明显。
图13为配筋率对FRP筋/混凝土拉伸刚化的影响。由于在相同拉力作用下,配筋率高的构件能分担拉力的混凝土量小于配筋率低的构件,因此在相同黏结长度下,高配筋率构件的混凝土正应力远大于低配筋率构件,可以在初次开裂荷载中体现。可以看出,增大配筋率将减小拉伸刚化效应,但配筋率对初期刚度影响甚微。
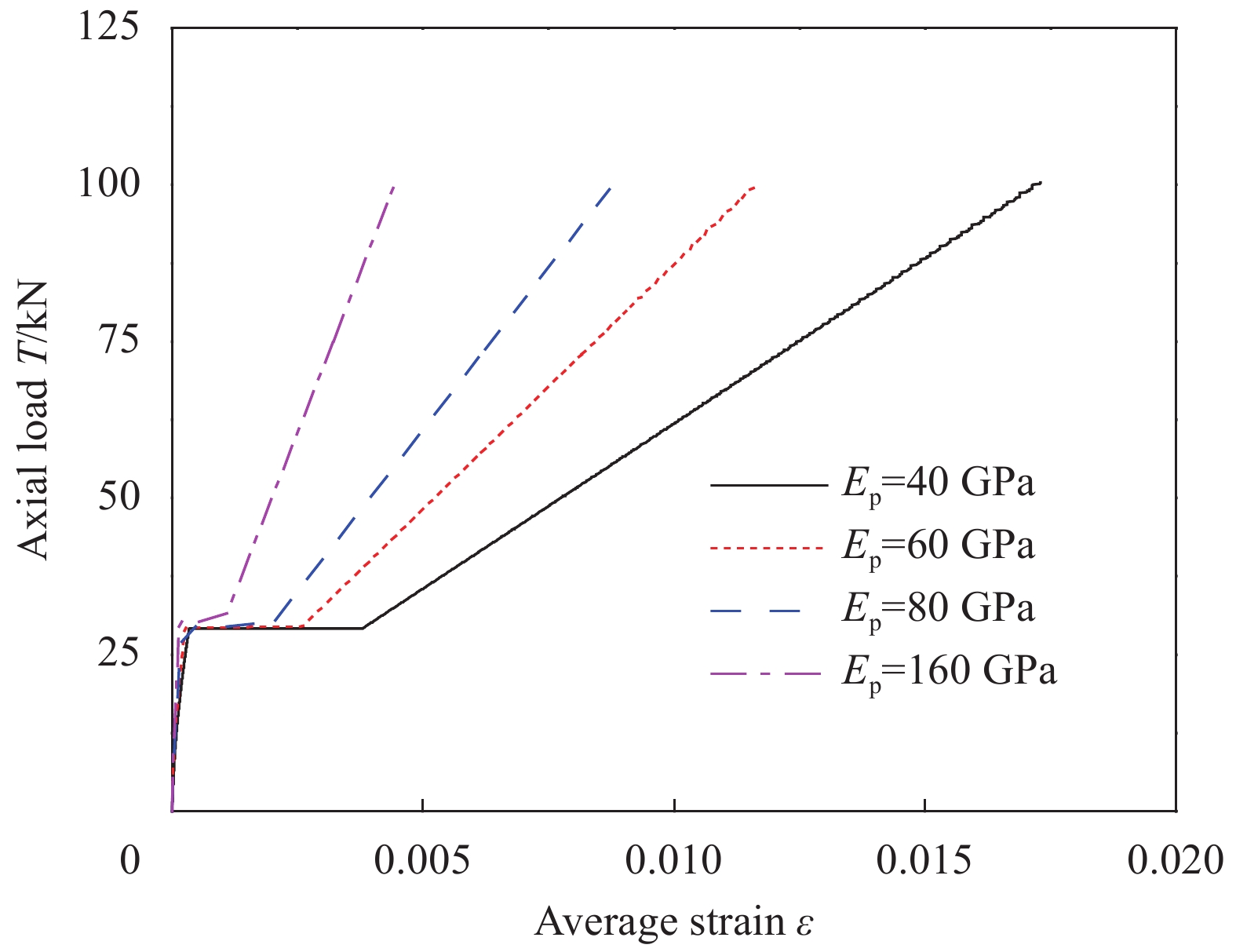
图14为FRP筋弹性模量对FRP筋/混凝土拉伸刚化的影响。可以看出,弹性模量对构件的初期刚度和初次开裂荷载影响不大,但对后期刚度影响较大,且弹性模量越小,拉伸刚化效应越明显,与已有的试验结果一致[8,22]。
5. 结 论
(1) 基于BPE改进模型提出的四线性简化黏结-滑移模型适用于纤维增强树脂复合材料(FRP)筋/混凝土黏结-滑移各阶段分析。该模型中弹性阶段结束时对应的滑移值
{\delta ^*} 建议取值在0.005~0.05 mm之间。(2) 基于简化黏结-滑移模型结合混凝土开裂判断准则提出的FRP筋/混凝土轴拉构件变形计算方法的计算结果与既有文献中试验结果吻合良好,能够有效确定轴拉构件变形过程中的刚度退化过程。
(3) 参数分析表明,提高混凝土强度对于初次开裂荷载影响较大,但对黏结效果提高不明显,因此对拉伸刚化作用影响不大;保证截面尺寸不变时,由于分担拉力的混凝土随配筋率提高而减少,因此增大配筋率将减小拉伸刚化效应;FRP筋弹性模量对拉伸刚化效应影响明显。
-
表 1 FRP筋/混凝土轴拉试件几何及材料参数
Table 1 Geometric and material parameters of FRP bars/concrete axial tensile specimens
Reference Specimen 2L/mm b/mm h/mm d/mm {f'_{\rm{c}}}/MPa {f_{\rm{t}}}/MPa {E_{\rm{c}}}/GPa {f_{{\rm{fu}}}}/MPa {E_{\rm{p}}}/GPa {\delta _1}/mm {\delta _{\rm{f}}}/mm [12] 13-170 1200 170 170 13.7 48.1 1.8 27.4 770 37.6 0.29 2.83 16-170 1200 170 170 16.9 46.6 2.6 34.6 1030 41.7 0.29 2.83 19-170 1200 170 170 19.1 56.2 2.1 33.3 637 40.8 0.29 2.83 [21] C30-12A-100(1) 1000 100 100 13.0 37.7 2.8 34.8 983 50.3 0.29 2.83 C85-16C-100(1) 1000 100 100 20.0 116.4 4.1 54.1 1236 63.8 1.50 10.00 [22] C50/13/100 1500 100 100 12.7 52.0 2.9 36.2 792 42.9 1.50 10.00 C50/19/150 1300 150 150 19.1 52.0 2.9 36.2 715 41.9 1.50 10.00 C90/19/150 1300 200 200 19.1 91.0 5.2 48.3 715 41.9 1.50 10.00 Notes:2L—Effective length of specimens; b, h—Width and height of cross sections, respectively; d—Perimeter of FRP bars; {f'_{\rm{c}}}—Compressive strength of concrete; {f_{\rm{t}}}—Tensile strength of concrete; {E_{\rm{c}}}, {E_{\rm{p}}}—Elastic modulus of concrete and FRP bars, respectively; {f_{\rm{fu}}}—Ultimate tensile strength of FRP bars; {\delta _1}, {\delta _{\rm{f}}}—Maximum slip in hardening stage and softening stage, respectively. 表 2 BPE模型黏结-滑移参数
Table 2 Bond-slip parameters for BPE model
Parameter Rough surface and medium strength concrete Smooth surface and medium strength concrete Rough surface and low strength concrete Rough surface and high strength concrete α 0.25 0.16 0.39 0.12 { {\delta } }_{ {{1} } }/mm 0.29 0.42 0.61 0.24 { {\delta } }_{ {{2} } }/mm 0.76 2.54 1.18 0.37 { {\delta } }_{ {{3} } }/mm 2.83 4.23 3.74 3.79 { {\tau } }_{ {{\rm{max}}} }/MPa 0.93 0.50 0.78 3.13 Notes: \alpha —A constant which controls initial nonlinear curvature; {\delta _1}, {\delta _2}, {\delta _3}— Maximum slip at nonlinear ascent stage, constant maximum bond stress stage and linear descent stage, respectively; {\tau _{\max }}— Maximum bond stress. -
[1] BENMOKRANE B, EL-SALAKAWY E, EL-RAGABY A, et al. Designing and testing of concrete bridge decks reinforced with glass FRP bars[J]. Journal of Bridge Engineering,2006,11(2):217-229. DOI: 10.1061/(ASCE)1084-0702(2006)11:2(217)
[2] GANGARAO H V, TALY N, VIJAY P V. Reinforced concrete design with FRP composites[M]. Florida: CRC Press, 2006.
[3] TORRES L, LÓPEZ-ALMANSA F, BOZZO L M. Tension-stiffening model for cracked flexural concrete members[J]. Journal of Structural Engineering,2004,130(8):1242-1251. DOI: 10.1061/(ASCE)0733-9445(2004)130:8(1242)
[4] DAI J G, UEDA T, SATO Y, et al. Modeling of tension stiffening behavior in FRP-strengthened RC members based on rigid body spring networks[J]. Computer-Aided Civil and Infrastructure Engineering,2012,27(6):406-418. DOI: 10.1111/j.1467-8667.2011.00741.x
[5] STRAMANDINOLI R S B, LA ROVERE H L. An efficient tension-stiffening model for nonlinear analysis of reinforced concrete members[J]. Engineering Structures,2008,30(7):2069-2080. DOI: 10.1016/j.engstruct.2007.12.022
[6] BISCHOFF P H, GROSS S, OSPINA C E. The story behind proposed changes to ACI 440 deflection requirements for FRP-reinforced concrete[CD]. New York: Curran Associates, Inc., 2010.
[7] NARAYANAN R S, BEEBY A W. Designers’ guide to EN 1992-1-1 and EN 1992-1-2. Eurocode 2: Design of concrete structures: General rules and rules for buildings and structural fire design[M]. Thomas Telford, 2005.
[8] BISCHOFF P H, PAIXAO R. Tension stiffening and cracking of concrete reinforced with glass fiber reinforced polymer (GFRP) bars[J]. Canadian Journal of Civil Engineering,2004,31(4):579-588. DOI: 10.1139/l04-025
[9] BAENA M, TORRES L, TURON A, et al. Analysis of cracking behavior and tension stiffening in FRP reinforced concrete tensile elements[J]. Composites Part B: Engineering,2013,45(1):1360-1367. DOI: 10.1016/j.compositesb.2012.07.026
[10] MIGLIETTA P C, GRASSELLI G, BENTZ E C. Finite/discrete element model of tension stiffening in GFRP reinforced concrete[J]. Engineering Structures,2016,111:494-504. DOI: 10.1016/j.engstruct.2015.12.037
[11] GHIASSI B, SOLTANI M, RAHNAMAYE S S. Micromechanical modeling of tension stiffening in FRP-strengthened concrete elements[J]. Journal of Composite Materials,2018,52(19):2577-2596. DOI: 10.1177/0021998317751248
[12] BAENA M, TURON A, TORRE L, et al. Experimental study and code predictions of fibre reinforced polymer reinforced concrete (FRP RC) tensile members[J]. Composite Structures,2011,93(10):2511-2520. DOI: 10.1016/j.compstruct.2011.04.012
[13] VILANOVA I, TORRES L, BAENA M, et al. Experimental study of tension stiffening in GFRP RC tensile members under sustained load[J]. Engineering Structures,2014,79:390-400. DOI: 10.1016/j.engstruct.2014.08.037
[14] LIN X S, ZHANG Y X. Evaluation of bond stress-slip models for FRP reinforcing bars in concrete[J]. Composite Structures,2014,104:131-141.
[15] ELIGEHAUSEN R, POPOV E P, BERTERO V V. Local bond stress-slip relationships of deformed bars under generalized excitations: Experimental results and analytical model[R]. Berkeley: Earthquake Engineering Research Center, 1983.
[16] COSENZA E, MANFREDI G, REALFONZO R. Behavior and modeling of bond of FRP rebars to concrete[J]. Journal of Composites for Construction,1997,1(2):40-51. DOI: 10.1061/(ASCE)1090-0268(1997)1:2(40)
[17] HARAJLI M H, HOUT M, JALKH W. Local bond stress-slip behavior of reinforcing bars embedded in plain and fiber concrete[J]. ACI Materials Journal,1995,92(4):343-354.
[18] HARAJLI M, HAMAD B, KARAM K. Bond-slip response of reinforcing bars embedded in plain and fiber concrete[J]. Journal of Materials in Civil Engineering,2002,14(6):503-511. DOI: 10.1061/(ASCE)0899-1561(2002)14:6(503)
[19] HARAJLI M H. Bond stress-slip model for steel bars in unconfined or steel, FRC, or FRP confined concrete under cyclic loading[J]. Journal of Structural Engineering,2009,135(5):509-518. DOI: 10.1061/(ASCE)0733-9445(2009)135:5(509)
[20] GUPTA A K, MAESTRINI S R. Tension-stiffness model for reinforced concrete bars[J]. Journal of Structural Engineering,1990,116(3):769-790. DOI: 10.1061/(ASCE)0733-9445(1990)116:3(769)
[21] SOORIYAARACHCHI H, PILAKOUTAS K, BYARS E. Tension stiffening behavior of GFRP-reinforced concrete[C]//Fiber-Reinforced Polymer (FRP) Reinforcement for Concrete Structures. Kansas City: American Concrete Institute, 2005: 975-990.
[22] KHARAL Z. Tension stiffening and cracking behavior of GFRP reinforced concrete[D]. Toronto: University of Toronto, 2014.
[23] ROSSETTI V A, GALEOTA D, GIAMMATTEO M M. Local bond stress-slip relationships of glass fiber reinforced plastic bars embedded in concrete[J]. Materials and Structures,1995,28:340-344. DOI: 10.1007/BF02473149
[24] BISCHOFF P H. Effects of shrinkage on tension stiffening and cracking in reinforced concrete[J]. Canadian Journal of Civil Engineering,2001,28(3):363-374. DOI: 10.1139/l00-117
-
期刊类型引用(3)
1. 关纪文,陈红梅,韦丽兰,梁淑嘉. 结构用GFRP筋受压力学性能试验. 湖南科技大学学报(自然科学版). 2023(04): 37-43 .  百度学术
百度学术
2. 陈国雄,安茹,符师桦. FRP筋混凝土梁拉伸刚化效应模型研究. 复合材料科学与工程. 2022(02): 11-18 .  百度学术
百度学术
3. 李艳玲,李军阳. 硫酸钠掺量对高分子聚合物混凝土增强剂的性能影响分析. 粘接. 2021(07): 34-37 .  百度学术
百度学术
其他类型引用(2)
-




 下载:
下载: