复合材料缠绕接头设计

张庆茂; 陈建农; 刘伟先; 郭丽君; 周光明

doi:10.13801/j.cnki.fhclxb.20200622.002

复合材料缠绕接头设计

1.
成都飞机设计研究所，成都 610091
2.
中航工业南京机电科技有限公司，南京 211113
3.
南京航空航天大学　航空宇航学院，南京 210016

详细信息

通讯作者:
张庆茂，博士，研究员，博士生导师，研究方向为飞机复合材料结构设计　 E-mail：qmzhang611@sina.com

中图分类号: TB332；V214.8
计量
- 文章访问数: 1445
- HTML全文浏览量: 445
- PDF下载量: 121
出版历程
- 收稿日期: 2020-04-26
- 录用日期: 2020-06-06
- 网络出版日期: 2020-06-22
- 刊出日期: 2021-02-14

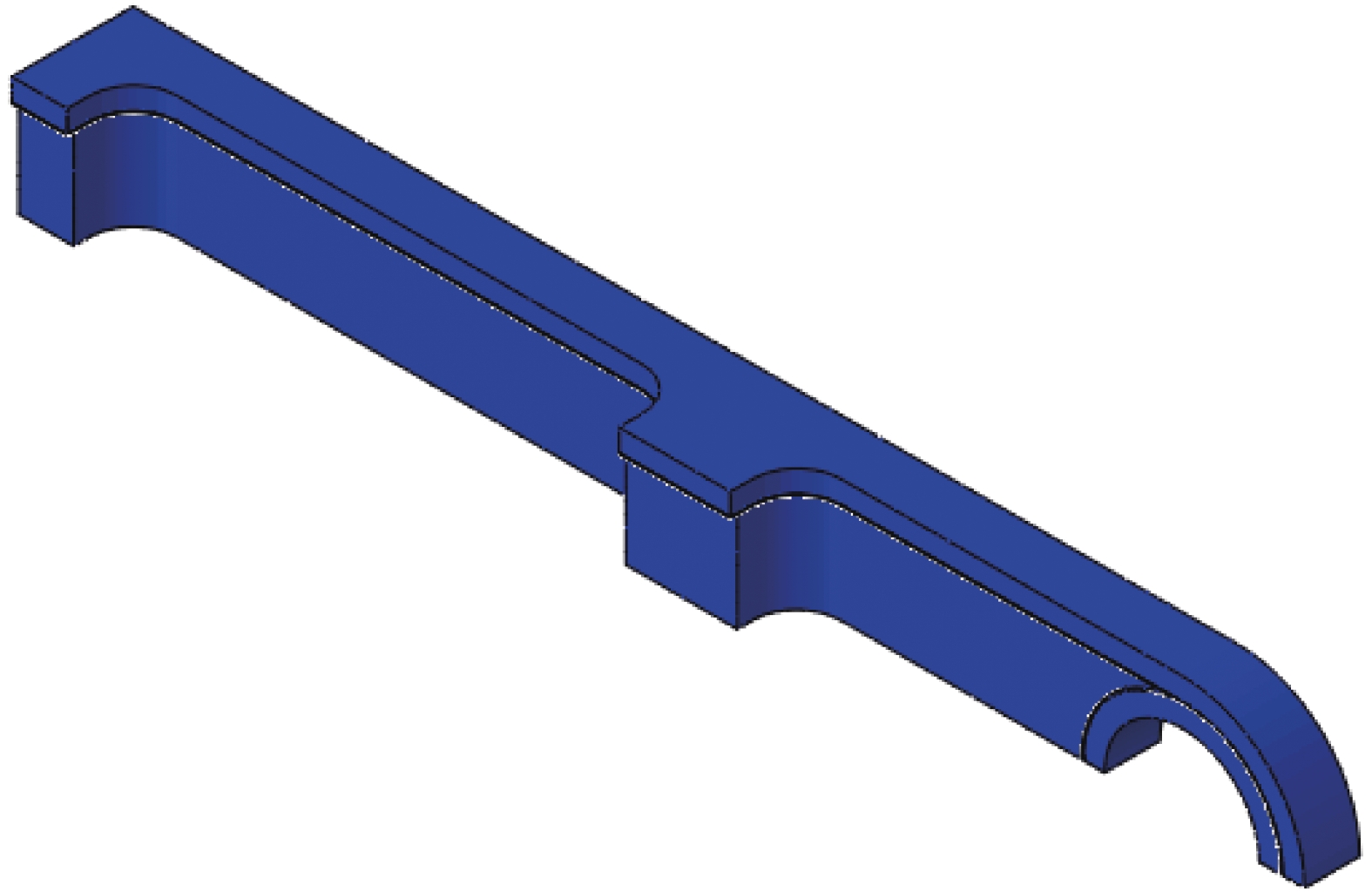
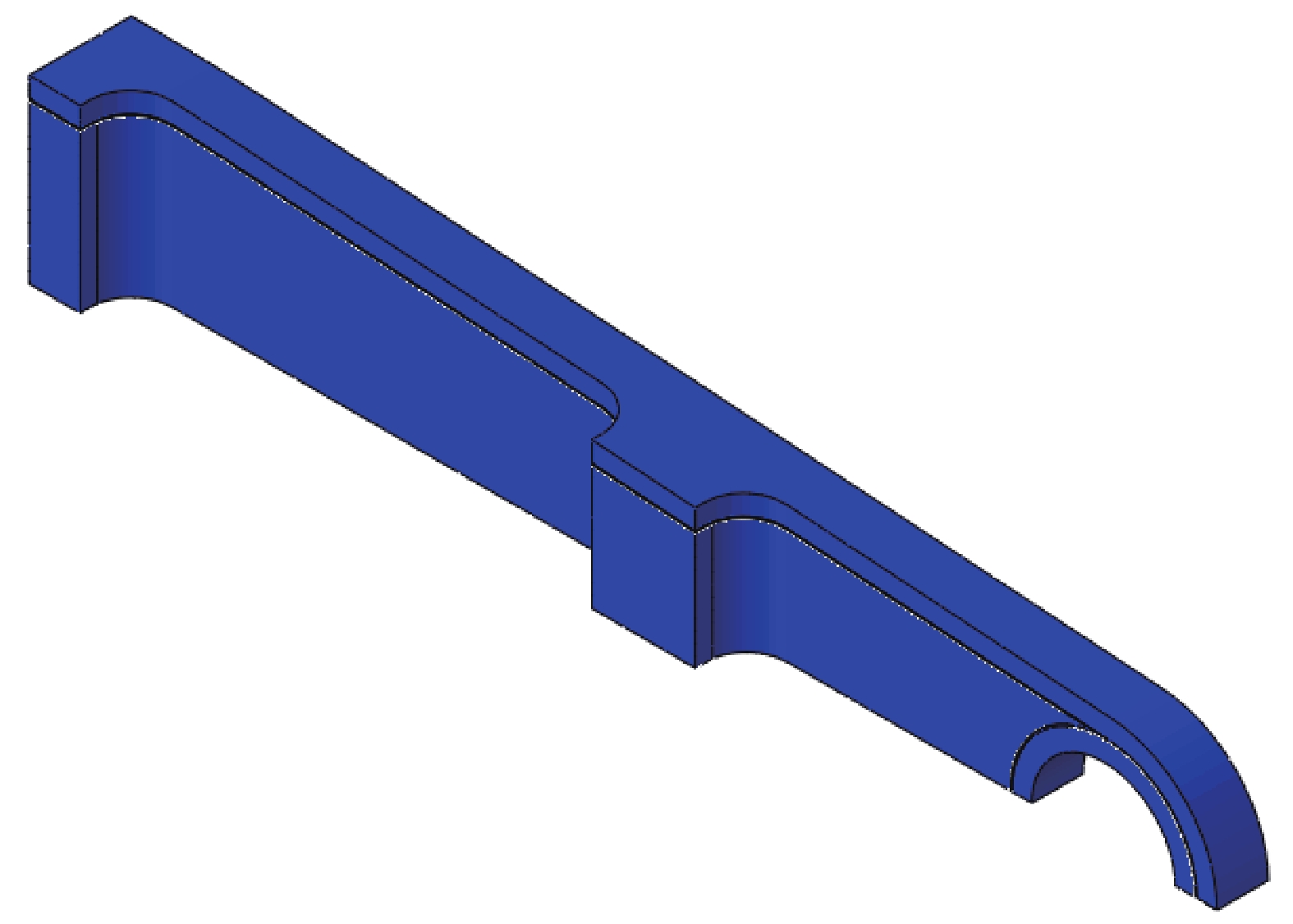
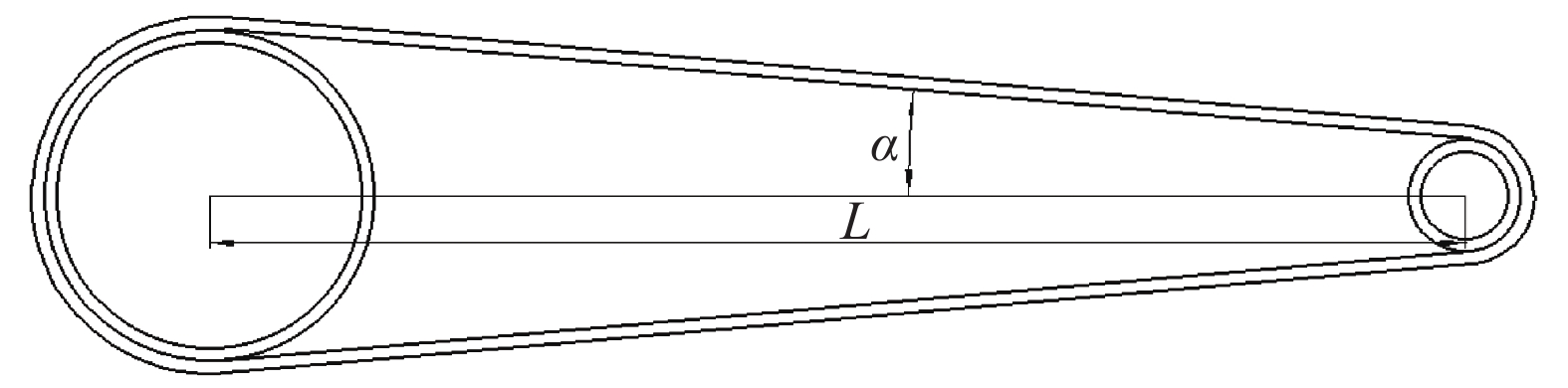
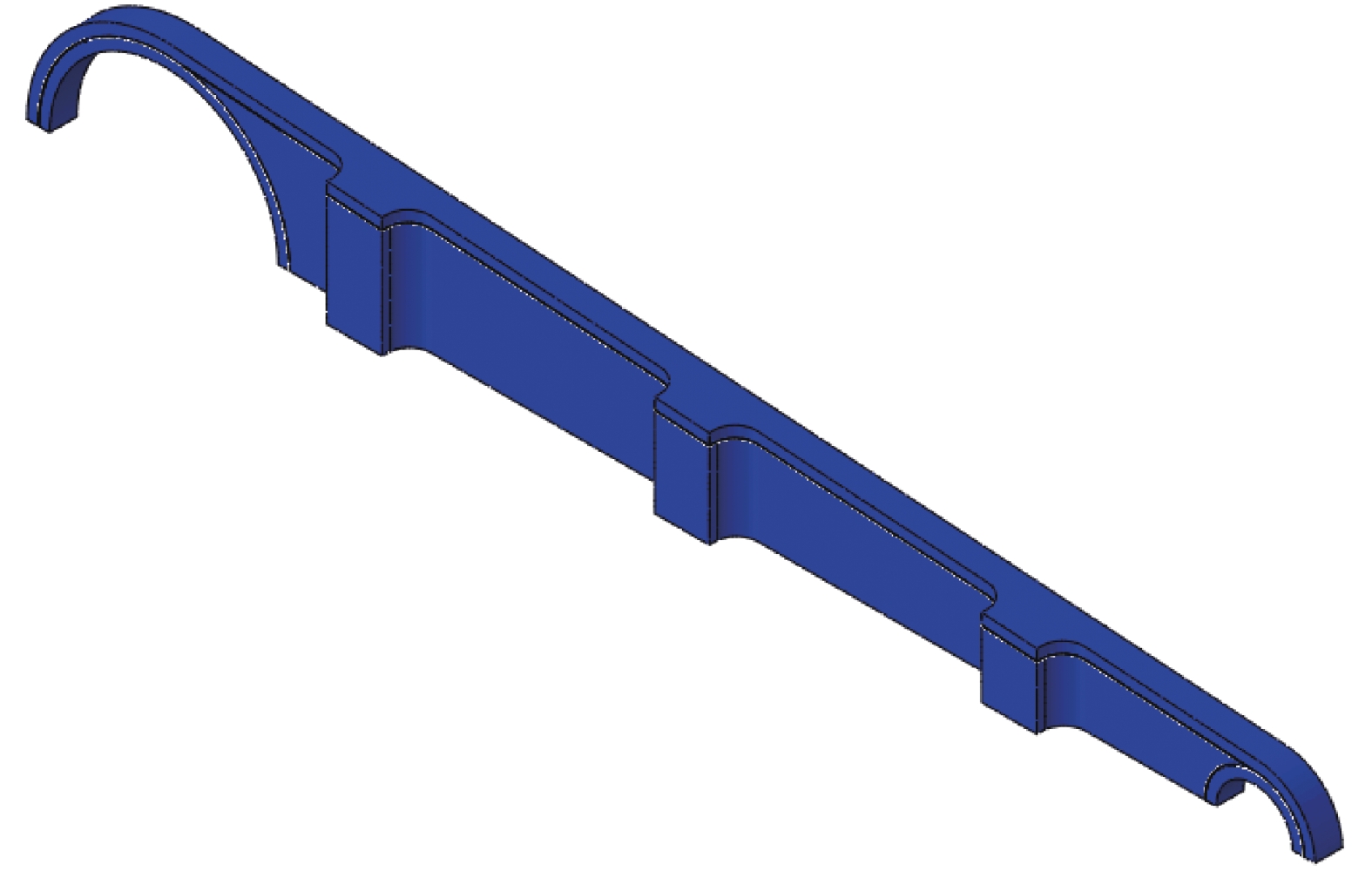
Design of composite winding joints

1.
Chengdu Aircraft Design & Research Institute, Chengdu 610091, China
2.
AVIC Nanjing Electromechanical Technology Co. Ltd., Nanjing 211113, China
3.
College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China

摘要

摘要: 复合材料接头由于其轻质、高强及可设计性好等特点，被越来越多地运用于国外大型民用飞机的结构设计中。本文通过有限元建模，对一种新型的复合材料缠绕接头在拉伸和压缩载荷下的力学响应进行研究。主要围绕基础型、梭型和锥型三种典型的接头形式，比较了不同构型对缠绕接头力学性能的影响。结果表明，三种典型构型的复合材料缠绕接头均具有较好的极限载荷。在此基础上，研究了梭型和锥型构件的力学性能随斜角的变化，从而增加复合材料缠绕接头的应用方式，扩大复合材料缠绕接头的应用范围。
- 复合材料缠绕 /
- 链环 /
- 内衬环 /
- 界面失效 /
- 连接效率 /
- 设计准则
Abstract: The composite joints are increasingly used in foreign civil large-scale aircraft due to their light weight, high strength and designable structure. This work focused on the mechanical behaviour of a newly designed composite wound joints under tension and compression using finite element modelling method. Three typical structures, i.e., basic configuration, shuttle configuration, cone configuration, were compared to get the influence of different configurations on the mechanical behaviour of composite joints. Results show that all three structures have satisfying strength. The slope angles of shuttle and cone configurations were furtherly studied to increase the application of composite wound joints.
- composite winding /
- chain link /
- inner ring /
- interface effectiveness /
- connection efficiency /
- design criteria

HTML全文

连续碳化硅纤维增韧碳化硅陶瓷基复合材料(SiC/SiC)具备高强度、耐高温、低密度等特点，可作为新型航空发动机的优选材料之一^[1-5]。随着SiC/SiC复合材料应用范围愈加广泛，不仅应用于航空领域，在化工领域中也是制造密封环的理想材料，在核聚变反应堆中可用于包层结构、包层流道内衬和转换器等方面^[6]，这些尖端领域均对复合材料的稳定性提出要求。化学气相渗透法(CVI)工艺导致陶瓷基复合材料(CMC)内部普遍存在一些缺陷(束内外孔隙、分层、预制体铺层错位和基体开裂等)，故其力学性能具有较大的离散性，强度作为结构设计的一项重要参数势必会受到其离散性的影响，从而限制结构的高可靠性设计。

CMC成型编织和致密化工艺复杂，易形成损伤源，有必要综合考虑制备工艺中的损伤对复合材料力学性能的影响，建立概率论可靠性模型^[7]。大量研究表明CMC拉伸强度服从Weibull分布^[8-13]。陶永强等^[14]通过渐进损伤的简化剪滞理论得到了各层应力分布及90°层裂纹密度与施加应力之间的关系；Curtin等^[15]基于基体裂纹随机开裂、纤维随机破坏理论，对单向增强CMC的应力-应变行为进行了模拟；孟志新等^[16]探究了不同纤维束下SiC CMC的拉伸行为；Vagaggini等^[17]计算了界面性能参数对复合材料拉伸行为的影响，表明增大界面脱粘能和界面滑移应力利于提高拉伸强度。目前CMC已实现工程化应用，评估工艺放大对复合材料性能分散性的影响成为主要的技术问题，分析单向纤维束复合材料拉伸强度的可靠性，评估结构单元和微结构特征对分散性的影响，也是该材料由小试走向中试的重要环节，小试指实验室开发优化阶段，中试指在小试的基础上继续放大、量产化。关于各组元对CMC性能影响的研究已有很多报道，但是关于小试炉与中试炉对CMC力学性能及其各组元影响的研究鲜有报道。

本文采用CVI技术分别在小试炉与中试炉中制备了单向纤维束SiC/SiC复合材料(Mini-SiC/SiC)的两批试样，探究工艺放大制备对复合材料力学性能离散的影响，并讨论造成复合材料力学性能离散的来源。其中小试炉为实验室制备，一台CVI沉积炉，中试为90台沉积炉，小试炉膛直径为600 mm，中试炉膛直径为1200 mm。通过双参数Weibull分布模型对Mini-SiC/SiC复合材料强度分布和可靠性进行分析，并基于双参数Weibull分布损伤模型建立拉伸载荷-位移关系，最终采用ORS Dragonfly软件分割各组元，结合基体间距裂纹公式分析分散性对可靠性的影响。

1. 材料制备与测试分析

1.1 Mini-SiC/SiC复合材料的制备

采用CVI法制备Mini-SiC/SiC复合材料，见图1。首先，均匀地将SiC纤维束缠绕到石墨框上，获得纤维预制体。然后，在纤维预制体表面沉积BN界面层，其中以BCl₃作为硼源，NH₃作为氨源，Ar为稀释气体，沉积温度600℃^[18]。最后，将沉积BN界面层的SiC纤维预制体在化学气相沉积炉中浸渗SiC基体，选择三氯甲基硅烷(MTS)为SiC基体的源物质，以H₂为载气，Ar为稀释气体，MTS与H₂摩尔比1∶10，沉积温度1150℃。Mini-SiC/SiC复合材料制备工艺参数如表1所示，Mini-SiC/SiC A为小试炉制备(炉膛直径为600 mm)，Mini-SiC/SiC B为中试炉制备(炉膛直径为1200 mm)，小试炉制备复合材料平均密度为3.09 g/cm²，中试炉制备复合材料平均密度为3.07 g/cm²。SiC纤维耐温为1350℃，故制备温度对其影响不大。

图 1 单向纤维束SiC/SiC (Mini-SiC/SiC)复合材料制备示意图

Figure 1. Schematic diagram of preparation of unidirectional fiber bundle SiC/SiC (Mini-SiC/SiC) composites

MTS—Methyltrichlorosilane

下载: 全尺寸图片幻灯片

表 1 Mini-SiC/SiC复合材料的制备工艺参数

Table 1. Process parameters of Mini-SiC/SiC composites

Material name	Deposition time/h		Inside diameter/mm
Material name	BN interface	SiC matrix	Inside diameter/mm
Mini-SiC/SiC A	100	160	600
Mini-SiC/SiC B	100	160	1200
Notes: Mini-SiC/SiC A—Preparation in a small test furnace (Furnace diameter of 600 mm); Mini-SiC/SiC B—Preparation in a pilot test furnace (Furnace diameter of 1200 mm).

下载: 导出CSV

| 显示表格

1.2 力学测试与分析方法

拉伸测试在美特斯(MTS)公司生产的CMT6203型微机控制电子万能试验机上进行。实验执行标准为GB/T 1040.5—2008^[19]，标距50 mm，加载速度3 mm/min。其拉伸测试特定夹具组件见图2。

图 2 拉伸测试特定夹具组件

Figure 2. Stretch test specific fixture assembly

F—Force

下载: 全尺寸图片幻灯片

Mini-SiC/SiC复合材料性能分析，采用以概率论为根据的结构可靠性模型，基于双参数Weibull分布模型对Mini-SiC/SiC复合材料的强度分布和可靠性进行分析。

1.3 表征与分析

采用扫描电子显微镜(SEM，SU3800，日本日立)观察Mini-SiC/SiC复合材料的显微结构和微观形貌。ORS Dragonfly软件在阈值分割的基础上，对Mini-SiC/SiC复合材料断层扫描(CT，AX-2000，宁波奥影检测)图像使用深度学习工具分割出灰度值相近的部分进行处理^[20]。

2. 结果与讨论

2.1 Mini-SiC/SiC复合材料非线性拉伸行为

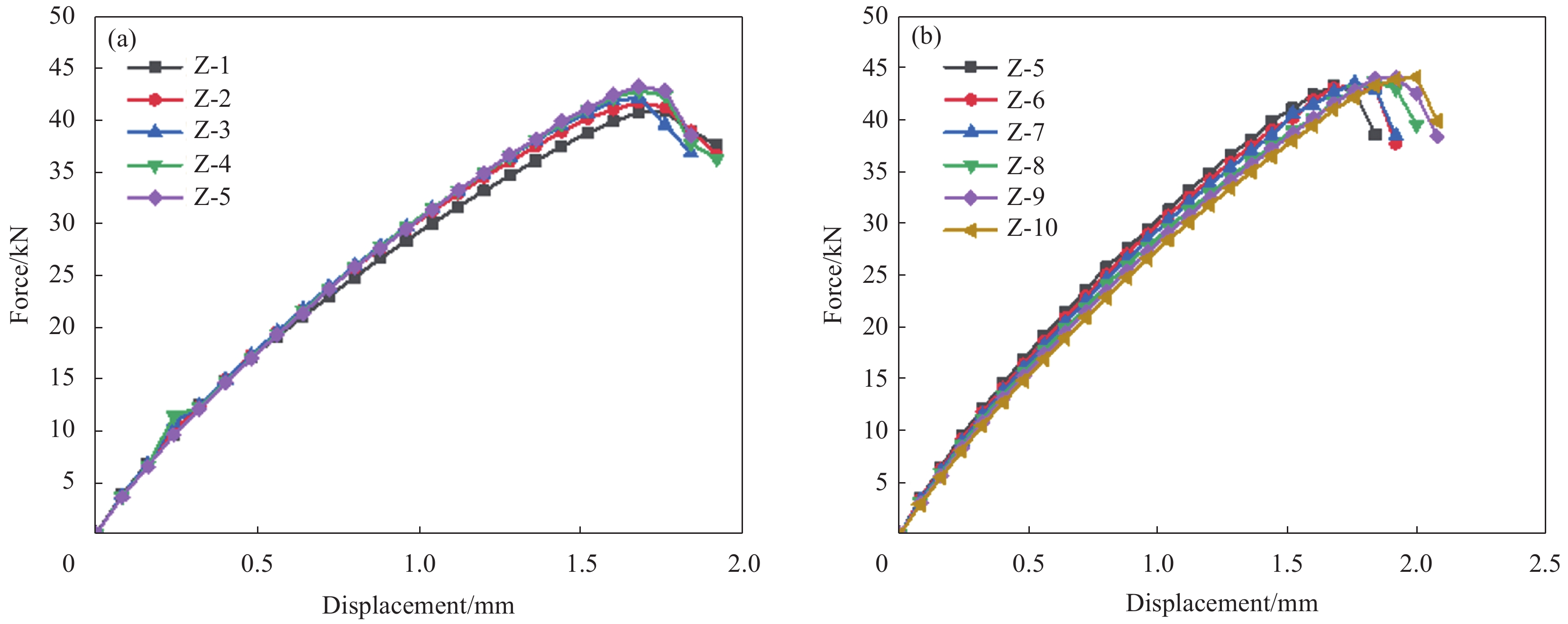
图3为典型Mini-SiC/SiC复合材料载荷-位移曲线。该图由两组曲线组成，图3(a)、3(b)分别为小试炉与中试炉制备，可见曲线规律一致，故各选取其中一条曲线分析，曲线分三阶段：第一阶段加载初期，复合材料整体发生弹性变形，拉伸曲线斜率保持不变；第二阶段曲线呈非线性，且斜率逐渐减小，SiC基体产生新裂纹，随应力增加而增多；当达到最大载荷时曲线进入第三阶段，该阶段曲线未表现出韧性现象，呈现当基体裂纹达到饱和时，直接发生脆性断裂，其断口主要以纤维单丝形式拔出，未出现纤维簇形式拔出。

图 3 Mini-SiC/SiC复合材料典型的拉伸载荷-位移曲线

Figure 3. Typical tensile load-displacement curves of Mini-SiC/SiC composites

下载: 全尺寸图片幻灯片

2.2 Mini-SiC/SiC复合材料拉伸强度统计分布规律

采用中位估计法获取材料强度分布，计算每个强度所对应的失效概率，该失效概率为试验估计值。中位估计法失效概率估计值F_n可表示为

${F}_{\mathrm{n}}\left(\sigma \right)=\frac{i-0.5}{N}$

(1)

式中：i为强度从小到大排列的序数，即强度σ所对应的序号，i的最大值为 N；N为样本总量。

双参数Weibull分布模型累积失效分布函数F(σ) 数学表达式为

$F\left(\sigma \right)=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{\sigma }{{\sigma }_{0}}\right)}^{m}\right]$

(2)

式中： ${\sigma }_{0}$ 为尺度参数，当 σ₀=σ时，Weibull函数取最大值；m为形状参数，表示材料强度的分布规则，m越大，强度分散性越小。

将式(2)整理得：

$\mathrm{ln}\left\{\mathrm{ln}\left[\frac{1}{1-F\left(\sigma \right)}\right]\right\}=m\mathrm{ln}\sigma -m\mathrm{ln}{\sigma }_{0}$

(3)

由式(3)将 $\mathrm{ln}\left\{\mathrm{ln}\left[{1}/({1-F\left(\sigma \right)})\right]\right\}$ 作为y轴，lnσ作为x轴，可得：

$y=mx-m\mathrm{ln}{\sigma }_{0}$

(4)

将式(4)进行作图，并线性拟合分析，由此可得m和σ₀值。

2.2.1 参数估计方法

Weibull分布参数求解及检验主要数据(见附录表4)，线性拟合如图4所示。以Mini-SiC/SiC A复合材料为例，进行双参数Weibull分布模型的参数估计。

图 4 Mini-SiC/SiC复合材料拉伸强度Weibull分布的线性拟合图

Figure 4. Linear fitting diagram of Weibull distribution of tensile strength of Mini-SiC/SiC composites

F_n(σ)—Failure probability; σ—Strength value

下载: 全尺寸图片幻灯片

由图4(a)可得，Mini-SiC/SiC A线性拟合曲线函数为

$y=20.59x-122.03$

(5)

由此可知，m=20.59，σ₀=374.79 MPa。同理可得，Mini-SiC/SiC B的m=5.01，σ₀=400.74 MPa，前者m值大于后者，表明小试炉制备稳定性更优。此外，Weibull分布参数和线性相关系数如表2所示。由表可得，线性相关系数r都接近于1，变量之间存在高度相关性，线性拟合合理，因此m与σ₀接近真实值。

表 2 两种Mini-SiC/SiC复合材料拉伸强度双参数Weibull分布的参数和线性相关系数

Table 2. Parameters and linear correlation coefficient of two-parameter Weibull distribution for tensile strength of two Mini-SiC/SiC composites

Name	Shape parameter b	Scale parameter a/mm	r
Mini-SiC/SiC A	20.59	374.79	0.94
Mini-SiC/SiC B	5.01	400.74	0.98

下载: 导出CSV

| 显示表格

将上述得到的m和σ₀代入式(2)，Mini-SiC/SiC A复合材料的双参数Weibull累积失效分布函数可表示为

$F\left(\sigma \right)=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{\sigma }{374.79}\right)}^{20.59}\right]$

(6)

同理可得，Mini-SiC/SiC B的双参数Weibull累积失效分布函数可表示为

$F\left(\sigma \right)=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{\sigma }{400.74}\right)}^{5.01}\right]$

(7)

图5为两种Mini-SiC/SiC复合材料双参数Weibull累积失效分布函数曲线与中位估计数据曲线对比图。分析可知，分别采用式(6)、式(7)计算的曲线与中位估计法得到的曲线能够较好吻合。因此，拉伸强度分布规律能够采用双参数Weibull分布模型表征，且效果较好。

图 5 Mini-SiC/SiC复合材料Weibull累积分布函数曲线与中位估计数据的对比

Figure 5. Weibull cumulative distribution function curve compared with the median estimated data for Mini-SiC/SiC composites

下载: 全尺寸图片幻灯片

为检验Mini-SiC/SiC A复合材料拉伸强度与双参数Weibull分布的拟合优度。本文引入Kolmogorov-Smirnov(K-S)检验，可通过样本观测值的失效概率估计值F_n(σ)与假设的双参数Weibull累积失效概率分布F(σ)的差值进行对比分析，从而确定该失效概率的分布类型。

F_n(σ)与F(σ)的最大差值D_N由下式得出：

${D}_{\mathrm{N}}=\mathrm{m}\mathrm{a}\mathrm{x}\left|{F}_{\mathrm{n}}\left(\sigma \right)-F\left(\sigma \right)\right|$

(8)

F_n(σ)和F(σ)在上文中已完成计算，前者由中位估计法获得，后者则通过双参数Weibull分布函数计算得到，都代表材料在强度达到σ时发生失效的概率。D_N数据见附录表4。

工程上一般采取显著水平α＝0.05或α=0.01。经查阅D_N临界值表，当N大于35，D_N临界值等于D₃₅与 $\sqrt{N}$ 的比值，如附录表1所示。

当复合材料Mini-SiC/SiC A拉伸强度为356.48 MPa时(附录表4)，Kolmogorov距离取最大值D_N=0.1252<D_60,0.05=0.1756<D_60,0.01=0.2104，可知D_N小于显著水平α=0.05和α=0.01的D_N临界标准值。

采用相同方法可检验Mini-SiC/SiC B拉伸强度是否服从双参数Weibull分布，检验结果数据如附录表2所示。由表可知，D_N分别为0.0995均小于D_60,0.01和D_60,0.05，故拉伸强度均服从双参数Weibull分布，且拟合优度良好。

根据K-S检验可知，D_N小于显著水平α＝0.05和α=0.01的D_N临界标准值。故拉伸强度均服从双参数Weibull分布，且拟合优度良好。

可靠度R是度量可靠性的标准，其与失效概率关系可表示为

$R\left(\sigma \right)=1-F\left(\sigma \right)$

(9)

该式意味着给定任意强度，都可计算出其可靠度为多大，并随着强度增大，失效概率会增大，可靠度会减小。由于给出任意强度数据便可计算其可靠度，因此对于每个给定的可靠度，也可以计算出相应的可靠拉伸强度。联立式(2)和式(9)并求反函数，可获得给定可靠度下的可靠拉伸强度σ如下式：

$\sigma \left(R\right)={\sigma }_{0}{\left(\mathrm{ln}\frac{1}{R}\right)}^{\frac{1}{m}}$

(10)

由此就可获得任意可靠度所对应的可靠强度值。在工程上，一般将5%、25%、50%、75%、95%可靠度作为可靠质量标准。5个可靠度下的可靠拉伸强度值如附录表3所示。同时，不同可靠度下的可靠拉伸强度如附录图1所示。

研究表明，可靠度为50%时的可靠拉伸强度与平均拉伸强度较为接近，表3给出了可靠度为50%的可靠拉伸强度与平均拉伸强度。由表中数据通过计算绝对偏差和相对偏差可知：最大绝对偏差仅4.69 MPa，最大相对偏差仅1.2%。因此，采用平均拉伸强度可准确预测50%可靠度所对应的可靠强度，且误差较小。

表 3 两种Mini-SiC/SiC复合材料在可靠度50%时的可靠拉伸强度与平均拉伸强度

Table 3. Reliable tensile strength and average tensile strength of two Mini-SiC/SiC composites at 50% reliability

Name	Mean tensile strength/MPa	Tensile strength of 50% reliability/MPa	Absolute deviation/MPa	Relative deviation/%
Mini-SiC/SiC A	365.08	368.18	3.10	0.8
Mini-SiC/SiC B	367.78	372.47	4.69	1.2

下载: 导出CSV

| 显示表格

2.3 Mini-SiC/SiC复合材料拉伸载荷与位移关系的确定

复合材料拉伸应力σ与载荷P关系为

$\sigma =\frac{P}{S}$

(11)

复合材料拉伸应变ε与伸长量∆l关系为

$\varepsilon =\frac{\Delta l}{{l}_{0}}$

(12)

式中：S为材料截面积； ${l}_{0}$ 为标距，值为50 mm。

材料宏观损伤变量服从双参数Weibull分布，由式(2)与拉伸强度建立联系。在拉伸加载时，损伤贯穿整个过程，故累积损伤量和位移x同样服从双参数Weibull分布。因此累积损伤因子D_a随着位移x变化的分布函数可表示为类似于式(2)形式，如下所示：

${D}_{\mathrm{a}}=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x}{a}\right)}^{b}\right]$

(13)

由于SiC/SiC复合材料为脆性材料，为便于计算参数a、b，获取Weibull分布模型，因此将x视为断裂位移x_max。

将式(13)整理得：

$\mathrm{ln}\left\{\mathrm{ln}\left[\frac{1}{1-{D}_{\mathrm{a}}}\right]\right\}=b\mathrm{ln}{x}_{\mathrm{m}\mathrm{a}\mathrm{x}}-b\mathrm{ln}a$

(14)

可将 $\mathrm{ln}\left\{\mathrm{ln}\left[{1}/({1-{D}_{\mathrm{a}}})\right]\right\}$ 作为y轴，lnx_max作为x轴，得：

$y=b{x}_{\mathrm{m}\mathrm{a}\mathrm{x}}-b\mathrm{ln}a$

(15)

SiC/SiC复合材料中，SiC纤维和SiC基体均为脆性材料，各组分材料达到破坏极限前几乎未发生塑性变形。因此，基于双参数Weibull分布的弹性损伤模型表征Mini-SiC/SiC复合材料拉伸加载过程：

$P=k{\left(1-{D}_{\mathrm{a}}\right)}_{x}$

(16)

式中，k为抗拉刚度。

2.3.1 双参数Weibull分布模型参数估计

Weibull分布参数求解及检验的详细数据见附录表5，线性拟合如图6所示。以Mini-SiC/SiC A复合材料为例，进行双参数Weibull分布模型参数估计。

图 6 Mini-SiC/SiC复合材料断裂位移Weibull分布线性拟合

Figure 6. Linear fitting of Weibull distribution for fracture displacement of Mini-SiC/SiC composites

D_a—Cumulative damage factor

下载: 全尺寸图片幻灯片

Mini-SiC/SiC A复合材料拟合曲线函数为

$y=3.09x+0.42$

(17)

由此可得，b=3.09，a=0.87 mm。同理可得，Mini-SiC/SiC B的b=2.50，a=1.16 mm。此外，Weibull分布参数和线性相关系数r如表4所示。可知，线性相关系数都接近于1，变量之间存在高度相关关系，线性拟合合理，a与b接近真实数据。

表 4 两种Mini-SiC/SiC复合材料断裂位移双参数Weibull分布参数、线性相关系数

Table 4. Weibull distribution parameters and linear correlation coefficients of two Mini-SiC/SiC composites with two-parameter fracture displacement

Name	Shape parameter b	Scale parameter a/mm	r
Mini-SiC/SiC A	3.09	0.87	0.97
Mini-SiC/SiC B	2.50	1.16	0.99

下载: 导出CSV

| 显示表格

代入参数后，双参数Weibull累积损失因子损伤函数可分别表示为

${D}_{\mathrm{a}}=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x}{0.87}\right)}^{3.09}\right]$

(18)

${D}_{\mathrm{a}}=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x}{1.16}\right)}^{2.50}\right]$

(19)

图7为拉伸强度的Weibull累积损伤因子函数拟合结果与试验结果对比图。分析可知，中位估计数据分别和式(18)、式(19)函数曲线吻合较好，因此，双参数Weibull模型能较好地表征累积损伤因子分布规律。

图 7 Mini-SiC/SiC复合材料Weibull累积损伤因子分布函数曲线与中位估计数据的对比

Figure 7. Weibull cumulative damage factor distribution function curves for Mini-SiC/SiC composites compared with median estimated data

下载: 全尺寸图片幻灯片

D_N为Kolmogorov距离；D_60,0.01为样本总量为60，显著水平α取0.01；D_60,0.05为样本总量为60，显著水平α取0.05。

采用K-S检验进行拟合优度分析，计算估计值D和D_a最大差异值可获得D_N。如表5所示，经比对发现，两种材料D_N值均小于D_60,0.01、D_60,0.05，故断裂位移均服从双参数Weibull分布，且拟合优度良好。

表 5 Mini SiC/SiC复合材料的D_N与D_60,0.01、D_60,0.05

Table 5. D_N and D_60,0.01, D_60,0.05 of Mini SiC/SiC composites

Name	D_N	D_60,0.01	D_60,0.05
Mini-SiC/SiC A	0.1139	0.2104	0.1756
Mini-SiC/SiC B	0.1036	0.2104	0.1756
Notes: D_N—Kolmogorov distance; D_60,0.01—Total sample size is 60 and the significance level α is taken as 0.01; D_60,0.05—Total sample size is 60 and α is taken as 0.05.

下载: 导出CSV

| 显示表格

2.3.2 拉伸载荷与位移关系

将式(13)代入式(16)得拉伸载荷-位移关系模型：

$P=k\left(\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x}{a}\right)}^{b}\right]\right)x$

(20)

为求解k值，假设拉伸载荷-位移为线性关系。将每个试样断裂位移和最大载荷数据代入式(20)，可得每个试样值，取平均值，即为k值。经计算，两种材料k值分别为370.89 N/mm、251.09 N/mm。将a、b、k值代入式(20)，得Mini-SiC/SiC A、Mini-SiC/SiC B拉伸载荷-位移模型分别为

$P=370.89\left(\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x}{0.87}\right)}^{3.09}\right]\right)x$

(21)

$P=251.09\left(\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x}{1.16}\right)}^{2.50}\right]\right)x$

(22)

将拉伸应力和载荷关系(式(11))与拉伸应变和加载位移之间的关系(式(12))及拉伸载荷-位移模型(式(20))联立进行求解，得拉伸应力-应变关系如下式：

$\sigma =\frac{k\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({\varepsilon {l}_{0}}/{a}\right)}^{b}\right]\varepsilon {l}_{0}}{S}$

(23)

代入相关数据得上述两种材料拉伸应力-应变关系分别如下式所示：

$\sigma =\frac{370.89\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({ 50\varepsilon }/{0.87}\right)}^{3.09}\right] 50\varepsilon}{S}$

(24)

$\sigma =\frac{251.09\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({ 50\varepsilon }/{1.16}\right)}^{2.50}\right] 50\varepsilon }{S}$

(25)

为验证拉伸应力-应变关系合理性，抽取拉伸强度接近于平均值的试样进行检验。Mini-SiC/SiC A中选取最大载荷128.79 N，断裂位移0.83 mm的试样。Mini-SiC/SiC B中选取最大载荷132.60 N，断裂位移为1.03 mm的试样。求出试样断裂应变ε_max后，将该值分别代入式(24)、式(25)可获得采用拉伸应力-应变关系计算强度值(表6)。比对发现，与真实强度误差不超过7%。因此，该关系建立合理，可预测应力-应变关系。

表 6 Mini-SiC/SiC复合材料拉伸应力-应变关系检验过程主要数据

Table 6. Main data of the test process of tensile stress-strain relationship of Mini-SiC/SiC composites

Name	Mini-SiC/ SiC A	Mini-SiC/ SiC B
Maximum load P/N	128.79	132.60
Fracture displacement x_max/mm	0.83	1.03
True strength value σ/MPa	368.72	393.48
Fracture strain ε_max	0.0166	0.0205
Strength calculation value of con- stitutive model/MPa	373.50	366.40
Error between calculated value and real value	+1.2%	–6.8%

下载: 导出CSV

| 显示表格

2.4 基体对复合材料强度分散性的影响

源于CVI工艺的复杂性，故复合材料内部存在缺陷，这些缺陷导致复合材料宏观力学性能具有分散性。图8为Mini-SiC/SiC复合材料初始态与断口SEM图像。图8(a)为初始态单向纤维，可看出纤维束表面沉积基体较粗糙，存在参差不齐菜花状β-SiC，表明基体沉积状态具有不稳定性。由图8(b)、8(c)可见，Mini-SiC/SiC复合材料断口纤维呈纤维单丝形式拔出，基体裂纹未出现大范围偏转，表现瞬间断裂。当纤维束表面存在缺陷时，拉伸过程中会由于应力集中而成为断裂源，造成纤维早期破环，故降低纤维表面缺陷可提高纤维束强度，从而降低强度的分散性。

图 8 Mini-SiC/SiC复合材料初始态与断口SEM图像

Figure 8. SEM images of initial state and fracture of Mini-SiC/SiC composites

下载: 全尺寸图片幻灯片

图9采用ORS Dragonfly软件对Mini-SiC/SiC复合材料拉断CT图进行处理，图9(a)为初始状态下的正视断口，在阈值分割基础上采用深度学习方法提取拉伸断口裂纹分布(图9(b))情况，其中近似垂直于纤维且相互平行的线条为复合材料周期性裂纹。接着提取SiC纤维(图9(c))，可看出纤维分布并不均匀，纤维少的地方为基体与孔隙填充。随后，对断口俯视角度也进行学习处理(图9(d))，先提取SiC基体(图9(e))，可清楚看到纤维与基体分布状况，证实纤维少的地方由基体填充。最后，提取纤维表面BN界面相(图9(f))，可以看出界面相均匀覆盖纤维表面，形成一根根圆柱管。

图 9 ORS Dragonfly软件处理Mini-SiC/SiC复合材料断层扫描图像

Figure 9. ORS Dragonfly software for processing Mini-SiC/SiC composite tomography images

下载: 全尺寸图片幻灯片

由图8和图9从Mini-SiC/SiC复合材料宏观表面和分离复合材料内部各组元来看，制备态表面状态与复合材料内部纤维分布情况，会影响界面相与基体分布状态，导致复合材料分散性大，影响其可靠性。

复合材料拉伸断裂强度σ_u如下式所示：

${\sigma }_{\mathrm{u}}={\sigma }_{\mathrm{f}\mathrm{u}}{V}_{\mathrm{f}}$

(26)

式中： ${\sigma }_{\mathrm{f}\mathrm{u}}$ 为纤维断裂强度； ${V}_{\mathrm{f}}$ 为纤维体积分数。

由式(26)求得理论拉伸强度为499.45 MPa，但由于单向复合材料断裂时，连续纤维(l>30l_c)并非同时断裂，下式中载荷传递因子β为0.7，其纤维承载效率大于99%：

${\sigma }_{\mathrm{f}\mathrm{u}}={\sigma }_{\mathrm{f}\mathrm{u}}^{*}\left(1-\frac{1-\beta }{l/{l}_{\mathrm{c}}}\right)$

(27)

式中： ${\sigma }_{\mathrm{f}\mathrm{u}}^{*}$ 为纤维的原位断裂强度； $l/{l}_{\mathrm{c}}$ 为比长度；l为纤维长度；l_c为临界纤维长度。

此时求得理论拉伸强度为349.61 MPa，该值与实测拉伸强度365.08 MPa相差仅4.24%。表明纤维基本全部承载，纤维对复合材料分散性影响较小。

图10对Mini-SiC/SiC复合材料拉伸产生的周期性裂纹间距进行测量，最小裂纹间距为83.2 μm，最大裂纹为107.8 μm。根据图9(f)可知界面相均匀分布，故视界面滑移应力(τ)为定值，不影响复合材料的分散性。由式(28)可计算出(附录表8、表9) Mini-SiC/SiC复合材料基体裂纹宽度为89.43 μm，该宽度处于实际裂纹宽度范围内。验证了该式可以较好地描述Mini-SiC/SiC复合材料力学断裂行为。

图 10 ORS Dragonfly软件提取Mini-SiC/SiC复合材料周期性裂纹间距图

Figure 10. Extraction of periodic crack spacing diagram of Mini-SiC/SiC composites by ORS Dragonfly software

下载: 全尺寸图片幻灯片

将最小与最大裂纹间距代入式(25)，分别求出其对应拉伸强度为376.16 MPa和406.14 MPa，该值同样处于该批试样实际拉伸强度(331.02 MPa，407.82 MPa)内，表明基体裂纹间距具有离散性，基体是影响Mini-SiC/SiC复合材料可靠性的主要来源。

$\; \varsigma =\frac{{{b}_{2}{(1-{a}_{1}V_{\rm{f}})}^{2}R{{\sigma }_{\mathrm{p}}}^{2}}}{{4d{\tau }_{0}{E}_{\mathrm{m}}{V_{\rm{f}}}^{2} }}$

(28)

式中：V_f为纤维体积分数； ${\sigma }_{\rm{p}}$ 为峰值应力；R为纤维半径；d为裂纹间距；E_m为基体模量。

通过双参数Weibull分布模型可知，小试炉与中试炉拟合良好，故裂纹间距仍选用图10。此时中试炉试样拉伸强度(附录表6)范围为(161.09 MPa，540.95 MPa)，该范围大于小试炉试样拉伸强度范围，这是由于中试炉沉积基体工艺的放大化所导致，这种现象与m值对应，表明中试炉具有更大离散性(图3)。最大和最小裂纹间距对应的拉伸强度仍处于该范围内。

图11为基体影响复合材料形状参数m与力学性能离散的机制图。根据图9(f)与式(26)、式(27)可知，纤维与界面对复合材料性能离散的影响不大，故基体为影响复合材料可靠性的重要原因。m值影响应力-应变曲线非线性段的平稳性^[21]，m越大非线性段越平稳，表明复合材料在达到基体最大开裂后曲线越规律，离散性越小。图3与表2可明显看出小试炉制备的复合材料更加稳定，这是由于在小试炉中CVI沉积复合材料基体更加均匀，复合材料孔隙分布集中在内部中心区域(图11(a))，该区域的形成主要原因是基体在沉积时会形成沉积梯度，靠近表层区域的部分复合材料密度大、孔隙被充分填充，致使复合材料内部孔隙无法填充。反观中试炉制备，CVI工艺得到放大，同批次制备试样大大增多，造成复合材料内部孔隙发生不均匀分布现象(图11(b))，进而导致制备出的试样离散性增大、m值减小，影响其可靠性。

图 11 基体对Mini-SiC/SiC复合材料形状参数m与力学性能离散的影响

Figure 11. Matrix effects on the shape parameter m and mechanical property dispersion of Mini-SiC/SiC composites

下载: 全尺寸图片幻灯片

3. 结论

(1) 双参数Weibull分布模型可准确表征小试炉制备单向纤维束 SiC/SiC (Mini-SiC/SiC A)、中试炉制备Mini-SiC/SiC B拉伸强度分布，其拉伸强度分别为365.08 MPa和367.78 MPa，形状参数分别为20.59和5.01。

(2) 基于双参数Weibull分布模型建立的可靠度分析模型可准确预测不同可靠度下的可靠强度。其中，当可靠度为50%时，可靠强度与拉伸强度最大误差为1.2%，故在工程中可采用材料的平均拉伸强度预测50%可靠拉伸强度。

(3) 基于双参数Weibull分布模型建立的拉伸载荷-位移关系可准确预测拉伸应力-应变关系，与真实强度误差不超过7%。

(4) 复合材料内部界面相均匀包裹纤维，界面相滑移应力视为定值；连续纤维承载大于99%，纤维对复合材料性能离散性影响较小；通过基体裂纹间距公式可知，最小和最大裂纹间距所对应的拉伸强度为376.16 MPa和406.14 MPa，该值均处于Mini-SiC/SiC A复合材料拉伸强度(331.02 MPa，407.82 MPa)和Mini-SiC/SiC B复合材料拉伸强度(161.09 MPa，540.95 MPa)范围内。然而，Mini-SiC/SiC B复合材料拉伸强度范围大于Mini-SiC/SiC A，且前者 Weibull模数5.01比后者 Weibull模数 20.59低75.7%，中试分散性更大是由于中试炉尺寸放大所致，基体非均匀性是影响复合材料可靠性的主要原因。

图 1 基础型缠绕接头受拉/压构型示意图

Figure 1. Schematic diagrams of basic winding joint tension/compression configurations

下载: 全尺寸图片幻灯片

图 2 基础型缠绕接头受拉构型结构形式

Figure 2. Basic winding joint tension configuration structure

D₁—Diameter of the inner surface of inner ring; D₂—Diameter of the outer surface of inner ring; L—Length of the laminate; Φ—Diameter of the laminate; W—Width of the joint

下载: 全尺寸图片幻灯片

图 3 基础型缠绕接头受拉构型尺寸

Figure 3. Tension configuration dimensions of basic winding joint

下载: 全尺寸图片幻灯片

图 4 基础型缠绕接头受压构型尺寸

Figure 4. Compression configuration dimensions of basic winding joint

R—Chamfer

下载: 全尺寸图片幻灯片

图 5 基础型缠绕接头受拉构型有限元模型约束加载示意图

Figure 5. Schematic diagram of constraint and load for finite element model of basic winding joint tension configuration

下载: 全尺寸图片幻灯片

图 6 拉伸工况下基础型缠绕接头受拉构型载荷-位移曲线

Figure 6. Load-displacement curve of basic winding joint tension configuration under tensile condition

下载: 全尺寸图片幻灯片

图 7 拉伸工况下基础型缠绕接头受拉构型链环损伤演化

Figure 7. Damage evolution of loop under tensile condition for basic winding joint tension configuration

下载: 全尺寸图片幻灯片

图 8 压缩工况下基础型缠绕接头受拉构型载荷-位移曲线

Figure 8. Load-displacement curve of basic winding joint tension configuration under compression condition

下载: 全尺寸图片幻灯片

图 9 压缩工况下基础型缠绕接头受拉构型损伤演化

Figure 9. Damage evolution of basic winding joint tension configuration under compression condition

下载: 全尺寸图片幻灯片

图 10 基础型缠绕接头受压构型三维模型

Figure 10. 3D model of the basic winding joint compression configuration

下载: 全尺寸图片幻灯片

图 11 基础型缠绕接头受拉构型和受压构型压缩工况下载荷-位移曲线对比

Figure 11. Comparison of load-displacement curves of basic winding joint tension configuration and compression configuration under compression

下载: 全尺寸图片幻灯片

图 12 压缩工况下基础型缠绕接头受压构型损伤演化

Figure 12. Damage evolution of basic winding joint compression configuration under compression condition

下载: 全尺寸图片幻灯片

图 13 梭型缠绕接头x-y平面示意图

Figure 13. x-y plane diagram of shuttle winding joint

下载: 全尺寸图片幻灯片

图 14 梭型缠绕接头受拉构型三维模型

Figure 14. 3D model of shuttle winding joint tension configuration

下载: 全尺寸图片幻灯片

图 15 模型S-1~S-10载荷-位移曲线

Figure 15. Load-displacement curves of model S-1 - S-10

下载: 全尺寸图片幻灯片

图 16 梭型缠绕接头受拉构型各阶段载荷随α角变化的曲线

Figure 16. Curves of force changing with α angle of shuttle winding joint tension configuration at each stage

下载: 全尺寸图片幻灯片

图 17 梭型缠绕接头受压构型三维模型

Figure 17. 3D model of shuttle winding joint compression configuration

下载: 全尺寸图片幻灯片

图 18 模型SY-1~SY-5载荷-位移曲线

Figure 18. Load-displacement curves of model SY-1 - SY-5

下载: 全尺寸图片幻灯片

图 19 压缩工况下模型SY-1~SY-5各损伤起始点随α角的变化

Figure 19. Changes of each damage starting point with α of model SY-1 - SY-5 under compression condition

下载: 全尺寸图片幻灯片

图 20 锥型缠绕接头X-Y平面示意图

Figure 20. X-Y plane diagram of tapered winding joint

下载: 全尺寸图片幻灯片

图 21 锥型缠绕接头受拉/压构型X-Z平面示意图

Figure 21. X-Z plane diagram of tapered winding joint tension/compression configuration

下载: 全尺寸图片幻灯片

图 22 锥型缠绕接头受拉构型三维模型

Figure 22. 3D model of tapered winding joint tension configuration

下载: 全尺寸图片幻灯片

图 23 模型Z-1~Z-10载荷-位移曲线

Figure 23. Load-displacement curves of model Z-1-Z-10

下载: 全尺寸图片幻灯片

图 24 模型Z-1~Z-10各阶段载荷随α角变化的曲线

Figure 24. Changes of force with α angle of model Z-1–Z-10 at each stage

下载: 全尺寸图片幻灯片

图 25 锥型缠绕接头受压构型三维模型

Figure 25. 3D model of tapered winding joint compression configuration

下载: 全尺寸图片幻灯片

图 26 模型ZY-1~ZY-5载荷-位移曲线

Figure 26. Load-displacement curves of model ZY-1-ZY-5

下载: 全尺寸图片幻灯片

图 27 压缩工况下模型ZY-1~ZY-5各损伤起始点随α角的变化

Figure 27. Changes of each damage starting point with α angle of model ZY-1 - ZY-5 under compression condition

下载: 全尺寸图片幻灯片

表 1 复合材料参数

Table 1 Composite material parameters

Property	CCF300/BA9916-Ⅱ	CF3031/BA9916-Ⅱ
${E_1}$ /GPa	120	60
${E_2}$ /GPa	7.7	59
${E_3}$ /GPa	7.7	7.7
${\nu _{12} } = {\nu _{13} } = {\nu _{23} }$	0.05	0.27
${G_{12}} = {G_{13}}$ /GPa	5.5	6.4
${G_{23}}$ /GPa	5.5	6.4
${X_{\rm{T}}}$ /MPa	1 400	500
${X_{\rm{C}}}$ /MPa	1 300	450
${Y_{\rm{T}}} = {Z_{\rm{T}}}$ /MPa	35	450
${Y_{\rm{C}}} = {Z_{\rm{C}}}$ /MPa	160	455
${S_{12}} = {S_{13}}$ /MPa	163	105
${S_{23}}$ /MPa	86	83
Notes：E_i (i, j=1, 2, 3)—Elastic modulus in the direction of fibre, perpendicular to the fibre in the plane and out of plane; X_T, Y_T and Z_T—Tensile strength in the three directions above, respectively; X_C, Y_C and Z_C—Compress strength in the three directions above, respectively; ν_ij, G_ij and S_ij (i, j=1, 2, 3)—Poisson’s ratio, shear modulus and shear strength for 1-2, 1-3, 2-3 plane, respectively.

下载: 导出CSV

表 2 J-116B结构胶材料参数

Table 2 Material parameters of J-116B

$E/{E_{{\rm{nn}}}}$ /(MPa·mm⁻¹)	${G_1}/{E_{{\rm{ss}}}}$ /(MPa·mm⁻¹)	${G_2}/{E_{{\rm{tt}}}}$ /(MPa·mm⁻¹)	$t_{\rm{n}}^0$ /MPa	$t_{\rm{s}}^0$ /MPa	$t_{\rm{t}}^0$ /MPa
1000	300	300	20	30	30
Notes： $E/{E_{{\rm{nn}}}}$ , ${G_1}/{E_{{\rm{ss}}}}$ and ${G_2}/{E_{{\rm{tt}}}}$ —Interface stiffness for three directions, respectively; $t_{\rm{n}}^0$ , $t_{\rm{t}}^0$ and $t_{\rm{t}}^0$ —Interface strength for three directions, respectively.

下载: 导出CSV

表 3 梭型缠绕接头模型编号

Table 3 Model number of shuttle winding joint

Tension		Compression
Model	Angle/(°)	model	Angle/(°)
S-1	1	SY-1	2
S-2	2	SY-2	4
S-3	3	SY-3	6
S-4	4	SY-4	8
S-5	5	SY-5	10
S-6	6
S-7	7
S-8	8
S-9	9
S-10	10

下载: 导出CSV

表 4 模型S-1~S-10各阶段载荷及对应位移

Table 4 Loads and corresponding displacements of model S-1 - S-10 at each stage

Stage	Property	S-1	S-2	S-3	S-4	S-5	S-6	S-7	S-8	S-9	S-10
Initial damage of interface	Force/kN	10.92	11.15	11.31	11.48	11.65	11.81	11.97	12.09	12.20	12.32
Initial damage of interface	Displacement/mm	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30
Failure of interface	Force/kN	34.96	35.46	35.78	36.10	36.42	36.62	36.87	37.05	37.19	37.35
Failure of interface	Displacement/mm	1.40	1.40	1.40	1.40	1.40	1.40	1.40	1.40	1.40	1.40
Initial damage of chain link	Force/kN	36.85	37.33	37.64	37.95	38.26	38.51	38.70	38.86	39.00	39.14
Initial damage of chain link	Displacement/mm	1.50	1.50	1.50	1.50	1.50	1.50	1.50	1.50	1.50	1.50
Failure of winding joint	Force/kN	40.66	40.78	41.05	41.36	41.67	42.21	42.74	43.28	43.42	43.59
Failure of winding joint	Displacement/mm	1.80	1.80	1.80	1.80	1.80	1.80	1.80	1.80	1.90	1.90

下载: 导出CSV

表 5 压缩工况下模型SY-1~SY-5损伤起始点

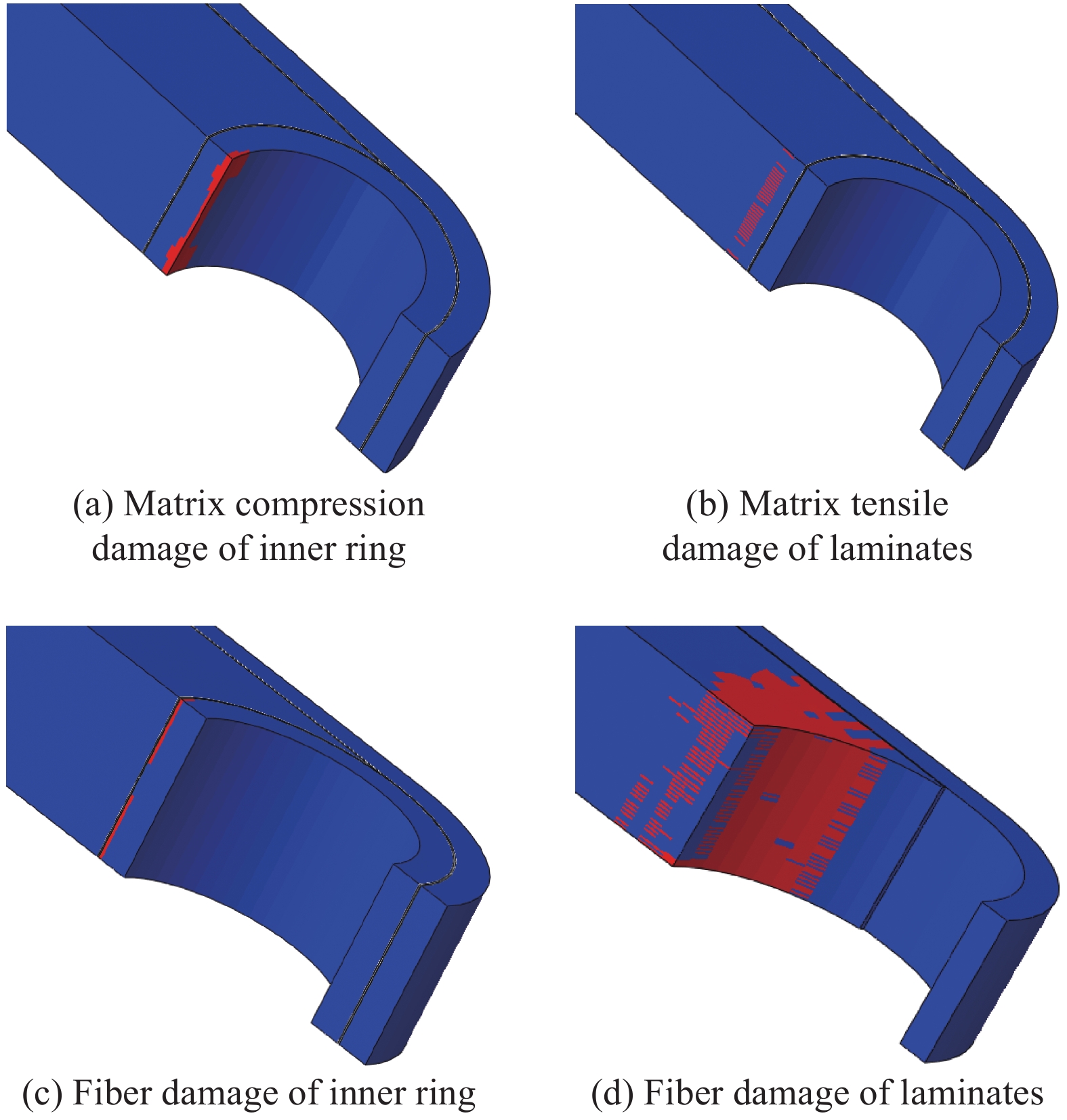
Table 5 Damage starting points of model SY-1 - SY-5 under compression condition

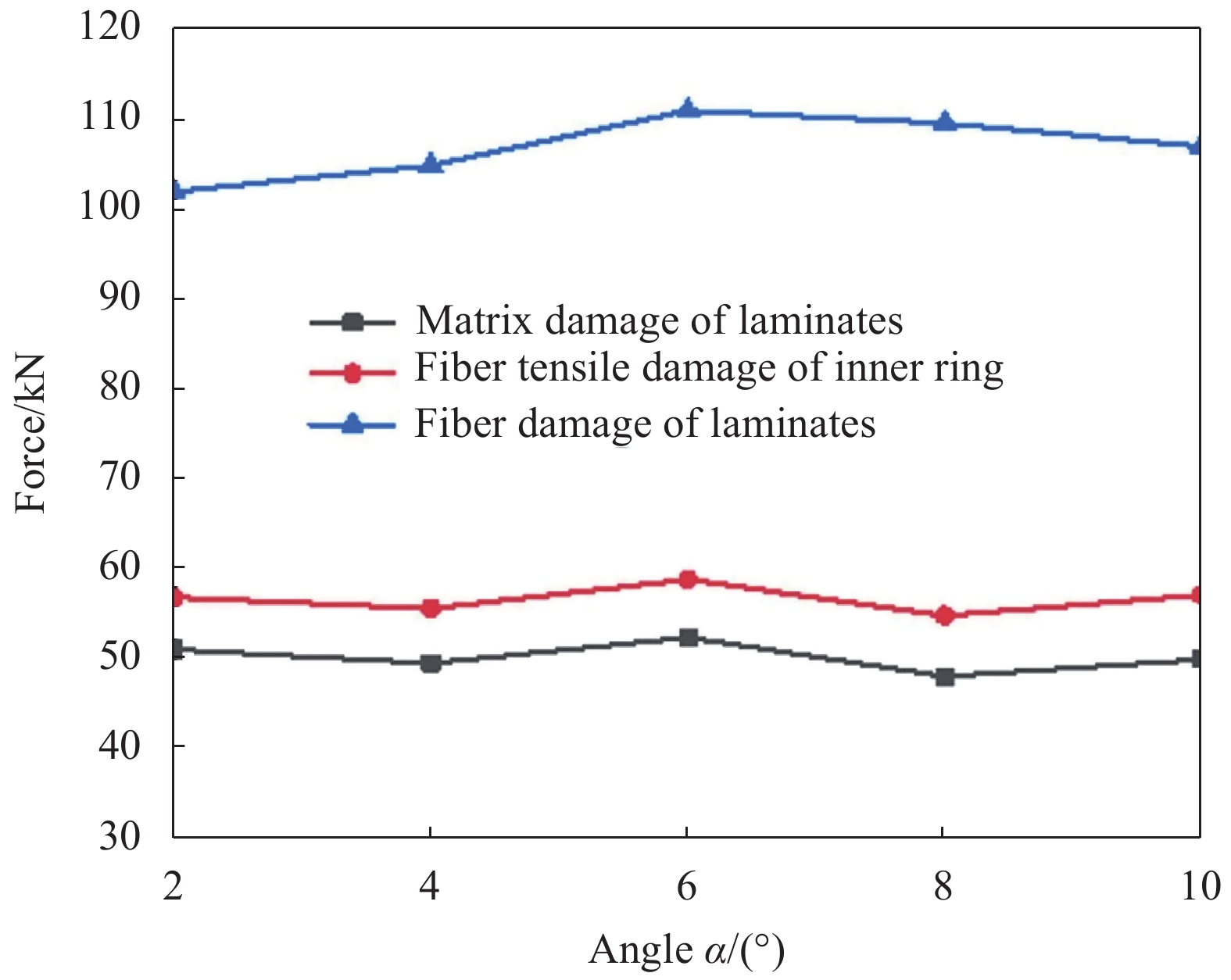
Stage	Property	SY-1	SY-2	SY-3	SY-4	SY-5
Matrix compression damage of inner ring	Force/kN	50.97	49.44	52.30	47.98	49.83
Matrix compression damage of inner ring	Displacement/mm	0.72	0.64	0.64	0.56	0.56
Matrix damage of laminates	Force/kN	50.97	49.44	52.30	47.98	49.83
Matrix damage of laminates	Displacement/mm	0.72	0.64	0.64	0.56	0.56
Fiber tensile damage of inner ring	Force/kN	56.76	55.51	58.74	54.73	57.01
Fiber tensile damage of inner ring	Displacement/mm	0.80	0.72	0.72	0.64	0.64
Fiber damage of laminates	Force/kN	101.90	104.82	110.93	109.51	106.93
Fiber damage of laminates	Displacement/mm	1.44	1.36	1.36	1.28	1.20

下载: 导出CSV

表 6 锥形缠绕接头模型编号

Table 6 model number of tapered winding joint

Tension		Compression
No.	Angle/(°)	No.	Angle/(°)
Z-1	1	Z-1	2
Z-2	2	Z-2	4
Z-3	3	Z-3	6
Z-4	4	Z-4	8
Z-5	5	Z-5	10
Z-6	6
Z-7	7
Z-8	8
Z-9	9
Z-10	10

下载: 导出CSV

表 7 模型Z-1~Z-10各阶段载荷及对应位移

Table 7 Loads and corresponding displacements of model Z-1-Z-10 at each stage

Stage	Property	Z-1	Z-2	Z-3	Z-4	Z-5	Z-6	Z-7	Z-8	Z-9	Z-10
Initial damage of interface	Force/kN	9.53	10.02	10.76	11.31	12.11	11.82	11.52	11.22	10.86	10.52
Initial damage of interface	Displacement/mm	0.24	0.24	0.24	0.24	0.32	0.32	0.32	0.32	0.32	0.32
Failure of interface	Force/kN	34.64	36.01	36.48	36.51	36.65	35.92	35.40	34.50	34.11	33.41
Failure of interface	Displacement/mm	1.28	1.28	1.28	1.28	1.28	1.28	1.28	1.28	1.28	1.28
Initial damage of chain link	Force/kN	37.46	38.88	39.46	39.64	39.90	40.15	40.59	41.11	41.57	42.17
Initial damage of chain link	Displacement/mm	1.44	1.44	1.44	1.44	1.44	1.52	1.52	1.60	1.68	1.76
Failure of winding joint	Force/kN	40.82	41.71	42.17	42.81	43.26	43.27	43.59	43.75	44.05	44.14
Failure of winding joint	Displacement/mm	1.76	1.68	1.68	1.68	1.68	1.76	1.76	1.84	1.92	2.00

下载: 导出CSV

表 8 压缩工况下模型ZY-1~ZY-5损伤起始点

Table 8 Damage starting points of model ZY-1-ZY-5 under compression condition

Stage	Property	ZY-1	ZY-2	ZY-3	ZY-4	ZY-5
Fiber tensile damage of right inner ring	Force/kN	29.00	31.87	32.12	33.43	32.79
Fiber tensile damage of right inner ring	Displacement/mm	0.48	0.48	0.44	0.44	0.40
Matrix damage of right side of laminates	Force/kN	40.98	45.32	46.78	48.66	45.98
Matrix damage of right side of laminates	Displacement/mm	0.68	0.68	0.64	0.64	0.56
Matrix compression damage of right inner ring	Force/kN	45.79	50.47	55.45	54.53	52.63
Matrix compression damage of right inner ring	Displacement/mm	0.76	0.76	0.76	0.72	0.64
Matrix damage of left side of laminates	Force/kN	60.34	72.10	75.66	78.92	78.83
Matrix damage of left side of laminates	Displacement/mm	1.00	1.08	1.04	1.04	0.96
Fiber tensile damage of left inner ring	Force/kN	77.42	85.36	101.89	108.60	104.93
Fiber tensile damage of left inner ring	Displacement/mm	1.28	1.28	1.40	1.44	1.28
Fiber damage of right side of laminates	Force/kN	98.89	106.29	113.34	123.40	118.11
Fiber damage of right side of laminates	Displacement/mm	1.64	1.60	1.56	1.64	1.44

下载: 导出CSV

参考文献(17)

[1]	杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1):1-12. DOI: 10.3321/j.issn:1000-3851.2007.01.001 DU S Y. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica,2007,24(1):1-12(in Chinese). DOI: 10.3321/j.issn:1000-3851.2007.01.001
[2]	赵渠森. 先进复合材料手册[M]. 北京: 机械工业出版社, 2003: 872-873. ZHAO Q S. Handbook of Advanced Composite Materials[M]. Beijing: Mechanical Industry Press, 2003: 872-873(in Chinese).
[3]	王琪. 耳片接头结构的拓扑优化与参数化设计研究[D]. 南京: 南京航空航天大学, 2016. WANG Q. Research on topology optimization and parametric design of lug connectors[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2016(in Chinese).
[4]	SCHULZ D. Develpoment of the A320 fin in modern composite fiber construction[C]//ICAS-80-16.2. 1988: 1828.
[5]	HAVAR T, DRECHSLER K. Design and progressive failure analysis of 3d-reinforced composite force introduction loops[C]. 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. 2008.
[6]	HAVAR T, MIDDENDORF J, WERCHNER C. Design and manufacturing of composite aerospace load introduction structures[C]//52th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. 2011: 1713.
[7]	张文荣. 复合材料耳片接头承载能力试验[J]. 洪都科技, 2001(1):38-42. ZHANG W R. Bearing capacity test of composite lug joint[J]. Hongdu Science and Technology,2001(1):38-42(in Chinese).
[8]	孙旋, 童明波, 陈智, 等. 碳纤维复合材料接头力学性能试验与仿真分析[J]. 复合材料学报, 2016, 33(11):2517-2527. SUN X, TONG M B, CHEN Z, et al. Test and simulation analysis of mechanical properties of carbon fiber composite joints[J]. Acta Materiae Compositae Sinica,2016,33(11):2517-2527(in Chinese).
[9]	郑锡涛, 孙秦, 柴亚南, 等. 复合材料编织接头承载能力的试验研究[J]. 航空学报, 2007, 28(2):348-351. DOI: 10.3321/j.issn:1000-6893.2007.02.019 ZHENG X T, SUN Q, CHAI Y N, et al. Experimental study on bearing capacity of composite braided joints[J]. Acta Aeronautica Sinica,2007,28(2):348-351(in Chinese). DOI: 10.3321/j.issn:1000-6893.2007.02.019
[10]	郑锡涛, 郭英男, 孙秦, 等. 三维四向编织复合材料接头承载能力分析[J]. 机械强度, 2006, 28(6):923-926. DOI: 10.3321/j.issn:1001-9669.2006.06.027 ZHENG X T, GUO Y N, SUN Q, et al. Analysis of bearing capacity of 3d four-way braided composite joints[J]. Mechanical Strength,2006,28(6):923-926(in Chinese). DOI: 10.3321/j.issn:1001-9669.2006.06.027
[11]	程家林. 层压复合材料连接接头设计及其在大飞机中的应用[J]. 航空学报, 2008(3):640-644. DOI: 10.3321/j.issn:1000-6893.2008.03.017 CHENG J L. Laminated composite joint design and its application in large aircraft[J]. Acta Aeronautica Sinica,2008(3):640-644(in Chinese). DOI: 10.3321/j.issn:1000-6893.2008.03.017
[12]	史坚忠. 复合材料主承力接头设计技术研究[D]. 南京: 南京航空航天大学, 1999. SHI J Z. Research on design technology of composite main bearing joint[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 1999(in Chinese).
[13]	史坚忠, 黄维杨. 复合材料承力接头设计的相关理论与应用概述[J]. 华东交通大学学报, 1998, 12(15):38-44. SHI J Z, HUANG W Y. Theory and application of composite bearing joint design[J]. Journal of east China Jiaotong University,1998,12(15):38-44(in Chinese).
[14]	雷良超, 周光明, 陆方舟, 等. 复合材料缠绕接头拉伸失效性能有限元分析[J]. 兵器装备工程学报, 2018, 39(4):174-178. DOI: 10.11809/bqzbgcxb2018.04.037 LEI L C, ZHOU G M, LU F Z, et al. Finite element analysis on tensile properties of composite winding joint[J]. Journal of Ordnance Equipment Engineering,2018,39(4):174-178(in Chinese). DOI: 10.11809/bqzbgcxb2018.04.037
[15]	雷良超. 复合材料缠绕接头力学性能研究[D]. 南京: 南京航空航天大学, 2018. LEI L C. Research on mechanical properties of the winding composite lug[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2018(in Chinese).
[16]	HASHIN Z. Failure criteria for unidirectional fiber compo-sites[J]. Journal of Applied Mechanics,1980,47(2):329-334. DOI: 10.1115/1.3153664
[17]	CAMANHO P P. A progressive damage model for mechanically fastened joints in composite laminates[J]. Journal of Composite Materials,1999,33(24):2248-2280. DOI: 10.1177/002199839903302402