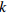Free vibration characteristics of corrugated sandwich plates under different boundary conditions
-
摘要: 波纹夹芯板作为一种特殊的复合材料结构，边界条件对其振动特性有重要影响。根据不同剪切方式下的剪切变形理论和基尔霍夫经典板理论(CLPT)，利用Hamilton原理建立波纹夹芯板的动力学方程。其中，波纹芯层等效成各向异性均质体。根据四边简支、四边固支、对边简支和固支、一边固支三边简支的边界条件，推导出位移形式的偏微分动力学方程。求解得到波纹夹芯板在不同边界条件下自由振动的固有频率，与有限元仿真结果进行对比，验证了理论结果的正确性。在此基础上，基于指数剪切变形理论(ESDT)，分析了不同边界条件下波纹夹芯板的基频随材料参数和结构几何参数的变化规律。结果表明，材料和几何参数对不同边界条件下波纹夹芯板的振动特性有重要影响。相关研究结果将对波纹夹芯板在工程应用中的减振设计及优化分析提供一定的理论依据。Abstract: As a special composite structure, the vibration characteristics of corrugated sandwich panel are greatly influenced by the boundary conditions. According to the shear deformation theory of different shear modes and Kirchhoff's classical plate theory(CLPT), the dynamic equation of corrugated sandwich plates was established by Hamilton principle. Among them, the corrugated core layer was equivalent to an anisotropic homogeneous body. According to the boundary conditions of four sides simply supported, four sides clamped, opposite sides simply supported and clamped, one side fixed and three edges clamped, the partial differential dynamic equation relative to the displacements was derived. By solving the equation, the natural frequencies of the corrugated sandwich plates under different boundary conditions were obtained. Compared with the finite element simulation results, the correctness of the theoretical results was verified. On this basis, based on the exponential shear deformation theory(ESDT), the variation of fundamental frequency of the corrugated sandwich plate with material parameters and structural geometric parameters under different boundary conditions was analyzed. The results show that the material and structural geometric parameters have an important influence on the vibration characteristics of the corrugated sandwich plates under different boundary conditions. Relevant research results will provide a theoretical basis for the vibration reduction design and optimization analysis of corrugated sandwich plates in engineering application.
-
随着电子信息的发展，电子材料的集成度越来越高，电子设备运行过程中，输出功率只占一部分，其他功率通过元器件热能形式散发出来。如果热量无法得到有效散发，设备温度将不断提高，当超过极限温度元器件会发生损坏[1-2]。日益突出的散热问题推动了电子封装材料的发展，传统电子封装材料已经无法满足新时代电子元器件散热的需求，因此研究新型的电子封装材料是信息技术发展的当务之急[3-4]。
近年来，石墨膜/铝复合材料在热管理领域备受关注[5-7]，是得益于石墨膜平面方向热导率超过
1200 W/(m·K)[8]。与铝基复合，能够弥补石墨膜自身易碎的缺点，同时也实现了石墨膜间的无胶复合。石墨膜/铝复合材料在面内方向展现出较高的热导率，是一种优异的电子封装材料。目前，石墨膜/铝复合材料研究主要在于材料的制备[9]和界面优化[10-12]等方面，其优势体现在面内方向导热能力较好。但由于石墨膜晶体的结构与石墨一致，呈现出高度的各向异性，在石墨膜厚度方向上的热导率仅为38 W/(m·K)[13-14]，因此随着石墨膜体积分数的增加，石墨膜/铝复合材料纵向导热能力逐渐削弱。黄宇[6]使用真空热压法制备了石墨膜体积分数为17.4vol%~69.4vol%的石墨膜/铝层叠复合材料，复合材料面内热导率从356 W/(m·K)增加到902 W/(m·K)，纵向热导率从63.3 W/(m·K)降低到7.2 W/(m·K)。Chang等[8]使用压力渗透法制备石墨膜/铝层叠复合材料，将石墨膜与铝箔叠放于模具烧结及铝基体浸渍。结果发现层叠复合材料由于合金中Si的存在没有界面反应物生成，面内热导率可高达743 W/(m·K)，但纵向热导率最高仅为18 W/(m·K)。田聪[9]制备三明治结构的石墨膜/环氧树脂/铝导热基板，所制备的复合材料面内热导率在448.1~491.1 W/(m·K)之间，而纵向热导率为35.9 W/(m·K)。目前大部分石墨膜/铝复合材料的热导率在纵向和面内方向上存在数量级差异的问题，然而材料纵向导热能力对于新型电子封装材料至关重要[15]，这限制了该系列复合材料在散热材料领域方面的应用。近期，复合材料增强相构型逐渐被相关学者所重视。通过合理的构型设计可以使高导热增强相成为复合材料中的导热通道，有利于减少热量在界面传导的损失，从而提升复合材料的热导率。如Lin等[16]使用糖模板法将氮化硼纳米片(BNNS)作为互连填料，随后通过注入聚二甲基硅氧烷(PDMS)并采用热压法制备复合材料。结果表明，相较于缺乏互连结构的复合材料，具有互连构型的复合材料在面内和面外导热系数分别提高了14倍和4倍。Yang 等[17]使用真空浸渗法将经过氧化石墨烯膜(GO)和石墨烯纳米片(GNP)组成的石墨烯气凝胶(HGA)引入聚乙二醇(PEG)，在基体材料中形成连续的导热通道，当HGA质量分数仅为2.2wt%，复合材料热导率上升了361%。高导热增强相充当导热通道已经证明了其对研究电子封装领域材料热性能有提升作用。
金刚石具有很好的热性能，室温下热导率为700~
2200 W/(m·K)[18]，可以作为石墨膜/铝复合材料高导热增强相。目前在石墨叠层增强金属基复合材料中，鲜有关于高导热增强相作为导热通道设计的研究报道。本文提出了一种在石墨膜/铝复合材料中引入金刚石作为导热通道的设计方法，金刚石嵌入铝基体的同时，作为桥梁连接上下石墨膜，已达到提高复合材料纵向热导率的目的。金刚石引入石墨膜/铝复合材料后，金刚石与铝基体的界面问题仍需考虑。有研究学者发现，金刚石通过表面镀覆Ti[19]、WC[20]或W[21–24]镀层后，可以提高金刚石与铝基体的界面结合，降低界面热阻。由于W镀层具有自身热导率最高178 W/(m·K)、且在铝中固溶度最小等优点[25] ，本文使用磁控溅射法对金刚石表面进行钨层镀覆以改善金刚石增强石墨膜/铝复合材料界面问题，随后采用快速热压烧结法(FHP)制备金刚石增强石墨膜/铝复合材料。通过改变芯层厚度改变金刚石体积分数(0vol%~30vol%)并揭示其对复合材料导热性能的影响规律。1. 实验部分
1.1 原材料
本文采用郑州黄河旋风有限公司生产的金刚石，平均粒径约为300 μm，密度为3.5 g/cm3；石墨膜源于苏州达昇电子材料有限公司，厚度约为70 μm，密度为1.7 g/cm3；Al-12Si粉体源于河北峰烨金属材料有限公司，平均粒径约为30 μm且纯度大于99.7%。采用物理气相沉积(PVD)技术在金刚石镀覆金属钨层，其XRD图谱如图1(c)所示。镀钨金刚石表面主要是WC、W2C与金刚石的衍射峰。镀钨金刚石SEM图像如图1(a)所示，金刚石颗粒的各个晶面都被完整地包裹，并且钨镀层呈现出平整致密的特征。图1(b)和图1(d)分别为金刚石(100)晶面与(111)晶面部分区域EDS分析，值得注意的是，与(111)晶面相比，镀钨金刚石的(100)晶面呈现出更加致密的特性。
![]()
图 1 (a) 镀钨金刚石颗粒的SEM图像；(b) 镀钨金刚石(100)晶面EDS分析；(c) 镀钨金刚石XRD图谱；(d) 镀钨金刚石(111)晶面EDS分析Figure 1. (a) SEM image of W-coated diamond particle; (b) EDS analysis of W-coated diamond particles on (100) facet; (c) XRD pattern of W-coated diamond particle; (d) EDS analysis of W-coated diamond particles on (111) facet1.2 金刚石增强石墨膜/铝复合材料制备
使用快速热压烧结法(FHP)制备金刚石增强石墨膜/铝复合材料。为了研究金刚石表面对复合材料界面的影响，设置镀钨金刚石与未镀金刚石两组对照组。将不同体积分数(0vol%~30vol%)的金刚石颗粒与Al-12Si粉体均匀混合。随后将混合粉体放入底部带有石墨膜的模具中，并在混合粉体整体表面覆盖一层石墨膜，形成石墨膜-金刚石/铝夹芯-石墨膜三明治结构。将模具放入炉中，抽真空至10 Pa以内开始加热，以100℃/min升至400℃，之后以30℃/min升至540℃。加载压力维持在40 MPa，保温10 min后，随炉冷却至室温，最终得到金刚石增强石墨膜/铝复合材料。
1.3 表征方法
通过扫描电子显微镜(TESCAN Mira4)观察复合材料微观结构。使用阿基米德排水法测量样品密度。在室温条件下采用热分析设备(NETZSCH LFA467)测试了复合材料热扩散系数(α)，为确保数据的准确性，使用3个闪射点测量样品，得到样品3个热扩散数值，通过下式计算热导率：
λ=αρCp (1) 其中：λ为热导率；Cp为比热容，通过理论计算得出；密度ρ采用阿基米德排水法测得，为了更方便直观地评估样品导热能力，采用红外热成像分析仪(FLIR SC300)输出样品在受热条件下表面温度的红外图像。
2. 结果与讨论
2.1 金刚石增强相构型设计
本文采用高导热金刚石作为石墨膜/铝复合材料的增强相，为了达到金刚石能够充当石墨膜/铝复合材料导热通道目的，金刚石需要穿透Al-12Si芯层并且不会将石墨膜刺穿，理想效果如图2所示。其中图2(a)为快速热压烧结示意图。图2(b)展示了理想复合材料结构。图2(c)为图2(b)放大图，即所有金刚石均都够贯穿Al-12Si芯层，芯层上下表面都可观察到金刚石的突起，并且突起的部分刺入了上下两层石墨膜。这种金刚石穿透Al-12Si层，刺入上下石墨膜中构建了石墨膜-金刚石-石墨膜的导热通道。换言之，金刚石在复合膜中起到了“顶梁柱”的作用。
![]()
2.2 复合材料微观形貌
如前所述，金刚石能否贯穿中间的铝层并刺入上下石墨膜中，是导热通道构建的关键。本文首先对未镀金刚石制备的金刚石增强石墨膜/铝复合材料进行观察，看金刚石是否能够穿透Al-12Si芯层并且一定程度刺入上下两层石墨膜。表征方法如下：将样品表面石墨膜沿边缘撕去，分别观察芯层上表面是否有金刚石突起及上下层石墨膜是否有金刚石刺入的痕迹。芯层表面和上下两层石墨膜宏观形貌分别为图3(a)与图3(c)所示。在图3(a)中，芯层表面框线区域内出现凸出的金刚石颗粒，这些金刚石颗粒突出Al-12Si芯层表面。采用SEM对芯层表面进行观察。图3(b)展示了复合材料芯层表面金刚石颗粒的放大区域，可清晰观察到金刚石突出Al-12Si芯层表面。图3(c)中虚线区域展示了金刚石颗粒在上下两层石墨膜各自留下对称压痕，表明金刚石在复合材料中发挥支撑作用。两种现象验证了金刚石成功穿透Al-12Si芯层并连接上下两层石墨膜。
![]()
图 3 (a) 金刚石穿透铝基宏观图(已去除上下表面石墨膜)；(b) 金刚石颗粒的SEM图像；(c) 石墨膜上压痕宏观图；(d) 石墨膜上压痕的SEM图像Figure 3. (a) Macroscopic morphology of diamond penetration of aluminum base (with upper and lower surface graphite film removed); (b) SEM image of diamond particle; (c) Macroscopic morphology of graphite film indentations; (d) SEM image of indentation on graphite film图3(d)展示了金刚石在石墨膜表面形成的个别压痕，说明当金刚石突出铝基层并接触到石墨膜后，会对石墨膜内部结构造成损伤。这种损伤可能会对石墨膜自身热导率出现影响。图4展示了石墨膜表面凹痕对其热导率的影响，可以看到表面凹痕小于20 μm对石墨膜本征热导率影响小于4%。因此，需要将金刚石的刺入深度控制在20 μm左右。本文通过石墨膜厚度(70 μm)、金刚石(300 μm)粒径叠加高度和控制复合材料中间Al-12Si芯层厚度计算，复合材料样品总厚度约为440 μm时，在保证可以实现金刚石穿透铝基连接上下两层石墨膜的构型设计前提下，能够有效维持石墨膜本身的高热导率特性。
![]()
图 4 压痕深度对石墨膜面内热导率影响Figure 4. Effect of pit depth on thermal conductivity of graphite film surface图5(a)与图5(b)展示了本文制备的未镀金刚石增强石墨膜/铝复合材料横截面宏观特征及SEM形貌。可以观察到石墨膜与Al-12Si芯层没有明显孔洞或裂纹，说明石墨膜与Al-12Si芯层结合良好。图5(c)呈现了经过剪切处理后的复合材料断口的宏观特征，在剪切力作用下石墨膜与芯层仍保持良好的结合。金刚石颗粒所在断口区域的SEM图像如图5(d)所示。可以发现金刚石颗粒连接上下两层石墨膜在复合材料中充当“顶梁柱”作用，从另一角度验证了连通结构已经建立。同时金刚石颗粒与基体的结合情况是重要观察部位，图5(d)中实线所指的是金刚石的(111)晶面与铝基体间的孔隙，其来源可能是烧结过程中金刚石与铝基结合较差，这种较弱的界面结合会对复合材料的导热性能产生不利影响[26]，也有可能是金刚石在剪切力作用下与铝基体分离。Che等[27]研究表明，相比(100)晶面，Al4C3更难在金刚石(111)晶面生成，因此金刚石(111)晶面与铝基的结合效果不佳。
研究表明，对金刚石进行表面镀钨处理可以有效改善与铝基体的界面结合[28]。采用SEM对剪切后镀钨金刚增强石墨膜/铝复合材料断口及撕开石墨膜后芯层表面进行观察。如图6(a)所示，镀钨金刚石与上下表面联通。从图6(b)可以观察到，撕开复合材料上层石墨膜后，镀钨金刚石在Al-12Si芯层中凸显出来。此外，根据图6(c)所示的EDS分析结果显示，在突出的镀钨金刚石表面上粘附有残留的石墨膜，这说明石墨膜与镀钨金刚石之间存在良好结合。图6(d)展示了镀钨金刚石增强石墨膜/铝复合材料断口形貌，可观察到嵌在铝基体中的镀钨金刚石与基体结合较紧密，没有出现孔洞，说明镀层的存在改善了金刚石与铝基体的润湿性。此外，复合材料经过剪切后金刚石顶部和底部连接石墨膜，表明复合材料内部已形成连通结构。通过EDS分析镀钨金刚石(111)晶面，从图6(f)中观察到铝基体残留在其表面，这说明引入钨镀层可以增强铝基体在金刚石表面的附着力，避免了金刚石与铝基体的选择性粘附[29]。与图5(c)未镀金刚石增强复合材料断口形貌相比，镀钨金刚石增强复合材料具有更高的内部界面强度，从而减少界面孔隙对复合材料的影响。
![]()
![]()
图 6 (a) 镀钨复合材料断口的SEM图像；(b) 撕开石墨膜后镀钨复合材料芯层表面的SEM图像；(c) 图6(b)的EDS分析；(d) 图6(a)中放大的镀钨金刚石颗粒SEM图像；(e) 图6(d)的EDS分析；(f) 镀钨金刚石(111) 晶面EDS分析Figure 6. (a) SEM image of W-coated composites fracture; (b) SEM image of the composite core surface after tearing the graphite film; (c) EDS analysis of Fig.6(b); (d) Enlarged SEM image of W-coated diamond particles in Fig.6(a); (e) EDS analysis of Fig.6(d); (f) EDS analysis of W-coated diamond (111) facet2.3 金刚石体积分数对金刚石增强石墨/铝复合材料热性能影响
分别对未镀金刚石与镀钨金刚石增强石墨膜/铝复合材料进行面内方向和厚度方向上热导率测试，结果如图7(a)所示。当未镀金刚石体积分数为10vol%时，复合材料面内热导率可达到最高为614 W/(m·K)。随着金刚石体积分数超过10vol%，复合材料面内热导率逐渐降低。当未镀金刚石体积分数为30vol%时，复合材料面内热导率降低至498 W/(m·K)。这种低热导率可能是由复合材料内部的缺陷导致的[30]，如孔隙、内应力、氧化等。根据前文中未镀金刚石增强复合材料断口微观结构特征分析，主要原因是复合材料内部存在界面孔隙。与此同时，如图7(b)所示，随着金刚石体积分数的增加，复合材料纵向热导率不断提升。当金刚石体积分数为30vol%时，复合材料纵向热导率达到最高值153 W/(m·K)。这是由于金刚石的引入为石墨膜/铝复合材料提供纵向导热通道，如图7(f)所示。复合材料纵向导热通道数量逐渐增多，金刚石“顶梁柱”的作用愈发凸显，从而使复合材料纵向导热能力效果不断提升。金属导热是以自由电子为主，金刚石的热传递是由声子主导。由此，金刚石与金属基材料构成复合材料是通过金刚石的声子与金属中的电子耦合完成的。相较于未镀金刚石增强复合材料，金刚石表面碳化物的构成可以有效地将电子与声子匹配，从而提高所在复合材料的导热性能。当镀钨金刚石体积分数为10vol%时，镀钨金刚石增强石墨膜/铝复合材料在面内方向上热导率达到658 W/(m·K)，相较于未镀金刚石增强复合材料提高了7%。当镀钨金刚石体积分数为30vol%时，纵向热导率达到177 W/(m·K)，相较于未镀金刚石增强复合材料提高了34%。该结果表明，高导热金刚石在引入镀层后，可以显著提升复合材料在面内方向和纵向上的热导率。为了更直接观察金刚石增强石墨膜/铝复合材料的导热性能，使用热成像设备对样品进行分析，如图7(c)所示。在相同金刚石体积分数与时间条件下，镀钨金刚石增强石墨膜/铝复合材料表面温度相较于未镀金刚石增强复合材料均提高了0.5℃。这说明在模拟应用中，镀钨金刚石增强复合材料具有更出色的导热性能。
![]()
图 7 镀钨金刚石增强石墨膜/铝复合材料热导率与未镀对比：(a) 面内方向；(b) 厚度方向；(c) 未镀金刚石所在复合材料热成像图；(d) 镀钨金刚石所在复合材料热成像图；(e) 石墨膜/铝复合材料模拟热流图；(f) 金刚石增强石墨膜/铝复合材料模拟热流图Figure 7. Comparison of thermal conductivity of W-coated diamond reinforced graphite film/aluminum composite with original: (a) In-plane direction; (b) Thickness direction; (c) Diamond in the composite material by infrared thermal imagery; (d) W-coated diamond in the composite by infrared thermal imagery; (e) Simulated heat flow diagram of graphite film/aluminum composite; (f) Diamond reinforced graphite film/aluminum composite simulation heat flow diagram3. 结 论
本文采用快速热压烧结法成功制备了镀钨金刚石与未镀金刚石增强石墨膜/铝复合材料，探究了金刚石体积分数及其表面改性处理对复合材料导热性能的影响，主要结论如下：
(1)通过在石墨膜/铝复合材料引入高导热金刚石，成功在复合材料内部构建了纵向导热通道；
(2)随着金刚石体积分数(0vol%~30vol%)的增加，复合材料在面内方向上的热导率呈现出先上升后降低的趋势。当金刚石体积分数为10vol%时，复合材料在面内方向的热导率达到最高值为614 W/(m·K)。与此同时，复合材料纵向热导率持续增加。当金刚石体积分数为30vol%时，复合材料纵向热导率达到最高值为132 W/(m·K)；
(3)金刚石表面包裹W镀层显著提高金刚石与铝基体的结合强度。当镀钨金刚石体积分数为10vol%时，镀钨金刚石增强石墨/铝复合材料相较于未镀金刚石增强复合材料在面内方向上的热导率提升了7%，达到658 W/(m·K)。同时，在纵向热传导方面也会有所增强，当镀钨金刚石体积分数达到30vol%，相较于未镀金刚石增强复合材料提升了34%，达到177 W/(m·K)。
-
![]()
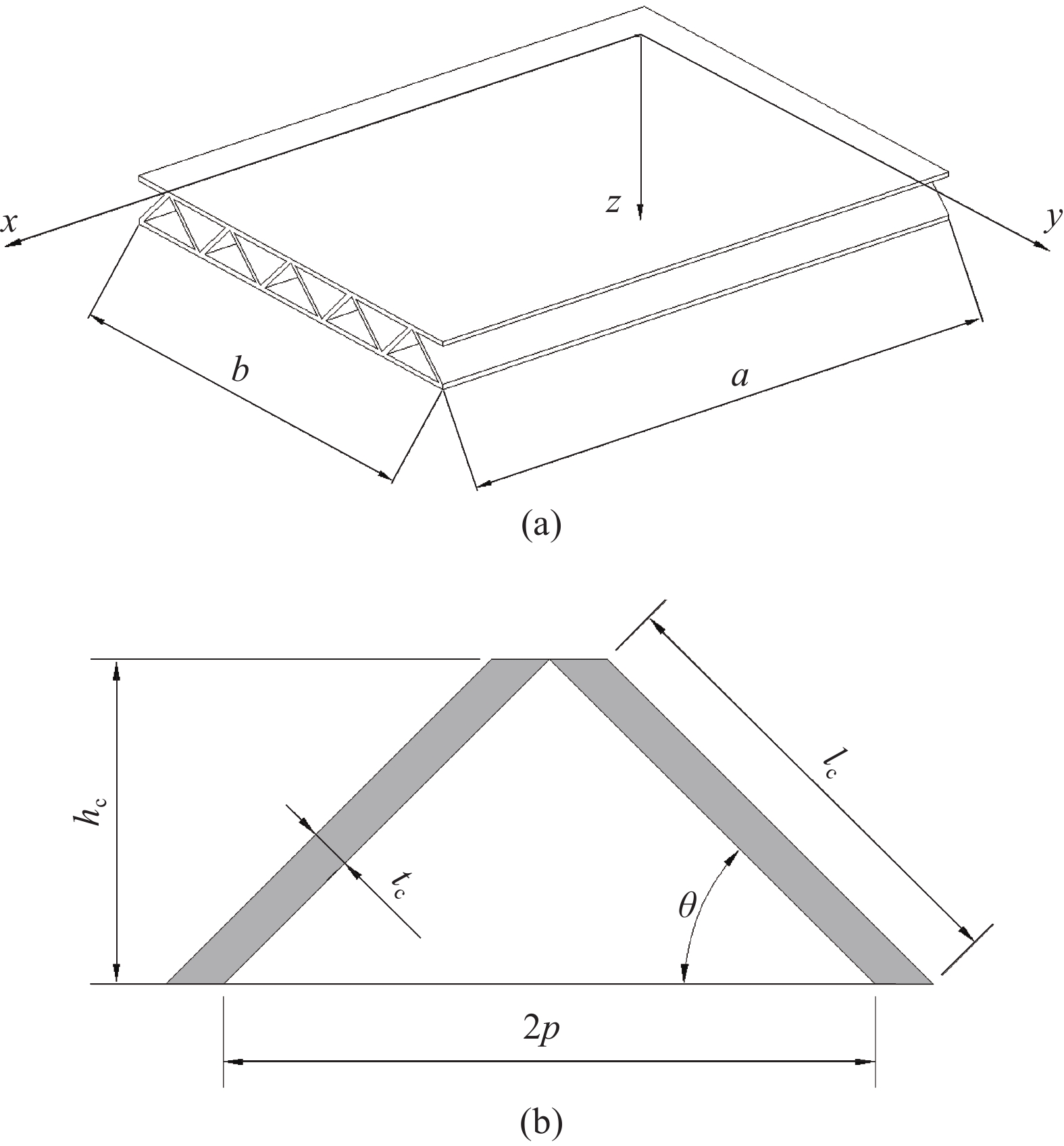
图 1 波纹夹芯板的模型(a)和波纹单胞示意图(b)
Figure 1. Model diagrams of corrugated sandwich panel (a) and corrugated cell (b)
a—Length of corrugated sandwich panel; b—Width of corrugated sandwich panel; lc—Length of the hypotenuse; hc—Height of core layer; tc—Wall thickness; θ—Corrugation angle; p—Length of bottom side
![]()
图 3 波纹夹芯板前五阶振型图
Figure 3. The first five mode shapes of the corrugated sandwich plates
![]()
图 4 不同边界条件下波纹夹芯板一阶振型图
Figure 4. The first mode shapes of corrugated sandwich plates under different boundary conditions
![]()
图 5 波纹与面板夹角对波纹夹芯板基频的影响
Figure 5. Influence of the angle between corrugation and panel on the fundamental frequency of corrugated sandwich panel
![]()
图 6 波纹芯层高度占比对波纹夹芯板基频的影响
Figure 6. Influence of corrugated core height ratio on the fundamental frequency of corrugated sandwich panel
![]()
图 7 波纹壁厚度对波纹夹芯板基频的影响
Figure 7. Influence of corrugated wall thickness on the fundamental frequency of corrugated sandwich panel
![]()
图 8 波纹夹芯板厚度
h 对波纹夹芯板基频的影响Figure 8. Influence of corrugated plate thickness on the fundamental frequency of corrugated sandwich panel
![]()
图 9 比例因子
k 对波纹夹芯板基频的影响Figure 9. Influence of scale factor on the fundamental frequency of corrugated sandwich panel
表 1 不同板理论对应的剪切形状函数
Table 1 Shear shape functions corresponding to different plate theories
Shear theory Function f (z) CLPT f(z)=0 FSDT f(z)=z SSDT f(z)=hπsin(πzh) TSDT f(z)=z[1−43(zh)2] ESDT f(z)=ze−2(zh)2 Notes: CLPT—Classical plate theory; FSDT—First-order shear plate theory; SSDT—Sinusoidal shear deformation theory; TSDT—Third-order shear deformation theory; ESDT—Exponential shear deformation theory. 
下载: 导出CSV
表 2 不同边界条件下的函数Xm(x) 和 Yn(y)
Table 2 Functions Xm(x) and Yn(y) for different boundary conditions
Boundary conditions Function Xm(x) Function Yn(y) SSSS sinαx sinβx CCCC 1−cos2αx 1−cos2βx CCSS 1−cos2αx sinβx CSSS sinαx(cosαx−1) sinβx Notes: SSSS—Four sides simply supported; CCCC—Four sides clamped; CCSS—Opposite sides simply supported and clamped; CSSS—One side fixed and three edges clamped; α=mπ/a; β=nπ/b; m, n—Half-wave numbers in two orthogonal coordinate directions respectively.
下载: 导出CSV
表 3 四边简支波纹夹芯板在不同理论下的固有频率理论解与有限元仿真结果
Table 3 Theoretical solutions and finite element simulation results of natural frequency of simply supported corrugated sandwich plates using different theories
Mode ABAQUS CLPT FSDT SSDT TSDT ESDT Result Error/% Result Error/% Result Error/% Result Error/% Result Error/% (1,1) 31.18 31.72 1.75 31.41 0.77 31.00 −0.57 31.01 −0.54 30.99 −0.58 (2,1) 65.39 69.52 6.32 68.09 4.13 65.82 0.66 65.88 0.75 65.79 0.61 (1,2) 86.48 88.51 2.36 86.23 −0.29 83.74 −3.16 83.78 −3.12 83.74 −3.17 (2,2) 116.13 125.70 8.24 121.21 4.38 115.60 −0.45 115.72 −0.35 115.57 −0.48 (3,1) 118.46 132.06 11.48 127.11 7.30 119.24 0.66 119.45 0.84 119.12 0.56
下载: 导出CSV
表 4 不同边界条件和板理论下波纹夹芯板的基频理论解与有限元仿真结果
Table 4 Theoretical solutions and finite element simulation results of fundamental frequency of corrugated sandwich plates with different boundary conditions and plate theories
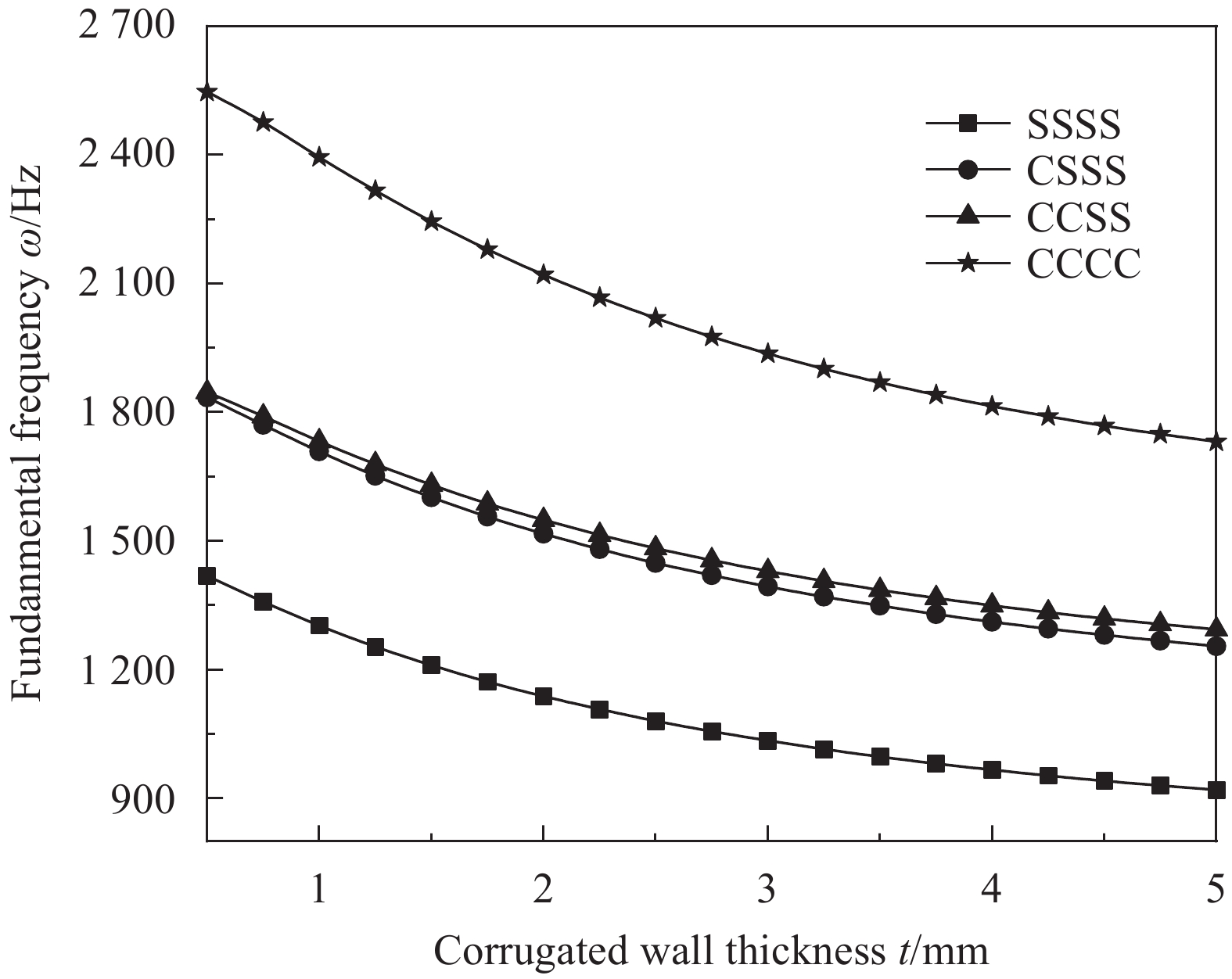
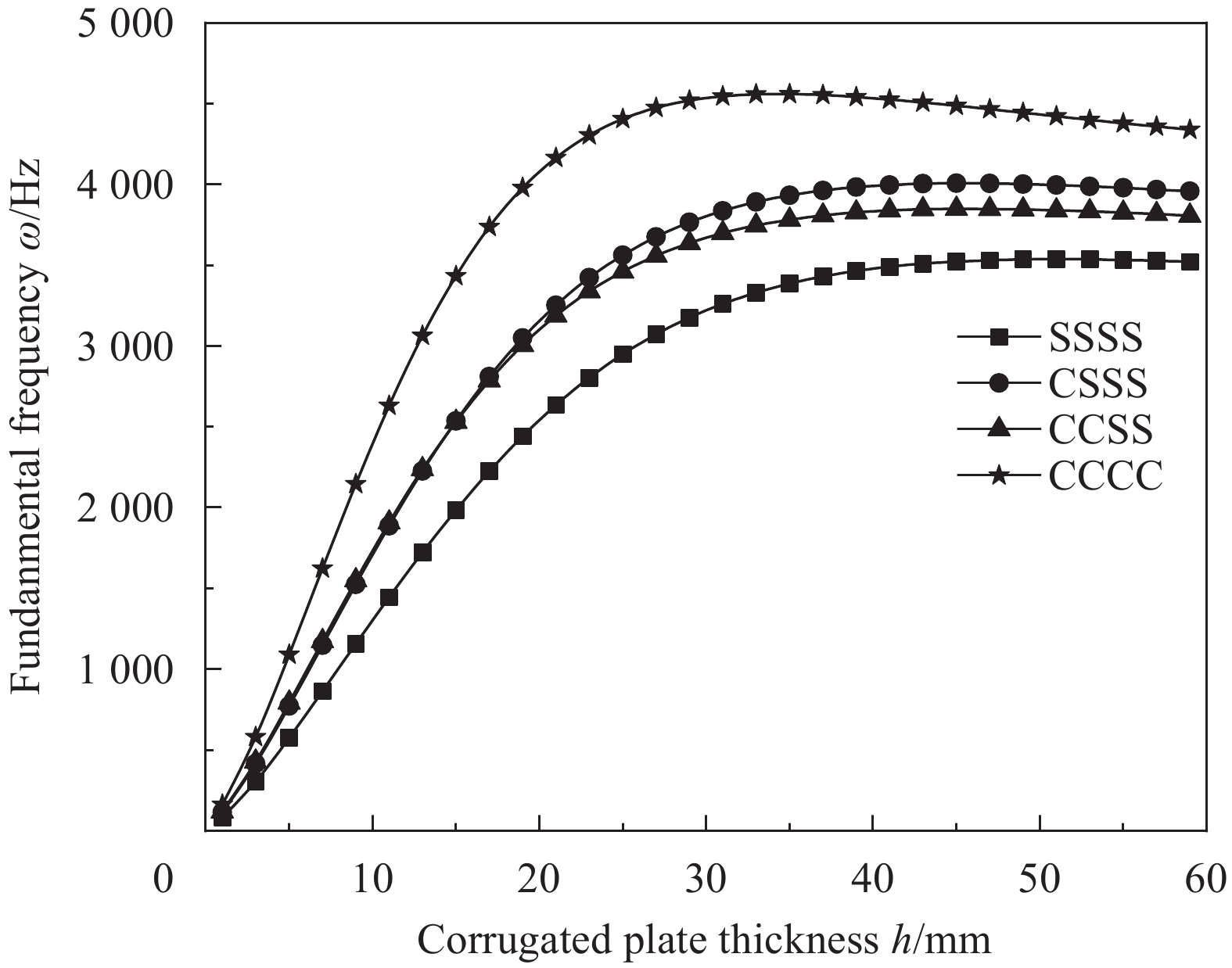
Boundary conditons ABAQUS CLPT FSDT SSDT TSDT ESDT Result Error/% Result Error/% Result Error/% Result Error/% Result Error/% SSSS 31.18 31.72 1.75 31.41 0.77 31.00 −0.57 31.01 −0.54 30.99 −0.58 CCCC 56.42 60.46 7.17 58.90 4.40 56.99 1.01 57.03 1.08 56.98 0.99 CCSS 40.47 43.19 6.71 42.44 4.87 41.23 1.88 41.26 1.96 41.22 1.84 CSSS 39.50 42.14 6.70 41.56 5.22 40.66 2.94 40.68 2.99 40.65 2.91
下载: 导出CSV
表 5 不同材料组合下波纹夹芯板的基频
Table 5 Fundamental frequencies of corrugated sandwich panels with different material combinations
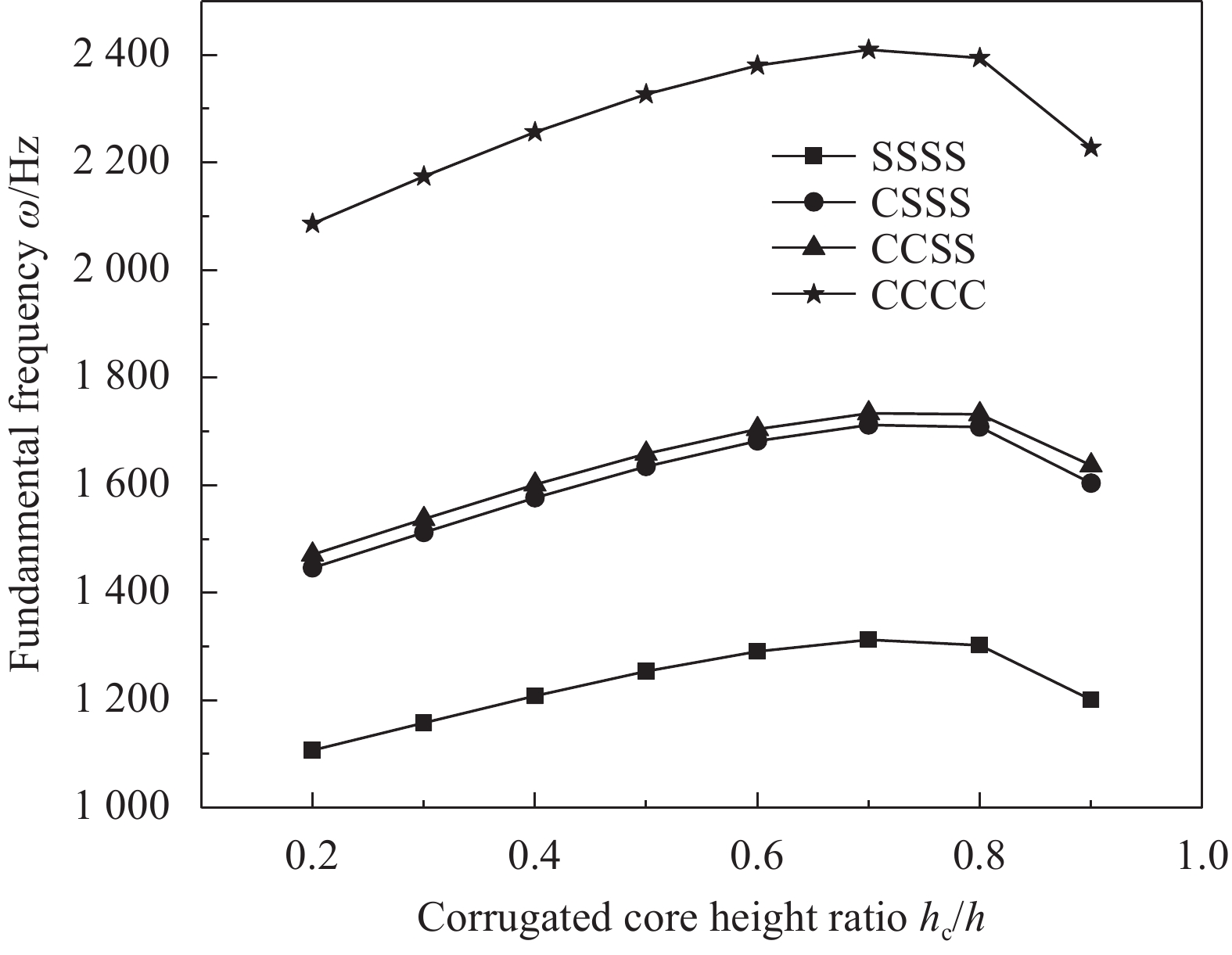
Boundary conditon Al-Al-Al Ti-Ti-Ti Al-Ti-Al Ti-Al-Ti SSSS 30.99 38.72 29.07 40.53 CCCC 56.98 71.16 54.31 71.99 CCSS 41.22 51.46 39.96 52.38 CSSS 40.65 50.76 39.03 52.17
下载: 导出CSV
-
[1] 岳灿甫, 吴始栋. 国外船用激光焊接波纹夹芯板的开发与应用[J]. 鱼雷技术, 2007, 15(4):1-5. YUE C F, WU S D. Introduction to development and applications of marine laser welded lightweight sandwich panel in the US navy and european countries[J]. Torpedo Technology,2007,15(4):1-5(in Chinese).
[2] 贺梦豪, 吴昊, 程远胜. 波纹夹芯杂交夹层板入水砰击动力响应特性研究[J]. 舰船科学技术, 2016, 38(8):11-17. HE M H, WU H, CHENG Y S. Dynamic response analysis of hybrid sandwich plate with corrugated-cores subjected to slam-ming impact[J]. Ship Science and Technology,2016,38(8):11-17(in Chinese).
[3] 孙小曼. 车用波纹夹芯板弯曲性能研究[D]. 大连: 大连理工大学, 2013. SUN X M. Analysis of bending performance of vehicle corrugated core sandwich structure[D]. Dalian: Dalian University of Technology, 2013(in Chinese).
[4] KUJALA P, KLANAC A. Steel sandwich panels in marine applications[J]. Brodogradnja,2005,56(4):305-314.
[5] PENG L X, LIEW K M, KITIPORNCHAI S. Analysis of stiffened corrugated plates based on the FSDT via the mesh-free method[J]. International Journal of Mechanical Sciences,2006,49(3):364-378.
[6] SEMENYUK N P, NESKHODOVSKAYA N A. On design models in stability problems for corrugated cylindrical shells[J]. International Applied Mechanics,2002,38(10):1245-1252. DOI: 10.1023/A:1022214630581
[7] BRIASSOULIS D. Equivalent orthotropic properties of corrugated sheets[J]. Computers & Structures,1986,23(2):129-138.
[8] SOHRAB K, DAN Z. Corrugated all-composite sandwich structures. Part 2: Failure mechanisms and experimental programme[J]. Composites Science and Technology,2009,69(7):920-925.
[9] TIAN Y S, LU T J. Optimal design of compression corrugated panels[J]. Thin-Walled Structures,2005,43(3):477-498. DOI: 10.1016/j.tws.2004.07.014
[10] SAMANTA A, MUKHOPADHYAY M. Finite element static and dynamic analyses of folded plates[J]. Engineering Structures,1999,21(3):277-287. DOI: 10.1016/S0141-0296(97)90172-3
[11] XIA Y, FRISWELL M I, FLORES E I S. Equivalent models of corrugated panels[J]. International Journal of Solids and Structures,2012,49(13):1453-1462. DOI: 10.1016/j.ijsolstr.2012.02.023
[12] LI X, WANG Z, ZHU F, et al. Response of aluminium corrugated sandwich panels under air blast loadings: Experiment and numerical simulation[J]. International Journal of Impact Engineering,2014,65:79-88. DOI: 10.1016/j.ijimpeng.2013.11.002
[13] 王红霞, 王德禹, 李喆. 三角形夹芯板夹心层的等效弹性常数[J]. 固体力学学报, 2007, 28(2):178-182. DOI: 10.3969/j.issn.0254-7805.2007.02.011 WANG H X, WANG D Y. LI Z. Equivalent elastic constants of truss-core sandwich plates[J]. Acta Mechanica Solida Sinica,2007,28(2):178-182(in Chinese). DOI: 10.3969/j.issn.0254-7805.2007.02.011
[14] 王青伟, 赵才其. 三角形桁架夹芯层等效弹性常数研究和夹芯板参数优化设计[J]. 特种结构, 2010, 27(5):61-66. DOI: 10.3969/j.issn.1001-3598.2010.05.015 WANG Q W, ZHAO C Q. Research of equivalent elastic constants of triangle truss-core sandwich panels and optimization design of constants of core sandwich panels[J]. Special Structures,2010,27(5):61-66(in Chinese). DOI: 10.3969/j.issn.1001-3598.2010.05.015
[15] 吴建均, 王永静, 谢敬尧, 等. 泡沫波纹复合夹心梁等效弹性常数的推导及其振动特性研究[J]. 西安交通大学学报, 2018, 52(11):73-80. WU J J, WANG Y J, XIE J Y, et al. Derivation of equivalent elastic constant and vibration analysis of foam-corrugated composite sandwich beam[J]. Journal of Xi'an Jiaotong University,2018,52(11):73-80(in Chinese).
[16] 崔岸, 刘芳芳, 张晗, 等. 车身泡沫填充铝合金波纹夹芯板结构性能分析与优化[J]. 汽车工程, 2019, 41(10):1221-1227. CUI A, LIU F F, ZHANG H, et al. Performance analysis and optimization of foam-filled aluminum-alloy corrugated sandwich panel structure for vehicle body[J]. Automotive Engineering,2019,41(10):1221-1227(in Chinese).
[17] 李静雯, 张博明, 孙义亮, 等. 不同铺层方式下连续玻璃纤维/聚丙烯复合材料波纹夹芯板的力学性能[J]. 复合材料学报, 2019, 36(5):1074-1082. LI J W, ZHANG B M, SUN Y L, et al. Mechanical properties of continuous glass fiber/polypropylene corrugated sandwich boards under different laminates[J]. Acta Materiae Compositae Sinica,2019,36(5):1074-1082(in Chinese).
[18] 刘昆, 王哲, 王自力. 波纹夹层板冲击响应理论计算方法研究[J]. 振动与冲击, 2019, 38(2):90-97. LIU K, WANG Z, WANG Z L. Theoretical calculation method for the impact responses of corrugated sandwich panels[J]. Journal of Vibration and Shock,2019,38(2):90-97(in Chinese).
[19] REDDY J N. Mechanics of laminated composite plates and shells: Theory and analysis[M]. New York: CRC Press, 2004.
[20] CROCE L D, VENINI P. Finite elements for functionally graded Reissner-Mindlin plates[J]. Computer Methods in Applied Mechanics and Engineering,2004,193(9–11):705-725.
[21] MATSUNAGA H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory[J]. Composite Structures,2008,82(4):499-512. DOI: 10.1016/j.compstruct.2007.01.030
[22] TALHA M, SINGH B N. Static response and free vibration analysis of FGM plates using higher order shear deformation theory[J]. Applied Mathematical Modelling,2010,34(12):3991-4011. DOI: 10.1016/j.apm.2010.03.034
[23] WU C P, LI H Y. An RMVT-based third-order shear deformation theory of multilayered functionally graded material plates[J]. Composite Structures,2010,92:2591-2605. DOI: 10.1016/j.compstruct.2010.01.022
[24] THAI H T, VO T P. A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates[J]. Applied Mathematical Modelling,2013,37:3269-3281. DOI: 10.1016/j.apm.2012.08.008
[25] 曹源, 雷剑. 基于正弦剪切变形理论的功能梯度材料三明治微梁的静动态特性[J]. 复合材料学报, 2020, 37(1):223-235. CAO Y, LEI J. Static and dynamic properties of functionally graded materials sandwich microbeams based on sinusoidal shear deformation theory[J]. Acta Materiae Compositae Sinica,2020,37(1):223-235(in Chinese).
[26] KARAMA M, AFAQ K S, MISTOU S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity[J]. International Journal of Solids and Structures,2003,40(6):1525-1546. DOI: 10.1016/S0020-7683(02)00647-9
[27] REDDY J N. Energy principles and variational methods in applied mechanics[M]. New York: John Wiley & Sons Inc, 2002.
-
期刊类型引用(3)
1. 李梦涵，魏娜，徐瑞琪，杨泽钰，崔洪芝. 三维碳纳米管/硅藻土基多孔陶瓷复合材料的制备及其光热水蒸发性能. 复合材料学报. 2023(08): 4577-4586 . 
本站查看
2. 吴玉萍，王乾廷，孙炜，周忠华，谢宗丽，宋铭雨. 含椭圆叶片状SiO_2/聚乙烯醇渗透汽化复合膜的制备与性能. 复合材料学报. 2022(06): 2783-2791 . 本站查看
3. 赵士雄. 反渗透复合膜制备及其改性方法研究进展. 云南化工. 2022(06): 20-21+38 . 百度学术
其他类型引用(1)
-
计量
- 文章访问数: 1473
- HTML全文浏览量: 521
- PDF下载量: 105
- 被引次数: 4
