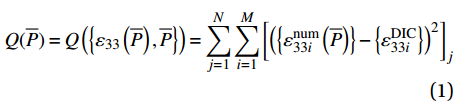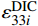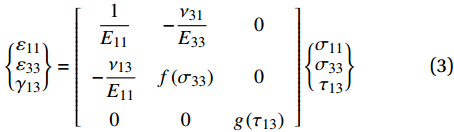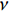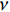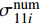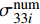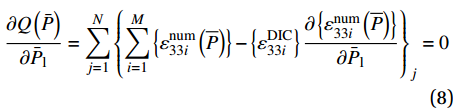数字图像相关方法辅助的IM7/8552碳纤维/环氧树脂复合材料单向带层合板沿厚度方向非线性本构参数识别

贺体人; 刘刘; 徐吉峰

doi:10.13801/j.cnki.fhclxb.20200316.001

数字图像相关方法辅助的IM7/8552碳纤维/环氧树脂复合材料单向带层合板沿厚度方向非线性本构参数识别

贺体人^1,,
刘刘^2, ,,
徐吉峰^1,

1.
中国商用飞机有限责任公司　北京民用飞机技术研究中心　民用飞机结构与复合材料北京市重点实验室，北京 102211
2.
北京理工大学　宇航学院，北京 100081

基金项目: 中国博士后科学基金面上资助(2019M651629)

详细信息

通讯作者:
刘刘，博士，副教授，博士生导师，研究方向为复合材料力学响应行为的实验　E-mail：liuliu@bit.edu.cn

中图分类号: TB332
计量
- 文章访问数: 2365
- HTML全文浏览量: 496
- PDF下载量: 137
出版历程
- 收稿日期: 2020-01-06
- 录用日期: 2020-03-03
- 网络出版日期: 2020-03-15
- 刊出日期: 2021-01-14

Digital image correlation aided method for identification of nonlinear constitutive parameters of IM7/8552 carbon fiber/epoxy composite unidirectional laminate along thickness directionction

HE Tiren^1,,
LIU Liu^2, ,,
XU Jifeng^1,

1.
Beijing Key Laboratory of Commercial Aircraft Structures and Composite Materials, BASTRI, COMAC, Beijing 102211, China
2.
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 提出了采用数字图像相关(DIC)方法和有限元模型修正(FEMU)技术相结合，通过短梁剪切(SBS)试验获得碳纤维增强环氧树脂(IM7/8552)正交各向异性复合材料单向带层合板沿厚度方向压缩本构关系参数的试验方法。该方法根据假设材料初始本构，采用3D有限元模型(FEM)计算获得主平面压头下方沿厚度方向的应力和应变分布，以DIC实测应变和有限元计算应变之间的方差建立目标函数，并在FEM中进行迭代更新，收敛后获得材料本构参数。由于选择的试样加载形式近似静定结构，试样表面的应力分布对材料本构关系及参数弱相关，上述迭代过程进一步转化为通过全场有限元计算应力和DIC实测应变之间的最小二乘回归识别假设本构关系及参数。因此，该方法具有以下优点：迭代过程中不需要建立针对识别参数的显式敏感度矩阵，识别效率高；识别过程对初始材料本构参数不敏感。
- 正交各向异性 /
- 压缩本构参数 /
- 数字图像相关(DIC) /
- 有限元模型修正(FEMU) /
- 复合材料
Abstract: A digital image correlation (DIC) aided method combined with finite element model updating (FEMU) technique was proposed to identify the compressive constitutive parameters along the thickness direction for carbon fiber/epoxy (IM7/8552) orthotropic composite unidirectional laminate through short beam shear (SBS) test. The stress and strain distributions on the loading plane along the thickness direction under the loading nose were calculated by 3D finite element model (FEM) with the initial trial parameters. A cost function of the square difference between DIC-measured and FEM-calculated strains was given accordingly and unknown constitutive parameters were determined iteratively through minimization of it. The stress distribution is weakly sensitive to the constitutive parameters since the SBS test configuration is nearly statically determinate. Thus minimization of the cost function can be achieved by the least squared linear regression between FEM-calculated stress and DIC-measured strain. The advantages of the proposed method include that an explicit sensitivity matrix is not required in the iterative procedure, the efficiency of the parameter identification is high, and it is not sensitive to the initial trial parameters.
- orthotropic /
- compressive constitutive parameters /
- digital image correlation (DIC) /
- finite element model updating (FEMU) /
- composite

HTML全文

横向载荷下的力学性能对于复合材料层合板的整体力学性能和失效模式有重要影响^[1]。在加载过程中，横向失效往往最先出现，并可能导致复合材料层合板其他铺层的进一步破坏^[2-4]。随着复合材料部件在实际工况中的受力情况越来越复杂，分析复合材料在横向载荷下的应变分布和变形机制是进一步研究复合材料力学性能的基础^[5-7]。

采用试验方法开展复合材料本构识别是获得复合材料力学性能参数的主要手段^[8-11]。数字图像相关(DIC)方法由于操作简单、非接触测量及数据的全场性等优点在复合材料本构参数识别试验中得到越来越广泛的应用^[12-14]。由试验获得的应变数据识别本构参数是一个典型的反问题，常用的求解方法有虚位移场(VFM)法^[15-17]和有限元模型修正(FEMU)法^[18-21]。VFM法利用全场变形实测数据，通过材料本构关系(含未知参数)及满足位移边界条件和连续性条件的虚位移场给出结构应变能表达式，根据虚功原理可得到实测变形、载荷与本构模型中未知材料参数之间的关系。FEMU法通过计算试验实测结果与有限元模型(FEM)数值结果之间的方差，建立目标函数，通过最小化目标函数获得优化的材料本构关系中多个参数，普适性强。

DIC法辅助的复合材料本构参数识别方面，薛康等^[22]采用文献[8]中碳纤维/环氧树脂(IM7/8552)复合材料单轴压缩试验结果，其横向压缩模量为8.4 GPa。Makeev等^[23]通过改进短梁剪切(SBS)试验识别了正交各向异性复合材料沿主方向三个对称面内本构参数。进而通过单轴拉伸试验测定IM7/8552复合材料单向带层合板层间拉伸模量E_33T，并与SBS试验获得的层间拉伸模量进行比较，验证了可以由SBS试验结合DIC和FEMU法获得正交各向异性复合材料层合板沿厚度方向的拉伸弹性模量^[24]。这些研究均表明DIC法结合力学试验在各向异性复合材料力学性能参数识别方面具有一定的潜力和优势。

在SBS试验中，压头下方材料的位移和应变水平高，梯度大，变形复杂，因此在SBS试验结合DIC法识别材料力学本构参数的研究中，主要采用在远离压头和支撑点的图像区域为感兴趣区域(ROI)^[25-26]，采用压头下方复杂高横向压缩正应变区域开展复合材料沿厚度方向压缩本构参数识别的研究不多见。Carpentier^[18]和Julia^[27]通过调整SBS试验中正交各向异性复合材料制备方向和加载平面，获得了IM7/8552复合材料层合板3-2面(垂直纤维方向为2方向)由基体主导的拉伸失效模式，并识别得到复合材料沿厚度方向(3方向)的拉伸和压缩弹性模量，研究成果验证了可以由SBS试验识别复合材料沿厚度方向的线性本构关系参数，但由于复合材料在2-3面拉伸失效模式下过早失效，试验难以获得复合材料沿厚度方向的高应变水平，因此研究中未涉及复合材料高应变区域的非线性本构参数识别。

本文采用FEMU法开展正交各向异性复合材料沿厚度方向压缩本构参数识别。通过调整SBS试验参数实现复合材料1-3面(纤维方向为1方向)压缩剪切复合失效模式，并根据压头下方局部复杂高梯度应变区域对IM7/8552复合材料单向带层合板沿厚度方向(横向)压缩本构关系参数进行识别。对于正交各向异性本构关系的表达，本文采用用户材料子程序(UMAT)定义材料的正交各向异性本构参数并代入到ABAQUS模型中进行计算^[18-20]；在非线性本构关系的表达方面，本文采用单参数幂指数塑性本构模型形式，表征复合材料层合板沿厚度方向的非线性本构关系^[18-20]。

1. 试验材料及方法

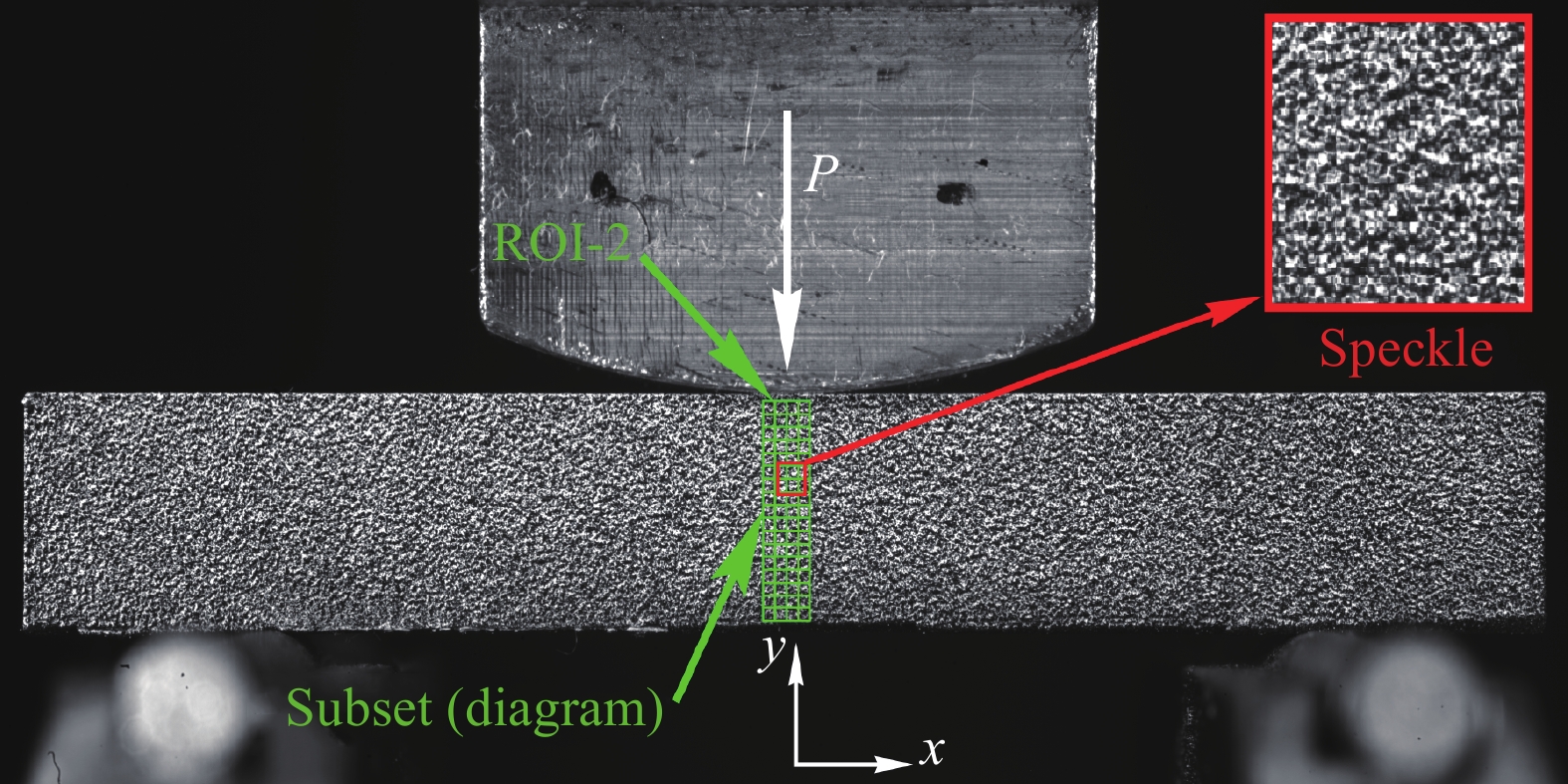
文中采用如图1所示的短梁剪切(SBS)试验形式，所用试样是由6.4 mm厚的31层正交各向异性碳纤维/环氧树脂(IM7/8552)复合材料单向带层合板切割而成。层合板固化温度为177℃，采用预浸制方法制作，试样形状为矩形横截面短梁，试样的材料方向如图2所示，其中纤维方向为1方向，垂直纤维方向为2方向，厚度方向为3方向。

图 1 改进短梁剪切试验(SBS)装置

Figure 1. Equipment setup of custom short-beam shear (SBS) test

下载: 全尺寸图片幻灯片

图 2 碳纤维/环氧树脂(IM7/8552)复合材料单向带层合板材料方向示意图

Figure 2. Schematic diagram of material directions of carbon fiber/epoxy (IM7/8552) composite unidirectional belt laminate

下载: 全尺寸图片幻灯片

参考ASTM D2344M—16^[28]，SBS试验参数为试样宽度与厚度的比值w/t=2，支撑点间距离与试样厚度的比值4<L/t<5，压头直径为6.4 mm (0.25 in)，支撑柱直径为3.2 mm (0.125 in)。为获得复合材料试样不同的失效模式，本文对ASTM D2344M—16^[28]中推荐的试验参数进行了调整，为保证在远离支撑点位置处应变沿试样宽度方向均匀分布，调整试样宽度与厚度的尺寸相等，即w/t=1；为避免试验中试样过早失效，试样厚度t由3.8 mm增加到6.4 mm，试样长度l=45.45 mm；压头的直径由D=6.4 mm (0.25 in)增大至D=50.8 mm (4 in)，支撑点之间距离L=30.5 mm，支撑点之间距离为试样厚度的4.77倍。支撑柱直径D_s=3.2 mm在本文的SBS试验中保持不变。该试验为常温实验，采用位移加载形式，加载速度为0.254 mm/min。试样典型的失效图像如图3所示。

图 3 IM7/8552复合材料单向带层合板压头下方挤压失效

Figure 3. Compressive failure of IM7/8552 composite unidirectional belt laminate under loading nose

下载: 全尺寸图片幻灯片

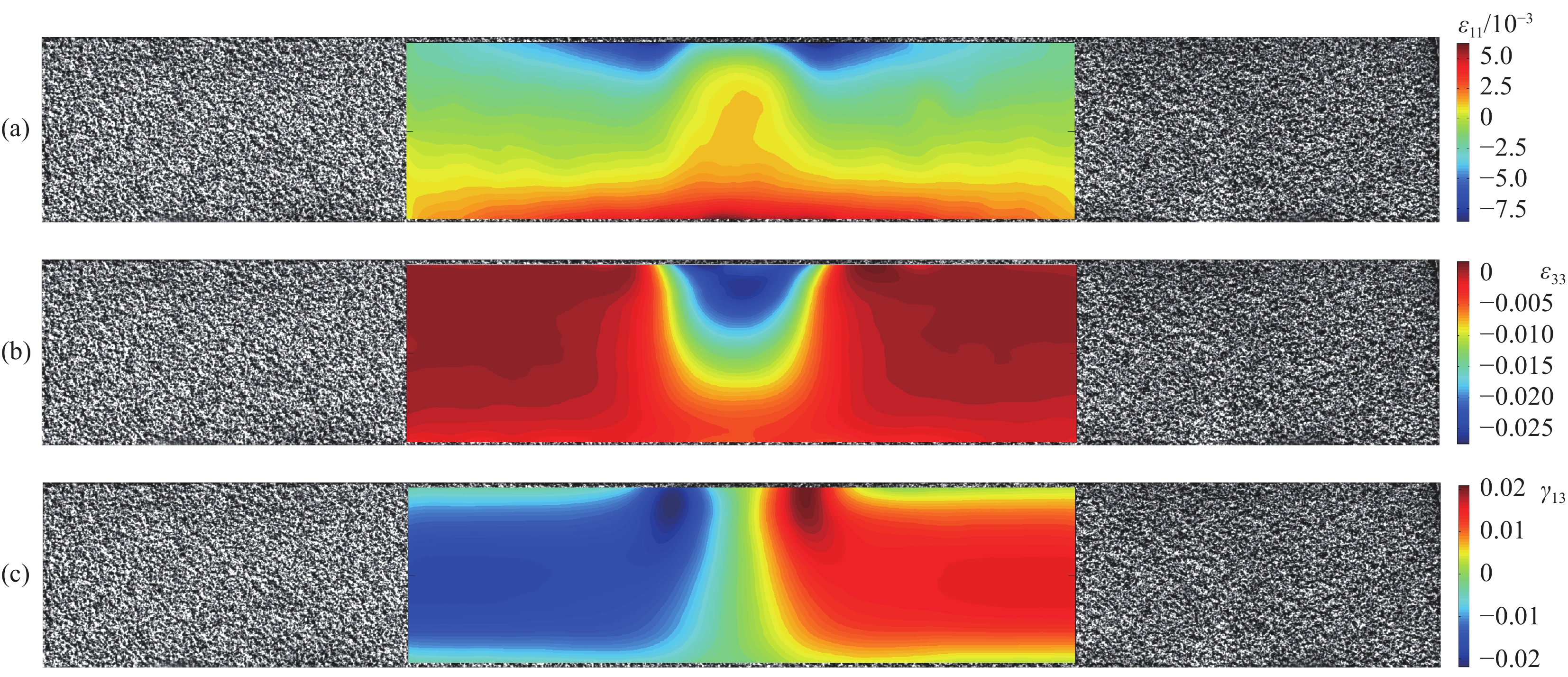
试验中由高分辨率相机、微距镜头、冷光源和三脚架共同组成DIC图像采集设备，图像采集频率为0.2 Hz。相机型号为IPX-16M3-L-1，分辨率为4 872×3 248 pixel，成像芯片为电荷耦合元件(CCD)。微距镜头型号为Sigma 105 mm f/2.8 EX DG，焦距为105 mm，光圈范围为f/2.8~C。试验过程中光圈值依据实验室光照强度进行设定，光线较强时光圈值为F1.6，光线较弱时光圈值为F2.8，镜头的变焦倍数为1。试验中镜头与试样表面之间距离为180 mm。DIC实测应变由数字图像相关软件VIC-2D计算获得，相关计算过程中涉及的参数相关窗为29×29 pixel，步长因子为7 pixel，平滑因子为15 pixel，计算区域内共包含10 260个数据点。应变云图如图4所示，其中图4(a)为沿纤维方向的正应变云图，图4(b)为沿厚度方向的正应变云图，图4(c)为剪应变云图。

图 4 数字图像相关(DIC)方法实测IM7/8552复合材料单向带层合板应变云图

Figure 4. Cloud images of strain of IM7/8552 composite unidirectional belt laminate from digital image correlation (DIC) aided method ((a) Normal axial strain; (b) Interlaminar strain; (c) Shear strain)

下载: 全尺寸图片幻灯片

2. IM7/8552单向带层合板可变参数3D有限元模型(FEM)

考虑到感兴趣区域(ROI)为压头正下方的矩形区域，且由于对称性，FEM采用1/2模型，模型中试样的宽度为实际试样的1/2，长度和厚度与实际试样相同。该模型包含几何非线性和材料非线性。模型在厚度方向划分了34层单元。在加载历程部分，共57个分析步，与DIC采集图像的数量相同。FEM的本构初值为材料制备方提供的线弹性本构参数。ROI-1区域如图5(a)中方框所示。考虑到压头下方应力水平较高，试样变形较复杂，应变梯度较大，且涉及到接近失效阶段的应力-应变行为，为提高应力分析精度，同时提高FEM在参数迭代修正过程中的效率，采用子模型分析技术。将图5(a)中的1/2模型作为全局模型，对压头下方区域建立如图5(b)所示的子模型，进行局部单元细化，以较小的计算代价取得更高精度的应力-应变结果，子模型中单元的长和高的尺寸均为2 pixel (0.226 mm)，沿2方向的宽为6 pixel (0.678 mm)。模型共含33 600个单元，为了在较低计算成本条件下获得精度较高的应力计算结果，单元类型选择为C3D8I^[29]。

图 5 SBS试验的IM7/8552复合材料单向带层合板3D有限元模型(FEM)的全局模型和子模型

Figure 5. 3D global and sub finite element model (FEM) of IM7/8552 composite unidirectional belt laminate of SBS test

ROI—Region of interest; L, w, h—Length, width and height of specimen, respectively

下载: 全尺寸图片幻灯片

子模型各个分析步的驱动变量为全局模型在该分析步的位移结果，即将全局模型在子模型边界上的位移结果作为边界条件来引入子模型。为避免边界条件设定对本构参数识别结果产生较大影响，本文采用有限元模拟数据开展边界条件对本构参数识别结果的影响进行研究，研究过程中首先在全局模型中给出材料沿厚度方向的本构参数杨氏模量E_33C=8 603 MPa，并根据上述边界条件建立子模型，开展沿厚度方向的本构参数识别，识别结果为E_33C=8 611 MPa，标准偏差为0.09%，由此可以确定该边界条件的施加不会对识别结果产生较大影响。

子模型的加载历程与全局模型相同，在与压头分析钢体表面耦合的参考点上施加集中力。考虑到在ROI-1区域内压头下方存在沿厚度方向的高水平压应力和剪应力，且应力之间的非线性耦合情况未知，为屏蔽剪应力与压应力非线性耦合行为对横向压缩本构参数识别结果的影响^[27]，选取图5(b)中ROI-2 (压头正下方向宽为0.9 mm，高为6 mm)区域进行应力-应变关系的识别，ROI-2区域的压应力较大，剪应力和沿1方向的正应力均较小，是识别材料横向压缩正应力-应变关系的理想区域。

3. 基于局部高梯度应变的IM7/8552单向带层合板非线性本构参数识别

本小节采用有限元模型修正(FEMU)法开展复合材料横向压缩本构参数识别，本构参数包括沿厚度方向的杨氏模量E_33C、非线性参数K_33C及n_33C。识别过程的参数初值是由材料制备方提供的线性本构参数。识别过程中通过如图6所示的压头下方ROI-2区域内FEM计算所得节点应变和由DIC实测应变插值到FEM节点处应变之间的方差建立目标函数。

图 6 开展本构参数识别感兴趣区域(ROI)

Figure 6. Region of interest(ROI) of identification process

P—External load of SBS test

下载: 全尺寸图片幻灯片

识别过程的收敛准则为本构参数的变化率小于0.5%或目标函数归一化平方根变化率小于1%，目标函数的计算如下：

$Q(\overline P ) = Q\left( {\left\{ {{\varepsilon _{33}}\left( {\overline P } \right),\overline P } \right\}} \right) = \sum\limits_{j = 1}^N {\sum\limits_{i = 1}^M {{{\left[ {{{\left( {\left\{ {\varepsilon _{33i}^{{\rm{num}}}\left( {\overline P } \right)} \right\} - \left\{ {\varepsilon _{33i}^{{\rm{DIC}}}} \right\}} \right)}^2}} \right]}_j}} }$

(1)

式中： $\left\{ {\overline P } \right\}$ 表示一系列待求的本构参数；N为FEM加载步的数量，也对应试验过程中DIC在试样失效前采集到的图像数量；M为FEM的每一个分析步中ROI-2区域内的节点个数；M×N为整个识别过程中所用的应力或应变数据点个数； ${\varepsilon _{33i}^{{\rm{num}}}}$ 和 ${\varepsilon _{33i}^{{\rm{DIC}}}}$ 分别表征在节点i处的有限元计算应变和DIC实测应变；i为节点编号。

目标函数 ${Q\left( {\overline P} \right)}$ 获得最小值时应满足下式：

$\frac{{\partial Q\left( {\overline P} \right)}}{{\partial {{\overline P }_l}}} = \sum\limits_{j = 1}^N {{{\left[ {\sum\limits_{i = 1}^M {\left( {\varepsilon _{33i}^{{\rm{num}}}\left( {\overline P } \right) - \varepsilon _{33i}^{{\rm{DIC}}}} \right)\frac{{\partial \varepsilon _{33i}^{{\rm{num}}}\left( {\overline P } \right)}}{{\partial {{\overline P }_l}}}} } \right]}_j}} = 0$

(2)

以试样的1-3面为例，正交各向异性复合材料单向带层合板的本构模型初始假设为

$\left\{ \begin{aligned} {\varepsilon _{11}} \\ {\varepsilon _{33}} \\ {\gamma _{13}} \end{aligned} \right\} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{E_{11}}}}}&{ - \dfrac{{{\nu _{31}}}}{{{E_{33}}}}}&0 \\ { - \dfrac{{{\nu _{13}}}}{{{E_{11}}}}}&{f\left( {{\sigma _{33}}} \right)}&0 \\ 0&0&{g\left( {{\tau _{13}}} \right)} \end{array}} \right]\left\{ \begin{aligned} {\sigma _{11}} \\ {\sigma _{33}} \\ {\tau _{13}} \end{aligned} \right\}$

(3)

式中：E₁₁为材料纵向的弹性模量；E₃₃为材料横向压缩弹性模量； $\nu$ ₃₁和 $\nu$ ₁₃分别为相应方向的泊松比；σ₁₁、σ₃₃和τ₁₃为有限元计算应力分量；ε₁₁、ε₃₃和γ₁₃为有限元计算应变分量；g(τ₁₃)表征剪切非线性本构关系；f (σ₃₃)表征横向压缩非线性本构关系。本文均选择采用单参数幂指数塑性本构模型表征非线性本构关系，剪切非线性本构关系如下：

${\gamma _{13}} = \frac{{{\tau _{13}}}}{{{G_{13}}}} + {\left( {\frac{{{\tau _{13}}}}{{{K_{13}}}}} \right)^{\frac{1}{{{n_{13}}}}}}$

(4)

式中：G₁₃为剪切模量；K₁₃为剪切非线性参数中的割线模量；n₁₃为指数相关的参数。在前期相关研究工作中采用远离压力和支撑点的中间区域，基于DIC全场应变数据识别得到该材料层间剪切非线性本构参数^[25]，本文重点讨论材料厚度方向压缩本构参数的识别。复合材料单向带层合板沿厚度方向压缩非线性本构关系如下：

${\varepsilon _{33}} = \frac{{{\sigma _{33}}}}{{{E_{33}}}} - \frac{{{\sigma _{11}}}}{{{E_{11}}}}{\nu _{13}} + {\left( {\frac{{{\sigma _{33}}}}{{{K_{33}}}}} \right)^{\frac{1}{{{n_{33}}}}}}$

(5)

式中，K₃₃和n₃₃为非线性参数。考虑到ROI-2区域内纵向正应力σ₁₁远小于横向正应力σ₃₃，因此识别过程中不考虑泊松比效果，横向压缩应力-应变关系可简写为

${\varepsilon _{33}} = \frac{{{\sigma _{33}}}}{{{E_{33}}}} + {\left( {\frac{{{\sigma _{33}}}}{{{K_{33}}}}} \right)^{\frac{1}{{{n_{33}}}}}}$

(6)

将式(6)代入式(1)可得到目标函数的展开式为

$Q\left( {\overline P } \right) \!=\! Q\left( {\varepsilon ,\overline P } \right)\! =\! \sum\limits_{j = 1}^N {{{\left\{ {\sum\limits_{i = 1}^M {\left[ {{{\left( {\frac{{\sigma _{33i}^{{\rm{num}}}}}{{{E_{33}}}} \!+\! {{\left( {\frac{{\sigma _{33i}^{{\rm{num}}}}}{{{K_{33}}}}} \right)}^{\frac{1}{{{n_{33}}}}}} \!-\! \varepsilon _{33i}^{{\rm{DIC}}}} \right)}^2}} \right]} } \right\}}_j}}$

(7)

由式(7)可知，FEMU法目标函数是与有限元计算应力 ${\sigma _{11i}^{{\rm{num}}}}$ 和 ${\sigma _{33i}^{{\rm{num}}}}$ 、实测应变 ${\varepsilon _{33i}^{{\rm{DIC}}}}$ 及待求本构参数相关的函数。将式(6)代入式(2)，则式(2)可表达为

$\frac{{\partial Q\left( {\bar P} \right)}}{{\partial {{\bar P}_{\rm{l}}}}} = \sum\limits_{j = 1}^N {{{\left\{ {\sum\limits_{i = 1}^M {\left\{ {\varepsilon _{33i}^{{\rm{num}}}\left( {\overline P } \right)} \right\} - \left\{ {\varepsilon _{33i}^{{\rm{DIC}}}} \right\}\frac{{\partial \left\{ {\varepsilon _{33i}^{{\rm{num}}}\left( {\overline P } \right)} \right\}}}{{\partial {{\bar P}_{\rm{l}}}}}} } \right\}}_j}} = 0$

(8)

采用FEMU法开展本构参数识别的流程图如图7所示。

图 7 有限元模型修正(FEMU)法沿厚度方向压缩本构参数识别流程图

Figure 7. Flowchart of thickness compressive constitutive parameters identification process using finite element model updating (FEMU) method

ε₃₃—Interlaminar compressive stress-strain; B.C.—Boundary conditions

下载: 全尺寸图片幻灯片

4. IM7/8552单向带层合板层间压缩本构参数的识别结果

采用有限元计算应力和DIC实测应变，结合FEMU技术识别得到的IM7/8552复合材料单向带层合板沿厚度方向本构参数识别结果、平均值和变异系数(COV)如表1所示。

表 1 IM7/8552复合材料单向带层合板厚度方向本构参数识别结果

Table 1. Convergence results of compressive constitutive parameters along thickness direction of IM7/8552 composite unidirectional belt laminate

	E_33C/MPa⁻¹	K_33C/MPa⁻¹	n_33C
1	8 603.86	786.50	3.59
2	8 879.12	861.30	3.54
3	8 688.18	794.21	3.63
4	8 592.68	785.48	3.59
5	8 418.64	717.23	3.66
AVG	8 636.49	788.94	3.60
COV/%	1.94	6.48	1.26
Notes: E_33C—Compressive elastic modulus in thickness direction; K_33C—Secant modulus in thickness direction; n_33C—Index number; COV—Coefficient of variation.

下载: 导出CSV

| 显示表格

表1中识别结果属于同厂家同一批次试样，试样均由BELL公司的IM7/8552正交各向异性复合材料单向带层合板切割而成，5个试样的识别结果几乎一致(变异系数小于10%)；且压缩模量E_33C与文献[8]中采用单轴压缩试验的识别结果接近(标准偏差为3.06%)，与文献[24]中识别结果的标准偏差为3.64%，因此证明该识别结果是可靠的。

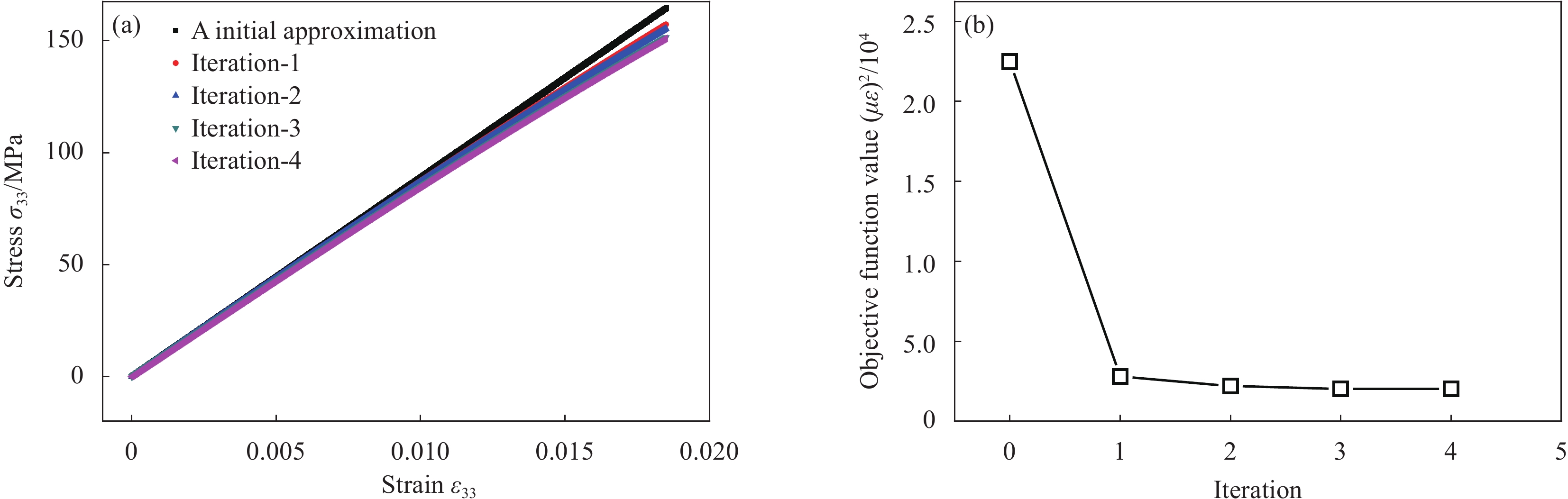
图8为在FEM中代入修正收敛的本构参数计算所得应力数据σ₃₃、DIC应变数据ε₃₃及最小二乘回归结果。数据包含压头下方ROI-2区域内整个加载历程中的应力-应变数据。优化过程经过5次迭代达到收敛，其中每一次迭代中的应力-应变曲线及目标函数值如图9所示。

图 8 IM7/8552复合材料单向带层合板横向压缩应力-应变数据和最小二乘回归结果

Figure 8. Interlaminar compressive stress-strain data and least-square convergence results of IM7/8552 composite unidirectional belt laminate

下载: 全尺寸图片幻灯片

图 9 IM7/8552复合材料单向带层合板沿厚度方向压缩正应力-应变关系识别结果(a)及目标函数值(b)随迭代次数的变化

Figure 9. Variation of constitutive curves (a) and objective function results (b) with iterations of IM7/8552 composite unidirectional belt laminate

下载: 全尺寸图片幻灯片

值得注意的是，在材料本构识别前，不失一般性的可假设材料初始本构关系为线性，不考虑非线性。图9(a)中A组的应力是通过DIC实测应变和初始假设的线性压缩弹性模量计算得到的，表征非线性特征的幂指数项为零，将初始假设的线性本构参数代入FEM后，通过有限元计算得到的应力和DIC实测应变数据。可见，压头下方沿试样厚度方向的压缩正应力-应变关系表现出一定的非线性，如图8所示。进而可修正假设的线性本构关系，采用式(6)三参数塑性本构模型表征其非线性行为。通过有限元计算应力和DIC实测应变，采用最小二乘回归，可识别得到式(6)中的非线性参数，结合FEMU，5次迭代后目标函数达到最小并收敛，识别得到了能够反映材料在目标区域的非线性力学响应的本构关系和参数。由图9(a)可见，初始假设的线性本构修正为收敛后的非线性本构。由图9(b)可见，目标函数值经过一次迭代后迅速降低，并逐渐趋于收敛。

5. 本构参数初值对识别结果的影响

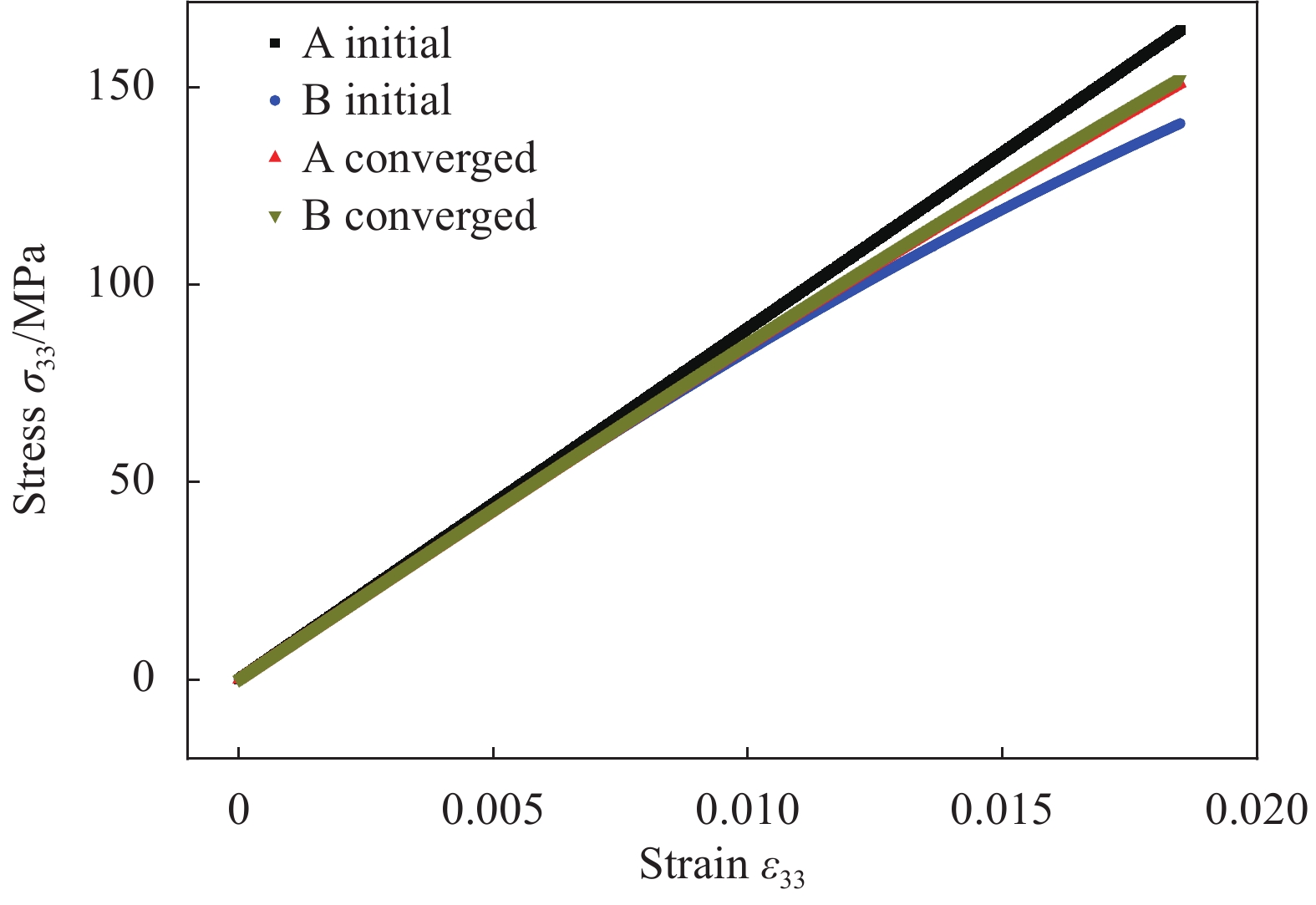
图10为采用A、B两组不同的初始本构关系假设开展识别结果的对比。

图 10 不同本构参数初值识别前和识别收敛后的应力-应变曲线

Figure 10. Stress-strain curves of different initial approximation before and after identification

A—Linear elastic initial approximation; B—Over inelastic initial approximation

下载: 全尺寸图片幻灯片

图10中A组本构参数为线弹性本构参数，B组本构参数为过非线性的本构参数，中间两条曲线分别为两组不同本构初值的识别结果。可见，采用A、B两组不同初值开展识别的最终收敛结果高度一致。A组本构参数初值的识别过程经过4次迭代达到收敛，B组本构参数初值的识别过程仅经过3次迭代达到收敛。其中A组本构初值并未考虑材料非线性行为，在识别过程的第一次迭代修正后即可根据有限元计算应力和DIC实测应变通过最小二乘回归确定非线性应力-应变关系，并通过式(6)对线弹性的本构关系的假设进行修正。由此可以说明，该识别方法采用压头下方较小区域内高水平压缩应变数据开展非线性本构参数的识别效率很高，对本构参数初值及本构关系的初始假设具有很强的鲁棒性，特别是在识别过程中通过对应力-应变数据开展最小二乘回归，可在每一次迭代过程中识别最优表达式对本构关系的初始假设进行修正。

6. 结论

(1)采用压头下方较小区域内高梯度压缩正应变数据识别得到碳纤维/环氧树脂(IM7/8552)复合材料单向带层合板厚度方向压缩本构参数，同厂家同批次试样的识别结果变异系数小于7%，与文献[8]中采用单轴压缩试验获得的压缩弹性模量标准偏差为3.06%，识别结果可靠。

(2)由于短梁剪切试验中试样近似为静定结构，因此本文采用的识别方法效率高，对于非线性本构参数只需5次迭代就可以得到正确结果。该方法在迭代过程中不需要求解应变数据对于待求本构参数的显式的敏感度矩阵。

(3)本文采用的识别方法对本构参数的初值和本构关系的初始假设不敏感；识别过程中可采用有限元计算应力和数字图像相关方(DIC)法实测应变通过最小二乘回归修正本构关系的初始假设。

(4) DIC辅助的复合材料单向带层合板短梁剪切试验，相较于复合材料单轴拉伸或压缩等标准试验方法，通过全场非均匀应变数据，识别横向压缩本构行为参数的同时，也可通过调整DIC中感兴趣区域(ROI)位置，获得复合材料纵向拉/压模量、层间剪切本构行为参数，提高力学行为参数测试效率。试验所用复合材料便于统一制备，经济性好。

(5)本文提出的识别方法可以识别均匀化后正交各向异性复合材料沿材料主方向宏观本构关系参数，但由于DIC散斑制备技术、变形识别分辨率等因素的制约，目前还不具备识别复合材料界面性能和微观组分本构关系参数的能力。

图 1 改进短梁剪切试验(SBS)装置

Figure 1. Equipment setup of custom short-beam shear (SBS) test

下载: 全尺寸图片幻灯片

图 2 碳纤维/环氧树脂(IM7/8552)复合材料单向带层合板材料方向示意图

Figure 2. Schematic diagram of material directions of carbon fiber/epoxy (IM7/8552) composite unidirectional belt laminate

下载: 全尺寸图片幻灯片

图 3 IM7/8552复合材料单向带层合板压头下方挤压失效

Figure 3. Compressive failure of IM7/8552 composite unidirectional belt laminate under loading nose

下载: 全尺寸图片幻灯片

图 4 数字图像相关(DIC)方法实测IM7/8552复合材料单向带层合板应变云图

下载: 全尺寸图片幻灯片

图 5 SBS试验的IM7/8552复合材料单向带层合板3D有限元模型(FEM)的全局模型和子模型

Figure 5. 3D global and sub finite element model (FEM) of IM7/8552 composite unidirectional belt laminate of SBS test

ROI—Region of interest; L, w, h—Length, width and height of specimen, respectively

下载: 全尺寸图片幻灯片

图 6 开展本构参数识别感兴趣区域(ROI)

Figure 6. Region of interest(ROI) of identification process

P—External load of SBS test

下载: 全尺寸图片幻灯片

图 7 有限元模型修正(FEMU)法沿厚度方向压缩本构参数识别流程图

Figure 7. Flowchart of thickness compressive constitutive parameters identification process using finite element model updating (FEMU) method

ε₃₃—Interlaminar compressive stress-strain; B.C.—Boundary conditions

下载: 全尺寸图片幻灯片

图 8 IM7/8552复合材料单向带层合板横向压缩应力-应变数据和最小二乘回归结果

Figure 8. Interlaminar compressive stress-strain data and least-square convergence results of IM7/8552 composite unidirectional belt laminate

下载: 全尺寸图片幻灯片

图 9 IM7/8552复合材料单向带层合板沿厚度方向压缩正应力-应变关系识别结果(a)及目标函数值(b)随迭代次数的变化

Figure 9. Variation of constitutive curves (a) and objective function results (b) with iterations of IM7/8552 composite unidirectional belt laminate

下载: 全尺寸图片幻灯片

图 10 不同本构参数初值识别前和识别收敛后的应力-应变曲线

Figure 10. Stress-strain curves of different initial approximation before and after identification

A—Linear elastic initial approximation; B—Over inelastic initial approximation

下载: 全尺寸图片幻灯片

表 1 IM7/8552复合材料单向带层合板厚度方向本构参数识别结果

Table 1 Convergence results of compressive constitutive parameters along thickness direction of IM7/8552 composite unidirectional belt laminate

	E_33C/MPa⁻¹	K_33C/MPa⁻¹	n_33C
1	8 603.86	786.50	3.59
2	8 879.12	861.30	3.54
3	8 688.18	794.21	3.63
4	8 592.68	785.48	3.59
5	8 418.64	717.23	3.66
AVG	8 636.49	788.94	3.60
COV/%	1.94	6.48	1.26
Notes: E_33C—Compressive elastic modulus in thickness direction; K_33C—Secant modulus in thickness direction; n_33C—Index number; COV—Coefficient of variation.

下载: 导出CSV

参考文献(29)

[1]	CHEN H X, CAO H J, HUANG X M. Simulation analysis of in-plane compression on three-dimensional spacer fabric composite[J]. Materials Science Forum,2019,971:36-44. DOI: 10.4028/www.scientific.net/MSF.971.36
[2]	KAMAE T, DRZAL L T. Carbon fiber/epoxy composite property enhancement through incorporation of carbon nanotubes at the fiber-matrix interphase Part Ⅰ: The development of carbon nanotube coated carbon fibers and the evaluation of their adhesion[J]. Composites Part A: Applied Science and Manufacturing,2012,43(9):1569-1577. DOI: 10.1016/j.compositesa.2012.02.016
[3]	RIZVI Z H, SEMBDNER K, SUMAN A, et al. Experimental and numerical investigation of thermo-mechanical properties for nano-geocomposite[J]. International Journal of Thermophysics,2019,40(5):54.
[4]	ZHOU Y, HOSUR M, JEELANI S, et al. Fabrication and characterization of carbon fiber reinforced clay/epoxy composite[J]. Journal of Materials Science,2012,47(12):5002-5012. DOI: 10.1007/s10853-012-6376-4
[5]	彭湃, 赵美英, 王文智. 细观力学模型预测复合材料横向强度性能研究[J]. 机械科学与技术, 2017, 36(10):1611-1618. PENG Pai, ZHAO Meiying, WANG Wenzhi. Transverse strength prediction of composite materials via micromechanics model[J]. Mechanical Science and Technology for Aerospace Engineering,2017,36(10):1611-1618(in Chinese).
[6]	QUICK T, SAFRIET S, MOLLENHAUER D, et al. Compression testing of micro-scale unidirectional polymer matrix composites[M]//BEESE A, ZEHNDER A, XIA S. Fracture, fatigue, failure and damage evolution, Volume 8. Springer Cham, 2016: 225-233.
[7]	HUSSIEN A, MOEHRING M, SCHWALL C, et al. On compressive response of IM7/8552 lamina: A theoretical & experimental review[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Hawaii: American Institute of Aeronautics and Astronantics, Inc., 2012.
[8]	KOERBER H, XAVIER J, CAMANHO P P. High strain rate characterisation of unidirectional carbon-epoxy IM7-8552 in transverse compression and in-plane shear using digital image correlation[J]. Mechanics of Materials,2010,42(11):1004-1019. DOI: 10.1016/j.mechmat.2010.09.003
[9]	KAWAI M, WATANABE K, HOSHI H, et al. Effect of specimen size on longitudinal strength of unidirectional carbon/epoxy composite laminates (part 1, unnotched strength)[J]. Advanced Composite Materials,2019,28(s2):53-71.
[10]	TAM J H, ONG Z C, ISMAIL Z, et al. Identification of material properties of composite materials using nondestructive vibrational evaluation approaches: A review[J]. Mechanics of Advanced Materials & Structures,2017,24(12):971-986.
[11]	KOERBER H, KUHN P, PLOECKL M, et al. Experimental characterization and constitutive modeling of the non-linear stress-strain behavior of unidirectional carbon-epoxy under high strain rate loading[J]. Advanced Modeling and Simulation in Engineering Sciences,2018,5:17.
[12]	王显, 马少鹏, 陈俊达, 等. 数字散斑相关方法的全场优化表述[J]. 北京理工大学学报, 2011, 31(5):505-508, 566. WANG Xian, MA Shaopeng, CHEN Junda, et al. Global optimization model for digital speckle correlation method[J]. Transactions of Beijing Institute of Technology,2011,31(5):505-508, 566(in Chinese).
[13]	GONZALEZ J F, ANTARTIS D A, MARTINEZ M, et al. Three-dimensional study of graphite-composite electrode chemo-mechanical response using digital volume correlation[J]. Experimental Mechanics,2018,58(9):573-583.
[14]	BARBARELLA E, ALLIX O, DAGHIA F, et al. Comparison of mechanical tests for the identification of composite defects using full-field measurements and the modified constitutive relation error[M]//SORIĆ J, WRIGGERS P, ALLIX O. Multiscale modeling of heterogeneous structures. Springer, Cham, 2018: 39-59.
[15]	AVRIL S, PIERRON F, PANNIER Y, et al. Stress reconstruction and constitutive parameter identification in plane-stress elasto-plastic problems using surface measurements of deformation fields[J]. Experimental Mechanics,2008,48(4):403-419. DOI: 10.1007/s11340-007-9084-2
[16]	GREDIAC M, TOUSSAINT E, PIERRON F. Special virtual fields for the direct determination of material parameters with the virtual fields method 2: Application to in-plane properties[J]. International Journal of Solids & Structures,2002,39(10):2707-2730.
[17]	GREDIAC M, PIERRON F, AVRIL S, et al. The virtual fields method for extracting constitutive parameters from full-field measurements: A review[J]. Strain,2010,42(4):233-253.
[18]	CARPENTIER A P. Advanced materials characterization based on full field deformation measurements[D]. Texas: University of Texas at Arlington, 2013.
[19]	贾利勇, 贾欲明, 于龙, 等. 基于多尺度模型的复合材料厚板G₁₃剪切失效分析[J]. 复合材料学报, 2017, 34(4):786-794. JIA Liyong, JIA Yuming, YU Long, et. al. Failure analysis of thick composite laminates with multi-scale modelling under G₁₃ out-of-plane shear loading[J]. Acta Materiae Compositae Sinica,2017,34(4):786-794(in Chinese).
[20]	JI X, HAO Z, SU L, et al. Characterizing the constitutive response of plain-woven fibre reinforced aerogel matrix composites using digital image correlation[J]. Composite Structures,2020,234:111652.
[21]	VIALA R, PLACET V, COGAN S. Identification of the anisotropic elastic and damping properties of complex shape composite parts using an inverse method based on finite element model updating and 3D velocity fields measurements (FEMU-3DVF): Application to bio-based composite violin soundboards[J]. Composites Part A: Applied Science and Manufacturing,2018,106:91-103.
[22]	薛康, 肖毅, 王杰, 等. 单向纤维增强聚合物复合材料压缩渐进破坏[J]. 复合材料学报, 2019, 36(6):1398-1412. XUE Kang, XIAO Yi, WANG Jie, et. al. Compression progressive failure of unidirectional fiber reinforced polymer composite[J]. Acta Materiae Compositae Sinica,2019,36(6):1398-1412(in Chinese).
[23]	MAKEEV A, HE Y, CARPENTIER P, et al. A method for measurement of multiple constitutive properties for composite materials[J]. Composites Part A: Applied Science and Manufacturing,2012,43(12):2199-2210. DOI: 10.1016/j.compositesa.2012.07.021
[24]	MAKEEV A, CARPENTIER P, SHONKWILER B. Methods to measure interlaminar tensile modulus of composites[J]. Composites Part A: Applied Science and Manufacturing,2014,56:256-261.
[25]	HE T, LIU L, MAKEEV A, et al. Characterization of stress-strain behavior of composites using digital image correlation and finite element analysis[J]. Composite Structures,2016,140:84-93. DOI: 10.1016/j.compstruct.2015.12.018
[26]	HE T, LIU L, MAKEEV A. Uncertainty analysis in composite material properties characterization using digital image correlation and finite element model updating[J]. Composite Structures,2017,184:337-351.
[27]	JULIA C. Accurate three-dimensional characterization of the nonlinear material constitutive properties for laminated composite materials[D]. Texas: University of Texas at Arlington, 2015.
[28]	ASTM International. Standard test method for short-beam strength of polymer matrix composite materials and their laminates: ASTM D2344M—16[S]. West Conshohocken: ASTM International, 2016.
[29]	HE Y, MAKEEV A. Nonlinear shear behavior and interlaminar shear strength of unidirectional polymer matrix composites: A numerical study[J]. International Journal of Solids and Structures,2014,51(6):1263-1273. DOI: 10.1016/j.ijsolstr.2013.12.014

施引文献(8)

期刊类型引用(3)

1.	邱伊健，郑萍，程香平，郭玉松. 随机多尺度短切碳纤维复合结构模型中RVE尺寸效应和方向模量的均一化响应. 兵工学报. 2023(03): 702-717 . 百度学术
2.	凌小康，张敬宗，钱鼎，宋义敏. 基于DSCM-FEM的花岗岩力学参数反演方法研究. 计算力学学报. 2022(02): 216-221 . 百度学术
3.	张志远，李伟，蒋鹏，张宏远，闫孝伟. 碳纤维复合材料层合板低速冲击损伤特性研究. 兵器材料科学与工程. 2021(04): 34-39 . 百度学术