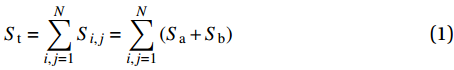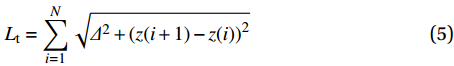Effect of macro fibers on flexural toughness and crack surface topography of concrete
-
摘要: 为了研究结构型聚丙烯纤维、结构型钢纤维及混杂纤维(包括结构型聚丙烯纤维和结构型钢纤维)对混凝土弯曲韧性及裂缝表面形态的影响，参照RILEM TC 162-TDF[10]标准进行混凝土开口梁的三点弯曲试验。利用激光扫描仪对每个试件裂缝表面形态进行信息采集。基于裂缝表面信息，计算了四种裂缝表面粗糙程度参数(即裂缝粗糙度(RN)、分形维数(D)、z坐标正态分布的标准差(σz)和裂缝曲折度(τ))，并比较分析了裂缝表面粗糙程度参数与弯曲韧性参数之间的相关性。研究表明：随着纤维掺量的增多，混凝土弯曲韧性和裂缝表面粗糙程度均随之增大。与结构型聚丙烯纤维和结构型钢纤维相比，混杂纤维在提高混凝土弯曲韧性和增大混凝土裂缝表面粗糙度方面均展现出正混杂效应。与分形维数D、z坐标正态分布标准差σz和裂缝曲折度τ相比，裂缝粗糙度RN与纤维增强混凝土梁弯曲韧性参数的相关性最为显著，且存在指数函数关系。基于该函数关系，可借助纤维增强混凝土梁的弯曲试验快速估测裂缝表面的粗糙程度。Abstract: In order to study the effect of different macro fibers (including macro polypropylene fiber, macro steel fiber and hybrid fiber of polypropylene fiber and steel fiber) on the flexural toughness and crack surface topography of concrete, three-point bending test was conducted on notched beams in accordance with RILEM TC 162-TDF[10]. The laser scanning equipment was utilized to measure the information of crack surface topography. The four roughness parameters (roughness number (RN), fractal dimension (D), standard deviation of height distribution (σz) and crack tortuosity (τ)) were calculated according to the information of crack surface topography and the correlation between four crack roughness parameters and flexural toughness parameters were then analyzed and compared. The results show that with the increasing of fiber content, the flexural toughness and crack surface roughness increase. Compared to polypropylene fiber and steel fiber, the hybrid fiber illustrates the positive synergistic effect on the flexural toughness and crack surface roughness of concrete. Compared to ractal dimension D, standard deviation of height distribution σz and crack tortuosity τ, the correlation between RN and flexural toughness of fiber reinforced concrete beam is the most satisfactory. Meanwhile, the relationship between roughness number RN and flexural toughness parameters follows the exponential function, which can be applied to quickly estimate crack surface roughness by the bending test of fiber reinforced concrete.
-
Keywords:
- macro fiber /
- flexural toughness /
- laser scanning /
- topography of crack surface /
- roughness
-
混凝土结构在正常使用阶段均带裂缝工作。当混凝土结构出现裂缝时，外界的水和空气会携带有害物质通过裂缝进入混凝土内部，从而加剧混凝土结构的腐蚀并影响结构的耐久性和使用寿命。已有研究[1-2] 表明，当裂缝宽度一定时，外界物质通过裂缝进入混凝土的难易程度主要取决于混凝土裂缝表面的粗糙程度，即裂缝表面越粗糙，外界物质越难渗入混凝土中。因此，增加混凝土裂缝表面粗糙程度是提高开裂混凝土结构耐久性的有效手段。
近些年，一些学者将研究重点集中在水泥基材料裂缝表面粗糙程度与其力学性能的相关性。Issa等[3]使用Slit-Island 测量法研究了普通混凝土断裂韧性与裂缝表面粗糙程度的关系并发现普通混凝土断裂面越粗糙，其断裂韧性越高。Kurtis等[4]借助共聚焦显微镜探究了纤维增强砂浆试件裂缝表面形态，并发现其断裂韧性和裂缝表面的粗糙程度具有线性关系。Ficker等[5]使用共聚焦显微镜分析了水灰比从0.4到1.0的混凝土抗压强度与其裂缝表面粗糙程度的关系，并发现裂缝表面粗糙度随水灰比的增加而逐渐增大，随抗压强度的增大而逐渐减小。Erdem等[6]研究了不同种类的粗骨料混凝土断裂能与裂缝表面形态的关系，并发现棱角较多的骨料会导致裂缝表面更加粗糙。Cai等[7]通过对冻融作用后碱矿渣混凝土断裂韧性的研究，发现随着冻融循环次数的增加，其断裂韧性逐渐降低，且裂缝表面粗糙程度逐渐增加。以上研究表明，普通混凝土和砂浆的断裂面粗糙程度与其韧性具有一定的相关性。但目前仍缺少关于纤维增强混凝土(FRC)的韧性与裂缝表面粗糙程度的相关研究。
FRC已成为应用广泛的建筑复合材料，其优势在于通过纤维改善混凝土脆性，并显著增加混凝土材料韧性性能。同时，纤维也会增加混凝土裂缝表面粗糙程度，降低裂缝的渗透率，进而提高开裂混凝土结构的耐久性和使用寿命[8-9]。然而，FRC耐久性试验(如气体/水渗透性能)存在试验操作复杂、试验结果离散程度大和试验时间长等缺点。考虑到FRC弯曲测试方法已经趋于成熟，主要规范包括RILEM TC 162—TDF[10]、ASTM C1609M—19a[11]、CECS 13∶2009[12]、JCI-S-001—2003[13]，相比于耐久性(气体/水渗透性能)试验，FRC的弯曲试验具有操作简单、时间短和结果离散程度低等优势，如果可通过FRC的弯曲韧性间接评估出其耐久性能，则可节省试验的时间和成本，并显著提高对FRC耐久性能评测的准确性，可为FRC结构设计做出指导性建议。
本研究定量分析了普通混凝土(NC)、结构型钢纤维增强混凝土(SF/NC)、结构型聚丙烯纤维增强混凝土(PP/NC)和钢-聚丙烯混杂纤维增强混凝土(SF-PP/NC)的弯曲韧性与裂缝表面粗糙程度的相关性。借鉴RILEM TC 162-TDF标准[10]，分别对各组试件开口梁进行三点弯曲试验，利用课题组自行设计的激光扫描仪对混凝土裂缝表面形态进行信息采集和重构。研究了结构型纤维对混凝土弯曲韧性及裂缝表面形态的影响，从而探究FRC裂缝表面粗糙程度与其弯曲韧性参数的相关性，并为FRC韧性与其耐久性能的相关性研究提供有力支撑。
1. 试验材料及方法
1.1 原材料与配比
普通硅酸盐水泥(P·O42.5R)；Ⅰ级粉煤灰；石英砂(粒径为0~5 mm，细度模数为2.65)；机制碎石(粒径为5~10 mm连续级配)；聚羧酸高效减水剂，减水率为30%。混凝土基准配比如表1所示。钢纤维为端部弯钩型钢纤维(SF)，聚丙烯纤维为平直型聚丙烯纤维(PP)。SF和PP的形状和参数分别如图1和表2所示。SF的掺量为20 kg/m3(0.25vol%)、40 kg/m3(0.5vol%)和60 kg/m3(0.75vol%)，PP的掺量为2.3 kg/m3(0.25vol%)、4.6 kg/m3 (0.5vol%)和6.9 kg/m3(0.75vol%)，混杂纤维掺量为2.3 kg/m3 PP和20 kg/m3 SF(纤维总体积掺量为0.5vol%)及2.3 kg/m3 PP和40 kg/m3SF(纤维总体积掺量为0.75vol%)，根据纤维掺量将试件编号分组，如SF40/NC，表示钢纤维掺量为40 kg/m3的混凝土试样。
表 1 混凝土基准配比Table 1. Basic mix proportion of concretekg·m–3 Cement Fly ash Fine aggregate Coarse aggregate Water Superplasticizer 390 155 822 848 272.5 5.5 ![]()
图 1 结构型钢纤维(SF)和结构型聚丙烯纤维(PP)的形状Figure 1. Geometries of macro steel fiber(SF) and macro polypropylene fiber(PP)1.2 试件制备
根据CECS 13∶2009[12]，采用强制式单卧轴混凝土搅拌机对拌合物进行搅拌。然后将混凝土分别装入100 mm×100 mm×400 mm和100 mm×100 mm×100 mm的钢模具中振捣。一天后拆模，并将试件放置在温度为(20±2)℃且相对湿度为95%的标准养护室养护至28天。养护完成后对立方体试件进行混凝土抗压试验，28天龄期混凝土试件抗压强度的试验结果如表3所示。在混凝土梁的侧面跨中位置处预制深度为10 mm、宽度为3 mm的开口，并进行三点弯曲试验。
1.3 三点弯曲试验
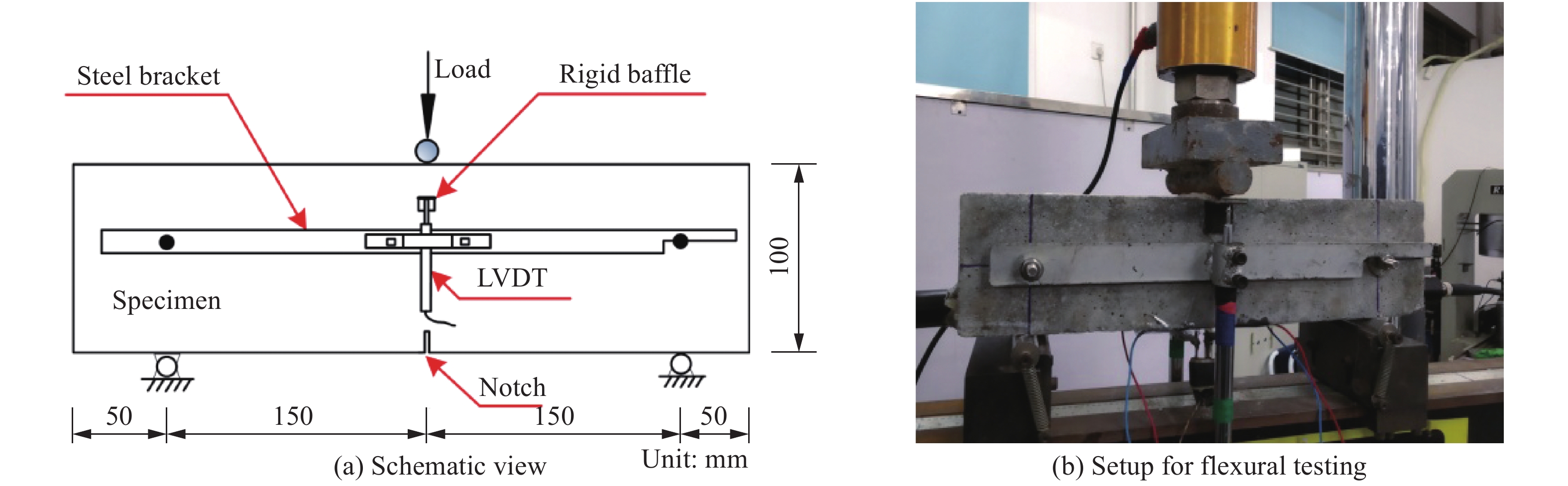
开口梁的三点弯曲试验借鉴RILEM TC 162-TDF[10]的试验方法。该试验在MTS Landmark®伺服试验机上进行。试验装置如图2所示。试验加载速度为0.2 mm/min，直到混凝土梁完全断开时试验停止。两个位移传感器(LVDT)分别布置于混凝土梁的两个侧面记录梁跨中变形。
表 2 纤维性能参数Table 2. Properties of fibersType Shape of fiber Length/mm Diameter/mm Aspect ratio Tensile
strength/MPaElastic
modulus/GPaNumber/
(104 pieces·kg−1)Macro PP Straight 45 0.75 60 490 3.9 5.76 Macro SF Hooked-end 35 0.55 65 1 150 200.0 1.45 表 3 28天龄期混凝土试件抗压强度Table 3. Compressive strength (28 d) of concrete specimensComposite SF PP Compressive strength/MPa NC — — 37.3 SF20/NC 20 kg/m3 (0.25vol%) — 41.7 SF40/NC 40 kg/m3 (0.5vol%) — 35.4 SF60/NC 60 kg/m3 (0.75vol%) — 34.1 PP2.3/NC — 2.3 kg/m3 (0.25vol%) 36.5 PP4.6/NC — 4.6 kg/m3 (0.5vol%) 35.4 PP6.9/NC — 6.9 kg/m3 (0.75vol%) 37.5 SF20-PP2.3/NC 20 kg/m3 (0.25vol%) 2.3 kg/m3 (0.25vol%) 37.2 SF40-PP2.3/NC 40 kg/m3 (0.5vol%) 2.3 kg/m3 (0.25vol%) 38.5 ![]()
图 2 混凝土开口梁弯曲试验Figure 2. Flexural test of concrete notched beamLVDT—Linear variable differential transformer1.4 裂缝表面形态测量方法
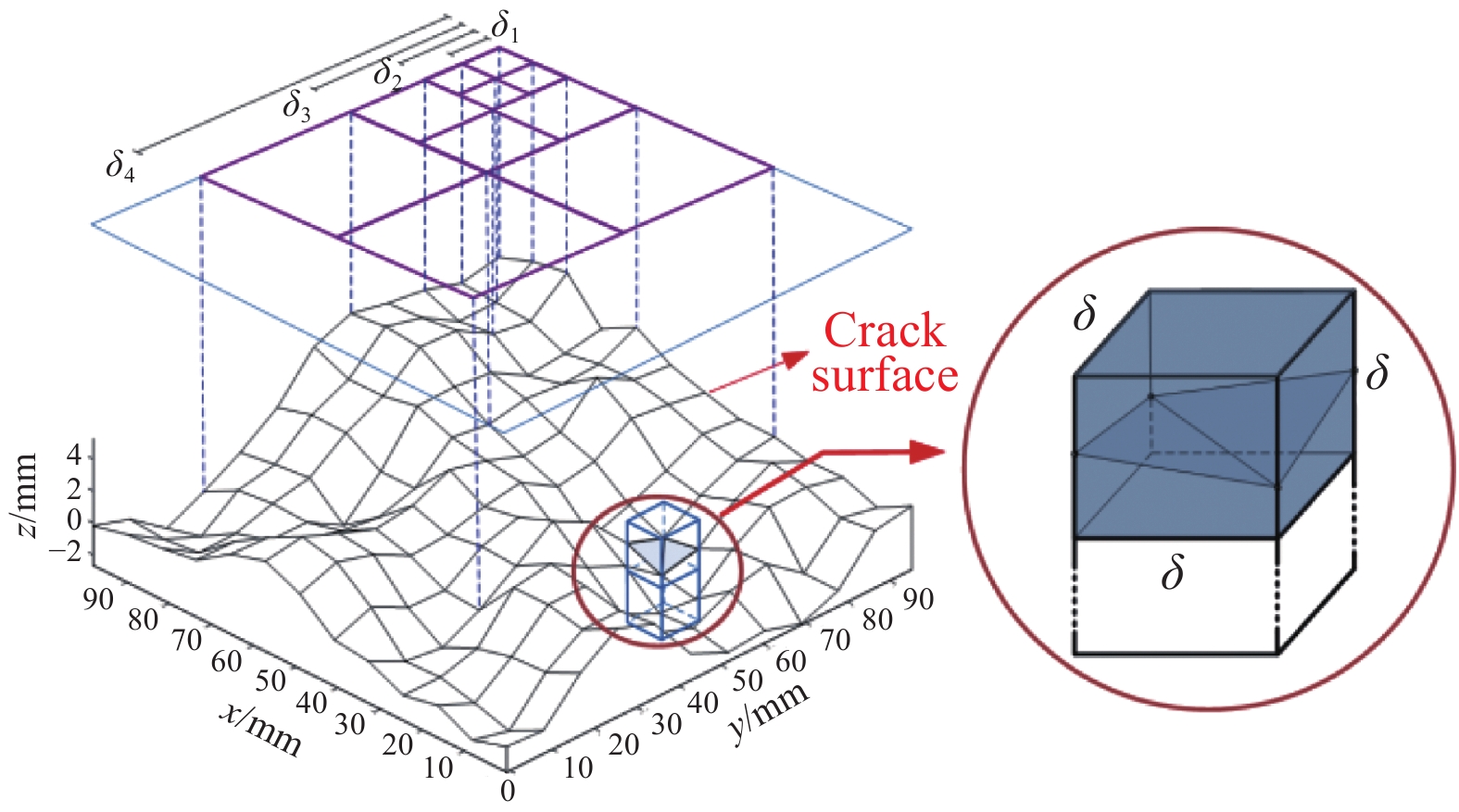
在三点弯曲试验结束后，混凝土梁沿裂缝被分为两部分。切断暴露于试件裂缝表面的纤维后使用自行设计的激光扫描仪对裂缝表面进行形貌扫描和信息收集(如图3所示)。利用Mach3程序编写G代码控制激光位移计的扫描路径，如图4所示。扫描区域投影尺寸为90 mm×100 mm。每个混凝土试件裂缝表面信息包含约23 000个数据点，每个数据点为裂缝表面各点的空间坐标(x, y, z)信息。其中，y轴坐标借助于扫描路径的数据获得，x轴和z轴坐标数据通过精度为7 μm的激光位移计采集。
1.5 粗糙程度参数
为表征各组混凝土裂缝表面粗糙程度的差异化，四种参数(裂缝粗糙度(RN)、分形维数(D)、z坐标正态分布的标准差(σz)和裂缝曲折度(τ))分别被用于衡量各组试件裂缝表面的粗糙程度。
1.5.1 裂缝粗糙度
图5为混凝土裂缝表面形态示意图，左图为裂缝表面网格示意图，So为扫描区域投影面积，即90 mm×100 mm；右图为裂缝表面St的一个单元网格模型。N为裂缝表面St中单元网格的个数。每个单元内的裂缝表面面积被分为两个三角形(Sa和Sb)，它们的面积根据Heron式[1]计算。裂缝粗糙度数RN计算方法如下式[5-6, 14-17] ：
St=N∑i,j=1Si,j=N∑i,j=1(Sa+Sb) (1) RN=StSo (2) 1.5.2 分形维数
由于混凝土裂缝具有分形特征，因此分形维数可用于评估混凝土裂缝表面的粗糙程度[18]。盒子计数法是分形维数常用的测量方法，其中“盒子”的尺寸δ和裂缝表面粗糙程度决定了裂缝表面所能覆盖“盒子”的最大数量N(δ)。随着“盒子”的尺寸δ变化，N(δ)也随之变化。因此裂缝表面的分形维数可以通过不同“盒子”的尺寸δ对应的 “盒子”最大数量N(δ)的关系计算得出，图6为盒子计数法示意图，“盒子”的尺寸δ与 “盒子”最大数量N(δ)的关系如下[3, 7, 14, 19-20] ：
N(δ)∼δ−D (3) 式中，D为裂缝表面分形维数。
1.5.3 z坐标正态分布标准差值
对每个混凝土试件裂缝表面信息中23 000个数据点的高程信息(即每个数据点的z坐标)进行统计和分析。研究发现，每组数据点的z坐标都有其独特的正态分布曲线，如图7所示。说明每组数据点z坐标的正态分布标准差σz可用于表征混凝土裂缝表面高程信息的离散程度，从而间接反映出混凝土试件裂缝表面的粗糙程度，z坐标的正态分布标准差σz计算如下[21]：
![]()
图 7 混凝土试件裂缝表面z坐标分布直方图Figure 7. Distribution histogram of z coordinates from concrete cracked surfaceσz=√N∑i=1(zi−¯z)2N (4) 式中：
ˉz 为扫描区域上所有数据点z坐标的平均值；N为数据点的个数。1.5.4 裂缝曲折度
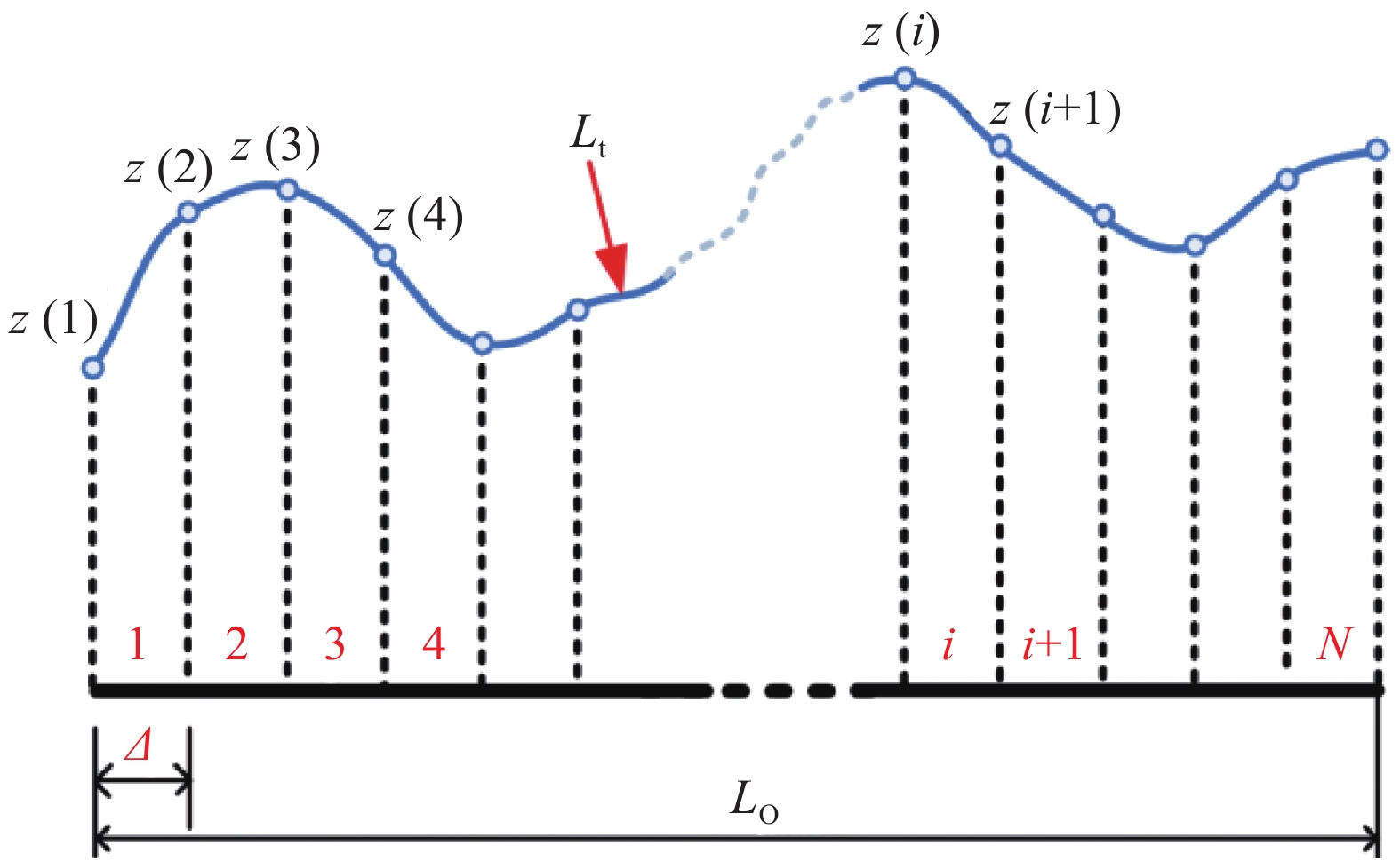
裂缝曲折度是用来衡量混凝土表面裂缝弯曲程度的常用指标，可用来间接反映裂缝表面的粗糙程度。图8为混凝土裂缝曲折度计算方法。混凝土裂缝曲折度计算如下[18, 22]：
Lt=N∑i=1√Δ2+(z(i+1)−z(i))2 (5) Lo=NΔ (6) τ=(LoLt)2 (7) 式中：Lo为混凝土表面的裂缝的投影长度；Lt为混凝土表面的裂缝实际长度；z(i)为数据点i所对应的z轴坐标值；各数据点投影的距离Δ为0.2 mm；N为混凝土表面裂缝数据点个数。
2. 结果与讨论
2.1 纤维增强混凝土(FRC)的弯曲性能
图9为NC、SF/NC、PP/NC和SF-PP/NC试件的荷载-挠度曲线。表4为NC、SF/NC、PP/NC和SF-PP/NC试件的比例极限荷载、极限荷载、弯曲韧性参数(能量吸收能力和等效抗弯强度)及桥接于裂缝表面的纤维根数。由于能量吸收能力和等效抗弯强度均为弯曲韧性参数[23]，且它们之间呈正比[10]，因此本文仅使用能量吸收能力(DfBZ,2和DfBZ,3)作为衡量FRC梁弯曲韧性的参数进行研究。
表 4 NC、SF/NC、PP/NC和SF-PP/NC试件的比例极限荷载、极限荷载、能量吸收能力、等效抗弯强度和裂缝表面纤维根数Table 4. Load at limit of proportionality, ultimate load, energy absorption capacity, equivalent flexural tensile strength and parameters of flexural toughness of NC, SF/NC, PP/NC and SF-PP/NC specimensFiber content/vol% Specimen FL/kN Fu/kN DfBZ,2/(N·m) feq,2/MPa DfBZ,3/(N·m) feq,3/MPa Nf 0 NC 10.0 10.0 0 0 0 0 0 0.25 SF20/NC 9.1 9.1 2.0 2.23 11.3 2.52 60.0 PP2.3/NC 9.7 9.7 1.1 1.20 7.4 1.65 50.7 0.50 SF40/NC 11.4 11.9 4.3 4.82 25.3 5.63 125.0 PP4.6/NC 9.8 9.8 1.4 1.53 9.7 2.16 108.0 SF20-PP2.3/NC 11.2 13.0 5.1 5.67 29.5 6.56 134.7 0.75 SF60/NC 12.4 18.4 9.1 10.12 45.1 10.03 199.3 PP6.9/NC 10.6 10.6 2.3 2.51 13.9 3.10 169.0 SF40-PP2.3/NC 12.3 15.7 6.2 6.89 36.2 8.04 194.3 Notes: FL—Maximum load in the interval of 0.05 mm; Fu—Ultimate load; DfBZ,2, DfBZ,3 —Energy absorption of the influence of fiber at the deflections of (δL+0.65 mm) and (δL+2.65 mm), respectively; feq,2, feq,3—Equivalent flexural tensile strengths by the deflections of (δL+0.65 mm) and (δL+2.65 mm), respectively; Nf—Number of fibers on the cracked surface. ![]()
图 9 普通混凝土(NC)、钢纤维增强混凝土(SF/NC)、聚丙烯纤维增强混凝土(PP/NC)和混杂纤维增强混凝土(SF-PP/NC)试件的荷载-挠度曲线Figure 9. Load-deflection curves of normal concrete(NC), steel fiber reinforced concrete(SF/NC), polypropylene fiber reinforced concrete(PP/NC) and hybrid fiber reinforced concrete(SF-PP/NC) specimens由表4可知，与PP2.3/NC试件相比，SF20/NC试件的DfBZ,2和DfBZ,3值分别增大了82%和53%。与PP4.6/NC试件相比，SF40/NC试件的DfBZ,2和DfBZ,3值分别增大了207%和161%, SF20-PP2.3/NC试件的DfBZ,2和DfBZ,3值分别增大了264%和204%。与PP6.9/NC试件相比，SF60/NC试件的DfBZ,2和DfBZ,3值分别增大了296%和224%, SF40-PP2.3/NC试件的DfBZ,2和DfBZ,3值分别增大了170%和160%。
对于SF/NC，与SF20/NC试件相比，SF40/NC试件的DfBZ,2和DfBZ,3值分别增大了115%和124%，SF60/NC试件的DfBZ,2和DfBZ,3值分别增大了355%和298%，且SF40/NC和SF60/NC试件裂缝表面上纤维根数分别增加了108%和232%。同时，SF20/NC和SF40/NC试件表现出挠度软化行为，SF60/NC试件表现出挠度硬化行为。
对于PP/NC，与PP2.3/NC试件相比，PP4.6/NC试件的DfBZ,2和DfBZ,3值分别增大了27%和31%，PP6.9/NC试件的DfBZ,2和DfBZ,3值分别增大了109%和88%，且PP4.6和PP6.9试件裂缝表面上纤维根数分别增加了118%和233%。同时，PP2.3/NC、PP4.6/NC和PP6.9/NC试件均表现出挠度软化行为。
综上所述，SF40/NC和SF60/NC试件的钢纤维掺量分别是SF20/NC试件的2倍和3倍，但SF40/NC和SF60/NC试件裂缝表面纤维数量分别为SF20/NC试件的2.08和3.32倍。且PFRC试件也有相似的现象。由此可以推断，随着纤维掺量的增加，裂缝表面的纤维数量增长率高于纤维掺量的增加率。
对于SF-PP/NC，结合表4可知，相比于PP2.3/NC试件和SF20/NC试件的能量吸收能力之和，SF20-PP2.3/NC试件的DfBZ,2和DfBZ,3值分别增大了65%和57%。同时，相比于PP2.3/NC和SF40/NC的能量吸收能力之和，SF40-P2.3/NC的DfBZ,2和DfBZ,3值分别增大了14%和10%。综上所述，混杂纤维对增强混凝土弯曲韧性展现出正混杂效应。
2.2 FRC裂缝的表面形态
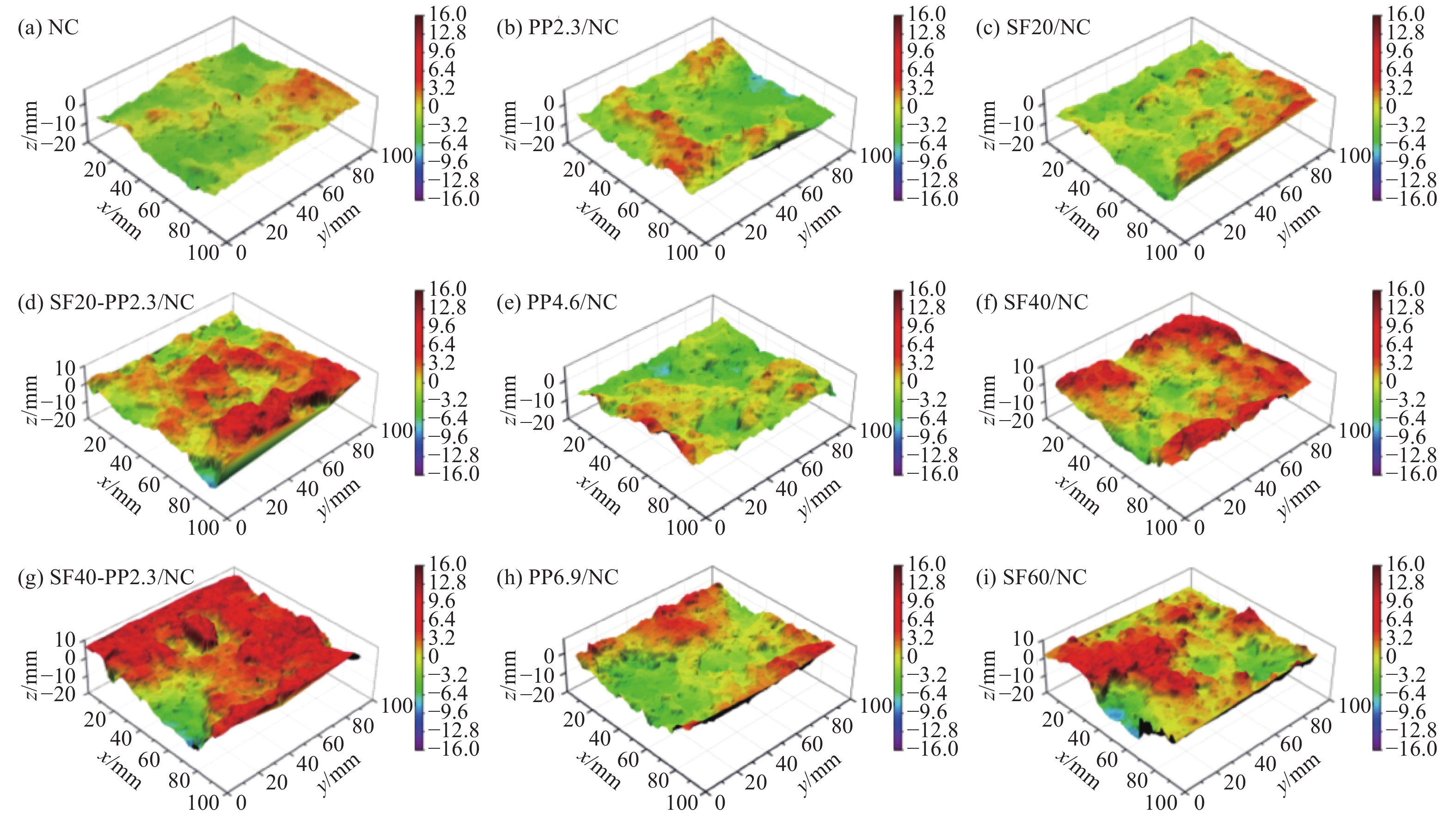
图10为NC、SF/NC、PP/NC和SF-PP/NC试件裂缝表面的重构图。可以发现，与NC试件相比，FRC试件的裂缝表面更加粗糙；对于相同纤维种类，随着纤维掺量的增加，混凝土裂缝表面粗糙程度随之增加；对于纤维体积掺量相同的FRC试件，SF-PP/NC和SF/NC较PP/NC具有更加粗糙的裂缝表面。
![]()
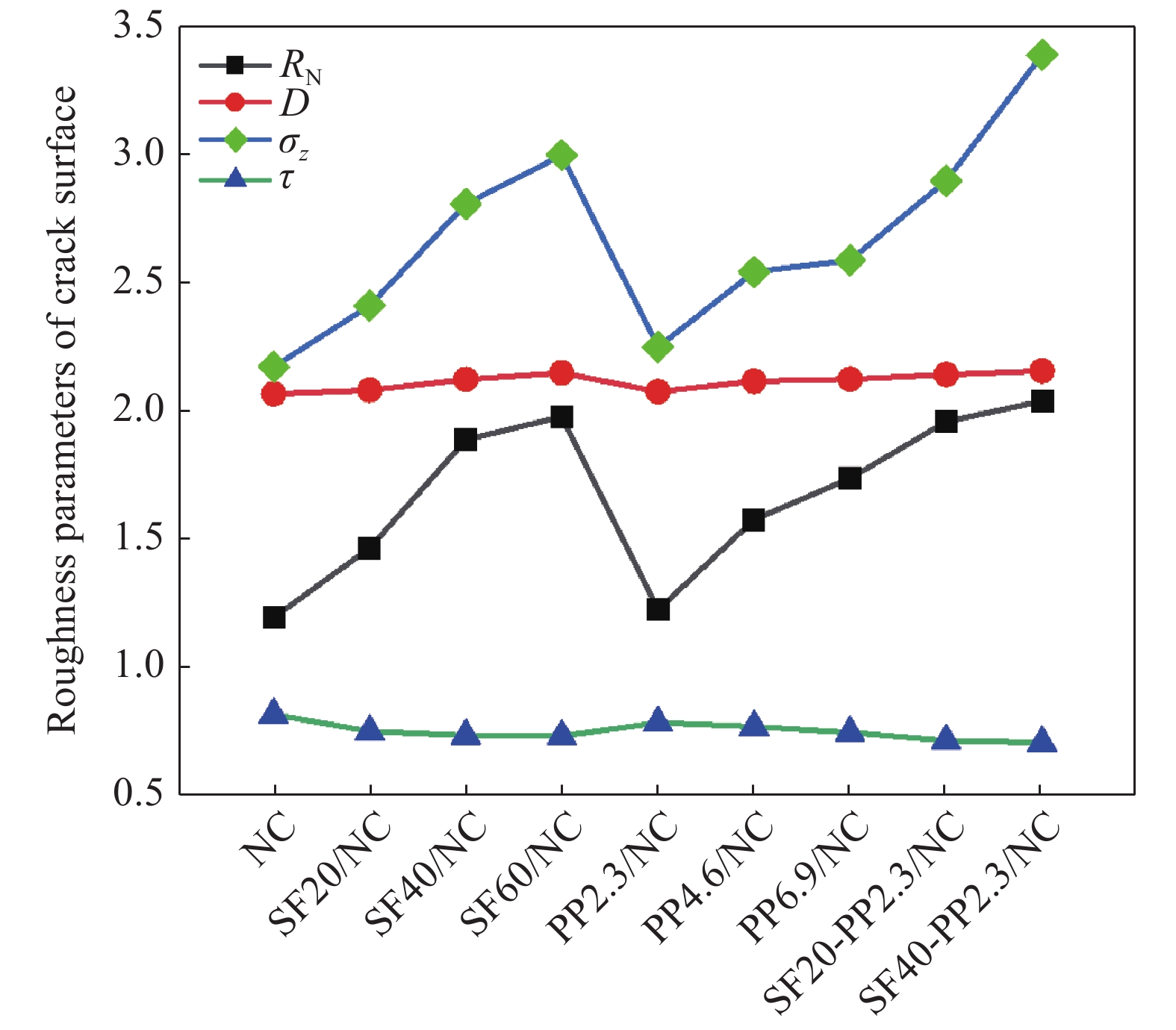
图 10 NC、SF/RC、PP/NC和SF-PP/NC试件裂缝表面的重构图Figure 10. Reconstruction views of cracked surface of NC, SF/RC, PP/NC and SF-PP/NC specimens为了量化不同组试件裂缝表面的粗糙程度，基于裂缝表面形貌信息得出四种粗糙程度参数，即裂缝粗糙度(RN)、分形维数(D)、z坐标正态分布标准差(σz)和裂缝曲折度(τ)，NC、SF/NC、PP/NC和SF-PP/NC试件粗糙程度参数的平均值如表5和图11所示。
表 5 NC、SF/NC、PP/NC和SF-PP/NC试件的裂缝表面粗糙程度参数Table 5. Roughness parameters of NC, SF/NC, PP/NC and SF-PP/NC specimensParameter NC SF20/NC SF40/NC SF60/NC PP2.3/NC PP4.6/NC PP6.9/NC SF20-PP2.3/NC SF40-PP2.3/NC RN 1.20
(Cv=2.5%)1.47
(Cv=4.8%)1.89
(Cv=2.0%)1.98
(Cv=3.3%)1.23
(Cv=5.9%)1.58
(Cv=3.2%)1.74
(Cv=2.3%)1.96
(Cv=0.9%)2.04
(Cv=1.6%)D 2.068
(Cv=3.5%)2.082
(Cv=1.9%)2.124
(Cv=5.0%)2.149
(Cv=4.0%)2.076
(Cv=2.0%)2.117
(Cv=1.7%)2.125
(Cv=2.3%)2.143
(Cv=2.9%)2.157
(Cv=5.1%)σz/mm 2.173
(Cv=3.4%)2.411
(Cv=3.0%)2.805
(Cv=1.9%)2.994
(Cv=2.8%)2.250
(Cv=2.2%)2.542
(Cv=1.0%)2.587
(Cv=5.5%)2.896
(Cv=3.5%)3.384
(Cv=2.5%)τ 0.824
(Cv=1.1%)0.758
(Cv=1.8%)0.742
(Cv=2.2%)0.740
(Cv=3.3%)0.792
(Cv=6.7%)0.777
(Cv=6.1%)0.754
(Cv=2.6%)0.722
(Cv=1.8%)0.715
(Cv=2.1%)Note: Cv—Coefficient of variation; RN—Roughness number; D—Fractal dimension; σz—Standard deviation of height distribution; τ—Crack tortuosity. ![]()
图 11 NC、SF/NC、PP/NC和SF-PP/NC试件的粗糙程度参数Figure 11. Roughness parameters of NC, SF/NC, PP/NC and SF-PP/NC specimens由表5可知，对于不同试件，裂缝粗糙度RN、分形维数D和z坐标正态分布标准差σz与裂缝表面粗糙程度呈正相关关系。而随着混凝土表面裂缝越曲折，裂缝曲折度τ越小。由图11可知，通过裂缝粗糙度RN、分形维数D、z坐标正态分布标准差σz和裂缝曲折度τ评价的NC、SF/NC、PP/NC和SF-PP/NC试件的裂缝粗糙程度展现出相似的排列顺序。
图12为混凝土裂缝表面粗糙程度参数与弯曲韧性参数的统计关系。可知，混凝土裂缝粗糙度RN与其弯曲韧性的相关系数R2分别为0.67 (RN-DfBZ,2)和0.74 (RN-DfBZ,3)，且高于其他参数与弯曲韧性的相关系数。说明相比于其他参数，裂缝粗糙度RN更适用于评估混凝土裂缝表面粗糙程度与其弯曲韧性的相关性。其原因可以归结为：(1)裂缝曲折度τ为裂缝表面粗糙程度在混凝土表面二维平面的显现形式，而裂缝曲折度的投影长度仅为90 mm，相比于针对混凝土裂缝表面的三维结构所计算的裂缝粗糙度RN，混凝土骨料大小、形状和纤维方向均会导致所计算的裂缝曲折度具有较大随机性；(2)对于裂缝表面分形维数D，由于该参数的基础值为2，试验中各组试件最大分形维数值仅为2.157，同时，混凝土试件具有较大的离散性，因此分形维数未能充分区分不同试件之间裂缝粗糙程度；(3)由于每组试件z坐标正态分布标准差σz和裂缝粗糙度RN均通过裂缝表面的形态信息统计获得，且对不同试件的裂缝表面区分程度较高，因此z坐标正态分布标准差σz和裂缝粗糙度RN均与混凝土梁弯曲韧性具有相对较高的相关系数R2，而裂缝粗糙度RN与混凝土梁弯曲韧性展现出更高的相关性。因此，本文使用裂缝粗糙度RN表征不同试件裂缝表面粗糙程度。
![]()
图 12 混凝土裂缝表面粗糙程度参数与弯曲韧性参数的统计关系Figure 12. Statistical relationship between roughness parameters and flexural toughness parameters of concrete2.3 FRC裂缝的粗糙度
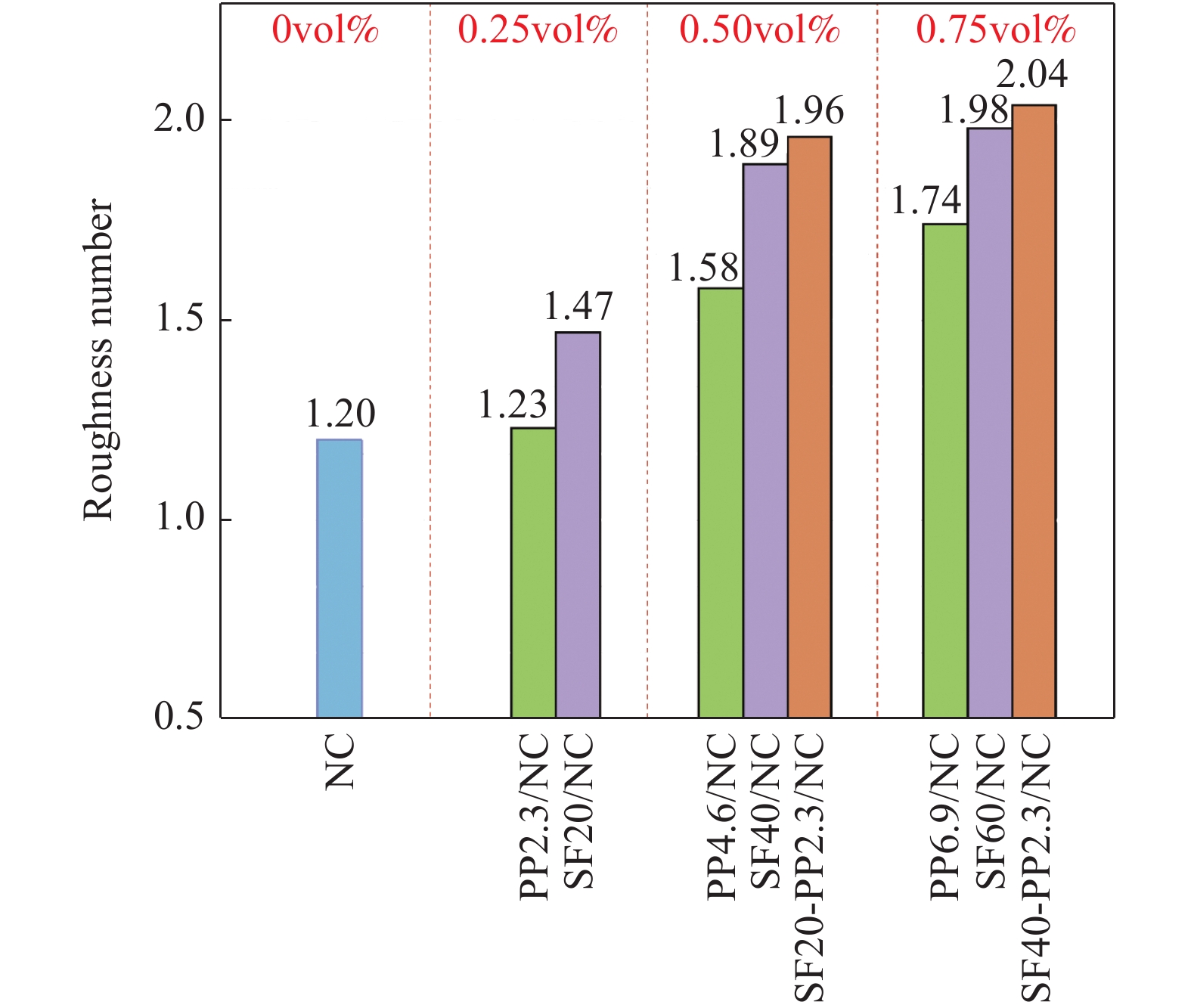
图13为NC、SF/NC、PP/NC和SF-PP/NC试件的裂缝粗糙度对比。可知，与NC相比，PP2.3/NC和SF20/NC试件裂缝粗糙度RN分别增加了2.5%和22.5%。与SF20/NC试件相比，SF40/NC和SF60/NC试件裂缝粗糙度RN分别增加了28.6%和34.7%。与PP2.3/NC试件相比，PP4.6/NC和PP6.9/NC试件裂缝粗糙度RN分别增加了28.5%和41.5%。与PP2.3/NC试件相比，SF20-PP2.3/NC和SF40-PP2.3/NC试件的裂缝粗糙度RN分别增加了59.3%和65.9%。
![]()
图 13 NC、SF/NC、PP/NC和SF-PP/NC试件的裂缝粗糙度RN对比Figure 13. Comparison of crack surface roughness number RN of NC, SF/NC, PP/NC and SF-PP/NC specimens此外，SF-PP/NC试件的裂缝粗糙度RN高于相同纤维体积掺量的SF/NC和PP/NC试件。即与SF40/NC和PP4.6/NC试件相比，SF20-PP2.3/NC试件的裂缝表面RN分别增加了3.7%和24.1%。与SF60/NC和PP6.9/NC试件相比，SF40-PP2.3/NC试件的裂缝粗糙度RN分别增加了3.0%和17.2%。
综上所述，纤维增加了混凝土裂缝表面粗糙程度，且随着纤维掺量的增加，混凝土裂缝表面的粗糙程度也随之提高。Armandei 等[24]研究发现，纤维会将混凝土中的骨料和净浆组成更加坚固的区域，该区域的强度比混凝土基体更高且尺寸比混凝土中的粗骨料更大。根据已有研究[3, 25] 可知，混凝土裂缝表面的粗糙程度与粗骨料粒径呈正相关关系。而纤维、骨料和净浆组成了尺寸更大、强度更高的“粗骨料”，可有效阻止裂缝穿过该区域，并使裂缝路径偏向强度较低的混凝土基体区域继续扩展，从而改变了裂缝的扩展方向，增加了裂缝表面的粗糙程度。
同时，当纤维体积掺量相同时，SF-PP/NC较单掺纤维的SF/NC和PP/NC具有更粗糙的裂缝表面。由此可推断，混杂纤维对增强混凝土裂缝表面粗糙程度展现出正混杂效应。
2.4 裂缝粗糙度RN与FRC梁弯曲韧性的关系
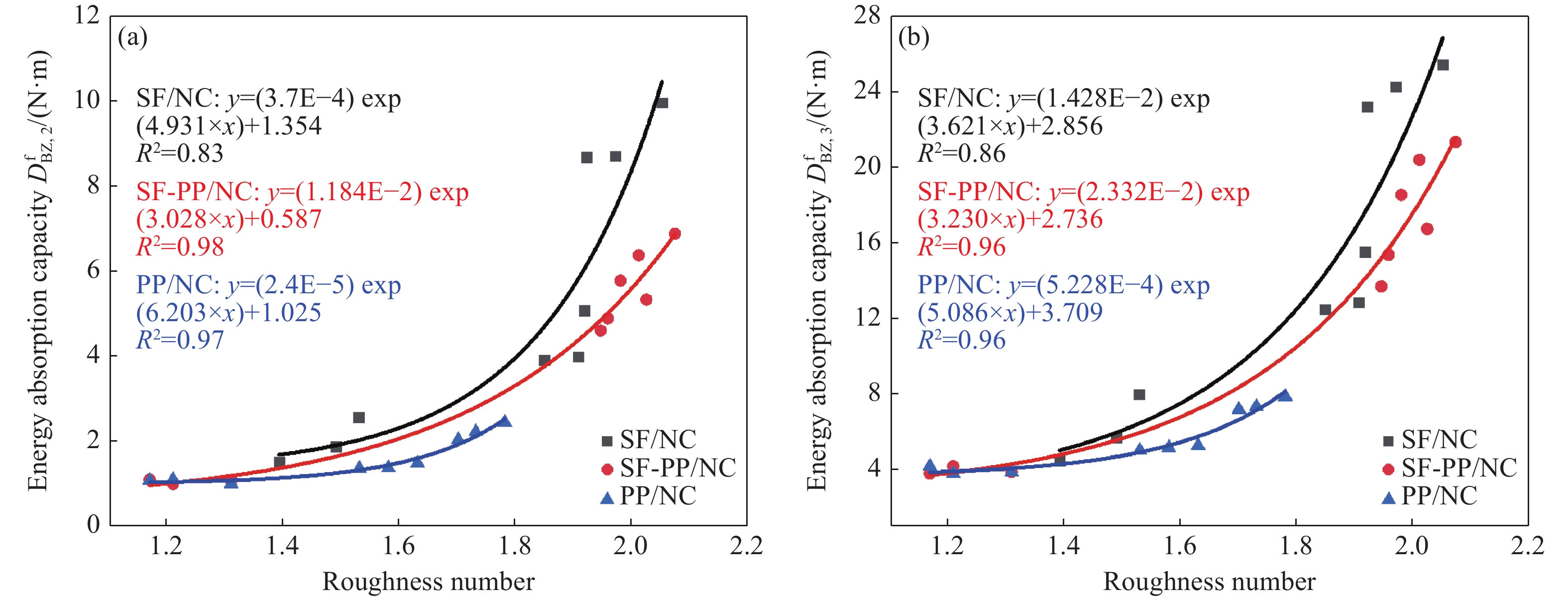
图14为SF/NC、PP/NC和SF-PP/NC试件裂缝表面粗糙程度与弯曲韧性参数关系曲线。其中，SF-PP/NC试件包括SF20-PP2.3/NC和SF40-PP2.3/NC，PP2.3/NC试件可作为对照组被用于表征SF-PP/NC试件裂缝表面形态与其弯曲韧性的关系。可知，FRC裂缝表面粗糙度参数RN与能量吸收能力(DfBZ,2和DfBZ,3)即弯曲韧性参数之间存在指数函数关系，如下式：
![]()
图 14 SF/NC、PP/NC和SF-PP/NC试件裂缝粗糙度与弯曲韧性的关系Figure 14. Relationship between cracked surface roughness and parameters of flexural toughness of SF/NC, PP/NC and SF-PP/NC specimensY=a⋅exp(b⋅X)+c (8) 式中：a、b和c为拟合参数；X为裂缝粗糙度RN值；Y为FRC梁能量吸收能力(DfBZ,2和DfBZ,3)值。
由图14还可以看到，随着粗糙度参数RN的增加，SF/NC、PP/NC和SF-PP/NC试件的弯曲韧性参数呈指数函数增长，且与Kurtis等[4]和Ding[26]的研究数据展示出相似的结果。说明本研究所得结果具有普遍适用性。原因可归结为：当纤维在混凝土基体中呈三维乱向分布时，随着纤维掺量的增加，裂缝表面的粗糙程度随之增大，即裂缝表面积变大，进而增加了桥接裂缝的纤维数量。由于桥接于裂缝的纤维数量由试件的纤维掺量和裂缝表面积决定，导致随纤维掺量的增加，桥接于裂缝表面纤维数量的增加率高于纤维掺量的增长率。进而导致随纤维掺量的增加，FRC梁弯曲韧性的增长率也显著增加(如表4所示)。然而通过试验可发现，裂缝表面粗糙程度的增长率随纤维掺量的增加而逐渐减小(如图13所示)。说明随着纤维掺量的增加，FRC梁的弯曲韧性较裂缝表面粗糙程度增长更快。因此，裂缝表面粗糙程度与弯曲韧性之间的关系呈指数函数关系。
基于不同FRC的裂缝表面粗糙度与弯曲韧性函数关系，可通过弯曲韧性试验快速且方便地评估出裂缝表面的粗糙程度。由于混凝土裂缝粗糙度与其耐久性能(渗透性能)之间存在密切的关系，未来的研究将专注于建立混凝土裂缝形态与开裂混凝土耐久性能之间的关系，从而为通过混凝土力学性能试验快速准确地评估开裂混凝土结构耐久性能的研究提供理论支持。
3. 结 论
(1)采用自行设计的激光扫描仪可有效获取混凝土裂缝表面形态信息，进而可计算出用于表征裂缝表面粗糙程度的参数，即裂缝粗糙度(RN)、分形维数(D)、z坐标正态分布标准差(σz)和裂缝曲折度(τ)。
(2)与分形维数D、z坐标正态分布标准差σz和裂缝曲折度τ相比，纤维增强混凝土(FRC)裂缝粗糙度RN与弯曲韧性参数的相关性最为显著。
(3)与结构型钢纤维和结构聚丙烯纤维相比，混杂纤维在提高混凝土弯曲韧性和增大混凝土裂缝表面粗糙程度方面均展现出正混杂效应。
(4) FRC裂缝表面粗糙度与其弯曲韧性参数展现出指数函数关系。基于该函数关系，可以通过FRC梁的弯曲试验快速估测裂缝表面的粗糙程度，并为FRC韧性与其耐久性能的相关性研究提供理论支持。
-
![]()
图 1 结构型钢纤维(SF)和结构型聚丙烯纤维(PP)的形状
Figure 1. Geometries of macro steel fiber(SF) and macro polypropylene fiber(PP)
![]()
图 2 混凝土开口梁弯曲试验
Figure 2. Flexural test of concrete notched beam
LVDT—Linear variable differential transformer
![]()
图 7 混凝土试件裂缝表面z坐标分布直方图
Figure 7. Distribution histogram of z coordinates from concrete cracked surface
![]()
图 9 普通混凝土(NC)、钢纤维增强混凝土(SF/NC)、聚丙烯纤维增强混凝土(PP/NC)和混杂纤维增强混凝土(SF-PP/NC)试件的荷载-挠度曲线
Figure 9. Load-deflection curves of normal concrete(NC), steel fiber reinforced concrete(SF/NC), polypropylene fiber reinforced concrete(PP/NC) and hybrid fiber reinforced concrete(SF-PP/NC) specimens
![]()
图 10 NC、SF/RC、PP/NC和SF-PP/NC试件裂缝表面的重构图
Figure 10. Reconstruction views of cracked surface of NC, SF/RC, PP/NC and SF-PP/NC specimens
![]()
图 11 NC、SF/NC、PP/NC和SF-PP/NC试件的粗糙程度参数
Figure 11. Roughness parameters of NC, SF/NC, PP/NC and SF-PP/NC specimens
![]()
图 12 混凝土裂缝表面粗糙程度参数与弯曲韧性参数的统计关系
Figure 12. Statistical relationship between roughness parameters and flexural toughness parameters of concrete
![]()
图 13 NC、SF/NC、PP/NC和SF-PP/NC试件的裂缝粗糙度RN对比
Figure 13. Comparison of crack surface roughness number RN of NC, SF/NC, PP/NC and SF-PP/NC specimens
![]()
图 14 SF/NC、PP/NC和SF-PP/NC试件裂缝粗糙度与弯曲韧性的关系
Figure 14. Relationship between cracked surface roughness and parameters of flexural toughness of SF/NC, PP/NC and SF-PP/NC specimens
表 1 混凝土基准配比
Table 1 Basic mix proportion of concrete
kg·m–3 Cement Fly ash Fine aggregate Coarse aggregate Water Superplasticizer 390 155 822 848 272.5 5.5 
下载: 导出CSV
表 2 纤维性能参数
Table 2 Properties of fibers
Type Shape of fiber Length/mm Diameter/mm Aspect ratio Tensile
strength/MPaElastic
modulus/GPaNumber/
(104 pieces·kg−1)Macro PP Straight 45 0.75 60 490 3.9 5.76 Macro SF Hooked-end 35 0.55 65 1 150 200.0 1.45
下载: 导出CSV
表 3 28天龄期混凝土试件抗压强度
Table 3 Compressive strength (28 d) of concrete specimens
Composite SF PP Compressive strength/MPa NC — — 37.3 SF20/NC 20 kg/m3 (0.25vol%) — 41.7 SF40/NC 40 kg/m3 (0.5vol%) — 35.4 SF60/NC 60 kg/m3 (0.75vol%) — 34.1 PP2.3/NC — 2.3 kg/m3 (0.25vol%) 36.5 PP4.6/NC — 4.6 kg/m3 (0.5vol%) 35.4 PP6.9/NC — 6.9 kg/m3 (0.75vol%) 37.5 SF20-PP2.3/NC 20 kg/m3 (0.25vol%) 2.3 kg/m3 (0.25vol%) 37.2 SF40-PP2.3/NC 40 kg/m3 (0.5vol%) 2.3 kg/m3 (0.25vol%) 38.5
下载: 导出CSV
表 4 NC、SF/NC、PP/NC和SF-PP/NC试件的比例极限荷载、极限荷载、能量吸收能力、等效抗弯强度和裂缝表面纤维根数
Table 4 Load at limit of proportionality, ultimate load, energy absorption capacity, equivalent flexural tensile strength and parameters of flexural toughness of NC, SF/NC, PP/NC and SF-PP/NC specimens
Fiber content/vol% Specimen FL/kN Fu/kN DfBZ,2/(N·m) feq,2/MPa DfBZ,3/(N·m) feq,3/MPa Nf 0 NC 10.0 10.0 0 0 0 0 0 0.25 SF20/NC 9.1 9.1 2.0 2.23 11.3 2.52 60.0 PP2.3/NC 9.7 9.7 1.1 1.20 7.4 1.65 50.7 0.50 SF40/NC 11.4 11.9 4.3 4.82 25.3 5.63 125.0 PP4.6/NC 9.8 9.8 1.4 1.53 9.7 2.16 108.0 SF20-PP2.3/NC 11.2 13.0 5.1 5.67 29.5 6.56 134.7 0.75 SF60/NC 12.4 18.4 9.1 10.12 45.1 10.03 199.3 PP6.9/NC 10.6 10.6 2.3 2.51 13.9 3.10 169.0 SF40-PP2.3/NC 12.3 15.7 6.2 6.89 36.2 8.04 194.3 Notes: FL—Maximum load in the interval of 0.05 mm; Fu—Ultimate load; DfBZ,2, DfBZ,3 —Energy absorption of the influence of fiber at the deflections of (δL+0.65 mm) and (δL+2.65 mm), respectively; feq,2, feq,3—Equivalent flexural tensile strengths by the deflections of (δL+0.65 mm) and (δL+2.65 mm), respectively; Nf—Number of fibers on the cracked surface.
下载: 导出CSV
表 5 NC、SF/NC、PP/NC和SF-PP/NC试件的裂缝表面粗糙程度参数
Table 5 Roughness parameters of NC, SF/NC, PP/NC and SF-PP/NC specimens
Parameter NC SF20/NC SF40/NC SF60/NC PP2.3/NC PP4.6/NC PP6.9/NC SF20-PP2.3/NC SF40-PP2.3/NC RN 1.20
(Cv=2.5%)1.47
(Cv=4.8%)1.89
(Cv=2.0%)1.98
(Cv=3.3%)1.23
(Cv=5.9%)1.58
(Cv=3.2%)1.74
(Cv=2.3%)1.96
(Cv=0.9%)2.04
(Cv=1.6%)D 2.068
(Cv=3.5%)2.082
(Cv=1.9%)2.124
(Cv=5.0%)2.149
(Cv=4.0%)2.076
(Cv=2.0%)2.117
(Cv=1.7%)2.125
(Cv=2.3%)2.143
(Cv=2.9%)2.157
(Cv=5.1%)σz/mm 2.173
(Cv=3.4%)2.411
(Cv=3.0%)2.805
(Cv=1.9%)2.994
(Cv=2.8%)2.250
(Cv=2.2%)2.542
(Cv=1.0%)2.587
(Cv=5.5%)2.896
(Cv=3.5%)3.384
(Cv=2.5%)τ 0.824
(Cv=1.1%)0.758
(Cv=1.8%)0.742
(Cv=2.2%)0.740
(Cv=3.3%)0.792
(Cv=6.7%)0.777
(Cv=6.1%)0.754
(Cv=2.6%)0.722
(Cv=1.8%)0.715
(Cv=2.1%)Note: Cv—Coefficient of variation; RN—Roughness number; D—Fractal dimension; σz—Standard deviation of height distribution; τ—Crack tortuosity.
下载: 导出CSV
-
[1] DING Y, LI D, ZHANG Y. Quantitative analysis of macro steel fiber influence on crack geometry and water permeability of concrete[J]. Composite Structures,2018,187:325-335. DOI: 10.1016/j.compstruct.2017.12.074
[2] RASTIELLO G, BOULAY C, PONT S D, et al. Real-time water permeability evolution of a localized crack in concrete under loading[J]. Cement and Concrete Research,2014,56:20-28. DOI: 10.1016/j.cemconres.2013.09.010
[3] ISSA M A, ISSA M A, ISLAM M S, et al. Fractal dimension: A measure of fracture roughness and toughness of concrete[J]. Engineering Fracture Mechanics,2003,70(1):125-137. DOI: 10.1016/S0013-7944(02)00019-X
[4] KURTIS K E, EL-ASHKAR N H, COLLINS C L, et al. Examining cement-based materials by laser scanning confocal microscopy[J]. Cement <italic>&</italic> Concrete Composites,2003,25(7):695-701.
[5] FICKER T, MARTIŠEK D, JENNINGS H M. Roughness of fracture surfaces and compressive strength of hydrated cement pastes[J]. Cement and Concrete Research,2010,40(6):947-955. DOI: 10.1016/j.cemconres.2010.02.002
[6] ERDEM S, BLANKSON M A. Fractal-fracture analysis and characterization of impact-fractured surfaces in different types of concrete using digital image analysis and 3D nanomap laser profilometery[J]. Construction and Building Materials,2013,40:70-76. DOI: 10.1016/j.conbuildmat.2012.11.013
[7] CAI W, CEN G, WANG H. Fracture surface fractal characteristics of alkali-slag concrete under freeze-thaw cycles[J]. Advances in Materials Science and Engineering,2017,2017:1689893.
[8] 丁一宁, 郝晓卫, 门旭. 纤维对混凝土裂缝宽度、曲折度及渗透性的影响[J]. 复合材料学报, 2019, 36(2):491-497. DING Yining, HAO Xiaowei, MEN Xu. Effect of fiber on the crack width, tortuosity and permeability of concrete[J]. Acta Materiae Compositae Sinica,2019,36(2):491-497(in Chinese).
[9] 邓宗才. 混杂纤维增强超高性能混凝土弯曲韧性与评价方法[J]. 复合材料学报, 2016, 33(6):1274-1280. DENG Zongcai. Flexural toughness and characterization method of hybrid fibers reinforced ultra-high performance concrete[J]. Acta Materiae Compositae Sinica,2016,33(6):1274-1280(in Chinese).
[10] RILEM Technical Committees. Test and design methods for steel fiber reinforced concrete: Bending test: Rilem TC 162-TDF[J]. Materials and Structures,2002,35(9):579-582.
[11] ASTM International. Standard test method for flexural performance of fiber reinforced concrete (using beam with three-point loading): ASTM C1609—19a[S]. Weat Conshohocken: ASTM International, 2012.
[12] 中国工程建设标准化协会. 纤维混凝土试验方法标准: CECS 13∶2009[S]. 北京: 中国计划出版社, 2010. China Association for Engineering Construction Standardization. Standard test methods for fiber reinforced concrete: CECS 13∶2009[S]. Beijing: China Planning Press, 2010(in Chinese).
[13] Japan Concrete Institute. Method of test for fracture energy of concrete by use of notched beam: JCI-S-001-2003[S]. Tokyo: Japan Concrete Institute, 2003.
[14] XIN Y B, HSIA K J, LANGE D A. Quantitative characterization of the fracture surface of Si single crystals by confocal microscopy[J]. Journal of the American Ceramic Society,2010,78(12):3201-3208.
[15] APEDO K L, MONTGOMERY P, SERRES N, et al. Geometrical roughness analysis of cement paste surfaces using coherence scanning interferometry and confocal microscopy[J]. Materials Characterization,2016,118:212-224. DOI: 10.1016/j.matchar.2016.05.023
[16] LANGE D A, JENNINGS H M, SHAH S P. Relationship between fracture surface roughness and fracture behavior of cement paste and mortar[J]. Journal of the American Ceramic Society,1993,76(3):589-597. DOI: 10.1111/j.1151-2916.1993.tb03646.x
[17] ZHOU H W, XIE H. Direct estimation of the fractal dimensions of a fracture surface of Rock[J]. Surface Review <italic>&</italic> Letters,2008,10(5):751-762.
[18] AKHAVAN A, SHAFAATIAN S M H, RAJABIPOUR F. Quantifying the effects of crack width, tortuosity, and roughness on water permeability of cracked mortars[J]. Cement and Concrete Research,2012,42(2):313-320. DOI: 10.1016/j.cemconres.2011.10.002
[19] FICKER T, MARTIŠEK D. Roughness and fractality of fracture surfaces as indicators of mechanical quantities of porous solids[J]. Central European Journal of Physics,2011,9(6):1440-1445.
[20] CARPINTERI A. A fractal analysis of size effect on fatigue crack growth[J]. International Journal of Fatigue,2004,26(2):125-133. DOI: 10.1016/S0142-1123(03)00142-7
[21] LIMANDRI S, GALVÁN JOSA V, VALENTINUZZI M C, et al. 3D scanning electron microscopy applied to surface characterization of fluorosed dental enamel[J]. Micron,2016,84:54-60. DOI: 10.1016/j.micron.2016.02.001
[22] BEAR J. Dynamics of fluids in porous media[M]. New York: American Elsevier Publishing Company, Inc., 1972.
[23] DING Y, AZEVEDO C, AGUIAR J B, et al. Study on residual behaviour and flexural toughness of fibre cocktail reinforced self compacting high performance concrete after exposure to high temperature[J]. Construction and Building Materials,2011,26(1):21-31.
[24] ARMANDEI M, FILHO E D S S. Correlation between fracture roughness and material strength parameters in SFRCs using 2D image analysis[J]. Construction and Building Materials,2017,140:82-90. DOI: 10.1016/j.conbuildmat.2017.02.103
[25] YAN A, WU K R, ZHANG D, et al. Effect of fracture path on the fracture energy of high-strength concrete[J]. Cement and Concrete Research,2001,31(11):1601-1606. DOI: 10.1016/S0008-8846(01)00610-X
[26] DING Y. Investigations into the relationship between deflection and crack mouth opening displacement of SFRC beam[J]. Construction and Building Materials,2011,25(5):2432-2440. DOI: 10.1016/j.conbuildmat.2010.11.055
-
期刊类型引用(3)
1. 栗罡，巴林，陈明，董伟. 基于数字图像相关法的钢纤维混凝土断裂性能研究. 水利与建筑工程学报. 2024(01): 25-30 . 
百度学术
2. 陈聪聪，吴泽媚，胡翔，史才军. 钢纤维形状和养护制度对超高性能混凝土强度及韧性的影响. 材料导报. 2024(15): 139-149 . 百度学术
3. 孙文昊，梁钰涛，谢俊，陈俊伟. 不同结构型纤维对混凝土弯曲性能的混杂效应. 混凝土. 2023(08): 14-17+22 . 百度学术
其他类型引用(5)
-
计量
- 文章访问数: 1151
- HTML全文浏览量: 306
- PDF下载量: 39
- 被引次数: 8
