Impact resistance of composite panels under in-plane preloading
-
摘要: 考虑面内初始载荷作用，开展复合材料层合板高速冲击响应与损伤特性研究。设计一种面内拉伸/压缩/剪切初始载荷施加装置，结合气炮试验装置，提出一种初始载荷复合材料高速冲击试验方法，针对X850/IM+和M21C/IMA两种牌号复合材料层合板开展高速冲击试验。结果表明：面内初始载荷对复合材料层合板高速冲击响应和损伤特性有显著影响；相比无初始载荷冲击情况，面内拉伸载荷作用提高了结构抗弯刚度，使冲击剩余速度提高，穿透速度降低，分层损伤面积减小；而面内压缩载荷则反之。Abstract: Taking the effect of the in-plane preloading into consideration, the impact behavior of composite panels was studied. A kind of in-plane loading device was designed to apply tension, compression and shear loads. The high-speed impact test method of preloaded composite structures was proposed with the gas gun and the in-plane loading device. Then high-speed impact tests for X850/IM+ and M21C/IMA composite panels were conducted. The test results show that the in-plane preload has a significant influence on the impact response. Compared with the non-preloaded impact process, the in-plane pre-tension raises the structural bending stiffness and the residual speed, resulting in a decrease of the penetration velocity and delamination area, while the effect of the in-plane pre-compression is opposite.
-
在住宅建筑中，通过外墙的传热量约占围护结构总传热量的60%，围护结构损失的热量占建筑总能耗的80%[1]，提升外墙的保温隔热能力是实现建筑节能的重要路径。而预制夹心墙体具有良好的力学与热工性能，有效提高了建筑节能效率，并可以实现保温层与主体结构同寿命，目前已广泛用作装配式建筑的外墙[2-3]。保温连接件是使预制夹心墙体内、外叶板与保温夹层共同工作的重要传力构件，由于外部荷载的不确定性，保温连接件应具有良好的剪切与轴向受力性能以保证墙体的安全[4-5]。此外，随着超低能耗建筑的推广，预制夹心墙体的保温层厚度可能会超过150 mm[6]，这对保温连接件的力学性能提出了更高的要求。
根据保温连接件主体原材料的不同可分为金属连接件与非金属连接件。金属连接件力学性能良好，但由于其导热系数大，易使墙体中产生大量“冷热桥”[7]，而用于超低能耗建筑的预制夹心墙体应避免“冷热桥”的出现，因此导热系数较低的非金属连接件具有技术优势，但非金属连接件的抗剪强度通常较弱，需通过合理的截面设计以满足其力学性能要求[8]。用于制作保温连接件的非金属材料有玄武岩纤维增强复合材料(Basalt Fiber Reinforced Plastic，BFRP)、碳纤维增强复合材料(Carbon Fiber Reinforced Polymer，CFRP)与玻璃纤维增强复合材料(Glass Fiber Reinforced Polymer，GFRP)等，其中关于GFRP保温连接件的研究与应用最为广泛[9]。截面形式对保温连接件的受力性能具有重要影响，仅能抵抗单向剪力作用的保温连接件被称为单向受力连接件，可以抵抗双向正交剪切作用的保温连接件被称为双向受力连接件，值得注意的是单向受力连接件连接件可有效抵抗面内剪切作用，但在面外抗剪能力较差，而双向受力连接件在面内、面外具有相似的抗剪性能[10]，具有巨大的研发潜力。现有GFRP保温连接件大多为单向受力连接件，其截面类型为实心棒式、针式、板式、波纹式、网格式等[11-14]，仅有Huang[15]提出的GFRP六角形管式保温连接件可作为非金属双向受力连接件。
目前，国内外学者针对GFRP保温连接件的力学性能开展了大量研究。杨佳林[16]研究了用于70 mm厚保温夹层的板式GFRP连接件的剪切与拔出性能，结果表明该连接件的抗剪承载力为15.3 kN，抗拔承载力为11.2 kN，满足工程设计需求。赵朝亮[17] 开展了3个用于50 mm厚GFRP针式连接件双剪试件推出试验，试验结果表明GFRP针式连接件最终在锚固端薄弱处发生了剪断破坏。郝锦涛[18]对用于保温层厚度为200 mm的GFRP棒式连接件与板式连接件的抗剪性能进行了对比分析，并基于结构力学与材料力学方法提出了GFRP连接件抗剪承载力计算公式。何之舟[19] 研究了保温层厚度为150 mm的工字型截面GFRP连接件的轴向受力性能，结果表明其轴拉与轴压承载力分别为25.6 kN和36.8 kN。此外，也有学者对保温板与内、外叶板之间的界面性能进行了研究。李雨珊[20]通过推出试验研究了ECC面层与不同厚度EPS保温板(50 mm、70 mm、100 mm)之间的界面粘结性能，并结合Teixeira的分析理论推导了理论承载力。
总结上述研究可以发现，目前研究大多集中在用于较薄保温层的GFRP保温连接件，而关于GFRP超长保温连接件力学性能的研究与应用十分匮乏；双向受力连接件力学性能好且具有降低设计难度和施工成本的优势，但现有可供选择的双向受力连接件种类十分匮乏；超厚EPS保温板与保温连接件在剪切作用下的协同工作机制与承载力贡献仍需进一步研究。与此同时，预制夹心墙体在生产、运输与施工阶段需要水平贮存，在夹心墙体使用阶段需考虑风荷载、面外地震荷载等面外荷载的作用，因此亟需对GFRP超长保温连接件(GFRP UT连接件)的轴向受力性能开展研究。
基于上述问题，本文提出一种以环氧树脂基GFRP圆管型材为主体，端部设置双层双向锚固钢筋的新型GFRP UT连接件，其具有以下几点技术优势：
(1) GFRP UT连接件主体为GFRP圆管，在横截面上两个方向(竖向与水平)具有相同惯性矩，可抵抗双向面内剪切作用，在夹心墙中布置连接件时无需考虑其设置方向，可简化保温连接件体系的设计；与相同面积的实心棒状截面相比，圆管具有更好的抗弯剪能力，提高了连接件主体材料的利用效率。
(2)现有连接件大多通过改变连接件端部构造形式以实现其与内外叶板的锚固，但会使制作连接件的模具更加复杂，而GFRP UT连接件端部采用锚固钢筋，因此其构造简单、连接可靠且便于施工人员定位与安装。
(3) GFRP UT连接件主体采用环氧树脂基GFRP拉挤型材，其强度高、导热系数低且易于工厂批量化生产，可用于具有超厚保温层(150 mm)的夹心墙体，而现有保温连接件在此条件下大多难以保证安全工作；同时，其良好的力学性能也可以减少夹心墙体中布置该连接件的数量，进一步降低了人工与材料成本。
为研究GFRP UT连接件的力学性能，本文开展了GFRP UT连接件的推出试验与轴压试验，研究其剪切与轴向受力性能及破坏模式，结合有限元分析深入探究试件的损伤作用机制，并建立了GFRP UT连接件的抗剪与轴压承载力计算公式，该计算方法可为其在超低能耗夹心墙体中的设计与布置提供理论依据，并对其工程应用提供技术支撑。
1. 推出试验
1.1 试件设计
推出试验研究的参数包括混凝土强度(C35、C40)与保温层构造(去除、保留EPS保温板)，参数设置与试件编号如表1所示。剪切试件分为3组，为消除随机误差，每组2个相同试件，共6个剪切试件；根据试件类型、混凝土强度与保温层构造的顺序对试件进行命名。例如SC-C35-EPS表示保留EPS保温板的混凝土强度等级为C35的剪切试件。GFRP UT连接件由环氧树脂基GFRP圆管与锚固钢筋组成，具体尺寸见图1。每个剪切试件由4个GFRP UT连接件、3块钢筋混凝土板与2块EPS保温板组成，其中外侧2块钢筋混凝土板模拟夹心墙体的外叶板，中间1块钢筋混凝土板模拟夹心墙体的内叶板，GFRP连接件居中对称布置，剪切试件的具体尺寸与配筋如图2所示。除SC-C35-EPS组外，其余的剪切试件在试验开始前去除了EPS保温板。
表 1 GFRP UT连接件剪切试件参数Table 1. Parameters of shear specimen of GFRP UT connectorsSpecimen Concrete Insulation Number SC-C35 C35 None 2 SC-C40 C40 None 2 SC-C35-EPS C35 EPS 2 Notes: SC is shear specimen for circular tube connectors; C35 and C40 are the concrete strength of shear specimens; EPS is EPS insulation board. ![]()
图 1 GFRP UT连接件详细尺寸(单位：mm)Figure 1. Detailed dimensions of GFRP UT connectors (Unit: mm)本次试验的全部试件由陕西中天建筑工业有限公司生产，在试验开始前对各组成材料进行材性测试，其中C35混凝土实测立方体抗压强度为36.46 MPa，C40混凝土实测立方体抗压强度为41.98 MPa；钢筋屈服强度为511.61 MPa，极限强度为630.43 MPa；环氧树脂基GFRP圆管由南通时瑞塑胶制品有限公司通过拉挤工艺生产，其依据规范GB/T
1447 -2005[21]、GB/T1448 -2005[22]、GB/T3355 -2014[23]测试其力学性能，测试结果如表2所示。表 2 GFRP材性测试结果Table 2. GFRP material property test resultsMaterial property Value Test method Longitudinal tensile strength 1228.19 MPaGB/T 1447-2005[21] Transverse tensile strength 63.56 MPa Longitudinal modulus of elasticity 54.98 GPa Transverse modulus of elasticity 16.14 GPa Longitudinal compressive strength 367.18 MPa GB/T 1448-2005[22] Transverse compressive strength 145.86 MPa Shear strength 53.91 Mpa GB/T 3355-2014[23] Shear modulus of elasticity 6.07 GPa 1.2 试验加载
推出试验采用WAW-1000液压伺服万能试验机(上海华龙测试仪器有限公司)作为加载设备，在内叶板顶部与外叶板底部分别放置厚钢板以使剪切试件受力均匀，如图3所示。试验采用单调加载方式，加载速度控制为0.5 mm/min，匀速加载直至承载力降低为峰值荷载的85%。
在内叶板与外叶板底部分别设置一个竖向位移计以测量内、外叶板在加载过程中的相对位移。此外，为研究加载过程中保温材料与内、外叶板混凝土间的界面粘结性能与保温材料损伤机制，采用数字图像(DIC)技术对试件SC-C35-EPS的变形情况进行监测，如图3(a)所示。
1.3 试验结果与分析
1.3.1 受力过程与破坏形态
GFRP UT连接件剪切试件的屈服荷载($ P{\text{y = }} 0.6 P{\text{u}} $)、屈服滑移($ \Delta {\text{y}} $)、峰值荷载($ P{\text{u}} $)与峰值滑移($ \Delta {\text{u}} $)如表1所示。
剪切试件的最终破坏形态如图4所示，通过对试验过程中剪切试件的裂缝发展状况与破坏形态进行分析可以发现，加载前期试件无明显现象发生，此时剪切试件处于弹性工作状态；随着位移的持续增加，混凝土外叶板外侧逐渐出现横向水平细微裂缝，在荷载作用下持续延展且裂缝数量在不断增加；在加载后期，与GFRP UT连接件根部相连的内、外叶板锚固区混凝土出现明显损伤，部分混凝土发生脱落，而GFRP UT连接件仅在根部出现了轻微损伤。图5为试件的DIC分析结果，通过对比不同受力阶段试件SC-C35-EPS中EPS保温板的损伤程度，可知EPS保温板与混凝土内、外叶板界面粘结良好，未出现脱粘现象，而EPS保温板最终出现了斜向45°撕裂，说明EPS保温板通过摩擦作用参与了受力并最终出现了剪切破坏。通过对比表3中的SC-C35-EPS组与SC-C35组的平均峰值承载力亦可知EPS保温板对GFRP UT连接件的抗剪性能具有显著贡献。此外，由图4(b)可知，EPS保温层未改变GFRP UT连接件剪切试件的破坏模式。
表 3 GFRP UT连接件剪切试验结果Table 3. Shear test results of GFRP UT connectorsSpecimen Yield load
$ P{\text{y}} $/kNYield slip
$ \Delta {\text{y}} $/mmPeak load
$ P{\text{u}} $/kNPeak slip
$ \Delta {\text{u}} $/mmSC-C35-1 50.29 2.98 83.81 8.14 SC-C35-2 50.54 2.66 84.23 6.68 Average value 50.42 2.82 84.02 7.41 SC-C40-1 52.60 3.11 87.70 8.35 SC-C40-2 52.13 2.98 86.88 6.21 Average value 52.37 3.05 87.29 7.28 SC-C35-EPS-1 67.04 3.26 111.73 7.71 SC-C35-EPS-2 63.66 2.96 106.10 7.36 Average value 65.35 3.11 108.92 7.54 1.3.2 荷载-滑移曲线
剪切试件的荷载-滑移曲线如图6所示，曲线由三阶段组成，分别为弹性阶段($ P < 0.6 P{\text{u}} $)、弹塑性阶段($ 0.6 P{\text{u}} < P < P{\text{u}} $)和下降阶段。在弹性阶段，GFRP UT连接件与混凝土间的滑移变形很小，荷载-滑移曲线近似为直线；在弹塑性阶段，滑移量逐渐增加，内、外叶板混凝土逐渐出现损伤，试件的刚度不断退化；在下降阶段，所有剪切试件均表现出了缓慢下降的趋势，呈现出延性破坏的特征。
此外，根据图6与表3可以知，所有试件中SC-C35组的峰值承载力最低，SC-C40组的峰值承载力为SC-C35组的1.04倍，SC-C35-EPS组的峰值承载力为SC-C35组的1.30倍，表明提高混凝土强度与填充EPS保温板均可提升GFRP UT连接件剪切试件的承载能力。
1.3.3 刚度与延性
为了对比不同试件的刚度与延性，定义荷载-滑移曲线上升段中0.6倍峰值荷载处为屈服点，取该点的荷载与位移比值作为试件的刚度：
$$ K = \frac{{P{\text{y}}}}{{\Delta {\text{y}}}} $$ (1) 式中：$ K $表示刚度(kN/mm)；$ P{\text{y}} $表示屈服荷载值(kN)，等于$ 0.6 P{\text{u}} $；$ \Delta {\text{y}} $表示屈服荷载对应滑移量(mm)。
图7(a)为剪切试件的刚度与平均刚度对比，SC-C35组与SC-C40组试件的刚度较为接近，说明混凝土强度对剪切试件刚度影响较小；而SC-C35-EPS组试件的平均刚度较SC-C35组提升了17.22%，说明加载前期EPS保温板与GFRP UT连接件共同参与了剪切试件的受力，EPS保温板对剪切试件的刚度具有一定贡献。
![]()
图 7 剪切试件刚度与延性系数对比Figure 7. Comparison of shear specimen stiffness and ductility coefficient此外，采用延性系数表示试件的延性，其数值越大表示试件的延性越好：
$$ \mu = \frac{{\Delta {{u}}}}{{\Delta {{y}}}} $$ (2) 式中：$ \mu $表示延性系数；$ \Delta {{u}} $表示峰值荷载对应的滑移量(mm)；$ \Delta {{y}} $表示屈服荷载对应滑移量(mm)。
图7(b)为剪切试件的延性系数与平均延性系数对比图，可以发现SC-C40组和SC-C35-EPS组的延性系数均较SC-C35有所提升，其中SC-C40组提高了13.16%，SC-C35-EPS组提高了7.89%。
1.3.4 损伤演变
试件的损伤随着加载过程的进行而不断发展，参考连续损伤力学理论，通过定义损伤场变量描述试件的损伤演变情况[24]：
$$ D = 1 - \frac{{{S^*}}}{{S_0}} $$ (3) 式中：$ D $表示相对于界面外法线$ n $方向的局部损伤变量；$ S_0 $与$ {S^*} $分别表示界面外法线$ n $方向在损伤前后的面积。
由于$ \sigma \cdot S_0 = {\sigma ^*} \cdot {S^*} $，根据等效应变假设：
$$ D = 1 - \frac{{{E^*}}}{{E_0}} $$ (4) 式中：$ E_0 $为界面未损伤状态下界面的弹性刚度，本文取为荷载-滑移曲线上升段0.6倍峰值荷载处的割线斜率；$ {E^*} $为界面损伤后的割线刚度。
图8为各组剪切试件的损伤演变过程，加载初期为第1阶段，试件损伤非常小，损伤场变量$ D $近似为0；随着混凝土逐渐出现损伤和EPS保温板开裂，损伤进入第2阶段，在该阶段中损伤场变量$ D $在0~0.7范围内快速增长；随后损伤进入第3阶段，该阶段损伤场变量$ D $由0.7逐渐增加至0.9左右并不再增加，损伤变化过程趋于平缓，表明此时试件已经破坏。由图8可知，EPS保温板延缓了剪切试件的损伤发展，但提高混凝土强度对剪切试件抵抗损伤能力的影响较小。
2. 轴压试验
2.1 试件设计
受压试件参数为混凝土强度(C35、C40)，试件编号如表4所示，为消除随机误差影响，每组2个相同试件，根据试件类型与混凝土强度对试件进行命名，例如CC-C35表示混凝土强度等级为C35的轴压试件。
表 4 GFRP超长双向受力保温连接件受压试件参数Table 4. Parameters of compression specimen of GFRP extra-long bi-directional thermal insulation connectorsSpecimen Concrete strength grade Insulation layer Number CC-C35 C35 None 2 CC-C40 C40 None 2 Notes: CC is compression specimen for circular tube connectors; C35 and C40 are the concrete strength of compression specimens. 受压试件的具体尺寸如图9所示，每个受压试件由1个居中且垂直的GFRP UT连接件和2块钢筋混凝土板组成。在轴压试验过程中，GFRP UT连接件与EPS保温板同时承受轴向压力，试件的受压性能为二者受压性能的直接叠加，且EPS保温板的抗压强度仅为76.1 kPa，对试件受压性能的贡献很小，为更好的观测加载过程中GFRP UT连接件的受力状态，在加载前去除受压试件中的EPS保温材料。
2.2 加载装置与量测方案
轴压试验加载设备也采用WAW-1000液压伺服万能试验机(上海华龙测试仪器有限公司)，如图10所示，试验采用单调加载方式，加载速度控制为0.5 mm/min，当试件承载力下降为峰值荷载的85%时停止试验。为给GFRP UT连接件的轴向移动提供空间，同时避免加载平台限制钢筋混凝土板的变形与破坏，在受压试件顶部与底部分别放置一块环形钢板，如图11所示。此外，在上下两块钢筋混凝土板侧分别设置一个竖向位移计以测量拉结件轴向相对位移，布置方式见图10。
2.3 试验结果与分析
2.3.1 受力过程与破坏形态
GFRP UT连接件受压试件的屈服荷载($ P_{\text{y = }}0.6 P_{\text{u}} $)、屈服滑移($ \Delta {\text{y}} $)、峰值荷载($ P_{\text{u}} $)与峰值滑移($ \Delta _{\text{u}} $)如表5所示。
表 5 GFRP UT连接件受压试验结果Table 5. Compression test results of GFRP UT connectorsSpecimen Yield load
$ P{\text{y}} $/kNYield slip
$ \Delta {\text{y}} $/mmPeak load
$ P{\text{u}} $/kNPeak slip
$ \Delta {\text{u}} $/mmCC-C35-1 15.04 1.82 25.06 5.04 CC-C35-2 14.80 1.82 24.67 5.39 Average value 14.92 1.82 24.87 5.22 CC-C40-1 17.22 2.03 28.70 5.35 CC-C40-2 15.70 1.84 26.17 4.78 Average value 16.46 1.94 27.44 5.07 受压试件的最终破坏形态如图12所示，所有试件均表现出明显的冲切破坏特征。加载前期试件无明显损伤，可认为其处于弹性阶段；由于试件顶部与底部垫有回形钢板，与之相连的钢筋混凝土板会受到弯矩作用，加载至0.6倍峰值荷载左右时，混凝土板侧面边缘出现沿板厚方向的纵向裂缝，如图12(a)所示；随着荷载持续增加，纵向裂缝裂缝不断扩展，钢筋混凝土板内侧出现明显弯曲变形， 但未观察到有明显损伤。试验过程中无法观察到钢筋混凝土板外侧的损伤状态，因此只能在试验结束后将试件从加载设备中取出观察钢筋混凝土板外侧(试件顶面、底面)的裂缝，可以发现其具有内外两圈环状贯通混凝土裂缝，两圈裂缝之间还具有散射状裂缝，如图12(b)所示。其中内圈混凝土裂缝近似圆形，分析其是由GFRP UT连接件端部冲切混凝土形成的，而外圈混凝土裂缝近似方形，分析其是由双层双向布置的锚固筋在压力作用下对混凝土造成的冲切破坏。在加载全过程中， GFRP UT连接件保持完好，未见明显损伤，说明受压试件的峰值荷载由混凝土冲切破坏控制。
2.3.2 荷载-滑移曲线
受压试件的荷载-滑移曲线如图13所示。前期曲线基本呈线性增长，即处于弹性阶段；当荷载-滑移曲线到达峰值荷载的0.6倍处左右时，曲线斜率开始下降，这是由于混凝土侧面出现了裂缝；随后荷载继续增加，直至达到峰值荷载；加载末期，由于试件中混凝土冲切破坏面不断延展贯通，试件的承载力持续下降。结合图13与表5可知，CC-C40组的平均承载力比CC-C35组的提高了10.33%，表明提高混凝土强度可显著提升GFRP UT连接件受压试件的承载能力。
2.3.3 刚度与延性
受压试件的刚度与延性对比如图14所示，刚度与延性系数的计算方法与剪切试件相同，通过对比可知CC-C40组试件比CC-C35组的刚度提高了3.78%，而延性系数降低了8.71%，表明提高混凝土强度有助于提升试件的刚度表现，但同时会引起试件延性的降低。
![]()
图 14 受压试件刚度与延性系数对比Figure 14. Comparison of compression specimen stiffness and ductility coefficient2.3.4 损伤演变
图15为受压试件的损伤演变过程，第1阶段的损伤非常小，损伤场变量$ D $约为0；与剪切试件损伤演变过程不同的是当损伤进入第2阶段后，$ D $值从0~0.8范围内几乎呈直线增长，说明在该阶段中钢筋混凝土板内的损伤不断累积，并逐渐形成了冲切破坏面；当损伤第3阶段，即$ D $值大于0.8时损伤趋于变缓，但最终$ D $值未超过0.9，这是由于受压试件的冲切破坏面一旦形成，试件将立刻失效，为脆性破坏。对比CC-C35组与CC-C40组试件的损伤演化过程，可以发现提高混凝土强度可增强试件抵抗受压损伤的能力。
3. 有限元模型
为深入研究GFRP UT连接件剪切试件与受压试件的受力机制，并为建立其抗剪与抗压承载力计算方法提供支撑，通过ABAQUS软件分别建立了剪切试件与受压试件的有限元模型。
3.1 模型建立
有限元模型参考实际试件尺寸建立，其中剪切试件模型包括混凝土、分布钢筋、GFRP连接件(包含GFRP圆管与锚固钢筋)与保温层四部分，如图16(a)所示。混凝土、EPS保温板与回形钢板采用C3D8R实体单元，GFRP圆管采用S4R壳单元，分布钢筋与锚固钢筋采用C3D2线单元。GFRP圆管与锚固钢筋通过“合并”命令合并为一体，其锚固钢筋部分与分布钢筋均通过“嵌入区域”命令内置于内、外叶板混凝土中，GFRP圆管嵌入混凝土部分切向罚接触，摩擦系数设置为0.6，法向为硬接触。结合图5所示的DIC分析结果与图6(b)可知，保温层与混凝土界面粘结性能良好，EPS保温板通过摩擦作用参与了试件的剪切受力，因此将保温层与内外叶板混凝土间亦设置为切向罚接触，摩擦系数设为0.6。有限元模型的边界条件设置情况如下，对于剪切试件模型，在内叶板混凝土顶面耦合一参考点作为加载点，两侧外叶板底部设置为完全固定；对于受压试件模型，为使有限元模型的边界条件更符合试验加载的真实情况，在受压试件模型中建立了回形钢板，如图16(b)所示，在上部回形钢板顶面耦合一参考点作为加载点，并将上部回形钢板底面设置为完全固定。
![]()
图 16 GFRP UT连接件有限元数值模型Figure 16. Finite element numerical model of GFRP UT connectors3.2 材料本构
混凝土材料通过塑性损伤模型模拟其塑性行为，采用《混凝土结构设计规范》GB50010-2010[25]中的本构关系定义混凝土应力-应变曲线；保温材料定义为弹性材料；钢筋材料采用二折线本构定义其塑性行为；GFRP材料采用Hashin损伤模型定义其塑性行为。
3.3 模型验证
根据试验结果，剪切试件的最终状态为混凝土端部锚固区开裂，轴压试件的最终状态为混凝土冲切破坏，两类破坏均是由于混凝土受拉损伤引起的，因此可通过有限元模型中的混凝土受拉损伤指标(DAMAGET)判断试件的受力状态。DAMAGET用于表征混凝土受拉损伤程度，其数值范围为0~1，数值越大表明其损伤程度越大，当达到1时说明该区域混凝土已经完全破坏。图17与图18为剪切试件和受压试件的有限元模型云图与试验现象的对比，可以发现模型中指标数值较大的区域与试验过程中混凝土损伤严重的区域基本吻合；图19与图20为剪切试件和受压试件的试验与有限元模型的荷载滑移曲线对比，说明有限元模型可高精度复现试验结果。
![]()
图 17 剪切试件破坏模式有限元模型验证Figure 17. Verification of finite element model for shear specimen failure mode![]()
图 18 受压试件破坏模式有限元模型验证Figure 18. Verification of finite element model for compression specimen failure mode![]()
图 19 剪切试件试验与有限元模拟荷载-滑移曲线对比Figure 19. Comparison of load-slip curves between shear specimen test and FE simulation![]()
图 20 受压试件试验与有限元模拟荷载-滑移曲线对比Figure 20. Comparison of load-slip curves between compression specimen test and FE simulation3.4 参数化分析
为进一步探究GFRP UT连接件的抗剪与轴压性能，扩充分析参数对其力学性能的影响，有限元模型的荷载-滑移曲线见图21与图22，其峰值承载力统计于表6与表7。
![]()
图 22 受压试件有限元参数拓展分析Figure 22. Expansion analysis of FE parameters of compression specimen表 6 剪切试验与有限元模拟结果与计算值对比Table 6. Comparison of shear test and FE simulation results with calculated valuesSpecimen Test (FE)
value/kNTheoretical value/kN Test (FE) value/
Theoretical valueSC-C35-1 83.81 81.78 1.02 SC-C35-2 84.23 81.78 1.03 SC-C40-1 87.70 88.67 0.99 SC-C40-2 86.88 88.67 0.98 SC-C35-EPS-1 111.73 102.70 1.09 SC-C35-EPS-2 106.10 102.70 1.03 C25-150-W60 (FE) 72.85 66.57 1.09 C30-150-W60 (FE) 78.54 73.59 1.07 C35-150-W60 (FE) 83.78 80.10 1.05 C40-150-W60 (FE) 89.86 86.20 1.04 C45-150-W60 (FE) 94.27 91.97 1.03 C35-100-W60 (FE) 96.40 98.90 0.97 C35-125-W60 (FE) 90.08 88.75 1.01 C35-175-W60 (FE) 75.88 72.72 1.04 C35-200-W60 (FE) 67.76 66.41 1.02 C35-150-W65 (FE) 85.84 89.96 0.95 C35-150-W70 (FE) 87.48 87.64 1.00 C35-150-W75 (FE) 88.69 89.31 0.99 C35-150-W80 (FE) 90.60 90.99 1.00 表 7 受压试验结果与计算值对比Table 7. Comparison of compression test results and calculated valuesSpecimen Test (FE)
value/kNTheoretical
value/kNTest (FE) value/
Theoretical valueCC-C35-1 25.06 26.28 0.95 CC-C35-2 24.67 26.28 0.94 CC-C40-1 28.70 28.49 1.01 CC-C40-2 26.17 28.49 0.92 C25-W60 (FE) 22.39 21.39 1.05 C30-W60 (FE) 23.57 23.65 1.00 C35-W60 (FE) 24.63 25.74 0.96 C40-W60 (FE) 26.61 27.70 0.96 C45-W60 (FE) 28.15 29.55 0.95 C35-W65 (FE) 27.44 28.34 0.97 C35-W70 (FE) 30.83 31.37 0.98 C35-W75 (FE) 32.98 33.94 0.97 C35-W80 (FE) 34.69 35.94 0.97 对于剪切试件有限元模型扩充分析的参数为混凝土强度、保温层厚度与外叶板厚度，模型编号以混凝土强度、保温层厚度、外叶板厚度的顺序命名。结合受压试验与有限元模拟验证结果可以发现，受压试件的峰值荷载由混凝土冲切破坏面控制，而保温层厚度对轴压试件形成的混凝土冲切破坏面影响较小，因此对于受压试件有限元模型扩充分析的参数为混凝土强度、保温层厚度，模型编号以混凝土强度、保温层厚度、外叶板厚度的顺序命名。
对于GFRP UT连接件剪切试件，与混凝土强度等级为C25的剪切试件相比，混凝土强度等级为C30、C35、C40、C45的试件抗剪承载力分别提升了7.8%、15.0%、23.3%、29.4%；当保温层厚度由100 mm增大到200 mm时，试件抗剪承载力降低了29.7%，这是由于保温层厚度增大，连接件端部所承受的弯矩增大，端部锚固区混凝土更易发生损伤；当外叶板厚度由60 mm增加至80 mm，试件抗剪承载力提升了8.1%，说明外叶板厚度对试件抗剪承载力具有一定影响。
对于GFRP UT连接件受压试件，当混凝土强度等级从C25至C45时，轴压承载力提升了25.86%；与外叶板厚度为60 mm的受压试件相比，外叶板厚度65 mm、70 mm、75 mm、80 mm的受压试件承载力分别提升了11.4%、25.2%、33.9%、40.8%，可发现增大外叶板厚度可提升试件轴压承载力，而承载力增量逐渐减小，这是由于增大外叶板厚度会提升混凝土破坏面面积，但当其厚度较大时，破坏面面积不会持续增加。
4. 承载力计算
4.1 抗剪承载力
结合试验与有限元模型结果对剪切试件的受力机制进行分析，如图17与图23所示。剪切试件的抗剪承载力$ {F_{\text{V}}} $由GFRP UT连接件的抗剪承载力$ {F_{\text{G}}} $与EPS保温板的抗剪承载力$ {F_{\text{E}}} $组成，即
$$ {F_{\text{V}}} = {F_{\text{G}}} + {F_{\text{E}}} $$ (5) 在竖向荷载作用下，内叶板向下移动，将剪力与弯矩通过GFRP UT连接件传递至外叶板端部，随即引起锚固区混凝土的损伤，结合试验与有限元分析结果可知锚固区混凝土最终破坏，而连接件未见明显损伤，因此剪切试件的极限承载力由锚固区混凝土控制。该区域的混凝土为三维应力单元，但由于剪切试件未受到水平作用力，其平面外应力非常小，因此可对该区域混凝土的平面应力单元进行分析。文献[26]基于最大主拉应力准则建立了工字截面连接件的抗剪承载力计算方法：
$$ {F_{\text{G}}} = \frac{1}{{\left( {\dfrac{{k_1}}{{2{f_{\text{t}}}}}L + \sqrt {{{\left( {\dfrac{{k_1}}{{2{f_{\text{t}}}}}} \right)}^2}{L^2} + {{\left( {\dfrac{{k_2}}{{{f_{\text{t}}}}}} \right)}^2}} } \right)}} $$ (6) 式中：$ k_1 $为弯矩影响系数；$ k_2 $为剪力影响系数；$ {f_{\text{t}}} $为混凝土抗拉强度(MPa)；$ L $为保温层厚度(mm)。
由于GFRP UT连接件剪切试件的受力机制和破坏模式与之相似，可参考上述方法建立GFRP UT连接件的抗剪承载力计算公式，结合本文推出试验结果对式(6)进行修正：
$$ {F_{\text{G}}} = \frac{1}{{\left( {\dfrac{{6.95 \times {{10}^{ - 4}}}}{{2f_{\text{t}}}}L + \sqrt {{{\left( {\dfrac{{6.95 \times {{10}^{ - 4}}}}{{2f_{\text{t}}}}} \right)}^2}{L^2} + {{\left( {\dfrac{{0.07}}{{f_{\text{t}}}}} \right)}^2}} } \right)}} $$ (7) 然而，上式中所包含的变量主要为混凝土强度与保温层厚度，然而由图21(c)可知，外叶板厚度对剪切试件承载力也有影响，因此本文提出抗剪承载力外叶板厚度影响系数$ \alpha $，结合数值模拟分析结果进行拟合，可得$ \alpha = 0.004 t{\text{ + 0}}{\text{.766}} $，其中$ t $为外叶板厚度。GFRP UT连接件的抗剪承载力计算公式见下式。值得注意的是，每个剪切试件包含4个GFRP UT连接件，因此剪切试件的抗剪承载力计算值为下式计算结果的4倍：
$$ {F_{\text{G}}} = \alpha \dfrac{1}{{\left( {\dfrac{{6.95 \times {{10}^{ - 4}}}}{{2f_{\text{t}}}}L + \sqrt {{{\left( {\dfrac{{6.95 \times {{10}^{ - 4}}}}{{2f_{\text{t}}}}} \right)}^2}{L^2} + {{\left( {\dfrac{{0.07}}{{f_{\text{t}}}}} \right)}^2}} } \right)}} $$ (8) 根据图5与图17(c)中EPS保温板的破坏形态可以发现，EPS保温板参与了试件的抗剪作用，并最终发生了斜向45°撕裂破坏，文献[20]考虑了保温层对试件抗剪承载力的贡献：
$$ {F_{\text{E}}} = \frac{{{G_{\text{E}}}{A_{\text{E}}}{\delta _1}}}{L} $$ (9) 式中：$ {G_{\text{E}}} $为保温材料的剪切模量(MPa)，EPS保温材料为2.27 MPa；$ {A_{\text{E}}} $为EPS保温材料受剪切的剪切面面积(mm2)；$ {\delta _1} $为相对滑移量(mm)，即荷载-滑移曲线首次突降点对应的滑移量。
剪切试件的抗剪承载力为GFRP UT连接件的抗剪承载力与EPS保温板的抗剪承载力之和，计算方法见下式：
$$ \begin{split} &{F_{\text{V}}} = \left( {0.004t + 0.766} \right)\\ &\;\;\frac{1}{{\left( {\frac{{6.95 \times {{10}^{ - 4}}}}{{2f_{\text{t}}}}L + \sqrt {{{\left( {\dfrac{{6.95 \times {{10}^{ - 4}}}}{{2f_{\text{t}}}}} \right)}^2}{L^2} + {{\left( {\dfrac{{0.07}}{{f_{\text{t}}}}} \right)}^2}} } \right)}} + \dfrac{{{G_{\text{E}}}{A_{\text{E}}}{\delta _1}}}{L} \end{split} $$ (10) GFRP UT连接件剪切试件的抗剪承载力试验与有限元模拟值和计算值的对比如表6所示，可以看出，所有试件的计算误差均小于10%，该抗剪承载力计算方法具有较高的精度。
4.2 轴压承载力
根据轴压试验结果，轴压试件的破坏模式为混凝土发生了冲切破坏，而GFRP UT连接件几乎完好，说明试件的轴向承载力主要由混凝土冲切承载力控制，因此可通过确定混凝土冲切破坏面计算试件的轴压承载力。
由图18(b)可知，轴压试件端部混凝土板底部出现了内、外两圈贯通裂缝，表明其存在内、外两层混凝土冲切破坏面，内层破坏面包含于外层破坏面中，因此可认为外层混凝土破坏面的抗冲切承载力即为试件的轴压承载力，如图24所示。
由图24可知，外层混凝土破坏面由GFRP UT连接件中双层双向布置的锚固钢筋与混凝土之间相互挤压形成，混凝土损伤从锚固钢筋根部大致沿斜向45°向外发展至混凝土表面。
GFRP UT连接件中的锚固钢筋为双层双向布置，每层的两根锚固钢筋间距较小，其会形成一个整体破坏面，如图25所示。
![]()
图 25 混凝土冲切破坏面宽度Figure 25. Width of concrete punching failure surface$ {h_0} $ is the anchorage depth of anchorage steel bar; $ l $ is the spacing of anchorage steel bar; $ d $ is the diameter of anchorage steel bar由图25可知，由于混凝土裂缝发展角度近似45°，因此混凝土冲切破坏面宽度$ b $的计算方法如下：
$$ b = l + d + 2{h_0} $$ (11) 式中：$ l $为锚固钢筋间距(mm)，为20 mm；$ d $为锚固钢筋直径(mm)，为8 mm；$ {h_0} $为锚固钢筋的锚固深度(mm)，第一层锚固钢筋为25 mm，第二层锚固钢筋为45 mm。
锚固钢筋造成的混凝土冲切破坏面是一个三维冲切面，将三维破坏面沿GFRP UT连接件轴向进行投影，每层锚固钢筋会在连接件两侧分别形成一个近似梯形的混凝土冲切破坏面投影，如图26示。
![]()
图 26 混凝土冲切破坏面投影Figure 26. Projection of concrete punching failure surface$ {A_{{\text{P1}}}} $ and $ {A_{{\text{P2}}}} $ are the projected areas of concrete shear failure caused by anchoring steel bars in the first and second layers; $ {h_0} $ is the anchorage depth of anchorage steel bar因此，每层锚固钢筋引起的混凝土冲切破坏面投影面积$ {A_{\text{P}}} $计算方法为
$$ {A_{\text{P}}} = 2 \times (l + d + b) \times {h_0}/2 $$ (12) 由式(12)可得，第一层与第二层锚固钢筋的混凝土冲切破坏面投影面积$ {A_{{\text{P1}}}} $与$ {A_{{\text{P2}}}} $分别为
2650 mm2与6570 mm2。在确定了混凝土冲切破坏面投影面积后便可计算受压试件的轴压承载力：$$ {F_{\text{C}}} = ({A_{{\text{p1}}}} + {A_{{\text{p2}}}}){f_{\text{t}}} $$ (13) 然而，通过对比图22(b)所示的不同外叶板厚度模拟结果与上式的计算结果可知，当外叶板厚度越大时，其有限元模拟结果与理论计算结果误差越大，这主要是由于当外叶板厚超过一定范围后，受压试件的混凝土冲切破坏面面积不会继续扩展，因此本文提出轴压承载力外叶板厚度影响系数$ \beta $对上式进行修正，结合图22(b)中的模拟结果进行拟合可得$ \beta = - 0.014 t{\text{ + 1}}{\text{.81}} $。则受压试件的轴压承载力计算公式如下：
$$ {F_{\text{C}}} = ( - 0.014t + 1.81)({A_{{\text{p1}}}} + {A_{{\text{p2}}}}){f_{\text{t}}} $$ (14) GFRP UT连接件受压试件的轴压承载力试验值与计算值对比如表7所示，试验值与理论值吻合良好，误差均小于10%，可用于预测GFRP UT连接件的轴向承载力。
5. 结 论
(1)玻璃纤维增强复合材料超长双向受力保温连接件(GFRP UT连接件)剪切试件的破坏模式为锚固区混凝土破坏，而GFRP UT连接件未见明显损伤；典型的荷载-滑移曲线可分为弹性、弹塑性和下降三个阶段，具有延性破坏特征。
(2)当剪切试件的混凝土强度由C35提升至C40时，试件峰值承载力与延性分别提升了4%和13.16%，但刚度变化不显著；填充EPS保温板的剪切试件相比于去除EPS保温板的剪切试件峰值承载力、延性与刚度分别提升了29.64%、7.89%和17.22%，且损伤发展较缓。
(3) GFRP UT连接件受压试件顶面与底面最终出现了内、外两圈环状贯通混凝土裂缝，其破坏模式为混凝土冲切破坏。
(4)当轴压试件的混凝土强度由C35提升至C40时，试件抵抗损伤的能力也随之提高，且峰值承载力与刚度分别提高了10.33%和3.78%，但延性系数降低了8.71%。
(5)结合试验与有限元模型研究了GFRP UT连接件在剪切与轴压作用下的受力机制，建立了GFRP UT连接件的抗剪与轴压承载力计算方法，试验值与计算值吻合良好，可为GFRP UT连接件在超低能耗夹心墙体中的工程设计与应用提供参考。
-
![]()
图 2 复合材料层合板高速冲击试验原理图
Figure 2. Schematic diagram of high-speed impact test for composite laminates
![]()
图 3 X850/IM+复合材料层合板冲击反射/透射速度
Figure 3. Impact rebound/penetration speeds of X850/IM+ composite laminates
![]()
图 4 M21C/IMA复合材料牌号层合板冲击反射/透射速度
Figure 4. Impact rebound/penetration speeds of M21C/IMA composite laminates
![]()
图 5 X850/IM+层合板冲击损伤C扫描图像
Figure 5. Impact damage C-scanning images of X850/IM+ laminates
![]()
图 6 M21C/IMA复合材料层合板冲击损伤C扫描图像
Figure 6. Impact damage C-scanning images of M21C/IMA composite laminates
![]()
图 7 5×10−3拉伸X850/IM+复合材料层合板冲击后背面纤维撕裂
Figure 7. Torn fiber on the back of X850/IM+ composite laminatesunder 5×10−3 pretension
表 1 复合材料层合板高速冲击试验矩阵
Table 1 High-speed impact test matrix for composite laminates
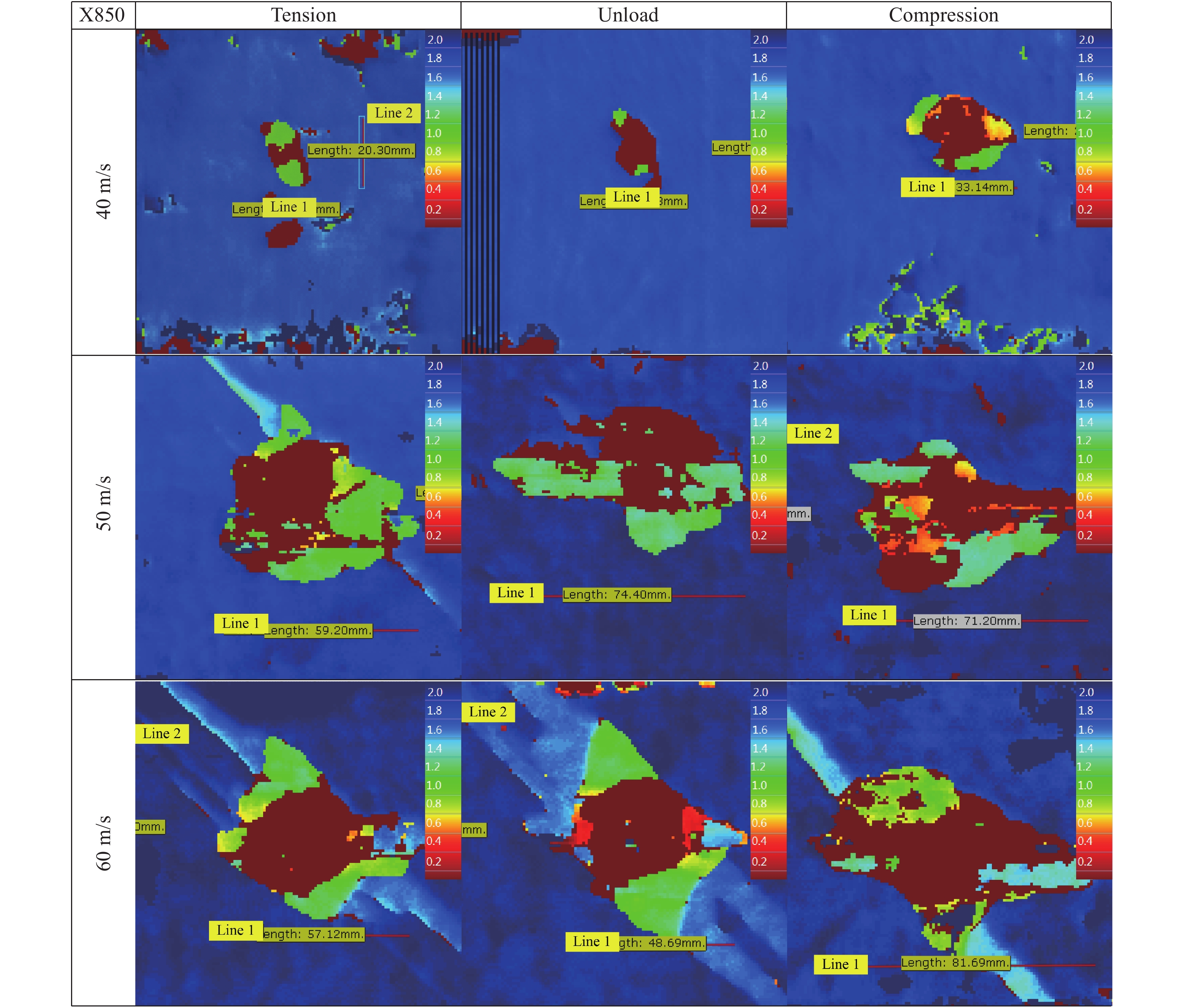
Initial velocity/(m·s−1) Preloading −5.0×10−3 0 5.0×10−3 40 4 pieces 4 pieces 4 pieces 50 4 pieces 4 pieces 4 pieces 60 4 pieces 4 pieces 4 pieces 
下载: 导出CSV
表 2 X850/IM+复合材料层合板冲击损伤面积
Table 2 Impact damage areas of X850/IM+ composite laminates
Initial velocity/
(m·s−1)Tension/
mm2Unload/
mm2Compression/
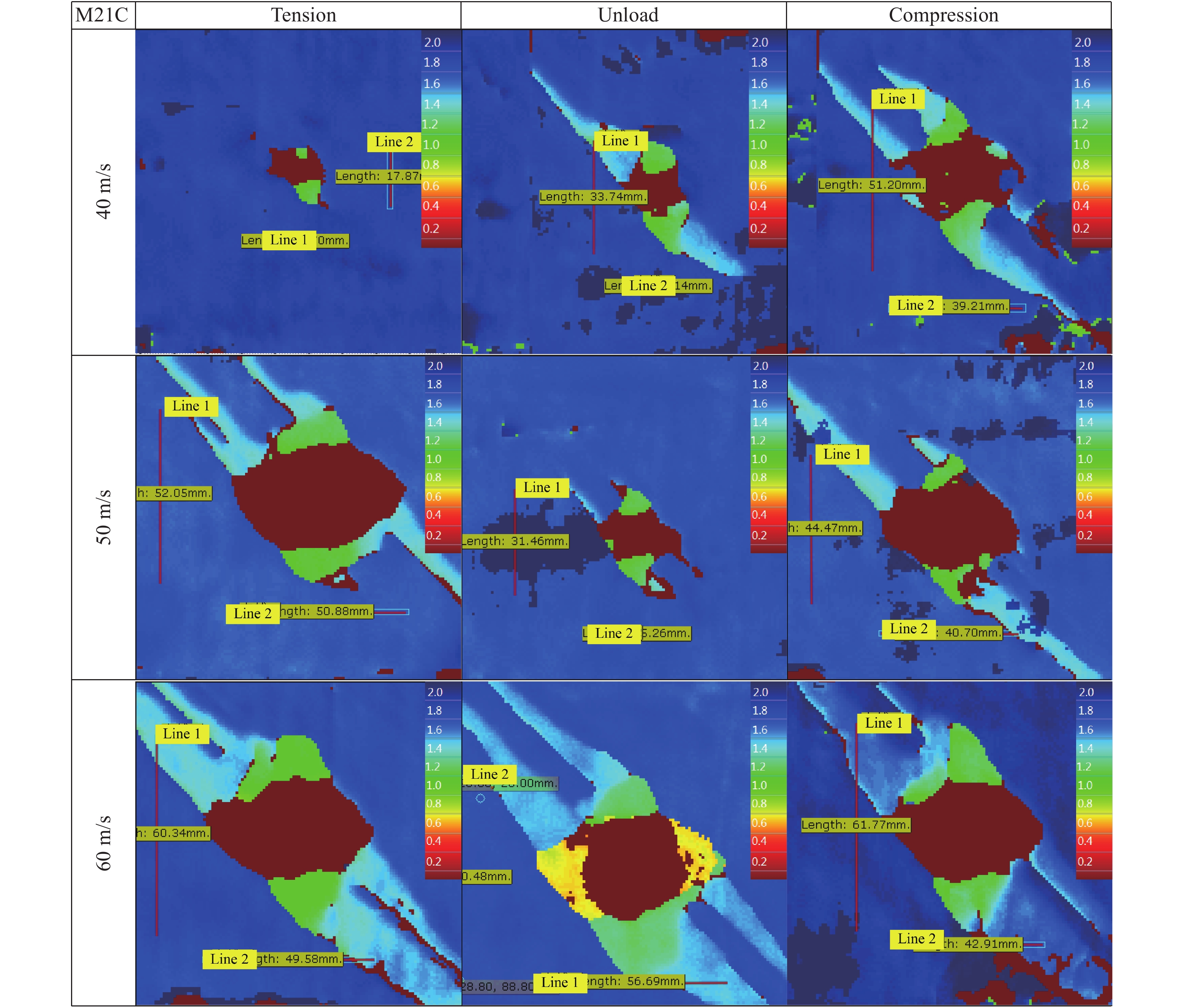
mm240 215 224 573 50 2 068 1 878 2 151 60 1 950 2 001 2 614
下载: 导出CSV
表 3 M21C/IMA层合板冲击损伤面积
Table 3 Impact damage areas of M21C/IMA laminates
Initial velocity/(m·s−1) Tension/
mm2Unload/
mm2Compression/
mm240 236 559 986 50 1 929 536 1 287 60 1 804 1 888 1 867
下载: 导出CSV
-
[1] 邵青, 何宇廷, 张腾, 等. 复合材料加筋板低速冲击损伤及剩余压缩强度试验研究[J]. 复合材料学报, 2014, 31(1):200-206. DOI: 10.3969/j.issn.1000-3851.2014.01.029 SHAO Q, HE Y T, ZHANG T, et al. Experimental research on low-velocity impact and residual compressive strength of composite stiffened panels[J]. Acta Materiae Compositae Sinica,2014,31(1):200-206(in Chinese). DOI: 10.3969/j.issn.1000-3851.2014.01.029
[2] 王念. 复合材料层合板冲击损伤及损伤容限研究[D]. 南京: 南京航空航天大学, 2014. WANG N. Research on impact damage and damage tolerance of composites laminates[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014(in Chinese).
[3] WILLIAMS J G, ANDERSON M S, RHODES M D, et al. Recent developments in the design, testing and impact-damage tolerance of stiffened composite panels[M]//Fibrous Composites in Structural Design. US: Springer, 1980: 259-291.
[4] SODERQUIST J R. Certification of civil composite aircraft structure[C]. SAE Technical Paper, 1981.
[5] NETTLES A T, LANCE D G. The effect of compressive preload on the compression-after-impact strength of carbon/epox[R]. NASA Technical Paper TP3303. Washington: NASA, 1992.
[6] HEIMBS S, BERGMANN T, SCHUELER D, et al. High velocity impact on preloaded composite plates[J]. Composite Structures,2014,111:158-168. DOI: 10.1016/j.compstruct.2013.12.031
[7] TOSO N, JOHNSON A. LIBCOS—Significance of load upon impact behavior of composite structure, DLR/C EASA2009OP24[R]. Stuttgart: German Aerospace Center, 2009.
[8] FAA Advisory Circular. Composite aircraft structures: AC 20.107B[S]. American: Federal Aviation Administration, 2009.
[9] KELKAR A D, SANKAR J, GRACE C, et al. Behavior of tensile preloaded composites subjected to low-velocity impact loads[C]. PVP-American Society of Mechanical Engineers. Pressure Vessels and Piping Division Newsletter, 1997.
[10] MITREVSKI T, MARSHALL I H, THOMSON R S, et al. Low-velocity impacts on preloaded GFRP specimens with various impactor shapes[J]. Composite Structure,2006,76(3):209-217. DOI: 10.1016/j.compstruct.2006.06.033
[11] KURSUN A, ŞENEL M. Investigation of the effect of low-velocity impact on composite plates with preloading[J]. Experimental Techniques, 2013, 37.6: 41-48.
[12] KURSUN A, SENEL M, ENGINSOY H M. Experimental and numerical analysis of low velocity impact on a preloaded composite plate[J]. Advances in Engineering Software,2015,90:41-52. DOI: 10.1016/j.advengsoft.2015.06.010
[13] STARNES J H, RHODES M D, WILLIAMS J G. Effect of impact damage and holes on the compressive strength of a graphite/epoxy laminate[J]. Nondestructive Evaluation and Flaw Criticality for Composite Materials,1979,696:145-171.
[14] HERSZBERG I, WELLER T. Impact damage resistance of buckled carbon/epoxy panels[J]. Composite Structures, 2006, 73(2): 130-137.
[15] HEIMBS S, HELLER S, MIDDENDORF P, et al. Low velocity impact on CFRP plates with compressive preload: Test and modelling[J]. International Journal of Impact Engineering,2009,36(10):1182-1193.
[16] HEIMBS S, BERGMANN T. High-velocity impact behaviour of prestressed composite plates under bird strike loading[J]. International Journal of Aerospace Engineering,2012,2012:372167.
[17] CHOI I H. Low-velocity impact analysis of composite laminates under initial in-plane load[J]. Composite Structures,2008,86(1):251-257.
[18] SUN C T, CHEN J K. On the impact of initially stressed composite laminates[J]. Journal of Composite Materials,1985,19(6):490-504. DOI: 10.1177/002199838501900601
[19] SUN C T, CHATTOPADHYAY S. Dynamic response of anisotropic laminated plates under initial stress to impact of a mass[J]. Journal of Applied Mechanics,1975,42(3):693-698. DOI: 10.1115/1.3423664
[20] 王计真, 刘小川. 预加载复合材料层合薄板低速冲击理论分析[J]. 应用力学学报, 2018, 35(6):1248-1253. WANG Jizhen, LIU Xiaochuan. Analysis of low-speed impact of preloaded composite laminates[J]. Chinese Journal of Applied Mechanics,2018,35(6):1248-1253(in Chinese).
[21] 王计真. 预应力状态下复合材料板冲击响应数值方法研究[J]. 科学技术与工程, 2017, 17(4):25-31. DOI: 10.3969/j.issn.1671-1815.2017.04.003 WANG Jizhen. Numerical method of impact response of composite plates under prestressed state[J]. Science Technology and Engineering,2017,17(4):25-31(in Chinese). DOI: 10.3969/j.issn.1671-1815.2017.04.003
-
期刊类型引用(3)
1. 马晓东，赵佳琪，饶青青，袁炳楠，况燚. 温度响应型磁性分子印迹聚合物的制备及其吸附性能. 林业工程学报. 2025(01): 70-79 . 
百度学术
2. 杨帅，宋雨方，钟炜锋，龚立昊，张学君，王梁彬，张洪吉. 温度响应性聚丙烯酸酯分散体的制备及性能研究. 涂料工业. 2024(02): 20-28 . 百度学术
3. 宋丹丹，马越，郭文娟. 聚丙烯酰胺荧光纳米纤维制备及温敏性能研究. 针织工业. 2023(08): 27-31 . 百度学术
其他类型引用(3)
-
计量
- 文章访问数: 808
- HTML全文浏览量: 313
- PDF下载量: 80
- 被引次数: 6
