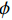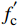纤维增强树脂复合材料约束超高性能混凝土轴压性能的细观数值模拟

田会文; 周臻; 陆纪平; 彭振

doi:10.13801/j.cnki.fhclxb.20190827.001

纤维增强树脂复合材料约束超高性能混凝土轴压性能的细观数值模拟

东南大学　混凝土及预应力混凝土结构教育部重点实验室，南京 210096

基金项目: 国家重点研发计划(2017YFC0703700)

详细信息

通讯作者:
周臻，教授，博士，博士生导师，研究方向为新材料与新型组合结构、损伤可控结构体系　E-mail：seuhj@163.com

中图分类号: TU375.4
计量
- 文章访问数: 1295
- HTML全文浏览量: 316
- PDF下载量: 75
出版历程
- 收稿日期: 2019-07-11
- 录用日期: 2019-08-18
- 网络出版日期: 2019-08-27
- 刊出日期: 2020-07-14

Meso-scale numerical simulation of axial compression performance of fiber reinforced polymer composite-confined ultra-high performance concrete

Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education, Southeast University, Nanjing 210096, China

摘要

摘要: 利用LS-DYNA有限元分析软件建立纤维增强树脂(FRP)复合材料约束超高性能混凝土(UHPC)圆柱细观有限元模型，以研究其单轴受压性能。通过已有试验数据验证了模型的有效性，并建立了能准确反映FRP复合材料约束作用的K&C模型的剪切膨胀参数预测公式。在此基础上进行参数分析，研究FRP复合材料厚度、纤维缠绕角度和钢纤维掺量的影响。结果表明，本文模型不仅能模拟随机分布钢纤维对试件应力分布的影响，且能较准确反映FRP复合材料约束作用对核心UHPC强度和延性的提高效果。模型在轴压作用下的破坏模式和应力-应变曲线与试验结果基本一致。参数分析表明，随FRP复合材料厚度或纤维缠绕角度的增大，试件极限承载力和延性均增大，而增大钢纤维掺量虽可限制核心UHPC斜裂缝的开展，但对试件强度和延性影响较小。
- 超高性能混凝土 /
- 纤维增强树脂(FRP)复合材料约束 /
- 轴压性能 /
- 细观模型 /
- 数值模拟
Abstract: To investigate the axial compressive performance of fiber reinforced polymer (FRP) composite-confined ultra-high performance concrete (UHPC) cylindrical specimens, the meso-scale finite element model was established in LS-DYNA and validated by the comparison of the experimental data. The formula of shear dilation parameter of K&C model was proposed, which could accurately reflect the FRP composites confinement for UHPC. Based on the validated model, a parametric analysis was conducted to investigate the influence of FRP composite tube thickness, FRP composites fiber winding angle and steel fiber content. The results show that the model can not only capture the effect of random distributed steel fibers on the specimen stress distribution, but also accurately reflect the enhancement of strength and ductility of UHPC core subjected to FRP composite confinement. Good agreement is found in failure modes and stress-strain curves between simulation and experimental results. Parametric studies show that with the increase of FRP composite tubes thickness and FRP composite fiber winding angle, the strength and ductility of the FRP composite-confined UHPC specimens are significantly enhanced. An increase in steel fiber content can effectively restrain the inclined shear cracks in UHPC core, but has little effect on the strength and ductility of the specimens.
- ultra-high performance concrete /
- fiber reinforced polymer (FRP) composite confinement /
- axial compressive performance /
- meso-scale model /
- numerical simulation

HTML全文

超高性能混凝土(UHPC)是一种新型水泥基复合材料，其具有超高强度、高韧性和高耐久性等优良特性，目前在桥梁工程、房屋建筑和海洋工程中有大量应用^[1-4]。

纤维增强树脂(FRP)复合材料约束可有效提高普通混凝土( NSC)和高强混凝土(HSC)的强度和延性已被广泛验证^[5-7]，而UHPC不仅具有超高的强度，同时具有比HSC更好的横向变形能力，有利于更好地发挥FRP复合材料的被动约束作用。Zohrevand等^[8]首次开展了FRP复合材料布缠绕约束UHPC圆柱的轴压力学性能试验，证明了FRP复合材料约束可大幅提高UHPC柱的抗压强度和极限应变。Guler^[9]和Wang等^[10]的研究则表明，相比于NSC和HSC，UHPC需要更大约束刚度的FRP复合材料才能实现试件延性的大幅提升。田会文等^[11]的研究表明，钢纤维掺量对FRP复合材料约束UHPC的影响在约束刚度较小的试件中更明显，当约束刚度较大时，钢纤维影响较小。

随着计算机技术的快速发展，细观数值模拟开始被广泛用于研究混凝土的力学性能，以解决单一均质材料无法模拟多相复合材料中材料组分随机性影响的难题。NSC和HSC因含有粗骨料、细骨料、砂浆、气孔和界面层等，其细观模型一般需单独建立各相材料组分^[12]。在纤维增强混凝土(FRC)的细观模拟中，有学者建议采用包含骨料、砂浆和纤维三种组分的模型^[13]，也有学者简化为仅包含混凝土基体和纤维两种组分的模型并取得较好模拟效果^[14]。UHPC因不含粗、细骨料，一般采用钢纤维和基体二相材料的细观模型^[15-16]。

目前，采用三维细观模型研究UHPC受力性能的报道较少，而针对FRP复合材料约束UHPC的细观模拟未见公开报道，因此有必要建立其细观有限元模型并进行参数分析。本文通过与试验对比来验证模型有效性，并提出适用于FRP复合材料约束UHPC的K&C模型剪胀参数公式。在此基础上，通过参数分析研究FRP复合材料厚度、FRP复合材料纤维缠绕角度和钢纤维掺量等主要参数对试件破坏模式、抗压强度和延性等的影响。

1. 数值模型的建立

1.1 模型概述

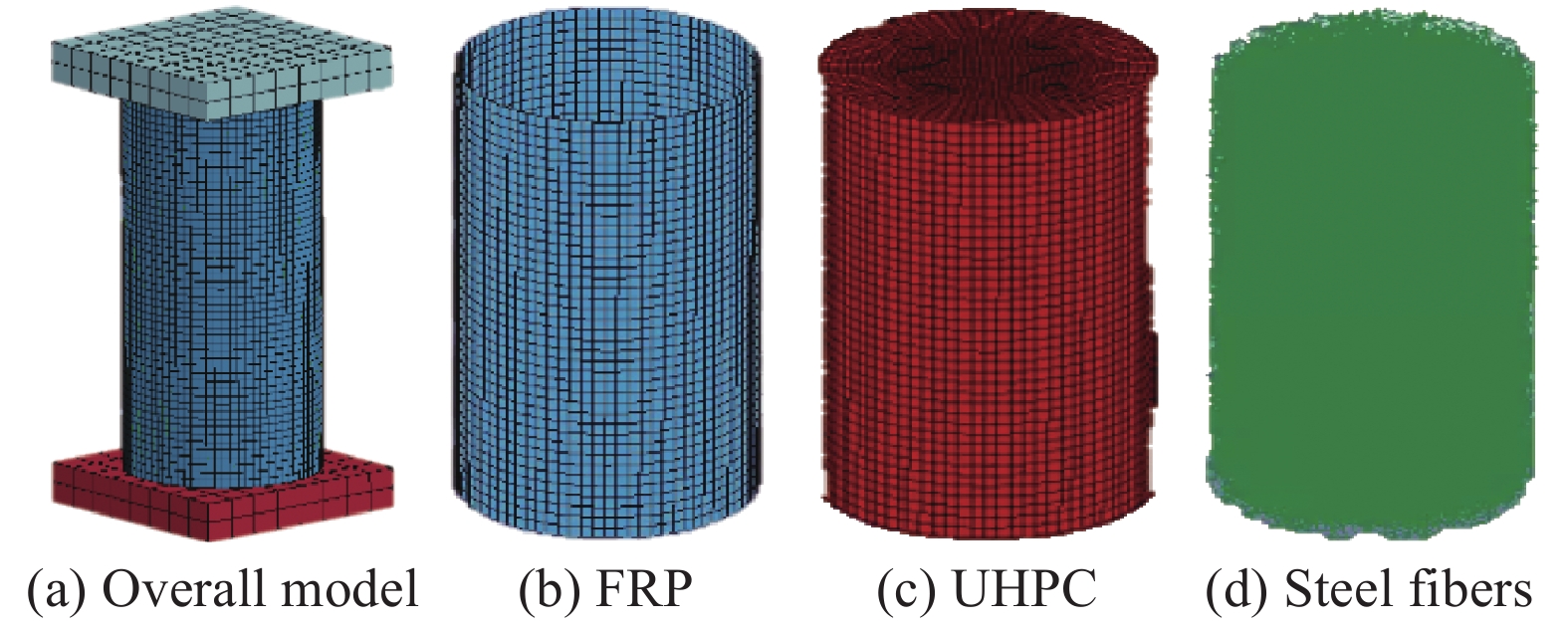
纤维增强树脂(FRP)复合材料约束超高性能混凝土(UHPC)细观模型可分为三部分：FRP复合材料外管、核心UHPC基体及随机分布其中的钢纤维，如图1所示。FRP复合材料采用可考虑壳单元弯曲和剪切变形能力的四节点壳单元，单元算法采用Belytschko-Tsay算法。UHPC基体采用三维八节点常应力实体单元，单点高斯积分求解，同时采用沙漏系数为0.06的刚体沙漏控制，以避免出现零能模式。钢纤维采用具有良好计算效率和鲁棒性的Hughes-Liu梁单元。

图 1 纤维增强树脂(FRP)复合材料约束超高性能混凝土(UHPC)轴压有限元分析模型

Figure 1. Finite element model of axial compression of fiber reinforced polymer(FRP) composite-confined ultra-high performance concrete(UHPC)

下载: 全尺寸图片幻灯片

模拟FRP复合材料与UHPC之间的接触关系时采用面面接触，即LS-DYNA中的CONTACT_SURFACE_ TO_SURFACE命令，其中：FRP复合材料内表面为从面，UHPC外表面为主面，两面之间法向可传递压力，切向不考虑滑动，摩擦系数取1.0。根据Elsanadedy等^[17]的研究结果，划分网格时，使FRP复合材料和混凝土的网格尺寸相同，且二者接触面节点处于相同位置，可更好地模拟接触关系。

建立上下刚体加载端板用于模拟边界条件，同样采用面面接触模拟端板与试件之间的接触关系，端板面为主面，试件上下端面为从面，摩擦系数为0.6^[15]。下加载板约束所有自由度，上加载板仅保留竖向自由度，对上加载板施加速度为0.01 mm/s的位移实现加载。

1.2 三维随机钢纤维模型

钢纤维的生成采用MATLAB伪随机数法生成，具体流程如图2所示。由于生成的钢纤维单元数量较大，考虑钢纤维与混凝土基体之间相互作用会导致计算成本的成倍增加，且收敛性较差。因此，利用CONSTRAINED_LAGRANGE_IN_SOLID命令将钢纤维与混凝土基体绑定。已有研究^[15-16]表明，不考虑两者之间相互作用，亦能得到较好的模拟效果。

图 2 钢纤维生成流程

Figure 2. Generation of steel fibers

下载: 全尺寸图片幻灯片

1.3 材料本构

钢纤维采用双线性塑性随动强化材料MAT_ PLASTIC_KINEMATIC作为本构，弹性模量和屈服应力分别取210 GPa和1 480 MPa，屈服后强化系数取0.01。FRP复合材料外壳采用弹性正交材料MAT_ ORTHOTROPIC_ELASTIC作为本构。对于单向FRP复合材料布缠绕约束试件，仅指定FRP复合材料轴向弹性模量，并设置泊松比为零，以忽略其他方向纤维相互作用的影响^[18]。采用MAT_ADD_EROSION中的最大应变准则来控制FRP复合材料单元的删除，FRP复合材料极限应变与其他基本力学参数取文献试验值。文献[8]中FRP复合材料板基本参数如表1所示。

表 1 FRP复合材料板力学性能

Table 1. Mechanical properties of FRP composite laminate

Type	Tensile strength/MPa	Elastic modulus/GPa
GFRP	610	26.1
CFRP	850	70.6
Notes: GFRP—Glass fiber reinforced polymer composite; CFRP—Carbon fiber reinforced polymer composite.

下载: 导出CSV

| 显示表格

UHPC本构选择K&C材料模型，即LS-DYNA中的MAT_CONCRETE_DAMAGE_REL3材料，该模型能够模拟混凝土的应变软化、剪切膨胀等行为，被广泛应用于混凝土的非线性模拟，模型具体介绍请参考文献[19]。K&C模型可通过仅指定抗压强度自动计算其他参数，但该方法是基于45.4 MPa普通混凝土提出，用于UHPC时需校正参数。Xu等^[20]证明了K&C模型用于模拟UHPC力学性能的可行性，并提出了确定模型部分参数的方法。影响本文模拟结果的主要参数为强度面参数、损伤参数、状态方程和剪切膨胀参数，以下逐一介绍。

K&C模型通过引入初始屈服面、极限强度面和残余强度面，分别描述混凝土的初始屈服强度、极限强度及残余强度的变化规律。根据Xu等^[20]提出的方法可确定文献[8]中189 MPa的UHPC的强度面参数，见表2所示。其他强度等级的UHPC可根据实际抗压强度值按下式缩放得到：

$a_{0i}^{{\rm{new }}} = \phi a_{0i}^{{\rm{old }}}\;\;\;a_{1i}^{{\rm{new }}} = a_{1i}^{{\rm{old }}}\;\;a_{2i}^{{\rm{new }}} = a_{2i}^{{\rm{old }}}/\phi$

(1)

式中：a_0i、a_1i和a_2i为强度面参数； $\phi$ 为缩放参数，由下式确定：

$\phi = f_{\rm{c}}^{'{\rm{new}}}/f_{\rm{c}}^{'{\rm{old}}}$

(2)

式中： $f_{\rm{c}}^{'{\rm{old}}}$ 为已知强度面参数的未约束混凝土强度； $f_{\rm{c}}^{'{\rm{new}}}$ 为拟求强度面参数的未约束混凝土强度。

表 2 UHPC本构模型强度面参数

Table 2. Shear failure surfaces parameters of UHPC

a₀	a₁	a₂	a_0f	a_1f	a_1f	a_2f
6.046	0.366	0.00639	2.722	0.813	0.366	0.00639

下载: 导出CSV

| 显示表格

损伤参数b₁、b₂及b₃的取值影响混凝土的损伤演化规律，本文通过试算并对比文献[8]和文献[11]试验结果确定该参数，如表3所示。状态方程是混凝土体积应变、静水压力和卸载体积模量的关系，用来控制混凝土的软化，一般通过试验确定。K&C材料模型通过EOS_TABULATED_COMPACTION定义状态方程曲线，本文采用Guler^[9]建议的曲线。此外，可通过MAT_ADD_EROSION控制UHPC单元失效准则。尽管单元失效不代表材料的实际特性，但能表征试件宏观损伤并克服单元畸变造成的收敛性问题^[15]。实验结果表明，核心UHPC为受压剪切破坏^[10]，因此本文采用最大等效应变准则，当最大等效应变达到0.0245时，UHPC单元被删除。

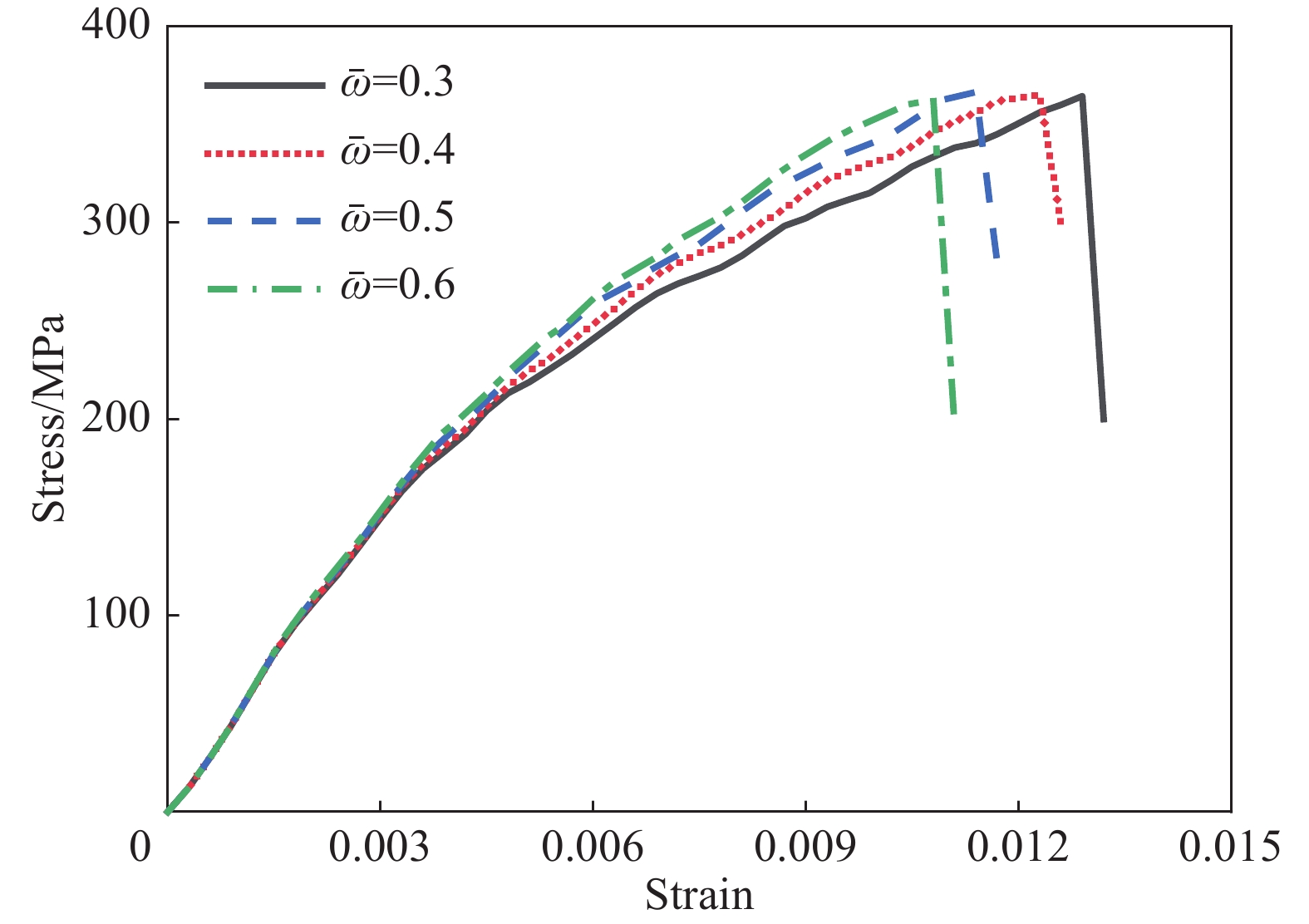
表 3 UHPC本构模型损伤演化参数

Table 3. Damage scaling parameters of UHPC

b₁	b₂	b₃
1.60	1.701	1.449

下载: 导出CSV

| 显示表格

UHPC的膨胀性能是影响FRP复合材料约束UHPC受压力学性能的关键参数。在K&C模型中，剪切膨胀参数ϖ决定了塑性应变的体积分量和偏分量的比值。ϖ正值代表混凝土体积膨胀，负值代表体积缩小^[21]。通过ϖ可捕捉混凝土开裂时的剪切膨胀效应，此时如果有较充分的箍筋或FRP复合材料约束，则会产生较大的约束应力，从而提高被约束UHPC的强度和延性。因此，在FRP复合材料约束UHPC的模拟中，ϖ的准确性直接影响模拟的精度。图3为计算参数取文献[8]的剪胀参数ϖ对FRP复合材料约束UHPC轴压力学性能的影响。可以看出，ϖ不仅显著影响FRP复合材料约束UHPC在塑性阶段的应力-应变曲线斜率，且对试件的极限应变和强度有较大影响。Youssf等^[21]提出过针对FRP复合材料约束普通混凝土(NSC)计算剪切膨胀参数的经验公式，但该公式对FRP复合材料约束UHPC不适用。因此，本文采用试算的方法确定ϖ数值，并在2.3节将根据已经得到的大量的特定FRP复合材料环向刚度与UHPC强度对应的ϖ拟合预测公式，用于参数分析。

图 3 剪胀参数ϖ对FRP复合材料约束UHPC轴压力学性能的影响

Figure 3. Influence of shear dilation parameter ϖ on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

1.4 网格敏感性

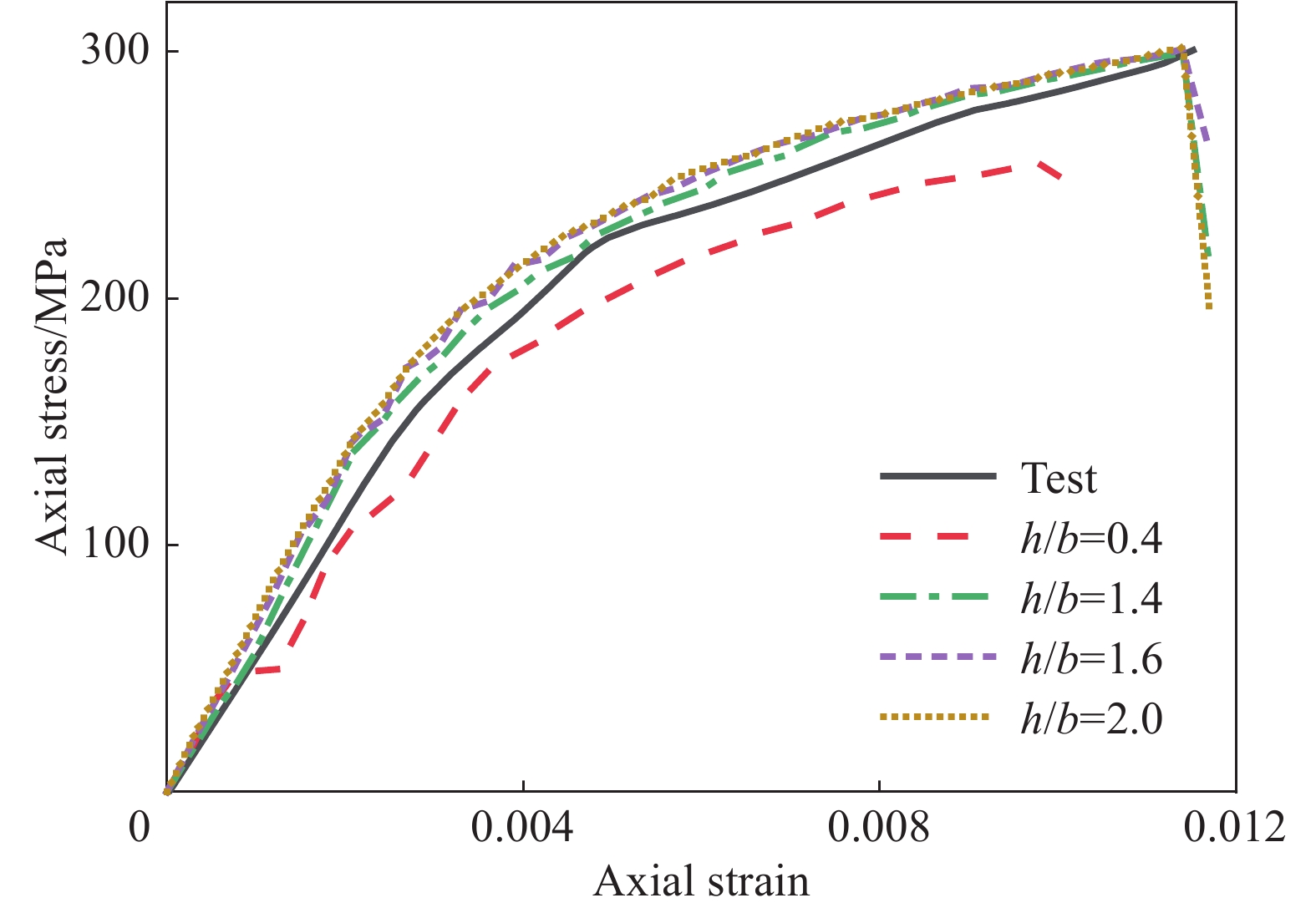
为确定计算效率与精度相平衡的有限元模型单元尺寸，以文献[8]的UHPC试件为例，进行单元网格尺寸敏感性分析。钢纤维划分3个单元，混凝土保持单元宽度为5 mm不变，在0.4~2.0的范围内改变单元高宽比h/b，同时保证壳单元网格与混凝土外表面单元网格节点一一对应。图4为单元网格高宽比h/b对FRP复合材料约束UHPC轴压力学性能的影响。可以看出，当单元的高宽比为1.0时，模拟结果与试验结果最接近，此时的实体单元数量为48 000，而壳单元的数量为11 200个。

图 4 单元网格高宽比h/b对FRP复合材料约束UHPC轴压力学性能的影响

Figure 4. Influence of aspect ratio h/b of element mesh on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

2. 数值模型验证

2.1 模型结果与试验对比

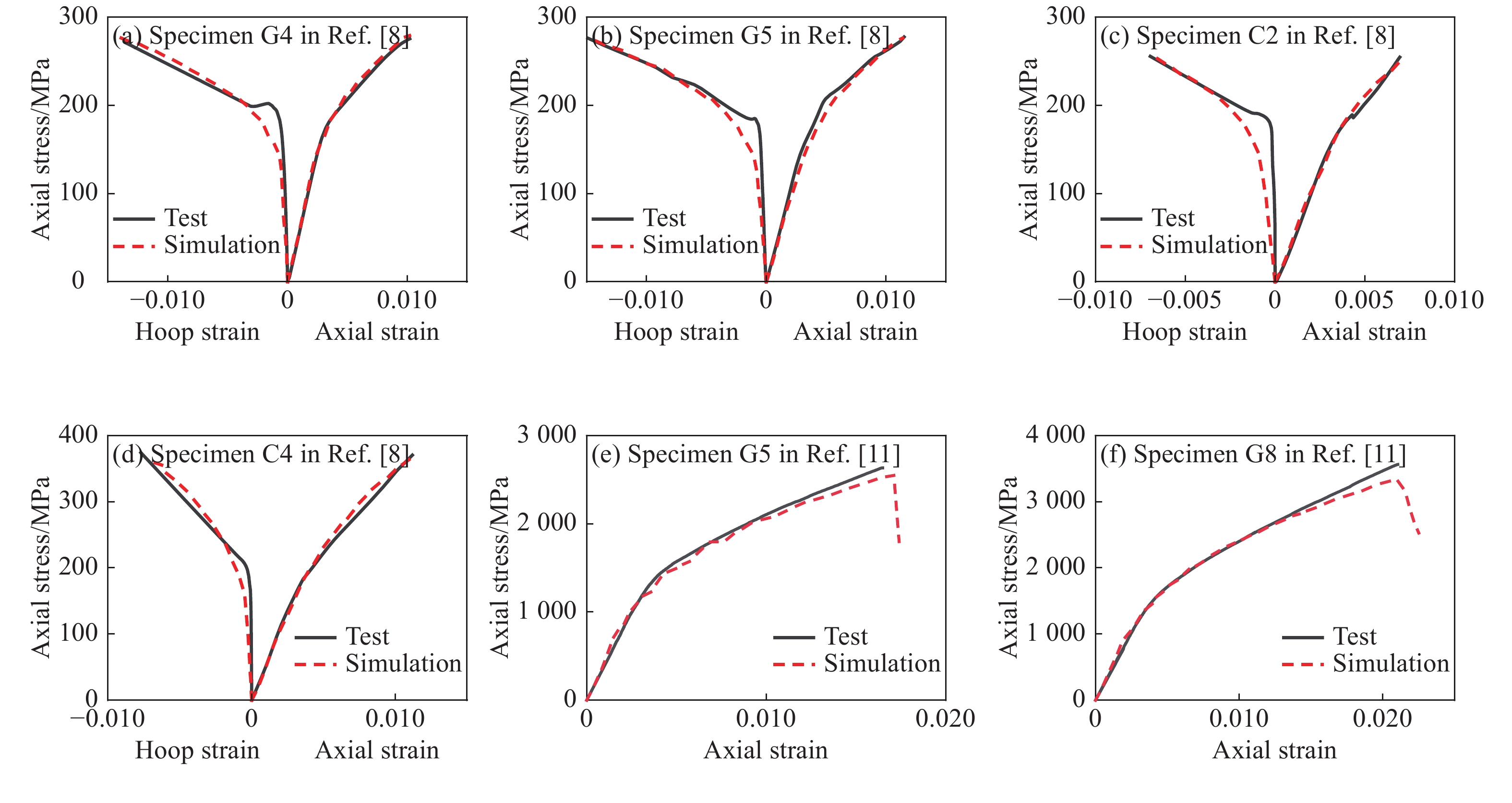
选取文献[8]和文献[11]中的试件进行模拟验证，各参数见表4所示，其中ϖ通过试算得到。图5为试验与模拟应力-应变曲线的对比。可以看出，试验与模拟两曲线在各关键点和总体趋势上十分接近。表5为试验与模拟极限状态的误差对比。可知，峰值应力模拟值与实验值误差在0.20%~2.07%，极限轴向应变模拟值与实验值误差在0.86%~5.87%，极限环向应变模拟值与实验值误差在3.03%~10.55%，因此该模型能较好地模拟FRP复合材料约束UHPC的应力-应变曲线和极限状态。

表 4 FRP复合材料约束UHPC试验数据库

Table 4. Test database for FRP composite confined UHPC

Ref.	Specimen	$f_{\rm{c}}^{'}$ /MPa	E_FRP/GPa	t_FRP/mm	D/mm	E₁/MPa	E₁/ $f_{\rm{c}}^{'}$	ϖ
[8]	G4	189	26.10	4.08	108	986.00	10.43	0.290
[8]	G5	189	26.10	5.10	108	1 972.00	13.04	0.321
[8]	C2	189	70.60	2.04	108	2 465.00	14.11	0.358
[8]	C4	189	70.60	4.08	108	2 667.11	28.22	0.585
[11]	G5	130	41.58	5.07	100	4 158.00	31.98	0.647
[11]	G8	130	41.58	8.05	100	6 652.80	51.17	0.968
Notes: $f_{\rm{c}}^{'}$ —Unconfined strength of UHPC; E_FRP, t_FRP—Elastic modulus and thickness of FRP composite tubes, respectively; D—Diameter of specimens; E₁—Confinement stress provided by FRP composite tubes; ϖ—Shear dilation parameter.

下载: 导出CSV

| 显示表格

图 5 FRP复合材料约束UHPC的模拟与试验应力-应变曲线对比

Figure 5. Comparison of simulation and test stress-strain curves of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

表 5 FRP复合材料约束UHPC的模拟与试验极限状态对比

Table 5. Comparison of simulation and test ultimate condition of FRP composite confined UHPC

Ref.	Specimen	Strength/MPa		Error/%	Ultimate axial strain		Error /%	Hoop rupture strain		Error /%
Ref.	Specimen	Test	Simulation	Error/%	Test	Simulation	Error /%	Test	Simulation	Error /%
[8]	G4	273.5	279.2	2.07	0.01060	0.0102	3.78	0.0135	0.0148	9.84
[8]	G5	298.9	299.5	0.20	0.01150	0.0114	0.86	0.0140	0.0152	8.30
[8]	C2	254.1	255.0	0.36	0.00680	0.0072	5.87	0.0069	0.0067	3.03
[8]	C4	372.2	366.3	1.59	0.01050	0.0111	5.71	0.0080	0.0072	10.55
[11]	G5	2 634.8	2 558.6	2.89	0.01648	0.0171	3.76	−	−	−
[11]	G8	3 564.3	3 323.8	6.75	0.02105	0.0210	0.19	−	−	−

下载: 导出CSV

| 显示表格

2.2 FRP复合材料约束UHPC破坏全过程

为进一步验证所建细观模型的有效性并研究其受力机制，以文献[8]中G5试件为例，研究试件受压破坏全过程，并对比试验与模拟的试件破坏模式。图6为文献[8]中试件典型破坏形态。可知，中部FRP复合材料拉断后试件失效，核心UHPC为受压剪切破坏。

图 6 文献[8]中GFRP约束UHPC试件典型破坏形态

Figure 6. Typical failure mode of GFRP confined UHPC specimen in Ref. [8]

下载: 全尺寸图片幻灯片

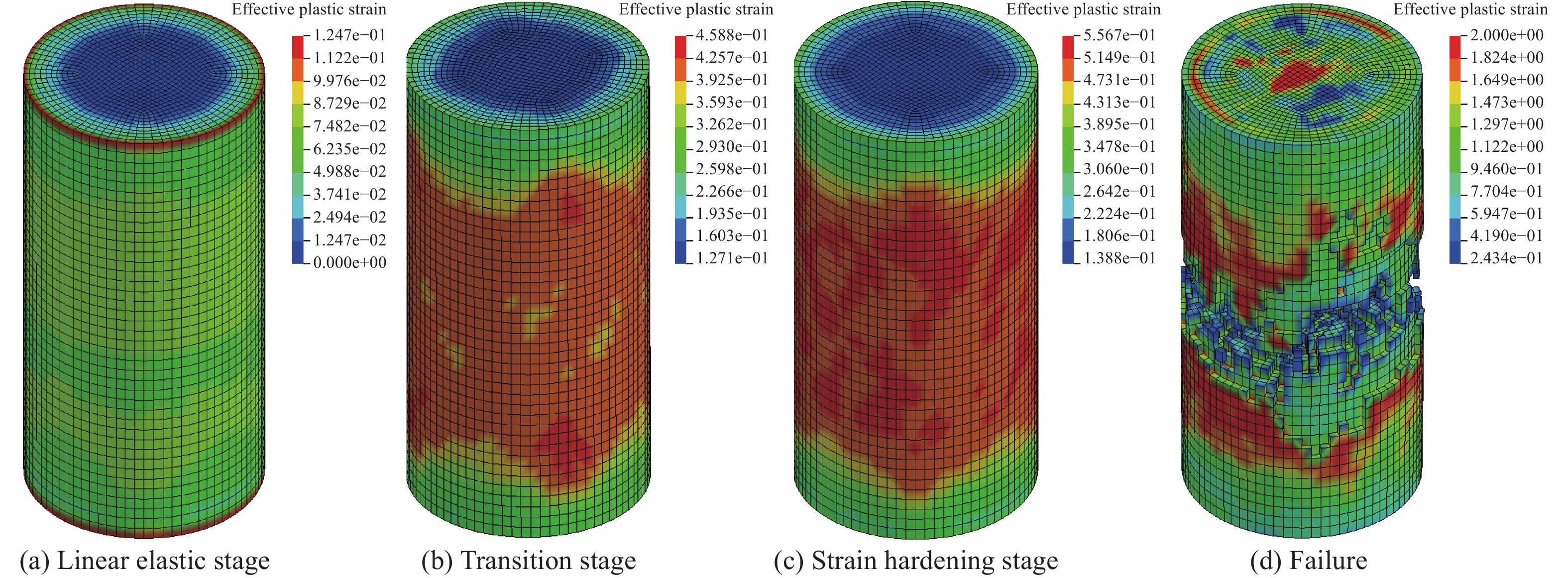
图7为FRP复合材料约束UHPC受压应力-应变曲线各阶段示意图，包括弹性阶段、过渡阶段、线性强化阶段和破坏。图8~10为模拟的受压破坏各阶段混凝土基体等效塑性应变云、FRP复合材料环向应力、钢纤维轴向应力。

图 7 FRP复合材料约束UHPC受压应力-应变曲线各阶段示意图

Figure 7. Illustration of different stages of stress-strain curves of FRP composite confined UHPC under axial compression

下载: 全尺寸图片幻灯片

图 9 文献[8]中G5试件FRP复合材料环向应力

Figure 9. Hoop stress of FRP composite of specimen G5 in Ref. [8]

下载: 全尺寸图片幻灯片

图 10 文献[8]中G5试件钢纤维轴向应力

Figure 10. Axial stress of steel fibers of specimen G5 in Ref. [8]

下载: 全尺寸图片幻灯片

(1) 线弹性阶段：当荷载较小时试件处于弹性阶段，混凝土等效塑性应变总体较小，仅端部应力集中部分进入塑性。由于混凝土膨胀较小且其泊松比小于FRP复合材料管泊松比，FRP复合材料此时未对核心混凝土产生约束作用。钢纤维作用较弱且大部分处于受压状态。

(2) 过渡阶段：随着荷载增大，中部混凝土单元开始出现损伤，环向应变持续增大从而激活了FRP复合材料管的约束作用，混凝土开始处于三向受压状态。试件中部混凝土膨胀较大区域的钢纤维开始由受压转为受拉状态，限制混凝土的侧向膨胀。

(3) 强化阶段：由于FRP复合材料提供了有效的约束作用，混凝土处于三向受压状态，塑性区进一步增大，并沿45°斜向扩展，混凝土最大受压应力超过混凝土单轴抗压强度。试件中部因UHPC膨胀较大导致处于受拉状态的钢纤维数量增多，部分钢纤维进入塑性，而试验中钢纤维在进入塑性之前将与混凝土出现黏结滑移，模拟中未考虑黏结滑移则过高地估计了钢纤维的影响。

(4) 破坏阶段：试件中部FRP复合材料纤维环向应变首先断裂，对应位置的混凝土单元失去约束后迅速达到失效应变，单元开始删除，试件破坏。

根据上述分析可知，本文建立的三维细观有限元模型能模拟FRP复合材料约束UHPC试件的受压破坏全过程，且模拟得到的破坏形态与试验基本一致。

图 8 文献[8]中G5试件UHPC基体等效塑性应变

Figure 8. Equivalent plastic strain of UHPC matrix of specimen G5 in Ref. [8]

下载: 全尺寸图片幻灯片

2.3 剪切膨胀参数计算公式

在2.2节模型验证时得到了大量特定FRP复合材料环向刚度E₁与UHPC强度 $f_{\rm{c}}^{'}$ 对应的ϖ值，将其汇总如图11所示，可发现ϖ与E₁/ $f_{\rm{c}}^{'}$ 呈线性关系。因此，提出适用于FRP复合材料约束UHPC的剪切膨胀参数公式为

图 11 剪胀参数ϖ拟合公式

Figure 11. Fitted equation of shear dilation parameter ϖ

下载: 全尺寸图片幻灯片

$\varpi = 0.0167{E_1}/f_{\rm{c}}^{'} + 0.1137$

(3)

其中，E₁可由下式计算得到：

${E_1} = 2{t_{{\rm{FRP}}}} {E_{{\rm{FRP}}}}/D$

(4)

式中：E_FRP和t_FRP分别为FRP复合材料弹性模量和厚度；D为试件直径。以上公式可用于参数分析时预测ϖ。

3. 各参数对FRP约束UHPC轴压性能的影响

以文献[8]中G5试件为基准，具体参数见表4所示。通过改变FRP复合材料厚度、FRP复合材料纤维角度和钢纤维掺量等参数，研究其对试件轴压性能的影响。

3.1 FRP厚度对FRP约束UHPC轴压性能的影响

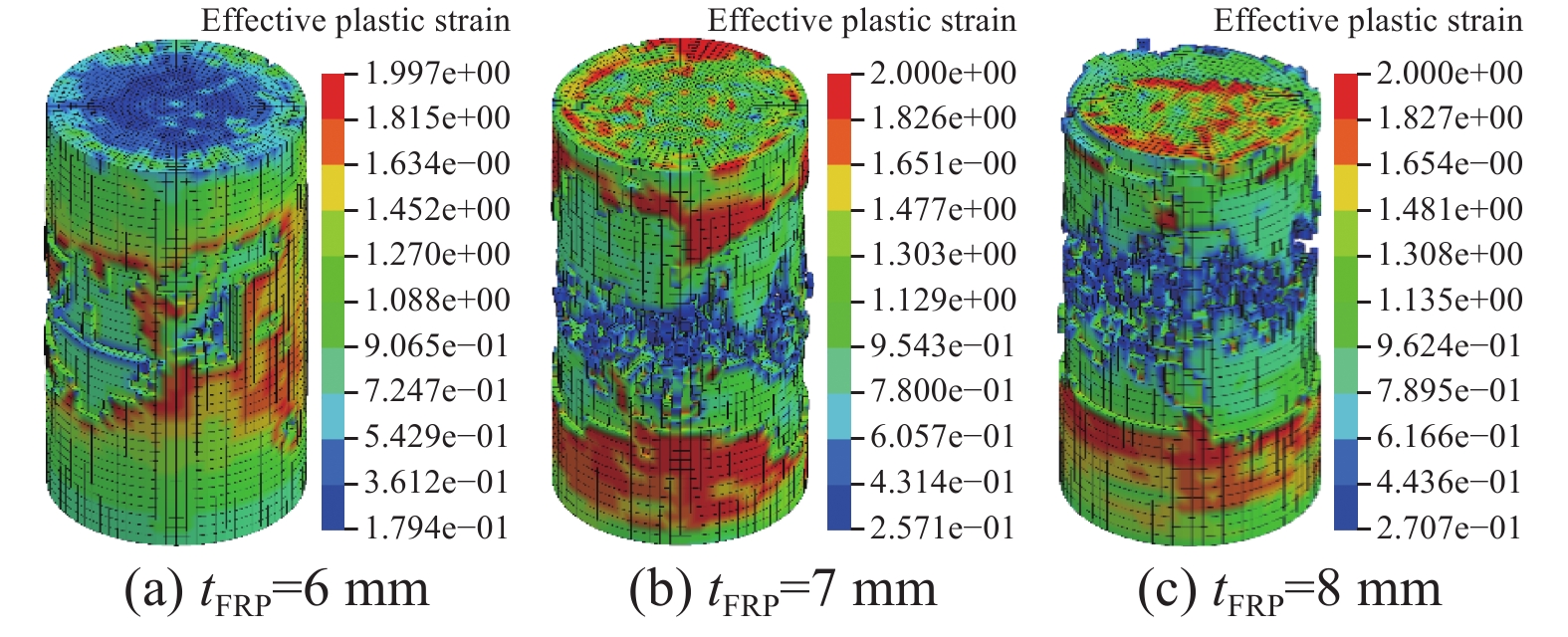
保持UHPC参数、FRP复合材料角度和钢纤维掺量不变，改变FRP复合材料厚度(t_FRP=5 mm、6 mm、7 mm、8 mm)进行参数分析。图12为不同FRP复合材料厚度的FRP复合材料约束UHPC的应力-应变曲线。可以看出，不同FRP复合材料厚度的FRP复合材料约束UHPC在弹性阶段的受压性能基本相同，主要原因是此阶段混凝土膨胀较小，FRP复合材料约束作用未被激活，试件性能主要受未约束UHPC受压性能的影响。在强化阶段，随FRP复合材料厚度增加，FRP复合材料提供的环向约束力增大，试件的强度和极限应变有较大提升。通过等效塑性应变分布可表征UHPC核心的破坏形态。图13为不同FRP复合材料管厚时核心UHPC的破坏形态，其中t_FRP=5 mm试件如图8所示。可以看出，UHPC均首先在中部达到失效准则而删除，这是由于试件两端部受到加载端板摩擦力的“环箍效应”导致强度提高，且侧向膨胀减小。

图 12 FRP复合材料厚度对FRP复合材料约束UHPC轴压力学性能的影响

Figure 12. Influence of FRP composite thickness on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 13 不同FRP复合材料管厚时核心UHPC破坏形态

Figure 13. Failure modes of UHPC core with different FRP composite tube thicknesses

下载: 全尺寸图片幻灯片

3.2 FRP纤维角度对FRP约束UHPC轴压性能的影响

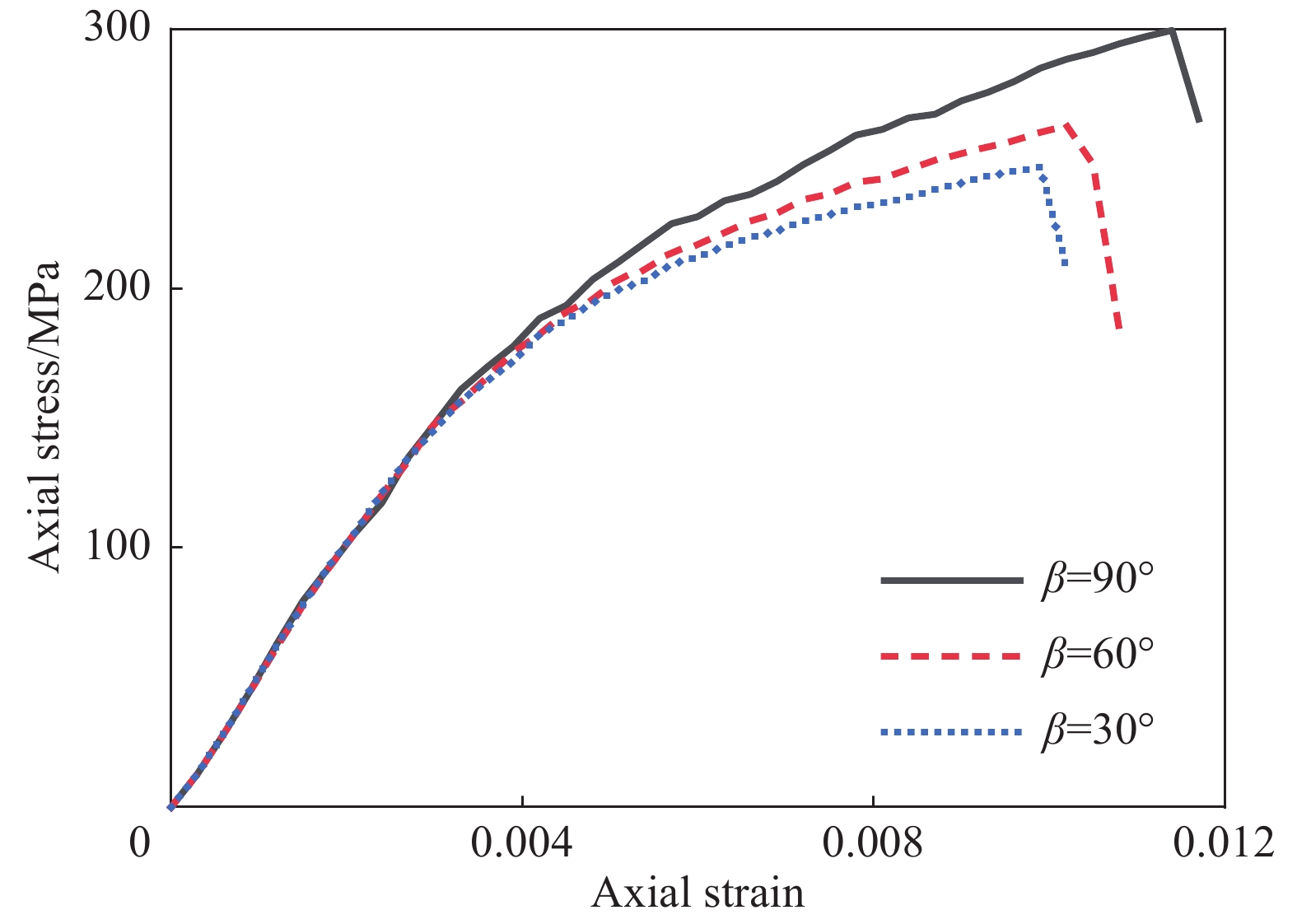
保持UHPC参数、FRP复合材料厚度和钢纤维掺量不变，改变FRP复合材料纤维角度(β=30°、60°、90°)进行参数分析。本文模拟FRP复合材料采用的MAT_ORTHOTROPIC_ ELASTIC模型允许用户定义FRP复合材料在三维空间的属性，通过改变BETA参数即可改变FRP复合材料纤维的方向。图14为三种不同FRP复合材料纤维角度下FRP复合材料约束UHPC应力-应变曲线，其中缠绕角度为纤维与试件纵向所呈角度。可以看出，在弹性阶段，三组试件曲线基本重合。随着荷载进一步增大，试件进入强化阶段，此时核心混凝土逐渐膨胀，FRP复合材料环向拉应力逐渐增大。环向布置更多的纤维，即缠绕角度越接近90°，FRP复合材料提供的约束越大，从而使试件表现出更高的承载力和极限应变。相比缠绕角度60°和30°的试件，缠绕角度为90°时试件的承载力分别提高了14.0%和24.4%，极限应变分别提高了11.8%和15.1%。因此更多纤维布置在环向能实现更好的受压性能。

图 14 FRP复合材料纤维角度β对FRP复合材料约束UHPC轴压力学性能的影响

Figure 14. Influence of FRP composite fiber winding angle β on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图15为不同FRP复合材料纤维角度时核心UHPC破坏形态，其中β=90°试件如图8所示。可以看出，试件均在中部首先破坏，且纤维角度越小，由等效塑性应变分布和单元删除表征的剪切斜裂缝的发展越显著。这是由于纤维角度越小，试件越接近无约束状态，而无约束UHPC圆柱典型破坏模式即为上下贯通的剪切斜裂缝^[10-11]。

图 15 不同FRP复合材料纤维角度时核心UHPC破坏形态

Figure 15. Failure modes of UHPC core with different FRP composite fiber winding angles

下载: 全尺寸图片幻灯片

3.3 钢纤维掺量对FRP约束UHPC轴压性能的影响

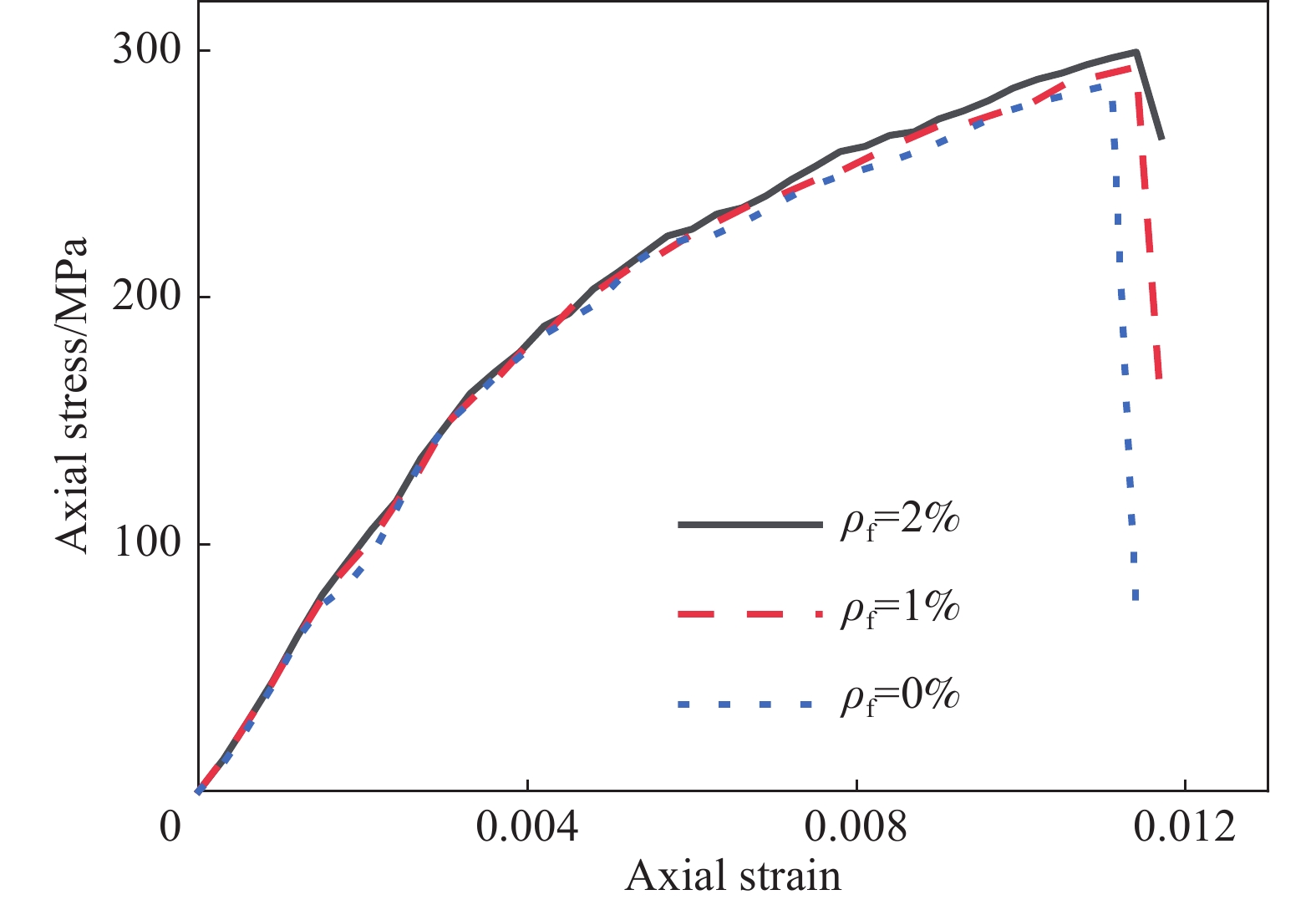
保持UHPC和FRP复合材料参数不变，改变钢纤维掺量(ρ_f=0%、1%、2%)进行参数分析。图16为三种不同钢纤维掺量下FRP复合材料约束UHPC的应力-应变曲线。可以看出，在弹性阶段，三条曲线几乎重合，增大钢纤维掺量对FRP复合材料约束UHPC试件的初始弹性模量影响较小，与未约束UHPC试件规律相同^[22]。但在强化阶段，钢纤维掺量对试件抗压强度和极限应变的影响明显小于其对未约束UHPC试件的影响^[22]。说明在约束状态下，钢纤维桥接裂缝以增韧的作用减弱。

图 16 钢纤维掺量ρ_f对FRP复合材料约束UHPC轴压力学性能的影响

Figure 16. Influence of steel fiber content ρ_f on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

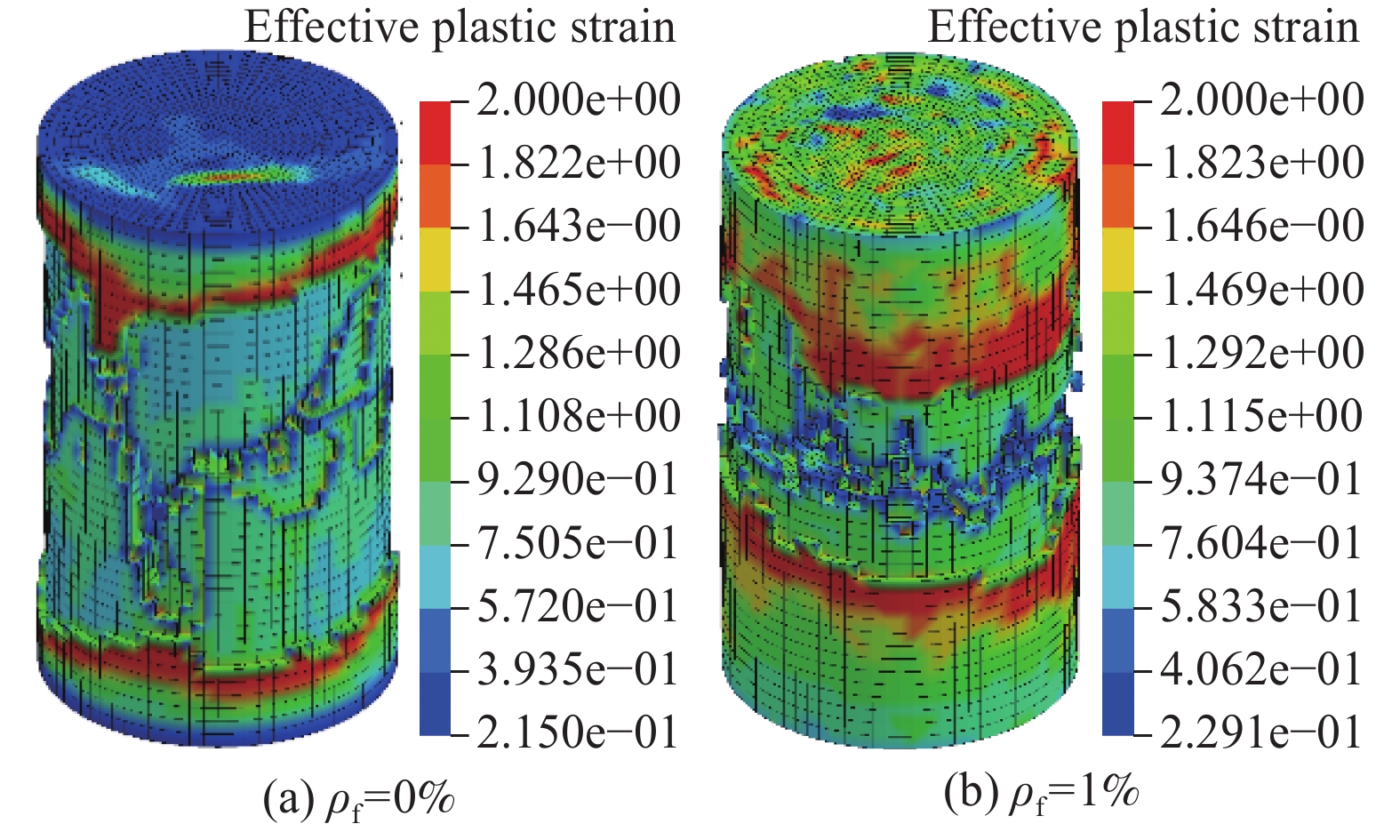
图17为不同钢纤维掺量下核心UHPC破坏形态对比，其中ρ_f=2%试件如图8所示。可以看出，不含钢纤维的试件裂缝呈45°斜向分布，整个试件高度范围内大量混凝土单元达到失效准则而被删除。随着钢纤维掺量增加，在极限荷载时混凝土单元删除的数量减少，且集中在中部区域，说明钢纤维的加入有效限制了剪切斜裂缝的开展。

图 17 不同钢纤维体掺量时核心UHPC破坏形态

Figure 17. Failure modes of UHPC core with different steel fiber contents

下载: 全尺寸图片幻灯片

4. 结论

建立纤维增强树脂(FRP)复合材料约束超高性能混凝土(UHPC)细观有限元模型，并通过现有试验数据验证该模型的正确性，在此基础上，研究各参数对FRP复合材料约束UHPC轴压性能的影响。

(1) 本文所建立的FRP复合材料约束UHPC圆柱细观有限元模型不仅能模拟随机分布钢纤维对试件应力分布的影响，且能较准确反映UHPC受压膨胀后激活的FRP复合材料约束作用对核心UHPC强度和延性的提高效果。模型在轴压作用下的破坏模式和应力-应变曲线与试验结果基本一致，表明了模型的有效性。

(2) 混凝土剪胀参数在FRP复合材料约束混凝土数值模拟中十分重要。与普通混凝土相比，在高约束条件下UHPC并不会出现剪缩现象。本文提出的剪胀参数公式对模拟FRP复合材料约束UHPC试件具有参考意义。

(3) 参数分析结果表明，随着FRP复合材料厚度的增加或FRP复合材料纤维缠绕角度的增大，FRP复合材料约束UHPC圆柱的极限承载力和延性均增大，但钢纤维掺量对试件的受压性能影响较小。

图 1 纤维增强树脂(FRP)复合材料约束超高性能混凝土(UHPC)轴压有限元分析模型

Figure 1. Finite element model of axial compression of fiber reinforced polymer(FRP) composite-confined ultra-high performance concrete(UHPC)

下载: 全尺寸图片幻灯片

图 2 钢纤维生成流程

Figure 2. Generation of steel fibers

下载: 全尺寸图片幻灯片

图 3 剪胀参数ϖ对FRP复合材料约束UHPC轴压力学性能的影响

Figure 3. Influence of shear dilation parameter ϖ on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 4 单元网格高宽比h/b对FRP复合材料约束UHPC轴压力学性能的影响

Figure 4. Influence of aspect ratio h/b of element mesh on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 5 FRP复合材料约束UHPC的模拟与试验应力-应变曲线对比

Figure 5. Comparison of simulation and test stress-strain curves of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 6 文献[8]中GFRP约束UHPC试件典型破坏形态

Figure 6. Typical failure mode of GFRP confined UHPC specimen in Ref. [8]

下载: 全尺寸图片幻灯片

图 7 FRP复合材料约束UHPC受压应力-应变曲线各阶段示意图

Figure 7. Illustration of different stages of stress-strain curves of FRP composite confined UHPC under axial compression

下载: 全尺寸图片幻灯片

图 9 文献[8]中G5试件FRP复合材料环向应力

Figure 9. Hoop stress of FRP composite of specimen G5 in Ref. [8]

下载: 全尺寸图片幻灯片

图 10 文献[8]中G5试件钢纤维轴向应力

Figure 10. Axial stress of steel fibers of specimen G5 in Ref. [8]

下载: 全尺寸图片幻灯片

图 8 文献[8]中G5试件UHPC基体等效塑性应变

Figure 8. Equivalent plastic strain of UHPC matrix of specimen G5 in Ref. [8]

下载: 全尺寸图片幻灯片

图 11 剪胀参数ϖ拟合公式

Figure 11. Fitted equation of shear dilation parameter ϖ

下载: 全尺寸图片幻灯片

图 12 FRP复合材料厚度对FRP复合材料约束UHPC轴压力学性能的影响

Figure 12. Influence of FRP composite thickness on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 13 不同FRP复合材料管厚时核心UHPC破坏形态

Figure 13. Failure modes of UHPC core with different FRP composite tube thicknesses

下载: 全尺寸图片幻灯片

图 14 FRP复合材料纤维角度β对FRP复合材料约束UHPC轴压力学性能的影响

Figure 14. Influence of FRP composite fiber winding angle β on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 15 不同FRP复合材料纤维角度时核心UHPC破坏形态

Figure 15. Failure modes of UHPC core with different FRP composite fiber winding angles

下载: 全尺寸图片幻灯片

图 16 钢纤维掺量ρ_f对FRP复合材料约束UHPC轴压力学性能的影响

Figure 16. Influence of steel fiber content ρ_f on axial compressive behavior of FRP composite confined UHPC

下载: 全尺寸图片幻灯片

图 17 不同钢纤维体掺量时核心UHPC破坏形态

Figure 17. Failure modes of UHPC core with different steel fiber contents

下载: 全尺寸图片幻灯片

表 1 FRP复合材料板力学性能

Table 1 Mechanical properties of FRP composite laminate

Type	Tensile strength/MPa	Elastic modulus/GPa
GFRP	610	26.1
CFRP	850	70.6
Notes: GFRP—Glass fiber reinforced polymer composite; CFRP—Carbon fiber reinforced polymer composite.

下载: 导出CSV

表 2 UHPC本构模型强度面参数

Table 2 Shear failure surfaces parameters of UHPC

a₀	a₁	a₂	a_0f	a_1f	a_1f	a_2f
6.046	0.366	0.00639	2.722	0.813	0.366	0.00639

下载: 导出CSV

表 3 UHPC本构模型损伤演化参数

Table 3 Damage scaling parameters of UHPC

b₁	b₂	b₃
1.60	1.701	1.449

下载: 导出CSV

表 4 FRP复合材料约束UHPC试验数据库

Table 4 Test database for FRP composite confined UHPC

Ref.	Specimen	$f_{\rm{c}}^{'}$ /MPa	E_FRP/GPa	t_FRP/mm	D/mm	E₁/MPa	E₁/ $f_{\rm{c}}^{'}$	ϖ
[8]	G4	189	26.10	4.08	108	986.00	10.43	0.290
[8]	G5	189	26.10	5.10	108	1 972.00	13.04	0.321
[8]	C2	189	70.60	2.04	108	2 465.00	14.11	0.358
[8]	C4	189	70.60	4.08	108	2 667.11	28.22	0.585
[11]	G5	130	41.58	5.07	100	4 158.00	31.98	0.647
[11]	G8	130	41.58	8.05	100	6 652.80	51.17	0.968
Notes: $f_{\rm{c}}^{'}$ —Unconfined strength of UHPC; E_FRP, t_FRP—Elastic modulus and thickness of FRP composite tubes, respectively; D—Diameter of specimens; E₁—Confinement stress provided by FRP composite tubes; ϖ—Shear dilation parameter.

下载: 导出CSV

表 5 FRP复合材料约束UHPC的模拟与试验极限状态对比

Table 5 Comparison of simulation and test ultimate condition of FRP composite confined UHPC

Ref.	Specimen	Strength/MPa		Error/%	Ultimate axial strain		Error /%	Hoop rupture strain		Error /%
Ref.	Specimen	Test	Simulation	Error/%	Test	Simulation	Error /%	Test	Simulation	Error /%
[8]	G4	273.5	279.2	2.07	0.01060	0.0102	3.78	0.0135	0.0148	9.84
[8]	G5	298.9	299.5	0.20	0.01150	0.0114	0.86	0.0140	0.0152	8.30
[8]	C2	254.1	255.0	0.36	0.00680	0.0072	5.87	0.0069	0.0067	3.03
[8]	C4	372.2	366.3	1.59	0.01050	0.0111	5.71	0.0080	0.0072	10.55
[11]	G5	2 634.8	2 558.6	2.89	0.01648	0.0171	3.76	−	−	−
[11]	G8	3 564.3	3 323.8	6.75	0.02105	0.0210	0.19	−	−	−

下载: 导出CSV

参考文献(22)

[1]	郑文忠, 吕雪源. 活性粉末混凝土研究进展[J]. 建筑结构学报, 2015, 36(10):44-58. ZHENG Wenzhong, LV Xueyuan. Literature review of reactive powder concrete[J]. Journal of Building Structures,2015,36(10):44-58(in Chinese).
[2]	梁兴文, 胡翱翔, 于婧, 等. 钢纤维对超高性能混凝土抗弯力学性能的影响[J]. 复合材料学报, 2018, 35(3):722-731. LIANG Xingwen, HU Aoxiang, YU Jing, et al. Effect of steel fibers on the flexural response of ultra-high performance concrete[J]. Acta Materiae Compositae Sinica,2018,35(3):722-731(in Chinese).
[3]	管品武, 涂雅筝, 张普, 等. 超高性能混凝土单轴拉压本构关系研究[J]. 复合材料学报, 2019, 36(5):1295-1305. GUAN Pinwu, TU Yazheng, ZHANG Pu, et al. A review on constitutive relationship of ultra-high performance concrete under uniaxial compression andtension[J]. Acta Materiae Compositae Sinica,2019,36(5):1295-1305(in Chinese).
[4]	SHI C, WU Z, XIAO J, et al. A review on ultra high performance concrete Part Ⅰ: Raw materials and mixture design[J]. Construction and Building Materials,2015,101:741-751. DOI: 10.1016/j.conbuildmat.2015.10.088
[5]	WEI Y Y, WU Y F. Unified stress-strain model of concrete for FRP-confined columns[J]. Construction and Building Materials,2012,26(1):381-392. DOI: 10.1016/j.conbuildmat.2011.06.037
[6]	潘毅, 万里, 吴晓飞, 等. 负载下碳纤维布约束混凝土柱应力-应变关系的有限元分析[J]. 工业建筑, 2015, 45(s2):6-11. PAN Yi, WAN Li, WU Xiaofei, et al. Finite element analysis of the axial stress-strain relationship of concrete columns confined by CFRP under preload[J]. Industrial Construction,2015,45(s2):6-11(in Chinese).
[7]	YU T, ZHANG B, TENG J G. Unified cyclic stress-strain model for normal and high strength concrete confined with FRP[J]. Engineering Structures,2015,102:189-201. DOI: 10.1016/j.engstruct.2015.08.014
[8]	ZOHREVAND P, MIRMIRAN A. Behavior of ultrahigh-performance concrete confined by fiber-reinforced polymers[J]. Journal of Materials in Civil Engineering,2011,23(12):1727-1734. DOI: 10.1061/(ASCE)MT.1943-5533.0000324
[9]	GULER S. Axial behavior of FRP-wrapped circular ultra-high performance concrete specimens[J]. Structural Engineering & Mechanics,2014,50(6):709-722.
[10]	WANG W Q, WU C Q, LIU Z X, et al. Compressive behavior of ultra-high performance fiber-reinforced concrete (UHPFRC) confined with FRP[J]. Composite Structures,2018,204:419-437. DOI: 10.1016/j.compstruct.2018.07.102
[11]	田会文, 周臻, 陆纪平, 等. 钢纤维掺量对FRP管约束超高性能混凝土轴压性能的影响[J]. 东南大学学报(自然科学版), 2019, 49(3):481-487. DOI: 10.3969/j.issn.1001-0505.2019.03.011 TIAN Huiwen, ZHOU Zhen, LU Jiping, et al. Effects of steel fiber content on axial compression performance of UHPC filled FRP tubes[J]. Journal of Southeast University (Natural Science Edition),2019,49(3):481-487(in Chinese). DOI: 10.3969/j.issn.1001-0505.2019.03.011
[12]	金浏, 杜修力. 钢筋混凝土构件细观数值模拟分析[J]. 水利学报, 2012, 43(10):1230-1236. JIN Liu, DU Xiuli. Meso numerical simulation of reinforced concrete members[J]. Journal of Hydraulic Engineering,2012,43(10):1230-1236(in Chinese).
[13]	XU Z, HAO H, LI H N. Mesoscale modelling of fibre reinforced concrete material under compressive impact loading[J]. Construction and Building Materials,2012,26(1):274-288. DOI: 10.1016/j.conbuildmat.2011.06.022
[14]	LIANG X, WU C. Meso-scale modelling of steel fibre reinforced concrete with high strength[J]. Construction and Building Materials,2018,165:187-198. DOI: 10.1016/j.conbuildmat.2018.01.028
[15]	赵秋山, 徐慎春, 刘中宪. 钢纤维增强超高性能混凝土抗压性能的细观数值模拟[J]. 复合材料学报, 2018, 35(6):1661-1673. ZHAO Qiushan, XU Shenchun, LIU Zhongxian. Microscopic numerical simulation of the uniaxial compression of steel fiber reinforced ultra-high performance concrete[J]. Acta Materiae Compositae Sinica,2018,35(6):1661-1673(in Chinese).
[16]	XU S, WU C, LIU Z, et al. Numerical study of ultra-high-performance steel fibre-reinforced concrete columns under monotonic push loading[J]. Advances in Structural Engineering,2018,21(8):1234-1248. DOI: 10.1177/1369433217747710
[17]	ELSANADEDY H M, AL-SALLOUM Y A, ALSAYED S H, et al. Experimental and numerical investigation of size effects in FRP-wrapped concrete columns[J]. Construction and Building Materials,2012,29:56-72. DOI: 10.1016/j.conbuildmat.2011.10.025
[18]	FERROTTO M F, FISCHER O, CAVALERI L. A strategy for the finite element modeling of FRP-confined concrete columns subjected to preload[J]. Engineering Structures,2018,173:1054-1067. DOI: 10.1016/j.engstruct.2018.07.047
[19]	WU Y, CRAWFORD J E. Numerical modeling of concrete using a partially associative plasticity model[J]. Journal of Engineering Mechanics,2015,141(12):04015051. DOI: 10.1061/(ASCE)EM.1943-7889.0000952
[20]	XU M, WILLE K. Calibration of K&C concrete model for UHPC in LS-DYNA[J]. Advanced Materials Research,2015,1081:254-259.
[21]	YOUSSF O, ELGAWADY M A, MILLS J E, et al. Finite element modelling and dilation of FRP-confined concrete columns[J]. Engineering Structures,2014,79:70-85. DOI: 10.1016/j.engstruct.2014.07.045
[22]	WU Z, SHI C, HE W, et al. Effects of steel fiber content and shape on mechanical properties of ultra high performance concrete[J]. Construction and Building Materials,2016,103:8-14. DOI: 10.1016/j.conbuildmat.2015.11.028

施引文献(21)

期刊类型引用(12)

1.	朱昌星，吴大志，孙家鑫. 碳纤维增韧注浆体试块动态压缩力学特性及其数值模拟. 中国矿业大学学报. 2024(03): 600-612 . 百度学术
2.	张景杭，夏樟华，姜绍飞，洪俊贤，朱朴，范千. BFRP模壳不排水加固RC墩柱恢复力模型. 振动与冲击. 2024(16): 192-203 . 百度学术
3.	马恺泽，韩潇，何腾伟，白景柱. FRP约束UHPC圆形短柱轴心受压性能研究. 西南交通大学学报. 2024(05): 1132-1139 . 百度学术
4.	游俊，李峰. 单丝20 mm碳纤维含量对CFRC梁抗弯性能的影响试验. 混凝土. 2023(05): 124-127+133 . 百度学术
5.	李庆文，禹萌萌，刘艺伟，曹行，高森林，聂帆帆，李玲. GFRP布被动约束标准煤矸石混凝土圆柱轴压性能细观模拟. 硅酸盐通报. 2023(07): 2458-2471 . 百度学术
6.	李庆文，曾杏钢，张向东，禹萌萌，刘艺伟，曹行. 碳纤维布层数对煤圆柱力学特性影响的细观研究. 煤炭科学技术. 2023(08): 73-85 . 百度学术
7.	郭润兰，范雅琼，王广书，史方青，黄华. 基于PFC~(3D)的机床床身用树脂矿物复合材料损伤性能细观研究. 复合材料学报. 2022(02): 834-844 . 本站查看
8.	赵伟，李峰. 不同量16mm碳纤维增强混凝土梁落锤冲击试验. 高科技纤维与应用. 2022(02): 17-21 . 百度学术
9.	中国桥梁工程学术研究综述·2021. 中国公路学报. 2021(02): 1-97 . 百度学术
10.	胡良鹏，陈徐东，董文. 不同骨料粒径刚玉球混凝土力学特性与细观破坏机理. 混凝土. 2021(10): 70-75 . 百度学术
11.	高轩晋. 新型复合材料在混凝土中的应用研究. 造纸装备及材料. 2021(10): 31-33 . 百度学术
12.	张霓，郑晨阳，羡丽娜，王连广. 玻璃纤维增强树脂复合材料管-钢筋/混凝土空心构件抗弯性能. 复合材料学报. 2020(12): 3052-3063 . 本站查看