Failure strength prediction of composite laminates using 3D damage constitutive model with nonlinear shear effects
-
摘要: 基于连续损伤力学,建立了同时考虑复合材料剪切非线性效应和损伤累积导致材料属性退化的三维损伤本构模型。模型能够区分纤维损伤、基体损伤和分层损伤不同的失效模式,并定义了相应损伤模式的损伤变量。复合材料层合板层内纤维初始损伤采用最大应力准则判定,基体初始损伤采用三维Puck准则中的基体失效准则判定,分层初始损伤采用三维Hou准则中的分层破坏准则判定,为了计算Puck失效理论中的基体失效断裂面角度,本文提出了分区抛物线法,通过Matlab软件编写计算程序并进行分析。结果表明,与Puck遍历法和分区黄金分割法对比,本文提出的分区抛物线法有效地降低了求解断裂面角度的计算次数,提高了计算效率和计算精度。推导了本构模型的应变驱动显式积分算法以更新应力和解答相关的状态变量,开发了包含数值积分算法的用户自定义子程序VUMAT,并嵌于有限元程序Abaqus v6.14中。通过对力学行为展现显著非线性效应的AS4碳纤维/3501-6环氧树脂复合材料层合板进行渐进失效分析,验证了本文提出的材料本构模型的有效性。结果显示,已提出的模型能够较准确地预测此类复合材料层合板的力学行为及其失效强度,为复合材料构件及其结构设计提供一种有效的分析方法。Abstract: Based on the continuum damage mechanics, a 3D damage constitutive model which takes into account the nonlinear shear behavior of composites and material properties degradation due to damage development was proposed. The model differentiates between different failure modes, such as fiber failure mode, matrix failure mode and delamination. The damage variables corresponding to each failure mode were defined. The onsets of fiber damage, matrix damage and delamination of composite laminates were predicted using maximum stress failure criteria, Puck’s matrix failure criteria and Hou’s delamination criteria, respectively. In order to predict the angle of fracture surface in Puck’s matrix fracture failure theory, a selective parabola algorithm was proposed and coded using Matlab procedure. Compared with the Puck’s algorithm and the selective range golden section search algorithm, it shows that the selective parabola algorithm effectively reduces the number of calculations and improves the calculation efficiency and accuracy. A strain-driven explicit integration algorithm for the proposed material constitutive model was developed to update stresses and solution dependent state variables. The user-defined material subroutine VUMAT containing the numerical integration algorithm was coded and implemented in the finite element procedure Abaqus v6.14. The efficiency of the material constitutive model was demonstrated through progressive failure analyses of AS4 carbon fiber/3501-6 epoxy composite laminates, the mechanical behavior of which demonstrates significant nonlinear shear effects. The numerical results show that the proposed model is able to predict the mechanical behavior and failure strength of composites with sufficient accuracy. The proposed approach provides an efficient method for the design of composite components and structures.
-
表 1 三种典型的三维应力状态及材料参数
Table 1. Typical 3D stress states and material properties
Material property Stress state ${\sigma _2}$/
MPa${\sigma _3}$/
MPa${\tau _{12}}$/
MPa${\tau _{13}}$/
MPa${\tau _{23}}$/
MPa$R_ {\bot} ^{\rm{t}}/{\rm{MPa}}$ 25 Case 1 0 0 0 0 59.1 $R_ {\bot} ^{\rm{c}}/{\rm{MPa}}$ 120 Case 2 −231.2 0 0 0 0 $R_{ \bot \parallel }^{\rm{A}}/{\rm{MPa}}$ 70 Case 3 34.0 −87.0 22.0 46.0 29.0 Notes: $R_ {\bot} ^{\rm{t}}$, $R_ {\bot} ^{\rm{c}}$—Tensile strength and compressive strength in the transverse direction,respectively; $R_{ \bot \parallel }^{\rm{A}}$—Strength of the fracture plane against failure due to longitudinal shear stress; ${\sigma _2}$, ${\sigma _3}$—Normal stresses in the transverse and through-thickness directions, respectively; ${\tau _{12}}$, ${\tau _{13}}$, ${\tau _{23}}$—Shear stresses for the 1-2, 1-3, 2-3 plane, respectively. 表 2 三种典型三维应力状态下断裂角计算精度和计算效率对比
Table 2. Comparison of accuracy and efficiency for fracture angle calculation under three typical 3D stress states
Stress state Precision/(°) Theoretical
solution/(°)Puck’s algorithm[11] SRGSS[16] Proposed method θ/(°) N T/s θ/(°) N T/s θ/(°) N T/s Case 1 1 45.000 45.0 180 0.437 44.854 24 0.107 45.000 19 0.101 0.1 45.0 1 800 4.160 44.985 29 0.148 45.000 19 0.101 Case 2 1 ±51.137 51.0 180 0.428 51.245 31 0.109 51.044 21 0.104 0.1 51.1 1 800 4.162 51.145 41 0.151 51.044 21 0.104 Case 3 1 14.901 15.0 180 0.432 14.854 38 0.112 14.974 23 0.107 0.1 14.9 1 800 4.187 14.916 53 0.156 14.974 23 0.107 Notes: θ—Fracture angle; N—Number of state points; T—Calculated time by different search methods; SRGSS—Selective range golden section search algorithm. 表 3 AS4碳纤维/3501-6环氧树脂复合材料单向板材料属性
Table 3. Material properties of unidirectional AS4 carbon fiber/3501-6 epoxy composite laminate
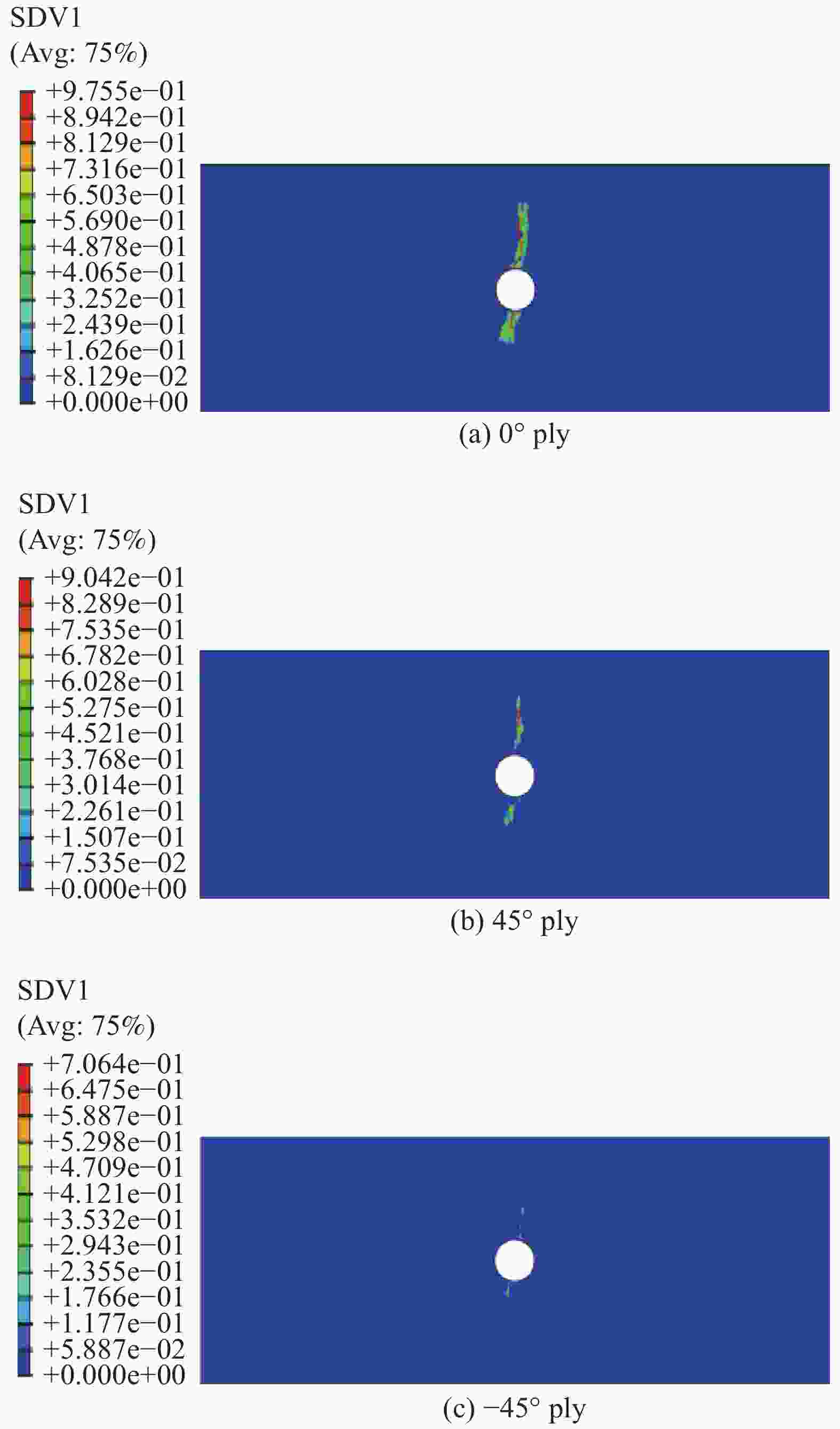
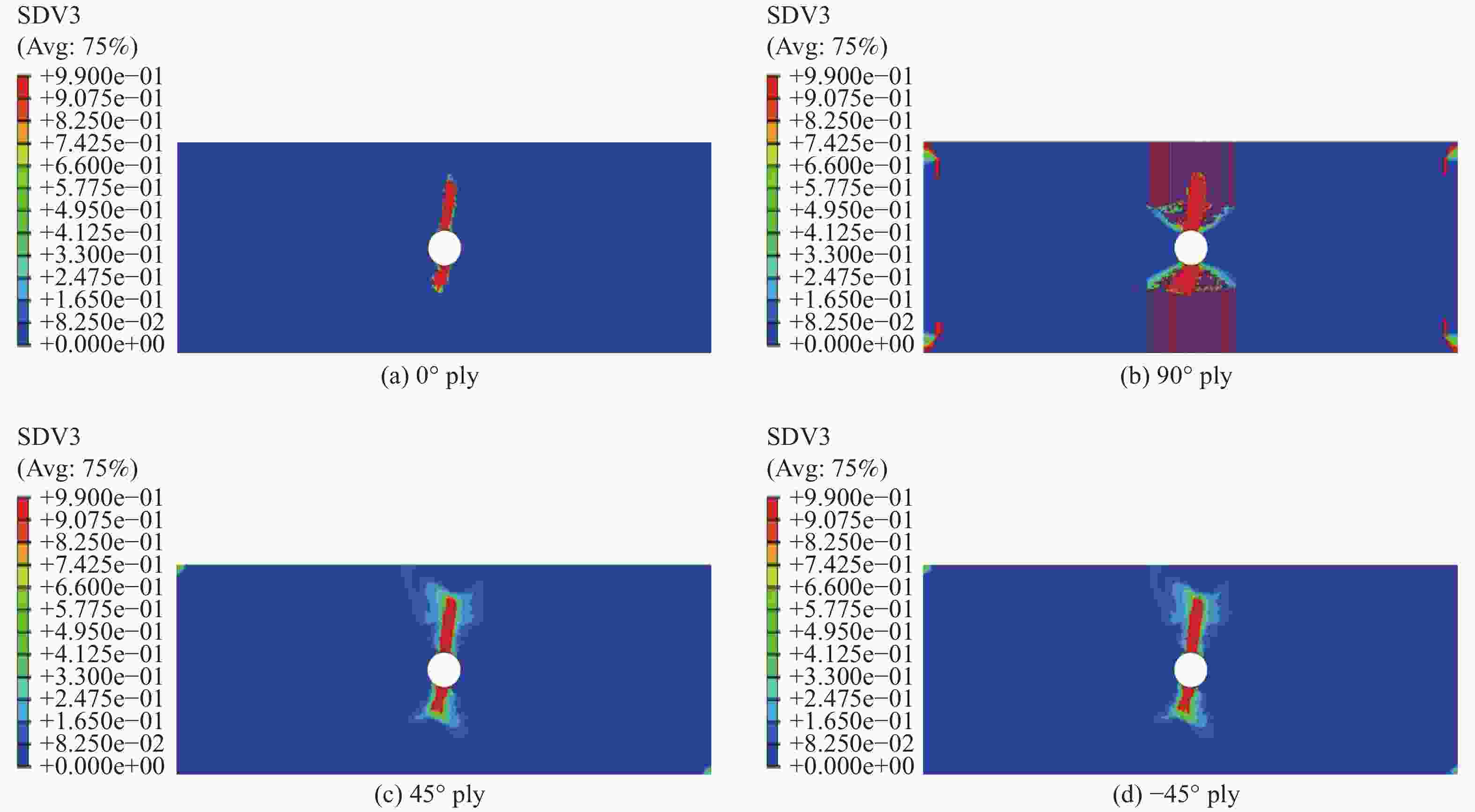
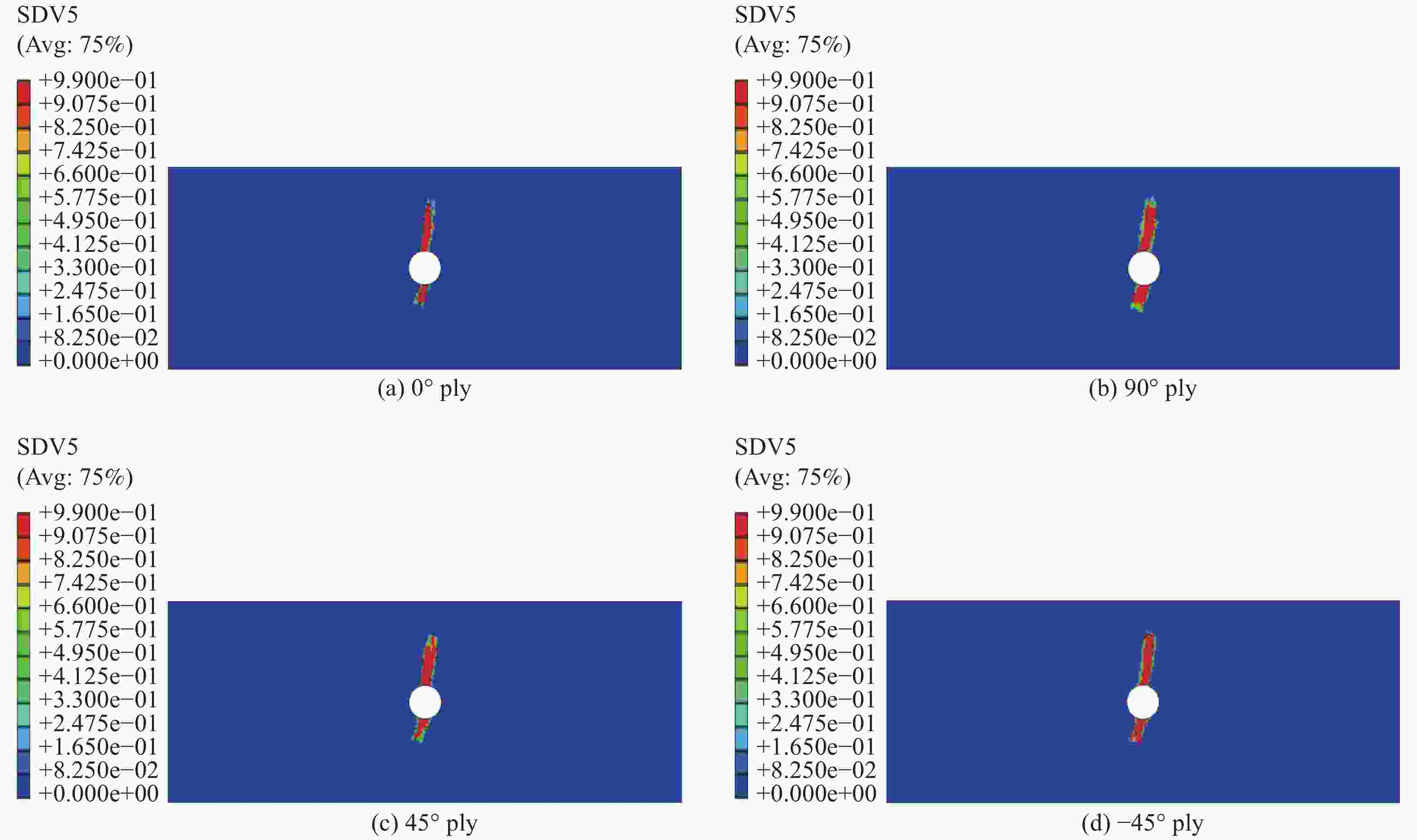
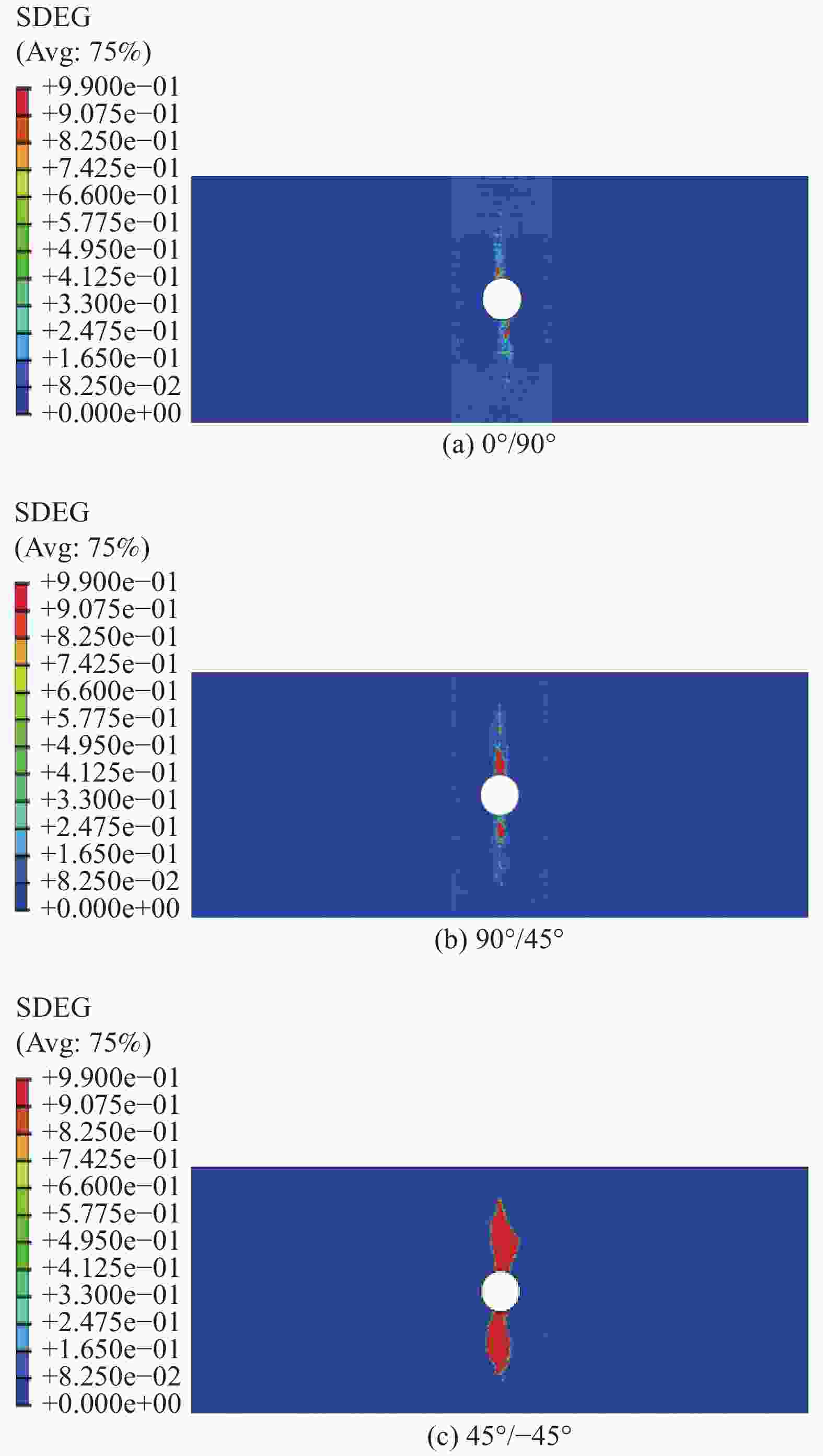
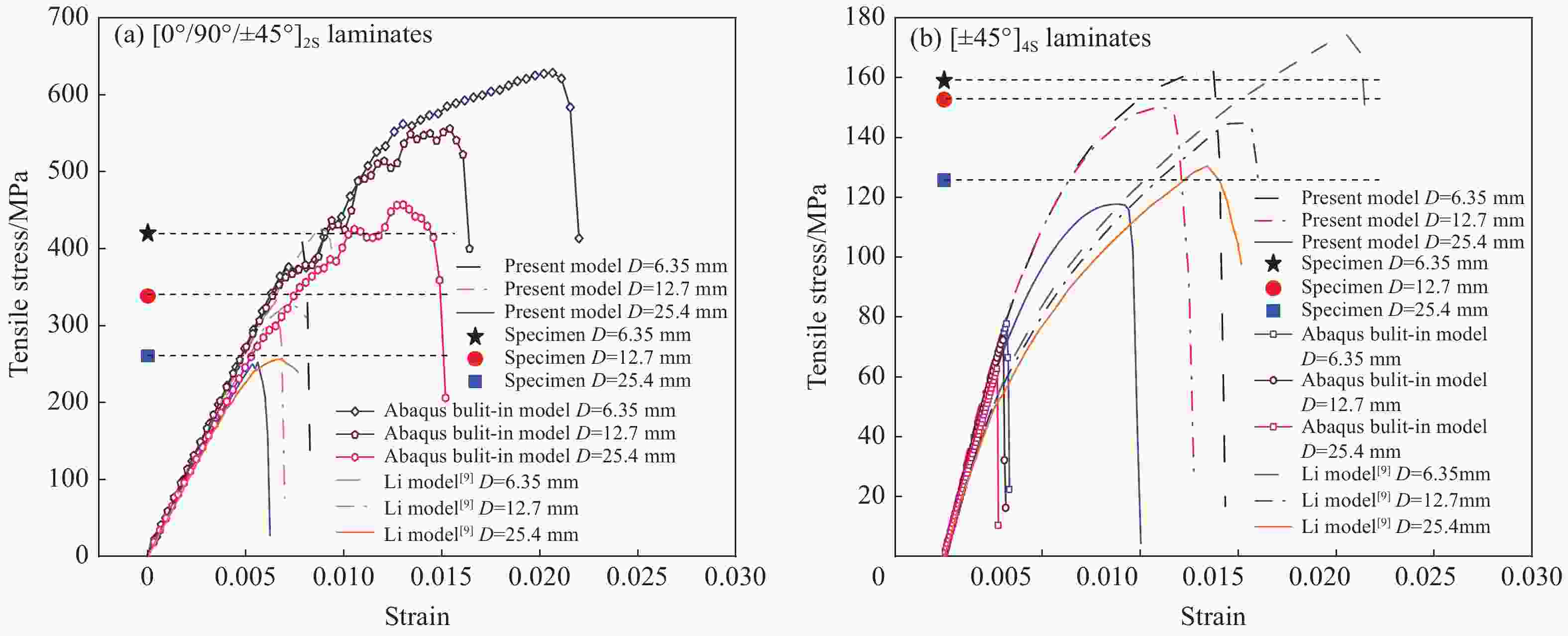
$\begin{aligned}&{E_1}/{\rm{GPa}}\end{aligned}$ $\begin{aligned}&{E_2} = {E_3}/{\rm{GPa}}\end{aligned}$ $\begin{aligned}&{S_{{\rm{fc}}}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}&{S_{{\rm{ft}}}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}&{G_{12}} = {G_{13}}/{\rm{GPa}}\end{aligned}$ $\begin{aligned}&{G_{23}}/{\rm{GPa}}\end{aligned}$ $\begin{aligned}{\nu _{23}}\end{aligned}$ 138 10.1 1690 1450 7.0 1.57 0.34 $\begin{aligned}{\nu _{12}} = {\nu _{13}}\end{aligned}$ $\begin{aligned}R_ {\bot} ^{\rm{t}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}R_ {\bot} ^{\rm{c}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}{S_{{\rm{zt}}}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}{S_{{\rm{zc}}}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}{S_{13}} = {S_{23}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}A\end{aligned}$ 0.29 65 285 65 285 81 1.3 $\begin{aligned}R_{ \bot \parallel }^{\rm{A}}/{\rm{MPa}}\end{aligned}$ $\begin{aligned}{G_{{\rm{ft}}}}\end{aligned}$/(N·mm−1) $\begin{aligned}{G_{{\rm{fc}}}}\end{aligned}$/(N·mm−1) $\begin{aligned}{G_{ {\simfont\text{Ⅰ} }\!\!\!{\rm{C} } } }\end{aligned}$/(N·mm−1) $\begin{aligned}{G_{ {\simfont\text{Ⅱ} }\!\!{\rm{C} } } }\end{aligned}$/(N·mm−1) ${G_{ {\simfont\text{Ⅲ} } {\rm{C} } } }$/(N·mm−1) 81 220.6 220.6 0.22 0.65 0.65 Notes: $\begin{aligned}{E_1}\end{aligned}$, $\begin{aligned}{E_2}\end{aligned}$, $\begin{aligned}{E_3}\end{aligned}$—Elastic moduli in the fiber, transverse and through-thickness directions; $\begin{aligned}{S_{{\rm{fc}}}}\end{aligned}$, $\begin{aligned}{S_{{\rm{ft}}}}\end{aligned}$—Tensile strength and compressive strength in the fiber direction; $\begin{aligned}{S_{{\rm{zt}}}}\end{aligned}$, $\begin{aligned}{S_{{\rm{zc}}}}\end{aligned}$— Tensile and compressive strengths in the through-thickness directions; $\begin{aligned}{\nu _{ij}}\end{aligned}$, $\begin{aligned}{G_{ij}}\end{aligned}$(ij=12, 13, 23)—Poisson’s ratios and shear moduli for 1-2, 1-3, 2-3 plane, respectively; $\begin{aligned}{S_{13}}\end{aligned}$, $\begin{aligned}{S_{23}}\end{aligned}$—Shear strengths for 1-3 and 2-3 planes; $\begin{aligned}{G_{{\rm{ft}}}}\end{aligned}$ and $\begin{aligned}{G_{{\rm{fc}}}}\end{aligned}$—Tensile and compressive fracture energies in the fiber direction; $\begin{aligned}{G_{ {\simfont\text{Ⅰ} }\!\!\!{\rm{C} } } }\end{aligned}$, $\begin{aligned}{G_{ {\simfont\text{Ⅱ} }\!\!{\rm{C} } } }\end{aligned}$, $\begin{aligned}{G_{ {\simfont\text{Ⅲ} }{\rm{C} } } }\end{aligned}$—Fracture energies for mode Ⅰ, Ⅱ and Ⅲ in the through-thickness direction, respectively; A—Parameter in the Soutis’ formula related to the composite material. 表 4 [0°/90°/±45°]2S及[±45°]4S带孔层合板拉伸破坏强度预测值与试验结果对比
Table 4. Comparison between predicted and experimental tensile failure strengths of [0°/90°/±45°]2S and [±45°]4S composite laminates
Lay-up D/
mmTest value/
MPaPresent model Li model[9] Abaqus built-in model Predicted
value/MPaError/
%Predicted
value/MPaError/
%Predicted
value/MPaError/
%6.35 420±25 416 −1.0 426 1.4 629 49.8 [0°/90°/±45°]2S 12.70 340±13 338 −0.6 352 3.5 557 63.8 25.40 262±3 253 −3.4 256 −2.3 458 74.8 6.35 159±7 163 2.5 174 9.4 78 −50.9 [±45°]4S 12.70 153±7 150 −2.0 148 −3.2 74 −51.6 25.40 126±2 118 −6.3 130 3.2 63 −50.0 -
[1] LAFARIE-FRENOT M C, TOUCHARD F. Comparative in-plane shear behaviour of long-carbon-fibre composites with thermoset or thermoplastic matrix[J]. Composites Science and Technology,1994,52(3):417-425. doi: 10.1016/0266-3538(94)90176-7 [2] CARLSSON L A, ARONSSON C G, BÄCKLUND J. Notch sensitivity of thermoset and thermoplastic laminates loaded in tension[J]. Journal of Materials Science,1989,24(5):1670-1682. doi: 10.1007/BF01105690 [3] CHANG F K, LESSARD L B. Damage tolerance of laminated composites containing an open hole and subjected to compressive loadings Part I: Analysis[J]. Journal of Composite Materials,1991,25(1):2-43. doi: 10.1177/002199839102500101 [4] TAN S C. A progressive failure model for composite laminates containing openings[J]. Journal of Composite Materials,1991,25(5):556-577. doi: 10.1177/002199839102500505 [5] MATZENMILLER A, LUBLINER J, TAYLOR R L. A constitutive model for anisotropic damage in fiber-composites[J]. Mechanics of Materials,1995,20(2):125-152. doi: 10.1016/0167-6636(94)00053-0 [6] 龙舒畅. 含初始缺陷复合材料的低速冲击损伤与剩余强度研究[D]. 广州: 华南理工大学, 2014.LONG S C. The research on low energy impact damage and residual strength of composites with initial imperfection[D]. Guangzhou: South China University of Technology, 2014(in Chinese). [7] 李力, 黄哲峰, 杨增钦, 等. 基于三维Puck失效准则及唯象模量退化的复合材料臂杆屈曲分析[J]. 复合材料学报, 2019, 36(2):42-52.LI L, HUANG Z F, YANG Z Q, et al. Bulking analysis of composite arm based on 3D Puck failure criterion and phenomenological modulus degradation method[J]. Acta Materiae Compositae Sinica,2019,36(2):42-52(in Chinese). [8] 吴义韬, 姚卫星, 吴富强. 复合材料层合板面内渐进损伤分析的CDM模型[J]. 力学学报, 2014, 46(1):94-104. doi: 10.6052/0459-1879-13-106WU Y T, YAO W X, WU F Q. CDM model for intarlaminar progressive damage analysis of composite laminates[J]. Chinese Journal of Theoretical and Applied Mechanics,2014,46(1):94-104(in Chinese). doi: 10.6052/0459-1879-13-106 [9] 李秋漳, 姚卫星, 陈方. 复合材料层合板缺口强度的CDM三维数值模型[J]. 复合材料学报, 2016, 33(12):2766-2774.LI Q Z, YAO W X, CHEN F. CDM three-dimensional numerical model for notched strength of composite laminates[J]. Acta Materiae Compositae Sinica,2016,33(12):2766-2774(in Chinese). [10] PAUL B. A modification of the Coulomb-Mohr theory of fracture[J]. Journal of Applied Mechanics,1961,28(2):259-268. doi: 10.1115/1.3641665 [11] PUCK A, SCHRMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models[M]//HINTON M J, KADDOUR A S, SODEN P D. Failure criteria in fibre-reinforced-polymer composites. Oxford: Elsevier, 2004: 832-876. [12] DEUSCHLE H M, KRÖPLIN B H. Finite element implementation of Puck’s failure theory for fibre-reinforced composites under three-dimensional stress[J]. Journal of Composite Materials,2012,46(19-20):2485-2513. doi: 10.1177/0021998312451480 [13] XIAO X R. Modeling energy absorption with a damage mechanics based composite material model[J]. Journal of Composite Materials,2009,43(5):427-444. doi: 10.1177/0021998308097686 [14] PINHO S T, IANNUCCI L, ROBINSON P. Physically-based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking Part I: Development[J]. Composites Part A: Applied Science and Manufacturing,2006,37(1):63-73. [15] WIEGAND J, PETRINIC N, ELLIOTT B. An algorithm for determination of the fracture angle for the three-dimensional Puck matrix failure criterion for UD composites[J]. Composites Science and Technology,2008,68(12):2511-2517. doi: 10.1016/j.compscitech.2008.05.004 [16] SCHIRMAIER F J, WEILAND J, KÄRGER L, et al. A new efficient and reliable algorithm to determine the fracture angle for Puck’s 3D matrix failure criterion for UD composites[J]. Composites Science and Technology,2014,100:19-25. doi: 10.1016/j.compscitech.2014.05.033 [17] HOU J P, PETRINIC N, RUIZ C. A delamination criterion for laminated composites under low-velocity impact[J]. Composites Science and Technology,2001,61(14):2069-2074. [18] CHANG F K, CHANG K Y. A progressive damage model for laminated composites containing stress concentrations[J]. Journal of Composite Materials,1987,21(9):834-855. doi: 10.1177/002199838702100904 [19] DEUSCHLE H M, PUCK A. Application of the Puck failure theory for fibre-reinforced composites under three-dimensional stress: Comparison with experimental results[J]. Journal of Composite Materials,2013,47(6-7):827-846. doi: 10.1177/0021998312462158 [20] 贾利勇, 廖斌斌, 于龙, 等. 基于Puck理论的复合材料层合板横向剪切失效分析[J]. 复合材料学报, 2019, 36(10):2286-2293.JIA L Y, LIAO B B, YU L, et al. Failure analysis of composite laminates with Puck’s theory under transverse shear load[J]. Acta Materiae Compositae Sinica,2019,36(10):2286-2293(in Chinese). [21] BAŽANT Z P, OH B H. Crack band theory for fracture of concrete[J]. Matériaux et Construction,1983,16(3):155-177. doi: 10.1007/BF02486267 [22] DEUSCHLE H M. 3D failure analysis of UD fibre reinforced composites: Puck’s theory within FEA[D]. Stuttgart: University of Stuttgart, 2010. [23] CHEN J F, MOROZOV E V, SHANKAR K. Simulating progressive failure of composite laminates including in-ply and delamination damage effects[J]. Composites Part A: Applied Science and Manufacturing,2014,61:185-200. doi: 10.1016/j.compositesa.2014.02.013 [24] 李彪. 基于失效机理的复合材料层合板强度分析方法[D]. 西安: 西北工业大学, 2015.LI B. Failure mechanism based strength analysis method for laminated composites[D]. Xi’an: Northwestern Polytechnical University, 2015(in Chinese). [25] SHI Y, SWAIT T, SOUTIS C. Modelling damage evolution in composite laminates subjected to low velocity impact[J]. Composite Structures,2012,94(9):2902-2913. doi: 10.1016/j.compstruct.2012.03.039 [26] 罗鹏. 含率相关非线性剪切关系的复合材料损伤模型[D]. 广州: 暨南大学, 2018.LUO P. Composite material damage model including strain rate-dependent nonlinear shear stress strain relationship[D]. Guangzhou: Jinan University, 2018(in Chinese). [27] DANIEL I M, WERNER B T, FENNER J S. Strain-rate-dependent failure criteria for composites[J]. Composites Science and Technology,2011,71(3):357-364. doi: 10.1016/j.compscitech.2010.11.028 [28] 陈静芬. 基于弹塑性损伤本构模型的复合材料层合板破坏荷载预测[J]. 复合材料学报, 2017, 34(4):545-557.CHEN J F. Failure loads prediction of composite laminates using a combined elastoplastic damage model[J]. Acta Materiae Compositae Sinica,2017,34(4):545-557(in Chinese). -






 下载:
下载: