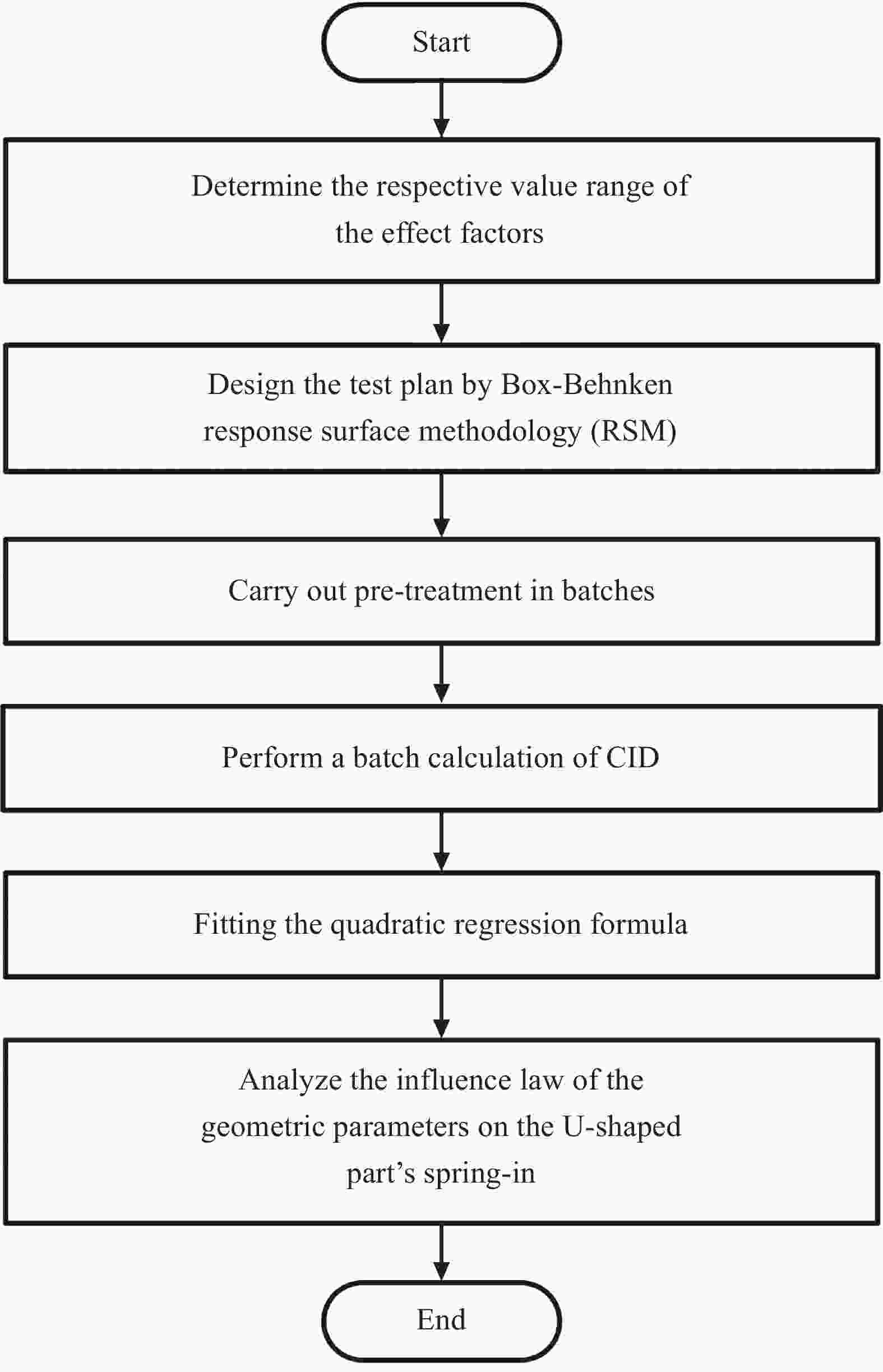
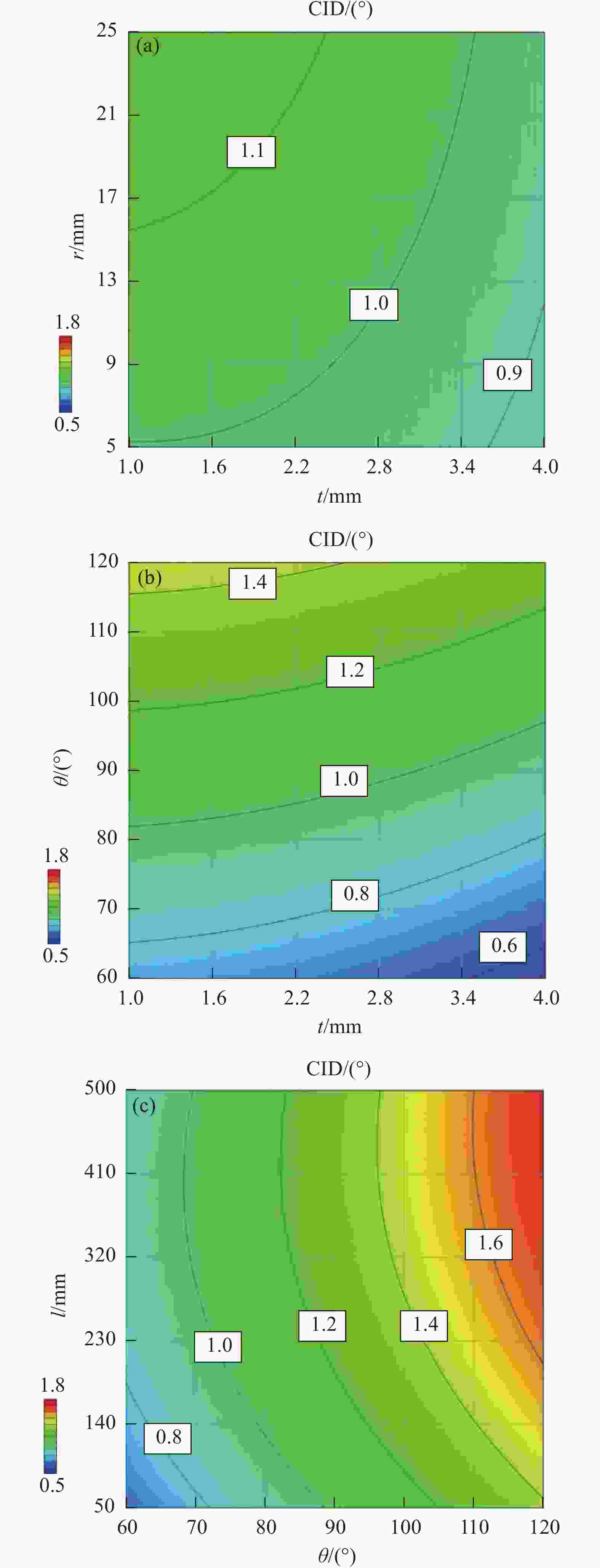
Prediction and analysis of cure-induced deformation of composite U-shaped parts with variable thickness
-
摘要: 为了准确预测变厚度CCF800H/AC531碳纤维/环氧树脂复合材料U型零件的固化变形，并分析弯边以及变厚区参数对变形的影响。首先，利用自洽方法确定了单层复合材料力学性能，采用细观有限元方法预测了层合板的整体性能以避免仿真建模时复杂的铺层设置。而后结合固化硬化瞬时线弹性模型建立了零件的固化变形预测方法并进行了验证。变厚区对相邻区域的变形的影响规律由变厚区结构参数确定，与铺层方式和材料种类无关。运用Box-Behnken响应面方法，拟合了两个二次模型以分析弯边参数和变厚度结构参数对固化变形的影响规律。变厚区对较薄区域的影响较大，变形最大减小幅度达15%，而对较厚区域的影响可以忽略。采用方差分析比较了不同因素的影响，变厚区的宽度变化对变形的影响较小。当截面距变厚区的距离大于150 mm时，变厚区对较薄区域的影响接近为0。Abstract: The micromechanics and the finite element analysis method (FEA) were used to predict the cure-induced deformation (CID) of CCF800H/AC531 carbon fiber/epoxy composite U-shaped parts with variable thickness. The effects of flange and various thickness area parameters on CID were studied by response surface methodology (RSM). The material properties of unidirectional composite were determined by self-consistent method, and the equivalent properties of laminates were calculated by FEA based micromechanical model to avoid the complex layer division and direction definition of the numerical model. The CID of U-shaped parts was predicted by the curing hardening instantaneous linear elastic model (CHILE). A case part was manufactured to verify the accuracy of the FEA. It can be found that the lay-ups and material types have no influence on the law of variable thickness area’s effect on adjacent areas. Then two plans were designed by the Box-Behnken RSM method to analyze the influence of flange parameters and variable thickness area parameters, and two quadratic regression models were fitted, respectively. The investigation reveals that the variable thickness area greatly influences the thinner area, with a maximum reduction of CID of about 15%. The variable thickness area has little effect on the thicker area. Besides, the CID is unaffected by the width of the variable thickness area. The variable thickness area has no effect on the CID of a cross section if it is 150 mm or more away from the cross section.
-
图 1 变厚度U型零件的结构参数与固化变形(CID)
Figure 1. Geometric parameters and cure-induced deformation (CID) of variable thickness U-shaped part
图 2 变厚度U型零件残余应力的累计与释放
Figure 2. Stress accumulation and release of variable thickness U-shaped part
图 3 变厚度U型零件的CID：(a) 剪切模量很小；(b) 剪切模量很大
Figure 3. CID of variable thickness U-shaped part: (a) Shear modulus stiff; (b) Shear modulus flexible
图 4 变厚度U型零件弯边CID：(a) 变厚度弯边；(b) 由A点到B点的CID示意图
Figure 4. Flange’s CID of variable thickness U-shaped part: (a) Flange with a variable thickness area; (b) CID schematic diagram from A to B
图 6 层合板截面属性的赋予：(a) 铺层划分与单层方向定义；(b) 等效性能的赋予
Figure 6. Definition of section properties of laminates: (a) Layer division and direction definition; (b) Definition of equivalent properties
图 7 代表性体积单元(RVE)的有限元模型
Figure 7. Finite element model of representative volume element (RVE)
图 8 进行等效性能预测时RVE的位移云图
Figure 8. Displacement cloud maps of RVE for different equivalent properties
图 9 变厚度U型零件不同厚度区域的网格划分与组装
Figure 9. Meshing and assembling elements of variable thickness U-shaped part
图 10 变厚度U型零件固化变形变厚区仿真边界条件
Figure 10. Constraints on the variable thickness area of variable thickness U-shaped part
图 11 变厚度U型件每个截面脱模前后施加的边界条件
Figure 11. Constraints applied to each cross-section of variable thickness U-shaped part before and after curing
图 12 变厚度U型零件CID计算：(a)仿真结果；(b)变形角度
Figure 12. Calculation of CID of variable thickness U-shaped part: (a) FEA result; (b) Spring-in angle
U—Displacement
图 14 变厚度U型零件CID试验值与预测值：(a)弯边1；(b)弯边2
Figure 14. Experimental and predicted CID data for the variable thickness U-shaped part: (a) Flange 1; (b) Flange 2
图 15 不同铺层的变厚度U型零件的CID
Figure 15. CID data for the variable thickness U-shaped parts with different lay-ups
图 16 不同材料的变厚度U型零件的CID
Figure 16. CID data for the variable thickness U-shaped parts with different materials
图 17 Box-Behnken响应面方法设计点
Figure 17. Design points of Box-Behnken response surface methodology
图 19 等厚度U型零件各弯边参数对CID影响的等高云图：(a) 厚度(t)和半径(r)；(b) t和角度(θ)；(c) θ和弯边长度(l)
Figure 19. Contour plot of the influence of flange parameters on CID of equal thickness U-shaped parts: (a) Thickness (t) and radius (r); (b) t and flange angle (θ); (c) θ and flange length (l)
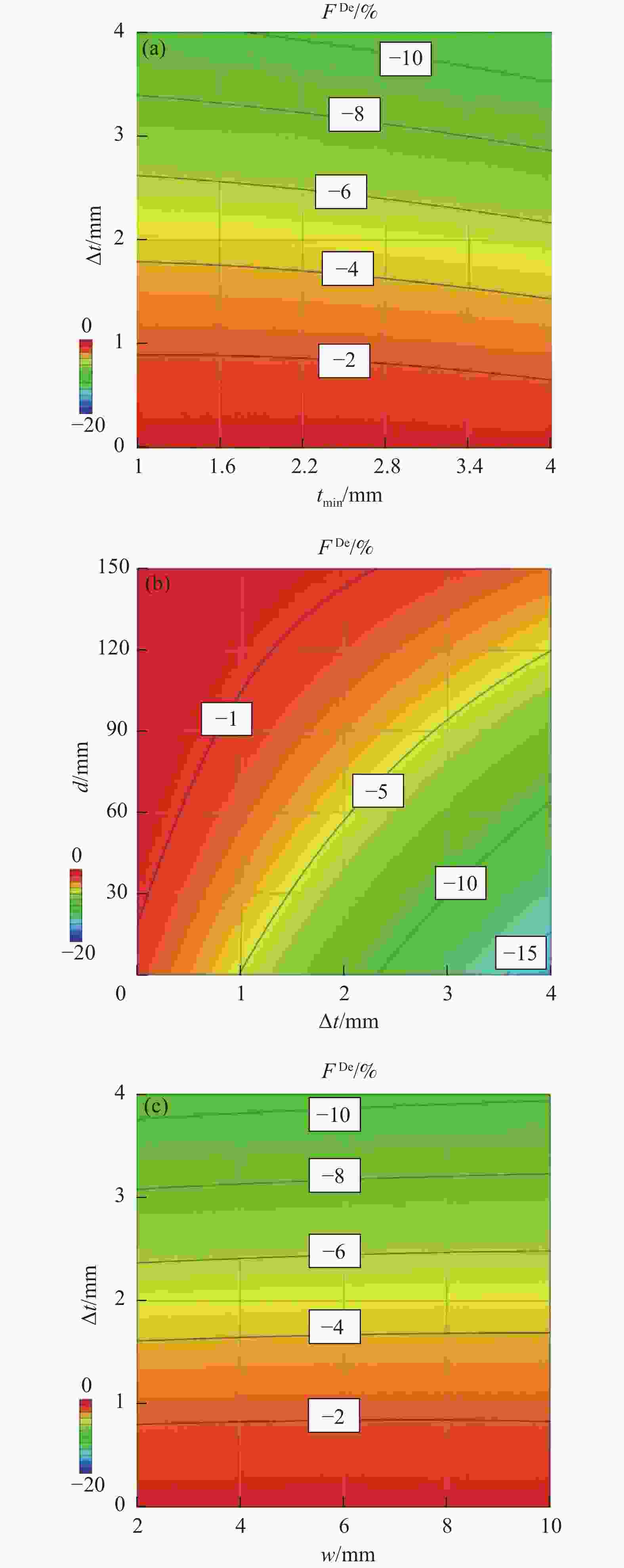
图 20 各变厚区参数对变厚度U型零件CID影响的等高云图：(a) tmin和Δt；(b) Δt和d；(c) w和Δt
Figure 20. Contour plot of the influence of variable thickness area parameters on CID of variable thickness U-shaped parts: (a) tmin and Δt; (b) Δt and d; (c) w and Δt
FDe—Reduction of cure-induced deformation in the thinner area; d—Distance from cross-section to variable thickness area
表 1 AC531树脂固化动力学参数
Table 1. Cure kinetics parameters of AC531
Parameter Value A1/s−1 3384 A2/s−1 7536410 m 0.6062 n1 3.6286 n2 0.8712 Q1/(J·mol−1) 55575 Q2/(J·mol−1) 94596 R/(J·(mol·K)−1) 8.314 Notes: A1 and A2—Pre-exponential coefficients; Q1 and Q2—Reaction activation energy; R—Universal gas constant; m—First exponential constant; n1 and n2—Second exponential constants. 
下载: 导出CSV
表 2 CCF800H/AC531碳纤维/环氧树脂体系热机械性能
Table 2. Thermo-mechanical properties of the CCF800H/AC531 carbon/epoxy
Parameter Value Tg(0)/K 274.98 ρ/(kg·m−3) 1540 ρr/(kg·m−3) 1300 g1 3.244 g2 7.528 Vf/% 57.4 Notes: Tg(0)—Glass transition temperature at curing degree 0; ρ and ρr—Densities of the composite and resin; g1 and g2—Fitting coefficients; Vf—Volume fraction of the fiber.
下载: 导出CSV
Mechanical
propertiesAC531 resin CCF800H fiber E11/GPa 4.74 294 E22/GPa 4.74 14 $v_{12} $ 0.38 0.2 $v_{23} $ 0.38 0.5 G12/GPa 1.72 15 G23/GPa 1.72 5.5 $ M_{\text{1}}^{\text{T}} $/(10−6·°C−1) 35 −0.56 $ M_{\text{2}}^{\text{T}} $/(10−6·°C−1) 35 10.1 $ M_{\text{1}}^{\text{S}} $ −0.6% — Notes: E11, E22—Elastic moduli; $v_{12} $, $v_{23} $—Poisson’s ratios; G12, G23—Shear moduli; $ M_{\text{1}}^{\text{T}} $ and $ M_{\text{2}}^{\text{T}} $—Thermal expansion coefficients; $ M_{\text{1}}^{\text{S}} $—Chemical shrinkage coefficient.
下载: 导出CSV
表 4 边界条件
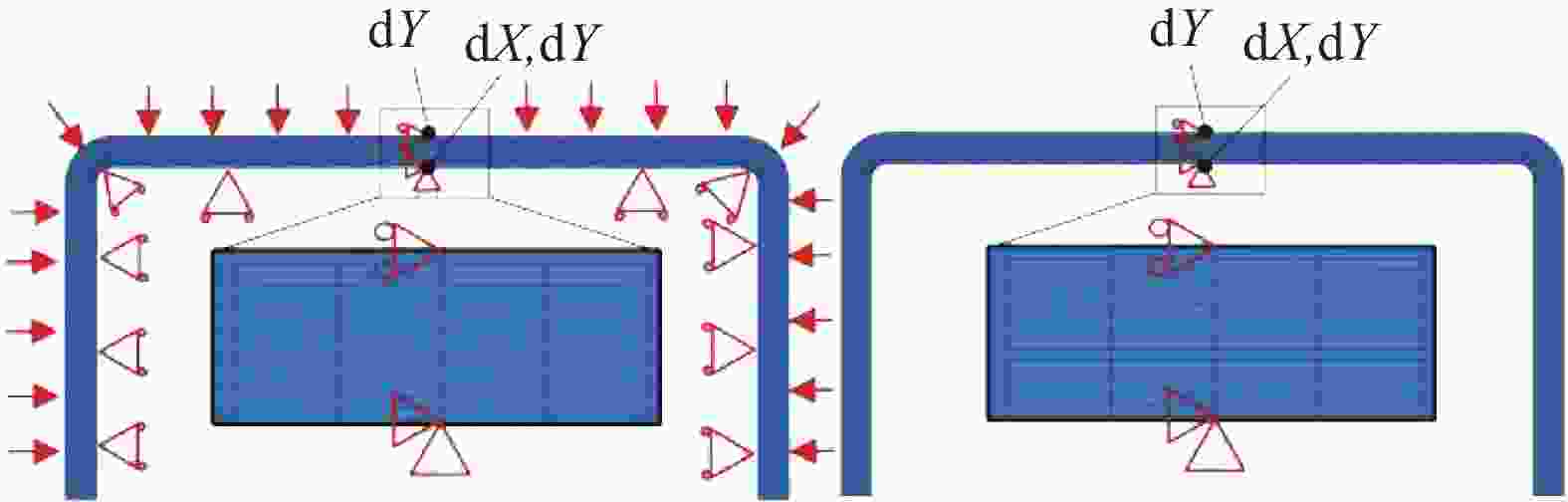
Table 4. Boundary conditions
Plane BC1 Plane BC2 BC3 BC4 Y=−L S X=0 S S S Y=L S X=L UX S S Z=−H RY/UZ Y=0 S S S Z=H RY/RZ Y=L S UY S X=−L F Z=0 S S S X=L F Z=H S S UZ Notes: U—Apply a uniform displacement to the plane; S—Apply a symmetrical constraint to the plane; R—Limit the displacement of the plane; F—No constraints are imposed.
下载: 导出CSV
表 5 [0, 90]ns铺层CCF800H/AC531复合材料等效性能
Table 5. Equivalent material properties of CCF800H/AC531 composite with [0, 90]ns layup
Property Value E11/MPa 91237 E33/MPa 18406 G12/MPa 4597 G23/MPa 3709 ${v_{12}} $ 0.031 ${v_{13}} = {v_{23}} $ 0.566 $ M_{\text{1}}^{\text{T}} $/(10−6 K−1) 1.88 $ M_{\text{3} }^{\text{T} } $/(10−5 K−1) 4.27 $ M_{\text{1}}^{\text{S}} $ 0 $ M_{\text{3} }^{\text{S} } $ −0.76%
下载: 导出CSV
表 6 等厚度U型零件弯边参数的范围
Table 6. Range of flange parameters of equal thickness U-shaped parts
Parameter t/mm r/mm $\theta $/(°) l/mm Lower bound 1 5 60 50 Upper bound 4 25 120 500 Notes: t—Part’s thickness; r—Flange radius; $ \theta $—Flange angle; l—Flange length.
下载: 导出CSV
表 7 变厚度U型零件参数的范围
Table 7. Range of parameters of variable thickness U-shaped parts
Parameters tmin/mm Δt/mm d/mm w/mm Lower bound 1 0 0 2 Upper bound 4 4 35/150 20 Notes: tmin—Thickness of the thinner area; Δt—Value of variable thickness; d—Distance between the cross-section and the variable thickness area; w—Width of the variable thickness area.
下载: 导出CSV
-
[1] 蒋诗才, 安学锋, 闫丽, 等. 国产T800级高韧性环氧树脂基复合材料C梁热隔膜预成型工艺研究[J]. 复合材料科学与工程, 2020(12):109-114. doi: 10.3969/j.issn.1003-0999.2020.12.018JIANG Shicai, AN Xuefeng, YAN Li, et al. Study on preform technology of C-beam hot diaphragm of domestic T800 high toughness epoxy resin martix composite[J]. Composites Science and Engineering,2020(12):109-114(in Chinese). doi: 10.3969/j.issn.1003-0999.2020.12.018 [2] 李伟, 张晨乾, 叶宏军, 等. 固化工艺参数对国产T800增强高韧性复合材料性能的影响[J]. 复合材料科学与工程, 2020(6):98-104. doi: 10.3969/j.issn.1003-0999.2020.06.017LI Wei, ZHANG Chenqian, YE Hongjun, et al. Effect of curing process parameters on the properties of high toughness composites reinforced by domestic carbon fiber[J]. Composites Science and Engineering,2020(6):98-104(in Chinese). doi: 10.3969/j.issn.1003-0999.2020.06.017 [3] DING A, LI S, SUN J, et al. A thermoviscoelastic model of process-induced residual stresses in composite structures with considering thermal dependence[J]. Composite Structures,2016,136:34-43. doi: 10.1016/j.compstruct.2015.09.014 [4] 谭华, 晏石林. 热固性树脂基复合材料固化过程的三维数值模拟[J]. 复合材料学报, 2004, 21(6):167-172. doi: 10.3321/j.issn:1000-3851.2004.06.029TAN Hua, YAN Shilin. Three-dimensional simulation of curing process for thermoset composites[J]. Acta Materiae Compositae Sinica,2004,21(6):167-172(in Chinese). doi: 10.3321/j.issn:1000-3851.2004.06.029 [5] BELLINI C, SORRENTINO L. Analysis of cure induced deformation of CFRP U-shaped laminates[J]. Composite Structures,2018,197:1-9. doi: 10.1016/j.compstruct.2018.05.038 [6] 马晓东, 孙志杰, 顾轶卓. 变厚度复合材料热压罐工艺层板厚度控制的实验研究[J]. 复合材料学报, 2009, 26(5):14-19. doi: 10.3321/j.issn:1000-3851.2009.05.003MA Xiaodong, SUN Zhijie, GU Yizhuo. Experimental analysis on thickness control of variable thickness composite laminates during autoclave process[J]. Acta Materiae Compositae Sinica,2009,26(5):14-19(in Chinese). doi: 10.3321/j.issn:1000-3851.2009.05.003 [7] BELLINI C, SORRENTINO L. Spring-in analysis of CFRP thin laminates: Numerical and experimental results[J]. Composite Structures,2017,173:17-24. doi: 10.1016/j.compstruct.2017.03.105 [8] GROH F, KAPPEL E, HUEHNE C. Investigation of fast curing epoxy resins regarding process induced distortions of fibre reinforced composites[J]. Composite Structures,2019,207:923-934. doi: 10.1016/j.compstruct.2018.09.003 [9] WISNOM M R, POTTER K D, ERSOY N. Shear-lag analysis of the effect of thickness on spring-in of curved composites[J]. Journal of Composite Material,2007,41:1311-1324. doi: 10.1177/0021998306068072 [10] OLSSON A, SANDBER G E. Latin hypercube sampling for stochastic finite element analysis[J]. Journal of Engineering Mechanics,2002,128(1):121-125. doi: 10.1061/(ASCE)0733-9399(2002)128:1(121) [11] ABLIZ D, ARTYS T, ZIEGMANN G. Influence of model parameter estimation methods and regression algorithms on curing kinetics and rheological modelling[J]. Journal of Applied Polymer Science,2017,134(30):45137. doi: 10.1002/app.45137 [12] BARAN I, TUTUM C C, NIELSEN M W. Process induced residual stresses and distortions in pultrusion[J]. Composites Part B: Engineering,2013,51:148-161. doi: 10.1016/j.compositesb.2013.03.031 [13] DING A, LI S, WANG J. Prediction of process-induced distortions in L-shaped composite profiles using path-dependent constitutive law[J]. Applied Composite Materials,2016,23(5):1027-1045. doi: 10.1007/s10443-016-9501-8 [14] BOGETTI T A, GILLSEPIE J W. Process-induced stress and deformation in thick-section thermoset composite laminates[J]. Journal of Composite Material,1992,26(5):626-660. doi: 10.1177/002199839202600502 [15] ZOCHER M A, GROVES S E, ALLEN D H. A three-dimensional finite element formulation for thermo viscoelastic orthotropic media[J]. International Journal for Numerical Methods in Engineering,1997,40(12):2267-2288. doi: 10.1002/(SICI)1097-0207(19970630)40:12<2267::AID-NME156>3.0.CO;2-P [16] BARAN I, CINAR K, ERSOY N. A review on the mechanical modeling of composite manufacturing processes[J]. Archives of Computational Methods in Engineering,2017,24(2):365-395. doi: 10.1007/s11831-016-9167-2 [17] LIANG Y Z, FANG K T, XU Q S. Uniform design and its applications in chemistry and chemical engineering[J]. Chemometrics & Intelligent Laboratory Systems,2001,58(1):43-57. doi: 10.1016/S0169-7439(01)00139-3 [18] CHEN J L, AU K C, WONG Y S, et al. Using orthogonal design to determine optimal conditions for biodegradation of phenanthrene in mangrove sediment slurry[J]. Journal of Hazardous Materials,2010,176(1-3):666-671. doi: 10.1016/j.jhazmat.2009.11.083 [19] MOSALLANEZHAD A, KALANTARIASL A. Performance prediction of ion-engineered water injection (EWI) in chalk reservoirs using response surface methodology (RSM)[J]. Energy Reports,2021,7:2916-2929. doi: 10.1016/j.egyr.2021.05.012 [20] PALANIKUMAR K. Modeling and analysis for surface roughness in machining glass fibre reinforced plastics using response surface methodology[J]. Materials and Design,2007,28(10):2611-2618. doi: 10.1016/j.matdes.2006.10.001 [21] KAMAL M R. Thermoset characterization for moldability analysis[J]. Polymer Engineer and Science,1974,14(3):231-239. doi: 10.1002/pen.760140312 [22] HUI X, XU Y, ZHANG W. An integrated modeling of the curing process and transverse tensile damage of unidirectional CFRP composites[J]. Composite Structure,2021,263:113681. doi: 10.1016/j.compstruct.2021.113681 [23] JOHNSTON A, VAZIRI R, POURSARTIP A. A plane strain model for process-induced deformation of laminated composite structures[J]. Journal of Composite Materials,2001,35(16):1435-1469. doi: 10.1106/YXEA-5MH9-76J5-BACK [24] SIMON S L, MCKENNA G B, SINDT O. Modeling the evolution of the dynamic mechanical properties of a commercial epoxy during cure after gelation[J]. Journal of Applied Polymer Science,2000,76(4):495-508. doi: 10.1002/(SICI)1097-4628(20000425)76:4<495::AID-APP7>3.0.CO;2-B [25] SVANBERG J, HOLMBERG J. Prediction of shape distortions part II. Experimental validation and analysis of boundary conditions[J]. Composite Part A: Applied Science and Manufacture,2004,35(6):723-734. doi: 10.1016/j.compositesa.2004.02.006 [26] FERREIRA S, BRUNS R E, FERREIRA H S, et al. Box-Behnken design: An alternative for the optimization of analytical methods[J]. Analytica Chimica Acta,2007,597(2):179-186. doi: 10.1016/j.aca.2007.07.011 [27] MONTGOMERY D C. Design and analysis of experiments[M]. New York: Wiley, 2001. -
下载:
点击查看大图
计量
- 文章访问数: 1116
- HTML全文浏览量: 890
- PDF下载量: 111
- 被引次数: 0
